INTRODUCTION
Many experimental studies performed in last two decades have demonstrated that materials with the skutterudite structure (general formula MX 3 where M = Co, Ir or Rh; X = P, As or Sb) offer great potential for thermoelectric applications (Uher Reference Uher, Kanatzidis, Mahanti and Hogan2003; Fleurial et al., Reference Fleurial, Caillat and Borshchevsky1997). The crystal structure of skutterudite (space group Im 3) is a derivative of the perovskite structure AMX 3 and is characterized by large tilting of the [MX 6] octahedra (tilt system a +a +a +) (Mitchell, Reference Mitchell2002). The A-site, occupied in the perovskite structure, is vacant.
The tilting of the octahedra results in the proximity of X anions forming [X 4] rectangles in which the homonuclear X-X bonds occur. Besides binary skutterudites, ternary skutterudites have been also synthesized. These phases can be obtained by isoelectronic substitution either on the cation site M by a pair of elements from 8 and 10 groups, e.g., Fe0.5Ni0.5Sb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974) or by analogous substitution on the anion site X by a pair of elements from 14 and 16 groups of the periodical system, e.g., CoGe1.5Te1.5 (Vaqueiro et al., Reference Vaqueiro, Sobany, Powell and Knight2006). The crystallographic studies of (Vaqueiro et al., Reference Vaqueiro, Sobany, Powell and Knight2006, Reference Vaqueiro, Sobany and Powel2010) on AB 1.5Te1.5 (A = Co, Rh, Ir; B = Ge, Sn) ternary skutterudites showed a long-range ordering of B and Te atoms resulting in lowering of the symmetry from cubic to rhombohedral. The phase RuSb2Te is mentioned in the list of prospective thermoelectric materials with skutterudite structure of Fleurial et al. (Reference Fleurial, Caillat and Borshchevsky1997), however, no detailed information concerning the crystal structure and powder diffraction data is available in the literature and in crystallographic databases [ICDD (Reference Kabekkodu2010), Fiz Karlsruhe and NIST (2010) and Linus Pauling File (2011)].
The aim of this work is synthesis and Rietveld structure analysis of the ternary skutterudite RuSb2Te. Powder diffraction data up to 110° 2θ (Cu Kα) are reported.
EXPERIMENTAL
The RuSb2Te ternary compound was synthesized from individual elements by high-temperature solid-state reaction. Stoichiometric amounts of Ru (99.9%), Sb (99.999%), and Te (99.999%) were sealed into an evacuated carbon-coated silica glass tube and heated up to 1050 °C for 48 h in a furnace. After quenching into a cold-water bath, the same tube was placed into furnace and annealed at 550 °C for 120 h. After regrinding under acetone, the resultant material was pelletized and heated again at 550 °C for 120 h. The completion of the solid-state reaction of obtained powder samples was verified by powder X-ray diffraction.
Powder X-ray diffraction data of RuSb2Te were obtained in the Bragg-Brentano geometry on a Bruker D8-Advance diffractometer. Cu Kα radiation was used. To minimize the background, the specimen of RuSb2Te was placed on a flat low-background silicon wafer. The generator was operated at 40 kV and 40 mA, respectively. The details of data collection are summarized in Table I. The observed powder diffractogram is shown in Figure 1. A full width at half maximum of 0.053° 2θ X-ray powder data was observed at 13.503° 2θ, indicating good crystallinity of the investigated specimen.
STRUCTURE REFINEMENT
The crystal structure of RuSb2Te was refined using the Rietveld method for X-ray powder diffraction data by means
TABLE I. Experimental conditions.


Figure 1. (Color online) Observed (circles), calculated (solid line), and difference Rietveld profiles for RuSb2Te. The vertical bars indicate the positions of Bragg reflections.
of the program FULLPROF (Rodríguez-Carvajal, Reference Rodríguez-Carvajal1990). All peaks in the powder diffraction pattern were indexed on a cubic body-centred cell analogous to CoSb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974). Consequently, the crystal structure of CoSb3 was used as a starting structural model in the Rietveld refinement.
The refined parameters include those describing peak shape and width, peak asymmetry (two parameters), unit-cell parameters and fractional coordinates. The pseudo-Voigt function was used to model the line shape of the diffraction profiles. The background was determined by linear interpolation between consecutive breakpoints in the diffraction pattern.
The convergence criterion, ε, forcing the termination of the refinement when parameter shifts < ε × σ, was set to 0.1. In total, 13 parameters were refined. The Sb and Te randomly occupy the 24g position in the Im 3 space group; their occupancy factors were assigned according to the RuSb2Te chemical composition (i.e., 0.67 and 0.33 for Sb and Te, respectively). The final cycles of refinement converged to the satisfactory values of agreement factors: R p = 4.69%, R wp = 6.30%, R B = 3.68%, and χ2 = 1.05).
It is worth noting that a relatively large group of anion-ordered ternary skutterudites MX 1.5Y 1.5 with R 3 symmetry has been described [e.g., IrGe1.5Se1.5 (Laufek and Navrátil, Reference Laufek and Navrátil2010), RhGe1.5Se1.5 (Liang et al., Reference Liang, Schnelle, Oeschler, Budnyk and Grin2011), CoSn1.5Te1.5 (Laufek et al., Reference Laufek, Navrátil and Goliáš2008)]. The refinement of RuSb2Te based on the anion-ordered structure model of CoSn1.5Te1.5 (space group R 3) was also attempted. Although this refinement resulted in approximately the same values of profile agreement parameters (R p = 4.77%, R wp = 6.34%, R B = 5.63%,
TABLE II. Refined parameters for RuSb2Te [room temperature, space group Im 3, a = 9.2665(1) Å, V = 795.70(1) Å3, Z = 8, D c = 7.88 g/cm3, R p = 4.69%, R wp = 6.30%, and R B = 3.68%). The displacement parameters of Sb and Te were constrained to be equal in the Rietveld refinement.

TABLE III. Powder diffraction data for RuSb2Te. Reflections with I calc and I obs < 1% are not shown in the table.


Figure 2. (Color online) (a) Polyhedral and (b) ball-and-stick representation of the RuSb2Te structure showing the corner sharing arrangement of the [Ru(Sb/Te)6] octahedra. (c) Comparison of four-member [(Sb/Te)4] and [Sb4] rings found in the RuSb2Te and CoSb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974) structures, respectively.
and χ2 = 0.94 for 23 refined parameters) as for disordered structure (Im 3, see above), it failed to reach convergence. Moreover, the application of Platon ADDSYM Program (Spek Reference Spek1988, Reference Spek2003) to identify the missing symmetry elements to this structure (space group R 3) indicated missing symmetry elements. Therefore, the proper symmetry of the RuSb2Te structure should be Im 3.
To support this conclusion, powder diffraction patterns for ordered and disordered structural models of RuSb2Te were calculated. The POWDERCELL 2.4.program (Kraus and Nolze, Reference Kraus and Nolze2000) was used for the calculations. Although the scattering factors of Sb and Te for X-rays (Cu Kα radiation) are very similar, a comparison of these two calculated patterns has showed that weak superstructure diffractions indicating the structural ordering can be detected by conventional powder X-ray diffraction. However, neither superstructure reflections nor peak splitting was observed for RuSb2Te.
The experimental conditions of diffraction-data collection are given in Table I, and Table II shows refined structural parameters for RuSb2Te. The final Rietveld plot is depicted in Figure 1.
RESULTS AND DISCUSSION
The powder diffraction data are listed in Table III. The observed values of diffraction positions, d-spacing and intensities were extracted by the program XFIT (Coelho and Cheary, Reference Coelho and Cheary1997) employing the split Pearson VII profile function. The 2θobs and d obs were corrected for the refined zero-point shift of 0.013° 2θ.
The RuSb2Te crystallizes in the skutterudite-type structure. Its atomic architecture is shown in Figure 2. In this structure, each Ru atom is surrounded by six Sb/Te atoms showing a weakly distorted octahedral arrangement. The [Ru(Sb/Te)6] octahedra share all six corners forming a perovskite-like three dimensional framework. Table IV shows a comparison of selected bond distance and bond angles for isostructural compounds RuSb2Te and CoSb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974). As can be seen from Table IV, the Ru-Sb/Te bond distance is slightly longer than the corresponding Co-Sb bond distance in CoSb3. Neglecting the small difference in the covalent radii of Sb (r Sb = 1.41 Å) and Te (r Te = 1.37 Å) (Emsley, Reference Emsley1989), this can be explained by the considerably lower covalent radius of Co (r Co = 1.16 Å) with respect to that of Ru (r Ru = 1.24 Å) (Emsley, Reference Emsley1989).
As was noted by Mitchell (Reference Mitchell2002) and Vaqueiro et al. (Reference Vaqueiro, Sobany and Stindl2008), the skutterudite structure can be derived from the perovskite structure ABX 3 by omission of the A atom and by tilting of the BX 6 octahedra (tilt system a +a +a +). The tilt angle (φ) can be calculated from the unit-cell parameter a and the Ru-(Sb/Te) bond distance according to a relationship given by O’Keefe and Hyde (Reference O’Keefe and Hyde1977)
Using this expression, we have calculated the values of 33.5° and 32.4° for RuSb2Te (this work) and CoSb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974), respectively. Once again
TABLE IV. Selected interatomic distances and bond angles for RuSb2Te and CoSb3 (Kjekshus and Rakke, Reference Kjekshus and Rakke1974).
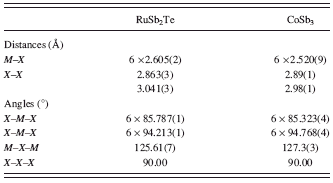
neglecting the small difference in the covalent radii of Sb and Te (see above), these values of tilt angles are in accordance with a general trend observed in skutterudites: for a given anion the tilt angle (φ) increases with increasing size of the cation (Mitchell, Reference Mitchell2002).
Because of the tilting of [Ru(Sb/Te)6] octahedra according to a +a +a + tilt system, the Sb/Te atoms form the four-membered rings [(Sb/Te)4] of rectangular shape. These rings are a hallmark of the skutterudite crystal structure. As is indicated in Figure 2(c), the short [2.863(3) Å] and long [3.041(3) Å] (Sb/Te)-(Sb/Te) bond distances alternate within the [(Sb/Te)4] rings in the RuSb2Te crystal structure. These distances are more or less comparable with Sb-Sb distance of 2.869(1) Å and Te-Te distance of 2.863(5) Å found in the crystal structures of marcasite-type phases RuTe2 (Koehler, Reference Koehler1997) and RuSb2 (Kjekshus et al. Reference Kjekshus, Rakke and Andresen1977), respectively. In comparison to [Sb4] rings found in the CoSb3 structure (Kjekshus and Rakke, Reference Kjekshus and Rakke1974), the Sb/Te rings show slightly more deviation from squared shape to rectangular (Figure 2(c)). The ratio of two Sb-Sb distances is 1.03 for CoSb3 structure, whereas for RuSb2Te structure the ratio of two (Sb/Te)-(Sb/Te) distances has a value of 1.06.
The RuSb2Te phase does not show any indication of structural ordering of Sb and Te atoms. It is worth noting that the structural ordering of anions was only observed in ternary skutterudites with MY 1.5X 1.5 stoichiometry (M = Co, Ir, and Rh; X = Ge and Sn; Y = S, Se, and Te), i.e., with anion ratio of 1:1. The RuSb2Te phase shows a different ratio of anions, i.e., 1:2, and consequently crystallizes in a cubic disordered structure.
It should be also noted that the description of the skutterudites using ionic formula M 43+[X 4]34- is only formal. For example, in the RuSb2Te compound, the electronegativities of Ru, Sb, and Te are almost comparable (Pauling electronegativities: Ru 2.2, Te 2.1, and Sb 2.05), which indicates that the strict division of atoms into electropositive cations and electronegative anions is not valid. Hence, the covalent radii should be used in bond lengths considerations. Further details about bonding and band structure calculations on skutterudite-type compounds can be found in the work of Partik and Lutz (Reference Partik and Lutz1999).
ACKNOWLEDGMENTS
This study was supported by an internal project of Czech Geological Survey (Project No. 332300) and by the Grant Agency of the Czech Republic (Project No. P108/10/1315).








