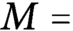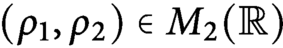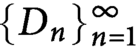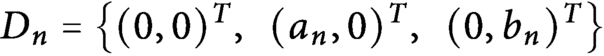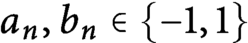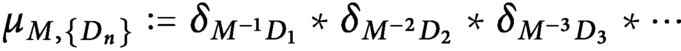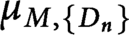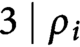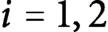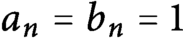1 Introduction
It is well known that the family
$\{e^{2\pi i \langle n,x\rangle }: n\in {\mathbb Z}^d\}$
of exponential functions forms an orthonormal basis for
$L^2([0,1]^d)$
. This result is now one of the basic pillars of modern mathematics. It is natural to ask what other measures have this property, or whether there is a family of exponential functions that forms an orthogonal basis of their
$L^2$
-space?
Let
$\mu $
be a Borel probability measure with compact support on
${\mathbb R}^d$
, and let
$\langle \cdot , \cdot \rangle $
denote the standard inner product on
${\mathbb R}^d$
. We call
$\mu $
a spectral measure if there exists a countable set
$\Lambda \subset {\mathbb R}^d$
such that
$E(\Lambda ):=\{e^{-2\pi i \langle \lambda , x \rangle }: \lambda \in \Lambda \}$
forms an orthonormal basis for
$L^2(\mu )$
. The set
$\Lambda $
is then called a spectrum of
$\mu $
. The existence and nonexistence of a spectrum for
$\mu $
is a basic problem in harmonic analysis. The question was originally studied by Fuglede [Reference Fuglede20] in 1974, where he proposed a famous conjecture: a Lebesgue measurable set
$\Omega $
is a spectral set in
${\mathbb R}^d$
if and only if it tiles
${\mathbb R}^d$
by translations. Although the conjecture was proven to be false in
${\mathbb R}^d$
,
$d\geq 3$
[Reference Kolountzakis and Matolcsi25, Reference Tao30], the problem generated a lot of interest on the study of a measure to be spectral. This opened up a new possibility of applying the well developed Fourier analysis techniques to certain classes of fractals. In 1998, Jorgensen and Pedersen [Reference Jorgensen and Pedersen24] gave the first singular spectral measure: the standard middle-fourth Cantor measure. Following these discoveries, many more examples of fractal spectral measures have been constructed, such as self-similar measures [Reference Dai4, Reference Laba and Wang26], self-affine measures [Reference Dutkay, Haussermann and Lai11, Reference Dai, Fu and Yan17, Reference Wang31] and Moran measures [Reference An, He and He2, Reference An and He3, Reference Fu and Wen19]. It is surprising that there are many distinctive phenomena that singular spectral measures do have but the absolutely continuous ones do not. For instance, (1) the convergence of the associated Fourier series is very different for distinct spectra in the space of continuous functions [Reference Dutkay, Han and Sun10, Reference Strichartz29]; (2) there exists a singular spectral measure
$\mu $
with two spectra
$\Lambda $
and
$k\Lambda $
for some integer
$k>1$
[Reference Dutkay and Jorgensen15, Reference Laba and Wang26]; and (3) there exists a singular spectral measure
$\mu $
with two spectra such that the Beurling dimensions of them are different [Reference Dai, He and Lai5, Reference Dai and Sun7, Reference Dutkay, Han, Sun and Weber13]. In addition, the theory of spectral measures has been widely used in the study of quasi-crystal [Reference Greenfeld and Lev21], p-adic fields
${\mathbb Q}_p$
[Reference Fan, Fan, Liao and Shi16], Gabor bases [Reference Liu and Wang27] and wavelets [Reference Dutkay and Jorgensen14].
The aim of this paper is to study a class of singular spectral measures on
${\mathbb R}^2$
. Let
$M= \left (\!\!\!\begin {array}{cc}\rho _1 & 0\\0 & \rho _2\\\end {array}\!\!\!\right )\in M_2({\mathbb R})$
be an expanding matrix. Let
$\{D_n\}_{n=1}^{\infty }$
be a sequence of digit sets in
${\mathbb Z}^2$
, where
$$ \begin{align*} D_n=\left\{\begin{pmatrix} 0\\ 0 \end{pmatrix},\,\,\,\begin{pmatrix} a_n\\ 0 \end{pmatrix}, \,\,\, \begin{pmatrix} 0\\ b_n \end{pmatrix} \right\},\quad a_n,b_n\in \{-1,1\}. \end{align*} $$
Then associated with them there exists a Borel probability measure
$\mu _{M, \{D_n\}}$
, which is defined by the following infinite convolutions of discrete measures as
$$ \begin{align} \mu_{M, \{D_n\}}=\delta_{M^{-1}D_1}\ast \delta_{M^{-2}D_2}\ast \delta_{M^{-3}D_3}\ast \cdots, \end{align} $$
where the convergence is in a weak sence. Here
$\delta _E=\frac {1}{\#E}\sum _{e\in E}$
supported on a finite set E, where
$\delta _e$
is a Dirac measure at e and
$\#E$
denotes the cardinality of E. The measure
$\mu _{M, \{D_n\}}$
is called a Moran Sierpinski-type measure.
If
$a_n=b_n=1$
, the corresponding measure
$\mu _{M,D}$
is a Sierpinski-type measure. Dai et al. [Reference Dai, Fu and Yan17] and Deng et al. [Reference Deng and Lau9] proved that
$\mu _{M,D}$
is a spectral measure if and only if
$3\mid \rho _i$
,
$i=1,2$
. More recently, Wang [Reference Wang31] gave the analogous result of a class of spectral measure
$\mu _{M,D}$
, where the digit set D satisfies certain conditions. For general Moran measures on
${\mathbb R}^d$
, the spectral property of such measures were first studied by Strichartz in [Reference Strichartz28]. In 2017, Dutkay and Lai [Reference Dutkay and Lai12] studied Moran spectral measures determined by a finite number of Hadamard triples. They showed that if we randomly take convolution on these Hadamard triples, then under certain conditions, almost all Moran measures are spectral. Furthermore, some results of Moran spectral measures have appeared in many papers, see e.g., [Reference An, Fu and Lai1, Reference Fu, He and Wen18, Reference He and He22]. We note that in all these papers, they assume either under the condition of Hadamard triple, or
$d=1$
. We will extend the spectral property of these measures to the Moran measures
$\mu _{M,\{D_n\}}$
defined as in equation (1.1). The main result of this paper is the following:
Theorem 1.1 Let
$\mu _{M, \{D_n\}}$
be the Moran Sierpinski-type measure defined by equation (1.1). Then
$\mu _{M, \{D_n\}}$
is a spectral measure if and only if
$3\mid \rho _i$
,
$i=1,2$
.
Remark 1.2 It is easy to see that there may not be a common C such that
$(D_n, C)$
forms a compatible pair for each
$n\in {\mathbb N}$
by the difference of the zero set
${\mathcal Z}(\hat {\delta }_{D_n})$
for
$n\in {\mathbb N}$
, which yields difficulty to deal with the construction of the orthogonal family of exponentials in
$L^2(\mu _{M,\{D_n\}})$
.
The sufficiency of Theorem 1.1 is to construct a spectrum
$\Lambda $
for
$\mu _{M, \{D_n\}}$
. Here, the main difficulty is the completeness of
$\Lambda $
. The method in this paper is different from the other existing proofs in literatures, see e.g., [Reference An, He and He2, Reference An and He3, Reference He and He22], where the completeness is established by considering only one variable.
The subtle part is the necessity of Theorem 1.1. Our strategy is to analyze the structure of the orthogonal set of the measure
$\mu _{M, \{D_n\}}$
. We first obtain that
Theorem 1.3 The Moran Sierpinski-type measure
$\mu _{M, \{D_n\}}$
admits an infinite orthogonal set if and only if
$\rho _i=(\frac {3p_i}{q_i})^{1/r_i}$
for some
$r_i,p_i,q_i\in {\mathbb N}^+$
with
$\gcd (3p_i,q_i)=1$
,
$i = 1, 2$
.
According to Theorem 1.3, we prove Theorem 1.1 by elimination that each of the following cases can NOT admit a spectrum:
-
(i) For
$i=1, 2$
,
$\rho _i= (\frac {3p_i}{q_i})^{1/r_i}$
for
$r_1> 1$
or
$r_2> 1$
. -
(ii) For
$i=1, 2$
,
$\rho _i=\frac {3p_i}{q_i}$
for
$q_1>1$
or
$q_2>1$
.
Here, we assume that
$r_i$
is the smallest positive integer such that
$\rho _i^{r_i}\in {\mathbb Q}$
,
$i=1,2$
. The most subtle part of the proof is (ii). We need to show that there is a special decomposition of the spectrum. The method to find a special decomposition of the spectrum is of independent interest, which can be used for the study of the spectrality of more general singular measures.
We organize the paper as follows. In Section 2, we set up the notations, the basic criteria of spectrum, and the proof of the sufficiency of Theorem 1.1. In Section 3, we prove Theorem 1.3 and settle case (i). In Section 4 we give a detailed study of the spectrum
$\Lambda $
, which is used in Section 5 to consider the case (ii).
2 Preliminaries and the sufficiency of Theorem 1.1
Let
$\mu $
be a Borel probability measure with compact support in
${\mathbb R}^d$
. The Fourier transform of
$\mu $
is defined as usual,
$$ \begin{align} \hat{\mu}(\xi)=\int e^{-2\pi i \langle\xi, x \rangle}\,\text{d}\mu(x). \end{align} $$
Let
$\Lambda \subset {\mathbb R}^d$
be a countable set and denote
$E(\Lambda ):=\{e^{-2\pi i \langle \lambda , x\rangle }: \lambda \in \Lambda \}$
. We say that
$\Lambda $
is an orthogonal set (a spectrum) of
$\mu $
if
$E(\Lambda )$
forms an orthogonal family (an orthonormal basis) for
$L^2(\mu )$
. It is easy to check that the orthogonality of
$E(\Lambda )$
is equivalent to the condition
$(\Lambda -\Lambda ) \setminus \{0\}\subset {\mathcal Z}(\hat {\mu })$
, where
${\mathcal Z}{\left (f\right )}$
denotes the zero set of the function f, i.e.,
${\mathcal Z}{\left (f\right )}=\{x: f(x)=0\}$
. Moreover, we call
$\Lambda $
is a maximal orthogonal set if for any
$r\in {\mathbb R}^d\setminus \Lambda $
,
$\{r\}\cup \Lambda $
is not an orthogonal set of
$\mu $
. Since orthogonal sets are invariant under translations, without loss of generality, we always assume
$0\in \Lambda $
. For any
$\xi \in {{\mathbb R}^d}$
, we define
$ Q_{\Lambda }(\xi )=\sum _{\lambda \in \Lambda }|\hat {\mu }(\xi +\lambda )|^2.$
By using the Parseval identity, we have the following basic criterion for the orthogonality (spectrality) of
$\mu $
.
Theorem 2.1[Reference Jorgensen and Pedersen24]
Let
$\mu $
be a Borel probability measure with compact support in
${\mathbb R}^d$
, and let
$\Lambda \subset {\mathbb R}^d$
be a countable subset. Then
-
(i)
$\Lambda $
is an orthogonal set of
$\mu $
if and only if
$Q_\Lambda (\xi )\le 1$
for
$\xi \in {\mathbb R}^d$
. In this case,
$Q_\Lambda (z)$
is an entire function in
${\mathbb C}^d$
. -
(ii)
$\Lambda $
is a spectrum of
$\mu $
if and only if
$Q_\Lambda (\xi )\equiv 1$
for
$\xi \in {\mathbb R}^d$
.
As a simple consequence of Theorem 2.1, we have the following useful lemma, which was proved in [Reference Dai, He and Lau6].
Lemma 2.2 Let
$\mu =\mu _0\ast \mu _1$
be the convolution of two probability measures
$\mu _i$
,
$i=0, 1$
, and they are not Dirac measures. Suppose that
$\Lambda $
is an orthogonal set of
$\mu _0$
, then
$\Lambda $
is also an orthogonal set of
$\mu $
, but cannot be a spectrum of
$\mu $
.
Let
$\mu _{M, \{D_n\}}$
be the Moran Sierpinski-type measure defined in equation (1.1). It follows from equation (2.1) that
$$ \begin{align*} \hat{\mu}_{M,\{D_n\}}(\xi)=\prod_{k=1}^{\infty}m_{D_k}(M^{*-k}\xi),\quad \xi\in {\mathbb R}^2, \end{align*} $$
where
$m_{D_k}(\xi ) =\frac {1}{3}\sum _{d\in D_k}e^{-2\pi i \langle d, \xi \rangle }$
is the mask function of
$D_k$
and
$M^*$
denotes the transposed conjugate matrix of M. Then the zero set of
$m_{D_{k}}(x)$
is
$$ \begin{align*} {\mathcal Z}(m_{D_{k}})= \left\{\!\!\!\begin{array}{ll} A_1\bigcup A_2, \,\, & a_k= b_k=-1\,\, \mathrm {or} \,\, a_k= b_k=1;\\ A_3\bigcup A_4, \,\,& a_k=-1, b_k=1 \,\, \mathrm{or} \,\, a_k=1, b_k=-1.\nonumber\\ \end{array}\right. \end{align*} $$
where
$$ \begin{align} A_1&=\frac{1}{3} \begin{pmatrix} 1\\ 2 \end{pmatrix}+{\mathbb Z}^2 ,\, A_2=\frac{1}{3} \begin{pmatrix} 2\\ 1 \end{pmatrix} +{\mathbb Z}^2 ,\nonumber \\ A_3&=\frac{1}{3} \begin{pmatrix} 1\\ 1 \end{pmatrix}+{\mathbb Z}^2 , \, A_4=\frac{1}{3} \begin{pmatrix} 2\\ 2 \end{pmatrix} +{\mathbb Z}^2. \end{align} $$
Then we obtain the following relationship
$$ \begin{align} {\mathcal Z} \left(\hat{\mu}_{M, \{D_n\}}\right)=\bigcup_{k=1}^{\infty}M^{k}{\mathcal Z} \left(m_{D_k}\right)\subset \bigcup_{k=1}^{\infty}M^{k}(A_1\cup A_2\cup A_3\cup A_4). \end{align} $$
In the rest of this section, we will prove the sufficiency of Theorem 1.1. Our goal is to construct a spectrum for
$\mu _{M,\{D_n\}}$
. This construction is based on the central idea of Hadamard triple, as described below.
Definition 2.1 Let
$M\in M_2({\mathbb Z})$
be an expansive matrix with integer entries. Let
$D, C \subset {\mathbb Z}^{2}$
be two finite subsets of integer vectors with
$\#D=\#C$
. We say that the system
$(M, D, C)$
forms a Hadamard triple (or
$(M^{-1}D, C)$
is a compatible pair) if the matrix
$H= \frac {1}{\sqrt {\#D}}\left [e^{2 \pi i \langle M^{-1}d,c\rangle }\right ]_{d\in D,c \in C}$
is unitary, i.e.,
$H^{*}H=I$
.
Let
$3\mid \rho _i$
for each
$i=1,2$
, it is easy to check that
$(M^{-1}D_k, MC_k)$
is a compatible pair, where
$$ \begin{align} C_k= \left\{\!\!\!\!\begin{array}{ll} \left\{\begin{pmatrix} 0\\ 0 \end{pmatrix}, \begin{pmatrix} \frac{1}{3}\\-\frac{1}{3} \end{pmatrix}, \begin{pmatrix} -\frac{1}{3}\\ \frac{1}{3} \end{pmatrix}\right\}, \,\, a_k= b_k=-1\,\mathrm{or} \, a_k= b_k=1;\\ \left\{\begin{pmatrix} 0\\ 0 \end{pmatrix}, \begin{pmatrix} \frac{1}{3} \\ \frac{1}{3} \end{pmatrix}, \begin{pmatrix} -\frac{1}{3}\\ -\frac{1}{3} \end{pmatrix}\right\}, \,\, a_k=-1, b_k=1 \, \mathrm{or} \, a_k=1, b_k=-1.\\ \end{array}\right. \end{align} $$
Denote
$\Lambda _n:=\sum _{k=1}^{n}M^kC_k$
for any
$n\geq 1$
and
$\Lambda :=\bigcup _{k=1}^{\infty }\Lambda _n.$
Define
$$ \begin{align*} \mu_{n}&=\delta_{M^{-1}D_1}\ast \cdots \ast \delta_{M^{-n}D_n},\nonumber\\ \mu_{>n}&=\delta_{M^{-(n+1)}D_{n+1}}\ast \delta_{M^{-(n+2)}D_{n+2}}\ast \cdots.\nonumber \end{align*} $$
Then
$\mu _{M,\{D_n\}}=\mu _n * \mu _{>n}$
. Thus, we have that
$\Lambda _n$
is a spectrum of
$\mu _n$
and
$\Lambda $
is an orthogonal set of
$\mu _{M, \{D_n\}}$
. The following lemma is motivated by Theorem 2.3 in [Reference An, He and He2] and easy to prove.
Lemma 2.3 Let
$\mu $
be a Borel probability measure with compact support in
${\mathbb R}^d$
and
$\xi \in {\mathbb R}^d$
with
$\|\xi \|\leq 1$
. Suppose that
$\Lambda =\bigcup _{n=1}^{\infty }\Lambda _{\alpha _n} $
is an orthogonal set of
$\mu $
and
$\{\alpha _n\}_{n=1}^{\infty }$
is an increasing sequence of integers. If
$\Lambda _{\alpha _n}$
is a spectrum of
$\mu _{\alpha _n}$
and
$$ \begin{align*}\inf_{\lambda \in \Lambda_{\alpha_{n+s}} \backslash \Lambda_{\alpha_n}} \vert \hat\mu_{>\alpha_{n+s}}\left(\xi +\lambda\right)\vert ^2 \geq c > 0\end{align*} $$
for all
$n ,s \geq 1$
, then
$\Lambda $
is a spectrum of
$\mu $
.
We now prove the sufficiency of Theorem 1.1, which is restated as follows.
Theorem 2.4 Let
$\mu _{M, \{D_n\}}$
be the Moran Sierpinski-type measure defined as in equation (1.1). If
$3\mid \rho _i$
for each
$i=1,2$
, then
$\mu _{M, \{D_n\}}$
is a spectral measure with a spectrum
$$ \begin{align*}\Lambda=\left\{ \sum_{k=1}^{n}M^kc_k: c_k\in C_k, n\geq 1 \right\},\end{align*} $$
where
$C_k$
is defined as in equation (2.4).
Proof Denote
$\rho _i:=3p_i$
, where
$p_i\in {\mathbb N}^+$
for
$i=1, 2$
. By Lemma 2.3, we need to prove that there exists a constant
$c>0$
such that for any
$\xi \in {\mathbb R}^2$
with
$\parallel \xi \parallel \leq \frac 13$
, we have
$\left \vert \hat {\mu }_{>n}(\xi +\lambda )\right \vert ^2\geq c>0$
for any
$\lambda \in \Lambda _n$
and
$n\geq 1.$
Note that
$ \left \vert \hat {\mu }_{>n}(\xi +\lambda )\right \vert ^2 =\prod _{k=n+1}^{\infty }\left \vert \hat {\delta }_{M^{-k}D_k}(\xi +\lambda )\right \vert ^2.$
So, we need to estimate
$\left \vert \hat {\delta }_{M^{-k}D_k}(\xi +\lambda )\right \vert ^2$
for all
$k\geq n+1$
. Take any
$\lambda \in \Lambda _n$
and write
$\lambda =\begin {pmatrix} \lambda _1\\ \lambda _2\end {pmatrix} =\begin {pmatrix} \sum _{i=1}^{n}(3p_1)^ic_{i1}\\ \sum _{i=1}^{n}(3p_2)^ic_{i2} \end {pmatrix},$
where
$\begin {pmatrix} c_{i1}\\ c_{i2} \end {pmatrix}\in C_i$
. Let
$p=\min \{p_1, p_2\}$
. For any
$k\geq n+1$
and
$j=1,2$
, we have
$$ \begin{align} \left|\frac{\xi_j+\lambda_j}{(3p_j)^{k}}\right| \leq\frac{1}{3}\left|\frac{1}{(3p_j)^k}+\cdots \frac{1}{(3p_j)^{k-n}}\right| \leq\frac{1}{6}\frac{1}{(3p)^{k-n-1}}. \end{align} $$
A direct calculation shows
$$ \begin{align} \left\vert \hat{\delta}_{M^{-k}D_k}(\xi+\lambda)\right\vert^2 =&\left\vert\frac{1}{3}\left(1+e^{-2\pi i a_k(3p_1)^{-k} (\xi_1+\lambda_1)}+e^{-2\pi i b_k(3p_2)^{-k} (\xi_2+\lambda_2)}\right)\right \vert^2 \nonumber\\ =& \frac{1}{9}\left\vert 3+2\left(\cos\frac{2\pi (\xi_1+\lambda_1)}{(3p_1)^{k}}+\cos\frac{2\pi (\xi_2+\lambda_2)}{(3p_2)^{k}}\right)\right.\nonumber\\ &\left.+2\cos\left(\frac{2\pi (\xi_1+\lambda_1)}{(3p_1)^{k}}\pm \frac{2\pi (\xi_2+\lambda_2)}{(3p_2)^{k}}\right) \right\vert. \end{align} $$
For
$k=n+1$
, equation (2.5) shows that
$\cos \frac {2\pi (\xi _j+\lambda _j)}{(3p_j)^{k}}\geq \cos \frac {\pi }{3}$
for
$ j=1, 2$
. By equation (2.6),
$$ \begin{align*} \left\vert \hat{\delta}_{M^{-(n+1)}D_{n+1}}(\xi+\lambda)\right\vert^2 \geq\frac{1}{9}\left\vert 5 +2\cos\left(\frac{2\pi (\xi_1+\lambda_1)}{(3p_1)^{k}}\pm \frac{2\pi (\xi_2+\lambda_2)}{(3p_2)^{k}}\right) \right\vert \geq\frac{1}{3}. \end{align*} $$
For
$k\geq n+2$
, according to
$\cos x \geq 1-x^2$
, we have
$$ \begin{align*} \cos\frac{2\pi (\xi_j+\lambda_j)}{(3p_j)^{k}} \geq 1-\frac{\pi^2}{9}\frac{1}{(9p^2)^{k-n-1}},\quad j=1, 2, \end{align*} $$
$$ \begin{align*} \cos\left(\frac{2\pi(\xi_1+\lambda_1)}{(3p_1)^{k}}\pm \frac{2\pi(\xi_2+\lambda_2)}{(3p_2)^{k}}\right) \geq 1-\frac{4\pi^2}{9}\frac{1}{(9p^2)^{k-n-1}}. \end{align*} $$
By equation (2.6),
$$ \begin{align*} \left\vert \hat{\delta}_{M^{-k}D_k}(\xi+\lambda)\right\vert^2 \geq1-\frac{4\pi^2}{9}\frac{1}{(9p^2)^{k-n-1}}. \end{align*} $$
Hence,
$$ \begin{align*} \left\vert \hat{\mu}_{>n}(\xi+\lambda)\right\vert^2 \geq \frac{1}{3}\prod_{k=1}^{\infty} \left(1-\frac{4\pi^2}{9}\frac{1}{(9p^2)^{k}}\right):=c>0.\end{align*} $$
▪
3 Spectrality for irrational contraction
3.1 Infinite orthogonal set of
$\mu _{M, \{D_n\}}$
We know that the self-similar measure
$\mu _{\rho ,\{0,1,2\}}$
on
${\mathbb R}$
is defined as
$\mu _{\rho ,\{0,1,2\}}(\cdot )=\frac {1}{3}\sum _{i=0}^{2}\mu _{\rho ,\{0,1,2\}} (\rho (\cdot )-i)$
. And the zero set of
$\hat {\mu }_{\rho ,\{0,1,2\}}$
is
${\mathcal Z}(\hat {\mu }_{\rho ,\{0,1,2\}})=\bigcup _{n=1}^{\infty } \rho ^n \frac {\{1,2\}+3{\mathbb Z}}{3}$
. The following theorem gives the existence condition of infinite orthogonal set of
$\mu _{\rho ,\{0,1,2\}}$
, which was proved in [Reference Deng8, Reference Hu and Lau23].
Theorem 3.1
$\mu _{\rho ,\{0,1,2\}}$
admits an infinite orthogonal set if and only if
$\rho =\left (\frac {3p}{q}\right )^{1/r}$
for some
$r, p, q\in {\mathbb N}^+$
with
$\gcd (3p,q)=1$
.
Proof of Theorem 1.3 Suppose that
$0\in \Lambda $
is an infinite orthogonal set of
$\mu _{M, \{D_n\}}$
. Denote
$\pi _i(\Lambda )=\{x_i: (x_1,x_2)^T\in \Lambda \}$
,
$i=1,2$
. By equations (2.2) and (2.3), we have
$$ \begin{align*} (\pi_i(\Lambda)-\pi_i(\Lambda))\setminus\{0\}\subseteq \bigcup_{n=1}^{\infty}{\rho_i}^{n} \frac{\{1,2\}+3{\mathbb Z}}{3}, \quad i=1,2. \end{align*} $$
This implies that
$\pi _i(\Lambda )$
is an orthogonal set of
$\mu _{\rho _i,\{0,1,2\}}$
for each
$i=1,2$
. We prove that
$\pi _i(\Lambda )$
is infinite for each
$i=1,2$
. Otherwise, without loss of generality, let
$\pi _1(\Lambda )$
is finite. The pigeon hole principle shows that there exist
$\lambda ^{\prime }\neq \lambda ^{\prime \prime } \in \Lambda $
such that
$\lambda ^{\prime }=(\lambda _1^{\prime }, \lambda _2^{\prime })^T$
and
$\lambda ^{\prime \prime }=(\lambda _1^{\prime }, \lambda _2^{\prime \prime })^T$
. Note that
$\lambda ^{\prime }-\lambda ^{\prime \prime }\notin {\mathcal Z} \left (\hat {\mu }_{M,\{D_n\}}\right )$
. This is a contradiction to the orthogonality of
$\Lambda $
. Hence,
$\pi _i(\Lambda )$
is an infinite orthogonal set of
$\mu _{\rho _i, \{0,1,2\}}$
,
$i=1,2$
. With Theorem 3.1, we get that
$\rho _i=(\frac {q_i}{p_i})^{1/r_i}$
for some
$r_i, p_i, q_i\in {\mathbb N}^+$
,
$i=1,2$
.
For the converse, let
$r=r_1r_2$
. We write
$$ \begin{align*} \hat{\mu}_{M, \{D_n\}}(\xi) =\prod_{j=1}^{\infty}\hat{\delta}_{D_j}(M^{-j}\xi) =\prod_{i=1}^{r}\prod_{j=0}^{\infty}\hat{\delta}_{D_{i+jr}}(M^{-(i+rj)}\xi). \end{align*} $$
Define the probability measures
$\nu _i=\delta _{M^{-i}D_i}*\delta _{M^{-(i+r)}D_{i+r}} *\delta _{M^{-(i+2r)}D_{i+2r}}*\cdots $
,
$1\leq i\leq r$
. Then
$ \hat {\mu }_{M, \{D_n\}}(\xi )=\prod _{i=1}^{r}\hat {\nu }_{i}(\xi )$
and
${\mathcal Z}(\hat {\mu }_{M,\{D_n\}})=\bigcup _{i=1}^{r}{\mathcal Z}(\hat {\nu }_i)$
, where
$\hat {\nu }_{i}(\xi ) =\prod _{j=0}^{\infty }\hat {\delta }_{D_{i+jr}}(M^{-(i+rj)}\xi )$
for
$1\leq i\leq r$
. By the pigeon hole principle, there exist
$a,b\in \{-1,1\}$
and infinite set J such that
$a_{1+jr}= a$
and
$b_{1+jr}= b$
for any
$j\in J$
. Without loss of generality let
$a=b=1$
. Then for any
$j\in J$
, we have
${\mathcal Z}(\hat {\delta }_{D_{1+jr}})=\left ( \frac {1}{3} \begin {pmatrix} 1\\ 2 \end {pmatrix}+{\mathbb Z}^2 \right ) \bigcup \left (\frac {1}{3} \begin {pmatrix} 2\\ 1 \end {pmatrix} +{\mathbb Z}^2 \right ).$
Let
$a= \begin {array}{cc}1\\ \overline {3} \\ \end {array} \begin {pmatrix} 1\\ 2 \end {pmatrix}$
and
$R=q_1^{r_2}q_2^{r_1}M^r$
. We take
$\Lambda =\{MR^{j} a: j\in J\}\cup \{0\}.$
Then
$\Lambda $
is infinite since J is infinite. For any distinct
$\lambda _1=MR^{j_1}a, \lambda _2=MR^{j_2}a\in \Lambda $
with
$j_1,j_2\in J$
and
$j_1<j_2$
, we have
$\lambda _1=M^{1+rj_1} \frac {q_1^{r_2 j_1}q_2^{r_1 j_1}}{3}\begin {pmatrix} 1\\ 2 \end {pmatrix}$
and
$$ \begin{align*} \lambda_2-\lambda_1 = M^{1+rj_1} \frac{q_1^{r_2 j_1}q_2^{r_1 j_1}}{3}\begin{pmatrix} (3p_1)^{r_2(j_2-j_1)}q_2^{r_1(j_2-j_1)}-1 \\ 2(3p_2)^{r_1(j_2-j_1)}q_1^{r_2(j_2-j_1)}-2 \end{pmatrix}. \end{align*} $$
Hence,
$\lambda _1, \lambda _2-\lambda _1\in \bigcup _{j\in J}M^{1+rj}{\mathcal Z}(\hat {\delta }_{D_{1+jr}}) \subseteq {\mathcal Z}(\hat {\nu }_1)$
. Thus,
$\Lambda $
is an infinite orthogonal set of
$\nu _1$
. From Lemma 2.2, it is clear that
$\Lambda $
is an infinite orthogonal set of
$\mu _{M, \{D_n\}}$
. ▪
3.2 The case of
$\rho _i=(\frac {3p_i}{q_i})^{1/r_i}$
for
$r_1>1$
or
$r_2>1$
We state a lemma as follows, which has been proved in [Reference Deng8].
Lemma 3.2 Assume that
$b\in {\mathbb R}$
admits a minimal integer polynomial
$p x^r-q$
and satisfies that
$a_1b^{l_1}+a_2b^{l_2}=a_3b^{l_3}$
, where
$a_1,a_2,a_3\in {\mathbb Z}\setminus \{0\}$
and
$l_1, l_2, l_3\geq 0$
. Then
$l_1\equiv l_2 \equiv l_3 (\mathrm {mod}~r)$
.
Theorem 3.3 If
$\rho _i=(\frac {3p_i}{q_i})^{1/r_i}$
for
$r_1>1$
or
$r_2>1$
, then the Moran Sierpinski-type measure
$\mu _{M, \{D_n\}}$
is not a spectral measure.
Proof Without loss of generality let
$r_1>1$
. Then
$q_1x^{r_1}-3p_1$
is the minimal polynomial of
$\rho _1$
. Denote
$\nu _i=\delta _{M^{-i}D_i}*\delta _{M^{-(i+r_1)}D_{i+r_1}} *\delta _{M^{-(i+2r_1)}D_{i+2r_1}}*\cdots $
for
$1\leq i\leq r_1.$
Then
$\hat {\nu }_{i}(\xi ) =\prod _{j=0}^{\infty }\hat {\delta }_{D_{i+jr}}(M^{-(i+rj)}\xi )$
,
$1\leq i\leq r_1.$
Let
$0\in \Lambda $
be any infinite orthogonal set of
$\mu _{M, \{D_n\}}$
. For any
$\lambda _1\neq \lambda _2 \in \Lambda $
, write
$ \lambda _1=M^{l_1} \begin {pmatrix} a_{11}\\ a_{12} \end {pmatrix}\in M^{l_1}{\mathcal Z}(m_{D_{l_1}})$
,
$\lambda _2=M^{l_2} \begin {pmatrix} a_{21}\\ a_{22} \end {pmatrix}\in M^{l_2}{\mathcal Z}(m_{D_{l_2}}),$
where
$l_1,l_2\geq 1$
. There exist
$l_3\geq 1$
and
$\begin {pmatrix} a_{31}\\ a_{32} \end {pmatrix} \in {\mathcal Z}(m_{D_{l_3}})$
such that
$\lambda _1-\lambda _2=M^{l_3} \begin {pmatrix} a_{31}\\ a_{32} \end {pmatrix}.$
It follows that
$a_{11}\rho _1^{l_1}-a_{21}\rho _1^{l_2}=a_{31}\rho _1^{l_3}.$
Combining equation (2.2) and Lemma 3.2, we obtain
$l_1\equiv l_2\equiv l_3 (\mathrm {mod}~r_1)$
. This shows that there exists
$i_0\in \{1,2,\ldots ,r_1\}$
with
$i_0\equiv l_1 (\mathrm {mod}~r_1)$
such that
$\Lambda $
is an orthogonal set of
$\nu _{i_0}$
. Using Lemma 2.2, we conclude that
$\Lambda $
is not a spectrum of
$\mu _{M, \{D_n\}}$
and the theorem is proved. ▪
4 Structure of spectrum for rational contraction
In this section, let
$\rho _i=\frac {3p_i}{q_i}$
for some
$p_i, q_i\in {\mathbb N}^+$
,
$i=1, 2$
. These sets
$A_i$
,
$1\leq i\leq 4$
, are defined as in equation (2.2). Suppose that
$\mu _{M, \{D_n\}}$
is a spectral measure. We will characterize the structure of spectrum
$\Lambda $
and estimate the growth rate of elements in
$\Lambda $
.
Lemma 4.1 Let
$\gcd (q_i, 3)=1$
for
$i=1,2$
. Suppose that
$\alpha \in \begin {array}{cc}1\\ \overline {3} \\ \end {array}\left (\!\!\!\begin {array}{cc}q_1 & 0 \\ 0 & q_2\\ \end {array}\!\!\!\right ){\mathbb Z}^2 \cap (\bigcup _{i=1}^{4}A_i)$
. Then
$\left (\!\!\!\begin {array}{cc}q_1^{-1} & 0 \\ 0 & q_2^{-1}\\ \end {array}\!\!\!\right )\alpha \in \bigcup _{i=1}^{4}A_i.$
Proof Denote
$\alpha =\begin {array}{cc}1\\ \overline {3} \\ \end {array}\left (\!\!\!\begin {array}{cc}q_1 & 0 \\ 0 & q_2\\ \end {array}\!\!\!\right )\begin {pmatrix} z_1\\ z_2 \end {pmatrix}$
for some
$z_1,z_2\in {\mathbb Z}$
. Without loss of generality let
$\alpha \in A_1$
. From equation (2.2), we get
$\begin {pmatrix} q_1z_1\\ q_2z_2 \end {pmatrix}\equiv \begin {pmatrix} 1\\ 2 \end {pmatrix} (\mathrm {mod}~3{\mathbb Z}^2).$
If
$q_1\equiv q_2 (\mathrm {mod}~3)$
, then
$z_1 \not \equiv z_2 (\mathrm {mod}~3)$
. This implies that
$\left (\!\!\!\begin {array}{cc}q_1^{-1} & 0 \\ 0 & q_2^{-1}\\ \end {array}\!\!\!\right )\alpha =\begin {array}{cc}1\\ \overline {3} \\ \end {array} \begin {pmatrix} z_1\\ z_2 \end {pmatrix}\in A_1\cup A_2$
. If
$q_1\not \equiv q_2 (\mathrm {mod}~3)$
, then
$z_1\equiv z_2 (\mathrm {mod}~3)$
. This implies that
$\left (\!\!\!\begin {array}{cc}q_1^{-1} & 0 \\ 0 & q_2^{-1}\\ \end {array}\!\!\!\right )\alpha =\begin {array}{cc}1\\ \overline {3} \\ \end {array} \begin {pmatrix} z_1\\ z_2 \end {pmatrix}\in A_3\cup A_4$
. We complete the proof. ▪
In rest of the section, we will analyze the structure of spectrum
$\Lambda $
. Denote
$M=M' R^{-1}$
, where
$M'=\left (\!\!\! \begin {array}{cc} 3p_1 & 0 \\ 0 & 3p_2\\ \end {array} \!\!\!\right )$
and
$R=\left (\!\!\! \begin {array}{cc} q_1 & 0 \\ 0 & q_2\\ \end {array} \!\!\!\right ).$
Theorem 4.2 Let
$\rho _i=\frac {3p_i}{q_i}$
for
$p_i,q_i\in {\mathbb N}^+$
. If
$0\in \Lambda $
is an orthogonal set of
$\mu _{M,\{D_n\}}$
, then there exists
$t\in {\mathbb N}^+$
such that
$$ \begin{align} (\Lambda-\Lambda)\setminus\{0\}\subseteq M^t \bigcup_{n=0}^{\infty}M^{{\prime}n}(A_1\cup A_2\cup A_3 \cup A_4). \end{align} $$
Moreover, if
$0\in \Lambda $
is a spectrum of
$\mu _{M,\{D_n\}}$
, then
$t=1$
.
Proof If
$\# \Lambda \leq 2$
, the statement is trivial since
$0\in \Lambda $
. We now assume that
$\# \Lambda \geq 3$
. Let t be the smallest integer such that
$(\Lambda -\Lambda )\cap M^t({\mathcal Z}\left (m_{D_t}\right ))\neq \emptyset $
. Then there exist
$\lambda _1\neq \lambda _0\in \Lambda $
such that
$\lambda _1-\lambda _0 = M^t \alpha $
for some
$\alpha \in {\mathcal Z}\left (m_{D_t}\right )$
. For any
$\lambda _2\in \Lambda \setminus \{\lambda _0,\lambda _1\}$
, the orthogonality of
$\Lambda $
implies that
$\lambda _2-\lambda _0=M^{t+k}\beta $
and
$\lambda _2-\lambda _1=M^{t+l}\gamma $
for some
$\beta \in {\mathcal Z}\left (m_{D_{t+k}}\right ), \gamma \in {\mathcal Z}\left (m_{D_{t+l}}\right )$
and
$k,l \geq 0$
. Then
$M^{k}\beta -M^{l}\gamma =\alpha $
. With
$M=M'R^{-1}$
, it is clear that
$$ \begin{align} R^l M^{{\prime}k} \beta- R^k M^{{\prime}l} \gamma=R^{k+l} \alpha. \end{align} $$
We claim that
$k=0$
or
$l=0$
. Indeed, if
$k,l>0$
, the left hand side of equation (4.2) must be integer vector but the right hand side belongs to
$\frac {{\mathbb Z}^2}{3}\setminus {\mathbb Z}^2$
. This is a contradiction. Hence the claim follows.
If
$k=0$
, then
$\lambda _2-\lambda _0=M^t \beta \in M^t({\mathcal Z}\left (m_{D_t}\right ))\subset M^t(\bigcup _{i=1}^{4}A_i)$
. If
$k>0$
, then
$l=0$
. Equation (4.2) implies
$\beta =R^k M^{{\prime }^{-k}}(\alpha +\gamma ).$
Note that
$\alpha ,\beta ,\gamma \in \bigcup _{i=1}^{4}A_i\subseteq \frac {{\mathbb Z}^2}{3}$
and
$\gcd (3p_i,q_i)=1$
for
$i=1,2$
. Then
$\beta \in \frac {R^k}{3}{\mathbb Z}^2 \cap (\bigcup _{i=1}^{4}A_i).$
By Lemma 4.1, we have
$R^{-k}\beta \in \bigcup _{i=1}^{4}A_i$
. This implies that
$\lambda _2-\lambda _0 \in M^t M^{{\prime }^{k}}(\bigcup _{i=1}^{4}A_i).$
Since
$\lambda _2$
is arbitrary, it follows that
$$ \begin{align*} (\Lambda-\lambda_0)\setminus\{0\}\subseteq M^t \bigcup_{n=0}^{\infty}M^{{\prime}^n}\left(\bigcup_{i=1}^{4}A_i\right). \end{align*} $$
On the other hand, for any
$\lambda _3\neq \lambda _4\in \Lambda \setminus \{\lambda _0\}$
, we have
$$ \begin{align*}\lambda_3-\lambda_0=M^{t+k'}\beta',\quad \lambda_4-\lambda_0=M^{t+l'}\gamma',\quad \lambda_3-\lambda_4=M^{t+s'}\alpha'\end{align*} $$
for some
$\alpha '\in {\mathcal Z} (m_{D_{t+k'}} ), \beta '\in {\mathcal Z} (m_{D_{t+l'}} ), \gamma '\in {\mathcal Z} (m_{D_{t+s'}} )$
and
$k',l', s'\geq 0$
. Then
$M^{s'}\alpha '=M^{k'}\beta '-M^{l'}\gamma '.$
Thus, by the similar arguments to the above proof, we obtain
$\lambda _3-\lambda _4\in M^t M^{{\prime }^{s'}}(\bigcup _{i=1}^{4}A_i).$
By the arbitrariness of
$\lambda _3, \lambda _4$
, we get
$$ \begin{align*} (\Lambda-\Lambda)\setminus\{0\}\subseteq M^t \bigcup_{n=0}^{\infty}M^{{\prime}^n}\left(\bigcup_{i=1}^{4}A_i\right). \end{align*} $$
Moreover, suppose to the contrary that
$t\geq 2$
. For any
$\lambda _1\neq \lambda _2\in \Lambda $
, we have
$\lambda _1-\lambda _2=M^t M^{{\prime }^i} \alpha =M^j \beta $
for some
$i\geq 0, j\geq t\geq 2$
,
$\alpha \in \bigcup _{i=1}^{4}A_i$
and
$\beta \in {\mathcal Z}\left (m_{D_j}\right )$
. This shows that
$$ \begin{align*} M^{-1}(\lambda_1-\lambda_2)=M^{j-1}\beta \in M^{j-1}{\mathcal Z}(m_{D_j})\subset \bigcup_{n=1}^{\infty}M^n{\mathcal Z}\left(m_{D_{n+1}}\right). \end{align*} $$
Then
$M^{-1}\Lambda $
is an orthogonal set of
$\delta _{M^{-1}D_2}\ast \delta _{M^{-2}D_3}\ast \cdots $
, and hence
$\Lambda $
is an orthogonal set of
$\delta _{M^{-2}D_2}\ast \delta _{M^{-3}D_3}\ast \cdots $
. Note that
$\mu _{M,\{D_n\}}=\delta _{M^{-1}D_1}*(\delta _{M^{-2}D_2}\ast \delta _{M^{-3}D_3}\ast \cdots )$
. Lemma 2.2 implies that
$\Lambda $
cannot be a spectrum of
$\mu _{M, \{D_n\}}$
. That is a contradiction. Thus,
$t=1$
. ▪
For further analysis, we need the measures
$$ \begin{align} \nu_{>n}(\cdot)=\mu_{>n}(M^{-n} \cdot)=\delta_{M^{-1}D_{n+1}}\ast \delta_{M^{-2}D_{n+2}}\ast \cdots. \end{align} $$
The following theorem analogous to Theorem 4.2 and thus we omit the proof.
Theorem 4.3 Let
$\rho _i=\frac {3p_i}{q_i}$
for some
$p_i,q_i\in {\mathbb N}^+$
with
$\gcd (3p_i,q_i)=1$
,
$i=1, 2$
. If
$0\in \Lambda $
is a spectrum of
$\nu _{>n}$
. Then
$(\Lambda -\Lambda )\setminus \{0\}\subseteq M \bigcup \limits _{n=1}^\infty M^{{\prime }^n}(\bigcup _{i=1}^{4}A_i).$
Note that
$M^{{\prime }^n}(\bigcup _{i=1}^{4}A_i)\subset {\mathbb Z}^2$
,
$n\geq 1$
. Hence,
$M \bigcup _{n=0}^{\infty }M^{{\prime }^n}(\bigcup _{i=1}^{4}A_i)\subseteq \bigcup _{i=1}^{4} MA_i\cup M{\mathbb Z}^2.$
Combining this with Theorem 3.1, we have
$$ \begin{align} (\Lambda-\Lambda) \subseteq \bigcup_{i=1}^{4} MA_i\cup M{\mathbb Z}^2. \end{align} $$
Theorem 4.4 Let
$\mu _{M,\{D_n\}}$
be the Moran Sierpinski-type measure defined as in equation (1.1). Suppose that
$\Lambda $
is a spectrum of
$\mu _{M,\{D_n\}}$
. Then
$\Lambda $
can be decomposed as
$ \Lambda =\bigcup _{k=0}^{2}(\lambda _k+ M\Lambda _k), $
where
-
(i)
$0\in \Lambda _k\subseteq {\mathbb Z}^2$
is a spectrum of
$\nu _{>1}$
for each
$k\in \{0, 1, 2\}$
. -
(ii)
$\{\lambda _k: k=0, 1, 2\}$
is a spectrum of
$\delta _{M^{-1}D_1}$
with
$\lambda _0\in \Lambda \cap M{\mathbb Z}^2$
and for each
$k=1,2$
,
$$ \begin{align*} \lambda_k\in \left\{\begin{array}{ll} \Lambda\cap MA_k,\quad &a_1= b_1=-1\,\, or \,\,a_1= b_1=1;\\ \Lambda\cap MA_{k+2},\quad &a_1=-1, b_1=1\,\,or\,\,a_1=1, b_1=-1.\\ \end{array}\right. \end{align*} $$
Proof If
$a_1= b_1=-1$
, we have
$$ \begin{align*}(\Lambda-\Lambda)\setminus\{0\}\subset {\mathcal Z}(\hat{\mu}_{M,\{D_n\}}) \subset M(A_1\cup A_2)\cup \bigcup_{n=2}^{\infty}M^n\left(\bigcup_{i=1}^{4}A_i\right).\end{align*} $$
Since
$M(A_3\cup A_4)\cap M^n(\bigcup _{i=1}^{4}A_i)=\emptyset $
for all
$n\geq 2$
. Combining this with equation (4.4), we obtain
$(\Lambda -\Lambda ) \subseteq M(A_1\cup A_2)\cup M{\mathbb Z}^2.$
We claim that
$\Lambda \cap MA_k\neq \emptyset $
for each
$k=1, 2$
. Otherwise, without loss of generality let
$\Lambda \cap MA_1=\emptyset $
. Then
$\Lambda \subseteq MA_2\cup M{\mathbb Z}^2$
. Let
$\lambda '\in MA_1$
. We note that
$\lambda -\lambda '\in {\mathcal Z}(\hat {\mu }_{M,\{D_n\}})$
for any
$\lambda \in \Lambda $
. This implies that
$\{\lambda '\}\cup \Lambda $
is an orthogonal set of
$\mu _{M,\{D_n\}}$
, which contradicts the maximality of
$\Lambda $
. Hence, the claim follows.
We choose
$\lambda _0\in \Lambda \cap M{\mathbb Z}^2$
and
$\lambda _k\in \Lambda \cap MA_k$
,
$k=1,2.$
It is clear that
$\{\lambda _0, \lambda _1, \lambda _2\}$
is a spectrum of
$\delta _{M^{-1}D_1}$
. Let
$$ \begin{align} \Lambda_k=M^{-1}(\Lambda-\lambda_k)\cap {\mathbb Z}^2, \quad k=0, 1, 2. \end{align} $$
This shows that
$$ \begin{align*}0\in \Lambda_k \subseteq {\mathbb Z}^2 \quad \mathrm{and} \quad \lambda_k+M\Lambda_k=\Lambda\cap (\lambda_k+M{\mathbb Z}^2), \quad k=0, 1, 2.\end{align*} $$
Then
$\lambda _0+M{\mathbb Z}^2=M{\mathbb Z}^2$
and
$\lambda _k+M{\mathbb Z}^2=MA_k$
,
$k=1, 2.$
Hence,
$$ \begin{align*}\bigcup_{k=0}^{2}(\lambda_k+M\Lambda_k)=\Lambda\cap \bigcup_{k=0}^{2}(\lambda_k+M{\mathbb Z}^2)=\Lambda,\end{align*} $$
where
$\lambda _k+M\Lambda _k$
(
$k=0, 1, 2$
) are pairwise disjoint. From equation (4.5),
$$ \begin{align*} (\Lambda_k-\Lambda_k)\setminus\{0\} \subseteq M^{-1}(\Lambda-\Lambda)\cap {\mathbb Z}^2 \subseteq \left(\bigcup_{n=1}^{\infty}M^{n}{\mathcal Z}(m_{D_{n+1}})\right)={\mathcal Z}(\hat{\nu}_{>1}). \end{align*} $$
This implies that
$\Lambda _k$
is an orthogonal set of
$\nu _{>1}$
. By Theorem 2.1(i),
$\sum _{\alpha _{k}\in \Lambda _{k}}\vert \hat {\nu }_{>1}\left (\xi +\alpha _{k}\right ) \vert ^2\leq 1$
for any
$\xi \in {\mathbb R}^2$
,
$k\in \{0, 1, 2\}.$
Hence,
$$ \begin{align*} 1 &= \sum_{\lambda\in \Lambda}\left\vert \hat{\mu}_{M,\{D_n\}}\left(\xi +\lambda\right)\right\vert^2\\ &=\sum_{k=0}^2 \sum_{\alpha_k\in \Lambda_k} \left\vert \hat{\delta}_{D_1}\left(M^{-1} (\xi+\lambda_k)+\alpha_k\right)\right\vert^2 \left\vert\hat{\nu}_{>1} \left(M^{-1}(\xi+\lambda_k)+\alpha_k)\right)\right\vert ^2\\ &= \sum_{k=0}^2 \left\vert \hat{\delta}_{D_1}\left(M^{-1}(\xi+\lambda_k)\right)\right\vert^2 \sum_{\alpha_k\in \Lambda_k}\left\vert \hat{\nu}_{>1}\left(M^{-1}(\xi+ \lambda_k)+\alpha_k)\right)\right\vert^2\\ &\leq \sum_{k=0}^2 \left\vert \hat{\delta}_{D_1}\left(M^{-1}(\xi+\lambda_k)\right)\right\vert^2 =1 \end{align*} $$
for any
$\xi \in {\mathbb R}^2$
. This forces that
$\sum _{\alpha _{k}\in \Lambda _{k}}\vert \hat {\nu }_{>1}\left (\xi +\alpha _{k}\right )\vert ^2= 1$
for all
$k=0, 1, 2.$
Thus, it follows from Theorem 2.1(ii) that
$\Lambda _{k}$
is a spectrum of
$\nu _{>1}$
for each
$k\in \{0, 1, 2\}$
.
Similarly, the other cases of
$a_1= b_1=1$
,
$a_1=-1, b_1=1$
and
$a_1=1, b_1=-1$
follow from the same argument and this completes the proof. ▪
Combining the above Theorems 4.3 and 4.4, we have the following corollary. In order to illustrate the further structure of spectrum of
$\mu _{M,\{D_n\}}$
, we denote
$\Omega =\{0, 1, 2\}$
,
$\Omega ^m=\{K=k_1 k_2\cdots k_m:k_i \in \Omega,\,1\leq\,i\leq\,m \}$
to be the set of all words with length m, and
$\Omega ^*=\bigcup _{m=1}^{\infty }\Omega ^m$
to be the set of finite words.
Theorem 4.5 Let
$\Lambda $
be a spectrum of
$\mu _{M,\{D_n\}}$
. Then
-
(i) For each
$m\geq 1$
, there is a decomposition (4.6)where
$$ \begin{align} \Lambda=\bigcup_{k_1\cdots k_m\in \Omega^m}\left(\lambda_{k_1} +\cdots +M^{m-1}\lambda_{k_1\cdots k_m}+M^m\Lambda_{k_1\cdots k_m}\right), \end{align} $$
$\{\lambda _{k_1\cdots k_m}: k_m=0, 1, 2\}$
is a spectrum of
$\delta _{M^{-1}D_m}$
with
$\lambda _{k_1\cdots k_{m-1}0}\in \Lambda _{k_1\cdots k_{m-1}}\cap M{\mathbb Z}^2$
and for each
$$ \begin{align*} \lambda_{k_1\cdots k_m}\in \left\{\!\!\!\begin{array}{ll} \Lambda_{k_1\cdots k_{m-1}}\cap MA_{k_m},\,\, &a_m= b_m=-1\,\, or \,\,a_m= b_m=1\\ \Lambda_{k_1\cdots k_{m-1}}\cap MA_{k_m+2},\,\, &a_m=-1, b_m=1\,\,or\,\,a_m=1, b_m=-1\\ \end{array}\right. \end{align*} $$
$k_m=1,2$
. For
$k_m=0, 1, 2$
, each
$\Lambda _{k_1\cdots k_m}$
is a spectrum of
$\nu _{>m}$
with
$0\in \Lambda _{k_1\cdots k_m}=M^{-1}(\Lambda _{k_1\cdots k_{m-1}}-\lambda _{k_1\cdots k_m})\cap {\mathbb Z}^2.$
Moreover (4.7)
$$ \begin{align} \Lambda_{k_1\cdots k_m}\subseteq \begin{pmatrix} q_1^{m-1} & 0 \\ 0 & q_2^{m-1} \end{pmatrix} {\mathbb Z}^2. \end{align} $$
-
(ii) Let
$\Gamma _m:=\{\lambda _{k_1}+\cdots +M^{m-1}\lambda _{k_1k_2\cdots k_m}: k_1k_2\cdots k_m\in \Omega ^m\}.$
Then
$\Gamma _m$
is a spectrum of the measure
$\mu _m$
.
Proof For (i), applying the procedures in Theorem 4.4 repeatedly, then we get the decomposition. By equation (4.6),
$M^m(\Lambda _{k_1\cdots k_m}-\Lambda _{k_1\cdots k_m})\subseteq \Lambda -\Lambda \subseteq M\frac {{\mathbb Z}^2}{3}.$
This implies that
$$ \begin{align*} \Lambda_{k_1\cdots k_m}-\Lambda_{k_1\cdots k_m}\subseteq M^{1-m}\frac{{\mathbb Z}^2}{3} \subseteq \left(\!\!\! \begin{array}{cc} q_1^{m-1} & 0 \\ 0 & q_2^{m-1}\\ \end{array} \!\!\!\right){\mathbb Z}^2. \end{align*} $$
Hence, equation (4.7) holds.
We prove (ii) by mathematical induction. when
$m=1$
, the statement is true by Theorem 4.4. Assume now it is true for
$m-1$
. Then
$$ \begin{align*} &~\sum_{\lambda\in \Gamma_m}\left\vert \hat{\mu}_{m}\left(\xi +\lambda\right)\right\vert^2 =\sum_{\lambda\in \Gamma_m}\left\vert\hat{\mu}_{m-1}\left(\xi +\lambda\right)\right\vert^2 \left\vert \hat{\delta}_{D_m}\left(M^{-m} (\xi+\lambda\right)\right\vert^2 \\ &=\sum_{\lambda'\in \Gamma_{m-1}}\left\vert\hat{\mu}_{m-1}\left(\xi +\lambda'\right)\right\vert^2 \sum_{k_m=0}^{2}\left\vert \hat{\delta}_{D_m}\left(M^{-m} (\xi+\lambda')+M^{-1}\lambda_{k_1\cdots k_m}\right)\right\vert^2 \\ &= \sum_{k_m=0}^2 \left\vert \hat{\delta}_{D_m}\left(M^{-m}(\xi+\lambda_k)+M^{-1}\lambda_{k_1\cdots k_m}\right)\right\vert^2=1.\end{align*} $$
▪
We observe that in the proof of Theorem 4.4,
$\{\lambda _k: k=0, 1, 2\}$
can be chosen freely. In order to estimate the ranges of the elements in
$\Lambda $
, we introduce two special types of decomposition by selecting the first or the second coordinate of
$\lambda _{k_1\cdots k_m}$
to be the “smallest” one respectively step by step. For convenience, we denote
$$ \begin{align} \Lambda_{k_1\cdots k_{m-1}}^{\prime}=\left\{\!\!\!\begin{array}{ll} \Lambda_{k_1\cdots k_{m-1}}\cap MA_{k_m},\,\,a_m= b_m=-1\,\, or \,\,a_m= b_m=1;\\ \Lambda_{k_1\cdots k_{m-1}}\cap MA_{k_m+2},\,\,a_m=-1, b_m=1\,\,or\,\,a_m=1, b_m=-1.\\ \end{array}\right. \end{align} $$
For a fixed
$j\in \{1, 2\}$
, we define the j-type decomposition system of the spectrum
$\Lambda $
as follows.
Step 1: Let
$\lambda _0=0$
and
$$ \begin{align*} \lambda_{k_1}\in\Lambda'= \left\{\!\!\!\begin{array}{ll} \Lambda\cap MA_{k_1},\quad &a_1= b_1=-1\,\,\, or \,\,\,a_1= b_1=1\\ \Lambda\cap MA_{k_1+2},\quad &a_1=-1, b_1=1\,\,\,or\,\,\,a_1=1, b_1=-1\\ \end{array}\right. \end{align*} $$
for each
$k_1=1,2$
such that
$$ \begin{align} \left|\pi_j(\lambda_{k_1})\right|=\min \left\{\left|\pi_j(\lambda)\right|: \lambda\in \Lambda'\right\}. \end{align} $$
Let
$\Lambda _{k_1}=M^{-1}(\Lambda -\lambda _{k_1})\cap {\mathbb Z}^2$
,
$k_1=0, 1, 2.$
Step 2: Suppose that
$\lambda _{k_1k_2\cdots k_{m-1}}$
and
$\Lambda _{k_1\cdots k_{m-1}}$
have been defined for all
$k_1\cdots k_{m-1}\in \Omega ^{m-1}$
. We take
$\lambda _{k_1k_2\cdots k_{m-1}0}=0$
and
$\lambda _{k_1\cdots k_m}\in \Lambda _{k_1\cdots k_{m-1}}^{\prime }$
for
$k_m=1,2$
such that
$$ \begin{align} \begin{array}{rl} & \left|\pi_j\left(\lambda_{k_1}+\cdots +M^{m-1}\lambda_{k_1\cdots k_m}\right)\right|\\ =& \min \left\{\left|\pi_j(\lambda)\right|: \lambda\in \lambda_{k_1} +\cdots +M^{m-2}\lambda_{k_1\cdots k_{m-1}}+M^{m-1}\Lambda_{k_1\cdots k_{m-1}}^{\prime}\right\}. \end{array} \end{align} $$
Let
$\Lambda _{k_1k_2\cdots k_m}=M^{-1}(\Lambda _{k_1\cdots k_{m-1}}-\lambda _{k_1\cdots k_m})\cap {\mathbb Z}^2$
,
$k_m=0, 1, 2.$
Note that
$\bigcup _{i=1}^{4}A_i\subset \frac {{\mathbb Z}^2}{3}$
. Then the equations (4.9) and (4.10) are well-defined. Therefore, we get the j-type decomposition system by induction.
We now give a key theorem, this will be used in the following section.
Theorem 4.6 Let
$\Lambda $
be a spectrum of
$\mu _{M,\{D_n\}}$
and
$\{\lambda _{k_1k_2\cdots k_m}, \Lambda _{k_1k_2\cdots k_m}: k_1k_2\cdots k_m\in \Omega ^*\}$
be a j-type decomposition system of
$\Lambda $
. Then
-
(i) If
$k_m\neq 0$
, then
$\left |\pi _j(\lambda _{k_1}+\cdots +M^{m-1}\lambda _{k_1k_2\cdots k_m})\right |\geq \frac {(3p_j)^{m-1}}{2q_j}$
. -
(ii)
$\Lambda =\bigcup _{m=1}^{\infty }\Gamma _m$
.
Proof Without loss of generality, we assume that
$j=1$
. We prove (i). For each
$\lambda _{k_1\cdots k_m}$
with
$k_m\neq 0$
,
$\lambda _{k_1\cdots k_m}\in \Lambda _{k_1\cdots k_{m-1}}$
and by Theorem 4.5, we get
$$ \begin{align*} M^{m-1}\lambda_{k_1\cdots k_m}\in \begin{pmatrix} \frac{(3p_1)^{m-1}}{q_1} & 0 \\ 0 & \frac{(3p_2)^{m-1}}{q_2} \end{pmatrix}{\mathbb Z}^2. \end{align*} $$
Note that
$\lambda _{k_1\cdots k_m}\in \Lambda _{k_1\cdots k_{m-1}}^{\prime }$
and
$\bigcup _{i=1}^{4}A_i\subseteq \frac {{\mathbb Z}^2}{3}\setminus {\mathbb Z}^2$
. This implies that
$\pi _1(\lambda _{k_1\cdots k_m})\neq 0$
. Hence,
$\left |\pi _1\left (M^{m-1}\lambda _{k_1\cdots k_m}\right )\right |\geq \frac {(3p_1)^{m-1}}{q_1}.$
By (4.10),
$$ \begin{align*} &~2\left|\pi_1\left(\lambda_{k_1}\cdots +M^{m-1}\lambda_{k_1\cdots k_m}\right)\right|\\ &\geq \left|\pi_1\left(\lambda_{k_1}+\cdots +M^{m-1}\lambda_{k_1\cdots k_m}\right) -\pi_1\left(\lambda_{k_1}+\cdots +M^{m-2}\lambda_{k_1\cdots k_{m-1}}\right)\right|\\ &= \left|\pi_1\left(M^{m-1}\lambda_{k_1\cdots k_m}\right)\right|\geq\frac{(3p_1)^{m-1}}{q_1}. \end{align*} $$
To prove (ii), note that
$\bigcup _{m=1}^{\infty }\Gamma _m\subseteq \Lambda $
by Theorem 4.5, we just to prove
$\Lambda \subseteq \bigcup _{m=1}^{\infty }\Gamma _m$
. Suppose on the contrary that there exists
$\lambda \in \Lambda $
but
$\lambda \notin \bigcup _{m=1}^{\infty }\Gamma _m$
. Then there is
$m_0$
large enough such that
$\left |\pi _1(\lambda )\right |<\frac {(3p_1)^{m_0}}{2q_1}$
. By equation (4.6), there exists
$k_1\cdots k_{m_0}\in \Omega ^{m_0}$
such that
$ \lambda \in \lambda _{k_1}+M\lambda _{k_1 k_2}+\cdots +M^{m_0-1}\lambda _{k_1\cdots k_{m_0}} +M^{m_0}\Lambda _{k_1\cdots k_{m_0}}.$
From equation (4.7),
$$ \begin{align*} \lambda-\left(\lambda_{k_1}+\cdots +M^{m_0-1}\lambda_{k_1\cdots k_{m_0}}\right)\in M^{m_0}\Lambda_{k_1 \cdots k_{m_0}}\subseteq \begin{pmatrix} \frac{(3p_1)^{m_0}}{q_1} & 0 \\ 0 & \frac{(3p_2)^{m_0}}{q_2} \end{pmatrix} {\mathbb Z}^2. \end{align*} $$
Using a similar argument to (i), we have
$$ \begin{align*} 2\left|\pi_1(\lambda)\right| \geq \left|\pi_1\left(\lambda\right) -\pi_1\left(\lambda_{k_1}+M\lambda_{k_1 k_2}+\cdots +M^{m_0-1}\lambda_{k_1\cdots k_{m_0}}\right)\right|\geq\frac{(3p_1)^{m_0}}{q_1}. \end{align*} $$
This contradicts to the assumption for
$m_0$
. We complete the proof of (ii). ▪
5 Proof of the necessity of Theorem 1.1
In this section, we will complete the proof of the necessity of Theorem 1.1 when
$\rho _i=\frac {3p_i}{q_i}$
for
$q_1>1$
or
$q_2>1$
(Theorem 5.3). Here, a few technical lemmas are needed.
For any
$x\in {\mathbb R}$
, let
$\|x\|=|\langle x\rangle |$
, where
$\langle x\rangle $
is the unique number such that
$\langle x\rangle \in (-\frac {1}{2}, \frac {1}{2}]$
and
$x-\langle x\rangle =[x] \in {\mathbb Z}$
. Clearly
$\|x\|$
is the distance from x to
${\mathbb Z}$
.
Lemma 5.1 Let
$a_j=\ln q_j/\ln (3p_j)$
and
$c_j=\frac {1}{3}\left (\left |1+e^{\pi i/ 3p_j}\right |+1\right )$
for
$j=1, 2$
. Fix
$j\in \{1, 2\}$
. Then for any
$x=(x_1, x_2)^T\in {\mathbb R}^2$
with
$|x_j|>1$
, there exist
$n_j\in {\mathbb N}^+$
and
$y=(y_1, y_2)^T\in {\mathbb R}^2$
such that
$$ \begin{align*} \rho_j^{-2}|x_j|^{a_j}\leq |y_j|\leq \rho_j^{-1}|x_j|\quad \mathrm{and}\quad \left| \hat{\mu}_{M,\{D_n\}}(x) \right|\leq c_j \left|\hat{\nu}_{>n_j}(y)\right|. \end{align*} $$
Proof Without loss of generality, we let
$j=1$
. If
$\left \|\rho _1^{-1}x_1\right \|\geq \frac {1}{6p_1}$
, then
$$ \begin{align*} \left\vert \hat{\delta}_{M^{-1}D_n}\left(x\right)\right\vert \leq\frac{1}{3}\left(\left|1+e^{2\pi i \langle\rho_1^{-1}x_1\rangle}\right|+1\right) \leq\frac{1}{3}\left(\left|1+e^{\pi i \frac{1}{3p_1}}\right|+1\right). \end{align*} $$
This implies that
$$ \begin{align*} \left\vert \hat{\mu}_{M,\{D_n\}}\left(x\right)\right\vert &=\left\vert \hat{\delta}_{M^{-1}D_1}\left(x\right)\right\vert \left\vert \hat{\mu}_{>1}\left(x\right)\right\vert\\ &=\left\vert \hat{\delta}_{M^{-1}D_1}\left(x\right)\right\vert \left\vert \hat{\nu}_{>1}\left(M^{-1}x\right)\right\vert \leq c_1\left\vert \hat{\nu}_{>1}\left(M^{-1}x\right)\right\vert. \end{align*} $$
Hence, our statement follows by taking
$n_1=1$
and
$y=M^{-1}x$
.
If
$\left \|\rho _1^{-1}x_1\right \|< \frac {1}{6p_1}$
, note that
$\left |\rho _1^{-1}x_1\right |=\left |\frac {q_1}{3p_1}x_1\right |>\frac {1}{3p_1}$
, we can write
$\rho _1^{-1}x_1=(3p_1)^s\xi +\langle \rho _1^{-1}x_1\rangle $
with
$3p_1\not \mid \xi $
and
$s\geq 0$
. Then
$ \rho _1^{-(s+2)}x_1=\frac {q_1^{s+1}\xi }{3p_1}+\rho _1^{-(s+1)} \langle \rho _1^{-1}x_1\rangle . $
Denote
$q_1^{s+1}\xi =3p_1\eta +t$
with
$\eta \in {\mathbb Z}$
and
$t\in \{1, 2, \ldots , 3p_1-1\}$
. Then
$$ \begin{align*} \left\|\rho_1^{-(s+2)}x_1\right\|=\left\|\frac{t}{3p_1}+\rho_1^{-(s+1)} \langle\rho_1^{-1}x_1\rangle \right\|>\frac{1}{3p_1}-\frac{1}{6p_1}=\frac{1}{6p_1}. \end{align*} $$
This shows that
$\left \vert \hat {\delta }_{M^{-(s+2)}D_{s+2}}\left (x\right )\right \vert \leq \frac {1}{3}\left (\left |1+e^{\pi i \frac {1}{3p_1}}\right |+1\right ).$
Therefore,
$$ \begin{align*} \left\vert \hat{\mu}_{M, \{D_n\}}\left(x\right)\right\vert &=\prod_{j=1}^{s+2}\left\vert \hat{\delta}_{M^{-j}D_j}\left(x\right)\right\vert \left\vert \hat{\mu}_{>s+2}\left(x\right)\right\vert\\ &\leq\left\vert \hat{\delta}_{M^{-{s+2}}D_{s+2}}\left(x\right)\right\vert \left\vert \hat{\nu}_{>s+2}\left(M^{-(s+2)}x\right)\right\vert\\ &\leq c_1\left\vert \hat{\nu}_{>s+2}\left(M^{-(s+2)}x\right)\right\vert. \end{align*} $$
Let
$y=M^{-(s+2)}x=\begin {pmatrix} \rho _1^{-(s+2)}x_1\\ \rho _2^{-(s+2)}x_2 \end {pmatrix}$
. Then
$\left |y_1\right |\leq \rho _1^{-1}\left |x_1\right |$
. Since
$ \left |\rho _1^{-1}x_1\right |\geq \left |[\rho _1^{-1}x_1]\right |-\left \|\rho _1^{-1}x_1\right \| \geq \rho _1^{-1}(3p_1)^s. $
We have
$|x_1|\geq (3p_1)^s$
. Then
$$ \begin{align*} \left|y_1\right|=\rho_1^{-(s+2)}\left|x_1\right| =\frac{q_1^s}{(3p_1)^s}\rho_1^{-2}|x_1| =\frac{(3p_1)^{a_1s}}{(3p_1)^s}\rho_1^{-2}|x_1| \geq \rho_1^{-2}|x_1|^{a_1}. \end{align*} $$
Hence, our statement follows by taking
$n_1=s+2$
and
$y=M^{-(s+2)}x$
. ▪
Lemma 5.2 Let
$r_j>\frac {\ln a_j}{\ln c_j}+1$
be an integer for
$j=1, 2$
, where
$a_j, c_j$
are as in Lemma 5.1. Fix
$j\in \{1, 2\}$
. Then there exist constant
$\alpha _j>1$
,
$C_j>1$
and
$n_{0,j}$
large enough such that for any
$\lambda \in \Gamma _{(n+1)^{r_j}}\setminus \Gamma _{n^{r_j}}$
with
$n>n_{0,j}$
and
$x\in (0,1)\times (0,1)$
, we have
$$ \begin{align*} \left|\hat{\nu}_{>(n+1)^{r_j}}(M^{-(n+1)^{r_j}}(x+\lambda))\right| \leq \frac{C_j}{n^{\alpha_j}}. \end{align*} $$
Proof Without loss of generality, we let
$j=1$
. By Theorem 4.6(i), for any
$\lambda \in \Gamma _{(n+1)^{r_1}}\setminus \Gamma _{n^{r_1}}$
, we have
$|\pi _1(\lambda )|\geq \frac {1}{2q_1}(3p_1)^{n^{r_1}}.$
Let
$\eta =\begin {pmatrix} \eta _1\\ \eta _2 \end {pmatrix}:=\begin {pmatrix} (M^{-(n+1)^{r_1}}(x+\lambda ))_1\\ (M^{-(n+1)^{r_1}}(x+\lambda ))_2 \end {pmatrix}$
. Then
$$ \begin{align*} \left\vert \eta_1\right\vert =\left\vert \frac{q_1^{(n+1)^{r_1}}}{(3p_1)^{(n+1)^{r_1}}}\pi_1(x+\lambda)\right\vert \geq\frac{1}{2q_1}(3p_1)^{n^{r_1}} \frac{q_1^{(n+1)^{r_1}}}{(3p_1)^{(n+1)^{r_1}}} -\frac{q_1^{(n+1)^{r_1}}}{(3p_1)^{(n+1)^{r_1}}}. \end{align*} $$
We take sufficiently large
$n_{0,1}$
such that
$(n+1)^{r_1}\leq n^{r_1}+{r_1}^2n^{r_1-1}-3$
,
$(3p_1)^{n^{r_1}}>4q_1$
and
$q_1^n>(3p_1)^{r_1^2+1}$
whenever
$n\geq n_{0,1}$
. Hence, for
$n\geq n_{0,1}$
, we get
$$ \begin{align*} \left\vert \eta_1\right\vert &\geq\left(\frac{q_1^n}{(3p_1)^{{r_1}^2}}\right)^{n^{r_1-1}} \frac{(3p_1)^3((3p_1)^{n^{r_1}}-2q_1)}{(3p_1)^{n^{r_1}}(2q_1)}\\ &\geq\left(\frac{q_1^n}{(3p_1)^{{r_1}^2}}\right)^{n^{r_1-1}} \geq (3p_1)^{n^{r_1-1}}>1. \end{align*} $$
Let
$d^{(0)}=\begin {pmatrix} d_1^{(0)}\\ d_2^{(0)} \end {pmatrix}\in {\mathbb R}^2$
with
$d_1^{(0)}=\eta _1$
. Applying Lemma 5.1 several times, we obtain an sequence of positive integers
$n_1<n_2<\cdots $
and
$d^{(i)}=\begin {pmatrix} d_1^{(i)}\\ d_2^{(i)} \end {pmatrix}$
satisfying that
$\rho _1^{-2}\left |d_1^{(i)}\right |^{a_1}\leq \left |d_1^{(i+1)}\right |\leq \rho _1^{-1}\left |d_1^{(i)}\right |$
for all
$i\geq 0$
, and for any
$\left |d_1^{(l)}\right |>1$
,
$$ \begin{align*} \left|\hat{\mu}_{M,\{D_n\}}(\eta)\right|\leq c_1 \left|\hat{\nu}_{>n_1}(d^{(1)})\right|\leq c_1^2 \left|\hat{\nu}_{>n_2}(d^{(2)})\right|\leq \cdots \leq c_1^l \left|\hat{\nu}_{>n_l}(d^{(l)})\right|\leq \cdots. \end{align*} $$
Take
$l=\lfloor \log _{a_1} \frac {2n^{1-r_1}}{1-a_1} \rfloor $
, where the symbol
$\lfloor x \rfloor $
denotes the biggest integer smaller or equal to x. Then
$$ \begin{align*} \left|d_1^{(l)}\right| \geq\rho_1^{-2(1+a_1+\cdots+a_1^{l-1})}\left|\eta_1\right|^{a_1^l} \geq q_1^{\frac{2}{1-a_1}}(3p_1)^{-\frac{2}{1-a_1}}(3p_1)^{n^{r_1-1}a_1^l}>1. \end{align*} $$
This implies that
$$ \begin{align*} \left|\hat{\mu}_{M,\{D_n\}}(\eta)\right|\leq c_1^l \leq c_1^{\log_{a_1} \frac{2n^{1-r_1}}{1-a_1}} =c_1^{\log_{a_1} \frac{2}{1-a_1}} n^{-(r_1-1)\ln c_1/ \ln a_1}. \end{align*} $$
We assume
$C_1:=c_1^{\log _{a_1} \frac {2}{1-a_1}}$
and
$\alpha _1:=(r_1-1)\ln c_1/ \ln a_1$
, this completes the proof. ▪
We are now ready to prove the case of
$\rho _i=\frac {3p_i}{q_i}$
for
$q_1>1$
or
$q_2>1$
, which is restated as follows.
Theorem 5.3 Let
$\mu _{M,\{D_n\}}$
be the Moran Sierpinski-type measure defined as in equation (1.1). If
$\rho _i=\frac {3p_i}{q_i}$
for
$q_1>1$
or
$q_2>1$
,
$i=1, 2$
, then
$\mu _{M,\{D_n\}}$
is not a spectral measure.
Proof Without loss of generality, we assume that
$q_1>1$
. Suppose on the contrary that
$\mu _{M,\{D_n\}}$
is a spectral measure. Let
$\Lambda $
be a spectrum of
$\mu _{M,\{D_n\}}$
and
$\{\lambda _{k_1k_2\cdots k_m}, \Lambda _{k_1k_2\cdots k_m}: k_1k_2\cdots k_m\in \Omega ^*\}$
be a j-type decomposition system of
$\Lambda $
. Then
$\Lambda =\bigcup _{m=1}^{\infty }\Gamma _m$
by Theorem 4.6(ii). We assume all the parameters in Lemma 5.2. Denote
$$ \begin{align*} Q_n(x)=\sum_{\lambda\in \Gamma_n}\left|\hat{\mu}_{M,\{D_n\}}(x+\lambda)\right|^2 \quad \mathrm{and} \quad Q(x)=\sum_{\lambda\in \Lambda}\left|\hat{\mu}_{M,\{D_n\}}(x+\lambda)\right|^2. \end{align*} $$
Combining Theorem 4.5(ii) and Lemma 5.2, for any
$n\geq n_{0,1}$
and
$x\in (0,1)\times (0,1)$
, we get
$$ \begin{align*} &~Q_{(n+1)^{r_1}}(x)=Q_{n^{r_1}}(x)+\sum_{\lambda\in \Gamma_{(n+1)^{r_1}}\setminus\Gamma_{n^{r_1}}} \left|\hat{\mu}_{M,\{D_n\}}(x+\lambda)\right|^2\\ &= Q_{n^{r_1}}(x)+\sum_{\lambda\in \Gamma_{(n+1)^{r_1}}\setminus\Gamma_{n^{r_1}}} \left|\hat{\mu}_{(n+1)^{r_1}}(x+\lambda)\right|^2 \left|\hat{\nu}_{>(n+1)^{r_1}}(M^{-(n+1)^{r_1}}(x+\lambda)\right|^2\\ &\leq Q_{n^{r_1}}(x)+\frac{C_1^2}{n^{2\alpha_1}}\sum_{\lambda\in \Gamma_{(n+1)^{r_1}}\setminus\Gamma_{n^{r_1}}} \left|\hat{\mu}_{(n+1)^{r_1}}(x+\lambda)\right|^2\\ &\leq Q_{n^{r_1}}(x)+\frac{C_1^2}{n^{2\alpha_1}}\left(1- Q_{n^{r_1}}(x)\right). \end{align*} $$
This implies that
$$ \begin{align*} &~1-Q_{(n+1)^{r_1}}(x)\geq (1-Q_{n^{r_1}}(x))(1-\frac{C_1^2}{n^{2\alpha_1}})\geq\cdots\\ &\geq(1-Q_{n_{0,1}^{r_1}}(x))\prod_{k=n_{0,1}}^{n} \left(1-\frac{C_1^2}{k^{2\alpha_1}}\right). \end{align*} $$
By taking
$n\rightarrow \infty $
, we obtain that
$ (1-Q_{n_{0,1}^{r_1}}(x))\prod _{k=n_{0,1}}^{\infty } \left (1-\frac {C_1^2}{k^{2\alpha _1}}\right )\leq 0$
. Note that
$\prod _{k=n_{0,1}}^{\infty } \left (1-\frac {C_1^2}{k^{2\alpha _1}}\right )\neq 0$
. Then
$Q_{n_{0,1}^{r_1}}(x)\equiv 1$
for any
$x\in (0,1)\times (0,1)$
. This means that
$\Gamma _{n_{0,1}^{r_1}}$
is a spectrum of
$\mu _{M,\{D_n\}}$
by Theorem 2.1(ii). This contradicts the fact that
$\Gamma _{n_{0,1}^{r_1}}$
is a finite set. Hence we complete the proof. ▪
Acknowledgment
The author would like to thank editor in handling the manuscript and the anonymous referee for their helpful comments. This work is supported by the National Natural Science Foundation of China (Grant No. 11971194). The author is thankful to Professor Xing-Gang He for many helpful suggestions.
