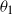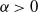1. Introduction
The Chinese restaurant process (CRP) is a discrete-time stochastic process which generates exchangeable random partitions. This process is first mentioned in David Aldous’s lecture notes [Reference Aldous1, p. 92] on exchangeability and goes back to ideas of Jim Pitman and Lester Dubins. The one-parameter CRP can be generated [Reference James16,Reference Lo, Brunner and Chan23] from a Dirichlet process, being strongly related to the Blackwell and MacQueen urn [Reference Blackwell and MacQueen4]. Similarly, the two-parameter CRP can be constructed from the two-parameter Poisson–Dirichlet process, also called the Pitman–Yor process [Reference Pitman and Yor31]. Constructions of this form have been generalized using normalized completely random measures [Reference James16,Reference James17] and the Poisson–Kingman process (see also [Reference Pitman, Speed and Goldstein29]). Pitman [Reference Pitman27,Reference Pitman28,Reference Pitman30] further developed the related theory on (partially) exchangeable random partitions. The CRP and the associated random measures have applications in several disciplines, for example in Bayesian statistics [Reference Green, Bingham and Goldie11,Reference James16,Reference James17] and in mathematical population genetics. We mention here Kingman’s work [Reference Kingman22] on random partitions in population genetics, and that the Ewens sampling formula [Reference Ewens8] arises naturally from the CRP or from the Dirichlet process (see [Reference Antoniak2]).
We are interested in the following extension of the CRP. Fix three real parameters
![]() $\alpha$
,
$\alpha$
,
![]() $\theta_1$
, and
$\theta_1$
, and
![]() $\theta_2$
. The precise range of these parameters will be provided shortly. Imagine a restaurant having an infinite number of tables with labels
$\theta_2$
. The precise range of these parameters will be provided shortly. Imagine a restaurant having an infinite number of tables with labels
![]() $i\in\mathbb{N}\,:\!=\,\{1,2,\ldots\}$
and a cocktail bar. All tables and the bar are assumed to have infinite capacity. At the beginning (opening) the restaurant is empty. If at stage
$i\in\mathbb{N}\,:\!=\,\{1,2,\ldots\}$
and a cocktail bar. All tables and the bar are assumed to have infinite capacity. At the beginning (opening) the restaurant is empty. If at stage
![]() $n\in\mathbb{N}_0\,:\!=\,\{0,1,\ldots\}$
there are
$n\in\mathbb{N}_0\,:\!=\,\{0,1,\ldots\}$
there are
![]() $n_0\in\mathbb{N}_0$
customers at the bar and
$n_0\in\mathbb{N}_0$
customers at the bar and
![]() $k\in\mathbb{N}_0$
occupied tables with
$k\in\mathbb{N}_0$
occupied tables with
![]() $n_i\in\mathbb{N}$
customers at the ith table,
$n_i\in\mathbb{N}$
customers at the ith table,
![]() $i\in\{1,\ldots,k\}$
, the next customer is seated
$i\in\{1,\ldots,k\}$
, the next customer is seated
-
• at the bar with probability
 $(n_0+\theta_2-\theta_1)/(n+\theta_2)$
,
$(n_0+\theta_2-\theta_1)/(n+\theta_2)$
, -
• at occupied table
 $i\in\{1,\ldots,k\}$
with probability
$i\in\{1,\ldots,k\}$
with probability
 $(n_i-\alpha)/(n+\theta_2)$
, and
$(n_i-\alpha)/(n+\theta_2)$
, and -
• at the new table
 $k+1$
with probability
$k+1$
with probability
 $(\alpha k+\theta_1)/(n+\theta_2)$
,
$(\alpha k+\theta_1)/(n+\theta_2)$
,
where
![]() $n\,:\!=\,\sum_{i=0}^kn_i$
. In particular, customer 1 is seated at table 1 with probability
$n\,:\!=\,\sum_{i=0}^kn_i$
. In particular, customer 1 is seated at table 1 with probability
![]() $\theta_1/\theta_2$
and at the bar with probability
$\theta_1/\theta_2$
and at the bar with probability
![]() $1-\theta_1/\theta_2$
. In order to fulfill the axioms of probability it is assumed that either
$1-\theta_1/\theta_2$
. In order to fulfill the axioms of probability it is assumed that either
![]() $0\le\alpha\le 1$
and
$0\le\alpha\le 1$
and
![]() $0<\theta_1\le\theta_2<\infty$
or that
$0<\theta_1\le\theta_2<\infty$
or that
![]() $\alpha=-\kappa<0$
for some
$\alpha=-\kappa<0$
for some
![]() $\kappa>0$
,
$\kappa>0$
,
![]() $\theta_1=m\kappa$
for some
$\theta_1=m\kappa$
for some
![]() $m\in\mathbb{N}$
, and
$m\in\mathbb{N}$
, and
![]() $\theta_1\le \theta_2<\infty$
. The case
$\theta_1\le \theta_2<\infty$
. The case
![]() $\theta_1=0$
is excluded, since in this case all customers would sit at the bar. For
$\theta_1=0$
is excluded, since in this case all customers would sit at the bar. For
![]() $\theta_1=\theta_2$
the bar can be neglected (stays empty) and the model coincides with Pitman’s [Reference Pitman30] two-parameter
$\theta_1=\theta_2$
the bar can be neglected (stays empty) and the model coincides with Pitman’s [Reference Pitman30] two-parameter
![]() $(\alpha,\theta)$
-Chinese restaurant model with
$(\alpha,\theta)$
-Chinese restaurant model with
![]() $\theta\,:\!=\,\theta_1>0$
. Green [Reference Green, Bingham and Goldie11] studied mixed Dirichlet processes in which not all clusters have equal standing. For example (see [Reference Green, Bingham and Goldie11, Section 5.3]), we may think about a distinguished ‘background’ cluster behaving differently from all other clusters. The cocktail bar can be viewed as such a background cluster. For details on the random probability measure associated to the restaurant process with cocktail bar we refer the reader to the remark at the end of Section 5.
$\theta\,:\!=\,\theta_1>0$
. Green [Reference Green, Bingham and Goldie11] studied mixed Dirichlet processes in which not all clusters have equal standing. For example (see [Reference Green, Bingham and Goldie11, Section 5.3]), we may think about a distinguished ‘background’ cluster behaving differently from all other clusters. The cocktail bar can be viewed as such a background cluster. For details on the random probability measure associated to the restaurant process with cocktail bar we refer the reader to the remark at the end of Section 5.
After
![]() $n\in\mathbb{N}_0$
customers have been seated, typical quantities of interest are the number
$n\in\mathbb{N}_0$
customers have been seated, typical quantities of interest are the number
![]() $N_{n,0}$
of customers seated at the bar, the number
$N_{n,0}$
of customers seated at the bar, the number
![]() $N_{n,i}$
of customers seated at table
$N_{n,i}$
of customers seated at table
![]() $i\in\mathbb{N}$
, and the number
$i\in\mathbb{N}$
, and the number
![]() $K_n$
of occupied (nonempty) tables. Note that
$K_n$
of occupied (nonempty) tables. Note that
![]() $N_{n,i}=0$
for
$N_{n,i}=0$
for
![]() $i>K_n$
and
$i>K_n$
and
![]() $\sum_{i=0}^{K_n} N_{n,i}=n$
. The process
$\sum_{i=0}^{K_n} N_{n,i}=n$
. The process
![]() $(N_n)_{n\in\mathbb{N}_0}$
, defined via
$(N_n)_{n\in\mathbb{N}_0}$
, defined via
![]() $N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
for all
$N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
for all
![]() $n\in\mathbb{N}_0$
, is a Markov chain with
$n\in\mathbb{N}_0$
, is a Markov chain with
![]() $N_0=(0)$
and transition probabilities
$N_0=(0)$
and transition probabilities
![]() $\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_0 \mid N_n=\textbf{n})=(n_0+\theta_2-\theta_1)/(n+\theta_2)$
,
$\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_0 \mid N_n=\textbf{n})=(n_0+\theta_2-\theta_1)/(n+\theta_2)$
,
![]() $\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_i \mid N_n=\textbf{n}) = (n_i-\alpha)/(n+\theta_2)$
,
$\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_i \mid N_n=\textbf{n}) = (n_i-\alpha)/(n+\theta_2)$
,
![]() $i\in\{1,\ldots,k\}$
, and
$i\in\{1,\ldots,k\}$
, and
![]() $\mathbb{P}(N_{n+1}=(n_0,\ldots,n_k,1) \mid N_n=\textbf{n}) = (\alpha k+\theta_1)/(n+\theta_2)$
for all
$\mathbb{P}(N_{n+1}=(n_0,\ldots,n_k,1) \mid N_n=\textbf{n}) = (\alpha k+\theta_1)/(n+\theta_2)$
for all
![]() $\textbf{n}=(n_0,\ldots,n_k)$
with
$\textbf{n}=(n_0,\ldots,n_k)$
with
![]() $k,n_0\in\mathbb{N}_0$
,
$k,n_0\in\mathbb{N}_0$
,
![]() $n_1,\ldots,n_k\in\mathbb{N}$
, and
$n_1,\ldots,n_k\in\mathbb{N}$
, and
![]() $n_0+\cdots+n_k=n$
, where
$n_0+\cdots+n_k=n$
, where
![]() $\textbf{e}_i$
denotes the ith unit vector in
$\textbf{e}_i$
denotes the ith unit vector in
![]() $\mathbb{R}^{\{0,\ldots,k\}}$
,
$\mathbb{R}^{\{0,\ldots,k\}}$
,
![]() $i\in\{0,\ldots,k\}$
.
$i\in\{0,\ldots,k\}$
.
The article is organized as follows. In Section 2 the model is reinterpreted in terms of a mixture of a two-type Pólya urn and a two-parameter CRP. Section 3 focuses on the number
![]() $N_{n,0}$
of customers at the bar at stage n. In Section 4, in analogy to the construction provided by Pitman [Reference Pitman30], a general restaurant process with cocktail bar and random seating plan is introduced; this is useful to derive results on the joint distribution and asymptotics of
$N_{n,0}$
of customers at the bar at stage n. In Section 4, in analogy to the construction provided by Pitman [Reference Pitman30], a general restaurant process with cocktail bar and random seating plan is introduced; this is useful to derive results on the joint distribution and asymptotics of
![]() $N_{n,i}$
,
$N_{n,i}$
,
![]() $i\in\mathbb{N}_0$
, which is done in Section 5. The number
$i\in\mathbb{N}_0$
, which is done in Section 5. The number
![]() $K_n$
of occupied tables is studied in Section 6. A formula in terms of generalized Stirling numbers for the distribution of
$K_n$
of occupied tables is studied in Section 6. A formula in terms of generalized Stirling numbers for the distribution of
![]() $K_n$
is provided in (14). The simple case
$K_n$
is provided in (14). The simple case
![]() $\alpha=0$
is studied briefly in Section 6.1. The main part (Section 6.2) concentrates on the case
$\alpha=0$
is studied briefly in Section 6.1. The main part (Section 6.2) concentrates on the case
![]() $\alpha\ne 0$
. For
$\alpha\ne 0$
. For
![]() $\alpha\ne 0$
, Corollary 1 provides an exact formula for the moments of
$\alpha\ne 0$
, Corollary 1 provides an exact formula for the moments of
![]() $K_n$
. Theorem 3 states that, for
$K_n$
. Theorem 3 states that, for
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $K_n/n^\alpha$
is asymptotically three-parameter Mittag–Leffler distributed. The restaurant process with cocktail bar can hence be viewed as a basic model where the three-parameter Mittag–Leffler distribution arises naturally in the limit. The work finishes with an independent part (Section 7) on the three-parameter Mittag–Leffler distribution and a more applied part (Section 8) containing new distributional representations for the two- (see Proposition 4) and three-parameter Mittag–Leffler distribution (see Corollary 3) leading to accurate and efficient random number generators for these distributions.
$K_n/n^\alpha$
is asymptotically three-parameter Mittag–Leffler distributed. The restaurant process with cocktail bar can hence be viewed as a basic model where the three-parameter Mittag–Leffler distribution arises naturally in the limit. The work finishes with an independent part (Section 7) on the three-parameter Mittag–Leffler distribution and a more applied part (Section 8) containing new distributional representations for the two- (see Proposition 4) and three-parameter Mittag–Leffler distribution (see Corollary 3) leading to accurate and efficient random number generators for these distributions.
The proofs draw heavily from methods known for random partitions [Reference Pitman27,Reference Pitman28,Reference Pitman30], from martingale methods and results known for Pólya urns and related urn models (see, for example, [Reference Janson18,Reference Janson19]), and from (asymptotic) results known for the two-parameter CRP [Reference Pitman30].
The restaurant process with cocktail bar turns out to be a mathematically well tractable extension of the two-parameter CRP having strong relations to martingales, Pólya urns, and random partitions. Moreover, in the analytic community there is interest (see, for example, [Reference Tomovski, Pogány and Srivastava40]) on (extensions of) Prabhakar’s [Reference Prabhakar32] three-parameter Mittag–Leffler function, which is (up to a factor) the Laplace transform of the three-parameter Mittag–Leffler distribution being the limiting distribution of the number of occupied tables in the restaurant model with cocktail bar provided that
![]() $\alpha>0$
(see Theorem 3). The restaurant process with cocktail bar therefore sheds some new light on the three-parameter Mittag–Leffler distribution and therefore bridges analytic and probabilistic aspects around Mittag–Leffler functions. The model may also find its way into applications, for example in the context of extensions of sampling formulas in mathematical population genetics. We refer the reader to the remarks at the end of Section 5 for some more details pointing in this direction.
$\alpha>0$
(see Theorem 3). The restaurant process with cocktail bar therefore sheds some new light on the three-parameter Mittag–Leffler distribution and therefore bridges analytic and probabilistic aspects around Mittag–Leffler functions. The model may also find its way into applications, for example in the context of extensions of sampling formulas in mathematical population genetics. We refer the reader to the remarks at the end of Section 5 for some more details pointing in this direction.
Throughout the article,
![]() $\beta(a,b)$
denotes the beta distribution with parameters
$\beta(a,b)$
denotes the beta distribution with parameters
![]() $a,b>0$
having density
$a,b>0$
having density
![]() $x\mapsto ({\rm B}(a,b))^{-1}x^{a-1}(1-x)^{b-1}$
,
$x\mapsto ({\rm B}(a,b))^{-1}x^{a-1}(1-x)^{b-1}$
,
![]() $x\in (0,1)$
, with respect to Lebesgue measure on (0,1), where
$x\in (0,1)$
, with respect to Lebesgue measure on (0,1), where
![]() ${\rm B}(.,.)$
denotes the beta function. We furthermore use for
${\rm B}(.,.)$
denotes the beta function. We furthermore use for
![]() $a,b>0$
the convention
$a,b>0$
the convention
![]() $\beta(0,b)\,:\!=\,\delta_0$
(Dirac measure at 0) and
$\beta(0,b)\,:\!=\,\delta_0$
(Dirac measure at 0) and
![]() $\beta(a,0)\,:\!=\,\delta_1$
(Dirac measure at 1).
$\beta(a,0)\,:\!=\,\delta_1$
(Dirac measure at 1).
2. Reinterpretation as an urn model
The restaurant with cocktail bar can be reinterpreted as a mixture of a two-type Pólya urn with initial weights
![]() $\theta_2-\theta_1$
and
$\theta_2-\theta_1$
and
![]() $\theta_1$
and a standard CRP with parameters
$\theta_1$
and a standard CRP with parameters
![]() $\alpha$
and
$\alpha$
and
![]() $\theta_1$
as follows. Consider an urn with balls of two main colors, white and red. Assume furthermore that there is an entire (countable infinite) graduation of red colors, the red balls being split into balls of red subcolors. Let
$\theta_1$
as follows. Consider an urn with balls of two main colors, white and red. Assume furthermore that there is an entire (countable infinite) graduation of red colors, the red balls being split into balls of red subcolors. Let
![]() $(W_n,R_{n,1},\ldots,R_{n,K_n})$
be the number of balls of the different colors present after n steps, the total number of red balls being
$(W_n,R_{n,1},\ldots,R_{n,K_n})$
be the number of balls of the different colors present after n steps, the total number of red balls being
![]() $R_n=\sum_{i=1}^{K_n}R_{n,i}$
. Let
$R_n=\sum_{i=1}^{K_n}R_{n,i}$
. Let
![]() $W_0\,:\!=\,K_0\,:\!=\,0$
. Then, recursively, given
$W_0\,:\!=\,K_0\,:\!=\,0$
. Then, recursively, given
![]() $(W_n,R_{n,1},\ldots,R_{n,K_n})$
at step n, one adds a white ball with probability
$(W_n,R_{n,1},\ldots,R_{n,K_n})$
at step n, one adds a white ball with probability
![]() $(W_n+\theta_2-\theta_1)/(n+\theta_2)$
or a ball of red subcolor i with probability
$(W_n+\theta_2-\theta_1)/(n+\theta_2)$
or a ball of red subcolor i with probability
![]() $(R_{n,i}-\alpha)/(n+\theta_2)$
,
$(R_{n,i}-\alpha)/(n+\theta_2)$
,
![]() $i\in\{1,\ldots,K_n\}$
, or a ball with new red subcolor
$i\in\{1,\ldots,K_n\}$
, or a ball with new red subcolor
![]() $K_n+1$
with probability
$K_n+1$
with probability
![]() $(\alpha K_n+\theta_1)/(n+\theta_2)$
. This setting corresponds to the restaurant model with cocktail bar with
$(\alpha K_n+\theta_1)/(n+\theta_2)$
. This setting corresponds to the restaurant model with cocktail bar with
![]() $N_{n,0}=W_n$
and
$N_{n,0}=W_n$
and
![]() $N_{n,i}=R_{n,i}$
. Now observe that
$N_{n,i}=R_{n,i}$
. Now observe that
![]() $(W_n+\theta_2-\theta_1,R_n+\theta_1)_{n\in\mathbb{N}_0}$
is a two-type Pólya urn with initial weights
$(W_n+\theta_2-\theta_1,R_n+\theta_1)_{n\in\mathbb{N}_0}$
is a two-type Pólya urn with initial weights
![]() $\theta_2-\theta_1$
and
$\theta_2-\theta_1$
and
![]() $\theta_1$
. Indeed, conditional that there are
$\theta_1$
. Indeed, conditional that there are
![]() $W_n=k$
white balls (and hence
$W_n=k$
white balls (and hence
![]() $R_n=n-k$
red balls) in the urn, a white ball is drawn from the urn with probability
$R_n=n-k$
red balls) in the urn, a white ball is drawn from the urn with probability
and returned to the urn together with an additional white ball. Moreover, the jump evolution of the process
![]() $(R_{n,1},\ldots,R_{n,K_n})$
is a standard CRP (see [Reference Pitman30]) with parameters
$(R_{n,1},\ldots,R_{n,K_n})$
is a standard CRP (see [Reference Pitman30]) with parameters
![]() $\alpha$
and
$\alpha$
and
![]() $\theta_1$
independent of the Pólya urn. For
$\theta_1$
independent of the Pólya urn. For
![]() $${\theta _1} = {\theta _2} = :\theta $$
and
$${\theta _1} = {\theta _2} = :\theta $$
and
![]() $\alpha=0$
the model coincides with the Pólya-like urns studied in [Reference Donnelly7,Reference Hoppe12,Reference Hoppe13,Reference Trieb41], being related to the Ewens sampling formula [Reference Ewens8].
$\alpha=0$
the model coincides with the Pólya-like urns studied in [Reference Donnelly7,Reference Hoppe12,Reference Hoppe13,Reference Trieb41], being related to the Ewens sampling formula [Reference Ewens8].
3. Number of customers at the cocktail bar
One of the simplest functionals is the number
![]() $N_{n,0}$
of customers seated at the cocktail bar after
$N_{n,0}$
of customers seated at the cocktail bar after
![]() $n\in\mathbb{N}_0$
customers have entered the restaurant. Clearly,
$n\in\mathbb{N}_0$
customers have entered the restaurant. Clearly,
![]() $N_{n,0}$
coincides with the number
$N_{n,0}$
coincides with the number
![]() $W_n$
of white balls of the Pólya urn
$W_n$
of white balls of the Pólya urn
![]() $(W_n+\theta_2-\theta_1,R_n+\theta_1)_{n\in\mathbb{N}_0}$
introduced in Section 2. The following results on
$(W_n+\theta_2-\theta_1,R_n+\theta_1)_{n\in\mathbb{N}_0}$
introduced in Section 2. The following results on
![]() $N_{n,0}=W_n$
are therefore known from standard theory on Pólya urns and we hence keep this section relatively short. From the model it follows that
$N_{n,0}=W_n$
are therefore known from standard theory on Pólya urns and we hence keep this section relatively short. From the model it follows that
![]() $(W_n)_{n\in\mathbb{N}_0}$
is a Markov chain with state space
$(W_n)_{n\in\mathbb{N}_0}$
is a Markov chain with state space
![]() $\mathbb{N}_0$
,
$\mathbb{N}_0$
,
![]() $W_0=0$
, and transition probabilities
$W_0=0$
, and transition probabilities
The distribution of
![]() $W_n$
depends only on
$W_n$
depends only on
![]() $\theta_1$
and
$\theta_1$
and
![]() $\theta_2$
but not on
$\theta_2$
but not on
![]() $\alpha$
. It is easily checked by induction on
$\alpha$
. It is easily checked by induction on
![]() $n\in\mathbb{N}_0$
that
$n\in\mathbb{N}_0$
that
![]() $W_n$
has distribution
$W_n$
has distribution
where
![]() $[x]_0\,:\!=\,1$
,
$[x]_0\,:\!=\,1$
,
![]() $[x]_k\,:\!=\,x(x+1)\cdots(x+k-1)$
for
$[x]_k\,:\!=\,x(x+1)\cdots(x+k-1)$
for
![]() $x\in\mathbb{R}$
and
$x\in\mathbb{R}$
and
![]() $k\in\mathbb{N}$
, and
$k\in\mathbb{N}$
, and
![]() $P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. The occurrence of
$P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. The occurrence of
![]() $P_0$
is well known from Pólya urns and will also become clearer in Sections 4 and 5. From (2) it follows that, given
$P_0$
is well known from Pólya urns and will also become clearer in Sections 4 and 5. From (2) it follows that, given
![]() $P_0$
, the distribution of
$P_0$
, the distribution of
![]() $W_n$
is binomial with parameters n and
$W_n$
is binomial with parameters n and
![]() $P_0$
. In particular,
$P_0$
. In particular,
![]() $W_n$
has descending factorial moments
$W_n$
has descending factorial moments
where
![]() $(x)_0\,:\!=\,1$
and
$(x)_0\,:\!=\,1$
and
![]() $(x)_j\,:\!=\,x(x-1)\cdots(x-j+1)$
for
$(x)_j\,:\!=\,x(x-1)\cdots(x-j+1)$
for
![]() $x\in\mathbb{R}$
and
$x\in\mathbb{R}$
and
![]() $j\in\mathbb{N}$
. For
$j\in\mathbb{N}$
. For
![]() $\theta_1=\theta_2$
the bar stays empty (
$\theta_1=\theta_2$
the bar stays empty (
![]() $W_n=0$
). We therefore focus without loss of generality on the case
$W_n=0$
). We therefore focus without loss of generality on the case
![]() $0<\theta_1<\theta_2$
. Conditional on
$0<\theta_1<\theta_2$
. Conditional on
![]() $P_0$
, each ball is independently white with probability
$P_0$
, each ball is independently white with probability
![]() $P_0$
. Thus, if
$P_0$
. Thus, if
![]() $0<\theta_1<\theta_2$
and, hence,
$0<\theta_1<\theta_2$
and, hence,
![]() $P_0>0$
almost surely, it follows that
$P_0>0$
almost surely, it follows that
![]() $W_n\to\infty$
almost surely as
$W_n\to\infty$
almost surely as
![]() $n\to\infty$
.
$n\to\infty$
.
Theorem 1. (Convergence of scaled
![]() $W_n$
.) Assume that
$W_n$
.) Assume that
![]() $0<{\theta}_{1}\le\theta_{2}$
. Then, as
$0<{\theta}_{1}\le\theta_{2}$
. Then, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $W_n/n\to P_0$
almost surely and in
$W_n/n\to P_0$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $P_0 \stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. In particular, the convergence
$P_0 \stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. In particular, the convergence
![]() $\lim_{n\to\infty}\mathbb{E}((W_n/n)^p)=\mathbb{E}(P_0^p)$
,
$\lim_{n\to\infty}\mathbb{E}((W_n/n)^p)=\mathbb{E}(P_0^p)$
,
![]() $p\ge 0$
, of all moments holds.
$p\ge 0$
, of all moments holds.
Remark 1. For
![]() $\theta_1=\theta_2$
the bar stays empty and the result holds with
$\theta_1=\theta_2$
the bar stays empty and the result holds with
![]() $P_0\stackrel{\textrm{d}}{=}\delta_0=\beta(0,\theta_1)$
.
$P_0\stackrel{\textrm{d}}{=}\delta_0=\beta(0,\theta_1)$
.
Proof. For
![]() $\theta_1=\theta_2$
the bar stays empty and the result holds with
$\theta_1=\theta_2$
the bar stays empty and the result holds with
![]() $P_0\stackrel{\textrm{d}}{=}\delta_0=\beta(0,\theta_1)$
. Assume now that
$P_0\stackrel{\textrm{d}}{=}\delta_0=\beta(0,\theta_1)$
. Assume now that
![]() $\theta_1<\theta_2$
. The proof is based on a martingale method known from Pólya urns. For
$\theta_1<\theta_2$
. The proof is based on a martingale method known from Pólya urns. For
![]() $n\in\mathbb{N}_0$
define
$n\in\mathbb{N}_0$
define
![]() $M_n\,:\!=\,(W_n+\theta_2-\theta_1)/(n+\theta_2)$
. Using (1) it is easily checked that
$M_n\,:\!=\,(W_n+\theta_2-\theta_1)/(n+\theta_2)$
. Using (1) it is easily checked that
![]() $\mathbb{E}(M_{n+1} \mid W_n)=M_n$
almost surely,
$\mathbb{E}(M_{n+1} \mid W_n)=M_n$
almost surely,
![]() $n\in\mathbb{N}_0$
. Thus,
$n\in\mathbb{N}_0$
. Thus,
![]() $(M_n)_{n\in\mathbb{N}_0}$
is a nonnegative martingale with respect to the filtration
$(M_n)_{n\in\mathbb{N}_0}$
is a nonnegative martingale with respect to the filtration
![]() $(\mathcal{F}_n)_{n\in\mathbb{N}_0}$
, where
$(\mathcal{F}_n)_{n\in\mathbb{N}_0}$
, where
![]() $\mathcal{ F}_n$
denotes the
$\mathcal{ F}_n$
denotes the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $W_0,\ldots,W_n$
. By martingale convergence there exists
$W_0,\ldots,W_n$
. By martingale convergence there exists
![]() $M_\infty$
such that
$M_\infty$
such that
![]() $M_n\to M_\infty$
almost surely as
$M_n\to M_\infty$
almost surely as
![]() $n\to\infty$
. Since
$n\to\infty$
. Since
![]() $W_n\to\infty$
almost surely as
$W_n\to\infty$
almost surely as
![]() $n\to\infty$
, it follows that
$n\to\infty$
, it follows that
![]() $M_n\sim W_n/n$
and, hence,
$M_n\sim W_n/n$
and, hence,
![]() $W_n/n\to M_\infty$
almost surely. The distribution of
$W_n/n\to M_\infty$
almost surely. The distribution of
![]() $M_\infty$
is obtained as follows. Let
$M_\infty$
is obtained as follows. Let
![]() $P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. For all
$P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. For all
![]() $j\in\mathbb{N}_0$
, by (3),
$j\in\mathbb{N}_0$
, by (3),
![]() $\mathbb{E}((W_n)_j)=(n)_j\mathbb{E}(P_0^j)\sim n^j\mathbb{E}(P_0^j)$
,
$\mathbb{E}((W_n)_j)=(n)_j\mathbb{E}(P_0^j)\sim n^j\mathbb{E}(P_0^j)$
,
![]() $n\to\infty$
. Thus, the convergence
$n\to\infty$
. Thus, the convergence
![]() $\lim_{n\to\infty}\mathbb{E}((W_n/n)^j)=\mathbb{E}(P_0^j)$
,
$\lim_{n\to\infty}\mathbb{E}((W_n/n)^j)=\mathbb{E}(P_0^j)$
,
![]() $j\in\mathbb{N}_0$
, of all moments holds. Since
$j\in\mathbb{N}_0$
, of all moments holds. Since
![]() $\beta(\theta_2-\theta_1,\theta_1)$
is uniquely determined by its moments, this convergence of moments implies (see, for example, [Reference Billingsley3, Theorem 30.2]) the convergence
$\beta(\theta_2-\theta_1,\theta_1)$
is uniquely determined by its moments, this convergence of moments implies (see, for example, [Reference Billingsley3, Theorem 30.2]) the convergence
![]() $W_n/n\to P_0$
in distribution as
$W_n/n\to P_0$
in distribution as
![]() $n\to\infty$
. In particular, the distribution of the almost sure limit
$n\to\infty$
. In particular, the distribution of the almost sure limit
![]() $M_\infty$
must coincide with the distribution
$M_\infty$
must coincide with the distribution
![]() $\beta(\theta_2-\theta_1,\theta_1)$
of the distributional limit
$\beta(\theta_2-\theta_1,\theta_1)$
of the distributional limit
![]() $P_0$
. The almost sure convergence implies the convergence in probability. Convergence in probability together with the convergence of all moments implies (see, for example, [Reference Kallenberg20, p. 68, Proposition 4.12]) the convergence in
$P_0$
. The almost sure convergence implies the convergence in probability. Convergence in probability together with the convergence of all moments implies (see, for example, [Reference Kallenberg20, p. 68, Proposition 4.12]) the convergence in
![]() $L^p$
and, hence, the convergence of the pth moments for any
$L^p$
and, hence, the convergence of the pth moments for any
![]() $p>0$
.
$p>0$
.
Remark 2. Under the assumption
![]() $0<\theta_1<\theta_2<\infty$
the first passage times
$0<\theta_1<\theta_2<\infty$
the first passage times
![]() $\tau_k\,:\!=\,\inf\{n\in\mathbb{N}_0:W_n=k\}$
,
$\tau_k\,:\!=\,\inf\{n\in\mathbb{N}_0:W_n=k\}$
,
![]() $k\in\mathbb{N}_0$
, satisfy
$k\in\mathbb{N}_0$
, satisfy
![]() $\tau_k/k\to\tau\,:\!=\,1/P_0$
almost surely as
$\tau_k/k\to\tau\,:\!=\,1/P_0$
almost surely as
![]() $k\to\infty$
, where
$k\to\infty$
, where
![]() $\tau$
has an inverted beta distribution with density
$\tau$
has an inverted beta distribution with density
![]() $x\mapsto ({\rm B}(\theta_2-\theta_1,\theta_1))^{-1}x^{-\theta_2}(x-1)^{\theta_1-1}$
,
$x\mapsto ({\rm B}(\theta_2-\theta_1,\theta_1))^{-1}x^{-\theta_2}(x-1)^{\theta_1-1}$
,
![]() $x>1$
.
$x>1$
.
Remark 3. The number
![]() $\sum_{i=1}^{K_n}N_{n,i}$
of customers seated at all tables coincides with the number
$\sum_{i=1}^{K_n}N_{n,i}$
of customers seated at all tables coincides with the number
![]() $R_n$
of red balls of the Pólya urn introduced in Section 2. Under the assumption
$R_n$
of red balls of the Pólya urn introduced in Section 2. Under the assumption
![]() $0<\theta_1\le\theta_2$
it follows from
$0<\theta_1\le\theta_2$
it follows from
![]() $W_n+R_n=n$
and Theorem 1 that, as
$W_n+R_n=n$
and Theorem 1 that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $R_n/n\to R$
almost surely and in
$R_n/n\to R$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $R\,:\!=\,1-P_0\stackrel{\textrm{d}}{=}\beta(\theta_1,\theta_2-\theta_1)$
. In particular, the convergence
$R\,:\!=\,1-P_0\stackrel{\textrm{d}}{=}\beta(\theta_1,\theta_2-\theta_1)$
. In particular, the convergence
![]() $\lim_{n\to\infty}\mathbb{E}((R_n/n)^p)=\mathbb{E}(R^p)$
,
$\lim_{n\to\infty}\mathbb{E}((R_n/n)^p)=\mathbb{E}(R^p)$
,
![]() $p\ge 0$
, of all moments holds.
$p\ge 0$
, of all moments holds.
In order to study the number of customers
![]() $N_{n,i}$
at table
$N_{n,i}$
at table
![]() $i\in\mathbb{N}$
after n customers have entered the restaurant it will be helpful to introduce the following more general restaurant process.
$i\in\mathbb{N}$
after n customers have entered the restaurant it will be helpful to introduce the following more general restaurant process.
4. Random seating plan
We slightly extend Pitman’s [Reference Pitman30, p. 59] random seating plan model as follows. Let
![]() $P_0, P_1,\ldots$
be random variables with
$P_0, P_1,\ldots$
be random variables with
![]() $P_i\ge 0$
and
$P_i\ge 0$
and
![]() $\sum_{i=0}^\infty P_i\le 1$
. Given
$\sum_{i=0}^\infty P_i\le 1$
. Given
![]() $P_0,P_1,\ldots$
, if at stage
$P_0,P_1,\ldots$
, if at stage
![]() $n\in\mathbb{N}_0$
there are k occupied tables the next customer is seated
$n\in\mathbb{N}_0$
there are k occupied tables the next customer is seated
-
• at the bar with probability
 $P_0$
,
$P_0$
, -
• at occupied table
 $i\in\{1,\ldots,k\}$
with probability
$i\in\{1,\ldots,k\}$
with probability
 $P_i$
, and
$P_i$
, and -
• at the new table
 $k+1$
with probability
$k+1$
with probability
 $1-\sum_{i=0}^k P_i$
.
$1-\sum_{i=0}^k P_i$
.
In particular, the first customer is seated at the cocktail bar with probability
![]() $\mathbb{E}(P_0)$
and at table 1 with probability
$\mathbb{E}(P_0)$
and at table 1 with probability
![]() $1-\mathbb{E}(P_0)$
. For
$1-\mathbb{E}(P_0)$
. For
![]() $P_0=0$
the bar stays empty, hence
$P_0=0$
the bar stays empty, hence
![]() $K_1=1$
and the model coincides with that of [Reference Pitman30, p. 59]. Let
$K_1=1$
and the model coincides with that of [Reference Pitman30, p. 59]. Let
![]() $i\in\mathbb{N}_0$
. The law of large numbers ensures that
$i\in\mathbb{N}_0$
. The law of large numbers ensures that
![]() $N_{n,i}/n\to P_i$
almost surely as
$N_{n,i}/n\to P_i$
almost surely as
![]() $n\to\infty$
. The latter convergence also holds in
$n\to\infty$
. The latter convergence also holds in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, since
$p>0$
, since
![]() $0\le N_{n,i}/n\le 1$
for all
$0\le N_{n,i}/n\le 1$
for all
![]() $n\in\mathbb{N}_0$
. The dominated convergence theorem yields
$n\in\mathbb{N}_0$
. The dominated convergence theorem yields
By conditioning on
![]() $(P_0,P_1,\ldots)$
it follows that
$(P_0,P_1,\ldots)$
it follows that
![]() $N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
has distribution
$N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
has distribution
![]() $\textbf{n}=(n_0,\ldots,n_k)$
with
$\textbf{n}=(n_0,\ldots,n_k)$
with
![]() $k,n_0\in\mathbb{N}_0$
,
$k,n_0\in\mathbb{N}_0$
,
![]() $n_1,\ldots,n_k\in\mathbb{N}$
, and
$n_1,\ldots,n_k\in\mathbb{N}$
, and
![]() $n_0+\cdots+n_k=n$
, where
$n_0+\cdots+n_k=n$
, where
 \begin{equation} p(\textbf{n}) \,:\!=\, \mathbb{E}\bigg( P_0^{n_0}\prod_{i=1}^k P_i^{n_i-1} \prod_{i=0}^{k-1}\bigg(1-\sum_{j=0}^i P_j\bigg)\bigg) \end{equation}
\begin{equation} p(\textbf{n}) \,:\!=\, \mathbb{E}\bigg( P_0^{n_0}\prod_{i=1}^k P_i^{n_i-1} \prod_{i=0}^{k-1}\bigg(1-\sum_{j=0}^i P_j\bigg)\bigg) \end{equation}
and the combinatorial factor
counts the number of permutations of the n-tuple
such that left to the first 1 there are only 0s, left to the first 2 there are only 0s and 1s,
![]() $\ldots$
, left to the first k there are only 0s, 1s,
$\ldots$
, left to the first k there are only 0s, 1s,
![]() $\ldots$
,
$\ldots$
,
![]() $(k-1)$
s. Let
$(k-1)$
s. Let
![]() $S_k$
denote the set of all permutations of
$S_k$
denote the set of all permutations of
![]() $\{1,\ldots,k\}$
. From the identity
$\{1,\ldots,k\}$
. From the identity
![]() $\sum_{\sigma\in S_k}\prod_{i=1}^k 1/(n_{\sigma i}+\cdots+n_{\sigma k})=1/(n_1\cdots n_k)$
it follows that
$\sum_{\sigma\in S_k}\prod_{i=1}^k 1/(n_{\sigma i}+\cdots+n_{\sigma k})=1/(n_1\cdots n_k)$
it follows that
For
![]() $k=0$
, (4) reduces to
$k=0$
, (4) reduces to
![]() $\mathbb{P}((N_{n,0},\ldots,N_{n,K_n})=(n))=\mathbb{P}(N_{n,0}=n,K_n=0)=\mathbb{E}(P_0^n)$
, which is the probability that the first n customers all sit at the bar. For
$\mathbb{P}((N_{n,0},\ldots,N_{n,K_n})=(n))=\mathbb{P}(N_{n,0}=n,K_n=0)=\mathbb{E}(P_0^n)$
, which is the probability that the first n customers all sit at the bar. For
![]() $P_0=0$
(and hence
$P_0=0$
(and hence
![]() $n_0=0$
) the three formulas (4), (5), and (6) are in agreement with the corresponding formulas (see [Reference Pitman27, Eqs. (21), (7), and (20)]) for partially exchangeable partitions. An adaptation of [Reference Pitman27, Corollary 17] yields the following. Given
$n_0=0$
) the three formulas (4), (5), and (6) are in agreement with the corresponding formulas (see [Reference Pitman27, Eqs. (21), (7), and (20)]) for partially exchangeable partitions. An adaptation of [Reference Pitman27, Corollary 17] yields the following. Given
![]() $P_0$
, the number
$P_0$
, the number
![]() $N_{n,0}$
of customers at the bar has a binomial distribution with parameters n and
$N_{n,0}$
of customers at the bar has a binomial distribution with parameters n and
![]() $P_0$
. Thus,
$P_0$
. Thus,
![]() $\mathbb{P}(N_{n,0}=k)=\binom{n}{k}\mathbb{E}(P_0^k(1-P_0)^{n-k})$
,
$\mathbb{P}(N_{n,0}=k)=\binom{n}{k}\mathbb{E}(P_0^k(1-P_0)^{n-k})$
,
![]() $k\in\{0,\ldots,n\}$
. For
$k\in\{0,\ldots,n\}$
. For
![]() $i\in\mathbb{N}_0$
, given
$i\in\mathbb{N}_0$
, given
![]() $P_0,\ldots,P_{i+1}$
and
$P_0,\ldots,P_{i+1}$
and
![]() $N_{n,0},\ldots,N_{n,i}$
with
$N_{n,0},\ldots,N_{n,i}$
with
![]() $N_{n,0}+\cdots+N_{n,i}<n$
, the random variable
$N_{n,0}+\cdots+N_{n,i}<n$
, the random variable
![]() $N_{n,i+1}-1$
has a binomial distribution with parameters
$N_{n,i+1}-1$
has a binomial distribution with parameters
![]() $n-\sum_{j=0}^i{N_{n,j}}-1$
and
$n-\sum_{j=0}^i{N_{n,j}}-1$
and
![]() $W_{i+1}\,:\!=\,P_{i+1}/(1-\sum_{j=0}^i P_j)$
.
$W_{i+1}\,:\!=\,P_{i+1}/(1-\sum_{j=0}^i P_j)$
.
The model generates a random partition
![]() $\Pi$
of
$\Pi$
of
![]() $\mathbb{N}$
by defining
$\mathbb{N}$
by defining
![]() $i,j\in\mathbb{N}$
to belong to the same block of
$i,j\in\mathbb{N}$
to belong to the same block of
![]() $\Pi$
if and only if customers i and j are both seated at the bar or at the same table. Let
$\Pi$
if and only if customers i and j are both seated at the bar or at the same table. Let
![]() $C_0$
be the set of customers at the bar and
$C_0$
be the set of customers at the bar and
![]() $C_i$
the set of customers at table
$C_i$
the set of customers at table
![]() $i\in\mathbb{N}$
. In general,
$i\in\mathbb{N}$
. In general,
![]() $\Pi=\{C_i:i\in\mathbb{N}_0,C_i\ne\emptyset\}$
is not exchangeable, but given
$\Pi=\{C_i:i\in\mathbb{N}_0,C_i\ne\emptyset\}$
is not exchangeable, but given
![]() $C_0$
, the partition corresponding to the blocks
$C_0$
, the partition corresponding to the blocks
![]() $C_i$
,
$C_i$
,
![]() $i\in\mathbb{N}$
with
$i\in\mathbb{N}$
with
![]() $C_i\ne\emptyset$
, is a partially exchangeable partition of
$C_i\ne\emptyset$
, is a partially exchangeable partition of
![]() $\mathbb{N}\setminus C_0$
in the sense of [Reference Pitman27].
$\mathbb{N}\setminus C_0$
in the sense of [Reference Pitman27].
5. Joint convergence
We now come back to the model introduced in Section 1 and study the asymptotics of
![]() $N_{n,i}$
,
$N_{n,i}$
,
![]() $i\in\mathbb{N}_0$
, as
$i\in\mathbb{N}_0$
, as
![]() $n\to\infty$
. Our main result is the following.
$n\to\infty$
. Our main result is the following.
Theorem 2. Assume that
![]() $0\le\alpha\le 1$
and
$0\le\alpha\le 1$
and
![]() $0<\theta_1\le\theta_2<\infty$
. Then, as
$0<\theta_1\le\theta_2<\infty$
. Then, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $(N_{n,i}/n)_{i\in\mathbb{N}_0}\to (P_i)_{i\in\mathbb{N}_0}$
almost surely, where
$(N_{n,i}/n)_{i\in\mathbb{N}_0}\to (P_i)_{i\in\mathbb{N}_0}$
almost surely, where
![]() $(P_i)_{i\in\mathbb{N}_0}$
is a stick-breaking sequence satisfying
$(P_i)_{i\in\mathbb{N}_0}$
is a stick-breaking sequence satisfying
![]() $(P_i)_{i\in\mathbb{N}_0}\stackrel{\textrm{d}}{=}((B_i)\prod_{j=0}^{i-1}(1-B_j))_{i\in\mathbb{N}_0}$
with independent random variables
$(P_i)_{i\in\mathbb{N}_0}\stackrel{\textrm{d}}{=}((B_i)\prod_{j=0}^{i-1}(1-B_j))_{i\in\mathbb{N}_0}$
with independent random variables
![]() $B_0,B_1,\ldots$
having beta distributions
$B_0,B_1,\ldots$
having beta distributions
![]() $B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
$B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
![]() $B_i\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha i+\theta_1)$
,
$B_i\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha i+\theta_1)$
,
![]() $i\in\mathbb{N}$
. Moreover, the convergence
$i\in\mathbb{N}$
. Moreover, the convergence
of all finite joint moments holds.
Remark 4. For
![]() $\alpha=1$
each customer is seated either at the bar or at a new table. Thus,
$\alpha=1$
each customer is seated either at the bar or at a new table. Thus,
![]() $N_{n,i}=1$
,
$N_{n,i}=1$
,
![]() $i\in\{1,\ldots,K_n\}$
, and the theorem holds with
$i\in\{1,\ldots,K_n\}$
, and the theorem holds with
![]() $P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
$P_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
![]() $P_i=0$
for all
$P_i=0$
for all
![]() $i\in\mathbb{N}$
.
$i\in\mathbb{N}$
.
Two proofs of Theorem 2 are provided. The first is self-contained and based on the random seating plan model introduced in Section 4. The second exploits the reinterpretation in terms of a mixture of a Pólya urn and a two-parameter CRP described in Section 2.
Proof 1 of Theorem 2. Let
![]() $B_0,B_1,\ldots$
be independent random variables with
$B_0,B_1,\ldots$
be independent random variables with
![]() $B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
$B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
and
![]() $B_i\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha i+\theta_1)$
,
$B_i\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha i+\theta_1)$
,
![]() $i\in\mathbb{N}$
. Note that
$i\in\mathbb{N}$
. Note that
![]() $B_0=0$
if
$B_0=0$
if
![]() $\theta_1=\theta_2$
and that
$\theta_1=\theta_2$
and that
![]() $B_i=0$
for all
$B_i=0$
for all
![]() $i\in\mathbb{N}$
if
$i\in\mathbb{N}$
if
![]() $\alpha=1$
. For
$\alpha=1$
. For
![]() $i\in\mathbb{N}_0$
define
$i\in\mathbb{N}_0$
define
![]() $\overline{B}_i\,:\!=\,1-B_i$
and
$\overline{B}_i\,:\!=\,1-B_i$
and
![]() $P_i\,:\!=\,\overline{B}_0\cdots\overline{B}_{i-1}B_i$
. Clearly,
$P_i\,:\!=\,\overline{B}_0\cdots\overline{B}_{i-1}B_i$
. Clearly,
![]() $1-\sum_{j=0}^iP_j=\overline{B}_0\cdots\overline{B}_i$
,
$1-\sum_{j=0}^iP_j=\overline{B}_0\cdots\overline{B}_i$
,
![]() $i\in\mathbb{N}_0$
. For
$i\in\mathbb{N}_0$
. For
![]() $\textbf{n}\,:\!=\,(n_0,\ldots,n_k)$
with
$\textbf{n}\,:\!=\,(n_0,\ldots,n_k)$
with
![]() $k,n_0\in\mathbb{N}_0$
and
$k,n_0\in\mathbb{N}_0$
and
![]() $n_1,\ldots,n_k\in\mathbb{N}$
,
$n_1,\ldots,n_k\in\mathbb{N}$
,
 \begin{align*} p(\textbf{n}) & \,:\!=\, \mathbb{E}\bigg(P_0^{n_0}\prod_{i=1}^k P_i^{n_i-1}\prod_{i=0}^{k-1}\bigg(1-\sum_{j=0}^i P_j\bigg)\bigg)\\[3pt] & = \mathbb{E}\big(B_0^{n_0}\overline{B}_0^{n_1+\cdots+n_k}\big)\prod_{i=1}^k \mathbb{E}\big(B_i^{n_i-1}\overline{B_i}^{n_{i+1}+\cdots+n_k}\big)\\[3pt] & = \frac{[\theta_2-\theta_1]_{n_0}[\theta_1]_{n_1+\cdots+n_k}}{[\theta_2]_n} \prod_{i=1}^k \frac{[1-\alpha]_{n_i-1}[\alpha i+\theta_1]_{n_{i+1}+\cdots+n_k}} {[1+\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k-1}}, \end{align*}
\begin{align*} p(\textbf{n}) & \,:\!=\, \mathbb{E}\bigg(P_0^{n_0}\prod_{i=1}^k P_i^{n_i-1}\prod_{i=0}^{k-1}\bigg(1-\sum_{j=0}^i P_j\bigg)\bigg)\\[3pt] & = \mathbb{E}\big(B_0^{n_0}\overline{B}_0^{n_1+\cdots+n_k}\big)\prod_{i=1}^k \mathbb{E}\big(B_i^{n_i-1}\overline{B_i}^{n_{i+1}+\cdots+n_k}\big)\\[3pt] & = \frac{[\theta_2-\theta_1]_{n_0}[\theta_1]_{n_1+\cdots+n_k}}{[\theta_2]_n} \prod_{i=1}^k \frac{[1-\alpha]_{n_i-1}[\alpha i+\theta_1]_{n_{i+1}+\cdots+n_k}} {[1+\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k-1}}, \end{align*}
since
![]() $X\stackrel{\textrm{d}}{=}\beta(a,b)$
satisfies
$X\stackrel{\textrm{d}}{=}\beta(a,b)$
satisfies
![]() $\mathbb{E}(X^n(1-X)^m)=[a]_n[b]_m/[a+b]_{n+m}$
for all
$\mathbb{E}(X^n(1-X)^m)=[a]_n[b]_m/[a+b]_{n+m}$
for all
![]() $n,m\in\mathbb{N}_0$
. Define
$n,m\in\mathbb{N}_0$
. Define
![]() $[x|y]_0\,:\!=\,1$
and
$[x|y]_0\,:\!=\,1$
and
![]() $[x|y]_k\,:\!=\,\prod_{j=0}^{k-1}(x+jy)$
for
$[x|y]_k\,:\!=\,\prod_{j=0}^{k-1}(x+jy)$
for
![]() $x,y\in\mathbb{R}$
and
$x,y\in\mathbb{R}$
and
![]() $k\in\mathbb{N}$
. Since
$k\in\mathbb{N}$
. Since
![]() $[1+\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k-1}=[\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k}/(\alpha(i-1)+\theta_1)$
, the formula above reduces to
$[1+\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k-1}=[\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k}/(\alpha(i-1)+\theta_1)$
, the formula above reduces to
 \begin{align} p(\textbf{n}) & = \frac{[\theta_2-\theta_1]_{n_0}[\theta_1]_{n_1+\cdots+n_k}} {[\theta_2]_n} \prod_{i=1}^k (\alpha(i-1)+\theta_1) \frac{[1-\alpha]_{n_i-1}[\alpha i+\theta_1]_{n_{i+1}+\cdots+n_k}} {[\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k}}\nonumber\\[3pt] & = \frac{[\theta_2-\theta_1]_{n_0}}{[\theta_2]_n} [\theta_1 \mid \alpha]_k \prod_{i=1}^k [1-\alpha]_{n_i-1}. \end{align}
\begin{align} p(\textbf{n}) & = \frac{[\theta_2-\theta_1]_{n_0}[\theta_1]_{n_1+\cdots+n_k}} {[\theta_2]_n} \prod_{i=1}^k (\alpha(i-1)+\theta_1) \frac{[1-\alpha]_{n_i-1}[\alpha i+\theta_1]_{n_{i+1}+\cdots+n_k}} {[\alpha(i-1)+\theta_1]_{n_i+\cdots+n_k}}\nonumber\\[3pt] & = \frac{[\theta_2-\theta_1]_{n_0}}{[\theta_2]_n} [\theta_1 \mid \alpha]_k \prod_{i=1}^k [1-\alpha]_{n_i-1}. \end{align}
Note that (9) is symmetric in
![]() $n_1,\ldots,n_k$
(excluding
$n_1,\ldots,n_k$
(excluding
![]() $n_0$
). From (9) it follows (by distinguishing the cases
$n_0$
). From (9) it follows (by distinguishing the cases
![]() $i=0$
and
$i=0$
and
![]() $i\in\{1,\ldots,k\}$
) that
$i\in\{1,\ldots,k\}$
) that
![]() $N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
satisfies
$N_n\,:\!=\,(N_{n,0},\ldots,N_{n,K_n})$
satisfies
![]() $\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_i \mid N_n=\textbf{n}) = p(\textbf{n}+\textbf{e}_i)/p(\textbf{n})$
for
$\mathbb{P}(N_{n+1}=\textbf{n}+\textbf{e}_i \mid N_n=\textbf{n}) = p(\textbf{n}+\textbf{e}_i)/p(\textbf{n})$
for
![]() $i\in\{0,\ldots,k\}$
and
$i\in\{0,\ldots,k\}$
and
![]() $\textbf{n}=(n_0,\ldots,n_k)$
with
$\textbf{n}=(n_0,\ldots,n_k)$
with
![]() $k,n_0\in\mathbb{N}_0$
,
$k,n_0\in\mathbb{N}_0$
,
![]() $n_1,\ldots,n_k\in\mathbb{N}$
, and
$n_1,\ldots,n_k\in\mathbb{N}$
, and
![]() $n\,:\!=\,n_0+\cdots+n_k$
. We are therefore in the situation of the model with random seating plan studied in Section 4 corresponding to the sequence
$n\,:\!=\,n_0+\cdots+n_k$
. We are therefore in the situation of the model with random seating plan studied in Section 4 corresponding to the sequence
![]() $(P_0,P_1,\ldots)$
. From the results in Section 4 it follows that, for every
$(P_0,P_1,\ldots)$
. From the results in Section 4 it follows that, for every
![]() $i\in\mathbb{N}_0$
, as
$i\in\mathbb{N}_0$
, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $N_{n,i}/n\to P_i$
almost surely and in
$N_{n,i}/n\to P_i$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
. Moreover, the convergence (8) of all finite joint moments holds.
$p>0$
. Moreover, the convergence (8) of all finite joint moments holds.
Proof 2 of Theorem 2. Recall the reinterpretation of the model as a mixture of a Pólya urn and a two-parameter CRP (see Section 2). The number
![]() $N_{n,0}$
of customers at the bar coincides with the number
$N_{n,0}$
of customers at the bar coincides with the number
![]() $W_n$
of white balls in the urn. From standard theory on Pólya urns (see also Section 3) it therefore follows that, as
$W_n$
of white balls in the urn. From standard theory on Pólya urns (see also Section 3) it therefore follows that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $N_{n,0}/n=W_n/n\to B_0$
almost surely, where
$N_{n,0}/n=W_n/n\to B_0$
almost surely, where
![]() $B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. Let
$B_0\stackrel{\textrm{d}}{=}\beta(\theta_2-\theta_1,\theta_1)$
. Let
![]() $i\in\mathbb{N}$
. The number
$i\in\mathbb{N}$
. The number
![]() $N_{n,i}$
of customers at table i coincides with the number
$N_{n,i}$
of customers at table i coincides with the number
![]() $R_{n,i}$
of balls of red subcolor i. Therefore,
$R_{n,i}$
of balls of red subcolor i. Therefore,
As
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $R_n/n=1-W_n/n\to 1-B_0$
almost surely. Since the jump evolution of the process
$R_n/n=1-W_n/n\to 1-B_0$
almost surely. Since the jump evolution of the process
![]() $(R_{n,1},\ldots,R_{n,K_n})$
is a two-parameter CRP with parameters
$(R_{n,1},\ldots,R_{n,K_n})$
is a two-parameter CRP with parameters
![]() $\alpha$
and
$\alpha$
and
![]() $\theta_1$
independent of the Pólya urn, it follows from [Reference Pitman30, Theorem 3.2] (see also [Reference Pitman27]) that, as
$\theta_1$
independent of the Pólya urn, it follows from [Reference Pitman30, Theorem 3.2] (see also [Reference Pitman27]) that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $R_{n,i}/R_n\to B_i\prod_{j=1}^{i-1}(1-B_j)$
almost surely, where
$R_{n,i}/R_n\to B_i\prod_{j=1}^{i-1}(1-B_j)$
almost surely, where
![]() $B_1,B_2,\ldots$
are independent (and independent of
$B_1,B_2,\ldots$
are independent (and independent of
![]() $B_0$
) with
$B_0$
) with
![]() $B_j\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha j+\theta_1)$
. Thus,
$B_j\stackrel{\textrm{d}}{=}\beta(1-\alpha,\alpha j+\theta_1)$
. Thus,
![]() $N_{n,i}/n\to P_i$
almost surely as
$N_{n,i}/n\to P_i$
almost surely as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $i\in\mathbb{N}_0$
, with
$i\in\mathbb{N}_0$
, with
![]() $P_i$
as given in Theorem 2. By dominated convergence the convergence (8) holds.
$P_i$
as given in Theorem 2. By dominated convergence the convergence (8) holds.
Remark 5. Let
![]() $i\in\mathbb{N}$
. The almost sure convergence of
$i\in\mathbb{N}$
. The almost sure convergence of
![]() $N_{n,i}/n$
as
$N_{n,i}/n$
as
![]() $n\to\infty$
can alternatively be derived via a martingale method as follows. Define
$n\to\infty$
can alternatively be derived via a martingale method as follows. Define
For
![]() $k\in\mathbb{N}$
we have
$k\in\mathbb{N}$
we have
![]() $N_{n+1,i}\ge 1$
on
$N_{n+1,i}\ge 1$
on
![]() $\{N_{n,i}=k\}$
and, hence,
$\{N_{n,i}=k\}$
and, hence,
 \begin{eqnarray*} & & \mathbb{E}(M_{n+1,i} \mid N_{n,i}=k) = \mathbb{E}\bigg(\frac{N_{n+1,i}-\alpha}{n+1+\theta_2} \,\Big|\, N_{n,i}=k\bigg)\\[3pt] & = & \frac{k-\alpha}{n+1+\theta_2} \bigg(1-\frac{k-\alpha}{n+\theta_2}\bigg) + \frac{k+1-\alpha}{n+1+\theta_2}\frac{k-\alpha}{n+\theta_2}\\[3pt] & = & \frac{k-\alpha}{n+1+\theta_2} \bigg(1-\frac{k-\alpha}{n+\theta_2}+\frac{k+1-\alpha}{n+\theta_2}\bigg) = \frac{k-\alpha}{n+\theta_2},\qquad n\in\mathbb{N}_0,\ k\in\mathbb{N}. \end{eqnarray*}
\begin{eqnarray*} & & \mathbb{E}(M_{n+1,i} \mid N_{n,i}=k) = \mathbb{E}\bigg(\frac{N_{n+1,i}-\alpha}{n+1+\theta_2} \,\Big|\, N_{n,i}=k\bigg)\\[3pt] & = & \frac{k-\alpha}{n+1+\theta_2} \bigg(1-\frac{k-\alpha}{n+\theta_2}\bigg) + \frac{k+1-\alpha}{n+1+\theta_2}\frac{k-\alpha}{n+\theta_2}\\[3pt] & = & \frac{k-\alpha}{n+1+\theta_2} \bigg(1-\frac{k-\alpha}{n+\theta_2}+\frac{k+1-\alpha}{n+\theta_2}\bigg) = \frac{k-\alpha}{n+\theta_2},\qquad n\in\mathbb{N}_0,\ k\in\mathbb{N}. \end{eqnarray*}
On
![]() $\{N_{n,i}=0\}$
the random variable
$\{N_{n,i}=0\}$
the random variable
![]() $N_{n+1,i}$
takes the two values 0 and 1. From (10) we conclude that, on
$N_{n+1,i}$
takes the two values 0 and 1. From (10) we conclude that, on
![]() $\{N_{n,i}=0\}$
, the random variable
$\{N_{n,i}=0\}$
, the random variable
![]() $M_{n+1,i}$
is constant, equal to
$M_{n+1,i}$
is constant, equal to
![]() $(1-\alpha)/(n+1+\theta_2)$
. Thus,
$(1-\alpha)/(n+1+\theta_2)$
. Thus,
![]() $\mathbb{E}(M_{n+1,i} \mid N_{n,i}=0) =(1-\alpha)/(n+1+\theta_2)\le(1-\alpha)/(n+\theta_2)$
. Clumping the two cases
$\mathbb{E}(M_{n+1,i} \mid N_{n,i}=0) =(1-\alpha)/(n+1+\theta_2)\le(1-\alpha)/(n+\theta_2)$
. Clumping the two cases
![]() $k\in\mathbb{N}$
and
$k\in\mathbb{N}$
and
![]() $k=0$
together leads to
$k=0$
together leads to
![]() $\mathbb{E}(M_{n+1,i} \mid N_{n,i}) \le (\max(N_{n,i},1)-\alpha)/(n+\theta_2)=M_{n,i}$
almost surely. Thus,
$\mathbb{E}(M_{n+1,i} \mid N_{n,i}) \le (\max(N_{n,i},1)-\alpha)/(n+\theta_2)=M_{n,i}$
almost surely. Thus,
![]() $(M_{n,i})_{n\in\mathbb{N}_0}$
is a nonnegative supermartingale with respect to the filtration
$(M_{n,i})_{n\in\mathbb{N}_0}$
is a nonnegative supermartingale with respect to the filtration
![]() $(\mathcal{ F}_n)_{n\in\mathbb{N}_0}$
, where
$(\mathcal{ F}_n)_{n\in\mathbb{N}_0}$
, where
![]() $\mathcal{ F}_n$
denotes the
$\mathcal{ F}_n$
denotes the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $N_{0,i},\ldots,N_{n,i}$
. By martingale convergence there exists
$N_{0,i},\ldots,N_{n,i}$
. By martingale convergence there exists
![]() $M_{\infty,i}$
such that
$M_{\infty,i}$
such that
![]() $M_{n,i}\to M_{\infty,i}$
almost surely as
$M_{n,i}\to M_{\infty,i}$
almost surely as
![]() $n\to\infty$
. For
$n\to\infty$
. For
![]() $\alpha<1$
it can be checked that
$\alpha<1$
it can be checked that
![]() $N_{n,i}\to\infty$
as
$N_{n,i}\to\infty$
as
![]() $n\to\infty$
. Thus,
$n\to\infty$
. Thus,
![]() $M_{n,i}\sim N_{n,i}/n$
and, hence,
$M_{n,i}\sim N_{n,i}/n$
and, hence,
![]() $N_{n,i}/n\to M_{\infty,i}$
almost surely as
$N_{n,i}/n\to M_{\infty,i}$
almost surely as
![]() $n\to\infty$
.
$n\to\infty$
.
However, this martingale approach alone does not seem to be useful to derive the distribution of
![]() $M_{\infty,i}$
. Proof 1 based on the random seating plan model has the advantage that the limiting beta distributions are obvious by construction. In the second proof the limiting beta distributions follow from the asymptotic results known for Pólya urns and for the two-parameter CRP.
$M_{\infty,i}$
. Proof 1 based on the random seating plan model has the advantage that the limiting beta distributions are obvious by construction. In the second proof the limiting beta distributions follow from the asymptotic results known for Pólya urns and for the two-parameter CRP.
Remark 6. (Sampling formula) Define
Since
![]() $p(\textbf{n})$
is in our case (see (9)) symmetric in
$p(\textbf{n})$
is in our case (see (9)) symmetric in
![]() $n_1,\ldots,n_k$
, it follows from (4) and (7) that
$n_1,\ldots,n_k$
, it follows from (4) and (7) that
 \begin{equation} \tilde{p}(\textbf{n}) = \frac{n!}{k!\,n_0!\cdots n_k!}\,p(\textbf{n}) = \frac{n!}{k!n_0!\cdots n_k!}\frac{[\theta_2-\theta_1]_{n_0}}{[\theta_2]_n} [\theta_1 \mid \alpha]_k \prod_{i=1}^k [1-\alpha]_{n_i-1}, \end{equation}
\begin{equation} \tilde{p}(\textbf{n}) = \frac{n!}{k!\,n_0!\cdots n_k!}\,p(\textbf{n}) = \frac{n!}{k!n_0!\cdots n_k!}\frac{[\theta_2-\theta_1]_{n_0}}{[\theta_2]_n} [\theta_1 \mid \alpha]_k \prod_{i=1}^k [1-\alpha]_{n_i-1}, \end{equation}
where the last equality holds by (9). The sampling formula (11) for the restaurant process with cocktail bar is symmetric in
![]() $n_1,\ldots,n_k$
but not in
$n_1,\ldots,n_k$
but not in
![]() $n_0,\ldots,n_k$
. Formulas of this form might be of interest for applications in mathematical population genetics, where a distinguished type 0 occurs in the population. Clearly, for
$n_0,\ldots,n_k$
. Formulas of this form might be of interest for applications in mathematical population genetics, where a distinguished type 0 occurs in the population. Clearly, for
![]() $\theta_1=\theta_2 \!=: \theta>0$
the cocktail bar stays empty (
$\theta_1=\theta_2 \!=: \theta>0$
the cocktail bar stays empty (
![]() $n_0=0$
) and (11) turns into the symmetric formula for the two-parameter CRP,
$n_0=0$
) and (11) turns into the symmetric formula for the two-parameter CRP,
 \begin{equation*} \tilde{p}(n_1,\ldots,n_k)\ =\ \frac{n!}{k!} \frac{[\theta|\alpha]_k}{[\theta]_n}\prod_{i=1}^k \frac{[1-\alpha]_{n_i-1}}{n_i!}, \end{equation*}
\begin{equation*} \tilde{p}(n_1,\ldots,n_k)\ =\ \frac{n!}{k!} \frac{[\theta|\alpha]_k}{[\theta]_n}\prod_{i=1}^k \frac{[1-\alpha]_{n_i-1}}{n_i!}, \end{equation*}
![]() $1\le k\le n$
,
$1\le k\le n$
,
![]() $n_1,\ldots,n_k\in\mathbb{N}$
,
$n_1,\ldots,n_k\in\mathbb{N}$
,
![]() $n_1+\cdots+n_k=n$
, which for
$n_1+\cdots+n_k=n$
, which for
![]() $\alpha=0$
is in agreement with Ewens’s sampling formula (see, for example, [Reference Möhle25, Eq. (1)]),
$\alpha=0$
is in agreement with Ewens’s sampling formula (see, for example, [Reference Möhle25, Eq. (1)]),
![]() $\tilde{p}(n_1,\ldots,n_k)=n!\theta^k/(k![\theta]_n n_1\cdots n_k)$
,
$\tilde{p}(n_1,\ldots,n_k)=n!\theta^k/(k![\theta]_n n_1\cdots n_k)$
,
![]() $1\le k\le n$
,
$1\le k\le n$
,
![]() $n_1,\ldots,n_k\in\mathbb{N}$
,
$n_1,\ldots,n_k\in\mathbb{N}$
,
![]() $n_1+\cdots+n_k=n$
.
$n_1+\cdots+n_k=n$
.
Remark 7. (Random probability measure, RPM) Section 5 of [Reference Green, Bingham and Goldie11] studies Dirichlet mixtures of Dirichlet processes of the form
![]() $\xi\,:\!=\,\sum_j W_j \xi_j$
, where the
$\xi\,:\!=\,\sum_j W_j \xi_j$
, where the
![]() $\xi_j$
are independent Dirichlet processes and
$\xi_j$
are independent Dirichlet processes and
![]() $(W_j)_j$
is Dirichlet distributed and independent of
$(W_j)_j$
is Dirichlet distributed and independent of
![]() $(\xi_j)_j$
. Note that each
$(\xi_j)_j$
. Note that each
![]() $\xi_j$
is an RPM on some appropriate measure space, say
$\xi_j$
is an RPM on some appropriate measure space, say
![]() $(S,\mathcal{S})$
. The construction is easily generalized by allowing
$(S,\mathcal{S})$
. The construction is easily generalized by allowing
![]() $\xi_j$
to be, for example, a two-parameter Poisson–Dirichlet process or a general RPM
$\xi_j$
to be, for example, a two-parameter Poisson–Dirichlet process or a general RPM
![]() $\xi_j:\Omega\times\mathcal{ S}\to [0,1]$
.
$\xi_j:\Omega\times\mathcal{ S}\to [0,1]$
.
Our model has two colors
![]() $j\in\{0,1\}$
(white and red), and
$j\in\{0,1\}$
(white and red), and
![]() $(W_0,W_1)$
is Dirichlet distributed with parameters
$(W_0,W_1)$
is Dirichlet distributed with parameters
![]() $\theta_2-\theta_1$
and
$\theta_2-\theta_1$
and
![]() $\theta_1$
, the initial weights of the two-type Pólya urn from Section 2. Comparing the stick-breaking construction from [Reference Green, Bingham and Goldie11, p. 16] with Theorem 2, we see that
$\theta_1$
, the initial weights of the two-type Pólya urn from Section 2. Comparing the stick-breaking construction from [Reference Green, Bingham and Goldie11, p. 16] with Theorem 2, we see that
![]() $\xi_1$
is a two-parameter Poisson–Dirichlet process
$\xi_1$
is a two-parameter Poisson–Dirichlet process
![]() $\xi_1={\rm PDP}(\alpha,\theta_1,Q_1)$
with parameters
$\xi_1={\rm PDP}(\alpha,\theta_1,Q_1)$
with parameters
![]() $\alpha$
and
$\alpha$
and
![]() $\theta_1$
. Here,
$\theta_1$
. Here,
![]() $Q_1$
denotes some given (usually diffuse) base probability measure on
$Q_1$
denotes some given (usually diffuse) base probability measure on
![]() $(S,\mathcal{ S})$
. Moreover,
$(S,\mathcal{ S})$
. Moreover,
![]() $\xi_0$
has the form
$\xi_0$
has the form
![]() $\xi_0(\omega,A)=\delta_{X_0(\omega)}(A)$
,
$\xi_0(\omega,A)=\delta_{X_0(\omega)}(A)$
,
![]() $\omega\in\Omega$
,
$\omega\in\Omega$
,
![]() $A\in\mathcal{ S}$
, with
$A\in\mathcal{ S}$
, with
![]() $X_0\stackrel{\textrm{d}}{=}Q_0$
, where again
$X_0\stackrel{\textrm{d}}{=}Q_0$
, where again
![]() $Q_0$
is a base probability measure on
$Q_0$
is a base probability measure on
![]() $(S,\mathcal{ S})$
. Note that
$(S,\mathcal{ S})$
. Note that
![]() $\xi_0$
can be viewed as a degenerate Dirichlet process
$\xi_0$
can be viewed as a degenerate Dirichlet process
![]() ${\rm DP}(a,Q_0)$
in the limit
${\rm DP}(a,Q_0)$
in the limit
![]() $a\to 0$
, corresponding to the fact that the white-colored segment of the stick does not undergo any stick-breaking procedure. As noted in [Reference James16, Eq. (6)],
$a\to 0$
, corresponding to the fact that the white-colored segment of the stick does not undergo any stick-breaking procedure. As noted in [Reference James16, Eq. (6)],
![]() $\xi_1$
can be represented as
$\xi_1$
can be represented as
![]() $\xi_1(\omega,A)=\sum_{i\ge 1}J_i(\omega) \delta_{X_i(\omega)}(A)$
,
$\xi_1(\omega,A)=\sum_{i\ge 1}J_i(\omega) \delta_{X_i(\omega)}(A)$
,
![]() $\omega\in\Omega$
,
$\omega\in\Omega$
,
![]() $A\in\mathcal{ S}$
, where
$A\in\mathcal{ S}$
, where
![]() $X_1,X_2,\ldots$
are independent and identically distributed with distribution
$X_1,X_2,\ldots$
are independent and identically distributed with distribution
![]() $Q_1$
and
$Q_1$
and
![]() $J=(J_1,J_2,\ldots)$
has the two-parameter Poisson–Dirichlet distribution
$J=(J_1,J_2,\ldots)$
has the two-parameter Poisson–Dirichlet distribution
![]() ${\rm PD}(\alpha,\theta_1)$
and is independent of
${\rm PD}(\alpha,\theta_1)$
and is independent of
![]() $(X_i)_{i\in\mathbb{N}}$
. Note that
$(X_i)_{i\in\mathbb{N}}$
. Note that
![]() $J_1>J_2>\cdots$
and
$J_1>J_2>\cdots$
and
![]() $\sum_{i\ge 1} J_i=1$
. The RPM
$\sum_{i\ge 1} J_i=1$
. The RPM
![]() $\xi$
associated to the restaurant process with cocktail bar thus has the form
$\xi$
associated to the restaurant process with cocktail bar thus has the form
6. Number of occupied tables
In order to analyze the number of occupied tables it will turn out to be convenient to introduce, for
![]() $a,b,r\in\mathbb{R}$
, the generalized Stirling numbers
$a,b,r\in\mathbb{R}$
, the generalized Stirling numbers
![]() $S(n,k;a,b,r)$
,
$S(n,k;a,b,r)$
,
![]() $n,k\in\mathbb{N}_0$
, having vertical generating function (see [Reference Hsu and Shiue14, Theorem 2])
$n,k\in\mathbb{N}_0$
, having vertical generating function (see [Reference Hsu and Shiue14, Theorem 2])
 \begin{equation} k!\sum_{n\ge 0}S(n,k;a,b,r)\frac{t^n}{n!} = \left\{ \begin{array}{cl} \displaystyle(1+at)^{r/a}\bigg(\frac{(1+at)^{b/a}-1}{b}\bigg)^k & \mbox{if $ab\ne 0$,}\\[3pt] \displaystyle \textrm{e}^{rt}\bigg(\frac{\textrm{e}^{bt}-1}{b}\bigg)^k & \mbox{if $a=0$ and $b\ne 0$,}\\[3pt] \displaystyle(1+at)^{r/a}\bigg(\frac{\log(1+at)}{a}\bigg)^k & \mbox{if $a\ne 0$ and $b=0$,}\\[3pt] \textrm{e}^{rt}t^k & \mbox{if $a=b=0$.} \end{array} \right.\end{equation}
\begin{equation} k!\sum_{n\ge 0}S(n,k;a,b,r)\frac{t^n}{n!} = \left\{ \begin{array}{cl} \displaystyle(1+at)^{r/a}\bigg(\frac{(1+at)^{b/a}-1}{b}\bigg)^k & \mbox{if $ab\ne 0$,}\\[3pt] \displaystyle \textrm{e}^{rt}\bigg(\frac{\textrm{e}^{bt}-1}{b}\bigg)^k & \mbox{if $a=0$ and $b\ne 0$,}\\[3pt] \displaystyle(1+at)^{r/a}\bigg(\frac{\log(1+at)}{a}\bigg)^k & \mbox{if $a\ne 0$ and $b=0$,}\\[3pt] \textrm{e}^{rt}t^k & \mbox{if $a=b=0$.} \end{array} \right.\end{equation}
We now turn to the number
![]() $K_n$
of occupied tables at stage
$K_n$
of occupied tables at stage
![]() $n\in\mathbb{N}_0$
. Clearly,
$n\in\mathbb{N}_0$
. Clearly,
![]() $(K_n)_{n\in\mathbb{N}_0}$
is a Markov chain with state space
$(K_n)_{n\in\mathbb{N}_0}$
is a Markov chain with state space
![]() $\mathbb{N}_0$
,
$\mathbb{N}_0$
,
![]() $K_0=0$
, and transition probabilities
$K_0=0$
, and transition probabilities
Exploiting the recursion [Reference Hsu and Shiue14, Theorem 1] for the generalized Stirling numbers it is easily checked by induction on
![]() $n\in\mathbb{N}_0$
that
$n\in\mathbb{N}_0$
that
![]() $K_n$
has distribution
$K_n$
has distribution
For
![]() $\alpha=-\kappa<0$
and
$\alpha=-\kappa<0$
and
![]() $\theta_1=m\kappa$
it follows that
$\theta_1=m\kappa$
it follows that
![]() $[\theta_1 \mid \alpha]_k=[m\kappa \mid-\kappa ]_k=0 $
for
$[\theta_1 \mid \alpha]_k=[m\kappa \mid-\kappa ]_k=0 $
for
![]() $k>m$
, confirming that
$k>m$
, confirming that
![]() $\mathbb{P}(K_n\le m)=1$
in this case. For
$\mathbb{P}(K_n\le m)=1$
in this case. For
![]() $\theta_1=\theta_2 \!=: \theta$
, the random variable
$\theta_1=\theta_2 \!=: \theta$
, the random variable
![]() $K_n$
counts the number of occupied tables in Pitman’s [Reference Pitman30] two-parameter
$K_n$
counts the number of occupied tables in Pitman’s [Reference Pitman30] two-parameter
![]() $(\alpha,\theta)$
-CRP. Although the distribution (14) of
$(\alpha,\theta)$
-CRP. Although the distribution (14) of
![]() $K_n$
is known, it will turn out to be helpful to derive recursions for some functionals of
$K_n$
is known, it will turn out to be helpful to derive recursions for some functionals of
![]() $K_n$
such as the moments and the Laplace transform.
$K_n$
such as the moments and the Laplace transform.
Lemma 1. (Recursion for the moments and the Laplace transform of
![]() $K_n.$
)
$K_n.$
)
The moments
![]() $\mu_{n,m}\,:\!=\,\mathbb{E}(K_n^m)$
,
$\mu_{n,m}\,:\!=\,\mathbb{E}(K_n^m)$
,
![]() $n,m\in\mathbb{N}_0$
, of
$n,m\in\mathbb{N}_0$
, of
![]() $K_n$
satisfy the linear recursion
$K_n$
satisfy the linear recursion
 \begin{equation} \mu_{n+1,m} = \frac{n+\theta_2+\alpha m}{n+\theta_2}\mu_{n,m} + \frac{1}{n+\theta_2}\sum_{j=0}^{m-1} \bigg(\alpha\binom{m}{j-1}+\theta_1\binom{m}{j}\bigg)\mu_{n,j}, \end{equation}
\begin{equation} \mu_{n+1,m} = \frac{n+\theta_2+\alpha m}{n+\theta_2}\mu_{n,m} + \frac{1}{n+\theta_2}\sum_{j=0}^{m-1} \bigg(\alpha\binom{m}{j-1}+\theta_1\binom{m}{j}\bigg)\mu_{n,j}, \end{equation}
![]() $n,m\in\mathbb{N}_0$
, with initial conditions
$n,m\in\mathbb{N}_0$
, with initial conditions
![]() $\mu_{0,m}\,:\!=\,\delta_{0,m}$
(Kronecker symbol),
$\mu_{0,m}\,:\!=\,\delta_{0,m}$
(Kronecker symbol),
![]() $m\in\mathbb{N}_0$
, and the usual convention
$m\in\mathbb{N}_0$
, and the usual convention
![]() $\binom{m}{j-1}\,:\!=\,0$
for
$\binom{m}{j-1}\,:\!=\,0$
for
![]() $j=0$
. The Laplace transform
$j=0$
. The Laplace transform
![]() $\psi_n$
of
$\psi_n$
of
![]() $K_n$
satisfies
$K_n$
satisfies
![]() $\psi_0(\lambda)=1$
and
$\psi_0(\lambda)=1$
and
Proof. Clearly,
![]() $\mu_{0,m}=\delta_{0,m}$
and
$\mu_{0,m}=\delta_{0,m}$
and
![]() $\psi_0(\lambda)=1$
, since
$\psi_0(\lambda)=1$
, since
![]() $K_0=0$
. For
$K_0=0$
. For
![]() $n\in\mathbb{N}_0$
and
$n\in\mathbb{N}_0$
and
![]() $k\in\{1,\ldots,n\}$
,
$k\in\{1,\ldots,n\}$
,
 \begin{align*} \mathbb{E}(K_{n+1}^m \mid K_n=k) & = k^m\bigg(1-\frac{\alpha k+\theta_1}{n+\theta_2}\bigg) + (k+1)^m\frac{\alpha k+\theta_1}{n+\theta_2}\\[3pt] & = k^m + \frac{\alpha k+\theta_1}{n+\theta_2}\big((k+1)^m-k^m\big)\\[3pt] & = k^m+\frac{\alpha k+\theta_1}{n+\theta_2} \sum_{j=0}^{m-1}\binom{m}{j}k^j\\[3pt] & = \bigg(1+\frac{\alpha m}{n+\theta_2}\bigg)k^m + \frac{1}{n+\theta_2}\sum_{j=0}^{m-1} \bigg(\alpha\binom{m}{j-1}+\theta_1\binom{m}{j}\bigg)k^j, \end{align*}
\begin{align*} \mathbb{E}(K_{n+1}^m \mid K_n=k) & = k^m\bigg(1-\frac{\alpha k+\theta_1}{n+\theta_2}\bigg) + (k+1)^m\frac{\alpha k+\theta_1}{n+\theta_2}\\[3pt] & = k^m + \frac{\alpha k+\theta_1}{n+\theta_2}\big((k+1)^m-k^m\big)\\[3pt] & = k^m+\frac{\alpha k+\theta_1}{n+\theta_2} \sum_{j=0}^{m-1}\binom{m}{j}k^j\\[3pt] & = \bigg(1+\frac{\alpha m}{n+\theta_2}\bigg)k^m + \frac{1}{n+\theta_2}\sum_{j=0}^{m-1} \bigg(\alpha\binom{m}{j-1}+\theta_1\binom{m}{j}\bigg)k^j, \end{align*}
where
![]() $\binom{m}{j-1}\,:\!=\,0$
for
$\binom{m}{j-1}\,:\!=\,0$
for
![]() $j=0$
. Multiplying by
$j=0$
. Multiplying by
![]() $\mathbb{P}(K_n=k)$
and summing over all k yields (15). Similarly,
$\mathbb{P}(K_n=k)$
and summing over all k yields (15). Similarly,
![]() $\mathbb{E}(\textrm{e}^{-\lambda K_{n+1}} \mid K_n=k) = \big(1-\frac{\alpha k+\theta_1}{n+\theta_2}\big)\textrm{e}^{-\lambda k}+\frac{\alpha k+\theta_1}{n+\theta_2}\textrm{e}^{-\lambda(k+1)} = \big(1-(1-\textrm{e}^{-\lambda})\frac{\alpha k+\theta_1}{n+\theta_2}\big)\textrm{e}^{-\lambda k}$
,
$\mathbb{E}(\textrm{e}^{-\lambda K_{n+1}} \mid K_n=k) = \big(1-\frac{\alpha k+\theta_1}{n+\theta_2}\big)\textrm{e}^{-\lambda k}+\frac{\alpha k+\theta_1}{n+\theta_2}\textrm{e}^{-\lambda(k+1)} = \big(1-(1-\textrm{e}^{-\lambda})\frac{\alpha k+\theta_1}{n+\theta_2}\big)\textrm{e}^{-\lambda k}$
,
![]() $\lambda\ge 0$
. Multiplication by
$\lambda\ge 0$
. Multiplication by
![]() $\mathbb{P}(K_n=k)$
and summation over all k yields (16).
$\mathbb{P}(K_n=k)$
and summation over all k yields (16).
Remark 8. (First passage time) For
![]() $k\in\mathbb{N}_0$
let
$k\in\mathbb{N}_0$
let
![]() $T_k\,:\!=\,\inf\{n\in\mathbb{N}_0:K_n=k\}$
denote the time the chain K reaches state k. In other words,
$T_k\,:\!=\,\inf\{n\in\mathbb{N}_0:K_n=k\}$
denote the time the chain K reaches state k. In other words,
![]() $T_k$
is the first hitting time or first passage time of the state k. Clearly,
$T_k$
is the first hitting time or first passage time of the state k. Clearly,
![]() $T_0=0$
, since
$T_0=0$
, since
![]() $K_0=0$
. For
$K_0=0$
. For
![]() $k\in\mathbb{N}$
the distribution of
$k\in\mathbb{N}$
the distribution of
![]() $T_k$
is given by
$T_k$
is given by
 \begin{align} \mathbb{P}(T_k=n) & = \mathbb{P}(K_n=k,K_{n-1}=k-1)\nonumber\\[3pt] & = \mathbb{P}(K_n=k \mid K_{n-1}=k-1)\mathbb{P}(K_{n-1}=k-1)\nonumber\\[3pt] & = \frac{\alpha(k-1)+\theta_1}{n-1+\theta_2}\mathbb{P}(K_{n-1}=k-1), \qquad n\in\{k,k+1,\ldots\}. \end{align}
\begin{align} \mathbb{P}(T_k=n) & = \mathbb{P}(K_n=k,K_{n-1}=k-1)\nonumber\\[3pt] & = \mathbb{P}(K_n=k \mid K_{n-1}=k-1)\mathbb{P}(K_{n-1}=k-1)\nonumber\\[3pt] & = \frac{\alpha(k-1)+\theta_1}{n-1+\theta_2}\mathbb{P}(K_{n-1}=k-1), \qquad n\in\{k,k+1,\ldots\}. \end{align}
From (14) we conclude that
 \begin{align} \mathbb{P}(T_k=n) & = \frac{\alpha(k-1)+\theta_1}{n-1+\theta_2} \frac{[\theta_1 \mid \alpha]_{k-1}}{[\theta_2]_{n-1}}S(n-1,k-1;-1,-\alpha,\theta_2-\theta_1)\nonumber\\[3pt] & = \frac{[\theta_1 \mid \alpha]_k}{[\theta_2]_n} S(n-1,k-1;-1,-\alpha,\theta_2-\theta_1),\qquad n\in\{k,k+1,\ldots\} . \end{align}
\begin{align} \mathbb{P}(T_k=n) & = \frac{\alpha(k-1)+\theta_1}{n-1+\theta_2} \frac{[\theta_1 \mid \alpha]_{k-1}}{[\theta_2]_{n-1}}S(n-1,k-1;-1,-\alpha,\theta_2-\theta_1)\nonumber\\[3pt] & = \frac{[\theta_1 \mid \alpha]_k}{[\theta_2]_n} S(n-1,k-1;-1,-\alpha,\theta_2-\theta_1),\qquad n\in\{k,k+1,\ldots\} . \end{align}
The asymptotics of
![]() $K_n$
as
$K_n$
as
![]() $n\to\infty$
and of
$n\to\infty$
and of
![]() $T_k$
as
$T_k$
as
![]() $k\to\infty$
are provided in Sections 6.1 and 6.2 for
$k\to\infty$
are provided in Sections 6.1 and 6.2 for
![]() $\alpha=0$
and
$\alpha=0$
and
![]() $\alpha\ne 0$
respectively.
$\alpha\ne 0$
respectively.
6.1. The case
 ${\alpha=0}$
${\alpha=0}$
We briefly discuss the behavior of
![]() $K_n$
for
$K_n$
for
![]() $\alpha=0$
. In this case it follows, for example from (16), that
$\alpha=0$
. In this case it follows, for example from (16), that
![]() $K_n\stackrel{\textrm{d}}{=}\sum_{j=0}^{n-1}B_j$
,
$K_n\stackrel{\textrm{d}}{=}\sum_{j=0}^{n-1}B_j$
,
![]() $n\in\mathbb{N}$
, where
$n\in\mathbb{N}$
, where
![]() $B_0,B_1,\ldots$
are independent Bernoulli random variables with mean
$B_0,B_1,\ldots$
are independent Bernoulli random variables with mean
![]() $\mathbb{E}(B_j)=\theta_1/(j+\theta_2)$
,
$\mathbb{E}(B_j)=\theta_1/(j+\theta_2)$
,
![]() $j\in\mathbb{N}_0$
. Thus,
$j\in\mathbb{N}_0$
. Thus,
![]() $K_n$
has probability-generating function
$K_n$
has probability-generating function
 \begin{equation*} f_n(s) = \prod_{j=0}^{n-1} \frac{j+\theta_2-\theta_1+\theta_1 s}{j+\theta_2} = \frac{\Gamma(\theta_2)\Gamma(n+\theta_2-\theta_1+\theta_1 s)} {\Gamma(n+\theta_2)\Gamma(\theta_2-\theta_1+\theta_1 s)}, \qquad n\in\mathbb{N}_0,s\in\mathbb{C},\end{equation*}
\begin{equation*} f_n(s) = \prod_{j=0}^{n-1} \frac{j+\theta_2-\theta_1+\theta_1 s}{j+\theta_2} = \frac{\Gamma(\theta_2)\Gamma(n+\theta_2-\theta_1+\theta_1 s)} {\Gamma(n+\theta_2)\Gamma(\theta_2-\theta_1+\theta_1 s)}, \qquad n\in\mathbb{N}_0,s\in\mathbb{C},\end{equation*}
and integer moments
 \begin{align*} \mathbb{E}(K_n^m) & = \mathbb{E}((B_0+\cdots+B_{n-1})^m)\\[3pt]
& = \sum_{\genfrac{}{}{0pt}{2}{m_0,\ldots,m_{n-1}\ge 0}{m_0+\cdots+m_{n-1}=m}} \frac{m!}{m_0!\cdots m_{n-1}!} \mathbb{E}\big(B_0^{m_0}\big)\cdots\mathbb{E}\big(B_{n-1}^{m_{n-1}}\big)\\[3pt]
& = m!\sum_{I\subseteq\{0,\ldots,n-1\}} \sum_{\genfrac{}{}{0pt}{2}{m_i,i\in I}{\sum_{i\in I} m_i=m}} \prod_{i\in I}\frac{\mathbb{E}(B_i)}{m_i!}\\[3pt] & = m!\sum_{I\subseteq\{0,\ldots,n-1\}} \bigg(\prod_{i\in I}\mathbb{E}(B_i)\bigg) \sum_{\genfrac{}{}{0pt}{2}{m_i,i\in I}{\sum_{i\in I}m_i=m}} \prod_{i\in I}\frac{1}{m_i!}\\[3pt] & = \sum_{I\subseteq\{0,\ldots,n-1\}}|I|!S(m,|I|) \bigg(\prod_{i\in I}\mathbb{E}(B_i)\bigg)\\[3pt] & = \sum_{j=1}^m S(m,j) \sum_{\genfrac{}{}{0pt}{2}{i_1,\ldots,i_j=0}{\rm all\;distinct}}^{n-1} \mathbb{E}(B_{i_1})\cdots\mathbb{E}(B_{i_j})\\[3pt] & = \sum_{j=1}^m S(m,j) \sum_{\genfrac{}{}{0pt}{2}{i_1,\ldots,i_j=0}{\rm all\;distinct}}^{n-1} \frac{\theta_1^j}{(i_1+\theta_2)\cdots(i_j+\theta_2)}, \qquad n,m\in\mathbb{N},\end{align*}
\begin{align*} \mathbb{E}(K_n^m) & = \mathbb{E}((B_0+\cdots+B_{n-1})^m)\\[3pt]
& = \sum_{\genfrac{}{}{0pt}{2}{m_0,\ldots,m_{n-1}\ge 0}{m_0+\cdots+m_{n-1}=m}} \frac{m!}{m_0!\cdots m_{n-1}!} \mathbb{E}\big(B_0^{m_0}\big)\cdots\mathbb{E}\big(B_{n-1}^{m_{n-1}}\big)\\[3pt]
& = m!\sum_{I\subseteq\{0,\ldots,n-1\}} \sum_{\genfrac{}{}{0pt}{2}{m_i,i\in I}{\sum_{i\in I} m_i=m}} \prod_{i\in I}\frac{\mathbb{E}(B_i)}{m_i!}\\[3pt] & = m!\sum_{I\subseteq\{0,\ldots,n-1\}} \bigg(\prod_{i\in I}\mathbb{E}(B_i)\bigg) \sum_{\genfrac{}{}{0pt}{2}{m_i,i\in I}{\sum_{i\in I}m_i=m}} \prod_{i\in I}\frac{1}{m_i!}\\[3pt] & = \sum_{I\subseteq\{0,\ldots,n-1\}}|I|!S(m,|I|) \bigg(\prod_{i\in I}\mathbb{E}(B_i)\bigg)\\[3pt] & = \sum_{j=1}^m S(m,j) \sum_{\genfrac{}{}{0pt}{2}{i_1,\ldots,i_j=0}{\rm all\;distinct}}^{n-1} \mathbb{E}(B_{i_1})\cdots\mathbb{E}(B_{i_j})\\[3pt] & = \sum_{j=1}^m S(m,j) \sum_{\genfrac{}{}{0pt}{2}{i_1,\ldots,i_j=0}{\rm all\;distinct}}^{n-1} \frac{\theta_1^j}{(i_1+\theta_2)\cdots(i_j+\theta_2)}, \qquad n,m\in\mathbb{N},\end{align*}
where
![]() $S(\!\cdot\,,\cdot\!)$
denote Stirling numbers of the second kind. Clearly,
$S(\!\cdot\,,\cdot\!)$
denote Stirling numbers of the second kind. Clearly,
 \begin{equation*} \mathbb{E}(K_n) = \sum_{i=0}^{n-1}\frac{\theta_1}{i+\theta_2} \sim \theta_1\log n,\qquad n\to\infty,\end{equation*}
\begin{equation*} \mathbb{E}(K_n) = \sum_{i=0}^{n-1}\frac{\theta_1}{i+\theta_2} \sim \theta_1\log n,\qquad n\to\infty,\end{equation*}
and
 \begin{equation*} {\rm Var}(K_n) = \sum_{i=0}^{n-1}\frac{\theta_1(i+\theta_2-\theta_1)}{(i+\theta_2)^2} \sim \theta_1\log n,\qquad n\to\infty.\end{equation*}
\begin{equation*} {\rm Var}(K_n) = \sum_{i=0}^{n-1}\frac{\theta_1(i+\theta_2-\theta_1)}{(i+\theta_2)^2} \sim \theta_1\log n,\qquad n\to\infty.\end{equation*}
By the central limit theorem,
![]() $(K_n-\theta_1\log n)/\sqrt{\theta_1\log n}$
is asymptotically standard normal distributed. This convergence holds also locally, i.e.
$(K_n-\theta_1\log n)/\sqrt{\theta_1\log n}$
is asymptotically standard normal distributed. This convergence holds also locally, i.e.
which follows from [Reference Petrov26, p.193, Theorem 3].
Let us now turn to the first passage time
![]() $T_k$
.
$T_k$
.
Proposition 1. If
![]() $\alpha=0$
then, as
$\alpha=0$
then, as
![]() $k\to\infty$
,
$k\to\infty$
,
![]() $(\theta_1\log T_k-k)/\sqrt{k}$
is asymptotically standard normal distributed.
$(\theta_1\log T_k-k)/\sqrt{k}$
is asymptotically standard normal distributed.
Proof. We known that
![]() $(K_n-\theta_1\log n)/\sqrt{\theta_1\log n}$
converges in distribution to the standard normal law. Fix
$(K_n-\theta_1\log n)/\sqrt{\theta_1\log n}$
converges in distribution to the standard normal law. Fix
![]() $x\in\mathbb{R}$
. For
$x\in\mathbb{R}$
. For
![]() $k\in\mathbb{N}$
define
$k\in\mathbb{N}$
define
![]() $n\,:\!=\,n(k)\,:\!=\,\lfloor\exp((x\sqrt{k}+k)/\theta_1)\rfloor\in\mathbb{N}_0$
. For all
$n\,:\!=\,n(k)\,:\!=\,\lfloor\exp((x\sqrt{k}+k)/\theta_1)\rfloor\in\mathbb{N}_0$
. For all
![]() $k\in\mathbb{N}$
we have
$k\in\mathbb{N}$
we have
 \begin{align*} \mathbb{P}\bigg(\frac{\theta_1\log T_k-k}{\sqrt{k}}\le x\bigg) & = \mathbb{P}(T_k\le n) = \mathbb{P}(K_n\ge k) = 1-\mathbb{P}(K_n\le k-1)\\[3pt] & = 1-\mathbb{P}\bigg( \frac{K_n-\theta_1\log n}{\sqrt{\theta_1\log n}}\le\frac{k-1-\theta_1\log n}{\sqrt{\theta_1\log n}} \bigg)\\[3pt] & \to 1-\Phi(-x)\ =\ \Phi(x) \end{align*}
\begin{align*} \mathbb{P}\bigg(\frac{\theta_1\log T_k-k}{\sqrt{k}}\le x\bigg) & = \mathbb{P}(T_k\le n) = \mathbb{P}(K_n\ge k) = 1-\mathbb{P}(K_n\le k-1)\\[3pt] & = 1-\mathbb{P}\bigg( \frac{K_n-\theta_1\log n}{\sqrt{\theta_1\log n}}\le\frac{k-1-\theta_1\log n}{\sqrt{\theta_1\log n}} \bigg)\\[3pt] & \to 1-\Phi(-x)\ =\ \Phi(x) \end{align*}
as
![]() $k\to\infty$
, since
$k\to\infty$
, since
![]() $(k-1-\theta_1\log n)/\sqrt{\theta_1\log n}\to-x$
as
$(k-1-\theta_1\log n)/\sqrt{\theta_1\log n}\to-x$
as
![]() $k\to\infty$
.
$k\to\infty$
.
Remark 9. Useful formulas for some functionals of
![]() $T_k$
are available for
$T_k$
are available for
![]() $\alpha=0$
and
$\alpha=0$
and
![]() $\theta_1=\theta_2=1$
. In this case it follows from (17) and (18) that
$\theta_1=\theta_2=1$
. In this case it follows from (17) and (18) that
![]() $T_k$
has distribution
$T_k$
has distribution
where
![]() $s(\cdot\,,\cdot)$
are the Stirling numbers of the first kind. It follows that
$s(\cdot\,,\cdot)$
are the Stirling numbers of the first kind. It follows that
![]() $T_k$
has probability-generating function
$T_k$
has probability-generating function
 \begin{align*} \mathbb{E}(s^{T_k}) & = \sum_{n=k}^\infty |s(n-1,k-1)|\frac{s^n}{n!}\\[3pt] & = \int_0^s \sum_{n=k}^\infty |s(n-1,k-1)|\frac{u^{n-1}}{(n-1)!}\,{\rm d}u\\[3pt] & = \int_0^s \frac{(-\log(1-u))^{k-1}}{(k-1)!}\,{\rm d}u\\[3pt] & = 1-(1-s)\sum_{j=0}^{k-1}\frac{(-\log(1-s))^j}{j!},\qquad 0\le s\le 1. \end{align*}
\begin{align*} \mathbb{E}(s^{T_k}) & = \sum_{n=k}^\infty |s(n-1,k-1)|\frac{s^n}{n!}\\[3pt] & = \int_0^s \sum_{n=k}^\infty |s(n-1,k-1)|\frac{u^{n-1}}{(n-1)!}\,{\rm d}u\\[3pt] & = \int_0^s \frac{(-\log(1-u))^{k-1}}{(k-1)!}\,{\rm d}u\\[3pt] & = 1-(1-s)\sum_{j=0}^{k-1}\frac{(-\log(1-s))^j}{j!},\qquad 0\le s\le 1. \end{align*}
6.2. The case
 ${\alpha\ne 0}$
${\alpha\ne 0}$
For
![]() $\alpha\ne 0$
the right-hand side of the recursion (16) for the Laplace transform
$\alpha\ne 0$
the right-hand side of the recursion (16) for the Laplace transform
![]() $\psi_n$
of
$\psi_n$
of
![]() $K_n$
depends not only on
$K_n$
depends not only on
![]() $\psi_n$
but also on the derivative of
$\psi_n$
but also on the derivative of
![]() $\psi_n$
and is hence much more involved than for
$\psi_n$
and is hence much more involved than for
![]() $\alpha=0$
. Therefore, at first glance it seems to be hopeless to solve the recursion (16). The following proposition, however, provides a rather useful solution to this recursion on the interval
$\alpha=0$
. Therefore, at first glance it seems to be hopeless to solve the recursion (16). The following proposition, however, provides a rather useful solution to this recursion on the interval
![]() $[0,\log 2)$
.
$[0,\log 2)$
.
Proposition 2. (Laplace transform of
![]() $K_n$
.) If
$K_n$
.) If
![]() $\alpha\ne 0$
then the Laplace transform
$\alpha\ne 0$
then the Laplace transform
![]() $\psi_n$
of
$\psi_n$
of
![]() $K_n$
satisfies
$K_n$
satisfies
 \begin{equation} \psi_n(\lambda) = \textrm{e}^{\gamma\lambda}\sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}(1-\textrm{e}^\lambda)^j, \qquad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2, \end{equation}
\begin{equation} \psi_n(\lambda) = \textrm{e}^{\gamma\lambda}\sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}(1-\textrm{e}^\lambda)^j, \qquad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2, \end{equation}
where
![]() $\gamma\,:\!=\,\theta_1/\alpha$
.
$\gamma\,:\!=\,\theta_1/\alpha$
.
Remark 10. For
![]() $\alpha>0$
the series on the right-hand side of (19) is absolutely convergent since
$\alpha>0$
the series on the right-hand side of (19) is absolutely convergent since
![]() $|1-\textrm{e}^\lambda|<1$
for
$|1-\textrm{e}^\lambda|<1$
for
![]() $0\le\lambda<\log 2$
. For
$0\le\lambda<\log 2$
. For
![]() $\alpha=-\kappa<0$
and
$\alpha=-\kappa<0$
and
![]() $\theta_1=m\kappa$
for some
$\theta_1=m\kappa$
for some
![]() $m\in\mathbb{N}$
we have
$m\in\mathbb{N}$
we have
![]() $\gamma\,:\!=\,\theta_1/\alpha=-m\in-\mathbb{N}$
and the series on the right-hand side in (19) reduces to a finite sum, since in this case
$\gamma\,:\!=\,\theta_1/\alpha=-m\in-\mathbb{N}$
and the series on the right-hand side in (19) reduces to a finite sum, since in this case
![]() $[\gamma]_j=0$
for
$[\gamma]_j=0$
for
![]() $j>m$
. Clearly, knowledge of the Laplace transform
$j>m$
. Clearly, knowledge of the Laplace transform
![]() $\psi_n$
on the interval
$\psi_n$
on the interval
![]() $[0,\log 2)$
fully determines the distribution of
$[0,\log 2)$
fully determines the distribution of
![]() $K_n$
.
$K_n$
.
Proof. It suffices to verify that
![]() $\psi_n$
, defined via (19), solves the recursion (16) with initial condition
$\psi_n$
, defined via (19), solves the recursion (16) with initial condition
![]() $\psi_0\equiv 1$
. Equivalently, it suffices to verify that
$\psi_0\equiv 1$
. Equivalently, it suffices to verify that
![]() $(f_n)_{n\in\mathbb{N}_0}$
, defined via
$(f_n)_{n\in\mathbb{N}_0}$
, defined via
 \begin{equation} f_n(\lambda) \,:\!=\, \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}\big(1-\textrm{e}^\lambda\big)^j, \qquad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2, \end{equation}
\begin{equation} f_n(\lambda) \,:\!=\, \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}\big(1-\textrm{e}^\lambda\big)^j, \qquad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2, \end{equation}
solves the recursion
with initial condition
![]() $f_0(\lambda)=\textrm{e}^{-\gamma\lambda}$
,
$f_0(\lambda)=\textrm{e}^{-\gamma\lambda}$
,
![]() $0\le\lambda<\log 2$
. Obviously,
$0\le\lambda<\log 2$
. Obviously,
 \begin{equation*} f_0(\lambda)=\sum_{j=0}^\infty \binom{j+\gamma-1}{j}(1-\textrm{e}^\lambda)^j=\sum_{j=0}^\infty \binom{-\gamma}{j}(\textrm{e}^\lambda-1)^j=\big(1+\big(\textrm{e}^\lambda-1\big)\big)^{-\gamma}=\textrm{e}^{-\gamma\lambda} \end{equation*}
\begin{equation*} f_0(\lambda)=\sum_{j=0}^\infty \binom{j+\gamma-1}{j}(1-\textrm{e}^\lambda)^j=\sum_{j=0}^\infty \binom{-\gamma}{j}(\textrm{e}^\lambda-1)^j=\big(1+\big(\textrm{e}^\lambda-1\big)\big)^{-\gamma}=\textrm{e}^{-\gamma\lambda} \end{equation*}
for all
![]() $0\le\lambda<\log 2$
by binomial series expansion. Taking the derivative with respect to
$0\le\lambda<\log 2$
by binomial series expansion. Taking the derivative with respect to
![]() $\lambda$
in (20) yields
$\lambda$
in (20) yields
 \begin{equation*} {f\kern0.5pt}_n{\!\!'}\kern2pt(\lambda) = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!} j\big(1-\textrm{e}^\lambda\big)^{j-1}\big(-\textrm{e}^\lambda\big). \end{equation*}
\begin{equation*} {f\kern0.5pt}_n{\!\!'}\kern2pt(\lambda) = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!} j\big(1-\textrm{e}^\lambda\big)^{j-1}\big(-\textrm{e}^\lambda\big). \end{equation*}
Multiplication by
![]() $1-\textrm{e}^{-\lambda}$
leads to
$1-\textrm{e}^{-\lambda}$
leads to
 \begin{equation} (1-\textrm{e}^{-\lambda}){f\kern0.5pt}_n{\!\!'}\kern1pt(\lambda) = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}j\big(1-\textrm{e}^\lambda\big)^j. \end{equation}
\begin{equation} (1-\textrm{e}^{-\lambda}){f\kern0.5pt}_n{\!\!'}\kern1pt(\lambda) = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!}j\big(1-\textrm{e}^\lambda\big)^j. \end{equation}
Now, by (20),
 \begin{align*} f_{n+1}(\lambda) & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_{n+1}}{[\theta_2]_{n+1}} \frac{[\gamma]_j}{j!}\big(1-\textrm{e}^\lambda\big)^j\\[3pt] & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \bigg(1+\frac{\alpha j}{\theta_2+n}\bigg) \frac{[\gamma]_j}{j!} \big(1-\textrm{e}^\lambda\big)^j\\[3pt] & = f_n(\lambda) + \frac{\alpha}{\theta_2+n} \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!} j\big(1-\textrm{e}^\lambda\big)^j\\[3pt] &
= f_n(\lambda) + \frac{\alpha}{\theta_2+n}\big(1-\textrm{e}^{-\lambda}\big)\kern1pt{f\kern0.5pt}_n{\!\!'}\kern1pt (\lambda), \end{align*}
\begin{align*} f_{n+1}(\lambda) & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_{n+1}}{[\theta_2]_{n+1}} \frac{[\gamma]_j}{j!}\big(1-\textrm{e}^\lambda\big)^j\\[3pt] & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \bigg(1+\frac{\alpha j}{\theta_2+n}\bigg) \frac{[\gamma]_j}{j!} \big(1-\textrm{e}^\lambda\big)^j\\[3pt] & = f_n(\lambda) + \frac{\alpha}{\theta_2+n} \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} \frac{[\gamma]_j}{j!} j\big(1-\textrm{e}^\lambda\big)^j\\[3pt] &
= f_n(\lambda) + \frac{\alpha}{\theta_2+n}\big(1-\textrm{e}^{-\lambda}\big)\kern1pt{f\kern0.5pt}_n{\!\!'}\kern1pt (\lambda), \end{align*}
where the last equality holds by (22). Hence,
![]() $(f_n)_{n\in\mathbb{N}_0}$
solves the recursion (21).
$(f_n)_{n\in\mathbb{N}_0}$
solves the recursion (21).
Corollary 1 provides a formula for
![]() $\mathbb{E}(K_n^i)$
,
$\mathbb{E}(K_n^i)$
,
![]() $i\in\mathbb{N}_0$
, showing that
$i\in\mathbb{N}_0$
, showing that
![]() $\mathbb{E}(K_n^i)$
is a linear combination of terms of the form
$\mathbb{E}(K_n^i)$
is a linear combination of terms of the form
![]() $[\theta_2+\alpha j]_n/[\theta_2]_n$
,
$[\theta_2+\alpha j]_n/[\theta_2]_n$
,
![]() $j\in\{0,\ldots,i\}$
, where each term occurs according to a particular weight
$j\in\{0,\ldots,i\}$
, where each term occurs according to a particular weight
![]() $\kappa_{i,j}$
. Similar formulas have been obtained in [Reference Zhang, Chen and Mahmoud42, Theorem 3.1] for the moments of the number of balls of a given type for balanced triangular Pólya urns. The proof in [Reference Zhang, Chen and Mahmoud42] is elementary but based on a double induction on n and i. Slightly less precise statements (the weights
$\kappa_{i,j}$
. Similar formulas have been obtained in [Reference Zhang, Chen and Mahmoud42, Theorem 3.1] for the moments of the number of balls of a given type for balanced triangular Pólya urns. The proof in [Reference Zhang, Chen and Mahmoud42] is elementary but based on a double induction on n and i. Slightly less precise statements (the weights
![]() $\kappa_{i,j}$
of the linear combinations are not provided explicitly) for certain urn models can be also found in [Reference Flajolet, Dumas and Puyhaubert10, Proposition 15]. Our result follows directly from our Proposition 2.
$\kappa_{i,j}$
of the linear combinations are not provided explicitly) for certain urn models can be also found in [Reference Flajolet, Dumas and Puyhaubert10, Proposition 15]. Our result follows directly from our Proposition 2.
Corollary 1. (Moments of
![]() $K_n$
.) If
$K_n$
.) If
![]() $\alpha\ne 0$
then
$\alpha\ne 0$
then
 \begin{equation} \mathbb{E}(K_n^i) = \frac{1}{[\theta_2]_n} \sum_{j=0}^i \kappa_{i,j} [\theta_2+\alpha j]_n,\qquad n,i\in\mathbb{N}_0, \end{equation}
\begin{equation} \mathbb{E}(K_n^i) = \frac{1}{[\theta_2]_n} \sum_{j=0}^i \kappa_{i,j} [\theta_2+\alpha j]_n,\qquad n,i\in\mathbb{N}_0, \end{equation}
where the coefficients
![]() $\kappa_{i,j}$
only depend on
$\kappa_{i,j}$
only depend on
![]() $\gamma\,:\!=\,\theta_1/\alpha$
and are given by
$\gamma\,:\!=\,\theta_1/\alpha$
and are given by
with
![]() $S_\gamma(i,j)\,:\!=\,S(i,j;0,1,\gamma)$
; see (12). In particular, if
$S_\gamma(i,j)\,:\!=\,S(i,j;0,1,\gamma)$
; see (12). In particular, if
![]() $\alpha>0$
then, for all
$\alpha>0$
then, for all
![]() $i\in\mathbb{N}_0$
,
$i\in\mathbb{N}_0$
,
and, if
![]() $\alpha<0$
, then, for all
$\alpha<0$
, then, for all
![]() $i\in\mathbb{N}_0$
,
$i\in\mathbb{N}_0$
,
Remark 11. Roughly speaking, for
![]() $\alpha>0$
the ith moment
$\alpha>0$
the ith moment
![]() $\mathbb{E}(K_n^i)$
is of order
$\mathbb{E}(K_n^i)$
is of order
![]() $n^{\alpha i}$
, whereas for
$n^{\alpha i}$
, whereas for
![]() $\alpha<0$
the ith moment
$\alpha<0$
the ith moment
![]() $\mathbb{E}(K_n^i)$
is bounded and converges to
$\mathbb{E}(K_n^i)$
is bounded and converges to
![]() $m^i$
as
$m^i$
as
![]() $n\to\infty$
, in agreement with the fact that, for
$n\to\infty$
, in agreement with the fact that, for
![]() $\alpha<0$
, the number of occupied tables never exceeds m.
$\alpha<0$
, the number of occupied tables never exceeds m.
Proof. Plugging the expansion
 \begin{equation*} \textrm{e}^{\gamma\lambda}\big(1-\textrm{e}^\lambda\big)^j = (-1)^j \textrm{e}^{\gamma\lambda}(\textrm{e}^\lambda-1)^j = (-1)^jj!\sum_{i=j}^\infty S_\gamma(i,j)\frac{\lambda^i}{i!} \end{equation*}
\begin{equation*} \textrm{e}^{\gamma\lambda}\big(1-\textrm{e}^\lambda\big)^j = (-1)^j \textrm{e}^{\gamma\lambda}(\textrm{e}^\lambda-1)^j = (-1)^jj!\sum_{i=j}^\infty S_\gamma(i,j)\frac{\lambda^i}{i!} \end{equation*}
into (19) leads to
 \begin{align*} \mathbb{E}(\textrm{e}^{-\lambda K_n}) & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} [\gamma]_j(-1)^j \sum_{i=j}^\infty S_\gamma(i,j)\frac{\lambda^i}{i!}\\[3pt] & = \sum_{i=0}^\infty \frac{(-\lambda)^i}{i!} \sum_{j=0}^i \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} [\gamma]_j (-1)^{i-j} S_\gamma(i,j), \quad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2. \end{align*}
\begin{align*} \mathbb{E}(\textrm{e}^{-\lambda K_n}) & = \sum_{j=0}^\infty \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} [\gamma]_j(-1)^j \sum_{i=j}^\infty S_\gamma(i,j)\frac{\lambda^i}{i!}\\[3pt] & = \sum_{i=0}^\infty \frac{(-\lambda)^i}{i!} \sum_{j=0}^i \frac{[\theta_2+\alpha j]_n}{[\theta_2]_n} [\gamma]_j (-1)^{i-j} S_\gamma(i,j), \quad n\in\mathbb{N}_0,\ 0\le\lambda<\log 2. \end{align*}
Comparing the coefficients in this expansion with those of
shows that
![]() $K_n$
has moments (23) with weights
$K_n$
has moments (23) with weights
![]() $\kappa_{i,j}$
defined via (24). The asymptotic formulas (25) and (26) follow immediately.
$\kappa_{i,j}$
defined via (24). The asymptotic formulas (25) and (26) follow immediately.
We now study the asymptotics of
![]() $K_n$
as
$K_n$
as
![]() $n\to\infty$
and start with the rather simple case
$n\to\infty$
and start with the rather simple case
![]() $\alpha=-\kappa<0$
and
$\alpha=-\kappa<0$
and
![]() $\theta_1=m\kappa$
for some
$\theta_1=m\kappa$
for some
![]() $m\in\mathbb{N}$
. In this case we conclude from (14) and
$m\in\mathbb{N}$
. In this case we conclude from (14) and
![]() $[\theta_1|\alpha]_k=[m\kappa|-\kappa]_k=\kappa^km!/(m-k)!$
that, for
$[\theta_1|\alpha]_k=[m\kappa|-\kappa]_k=\kappa^km!/(m-k)!$
that, for
![]() $k\in\{0,\ldots,m\wedge n\}$
,
$k\in\{0,\ldots,m\wedge n\}$
,
 \begin{align*} \mathbb{P}(K_n=k) & = \frac{[\theta_1|\alpha]_k}{[\theta_2]_n} S(n,k;-1,\kappa,\theta_2-\theta_1)\nonumber\\[3pt] & = \kappa^k\frac{m!}{(m-k)!} \frac{1}{[\theta_2]_n}S(n,k;-1,\kappa,\theta_2-\theta_1).\end{align*}
\begin{align*} \mathbb{P}(K_n=k) & = \frac{[\theta_1|\alpha]_k}{[\theta_2]_n} S(n,k;-1,\kappa,\theta_2-\theta_1)\nonumber\\[3pt] & = \kappa^k\frac{m!}{(m-k)!} \frac{1}{[\theta_2]_n}S(n,k;-1,\kappa,\theta_2-\theta_1).\end{align*}
Proposition 3. If
![]() $\alpha=-\kappa<0$
and
$\alpha=-\kappa<0$
and
![]() $\theta_1=m\kappa$
for some
$\theta_1=m\kappa$
for some
![]() $m\in\mathbb{N}$
, then, as
$m\in\mathbb{N}$
, then, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $K_n\to m$
almost surely and in
$K_n\to m$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
.
$p>0$
.
Proof. For
![]() $\alpha<0$
the chain
$\alpha<0$
the chain
![]() $(K_n)_{n\in\mathbb{N}_0}$
has finite state space
$(K_n)_{n\in\mathbb{N}_0}$
has finite state space
![]() $\{0,\ldots,m\}$
. Thus, as
$\{0,\ldots,m\}$
. Thus, as
![]() $n\to\infty$
, the chain converges almost surely to its absorbing state m. For all
$n\to\infty$
, the chain converges almost surely to its absorbing state m. For all
![]() $i\in\mathbb{N}_0$
, by (26),
$i\in\mathbb{N}_0$
, by (26),
![]() $\lim_{n\to\infty}\mathbb{E}(K_n^i)=m^i$
. This convergence of all moments together with the almost sure convergence implies (see [Reference Kallenberg20, p. 68, Proposition 4.12]) the convergence
$\lim_{n\to\infty}\mathbb{E}(K_n^i)=m^i$
. This convergence of all moments together with the almost sure convergence implies (see [Reference Kallenberg20, p. 68, Proposition 4.12]) the convergence
![]() $K_n\to m$
in
$K_n\to m$
in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
.
$p>0$
.
Example 1. For
![]() $\kappa=1$
the Stirling numbers
$\kappa=1$
the Stirling numbers
![]() $S(n,k;-1,\kappa,0)$
coincide with the Lah numbers
$S(n,k;-1,\kappa,0)$
coincide with the Lah numbers
![]() $S(n,k;-1,1,0)=\frac{n!}{k!}\binom{n-1}{k-1}$
. Choosing in addition
$S(n,k;-1,1,0)=\frac{n!}{k!}\binom{n-1}{k-1}$
. Choosing in addition
![]() $\theta_2\,:\!=\,\theta_1$
(
$\theta_2\,:\!=\,\theta_1$
(
![]() $=m$
) yields
$=m$
) yields
 \begin{equation*} \mathbb{P}(K_n=k) = \frac{m!}{(m-k)!}\frac{(m-1)!}{(m+n-1)!} \frac{n!}{k!}\binom{n-1}{k-1} = \frac{\binom{m-1}{k-1}\binom{n}{k}} {\binom{m+n-1}{n-1}}, \quad k\in\{0,\ldots,m\wedge n\}, \end{equation*}
\begin{equation*} \mathbb{P}(K_n=k) = \frac{m!}{(m-k)!}\frac{(m-1)!}{(m+n-1)!} \frac{n!}{k!}\binom{n-1}{k-1} = \frac{\binom{m-1}{k-1}\binom{n}{k}} {\binom{m+n-1}{n-1}}, \quad k\in\{0,\ldots,m\wedge n\}, \end{equation*}
so
![]() $K_n-1$
has a hypergeometric distribution with parameters
$K_n-1$
has a hypergeometric distribution with parameters
![]() $m+n-1$
,
$m+n-1$
,
![]() $m-1$
, and
$m-1$
, and
![]() $n-1$
.
$n-1$
.
More exciting is the case
![]() $\alpha>0$
. Before we state the main result (Theorem 3), let us turn to Mittag–Leffler distributions. Let
$\alpha>0$
. Before we state the main result (Theorem 3), let us turn to Mittag–Leffler distributions. Let
![]() $0\le\alpha\le 1$
and
$0\le\alpha\le 1$
and
![]() $\beta,\gamma>0$
with
$\beta,\gamma>0$
with
![]() $\beta\ge\alpha\gamma$
. By Lemma 2 provided in Section 7 there exists a positive random variable
$\beta\ge\alpha\gamma$
. By Lemma 2 provided in Section 7 there exists a positive random variable
![]() $\eta$
uniquely determined by its integer moments,
$\eta$
uniquely determined by its integer moments,
Since the Laplace transform
![]() $\psi$
of
$\psi$
of
![]() $\eta$
is related to Prabhakar’s [Reference Prabhakar32] three-parameter Mittag–Leffler function
$\eta$
is related to Prabhakar’s [Reference Prabhakar32] three-parameter Mittag–Leffler function
![]() $E_{\alpha,\beta}^\gamma$
via
$E_{\alpha,\beta}^\gamma$
via
![]() $\psi(\lambda)=\Gamma(\beta)E_{\alpha,\beta}^\gamma(-\lambda)$
,
$\psi(\lambda)=\Gamma(\beta)E_{\alpha,\beta}^\gamma(-\lambda)$
,
![]() $\lambda\ge 0$
, we call the distribution of
$\lambda\ge 0$
, we call the distribution of
![]() $\eta$
the three-parameter Mittag–Leffler distribution and denote it by
$\eta$
the three-parameter Mittag–Leffler distribution and denote it by
![]() ${\rm ML}(\alpha,\beta,\gamma)$
. The distribution
${\rm ML}(\alpha,\beta,\gamma)$
. The distribution
![]() ${\rm ML}(\alpha,\beta)\,:\!=\,{\rm ML}(\alpha,\beta,\beta/\alpha)$
is called the two-parameter Mittag–Leffler distribution and for
${\rm ML}(\alpha,\beta)\,:\!=\,{\rm ML}(\alpha,\beta,\beta/\alpha)$
is called the two-parameter Mittag–Leffler distribution and for
![]() $\beta\,:\!=\,\gamma\,:\!=\,1$
we recover the one-parameter Mittag–Leffler distribution
$\beta\,:\!=\,\gamma\,:\!=\,1$
we recover the one-parameter Mittag–Leffler distribution
![]() ${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
having moments
${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
having moments
![]() $\Gamma(j+1)/\Gamma(\alpha j+1)$
,
$\Gamma(j+1)/\Gamma(\alpha j+1)$
,
![]() $j\in\mathbb{N}_0$
. For more information on Mittag–Leffler distributions we refer the reader to Sections 7 and 8. Pitman [Reference Pitman30, Theorem 3.8] showed for the two-parameter CRP with parameters
$j\in\mathbb{N}_0$
. For more information on Mittag–Leffler distributions we refer the reader to Sections 7 and 8. Pitman [Reference Pitman30, Theorem 3.8] showed for the two-parameter CRP with parameters
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\theta>-\alpha$
that, as
$\theta>-\alpha$
that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $K_n/n^\alpha\to K$
almost surely and in
$K_n/n^\alpha\to K$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\theta)$
. The following convergence result is the natural extension for the restaurant process with cocktail bar.
$K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\theta)$
. The following convergence result is the natural extension for the restaurant process with cocktail bar.
Theorem 3. (Convergence of scaled
![]() $K_n$
.) If
$K_n$
.) If
![]() $\alpha>0$
then, as
$\alpha>0$
then, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $K_n/n^\alpha\to K$
almost surely and in
$K_n/n^\alpha\to K$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is three-parameter Mittag–Leffler distributed with parameters
$K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is three-parameter Mittag–Leffler distributed with parameters
![]() $0<\alpha<1$
,
$0<\alpha<1$
,
![]() $\beta\,:\!=\,\theta_2$
, and
$\beta\,:\!=\,\theta_2$
, and
![]() $\gamma\,:\!=\,\theta_1/\alpha$
. In particular, the convergence
$\gamma\,:\!=\,\theta_1/\alpha$
. In particular, the convergence
of all moments holds.
Two proofs are provided. The first is self-contained, more elementary than that provided in [Reference Pitman30] for the two-parameter CRP, and based on a martingale argument similar to those used in the context of Pólya urns. The distribution of K is determined via Corollary 1. The second proof is based on reinterpretation of the model in terms of a mixture of a Pólya urn and a two-parameter CRP. Both proofs are relatively short.
First proof of Theorem 3. For
![]() $n\in\mathbb{N}_0$
define
$n\in\mathbb{N}_0$
define
For all
![]() $n\in\mathbb{N}_0$
, by (13),
$n\in\mathbb{N}_0$
, by (13),
 \begin{align*} \mathbb{E}(K_{n+1}+\gamma \mid K_n) & = (K_n+\gamma)\bigg(1-\frac{\alpha(K_n+\gamma)}{n+\beta}\bigg) + (K_n+1+\gamma)\frac{\alpha(K_n+\gamma)}{n+\beta}\\[3pt] & = (K_n+\gamma)\bigg(1-\frac{\alpha(K_n+\gamma)}{n+\beta} +\frac{\alpha(K_n+1+\gamma)}{n+\beta} \bigg)\\[3pt] & = (K_n+\gamma)\bigg(1+\frac{\alpha}{n+\beta}\bigg) = (K_n+\gamma)\frac{n+\alpha+\beta}{n+\beta} \end{align*}
\begin{align*} \mathbb{E}(K_{n+1}+\gamma \mid K_n) & = (K_n+\gamma)\bigg(1-\frac{\alpha(K_n+\gamma)}{n+\beta}\bigg) + (K_n+1+\gamma)\frac{\alpha(K_n+\gamma)}{n+\beta}\\[3pt] & = (K_n+\gamma)\bigg(1-\frac{\alpha(K_n+\gamma)}{n+\beta} +\frac{\alpha(K_n+1+\gamma)}{n+\beta} \bigg)\\[3pt] & = (K_n+\gamma)\bigg(1+\frac{\alpha}{n+\beta}\bigg) = (K_n+\gamma)\frac{n+\alpha+\beta}{n+\beta} \end{align*}
almost surely. Multiplication by
![]() $\Gamma(n+1+\beta)/\Gamma(n+1+\alpha+\beta)$
yields
$\Gamma(n+1+\beta)/\Gamma(n+1+\alpha+\beta)$
yields
![]() $\mathbb{E}(M_{n+1} \mid K_n)=M_n$
almost surely for all
$\mathbb{E}(M_{n+1} \mid K_n)=M_n$
almost surely for all
![]() $n\in\mathbb{N}_0$
. Thus,
$n\in\mathbb{N}_0$
. Thus,
![]() $(M_n)_{n\in\mathbb{N}_0}$
is a nonnegative martingale with respect to the filtration
$(M_n)_{n\in\mathbb{N}_0}$
is a nonnegative martingale with respect to the filtration
![]() $(\mathcal{ F}_n)_{n\in\mathbb{N}_0}$
, where
$(\mathcal{ F}_n)_{n\in\mathbb{N}_0}$
, where
![]() $\mathcal{ F}_n$
denotes the
$\mathcal{ F}_n$
denotes the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $K_0,\ldots,K_n$
. By martingale convergence there exists K such that
$K_0,\ldots,K_n$
. By martingale convergence there exists K such that
![]() $M_n\to K$
almost surely as
$M_n\to K$
almost surely as
![]() $n\to\infty$
. Note that
$n\to\infty$
. Note that
![]() $K_n\to\infty$
almost surely as
$K_n\to\infty$
almost surely as
![]() $n\to\infty$
, which follows from Theorem 2 and the fact that all of the
$n\to\infty$
, which follows from Theorem 2 and the fact that all of the
![]() $P_i$
,
$P_i$
,
![]() $i\in\mathbb{N}$
, are strictly positive almost surely. Thus, it follows from (28) that
$i\in\mathbb{N}$
, are strictly positive almost surely. Thus, it follows from (28) that
![]() $M_n\sim (K_n+\gamma)/n^\alpha\sim K_n/n^\alpha$
almost surely as
$M_n\sim (K_n+\gamma)/n^\alpha\sim K_n/n^\alpha$
almost surely as
![]() $n\to\infty$
, and hence
$n\to\infty$
, and hence
![]() $K_n/n^\alpha\to K$
almost surely.
$K_n/n^\alpha\to K$
almost surely.
Now Corollary 1 is used to determine the distribution of K. Let
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
be three-parameter Mittag–Leffler distributed with parameters
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
be three-parameter Mittag–Leffler distributed with parameters
![]() $\alpha,\beta\,:\!=\,\theta_2$
and
$\alpha,\beta\,:\!=\,\theta_2$
and
![]() $\gamma\,:\!=\,\theta_1/\alpha$
. For all
$\gamma\,:\!=\,\theta_1/\alpha$
. For all
![]() $j\in\mathbb{N}_0$
, by (25) and (27),
$j\in\mathbb{N}_0$
, by (25) and (27),
Thus,
![]() $\lim_{n\to\infty}\mathbb{E}((K_n/n^\alpha)^j)=\mathbb{E}(\eta^j)$
,
$\lim_{n\to\infty}\mathbb{E}((K_n/n^\alpha)^j)=\mathbb{E}(\eta^j)$
,
![]() $j\in\mathbb{N}_0$
. Since (see Section 7, Lemma 2) the distribution
$j\in\mathbb{N}_0$
. Since (see Section 7, Lemma 2) the distribution
![]() ${\rm ML}(\alpha,\beta,\gamma)$
of
${\rm ML}(\alpha,\beta,\gamma)$
of
![]() $\eta$
is uniquely determined by its moments, this convergence of moments implies (see, for example, [3, Theorem 30.2]) the convergence
$\eta$
is uniquely determined by its moments, this convergence of moments implies (see, for example, [3, Theorem 30.2]) the convergence
![]() $K_n/n^\alpha\to\eta$
in distribution as
$K_n/n^\alpha\to\eta$
in distribution as
![]() $n\to\infty$
. In particular, the distribution of the almost sure limit K must coincide with the distribution
$n\to\infty$
. In particular, the distribution of the almost sure limit K must coincide with the distribution
![]() ${\rm ML}(\alpha,\beta,\gamma)$
of the distributional limit
${\rm ML}(\alpha,\beta,\gamma)$
of the distributional limit
![]() $\eta$
. By (41), K has moments
$\eta$
. By (41), K has moments
![]() $\mathbb{E}(K^p)=(\Gamma(\beta)\Gamma(p+\gamma))/(\Gamma(\gamma)\Gamma(\alpha p+\beta))$
,
$\mathbb{E}(K^p)=(\Gamma(\beta)\Gamma(p+\gamma))/(\Gamma(\gamma)\Gamma(\alpha p+\beta))$
,
![]() $p\ge 0$
. The rest of the proof works as in the proof of Theorem 1.
$p\ge 0$
. The rest of the proof works as in the proof of Theorem 1.
Second proof of Theorem 3. Recall the reinterpretation of the model in terms of a mixture of a two-type Pólya urn and a standard CRP described in Section 2. We have
Since the jump evolution of the process
![]() $(R_{n,1},\ldots,R_{n,K_n})_{n\in\mathbb{N}}$
is a standard CRP with parameters
$(R_{n,1},\ldots,R_{n,K_n})_{n\in\mathbb{N}}$
is a standard CRP with parameters
![]() $\alpha$
and
$\alpha$
and
![]() $\theta_1$
, it follows from [Reference Pitman30, Theorem 3.8] that, as
$\theta_1$
, it follows from [Reference Pitman30, Theorem 3.8] that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $K_n/R_n^\alpha\to L$
almost surely and in
$K_n/R_n^\alpha\to L$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\theta_1)$
. By standard results for Pólya urns (see also the remark at the end of Section 3), as
$L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\theta_1)$
. By standard results for Pólya urns (see also the remark at the end of Section 3), as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $R_n/n\to R$
almost surely and in
$R_n/n\to R$
almost surely and in
![]() $L^p$
for any
$L^p$
for any
![]() $p>0$
, where
$p>0$
, where
![]() $R\stackrel{\textrm{d}}{=}\beta(\theta_1,\theta_2-\theta_1)$
. Thus,
$R\stackrel{\textrm{d}}{=}\beta(\theta_1,\theta_2-\theta_1)$
. Thus,
![]() $K_n/n^\alpha\to LR^\alpha \!=: K$
almost surely. Moreover, L and R are independent. By the independence structure we also have convergence of all moments
$K_n/n^\alpha\to LR^\alpha \!=: K$
almost surely. Moreover, L and R are independent. By the independence structure we also have convergence of all moments
![]() $\mathbb{E}((K_n/n^\alpha)^j)=\mathbb{E}((K_n/R_n^\alpha)^j)\mathbb{E}((R_n/n)^{\alpha j})\to\mathbb{E}(L^j)\mathbb{E}(R^{\alpha j})=\mathbb{E}(K^j)$
,
$\mathbb{E}((K_n/n^\alpha)^j)=\mathbb{E}((K_n/R_n^\alpha)^j)\mathbb{E}((R_n/n)^{\alpha j})\to\mathbb{E}(L^j)\mathbb{E}(R^{\alpha j})=\mathbb{E}(K^j)$
,
![]() $j\in\mathbb{N}_0$
. The almost sure convergence implies convergence in probability. Convergence in probability together with the convergence of all moments implies (see, for example, [Reference Kallenberg20, p. 68, Proposition 4.12]) convergence in
$j\in\mathbb{N}_0$
. The almost sure convergence implies convergence in probability. Convergence in probability together with the convergence of all moments implies (see, for example, [Reference Kallenberg20, p. 68, Proposition 4.12]) convergence in
![]() $L^p$
and, hence, the convergence of the pth moments for any
$L^p$
and, hence, the convergence of the pth moments for any
![]() $p>0$
.
$p>0$
.
The distribution of K is determined via moment calculations as follows. Using the density formula [Reference Pitman30, Eq. (3.27)] of L it is easily checked that L has moments (see also [Reference Pitman30, Eq. (3.47)])
 \begin{equation} \mathbb{E}(L^j) = \frac{\Gamma(\theta_1)\Gamma\Big(j+\frac{\theta_1}{\alpha}\Big)} {\Gamma\Big(\frac{\theta_1}{\alpha}\Big)\Gamma(\alpha j+\theta_1)}, \qquad j\in\mathbb{N}_0. \end{equation}
\begin{equation} \mathbb{E}(L^j) = \frac{\Gamma(\theta_1)\Gamma\Big(j+\frac{\theta_1}{\alpha}\Big)} {\Gamma\Big(\frac{\theta_1}{\alpha}\Big)\Gamma(\alpha j+\theta_1)}, \qquad j\in\mathbb{N}_0. \end{equation}
Moreover, the beta distributed random variable R satisfies
Since L and R are independent it follows from (29) and (30) that
![]() $K=LR^\alpha$
has moments
$K=LR^\alpha$
has moments
 \begin{equation*} \mathbb{E}(K^j) = \mathbb{E}(L^j)\mathbb{E}(R^{\alpha j}) = \frac{\Gamma(\theta_2)\Gamma\Big(j+\frac{\theta_1}{\alpha}\Big)} {\Gamma\Big(\frac{\theta_1}{\alpha}\Big)\Gamma(\alpha j+\theta_2)} = \frac{\Gamma(\beta)\Gamma(j+\gamma)}{\Gamma(\gamma)\Gamma(\alpha j+\beta)},\qquad j\in\mathbb{N}_0. \end{equation*}
\begin{equation*} \mathbb{E}(K^j) = \mathbb{E}(L^j)\mathbb{E}(R^{\alpha j}) = \frac{\Gamma(\theta_2)\Gamma\Big(j+\frac{\theta_1}{\alpha}\Big)} {\Gamma\Big(\frac{\theta_1}{\alpha}\Big)\Gamma(\alpha j+\theta_2)} = \frac{\Gamma(\beta)\Gamma(j+\gamma)}{\Gamma(\gamma)\Gamma(\alpha j+\beta)},\qquad j\in\mathbb{N}_0. \end{equation*}
These are the moments of
![]() ${\rm ML}(\alpha,\beta,\gamma)$
. Since (see Section 7, Lemma 2) the distribution
${\rm ML}(\alpha,\beta,\gamma)$
. Since (see Section 7, Lemma 2) the distribution
![]() ${\rm ML}(\alpha,\beta,\gamma)$
is uniquely determined by its moments, it follows that
${\rm ML}(\alpha,\beta,\gamma)$
is uniquely determined by its moments, it follows that
![]() $K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
.
$K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
.
Let us now turn to the first passage times
![]() $T_k\,:\!=\,\inf\{n\in\mathbb{N}_0:K_n=k\}$
,
$T_k\,:\!=\,\inf\{n\in\mathbb{N}_0:K_n=k\}$
,
![]() $k\in\mathbb{N}_0$
.
$k\in\mathbb{N}_0$
.
Corollary 2. If
![]() $\alpha>0$
then, as
$\alpha>0$
then, as
![]() $k\to\infty$
,
$k\to\infty$
,
![]() $T_k/k^{1/\alpha}\to K^{-1/\alpha}$
almost surely, where
$T_k/k^{1/\alpha}\to K^{-1/\alpha}$
almost surely, where
![]() $K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
with
$K\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
with
![]() $\beta\,:\!=\,\theta_2$
and
$\beta\,:\!=\,\theta_2$
and
![]() $\gamma\,:\!=\,\theta_1/a$
.
$\gamma\,:\!=\,\theta_1/a$
.
Proof. From
![]() $K_n\to\infty$
almost surely as
$K_n\to\infty$
almost surely as
![]() $n\to\infty$
it follows that
$n\to\infty$
it follows that
![]() $T_k\to\infty$
almost surely as
$T_k\to\infty$
almost surely as
![]() $k\to\infty$
. Therefore, as
$k\to\infty$
. Therefore, as
![]() $k\to\infty$
,
$k\to\infty$
,
![]() $k/T_k^\alpha=K_{T_k}/T_k^\alpha\to K$
almost surely by Theorem 3, or, equivalently,
$k/T_k^\alpha=K_{T_k}/T_k^\alpha\to K$
almost surely by Theorem 3, or, equivalently,
![]() $T_k/k^{1/\alpha}\to K^{-1/\alpha}$
almost surely.
$T_k/k^{1/\alpha}\to K^{-1/\alpha}$
almost surely.
Remark 12. (Siegmund duality) It is readily seen that the chain
![]() $K=(K_n)_{n\in\mathbb{N}_0}$
is stochastically monotone, i.e.
$K=(K_n)_{n\in\mathbb{N}_0}$
is stochastically monotone, i.e.
![]() $\mathbb{P}(K_{n+1}\ge j \mid K_n=i)$
is increasing in
$\mathbb{P}(K_{n+1}\ge j \mid K_n=i)$
is increasing in
![]() $i\in\mathbb{N}_0$
for all
$i\in\mathbb{N}_0$
for all
![]() $n,j\in\mathbb{N}_0$
. Moreover,
$n,j\in\mathbb{N}_0$
. Moreover,
![]() $\mathbb{P}(K_{n+1}\ge j \mid K_n=i)\to 1$
as
$\mathbb{P}(K_{n+1}\ge j \mid K_n=i)\to 1$
as
![]() $i\to\infty$
for all
$i\to\infty$
for all
![]() $n,j\in\mathbb{N}_0$
. Thus, there exists a Markov chain
$n,j\in\mathbb{N}_0$
. Thus, there exists a Markov chain
![]() $X=(X_n)_{n\in\mathbb{N}_0}$
which is Siegmund dual to K, i.e.
$X=(X_n)_{n\in\mathbb{N}_0}$
which is Siegmund dual to K, i.e.
![]() $\mathbb{P}(X_{n+1}\le j \mid X_n=i)=\mathbb{P}(K_{n+1}\ge i \mid K_n=j)$
for all
$\mathbb{P}(X_{n+1}\le j \mid X_n=i)=\mathbb{P}(K_{n+1}\ge i \mid K_n=j)$
for all
![]() $n,i,j\in\mathbb{N}_0$
. For general information on Siegmund duality we refer the reader to [Reference Siegmund34]. It is easily seen that the chain X has absorbing state 0 and transition probabilities
$n,i,j\in\mathbb{N}_0$
. For general information on Siegmund duality we refer the reader to [Reference Siegmund34]. It is easily seen that the chain X has absorbing state 0 and transition probabilities
It might be interesting to study properties of the chain X. The same could be done for
![]() $N_{n,i}$
(i fixed) instead of
$N_{n,i}$
(i fixed) instead of
![]() $K_n$
.
$K_n$
.
7. The three-parameter Mittag–Leffler distribution
We provide an independent section on a natural extension of the one- and two-parameter Mittag–Leffler distributions. At least two types of Mittag–Leffler distributions are known from the literature. Type 1 distributions are heavy tailed, whereas type 2 distributions have finite moments of all orders. We are dealing here with the three-parameter Mittag–Leffler distribution of type 2. The key lemma is the following.
Lemma 2. Let
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta,\gamma>0$
with
$\beta,\gamma>0$
with
![]() $\beta\ge\alpha\gamma$
. There exists a strictly positive random variable
$\beta\ge\alpha\gamma$
. There exists a strictly positive random variable
![]() $\eta$
uniquely determined by its integer moments
$\eta$
uniquely determined by its integer moments
The random variable
![]() $\eta$
has strictly positive density
$\eta$
has strictly positive density
with respect to Lebesgue measure on
![]() $(0,\infty)$
, with the usual convention that
$(0,\infty)$
, with the usual convention that
![]() $1/\Gamma(s)\,:\!=\,0$
for
$1/\Gamma(s)\,:\!=\,0$
for
![]() $s\in-\mathbb{N}_0\,:\!=\,\{0,-1,-2,\ldots\}$
.
$s\in-\mathbb{N}_0\,:\!=\,\{0,-1,-2,\ldots\}$
.
Remark 13. It will be clarified later (see (41)) that (31) also holds with j replaced by any real number
![]() $p>-\gamma$
.
$p>-\gamma$
.
Proof. For
![]() $j\in\mathbb{N}_0$
define
$j\in\mathbb{N}_0$
define
![]() $a_j\,:\!=\,\Gamma(\beta)\Gamma(j+\gamma)/(j!\Gamma(\gamma)\Gamma(\alpha j+\beta))$
. Clearly,
$a_j\,:\!=\,\Gamma(\beta)\Gamma(j+\gamma)/(j!\Gamma(\gamma)\Gamma(\alpha j+\beta))$
. Clearly,
as
![]() $j\to\infty$
. The series
$j\to\infty$
. The series
![]() $\sum_{j=0}^\infty a_jt^j$
is therefore absolutely convergent for every
$\sum_{j=0}^\infty a_jt^j$
is therefore absolutely convergent for every
![]() $t\in\mathbb{R}$
. In particular, the function
$t\in\mathbb{R}$
. In particular, the function
![]() $\psi:[0,\infty)\to\mathbb{R}$
, defined via
$\psi:[0,\infty)\to\mathbb{R}$
, defined via
 \begin{equation} \psi(\lambda) \,:\!=\, \sum_{j=0}^\infty a_j(-\lambda)^j = \frac{\Gamma(\beta)}{\Gamma(\gamma)}\sum_{j=0}^\infty \frac{\Gamma(j+\gamma)}{\Gamma(\alpha j+\beta)} \frac{(-\lambda)^j}{j!}, \qquad\lambda\ge 0, \end{equation}
\begin{equation} \psi(\lambda) \,:\!=\, \sum_{j=0}^\infty a_j(-\lambda)^j = \frac{\Gamma(\beta)}{\Gamma(\gamma)}\sum_{j=0}^\infty \frac{\Gamma(j+\gamma)}{\Gamma(\alpha j+\beta)} \frac{(-\lambda)^j}{j!}, \qquad\lambda\ge 0, \end{equation}
is well defined. Clearly,
![]() $\psi(0)=1$
. Moreover,
$\psi(0)=1$
. Moreover,
![]() $\psi(\lambda)=\Gamma(\beta) E_{\alpha,\beta}^\gamma(-\lambda)$
, where
$\psi(\lambda)=\Gamma(\beta) E_{\alpha,\beta}^\gamma(-\lambda)$
, where
![]() $E_{\alpha,\beta}^\gamma$
denotes Prabhakar’s [Reference Prabhakar32] three-parameter Mittag–Leffler function. Equation (22) of [Reference Tomovski, Pogány and Srivastava40], which is valid for
$E_{\alpha,\beta}^\gamma$
denotes Prabhakar’s [Reference Prabhakar32] three-parameter Mittag–Leffler function. Equation (22) of [Reference Tomovski, Pogány and Srivastava40], which is valid for
![]() $t\,:\!=\,1$
,
$t\,:\!=\,1$
,
![]() $0<\alpha<1$
, and
$0<\alpha<1$
, and
![]() $\beta,\gamma>0$
satisfying
$\beta,\gamma>0$
satisfying
![]() $\beta\ge\alpha\gamma$
, implies that
$\beta\ge\alpha\gamma$
, implies that
![]() $\psi(\lambda)=\int_0^\infty \textrm{e}^{-\lambda x}g(x)\,{\rm d}x$
, where
$\psi(\lambda)=\int_0^\infty \textrm{e}^{-\lambda x}g(x)\,{\rm d}x$
, where
![]() $g(x)\,:\!=\, (\Gamma(\beta)/\Gamma(\gamma))x^{(\beta-1)/\alpha-1}\Psi(\alpha,\beta,\gamma;x^{-1/\alpha})$
,
$g(x)\,:\!=\, (\Gamma(\beta)/\Gamma(\gamma))x^{(\beta-1)/\alpha-1}\Psi(\alpha,\beta,\gamma;x^{-1/\alpha})$
,
![]() $x>0$
, and
$x>0$
, and
![]() $\Psi$
is defined as in [Reference Tomovski, Pogány and Srivastava40, Eq. (21)]. By [36, p. 122] (see also [Reference Stanković35]),
$\Psi$
is defined as in [Reference Tomovski, Pogány and Srivastava40, Eq. (21)]. By [36, p. 122] (see also [Reference Stanković35]),
![]() $\Psi$
, and hence g, is strictly positive. Thus,
$\Psi$
, and hence g, is strictly positive. Thus,
![]() $\psi$
is completely monotone and, consequently, a Laplace transform of some nonnegative random variable, say
$\psi$
is completely monotone and, consequently, a Laplace transform of some nonnegative random variable, say
![]() $\eta$
. From (33) we conclude that
$\eta$
. From (33) we conclude that
![]() $\eta$
has moments (31). The moment-generating function
$\eta$
has moments (31). The moment-generating function
![]() $t\mapsto\sum_{j=0}^\infty a_jt^j=\sum_{j=0}^\infty t^j\mathbb{E}(\eta^j)/j!$
of
$t\mapsto\sum_{j=0}^\infty a_jt^j=\sum_{j=0}^\infty t^j\mathbb{E}(\eta^j)/j!$
of
![]() $\eta$
has infinite radius of convergence. The distribution of
$\eta$
has infinite radius of convergence. The distribution of
![]() $\eta$
is hence (see [3, Theorem 30.1]) uniquely determined by its moments. Obviously, g is a density of
$\eta$
is hence (see [3, Theorem 30.1]) uniquely determined by its moments. Obviously, g is a density of
![]() $\eta$
. The series formula (32) for g(x) follows from [Reference Tomovski, Pogány and Srivastava40, Eqs. (19), (21)].
$\eta$
. The series formula (32) for g(x) follows from [Reference Tomovski, Pogány and Srivastava40, Eqs. (19), (21)].
The proof shows that the Laplace transform
![]() $\psi$
of
$\psi$
of
![]() $\eta$
is related to Prabhakar’s [Reference Prabhakar32] generalized three-parameter Mittag–Leffler function
$\eta$
is related to Prabhakar’s [Reference Prabhakar32] generalized three-parameter Mittag–Leffler function
![]() $E_{\alpha,\beta}^\gamma$
via
$E_{\alpha,\beta}^\gamma$
via
![]() $\psi(\lambda)=\Gamma(\beta)E_{\alpha,\beta}^\gamma(-\lambda)$
. The following definition is hence natural.
$\psi(\lambda)=\Gamma(\beta)E_{\alpha,\beta}^\gamma(-\lambda)$
. The following definition is hence natural.
Definition 1. (Three-parameter Mittag–Leffler distribution.) Let
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta,\gamma>0$
with
$\beta,\gamma>0$
with
![]() $\beta\ge\alpha\gamma$
. The distribution of the random variable
$\beta\ge\alpha\gamma$
. The distribution of the random variable
![]() $\eta$
from Lemma 2 is called the three-parameter Mittag–Leffler distribution (of type 2). We denote this distribution by
$\eta$
from Lemma 2 is called the three-parameter Mittag–Leffler distribution (of type 2). We denote this distribution by
![]() ${\rm ML}(\alpha,\beta,\gamma)$
.
${\rm ML}(\alpha,\beta,\gamma)$
.
Remark 14. The density (32) and the Mellin transform
of
![]() ${\rm ML}(\alpha,\beta,\gamma)$
occur (with other parameter notation and without mentioning the name of the distribution) in [Reference Flajolet, Dumas and Puyhaubert10, Eqs. (80), (81)]. The moments of this distribution also occur (with other parameter notation) in [Reference Janson19, Theorem 8.8].
${\rm ML}(\alpha,\beta,\gamma)$
occur (with other parameter notation and without mentioning the name of the distribution) in [Reference Flajolet, Dumas and Puyhaubert10, Eqs. (80), (81)]. The moments of this distribution also occur (with other parameter notation) in [Reference Janson19, Theorem 8.8].
Remark 15. The distribution
![]() ${\rm ML}(\alpha,\beta,\gamma)$
is also defined for
${\rm ML}(\alpha,\beta,\gamma)$
is also defined for
![]() $\alpha=0$
and
$\alpha=0$
and
![]() $\alpha=1$
. For
$\alpha=1$
. For
![]() $\alpha=0$
the density (32) reduces to
$\alpha=0$
the density (32) reduces to
![]() $g(x)=x^{\gamma-1}\textrm{e}^{-x}/\Gamma(\gamma)$
, showing that it is appropriate to define
$g(x)=x^{\gamma-1}\textrm{e}^{-x}/\Gamma(\gamma)$
, showing that it is appropriate to define
![]() ${\rm ML}(0,\beta,\gamma)$
to be the gamma distribution with shape parameter
${\rm ML}(0,\beta,\gamma)$
to be the gamma distribution with shape parameter
![]() $\gamma$
and scale parameter 1 (independent of
$\gamma$
and scale parameter 1 (independent of
![]() $\beta$
). For
$\beta$
). For
![]() $\alpha=1$
the moments (31) coincide with those of the beta distribution with parameters
$\alpha=1$
the moments (31) coincide with those of the beta distribution with parameters
![]() $\gamma$
and
$\gamma$
and
![]() $\beta-\gamma$
(with the usual convention to be the Dirac measure in 1 for
$\beta-\gamma$
(with the usual convention to be the Dirac measure in 1 for
![]() $\beta=\gamma$
). It is hence appropriate to define
$\beta=\gamma$
). It is hence appropriate to define
![]() ${\rm ML}(1,\beta,\gamma)$
to be the beta distribution with parameters
${\rm ML}(1,\beta,\gamma)$
to be the beta distribution with parameters
![]() $\gamma$
and
$\gamma$
and
![]() $\beta-\gamma$
.
$\beta-\gamma$
.
Remark 16. Let us clarify the relation to the classical one-parameter Mittag–Leffler distribution
![]() ${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
. For
${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
. For
![]() $\beta=\gamma=1$
the density (32) reduces to
$\beta=\gamma=1$
the density (32) reduces to
 \begin{align*} g_\alpha(x) & \,:\!=\, g_{\alpha,1,1}(x) = \sum_{n=0}^\infty \frac{(-x)^n}{n!}\frac{1}{\Gamma(1-\alpha(n+1))} = \sum_{k=1}^\infty \frac{(-x)^{k-1}}{(k-1)!}\frac{1}{\Gamma(1-\alpha k)}\\[3pt] & = \sum_{k=1}^\infty \frac{(-x)^{k-1}}{(k-1)!} \frac{1}{(-\alpha k)\Gamma(-\alpha k)} = \frac{1}{\alpha}\sum_{k=1}^\infty \frac{(-1)^kx^{k-1}}{k!} \frac{1}{\Gamma(-\alpha k)},\qquad x>0. \end{align*}
\begin{align*} g_\alpha(x) & \,:\!=\, g_{\alpha,1,1}(x) = \sum_{n=0}^\infty \frac{(-x)^n}{n!}\frac{1}{\Gamma(1-\alpha(n+1))} = \sum_{k=1}^\infty \frac{(-x)^{k-1}}{(k-1)!}\frac{1}{\Gamma(1-\alpha k)}\\[3pt] & = \sum_{k=1}^\infty \frac{(-x)^{k-1}}{(k-1)!} \frac{1}{(-\alpha k)\Gamma(-\alpha k)} = \frac{1}{\alpha}\sum_{k=1}^\infty \frac{(-1)^kx^{k-1}}{k!} \frac{1}{\Gamma(-\alpha k)},\qquad x>0. \end{align*}
Applying the formula
![]() $\pi/\Gamma(1-z)=\Gamma(z)\sin(\pi z)$
with
$\pi/\Gamma(1-z)=\Gamma(z)\sin(\pi z)$
with
![]() $z\,:\!=\,\alpha k+1$
we recover the density formula (see, for example, [Reference Pitman30, p. 11, Eq. (0.43)])
$z\,:\!=\,\alpha k+1$
we recover the density formula (see, for example, [Reference Pitman30, p. 11, Eq. (0.43)])
 \begin{align*} g_\alpha(x) & = \frac{1}{\pi\alpha}\sum_{k=1}^\infty \frac{(-1)^kx^{k-1}}{k!}\Gamma(\alpha k+1)\sin(\pi(\alpha k+1))\\[3pt] & = \frac{1}{\pi\alpha}\sum_{k=1}^\infty \frac{(-x)^{k-1}}{k!}\Gamma(\alpha k+1)\sin(\pi\alpha k), \qquad x>0. \end{align*}
\begin{align*} g_\alpha(x) & = \frac{1}{\pi\alpha}\sum_{k=1}^\infty \frac{(-1)^kx^{k-1}}{k!}\Gamma(\alpha k+1)\sin(\pi(\alpha k+1))\\[3pt] & = \frac{1}{\pi\alpha}\sum_{k=1}^\infty \frac{(-x)^{k-1}}{k!}\Gamma(\alpha k+1)\sin(\pi\alpha k), \qquad x>0. \end{align*}
In this case
![]() $\eta$
has moments
$\eta$
has moments
![]() $\mathbb{E}(\eta^j)=\Gamma(j+1)/\Gamma(\alpha j+1)$
,
$\mathbb{E}(\eta^j)=\Gamma(j+1)/\Gamma(\alpha j+1)$
,
![]() $j\in\mathbb{N}_0$
. Alternatively, the density
$j\in\mathbb{N}_0$
. Alternatively, the density
![]() $g_\alpha$
is obtained from the density
$g_\alpha$
is obtained from the density
![]() $g_{\alpha,\beta,\gamma}$
of
$g_{\alpha,\beta,\gamma}$
of
![]() ${\rm ML}(\alpha,\beta,\gamma)$
by choosing
${\rm ML}(\alpha,\beta,\gamma)$
by choosing
![]() $\gamma=\beta/\alpha$
and letting
$\gamma=\beta/\alpha$
and letting
![]() $\beta\to 0$
, since, by (32), for all
$\beta\to 0$
, since, by (32), for all
![]() $x>0$
,
$x>0$
,
as
![]() $\beta\to 0$
.
$\beta\to 0$
.
Remark 17. We collect here some properties of
![]() ${\rm ML}(\alpha)$
. It is known (see, for example, [Reference Feller9, p. 453]) that
${\rm ML}(\alpha)$
. It is known (see, for example, [Reference Feller9, p. 453]) that
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha)$
satisfies
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha)$
satisfies
![]() $\eta\stackrel{\textrm{d}}{=}\xi^{-\alpha}$
, where
$\eta\stackrel{\textrm{d}}{=}\xi^{-\alpha}$
, where
![]() $\xi$
is a positive
$\xi$
is a positive
![]() $\alpha$
-stable random variable with Laplace transform
$\alpha$
-stable random variable with Laplace transform
![]() $\lambda\mapsto \textrm{e}^{-\lambda^\alpha}$
,
$\lambda\mapsto \textrm{e}^{-\lambda^\alpha}$
,
![]() $\lambda\ge 0$
. In particular, the density
$\lambda\ge 0$
. In particular, the density
![]() $g_\alpha$
of
$g_\alpha$
of
![]() $\eta$
satisfies
$\eta$
satisfies
where
![]() $f_\alpha$
denotes the density of
$f_\alpha$
denotes the density of
![]() $\xi$
having series representation
$\xi$
having series representation
From the representation
![]() $\eta\stackrel{\textrm{d}}{=}\xi^{-\alpha}$
and [Reference Kanter21, Corollary 4.1] (see also [Reference Chambers, Mallows and Stuck5]), it follows that
$\eta\stackrel{\textrm{d}}{=}\xi^{-\alpha}$
and [Reference Kanter21, Corollary 4.1] (see also [Reference Chambers, Mallows and Stuck5]), it follows that
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha)$
satisfies
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha)$
satisfies
where U and E are independent, U is uniformly distributed on
![]() $(0,\pi)$
, E is standard exponentially distributed, and
$(0,\pi)$
, E is standard exponentially distributed, and
![]() $a(\varphi)\,:\!=\,a_\alpha(\varphi)$
is defined via
$a(\varphi)\,:\!=\,a_\alpha(\varphi)$
is defined via
 \begin{align} a_\alpha(\varphi) & \,:\!=\, \bigg(\frac{\sin(\alpha\varphi)}{\sin\varphi}\bigg)^{1/(1-\alpha)} \frac{\sin((1-\alpha)\varphi)}{\sin(\alpha\varphi)}\nonumber\\[3pt] & = \bigg( \frac{\sin(\alpha\varphi)}{\sin\varphi} \bigg)^{\alpha/(1-\alpha)} \frac{\sin((1-\alpha)\varphi)}{\sin\varphi}, \qquad 0<\varphi<\pi. \end{align}
\begin{align} a_\alpha(\varphi) & \,:\!=\, \bigg(\frac{\sin(\alpha\varphi)}{\sin\varphi}\bigg)^{1/(1-\alpha)} \frac{\sin((1-\alpha)\varphi)}{\sin(\alpha\varphi)}\nonumber\\[3pt] & = \bigg( \frac{\sin(\alpha\varphi)}{\sin\varphi} \bigg)^{\alpha/(1-\alpha)} \frac{\sin((1-\alpha)\varphi)}{\sin\varphi}, \qquad 0<\varphi<\pi. \end{align}
The functions
![]() $a_\alpha(\!\cdot\!)$
are strictly increasing on
$a_\alpha(\!\cdot\!)$
are strictly increasing on
![]() $(0,\pi)$
and have the symmetry property
$(0,\pi)$
and have the symmetry property
Note that
![]() $a_\alpha(\varphi)={\rm Re}(z^\alpha-z)$
is the real part of
$a_\alpha(\varphi)={\rm Re}(z^\alpha-z)$
is the real part of
![]() $z^\alpha-z$
for those complex numbers
$z^\alpha-z$
for those complex numbers
![]() $z=r\textrm{e}^{i\varphi}\in\mathbb{C}$
for which the imaginary part
$z=r\textrm{e}^{i\varphi}\in\mathbb{C}$
for which the imaginary part
![]() ${\rm Im}(z^\alpha-z)$
vanishes. The representation (35) yields an efficient and accurate pseudo-random number generator for
${\rm Im}(z^\alpha-z)$
vanishes. The representation (35) yields an efficient and accurate pseudo-random number generator for
![]() ${\rm ML}(\alpha)$
. From (35) a straightforward calculation shows that
${\rm ML}(\alpha)$
. From (35) a straightforward calculation shows that
![]() $\mathbb{P}(\eta\le x)=\pi^{-1}\int_0^\pi (1-\exp(-a(\varphi)x^{\frac{1}{1-\alpha}}))\,{\rm d}\varphi$
. Taking the derivative with respect to x yields
$\mathbb{P}(\eta\le x)=\pi^{-1}\int_0^\pi (1-\exp(-a(\varphi)x^{\frac{1}{1-\alpha}}))\,{\rm d}\varphi$
. Taking the derivative with respect to x yields
This integral formula is useful for computing the density
![]() $g_\alpha$
of
$g_\alpha$
of
![]() ${\rm ML}(\alpha)$
numerically. The analogous integral formula for the density
${\rm ML}(\alpha)$
numerically. The analogous integral formula for the density
![]() $f_\alpha$
of the
$f_\alpha$
of the
![]() $\alpha$
-stable random variable
$\alpha$
-stable random variable
![]() $\xi$
can be traced back to [Reference Ibragimov and Chernin15, p. 456] and [Reference Mikusiński24, Eq. (2)].
$\xi$
can be traced back to [Reference Ibragimov and Chernin15, p. 456] and [Reference Mikusiński24, Eq. (2)].
For particular parameter choices the density of
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is explicitly known. The following examples show that the half-normal distribution and the Rayleigh distribution belong to the class of three-parameter Mittag–Leffler distributions.
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is explicitly known. The following examples show that the half-normal distribution and the Rayleigh distribution belong to the class of three-parameter Mittag–Leffler distributions.
Example 2. For
![]() $(\alpha,\beta,\gamma)=(\frac{1}{2},1,1)$
the random variable
$(\alpha,\beta,\gamma)=(\frac{1}{2},1,1)$
the random variable
![]() $\eta$
is half-normal distributed with density
$\eta$
is half-normal distributed with density
![]() $x>0$
, having moments
$x>0$
, having moments
![]() $\mathbb{E}(\eta^j)=\Gamma(j+1)/\Gamma\big(\frac{j}{2}+1\big)=2^j\Gamma\big(\frac{j+1}{2}\big)/\sqrt{\pi}$
, where the last equality holds by Legendre’s duplication formula
$\mathbb{E}(\eta^j)=\Gamma(j+1)/\Gamma\big(\frac{j}{2}+1\big)=2^j\Gamma\big(\frac{j+1}{2}\big)/\sqrt{\pi}$
, where the last equality holds by Legendre’s duplication formula
![]() $\Gamma\big(\frac{x}{2}\big)\Gamma\big(\frac{x+1}{2}\big)=2^{1-x}\sqrt{\pi}\Gamma(x)$
.
$\Gamma\big(\frac{x}{2}\big)\Gamma\big(\frac{x+1}{2}\big)=2^{1-x}\sqrt{\pi}\Gamma(x)$
.
Example 3. For
![]() $(\alpha,\beta,\gamma)=\big(\frac{1}{2},\beta,2\beta\big)$
the random variable
$(\alpha,\beta,\gamma)=\big(\frac{1}{2},\beta,2\beta\big)$
the random variable
![]() $\eta$
has moments
$\eta$
has moments
![]() $\mathbb{E}(\eta^j)=\Gamma(\beta)\Gamma(j+2\beta)/\big(\Gamma(2\beta)\Gamma\big(\frac{j}{2}+\beta\big)\big)=2^j\Gamma\big(\frac{j+1}{2}+\beta\big)/\Gamma\big(\beta+\frac{1}{2}\big)$
,
$\mathbb{E}(\eta^j)=\Gamma(\beta)\Gamma(j+2\beta)/\big(\Gamma(2\beta)\Gamma\big(\frac{j}{2}+\beta\big)\big)=2^j\Gamma\big(\frac{j+1}{2}+\beta\big)/\Gamma\big(\beta+\frac{1}{2}\big)$
,
![]() $j\in\mathbb{N}_0$
, where the last equality again holds by Legendre’s duplication formula. Moreover,
$j\in\mathbb{N}_0$
, where the last equality again holds by Legendre’s duplication formula. Moreover,
![]() $\eta$
has density
$\eta$
has density
For
![]() $\beta=\frac{1}{2}$
it follows that
$\beta=\frac{1}{2}$
it follows that
![]() $\eta$
is Rayleigh distributed with density
$\eta$
is Rayleigh distributed with density
![]() $x\mapsto (x/2)\textrm{e}^{-x^2/4}$
,
$x\mapsto (x/2)\textrm{e}^{-x^2/4}$
,
![]() $x>0$
.
$x>0$
.
Example 4. A technical but straightforward calculation shows that
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}\big(\frac{1}{2},2,2\big)$
has density
$\eta\stackrel{\textrm{d}}{=}{\rm ML}\big(\frac{1}{2},2,2\big)$
has density
![]() $x\mapsto x\big(1-\pi^{-1/2}\int_0^x \textrm{e}^{-u^2/4}\,{\rm d}u\big)=x(1-\mathbb{P}(|X|\le x))$
,
$x\mapsto x\big(1-\pi^{-1/2}\int_0^x \textrm{e}^{-u^2/4}\,{\rm d}u\big)=x(1-\mathbb{P}(|X|\le x))$
,
![]() $x>0$
, where
$x>0$
, where
![]() $X\stackrel{\textrm{d}}{=}N(0,2)$
is normal distributed with variance 2.
$X\stackrel{\textrm{d}}{=}N(0,2)$
is normal distributed with variance 2.
For
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta>0$
the distribution
$\beta>0$
the distribution
![]() ${\rm ML}(\alpha,\beta)\,:\!=\,{\rm ML}(\alpha,\beta,\beta/\alpha)$
is usually called the two-parameter Mittag–Leffler distribution. The following corollary provides a characterization of
${\rm ML}(\alpha,\beta)\,:\!=\,{\rm ML}(\alpha,\beta,\beta/\alpha)$
is usually called the two-parameter Mittag–Leffler distribution. The following corollary provides a characterization of
![]() ${\rm ML}(\alpha,\beta,\gamma)$
in terms of a beta distribution and a two-parameter Mittag–Leffler distribution.
${\rm ML}(\alpha,\beta,\gamma)$
in terms of a beta distribution and a two-parameter Mittag–Leffler distribution.
Corollary 3. Let
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta,\gamma>0$
with
$\beta,\gamma>0$
with
![]() $\beta\ge\alpha\gamma$
. If
$\beta\ge\alpha\gamma$
. If
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is three-parameter Mittag–Leffler distributed with parameters
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
is three-parameter Mittag–Leffler distributed with parameters
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
, and
$\beta$
, and
![]() $\gamma$
then the distributional factorization
$\gamma$
then the distributional factorization
holds, where B and L are independent,
![]() $B\stackrel{\textrm{d}}{=}{\rm ML}(1,\beta/\alpha,\gamma)$
is beta distributed with parameters
$B\stackrel{\textrm{d}}{=}{\rm ML}(1,\beta/\alpha,\gamma)$
is beta distributed with parameters
![]() $\gamma$
and
$\gamma$
and
![]() $\beta/\alpha-\gamma$
, and
$\beta/\alpha-\gamma$
, and
![]() $L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
is two-parameter Mittag–Leffler distributed.
$L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
is two-parameter Mittag–Leffler distributed.
Proof. Clearly, B has moments
![]() $\mathbb{E}(B^j)=\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(j+\gamma)/(\Gamma(\gamma)\Gamma\big(j+\frac{\beta}{\alpha}\big))$
,
$\mathbb{E}(B^j)=\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(j+\gamma)/(\Gamma(\gamma)\Gamma\big(j+\frac{\beta}{\alpha}\big))$
,
![]() $j\in\mathbb{N}_0$
. By (31), L has moments
$j\in\mathbb{N}_0$
. By (31), L has moments
![]() $\mathbb{E}(L^j)=\Gamma(\beta)\Gamma\big(j+\frac{\beta}{\alpha}\big)/(\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha j+\beta))$
,
$\mathbb{E}(L^j)=\Gamma(\beta)\Gamma\big(j+\frac{\beta}{\alpha}\big)/(\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha j+\beta))$
,
![]() $j\in\mathbb{N}_0$
. Since B and L are independent, it follows that BL has moments
$j\in\mathbb{N}_0$
. Since B and L are independent, it follows that BL has moments
 \begin{align*} \mathbb{E}((BL)^j) = \mathbb{E}(B^j)\,\mathbb{E}(L^j) & = \frac{\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(j+\gamma)} {\Gamma(\gamma)\Gamma\big(j+\frac{\beta}{\alpha}\big)} \frac{\Gamma(\beta)\Gamma\big(j+\frac{\beta}{\alpha}\big)} {\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha j+\beta)}\\[3pt] & = \frac{\Gamma(\beta)\Gamma(j+\gamma)} {\Gamma(\gamma)\Gamma(\alpha j+\beta)},\qquad j\in\mathbb{N}_0. \end{align*}
\begin{align*} \mathbb{E}((BL)^j) = \mathbb{E}(B^j)\,\mathbb{E}(L^j) & = \frac{\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(j+\gamma)} {\Gamma(\gamma)\Gamma\big(j+\frac{\beta}{\alpha}\big)} \frac{\Gamma(\beta)\Gamma\big(j+\frac{\beta}{\alpha}\big)} {\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha j+\beta)}\\[3pt] & = \frac{\Gamma(\beta)\Gamma(j+\gamma)} {\Gamma(\gamma)\Gamma(\alpha j+\beta)},\qquad j\in\mathbb{N}_0. \end{align*}
These moments coincide with those (see (31)) of
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
. Thus,
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
. Thus,
![]() $\eta\stackrel{\textrm{d}}{=}BL$
.
$\eta\stackrel{\textrm{d}}{=}BL$
.
Remark 18. The factorization (39) allows us to define the three-parameter Mittag–Leffler distribution from the two-parameter Mittag–Leffler distribution. Equation (39) also yields a random number generator for the three-parameter Mittag–Leffler distribution. Accurate and efficient sampling methods for the two-parameter Mittag–Leffler distribution are provided in Section 8.
Remark 19. The random variable
![]() $L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
in Corollary 3 has density (see, for example, [Reference Pitman30, p. 68, Eq. (3.27)])
$L\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
in Corollary 3 has density (see, for example, [Reference Pitman30, p. 68, Eq. (3.27)])
where
![]() $g_\alpha$
is the density of the one-parameter Mittag–Leffler distribution
$g_\alpha$
is the density of the one-parameter Mittag–Leffler distribution
![]() ${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
having moments
${\rm ML}(\alpha)\,:\!=\,{\rm ML}(\alpha,1,1)$
having moments
![]() $\Gamma(p+1)/\Gamma(\alpha p+1)$
,
$\Gamma(p+1)/\Gamma(\alpha p+1)$
,
![]() $p>-1$
. In other words,
$p>-1$
. In other words,
![]() $g_{\alpha,\beta}$
is the
$g_{\alpha,\beta}$
is the
![]() $(\beta/\alpha)$
-size-biased density of
$(\beta/\alpha)$
-size-biased density of
![]() $g_\alpha$
. From (40) it follows that
$g_\alpha$
. From (40) it follows that
![]() $L^{-1/\alpha}$
has density
$L^{-1/\alpha}$
has density
where
![]() $f_\alpha$
is the density (34) of the positive
$f_\alpha$
is the density (34) of the positive
![]() $\alpha$
-stable random variable
$\alpha$
-stable random variable
![]() $\xi$
with Laplace transform
$\xi$
with Laplace transform
![]() $\lambda\mapsto \textrm{e}^{-\lambda^\alpha}$
,
$\lambda\mapsto \textrm{e}^{-\lambda^\alpha}$
,
![]() $\lambda\ge 0$
. Thus,
$\lambda\ge 0$
. Thus,
![]() $L^{-1/\alpha}$
is the
$L^{-1/\alpha}$
is the
![]() $(-\beta)$
-size-biased random variable of
$(-\beta)$
-size-biased random variable of
![]() $\xi$
.
$\xi$
.
Remark 20. The moment formula
 \begin{align*} \mathbb{E}(L^p) & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \int_0^\infty x^{p+\frac{\beta}{\alpha}} g_\alpha(x)\,{\rm d}x\\[3pt] & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \frac{\Gamma\big(p+\frac{\beta}{\alpha}+1\big)}{\Gamma\big(\alpha\big(p+\frac{\beta}{\alpha}\big)+1\big)} = \frac{\Gamma(\beta)\Gamma\big(p+\frac{\beta}{\alpha}\big)}{\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha p+\beta)} \end{align*}
\begin{align*} \mathbb{E}(L^p) & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \int_0^\infty x^{p+\frac{\beta}{\alpha}} g_\alpha(x)\,{\rm d}x\\[3pt] & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \frac{\Gamma\big(p+\frac{\beta}{\alpha}+1\big)}{\Gamma\big(\alpha\big(p+\frac{\beta}{\alpha}\big)+1\big)} = \frac{\Gamma(\beta)\Gamma\big(p+\frac{\beta}{\alpha}\big)}{\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma(\alpha p+\beta)} \end{align*}
holds for all
![]() $p>-\frac{\beta}{\alpha}$
. The calculations in the proof of Corollary 3 thus also hold with j replaced by any real parameter
$p>-\frac{\beta}{\alpha}$
. The calculations in the proof of Corollary 3 thus also hold with j replaced by any real parameter
![]() $p>-\gamma$
. In particular, if
$p>-\gamma$
. In particular, if
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
, then
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
, then
For
![]() $p>-\gamma$
the p-size-biased random variable
$p>-\gamma$
the p-size-biased random variable
![]() $\eta^*$
of
$\eta^*$
of
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
satisfies
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
satisfies
![]() $\eta^*\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta+\alpha p,\gamma+p)$
, since it is seen from (41) and (32) that the density
$\eta^*\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta+\alpha p,\gamma+p)$
, since it is seen from (41) and (32) that the density
![]() $x\mapsto x^pg_{\alpha,\beta,\gamma}(x)/\mathbb{E}(\eta^p)$
,
$x\mapsto x^pg_{\alpha,\beta,\gamma}(x)/\mathbb{E}(\eta^p)$
,
![]() $x>0$
, of
$x>0$
, of
![]() $\eta^*$
coincides with
$\eta^*$
coincides with
![]() $g_{\alpha,\beta+\alpha p,\gamma+p}$
. In particular, for every
$g_{\alpha,\beta+\alpha p,\gamma+p}$
. In particular, for every
![]() $p>0$
the family of three-parameter Mittag–Leffler distributions is closed under p-size-biasing.
$p>0$
the family of three-parameter Mittag–Leffler distributions is closed under p-size-biasing.
Remark 21. Corollary 3 is easily generalized as follows. Let
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta,\gamma,\gamma'>0$
with
$\beta,\gamma,\gamma'>0$
with
![]() $\gamma\le\gamma'$
and
$\gamma\le\gamma'$
and
![]() $\beta\ge\alpha\gamma'$
. If
$\beta\ge\alpha\gamma'$
. If
![]() $\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
and
$\eta\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma)$
and
![]() $\eta'\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma')$
then the distributional factorization
$\eta'\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta,\gamma')$
then the distributional factorization
![]() $\eta\stackrel{\textrm{d}}{=}B\eta'$
holds, where
$\eta\stackrel{\textrm{d}}{=}B\eta'$
holds, where
![]() $B\stackrel{\textrm{d}}{=}\beta(\gamma,\gamma'-\gamma)$
is independent of
$B\stackrel{\textrm{d}}{=}\beta(\gamma,\gamma'-\gamma)$
is independent of
![]() $\eta'$
. We have not been able to find a natural explanation of this factorization in terms of an urn model or some combinatorial construction, and leave this question as an open problem for future research.
$\eta'$
. We have not been able to find a natural explanation of this factorization in terms of an urn model or some combinatorial construction, and leave this question as an open problem for future research.
8. Sampling from the two- and three-parameter Mittag–Leffler distribution
By Corollary 3 and Remark 18 thereafter it suffices to focus on the two-parameter Mittag–Leffler distribution
![]() ${\rm ML}(\alpha,\beta)$
. To the best of the author’s knowledge random number generators for
${\rm ML}(\alpha,\beta)$
. To the best of the author’s knowledge random number generators for
![]() ${\rm ML}(\alpha,\beta)$
are not known from the literature. The key to developing random number generators is the following Proposition 4, which provides a useful distributional representation for
${\rm ML}(\alpha,\beta)$
are not known from the literature. The key to developing random number generators is the following Proposition 4, which provides a useful distributional representation for
![]() ${\rm ML}(\alpha,\beta)$
.
${\rm ML}(\alpha,\beta)$
.
Proposition 4. Let
![]() $L=L_{\alpha,\beta}\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
be two-parameter Mittag–Leffler distributed with parameters
$L=L_{\alpha,\beta}\stackrel{\textrm{d}}{=}{\rm ML}(\alpha,\beta)$
be two-parameter Mittag–Leffler distributed with parameters
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta>0$
. Then the distributional representation
$\beta>0$
. Then the distributional representation
holds, where G is gamma distributed with shape parameter
![]() $\frac{\beta}{\alpha}(1-\alpha)+1$
and scale parameter 1 having density
$\frac{\beta}{\alpha}(1-\alpha)+1$
and scale parameter 1 having density
![]() $f_G(x)\,:\!=\,x^{\frac{\beta}{\alpha}(1-\alpha)}\textrm{e}^{-x} /\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)$
,
$f_G(x)\,:\!=\,x^{\frac{\beta}{\alpha}(1-\alpha)}\textrm{e}^{-x} /\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)$
,
![]() $x>0$
, the function
$x>0$
, the function
![]() $a(\!\cdot\!)=a_\alpha(\!\cdot\!)$
is defined via (36), and the
$a(\!\cdot\!)=a_\alpha(\!\cdot\!)$
is defined via (36), and the
![]() $(0,\pi)$
-valued random variable V is independent of G and has density
$(0,\pi)$
-valued random variable V is independent of G and has density
with normalizing constant
 \begin{equation*} c_{\alpha,\beta} \,:\!=\, \frac{\Gamma(\beta+1)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\pi\Gamma\big(\frac{\beta}{\alpha}+1\big)}. \end{equation*}
\begin{equation*} c_{\alpha,\beta} \,:\!=\, \frac{\Gamma(\beta+1)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\pi\Gamma\big(\frac{\beta}{\alpha}+1\big)}. \end{equation*}
Proof. For
![]() $0<\varphi<\pi$
define
$0<\varphi<\pi$
define
![]() $W_\varphi\,:\!=\,(G/a(\varphi))^{1-\alpha}$
. Taking the derivative with respect to x in the equation
$W_\varphi\,:\!=\,(G/a(\varphi))^{1-\alpha}$
. Taking the derivative with respect to x in the equation
![]() $\mathbb{P}(W_\varphi\le x)=\mathbb{P}\big(G\le a(\varphi)x^{\frac{1}{1-\alpha}}\big)$
shows that
$\mathbb{P}(W_\varphi\le x)=\mathbb{P}\big(G\le a(\varphi)x^{\frac{1}{1-\alpha}}\big)$
shows that
![]() $W_\varphi$
has density
$W_\varphi$
has density
![]() $w_\varphi$
given by
$w_\varphi$
given by
 \begin{align*} w_\varphi(x) & \,:\!=\, \frac{a(\varphi)}{1-\alpha}x^{\frac{1}{1-\alpha}-1} f_G\big(a(\varphi)x^{\frac{1}{1-\alpha}}\big)\\[3pt] & = \frac{(a(\varphi))^{\frac{\beta}{\alpha}(1-\alpha)+1}} {(1-\alpha)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} x^{\frac{\beta}{\alpha}+\frac{1}{1-\alpha}-1} \exp\big(-a(\varphi)x^{\frac{1}{1-\alpha}}\big),\qquad x>0. \end{align*}
\begin{align*} w_\varphi(x) & \,:\!=\, \frac{a(\varphi)}{1-\alpha}x^{\frac{1}{1-\alpha}-1} f_G\big(a(\varphi)x^{\frac{1}{1-\alpha}}\big)\\[3pt] & = \frac{(a(\varphi))^{\frac{\beta}{\alpha}(1-\alpha)+1}} {(1-\alpha)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} x^{\frac{\beta}{\alpha}+\frac{1}{1-\alpha}-1} \exp\big(-a(\varphi)x^{\frac{1}{1-\alpha}}\big),\qquad x>0. \end{align*}
Note that
![]() $w_\varphi$
is the density of a
$w_\varphi$
is the density of a
![]() $(\beta/\alpha)$
-size-biased Weibull distribution with distribution function
$(\beta/\alpha)$
-size-biased Weibull distribution with distribution function
![]() $x\mapsto 1-\exp\big(-a(\varphi)x^{\frac{1}{1-\alpha}}\big)$
,
$x\mapsto 1-\exp\big(-a(\varphi)x^{\frac{1}{1-\alpha}}\big)$
,
![]() $x>0$
. Now, by (40) and (38), L has density
$x>0$
. Now, by (40) and (38), L has density
 \begin{align} g_{\alpha,\beta}(x) & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} x^{\frac{\beta}{\alpha}}g_\alpha(x)\nonumber\\[3pt]
& = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \frac{x^{\frac{\beta}{\alpha}+\frac{1}{1-\alpha}-1}}{\pi(1-\alpha)} \int_0^\pi a(\varphi) \exp\Big(-a(\varphi)x^{\frac{1}{1-\alpha}}\Big) \,{\rm d}\varphi\nonumber\\[3pt]
& = \int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi) \,{\rm d}\varphi, \qquad x>0, \end{align}
\begin{align} g_{\alpha,\beta}(x) & = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} x^{\frac{\beta}{\alpha}}g_\alpha(x)\nonumber\\[3pt]
& = \frac{\Gamma(\beta+1)}{\Gamma\big(\frac{\beta}{\alpha}+1\big)} \frac{x^{\frac{\beta}{\alpha}+\frac{1}{1-\alpha}-1}}{\pi(1-\alpha)} \int_0^\pi a(\varphi) \exp\Big(-a(\varphi)x^{\frac{1}{1-\alpha}}\Big) \,{\rm d}\varphi\nonumber\\[3pt]
& = \int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi) \,{\rm d}\varphi, \qquad x>0, \end{align}
with
![]() $w_\varphi(x)$
as defined above and
$w_\varphi(x)$
as defined above and
![]() $h_{\alpha,\beta}(\varphi)$
defined via (43). From
$h_{\alpha,\beta}(\varphi)$
defined via (43). From
![]() $\int_0^\infty w_\varphi(x)\,{\rm d}x=1$
we conclude, by Fubini’s theorem, that
$\int_0^\infty w_\varphi(x)\,{\rm d}x=1$
we conclude, by Fubini’s theorem, that
![]() $\int_0^\pi h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi =\int_0^\infty \int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi) \,{\rm d}\varphi\,{\rm d}x=\int_0^\infty g_{\alpha,\beta}(x)\,{\rm d}x=1$
, so
$\int_0^\pi h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi =\int_0^\infty \int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi) \,{\rm d}\varphi\,{\rm d}x=\int_0^\infty g_{\alpha,\beta}(x)\,{\rm d}x=1$
, so
![]() $h_{\alpha,\beta}$
is a density of some
$h_{\alpha,\beta}$
is a density of some
![]() $(0,\pi)$
-valued random variable V, which can be chosen such that it is independent of G. Therefore,
$(0,\pi)$
-valued random variable V, which can be chosen such that it is independent of G. Therefore,
![]() $(G/a(V))^{1-\alpha}$
has distribution function
$(G/a(V))^{1-\alpha}$
has distribution function
![]() $x\mapsto\mathbb{P}((G/a(V))^{1-\alpha}\le x) =\int_0^\pi \mathbb{P}((G/a(\varphi))^{1-\alpha}\le x) \,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi =\int_0^\pi \mathbb{P}(W_\varphi\le x) \,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi$
and hence density
$x\mapsto\mathbb{P}((G/a(V))^{1-\alpha}\le x) =\int_0^\pi \mathbb{P}((G/a(\varphi))^{1-\alpha}\le x) \,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi =\int_0^\pi \mathbb{P}(W_\varphi\le x) \,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi$
and hence density
![]() $x\mapsto\int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi$
,
$x\mapsto\int_0^\pi w_\varphi(x)\,h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi$
,
![]() $x>0$
, which coincides with the density (44) of L.
$x>0$
, which coincides with the density (44) of L.
Remark 22. Only particular functionals of V are explicitly known. For example, from (42) it follows that the reciprocal of
![]() $a_\alpha(V)$
has moments
$a_\alpha(V)$
has moments
 \begin{align*} \mathbb{E}((a_\alpha(V))^{-q}) & = \frac{\mathbb{E}\big(L^{\frac{q}{1-\alpha}}\big)}{\mathbb{E}(G^q)}\\[3pt] & = \frac{\Gamma(\beta)\Gamma\big(\frac{q}{1-\alpha}+\frac{\beta}{\alpha}\big)} {\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma\big(\alpha\frac{q}{1-\alpha}+\beta\big)} \frac{\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)}{\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+q+1\big)}, \qquad q>-\frac{\beta}{\alpha}(1-\alpha). \end{align*}
\begin{align*} \mathbb{E}((a_\alpha(V))^{-q}) & = \frac{\mathbb{E}\big(L^{\frac{q}{1-\alpha}}\big)}{\mathbb{E}(G^q)}\\[3pt] & = \frac{\Gamma(\beta)\Gamma\big(\frac{q}{1-\alpha}+\frac{\beta}{\alpha}\big)} {\Gamma\big(\frac{\beta}{\alpha}\big)\Gamma\big(\alpha\frac{q}{1-\alpha}+\beta\big)} \frac{\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)}{\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+q+1\big)}, \qquad q>-\frac{\beta}{\alpha}(1-\alpha). \end{align*}
For particular parameter values the density (43) of
![]() $V=V_{\alpha,\beta}$
further simplifies. For example, for
$V=V_{\alpha,\beta}$
further simplifies. For example, for
![]() $\alpha=\frac{1}{2}$
, (36) reduces to
$\alpha=\frac{1}{2}$
, (36) reduces to
![]() $a_{\frac{1}{2}}(\varphi)=\big(\sin\big(\frac{\varphi}{2}\big)/\sin(\varphi)\big)^2 =1/\big(2\cos\big(\frac{\varphi}{2}\big)\big)^2$
and Legendre’s duplication formula
$a_{\frac{1}{2}}(\varphi)=\big(\sin\big(\frac{\varphi}{2}\big)/\sin(\varphi)\big)^2 =1/\big(2\cos\big(\frac{\varphi}{2}\big)\big)^2$
and Legendre’s duplication formula
![]() $\Gamma\big(\frac{x}{2}\big)\Gamma\big(\frac{x+1}{2}\big)=2^{1-x}\sqrt{\pi}\Gamma(x)$
, applied with
$\Gamma\big(\frac{x}{2}\big)\Gamma\big(\frac{x+1}{2}\big)=2^{1-x}\sqrt{\pi}\Gamma(x)$
, applied with
![]() $x\,:\!=\,2\beta+1$
, leads to
$x\,:\!=\,2\beta+1$
, leads to
It follows that
where
![]() $B_\beta$
is beta distributed with parameters
$B_\beta$
is beta distributed with parameters
![]() $\beta+\frac{1}{2}$
and
$\beta+\frac{1}{2}$
and
![]() $\frac{1}{2}$
, and
$\frac{1}{2}$
, and
![]() $G_\beta$
is independent of
$G_\beta$
is independent of
![]() $B_\beta$
and gamma distributed with shape parameter
$B_\beta$
and gamma distributed with shape parameter
![]() $\beta+1$
and scale parameter 1 having density
$\beta+1$
and scale parameter 1 having density
![]() $x\mapsto x^\beta \textrm{e}^{-x}/\Gamma(\beta+1)$
,
$x\mapsto x^\beta \textrm{e}^{-x}/\Gamma(\beta+1)$
,
![]() $x>0$
. The last formula in (45) yields an efficient random number generator for
$x>0$
. The last formula in (45) yields an efficient random number generator for
![]() ${\rm ML}(\frac{1}{2},\beta)$
. Proposition 4 also holds for
${\rm ML}(\frac{1}{2},\beta)$
. Proposition 4 also holds for
![]() $\beta=0$
. In this case V is uniformly distributed on
$\beta=0$
. In this case V is uniformly distributed on
![]() $(0,\pi)$
, G is standard exponentially distributed, and (42) reduces to (35). From the symmetry relation (37) it follows that
$(0,\pi)$
, G is standard exponentially distributed, and (42) reduces to (35). From the symmetry relation (37) it follows that
![]() $h_{\alpha,\beta}=h_{\tilde\alpha,\tilde\beta}$
with
$h_{\alpha,\beta}=h_{\tilde\alpha,\tilde\beta}$
with
![]() $\tilde\alpha\,:\!=\,1-\alpha$
and
$\tilde\alpha\,:\!=\,1-\alpha$
and
![]() $\tilde\beta\,:\!=\,\beta(1-\alpha)/\alpha$
.
$\tilde\beta\,:\!=\,\beta(1-\alpha)/\alpha$
.
Remark 23. (Random number generator) The representation (42) yields a sampling method for
![]() ${\rm ML}(\alpha,\beta)$
. Generators for the gamma distribution are well known (see, for example, [Reference Devroye6, Section IX 3.2]). Sampling from V can be implemented by the following rejection technique. Since
${\rm ML}(\alpha,\beta)$
. Generators for the gamma distribution are well known (see, for example, [Reference Devroye6, Section IX 3.2]). Sampling from V can be implemented by the following rejection technique. Since
![]() $a(\!\cdot\!)$
is strictly increasing on
$a(\!\cdot\!)$
is strictly increasing on
![]() $(0,\pi)$
it follows that the density (43) of V is strictly decreasing and hence bounded by
$(0,\pi)$
it follows that the density (43) of V is strictly decreasing and hence bounded by
![]() $h_{\alpha,\beta}(0+)=c_{\alpha,\beta} (a(0+))^{-\frac{\beta}{\alpha}(1-\alpha)}<\infty$
. The constant
$h_{\alpha,\beta}(0+)=c_{\alpha,\beta} (a(0+))^{-\frac{\beta}{\alpha}(1-\alpha)}<\infty$
. The constant
![]() $a(0+)=(1-\alpha)\alpha^{\alpha/(1-\alpha)}$
is known. A simple rejection method (see [Reference Devroye6, p. 42]) to sample from V therefore works via Algorithm 1.
$a(0+)=(1-\alpha)\alpha^{\alpha/(1-\alpha)}$
is known. A simple rejection method (see [Reference Devroye6, p. 42]) to sample from V therefore works via Algorithm 1.

The normalizing constant
![]() $c_{\alpha,\beta}$
is not involved in this algorithm. Note that the inequality
$c_{\alpha,\beta}$
is not involved in this algorithm. Note that the inequality
![]() $u\le (a(0+)/a(v))^{\beta(1-\alpha)/\alpha}$
is equivalent to the standard acceptance condition
$u\le (a(0+)/a(v))^{\beta(1-\alpha)/\alpha}$
is equivalent to the standard acceptance condition
![]() $uh_{\alpha,\beta}(0+)\le h_{\alpha,\beta}(v)$
. The efficiency of Algorithm 1 is discussed in Remark 24. A more efficient rejection method (Algorithm 2) is provided afterwards.
$uh_{\alpha,\beta}(0+)\le h_{\alpha,\beta}(v)$
. The efficiency of Algorithm 1 is discussed in Remark 24. A more efficient rejection method (Algorithm 2) is provided afterwards.
Our next result concerns the asymptotic behavior of
![]() $V=V_{\alpha,\beta}$
as
$V=V_{\alpha,\beta}$
as
![]() $\alpha\to 0$
and as
$\alpha\to 0$
and as
![]() $\beta\to\infty$
respectively. It is remarkable that
$\beta\to\infty$
respectively. It is remarkable that
![]() $V_{\alpha,\beta}$
has a nondegenerate limit as
$V_{\alpha,\beta}$
has a nondegenerate limit as
![]() $\alpha\to 0$
.
$\alpha\to 0$
.
Proposition 5.
-
(a) As
 $\alpha\to 0$
the density
$\alpha\to 0$
the density
 $h_{\alpha,\beta}$
of
$h_{\alpha,\beta}$
of
 $V_{\alpha,\beta}$
converges uniformly on
$V_{\alpha,\beta}$
converges uniformly on
 $(0,\pi)$
to
$(0,\pi)$
to
 $h_{0,\beta}$
defined via
(46)
$h_{0,\beta}$
defined via
(46) \begin{equation} h_{0,\beta}(\varphi) \,:\!=\, \frac{\Gamma(\beta+1)}{\pi} \bigg(\frac{\sin\varphi}{\beta\varphi}\bigg)^\beta \exp(\beta\varphi\cot\varphi), \qquad 0<\varphi<\pi. \end{equation}
\begin{equation} h_{0,\beta}(\varphi) \,:\!=\, \frac{\Gamma(\beta+1)}{\pi} \bigg(\frac{\sin\varphi}{\beta\varphi}\bigg)^\beta \exp(\beta\varphi\cot\varphi), \qquad 0<\varphi<\pi. \end{equation}
In particular,
 $V_{\alpha,\beta}\to V_{0,\beta}$
in distribution as
$V_{\alpha,\beta}\to V_{0,\beta}$
in distribution as
 $\alpha\to 0$
, where
$\alpha\to 0$
, where
 $V_{0,\beta}$
has density (46).
$V_{0,\beta}$
has density (46). -
(b) As
 $\beta\to\infty$
the map
$\beta\to\infty$
the map
 $x\mapsto\beta^{-1/2} h_{\alpha,\beta}(\beta^{-1/2}x)$
converges uniformly on
$x\mapsto\beta^{-1/2} h_{\alpha,\beta}(\beta^{-1/2}x)$
converges uniformly on
 $(0,\infty)$
to
$(0,\infty)$
to
 $h_\alpha$
defined via
(47)In particular,
$h_\alpha$
defined via
(47)In particular, \begin{equation} h_\alpha(x) \,:\!=\, \sqrt{\frac{2(1-\alpha)}{\pi}} \exp\bigg(-\frac{1-\alpha}{2}x^2\bigg),\qquad x>0. \end{equation}
\begin{equation} h_\alpha(x) \,:\!=\, \sqrt{\frac{2(1-\alpha)}{\pi}} \exp\bigg(-\frac{1-\alpha}{2}x^2\bigg),\qquad x>0. \end{equation}
 $\sqrt{\beta}V_{\alpha,\beta}\to V_\alpha$
in distribution as
$\sqrt{\beta}V_{\alpha,\beta}\to V_\alpha$
in distribution as
 $\beta\to\infty$
, where
$\beta\to\infty$
, where
 $V_\alpha$
is half-normal distributed with density (47).
$V_\alpha$
is half-normal distributed with density (47).
Proof.
-
(a) An application of Stirling’s formula
 $\Gamma(x+1)\sim (x/\textrm{e})^x\sqrt{2\pi x}$
,
$\Gamma(x+1)\sim (x/\textrm{e})^x\sqrt{2\pi x}$
,
 $x\to\infty$
, shows that the normalizing constants
$x\to\infty$
, shows that the normalizing constants
 $c_{\alpha,\beta}$
satisfy
$c_{\alpha,\beta}$
satisfy
 $c_{\alpha,\beta}\sim\pi^{-1}\Gamma(\beta+1)(\alpha/\beta)^\beta$
as
$c_{\alpha,\beta}\sim\pi^{-1}\Gamma(\beta+1)(\alpha/\beta)^\beta$
as
 $\alpha\to 0$
. Fix
$\alpha\to 0$
. Fix
 $0<\varphi<\pi$
. From
as
$0<\varphi<\pi$
. From
as \begin{align*} \bigg(\frac{\sin((1-\alpha)\varphi)}{\sin\varphi}\bigg)^{\frac{1}{\alpha}} & = ( \cos(\alpha\varphi)-\sin(\alpha\varphi)\cot\varphi )^{\frac{1}{\alpha}}\\[3pt] & = ( 1 - \alpha\varphi\cot\varphi + O(\alpha^2) )^{\frac{1}{\alpha}} \to \exp(-\varphi\cot\varphi) \end{align*}
\begin{align*} \bigg(\frac{\sin((1-\alpha)\varphi)}{\sin\varphi}\bigg)^{\frac{1}{\alpha}} & = ( \cos(\alpha\varphi)-\sin(\alpha\varphi)\cot\varphi )^{\frac{1}{\alpha}}\\[3pt] & = ( 1 - \alpha\varphi\cot\varphi + O(\alpha^2) )^{\frac{1}{\alpha}} \to \exp(-\varphi\cot\varphi) \end{align*}
 $\alpha\to 0$
we conclude that
as
$\alpha\to 0$
we conclude that
as \begin{equation*} (a_\alpha(\varphi))^{\frac{1}{\alpha}} = \bigg(\frac{\sin(\alpha\varphi)}{\sin\varphi}\bigg)^{1-\alpha} \bigg(\frac{\sin((1-\alpha)\varphi)}{\sin\varphi}\bigg)^{\frac{1}{\alpha}} \sim \frac{\alpha\varphi}{\sin\varphi}\exp(-\varphi\cot\varphi) \end{equation*}
\begin{equation*} (a_\alpha(\varphi))^{\frac{1}{\alpha}} = \bigg(\frac{\sin(\alpha\varphi)}{\sin\varphi}\bigg)^{1-\alpha} \bigg(\frac{\sin((1-\alpha)\varphi)}{\sin\varphi}\bigg)^{\frac{1}{\alpha}} \sim \frac{\alpha\varphi}{\sin\varphi}\exp(-\varphi\cot\varphi) \end{equation*}
 $\alpha\to 0$
. Putting these formulas together shows that
This pointwise convergence holds uniformly on
$\alpha\to 0$
. Putting these formulas together shows that
This pointwise convergence holds uniformly on \begin{align*} h_{\alpha,\beta}(\varphi) & = c_{\alpha,\beta} \bigg(\frac{1}{(a_\alpha(\varphi))^{\frac{1}{\alpha}}}\bigg)^{(1-\alpha)\beta}\\[3pt] & \to \frac{\Gamma(\beta+1)}{\pi} \bigg(\frac{\sin\varphi}{\beta\varphi}\bigg)^\beta \exp(\beta\varphi\cot\varphi) = h_{0,\beta}(\varphi),\qquad \alpha\to 0. \end{align*}
\begin{align*} h_{\alpha,\beta}(\varphi) & = c_{\alpha,\beta} \bigg(\frac{1}{(a_\alpha(\varphi))^{\frac{1}{\alpha}}}\bigg)^{(1-\alpha)\beta}\\[3pt] & \to \frac{\Gamma(\beta+1)}{\pi} \bigg(\frac{\sin\varphi}{\beta\varphi}\bigg)^\beta \exp(\beta\varphi\cot\varphi) = h_{0,\beta}(\varphi),\qquad \alpha\to 0. \end{align*}
 $(0,\pi)$
, since all involved functions
$(0,\pi)$
, since all involved functions
 $h_{\alpha,\beta}$
and
$h_{\alpha,\beta}$
and
 $h_{0,\beta}$
can be continuously extended to
$h_{0,\beta}$
can be continuously extended to
 $[0,\pi]$
via
$[0,\pi]$
via
 $h_{\alpha,\beta}(\pi)\,:\!=\,0$
,
$h_{\alpha,\beta}(\pi)\,:\!=\,0$
,
 $h_{0,\beta}(\pi)\,:\!=\,0$
,
$h_{0,\beta}(\pi)\,:\!=\,0$
,
 $h_{\alpha,\beta}(0)\,:\!=\,c_{\alpha,\beta}(a_\alpha(0+))^{\beta(1-\alpha)/\alpha}$
and
$h_{\alpha,\beta}(0)\,:\!=\,c_{\alpha,\beta}(a_\alpha(0+))^{\beta(1-\alpha)/\alpha}$
and
 $h_{0,\beta}(0)\,:\!=\,\pi^{-1}\Gamma(\beta+1)(\textrm{e}/\beta)^\beta$
and all these functions are decreasing, continuous, and bounded on
$h_{0,\beta}(0)\,:\!=\,\pi^{-1}\Gamma(\beta+1)(\textrm{e}/\beta)^\beta$
and all these functions are decreasing, continuous, and bounded on
 $[0,\pi]$
. In particular
$[0,\pi]$
. In particular
 $\int_0^\pi h_{0,\beta}(\varphi)\,{\rm d}\varphi=\lim_{\alpha \to 0}\int_0^\pi h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi=1$
, so
$\int_0^\pi h_{0,\beta}(\varphi)\,{\rm d}\varphi=\lim_{\alpha \to 0}\int_0^\pi h_{\alpha,\beta}(\varphi)\,{\rm d}\varphi=1$
, so
 $h_{0,\beta}$
is a density of some
$h_{0,\beta}$
is a density of some
 $(0,\pi)$
-valued random variable
$(0,\pi)$
-valued random variable
 $V_{0,\beta}$
. Clearly, the uniform convergence of the densities implies the convergence
$V_{0,\beta}$
. Clearly, the uniform convergence of the densities implies the convergence
 $V_{\alpha,\beta}\to V_{0,\beta}$
in distribution as
$V_{\alpha,\beta}\to V_{0,\beta}$
in distribution as
 $\alpha\to 0$
.
$\alpha\to 0$
.
-
(b) An application of Stirling’s formula yields
 $c_{\alpha,\beta}\sim\sqrt{2(1-\alpha)\beta/\pi}(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}$
as
$c_{\alpha,\beta}\sim\sqrt{2(1-\alpha)\beta/\pi}(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}$
as
 $\beta\to\infty$
. Straightforward calculations show that the function
$\beta\to\infty$
. Straightforward calculations show that the function
 $a_\alpha(\!\cdot\!)$
in (36) has Taylor expansion
$a_\alpha(\!\cdot\!)$
in (36) has Taylor expansion
 $a_\alpha(\varphi)=a_\alpha(0+)(1+\frac{\alpha}{2}\varphi^2+O(\varphi^4))$
. Thus, for all
$a_\alpha(\varphi)=a_\alpha(0+)(1+\frac{\alpha}{2}\varphi^2+O(\varphi^4))$
. Thus, for all
 $x>0$
and all sufficiently large
$x>0$
and all sufficiently large
 $\beta$
,
$\beta$
,
 \begin{align*} \frac{1}{\sqrt{\beta}}h_{\alpha,\beta}\bigg(\frac{x}{\sqrt{\beta}\,}\bigg) & = \frac{c_{\alpha,\beta}}{\sqrt{\beta}\,} \frac{1}{\big(a_\alpha\big(\frac{x}{\sqrt{\beta}}\big)\big)^{\frac{\beta}{\alpha}(1-\alpha)}} \sim \sqrt{\frac{2(1-\alpha)}{\pi}} \frac{1}{\big(1+\frac{\alpha}{2}\frac{x^2}{\beta}+O(x^4)\big)^{\frac{\beta}{\alpha}(1-\alpha)}}\\[3pt] & \to \sqrt{\frac{2(1-\alpha)}{\pi}}\exp\bigg(-\frac{1-\alpha}{2}x^2\bigg)\ =\ h_\alpha(x), \qquad \beta\to\infty. \end{align*}
\begin{align*} \frac{1}{\sqrt{\beta}}h_{\alpha,\beta}\bigg(\frac{x}{\sqrt{\beta}\,}\bigg) & = \frac{c_{\alpha,\beta}}{\sqrt{\beta}\,} \frac{1}{\big(a_\alpha\big(\frac{x}{\sqrt{\beta}}\big)\big)^{\frac{\beta}{\alpha}(1-\alpha)}} \sim \sqrt{\frac{2(1-\alpha)}{\pi}} \frac{1}{\big(1+\frac{\alpha}{2}\frac{x^2}{\beta}+O(x^4)\big)^{\frac{\beta}{\alpha}(1-\alpha)}}\\[3pt] & \to \sqrt{\frac{2(1-\alpha)}{\pi}}\exp\bigg(-\frac{1-\alpha}{2}x^2\bigg)\ =\ h_\alpha(x), \qquad \beta\to\infty. \end{align*}
This convergence holds uniformly for all
![]() $x>0$
since all involved functions are continuous, monotone decreasing, and bounded. In particular,
$x>0$
since all involved functions are continuous, monotone decreasing, and bounded. In particular,
![]() $\sqrt{\beta}V_{\alpha,\beta}\to V_\alpha$
in distribution as
$\sqrt{\beta}V_{\alpha,\beta}\to V_\alpha$
in distribution as
![]() $\beta\to\infty$
, where
$\beta\to\infty$
, where
![]() $V_\alpha$
is half-normal distributed with density (47).
$V_\alpha$
is half-normal distributed with density (47).
Remark 24. (Efficiency of Algorithm 1) Let N denote the number of steps the rejection algorithm for V (Algorithm 1) needs to terminate. Clearly,
![]() $\mathbb{P}(N=n)=p(1-p)^{n-1}$
,
$\mathbb{P}(N=n)=p(1-p)^{n-1}$
,
![]() $n\in\mathbb{N}$
, where
$n\in\mathbb{N}$
, where
![]() $p\,:\!=\,1/(\pi h_{\alpha,\beta}(0+))$
denotes the acceptance probability. The rejection algorithm therefore needs, on average,
$p\,:\!=\,1/(\pi h_{\alpha,\beta}(0+))$
denotes the acceptance probability. The rejection algorithm therefore needs, on average,
 \begin{align*} \mathbb{E}(N) & = \frac{1}{p} = \pi h_{\alpha,\beta}(0+) = \frac{\pi c_{\alpha,\beta}} {(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}}\\[3pt] & = \frac{\Gamma(\beta+1)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\Gamma\big(\frac{\beta}{\alpha}+1\big)} \big(\alpha(1-\alpha)^{\frac{1-\alpha}{\alpha}}\big)^{-\beta} \end{align*}
\begin{align*} \mathbb{E}(N) & = \frac{1}{p} = \pi h_{\alpha,\beta}(0+) = \frac{\pi c_{\alpha,\beta}} {(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}}\\[3pt] & = \frac{\Gamma(\beta+1)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\Gamma\big(\frac{\beta}{\alpha}+1\big)} \big(\alpha(1-\alpha)^{\frac{1-\alpha}{\alpha}}\big)^{-\beta} \end{align*}
steps to terminate. An application of Stirling’s formula yields
![]() $\mathbb{E}(N)\sim\sqrt{2\pi(1-\alpha)\beta}$
as
$\mathbb{E}(N)\sim\sqrt{2\pi(1-\alpha)\beta}$
as
![]() $\beta\to\infty$
. Moreover, it can be checked that
$\beta\to\infty$
. Moreover, it can be checked that
![]() $\mathbb{E}(N)$
is decreasing in
$\mathbb{E}(N)$
is decreasing in
![]() $\alpha\in (0,1)$
. Hence, by Proposition 5(a), we obtain, uniformly for all
$\alpha\in (0,1)$
. Hence, by Proposition 5(a), we obtain, uniformly for all
![]() $\alpha\in (0,1)$
, the upper bound
$\alpha\in (0,1)$
, the upper bound
For example, for
![]() $\beta=1$
the rejection algorithm needs (independently of
$\beta=1$
the rejection algorithm needs (independently of
![]() $\alpha$
) on average not more than
$\alpha$
) on average not more than
![]() $\textrm{e} \approx 2.71828$
steps to terminate. For large values of
$\textrm{e} \approx 2.71828$
steps to terminate. For large values of
![]() $\beta$
the algorithm becomes less efficient and the average number of steps to terminate grows like
$\beta$
the algorithm becomes less efficient and the average number of steps to terminate grows like
![]() $\sqrt{2\pi(1-\alpha)\beta}$
as
$\sqrt{2\pi(1-\alpha)\beta}$
as
![]() $\beta\to\infty$
. In summary, Algorithm 1, the rejection algorithm for V, is sufficiently efficient as long as
$\beta\to\infty$
. In summary, Algorithm 1, the rejection algorithm for V, is sufficiently efficient as long as
![]() $\beta$
is not too large. An alternative rejection method (Algorithm 2) is provided which is highly efficient for all parameter values
$\beta$
is not too large. An alternative rejection method (Algorithm 2) is provided which is highly efficient for all parameter values
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta>0$
. For very large values of
$\beta>0$
. For very large values of
![]() $\beta$
one may alternatively approximate the distribution of V using the half-normal limit from Proposition 5(b).
$\beta$
one may alternatively approximate the distribution of V using the half-normal limit from Proposition 5(b).
Remark 25. As a side effect, Proposition 5(a) implies that the reciprocal gamma function has the integral representation
By the identity theorem for holomorphic functions, (48) even holds for all
![]() $\beta\in\mathbb{H}\,:\!=\,\{z\in\mathbb{C}:{\rm Re}(z)>0\}$
. Note that both expressions on the left- and right-hand sides in (48) are well-defined holomorphic functions in
$\beta\in\mathbb{H}\,:\!=\,\{z\in\mathbb{C}:{\rm Re}(z)>0\}$
. Note that both expressions on the left- and right-hand sides in (48) are well-defined holomorphic functions in
![]() $\beta\in\mathbb{H}$
. For the left-hand side this is clear since the map
$\beta\in\mathbb{H}$
. For the left-hand side this is clear since the map
![]() $\beta\mapsto\beta^\beta$
and
$\beta\mapsto\beta^\beta$
and
![]() $\Gamma(\!\cdot\!)$
are holomorphic on
$\Gamma(\!\cdot\!)$
are holomorphic on
![]() $\mathbb{H}$
. By the differentiation lemma the right-hand side in (48) is also complex differentiable in any point
$\mathbb{H}$
. By the differentiation lemma the right-hand side in (48) is also complex differentiable in any point
![]() $\beta\in\mathbb{H}$
, and it is allowed to take the derivative below the integral.
$\beta\in\mathbb{H}$
, and it is allowed to take the derivative below the integral.
Temme ([Reference Temme38, p. 4, Eq. (2.1.8)], [Reference Temme39, p. 71, Eq. (3.38)]) derives (48), in a slightly different form, via an appropriate contour integration of the reciprocal gamma function and focuses on its usefulness for numerical computations of the gamma function (see also [Reference Schmelzer and Trefethen33]). Despite its elegance and usefulness, (48) does not seem to have achieved much attention in the literature. For one further application of (48) we refer the reader to Example 11.16 of [Reference Steutel and Van Harn37].
We have seen that Algorithm 1 is not very efficient for large values of
![]() $\beta$
. The following more sophisticated rejection algorithm for V will turn out to be efficient for all parameters
$\beta$
. The following more sophisticated rejection algorithm for V will turn out to be efficient for all parameters
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $\beta>0$
. Assume first that
$\beta>0$
. Assume first that
![]() $\alpha\le\frac{1}{2}$
. In this case it can be checked that
$\alpha\le\frac{1}{2}$
. In this case it can be checked that
![]() $h_{\alpha,\beta}(\varphi) \le d_{\alpha,\beta}h_{\frac{1}{2},\beta}(\varphi)$
,
$h_{\alpha,\beta}(\varphi) \le d_{\alpha,\beta}h_{\frac{1}{2},\beta}(\varphi)$
,
![]() $ 0<\varphi<\pi$
,
$ 0<\varphi<\pi$
,
![]() $\beta>0$
, with constant
$\beta>0$
, with constant
 \begin{equation*} d_{\alpha,\beta} \,:\!=\, \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} = \frac{c_{\alpha,\beta}{\rm B}\big(\beta+\frac{1}{2},\frac{1}{2}\big)} {(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}} = \frac{\Gamma\big(\beta+\frac{1}{2}\big)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\sqrt{\pi}\Gamma\big(\frac{\beta}{\alpha}+1\big)\alpha^\beta(1-\alpha)^{\frac{\beta}{\alpha}(1-\alpha)}}.\end{equation*}
\begin{equation*} d_{\alpha,\beta} \,:\!=\, \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} = \frac{c_{\alpha,\beta}{\rm B}\big(\beta+\frac{1}{2},\frac{1}{2}\big)} {(a_\alpha(0+))^{\frac{\beta}{\alpha}(1-\alpha)}} = \frac{\Gamma\big(\beta+\frac{1}{2}\big)\Gamma\big(\frac{\beta}{\alpha}(1-\alpha)+1\big)} {\sqrt{\pi}\Gamma\big(\frac{\beta}{\alpha}+1\big)\alpha^\beta(1-\alpha)^{\frac{\beta}{\alpha}(1-\alpha)}}.\end{equation*}
Thus, for
![]() $\alpha\le\frac{1}{2}$
and
$\alpha\le\frac{1}{2}$
and
![]() $\beta>0$
, an alternative rejection algorithm for V works via Algorithm 2 (see [Reference Devroye6, p. 42]).
$\beta>0$
, an alternative rejection algorithm for V works via Algorithm 2 (see [Reference Devroye6, p. 42]).

Sampling from
![]() $V_{\frac{1}{2},\beta}$
is straightforward by the first formula in (45). The value t simplifies to
$V_{\frac{1}{2},\beta}$
is straightforward by the first formula in (45). The value t simplifies to
 \begin{align*} t = \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} \frac{h_{\frac{1}{2},\beta}(v)}{h_{\alpha,\beta}(v)} & = \bigg( \frac{a_{\frac{1}{2}}(0+)}{a_{\frac{1}{2}}(v)} \bigg)^\beta \bigg( \frac{a_\alpha(v)}{a_\alpha(0+)} \bigg)^{\frac{\beta}{\alpha}(1-\alpha)}\\[3pt] & = \cos^{2\beta}\bigg(\frac{v}{2}\bigg) \bigg(\frac{a_\alpha(v)}{a_\alpha(0+)}\bigg)^{\frac{\beta}{\alpha}(1-\alpha)}\end{align*}
\begin{align*} t = \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} \frac{h_{\frac{1}{2},\beta}(v)}{h_{\alpha,\beta}(v)} & = \bigg( \frac{a_{\frac{1}{2}}(0+)}{a_{\frac{1}{2}}(v)} \bigg)^\beta \bigg( \frac{a_\alpha(v)}{a_\alpha(0+)} \bigg)^{\frac{\beta}{\alpha}(1-\alpha)}\\[3pt] & = \cos^{2\beta}\bigg(\frac{v}{2}\bigg) \bigg(\frac{a_\alpha(v)}{a_\alpha(0+)}\bigg)^{\frac{\beta}{\alpha}(1-\alpha)}\end{align*}
and can hence be computed without much effort. The constants
![]() $c_{\alpha,\beta}$
and
$c_{\alpha,\beta}$
and
![]() $d_{\alpha,\beta}$
are not needed during the calculations. Algorithm 2 takes (see [Reference Devroye6, p. 42]) on average
$d_{\alpha,\beta}$
are not needed during the calculations. Algorithm 2 takes (see [Reference Devroye6, p. 42]) on average
![]() $\mathbb{E}(N)=d_{\alpha,\beta}$
steps to terminate. Since
$\mathbb{E}(N)=d_{\alpha,\beta}$
steps to terminate. Since
![]() $h_{\alpha,\beta}(0+)$
and hence
$h_{\alpha,\beta}(0+)$
and hence
![]() $d_{\alpha,\beta}$
is decreasing in
$d_{\alpha,\beta}$
is decreasing in
![]() $\alpha$
it follows that
$\alpha$
it follows that
 \begin{align*} \mathbb{E}(N) & = \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} \le \frac{h_{0,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)}\\[3pt] & = \frac{1}{\pi}\Gamma(\beta+1)\bigg(\frac{\textrm{e}}{\beta}\bigg)^\beta {\rm B}\big(\beta+\mbox{$\frac{1}{2}$},\mbox{$\frac{1}{2}$}\big) = \frac{1}{\sqrt{\pi}\,}\bigg(\frac{\textrm{e}}{\beta}\bigg)^\beta \Gamma\big(\beta+\mbox{$\frac{1}{2}$}\big).\end{align*}
\begin{align*} \mathbb{E}(N) & = \frac{h_{\alpha,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)} \le \frac{h_{0,\beta}(0+)}{h_{\frac{1}{2},\beta}(0+)}\\[3pt] & = \frac{1}{\pi}\Gamma(\beta+1)\bigg(\frac{\textrm{e}}{\beta}\bigg)^\beta {\rm B}\big(\beta+\mbox{$\frac{1}{2}$},\mbox{$\frac{1}{2}$}\big) = \frac{1}{\sqrt{\pi}\,}\bigg(\frac{\textrm{e}}{\beta}\bigg)^\beta \Gamma\big(\beta+\mbox{$\frac{1}{2}$}\big).\end{align*}
This expression is increasing in
![]() $\beta$
and bounded with limit
$\beta$
and bounded with limit
![]() $\sqrt{2}$
as
$\sqrt{2}$
as
![]() $\beta\to\infty$
, leading to
$\beta\to\infty$
, leading to
![]() $\mathbb{E}(N)\le \sqrt{2}$
uniformly for all
$\mathbb{E}(N)\le \sqrt{2}$
uniformly for all
![]() $\alpha\le\frac{1}{2}$
and
$\alpha\le\frac{1}{2}$
and
![]() $\beta>0$
. Algorithm 2 therefore takes on average never more than
$\beta>0$
. Algorithm 2 therefore takes on average never more than
![]() $\sqrt{2}$
steps to terminate and is hence quite efficient. The case
$\sqrt{2}$
steps to terminate and is hence quite efficient. The case
![]() $\alpha>\frac{1}{2}$
can be transformed in advance into
$\alpha>\frac{1}{2}$
can be transformed in advance into
![]() $\alpha<\frac{1}{2}$
using the relation
$\alpha<\frac{1}{2}$
using the relation
![]() $h_{\alpha,\beta}=h_{\tilde\alpha,\tilde\beta}$
with
$h_{\alpha,\beta}=h_{\tilde\alpha,\tilde\beta}$
with
![]() $\tilde\alpha\,:\!=\,1-\alpha$
and
$\tilde\alpha\,:\!=\,1-\alpha$
and
![]() $\tilde\beta\,:\!=\,\beta(1-\alpha)/\alpha$
.
$\tilde\beta\,:\!=\,\beta(1-\alpha)/\alpha$
.
Acknowledgements
The author would like to thank two anonymous referees for their constructive reports leading to a significant improvement of the article. He furthermore thanks Helmut Pitters for fruitful discussions and Fernando Cordero for pointing out the integral representation (3.38) on p. 71 of [Reference Temme39].