Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T08:07:34.607Z Has data issue: false hasContentIssue false
  • English
  • Français

A CENTRAL LIMIT THEOREM FOR MIXING TRIANGULAR ARRAYS OF VARIABLES WHOSE DEPENDENCE IS ALLOWED TO GROW WITH THE SAMPLE SIZE

Published online by Cambridge University Press:  23 September 2005

Christian Francq  and
Jean-Michel Zakoïan
Christian Francq
Affiliation:
Université Lille III, GREMARS
Jean-Michel Zakoïan
Affiliation:
Université Lille III, GREMARS and CREST
Rights & Permissions [Opens in a new window]

Abstract

Conditions ensuring a central limit theorem for strongly mixing triangular arrays are given. Larger samples can show longer range dependence than shorter samples. The result is obtained by constraining the rate growth of dependence as a function of the sample size, with the usual trade-off of memory and moment conditions. An application to heteroskedasticity and autocorrelation consistent estimators is proposed.

Type
Notes and Problems
Information
Econometric Theory , Volume 21 , Issue 6 , December 2005 , pp. 1165 - 1171
Copyright
© 2005 Cambridge University Press

1. PROBLEM AND MOTIVATION

For statistical purposes, it may be required to use a central limit theorem (CLT) for triangular sequences (xn,t) of the form xn,t = fn(ut−hn,…,ut+hn), where fn is some measurable function, hn → ∞, and (ut) is a mixing process. There exist a variety of CLTs available for triangular sequences. Unfortunately, many of them are difficult to verify on particular cases or impose conditions such as supn αn(h) → 0 as h → ∞ where (αn(h))h is the sequence of strong mixing coefficients of (xn,t)t (see, e.g., Withers, 1981). It follows from the definition of xn,t that αn(h) ≤ α(h − 2hn), where (α(h))h is the sequence of strong mixing coefficients of (ut). Because

, in general, the latter inequality is of no help to establish supn αn(h) = o(h).

Let (xn,t)n≥1,1≤t≤n be a triangular array of centered real-valued random variables. In the sequel, we no longer assume that (xnt) is subordinated to some process (ut). For each n ≥ 2 and h = 1,…,n − 1, let the strong mixing coefficients of xn,1,…,xn,n be defined by

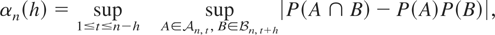
where

. By convention, we set

for h ≤ 0 and αn(h) = 0 for h ≥ n. Put

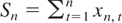
and assume that

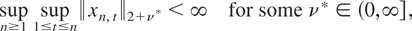
there exist a sequence of integers (Tn) such that

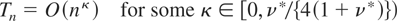
and a sequence {α(h)}h≥1 such that

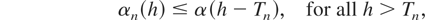
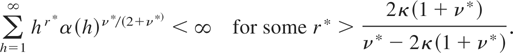
The problem is to show the following CLT:

Under assumptions (1)–(5),

.

2. SOLUTION AND DISCUSSION

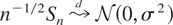
Note that the preceding result can be viewed as an extension to triangular arrays of the CLT given by Herrndorf (1984). Condition (2) is of course a standard assumption to obtain an asymptotic nondegenerate Gaussian distribution for the sequence n−1/2Sn. To illustrate the other conditions, suppose that (xnt) is defined as in the beginning of this note, with α(h) decreasing to 0 at exponential rate. Then (5) is automatically satisfied; (4) is satisfied with Tn = 2hn. Conditions (1) and (3) impose a balance between the existence of moments and the number, 2hn, of terms us allowed in the definition of xn,t. Now we prove the announced result.

Proof of the CLT. Let κ1 and κ2 be constants such that

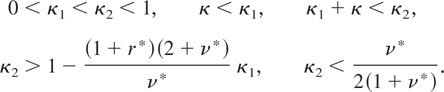
Figure 1 shows that these inequalities are compatible. Define sequences of integers (kn), (mn), (qn), and (pn) by

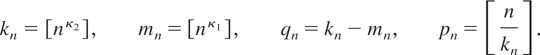
Note that

as n → ∞. Employing a standard technique, we split the sum

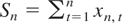
into pn alternate “big” blocks of length qn and “small” blocks of length mn. More precisely, write Sn = Sn′ + Sn′′, where

To prove the CLT it suffices to show that for n → ∞

Indeed, (i) implies that n−1/2Sn and n−1/2Sn′ have the same asymptotic distribution, (ii) implies that the characteristic function of n−1/2Sn′ is asymptotically equivalent to that of

where the ξn,[ell ]′ are independent and are distributed like ξn,[ell ], and (iii) is simply the Lindeberg condition ensuring the CLT for independent, but not necessarily identically distributed, random variables.

Illustration of Inequalities (6). Let . We have .

Using the Davydov (1968) inequality, there exists a universal constant K0 (one can take K0 = 4), such that for ν* < ∞,

Using inequality (1.4) in Ibragimov (1962), the same inequalities hold when ν* = ∞ (with 2 + ν* = ∞ and ν*/(2 + ν*) = 1). Thus

for some positive constant K. Hence (i) holds because, in view of (6), pn mn(Tn + 1)/n ∼ n−κ2+κ1+κ → 0, kn2/n ∼ n2κ2−1 → 0, and qn − Tn ∼ nκ2 → ∞.

Using the Ibragimov (1962) inequality and the fact that un = O(n−r*−1) when un ↓ 0 and [sum ]n nr*un < ∞, we obtain

which establishes (ii).

When ν* < ∞, by the Hölder and Markov inequalities, we have

which establishes (iii) in the case ν* < ∞. Finally, when M := supn≥1 sup1≤t≤n∥xn,t∥∞ < ∞, we have

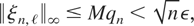
and the sum in (iii) equals 0, for sufficiently large n. The proof is complete. █

2.1. Application

Suppose we are interested in estimating a matrix of the form

where Γ(j) is the jth autocovariance of some mixing stationary process (ut). Such problems have been extensively considered in the econometric literature, e.g., by Andrews (1991). The limit of Jn, when n goes to infinity, equals 2π times the spectral density of (ut) evaluated at the frequency 0. This framework is encountered in the estimation of the optimal weighting matrix for general method of moments estimators, the estimation of the covariance matrix of the error term in unit root tests, or the estimation of the asymptotic variance of sample autocovariances of nonlinear processes. See, e.g., Francq and Zakoïan (2005) for references. For simplicity, assume that ut is real-valued and centered.

We consider HAC (heteroskedasticity and autocorrelation consistent) estimators of Jn given by

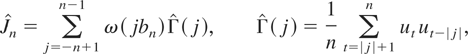
where ω(·) is a kernel function and bn is a size-dependent bandwidth parameter such that bn → 0 and nbn → ∞ as n → ∞. We assume that

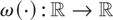
satisfies the standard assumptions: ω(0) = 1, ω(·) is even, with support [−1,1], and is continuous on [−1,1]. To derive the asymptotic distribution of the HAC estimator, write

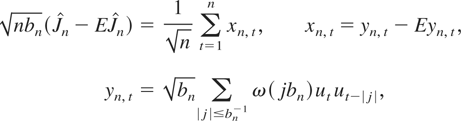
where, by convention, ut = 0 when t < 1 or t > n. This form suggests trying to apply a CLT for processes that are near epoch dependent on an α-mixing process ((ut) in our framework), such as Theorem 10.2. in Pötscher and Prucha (1997) or Theorem 24.6 in Davidson (1994). This requires verifying that

tends to zero with a sufficient rate as m goes to infinity. We have

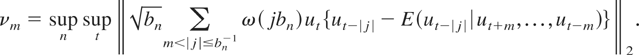
Unfortunately, νm does not converge to zero in general. To see this, take, e.g., the case where (ut) is independent and identically distributed (i.i.d.), with the truncated window ω(x) = 1 for |x| ≤ 1. We have, denoting by [x] the integer part of x,

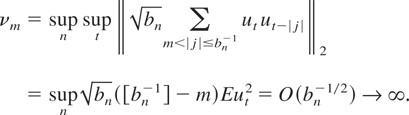
Thus we have shown that the standard CLTs for dependent processes can not be directly applied to establish the asymptotic normality of HAC-type estimators. Now let us try to apply the CLT proposed in this note. For simplicity, assume that the sequence (α(h))h of the strong mixing coefficients of (ut) decreases to 0 at exponential rate and suppose that Eut8 < ∞. Because ω is bounded, we have

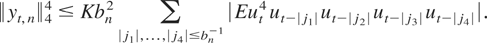
Using the Davydov (1968) inequality it can be easily shown (see Francq and Zakoïan, 2005) that

Note that (9) is obvious when the sequence (ut) is i.i.d. and that the result remains true when the mixing coefficients tend to zero at a sufficiently high rate. Now using (9), (8) gives supn≥1 sup1≤t≤n∥yt,n∥44 < ∞, and (1) is satisfied with ν* = 2. By Lemma 1 and Proposition 1(a) of Andrews (1991),

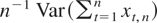
converges to

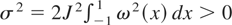
when J = limn→∞ Jn > 0. Thus (2) holds. Under our mixing assumption, (5) is satisfied for all κ. Clearly (4) is satisfied for Tn = [2/bn]. Finally (3) is satisfied when lim infn→∞ nbnτ > 0 for some τ > 6. Thus applying our CLT, we can conclude that

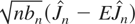
has an asymptotic centered normal distribution with variance σ2.

A more elaborate application of the result of this paper can be found in Francq and Zakoïan (2005).

References

REFERENCES

Andrews, D.W.K. (1991) Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59, 817–858.Google Scholar
Davidson, J. (1994) Stochastic Limit Theory. Oxford University Press.
Davydov, Y.A. (1968) Convergence of distributions generated by stationary stochastic processes. Theory of Probability and Its Applications 13, 691–696.Google Scholar
Francq, C. & J.-M. Zakoïan (2005) HAC Estimation and Strong Linearity Testing in Weak ARMA Models. Manuscript, http://www.crest.fr/pageperso/ls/zakoian/zakoian.htm. CREST.
Herrndorf, N. (1984) A functional central limit theorem for weakly dependent sequences of random variables. Annals of Probability 12, 141–153.Google Scholar
Ibragimov, I.A. (1962) Some limit theorems for stationary processes. Theory of Probability and Its Applications 7, 349–382.Google Scholar
Pötscher, B.M. & I.R. Prucha (1997) Dynamic Nonlinear Econometric Models. Springer Verlag.
Withers, C.S. (1981) Central limit theorems for dependent variables. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandete Gebiete 57, 509–534.Google Scholar
Figure 0

Illustration of Inequalities (6). Let . We have .