1. Introduction
In the early beginning of acoustics, Helmholtz (Reference Helmholtz1870) already formulated the well known reciprocity principle: ‘a disturbance produced at a source location ![]() $A$ and recorded at a receiver point
$A$ and recorded at a receiver point ![]() $B$, is identical to what would have been recorded at the source location
$B$, is identical to what would have been recorded at the source location ![]() $A$ if the same disturbance occurred in
$A$ if the same disturbance occurred in ![]() $B$’. This principle, generalised to dissipative systems by Lord Rayleigh (Strutt Reference Strutt1877, §§72–78, §§107–111), indicates that sound propagation is not a matter of the features of the sound emitter or receiver, but only depends on the property of the considered medium. Despite this early discovery, the reciprocity principle has not been widely used by the acoustics community. Eversman (Reference Eversman1976) and Cho (Reference Cho1980) for ducted systems, and Bojarski (Reference Bojarski1983) for the free-field problem, derived general reciprocity relations for acoustic media at rest. An outstanding work was done by Levine & Schwinger (Reference Levine and Schwinger1948) who first used the reciprocity principle to determine the directivity pattern of a complex sound propagation problem. In their investigation of the far-field radiation from an unflanged duct, the authors exchanged observer and source positions, and turned the complex radiation problem into the equivalent problem of a plane wave coming from infinity and impinging at the duct end. In the same spirit, later the reciprocity principle has also been employed by Crighton & Leppington (Reference Crighton and Leppington1970, Reference Crighton and Leppington1971, Reference Crighton and Leppington1973) to analytically derive the far-field radiation of an acoustic source in the vicinity of a refracting body. These contributions permitting the continuation of a near-field acoustic solution to the far-field are important, because they have since motivated most of the investigations involving the reciprocity principle in aeroacoustics.
$B$’. This principle, generalised to dissipative systems by Lord Rayleigh (Strutt Reference Strutt1877, §§72–78, §§107–111), indicates that sound propagation is not a matter of the features of the sound emitter or receiver, but only depends on the property of the considered medium. Despite this early discovery, the reciprocity principle has not been widely used by the acoustics community. Eversman (Reference Eversman1976) and Cho (Reference Cho1980) for ducted systems, and Bojarski (Reference Bojarski1983) for the free-field problem, derived general reciprocity relations for acoustic media at rest. An outstanding work was done by Levine & Schwinger (Reference Levine and Schwinger1948) who first used the reciprocity principle to determine the directivity pattern of a complex sound propagation problem. In their investigation of the far-field radiation from an unflanged duct, the authors exchanged observer and source positions, and turned the complex radiation problem into the equivalent problem of a plane wave coming from infinity and impinging at the duct end. In the same spirit, later the reciprocity principle has also been employed by Crighton & Leppington (Reference Crighton and Leppington1970, Reference Crighton and Leppington1971, Reference Crighton and Leppington1973) to analytically derive the far-field radiation of an acoustic source in the vicinity of a refracting body. These contributions permitting the continuation of a near-field acoustic solution to the far-field are important, because they have since motivated most of the investigations involving the reciprocity principle in aeroacoustics.
The failure of the standard reciprocity principle in arbitrary media was also quickly identified. Rayleigh (Strutt Reference Strutt1877, §111) already stated that: ‘It is important to remember that the Principle of Reciprocity is limited to systems which vibrate about a configuration of equilibrium, and is therefore not to be applied without reservation to such a problem as that presented by the transmission of sonorous waves through the atmosphere when disturbed by wind’. Several contributions thus aimed at properly delimiting its domain of validity. Landau & Lifshitz (Reference Landau and Lifshitz1959) proved the reciprocity principle for a variable index of refraction. Lyamshev (Reference Lyamshev1961) generalised the reciprocity principle in the presence of a uniform mean flow with the so-called flow reversal theorem (FRT), illustrated in figure 1. A similar formulation was used by Dowling, Ffowcs Williams & Goldstein (Reference Dowling, Ffowcs Williams and Goldstein1978) and by Dowling (Reference Dowling1983) for piecewise uniform flows. Howe (Reference Howe1975) proved the reciprocity principle for potential mean flows to first order in Mach number. Möhring then extended the FRT to all potential mean flows (Möhring Reference Möhring1978, Reference Möhring1979) and gave indications on reciprocity for rotational flow (Möhring Reference Möhring2001). Godin et al. attempted to generalise the FRT to arbitrary mean flows (Godin Reference Godin1997), and proved a general version of Fermat's principle for ray acoustics (Godin & Voronovich Reference Godin and Voronovich2004). One of the objectives of this study is to carry out computations of reciprocal solutions involving the FRT in order to assess the validity of this technique for propagation problems in complex mean flows.

Figure 1. ![]() $(a)$ Green's function for the acoustic pressure field
$(a)$ Green's function for the acoustic pressure field ![]() $G_{\boldsymbol {x}_A}$ generated by a harmonic source in a uniform mean flow with an observer set at
$G_{\boldsymbol {x}_A}$ generated by a harmonic source in a uniform mean flow with an observer set at ![]() $\boldsymbol {x}_B$;
$\boldsymbol {x}_B$; ![]() $(b)$
$(b)$![]() $G^-_{\boldsymbol {x}_B}$ for the reversed flow is depicted where source and receiver locations have been switched. The FRT states that
$G^-_{\boldsymbol {x}_B}$ for the reversed flow is depicted where source and receiver locations have been switched. The FRT states that ![]() $G_{ \boldsymbol {x}_A }(\boldsymbol {x}_B) = G^-_{\boldsymbol {x}_B}(\boldsymbol {x}_A )$.
$G_{ \boldsymbol {x}_A }(\boldsymbol {x}_B) = G^-_{\boldsymbol {x}_B}(\boldsymbol {x}_A )$.
A proper mathematical generalisation of the reciprocity principle, however, requires the introduction of the adjoint formalism (Morse & Feshbach Reference Morse and Feshbach1953, § 7.5; Lamb Jr. Reference Lamb1995, § 4.6.1; Stone & Goldbart Reference Stone and Goldbart2009, § 4.2.1). Although the use of the adjoint formalism is long-standing in the flow receptivity community (Roberts Reference Roberts1960; Hill Reference Hill1995; Luchini & Bottaro Reference Luchini and Bottaro1998; Barone & Lele Reference Barone and Lele2005) and became a staple in optimisation and control (Jameson Reference Jameson1988; Giles & Pierce Reference Giles and Pierce1997; Wei & Freund Reference Wei and Freund2006), its use in aeroacoustic computations is fairly recent. The first correct generalisation of the reciprocity principle to tackle acoustic propagation in arbitrary mean flows was formulated by Tam & Auriault (Reference Tam and Auriault1998) for the linearised Euler equations (LEE) and for Lilley's equation (Lilley et al. Reference Lilley, Plumblee, Strahle, Ruo and Doak1972). Another aim of this study is to recall the adjoint methodology in a synoptic and broader way.
Besides the general derivation of the methodology, Tam & Auriault (Reference Tam and Auriault1998) mainly focuses on the formulation of the adjoint as the sum of a quasi-analytical solution of a propagation problem on an axisymmetric parallel mean flow for the adjoint Lilley equation, and an additional contribution induced by the jet spreading is solved numerically using a Fourier mode decomposition. This remarkable analytical solution has since been widely reused in the literature to assess jet noise polar directivity (Tam & Auriault Reference Tam and Auriault1999; Khavaran & Bridges Reference Khavaran and Bridges2005; Tam, Pastouchenko & Viswanathan Reference Tam, Pastouchenko and Viswanathan2005; Afsar, Dowling & Karabasov Reference Afsar, Dowling and Karabasov2006; Raizada & Morris Reference Raizada and Morris2006; Miller Reference Miller2014b; Gryazev, Markesteijn & Karabasov Reference Gryazev, Markesteijn and Karabasov2018), and has been simplified by Afsar (Reference Afsar2009). This handy analytical model has been improved by Goldstein & Leib (Reference Goldstein and Leib2008) in the low-frequency range to include jet spreading and then used repeatedly (Afsar Reference Afsar2010; Goldstein, Sescu & Afsar Reference Goldstein, Sescu and Afsar2012; Afsar etal. Reference Afsar, Sescu, Sassanis, Towne, Bres and Lele2016b; Afsar, Sescu & Leib Reference Afsar, Sescu and Leib2016a). Afsar et al. (Reference Afsar, Sescu, Sassanis and Lele2017) improved the formulation further with a composite solution for Green's function uniformly valid for all frequencies. In the same line, Cheung et al. (Reference Cheung, Pastouchenko, Mani and Paliath2015) developed a method to solve semi-analytically Lilley's equation for non-axisymmetric parallel flows to address azimuthal directivity, yet without falling back to an adjoint formalism.
In numerous relevant configurations, the mean flow topology in which acoustics propagates is complex, e.g. consider the dissymmetric dual stream hot jet flow behind an aircraft engine as computed by Mosson, Binet & Caprile (Reference Mosson, Binet and Caprile2014), and computational aeroacoustics tools are needed to address correctly the propagation problem. In the present work a purely numerical method is therefore presented to solve adjoint-based propagation problems. The aeroacoustics community has already computed numerically adjoint Green's function for arbitrary mean flows: Tam & Pastouchenko (Reference Tam and Pastouchenko2002), Pastouchenko & Tam (Reference Pastouchenko and Tam2007), and recently Xu et al. (Reference Xu, He, Li and Hu2015), used the method to assess the azimuthal directivity of non-axisymmetric jets. Tam, Pastouchenko & Viswanathan (Reference Tam, Pastouchenko and Viswanathan2010) also achieved with this method, continuation of a near-field acoustic solution to the far-field in the presence of flow heterogeneities. In parallel to these studies, the group of Karabasov et al. implemented the adjoint linearised Euler equations, first two-dimensionally (Karabasov & Hynes Reference Karabasov and Hynes2005) then three-dimensionally (Semiletov & Karabasov Reference Semiletov and Karabasov2013), and tackled numerically the acoustic far-field radiation for an arbitrary jet profile (Karabasov, Bogey & Hynes Reference Karabasov, Bogey and Hynes2013; Depuru Mohan et al. Reference Depuru Mohan, Dowling, Karabasov, Xia, Graham, Hynes and Tucker2015). Nevertheless, except some scarce contributions (Alonso & Burdisso Reference Alonso and Burdisso2007), in all the studies mentioned above, the adjoint solution is always sought as the solution to a scattering problem, with furthermore the adjoint source set in the far-field. In the present study, the adjoint method is recalled in a systematic and general way valid for any linear operator, any propagation media and propagation distance. Even if some adjoint computations including surfaces have been conducted (Pastouchenko & Tam Reference Pastouchenko and Tam2007; Tam et al. Reference Tam, Pastouchenko and Viswanathan2010; Xu et al. Reference Xu, He, Li and Hu2015), including liners in Alonso & Burdisso (Reference Alonso and Burdisso2007), as pointed out by Miller (Reference Miller2014a) the currently used formulation of the adjoint method cannot account for diffraction at surface edges. This is because the adjoint field is already sought as the solution to a scattering problem to account for flow refraction effects. Analogously with Barone & Lele (Reference Barone and Lele2005), the adjoint method as presented here has the capability to tackle adequately diffraction phenomena.
The general derivation of the adjoint methodology, its validation for a non-trivial case, and its comparison against the FRT are the main purposes of this study. To achieve these objectives, two different wave equations – Pierce's wave equation (Pierce Reference Pierce1990) which is self-adjoint, and Lilley's wave equation (Lilley et al. Reference Lilley, Plumblee, Strahle, Ruo and Doak1972) – are considered. This paper is organised as follows: the theoretical background of the adjoint formalism is laid out in § 2, the adjoint method is then executed for a well-documented sheared and stratified mean flow case for Lilley's equation and compared with results obtained with the FRT in § 3. In § 4 both methodology are compared for Pierce's wave equation to illustrate numerically the equivalence between the adjoint approach and the FRT for a self-adjoint wave equation. Concluding remarks are finally drawn.
2. The adjoint method in the propagation problem
2.1. Lagrange's identity
In the framework of the adjoint method, the physical relevant problem is often qualified as direct in opposition to what is defined as the adjoint problem. Consider a pressure field ![]() $p$ and a source term
$p$ and a source term ![]() $s$, a linear acoustic propagation problem may be described by a linear operator
$s$, a linear acoustic propagation problem may be described by a linear operator ![]() $\mathcal {L}_0$ so that the physical problem of interest – the direct problem – may be written over a domain
$\mathcal {L}_0$ so that the physical problem of interest – the direct problem – may be written over a domain ![]() $\Omega$ as
$\Omega$ as
 \begin{equation} \begin{cases} \mathcal{L}_0\ p = s & \text{in}\ \Omega,\\ \mathcal{B}_0\ p = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathcal{L}_0\ p = s & \text{in}\ \Omega,\\ \mathcal{B}_0\ p = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}
with ![]() $\mathcal {B}_0$ the boundary conditions that are necessary for the problem to be well-posed. A cornerstone for the adjoint method is Lagrange's identity (Morse & Feshbach Reference Morse and Feshbach1953, § 7.5; Stone & Goldbart Reference Stone and Goldbart2009, § 4.2.1) which relates the direct and adjoint fields with help of a scalar product and reads: given a scalar product
$\mathcal {B}_0$ the boundary conditions that are necessary for the problem to be well-posed. A cornerstone for the adjoint method is Lagrange's identity (Morse & Feshbach Reference Morse and Feshbach1953, § 7.5; Stone & Goldbart Reference Stone and Goldbart2009, § 4.2.1) which relates the direct and adjoint fields with help of a scalar product and reads: given a scalar product ![]() $\langle, \rangle$, there exists a unique operator
$\langle, \rangle$, there exists a unique operator ![]() ${\mathcal {L}}^\dagger _0$ and specific boundary conditions
${\mathcal {L}}^\dagger _0$ and specific boundary conditions ![]() ${\mathcal {B}}^\dagger _0$ (Giles & Pierce Reference Giles and Pierce1997) such that for any field
${\mathcal {B}}^\dagger _0$ (Giles & Pierce Reference Giles and Pierce1997) such that for any field ![]() ${p}^\dagger$:
${p}^\dagger$:
where ![]() ${p}^\dagger$ is referred to as the adjoint field. Introducing the adjoint source
${p}^\dagger$ is referred to as the adjoint field. Introducing the adjoint source ![]() ${s}^\dagger$, such that
${s}^\dagger$, such that ![]() ${s}^\dagger = {\mathcal {L}}^\dagger _0\ {p}^\dagger$, the adjoint problem associated with (2.1) with respect to
${s}^\dagger = {\mathcal {L}}^\dagger _0\ {p}^\dagger$, the adjoint problem associated with (2.1) with respect to ![]() $\langle, \rangle$ may be written as
$\langle, \rangle$ may be written as
 \begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {p}^\dagger = {s}^\dagger & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {p}^\dagger = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {p}^\dagger = {s}^\dagger & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {p}^\dagger = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}Lagrange's identity can then be recast in the following convenient form:
From this relation it is clear that there is no strict equality between the direct field ![]() $p$ and the adjoint field
$p$ and the adjoint field ![]() ${p}^\dagger$. Only the source and field projections are cross-related as defined in (2.4). Adjoint fields
${p}^\dagger$. Only the source and field projections are cross-related as defined in (2.4). Adjoint fields ![]() ${p}^\dagger$ and sources
${p}^\dagger$ and sources ![]() ${s}^\dagger$ are mathematical entities with consistent units. Let
${s}^\dagger$ are mathematical entities with consistent units. Let ![]() $\boldsymbol {X}_m$ be the coordinate of a microphone point, then adjoint Green's function
$\boldsymbol {X}_m$ be the coordinate of a microphone point, then adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {X}_m}$ for an impulse Dirac source
${G}^\dagger _{\boldsymbol {X}_m}$ for an impulse Dirac source ![]() $\delta _{\boldsymbol {X}_m}$ is defined by
$\delta _{\boldsymbol {X}_m}$ is defined by
 \begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {G}^\dagger_{\boldsymbol{X}_m} = \delta_{\boldsymbol{X}_m} & \text{in}\ \Omega, \\ {\mathcal{B}}^\dagger_0\ {G}^\dagger_{\boldsymbol{X}_m} = 0 & \text{on}\ \partial\Omega, \end{cases}\end{equation}
\begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {G}^\dagger_{\boldsymbol{X}_m} = \delta_{\boldsymbol{X}_m} & \text{in}\ \Omega, \\ {\mathcal{B}}^\dagger_0\ {G}^\dagger_{\boldsymbol{X}_m} = 0 & \text{on}\ \partial\Omega, \end{cases}\end{equation}Lagrange's relation then directly gives the formula used in practice to rebuild the direct solution from the adjoint one:
These statements are general and apply in the time domain, where ![]() $\boldsymbol {X}_m \equiv (\boldsymbol {x}_m; t_m)$ and
$\boldsymbol {X}_m \equiv (\boldsymbol {x}_m; t_m)$ and ![]() $\delta _{\boldsymbol {X}_m} \equiv \delta (\boldsymbol {x}-\boldsymbol {x}_m) \delta (t-t_m)$, as well as in the Fourier domain for which
$\delta _{\boldsymbol {X}_m} \equiv \delta (\boldsymbol {x}-\boldsymbol {x}_m) \delta (t-t_m)$, as well as in the Fourier domain for which ![]() $\boldsymbol {X}_m \equiv \boldsymbol {x}_m$ and
$\boldsymbol {X}_m \equiv \boldsymbol {x}_m$ and ![]() $\delta _{\boldsymbol {X}_m} \equiv \delta (\boldsymbol {x}-\boldsymbol {x}_m)$. In the rest of this study for the sake of simplicity only scalar wave equations are considered, but it is straightforward to transpose these results to multivariable linear operators (Wapenaar Reference Wapenaar1996) by making use of a multivariable Hermitian scalar product, resulting in turn in the computation of vector adjoint Green's functions.
$\delta _{\boldsymbol {X}_m} \equiv \delta (\boldsymbol {x}-\boldsymbol {x}_m)$. In the rest of this study for the sake of simplicity only scalar wave equations are considered, but it is straightforward to transpose these results to multivariable linear operators (Wapenaar Reference Wapenaar1996) by making use of a multivariable Hermitian scalar product, resulting in turn in the computation of vector adjoint Green's functions.
In the literature, the relation (2.6) is sometimes referred to as the representation theorem (Vasconcelos, Snieder & Douma Reference Vasconcelos, Snieder and Douma2009). In their pioneering work, Tam & Auriault (Reference Tam and Auriault1998, equation (A 12)), derived a first version of this relation enabling fluctuating pressure predictions for sources of the momentum equations. An extension to sources set in the energy equation has been given by Afsar et al. (Reference Afsar, Dowling and Karabasov2006) and Afsar, Dowling & Karabasov (Reference Afsar, Dowling and Karabasov2007). The expression given here is its general expression and handles any linear operator ![]() $\mathcal {L}_0$ and any scalar product, any source term
$\mathcal {L}_0$ and any scalar product, any source term ![]() $s$ can be used to rebuild any field variable
$s$ can be used to rebuild any field variable ![]() $p$ from the considered linear operator
$p$ from the considered linear operator ![]() $\mathcal {L}_0$ if corresponding adjoint Green's function
$\mathcal {L}_0$ if corresponding adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {X}_m}$ is computed.
${G}^\dagger _{\boldsymbol {X}_m}$ is computed.
One convenient feature of the adjoint method, is to change the convolution nature of Green's integral representation of the solution into a correlation type representation (Vasconcelos et al. Reference Vasconcelos, Snieder and Douma2009). As an illustration, consider a time domain problem, with ![]() $\langle \, f,g\rangle = \int _\mathbb {R}\,\textrm {d}t \int _{\Omega }\,\textrm {d}\boldsymbol {x}\ f(\boldsymbol {x},t) g(\boldsymbol {x},t)$, then Green's formula reads
$\langle \, f,g\rangle = \int _\mathbb {R}\,\textrm {d}t \int _{\Omega }\,\textrm {d}\boldsymbol {x}\ f(\boldsymbol {x},t) g(\boldsymbol {x},t)$, then Green's formula reads
where for the sake of clarity boundary conditions have been omitted. If now a shift-invariant problem is considered, i.e. ![]() $G_{\boldsymbol {x}_s,t_s}(\boldsymbol {x}_m,t_m) \equiv G(\boldsymbol {x}_m-\boldsymbol {x}_s,t_m-t_s)$, the previous expression can be expressed as a double convolution product over the source position
$G_{\boldsymbol {x}_s,t_s}(\boldsymbol {x}_m,t_m) \equiv G(\boldsymbol {x}_m-\boldsymbol {x}_s,t_m-t_s)$, the previous expression can be expressed as a double convolution product over the source position ![]() $\boldsymbol {x}_s$ and emission time
$\boldsymbol {x}_s$ and emission time ![]() $t_s$. In contrast, the operational expression of Lagrange's identity given in (2.6) writes
$t_s$. In contrast, the operational expression of Lagrange's identity given in (2.6) writes
Relying on conventional Green's integral method, ![]() $G_{\boldsymbol {x}_s,t_s}$ should be recomputed for each
$G_{\boldsymbol {x}_s,t_s}$ should be recomputed for each ![]() $\boldsymbol {x}_s$, whereas if the solution
$\boldsymbol {x}_s$, whereas if the solution ![]() $p$ of the propagation problem is sought at one single point
$p$ of the propagation problem is sought at one single point ![]() $\boldsymbol {x}_m$, the adjoint method requires only a single calculation of
$\boldsymbol {x}_m$, the adjoint method requires only a single calculation of ![]() ${G}^\dagger _{\boldsymbol {x}_m,t_m}$ at
${G}^\dagger _{\boldsymbol {x}_m,t_m}$ at ![]() $\boldsymbol {x}_m$. This approach shows to be very efficient from a computational point of view, for acoustic prediction to a finite number of points of widespread stochastic sources; this is precisely the appeal of this technique. What is more, as long as the mean flow of the propagation problem and the observer are unchanged, adjoint Green's function
$\boldsymbol {x}_m$. This approach shows to be very efficient from a computational point of view, for acoustic prediction to a finite number of points of widespread stochastic sources; this is precisely the appeal of this technique. What is more, as long as the mean flow of the propagation problem and the observer are unchanged, adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {x}_m,t_m}$ can be reused.
${G}^\dagger _{\boldsymbol {x}_m,t_m}$ can be reused.
At last, recall that the adjoint representation is not unique (Roberts Reference Roberts1960), different scalar products lead indeed to different adjoint formulations. Attention must therefore be paid when comparing, for instance, the adjoint pressure ![]() ${p}^\dagger$ computed from the set of adjoint LEE with the adjoint pressure
${p}^\dagger$ computed from the set of adjoint LEE with the adjoint pressure ![]() ${p}^\dagger$ computed with adjoint Lilley's equation (Tam & Auriault Reference Tam and Auriault1998, figure 9), in general those both variables have no common points.
${p}^\dagger$ computed with adjoint Lilley's equation (Tam & Auriault Reference Tam and Auriault1998, figure 9), in general those both variables have no common points.
2.2. Reciprocity relation and the notion of self-adjointness
Adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {x}_m,t_m}$ for a source position
${G}^\dagger _{\boldsymbol {x}_m,t_m}$ for a source position ![]() $\boldsymbol {x}_m$ at time
$\boldsymbol {x}_m$ at time ![]() $t_m$, is defined by
$t_m$, is defined by
 \begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {G}^\dagger_{\boldsymbol{x}_m,t_m}(\boldsymbol{x},t) = \delta(\boldsymbol{x}-\boldsymbol{x}_m)\delta(t-t_m) & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {G}^\dagger_{\boldsymbol{x}_m,t_m}(\boldsymbol{x},t) = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {G}^\dagger_{\boldsymbol{x}_m,t_m}(\boldsymbol{x},t) = \delta(\boldsymbol{x}-\boldsymbol{x}_m)\delta(t-t_m) & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {G}^\dagger_{\boldsymbol{x}_m,t_m}(\boldsymbol{x},t) = 0 & \text{on}\ \partial\Omega, \end{cases} \end{equation}
when instead of the physical problem defined in (2.1), an impulsive problem at position ![]() $\boldsymbol {x}_s$ and time
$\boldsymbol {x}_s$ and time ![]() $t_s$ is considered:
$t_s$ is considered:
 \begin{equation} \begin{cases} \mathcal{L}_0\ G_{\boldsymbol{x}_s,t_s}(\boldsymbol{x},t) = \delta(\boldsymbol{x}-\boldsymbol{x}_s)\delta(t-t_s) & \text{in}\ \Omega,\\ \mathcal{B}_0\ G_{\boldsymbol{x}_s,t_s}(\boldsymbol{x},t) = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathcal{L}_0\ G_{\boldsymbol{x}_s,t_s}(\boldsymbol{x},t) = \delta(\boldsymbol{x}-\boldsymbol{x}_s)\delta(t-t_s) & \text{in}\ \Omega,\\ \mathcal{B}_0\ G_{\boldsymbol{x}_s,t_s}(\boldsymbol{x},t) = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
The general scalar reciprocity principle is recovered with help of Lagrange's identity (2.4) and the above-introduced scalar product ![]() $\langle, \rangle$:
$\langle, \rangle$:
As the direct problem is causal, its adjoint is then necessary anti-causal, e.g. (Goldstein Reference Goldstein2006, equation (A8)),
This complies with the analysis of Karabasov et al. (Semiletov & Karabasov Reference Semiletov and Karabasov2013; Karabasov & Sandberg Reference Karabasov and Sandberg2015) and Afsar et al. (Reference Afsar, Sescu, Sassanis and Lele2017) who stressed that, the adjoint source acts as a sink and that the adjoint acoustic solution is inward-going, but goes beyond. The adjoint solution needs furthermore to go backward in time and is intrinsically anti-causal (Lamb Jr. Reference Lamb1995, §§ 4.5 and 4.6; Stone & Goldbart Reference Stone and Goldbart2009, § 4.2). This has been pointed out in the flow receptivity community by Luchini & Bottaro (Reference Luchini and Bottaro1998) and since then is well-established (Barone & Lele Reference Barone and Lele2005; Wei & Freund Reference Wei and Freund2006). A proof for this can be found in the literature for the heat equation (Stone & Goldbart Reference Stone and Goldbart2009, § 6.4.2) and is given in appendix B. for the convected Helmholtz's wave equation.
As a consequence, only some very specific problems may verify (2.1) ![]() $\equiv$ (2.3). Such problems are referred to as self-adjoint (or symmetric) for which the well known symmetry property of Green's function is recovered. Strictly speaking, due to the boundary conditions, no self-adjoint problem exists for time-dependant problems. The solution would indeed need to be causal and anti-causal at the same time. In this work, the mathematical self-adjoint definition is gently relaxed so to also call self-adjoint, time problems for which Green's function, for the usual scalar product, verifies
$\equiv$ (2.3). Such problems are referred to as self-adjoint (or symmetric) for which the well known symmetry property of Green's function is recovered. Strictly speaking, due to the boundary conditions, no self-adjoint problem exists for time-dependant problems. The solution would indeed need to be causal and anti-causal at the same time. In this work, the mathematical self-adjoint definition is gently relaxed so to also call self-adjoint, time problems for which Green's function, for the usual scalar product, verifies ![]() ${G}^\dagger _{\boldsymbol {x}_m,t_m}(\boldsymbol {x}_s,t_s) = G_{\boldsymbol {x}_s,-t_s}(\boldsymbol {x}_m,-t_m)$. From this standpoint, the acoustic problem governed by Helmholtz's equation is self-adjoint, see Morse & Feshbach (Reference Morse and Feshbach1953, § 7.3) or Eisler (Reference Eisler1969). Skew-symmetric problems are also included in this enlarged definition of self-adjointness. This seems reasonable, since for some well-chosen scalar products, the LEE for a uniform and steady mean flow are skew-symmetric while Helmholtz's equation, which is physically equivalent in its description, is symmetric. This result, moreover, complies with the work of Möhring (Reference Möhring2001), in which the classical reciprocity principle is derived from antisymmetric relations. Thus for an acoustic propagation problem with ordinary boundary conditions to verify this enlarged definition of self-adjointness, it is sufficient that
${G}^\dagger _{\boldsymbol {x}_m,t_m}(\boldsymbol {x}_s,t_s) = G_{\boldsymbol {x}_s,-t_s}(\boldsymbol {x}_m,-t_m)$. From this standpoint, the acoustic problem governed by Helmholtz's equation is self-adjoint, see Morse & Feshbach (Reference Morse and Feshbach1953, § 7.3) or Eisler (Reference Eisler1969). Skew-symmetric problems are also included in this enlarged definition of self-adjointness. This seems reasonable, since for some well-chosen scalar products, the LEE for a uniform and steady mean flow are skew-symmetric while Helmholtz's equation, which is physically equivalent in its description, is symmetric. This result, moreover, complies with the work of Möhring (Reference Möhring2001), in which the classical reciprocity principle is derived from antisymmetric relations. Thus for an acoustic propagation problem with ordinary boundary conditions to verify this enlarged definition of self-adjointness, it is sufficient that ![]() ${\mathcal {L}}^\dagger _0 = {\pm }\mathcal {L}_0$.
${\mathcal {L}}^\dagger _0 = {\pm }\mathcal {L}_0$.
3. Application to Lilley's equation
3.1. Derivation of Lilley's adjoint problem
Acoustic propagation in a steady parallel mean flow is considered. In spite of their apparent limitations, these mean flows are of practical importance since they correspond to configurations encountered in jets and many subtle phenomena can be described with them. The equation derived by Lilley et al. (Reference Lilley, Plumblee, Strahle, Ruo and Doak1972) is known to take exactly the acoustic propagation effects over such parallel mean flows into account. This section shows how an adjoint method based upon this wave equation can be used.
From now on, and in later sections, all results will be derived in the frequency domain for a pulsation frequency ![]() $\omega$, which is related to the time domain through Fourier transform,
$\omega$, which is related to the time domain through Fourier transform,
Following this convention, the material derivative along the mean flow writes as ![]() $D_{\boldsymbol {u}_0} = \{-{\rm i}\omega + \boldsymbol {u}_0 \boldsymbol{\cdot} \boldsymbol {\nabla }\}$. Consistently, the canonical scalar product for complex valued functions, defined for
$D_{\boldsymbol {u}_0} = \{-{\rm i}\omega + \boldsymbol {u}_0 \boldsymbol{\cdot} \boldsymbol {\nabla }\}$. Consistently, the canonical scalar product for complex valued functions, defined for ![]() $f$ and
$f$ and ![]() $g$ by
$g$ by
is considered, where ![]() ${f}^*$ denotes the complex conjugate of
${f}^*$ denotes the complex conjugate of ![]() $f$. Let
$f$. Let ![]() $\boldsymbol {u}_0 = u_{0,1}\boldsymbol {e}_1$ be the mean velocity field with
$\boldsymbol {u}_0 = u_{0,1}\boldsymbol {e}_1$ be the mean velocity field with ![]() $\boldsymbol {e}_1$ a unit vector in the flow direction,
$\boldsymbol {e}_1$ a unit vector in the flow direction, ![]() $\rho _0$ the mean density and
$\rho _0$ the mean density and ![]() $p_0$ the mean pressure considered. The evolution of the fluctuating pressure
$p_0$ the mean pressure considered. The evolution of the fluctuating pressure ![]() $p$ is governed by Lilley's equation and obeys some radiating boundary condition
$p$ is governed by Lilley's equation and obeys some radiating boundary condition ![]() $\mathcal {B}_0$, leading to the direct problem
$\mathcal {B}_0$, leading to the direct problem
 \begin{equation} \begin{cases} \mathcal{L}_0\ p = D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}(p) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} p) \right) + 2a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial p}{\partial x_1} \right) = S_{Lilley} & \text{in}\ \Omega,\\ \mathcal{B}_0\ p = 0 & \text{on} \ \partial\Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathcal{L}_0\ p = D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}(p) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} p) \right) + 2a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial p}{\partial x_1} \right) = S_{Lilley} & \text{in}\ \Omega,\\ \mathcal{B}_0\ p = 0 & \text{on} \ \partial\Omega, \end{cases} \end{equation}
where ![]() $a_0 = \sqrt {\gamma p_0/\rho _0}$ is the mean speed of sound. The source term
$a_0 = \sqrt {\gamma p_0/\rho _0}$ is the mean speed of sound. The source term ![]() $S_{Lilley}$ of Lilley's equation can be expressed with some generic source term definition
$S_{Lilley}$ of Lilley's equation can be expressed with some generic source term definition ![]() $(S_{\rho },\boldsymbol {S}_{\boldsymbol {u}},S_p)$ of the LEE, and can be found in the literature, e.g. in Bailly, Bogey & Candel (Reference Bailly, Bogey and Candel2010, equation (26)),
$(S_{\rho },\boldsymbol {S}_{\boldsymbol {u}},S_p)$ of the LEE, and can be found in the literature, e.g. in Bailly, Bogey & Candel (Reference Bailly, Bogey and Candel2010, equation (26)),
To define the corresponding adjoint problem, the linear operator ![]() ${\mathcal {L}}^\dagger _0$ and adjoint boundary conditions
${\mathcal {L}}^\dagger _0$ and adjoint boundary conditions ![]() ${\mathcal {B}}^\dagger _0$ which fulfil Lagrange's identity are now sought. Starting with the left-hand side of Lagrange's identity (2.2)
${\mathcal {B}}^\dagger _0$ which fulfil Lagrange's identity are now sought. Starting with the left-hand side of Lagrange's identity (2.2)
the right-hand side of the equality is obtained after using integration by parts and other vector calculus formulas, leading to
 \begin{align} \langle {p}^\dagger,\mathcal{L}_0\ p\rangle &= \displaystyle \int_\Omega \,\textrm{d}\boldsymbol{x}\ \left\{\vphantom{\left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right)} -D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}\left({p}^\dagger\right) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} {p}^\dagger) \right)\right.\nonumber\\ &\quad \left. \displaystyle + 4 a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right) + 3 \boldsymbol{\nabla} \boldsymbol{\cdot} \left( a_0^2 \boldsymbol{\nabla} u_{0,1} \right) \dfrac{\partial {p}^\dagger}{\partial x_1} \right\}^{\ast} p \nonumber\\ &\quad \displaystyle + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \left( { D^2_{\boldsymbol{u}_0}({p}^\dagger) }^* p - {D_{\boldsymbol{u}_0}({p}^\dagger) }^* D_{\boldsymbol{u}_0}(p) \right) \boldsymbol{u}_0 \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ {{p}^\dagger}^* \left( D^2_{\boldsymbol{u}_0}(p) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} p) \right) \boldsymbol{u}_0 \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \left( -2 a_0^2 { \dfrac{\partial {p}^\dagger}{\partial x_1} }^* \boldsymbol{\nabla} u_{0,1} - a_0^2 { \boldsymbol{\nabla}( D_{\boldsymbol{u}_0}({p}^\dagger) ) }^* \right) p \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ - 2a_0^2 { {p}^\dagger }^* (\boldsymbol{\nabla} p \boldsymbol{\cdot} \boldsymbol{\nabla} u_{0,1})\boldsymbol{x_1} + a_0^2 { D_{\boldsymbol{u}_0}({p}^\dagger) }^* \boldsymbol{\nabla} p \right]. \end{align}
\begin{align} \langle {p}^\dagger,\mathcal{L}_0\ p\rangle &= \displaystyle \int_\Omega \,\textrm{d}\boldsymbol{x}\ \left\{\vphantom{\left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right)} -D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}\left({p}^\dagger\right) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} {p}^\dagger) \right)\right.\nonumber\\ &\quad \left. \displaystyle + 4 a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right) + 3 \boldsymbol{\nabla} \boldsymbol{\cdot} \left( a_0^2 \boldsymbol{\nabla} u_{0,1} \right) \dfrac{\partial {p}^\dagger}{\partial x_1} \right\}^{\ast} p \nonumber\\ &\quad \displaystyle + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \left( { D^2_{\boldsymbol{u}_0}({p}^\dagger) }^* p - {D_{\boldsymbol{u}_0}({p}^\dagger) }^* D_{\boldsymbol{u}_0}(p) \right) \boldsymbol{u}_0 \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ {{p}^\dagger}^* \left( D^2_{\boldsymbol{u}_0}(p) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} p) \right) \boldsymbol{u}_0 \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \left( -2 a_0^2 { \dfrac{\partial {p}^\dagger}{\partial x_1} }^* \boldsymbol{\nabla} u_{0,1} - a_0^2 { \boldsymbol{\nabla}( D_{\boldsymbol{u}_0}({p}^\dagger) ) }^* \right) p \right]\nonumber\\ & \displaystyle \quad + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ - 2a_0^2 { {p}^\dagger }^* (\boldsymbol{\nabla} p \boldsymbol{\cdot} \boldsymbol{\nabla} u_{0,1})\boldsymbol{x_1} + a_0^2 { D_{\boldsymbol{u}_0}({p}^\dagger) }^* \boldsymbol{\nabla} p \right]. \end{align}
The Green–Ostrogradsky theorem helps to express the divergence term as a contour integral. ![]() ${\mathcal {B}}^\dagger _0$ is defined so that together with
${\mathcal {B}}^\dagger _0$ is defined so that together with ![]() $\mathcal {B}_0$ this boundary term is zero. Thus, if
$\mathcal {B}_0$ this boundary term is zero. Thus, if ![]() $p$ and
$p$ and ![]() ${p}^\dagger$, respectively, satisfy their boundary conditions, the previous contour integral does not contribute and Lagrange's identity,
${p}^\dagger$, respectively, satisfy their boundary conditions, the previous contour integral does not contribute and Lagrange's identity, ![]() $\left \langle {p}^\dagger,\mathcal {L}_0\ p\right \rangle = \left \langle {\mathcal {L}}^\dagger _0\ {p}^\dagger, p\right \rangle$ is retrieved. Finally by identification, the adjoint problem associated with Lilley's equation is obtained as
$\left \langle {p}^\dagger,\mathcal {L}_0\ p\right \rangle = \left \langle {\mathcal {L}}^\dagger _0\ {p}^\dagger, p\right \rangle$ is retrieved. Finally by identification, the adjoint problem associated with Lilley's equation is obtained as
 \begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {p}^\dagger = \displaystyle - D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}({p}^\dagger) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} {p}^\dagger) \right) + 4 a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right) & \\ \qquad\quad\ \ + 3a_0^2 {\rm \Delta} u_{0,1} \dfrac{\partial {p}^\dagger}{\partial x_1} + 3 \dfrac{\partial {p}^\dagger}{\partial x_1} \boldsymbol{\nabla} a_0^2 \boldsymbol{\cdot} \boldsymbol{\nabla} u_{0,1} & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {p}^\dagger = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
\begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {p}^\dagger = \displaystyle - D_{\boldsymbol{u}_0}\left( D^2_{\boldsymbol{u}_0}({p}^\dagger) - \boldsymbol{\nabla} \boldsymbol{\cdot} (a_0^2 \boldsymbol{\nabla} {p}^\dagger) \right) + 4 a_0^2 \boldsymbol{\nabla} u_{0,1} \boldsymbol{\cdot} \boldsymbol{\nabla} \left( \dfrac{\partial {p}^\dagger}{\partial x_1} \right) & \\ \qquad\quad\ \ + 3a_0^2 {\rm \Delta} u_{0,1} \dfrac{\partial {p}^\dagger}{\partial x_1} + 3 \dfrac{\partial {p}^\dagger}{\partial x_1} \boldsymbol{\nabla} a_0^2 \boldsymbol{\cdot} \boldsymbol{\nabla} u_{0,1} & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {p}^\dagger = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
One has ![]() ${\mathcal {L}}^\dagger _0 \neq \pm \mathcal {L}_0$ and Lilley's equation is therefore not self-adjoint.
${\mathcal {L}}^\dagger _0 \neq \pm \mathcal {L}_0$ and Lilley's equation is therefore not self-adjoint.
In the following, a numerical execution of the adjoint method is conducted for a sheared and stratified mean flow, for which Lilley's equation and its adjoint are solved. Computations are achieved with PROPA, an in-house frequency domain code using a direct inversion method. Care must be taken in the implementation of the adjoint anti-causality conditions. A description of the numerical procedure is provided in appendix A..
3.2. Solution to the direct problem
The direct problem under consideration here is the two-dimensional radiation of an acoustic source set in a sheared and stratified flow and corresponds to the well-documented mean flow analysed in the fourth computational aeroacoustic workshop (Dahl Reference Dahl2004). The mean velocity profile follows a Gaussian evolution in the transverse direction
where ![]() $\boldsymbol {x} = (x_1, x_2)$,
$\boldsymbol {x} = (x_1, x_2)$, ![]() $u_j = M_ja_j$,
$u_j = M_ja_j$, ![]() $a_j = \sqrt {\gamma R T_j}$ and
$a_j = \sqrt {\gamma R T_j}$ and ![]() $\sigma = \sqrt {0.845 \, \log (2)}$ m is its standard deviation. To model a high-speed and heated jet flow, the following values are taken:
$\sigma = \sqrt {0.845 \, \log (2)}$ m is its standard deviation. To model a high-speed and heated jet flow, the following values are taken: ![]() $M_j =0.756$,
$M_j =0.756$, ![]() $T_j = 600\ \textrm {K}$,
$T_j = 600\ \textrm {K}$, ![]() $T_\infty = 300\ \textrm {K}$,
$T_\infty = 300\ \textrm {K}$, ![]() $\gamma = 1.4$ and
$\gamma = 1.4$ and ![]() $R = 287\ \textrm {m}^{2}\,\textrm {s}^{-2}\,\textrm {K}^{-1}$. Considering
$R = 287\ \textrm {m}^{2}\,\textrm {s}^{-2}\,\textrm {K}^{-1}$. Considering ![]() $\rho _j = \gamma p_0 / a_j^2$ and
$\rho _j = \gamma p_0 / a_j^2$ and ![]() $p_0 = 103\,330\ \textrm {Pa}$, the mean density
$p_0 = 103\,330\ \textrm {Pa}$, the mean density ![]() $\rho _0(x_2)$ is defined with Crocco–Busemann's law
$\rho _0(x_2)$ is defined with Crocco–Busemann's law
The stability analysis of this mean flow profile has been performed and the spatial growth rate of the Kelvin–Helmholtz instability wave is given in Bailly & Bogey (Reference Bailly and Bogey2003, figure 1). To avoid the triggering of these hydrodynamic waves, a source pulsation of ![]() $\omega = 200 {\rm \pi}\ \textrm {rad}\,\textrm {s}^{-1}$ is chosen, which ensures possible vortical disturbances are damped and do not corrupt the acoustic solution. This frequency corresponds to a Strouhal number of
$\omega = 200 {\rm \pi}\ \textrm {rad}\,\textrm {s}^{-1}$ is chosen, which ensures possible vortical disturbances are damped and do not corrupt the acoustic solution. This frequency corresponds to a Strouhal number of ![]() $St_{2 \sigma } = 2 \sigma f/u_j =0.60$ and to
$St_{2 \sigma } = 2 \sigma f/u_j =0.60$ and to ![]() $\omega b /u_j = 2.20$ according to the notation given in Bailly & Bogey (Reference Bailly and Bogey2003). The source for Lilley's equation chosen here corresponds to a quadrupole source
$\omega b /u_j = 2.20$ according to the notation given in Bailly & Bogey (Reference Bailly and Bogey2003). The source for Lilley's equation chosen here corresponds to a quadrupole source ![]() $\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ of unitary amplitude, computed as the gradient of a Gaussian monopolar source
$\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ of unitary amplitude, computed as the gradient of a Gaussian monopolar source ![]() $S_m$ whose spatial variation is given by
$S_m$ whose spatial variation is given by ![]() $S_m= \sigma _s \sqrt {e}\ \exp ({-(x_1^2 + x_2^2)/(2 \sigma _s^2)})$, where
$S_m= \sigma _s \sqrt {e}\ \exp ({-(x_1^2 + x_2^2)/(2 \sigma _s^2)})$, where ![]() $\sigma _s = \sigma /4$. This sound source for the direct problem
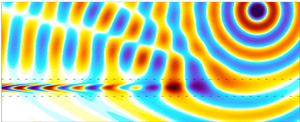
$\sigma _s = \sigma /4$. This sound source for the direct problem ![]() $\rho _0 \boldsymbol {S}_{\boldsymbol {u}} = \boldsymbol {\nabla } S_m$ is taken into account in Lilley's equation with the relation (3.4), and is depicted in figure 2(a,b). The channelling of acoustic waves propagating in the opposite direction to the mean flow inside the jet, and the generation of a cone of silence downstream, can be easily identified in the computed fields; however, the quadrupole nature of the acoustic source is not.
$\rho _0 \boldsymbol {S}_{\boldsymbol {u}} = \boldsymbol {\nabla } S_m$ is taken into account in Lilley's equation with the relation (3.4), and is depicted in figure 2(a,b). The channelling of acoustic waves propagating in the opposite direction to the mean flow inside the jet, and the generation of a cone of silence downstream, can be easily identified in the computed fields; however, the quadrupole nature of the acoustic source is not.

Figure 2. Direct problem for Lilley's wave equation. ![]() $(a,b)$ Linearised Euler equations equivalent quadrupole source
$(a,b)$ Linearised Euler equations equivalent quadrupole source ![]() $\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ forcing the direct problem (
$\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ forcing the direct problem (![]() $(a)$
$(a)$![]() $\rho _0 S_{u_1}$ and
$\rho _0 S_{u_1}$ and ![]() $(b)$
$(b)$![]() $\rho _0 S_{u_2}$).
$\rho _0 S_{u_2}$). ![]() $(c,d)$ Mach number
$(c,d)$ Mach number ![]() $M_0$ and density
$M_0$ and density ![]() $\rho _0$ profiles of the parallel mean flow considered, and the real part of the pressure field is shown. Dashed lines represent the position of maximal shearing (
$\rho _0$ profiles of the parallel mean flow considered, and the real part of the pressure field is shown. Dashed lines represent the position of maximal shearing (![]() $x_2/\sigma = 1$).
$x_2/\sigma = 1$).
3.3. Reconstruction of the solution with the adjoint method
The adjoint method is now used to recover the direct field solution. For this analysis a sample of 69 equispaced adjoint sources along a line ![]() $\boldsymbol {x}_2/\sigma = 9.0$ is considered. For each of these adjoint sources the anti-causal adjoint Lilley's problem (3.7) is solved. The same base flow, the same mesh and the same frequency as for the direct problem are considered. Figure 3 shows two samples of adjoint Green's problem solved among a total set of
$\boldsymbol {x}_2/\sigma = 9.0$ is considered. For each of these adjoint sources the anti-causal adjoint Lilley's problem (3.7) is solved. The same base flow, the same mesh and the same frequency as for the direct problem are considered. Figure 3 shows two samples of adjoint Green's problem solved among a total set of ![]() $69$. Wherever the mean velocity gradient is zero, the adjoint Lilley equation behaves like a classical acoustic propagation operator. This can be observed in figure 3 and inferred from the self-adjoint property of Lilley's equation for a constant flow profile (compare (3.3) and (3.7)). Yet wherever the mean flow is sheared, the propagation problem ceases to be self-adjoint and specific features of the adjoint formulation (3.7) are expected. The wave patterns warped in the flow channel for numerical adjoint Green's function computed at
$69$. Wherever the mean velocity gradient is zero, the adjoint Lilley equation behaves like a classical acoustic propagation operator. This can be observed in figure 3 and inferred from the self-adjoint property of Lilley's equation for a constant flow profile (compare (3.3) and (3.7)). Yet wherever the mean flow is sheared, the propagation problem ceases to be self-adjoint and specific features of the adjoint formulation (3.7) are expected. The wave patterns warped in the flow channel for numerical adjoint Green's function computed at ![]() $\boldsymbol {x}_m/\sigma = (25,9.0)$ and shown in figure 3 is such a phenomenon. Recall that the fields presented in figure 3 are anti-causal and focus toward the adjoint source.
$\boldsymbol {x}_m/\sigma = (25,9.0)$ and shown in figure 3 is such a phenomenon. Recall that the fields presented in figure 3 are anti-causal and focus toward the adjoint source.

Figure 3. Numerical adjoint Green's problems associated with Lilley's equation at ![]() $\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions
$\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions ![]() $x_1/\sigma = 0.0$,
$x_1/\sigma = 0.0$, ![]() $x_1/\sigma = 25$ and
$x_1/\sigma = 25$ and ![]() $x_2/\sigma =9.0$.
$x_2/\sigma =9.0$. ![]() $(a,c)$ Adjoint Gaussian source terms
$(a,c)$ Adjoint Gaussian source terms ![]() ${S}^{\dagger,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing, and
${S}^{\dagger,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing, and ![]() $(b,d)$ the associated adjoint fields
$(b,d)$ the associated adjoint fields ![]() ${p}^\dagger$ regarded as numerical adjoint Green's functions
${p}^\dagger$ regarded as numerical adjoint Green's functions ![]() ${G}^{\dagger,N}_{\boldsymbol {x}_m}$.
${G}^{\dagger,N}_{\boldsymbol {x}_m}$.
To properly define adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {x}_m}$, the impulse response of the linear operator
${G}^\dagger _{\boldsymbol {x}_m}$, the impulse response of the linear operator ![]() ${\mathcal {L}}^\dagger _0$ should be considered, that is
${\mathcal {L}}^\dagger _0$ should be considered, that is ![]() ${\mathcal {L}}^\dagger _0\ {G}^\dagger _{\boldsymbol {x}_m} = \delta _{\boldsymbol {x}_m}$. For most numerical solvers, computing the solution to an exact Dirac delta function
${\mathcal {L}}^\dagger _0\ {G}^\dagger _{\boldsymbol {x}_m} = \delta _{\boldsymbol {x}_m}$. For most numerical solvers, computing the solution to an exact Dirac delta function ![]() $\delta _{\boldsymbol {x}_m}$ is tricky. A bypass to this is considered here; narrow Gaussian sources are chosen to force the linear operator
$\delta _{\boldsymbol {x}_m}$ is tricky. A bypass to this is considered here; narrow Gaussian sources are chosen to force the linear operator ![]() ${\mathcal {L}}^\dagger _0$ given in (3.7). Then when the size
${\mathcal {L}}^\dagger _0$ given in (3.7). Then when the size ![]() $L$ of the numerical adjoint source
$L$ of the numerical adjoint source ![]() ${S}^{\dagger,N}_{\boldsymbol {x}_m}$ is small with respect to the acoustic wavelength
${S}^{\dagger,N}_{\boldsymbol {x}_m}$ is small with respect to the acoustic wavelength ![]() $\lambda$, mathematical Green's function
$\lambda$, mathematical Green's function ![]() ${G}^\dagger _{\boldsymbol {x}_m}$ can be approximated with the following normalisation of numerical Green's function
${G}^\dagger _{\boldsymbol {x}_m}$ can be approximated with the following normalisation of numerical Green's function ![]() ${G}^{\dagger,N}_{\boldsymbol {x}_m}$:
${G}^{\dagger,N}_{\boldsymbol {x}_m}$:
where ![]() ${S}^{\dagger,N}_{\boldsymbol {x}_m}$ is the numerical source term of the adjoint problem, chosen presently to be a sharp Gaussian around
${S}^{\dagger,N}_{\boldsymbol {x}_m}$ is the numerical source term of the adjoint problem, chosen presently to be a sharp Gaussian around ![]() ${\boldsymbol {x}_m}$. For a Gaussian source, its size
${\boldsymbol {x}_m}$. For a Gaussian source, its size ![]() $L$ is measured by its standard deviation
$L$ is measured by its standard deviation ![]() $\sigma _{s}$, for the present analysis,
$\sigma _{s}$, for the present analysis, ![]() $\lambda /\sigma _{s}\approx 23$. Following this procedure, for each adjoint solution, adjoint Green's function
$\lambda /\sigma _{s}\approx 23$. Following this procedure, for each adjoint solution, adjoint Green's function ![]() ${G}^\dagger _{\boldsymbol {x}_m}$ is defined. Lagrange's identity (2.2) then readily gives at each sample position
${G}^\dagger _{\boldsymbol {x}_m}$ is defined. Lagrange's identity (2.2) then readily gives at each sample position ![]() $\boldsymbol {x}_m$ the physical pressure field
$\boldsymbol {x}_m$ the physical pressure field ![]() $p(\boldsymbol {x}_m)$:
$p(\boldsymbol {x}_m)$:
Results obtained for the investigated sampled line are compared in figure 4 against the direct problem solution seen as a reference. Figure 4 shows an almost perfect reconstruction of the reference field with the adjoint method, demonstrating thus the viability of the approach, and gives an a posteriori validation of the utilised numerical trick to compute an anti-causal solution (refer to appendix B.). In practice, the only limitation of the method is the ability to properly compute numerical adjoint Green's function. The bypass procedure, given in (3.10), requiring that the adjoint source is compact (![]() $\lambda /L\gg 1$) proves to work correctly as well.
$\lambda /L\gg 1$) proves to work correctly as well.

Figure 4. Validation of the adjoint method along the line ![]() $x_2/\sigma = 9.0$ for Lilley's equation. Reference data for the pressure
$x_2/\sigma = 9.0$ for Lilley's equation. Reference data for the pressure ![]() $p$ (real part, ——; imaginary part, - - - -) is taken from the direct field computation presented in figure 2. Rebuilt pressure field
$p$ (real part, ——; imaginary part, - - - -) is taken from the direct field computation presented in figure 2. Rebuilt pressure field ![]() $p$ (real part,
$p$ (real part, ![]() $\circ$; imaginary part,
$\circ$; imaginary part, ![]() $+$) is obtained with Lagrange's identity.
$+$) is obtained with Lagrange's identity.
3.4. Reconstruction of the solution with the FRT
The FRT introduced by Lyamshev (Reference Lyamshev1961) and Howe (Reference Howe1975), and formulated in a more general statement by Godin (Reference Godin1997), exploits alternatively the reciprocity principle to rebuild the physical field. The FRT is used here and applied to Lilley's wave equation to enable comparison with the adjoint method.
In the framework of the FRT, the reciprocal problem is obtained from the direct one (2.1) by turning the velocity dependences in ![]() $\boldsymbol {u}_0$ in the linear operators
$\boldsymbol {u}_0$ in the linear operators ![]() $\mathcal {L}_0$ and
$\mathcal {L}_0$ and ![]() $\mathcal {B}_0$ into
$\mathcal {B}_0$ into ![]() $-\boldsymbol {u}_0$. The corresponding operators will be referred to as
$-\boldsymbol {u}_0$. The corresponding operators will be referred to as ![]() $\mathcal {L}^-_0$ and
$\mathcal {L}^-_0$ and ![]() $\mathcal {B}^-_0$, the reciprocal field
$\mathcal {B}^-_0$, the reciprocal field ![]() $p^-$ is then governed by the FRT equations
$p^-$ is then governed by the FRT equations
 \begin{equation} \begin{cases} \mathcal{L}^-_0\ p^- = s^- & \text{in} \ \Omega\\ \mathcal{B}^-_0\ p^- = 0 & \text{on} \ \partial\Omega \end{cases}, \end{equation}
\begin{equation} \begin{cases} \mathcal{L}^-_0\ p^- = s^- & \text{in} \ \Omega\\ \mathcal{B}^-_0\ p^- = 0 & \text{on} \ \partial\Omega \end{cases}, \end{equation}
where ![]() $s^-$ is the source for the FRT problem considered. In practice, it is sufficient to invert the mean flow
$s^-$ is the source for the FRT problem considered. In practice, it is sufficient to invert the mean flow ![]() $\boldsymbol {u}_0$ direction in the direct problem solver to compute
$\boldsymbol {u}_0$ direction in the direct problem solver to compute ![]() $p^-$. This has been achieved for Lilley's wave equation for which simulations are conducted for the same sampling of sources as for the adjoint problem presented in the previous paragraph, that is by taking
$p^-$. This has been achieved for Lilley's wave equation for which simulations are conducted for the same sampling of sources as for the adjoint problem presented in the previous paragraph, that is by taking ![]() $s^- \equiv {s}^\dagger$. The same mean density
$s^- \equiv {s}^\dagger$. The same mean density ![]() $\rho _0$, pulsation frequency
$\rho _0$, pulsation frequency ![]() $\omega$ and mesh as for the direct problem are considered. Again, Green's solutions to
$\omega$ and mesh as for the direct problem are considered. Again, Green's solutions to ![]() $\mathcal {L}^-_0$ are considered and (3.4) is therefore discarded. Some realisations for the reciprocal field
$\mathcal {L}^-_0$ are considered and (3.4) is therefore discarded. Some realisations for the reciprocal field ![]() $p^-$ for different sample locations are shown in figure 5.
$p^-$ for different sample locations are shown in figure 5.

Figure 5. Numerical FRT Green's problems associated with Lilley's equation at ![]() $\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions
$\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions ![]() $x_1/\sigma = 0.0$,
$x_1/\sigma = 0.0$, ![]() $x_1/\sigma = 25$ and
$x_1/\sigma = 25$ and ![]() $x_2/\sigma =9.0$.
$x_2/\sigma =9.0$. ![]() $(a,c)$ Gaussian source terms
$(a,c)$ Gaussian source terms ![]() $S^{-,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing and
$S^{-,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing and ![]() $(b,d)$ the associated reciprocal fields
$(b,d)$ the associated reciprocal fields ![]() $p^-$ regarded as numerical FRT Green's functions
$p^-$ regarded as numerical FRT Green's functions ![]() $G^{-,N}_{\boldsymbol {x}_m}$. The same range for the colourmaps as in figure 3 is used.
$G^{-,N}_{\boldsymbol {x}_m}$. The same range for the colourmaps as in figure 3 is used.
A normalisation procedure similar to (3.10) is used to compute FRT reciprocal Green's function ![]() $G^-_{\boldsymbol {x}_m}$ from the numerical FRT field
$G^-_{\boldsymbol {x}_m}$ from the numerical FRT field ![]() $G^{-,N}_{\boldsymbol {x}_m}$. In a similar fashion to (2.2), the pressure field
$G^{-,N}_{\boldsymbol {x}_m}$. In a similar fashion to (2.2), the pressure field ![]() $p$ solution of the direct problem is rebuilt with
$p$ solution of the direct problem is rebuilt with
where the scalar product for real-valued functions ![]() $\langle, \rangle _{\mathbb {R}}$ should be used, according to Lyamshev (Reference Lyamshev1961, equation (14)), defined for the functions
$\langle, \rangle _{\mathbb {R}}$ should be used, according to Lyamshev (Reference Lyamshev1961, equation (14)), defined for the functions ![]() $f$ and
$f$ and ![]() $g$ by
$g$ by
The explanation why a non-Hermitian scalar product is needed in the application of the FRT is discussed later in § 4.3. The pressure field ![]() $p$ obtained along the sampled line with the FRT is compared in figure 6 against the direct problem solution taken as reference.
$p$ obtained along the sampled line with the FRT is compared in figure 6 against the direct problem solution taken as reference.

Figure 6. Validation of the FRT method along the line ![]() $x_2/\sigma = 9.0$ for Lilley's equation. Reference data for the pressure
$x_2/\sigma = 9.0$ for Lilley's equation. Reference data for the pressure ![]() $p$ (real part, ——; imaginary part, - - - -) is taken from the direct field computation presented in figure 2. Rebuilt pressure field
$p$ (real part, ——; imaginary part, - - - -) is taken from the direct field computation presented in figure 2. Rebuilt pressure field ![]() $p$ (real part,
$p$ (real part, ![]() $\circ$; imaginary part,
$\circ$; imaginary part, ![]() $+$) is obtained with(3.13).
$+$) is obtained with(3.13).
In this example, the FRT recovers very poorly the direct problem solution both qualitatively as quantitatively. In this configuration a relative error greater than ![]() $300\,\%$ is observed at some observer locations, this error grows when the considered pulsation frequency
$300\,\%$ is observed at some observer locations, this error grows when the considered pulsation frequency ![]() $\omega$ decreases. A comparative look at the reciprocal fields obtained with the FRT, in figure 5, and with the adjoint method, in figure 3, reveals striking differences in both computed reciprocal fields. Subtle phenomena seem indeed to occur in the region of flow gradients in the adjoint approach which are not described by the FRT methodology; note that this region coincides with the region for which
$\omega$ decreases. A comparative look at the reciprocal fields obtained with the FRT, in figure 5, and with the adjoint method, in figure 3, reveals striking differences in both computed reciprocal fields. Subtle phenomena seem indeed to occur in the region of flow gradients in the adjoint approach which are not described by the FRT methodology; note that this region coincides with the region for which ![]() $\mathcal {L}_0$ is not self-adjoint. Furthermore this region of flow gradient is precisely where the source
$\mathcal {L}_0$ is not self-adjoint. Furthermore this region of flow gradient is precisely where the source ![]() $S_{Lilley}$ for the direct problem is located and, according to (3.11) and (3.13), it is the part of the reciprocal fields that contributes to the value of the rebuilt pressure
$S_{Lilley}$ for the direct problem is located and, according to (3.11) and (3.13), it is the part of the reciprocal fields that contributes to the value of the rebuilt pressure ![]() $p$ at the sample locations
$p$ at the sample locations ![]() $\boldsymbol {x}_m$. This paragraph highlights hence, that the rigorous computation of an acoustic field over a shear mean flow is typically a case for which the commonly used reciprocity principle – even if extended with the FRT – fails and where the general adjoint framework is required.
$\boldsymbol {x}_m$. This paragraph highlights hence, that the rigorous computation of an acoustic field over a shear mean flow is typically a case for which the commonly used reciprocity principle – even if extended with the FRT – fails and where the general adjoint framework is required.
4. Application to Pierce's equation
The adjoint method is a general and powerful technique which could be applied to any linearised operator. However, to compute acoustic propagation with this technique, there is an interest in operators which are self-adjoint. Reasons for this are twofold. First, from a practical point of view, if a self-adjoint operator is chosen, the set of equations governing the direct and the adjoint problem are identical apart from the causality/anti-causality conditions, leading obviously to an easier implementation of the technique and enabling the use of some off-the-shelf solvers. Second, the adjoint method suffers from the same stumbling block as for the direct problem, in particular when the mean flow field considered is sheared, instability waves may also occur in the adjoint space (Karabasov & Hynes Reference Karabasov and Hynes2005) and corrupt the acoustic solution. Möhring (Reference Möhring1999) pointed out that self-adjoint propagation operators are energy preserving and, in turn, do not trigger any instability waves. Choosing a self-adjoint operator is then an elegant means to guarantee the stability of the acoustic propagation problem.
In the present section, the study conducted for Lilley's wave equation is repeated for Pierce's wave equation (Pierce Reference Pierce1990). This wave operator is self-adjoint for the usual scalar product (3.2) and relies on a potential description of acoustic fluctuations. From the authors’ investigations, this wave equation has been found to be among the most accurate stable operator governing acoustic propagation in an arbitrary mean flow. Note that, unlike Blokhintzev's wave equation for the acoustic potential (Blokhintzev Reference Blokhintzev1946) or the acoustic perturbation equations (Ewert & Schröder Reference Ewert and Schröder2003), no barotropic assumption of the mean flow is required. If ![]() $\phi$ refers to the acoustic velocity potential, Pierce's wave equation reads
$\phi$ refers to the acoustic velocity potential, Pierce's wave equation reads
 \begin{equation} \begin{cases} p = - D_{\boldsymbol{u}_0}(\phi), \\ D_{\boldsymbol{u}_0}^2(\phi) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} \phi) = S_{Pierce} \equiv D_{\boldsymbol{u}_0}(S_m) - S_p, \\ {\rm \Delta} S_m = \boldsymbol{\nabla} \boldsymbol{\cdot} (\rho_0 \boldsymbol{S}_{\boldsymbol{u}}), \end{cases} \end{equation}
\begin{equation} \begin{cases} p = - D_{\boldsymbol{u}_0}(\phi), \\ D_{\boldsymbol{u}_0}^2(\phi) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} \phi) = S_{Pierce} \equiv D_{\boldsymbol{u}_0}(S_m) - S_p, \\ {\rm \Delta} S_m = \boldsymbol{\nabla} \boldsymbol{\cdot} (\rho_0 \boldsymbol{S}_{\boldsymbol{u}}), \end{cases} \end{equation}
where the first equation relates the fluctuating pressure ![]() $p$ to the velocity potential
$p$ to the velocity potential ![]() $\phi$ (Pierce Reference Pierce1990, equation (26)). Because this wave equation relies upon a potential field for the solution, the source term should be potential as well. The third equation links the linearised momentum equation source term
$\phi$ (Pierce Reference Pierce1990, equation (26)). Because this wave equation relies upon a potential field for the solution, the source term should be potential as well. The third equation links the linearised momentum equation source term ![]() $\boldsymbol {S}_{\boldsymbol {u}}$ to the corresponding filtered potential term
$\boldsymbol {S}_{\boldsymbol {u}}$ to the corresponding filtered potential term ![]() $S_m$. The adjoint method could be applied to the first and second equations of (4.1) taken as a whole, provided that a suitable multivariable scalar product is defined. But for the sake of considering an unambiguous self-adjoint operator in the sense of § 2.2 and for simplicity, the adjoint method and the FRT will only be applied here to the wave equation for
$S_m$. The adjoint method could be applied to the first and second equations of (4.1) taken as a whole, provided that a suitable multivariable scalar product is defined. But for the sake of considering an unambiguous self-adjoint operator in the sense of § 2.2 and for simplicity, the adjoint method and the FRT will only be applied here to the wave equation for ![]() $\phi$ and for the scalar product (3.2). The fluctuating pressure
$\phi$ and for the scalar product (3.2). The fluctuating pressure ![]() $p$ will be rebuilt subsequently.
$p$ will be rebuilt subsequently.
4.1. Solution to the direct problem
The direct problem under consideration is made of Pierce's wave equation completed with some radiating boundary conditions ![]() $\mathcal {B}_0$
$\mathcal {B}_0$
 \begin{equation} \begin{cases} \mathcal{L}_0\ \phi = D_{\boldsymbol{u}_0}^2(\phi) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} \phi) = S_{Pierce} & \text{in} \ \Omega,\\ \mathcal{B}_0\ \phi = 0 & \text{on} \ \partial\Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathcal{L}_0\ \phi = D_{\boldsymbol{u}_0}^2(\phi) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} \phi) = S_{Pierce} & \text{in} \ \Omega,\\ \mathcal{B}_0\ \phi = 0 & \text{on} \ \partial\Omega, \end{cases} \end{equation}
where ![]() $S_{Pierce}$ is built according to (4.1) and is based on the same LEE equivalent source terms
$S_{Pierce}$ is built according to (4.1) and is based on the same LEE equivalent source terms ![]() $(S_{\rho },\boldsymbol {S}_{\boldsymbol {u}},S_p)$ as used for
$(S_{\rho },\boldsymbol {S}_{\boldsymbol {u}},S_p)$ as used for ![]() $S_{Lilley}$. For simplicity, the quadrupole source
$S_{Lilley}$. For simplicity, the quadrupole source ![]() $\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ considered in § 3.2 was chosen in this study to derive from a potential source
$\rho _0 \boldsymbol {S}_{\boldsymbol {u}}$ considered in § 3.2 was chosen in this study to derive from a potential source ![]() $S_m$. For arbitrary sources, a filtering process based on a Poisson solver has proved to give very satisfactory results for Pierce's equation when compared with the solution for the unfiltered source computed with Lilley's equation. The computation of
$S_m$. For arbitrary sources, a filtering process based on a Poisson solver has proved to give very satisfactory results for Pierce's equation when compared with the solution for the unfiltered source computed with Lilley's equation. The computation of ![]() $\phi$ described in Pierce's direct problem (4.2) is achieved with the in-house code PROPA. The same mean flow field and the same frequency are analysed as previously for Lilley's wave equation. The fluctuating pressure
$\phi$ described in Pierce's direct problem (4.2) is achieved with the in-house code PROPA. The same mean flow field and the same frequency are analysed as previously for Lilley's wave equation. The fluctuating pressure ![]() $p$ is then straightforwardly rebuilt with
$p$ is then straightforwardly rebuilt with ![]() $p = - D_{\boldsymbol {u}_0}(\phi )$ and is shown in figure 7.
$p = - D_{\boldsymbol {u}_0}(\phi )$ and is shown in figure 7.

Figure 7. Direct problem for Pierce's wave equation. ![]() $(a)$ Source for Pierce's potential acoustic wave equation
$(a)$ Source for Pierce's potential acoustic wave equation ![]() $S_m$ equivalent to the quadrupole
$S_m$ equivalent to the quadrupole ![]() $\rho _0 \boldsymbol {S}_{\boldsymbol {u}} (= \boldsymbol {\nabla } S_m)$ shown in figure 2.
$\rho _0 \boldsymbol {S}_{\boldsymbol {u}} (= \boldsymbol {\nabla } S_m)$ shown in figure 2. ![]() $(b,c)$ Mach number
$(b,c)$ Mach number ![]() $M_0$ and density
$M_0$ and density ![]() $\rho _0$ profiles of the parallel mean flow considered and the real part of the pressure field
$\rho _0$ profiles of the parallel mean flow considered and the real part of the pressure field ![]() $p = -D_{\boldsymbol {u}_0}(\phi )$ is shown with the same range for the colourmap as in figure 2. Dashed lines represent the position of maximal shearing (
$p = -D_{\boldsymbol {u}_0}(\phi )$ is shown with the same range for the colourmap as in figure 2. Dashed lines represent the position of maximal shearing (![]() $x_2/\sigma = 1$).
$x_2/\sigma = 1$).
4.2. Reconstruction of the solution with the adjoint method
Repeating the procedure given in § 3.3, the adjoint method is used here to recover the velocity potential ![]() $\phi$ associated with the direct field. The fluctuating pressure
$\phi$ associated with the direct field. The fluctuating pressure ![]() $p$ is rebuilt subsequently. The same sampling of adjoint sources used previously, partly shown in figure 3, is considered here. Each of these adjoint sources is defined as a sink term to the anti-causal adjoint Pierce problem
$p$ is rebuilt subsequently. The same sampling of adjoint sources used previously, partly shown in figure 3, is considered here. Each of these adjoint sources is defined as a sink term to the anti-causal adjoint Pierce problem
 \begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {\phi}^\dagger = D_{\boldsymbol{u}_0}^2({\phi}^\dagger) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} {\phi}^\dagger) & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {\phi}^\dagger = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
\begin{equation} \begin{cases} {\mathcal{L}}^\dagger_0\ {\phi}^\dagger = D_{\boldsymbol{u}_0}^2({\phi}^\dagger) - \boldsymbol{\nabla} \boldsymbol{\cdot} ( a_0^2 \boldsymbol{\nabla} {\phi}^\dagger) & \text{in}\ \Omega,\\ {\mathcal{B}}^\dagger_0\ {\phi}^\dagger = 0 & \text{on}\ \partial\Omega. \end{cases} \end{equation}
Because Pierce's wave equation is self-adjoint for the scalar product (3.2) chosen here, its associated adjoint problem is nothing other than Pierce's wave equation completed with some anti-radiating boundary conditions ![]() ${\mathcal {B}}^\dagger _0$. The same features for the mean flow and the numerical settings as for previous calculations are considered. Figure 8 shows the adjoint velocity potential fields
${\mathcal {B}}^\dagger _0$. The same features for the mean flow and the numerical settings as for previous calculations are considered. Figure 8 shows the adjoint velocity potential fields ![]() ${\phi }^\dagger$ solution to Pierce's adjoint problem taken at two sample locations.
${\phi }^\dagger$ solution to Pierce's adjoint problem taken at two sample locations.

Figure 8. Numerical adjoint Green's problems associated with Pierce's equation at ![]() $\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions
$\boldsymbol {x}_m = (x_1,x_2)$ for the axial positions ![]() $x_1/\sigma = 0.0$,
$x_1/\sigma = 0.0$, ![]() $x_1/\sigma = 25$ and
$x_1/\sigma = 25$ and ![]() $x_2/\sigma =9.0$.
$x_2/\sigma =9.0$. ![]() $(a,c)$ adjoint Gaussian source terms
$(a,c)$ adjoint Gaussian source terms ![]() ${S}^{\dagger,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing and
${S}^{\dagger,N}_{\boldsymbol {x}_m}$ considered to mimic an impulse forcing and ![]() $(b,d)$ the associated adjoint fields
$(b,d)$ the associated adjoint fields ![]() ${\phi }^\dagger$ regarded as numerical adjoint Green's functions
${\phi }^\dagger$ regarded as numerical adjoint Green's functions ![]() ${G}^{\dagger,N}_{\boldsymbol {x}_m}$. The range for the colourmaps used here differs from the one used in figures 3 and 5.
${G}^{\dagger,N}_{\boldsymbol {x}_m}$. The range for the colourmaps used here differs from the one used in figures 3 and 5.
As previously, adjoint Green's functions ![]() ${G}^\dagger _{\boldsymbol {x}_m}$ are computed from previous numerical adjoint functions
${G}^\dagger _{\boldsymbol {x}_m}$ are computed from previous numerical adjoint functions ![]() ${G}^{\dagger,N}_{\boldsymbol {x}_m}$ using the compacity assumption of the adjoint source. Lagrange's identity then gives straightforwardly at each sample position
${G}^{\dagger,N}_{\boldsymbol {x}_m}$ using the compacity assumption of the adjoint source. Lagrange's identity then gives straightforwardly at each sample position ![]() $\boldsymbol {x}_m$,
$\boldsymbol {x}_m$,
and subsequently the acoustic pressure ![]() $p = - D_{\boldsymbol {u}_0}(\phi )$. Results obtained for the fluctuating pressure
$p = - D_{\boldsymbol {u}_0}(\phi )$. Results obtained for the fluctuating pressure ![]() $p$ along the sampled line are compared in figure 9 against Pierce's direct problem solution taken as reference.
$p$ along the sampled line are compared in figure 9 against Pierce's direct problem solution taken as reference.

Figure 9. Validation of the adjoint method along the line ![]() $x_2/\sigma = 9.0$ for Pierce's equation. Reference data for the pressure
$x_2/\sigma = 9.0$ for Pierce's equation. Reference data for the pressure ![]() $p$ (real part, ——; imaginary part, - - - -) is rebuilt from the direct field computation using
$p$ (real part, ——; imaginary part, - - - -) is rebuilt from the direct field computation using ![]() $p = - D_{\boldsymbol {u}_0}(\phi )$ as presented in figure 7. Similarly, the rebuilt pressure field
$p = - D_{\boldsymbol {u}_0}(\phi )$ as presented in figure 7. Similarly, the rebuilt pressure field ![]() $p$ (real part,
$p$ (real part, ![]() $\circ$;imaginary part,
$\circ$;imaginary part, ![]() ${+}$) is computed from the velocity potential field
${+}$) is computed from the velocity potential field ![]() $\phi$ computed with Lagrange's identity. Dotted lines,
$\phi$ computed with Lagrange's identity. Dotted lines, ![]() $\cdots \cdots$, display the corresponding real and imaginary parts of the pressure
$\cdots \cdots$, display the corresponding real and imaginary parts of the pressure ![]() $p$ solution to Lilley's equation given in figure 4.
$p$ solution to Lilley's equation given in figure 4.
Again in figure 9, an almost perfect reconstruction of the reference pressure field ![]() $p$ is obtained with the adjoint method. On an indicative basis, figure 9 also shows the pressure field
$p$ is obtained with the adjoint method. On an indicative basis, figure 9 also shows the pressure field ![]() $p$ computed previously with Lilley's wave equation. The satisfactory ability of Pierce's wave equation to compute acoustic refraction effects for the high-speed heated sheared mean flow encountered here is enlightening. This potential acoustic prediction is all the more satisfactory, since Pierce's equation is known to be accurate in the high-frequency limit (Pierce Reference Pierce1990), which is not fulfilled here,
$p$ computed previously with Lilley's wave equation. The satisfactory ability of Pierce's wave equation to compute acoustic refraction effects for the high-speed heated sheared mean flow encountered here is enlightening. This potential acoustic prediction is all the more satisfactory, since Pierce's equation is known to be accurate in the high-frequency limit (Pierce Reference Pierce1990), which is not fulfilled here, ![]() $\lambda / \sigma \approx 3$.
$\lambda / \sigma \approx 3$.
4.3. The adjoint method and the FRT equivalence for self-adjoint operators
In this study on Pierce's wave equation, the field reconstruction achieved with the FRT is not shown. Rigorously the same results as those presented for the adjoint method in figures 8 and 9 would have indeed been obtained. This is because the adjoint method and the FRT are fully equivalent for self-adjoint operators. A proof for this is given here for Helmholtz's wave equation written for a uniform steady background flow. Three-dimensional Green's function for the latter is recalled in appendix B. and solutions to the direct and adjoint propagation problems can be expressed as
 \begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x},\omega) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_s) }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_s} \right) }{4{\rm \pi} r_{\boldsymbol{x}_s}} \end{equation}
\begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x},\omega) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_s) }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_s} \right) }{4{\rm \pi} r_{\boldsymbol{x}_s}} \end{equation}and
 \begin{equation} {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x},\omega) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_m) }{1-M_0^2} \right) \dfrac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_m} \right) }{4{\rm \pi} r_{\boldsymbol{x}_m}}, \end{equation}
\begin{equation} {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x},\omega) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_m) }{1-M_0^2} \right) \dfrac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_m} \right) }{4{\rm \pi} r_{\boldsymbol{x}_m}}, \end{equation}
where ![]() $r_{\boldsymbol {x}_i} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_i|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_i))^2}$ and
$r_{\boldsymbol {x}_i} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_i|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_i))^2}$ and ![]() $\boldsymbol {M}_0 = \boldsymbol {u}_0/a_0$ is the vectorial Mach number. Furthermore, let
$\boldsymbol {M}_0 = \boldsymbol {u}_0/a_0$ is the vectorial Mach number. Furthermore, let ![]() $G_{\boldsymbol {x}_m}^-$ be Green's function in
$G_{\boldsymbol {x}_m}^-$ be Green's function in ![]() $\boldsymbol {x}_m$ solution of the FRT. Then
$\boldsymbol {x}_m$ solution of the FRT. Then ![]() $G_{\boldsymbol {x}_m}^-$ can be deduced from the expression of
$G_{\boldsymbol {x}_m}^-$ can be deduced from the expression of ![]() $G_{\boldsymbol {x}_s}$ by switching the source
$G_{\boldsymbol {x}_s}$ by switching the source ![]() $\boldsymbol {x}_s$ and the observer
$\boldsymbol {x}_s$ and the observer ![]() $\boldsymbol {x}_m$ positions and reversing the mean velocity
$\boldsymbol {x}_m$ positions and reversing the mean velocity ![]() $\boldsymbol {u}_0$ direction. Consistently with what is carried out for the numerical simulations in the frequency domain, it is argued that the anti-causal solution for the adjoint problem
$\boldsymbol {u}_0$ direction. Consistently with what is carried out for the numerical simulations in the frequency domain, it is argued that the anti-causal solution for the adjoint problem ![]() ${G}^\dagger _{\boldsymbol {x}_m}$ can be selected considering the usual radiating solution, but for an opposite pulsation frequency
${G}^\dagger _{\boldsymbol {x}_m}$ can be selected considering the usual radiating solution, but for an opposite pulsation frequency ![]() $\omega$. From the above obtained analytical expressions, the equivalence of the reciprocal fields computed with the adjoint method or the FRT are then easily verified:
$\omega$. From the above obtained analytical expressions, the equivalence of the reciprocal fields computed with the adjoint method or the FRT are then easily verified:
Since analytical solutions to acoustic propagation problems are scarce, directly assessing this symmetry with respect to the flow reversal on general analytical solutions is hopeless. However, this symmetry in the exchange of the mean flow direction and the sign of the pulsation frequency ![]() $\omega$ of the acoustic solution can already be assessed from the linear operator
$\omega$ of the acoustic solution can already be assessed from the linear operator ![]() $\mathcal {L}_0$ governing the wave propagation. And effectively, in Pierce's wave operator, changing the sign of
$\mathcal {L}_0$ governing the wave propagation. And effectively, in Pierce's wave operator, changing the sign of ![]() $\omega$ or
$\omega$ or ![]() $\boldsymbol {u}_0$ appears to be fully equivalent. This remark holds for all self-adjoint wave equations describing acoustic propagation over a moving flow, namely the ones introduced by Galbrun (Reference Galbrun1931), Phillips (Reference Phillips1960), Goldstein (Reference Goldstein1978), Godin (Reference Godin1997) and Möhring (Reference Möhring1999).
$\boldsymbol {u}_0$ appears to be fully equivalent. This remark holds for all self-adjoint wave equations describing acoustic propagation over a moving flow, namely the ones introduced by Galbrun (Reference Galbrun1931), Phillips (Reference Phillips1960), Goldstein (Reference Goldstein1978), Godin (Reference Godin1997) and Möhring (Reference Möhring1999).
On top of that, a critical literature review reveals that in the studies illustrating the FRT, only self-adjoint wave equations written in the frequency domain are considered. The proof for the FRT reciprocity relation, classically starts with the multiplication of the wave equation governing the direct propagation problem by a field variable, and its integration over the entire propagation domain. In fact, this operation closely resembles a scalar product multiplication with a test function or a Lagrange multiplier. Integration by parts of the direct problem wave equation then frees the direct field variable and defines the reciprocal wave equation with reversed flow to which the previously introduced test function is subject, i.e. the FRT for the considered wave equation is readily demonstrated. The difference with the adjoint method lies in the scalar product which is not well-posed for the FRT. As a matter of fact, manipulating a wave equation written in the frequency domain requires the introduction of a Hermitian scalar products. If the latter condition were fulfilled in the FRT proof, the self-adjoint property of the equation would have been retrieved and in turn no flow reversal needed. It appears now clearly why only ![]() $\mathbb {R}$ space scalar products should be considered in the final solution reconstruction with the FRT, to say,
$\mathbb {R}$ space scalar products should be considered in the final solution reconstruction with the FRT, to say,
The reciprocal field ![]() $G_{\boldsymbol {x}_m}^-$ computed with the FRT is in fact, the complex conjugate of the adjoint field
$G_{\boldsymbol {x}_m}^-$ computed with the FRT is in fact, the complex conjugate of the adjoint field ![]() ${G}^\dagger _{\boldsymbol {x}_m}$. This is easily seen, taking benefit of the Fourier transform property of a real-valued field
${G}^\dagger _{\boldsymbol {x}_m}$. This is easily seen, taking benefit of the Fourier transform property of a real-valued field ![]() $G_{\boldsymbol {x}_m}^-(\boldsymbol {x},-\omega )={G^-}^*_{\boldsymbol {x}_m}(\boldsymbol {x},\omega )$ for which it follows from (4.7):
$G_{\boldsymbol {x}_m}^-(\boldsymbol {x},-\omega )={G^-}^*_{\boldsymbol {x}_m}(\boldsymbol {x},\omega )$ for which it follows from (4.7):
The equivalence between the adjoint method and the FRT for self-adjoint operators has pragmatic implications. The solving of anti-causal adjoint equations can indeed be advantageously replaced by direct computations over reversed flow. An interesting question to answer is whether some linear operators may all at once describe exactly acoustic propagation over a sheared mean flow and be self-adjoint. Möhring (Reference Möhring1999) answered this question and illustrated how from a self-adjoint operator an energy-conserving law could be derived for the acoustic field. Yet, it is well known that for sheared flows, instability waves may occur converting acoustic energy into vortical energy (Yates Reference Yates1978; Maestrello, Bayliss & Turkel Reference Maestrello, Bayliss and Turkel1981) and thus that no such conservation law for acoustic energy exist. Hence for arbitrary mean flows, acoustic energy is not preserved, and a linear operator which is twofold self-adjoint and exactly describes acoustic propagation does not exist. If acoustic propagation in a complex media needs to be conducted very accurately, a non-self-adjoint operator needs therefore to be considered. Nevertheless if a decoupling of the acoustic with the vortical mode is required for stability purposes, and approximations tolerated, Pierce's wave equation seems to achieve nicely the prediction of flow refraction effects on sound.
5. Conclusion
In the present study, the adjoint method is analysed in-depth and demonstratively applied to the model problem of a source radiating in a sheared and stratified mean flow. This approach offers a fully equivalent alternative to ordinary computational aeroacoustics to rebuild locally the solution of a non-trivial propagation problem. With respect to the pioneering work of Tam & Auriault (Reference Tam and Auriault1998), the adjoint field is not sought as the solution of a scattering problem. The presented approach wraps around Lagrange's identity, which offers a robust mathematical basis for the method. A well-defined scalar product is considered leading to a consistent expression of the representation formula. The anti-causality of the adjoint field is also stressed. In addition, the adjoint method is compared against the flow reversal theorem, that is shown to work properly only for self-adjoint wave equations. This property is sometimes overseen or confusingly addressed in aeroacoustics. Finally, solving an adjoint problem can be sometimes cumbersome due to the presence of instability waves, and to the numerical implementation of anti-causality boundary conditions, for instance. Another contribution of this work is to propose a stable and accurate alternative methodology based on Pierce's equation and the rigorous use of the flow reversal theorem. A general expression of the source term is derived that enables the prediction of aerodynamic noise. No limitation on the physical source is imposed, and this method has already changed the game for computation of acoustic radiation of widely distributed physical sources such as those found in jets (Tam & Auriault Reference Tam and Auriault1999; Morris & Farassat Reference Morris and Farassat2002; Raizada & Morris Reference Raizada and Morris2006), and there is some interest in computing accurately the quantities appearing in the model for complex configurations. Compared with the classical adjoint formulation encountered in aeroacoustics, the presented approach has the ability to account for acoustic diffraction at surface edges (Barone & Lele Reference Barone and Lele2005) and describes near-field propagation as well. Future contributions should verify the ability of the technique to properly account for realistic configurations.
Acknowledgements
The authors gratefully acknowledge Dr G. Bodard for the constructive technical monitoring of this work. The first author is funded by Safran Aircraft Engines (CIFRE ![]() $2017/0229$), with also the support of the Labex CeLyA of the Université de Lyon, within the programme ‘Investissements d'Avenir’ (ANR-10-LABX-0060/ANR-11-IDEX-0007) operated by the French National Research Agency (ANR).
$2017/0229$), with also the support of the Labex CeLyA of the Université de Lyon, within the programme ‘Investissements d'Avenir’ (ANR-10-LABX-0060/ANR-11-IDEX-0007) operated by the French National Research Agency (ANR).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Details on the code PROPA
PROPA is a high-order finite difference code designed to solve different linear acoustic operators and their adjoint. It handles free-field problems with arbitrary source and mean flow definitions for two-dimensional or axisymmetric configurations. The code is written in the frequency domain, in a Matlab environment, and uses a direct inversion method relying on UMFPACK solver, which is Matlab's direct inversion multithreaded algorithm for sparse and unsymmetric system (Davis Reference Davis2004). The finite difference scheme used is the 11 point stencil from Bogey & Bailly (Reference Bogey and Bailly2004) and Berland et al. (Reference Berland, Bogey, Marsden and Bailly2007), and the grids considered are uniform. Radiating boundary conditions are achieved using a perfectly matched layer (PML) reformulation of the spatial derivatives in the sponge layer as presented by Hu (Reference Hu2008). The sponge layer width, and the amplitude of the damping which follows a cubic law, is defined by trial and error so to avoid visible PML reflection and in a way so that in the extremity of the sponge layer, the signal has been damped by at least 10 orders of magnitude. The computations presented here are obtained on a regular mesh composed of ![]() $800\times 450$ elements including
$800\times 450$ elements including ![]() $50$ cells-thick PML layers (not shown). Calculations have been done on a 16 core Dell T7810 computer of 64 GB (CPU: Xeon E5-2609v4). Each run required approximately 50 GB of RAM.
$50$ cells-thick PML layers (not shown). Calculations have been done on a 16 core Dell T7810 computer of 64 GB (CPU: Xeon E5-2609v4). Each run required approximately 50 GB of RAM.
Care must be taken in the implementation of the boundary conditions associated with the adjoint problem, since adjoint problems are anti-causal and thus non-radiating ones. Stated differently, an adjoint source acts as a well of energy. In the next paragraph, some evidence is given for the convected Helmholtz's equation. In practice, some anti-radiating boundary conditions should be developed to tackle properly the adjoint of acoustic free-field propagation problems. This could be fairly easily achieved in the frequency domain, for instance, with a PML-like formulation by changing the sign of the damping parameter so to allow only incoming waves entering the domain. But an other approach does exist and has been retained in this study. Recalling that the adjoint field ![]() ${p}^\dagger$ is real-valued in the time-domain, the following symmetry property of its Fourier transform exists:
${p}^\dagger$ is real-valued in the time-domain, the following symmetry property of its Fourier transform exists: ![]() ${p}^\dagger (-\omega ) = {{p}^\dagger }^*(\omega )$. Relying on this symmetry, it is possible to turn the adjoint non-radiating problem into a radiating problem where the conjugate of the adjoint field is computed by changing
${p}^\dagger (-\omega ) = {{p}^\dagger }^*(\omega )$. Relying on this symmetry, it is possible to turn the adjoint non-radiating problem into a radiating problem where the conjugate of the adjoint field is computed by changing ![]() $\omega$ into
$\omega$ into ![]() $-\omega$ in the solved linear problem. An illustration of this symmetry property is given in the next section.
$-\omega$ in the solved linear problem. An illustration of this symmetry property is given in the next section.
Appendix B. Anti-causality of the adjoint Helmholtz's equation
The purpose of this section is a reminder that if the direct problem is radiating, its adjoint is not. Illustration for this is given in the frequency domain for the convected Helmholtz's equation.
B.1. Green's function for the direct problem
Introducing the vectorial Mach number ![]() $\boldsymbol {M}_0 = \boldsymbol {u}_0/a_0$, the homogeneous solution
$\boldsymbol {M}_0 = \boldsymbol {u}_0/a_0$, the homogeneous solution ![]() $F$ to Helmholtz's equation is defined as
$F$ to Helmholtz's equation is defined as
If ![]() $F_1$ and
$F_1$ and ![]() $F_2$ are two independent solutions of the problem, any solution of the homogeneous problem can be expressed in the (
$F_2$ are two independent solutions of the problem, any solution of the homogeneous problem can be expressed in the (![]() $F_1$,
$F_1$,![]() $F_2$) basis as,
$F_2$) basis as, ![]() $F(\boldsymbol {x}) = A_1\ F_1(\boldsymbol {x}) + A_2\ F_2(\boldsymbol {x})$, where the values of the
$F(\boldsymbol {x}) = A_1\ F_1(\boldsymbol {x}) + A_2\ F_2(\boldsymbol {x})$, where the values of the ![]() $A_1$,
$A_1$, ![]() $A_2$ constants are determined from the boundary conditions. One can verify that the following expressions for
$A_2$ constants are determined from the boundary conditions. One can verify that the following expressions for ![]() $F_1$ and
$F_1$ and ![]() $F_2$ are independent and are solutions of the homogeneous problem:
$F_2$ are independent and are solutions of the homogeneous problem:
 \begin{equation} \begin{cases} F_1(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{x} }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} \tilde{x} \right) }{4{\rm \pi} \tilde{x}},\\ F_2(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{x} }{1-M_0^2} \right) \dfrac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} \tilde{x} \right) }{4{\rm \pi} \tilde{x}}, \end{cases} \end{equation}
\begin{equation} \begin{cases} F_1(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{x} }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} \tilde{x} \right) }{4{\rm \pi} \tilde{x}},\\ F_2(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{x} }{1-M_0^2} \right) \dfrac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} \tilde{x} \right) }{4{\rm \pi} \tilde{x}}, \end{cases} \end{equation}
where ![]() $\tilde {x} = \sqrt {(1-M_0^2) |\boldsymbol {x}|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} \boldsymbol {x})^2}$. Without flow, the boundary condition of the radiating problem is given by the Sommerfeld conditions. The far-field asymptotic solution to the radiating problem for a uniform mean flow are given by Tam & Webb (Reference Tam and Webb1993) in two dimensions, and by Bogey & Bailly (Reference Bogey and Bailly2002) in three dimensions. In the frequency domain, boundary conditions for the three-dimensional uniform flow case are given by
$\tilde {x} = \sqrt {(1-M_0^2) |\boldsymbol {x}|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} \boldsymbol {x})^2}$. Without flow, the boundary condition of the radiating problem is given by the Sommerfeld conditions. The far-field asymptotic solution to the radiating problem for a uniform mean flow are given by Tam & Webb (Reference Tam and Webb1993) in two dimensions, and by Bogey & Bailly (Reference Bogey and Bailly2002) in three dimensions. In the frequency domain, boundary conditions for the three-dimensional uniform flow case are given by
with
From the expression given for ![]() $F$, it can be now deduced that radiating solutions are given by
$F$, it can be now deduced that radiating solutions are given by ![]() $F \propto F_1$, thus that the
$F \propto F_1$, thus that the ![]() $F_2$ solution to the Helmholtz's equation is not a radiating one. The remaining constant is determined with the forcing term of the problem. It is now possible to define properly Green's function
$F_2$ solution to the Helmholtz's equation is not a radiating one. The remaining constant is determined with the forcing term of the problem. It is now possible to define properly Green's function ![]() $G_{\boldsymbol {x}_s}$ associated with Helmholtz's radiation problem for a source term in
$G_{\boldsymbol {x}_s}$ associated with Helmholtz's radiation problem for a source term in ![]() $\boldsymbol {x}_s$ as
$\boldsymbol {x}_s$ as
 \begin{equation} \begin{cases} \left(-\textrm{i} \omega/a_0 + \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \right)^2 G_{\boldsymbol{x}_s}(\boldsymbol{x}) - {\rm \Delta} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \delta(\boldsymbol{x}_s-\boldsymbol{x})\\ \text{for}\ |\boldsymbol{x}| \rightarrow \infty, \quad \left\{ -\textrm{i}\omega + v_{g,\infty} \left( \dfrac{\partial}{\partial |\boldsymbol{x}|} + \dfrac{1}{|\boldsymbol{x}|}\right)\right\} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = O\left(\dfrac{1}{|\boldsymbol{x}|}\right),\end{cases} \end{equation}
\begin{equation} \begin{cases} \left(-\textrm{i} \omega/a_0 + \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \right)^2 G_{\boldsymbol{x}_s}(\boldsymbol{x}) - {\rm \Delta} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \delta(\boldsymbol{x}_s-\boldsymbol{x})\\ \text{for}\ |\boldsymbol{x}| \rightarrow \infty, \quad \left\{ -\textrm{i}\omega + v_{g,\infty} \left( \dfrac{\partial}{\partial |\boldsymbol{x}|} + \dfrac{1}{|\boldsymbol{x}|}\right)\right\} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = O\left(\dfrac{1}{|\boldsymbol{x}|}\right),\end{cases} \end{equation}for which the solution is uniquely defined as
 \begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_s) }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_s} \right) }{4{\rm \pi} r_{\boldsymbol{x}_s}}, \end{equation}
\begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \exp\left( -\textrm{i} \dfrac{\omega}{a_0} \dfrac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_s) }{1-M_0^2} \right) \dfrac{\exp\left( \textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_s} \right) }{4{\rm \pi} r_{\boldsymbol{x}_s}}, \end{equation}
where ![]() $r_{\boldsymbol {x}_s} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_s|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_s))^2}$. It is interesting to note that for the impulse problem, the far-field boundary conditions are more than just an asymptotic solution. In the impulse problem, since the source term is infinitely small, boundaries are always far from the source and the above given far-field solution is everywhere exact for Green's problem, so that the second-order radiating Helmholtz's problem is equivalent to the following first-order problem:
$r_{\boldsymbol {x}_s} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_s|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_s))^2}$. It is interesting to note that for the impulse problem, the far-field boundary conditions are more than just an asymptotic solution. In the impulse problem, since the source term is infinitely small, boundaries are always far from the source and the above given far-field solution is everywhere exact for Green's problem, so that the second-order radiating Helmholtz's problem is equivalent to the following first-order problem:
with
B.2. Green's function for the adjoint problem
It is well known that Helmholtz's operator is formally self-adjoint, but that the radiation problem governed by Helmholtz's equation is not, due to non-symmetries of the boundary conditions. Thus, the solution of the adjoint problem is different from the one of the direct problem. This complies with the reciprocity principle for complex valued scalar functions which can be deduced from Lagrange's identity (Alonso & Burdisso Reference Alonso and Burdisso2007, equation (48); Stone & Goldbart Reference Stone and Goldbart2009, § 5.3.1):
The adjoint solution to the considered problem can be deduced from the previous fundamental relation
 \begin{equation} {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x}) = \exp\left( -\textrm{i} \frac{\omega}{a_0} \frac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_m) }{1-M_0^2} \right) \frac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_m} \right) }{4{\rm \pi} r_{\boldsymbol{x}_m}}, \end{equation}
\begin{equation} {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x}) = \exp\left( -\textrm{i} \frac{\omega}{a_0} \frac{ \boldsymbol{M}_0 \boldsymbol{\cdot} (\boldsymbol{x}-\boldsymbol{x}_m) }{1-M_0^2} \right) \frac{\exp\left( -\textrm{i} \dfrac{1}{1-M_0^2} \dfrac{\omega}{a_0} r_{\boldsymbol{x}_m} \right) }{4{\rm \pi} r_{\boldsymbol{x}_m}}, \end{equation}
where ![]() $r_{\boldsymbol {x}_m} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_m|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_m))^2}$. In turns out that the adjoint solution corresponds to the
$r_{\boldsymbol {x}_m} = \sqrt {(1-M_0^2) |\boldsymbol {x} - \boldsymbol {x}_m|^2 + (\boldsymbol {M}_0 \boldsymbol{\cdot} (\boldsymbol {x}-\boldsymbol {x}_m))^2}$. In turns out that the adjoint solution corresponds to the ![]() $F_2$ solution of the homogeneous convected equation studied above. One can verify that this solution has indeed a non-radiating behaviour in the far-field. From the solution to the direct problem and adjoint problem, the classical out-going (causal) and in-going (anti-causal) waves solution of Helmholtz's equation without flow can be retrieved:
$F_2$ solution of the homogeneous convected equation studied above. One can verify that this solution has indeed a non-radiating behaviour in the far-field. From the solution to the direct problem and adjoint problem, the classical out-going (causal) and in-going (anti-causal) waves solution of Helmholtz's equation without flow can be retrieved:
 \begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \frac{\exp\left( \textrm{i} \dfrac{\omega}{a_0} |\boldsymbol{x} - \boldsymbol{x}_s| \right) }{4{\rm \pi} |\boldsymbol{x} - \boldsymbol{x}_s|},\quad {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x}) = \frac{\exp\left( - \textrm{i} \dfrac{\omega}{a_0} |\boldsymbol{x} - \boldsymbol{x}_m| \right) }{4{\rm \pi} |\boldsymbol{x} - \boldsymbol{x}_m|}, \end{equation}
\begin{equation} G_{\boldsymbol{x}_s}(\boldsymbol{x}) = \frac{\exp\left( \textrm{i} \dfrac{\omega}{a_0} |\boldsymbol{x} - \boldsymbol{x}_s| \right) }{4{\rm \pi} |\boldsymbol{x} - \boldsymbol{x}_s|},\quad {G}^\dagger_{\boldsymbol{x}_m}(\boldsymbol{x}) = \frac{\exp\left( - \textrm{i} \dfrac{\omega}{a_0} |\boldsymbol{x} - \boldsymbol{x}_m| \right) }{4{\rm \pi} |\boldsymbol{x} - \boldsymbol{x}_m|}, \end{equation}where the causal and anti-causal behaviour of the solution is more easily seen.
B.3. Recovering the anti-causal adjoint solution
From Green's function of the direct problem, it can be seen that the solution is invariant under source–observer position exchange and flow direction reversal. This is an example where the FRT could be used. In this study the symmetry of the problem with respect to time is used to simplify the numerical implementation. Unlike symmetries from space on which the FRT relies, the time symmetry of the operator cannot be violated. Indeed for real-valued signals ![]() $p(t)$, their Fourier transform always verify
$p(t)$, their Fourier transform always verify ![]() $p(\omega ) = {p}^*(-\omega )$. Applying this rule to the reciprocity principle yields
$p(\omega ) = {p}^*(-\omega )$. Applying this rule to the reciprocity principle yields
As can be inferred for the case of previously treated convected Helmholtz's equation, solving the non-radiating adjoint equation for positive pulsation ![]() $\omega$ or solving the radiating problem, that is complex conjugated to the latter, for negative pulsation
$\omega$ or solving the radiating problem, that is complex conjugated to the latter, for negative pulsation ![]() $-\omega$ are equivalent. The generality of this property is assumed. Instead of developing and coding anti-radiation numerical boundary conditions, standard PML conditions are used. The anti-causality of the adjoint field is accounted for by changing the sign of the pulsation
$-\omega$ are equivalent. The generality of this property is assumed. Instead of developing and coding anti-radiation numerical boundary conditions, standard PML conditions are used. The anti-causality of the adjoint field is accounted for by changing the sign of the pulsation ![]() $\omega$ in the adjoint linear operator
$\omega$ in the adjoint linear operator ![]() ${\mathcal {L}}^\dagger _0$. The capability of the adjoint method, using this numerical trick, to recover the direct field serves as a verification for the latter assumption.
${\mathcal {L}}^\dagger _0$. The capability of the adjoint method, using this numerical trick, to recover the direct field serves as a verification for the latter assumption.