1. INTRODUCTION
Satellite navigation continues to be a foundation subject (Sandford, Reference Sandford1999) not only in the area of navigation, but in industry, everyday life, global economy, geostrategy and geopolitics. The marked importance of satellite navigation requires sustained satellite navigation system performance. In order to provide robust and reliable positioning, a strict control of the causes of satellite positioning errors is demanded (Sandford, Reference Sandford1999, Misra and Enge, Reference Misra and Enge.2004). General sources of the satellite positioning errors are well identified (Parkinson and Spilker, Reference Parkinson and Spilker1996, Misra and Enge, Reference Misra and Enge.2004). However, the question of their proper modelling still continues (Parkinson and Spilker, Reference Parkinson and Spilker1996, Misra and Enge, Reference Misra and Enge.2004). This especially applies to the impact of the ionosphere, which is the most important cause of satellite positioning errors (Parkinson and Enge, Reference Parkinson and Spilker1996, Klobuchar, Reference Klobuchar1987). Usually expressed as the ionospheric delay in mid-latitudes, the influence of the ionosphere on satellite positioning performance is the result of a very complex process involving the impact of both extraterrestrial (space weather) and terrestrial (local ionospheric disturbances around the observation site) (Klobuchar, Reference Klobuchar1987, Parkinson and Spilker, Reference Parkinson and Spilker1996, Misra and Enge, 2004, Sandford, Reference Sandford1999, Langley, Reference Langley2000, Filjar, Reference Filjar2001) influences.
The ionospheric impact on the satellite navigation performance has been a research subject since the introduction of radio navigation systems (Klobuchar, Reference Klobuchar1987, Klobuchar et al, Reference Klobuchar2002, Lockwood, Reference Lockwood1999). The international community (consisting mostly of scientists and engineers, but also of radio amateurs, amateur radio astronomers and other enthusiasts) has performed numerous field campaigns in related research areas. Collected observations have provided invaluable material for development of better understanding of ionospheric processes. However, the present knowledge provides enough evidence only for the general understanding of ionospheric processes in stable space weather and ionospheric conditions (Davis, Reference Davis1990, Parkinson and Enge, 1996, Klobuchar, Reference Klobuchar1987). Successful modelling and forecasting of the ionospheric behaviour is essential for the elimination of the satellite positioning ionospheric error. This task still remains an open research issue, especially in periods of severely disturbed space weather and ionosphere (Sandford, Reference Sandford1999, Lockwood, Reference Lockwood1999, Filjar and Kos, Reference Filjar and Kos.2006).
2. SPACE WEATHER
Space weather is a common name for a variety of processes in the vast space between the Sun and the Earth, generated by solar activity and influencing the Earth's surroundings (Davis, Reference Davis1990, Sandford, Reference Sandford1999). Solar activity generates occasional ejections of particles and energy into outer space. Expelled from the Sun, the particles and energy form the solar wind. If aligned in a certain way, this solar wind can bring a huge amount of mass and energy to the Earth's surroundings, affecting the state and composition of the Earth's magnetic field (magnetosphere) and the atmosphere (ionosphere) (Davis, Reference Davis1990). In general terms, the solar activity affects the vertical distribution of free charged particles (especially free electrons) in the ionosphere, causing the ionospheric disturbances that affect considerably the propagation of radio waves (Davis, Reference Davis1990). Although the theoretical description is well known, the complexity of the Sun-Earth relationship is still able to produce a variety of strong and unpredictable ionospheric disturbances (Davis, Reference Davis1990, Klobuchar, Reference Klobuchar1987, Klobuchar et al, Reference Klobuchar2002, Parkinson and Spilker, Reference Parkinson and Spilker1996, Filjar and Kos, Reference Filjar and Kos.2006).
The state of the space weather can be measured and quantified in terms of a number of space weather parameters (Davis, Reference Davis1990, McNamara, Reference McNamara1991, Filjar and Kos, Reference Filjar and Kos.2006). In support of this discussion, only the most common parameters will be briefly introduced here. Space weather parameters can be roughly divided into three main groups:
• parameters describing solar activity
• parameters of the Earth's magnetic (geomagnetic) field
• ionospheric parameters.
2.1. Solar Activity
The sunspot number (Davis, Reference Davis1990) is the most traditional way of describing solar activity. During the intervals of particularly strong solar activity, a number of areas on the Sun can be formed that have considerably lower temperature than neighbouring areas. This temperature difference shows as a form of dark patches on the Sun's disc that are easily visible from the Earth. The ancient Chinese astronomers conducted the first observations of the solar disc in search of dark spots. Monitoring of the solar activity continued through centuries, with the observation records available since the beginning of the 18th century. The sunspot number is measured through the special procedure that yields the Zurich number, combining the observation of both single sunspots and the groups of sunspots. Increased solar activity will increase the sunspot number. A quiet Sun is characterised by a very low number of sunspots (zero is not at all an uncommon observation result), while during very disturbed space weather an active Sun can yield a sunspot number in excess of 300. Since solar activity produces considerable ejections of matter and energy, the level of solar activity can be measured by observation of the intensity of solar radiation. Especially suitable is monitoring of certain lines in the electromagnetic spectrum of the solar flux (Davis, Reference Davis1990), of which the 280·37 GHz radio signal (10·7 cm wavelength) has become a de facto standard in solar activity monitoring.
2.2. Geomagnetic Field
The Earth's magnetic (geomagnetic) field is described by a number of parameters (field strength in various directions, angles between the appropriate vectors of geomagnetic field components etc.) (Davis, Reference Davis1990). Here we concentrate on the parameters describing disturbances of geomagnetic field, of which the most important are the planetary K p and A p indices. The K index measures the relative intensity of magnetic disturbance, with the scaleset between 0 and 9. Each geomagnetic observatory determines its own absolute values of the magnetic field component disruptions related to the K index scale. The maximum geomagnetic component deviation from the quiet day magnetic curve of a particular geomagnetic observatory is selected for conversion to the K index at the 3-hours interval, starting at 00.00 GMT each day. Selected maximum geomagnetic component deviation is then converted into the 3-hours K index for the geomagnetic observatory in question using the observatory-specific algorithm. A common approach to the K index definition in relation to the intensity of the geomagnetic disturbance (storm) is presented in Table 1. The planetary K p index is compiled from separate measurements of 3-hours K indices collected at 12 reference stations distributed around the globe in the belt between 63° N and 48° S. Due to the quasi-logarithmic nature of the K p index, the A p index is introduced, with the values based on K indices processed in a separate way.
Table 1. K index definition.

2.3. Ionosphere
The Earth's ionosphere is described in terms of its layers. With the D, E, F1 and F2 layers active during the course of an average day, and with only E and F2 layers active during the night, the Earth's ionosphere appears to be a vast area of complex physical and chemical processes (Davis, Reference Davis1990). Every ionospheric layer is formed as a consequence of solar radiations at particular segment of the radio spectrum (Davis, Reference Davis1990, Parkinson and Spilker, Reference Parkinson and Spilker1996) emerging from the Sun, but each of them can be described fairly well using a semi-parabolic model. Using this model, one can identify the following parameters as the most convenient for an ionospheric layer description (Davis, Reference Davis1990):
• y mX … semi-thickness of the layer X
• h mX … height of a local maximum of a free electron density for the layer X
• f 0X … layer X critical frequency
• N mX … local maximum of a free electron density for the layer X
3. GPS IONOSPHERIC DELAY
The GPS Ionospheric Delay on the radio ray path between satellite and receiver is defined in the following way (Parkinson and Spilker, Reference Parkinson and Spilker1996):
![\Delta t \equals {1 \over c}\int\limits_{satellite}^{receiver} \!\!\!{\left[ {n\left( l \right) \minus 1} \right]dl}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022093631899-0954:S0373463307004420_eqn1.gif?pub-status=live)
where: Δt … GPS ionospheric delay; c … velocity of light; n(l) … refraction index on the path l. The equivalent GPS ionospheric delay related to distance measurements can be defined using the following relation (Parkinson and Spilker, Reference Parkinson and Spilker1996):
![\Delta \rho \equals {1 \over c}\int\limits_{satellite}^{receiver} \!\!\!{\left[ {n\left( l \right) \minus 1} \right]dl}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022093631899-0954:S0373463307004420_eqn2.gif?pub-status=live)
where Δρ … equivalent GPS ionospheric delay.
Appleton's formula provides a reasonable approximation for the relationship between refraction index and the free electron density distribution (Davis, Reference Davis1990, Parkinson and Spilker, Reference Parkinson and Spilker1996):
where N(h) … vertical distribution of the free electron density over the height h above the surface of the Earth and f … frequency of the radio signal.
The combination of (1) and (3) yields the equation that directly describes the relationship between free electron density profile and the GPS ionospheric delay (Parkinson and Spilker, Reference Parkinson and Spilker1996):
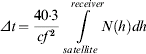
The integral on the right side of (4) is called the Total Electron Content (TEC) (Parkinson and Spilker, Reference Parkinson and Spilker1996):

Using equation (5), (4) can be written as:
Following the same analogy, the equation for the equivalent GPS ionospheric delay becomes:
Considering the pseudorange measurements taken on both GPS transmitting frequencies (f 1=1575·42 MHz and f 2=1227·60 MHz) and with utilisation of the equation (7), the following relation between the TEC and GPS pseudorange measurements can be established (Parkinson and Spilker, Reference Parkinson and Spilker1996):
Equation (8) can be transformed in order to yield the TEC determining equation:
Using a dual-frequency GPS receiver and equation (9), the real TEC value can be determined directly. Still, with the applied restrictions for GPS dual-frequency receiver usage among common users, another method for indirect determination of TEC and GPS ionospheric delay should be utilised. The most common of them is a standard GPS ionospheric delay model, also known as the Klobuchar model, after its inventor (Klobuchar, Reference Klobuchar1987, Misra and Enge, 2004, Parkinson and Spilker, Reference Parkinson and Spilker1996). The Klobuchar model presumes a cosine-like daily dynamic of the GPS ionospheric delay values, with the maximum GPS ionospheric delay emerging around 14.00 local time (Klobuchar, Reference Klobuchar1987). The model is comprehensively described using the equation (10).
where: Δt … GPS ionospheric delay; F … slant factor; t n … nighttime value of the GPS ionospheric delay; A … GPS ionospheric delay daily maximum; P … period of the cosine GPS ionospheric delay daily walk; t … time instant for which the GPS ionospheric delay is calculated (in seconds since the start of current day); t 0 … time of the GPS ionospheric delay maximum (set to 14.00 local time, in seconds).
The Klobuchar model provides reasonably good GPS ionospheric delay corrections when applied during quiet or mildly disturbed space weather and ionospheric conditions. Its performance deteriorates considerably during extreme space weather conditions and around the Earth's poles (Parkinson and Spilker, Reference Parkinson and Spilker1996, Filjar and Kos, Reference Filjar and Kos.2006).
4. SEVERE SPACE WEATHER CONDITIONS IN AUTUMN 2003
Observation records show marked solar activity during October and November 2003 (Space Physics Interactive Data Resource, 2006, National Weather Service, 2004, Oler, Reference Oler2004). Three large solar flares expelled considerable amounts of material and radiation, two of them beaming solar wind towards the Earth, causing the emergence of several geomagnetic and ionospheric storms (National Weather Service, 2004). Figure 1 shows the daily sunspot number values for the year 2003. Two important outbreaks of severe space weather occurred during October and November, with the general solar activity unexpectedly high for a ceasing solar cycle. The severity of space weather in the period in question is confirmed by the observation of the solar flux. Again, two most notable events of increased solar flux values were observed in the October–November 2003 period, as presented in Figure 2. Figure 3 shows linear relation between solar flux and sunspot number values in the period in question. There is a bias value of the solar flux remaining in days with no sunspots observed.

Figure 1. Sunspot number values during the year 2003.

Figure 2. Solar flux during the year 2003.

Figure 3. Linear relationship between solar flux and sunspot number, as observed during the October–November 2003 period.
Extreme solar activity in Autumn 2003 had a direct impact on geomagnetic conditions. The two largest disruptions of geomagnetic field take place during severe space weather conditions in October and November 2003. With the A p index usually well below 30, the most marked geomagnetic field deterioration observed around 29 October (day 302) raised the A p index value more than 6-fold (to almost 200), as shown on Figure 4. There was only one comparable event in Summer 2003, with geomagnetic disturbance far less pronounced than during the second outbreak in October–November 2003 period.

Figure 4. A p index values in the year 2003.
A detailed insight into the behaviour of all three space weather indices during the October–November 2003 period (Figure 5) shows a very good correlation between them. Additionally, a certain delay in response to severe space weather outbreak can be observed. Solar flux responds in the fastest way, with the A p and sunspot number indices acting with a delay of several hours and several days, respectively.

Figure 5. Combined diagram of sunspot number (black), solar flux (red), and A p (green) indices values during the October–November 2003 period.
5. GPS IONOSPHERIC DELAY IN CROATIA DURING AUTUMN 2003
GPS ionospheric delay dynamics can be observed in real time using dual-frequency geodetic GPS receivers, as presented in section 3, equation (9). At the time of the severe space weather outbreak in 2003, two geodetic GPS reference stations were set in Croatia as a part of a larger European geodetic network, one of them situated in Osijek, eastern Croatia. Archived pseudorange measurements taken during the period in question are available on the Internet. The RINEX observation (Institut Geographique National, 2006) and navigation (US National Geodetic Survey – CORS, 2006) files have been retrieved in order to reconstruct the real ionospheric situation over Croatia during October and November 2003. Observed dual-frequency pseudorange measurements were used for the determination of actual TEC and GPS ionospheric delay values. Archived RINEX navigation files were used to extract the information needed for determination of A and P parameters of Klobuchar model (equation (10)). The main aims were to research the actual GPS ionospheric delay dynamics and investigate the behaviour of the Klobuchar model during severe space weather conditions. Both tasks were performed satisfactorily.
A series of GPS ionospheric delay values taken every 15 minutes during the October–November period at Osijek, Croatia reference station are shown in Figure 6. The actual GPS ionospheric delay values were derived from the RINEX observation files, while modelled values were determined according to Klobuchar. The time series of actual GPS ionospheric delays show the appearance of three ionospheric storms between days 300 and 325 in the year 2003. These storms had an usual life cycle (Davis, Reference Davis1990, Booker, Reference Booker1954), consisting of the initial, negative and recovery phase. The initial phases raised the maximum daily GPS ionospheric delay to values of 7–8 m, which is in accordance with previous observations elsewhere, as presented in references. The negative phases lowered the maximum daily GPS ionospheric delay below the average value (4 m). The recovery phases returned the daily GPS ionospheric delay to normal (long-term average in quiet conditions) value, with the exemption of the first ionospheric storm (on 29 October) being followed by the second one too soon to allow the recovery phase.

Figure 6. Actual (derived from dual frequency GPS pseudorange measurements, black) and modelled (according to Klobuchar, red) GPS ionospheric delay above Osijek, Croatia.
The drawbacks of the Klobuchar model utilisation during severe space weather conditions are apparent, and can be summarised as follows.
• The Klobuchar model responds to immediate outbreaks of severe space weather with considerable delay (as much as a couple of days).
• Estimated values of the GPS ionospheric delay are considerably larger than the actual ones. This means that the application of the model in severe space weather conditions generates positioning errors, instead of error correction provision.
• Response of the Klobuchar model to short-term disturbances is slow and it has pronounced and sustained impact long after the triggering disturbance fades away.
• The Klobuchar model in its standard form does not take into account local ionospheric characteristics.
6. MODELLING RELATIONSHIP BETWEEN SPACE WEATHER PARAMETERS AND GPS IONOSPHERIC DELAY
The dynamics of extracted actual maximum daily GPS ionospheric delay values was analysed in relation to the dynamics of space weather parameters. Two models have arisen as the result of the analysis providing the foundation for a more detailed analysis of the regional impact of severe space weather on GPS ionospheric delay. Both models take advantage of the existence of various types of space weather conditions (quiet, mildly disturbed, severe) to correlate measured (actual) maximum daily GPS ionospheric delay observed in Osijek, Croatia with space weather parameters. The parameters of both models are presented in Table 2.
Table 2. Parameters of established experimental models.

One linear model (Model 1) has been established to describe a direct relation between the actual maximum daily equivalent GPS ionospheric delay and sunspot number (Figure 7), while the other (Model 2) describes the relationship between the actual maximum daily GPS ionospheric delay and the solar flux (Figure 8). An attempt was made to establish the similar model for the A p index (Figure 9) However, this was not successful due to a lack of even distribution of the A p index values in a wider range.

Figure 7. Actual maximum daily equivalent GPS ionospheric delay in relation to sunspot number.

Figure 8. Actual maximum daily equivalent GPS ionospheric delay in relation to solar flux.

Figure 9. Actual maximum daily equivalent GPS ionospheric delay in relation to the A p index.
7. DISCUSSION
The two experimental models present several interesting issues in relation to direct impact of space weather conditions on the maximum daily GPS ionospheric delay in Croatia. First, the slope parameter (a) has practically the same value in both models. Then, Model 1 yields the maximum daily equivalent GPS ionospheric delay of 3·44 m in quiet space weather conditions, which is within a 1 m-error range when compared with the actual observations. Additionally, it provides the maximum daily GPS ionospheric delay of 7·00 m during severe space weather conditions, which is in accordance with observed values, both in Osijek, Croatia and elsewhere.
Model 2 yields the maximum daily equivalent GPS ionospheric delay of 2·41 m in quiet space weather conditions, which is in a very good accordance with the actual observations. Furthermore, it shows the maximum daily GPS ionospheric delay of 7·00 m during severe space weather conditions, which is in accordance with observed values, both in Osijek, Croatia and elsewhere.
Finally, considering the relation between sunspot number and solar flux expressed in Figure 3, both models yield a correct (according to measurements) and identical value of the maximum daily GPS ionospheric delay in severe space weather conditions (sunspot number=300, solar flux=300, maximum daily GPS ionospheric delay=7 m).
8. CONCLUSION AND FUTURE WORK
The October–November 2003 severe space weather event provided an excellent opportunity for a study of the direct impact of severe space weather conditions on the GPS ionospheric delay. Availability of the RINEX observation and navigation archives has enabled detailed research targeting the area of Croatia and surrounding region. Development of the severe space weather conditions has been analysed through an examination of the space weather parameters (sunspot number, solar flux and geomagnetic field planetary A p index). Ionospheric conditions over eastern Croatia related to the GPS ionospheric delay have been reconstructed from the RINEX files. The considerable impact of the severe space weather on the GPS ionospheric delay has been observed. Limitations of the standard (Klobuchar) GPS ionospheric delay model have been identified. Two experimental models describing the direct relation between maximum daily GPS ionospheric delay, and sunspot number and solar flux (respectively) have been established.
Although the achievements presented in this paper are considerable, they only build a foundation for a more extended work aiming to better shape existing models of the GPS ionospheric delays, to investigate local ionospheric characteristics in south-eastern Europe and to establish a more accurate regional GPS ionospheric delay model.













