INTRODUCTION
Lymphatic filariasis (LF) is a parasitic disease caused by the infection with one or several of a group of filarial nematodes dwelling in the lymph system and being transmitted by mosquito vectors. Recently, revised figures estimate that LF is endemic in 83 countries and that 119 million people are infected worldwide. LF is a major cause of morbidity, with the loss of 4·6 million DALYs (disability-adjusted life years) (Remme et al. Reference Remme, Feenstra, Lever, Medici, Morel, Noma, Ramaiah, Richards, Sékétéli, Schmunis, van Brakel, Vassall, Jamison, Breman, Measham, Alleyne, Claeson, Evans, Jha, Mills and Musgrove2006), severely affecting socio-economic development in endemic areas (Ramaiah et al. Reference Ramaiah, Guyatt, Ramu, Vanamail, Pani and Das1999; Zagaria and Savioli, Reference Zagaria and Savioli2002). The Global Programme to Eliminate Lymphatic Filariasis (GPELF), launched in 2000, involves community-wide annual treatment with the broad-spectrum anthelmintic albendazole (ABZ) in combination with ivermectin (IVM) or diethylcarbamazine (DEC). The combination chosen depends on whether or not human onchocerciasis is co-endemic (Maher and Ottesen, Reference Maher and Ottesen2000; Ottesen, Reference Ottesen2000, Reference Ottesen2002; Dean, Reference Dean2002; Zagaria and Savioli, Reference Zagaria and Savioli2002).
Resistance to both benzimidazoles (including ABZ) and macrocyclic lactones (MLs, to which IVM belongs), has been documented in many parasitic nematodes affecting livestock (Prichard et al. Reference Prichard, Hall, Kelly, Martin and Donald1980; Prichard, Reference Prichard1990; Wolstenholme et al. Reference Wolstenholme, Fairweather, Prichard, von Samson-Himmelstjerna and Sangster2004), suggesting that the possibility of resistance developing in lymphatic filariae of humans should not be dismissed. There have been some reports of tolerance to DEC by filarial parasites (Eberhard et al. Reference Eberhard, Lowrie and Lammie1988, Reference Eberhard, Lammie, Dickinson and Roberts1991), and we have shown that a polymorphism, known to be associated with benzimidazole resistance in veterinary parasites, is present in West African populations of Wuchereria bancrofti (see Schwab et al. Reference Schwab, Boakye, Kyelem and Prichard2005). ABZ resistance is known to be associated with selection on β-tubulin and is thought to be recessive in most helminths of veterinary importance (Elard and Humbert, Reference Elard and Humbert1999; Prichard, Reference Prichard2001; Silvestre and Cabaret, Reference Silvestre and Cabaret2002).
Schwab et al. (Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006) incorporated population genetics into the deterministic mathematical model EPIFIL, which examines the population dynamics of W. bancrofti (see Chan et al. Reference Chan, Srividya, Norman, Pani, Ramaiah, Vanamail, Michael, Das and Bundy1998, Reference Chan, Norman, Michael, Bundy, Das, Pani and Ramaiah1999; Norman et al. Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000), with the aim of investigating the impact of mass drug administration (MDA) on the development of ABZ resistance in the absence of resistance to either DEC or IVM. The model suggested that if 10 annual treatments with ABZ+DEC were applied, this would lead to a 5-fold increase in a (homozygous) ABZ resistant genotype, whereas, in the case of the ABZ+IVM combination, the increase in ABZ resistance would be less pronounced.
Recently, it has been documented that in areas of Ghana endemic for the related filarial nematode Onchocerca volvulus, in which humans have been treated more than 9 times with IVM, some infected individuals exhibit a suboptimal response phenotype and experience a faster recovery of microfilaridermia after treatment than normal responders (Awadzi et al. Reference Awadzi, Attah, Addy, Opoku, Quartey, Lazdins-Helds, Ahmed, Boatin, Boakye and Edwards2004a, Reference Awadzi, Boakye, Edwards, Opoku, Attah, Osei-Atweneboana, Lazdins-Helds, Ardrey, Addy, Quartey, Ahmed, Boatin and Soumbey-Alleyb). Whether this phenotype is associated with genetic changes indicative of selection under IVM pressure has not yet been ascertained. However, there is genetic evidence that selection by IVM treatment may indeed be occurring in O. volvulus populations. Significant differences in allele frequencies between worms obtained from untreated and IVM-treated human populations were found for β-tubulin, P-glycoprotein and other ABC transporter genes (Eng and Prichard, Reference Eng and Prichard2005; Ardelli and Prichard, Reference Ardelli and Prichard2004; Ardelli et al. Reference Ardelli, Guerriero and Prichard2005, Reference Ardelli, Guerriero and Prichard2006a, Reference Ardelli, Guerriero and Prichardb; Eng et al. Reference Eng, Blackhall, Osei-Atweneboana, Bourguinat, Galazzo, Beech, Unnasch, Awadzi, Lubega and Prichard2006).
In Haemonchus contortus, the barber's pole worm of small ruminants, more than one gene appears to be under selection by repeated treatments with IVM or other MLs (Blackhall et al. Reference Blackhall, Pouliot, Prichard and Beech1998a, Reference Blackhall, Liu, Xu, Prichard and Beechb; Prichard, Reference Prichard2005). Although previous reports had concluded that IVM resistance in H. contortus was a monogenic trait (Le Jambre et al. Reference Le Jambre, Gill, Lenane and Baker2000), more recent evidence, based on the responses of field isolates of resistant H. contortus and Trichostrongylus colubriformis to MLs, suggests that ML resistance is likely to be polygenic (Le Jambre et al. Reference Le Jambre, Geoghegan and Lyndal-Murphy2005). The results of a mathematical model investigating anthelmintic resistance in sheep parasites examined concurrent selection by more than one drug upon multiple resistance genes, and concluded that under the assumption of linkage equilibrium, resistance is selected more slowly when it is polygenic rather than monogenic (Barnes et al. Reference Barnes, Dobson and Barger1995).
Little is known about the relative dominance of alleles conferring ML resistance in parasitic nematodes. Mathematical models have demonstrated how the mode of inheritance of drug resistance has a large impact on its selection, with dominant traits being selected more rapidly (Barnes et al. Reference Barnes, Dobson and Barger1995). In H. contortus, in particular, it has been speculated that IVM resistance is a completely dominant trait (Le Jambre et al. Reference Le Jambre, Gill, Lenane and Baker2000; Barnes et al. Reference Barnes, Dobson, Stein, Le Jambre and Lenane2001), whereas Le Jambre et al. (Reference Le Jambre, Geoghegan and Lyndal-Murphy2005) have suggested that resistance to moxidectin and abamectin, also members of the ML family, are semi-recessive and semi-dominant, respectively. Another study has shown that the mode of inheritance of ML resistance to moxidectin in Teladorsagia circumcincta may be semi-dominant or recessive (Sutherland et al. Reference Sutherland, Leathwick, Moen and Bisset2002).
In this paper, we expand our previous work (Schwab et al. Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006) to include the possibility of concurrent selection for resistance to ABZ and IVM in W. bancrofti. We have chosen to consider resistance to IVM and not to DEC, because, unlike the many cases of IVM resistance in veterinary nematodes, resistance against DEC has not been unequivocally demonstrated to date.
DEVELOPMENT OF THE MODEL
Population dynamics
The model described in this paper is based on EPIFIL (Chan et al. Reference Chan, Norman, Michael, Bundy, Das, Pani and Ramaiah1999; Norman et al. Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000), into which genetic structure was incorporated by Schwab et al. (Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006), where all equations and parameters for EPIFIL may be found. Since EPIFIL was initially parameterized for the locality of Pondicherry, India, where age-specific microfilarial infection profiles peak in young humans, the model assumes some degree of protective immunity against incoming infective larvae. This conjecture has been maintained in the work presented here. Parameters determining the intensity of transmission and the particular epidemiology in the model are such that the annual biting rate (by Culex quinquefasciatus) is ∼70 000 bites per person per year, the annual transmission potential is 940 third-stage larvae per person per year, the mean microfilaraemia is 0·85 per 20 μl of blood, and the prevalence of microfilarial infection is 8% prior to the introduction of chemotherapy, based on the EPIFIL model (Norman et al. Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000).
Population genetics
Analysis of patients from villages in Burkina Faso, prior to the introduction of anti-LF chemotherapy, indicated that the β-tubulin genotype distribution of W. bancrofti microfilariae deviates from the Hardy-Weinberg equilibrium (Schwab et al. Reference Schwab, Boakye, Kyelem and Prichard2005). The non-random mating of W. bancrofti causes a deficiency in the proportion of heterozygote offspring, which can be described using Wright's inbreeding F-statistic (Wright, Reference Wright1951). W. bancrofti from the untreated population in Burkina Faso was shown to have an overall inbreeding coefficient of F IT=0·44 (Churcher, Reference Churcher2006). A detailed description of this calculation and a discussion of the possible mechanisms generating homozygosity in W. bancrofti will be presented elsewhere. Throughout this paper, and unless otherwise stated, the genotype distribution for microfilariae shall be altered to account for this degree of non-random mating (see Tables B.1. and C.1 of Appendices B and C), as was done in the previous study (Schwab et al. Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006).
We have assumed that there are no costs or trade-offs associated with the resistance alleles (i.e., resistant and susceptible W. bancrofti have identical fitness prior to the introduction of chemotherapy). We have also assumed that resistance to ABZ is associated with a single autosomal locus with 2 alleles, with the resistance allele being recessive. IVM resistance was assumed to be associated with either 1 autosomal locus with 2 alleles (i.e., to be monogenic), or with 2 autosomal loci with 2 alleles each (i.e., to be polygenic). In the default setting, IVM resistance was assumed to be dominant, but this assumption was later relaxed in order to explore the influence of different modes of inheritance, ranging from a fully dominant to a fully recessive trait. Unless otherwise stated, the initial frequencies of the ABZ and IVM resistance alleles were (respectively) set to 0·2 (based on Schwab et al. Reference Schwab, Boakye, Kyelem and Prichard2005) and 0·05 (loosely based on polymorph/allele frequencies observed in O. volvulus; Eng and Prichard, Reference Eng and Prichard2005; Eng et al. Reference Eng, Blackhall, Osei-Atweneboana, Bourguinat, Galazzo, Beech, Unnasch, Awadzi, Lubega and Prichard2006). In order to test the sensitivity of model outcomes to assuming lower initial values, we also conducted simulations using 0·02 for both putative ABZ and IVM resistance allele frequencies.
Monogenic ivermectin resistance
When ABZ and IVM resistances were both considered and each was assumed to be monogenic, each of the EPIFIL equations for adult worms, microfilariae and infective larvae populations, was written to represent parasites which were either: (i) drug sensitive for both drugs; (ii) ABZ-sensitive and IVM-resistant; (iii) ABZ-resistant and IVM-sensitive, or (iv) resistant to both drugs. It is thought that ABZ and IVM resistance may both involve the β-tubulin gene (Prichard, Reference Prichard2001; Eng and Prichard, Reference Eng and Prichard2005; Eng et al. Reference Eng, Blackhall, Osei-Atweneboana, Bourguinat, Galazzo, Beech, Unnasch, Awadzi, Lubega and Prichard2006), such that there is a chance that the loci conferring ABZ and IVM resistance may be completely or partially linked. Various degrees of dominance of IVM resistance and linkage, with recessive ABZ resistance, were considered by altering assumptions regarding drug efficacy and the degree of recombination between ABZ and IVM resistance loci (full equations are given in Appendices A and B).
Polygenic ivermectin resistance
For the situation in which IVM resistance would be conferred by 2 loci, we assumed that one of these loci is completely linked to ABZ resistance (i.e., no recombination between loci), as would be the case if both ABZ and IVM resistance were to involve β-tubulin. The other IVM resistance locus was assumed to be unlinked (e.g., involving a P-glycoprotein or another gene), resulting in worm populations with 30 possible genotype combinations. We considered 3 different scenarios: (1) one IVM resistance locus was responsible for IVM resistance in adult nematodes and a second locus for IVM resistance in microfilariae, as may be the case if adults and microfilariae have different resistance mechanisms, a scenario which may be consistent with the differences in the responses of adult worms and microfilariae to IVM; (2) neither locus on its own led to IVM resistance, but selection on both loci together was required for resistance, which will occur if genetic change at both loci is required for the resistance mechanism to be functional; and (3) one locus conferred resistance in all microfilariae and 70% of adults, and a second locus conferred resistance in the remaining 30% of adults, suggesting that one mechanism of resistance protects all microfilariae and most adults, and that a second mechanism has developed in the adult worms that survive treatment. This scenario may again, in part, reflect differences in the responses of macrofilariae and microfilariae to IVM. Linkage equilibrium was assumed between the 2 IVM loci.
Treatment-related parameters
Once the model is run to equilibrium, and unless otherwise stated, MDA with the ABZ+IVM combination starts in year 1 and proceeds annually for 10 years uninterruptedly. (Although the main strategy of GPELF is based on a programme duration of 5 years in each endemic area, doubts have been raised as to whether this would be enough to attain intended goals in all regions (Michael et al. Reference Michael, Malecela-Lazaro, Simonsen, Pedersen, Barker, Kumar and Kazura2004).) In order to reflect therapeutic coverage (set at a default level of 85% of the total population), treated and untreated parasite populations were modelled separately. At the point of transmission, the contributions of each population of infective larvae, from treated and untreated people, respectively (depending on coverage level), were introduced into the equations for adult worms. Due to the constraints imposed by a deterministic model which considers population averages, and to reflect that often the same individuals fail to comply with treatment in successive years, the model assumes that the same section of the host population is treated at each round. After cessation of chemotherapy, no further treatments take place, but the model is run for 10 more years. Model outputs regarding microfilarial genotype frequencies (expressed as percentages) and host microfilaraemia (expressed as microfilariae per 20 μl of blood) are shown up to years 15 and 20, respectively.
Assumptions on drug efficacy were based on those made by Michael et al. (Reference Michael, Malecela-Lazaro, Simonsen, Pedersen, Barker, Kumar and Kazura2004) and other published drug trials (Addiss et al. Reference Addiss, Beach, Streit, Lutwick, LeConte, Lafontant, Hightower and Lammie1997; Ismail et al. Reference Ismail, Jayakody, Weil, Nirmalan, Jayasinghe, Abeyewickrema, Rezvi Sheriff, Rajaratnam, Amarasekera, de Silva, Michalski and Dissanaike1998; Dunyo et al. Reference Dunyo, Nkrumah and Simonsen2000) and have been summarized in Table 1. Treatment was modelled as instantaneous reductions in adult worms (macrofilaricidal effect), microfilarial populations (microfilaricidal effect), or female worm reproduction rate (sterilizing effect) by the percentage efficacy given in Table 1. Following chemotherapy, sterilized females did not resume microfilarial production for a period of time specified for each drug. Model outcomes in this paper examine the effect, during and up to 5 years after the cessation of MDA, of 10 annual treatments on the genotype distribution of the microfilariae (the stage more feasibly sampled for genetic analyses), and up to 10 years after the cessation of MDA on the mean microfilaraemia.
Table 1. Efficacy assumptions for ABZ+IVM treatment on drug-susceptible (adapted from Michael et al. Reference Michael, Malecela-Lazaro, Simonsen, Pedersen, Barker, Kumar and Kazura2004) and drug-resistant Wuchereria bancrofti
All equations for the models explored are given in Appendices A–C and Tables B.1 and C.1. Model code was written using the JSim numerical integration software, available from http://nsr.bioeng.washington.edu/PLN/Members/butterw/JSIMDOC1.6/JSim_Home.stx/view. Differential equations were solved using the Euler method (Edwards and Penney, Reference Edwards and Penney1989). Prior to the initiation of control perturbations, W. bancrofti populations were assumed to be at endemic equilibrium, as it has been ascertained that prevalences of infection in areas of Burkina Faso have remained relatively stable for at least 30 years (Gyapong et al. Reference Gyapong, Kyelem, Kleinschmidt, Agbo, Ahouandogbo, Gaba, Owusu-Banahene, Sanou, Sodahlon, Biswas, Kale, Molyneux, Roungou, Thomson and Remme2002).
RESULTS
MONOGENIC IVERMECTIN RESISTANCE
Influence of parasite inbreeding
Model outputs indicate that parasite non-random mating (which results in increased offspring homozygosity) increases the projected rate at which ABZ and IVM-resistant genotypes would spread throughout the genome of W. bancrofti. Increased microfilarial homozygosity (as reflected by the value of F IT) increases the frequency of the dominant IVM-resistant genotypes during MDA. For F IT=0·44 (the value of homozygosity observed in Burkina Faso), the frequency of IVM-resistant genotypes in year 10 (63%) is 8 times higher than that prior to the initiation of control (8%), whereas for F IT=0 (no excess homozygosity), the frequency in year 10 is 6 times as high (Fig. 1A). If initial allele frequencies are assumed to be lower (0·02 for both ABZ and IVM), the frequency of IVM-resistant microfilariae would increase 17-fold (from 3% to 51%) when F IT=0·44, but only about 6-fold (from 4% to 24%) if random mating is assumed. It is important to note that this increase only occurs in the presence of ABZ resistance. At the cessation of treatment, the percentage of microfilarial genotypes resistant to both ABZ and IVM would have increased to 52% in the case of F IT=0·44 as opposed to 8% when F IT=0 and parasite mating is random (Fig. 1B). The higher frequency of resistant genotypes caused by parasite non-random mating is reflected in higher levels of microfilaraemia, particularly after 5 years of MDA (Fig. 1C).
Fig. 1. The effect of increasing levels of parasite inbreeding (i.e., increased homozygosity) as measured by Wright's F-statistic, F IT, on the development of anthelmintic-resistant Wuchereria bancrofti, during 10 annual treatments at 85% therapeutic coverage with the ABZ+IVM combination, and after 5 (genotype frequency) or 10 years (microfilaraemia) following cessation of mass drug administration (MDA). The initial ABZ and IVM resistance allele frequencies were set, respectively, at 0·2 and 0·05. IVM resistance is assumed to be a fully dominant trait. (A) The average frequency (expressed as percentage) of IVM-resistant microfilarial genotypes; (B) the average frequency (%) of microfilarial genotypes resistant to both ABZ and IVM, and (C) the mean microfilaraemia per 20 μl of blood in the human host population, with chemotherapy starting in year 1.
Concurrent development of ABZ and IVM resistance
Model outputs indicate that when the initial frequencies of the ABZ and IVM resistance alleles is 0·2 and 0·05, respectively, MDA with ABZ+IVM would increase the frequency of microfilarial genotypes resistant to both drugs from under 1% prior to control to 52% at its cessation (Fig. 2A), or to 40% when initial resistance allele frequency to both drugs is 0·02. The presence of IVM resistance increases the rate of ABZ resistance development. In the absence of IVM resistance, the frequency of ABZ-resistant homozygotes only increases from 12% at year 0 to 14% at year 10, and to 40% 5 years after halting MDA (Schwab et al. Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006). If the IVM resistance gene is present at an initial allele frequency of 0·05, the frequency of ABZ-resistant homozygotes would reach 57% and 70%, following the same treatment schedule at years 10 and 15, respectively (Fig. 2A). If the initial resistance allele frequency, in relation to both drugs, is 0·02, the frequency of the ABZ-resistant homozygotes would reach 39% and 54% at years 10 and 15, respectively. The rate of IVM resistance spread is similarly affected by the concurrent selection for the ABZ-resistant genotype (results not shown). The presence of IVM resistance would also increase the average microfilaraemia relative to that with no resistance, and this is particularly marked after 5 rounds of MDA (Fig. 2B).
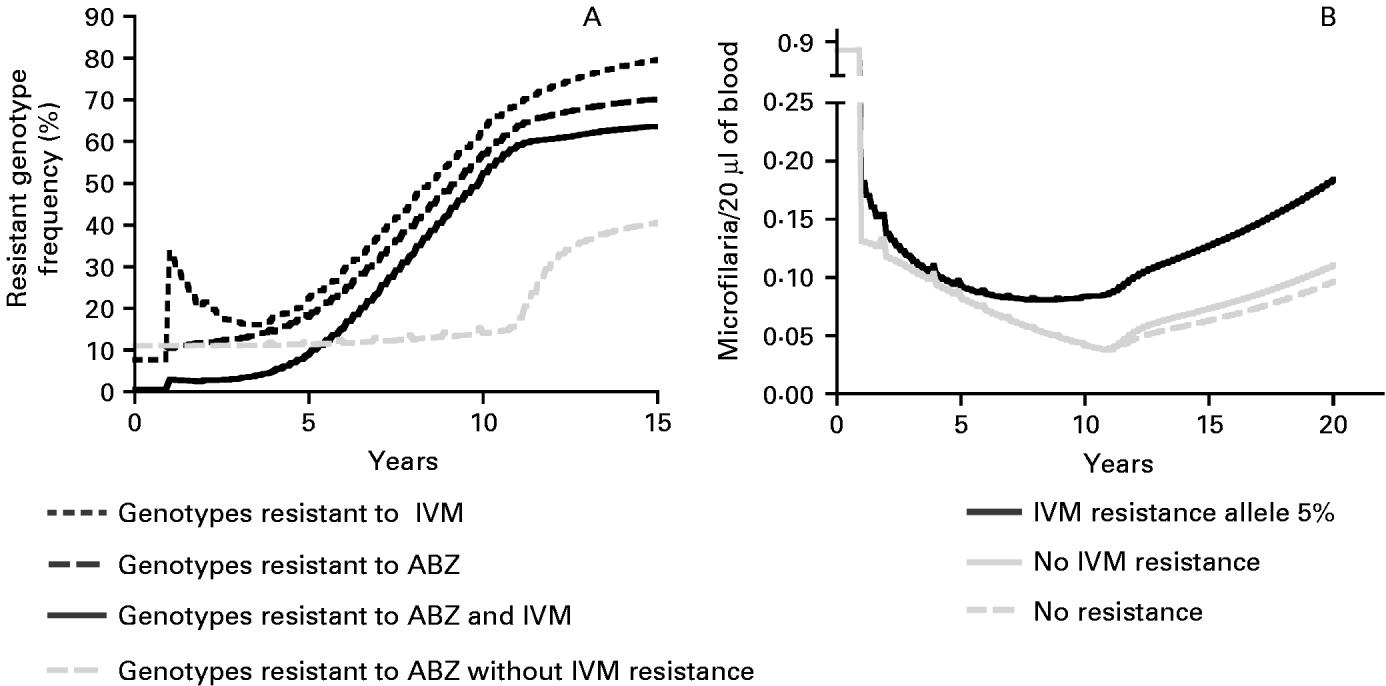
Fig. 2. Estimated development of anthelmintic resistance in Wuchereria bancrofti during 10 annual treatments with ABZ+IVM at 85% coverage and after 5 (genotype frequency) or 10 years (microfilaraemia) following cessation of MDA. (A) The average frequency (%) of microfilarial genotypes resistant to ABZ, IVM, or to both ABZ and IVM, where resistance to both ABZ and IVM can develop, or if only ABZ resistance occurs, and (B) the mean microfilaraemia per 20 μl of blood in the human host population, with chemotherapy starting in year 1, if there is no drug resistance, resistance to ABZ, but not to IVM or when resistance can develop to both ABZ and IVM.
The frequency of resistant genotypes, following the cessation of treatment, increased with the number of years of annual MDA treatment. Fifteen years after the commencement of treatment, the frequencies of microfilariae resistant to both ABZ and IVM were estimated to be 20%, 40% and 65%, after 5, 7 and 10 years of MDA (combination treatment), respectively. The same trend was observed with the lower initial allele frequencies (results not shown).
Age-specific profiles of ABZ and IVM-resistant genotypes
The proportion of resistant microfilariae that a host harbours will depend on the age of the host and the time since the start of chemotherapy. Fig. 3 indicates that, in a treatment programme of 10 years duration and following the onset of MDA, the proportion of resistant genotypes will be highest in the youngest hosts, and this is particularly marked 5 and 10 years into the programme. The peak resistant genotype frequency shifts towards older ages (teenagers and young adults) 5 and 10 years after the cessation of treatment, whilst the frequency in children starts returning to that in the overall population. Hosts which were young at the start of chemotherapy continue to have a higher than average number of resistant parasites for a number of years after treatment ceases, and this result reflects the assumption of acquired protective immunity as a function of established worm burden embedded in EPIFIL. The same effect was observed with the lower initial allele frequencies.
Fig. 3. Host age-specific profiles of the proportion of microfilariae which are resistant to ABZ and IVM, 5, 10, 15 and 20 years after commencement of 10 annual rounds of MDA with ABZ+IVM with 85% therapeutic coverage. Initial ABZ and IVM resistance allele frequencies, were 0·2 and 0·05, respectively, with F IT=0·44.
Variable ivermectin resistance dominance
The default parameters of the model assume that the IVM resistance allele is fully dominant. However, although it is generally believed that the ABZ resistance allele will be recessive (benzimidazole resistance has been found to be recessive in nematodes of non-human animals), it is still unclear how IVM resistance would be inherited. We examined the effect of varying the degree of dominance of the IVM resistance allele. Results (not shown) indicate that varying the dominance of IVM resistance has a small impact on ABZ resistance. The frequency of the ABZ-resistant genotype is marginally higher if the IVM resistance allele is recessive (74·5% 5 years after the cessation of treatment) than if it is dominant (71·2%). As may be expected, the frequency of the IVM-resistant genotype increases with the dominance of IVM resistance. Projected host microfilaraemia, after 10 years of chemotherapy, will be slightly higher if the IVM resistance gene is recessive. However, this increase is relatively minor (0·198 microfilariae per 20 μl of blood after treatment if IVM resistance is recessive vs 0·184 microfilariae per 20 μl of blood if it is dominant). Dominance of IVM resistance has the same impact at the lower initial allele frequencies of 0·02 for both drugs.
Dependence of selection on linkage
In the monogenic IVM resistance model, the rate of increase in the frequency of resistant genotypes was relatively insensitive to whether the loci conferring ABZ and IVM resistance were unlinked, partially linked, or fully linked, as long as prior to the introduction of chemotherapy, the resistance loci were in random association within the parasite genome (i.e., genotypes were at linkage equilibrium, outputs not shown). However, if both loci were 100% linked (i.e., no recombination occurs between the 2 loci at meiosis), the result of selection would be affected by the number of chromosomes in the W. bancrofti population bearing only IVM resistance or both ABZ and IVM resistance before the start of treatment (initial linkage disequilibrium). If the (linked) alleles conferring ABZ and IVM resistance were assumed to be always on the opposite strands of a chromosome (high initial linkage disequilibrium with discordant alleles), the ABZ and IVM-resistant genotypes would be less frequent in the population after treatment than would be the case if they were initially at linkage equilibrium. The highest frequency of resistant genotypes would result from initially high linkage disequilibrium when both ABZ and IVM resistance alleles are located on the same chromosome (concordant alleles). These results are illustrated in Fig. 4. The effect of linkage was the same when the lower initial frequencies were assumed (data not shown).
Fig. 4. The estimated effect, on the development of ABZ and IVM resistance, of 100% linkage between the alleles conferring these traits during 10 annual treatments with ABZ+IVM at 85% coverage. The initial ABZ and IVM resistance allele frequencies, and the value of F IT are as in Fig. 3. (A) The average frequency (%) of ABZ-resistant microfilarial genotypes; (B) the average frequency (%) of IVM-resistant microfilarial genotypes; (C) the average frequency (%) of ABZ and IVM-resistant microfilarial genotypes and (D) the mean microfilaraemia per 20 μl of blood in the human host, with chemotherapy starting in year 1. Linkage disequilibrium was calculated after Hartl and Clark (Reference Hartl and Clark1997) ; standardized linkage disequilibrium (D′) was calculated after Lewontin (Reference Lewontin1988).
POLYGENIC IVERMECTIN RESISTANCE
The rate of increase of IVM resistance will be higher if it is inherited as a single gene rather than as a 2-gene system, although the difference will depend on the initial allele frequencies and the selective advantage that the different IVM resistance genes confer individually. If 2 genes are both required for complete IVM resistance and individually they do not confer any resistance, the development of resistance will be delayed if the resistance alleles are at a low initial frequency. However, the development of monogenic and polygenic IVM resistance is relatively similar at higher initial allele frequencies, as a high proportion of worms will already have both IVM resistance genes (Fig. 5). Results also indicate that the development of polygenic IVM resistance will be influenced by the life-cycle stage of the parasite at which resistance is manifested. If one gene conferred IVM resistance to microfilariae (impeding microfilaricidal effects) and the other gene conferred resistance to all adult worms (preventing macrofilaricidal or anti-fecundity effects in 100% of the worms), treatment failure, under our model assumptions, would develop more rapidly than would be the case if the first gene was, for instance, responsible for both microfilarial resistance and resistance in 70% of adults, and the second gene conferred resistance to the remaining 30% of the macrofilariae. These conclusions were the same when the lower initial allele frequencies were assumed.
Fig. 5. The estimated effect of selection on 1 ABZ resistance gene and 2 IVM resistance genes on the development of ABZ and IVM resistance during 10 annual treatments with ABZ+IVM at 85% coverage. The initial ABZ and IVM resistance allele frequencies, and the value of F IT are as in Fig. 3. (A) The average frequency (%) of IVM-resistant microfilarial genotypes; (B) the average frequency (%) of microfilarial genotypes resistant to both ABZ and IVM, and (C) the mean microfilaraemia per 20 μl of blood in the human host, with chemotherapy starting in year 1.
DISCUSSION
Combination therapy with 2 anthelmintics will influence the rates of development of single and multi-drug-resistant parasites according to the efficacies of the drugs (in combination and individually) and the underlying genetics conferring resistance. Due to the many uncertainties regarding the population dynamics of the parasite (e.g., operation of acquired protective immunity) and the inheritance of IVM resistance (e.g., whether it is dominant), among others, the results of this study provide qualitative insight (rather than quantitative predictions) into how assumptions regarding the genetics of IVM resistance may influence the development of drug resistance in W. bancrofti under a combination treatment with ABZ+IVM.
The models highlight a number of results which may be of interest to those investigating the possibility of resistance developing, following prolonged co-administration of 2 anthelmintics. One salient prediction was the peak and subsequent temporary decline in the proportion of microfilariae resistant to IVM following the first round of chemotherapy. Results suggest that molecular epidemiological surveys conducted in the first 3 years of treatment might conclude that the genes conferring drug resistance had negative pleiotropic effects, therefore reducing the chance that IVM resistance will impede parasite elimination. However, the model indicates that the decline in microfilariae resistant to IVM may mask an increase in the number of adult worms resistant to both ABZ and IVM. The initial peak in IVM resistance is caused by the relative dominance of the alleles conferring ABZ and IVM resistance, and the assumed efficacies of the 2 drugs against the different life-cycle stages of the parasite. Microfilariae resistant to IVM prior to the start of chemotherapy survive the first round of treatment, but subsequently start to decrease in number as ABZ would have sterilized the majority of IVM-resistant adult worms. The rate of decline observed in the proportion of microfilariae resistant to IVM is highly sensitive to the assumed life-span of microfilariae, a parameter particularly difficult to quantify, with estimates ranging from 6 months to 2 years (Plaisier et al. Reference Plaisier, Cao, Van Oortmarssen and Habbema1999). It should be noted that if multiple genes are associated with different pharmacodynamic properties of a drug or drug combination, then examining the changes at single loci may produce misleading results.
Previous work had indicated that the change in proportion of ABZ-resistant microfilariae may only become apparent after the end of the treatment period, due to the small amount of reproduction that occurs in the treated population while chemotherapy is in progress and the fact that the microfilariae population is, at that time, composed primarily of parasites from untreated patients (Schwab et al. Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006). However, the present work suggests that concurrent selection of both ABZ and IVM resistance may cause observable changes in the proportion of ABZ, IVM, and ABZ and IVM-resistant microfilariae during the treatment period, as some parasites can overcome the combined action of both drugs and are able to reproduce. According to model outcomes, the presence of IVM resistance would enhance the rate of increase of any ABZ resistance, and vice versa, as a parasite resistant to both drugs has a higher probability of completing its life-cycle.
There is considerable debate as to the number of years that combination chemotherapy should be provided under the current GPELF programmes for achieving the goals of elimination. The number of years of annual combination treatment influences the proportion of the microfilarial population with ABZ and IVM-resistant genotypes following the cessation of treatment. The higher frequency of resistant genotypes that follows a longer period of treatment indicates that for a given location, if transmission has not been interrupted by the programme and the parasite population has not been eliminated, a return to chemotherapy would be considerably less effective if the initial phase of treatment had lasted for 10 years rather than for 5 years. However, the present (deterministic) framework is not appropriate to explore the probability of parasite elimination with duration of control. In most of the scenarios explored here, levels of microfilaraemia which might cause concern would not be evident until after 5 years into the programme. Also, although the levels of parasite inbreeding used here are those estimated for W. bancrofti populations in West Africa, vector parameters derived from Culex (a vector for which the per microfilariae probability of completing its development within the mosquito increases with decreasing microfilaraemia) were used. LF in West Africa is transmitted by Anopheles species (for which the per-microfilaria probability of development may decrease markedly at low levels of microfilaraemia due to the increased proportion of ingested microfilariae damaged by the cibarial armatures of these vectors) (Bryan and Southgate, Reference Bryan and Southgate1988; Bryan et al. Reference Bryan, McMahon and Barnes1990).
An interesting result is that hosts of different ages may harbour different proportions of resistant microfilariae. Following the start of chemotherapy, the model indicates that children will, on average, acquire a higher proportion of resistant W. bancrofti than adult hosts, because they are becoming infected with new parasites at a faster rate. The exact age-profile of resistance will depend on the age-dependent heterogeneity in exposure, the acquisition of protective immune responses, and the time since the start of chemotherapy at which genetic surveys are undertaken. The model outputs in this study depend on the ability of EPIFIL to represent adequately the processes regulating W. bancrofti population abundance. EPIFIL assumes that the acquisition of new infections may be reduced in adult hosts due to acquired immunological responses protecting against incoming infection (Norman et al. Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000), but this has not yet been confirmed in different geographical locations (Stolk et al. Reference Stolk, Ramaiah, Van Oortmarssen, Das, Habbema and De Vlas2004). Regardless of the mechanisms underlying infection age-profiles, molecular epidemiological surveys should take into consideration that, after the start of chemotherapy, hosts which acquire new infections at the fastest rate will have the highest resistance allele frequency. This also has implications if vector control is added to annual chemotherapy, because vector control would reduce the acquisition of new parasites and thus assist in reducing the proportion of resistant genotypes in the parasite population.
An analysis of the microfilarial data collected by Schwab et al. (Reference Schwab, Boakye, Kyelem and Prichard2005) indicates that genetic differentiation in W. bancrofti between hosts, and assortative parasite mating may cause excess homozygosity to a degree equivalent to Wright's inbreeding F-statistic of F IT=0·44 (Churcher, Reference Churcher2006). Helminth inbreeding typically enhances the spread of recessive alleles but is not expected to increase selection for alleles which are dominant, as excess homozygosity will reduce the number of offspring with the resistance allele. Model outputs suggest that, under the assumed modes of inheritance of IVM and ABZ resistances, and in the presence of ABZ resistance, helminth inbreeding would increase markedly the spread of IVM and of ABZ and IVM-resistant parasites. This is because the selective advantage conferred by the more rapid increase in ABZ resistance (which is increased by parasite inbreeding) outweighs the loss of microfilariae which are heterozygous at the IVM resistance locus (thus being resistant to IVM). How the degree of parasite inbreeding will influence the frequency of parasites resistant to both ABZ and IVM will depend on the different efficacies of the 2 drugs and the relative dominance of the resistance alleles under selection.
Based on the assumptions made here regarding inheritance, linkage between the genes conferring ABZ and IVM resistance is unlikely to influence the incidence of combination treatment failure, unless the genes are completely linked and are at linkage disequilibrium. The model was not extended to investigate how linkage would influence the development of polygenic IVM resistance, so we cannot speculate on more complicated genetic scenarios. If the genes conferring resistance to both drugs were always present in the same gamete, selection for one type of resistance would also lead to selection for resistance against the second drug, reducing the time that it takes for widespread treatment failure. A recent study indicates that this may be the case for the 2 genes under consideration here, as an increase in the frequency of the Phe200Tyr polymorphism in the β-tubulin gene was observed after the selection of H. contortus with IVM and in IVM-resistant worms (Eng et al. Reference Eng, Blackhall, Osei-Atweneboana, Bourguinat, Galazzo, Beech, Unnasch, Awadzi, Lubega and Prichard2006).
Model outcomes suggest, under our assumptions and parameterization, that microfilarial intensity would decrease to as low as 0·04 microfilariae per 20 μl of blood by the end of MDA in our simulations. Using the calculations proposed by Norman et al. (Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000), this would translate into a microfilarial prevalence of 1%. There has been some debate about the threshold prevalence below which it is deemed that transmission can no longer occur, with the 1% cut-off microfilaraemia stemming from the Chinese experience in eliminating (bancroftian and brugian) LF transmitted by Culex quinquefasciatus and Anopheles sinensis (see WHO, 2003). Michael et al. (Reference Michael, Malecela-Lazaro, Simonsen, Pedersen, Barker, Kumar and Kazura2004) assumed the threshold prevalence to be 0·5%. In Western Samoa, transmission was not interrupted even after the microfilarial prevalence fell to 0·2% due to mass DEC administration (Esterre et al. Reference Esterre, Plichart, Séchan and Nguyen2001). It is thus likely that transmission would continue in the scenarios explored by our model and that resistance could develop. However, we stress that stochastic frameworks (Plaisier et al. Reference Plaisier, Subramanian, Das, Souza, Lapa, Furtado, Van der Ploeg, Habbema and van Oortmarssen1998) are more suitable than deterministic models (Norman et al. Reference Norman, Chan, Srividya, Pani, Ramaiah, Vanamail, Michael, Das and Bundy2000) to investigate the probability of parasite elimination or recrudescence ensuing the cessation of MDA.
Notwithstanding modelling approaches, the presence of multi-drug resistance would hinder the success of combination chemotherapy control programmes and may prevent parasite elimination. However, it is important to note that even though our models have relatively high resistance allele frequencies prior to the introduction of chemotherapy, as default values, the presence of resistance will only become phenotypically manifested in the temporal trends of host microfilaraemia a number of years after the start of treatment (in the present model, typically after 5 years). It should also be noted that the frequency of a potentially ABZ-resistant genotype was found to be already high in West African populations of W. bancrofti microfilariae before the introduction of LF chemotherapy (Schwab et al. Reference Schwab, Boakye, Kyelem and Prichard2005). It is also important to recall that none of the anthelmintics used for LF control is very effective at eliminating the parasite from the host, because W. bancrofti is relatively tolerant to all of the anthelmintics used by the GPELF (Michael et al. Reference Michael, Malecela-Lazaro, Simonsen, Pedersen, Barker, Kumar and Kazura2004). If anthelmintic resistance genes were present in the population prior to the onset of MDA, and assuming that they are randomly distributed among the worm population initially, relatively few parasites will be resistant to both drugs at the first round of treatment. Successive rounds of MDA are likely to promote assortative mating within the surviving (fertile) worm population, thus increasing the number of parasites resistant to both drugs. Only after the genes have re-assorted in the parasite population in this way will treatment failure start to become apparent. With this in mind, it is advisable to implement promptly the monitoring and evaluation of possible changes in the parasite genome, by means of appropriate molecular markers, and to link this to the monitoring of responses to treatment in the host population. These actions may identify, before anthelmintic resistance becomes a major public health concern, treatment factors that could enhance the spread of drug resistance. Although it is typically thought that combination therapy should delay the emergence of treatment failure, factors such as moderately high initial resistance allele frequencies to both drugs, dominance, genetic linkage, parasite inbreeding and high treatment coverage in MDA programmes may cause multi-drug resistance to hinder the achievement of GPELF's goals. Continued updating and improvement of transmission models, particularly those which merge the population dynamics and population genetics of the parasite, should be essential components of any epidemiological surveillance system implemented to protect the investments made by the Global Alliance to Eliminate Lymphatic Filariasis and its donors (Dadzie et al. Reference Dadzie, Basáñez and Richards2004; Michael et al. Reference Michael, Malecela-Lazaro, Maegga, Fischer and Kazura2006; Schwab et al. Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006).
We would like to thank Dr M.-S. Chan and co-workers for providing us with the source code of EPIFIL, the National Simulation Resource of the University of Washington for the JSim software, Dr R. Beech for useful discussions, the National Science and Engineering Research Council of Canada, the Centre for Host Parasite Interactions, Quebec, GlaxoSmithKline, and the Medical Research Council, UK (T. S. C. and M.-G. B.) for financial support.
APPENDIX A. INCORPORATION OF PARASITE POPULATION GENETICS INTO EPIFIL
The EPIFIL model is extended by incorporating genetic structure into the worm population in order to examine the development of ABZ, IVM, and ABZ and IVM resistances. The mathematical models track the number of worms, in both the treated and untreated sections of the human host population, of each of 10 genotype combinations in the case of the ABZ monogenic-IVM monogenic model (2 loci with 2 alleles each), and 30 genotype combinations in the case of the ABZ monogenic-IVM polygenic model (3 loci with 2 alleles each). ABZ resistance is assumed to be recessive throughout, whilst the model investigates the effects of variable IVM resistance dominance, with the default setting assuming that IVM resistance is fully dominant. For each of these loci the different genotypes are identified using the following system: 0 corresponds to the susceptible homozygote, 1 to the heterozygote, and 2 to the resistant homozygote. The mean number of adult worms per person of each genotype is denoted, after dropping the age and time dependency, by W bcde, with subscript b indicating the treatment category (b=T or b=U for worms within, respectively, hosts treated or untreated with ABZ+IVM), and the superscripts c, d and e specifying the worm genotype at each of the different loci (c=the ABZ resistance locus, d=the first, linked IVM resistance locus, and e=the second unlinked IVM resistance locus). If IVM resistance is conferred by a single locus (the IVM monogenic model) the superscript e is dropped and superscript d indicates resistance to macrofilaricidal/inhibition of reproduction and embryostatic effects of IVM. For example, W b00 denotes the mean number of adult worms (in the IVM monogenic model) which have the homozygote susceptible genotype at both the ABZ and IVM resistance loci; W b201 indicates the mean number of worms (in the IVM polygenic model) which are homozygous resistant at the ABZ resistance locus, homozygous susceptible at the linked, IVM resistance locus, and heterozygous at the second, unlinked IVM resistance locus. Similar notation is used to represent the mean number of microfilariae per 20 μl blood, M bcde, and the mean number of L3 larvae per mosquito, L bcde. The level of acquired immunity in the treated and untreated human population is specified by, respectively, I T and I U. The modified EPIFIL equations are as follows,
![L^{\ast cde} \equals\hskip-1 \left[ {C{{L_{T}^{\ast cde} } \over {L_{T}^{\ast } }} \plus \left( {1 \minus C} \right){{L_{U}^{\ast cde} } \over {L_{U}^{\ast } }}} \right]\hskip-2 \left[ {CL_{T}^{\ast } \plus \lpar 1 \minus C\rpar L_{U}^{\ast } } \right]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn4.gif?pub-status=live){kind=small}
where λ is the biting rate per mosquito on humans; V/H is the vector to human ratio; ϕ1 is the proportion of L3 larvae that leave the mosquito's proboscis at the time of biting and are deposited onto a human's skin; ϕ2 is the proportion of the latter which enter the host through the wound caused by the mosquito bite; s 2 is the proportion of larvae that having entered the host will develop into adult worms; h(a) is the proportion of hosts of age a that are bitten, thereby making the biting rate on humans age-dependent (it is assumed that this proportion increases linearly until the age of 9 years and becomes unity thereafter); β is the severity by which larval establishment is decreased by acquired immunity I (which is assumed to increase with cumulative worm burden or worm experience and decay at a rate Δ); μ, γ and σ are, respectively, the per capita death rates of adult worms, microfilariae and L3 larvae; α is the per capita reproductive rate of adult worms (the rate at which fertilized females produce microfilariae per 20 μl of blood), and ωbcde is the proportion of microfilariae with the cde genotype (calculated as described in Appendix B). The proportion of the total host population treated (therapeutic coverage) is denoted by C; 
and . The expression for L*cde determines the average number of L3 larvae per mosquito for each genotype that infect the treated and untreated sections of the population. As with EPIFIL, the L3 population is assumed to be at equilibrium (denoted by the asterisk) and is calculated using equation (A5). In this equation, the function that models larval development within the (Culex-type) mosquito vector as dependent on the level of microfilaraemia, f(M b), is calculated separately for treated and untreated sections of the host population with expression,
![f\lpar M_{b} \rpar \equals 1 \minus \left\{ {1 \plus {{M_{b} } \over {k_{b} }}\left[ {1 \minus \exp\hskip-1 \lpar \minus \rho \sol \kappa \rpar } \right]} \right\}^{ \minus k_{b} },](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn6.gif?pub-status=live){kind=small}
where ρ is the initial, linear rate of increase in L3 larvae per microfilaria in 20 μl of blood, ρ/κ the severity of density-dependent constraints upon larval uptake and/or development; κ the level at which the function saturates (the maximum number of L3 produced per mosquito as microfilaraemia increases), and k b the overdispersion parameter of the negative binomial. In the remainder of equation (A5), g is the proportion of bites which result in infection of mosquitoes, and π(a) is the proportion of the host population surviving to age a, based on a population in Pondicherry, India (for which EPIFIL was first parameterized). The equation for π(a) is given by,
![\pi \lpar a\rpar \equals {{\exp\hskip-1 \lpar \minus a\sol m\rpar } \over m}\left[ {1 \minus \exp\hskip-1 \lpar \minus n\sol m\rpar } \right]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn7.gif?pub-status=live){kind=small}
with m=29 and n=65. Finally, it is assumed (motivated by data), that the overdispersion parameter of the negative binomial distribution of microfilariae in the host population is itself a density-dependent function with expression , representing a degree of overdispersion which depends linearly on microfilaraemia and will therefore increase in the treated sections of the population under microfilaricidal therapy. All the parameter values of the basic EPIFIL model have been listed in Schwab et al. (Reference Schwab, Churcher, Schwab, Basáñez and Prichard2006).
APPENDIX B. IVM Monogenic Model
In the IVM monogenic model we allow the IVM resistance locus to be either linked or unlinked to the ABZ resistance locus. Linkage increases the number of possible genotype combinations a parasite can have as helminths which are heterozygous for both ABZ and IVM resistance can either have both resistance alleles on the same chromosome (alleles are concordant, denoted by superscript C), or have resistance alleles on the opposite, partner chromosome (alleles are discordant, denoted by superscript D). The different genotype combinations for the 2-loci model and their associated abbreviations are listed in Table B1.
Table B.1. The abbreviations and genotype equations used for the ABZ monogenic-IVM monogenic (2-loci) model. For the linked loci it is specified on which chromosome (denoted Ch.) the susceptibility and resistance alleles occur
Parameter F adjusts for excess homozygosity (see main text).
The genotype distribution of microfilariae in the next generation is determined by the allele frequency of the adult worm population using simple Mendelian genetics. The frequency of gametes produced by the adult worm population is denoted by . Gametes can have either the resistance or susceptibility allele at each of the loci under investigation (where h denotes the ABZ resistance locus and i denotes the IVM resistance locus, with resistance in both cases referring to macrofilarial resistance as described above). For the 2-loci model the gamete frequencies are calculated as follows,
![G_{b}^{SS} \equals w_{b}^{\setnum{00}} \plus 0 \mdot 5\hskip-1 \left[ {w_{b}^{\setnum{01}} \plus \lpar 1 \minus r\rpar \,w_{b}^{\setnum{11}^{C} } \plus r\,w_{b}^{\setnum{11}^{D} } \plus w_{b}^{\setnum{10}} } \right]\hskip-4](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn8.gif?pub-status=live){kind=small}
![G_{b}^{SR} \equals w_{b}^{\setnum{02}} \plus 0 \mdot 5 \hskip-1\left[ {w_{b}^{\setnum{01}} \plus r\,w_{b}^{\setnum{11}^{C} } \plus \lpar 1 \minus r\rpar \,w_{b}^{\setnum{11}^{D} } \plus w_{b}^{\setnum{12}} } \right]\hskip-5](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn9.gif?pub-status=live){kind=small}
![G_{b}^{RS} \equals w_{b}^{\setnum{20}} \plus 0 \mdot 5\hskip-1 \left[ {w_{b}^{\setnum{10}} \plus r\,w_{b}^{\setnum{11}^{C} } \plus \lpar 1 \minus r\rpar \,w_{b}^{\setnum{11}^{D} } \plus w_{b}^{\setnum{21}} } \right]\hskip-5](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn10.gif?pub-status=live){kind=small}
![G_{b}^{RR} \equals w_{b}^{\setnum{22}} \plus 0 \mdot 5 \hskip-1\left[ {w_{b}^{\setnum{12}} \plus \lpar 1 \minus r\rpar \,w_{b}^{\setnum{11}^{C} } \plus r\,w_{b}^{\setnum{11}^{D} } \plus w_{b}^{\setnum{21}} } \right]\hskip-5](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921021940953-0066:S0031182007002363:S0031182007002363_eqn11.gif?pub-status=live){kind=small}
where w bcd is the proportion of the adult worm population with the cd genotype (given by ). The proportion of new microfilariae with the cd genotype, , is calculated from the different gamete frequencies; for individual equations see Table B.1. Parameter r is the recombination fraction between the two loci or the proportion of recombinant gametes that are produced by a double heterozygote (Hartl and Clark, Reference Hartl and Clark1997). Genes that are not linked have a recombination fraction r=0·5. Genes which are linked have a value of r<0·5. When genes are 100% linked, r=0 (i.e., no recombination occurs between the two loci). Unless otherwise stated, the model assumes non-random parasite mating, with F (see Tables B.1 and C.1) set at 0·44 (the value of F IT estimated for untreated populations in Burkina Faso, see main text).
APPENDIX C. IVM Polygenic Model
Here we model the parasite genotype frequency when there are 3 loci associated with resistance; one which determines ABZ resistance and another 2 loci that determine IVM resistance. The 3-loci model assumes that one of the IVM resistance loci is completely linked to the ABZ locus (with no recombination occurring between the loci), with the other remaining loci being unlinked to either of the first 2 loci. The frequencies of parental gametes can be derived from the 2-loci case as follows:
where w bcde is the frequency of the adult worm population with the cde genotype (given by ). G bghS denotes the frequency of the gamete G bgh with the susceptibility allele at the third, unlinked locus, and G bghR denotes the frequency of the gamete G bgh bearing the resistance allele at the third unlinked locus. For individual equations calculating the proportion of new microfilariae with the cde genotype see Table C.1.
Table C.1. The abbreviations and genotype equations used for the ABZ-monogenic-IVM polygenic (3-loci) model. Allele location on chromosomes and parameter F as in Table B.1
