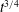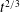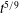1. Introduction
Volcanic ash presents a considerable hazard both close to the volcano, where a large volume of ash may accumulate on the ground, and on a regional scale, where airborne fine ash particles are potentially hazardous to aviation (Miller & Casadevall Reference Miller, Casadevall and Sigurdsson2000; Bonadonna et al. Reference Bonadonna, Genco, Gouhier, Pistolesi, Cioni, Alfano, Hoskuldsson and Ripepe2011). Volcanic ash is transported into the atmosphere during an eruption by a sustained buoyant plume of gas and particles (Sparks Reference Sparks1986). As the plume ascends it mixes with the atmosphere, broadening its width and reducing its density deficit (Morton, Taylor & Turner Reference Morton, Taylor and Turner1956; Woods Reference Woods1988; Woodhouse et al. Reference Woodhouse, Hogg, Phillips and Sparks2013). The decreasing density of the atmosphere with height means that the bulk density of the plume eventually becomes equal to that of the atmosphere, and, after an inertial overshoot, the column spreads horizontally about this altitude to form a thin intrusion (Bursik, Carey & Sparks Reference Bursik, Carey and Sparks1992a ; Bonadonna & Phillips Reference Bonadonna and Phillips2003).
Two morphologies of intrusions are commonly observed (Sparks et al.
Reference Sparks, Bursik, Carey, Gilbert, Glaze, Sigurdsson and Woods1997). In the absence of significant atmospheric wind (when the wind speed is much slower than the spreading rate of the intrusion), the plume spreads radially, forming an axisymmetric intrusion known as an umbrella cloud. When the wind is significant, however, the plume may be bent over as it rises, and an intrusion is formed which is predominantly advected downwind of the volcano, but which also exhibits lateral spreading. In both cases, the cloud is of relatively uniform density, but intrudes into a stratified atmosphere. The resulting pressure distribution causes variations in the thickness of the cloud to drive a predominantly horizontal spreading flow, which is resisted by inertial drag and by turbulent drag between the intrusion and the surrounding atmosphere. Importantly, the ash plays relatively little dynamical role in this spreading, because it is sufficiently dilute that it does not contribute significantly to the overall bulk density: the volumetric concentration of ash at the elevation where the plume reaches neutral buoyancy is typically as low as
$10^{-6}$
, due to entrainment of ambient air and particle fallout during the rise of the plume, leading to a density contribution of approximately 1 part in
$10^{3}$
(Woodhouse et al.
Reference Woodhouse, Hogg, Phillips and Sparks2013).
The spreading of volcanic plumes is simply a consequence of the sustained plume forming a region of mixed fluid, located around its neutral buoyancy height, within a stratified ambient (see, e.g., Wu Reference Wu1969; Amen & Maxworthy Reference Amen and Maxworthy1980; Ungarish Reference Ungarish2005, and references therein). This mechanism occurs much more generally in environmental flows, for example in oceanic dispersal of pollutants (Chen Reference Chen1980; Lemckert & Imberger Reference Lemckert and Imberger1993; Akar & Jirka Reference Akar and Jirka1994, Reference Akar and Jirka1995) and in river interflows (Alavian et al. Reference Alavian, Jirka, Denton, Johnson and Stefan1992). While we present our analysis in the context of the spreading of volcanic plumes, our results apply more generally to high-Reynolds-number intrusions into a continuously stratified ambient.
In the absence of significant drag or mixing effects, intrusions at high Reynolds number are governed by conservation of mass and momentum, and by a linear relationship between the thickness and the propagation speed of the front of the intrusion (Benjamin Reference Benjamin1968; Ungarish Reference Ungarish2009). The ‘inertia-buoyancy’ scalings that originate from these mechanisms have been applied previously to both axisymmetric and wind-blown spreading volcanic plumes.
In the axisymmetric case, the focus of many experimental and theoretical studies has been on obtaining the long-time growth rate of the intrusion. Using scaling arguments and simplified models, Chen (Reference Chen1980), Lemckert & Imberger (Reference Lemckert and Imberger1993) and Woods & Kienle (Reference Woods and Kienle1994) suggest that the intrusion radius
$r_{f}(t)$
grows with time
$t$
as
$r_{f}\sim t^{2/3}$
. In a large-scale experimental study of continuously supplied axisymmetric intrusions into a stratified water ambient, Lemckert & Imberger (Reference Lemckert and Imberger1993) found that the growing radius of the intrusion (typically greater than 100 m in their experiments) was best described as a power law
$r_{f}(t)\sim t^{0.72}$
, which they associated with this buoyancy-inertial regime, despite the difference between this exponent and the value of
$2/3$
suggested by their scaling argument. In laboratory-scale experiments, Kotsovinos (Reference Kotsovinos2000) observed a range of growth rates from
$r_{f}\sim t$
to
$r_{f}\sim t^{1/2}$
, associated with the initiation of the intrusion and the onset of drag, which occurs quite rapidly at smaller scales. Richards, Aubourg & Sutherland (Reference Richards, Aubourg and Sutherland2014) observed continuously supplied axisymmetric intrusions with a growth rate of approximately
$r_{f}\sim t^{3/4}$
in laboratory experiments, and attributed this growth rate to a constant buoyancy flux within the intrusion.
In this paper we focus on obtaining time-dependent solutions to the shallow-layer equations that describe continuously supplied horizontal intrusions into a stratified ambient. In the case of a continuously supplied axisymmetric intrusion we find a surprising result: the scaling
$r_{f}\sim t^{2/3}$
for the growth of such an intrusion, although widely used (e.g. Woods & Kienle Reference Woods and Kienle1994; Suzuki & Koyaguchi Reference Suzuki and Koyaguchi2009; Costa, Folch & Macedonio Reference Costa, Folch and Macedonio2013), is not in fact realised by solutions of the shallow-layer model. Instead, the solution takes the form of a time-dependent outer ‘head’ region, connected by a jump to a time-independent steady inner ‘tail’, with the intrusion radius growing as
$r_{f}\sim t^{3/4}$
. This type of solution is not of self-similar form, and the simple scaling arguments that rely on similarity, which are used to predict the temporal evolution of
$r_{f}\sim t^{2/3}$
, are not substantiated by our numerical solutions of the governing shallow-layer equations. We analyse the equations asymptotically to understand the origin of the
$r_{f}\sim t^{3/4}$
scaling. Additionally, we use dimensional analysis to suggest that the reason for this non-self-similar behaviour in continuously supplied axisymmetric intrusions originating from a point source is the occurrence of two dimensional groups in the parameters that govern the equations, and therefore different time-dependent length scales can be constructed. This is in contrast to the two-dimensional intrusions that originate from a line source, and to instantaneous releases of a constant volume of mixed fluid in either geometry, in which only one time-dependent length scale can be constructed.
Some previous studies have suggested scaling arguments that lead to a radial growth rate of
$t^{3/4}$
for continuously supplied axisymmetric intrusions, and these rely implicitly on the assumption that the intrusion adopts a similarity form. However, such a similarity solution is not in accord with either our numerical computations or our asymptotic solutions. Kotsovinos (Reference Kotsovinos2000) presents a model for intrusions in which the difference between the density of the ambient fluid immediately above and below the intrusion is assumed to be independent of the flow thickness. This assumption is appropriate for dense gravity currents or for intrusions that flow along a sharp interface between two unstratified fluids of different density, but is not applicable to intrusions into continuously stratified environments. In fact, the scaling argument presented by Kotsovinos (Reference Kotsovinos2000) is equivalent to that developed by Didden & Maxworthy (Reference Didden and Maxworthy1982) for axisymmetric gravity currents, as discussed below. It will be shown that this result is also not realised by the governing equations. Richards et al. (Reference Richards, Aubourg and Sutherland2014) show that a scaling of
$r_{f}\sim t^{3/4}$
can be obtained for axisymmetric continuously supplied intrusions by assuming that a quantity associated with the buoyancy flux of the intrusion is constant, rather than the volume flux. The quantity conserved in the scalings of Richards et al. (Reference Richards, Aubourg and Sutherland2014) is the buoyancy in the upper half of the intrusion (the total buoyancy flux of the intrusion being zero, due to symmetry about the level of neutral buoyancy). However, unlike in a gravity current, where the total excess buoyancy of the current is conserved even when ambient fluid is entrained into the current, buoyancy is not conserved in the upper half of an intrusion, due to the flux of buoyancy between the upper and lower halves of the intrusion required to keep the intrusion well mixed.
The non-self-similar evolution that we derive in this paper occurs also in axisymmetric compositional gravity currents driven by a sustained point source that move over a horizontal boundary through an otherwise stationary uniform environment (Garvine Reference Garvine1984; Bonnecaze et al.
Reference Bonnecaze, Hallworth, Huppert and Lister1995; Slim & Huppert Reference Slim and Huppert2011). As alluded to previously, naïve scaling on the assumption that these gravity currents are self-similar would assert that
$r_{f}\sim t^{3/4}$
(Chen Reference Chen1980; Didden & Maxworthy Reference Didden and Maxworthy1982; Kotsovinos Reference Kotsovinos2000). However, numerical integration of the equations and an analysis of the flow (Slim & Huppert Reference Slim and Huppert2011) reveal that the current is not self-similar, but instead features a steady tail and time-dependent front similar to those that occur in continuously supplied axisymmetric intrusions, growing as
$r_{f}\sim t^{4/5}$
. A simple scaling analysis therefore fails, and in appendix A we calculate this growth rate through an asymptotic solution for the flow at late times.
The effects of drag progressively influence the motion of sustained intrusions. While the dynamics is controlled by fluid inertia and gradients of the hydrostatic pressure sufficiently close to source, drag becomes dominant in the far field. We analyse the transition to drag-dominated behaviour in the absence of wind and identify a new radial spreading regime
$r_{f}\sim t^{5/9}$
when the dynamical balance is between the pressure gradient and the hydraulic resistance, analogous to the transition from the inertial-buoyancy regime to the drag state shown by Hogg & Woods (Reference Hogg and Woods2001) for compositionally driven gravity currents in a uniform environment.
A volcanic plume affected by wind no longer spreads radially. The intrusion instead moves preferentially downstream as it is accelerated to the ambient wind speed. Bursik et al. (Reference Bursik, Carey and Sparks1992a
) used scaling arguments to predict that the steady width of the spreading intrusion far downwind scales as
$x^{1/2}$
, where
$x$
is the distance downstream of the source. Akar & Jirka (Reference Akar and Jirka1994, Reference Akar and Jirka1995) formulated a shallow-layer model for continuously supplied intrusions and gravity currents into flowing ambients, obtaining numerical solutions to the model close to the source and width-averaged equations describing the spreading of the plume far downstream. Akar & Jirka found good agreement between these theoretical results and field measurements of gravity currents arising from discharges of warm water into the ocean. Using a similar shallow-layer model, Baines (Reference Baines2013) formulated steady solutions by assuming energy conservation and an irrotational flow, also finding an intrusion width proportional to
$x^{1/2}$
. Contrary to the suggestion of Baines (Reference Baines2013), we show that the presence of drag must alter the lateral balance of forces far from source in wind-affected intrusions and result in a width far downstream that is asymptotically smaller than
$x^{1/2}$
. We find that the model of Bursik et al. (Reference Bursik, Carey and Sparks1992a
) describes an intermediate asymptotic regime, and identify a new spreading regime, which becomes established further downstream, in which the lateral motion is balanced by drag and the intrusion width scales as
$x^{1/3}$
.
Sufficiently far from source, the ash particles within a volcanic intrusion act as tracers due to their negligible contribution to the density, and are advected horizontally with the intrusion velocity. In the vertical direction, the gravitational settling of the ash particles is countered by their redistribution throughout the thickness of the intrusion, due to turbulent fluid motion. This results in a flux of particles settling out of the base of the intrusion proportional to the product of the vertically averaged particle concentration and the particle settling velocity (Hazen Reference Hazen1904; Sparks, Carey & Sigurdsson Reference Sparks, Carey and Sigurdsson1991). We integrate a model based on these processes to obtain the temporal and spatial distribution of particles within the intrusion. This distribution of particles is of direct relevance to the prediction of hazards to aviation, and provides a time-dependent source for models of particle settling in the atmosphere, used to predict the location of ash deposits (Bursik et al. Reference Bursik, Carey and Sparks1992a ; Sparks et al. Reference Sparks, Bursik, Carey, Gilbert, Glaze, Sigurdsson and Woods1997; Bonadonna & Phillips Reference Bonadonna and Phillips2003).
This paper is structured as follows. In § 2 we present the shallow-layer intrusion model. In § 3 we find time-dependent solutions of this model for continuously supplied axisymmetric intrusions in the absence of drag, obtaining an unexpected non-similarity structure for the solution, and find an asymptotic description of these non-similarity solutions at intermediate times. In § 3.4 we demonstrate how the inclusion of drag, which becomes significant at late times, alters this axisymmetric flow. In § 4 we show how the addition of an ambient wind results in an intrusion that is primarily advected downstream, and calculate explicitly the shape of the plume and rate of spreading in the drag-dominated regime far downstream. In § 5 we couple the intrusions calculated thus far to a particle transport and settling model appropriate for volcanic intrusions. In § 6 we discuss the important role that buoyancy-driven intrusions play in transporting volcanic ash in the atmosphere, and in § 7 we summarise and draw conclusions. In appendix A we analyse the related problem of a continuously fed axisymmetric gravity current moving along a horizontal boundary through a uniform environment, deriving the solution in the form of an asymptotic series at late times. For this flow, analogously to § 3, we demonstrate the non-similarity spreading and use asymptotic arguments to calculate the solution for height and velocity of the current. In appendix B we use related asymptotic techniques to evaluate higher-order corrections to the leading-order long-time solution derived in § 3 for a continuously fed axisymmetric intrusion.
2. Shallow-layer model
We model the intrusion of fluid from a sustained source of volume flux
$2{\rm\pi}Q^{\star }$
at the height of neutral buoyancy, through an environment that is stably stratified with constant buoyancy frequency,
$N^{\star }$
(hereafter, dimensional variables are denoted with a star, and dimensionless variables are unadorned).
The intruding fluid is assumed to spread symmetrically about its vertical level of neutral buoyancy as a relatively thin layer so that the vertical accelerations are negligible and the pressure adopts a hydrostatic distribution. It is further assumed that the density of fluid within the intruding layer is vertically uniform due to turbulent mixing, and this implies that there are horizontal pressure gradients due to variations in the thickness of the layer; these drive the motion.
We follow the approach of Ungarish & Huppert (Reference Ungarish and Huppert2002) in modelling the flow in terms of the dimensionless thickness of the intruding layer,
$h$
, and the dimensionless horizontal velocity field,
$\boldsymbol{u}=(u,v)$
, with the coordinate axes aligned so that the
$x$
and
$y$
axes are horizontal and the
$z$
axis is vertical. Length and time scales are rendered dimensionless with respect to
$(Q^{\star }/N^{\star })^{1/3}$
and
$N^{\star -1}$
respectively. For a volcanic intrusion into the atmosphere, the typical flux per radian at the plume top
$Q^{\star }$
ranges from
$10^{4}$
to
$10^{10}~\text{m}^{3}~\text{s}^{-1}$
, and a typical atmospheric buoyancy frequency is
$0.01~\text{s}^{-1}$
(Sparks et al.
Reference Sparks, Bursik, Carey, Gilbert, Glaze, Sigurdsson and Woods1997). Thus, the length scale
$(Q^{\star }/N^{\star })^{1/3}$
used for non-dimensionalisation is in the range 100 m–10 km. The time scale
$N^{\star -1}$
, by contrast, is independent of the size of the eruption.
We model the intrusions as incompressible and, in order to do so, make two assumptions. First, we assume that the variation of atmospheric pressure over the thickness of the intrusion is small; that is, the intrusions are much thinner than the density scale height (the height over which the atmospheric density varies by a factor of
$e$
), approximately 7 km (Gill Reference Gill1982). Second, the Mach number of the intrusions is very small (they are much slower than the speed of sound,
${\approx}300~\text{m}~\text{s}^{-1}$
). Conservation of mass is then given by
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}(hu)+\frac{\partial }{\partial y}(hv)=C_{E}|\boldsymbol{U}-\boldsymbol{u}|,\end{eqnarray}$$
where
$C_{E}$
is a coefficient of entrainment, which in general is dependent on the flow variables, and
$\boldsymbol{U}=(U,0)$
is the ambient wind speed (assumed to be constant and in the
$x$
direction).
To describe the balance of momentum we make the assumption that the dominant processes influencing the energy and momentum of the intrusion are the influx of mixed fluid at the plume source, the inertial resistance at the advancing flow front and turbulent drag (Barenblatt Reference Barenblatt1996, § 11.6; Ungarish & Huppert Reference Ungarish and Huppert2002; Bolster, Hang & Linden Reference Bolster, Hang and Linden2008). We assume that, compared with these processes, relatively little momentum or energy is transferred to any excited internal wavefields or other distortions to the background density gradient. It has been inferred that internal gravity waves do play a significant role in some intrusive flows through stratified fluids, such as in the collapse of a mixed region (Amen & Maxworthy Reference Amen and Maxworthy1980). In other flows, however, such as the lock-release currents of Maurer & Linden (Reference Maurer and Linden2014), energy loss to gravity waves was observed to have a relatively small effect on the propagation of the intrusion. Ansong & Sutherland (Reference Ansong and Sutherland2010) made direct experimental observations of gravity waves generated by the scenario that we consider in this paper, namely a buoyant plume and subsequent radial intrusion into a stratified environment. They measured the energy extracted by gravity waves to be small, approximately 4 % of the energy of the plume at the neutral buoyancy height, and observed that these waves originated largely from the region of inertial overshoot immediately above the rising plume, rather than from the horizontally spreading intrusion itself. These observations support our assumption that gravity waves play only a relatively small role in the propagation of the volcanic intrusions that we consider. Nevertheless, the onset of viscous effects in laboratory-scale flows means that observations of high-Reynolds-number intrusions, including those made by Ansong & Sutherland (Reference Ansong and Sutherland2010), can only be made at relatively early non-dimensional times, compared with the duration of volcanic intrusions. Large-scale experiments (similar to those of Lemckert & Imberger Reference Lemckert and Imberger1993), or even field observations of gravity wave generation by volcanic intrusions, may therefore be invaluable in determining the influence of gravity waves on the spread of volcanic intrusions, and the extent to which our modelling idealisations are justified.
Under the assumption that gravity wave effects can be neglected, and also that Coriolis forces are negligible, the balance of momentum in the downwind and cross-wind directions respectively yields
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}(hu)+\frac{\partial }{\partial x}\left(hu^{2}+\frac{h^{3}}{12}\right)+\frac{\partial }{\partial y}(huv)=C_{D}(U-u)|\boldsymbol{U}-\boldsymbol{u}|+C_{E}U|\boldsymbol{U}-\boldsymbol{u}|, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}(hv)+\frac{\partial }{\partial x}(huv)+\frac{\partial }{\partial y}\left(hv^{2}+\frac{h^{3}}{12}\right)=-C_{D}v|\boldsymbol{U}-\boldsymbol{u}|. & \displaystyle\end{eqnarray}$$
$C_{D}$
is the drag coefficient that parametrises the relationship between the interfacial stresses and the velocity difference between the motion of the flowing layer and the surrounding environment.
For simplicity we assume that the drag coefficient
$C_{D}$
is constant. This parametrisation of drag is a simple model for the tangential stresses at the interface between the intrusion and the ambient, which may arise from wind stress or from thin mixing layers, which form above and below the intrusion but do not result in significant entrainment (Abraham, Karelse & Van Os Reference Abraham, Karelse and Van Os1979; Baines Reference Baines2013). The final term of (2.2) expresses the momentum of the fluid entrained into the current. This results in an additional drag on the intrusion, which, like the drag parametrised in our model through
$C_{D}$
, is proportional to the square of the difference in velocity between the intrusion and the ambient.
While there are well-accepted shallow-water parametrisations for the entrainment coefficient
$C_{E}$
for gravity currents (see, for example, Parker, Fukushima & Pantin Reference Parker, Fukushima and Pantin1986; Johnson & Hogg Reference Johnson and Hogg2013), the rate of mixing into intrusions through stratified environments (and potential resultant stratification within the intrusion) is not well understood. We make the assumption that, for the continuously supplied intrusions described in this paper, the flux of fluid entrained into the intrusion is much smaller than the source flux
$Q^{\star }$
, and thus that the effect of entrainment on the current volume is negligible. Hereafter we therefore set
$C_{E}=0$
, anticipating that future experimental testing may provide the means to refine this approximation.
Our shallow model for intrusions (2.1)–(2.3) follows an established approach of using depth-integrated equations to model flows into stratified environments (e.g. Ungarish Reference Ungarish2005; Baines Reference Baines2013). Although we do not model details of the fully three-dimensional turbulent flow, by including radial and temporal variability in the flow fields our equations provide a much more complete model for intrusions than the balance of flow forces, which has been used previously to estimate the behaviour of intrusions (Chen Reference Chen1980; Lemckert & Imberger Reference Lemckert and Imberger1993; Woods & Kienle Reference Woods and Kienle1994; Kotsovinos Reference Kotsovinos2000; Richards et al. Reference Richards, Aubourg and Sutherland2014).
Solutions to the hyperbolic equations (2.1)–(2.3) may form discontinuities and, once these discontinuities are present, the continuum equations alone are no longer sufficient to specify the future evolution of the system. To resolve this we specify internal jump conditions (akin to the Rankine–Hugoniot conditions in gas dynamics), which determine how the flow variables
$\boldsymbol{u}$
and
$h$
are linked across the discontinuity. We specify that the mass and momentum fluxes of the intrusion are conserved across the jump, leading to the conditions
$$\begin{eqnarray}[h(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}-c)]_{-}^{+}=0\quad \text{and}\quad [h\boldsymbol{u}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}-c)+\boldsymbol{n}h^{3}/12]_{-}^{+}=0,\end{eqnarray}$$
where
$c$
is the propagation speed of the shock in the direction of the unit shock normal vector
$\boldsymbol{n}$
and
$[\cdot ]_{-}^{+}$
denotes the difference in flow variables across the jump (cf. Chapman Reference Chapman2000). In specifying continuity of mass and momentum fluxes we assume that any additional processes at the jump, such as generation of internal waves or entrainment of ambient fluid, play only a small role. The rate of entrainment at internal jumps is limited by energy and entropy considerations (Jacobson, Milewski & Tabak Reference Jacobson, Milewski and Tabak2008), but obtaining a quantitative parametrisation of this entrainment rate remains a challenging problem, especially in the case of a stratified ambient fluid (see, for example, Thorpe Reference Thorpe2010).
The source of the intrusion is located at the origin. We describe the source by imposing a volume flux across a cylinder of radius
$r_{0}$
enclosing the origin, such that
$$\begin{eqnarray}\int _{r=r_{0}}h\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{r}}\text{d}{\it\theta}=2{\rm\pi},\end{eqnarray}$$
where
$\hat{\boldsymbol{r}}$
is a unit radial vector. We discuss the definition of
$r_{0}$
further in the following section.
3. Axisymmetric flow
In the absence of wind
$(U=0)$
the ensuing motion is purely radial with velocity field
$u_{r}=(u^{2}+v^{2})^{1/2}$
, and the governing equations (2.1)–(2.3) become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}(hu_{r})+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}^{2}h)+\frac{\partial }{\partial r}\left(\frac{h^{3}}{12}\right)=-C_{D}u_{r}|u_{r}|, & \displaystyle\end{eqnarray}$$
$r=(x^{2}+y^{2})^{1/2}$
. These equations are hyperbolic conservation laws, possessing two characteristics with speeds
$u_{r}\pm h/2$
. We define the Froude number for these axisymmetric flows with no azimuthal motion as the ratio of the radial flow speed to the speed of the characteristics in a stationary flow, 
$$\begin{eqnarray}\mathit{Fr}=2|u_{r}|/h.\end{eqnarray}$$
In an axisymmetric geometry, the boundary condition specifying the source flux (2.5) becomes
$$\begin{eqnarray}ru_{r}h=1\quad \text{at }r=r_{0}.\end{eqnarray}$$
At the flow front we impose a kinematic boundary condition
$\text{d}r_{f}/\text{d}t=u_{r}(r=r_{f})$
and a dynamic boundary condition which specifies a constant Froude number
$\mathit{Fr}_{f}$
, which is of order unity, at the front of the intrusion (Ungarish Reference Ungarish2006),
$$\begin{eqnarray}u_{r}={\textstyle \frac{1}{2}}\mathit{Fr}_{f}h\quad \text{at }r=r_{f}(t).\end{eqnarray}$$
3.1. Steady drag-free flow
We seek fully time-dependent solutions to (3.1), (3.2) in which the drag is negligible (
$C_{D}=0$
), but, as previously noted, will find that these time-dependent solutions are in non-similarity form, and much of the time-dependent solution is in fact steady. We therefore first look for steady solutions. The governing equations (3.1) and (3.2) can be written in steady-state form as
$$\begin{eqnarray}\frac{\text{d}}{\text{d}r}(ru_{r}h)=0\quad \text{and}\quad \frac{\text{d}}{\text{d}r}\left(u_{r}^{2}+\frac{1}{4}h^{2}\right)=0,\end{eqnarray}$$
where (3.6b ) follows directly from a simplification of (3.2). Integration of these ordinary differential equations, which correspond to mass conservation and a Bernoulli equation, requires two boundary conditions. The constant associated with (3.6a ) is supplied by the condition (3.4) at source. The constant associated with (3.6b ) cannot be supplied by the front condition (3.5), since the inherently unsteady front condition cannot apply to a steady-state intrusion. We instead specify the constant of integration of (3.6b ), writing
$$\begin{eqnarray}u_{r}^{2}+{\textstyle \frac{1}{4}}h^{2}=E,\end{eqnarray}$$
where
$E$
is for now an arbitrary positive constant, which we shall show is determined at the source of the intrusion.
With these constants determined, the solutions to (3.6a,b
) can be obtained algebraically (Baines Reference Baines2013). There are two solutions for the velocity and thickness fields: a supercritical solution in which
$\mathit{Fr}=2|u_{r}|/h\geqslant 1$
,
$$\begin{eqnarray}u_{r}^{2}=\frac{E}{2}(1+{\it\Psi})\quad \text{and}\quad h^{2}=2E(1-{\it\Psi}),\end{eqnarray}$$
and a subcritical solution in which
$\mathit{Fr}\leqslant 1$
,
$$\begin{eqnarray}u_{r}^{2}=\frac{E}{2}(1-{\it\Psi})\quad \text{and}\quad h^{2}=2E(1+{\it\Psi}),\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\Psi}=\left(1-\frac{1}{E^{2}r^{2}}\right)^{1/2}.\end{eqnarray}$$
Both of these solutions exist only for
$r\geqslant 1/E$
, and at
$r=1/E$
the flow is critical, i.e.
$\mathit{Fr}=1$
. We will show that it is always the supercritical solution (3.8) that is realised as part of the fully time-dependent motion, and plot this supercritical solution in figure 1, scaling
$h$
and
$u_{r}$
by
$E^{-1/2}$
and
$r$
by
$E$
to remove the dependence on the parameter
$E$
. In the supercritical solutions,
$u_{r}$
tends to a constant and
$h$
decays with increasing radial distance
$r$
, meaning that the Froude number
$\mathit{Fr}=2|u_{r}|/h$
diverges with increasing
$r$
.
Figure 1. The scaled velocity
$u_{r}/\sqrt{E}$
(dashed line) and thickness
$h/\sqrt{E}$
(solid line) of the steady supercritical axisymmetric intrusion as a function of the scaled radial distance
$rE$
, given by (3.8). This solution illustrates both the radial thinning and the constant velocity obtained for
$rE\gg 1$
. The constant far-field velocity is approached rapidly:
$u/\sqrt{E}$
is within 4 % of its far-field value by
$rE=2$
.
The time-dependent evolution of a radial intrusion, specified by the hyperbolic equations (3.1) and (3.2), requires two boundary conditions to be imposed at the source
$r=r_{0}$
, because it is supercritical, since two characteristics leave this boundary (Whitham Reference Whitham1974). Both the flux condition (3.4) and the Bernoulli constant (3.7) used to determine the steady supercritical solution (3.8) are therefore specified at the source. We may identify the parameter
$E$
in terms of a source Froude number,
$\mathit{Fr}_{0}=2|u_{r}|/h$
at
$r=r_{0}$
(where for this supercritical flow
$\mathit{Fr}_{0}\geqslant 1$
), from which we obtain
$$\begin{eqnarray}E=\frac{\mathit{Fr}_{0}^{2}+1}{2r_{0}\mathit{Fr}_{0}}.\end{eqnarray}$$
In the solutions that follow, the quantities
$\mathit{Fr}_{0}$
and
$r_{0}$
occur only through
$E$
, and we may therefore specify without loss of generality either
$\mathit{Fr}_{0}$
or
$r_{0}$
. A natural choice for axisymmetric intrusions is to fix
$\mathit{Fr}_{0}=1$
; that is, to identify
$r_{0}$
as the radius at which the flow is critical. In this case, from (3.11), we obtain
$r_{0}=1/E$
.
In volcanic eruptions, the axisymmetric shallow intrusions that form are fed by a rising plume. Near the origin, the flow transitions from a near-vertical plume to a near-horizontal intrusion, and flow in this region is fully three-dimensional. In this section we have demonstrated that, once the intrusion has become shallow, the parameters at source that determine its behaviour are the volume flux and the parameter
$E$
. While the volume flux is frequently calculated from observations of volcanic plumes, we note that
$E$
may be more difficult to infer. In particular, our identification of
$r_{0}=1/E$
as the radius at which the flow becomes critical is not the same as the commonly used ‘corner radius’ of a volcanic umbrella cloud (Sparks et al.
Reference Sparks, Bursik, Carey, Gilbert, Glaze, Sigurdsson and Woods1997), a parameter characterising the radius at which the vertical flow in the rising plume transitions to a horizontal flow in the intrusion. The fully three-dimensional flow in the region at which the corner radius is defined means that there may be no simple relationship between the corner radius and the parameter
$E=1/r_{0}$
which determines the behaviour of the intrusion. However, we will show that the growth rate of the intrusion at late times depends only very weakly on
$E$
(the growth rate is proportional to
$E^{1/8}$
), indicating that accurate measurement of
$E$
may not be necessary to obtain good predictions of the growth of volcanic intrusions.
3.2. Unsteady drag-free flow
We now examine the unsteady radial motion. We numerically integrate the unsteady radially symmetric equations (3.1), (3.2), with boundary conditions (3.4), (3.7) and (3.5). Here and throughout this paper we use the shock-capturing method of Kurganov & Tadmor (Reference Kurganov and Tadmor2000), which ensures that (2.4) is enforced at any discontinuities in the solution. We obtain the thickness field
$h$
as a function of time (figure 2
a), along with the temporal evolution of the radial front
$r_{f}(t)$
(figure 2
b). This evolution and the approach to steady state take a rather unusual form: rather than progressing as a straightforward similarity solution, as is common for many models of gravity current motion (see, for example, Ungarish Reference Ungarish2009), the time-dependent solution is steady everywhere except in a time-dependent region close to the front. The steady inner tail region is described exactly by the steady supercritical solution (3.8a,b
). The convergence of hyperbolic characteristics at the interface between this tail and the time-dependent frontal region means that the two regions are connected by an outward-propagating jump or shock (see, for example, Whitham Reference Whitham1974). We denote the radial position of this shock as
$r_{s}(t)$
, which is determined as part of the solution (figure 2
a).
Figure 2. Numerical time-dependent solutions of an axisymmetric intrusion in the absence of drag (
$\mathit{Fr}_{f}=1,E=1$
). (a) The flow thickness
$h$
, centred on the neutral buoyancy height
$z=0$
, as a function of radial position at times
$t=2,10,25,50,100$
. The radial positions of the front of the intrusion
$r_{f}(t)$
and of the internal jump
$r_{s}(t)$
are indicated for
$t=100$
. (b) The radial position of the front of the intrusion
$r_{f}$
and width of the time-dependent frontal region
$r_{f}-r_{s}$
as a function of time. Dashed lines indicate the theoretical late-time predictions (3.24) and (3.25) for the current radius
$r_{f}$
and the width of the time-dependent frontal region
$r_{f}-r_{s}$
respectively.
Importantly, this two-region structure implies that the rate of radial spreading is rather different from what might have been anticipated on the basis of simple scaling arguments (see, for example, Lemckert & Imberger Reference Lemckert and Imberger1993; Woods & Kienle Reference Woods and Kienle1994). Such scaling arguments advance by requiring that the time dependence of the current length and flow variables are governed by similarity scalings. In a scaling argument, the linear increase in current volume due to the continuous source would imply that
$r_{f}^{2}h\sim t$
, while at the intrusion front,
$u_{r}\sim r_{f}/t$
is required for kinematic consistency and
$u_{r}\sim h$
to match the imposed frontal Froude number. Together these would imply that
$r_{f}\sim t^{2/3}$
. Our numerical solutions of the governing equations indicate that instead
$r_{f}$
varies as a power of time that approaches
$t^{0.75}$
at late times (figure 2
b), close to the rate
$r_{f}\sim t^{0.72}$
found experimentally for large-scale continuously supplied intrusions by Lemckert & Imberger (Reference Lemckert and Imberger1993).
The form of the numerical solutions indicates that this discrepancy in growth rate between numerical solutions and scaling arguments is because the bulk of the motion away from the front does not scale in a manner determined by the conditions at the intrusion front, but is instead independent of time. The existence of time dependence only near the current front is entirely analogous to that found by Garvine (Reference Garvine1984) and Slim & Huppert (Reference Slim and Huppert2011) for axisymmetric gravity currents propagating over a horizontal boundary through a uniform environment due to a sustained source. In appendix A we show that the asymptotic arguments developed below may be applied also to such gravity currents. In fact the non-existence of the similarity solution for a sustained axisymmetric gravity current was established by Grundy & Rottman (Reference Grundy and Rottman1986), although they did not demonstrate what might occur instead. For both intrusions and gravity currents, we find numerically that the ordinary differential equations (ODEs) that result from assuming that the current is self-similar become singular in the interior of the flow, and cannot be integrated to satisfy the boundary conditions at both the source and the front of the intrusion.
We now explain why the similarity solution is not achieved and how this behaviour can be identified at the outset, without numerical solution of the governing equations. In contrast to the axisymmetric continuously supplied flows described above, gravity currents generated by a line source (e.g. Gratton & Vigo Reference Gratton and Vigo1994) do attain a similarity form, and the scalings of these can be obtained by simple scaling arguments. We therefore identify a fundamental difference between radial flows supplied by a point source (either gravity currents or intrusions) and ‘two-dimensional’ flows generated by a line source. This difference can be explained by dimensional analysis. If a unique time-dependent length scale can be constructed from time and the parameters that feature in the problem, a similarity solution for the current is expected (Barenblatt Reference Barenblatt1996). In this case there is exactly one dimensional group that can be constructed from the parameters of the problem. When more than one dimensional group can be constructed, a similarity solution may be obtained asymptotically at late times, but a non-similarity form is also possible.
The governing equations for an axisymmetric intrusion, (3.1) and (3.2), contain no parameters when redimensionalised and written in terms of
$u_{r}^{\star }$
and
$b^{\star }=N^{\star }h^{\star }$
: the parameters occur only in the boundary conditions. One dimensionless parameter
$\mathit{Fr}_{f}$
enters into the problem in the boundary condition at the flow front (3.5), and at the source of an axisymmetric flow we write the two boundary conditions required for a supercritical flow as
$$\begin{eqnarray}\displaystyle & b^{\star }u_{r}^{\star }r^{\star }=Q^{\star }N^{\star }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & u_{r}^{\star 2}+b^{\star 2}/4=E^{\star }. & \displaystyle\end{eqnarray}$$
$[Q^{\star }N^{\star }]\equiv L^{3}T^{-2}$
and
$[E^{\star }]\equiv L^{2}T^{-2}$
have differing dimensions, and consequently the only dimensionless parameter that can be constructed from them,
$(Q^{\star }N^{\star })^{2}/(E^{\star 3}t^{\star 2})$
, is time-dependent. Dimensional analysis then indicates that the current radius at late times is given by
$r_{f}=(Q^{\star }N^{\star }/E^{\star })f[\mathit{Fr}_{f},(Q^{\star }N^{\star })^{2}/(E^{\star 3}t^{\star 2})]$
, where
$f$
is an arbitrary function of all the non-dimensional parameters in the problem. The occurrence of a time-dependent argument of the undetermined function
$f$
means that the time dependence of the system is also undetermined, and a simple similarity solution is not necessarily expected.
In contrast, for an intrusion supplied by a line source of volume flux
$Q_{l}^{\star }$
per unit width, the boundary conditions to be applied at source are
$$\begin{eqnarray}\displaystyle & b^{\star }u^{\star }=Q_{l}^{\star }N^{\star }\quad \text{and} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & u_{r}^{\star 2}+b^{\star 2}/4=E^{\star }. & \displaystyle\end{eqnarray}$$
$[Q_{l}^{\star }N^{\star }]\equiv [E^{\star }]\equiv L^{2}T^{-2}$
. We can then determine that the current length
$x_{f}$
attains a similarity form
$x_{f}=(Q_{l}^{\star }N^{\star })^{1/2}t^{\star }f(\mathit{Fr}_{f},Q_{l}^{\star }N^{\star }/E^{\star })$
, where
$f$
is again a function of all the non-dimensional parameters in the problem, but in this case with no time-dependent parameters.
In contrast to the intrusions supplied by a source of constant flux, intrusions that result from an instantaneous release of a fixed volume of mixed fluid are governed by similarity solutions both in ‘two-dimensional’ and axisymmetric geometries (Ungarish Reference Ungarish2005; Ungarish & Zemach Reference Ungarish and Zemach2007). In such constant-volume releases, neither the dimensional governing equations (when written in terms of
$u_{r}^{\star }$
and
$b^{\star }=N^{\star }h^{\star }$
) nor the boundary conditions involve a dimensional parameter: the only dimensional parameters occur in the specification of the initial conditions. In general, the parameters describing the initial conditions would not be expected to affect the current at late times. However, integrating the equation of conservation of mass across the current and applying the kinematic condition at the flow front implies that one of these parameters, the total current volume multiplied by
$N^{\star }$
, is conserved throughout the time evolution of the current, and therefore plays a role in the buoyancy-inertial similarity solutions attained at late time. Importantly, no other parameter resulting from the initial conditions is conserved, so at late times the problem is described by only one dimensional parameter. In two-dimensional intrusions, the conserved quantity is
$\int _{0}^{x_{f}^{\star }}b^{\star }\text{d}x^{\star }$
(where
$x_{f}^{\star }$
is the location of the front of the current), which has dimensions
$[L^{2}T^{-1}]$
, leading to a current that grows as
$t^{1/2}$
(Ungarish Reference Ungarish2005). In axisymmetric intrusions, this conserved quantity is
$\int _{0}^{r_{f}^{\star }}rb^{\star }\text{d}r^{\star }$
, with dimensions
$[L^{3}T^{-1}]$
, leading to a current that grows as
$t^{1/3}$
(Ungarish & Zemach Reference Ungarish and Zemach2007).
The results of a dimensional analysis for gravity currents flowing over a horizontal surface through an unstratified ambient are entirely analogous those obtained above for intrusions. As with intrusions, only a single dimensional parameter can be constructed for instantaneous releases of dense fluid in either two-dimensional or axisymmetric geometries, and for two-dimensional gravity currents supplied by a constant source of buoyancy, leading to similarity solutions in these three cases (Hoult Reference Hoult1972; Gratton & Vigo Reference Gratton and Vigo1994). For axisymmetric gravity currents resulting from a constant source of buoyancy, two dimensional parameters can be constructed and a non-similarity solution results (appendix A).
3.3. Details of the unsteady drag-free motion
We seek an analytical form for the non-similarity solution describing axisymmetric continuously supplied intrusions at late times that is suggested by dimensional analysis and by our numerical computations (figure 2). In constructing such an analytical form we obtain algebraically the observed
$t^{3/4}$
growth rate of the current, and how this growth rate arises from the interaction of the two regions in the current, the time-dependent front and the steady inner tail. The jump at at
$r=r_{s}(t)$
separating these two regions plays an important role in the dynamics of the motion. For this radial flow the jump conditions for mass and radial momentum (2.4) that act across this discontinuity become
$$\begin{eqnarray}\left[(u_{r}-c)h\right]_{r_{s}^{-}}^{r_{s}^{+}}=0\quad \text{and}\quad \left[u_{r}(u_{r}-c)h+{\textstyle \frac{1}{12}}h^{3}\right]_{r_{s}^{-}}^{r_{s}^{+}}=0,\end{eqnarray}$$
where the shock speed
$c=\text{d}r_{s}/\text{d}t$
and where
$r_{s}^{+}$
and
$r_{s}^{-}$
denote values of the radius
$r$
immediately downstream and upstream of the shock respectively. On the source side of the discontinuity
$(r<r_{s})$
the flow is described by the steady supercritical solution (3.8) and in particular when
$r\gg r_{0}$
we find that
$$\begin{eqnarray}u_{r}(r_{s}^{-})=E^{1/2}+\cdots \quad \text{and}\quad h(r_{s}^{-})=E^{-1/2}\frac{1}{r_{s}^{-}}+\cdots \,.\end{eqnarray}$$
Since
$h(r_{s}^{+})\gg h(r_{s}^{-})$
, we may deduce the leading-order contributions from the jump conditions (3.16), namely that
$c=u_{r}(r_{s}^{+})$
and that
$(1/12)h(r_{s}^{+})^{3}=u_{r}(r_{s}^{-})^{2}h(r_{s}^{-})$
.
The decrease in Froude number that occurs as fluid passes through the shock allows the steady supercritical flow, which has a Froude number that increases with increasing radial distance from source (
$\mathit{Fr}=2u_{r}/h\sim r$
at for
$r\gg r_{0}$
), to match onto the boundary condition of constant Froude number at the flow front (3.5). It is for this reason that only the supercritical steady solution (3.8) is relevant to the time-dependent flow. The Froude number in the subcritical steady solution (3.9) decreases with increasing radius (
$\mathit{Fr}\sim 1/r$
for
$r\gg r_{0}$
). If this steady subcritical solution were connected with a shock to the constant Froude number front condition (3.5), at large radial distances, fluid passing through this shock would move from a region in which
$\mathit{Fr}\ll 1$
to a region in which
$\mathit{Fr}$
is of order unity. Such an increase in Froude number is associated with production of energy at the shock (Whitham Reference Whitham1974), which is physically inadmissible. Thus, the supercritical steady solution is selected in time-dependent flows by the constant Froude number at the flow front (3.5).
We now seek the powers of time that govern the intrusion radius, shock position and flow variables in the front region. The momentum jump condition and asymptotic form of the steady inner tail solution (3.17) for
$r\gg r_{0}$
imply a scaling on the flow thickness in the outer frontal region just downstream of the shock,
$$\begin{eqnarray}h(r_{s}^{+})^{3}\sim 1/r_{s}.\end{eqnarray}$$
The dynamic and kinematic boundary conditions at the current front imply a scaling on the flow thickness at the front,
$$\begin{eqnarray}h(r_{f})\sim u(r_{f})\sim r_{f}/t.\end{eqnarray}$$
Assuming that the positions of the shock
$r_{s}$
and intrusion front
$r_{f}$
scale as the same power of time at late times (
$r_{f}\sim r_{s}$
) and that the flow thickness likewise scales uniformly with time throughout the frontal region [
$h(r_{f})\sim h(r_{s})$
] allows us to combine the scalings (3.18) and (3.19) to obtain that
$r_{f}\sim r_{s}\sim t^{3/4}$
and that, in the frontal region,
$u\sim h\sim t^{-1/4}$
. This scaling of
$r_{f}(t)$
is consistent with the exponent determined by our numerical solutions (figure 2
b).
We therefore write
$r_{f}=Kt^{3/4}+\cdots \,$
and
$r_{s}=K_{s}t^{3/4}+\cdots \,$
, where
$K$
and
$K_{s}$
are constants to be determined, and pose similarity solutions for the thickness and velocity field within the frontal region of the form
$h=t^{-1/4}H_{0}(r/r_{f})$
and
$u_{r}=t^{-1/4}U_{0}(r/r_{f})$
. Two distinct current structures are possible with this ansatz. If
$K_{s}<K$
, the width of the frontal region
$r_{f}-r_{s}\sim t^{3/4}$
and the spatial variation of
$h$
and
$u$
within the frontal region is determined by the functions
$H_{0}$
and
$U_{0}$
. Alternatively, if
$K_{s}=K$
, the width of the frontal region
$r_{f}-r_{s}$
must grow more slowly than
$t^{3/4}$
, and the thickness and velocity within the frontal region are spatially constant to leading order, taking the form
$h=t^{-1/4}H_{0}(1)$
and
$u=t^{-1/4}U_{0}(1)$
. We show now that this latter situation is the case.
The mass conservation equation (3.1), when integrated across the frontal region, yields
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\int _{r_{s}}^{r_{f}}hr\text{d}r=r_{s}h(r_{s}^{+})[u(r_{s}^{+})-c].\end{eqnarray}$$
At leading order we have found that
$c=u(r_{s}^{+})$
, but by substituting the leading-order expressions and asymptotic form of the steady solution (3.17) into the jump condition for mass (3.16a
), we obtain that at the next order,
$$\begin{eqnarray}h(r_{s}^{+})[u(r_{s}^{+})-c]=u_{r}(r_{s}^{-})h(r_{s}^{-})+\cdots =\frac{1}{r_{s}}.\end{eqnarray}$$
Thus, on integrating (3.20), we obtain
$$\begin{eqnarray}\int _{r_{s}}^{r_{f}}hr\text{d}r=t+\cdots \,.\end{eqnarray}$$
Using the leading-order expressions for
$r_{s}$
,
$r_{f}$
and
$h$
in (3.22), we find that the powers of time on either side of the equation can balance only if
$K_{s}=K$
.
Thus, to leading order the shock and the front move at the same speed. Substituting the leading-order expressions
$h=t^{-1/4}H_{0}(1)$
and
$u=t^{-1/4}U_{0}(1)$
into the kinematic and dynamic boundary conditions at
$r=r_{f}$
, we obtain
$U_{0}(1)=3K/4$
and
$H_{0}(1)=3K/(2\mathit{Fr}_{f})$
respectively. From the momentum jump condition (3.16b
),
$$\begin{eqnarray}\frac{1}{12}[H_{0}(1)]^{3}=\frac{E^{1/2}}{K},\end{eqnarray}$$
which determines that the coefficient multiplying the intrusion radius
$r_{f}=Kt^{3/4}$
is
$$\begin{eqnarray}K=(32/9)^{1/4}E^{1/8}\mathit{Fr}_{f}^{3/4}.\end{eqnarray}$$
The width of the frontal region at late times can be determined by substituting the similarity forms into (3.22), from which we obtain
$$\begin{eqnarray}r_{f}(t)-r_{s}(t)=\frac{t^{1/2}}{KH_{0}(1)}+\cdots =(144K^{4}E)^{-1/6}t^{1/2}.\end{eqnarray}$$
This predicted width, and the current radius (3.24), compare well with those calculated from our time-dependent numerical computation (figure 2
b). We note that at late times, (3.22) implies that the volume of the fluid within the outer frontal region of the intrusion scales as
$r_{f}(r_{f}-r_{s})h\sim t$
, whereas the volume of fluid within the tail region
$\int _{0}^{r_{s}}rh\,\text{d}r\sim t^{3/4}$
. Thus, in the asymptotic regime of late time, the bulk of the intrusion volume is contained within the time-dependent frontal region (cf. figure 2).
We demonstrate in appendix B that the long-time behaviour of the current can also be derived by posing an asymptotic expansion for the flow variables. In doing so we obtain a more accurate description of the flow at long times, by calculating next-order corrections to the leading-order solution above.
3.4. Unsteady axisymmetric flow with drag
Our solutions so far have neglected the effect of drag on the radial intrusions. The neglect of drag is an appropriate dynamical regime provided the drag force
$(C_{D}u_{r}|u_{r}|)$
is much smaller than the inertia
$\partial (u_{r}h)/\partial t$
. By comparing the magnitudes of these terms in the frontal region at late times, we deduce that drag may be neglected here if
$C_{D}\mathit{Fr}_{f}t\ll 1$
. Numerical time-dependent solutions of the axisymmetric equations with drag (figure 3
a) are consistent with this view, with solutions with
$C_{D}\mathit{Fr}_{f}t\ll 1$
closely resembling those in the drag-free case (figure 2
a).
Figure 3. Time-dependent solutions of an axisymmetric intrusion including effects of drag. (a) Illustration of the flow thickness
$h$
centred on the neutral buoyancy height
$z=0$
, with
$C_{D}=0.01$
and parameters otherwise as in figure 2 at times
$t=2,10,25,50,100,200$
. (b) Current front position
$r_{f}$
as a function of time, for
$C_{D}=0.1$
, 0.01 and 0.001. The dashed line indicates the theoretical growth rate at late times of the current with
$C_{D}=0.1$
. (c) Numerical solutions of the time-dependent equations with
$C_{D}=0.1$
at time
$t=2\times 10^{3}$
, rescaled to similarity variables (solid curves), compared with solutions to the similarity ODEs (3.28) for the drag-dominated regime (dashed curves).
In dimensional form, we therefore have that drag becomes significant when
$t^{\star }\gg 1/(N^{\star }C_{D}\mathit{Fr}_{f})$
. This time is independent of the volume flux of the eruption. The value of
$C_{D}$
for an intrusion at high Reynolds number is poorly constrained, but by analogy with the turbulent drag that results from entrainment (e.g. Fernando Reference Fernando1991) we anticipate values between 0.001 and 0.1. With
$C_{D}=0.01$
the estimate above, with typical atmospheric stratification of
$N^{\star }=0.01~\text{s}$
, indicates that drag may become important after approximately 3 h.
When
$C_{D}\mathit{Fr}_{f}t\approx 1$
(for example, the solutions at
$t=50$
, 100 and 200 in figure 3
a) the effects of drag become significant. In figure 3(a) the reduction in velocity in the steady supercritical tail due to drag results in a thicker intrusion in this region, compared with the drag-free case illustrated in figure 2(a). The time-dependent frontal region is both wider and thinner than in the drag-free case, resulting in an intrusion with a much smaller change in thickness across the jump linking the two regions. The width of the frontal region grows rapidly with time when
$C_{D}\mathit{Fr}_{f}t>1$
, as drag becomes increasingly significant, with this frontal region at late times forming the majority of the intrusion.
When
$C_{D}\mathit{Fr}_{f}t\gg 1$
a new dominant momentum balance is established between the radial pressure gradient and the drag. Then, similarly to gravity current motion in a uniform environment (Hatcher, Hogg & Woods Reference Hatcher, Hogg and Woods2000; Hogg & Woods Reference Hogg and Woods2001), the flow undergoes a transition so that the dimensionless governing equations for the radial motion are
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}h)=0\quad \text{and}\quad \frac{h^{2}}{4}\frac{\partial h}{\partial r}=-C_{D}|u_{r}|u_{r}.\end{eqnarray}$$
These parabolic equations are subject to the source condition (3.4). In this drag-dominated regime, there is a new class of similarity solutions for the ensuing motion, and scaling can be usefully employed to determine the similarity exponents. To this end, we note from integrating (3.26a
) across the intrusion that mass conservation demands
$r_{f}^{2}h\sim t$
, while from (3.26b
) the dynamical balance requires
$h^{3}/r_{f}\sim C_{D}r_{f}^{2}/t^{2}$
. Thus, we deduce that the similarity variable
$r_{f}\sim C_{D}^{-1/9}t^{5/9}$
and seek solutions of the form
$$\begin{eqnarray}h={\it\kappa}C_{D}^{2/9}t^{-1/9}\mathscr{H}({\it\eta}),\quad u_{r}={\it\kappa}C_{D}^{-1/9}t^{-4/9}\mathscr{U}({\it\eta})\quad \text{and}\quad r_{f}={\it\kappa}C_{D}^{-1/9}t^{5/9},\end{eqnarray}$$
where
${\it\eta}=r/r_{f}(t)$
and
${\it\kappa}$
is a dimensionless constant to be determined. On substitution of (3.27) into the governing equations (3.26), we obtain
$$\begin{eqnarray}\frac{1}{{\it\eta}}({\it\eta}\mathscr{U}\mathscr{H})^{\prime }-\frac{5{\it\eta}}{9}\mathscr{H}^{\prime }-\frac{1}{9}\mathscr{H}=0\quad \text{and}\quad \frac{\mathscr{H}^{2}}{4}\mathscr{H}^{\prime }=-\mathscr{U}|\mathscr{U}|,\end{eqnarray}$$
where the prime denotes differentiation with respect to
${\it\eta}$
. These are subject to boundary conditions
$\mathscr{U}(1)=5/9$
and
$\mathscr{H}(1)=0$
, where the former imposes kinematic consistency at the front and the latter is the Froude number condition in the regime
$C_{D}t\gg 1$
. Finally, the specification of the source flux is most easily enforced by integrating the mass conservation equation (3.26a
) from
$r=r_{0}$
to
$r=r_{f}$
, which yields
$$\begin{eqnarray}{\it\kappa}^{3}\int _{0}^{1}{\it\eta}\mathscr{H}\text{d}{\it\eta}=1,\end{eqnarray}$$
because
$r_{0}/r_{f}(t)\ll 1$
when
$C_{D}t\gg 1$
. Only one boundary condition at source is required for these subcritical drag-dominated flows. The ordinary differential equations (3.28) are readily integrated numerically (for example, using a Runge–Kutta method), and applying (3.29) we find that
${\it\kappa}=1.222$
. The profiles of
$\mathscr{H}$
and
$\mathscr{U}$
, illustrated in figure 3(c), closely match the numerical solution to the time-dependent equations (3.1) and (3.2) at late times. In the similarity regime both the flow thickness and the velocity decay monotonically with increasing radius, with the intrusion exhibiting a rounded flow front.
The existence of a similarity solution in this drag-dominated regime (in contrast to the non-similarity solution obtained in the drag-free regime) may be anticipated from dimensional analysis. By writing (3.26a,b
) in terms of a new variable
$hN^{2/3}$
, we find that the problem can be written in terms of only a single dimensional parameter,
$N^{\star 2}Q^{\star 3}$
, with dimensions
$[N^{\star 2}Q^{\star 3}]\equiv L^{9}T^{-5}$
. Thus, as in the analysis for an intrusion generated by a line source in § 3.2, the only length scale is a similarity length scale, which in this case grows as
$t^{5/9}$
, and a similarity solution to the equations must result.
We note that for
${\it\eta}\ll 1$
the solution has the form
$\mathscr{H}({\it\eta})\sim {\it\eta}^{-1/5}+\cdots \,$
and
$\mathscr{U}({\it\eta})={\it\eta}^{-4/5}+\cdots \,$
, and thus the original dimensionless variables
$h$
and
$u_{r}$
are independent of time for
$r\ll r_{f}$
. To first order in
$r/r_{f}$
, mass conservation (3.26a
) then implies that
$ru_{r}h$
is constant, from which we find
$$\begin{eqnarray}h=(20C_{D})^{1/5}r^{-1/5}+\cdots \quad \text{and}\quad u_{r}=(20C_{D})^{-1/5}r^{-4/5}+\cdots \,.\end{eqnarray}$$
These leading-order terms were obtained by Baines (Reference Baines2013) under the assumption of a steady flow. We have shown that that once drag has become dominant, this steady solution is in fact attained by the attracting time-dependent similarity solution, but only in the regime
$r\ll r_{f}$
. Thus, the flow is time-dependent close to the front of the intrusion, but a steady intrusion is ‘laid down’ asymptotically, closer to the source.
4. Two-dimensional flow with wind drag
In the presence of an ambient wind, the intrusion no longer spreads radially, but is preferentially deflected downwind sufficiently far from source, due to drag between the intrusion and the ambient fluid. While initially the intrusion spreads nearly axisymmetrically, at later times (when
$\text{d}r_{f}/\text{d}t\ll U$
) the intrusion is predominantly advected downwind. In this latter phase, the front of the intrusion moves downwind approximately at speed
$U$
, leaving behind a steady intrusion that spreads laterally downwind. A typical numerically calculated steady-state solution to (2.1)–(2.3) that is established in this case is illustrated in figure 4.
Figure 4. A solution of (2.1)–(2.3) with
$C_{D}=0.1,U=1$
that has reached steady state. (a) The intrusion thickness
$h$
, indicated by grey contours (at intervals of 0.025) and black contours (at intervals of 0.1). (b) Flow streamlines (grey curves) and
$\log ({\it\phi})$
, indicated by black contours. We have enforced the flux at source (2.5) by adding the source flux as applied over a region of radius 3.18 in non-dimensional units: we have chosen this as a typical radius at the neutral buoyancy height of a buoyant plume originating from a volcano, calculated using the model of Woodhouse et al. (Reference Woodhouse, Hogg, Phillips and Sparks2013). The flow far downstream is independent of this radius.
Close to the source, one of two behaviours is observed. For sufficiently low ambient flow speed or sufficiently small coefficient of drag, the motion close to the source is approximately radial, but ambient atmospheric wind arrests the upwind motion some distance from the source, leading to a stagnation point. For sufficiently large
$U$
or
$C_{D}$
the flow direction is predominantly downwind everywhere. In flows exhibiting a stagnation point, including that illustrated in figure 4, the transfer of the initially upstream-propagating part of the intrusion to the lateral margins of the flow downstream results in thickening of the intrusion close to its boundary.
Our primary focus is on the flow far downstream of the source, where the component of the intrusion velocity aligned with the wind becomes close to the wind speed, but lateral pressure gradients associated with the cross-wind gradients of the intrusion thickness result in the current continuing to broaden. As a consequence of this broadening and of mass conservation, the thickness of the intrusion continues to diminish with distance from the source. Close to the source the flow has a bilobate form, caused by deflection of the initially axisymmetric inflow by the wind, and indicated by the contours of height in figure 4(a). At large distances from the source, the flow always forms a single central maximum in flow thickness. The behaviour sufficiently far downwind of the source may be analysed asymptotically based upon the cross-wind velocity being much smaller than the downwind velocity (
$|v/u|\ll 1$
), which in turn implies that downwind length scales far exceed cross-wind ones. To exploit this asymptotic regime, it is convenient to introduce an ordering parameter
${\it\epsilon}\sim |v/u|$
and write the downwind and cross-wind velocity components and intrusion thickness as
$$\begin{eqnarray}u=U-{\it\epsilon}^{2}\tilde{U} ,\quad v={\it\epsilon}V\quad \text{and}\quad h={\it\epsilon}^{1/2}H,\end{eqnarray}$$
where
$\tilde{U} ,V$
and
$H$
are functions of
$X\equiv {\it\epsilon}^{3/2}x$
and
$Y\equiv {\it\epsilon}^{1/2}y$
. By substituting these definitions into the governing equations (2.1)–(2.3) and obtaining the equations at leading order when
${\it\epsilon}\ll 1$
, we find that conservation of mass (2.1) is given by
$$\begin{eqnarray}U\frac{\partial H}{\partial X}+\frac{\partial }{\partial Y}(HV)=0,\end{eqnarray}$$
and the components of the momentum equations (2.2) and (2.3) are given by
$$\begin{eqnarray}\frac{H^{2}}{4}\frac{\partial H}{\partial X}=-C_{D}\tilde{U} |V|\quad \text{and}\quad \frac{H^{2}}{4}\frac{\partial H}{\partial Y}=-C_{D}V|V|\end{eqnarray}$$
respectively. Integrating (4.2) across the width of the flow and applying the global conservation of mass, which implies that the flow across any downstream section of the flow is equal to that supplied by the source, gives
$$\begin{eqnarray}U\int _{-W(X)}^{W(X)}H\text{d}Y=2{\rm\pi},\end{eqnarray}$$
where the half-width of the intrusion is denoted by
$w(x)={\it\epsilon}^{-1/2}W(X)$
. This far-field set of governing equations admits similarity solutions. First, from flux conservation (4.4), we deduce
$UHY\sim 1$
, while from mass conservation (4.2),
$U/X\sim V/Y$
. Finally, the cross-wind momentum (4.3) yields
$H^{3}/Y\sim C_{D}V^{2}$
. Together these identify the similarity scaling
$H\sim (C_{D}/U)^{1/6}X^{-1/3}$
and we seek a solution of the form
$$\begin{eqnarray}H=\left(\frac{C_{D}}{U}\right)^{1/6}\frac{{\hat{C}}}{X^{1/3}}{\hat{H}}({\it\xi})\quad \text{and}\quad W={\hat{C}}\left(\frac{X^{2}}{U^{5}C_{D}}\right)^{1/6},\end{eqnarray}$$
where
${\it\xi}=Y/W(X)$
and
${\hat{C}}$
is a constant that is to be determined as part of the solution. On substitution of (4.5) into the governing equations (4.3), integrating them and applying the boundary condition that
${\hat{H}}(1)=0$
, we find that
$$\begin{eqnarray}{\hat{H}}({\it\xi})=\left({\textstyle \frac{2}{3}}\right)^{2/3}(1-|{\it\xi}|^{3})^{1/3}.\end{eqnarray}$$
Substituting (4.6) into (4.4) we find
${\hat{C}}=2.159$
. Furthermore, we find that
$$\begin{eqnarray}V=\frac{UY}{3X}\quad \text{and}\quad \tilde{U} =\frac{{\hat{C}}^{3}}{9C_{D}^{1/2}U^{3/2}|Y|X}-\frac{2UY^{2}}{9X^{2}}.\end{eqnarray}$$
The arbitrary ordering parameter is eliminated when this solution is written in terms of the original dimensionless independent variables. The asymptotic regime within which the similarity solutions are valid is then given by
$w/x\ll 1$
, which corresponds to
$x\gg U^{-5/2}C_{D}^{-1/4}$
. An additional constraint on the applicability of these solutions arises from the fact that, near the axis
$y=0$
, inertial terms in (2.3) that are neglected in (4.3b
) are of comparable size to the drag and pressure forces. Comparing the size of the neglected terms with the terms in (4.3b
), we find that the solutions above are valid when
$|y|\gg (x^{2}C_{D}^{5}U)^{-1/6}$
, or, in other words, are valid for all but a negligible fraction of the width of the intrusion when
$x\gg U/C_{D}$
. Comparison of the similarity solutions with numerical computations of the governing equations (2.1)–(2.3) (figure 5) indicates that the similarity solution is indeed realised far downstream.
Figure 5. Cross-sections of the thickness of the intrusion shown in figure 4, scaled to the similarity variables
${\hat{H}}$
and
${\it\xi}$
. Cross-sections are taken at non-dimensional distances downstream of the source of
$x=200$
(dash-dotted curve), 1000 (dashed curve) and 2500 (dotted curve). The similarity solution (4.6) is indicated by the solid curve.
4.1. Downwind spreading regimes
Our calculation of current width spreading as
$w\sim x^{1/3}$
far downstream differs from the prediction of
$w\sim x^{1/2}$
of Bursik et al. (Reference Bursik, Carey and Sparks1992a
). Their prediction is made under the assumption that the downstream speed of the intrusion is equal to the ambient wind speed
$U$
due to drag, but that the lateral spreading far downstream is in an inertia-buoyancy regime, governed by the constant Froude number condition at the flow extremities, rather than being governed by the balance between lateral pressure gradients (4.3) and drag. Drag becomes increasingly important in this lateral spreading at late times (or, equivalently, far downwind of the source), and thus we expect a transition some distance downwind from an intrusion spreading in the inertia-buoyancy regime of Bursik et al. (Reference Bursik, Carey and Sparks1992a
) to one spreading in the drag-dominated regime, as described in § 4. We seek the location of this transition.
The width of a wind-dominated intrusion in the inertia-buoyancy spreading regime is given by Bursik et al. (Reference Bursik, Carey and Sparks1992a
), up to an undetermined parameter, postulated to be of order unity, depending on the flow geometry. We now calculate this parameter within the context of the model proposed by Bursik et al. (Reference Bursik, Carey and Sparks1992a
) in which the downstream intrusion velocity is exactly equal to the wind speed,
$u=U$
. Under this assumption the steady governing equations in the absence of drag become
$$\begin{eqnarray}\displaystyle & \displaystyle U\frac{\partial h}{\partial x}+\frac{\partial }{\partial y}(hv)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U\left[U\frac{\partial h}{\partial x}+\frac{\partial }{\partial y}(hv)\right]=-\frac{\partial }{\partial x}\left(\frac{h^{3}}{12}\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}U\frac{\partial }{\partial x}(hv)+\frac{\partial }{\partial y}(hv^{2})=-\frac{\partial }{\partial y}\left(\frac{h^{3}}{12}\right).\end{eqnarray}$$
Identifying the quantity
$U\partial /\partial x$
with the temporal derivative in a frame moving downstream at velocity
$U$
, as Bursik et al. (Reference Bursik, Carey and Sparks1992a
) do, we see that (4.8) and (4.10) are simply the equations of mass and lateral momentum conservation for a one-dimensional intrusion, with the dynamic boundary condition
$v=\mathit{Fr}_{f}h$
at the flow front. The width of the steady laterally spreading intrusion can therefore be determined by solutions to the unsteady one-dimensional system (4.8) and (4.10), which has been studied previously in the context of intrusions resulting from the instantaneous release of a constant volume of mixed fluid. At late times a similarity solution describes the spreading (Ungarish Reference Ungarish2009), and predicts a thickness profile for the intrusion
$$\begin{eqnarray}h(x,y)=\tilde{C}x^{-1/2}\left(\frac{y^{2}}{w_{i}(x)^{2}}+\frac{1}{\mathit{Fr}_{f}^{2}}-1\right)^{1/2},\end{eqnarray}$$
where the intrusion half-width
$w_{i}(x)$
is given by
$$\begin{eqnarray}w_{i}(x)=\tilde{C}x^{1/2}/U\end{eqnarray}$$
and
$\tilde{C}$
is a function of the frontal Froude number. We note that under the scalings implied far downstream by (4.11) and (4.12), the term on the right-hand side of (4.9) is asymptotically small, and thus this equation is also satisfied by any solution of (4.8).
Integrating the thickness profile (4.11) across the width of the flow, and requiring, as in (4.4), that the flux through this profile is equal to the source flux gives
$$\begin{eqnarray}\tilde{C}^{2}\int _{-1}^{1}({\it\eta}^{2}+\mathit{Fr}_{f}^{-2}-1)^{1/2}\text{d}{\it\eta}=2{\rm\pi}.\end{eqnarray}$$
Evaluating this integral for the value of the Froude number suggested by Ungarish (Reference Ungarish2009),
$\mathit{Fr}_{f}=1.19/\sqrt{2}$
, we then obtain
$\tilde{C}=1.926$
. It is notable that the thickness profile in the buoyancy-inertial spreading regime (4.11) is qualitatively very different from that found in the drag-dominated regime (4.6), with the minimum intrusion thickness occurring along the centreline,
$y=0$
.
Equating the half-width
$w_{i}$
given by (4.12) with the half-width predicted for the drag-dominated current (4.6), we find that the spreading becomes drag dominated at an approximate distance
$$\begin{eqnarray}x_{t}\approx 2.0U/C_{D}\end{eqnarray}$$
downwind of the intrusion source. As we have noted, the value of
$C_{D}$
for an intrusion at high Reynolds number is very poorly constrained, but using
$C_{D}=0.01$
with realistic atmospheric values of
$N^{\star }=0.01~\text{s}^{-1}$
and
$U^{\star }=10~\text{m s}^{-1}$
, (4.14) indicates that the transition from inertia-limited to drag-limited spreading occurs in the region of 200 km downstream of the source. While the uncertainty in
$C_{D}$
limits the accuracy of this estimate, the order of magnitude suggests that both regimes are likely to be observable in volcanic plumes, which can reach over 1000 km downwind (Pouget et al.
Reference Pouget, Bursik, Webley, Dehn and Pavolonis2013). It is notable that the flux
$Q^{\star }$
does not enter into the redimensionalised form of (4.14),
$x_{t}^{\star }\approx 2.0U^{\star }/(C_{D}N^{\star })$
; this estimate is therefore independent of the plume flux.
5. Particle transport
Motivated by the atmospheric transport of volcanic ash, we now analyse models of the transport of particles within horizontally flowing intrusions. The concentration of suspended particulate is assumed to be sufficiently dilute that it does not significantly alter the density of the intrusion, but rather it is advected by the fluid motion and settles under gravity. We assume that the particles are maintained in suspension by the action of fluid turbulence, and that this turbulence is sufficiently energetic to keep the suspension vertically well mixed. It is assumed that there is no flux of particles across the upper surface of the intrusion, but that particles may settle across the lower surface. At the lower interface, the flux per unit area is
$v_{s}{\it\phi}$
, where
${\it\phi}$
is the volume fraction of particles within the intrusion and
$v_{s}$
is the dimensionless settling velocity. Then, the equation governing the evolution of the volume fraction within the intrusion is given by
$$\begin{eqnarray}\frac{\partial }{\partial t}(h{\it\phi})+\frac{\partial }{\partial x}(uh{\it\phi})+\frac{\partial }{\partial y}(vh{\it\phi})=-v_{s}{\it\phi},\end{eqnarray}$$
or, equivalently,
$$\begin{eqnarray}\frac{\text{D}{\it\phi}}{\text{D}t}=-\frac{v_{s}}{h}{\it\phi},\end{eqnarray}$$
where
$\text{D}/\text{D}t=\partial /\partial t+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}$
. This model is a form of Hazen’s law (Hazen Reference Hazen1904; Sparks et al.
Reference Sparks, Carey and Sigurdsson1991; Bursik et al.
Reference Bursik, Sparks, Gilbert and Carey1992b
). The mean settling velocity
$v_{s}$
of a particle in turbulence is close in value to its settling velocity in a still fluid, but may differ slightly from this due to inertial effects (Maxey Reference Maxey1987). The assumption of a well-mixed intrusion requires the particle settling velocity to be much smaller than the turbulent velocity scales within the flow. This is true of the fine ash particles (diameter
${\leqslant}50~{\rm\mu}\text{m}$
, for which
$v_{s}\ll 1~\text{m}~\text{s}^{-1}$
) which comprise a substantial portion of the ash in the intrusion (Bonadonna & Phillips Reference Bonadonna and Phillips2003).
As with the dynamical evolution of the plume, we consider the case where the source conditions are steady. The volume fraction of particles at the source of the intrusion is then a constant
${\it\phi}_{0}$
, and both
${\it\phi}_{0}$
and the settling velocity
$v_{s}$
can be scaled out of the problem by defining
$$\begin{eqnarray}{\it\Phi}=({\it\phi}/{\it\phi}_{0})^{1/v_{s}},\end{eqnarray}$$
which results in a particle transport equation
$$\begin{eqnarray}\frac{\text{D}{\it\Phi}}{\text{D}t}=-\frac{{\it\Phi}}{h},\end{eqnarray}$$
with boundary condition
${\it\Phi}=1$
at the source. This transformation could be useful for analysing polydisperse suspensions (Harris, Hogg & Huppert Reference Harris, Hogg and Huppert2002), in which case the volume fraction of every class of particles, each with a different settling velocity, is related to the evolution of the single field
${\it\Phi}$
.
When the flow is purely radial, the governing equation (5.1) becomes
$$\begin{eqnarray}\frac{\partial }{\partial t}(h{\it\phi})+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}h{\it\phi})=-v_{s}{\it\phi}.\end{eqnarray}$$
For steady flows, by noting that volume flux conservation imposes
$ru_{r}h=1$
, we find that if the source particle concentration
${\it\phi}_{0}$
is time-independent, the volume fraction of particles in the intrusion attains the steady distribution (Sparks et al.
Reference Sparks, Carey and Sigurdsson1991)
$$\begin{eqnarray}\frac{{\it\phi}}{{\it\phi}_{0}}=\exp \left(-\frac{v_{s}(r^{2}-r_{0}^{2})}{2}\right).\end{eqnarray}$$
This distribution occurs both in the steady tail region of the drag-free currents and, asymptotically, in the region close to the source of the drag-dominated current, where the steady flow (3.30) is established.
In figure 6 we show the particle concentration in the drag-free radial intrusion illustrated in figure 2, calculated from time-dependent solutions of (5.5). In these computations we have chosen
$v_{s}=0.01$
. We note, however, that the scaling (5.3) implies that these numerical solutions can be rescaled to obtain the solution for arbitrary settling velocity. In the steady tail region (for
$r<r_{s}$
), the particle concentration is equal to the steady solution (5.6). For material points within the time-dependent frontal region, the late-time behaviour of the intrusion thickness is
$h\sim t^{-1/4}$
, which, when substituted into the characteristic equation (5.2) and integrated, implies that
$\log ({\it\phi})\sim -t^{5/4}$
. Expressing
$t$
in terms of the radial position of this frontal region
$r\sim t^{3/4}$
, we obtain a radial decrease in particle concentration
$\log ({\it\phi})\sim -r^{5/3}$
, slower than the decay in the tail region. Thus, the particle concentration in the unsteady frontal region may be significantly larger than that which would be estimated if a steady-state particle distribution were assumed. The higher concentration of particles in the flow head, compared with that in the adjacent region of the steady tail, is due to the thicker flow in the head, which from (5.2) results in reduced sedimentation. Qualitatively similar profiles of
${\it\phi}$
are obtained in continuously supplied radial particle-driven gravity currents (Bonnecaze et al.
Reference Bonnecaze, Hallworth, Huppert and Lister1995).
Figure 6. Particle concentration
${\it\phi}/{\it\phi}_{0}$
as a function of radial position for a drag-free intrusion with parameters as in figure 2 and a non-dimensional settling velocity
$v_{s}=0.01$
, at times
$t=10$
, 25, 50 and 100 (solid lines). The particle concentration in the steady tail region is described by steady solution (5.6) (dashed line), decaying as
$\log ({\it\phi})\sim -r^{2}$
. In the time-dependent head region (highlighted with dotted lines for
$t=100$
), the particle concentration varies widely, with the concentration at the flow front decaying more slowly than the tail region, as
$\log ({\it\phi})\sim -r^{5/3}$
at large
$r$
.
In wind-driven non-axisymmetric intrusions, numerical solutions for the particle concentration can be obtained by integrating the hyperbolic equation (5.1) alongside the equations governing the intrusion dynamics, equations (2.1)–(2.3). Such a solution is illustrated in figure 4(b). We have established in § 4 that, far downwind of the source, the intrusion adopts a steady state given by the similarity solution (4.6) and (4.7). Substituting for the velocity and thickness fields in (5.2), we obtain
$$\begin{eqnarray}U\frac{\partial {\it\phi}}{\partial x}+\frac{Uy}{3x}\frac{\partial {\it\phi}}{\partial y}=-\frac{v_{s}}{U}\left(\frac{U}{C_{D}}\right)^{1/6}\left(\frac{3}{2}\right)^{2/3}\frac{{\it\phi}}{{\hat{C}}(1-y^{3}/w^{3})^{1/3}}.\end{eqnarray}$$
This governing equation may then be integrated along the characteristics, which are described by
$\text{d}y/\text{d}x=y/3x$
, to find that
$$\begin{eqnarray}\frac{{\it\phi}}{{\it\phi}_{0}}=k\exp \left(-\frac{v_{s}}{U}\left(\frac{U}{C_{D}}\right)^{1/6}\left(\frac{3}{2}\right)^{5/3}\frac{x^{4/3}}{2{\hat{C}}(1-y^{3}/w(x)^{3})^{1/3}}\right).\end{eqnarray}$$
The coefficient
$k$
is constant on each characteristic, and must be determined by integrating (5.2) along the characteristic from the boundary condition at the source,
${\it\phi}={\it\phi}_{0}$
, to the region far downstream, where the asymptotic form (5.8) is obtained.
We note that by making only two assumptions, that the downwind velocity of the intrusion is constant and that its thickness decays downwind as
$x^{-1/3}$
(as implied by (4.5)), we obtain from integrating (5.2) that
$\log ({\it\phi}/{\it\phi}_{0})\sim -x^{4/3}$
. This straightforward scaling captures the overall dependence of particle concentration on downwind distance that occurs in the asymptotic solution for particle concentration (5.8).
6. Discussion
Our results have important consequences for the modelling of volcanic ash transport in the atmosphere, as we discuss below. In particular, we examine the implications of our study on the modelling strategies currently used to forecast volcanic ash transport in the atmosphere.
The disruption that can be caused by volcanic ash in the atmosphere to both aviation and infrastructure on the ground necessitates the forecasting of ash transport over large areas. Currently, the majority of models used to predict ash transport in the atmosphere, a class of models known as Volcanic Ash Transport and Dispersion (VATD) models, are based on the advection of ash particles by (persistent) atmospheric winds and the diffusion of ash, primarily by atmospheric turbulence (Folch Reference Folch2012). These advection-diffusion models are appealing in operational applications, where rapid forecasts are required during volcanic crises, because efficient numerical schemes can be employed for their computation. However, advection–diffusion models currently work under the assumption that the wind field within the intrusion does not differ from the ambient atmospheric wind, thereby neglecting the effect of buoyancy-induced motion within the intrusion.
An important aspect of ash cloud behaviour is the observation that the ash layers are characteristically quite thin in the far field at hundreds of kilometres from the source (Hobbs et al. Reference Hobbs, Radke, Lyons, Ferek and Coffman1991; Schumann et al. Reference Schumann, Weinzierl, Reitebuch, Schlager, Minikin, Forster, Baumann, Sailer, Graf, Mannstein, Voigt, Rahm, Simmet, Scheibe, Lichtenstern, Stock, Rüba, Schäuble, Tafferner, Rautenhaus, Gerz, Ziereis, Krautstrunk, Mallaun, Gayet, Lieke, Kandler, Ebert, Weinbruch, Stohl, Gasteiger, Gross, Freudenthaler, Wiegner, Ansmann, Tesche, Olafsson and Sturm2011). Whereas ash clouds can be several kilometres thick near the source (Sparks et al. Reference Sparks, Bursik, Carey, Gilbert, Glaze, Sigurdsson and Woods1997), thinning occurs rapidly with distance from the source (e.g. Dellino et al. Reference Dellino, Gudmundsson, Larsen, Mele, Stevenson, Thordarson and Zimanowski2012, figure 1) and the far-field thickness is typically a few hundred metres. The buoyancy-driven radial flow that results in thinning of the intrusion (figure 1) is absent from models invoking the advection–diffusion description, and vertical diffusion in these models then typically results in a predicted thickening of ash clouds. Thinning of ash clouds is, however, a key feature of buoyancy-driven intrusion models, and is seen in laboratory studies (Wu Reference Wu1969; Amen & Maxworthy Reference Amen and Maxworthy1980; Faust & Plate Reference Faust and Plate1984; Holasek, Woods & Self Reference Holasek, Woods and Self1996b ; Richards et al. Reference Richards, Aubourg and Sutherland2014) and numerical investigations (Herzog, Oberhuber & Graf Reference Herzog, Oberhuber and Graf2003; Koyaguchi, Ochiai & Suzuki Reference Koyaguchi, Ochiai and Suzuki2009; Suzuki & Koyaguchi Reference Suzuki and Koyaguchi2009). Thus, models that include buoyancy appear to be more consistent with observations of thin far-field ash layers.
Advection–diffusion models of volcanic ash dispersion can predict the formation of thin ash layers only through the action of vertical wind shear, which can transport ash at different altitudes in different directions. The sensitivity of advection–diffusion descriptions of ash transport to the direction of the ambient wind field at different altitudes can lead to predictions of ash at altitudes and locations where no (or very little) ash has been observed (Dacre et al. Reference Dacre, Grant, Hogan, Belcher, Thomson, Devenish, Marenco, Hort, Haywood, Ansmann, Mattis and Clarisse2011; Devenish et al. Reference Devenish, Francis, Johnson, Sparks and Thomson2012), and requires a precise description of the vertical distribution of ash above the volcanic source (Dacre et al. Reference Dacre, Grant, Hogan, Belcher, Thomson, Devenish, Marenco, Hort, Haywood, Ansmann, Mattis and Clarisse2011; Devenish et al. Reference Devenish, Francis, Johnson, Sparks and Thomson2012; Kristiansen et al. Reference Kristiansen, Stohl, Prata, Bukowiecki, Dacre, Eckhardt, Henne, Hort, Johnson, Marenco, Neininger, Reitebuch, Seibert, Thomson, Webster and Weinzierl2012). Furthermore, the formation of thin ash layers in advection–diffusion models is dependent on specific ambient wind conditions, whereas the thinning of ash layers is an intrinsic feature of the radial wind fields (or, far downwind, laterally diverging wind fields) that result from buoyancy-driven spreading.
Correctly forecasting the thickness of the ash cloud is an important factor in forecasting the peak ash concentration within an intrusion, which has become a critical aspect of ash hazard management for aviation (a concentration of
$2~\text{mg}~\text{m}^{-3}$
has become the threshold above which flying is regarded as a concern). Satellite observations of ash in the atmosphere can provide the total vertically integrated mass of ash at each horizontal location in the plume (Francis, Cooke & Saunders Reference Francis, Cooke and Saunders2012), but estimates of ash concentration cannot be made without prior knowledge of the thickness of the ash layer (Prata & Prata Reference Prata and Prata2012). Thin layers of ash will lead to higher peak ash concentrations than if the same mass of ash were distributed in a thicker vertically diffuse layer.
The importance of buoyancy-driven motion in volcanic intrusions is highlighted by the significant spreading in the upwind and cross-wind directions observed in ‘strong’ volcanic plumes (plumes that rise predominately vertically, with little effect of atmospheric wind on the ascent of the plume). For large volcanic eruptions the buoyancy-driven spreading of the intrusion can be strongly dominant over the ambient wind field over large areas. For example, satellite observations of the ash cloud from the 1991 eruption of Mount Pinatubo, Philippines, showed an approximately axisymmetric spreading of the ash cloud to a distance of 300 km (Holasek, Self & Woods Reference Holasek, Self and Woods1996a ) despite strong atmospheric winds (Oswalt, Nichols & O’Hara Reference Oswalt, Nichols, O’Hara, Newhall and Punongbayan1996). Similarly, satellite observations showed significant upwind and cross-wind spreading of the ash cloud formed during the 18 May 1980 eruption of Mount St. Helens, USA (Sarna-Wojcicki et al. Reference Sarna-Wojcicki, Shipley, Waitt, Dzurisin, Hays, Davis, Wood, Bateridge, Lipman and Mullineaux1980; Sparks, Moore & Rice Reference Sparks, Moore and Rice1986), and photographs from aircraft and satellites of the ash cloud from Córdon Caulle, Chile, showed some upwind ash transport and cross-wind spreading of the intrusion, while the majority of the ash cloud was transported downwind (Collini et al. Reference Collini, Soledad Osores, Folch, Viramonte, Villarosa and Salmuni2013). The advection–diffusion descriptions of ash transport currently used in VATD models are unable to describe significant motion of ash against the wind (any upwind motion is due only to transport by diffusion, which is negligible in comparison to advection by the wind field unless the wind speed is small), and cross-wind motion is driven by atmospheric turbulence, so it is dependent on the ambient meteorology. In contrast, models that include the effect of buoyancy have the potential to capture the upwind and lateral transport of ash (Baines Reference Baines2013). The correct prediction of this transport is essential for confident forecasts and interpretation of the distribution of ash deposits following volcanic eruptions. Costa et al. (Reference Costa, Folch and Macedonio2013) have demonstrated that an advection–diffusion model of ash transport from the 1991 eruption of Mount Pinatubo is unable to capture the upwind and cross-wind spreading of ash near the volcanic source that is observed in satellite observations, and suggest that buoyancy-driven spreading is necessary in order to describe the observed ash distribution.
From our modelling of wind-blown plumes in § 4 we expect that, far from source, weaker volcanic plumes will be advected downstream by wind, while spreading laterally due to buoyancy. Bursik et al. (Reference Bursik, Carey and Sparks1992a
) showed that the spreading of the cloud from the 1980 eruption of Mount St. Helens could indeed be explained by lateral buoyant spreading to distances of several hundred kilometres downwind. However, we expect that even further downwind than this, the advection of particles by the buoyancy-driven component of the motion will diminish in importance relative to the dispersion of particles due to atmospheric diffusion. The motion then becomes dominated in the downwind direction by advection due to the ambient wind and dominated in the vertical and/or cross-wind directions by the diffusive transport due to (transient) turbulent winds, as described by the current VATD models. We estimate the distance from source within which the buoyancy-driven motion is dominant by constructing Peclet numbers in the lateral and vertical directions. These Peclet numbers quantify the relative strength of buoyancy-driven spreading and thinning of a wind-blown plume, as described in § 4, compared with dispersion in the horizontal and vertical directions due to atmospheric turbulence, which can be parametrised by a linear diffusion with horizontal and vertical diffusion coefficients
$D_{h}$
and
$D_{v}$
respectively. The Peclet numbers
$\mathit{Pe}_{h}$
and
$\mathit{Pe}_{v}$
in the lateral and vertical directions respectively represent the ratio of the time scale for turbulent diffusive transport across the intrusion (given by
$w^{2}/D_{h}$
for horizontal diffusion and
$h^{2}/D_{v}$
for vertical diffusion) to the time scale of buoyancy-driven spreading of the intrusion (given by
$w/v$
for lateral motion and
$h/{\dot{h}}$
for vertical motion, where
${\dot{h}}$
is a vertical velocity scale). The intrusion length scales in the lateral and vertical directions are
$w$
and
$h$
respectively. The lateral velocity scale is
$v$
, and from differentiating the scaling
$wh\sim \text{constant}$
, obtained from (4.4), we find
${\dot{h}}=hv/w$
. The horizontal and vertical Peclet numbers are therefore
$$\begin{eqnarray}\mathit{Pe}_{h}=\frac{wv}{D_{h}}\quad \text{and}\quad Pe_{v}=\frac{h^{2}v}{wD_{v}}\end{eqnarray}$$
respectively. When buoyancy-driven lateral spreading is dominant over turbulent diffusion (as expected near source) we have
$\mathit{Pe}\gg 1$
, whereas when atmospheric turbulent diffusion dominates buoyant motion, which may occur very far from source, we have
$\mathit{Pe}\ll 1$
. For
$\mathit{Pe}\sim 1$
both buoyancy and diffusion contribute to the dispersion of ash. On substituting into (6.1) the asymptotic forms for
$w$
,
$v$
and
$h$
in the drag-dominated spreading regime of a wind-driven plume (from (4.5) and (4.7)) and equating the Peclet numbers to 1, we obtain dimensional estimates for the distance downstream at which atmospheric diffusion becomes significant in the lateral and vertical directions,
$$\begin{eqnarray}x_{h}^{\star }\sim \frac{{Q^{\star }}^{3}{N^{\star }}^{2}}{C_{D}{U^{\star }}^{2}{D_{h}^{\star }}^{3}}\quad \text{and}\quad x_{v}^{\star }\sim \left(\frac{{Q^{\star }}^{3}{U^{\star }}^{2}C_{D}}{{N^{\star }}^{2}{D_{v}^{\star }}^{3}}\right)^{1/5}\end{eqnarray}$$
respectively. In the upper troposphere and lower stratosphere, horizontal diffusivities
$D_{h}^{\star }$
are typically
$5{-}20~\text{m}^{2}~\text{s}^{-1}$
, with vertical diffusivities
$D_{v}^{\star }$
approximately a factor of 100 smaller (e.g. Cadet Reference Cadet1977; Woodman & Rastogi Reference Woodman and Rastogi1984; Schumann et al.
Reference Schumann, Konopka, Baumann, Busen, Gerz, Schlager, Schulte and Volkert1995). Taking other parameters appropriate to volcanic intrusions in the atmosphere, we find that vertical diffusion becomes significant long before horizontal diffusion (
$x_{v}^{\star }\ll x_{h}^{\star }$
). With
$Q^{\star }=10^{7}~\text{m}^{3}~\text{s}^{-1}$
, a value indicative of a moderately sized volcanic eruption column, the vertical diffusion becomes significant approximately 1000 km downstream. Although only an order-of-magnitude estimate, this suggests that in larger volcanic eruptions, buoyancy-driven spreading (in particular the drag-dominated regime that we describe in § 4) is the dominant process through which volcanic intrusions spread and by which ash is dispersed, even very far from source.
A consequence of this buoyancy-driven horizontal dispersal of ash is that suspended ash is advected to the margins of an ash cloud, which can result in an ash cloud with quite sharp edges, consistent with observations (Prata & Prata Reference Prata and Prata2012; Spinetti et al. Reference Spinetti, Barsotti, Neri, Buongiorno, Doumaz and Nannipieri2013). In an advection–diffusion framework, horizontal spreading of ash is driven only by horizontal gradients in the ash concentration, which implies a diffuse outer zoning and decreasing concentrations of ash towards the flow margins.
Predictions of the vertical distribution of ash within an intrusion also differ between advection–diffusion and buoyancy-driven spreading models. In a buoyancy-driven intrusion, the difference in velocity between a volcanic intrusion and the surrounding atmosphere results in the generation of internal turbulence within the intrusion. This turbulence can keep ash particles in suspension throughout the layer, which underlies our use in § 5 of a particle settling flux based on a uniform distribution of ash throughout the height of the intrusion. In advection–diffusion models, the only source of vertical mixing is the much weaker atmospheric turbulence, which is less effective at keeping ash particles suspended. Vertical mixing due to buoyancy can keep quite large particles in suspension and may explain why particles of up to
$100~{\rm\mu}\text{m}$
were transported to the UK during the Eyjafjallajökull eruption in 2010 (Stevenson et al.
Reference Stevenson, Loughlin, Rae, Thordarson, Milodowski, Gilbert, Harangi, Lukács, Højgaard, Árting, Pyne-O’Donnell, MacLeod, Whitney and Cassidy2012).
7. Summary and conclusions
We have presented solutions to a depth-integrated model for continuously supplied intrusions into a linearly stratified atmosphere. For an axisymmetric intrusion in which the drag between the intrusion and the surrounding atmosphere is negligible, the intrusion grows in a manner that is completely different from that previously suggested by simple scaling arguments. While scaling arguments suggest that the radius of a continuously supplied axisymmetric intrusion should grow as
$r_{f}\sim t^{2/3}$
, we find that the solution of the depth-integrated model is not a similarity solution, and an asymptotic growth rate of
$r_{f}\sim t^{3/4}$
is established instead. This suggests a need to re-evaluate interpretations of volcanic plumes, such as those of Costa et al. (Reference Costa, Folch and Macedonio2013) and references therein, that are predicated on the assumption that
$r_{f}\sim t^{2/3}$
.
We have demonstrated that this non-similarity behaviour is anticipated from dimensional arguments, and that the simple scalings break down due to an internal jump in the flow, which results from the need to connect the Froude number of the steady solution in the inner tail (3.8) to the Froude number at the current front
$\mathit{Fr}_{f}$
, which is of order unity. Such a jump allows the current volume to be contained almost entirely within a thin annulus near the current front, a distribution different from that anticipated in the scalings of Lemckert & Imberger (Reference Lemckert and Imberger1993) and Woods & Kienle (Reference Woods and Kienle1994). We note the similarity with entraining gravity currents, in which the restriction of the current buoyancy to a thin boundary layer also results in a solution different from that predicted by simple scaling arguments (Johnson & Hogg Reference Johnson and Hogg2013). A consequence of the non-similarity behaviour of these intrusions is that, even though the flow near the front of the intrusion is evolving, the intrusion near the source is steady, exhibiting an approximately constant radial velocity and rapid radial thinning.
When the ambient is moving relative to the source of the intrusion, buoyancy effects result in a pronounced thinning and lateral spreading with increasing distance downstream. Far downstream, the predominant motion of the flow is due to advection by wind, but our far-field solution (4.6) demonstrates that even far from source, buoyancy effects play a role in thinning and spreading an intrusion.
We have shown that drag increasingly influences the motion of an intrusion at late times. The time and location of this transition to a drag-influenced current are dependent on the poorly constrained drag coefficient
$C_{D}$
. However, for typical atmospheric conditions, and an order-of-magnitude estimate of
$C_{D}=0.01$
which is consistent with the mechanism of drag through turbulent mixing, we have shown in § 4 that drag becomes important after approximately 3 h for axisymmetric plumes, and in § 4.1 that for intrusions in a moving ambient, drag dominates the lateral force balance and changes the spreading regime after approximately 200 km. Both these estimates are independent of the source flux of the intrusion, and are of a magnitude that suggests that volcanic plumes may often be in a transitional regime where the effects of drag are neither negligible nor dominant.
Acknowledgements
The authors thank M. Ungarish for helpful discussions, and acknowledge support from NERC through the Vanaheim project ‘Characterisation of the near-field Eyjafjallajokull volcanic plume and its long-range influence’ (NE/I01554X/1). M.J.W., A.J.H. and J.C.P. were additionally funded by the European Union Seventh Framework Programme (FP7, 2007–2013) under grant agreement number 208377, FutureVolc, and A.J.H. and C.G.J. by EPSRC through grant EP/G066353/1. R.S.J.S. acknowledges the support of a European Research Council Advanced Grant. This research was supported in part by the National Science Foundation under Grant No. NSF PHY11-25915.
Appendix A. Continuously supplied axisymmetric gravity currents in a homogeneous ambient
In §§ 3.2 and 3.3 we demonstrated that a continuously supplied axisymmetric intrusion exhibits a steady inner tail region coupled to an unsteady frontal region, and a growth rate
$r_{f}\sim t^{3/4}$
that differs from that obtained from direct scaling arguments. In this appendix we demonstrate that the same arguments predict a very similar structure in the case of an axisymmetric gravity current in an unstratified ambient, which was previously observed by Garvine (Reference Garvine1984) and analysed by Slim & Huppert (Reference Slim and Huppert2011). This emphasises that the non-similarity two-region solution structure is not a property specific to intrusions, but is a more generic phenomenon resulting from the continuous supply of fluid to a high-Reynolds-number current in an axisymmetric geometry.
Defining the dimensional reduced gravity
$g^{\prime \star }=g^{\star }({\it\rho}^{\star }-{\it\rho}_{0}^{\star })/{\it\rho}_{0}^{\star }$
, where
${\it\rho}^{\star }$
and
${\it\rho}_{0}^{\star }$
are the current and ambient fluid densities respectively and
$g^{\star }$
is the acceleration due to gravity, in this appendix we non-dimensionalise lengths by
$(Q^{\star 2}/g^{\prime \star })^{1/5}$
and times by
$(Q^{\star }/g^{\prime \star 3})^{1/5}$
. The axisymmetric shallow-water equations for a gravity current flowing over a horizontal surface are then
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}(hu)+\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}^{2}h)+\frac{\partial }{\partial r}\left(\frac{h^{2}}{2}\right)=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}u_{r}=\mathit{Fr}_{f}\sqrt{h},\quad \text{at }r=r_{f}(t).\end{eqnarray}$$
Simple scaling arguments for such a gravity current would suggest that conservation of mass is given by
$hr_{f}^{2}\sim t$
, while the dynamical balance of buoyancy and inertia requires that
$h\sim (r_{f}/t)^{2}$
. Together, these suggest that
$r_{f}\sim t^{3/4}$
(Chen Reference Chen1980; Didden & Maxworthy Reference Didden and Maxworthy1982; Bonnecaze et al.
Reference Bonnecaze, Hallworth, Huppert and Lister1995). However, numerical solutions of (A 1) and (A 2) (figure 7) indicate that the solution is not in similarity form, but has a steady inner tail region connecting to a time-dependent frontal region through a discontinuity.
Figure 7. Numerical time-dependent solutions of an axisymmetric gravity current (
$\mathit{Fr}_{f}=1.19$
,
$\mathit{Fr}_{0}=1$
,
$r_{0}=1$
). (a) Flow thickness
$h$
at times
$t=2,10,25,50$
. (b) Current front position
$r_{f}$
and width of the time-dependent frontal region
$r_{f}-r_{s}$
as a function of time. The dashed lines of gradient
$4/5$
and
$3/5$
indicate the theoretical late-time predictions (A 19) and (A 28) for
$r_{f}$
and
$r_{f}-r_{s}$
respectively.
Seeking a steady solution that we anticipate will form the tail region, we discard time derivatives and the front condition, and as before obtain two conservation equations
$$\begin{eqnarray}\frac{\text{d}}{\text{d}r}\left(ru_{r}h\right)=0\quad \text{and}\quad \frac{\text{d}}{\text{d}r}\left(\frac{u_{r}^{2}}{2}+h\right)=0.\end{eqnarray}$$
We apply the source conditions
$$\begin{eqnarray}ru_{r}h=1\quad \text{and}\quad u_{r}^{2}/2+h=\tilde{E}\quad \text{at }r=r_{0},\end{eqnarray}$$
which represent the constant mass flux and the energy density (Bernoulli constant) respectively. By substituting (A 5a
) and the Froude number condition at source,
$\mathit{Fr}_{0}=u/\sqrt{h}$
at
$r=r_{0}$
, into (A 5b
), we obtain an expression for the Bernoulli constant
$\tilde{E}$
in terms of the source Froude number,
$$\begin{eqnarray}\tilde{E}=[\mathit{Fr}_{0}^{-2/3}+(1/2)\mathit{Fr}_{0}^{4/3}]r_{0}^{-2/3}.\end{eqnarray}$$
The expressions for
$h$
and
$u$
, analogous to (3.8a,b
), are solutions to a cubic equation, and as in the case of intrusions, both a subcritical and a supercritical solution exist (Garvine Reference Garvine1984). Selecting the supercritical solution as before, we find that for
$r\gg r_{0}$
,
$$\begin{eqnarray}u_{r}(r)=(2\tilde{E})^{1/2}+\cdots \quad \text{and}\quad h(r)=(2\tilde{E})^{-1/2}\frac{1}{r}+\cdots \,.\end{eqnarray}$$
As with the radial intrusions, the supercritical flow at source means that two source boundary conditions (A 5a,b
) are specified. The solution in the supercritical region flow is fully specified by these conditions through integrating (A 4), and is therefore steady because the source conditions are steady. Our specification of both the required source boundary conditions (A 5a
) and (A 5b
) introduces the additional dimensional parameter
$\tilde{E}^{\star }$
(where
$[\tilde{E}^{\star }]=L^{2}T^{-2}$
), which allows for a non-similarity solution.
We contrast this with the approach of Bonnecaze et al. (Reference Bonnecaze, Hallworth, Huppert and Lister1995), who attempt to construct a similarity solution to the problem of a radial continuously supplied gravity current, based on the simple scaling arguments that suggest
$r_{f}\sim t^{3/4}$
. Bonnecaze et al. (Reference Bonnecaze, Hallworth, Huppert and Lister1995) construct a discontinuous solution to the resulting similarity ordinary differential equations with an unsteady supercritical region near the source. However, this supercritical region does not satisfy the source condition (A 5b
). More problematically, the similarity solution suggested by Bonnecaze et al. (Reference Bonnecaze, Hallworth, Huppert and Lister1995), and illustrated in their figure 1(b), has a singularity within the domain of the intrusion, and cannot be integrated back to the origin in similarity space, where the source boundary conditions (A 5a,b
) must be applied. Numerically integrating the similarity equations with the parameters chosen by Bonnecaze et al. (Reference Bonnecaze, Hallworth, Huppert and Lister1995), we find that the singularity is at
$y=0.019$
, where
$y$
is their similarity variable. Thus, the result of Bonnecaze et al. (Reference Bonnecaze, Hallworth, Huppert and Lister1995) is not a solution to the problem of a gravity current originating from a continuous source of buoyancy of fixed size.
The procedure for obtaining the non-similarity solution for the time-dependent frontal region is analogous to that in § 3.3 and shares some features with Slim & Huppert (Reference Slim and Huppert2011), although importantly it differs in detail from their construction. The outer frontal region is connected to the inner steady tail through a shock or discontinuity at
$r=r_{s}(t)$
. The jump conditions across this shock for a gravity current in a homogeneous ambient, assuming conservation of mass and momentum, are
$$\begin{eqnarray}\left[(u_{r}-c)h\right]_{r_{s}^{-}}^{r_{s}^{+}}=0\quad \text{and}\quad \left[u_{r}(u_{r}-c)h+{\textstyle \frac{1}{2}}h^{2}\right]_{r_{s}^{-}}^{r_{s}^{+}}=0.\end{eqnarray}$$
As in § 3.3, we seek a similarity solution for the frontal region and pose that
$h(r_{s}^{+})\sim u_{r}(r_{s}^{+})^{2}$
, while noting that
$u_{r}(r_{s}^{-})^{2}h(r_{s}^{-})\sim 1/r_{s}$
and
$c\sim r_{s}/t$
. Thus, we anticipate that
$r_{f}=r_{f0}t^{4/5}$
and
$r_{s}=r_{s0}t^{4/5}$
, where
$r_{f0}$
and
$r_{s0}$
are constants to be determined. This ansatz is identical to the formulation of Slim & Huppert (Reference Slim and Huppert2011). However, it is not the complete solution because it does not satisfy the shock conditions exactly: the largest omitted term in the balance of momentum flux across the shock (A 8) is
$u_{r}(r_{s}^{-})ch(r_{s}^{-})$
, and this is
$O(t^{-1})$
, while the leading-order terms are
$O(t^{-4/5})$
. Furthermore, we show below that
$r_{f0}=r_{s0}$
and thus, as Slim & Huppert (Reference Slim and Huppert2011) anticipate, their similarity solutions for the frontal region are only valid for a region of vanishing width, because to leading order the front and the shock move at the same speed. Thus, in order to obtain a more complete description of the solution within the frontal region at late times, we must account for the non-self-similar evolution of the height and velocity fields.
To do this, we examine the asymptotic form of the height and velocity fields in the regime
$t\gg 1$
, extending the solution beyond the leading-order description deduced above by extending the matching of mass and momentum fluxes (A 8) across the shock to next order. We pose expansions for the front and shock positions and the height and velocity fields that account for the first correction terms to the leading-order terms. These corrections are
$O(t^{-1/5})$
smaller than the leading-order terms, due to the magnitude of the first omitted terms in the shock conditions, as identified above. Thus, we write
$$\begin{eqnarray}\displaystyle r_{f}(t) & = & \displaystyle r_{f0}t^{4/5}+r_{f1}t^{3/5}+O(t^{2/5}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{s}(t) & = & \displaystyle r_{s0}t^{4/5}+r_{s1}t^{3/5}+O(t^{2/5}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(r,t) & = & \displaystyle r_{f0}^{2}t^{-2/5}H_{0}({\it\eta})+r_{f1}r_{f0}t^{-3/5}H_{1}({\it\eta})+O(t^{-4/5}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u(r,t) & = & \displaystyle r_{f0}t^{-1/5}U_{0}({\it\eta})+r_{f1}t^{-2/5}U_{1}({\it\eta})+O(t^{-3/5}),\end{eqnarray}$$
${\it\eta}=r/r_{f}(t)$
. Denoting differentiation with respect to
${\it\eta}$
by a prime, we find that the leading-order expressions of mass and momentum conservation are given by 
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{2}{5}}{\it\eta}H_{0}-{\textstyle \frac{4}{5}}{\it\eta}^{2}H_{0}^{\prime }+({\it\eta}U_{0}H_{0})^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{1}{5}}U_{0}-{\textstyle \frac{4}{5}}{\it\eta}U_{0}^{\prime }+U_{0}U_{0}^{\prime }+H_{0}^{\prime }=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}U_{0}(1)=\frac{4}{5}\quad \text{and}\quad H_{0}(1)=\frac{16}{25\mathit{Fr}_{f}^{2}}.\end{eqnarray}$$
Straightforwardly, from the governing equations (A 13) and (A 14), we find
$U_{0}^{\prime }(1)=-2/5$
and
$H_{0}^{\prime }(1)=4/25$
; these values will be needed in the analysis that follows. Differentiating (A 10) gives the speed of the shock,
$$\begin{eqnarray}c={\textstyle \frac{4}{5}}r_{s0}t^{-1/5}+{\textstyle \frac{3}{5}}r_{s1}t^{-2/5}+O(t^{-3/5}),\end{eqnarray}$$
and the leading-order expressions from the balance of mass and momentum fluxes at the shock (A 8) then yield
$$\begin{eqnarray}U_{0}({\it\eta}_{s})=\frac{4{\it\eta}_{s}}{5}\quad \text{and}\quad H_{0}({\it\eta}_{s})^{2}=\frac{2(2\tilde{E})^{1/2}}{r_{f0}^{5}{\it\eta}_{s}},\end{eqnarray}$$
where
${\it\eta}_{s}=r_{s0}/r_{f0}$
. From (A 13), and using (A 15) and (A 17), we deduce
$$\begin{eqnarray}\int _{{\it\eta}_{s}}^{1}\frac{6}{5}{\it\eta}H_{0}\text{d}{\it\eta}=-\!\left[{\it\eta}H_{0}\left(U_{0}-\frac{4}{5}{\it\eta}\right)\right]_{{\it\eta}_{s}}^{1}=0.\end{eqnarray}$$
Since
$H_{0}$
is strictly positive, we deduce that
$r_{s0}=r_{f0}$
and thus, from (A 15) and (A 17), that
$$\begin{eqnarray}r_{f0}^{5}=\frac{5^{4}\mathit{Fr}_{f}^{4}\tilde{E}^{1/2}}{2^{13/2}}.\end{eqnarray}$$
In summary, to leading order the front and the shock move at the same speed, and, to the same order of truncation when
$t\gg 1$
, the frontal region is of vanishing width. The value of
$r_{f0}$
(A 19) is identical to that derived by Slim & Huppert (Reference Slim and Huppert2011) and compares favourably with our numerical computations (see figure 7).
However, our subsequent analysis, in which we compute the solution at the next order, differs from Slim & Huppert (Reference Slim and Huppert2011) because the frontal region is not in precise similarity form. First, we evaluate the shock conditions at next order, and to this end we require the height and velocity fields at
$r=r_{s}^{+}$
, given by
$$\begin{eqnarray}\displaystyle & u(r_{s}^{+},t)=r_{f0}U_{0}(1)t^{-1/5}+\left(U_{0}^{\prime }(1)(r_{s1}-r_{f1})+r_{f1}U_{1}(1)\right)t^{-2/5}+O(t^{-3/5}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & h(r_{s}^{+},t)=r_{f0}^{2}H_{0}(1)t^{-2/5}+r_{f0}\left(H_{0}^{\prime }(1)(r_{s1}-r_{f1})+r_{f1}H_{1}(1)\right)t^{-3/5}+O(t^{-4/5}).\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r_{f0}^{3}H_{0}(1)}=r_{f1}(U_{1}(1)-U_{0}^{\prime }(1))+r_{s1}\left(-\frac{3}{5}+U_{0}^{\prime }(1)\right)\end{eqnarray}$$
and from the balance of momentum fluxes we find
$$\begin{eqnarray}-\!\frac{8}{5r_{f0}^{3}H_{0}(1)}=\left(H_{0}^{\prime }(1)+\frac{1}{2}H_{0}(1)\right)r_{s1}+(H_{1}(1)-H_{0}^{\prime }(1))r_{f1}.\end{eqnarray}$$
With the boundary conditions at the current front
$U_{1}(1)=3/5$
and
$H_{1}(1)=24/(25\mathit{Fr}_{f}^{2})$
, obtained in the same way as the boundary conditions on the leading-order functions (A 15), we obtain from (A 22) and (A 23) values for
$r_{s1}$
and
$r_{f1}$
,
$$\begin{eqnarray}r_{s1}=\frac{1}{8r_{f0}^{3}H_{0}(1)}(-6-9\mathit{Fr}_{f}^{2})\quad \text{and}\quad r_{f1}=\frac{1}{8r_{f0}^{3}H_{0}(1)}(2-9\mathit{Fr}_{f}^{2}).\end{eqnarray}$$
The width of the frontal region is then
$$\begin{eqnarray}r_{f}(t)-r_{s}(t)=(r_{f1}-r_{rs1})t^{3/5}+O(t^{2/5})=\frac{t^{3/5}}{r_{f0}^{3}H_{0}(1)}+O(t^{2/5}).\end{eqnarray}$$
This asymptotic result is compared with the numerical output in figure 7, again showing good agreement between the two when
$t\gg 1$
. To complete the formulation at this order, we find the following governing equations:
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{3}{5}}{\it\eta}H_{1}-{\textstyle \frac{4}{5}}{\it\eta}^{2}H_{1}^{\prime }+({\it\eta}(U_{0}H_{1}+U_{1}H_{0}))^{\prime }=-{\textstyle \frac{1}{5}}{\it\eta}^{2}H_{0}^{\prime }+({\it\eta}H_{0}U_{0})^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{2}{5}}U_{1}-{\textstyle \frac{4}{5}}{\it\eta}U_{1}^{\prime }+(U_{0}U_{1})^{\prime }+H_{1}^{\prime }=-{\textstyle \frac{1}{5}}{\it\eta}U_{0}^{\prime }+U_{0}U_{0}^{\prime }+H_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$H_{1}$
and
$U_{1}$
.
As in the case of an intrusion, global mass conservation can be used to determine a part of the solution at this order (the width of the frontal region
$r_{f}(t)-r_{s}(t)$
), without the need to exploit fully the underlying asymptotic structure of the solution. The analysis proceeds by noting that
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\int _{r_{s}(t)}^{r_{f}(t)}rh\text{d}r=r_{s}(u(r_{s}^{-})-c)h(r_{s}^{-})=1+\cdots \,.\end{eqnarray}$$
Then, to leading order
$r_{f}(r_{f}-r_{s})h(r_{f})=t+\cdots \,$
, and this leads to (A 25).
Appendix B. Asymptotic expansion for an intrusion close to the front
In § 3.3 we calculated the leading-order expressions for the radius and for the flow velocity and thickness of a continuously supplied radial intrusion. Here, we extend this analysis to obtain the next-order terms describing the flow at late times, by posing an asymptotic expansion within the time-dependent head region. This derivation is analogous to that performed for gravity currents through a homogeneous environment in appendix A. Guided by the leading-order behaviour of an intrusion at late times derived in § 3.3, and the magnitude of the neglected terms when this leading-order solution is substituted into the governing equations, we pose the following asymptotic expansion for the intrusion at late times:
$$\begin{eqnarray}\displaystyle r_{f}(t) & = & \displaystyle r_{f0}t^{3/4}+r_{f1}t^{1/2}+O(t^{1/4}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{s}(t) & = & \displaystyle r_{s0}t^{3/4}+r_{s1}t^{1/2}+O(t^{1/4}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(r,t) & = & \displaystyle r_{f0}t^{-1/4}H_{0}({\it\eta})+r_{f1}t^{-1/2}H_{1}({\it\eta})+O(t^{-3/4}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u(r,t) & = & \displaystyle r_{f0}t^{-1/4}U_{0}({\it\eta})+r_{f1}t^{-1/2}U_{1}({\it\eta})+O(t^{-3/4}),\end{eqnarray}$$
${\it\eta}=r/r_{f}(t)$
. The leading-order expressions of mass and momentum conservation are then given by 
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{1}{4}}{\it\eta}H_{0}-{\textstyle \frac{3}{4}}{\it\eta}^{2}H_{0}^{\prime }+({\it\eta}U_{0}H_{0})^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{1}{4}}U_{0}-{\textstyle \frac{3}{4}}{\it\eta}U_{0}^{\prime }+U_{0}U_{0}^{\prime }+{\textstyle \frac{1}{4}}H_{0}H_{0}^{\prime }=0, & \displaystyle\end{eqnarray}$$
${\it\eta}$
. The kinematic and dynamic boundary conditions at the front of the motion, when applied to (B 1), (B 3) and (B 4), imply that 
$$\begin{eqnarray}U_{0}(1)=\frac{3}{4}\quad \text{and}\quad H_{0}(1)=\frac{3}{2\mathit{Fr}_{f}},\end{eqnarray}$$
and, from the governing equations (B 5) and (B 6), we find
$U_{0}^{\prime }(1)=-1/2$
and
$H_{0}^{\prime }(1)=\mathit{Fr}_{f}/2$
. These values will be needed in the analysis that follows. The speed of the shock is given by
$$\begin{eqnarray}c={\textstyle \frac{3}{4}}r_{s0}t^{-1/4}+{\textstyle \frac{1}{2}}r_{s1}t^{-1/2}+O(t^{-3/4}),\end{eqnarray}$$
and the leading-order expressions from the balance of mass and momentum fluxes at the shock (3.16) then yield
$$\begin{eqnarray}U_{0}({\it\eta}_{s})=\frac{3{\it\eta}_{s}}{4}\quad \text{and}\quad H_{0}({\it\eta}_{s})^{3}=\frac{12E^{1/2}}{r_{f0}^{4}{\it\eta}_{s}},\end{eqnarray}$$
where
${\it\eta}_{s}=r_{s0}/r_{f0}$
. Integrating (B 5), and using (B 7) and (B 9), we deduce
$$\begin{eqnarray}\int _{{\it\eta}_{s}}^{1}\frac{5}{4}{\it\eta}H_{0}\text{d}{\it\eta}=-\!\left[{\it\eta}H_{0}\left(U_{0}-\frac{3}{4}{\it\eta}\right)\right]_{{\it\eta}_{s}}^{1}=0.\end{eqnarray}$$
Since
$H_{0}$
is strictly positive, we find that
$r_{s0}=r_{f0}$
and thus, from (B 7) and (B 9), that
$$\begin{eqnarray}r_{f0}^{4}=\frac{32\mathit{Fr}_{f}^{3}E^{1/2}}{9},\end{eqnarray}$$
which is consistent with our existing leading-order result (3.24).
At next order we first evaluate the shock conditions, for which we require the height and velocity fields at
$r=r_{s}^{+}$
, given by
$$\begin{eqnarray}\displaystyle & u(r_{s}^{+},t)=r_{f0}U_{0}(1)t^{-1/4}+\left(U_{0}^{\prime }(1)(r_{s1}-r_{f1})+r_{f1}U_{1}(1)\right)t^{-1/2}+O(t^{-3/4}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & h(r_{s}^{+},t)=r_{f0}H_{0}(1)t^{-1/4}+\left(H_{0}^{\prime }(1)(r_{s1}-r_{f1})+r_{f1}H_{1}(1)\right)t^{-1/2}+O(t^{-3/4}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r_{f0}^{2}H_{0}(1)}=r_{f1}(U_{1}(1)-U_{0}^{\prime }(1))+r_{s1}\left(-\frac{1}{2}+U_{0}^{\prime }(1)\right)\end{eqnarray}$$
and from the balance of momentum fluxes we find
$$\begin{eqnarray}-\!\frac{6}{r_{f0}^{2}H_{0}(1)^{2}}=\left(H_{0}^{\prime }(1)+\frac{1}{2}H_{1}(1)\right)r_{s1}+(H_{1}(1)-H_{0}^{\prime }(1))r_{f1}.\end{eqnarray}$$
With the boundary conditions at the current front
$U_{1}(1)=1/3$
and
$H_{1}(1)=1/\mathit{Fr}_{f}$
, obtained in the same way as the boundary conditions on the leading-order functions (B 7), we obtain from (B 14) and (B 15) that
$$\begin{eqnarray}r_{f1}=\frac{2\mathit{Fr}_{f}}{9r_{f0}^{2}}(1-7\mathit{Fr}_{f}^{2})\quad \text{and}\quad r_{s1}=\frac{2\mathit{Fr}_{f}}{9r_{f0}^{2}}(-2-7\mathit{Fr}_{f}^{2}).\end{eqnarray}$$
In calculating both
$r_{f1}$
and
$r_{s1}$
explicitly, with this calculation we extend the results in § 3.3, where only the leading-order width of the front
$(r_{f1}-r_{s1})t^{1/2}$
was obtainable. The governing equations at this order,
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{1}{2}}{\it\eta}H_{1}-{\textstyle \frac{3}{4}}{\it\eta}^{2}H_{1}^{\prime }+({\it\eta}(U_{0}H_{1}+U_{1}H_{0}))^{\prime }=-{\textstyle \frac{1}{4}}{\it\eta}^{2}H_{0}^{\prime }+({\it\eta}H_{0}U_{0})^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\textstyle \frac{1}{2}}U_{1}-{\textstyle \frac{3}{4}}{\it\eta}U_{1}^{\prime }+(U_{0}U_{1})^{\prime }+{\textstyle \frac{1}{4}}(H_{0}H_{1})^{\prime }=-{\textstyle \frac{1}{4}}{\it\eta}U_{0}^{\prime }+U_{0}U_{0}^{\prime }+{\textstyle \frac{1}{4}}H_{0}H_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$H_{1}$
and
$U_{1}$
.
