INTRODUCTION
Monochromaticity and coherence are two significant properties of laser radiation; laser matter interaction is one of the most important and substantial of these properties. Laser matter interaction has many applications in the field of atomic physics, non-linear optics, plasma physics, condensed matter physics, quantum electronic, and nanotechnology. Like with many other technical discoveries, various laser applications were neither foreseen initially, nor were their consequences which developed as a consequence naturally fueled by the evolution of theoretical studies. After demonstration of the first laser, early studies were predominantly theoretical investigations on the laser target interaction. Experiments were carried out to verify the theoretical models. Later, these experiments became pillars of many practical applications (Chrisey & Hubler, 1994).
The generation of ultra short laser pulses started many exciting research topics (Eliezer et al., 2005; Glinec et al., 2005; Gamaly et al., 2005; Rafique et al., 2005; Gavrilov et al., 2004). Development of high power laser systems generating ultra short pulses down to the sub-picoseconds regime has led to many exciting studies on the response of atoms molecules, clusters, and solids to intense electromagnetic fields (Fukuda et al., 2004; Greschik & Kull, 2004; Kanapathipillai, 2006). The study of laser matter interaction gave many new ways for development of laser-based accelerators (Borghesi et al., 2005; Roth et al., 2005; Brambrink et al., 2006), inertial confinement fusion (ICF), microelectronics, and others. Pulsed laser interaction was also utilized to produce high electron current emission in the form of pulses from metals (Kawamura et al., 1984; Fujimoto et al., 1984).
Free electrons inside metals behave like the gas of electrons inside fixed metal ions (Wahab, 1999), that is why when laser radiation falls on metals, most of the energy is absorbed by free electrons by inverse bremstruhlung (Chichkov et al., 1996). It was observed by Kaganov et al. (1957) that electrons can exist out of equilibrium in lattice for time less than the electron energy relaxation time τR. Electrons can convert their energy to lattice by collisions after time τR (relaxation time for hot electrons on the surface of the metal) (Wahab, 1999), which can cause the production of phonons (lattice vibrations quantized particles), or thermal energy into the material. The absorbed thermal energy can melt and ablate the target material depends on properties of laser beam and target material properties (Chrisey & Hubler, 1994 Fisher et al., 2005, 2006).
It has been seen by time of flight measurements that heat transit time scales linearly with sample thickness (Brorson et al., 1987) and transport occurs at the Fermi velocity VF in gold. Free electrons gain energy from laser and transfer it to lattice with production of phonons, thus thermal energy diffuses into the material that can be analyzed by using two temperature model (TTM). Theoretical models calculation suggest that it should be possible to heat the electron gas to a temperature Te of up to several thousands of K for a few ps while keeping the lattice temperature Tl relatively cool (Kaganov et al., 1957), because electrons heat capacity is less than the lattice heat capacity.
The problem of hot electron relaxation dynamics in metals after the excitation by a femtosecond laser pulse has been intensively studied during last couple of decades (Fujimoto et al., 1984; Brorson et al., 1987; Wang et al., 1994; Schoenlein et al., 1987; Fann et al., 1992a, 1992b; Limpouch et al., 2004). The models, which deal with the heat transport in non-equilibrium, are called microscopic two-step model. There are two models of this kind. The first one was modified by Fujimoto et al. (1984). The second one is hyperbolic two-step model developed by Qiu and Tien (1993). This second model is based on macroscopic averages of electric and heat currents carried by electrons in the momentum space. There are different solutions for this model based on different operating boundary conditions and methodologies (Al-Nimr et al., 2003). This model in its simplest form involved three coupled equations, it does not account for the conduction of heat by phonons and for the absorption of the incident laser energy by the electron gas (Tzov, 1995). When these effects are included, the model leads to four coupled equations, which are difficult to solve (Al-Nimr et al., 2003; Chen et al., 2002) with a reformulated generalized governing equation of the hyperbolic two-step model by the perturbation techniques.
Sze et al. (1964, 1966) observed that electrons scattering in a mean free path is around 1000 Å at the energy of 1 eV above Fermi energy, and for 0.4 eV the scattering lifetime should be around 0.6 μm. According to simple scaling law, this result is consistent with Fann et al. (1992a, 1992b) measurements. Fann et al. (1992a, 1992b) studied electron energy distribution in a gold film with approximately 700 fs time resolved photoemission spectroscopy following the laser heating by a 400 fs visible laser pulse. The measured distribution can be fitted by Fermi-Dirac function at an elevated temperature except within 800 fs of heating pulse. They examined relaxation dynamics of electron temperature by electron-phonon coupling model. This model is consistent on two coupled sub-systems, one for electrons with Fermi Dirac distribution at temperature Te, and one for phonons with Bose-Einstein distribution at lattice temperature Tl. The coupling within two systems occurs via electron–phonon interaction characterized by an exchange of energy at a rate proportional to Te − Tl.
If the laser is polarized in the plane of incidence, plasma waves are generated at typical density nc, there they feed energy into plasma (Friedberg et al., 1972). This dissipation introduces a phase lag between the electron oscillatory motion and the wave, causing the electrons to experience a time-averaged force. The force on the electrons determines a DC electric field (via Ohm's Law), which is solenoidal for geometry of resonance absorption. At resonance absorption (Friedberg et al., 1972), the production of DC electric fields and current density ‘J’ can also be produced inside the metal in a certain direction, so heat transport for sub-picoseconds laser pulse inside a metal should be in a particular direction due to the current density produced by laser interaction.
The thermal conduction is more important if electron energy relaxation time is greater than laser pulse duration. The model presented in this paper provides theoretical evidences that heat energy would conduct due to the electrons in a particular direction from the focal spot. The production of current density by laser metal interaction is responsible for such heat conduction. This model will provide a deep insight picture for new research topics in the field of shot pulsed laser interaction with metals.
THEORETICAL MODEL
Laser is a rich source of electromagnetic energy that can be transformed into excitation energy (Chrisey & Hubler, 1994) during the laser metal interaction. The energy transformed to the lattice through the electron phonon interaction, is responsible for the melting and vaporization of the target metals. Thermal energy increases the collective atomic motion of the target atoms that associates with relaxation of laser induced stresses (Leonid & Zhigilei, 2005). The presence of channels of energy dislocation, that is not accounting for the conventional TTM (Santala et al., 2001), the fraction of non thermal energy in the laser energy partitioning increases with increasing laser fluence (Santala et al., 2001).
Lattice vibrations (Phonons) are the main contributors for the conduction of heat in solid materials. In non-magnetic materials, lattice vibrations are the only contributors. But for metals, electrons become the main contributors (Srivastava, 2003). The free electrons in the metal are called conduction electrons. Collectively, these electrons contributed by individual metal atoms are conventionally interpreted as free electron gas that occupies most of the volume of the metal (Srivastava, 2003).
The theoretical thermal conductivity of a material can be defined as,
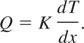
Where, K is the thermal conductivity of the material, Q is the energy per unit area per unit time. For thermal conductivity of metals, electrons play an important role in the conduction of thermal energy (Chichkov et al., 1996). So to find the temperature distribution and heat conduction, the following assumptions are made;
(1) Laser radiation is plane polarized with plane of target.
(2) Whole of pulsed energy is absorbed by free electrons.
(3) Electrons transfer their energy to lattice by collision in time τR after covering mean free path.
Under these assumptions, above Eq. (1) can be written for electrons as,
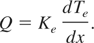
Where, Ke is the electronic thermal conductivity and Te is the electron temperature. Eq. (2) can be solved as,
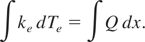
The heat energy deposited by laser pulse into the target material can be formulated as (Chrisey & Hubler, 1994).

In this above equation, R is the reflectivity of the material and I(x) is the intensity of laser radiation at any point inside the target material.
Let us suppose that laser pulse with initial intensity Io interacted with metal surface for a time τP (laser pulse duration). Laser radiation is absorbed into the target with in skin depth Lo as shown in the Figure 1. The intensity profile into the target is represented by a well know exponential relation,

The average temperature produced in volume of skin depth can be calculated by using Eqs. (3), (4), and (5)
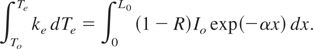
The limits of integral on the left-side are taken from To (temperature of the target electrons before the laser pulse interaction) to Te (temperature after the laser pulse). The integral on the right-side is taken over the entire optical or penetration depth (Lo ∼ α−1).

Schematic of Laser metal interaction.
Then

The absorbed heat energy is then transferred into the material from focal spot volume VS to surrounding target. Heat transformation depends not only on thermal conductivity but also on laser pulse duration τP. The thermal diffusion length of thermal energy within time τP for target material is given by (Chrisey & Hubler, 1994).

The above relation indicates that thermal diffusion length depends on half power of laser pulse duration. Eq. (8) can be written for electron thermal diffusion length,
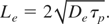
Where De is the electron thermal diffusivity i.e., given by,
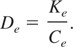
Where Ce is the heat capacity for electrons, Ce is given by the sommerfeld equation,
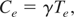
γ is the sommerfeld constant that explains the electron density of states at Fermi energy that is given by,

With the use of Eqs. (9), (10), and (11), electronic thermal conductivity can be calculated in terms of electron temperature and thermal diffusion length.
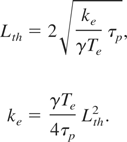
This above equations shows that ke ∼ Te. After putting Eq. (13) into Eq. (7), we get a solvable relation for electron temperature.
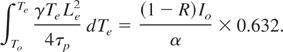
By utilizing the condition Te >> To
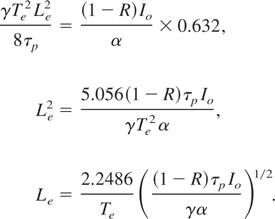
Eq. (15) is the relation for electron thermal diffusion length versus laser radiation intensity that can also be represented in terms of laser Fluence, and heat density deposited onto the target material is as follows,
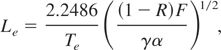
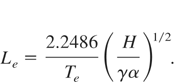
Eq. (16) is for laser fluence and Eq. (17) is for heat density deposited into the target material.
Laser radiation is a rich source of electromagnetic energy that can develop an electric field inside the target material. The value of laser induced electric field can be calculated by the following formula (Chrisey & Hubler, 1994).
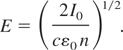
Laser induced electric field can accelerate the electrons from focal spot with velocity,
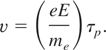
Putting Eq. (19) into Eq. (20) to get the velocity of electrons in terms of laser radiation intensity,
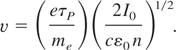
In consequence, the laser induced electric field and an electron current density would be generated onto the target, which is given by a renounced formula,
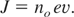
Current density can be related with the intensity of the laser radiation,
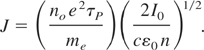
From the above equations, laser intensity can be deduced as,
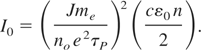
Now putting Eq. (24) into Eq. (15), we get,

Where S is a constant that depends on physical properties of the target, it is called Shahbaz constant in our Appendix. Eq. (25) indicates that electrons thermal diffusion length is directly proportional to the laser induced current density onto the target material that would be dominant in case of metal target, because electronic conduction can be explained (Wahab, 1999) on the basis of free electron gas model. That relation also reveals that electron diffusion length is inversely proportional to the electron temperature. So for, higher values of Te, the electron lattice coupling rate will also be very high. The relation of Le with J gives favor to heat energy conduction in particular direction along current density as shown in Figure 2. The relaxation of non-thermalized electrons to a thermal Fermi Dirac distribution is a complicated many body problem. According to Fermi liquid theory, the single particle lifetime above the Fermi level, scales as (E − EF)−2. The higher the energy, the faster the relaxation time, and a particle just at the Fermi level should have an infinite lifetime.

Schematic of shifting the isotherms along the current density Jy induced by laser radiation.
The important result of the above equation is the relation of Le with laser pulse duration time τP. Le is proportional to minus half power of τP which also indicates that electron heat conduction for metals during interaction with laser would be dominant for shorter laser pulse, which is sported by the graph between the laser pulse duration and thermal diffusion length shown in the Figure 3. Electrons take time of the order of sub-picoseconds to transfer the absorbed energy by coupling or scattering from lattice. Thus, heat conduction phenomenon in a particular direction will be dominant for laser pulse duration less than sub-picoseconds. If pulse duration is less than sub-picoseconds, then heat diffusion continues after laser pulse (Chichkov et al., 1996) into the metal by electrons and phonons. But during the pulse of that range, the heat energy conducts only due to the electrons. Thus heat conduction can be studied separately into the electron gas and lattice during laser pulse and after laser pulse for (τP < τR). The heat flow in electron gas and lattice has been studied separately due the fact that phonon–electron thermal relaxation is of the order of sub-picoseconds (Fujimoto et al., 1984; Qiu & Tien, 1992, 1993, 1994). Thus such separation is valid for pulse duration less than electron relaxation time.

Graph between laser pulse duration and heat diffusion length. Darck line is for electron heat conduction and light line for over all heat conduction due to material.
It is also observed (Pukhov, 2001) by three-dimensional simulation that at higher intensities of the order of 1019 W/cm2, pondromotive force can push electrons inward to the target. Such type of charge separation would generate the electric field inside the target. Thus, pondromotive force can also play a very important role in transport of heat energy in certain direction, not only for τP of the order of sub-picoseconds but also for nanoseconds. Experimental results (Valette, 2005) about competitive study of femtosecond and nanosecond pulse interaction with metals reveal that heat affected zone is 2 μm and 30–40 μm, respectively.
Laser metal interaction is very important especially for the ICF (Tabak et al., 1994). In the case of plasma inertial confinement (PIC), the energy distributed into electronic excitation, thermal energy, and mechanical or compression energy in the fuel pellet. The heating of the fuel pellet to sufficiently large temperature is then achieved using fast electrons generating during laser pellet interaction. A large amount of laser pulse energy is transformed to electrons that have been conformed experimentally (Santala et al., 2001).
CONCLUSIONS
Heat conduction during laser metal interaction would be conducted in particular direction along the current density induced by laser radiation. Electronic heat conduction along current density is dominant for ultra short laser pulse less than relaxation time for hot electrons at the surface of target metal. The calculations made will open the door for certain new areas and will also be helpful for laser cutting and drilling.
ACKNOWLEDGMENT
The author is thankful to Dr. D.H.H. Hoffmann, for kind help in preparing this paper.
APPENDIX
The value of S (Shahbaz constant) constant,
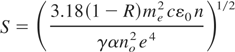
Focal spot volume
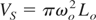
Where, ωo is the radius of focal spot and Lo is the skin depth. Then no can be formulated as,
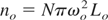
In this above relation N is the number of free electrons per unit volume.





