INTRODUCTION
Since the invention of chirped pulse amplification, the construction of compact ultra-intense and ultra-short laser pulses has become feasible. Propagation of such laser pulses has been investigated in various plasma conditions (Wang et al., Reference Wang, Lin, Sheng, Liu, Zhao, Guo, Lu, He, Chen and Yan2011; Sadighi-Bonabi et al., Reference Sadighi-Bonabi and Moshkelgosha2011) resulted in generation of mono-energetic electrons (Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Sadighi-Bonabi et al., Reference Sadighi-Bonabi and Rahmatollahpur2010; Yazdanpanah et al., Reference Yazdanpanah and Anvari2014) protons and ions (Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernández2006; Yazdani et al., Reference Yazdani, Cang, Sadighi-Bonabi, Hora and Osman2009; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Hora, Riazi, Yazdani and Sadighi2010; Hora et al., Reference Hora, Sadighi-Bonabi, Yazdani, Afarideh, Nafari and Ghorannevis2012) and X-rays (Nikzad et al., Reference Nikzad, Sadighi-Bonabi, Riazi, Mohammadi and Heydarian2012; Shirozhen et al., Reference Shirozhan, Moshkelgosha and Sadighi-Bonabi2014). Laser based ion acceleration is highly attractive due to its potential applications, including fast ignition (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001), proton radiography (Borghesi et al., Reference Borghesi, Fuchs, Bulanov, Mackinnon, Patel and Roth2006), and so on. One of the critical issues for the development of the laser-driven ion source is enhancement of the ion energy, which is a fundamental requirement of various applications including medical purposes (Malka et al., Reference Malka, Fritzler, Lefebvre, D'humieres, Ferrand, Grillon, Albaret, Meyroneinc, Chambaret, Antonetti and Hulin2004; Borghesi et al., Reference Borghesi, Toncian, Fuchs, Cecchetti, Romagnani, Kar, Quinn, Ramakrishna, Wilson, Antici, Audebert, Brambrink, Pipahl, Jung, Amin, Willi, Larke, Notley, Mora, Grismayer, D'humières and Sentoku2009).
Various mechanisms of laser-ion acceleration have been proposed to explain the acceleration methods including target normal sheath acceleration (TNSA) (Hattchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Mackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Wilks and Yasuike2000), shock acceleration (Henig et al., Reference Henig, Kiefer, Geissler, Rykovanov, Ramis, Hörlein, Osterhoff, Major, Veisz, Karsch, Krausz, Habs and Schreiber2009), Coulomb explosion (Bulanov et al., Reference Bulanov, Brantov, Bychenkov, Chvykov, Kalinchenko, Matsuoka, Rousseau, Reed, Yanovsky, Litzenberg, Krushelnick and Maksimchuk2008), radiation pressure acceleration or skin-layer ponderomotive acceleration (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Yazdani et al., Reference Yazdani, Cang, Sadighi-Bonabi, Hora and Osman2009), and laser break-out afterburner acceleration (Jung et al., Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albright2013). At present accessible laser intensities, only indirect ion acceleration is possible. In the TNSA model, ions are accelerated on the rear surface of a thin target by a quasi-electrostatic field created by the fast electrons propagating from the target front side. In this regime, proton beams with energies up to 65 MeV have been reported (Gaillard et al., Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan2011).
Many proposals have been suggested to improve the laser absorption by modification in laser and target parameters such as pulse contrast, laser beam shaping, polarization (Daido et al., Reference Daido, Nishiuchi and Pirozhkov2012), mass limited target (Limpouch et al., Reference Limpouch, Psikal, Andreev, Platonov and Kawata2008), micro-structured surface target for the ion energy enhancement (Margarone et al., Reference Margarone, Klimo, Kim, Prokupek, Limpouch, Jeong, Mocek, Psikal, Kim, Proska, Hnam, Stolcova, Choi, Lee, Sung, Yu and Korn2012; Ceccotti et al. Reference Ceccotti, Floquet, Sgattoni, Bigongiari, Raynaud, Riconda, Heron, Baffigi, Labate, Gizzi, Vassura, Fuchs, Passoni, Kveton, Novotny, Possolt, Prokupek, Proska, Psikal, Stolcova, Velyhan, Bougeard, D'oliveira, Tcherbakoff, Reau, Martin and Macchi2013), and decreasing of target thickness to boost the electron recirculation (Mackinnon et al., Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman2002). Furthermore, particular attention has been paid to near critical target for ion acceleration due to advantages of higher energy coupling from laser to electrons (Bulanov et al., Reference Bulanov, Bychenkov, Chvykov, Kalinchenko, Litzenberg, Matsuoka, Thomas, Willingale, Yanovsky, Krushelnick and Maksimchuk2010; Willingale et al., Reference Willingale, Nilson, Thomas, Bulanov, Maksimchuk, Nazarov, Sangster, Stoeckl and Krushelnick2011). The interaction of laser beam with electrons is greatly influenced by target density. In the solid target, the interaction takes place on the surface. On the other hand, the laser beam is able to go through the target if the density is sub-critical, as in the case of a gas jet. Such a low density target introduces an extended interaction length to the laser and enables a higher energy gain for the electrons. Creating a near-critical density plasma for wavelength around 1 µm (n c = 1021 cm−3) with sharp density gradient is challenging experimentally. Solid targets have a very high plasma density in a range of 1023–1024 cm−3 in ionized condition. The critical density takes places somewhere within the expanding plasma, but it would not be in a sharp boundary or in a region with constant near-critical density over a significant distance. Supersonic gas jet targets are useful for producing plasma densities in the range of 1018–1020 cm−3, but not much higher (Sylla et al., Reference Sylla, Flacco, Kahaly, Veltcheva, Lifschitz, Malka, D'humieres, Andriyash and Tikhonchuk2013). Although this is a useful method to produce critical densities for far infra-red wavelengths such as in carbon dioxide lasers, it is far below the quantities needed for near infrared or visible ranges, for example, in Nd:YAG lasers. To produce near-critical density plasma with these lasers, low density foam targets are excellent choices where the produced long uniform initial plasma density can be determined by the initial target size. A foam material is defined by reduction of mass density down to 10−3 of solid target density and it can only be a few mg/cc. More recently, a foam material with a thickness of 5–80 micron and density of 1–1000 mg/cc has been manufactured (Zani et al., Reference Zani, Dellasega, Russo and Passoni2013). This can provide an ideal near-critical density for high contrast lasers such as Ti:sapphire laser.
In a three layer target configuration (with one layer foam) proposed by Nakamura et al. (Reference Nakamura, Tampo, Kodama, Bulanovs and Kando2010) and Sgattoni et al. (Reference Sgattoni, Londrillo, Macchi and Passoni2012), it was found that the presence of near-critical plasma increases the conversion efficiency, significantly, and leads to enhancement of proton acceleration. This important result led to the motivation to study multi-layer foams with near critical densities. In this work, interaction of short laser pulse with a new target assembly composed of three foam layers with uprising densities in front of Al target is presented. The accelerated electron beams during interaction with near critical density layers have been investigated and categorized to explain the proton energy enhancement in comparison to bare solid target. It is noticed that in three layer target arrangement the relativistic self-focusing is increased considerably by using a foam target. However, it is further improved in multi-layer assembled target and the spot size is reduced from 5 µm to 1.7 µm. Furthermore, a considerable increasing on the accelerated proton energy is achieved. This is explained in more detail.
SIMULATION PARAMETERS
The simulations are performed by using the parallel PIC code extreme laser-matter interaction simulator (ELMIS; http://www.ipfran.ru/english/structure/lab334/simlight.html; Gonoskov et al., Reference Gonoskov, Korzhimanov, Eremin, Kim and Sergeev2009). In the relativistic code of ELMIS, Maxwell's equations are solved by using a parallel fast Fourier transform technique. The target consists of foam layers with an electron density from 0.3n c to 1.2n c, located in 64 < x < 85 and −8 < y < 8, where n c is critical density, x and y are in micrometer; with thickness of 7 µm for each layer, a 0.5 µm Al solid layer with electron density of 45n c and a 60 nm contaminant layer of protons and electrons with a density of 8n c as the last layer in the target design.
In our simulations, a linearly polarized laser pulse with duration of τL = 80 fs (FWHM, Gaussian profile) and wavelength of λL = 1 µm is focused into spot of 5 µm on the target surface. The maximum laser intensity used in this simulation is 2 × 1020 Wcm−2. The size of simulation box is 128 µm × 32 µm (8192 × 2048 cells) with absorbing boundaries for the fields and particles. The initial plasma temperature is set to 0.3 keV, and the cell size is 15.625 nm, which is four times of the Debye length for the considered plasma. The time steps are set to (2π/ωp)/16 ≈ 3.0 × 10−17 s, where ωp = (4πe45n c/m e)1/2 is the plasma frequency. Structure of the multi-layer target assembly is shown in Figure 1.

Fig. 1. Structure of the multi-layer target assembly.
RESULTS AND DISCUSSION
The incident laser pulse at relativistic intensity of 2 × 1020 Wcm−2 is self-focused as it propagates in the foam layer, as it is shown in Figure 2 at t = 49τ, where, τ is the time of one laser cycle (τ = λc is the speed of light, for wavelength λ = 1 µm; τ comes out to be 3.33 fs). A laser pulse experiences relativistic self-focusing in the condition when the laser power exceeds the critical power of Pcr ≈ 17(ω0/ωp)2 GW, where ω0 and ωp are plasma and laser frequencies, respectively (Hora, Reference Hora1973; Reference Hora1975). For the foam layer with average density of about 0.3n c the critical power becomes Pcr ~ 1.8 × 1011 W; this is related to the laser intensity of I = 7.2 × 1017 W/cm2 with 5 µm spot radius. Figure 2 shows the laser envelope, E y, along the laser propagation axis. It can be realized that the laser pulse is self-focused rapidly in the foam layers in a tight focal spot with the diameter of 1.7 µm before interaction with the solid layer. It should be mentioned that the foam thickness is selected in a way to provide the maximum focusing along it. Therefore, there is a careful matching between the optimum self-focusing and foam thickness at the defined densities.

Fig. 2. Indicates the laser envelope E y along the laser propagation axis at t = 49τ for multi-layer target. The laser intensity is 2 × 1020 Wcm−2 with 80 fs laser pulse duration. The initial laser spot size is 5 µm.
Two typical groups of electrons are recognized from the simulation, which are shown in Figure 3. The first group of the electrons with densities much higher than the background electrons is created by ponderomotive force of the focused pulse that expels the local plasma electrons, leads to an ion channel formation behind it. The second group of electrons experiences the direct laser acceleration (DLA) via betatron resonance which was proposed by Pukhov et al. (Reference Pukhov, Sheng and Meyer-Ter-Vehn1999). It should be noticed that high energy electrons are produced via several mechanisms in underdense plasma, such as: DLA, stochastic heating, LWFA, and nonlinear self-focusing. In this study, the contribution of LWFA is ignored due to much larger laser pulse duration in comparison to the plasma wavelength and limitation of the acceleration distance (Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004). Relativistic self-focusing and DLA regime explained by transverse betatron oscillation of energetic electrons are the dominant approaches in the present simulation. Under these circumstances, when the laser frequency is close to the betatron frequency of electrons, an efficient energy exchange is possible.

Fig. 3. Electron density map at t = 49τ for multi-layer target.
Figure 4 illustrates that the transverse momentum of the electrons increases with the laser penetration distance and can reach to a maximum of about 22m ec. This is about two times higher than the amount given by p y = a 0m ec, (12 m ec is the amount of the relativistic electron in plane electromagnetic wave in vacuum) (Yu et al., Reference Yu, Bychenkov, Sentoku, Yu, Sheng and Mima2000). The transverse momentum of the electrons, p y, is converted into longitudinal momentum, P x, via V × B interaction; for the fast electrons P x can reach to 134m ec, as it is observed in Figure 5. This is about 80% more than the amount achieved by P x = a 02m ec/2 = 72m ec in vacuum (Yu et al., Reference Yu, Bychenkov, Sentoku, Yu, Sheng and Mima2000; Gahn et al., Reference Gahn, Tsakiris, Pukhov, Meyer-Ter-Vehn, Pretzler, Thirolf, Habs and Witte1999). These electrons with momentum exceeding a 02m ec/2 could be called super-hot electrons due to their much higher temperature compared to the ponderomotive scaling of electrons defined by Wilks et al. (Reference Wilks, Kruer, Tabak and Langdon1992). The oscillation frequency of the longitudinal momentum is twice that of the transverse momentum (ω0). The reason of ion energy increment is obviously due to the fact that the laser wavelength λ0 has a relativistic increase λ = λ0/n(I) (Hora, Reference Hora1975). The nonlinear optical properties of plasma due to the relativistic electron motion in an intense laser field are of fundamental importance in generation of laser driven sources of particles.

Fig. 4. Transverse momentum, p y, of the electrons for target with multi-layer foam layer at t = 65τ is indicated.

Fig. 5. Longitudinal momentum, px, of the electrons for target with multi-layer foam at t = 65τ is presented.
Three types of cold, hot, and super-hot electrons are generated in interaction of laser with the multi-layer target assembly. As mentioned before, TNSA is an ion acceleration regime by thermal electrons (Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, Mackinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000) and it is valid for solid targets with a wide thickness range: hundreds of nanometers to a few micrometers. The thermal electron temperature obtained by the relativistic oscillation energy so called hot electrons (Wilks et al., Reference Wilks, Kruer, Tabak and Langdon1992):
where m e is the electron mass, c is the speed of light, and a 0 is the normalized laser amplitude. The electrons with temperatures lower than T e of Eq. (1) are called cold, and those with temperature larger than T e are named super-hot electrons, where the latter are produced by interaction of an intense laser with a solid target covered by foam layers.
The electron energy spectrum at 71τ is shown in Figures 6a and 6b. It demonstrates an exponential dependence of dN/dE to −1/T e, from dN/dE∝exp (−E/T e), where E is electron energy and T e refers to effective temperature. In Figure 6a for the multi-layer foam target, in the selected range of E from 10 to 50 MeV, T e is 7.9 MeV, which is 45% more than the estimated amount by the ponderomotive or hot electron scaling, Eq. (1). In Figure 6b for the bare solid target, the effective temperature in the selected range of E from 5 to 18 MeV, T e is 2.2 MeV. It should be emphasized that with introducing a near critical density layer, not only the domain of hot electrons is increased, but also much higher energy cut-off is realized due to dominant regime of DLA. Figure 6c presents the evolution of effective temperature for the energetic electrons with an estimation of the maximum temperature for different target configurations. For the attached foam to the solid foil, T e increases almost linearly versus time to a maximum of about 8 MeV at t ~ 71τ. The comparison of Figures 6a and 6b represents that by increasing the interaction time, decreasing of T e in the target with foam is larger and faster than the solid target due to the status of energy transfer from electrons to ions. This is observed more clearly in Figure 6c.

Fig. 6. The energy spectrum of the electrons at t = 71τ for case of multi-layer foam (a) and for bare solid target (b). The evolution of the energetic electrons temperature for different target compositions (c) is shown.
Figure 7 shows the proton energy spectrum for different target compositions. It is noticed that the proton cut-off energy for the multi-layer foam configuration has the highest amount; it is about 2.7 times of the bare solid target. It can also be seen that the proton energy spectrum has a smooth cut-off and the number of high energy protons is increased for this target, which is demanding in some applications.

Fig. 7. The energy spectrum of protons at t = 109τ for bare solid (black) and multi-layer foam attached to the solid target (blue) are presented.
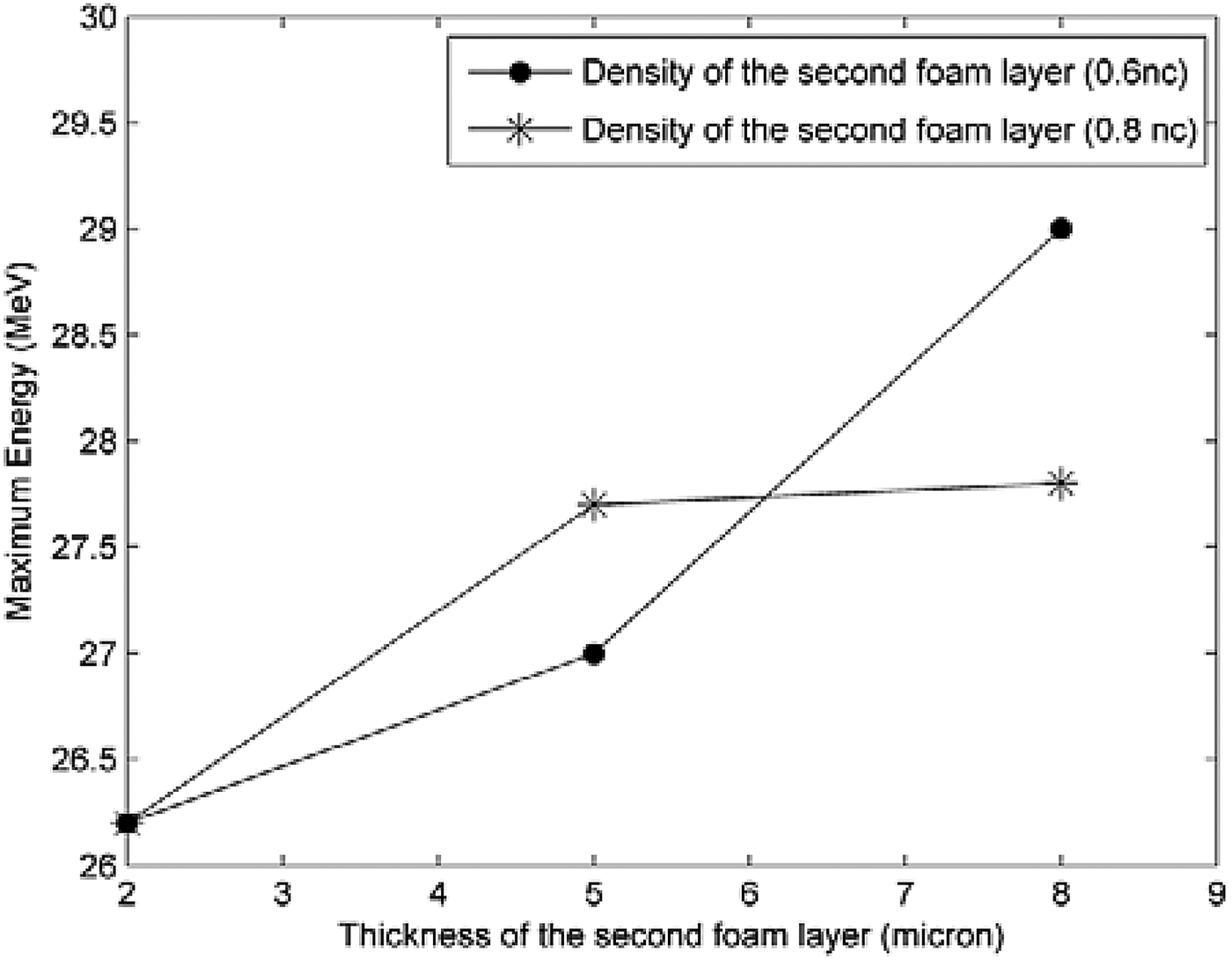
When the laser pulse propagates through the foam layer, the laser penetration length and self-focusing are increased, resulting in the enhancement of interaction intensity to higher values. In low density foam, by increasing of the laser propagation through the plasma, laser energy absorption by electrons is decreased. But for foam with slightly higher density, laser energy absorption by electrons due to the volume interaction is dominated. The simultaneous effects of these factors result in an optimum condition for effective energy transformation to the electrons. The optimum amounts of density and thickness for the foam layer has been determined in Sgattoni et al. (Reference Sgattoni, Londrillo, Macchi and Passoni2012). In this study, it is shown that by adding an extra foam layer with slightly lower density to the optimum condition of the Sgattoni's work, the laser self-focusing is stimulated and therefore further energy absorption and heating experienced by ions and electrons. The new simulations are carried out by using the optimum parameters for the first foam layer with 2 µm thickness and 2n c density, and the second foam layer with series of data: 0.6n c–0.8n c for density and thickness of 0, 5, and 8 µm and the same laser parameters of Sgattoni's work (Sgattoni et al., Reference Sgattoni, Londrillo, Macchi and Passoni2012) are employed. Figure 8 shows that in this new arrangement, furtherer improvement is achieved in maximum proton energy and confirms the priority of a multi-layer arrangement in comparison using only one foam target. For more clarification, the electron density map at 27τ Figure 9a. and the proton energy spectrum for multi-layer target which contain two foam layers with 8 µm and 2 µm thickness and density of 0.6n c and 2n c, respectively, in Figure 9b are indicated.

Fig. 8. Shows the maximum proton energy versus different density and thickness of the second foam layer.

Fig. 9. The electron density map at 27τ (a) and the proton energy spectrum (b) are presented.
CONCLUSION
In this work, proton acceleration from interaction of ultra-intense linearly polarized laser pulse with a multi-layer assembled target is studied by using two-dimensional particle-in-cell simulation. In this assembled target, electron heating is improved under the action of DLA and laser pulse self-focusing which leads to stronger electrostatic field generation at the target back for relatively long time. In this arrangement, the maximum proton energy is increased up to 2.7 times of the amount produced without sub-critical density plasma. The amount of the accelerated protons with higher energy is also increased, considerably, and the cut-off energy is obtained following a smooth reduction of protons number. Furthermore, it is noticed that with the mentioned arrangement, additional improvement is achieved in maximum proton energy and confirms the priority of a multi-layer arrangement in comparison using only one foam target. Based on the achieved outcomes and due to the possible technology for fabrication of new foam targets, it is suggested to do further investigation on electron heating via interaction of ultra-intense laser pulses with these targets at the critical density and even at the related effective critical density, which are not feasible at the common solid targets.
ACKNOWLEDGEMENT
The authors would like to acknowledge Prof. C. G. Wahlstrom, Prof. M. Marklund, Dr. A. V. Korzhimanov, Dr. O. Lundh and Dr. L. Nikzad for their supports. Special thanks to Dr. A. Gonoskov for his PIC code and useful comments.