Introduction
Fertility is a fitness-related trait that affects profitability in dairy cattle production systems. Over the past several decades, fertility traits have been included in selection indices for dairy cattle (Refsdal, Reference Refsdal2007; Butler, Reference Butler2013) and genetic evaluations of fertility traits have been conducted using an additive genetic model while previous studies support the hypothesis that dominance variance contributes to the phenotypic variance of fertility traits (Tempelman and Burnside, Reference Tempelman and Burnside1990; Hoeschele, Reference Hoeschele1991). If dominance genetic effects exist but are not included in a linear mixed model, it could lead to bias in the prediction of breeding values (BVs) as well as the estimate of additive genetic variance (Toro and Varona, Reference Toro and Varona2010). Fertility traits usually have low heritability and large non-additive genetic effects such as dominance effects (González-Recio and Alenda, Reference González-Recio and Alenda2005; Jamrozik et al., Reference Jamrozik, Fatehi, Kistemaker and Schaeffer2005; Ghiasi et al., Reference Ghiasi, Pakdel, Nejati-Javaremi, Mehrabani-Yeganeh, Honarvar, González-Recio, Carabaño and Alenda2011).
Accurate estimation of non-additive variance is difficult because it is often confounded with other genetic and environmental effects such as common environment or maternal effects (Fuerst and Solkner, Reference Fuerst and Solkner1994). Consequently, estimates of non-additive genetic variance may be biased upwards. Including dominance effects in genetic evaluations will avoid overestimation of additive genetic variance and allow prediction of dominance genetic merit that can be used in mate selection programmes (Van Tassell et al., Reference Van Tassell, Misztal and Varona2000). The dominance effect is rarely included in genetic evaluation due to the computational complexity and family structure of the data. In order to estimate dominance variance, a large number of full-sibs is required (Misztal, Reference Misztal2001; Toro and Varona, Reference Toro and Varona2010). Recently, new computational procedures to estimate the genetic parameters of models, including the dominance effect, have become feasible. For instance, Wolak (Reference Wolak2012) developed an R package (Nadiv) to construct non-additive genetic relationship matrices for estimating non-additive genetic variance that can be used in routine software, such as ASReml (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2009), in the animal breeding industry.
For fertility traits, Palucci et al. (Reference Palucci, Schaeffer, Miglior and Osborne2007) reported that the dominance genetic variance for age to first service, heifer non-return rate and the interval from calving to the first service was greater than the additive genetic variances. Hoeschele (Reference Hoeschele1991) found that dominance variance is 1.1–1.6 times larger than additive genetic variance for dairy cow fertility traits. To our knowledge, no previous studies have estimated non-additive genetic variance for female fertility traits in Iranian Holstein cows. Therefore, the aim of the current study was to estimate the dominance variance for days from calving to first service (DFS), a number of services to conception (NSC) and days open (DO) in Iranian Holstein cows.
Materials and methods
The data available consisted of 25 518 fertility records from first parity dairy cows collected from 1981 to 2012 in 15 large Holstein herds of Iran. These herds were distributed in ten different provinces of Iran. The management of all herds was similar. The oestrus signs were detected by visual observations. Cows were inseminated with semen mostly imported from North America and Canada. Pregnancy diagnosis was performed 56 days after artificial insemination (AI) by rectal palpation method.
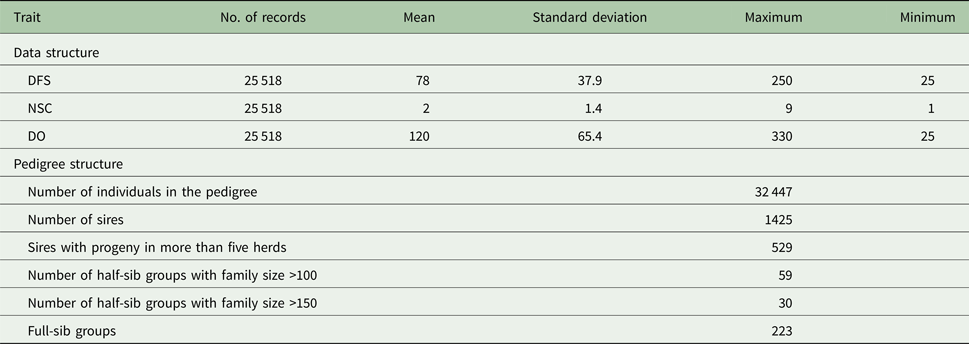
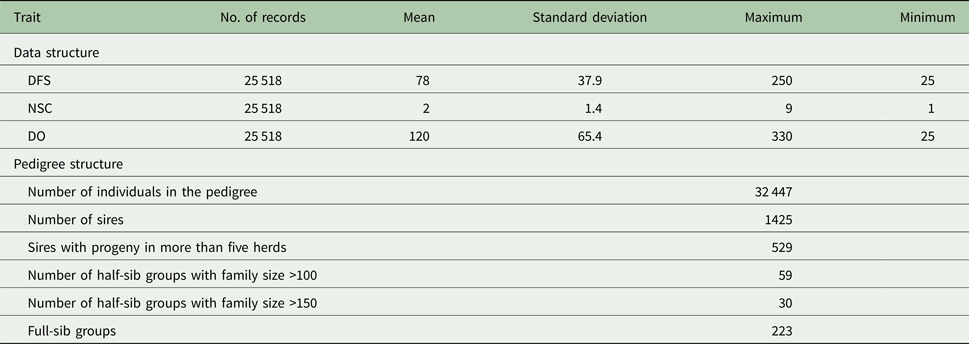
The evaluated fertility traits were DFS, NSC and DO. Cows were required to be at least 18-months old at first service. Days from calving to the first service ranged from 25 to 250 days. If NSC was greater than 10, then NSC was assigned to 10 and DO was required to be between 30 and 330 days. Descriptive statistics for the data used for analysis are presented in Table 1. These data were provided by the Dairy Herd Improvement Program of the Animal Breeding Centre of Iran. Artificial insemination technician's record all insemination data and are in charge of providing an accurate dataset. Two statistical models were used to estimate the variance components:
Table 1. Descriptive statistics of data and pedigree for days from calving to the first service (DFS) and number of services to conception (NSC) and days open (DO)
Model 1. A linear mixed model, including only additive genetic effect:
$${\bf y} = {\bf Xb} + {\bf Z}_{\bf a}{\bf a} + {\bf e}$$Model 2. A linear mixed model, including both additive and dominance genetic effects (additive-dominance genetic model):
$${\bf y} = {\bf Xb} + {\bf Z}_{\bf a}{\bf a} + {\bf Z}_{\bf d}{\bf d} + {\bf e}$$where y is the vector of observations; b is the vector of fixed effects; a is the vector of the random additive genetic effect, d is the vector of the random dominance effect, e is the vector of the random residual effect and X, Za and Zd are incidence matrices relating observations to fixed, additive and dominance effects, respectively.
Fixed effects in the model for DO and NSC were the age at previous calving (20 levels), effects of parity (six levels), herd-year-season (1620 levels) and month of first insemination (12 levels). Fixed effects for DFS were herd-year of calving (953 levels), age at previous calving (20 levels), effects of parity (six levels) and previous month of calving (12 levels).
The assumptions of the models are:
$$\left( {\matrix{ {\bf a} \cr {\bf d} \cr {\bf e} \cr}} \right) \sim N\left[ {0,\left( {\matrix{ {{\bf A}\sigma _{\rm a}^2} & 0 & 0 \cr 0 & {{\bf D}\sigma _{\rm d}^2} & 0 \cr 0 & 0 & {{\bf I}\sigma _{\rm e}^2} \cr}} \right)} \right]$$a, d and e are the vectors of the random additive genetic effect, random dominance effect and random residual effects, all with a normal distribution (N), respectively.
$\sigma _{\rm a}^2, \sigma _{\rm d}^2 $, and 
$\sigma _{\rm e}^2 \; $ are the additive genetic variance, dominance variance and residual variance, respectively. I is the identity matrix of order 25 518 for a number of records; A and D are the additive and dominance genetic relationship matrices both with equal order 32 447 × 32 447 for a number of animals in pedigree.
ASReml software (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2009) was used to estimate the variance components. In order to estimate the additive variance and the dominance variance simultaneously, the inverse of matrices A and D was externally calculated using the Nadiv package (Wolak, Reference Wolak2012), and then the non-zero elements of the lower triangle of each inverse of matrices A and D were stored. The inverse of A and D matrices was supplied to the ASReml software as arbitrary (co)variance matrices to estimate variance components and predict BVs. The estimated variance components were presented as ratios of the total phenotypic variance 
${\rm (}\sigma _{\rm p}^2 )$ for each model: the additive genetic variance ratio or heritability as 
$h^{\rm 2} = \sigma _{\rm a}^2 /\sigma _{\rm p}^2 $ and the dominance genetic variance ratio as 
$d^2 = \; \sigma _{\rm d}^2 /\sigma _{\rm p}^2 $.
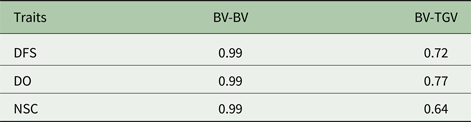
The comparison of models was assessed by Akaike's information criterion (AIC) and the Spearman's rank correlation between BV predicted from additive and additive-dominance model and Spearman's correlation between BVs and total genetic values (TGV) was also computed.
Results
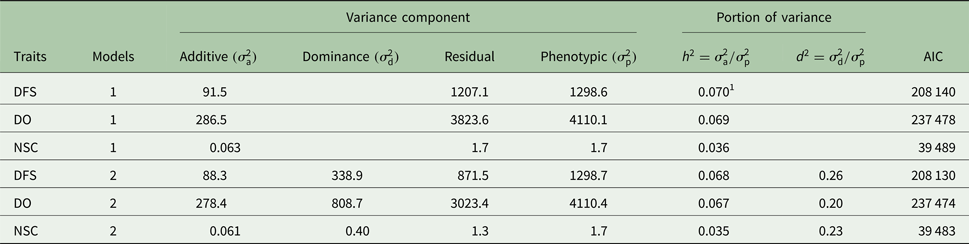
Descriptive statistics of the traits studied are presented in Table 1. The mean of DFS and DO were 78 and 120 days, respectively. The average NSC in the studied population was 2. The AIC criteria for comparing additive genetic model and additive-dominance model are presented in Table 2. The value of AIC in additive-dominance model was lower than AIC in the additive genetic model for all studied traits. The variance components using the additive genetic model and the model fitting both additive and dominance genetic effects are presented in Table 2. The difference between heritability in the additive genetic model (Model 1) and heritability in the additive-dominance model (Model 2) for all the traits was low. In general, the estimated dominance variance was larger than the estimated additive genetic variance irrespective of the trait under study. The estimated narrow sense heritability was 0.07 for DFS, 0.04 for NSC and 0.07 for DO. In the dominance model, the values of d 2 were 0.260, 0.231 and 0.196 for DFS, NSC and DO, respectively. The values of d 2 were 3.8, 6.6 and 2.9 times greater than the estimated narrow heritability for DFS, NSC and DO, respectively. Amount of heritability and additive genetic variance were nearly the same in additive genetic and additive-dominance models for all traits. Spearman's rank correlation between the BVs in additive genetic and additive-dominance models was 0.99 for all studied traits. The moderate Spearman's rank correlation (ranged from 0.64 to 0.77) was calculated between the predicted BVs and the TGV in the dominance model for three fertility traits (Table 3).
Table 2. Estimates of variance components using additive model (1) and additive-dominance model (2) for days from calving to first service (DFS), number of services to conception (NSC) and days open (DO) and Akaike's information criterion (AIC)
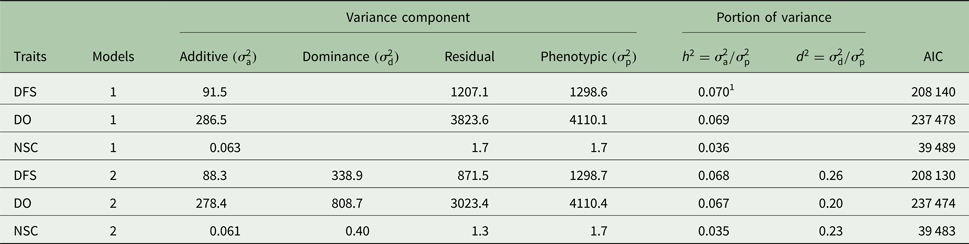
1 Standard errors for h 2 and d 2 were <0.005 and 0.09, respectively.
Table 3. Spearman's rank correlation between predicted breeding values (BV) using additive and additive-dominance models and rank correlation between BV and total genetic value in additive-dominance models (TGV)1
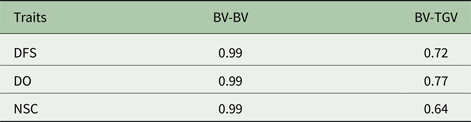
1 TGV = breeding value + dominance value.
Discussion
In order to separate dominance genetic variance from additive genetic variance, data should include individuals having non-zero dominance relationships to each other. Van Tassell et al. (Reference Van Tassell, Misztal and Varona2000) argued that a minimum of 20% full sibs in the population is required to successfully estimate non-additive genetic variation. Recently, utilization of multiple ovulation and embryo transfer in Iranian dairy cattle have produced sufficient groups of close relatives which share additive and non-additive genetic effects.
The AIC criteria indicated that the model fitting both additive and dominance genetic effects is the most appropriate model for analysing three fertility traits. Hence, for genetic evaluation of fertility traits, non-additive effects should be included in the statistical model in addition to the additive genetic effects. Van der Werf and De Boer (Reference Van Der Werf and De Boer1989) pointed out that in dairy cattle the prediction of BV will be biased with models including only additive effects. Hoeschele (Reference Hoeschele1991) recommended that fertility traits in dairy cattle should be analysed using animal models including additive, dominance and additive × additive interaction together. Fuerst and Solkner (Reference Fuerst and Solkner1994) concluded that dominance variance is an important component for fertility traits and estimates of heritability without considering dominance effect in the model are overestimated. Palucci et al. (Reference Palucci, Schaeffer, Miglior and Osborne2007) showed that in order to estimate genetic parameters and predict BVs for fertility traits, the genetic evaluation must account for non-additive genetic effects.
In the current study, the estimated dominance variances for all studied traits were greater than the estimated additive genetic variances in the additive-dominance model. Traits related to fitness such as fertility traits are commonly found to show inbreeding depression and heterosis (Charlesworth and Willis, Reference Charlesworth and Willis2009), which is usually supported by directional dominance at loci that control these traits. According to the interpretation of Fisher's fundamental theorem of natural selection (Fisher, Reference Fisher1930), the traits associated with fitness are expected to have lower heritability than other traits because alleles conferring the highest fitness will be driven to fixation quickly due to natural selection (Jones, Reference Jones1987). Therefore, it is expected that the non-additive genetic variance for fertility traits will be higher than additive genetic variance. Heterosis and inbreeding depression was reported for reproductive performance in Holstein cattle (Beckett et al., Reference Beckett, Ludwick, Rader, Hines and Pearson1979; González-Recio et al., Reference González-Recio, Lopez De Maturana and Gutiérrez2007; Pryce et al., Reference Pryce, Haile-Mariam, Goddard and Hayes2014). In the literature, heritability reported for fertility traits is small and ranged from 0.02 to 0.076 (González-Recio and Alenda, Reference González-Recio and Alenda2005; Ghiasi et al., Reference Ghiasi, Pakdel, Nejati-Javaremi, Mehrabani-Yeganeh, Honarvar, González-Recio, Carabaño and Alenda2011). In line with the current findings, Hoeschele (Reference Hoeschele1991) reported that the amount of dominance variance was larger than additive genetic variance for days between first and last insemination and DO in Holstein cows. Moreover, similar results were obtained for fertility traits in Canadian Holstein cow by Palucci et al. (Reference Palucci, Schaeffer, Miglior and Osborne2007), who reported that for age to the first service, heifer non-return rate and the interval from calving to first service amount of dominance variance is larger than additive variance. In a study by Fuerst and Solkner (Reference Fuerst and Solkner1994), the estimated dominance variance was larger than additive variance for calving interval. Palucci et al. (Reference Palucci, Schaeffer, Miglior and Osborne2007) reported that d 2 for DFS was 0.073, which was smaller than d 2 for DFS found in the present study. A high genetic correlation (>0.99) between calving interval and DO has been reported (González-Recio and Alenda, Reference González-Recio and Alenda2005; Ghiasi et al., Reference Ghiasi, Pakdel, Nejati-Javaremi, Mehrabani-Yeganeh, Honarvar, González-Recio, Carabaño and Alenda2011). Aliloo et al. (Reference Aliloo, Pryce, González-Recio, Cocks and Hayes2016) estimated genomic dominance variance for calving interval traits in Holstein and Jersey cows; they concluded that the ratio of dominance variance to phenotypic variance for this fertility trait was 0.012 and close to zero for Holstein and Jersey cows, respectively, which was lower than the estimated value for DO in the present study using pedigree data. The ratio of dominance variance to the phenotypic variance for age at first detected corpus luteum and post-partum anoestrus interval traits in beef cattle using genomic data was reported between 0 and 0.18 (Bolormaa et al., Reference Bolormaa, Pryce, Zhang, Reverter, Barendse, Hayes and Goddard2015), which is in conflict with results obtained in the current study.
There is a minor difference between estimated additive genetic variance from the additive genetic model and from the additive-dominance model, but the residual variance largely decreased in the additive-dominance model. These results show that when the dominance component was dropped from the model the amount of dominance variance moved to residual variance. Also, there is a minor difference between the amount of heritability in the additive genetic model and additive-dominance model for all traits. In general, the amount of heritability and additive genetic variance slightly was larger in the additive genetic model compared with additive-dominance model. These results show that there is no confounding between the dominance variance and the additive genetic variance components for fertility traits in the current study. It should be noted that the pedigree structure, especially numbers of full-sib groups were small. Therefore, one should interpret estimates of additive and dominance variances with caution. The current findings are not in agreement with results obtained by Hoeschele (Reference Hoeschele1991) and Palucci et al. (Reference Palucci, Schaeffer, Miglior and Osborne2007). Heritability in the additive genetic model was lower than the heritability in additive-dominance model for fertility traits in Holstein cow (Palucci et al., Reference Palucci, Schaeffer, Miglior and Osborne2007). Hoeschele (Reference Hoeschele1991) pointed out the estimates of heritability in the broad sense were larger than estimates of heritability in a narrow sense for DO and service period, indicating confounding between dominance variance and the additive genetic variance. No confounding between the dominance variance and the additive genetic variance was observed for production traits (milk, fat and protein yield) in Holstein cows (Miglior et al., Reference Miglior, Burnside and Kennedy1995). In other species, confounding between the dominance and additive genetic variance components has been reported for litter size in rabbits (Nagy et al., Reference Nagy, Farkas, Curik, Gorjanc, Gyovai and Szendrő2014), pig longevity traits (Serenius et al., Reference Serenius, Stalder and Puonti2006) and the egg production traits of laying hens (Wei and Van Der Werf, Reference Wei and Van Der Werf1993).
Spearman's rank correlation was calculated to determine the differences in the BVs predicted in the additive and additive-dominance models. Even though according to the AIC criteria, the additive-dominance model was better than the additive genetic model for analysing, DFS, NSC and DO in the current study, Spearman's rank correlation between the BVs in the additive genetic model and additive-dominance model was high (0.99). Spearman's high-rank correlation indicates that the predicted BV by the additive genetic and additive-dominance models rank the animals similarly. The high Spearman's rank correlation obtained between the BVs in the additive and additive-dominance models is due to the no confounding between additive and dominance variance for fertility traits in the current study. Although including the dominance effect in the model did not affect the ranking of the animals based on the predicted BVs in comparison with the additive model, the dominance effects can be predicted in addition to the BVs using the additive-dominance models. Spearman's rank correlations between the predicted BVs and the TGV in additive-dominance models were moderate for all the fertility traits in the current study. These results indicate that ranking animals based on BV will be different from ranking animals based on TGV. The joint estimation of additive and dominance genetic effect could be utilized in mate allocation programs to improve total genetic merit of fertility traits. Toro and Varona (Reference Toro and Varona2010) reported that utilizing the dominance effect in genomic evaluation increases the accuracy of predicted BVs and it gains an extra genetic response from mate allocation techniques. Lawlor et al. (Reference Lawlor, Weigel and Misztal1993) showed that considering the dominance effect in mating allocation systems would increase income approximately US$28 in Holstein cows.
Conclusions
The estimates of dominance genetic variance for fertility traits were larger than the additive genetic variance. Ignoring the dominance effect in the model resulted in the overestimation of residual variance, whereas, a very slight overestimation was observed for an additive variance. Ranking the animals based on predicted BV was the same in the additive genetic model and the dominance model. The moderate rank correlation was found between the predicted BVs and the TGVs. Including the dominance effect in a model is important for prediction of dominance effect and it can be used to calculate the TGV for mate allocation programmes.
Financial support
This project was financially supported by Payame Noor University.
Conflict of interest
None.
Ethical standards
Not applicable.
