4 Isolated single droplet: a control study

The distribution of evaporation flux $(J(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}))$ around a sessile droplet is a function of its shape alone (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997). For a sessile droplet evaporating on a hydrophobic substrate, the evaporation flux distribution is symmetric along the azimuthal direction $(\unicode[STIX]{x2202}J/\unicode[STIX]{x2202}\unicode[STIX]{x1D711}\approx 0)$ ; however, it varies along the polar direction $(\unicode[STIX]{x2202}J/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\neq 0)$ as depicted in figure 2. For a sessile droplet on a hydrophilic substrate, the evaporation flux is maximum at the three phase contact line $(\unicode[STIX]{x1D703}=0)$ , while it is minimum at the apex region $(\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2)$ (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997). However, for a hydrophobic sessile droplet, a wedge-like region of enhanced vapour concentration reduces the evaporation flux near the three phase contact line. Therefore, for a hydrophobic sessile droplet, evaporation flux is maximum at the apex point $(\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2)$ and minimum at the three phase droplet contact line $(\unicode[STIX]{x1D703}=0)$ (Jyoti et al. Reference Jyoti, Shaikeea and Basu2016). Evaporation rate and flux distribution govern the contact line dynamics and internal flow features (strength and pattern). Based on transient contact line dynamics, there exist two distinct modes of evaporation, namely, CCR (constant contact radius) and CCA (constant contact angle) (Nguyen & Nguyen Reference Nguyen and Nguyen2012; Yu, Wang & Zhao Reference Yu, Wang and Zhao2012; Jyoti et al. Reference Jyoti, Shaikeea, Basu and Bansal2017). In addition, numerous studies have reported a mixed mode of evaporation where both contact radius and contact angle undergo simultaneous changes (Nguyen & Nguyen Reference Nguyen and Nguyen2012). In general, CCR and CCA modes of evaporation are tools to characterise the wettability of the surface. For example, sessile droplets evaporating on super-hydrophilic surfaces generally show pinned contact line behaviour resulting in the CCR mode of evaporation with high contact angle hysteresis. On the other hand, superhydrophobic surfaces generally support the CCA mode of droplet evaporation with negligible contact angle hysteresis. In the present case (control study), an isolated sessile droplet (ID) on a PDMS substrate shows an initial contact angle of $110^{\circ }\pm 2^{\circ }$ , with an overall standard deviation of 6 %. The ID evaporating on a PDMS substrate shows a buoyancy-driven double toroid flow pattern. Figure 4(a,d) shows the side and bottom view PIV flow field. The bottom view vector field indicates an average velocity ${\sim}6{-}8~\unicode[STIX]{x03BC}\text{m}~\text{sec}^{-1}$ (at around $t/t_{e,ID}\approx 0.1$ ). Glass substrate and silicon wafer offer an initial contact angle of $45^{\circ }\pm 3^{\circ }$ and $72^{\circ }\pm 3^{\circ }$ respectively. Internal flow fields of sessile droplets resting on such hydrophilic substrates show the traditional radially outward capillary flow (as seen in the coffee ring effect) (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997).

Apart from the local dynamics such as contact line movement and the internal flow field, global parameters such as total evaporation time scales form an important aspect of sessile droplet evaporation. For a diffusion-based evaporation model (negligible external convective effects), the rate of droplet volume change is given by Fick’s law (Jyoti et al. Reference Jyoti, Shaikeea and Basu2016; Bansal et al. Reference Bansal, Hatte, Basu and Chakraborty2017; Hatte et al. Reference Hatte, Dhar, Bansal, Chakraborty and Basu2019):

(4.1) $$\begin{eqnarray}\frac{\text{d}V}{\text{d}t}=\frac{-J_{avg}A_{d}}{\unicode[STIX]{x1D70C}}=\frac{-2\unicode[STIX]{x03C0}DMR_{c}\,f(\unicode[STIX]{x1D703}_{c})(c_{s}-c_{\infty })}{\unicode[STIX]{x1D70C}},\end{eqnarray}$$

where, $V$ is the instantaneous droplet volume, $J_{avg}$ is the global evaporation flux value averaged around the droplet surface, $A_{d}$ is the instantaneous droplet surface area, $\unicode[STIX]{x1D70C}$ is the density of working fluid, $D$ is the diffusion constant of vapour in air, $R_{c}$ and $\unicode[STIX]{x1D703}_{c}$ are the instantaneous droplet contact radius and contact angle respectively and $C_{s}$ and $C_{\infty }$ are the vapour concentrations near and far away from the interface respectively. For $\unicode[STIX]{x1D703}_{c}>10^{\circ }$ , $f(\unicode[STIX]{x1D703}_{c})=(0.00008957+0.633\unicode[STIX]{x1D703}_{c}+0.116\unicode[STIX]{x1D703}_{c}^{2}-0.08878\unicode[STIX]{x1D703}_{c}^{3}+0.01033\unicode[STIX]{x1D703}_{c}^{4})/\text{sin}(\unicode[STIX]{x1D703}_{c})$ (Picknett & Bexon Reference Picknett and Bexon1977); $f(\unicode[STIX]{x1D703}_{c})$ is a geometric factor that takes into account the incomplete spherical shape of a sessile droplet. Instantaneous contact line parameters ( $R_{c}$ and $\unicode[STIX]{x1D703}_{c}$ ) strongly affect the vaporisation time scales. In the present case, the average evaporation rate is represented in terms of its initial contact line parameters (discussed later). The basic assumption underlying (4.1) is the presence of uniform infinite medium for the diffusion of vapour. However, this assumption is not valid in practical cases where vapour diffusing out from the liquid–air interface experiences reduced mobility.

5 An interacting linear three-droplet system

An evaporating sessile droplet interacts with its surrounding entities. In diffusion-based systems, these interactions are mediated through the vapour field. For an interacting hydrophobic three-droplet system, a wedge-like confinement forms naturally between the CD and SD (figure 2). Due to the close proximity of the droplets, an additional region of vapour confinement is formed (figure 2). For the case of an interacting three-droplet system over a hydrophilic substrate, due to the absence of a wedge-like confinement region, it is only the proximity of neighbouring droplets that gives rise to the formation of the vapour confinement zone, as depicted in figure 2. We will show in subsequent sections that the present model is valid for both hydrophilic and hydrophobic droplet systems. The dimensions of this vapour confinement space depend strongly on the separation distance between CD and SD. The wedge leads to reduced mobility (diminished tendency to diffuse out to the ambient) forcing the vapour to accumulate in the confinement resulting in relatively enhanced local vapour concentration $c_{\infty }^{\prime }(c_{\infty }<c_{\infty }^{\prime }<c_{s})$ . Hence, the extent of vapour-mediated interactions depends on the geometric parameters that create the region of confinement in the first place. The spatial variation of vapour concentration for CD and SD results in the redistribution of evaporation flux pattern as shown in figure 2 (compared to the isolated droplet counterpart). Figure 2(b,d) shows that for SD, the liquid–air interface close to the wedge shows relative suppression of the evaporation flux. CD however suffers an overall degradation in evaporation rate as well as strong spatial variations in both azimuthal and polar directions. In the subsequent sections, vapour-mediated interaction induced effects on the evaporation dynamics of a three-droplet system is studied for a range of droplet separation values $(L/D_{e}\in [1.1,2.6])$ . We will focus on the details pertaining to a PDMS substrate unless stated otherwise. However, we will show that the evaporation lifetime scaling is equally applicable to other substrates as well.

Figure 3. CD contact line dynamics. Transient variation of (a) contact radius (b) contact angle and (c) droplet volume for different cases of droplet separation values. Inadequacy of the normalising time scale is evident in all the plots.

6 Contact line dynamics

In the current set of experiments, the sessile droplets can be approximated as a spherical cap since the contact radius of 0.75 mm (for $2~\unicode[STIX]{x03BC}\text{l}$ volume) is much lower than the corresponding capillary length; $\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}\approx 2.7$  mm. Initial contact radius and contact angle of a sessile droplet are dependent on the wettability of the substrate. However, with progressive evaporation, the dynamics is characterised by the transient variation in droplet contact line parameters; contact radius ( $R_{c}$ ) and contact angle ( $\unicode[STIX]{x1D703}_{c}$ ). For all values of SD–CD separation ( $L$ ) considered in the experiments, the range of droplet contact radius (PDMS substrate) is observed as: initial contact radius ${\sim}0.75$  mm; final contact radius ${\sim}0.48$  mm. Assuming a spherical cap geometry, the transient variation of droplet volume is shown in figure 3(c). There are two important observations from the volume regression plot (figure 3 c). First, the variation of droplet volume is nonlinear in nature. It is well known that the initial linearity in droplet volume regression is lost due to the inherent slip of the contact line (Bansal et al. Reference Bansal, Hatte, Basu and Chakraborty2017; Hatte et al. Reference Hatte, Dhar, Bansal, Chakraborty and Basu2019). Second, the evaporation lifetime is significantly different for different values of droplet spacing ( $L/D_{e}$ ). In the present study, a maximum of 65 % increase in evaporation lifetime (compared to ID) is observed for a droplet spacing of $L/D_{e}\approx 1.1$ . It is tempting to scale the evaporative lifetime of a three-droplet system with that of the single droplet (ID), as shown in figure 3. However, this scaling causes significant divergence in contact line parameters for different $L/D$ ratios. This consequently proves the inadequacy of the time scale involving ID. Hence, for an interacting three-droplet system, a different time scale is necessary which ideally should unify the transient data (contact line parameters, volume) across all $L/D$ values.

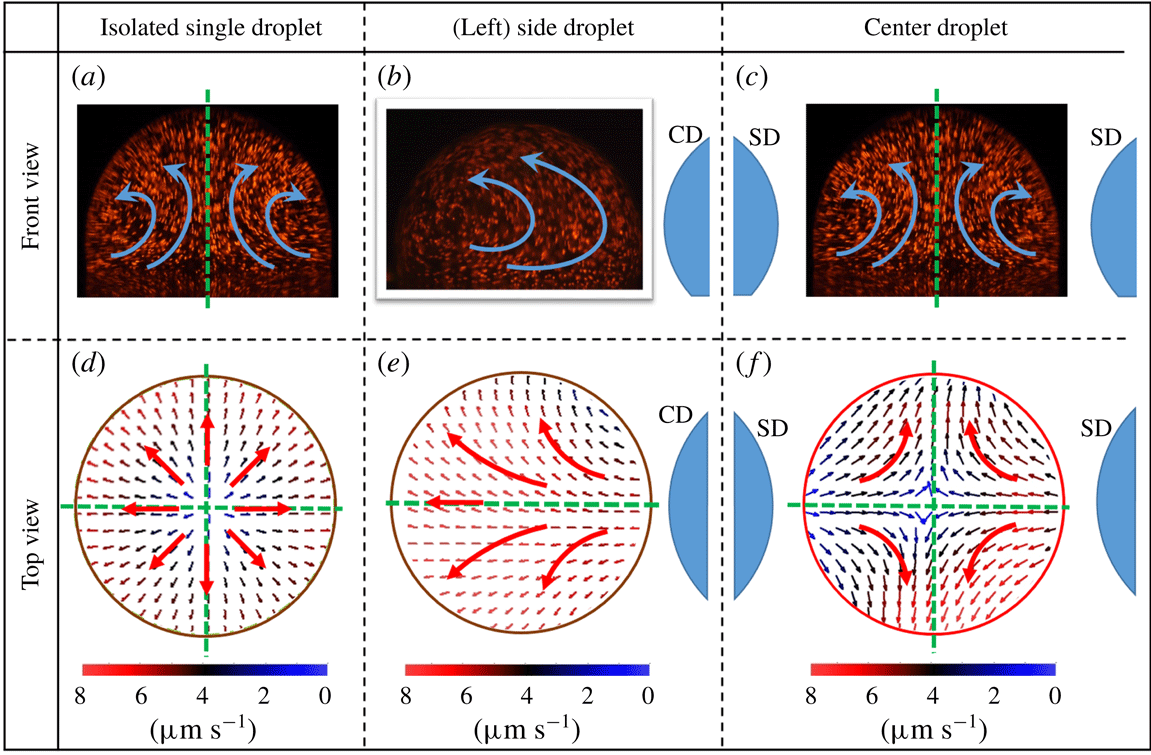
Figure 4. Internal flow dynamics. Flow field visualisation from front view for (a) an isolated sessile droplet (b) CD, (c) SD and flow vector characterisation from bottom view for (d) an isolated sessile droplet (e) CD and (f) SD. Droplet separation value of $L/D_{e}=1$ is considered for symmetric interacting three-droplet system. Arrows denote the direction of internal flow and green dotted lines indicate the axes of symmetry.

7 Internal flow dynamics

Evaporation flux distribution around a sessile droplet governs its internal flow dynamics as discussed in the previous section. The same is evident from the equal number of axes of symmetries in evaporation flux distributions (figure 2) and corresponding internal flow fields (figure 4). As a result, for an interacting three-droplet system, vapour-mediated interaction induced redistribution of the evaporation flux causes alterations in the internal flow patterns of CD and SD (compared to its ID counterpart). In the present case, internal flow dynamics of CD and SD is studied for two cases; first, for lower value of droplet separation $L/D_{e}\approx 1$ , and symmetric placement of CD; second, for an asymmetric placement of CD.

For a CD, in symmetric three-droplet system, the presence of two SDs at opposite ends affects the evaporation flux distribution as represented in figure 2(b,d,f). As a result, the bottom view flow field appears to be originating from the region of high vapour confinement and directed towards the relatively relaxed region at ambient conditions (figure 4 f). It is interesting to note that the side view flow field exhibiting a double toroid flow pattern is similar to its ID counterpart (with two axes of symmetry) because of the symmetric placement of CD (figure 4 a,c). However, due to a suppressed evaporation flux, the magnitude of the internal flow field for CD ( $3.5~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ ) is lower than the corresponding ID ( ${\sim}7~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ ). For a SD, there exists a highly asymmetric evaporation flux distribution (figure 2 b,d) mainly due to preferential vapour accumulation on one side and ambient conditions on the other. As a result, a unidirectional flow field is observed from bottom view particle image velocimetry (PIV), as shown in figure 4(e), as opposed to a divergent flow as encountered in ID (isolated droplet). The flow is essentially directed towards the droplet side that is exposed to the ambient (zone of relaxed concentration). In addition, from figure 4(b), it is observed that the side view PIV flow field for SD shows a transition from double toroid (ID counterpart) to a single toroid flow pattern directed away from CD. SD flow field with progression in evaporation develops a pair of vortices on the side facing the CD as shown in figure 5(c). The formation of vortices is attributed to restoration of the SD flow field from unidirectional to the divergent double toroidal flow pattern (bottom view PIV for ID). However, with progressive evaporation, as the dynamic separation between the SD and CD increases, the initial vapour field is relaxed, thereby restoring the symmetric distribution of evaporation flux for SD. As a result, during the later part of the evaporation lifetime $(t/t_{e}\approx 0.8)$ , the SD flow field transitions from a single toroid to double toroid flow field exhibiting a pair of transient intermediate vortical structures. The same pair of vortices are observed from the side view PIV of SD at a plane perpendicular to the line joining the three droplets as shown in figure 5(d). These vortical structures are repeatable across all experimental realisations. Further, at sufficiently higher values of droplet spacing $L/D_{e}>2.6$ , internal flow field patterns of CD and SD in a three-droplet interacting system are observed to be strikingly similar to an ID. Hence, it is stated that for droplet spacing of $L/D_{e}>2.6$ , the three-droplet system shows insignificant vapour-mediated interactions and behave as three individual IDs. Mathematical reasoning for this critical/threshold magnitude $(L/D_{e}>2.6)$ is explained in following section.

Figure 5. Bottom view flow field of an interacting three -droplet system. Bottom view flow field of (left) SD for a symmetric placement of CD at (a)  $(t/t_{e}\approx 0.1)$ , (b)  $(t/t_{e}\approx 0.5)$ , (c)  $(t/t_{e}\approx 0.8)$ and (d) side view flow field in a plane perpendicular to the line joining the three linear droplets. (c) Shows formation of vortices near the end of the evaporation lifetime. Bottom view flow field of CD for extreme levels of asymmetric placement of CD, (e)  $L1/D=1.7$ , $L2/D=3.4$ and (f)  $L1/D=1.7$ , $L2/D=8.5$ . Smaller circular objects represent the position of CD and/or SD to highlight the position of the droplet under observation.

For an asymmetric droplet system (the CD is not equidistant from the two SDs), the internal flow field in the CD differs significantly from the case of a symmetric droplet system. Relatively higher vapour accumulation on one side compared to the other results in a unidirectional flow field as observed from the bottom view PIV flow field (figure 5 e,f) for two asymmetric configurations. In both cases (figure 5 e,f), the relative separations ( $L2/L1$ ) are varied from 2 to 5. The flow field pattern remain sufficiently similar.

8 Droplet lifetime scaling

Figure 3(c) shows that the lifetime of CD from the interacting three-droplet system is higher than its ID counterpart. In addition, figure 3 also shows that the correct scaling of CD lifetime should incorporate the relative separation ( $L/D_{e}$ ). Figure 6 illustrates the wedge region responsible for the accumulation of vapour thereby slowing down the evaporation process.

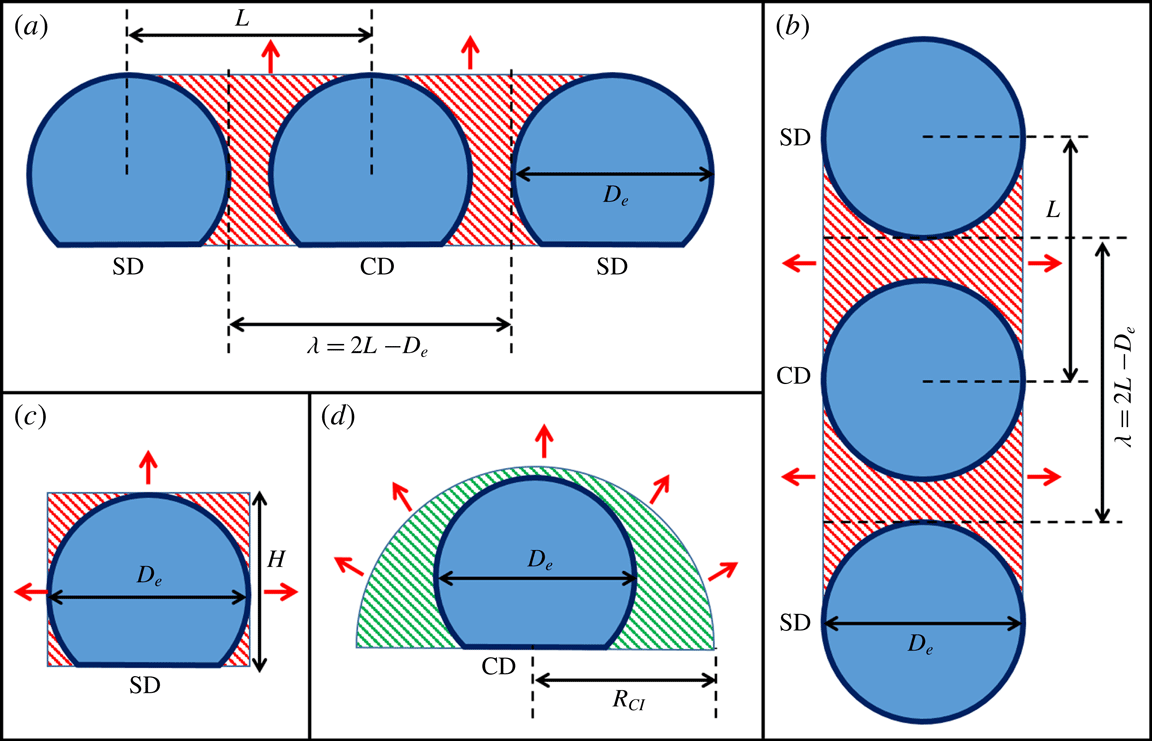
Figure 6. Schematic of the region of vapour entrapment with enhanced vapour concentration of $c_{\infty }^{\prime }$ . (a) Front view and (b) top view of the cuboid and equivalent half-cylindrical region of vapour entrapment, (c) side view of the cuboidal region of vapour entrapment and (d) side view of the equivalent half-cylindrical region of vapour entrapment. Red arrows denote the direction of vapour front propagation.

In order to develop a mathematically consistent scaling argument, a region of vapour-mediated interaction is first defined. Geometric parameters that define the extent and region of vapour confinement are – droplet spacing ( $L$ ), droplet contact radius ( $R_{c}$ ), droplet equatorial diameter ( $D_{e}$ ), droplet height ( $H$ ) and contact angle ( $\unicode[STIX]{x1D703}_{c}$ ). Along the direction of droplet placement, the CD vapour field is obstructed by the presence of two SDs each at spacing  $L$ . In order to establish a mathematical model encompassing the aforementioned geometric parameters, a lumped model is proposed.

We arrive at a simple new unified theory on the evaporating droplet lifetime by replacing the traditionally described single-step process with a two-step diffusion model. The first step physically signifies the fact that vapour leaving the liquid–air interface is accumulated in the region of vapour entrapment, exhibiting an enhanced vapour concentration of $c_{\infty }^{\prime }$ (figure 6) in the ambient. Instantaneous rate of droplet volume decay in this step is expressed in terms of its governing parameters as per Fick’s law:

(8.1) $$\begin{eqnarray}\frac{\text{d}V}{\text{d}t}=\frac{-2\unicode[STIX]{x03C0}DMR_{c}\,f(\unicode[STIX]{x1D703})(c_{s}-c_{\infty }^{\prime })}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$

In the second step, it is assumed that the entrapped vapour field diffuses out in a linear fashion to the ambient $(c_{\infty })$ over a length scale $\overline{La}$ .

(8.2) $$\begin{eqnarray}\frac{\text{d}V}{\text{d}t}_{avg}=-\frac{DM(A_{c})(c_{\infty }^{\prime }-c_{\infty })}{\unicode[STIX]{x1D70C}\overline{L_{a}}},\end{eqnarray}$$

where, $A_{c}$ is the surface area of the vapour field front (discussed later). These two processes are in equilibrium with very little variation of $c_{\infty }^{\prime }$ almost throughout the lifetime of CD. The average rate of droplet volume decay can be cast in terms of its initial geometric parameters:

(8.3) $$\begin{eqnarray}\frac{\text{d}V}{\text{d}t}_{avg}=A\frac{-2\unicode[STIX]{x03C0}DMR_{ci}\,f(\unicode[STIX]{x1D703}_{ci})(c_{s}-c_{\infty }^{\prime })}{\unicode[STIX]{x1D70C}},\end{eqnarray}$$

where $A$ is a fitting parameter (of the order of unity), with specific value (as fitted from a wide range of experimental data) of approximately 0.74 i.e. ${\sim}O(1)$ . Equation (8.3) shows excellent agreement with experimental data (insignificant deviation of 2.7 %). Equating (8.2) and (8.3) we get,

(8.4) $$\begin{eqnarray}-\frac{DM(A_{c})(c_{\infty }^{\prime }-c_{\infty })}{\unicode[STIX]{x1D70C}\overline{L_{a}}}=A\frac{-2\unicode[STIX]{x03C0}DMR_{ci}\,f(\unicode[STIX]{x1D703}_{ci})(c_{s}-c_{\infty }^{\prime })}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$

Rearranging (8.4) we get,

(8.5) $$\begin{eqnarray}(c_{\infty }^{\prime }-c_{\infty })=\frac{\overline{L_{a}}}{A_{c}}\times A2\unicode[STIX]{x03C0}R_{ci}\,f(\unicode[STIX]{x1D703}_{ci})(c_{s}-c_{\infty }^{\prime }).\end{eqnarray}$$

From (8.5), $c_{\infty }^{\prime }$ is represented in terms of $c_{s}$ and $c_{\infty }$ as,

(8.6) $$\begin{eqnarray}c_{\infty }^{\prime }=\frac{\overline{L_{a}}A2\unicode[STIX]{x03C0}R_{ci}\,f(\unicode[STIX]{x1D703}_{ci})c_{s}+A_{c}c_{\infty }}{(A_{c}+\overline{L_{a}}A2\unicode[STIX]{x03C0}R_{ci}\,f(\unicode[STIX]{x1D703}_{ci}))}.\end{eqnarray}$$

Multiplying (8.6) by $-1$ and adding $c_{s}$ on both sides we get,

(8.7) $$\begin{eqnarray}(c_{S}-c_{\infty }^{\prime })=c_{S}-\frac{\overline{L_{a}}A2\unicode[STIX]{x03C0}R_{ci}\,f(\unicode[STIX]{x1D703}_{ci})c_{s}+A_{c}c_{\infty }}{(A_{c}+\overline{L_{a}}A2\unicode[STIX]{x03C0}R_{ci}\,f(\unicode[STIX]{x1D703}_{ci}))}.\end{eqnarray}$$

Rearranging (8.7) we get $(c_{S}-c_{\infty }^{\prime })$ in terms of $(c_{s}-c_{\infty })$ as,

(8.8) $$\begin{eqnarray}(c_{S}-c_{\infty }^{\prime })=\frac{A_{c}(C_{S}-c_{\infty })}{(A2\unicode[STIX]{x03C0}R_{Ci}\,f(\unicode[STIX]{x1D703}_{ci})\overline{L_{a}}+A_{c})}.\end{eqnarray}$$

Substituting (8.8) in (8.3), and rewriting $|(\text{d}V/\text{d}t)_{avg}|\approx V_{d}/t_{e,CD}$ , we get,

(8.9) $$\begin{eqnarray}\frac{t_{e,CD}}{V_{d}}=\frac{\overline{L_{a}}}{\unicode[STIX]{x1D6FC}A_{c}}+\frac{1}{\unicode[STIX]{x1D6FC}(2\unicode[STIX]{x03C0}AR_{ci}\,f(\unicode[STIX]{x1D703}_{ci}))},\end{eqnarray}$$

where, $t_{e,CD}$ is the lifetime of the CD, $V_{d}$ is the initial droplet volume and $\unicode[STIX]{x1D6FC}=(2\unicode[STIX]{x03C0}DM(c_{s}-c_{\infty }))/\unicode[STIX]{x1D70C}$ .

Average vapour accumulation length $\overline{L_{a}}$ depends on the geometric parameters of the interacting three-droplet system. In order to quantify this dependency, a vapour concentration field along the radially outward direction from the liquid–air interface is simulated for an isolated spherical droplet, as shown in figure 7.

Figure 7. Variation of vapour concentration along the radial direction for a spherical isolated droplet.

The obtained value of $\unicode[STIX]{x1D6FD}\sim 4$ , indicates the radial distance $(r=\unicode[STIX]{x1D6FD}D_{e})$ at which the vapour concentration gradient is ${\sim}0$ (i.e. $\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}r|_{r=\unicode[STIX]{x1D6FD}D_{e}}\approx 0$ ). The average accumulation length can thereby be written as $\overline{L_{a}}=K\times \unicode[STIX]{x1D6FD}\times D_{e}$ where $K$ is of the order of unity. Now, the volume of a sessile droplet is defined by two independent parameters out of four, namely, contact radius, contact angle, equatorial diameter and droplet height. Using sessile droplet geometry, equatorial diameter $D_{e}=2R_{c}\cos ec(\unicode[STIX]{x1D703}_{ci})$ is substituted to obtain $\overline{L_{a}}$ as:

(8.10) $$\begin{eqnarray}\overline{L_{a}}=2K\unicode[STIX]{x1D6FD}R_{c}\cos ec(\unicode[STIX]{x1D703}_{ci}).\end{eqnarray}$$

Substituting $\overline{L_{a}}$ from (8.10) in (8.9) and rearranging, we get,

(8.11) $$\begin{eqnarray}t_{e,CD}=\frac{2V_{d}K\unicode[STIX]{x1D6FD}R_{c}\cos ec(\unicode[STIX]{x1D703}_{ci})}{\unicode[STIX]{x1D6FC}A_{c}}+\frac{V_{d}}{\unicode[STIX]{x1D6FC}(2\unicode[STIX]{x03C0}AR_{ci}\,f(\unicode[STIX]{x1D703}_{ci}))}.\end{eqnarray}$$

Second term on the right-hand side of (8.11) corresponds to the lifetime of an isolated droplet $(t_{e,ID})$ as per (8.3). Therefore, equation (8.11) is written in the form:

(8.12) $$\begin{eqnarray}\frac{t_{e,CD}}{t_{e,ID}}=\frac{AK\unicode[STIX]{x1D6FD}\cos ec(\unicode[STIX]{x1D703}_{ci})A_{d,i}}{A_{c}}+1,\end{eqnarray}$$

where, $A_{d,i}=4\unicode[STIX]{x03C0}R_{ci}^{2}\,f(\unicode[STIX]{x1D703}_{ci})$ is the initial CD surface area. The value of $A_{c}$ (vapour field front area) depends on the geometry of the region of vapour entrapment.

The presence of two SDs creates a vapour entrapment region with the shape of a cuboid as shown in figure 6. The accumulated vapour front with progression in evaporation propagates in two different directions (figure 6). In the simple lumped parameter-based modelling approach adopted here, the vapour field propagation in two directions is converted into a unidirectional case by assuming an equivalent half-cylindrical vapour field of cross-sectional area $A_{c}$ (figure 6) propagating radially outward towards the ambient. To calculate the equivalent cylindrical geometric parameters, the total volume of the accumulated vapour field is conserved as:

(8.13) $$\begin{eqnarray}\unicode[STIX]{x1D706}\times D_{e}\times H=\frac{\unicode[STIX]{x03C0}r_{cl}^{2}\unicode[STIX]{x1D706}}{2},\end{eqnarray}$$

where, $H=R_{ci}(1+\sin \unicode[STIX]{x1D703}_{ci})$ is the initial droplet height, $D_{e}=2R_{ci}\cos ec\unicode[STIX]{x1D703}_{ci}$ is the initial equatorial diameter of the droplet and $\unicode[STIX]{x1D706}=2L-D_{e}$ is the space between the edges of two SDs facing the CD. Using the equivalent radius obtained from (8.13), the available equivalent surface area of the assumed half-cylindrical geometry is given as:

(8.14) $$\begin{eqnarray}A_{c}=\unicode[STIX]{x03C0}r_{cl}\unicode[STIX]{x1D706}=2R_{ci}\unicode[STIX]{x1D706}\sqrt{\unicode[STIX]{x03C0}(1+\cos ec\unicode[STIX]{x1D703}_{ci})}.\end{eqnarray}$$

Area ratio defined as $A_{R}=A_{d,i}/A_{c}$ is the relative surface area of CD to the surface area of the accumulated vapour field in the region of confinement. In the present framework, $A_{R}=A_{d,i}/A_{c}$ is termed as the extent of confinement the CD is subjected to. Decrease of $L/D$ leads to reduction of the vapour field front area ( $A_{c}$ ) thereby increasing the extent of confinement $(A_{R}=A_{d,i}/A_{c})$ . Similarly, with increasing separation, the vapour field front area ( $A_{c}$ ) is increased and the extent of confinement $(A_{R}=A_{d,i}/A_{c})$ is decreased. In an asymptotic limit, three droplets placed at sufficiently large spacing thus behave like individual IDs.

Equation (8.12) predicts the theoretical lifetime of CD compared to its ID counterpart. In (8.12), the constant term $AK\unicode[STIX]{x1D6FD}\approx 0.47$ is of the order of $O(1)$ . Hence it is inferred that the evaporation lifetime scaling $(t_{e,CD}/t_{e,ID})$ is of the same order as the extent of confinement $(A_{R}=A_{d,i}/A_{c})$ . Droplet geometric parameters $R_{ci},\cos ec(\unicode[STIX]{x1D703}_{ci})$ and $f(\unicode[STIX]{x1D703}_{ci})$ take into account the initial droplet volume and wettability of the substrate respectively. It is noted that no particular restriction exists on $R_{ci}$ and $\unicode[STIX]{x1D703}_{ci}$ values. Consequently, the present scaling approach is believed to be applicable for a range of initial droplet volumes across all possible substrate–fluid combinations. For a given initial contact angle, theoretical lifetime scaling as per (8.12) shows linear dependence on the extent of confinement $(A_{R}=A_{d,i}/A_{c})$ values. Hence, for no confinement, the theoretical scaling argument should approach the classical case of an ID. In addition, for the maximum possible confinement, there should exist a theoretical upper limit on the scaling of the CD lifetime. 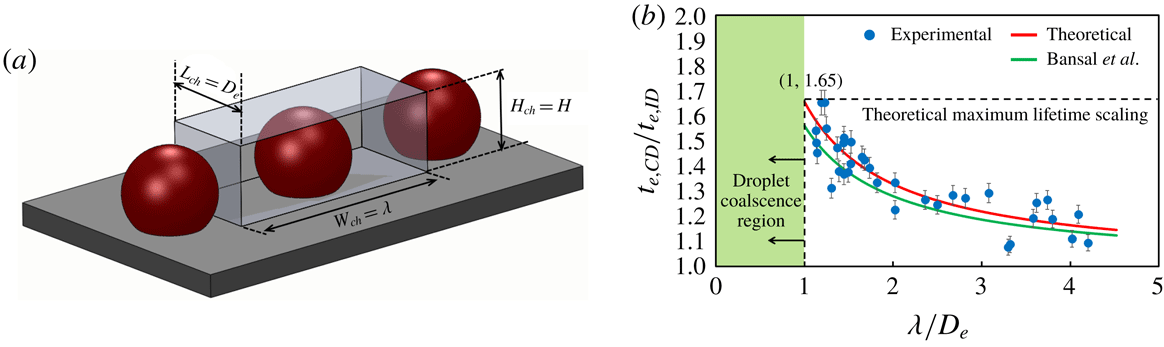In order to validate the theoretical universal lifetime scaling, extensive experiments are conducted for different levels of CD confinement (by changing the separation $L$ between CD and SD). Experimental values show excellent agreement with the semi-analytical formulation (8.12) as shown in figure 8. Figure 8 also shows the two asymptotic regions. In region 1, as the distance ( $L$ ) between the CD and SD is increased beyond a certain value, the extent of confinement tends to zero and the corresponding scaling of CD lifetime approaches the classical case of ID $(t_{e,CD}/t_{e,ID}\approx 1)$ . In the present experiments, the minimum value of $A_{R}$ ( $=0.33$ ) corresponding to the relative spacing of $L/D_{e}=2.6$ , gives the lifetime scaling of 1.06 which is approximately ${\sim}1$ . Repeated experiments for higher droplet–droplet separation values $(L/D_{e}>2.6)$ confirm that the lifetime scaling approaches 1. This relative critical droplet separation value of $L/D_{e}=2.6$ , where the three-droplet system starts behaving as a set of three isolated droplets, is almost same as the value of $L/D\approx 2.5$ for an interacting two-droplet system obtained by Jyoti et al. (Reference Jyoti, Shaikeea and Basu2016). In the asymptotic region of highest confinement, the minimum separation between CD and SD can at most be equal to the equatorial diameter of the sessile droplet ( $D_{e}$ ). Hence, the maximum extent of confinement value (for $L/D_{e}\approx 1^{+}$ ) is ${\sim}1.3$ while the corresponding CD lifetime scaling obtained from (8.12) is ${\sim}1.65$ . This value puts an upper limit on any evaporating three-droplet system (irrespective of volume, substrate wettability and experimental conditions). Hence the theoretical bounds of the present framework of three interacting linear sessile droplets can be written as domain: $A_{r}\in (0,1.3)$ and range: $t_{e,CD}/t_{e,ID}\in (1,1.65)$ . It therefore can be inferred that the lifetime of any CD in an $n$ -droplet array $(n\geqslant 3)$ can at most be extended by 65 % compared to its isolated counterpart. The upper limit of 1.65 for scaling in evaporation lifetime can only be extended by increasing the maximum amount of confinement a droplet can be subjected to. This can be achieved by changing the form of confinement as in the case of two-dimensional droplet arrays or droplets trapped in narrow channels.

Figure 8. Evaporation lifetime scaling. Relative increase in evaporation lifetime of CD in an interacting three-droplet system with the extent of confinement $(A_{R}=A_{d,i}/A_{c})$ .

As mentioned previously, the present framework of an interacting three-droplet system acts as a fundamental unit for a linear array of $n$ -droplets $(n\geqslant 3)$ . In order to check the validity of this hypothesis, a systematic set of experiments are conducted by varying the experimental parameter space. First, in order to vary the initial droplet contact angle and contact radius, two different types of substrates namely, glass and silicon wafers are considered. Figure 8 shows a good agreement of the experimental values with the theoretical formulation (8.12) for glass and silicon substrates for a range of droplet separation values.

In order to verify the independence of the scaling on the number of participating droplets $(n\geqslant 3)$ , the lifetime scaling of two CDs of an interacting four-droplet system as depicted in figure 9(a) for four different values of droplet separation length $L$ is calculated. Figure 8 shows that even for a four-droplet system, the two CDs (figure 9 a) obey the lifetime scaling as represented by (8.12). Therefore, the evaporation dynamics of a linear array of $n$ -droplets $(n\geqslant 3)$ excluding the edge droplets can be uniquely represented using (8.12).

In addition, in the present experiments, the position of CD is equidistant (symmetric) from the two SDs. However, in the formulation stated by (8.12) the region of vapour confinement relates to the distance between the edges of two SDs denoted by $\unicode[STIX]{x1D706}=2L-D_{e}$ . Position of CD (placed anywhere in between the two SDs) does not affect the total region of vapour confinement. Therefore, even the asymmetrically placed CD should follow the scaling formulation. In order to validate this hypothesis, experiments are repeated for an asymmetric placement of CD as shown in figure 9(b). In this context, the separation distance is now written as $\unicode[STIX]{x1D706}=L1+L2-D_{e}$ , where $L1$ and $L2$ are the centre-to-centre distances of the CD from the left and right SDs respectively as shown in figure 9(b). The absolute values of $L1$ and $L2$ are as shown in table 1.

Figure 9. An interacting system of (a) four sessile droplets placed in a linear arrangement at a uniform separation of $L$ and (b) three droplets with asymmetric position of CD.

Table 1. Absolute values of $L1$ and $L2$ covered in the experiments for the asymmetric placement of CD.

Figure 8 again shows an excellent agreement between the experimental and theoretical lifetime scalings for asymmetrically placed CD. If a CD is moved towards one of the SD droplets from an initially symmetric configuration, then the two regions created show a slightly differential extent of vapour confinement. The increase in evaporation flux on the right-hand side is compensated by the decrease in vaporisation from the left-hand side. Consequently, in a global sense, the lifetime scaling does not change as compared to the symmetric configuration. In addition, two cases of extreme CD asymmetry as (illustrated in figure 5), are in good agreement with the theoretical lifetime scaling argument as per (8.12), as seen from figure 8. Therefore, it can be confidently stated that the asymmetry of CD in an interacting three-droplet system does not affect its lifetime scaling and is only dependent on the total vapour accumulation region defined by $L1+L2$ . However, from the preceding section on internal flow dynamics, it is evident that the internal flow will be altered because of the redistribution of evaporation flux.

The average total error between the theoretical and experimental values is within 2 %, and the average positive and negative errors are within 6.8 % and 4.7 % respectively. In addition, it is noted that more than 50 % of data points have their standard deviation error bounds encompassing the corresponding theoretical values. In addition, an $R^{2}$ value of 0.75 is obtained corresponding to the fitted linear regression line. In the absence of analytical formulations, the present scaling approach does a good job of establishing a functional dependence of the evaporation lifetime scaling on the characteristic governing parameters. Considering the extreme variation of evaporation lifetime in an interacting droplet array, it is asserted that the obtained $R^{2}=0.75$ value signifies statistical closeness of the experimental data. In addition, to understand the closeness of the data for different parameter space (changes in the governing parameters) a $t$ -test is performed. The experimental data are divided into two categories. Category-1, is the values corresponding to symmetric three-droplet system on PDMS and category-2 is the rest of the data that correspond to the variation of the governing parameter space. Owing to the different sizes of two data sets (categories) we opt for a $t$ -test of two samples assuming unequal variances. The null hypothesis of the $t$ -test is the zero mean difference. Using the standard significance level of 0.05 the $t$ -test parameters are tabulated.

Table 2. Statistical $t$ -test parameters for experimental data divided into two categories. Category-1: interacting three-droplet system on PDMS, and category-2: data corresponding to the variation of the governing parameter space.

Table 2 lists a $t$ -stat (0.14) value that is very much less that the corresponding $t$ -critical values (2.01), hence the difference between the two samples (categories) is considered to be insignificant. In addition, $p$ -value of 0.88 is significantly higher than the significance level value ( $\gg 0.05$ ), which indicates that there is 88 % probability that the two samples (categories) are consistent and come from the same model (behaviour). With these statistical inferences it is put forward that the current analytical model is consistent with the experimental values across a wide range of parameter space.

Figure 10. Universal merger of individual droplet parameters namely, (a) contact radius (b) contact angle and (c) droplet volume across all cases of spacing values.

9 Mode merger

Next the transient behaviour of individual contact line parameters, namely contact radius $(R_{c})$ and contact angle $(\unicode[STIX]{x1D703}_{c})$ , are revisited to study their convergence across all $L/D$ values using the droplet lifetime scaling approach. Figure 10 shows the merger of transient contact line parameters when they are scaled with their individual theoretical lifetimes, as obtained from (8.12). Overall standard deviations observed in contact radius, contact angle and droplet volume values are ${\sim}9.8\,\%$ , ${\sim}2.6\,\%$ and ${\sim}6.1\,\%$ respectively. The participation of ID in the universal collapse of contact line data shows that vapour-mediated interactions affect only the time scale of evaporation, but not the time spent by droplets in their characteristic evaporation modes which remain intact for CD, SD and ID. Therefore, in addition to evaporation lifetime values, the merger plots can be used to predict the instantaneous state of an evaporating three-droplet system across a range of $L/D$ values.

Figure 11. Confined droplet lifetime scaling analogy. (a) Schematic representing the confinement of CD (of an interacting three-droplet system) by a rectangular channel of dimensions: $L_{ch}\times W_{ch}\times H_{ch}$ . (b) Evaporation lifetime scaling of CD (of an interacting three-droplet system) with droplet separation values for two different forms of confinement (droplet–droplet and rectangular channel confinement).

10 Analogy with other confinement forms

Previous studies by Bansal et al. (Reference Bansal, Hatte, Basu and Chakraborty2017) and Hatte et al. (Reference Hatte, Dhar, Bansal, Chakraborty and Basu2019) have considered a different form of confinement wherein a single sessile droplet was symmetrically placed in a rectangular channel. In order to create an analogy between the present form of confinement (interacting three-droplet system) and the rectangular channel geometry, CD is assumed to be surrounded by a rectangular channel as depicted in figure 11(a). In order to establish an analogy, we cast the channel dimensions in terms of our three-droplet parameters as; $W_{ch}=\unicode[STIX]{x1D706}$ , $L_{ch}=D_{e}$ and $H_{ch}=H$ .

Equation (8.12) is rearranged in the following form:

(10.1) $$\begin{eqnarray}\frac{t_{e,CD}}{t_{e,ID}}=\frac{AK\unicode[STIX]{x1D6FD}\cos ec(\unicode[STIX]{x1D703}_{ci})A_{d,i}}{2R_{ci}\unicode[STIX]{x1D706}\sqrt{\unicode[STIX]{x03C0}(1+\cos ec\unicode[STIX]{x1D703}_{ci})}}+1.\end{eqnarray}$$

Using the values of channel dimensions from the analogy, the lifetime scaling formulation proposed by Bansal et al. (Reference Bansal, Hatte, Basu and Chakraborty2017) can be rearranged as follows:

(10.2) $$\begin{eqnarray}\frac{t_{e,CD}}{t_{e,ID}}=\frac{AKA_{d,i}}{0.7\times 2R_{ci}\unicode[STIX]{x1D706}}+1.\end{eqnarray}$$

In order to compare these two forms, the scaled evaporation lifetime of a CD (with respect to its ID counterpart) is plotted against variation of droplet separation values; $\unicode[STIX]{x1D706}=2L-D_{e}$ . A near perfect agreement (as seen from figure 11 b) with the present model and previous models for channel confinement (Bansal et al. Reference Bansal, Hatte, Basu and Chakraborty2017) indicates the robustness of the scaling approach irrespective of the form of confinement. To establish the universality of the evaporation lifetime scaling, the present model must be extended for a two-dimensional array of sessile droplets. In addition, the scaling approach can be verified for working fluids with significant vapour pressure differential.