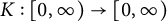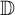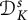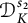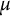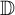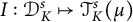1 Introduction
Let
![]() $\mathbb {D}=\{z\in \mathbb {C}: |z|<1\}$
denote the open unit disk in the complex plane
$\mathbb {D}=\{z\in \mathbb {C}: |z|<1\}$
denote the open unit disk in the complex plane
![]() $\mathbb {C}$
and let
$\mathbb {C}$
and let
![]() $H(\mathbb {D})$
be the space of all analytic functions in
$H(\mathbb {D})$
be the space of all analytic functions in
![]() $\mathbb {D}$
endowed with the topology of uniform convergence in compact subsets. For
$\mathbb {D}$
endowed with the topology of uniform convergence in compact subsets. For
![]() $-1<s<\infty $
, a function
$-1<s<\infty $
, a function
![]() $f\in H(\mathbb {D})$
belongs to the weighted Dirichlet spaces
$f\in H(\mathbb {D})$
belongs to the weighted Dirichlet spaces
![]() $\mathcal {D}_s$
if
$\mathcal {D}_s$
if
Here,
![]() $\mathrm {d}A$
is the normalized area measure on
$\mathrm {d}A$
is the normalized area measure on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Through this paper, we assume that
![]() $K: [0, \infty)\rightarrow [0, \infty)$
is a right-continuous and nondecreasing function, not identically zero. For
$K: [0, \infty)\rightarrow [0, \infty)$
is a right-continuous and nondecreasing function, not identically zero. For
![]() $0<s<\infty $
, a function
$0<s<\infty $
, a function
![]() $f\in H(\mathbb {D})$
belongs to the Morrey type space
$f\in H(\mathbb {D})$
belongs to the Morrey type space
![]() $\mathcal {D}^{s}_{K}$
if
$\mathcal {D}^{s}_{K}$
if
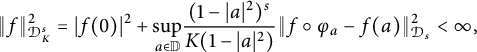 $$ \begin{align} \|f\|^{2}_{\mathcal{D}^{s}_{K}}=|f(0)|^2+\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^s}{K(1-|a|^2)}\|f\circ\varphi_{a}-f(a)\| ^{2}_{\mathcal{D}_s}<\infty, \end{align} $$
$$ \begin{align} \|f\|^{2}_{\mathcal{D}^{s}_{K}}=|f(0)|^2+\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^s}{K(1-|a|^2)}\|f\circ\varphi_{a}-f(a)\| ^{2}_{\mathcal{D}_s}<\infty, \end{align} $$
where
![]() $\varphi _{a}(z)=\frac {a-z}{1-\bar {a}z}$
is a Möbius transformation of
$\varphi _{a}(z)=\frac {a-z}{1-\bar {a}z}$
is a Möbius transformation of
![]() $\mathbb {D}$
. From the definition, we know that
$\mathbb {D}$
. From the definition, we know that
![]() $\mathcal {D}^{s}_{K}$
mainly depends on the behavior of the function
$\mathcal {D}^{s}_{K}$
mainly depends on the behavior of the function
![]() $K(t)$
for small t.
$K(t)$
for small t.
It is clear that
![]() $\mathcal {D}^{s}_{K}$
is always a subspace of
$\mathcal {D}^{s}_{K}$
is always a subspace of
![]() $\mathcal {D}_s$
for
$\mathcal {D}_s$
for
![]() $0<s<\infty $
, and
$0<s<\infty $
, and
![]() $\mathcal {D}^{s_1}_{K}\subseteq \mathcal {D}^{s_2}_{K}$
for
$\mathcal {D}^{s_1}_{K}\subseteq \mathcal {D}^{s_2}_{K}$
for
![]() $0<s_1\leq s_2<\infty $
. Some choices of s and K give known spaces. For example, if
$0<s_1\leq s_2<\infty $
. Some choices of s and K give known spaces. For example, if
![]() $K(t)=t^{s\lambda }$
,
$K(t)=t^{s\lambda }$
,
![]() $0\leq s, \lambda \leq 1$
, then
$0\leq s, \lambda \leq 1$
, then
![]() $\mathcal {D}^{s}_{K}=\mathcal {D}^{\lambda }_s$
, which was considered in [Reference Galanopoulos, Merchán and Siskakis6]; if
$\mathcal {D}^{s}_{K}=\mathcal {D}^{\lambda }_s$
, which was considered in [Reference Galanopoulos, Merchán and Siskakis6]; if
![]() $s=1$
,
$s=1$
,
![]() $\mathcal {D}^{s}_{K}$
gives
$\mathcal {D}^{s}_{K}$
gives
![]() $H^2_K$
, and if
$H^2_K$
, and if
![]() $K(t)=t^s$
,
$K(t)=t^s$
,
![]() $0<s<\infty $
, then
$0<s<\infty $
, then
![]() $\mathcal {D}^{s}_{K}=\mathcal {Q}_s$
; see [Reference Wulan and Zhou24] for
$\mathcal {D}^{s}_{K}=\mathcal {Q}_s$
; see [Reference Wulan and Zhou24] for
![]() $H^2_K$
and [Reference Xiao26, Reference Xiao27] for the theory of
$H^2_K$
and [Reference Xiao26, Reference Xiao27] for the theory of
![]() $\mathcal {Q}_s$
spaces.
$\mathcal {Q}_s$
spaces.
Denote by
![]() $\mathcal Q_K$
the space of all functions
$\mathcal Q_K$
the space of all functions
![]() $f\in H(\mathbb {D})$
for which
$f\in H(\mathbb {D})$
for which
where
![]() $g(z,a)=\mathrm {log}|\frac {1-\bar {a}z}{z-a}|$
is the Green function of
$g(z,a)=\mathrm {log}|\frac {1-\bar {a}z}{z-a}|$
is the Green function of
![]() $\mathbb {D}$
with logarithmic singularity at
$\mathbb {D}$
with logarithmic singularity at
![]() $a\in \mathbb {D}$
. If
$a\in \mathbb {D}$
. If
![]() $K(t)=t^{s}, 0<s<\infty $
, then
$K(t)=t^{s}, 0<s<\infty $
, then
![]() $\mathcal Q_{K}=\mathcal Q_{s}$
. See [Reference Essén and Wulan4, Reference Essén, Wulan and Xiao5, Reference Wulan and Zhu25] for more results of
$\mathcal Q_{K}=\mathcal Q_{s}$
. See [Reference Essén and Wulan4, Reference Essén, Wulan and Xiao5, Reference Wulan and Zhu25] for more results of
![]() $\mathcal Q_{K}$
spaces.
$\mathcal Q_{K}$
spaces.
In 1938, Morrey spaces were introduced for solutions of partial differential equations and were subsequently studied as function classes in harmonic analysis on Euclidean spaces; see [Reference Morrey12, Reference Peetre18, Reference Zorko31]. The analytic Morrey spaces have attracted a lot of attention in recent years, for example, [Reference Galanopoulos, Merchán and Siskakis6, Reference Li, Liu and Lou9, Reference Liu and Lou10, Reference Wu and Xie23, Reference Wulan and Zhou24].
The purpose of this article is to study a more general analytic Morrey type space
![]() $\mathcal {D}^s_K$
with a nondecreasing function K. Firstly, a characterization of
$\mathcal {D}^s_K$
with a nondecreasing function K. Firstly, a characterization of
![]() $\mathcal {D}^s_K$
is given by introducing K-Carleson measure. Secondly, as an extension of known results, we find a sufficient or necessary condition for the embedding map
$\mathcal {D}^s_K$
is given by introducing K-Carleson measure. Secondly, as an extension of known results, we find a sufficient or necessary condition for the embedding map
![]() $I: \mathcal {D}^s_K\mapsto \mathcal {T}^s_{K}(\mu)$
to be bounded. Finally, we obtain a feature of
$I: \mathcal {D}^s_K\mapsto \mathcal {T}^s_{K}(\mu)$
to be bounded. Finally, we obtain a feature of
![]() $\mathcal {D}_K^s$
in terms of the fractional order derivatives, and build a bridge between two spaces
$\mathcal {D}_K^s$
in terms of the fractional order derivatives, and build a bridge between two spaces
![]() $\mathcal {D}^{s_1}_K$
and
$\mathcal {D}^{s_1}_K$
and
![]() $\mathcal {D}^{s_2}_K$
by the fractional order derivatives.
$\mathcal {D}^{s_2}_K$
by the fractional order derivatives.
We will write
![]() $A\lesssim B$
, if there exists a constant
$A\lesssim B$
, if there exists a constant
![]() $C>0$
such that
$C>0$
such that
![]() $A\leq CB$
. Also, the symbol
$A\leq CB$
. Also, the symbol
![]() $A\approx B$
means that
$A\approx B$
means that
![]() $A\lesssim B\lesssim A$
.
$A\lesssim B\lesssim A$
.
2 Spaces
 $\mathcal {D}^{s}_{K}$
via K-Carleson measures
$\mathcal {D}^{s}_{K}$
via K-Carleson measures
We say K satisfies the doubling condition if there exist positive constants C and M such that
In many situations, we will need to consider two conditions on K as follows:
and
where
It is clear that the function
![]() $K(t)=t^p$
satisfies (2.1) for all p,
$K(t)=t^p$
satisfies (2.1) for all p,
![]() $0<p<\infty $
, and satisfies (2.2) whenever
$0<p<\infty $
, and satisfies (2.2) whenever
![]() $0<p<\sigma $
. The following results about the weight function will be needed ([Reference Essén, Wulan and Xiao5, Lemmas 2.1 and 2.2] or [Reference Wulan and Zhu25, Theorems 3.4 and 3.5]).
$0<p<\sigma $
. The following results about the weight function will be needed ([Reference Essén, Wulan and Xiao5, Lemmas 2.1 and 2.2] or [Reference Wulan and Zhu25, Theorems 3.4 and 3.5]).
Lemma A Suppose K satisfies condition (2.1) and the doubling condition on
![]() $(0,1)$
. Then there exists a weight function
$(0,1)$
. Then there exists a weight function
![]() $K_{1}$
such that
$K_{1}$
such that
![]() $K_{1}$
is comparable with K on
$K_{1}$
is comparable with K on
![]() $(0,1)$
, and the function
$(0,1)$
, and the function
![]() $\frac {K_1(t)}{t^c}$
is increasing on
$\frac {K_1(t)}{t^c}$
is increasing on
![]() $(0,1)$
for all sufficiently small positive constants c.
$(0,1)$
for all sufficiently small positive constants c.
Lemma B Suppose K satisfies condition (2.2) for some
![]() $\sigma>0$
. Then there exists a weight function
$\sigma>0$
. Then there exists a weight function
![]() $K_{2}$
such that
$K_{2}$
such that
![]() $K_{2}$
is comparable with K on (0,1), and the functions
$K_{2}$
is comparable with K on (0,1), and the functions
![]() $\frac {K_2(t)}{t^\sigma }$
and
$\frac {K_2(t)}{t^\sigma }$
and
![]() $\frac {K_2(t)}{t^{\sigma -c}}$
are both decreasing on
$\frac {K_2(t)}{t^{\sigma -c}}$
are both decreasing on
![]() $(0,1)$
for all sufficiently small positive constants c.
$(0,1)$
for all sufficiently small positive constants c.
Remark 2.1 If K satisfies condition (2.2) for some
![]() $\sigma>0$
, we are able to obtain some results as follows.
$\sigma>0$
, we are able to obtain some results as follows.
-
(i) For
 $0<t\leq r<\infty $
, it is easy to see that for all sufficiently small positive constants
$0<t\leq r<\infty $
, it is easy to see that for all sufficiently small positive constants $$ \begin{align*}\frac{K(r)}{K(t)}=\frac{K(r)t^{\sigma-c}}{r^{\sigma-c}K(t)}\bigg(\frac{r}{t}\bigg)^{\sigma-c}\leq\bigg(\frac{r}{t}\bigg)^{\sigma-c} \leq\bigg(\frac{r}{t}\bigg)^\sigma \end{align*} $$
$$ \begin{align*}\frac{K(r)}{K(t)}=\frac{K(r)t^{\sigma-c}}{r^{\sigma-c}K(t)}\bigg(\frac{r}{t}\bigg)^{\sigma-c}\leq\bigg(\frac{r}{t}\bigg)^{\sigma-c} \leq\bigg(\frac{r}{t}\bigg)^\sigma \end{align*} $$
 $c<\sigma $
.
$c<\sigma $
.
-
(ii) The function K satisfies the doubling condition [Reference Wulan and Zhu25, Corollary 3.2].
-
(iii)
 $\mathcal Q_s\subseteq \mathcal {D}^{s}_K$
for
$\mathcal Q_s\subseteq \mathcal {D}^{s}_K$
for
 $\sigma \leq s<\infty $
.
$\sigma \leq s<\infty $
. -
(iv) Furthermore, if K satisfies (2.1), then
 $\mathcal {D}^{c}_K\subseteq \mathcal Q_K \subseteq \mathcal {D}^{\sigma }_K$
for all sufficiently small positive constants
$\mathcal {D}^{c}_K\subseteq \mathcal Q_K \subseteq \mathcal {D}^{\sigma }_K$
for all sufficiently small positive constants
 $c<\sigma $
.
$c<\sigma $
.
Proposition 2.1 Let
![]() $0<s< \infty $
. Then
$0<s< \infty $
. Then
![]() $\mathcal {D}^{s}_{K}\subseteq \mathcal {D}_{s}$
and moreover,
$\mathcal {D}^{s}_{K}\subseteq \mathcal {D}_{s}$
and moreover,
![]() $\mathcal {D}^{s}_{K}=\mathcal {D}_{s}$
if and only if
$\mathcal {D}^{s}_{K}=\mathcal {D}_{s}$
if and only if
![]() $K(0)>0$
.
$K(0)>0$
.
Proof Note that
![]() $\mathcal {D}^{s}_{K}\subseteq \mathcal {D}_{s}$
is obvious. Assume that
$\mathcal {D}^{s}_{K}\subseteq \mathcal {D}_{s}$
is obvious. Assume that
![]() $K(0)>0$
and
$K(0)>0$
and
![]() $f\in \mathcal {D}_s$
. Since K is nondecreasing, we have
$f\in \mathcal {D}_s$
. Since K is nondecreasing, we have
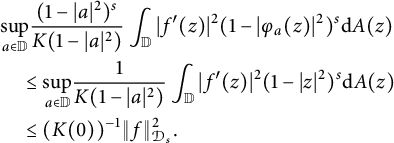 $$ \begin{align*} &\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^s}{K(1-|a|^2)} \int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z)\\ &\quad\leq\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)} \int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|z|^2)^{s}\mathrm{d}A(z)\\ &\quad \leq (K(0))^{-1}\|f\|^2_{\mathcal{D}_s}. \end{align*} $$
$$ \begin{align*} &\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^s}{K(1-|a|^2)} \int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z)\\ &\quad\leq\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)} \int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|z|^2)^{s}\mathrm{d}A(z)\\ &\quad \leq (K(0))^{-1}\|f\|^2_{\mathcal{D}_s}. \end{align*} $$
Thus,
![]() $f\in \mathcal {D}^{s}_{K}$
and so
$f\in \mathcal {D}^{s}_{K}$
and so
![]() $\mathcal {D}^{s}_{K}=\mathcal {D}_s$
.
$\mathcal {D}^{s}_{K}=\mathcal {D}_s$
.
Conversely, for
![]() $0<r<1$
, let
$0<r<1$
, let
![]() $\mathbb {D}(c,r)=\{z\in \mathbb {D}: |\varphi _{c}(z)| < r \}$
be a pseudo-hyperbolic disk centered at
$\mathbb {D}(c,r)=\{z\in \mathbb {D}: |\varphi _{c}(z)| < r \}$
be a pseudo-hyperbolic disk centered at
![]() $c\in \mathbb {D}$
. It is well-known that
$c\in \mathbb {D}$
. It is well-known that
for all
![]() $z\in \mathbb {D}(c,r)$
. Assume that
$z\in \mathbb {D}(c,r)$
. Assume that
![]() $\mathcal {D}^{s}_{K}=\mathcal {D}_s, 0 < s < \infty $
. The closed graph theorem yields that the identity map from
$\mathcal {D}^{s}_{K}=\mathcal {D}_s, 0 < s < \infty $
. The closed graph theorem yields that the identity map from
![]() $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
![]() $\mathcal {D}^{s}_{K}$
is continuous. Thus, there exists a positive constant C such that
$\mathcal {D}^{s}_{K}$
is continuous. Thus, there exists a positive constant C such that
for all
![]() $f\in \mathcal {D}_s$
. For
$f\in \mathcal {D}_s$
. For
![]() $c\in \mathbb {D}$
, we consider the test function
$c\in \mathbb {D}$
, we consider the test function
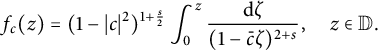 $$ \begin{align*}f_c(z)=(1-|c|^2)^{1+\frac{s}{2}}\int_{0}^{z}\frac{\mathrm{d}\zeta}{(1-\bar{c}\zeta)^{2+s}}, \quad z\in \mathbb{D}. \end{align*} $$
$$ \begin{align*}f_c(z)=(1-|c|^2)^{1+\frac{s}{2}}\int_{0}^{z}\frac{\mathrm{d}\zeta}{(1-\bar{c}\zeta)^{2+s}}, \quad z\in \mathbb{D}. \end{align*} $$
The use of [Reference Zhu30, Lemma 3.10] yields
see [Reference Pau and Peláez16, Theorem 3.1]. Combining this with (2.3) gives that
Hence,
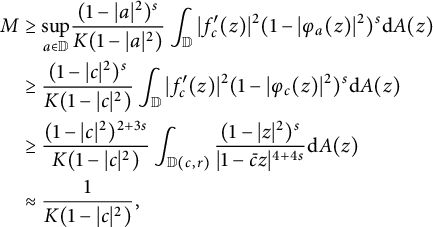 $$ \begin{align*} M&\geq\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^{s}}{K(1-|a|^2)} \int_{\mathbb{D}}|f_c^{\prime}(z)|^{2}(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z)\\ &\geq\frac{(1-|c|^2)^{s}}{K(1-|c|^2)} \int_{\mathbb{D}}|f_c^{\prime}(z)|^{2}(1-|\varphi_c(z)|^{2})^{s}\mathrm{d}A(z)\\ &\geq\frac{(1-|c|^2)^{2+3s}}{K(1-|c|^2)} \int_{\mathbb{D}(c,r)}\frac{(1-|z|^2)^{s}}{|1-\bar{c}z|^{4+4s}}\mathrm{d}A(z)\\ &\approx\frac{1}{K(1-|c|^2)}, \end{align*} $$
$$ \begin{align*} M&\geq\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^{s}}{K(1-|a|^2)} \int_{\mathbb{D}}|f_c^{\prime}(z)|^{2}(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z)\\ &\geq\frac{(1-|c|^2)^{s}}{K(1-|c|^2)} \int_{\mathbb{D}}|f_c^{\prime}(z)|^{2}(1-|\varphi_c(z)|^{2})^{s}\mathrm{d}A(z)\\ &\geq\frac{(1-|c|^2)^{2+3s}}{K(1-|c|^2)} \int_{\mathbb{D}(c,r)}\frac{(1-|z|^2)^{s}}{|1-\bar{c}z|^{4+4s}}\mathrm{d}A(z)\\ &\approx\frac{1}{K(1-|c|^2)}, \end{align*} $$
which clearly implies
![]() $K(0)>0$
. The proof is complete. ▪
$K(0)>0$
. The proof is complete. ▪
Proposition 2.2 Suppose K satisfies condition (2.2) for some
![]() $\sigma>0$
. Then
$\sigma>0$
. Then
![]() $\mathcal {D}^{s}_{K}=\mathcal Q_s$
if and only if
$\mathcal {D}^{s}_{K}=\mathcal Q_s$
if and only if
![]() $K(t)\approx t^s, 0 < s < \infty $
.
$K(t)\approx t^s, 0 < s < \infty $
.
Proof The proof is easily completed by the following estimates:
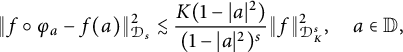 $$ \begin{align*}\|f\circ\varphi_{a}-f(a)\| ^{2}_{\mathcal{D}_s}\lesssim\frac{K(1-|a|^2)}{(1-|a|^2)^s}\|f\|^{2}_{\mathcal{D}_K^s},\quad a\in\mathbb{D}, \end{align*} $$
$$ \begin{align*}\|f\circ\varphi_{a}-f(a)\| ^{2}_{\mathcal{D}_s}\lesssim\frac{K(1-|a|^2)}{(1-|a|^2)^s}\|f\|^{2}_{\mathcal{D}_K^s},\quad a\in\mathbb{D}, \end{align*} $$
and
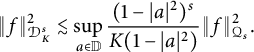 $$ \begin{align*}\|f\|^{2}_{\mathcal{D}_K^s}\lesssim\mathop{\mathrm{sup}}\limits_{a\in\mathbb{D}}\frac{(1-|a|^2)^s}{K(1-|a|^2)}\|f\|^{2}_{\mathcal Q_s}. \end{align*} $$
$$ \begin{align*}\|f\|^{2}_{\mathcal{D}_K^s}\lesssim\mathop{\mathrm{sup}}\limits_{a\in\mathbb{D}}\frac{(1-|a|^2)^s}{K(1-|a|^2)}\|f\|^{2}_{\mathcal Q_s}. \end{align*} $$
▪
Let
![]() $|I|$
be the normalized length of arc I on the unit circle
$|I|$
be the normalized length of arc I on the unit circle
![]() $\mathbb {T}$
, and let
$\mathbb {T}$
, and let
![]() $S(I)$
be the Carleson box defined by
$S(I)$
be the Carleson box defined by
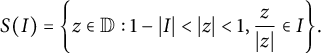 $$ \begin{align*}S(I)=\bigg\{z\in\mathbb{D}: 1-|I|<|z|<1, \frac{z}{|z|}\in I\bigg\}. \end{align*} $$
$$ \begin{align*}S(I)=\bigg\{z\in\mathbb{D}: 1-|I|<|z|<1, \frac{z}{|z|}\in I\bigg\}. \end{align*} $$
A positive Borel measure
![]() $\mu $
is a K-Carleson measure on
$\mu $
is a K-Carleson measure on
![]() $\mathbb {D}$
if
$\mathbb {D}$
if
For
![]() $0<s<\infty, 0\leq \alpha <\infty $
, if we choose
$0<s<\infty, 0\leq \alpha <\infty $
, if we choose
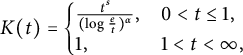 $$ \begin{align*} K(t)=\left\{\begin{array}{@{}ll} \frac{t^s}{(\log\frac{e}{t})^\alpha}, & 0 < t \leq1,\\ 1, & 1 < t < \infty, \end{array} \right. \end{align*} $$
$$ \begin{align*} K(t)=\left\{\begin{array}{@{}ll} \frac{t^s}{(\log\frac{e}{t})^\alpha}, & 0 < t \leq1,\\ 1, & 1 < t < \infty, \end{array} \right. \end{align*} $$
then
![]() $\mu $
is
$\mu $
is
![]() $(\alpha, s)$
-logarithmic Carleson measure [Reference Zhao29]; if
$(\alpha, s)$
-logarithmic Carleson measure [Reference Zhao29]; if
![]() $\alpha =0$
, the
$\alpha =0$
, the
![]() $(0, s)$
-logarithmic Carleson measure coincides with s-Carleson measure.
$(0, s)$
-logarithmic Carleson measure coincides with s-Carleson measure.
Theorem 2.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\mu $
is a positive Borel measure on
$\mu $
is a positive Borel measure on
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
![]() $\mu $
is a K-Carleson measure if and only if
$\mu $
is a K-Carleson measure if and only if
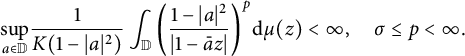 $$ \begin{align} \underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}} \bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z)<\infty, \quad \sigma\leq p<\infty. \end{align} $$
$$ \begin{align} \underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}} \bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z)<\infty, \quad \sigma\leq p<\infty. \end{align} $$
Proof Assume that (2.4) holds. For an interval
![]() $I\subseteq \mathbb {T}$
, let
$I\subseteq \mathbb {T}$
, let
![]() $e^{i\theta }$
,
$e^{i\theta }$
,
![]() $\theta \in [0,2\pi)$
, be the midpoint of I and
$\theta \in [0,2\pi)$
, be the midpoint of I and
![]() $a=(1-|I|)e^{i\theta }$
. Note that
$a=(1-|I|)e^{i\theta }$
. Note that
By the doubling condition, we have
Thus,
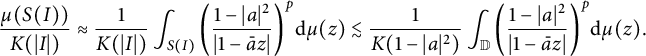 $$ \begin{align*} \frac{\mu(S(I))}{K(|I|)}\approx\frac{1}{K(|I|)}\int_{S(I)}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) \lesssim\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z). \end{align*} $$
$$ \begin{align*} \frac{\mu(S(I))}{K(|I|)}\approx\frac{1}{K(|I|)}\int_{S(I)}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) \lesssim\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z). \end{align*} $$
Therefore,
![]() $\mu $
is a K-Carleson measure.
$\mu $
is a K-Carleson measure.
On the other hand, suppose
![]() $\mu $
is K-Carleson measure and
$\mu $
is K-Carleson measure and
![]() $2^nI$
denotes the arc with the same center as I and the length
$2^nI$
denotes the arc with the same center as I and the length
![]() $2^n|I|$
. Then we have the following estimate:
$2^n|I|$
. Then we have the following estimate:
which implies for
![]() $\sigma \leq p<\infty $
$\sigma \leq p<\infty $
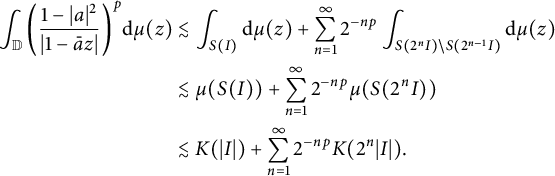 $$ \begin{align*} \int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) &\lesssim\int_{S(I)}\mathrm{d}\mu(z)+ \sum^{\infty}_{n=1}2^{-np}\int_{S(2^{n}I)\backslash S(2^{n-1}I)}\mathrm{d}\mu(z)\\ &\lesssim\mu(S(I))+\sum^{\infty}_{n=1}2^{-np}\mu(S(2^{n}I))\\ &\lesssim K(|I|)+\sum^{\infty}_{n=1}2^{-np}K(2^{n}|I|). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) &\lesssim\int_{S(I)}\mathrm{d}\mu(z)+ \sum^{\infty}_{n=1}2^{-np}\int_{S(2^{n}I)\backslash S(2^{n-1}I)}\mathrm{d}\mu(z)\\ &\lesssim\mu(S(I))+\sum^{\infty}_{n=1}2^{-np}\mu(S(2^{n}I))\\ &\lesssim K(|I|)+\sum^{\infty}_{n=1}2^{-np}K(2^{n}|I|). \end{align*} $$
By Lemma B, there exists a sufficiently small positive constant c such that
Consequently,
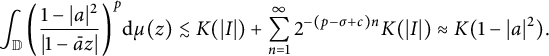 $$ \begin{align*} \int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) \lesssim K(|I|)+\sum^{\infty}_{n=1}2^{-(p-\sigma+c)n}K(|I|)\approx K(1-|a|^2). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}}\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^p\mathrm{d}\mu(z) \lesssim K(|I|)+\sum^{\infty}_{n=1}2^{-(p-\sigma+c)n}K(|I|)\approx K(1-|a|^2). \end{align*} $$
This completes the proof of Theorem 2.1. ▪
Note that Theorem 2.1 gives a new characterization of
![]() $\mathcal {D}^{s}_{K}$
space in terms of K-Carleson measure by replacing
$\mathcal {D}^{s}_{K}$
space in terms of K-Carleson measure by replacing
![]() $\mathrm {d}\mu (z)$
by
$\mathrm {d}\mu (z)$
by
![]() $|f^{\prime }(z)|^2(1-|z|^2)^s\mathrm {d}A(z)$
and putting
$|f^{\prime }(z)|^2(1-|z|^2)^s\mathrm {d}A(z)$
and putting
![]() $p=2s$
.
$p=2s$
.
Theorem 2.2 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\frac {\sigma }{2}\leq s<\infty $
. Then
$\frac {\sigma }{2}\leq s<\infty $
. Then
![]() $f\in \mathcal {D}^{s}_{K}$
if and only if
$f\in \mathcal {D}^{s}_{K}$
if and only if
3 The embedding map from
 $\mathcal {D}^{s}_{K}$
to
$\mathcal {D}^{s}_{K}$
to
 $\mathcal {T}^s_{K}(\mu)$
$\mathcal {T}^s_{K}(\mu)$
Let X be a space of analytic functions in
![]() $\mathbb D$
. For
$\mathbb D$
. For
![]() $0 <p<\infty $
, a positive Borel measure
$0 <p<\infty $
, a positive Borel measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {D}$
is said to be a p-Carleson measure for the space X if the embedding map
$\mathbb {D}$
is said to be a p-Carleson measure for the space X if the embedding map
![]() $I: X \mapsto L^p(d\mu)$
is a bounded operator, i.e., there is a constant
$I: X \mapsto L^p(d\mu)$
is a bounded operator, i.e., there is a constant
![]() $C>0$
such that
$C>0$
such that
for all functions
![]() $f\in X$
. When the parameter
$f\in X$
. When the parameter
![]() $p=2$
, we always simply leave out the p in front of the Carleson measure. Note that the following two notations are different:
$p=2$
, we always simply leave out the p in front of the Carleson measure. Note that the following two notations are different:
-
(i)
 $\mu $
is a p-Carleson measure on
$\mu $
is a p-Carleson measure on
 $\mathbb D$
and
$\mathbb D$
and -
(ii)
 $\mu $
is a p-Carleson measure for a space X.
$\mu $
is a p-Carleson measure for a space X.
Carleson’s embedding theorem [Reference Carleson3] shows that
![]() $\mu $
is a Carleson measure on
$\mu $
is a Carleson measure on
![]() $\mathbb D$
if and only if
$\mathbb D$
if and only if
![]() $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for
![]() $H^2$
. Similar results for some Bergman spaces and Dirichlet type spaces can be found in [Reference Oleinik13, Reference Stegenga21, Reference Wu22]. However, Stegenga [Reference Stegenga21] proved that
$H^2$
. Similar results for some Bergman spaces and Dirichlet type spaces can be found in [Reference Oleinik13, Reference Stegenga21, Reference Wu22]. However, Stegenga [Reference Stegenga21] proved that
![]() $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for
![]() $\mathcal {D}_s$
implies that
$\mathcal {D}_s$
implies that
![]() $\mu $
is an s-Carleson measure on
$\mu $
is an s-Carleson measure on
![]() $\mathbb D$
for
$\mathbb D$
for
![]() $0<s<\infty $
but the converse is true only for
$0<s<\infty $
but the converse is true only for
![]() $s\ge 1$
. There are many research works on these topics for different function spaces; see, for example, [Reference Girela and Peláez7, Reference Kerman and Sawyer8, Reference Liu, Lou and Zhu11, Reference Xiao27].
$s\ge 1$
. There are many research works on these topics for different function spaces; see, for example, [Reference Girela and Peláez7, Reference Kerman and Sawyer8, Reference Liu, Lou and Zhu11, Reference Xiao27].
For
![]() $0<s<\infty $
and a positive Borel measure
$0<s<\infty $
and a positive Borel measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {D}$
, we define a new space
$\mathbb {D}$
, we define a new space
![]() $\mathcal {T}^s_{K}(\mu)$
consisting of functions
$\mathcal {T}^s_{K}(\mu)$
consisting of functions
![]() $f\in H(\mathbb {D})$
for which
$f\in H(\mathbb {D})$
for which
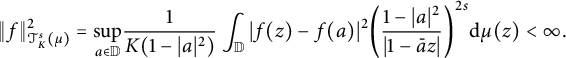 $$ \begin{align*}\|f\|^2_{\mathcal{T}^s_{K}(\mu)}=\underset{a\in\mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)} \int_{\mathbb{D}}|f(z)-f(a)|^2\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^{2s}\mathrm{d}\mu(z)<\infty. \end{align*} $$
$$ \begin{align*}\|f\|^2_{\mathcal{T}^s_{K}(\mu)}=\underset{a\in\mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)} \int_{\mathbb{D}}|f(z)-f(a)|^2\bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^{2s}\mathrm{d}\mu(z)<\infty. \end{align*} $$
We will consider the embedding map
![]() $I: \mathcal {D}^s_K\mapsto \mathcal {T}^s_{K}(\mu)$
and find sufficient or necessary condition for the operator I to be bounded. As an extension of results of [Reference Galanopoulos, Merchán and Siskakis6, Reference Liu, Lou and Zhu11, Reference Pau and Peláez15, Reference Qian and Li19, Reference Xiao28], we state the following theorem.
$I: \mathcal {D}^s_K\mapsto \mathcal {T}^s_{K}(\mu)$
and find sufficient or necessary condition for the operator I to be bounded. As an extension of results of [Reference Galanopoulos, Merchán and Siskakis6, Reference Liu, Lou and Zhu11, Reference Pau and Peláez15, Reference Qian and Li19, Reference Xiao28], we state the following theorem.
Theorem 3.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\frac {\sigma }{2}\leq s<\infty $
. For a positive Borel measure
$\frac {\sigma }{2}\leq s<\infty $
. For a positive Borel measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {D}$
, the following results are true.
$\mathbb {D}$
, the following results are true.
-
(i) If
 $I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded, then
$I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded, then
 $\mu $
is an s-Carleson measure on
$\mu $
is an s-Carleson measure on
 $\mathbb D$
.
$\mathbb D$
. -
(ii) If
 $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for
 $\mathcal {D}_s$
, then
$\mathcal {D}_s$
, then
 $I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded.
$I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded.
The following Lemmas will be used in the proof of Theorem 3.1.
Lemma C ([Reference Ortega and Fàbrega14, Reference Pau and Zhao17])
If
![]() $s>-1$
,
$s>-1$
,
![]() $r, t>0$
with
$r, t>0$
with
![]() $r+t-s-2>0$
, then
$r+t-s-2>0$
, then
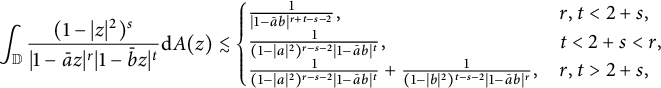 $$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{a}z|^r|1-\bar{b}z|^t}\mathrm{d}A(z)\lesssim\left\{ \begin{array}{@{}ll} \frac{1}{|1-\bar{a}b|^{r+t-s-2}}, & r,t < 2+s,\\ \frac{1}{(1-|a|^2)^{r-s-2}|1-\bar{a}b|^{t}}, & t < 2+s < r,\\ \frac{1}{(1-|a|^2)^{r-s-2}|1-\bar{a}b|^{t}} +\frac{1}{(1-|b|^2)^{t-s-2}|1-\bar{a}b|^{r}}, & r,t > 2+s,\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{a}z|^r|1-\bar{b}z|^t}\mathrm{d}A(z)\lesssim\left\{ \begin{array}{@{}ll} \frac{1}{|1-\bar{a}b|^{r+t-s-2}}, & r,t < 2+s,\\ \frac{1}{(1-|a|^2)^{r-s-2}|1-\bar{a}b|^{t}}, & t < 2+s < r,\\ \frac{1}{(1-|a|^2)^{r-s-2}|1-\bar{a}b|^{t}} +\frac{1}{(1-|b|^2)^{t-s-2}|1-\bar{a}b|^{r}}, & r,t > 2+s,\\ \end{array} \right. \end{align*} $$
for all
![]() $a,b\in \mathbb {D}$
.
$a,b\in \mathbb {D}$
.
Lemma 3.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\frac {\sigma }{2}\leq s<\infty $
. Then the functions
$\frac {\sigma }{2}\leq s<\infty $
. Then the functions
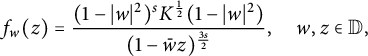 $$ \begin{align*}f_{w}(z)=\frac{(1-|w|^2)^sK^{\frac{1}{2}}(1-|w|^2)}{(1-\bar{w}z)^{\frac{3s}{2}}}, \quad w, z\in\mathbb{D}, \end{align*} $$
$$ \begin{align*}f_{w}(z)=\frac{(1-|w|^2)^sK^{\frac{1}{2}}(1-|w|^2)}{(1-\bar{w}z)^{\frac{3s}{2}}}, \quad w, z\in\mathbb{D}, \end{align*} $$
belong to
![]() $\mathcal {D}^{s}_{K}$
and
$\mathcal {D}^{s}_{K}$
and
Proof By a simple calculation,
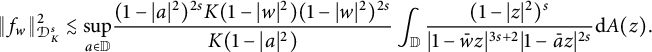 $$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 \lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^{2s}K(1-|w|^2)(1-|w|^2)^{2s}}{K(1-|a|^2)} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{w}z|^{3s+2}|1-\bar{a}z|^{2s}}\mathrm{d}A(z). \end{align*} $$
$$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 \lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{(1-|a|^2)^{2s}K(1-|w|^2)(1-|w|^2)^{2s}}{K(1-|a|^2)} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{w}z|^{3s+2}|1-\bar{a}z|^{2s}}\mathrm{d}A(z). \end{align*} $$
Case 1. For
![]() $\frac {\sigma }{2}\leq s<2$
, it follows from Lemma C that
$\frac {\sigma }{2}\leq s<2$
, it follows from Lemma C that
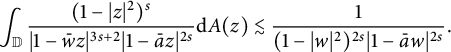 $$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{w}z|^{3s+2}|1-\bar{a}z|^{2s}}\mathrm{d}A(z) \lesssim\frac{1}{(1-|w|^2)^{2s}|1-\bar{a}w|^{2s}}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^s}{|1-\bar{w}z|^{3s+2}|1-\bar{a}z|^{2s}}\mathrm{d}A(z) \lesssim\frac{1}{(1-|w|^2)^{2s}|1-\bar{a}w|^{2s}}. \end{align*} $$
Thus,
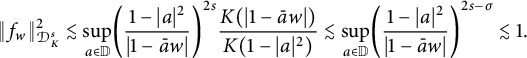 $$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 \lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s}\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)} \lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s-\sigma}\lesssim 1. \end{align*} $$
$$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 \lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s}\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)} \lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s-\sigma}\lesssim 1. \end{align*} $$
Case 2. For
![]() $s=2$
, choosing a number
$s=2$
, choosing a number
![]() $\delta, 0<\delta \leq \sigma $
, and applying Lemma C, we have
$\delta, 0<\delta \leq \sigma $
, and applying Lemma C, we have
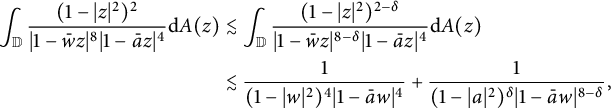 $$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^2}{|1-\bar{w}z|^{8}|1-\bar{a}z|^{4}}\mathrm{d}A(z) &\lesssim\int_{\mathbb{D}}\frac{(1-|z|^2)^{2-\delta}}{|1-\bar{w}z|^{8-\delta}|1-\bar{a}z|^{4}}\mathrm{d}A(z)\\ &\lesssim\frac{1}{(1-|w|^2)^{4}|1-\bar{a}w|^{4}}+\frac{1}{(1-|a|^2)^{\delta}|1-\bar{a}w|^{8-\delta}}, \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}}\frac{(1-|z|^2)^2}{|1-\bar{w}z|^{8}|1-\bar{a}z|^{4}}\mathrm{d}A(z) &\lesssim\int_{\mathbb{D}}\frac{(1-|z|^2)^{2-\delta}}{|1-\bar{w}z|^{8-\delta}|1-\bar{a}z|^{4}}\mathrm{d}A(z)\\ &\lesssim\frac{1}{(1-|w|^2)^{4}|1-\bar{a}w|^{4}}+\frac{1}{(1-|a|^2)^{\delta}|1-\bar{a}w|^{8-\delta}}, \end{align*} $$
and hence
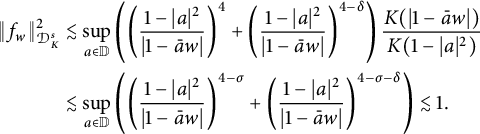 $$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 &\lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\delta}\right)\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)}\\ &\lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\sigma}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\sigma-\delta}\right)\lesssim 1. \end{align*} $$
$$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 &\lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\delta}\right)\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)}\\ &\lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\sigma}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{4-\sigma-\delta}\right)\lesssim 1. \end{align*} $$
Case 3. For
![]() $2< s<\infty $
, we similarly obtain that
$2< s<\infty $
, we similarly obtain that
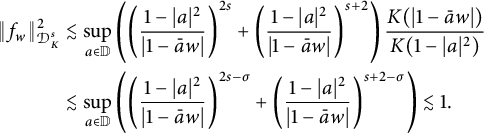 $$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 &\lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{s+2}\right)\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)}\\ &\lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s-\sigma}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{s+2-\sigma}\right)\lesssim 1. \end{align*} $$
$$ \begin{align*} \|f_w\|_{\mathcal{D}^s_K}^2 &\lesssim\underset{a\in\mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{s+2}\right)\frac{K(|1-\bar{a}w|)}{K(1-|a|^2)}\\ &\lesssim\underset{a\in \mathbb{D}}{\mathrm{sup}}\left(\bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{2s-\sigma}+ \bigg(\frac{1-|a|^2}{|1-\bar{a}w|}\bigg)^{s+2-\sigma}\right)\lesssim 1. \end{align*} $$
Therefore, (3.2) is checked. ▪
The following result gives an estimate on the growth of a function f in
![]() $\mathcal {D}^{s}_{K}$
.
$\mathcal {D}^{s}_{K}$
.
Lemma 3.2 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\frac {\sigma }{2}\leq s<\infty $
. Then for any
$\frac {\sigma }{2}\leq s<\infty $
. Then for any
![]() $f\in \mathcal {D}^{s}_{K}$
,
$f\in \mathcal {D}^{s}_{K}$
,
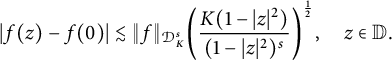 $$ \begin{align} |f(z)-f(0)|\lesssim\|f\|_{\mathcal{D}^{s}_{K}}\bigg(\frac{K(1-|z|^2)}{(1-|z|^2)^s}\bigg)^{\frac{1}{2}}, \quad z\in\mathbb{D}. \end{align} $$
$$ \begin{align} |f(z)-f(0)|\lesssim\|f\|_{\mathcal{D}^{s}_{K}}\bigg(\frac{K(1-|z|^2)}{(1-|z|^2)^s}\bigg)^{\frac{1}{2}}, \quad z\in\mathbb{D}. \end{align} $$
Proof Let
![]() $\mathbb {D}(w,r)=\{z\in \mathbb {D}: |\varphi _{w}(z)| < r \}, w\in \mathbb {D}, 0 < r < 1$
. Using the submean value property of
$\mathbb {D}(w,r)=\{z\in \mathbb {D}: |\varphi _{w}(z)| < r \}, w\in \mathbb {D}, 0 < r < 1$
. Using the submean value property of
![]() $|f^{\prime }(z)|^{2}$
, we get
$|f^{\prime }(z)|^{2}$
, we get
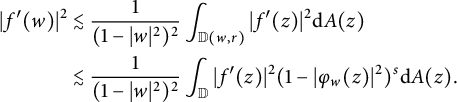 $$ \begin{align*} |f^{\prime}(w)|^{2}&\lesssim\frac{1}{(1-|w|^2)^{2}}\int_{\mathbb{D}(w,r)}|f^{\prime}(z)|^{2}\mathrm{d}A(z)\\ &\lesssim\frac{1}{(1-|w|^2)^{2}}\int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|\varphi_{w}(z)|^2)^{s}\mathrm{d}A(z). \end{align*} $$
$$ \begin{align*} |f^{\prime}(w)|^{2}&\lesssim\frac{1}{(1-|w|^2)^{2}}\int_{\mathbb{D}(w,r)}|f^{\prime}(z)|^{2}\mathrm{d}A(z)\\ &\lesssim\frac{1}{(1-|w|^2)^{2}}\int_{\mathbb{D}}|f^{\prime}(z)|^{2}(1-|\varphi_{w}(z)|^2)^{s}\mathrm{d}A(z). \end{align*} $$
Hence,
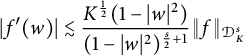 $$ \begin{align*}|f^{\prime}(w)|\lesssim\frac{K^{\frac{1}{2}}(1-|w|^2)}{(1-|w|^2)^{\frac{s}{2}+1}}\|f\|_{\mathcal{D}^{s}_{K}} \end{align*} $$
$$ \begin{align*}|f^{\prime}(w)|\lesssim\frac{K^{\frac{1}{2}}(1-|w|^2)}{(1-|w|^2)^{\frac{s}{2}+1}}\|f\|_{\mathcal{D}^{s}_{K}} \end{align*} $$
and
 $$ \begin{align} |f(w)-f(0)|=\bigg|w\int^1_0f^{\prime}(wt)\mathrm{d}t\bigg|\lesssim\|f\|_{\mathcal{D}^{s}_{K}} \int^1_0\frac{K^{\frac{1}{2}}(1-|wt|^2)}{(1-|wt|^2)^{\frac{s}{2}+1}}|w|\mathrm{d}t. \end{align} $$
$$ \begin{align} |f(w)-f(0)|=\bigg|w\int^1_0f^{\prime}(wt)\mathrm{d}t\bigg|\lesssim\|f\|_{\mathcal{D}^{s}_{K}} \int^1_0\frac{K^{\frac{1}{2}}(1-|wt|^2)}{(1-|wt|^2)^{\frac{s}{2}+1}}|w|\mathrm{d}t. \end{align} $$
Under the preliminary assumption that K satisfies condition (2.2) for some
![]() $\sigma $
, there exists a sufficiently small positive constant c such that
$\sigma $
, there exists a sufficiently small positive constant c such that
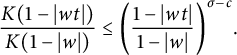 $$ \begin{align*} \frac{K(1-|wt|)}{K(1-|w|)}\leq\bigg(\frac{1-|wt|}{1-|w|}\bigg)^{\sigma-c}. \end{align*} $$
$$ \begin{align*} \frac{K(1-|wt|)}{K(1-|w|)}\leq\bigg(\frac{1-|wt|}{1-|w|}\bigg)^{\sigma-c}. \end{align*} $$
Consequently, the integral on the right-hand side of (3.4) is dominated by
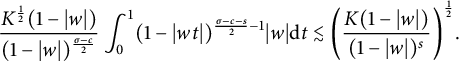 $$ \begin{align*} \frac{K^{\frac{1}{2}}(1-|w|)}{(1-|w|)^{\frac{\sigma-c}{2}}}\int^1_0(1-|wt|)^{\frac{\sigma-c-s}{2}-1}|w|\mathrm{d}t \lesssim\bigg(\frac{K(1-|w|)}{(1-|w|)^s}\bigg)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \frac{K^{\frac{1}{2}}(1-|w|)}{(1-|w|)^{\frac{\sigma-c}{2}}}\int^1_0(1-|wt|)^{\frac{\sigma-c-s}{2}-1}|w|\mathrm{d}t \lesssim\bigg(\frac{K(1-|w|)}{(1-|w|)^s}\bigg)^{\frac{1}{2}}. \end{align*} $$
Here, we choose
![]() $0<c<\sigma $
such that
$0<c<\sigma $
such that
![]() $\sigma -s-c>0$
for
$\sigma -s-c>0$
for
![]() $\sigma -s>0$
and choose
$\sigma -s>0$
and choose
![]() $0<c<\sigma $
such that
$0<c<\sigma $
such that
![]() $\sigma -s-c<0$
for
$\sigma -s-c<0$
for
![]() $\sigma -s\le 0$
. Thus, we obtain the desired growth inequality (3.3). ▪
$\sigma -s\le 0$
. Thus, we obtain the desired growth inequality (3.3). ▪
Proof Proof of Theorem 3.1
Suppose condition (i) holds; that is there exists a constant
![]() $C>0$
such that
$C>0$
such that
holds for all
![]() $f\in \mathcal {D}^s_K$
. For
$f\in \mathcal {D}^s_K$
. For
![]() $I\subseteq \mathbb {T}$
, let
$I\subseteq \mathbb {T}$
, let
![]() $e^{i\theta }$
,
$e^{i\theta }$
,
![]() $\theta \in [0,2\pi)$
, be the midpoint of I. Choose
$\theta \in [0,2\pi)$
, be the midpoint of I. Choose
![]() $w=(1-2|I|)e^{i\theta }$
and
$w=(1-2|I|)e^{i\theta }$
and
![]() $|I|<\frac {1}{8}$
. A simple geometric argument shows that
$|I|<\frac {1}{8}$
. A simple geometric argument shows that
Consider the test function
![]() $f_{w}\in \mathcal {D}^s_K$
of Lemma 3.1, we have
$f_{w}\in \mathcal {D}^s_K$
of Lemma 3.1, we have
By (3.6), we obtain
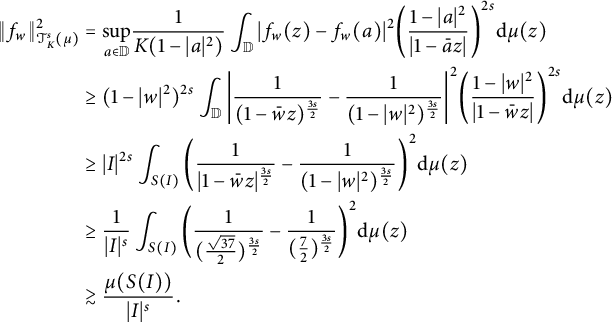 $$ \begin{align*} \|f_w\|^{2}_{ \mathcal{T}^s_{K}(\mu)} &=\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}|f_w(z)-f_w(a)|^2 \bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^{2s}\mathrm{d}\mu(z)\\ &\geq(1-|w|^2)^{2s}\int_{\mathbb{D}}\bigg|\frac{1}{(1-\bar{w}z)^{\frac{3s}{2}}}-\frac{1}{(1-|w|^2)^{\frac{3s}{2}}} \bigg|^2\bigg(\frac{1-|w|^2}{|1-\bar{w}z|}\bigg)^{2s}\mathrm{d}\mu(z)\\ &\geq|I|^{2s}\int_{S(I)}\bigg(\frac{1}{|1-\bar{w}z|^{\frac{3s}{2}}}-\frac{1}{(1-|w|^2)^{\frac{3s}{2}}}\bigg)^2\mathrm{d}\mu(z)\\ &\geq\frac{1}{|I|^s}\int_{S(I)}\bigg(\frac{1}{(\frac{\sqrt{37}}{2})^{\frac{3s}{2}}}-\frac{1}{(\frac{7}{2})^{\frac{3s}{2}}} \bigg)^2\mathrm{d}\mu(z)\\ &\gtrsim\frac{\mu(S(I))}{|I|^s}. \end{align*} $$
$$ \begin{align*} \|f_w\|^{2}_{ \mathcal{T}^s_{K}(\mu)} &=\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}|f_w(z)-f_w(a)|^2 \bigg(\frac{1-|a|^2}{|1-\bar{a}z|}\bigg)^{2s}\mathrm{d}\mu(z)\\ &\geq(1-|w|^2)^{2s}\int_{\mathbb{D}}\bigg|\frac{1}{(1-\bar{w}z)^{\frac{3s}{2}}}-\frac{1}{(1-|w|^2)^{\frac{3s}{2}}} \bigg|^2\bigg(\frac{1-|w|^2}{|1-\bar{w}z|}\bigg)^{2s}\mathrm{d}\mu(z)\\ &\geq|I|^{2s}\int_{S(I)}\bigg(\frac{1}{|1-\bar{w}z|^{\frac{3s}{2}}}-\frac{1}{(1-|w|^2)^{\frac{3s}{2}}}\bigg)^2\mathrm{d}\mu(z)\\ &\geq\frac{1}{|I|^s}\int_{S(I)}\bigg(\frac{1}{(\frac{\sqrt{37}}{2})^{\frac{3s}{2}}}-\frac{1}{(\frac{7}{2})^{\frac{3s}{2}}} \bigg)^2\mathrm{d}\mu(z)\\ &\gtrsim\frac{\mu(S(I))}{|I|^s}. \end{align*} $$
Combining this with (3.5), we find
which means that
![]() $\mu $
is an s-Carleson measure.
$\mu $
is an s-Carleson measure.
To prove (ii), we first show that if
![]() $f\in \mathcal {D}^{s}_{K}$
then
$f\in \mathcal {D}^{s}_{K}$
then
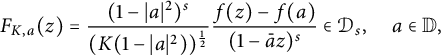 $$ \begin{align} F_{K,a}(z)=\frac{(1-|a|^2)^{s}}{(K(1-|a|^2))^{\frac12}}\frac{f(z)-f(a)}{(1-\bar{a}z)^s}\in \mathcal{D}_s, \quad a\in \mathbb{D}, \end{align} $$
$$ \begin{align} F_{K,a}(z)=\frac{(1-|a|^2)^{s}}{(K(1-|a|^2))^{\frac12}}\frac{f(z)-f(a)}{(1-\bar{a}z)^s}\in \mathcal{D}_s, \quad a\in \mathbb{D}, \end{align} $$
and
Thus, if
![]() $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for
![]() $\mathcal {D}_s$
, then there is a constant
$\mathcal {D}_s$
, then there is a constant
![]() $C>0$
such that
$C>0$
such that
holds for all
![]() $f\in \mathcal {D}_s$
. Collecting all estimates above, we have that
$f\in \mathcal {D}_s$
. Collecting all estimates above, we have that
which is the desired conclusion.
Now, we are going to check (3.7) and (3.8). In fact,
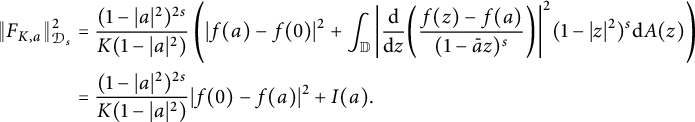 $$ \begin{align*} \|F_{K,a}\|^2_{\mathcal{D}_s} &=\frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}\left(|f(a)-f(0)|^2+\int_{\mathbb{D}}\bigg|\frac{\mathrm{d}}{\mathrm{d}z} \bigg(\frac{f(z)-f(a)}{(1-\bar{a}z)^s}\bigg)\bigg|^{2}(1-|z|^{2})^{s}\mathrm{d}A(z)\right)\\ &=\frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}|f(0)-f(a)|^2+I(a). \end{align*} $$
$$ \begin{align*} \|F_{K,a}\|^2_{\mathcal{D}_s} &=\frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}\left(|f(a)-f(0)|^2+\int_{\mathbb{D}}\bigg|\frac{\mathrm{d}}{\mathrm{d}z} \bigg(\frac{f(z)-f(a)}{(1-\bar{a}z)^s}\bigg)\bigg|^{2}(1-|z|^{2})^{s}\mathrm{d}A(z)\right)\\ &=\frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}|f(0)-f(a)|^2+I(a). \end{align*} $$
By Lemma 3.2, the first term in the last sum is
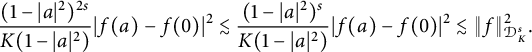 $$ \begin{align*} \frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}|f(a)-f(0)|^2\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}|f(a)-f(0)|^2 \lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}. \end{align*} $$
$$ \begin{align*} \frac{(1-|a|^2)^{2s}}{K(1-|a|^2)}|f(a)-f(0)|^2\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}|f(a)-f(0)|^2 \lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}. \end{align*} $$
For the second term, we have
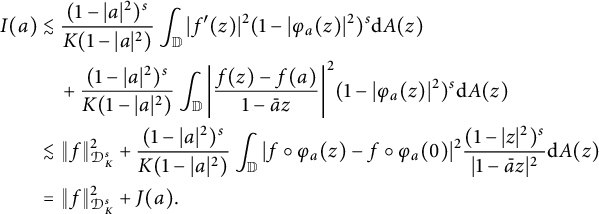 $$ \begin{align*} I(a)&\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}} |f^{\prime}(z)|^2(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z) \\ & \quad + \frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg|\frac{f(z)-f(a)}{1-\bar{a}z}\bigg|^{2}(1-|\varphi_a(z)|^{2})^{s} \mathrm{d}A(z)\\ &\lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}+\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}} |f\circ\varphi_a(z)-f\circ\varphi_a(0)|^{2}\frac{(1-|z|^{2})^{s}}{|1-\bar{a}z|^2}\mathrm{d}A(z)\\ &=\|f\|^2_{\mathcal{D}^{s}_{K}}+J(a). \end{align*} $$
$$ \begin{align*} I(a)&\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}} |f^{\prime}(z)|^2(1-|\varphi_a(z)|^{2})^{s}\mathrm{d}A(z) \\ & \quad + \frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg|\frac{f(z)-f(a)}{1-\bar{a}z}\bigg|^{2}(1-|\varphi_a(z)|^{2})^{s} \mathrm{d}A(z)\\ &\lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}+\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}} |f\circ\varphi_a(z)-f\circ\varphi_a(0)|^{2}\frac{(1-|z|^{2})^{s}}{|1-\bar{a}z|^2}\mathrm{d}A(z)\\ &=\|f\|^2_{\mathcal{D}^{s}_{K}}+J(a). \end{align*} $$
By the reproducing formula of Rochberg and Wu [Reference Rochberg and Wu20], we get
where
![]() $s>-1$
and
$s>-1$
and
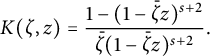 $$ \begin{align*} K(\zeta,z)=\frac{1-(1-\bar{\zeta}z)^{s+2}}{\bar{\zeta}(1-\bar{\zeta}z)^{s+2}}. \end{align*} $$
$$ \begin{align*} K(\zeta,z)=\frac{1-(1-\bar{\zeta}z)^{s+2}}{\bar{\zeta}(1-\bar{\zeta}z)^{s+2}}. \end{align*} $$
Obviously,
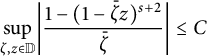 $$ \begin{align*} \underset{\zeta,z\in \mathbb{D}}{\mathrm{sup}}\bigg|\frac{1-(1-\bar{\zeta}z)^{s+2}}{\bar{\zeta}}\bigg|\leq C \end{align*} $$
$$ \begin{align*} \underset{\zeta,z\in \mathbb{D}}{\mathrm{sup}}\bigg|\frac{1-(1-\bar{\zeta}z)^{s+2}}{\bar{\zeta}}\bigg|\leq C \end{align*} $$
holds for some constant
![]() $C>0$
. Choosing
$C>0$
. Choosing
![]() $0 < \varepsilon < s $
and by the Cauchy–Schwarz inequality,
$0 < \varepsilon < s $
and by the Cauchy–Schwarz inequality,
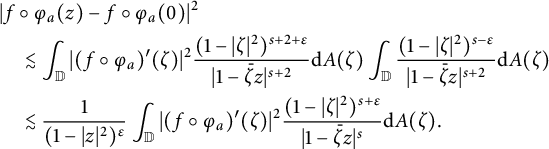 $$ \begin{align*} &|f\circ\varphi_a(z)-f\circ\varphi_a(0)|^2\\ &\quad \lesssim\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2\frac{(1-|\zeta|^2)^{s+2+\varepsilon}}{|1-\bar{\zeta}z|^{s+2}} \mathrm{d}A(\zeta) \int_{\mathbb{D}}\frac{(1-|\zeta|^2)^{s-\varepsilon}}{|1-\bar{\zeta}z|^{s+2}}\mathrm{d}A(\zeta)\\ &\quad \lesssim\frac{1}{(1-|z|^2)^{\varepsilon}}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2 \frac{(1-|\zeta|^2)^{s+\varepsilon}}{|1-\bar{\zeta}z|^{s}}\mathrm{d}A(\zeta). \end{align*} $$
$$ \begin{align*} &|f\circ\varphi_a(z)-f\circ\varphi_a(0)|^2\\ &\quad \lesssim\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2\frac{(1-|\zeta|^2)^{s+2+\varepsilon}}{|1-\bar{\zeta}z|^{s+2}} \mathrm{d}A(\zeta) \int_{\mathbb{D}}\frac{(1-|\zeta|^2)^{s-\varepsilon}}{|1-\bar{\zeta}z|^{s+2}}\mathrm{d}A(\zeta)\\ &\quad \lesssim\frac{1}{(1-|z|^2)^{\varepsilon}}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2 \frac{(1-|\zeta|^2)^{s+\varepsilon}}{|1-\bar{\zeta}z|^{s}}\mathrm{d}A(\zeta). \end{align*} $$
By Fubini’s theorem and Lemma C, we get
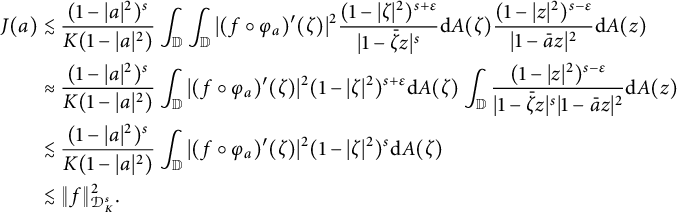 $$ \begin{align*} J(a)&\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2 \frac{(1-|\zeta|^2)^{s+\varepsilon}}{|1-\bar{\zeta}z|^{s}}\mathrm{d}A(\zeta)\frac{(1-|z|^{2})^{s-\varepsilon}}{|1-\bar{a}z|^2} \mathrm{d}A(z)\\ &\approx\frac{(1-|a|^2)^s}{K(1-|a|^2)} \int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2(1-|\zeta|^2)^{s+\varepsilon}\mathrm{d}A(\zeta) \int_{\mathbb{D}}\frac{(1-|z|^{2})^{s-\varepsilon}}{|1-\bar{\zeta}z|^{s}|1-\bar{a}z|^2}\mathrm{d}A(z)\\ &\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2(1-|\zeta|^2)^{s}\mathrm{d}A(\zeta)\\ &\lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}. \end{align*} $$
$$ \begin{align*} J(a)&\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2 \frac{(1-|\zeta|^2)^{s+\varepsilon}}{|1-\bar{\zeta}z|^{s}}\mathrm{d}A(\zeta)\frac{(1-|z|^{2})^{s-\varepsilon}}{|1-\bar{a}z|^2} \mathrm{d}A(z)\\ &\approx\frac{(1-|a|^2)^s}{K(1-|a|^2)} \int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2(1-|\zeta|^2)^{s+\varepsilon}\mathrm{d}A(\zeta) \int_{\mathbb{D}}\frac{(1-|z|^{2})^{s-\varepsilon}}{|1-\bar{\zeta}z|^{s}|1-\bar{a}z|^2}\mathrm{d}A(z)\\ &\lesssim\frac{(1-|a|^2)^s}{K(1-|a|^2)}\int_{\mathbb{D}}|(f\circ\varphi_a)^{\prime}(\zeta)|^2(1-|\zeta|^2)^{s}\mathrm{d}A(\zeta)\\ &\lesssim\|f\|^2_{\mathcal{D}^{s}_{K}}. \end{align*} $$
For
![]() $1\leq s<\infty $
, we know that
$1\leq s<\infty $
, we know that
![]() $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for
![]() $\mathcal {D}_{s}$
if and only if
$\mathcal {D}_{s}$
if and only if
![]() $\mu $
is an s-Carleson measure on
$\mu $
is an s-Carleson measure on
![]() $\mathbb {D}$
; see [Reference Stegenga21, Theorem 1.2]. However, this is no longer true for
$\mathbb {D}$
; see [Reference Stegenga21, Theorem 1.2]. However, this is no longer true for
![]() $0<s<1$
; see [Reference Aleman, Carlsson and Persson1, Reference Arcozzi, Rochberg and Sawyer2]. Thus, we obtain the following result.
$0<s<1$
; see [Reference Aleman, Carlsson and Persson1, Reference Arcozzi, Rochberg and Sawyer2]. Thus, we obtain the following result.
Theorem 3.2 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $1\leq s<\infty $
. For a positive Borel measure
$1\leq s<\infty $
. For a positive Borel measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {D}$
, the embedding map
$\mathbb {D}$
, the embedding map
![]() $I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded if and only if
$I: \mathcal {D}^{s}_{K} \mapsto \mathcal {T}^s_{K}(\mu)$
is bounded if and only if
![]() $\mu $
is an s-Carleson measure.
$\mu $
is an s-Carleson measure.
Remark 3.1
-
(i) If
 $K(t)=t^{s\lambda }$
,
$K(t)=t^{s\lambda }$
,
 $0<s, \lambda <1$
, Theorem 3.1
gives [Reference Galanopoulos, Merchán and Siskakis6, Theorems 3.4 and 3.5(2)].
$0<s, \lambda <1$
, Theorem 3.1
gives [Reference Galanopoulos, Merchán and Siskakis6, Theorems 3.4 and 3.5(2)]. -
(ii) If
 $K(t)=t^s$
, Theorem 3.1
implies [Reference Liu, Lou and Zhu11, Theorem 5] and [Reference Xiao28, Theorem 1.1] (or [Reference Pau and Peláez15, Theorem 1]).
$K(t)=t^s$
, Theorem 3.1
implies [Reference Liu, Lou and Zhu11, Theorem 5] and [Reference Xiao28, Theorem 1.1] (or [Reference Pau and Peláez15, Theorem 1]). -
(iii) If K satisfies condition (2.2) for
 $\sigma =1$
, Theorem 3.2
was obtained by Qian and Li [Reference Qian and Li19, Theorem 2] for
$\sigma =1$
, Theorem 3.2
was obtained by Qian and Li [Reference Qian and Li19, Theorem 2] for
 $s=1$
and
$s=1$
and
 $\mathrm {d}\mu (z)=|g^{\prime }(z)|^2(1-|z|^2)\mathrm {d}A(z)$
.
$\mathrm {d}\mu (z)=|g^{\prime }(z)|^2(1-|z|^2)\mathrm {d}A(z)$
.
4 Fractional order derivatives and
 $\mathcal{D}_K^s$
spaces
$\mathcal{D}_K^s$
spaces
For fixed
![]() $b>1$
, consider the t-order derivative of a function
$b>1$
, consider the t-order derivative of a function
![]() $f\in H(\mathbb {D})$
defined by
$f\in H(\mathbb {D})$
defined by
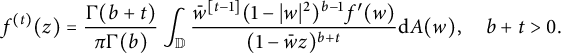 $$ \begin{align*} f^{(t)}(z)=\frac{\Gamma(b+t)}{\pi\Gamma(b)}\int_{\mathbb{D}} \frac{{\bar{w}}^{[t-1]}(1-|w|^2)^{b-1}f^{\prime}(w)}{(1-\bar{w}z)^{b+t}}\mathrm{d}A(w), \quad b+t>0. \end{align*} $$
$$ \begin{align*} f^{(t)}(z)=\frac{\Gamma(b+t)}{\pi\Gamma(b)}\int_{\mathbb{D}} \frac{{\bar{w}}^{[t-1]}(1-|w|^2)^{b-1}f^{\prime}(w)}{(1-\bar{w}z)^{b+t}}\mathrm{d}A(w), \quad b+t>0. \end{align*} $$
Here,
![]() $[x]$
stands for the smallest integer greater than or equal to
$[x]$
stands for the smallest integer greater than or equal to
![]() $x\in \mathbb {R}$
, and
$x\in \mathbb {R}$
, and
![]() $\Gamma (\cdot)$
is the Gamma function. Note that
$\Gamma (\cdot)$
is the Gamma function. Note that
![]() $(f^{(t)})^{\prime }=f^{(t+1)}$
.
$(f^{(t)})^{\prime }=f^{(t+1)}$
.
A direct computation yields
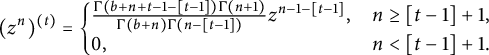 $$ \begin{align*} (z^n)^{(t)}=\left\{ \begin{array}{@{}ll} \frac{\Gamma(b+n+t-1-[t-1])\Gamma(n+1)}{\Gamma(b+n)\Gamma(n-[t-1])}z^{n-1-[t-1]},& n\geq[t-1]+1,\\ 0,& n<[t-1]+1.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} (z^n)^{(t)}=\left\{ \begin{array}{@{}ll} \frac{\Gamma(b+n+t-1-[t-1])\Gamma(n+1)}{\Gamma(b+n)\Gamma(n-[t-1])}z^{n-1-[t-1]},& n\geq[t-1]+1,\\ 0,& n<[t-1]+1.\\ \end{array} \right. \end{align*} $$
It is easy to conclude that the t-fractional order derivative is just the usual tth order derivative if t is a positive integer.
In [Reference Wu and Xie23], Wu and Xie revealed that a function
![]() $f\in \mathcal Q_s$
can be viewed as its fractional order derivative in a Morrey space. In [Reference Wulan and Zhou24], Zhou and Wulan showed a connection between
$f\in \mathcal Q_s$
can be viewed as its fractional order derivative in a Morrey space. In [Reference Wulan and Zhou24], Zhou and Wulan showed a connection between
![]() $H^2_K$
and
$H^2_K$
and
![]() $\mathcal Q_K$
by using the fractional order derivative. In this section, a characterization of
$\mathcal Q_K$
by using the fractional order derivative. In this section, a characterization of
![]() $\mathcal {D}^{s}_K$
in terms of the fractional order derivative is given. As a by-product, we build a bridge between two spaces
$\mathcal {D}^{s}_K$
in terms of the fractional order derivative is given. As a by-product, we build a bridge between two spaces
![]() $\mathcal {D}^{s_1}_K$
and
$\mathcal {D}^{s_1}_K$
and
![]() $\mathcal {D}^{s_2}_K$
by the fractional order derivatives.
$\mathcal {D}^{s_2}_K$
by the fractional order derivatives.
Theorem 4.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
and
$0<\sigma <2$
and
![]() $\frac {\sigma }{2}\leq s<\infty $
. Then
$\frac {\sigma }{2}\leq s<\infty $
. Then
![]() $f\in \mathcal {D}_K^s$
if and only if
$f\in \mathcal {D}_K^s$
if and only if
is a K-Carleson measure.
Theorem 4.1 actually gives a relationship between two spaces
![]() $\mathcal {D}_K^{s_1}$
and
$\mathcal {D}_K^{s_1}$
and
![]() $\mathcal {D}_K^{s_2}$
as follows.
$\mathcal {D}_K^{s_2}$
as follows.
Corollary 4.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
. For
$0<\sigma <2$
. For
![]() $\frac {\sigma }{2}\leq s_1, s_2<\infty $
with
$\frac {\sigma }{2}\leq s_1, s_2<\infty $
with
![]() $s_1< s_2+2$
, the following statements are equivalent:
$s_1< s_2+2$
, the following statements are equivalent:
-
(i)
 $f\in \mathcal {D}_K^{s_1}$
.
$f\in \mathcal {D}_K^{s_1}$
. -
(ii)
 $f^{(\frac {s_2-s_1}{2})}\in \mathcal {D}^{s_2}_K$
.
$f^{(\frac {s_2-s_1}{2})}\in \mathcal {D}^{s_2}_K$
.
The following lemma will be used in the proof of Theorem 4.1.
Lemma 4.1 Suppose K satisfies (2.2) for some
![]() $0<\sigma <2$
. For
$0<\sigma <2$
. For
![]() $0\leq s<\infty $
, let
$0\leq s<\infty $
, let
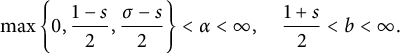 $$ \begin{align*} \max\bigg\{0, \frac{1-s}{2}, \frac{\sigma-s}{2}\bigg\} < \alpha < \infty, \quad \frac{1+s}{2} < b < \infty. \end{align*} $$
$$ \begin{align*} \max\bigg\{0, \frac{1-s}{2}, \frac{\sigma-s}{2}\bigg\} < \alpha < \infty, \quad \frac{1+s}{2} < b < \infty. \end{align*} $$
For
![]() $f\in L^1(\mathbb {D}, \mathrm {d}A)$
, define
$f\in L^1(\mathbb {D}, \mathrm {d}A)$
, define
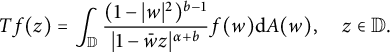 $$ \begin{align*} Tf(z)=\int_{\mathbb{D}}\frac{(1-|w|^2)^{b-1}}{|1-\bar{w}z|^{\alpha+b}}f(w)\mathrm{d}A(w), \quad z\in\mathbb{D}. \end{align*} $$
$$ \begin{align*} Tf(z)=\int_{\mathbb{D}}\frac{(1-|w|^2)^{b-1}}{|1-\bar{w}z|^{\alpha+b}}f(w)\mathrm{d}A(w), \quad z\in\mathbb{D}. \end{align*} $$
If
![]() $|f(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure, then
$|f(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure, then
is also a K-Carleson measure.
Proof For given s, write
and
We verify that
![]() $\|\mu _f\|_K<\infty $
yields
$\|\mu _f\|_K<\infty $
yields
![]() $\|\mu _{Tf}\|_K<\infty $
. To this end, for
$\|\mu _{Tf}\|_K<\infty $
. To this end, for
![]() $I\subset \mathbb {T}$
, we set
$I\subset \mathbb {T}$
, we set
![]() $2^nI$
as the subarc of
$2^nI$
as the subarc of
![]() $\mathbb {T}$
with the same center as I and length
$\mathbb {T}$
with the same center as I and length
![]() $2^n|I|$
for
$2^n|I|$
for
![]() $n\in \mathbb {N^+}$
. Then
$n\in \mathbb {N^+}$
. Then
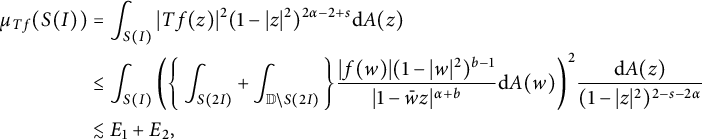 $$ \begin{align*} \mu_{Tf}(S(I))&=\int_{S(I)}|Tf(z)|^{2}(1-|z|^{2})^{2\alpha-2+s}\mathrm{d}A(z)\\ &\leq\int_{S(I)} \bigg(\bigg\{\int_{S(2I)}+\int_{\mathbb{D}\backslash S(2I)}\bigg\}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}\\ &\lesssim E_1+E_2, \end{align*} $$
$$ \begin{align*} \mu_{Tf}(S(I))&=\int_{S(I)}|Tf(z)|^{2}(1-|z|^{2})^{2\alpha-2+s}\mathrm{d}A(z)\\ &\leq\int_{S(I)} \bigg(\bigg\{\int_{S(2I)}+\int_{\mathbb{D}\backslash S(2I)}\bigg\}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}\\ &\lesssim E_1+E_2, \end{align*} $$
where
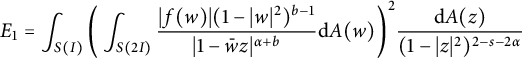 $$ \begin{align*} E_1=\int_{S(I)}\bigg(\int_{S(2I)}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}} \end{align*} $$
$$ \begin{align*} E_1=\int_{S(I)}\bigg(\int_{S(2I)}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}} \end{align*} $$
and
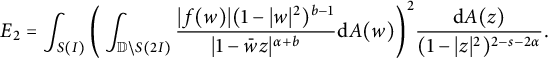 $$ \begin{align*} E_2=\int_{S(I)} \bigg(\int_{\mathbb{D}\backslash S(2I)}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}. \end{align*} $$
$$ \begin{align*} E_2=\int_{S(I)} \bigg(\int_{\mathbb{D}\backslash S(2I)}\frac{|f(w)|(1-|w|^{2})^{b-1}}{|1-\bar{w}z|^{\alpha+b}}\mathrm{d}A(w)\bigg)^2 \frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}. \end{align*} $$
For
![]() $E_1$
, we shall apply the classical Schur’s test [Reference Zhu30, Corollary 3.7] to a bounded operator on
$E_1$
, we shall apply the classical Schur’s test [Reference Zhu30, Corollary 3.7] to a bounded operator on
![]() $L^2(\mathbb {D})$
. Indeed, we consider
$L^2(\mathbb {D})$
. Indeed, we consider
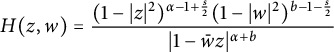 $$ \begin{align*} H(z,w)=\frac{(1-|z|^{2})^{\alpha-1+\frac{s}{2}}(1-|w|^{2})^{b-1-\frac{s}{2}}}{|1-\bar{w}z|^{\alpha+b}} \end{align*} $$
$$ \begin{align*} H(z,w)=\frac{(1-|z|^{2})^{\alpha-1+\frac{s}{2}}(1-|w|^{2})^{b-1-\frac{s}{2}}}{|1-\bar{w}z|^{\alpha+b}} \end{align*} $$
and the integral operator
Using [Reference Zhu30, Lemma 3.10], we derive that for
we obtain that
and
Accordingly, the operator
![]() $T_{H}$
is bounded from
$T_{H}$
is bounded from
![]() $L^2(\mathbb {D})$
to
$L^2(\mathbb {D})$
to
![]() $L^2(\mathbb {D})$
. Applying this to the function
$L^2(\mathbb {D})$
. Applying this to the function
where
![]() $\mathcal {X}_{S(2I)}$
is the characteristic function of
$\mathcal {X}_{S(2I)}$
is the characteristic function of
![]() $S(2I)$
, we get
$S(2I)$
, we get
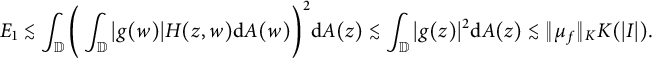 $$ \begin{align*} E_1\lesssim\int_{\mathbb{D}}\bigg(\int_{\mathbb{D}}|g(w)|H(z,w)\mathrm{d}A(w)\bigg)^2\mathrm{d}A(z)\lesssim \int_{\mathbb{D}}|g(z)|^2\mathrm{d}A(z)\lesssim\|\mu_f\|_K K(|I|). \end{align*} $$
$$ \begin{align*} E_1\lesssim\int_{\mathbb{D}}\bigg(\int_{\mathbb{D}}|g(w)|H(z,w)\mathrm{d}A(w)\bigg)^2\mathrm{d}A(z)\lesssim \int_{\mathbb{D}}|g(z)|^2\mathrm{d}A(z)\lesssim\|\mu_f\|_K K(|I|). \end{align*} $$
To handle
![]() $E_2$
, we note that both
$E_2$
, we note that both
and
hold for all
![]() $n\in \mathbb {N}$
. Using
$n\in \mathbb {N}$
. Using
![]() $\alpha>\mathrm {max}\big \{0, \frac {1-s}{2}, \frac {\sigma -s}{2}\big \}$
, we get
$\alpha>\mathrm {max}\big \{0, \frac {1-s}{2}, \frac {\sigma -s}{2}\big \}$
, we get
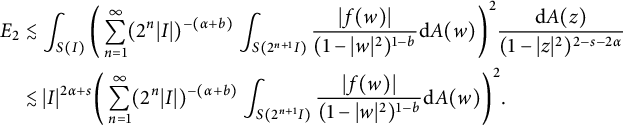 $$ \begin{align*} E_2 &\lesssim\int_{S(I)} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-(\alpha+b)}\int_{S(2^{n+1}I)}\frac{|f(w)|}{(1-|w|^{2})^{1-b}} \mathrm{d}A(w)\bigg)^2\frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}\\ &\lesssim|I|^{2\alpha+s} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-(\alpha+b)}\int_{S(2^{n+1}I)}\frac{|f(w)|}{(1-|w|^{2})^{1-b}}\mathrm{d}A(w)\bigg)^2. \end{align*} $$
$$ \begin{align*} E_2 &\lesssim\int_{S(I)} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-(\alpha+b)}\int_{S(2^{n+1}I)}\frac{|f(w)|}{(1-|w|^{2})^{1-b}} \mathrm{d}A(w)\bigg)^2\frac{\mathrm{d}A(z)}{(1-|z|^{2})^{2-s-2\alpha}}\\ &\lesssim|I|^{2\alpha+s} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-(\alpha+b)}\int_{S(2^{n+1}I)}\frac{|f(w)|}{(1-|w|^{2})^{1-b}}\mathrm{d}A(w)\bigg)^2. \end{align*} $$
Note that
![]() $\|\mu _f\|_K<\infty $
. By Hölder’s inequality and Remark 2.1 (i),
$\|\mu _f\|_K<\infty $
. By Hölder’s inequality and Remark 2.1 (i),
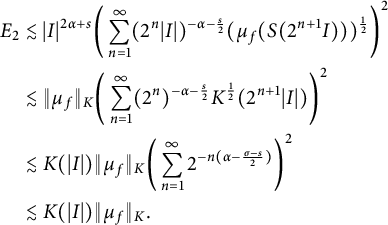 $$ \begin{align*} E_2&\lesssim|I|^{2\alpha+s} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-\alpha-\frac{s}{2}}(\mu_f(S(2^{n+1}I)))^{\frac{1}{2}}\bigg)^2\\ &\lesssim\|\mu_f\|_K\bigg(\sum_{n=1}^{\infty}(2^n)^{-\alpha-\frac{s}{2}}K^{\frac{1}{2}}(2^{n+1}|I|)\bigg)^2\\ &\lesssim K(|I|)\|\mu_f\|_K\bigg(\sum_{n=1}^{\infty}2^{-n(\alpha-\frac{\sigma-s}{2})}\bigg)^2\\ &\lesssim K(|I|)\|\mu_f\|_K. \end{align*} $$
$$ \begin{align*} E_2&\lesssim|I|^{2\alpha+s} \bigg(\sum_{n=1}^{\infty}(2^n|I|)^{-\alpha-\frac{s}{2}}(\mu_f(S(2^{n+1}I)))^{\frac{1}{2}}\bigg)^2\\ &\lesssim\|\mu_f\|_K\bigg(\sum_{n=1}^{\infty}(2^n)^{-\alpha-\frac{s}{2}}K^{\frac{1}{2}}(2^{n+1}|I|)\bigg)^2\\ &\lesssim K(|I|)\|\mu_f\|_K\bigg(\sum_{n=1}^{\infty}2^{-n(\alpha-\frac{\sigma-s}{2})}\bigg)^2\\ &\lesssim K(|I|)\|\mu_f\|_K. \end{align*} $$
The foregoing estimates on
![]() $E_1$
and
$E_1$
and
![]() $E_2$
give
$E_2$
give
![]() $\mu _{Tf}$
is a K-Carleson measure. ▪
$\mu _{Tf}$
is a K-Carleson measure. ▪
Now we are ready to prove Theorem 4.1. Let
![]() $f\in \mathcal {D}_K^{s}$
. By Theorem 2.2, we know that
$f\in \mathcal {D}_K^{s}$
. By Theorem 2.2, we know that
![]() $|f^{\prime }(z)|^{2}(1-|z|^{2})^{s}\mathrm {d}A(z)$
is a K-Carleson measure. Since
$|f^{\prime }(z)|^{2}(1-|z|^{2})^{s}\mathrm {d}A(z)$
is a K-Carleson measure. Since
 $$ \begin{align*} |f^{(t)}(z)|\leq\frac{\Gamma(b+t)}{\pi\Gamma(b)}\int_{\mathbb{D}} \frac{(1-|w|^2)^{b-1}|f^{\prime}(w)|}{|1-\bar{w}z|^{b+t}}\mathrm{d}A(w), \quad \mathrm{max}\left\{1,\frac{1+s}{2}\right\} < b < \infty, \end{align*} $$
$$ \begin{align*} |f^{(t)}(z)|\leq\frac{\Gamma(b+t)}{\pi\Gamma(b)}\int_{\mathbb{D}} \frac{(1-|w|^2)^{b-1}|f^{\prime}(w)|}{|1-\bar{w}z|^{b+t}}\mathrm{d}A(w), \quad \mathrm{max}\left\{1,\frac{1+s}{2}\right\} < b < \infty, \end{align*} $$
we obtain by Lemma 4.1 that
is a K-Carleson measure.
Conversely, suppose
![]() $|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm {d}A(z)$
is a K-Carleson measure. Now we consider the function:
$|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm {d}A(z)$
is a K-Carleson measure. Now we consider the function:
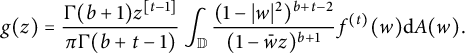 $$ \begin{align*} g(z)=\frac{\Gamma(b+1)z^{[t-1]}}{\pi\Gamma(b+t-1)}\int_{\mathbb{D}} \frac{(1-|w|^2)^{b+t-2}}{(1-\bar{w}z)^{b+1}}f^{(t)}(w)\mathrm{d}A(w). \end{align*} $$
$$ \begin{align*} g(z)=\frac{\Gamma(b+1)z^{[t-1]}}{\pi\Gamma(b+t-1)}\int_{\mathbb{D}} \frac{(1-|w|^2)^{b+t-2}}{(1-\bar{w}z)^{b+1}}f^{(t)}(w)\mathrm{d}A(w). \end{align*} $$
It follows from Lemma 4.1 that
![]() $|g(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure. To establish a relationship between g and
$|g(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure. To establish a relationship between g and
![]() $f^{\prime }$
, we express f and
$f^{\prime }$
, we express f and
![]() $f^{(t)}$
as Taylor series below:
$f^{(t)}$
as Taylor series below:
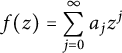 $$ \begin{align*} f(z)=\sum_{j=0}^{\infty}a_jz^j \end{align*} $$
$$ \begin{align*} f(z)=\sum_{j=0}^{\infty}a_jz^j \end{align*} $$
and
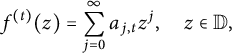 $$ \begin{align*} f^{(t)}(z)=\sum_{j=0}^{\infty}a_{j,t}z^j, \quad z\in\mathbb{D}, \end{align*} $$
$$ \begin{align*} f^{(t)}(z)=\sum_{j=0}^{\infty}a_{j,t}z^j, \quad z\in\mathbb{D}, \end{align*} $$
where
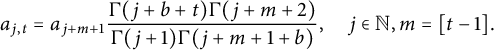 $$ \begin{align*} a_{j,t}=a_{j+m+1}\frac{\Gamma(j+b+t)\Gamma(j+m+2)}{\Gamma(j+1)\Gamma(j+m+1+b)}, \quad j\in\mathbb{N}, m=[t-1]. \end{align*} $$
$$ \begin{align*} a_{j,t}=a_{j+m+1}\frac{\Gamma(j+b+t)\Gamma(j+m+2)}{\Gamma(j+1)\Gamma(j+m+1+b)}, \quad j\in\mathbb{N}, m=[t-1]. \end{align*} $$
Obviously,
![]() $m\geq 0$
. Rewrite
$m\geq 0$
. Rewrite
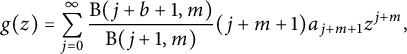 $$ \begin{align*} g(z) =\sum_{j=0}^{\infty}\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}(j+m+1)a_{j+m+1}z^{j+m}, \end{align*} $$
$$ \begin{align*} g(z) =\sum_{j=0}^{\infty}\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}(j+m+1)a_{j+m+1}z^{j+m}, \end{align*} $$
where
![]() $\mathrm {B}(\cdot,\cdot)$
is the Beta function. Note that
$\mathrm {B}(\cdot,\cdot)$
is the Beta function. Note that
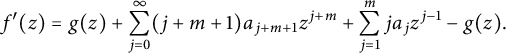 $$ \begin{align*} f^{\prime}(z) =g(z)+\sum_{j=0}^{\infty}(j+m+1)a_{j+m+1}z^{j+m}+\sum_{j=1}^{m}j a_jz^{j-1}-g(z). \end{align*} $$
$$ \begin{align*} f^{\prime}(z) =g(z)+\sum_{j=0}^{\infty}(j+m+1)a_{j+m+1}z^{j+m}+\sum_{j=1}^{m}j a_jz^{j-1}-g(z). \end{align*} $$
By setting
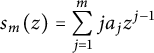 $$ \begin{align*} s_m(z)=\sum^{m}_{j=1}ja_jz^{j-1} \end{align*} $$
$$ \begin{align*} s_m(z)=\sum^{m}_{j=1}ja_jz^{j-1} \end{align*} $$
and
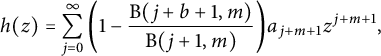 $$ \begin{align*} h(z)=\sum_{j=0}^{\infty}\bigg(1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\bigg)a_{j+m+1}z^{j+m+1}, \end{align*} $$
$$ \begin{align*} h(z)=\sum_{j=0}^{\infty}\bigg(1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\bigg)a_{j+m+1}z^{j+m+1}, \end{align*} $$
we obtain
Case 1:
![]() $m=0$
. A simple calculation gives that
$m=0$
. A simple calculation gives that
![]() $f^{\prime }=g$
. Therefore,
$f^{\prime }=g$
. Therefore,
![]() $|f^{\prime }(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure.
$|f^{\prime }(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure.
Case 2:
![]() $m>0$
. Note that
$m>0$
. Note that
![]() $|g(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure and
$|g(z)|^2(1-|z|^2)^{s}\mathrm {d}A(z)$
is a K-Carleson measure and
![]() $s_m$
is a polynomial. It remains to deal with the function
$s_m$
is a polynomial. It remains to deal with the function
![]() $h'$
in (4.1). It is enough to show that
$h'$
in (4.1). It is enough to show that
![]() $h\in \mathcal {D}_{s-\sigma }$
by the following argument:
$h\in \mathcal {D}_{s-\sigma }$
by the following argument:
Notice that
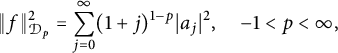 $$ \begin{align} \|f\|^2_{\mathcal{D}_p}=\sum^{\infty}_{j=0}(1+j)^{1-p}|a_j|^2, \quad -1 < p < \infty, \end{align} $$
$$ \begin{align} \|f\|^2_{\mathcal{D}_p}=\sum^{\infty}_{j=0}(1+j)^{1-p}|a_j|^2, \quad -1 < p < \infty, \end{align} $$
(see [Reference Stegenga21]) and a standard estimate
 $$ \begin{align*} 0<1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\leq\frac{(b+1)m}{j+m+1}, \quad j\in\mathbb{N}. \end{align*} $$
$$ \begin{align*} 0<1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\leq\frac{(b+1)m}{j+m+1}, \quad j\in\mathbb{N}. \end{align*} $$
Accordingly,
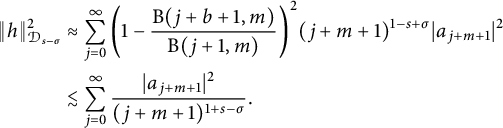 $$ \begin{align*} \|h\|^2_{\mathcal{D}_{s-\sigma}} &\approx\sum_{j=0}^{\infty}\bigg(1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\bigg)^2(j+m+1)^{1-s+\sigma}|a_{j+m+1}|^2\\ &\lesssim\sum_{j=0}^{\infty}\frac{|a_{j+m+1}|^2}{(j+m+1)^{1+s-\sigma}}. \end{align*} $$
$$ \begin{align*} \|h\|^2_{\mathcal{D}_{s-\sigma}} &\approx\sum_{j=0}^{\infty}\bigg(1-\frac{\mathrm{B}(j+b+1,m)}{\mathrm{B}(j+1,m)}\bigg)^2(j+m+1)^{1-s+\sigma}|a_{j+m+1}|^2\\ &\lesssim\sum_{j=0}^{\infty}\frac{|a_{j+m+1}|^2}{(j+m+1)^{1+s-\sigma}}. \end{align*} $$
In addition, by Theorem 2.1 for any q,
![]() $\sigma \leq q<\infty $
,
$\sigma \leq q<\infty $
,
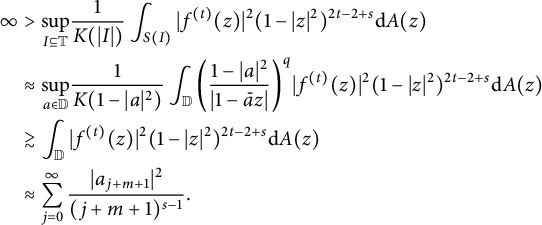 $$ \begin{align*} \infty&>\underset{I\subseteq \mathbb{T}}{\mathrm{sup}}\frac{1}{K(|I|)}\int_{S(I)}|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\approx\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg(\frac{1-|a|^{2}}{|1-\bar{a}z|}\bigg)^q|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\gtrsim\int_{\mathbb{D}}|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\approx\sum^{\infty}_{j=0}\frac{|a_{j+m+1}|^2}{(j+m+1)^{s-1}}. \end{align*} $$
$$ \begin{align*} \infty&>\underset{I\subseteq \mathbb{T}}{\mathrm{sup}}\frac{1}{K(|I|)}\int_{S(I)}|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\approx\underset{a\in \mathbb{D}}{\mathrm{sup}}\frac{1}{K(1-|a|^2)}\int_{\mathbb{D}}\bigg(\frac{1-|a|^{2}}{|1-\bar{a}z|}\bigg)^q|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\gtrsim\int_{\mathbb{D}}|f^{(t)}(z)|^2(1-|z|^2)^{2t-2+s}\mathrm{d}A(z)\\ &\approx\sum^{\infty}_{j=0}\frac{|a_{j+m+1}|^2}{(j+m+1)^{s-1}}. \end{align*} $$
Here, the latter part holds by using (4.2) and the Stirling’s formula:
Therefore,
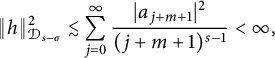 $$ \begin{align*} \|h\|^2_{\mathcal{D}_{s-\sigma}}\lesssim\sum^{\infty}_{j=0}\frac{|a_{j+m+1}|^2}{(j+m+1)^{s-1}}<\infty, \end{align*} $$
$$ \begin{align*} \|h\|^2_{\mathcal{D}_{s-\sigma}}\lesssim\sum^{\infty}_{j=0}\frac{|a_{j+m+1}|^2}{(j+m+1)^{s-1}}<\infty, \end{align*} $$
which is the desired result.