1. Introduction
The problem of acute water shortage affects many developing regions. Population growth and economic development, coupled with rising scarcity of water, have led to increasing costs of water supply development. This is threatening the economy of many river basins, and thus drawing countries that share these basins into possible water conflicts (Spulber and Sabbaghi, Reference Spulber, Sabbaghi, Dinar and Zilberman1994; see also Just and Netanyahu, Reference Just, Netanyahu, Just and Netanyahu1998; Beach et al., Reference Beach, Hamner, Hewitt, Kaufman, Kurki, Oppeneimer and Wolf2000; Biswas, Reference Biswas, Biswas and Uitto2001; Dinar et al., 1994; and Dinar and Dinar, Reference Dinar and Dinar2000). Although transboundary water resources can promote hostility, the historical record has shown that cooperation has consistently prevailed over acute conflict with respect to international water resources (Wolfe, Reference Wolfe2001).Footnote 1 In many cases – for example the transboundary water agreements between Egypt and Sudan in 1959, Israel and Jordan in 1994, and India and Bangladesh in 1996 – ‘political altruism’ has motivated countries to reach an agreement on water sharing, where upstream countries agree to transfer ‘claims’ to water along a shared watercourse.Footnote 2 Changes in political altruism factors, however, could entice upstream countries to exercise unilateral diversion. Under such ‘no win’ situations, there is a need for alternative institutional arrangements for downstream countries to meet increasing water scarcity, where water sharing is based on an existing agreement or treaty.Footnote 3
Thus an alternative solution is to tackle directly the problem of growing scarcity of freshwater in a river basin by augmenting supplies. However, creating new sources to augment water supply requires large investments and effective institutions for allocating water. Implementation of these measures in a transboundary river basin requires cooperation and coordination between the various countries sharing the water. One possible approach is a market-based water transfer (Green and O'Connor, Reference Green and O'Connor2001; Howe et al., Reference Howe, Schurmeier and Shaw1986). Water transfers have been used in different ways, but the main purpose has been the diversion of water within a given river basin system, such as from a water-surplus part of the basin to one or more water-deficit areas.
Water transfers may also prove a useful way of augmenting existing water-sharing treaties for an international river basin, especially when growing water demands threaten the long-term viability of the agreements. Just and Netanyahu (Reference Just, Netanyahu, Just and Netanyahu1998) point out that 53 international river basins in the world are shared by three or more nations, and are managed according to bilateral or even trilateral treaties or initiatives that are subject to limited scope for cooperation.Footnote 4 Under such conditions, there is a possibility of attaining bilateral or even multilateral agreement on international river basin management, through ‘linking’ the agreement between the parties to an additional issue of mutual interest to the parties. Similarly, Bennett et al. (Reference Bennett, Ragland, Yolles, Just and Netanyahu1998) demonstrate how issue linkage can facilitate agreement on a number of international river basin issues, and strengthen the enforceability of existing agreements.
The following paper makes two contributions. We develop a model of market-based transfer in an international river basin to illustrate how such a water transfer can influence the water-sharing decisions of two countries in the basin. To the best of our knowledge, this contribution represents the first analysis to explore the potential of market-based water transfers as a means of facilitating international river basin management and the resolution of water conflict.
The second contribution of the paper is to illustrate the example of water sharing of the Ganges River between India and Bangladesh, with possible augmentation of the entire Ganges River flow through transfers from water stored in Nepal (see figure 1).Footnote 5 Throughout the long history of negotiations between India and Bangladesh over sharing the water of the Ganges River Basin, the possibility of augmenting water supply in the Basin through transfers from water-rich Nepal has been consistently proposed. As outlined by Shah (Reference Shah, Biswas and Uitto2001) and Onta (Reference Onta, Biswas and Uitto2001), the most likely proposal is the building in Nepal of a dam on the Kosi tributary of the Ganges, with the stored waters then used to augment the lean flows in the Ganges upstream of Farakka. Thus our paper also makes a contribution to analyzing an important policy proposal concerning transboundary water sharing in the Ganges River Basin. To understand the importance of this water transfer proposal, it is necessary to explore further the background to transboundary water sharing of the Ganges River.
Figure 1. Potential water transfer from Nepal
The Ganges River originates in China, and along its 2,500 km long course, the river flows through northern India and passes through the state of West Bengal in India and then enters Bangladesh. In central Bangladesh, the Ganges is joined by the Brahmaputra and Meghna Rivers before the combined flows empty into the Bay of Bengal (see figure 1). In Bangladesh, which is the final downstream country along the Ganges, freshwater availability depends on the share of water diverted by India, which is the next country upstream. However, for many decades, India and Bangladesh failed to resolve issues of sharing the water of the Ganges River, particularly the dry season flow, as well as possibly augmenting the entire river flow through cooperation with Nepal.Footnote 6 This situation developed into a serious water conflict issue when in 1975 India constructed a dam at Farakka on the Ganges River near the border with Bangladesh to divert water unilaterally for agricultural irrigation and to improve the navigability of Calcutta Port.Footnote 7 The decline in water flowing to Bangladesh has in turn impacted its agriculture, fisheries, and river navigation downstream (Varghese, Reference Varghese1997). However, in 1996 India and Bangladesh signed a major new agreement on water sharing, which is called the Ganges River Treaty. It is believed that the Treaty has been an outcome of political altruism or good political relationships between the two countries (Bhaduri, Reference Bhaduri2005). But a change in altruistic concern could induce India to unilaterally divert water. In addition, the current concern is that in the near future there may not be enough water flow in the Ganges River to fulfil the water requirements of both India and Bangladesh. Also recognizing that the Ganges flows during the dry season are not adequate to meet the requirements of both India and Bangladesh, it was agreed by both the countries to cooperate with each other in finding a solution to the long-term problem of augmenting the flows of the River during the dry season.
One of the possible ways, as proposed by Bangladesh, is to augment the flow of water in Bangladesh by water transfer from a resource abundant neighbouring third country, Nepal.Footnote 8 The surplus water in Nepal could be used to augment dry season flows in Bangladesh by constructing a water storage facility using a dam on the Kosi River.Footnote 9 Due to the local geography, water cannot be directly transferred to the downstream country, Bangladesh (see figure 1). Water can only be transferred from Nepal to Bangladesh through the upstream country, India.
Here, a water-sharing model is formulated to determine the optimal amount of water transfer. The model includes the possibility of an ‘outside option’ for the downstream country, Bangladesh, to buy water from a third country, Nepal. Transfer of water entails a high cost, which may include building storage dams, canals, or pipelines. The presence of the transfer cost of water and the scarcity value of water are crucial to the outcomes of the model. This would induce Nepal, the water seller country, to charge a monopoly price, assuming its ability as a monopoly seller of water.
Even though the water is transferred through India, the latter country would have little incentive to exploit the opportunity to control the water transferred from Nepal. If political willingness has induced the countries to allocate water according to a treaty, then India may have no incentive to influence the amount of water transferred due to the risk of breakdown of the existing treaty. In the absence of any treaty, the upstream country, India, would not use a proportion of water transferred for India, as water usage above the optimal consumption would entail a decreased profit.Footnote 10 This case will yield results very similar to the case where water is directly transferred. Here the third country has the ability to be a monopoly seller of water, having exclusive control over the price of water. The outcome would be different if India gains positive benefits from water transfer as positive externalities. The positive externalities could be in the form of flood mitigation, improved navigation, and generation of hydroelectric power. We demonstrate that under a ‘no treaty’ condition, if India gains positive externalities from water transfer, then it would influence the water allocation between the two countries. In the setting of the Ganges Treaty, positive externalities could induce India to buy water jointly with Bangladesh. We explore whether water transfer offers sufficient additional benefits to India to allow a coalition among the involved countries, and to create a potential Pareto improvement.
Thus the paper illustrates the example of water transfer in an international river basin by focusing on Bangladesh's proposal to transfer water from Nepal. The model also examines different scenarios under which such a transfer could take place. The findings of the paper clearly indicate the situations under which both India and Bangladesh could be better off if they jointly agree to transfer water from Nepal. Such outcomes not only demonstrate how such a water transfer would alleviate emerging problems of scarcity in the lower Basin, but also how such a ‘linkage’ water augmentation agreement would facilitate the sustainability of the existing 1996 water-sharing Ganges Treaty between India and Bangladesh.
We have structured the paper as follows. In the next section, we develop an international river basin model of water sharing between an upstream and a downstream country. The subsequent section illustrates the case of indirect market-based water transfer from Nepal. In section 4 we explore market-based water transfer to Bangladesh with positive externalities to India. In the following section we present the possible case of water transfer to both India and Bangladesh under treaty conditions. Section 6 discusses the policy implications of water transfer. Finally, the conclusion summarizes the main findings and results of the paper.
2. A model of water sharing in an international river basin
In this section, we develop an international river basin model of water sharing between an upstream country and a downstream country and the possibility of direct market-based water transfer to meet the excess demand for water in the downstream country. Consider the allocation of river water between India and Bangladesh of the Ganges River Basin. India is an upstream country and has the opportunity to divert water unilaterally; while Bangladesh is a downstream country where the freshwater availability depends on the water usage of the upstream country. We assume that the flow of water, W, is non-stochastic. The proportion of water diverted in India is α, whereas the proportion of water allocated to the downstream country, Bangladesh, is 1−α, with 0 < α < 1. As the flow of water, W, is invariant, the consumptive usage of water by India (I) and Bangladesh (B) is a function of the share of water, α, diverted in India. The contribution of α to the consumptive usage of water, wi, in country i (i = I,B) can be represented by
Consider an agricultural production function qi = f(wi, xi) for i = I, B, where wi is the amount of water usage and xi is an indicator for all other inputs.Footnote 11 The production function is assumed to be strictly concave for all possible values of w and x.
The cost function of withdrawing water from the river and for distribution is ciw(wi), and is assumed to be increasing and convex for all values of w. The marginal cost of other factors, cix, is constant for all values of x. The price of the agricultural good is pi, and is determined exogenously in the international market. The payoff to each country is represented by the aggregate profit of the agricultural sector.
The payoff functions of India (I) and Bangladesh (B) are represented as
As in most river basins, the water flows of the Ganges River are sufficient to meet the water demand of the upstream country, India. India diverts a share of water to meet its optimal water consumption needs.
India will determine the optimal share of water diversion upstream by choosing α to maximize its payoff πI = pI qI(wI, xI) − cI w(wI) − cI X xI, given the constraint wI = αW α ∈ (0, 1). The first-order condition of the above problem can be represented as
![\begin{equation}
\left[ {p^I \frac{{\partial q^I}}{{\partial w^I}}\frac{{\partial w^I}}{{\partial \alpha}} - \frac{{\partial c_w ^I}}{{\partial w^I}}\frac{{\partial w^I}}{{\partial \alpha}}} \right] \,{=}\, 0\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:70809:20160411115532095-0698:S1355770X07004056_eqnU4.gif?pub-status=live){kind=small}
As W > 0, the above first-order equation can be simplified to
![\begin{equation}
\left[ {p^I \frac{{\partial q^I}}{{\partial w^I}} - \frac{{\partial c_w ^I}}{{\partial w^I}}} \right] \,{=}\, 0
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:72488:20160411115532095-0698:S1355770X07004056_eqn5.gif?pub-status=live){kind=small}
The above expression implies that India's payoff will be maximized when the net marginal benefit of water consumption is equal to zero.
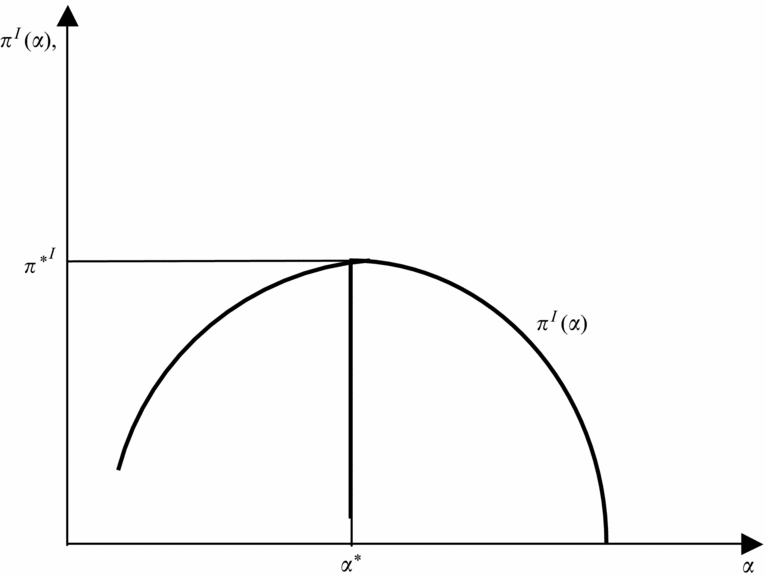
The solution to the above maximization problem is α* = α(pI, xI), where the optimal amount of water usage by the upstream country depends on the price of agricultural good, pI, and usage of other inputs for agriculture. Figure 2 illustrates India's, the upstream country, payoff, πI(α) as a function of the share of water diversion, α. Since qI(wI, xI) is strictly concave, it follows that the slope of the profit function with respect to the share of water diverted is positive for α < α*, and, conversely, is negative for α* > α(see figure 2).
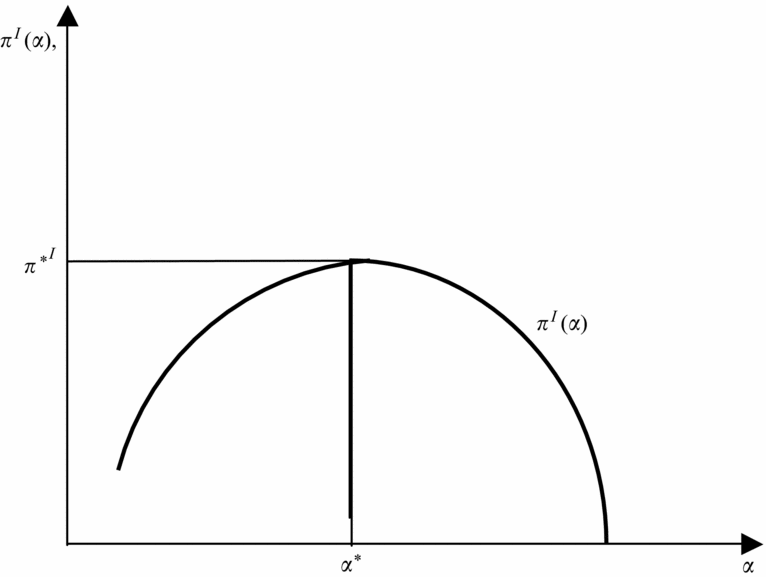
Figure 2. India's payoff as a function of share of water diversion
Assuming that consumptive usage of water is a fixed proportion of the available water, α, a lower rate of water utilization would require a lower value of α, thus under-utilization of water for a lower value of α will result in lower profit for producers. Similarly, over-utilization of water will ensure a lower profit π < π*I because of diminishing marginal productivity of water and the negative second-order profit condition (see figure 2). Given that there is no water-sharing agreement, India will maximize its profit π*I by diverting α*share of water upstream and allowing the rest to flow downstream to Bangladesh (see figure 2).
The freshwater availability to the downstream country, Bangladesh, is dependent on the share of water diverted in the upstream country, India. Bangladesh's problem is to maximize its profit function and can be represented as follows
![\begin{equation}
\mathop {Max}\limits_{w^B} \pi ^B \,{=}\, p^B q^B (w^B,\,x^B) - c_w^B (w^B) - c_X^B x^B\]% {\rm subject}\,{\rm to}\,w^B \le (1 - \alpha)W.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:21052:20160411115532095-0698:S1355770X07004056_eqn6.gif?pub-status=live)
Bangladesh faces two possible regimes while maximizing its agricultural profit function:
(I) The constraint is binding wB = (1 − α)W, implying that there is scarcity of water in the river basin.
(II) The physical water availability constraint is non-binding wB < (1 − α)W.
If the water availability constraint is binding, then the solution of the above problem (5) is w*B = wB(α). In the absence of any water-sharing treaty, Bangladesh's water consumption, w*B, depends on the optimal share of water diverted in India, α*, and thus is influenced by India's domestic agricultural price and usage of other inputs. A rise in agricultural production subsidies in India, for instance, will increase the demand for water there. Higher consumption of water in the upstream country will thus affect the water consumption in the downstream country. If there is water scarcity, then the solution w*B = wB(α*) represents the actual supply of freshwater to Bangladesh. The profit level of Bangladesh under regime (I) will be π*B(pB, xB, α).
Water can also be shared according to an agreement between an upstream and a downstream country. Suppose α is the share of water allocation determined by such an existing treaty between India and Bangladesh. The actual supply of freshwater to the downstream country will be w*B = w B (α).
If the water availability constraint is non-binding, then the solution to the problem is w*B = w(pB, xB). The solution represents Bangladesh's desired demand for water, which approximates the profit-maximizing optimal water consumption in the case where there is no water scarcity. The solution suggests that the consumptive usage of water in Bangladesh is independent of water usage in the upstream country, India, and can only be influenced by domestic price and other factor usage. The profit level of Bangladesh under this regime is πB(pB, cB x, xB).
Measuring the ex ante amount of water needed for Bangladesh to approximate the maximized profit when there is no scarcity of water in the downstream country, the excess demand for water in Bangladesh to attain the profit-maximizing optimum can be represented by
where α = α* in the case without treaty, while α = α is the share of water diverted by the upstream country under an existing water-sharing treaty.
According to (6) excess demand for water, EDB, arises when Bangladesh faces water scarcity, and is dependent on the share of water, α, diverted by the upstream country, India. The excess demand for water also depends on the agricultural price, pB, and usage of other production factors, xB, of Bangladesh. In order to make the problem tractable, we consider these factors influencing the excess demand to be exogenously determined, thus making the excess demand of Bangladesh, EDB, a function of α only.
Equation (6) also allows us to consider how Bangladesh can meet its excess demand for water through transfers from a water-abundant third country. Bangladesh can meet its shortage of water by buying the amount of water, D, depending on the price of water from a water-abundant third country. The range of D lies between zero and EDB. In the case of the Ganges River Basin, Nepal, a relatively freshwater-abundant country, is the only potential supplier of water to Bangladesh. However, due to the local geography, water cannot be directly transferred to Bangladesh (see figure 1). Water can only be affordably transferred from Nepal to Bangladesh through India. Such water transfers would influence the water flow in India.
From a political altruism perspective, a country's concern about the other country is moulded by political objectives. Under the present condition with the Ganges Treaty, where altruistic concerns may have induced India to sacrifice water for Bangladesh, India may have no incentive to control the amount of water transferred to Bangladesh due to the risk of causing a breakdown of the existing Ganges Treaty. If India altruistically cares about Bangladesh, then any plan by the latter country to augment its flow of water will not be threatened. Even in the absence of altruism, India may have little incentive to use a proportion of the water transferred for Bangladesh because water usage above the optimal level would entail a higher marginal cost and decreased profit. This case will yield a result very similar to the case where water is directly transferred.
We also consider the possible case where India gains additional benefits from water transfer as positive externalities when water is indirectly transferred to Bangladesh through India. We explore the conditions under which water transfer from Nepal influences the water allocation between India and Bangladesh.
3. Market-based water transfer to Bangladesh without positive externalities to India
Assume here that water can be transferred to Bangladesh from Nepal through India, influencing its water consumption. Suppose Nepal forgoes some amount of domestic water consumption and also incurs a water transfer cost in supplying water to Bangladesh. Suppose WN, the water supply in Nepal, is deterministic. If Nepal transfers an amount of water, D, to Bangladesh and wN is the domestic water consumption of Nepal, then the water availability constraint can be represented as
The cost function of withdrawing water from the river and of distribution in Nepal for domestic consumption is cNw(wi), and is assumed to be increasing and convex for all values of w. The marginal cost of other factors, cNx, is constant for all values of x. The price of the agricultural good is pN, and is determined exogenously in the domestic market of Nepal. The cost of transferring water, TN, can be expressed as
where T is the fixed cost of water supply and tN is the variable cost of water supply. We also assume the marginal cost of water transfer, T′(D), is increasing. If Nepal sets a price, r, for each unit of water transferred to Bangladesh, the payoff of Nepal is represented by
Bangladesh, facing the price of water from Nepal and the share of water diverted by India, will buy the desired amount of water, D, represented by the equation
Water consumption in Bangladesh is wB = (1 − α)W + D. The payoff function for Bangladesh is represented as
The sequence of the countries' move is as follows:
1. Nepal sets the price of water, r.
2. Bangladesh observes r, and then chooses the amount of water to be bought from Nepal.
To solve the backward-induction outcome of the model, we first compute Bangladesh's reaction to an arbitrary share of water diverted by India, and the price of water charged by Nepal, RB(α, r).Footnote 12
![\begin{equation}
\mathop {Max}\limits_{D > 0} \pi ^B {=} p^B q^B (w^B,\,x^B) \,{-}\, c_w^B (w^B) \,{-}\, c_X^B x^B \,{-}\, rD\,{\rm subject}\,{\rm to}\,w^B \,{=}\, (1 \,{-}\, \alpha)W {+} D
\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:96114:20160411115532095-0698:S1355770X07004056_eqnU13.gif?pub-status=live){kind=small}
The first-order condition of the above problem can be expressed as
![\begin{equation}
p^B \frac{{\partial q^B}}{{\partial w^B}}\frac{{\partial w^B}}{{\partial D}} - \frac{{\partial c_w^B}}{{\partial w^B}}\frac{{\partial w^B}}{{\partial D}} - r \,{=}\, 0.\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:63458:20160411115532095-0698:S1355770X07004056_eqnU14.gif?pub-status=live){kind=small}
The above first-order condition can be simplified to
The above expression implies that Bangladesh will demand an optimal amount of water transfer from Nepal when the net marginal benefit of water transfer ![$[{p^B \frac{{\partial q^B}}{{\partial w^B}} - \frac{{\partial c_w^B}}{{\partial w^B}}}]$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:32922:20160411115532095-0698:S1355770X07004056_inline4.gif?pub-status=live){kind=small}
is equal to its opportunity cost, r.
The demand function for excess water can be derived by solving equation (12)
In the absence of any water-sharing treaty, India always has the option of unilaterally diverting any share of water. India determines the optimal share of water, α*, maximizing its profit function. Bangladesh's demand function for water will be D = D(r, α*).
In the case of a water-sharing treaty, Bangladesh's demand for water will be modified to D = D(r, α), where α is the share of water agreed by a treaty. As the upstream country, India, forgoes water in the case of an altruistic water-sharing agreement, the share of water diverted, α, will be less than the share of water, α*, in the case without water-sharing agreement. The downstream country, Bangladesh, will demand less water when water is shared according to agreement.
Given perfect information, Nepal knows there is a water-sharing agreement between India and Bangladesh, and the associated water share, α. Nepal also knows that if there is no water-sharing treaty, then India will divert α* share of water.
Since Nepal can solve Bangladesh's problems as well, Nepal should anticipate the amount of water bought, given the reaction function, D(r, α). Thus Nepal's problem amounts to
subject to D = D(r, α); TN = T + tN(D) and wN + D = WN.
The first-order condition is
![\begin{equation}
p^N \frac{{\partial q^N}}{{\partial w^N}}\frac{{\partial w^N}}{{\partial D}}\frac{{\partial D}}{{\partial r}} - \frac{{\partial c_w^N}}{{\partial w^N}}\frac{{\partial w^N}}{{\partial D}}\frac{{\partial D}}{{\partial r}} + D + r\frac{{\partial D}}{{\partial r}} - \frac{{\partial t^N}}{{\partial r}} \,{=}\, 0.
\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:70220:20160411115532095-0698:S1355770X07004056_eqnU18.gif?pub-status=live){kind=small}
Simplifying the above expression we get
![\begin{equation}
D + r\frac{{\partial D}}{{\partial r}} \,{=}\, \frac{{\partial D}}{{\partial r}}\left[ {p^N \frac{{\partial q^N}}{{\partial w^N}} - \frac{{\partial c_w^N}}{{\partial w^N}}} \right] + \frac{{\partial t^N}}{{\partial r}}.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:72874:20160411115532095-0698:S1355770X07004056_eqn19.gif?pub-status=live){kind=small}
The above first-order condition suggests that Nepal will charge a water transfer price such that the marginal revenue of water transfer 
equals the marginal benefit forgone in domestic consumption 
and the marginal cost of water transfer 
.
Knowing the share of water diversion by the upstream country, α, Nepal sets a price r*, while Bangladesh, observing the price, will buy D* amount of water from Nepal. Nepal is the monopoly seller of water to Bangladesh and has exclusive control over the price of water, and so will charge a higher monopoly price for the share of water, α, diverted by the upstream country. Bangladesh is the only buyer of water from Nepal and has exclusive control over the amount of excess water to be bought. Observing a higher price, Bangladesh will buy a smaller amount of water (see Appendix notes).
The question remaining is whether it is better than the outcomes without market-based water transfer? The answer to the question depends on how a market-based transfer will affect the water allocation of the countries relative to the socially optimal allocation, and is demonstrated using figure 3. Let S 1 be the supply curve of water, which measures the marginal cost of water transfer from Nepal (see figure 3). The water demand function that measures the marginal benefit of water consumption with no transaction cost is D 1. Start with a quantity, w*B(α*), as the initial allocation of water to Bangladesh in the case with no market-based water allocation. According to the Coase theorem, the social planner will choose a water allocation on the Pareto efficient frontier that is equivalent to maximizing the joint benefits of the countries from the water transfer. The joint benefits of the countries from the water transfer can be represented as
The efficient allocation of water between the countries is determined by maximizing the above function subject to WN = wN + wB.
Figure 3. Market-based water transfer and resource allocation
As indicated in figure 3, the optimal water allocation by a social planner, Bangladesh's water demand D 1 is equal to S 1 at wB 1. According to this efficient market-based water allocation, Bangladesh receives an additional amount of water wB 1 − w*B(α*). If Nepal charges the monopoly price for the excess water transferred to Bangladesh, then the optimal allocation of water, wB 2, to the latter country will be determined where MR 1 = MC (see figure 3).
Bangladesh will buy less and the outcome will be inefficient, but still better than the outcome without any market-based water transfer. There can be transaction costs involved in such market-based water transfers. They can result from political action by third parties who are concerned about in-stream water use, environmental quality, and the economic impacts on regional sales caused by reduced agricultural production.
In many countries, buyers pay such transaction costs. If the transaction costs of administering the water trades are included, Bangladesh's demand curve for water will shift from D 1 to D 2 (see figure 3).
With the shift of the MR curve, the allocation with transaction costs included becomes wB 3, where MC = MR 2. Nepal will have no incentive to reduce these transaction costs if Bangladesh pays them and this, therefore, yields an inefficient outcome.
We have seen that the uncooperative static equilibrium produces an inefficient outcome. There are other bargains where both countries can be made better off. If the game is repeated, the loss from non-cooperation will accumulate and there will be strong incentives for both countries to reach an agreement better than the uncooperative equilibrium. Each year, countries face scarcity of water and can re-negotiate the amount of water transfer and the price for it. Clearly, one could argue that choosing a cooperative solution is a much better outcome, so both the countries could implicitly create a mechanism that deters deviation from a cooperative outcome to reach a stable Pareto superior outcome.
4. Indirect market-based water transfer to Bangladesh with positive externalities to India
Here we demonstrate a case where water transfer to the downstream country, Bangladesh, provides positive externalities to India. The benefits may include flood mitigation, improved navigation, and generation of hydroelectric power. Such positive externalities generated from water transfer by Nepal may influence the water share between the two countries. We consider the case in a setting with no water-sharing treaty between India and Bangladesh where the latter has indirect transfer of water from a third country. Positive externalities are assumed to benefit only the upstream country, India, through which the water is transferred.
Additional water from Nepal may influence the water share diverted by India. Given this situation, the key issues are: (1) how do positive externalities from water transfers affect India's welfare and (2) with these welfare effects in mind, would India change its optimal water share? The analysis now focuses on how consumptive usage of river water is optimized over the two countries given water transfers from Nepal.
In the framework of a game theoretic model, we determine the optimal share of water diversion by India, with provision to Bangladesh augmented by water transfers from Nepal. Bangladesh's decision regarding the amount of water to buy depends on the price of water and the share of water diverted by India. Given the reaction function of Bangladesh, India, the upstream country, decides the optimal share of water diversion. Finally, Nepal, the water seller, charges a monopoly price given the reaction functions of both India and Bangladesh.
Here, in the model, we assume, in the absence of a water-sharing agreement, water is shared proportionately between India and Bangladesh. The proportion of water, α*, allocated for domestic consumption is optimally chosen by India, while the rest of the water flows to Bangladesh. We also assume that water flows to Bangladesh can be augmented by additional water transfers or releases from Nepal. Bangladesh determines D by observing the excess demand for water EDB = wB(pB, xB) − wB(α), so D, the amount of water Bangladesh is willing to buy from Nepal to meet the excess demand, is the choice variable for Bangladesh, where D ∈ ⌊0, EDB(α)⌋.
Water transfer from Nepal may produce positive externalities in the form of benefits to India. The benefits can affect India's welfare and may alter the water-sharing allocation. The benefit function, G, is dependent on the total water transfer, D, from Nepal.Footnote 13 The benefit function, G(D), is also assumed to be concave in the model.
As the positive externalities affect only upstream India, the payoff function for India is modified and is represented as
In the absence of a water-sharing treaty, the timing of the sequential game is as follows:
1. Nepal sets the price of water, r.
2. India chooses α, the share of water diverted.
3. Bangladesh observes the actions of both the players and chooses to buy D amount of water.
To solve the backward-induction outcome of this game, we first compute Bangladesh's reaction to an arbitrary share of water diverted by India, and the price of water charged by Nepal, D(α, r), as in problem (11).
Using the implicit function theorem, we derive the slope of the reaction function from the first condition (see equation (12)). Assuming no change in the price of water, r, Bangladesh's reaction to an arbitrary change in the share of water diversion by the upstream country, India, can be derived as follows
The above expression suggests that with an increase in the share of water, α, diverted by India, Bangladesh will react by buying more water from Nepal.
Given Bangladesh's reaction function, India will determine the optimal share of water diversion to Nepal by solving the following problem
![\begin{equation}
\pi ^I \,{=}\, p^I q^I (w^I,x^I) - c_w^I (w^I) - c_X^I x^I + G(D)\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:56978:20160411115532095-0698:S1355770X07004056_eqnU23.gif?pub-status=live){kind=small}
given the constraints: D = D(α, r) and wI = αW. The first-order condition of the above problem can be stated as follows
![\begin{equation}
p^I \left[ {\frac{{\partial q^I}}{{\partial w^I}}\frac{{\partial w^I}}{{\partial \alpha}}} \right] - \left[ {\frac{{\partial c_w ^I}}{{\partial w^I}}\frac{{\partial w^I}}{{\partial \alpha}}} \right] + \frac{{\partial G}}{{\partial D}}\frac{{\partial D}}{{\partial \alpha}} \,{=}\, 0\]%
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:26905:20160411115532095-0698:S1355770X07004056_eqnU24.gif?pub-status=live){kind=small}
Simplifying the above expression we get
![\begin{equation}
\left[ {p^I \frac{{\partial q^I}}{{\partial w^I}} - \frac{{\partial c_w ^I}}{{\partial w^I}}} \right] \,{=}\, \frac{{\left[ { - \frac{{\partial G}}{{\partial D}}} \right]\frac{{\partial D}}{{\partial \alpha}}}}{W} < 0.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:37018:20160411115532095-0698:S1355770X07004056_eqn25.gif?pub-status=live){kind=small}
Solving the above condition will result in India's reaction function, α = α(r).
The first-order condition (equation (19)) suggests that when there is water transfer from a third country (Nepal) at a given price, r, the value of the marginal benefit from water consumption to India 
will be less than the marginal cost of water usage 
at equilibrium if the marginal benefit to India of water transfer from Nepal 
is positive.
Given the reaction function of India and Bangladesh, Nepal will set a price of water transfer by solving the maximization problem as in equation (14) subject to the constraint D = D(α, r) and α = α(r). Solving the first-order condition (see equation (15)) yields the optimal price, r*, charged by Nepal. Given the reaction functions α = α(r) and D = D(α, r), India and Bangladesh will determine the optimal share of water diversion, α**, and the demand for water, D*, respectively. Figure 4 illustrates India's payoff and its optimal water diversion given Bangladesh's reaction function. With positive externalities from water transfer, India's payoff function, πI(α), has shifted upward by the amount of benefits, G. Without positive externalities, India diverts α* share of water (see figure 4). If India gains sufficiently large benefits from the water transfer, then, given Bangladesh's demand function for water, it might reduce the share of the water diverted to Bangladesh.
Figure 4. India's payoff and Bangladesh's reaction function in water transfer with positive externalities to upstream country
Knowing Bangladesh's reaction function, D(α, r(α)), India would divert less water to Bangladesh, so that Bangladesh, getting less water from India, would buy more water from Nepal. Thus, if there is a water transfer between Nepal and Bangladesh, and India gains sufficient benefits from the water transfer, then India's optimal share of water, α**, will be more than its optimal share of water, α*, the amount it would divert in the unconstrained case (see figure 4). It is evident that if water transfer from Nepal produces sufficient benefits to India, then it will increase the payoff to the latter country. India's payoff will increase from π*I to π**I (see figure 4). The magnitude of the increase in payoff depends on Bangladesh's demand function and the amount of benefits, G, that India receives from the water transfer.
There are two effects of such water transfers on Bangladesh. First, as India decreases the share of water diverted to Bangladesh, the demand for water by Bangladesh from Nepal at a given price of water will increase. Second, knowing India and Bangladesh's reaction function, Nepal will charge a higher price for each unit of water transferred. Facing a higher price, Bangladesh will buy even less water than in the case where water is transferred directly, leading to no additional benefits to India, and thus an even less efficient outcome.
The outcome can be influenced by the degree of benefits of the water transfer to India. If the potential benefits are high, then Bangladesh would face higher price, and as a consequence will buy less water. Overall, the results of the model suggest that if a water transfer to Bangladesh provides positive externalities to India, then it will affect the amount of water transferred. In an extreme case, if the potential effect of the positive externality is large enough, Bangladesh may prefer not to buy water from the third country, i.e. Nepal.
The outcome of the model would be different if the downstream country, Bangladesh, had the option to buy water in the presence of a water-sharing agreement with the upstream country, India. India would enjoy positive externalities from water transferred to the downstream country, and might prefer not to influence the share of water diverted as it would cause a breakdown of the water-sharing treaty. If a water-sharing treaty between India and Bangladesh arises from altruistic concerns, India would not take any action that hindered the beneficial effects to Bangladesh of water transfer.
5. Market-based water transfer to both India and Bangladesh
As India's benefits depend on the amount of water transfer, large benefits could entice India to buy water jointly with Bangladesh. Bhaduri (Reference Bhaduri2005) demonstrated that political altruism could encourage an upstream country to sacrifice water for the benefit of the downstream country and could induce countries to share water, according to an agreement.
If countries buy water together, then it could guarantee a potential Pareto improvement. In this framework, we present a simple altruistic model where both India and Bangladesh buy water from Nepal. Following a cooperative approach, the countries decide the share and amount of water transfer. We assume that water is shared proportionately between India and Bangladesh according to a water-sharing agreement.Footnote 14 The proportion of water allocated to India is α, while a proportion of water, (1 − α), flows downstream to Bangladesh. We also assume that water flows can be augmented by additional water transfers or releases from Nepal. We denote the amount of water released from Nepal as D, of which a proportion, β, flows downstream to India and (1–β) flows even further downstream to Bangladesh, with 0 < β < 1. The contribution of β and D to the consumptive usage of water, wi, in country i(i = I,B) respectively can be represented by
As assumed earlier, India gains benefits, G, from water transfer D. The countries share the cost of water according to the proportions in which they receive additional water. If India pays rβD, then Bangladesh will pay r(1 − β)D for joint water demand D at a price r charged by Nepal. A general model is presented, where the net benefit NBi of country i (i = I, B), in the framework of a system of interdependent utility functions, depends on own private benefit, Bi, cost of water transfer, and weighted net benefit of the other country, kiNBj (j ≠ i). The weights ki are the altruistic concerns of country i.
The net benefit functions of the countries are represented as
The private benefits of India, BI, include agricultural profits, πA, and benefits from water transfer, G(D). Bangladesh's private benefit includes only the agricultural profits.
Substituting BI = πI + G(D) and BB = πB in equations (24) and (25), the net benefit of the countries can be modified as
The joint net benefit of the countries is the aggregate of the net benefit functions of both the countries, which is expressed as follows
![\begin{equation}
V &=& NB^I + NB^B \,{=}\, \frac{1}{{1 - k^I k^B}}\langle (1 + k^B)[ {\pi ^I (w^I) + G(D) - r\beta D} ]\nonumber\\
&& {+}\, (1 + k^I)[ {\pi ^B (w^B) - r(1 - \beta)D} ] \rangle.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:80833:20160411115532095-0698:S1355770X07004056_eqn31.gif?pub-status=live)
Following a cooperative approach, the countries decide on the amount of water transfer, D.
If both the countries care about each other, then a cooperative outcome can be determined by choosing D and β to maximize the joint net benefit of the countries
![\begin{equation}
V &=& \frac{1}{{1 - k^I k^B}}\langle {(1 + k^B)[ \pi ^I (w^I) + G(D) - r\beta D} ]\nonumber\\
&& + (1 + k^I)[ {\pi ^B (w^B) - r(1 - \beta)D} ] \rangle
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:96187:20160411115532095-0698:S1355770X07004056_eqn32.gif?pub-status=live)
given the constraints wI = αW + βD; 
.
Assuming the stability condition kI kB, the first-order conditions of the above problem can be represented as
![\begin{equation}
\frac{{\partial V}}{{\partial D}} \,{=}\, (1 + k^B)\left[ {\frac{{\partial \pi ^I}}{{\partial w^I}}\beta + \frac{{\partial G(D)}}{{\partial D}} - r\beta} \right] + (1 + k^I)(1 - \beta)\left[ {\frac{{\partial \pi ^B}}{{\partial w^B}} - r} \right] \,{=}\, 0
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:32512:20160411115532095-0698:S1355770X07004056_eqn33.gif?pub-status=live){kind=small}
![\begin{equation}
\frac{{\partial V}}{{\partial \beta}} \,{=}\, \left[ {(1 + k^B)\frac{{\partial \pi ^I}}{{\partial w^I}} - (1 + k^I)\frac{{\partial \pi ^B}}{{\partial w^B}}} \right]D \,{=}\, 0
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:84732:20160411115532095-0698:S1355770X07004056_eqn34.gif?pub-status=live){kind=small}
Substituting equation (28) in (27), we get
The above equation (29) implies that the ratio of the net benefit of water transfer of India and Bangladesh equals the ratio of altruistic concerns.
Solving the first-order condition (27) yields the reaction functions D(r). Given the demand function of water D(r), Nepal will set a price of water transfer r* by solving the maximization problem as in (14). The third country will charge a high price but the outcome would be better with regard to efficiency than in the case without any sharing treaty.
The above model has important policy implications. India may gain benefits from indirect water transfer. India, in the setting of a water-sharing treaty, is unlikely to influence the water-sharing allocation. Greater benefits, however, could entice the upstream country (India) to buy water with the downstream country (Bangladesh). Bangladesh's payoff from a water transfer will be greater than the case without any water transfer, as it would augment the flow of water during the dry seasons and periods of drought; thus Bangladesh would buy water from the third country, Nepal. Nepal's gain is evident as it maximizes its profit by charging a monopoly price for water transfer. With all three countries gaining, it is possible that if a market-based water transfer offers sufficient benefits to the upstream country (India), then a grand coalition among the countries involved can guarantee potential Pareto improvement. Overall, we are able to demonstrate the conditions under which issue linkage, in this case water augmentation, can facilitate the water-sharing agreement between India and Bangladesh to be sustained in the long run.
6. Policy implications of market-based water transfer in a river basin
A market-based water transfer has great relevance in resolving the transboundary water conflict in a river basin. Water transfers would augment the flow of water in the river basins during dry seasons and periods of drought. If the price of water transferred is demand-determined, then water can be used efficiently in the countries and thus it can help in mitigating the water scarcity problem. Moreover, market-based water transfer has the potential to facilitate international river basin management and the resolution of water conflict.
In this paper, we have identified different scenarios under which a market-based water transfer can take place. Water transfer can take place in the cases both with and without a water-sharing agreement. The analysis in the paper suggests that only downstream countries would buy water to meet water scarcity. There are two ways in which a third country can transfer water to the downstream water scarce country, based on geographical location of the third country relative to the downstream country: direct water transfer and indirect water transfer through other riparian countries.
In table 1 we have listed all the possible scenarios in which water transfer can take place. We also rank the scenarios in terms of efficiency and welfare effects of the downstream country. The ranking is based on the theoretical results derived in the paper. According to the rankings, the worst scenario occurs when water is shared without any treaty and without any provision for transfer to the downstream country. The results also suggest that even a treaty-based water allocation is better with regard to efficient allocation; water transfer can also provide a similar outcome in the case without any water-sharing treaty. The second-best scenarios occur when the downstream country can buy water in the setting of a water-sharing agreement. In such scenarios, the downstream country faces a lower demand for water as the upstream country forgoes some amount of water.
Table 1. Relevance of market-based water transfer under different scenarios
Note: 1 Under treaty conditions, water share α is fixed.
2 The ranking is based on the welfare effects of the downstream country.
We found the best scenario is where both the upstream and downstream countries could supplement the water-sharing treaty with an additional provision of water transfer from a third country. In this case, water transfer could guarantee a potential Pareto improvement and facilitate the water-sharing agreement between the upstream and downstream countries to be sustained in the long run.
7. Conclusion
In the paper, we have explored market-based water transfer and its significance in mitigating water scarcity and resolving transboundary water conflict in the Ganges River Basin. In 1975 India constructed a dam at Farakka near the border with Bangladesh so that it could divert water unilaterally.
Although the 1996 Ganges River Treaty has established provisions for water releases from the Farakka Dam to ameliorate the impact of the dam on economic development in Bangladesh, the latter country is still vulnerable to unilateral water diversion by India. Changes in the political altruism factors could induce India to deviate from an agreement and divert water unilaterally. In addition, there is concern that there may be insufficient water flow in the entire Ganges River Basin to meet the future demands of both Bangladesh and India. To prevent this from occurring and to reinforce the water-sharing agreement, Bangladesh may buy water from a third country, Nepal.
In the paper we have analyzed the case where water from Nepal can be transferred to Bangladesh through the upstream country, India, as the local geography only permits such water transfer. The upstream country, India, through which water is transferred, has little incentive to use a proportion of the water transferred to Bangladesh because water usage above the optimal consumption would entail a higher marginal cost and a decreased profit under the assumptions of the model.
The outcome will be different if India gains positive externalities from water transfer. The positive externalities generated from water transfer from Nepal may influence the water share of the upstream and the downstream countries. In the absence of altruism, India would allow less water to flow to Bangladesh. India will be able to afford to overuse the water to the extent that the additional cost of water usage is compensated for by the positive externalities from water transfer. We have also explored whether positive externalities could induce India to buy water jointly with Bangladesh, and such a case will only occur if the countries possess altruistic concerns and share water according to an agreement. Following a cooperative approach, both India and Bangladesh decide about the share and amount of water transfer. We have demonstrated the conditions under which issue linkage, in this case water augmentation, can guarantee a potential Pareto improvement and facilitate the water-sharing agreement between the upstream and downstream countries to be sustained in the long run.
The effects of stochastic events, such as periodic drought, on the in-stream flows of the river, have not been considered in the model. If the amount of water available is subject to stochastic fluctuations, then this may alter the outcome of model. Further work could consider a stochastic version of the model.
Appendix notes
Figure A.1 illustrates the isoprofit curves of Bangladesh and Nepal, and the inverse demand for water. In the figure we measure D, the amount of water transfer on the horizontal axis and the price of water transfer, r, on the vertical axis. Lower isoprofit curves represent higher profit for Bangladesh as, holding D constant, the country does better when r is lower dπB|dD=0 = −Ddr. Isoprofit curve (IC)2B represents a higher profit than the isoprofit curve (IC)1B. In contrast, holding D fixed, Nepal does better when r is higher as dπN|dD=0 = Ddr>0, so higher isoprofit curve (IC)2N represents higher profit for Nepal. It suggests that Nepal charges a higher price, r*, and Bangladesh buys a lower amount of water, D*. The outcome is depicted in the figure at point F. The outcome (r*, D(r*)) at point F is not efficient, because there are other bargains in which both countries can be better off. Both countries' profits would be increased if r and D were in the shaded region (say point E).
Figure A.1. Isoprofit curves and efficient bargaining
