Transformer structure and design formula

This work considers two operating frequencies, f ₁ and f ₂, which are arbitrary and uncorrelated. The frequency ratio is defined as α ≡ f ₂/f ₁. The load is considered to have a frequency-dependent complex impedance, i.e. the load impedances at the two operating frequencies are different. Figure 1 shows the structure of the proposed switched band impedance transformer. The electrical lengths of the transmission lines and stubs are measured at frequency f ₁.

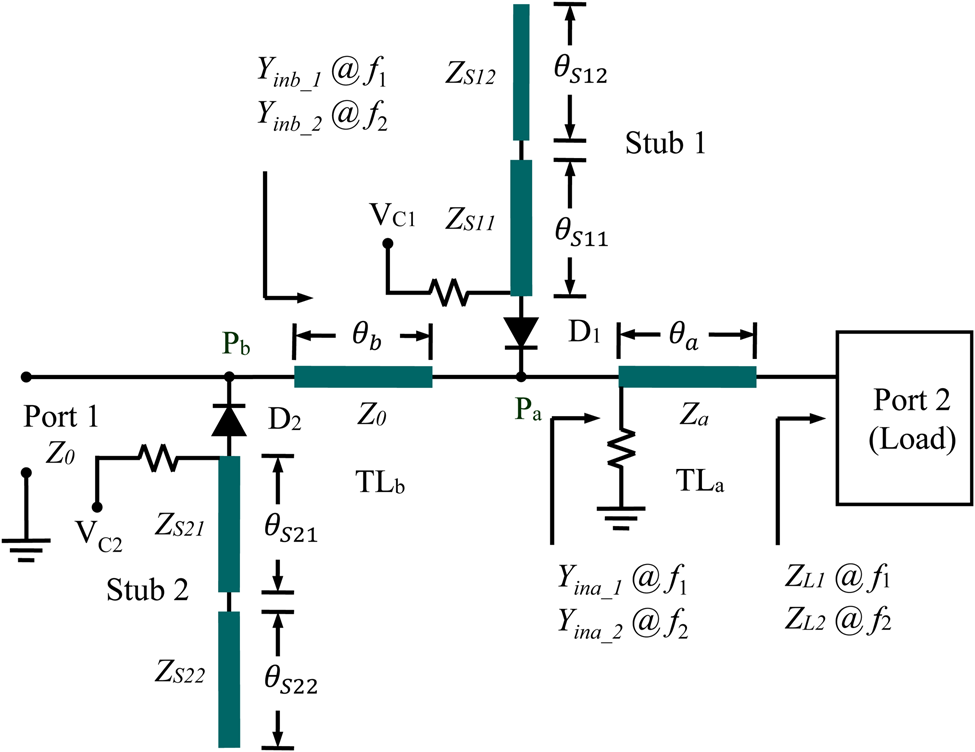
Fig. 1. The proposed switched band impedance transformer.

If transmission line TL_a and stub 1 are used to match the lower frequency, f ₁, the functions of the transmission lines and stubs as well as the design concept are described below. Transmission line TL_a is used to obtain an input admittance $Y_{ina\_1}$, seen by looking into the load and having the form $Y_0 + jB_{ina\_1}$ at frequency f ₁. If the load impedances at the two operating frequencies are Z _L1 = R _L1 + jX _L1 at f ₁ and Z _L2 = R _L2 + jX _L2 at f ₂, the electric length, θ _a, of transmission line TL_a can be determined as

(1)$$\theta _a = \tan ^{{-}1}\left({\displaystyle{{Z_aX_{L1} \pm \sqrt {Z_a^2 X_{L1}^2 -\lpar Z_a^2 -Z_0R_{L1}\rpar \lpar \vert Z_{L1}\vert^2-Z_0R_{L1}\rpar } } \over {Z_0R_{L1}-Z_a^2 }}} \right)\comma \;$$

where the characteristic impedance Z_a is a user-set parameter. Comparing with the previous study [Reference Norouzian and Gardner17], Z_a can be an arbitrary value instead of Z ₀.

Once the input admittance is calculated, a shunt stub is added to cancel the input susceptance. When diode D ₁ is forward biased and diode D ₂ is reverse biased, stub 1 is connected to transmission line TL_a at junction P_a and stub 2 is disconnected. Uniform-impedance stub¹⁴ can be used to cancel the input susceptance at f ₁ but not guarantee to block the signal at f ₂. In this study, stub 1, which has a stepped impedance, is used to cancel input susceptance B_{ina_ 1} at f ₁ and generate a transmission zero (total reflection), to block the signal at f ₂. Therefore, the lengths and the characteristic impedance of stub 1 must meet equations (2) and (3).

(2)$$\displaystyle{1 \over {Z_{S11}}}\displaystyle{{Z_{S11} + Z_{S12}\cot \lpar \theta _{S12}\rpar {\rm tan\lpar }\theta _{S11}\rpar } \over {Z_{S11}\tan \lpar \theta _{S11}\rpar -Z_{S12}\cot \lpar \theta _{S12}\rpar }} = {-}B_{ina\_1}\comma \;$$

(3)$$Z_{S11}\displaystyle{{Z_{S11}\tan \lpar \alpha \theta _{S11}\rpar -Z_{S12}\cot \lpar \alpha \theta _{S12}\rpar } \over {Z_{S11} + Z_{S12}\cot \lpar \alpha \theta _{S12}\rpar \tan \lpar \alpha \theta _{S11}\rpar }} = 0.$$

Solving these simultaneous equations for Z _S11 and Z _S12 yields

(4)$$Z_{S11} = \displaystyle{1 \over {B_{ina\_1}}}\displaystyle{{1 + \tan \lpar \theta _{S11}\rpar \cot \lpar \theta _{S12}\rpar \tan \lpar \alpha \theta _{S11}\rpar \tan \lpar \alpha \theta _{S12}\rpar } \over {\tan \lpar \theta _{S11}\rpar -\cot \lpar \theta _{S12}\rpar \tan \lpar \alpha \theta _{S11}\rpar \tan \lpar \alpha \theta _{S12}\rpar }}\comma \;$$

(5)$$Z_{S12} = Z_{S11}\tan \lpar \theta _{S11}\rpar \tan \lpar \alpha \theta _{S12}\rpar \comma \;$$

where the electrical lengths θ _S11 and θ _S12 are user-set parameters. Thus, the load impedance is transformed to Z ₀ at f ₁ and short-circuited at f ₂.

To achieve matching at frequency f ₂, diode D ₁ is reverse biased and D ₂ is forward biased. Thus, stub 1 is disconnected and stub 2 is connected to transmission line TL_b at junction P_b. Transmission lines TL_a and TL_b are used to obtain the input admittance $Y_{inb\_2}$, at junction P_b, seen by looking into the load and have the form $Y_0 + jB_{inb\_2}$ at frequency f ₂. The characteristic impedance of transmission line TL_b is chosen as Z ₀ so that it does not affect the matching condition at f ₁.

The electrical length, θ _b, of transmission line TL_b at frequency f ₁ can be determined as

(6)$$\theta _b = \displaystyle{1 \over \alpha }\tan ^{{-}1}\left({\displaystyle{{X_{ina\_2} \pm \sqrt {R_{ina\_2} [ {\lpar Z_0-R_{ina\_2}\rpar }^2 + X_{ina\_2}^2 ] /Z_0} } \over {R_{ina\_2}-Z_0}}} \right)\comma \;$$

where the input impedance at junction P_a without stub 1 is $R_{ina\_2} + jX_{ina\_2}$ at frequency f ₂.

Once the input conductance is obtained, stub 2 is used to cancel input susceptance B_{inb_ 2} at f ₂ and generate a virtual ground to block the signal at f ₁. Therefore, the lengths and the characteristic impedance of stub 2 must satisfy equations (7) and (8) simultaneously.

(7)$$Z_{S21}\displaystyle{{Z_{S21}\tan \lpar {\theta_{S21}} \rpar -Z_{S22}\cot \lpar {\theta_{S22}} \rpar } \over {Z_{S21} + Z_{S22}\cot \lpar \theta _{S22}\rpar \tan \lpar {\theta_{S21}} \rpar }} = 0\;\comma \;$$

(8)$$\displaystyle{1 \over {Z_{S21}}}\displaystyle{{Z_{S21} + Z_{S22}\cot \lpar {\alpha \theta_{S22}} \rpar \tan \lpar \alpha \theta _{S21}\rpar } \over {Z_{S21}\tan \lpar \alpha \theta _{S21}\rpar -Z_{S22}\cot \lpar \alpha \theta _{S22}\rpar }} = {-}B_{inb\_2}.$$

Solving these equations for Z _S21 and Z _S22 yields

(9)$$Z_{S21} = \displaystyle{1 \over {B_{inb\_2}}}\displaystyle{{1 + \tan \lpar \theta _{S21}\rpar \cot \lpar {\theta_{S22}} \rpar \tan \lpar {\alpha \theta_{S21}} \rpar \tan \lpar {\alpha \theta_{S22}} \rpar } \over {\tan \lpar {\theta_{S21}} \rpar -\cot \lpar \theta _{S22}\rpar \tan \lpar {\alpha \theta_{S21}} \rpar \tan \lpar {\alpha \theta_{S22}} \rpar }}\comma \;$$

(10)$$Z_{S22} = Z_{S21}\tan \lpar \theta _{S21}\rpar \tan \lpar {\theta_{S22}} \rpar \comma \;$$

where the electrical lengths θ _S21 and θ _S22 are user-set parameters. Thus, the load impedance is transformed to Z ₀ at f ₂ and short-circuited at f ₁. For convenience, the above solution is called Type 1.

The functions of the transmission lines and stubs can be interchanged with the same circuit structure. For convenience, this solution is called Type 2. Specifically, transmission line TL_a and stub 1 in Type 1 are used to match the lower frequency, f ₁, while transmission line TL_a and stub 1 in Type 2 are used to match the higher frequency, f ₂.

In Type 2, transmission line TL_a is used to obtain an input admittance seen by looking into the load and having unit conductance at frequency f ₂ while stub 1 is used to cancel the susceptance arising from transmission line TL_a at frequency f ₂ and to generate a transmission zero at frequency f ₁ when diode D ₁ is forward biased and diode D ₂ is reverse biased. For matching at frequency f ₁, diode D ₁ is reverse biased and D ₂ is forward biased. Thus, stub 1 is disconnected and stub 2 is connected to transmission line TL_b. Transmission lines TL_a and TL_b are used to obtain a certain input admittance so as to have unit admittance at frequency f ₁. Stub 2 is used to cancel the susceptance arising from transmission lines TL_a and TL_b at frequency f ₁ and to generate a transmission zero (total reflection), at frequency f ₂. In this case, the design formula is modified as equations (11)–(16).

(11)$$\theta _a = \displaystyle{1 \over \alpha }\tan ^{{-}1}\left({\displaystyle{{Z_aX_{L2} \pm \sqrt {Z_a^2 X_{L2}^2 -\lpar Z_a^2 -Z_0R_{L2}\rpar \lpar \vert Z_{L2}\vert^2-Z_0R_{L2}\rpar } } \over {Z_0R_{L2}-Z_a^2 }}} \right)\comma \;$$

(12)$$Z_{S11} = \displaystyle{1 \over {B_{ina\_2}}}\displaystyle{{1 + \tan \lpar \theta _{S11}\rpar \tan \lpar \theta _{S12}\rpar \tan \lpar \alpha \theta _{S11}\rpar \tan \lpar \alpha \theta _{S12}\rpar } \over {\tan \lpar \alpha \theta _{S11}\rpar -\tan \lpar \theta _{S11}\rpar \tan \lpar \theta _{S12}\rpar \cot \lpar \alpha \theta _{S12}\rpar }}\comma \;$$

(13)$$Z_{S12} = Z_{S11}\tan \lpar \theta _{S11}\rpar \tan \lpar \theta _{S12}\rpar \comma \;$$

and

(14)$$\theta _b = \tan ^{{-}1}\left({\displaystyle{{X_{ina\_1} \pm \sqrt {R_{ina\_1}[ {\lpar Z_0-R_{ina\_1}\rpar }^2 + X_{ina_1}^2 ] /Z_0} } \over {R_{ina\_1}-Z_0}}} \right)\comma \;$$

(15)$$Z_{S21} = \displaystyle{1 \over {B_{inb\_1}}}\displaystyle{{1 + \tan \lpar \theta _{S21}\rpar \cot \lpar \theta _{S22}\rpar \tan \lpar \alpha \theta _{S21}\rpar \tan \lpar \alpha \theta _{S22}\rpar } \over {\tan \lpar \theta _{S21}\rpar -\cot \lpar \theta _{S22}\rpar \tan \lpar \alpha \theta _{S21}\rpar \tan \lpar \alpha \theta _{S22}\rpar }}\comma \;$$

(16)$$Z_{S22} = Z_{S21}{\rm tan\lpar }\alpha \theta _{S21}{\rm \rpar tan\lpar }\alpha \theta_{S22}\rpar.$$

In these equations, B_{ina_ 2} denotes the input susceptance at frequency f ₂ at junction P_a, $R_{ina\_1} + jX_{ina\_1}$ denotes the input impedance at frequency f ₁ at junction P_a without stub 1, and B_{inb_ 1} denotes the input susceptance at frequency f ₁ at junction P_b.

Design example

To verify the proposed structure and design procedure, a switched band impedance transformer using microstrips was designed, fabricated, and measured. The arbitrary two operating frequencies used were 0.9 and 2.1 GHz. The transformer was designed and fabricated on a 1.6 mm-thick FR4 substrate with a dielectric constant of 4.35 and a loss tangent of 0.016. The load used was a 100 Ω resistor and an SMA connector shunt connected with a 1 pF capacitor. The corresponding load impedances were 87.24-j74.00 and 30.50-j60.38 Ω at the two operating frequencies, respectively.

Figure 2 shows the variation of the required electrical length θ_a versus the characteristic impedance Z_a of transmission line TL_a for Type 1. In this case, the length θ_a decreases as the impedance Z_a increases. Because Z_a is a user-set parameter, the designer can choose a suitable value to minimize θ_a under PCB fabrication constrains, such as width limitations. In contrast, traditional single-frequency matching networks or previous switched matching networks¹⁴ often use a 50 Ω transmission line, such that the circuit size is fixed and cannot be reduced. For example, the required length θ_a is about 60° if Z_a was chosen as 100 Ω which is a typical upper value of general PCB technique. While if Z_a was chosen to be equal to the traditional value of 50 Ω, the required length θ_a would be more than 100°. The proposed structure can reduce the required length by 60%. In this example, Z_a was chosen as 75 Ω and the required θ_a was 82.80° at 0.9 GHz.

Fig. 2. Variation of the required electrical length θ_a (at 0.9 GHz) versus the characteristic impedance Z_a of transmission line TL_a for Type 1.

As to transmission line TL_b, there were two solutions that could be chosen. In this example, θ_b was chosen as 29.32° at 0.9 GHz. Figure 3(a) demonstrates the variations of the required Z_{S 11} and Z_{S 12} versus θ_{S 12} for different values of θ_{S 11}. Because θ_{S 12} and θ_{S 11} are user-set parameters, suitable values can be chosen to obtain reasonable stub impedances, i.e. neither extremely high nor extremely low. For example, Z_{S 11} and Z_{S 12} are between 25 and 100 Ω when θ_{S 11} = 10° and 13° < θ_{S 12} < 35°. Figure 3(b) shows a similar phenomenon for stub 2.

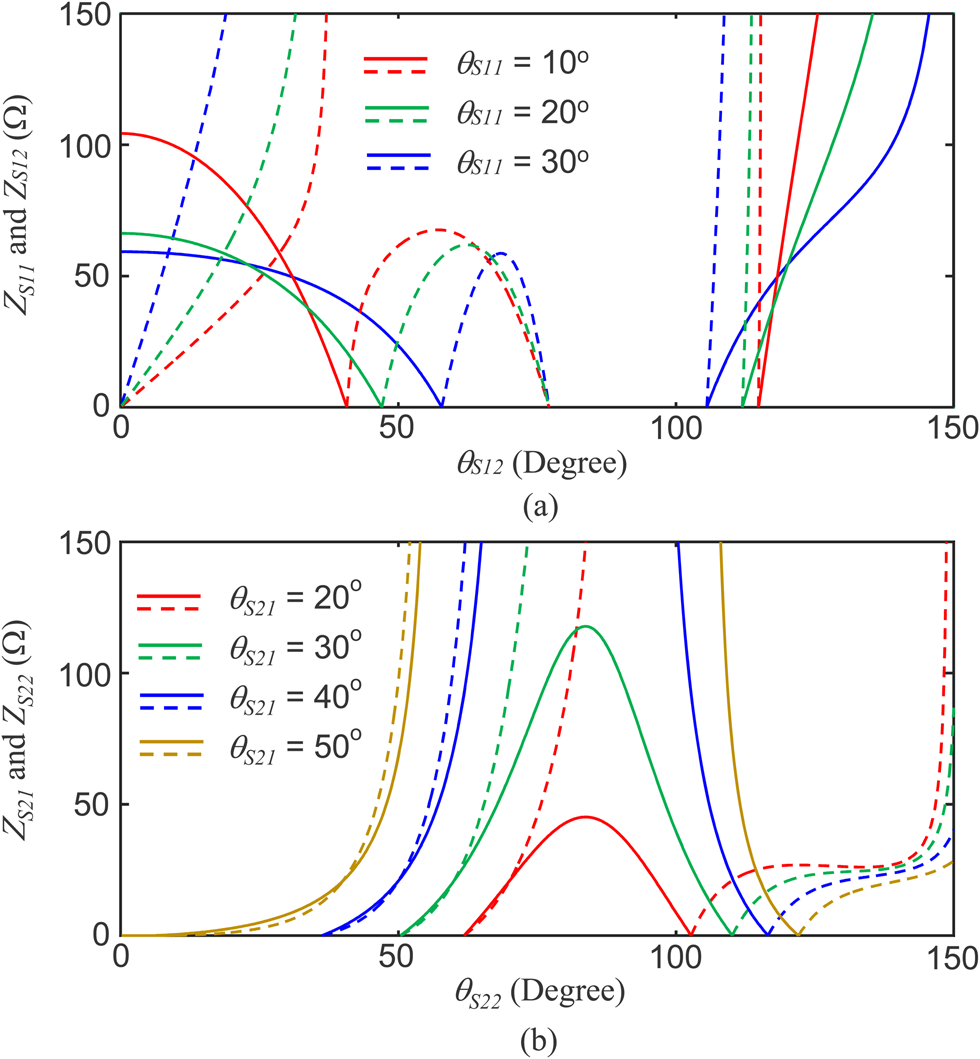
Fig. 3. Variation of the required stub impedances versus stub lengths, (a) Z_{S 11} (solid line) and Z_{S 12} (dashed line) against θ_{S 12} for different θ_{S 11}, (b) Z_{S 21} (solid line) and Z_{S 22} (dashed line) against θ_{S 22} for different θ_{S 21}.

For Type 2, Fig. 4 demonstrates the variation of the required electrical length θ_a versus the characteristic impedance Z_a of transmission line TL_a. Figure 4 shows that a higher impedance transmission line requires a shorter length. As Type 1, the designer can choose a suitable value to minimize θ_a under PCB fabrication constrain, such as width limitations. Here Z_a was chosen to be 75 Ω as Type 1 and thus the required length θ_a was 26.09° at 0.9 GHz. In contrast, the switched matching network that uses a 50 Ω transmission line requires θ_a of more than 34°. The choice of the characteristic impedances and lengths of stubs 1 and 2 is similar to Type 1.

Fig. 4. Variation of the required electrical length θ_a (at 0.9 GHz) versus the characteristic impedance Z_a of transmission line TL_a for Type 2.

Table 1 lists the parameters of the two designed circuits, where the underlined values denote user-set parameters and the rest were obtained using the proposed design formula. Figure 5 shows the frequency responses of the two designed switchable transformers which were simulated using Ansoft Designer (now called ANSYS HFSS-Circuit) with ideal transmission line model. The diodes were considered as ideal in our numerical simulation, i.e. open when zero-biased and shorted when forward-biased. In the lower-band mode, diode D ₁ is forward-biased and diode D ₂ is zero-biased. In this mode, the frequency response showed a good matching exactly at the operating frequency, 0.9 GHz, and a reflection of 0 dB at the non-operating frequency, 2.1 GHz. In the higher-band mode, diode D ₁ is zero-biased and diode D ₂ is forward-biased. The frequency response showed a good matching exactly at 2.1 GHz and a reflection of 0 dB at 0.9 GHz. Due to the restriction of total reflection at the non-operating frequency, the matching bandwidth of the presented impedance transformer is narrower than the traditional single-band impedance transformer which does not concern with total reflection at other frequencies.

Fig. 5. Simulated reflection coefficients of the two designed switch-band impedance transformers with different diode biasing conditions.

Table 1. Circuit parameters of the designed switched band impedance transformers where parameters with underline are user-setting.

The electrical lengths are measured at 0.9 GHz.

Figure 6 compares the numerical results of Type 1 using stepped-impedance stubs and traditional structure using uniform-impedance stubs. If the matching frequency is 2.1 GHz, the structure using stepped-impedance has S ₁₁ of 0 dB at 0.9 GHz while the structure using uniform-impedance stub has S ₁₁ of −12 dB. It is clear that the circuit using stepped-impedance stub can suppress signal at the non-operating frequency and the one using uniform-impedance stub has no such function.

Fig. 6. Comparison between impedance transformers with uniform-impedance stubs and stepped-impedance stubs.

Figure 7 shows a comparison of the numerical and measured frequency responses where the fabricated transformer Type 1 is embedded. This work used Infineon BAR63-02V PIN diodes. The experimental results were obtained using an R&S ZVA40 network analyzer. In the lower-band mode, the simulation revealed a good match at 0.9 GHz and total reflection (0 dB) at 2.1 GHz. The measurements showed good matching at 0.9 GHz and a reflection of −2.4 dB at 2.1 GHz. The bandwidths of the simulations and measurement are 338 and 383 MHz, respectively. In the higher-band mode, the simulation revealed a good match at 2.1 GHz and total reflection at 0.9 GHz. The bandwidths of the simulations and measurement are 98 and 113 MHz, respectively. The measurements showed a good match at 2.1 GHz and a reflection of −1.4 dB at 0.9 GHz. The deviations between the simulated and measured results may be due to fabrication errors, discontinuity effects, substrate losses, and non-ideal diodes. These factors were not considered in the design formula and simulation. The non-zero forward resistance of the PIN diode in the ON state, which degrades the virtual ground at junctions P_a and P_b, can be improved by replacing the PIN diode with an MEM switch, which has a very low insertion loss in the ON state, may improve the measured reflection at the non-operating frequency.

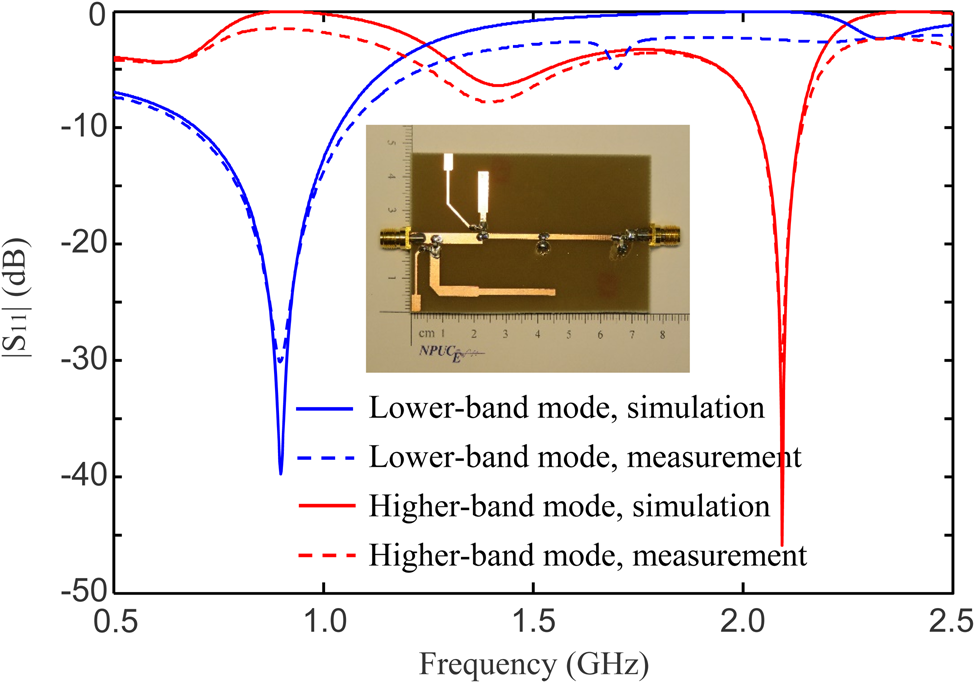
Fig. 7. Simulated and measured reflection coefficients of the fabricated switched band impedance transformer with different diode biasing conditions.

Table 2 compares this work and published researches about switched-band impedance transformers.

Table 2. Comparison between this work and other researches