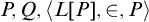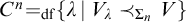1 Introduction
In this paper we consider inner models of the
$ZFC$
axioms using constructibility relative to a predicate consisting of a closed and unbounded (cub) class of ordinals. Such models, so of the form
${\langle L[P],\in , P \rangle }$
, are easily defined (see Kanamori [Reference Kanamori6]). There are a number of questions one may ask about such: what structural properties they may have—are they models of
$GCH$
? of
$V=HOD$
? Does
$\square $
hold in them? How do they relate to other well known inner models—are they fine structural? What are their reals? What are their grounds?
Of course if the universe is too thin, these dissolve into triviality, for example if
$V=L$
in the first place. Forcing constructions over L also give some not terribly interesting consistency results. However it turns out that with a modest large cardinal assumptions in the universe (that there is a measurable limit of measurable cardinals, or more precisely that there exists an elementary embedding of an inner model with a proper class of measurable cardinals to itself—we’ll call the latter assumption
$O^{k} (= O^{kukri})$
), then we have the following perhaps surprising theorem:
Theorem 1.1 (ZFC)
Suppose
$O^{k}$
exists. There is a definable proper class
$C { \,\subseteq \, } On$
that is cub beneath every uncountable cardinal, so that for any definable cub subclasses
$P,Q { \,\subseteq \, } C{:}$
$$ \begin{align*} \mathbb{R}^{L[P]}=\mathbb{R}^{L[Q]}; \quad {\langle L[P],\in, P \rangle} \equiv {\langle L[Q],\in, Q \rangle}, \end{align*} $$
where the elementary equivalence is in the language
$ {\mathcal {L}}_{\dot \in , \dot P}$
with a predicate symbol
$\dot P$
. Consequently these models are all similar to one another: they have the same reals, and their theories are invariant into outer models, in particular under
$ZFC$
-preserving class forcing. Moreover, this holds into
$ZFC$
-preserving extensions: if
$V[G]$
is any
$ZFC$
preserving class generic extension of V, and if Q is any definable, in
$V[G]$
, cub subclass of
$O^{k}$
, with P such defined in V, then this result holds between
$L[P]$
and
$L[Q]$
.
One might prima facie have surmised that a clever choice of elements for such a P might have allowed some coding of interesting sets in order that at the very least the theories of two such models would be different. But apparently not. A particular example of course is when
$P=Card$
itself, the latter the class of uncountable cardinals. Other examples are the classes
$C^{n}= \{ \beta \, | \, V_{\beta } \prec _{\Sigma _{n}} V\}$
: then
${\langle L[C^{2}],\in , C^{2} \rangle } \equiv {\langle L[C^{7}],\in , C^{7} \rangle }$
—one might have thought that the classes alone would have yielded some intrinsic informational content when used as predicates in this way. These models
$L[P]$
all have a rich structure and we have a complete picture of them: they can be considered as a form of generalised příkrý class generic extensions of a fine structural model with a proper class of measurables (hence the need for the hypothesis
$O^{k}$
). This fine structural model will naturally form the core model of the class
$L[P]$
, for such P. They thus have nice combinatorics:
$\square _{\lambda }$
holds everywhere, and
$GCH$
holds. They all have the same set of reals. The elements of P are all Jónsson in the model
$L[P]$
, but not much more. (See Corollary 2.4 below for a listing of such properties.) Perhaps again prima facie remarkable is that these theories are fixed not under just set forcing but by class forcing (by which we mean
$ZFC$
-preserving forcings). We should point out that these results can be extended easily to considering sequences
$P,Q$
from C of the same bounded but limit order type: again the displayed formulae of Theorem 1.1 would hold for such
$L[P]$
and
$L[Q]$
too.
We may apply this to solve the question of the identity of the Härtig quantifier model (which was the starting point for this paper). In [Reference Kennedy, Magidor and Väänänen7] the authors consider the possibilities of using the Gödel method of defining a hierarchy of constructible sets, but augmenting the logic from straightforward first order definability to one where a new quantifier
$\mathsf {Q}$
is added to the language. If the enhanced language is called
$ {\mathcal {L}}^{\ast }$
they build a model as follows:
$$ \begin{align*} \begin{array}{lcr} L_0^{\mathsf{Q}}& = & {\varnothing},\\ L_{\alpha+1}^{\mathsf{Q}} &=& \textit{Def}_{ {\mathcal{L}}^{*}}(L_{\alpha}^{\mathsf{Q}}), \\ L_{\lambda}^{\mathsf{Q}} & = & \bigcup_{\alpha < \lambda}L_{\alpha}^{\mathsf{Q}}, \end{array} \end{align*} $$
and then
$L^{\mathsf {Q}}= \bigcup _{\alpha \in On}L_{\alpha }^{\mathsf {Q}}$
.
If the quantifier
$\mathsf {Q}$
is the Härtig quantifier I, they dub the model
$C(I)$
.
Definition 1.2. The Härtig quantifier I has the following interpretation:
$$ \begin{align*} I x y \varphi(x,\vec p)\psi(y,\vec p) {\,\longleftrightarrow\,} |\{a : \varphi(a,\vec p) \}| = |\{b : \psi(b,\vec p) \}|. \end{align*} $$
For a summary of facts concerning this quantifier see [Reference Herre, Krynicki, Pinus and Väänänen4]. It is an important point to note that the construction of an
$L^{\mathsf {Q}}$
-hierarchy in such cases feeds in information from V. We would not expect the construction of such a hierarchy to be in any way absolute. Other than in trivial cases (such as when
$V=L$
) we should not expect that
$(V=L^{\mathsf {Q}})^{L^{\mathsf {Q}}}$
for example.
The paper [Reference Kennedy, Magidor and Väänänen7] shows, inter alia, the following results:
-
• If
$L^{\mu }$
, the least inner model of a measurable cardinal, exists then
$L^{\mu } { \,\subseteq \, } C(I)$
. -
•
$Con(ZFC + \exists \kappa (\kappa\ \textit{supercompact}) ) \Rightarrow Con(ZFC + C(I)\neq HOD)$
.
However it is left open as to exactly what model
$C(I)$
is, or of what kind. It is easy to see with
$\mathsf {Q}=I$
, that
$C(I)=L[Card]$
where
$Card$
is a one place predicate true of the infinite cardinals (and
$L[Card]$
is defined from the usual first order relativised constructibility hierarchy using the predicate). But that alone tells one very little about the structure of
$C(I)$
, for example whether it has large cardinals, or the
$(G)CH$
holds there. However
$Card$
is a cub class contained in the C of the theorem above. The theorem and its proof are thus applicable to
$L[Card]$
. It is important to require the closure of the classes P of Theorem 1.1: let
${Reg}$
be the class of regular cardinals; then we can show that
$L[Card]$
is, barring trivialities, a proper subclass of
$L[Reg]$
.
We shall have:
Theorem 5.1.
$\neg O^{k} {\,\Longleftrightarrow \,} K^{I} = K$
.
Here we shall set
$K^{I}= (K)^{C(I)}$
. Here K is the core model, which we regard here as constructed à la Jensen for which see the original manuscript of [Reference Jensen5], where the discussion is about mice with measures of order zero, which is all that we shall deal with here. Similarly the first part of [Reference Zeman14] gives a full exposition of this theory. Such a model is one of a family of models of the form
${\langle L[E],\in ,E \rangle }$
where E is a coherent sequence of extenders. In this context the extenders can be rendered as simply filters (again see [Reference Zeman14]). These models possess fine structure, have global wellorders of their domains, satisfy a strong form of the
$GCH$
, and have strong combinatorial properties, such as Jensen’s
$\Box _{\kappa }$
-property everywhere. For ‘small’ or ‘thin’
$L[E]$
models, they will, like L, be models of the statement ‘I am
$C(I)$
’:
Corollary 5.2.
$(V=L[E]) \,\, \neg O^{k}{\,\longleftrightarrow \,} V=C(I)$
.
This note, assuming large cardinals, rather just that
$O^{k}$
exists, identifies this model:
$C(I)$
is a generalised příkrý forcing extension of (an iterate of) the smallest inner model with a proper class of measurable cardinals. One way to express this is to say that, for limit ordinals
$\lambda $
the
$\omega $
-sequences of successor cardinals
$c_{\lambda }{=_{{\operatorname {df}}}} {\langle \aleph _{\lambda +i}\,\, | \, \, 0<i<\omega \rangle }$
form příkrý-sequences for the
$L[E]$
model which is the least inner model with a measurable cardinal on every
$\aleph _{\lambda + \omega }$
. We do this in such a manner that the class
${\langle c_{\lambda }\, | \, \lambda \in Lim \rangle }$
is
$\mathbb {P}^{\infty }$
-generic over the model
$L[E]$
for a certain class forcing
$\mathbb {P}^{\infty }= \mathbb {P}^{Card,\infty }$
. The source of this forcing is Magidor’s iterated příkrý-forcing ([Reference Magidor9] or see [Reference Gitik, Foreman and Kanamori3]) which has a full support; however as the measures in the model
$L[E]$
are sparsely distributed (there are inaccessible limits of measurables, but no measurable limits of measurables) the forcing can be simplified. Here we use such a simplified version as was used for countable sequences in [Reference Welch12], but more relevant here, for any set sized sequences of measurables—again with no measurable limits of measurables—analysed in detail by Fuchs [Reference Fuchs2]. That
$C(I)\neq HOD$
will now follow from the existence of
$O^{k}$
(Corollary 5.2).
In a final section we make a few remarks about the relationship between
$C(I)$
and
$C^{\ast }$
, the latter being the inner model defined using the additional ‘cofinality
$\omega $
’-quantifier
$\mathsf {Q}^{\omega }$
. (
$C^{\ast }$
is coextensive with
$L[{\operatorname {Cof}}_{\omega }]$
where
${\operatorname {Cof}}_{\omega }$
is the class of ordinals of cofinality
$\omega $
.) There is extensive discussion in [Reference Kennedy, Magidor and Väänänen7] on this model. A model may be large in one sense, even if it does not have any, say measurable cardinals, of its own: it may have inner models with very large cardinals instead, and this would surely count as the model being ‘large’. However in all of the results there, some of which assume very large cardinals in V, the outcomes for
$C^{\ast }$
are nevertheless all consistent with it being also a thin model. We show here that it must be larger than
$C(I)$
, but not by much, only in that
$O^{k}\in C(I)$
. So, one might conjecture that
$C^{\ast }$
is also thin:
Conjecture:
$C^{\ast }$
does not contain a mouse with a measurable of Mitchell order
$\omega _{1}$
. Or alternatively no mouse with a measurable limit of measurable cardinals with Mitchell order
$\omega _{1}$
.
Our result here does not imply that a mouse with a measure of Mitchell order
$> 0$
, if such exist, is in
$C(I)$
.
2 The model
$L[E_{0}]$
The principal model
$L[E_{0}]$
we shall use can be derived as follows.
Definition 2.1. Let
$O^{k}$
nameFootnote
1
$M_{0}$
being the least
$($
with respect to the mouse ordering
$<^{\ast })$
sound active mouse of the form
$M_{0}{=_{{\operatorname {df}}}} {\langle J^{E^{M_{0}}}_{\alpha _{0}}, E^{M_{0}}, F_{0} \rangle }$
so that
$M_{0}\models $
“
$F_{0}$
is a normal measure on
$\tau _{0} \wedge \forall \delta <\tau _{0}\exists \lambda < \tau _{0}( \delta < \lambda \wedge \lambda $
a measurable cardinal)”.
Here we mean a mouse in the sense of, e.g., [Reference Zeman14], and the
$E^{M_{0}}$
sequence is a coherent sequence of filters from which we are constructing. Then the following list of Facts are either common knowledge or are easily derived from standard arguments:
-
(i)
$M_{0}$
is a countable mouse with
$\rho ^{1}_{M_{0}} = \omega $
—the first projectum drops to
$\omega $
and there is a
$\Sigma _{1}^{M_{0}}$
definable map of
$\omega $
onto
$J^{E^{M_{0}}}_{\alpha _{0}}$
. -
(ii) We may form iterated ultrapowers of
$M_{0}$
repeatedly using the top measure
$F_{0}$
and its images to form iterates
$ M_{\iota }{=_{{\operatorname {df}}}} {\langle J^{E^{M_{\iota }}}_{\alpha _{\iota }}, E_{M_{\iota }}, F_{\iota } \rangle }$
so that
$ M_{\iota }\models $
“
$F_{\iota }$
is a normal measure on
$\tau _{\iota }$
”. -
(iii) These iterations generate, or “leave behind”, an inner model
$L[E_{0}] {=_{{\operatorname {df}}}} \bigcup _{\iota \in On } H_{\tau _{\iota }}^{M_{\iota }}$
with
$E_{0}= \bigcup _{\iota \in On}E^{M_{\iota }}{\upharpoonright } \tau _{\iota }$
. -
(iv) The cub class of critical points
$C_{M_{0}}={\langle \tau _{\iota }\, | \, \iota \in On \rangle } $
forms a class of indiscernibles that is cub beneath each uncountable cardinal, for the inner model
$L[E_{0}]$
. Indeed an elementary Skolem hull argument shows that the
$\{\tau _{\iota }\}$
form a class of generating indiscernibles for
$L[E_{0}]$
just as the Silver indiscernibles from
$O^{\sharp }$
do for L. -
(v) From (iii) we have that for any
$\iota <\nu $
that
$L_{\tau _{\iota }}[E_{0}] \prec L_{\tau _{\nu }}[E_{0}] \prec L[E_{0}]$
. Moreover for any
$\iota \in On$
we have that
$H_{\tau _{\iota }^{+}}^{L[E_{0}]}= |J^{E^{M_{\iota }}}_{\alpha _{\iota }}| $
, where
$\tau _{\iota }^{+}$
is the successor cardinal of
$\tau _{\iota }$
in the sense of
$L[E_{0}]$
and is thus identical to
$\alpha _{\iota }$
. If
$j_{\iota ,\nu }: M_{\iota } \longrightarrow M_{\nu }$
is the iteration map between the iterates displayed, we shall thus have that also
$j_{\iota ,\nu }: H_{\tau _{\iota }^{+}}^{L[E_{0}]}\longrightarrow H_{\tau _{\nu }^{+}}^{L[E_{0}]}$
is an elementary embedding, which extends to an elementary map
$\widetilde {\jmath } _{\iota ,\nu }: {L[E_{0}]}\longrightarrow {L[E_{0}]}$
. (Again this is similar to the corresponding fact in the embeddings of L coming from iterations of the “
$O^{\sharp }$
-mouse”: for
$\mu < \nu $
Silver indiscernibles for L, we have an elementary map
$j_{\mu ,\nu }: L_{\mu ^{+}}\longrightarrow L_{\nu ^{+}}$
, which extends to a map
$\widetilde {\jmath }_{\mu ,\nu }: L\longrightarrow L$
.) -
(vi) We may if we wish think of
$L[E_{0}]$
as having the same domain as the model
$L[\vec U]$
where
$\vec U$
is a sequence of filters on the
$\tau _{\iota }$
which are normal measures in
$L[\vec U]$
. The fine structure of the latter model was originally done à la Dodd–Jensen [Reference Dodd1] rather than the
$L[E]$
style of Jensen in [Reference Zeman14]. But the models have the same domain of sets.
We call a class P of ordinals appropriate if
$P { \,\subseteq \, } C_{M_{0}}$
is closed and unbounded. For such an appropriate P let
$ {\langle \lambda _{\iota } | \iota \in On \rangle }$
be its strictly increasing enumeration. Further, for
$\alpha \in On$
we set
$c({\alpha }) = c^{P}({\alpha }) ={\langle \lambda _{\omega \alpha +k}\, | \, 0<k<\omega \rangle }$
and
$\mu _{\alpha }=\mu _{\alpha }^{P} {=_{{\operatorname {df}}}} \lambda _{\omega \alpha +\omega }$
. Note the particular case of interest for latter is the appropriate class
$P=Card$
. With this notation then we shall see the following:
Theorem 2.2. Assume that
$O^{k}$
exists and P is an appropriate class.
-
(i)
$K^{L[P]}= L[ E^{P}]$
where
$ E^{P}$
is a coherent filter sequence so that
$L[ E^{P}]\models $
“
$\kappa $
is measurable” if and only if
$\kappa = \mu _{\alpha }$
for some
$\alpha $
. -
(ii) The class
${\langle c^{P}({\alpha }) \rangle } {=_{{\operatorname {df}}}}{\langle c^{P}({\alpha })\, | \, \alpha \in On \rangle }$
of
$\omega $
-sequences is příkrý-generic over
$L[E^{P}]$
for the forcing
$\mathbb {P}^{P}$
and
$L[P] = L[E^{P}][ {\langle c^{P}({\alpha }) \rangle }]$
.
A corollary of (the proof of) our theorem will be the following (a restatement of Theorem 1.1):
Theorem 2.3. Assume that
$O^{k}$
exists. Let
$P,Q { \,\subseteq \, } C_{M_{0}}$
be any two appropriate classes. Then
$$ \begin{align*} \mathbb{R}^{L[P]}=\mathbb{R}^{L[Q]}; \quad {\langle L[P],\in, P \rangle} \equiv {\langle L[Q],\in, Q \rangle}, \end{align*} $$
where the elementary equivalence is in the language
$ {\mathcal {L}}_{\dot \in , \dot P}$
with a predicate symbol
$\dot P$
.
Corollary 2.4. Assume
$O^{k}$
exists. Let P be any appropriate class. Then in
$L[P]:$
-
(i) Each
$\mu _{\alpha }$
is Jónsson, and
${c_{\alpha }}$
forms a coherent sequence of Ramsey cardinals below
$\mu _{\alpha } ($
see Koepke [Reference Koepke8]
$)$
. But there are no measurable cardinals. -
(ii) For any
$L[P]$
-cardinal
$\kappa $
we have
$\Diamond _{\kappa }$
,
${\Box }_{\kappa }$
,
$(\kappa ,1)$
-morasses, etc. -
(iii) The
$GCH$
holds but
$V\neq HOD$
. -
(iv) There is a
$\Delta ^{1}_{3}$
wellorder of
$\mathbb {R}= \mathbb {R}^{K^{L[P]}}; Det(\alpha $
-
${\boldsymbol {{\Pi }^{1}_{1}}})$
holds for any countable
$\alpha \ ($
see [Reference Welch12]
$)$
, but
$Det({\boldsymbol {\Sigma ^{0}_{1}}}({\boldsymbol {\Pi ^{1}_{1}}}))$
fails
$($
Simms, Steel, see [Reference Steel10]
$)$
.
Indeed we may add anything else that holds after a příkrý-generic extension of the
$L[E^{P}]$
model. Notice that
$(Card)^{L[Card]}$
will be very far from
$Card$
as any
$\mu \in Card$
will be in
$L[Card]$
a Ramsey cardinal (hence weakly compact) or a limit of such.
We note the following for latter use.
Lemma 2.5. Suppose
$O^{k}$
exists. Let
$L[E_{0}]$
be the model defined above. Let
$L[E']$
be any other model with a proper class of measurable cardinals, with
$L[E_{0}]=^{\ast }L[E']$
in the mouse/weasel ordering. Then
$L[E']$
is a simple iterate of
$L[E_{0}]$
.
Proof As the models are
$=^{*}$
equivalent the comparison of the models will be simple iterations on both sides. The claim is that the iteration on the
$L[E']$
side is trivial, i.e., no ultrapower is ever taken. We have noted above at (iii) that
$M_{0}$
is the unique sound mouse that ‘generates’
$L[E_{0}]$
. Thus in the mouse/weasel ordering it is the
$<^{*}$
-least sound mouse M with
$L[E_{0}]<^{*}M$
. But then it is the
$<^{*}$
-least sound mouse N with
$L[E']<^{*}N$
.
However note that if
$N_{0}$
is the least sound mouse that generates
$L[E']$
then
$N_{0}= M_{0}= O^{k}$
. Then the iteration of
$L[E_{0}]$
that yields
$L[E']$
is the iteration of
$M_{0}$
that generates
$L[E']$
but reindexed to omit any indices of the topmost measure of any model
$M_{\iota }$
.
In one obvious sense then
$L[E_{0}]$
is the ‘minimal’ model with a proper class of measurable cardinals.
Woodin in [Reference Woodin13] considered the question of what occurs when an
$\omega $
-sequence of ordinals is added to L. Besides reals added by forcing of course, much can happen. He shows that if s is an
$\omega $
-sequence of ordinals then
$L[s]$
is a model of GCH. This also used a příkrý-forcing and a short core model analysis. We comment below on what happens when we choose an
$\omega $
sequence or indeed any limit length sequences P contained in C.
2.1 Universal iterations
We place here a general discussion on universal iterations of a mouse, which we shall use only here as a device to ensure that certain iterations of a model, although defined externally to the model, leave inaccessibles of the model fixed. These results appeared in a somewhat more recherché form in [Reference Steel and Welch11], and are valid for mice below
$O^{pistol}$
. The overarching idea is that any iteration of a mouse can be embedded back into such an iteration which is internally definable. This enables one to have control over the movement of ordinals, calculations of cardinal successors, etc. Actually we only need a simple consequence. Apart from Lemma 2.10 below, the reader may omit this subsection, which does not really require this apparatus and can be proven directly.
Definition 2.6 [Reference Steel and Welch11]
Let M be a mouse and
$ \theta> On^{M}$
be an M-admissible ordinal. Then
${\langle M_{\eta }, \langle \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }, \langle \kappa _{\eta } \rangle_{\eta \leq \theta } \rangle }$
with indices
$\langle \nu _{\eta } \rangle_{\eta \leq \theta }$
, iteration embeddings
$\langle \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }$
, and critical points
$\langle \kappa _{\eta }\rangle _{\eta \leq \theta }$
, is an n-universal iteration of
$M= M_{0}$
of length
$\theta $
, if:
-
(i) there are no truncations and dropping of degree of the iteration at any stage
$\alpha < \theta $
and -
(ii) for any measure
$F= E^{M_{\alpha }}_{\nu }$
with
$crit(F)< \rho ^{n}_{M_{\alpha }}$
there is
$\beta <\theta $
,
$\alpha < \beta $
with
$E^{M_{\beta }}_{\nu _{\beta }}= \upsilon _{\alpha ,\beta }(F)$
.
Thus, in a universal iteration, every extender (or its image under the iteration so far) appearing on any extender sequence of the iteration is used unboundedly often before
$\theta $
. We shall be using the simplified version of the above where
$n=\omega $
and the extenders are measures of all elements of the models appearing, which are themselves
$ZF^{-}$
models (and so
$ \rho ^{\omega }_{M_{\alpha }}= On \cap M_{\alpha }$
throughout). The next lemma states that, although there can be many universal iterations of given length, any two such end up with isomorphic results.
Theorem 2.7 [Reference Steel and Welch11, Theorem 2.9]
Let
$\theta> On^{M}$
be an M-admissible ordinal. If
${\mathcal {U}} = \langle M_{\eta }, \langle \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }, {\kappa _{\eta }} \rangle_{\eta \leq \theta }$
and
$\,\overline {{\mathcal {U}}} = \langle \bar M_{\eta }, \langle \bar \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }, {\bar \kappa _{\eta }} \rangle_{\eta \leq \theta }$
are any two n-universal iterations of
$M=M_{0}=\bar M_{0}$
of length
$\theta $
then
$M_{\theta } = \bar M_{\theta }$
.
We may define a universal iteration in
$L[M]$
:
Lemma 2.8 [Reference Steel and Welch11, Definition 2.8]
Let
$\theta < \theta _{0}$
be two M-admissible ordinals. Then there is an n-universal iteration of M up to
$\theta $
which is an element of
$L_{\theta _{0}}[M]$
.
The point of a universal iteration is that any other iteration of the first model of a shorter length can be embedded into the universal iteration. We formulate that as follows.
Theorem 2.9 [Reference Steel and Welch11, Theorem 2.10]
Let
$\theta $
be an M-admissible ordinal. If
${\mathcal {U}} = \langle M_{\eta }, \langle \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }, {\kappa _{\eta }} \rangle_{\eta \leq \theta }$
is an n-universal iteration of
$M=M_{0}$
up to
$\theta $
, and
$ {\mathcal {J}} = \langle {N_{\iota }}, \langle \pi _{\iota ,j} \rangle_{\iota \leq j\leq \mu }, {\bar \kappa _{\iota }} \rangle_{\iota \leq \mu } $
is any length
$\mu +1< \theta\ n$
-iteration of
$M= N_{0} \ ($
with no truncations or drops in degree
$)$
, then there is an iteration
${\mathcal {I}} = \langle {P_{\iota }}, \langle \sigma _{\iota ,j} \rangle_{\iota \leq j\leq \xi }, {\lambda _{\iota }} \rangle_{\iota \leq \xi }$
of
$P_{0}= N_{\mu }$
of length some
$\xi +1< \theta \ ($
with no truncations or drops in degree
$)$
so that for some
$\beta $
,
$P_{\xi }= M_{\beta }$
.
We thus say that a universal iteration of length
$\theta $
absorbs all shorter length (appropriate) iterations of the first model. Let N be an inner model with only boundedly many measurable cardinals, bounded by some least N-regular cardinal
$\theta $
say. Then we may just as easily as above define a
$\theta +1$
length universal iteration of the proper class N using the measures which are all below
$\theta $
, and moreover we define this universal iteration in N. But to make it about sets, we consider just some sufficiently large initial segment
$N{\upharpoonright }\gamma $
where
$\gamma $
is an N-inaccessible limit of N-inaccessibles. (Our intended N will satisfy there are such.) We thus could consider the universal iteration to be on the first model
$Q_{0}= N{\upharpoonright }\gamma $
of the universal iteration
$ \langle Q_{\eta }, \langle \upsilon _{\eta ,\iota } \rangle_{\eta \leq \iota \leq \theta }, {\kappa _{\eta }} \rangle_{\eta \leq \theta }$
.
We then shall have:
Lemma 2.10. Let
$\pi : N_{0}\longrightarrow N_{\iota _{0}}$
be any simple iteration of
$N_{0}=N{\upharpoonright } \gamma $
with
$\gamma $
as above, of length
$\iota _{0}+1<\theta $
. Then for any N-inaccessible
$\bar \gamma \in (\theta ,\gamma )$
,
$\bar \gamma $
is a fixed point of
$\pi $
:
$\pi (\bar \gamma )=\bar \gamma $
.
Proof As alluded to above, this can be proven by a direct induction on
$\iota _{0} <\theta $
. Otherwise, as
$Q_{0}$
has inaccessible height in N, and letting
$\upsilon _{\alpha ,\beta }$
be the iteration maps from the universal iteration as defined above, then
$\upsilon _{0,\theta }``\gamma { \,\subseteq \,}\gamma $
and indeed
$\bar \gamma = \upsilon _{0,\theta }(\bar \gamma )$
for any N-inaccessible
$\bar \gamma $
in our chosen interval. (Proven by induction on
$j\leq \theta $
for the maps
$\upsilon _{0,j}$
by the usual counting of functions in the internally defined iteration
${\mathcal {U}}$
.) Further by Theorem 2.9 there is an iteration
${\mathcal {I}} = \langle {P_{\iota }}, \langle \sigma _{\iota ,j} \rangle_{\iota \leq j\leq \xi }, {\kappa _{\iota }} \rangle_{\iota \leq \xi }$
of
$P_{0}= N_{\iota _{0}}$
of length some
$\xi +1< \theta $
so that for some
$\beta < \theta $
,
$P_{\xi }= Q_{\beta }$
. However we have commuting maps
$\upsilon _{0,\beta } = \sigma _{0,\xi }\circ \pi : Q_{0}\longrightarrow Q_{\beta }$
. But
$\upsilon _{0,\beta }(\bar \gamma )=\bar \gamma $
as the N-inaccessibles are fixed points of these maps defined in N. So then
$\pi (\bar \gamma )=\bar \gamma $
too.
3 The generalized příkrý forcing
In [Reference Fuchs2] Fuchs developed a style of iterated příkrý forcing intended for use when there are no measurable limits of measurables. This considerably simplifies the format of the forcing as the manœuvres needed for names in the full Magidor iteration of [Reference Magidor9] are not needed. Moreover Fuchs proves a Mathias like characterisation (see Theorem 3.3 below) which we shall make use of. Section 3.2 thus borrows heavily from [Reference Fuchs2], but we shall adopt notation appropriate for this specific case.
3.1 The model
$L[E^{P}]$
We first defined a simple iteration of
$M_{0} = O^{k}$
by its top measure and its images used
$On$
times, that left behind the inner model
$L[E_{0}]$
. We fix an appropriate cub class P for this whole discussion. We may then define a normal iteration of
$L[E_{0}] \longrightarrow L[E^{P}]$
to line up the measures of
$L[E_{0}]$
onto the simple limit points of P, the
${\langle \mu ^{P}_{\alpha } \rangle }_{\alpha \in On}$
. We can reorganise these two into a single normal iteration.
${\langle M_{\iota }, {\langle \pi _{\eta ,\iota } \rangle }_{\eta \leq \iota <\infty }, {\kappa _{\iota }} \rangle }_{\iota \in On}$
where as usual at limit stages direct limits are taken. Indeed given the model
$L[E^{P}]$
, the comparison coiteration of
$(M_{0},L[E^{P}])$
(see [Reference Zeman14]) tells us what that iteration is by simply observing the
$M_{0}$
-side, as the
$L[E^{P}]$
model does not move in this. This iteration of
$M_{0}$
‘leaves behind’ or ‘generates’
$L[E^{P}]$
. Between ultrapowers where the top filter from the relevant model is used are the intermediate ultrapowers lining up each of the full measures with the appropriate
$\mu _{\alpha }$
. It is useful to identify the stages where the top measure is used: we let
$C= C_{P} $
be this class of indices. It is easy to see that
$C { \,\subseteq \, } C_{M_{0}}$
and is also cub in
$On$
. Thus with
$\iota <\nu $
both in C we shall have Fact (v) above (and the comments following) holding in this context, i.e., we have that for any
$\iota <\nu $
both in C, with
$\pi _{\iota ,\nu }: M_{\iota } \longrightarrow M_{\nu }$
:
-
(1) There is an extension of
$\pi _{\iota ,\nu }$
to
$\widetilde {\pi }_{\iota ,\nu }$
with
$\widetilde {\pi }_{\iota ,\nu }: L[E^{P}] \longrightarrow _{e} L[E^{P}] $
.
(Here
$\longrightarrow _{e}$
denotes that the embedding fully elementary, i.e., that it is
$\Sigma _{\omega }$
preserving in the language with a predicate for
$E^{P}$
.) Consequently we also have the
${\langle \kappa _{\iota } \rangle }_{\iota \in C} $
, which are
$\Sigma _{1}$
-indiscernibles for the
$M_{\iota }$
, will be full indiscernibles for
$L[E^{P}]$
, and inter alia that
$$ \begin{align*} L_{\kappa_{\iota}}[E^{P}] \prec L_{\kappa_{\eta}}[E^{P}] \prec L[E^{P}].\end{align*} $$
We shall thus have that also
$\pi _{\iota ,\nu }: H_{\kappa _{\iota }^{+}}^{L[E^{P}]}\longrightarrow H_{\kappa _{\nu }^{+}}^{L[E^{P}]}$
is a fully elementary embedding by noting that the domain of
$M_{\iota }$
is precisely this
$H_{\kappa _{\iota }^{+}}^{L[E^{P}]}$
in the model being left behind. We have then for each
$\nu \in C$
that it is an inaccessible limit of measurables in
$L[E^{P}]$
.
From the above, in
$L[E^{P}]$
we have that
${\langle \mu _{\alpha } \, | \, \alpha \in On \rangle }$
is a discrete proper class of ordinals, which constitute the measurable cardinals in
$L[E^{P}]$
with normal measures
$U_{\alpha }$
(which are indexed on the
$E^{P}$
-sequence by
$(\mu _{\alpha }^{+})^{L[E^{P}]}$
although that is not of much consequence in what follows). We note also the following:
Lemma 3.1. Fix
$\kappa \in C_{M_{0}}$
. Let
${\mathcal {I}} = {\langle N_{\iota }, {\langle \sigma _{\iota ,} \rangle }_{\iota \leq \theta } \rangle }$
where
$\theta < \kappa $
be a simple iteration of
$N_{0}= L[E_{0}]$
. Then
$\sigma _{0,\theta }(\kappa )= \kappa $
.
Proof First note
$\kappa $
is strongly inaccessible in
$L[E_{0}]$
as it is indiscernible there. The iteration
${\mathcal {I}} $
is divided into two parts: those measures used below
$\kappa $
and those above. It suffices to note that if the iteration below
$\kappa $
does not move
$\kappa $
the rest of the iteration using critical points
$\kappa _{k}\geq \kappa $
will not move
$\kappa $
as, in particular,
$\kappa $
is not measurable in
$L[E_{0}]$
. So it suffices to consider only those
${\mathcal {I}} $
with measures used below
$\kappa $
. However for such an iteration, although not necessarily internally definable in
$L[E_{0}]$
, one shows by induction on
$\theta $
that
$\sigma _{0,\theta }$
cannot move
$\kappa $
as
$\theta <\kappa $
.
As a consequence we have:
-
(2) Any
$\kappa \in C_{M_{0}}$
is only moved in such an iteration
$\sigma _{0,\theta }:L[E_{0}] \longrightarrow N_{\theta }$
if
$\theta \geq \kappa $
and for some
$\lambda <\kappa $
we have
$\sigma _{0,\theta }(\lambda ) \geq \kappa $
.
3.2 The forcing
We proceed to define the forcing in
$L[E^{P}]$
up to the
$L[E^{P}]$
-inaccessible cardinal
$\nu \in C$
.
Definition 3.2. For
$\nu \in C$
let
$\mathbb {P}^{\nu }= \mathbb {P}^{P,\nu }$
be the following set of function pairs
${\langle h,H \rangle }$
so that:
-
(i)
$H\in \prod _{\alpha < \nu } U_{\alpha },\, \text {dom}(h)=\nu $
, and
$\mathop {sp}(h)$
is finite, where the latter, the support of h, is:
$\mathop {sp}(h){=_{{\operatorname {df}}}} \{ x\in \text {dom}(h) \, | \, h(x)\neq {\varnothing }\}$
. -
(ii)
$\forall \alpha \in \mathop {sp}(h)\, h(i) \in [\mu _{\alpha }]^{<\omega }$
. -
(iii)
$\forall \alpha \in \mathop {sp}(h)\, h(\alpha ) { \,\subseteq \, } \min H(\alpha )$
. -
(iv)
$\forall \alpha \in \mathop {sp}(h)\, \forall \beta <\alpha ( \mu _{\beta }< \min (h({\alpha }))$
.
For
${\langle f,F \rangle }, {\langle g,G \rangle }\in \mathbb {P}^{\nu }$
set
${\langle f,F \rangle }\leq {\langle g,G \rangle }$
iff
$$ \begin{align*} \forall \alpha <\nu (\, F(\alpha)\subseteq G(\alpha)\,\wedge\,f(\alpha)\supseteq g(\alpha)\,\wedge\, f(\alpha)\backslash g(\alpha) { \,\subseteq\, } G(\alpha)).\end{align*} $$
The reader will recognise that we are using a form of příkrý forcing with full support up to
$\nu $
. (Those familiar with [Reference Fuchs2] will see that we have further simplified by only seeking příkrý sequences of length
$\omega $
in the generic extension.) We have the following basic properties (3)–(7) from Fuchs [Reference Fuchs2, p. 939].
Facts:
-
(3) For any
${\langle h,H \rangle }\in \mathbb {P}^{\nu }$
, any
$\alpha <\nu $
, and any
$n<\omega $
, there is
${\langle h',H' \rangle } \leq {\langle h,H \rangle } \wedge |h'(\alpha )|>n$
.
For the remainder of these Facts we let
$G^{\nu }$
be
$\mathbb {P}^{\nu }$
-generic over
$ L[E^{P}]$
, and we define
$c= c_{G^{\nu }}$
by
$c(\alpha )=\bigcup \{h(\alpha )\, | \, \exists H \langle h, H\rangle \in G^\nu\}$
for all
$\alpha < \nu $
.
-
(4) Then
$c\in \prod _{\alpha <\nu }(\mu _{\alpha }{\backslash } \bigcup _{\beta < \alpha }\mu _{\beta })^{\omega }$
. (Here
$(x)^{\omega }$
is the collection of sequences from x of order type
$\omega $
.) -
(5)
$G^{\nu } = G_{c} $
where the latter is The last then yields that
$$ \begin{align*} \hspace{-1.5pc} \{ {<h, H>} \mathbb{P}^{\nu}\, | \, {\forall} \alpha < \nu (h(\alpha) \ \textit{ is an initial segment of} \ c(\alpha)\wedge c(\alpha){\backslash} h(\alpha) { \,\subseteq\, } H(\alpha))\}. \end{align*} $$
$L[E^{P}][c]=L[E^{P}][G^{\nu }]$
.
-
(6)
$\mathbb {P}^{\nu }$
has the
$\nu ^{+}$
-c.c. (and this is best possible). -
(7) For every
$X\in (\prod _{\alpha <\nu }U_{\alpha })\cap L[E^{P}]$
, the set
$\bigcup _{\alpha <\nu } (c(\alpha ){\backslash } X(\alpha ))$
is finite.
We have the following crucial Mathias-like characterization of this product of forcings, stated in our terms:
Theorem 3.3 (Fuchs [Reference Fuchs2, Theorem 1])
A function
$d\in \prod _{\alpha <\nu }(\mu _{\alpha }{\backslash } \bigcup _{\beta < \alpha }\mu _{\beta })^{\omega }$
is
$\mathbb {P}^{\nu }$
-generic over
$L[E^{P}]$
if and only if for every
$$ \begin{align*} X\in (\prod_{\alpha <\nu}U_{\alpha})\cap L[E^{P}], \bigcup_{\alpha <\nu} (d(\alpha){\backslash} X(\alpha)) \end{align*} $$
is finite.
The combinatorics of this argument are somewhat involved so we don’t repeat this here. But a corollary to this, also observed by Fuchs, allows a version of weak homogeneity which we shall exploit later. Since we have full products but only finite supports and thus only finitely many příkrý-stems, if c is any
$\mathbb {P}^{\nu }$
-generic and p any condition, there is a finite perturbation d of c with
$p\in G_d$
. Using the Mathias characterisation of Theorem 3.3 this is the idea behind the following corollary.
Corollary 3.4 ([Reference Fuchs2, Corollary 1])
Let c be
$\mathbb {P}^{\nu }$
-generic over
$L[E^{P}]$
. Let
$p\in \mathbb {P}^{\nu }$
. Then there exists a sequence d which is
$\mathbb {P}^{\nu }$
-generic over
$L[E^{P}]$
so that:
-
(i)
$| \bigcup _{\alpha < \nu }(c(\alpha )\triangle d(\alpha ))|<\omega \,;$
-
(ii)
$p\in G_{d}$
.
But such a d is in
$L[E^{P}][c]$
and we have then this model equals
$L[E^{P}][d]$
. Consequently we have also:
Corollary 3.5. If
$\varphi (v_{0}, \ldots , v_{n-1})$
is any formula and
$\check a_{1},\ldots ,\check a_{n-1}$
any forcing names for elements of
$L[E^{P}]$
, and
$p\in \mathbb {P}^{\nu }$
we have
$$ \begin{align*} p\,{\Vdash}_{\mathbb{P}^{\nu}} \varphi(\check a_{1}, \ldots, \check a_{n-1}) {\,\Rightarrow\,} \mathbb{1}\Vdash_{\mathbb{P}^{\nu}} \varphi \check a_{1}, \ldots, \check a_{n-1}). \end{align*} $$
Again from Fuchs we have (8) and (9):
-
(8) For
$\gamma <\nu $
(not necessarily in C)
$\mathbb {P}^{\nu }$
can be decomposed as a product
$\mathbb {P}^{\gamma } \times \mathbb {P}^{\nu }_{\gamma }$
with elements of
$\mathbb {P}^{\gamma } $
functions with domain
$\gamma $
and those in
$\mathbb {P}^{\nu }_{\gamma }$
with domain
$[\gamma , \nu )$
. -
(9) Forcing with
$\mathbb {P}^{\nu }$
preserves all cardinals and cofinalities excepting the measurable cardinals below
$\nu $
, which are made cofinal with
$\omega $
by the addition of the generic function c.We also have: -
(10) Let
$\sigma $
be a sentence of the forcing language and
$p\in \mathbb {P}^{\nu }$
be a condition. Then there is a ‘pure’ or ‘direct’ extension
$q\in \mathbb {P}^{\nu }$
with
$q || \sigma $
, q deciding
$\sigma $
. That is if
$p={\langle h,H \rangle }$
, then such a q is the form
${\langle h,H' \rangle }$
where
$H'(\beta ) { \,\subseteq \, } H(\beta )$
for all
$\beta < \nu $
. (See Gitik [Reference Gitik, Foreman and Kanamori3, Lemma 6.2]). Further
$ \mathbb {P}^{\nu }_{\gamma }$
adds no bounded subsets of
$\kappa _{\gamma }$
—the
$\gamma $
th measurable cardinal of
$L[E^{P}]$
(ibid. Section 6.).
4 The class version: the full forcing
$\mathbb{P}^{\infty }=\mathbb{P}^{P,\infty }$
We may consider the forcings
$\mathbb {P}^{\iota },\mathbb {P}^{\nu }$
as above, as defined for such
$\iota ,\nu \in C$
,
$\iota <\nu $
, within
$L[E^{P}]$
.
-
(11)
$\widetilde {\pi }_{\iota ,\nu } (\mathbb {P}^{\iota }) = \mathbb {P}^{\nu }$
. -
(12) c is
$\mathbb {P}^{\iota }$
-generic over
$L[E^{P}]$
if and only if it is so over
$H_{\kappa _{\iota }^{+}}^{L[E^{P}]}$
.
Proof Let
$H^{\iota } {=_{{\operatorname {df}}}} H_{\kappa _{\iota }^{+}}^{L[E^{P}]}$
. Then
$H^{\iota }\models ZF^{-}$
. By ‘generic over
$H^{\iota }$
’ we mean that
$G^{\iota }_{c}$
meets every maximal antichain of
$ \mathbb {P}^{\iota }$
in
$H^{\iota }$
. We note that
$\mathbb {P}^{\iota }$
is itself a proper class of
$H^{\iota }$
; however by the
$\iota ^{+}$
-chain condition from (6), all maximal antichains of
$ \mathbb {P}^{\iota }$
in
$L[E^{P}]$
are elements of
$H^{\iota }$
. (12)
We may now define
$\Vdash _{\iota } $
the
$\mathbb {P}^{\iota }$
-forcing relation over
$H^{\iota }$
. Then we shall have:
-
(13) For
$\iota , \nu \in C$
,
$\iota < \nu $
,
$\widetilde {\pi }_{\iota ,\nu } : {\langle H^{\iota }, \mathbb {P}^{\iota }, \Vdash _{\iota } \rangle } \longrightarrow _{e} {\langle H^{\nu }, \mathbb {P}^{\nu }, \Vdash _{\nu } \rangle }$
.
Proof By (11) and (1). (13)
We let
$\langle M_{\infty }, E, {\langle \pi _{\iota ,\infty } \rangle }_{\iota \in C} \rangle {=_{{\operatorname {df}}}}\ \mathrm {dirlim}_{\iota \rightarrow \infty , \iota \in C} \ {\langle M_{\iota }, \in , {\langle \pi _{\iota ,\nu } \rangle } \rangle }_{\iota \leq \nu \in C}$
. We may consider
$M_{\infty }$
to be given by an
$\in $
-relation in the direct limit as some definable (in V) class
$E { \,\subseteq \, } V\times V$
. This domain we can identify with the domain
$ {\langle H^{\infty },E, {\langle \widetilde {\pi }_{\iota ,\infty } \rangle } \rangle } {=_{{\operatorname {df}}}}\ \mathrm {dirlim}_{\iota \rightarrow \infty , \iota \in C} \ {\langle H^{\iota }, \in , {\langle \widetilde {\pi }_{\iota ,\nu } \rangle } \rangle }$
, the sole difference being that the maps
$\widetilde {\pi }_{\iota ,\nu }$
, and so direct limit maps
$\widetilde {\pi }_{\iota ,\infty }$
are fully elementary:
$\widetilde {\pi }_{\iota ,\infty }:{\langle H^{\iota },\in \rangle }\rightarrow _{e} {\langle H^{\infty },E \rangle }$
. Of course if there were more ‘ordinals’ above
$On$
we would say that
$\langle H^{\infty },E \rangle $
is isomorphic to a model
${\langle \widetilde {H}, \in \rangle } \models ZFC^{-} +$
“
$On$
is the largest cardinal”. We define
$\mathbb {P}^{\infty }$
over
${\langle H^{\infty },E \rangle }$
. Note
$\mathbb {P}^{\infty }$
is also a proper class of
$H^{\infty }$
; but nevertheless we can still say that a
$\mathbb {P}^{\infty }$
-forcing relation
$\Vdash _{\infty } $
for
${\langle H^{\infty },E \rangle }$
is definable by taking the direct limit of the relations defined before (13) above. (It would be natural to want to formalise this whole discussion in Kelley–Morse class theory, noting that we have a strong class choice principle in the form of a global wellorder of
$H^{\infty }$
(a model of “
$V=L[E]$
”) which is
${\langle H^{\infty }, E \rangle }$
-definable. Our
$KM$
-theorem then would additionally talk naturally about all appropriate classes contained in C, rather than restricting to
$ZFC$
-definable ones.)
The Mathias condition in this context is obtained by treating
$On$
as another indiscernible in C:
-
(14) A proper class function
$d\in \prod _{\alpha <\infty }(\mu _{\alpha }{\backslash } \bigcup _{\beta < \alpha }\mu _{\beta })^{\omega }$
is
$\mathbb {P}^{\infty }$
-generic over
${\langle H^{\infty }, E \rangle }$
if and only if for every
$X\in \prod _{\alpha <\infty }U_{\alpha }$
, X coded in
$H^{\infty }$
satisfies that
$\bigcup _{\alpha <\infty } (d(\alpha ){\backslash } X(\alpha ))$
is finite.Another characterisation of being
$\mathbb {P}^{\infty }$
-generic is given below. From now on we let
$c = c^{P}$
be the sequence
$ {\langle c^{P}({\alpha })\, | \, \alpha \in On \rangle }$
where
$ {c^{P}({\alpha }) }$
is as defined above. Then
$\bigcup \{ \text {ran}\, c(\alpha )\, | \, \alpha \in On\}{\backslash } \omega = P{\backslash } P^{\ast }$
(where
$P^{\ast }$
is the set of limit points of P). -
(15) Let
$\iota \in C$
. Then
${c}{\upharpoonright } \iota $
is
$\mathbb {P}^{P,\iota }$
-generic over
${\langle H^{\iota },\in \rangle }$
.
Proof (The proof of (15) will take up until (22)). The assertion will follow from the Mathias condition characterized in Theorem 3.3. But for this we need to observe that for every
$X\in (\prod _{\alpha <\iota }U_{\alpha })\cap L[E^{P}]$
,
$\bigcup _{\alpha <\iota } (c(\alpha ){\backslash } X(\alpha ))$
is finite. Let X be such a sequence. Then
$X\in H^{\iota }$
and as such is in the domain of the direct limit model
$M_{\iota }$
. We thus have that
$X= \pi _{0,\iota }(f_{0})(\kappa _{i^{0}_{0}}, \, \ldots \, , \kappa _{i^{0}_{n(0)}})$
for some
$f_{0}\in M_{0}$
, and some indices
${i^{0}_{0}} <\, \cdots \, < {i^{0}_{n(0)}}< {\iota }$
. The iteration
$\pi _{i^{0}_{n(0)}+1,\iota }: M_{i^{0}_{n(0)}+1} \longrightarrow M_{\iota } $
only uses critical points
$\kappa _{j}> \kappa _{i^{0}_{n(0)}}$
and first lines up the next measure onto
$\lambda _{\omega {\alpha _{0}} + { \omega } }$
where
$\alpha _{0}$
is defined to be that least
$\alpha $
so that
$$ \begin{align*} \kappa_{{i^{0}_{n(0)}}} < \lambda_{\omega {\alpha} + { \omega} } \end{align*} $$
and then proceeds with the rest of the iteration to
$\iota $
. Define:
$$ \begin{align*} \widetilde{X}^{\tau}{=_{{\operatorname{df}}}} \pi_{0,\tau}(f_{0})(\kappa_{i^{0}_{0}}, \, \ldots \, , \kappa_{i^{0}_{n(0)}}) \text{ for }\iota \geq\tau> {i^{0}_{n(0)}}. \end{align*} $$
Then
-
(16)
$\pi _{\tau ,\iota }(\widetilde X^{\tau })= \widetilde X^{\iota }= X $
. -
(17) For
$\iota> \beta \geq \alpha _{0}$
we have:
$X(\beta ) = \widetilde X^{\tau }(\beta )$
for any
$\tau \geq \lambda _{\omega {\beta } + { \omega } }$
.
Proof For such a
$\tau $
, although
$\tau '< \lambda _{\omega {\beta } + { \omega } } \rightarrow \kappa _{\tau '}< \lambda _{\omega {\beta } + { \omega } }$
(as we are iterating up a smaller measure—meaning not the topmost measure—to
$ \lambda _{\omega {\beta } + { \omega } }$
),
$ \lambda _{\omega {\beta } + { \omega } }$
itself is not a critical point of the iteration, and thus
$\kappa _{\tau }> (\lambda _{\omega {\beta } + { \omega } }^{+})^{L[E^{P}]}$
. So
$\pi _{\tau ,\iota }{\upharpoonright } L_{\lambda _{\omega {\beta } + { \omega } }^{+}}[E^{P}] = \mathrm {id}{\upharpoonright } L_{\lambda _{\omega {\beta } + { \omega } }^{+}}[E^{P}] $
and so
$\widetilde X^{\tau }(\beta ) = \pi _{\tau ,\iota }(\widetilde X^{\tau }(\beta )) = \widetilde X^{\iota }(\beta ) = X(\beta )$
by (16).
-
(18) (i)
$c(\alpha _{0}){\backslash } \kappa _{i^{0}_{n(0)}+1} { \,\subseteq \, } X(\alpha _{0}) $
; thus at most finitely many elements of
$c(\alpha _{0})$
are not in
$X(\alpha _{0})$
. -
(ii) For
$\beta \in (\alpha _{0},\iota )$
,
$c(\beta ) { \,\subseteq \, } X(\beta )$
. -
(iii)
${c}{\upharpoonright } [\alpha _{0},\iota )$
fulfills the condition for
$\mathbb {P}_{\alpha _{0}}^{\iota }$
-genericity.
Proof To abbreviate, set
$\bar \lambda = \lambda _{\omega {\alpha _{0}} + { \omega } }$
,
$j ={i^{0}_{n(0)}+1}$
, and
$F= E^{M_{j}}_{\nu } $
where the latter is the full measure on
$\kappa _{j}$
that is being normally iterated up to
$\bar \lambda $
. Then
$\pi _{j,\bar \lambda } (F)=U_{\alpha _{0}}$
(the full measure on
$\bar \lambda $
in
$L[E^{P}]$
in the notation above). But
$\widetilde X^{j}(\alpha _{0})\in F$
. By normality of the measures in the iteration
$\kappa _{j}\in \pi _{j,\bar \lambda } (\widetilde X^{j}(\alpha _{0}))$
as well as the intermediate
$\kappa _{\tau '}$
for
$\tau '\in [j,\bar \lambda )$
. But the latter include, for some
$k<\omega $
, the ordinals
$\kappa _{\lambda _{\omega {\alpha _{0}} + { k} }}=\lambda _{\omega {\alpha _{0}} + { k} }> \kappa _{j}$
which form a co-finite tail of
$c(\alpha _{0})$
.
For (ii) a similar argument: for
$\beta> \alpha _{0}$
, there will be some
$j< {\lambda _{\omega {\beta } + { 1} }} (= \kappa _{\lambda _{\omega {\beta } + { 1} }})$
and some
$F\in M_{j}$
such that
$\pi _{j,\lambda _{\omega \beta +\omega }}(F)=U_{\beta }$
. Setting
$F' = \pi _{j,\lambda _{\omega \beta +1}}(F)$
this is a full measure on
${\lambda _{\omega {\beta } + { 1} }}$
in
$M_{{\lambda _{\omega {\beta } + { 1} }}}$
. Then
$\widetilde X^{{\lambda _{\omega {\beta } + { 1} }}}(\beta )\in ({P}({\lambda _{\omega {\beta } + { 1} }}))^{M_{{\lambda _{\omega {\beta } + { 1} }}}}$
will have
$F'$
measure
$1$
, and by normality of the iteration from
$M_{{\lambda _{\omega {\beta } + { 1} }}} $
to
$M_{{\lambda _{\omega {\beta } + { \omega } }}} $
, we have for all
$k>0$
:
$$ \begin{align*} {\lambda_{\omega {\beta} + { k} }}\in \pi_{{\lambda_{\omega {\beta} + { 1} }},{\lambda_{\omega {\beta} + { \omega} }}}( \widetilde X^{{\lambda_{\omega {\beta} + { 1} }}})(\beta) = \widetilde X^{{\lambda_{\omega {\beta} + { \omega} }}}(\beta) = X(\beta). \end{align*} $$
Thus
$c(\beta ) { \,\subseteq \, } X(\beta )$
. This concludes (ii) and with (i), (iii) is immediate.
We now repeat the process below
$\alpha _{0}$
obtaining a descending chain
$\alpha _{0}> \cdots > \alpha _{k}$
of ordinals verifying new, lower, pieces of the form
${c}{\upharpoonright } [\alpha _{l+1},\alpha _{l})$
of the condition for
${\langle c({\alpha }) \rangle }_{\alpha <\iota }$
. This process will halt with all of
${\langle c({\alpha }) \rangle }_{\alpha <\iota }$
so verified. These details follow.
Then
$X{\upharpoonright } [0,\alpha _{0}) \in H^{L[E^{P}]}_{\lambda _{\omega \alpha _{0}}^{+}}$
and as such is in the domain of the direct limit model
$M_{\lambda _{\omega \alpha _{0}}}$
. We thus have that
$X{\upharpoonright } [0,\alpha _{0})= \pi _{0,{\lambda _{\omega \alpha _{0}}}}(f_{1})(\kappa _{i^{1}_{0}}, \, \ldots \, , \kappa _{i^{1}_{n(1)}})$
for some
$f_{1}\in M_{0}$
, and some indices
${i^{1}_{0}} <\, \cdots \, < {i^{1}_{n(1)}}< {\lambda _{\omega \alpha _{0}}}$
. Let
$X_{\alpha _{0}}$
abbreviate
$X{\upharpoonright } [0,\alpha _{0})$
.
The iteration
$\pi _{i^{1}_{n(1)}+1,{\lambda _{\omega \alpha _{0}}}}: M_{i^{1}_{n(1)}+1} \longrightarrow M_{{\lambda _{\omega \alpha _{0}}}} $
only uses critical points
$\kappa _{j}> \kappa _{i^{1}_{n(1)}}$
and first lines up the next measure onto
$\lambda _{\omega {\alpha _{1}} + { \omega } }$
where
$\alpha _{1}$
is the least
$\alpha $
so that
$\kappa _{i^{1}_{n(1)}}< \lambda _{\omega {\alpha } + { \omega } } $
.
Define
$\widetilde {X}^{\tau }_{\alpha _{0}}{=_{{\operatorname {df}}}} \pi _{0,\tau }(f_{1})(\kappa _{i^{1}_{0}}, \, \ldots \, , \kappa _{i^{1}_{n(1)}})$
for
$\tau> \kappa _{i^{1}_{n(1)}} $
. Then
$\pi _{\tau ,{\lambda _{\omega \alpha _{0}}}}(\widetilde X^{\tau }_{\alpha _{0}})= \widetilde X^{{\lambda _{\omega \alpha _{0}}}}_{\alpha _{0}}= X_{\alpha _{0}} $
. Arguing just as for (17) and (18) above we have:
-
(19) For
$\alpha _{0}> \beta \geq \alpha _{1}$
:
$X_{\alpha _{0}}(\beta ) = \widetilde X^{\tau }_{\alpha _{0}}(\beta )$
for any
$\tau \geq \lambda _{\omega {\beta } + { \omega } }$
. -
(20) (i)
$c(\alpha _{1}){\backslash } \kappa _{i^{1}_{n(1)}+1} { \,\subseteq \, } X(\alpha _{1}) $
; thus at most finitely many elements of
$c(\alpha _{1})$
are not in
$X(\alpha _{1})$
. -
(ii) For
$\beta \in (\alpha _{1},\alpha _{0})$
,
$c(\beta ) { \,\subseteq \, } X(\beta )$
. -
(iii)
${c}{\upharpoonright } [\alpha _{1},\alpha _{0})$
fulfills the condition for
$\mathbb {P}_{\alpha _{1}}^{\alpha _{0}}$
-genericity.
We continue in this fashion defining a descending sequence of critical points
$\kappa _{i^{l+1}_{n(l+1)}}< \kappa _{i^{l}_{n(l)}} $
, and ordinals
$\alpha _{l+1}<\alpha _{l}$
, and deriving that
${c}{\upharpoonright } [\alpha _{l+1},\alpha _{i})$
fulfills the condition for
$\mathbb {P}_{\alpha _{l+1}}^{\alpha _{l}}$
-genericity. We then reach a point where
${i^{m+1}_{n(m+1)}} =0 $
in that for some
$f_{m+1} \in M_{0}$
we have that
$X{\upharpoonright } [0,\alpha _{m})= \pi _{0,{\lambda _{\omega \alpha _{m}}}}(f_{m+1})(\kappa _0)$
. As
$\kappa _{0}<\lambda _{0}$
we have that
$c(0) { \,\subseteq \, } X(0)$
and similarly
$c(\beta ) { \,\subseteq \, } X(\beta )$
for
$\beta \in (0,\alpha _{m})$
.
-
(21)
${c}{\upharpoonright } \iota $
is
$\mathbb {P}^{\iota }$
-generic over
$L[E^{P}]$
.
Proof Setting
$\alpha _{m+1}=0$
we then have:
${c}{\upharpoonright } \iota = \bigcup _{l<m+1}\{ {c}{\upharpoonright } [\alpha _{l+1},\alpha _{l})\} \cup {c}{\upharpoonright } [\alpha _{0},\iota ) $
, and
$c(\alpha ) { \,\subseteq \, } X(\alpha )$
for all
$\alpha $
not one of the
$\alpha _{l}$
. There are only finitely many
$\alpha _{l}$
, so this follows from (18)(i) and m instances of (20)(i).
This finishes (15).
-
(22) If
$\iota < \nu \in C$
,
$\widetilde {\pi }_{\iota ,j}:L[E^{P}]\longrightarrow _{e}L[E^{P}]$
, with
$\widetilde {\pi }_{\iota ,\nu }(\iota )=\nu =\kappa _{\nu }$
as above arising from the iteration maps
$\pi _{\iota ,\nu }:M_{\iota }\longrightarrow M_{\nu }$
, then with
$c{\upharpoonright }\iota $
, etc. as above, there is
$\overline \pi _{\iota ,\nu }\supset \widetilde {\pi }_{\iota ,\nu }$
with
$\overline \pi _{\iota ,\nu }: L[E^{P}][c{\upharpoonright } \iota ]\longrightarrow _{e}L[E^{P}][c{\upharpoonright }\nu ]$
, with
$\overline \pi _{\iota ,\nu }(c{\upharpoonright } \iota ) = c{\upharpoonright } \nu $
.
Proof As
$c{\upharpoonright } \iota $
is
$\mathbb {P}^{\iota } $
-generic (respectively,
$c{\upharpoonright } \nu $
is
$\mathbb {P}^{\nu } $
-generic) over
$L[E^{P}]$
and
$\widetilde {\pi }_{\iota ,\nu }\text {``}G_{c{\upharpoonright }\iota }\subset G_{c{\upharpoonright }\nu }$
, if we define
$\overline \pi _{\iota ,\nu }(\dot \tau _{G_{c{\upharpoonright }\iota }}) = \widetilde {\pi }_{\iota ,\nu }(\dot \tau )_{G_{c{\upharpoonright }\nu }} $
, then
$\overline \pi _{\iota ,\nu }$
will be well-defined and elementary, extending
$\widetilde {\pi }_{\iota ,\nu }$
. Furthermore
$\overline \pi _{\iota ,\nu }(c{\upharpoonright }\iota )=\overline \pi _{\iota ,\nu }(\dot \Gamma ^{\iota }_{G_{c{\upharpoonright }\iota }}) = \dot \Gamma ^{\nu }_{G_{c{\upharpoonright }\nu }} = c{\upharpoonright } \nu $
.
Consequently:
-
(23)
$\bigcup _{\iota \in C}c{\upharpoonright } \iota =c $
is
$\mathbb {P}^{\infty } $
-generic over
${\langle H^{\infty },E \rangle }$
.
Proof As we can see,
$c = \bigcup _{\iota \in C} c{\upharpoonright } \iota $
will be
$\mathbb {P}^{\infty }$
-generic over the direct limit model
${\langle H^{\infty },E \rangle }$
, as for any
$X\in (\prod _{\alpha <\infty }U_{\alpha })\cap L[E^{P}]$
, with X coded into
$H^{\infty }$
, the condition that
$\bigcup _{\alpha <\infty } (c(\alpha ){\backslash } X(\alpha )) = \bigcup _{\iota \in C}\bigcup _{\alpha <\iota } (c(\alpha ){\backslash } X_ \iota (\alpha ))$
be finite is fulfilled.
-
(24)
$L [ E^{P} ] [ c ] =L [ c ] .$
Proof We observe at the outset that
$L [ c ] =L [ P ]$
. The precursor of (24) is the observation that if d is a single Prikry generic
$\omega $
-sequence for the inner model
$L [ \mu ]$
with a single measurable cardinal, then
$L [ \mu ] [ d ] =L [ d ]$
. We check this analogous statement here for this larger model. We abbreviate by writing
$H=L [ E^{P} ] [ c ]$
, and we work in
${\langle H, \in ,c \rangle }$
. As c is
$\mathbb {P}^{P, \infty }$
-generic over
$L [ E^{P} ]$
we have that (
$ K{=_{{\operatorname {df}}}})\, K^{H} =K^{L [ E^{P} ]} =L [ E^{P} ]$
. (Usually one states that K is invariant under set forcing extensions, but here too for this class forcing extension, as
$\mathbb {P}_{0}^{\gamma } \times \mathbb {P}^{\infty }_{\gamma } =\mathbb {P}^{\infty }$
, with the top half adding no bounded subsets of
$\gamma ^{+}$
, for increasing cardinals
$\gamma $
we can perform the inductive definition of K in H, but in stages, thus, for increasing
$\gamma $
, in
$L [ E^{P} ] \left [ c {\upharpoonright } \gamma \right ]$
up to
$\gamma $
(where it produces
$L [ E^{P} ] {\upharpoonright } \gamma $
), and this will be the same as per the construction in H up to
$\gamma $
.)
Let
$K^{c} {=_{{\operatorname {df}}}} K^{L [ c ]}$
. (We use this notation just for this note (24) so there will be no danger of confusing this with the usual
$K^{c}$
-model.) Let
$M_{0} =K^{c}$
and
$N_{0} =K=L [ E^{P} ] $
.
Claim.
$M_{0} =N_{0}$
.The Claim gives (24):
$L [ E^{P} ]$
is then a definable inner model of
$L [ c ]$
.
Proof of Claim Still in H, if
$K^{c}$
is universal, as we are below a strong cardinal, there is an iteration embedding
$j:K {\,\longrightarrow \,} K^{c}$
, i.e., K iterates simply up to
$K^{c}$
without the latter moving. Suppose for a contradiction that
$j\neq {\operatorname {id}}$
. Let
$U_{\alpha }$
on
$\mu _{\alpha }$
be the first measure used in an ultrapower making up this map. As
$( {\operatorname {cf}} ( \mu _{\alpha } ) = \omega )^{L [ c ]}$
we have by the Weak Covering Lemma in
$L [ c ]$
that
$( \mu _{\alpha } $
is singular or measurable
$ )^{K^{c}}$
. But either alternative is absurd, as
$\mu _{\alpha }$
remains inaccessible but not measurable in
$K^{c}$
after the iteration
$K {\,\longrightarrow \,} K^{c}$
. So
$j= {\operatorname {id}}$
and we’d be done.
So suppose that
$K^{c}$
fails to be universal, then we have in terms of the mouse ordering, that
$K^{c} <^{\ast } K$
, but this can only be true if
$K^{c}$
has boundedly many measurable cardinals—as K is (an iterate of) the minimal inner model with a proper class of measurables. We show this leads to a contradiction. Again as we are below a strong cardinal, there is a set-sized initial segment of K,
$\overline {N}_{0} =N_{0} | \gamma $
for some least
$\gamma $
say, with, in the comparison of
$( M_{0,} \overline {N}_{0} )$
to
$( M_{\infty } , \overline {N}_{\infty } )$
, a tail of indices beyond some
$i_{0} < \infty $
(before which all the set many measures of
$M_{0}$
are lined up with those in iterates of
$\overline {N}_{0} $
), so that: (i) the M-side no longer moves, and thus
$M_{i_{0}} =M_{\infty }$
; and (ii) the iteration
$\overline {N}_{i_{0}} {\,\longrightarrow \,} \overline {N}_{\infty }$
consists merely of ultrapowers by its topmost measure out through all the ordinals. As
$\overline {N}_{i_{0}}$
is a set, this implies: (iii) all sufficiently large cardinals are limit points of the closed and unbounded class of the critical points
$\kappa _{j}$
in the iteration of
$\overline {N}_{i_{0}}$
by this topmost measure. Now pick, in
$L [ c ]$
, a sufficiently large limit point of c,
$\mu $
say, with
$\mu> {\operatorname {cf}}^{L [ c ]} ( \mu ) > \delta $
where we take
$\delta = |\overline {N}_{i_{0}}|^{+}$
. Note we can also assume that
${\operatorname {cf}}^{L[c]} ( \mu )$
is a sufficiently large cardinal as specified in (iii). Applying, still in
$L [ c ]$
, the Weak Covering Lemma over
$K^{c}$
, we have, just as above, that as
$( \mu \in {\operatorname {SingCard}} )^{L [ c ]}$
we have that
$( \mu \in {\operatorname {Sing}} \vee \mu $
is measurable
$)^{K^{c}}$
. The latter alternative is ruled out by our assumption that all measurables of
$M_{i_{0}}$
are below
$\delta $
. Thus we have
$\mu> {\operatorname {cf}}^{K^{c}} ( \mu ) > \delta $
. As this
$\tau {=_{{\operatorname {df}}}} {\operatorname {cf}}^{K^{c}} ( \mu )$
is a
$K^{c}$
-regular larger than any measurable cardinal used in the iteration
$M_{0} {\,\longrightarrow \,} M_{i_{0}}$
, we have that
$\pi ^{M}_{0,i_{0}} ( \mu ) = \mu $
, and
${\operatorname {cf}}^{M_{j}} ( \mu ) = \tau $
for
$0 \leq j \leq i_{0}$
also. But then
$( \mu \in {\operatorname {Sing}} )^{M_{i_{0}}}$
and
$M_{i_{0}} =M_{\infty }$
. However
$( \mu \in {\operatorname {Inacc}} )^{\overline {N}_{\infty }}$
, as we have remarked above, because all sufficiently large V-cardinals are critical points of the
$\overline {N}_{i_{0}}$
side of the iteration and hence are left behind as inaccessible in
$M_{\infty }$
. Contradiction! So this implies that
$K^{c}$
is universal after all, and that
$K=K^{c}$
. (Claim and (24))
We now finish:
Proof of Theorem 1.1 For C we take
$C_{M_{0}}$
the class of iteration points of the countable mouse
$M_{0}$
by its topmost measure. Given then any cub
$P,Q { \,\subseteq \, } C$
we shall have that there are normal iteration embeddings
$j:L[E_{0}]\longrightarrow L[E^{P}]$
and
$k:L[E_{0}]\longrightarrow L[E^{Q}]$
. The reals of all such models are thus the same. As the forcings
$\mathbb {P}^{C,\infty }$
(with the obvious definition),
$\mathbb {P}^{{P},\infty }$
and
$\mathbb {P}^{{Q},\infty }$
add no new bounded subsets of their least measurable we shall have that
$$ \begin{align*} L[P]=L[E^{P}][c] \text{ and } L[Q]=L[E^{Q}][d] \end{align*} $$
have the same reals (indeed subsets of
$\kappa _{0}$
, the least measurable cardinal of
$L[E_{0}]$
) where c, d are
$\mathbb {P}^{{P},\infty }$
- and
$\mathbb {P}^{{Q},\infty }$
-generic over
$L[E^{P}]$
, respectively,
$L[E^{Q}]$
. By the elementarity of
$j,k$
the topmost condition
$\mathbb {1}$
forces the same sentences in the forcing language over the respective models. Hence
$ Th({\langle L[P],\in ,P \rangle } ) = Th({\langle L[Q],\in ,Q \rangle } )$
.
Finally note that the preservation of these theories into forcing extensions (class or otherwise) follows simply from the absoluteness of
$O^{k}$
into such extensions.
Remark. If we are considering the theorem as one in
$KM$
, we should speak of
$KM$
-preserving extensions here.
Corollary 4.1. If P is appropriate,
$L[P]$
is a
$\mathbb {P}^{P,\infty }$
-generic extension of its core model—the latter being an iterate of the ‘minimal’ model of a proper class of measurable cardinals,
$L[E_{0}]$
.
Proof With
$c \ \mathbb {P}^{P,\infty }$
-generic over
$L[E^{P}]$
, c contains none of its limit points. But P is again just
$\bigcup \{ \text {ran}\, c(\alpha )\, | \, \alpha \in On\}{\backslash } \omega $
together with the latter’s closure. It is thus mutually interconstructible with c. Hence
$L[P]= L[c] =L[E^{P}][c] $
. However the invariance of K under the forcing
$\mathbb {P}^{P, \infty }$
(mentioned at the beginning of the proof of (24)) has that
$K^{L[P]}=K^{L[E^{P}]}$
. The latter equals
$L[E^{P}]$
as it is a model of “
$V=K$
”.
With less than a proper class sized P the reader will now see easily that similar results apply for set sequences
$P,Q { \,\subseteq \, } C$
of the same limit order type: any two such will have the same reals, the same theories and will look like the same příkrý-generic extensions of their inner models
$L[E^{P}] $
which now have only a bounded set of measurable cardinals, depending on the length of P or Q.
5 The Härtig quantifier model
$C(I)$
We apply the above analysis directly to
$C(I)= L[Card]$
. However first we show that below
$O^{k}$
,
$C(I)$
computes the canonical inner core model K of V. We then characterise
$C(I)$
inside
$L[E]$
models. This shows that below
$O^{k}$
the Härtig quantifier picks up all the sets of the model (and this is an equivalence to the non-existence of
$O^{k}$
). We shall let
$K^{I}= (K)^{C(I)}$
.
Theorem 5.1.
$\neg O^{k} \Leftrightarrow K^{I} = K$
.
Proof
$(\Leftarrow )$
follows from the work above: if
$O^{k}$
exists, it is not an element of
$C(I)$
and hence
$K^{I}$
cannot be K which contains
$O^{k}$
.
$(\Rightarrow )$
: we first note: Claim. Under
$\neg O^{k}$
, if W is a weasel with a proper class of measurable cardinals, it is universal.
Proof Assume for a contradiction that W has unboundedly many measurable cardinals, but is not universal, Then there would be some set-sized mouse P with
$W<^{\ast }P$
, where the coiteration of P with W would last
$On$
many steps, as P iterates past W. But this is absurd as P can have no measurable limit of measurables, by our assumption
$\neg O^{k}$
and hence can leave behind no such model as W if the latter has a proper class of such. We should thus conclude that W was universal.
We compare the models K which we shall label
$M_{0}$
(again, n.b., this is not the
$M_{0}$
of the earlier sections which equalled
$O^{k}$
) and
$K^{I}=N_{0}$
via coiteration
${\mathcal {I}} = \langle {M_{\iota }}, \langle \pi ^{M}_{\iota ,j} \rangle_{\iota \leq j\leq \theta }, {\kappa _{\iota }} \rangle_{\iota \leq \theta } $
and
${\mathcal {J}} = \langle {N_{\iota }}, \langle \pi ^{N}_{\iota ,j} \rangle_{\iota \leq j\leq \theta }, {\kappa _{\iota }} \rangle_{\iota \leq \theta } $
and with indices
${\langle \nu _{\iota } \rangle }_{\iota <\theta }$
where in this case
${\theta } \leq \infty $
—the comparison is class length.
-
(i)
$K^{I}$
is universal.
Proof Assume not. By the Claim
$K^{I}$
can only have boundedly many measurable cardinals. As there can be no truncation on the N-side of this coiteration (see, e.g., [Reference Zeman14, Lemma 5.3.1]), there is some least stage
$\iota _{0}$
such that for
$\mu \geq \iota _{0} \ \pi ^{N}_{\iota _{0},\mu }= {\operatorname {id}} {\upharpoonright } N_{\iota _{0}}$
. That is, all the full measures of
$N_{\iota _{0}}$
have been lined up with those of
$M_{\iota _{0}}$
. Thereafter
$N_{\mu }=N_{\iota _{0}}$
. On the M-side there may or may not have been a truncation but in any case if
$M_{\iota _{0}}$
is still a proper class, there is an initial segment of
$M_{0}$
, some
$M_{0}| \tau $
say, so that the coiteration of
$M_{0}|\tau $
with
$N_{0}$
yields the same outcome with the same indices and ultrapowers taken on both sides. We may thus assume that
$M_{0}$
is replaced by such an
$M_{0}|\tau $
. Furthermore that iteration is clearly of length
$On$
,
$M_{0}| \tau $
being a set and
$N_{0}$
a proper class. The point is that some set sized mouse will eventually iterate using repeatedly only some filter
$F_{{\iota }} = E^{M_{\iota }}_{\nu _{\iota }}$
and its images, with critical point
$\kappa _{\iota }$
, for
$\iota \geq \iota _{0}$
, past
$N_{\iota _{0}}$
leaving this model as
$N_{\infty }$
behind. Let
$ {\langle \lambda _{\alpha }\, | \, \alpha < \omega _{1} \rangle }$
increasingly enumerate the next
$\omega _{1} \ V$
-cardinals above
$|M_{\iota _{0}}|^{+ }=\lambda _{0}$
, and let their supremum be
$\lambda $
.
Then (a) the sequence
${\langle \lambda _{\alpha } \rangle }_{\alpha <\omega _{1}}\in C(I)$
; (b) as the cardinality of
$M_{\iota _{0}}<\lambda _{0}$
each of the
$\lambda _{\alpha }$
satisfy that
$\kappa _{\lambda _{\alpha }} = \lambda _{\alpha }$
and
$\pi ^{M}_{{\iota _{0}},\lambda _{\alpha }}(\kappa _{\iota _{0}})= \kappa _{\lambda _{\alpha }}= \lambda _{\alpha }$
. Consequently the filter
$F_{\lambda }= E^{M_{\lambda }}_{\nu _{\lambda }}$
to be used at stage
$\lambda $
is generated by the final segment filter using the sequence
${\langle \kappa _{\iota } \rangle }_{\iota _{0}<\iota <\lambda }$
, but also by the subsequence
${\langle \kappa _{\lambda _{\alpha }} \rangle }_{\alpha <\omega _{1}}= {\langle {\lambda _{\alpha }} \rangle }_{\alpha <\omega _{1}}$
. But at this stage
$\lambda $
we have
$({P}(\lambda ))^{M_{\lambda }}= ({P}(\lambda ))^{N_{\iota _{0}}}$
. We further have (c): the cardinals
$\lambda _{\alpha +1}$
are all fixed points of the embedding
$\pi ^{N}_{0,\iota _{0}}$
. We may thus, in
$C(I)$
, define
$\bar F$
on
$({P}(\lambda ))^{N_0}$
using the same final sequence
${\langle \kappa _{\lambda _{\alpha +1}} \rangle }_{\alpha <\omega _{1}}$
. Thus
$X\in \bar F {\,\longleftrightarrow \,} \pi ^{N}_{0,\iota _{0}}(X)\in F_{\lambda }$
. This is an
$N_{0}$
-normal amenable measure on
$\lambda $
, which is again
$\omega $
-complete. We have a contradiction as on the one hand
$K^{I}$
is universal in
$C(I)$
(it is the actual core model of
$C(I)$
), and thus by the theory of such models all
$\omega $
-complete normal measures amenable to it are on its
$E^{K^I}$
sequence; whilst on the other hand all the measurable cardinals of
$K^{I}$
are strictly below
$\kappa _{\iota _{0}}$
which is less than
$\lambda $
.
-
(ii)
$K= K^{I}$
.
Proof As we are below
$O^{pistol}$
(the sharp for the least model of a strong cardinal) it is a theorem of Jensen (see, e.g., [Reference Zeman14, Theorem 7.4.9]) that any universal weasel W, and by (i)
$K^{I}$
is such, is a simple iterate of K. If
$K^{I}$
contains no measurable cardinals then the result is proven: there are no measurables in K to iterate.
Suppose
$K\neq K^{I}$
for a contradiction. In the comparison of K with
$K^{I}$
let the first measurable to be moved on the K-side be
$\kappa $
, and let us suppose it to be iterated up to the measurable cardinal
$\kappa ^{I}$
in
$K^{I}$
. Suppose there is a further measurable cardinal in K above
$\kappa $
which has critical point
$\lambda $
(where we take
$\lambda $
least). Then the measure on
$\lambda $
here is to be iterated up to some measurable
$\lambda ^{I}> \kappa ^{I}$
in
$K^{I}$
. (The case of only the one
$\kappa $
measurable in K will be left to the reader.) So we suppose K (and so
$K^{I}$
) has at least two measurable cardinals.
Note that
$\kappa \leq \kappa ^{I}$
and
$\lambda \leq \lambda ^{I}$
. Let
$\lambda ^{I}<\mu $
where the latter is a strong limit V-cardinal of
$C(I)$
-cofinality greater than
$\tau $
, where we set
$\tau = |\kappa |^{+}$
.
In K iterate the measure on
$\lambda \ \mu $
-times, up to
$\mu $
and do the same in
$K^{I}$
sending
$\lambda ^{I}$
to
$\mu $
. Let the resulting models be
$\bar K$
and
$\bar K^{I}$
on the respective sides. Further let
$M= \bar K_{\mu }$
and
$N=\bar K^{I}_{\mu }$
be the initial segments of the two models cut down to
$\mu $
. These are
$ZFC$
-models. To compare these two all we have to do is to iterate the single measure
$F_{\kappa }$
on
$\kappa $
in M up to
$F^{I}_{\kappa ^{I}}$
on
$\kappa ^{I}$
in N. Let
$\sigma : M\longrightarrow N$
be this iteration map. If
${\langle } \lambda _{\alpha }\, | \, \alpha < \tau {\rangle }$
strictly increasingly enumerates the next
$\tau $
many successor elements of
$Card$
above
$\kappa ^{I ++}$
then all such
$\lambda _{\alpha }$
are less than
$\mu $
but are fixed points of the iteration map
$\sigma $
. Fix a set of definable Skolem functions for N, and so for M too by elementarity. Let
$H\prec N$
be the Skolem hull of:
$\kappa \cup \{ \lambda _{\alpha }\}_{\alpha < \tau }\cup {F^{I}_{\kappa ^{I}}}$
. Then
$H\cong H'$
where the latter is the Skolem hull of:
$\kappa \cup \{ \lambda _{\alpha }\}_{\alpha < \tau }\cup {F_{\kappa }}$
in M. (Note that we have
$\sigma (F_{\kappa }) = F^{I}_{\kappa ^{I}}$
and
$H\cap (\kappa , \kappa ^{I})={\varnothing }$
(the latter as
$\sigma (\kappa )=\kappa ^{I}$
).) Furthermore H is definable in
$C(I)$
since N and those components of the Skolem hull are. Let
$\pi : H \longrightarrow P$
be the Mostowski–Shepherdson Collapse, and thus
$|P| \geq \tau $
.
Check that
$\pi $
“
$F^{I}_{K^{I}} =F_{\kappa }$
, all inside
$C(I)$
. Hence, as
$\kappa ^{+K} =\kappa ^{+{K^{I}}} = \kappa ^{+M}$
we have
$E^{K}{\upharpoonright } \kappa ^{+} = E^{K^{I}}{\upharpoonright } \kappa ^{+}$
and then we have
$Q= {\langle J^{E^{K}}_{\kappa ^{+}}, E^{K}{\upharpoonright } \kappa ^{+}, F_{\kappa } \rangle } \in C(I)$
, and we may then proceed to build, in
$C(I)$
, a universal class model W with this structure as an initial segment. (In Jensen’s nomenclature Q is a ‘strong mouse’, cf. [Reference Zeman14, Section 7.1 and Lemma 7.1.1]). This is a contradiction since in
$C(I) \ K^{I}$
must simply iterate up to W and thus no such W can have a measurable cardinal on an ordinal less than
$\kappa ^{I}$
.
We then have easily that inside canonical models, if they are not too large then they are their own Härtig quantifier models:
Corollary 5.2.
$(V=L[E])$
$\neg O^{k}{\,\longleftrightarrow \,} V=C(I)$
.
Proof
$(\leftarrow )$
Again if
$O^{k}$
exists in V we have ensured it is outside of
$L[Card]= C(I)$
.
$(\rightarrow )$
If
$V=L[E]$
then
$V=K$
. If additionally
$\neg O^{k}$
then we also have
$K { \,\subseteq \, } C(I)$
.
For an inner model W let
$WCL(W)$
mean that for
${\forall } \tau (\tau \text { a singular cardinal } {\,\Rightarrow } (\tau ^+ = (\tau ^{+})^{W})$
.
Corollary 5.3.
$\neg O^{k}{\,\longleftrightarrow \,} WCL(C(I))$
.
Proof This is immediate since
$WCL(K)$
, and then
$WCL(C(I))$
will hold if
$K { \,\subseteq \, } C(I)$
.
Corollary 5.4. Assume
$ O^{k}$
exists. Then
$C(I)$
is a
$\mathbb {P}^{Card,\infty }$
-generic extension of its core model
$K^{I}$
, where
$\mathbb {P}^{Card,\infty }$
is as defined above as
$ \mathbb {P}^{P,\infty }$
for
$P=Card$
.
Corollary 5.5. Assume
$ O^{k}$
exists. Then
$C(I)\neq HOD$
.
Proof
$ O^{k}\notin C(I)$
, whilst
$ O^{k}\in HOD$
.
Corollary 5.6. Assume
$ O^{k}$
exists. Then
$C(I)^{C(I)}= K^{C(I)}$
. Consequently
${C(I)^{C(I)}} \models {``} V= {C(I)}{"}.$
Proof Note that by Corollary 5.4
$C(I)$
has the same cardinals as its core model
$K^{I}$
. Also
$K^{I}$
satisfies “
$V=L[E]$
”, thus by Corollary 5.2, we have
$C(I)^{C(I)} =C(I)^{K^I}= K^{I}$
.
The latter may consistently fail if
$\neg O^{k}$
: let M be the forcing extension of L that adds a Cohen real r, and then collapses
$\aleph _{2n+1}$
to
$\aleph _{2n}$
iff
$n\in r$
. Then
$(V=C(I)= C(I)^{C(I)})^{M}$
. But
$K^{M}=L$
.
6 The
${\operatorname {Cof}}_{\omega }$
model
$C^{\ast }$
We briefly make a few comments on the relationship between the Härtig quantifier model
$C(I)$
and the
${\operatorname {Cof}}_{\omega }$
model
$C^{\ast }$
of [Reference Kennedy, Magidor and Väänänen7]. For our purposes here we let
${\operatorname {Cof}}_{\omega } = \{\alpha \, | \, {\operatorname {cf}}(\alpha )=\omega \}$
, and then
$C^{\ast } = L[{\operatorname {Cof}}_{\omega }]$
. We show these models differ in that
$O^{k}\in C^{\ast }$
(if it exists) whilst we have shown this must fail for
$C(I)$
. We first note as an aside a generalisation of an argument of [Reference Kennedy, Magidor and Väänänen7] from a single measure to a sequence of such.
Theorem 6.1. Assume
$V= L[E]$
has measurable cardinals
${\langle \kappa _{\iota }\, | \, \iota < \theta < \kappa _{0} \rangle }$
with measures
$E_{\kappa _{\iota }}$
. Let
$L[E']$
be the simple iteration of
$L[E]$
where each measure is iterated in turn
$\omega ^{2}$
times with iteration points
${\langle \kappa _{\iota }^{\alpha }\, | \, \alpha < \omega ^{2} \rangle }$
. Then
$$ \begin{align*} C^{\ast} = L[E'][{\langle {\langle {\kappa_{\iota}^{\omega\cdot n}\, | \, 0< n < \omega} \rangle}\, | \, \iota < \theta \rangle}]. \end{align*} $$
Proof The assumption on the length of the sequence of ensures that all the measurable cardinals
$\kappa _{\iota }$
are discrete ordinals: there are no measurable limits of measurables, and thus those arguments in [Reference Kennedy, Magidor and Väänänen7] can, with some additional work, be used to get the result here.
We first show by methods of Theorem 5.1 that below
$O^{k}$
,
$K$
is universal. We then show that if
$O^{k}$
exists it must be in
$K^\ast$
. However first we give two lemmata about cofinalities of regular cardinals in iterates of mice. We do the case of
$M_{0}$
where the first projectum
$\rho ^{1}_{M_{0}}$
drops below the least measurable to
$\omega $
. We then just state the generalisation for the case of an
$n+1$
st projectum dropping below the least measurable of a mouse
$P_{0}$
for an
$n>0$
afterwards.
Lemma 6.2. Let
$\pi _{0,\theta }:M_{0}\longrightarrow M_{\theta }$
be a simple normal iteration of
$M_{0}$
, the
$O^{k}$
mouse
$($
i.e., without any truncations
$)$
, with critical points
${\langle \kappa _{\iota }\, | \, \iota < \theta \rangle }$
. Suppose that:
-
(i)
$M_{\theta }\models {``} \kappa $
is inaccessible, but not measurable”; (ii)
$\kappa \neq \kappa _{\iota }$
for any
$\iota <\theta $
.Then
$cf^{V}(\kappa )=\omega $
.
Proof We shall use the following observations:
Claim. If
$M_{\iota }= {\langle J_{\alpha _{\iota }}^{E^{M_{\iota }}},E^{M_{\iota }}, F_{\iota } \rangle }$
then
$cf(\alpha _{\iota })=\omega $
. Moreover, setting
$\widetilde {\kappa }_{\iota }{=_{{\operatorname {df}}}} \sup \{\kappa _{j}+1\, | \, j<\iota \}$
, then any
$\lambda \in (RegCard)^{M_{\iota }}$
with
$\lambda> \widetilde {\kappa }_{\iota }$
has V-cofinality
$\omega $
.
Proof We claim there is a
$\Sigma _{1}^{M_{\iota }}$
-definable sequence
${\langle \alpha ^{n}_{\iota } \rangle }_{n<\omega }$
which is increasing and cofinal in
$\alpha _{\iota }$
. Let
$\alpha ^{0}_{\iota }$
be the least
$\alpha $
greater than
${\operatorname {crit}}(F_{\iota })$
so that
$$ \begin{align*} {\exists} \beta \in ({\operatorname{crit}}(F_{{\kappa}_{\iota}},\alpha ) \, J_{\beta}^{E^{M_{\iota}}} \models ZF^{-}\wedge F_{\iota}\cap J_{\beta}^{E^{M_{\iota}}} \in J_{\alpha}^{E^{M_{\iota}}}. \end{align*} $$
By amenability of
${\langle M_{\iota },F_{\iota } \rangle } \alpha ^{0}_{\iota }$
and each
$\alpha ^{n+1}_{\iota }$
to follow is well defined. For this, let
$\alpha ^{n+1}_{\iota }$
be the least
$\alpha $
greater than
$\alpha ^{n}_{\iota }$
so that
$F_{\iota }\cap J_{\alpha ^{n}_{\iota }}^{E^{M_{\iota }}} \in J_{\alpha ^{n+1}_{\iota }}^{E^{M_{\iota }}} $
. Then
$\sup _{n}\alpha _{\iota }^{n} = \alpha _{\iota }$
: for if not then setting
$\alpha ' =\sup _{n}\alpha _{\iota }^{n} $
we should have that
$M'= {\langle J_{\alpha '}^{E^{M_{\iota }}},E^{M_{\iota }}, F_{\iota }\cap J_{\alpha '}^{E^{M_{\iota }}} \rangle }$
is an iterable premouse with an amenable topmost measure whose critical point is a measurable limit of measurables.
$M'$
is thus, being an initial segment of
$M_{\iota }$
, in the mouse ordering
$<^{\ast }$
below
$M_{0}$
which was defined to be the least such mouse. Contradiction! We thus have the first sentence of the Claim.
$M_{\theta }$
, being a simple iterate of
$M_{0}$
, has the first
$\Sigma _{1}$
-projectum dropping below its topmost critical point to
$\omega $
. The same is true of
$M_{\iota }$
and thus the latter is the
$\Sigma _{1}$
-Hull of
${\widetilde {\kappa }_{\iota }}$
in
$M_{\iota }$
(we write this as
$M_{\iota }{=_{{\operatorname {df}}}} \Sigma _{1}\text {-SH}^{M_{\iota }}({\widetilde {\kappa }_{\iota }})$
). Let
$H^{\iota }_{n}{=_{{\operatorname {df}}}} \Sigma _{1}\text {-SH}^{M_{\iota }|\alpha ^{n}_{\iota }}({\widetilde {\kappa }_{\iota }})$
, where
$M_{\iota }|\alpha ^{n}_{\iota } = {\langle J_{\alpha ^{n}_{\iota }}^{E^{M_{\iota }}},E^{M_{\iota }}, F_{\iota }\cap J_{\alpha ^{n}_{\iota }}^{E^{M_{\iota }}} \rangle }$
. Then
$H^{\iota }_{n}\in M_{\iota }$
and thus
$\tau ^{\iota }_ n( \lambda ,{\widetilde {\kappa }_{\iota }}) {=_{{\operatorname {df}}}} \sup H^{\iota }_{n} \cap \lambda $
must be less than
$\lambda $
for any
$M_{\iota }$
-regular
$\lambda> {\kappa }_{\iota }$
. However
$\sup _{n} \tau ^{\iota }_ n( \lambda ,{\widetilde {\kappa }_{\iota }}) =\lambda $
and the Claim then is proven.
The lemma is proved by induction on
$\theta $
, which now follows in the successor case: suppose
$\theta = \theta _{0}+1$
. If
$\kappa < \kappa _{\theta _{0}}$
then the result follows from the inductive hypothesis (and the normality of the iteration) as
$\pi _{\theta _{0},\theta _{0}+1}(\kappa )=\kappa $
. By assumption
$\kappa = \kappa _{\theta _{0}}$
is ruled out. For
$\kappa> \kappa _{\theta _{0}}$
as the iteration is normal
$\kappa> \widetilde {\kappa } _{\theta _{0}}$
, so we may apply the Claim with
$\kappa $
as
$\lambda>\widetilde {\kappa } _{\theta _{0}}$
.
Suppose now
${\operatorname {Lim}}(\theta )$
. Let
$\kappa $
satisfy (i) and (ii) of the lemma. As
$M_{\theta }$
is a direct limit model, for an
$\iota _{0}<\theta $
let
$\lambda _{\iota }\in M_{\iota }$
be such that
$\pi _{\iota ,\theta }(\lambda _{\iota })=\kappa $
, for
$\iota \in [\iota _{0},\theta )$
. By elementarity, for such
$\iota \geq \iota _{0} (\lambda _{\iota }$
is not measurable but is inaccessible)
$^{M_{\iota }}$
. Consequently
$\lambda _{\iota }\neq \kappa _{\iota }$
. If for some such
$\iota \ \lambda _{\iota }<\kappa _{\iota }$
then the conclusion of the lemma holds by the inductive hypothesis in
$M_{\iota }$
(as
$\pi _{\iota ,\theta }(\lambda _{\iota })=\lambda _{\iota }<\kappa _{\iota }$
). So we may assume
$\lambda _{\iota }>\kappa _{\iota }$
. (Note that this implies that
$\lambda _{\iota }>\widetilde {\kappa }_{\iota }$
since otherwise if we had equality here, then
$\kappa _{\iota }>\lambda _{\iota }$
.) However now each
$cf(\lambda _{\iota })=\omega $
by the inductive hypothesis, witnessed, as in the proof of the claim above, by the ordinals
$\tau ^{\iota }_ n( \lambda _{\iota },{\widetilde {\kappa }_{\iota _{0}}})$
. The
$\Sigma _{1}^{M_{\iota }}$
-definability of the sequence
${\langle \alpha ^{n}_{\iota } \rangle }_{n}$
yields the same for the sequence
${\langle \tau ^{\iota }_ n( \lambda _{\iota },{\widetilde {\kappa }_{\iota _{0}}}) \rangle }_{n} $
. Further
$\pi _{\iota ,\iota + 1}(\tau ^{\iota }_ n( \lambda _{\iota },{\widetilde {\kappa }_{\iota _{0}}}))=\tau ^{\iota +1}_ n( \lambda _{\iota +1},{\widetilde {\kappa }_{\iota _{0}}})$
. Proceeding to the direct limit we see that the image of this definable
$\omega $
-sequence will be an
$\omega $
-sequence cofinal in
$\kappa $
. This concludes the limit case and the lemma. (Lemma)
We state here the generalisation of this for other mice in this region. We say that an iteration
$\sigma : P_{0}\longrightarrow P_{\theta }$
has “no drops” if there are no truncations in the iteration, and there are no “drops in degree”, i.e., if
$n<\omega $
is such that
$\rho ^{n+1}_{P_{0}} \leq \kappa _{0}< \rho ^{n}_{P_{0}}$
then
${\forall } \iota <\theta (\rho ^{n+1}_{P_{i}} \leq \kappa _{\iota }< \rho ^{n}_{P_{i}})$
. (Hence the level at which the fine-structural ultrapowers are taken remains constant.) The lemma is proven by similar reasoning to the previous one, which is only an instance of the next with
$n=0$
.
Lemma 6.3. Let
$P_{0} \leq ^{\ast }M_{0}$
. Let
$\sigma : P_{0}\longrightarrow P_{\theta }$
have no drops in the above sense. Let n be least with
$\rho ^{n+1}_{P_{0}} \leq \kappa _{0}$
. Let
$\tau = {\operatorname {cf}}^{V}(\rho ^{n}_{P_{0}})$
. Suppose
$\rho ^{n+1}_{P_{\iota }} < \kappa < \rho ^{n}_{P_{\iota }}$
and that:
-
(i)
$P_{\theta }\models {``}\kappa $
is inaccessible but not measurable”; (ii)
$\,\kappa \neq \kappa _{\iota }$
for any
$\iota <\theta $
.
Then
$cf^{V}(\kappa )=\tau $
.
Proof We just sketch the main point: although n may be non-zero, the iteration map
$\pi _{\iota ,\iota +1} : M_{\iota } \longrightarrow M_{\iota +1}$
at each stage is
$\Sigma ^{(n)}_{0}$
-preserving and cofinal at the nth projectum level (and so
$\Sigma ^{(n)}_{1}$
-preserving; see [Reference Zeman14]). The map restricted to
$H^{M_{\iota }}_{\rho ^{n}_{M_{\iota }}}$
is thus cofinal into
$H^{M_{\iota +1}}_{\rho ^{n}_{M_{\iota +1}}}$
. (We recall that
$\rho ^{n+1}_{M_{\iota }}$
equals
$\rho ^{n+1}_{M_{0}}$
for any
$0< \iota \leq \theta $
.) Moreover we may pick a definition for a
$\Sigma ^{(n)}_{1}$
-definable partial, but cofinal, map
$\gamma :\rho ^{n+1}_{M_{{0}}}\longrightarrow \rho ^{n}_{M_{{0}}}$
which thus furnishes an increasing sequence
$\gamma ^{0}_{\eta }$
for
$\eta < {\operatorname {o.t.}}(\text {ran}(\gamma )) $
cofinal in
$\rho ^{n}_{M_{0}}$
. The range of
$\gamma $
is thus preserved by this definition throughout the iteration as a
$\Sigma ^{(n)}_{1}$
-definable set which we may write in increasing order as
$\gamma ^{\iota }_{\eta }$
for
$\eta < {\operatorname {o.t.}}(\text {ran}(\gamma )) $
, with
$\sup _{\eta }\gamma ^{\iota }_{\eta } = \rho ^{n}_{M_{\iota }}$
and
$\pi _{0,\iota }(\gamma ^{0}_{\eta }) = \gamma ^{\iota }_{\eta }$
. It is clear then that
$cf^{V}(\rho ^{n}_{M_{0}}) = cf^{V}(\rho ^{n}_{M_{\iota }})$
for all
$\iota \leq \theta $
. Now we can finish off as in the last lemma defining for any regular
$\kappa $
in the interval, sequences cofinal in the ordinal
$\kappa $
by defining appropriate Skolem hulls in the successor case, and using the mechanism of
$\gamma _{\eta }^{\iota }$
as analogues for the
$\alpha _{\iota }^{n}$
, and to define suitable
$\tau ^{\iota }_{\eta }(\lambda )$
, etc.
(The stipulation that P be below
$O^{k}$
in the mouse ordering is unnecessary, and the above holds much more generally.)
Theorem 6.4.
$\neg O^{k} \rightarrow K^{\ast } {=_{{\operatorname {df}}}} (K)^{C^{\ast }}$
is universal
$;$
thus
$K^{\ast }$
is a simple iterate of K.
Proof We argue as in the proof of (i) of Theorem 5.1 assuming that
$K^{\ast }$
is not universal for a contradiction, and thus it only has boundedly many measurable cardinals again. We set
$N_{0}=K^{\ast} $
and additionally require that
$\iota _{0}$
is such that there are no further drops on the
$K= M_{0}$
-side for
$\iota \geq \iota _{0}$
. Let
$\delta {=_{{\operatorname {df}}}} {\operatorname {cf}}^{V}(\kappa _{\iota _{0}}^{+})^{M_{\iota _{0}}}$
. Further, instead of setting
${\langle \lambda _{\alpha } \rangle }_{{0<\alpha <\omega _{1}}}$
as the next
$\omega _{1}\ V$
-cardinals above
$|M_{\iota _{0}}|^{+}$
, we take them as the next ordinals in increasing order satisfying:
-
(a)
${\operatorname {cf}}^V(\lambda _{\alpha }) = \omega , \text { if } \delta \neq \omega $
; or
$\neq \omega $
if
$\delta = \omega $
; -
(b)
$(\lambda _{\alpha }$
is inaccessible
$)^{K^\ast}$
.
Claim (i). Each
$\lambda _{\alpha }$
is a fixed point of
$\pi ^{N}_{0,\iota _{0}}$
.
Proof As each of the
$\lambda _{\alpha }$
is inaccessible in
$N_{0}$
they would be trivially fixed points for any iteration of
$N_{0}$
by measurable cardinals below
$\lambda _{0}$
. Let
$\theta $
be a regular cardinal of
$K^{\ast} $
bounding the measurable cardinals of
$N_{\iota _{0}}$
and so of
$N_{0}= K^{\ast} $
. By increasing the choice of
$\lambda _{0}$
if necessary, we shall assume without loss of generality that
$\lambda _{0}> \theta $
. Applying Lemma 2.10 for a
$\gamma> {\operatorname {sup}} \{\lambda _{\alpha }\, | \, \alpha < \omega _{1}\}$
which is in
$K^{\ast} $
an inaccessible limit of inaccessibles, then shows that the
$\lambda _{\alpha }$
are all fixed points of this map.
Claim (ii). Each
$\lambda _{\alpha }= \kappa _{\beta (\alpha )}$
for some critical point in the iteration
$\pi ^{M}_{\iota _{0},\infty }$
of
$M_{\iota _{0}}$
by the top measure
$F_{\iota _{0}}$
on
$\kappa _{\iota _{0}}$
.
Proof The instances of (ii) follow from the last two lemmata above.
We then finish off as follows: let
$\lambda {=_{{\operatorname {df}}}} \sup \{\lambda _{\alpha }\}_{\alpha < \omega _{1}}$
then
$\lambda = \kappa _{\lambda }$
and
$F_{\lambda }$
is generated by the final segment filter on
${\langle \lambda _{\alpha } \rangle }$
. As these are fixed points of the embedding
$\pi ^{N}_{0,\iota _{0}}$
we can define as before, in
$C^{\ast }$
,
$\widetilde {F}$
as this final segment filter generated by
${\langle \lambda _{\alpha } \rangle }$
on
${P}(\lambda )^{N_{0}}$
. As
$\widetilde {F}$
is then an
$\omega $
-complete measure, we get a contradiction as before.
The next corollary is just a particular example of the above.
Corollary 6.5. If
$\neg O^{\dagger }$
but there is an inner model
$L[U]\ ($
say with U’s critical point on the least possible ordinal
$)$
, then
$K^\ast$
is an iterate of
$L[U]$
.
Corollary 6.6. If there is an inner model with a proper class of measurable cardinals, then there is such an inner model in
$C^{\ast }$
.
Then the following ensures that
$C^{\ast }$
must be different from
$C(I)$
.
Theorem 6.7. If
$O^{k}$
exists, then it is in
$C^{\ast }$
.
Proof Assume for a contradiction that
$O^{k}\notin C^{\ast }$
. We coiterate
$P_{0}{=_{{\operatorname {df}}}} K$
with
$N_{0} {=_{{\operatorname {df}}}} K^{\ast} $
to models
$(P_{\infty }, N_{\infty })$
. By assumption
$K^{\ast} \leq ^{\ast } L[E_{0}]$
, the latter again the model left behind by the iteration out of
$M_{0}$
’s top measure.
Case 1.
$K^{\ast} $
has a proper class of measurable cardinals.
As
$O^{k}$
exists it is in K and indeed appears as an initial segment of K on the
$E^{K}$
sequence. The coiteration immediately starts with a truncation to a
$P_{0}^{\ast } = M_{0}$
of
$P_{0}$
, followed by an ultrapower
$\pi ^{P}_{0,1}:M_{0}\longrightarrow P_{1} $
and thereafter we have a comparison of
$P_{1}$
with
$N_{0}$
. Thus
$\pi ^{P}_{1, \infty }:M_{0}\longrightarrow P_{\infty }$
is a simple normal iteration of
$M_{0}$
that generates
$N_{\infty }$
. In this iteration
$K^{\ast} =N_{0}$
does not move, and thus
$N_{\infty } = N_{0}$
, by Lemma 2.5. Now consider
$\vec c $
an increasing
$\omega $
-sequence of ordinals
$\nu _{n}$
that (i) have uncountable V-cofinality; (ii) are limits of measurable cardinals in
$K^{\ast }$
, and (iii) are inaccessible in
$K^{\ast }$
. Such a sequence must exist as there is a cub class of
$\iota $
where the topmost measure
$F_{\iota }$
of
$P_{\iota }$
is used to form an ultrapower at stage
$\iota $
(and this leaves behind a non-measurable but inaccessible limit of measurables in
$L[E^{K^{\ast }}]$
). Such can be found in
$C^{\ast }$
as
$C^{\ast }= L[{\operatorname {Cof}}_{\omega }]$
. But conversely any
$\nu _{n}$
satisfying (i)–(iii) must itself be a critical point
$\kappa _{\iota (n)}$
, as by Lemma 6.2 the step
$\pi _{\iota (n),\iota (n) + 1}$
has to be an ultrapower step by the topmost measure
$F_{\iota (n)}$
of
$P_{\iota (n)}$
. If
${\iota ^{\ast }} = {\operatorname {sup}}_{n}\{{\iota (n)}\}$
, then in the direct limit model the topmost measure
$F_{\iota ^{\ast }}$
of
$ P_{\iota ^{\ast }}$
on
${P}(\kappa _{\iota ^{\ast }})\cap K^{\ast }={P}(\kappa _{\iota ^{\ast }})\cap P_{\iota ^{\ast }}$
is generated by the final segment filter on
$ {\langle \kappa _{\iota (n)} \rangle }_{n}\in C^{\ast }$
. But
$F_{\iota ^{\ast }}$
is then in
$C^{\ast }$
, and so
$P_{\iota ^{\ast }} \in C^{\ast }$
. But
$M_{0}= O^{k}= core(P_{\iota ^{\ast }})$
, that is, it is the (transitive collapse of) the
$\Sigma _{1}$
-SH
$^{P_{\iota ^{\ast }}}({\varnothing })$
, and thus is also in
$C^{\ast }$
.
Case 2. Otherwise.
We argue that this case also cannot occur. If it did, then
$K^{\ast} $
has a bounded set of measurable cardinals at most. Now argue as in the proof of Theorem 6.4. For some
$\iota _{0}$
there are no further truncations on the P-side of the iteration for
$\iota \geq \iota _{0}$
. We take
$\lambda _{\alpha }$
for
$0\leq \alpha <\omega _{1}$
an ascending sequence in
$C^{\ast }$
of ordinals beyond
$\kappa _{\iota _{0}}$
satisfying (a) and (b) there. (Again, apply the arguments of Lemma 2.10 that
$\pi ^{N}_{0,\eta }(\lambda _{\alpha })=\lambda _{\alpha }$
.) We again define an
$\widetilde {F}$
, an
$\omega $
-complete measure on
${P}(\lambda )^{K^\ast}$
for
$\lambda = \sup _{\alpha }\lambda _{\alpha }$
, with
$\widetilde {F} \in C^{\ast }$
. This is a contradiction just as before. So Case 2 cannot occur.
As discussed above, the exact nature of
$C^{\ast }$
remains open, but the above methods illustrate starkly how they do not apply to the least sword mouse
$O^{s}$
.
Acknowledgment
We should like to warmly thank the authors of [Reference Kennedy, Magidor and Väänänen7] for many discussions on their paper. We first presented this result at the CIRM-Luminy meeting in October 2017 to which we extend our thanks.
