2 Mathematical formulation

We consider thermally driven convection in the Boussinesq approximation of a three-dimensional, Cartesian layer of fluid rotating about the vertical. The fluid layer has depth $d$ , angular velocity $\unicode[STIX]{x1D6FA}$ , density $\unicode[STIX]{x1D70C}$ , kinematic viscosity $\unicode[STIX]{x1D708}$ , thermal diffusivity $\unicode[STIX]{x1D705}$ and magnetic diffusivity $\unicode[STIX]{x1D702}$ , all constant. Following standard practice, we adopt the layer depth $d$ , the thermal relaxation time $d^{2}/\unicode[STIX]{x1D705}$ and the temperature drop across the layer $\unicode[STIX]{x0394}T$ as the units of length, time and temperature respectively. We scale magnetic field intensities with $(2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D705}\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70C})^{1/2}$ , where $\unicode[STIX]{x1D707}_{0}$ is the magnetic permeability of the medium. With these units, and in standard notation, the evolution equations for a fluid with negligible inertia terms read

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{e}_{z}\times \boldsymbol{u}=-\unicode[STIX]{x1D735}p+\boldsymbol{J}\times \boldsymbol{B}+R\,\unicode[STIX]{x1D703}\boldsymbol{e}_{z}+E\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x2202}_{t}-q^{-1}\unicode[STIX]{x1D6FB}^{2})\boldsymbol{B}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{B}=\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x2202}_{t}-\unicode[STIX]{x1D6FB}^{2})\unicode[STIX]{x1D703}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}=w, & \displaystyle\end{eqnarray}$$

(2.4) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$

where $\boldsymbol{J}=\unicode[STIX]{x1D735}\times \boldsymbol{B}$ is the current density, $\unicode[STIX]{x1D703}$ denotes the temperature fluctuations relative to a linear background profile, and the velocity $\boldsymbol{u}=(u,v,w)$ . Three dimensionless numbers appear explicitly: the rotational Rayleigh number $R$ , the Ekman number $E$ and the Roberts number $q$ ; these are defined by

(2.5a-c ) $$\begin{eqnarray}\displaystyle & \displaystyle R=\frac{g\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}Td}{2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D705}},\quad E=\frac{\unicode[STIX]{x1D708}}{2\unicode[STIX]{x1D6FA}d^{2}},\quad q=\frac{\unicode[STIX]{x1D705}}{\unicode[STIX]{x1D702}}, & \displaystyle\end{eqnarray}$$

where $g$ is the gravitational acceleration and $\unicode[STIX]{x1D6FC}$ is the coefficient of thermal expansion. With the above standard non-dimensionalisation, the Rossby number $Ro$ scales as $E/Pr$ , where $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$ is the Prandtl number; thus, formally, at finite values of $E$ , infinitesimal values of $Ro$ correspond to infinite $Pr$ . It is crucial to note, though, that the physical basis for the smallness of the inertia terms (of order $Ro$ ) stems from the rapid rotation.

As noted in Paper 1, the linearity of (2.1) allows a decomposition of the velocity $\boldsymbol{u}$ as

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}=\boldsymbol{u}_{T}+\boldsymbol{u}_{M}, & \displaystyle\end{eqnarray}$$

where $\boldsymbol{u}_{T}$ and $\boldsymbol{u}_{M}$ satisfy, respectively, the equations

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{e}_{z}\times \boldsymbol{u}_{T}=-\unicode[STIX]{x1D735}p_{T}+R\,\unicode[STIX]{x1D703}\boldsymbol{e}_{z}+E\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{T}, & \displaystyle\end{eqnarray}$$

(2.8) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{e}_{z}\times \boldsymbol{u}_{M}=-\unicode[STIX]{x1D735}p_{M}+\boldsymbol{J}\times \boldsymbol{B}+E\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{M}, & \displaystyle\end{eqnarray}$$

with $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{T}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{M}=0$ and $p=p_{T}+p_{M}$ .

The component $\boldsymbol{u}_{T}$ is driven by buoyancy forces, whereas the component $\boldsymbol{u}_{M}$ is driven by magnetic forces, with the Coriolis force influencing both components. The velocity $\boldsymbol{u}_{T}$ exists even in the absence of magnetic fields, and defines the kinematic problem; $\boldsymbol{u}_{M}$ , on the other hand, exists only by virtue of the presence of the magnetic field. One can think of $\boldsymbol{u}_{M}$ as the means by which the system reacts to the presence of the magnetic field, leading eventually to the saturation of magnetic field growth. Note that in the saturated regime, the temperature distribution depends on both $\boldsymbol{u}_{T}$ and $\boldsymbol{u}_{M}$ , via (2.3), and hence $\boldsymbol{u}_{T}$ does not remain as the kinematic velocity.

If, however, the buoyancy force were to be prescribed, then $\boldsymbol{u}_{T}$ would always be independent of the magnetic field. This slightly simpler system, which we refer to as thermo-kinematic, provides, by comparison, useful insights into the behaviour of the full system. For the thermo-kinematic system, the governing equations (2.1), (2.2) and (2.4) are unchanged; however, the temperature equation (2.3) is replaced by

(2.9) $$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x2202}_{t}-\unicode[STIX]{x1D6FB}^{2})\unicode[STIX]{x1D703}+\boldsymbol{u}_{T}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}=w_{T}. & \displaystyle\end{eqnarray}$$

We adopt the same boundary conditions for the full and thermo-kinematic problems. In the horizontal directions we assume that all fields are periodic with periodicity $\unicode[STIX]{x1D706}$ – the aspect ratio. In the vertical we consider standard illustrative boundary conditions, namely that the boundaries are perfectly conducting, both thermally and electrically, impermeable and stress free. Formally these correspond to

(2.10) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}=w=\unicode[STIX]{x2202}_{z}u=\unicode[STIX]{x2202}_{z}v=B_{z}=\unicode[STIX]{x2202}_{z}B_{x}=\unicode[STIX]{x2202}_{z}B_{y}=0\quad \text{at}~z=0,1. & & \displaystyle\end{eqnarray}$$

We solve equations (2.2)–(2.4) numerically by standard pseudo-spectral methods. Details concerning the numerical methods can be found in Cattaneo, Emonet & Weiss (Reference Cattaneo, Emonet and Weiss2003). The numerical scheme requires at every time step a knowledge of the velocity $\boldsymbol{u}$ , which can be computed from the elliptical equation (2.1). The details of how this is performed are contained in appendix A of Paper 1.

3 Force projections

As discussed in the introduction, our chief aim in this paper is to understand the force balance in dynamos driven by rapidly rotating convection. One approach would be to consider the magnitude of the various forces in (2.1) (or, equivalently, (2.7) and (2.8)). The drawback with this approach is that the Coriolis, buoyancy and Lorentz terms are all non-solenoidal, and so have a gradient component; these are accommodated by the pressure gradient, which ensures that the flow remains solenoidal, but of itself is not of dynamical significance. A natural way to proceed (e.g. Dormy Reference Dormy2016) would be to take the curl of (2.1). This, however, introduces an extra derivative, which numerically can cause problems in simulations with high fluid and magnetic Reynolds numbers; indeed, the curl of the Lorentz force can be particularly unpleasant. Another possibility, and the one we adopt here, is to consider the projection of (2.7) and (2.8) onto the subspace of solenoidal vector functions. This takes care of the pressure whilst, importantly, not introducing any additional spatial derivatives. The price to pay though is that the interpretation of projected quantities is a little less intuitive than that of the full (non-projected) forces. In particular, such a projection tends to scramble the directional components; for example, the solenoidal projection of a purely vertical force, such as buoyancy, will have both vertical and horizontal components.

Implementation of this procedure in (2.7) and (2.8) leads to six projected forces, governed by the equations

(3.1) $$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{P}(R\,\unicode[STIX]{x1D703}\boldsymbol{e}_{z}-\boldsymbol{e}_{z}\times \boldsymbol{u}_{T})+E\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{T}=0, & \displaystyle\end{eqnarray}$$

(3.2) $$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{P}(\boldsymbol{J}\times \boldsymbol{B}-\boldsymbol{e}_{z}\times \boldsymbol{u}_{M})+E\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{M}=0, & \displaystyle\end{eqnarray}$$

where $\mathbb{P}$ denotes the solenoidal projection operator. Note that since the viscous terms are already solenoidal, these do not require projection.

We denote the projections of the magnetic, buoyancy, Coriolis and viscous forces by $M$ , $A$ , $C$ and $V$ , respectively. Since the system is strongly anisotropic, it is instructive to consider separately the horizontal and vertical components, which we denote by the subscripts $h$ and $v$ ; furthermore, since we are interested in the Coriolis and viscous forces for the thermal and magnetic velocities separately, we introduce the superscripts $T$ and $M$ for these projections.

4 Dynamo solutions

Our analysis is based on the study of three representative cases. The input parameter values for these are contained in table 1, together with $R_{c}$ , the critical Rayleigh number at the onset of convection. We also show $Rm$ , the magnetic Reynolds number, and the kinetic and magnetic Taylor microscales, all of which are output parameters. The numerical resolution is the same in all cases; to ensure that all quantities, included diagnostic ones, were fully resolved, we employed a higher resolution than that used in Paper 1. Certain aspects of these solutions have been discussed in Paper 1 and so here we give just a brief summary of their dynamo properties. In all three cases, the convection is vigorously time dependent and supports dynamo action; the essential difference between the three cases is in the manner in which the dynamo saturates. In Paper 1 we introduced the idea of weak and strong field dynamos categorised by the departure of the dynamic from the kinematic velocity. The three cases studied here correspond to a weak field dynamo (case 1, in which, in the decomposition (2.6), $\boldsymbol{u}\approx \boldsymbol{u}_{T}$ ), a strong field dynamo (case 2, in which both $\boldsymbol{u}_{T}$ and $\boldsymbol{u}_{M}$ contribute significantly to $\boldsymbol{u}$ ) and a super strong field dynamo (case 3, in which $\boldsymbol{u}\approx \boldsymbol{u}_{M}$ ). These three cases are illustrated in figure 1, which shows snapshots of the vertical components of $\boldsymbol{u}$ , $\boldsymbol{u}_{T}$ and $\boldsymbol{u}_{M}$ . As discussed in Paper 1, it is important to make the distinction between weak and strong field branches and what we refer to as weak and strong field solutions. Our nomenclature addresses the issue of the force balance that leads to dynamo saturation rather than the branch on which the solutions lie.

Table 1. Summary of the parameter values for the simulations. The input parameters are $E$ , $R$ , $q$ and $\unicode[STIX]{x1D706}$ . $R_{c}$ denotes the critical Rayleigh number for the onset of convection; the magnetic Reynolds number $Rm=q\langle \boldsymbol{u}^{2}\rangle ^{1/2}$ , where the root mean square (r.m.s.) velocity is obtained from a time average in the saturated state; $l_{v}$ and $l_{B}$ denote, respectively, the Taylor microscales for the velocity and the magnetic field, defined by $l_{v}^{2}=\langle |\boldsymbol{u}|^{2}\rangle /\langle |\unicode[STIX]{x1D735}\times \boldsymbol{u}|^{2}\rangle$ , $l_{B}^{2}=\langle |\boldsymbol{B}|^{2}\rangle /\langle |\unicode[STIX]{x1D735}\times \boldsymbol{B}|^{2}\rangle$ . The resolution for all cases is $1024\times 1024\times 257$ .

Figure 1. Snapshots of the vertical components of $\boldsymbol{u}$ (a,d,g), $\boldsymbol{u}_{T}$ (b,e,h) and $\boldsymbol{u}_{M}$ (c,f,i) for case 1 (a–c), case 2 (d–f) and case 3 (g–i) in a horizontal plane near the top of the domain. Each row is scaled consistently. Light (dark) tones correspond to upward (downward) moving fluid.

Historically, a problem of great interest in dynamo theory has been the generation of large-scale (mean) fields by helical convection, through what is referred to as the dynamo $\unicode[STIX]{x1D6FC}$ -effect. As expected, the influence of rotation on the convection does indeed introduce helicity into the flow; in Boussinesq convection, the helicity distribution is antisymmetric about the mid-plane (see Paper 1, figure 3). However, in the turbulent regimes studied here, the mean field generated is rather weak, despite the presence of helicity (see Paper 1, figure 10); it is worth noting that the absence of a mean field is not related to the neglect of inertia (see Cattaneo & Hughes Reference Cattaneo and Hughes2006). Thus, whether we are discussing weak or strong field dynamo solutions, they should not be regarded as mean-field-type dynamos.

5 Force balance

Figure 2. The r.m.s. values of the horizontal components of all six terms in (3.1) and (3.2) as a function of time, for case 2. The correspondence between symbols and projected forces is described in the legend, using the nomenclature of § 3.

Figure 3. Time-averaged r.m.s. values of the vertical (a,c,e) and horizontal (b,d,f) components of all six terms in  (3.1) and (3.2), for case 1 (a,b), case 2 (c,d), case 3 (e,f). The forces in (3.1) are shown in red, those in (3.2) in blue.

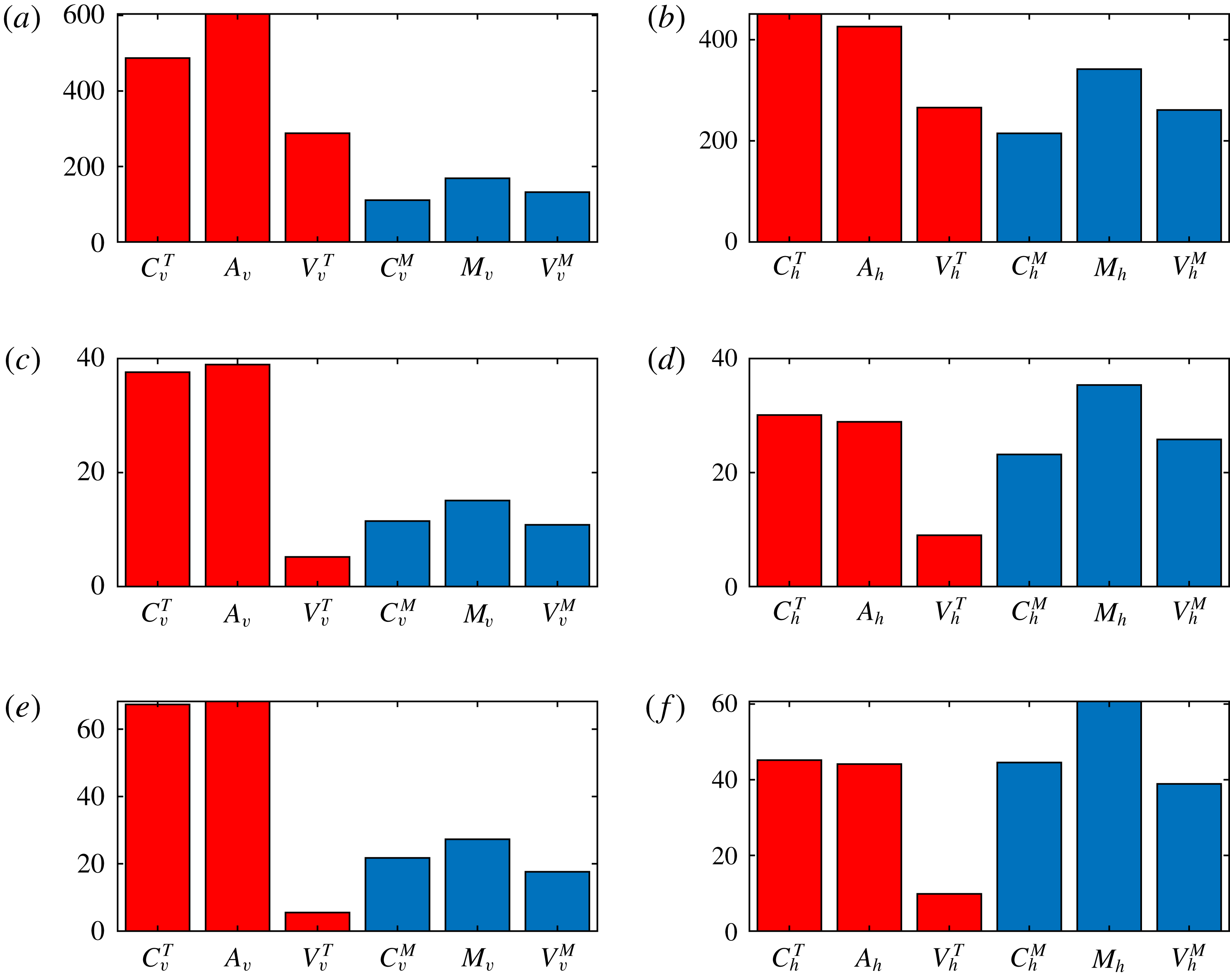
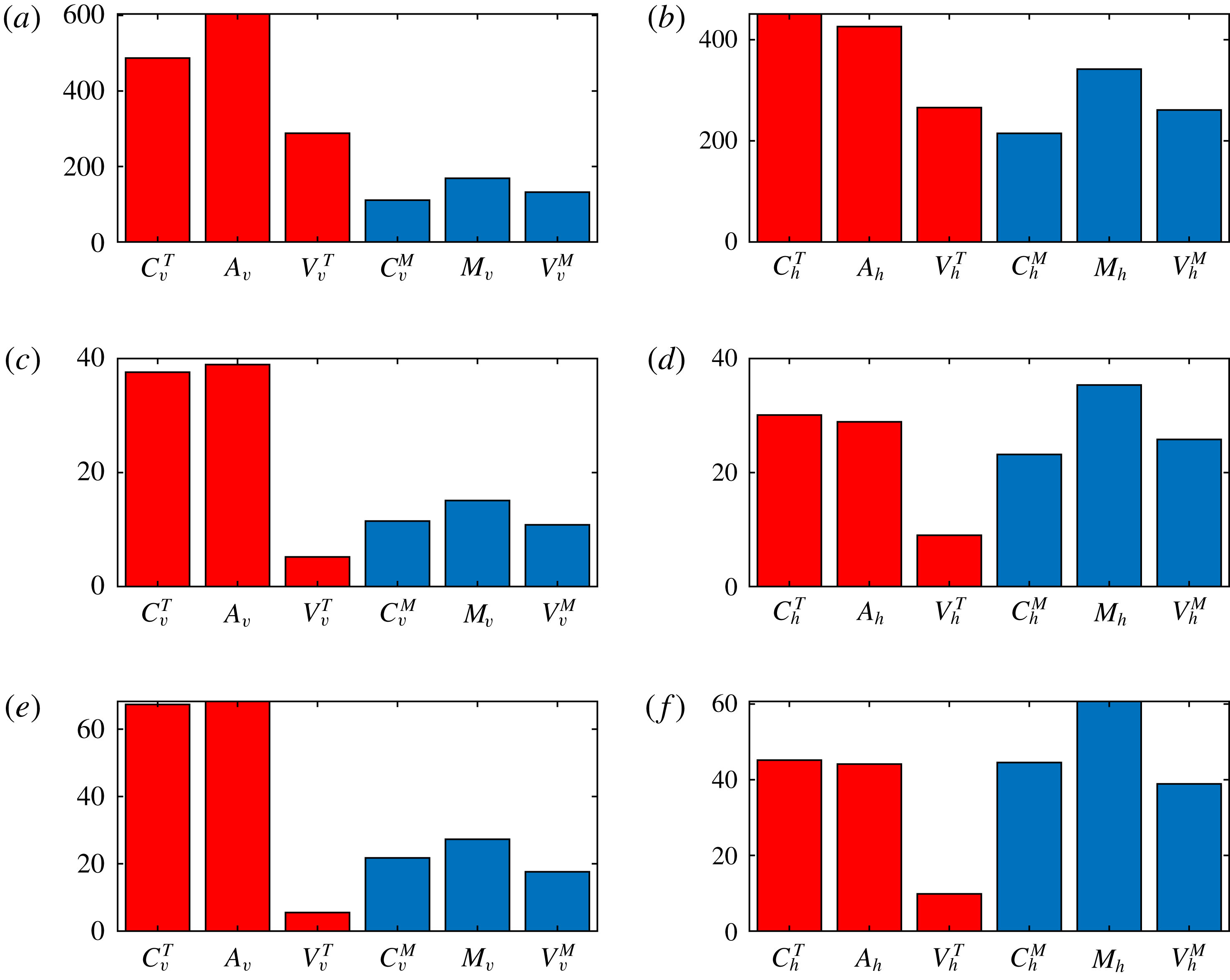
It is clear from inspection of figure 1 that the mechanism of dynamo saturation is very different in the three cases studied. In order to understand how this is achieved, it is necessary to analyse the means by which the exact force balance relations (3.1) and (3.2) are effected. Of course, this analysis must take into account the vectorial nature of the equations, but as a first step we can look at the magnitudes of the forces, separating the horizontal and vertical components of the various terms. Figure 2 plots the magnitudes of the horizontal components of the forces for the particular example of case 2. Two features are apparent. One is that there is a considerable range in the magnitudes of the various forces; the other is that, although there is some temporal variation in the magnitudes, this is small compared to their mean value. This is true for all three cases, for both the vertical and horizontal components. It therefore makes sense to consider the time-averaged quantities of the magnitudes of the forces, in which each term in (3.1) and (3.2) has both vertical and horizontal components. This then leads to a convenient graphical representation for the magnitudes of all of the terms in (3.1) and (3.2) in terms of bar charts.

Figure 3 shows the time-averaged r.m.s. values of the vertical and horizontal components of all six projected forces in (3.1) and (3.2), for all three cases studied. Several salient features are evident. In terms of the thermal force balance (3.1), the Coriolis and buoyancy forces dominate, in both the vertical and horizontal projections; indeed, in the progression from weak to strong to super strong solutions, the Coriolis and buoyancy forces become more and more balanced (i.e. $C_{v/h}^{T}\approx A_{v/h}$ ). For the magnetic force balance (3.2), the horizontal projections dominate for all three forces in all three cases. In the horizontal projections for the weak field solutions, all six forces are of comparable magnitude. In progressing to the strong and then super strong field solutions, the magnetic tension ( $M_{h}$ ) becomes dominant, with the thermal viscous stresses ( $V_{h}^{T}$ ) becoming progressively smaller; this trend for the diminishing of the thermal viscous stresses is also apparent in the vertical projections. Thus, as noted above, as one progresses from weak to super strong, there is a tendency in the thermal force balance equation for equality between Coriolis and buoyancy forces, with viscosity becoming irrelevant. This should be contrasted with the magnetic force balance equation, in which no such tendency is observed, with the viscous term ( $V_{v/h}^{M}$ ) always remaining important. This last result has some interesting implications for the role of viscous stresses in determining the nature of the solutions. For instance, if the solution approaches a Taylor state, with an exact balance between Coriolis, buoyancy and magnetic forces, then the viscous stresses would become irrelevant. Here, although the viscous stresses associated with the thermal component of the velocity ( $V_{v/h}^{T}$ ) do become small, this is not the case for those associated with the magnetic component ( $V_{v/h}^{M}$ ). If that is true in general, then this system does not have a tendency to approach a Taylor state; all three terms in (3.2) remain of comparable magnitude.

Figure 4. Vertical components of the projections of the Coriolis (a,c) and buoyancy (b,d) terms in the thermal force balance equation (3.1), for case 1 (a,b) and case 2 (c,d), in a horizontal plane near the top of the domain. Each row is scaled consistently. Light (dark) tones correspond to positive (negative) values.

Figure 5. Horizontal components of the projections of the Coriolis (a,c) and magnetic (b,d) terms in the magnetic force balance equation (3.2), for case 1 (a,b) and case 2 (c,d), in a horizontal plane near the top of the domain. Each row is scaled consistently. Light (dark) tones correspond to positive (negative) values.

Figure 6. Enlargement of a $\unicode[STIX]{x1D706}/4\times \unicode[STIX]{x1D706}/4$ section of figure 5 for case 2.

In order to gain some insight into the role of viscous stresses, it is useful to inspect the spatial distribution of the terms in (3.1) and (3.2). First we look at the vertical components of the thermal force balance equation (3.1). Figure 4 shows the horizontal planform, near the upper boundary, of the Coriolis and buoyancy terms for cases 1 and 2. Just as a reminder, it should be noted that for case 1, the aspect ratio is $\unicode[STIX]{x1D706}=5$ , whereas for case 2, $\unicode[STIX]{x1D706}=2$ . The Coriolis term is smoother than the corresponding buoyancy term, with the difference between them being accommodated by the viscous term. Clearly the difference between the two is reduced in the strong field solution. Indeed, this trend continues into the super strong regime, and it is conceivable that there will be regimes in which the Coriolis and buoyancy forces are arbitrarily close. This should be contrasted with the horizontal components of the magnetic force balance equation (3.2), shown in figure 5. Clearly the magnetic tension has a smooth component that can be balanced by the Coriolis term, but it also has a strongly intermittent, filamentary part that can be accommodated only by the viscous stresses; this can be seen particularly clearly in the blow-up of part of the domain shown in figure 6. The important feature is that this latter component does not appear to become any weaker in the progression from weak to strong field solutions. This intermittent component of the magnetic stresses is associated with current sheets, and there is no evidence here that these will ever disappear.

Figure 7. Time-averaged r.m.s. values of the vertical and horizontal components of all six terms in (3.1) and (3.2) for the thermo-kinematic problem, for case 1 (a,b), case 2 (c,d), case 3 (e,f). The forces in (3.1) are shown in red, those in (3.2) in blue.

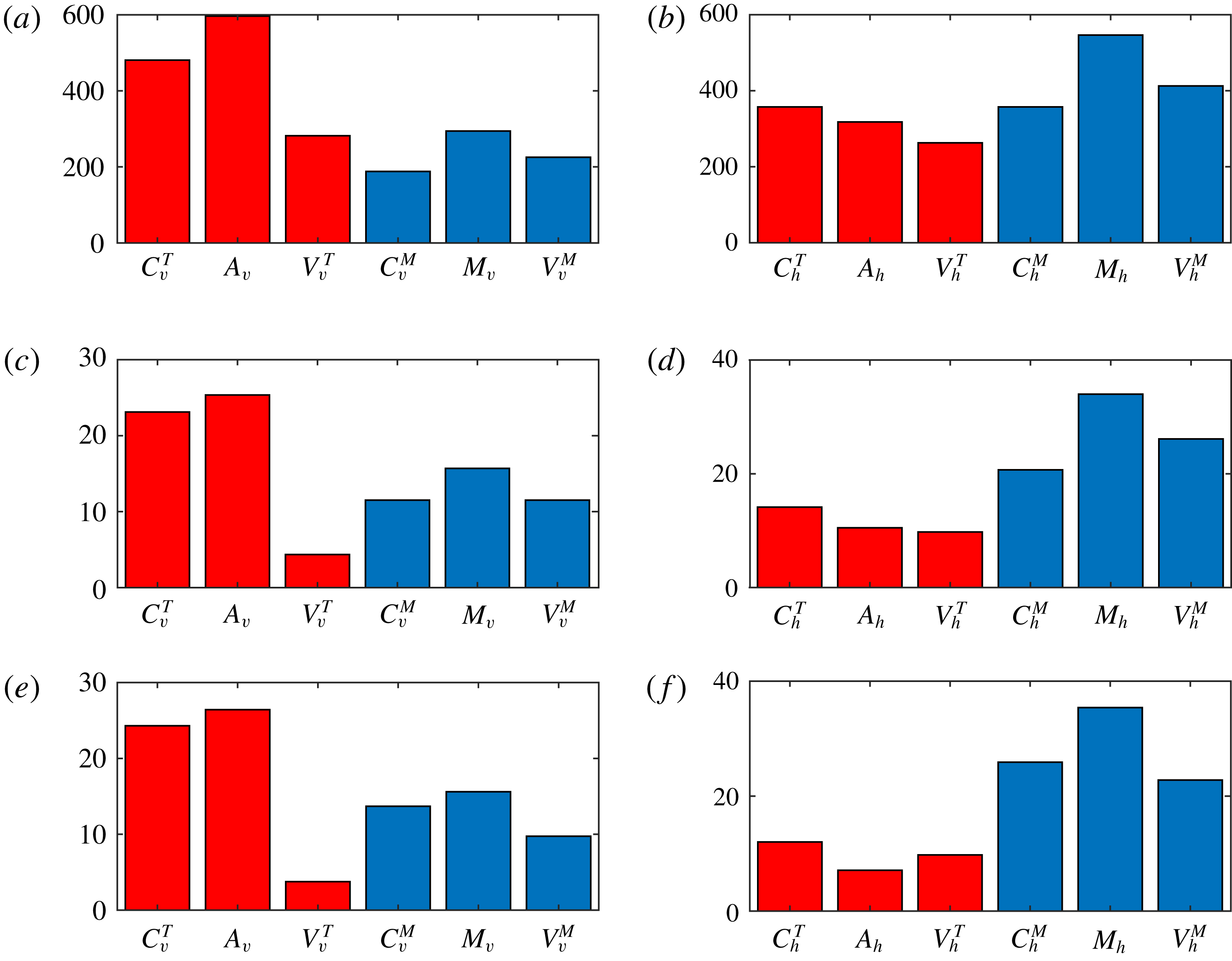
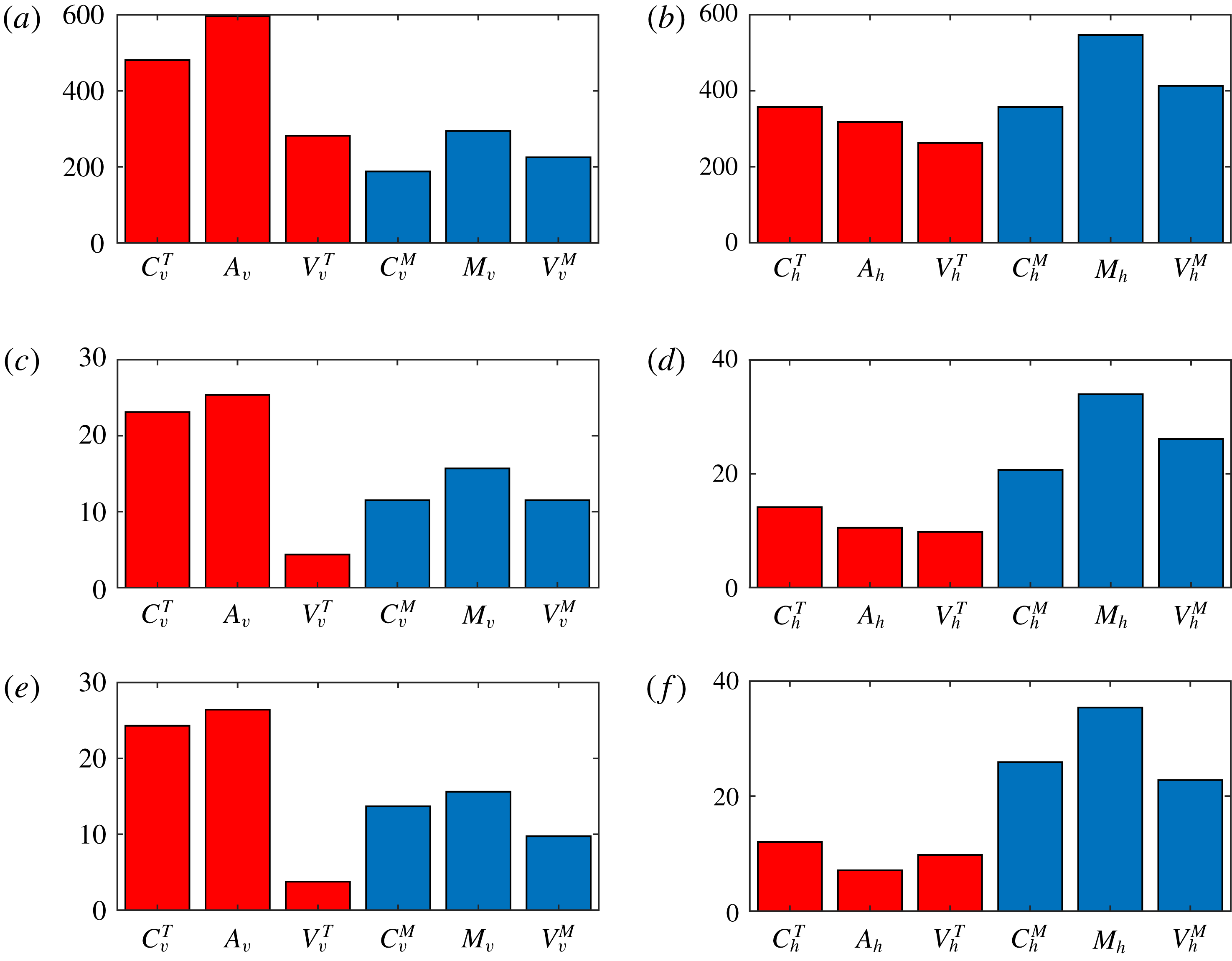
Further insight into the underlying physical processes can be gained from consideration of the thermo-kinematic problem, described in § 2. The key difference between the full and thermo-kinematic systems is that in the former the temperature is advected by the full velocity, and hence is influenced by the magnetic field, whereas in the latter, by construction, the temperature is what it would be in unmagnetised convection. In the full problem, the role of magnetic forces is twofold: to generate counter-vorticity and also to change the planform of convection, typically increasing its scale. In weak field solutions, this increase is only slight, whereas in strong field solutions it is substantial. By contrast, in the thermo-kinematic problem, in which the convective planform is fixed, there is only one route to saturation, namely the Lorentz force can only generate counter-vorticity.

Figure 7 shows the quantities corresponding to those in figure 3 for the thermo-kinematic problem with the same parameter values as cases 1 to 3. The magnitudes of the components in the magnetic force balance (3.2) are very similar to the corresponding quantities in the full problem. This is not surprising, since the magnetic part of the problem is unchanged. For the limiting case of a weak solution, the thermal forces in the full and thermo-kinematic problems will be identical, since that is precisely the definition of a weak solution. In our weak solution (case 1), there is however some weak coupling between the thermal forces and the magnetic field, which allows the dynamo to saturate at a lower level in comparison with the thermo-kinematic problem. For cases 2 and 3, the most striking difference is in the vertical components of the thermal forces, where the amplitude of the thermal forces is reduced relative both to those of the full system and also to the magnetic terms. This reduction in amplitude illustrates the vital role of the magnetic field in alleviating rotational constraints. For purely hydrodynamic convection, the rotational constraint manifests itself in a dependence of the horizontal scale of convection as $E^{1/3}$ for $E\ll 1$ ; this follows from the thermal force balance equation (2.7) and the temperature equation (2.3), which are precisely the thermo-kinematic equations. However, there is no such equivalent relationship deriving from the magnetic force balance equation (2.8) together with the induction equation (2.2). That being the case, for small $E$ , both the thermal velocity $\boldsymbol{u}_{T}$ and the temperature $\unicode[STIX]{x1D703}$ in the thermo-kinematic system can only be at small scales, whereas $\boldsymbol{u}_{M}$ can have, and indeed does have, a large-scale component. By contrast, in the full system, the presence of the large-scale $\boldsymbol{u}_{M}$ in the temperature equation (2.3) introduces a large-scale component in the temperature and therefore in the buoyancy force, which drives $\boldsymbol{u}_{T}$ towards larger scales. Thus the rotational constraint is released and the thermal velocity can attain larger amplitudes.

Figure 8. Time-averaged convective flux $\langle w\unicode[STIX]{x1D703}\rangle$ versus depth for case 2, with its constituent components $\langle w_{T}\unicode[STIX]{x1D703}\rangle$ and $\langle w_{M}\unicode[STIX]{x1D703}\rangle$ . Also shown is the convective flux $\langle w\unicode[STIX]{x1D703}\rangle _{tk}$ for the purely hydrodynamic (thermo-kinematic) case.

A particularly striking consequence of this effect is in the increased efficiency of the convection; this can be measured by the convective flux $F_{c}=\langle w\unicode[STIX]{x1D703}\rangle$ , where the average is taken over horizontal planes. For example, figure 8 shows the depth dependence, for case 2, of the time-averaged convective flux associated with the thermal velocity $w_{T}$ , the magnetic velocity $w_{M}$ and the full velocity $w$ (the sum of the two). We also show $F_{c}$ for the corresponding thermo-kinematic case, equivalent to purely hydrodynamic convection. Of note is the striking increase in convective efficiency in the magnetic system. Although the contribution to the heat transport from the thermal velocity has dropped slightly, this is more than compensated by the contribution from the induced magnetic velocity $\boldsymbol{u}_{M}$ , a fact that, in itself, is far from obvious. Thus, in rapidly rotating systems, hydromagnetic convection is considerably more efficient than its hydrodynamic counterpart, in contrast to non-rotating convection in which the influence of magnetic field is inhibiting (e.g. Cattaneo Reference Cattaneo1999).