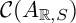0 Introduction
Cluster algebras were introduced by Fomin and Zelevinksy in [Reference Fomin and Zelevinksy6]–[Reference Fomin and Zelevinksy9]. Two different categorifications of cluster algebras were introduced independently in [Reference Buan, Marsh, Reineke, Reiten and Todorov4] and [Reference Caldero, Chapoton and Schiffler5]. Igusa and Todorov introduced a continuous version of a cluster category in [Reference Igusa and Todorov15].
In Part (I) [Reference Igusa, Rock and Todorov14], the authors defined continuous quivers of type A, generalizing quivers of type A, and proved results about decomposition of pointwise finite-dimensional representations and the category of finitely generated representations. In Part (II) [Reference Rock19], Rock introduced the Auslander–Reiten (AR) space, a continuous analog to the AR quiver, and proved results relating the AR-space to extensions in the representation category and distinguished triangles in the derived category. This paper is Part (III) of this series; the purpose is to form a continuous generalization of clusters and mutations.
We begin this work with classifying the derived categories of representations of continuous quivers of type A. In the finite case, the derived categories for any orientation of an
![]() $A_n$
quiver are all equivalent [Reference Happel11]. This is not true for the continuum:
$A_n$
quiver are all equivalent [Reference Happel11]. This is not true for the continuum:
Theorem A (Theorem 2.3.5)
Let
![]() $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
![]() $A_{{\mathbb {R}},S'}$
be possibly different orientations of continuous quivers of type A. Then
$A_{{\mathbb {R}},S'}$
be possibly different orientations of continuous quivers of type A. Then
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() $\mathcal {D}^b(A_{{\mathbb {R}},S'})$
are equivalent as triangulated categories if and only if one of the following holds:
$\mathcal {D}^b(A_{{\mathbb {R}},S'})$
are equivalent as triangulated categories if and only if one of the following holds:
-
(a) both
 $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
 $A_{{\mathbb {R}},S'}$
have finitely many sinks and sources,
$A_{{\mathbb {R}},S'}$
have finitely many sinks and sources, -
(b) the sinks and sources of
 $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
 $A_{{\mathbb {R}},S'}$
are each bounded on exactly one side, or
$A_{{\mathbb {R}},S'}$
are each bounded on exactly one side, or -
(c) the sinks and sources of
 $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
 $A_{{\mathbb {R}},S'}$
are unbounded on both sides.
$A_{{\mathbb {R}},S'}$
are unbounded on both sides.
We define the new “weak continuous cluster category”
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
(Definition 3.1.2) as the orbit category of the doubling of
${\mathcal {C}(A_{{\mathbb {R}},S})}$
(Definition 3.1.2) as the orbit category of the doubling of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
via almost-shift (same method as in [Reference Igusa and Todorov15]). The new categories
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
via almost-shift (same method as in [Reference Igusa and Todorov15]). The new categories
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
are related to the original categories
${\mathcal {C}(A_{{\mathbb {R}},S})}$
are related to the original categories
![]() $\mathcal D_\pi $
and
$\mathcal D_\pi $
and
![]() $\mathcal C_\pi $
by localizations:
$\mathcal C_\pi $
by localizations:
Theorem B (Theorems 3.3.3 and 3.3.4)
Assume
![]() $A_{{\mathbb {R}},S}$
has finitely many sinks and sources. Then there exist triangulated equivalences
$A_{{\mathbb {R}},S}$
has finitely many sinks and sources. Then there exist triangulated equivalences
where
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[\mathcal M^{-1}]$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[\mathcal M^{-1}]$
and
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[\mathcal N^{-1}]$
are triangulated localizations of
${\mathcal {C}(A_{{\mathbb {R}},S})}[\mathcal N^{-1}]$
are triangulated localizations of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
.
This new category
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
does not have a cluster structure. However, we define
${\mathcal {C}(A_{{\mathbb {R}},S})}$
does not have a cluster structure. However, we define
![]() $\mathbf E$
-clusters (Definition 4.3.1) in
$\mathbf E$
-clusters (Definition 4.3.1) in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
which is a weaker notion than clusters, in the sense that an
${\mathcal {C}(A_{{\mathbb {R}},S})}$
which is a weaker notion than clusters, in the sense that an
![]() $\mathbf E$
-cluster might not be mutated in the direction of each of its elements.
$\mathbf E$
-cluster might not be mutated in the direction of each of its elements.
Theorem C (Theorem 4.3.8)
Let T be an
![]() $\mathbf E$
-cluster and
$\mathbf E$
-cluster and
![]() $V\in T$
. Suppose that T can be mutated in the direction V. Then, there exists exactly one W, up to isomorphism, such that
$V\in T$
. Suppose that T can be mutated in the direction V. Then, there exists exactly one W, up to isomorphism, such that
![]() $(T\setminus \{V\})\cup \{W\}$
is an
$(T\setminus \{V\})\cup \{W\}$
is an
![]() $\mathbf E$
-cluster.
$\mathbf E$
-cluster.
The key difference between these new
![]() $\mathbf E$
-clusters and clusters in cluster structures (including the original
$\mathbf E$
-clusters and clusters in cluster structures (including the original
![]() $\mathcal C_\pi $
) is the weakening of the requirement for mutations similar to [Reference Holm and Jørgensen13]. Instead of there exists a unique choice, we require there exists none or one. This leads to our final contribution: that of cluster theories (Definition 4.1.1) which generalize cluster structures. A cluster theory on a skeletally small Krull–Schmidt additive category
$\mathcal C_\pi $
) is the weakening of the requirement for mutations similar to [Reference Holm and Jørgensen13]. Instead of there exists a unique choice, we require there exists none or one. This leads to our final contribution: that of cluster theories (Definition 4.1.1) which generalize cluster structures. A cluster theory on a skeletally small Krull–Schmidt additive category
![]() $\mathcal C$
is defined to be a groupoid
$\mathcal C$
is defined to be a groupoid
![]() $\mathscr T_{\mathbf P}(\mathcal C)$
of
$\mathscr T_{\mathbf P}(\mathcal C)$
of
![]() $\mathbf P$
-clusters induced by a pairwise compatibility condition
$\mathbf P$
-clusters induced by a pairwise compatibility condition
![]() $\mathbf P$
on
$\mathbf P$
on
![]() $\text {Ind}\,\mathcal C$
. In this language,
$\text {Ind}\,\mathcal C$
. In this language,
![]() $\mathbf E$
-clusters form the
$\mathbf E$
-clusters form the
![]() $\mathbf E$
-cluster theory
$\mathbf E$
-cluster theory
![]() $\mathscr T_{\mathbf E}(\mathcal C)$
of
$\mathscr T_{\mathbf E}(\mathcal C)$
of
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
which is given by compatibility condition
${\mathcal {C}(A_{{\mathbb {R}},S})}$
which is given by compatibility condition
![]() $\mathbf P=\mathbf E$
(Example 4.4.1). We give precise descriptions of embeddings of cluster theories (Definition 4.1.9):
$\mathbf P=\mathbf E$
(Example 4.4.1). We give precise descriptions of embeddings of cluster theories (Definition 4.1.9):
Theorem D (Theorems 5.1.6, 5.2.10, and 5.3.8)
There are embeddings of cluster theories given below, where general compatibility condition
![]() $\mathbf P$
is replaced by the symbol for each particular compatibility condition and where
$\mathbf P$
is replaced by the symbol for each particular compatibility condition and where
![]() $A_{\mathbb {R}}=A_{{\mathbb {R}},\emptyset }$
with straight descending orientation.
$A_{\mathbb {R}}=A_{{\mathbb {R}},\emptyset }$
with straight descending orientation.
-
•
 $\mathscr T_{\mathbf N_n}(\mathcal C(A_n))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for any
$\mathscr T_{\mathbf N_n}(\mathcal C(A_n))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for any
 $A_n$
quiver from [Reference Caldero, Chapoton and Schiffler5],
$A_n$
quiver from [Reference Caldero, Chapoton and Schiffler5], -
•
 $\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for the straight
$\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for the straight
 $A_\infty $
quiver from [Reference Holm and Jørgensen12], and
$A_\infty $
quiver from [Reference Holm and Jørgensen12], and -
•
 $\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for the original continuous cluster theories from [Reference Igusa and Todorov15].
$\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
for the original continuous cluster theories from [Reference Igusa and Todorov15].
The final part of this series (paper IV [Reference Rock20]) addresses the continuous generalizations of mutation, embedding and geometric models of cluster theories of type A.
1 Review of Parts (I) and (II) in This Series
1.1 Continuous Quivers of Type A and Their Representations
Fix a field k. We now recall relevant definitions and theorems about continuous quivers of type A and their representations from part (I), that is [Reference Igusa, Rock and Todorov14].

Figure 1 A visual depiction of a continuous quiver of type A.
Definition 1.1.1.
Continuous quivers of type A are triples
![]() $A_{{\mathbb {R}},S}=({\mathbb {R}},S,\preceq )$
s.t.
$A_{{\mathbb {R}},S}=({\mathbb {R}},S,\preceq )$
s.t.
-
1.
-
(a)
 $S\subset {\mathbb {R}}$
is a discrete subset, possibly empty, with no accumulation points.
$S\subset {\mathbb {R}}$
is a discrete subset, possibly empty, with no accumulation points. -
(b) Order on
 $S\cup \{\pm \infty \}$
is induced by the order of
$S\cup \{\pm \infty \}$
is induced by the order of
 ${\mathbb {R}}$
, and
${\mathbb {R}}$
, and
 $-\infty <s<+\infty $
for
$-\infty <s<+\infty $
for
 $\forall s\in S$
.
$\forall s\in S$
. -
(c) Elements of
 $S\cup \{\pm \infty \}$
are indexed by a subset of
$S\cup \{\pm \infty \}$
are indexed by a subset of
 ${\mathbb {Z}}\cup \{\pm \infty \}$
, so that
${\mathbb {Z}}\cup \{\pm \infty \}$
, so that
 $s_n$
denotes the element of
$s_n$
denotes the element of
 $S\cup \{\pm \infty \}$
with index n. The indexing must adhere to the following:
$S\cup \{\pm \infty \}$
with index n. The indexing must adhere to the following:-
i1 There exists
 $s_0\in S\cup \{\pm \infty \}$
.
$s_0\in S\cup \{\pm \infty \}$
. -
i2 If
 $m\leq n\in {\mathbb {Z}}\cup \{\pm \infty \}$
and
$m\leq n\in {\mathbb {Z}}\cup \{\pm \infty \}$
and
 $s_m,s_n\in S\cup \{\pm \infty \}$
then for all
$s_m,s_n\in S\cup \{\pm \infty \}$
then for all
 $p\in {\mathbb {Z}}\cup \{\pm \infty \}$
such that
$p\in {\mathbb {Z}}\cup \{\pm \infty \}$
such that
 $m\leq p \leq n$
the element
$m\leq p \leq n$
the element
 $s_p$
is in
$s_p$
is in
 $S\cup \{\pm \infty \}$
.
$S\cup \{\pm \infty \}$
.
-
-
-
2. New partial order
 $\preceq $
on
$\preceq $
on
 ${\mathbb {R}}$
, which we call the orientation of
${\mathbb {R}}$
, which we call the orientation of
 $A_{{\mathbb {R}},S}$
, is given by:
$A_{{\mathbb {R}},S}$
, is given by:-
p1 If n is even and
 $x,y\in [s_n,s_{n+1}]$
, then
$x,y\in [s_n,s_{n+1}]$
, then
 $x\preceq y$
iff
$x\preceq y$
iff
 $x\le y$
, and
$x\le y$
, and
 $s_n,s_{n+1}\in S\cup \{\pm \infty \}$
.
$s_n,s_{n+1}\in S\cup \{\pm \infty \}$
. -
p2 If n is odd and
 $x,y\in [s_n,s_{n+1}]$
, then
$x,y\in [s_n,s_{n+1}]$
, then
 $x\preceq y$
iff
$x\preceq y$
iff
 $x\ge y$
, and
$x\ge y$
, and
 $s_n,s_{n+1}\in S\cup \{\pm \infty \}$
.
$s_n,s_{n+1}\in S\cup \{\pm \infty \}$
.
-
When
![]() $A_{{\mathbb {R}},S}$
has straight descending orientation we sometimes denote it by
$A_{{\mathbb {R}},S}$
has straight descending orientation we sometimes denote it by
![]() $A_{\mathbb {R}}$
(as in [Reference Igusa and Todorov15]).
$A_{\mathbb {R}}$
(as in [Reference Igusa and Todorov15]).
Definition 1.1.2. Let
![]() $A_{{\mathbb {R}},S}=({\mathbb {R}},S\preceq )$
be a continuous quiver of type A and let k be a field. A k-representation V of
$A_{{\mathbb {R}},S}=({\mathbb {R}},S\preceq )$
be a continuous quiver of type A and let k be a field. A k-representation V of
![]() $A_{{\mathbb {R}},S}$
is the following data:
$A_{{\mathbb {R}},S}$
is the following data:
-
• A k-vector space
 $V(x)$
for each
$V(x)$
for each
 $x\in {\mathbb {R}}$
.
$x\in {\mathbb {R}}$
. -
• For every pair,
 $y\preceq x$
in
$y\preceq x$
in
 $A_{{\mathbb {R}},S}$
a k-linear map
$A_{{\mathbb {R}},S}$
a k-linear map
 $V(x,y):V(x)\to V(y)$
such that if
$V(x,y):V(x)\to V(y)$
such that if
 $z\preceq y \preceq x$
then
$z\preceq y \preceq x$
then
 $V(x,z)=V(y,z)\circ V(x,y)$
.
$V(x,z)=V(y,z)\circ V(x,y)$
.
We say V is pointwise finite-dimensional if
![]() $\dim _k V(x) < \infty $
for all
$\dim _k V(x) < \infty $
for all
![]() $x\in {\mathbb {R}}$
.
$x\in {\mathbb {R}}$
.
Definition 1.1.3. Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A and
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A and
![]() $I\subset {\mathbb {R}}$
be an interval. We denote by
$I\subset {\mathbb {R}}$
be an interval. We denote by
![]() $M_I$
the interval indecomposable representation of
$M_I$
the interval indecomposable representation of
![]() $A_{{\mathbb {R}},S}$
given by:
$A_{{\mathbb {R}},S}$
given by:
 $$ \begin{align*} M_I(x) &= \left\{ \begin{array}{ll} k, & x\in I, \\ 0, & \text{otherwise,} \end{array} \right. & M_I(x,y) &= \left\{ \begin{array}{ll} 1_k, & y\preceq x\in I, \\ 0, & \text{otherwise.} \end{array} \right. \end{align*} $$
$$ \begin{align*} M_I(x) &= \left\{ \begin{array}{ll} k, & x\in I, \\ 0, & \text{otherwise,} \end{array} \right. & M_I(x,y) &= \left\{ \begin{array}{ll} 1_k, & y\preceq x\in I, \\ 0, & \text{otherwise.} \end{array} \right. \end{align*} $$
Notation 1.1.4. Let
![]() $a<b\in {\mathbb {R}}\cup \{\pm \infty \}$
. By the notation
$a<b\in {\mathbb {R}}\cup \{\pm \infty \}$
. By the notation
![]() $|a,b|$
, we mean one of the following interval subsets of
$|a,b|$
, we mean one of the following interval subsets of
![]() ${\mathbb {R}}$
:
${\mathbb {R}}$
:
![]() $(a,b), (a,b], [a,b),[a,b]$
. For example,
$(a,b), (a,b], [a,b),[a,b]$
. For example,
![]() $M_{|a,b|}$
refers to one of
$M_{|a,b|}$
refers to one of
![]() $M_{(a,b)}$
,
$M_{(a,b)}$
,
![]() $M_{(a,b]}$
,
$M_{(a,b]}$
,
![]() $M_{[a,b)}$
,
$M_{[a,b)}$
,
![]() $M_{[a,b]}$
where intervals cannot be closed at
$M_{[a,b]}$
where intervals cannot be closed at
![]() $+\infty $
and
$+\infty $
and
![]() $-\infty $
.
$-\infty $
.
We need the following results from [Reference Igusa, Rock and Todorov14]. Note the last statement of the theorem recovers a result by Botnan and Crawley-Boevey in [Reference Botnan and Crawley-Boevey2].
Theorem 1.1.5 (Theorems 2.3.2 and 2.4.13 in [Reference Igusa, Rock and Todorov14])
Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A. For any interval
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A. For any interval
![]() $I\subset {\mathbb {R}}$
, the representation
$I\subset {\mathbb {R}}$
, the representation
![]() $M_I$
of
$M_I$
of
![]() $A_{{\mathbb {R}},S}$
is indecomposable. Any indecomposable pointwise finite-dimensional representation of
$A_{{\mathbb {R}},S}$
is indecomposable. Any indecomposable pointwise finite-dimensional representation of
![]() $A_{{\mathbb {R}},S}$
is isomorphic to
$A_{{\mathbb {R}},S}$
is isomorphic to
![]() $M_I$
for some interval I. Furthermore, for any indecomposable representations V and W of
$M_I$
for some interval I. Furthermore, for any indecomposable representations V and W of
![]() $A_{{\mathbb {R}},S}$
,
$A_{{\mathbb {R}},S}$
,
![]() $V\cong W$
if and only if
$V\cong W$
if and only if
![]() $\mathop {\text {supp}} V = \mathop {\text {supp}} W$
. Finally, any pointwise finite-dimensional representation V of
$\mathop {\text {supp}} V = \mathop {\text {supp}} W$
. Finally, any pointwise finite-dimensional representation V of
![]() $A_{{\mathbb {R}},S}$
is the direct sum of interval indecomposables.
$A_{{\mathbb {R}},S}$
is the direct sum of interval indecomposables.
Definition 1.1.6. Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A. By
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A. By
![]() $\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
, we denote the category of pointwise finite-dimensional representations of
$\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
, we denote the category of pointwise finite-dimensional representations of
![]() $A_{{\mathbb {R}},S}$
.
$A_{{\mathbb {R}},S}$
.
A description of projective representations is given in the next theorem and in Figure 2.

Figure 2 Supports for some indecomposable projectives described in Theorem 1.1.7.
Theorem 1.1.7 (Theorem 2.1.6 and Remark 2.4.16 in [Reference Igusa, Rock and Todorov14])
Let P be a projective indecomposable in
![]() $\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
. Then there exists
$\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
. Then there exists
![]() $a\in {\mathbb {R}}\cup \{\pm \infty \}$
such that P is isomorphic to one of the following indecomposables:
$a\in {\mathbb {R}}\cup \{\pm \infty \}$
such that P is isomorphic to one of the following indecomposables:
![]() $P_a$
,
$P_a$
,
![]() $P_{(a}$
, or
$P_{(a}$
, or
![]() $P_{a)}$
(see Figure 2.):
$P_{a)}$
(see Figure 2.):
 $$ \begin{align*} P_a(x) &= \left\{ \begin{array}{ll} k, & x \preceq a, \\ 0, & \text{otherwise,} \end{array}\right. & P_a(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a, \\ 0, & \text{otherwise,} \end{array}\right. \\ P_{(a}(x) &= \left\{\begin{array}{ll} k, & x\preceq a\text{ and } x>a\text{ in }{\mathbb{R}}, \\ 0, & \text{otherwise,} \end{array}\right. & P_{(a}(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a \text{ and } x,y>a, \\ 0, & \text{otherwise,} \end{array}\right. \\ P_{a)}(x) &= \left\{\begin{array}{ll} k, & x\preceq a\text{ and }x<a\text{ in }{\mathbb{R}}, \\ 0, & \text{otherwise,} \end{array}\right. & P_{a)}(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a \text{ and }x,y<a, \\ 0, & \text{otherwise.} \end{array}\right. \end{align*} $$
$$ \begin{align*} P_a(x) &= \left\{ \begin{array}{ll} k, & x \preceq a, \\ 0, & \text{otherwise,} \end{array}\right. & P_a(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a, \\ 0, & \text{otherwise,} \end{array}\right. \\ P_{(a}(x) &= \left\{\begin{array}{ll} k, & x\preceq a\text{ and } x>a\text{ in }{\mathbb{R}}, \\ 0, & \text{otherwise,} \end{array}\right. & P_{(a}(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a \text{ and } x,y>a, \\ 0, & \text{otherwise,} \end{array}\right. \\ P_{a)}(x) &= \left\{\begin{array}{ll} k, & x\preceq a\text{ and }x<a\text{ in }{\mathbb{R}}, \\ 0, & \text{otherwise,} \end{array}\right. & P_{a)}(x,y) &= \left\{\begin{array}{ll} 1_k, & y\preceq x \preceq a \text{ and }x,y<a, \\ 0, & \text{otherwise.} \end{array}\right. \end{align*} $$
Definition 1.1.8. Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A. By
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A. By
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, we denote the full subcategory of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, we denote the full subcategory of
![]() $\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
, whose objects are finitely generated by the indecomposable projectives of Theorem 1.1.7. Note that the indecomposable projectives in
$\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
, whose objects are finitely generated by the indecomposable projectives of Theorem 1.1.7. Note that the indecomposable projectives in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
![]() $\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
are the same.
$\operatorname {\mathrm {Rep}}_k^{\textrm {{pwf}}}(A_{{\mathbb {R}},S})$
are the same.
Theorem 1.1.9 ([Reference Igusa, Rock and Todorov14], Theorem 3.0.1)
Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A.
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A.
-
1. For any pair of indecomposable representations
 $M_I$
and
$M_I$
and
 $M_J$
in
$M_J$
in
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}},S})} (M_I,M_J)\cong k \text{ or }=0 \quad\text{ and }\quad \operatorname{\mathrm{Ext}}^1_{\operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}},S})} (M_I,M_J)\cong k \text{ or }=0. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}},S})} (M_I,M_J)\cong k \text{ or }=0 \quad\text{ and }\quad \operatorname{\mathrm{Ext}}^1_{\operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}},S})} (M_I,M_J)\cong k \text{ or }=0. \end{align*} $$
-
2. The category
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is abelian, Krull–Schmidt but not artinian.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is abelian, Krull–Schmidt but not artinian. -
3. The global dimension of
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is 1.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is 1. -
4. The category
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
has some, but not all, AR sequences (fully classified in [Reference Rock19, Table 3.1.3]).
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
has some, but not all, AR sequences (fully classified in [Reference Rock19, Table 3.1.3]).
1.2 The AR-space of
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
 ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
In this subsection, we recall the necessary definitions and theorems from part (II), that is [Reference Rock19]. The category
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is the category of bounded complexes of objects in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is the category of bounded complexes of objects in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with quasi-isomorphisms inverted; it is the derived category of a skeleton of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with quasi-isomorphisms inverted; it is the derived category of a skeleton of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. In order to define the AR-space of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. In order to define the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
[Reference Rock19, Defs. 4.1.9 and 5.2.5], we define functions
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
[Reference Rock19, Defs. 4.1.9 and 5.2.5], we define functions
![]() $\lambda _\kappa $
which are continuous analogue of certain sectional paths in classical AR-quivers. Using the functions
$\lambda _\kappa $
which are continuous analogue of certain sectional paths in classical AR-quivers. Using the functions
![]() $\lambda _\kappa $
, we define functions
$\lambda _\kappa $
, we define functions
![]() $\mathop {\boldsymbol {\Gamma }}$
and
$\mathop {\boldsymbol {\Gamma }}$
and
![]() $\mathop {\boldsymbol {\Gamma }}^b$
which describe the positions of objects in AR-spaces of
$\mathop {\boldsymbol {\Gamma }}^b$
which describe the positions of objects in AR-spaces of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
Definition 1.2.1. Let
![]() $z\in {\mathbb {R}}$
. Then
$z\in {\mathbb {R}}$
. Then
![]() $z=2n\pi + w$
for
$z=2n\pi + w$
for
![]() $n\in {\mathbb {Z}}$
and
$n\in {\mathbb {Z}}$
and
![]() $0\leq w \leq 2\pi $
. Let the functions
$0\leq w \leq 2\pi $
. Let the functions
![]() $\lambda :{\mathbb {R}}\to {\mathbb {R}}$
and
$\lambda :{\mathbb {R}}\to {\mathbb {R}}$
and
![]() $\lambda _\kappa :{\mathbb {R}}\to [-\frac {\pi }{2},\frac {\pi }{2}]$
,
$\lambda _\kappa :{\mathbb {R}}\to [-\frac {\pi }{2},\frac {\pi }{2}]$
,
![]() $\kappa \in [-\pi ,\pi )$
, be defined by:
$\kappa \in [-\pi ,\pi )$
, be defined by:
 $$ \begin{align*} \lambda(z)=\lambda(2n\pi + w) := \left\{\! \begin{array}{ll} w-\frac{\pi}{2}, & 0\leq w \leq \pi, \\ -w + \frac{3\pi}{2}, & \pi\leq w \leq 2\pi, \end{array} \right. \quad\text{ and }\quad \lambda_\kappa(x):= \lambda(x-\kappa). \end{align*} $$
$$ \begin{align*} \lambda(z)=\lambda(2n\pi + w) := \left\{\! \begin{array}{ll} w-\frac{\pi}{2}, & 0\leq w \leq \pi, \\ -w + \frac{3\pi}{2}, & \pi\leq w \leq 2\pi, \end{array} \right. \quad\text{ and }\quad \lambda_\kappa(x):= \lambda(x-\kappa). \end{align*} $$
Definition 1.2.2. The function
![]() $\mathop {\boldsymbol {\Gamma }}:\text {ind}(\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S}))\to {\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
, illustrated in Figure 3, is defined as follows (see [Reference Rock19, Sec. 2] for the full details).
$\mathop {\boldsymbol {\Gamma }}:\text {ind}(\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S}))\to {\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
, illustrated in Figure 3, is defined as follows (see [Reference Rock19, Sec. 2] for the full details).
-
•
 $\mathop {\boldsymbol {\Gamma }}(P_{s_0}):=(0,\tan ^{-1}(s_0)) $
$\mathop {\boldsymbol {\Gamma }}(P_{s_0}):=(0,\tan ^{-1}(s_0)) $
-
•
 $ \mathop {\boldsymbol {\Gamma }}(P_{s_n}) := \left ( \sum _{i=1}^{|n|} (-1)^{i+1} \left |\tan ^{-1}s_{\varepsilon i} - \tan ^{-1} s_{\varepsilon (i-1)}\right |,\ \tan ^{-1} s_n \right )$
,
$ \mathop {\boldsymbol {\Gamma }}(P_{s_n}) := \left ( \sum _{i=1}^{|n|} (-1)^{i+1} \left |\tan ^{-1}s_{\varepsilon i} - \tan ^{-1} s_{\varepsilon (i-1)}\right |,\ \tan ^{-1} s_n \right )$
,
 $n\neq 0$
,
$n\neq 0$
,
 $\varepsilon =$
sign of n
$\varepsilon =$
sign of n -
•
 $ \mathop {\boldsymbol {\Gamma }}(P_a) := t\cdot \mathop {\boldsymbol {\Gamma }}(P_{s_n}) + (1-t)\cdot \mathop {\boldsymbol {\Gamma }} (P_{s_{n+1}}), \quad s_n\lneq a\lneq s_{n+1}$
where t must satisfy:
$ \mathop {\boldsymbol {\Gamma }}(P_a) := t\cdot \mathop {\boldsymbol {\Gamma }}(P_{s_n}) + (1-t)\cdot \mathop {\boldsymbol {\Gamma }} (P_{s_{n+1}}), \quad s_n\lneq a\lneq s_{n+1}$
where t must satisfy:
 $\tan ^{-1}(a)=t \cdot \tan ^{-1}s_n + (1-t)\cdot \tan ^{-1}(s_{n+1})$
$\tan ^{-1}(a)=t \cdot \tan ^{-1}s_n + (1-t)\cdot \tan ^{-1}(s_{n+1})$
-
•
 $\mathop {\boldsymbol {\Gamma }}(P_{(a}):=\mathop {\boldsymbol {\Gamma }}(P_a)$
and
$\mathop {\boldsymbol {\Gamma }}(P_{(a}):=\mathop {\boldsymbol {\Gamma }}(P_a)$
and
 $\mathop {\boldsymbol {\Gamma }}(P_{a)}):=\mathop {\boldsymbol {\Gamma }}(P_a)$
$\mathop {\boldsymbol {\Gamma }}(P_{a)}):=\mathop {\boldsymbol {\Gamma }}(P_a)$
-
• If
 $\mathop {\boldsymbol {\Gamma }}(P_a)\in \text {graph}(\lambda _{\kappa '})$
,
$\mathop {\boldsymbol {\Gamma }}(P_a)\in \text {graph}(\lambda _{\kappa '})$
,
 $\mathop {\boldsymbol {\Gamma }}(P_b)\in \text {graph}(\lambda _\kappa ) $
and
$\mathop {\boldsymbol {\Gamma }}(P_b)\in \text {graph}(\lambda _\kappa ) $
and
 $a,b\notin S\cup \{\pm \infty \}$
,
$a,b\notin S\cup \{\pm \infty \}$
,
 $\mathop {\boldsymbol {\Gamma }}(M_{|a,b|})$
is the first intersection of the graphs of
$\mathop {\boldsymbol {\Gamma }}(M_{|a,b|})$
is the first intersection of the graphs of
 $\lambda _\kappa $
and
$\lambda _\kappa $
and
 $\lambda _{\kappa '}$
to the right of
$\lambda _{\kappa '}$
to the right of
 $\mathop {\boldsymbol {\Gamma }}(P_a)$
and
$\mathop {\boldsymbol {\Gamma }}(P_a)$
and
 $\mathop {\boldsymbol {\Gamma }}(P_b)$
. When a or b is in
$\mathop {\boldsymbol {\Gamma }}(P_b)$
. When a or b is in
 $S\cup \{\pm \infty \}$
there are additional details explained in part (II) [Reference Rock19].
$S\cup \{\pm \infty \}$
there are additional details explained in part (II) [Reference Rock19].

Figure 3 An example of a continuous quiver of type A and the image of
![]() $\mathop {\boldsymbol {\Gamma }}$
.
$\mathop {\boldsymbol {\Gamma }}$
.
The function
![]() $\mathop {\boldsymbol {\Gamma }}^b:\text {ind}({\mathcal {D}^b(A_{{\mathbb {R}},S})})\to {\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
is the natural extension of
$\mathop {\boldsymbol {\Gamma }}^b:\text {ind}({\mathcal {D}^b(A_{{\mathbb {R}},S})})\to {\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
is the natural extension of
![]() $\mathop {\boldsymbol {\Gamma }}$
to all the indecomposables of
$\mathop {\boldsymbol {\Gamma }}$
to all the indecomposables of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where
![]() $\mathop {\boldsymbol {\Gamma }}^b V[1] = (x+\pi ,-y)$
for each V with
$\mathop {\boldsymbol {\Gamma }}^b V[1] = (x+\pi ,-y)$
for each V with
![]() $\mathop {\boldsymbol {\Gamma }}^bV =(x,y)$
.
$\mathop {\boldsymbol {\Gamma }}^bV =(x,y)$
.
Remark 1.2.3. Each indecomposable object in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
have a (micro) position [Reference Rock19, Def. 4.1.2] 1, 2, 3, or 4 in the AR-space of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
have a (micro) position [Reference Rock19, Def. 4.1.2] 1, 2, 3, or 4 in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. (Micro) positions are to be thought of as occupying the four corners of a diamond; the diamonds correspond to AR triangles:
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. (Micro) positions are to be thought of as occupying the four corners of a diamond; the diamonds correspond to AR triangles:

In particular, two indecomposables V and W in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are isomorphic if and only if their (micro) position and image under
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are isomorphic if and only if their (micro) position and image under
![]() $\mathop {\boldsymbol {\Gamma }}$
or
$\mathop {\boldsymbol {\Gamma }}$
or
![]() $\mathop {\boldsymbol {\Gamma }}^b$
are the same. Thus, we sometimes identify indecomposables in
$\mathop {\boldsymbol {\Gamma }}^b$
are the same. Thus, we sometimes identify indecomposables in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with their corresponding points in the AR-spaces under
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with their corresponding points in the AR-spaces under
![]() $\mathop {\boldsymbol {\Gamma }}$
or
$\mathop {\boldsymbol {\Gamma }}$
or
![]() $\mathop {\boldsymbol {\Gamma }}^b$
.
$\mathop {\boldsymbol {\Gamma }}^b$
.
Example 1.2.4. The AR-space for
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}={\mathcal {D}^b(A_{{\mathbb {R}}})}$
is shown in Figure 4.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}={\mathcal {D}^b(A_{{\mathbb {R}}})}$
is shown in Figure 4.

Figure 4 Part of the AR-space of the bounded derived category
![]() ${\mathcal {D}^b(A_{{\mathbb {R}}})}$
.
${\mathcal {D}^b(A_{{\mathbb {R}}})}$
.
The AR-spaces of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are subsets of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are subsets of
![]() ${\mathbb {R}}^2$
. We consider rectangles and almost complete rectangles whose slopes are
${\mathbb {R}}^2$
. We consider rectangles and almost complete rectangles whose slopes are
![]() $\pm 1$
. These describe homomorphisms and extensions and play an important role in the proofs of the main results of this paper.
$\pm 1$
. These describe homomorphisms and extensions and play an important role in the proofs of the main results of this paper.
Theorem 1.2.5 ([Reference Rock19], Theorem 4.3.11)
Let
![]() $V\not \cong W$
be indecomposables in
$V\not \cong W$
be indecomposables in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then there is a nontrivial extension
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then there is a nontrivial extension
![]() $V\hookrightarrow E\twoheadrightarrow W$
if and only if there exists a rectangle or almost complete rectangle in the AR-space of
$V\hookrightarrow E\twoheadrightarrow W$
if and only if there exists a rectangle or almost complete rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with left-most corner V and right-most corner W. The other corners are the components of E.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with left-most corner V and right-most corner W. The other corners are the components of E.
-
• If the rectangle is complete, then E is a direct sum of two indecomposables.
-
• If the rectangle is almost complete, then E is indecomposable.
Furthermore, there is a bijection:

In the following theorem, we say “nontrivial triangle” to mean a distinguished triangle
![]() $A\to B\to C\to A[1]$
where
$A\to B\to C\to A[1]$
where
![]() $A,B,C\neq 0$
.
$A,B,C\neq 0$
.
Theorem 1.2.6 ([Reference Rock19], Theorem 5.2.10)
Let
![]() $V\not \cong W$
be indecomposables in
$V\not \cong W$
be indecomposables in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then there is a nontrivial distinguished triangle
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then there is a nontrivial distinguished triangle
![]() $V\to E\to W\to V[1]$
if and only if there exists a rectangle or almost complete rectangle in the AR-space of
$V\to E\to W\to V[1]$
if and only if there exists a rectangle or almost complete rectangle in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with left-most corner V and right-most corner W. The other corners are the components of E.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with left-most corner V and right-most corner W. The other corners are the components of E.
-
• If the rectangle is complete, then E is a direct sum of two indecomposables.
-
• If the rectangle is almost complete, then E is indecomposable.
Furthermore, there is a bijection:

Remark 1.2.7. It follows from Theorem 1.2.6 that the only AR triangles in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, for any continuous quiver of type A, are those of the following form, shown on the right, where each
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, for any continuous quiver of type A, are those of the following form, shown on the right, where each
![]() $V_i$
has (micro) position i and
$V_i$
has (micro) position i and
![]() $\mathop {\boldsymbol {\Gamma }}^b V_i=\mathop {\boldsymbol {\Gamma }}^b V_j \in {\mathbb {R}}\times (-\frac {\pi }{2},\frac {\pi }{2})$
for all
$\mathop {\boldsymbol {\Gamma }}^b V_i=\mathop {\boldsymbol {\Gamma }}^b V_j \in {\mathbb {R}}\times (-\frac {\pi }{2},\frac {\pi }{2})$
for all
![]() $i,j$
.
$i,j$
.
 $$ \begin{align*} V_1 \longrightarrow \begin{array}{c} V_2 \\ \oplus \\ V_3 \end{array} \longrightarrow V_4 \end{align*} $$
$$ \begin{align*} V_1 \longrightarrow \begin{array}{c} V_2 \\ \oplus \\ V_3 \end{array} \longrightarrow V_4 \end{align*} $$
2 Derived equivalence
In this section, we prove Theorem A classifying the derived categories of finitely generated representations of continuous quivers of type A, that is,
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
2.1 Some consequences of the octahedral axiom
We recall the octahedral axiom of a triangulated category, which we use in Lemma 2.2.7. Suppose the following are distinguished triangles:
Then the following distinguished triangles also exist:
where
![]() $h=j'\circ i$
,
$h=j'\circ i$
,
![]() $h'=j\circ i'$
,
$h'=j\circ i'$
,
![]() $i\circ g=i'\circ g'$
and
$i\circ g=i'\circ g'$
and
![]() $f[1]\circ j=f'\circ j'$
. This is often drawn as the lower and upper part of an octahedron. We use the following well-known results from [Reference Neeman18].
$f[1]\circ j=f'\circ j'$
. This is often drawn as the lower and upper part of an octahedron. We use the following well-known results from [Reference Neeman18].
Proposition 2.1.1. With the above notation, we have two distinguished triangles:

Lemma 2.1.2. Let
![]() $V\xrightarrow fW_1\xrightarrow g U_1\to V[1]$
and
$V\xrightarrow fW_1\xrightarrow g U_1\to V[1]$
and
![]() $V\xrightarrow {h\circ f}W_2\to U_2\to V[1]$
be distinguished triangles in a Krull–Schmidt triangulated category
$V\xrightarrow {h\circ f}W_2\to U_2\to V[1]$
be distinguished triangles in a Krull–Schmidt triangulated category
![]() $\mathcal D$
where
$\mathcal D$
where
![]() $h:W_1\to W_2$
, f and
$h:W_1\to W_2$
, f and
![]() $h\circ f$
are nonzero. Then the following is a distinguished triangle:
$h\circ f$
are nonzero. Then the following is a distinguished triangle:
2.2 Triangles and the geometry of the AR-space of
 ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
In this subsection, we show how the geometry of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is closely tied to the distinguished triangles in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is closely tied to the distinguished triangles in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. We use these connections in Section 2.3.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. We use these connections in Section 2.3.
We now define
![]() $\iota :{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
which is a triangulated equivalence of categories since the image of
$\iota :{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
which is a triangulated equivalence of categories since the image of
![]() $\iota $
is a skeleton of
$\iota $
is a skeleton of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Defining
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Defining
![]() $\iota $
is a process of choosing particularly nice representatives from each isomorphism class of objects.
$\iota $
is a process of choosing particularly nice representatives from each isomorphism class of objects.
Definition 2.2.1. Choose a total ordering on the isomorphism classes of indecomposables
![]() $M_I[n]$
in
$M_I[n]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
which is lexicographic in the pair
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
which is lexicographic in the pair
![]() $(I,n)$
. Then, shift
$(I,n)$
. Then, shift
![]() $[1]$
is order preserving. Let V be an object in
$[1]$
is order preserving. Let V be an object in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and let
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and let
![]() $V\cong \bigoplus _{i=1}^\ell M_{I_i}[n_i]$
for intervals
$V\cong \bigoplus _{i=1}^\ell M_{I_i}[n_i]$
for intervals
![]() $I_i$
and
$I_i$
and
![]() $n_i\in {\mathbb {Z}}$
. Let
$n_i\in {\mathbb {Z}}$
. Let
![]() $\iota V$
be defined by:
$\iota V$
be defined by:
-
1. left to right ordering of the summands of V according to the above chosen total order
-
2. associate them also in the same left to right order as, for example:
 $$ \begin{align*} \iota V=(((M_{I_1}[n_1] \oplus M_{I_2}[n_2])\oplus M_{I_3}[n_3])\oplus M_{I_4}[n_4] ) \oplus M_{I_5}[n_5]. \end{align*} $$
$$ \begin{align*} \iota V=(((M_{I_1}[n_1] \oplus M_{I_2}[n_2])\oplus M_{I_3}[n_3])\oplus M_{I_4}[n_4] ) \oplus M_{I_5}[n_5]. \end{align*} $$
Since every isomorphism class in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is a set, fix an isomorphim
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is a set, fix an isomorphim
![]() $\iota _V:V\to \iota V$
for each object V in
$\iota _V:V\to \iota V$
for each object V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Note that in some cases,
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Note that in some cases,
![]() $\iota _V$
be the identity. Since summands are ordered lexicographically, they keep the same order when shifted. So,
$\iota _V$
be the identity. Since summands are ordered lexicographically, they keep the same order when shifted. So,
![]() $\iota (V[1])=(\iota V)[1]$
.
$\iota (V[1])=(\iota V)[1]$
.
Let
![]() $f:V\to W$
be a morphism in
$f:V\to W$
be a morphism in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
![]() $\iota (f):=\iota _W\circ f\circ (\iota _V)^{-1}$
is the unique morphism
$\iota (f):=\iota _W\circ f\circ (\iota _V)^{-1}$
is the unique morphism
![]() $\iota (f):\iota (V)\to \iota (W)$
that makes the diagram on the right commute.
$\iota (f):\iota (V)\to \iota (W)$
that makes the diagram on the right commute.

In the next definition, the image of
![]() $\mathop {\boldsymbol {\Gamma }}^b$
(which is most or all of
$\mathop {\boldsymbol {\Gamma }}^b$
(which is most or all of
![]() ${\mathbb {R}}\times [-\frac \pi 2,\frac \pi 2]$
) plays a crucial role. For each
${\mathbb {R}}\times [-\frac \pi 2,\frac \pi 2]$
) plays a crucial role. For each
![]() $r\in {\mathbb {R}}$
, the map
$r\in {\mathbb {R}}$
, the map
![]() $T_r$
be defined for most objects in
$T_r$
be defined for most objects in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Suppose
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Suppose
![]() $(x,y)\in \mathop {\text {im}} \mathop {\boldsymbol {\Gamma }}^b$
. Then there is an object
$(x,y)\in \mathop {\text {im}} \mathop {\boldsymbol {\Gamma }}^b$
. Then there is an object
![]() $M_I[n]$
such that
$M_I[n]$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b(M_I[n])=(x,y)$
in each (micro) position
$\mathop {\boldsymbol {\Gamma }}^b(M_I[n])=(x,y)$
in each (micro) position
![]() $1,2,3,4$
if
$1,2,3,4$
if
![]() $y\neq -\frac \pi 2,\frac \pi 2$
, in position 3 if
$y\neq -\frac \pi 2,\frac \pi 2$
, in position 3 if
![]() $y=\frac \pi 2$
and in position 2 if
$y=\frac \pi 2$
and in position 2 if
![]() $y=-\frac \pi 2$
.
$y=-\frac \pi 2$
.
Definition 2.2.2. Let
![]() $V\cong \bigoplus V_i$
be an object in
$V\cong \bigoplus V_i$
be an object in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, where each
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, where each
![]() $V_i$
is indecomposable with
$V_i$
is indecomposable with
![]() $\mathop {\boldsymbol {\Gamma }}^b V_i=(x_i,y_i)$
. Let
$\mathop {\boldsymbol {\Gamma }}^b V_i=(x_i,y_i)$
. Let
![]() $r\in {\mathbb {R}}$
. If
$r\in {\mathbb {R}}$
. If
![]() $(x_i-r,y_i)\in \mathop {\text {im}} \mathop {\boldsymbol {\Gamma }}^b$
then there exists
$(x_i-r,y_i)\in \mathop {\text {im}} \mathop {\boldsymbol {\Gamma }}^b$
then there exists
![]() $M_{I_i}[n_i]$
such that
$M_{I_i}[n_i]$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b(M_{I_i}[n_i])=(x_i-r,y_i)$
and such that
$\mathop {\boldsymbol {\Gamma }}^b(M_{I_i}[n_i])=(x_i-r,y_i)$
and such that
![]() $V_i$
and
$V_i$
and
![]() $M_{I_i}[n_i]$
have the same (micro) position. Define
$M_{I_i}[n_i]$
have the same (micro) position. Define
![]() $T_rV_i:=M_{I_i}[n_i]$
and
$T_rV_i:=M_{I_i}[n_i]$
and
![]() $T_r(V) := \iota (\bigoplus M_{I_i}[n_i])$
. Since
$T_r(V) := \iota (\bigoplus M_{I_i}[n_i])$
. Since
![]() $\iota $
commutes with shift, so does
$\iota $
commutes with shift, so does
![]() $T_r$
, at least on objects:
$T_r$
, at least on objects:
![]() $T_rV[1]=(T_rV)[1]$
.
$T_rV[1]=(T_rV)[1]$
.
Let
![]() $f:V\to W$
where
$f:V\to W$
where
![]() $V=\bigoplus _{i\in I}V_i$
,
$V=\bigoplus _{i\in I}V_i$
,
![]() $W=\bigoplus _{j\in J}W_j$
and assume
$W=\bigoplus _{j\in J}W_j$
and assume
![]() $T_r(V),T_r(W)$
are defined. Let
$T_r(V),T_r(W)$
are defined. Let
![]() $f_{ij}:V_i\to W_j$
and
$f_{ij}:V_i\to W_j$
and
![]() $\iota (f_{ij}):\iota (V_i)=M_{I_i}[n_i]\to \iota (W_j)=M_{I_j}[m_j]$
. Then
$\iota (f_{ij}):\iota (V_i)=M_{I_i}[n_i]\to \iota (W_j)=M_{I_j}[m_j]$
. Then
![]() $T_r(\iota (f_{ij}):T_r(\iota (V_i)\to T_r(\iota (W_j)$
is given by multiplication by the same element of k as
$T_r(\iota (f_{ij}):T_r(\iota (V_i)\to T_r(\iota (W_j)$
is given by multiplication by the same element of k as
![]() $\iota (f_{ij})$
[Reference Rock19, Prop. 5.2.8 and Lem. 5.2.9]. Define
$\iota (f_{ij})$
[Reference Rock19, Prop. 5.2.8 and Lem. 5.2.9]. Define
![]() $T_rf=\iota \left (T_r(\iota (f_{ij})) \right )$
.
$T_rf=\iota \left (T_r(\iota (f_{ij})) \right )$
.
Remark 2.2.3. Note that
![]() $T_r$
depends only on r and
$T_r$
depends only on r and
![]() $\iota $
in Definition 2.2.1.
$\iota $
in Definition 2.2.1.
Definition 2.2.4. Let
![]() $V\cong \bigoplus V_i$
and
$V\cong \bigoplus V_i$
and
![]() $W\cong \bigoplus W_j$
be objects in
$W\cong \bigoplus W_j$
be objects in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where each
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where each
![]() $V_i$
and
$V_i$
and
![]() $W_j$
are indecomposable. Let
$W_j$
are indecomposable. Let
![]() $f:V\to W$
be a morphism. Consider the distinguished triangle
$f:V\to W$
be a morphism. Consider the distinguished triangle
![]() $V\stackrel {f}{\to } W\stackrel {g}{\to } U\stackrel {h}{\to }V[1]$
. We say U is determined by geometry and f if for any
$V\stackrel {f}{\to } W\stackrel {g}{\to } U\stackrel {h}{\to }V[1]$
. We say U is determined by geometry and f if for any
![]() $r\in {\mathbb {R}}$
such that
$r\in {\mathbb {R}}$
such that
![]() $T_r V$
and
$T_r V$
and
![]() $T_r W$
are defined, there exists a distinguished triangle
$T_r W$
are defined, there exists a distinguished triangle
![]() $T_r V\stackrel {T_r f}{\to } T_r W\to T_r U\to (T_rV)[1]$
in
$T_r V\stackrel {T_r f}{\to } T_r W\to T_r U\to (T_rV)[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
The following fact and notation are used in the proof of Lemma 2.2.7.
Proposition 2.2.5 ([Reference Rock19], Prop 4.4.2, Lemma 5.2.9)
Let
![]() $V\not \cong W$
be indecomposables in
$V\not \cong W$
be indecomposables in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S})}(V,W)\neq 0$
implies
$\operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S})}(V,W)\neq 0$
implies
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S})}(W,V)=0$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S})}(W,V)=0$
.
Notation 2.2.6. Let V and
![]() $W=\bigoplus W_j$
be objects in
$W=\bigoplus W_j$
be objects in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Let
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Let
![]() $X_{V,W}=\bigoplus W_{j_k}$
be a choice of summands of W giving the left minimal
$X_{V,W}=\bigoplus W_{j_k}$
be a choice of summands of W giving the left minimal
![]() $\mathop {\text {add}}(W)$
-approximation of V and let
$\mathop {\text {add}}(W)$
-approximation of V and let
![]() $Y_{V,W}$
be the other summands of W. Dually, let
$Y_{V,W}$
be the other summands of W. Dually, let
![]() ${_{V,W}}X$
denote summands of V giving the right minimal
${_{V,W}}X$
denote summands of V giving the right minimal
![]() $\mathop {\text {add}}(V)$
-approximation of W and let
$\mathop {\text {add}}(V)$
-approximation of W and let
![]() ${_{V,W}}Y$
denote the other summands of V.
${_{V,W}}Y$
denote the other summands of V.
A visual example of the proof technique to the following lemma is in Example 2.2.8.
Lemma 2.2.7. Let
![]() $V\stackrel {f}{\to } W\to U\to V[1]$
be a distinguished triangle in
$V\stackrel {f}{\to } W\to U\to V[1]$
be a distinguished triangle in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where either V or W is indecomposable. Then U is determined by geometry and f. Furthermore:
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
where either V or W is indecomposable. Then U is determined by geometry and f. Furthermore:
-
1. U has at most as many indecomposable summands as
 $V\oplus W$
.
$V\oplus W$
. -
2. If V is indecomposable, for each indecomposable summand
 $U_j$
of U, there is an indecomposable summand
$U_j$
of U, there is an indecomposable summand
 $W_i$
of W such that the line segment with endpoints
$W_i$
of W such that the line segment with endpoints
 $W_i$
and
$W_i$
and
 $U_j$
has slope
$U_j$
has slope
 $\pm (1,1)$
or
$\pm (1,1)$
or
 $W_i=U_j$
.
$W_i=U_j$
. -
3. If W is indecomposable, for each indecomposable summand
 $U_i$
of U, there is an indecomposable summand
$U_i$
of U, there is an indecomposable summand
 $V_j$
of V such that the line segment with endpoints
$V_j$
of V such that the line segment with endpoints
 $U_i[-1]$
and
$U_i[-1]$
and
 $V_j$
has slope
$V_j$
has slope
 $\pm (1,1)$
or
$\pm (1,1)$
or
 $W_i=U_j$
.
$W_i=U_j$
.
Proof.
Setup and Base Case. We assume V is indecomposable and prove the lemma by induction on the number of summands of W. Our base case is 1; that is W is also indecomposable. Note that, for any object, X in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, we have
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, we have
![]() $T_r(X[1])=(T_r(X))[1]$
. The base case then follows from Theorem 1.2.6 by rotating distinguished triangles.
$T_r(X[1])=(T_r(X))[1]$
. The base case then follows from Theorem 1.2.6 by rotating distinguished triangles.
Induction Setup and Trivial Case. For induction assume statements (1) and (2) hold when V is indecomposable and W has n or fewer indecomposable summands. Suppose
![]() $W\cong \bigoplus _{i=1}^n W_i$
where each
$W\cong \bigoplus _{i=1}^n W_i$
where each
![]() $W_i$
is indecomposable. For each summand
$W_i$
is indecomposable. For each summand
![]() $W_i$
, let
$W_i$
, let
![]() $f_i:V\to W_i$
be such that
$f_i:V\to W_i$
be such that
![]() $f=[f_1\, \cdots \, f_n]^t$
. Let
$f=[f_1\, \cdots \, f_n]^t$
. Let
![]() $W_{n+1}$
be an indecomposable and
$W_{n+1}$
be an indecomposable and
![]() $f_{n+1}:V\to W_{n+1}$
a morphism. If
$f_{n+1}:V\to W_{n+1}$
a morphism. If
![]() $f_{n+1}=0$
, the result follows using the induction hypothesis.
$f_{n+1}=0$
, the result follows using the induction hypothesis.
![]() $\textbf {Hom}{\boldsymbol {(}\mathbf{W}\boldsymbol {,}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {)}\boldsymbol {\neq } \mathbf{0}} \textbf { or } \textbf {Hom}{\boldsymbol {(}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {,}\mathbf{W}\boldsymbol {)}\boldsymbol {\neq } \mathbf{0}}$
. Assume
$\textbf {Hom}{\boldsymbol {(}\mathbf{W}\boldsymbol {,}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {)}\boldsymbol {\neq } \mathbf{0}} \textbf { or } \textbf {Hom}{\boldsymbol {(}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {,}\mathbf{W}\boldsymbol {)}\boldsymbol {\neq } \mathbf{0}}$
. Assume
![]() $f_{n+1}\neq 0$
. By exchanging the roles of a summand
$f_{n+1}\neq 0$
. By exchanging the roles of a summand
![]() $W_i$
of W and
$W_i$
of W and
![]() $W_{n+1}$
, we may assume, without loss of generality, that
$W_{n+1}$
, we may assume, without loss of generality, that
![]() $\operatorname {\mathrm {Hom}}(W_{n+1},W)\neq 0$
. Then there is at least one summand
$\operatorname {\mathrm {Hom}}(W_{n+1},W)\neq 0$
. Then there is at least one summand
![]() $W_j$
of W such that
$W_j$
of W such that
![]() $\operatorname {\mathrm {Hom}}(W_{n+1},W_j) \neq 0$
. Then
$\operatorname {\mathrm {Hom}}(W_{n+1},W_j) \neq 0$
. Then
![]() $f_j$
factor through
$f_j$
factor through
![]() $f_{n+1}$
and we may apply Lemma 2.1.2 to
$f_{n+1}$
and we may apply Lemma 2.1.2 to
![]() $f\oplus f_{n+1}$
and
$f\oplus f_{n+1}$
and
![]() $T_r(f\oplus f_{n+1})$
with
$T_r(f\oplus f_{n+1})$
with
![]() $W_j$
playing the role of
$W_j$
playing the role of
![]() $W_2$
in Lemma 2.1.2 and the statement follows by induction on n.
$W_2$
in Lemma 2.1.2 and the statement follows by induction on n.
![]() $\textbf {Hom}{\boldsymbol {(}\mathbf{W}\boldsymbol {,}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {)}\boldsymbol {=}\mathbf{0}\boldsymbol {=} \textbf {Hom}\boldsymbol {(}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {,}\mathbf{W}\boldsymbol {)}}$
. Suppose
$\textbf {Hom}{\boldsymbol {(}\mathbf{W}\boldsymbol {,}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {)}\boldsymbol {=}\mathbf{0}\boldsymbol {=} \textbf {Hom}\boldsymbol {(}\mathbf{W}_{\mathbf{n}\boldsymbol {+}\mathbf{1}}\boldsymbol {,}\mathbf{W}\boldsymbol {)}}$
. Suppose
![]() $f_{n+1}\neq 0$
,
$f_{n+1}\neq 0$
,
![]() $\operatorname {\mathrm {Hom}}(W,W_{n+1})=0$
, and
$\operatorname {\mathrm {Hom}}(W,W_{n+1})=0$
, and
![]() $\operatorname {\mathrm {Hom}}(W_{n+1},W)=0$
. Let
$\operatorname {\mathrm {Hom}}(W_{n+1},W)=0$
. Let
![]() $X_{V,W}$
be as in Notation 2.2.6. If
$X_{V,W}$
be as in Notation 2.2.6. If
![]() $X_{V,W}$
has fewer than n indecomposable summands then we are done since
$X_{V,W}$
has fewer than n indecomposable summands then we are done since
![]() $X_{V,W}\oplus W_{n+1}$
has n or fewer indecomposable summands and we may then apply the induction hypothesis.
$X_{V,W}\oplus W_{n+1}$
has n or fewer indecomposable summands and we may then apply the induction hypothesis.
Now suppose
![]() $X_{V,W}=W$
. Note
$X_{V,W}=W$
. Note
![]() $\operatorname {\mathrm {Hom}}(W,W_{n+1})=0$
but
$\operatorname {\mathrm {Hom}}(W,W_{n+1})=0$
but
![]() $f_i\neq 0$
for all
$f_i\neq 0$
for all
![]() $1\leq i\leq n+1$
. Thus the
$1\leq i\leq n+1$
. Thus the
![]() $W_i$
, for all
$W_i$
, for all
![]() $1\leq i \leq n+1$
, are totally ordered by y-coordinate and position (2 is greater than 1 and 4 which are greater than 3). Reindex the
$1\leq i \leq n+1$
, are totally ordered by y-coordinate and position (2 is greater than 1 and 4 which are greater than 3). Reindex the
![]() $W_i$
’s such that
$W_i$
’s such that
![]() $W_i < W_{i+1}$
in the total order and replace W with
$W_i < W_{i+1}$
in the total order and replace W with
![]() $\bigoplus _{i=1}^n W_i$
in the new index. We have the following distinguished triangles:
$\bigoplus _{i=1}^n W_i$
in the new index. We have the following distinguished triangles:

By our base case
![]() $U'$
has at most two indecomposable summands and by the rest of Theorem 1.2.6, the slopes of the line segments from
$U'$
has at most two indecomposable summands and by the rest of Theorem 1.2.6, the slopes of the line segments from
![]() $W_{n+1}$
to each summand of
$W_{n+1}$
to each summand of
![]() $U'$
is
$U'$
is
![]() $\pm (1,1)$
. By [Reference Rock19, Lem. 5.2.9],
$\pm (1,1)$
. By [Reference Rock19, Lem. 5.2.9],
![]() $W_n$
can map to at most one of the indecomposable summands of
$W_n$
can map to at most one of the indecomposable summands of
![]() $U'$
and that is the only possible summand that can map to
$U'$
and that is the only possible summand that can map to
![]() $W_n[1]$
.
$W_n[1]$
.
Thus W can map to at most one indecomposable summand of
![]() $U'$
. Then by induction E is determined by geometry and
$U'$
. Then by induction E is determined by geometry and
![]() $f\circ h'[-1]$
. By the octahedral axiom, we obtain the distinguished triangles:
$f\circ h'[-1]$
. By the octahedral axiom, we obtain the distinguished triangles:

Note that if we apply the base case to the first distinguished triangle, this proves statement 2. We repeat the same argument for
![]() $T_r$
applied to each morphism and indecomposable. Thus, E is determined by geometry and
$T_r$
applied to each morphism and indecomposable. Thus, E is determined by geometry and
![]() $[ f\, f_{n+1}]^t$
. Furthermore, the cone has the desired number of indecomposable summands. The case where W is indecomposable is similar.
$[ f\, f_{n+1}]^t$
. Furthermore, the cone has the desired number of indecomposable summands. The case where W is indecomposable is similar.
Example 2.2.8. As an example of Lemma 2.2.7, take
![]() $f:V\to \bigoplus _{i=1}^4 W_i$
as depicted in Figures 5 and 6. According to Lemma 2.2.7, the cone E should be the direct sum of no more than five indecomposables, the slopes between these indecomposables should be as described, and E should be determined by geometry and f.
$f:V\to \bigoplus _{i=1}^4 W_i$
as depicted in Figures 5 and 6. According to Lemma 2.2.7, the cone E should be the direct sum of no more than five indecomposables, the slopes between these indecomposables should be as described, and E should be determined by geometry and f.

Figure 5 Depiction of Example 2.2.8, where V is indecomposable and W has four indecomposable summands.
(Example 2.2.8 continued) We start with
![]() $V\to W_i$
for each i, then using the technique in the proof, splice together the triangles one by one. At each step
$V\to W_i$
for each i, then using the technique in the proof, splice together the triangles one by one. At each step
![]() $i>1$
, the new cone
$i>1$
, the new cone
![]() $E^i$
is given by using most of the old cone
$E^i$
is given by using most of the old cone
![]() $E^{i-1}$
with a slight change to account for the new indecomposable. For example, in Step 3 where
$E^{i-1}$
with a slight change to account for the new indecomposable. For example, in Step 3 where
![]() $n=2$
,
$n=2$
,
![]() $U,E,U'$
in the proof of Lemma 2.2.7 are given by
$U,E,U'$
in the proof of Lemma 2.2.7 are given by
![]() $U=E^2=E^2_1\oplus E^2_2\oplus E^2_3$
,
$U=E^2=E^2_1\oplus E^2_2\oplus E^2_3$
,
![]() $E=E^3=E^3_1\oplus E^3_2\oplus E^3_3\oplus E^3_4$
and
$E=E^3=E^3_1\oplus E^3_2\oplus E^3_3\oplus E^3_4$
and
![]() $U'=E^3_4\oplus Z$
.
$U'=E^3_4\oplus Z$
.
Theorem 2.2.9. Let
![]() $f:V\to W$
be a morphism in
$f:V\to W$
be a morphism in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and consider the distinguished triangle
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and consider the distinguished triangle
![]() Then U is determined by geometry and f.
Then U is determined by geometry and f.
Proof. The proof is by induction on the number of indecomposable summands of V, using Lemma 2.2.7 as the base case. Assume the lemma holds for all positive integers
![]() $\leq n$
and let
$\leq n$
and let
![]() $V_i$
for
$V_i$
for
![]() $1\leq i\leq n+1$
be indecomposables and let
$1\leq i\leq n+1$
be indecomposables and let
![]() $V=\bigoplus _{i=1}^n V_i$
. Let
$V=\bigoplus _{i=1}^n V_i$
. Let
![]() $f:V\to W$
and
$f:V\to W$
and
![]() $f_{n+1}:V_{n+1}\to W$
be nontrivial morphisms. Consider the following distinguished triangles:
$f_{n+1}:V_{n+1}\to W$
be nontrivial morphisms. Consider the following distinguished triangles:

Applying the octahedral axiom, we obtain the following distinguished triangles:

By the induction hypothesis, E is determined by geometry and
![]() $g_{n+1}\circ f$
.
$g_{n+1}\circ f$
.
2.3 Derived equivalence
In this subsection, we prove Theorem A (Theorem 2.3.5), the first main result of this paper: the bounded derived categories of two continuous quivers of type A are triangulated-equivalent if and only if they belong to the same of the following three disjoint classes: (a) finitely many sinks and sources, (b) the existence of a minimal sink/source or maximal sink/source, or (c) no minimal or maximal sink/source.
Lemma 2.3.1. Let
![]() $\mathcal G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to \mathcal D^b(A_{{\mathbb {R}},S'})$
be an equivalence of categories where
$\mathcal G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to \mathcal D^b(A_{{\mathbb {R}},S'})$
be an equivalence of categories where
![]() $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
![]() $A_{{\mathbb {R}},S'}$
are continuous quivers of type A. Let V and W be indecomposables in
$A_{{\mathbb {R}},S'}$
are continuous quivers of type A. Let V and W be indecomposables in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Suppose the line from V to W in the AR-space of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Suppose the line from V to W in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
has slope
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
has slope
![]() $\pm (1,1)$
. Then the line from
$\pm (1,1)$
. Then the line from
![]() $\mathcal G V$
to
$\mathcal G V$
to
![]() $\mathcal G W$
in the AR-space of
$\mathcal G W$
in the AR-space of
![]() $\mathcal D^b (A_{{\mathbb {R}},S'})$
has slope
$\mathcal D^b (A_{{\mathbb {R}},S'})$
has slope
![]() $\pm (1,1)$
.
$\pm (1,1)$
.
Proof. Suppose that the slope of the line segment from
![]() $\mathcal G V$
to
$\mathcal G V$
to
![]() $\mathcal G W$
in the AR-space of
$\mathcal G W$
in the AR-space of
![]() $\mathcal D^b (A_{{\mathbb {R}},S'})$
is greater than
$\mathcal D^b (A_{{\mathbb {R}},S'})$
is greater than
![]() $(1,1)$
or less than
$(1,1)$
or less than
![]() $-(1,1)$
. Then
$-(1,1)$
. Then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal G V,\mathcal G W)=0$
by [Reference Rock19, Lem. 5.2.9]. This contradicts that
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal G V,\mathcal G W)=0$
by [Reference Rock19, Lem. 5.2.9]. This contradicts that
![]() $\mathcal G$
is an equivalence of categories.
$\mathcal G$
is an equivalence of categories.
Now suppose the slope is less than
![]() $(1,1)$
and greater than
$(1,1)$
and greater than
![]() $-(1,1)$
. Then, by [Reference Rock19, Lem. 5.2.9],
$-(1,1)$
. Then, by [Reference Rock19, Lem. 5.2.9],
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal G W,\mathcal G V[1])\neq 0$
. By Theorem 1.2.6, we have a distinguished triangle
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal G W,\mathcal G V[1])\neq 0$
. By Theorem 1.2.6, we have a distinguished triangle
![]() $\mathcal G V \to U\oplus U' \to \mathcal G W\to \mathcal G V [1]$
and any morphism
$\mathcal G V \to U\oplus U' \to \mathcal G W\to \mathcal G V [1]$
and any morphism
![]() $f:\mathcal G V\to \mathcal G W$
factors through either U or
$f:\mathcal G V\to \mathcal G W$
factors through either U or
![]() $U'$
but not both. This contradicts the fact that any morphism from V to W in
$U'$
but not both. This contradicts the fact that any morphism from V to W in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that factors through some X and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that factors through some X and
![]() $X'$
factors through both either as
$X'$
factors through both either as
![]() $V\to X\to X'\to W$
or
$V\to X\to X'\to W$
or
![]() $V\to X'\to X\to W$
.
$V\to X'\to X\to W$
.
Definition 2.3.2. Let
![]() $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
![]() $A_{{\mathbb {R}},S'}$
be continuous quivers of type A. Suppose also that either (a) S,
$A_{{\mathbb {R}},S'}$
be continuous quivers of type A. Suppose also that either (a) S,
![]() $S'$
are both finite or (b)
$S'$
are both finite or (b)
![]() $S,S'$
are infinite but bounded on one side. We construct below a functor
$S,S'$
are infinite but bounded on one side. We construct below a functor
![]() $\mathcal {F}$
from
$\mathcal {F}$
from
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
to
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
to
![]() $\mathcal {D}^b(A_{{\mathbb {R}},S'})$
.
$\mathcal {D}^b(A_{{\mathbb {R}},S'})$
.
Define the translation
![]() $T={\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]\to {\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]$
as in Definition 2.2.2. In case (a), let
$T={\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]\to {\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]$
as in Definition 2.2.2. In case (a), let
![]() $T:=id$
. In case (b), by the proof of [Reference Rock19, Prop. 2.4.4], there is a function
$T:=id$
. In case (b), by the proof of [Reference Rock19, Prop. 2.4.4], there is a function
![]() $\lambda _\kappa $
(Definition 1.2.1) such that
$\lambda _\kappa $
(Definition 1.2.1) such that
![]() $graph(\lambda _\kappa )\cap \mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}^b)=\emptyset $
and
$graph(\lambda _\kappa )\cap \mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}^b)=\emptyset $
and
![]() $graph(\lambda _\kappa )\cup \mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}^b)={\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]$
and similarly for
$graph(\lambda _\kappa )\cup \mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}^b)={\mathbb {R}}\times \left [ -\frac \pi 2,\frac \pi 2\right ]$
and similarly for
![]() $\lambda _{\kappa '}$
. Let T be the translation so that
$\lambda _{\kappa '}$
. Let T be the translation so that
![]() $T(graph(\lambda _\kappa ))=graph(\lambda _{\kappa '})$
and therefore
$T(graph(\lambda _\kappa ))=graph(\lambda _{\kappa '})$
and therefore
![]() $T(\mathop {\text {im}} (\mathop {\boldsymbol {\Gamma }}^b))=\mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}')^b$
where
$T(\mathop {\text {im}} (\mathop {\boldsymbol {\Gamma }}^b))=\mathop {\text {im}}(\mathop {\boldsymbol {\Gamma }}')^b$
where
![]() $(\mathop {\boldsymbol {\Gamma }}')^b$
is the analogue of
$(\mathop {\boldsymbol {\Gamma }}')^b$
is the analogue of
![]() $\mathop {\boldsymbol {\Gamma }}^b$
for
$\mathop {\boldsymbol {\Gamma }}^b$
for
![]() $A_{{\mathbb {R}},S'}$
.
$A_{{\mathbb {R}},S'}$
.
Define
![]() $\mathcal F$
on objects: Let V be an indecomposable in
$\mathcal F$
on objects: Let V be an indecomposable in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Define
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Define
![]() $\mathcal F(V_i):=M_{I_i'}[n_i']$
in
$\mathcal F(V_i):=M_{I_i'}[n_i']$
in
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
such that
$\mathcal D^b(A_{{\mathbb {R}},S'})$
such that
![]() $(\mathop {\boldsymbol {\Gamma }}')^b(M_{I_i'}[n_i'])=T(\mathop {\boldsymbol {\Gamma }}^b(V_i))$
and
$(\mathop {\boldsymbol {\Gamma }}')^b(M_{I_i'}[n_i'])=T(\mathop {\boldsymbol {\Gamma }}^b(V_i))$
and
![]() $M_{I_i'}[n_i']$
has the same (micro) position as
$M_{I_i'}[n_i']$
has the same (micro) position as
![]() $V_i$
. Extend this definition to all objects
$V_i$
. Extend this definition to all objects
![]() $V=\bigoplus V_i$
by defining
$V=\bigoplus V_i$
by defining
![]() $\mathcal F(V):=\iota '(\bigoplus \mathcal F(V_i))$
. Since
$\mathcal F(V):=\iota '(\bigoplus \mathcal F(V_i))$
. Since
![]() $\iota '$
commutes with shift,
$\iota '$
commutes with shift,
![]() $\mathcal F(V[1])=(\mathcal FV)[1]$
.
$\mathcal F(V[1])=(\mathcal FV)[1]$
.
Define
![]() $\mathcal F$
on morphisms: Let
$\mathcal F$
on morphisms: Let
![]() $f=(f_{ij}):\bigoplus V_i\to \bigoplus W_j$
where
$f=(f_{ij}):\bigoplus V_i\to \bigoplus W_j$
where
![]() $V_i,W_j$
are indecomposable. Let
$V_i,W_j$
are indecomposable. Let
![]() $\iota (f_{ij})$
be the composition:
$\iota (f_{ij})$
be the composition:
![]() $\iota (f_{ij})=\iota _{W_j}\circ f_{ij}\circ \iota _{V_i}: M_{I_i}[n_i]\to M_{I_j}[m_j]$
. Then
$\iota (f_{ij})=\iota _{W_j}\circ f_{ij}\circ \iota _{V_i}: M_{I_i}[n_i]\to M_{I_j}[m_j]$
. Then
![]() $\iota (f_{ij})\in \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}( M_{I_i}[n_i], M_{I_j}[m_j])= k$
or
$\iota (f_{ij})\in \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}( M_{I_i}[n_i], M_{I_j}[m_j])= k$
or
![]() $0$
. Therefore,
$0$
. Therefore,
![]() $\iota (f_{ij})=c_{ij}\in k$
. Let
$\iota (f_{ij})=c_{ij}\in k$
. Let
![]() $\mathcal F(f_{ij}):=c_{ij}\in \operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S'})}( M_{I^{\prime }_i}[n^{\prime }_i], M_{I^{\prime }_j}[m^{\prime }_j])=k$
where
$\mathcal F(f_{ij}):=c_{ij}\in \operatorname {\mathrm {Hom}}_{\mathcal {D}^b(A_{{\mathbb {R}},S'})}( M_{I^{\prime }_i}[n^{\prime }_i], M_{I^{\prime }_j}[m^{\prime }_j])=k$
where
![]() $M_{I^{\prime }_i}[n^{\prime }_i]=\mathcal F(V_i)=\mathcal F(\iota V_i)=\mathcal F(M_{I_i}[n_i])$
and
$M_{I^{\prime }_i}[n^{\prime }_i]=\mathcal F(V_i)=\mathcal F(\iota V_i)=\mathcal F(M_{I_i}[n_i])$
and
![]() $M_{I^{\prime }_j}[m^{\prime }_j]=\mathcal F(W_j)=\mathcal F(\iota W_j)=\mathcal F(M_{I_j}[m_j])$
. Thus, for indecomposable
$M_{I^{\prime }_j}[m^{\prime }_j]=\mathcal F(W_j)=\mathcal F(\iota W_j)=\mathcal F(M_{I_j}[m_j])$
. Thus, for indecomposable
![]() $V_i,W_j$
,
$V_i,W_j$
,
![]() $\mathcal F$
gives an isomorphism
$\mathcal F$
gives an isomorphism
![]() $\mathcal F:\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V_i,W_j)\cong \operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal F(V_i),\mathcal F(W_j))$
. Finally, define:
$\mathcal F:\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V_i,W_j)\cong \operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}},S'})}(\mathcal F(V_i),\mathcal F(W_j))$
. Finally, define:
Lemma 2.3.3. Given
![]() $A_{{\mathbb {R}},S}$
and
$A_{{\mathbb {R}},S}$
and
![]() $A_{{\mathbb {R}},S'}$
in Definition 2.3.2,
$A_{{\mathbb {R}},S'}$
in Definition 2.3.2,
![]() $\mathcal F$
is a well-defined additive functor. Furthermore,
$\mathcal F$
is a well-defined additive functor. Furthermore,
![]() $\mathcal F$
is an equivalence of categories and
$\mathcal F$
is an equivalence of categories and
![]() $\mathcal F(V[1])= (\mathcal F V)[1]$
.
$\mathcal F(V[1])= (\mathcal F V)[1]$
.
Proof. By using the translation T in Definition 2.3.2 for any indecomposable V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
,
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
,
![]() $\mathcal F V$
is well-defined and indeed
$\mathcal F V$
is well-defined and indeed
![]() $\mathcal F$
induces a bijection on indecomposable objects. Furthermore, since
$\mathcal F$
induces a bijection on indecomposable objects. Furthermore, since
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
are both Krull–Schmidt, we have a bijection on all objects. By definition of
$\mathcal D^b(A_{{\mathbb {R}},S'})$
are both Krull–Schmidt, we have a bijection on all objects. By definition of
![]() $\mathcal F(f)$
given above,
$\mathcal F(f)$
given above,
![]() $\mathcal F$
gives an isomorphism
$\mathcal F$
gives an isomorphism
for all
![]() $V,W$
in
$V,W$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Therefore,
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Therefore,
![]() $\mathcal F$
is an additive equivalence of categories.
$\mathcal F$
is an additive equivalence of categories.
We have already pointed out that
![]() $\mathcal F(V[1])=(\mathcal FV)[1]$
on objects since
$\mathcal F(V[1])=(\mathcal FV)[1]$
on objects since
![]() $\iota $
and
$\iota $
and
![]() $T_r$
commute with shift on objects.
$T_r$
commute with shift on objects.
Lemma 2.3.4. Let
![]() $\mathcal F:{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to \mathcal D^b(A_{{\mathbb {R}},S'})$
be as in Lemma 2.3.3. Then, for every indecomposable object U in
$\mathcal F:{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to \mathcal D^b(A_{{\mathbb {R}},S'})$
be as in Lemma 2.3.3. Then, for every indecomposable object U in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, there is a natural isomorphism
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, there is a natural isomorphism
![]() $\Psi _U:\mathcal F(U[1])\cong (\mathcal FU)[1]$
(given by multiplication by
$\Psi _U:\mathcal F(U[1])\cong (\mathcal FU)[1]$
(given by multiplication by
![]() $c_V\neq 0\in k$
since
$c_V\neq 0\in k$
since
![]() $\mathcal F(U[1])=(\mathcal FU)[1]$
) so that, for a distinguished triangle,
$\mathcal F(U[1])=(\mathcal FU)[1]$
) so that, for a distinguished triangle,
![]() $U\xrightarrow f V\xrightarrow g W\xrightarrow h U[1]$
in
$U\xrightarrow f V\xrightarrow g W\xrightarrow h U[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, we have the following distinguished triangle in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, we have the following distinguished triangle in
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
.
$\mathcal D^b(A_{{\mathbb {R}},S'})$
.
Proof. First, suppose W is indecomposable.
By Theorem 1.2.6,
![]() $U\xrightarrow f V\xrightarrow g W$
is a rectangle or almost complete rectangle as shown on the right. Each hom set,
$U\xrightarrow f V\xrightarrow g W$
is a rectangle or almost complete rectangle as shown on the right. Each hom set,
![]() $\operatorname {\mathrm {Hom}}(U,V_1)$
,
$\operatorname {\mathrm {Hom}}(U,V_1)$
,
![]() $\operatorname {\mathrm {Hom}}(U,V_2)$
, and so on, is equal to k. So morphisms are given by scalars
$\operatorname {\mathrm {Hom}}(U,V_2)$
, and so on, is equal to k. So morphisms are given by scalars
![]() $a,b,c,d,e\in k$
. These scalars must satisfy
$a,b,c,d,e\in k$
. These scalars must satisfy
![]() $ad-bc=0$
. By an automorphism of the distinguished triangle we may assume
$ad-bc=0$
. By an automorphism of the distinguished triangle we may assume
![]() $(a,b,c,d)=(1,1,1,-1)$
.
$(a,b,c,d)=(1,1,1,-1)$
.

Take the morphism
![]() $\mathcal F W\to \mathcal F U[1]$
and complete it to a distinguished triangle in
$\mathcal F W\to \mathcal F U[1]$
and complete it to a distinguished triangle in
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
:
$\mathcal D^b(A_{{\mathbb {R}},S'})$
:
![]() $\mathcal FU\to X\to \mathcal FW\to \mathcal FU[1]$
. By Theorem 1.2.6,
$\mathcal FU\to X\to \mathcal FW\to \mathcal FU[1]$
. By Theorem 1.2.6,
![]() $\mathcal FU\to X\to \mathcal FW$
is a rectangle or almost complete rectangle. This forces
$\mathcal FU\to X\to \mathcal FW$
is a rectangle or almost complete rectangle. This forces
![]() $X\cong \mathcal FV$
. By the same argument as above, we may adjust the scalars corresponding to
$X\cong \mathcal FV$
. By the same argument as above, we may adjust the scalars corresponding to
![]() $a,b,c,d$
in the figure above and we obtain a distinguished triangle
$a,b,c,d$
in the figure above and we obtain a distinguished triangle
Since
![]() $\operatorname {\mathrm {Hom}}(\mathcal FW,\mathcal FU[1])\cong k$
,
$\operatorname {\mathrm {Hom}}(\mathcal FW,\mathcal FU[1])\cong k$
,
![]() $\varphi $
must be a scalar multiple of
$\varphi $
must be a scalar multiple of
![]() $\mathcal F(h)$
, say
$\mathcal F(h)$
, say
![]() $\varphi =c_V\mathcal F(h)$
.
$\varphi =c_V\mathcal F(h)$
.
We claim that the scalar
![]() $c_V$
is independent of V. This is easiest to see in the case when U is in (micro) position 1. In that case, there is a universal choice of V, call it
$c_V$
is independent of V. This is easiest to see in the case when U is in (micro) position 1. In that case, there is a universal choice of V, call it
![]() $\widetilde V$
, making
$\widetilde V$
, making
![]() $U\to \widetilde V\to \widetilde W$
and
$U\to \widetilde V\to \widetilde W$
and
![]() $\mathcal FU\to \mathcal F\widetilde V\to \mathcal F\widetilde W$
into almost split sequences. Any other distinguished triangle
$\mathcal FU\to \mathcal F\widetilde V\to \mathcal F\widetilde W$
into almost split sequences. Any other distinguished triangle
![]() $U\to V\to W\to U[1]$
or
$U\to V\to W\to U[1]$
or
![]() $\mathcal FU\to \mathcal FV\to W' \to \mathcal FU[1]$
is a pushout of these universal sequences as shown on the left side of the following diagram. Since W and
$\mathcal FU\to \mathcal FV\to W' \to \mathcal FU[1]$
is a pushout of these universal sequences as shown on the left side of the following diagram. Since W and
![]() $W'$
are determined by geometry, we must have
$W'$
are determined by geometry, we must have
![]() $W'\cong \mathcal FW$
as shown on the right side.
$W'\cong \mathcal FW$
as shown on the right side.

Then
![]() $h'$
must be equal to
$h'$
must be equal to
![]() $c_{\widetilde V}\mathcal Fh$
. This is clear when W is indecomposable. Otherwise we take a component
$c_{\widetilde V}\mathcal Fh$
. This is clear when W is indecomposable. Otherwise we take a component
![]() $W_i$
and complete
$W_i$
and complete
![]() $h_i:W_i\to U[1]$
to a distinguished triangle
$h_i:W_i\to U[1]$
to a distinguished triangle
![]() $U\to V_i\to W_i\to U[1]$
and we see that the ith component of
$U\to V_i\to W_i\to U[1]$
and we see that the ith component of
![]() $h'$
must be
$h'$
must be
![]() $c_{V_i}\mathcal Fh_i$
which is equal to
$c_{V_i}\mathcal Fh_i$
which is equal to
![]() $c_{\widetilde V}\mathcal Fh_i$
by the easy case. So, the lemma holds with
$c_{\widetilde V}\mathcal Fh_i$
by the easy case. So, the lemma holds with
![]() $\Psi _U$
being multiplication by
$\Psi _U$
being multiplication by
![]() $c_{\widetilde V}$
.
$c_{\widetilde V}$
.
When U is not in position 1, we take a “virtual almost split triangle” which is a family of distinguished triangles
![]() $U\to V_\varepsilon \to W_\varepsilon \to U[1]$
for
$U\to V_\varepsilon \to W_\varepsilon \to U[1]$
for
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
![]() $W_\varepsilon $
converging to U as
$W_\varepsilon $
converging to U as
![]() $\varepsilon \to 0$
. Then any distinguished triangle
$\varepsilon \to 0$
. Then any distinguished triangle
![]() $U\to V\to W\to U[1]$
is a pushout of such a triangle for sufficiently small
$U\to V\to W\to U[1]$
is a pushout of such a triangle for sufficiently small
![]() $\varepsilon $
and we can repeat the above argument. To show that
$\varepsilon $
and we can repeat the above argument. To show that
![]() $\Psi _U$
is a natural isomorphism, we need to show that
$\Psi _U$
is a natural isomorphism, we need to show that
![]() $c_V$
is independent of U. To do this, take
$c_V$
is independent of U. To do this, take
![]() $U,U'$
indecomposable, complete
$U,U'$
indecomposable, complete
![]() $U\to U'$
to a distinguished triangle, then rotate the triangle
$U\to U'$
to a distinguished triangle, then rotate the triangle
![]() $\mathcal FU\to \mathcal FU'\to \mathcal FW\to \mathcal FU[1]$
to see that the scalar for U is the same as that for
$\mathcal FU\to \mathcal FU'\to \mathcal FW\to \mathcal FU[1]$
to see that the scalar for U is the same as that for
![]() $U'$
.
$U'$
.
Theorem 2.3.5 (Theorem A)
The derived categories
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() $\mathcal {D}^b(A_{{\mathbb {R}},S'})$
are equivalent as triangulated categories if and only if one of the following hold:
$\mathcal {D}^b(A_{{\mathbb {R}},S'})$
are equivalent as triangulated categories if and only if one of the following hold:
-
(a)
 $S,S'$
are both finite,
$S,S'$
are both finite, -
(b) each of
 $S,S'$
is bounded on exactly one side, or
$S,S'$
is bounded on exactly one side, or -
(c)
 $S,S'$
are unbounded on both sides.
$S,S'$
are unbounded on both sides.
Proof. If (c) holds then by Proposition [Reference Igusa, Rock and Todorov14, Prop. 3.2.1] the representation categories are equivalent as abelian categories and so the derived categories are also be equivalent as triangulated categories. If (a) or (b) holds then the categories are already equivalent as additive categories, by Lemma 2.3.3. It remain to show that
![]() $\mathcal F$
is a equivalence of triangulated categories, that is, we need to extend Lemma 2.3.4 to the case when U is not indecomposable. So, let
$\mathcal F$
is a equivalence of triangulated categories, that is, we need to extend Lemma 2.3.4 to the case when U is not indecomposable. So, let
![]() $U\stackrel {f}{\to } V\stackrel {g}{\to } W \stackrel {h}{\to } U[1] $
be distinguished in
$U\stackrel {f}{\to } V\stackrel {g}{\to } W \stackrel {h}{\to } U[1] $
be distinguished in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
with
![]() $U=\bigoplus U_i$
. Then [Reference Neeman18, Def. 2.1.1] we need to show that
$U=\bigoplus U_i$
. Then [Reference Neeman18, Def. 2.1.1] we need to show that
is distinguished in
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
where
$\mathcal D^b(A_{{\mathbb {R}},S'})$
where
![]() $\Psi :\mathcal FU[1]\cong \mathcal FU[1]$
is multiplication by a fixed constant c. By Lemma 2.3.4, the analogous statement holds for
$\Psi :\mathcal FU[1]\cong \mathcal FU[1]$
is multiplication by a fixed constant c. By Lemma 2.3.4, the analogous statement holds for
![]() $U_i$
: completing the ith component
$U_i$
: completing the ith component
![]() $h_i:W\to U_i[1]$
to a distinguished triangle gives
$h_i:W\to U_i[1]$
to a distinguished triangle gives
![]() $U_i\stackrel {f_i}{\to } V_i\stackrel {g_i}{\to } W \stackrel {h_i}{\to } U_i[1] $
. Lemma 2.3.4 gives the distinguished triangle
$U_i\stackrel {f_i}{\to } V_i\stackrel {g_i}{\to } W \stackrel {h_i}{\to } U_i[1] $
. Lemma 2.3.4 gives the distinguished triangle
![]() $\mathcal FU_i\stackrel {\mathcal F f_i}{\to } \mathcal FV_i\stackrel {\mathcal Fg_i}{\to } W \stackrel {\Psi \circ \mathcal Fh_i}{\to } \mathcal FU_i[1] $
. This gives a morphism of distinguished triangles:
$\mathcal FU_i\stackrel {\mathcal F f_i}{\to } \mathcal FV_i\stackrel {\mathcal Fg_i}{\to } W \stackrel {\Psi \circ \mathcal Fh_i}{\to } \mathcal FU_i[1] $
. This gives a morphism of distinguished triangles:

However,
![]() $U\stackrel {f}{\to } V\stackrel {g}{\to } W$
is the pull back of
$U\stackrel {f}{\to } V\stackrel {g}{\to } W$
is the pull back of
![]() $U\to \bigoplus V_i\to \bigoplus W$
along the diagonal
$U\to \bigoplus V_i\to \bigoplus W$
along the diagonal
![]() $\Delta :W\to \bigoplus W$
. Since
$\Delta :W\to \bigoplus W$
. Since
![]() $\mathcal F$
is an equivalence of categories,
$\mathcal F$
is an equivalence of categories,
![]() $V'=\mathcal FV$
is the pull back in the diagram above and we conclude that
$V'=\mathcal FV$
is the pull back in the diagram above and we conclude that
![]() $(\ast )$
is a distinguished triangle. So,
$(\ast )$
is a distinguished triangle. So,
![]() $(\mathcal F,\Psi )$
is an equivalence of triangulated categories.
$(\mathcal F,\Psi )$
is an equivalence of triangulated categories.
Since every continuous quiver of type A with finitely many sinks and sources is derived equivalent we show that classes (b) and (c) are disjoint from (a) using the straight descending orientation. Afterwards, we show (b) and (c) are also disjoint.
Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A with infinitely many sinks and sources. Let
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A with infinitely many sinks and sources. Let
![]() $A_{{\mathbb {R}}}$
be the straight descending continuous quiver of type A. Let
$A_{{\mathbb {R}}}$
be the straight descending continuous quiver of type A. Let
![]() $\mathcal P$
be the set of indecomposable projectives of
$\mathcal P$
be the set of indecomposable projectives of
![]() $\text {rep}_k(A_{{\mathbb {R}}})$
included as indecomposables in degree 0 in
$\text {rep}_k(A_{{\mathbb {R}}})$
included as indecomposables in degree 0 in
![]() $\mathcal D^b(A_{{\mathbb {R}}})$
.
$\mathcal D^b(A_{{\mathbb {R}}})$
.
For contradiction, suppose there is an equivalence of categories
![]() $\mathcal G:\mathcal D^b(A_{{\mathbb {R}}})\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. By Lemma 2.3.1, we know that for any pair
$\mathcal G:\mathcal D^b(A_{{\mathbb {R}}})\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. By Lemma 2.3.1, we know that for any pair
![]() $P,P'\in \mathcal P$
, the slope of any line segment from
$P,P'\in \mathcal P$
, the slope of any line segment from
![]() $\mathcal G P$
to
$\mathcal G P$
to
![]() $\mathcal G P'$
(switching roles if necessary) is
$\mathcal G P'$
(switching roles if necessary) is
![]() $\pm (1,1)$
. Since
$\pm (1,1)$
. Since
![]() $\mathcal G$
is an equivalence we know that if there exists V in
$\mathcal G$
is an equivalence we know that if there exists V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\mathcal G P,V)\cong \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,\mathcal G P')\cong k$
for
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\mathcal G P,V)\cong \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,\mathcal G P')\cong k$
for
![]() $P,P'\in \mathcal P$
then
$P,P'\in \mathcal P$
then
![]() $V \cong \mathcal G P''$
for some
$V \cong \mathcal G P''$
for some
![]() $P''\in \mathcal P$
.
$P''\in \mathcal P$
.
Note that
![]() $\mathcal P$
induces an almost-complete line segment in the AR-space of
$\mathcal P$
induces an almost-complete line segment in the AR-space of
![]() $\mathcal D^b (A_{{\mathbb {R}}})$
. So, there does not exist an indecomposable object V in
$\mathcal D^b (A_{{\mathbb {R}}})$
. So, there does not exist an indecomposable object V in
![]() $\mathcal D^b(A_{{\mathbb {R}}})$
such that (i) V is not isomorphic to an element of
$\mathcal D^b(A_{{\mathbb {R}}})$
such that (i) V is not isomorphic to an element of
![]() $\mathcal P$
and (ii)
$\mathcal P$
and (ii)
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(V,P)\cong k$
for all
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(V,P)\cong k$
for all
![]() $P\in \mathcal P$
. We also know that if
$P\in \mathcal P$
. We also know that if
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(P_{+\infty },U)\cong \operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(P_{+\infty },U') \cong k$
then
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(P_{+\infty },U)\cong \operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(P_{+\infty },U') \cong k$
then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(U,U')\cong k$
or
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(U,U')\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(U',U)\cong k$
. Since
$\operatorname {\mathrm {Hom}}_{\mathcal D^b(A_{{\mathbb {R}}})}(U',U)\cong k$
. Since
![]() $\mathcal G$
is an equivalence of categories these properties are preserved. This forces the image
$\mathcal G$
is an equivalence of categories these properties are preserved. This forces the image
![]() $\mathcal G\mathcal P$
to induce an almost complete line segment whose existing endpoint
$\mathcal G\mathcal P$
to induce an almost complete line segment whose existing endpoint
![]() $\mathcal G P_{+\infty }$
is on the top or bottom boundary of the AR-space of
$\mathcal G P_{+\infty }$
is on the top or bottom boundary of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. We describe how we arrive at a contradiction and include pictures after this paragraph. Since
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. We describe how we arrive at a contradiction and include pictures after this paragraph. Since
![]() $A_{{\mathbb {R}},S}$
has infinitely many sinks and sources we must split the set
$A_{{\mathbb {R}},S}$
has infinitely many sinks and sources we must split the set
![]() $\mathcal G \mathcal P$
into (at least) two pieces since there is a missing graph of a
$\mathcal G \mathcal P$
into (at least) two pieces since there is a missing graph of a
![]() $\lambda $
function from the image of
$\lambda $
function from the image of
![]() $\mathop {\boldsymbol {\Gamma }}^b$
. The set
$\mathop {\boldsymbol {\Gamma }}^b$
. The set
![]() $\mathop {\boldsymbol {\Gamma }}^b \mathcal G\mathcal P$
is homeomorphic to the disjoint union of (at least) two intervals. The set
$\mathop {\boldsymbol {\Gamma }}^b \mathcal G\mathcal P$
is homeomorphic to the disjoint union of (at least) two intervals. The set
![]() $(\mathop {\boldsymbol {\Gamma }}')^b \mathcal P$
is homeomorphic to one interval. We cannot reorder the elements in the almost-complete line segment and we cannot allow a strict inclusion of
$(\mathop {\boldsymbol {\Gamma }}')^b \mathcal P$
is homeomorphic to one interval. We cannot reorder the elements in the almost-complete line segment and we cannot allow a strict inclusion of
![]() $\mathcal P$
into the almost-complete line segment in the AR-space of
$\mathcal P$
into the almost-complete line segment in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. This finally leads us to the contradiction. In Figure 7, we depict two of the issues with mapping the projectives by observing their image under
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. This finally leads us to the contradiction. In Figure 7, we depict two of the issues with mapping the projectives by observing their image under
![]() $\mathop {\boldsymbol {\Gamma }}^b$
.
$\mathop {\boldsymbol {\Gamma }}^b$
.

Figure 7 A visual depiction of the obstruction to a derived equivalence
![]() $\mathcal G:\mathcal D^b(A_{{\mathbb {R}}})\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
for
$\mathcal G:\mathcal D^b(A_{{\mathbb {R}}})\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
for
![]() $S={\mathbb {N}}$
and
$S={\mathbb {N}}$
and
![]() $S={\mathbb {Z}}$
in the proof of Theorem 2.3.5.
$S={\mathbb {Z}}$
in the proof of Theorem 2.3.5.
Now, we show that (b) and (c) are also disjoint. Suppose
![]() $A_{{\mathbb {R}},S}$
has half bounded sinks and sources and
$A_{{\mathbb {R}},S}$
has half bounded sinks and sources and
![]() $A_{{\mathbb {R}},S'}$
has unbounded sinks and sources on both sides. The image in
$A_{{\mathbb {R}},S'}$
has unbounded sinks and sources on both sides. The image in
![]() ${\mathbb {R}}^2$
under
${\mathbb {R}}^2$
under
![]() $\mathop {\boldsymbol {\Gamma }}^b$
of an almost complete line segment in the AR-space of
$\mathop {\boldsymbol {\Gamma }}^b$
of an almost complete line segment in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
has at most two path components. However, one may construct an almost complete line segment in the AR-space of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
has at most two path components. However, one may construct an almost complete line segment in the AR-space of
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
whose image in
$\mathcal D^b(A_{{\mathbb {R}},S'})$
whose image in
![]() ${\mathbb {R}}^2$
under
${\mathbb {R}}^2$
under
![]() $(\mathop {\boldsymbol {\Gamma }}')^b$
has three path components. Knowing this we apply a similar argument as before and see that an equivalence of categories cannot exist between
$(\mathop {\boldsymbol {\Gamma }}')^b$
has three path components. Knowing this we apply a similar argument as before and see that an equivalence of categories cannot exist between
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() $\mathcal D^b(A_{{\mathbb {R}},S'})$
.
$\mathcal D^b(A_{{\mathbb {R}},S'})$
.
3 New weak cluster category and relation to
 $\mathcal D_{\pi} $
and
$\mathcal D_{\pi} $
and
 $\mathcal C_{\pi} $
$\mathcal C_{\pi} $
This section is dedicated to the construction of the new weak cluster category
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
and the relation of
${\mathcal {C}(A_{{\mathbb {R}},S})}$
and the relation of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
to the continuous derived category
${\mathcal {C}(A_{{\mathbb {R}},S})}$
to the continuous derived category
![]() $\mathcal D_\pi $
and the continuous cluster category
$\mathcal D_\pi $
and the continuous cluster category
![]() $\mathcal C_\pi $
in [Reference Igusa and Todorov15].
$\mathcal C_\pi $
in [Reference Igusa and Todorov15].
3.1 Construction of
 ${\mathcal {C}(A_{{\mathbb {R}},S})}$
${\mathcal {C}(A_{{\mathbb {R}},S})}$
Following [Reference Garcia and Igusa10] and [Reference Igusa and Todorov15], we define
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
to be the orbit category of the double of the continuous derived category
${\mathcal {C}(A_{{\mathbb {R}},S})}$
to be the orbit category of the double of the continuous derived category
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
under the almost-shift functor.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
under the almost-shift functor.
Definition 3.1.1. Given any triangulated k-category
![]() $\mathcal D$
, we define the double
$\mathcal D$
, we define the double
![]() $\mathcal D^{(2)}$
of
$\mathcal D^{(2)}$
of
![]() $\mathcal D$
to be the category equivalent to
$\mathcal D$
to be the category equivalent to
![]() $\mathcal D$
whose objects are ordered pairs of objects
$\mathcal D$
whose objects are ordered pairs of objects
![]() $(X,Y)$
where
$(X,Y)$
where
![]() $X,Y$
are objects of
$X,Y$
are objects of
![]() $\mathcal D$
with morphisms given by
$\mathcal D$
with morphisms given by
The shift functor is defined on objects by
![]() $(X_1,X_2)[1]:=(X_1[1],X_2[1])$
and on morphisms by changing the signs of “cross morphisms,” that is,
$(X_1,X_2)[1]:=(X_1[1],X_2[1])$
and on morphisms by changing the signs of “cross morphisms,” that is,
 $$ \begin{align*} \left[\begin{matrix}f & g\\h & k\end{matrix} \right][1]=\left[\begin{matrix}f[1] & -g[1]\\-h[1] & k[1]\end{matrix} \right]. \end{align*} $$
$$ \begin{align*} \left[\begin{matrix}f & g\\h & k\end{matrix} \right][1]=\left[\begin{matrix}f[1] & -g[1]\\-h[1] & k[1]\end{matrix} \right]. \end{align*} $$
Finally, the distinguished triangles in
![]() $\mathcal D^{(2)}$
are:
$\mathcal D^{(2)}$
are:
is a distinguished triangle in
![]() $\mathcal D$
.
$\mathcal D$
.
The doubled category
![]() $\mathcal D^{(2)}$
has an self-equivalence F given by
$\mathcal D^{(2)}$
has an self-equivalence F given by
![]() $F(X,Y)=(Y[1],X[1])$
. We call this the almost-shift. It takes distinguished triangles to distinguished triangles.
$F(X,Y)=(Y[1],X[1])$
. We call this the almost-shift. It takes distinguished triangles to distinguished triangles.
Definition 3.1.2. Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A and
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A and
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
its bounded derived category. The new weak continuous cluster category (which we later call, in Definition 4.3.1, the continuous
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
its bounded derived category. The new weak continuous cluster category (which we later call, in Definition 4.3.1, the continuous
![]() $\mathbf E$
-cluster category), denoted
$\mathbf E$
-cluster category), denoted
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
, is the orbit category of the doubling of
${\mathcal {C}(A_{{\mathbb {R}},S})}$
, is the orbit category of the doubling of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
under the almost-shift functor F defined above. As in [Reference Garcia and Igusa10] and [Reference Igusa and Todorov15],
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
under the almost-shift functor F defined above. As in [Reference Garcia and Igusa10] and [Reference Igusa and Todorov15],
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
is also a triangulated category.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
is also a triangulated category.
Proposition 3.1.3. Let V and W be indecomposable objects in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)\cong k$
or
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)=0$
.
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)=0$
.
Proof. Suppose
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)\neq 0$
. We know
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)\neq 0$
. We know
 $$ \begin{align*}\operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(V,W)= \bigoplus_{n\in{\mathbb{Z}}}\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,W[n])\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(V,W)= \bigoplus_{n\in{\mathbb{Z}}}\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,W[n])\end{align*} $$
and so there exists at least one n such that
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[n])\cong k$
. By [Reference Rock19, Prop. 4.4.2 and Lem. 5.2.9], if
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[n])\cong k$
. By [Reference Rock19, Prop. 4.4.2 and Lem. 5.2.9], if
![]() $V\not \cong W$
we know that
$V\not \cong W$
we know that
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[m])=0$
for
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[m])=0$
for
![]() $m>n$
and
$m>n$
and
![]() $m<n$
. If
$m<n$
. If
![]() $V\cong W$
we note that, since
$V\cong W$
we note that, since
![]() $\operatorname {\mathrm {Ext}}^n_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,V)=0$
for
$\operatorname {\mathrm {Ext}}^n_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,V)=0$
for
![]() $n\neq 0$
,
$n\neq 0$
,
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(V,W)=\bigoplus_{n\in {\mathbb{Z}}}\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,V[n])=\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,V)\cong k. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(V,W)=\bigoplus_{n\in {\mathbb{Z}}}\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,V[n])=\operatorname{\mathrm{Hom}}_{{\mathcal{D}^b(A_{{\mathbb{R}},S})}}(V,V)\cong k. \end{align*} $$
Recall that by taking the orbit category, the class of objects in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
is the same as that in the doubling of
${\mathcal {C}(A_{{\mathbb {R}},S})}$
is the same as that in the doubling of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
even though the isomorphism classes have changed. Since the endomorphism ring of each indecomposable object is k, we obtain the following.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
even though the isomorphism classes have changed. Since the endomorphism ring of each indecomposable object is k, we obtain the following.
Proposition 3.1.4. The orbit category
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
is Krull–Schmidt.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
is Krull–Schmidt.
3.2 Localizations
In this section, we create a calculus of fractions in order to construct triangulated localizations of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We do this using a null system.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We do this using a null system.
Definition 3.2.1. An indecomposable object V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is called degenerate if
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is called degenerate if
![]() $\mathop {\boldsymbol {\Gamma }}^b(V)=(x,\pm \frac \pi 2)$
. Also,
$\mathop {\boldsymbol {\Gamma }}^b(V)=(x,\pm \frac \pi 2)$
. Also,
![]() $V=0$
is called degenerate. If V in
$V=0$
is called degenerate. If V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is degenerate then the orbit of V in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is degenerate then the orbit of V in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
is called degenerate. Let
${\mathcal {C}(A_{{\mathbb {R}},S})}$
is called degenerate. Let
![]() $V\cong \bigoplus V_i$
be an object in
$V\cong \bigoplus V_i$
be an object in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
,
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
,
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
where each
${\mathcal {C}(A_{{\mathbb {R}},S})}$
where each
![]() $V_i$
is indecomposable. If each
$V_i$
is indecomposable. If each
![]() $V_i$
is degenerate we say V is degenerate.
$V_i$
is degenerate we say V is degenerate.
Proposition 3.2.2. Let V and W be degenerate indecomposable objects in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
,
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
,
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
, and
${\mathcal {C}(A_{{\mathbb {R}},S})}$
, and
![]() $f:V\to W$
a morphism. Then f is either 0 or an isomorphism.
$f:V\to W$
a morphism. Then f is either 0 or an isomorphism.
Proof. When V and W are in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
this follows from [Reference Rock19, Sec. 4.2 and Lem. 5.2.9]. Now suppose V and W are in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
this follows from [Reference Rock19, Sec. 4.2 and Lem. 5.2.9]. Now suppose V and W are in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
and
${\mathcal {C}(A_{{\mathbb {R}},S})}$
and
![]() $f\neq 0$
. Since
$f\neq 0$
. Since
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)=\bigoplus _{n\in {\mathbb {Z}}} \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[n])$
some shift of W must be isomorphic to V in
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}}(V,W)=\bigoplus _{n\in {\mathbb {Z}}} \operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W[n])$
some shift of W must be isomorphic to V in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then f is an isomorphism since
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then f is an isomorphism since
![]() $\operatorname {\mathrm {Hom}}(V,V)\cong k$
and
$\operatorname {\mathrm {Hom}}(V,V)\cong k$
and
![]() $f\neq 0$
.
$f\neq 0$
.
Definition 3.2.3. Let
![]() $\mathcal D$
be a triangulated category. A null system in
$\mathcal D$
be a triangulated category. A null system in
![]() $\mathcal D$
is a full subcategory
$\mathcal D$
is a full subcategory
![]() $\mathcal N$
so that: (1) X is in
$\mathcal N$
so that: (1) X is in
![]() $\mathcal N$
if and only if
$\mathcal N$
if and only if
![]() $X[1]$
is in
$X[1]$
is in
![]() $\mathcal N$
and (2) if
$\mathcal N$
and (2) if
![]() $X\to Y\to Z\to X[1]$
is a distinguished triangle in
$X\to Y\to Z\to X[1]$
is a distinguished triangle in
![]() $\mathcal D$
and X and Z are both in
$\mathcal D$
and X and Z are both in
![]() $\mathcal N$
then so is Y.
$\mathcal N$
then so is Y.
We recall the following fact from [Reference Kashiwara and Schapira17, Th. 10.2.3(i)] as a proposition.
Proposition 3.2.4. Let
![]() $\mathcal D$
be a triangulated category and
$\mathcal D$
be a triangulated category and
![]() $\mathcal N$
a null system in
$\mathcal N$
a null system in
![]() $\mathcal D$
. Then
$\mathcal D$
. Then
![]() $\mathcal NQ:= \{ X\stackrel {f}{\to } Y : \exists \text { distinguished triangle }X\stackrel {f}{\to } Y\to Z\to X[1], Z\text { in }\mathcal N\} $
admits a left and right calculus of fractions in
$\mathcal NQ:= \{ X\stackrel {f}{\to } Y : \exists \text { distinguished triangle }X\stackrel {f}{\to } Y\to Z\to X[1], Z\text { in }\mathcal N\} $
admits a left and right calculus of fractions in
![]() $\mathcal D$
.
$\mathcal D$
.
Proposition 3.2.5. Let
![]() $\mathcal D$
be
$\mathcal D$
be
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Let
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Let
![]() $\mathcal N$
be the full, wide subcategory of
$\mathcal N$
be the full, wide subcategory of
![]() $\mathcal D$
whose objects are the degenerate objects in
$\mathcal D$
whose objects are the degenerate objects in
![]() $\mathcal D$
. Then
$\mathcal D$
. Then
![]() $\mathcal N$
is a null system and so
$\mathcal N$
is a null system and so
![]() $\mathcal N Q$
admits a left and right calculus of fractions.
$\mathcal N Q$
admits a left and right calculus of fractions.
Proof. If V is degenerate then
![]() $\mathop {\boldsymbol {\Gamma }}^b V=(x,\pm \frac \pi 2)$
. So,
$\mathop {\boldsymbol {\Gamma }}^b V=(x,\pm \frac \pi 2)$
. So,
![]() $\mathop {\boldsymbol {\Gamma }}^b V[1]=(x+\pi ,\mp \frac \pi 2)$
. So,
$\mathop {\boldsymbol {\Gamma }}^b V[1]=(x+\pi ,\mp \frac \pi 2)$
. So,
![]() $V[1]$
is degenerate if and only if V is degenerate. So,
$V[1]$
is degenerate if and only if V is degenerate. So,
![]() $\mathcal N$
satisfies the first condition to be a null system. By Proposition 3.2.2, it satisfies the second condition. Hence,
$\mathcal N$
satisfies the first condition to be a null system. By Proposition 3.2.2, it satisfies the second condition. Hence,
![]() $\mathcal N$
is a null system. It follows from Proposition. 3.2.4 that
$\mathcal N$
is a null system. It follows from Proposition. 3.2.4 that
![]() $\mathcal NQ$
admists a left and right calculus of fractions.
$\mathcal NQ$
admists a left and right calculus of fractions.
We now recall the following from [Reference Kashiwara and Schapira17, Th. 10.2.3(iii)].
Proposition 3.2.6. Let
![]() $\mathcal D$
be a triangulated category and
$\mathcal D$
be a triangulated category and
![]() $\mathcal N$
a null system in
$\mathcal N$
a null system in
![]() $\mathcal D$
. Then there exists a localization
$\mathcal D$
. Then there exists a localization
![]() $\mathcal D\to \mathcal D[(\mathcal {NQ})^{-1}]$
such that
$\mathcal D\to \mathcal D[(\mathcal {NQ})^{-1}]$
such that
![]() $\mathcal D[(\mathcal {NQ})^{-1}]$
is a triangulated category whose distinguished triangles are exactly the images of distinguished triangles in
$\mathcal D[(\mathcal {NQ})^{-1}]$
is a triangulated category whose distinguished triangles are exactly the images of distinguished triangles in
![]() $\mathcal D$
.
$\mathcal D$
.
Corollary 3.2.7. Let
![]() $\mathcal D$
be
$\mathcal D$
be
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
and
${\mathcal {C}(A_{{\mathbb {R}},S})}$
and
![]() $\mathcal N$
the full, wide subcategory of degenerate objects in
$\mathcal N$
the full, wide subcategory of degenerate objects in
![]() $\mathcal D$
. Then
$\mathcal D$
. Then
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
is a triangulated category whose distinguished triangles are images of distinguished triangles in
$\mathcal D[(\mathcal NQ)^{-1}]$
is a triangulated category whose distinguished triangles are images of distinguished triangles in
![]() $\mathcal D$
.
$\mathcal D$
.
Lemma 3.2.8.
(1) Let V and W be indecomposable nondegenerate in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Then
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
if and only if
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
if and only if
![]() $\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(W)$
.
$\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(W)$
.
(2) Let V and W be indecomposable nondegenerate in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
if and only if there exists
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
if and only if there exists
![]() $n\in {\mathbb {Z}}$
such that
$n\in {\mathbb {Z}}$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(W)$
.
$\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(W)$
.
Proof. In
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
,
${\mathcal {C}(A_{{\mathbb {R}},S})}$
,
![]() $W\cong W[n]$
for all
$W\cong W[n]$
for all
![]() $n\in {\mathbb {Z}}$
. Thus, by replacing W with
$n\in {\mathbb {Z}}$
. Thus, by replacing W with
![]() $W[n]$
, and choosing the appropriate n, we can prove (2) for
$W[n]$
, and choosing the appropriate n, we can prove (2) for
![]() $\mathop {\boldsymbol {\Gamma }}^b V= \mathop {\boldsymbol {\Gamma }}^b W$
.
$\mathop {\boldsymbol {\Gamma }}^b V= \mathop {\boldsymbol {\Gamma }}^b W$
.
First suppose
![]() $\mathop {\boldsymbol {\Gamma }}^b V =\mathop {\boldsymbol {\Gamma }}^b W$
in
$\mathop {\boldsymbol {\Gamma }}^b V =\mathop {\boldsymbol {\Gamma }}^b W$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Without loss of generality, first suppose
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Without loss of generality, first suppose
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W)\cong k$
. By Theorem 1.2.6 any nonzero indecomposable summands of U in the distinguished triangle
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(V,W)\cong k$
. By Theorem 1.2.6 any nonzero indecomposable summands of U in the distinguished triangle
![]() $W\to U\to V[1]\to W[1]$
in
$W\to U\to V[1]\to W[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are degenerate. Then U is degenerate and so
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
are degenerate. Then U is degenerate and so
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. Furthermore, if V and W are instead in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. Furthermore, if V and W are instead in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
then U is still degenerate and so
${\mathcal {C}(A_{{\mathbb {R}},S})}$
then U is still degenerate and so
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
.
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
.
Now suppose
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. Then U in the distinguished triangle
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. Then U in the distinguished triangle
![]() $W\to U\to V[1]\to W[1]$
in
$W\to U\to V[1]\to W[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is degenerate. We use Theorem 1.2.6 again and see
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
is degenerate. We use Theorem 1.2.6 again and see
![]() $\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b W$
. Now suppose
$\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b W$
. Now suppose
![]() $V\cong W$
in
$V\cong W$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
; so U is degenerate in the distinguished triangle
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
; so U is degenerate in the distinguished triangle
![]() $W\to U\to V\to W[1]$
in
$W\to U\to V\to W[1]$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. As an orbit category by almost-shift there are choices of lifts W, U, and
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. As an orbit category by almost-shift there are choices of lifts W, U, and
![]() $V[1]$
in
$V[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that yield the triangle in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that yield the triangle in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Again we apply Theorem 1.2.6 and see
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Again we apply Theorem 1.2.6 and see
![]() $\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b W$
.
$\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b W$
.
Lemma 3.2.9. Let
![]() $\mathcal D$
be either
$\mathcal D$
be either
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
and V and W be indecomposables in
${\mathcal {C}(A_{{\mathbb {R}},S})}$
and V and W be indecomposables in
![]() $\mathcal D$
. Let
$\mathcal D$
. Let
![]() $V_1$
be an indecomposable in
$V_1$
be an indecomposable in
![]() $\mathcal D$
such that
$\mathcal D$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b V_1$
and
$\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b V_1$
and
![]() $V_1$
has position 1. Then
$V_1$
has position 1. Then
![]() $ \operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)=0 \text { if and only if } \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)=0. $
$ \operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)=0 \text { if and only if } \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)=0. $
Proof. Suppose
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)=0$
. Consider a roof
$\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)=0$
. Consider a roof
 in
in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
. Since
$\mathcal D[(\mathcal NQ)^{-1}]$
. Since
![]() $f\in \mathcal NQ$
, we know (shifting if necessary in
$f\in \mathcal NQ$
, we know (shifting if necessary in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
) that
${\mathcal {C}(A_{{\mathbb {R}},S})}$
) that
![]() $\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b U$
. Then
$\mathop {\boldsymbol {\Gamma }}^b V=\mathop {\boldsymbol {\Gamma }}^b U$
. Then
![]() $\mathop {\boldsymbol {\Gamma }}^b V_1=\mathop {\boldsymbol {\Gamma }}^b U=\mathop {\boldsymbol {\Gamma }}^b V$
and so
$\mathop {\boldsymbol {\Gamma }}^b V_1=\mathop {\boldsymbol {\Gamma }}^b U=\mathop {\boldsymbol {\Gamma }}^b V$
and so
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,U)\cong k\cong \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,V)$
.
$\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,U)\cong k\cong \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,V)$
.
Let
![]() $s:V_1\to U$
be a nontrivial morphism. We then have the commutative diagram in
$s:V_1\to U$
be a nontrivial morphism. We then have the commutative diagram in
![]() $\mathcal D$
on the right. Since
$\mathcal D$
on the right. Since
![]() $f\circ s\in \mathcal NQ$
, we see that these two roofs are equivalent in
$f\circ s\in \mathcal NQ$
, we see that these two roofs are equivalent in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
. Denote the bottom roof by
$\mathcal D[(\mathcal NQ)^{-1}]$
. Denote the bottom roof by
![]() $\underline {f}'$
.
$\underline {f}'$
.

If
![]() $g=0$
then
$g=0$
then
![]() $\underline {f}$
was 0 all along. If
$\underline {f}$
was 0 all along. If
![]() $g\neq 0$
we have
$g\neq 0$
we have
![]() $g\circ s=0$
but
$g\circ s=0$
but
![]() $f\circ s\in \mathcal NQ$
and so
$f\circ s\in \mathcal NQ$
and so
![]() $\underline {f}'=0$
. Thus,
$\underline {f}'=0$
. Thus,
![]() $\underline {f}$
must be 0 and so
$\underline {f}$
must be 0 and so
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)=0$
.
$\operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)=0$
.
Now suppose
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)\neq 0$
. Choose nonzero morphisms
$\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)\neq 0$
. Choose nonzero morphisms
![]() $f:V_1\to V$
and
$f:V_1\to V$
and
![]() $g:V_1\to W$
. Then, we have the roof
$g:V_1\to W$
. Then, we have the roof
 . For contradiction, suppose
. For contradiction, suppose
![]() $\underline {f}=0$
.
$\underline {f}=0$
.
Then there is a roof

where
![]() $g'=0$
and the commuting diagram in
$g'=0$
and the commuting diagram in
![]() $\mathcal D$
shown on the right. However, this means (up to shifting in
$\mathcal D$
shown on the right. However, this means (up to shifting in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
)
${\mathcal {C}(A_{{\mathbb {R}},S})}$
)
![]() $\mathop {\boldsymbol {\Gamma }}^b \tilde {U}=\mathop {\boldsymbol {\Gamma }}^b V_1$
and so
$\mathop {\boldsymbol {\Gamma }}^b \tilde {U}=\mathop {\boldsymbol {\Gamma }}^b V_1$
and so
![]() $\tilde {U}\cong V_1$
, a contradiction as then the right side of the diagram would not commute.
$\tilde {U}\cong V_1$
, a contradiction as then the right side of the diagram would not commute.

Therefore, there exists a nonzero
![]() $\underline {f}\in \operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)$
.
$\underline {f}\in \operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W)$
.
Proposition 3.2.10. Let
![]() $\mathcal D$
be either
$\mathcal D$
be either
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
or
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Let V and W be indecomposable objects in
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. Let V and W be indecomposable objects in
![]() $\mathcal D[\mathcal N Q^{-1}]$
. Then
$\mathcal D[\mathcal N Q^{-1}]$
. Then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)\cong k$
or
$\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)=0$
.
$\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)=0$
.
Proof. Let V and W be indecomposable in
![]() $\mathcal D[\mathcal N Q^{-1}]$
so that
$\mathcal D[\mathcal N Q^{-1}]$
so that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)\neq 0$
. Let
$\operatorname {\mathrm {Hom}}_{\mathcal D[\mathcal N Q^{-1}]}(V,W)\neq 0$
. Let
![]() $V_1$
be an indecomposable in
$V_1$
be an indecomposable in
![]() $\mathcal D$
such that
$\mathcal D$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b V_1=\mathop {\boldsymbol {\Gamma }}^b V$
and the position of
$\mathop {\boldsymbol {\Gamma }}^b V_1=\mathop {\boldsymbol {\Gamma }}^b V$
and the position of
![]() $V_1$
is 1. By Lemmas 3.2.8 and 3.2.9, we know
$V_1$
is 1. By Lemmas 3.2.8 and 3.2.9, we know
![]() $V\cong _{\mathcal D[(\mathcal NQ)^{-1}]} V_1$
and
$V\cong _{\mathcal D[(\mathcal NQ)^{-1}]} V_1$
and
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)\neq 0$
. We show that
$\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W)\neq 0$
. We show that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W) \cong \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W) $
by defining two maps
$\operatorname {\mathrm {Hom}}_{\mathcal D[(\mathcal NQ)^{-1}]}(V,W) \cong \operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,W) $
by defining two maps
Fix a nonzero morphism
![]() $f':V_1\to V$
in
$f':V_1\to V$
in
![]() $\mathcal D$
. As we saw in the proof of Lemma 3.2.9 every nonzero morphism
$\mathcal D$
. As we saw in the proof of Lemma 3.2.9 every nonzero morphism
![]() $V\to W$
in
$V\to W$
in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
is equivalent to a roof whose middle term is
$\mathcal D[(\mathcal NQ)^{-1}]$
is equivalent to a roof whose middle term is
![]() $V_1$
. For contradiction, suppose
$V_1$
. For contradiction, suppose
![]() $\underline {f}=0$
. Then there is a roof
$\underline {f}=0$
. Then there is a roof
 in
in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
. Since
$\mathcal D[(\mathcal NQ)^{-1}]$
. Since
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,V)\cong k$
, there is a unique
$\operatorname {\mathrm {Hom}}_{\mathcal D}(V_1,V)\cong k$
, there is a unique
![]() $s:V_1\to V_1$
in
$s:V_1\to V_1$
in
![]() $\mathcal D$
such that
$\mathcal D$
such that
![]() $f\circ s= f'$
. Similarly, there is a unique
$f\circ s= f'$
. Similarly, there is a unique
![]() $g':V_1\to W$
in
$g':V_1\to W$
in
![]() $\mathcal D$
such that
$\mathcal D$
such that
![]() $g'=g\circ s$
. So we set
$g'=g\circ s$
. So we set
![]() $\Phi (\underline {f})=g'$
.
$\Phi (\underline {f})=g'$
.
Let
![]() $g':V_1\to W$
be a morphism in
$g':V_1\to W$
be a morphism in
![]() $\mathcal D$
. Then there is a roof
$\mathcal D$
. Then there is a roof
 in
in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
. So we set
$\mathcal D[(\mathcal NQ)^{-1}]$
. So we set
![]() $\Psi (g')=\underline {f}'$
.
$\Psi (g')=\underline {f}'$
.
Note that
![]() $\Psi \Phi (\underline {f})=\underline {f}'$
but the diagram on the right commutes in
$\Psi \Phi (\underline {f})=\underline {f}'$
but the diagram on the right commutes in
![]() $\mathcal D$
. Thus,
$\mathcal D$
. Thus,
![]() $\underline {f}'=\underline {f}$
in
$\underline {f}'=\underline {f}$
in
![]() $\mathcal D[(\mathcal NQ)^{-1}]$
and so
$\mathcal D[(\mathcal NQ)^{-1}]$
and so
![]() $\Psi \Phi (\underline {f})=\underline {f}$
. We see
$\Psi \Phi (\underline {f})=\underline {f}$
. We see
![]() $\Phi \Psi (g') = g'$
since in this case the s from our definition of
$\Phi \Psi (g') = g'$
since in this case the s from our definition of
![]() $\Phi ( \Psi (g) )$
is the identity. Therefore,
$\Phi ( \Psi (g) )$
is the identity. Therefore,
![]() $\Phi = \Psi ^{-1}$
and
$\Phi = \Psi ^{-1}$
and
![]() $\Psi = \Phi ^{-1}$
.
$\Psi = \Phi ^{-1}$
.

Finally, it is straightforward to check that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
preserve addition and send 0 to 0. Thus, we have the desired isomorphism and the proposition holds.
$\Psi $
preserve addition and send 0 to 0. Thus, we have the desired isomorphism and the proposition holds.
3.3 Triangulated equivalences
Here, we show the localization of the derived and new continuous cluster categories are triangulated equivalent to the previous derived and continuous cluster categories.
We recall the construction of the continuous derived category
![]() $\mathcal D_r$
from [Reference Igusa and Todorov15] as modified in [Reference Garcia and Igusa10]. The idea is that
$\mathcal D_r$
from [Reference Igusa and Todorov15] as modified in [Reference Garcia and Igusa10]. The idea is that
![]() $\mathcal D_\pi $
is the limit as
$\mathcal D_\pi $
is the limit as
![]() $n\to \infty $
of
$n\to \infty $
of
![]() $\mathcal D^b(\operatorname {\mathrm {rep}}_k(Q_n))$
where
$\mathcal D^b(\operatorname {\mathrm {rep}}_k(Q_n))$
where
![]() $Q_n$
is the quiver of type
$Q_n$
is the quiver of type
![]() $A_n$
with straight orientation. This is a topological category with a continuous triangulation. The original definition constructed
$A_n$
with straight orientation. This is a topological category with a continuous triangulation. The original definition constructed
![]() $\mathcal D_r$
for any positive real number r as the stable category of a Frobenius category. Here, we take the approach given in [Reference Garcia and Igusa10] which does not involve construction of an auxiliary category.
$\mathcal D_r$
for any positive real number r as the stable category of a Frobenius category. Here, we take the approach given in [Reference Garcia and Igusa10] which does not involve construction of an auxiliary category.
Definition 3.3.1. The object space of
![]() $\mathcal D_r$
is a subset of the plane:
$\mathcal D_r$
is a subset of the plane:
Equivalently,
![]() $x-r<y<x+r$
. We take the discrete topology on the field k and let
$x-r<y<x+r$
. We take the discrete topology on the field k and let
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathcal D_r}(X,Y)=\begin{cases} k, & \text{if } x_1\le x_2< y_1+r \text{ and } y_1\le y_2<x_1+r,\\ 0,& \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathcal D_r}(X,Y)=\begin{cases} k, & \text{if } x_1\le x_2< y_1+r \text{ and } y_1\le y_2<x_1+r,\\ 0,& \text{otherwise.} \end{cases} \end{align*} $$
Thus, for
![]() $X=(x,y)$
, the support of
$X=(x,y)$
, the support of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D_r}(X,-)$
is the half-open rectangle
$\operatorname {\mathrm {Hom}}_{\mathcal D_r}(X,-)$
is the half-open rectangle
and nonzero morphisms are specified by scalars in k. When Y converges to a limit point of this half-open interval, morphisms converge to zero. Then
![]() $\mathcal D_r$
is a topological k-category in the sense that the object and morphism sets are topological spaces and the structure maps of the category (source, target, composition, identity, and scalar multiplication) are continuous.
$\mathcal D_r$
is a topological k-category in the sense that the object and morphism sets are topological spaces and the structure maps of the category (source, target, composition, identity, and scalar multiplication) are continuous.
Following [Reference Garcia and Igusa10, Sec. 4.3], the distinguished triangles in
![]() $\mathcal D_r$
are constructed out of a family of distinguished triangles called universal virtual triangles. For each object
$\mathcal D_r$
are constructed out of a family of distinguished triangles called universal virtual triangles. For each object
![]() $X=(x,y)$
there is a family of distinguished triangles:
$X=(x,y)$
there is a family of distinguished triangles:
for sufficiently small
![]() $\varepsilon>0$
where
$\varepsilon>0$
where
![]() $I_1^\varepsilon X=(x,x+r-\varepsilon )$
,
$I_1^\varepsilon X=(x,x+r-\varepsilon )$
,
![]() $I_2^\varepsilon X=(y+r-\varepsilon ,y)$
and
$I_2^\varepsilon X=(y+r-\varepsilon ,y)$
and
![]() $T^\varepsilon X=(y+r-\varepsilon ,x+r-\varepsilon )$
. Morphisms are given by the indicated scalars. If X has several components, we take the direct sum of the virtual triangles (1) over all components of X. Note that, as
$T^\varepsilon X=(y+r-\varepsilon ,x+r-\varepsilon )$
. Morphisms are given by the indicated scalars. If X has several components, we take the direct sum of the virtual triangles (1) over all components of X. Note that, as
![]() $\varepsilon \to 0$
,
$\varepsilon \to 0$
,
![]() $T^\varepsilon X$
converges to
$T^\varepsilon X$
converges to
![]() $TX$
and
$TX$
and
![]() $T^\varepsilon X \xrightarrow { 1} T X$
converges to the identity morphism on
$T^\varepsilon X \xrightarrow { 1} T X$
converges to the identity morphism on
![]() $TX$
. The objects
$TX$
. The objects
![]() $I_1^\varepsilon X$
,
$I_1^\varepsilon X$
,
![]() $I_2^\varepsilon X$
converge to
$I_2^\varepsilon X$
converge to
![]() $0$
as
$0$
as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
The distinguished triangles in
![]() $\mathcal D_r$
are given as follows. For any morphism
$\mathcal D_r$
are given as follows. For any morphism
![]() $f:X\to Y$
in
$f:X\to Y$
in
![]() $\mathcal D_r$
, we define the distinguished triangle
$\mathcal D_r$
, we define the distinguished triangle
![]() $X\xrightarrow {f} Y\xrightarrow {g} Z\xrightarrow {h} TX$
to be the limit as
$X\xrightarrow {f} Y\xrightarrow {g} Z\xrightarrow {h} TX$
to be the limit as
![]() $\varepsilon \to 0$
of the following pushout diagram.
$\varepsilon \to 0$
of the following pushout diagram.

As
![]() $\varepsilon \to 0$
, the object
$\varepsilon \to 0$
, the object
![]() $Z^\varepsilon $
converges to an object Z. The morphisms
$Z^\varepsilon $
converges to an object Z. The morphisms
![]() $g,h$
also stabilize and the limit is well-defined (see [Reference Garcia and Igusa10] for details.)
$g,h$
also stabilize and the limit is well-defined (see [Reference Garcia and Igusa10] for details.)
In order to define a functor
![]() $G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]\to \mathcal D_\pi $
, we need a slight modification of the functor
$G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]\to \mathcal D_\pi $
, we need a slight modification of the functor
![]() $\iota :{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, (Definition 2.3.2).
$\iota :{\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, (Definition 2.3.2).

Figure 8 In this example,
![]() $Y=Y_1\oplus Y_2$
where
$Y=Y_1\oplus Y_2$
where
![]() $Y_1$
has the same y-coordinate as X. Then
$Y_1$
has the same y-coordinate as X. Then
![]() $Z^\varepsilon =I_1^\varepsilon \oplus Z_1\oplus Z_2^\varepsilon $
. As
$Z^\varepsilon =I_1^\varepsilon \oplus Z_1\oplus Z_2^\varepsilon $
. As
![]() $\varepsilon \to 0$
,
$\varepsilon \to 0$
,
![]() $I_1^\varepsilon $
moves to the right until it becomes
$I_1^\varepsilon $
moves to the right until it becomes
![]() $0$
,
$0$
,
![]() $Z_2^\varepsilon $
moves up to
$Z_2^\varepsilon $
moves up to
![]() $Z_2$
,
$Z_2$
,
![]() $Z_1$
stays where it is. Also,
$Z_1$
stays where it is. Also,
![]() $T^\varepsilon X$
goes to
$T^\varepsilon X$
goes to
![]() $ TX$
. Thus the distinguished triangle is
$ TX$
. Thus the distinguished triangle is
![]() $X\to Y_1\oplus Y_2\to Z_1\oplus Z_2\to TX$
. The support of
$X\to Y_1\oplus Y_2\to Z_1\oplus Z_2\to TX$
. The support of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal D_r}(X,-)$
is shaded.
$\operatorname {\mathrm {Hom}}_{\mathcal D_r}(X,-)$
is shaded.
Definition 3.3.2. Let V be an indecomposable in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
. Let
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]$
. Let
![]() $\mathop {\boldsymbol {\Gamma }}^b(V)=(x,y)$
. Define
$\mathop {\boldsymbol {\Gamma }}^b(V)=(x,y)$
. Define
![]() $G(V):=M(x-y,x+y)$
in
$G(V):=M(x-y,x+y)$
in
![]() $\mathcal D_\pi $
. We define G on morphisms
$\mathcal D_\pi $
. We define G on morphisms
![]() $f:V\to W$
where
$f:V\to W$
where
![]() $V,W$
are indecomposable. Let
$V,W$
are indecomposable. Let
![]() $\iota '(V)=M_I[n]$
, that is,
$\iota '(V)=M_I[n]$
, that is,
![]() $\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(M_I[n])$
and
$\mathop {\boldsymbol {\Gamma }}^b(V)=\mathop {\boldsymbol {\Gamma }}^b(M_I[n])$
and
![]() $M_{I[n]}$
is in position 1 in
$M_{I[n]}$
is in position 1 in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Similarly,
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. Similarly,
![]() $\iota '(W)=M_J[m]$
in position 1. Then
$\iota '(W)=M_J[m]$
in position 1. Then
![]() $\iota '(f)\in \operatorname {\mathrm {Hom}}(M_I[n],M_J[m])=k$
. Hence
$\iota '(f)\in \operatorname {\mathrm {Hom}}(M_I[n],M_J[m])=k$
. Hence
![]() $\iota '(f)=c_{VW}\in k$
. Define
$\iota '(f)=c_{VW}\in k$
. Define
![]() $G(f)$
to be
$G(f)$
to be
![]() $G(f):=c_{VW}\in \operatorname {\mathrm {Hom}}_{\mathcal D_\pi }(G(V),G(W))=k$
. Since both categories are Krull–Schmidt extend G bilinearly.
$G(f):=c_{VW}\in \operatorname {\mathrm {Hom}}_{\mathcal D_\pi }(G(V),G(W))=k$
. Since both categories are Krull–Schmidt extend G bilinearly.
Theorem 3.3.3. When S is finite,
![]() $G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]\to \mathcal D_\pi $
is a triangulated equivalence.
$G:{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal {NQ})^{-1}]\to \mathcal D_\pi $
is a triangulated equivalence.
Proof. One quickly verifies that G induces a bijection on isomorphism classes of objects and bijections on Hom spaces. It remains to show that cones in distinguished triangles are taken to cones in distinguished triangles.
Let
![]() $V \to U \to W\to V[1]$
be a distinguished triangle in
$V \to U \to W\to V[1]$
be a distinguished triangle in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
such that V, U, and W are all nonzero and distinct and V and W are indecomposable. Then this comes from a triangle
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
such that V, U, and W are all nonzero and distinct and V and W are indecomposable. Then this comes from a triangle
![]() $\tilde {V}\to \tilde {U}\to \tilde {W}\to \tilde {V}[1]$
in
$\tilde {V}\to \tilde {U}\to \tilde {W}\to \tilde {V}[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and so
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
and so
![]() $U=U_1\oplus U_2$
where
$U=U_1\oplus U_2$
where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are indecomposable and at most one is 0. Furthermore,
$U_2$
are indecomposable and at most one is 0. Furthermore,
![]() $\tilde {V}$
and
$\tilde {V}$
and
![]() $\tilde {W}$
are indecomposable. Then by Theorem 1.2.6, there is a rectangle or almost complete rectangle in the AR-space of
$\tilde {W}$
are indecomposable. Then by Theorem 1.2.6, there is a rectangle or almost complete rectangle in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
whose sides have slopes
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
whose sides have slopes
![]() $\pm (1,1)$
and whose left and right corner are
$\pm (1,1)$
and whose left and right corner are
![]() $\tilde {V}$
and
$\tilde {V}$
and
![]() $\tilde {W}$
, respectively. Thus,
$\tilde {W}$
, respectively. Thus,
![]() $\tilde {U}$
has at most two indecomposable summands.
$\tilde {U}$
has at most two indecomposable summands.
Since U is not 0,
![]() $\mathop {\boldsymbol {\Gamma }}^b \tilde {V}, \mathop {\boldsymbol {\Gamma }}^b\tilde {W}$
, and
$\mathop {\boldsymbol {\Gamma }}^b \tilde {V}, \mathop {\boldsymbol {\Gamma }}^b\tilde {W}$
, and
![]() $\mathop {\boldsymbol {\Gamma }}^b \tilde {U}$
form the corners of a rectangle in
$\mathop {\boldsymbol {\Gamma }}^b \tilde {U}$
form the corners of a rectangle in
![]() ${\mathbb {R}}^2$
whose left and right corners are
${\mathbb {R}}^2$
whose left and right corners are
![]() $\mathop {\boldsymbol {\Gamma }}^b \tilde {V}$
and
$\mathop {\boldsymbol {\Gamma }}^b \tilde {V}$
and
![]() $\mathop {\boldsymbol {\Gamma }}^b\tilde {W}$
, respectively. Since
$\mathop {\boldsymbol {\Gamma }}^b\tilde {W}$
, respectively. Since
![]() $U\neq 0$
no more than one indecomposable summand of
$U\neq 0$
no more than one indecomposable summand of
![]() $\tilde {U}$
may be sent to
$\tilde {U}$
may be sent to
![]() ${\mathbb {R}}\times (-\frac {\pi }{2},\frac {\pi }{2})$
by
${\mathbb {R}}\times (-\frac {\pi }{2},\frac {\pi }{2})$
by
![]() $\mathop {\boldsymbol {\Gamma }}^b$
.
$\mathop {\boldsymbol {\Gamma }}^b$
.
We give the coordinates of the image of
![]() $\mathop {\boldsymbol {\Gamma }}^b$
of the lifts of each indecomposable and compute G on each of our indecomposables below. First, a few notes. If one of
$\mathop {\boldsymbol {\Gamma }}^b$
of the lifts of each indecomposable and compute G on each of our indecomposables below. First, a few notes. If one of
![]() $\tilde {U}_1$
or
$\tilde {U}_1$
or
![]() $\tilde {U}_2$
is 0 then there is no
$\tilde {U}_2$
is 0 then there is no
![]() $\mathop {\boldsymbol {\Gamma }}^b$
of that indecomposable. If one of
$\mathop {\boldsymbol {\Gamma }}^b$
of that indecomposable. If one of
![]() $U_1$
or
$U_1$
or
![]() $U_2$
is 0 then G of that indecomposable will be 0. However, we compute
$U_2$
is 0 then G of that indecomposable will be 0. However, we compute
![]() $\mathop {\boldsymbol {\Gamma }}^b$
and G for both possibilities in each case for when those situations arise.
$\mathop {\boldsymbol {\Gamma }}^b$
and G for both possibilities in each case for when those situations arise.
 $$ \begin{align*} {\mathop{\boldsymbol{\Gamma}}}^b \tilde{V}\,& =(x,y), & GV\, &= M(x-y,x+y), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{U}_1& =(x+\alpha, y-\alpha), &GU_1 &= M(x-y+2\alpha,x+y), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{U}_2& =(x+\beta, y+\beta), &GU_2 &= M(x-y,x+y+2\beta), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{W}&= (x+\alpha+\beta,y-\alpha+\beta), &GW &= M(x-y+2\alpha,x+y+2\beta). \end{align*} $$
$$ \begin{align*} {\mathop{\boldsymbol{\Gamma}}}^b \tilde{V}\,& =(x,y), & GV\, &= M(x-y,x+y), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{U}_1& =(x+\alpha, y-\alpha), &GU_1 &= M(x-y+2\alpha,x+y), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{U}_2& =(x+\beta, y+\beta), &GU_2 &= M(x-y,x+y+2\beta), \\ {\mathop{\boldsymbol{\Gamma}}}^b \tilde{W}&= (x+\alpha+\beta,y-\alpha+\beta), &GW &= M(x-y+2\alpha,x+y+2\beta). \end{align*} $$
By the description in [Reference Igusa and Todorov15, Sec. 2.5] the four indecomposables in the image of G also form a distinguished triangle. In particular, if
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
are 0 then the distinguished triangles in
$\beta $
are 0 then the distinguished triangles in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
and
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
and
![]() $\mathcal D_\pi $
are split/trivial. With the same techniques used to prove Theorems 2.2.9 and 2.3.5, we see that G takes cones in distinguished triangles to cones in distinguished triangles.
$\mathcal D_\pi $
are split/trivial. With the same techniques used to prove Theorems 2.2.9 and 2.3.5, we see that G takes cones in distinguished triangles to cones in distinguished triangles.
Recall from [Reference Igusa and Todorov15] that
![]() $\mathcal C_\pi $
is the orbit category of
$\mathcal C_\pi $
is the orbit category of
![]() $\mathcal D_\pi $
given by the almost-shift functor on the double of
$\mathcal D_\pi $
given by the almost-shift functor on the double of
![]() $\mathcal D_\pi $
as described in Definitions 3.1.1 and 3.1.2.
$\mathcal D_\pi $
as described in Definitions 3.1.1 and 3.1.2.
Theorem 3.3.4. Assume
![]() $A_{{\mathbb {R}},S}$
has finitely many sinks and sources. Then there is a triangulated equivalence
$A_{{\mathbb {R}},S}$
has finitely many sinks and sources. Then there is a triangulated equivalence
![]() $H:{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]\to \mathcal C_\pi $
.
$H:{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]\to \mathcal C_\pi $
.
Proof. Let
![]() $\mathcal C$
be the orbit category of
$\mathcal C$
be the orbit category of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
via doubling and almost-shift as in Definitions 3.1.1 and 3.1.2. Since
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
via doubling and almost-shift as in Definitions 3.1.1 and 3.1.2. Since
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
is triangulated equivalent to
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
is triangulated equivalent to
![]() $\mathcal D_\pi $
, by Theorem 3.3.3, we see there must be a triangulated equivalence
$\mathcal D_\pi $
, by Theorem 3.3.3, we see there must be a triangulated equivalence
![]() $H_2:\mathcal C\to \mathcal C_\pi $
. We define a triangulated equivalence
$H_2:\mathcal C\to \mathcal C_\pi $
. We define a triangulated equivalence
![]() $H_1:{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}] \to \mathcal C$
. Afterwards we let
$H_1:{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}] \to \mathcal C$
. Afterwards we let
![]() $H = H_2 \circ H_1$
.
$H = H_2 \circ H_1$
.
Since
![]() $\mathcal C$
is an orbit category we choose our fundamental domain. We choose those indecomposables V that come from an indecomposable
$\mathcal C$
is an orbit category we choose our fundamental domain. We choose those indecomposables V that come from an indecomposable
![]() $\tilde {V}$
in
$\tilde {V}$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
![]() $(\alpha ,\beta )=\mathop {\boldsymbol {\Gamma }}^b V$
satisfy
$(\alpha ,\beta )=\mathop {\boldsymbol {\Gamma }}^b V$
satisfy
![]() $ -\frac {\pi }{2} < \beta < \frac {\pi }{2}$
and
$ -\frac {\pi }{2} < \beta < \frac {\pi }{2}$
and
![]() $ \beta \leq \alpha < \pi - \beta. $
This is precisely the image of the 0th degree indecomposables in
$ \beta \leq \alpha < \pi - \beta. $
This is precisely the image of the 0th degree indecomposables in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, excluding the injective indecomposables from
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, excluding the injective indecomposables from
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
Recall
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
has the same objects as
${\mathcal {C}(A_{{\mathbb {R}},S})}$
has the same objects as
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
but different isomorphism classes and similarly for
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
but different isomorphism classes and similarly for
![]() $\mathcal C$
and
$\mathcal C$
and
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
, respectively. For each indecomposable V in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
, respectively. For each indecomposable V in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
there exists a
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
there exists a
![]() $\tilde {V}$
in
$\tilde {V}$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
in degree 0 such that after taking the orbit,
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
in degree 0 such that after taking the orbit,
![]() $\tilde {V}$
is sent to V in the localization of
$\tilde {V}$
is sent to V in the localization of
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We define
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We define
![]() $H_1 V$
to be the indecomposable in
$H_1 V$
to be the indecomposable in
![]() $\mathcal C$
that comes from an indecomposable
$\mathcal C$
that comes from an indecomposable
![]() $\hat {V}$
in
$\hat {V}$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
that also comes from
${\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
that also comes from
![]() $\tilde {V}$
in
$\tilde {V}$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.
Let V and W be indecomposables in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. We show
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. We show
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)\cong k$
if and only if
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)\cong k$
if and only if
![]() $\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V, H_1 W)\cong k$
and similarly for 0 hom spaces. First, there are
$\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V, H_1 W)\cong k$
and similarly for 0 hom spaces. First, there are
![]() $\tilde {V}$
and
$\tilde {V}$
and
![]() $\tilde {W}$
in degree 0 in
$\tilde {W}$
in degree 0 in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that are sent to V and W after taking the orbit and localization. Then either
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
that are sent to V and W after taking the orbit and localization. Then either
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V},\tilde {W})\cong k$
or
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V},\tilde {W})\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V},\tilde {W}[1])\cong k$
. Let
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V},\tilde {W}[1])\cong k$
. Let
![]() $\tilde {V}_1$
be an indecomposable in
$\tilde {V}_1$
be an indecomposable in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
such that
![]() $\mathop {\boldsymbol {\Gamma }}^b \tilde {V}_1=\mathop {\boldsymbol {\Gamma }}^b \tilde {V}$
and
$\mathop {\boldsymbol {\Gamma }}^b \tilde {V}_1=\mathop {\boldsymbol {\Gamma }}^b \tilde {V}$
and
![]() $\tilde {V}_1$
has position 1. If
$\tilde {V}_1$
has position 1. If
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})$
and
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})$
and
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1])$
were both 0 then
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1])$
were both 0 then
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)$
would be 0. Since this is not the case,
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)$
would be 0. Since this is not the case,
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})\cong k$
or
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1])\cong k$
. Then
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1])\cong k$
. Then
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(\hat {V},\hat {W})\cong k$
or
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(\hat {V},\hat {W})\cong k$
or
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(\hat {V},\hat {W}[1])\cong k$
. In either case
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(\hat {V},\hat {W}[1])\cong k$
. In either case
![]() $\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)\cong k$
. In the case that
$\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)\cong k$
. In the case that
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)=0$
we have
$\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)=0$
we have
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})=0=\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1]$
and so
$\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W})=0=\operatorname {\mathrm {Hom}}_{{\mathcal {D}^b(A_{{\mathbb {R}},S})}}(\tilde {V}_1,\tilde {W}[1]$
and so
![]() $\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)=0$
as well.
$\operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)=0$
as well.
Now, as in Definition 2.3.2 for our triangulated equivalence of derived categories for different continuous quivers of type A, we can choose representatives from each isomorphism class of indecomposables and fix isomorphisms between indecomposables and their respective representatives. With such a construction we set
![]() $H_1 (\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)) := \operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)$
for each pair of representatives V and W in
$H_1 (\operatorname {\mathrm {Hom}}_{{\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]}(V,W)) := \operatorname {\mathrm {Hom}}_{\mathcal C}(H_1 V,H_1 W)$
for each pair of representatives V and W in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. This gives us an equivalence of categories but must still check triangles.
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
. This gives us an equivalence of categories but must still check triangles.
However, each distinguished triangle
![]() $U\to V\to W\to U[1]$
in
$U\to V\to W\to U[1]$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
comes from a triangle
${\mathcal {C}(A_{{\mathbb {R}},S})}[(\mathcal NQ)^{-1}]$
comes from a triangle
![]() $\tilde {U}\to \tilde {V}\to \tilde {W}\to \tilde {U}[1]$
in the doubling of
$\tilde {U}\to \tilde {V}\to \tilde {W}\to \tilde {U}[1]$
in the doubling of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. But after taking localization and then the orbit, the image of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. But after taking localization and then the orbit, the image of
![]() $\tilde {U}\to \tilde {V}\to \tilde {W}\to \tilde {U}$
is a distinguished triangle in
$\tilde {U}\to \tilde {V}\to \tilde {W}\to \tilde {U}$
is a distinguished triangle in
![]() $\mathcal C$
. This is, by definition, precisely the image of
$\mathcal C$
. This is, by definition, precisely the image of
![]() $U\to V\to W\to U[1]$
under
$U\to V\to W\to U[1]$
under
![]() $H_1$
. Thus,
$H_1$
. Thus,
![]() $H_1$
is a triangulated equivalence and so is
$H_1$
is a triangulated equivalence and so is
![]() $H=H_2\circ H_1$
.
$H=H_2\circ H_1$
.
4 Cluster theories
We introduce the notion of cluster theories (Definition 4.1.1). Cluster structures in the sense of [Reference Buan, Iyama, Reiten and Scott3] satisfy conditions of cluster theories, however, there are very natural cluster theories which do not have cluster structure. We prove the existence of several embeddings of cluster theories (Definition 4.1.9).
4.1 Cluster theories:
 $\mathscr T_{\mathbf P}(\mathcal C)$
$\mathscr T_{\mathbf P}(\mathcal C)$
This subsection is dedicated to providing a framework in which to talk about embedding cluster theories without requiring a functor between cluster categories. It should be noted that cluster theories are not necessarily cluster structures [Reference Buan, Marsh, Reineke, Reiten and Todorov4], [Reference Caldero, Chapoton and Schiffler5], [Reference Holm and Jørgensen12]. While cluster structures require each indecomposable in a cluster be mutable and mutation be given by approximations, cluster theories do not make such a requirement. Instead, we require that if an indecomposable is mutable then there is a unique choice for a replacement. In practice this is often related to some homological or other algebraic property.
Definition 4.1.1. Let
![]() $\mathcal C$
be a skeletally small Krull–Schmidt additive category in which there exists a pairwise compatibility condition
$\mathcal C$
be a skeletally small Krull–Schmidt additive category in which there exists a pairwise compatibility condition
![]() $\mathbf P$
on (isomorphism classes of) indecomposable objects. A set T of (isomorphism classes of) indecomposable objects is called maximally
$\mathbf P$
on (isomorphism classes of) indecomposable objects. A set T of (isomorphism classes of) indecomposable objects is called maximally
![]() $\mathbf P$
-compatible if for each
$\mathbf P$
-compatible if for each
![]() $Y\notin T$
there exists
$Y\notin T$
there exists
![]() $X\in T$
such that X and Y are not
$X\in T$
such that X and Y are not
![]() $\mathbf P$
-compatible. Suppose also that for each (isomorphism class of) indecomposable X in a maximally
$\mathbf P$
-compatible. Suppose also that for each (isomorphism class of) indecomposable X in a maximally
![]() $\mathbf P$
-compatible set T there exists none or one (isomorphism class of) indecomposable Y such that
$\mathbf P$
-compatible set T there exists none or one (isomorphism class of) indecomposable Y such that
![]() $\{X,Y\}$
is not
$\{X,Y\}$
is not
![]() $\mathbf P$
-compatible but
$\mathbf P$
-compatible but
![]() $(T\setminus \{X\})\cup \{Y\}$
is maximally
$(T\setminus \{X\})\cup \{Y\}$
is maximally
![]() $\mathbf P$
-compatible. Then
$\mathbf P$
-compatible. Then
-
• We call maximally
 $\mathbf P$
-compatible sets
$\mathbf P$
-compatible sets
 $\mathbf P$
-clusters.
$\mathbf P$
-clusters. -
• We call a function of the form
 $\mu :T\to (T\setminus \{X\})\cup \{Y\}$
such that
$\mu :T\to (T\setminus \{X\})\cup \{Y\}$
such that
 $\mu Z=Z$
when
$\mu Z=Z$
when
 $Z\neq X$
and
$Z\neq X$
and
 $\mu X=Y$
a
$\mu X=Y$
a
 $\mathbf P$
-mutation or
$\mathbf P$
-mutation or
 $\mathbf P$
-mutation at X.
$\mathbf P$
-mutation at X. -
• If there exists a
 $\mathbf P$
-mutation
$\mathbf P$
-mutation
 $\mu :T\to (T\setminus \{X\})\cup \{Y\}$
, we say
$\mu :T\to (T\setminus \{X\})\cup \{Y\}$
, we say
 $X\in T$
is
$X\in T$
is
 $\mathbf P$
-mutable.
$\mathbf P$
-mutable. -
• The subcategory
 $\mathscr T_{\mathbf P}(\mathcal C)$
of
$\mathscr T_{\mathbf P}(\mathcal C)$
of
 $\mathcal S\text {et}$
whose objects are
$\mathcal S\text {et}$
whose objects are
 $\mathbf P$
-clusters and whose morphisms are generated by
$\mathbf P$
-clusters and whose morphisms are generated by
 $\mathbf P$
-mutations (and identity maps) is called the
$\mathbf P$
-mutations (and identity maps) is called the
 $\mathbf P$
-cluster theory of
$\mathbf P$
-cluster theory of
 $\mathcal C$
.
$\mathcal C$
. -
• The inclusion functor
 $\mathscr T_{\mathbf P}(\mathcal C)\hookrightarrow \mathcal S\text {et}$
will be denoted
$\mathscr T_{\mathbf P}(\mathcal C)\hookrightarrow \mathcal S\text {et}$
will be denoted
 $I_{\mathbf P,\mathcal C}$
.
$I_{\mathbf P,\mathcal C}$
. -
• Since
 $\mathbf P$
-mutations are invertible,
$\mathbf P$
-mutations are invertible,
 $\mathscr T_{\mathbf P}(\mathcal C)$
is a groupoid.
$\mathscr T_{\mathbf P}(\mathcal C)$
is a groupoid.
We use
![]() $\mathbf P$
to indicate a general cluster theory given by an unspecified pairwise compatibility condition. Other more descriptive letters will be used for specific cases. We use “Krull–Schmidt category” to mean “skeletally small Krull–Schmidt additive category.”
$\mathbf P$
to indicate a general cluster theory given by an unspecified pairwise compatibility condition. Other more descriptive letters will be used for specific cases. We use “Krull–Schmidt category” to mean “skeletally small Krull–Schmidt additive category.”
Remark 4.1.2. Let
![]() $\mathcal C$
be a Krull–Schmidt category and
$\mathcal C$
be a Krull–Schmidt category and
![]() $\mathbf P$
a pairwise compatibility condition on the indecomposable objects in
$\mathbf P$
a pairwise compatibility condition on the indecomposable objects in
![]() $\mathcal C$
. If the
$\mathcal C$
. If the
![]() $\mathbf P$
-cluster theory of
$\mathbf P$
-cluster theory of
![]() $\mathcal C$
exists then it is determined by
$\mathcal C$
exists then it is determined by
![]() $\mathbf P$
. Thus, we say that
$\mathbf P$
. Thus, we say that
![]() $\mathbf P$
induces the
$\mathbf P$
induces the
![]() $\mathbf P$
-cluster theory of
$\mathbf P$
-cluster theory of
![]() $\mathcal C$
.
$\mathcal C$
.
Remark 4.1.3. Let
![]() $\mathcal C$
be a Krull–Schmidt category and
$\mathcal C$
be a Krull–Schmidt category and
![]() $\mathbf P$
a pairwise compatibility condition on
$\mathbf P$
a pairwise compatibility condition on
![]() $\text {Ind}(\mathcal C)$
. Using Zorn’s lemma, we note that there exist maximally
$\text {Ind}(\mathcal C)$
. Using Zorn’s lemma, we note that there exist maximally
![]() $\mathbf P$
-compatible sets of indecomposables of
$\mathbf P$
-compatible sets of indecomposables of
![]() $\mathcal C$
.
$\mathcal C$
.
Definition 4.1.4. Let
![]() $\mathcal C$
be a Krull–Schmidt category and
$\mathcal C$
be a Krull–Schmidt category and
![]() $\mathbf P$
a pairwise compatibility condition such that
$\mathbf P$
a pairwise compatibility condition such that
![]() $\mathbf P$
induces the
$\mathbf P$
induces the
![]() $\mathbf P$
-cluster theory of
$\mathbf P$
-cluster theory of
![]() $\mathcal C$
. If for every
$\mathcal C$
. If for every
![]() $\mathbf P$
-cluster T and
$\mathbf P$
-cluster T and
![]() $X\in T$
there is a
$X\in T$
there is a
![]() $\mathbf P$
-mutation at X then we call
$\mathbf P$
-mutation at X then we call
![]() $\mathscr T_{\mathbf P}(\mathcal C)$
the tilting
$\mathscr T_{\mathbf P}(\mathcal C)$
the tilting
![]() $\mathbf P$
-cluster theory.
$\mathbf P$
-cluster theory.
Remark 4.1.5. Sometimes an indecomposable X in a
![]() $\mathbf P$
-cluster T may not be
$\mathbf P$
-cluster T may not be
![]() $\mathbf P$
-mutable. However, we do not call X frozen. This is because in the next (and final) paper of this series, a continuous generalization of mutation is introduced in which some X which are not
$\mathbf P$
-mutable. However, we do not call X frozen. This is because in the next (and final) paper of this series, a continuous generalization of mutation is introduced in which some X which are not
![]() $\mathbf P$
-mutable may be mutated in the generalized type of mutation. The word frozen, then, should be reserved for indecomposables we have intentionally frozen.
$\mathbf P$
-mutable may be mutated in the generalized type of mutation. The word frozen, then, should be reserved for indecomposables we have intentionally frozen.
Proposition 4.1.6. Let
![]() $\mathcal C$
be a Krull–Schmidt category and
$\mathcal C$
be a Krull–Schmidt category and
![]() $\mathbf P$
a pairwise compatibility condition such that
$\mathbf P$
a pairwise compatibility condition such that
![]() $\mathbf P$
induces the
$\mathbf P$
induces the
![]() $\mathbf P$
-cluster theory of
$\mathbf P$
-cluster theory of
![]() $\mathcal C$
. Let T be a
$\mathcal C$
. Let T be a
![]() $\mathbf P$
-cluster and
$\mathbf P$
-cluster and
![]() $X\in T$
such that there exists a
$X\in T$
such that there exists a
![]() $\mathbf P$
-mutation
$\mathbf P$
-mutation
![]() $T\to (T\setminus \{X\})\cup \{Y\}$
. Then there exists a
$T\to (T\setminus \{X\})\cup \{Y\}$
. Then there exists a
![]() $\mathbf P$
-mutation
$\mathbf P$
-mutation
![]() $T'=(T\setminus \{X\})\cup \{Y\}\to (T'\setminus \{Y\})\cup \{X\}$
.
$T'=(T\setminus \{X\})\cup \{Y\}\to (T'\setminus \{Y\})\cup \{X\}$
.
Proof. We know
![]() $\{Y,X\}$
is not
$\{Y,X\}$
is not
![]() $\mathbf P$
-compatible but
$\mathbf P$
-compatible but
![]() $T=(T'\setminus \{Y\})\cup \{X\}$
is a
$T=(T'\setminus \{Y\})\cup \{X\}$
is a
![]() $\mathbf P$
-cluster.
$\mathbf P$
-cluster.
Example 4.1.7. In [Reference Caldero, Chapoton and Schiffler5], the authors describe the
![]() $A_n$
cluster structure as triangulations of the
$A_n$
cluster structure as triangulations of the
![]() $(n+3)$
-gon. This arises in a category
$(n+3)$
-gon. This arises in a category
![]() $\mathcal C(A_n)$
whose indecomposable objects are diagonals of the
$\mathcal C(A_n)$
whose indecomposable objects are diagonals of the
![]() $(n+3)$
-gon and compatibility is given by two diagonals not crossing.
$(n+3)$
-gon and compatibility is given by two diagonals not crossing.
Let
![]() $\mathbf N_n$
be the pairwise compatibility condition of not crossing. Let
$\mathbf N_n$
be the pairwise compatibility condition of not crossing. Let
![]() $\mathbf N_n$
-clusters be maximal sets of noncrossing diagonals and let
$\mathbf N_n$
-clusters be maximal sets of noncrossing diagonals and let
![]() $\mathbf N_n$
-mutations be the exchanging of one diagonal for another to produce a different triangulation. This is the tilting
$\mathbf N_n$
-mutations be the exchanging of one diagonal for another to produce a different triangulation. This is the tilting
![]() $\mathbf N_n$
-cluster theory of
$\mathbf N_n$
-cluster theory of
![]() $\mathcal C(A_n)$
.
$\mathcal C(A_n)$
.
Example 4.1.8. Our next example of a cluster theory is the cluster structure defined in [Reference Buan, Marsh, Reineke, Reiten and Todorov4] for cluster categories
![]() $\mathcal C(Q)$
of Dynkin quivers Q. Consider clusters in such cluster categories like those described in [Reference Buan, Marsh, Reineke, Reiten and Todorov4] as maximally rigid sets of indecomposables instead of the subcategories generated by those indecomposables.
$\mathcal C(Q)$
of Dynkin quivers Q. Consider clusters in such cluster categories like those described in [Reference Buan, Marsh, Reineke, Reiten and Todorov4] as maximally rigid sets of indecomposables instead of the subcategories generated by those indecomposables.
We define our pairwise compatibility condition
![]() $\mathbf R$
to be rigidity (
$\mathbf R$
to be rigidity (
![]() $\operatorname {\mathrm {Ext}}^1$
-orthogonality). Then the
$\operatorname {\mathrm {Ext}}^1$
-orthogonality). Then the
![]() $\mathbf R$
-clusters are maximally rigid sets of indecomposables in
$\mathbf R$
-clusters are maximally rigid sets of indecomposables in
![]() $\mathcal C(Q)$
and
$\mathcal C(Q)$
and
![]() $\mathbf R$
-mutations are traditional cluster tilting in
$\mathbf R$
-mutations are traditional cluster tilting in
![]() $\mathcal C(Q)$
. This yields the tilting
$\mathcal C(Q)$
. This yields the tilting
![]() $\mathbf R$
-cluster theory of
$\mathbf R$
-cluster theory of
![]() $\mathcal C(Q)$
.
$\mathcal C(Q)$
.
Definition 4.1.9. Let
![]() $\mathcal C$
and
$\mathcal C$
and
![]() $\mathcal D$
be two Krull–Schmidt categories with respective pairwise compatibility conditions
$\mathcal D$
be two Krull–Schmidt categories with respective pairwise compatibility conditions
![]() $\mathbf P$
and
$\mathbf P$
and
![]() $\mathbf Q$
. Suppose these compatibility conditions induce the
$\mathbf Q$
. Suppose these compatibility conditions induce the
![]() $\mathbf P$
-cluster theory and
$\mathbf P$
-cluster theory and
![]() $\mathbf Q$
-cluster theory of
$\mathbf Q$
-cluster theory of
![]() $\mathcal C$
and
$\mathcal C$
and
![]() $\mathcal D$
, respectively.
$\mathcal D$
, respectively.
Suppose there exists a functor
![]() $F:\mathscr T_{\mathbf P}(\mathcal C) \to \mathscr T_{\mathbf Q}(\mathcal D)$
such that F is an injection on objects and an injection from
$F:\mathscr T_{\mathbf P}(\mathcal C) \to \mathscr T_{\mathbf Q}(\mathcal D)$
such that F is an injection on objects and an injection from
![]() $\mathbf P$
-mutations to
$\mathbf P$
-mutations to
![]() $\mathbf Q$
-mutations. Suppose also there is a natural transformation
$\mathbf Q$
-mutations. Suppose also there is a natural transformation
![]() $\eta : I_{\mathbf P,\mathcal C} \to I_{\mathbf Q, \mathcal D}\circ F$
whose morphisms
$\eta : I_{\mathbf P,\mathcal C} \to I_{\mathbf Q, \mathcal D}\circ F$
whose morphisms
![]() $\eta _T: I_{\mathbf P,\mathcal C}(T) \to I_{\mathbf Q, \mathcal D}\circ F(T)$
are all injections. Then we call
$\eta _T: I_{\mathbf P,\mathcal C}(T) \to I_{\mathbf Q, \mathcal D}\circ F(T)$
are all injections. Then we call
![]() $(F,\eta ):\mathscr T_{\mathbf P}(\mathcal C) \to \mathscr T_{\mathbf Q}(\mathcal D)$
an embedding of cluster theories.
$(F,\eta ):\mathscr T_{\mathbf P}(\mathcal C) \to \mathscr T_{\mathbf Q}(\mathcal D)$
an embedding of cluster theories.
4.2 g-vectors
We follow Jørgensen and Yakimov in [Reference Jørgensen and Yakimov16] with the following definition.
Definition 4.2.1. Denote by
![]() $\mathcal P$
the collection of indecomposable objects in
$\mathcal P$
the collection of indecomposable objects in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
isomorphic to the images in
${\mathcal {C}(A_{{\mathbb {R}},S})}$
isomorphic to the images in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
of projective indecomposables in
${\mathcal {C}(A_{{\mathbb {R}},S})}$
of projective indecomposables in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Let V be an indecomposable in
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Let V be an indecomposable in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We define the g-vector or index of V to be the element
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We define the g-vector or index of V to be the element
![]() $g_V:=[P_V]-[Q_V]$
in
$g_V:=[P_V]-[Q_V]$
in
![]() $K_0^{\text {split}}(Add \mathcal P)$
such that
$K_0^{\text {split}}(Add \mathcal P)$
such that
![]() $Q_V\to P_V\to V\to Q_V[1]$
is a distinguished triangle in
$Q_V\to P_V\to V\to Q_V[1]$
is a distinguished triangle in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
that comes from the projective resolution of V.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
that comes from the projective resolution of V.
Definition 4.2.2. Let
![]() $[A]=\Sigma m_i[A_i]$
and
$[A]=\Sigma m_i[A_i]$
and
![]() $[B]=\Sigma n_j[B_j]$
be elements of
$[B]=\Sigma n_j[B_j]$
be elements of
![]() ${K_0^{\text {split}}({\mathcal {C}(A_{{\mathbb {R}},S})})}$
where the
${K_0^{\text {split}}({\mathcal {C}(A_{{\mathbb {R}},S})})}$
where the
![]() $A_i$
’s and
$A_i$
’s and
![]() $B_j$
’s are indecomposable. The Euler bilinear form
$B_j$
’s are indecomposable. The Euler bilinear form
![]() $\langle [A]\, ,\, [B]\rangle $
is defined:
$\langle [A]\, ,\, [B]\rangle $
is defined:
 $$ \begin{align*} \langle [A]\, ,\, [B] \rangle := \sum_i \sum_j \langle [A_i]\, ,\, [B_j] \rangle= \sum_i \sum_j(m_i\cdot n_j) (\dim_k\operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(A_i,B_j). \end{align*} $$
$$ \begin{align*} \langle [A]\, ,\, [B] \rangle := \sum_i \sum_j \langle [A_i]\, ,\, [B_j] \rangle= \sum_i \sum_j(m_i\cdot n_j) (\dim_k\operatorname{\mathrm{Hom}}_{{\mathcal{C}(A_{{\mathbb{R}},S})}}(A_i,B_j). \end{align*} $$
Since
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
is Krull–Schmidt, this is always a finite sum and thus well-defined.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
is Krull–Schmidt, this is always a finite sum and thus well-defined.
Definition 4.2.3. We say g-vectors
![]() $[P_V]-[Q_V]$
and
$[P_V]-[Q_V]$
and
![]() $[P_W]-[Q_W]$
are
$[P_W]-[Q_W]$
are
![]() $\mathbf E$
-compatible if
$\mathbf E$
-compatible if
We call this compatibility
![]() $\mathbf E$
-compatibility to align better with §4.1, where we introduced the general definition of a cluster theory (Definition 4.1.1).
$\mathbf E$
-compatibility to align better with §4.1, where we introduced the general definition of a cluster theory (Definition 4.1.1).
Proposition 4.2.4. Let
![]() $g_V=[P_V]-[Q_V]$
and
$g_V=[P_V]-[Q_V]$
and
![]() $g_W=[P_W]-[Q_W]$
be g-vectors of indecomposables V and W in
$g_W=[P_W]-[Q_W]$
be g-vectors of indecomposables V and W in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
, both in degree 0. Consider V and W as images of the composite
${\mathcal {C}(A_{{\mathbb {R}},S})}$
, both in degree 0. Consider V and W as images of the composite
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})\hookrightarrow {\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})\hookrightarrow {\mathcal {D}^b(A_{{\mathbb {R}},S})}\to {\mathcal {C}(A_{{\mathbb {R}},S})}$
. Then
![]() $g_V$
and
$g_V$
and
![]() $g_W$
are not
$g_W$
are not
![]() $\mathbf E$
-compatible if and only if there is an extension
$\mathbf E$
-compatible if and only if there is an extension
![]() $V\hookrightarrow U \twoheadrightarrow W$
or
$V\hookrightarrow U \twoheadrightarrow W$
or
![]() $W\hookrightarrow U\twoheadrightarrow V$
in
$W\hookrightarrow U\twoheadrightarrow V$
in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
Proof. Let
![]() $P_V$
,
$P_V$
,
![]() $P_W$
,
$P_W$
,
![]() $Q_V$
, and
$Q_V$
, and
![]() $Q_W$
be the projectives in
$Q_W$
be the projectives in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose image is in the isomorphism classes indicated by the g-vectors. If there is an extension
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose image is in the isomorphism classes indicated by the g-vectors. If there is an extension
![]() $V\hookrightarrow U\twoheadrightarrow W$
in
$V\hookrightarrow U\twoheadrightarrow W$
in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
then there is a nontrivial morphism
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
then there is a nontrivial morphism
![]() $W\to V[1]$
in
$W\to V[1]$
in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. By Theorem 1.1.9 there is, up to scaling and isomorphism, a unique extension. This extension exists because there is a morphism
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
. By Theorem 1.1.9 there is, up to scaling and isomorphism, a unique extension. This extension exists because there is a morphism
![]() $Q_W \to P_V$
that does not factor through
$Q_W \to P_V$
that does not factor through
![]() $Q_V\oplus P_W$
.
$Q_V\oplus P_W$
.
By the proof of [Reference Igusa, Rock and Todorov14, Prop. 3.2.4], we see this means there must be some indecomposable summand of
![]() $Q_W$
that maps to at least one indecomposable summand of
$Q_W$
that maps to at least one indecomposable summand of
![]() $P_V$
but does not factor through
$P_V$
but does not factor through
![]() $Q_V$
or
$Q_V$
or
![]() $P_W$
. By Theorem 1.1.7,
$P_W$
. By Theorem 1.1.7,
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is hereditary. So,
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
is hereditary. So,
![]() $Q_W$
is a subrepresentation of
$Q_W$
is a subrepresentation of
![]() $P_W$
and
$P_W$
and
![]() $Q_V$
is a subrepresentation of
$Q_V$
is a subrepresentation of
![]() $P_V$
. Thus,
$P_V$
. Thus,
![]() $\langle [P_V]-[Q_V]\, ,\, [P_W]-[Q_W] \rangle <0$
.
$\langle [P_V]-[Q_V]\, ,\, [P_W]-[Q_W] \rangle <0$
.
If we start with incompatible g-vectors then we reverse the argument and see that, up to symmetry, there is a morphism
![]() $Q_W\to P_V$
that does not factor through
$Q_W\to P_V$
that does not factor through
![]() $Q_V\oplus P_W$
. Thus there is an extension
$Q_V\oplus P_W$
. Thus there is an extension
![]() $V\hookrightarrow U\twoheadrightarrow W$
in
$V\hookrightarrow U\twoheadrightarrow W$
in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
.
Proposition 4.2.5. Let V and W be indecomposable objects in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
in the 0th degree. Then the g-vectors
${\mathcal {C}(A_{{\mathbb {R}},S})}$
in the 0th degree. Then the g-vectors
![]() $[P_V]-[Q_V]$
and
$[P_V]-[Q_V]$
and
![]() $[P_W]-[Q_W]$
are not
$[P_W]-[Q_W]$
are not
![]() $\mathbf E$
-compatible if and only if there is a rectangle or almost complete rectangle in the AR-space of
$\mathbf E$
-compatible if and only if there is a rectangle or almost complete rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, as a subspace of the AR-space of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, as a subspace of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, whose sides have slopes
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, whose sides have slopes
![]() $\pm (1,1)$
and whose left and right corners are V and W or W and V.
$\pm (1,1)$
and whose left and right corners are V and W or W and V.
Proof. Without loss of generality suppose V is the left corner and W is the right corner of a rectangle or almost complete rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then by Theorem 1.2.6 there is a distinguished triangle
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then by Theorem 1.2.6 there is a distinguished triangle
![]() $V\to U\to W\to V[1]$
. This corresponds to an extension
$V\to U\to W\to V[1]$
. This corresponds to an extension
![]() $V\hookrightarrow U\twoheadrightarrow W$
in
$V\hookrightarrow U\twoheadrightarrow W$
in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and so by Proposition 4.2.4, we know
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
and so by Proposition 4.2.4, we know
![]() $[P_V]-[Q_V]$
and
$[P_V]-[Q_V]$
and
![]() $[P_W]-[Q_W]$
are not
$[P_W]-[Q_W]$
are not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Now suppose
![]() $[P_V]-[Q_V]$
and
$[P_V]-[Q_V]$
and
![]() $[P_W]-[Q_W]$
are not
$[P_W]-[Q_W]$
are not
![]() $\mathbf E$
-compatible. Without loss of generality suppose
$\mathbf E$
-compatible. Without loss of generality suppose
![]() $\langle [P_W]-[Q_W]\, ,\, [P_V]-[Q_V] \rangle < 0$
. Then in
$\langle [P_W]-[Q_W]\, ,\, [P_V]-[Q_V] \rangle < 0$
. Then in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
there is an extension
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
there is an extension
![]() $V\hookrightarrow U\twoheadrightarrow W$
. Thus by Theorem 1.2.5, there is a rectangle or almost complete rectangle in the AR-space of
$V\hookrightarrow U\twoheadrightarrow W$
. Thus by Theorem 1.2.5, there is a rectangle or almost complete rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left corner is V and right corner is W.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left corner is V and right corner is W.
Example 4.2.6. In Figure 9, the bold lines are the isomorphism classes of objects
![]() $P[0]$
and
$P[0]$
and
![]() $P[1]$
where P is projective
$P[1]$
where P is projective
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. The objects V and W are two indecomposables whose g-vectors are not
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. The objects V and W are two indecomposables whose g-vectors are not
![]() $\mathbf E$
-compatible and are clearly the left and right corners of a rectangle in the AR-space of
$\mathbf E$
-compatible and are clearly the left and right corners of a rectangle in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
whose sides have slope
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
whose sides have slope
![]() $\pm (1,1)$
. The points labeled P and Q with subscripts
$\pm (1,1)$
. The points labeled P and Q with subscripts
![]() $Vi$
or
$Vi$
or
![]() $Wj$
are indecomposables of the objects
$Wj$
are indecomposables of the objects
![]() $P_V$
,
$P_V$
,
![]() $P_W$
,
$P_W$
,
![]() $Q_V$
, and
$Q_V$
, and
![]() $Q_W$
.
$Q_W$
.

Figure 9 A visual aide to compute Example 4.2.6.
We then perform the following computations:
 $$ \begin{align*} \langle [P_W]-[Q_W], [P_V] \rangle &= \langle [P_{W_1}] + [P_{W_2}] + [P_{W_3}] - [Q_{W_1}] - [Q_{W_2}] - [Q_{W_3}] ,\\ &\qquad[P_{V_1}] + [P_{V_2}] + [P_{V_3}] \rangle = -1 -1 -1= -3 \end{align*} $$
$$ \begin{align*} \langle [P_W]-[Q_W], [P_V] \rangle &= \langle [P_{W_1}] + [P_{W_2}] + [P_{W_3}] - [Q_{W_1}] - [Q_{W_2}] - [Q_{W_3}] ,\\ &\qquad[P_{V_1}] + [P_{V_2}] + [P_{V_3}] \rangle = -1 -1 -1= -3 \end{align*} $$
 $$ \begin{align*} \langle [P_W]-[Q_W], -[Q_V] \rangle = &\langle [P_{W_1}] + [P_{W_2}] + [P_{W_3}] - [Q_{W_1}] - [Q_{W_2}] - [Q_{W_3}] ,\\ &\qquad{}- [Q_{V_1}] - [Q_{V_2}] - [Q_{V_3}] \rangle = 1 + 1 + 0 =2 \end{align*} $$
$$ \begin{align*} \langle [P_W]-[Q_W], -[Q_V] \rangle = &\langle [P_{W_1}] + [P_{W_2}] + [P_{W_3}] - [Q_{W_1}] - [Q_{W_2}] - [Q_{W_3}] ,\\ &\qquad{}- [Q_{V_1}] - [Q_{V_2}] - [Q_{V_3}] \rangle = 1 + 1 + 0 =2 \end{align*} $$
And so we have
![]() $\langle [P_W] - [Q_W]\, ,\, [P_V] - [Q_V] \rangle = -1$
.
$\langle [P_W] - [Q_W]\, ,\, [P_V] - [Q_V] \rangle = -1$
.
4.3
 $\mathbf E$
-Clusters
$\mathbf E$
-Clusters
In this section, we define
![]() $\mathbf E$
-clusters in
$\mathbf E$
-clusters in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
and show how to mutate elements in a way similar to the usual notion of mutation.
${\mathcal {C}(A_{{\mathbb {R}},S})}$
and show how to mutate elements in a way similar to the usual notion of mutation.
Definition 4.3.1. Let T be a collection of (isomorphism classes of) indecomposable objects in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We say T is
${\mathcal {C}(A_{{\mathbb {R}},S})}$
. We say T is
![]() $\mathbf E$
-compatible if for any pair
$\mathbf E$
-compatible if for any pair
![]() $V, W\in T$
the g-vectors
$V, W\in T$
the g-vectors
![]() $g_V$
and
$g_V$
and
![]() $g_W$
are
$g_W$
are
![]() $\mathbf E$
-compatible. If, for each
$\mathbf E$
-compatible. If, for each
![]() $U\notin T$
, there exists a
$U\notin T$
, there exists a
![]() $V\in T$
such that
$V\in T$
such that
![]() $g_U$
and
$g_U$
and
![]() $g_V$
are not
$g_V$
are not
![]() $\mathbf E$
-compatible (i.e., T is maximally
$\mathbf E$
-compatible (i.e., T is maximally
![]() $\mathbf E$
-compatible), then T is called an
$\mathbf E$
-compatible), then T is called an
![]() $\mathbf E$
-cluster and, from now on,
$\mathbf E$
-cluster and, from now on,
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
be called the continuous
${\mathcal {C}(A_{{\mathbb {R}},S})}$
be called the continuous
![]() $\mathbf E$
-cluster category.
$\mathbf E$
-cluster category.
Example 4.3.2. Let
![]() $\mathcal P$
be the set of (isomorphism classes of) indecomposables P which are images in
$\mathcal P$
be the set of (isomorphism classes of) indecomposables P which are images in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
of projective objects in
${\mathcal {C}(A_{{\mathbb {R}},S})}$
of projective objects in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then
![]() $\mathcal P$
is
$\mathcal P$
is
![]() $\mathbf E$
-compatible. Let V be an indecomposable with g-vector
$\mathbf E$
-compatible. Let V be an indecomposable with g-vector
![]() $[P_V]-[Q_V]$
. Then
$[P_V]-[Q_V]$
. Then
![]() $[P_V]-[Q_V]$
is not
$[P_V]-[Q_V]$
is not
![]() $\mathbf E$
-compatible with
$\mathbf E$
-compatible with
![]() $[Q_V]$
. Therefore,
$[Q_V]$
. Therefore,
![]() $\mathcal P$
is an
$\mathcal P$
is an
![]() $\mathbf E$
-cluster.
$\mathbf E$
-cluster.
Lemma 4.3.3. Let
![]() $V \to U_1\oplus U_2\to W\to V[1]$
be a distinguished triangle in
$V \to U_1\oplus U_2\to W\to V[1]$
be a distinguished triangle in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
where V,
${\mathcal {C}(A_{{\mathbb {R}},S})}$
where V,
![]() $U_1$
,
$U_1$
,
![]() $U_2$
, and W are indecomposable. Suppose further that one may take representatives of each isomorphism class in degree 0 and obtain a (almost complete) rectangle entirely in the AR-space of
$U_2$
, and W are indecomposable. Suppose further that one may take representatives of each isomorphism class in degree 0 and obtain a (almost complete) rectangle entirely in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
as a subspace of the AR-space of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
as a subspace of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, where V is the left corner and W is the right corner. Then for any indecomposable X in
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
, where V is the left corner and W is the right corner. Then for any indecomposable X in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
if
${\mathcal {C}(A_{{\mathbb {R}},S})}$
if
![]() $\{X,V\}$
and
$\{X,V\}$
and
![]() $\{X,W\}$
are
$\{X,W\}$
are
![]() $\mathbf E$
-compatible so is
$\mathbf E$
-compatible so is
![]() $\{X,U_1,U_2\}$
. Suppose
$\{X,U_1,U_2\}$
. Suppose
![]() $X\not \cong V,W$
. Then, if
$X\not \cong V,W$
. Then, if
![]() $\{X,V,U_1,U_2\}$
or
$\{X,V,U_1,U_2\}$
or
![]() $\{X,W,U_1,U_2\}$
is
$\{X,W,U_1,U_2\}$
is
![]() $\mathbf E$
-compatible so are both
$\mathbf E$
-compatible so are both
![]() $\{X,W\}$
and
$\{X,W\}$
and
![]() $\{X,V\}$
.
$\{X,V\}$
.
Proof. We prove: if
![]() $\{X,U_1,U_2\}$
is not
$\{X,U_1,U_2\}$
is not
![]() $\mathbf E$
-compatible then either
$\mathbf E$
-compatible then either
![]() $\{X,W\}$
or
$\{X,W\}$
or
![]() $\{X,V\}$
is not
$\{X,V\}$
is not
![]() $\mathbf E$
-compatible. Thus, without loss of generality, we assume
$\mathbf E$
-compatible. Thus, without loss of generality, we assume
![]() $\{X,U_1\}$
is not
$\{X,U_1\}$
is not
![]() $\mathbf E$
-compatible. We need only to prove that
$\mathbf E$
-compatible. We need only to prove that
![]() $\{X,V\}$
or
$\{X,V\}$
or
![]() $\{X,W\}$
is not
$\{X,W\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Suppose one of
![]() $\{X,V\}$
or
$\{X,V\}$
or
![]() $\{X,W\}$
is
$\{X,W\}$
is
![]() $\mathbf E$
-compatible. We shall assume
$\mathbf E$
-compatible. We shall assume
![]() $\{X,V\}$
is
$\{X,V\}$
is
![]() $\mathbf E$
-compatible as the other assumption is symmetric. By Proposition 4.2.5, since
$\mathbf E$
-compatible as the other assumption is symmetric. By Proposition 4.2.5, since
![]() $\{X,U_1\}$
is not
$\{X,U_1\}$
is not
![]() $\mathbf E$
-compatible there is a (almost complete) rectangle in the AR-space of
$\mathbf E$
-compatible there is a (almost complete) rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left and right corners are X and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left and right corners are X and
![]() $U_1$
(possibly not respectively).
$U_1$
(possibly not respectively).
Since
![]() $\{X,V\}$
is
$\{X,V\}$
is
![]() $\mathbf E$
-compatible X must be to the left of
$\mathbf E$
-compatible X must be to the left of
![]() $U_1$
or else there would be a (almost complete) rectangle with left corner V and right corner X in the AR-space of
$U_1$
or else there would be a (almost complete) rectangle with left corner V and right corner X in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. But then there is a (almost complete) rectangle with left corner X and right corner W and so
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. But then there is a (almost complete) rectangle with left corner X and right corner W and so
![]() $\{X,W\}$
is not
$\{X,W\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Therefore, if
![]() $\{X,U_1,U_2\}$
is not
$\{X,U_1,U_2\}$
is not
![]() $\mathbf E$
-compatible then either
$\mathbf E$
-compatible then either
![]() $\{X,U_1\}$
or
$\{X,U_1\}$
or
![]() $\{X,U_2\}$
is not
$\{X,U_2\}$
is not
![]() $\mathbf E$
-compatible then at least one of
$\mathbf E$
-compatible then at least one of
![]() $\{X,V\}$
or
$\{X,V\}$
or
![]() $\{X,W\}$
is not
$\{X,W\}$
is not
![]() $\mathbf E$
-compatible. The partial converse statement follows from a similar argument.
$\mathbf E$
-compatible. The partial converse statement follows from a similar argument.
Definition 4.3.4. Let T be an
![]() $\mathbf E$
-cluster and
$\mathbf E$
-cluster and
![]() $V\in T$
. If there exists W such that
$V\in T$
. If there exists W such that
![]() $\{V,W\}$
is not
$\{V,W\}$
is not
![]() $\mathbf E$
-compatible but
$\mathbf E$
-compatible but
![]() $(T\setminus \{V\})\cup \{W\}$
is
$(T\setminus \{V\})\cup \{W\}$
is
![]() $\mathbf E$
-compatible we say V is
$\mathbf E$
-compatible we say V is
![]() $\mathbf E$
-mutable.
$\mathbf E$
-mutable.
Remark 4.3.5. Note that we have not required that
![]() $(T\setminus \{V\})\cup \{W\}$
be an
$(T\setminus \{V\})\cup \{W\}$
be an
![]() $\mathbf E$
-cluster. We only require that if V is replaced with W then the new set is
$\mathbf E$
-cluster. We only require that if V is replaced with W then the new set is
![]() $\mathbf E$
-compatible. We prove later (Theorem 4.3.8) that this means
$\mathbf E$
-compatible. We prove later (Theorem 4.3.8) that this means
![]() $(T\setminus \{V\})\cup \{W\}$
is indeed an
$(T\setminus \{V\})\cup \{W\}$
is indeed an
![]() $\mathbf E$
-cluster.
$\mathbf E$
-cluster.
Proposition 4.3.6. Let T be an
![]() $\mathbf E$
-cluster and
$\mathbf E$
-cluster and
![]() $V\in T$
be
$V\in T$
be
![]() $\mathbf E$
-mutable with choice W. Then one of the following is the distinguished triangle associated to the (almost complete) rectangle in Proposition 4.2.5 and whichever of
$\mathbf E$
-mutable with choice W. Then one of the following is the distinguished triangle associated to the (almost complete) rectangle in Proposition 4.2.5 and whichever of
![]() $U_1,U_2,U^{\prime }_1,U^{\prime }_2$
in the distinguished triangle are nonzero are in T.
$U_1,U_2,U^{\prime }_1,U^{\prime }_2$
in the distinguished triangle are nonzero are in T.

Proof. We prove the statement for (1) as (2) is similar. We know
![]() $\{V,U_1,U_2\}$
and
$\{V,U_1,U_2\}$
and
![]() $\{W,U_1,U_2\}$
are
$\{W,U_1,U_2\}$
are
![]() $\mathbf E$
-compatible by Proposition 4.2.5. We also know that for all
$\mathbf E$
-compatible by Proposition 4.2.5. We also know that for all
![]() $X\in T\backslash \{V\}$
both
$X\in T\backslash \{V\}$
both
![]() $\{X,V\}$
and
$\{X,V\}$
and
![]() $\{X,W\}$
are
$\{X,W\}$
are
![]() $\mathbf E$
-compatible. Then, by Lemma 4.3.3, for all
$\mathbf E$
-compatible. Then, by Lemma 4.3.3, for all
![]() $X\in T\backslash \{V\}$
we know
$X\in T\backslash \{V\}$
we know
![]() $\{X,U_1,U_2\}$
is
$\{X,U_1,U_2\}$
is
![]() $\mathbf E$
-compatible. Since T is an
$\mathbf E$
-compatible. Since T is an
![]() $\mathbf E$
-cluster, this means
$\mathbf E$
-cluster, this means
![]() $U_1,U_2\in T$
.
$U_1,U_2\in T$
.
Lemma 4.3.7. Let V, W, and
![]() $W'$
be indecomposables in
$W'$
be indecomposables in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
such that
${\mathcal {C}(A_{{\mathbb {R}},S})}$
such that
![]() $\{V,W\}$
and
$\{V,W\}$
and
![]() $\{V,W'\}$
are not
$\{V,W'\}$
are not
![]() $\mathbf E$
-compatible. Let
$\mathbf E$
-compatible. Let
![]() $U_1$
,
$U_1$
,
![]() $U_2$
,
$U_2$
,
![]() $U^{\prime }_1$
, and
$U^{\prime }_1$
, and
![]() $U^{\prime }_2$
be the indecomposables from the distinguished triangles in Proposition 4.2.5. If
$U^{\prime }_2$
be the indecomposables from the distinguished triangles in Proposition 4.2.5. If
![]() $W\not \cong W'$
then at least one of
$W\not \cong W'$
then at least one of
![]() $\{W, U^{\prime }_1, U^{\prime }_2\}$
,
$\{W, U^{\prime }_1, U^{\prime }_2\}$
,
![]() $\{W', U_1,U_2\}$
, or
$\{W', U_1,U_2\}$
, or
![]() $\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
$\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Proof. There are two cases: (1) when
![]() $\{W,W'\}$
is not
$\{W,W'\}$
is not
![]() $\mathbf E$
-compatible and (2) when
$\mathbf E$
-compatible and (2) when
![]() $\{W,W'\}$
is
$\{W,W'\}$
is
![]() $\mathbf E$
-compatible. By Proposition 4.2.5 this is equivalent to: (1) when there is a rectangle or almost complete rectangle in the AR-space of
$\mathbf E$
-compatible. By Proposition 4.2.5 this is equivalent to: (1) when there is a rectangle or almost complete rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left and right corners are W and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left and right corners are W and
![]() $W'$
and (2) when there is no such rectangle. By symmetry, we assume that, in the AR-space of
$W'$
and (2) when there is no such rectangle. By symmetry, we assume that, in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, W is never to the right of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
, W is never to the right of
![]() $W'$
.
$W'$
.
We assume (1) first. Then by our symmetry assumption W is the left corner and
![]() $W'$
is the right corner. We already know that there is a rectangle or almost complete rectangle with left and right corners W and V and similarly for
$W'$
is the right corner. We already know that there is a rectangle or almost complete rectangle with left and right corners W and V and similarly for
![]() $W'$
and V. There are then three possible places for V horizontally in the AR-space of
$W'$
and V. There are then three possible places for V horizontally in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
: (i) to the left of W, (ii) between W and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
: (i) to the left of W, (ii) between W and
![]() $W'$
, and (iii) to the right of
$W'$
, and (iii) to the right of
![]() $W'$
. We see that (i) and (iii) are similar so we just focus on (ii) and (iii). We have the schematics in the AR-space of
$W'$
. We see that (i) and (iii) are similar so we just focus on (ii) and (iii). We have the schematics in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
in Figure 10. In the two schematics, at least one of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
in Figure 10. In the two schematics, at least one of
![]() $X_1, X_2$
, at least one of
$X_1, X_2$
, at least one of
![]() $U_1,U_2$
, and both of
$U_1,U_2$
, and both of
![]() $U^{\prime }_1,U^{\prime }_2$
must be nonzero. In particular, if one of
$U^{\prime }_1,U^{\prime }_2$
must be nonzero. In particular, if one of
![]() $X_1,X_2$
is 0 we must be in case (1)(ii) so both
$X_1,X_2$
is 0 we must be in case (1)(ii) so both
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are nonzero and similarly for case (1)(iii).
$U_2$
are nonzero and similarly for case (1)(iii).

Figure 10 Schematics of Case (1)(ii) and Case (1)(iii) on the left and right, respectively, in the proof of Lemma 4.3.7.
In case (1)(ii), choose
![]() $X_i$
to be one of
$X_i$
to be one of
![]() $X_1$
or
$X_1$
or
![]() $X_2$
and nonzero. Let
$X_2$
and nonzero. Let
![]() $j\in \{1,2\}$
such that
$j\in \{1,2\}$
such that
![]() $\{i,j\}=\{1,2\}$
. Then
$\{i,j\}=\{1,2\}$
. Then
![]() $X_i$
and
$X_i$
and
![]() $U^{\prime }_j$
are the top and bottom corners of a rectangle in the AR-space of
$U^{\prime }_j$
are the top and bottom corners of a rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left corner is
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
whose left corner is
![]() $U_i$
and right corner is
$U_i$
and right corner is
![]() $W'$
. By Proposition 4.2.5 we see this means
$W'$
. By Proposition 4.2.5 we see this means
![]() $\{W',U_i\}$
is not
$\{W',U_i\}$
is not
![]() $\mathbf E$
-compatible and so
$\mathbf E$
-compatible and so
![]() $\{W',U_1,U_2\}$
is not
$\{W',U_1,U_2\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
In case (1)(iii) choose
![]() $U_i$
to be one of
$U_i$
to be one of
![]() $U_1$
or
$U_1$
or
![]() $U_2$
and nonzero and
$U_2$
and nonzero and
![]() $j\in \{1,2\}$
such that
$j\in \{1,2\}$
such that
![]() $\{i,j\}=\{1,2\}$
. We have a rectangle in the AR-space of
$\{i,j\}=\{1,2\}$
. We have a rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with left corner W, top and bottom corners
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
with left corner W, top and bottom corners
![]() $U_i$
and
$U_i$
and
![]() $X_j$
, and right corner
$X_j$
, and right corner
![]() $U^{\prime }_i$
By Proposition 4.2.5 again we have
$U^{\prime }_i$
By Proposition 4.2.5 again we have
![]() $\{W,U^{\prime }_1,U^{\prime }_2\}$
is not
$\{W,U^{\prime }_1,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Now we assume (2). This also comes with subcases. Either (i) W and
![]() $W'$
are on the “same side” of V in the AR-space of
$W'$
are on the “same side” of V in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or (ii) W and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or (ii) W and
![]() $W'$
are on “opposite sides” of V. In case (2)(i) this means
$W'$
are on “opposite sides” of V. In case (2)(i) this means
![]() $\mathop {\boldsymbol {\Gamma }}^b W$
and
$\mathop {\boldsymbol {\Gamma }}^b W$
and
![]() $\mathop {\boldsymbol {\Gamma }}^b W'$
both lie in the
$\mathop {\boldsymbol {\Gamma }}^b W'$
both lie in the
![]() $H_V$
as described in [Reference Rock19, Lem. 2.5.4]. By the same lemma, case (2)(ii) means one of
$H_V$
as described in [Reference Rock19, Lem. 2.5.4]. By the same lemma, case (2)(ii) means one of
![]() $\mathop {\boldsymbol {\Gamma }}^b W$
and
$\mathop {\boldsymbol {\Gamma }}^b W$
and
![]() $\mathop {\boldsymbol {\Gamma }}^b W'$
lies in
$\mathop {\boldsymbol {\Gamma }}^b W'$
lies in
![]() $H_V$
and the other in
$H_V$
and the other in
![]() $H_{V[-1]}$
. Since
$H_{V[-1]}$
. Since
![]() $\{W,W'\}$
is
$\{W,W'\}$
is
![]() $\mathbf E$
-compatible these are equivalent to either (i) one of W or
$\mathbf E$
-compatible these are equivalent to either (i) one of W or
![]() $W'$
being “above” the other in the AR-space of
$W'$
being “above” the other in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or (ii) W and
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
or (ii) W and
![]() $W'$
are “too far apart” to be the left and right corners of a rectangle or almost complete rectangle. In case (2)(ii), if we draw a rectangle with left and right corners
$W'$
are “too far apart” to be the left and right corners of a rectangle or almost complete rectangle. In case (2)(ii), if we draw a rectangle with left and right corners
![]() $\mathop {\boldsymbol {\Gamma }}^b W$
and
$\mathop {\boldsymbol {\Gamma }}^b W$
and
![]() $\mathop {\boldsymbol {\Gamma }}^b W'$
in
$\mathop {\boldsymbol {\Gamma }}^b W'$
in
![]() ${\mathbb {R}}^2$
one of the top or bottom corners will be in the image of the AR-space of
${\mathbb {R}}^2$
one of the top or bottom corners will be in the image of the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
under
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
under
![]() $\mathop {\boldsymbol {\Gamma }}$
. (Otherwise, W and
$\mathop {\boldsymbol {\Gamma }}$
. (Otherwise, W and
![]() $W'$
would not both lie in the AR-space of
$W'$
would not both lie in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
as a subspace of the AR-space of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
as a subspace of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.)
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
.)
In Figure 11, we have the following schematics (where the horizontal dashed line is the lower boundary of the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
) for cases (2)(i) and (2)(ii). At least one of
${\mathcal {D}^b(A_{{\mathbb {R}},S})}$
) for cases (2)(i) and (2)(ii). At least one of
![]() $U_2$
and
$U_2$
and
![]() $U^{\prime }_1$
must be nonzero in case (2)(i). Up to reversing roles, we see that there is a rectangle with left corner W, top and bottom corners
$U^{\prime }_1$
must be nonzero in case (2)(i). Up to reversing roles, we see that there is a rectangle with left corner W, top and bottom corners
![]() $U_2$
and
$U_2$
and
![]() $X_2$
, and right corner
$X_2$
, and right corner
![]() $U^{\prime }_2$
. Thus
$U^{\prime }_2$
. Thus
![]() $\{W,U^{\prime }_1,U^{\prime }_2\}$
is not
$\{W,U^{\prime }_1,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible. In case (2)(ii), we have argued that X must be nonzero so we have a rectangle with left corner
$\mathbf E$
-compatible. In case (2)(ii), we have argued that X must be nonzero so we have a rectangle with left corner
![]() $U_2$
, top and bottom corners X and V, and right corner
$U_2$
, top and bottom corners X and V, and right corner
![]() $U^{\prime }_2$
. This means
$U^{\prime }_2$
. This means
![]() $\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
$\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible because
$\mathbf E$
-compatible because
![]() $\{U_2,U^{\prime }_2\}$
is not
$\{U_2,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible. Therefore the proposition holds.
$\mathbf E$
-compatible. Therefore the proposition holds.
Theorem 4.3.8. Let T be an
![]() $\mathbf E$
-cluster. Let
$\mathbf E$
-cluster. Let
![]() $V\in T$
be
$V\in T$
be
![]() $\mathbf E$
-mutable with choice W. Then
$\mathbf E$
-mutable with choice W. Then
![]() $(T\setminus \{V\})\cup \{W\}$
is an
$(T\setminus \{V\})\cup \{W\}$
is an
![]() $\mathbf E$
-cluster and any other choice
$\mathbf E$
-cluster and any other choice
![]() $W'$
for V is isomorphic to W.
$W'$
for V is isomorphic to W.

Figure 11 Schematics of Case (2)(i) and Case (2)(ii) on the left and right, respectively, in the proof of Lemma 4.3.7.
Proof. First we prove the choice of W is unique up to isomorphism. By Proposition 4.3.6, we know there are two distinguished triangles with indecomposables
![]() $U_1$
,
$U_1$
,
![]() $U_2$
,
$U_2$
,
![]() $U^{\prime }_1$
, and
$U^{\prime }_1$
, and
![]() $U^{\prime }_2$
, all of which are in T. By Lemma 4.3.7, we know that if
$U^{\prime }_2$
, all of which are in T. By Lemma 4.3.7, we know that if
![]() $W\not \cong W'$
then one of
$W\not \cong W'$
then one of
![]() $\{W, U^{\prime }_1, U^{\prime }_2\}$
,
$\{W, U^{\prime }_1, U^{\prime }_2\}$
,
![]() $\{W', U_1,U_2\}$
, or
$\{W', U_1,U_2\}$
, or
![]() $\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
$\{U_1,U_2,U^{\prime }_1,U^{\prime }_2\}$
is not
![]() $\mathbf E$
-compatible. Therefore, since both W and
$\mathbf E$
-compatible. Therefore, since both W and
![]() $W'$
are choices for V we must have
$W'$
are choices for V we must have
![]() $W\cong W'$
.
$W\cong W'$
.
Now let X be an indecomposable in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
such that
${\mathcal {C}(A_{{\mathbb {R}},S})}$
such that
![]() $((T\setminus \{V\})\cup \{W\}) \cup \{X\}$
is
$((T\setminus \{V\})\cup \{W\}) \cup \{X\}$
is
![]() $\mathbf E$
-compatible. Then X is
$\mathbf E$
-compatible. Then X is
![]() $\mathbf E$
-compatible with
$\mathbf E$
-compatible with
![]() $U_1$
and
$U_1$
and
![]() $U_2$
from the distinguished triangle. By Lemma 4.3.3, since
$U_2$
from the distinguished triangle. By Lemma 4.3.3, since
![]() $\{X,W,U_1,U_2\}$
is
$\{X,W,U_1,U_2\}$
is
![]() $\mathbf E$
-compatible so is
$\mathbf E$
-compatible so is
![]() $\{X,V\}$
. Therefore
$\{X,V\}$
. Therefore
![]() $X\in T$
.
$X\in T$
.
4.4 Comparing the constructions
In this section, we highlight the differences and similarities between the previous cluster category
![]() $\mathcal C_\pi $
and the new category
$\mathcal C_\pi $
and the new category
![]() $\mathcal C(A_{{\mathbb {R}},S})$
. The cluster structure introduced by Igusa and Todorov in [Reference Igusa and Todorov15] requires that the clusters be discrete. This was required so that every object in the cluster be mutable. The new theory given in §4 does not come with this restriction; sometimes, an object in a cluster might not be
$\mathcal C(A_{{\mathbb {R}},S})$
. The cluster structure introduced by Igusa and Todorov in [Reference Igusa and Todorov15] requires that the clusters be discrete. This was required so that every object in the cluster be mutable. The new theory given in §4 does not come with this restriction; sometimes, an object in a cluster might not be
![]() $\mathbf E$
-mutable.
$\mathbf E$
-mutable.
Example 4.4.1. Let
![]() $A_{{\mathbb {R}},S}$
be a continuous quiver of type A. Consider again the
$A_{{\mathbb {R}},S}$
be a continuous quiver of type A. Consider again the
![]() $\mathbf E$
-cluster
$\mathbf E$
-cluster
![]() $\mathcal P$
of objects coming from projectives in Example 4.3.2. Let
$\mathcal P$
of objects coming from projectives in Example 4.3.2. Let
![]() $a\in {\mathbb {R}}$
such that a is neither a source nor a sink. By Theorem 1.1.7, there are exactly two projectives at a in
$a\in {\mathbb {R}}$
such that a is neither a source nor a sink. By Theorem 1.1.7, there are exactly two projectives at a in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Let P be the object in
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Let P be the object in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
that comes from
${\mathcal {C}(A_{{\mathbb {R}},S})}$
that comes from
![]() $P_a$
and Q the object that comes from
$P_a$
and Q the object that comes from
![]() $P_{(a}$
or
$P_{(a}$
or
![]() $P_{a)}$
, whichever exists in
$P_{a)}$
, whichever exists in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then we have a distinguished triangle
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. Then we have a distinguished triangle
![]() $Q\to P\to V\to Q[1]$
in
$Q\to P\to V\to Q[1]$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
where V is degenerate. In particular, there is no distinguished triangle
${\mathcal {C}(A_{{\mathbb {R}},S})}$
where V is degenerate. In particular, there is no distinguished triangle
![]() $P'\to W\to V\to P'[1]$
in
$P'\to W\to V\to P'[1]$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}},S})}$
where
${\mathcal {C}(A_{{\mathbb {R}},S})}$
where
![]() $P'$
is in
$P'$
is in
![]() $\mathcal P$
and not isomorphic to Q. Thus
$\mathcal P$
and not isomorphic to Q. Thus
![]() $(\mathcal P \setminus \{Q\})\cup \{V\}$
is
$(\mathcal P \setminus \{Q\})\cup \{V\}$
is
![]() $\mathbf E$
-compatible and so Q is
$\mathbf E$
-compatible and so Q is
![]() $\mathbf E$
-mutable.
$\mathbf E$
-mutable.
However, for any object V such that
![]() $\{V,P\}$
is not
$\{V,P\}$
is not
![]() $\mathbf E$
-compatible we have
$\mathbf E$
-compatible we have
![]() $\{V,P_{a+\varepsilon }\}$
is not
$\{V,P_{a+\varepsilon }\}$
is not
![]() $\mathbf E$
-compatible for
$\mathbf E$
-compatible for
![]() $0<\varepsilon <<1$
. Thus P is not
$0<\varepsilon <<1$
. Thus P is not
![]() $\mathbf E$
-mutable.
$\mathbf E$
-mutable.
We would like to mutate all the projectives from
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
into all the injectives from
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
into all the injectives from
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. However, this example appears to present a problem. The next paper in this series addresses this with a continuous generalization of mutation [Reference Rock20].
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}},S})$
. However, this example appears to present a problem. The next paper in this series addresses this with a continuous generalization of mutation [Reference Rock20].
5 Embeddings of cluster theories
In this section, we embed cluster theories of type
![]() $A_n$
,
$A_n$
,
![]() $A_\infty $
and
$A_\infty $
and
![]() $\mathcal C_\pi $
into the
$\mathcal C_\pi $
into the
![]() $\mathbf E$
-cluster theory of
$\mathbf E$
-cluster theory of
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
where
${\mathcal {C}(A_{{\mathbb {R}}})}$
where
![]() $A_{{\mathbb {R}}}=A_{{\mathbb {R}},\emptyset }$
with the straight descending orientation. We begin with the definition of an
$A_{{\mathbb {R}}}=A_{{\mathbb {R}},\emptyset }$
with the straight descending orientation. We begin with the definition of an
![]() $\mathbf E$
-compatible set
$\mathbf E$
-compatible set
![]() ${L}$
for
${L}$
for
![]() $A_{{\mathbb {R}}}$
we use in §5.1 and §5.2.
$A_{{\mathbb {R}}}$
we use in §5.1 and §5.2.
Definition 5.0.1. Let
![]() $\{a_i\}_{i\in {\mathbb {Z}}}$
be a collection of real numbers such that
$\{a_i\}_{i\in {\mathbb {Z}}}$
be a collection of real numbers such that
-
•
 $a_i < a_{i+1}$
for all
$a_i < a_{i+1}$
for all
 $i\in {\mathbb {Z}}$
and
$i\in {\mathbb {Z}}$
and -
•
 $a_i$
has two limits:
$a_i$
has two limits:
 $a_{-\infty }:=\displaystyle \lim _{i\to -\infty } a_i\in {\mathbb {Z}}$
and
$a_{-\infty }:=\displaystyle \lim _{i\to -\infty } a_i\in {\mathbb {Z}}$
and
 $a_{\infty }:=\displaystyle \lim _{i\to +\infty } a_i \in {\mathbb {Z}}$
.
$a_{\infty }:=\displaystyle \lim _{i\to +\infty } a_i \in {\mathbb {Z}}$
.
For each
![]() $i,j,\ell \in {\mathbb {Z}}$
such that
$i,j,\ell \in {\mathbb {Z}}$
such that
![]() $\ell \geq 0$
and
$\ell \geq 0$
and
![]() $0\leq j \leq 2^\ell $
define
$0\leq j \leq 2^\ell $
define
 $$ \begin{align*} a_{i,j,\ell} := a_i + \left(\frac{j}{2^\ell}\right)(a_{i+1} - a_i). \end{align*} $$
$$ \begin{align*} a_{i,j,\ell} := a_i + \left(\frac{j}{2^\ell}\right)(a_{i+1} - a_i). \end{align*} $$
For each
![]() $a_i$
, we define the following
$a_i$
, we define the following
![]() $\mathbf E$
-compatible set:
$\mathbf E$
-compatible set:
 $$ \begin{align*} A_i :=& \left\{ M_{(a_{i,j,\ell},\, a_{i,j+1,\ell})} :j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell\right\} \\ &\cup \left\{ M_{[x,x]} : x\in (a_i,a_i+1),\, x \neq a_{i,j,\ell} ,\,\, j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell\right\}. \end{align*} $$
$$ \begin{align*} A_i :=& \left\{ M_{(a_{i,j,\ell},\, a_{i,j+1,\ell})} :j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell\right\} \\ &\cup \left\{ M_{[x,x]} : x\in (a_i,a_i+1),\, x \neq a_{i,j,\ell} ,\,\, j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell\right\}. \end{align*} $$
Note that for any
![]() $a_i$
and
$a_i$
and
![]() $a_j$
we have
$a_j$
we have
![]() $A_i\cup A_j$
is
$A_i\cup A_j$
is
![]() $\mathbf E$
-compatible. Now, for each
$\mathbf E$
-compatible. Now, for each
![]() $i\in {\mathbb {Z}}$
such that
$i\in {\mathbb {Z}}$
such that
![]() $i< a_{-\infty }$
or
$i< a_{-\infty }$
or
![]() $i\geq a_{+\infty }$
define a similar type of
$i\geq a_{+\infty }$
define a similar type of
![]() $\mathbf E$
-compatible set:
$\mathbf E$
-compatible set:
 $$ \begin{align*} B_i :=& \left\{ M_{(i + j/2^\ell, i+ (j+1)/2^\ell)} : j,\ell\in{\mathbb{Z}},\, \ell\geq 0,\, 0\leq j < 2^\ell\right\} \cup \{P_{i+1}\}\\ & \cup \left\{ M_{[x,x]} : x\in (i,i+1),\, x \neq i + j/2^\ell,\, j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell \right\}. \end{align*} $$
$$ \begin{align*} B_i :=& \left\{ M_{(i + j/2^\ell, i+ (j+1)/2^\ell)} : j,\ell\in{\mathbb{Z}},\, \ell\geq 0,\, 0\leq j < 2^\ell\right\} \cup \{P_{i+1}\}\\ & \cup \left\{ M_{[x,x]} : x\in (i,i+1),\, x \neq i + j/2^\ell,\, j,\ell\in{\mathbb{Z}},\, \ell \geq 0,\, 0\leq j < 2^\ell \right\}. \end{align*} $$
The
![]() $\mathbf E$
-compatible set we want is
$\mathbf E$
-compatible set we want is
 $$ \begin{align*} {L} := \bigcup_{i\in{\mathbb{Z}}} A_i \cup \bigcup_{i< a_{-\infty} \text{ or } i \geq a_{+\infty}} B_i \cup \{M_{(a_{-\infty},a_{+\infty})}, P_{+\infty}\} \cup \left\{P_{i)} : i \leq a_{-\infty} \text{ or } i \geq a_{+\infty} \right\}. \end{align*} $$
$$ \begin{align*} {L} := \bigcup_{i\in{\mathbb{Z}}} A_i \cup \bigcup_{i< a_{-\infty} \text{ or } i \geq a_{+\infty}} B_i \cup \{M_{(a_{-\infty},a_{+\infty})}, P_{+\infty}\} \cup \left\{P_{i)} : i \leq a_{-\infty} \text{ or } i \geq a_{+\infty} \right\}. \end{align*} $$
5.1 Embeddings
 $\mathscr T_{\mathbf N_n} (\mathcal C(A_n)) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
$\mathscr T_{\mathbf N_n} (\mathcal C(A_n)) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
We use the
![]() $\mathbf N_n$
-cluster theory in Example 4.1.7. Label the vertices of the
$\mathbf N_n$
-cluster theory in Example 4.1.7. Label the vertices of the
![]() $(n+3)$
-gon counterclockwise, as shown on the right. Label diagonals by
$(n+3)$
-gon counterclockwise, as shown on the right. Label diagonals by
![]() $\alpha _{i,j}$
, where
$\alpha _{i,j}$
, where
![]() $i<j$
. A pair of diagonals
$i<j$
. A pair of diagonals
![]() $\{\alpha _{i,j},\alpha _{i',j'}\}$
cross if and only if
$\{\alpha _{i,j},\alpha _{i',j'}\}$
cross if and only if
![]() $i<i'<j<j'$
or
$i<i'<j<j'$
or
![]() $i'<i<j'<j$
. An
$i'<i<j'<j$
. An
![]() $\mathbf N_n$
-cluster is a maximal collection of noncrossing diagonals.
$\mathbf N_n$
-cluster is a maximal collection of noncrossing diagonals.

Definition 5.1.1. Let
![]() $a_i$
(for all
$a_i$
(for all
![]() $i\in {\mathbb {Z}}$
),
$i\in {\mathbb {Z}}$
),
![]() $a_{-\infty }$
, and
$a_{-\infty }$
, and
![]() $a_{+\infty }$
be as in Definition 5.0.1. Recall that
$a_{+\infty }$
be as in Definition 5.0.1. Recall that
![]() $M_I$
is the interval module with support
$M_I$
is the interval module with support
![]() $I\subset {\mathbb {R}}$
. Let
$I\subset {\mathbb {R}}$
. Let
It is straightforward to check that
![]() ${L}_n$
is
${L}_n$
is
![]() $\mathbf E$
-compatible in
$\mathbf E$
-compatible in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
.
${\mathcal {C}(A_{{\mathbb {R}}})}$
.
Let T be an
![]() $\mathbf N_n$
-cluster in
$\mathbf N_n$
-cluster in
![]() $\mathscr T_{\mathbf N_n}(\mathcal C(A_n))$
as described above. We construct an
$\mathscr T_{\mathbf N_n}(\mathcal C(A_n))$
as described above. We construct an
![]() $\mathbf E$
-cluster
$\mathbf E$
-cluster
![]() $F(T)$
in
$F(T)$
in
![]() $\mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
based on T. For that purpose, define
$\mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
based on T. For that purpose, define
![]() $M_{\alpha _{i,j}} := M_{(a_i,a_j)}$
.
$M_{\alpha _{i,j}} := M_{(a_i,a_j)}$
.
Proposition 5.1.2. A pair of diagonals
![]() $\{\alpha _{i,j},\alpha _{i',j'}\}$
is
$\{\alpha _{i,j},\alpha _{i',j'}\}$
is
![]() $\mathbf N_n$
-compatible if and only if the pair of objects
$\mathbf N_n$
-compatible if and only if the pair of objects
![]() $\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is
$\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is
![]() $\mathbf {E}$
-compatible.
$\mathbf {E}$
-compatible.
Proof. Suppose
![]() $\alpha _{i,j}$
is not
$\alpha _{i,j}$
is not
![]() $\mathbf N_n$
-compatible with
$\mathbf N_n$
-compatible with
![]() $\alpha _{i',j'}$
. Then, up to symmetry,
$\alpha _{i',j'}$
. Then, up to symmetry,
![]() $i<i'<j<j'$
. We then know there exists a rectangle in the AR-space of
$i<i'<j<j'$
. We then know there exists a rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
whose left corner is
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
whose left corner is
![]() $M_{\alpha _{i,j}}$
, top corner is
$M_{\alpha _{i,j}}$
, top corner is
![]() $M_{(a_i,a_{j'})}$
, bottom corner is
$M_{(a_i,a_{j'})}$
, bottom corner is
![]() $M_{(a_{i'}, a_j)}$
, and right corner is
$M_{(a_{i'}, a_j)}$
, and right corner is
![]() $M_{\alpha _{i',j'}}$
. Thus
$M_{\alpha _{i',j'}}$
. Thus
![]() $M_{\alpha _{i,j}}$
and
$M_{\alpha _{i,j}}$
and
![]() $M_{\alpha _{i',j'}}$
are not
$M_{\alpha _{i',j'}}$
are not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
If we start with
![]() $M_{\alpha _{i,j}}$
and
$M_{\alpha _{i,j}}$
and
![]() $M_{\alpha _{i',j'}}$
are not
$M_{\alpha _{i',j'}}$
are not
![]() $\mathbf E$
-compatible we get the rectangle in the AR-space of
$\mathbf E$
-compatible we get the rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
again which implies (up to symmetry) that
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
again which implies (up to symmetry) that
![]() $a_i < a_{i'} < a_j < a_{j'}$
and so
$a_i < a_{i'} < a_j < a_{j'}$
and so
![]() $i<i'<j<j'$
. Therefore,
$i<i'<j<j'$
. Therefore,
![]() $\alpha _{i,j}$
and
$\alpha _{i,j}$
and
![]() $\alpha _{i',j'}$
are not
$\alpha _{i',j'}$
are not
![]() $\mathbf N_n$
-compatible so the proposition holds.
$\mathbf N_n$
-compatible so the proposition holds.
Definition 5.1.3. Given an
![]() $\mathbf N_n$
-cluster T, define
$\mathbf N_n$
-cluster T, define
![]() $F(T) := {L}_n \cup \left \{M_{\alpha _{i,j}}: \alpha _{i,j} \in T\right \}$
.
$F(T) := {L}_n \cup \left \{M_{\alpha _{i,j}}: \alpha _{i,j} \in T\right \}$
.
With Proposition 5.1.2 it is straightforward to check
![]() $F(T)$
is
$F(T)$
is
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Proposition 5.1.4. If T is an
![]() $\mathbf N_n$
cluster, then
$\mathbf N_n$
cluster, then
![]() $F(T)$
is an
$F(T)$
is an
![]() $\mathbf E$
-cluster.
$\mathbf E$
-cluster.
Proof. Choose some indecomposable
![]() $M_{|c,d|}$
in
$M_{|c,d|}$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
such that
${\mathcal {C}(A_{{\mathbb {R}}})}$
such that
![]() $\{M_{|c,d|}\}\cup F(T)$
is
$\{M_{|c,d|}\}\cup F(T)$
is
![]() $\mathbf E$
-compatible. We show that
$\mathbf E$
-compatible. We show that
![]() $M_{|c,d|}\in F(T)$
. Recall (Notation 1.1.4) that
$M_{|c,d|}\in F(T)$
. Recall (Notation 1.1.4) that
![]() $M_{|c,d|}$
indicates
$M_{|c,d|}$
indicates
![]() $M_{(c,d)}$
,
$M_{(c,d)}$
,
![]() $M_{(c,d]}$
,
$M_{(c,d]}$
,
![]() $M_{[c,d)}$
or
$M_{[c,d)}$
or
![]() $M_{[c,d]}$
. We check the possible values of c; note that
$M_{[c,d]}$
. We check the possible values of c; note that
![]() $c < +\infty $
.
$c < +\infty $
.
Suppose
![]() $c =-\infty $
. Then either
$c =-\infty $
. Then either
![]() $d\leq a_{-\infty }$
or
$d\leq a_{-\infty }$
or
![]() $d\geq a_{+\infty }$
. If
$d\geq a_{+\infty }$
. If
![]() $d=a_{\pm \infty }$
then
$d=a_{\pm \infty }$
then
![]() $M_{|c,d|}=P_{a_{\pm \infty })}$
. If
$M_{|c,d|}=P_{a_{\pm \infty })}$
. If
![]() $d < a_{-\infty }$
or
$d < a_{-\infty }$
or
![]() $d>a_{+\infty }$
then
$d>a_{+\infty }$
then
![]() $d\in {\mathbb {Z}}$
or
$d\in {\mathbb {Z}}$
or
![]() $d=+\infty $
as
$d=+\infty $
as
![]() $M_{(i,i+1)}\in B_i$
from Definition 5.0.1. Thus, in all these cases,
$M_{(i,i+1)}\in B_i$
from Definition 5.0.1. Thus, in all these cases,
![]() $M_{|c,d|}$
must be
$M_{|c,d|}$
must be
![]() $P_{i)}$
for some
$P_{i)}$
for some
![]() $i\in {\mathbb {Z}}$
outside
$i\in {\mathbb {Z}}$
outside
![]() $(a_{-\infty },a_{+\infty })$
or
$(a_{-\infty },a_{+\infty })$
or
![]() $i=+\infty $
. If
$i=+\infty $
. If
![]() $-\infty < c < a_{-\infty }$
or
$-\infty < c < a_{-\infty }$
or
![]() $a_{+\infty }\leq c<+\infty $
then either (i)
$a_{+\infty }\leq c<+\infty $
then either (i)
![]() $c=i+j/2^\ell $
and
$c=i+j/2^\ell $
and
![]() $d=i+(j+1)/2^\ell $
for some i,
$d=i+(j+1)/2^\ell $
for some i,
![]() $\ell \geq 0$
,
$\ell \geq 0$
,
![]() $0\leq j < 2^\ell $
or (ii)
$0\leq j < 2^\ell $
or (ii)
![]() $c=d$
and
$c=d$
and
![]() $M_{|c,d|}=M_{[c,c]}$
.
$M_{|c,d|}=M_{[c,c]}$
.
Suppose
![]() $c=a_{-\infty }$
Then
$c=a_{-\infty }$
Then
![]() $d = a_1$
or
$d = a_1$
or
![]() $d =a_{+\infty }$
. Thus,
$d =a_{+\infty }$
. Thus,
![]() $M_{|c,d|}$
must be
$M_{|c,d|}$
must be
![]() $M_{(a_{-\infty },a_1)}$
or
$M_{(a_{-\infty },a_1)}$
or
![]() $M_{(a_{-\infty },a_{+\infty })}$
. Suppose
$M_{(a_{-\infty },a_{+\infty })}$
. Suppose
![]() $a_{-\infty } < c < a_{+\infty }$
and
$a_{-\infty } < c < a_{+\infty }$
and
![]() $c\neq a_i$
for any i. If
$c\neq a_i$
for any i. If
![]() $c=a_{i,j,\ell }$
for some
$c=a_{i,j,\ell }$
for some
![]() $i\in {\mathbb {Z}}$
,
$i\in {\mathbb {Z}}$
,
![]() $\ell \geq 0$
, and
$\ell \geq 0$
, and
![]() $0<j<(2^\ell )$
then, up to adjusting
$0<j<(2^\ell )$
then, up to adjusting
![]() $\ell $
,
$\ell $
,
![]() $d=a_{i,j+1,\ell }$
. If c is not of this form then
$d=a_{i,j+1,\ell }$
. If c is not of this form then
![]() $d=c$
and
$d=c$
and
![]() $M_{|c,d|}=M_{[c,c]}$
.
$M_{|c,d|}=M_{[c,c]}$
.
If
![]() $c=a_i$
, for some
$c=a_i$
, for some
![]() $i\notin \{1,\ldots , n+2\}$
, then either
$i\notin \{1,\ldots , n+2\}$
, then either
![]() $d=a_{i+1}$
,
$d=a_{i+1}$
,
![]() $d=a_1$
, or
$d=a_1$
, or
![]() $d=+\infty $
. Thus
$d=+\infty $
. Thus
![]() $M_{|c,d|}$
is one of
$M_{|c,d|}$
is one of
![]() $M_{(a_i,a_{i+1})}$
,
$M_{(a_i,a_{i+1})}$
,
![]() $M_{(a_i,a_1)}$
, or
$M_{(a_i,a_1)}$
, or
![]() $I_{(a_1}$
.
$I_{(a_1}$
.
Now, we check
![]() $c\in \{a_i\}_{i=1}^{n+2}$
. First assume
$c\in \{a_i\}_{i=1}^{n+2}$
. First assume
![]() $M_{|c,d|}\neq M_{\alpha _{i,j}}$
for any
$M_{|c,d|}\neq M_{\alpha _{i,j}}$
for any
![]() $\alpha _{i,j}$
. If
$\alpha _{i,j}$
. If
![]() $c=a_1$
, then either
$c=a_1$
, then either
![]() $d=a_{n+3}$
,
$d=a_{n+3}$
,
![]() $d=a_{+\infty }$
, or
$d=a_{+\infty }$
, or
![]() $d\in (a_1,a_2]$
. If
$d\in (a_1,a_2]$
. If
![]() $c=a_i$
for
$c=a_i$
for
![]() $1<i<n+3$
, then
$1<i<n+3$
, then
![]() $d\in (a_i,a_{i+1}]$
. In each case,
$d\in (a_i,a_{i+1}]$
. In each case,
![]() $M_{|c,d|}=M_{(a_1,a_{n+3})}$
,
$M_{|c,d|}=M_{(a_1,a_{n+3})}$
,
![]() $M_{|c,d|}=M_{(a_i, a_{i,j,l})}$
,
$M_{|c,d|}=M_{(a_i, a_{i,j,l})}$
,
![]() $M_{|c,d|}=M_{(a_1,a_{+\infty })}$
, or
$M_{|c,d|}=M_{(a_1,a_{+\infty })}$
, or
![]() $M_{|c,d|}=M_{(a_i,a_{i+1})}$
.
$M_{|c,d|}=M_{(a_i,a_{i+1})}$
.
Finally, we check
![]() $c\in \{a_i\}_{i=1}^{n+2}$
and
$c\in \{a_i\}_{i=1}^{n+2}$
and
![]() $M_{|c,d|}=M_{\alpha _{i,j}}$
for some
$M_{|c,d|}=M_{\alpha _{i,j}}$
for some
![]() $\alpha _{i,j}$
. For contradiction, assume
$\alpha _{i,j}$
. For contradiction, assume
![]() $\alpha _{i,j}\notin T$
. Then there is an
$\alpha _{i,j}\notin T$
. Then there is an
![]() $\alpha _{i',j'}\in T$
such that
$\alpha _{i',j'}\in T$
such that
![]() $\{\alpha _{i,j}, \alpha _{i',j'}\}$
is not
$\{\alpha _{i,j}, \alpha _{i',j'}\}$
is not
![]() $\mathbf N_n$
-compatible. By symmetry, suppose
$\mathbf N_n$
-compatible. By symmetry, suppose
![]() $i<i'<j<j'$
. However,
$i<i'<j<j'$
. However,
![]() $M_{\alpha _{i,j}} \to M_{(a_{i'}, a_j)}\oplus M_{(a_i, a_{j'})} \to M_{\alpha _{i',j'}}$
is an extension in
$M_{\alpha _{i,j}} \to M_{(a_{i'}, a_j)}\oplus M_{(a_i, a_{j'})} \to M_{\alpha _{i',j'}}$
is an extension in
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
. So, there is a rectangle in the AR-space of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
. So, there is a rectangle in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
whose left and right corners are
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
whose left and right corners are
![]() $M_{\alpha _{i,j}}$
and
$M_{\alpha _{i,j}}$
and
![]() $M_{\alpha _{i',j'}}$
, respectively (Theorem 1.2.5). Then
$M_{\alpha _{i',j'}}$
, respectively (Theorem 1.2.5). Then
![]() $\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is not
$\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is not
![]() $\mathbf E$
-compatible by Proposition 4.2.5. Since
$\mathbf E$
-compatible by Proposition 4.2.5. Since
![]() $M_{\alpha _{i',j'}}\in F(T)$
, we have a contradiction.
$M_{\alpha _{i',j'}}\in F(T)$
, we have a contradiction.
Lemma 5.1.5. Consider an
![]() $\mathbf N_n$
-cluster T and the induced
$\mathbf N_n$
-cluster T and the induced
![]() $\mathbf E$
-cluster
$\mathbf E$
-cluster
![]() $F(T)$
. Suppose
$F(T)$
. Suppose
![]() $T \to (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
is an
$T \to (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
is an
![]() $\mathbf N_n$
-mutation. Then
$\mathbf N_n$
-mutation. Then
![]() $F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
$F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
![]() $\mathbf E$
-mutation.
$\mathbf E$
-mutation.
Proof. It suffices to show that
![]() $\{M_{\alpha _{i,j}}, M_{\alpha _{i',j'}}\}$
is not
$\{M_{\alpha _{i,j}}, M_{\alpha _{i',j'}}\}$
is not
![]() $\mathbf E$
-compatible and
$\mathbf E$
-compatible and
![]() $(F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is
$(F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is
![]() $\mathbf E$
-compatible. By the proof of Proposition 5.1.4, we see that
$\mathbf E$
-compatible. By the proof of Proposition 5.1.4, we see that
![]() $\{M_{\alpha _{i,j}}, M_{\alpha _{i',j'}}\}$
is not
$\{M_{\alpha _{i,j}}, M_{\alpha _{i',j'}}\}$
is not
![]() $\mathbf E$
-compatible. Let
$\mathbf E$
-compatible. Let
![]() $T' = (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
. Note that
$T' = (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
. Note that
![]() $(F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\} = F(T')$
. By Proposition 5.1.4,
$(F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\} = F(T')$
. By Proposition 5.1.4,
![]() $F(T')$
is an
$F(T')$
is an
![]() $\mathbf E$
-cluster. Therefore,
$\mathbf E$
-cluster. Therefore,
![]() $F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
$F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
![]() $\mathbf E$
-mutation.
$\mathbf E$
-mutation.
Theorem 5.1.6. There is an embedding of cluster theories
![]() $\mathscr T_{\mathbf N_n}(\mathcal C(A_n))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
$\mathscr T_{\mathbf N_n}(\mathcal C(A_n))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
Proof. By Lemma 5.1.5, we see that, on objects, sending T to
![]() $F(T)$
and, on morphisms, sending each
$F(T)$
and, on morphisms, sending each
![]() $\mathbf N_n$
-mutation to the corresponding
$\mathbf N_n$
-mutation to the corresponding
![]() $\mathbf E$
-mutation described in the lemma yields a functor. Since
$\mathbf E$
-mutation described in the lemma yields a functor. Since
![]() $M_{\alpha _{i,j}}\not \cong M_{\alpha _{i',j'}}$
if
$M_{\alpha _{i,j}}\not \cong M_{\alpha _{i',j'}}$
if
![]() $i\neq i'$
or
$i\neq i'$
or
![]() $j\neq j'$
we see that if
$j\neq j'$
we see that if
![]() $T\neq T'$
, then
$T\neq T'$
, then
![]() $F(T)\neq F(T')$
. Furthermore, F is injective on clusters and generating morphisms between clusters.
$F(T)\neq F(T')$
. Furthermore, F is injective on clusters and generating morphisms between clusters.
Let
![]() $\eta _{T}: T\to F(T)$
be given by
$\eta _{T}: T\to F(T)$
be given by
![]() $\eta _{T} (\alpha _{i,j}) = M_{\alpha _{i,j}}$
. By Lemma 5.1.5, the
$\eta _{T} (\alpha _{i,j}) = M_{\alpha _{i,j}}$
. By Lemma 5.1.5, the
![]() $\eta _{T}$
’s commute with mutations. So,
$\eta _{T}$
’s commute with mutations. So,
![]() $(F,\eta )$
is an embedding of cluster theories.
$(F,\eta )$
is an embedding of cluster theories.
5.2 Embedding
 $\mathscr T_{\mathbf N_\infty } (\mathcal C(A_\infty )) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
$\mathscr T_{\mathbf N_\infty } (\mathcal C(A_\infty )) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
Here we embed the
![]() $\mathbb N_\infty $
-cluster theory of
$\mathbb N_\infty $
-cluster theory of
![]() $\mathcal C(A_\infty )$
into the
$\mathcal C(A_\infty )$
into the
![]() $\mathbf E$
-cluster theory of
$\mathbf E$
-cluster theory of
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
. We address the structure introduced by Holm and Jørgensen in [Reference Holm and Jørgensen12] using triangulations of the infinity-gon. Discussion on how to embed the closely related structure on the completed infinity-gon (introduced by Baur and Graz in [Reference Baur and Graz1]) is in the next paper of this series [Reference Rock20].
${\mathcal {C}(A_{{\mathbb {R}}})}$
. We address the structure introduced by Holm and Jørgensen in [Reference Holm and Jørgensen12] using triangulations of the infinity-gon. Discussion on how to embed the closely related structure on the completed infinity-gon (introduced by Baur and Graz in [Reference Baur and Graz1]) is in the next paper of this series [Reference Rock20].
Definition 5.2.1 (From [Reference Holm and Jørgensen12])
The infinity-gon has its vertices indexed by
![]() ${\mathbb {Z}}$
and no vertex at infinity. An arc is a pair of integers
${\mathbb {Z}}$
and no vertex at infinity. An arc is a pair of integers
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $i<j$
and
$i<j$
and
![]() $j-i\geq 2$
. Two arcs
$j-i\geq 2$
. Two arcs
![]() $(i,j)$
and
$(i,j)$
and
![]() $(i',j')$
are defined to cross if and only if
$(i',j')$
are defined to cross if and only if
![]() $i<i'<j<j'$
or
$i<i'<j<j'$
or
![]() $i'<i<j'<j$
. We call this pairwise compatibility condition
$i'<i<j'<j$
. We call this pairwise compatibility condition
![]() $\mathbf N_\infty $
. We write our arcs as
$\mathbf N_\infty $
. We write our arcs as
![]() $\alpha _{i,j}$
.
$\alpha _{i,j}$
.
The authors of [Reference Holm and Jørgensen12] show that there is a triangulated category whose indecomposables are the diagonals that are compatible if and only if they do not cross. We denote this category by
![]() $\mathcal C(A_\infty )$
.
$\mathcal C(A_\infty )$
.
Let
![]() $\{a_i\}$
be the sequence from Definition 5.0.1 and define
$\{a_i\}$
be the sequence from Definition 5.0.1 and define
![]() $M_{\alpha _{i,j}} := M_{(a_i,a_j)}$
. The following proposition is proved in the same fashion as Proposition 5.1.2.
$M_{\alpha _{i,j}} := M_{(a_i,a_j)}$
. The following proposition is proved in the same fashion as Proposition 5.1.2.
Proposition 5.2.2. The pair of arcs
![]() $\{\alpha _{i,j},\alpha _{i',j'}\}$
is
$\{\alpha _{i,j},\alpha _{i',j'}\}$
is
![]() $\mathbf N_\infty $
-compatible if and only if the pair of objects
$\mathbf N_\infty $
-compatible if and only if the pair of objects
![]() $\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is
$\{M_{\alpha _{i,j}},M_{\alpha _{i',j'}}\}$
is
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Definition 5.2.3. Let T be an
![]() $\mathbf N_\infty $
-cluster. Define
$\mathbf N_\infty $
-cluster. Define
![]() ${L}(T) := {L} \cup \{M_{\alpha _{i,j}}: \alpha _{i,j} \in T\}$
.
${L}(T) := {L} \cup \{M_{\alpha _{i,j}}: \alpha _{i,j} \in T\}$
.
By Proposition 5.2.2, similar to §5.1, it is straightforward that
![]() ${L}(T)$
is
${L}(T)$
is
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
It is not true that
![]() ${L}(T)$
is always an
${L}(T)$
is always an
![]() $\mathbf E$
-cluster. The clusters considered in [Reference Holm and Jørgensen12] form a proper subcategory of
$\mathbf E$
-cluster. The clusters considered in [Reference Holm and Jørgensen12] form a proper subcategory of
![]() $\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))$
. The
$\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))$
. The
![]() $\mathbf N_\infty $
-cluster theory includes what the authors in [Reference Holm and Jørgensen12] called “weak clusters.” Hence: the
$\mathbf N_\infty $
-cluster theory includes what the authors in [Reference Holm and Jørgensen12] called “weak clusters.” Hence: the
![]() $\mathbf N_\infty $
-cluster theory of
$\mathbf N_\infty $
-cluster theory of
![]() $\mathcal C(A_\infty )$
is not tilting.
$\mathcal C(A_\infty )$
is not tilting.
Example 5.2.4. Consider the
![]() $\mathbf N_\infty $
-cluster
$\mathbf N_\infty $
-cluster
![]() $T = \{ \alpha _{i,0}: i < -1\} \cup \{\alpha _{1,j} : j>2\}$
from [Reference Holm and Jørgensen12, Sketch 3, p. 279]. This is maximally
$T = \{ \alpha _{i,0}: i < -1\} \cup \{\alpha _{1,j} : j>2\}$
from [Reference Holm and Jørgensen12, Sketch 3, p. 279]. This is maximally
![]() $\mathbf N_\infty $
-compatible but
$\mathbf N_\infty $
-compatible but
![]() ${L}(T)$
is not maximally
${L}(T)$
is not maximally
![]() $\mathbf E$
-compatible. However,
$\mathbf E$
-compatible. However,
![]() ${L}(T) \cup \{M_{(a_{-\infty },a_0)}, M_{(a_{-\infty },a_1)}, M_{(a_1,a_{+\infty })}\}$
is maximally
${L}(T) \cup \{M_{(a_{-\infty },a_0)}, M_{(a_{-\infty },a_1)}, M_{(a_1,a_{+\infty })}\}$
is maximally
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
One issue with Example 5.2.4 is addressed by the authors in [Reference Holm and Jørgensen12]:
![]() $\mathop {\text {add}}(T)$
is not functorially finite in
$\mathop {\text {add}}(T)$
is not functorially finite in
![]() $\mathcal C(A_\infty )$
. On the other hand, there is not a problem with embedding too many cluster-like objects. Once the embedding has been established, one may take the subgroupoid of
$\mathcal C(A_\infty )$
. On the other hand, there is not a problem with embedding too many cluster-like objects. Once the embedding has been established, one may take the subgroupoid of
![]() $\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))$
consisting of only those
$\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))$
consisting of only those
![]() $\mathbf N_\infty $
-clusters that are part of the cluster structure in [Reference Holm and Jørgensen12]. Thus, there is still an embedding into the
$\mathbf N_\infty $
-clusters that are part of the cluster structure in [Reference Holm and Jørgensen12]. Thus, there is still an embedding into the
![]() $\mathbf E$
-cluster theory of
$\mathbf E$
-cluster theory of
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
.
${\mathcal {C}(A_{{\mathbb {R}}})}$
.
To create the embedding of cluster theories
![]() $\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
we need the following definitions adapted from [Reference Holm and Jørgensen12, Def. 3.2].
$\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
we need the following definitions adapted from [Reference Holm and Jørgensen12, Def. 3.2].
Definition 5.2.5. Let T be an
![]() $\mathbf N_\infty $
-compatible set of arcs.
$\mathbf N_\infty $
-compatible set of arcs.
-
• If, for all
 $n\in {\mathbb {Z}}$
, there are only finitely many arcs in the set
$n\in {\mathbb {Z}}$
, there are only finitely many arcs in the set
 $\{\alpha _{i,j} \in T : i=n \text { or }j=n\}$
we say T is locally finite.
$\{\alpha _{i,j} \in T : i=n \text { or }j=n\}$
we say T is locally finite. -
• If there exists
 $n\in {\mathbb {Z}}$
such that
$n\in {\mathbb {Z}}$
such that
 $\{\alpha _{i,j} \in T: j=n\}$
(respectively,
$\{\alpha _{i,j} \in T: j=n\}$
(respectively,
 $\{\alpha _{i,j} \in T: i = n\}$
) is infinite we call this set of arcs a left-fountain (respectively, right-fountain) at n.
$\{\alpha _{i,j} \in T: i = n\}$
) is infinite we call this set of arcs a left-fountain (respectively, right-fountain) at n. -
• If there exists n that has both a left- and right-fountains we say
 $\{\alpha _{i,j}\in T: i=n\text { or }j=n\}$
is a fountain.
$\{\alpha _{i,j}\in T: i=n\text { or }j=n\}$
is a fountain.
The authors note in [Reference Holm and Jørgensen12, Lem. 3.3] that if a left- or right-fountain exists in a
![]() $\mathbf N_\infty $
-cluster, then it must be unique. Just before the lemma, the authors of [Reference Holm and Jørgensen12] (who credit Collin Bleak for noticing) note that a left-fountain exists if and only if a right-fountain exists. This becomes quite important. It is also prudent to note that if there is a left-fountain at m and a right-fountain at n, then
$\mathbf N_\infty $
-cluster, then it must be unique. Just before the lemma, the authors of [Reference Holm and Jørgensen12] (who credit Collin Bleak for noticing) note that a left-fountain exists if and only if a right-fountain exists. This becomes quite important. It is also prudent to note that if there is a left-fountain at m and a right-fountain at n, then
![]() $m\leq n$
.
$m\leq n$
.
Definition 5.2.6. For an
![]() $\mathbf N_\infty $
-cluster T, we now define an
$\mathbf N_\infty $
-cluster T, we now define an
![]() $\mathbf E$
-cluster
$\mathbf E$
-cluster
![]() $F(T)$
.
$F(T)$
.
-
• If T is locally finite, then define
 $F(T) := {L}(T)$
.
$F(T) := {L}(T)$
. -
• If T has left- and right-fountains, then let m be the vertex with the left-fountain and n the vertex with the right-fountain (possibly,
 $m=n$
). Define
$m=n$
). Define  $$ \begin{align*} F(T) := {L}(T) \cup \{M_{(a_{-\infty},a_m)}, M_{(a_{-\infty},a_n)}, M_{(a_n,a_{+\infty})}\}. \end{align*} $$
$$ \begin{align*} F(T) := {L}(T) \cup \{M_{(a_{-\infty},a_m)}, M_{(a_{-\infty},a_n)}, M_{(a_n,a_{+\infty})}\}. \end{align*} $$
Proposition 5.2.7. Let T be an
![]() $\mathbf N_\infty $
-cluster. Suppose there exists
$\mathbf N_\infty $
-cluster. Suppose there exists
![]() $\ell \in {\mathbb {Z}}$
such that for all
$\ell \in {\mathbb {Z}}$
such that for all
![]() $\alpha _{i,j}\in T$
,
$\alpha _{i,j}\in T$
,
![]() $\ell \leq i $
or
$\ell \leq i $
or
![]() $j\leq \ell $
. Then there exists a left- and right-fountain in T.
$j\leq \ell $
. Then there exists a left- and right-fountain in T.
Proof. For contradiction, suppose T is locally finite. Let
By the maximality of T, we see that
![]() $0\leq i_\ell - j_\ell \leq 1$
and
$0\leq i_\ell - j_\ell \leq 1$
and
![]() $\ell \in \{i_\ell , j_\ell \}$
. Since we have assumed T is locally finite, let
$\ell \in \{i_\ell , j_\ell \}$
. Since we have assumed T is locally finite, let
We show
![]() $\alpha _{i_0,j_0}\in T$
, contradicting our assumption about
$\alpha _{i_0,j_0}\in T$
, contradicting our assumption about
![]() $\ell $
.
$\ell $
.
For contradiction, suppose there exists
![]() $\alpha _{i,j}\in T$
such that
$\alpha _{i,j}\in T$
such that
![]() $i_0 < i < j_0 < j$
. Since
$i_0 < i < j_0 < j$
. Since
![]() $i_0<i<j_0$
, we must have
$i_0<i<j_0$
, we must have
![]() $j_\ell \leq i \leq i_\ell $
. But then
$j_\ell \leq i \leq i_\ell $
. But then
![]() $i=i_\ell $
by our definition of
$i=i_\ell $
by our definition of
![]() $i_\ell $
. However
$i_\ell $
. However
![]() $j_0< j$
, contradiction our definition of
$j_0< j$
, contradiction our definition of
![]() $j_0$
. Thus, there cannot be such a
$j_0$
. Thus, there cannot be such a
![]() $\alpha _{i,j}\in T$
. Similarly, there can be no
$\alpha _{i,j}\in T$
. Similarly, there can be no
![]() $\alpha _{i',j'}\in T$
such that
$\alpha _{i',j'}\in T$
such that
![]() $i'<i_0<j'<j_0$
.
$i'<i_0<j'<j_0$
.
This means
![]() $\{\alpha _{i_0,j_0} \}\cup T$
is
$\{\alpha _{i_0,j_0} \}\cup T$
is
![]() $\mathbf N_\infty $
-compatible. Since T is an
$\mathbf N_\infty $
-compatible. Since T is an
![]() $\mathbf N_\infty $
-cluster we have
$\mathbf N_\infty $
-cluster we have
![]() $\alpha _{i_0,j_0}\in T$
. This contradicts our assumption about
$\alpha _{i_0,j_0}\in T$
. This contradicts our assumption about
![]() $\ell $
since
$\ell $
since
![]() $i_0<\ell < j_0$
. Therefore T is not locally finite; that is there exists a left- and right-fountain in T.
$i_0<\ell < j_0$
. Therefore T is not locally finite; that is there exists a left- and right-fountain in T.
Proposition 5.2.8. If T is an
![]() $\mathbf N_\infty $
-cluster, then
$\mathbf N_\infty $
-cluster, then
![]() $F(T)$
is an
$F(T)$
is an
![]() $\mathbf E$
-cluster.
$\mathbf E$
-cluster.
Proof. Recall
![]() $F(T)$
is an
$F(T)$
is an
![]() $\mathbf E$
-compatible set. Now suppose
$\mathbf E$
-compatible set. Now suppose
![]() $M_{|c,d|}$
is an indecomposable in
$M_{|c,d|}$
is an indecomposable in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
and
${\mathcal {C}(A_{{\mathbb {R}}})}$
and
![]() $F(T)\cup \{M_{|c,d|}\}$
is
$F(T)\cup \{M_{|c,d|}\}$
is
![]() $\mathbf E$
-compatible. We first assume
$\mathbf E$
-compatible. We first assume
![]() $M_{|c,d|}$
is not of the form
$M_{|c,d|}$
is not of the form
![]() $M_{\alpha _{i,j}}$
for any pair of integers
$M_{\alpha _{i,j}}$
for any pair of integers
![]() $i<j$
where
$i<j$
where
![]() $j-i\geq 2$
.
$j-i\geq 2$
.
Suppose
![]() $c=a_{-\infty }$
and T has a left- and right-fountains at m and n, respectively. Then
$c=a_{-\infty }$
and T has a left- and right-fountains at m and n, respectively. Then
![]() $d =a_m$
,
$d =a_m$
,
![]() $d=a_n$
, or
$d=a_n$
, or
![]() $d=a_{+\infty }$
. If
$d=a_{+\infty }$
. If
![]() $d=a_{+\infty }$
, then either
$d=a_{+\infty }$
, then either
![]() $c=a_{-\infty }$
or
$c=a_{-\infty }$
or
![]() $c=a_n$
. If T is locally finite, then
$c=a_n$
. If T is locally finite, then
![]() $c=a_{-\infty }$
if and only if
$c=a_{-\infty }$
if and only if
![]() $d=a_{+\infty }$
. The rest of the proof is similar to that of Proposition 5.1.4, using Proposition 5.2.2.
$d=a_{+\infty }$
. The rest of the proof is similar to that of Proposition 5.1.4, using Proposition 5.2.2.
The proofs of the following lemma and theorem follow the same logic as the proofs of Lemma 5.1.5 and Theorem 5.1.6.
Lemma 5.2.9. Consider an
![]() $\mathbf N_\infty $
-cluster T and the induced
$\mathbf N_\infty $
-cluster T and the induced
![]() $\mathbf E$
-cluster
$\mathbf E$
-cluster
![]() $F(T)$
. Suppose
$F(T)$
. Suppose
![]() $T \to (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
is an
$T \to (T \setminus \{\alpha _{i,j}\} )\cup \{\alpha _{i',j'}\}$
is an
![]() $\mathbf N_\infty $
-mutation. Then
$\mathbf N_\infty $
-mutation. Then
![]() $F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
$F(T) \to (F(T)\setminus \{M_{\alpha _{i,j}} \})\cup \{M_{\alpha _{i',j'}}\}$
is an
![]() $\mathbf E$
-mutation.
$\mathbf E$
-mutation.
Theorem 5.2.10. There is an embedding of cluster theories
![]() $\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
$\mathscr T_{\mathbf N_\infty }(\mathcal C(A_\infty ))\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
5.3 Embedding
 $\mathscr T_{\mathbf N_{{\mathbb {R}}}} (\mathcal C_{\pi }) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
$\mathscr T_{\mathbf N_{{\mathbb {R}}}} (\mathcal C_{\pi }) \to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
Now we embed the cluster theory of
![]() $\mathcal C_\pi $
into the new continuous cluster theory of
$\mathcal C_\pi $
into the new continuous cluster theory of
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
. In [Reference Igusa and Todorov15], the continuous cluster category
${\mathcal {C}(A_{{\mathbb {R}}})}$
. In [Reference Igusa and Todorov15], the continuous cluster category
![]() $\mathcal C_\pi $
is the orbit category of the doubling of
$\mathcal C_\pi $
is the orbit category of the doubling of
![]() $\mathcal D_\pi $
category (Definition 3.3.1) via almost-shift. Two indecomposables V and W in
$\mathcal D_\pi $
category (Definition 3.3.1) via almost-shift. Two indecomposables V and W in
![]() $\mathcal C_\pi $
are defined to be compatible if and only if
$\mathcal C_\pi $
are defined to be compatible if and only if
![]() $\dim (\operatorname {\mathrm {Ext}}_{\mathcal C_\pi }(V,W)\oplus \operatorname {\mathrm {Ext}}_{\mathcal C_\pi }(W,V)) \leq 1$
. We denote this compatibility condition by
$\dim (\operatorname {\mathrm {Ext}}_{\mathcal C_\pi }(V,W)\oplus \operatorname {\mathrm {Ext}}_{\mathcal C_\pi }(W,V)) \leq 1$
. We denote this compatibility condition by
![]() $\mathbf N_{{\mathbb {R}}}$
. Equivalently, V and W are not compatible in
$\mathbf N_{{\mathbb {R}}}$
. Equivalently, V and W are not compatible in
![]() $\mathcal C_\pi $
if there exists
$\mathcal C_\pi $
if there exists
![]() $n\in {\mathbb {Z}}$
such that there is a rectangle contained in
$n\in {\mathbb {Z}}$
such that there is a rectangle contained in
![]() $\mathcal D_\pi $
with lower left corner and upper right corner equal to V and
$\mathcal D_\pi $
with lower left corner and upper right corner equal to V and
![]() $W[n]$
and at most one of the other two corners on the boundary. There may be up to one point missing from the rectangle and it must be one of the corners not equal to V or W.
$W[n]$
and at most one of the other two corners on the boundary. There may be up to one point missing from the rectangle and it must be one of the corners not equal to V or W.
Indecomposables in
![]() $\mathcal D_\pi $
are
$\mathcal D_\pi $
are
![]() $M(x,y)$
where
$M(x,y)$
where
![]() $x,y\in {\mathbb {R}}$
with
$x,y\in {\mathbb {R}}$
with
![]() $|x-y|<\pi $
. Those in the fundamental domain (see figure below) are indecomposables in
$|x-y|<\pi $
. Those in the fundamental domain (see figure below) are indecomposables in
![]() $\mathcal C_\pi $
.
$\mathcal C_\pi $
.
We take our fundamental domain of
![]() $\mathcal C_\pi $
to be those indecomposables between the lines given by
$\mathcal C_\pi $
to be those indecomposables between the lines given by
![]() $M(0,y)$
and
$M(0,y)$
and
![]() $M(x,\pi )$
, including the
$M(x,\pi )$
, including the
![]() $M(0,y)$
indecomposables and excluding the
$M(0,y)$
indecomposables and excluding the
![]() $M(x,\pi )$
indecomposables, as shown in the figure on the right. This is the subset
$M(x,\pi )$
indecomposables, as shown in the figure on the right. This is the subset
![]() $X\subset {\mathbb {R}}^2$
in Definition 5.3.2.
$X\subset {\mathbb {R}}^2$
in Definition 5.3.2.

The line segment (without its endpoints) from
![]() $(-\frac {\pi }{2},-\frac {\pi }{2})$
to
$(-\frac {\pi }{2},-\frac {\pi }{2})$
to
![]() $(\frac {\pi }{2},\frac {\pi }{2})$
in
$(\frac {\pi }{2},\frac {\pi }{2})$
in
![]() ${\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
will be the image of the indecomposables in
${\mathbb {R}}\times [-\frac {\pi }{2},\frac {\pi }{2}]$
will be the image of the indecomposables in
![]() $\mathcal D_\pi $
of the form
$\mathcal D_\pi $
of the form
![]() $M(0,y)$
. It is also the image of the projective indecomposables from
$M(0,y)$
. It is also the image of the projective indecomposables from
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
in the 0th degree, with the exception of
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
in the 0th degree, with the exception of
![]() $P_{+\infty }$
, in
$P_{+\infty }$
, in
![]() ${\mathcal {D}^b(A_{{\mathbb {R}}})}$
. The dotted line bordering the fundamental domain in the picture are the indecomposables in
${\mathcal {D}^b(A_{{\mathbb {R}}})}$
. The dotted line bordering the fundamental domain in the picture are the indecomposables in
![]() $\mathcal D_\pi $
of the form
$\mathcal D_\pi $
of the form
![]() $M(x,\pi )$
.
$M(x,\pi )$
.

The following two definitions are useful in proving Theorem 5.3.8.
Definition 5.3.1. For each
![]() $M(x,y)$
in the fundamental domain in
$M(x,y)$
in the fundamental domain in
![]() $\mathcal C_\pi $
, set
$\mathcal C_\pi $
, set
Then
![]() $-\frac {\pi }{2} < \zeta _{x,y} < \frac {\pi }{2}$
and
$-\frac {\pi }{2} < \zeta _{x,y} < \frac {\pi }{2}$
and
![]() $\zeta _{x,y} \leq \xi _{x,y} < \pi -\zeta _{x,y}$
. The correspondence
$\zeta _{x,y} \leq \xi _{x,y} < \pi -\zeta _{x,y}$
. The correspondence
![]() $(x,y)\leftrightarrow (\xi ,\zeta )$
given by
$(x,y)\leftrightarrow (\xi ,\zeta )$
given by
![]() $(x,y)=(\xi -\zeta ,\xi +\zeta )$
and the above formula give a bijection
$(x,y)=(\xi -\zeta ,\xi +\zeta )$
and the above formula give a bijection
![]() $X\cong Y$
where
$X\cong Y$
where
 $$ \begin{align*} X &:= \{(x,y)\in {\mathbb{R}}^2 : |x-y|<\pi, x \geq 0, y < \pi \}= \text{ fundamental domain for}\ \mathcal C_\pi ,\\ Y &:= \left\{(\xi,\zeta)\in {\mathbb{R}}^2: -\frac{\pi}{2} < \zeta < \frac{\pi}{2} \text{ and } \zeta \leq \xi < \pi - \zeta \right\} = \text{AR-space of}\ \operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}}}). \end{align*} $$
$$ \begin{align*} X &:= \{(x,y)\in {\mathbb{R}}^2 : |x-y|<\pi, x \geq 0, y < \pi \}= \text{ fundamental domain for}\ \mathcal C_\pi ,\\ Y &:= \left\{(\xi,\zeta)\in {\mathbb{R}}^2: -\frac{\pi}{2} < \zeta < \frac{\pi}{2} \text{ and } \zeta \leq \xi < \pi - \zeta \right\} = \text{AR-space of}\ \operatorname{\mathrm{rep}}_k(A_{{\mathbb{R}}}). \end{align*} $$
These are indicated in the figures above. We set
 $$ \begin{align*} a_{x,y} &= \tan \left(\frac{\xi_{x,y}-\zeta_{x,y}-\pi}{2}\right) = \tan\left(\frac{x-\pi}2\right)& b_{x,y} &= \tan \left(\frac{\xi_{x,y}+\zeta_{x,y}}{2}\right)=\tan\left(\frac y2\right). \end{align*} $$
$$ \begin{align*} a_{x,y} &= \tan \left(\frac{\xi_{x,y}-\zeta_{x,y}-\pi}{2}\right) = \tan\left(\frac{x-\pi}2\right)& b_{x,y} &= \tan \left(\frac{\xi_{x,y}+\zeta_{x,y}}{2}\right)=\tan\left(\frac y2\right). \end{align*} $$
Using
![]() $\tan (\frac \pi 2)=-\infty $
, it is straightforward that the correspondences given in Definition 5.3.1:
$\tan (\frac \pi 2)=-\infty $
, it is straightforward that the correspondences given in Definition 5.3.1:
![]() $(x,y)\leftrightarrow (\xi _{x,y},\zeta _{x,y})\leftrightarrow (a_{x,y},b_{x,y})$
give bijections between
$(x,y)\leftrightarrow (\xi _{x,y},\zeta _{x,y})\leftrightarrow (a_{x,y},b_{x,y})$
give bijections between
![]() $X,Y$
and Z where
$X,Y$
and Z where
We interpret Z as the set of open intervals
![]() $(a,b)\subset {\mathbb {R}}$
where
$(a,b)\subset {\mathbb {R}}$
where
![]() $b<\infty $
. On objects:
$b<\infty $
. On objects:
-
•
 $M_{(a_{x,y},b_{x,y})}$
is the indecomposable in
$M_{(a_{x,y},b_{x,y})}$
is the indecomposable in
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
(and its image in
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
(and its image in
 ${\mathcal {D}^b(A_{{\mathbb {R}}})}$
and
${\mathcal {D}^b(A_{{\mathbb {R}}})}$
and
 ${\mathcal {C}(A_{{\mathbb {R}}})}$
) with support in the open interval
${\mathcal {C}(A_{{\mathbb {R}}})}$
) with support in the open interval
 ${(a_{x,y},b_{x,y})}\in Z$
.
${(a_{x,y},b_{x,y})}\in Z$
. -
•
 $(\xi _{x,y},\zeta _{x,y})=\mathop {\boldsymbol {\Gamma }}^b(M_{(a_{x,y},b_{x,y})})$
is the corresponding point in the AR-space Y of
$(\xi _{x,y},\zeta _{x,y})=\mathop {\boldsymbol {\Gamma }}^b(M_{(a_{x,y},b_{x,y})})$
is the corresponding point in the AR-space Y of
 $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
.
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
. -
•
 $M(x,y)=G(M_{(a_{x,y},b_{x,y})})$
,
$M(x,y)=G(M_{(a_{x,y},b_{x,y})})$
,
 $(x,y)\in X$
, is the corresponding object of
$(x,y)\in X$
, is the corresponding object of
 $\mathcal C_\pi $
where G is the functor given in Definition 3.3.2.
$\mathcal C_\pi $
where G is the functor given in Definition 3.3.2.
We denote by
![]() ${_{(x,y)}M}$
the indecomposable
${_{(x,y)}M}$
the indecomposable
![]() $M_{(a_{x,y},b_{x,y})}$
in
$M_{(a_{x,y},b_{x,y})}$
in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
.
${\mathcal {C}(A_{{\mathbb {R}}})}$
.
Definition 5.3.2. Let
![]() $\mathfrak f:X\to Z$
be the bijection given above. Thus
$\mathfrak f:X\to Z$
be the bijection given above. Thus
 $$ \begin{align*} \mathfrak f(x,y):=(a_{x,y},b_{x,y})=\left( \tan\left( \frac{x-\pi}{2} \right), \tan\left( \frac{y}{2} \right) \right). \end{align*} $$
$$ \begin{align*} \mathfrak f(x,y):=(a_{x,y},b_{x,y})=\left( \tan\left( \frac{x-\pi}{2} \right), \tan\left( \frac{y}{2} \right) \right). \end{align*} $$
With this notation we have
![]() ${_{(x,y)}M} =M_{\mathfrak f(x,y)}= M_{(a_{x,y}, b_{x,y})}$
. Let
${_{(x,y)}M} =M_{\mathfrak f(x,y)}= M_{(a_{x,y}, b_{x,y})}$
. Let
![]() $\mathfrak f_1(x,y)=a_{x,y}$
and
$\mathfrak f_1(x,y)=a_{x,y}$
and
![]() $\mathfrak f_2(x,y)=b_{x,y}$
be the endpoints of the open interval
$\mathfrak f_2(x,y)=b_{x,y}$
be the endpoints of the open interval
![]() $\mathfrak f(x,y)$
.
$\mathfrak f(x,y)$
.
Lemma 5.3.3. The pair
![]() $\{M(x,y), M(x',y')\}$
of indecomposables in
$\{M(x,y), M(x',y')\}$
of indecomposables in
![]() $\mathcal C_\pi $
is
$\mathcal C_\pi $
is
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible if and only if the pair
$\mathbf N_{{\mathbb {R}}}$
-compatible if and only if the pair
![]() $\{{_{(x,y)}M},{_{(x',y')}M}\}$
is
$\{{_{(x,y)}M},{_{(x',y')}M}\}$
is
![]() $\mathbf E$
-compatible in
$\mathbf E$
-compatible in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
.
${\mathcal {C}(A_{{\mathbb {R}}})}$
.
Proof. First suppose
![]() $\{M(x,y), M(x',y')\}$
is not
$\{M(x,y), M(x',y')\}$
is not
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible. Then
$\mathbf N_{{\mathbb {R}}}$
-compatible. Then
![]() $M(x',y)$
and
$M(x',y)$
and
![]() $M(x,y')$
are indecomposables in the fundamental domain of
$M(x,y')$
are indecomposables in the fundamental domain of
![]() $\mathcal C_\pi $
. This means
$\mathcal C_\pi $
. This means
![]() ${_{(x',y)}M}$
and
${_{(x',y)}M}$
and
![]() ${_{(x,y')}M}$
are well-defined indecomposables in
${_{(x,y')}M}$
are well-defined indecomposables in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
that, with
${\mathcal {C}(A_{{\mathbb {R}}})}$
that, with
![]() ${_{(x,y)}M}$
and
${_{(x,y)}M}$
and
![]() ${_{(x',y')}M}$
, form a rectangle in the AR-space of
${_{(x',y')}M}$
, form a rectangle in the AR-space of
![]() ${\mathcal {D}^b(A_{{\mathbb {R}}})}$
which is entirely contained in the AR-space of
${\mathcal {D}^b(A_{{\mathbb {R}}})}$
which is entirely contained in the AR-space of
![]() $\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
. Thus,
$\operatorname {\mathrm {rep}}_k(A_{{\mathbb {R}}})$
. Thus,
![]() $\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
$\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
![]() $\mathbf E$
-compatible.
$\mathbf E$
-compatible.
Now suppose
![]() $\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
$\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
![]() $\mathbf E$
-compatible. We reverse the argument and see that
$\mathbf E$
-compatible. We reverse the argument and see that
![]() $M(x',y)$
and
$M(x',y)$
and
![]() $M(x,y')$
are indecomposables forming a rectangle in the fundamental domain of
$M(x,y')$
are indecomposables forming a rectangle in the fundamental domain of
![]() $\mathcal C_\pi $
. Therefore,
$\mathcal C_\pi $
. Therefore,
![]() $\{M(x,y), M(x',y')\}$
is not
$\{M(x,y), M(x',y')\}$
is not
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible.
$\mathbf N_{{\mathbb {R}}}$
-compatible.
Definition 5.3.4. Let T be an
![]() $\mathbf N_{{\mathbb {R}}}$
-cluster in
$\mathbf N_{{\mathbb {R}}}$
-cluster in
![]() $\mathcal C_\pi $
. We define R in
$\mathcal C_\pi $
. We define R in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
:
${\mathcal {C}(A_{{\mathbb {R}}})}$
:
 $$ \begin{align*} R :=& \{P_{+\infty}\}\cup \left\{ {{}_{(x,y)}M} = M_{\mathfrak f(x,y)}=M_{(a_{x,y}, b_{x,y})} : M(x,y) \in T \right\} \\ & \cup \{ M_{[z,z]} :z \in{\mathbb{R}},\, \not\exists M(x,y)\in T \text{ such that } (\mathfrak f_1(x,y)= z \text{ or } \mathfrak f_2(x,y)=z)\}. \end{align*} $$
$$ \begin{align*} R :=& \{P_{+\infty}\}\cup \left\{ {{}_{(x,y)}M} = M_{\mathfrak f(x,y)}=M_{(a_{x,y}, b_{x,y})} : M(x,y) \in T \right\} \\ & \cup \{ M_{[z,z]} :z \in{\mathbb{R}},\, \not\exists M(x,y)\in T \text{ such that } (\mathfrak f_1(x,y)= z \text{ or } \mathfrak f_2(x,y)=z)\}. \end{align*} $$
Definition 5.3.5. For
![]() $(a,b)\subset {\mathbb {R}}$
,
$(a,b)\subset {\mathbb {R}}$
,
![]() $b<+\infty $
, define conditions
$b<+\infty $
, define conditions
![]() $S_\ell $
and
$S_\ell $
and
![]() $S_r$
as follows.
$S_r$
as follows.
-
 $S_\ell :$
Either (i)
$S_\ell :$
Either (i)
 $\exists M_{(c,a)}\in R$
or (ii)
$\exists M_{(c,a)}\in R$
or (ii)
 $\exists M_{(a,b')}\in R$
where
$\exists M_{(a,b')}\in R$
where
 $b'> b$
or (iii)
$b'> b$
or (iii)
 $a=-\infty $
.
$a=-\infty $
. -
 $S_r:$
Either (i)
$S_r:$
Either (i)
 $\exists M_{(b,c)}\in R$
or (ii)
$\exists M_{(b,c)}\in R$
or (ii)
 $\exists M_{(a',b)}\in R$
where
$\exists M_{(a',b)}\in R$
where
 $a' < a$
.
$a' < a$
.
For
![]() ${_{(x,y)}M}=M_{(a,b)}\in R$
, we define a set
${_{(x,y)}M}=M_{(a,b)}\in R$
, we define a set
![]() ${\rho }(a,b)$
that we use to construct
${\rho }(a,b)$
that we use to construct
![]() $F(T)$
.
$F(T)$
.
-
• If
 $(a,b)$
satisfies both
$(a,b)$
satisfies both
 $S_\ell $
and
$S_\ell $
and
 $S_r$
, let
$S_r$
, let
 ${\rho }(a,b)=\emptyset $
.
${\rho }(a,b)=\emptyset $
. -
• If
 $(a,b)$
satisfies
$(a,b)$
satisfies
 $S_\ell $
but not
$S_\ell $
but not
 $S_r$
, let
$S_r$
, let
 ${\rho }(a,b)=\{M_{(a,b]}\}$
.
${\rho }(a,b)=\{M_{(a,b]}\}$
. -
• If
 $(a,b)$
satisfies
$(a,b)$
satisfies
 $S_r$
but not
$S_r$
but not
 $S_\ell $
, let
$S_\ell $
, let
 ${\rho }(a,b)=\{M_{[a,b)}\}$
.
${\rho }(a,b)=\{M_{[a,b)}\}$
. -
• If
 $(a,b)$
satisfies neither
$(a,b)$
satisfies neither
 $S_\ell $
nor
$S_\ell $
nor
 $S_r$
, let
$S_r$
, let
 ${\rho }(a,b) = \{M_{[a,b]}, M_{[a,b)}\}$
.
${\rho }(a,b) = \{M_{[a,b]}, M_{[a,b)}\}$
.
Let
![]() $\mathcal P :=\{ P_{b)}: P_{b)}\in R, b < +\infty \}$
with total order
$\mathcal P :=\{ P_{b)}: P_{b)}\in R, b < +\infty \}$
with total order
![]() $P_{b)} \leq P_{b')}$
if
$P_{b)} \leq P_{b')}$
if
![]() $b \leq b'$
. Define
$b \leq b'$
. Define
![]() $F(T)$
:
$F(T)$
:
-
•
 $F(T) := \{I_{(b}\} \cup R\cup \displaystyle \bigcup _{P_{b)}\neq M_{(a,b)}\in R} {\rho }(a,b) $
if
$F(T) := \{I_{(b}\} \cup R\cup \displaystyle \bigcup _{P_{b)}\neq M_{(a,b)}\in R} {\rho }(a,b) $
if
 $P_{b)}\in \mathcal P$
is maximal.
$P_{b)}\in \mathcal P$
is maximal. -
•
 $F(T) := R\cup \displaystyle \bigcup _{M_{(a,b)}\in R} {\rho }(a,b) $
if
$F(T) := R\cup \displaystyle \bigcup _{M_{(a,b)}\in R} {\rho }(a,b) $
if
 $\mathcal P=\emptyset $
or
$\mathcal P=\emptyset $
or
 $\mathcal P$
has no maximal element.
$\mathcal P$
has no maximal element.
Proposition 5.3.6. If T is an
![]() $\mathbf N_{{\mathbb {R}}}$
-cluster in
$\mathbf N_{{\mathbb {R}}}$
-cluster in
![]() $\mathcal C_\pi $
, then
$\mathcal C_\pi $
, then
![]() $F(T)$
is an
$F(T)$
is an
![]() $\mathbf E$
-cluster in
$\mathbf E$
-cluster in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
.
${\mathcal {C}(A_{{\mathbb {R}}})}$
.
Proof. Using Lemma 5.3.3, it is straightforward to check that
![]() $F(T)$
is
$F(T)$
is
![]() $\mathbf E$
-compatible. Let
$\mathbf E$
-compatible. Let
![]() $M_{|c,d|}$
be an indecomposable in
$M_{|c,d|}$
be an indecomposable in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
such that
${\mathcal {C}(A_{{\mathbb {R}}})}$
such that
![]() $F(T)\cup \{M_{|c,d|}\}$
is
$F(T)\cup \{M_{|c,d|}\}$
is
![]() $\mathbf E$
-compatible. We show
$\mathbf E$
-compatible. We show
![]() $M_{|c,d|}\in F(T)$
.
$M_{|c,d|}\in F(T)$
.
As before we can check various values for c but in a different fashion than before. First suppose there exists
![]() $M(x,y)\in T$
such that
$M(x,y)\in T$
such that
![]() $\mathfrak f_1(x,y)=c$
. Then there is no
$\mathfrak f_1(x,y)=c$
. Then there is no
![]() $M(x',y')\in T$
such that
$M(x',y')\in T$
such that
![]() $\mathfrak f(x,y) = (a',b')$
and
$\mathfrak f(x,y) = (a',b')$
and
![]() $a' < d < b'$
. Thus, there exist
$a' < d < b'$
. Thus, there exist
![]() $M(x',y')\in T$
such that
$M(x',y')\in T$
such that
![]() $d=\mathfrak f_1(x',y')$
or
$d=\mathfrak f_1(x',y')$
or
![]() $d=\mathfrak f_2(x',y')$
. Then
$d=\mathfrak f_2(x',y')$
. Then
![]() $M_{[c,c]}$
and
$M_{[c,c]}$
and
![]() $M_{[d,d]}$
are not in
$M_{[d,d]}$
are not in
![]() $F(T)$
.
$F(T)$
.
Now we have
![]() $\{M_{(c,d)}\}\cup F(T)$
is
$\{M_{(c,d)}\}\cup F(T)$
is
![]() $\mathbf E$
-compatible. Since
$\mathbf E$
-compatible. Since
![]() $\mathfrak f:X\cong Z$
is a bijection, there is a
$\mathfrak f:X\cong Z$
is a bijection, there is a
![]() $M(x'',y'')$
that is compatible with T such that
$M(x'',y'')$
that is compatible with T such that
![]() $\mathfrak f(x'',y'')=(c,d)$
. However, since T is an
$\mathfrak f(x'',y'')=(c,d)$
. However, since T is an
![]() $\mathbf N_{{\mathbb {R}}}$
-cluster
$\mathbf N_{{\mathbb {R}}}$
-cluster
![]() $M(x'',y'')\in T$
and so
$M(x'',y'')\in T$
and so
![]() $M_{(c,d)}\in F(T)$
. If
$M_{(c,d)}\in F(T)$
. If
![]() $c\in |c,d|$
or
$c\in |c,d|$
or
![]() $c=-\infty $
, then there is no
$c=-\infty $
, then there is no
![]() $M_{(a,c)}\in F(T)$
and if
$M_{(a,c)}\in F(T)$
and if
![]() $d\in |c,d|$
there is no
$d\in |c,d|$
there is no
![]() $M_{(d,b)}\in F(T)$
. Thus, either
$M_{(d,b)}\in F(T)$
. Thus, either
![]() $|c,d|=(c,d)$
or
$|c,d|=(c,d)$
or
![]() $M_{|c,d|}\in {\rho }(c,d)$
. In either case
$M_{|c,d|}\in {\rho }(c,d)$
. In either case
![]() $M_{|c,d|}\in F(T)$
.
$M_{|c,d|}\in F(T)$
.
Now suppose there is no
![]() $M(x,y)\in T$
such that
$M(x,y)\in T$
such that
![]() $\mathfrak f_1(x,y)=c$
. For contradiction suppose
$\mathfrak f_1(x,y)=c$
. For contradiction suppose
![]() $d> c$
. Then
$d> c$
. Then
![]() $\{M(\mathfrak f^{-1}(c,d))\} \cup T$
is not
$\{M(\mathfrak f^{-1}(c,d))\} \cup T$
is not
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible and so by Lemma 5.3.3 there is
$\mathbf N_{{\mathbb {R}}}$
-compatible and so by Lemma 5.3.3 there is
![]() $M(x',y')\in T$
such that (i)
$M(x',y')\in T$
such that (i)
![]() $\mathfrak f(x',y')=(a,b)$
and (ii)
$\mathfrak f(x',y')=(a,b)$
and (ii)
![]() $a<c<b<d$
or
$a<c<b<d$
or
![]() $c<a<d<b$
. Thus,
$c<a<d<b$
. Thus,
![]() $\{M_{|c,d|}\}\cup F(T)$
is not
$\{M_{|c,d|}\}\cup F(T)$
is not
![]() $\mathbf E$
-compatible, a contradiction. Thus
$\mathbf E$
-compatible, a contradiction. Thus
![]() $d=c$
and
$d=c$
and
![]() $M_{|c,d|}=M_{[c,c]}$
. Then we know
$M_{|c,d|}=M_{[c,c]}$
. Then we know
![]() $d=c$
cannot be
$d=c$
cannot be
![]() $\mathfrak f_2(x',y')$
for some
$\mathfrak f_2(x',y')$
for some
![]() $M(x',y')\in T$
or else
$M(x',y')\in T$
or else
![]() $\{M_{[c,c]}\}\cup F(T)$
would not be
$\{M_{[c,c]}\}\cup F(T)$
would not be
![]() $\mathbf E$
-compatible. Therefore,
$\mathbf E$
-compatible. Therefore,
![]() $M_{[c,c]}$
is already in
$M_{[c,c]}$
is already in
![]() $R \subset F(T)$
.
$R \subset F(T)$
.
Lemma 5.3.7. Let T be an
![]() $\mathbf N_{{\mathbb {R}}}$
-cluster in
$\mathbf N_{{\mathbb {R}}}$
-cluster in
![]() $\mathcal C_\pi $
and
$\mathcal C_\pi $
and
![]() $F(T)$
the induced
$F(T)$
the induced
![]() $\mathbf E$
-cluster in
$\mathbf E$
-cluster in
![]() ${\mathcal {C}(A_{{\mathbb {R}}})}$
. If
${\mathcal {C}(A_{{\mathbb {R}}})}$
. If
![]() $T \to (T\setminus \{M(x,y)\})\cup \{M(x',y')\}$
is an
$T \to (T\setminus \{M(x,y)\})\cup \{M(x',y')\}$
is an
![]() $\mathbf N_{{\mathbb {R}}}$
-mutation, then
$\mathbf N_{{\mathbb {R}}}$
-mutation, then
![]() $F(T) \to (F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is an
$F(T) \to (F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is an
![]() $\mathbf E$
-mutation.
$\mathbf E$
-mutation.
Proof. By Lemma 5.3.3, we know
![]() $\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
$\{{_{(x,y)}M},{_{(x',y')}M}\}$
is not
![]() $\mathbf E$
-compatible. Thus it remains to show
$\mathbf E$
-compatible. Thus it remains to show
![]() $(F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is an
$(F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is an
![]() $\mathbf E$
-cluster. Without loss of generality, we assume
$\mathbf E$
-cluster. Without loss of generality, we assume
![]() $y'> y$
which implies
$y'> y$
which implies
![]() $x'> x$
, since
$x'> x$
, since
![]() $\{M(x,y),M(x',y')\}$
is not
$\{M(x,y),M(x',y')\}$
is not
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible. This also means
$\mathbf N_{{\mathbb {R}}}$
-compatible. This also means
![]() $x-\pi < x'-\pi <y<y'$
and
$x-\pi < x'-\pi <y<y'$
and
![]() $x<x' < \pi + y< \pi + y'$
.
$x<x' < \pi + y< \pi + y'$
.
Let
![]() $M(w,z)\in T$
such that
$M(w,z)\in T$
such that
![]() $(w,z)\neq (x,y)$
. Then both of
$(w,z)\neq (x,y)$
. Then both of
![]() $\{M(w,z), M(x,y)\}$
and
$\{M(w,z), M(x,y)\}$
and
![]() $\{M(w,z), M(x',y')\}$
are
$\{M(w,z), M(x',y')\}$
are
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible. We work with
$\mathbf N_{{\mathbb {R}}}$
-compatible. We work with
![]() $M(w,z)$
. First,
$M(w,z)$
. First,
![]() $x \leq w \leq x'$
if and only if
$x \leq w \leq x'$
if and only if
![]() $x-\pi < z \leq x'-\pi $
. Next,
$x-\pi < z \leq x'-\pi $
. Next,
![]() $\pi + y \leq w \leq \pi + y'$
if and only if
$\pi + y \leq w \leq \pi + y'$
if and only if
![]() $y < z \leq y'$
. Thus,
$y < z \leq y'$
. Thus,
![]() $\{M(w,z), M(x,x'), M(y,y')\}$
is
$\{M(w,z), M(x,x'), M(y,y')\}$
is
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible and so
$\mathbf N_{{\mathbb {R}}}$
-compatible and so
![]() $M(x,x'),M(y,y')\in T$
. We can similarly list all possibilities for z and check
$M(x,x'),M(y,y')\in T$
. We can similarly list all possibilities for z and check
![]() $\{M(w,z),M(x',y),M(x,y')\}$
is
$\{M(w,z),M(x',y),M(x,y')\}$
is
![]() $\mathbf N_{{\mathbb {R}}}$
-compatible. Thus,
$\mathbf N_{{\mathbb {R}}}$
-compatible. Thus,
![]() $M(x',y),M(x,y')\in T$
. Let
$M(x',y),M(x,y')\in T$
. Let
![]() $(a,b)=\mathfrak f(x,y)$
and
$(a,b)=\mathfrak f(x,y)$
and
![]() $(a',b')=\mathfrak f(x',y')$
. Then
$(a',b')=\mathfrak f(x',y')$
. Then
 $$ \begin{align*} (a',b) &= \mathfrak f(x',y), & (a,a') &= \mathfrak f(x,x'-\pi), \\ (a,b') &= \mathfrak f(x,y'), & (b,b') &= \mathfrak f(y+\pi,y'). \end{align*} $$
$$ \begin{align*} (a',b) &= \mathfrak f(x',y), & (a,a') &= \mathfrak f(x,x'-\pi), \\ (a,b') &= \mathfrak f(x,y'), & (b,b') &= \mathfrak f(y+\pi,y'). \end{align*} $$
Since
![]() $-\infty \le a<a'<b<b'<+\infty $
and
$-\infty \le a<a'<b<b'<+\infty $
and
![]() $M_{(a',b)},M_{(a,b')}\in R$
, we see that for
$M_{(a',b)},M_{(a,b')}\in R$
, we see that for
![]() $(a,b), (a,a')$
and
$(a,b), (a,a')$
and
![]() $(b,b')$
both
$(b,b')$
both
![]() $S_\ell $
and
$S_\ell $
and
![]() $S_r$
are satisfied. Thus
$S_r$
are satisfied. Thus
![]() $(F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is
$(F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
is
![]() $\mathbf E$
-compatible. Furthermore, let
$\mathbf E$
-compatible. Furthermore, let
![]() $T' = (T\setminus \{M(x,y)\})\cup \{M(x',y')\}$
. Then
$T' = (T\setminus \{M(x,y)\})\cup \{M(x',y')\}$
. Then
![]() $F(T') = (F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
. Therefore
$F(T') = (F(T)\setminus \{{_{(x,y)}M}\})\cup \{{_{(x',y')}M}\}$
. Therefore
![]() $F(T')$
is an
$F(T')$
is an
![]() $\mathbf E$
-cluster by Proposition 5.3.6 and the lemma holds.
$\mathbf E$
-cluster by Proposition 5.3.6 and the lemma holds.
Theorem 5.3.8. There is an embedding of cluster theories
![]() $\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
$\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
.
Proof. By Proposition 5.3.6 and Lemma 5.3.7, we see that, on objects, sending T to
![]() $F(T)$
and, on morphisms, sending each
$F(T)$
and, on morphisms, sending each
![]() $\mathbf N_{{\mathbb {R}}}$
-mutation to the corresponding
$\mathbf N_{{\mathbb {R}}}$
-mutation to the corresponding
![]() $\mathbf E$
-mutation yields a functor
$\mathbf E$
-mutation yields a functor
![]() $\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
. It is straightforward to check F is an injection on clusters and mutations.
$\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
. It is straightforward to check F is an injection on clusters and mutations.
Let
![]() $\eta _{T}:T\to F(T)$
be defined by
$\eta _{T}:T\to F(T)$
be defined by
![]() $\eta _{T} (M(x,y)) := {_{(x,y)}M}$
. This is an injection by definition and by Lemma 5.3.7 the
$\eta _{T} (M(x,y)) := {_{(x,y)}M}$
. This is an injection by definition and by Lemma 5.3.7 the
![]() $\eta $
’s commute with mutation. Therefore,
$\eta $
’s commute with mutation. Therefore,
![]() $(F,\eta )$
is an embedding of cluster theories.
$(F,\eta )$
is an embedding of cluster theories.
Remark 5.3.9. We observe that the embedding of cluster theories
![]() $\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
cannot be realized by a functor
$\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )\to \mathscr T_{\mathbf E}({\mathcal {C}(A_{{\mathbb {R}}})})$
cannot be realized by a functor
![]() $\mathcal C_\pi \to {\mathcal {C}(A_{{\mathbb {R}}})}$
since any embedding
$\mathcal C_\pi \to {\mathcal {C}(A_{{\mathbb {R}}})}$
since any embedding
![]() $\mathcal D_\pi \to {\mathcal {D}^b(A_{{\mathbb {R}}})}$
would need to use position 2 in even degrees and position 3 in odd degrees or vise versa (Remark 1.2.3) and compatibility for clusters would be violated when the positions switch.
$\mathcal D_\pi \to {\mathcal {D}^b(A_{{\mathbb {R}}})}$
would need to use position 2 in even degrees and position 3 in odd degrees or vise versa (Remark 1.2.3) and compatibility for clusters would be violated when the positions switch.
Remark 5.3.10. All clusters in
![]() $\mathcal C_\pi $
in [Reference Igusa and Todorov15] are
$\mathcal C_\pi $
in [Reference Igusa and Todorov15] are
![]() $\mathbf N_{{\mathbb {R}}}$
-clusters. However, there are
$\mathbf N_{{\mathbb {R}}}$
-clusters. However, there are
![]() $\mathbf N_{{\mathbb {R}}}$
-clusters that are not part of the cluster structure in [Reference Igusa and Todorov15]. For example, the vertical line
$\mathbf N_{{\mathbb {R}}}$
-clusters that are not part of the cluster structure in [Reference Igusa and Todorov15]. For example, the vertical line
![]() $\{M(0,y): -\pi < y < \pi \}$
is an
$\{M(0,y): -\pi < y < \pi \}$
is an
![]() $\mathbf N_{{\mathbb {R}}}$
-cluster but not part of the cluster structure in
$\mathbf N_{{\mathbb {R}}}$
-cluster but not part of the cluster structure in
![]() $\mathcal C_\pi $
.
$\mathcal C_\pi $
.
However, as with
![]() $A_\infty $
, this is not truly an issue. We have an injection on objects and so taking a subgroupoid of
$A_\infty $
, this is not truly an issue. We have an injection on objects and so taking a subgroupoid of
![]() $\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )$
that only contains the clusters in the cluster structure in
$\mathscr T_{\mathbf N_{{\mathbb {R}}}}(\mathcal C_\pi )$
that only contains the clusters in the cluster structure in
![]() $\mathcal C_\pi $
still embeds into
$\mathcal C_\pi $
still embeds into
![]() $\mathscr T_{\mathbf E}(\mathcal C_\pi )$
while preserving mutation. This is done in part (IV) [Reference Rock20].
$\mathscr T_{\mathbf E}(\mathcal C_\pi )$
while preserving mutation. This is done in part (IV) [Reference Rock20].
Acknowledgments
The authors would like to thank Ralf Schiffler for creating the Cluster Algebra Summer School in 2017 where the idea for this project was conceived. The second author would like to thank Eric Hanson for helpful discussions. The first author acknowledges support from the Simons Foundation. The majority of this work was completed while the second author was a graduate student at Brandeis University and they would like to thank the university for its hospitality. The authors are also grateful to the referee for numerous suggestions for improving this manuscript.