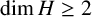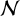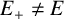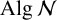1 Introduction
Let X be a Banach space and
![]() $B(X)$
the algebra of all bounded linear operators on X. Suppose that S is a subset of
$B(X)$
the algebra of all bounded linear operators on X. Suppose that S is a subset of
![]() $B(X)$
. Following [Reference Jiménez-Vargas, Li, Peralta, Wang and Wang4, Reference Li, Liu and Ren6], a map
$B(X)$
. Following [Reference Jiménez-Vargas, Li, Peralta, Wang and Wang4, Reference Li, Liu and Ren6], a map
![]() $\phi : X \rightarrow X$
(which is not assumed to be linear) is called a 2-local S-map if for any
$\phi : X \rightarrow X$
(which is not assumed to be linear) is called a 2-local S-map if for any
![]() $a, b \in X$
, there exists
$a, b \in X$
, there exists
![]() $\phi _{a, b} \in S$
, depending on a and b, such that
$\phi _{a, b} \in S$
, depending on a and b, such that
Here, X is said to be 2-S-reflexive if every 2-local S-map belongs to S.
The concept of a 2-local S-map dates back to the paper [Reference Šemrl13], where Šemrl investigated 2-local automorphisms and 2-local derivations, motivated by Kowalski and Słodkowski [Reference Kowalski and Słodkowski5]. Then in [Reference Molnár8], the earliest investigation of 2-local
![]() $\operatorname {Iso}(X)$
-maps (also called 2-local isometries in some papers) was carried out by Molnár, where
$\operatorname {Iso}(X)$
-maps (also called 2-local isometries in some papers) was carried out by Molnár, where
![]() $\operatorname {Iso}(X)$
denotes the set of all surjective linear isometries of X. By an isometry of X, we mean a function
$\operatorname {Iso}(X)$
denotes the set of all surjective linear isometries of X. By an isometry of X, we mean a function
![]() $\varphi : X \rightarrow X$
such that
$\varphi : X \rightarrow X$
such that
![]() $\|\varphi (a)-\varphi (b)\|=\|a-b\|$
for all
$\|\varphi (a)-\varphi (b)\|=\|a-b\|$
for all
![]() $a, b \in X$
. In [Reference Molnár8], Molnár proved that
$a, b \in X$
. In [Reference Molnár8], Molnár proved that
![]() $B(H)$
is 2-
$B(H)$
is 2-
![]() $\operatorname {Iso}(B(H))$
-reflexive, where H is an infinite-dimensional separable Hilbert space. Recently, there has been a growing interest in 2-
$\operatorname {Iso}(B(H))$
-reflexive, where H is an infinite-dimensional separable Hilbert space. Recently, there has been a growing interest in 2-
![]() $\operatorname {Iso}(X)$
-reflexive problems for several operator algebras and function algebras (see, for example, [Reference Al-Halees and Fleming1, Reference Molnár9, Reference Mori12]). However, the 2-
$\operatorname {Iso}(X)$
-reflexive problems for several operator algebras and function algebras (see, for example, [Reference Al-Halees and Fleming1, Reference Molnár9, Reference Mori12]). However, the 2-
![]() $\operatorname {Iso}(X)$
-reflexivity in the context of nest algebras has not yet been considered. In this paper, we study 2-
$\operatorname {Iso}(X)$
-reflexivity in the context of nest algebras has not yet been considered. In this paper, we study 2-
![]() $\operatorname {Iso}(X)$
-reflexivity in some nest algebras.
$\operatorname {Iso}(X)$
-reflexivity in some nest algebras.
Throughout, H will denote a separable Hilbert space over
![]() $\mathbb {C}$
with
$\mathbb {C}$
with
![]() $\dim H \geq 2$
, along with its dual space
$\dim H \geq 2$
, along with its dual space
![]() $H^*$
. For a subset
$H^*$
. For a subset
![]() $S \subseteq H$
, we set
$S \subseteq H$
, we set
![]() $S^\perp := \{f \in H^* : f(S)=0\}$
.
$S^\perp := \{f \in H^* : f(S)=0\}$
.
By a subspace lattice on H, we mean a collection
![]() $\mathcal {L}$
of closed subspaces of H with
$\mathcal {L}$
of closed subspaces of H with
![]() $(0)$
and H in
$(0)$
and H in
![]() $\mathcal {L}$
such that, for every family
$\mathcal {L}$
such that, for every family
![]() $\{E_r\}$
of elements of
$\{E_r\}$
of elements of
![]() $\mathcal {L}$
, both
$\mathcal {L}$
, both
![]() $\bigvee \{E_r\}$
and
$\bigvee \{E_r\}$
and
![]() $\bigwedge \{E_r\}$
belong to
$\bigwedge \{E_r\}$
belong to
![]() $\mathcal {L}$
, where
$\mathcal {L}$
, where
![]() $\bigvee \{E_r\}$
denotes the closed linear span of
$\bigvee \{E_r\}$
denotes the closed linear span of
![]() $\{E_r\}$
and
$\{E_r\}$
and
![]() $\bigwedge \{E_r\}$
denotes the intersection of
$\bigwedge \{E_r\}$
denotes the intersection of
![]() $\{E_r\}$
. We say a subspace lattice is a nest if it is totally ordered with respect to inclusion. When there is no confusion, we identify the closed subspace and the orthogonal projection on it.
$\{E_r\}$
. We say a subspace lattice is a nest if it is totally ordered with respect to inclusion. When there is no confusion, we identify the closed subspace and the orthogonal projection on it.
Let
![]() $\mathcal {L}$
be a subspace lattice on H and
$\mathcal {L}$
be a subspace lattice on H and
![]() $E \in \mathcal {L}$
. Define
$E \in \mathcal {L}$
. Define
 $$ \begin{align*} \begin{aligned} E_{-} & =\bigvee\{F \in \mathcal{L}: F \nsupseteq E\}\quad \text{for } E \neq (0);\quad (0)_-=(0),\\E_{+} & =\bigwedge\{F \in \mathcal{L}: F \nsubseteq E\}\quad \text{for } E \neq H;\quad H_+=H,\\\mathcal{J}(\mathcal{L}) & =\{E \in \mathcal{L}: E \neq(0) \text{ and } E_{-} \neq H\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} E_{-} & =\bigvee\{F \in \mathcal{L}: F \nsupseteq E\}\quad \text{for } E \neq (0);\quad (0)_-=(0),\\E_{+} & =\bigwedge\{F \in \mathcal{L}: F \nsubseteq E\}\quad \text{for } E \neq H;\quad H_+=H,\\\mathcal{J}(\mathcal{L}) & =\{E \in \mathcal{L}: E \neq(0) \text{ and } E_{-} \neq H\}. \end{aligned} \end{align*} $$
If
![]() $\mathcal {N}$
is a nest on H, then it is not difficult to verify that
$\mathcal {N}$
is a nest on H, then it is not difficult to verify that
It follows that the subspaces
![]() $\bigcup \{E: E \in \mathcal {J}(\mathcal {N})\}$
and
$\bigcup \{E: E \in \mathcal {J}(\mathcal {N})\}$
and
![]() $\bigcup \{E_{-}^{\perp }: E \in \mathcal {J}(\mathcal {N})\}$
are both dense in H and
$\bigcup \{E_{-}^{\perp }: E \in \mathcal {J}(\mathcal {N})\}$
are both dense in H and
![]() $H^*$
, respectively, where
$H^*$
, respectively, where
![]() $E_{-}^{\perp }=(E_{-})^{\perp }$
.
$E_{-}^{\perp }=(E_{-})^{\perp }$
.
Denote by
![]() $B(H)$
,
$B(H)$
,
![]() $K(H)$
and
$K(H)$
and
![]() $F(H)$
the algebra of all bounded linear operators on H, the algebra of all compact operators on H and the algebra of all bounded finite rank operators on H, respectively.
$F(H)$
the algebra of all bounded linear operators on H, the algebra of all compact operators on H and the algebra of all bounded finite rank operators on H, respectively.
By a nest algebra
![]() $\operatorname {Alg}\mathcal {N}$
, we mean the set of all operators in
$\operatorname {Alg}\mathcal {N}$
, we mean the set of all operators in
![]() $B(H)$
leaving each element in
$B(H)$
leaving each element in
![]() $\mathcal {N}$
invariant, that is,
$\mathcal {N}$
invariant, that is,
![]() $\operatorname {Alg}\mathcal {N}=\{T \in B(H): T E \subseteq E \text { for all } E \in \mathcal {N}\}$
. Denote
$\operatorname {Alg}\mathcal {N}=\{T \in B(H): T E \subseteq E \text { for all } E \in \mathcal {N}\}$
. Denote
![]() $F(\mathcal {N})=\operatorname {Alg}\mathcal {N}\cap F(H)$
and
$F(\mathcal {N})=\operatorname {Alg}\mathcal {N}\cap F(H)$
and
![]() $K(\mathcal {N})=\operatorname {Alg}\mathcal {N}\cap K(H)$
.
$K(\mathcal {N})=\operatorname {Alg}\mathcal {N}\cap K(H)$
.
For
![]() $x \in H$
and
$x \in H$
and
![]() $f \in H^*$
, the rank-one operator
$f \in H^*$
, the rank-one operator
![]() $x \otimes f$
is defined as the map
$x \otimes f$
is defined as the map
![]() $z \mapsto f(z)x$
. The following well-known result about rank-one operators will be repeatedly used.
$z \mapsto f(z)x$
. The following well-known result about rank-one operators will be repeatedly used.
Proposition 1.1 [Reference Longstaff7].
If
![]() $\mathcal {L}$
is a subspace lattice, then
$\mathcal {L}$
is a subspace lattice, then
![]() $x \otimes y \in \operatorname {Alg}\mathcal {L}$
if and only if there exists an element
$x \otimes y \in \operatorname {Alg}\mathcal {L}$
if and only if there exists an element
![]() $E \in \mathcal {L}$
such that
$E \in \mathcal {L}$
such that
![]() $x \in E$
and
$x \in E$
and
![]() $y \in E_-^\perp $
.
$y \in E_-^\perp $
.
2 Main result
Our main result is the following theorem.
Theorem 2.1. Let
![]() $\mathcal {N}$
be a nest on H such that
$\mathcal {N}$
be a nest on H such that
![]() $E_+ \neq E$
for any
$E_+ \neq E$
for any
![]() $E \neq H, E \in \mathcal {N}$
. If
$E \neq H, E \in \mathcal {N}$
. If
![]() $\phi $
is a 2-local isometry of
$\phi $
is a 2-local isometry of
![]() $\operatorname {Alg}\mathcal {N}$
, then
$\operatorname {Alg}\mathcal {N}$
, then
![]() $\phi $
is a surjective linear isometry.
$\phi $
is a surjective linear isometry.
The proof of Theorem 2.1 will be organised in a series of lemmas. In what follows,
![]() $\mathcal {N}$
is a nest on H such that
$\mathcal {N}$
is a nest on H such that
![]() $E_+ \neq E$
for any
$E_+ \neq E$
for any
![]() $E \neq H, E \in \mathcal {N}$
and
$E \neq H, E \in \mathcal {N}$
and
![]() $\phi $
is a 2-local isometry of
$\phi $
is a 2-local isometry of
![]() $\operatorname {Alg}\mathcal {N}$
. For
$\operatorname {Alg}\mathcal {N}$
. For
![]() $A, B \in \operatorname {Alg}\mathcal {N}$
, the symbol
$A, B \in \operatorname {Alg}\mathcal {N}$
, the symbol
![]() $\phi _{A, B}$
stands for a surjective linear isometry from
$\phi _{A, B}$
stands for a surjective linear isometry from
![]() $\operatorname {Alg}\mathcal {N}$
to itself such that
$\operatorname {Alg}\mathcal {N}$
to itself such that
![]() $\phi _{A, B}(A)=\phi (A)$
and
$\phi _{A, B}(A)=\phi (A)$
and
![]() $\phi _{A, B}(B)=\phi (B)$
. For a nest
$\phi _{A, B}(B)=\phi (B)$
. For a nest
![]() $\mathcal {M}$
, we denote by
$\mathcal {M}$
, we denote by
![]() $\mathcal {M}^{\perp }$
the nest
$\mathcal {M}^{\perp }$
the nest
![]() $\{I-E: E \in \mathcal {M}\}$
. A conjugation is a conjugate linear map on H such that
$\{I-E: E \in \mathcal {M}\}$
. A conjugation is a conjugate linear map on H such that
![]() $J^2=I$
and
$J^2=I$
and
![]() $ \langle J x, y\rangle = \langle J y, x\rangle $
for all
$ \langle J x, y\rangle = \langle J y, x\rangle $
for all
![]() $x, y \in H$
.
$x, y \in H$
.
Proposition 2.2 below is cited from the paper by Moore and Trent [Reference Moore and Trent11] where they summarise the results in [Reference Arazy and Solel2, Reference Moore and Trent10] and characterise the surjective linear isometries on nest algebras.
Proposition 2.2. Let
![]() $\mathcal {M}$
be a nest on H and
$\mathcal {M}$
be a nest on H and
![]() $\rho : \operatorname {Alg}\mathcal {M} \rightarrow \operatorname {Alg}\mathcal {M}$
be a surjective linear isometry. Then there are unitary operators U and V in
$\rho : \operatorname {Alg}\mathcal {M} \rightarrow \operatorname {Alg}\mathcal {M}$
be a surjective linear isometry. Then there are unitary operators U and V in
![]() $B(H)$
such that U and
$B(H)$
such that U and
![]() $U^*$
lie in
$U^*$
lie in
![]() $\operatorname {Alg}\mathcal {M}$
. Moreover, one of the following cases holds:
$\operatorname {Alg}\mathcal {M}$
. Moreover, one of the following cases holds:
-
(1)
 $\rho (A)=U V^* A V$
for every
$\rho (A)=U V^* A V$
for every
 $A \in \operatorname {Alg} \mathcal {M}$
and the map
$A \in \operatorname {Alg} \mathcal {M}$
and the map
 $E \mapsto V^* E V$
is an order isomorphism of
$E \mapsto V^* E V$
is an order isomorphism of
 $\mathcal {M}$
;
$\mathcal {M}$
; -
(2)
 $\rho (A)=U V^* J A^* J V$
for every
$\rho (A)=U V^* J A^* J V$
for every
 $A \in \operatorname {Alg}\mathcal {M}$
, where J is a conjugation on H such that
$A \in \operatorname {Alg}\mathcal {M}$
, where J is a conjugation on H such that
 $JE=EJ$
for each
$JE=EJ$
for each
 $E \in \mathcal {M}$
and the map
$E \in \mathcal {M}$
and the map
 $E \mapsto V^* J E J V$
is an order isomorphism from
$E \mapsto V^* J E J V$
is an order isomorphism from
 $\mathcal {M}$
onto
$\mathcal {M}$
onto
 $\mathcal {M}^{\perp }$
.
$\mathcal {M}^{\perp }$
.
Remark 2.3. (1) It can be easily verified that the map
![]() $T \mapsto JT^*J$
is a *-anti-isomorphism of
$T \mapsto JT^*J$
is a *-anti-isomorphism of
![]() $B(H)$
and J maps an orthonormal basis onto another orthonormal basis.
$B(H)$
and J maps an orthonormal basis onto another orthonormal basis.
(2) For any
![]() $a, b \in H$
,
$a, b \in H$
,
 $$ \begin{align*}\begin{aligned} \langle (Jf \otimes Jx)a, b \rangle&=\langle \langle a, Jx \rangle Jf, b\rangle= \langle a, Jx \rangle \langle Jf, b \rangle= \langle x, Ja\rangle \langle Jb, f \rangle\\ &= \langle \langle Jb,f \rangle x, Ja \rangle = \langle (x \otimes f)Jb, Ja \rangle = \langle a, J(x \otimes f)Jb\rangle, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \langle (Jf \otimes Jx)a, b \rangle&=\langle \langle a, Jx \rangle Jf, b\rangle= \langle a, Jx \rangle \langle Jf, b \rangle= \langle x, Ja\rangle \langle Jb, f \rangle\\ &= \langle \langle Jb,f \rangle x, Ja \rangle = \langle (x \otimes f)Jb, Ja \rangle = \langle a, J(x \otimes f)Jb\rangle, \end{aligned}\end{align*} $$
so
![]() $(Jf \otimes Jx)^*=J(x \otimes f)J$
.
$(Jf \otimes Jx)^*=J(x \otimes f)J$
.
(3) If
![]() $\rho $
is a surjective linear isometry of
$\rho $
is a surjective linear isometry of
![]() $\operatorname {Alg}\mathcal {M}$
, then according to Proposition 2.2, for any rank-one operator
$\operatorname {Alg}\mathcal {M}$
, then according to Proposition 2.2, for any rank-one operator
![]() $x \otimes f \in \operatorname {Alg} \mathcal {M}$
,
$x \otimes f \in \operatorname {Alg} \mathcal {M}$
,
![]() $\rho $
maps
$\rho $
maps
![]() $x \otimes f$
to either
$x \otimes f$
to either
![]() $UV^*x \otimes V^*f$
or
$UV^*x \otimes V^*f$
or
![]() $UV^*Jf \otimes V^*Jx$
, both of which are also rank-one operators. Since every finite rank operator in
$UV^*Jf \otimes V^*Jx$
, both of which are also rank-one operators. Since every finite rank operator in
![]() $\operatorname {Alg}\mathcal {M}$
can be written as a sum of finitely many rank-one operators in
$\operatorname {Alg}\mathcal {M}$
can be written as a sum of finitely many rank-one operators in
![]() $\operatorname {Alg}\mathcal {M}$
and
$\operatorname {Alg}\mathcal {M}$
and
![]() $\rho $
preserves linear independence, it follows that
$\rho $
preserves linear independence, it follows that
![]() $\rho $
preserves the rank of a finite rank operator. Since
$\rho $
preserves the rank of a finite rank operator. Since
![]() $\rho ^{-1}$
is also a surjective linear isometry,
$\rho ^{-1}$
is also a surjective linear isometry,
![]() $\rho $
preserves the rank in both directions.
$\rho $
preserves the rank in both directions.
Lemma 2.4.
![]() $\phi $
is rank preserving and
$\phi $
is rank preserving and
![]() $\phi |_{F(\mathcal {N})}$
is linear.
$\phi |_{F(\mathcal {N})}$
is linear.
Proof. It follows from Remark 2.3 that
![]() $\phi $
is rank preserving. According to Proposition 2.2,
$\phi $
is rank preserving. According to Proposition 2.2,
![]() $\phi _{A, B}(X)=U_{A, B}V_{A, B}^*XV_{A, B}$
or
$\phi _{A, B}(X)=U_{A, B}V_{A, B}^*XV_{A, B}$
or
![]() $\phi _{A, B}(X)=U_{A, B}V_{A, B}^*JX^*JV_{A, B}$
, where
$\phi _{A, B}(X)=U_{A, B}V_{A, B}^*JX^*JV_{A, B}$
, where
![]() $U_{A, B}$
and
$U_{A, B}$
and
![]() $V_{A, B}$
are unitary operators in
$V_{A, B}$
are unitary operators in
![]() $B(H)$
depending on
$B(H)$
depending on
![]() $A, B$
and
$A, B$
and
![]() $U_{A, B}, U_{A, B}^*$
lie in
$U_{A, B}, U_{A, B}^*$
lie in
![]() $\operatorname {Alg}\mathcal {N}$
.
$\operatorname {Alg}\mathcal {N}$
.
First, we show that
![]() $\phi $
is complex homogeneous. For any
$\phi $
is complex homogeneous. For any
![]() $A \in \operatorname {Alg}\mathcal {N}$
and
$A \in \operatorname {Alg}\mathcal {N}$
and
![]() $\lambda \in \mathbb {C}$
,
$\lambda \in \mathbb {C}$
,
![]() $\phi (\lambda A)=\phi _{A, \lambda A}(\lambda A)=\lambda \phi _{A, \lambda A}(A)=\lambda \phi (A)$
.
$\phi (\lambda A)=\phi _{A, \lambda A}(\lambda A)=\lambda \phi _{A, \lambda A}(A)=\lambda \phi (A)$
.
Next, we prove that
![]() $\phi $
is additive on
$\phi $
is additive on
![]() $F(\mathcal {N})$
. For any
$F(\mathcal {N})$
. For any
![]() $A, B \in F(\mathcal {N})$
, since
$A, B \in F(\mathcal {N})$
, since
![]() $\phi $
is rank preserving,
$\phi $
is rank preserving,
![]() $\phi (A)$
and
$\phi (A)$
and
![]() $\phi (B)$
are in
$\phi (B)$
are in
![]() $F(\mathcal {N})$
. We claim that
$F(\mathcal {N})$
. We claim that
![]() $\operatorname {tr}(\phi (A)\phi (B)^*)=\operatorname {tr}(AB^*)$
. Indeed, if
$\operatorname {tr}(\phi (A)\phi (B)^*)=\operatorname {tr}(AB^*)$
. Indeed, if
![]() $\phi _{A, B}(X)=U_{A, B}V_{A, B}^*XV_{A, B}$
, then
$\phi _{A, B}(X)=U_{A, B}V_{A, B}^*XV_{A, B}$
, then
If
![]() $\phi _{A, B}(X)=U_{A, B}V_{A, B}^*JX^*JV_{A, B}$
, then
$\phi _{A, B}(X)=U_{A, B}V_{A, B}^*JX^*JV_{A, B}$
, then
 $$ \begin{align*}\begin{aligned} \operatorname{tr}(\phi(A)\phi(B)^*)&=\operatorname{tr}(U_{A, B}V_{A, B}^*JA^*JV_{A, B}V^*_{A, B}(JB^*J)^*V_{A, B}U_{A, B}^*)\\ &=\operatorname{tr}(U_{A, B}V_{A, B}^*JA^*JV_{A, B}V^*_{A, B}JBJV_{A, B}U_{A, B}^*) =\operatorname{tr}(JA^*BJ) =\operatorname{tr}(AB^*). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \operatorname{tr}(\phi(A)\phi(B)^*)&=\operatorname{tr}(U_{A, B}V_{A, B}^*JA^*JV_{A, B}V^*_{A, B}(JB^*J)^*V_{A, B}U_{A, B}^*)\\ &=\operatorname{tr}(U_{A, B}V_{A, B}^*JA^*JV_{A, B}V^*_{A, B}JBJV_{A, B}U_{A, B}^*) =\operatorname{tr}(JA^*BJ) =\operatorname{tr}(AB^*). \end{aligned} \end{align*} $$
Thus, for any
![]() $A, A^\prime \in F(\mathcal {N})$
, by the linearity of
$A, A^\prime \in F(\mathcal {N})$
, by the linearity of
![]() $\operatorname {tr}$
,
$\operatorname {tr}$
,
By replacing B with
![]() $A+A^\prime $
, A and
$A+A^\prime $
, A and
![]() $A^\prime $
, we obtain
$A^\prime $
, we obtain
It follows that
![]() $\phi (A+A^{\prime })-\phi (A)-\phi (A^{\prime })=0$
, which means that
$\phi (A+A^{\prime })-\phi (A)-\phi (A^{\prime })=0$
, which means that
![]() $\phi $
is additive on
$\phi $
is additive on
![]() $F(\mathcal {N})$
.
$F(\mathcal {N})$
.
By Lemma 2.4 and [Reference Hou and Cui3, Corollary 2.2] where Hou and Cui characterise rank-1 preserving linear maps between nest algebras acting on Banach spaces, we can easily prove Lemma 2.5.
Lemma 2.5. One of the following statements holds.
-
(1) There exist injective linear transformations
such that $$ \begin{align*} D: \bigcup\{E: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H \quad\text{and}\quad C: \bigcup\{E_{-}^{\perp}: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H^* \end{align*} $$
$$ \begin{align*} D: \bigcup\{E: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H \quad\text{and}\quad C: \bigcup\{E_{-}^{\perp}: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H^* \end{align*} $$
 $\phi (x \otimes f)=D x \otimes C f$
for every
$\phi (x \otimes f)=D x \otimes C f$
for every
 $x \otimes f \in F(\mathcal {N})$
.
$x \otimes f \in F(\mathcal {N})$
.
-
(2) There exist injective linear transformations
such that $$ \begin{align*} D: \bigcup\{E_{-}^{\perp}: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H \quad\text{and}\quad C: \bigcup\{E: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H^* \end{align*} $$
$$ \begin{align*} D: \bigcup\{E_{-}^{\perp}: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H \quad\text{and}\quad C: \bigcup\{E: E \in \mathcal{J}(\mathcal{N})\} \rightarrow H^* \end{align*} $$
 $\phi (x \otimes f)=D f \otimes C x$
for every
$\phi (x \otimes f)=D f \otimes C x$
for every
 $x \otimes f \in F(\mathcal {N})$
.
$x \otimes f \in F(\mathcal {N})$
.
By categorising and discussing the two cases in Lemma 2.5, we can obtain the following result.
Lemma 2.6. One of the following statements holds.
-
(1) There exist unitary operators
 $C, D \in B(H)$
such that
$C, D \in B(H)$
such that
 $\phi (A)=DAC^*$
for any
$\phi (A)=DAC^*$
for any
 $A \in K(\mathcal {N})$
.
$A \in K(\mathcal {N})$
. -
(2) There exist bounded conjugate linear operators
 $C, D$
such that
$C, D$
such that
 $CJ, DJ \in B(H)$
are unitary operators and
$CJ, DJ \in B(H)$
are unitary operators and
 $\phi (A)=(DJ)JA^*J(CJ)^*$
for any
$\phi (A)=(DJ)JA^*J(CJ)^*$
for any
 $A \in K(\mathcal {N})$
.
$A \in K(\mathcal {N})$
.
Proof. We consider two cases.
Case 1. If Lemma 2.5(1) holds, then based on the assumption on
![]() $\mathcal {N}$
, there exist injective linear transformations
$\mathcal {N}$
, there exist injective linear transformations
![]() $D: \bigcup \{E : E \in \mathcal {J}(\mathcal {N})\}\rightarrow H $
and
$D: \bigcup \{E : E \in \mathcal {J}(\mathcal {N})\}\rightarrow H $
and
![]() $C: H^* \rightarrow H^*$
such that
$C: H^* \rightarrow H^*$
such that
![]() $\phi (x \otimes f)=D x \otimes C f$
for every
$\phi (x \otimes f)=D x \otimes C f$
for every
![]() $x \otimes f \in F(\mathcal {N})$
. Thus, for any
$x \otimes f \in F(\mathcal {N})$
. Thus, for any
![]() $x \otimes f \in \operatorname {Alg}\mathcal {N}$
,
$x \otimes f \in \operatorname {Alg}\mathcal {N}$
,
Fix
![]() $x_0 \neq 0 \in (0)_+$
. Then
$x_0 \neq 0 \in (0)_+$
. Then
![]() $x_0 \otimes f$
is in
$x_0 \otimes f$
is in
![]() $\operatorname {Alg}\mathcal {N}$
for any
$\operatorname {Alg}\mathcal {N}$
for any
![]() $f \neq 0, f \in ((0)_+)_-^\perp =H^*$
. It follows that
$f \neq 0, f \in ((0)_+)_-^\perp =H^*$
. It follows that
![]() $\|Dx_0\|\,\|Cf\| =\|x_0\|\,\|f\|$
. So
$\|Dx_0\|\,\|Cf\| =\|x_0\|\,\|f\|$
. So
![]() ${\|Cf\|}/{\|f\|}={\|x_0\|}/{\|Dx_0\|}$
for any
${\|Cf\|}/{\|f\|}={\|x_0\|}/{\|Dx_0\|}$
for any
![]() $f \neq 0, f \in H^*$
, which means that
$f \neq 0, f \in H^*$
, which means that
![]() $C \in B(H^*)$
and
$C \in B(H^*)$
and
![]() $\|C\|={\|x_0\|}/{\|Dx_0\|}$
.
$\|C\|={\|x_0\|}/{\|Dx_0\|}$
.
For any
![]() $E \in \mathcal {J}(\mathcal {N})$
, fix
$E \in \mathcal {J}(\mathcal {N})$
, fix
![]() $f_0 \neq 0, f \in E_-^\perp $
. Then
$f_0 \neq 0, f \in E_-^\perp $
. Then
![]() $x \otimes f_0 \in \operatorname {Alg}\mathcal {N}$
for any
$x \otimes f_0 \in \operatorname {Alg}\mathcal {N}$
for any
![]() $x \neq 0, x \in E$
. It follows that
$x \neq 0, x \in E$
. It follows that
![]() $\|Dx\|\,\|Cf_0\| =\|x\|\,\|f_0\|$
. Therefore,
$\|Dx\|\,\|Cf_0\| =\|x\|\,\|f_0\|$
. Therefore,
![]() ${\|Dx\|}/{\|x\|} ={\|f_0\|}/{\|Cf_0\|} ={\|Dx_0\|}/{\|x_0\|}$
, which means that
${\|Dx\|}/{\|x\|} ={\|f_0\|}/{\|Cf_0\|} ={\|Dx_0\|}/{\|x_0\|}$
, which means that
![]() $\|D|_E\| = {\|Dx_0\|}/{\|x_0\|}$
. Since
$\|D|_E\| = {\|Dx_0\|}/{\|x_0\|}$
. Since
![]() $\bigcup \{E : E \in \mathcal {J}(\mathcal {N})\}$
is dense in H, we can extend D to an operator in
$\bigcup \{E : E \in \mathcal {J}(\mathcal {N})\}$
is dense in H, we can extend D to an operator in
![]() $B(H)$
also denoted by D such that
$B(H)$
also denoted by D such that
![]() ${\|Dx\|}/{\|x\|}= {\|Dx_0\|}/{\|x_0\|}$
for any
${\|Dx\|}/{\|x\|}= {\|Dx_0\|}/{\|x_0\|}$
for any
![]() $x \neq 0, x \in H$
. So we can assume that
$x \neq 0, x \in H$
. So we can assume that
![]() $C, D$
are isometries. Since
$C, D$
are isometries. Since
![]() $\phi $
is an isometry, by the linearity of
$\phi $
is an isometry, by the linearity of
![]() $\phi |_{F(\mathcal {N})}$
and the continuity of
$\phi |_{F(\mathcal {N})}$
and the continuity of
![]() $\phi $
, we have
$\phi $
, we have
![]() $\phi (A)=DAC^*$
for all
$\phi (A)=DAC^*$
for all
![]() $A \in K(\mathcal {N})$
.
$A \in K(\mathcal {N})$
.
By the Riesz–Frechet theorem,
![]() $H^*$
can be identified with H through a conjugate linear surjective isometry. For any
$H^*$
can be identified with H through a conjugate linear surjective isometry. For any
![]() $E \neq H, E \in \mathcal {N}$
, we have
$E \neq H, E \in \mathcal {N}$
, we have
![]() $(E_+)_-=E$
by the hypothesis on
$(E_+)_-=E$
by the hypothesis on
![]() $\mathcal {N}$
. Thus, x is in
$\mathcal {N}$
. Thus, x is in
![]() $(E_+)_-^{\perp }$
for any
$(E_+)_-^{\perp }$
for any
![]() $x \in E_+ \ominus E$
, and so
$x \in E_+ \ominus E$
, and so
![]() $x \otimes x \in \operatorname {Alg}\mathcal {N}$
. Let
$x \otimes x \in \operatorname {Alg}\mathcal {N}$
. Let
![]() $\mathcal {N}=\{E_j:j \in \Omega \}$
and
$\mathcal {N}=\{E_j:j \in \Omega \}$
and
![]() $\{e_i^j : i \in \Lambda _j\}$
be an orthonormal basis of
$\{e_i^j : i \in \Lambda _j\}$
be an orthonormal basis of
![]() $(E_j)_+ \ominus E_j$
. Then
$(E_j)_+ \ominus E_j$
. Then
![]() $K:=\sum _{i,j} e_i^j \otimes e_i^j/(i\cdot j)$
is a compact operator in
$K:=\sum _{i,j} e_i^j \otimes e_i^j/(i\cdot j)$
is a compact operator in
![]() $\operatorname {Alg}\mathcal {N}$
. Moreover, K is an injective operator with dense range. We claim that
$\operatorname {Alg}\mathcal {N}$
. Moreover, K is an injective operator with dense range. We claim that
![]() $\phi (K)$
is also an injective operator with dense range.
$\phi (K)$
is also an injective operator with dense range.
For the case when
![]() $\phi (K)=U_{K, 0}V_{K, 0}^*KV_{K, 0}$
, since
$\phi (K)=U_{K, 0}V_{K, 0}^*KV_{K, 0}$
, since
![]() $U_{K, 0}, V_{K, 0}$
are unitary operators,
$U_{K, 0}, V_{K, 0}$
are unitary operators,
![]() $\phi (K)$
is also an injective operator with dense range.
$\phi (K)$
is also an injective operator with dense range.
For the case when
![]() $\phi (K)=U_{K, 0}V_{K, 0}^*JK^*JV_{K, 0}$
, since
$\phi (K)=U_{K, 0}V_{K, 0}^*JK^*JV_{K, 0}$
, since
![]() $\operatorname {Ker} K= (\operatorname {Ran} K^*)^\perp $
,
$\operatorname {Ker} K= (\operatorname {Ran} K^*)^\perp $
,
![]() $K^*$
is an injective operator with dense range. As J is a conjugate linear isometry, it follows that
$K^*$
is an injective operator with dense range. As J is a conjugate linear isometry, it follows that
![]() $\phi (K)$
is also an injective operator with dense range.
$\phi (K)$
is also an injective operator with dense range.
Therefore,
![]() $\phi (K)=\sum _{i,j} De_i^j \otimes Ce_i^j/(i\cdot j)$
is an injective operator with dense range, which implies D and C have dense ranges. Consequently, D and C are surjective isometries (unitary operators).
$\phi (K)=\sum _{i,j} De_i^j \otimes Ce_i^j/(i\cdot j)$
is an injective operator with dense range, which implies D and C have dense ranges. Consequently, D and C are surjective isometries (unitary operators).
Case 2. If Lemma 2.5(2) holds, then there exist injective linear transformations
![]() $D: H^* \rightarrow H$
and
$D: H^* \rightarrow H$
and
![]() $C: \bigcup \{E \in \mathcal {N} \mid E_{-} \neq H\} \rightarrow H^*$
such that
$C: \bigcup \{E \in \mathcal {N} \mid E_{-} \neq H\} \rightarrow H^*$
such that
![]() $\phi (x \otimes f)=D f \otimes C x$
for every
$\phi (x \otimes f)=D f \otimes C x$
for every
![]() $x \otimes f \in F(\mathcal {N})$
.
$x \otimes f \in F(\mathcal {N})$
.
According to the Riesz–Frechet theorem, we can consider D as an injective conjugate linear transformation from H to H, and C as an injective conjugate linear transformation from
![]() $\bigcup \{E \in \mathcal {N} \mid E_{-} \neq H\}$
to H. Similarly to Case 1, we can conclude that
$\bigcup \{E \in \mathcal {N} \mid E_{-} \neq H\}$
to H. Similarly to Case 1, we can conclude that
![]() $DJ$
and
$DJ$
and
![]() $CJ$
are unitary operators. By Remark 2.3,
$CJ$
are unitary operators. By Remark 2.3,
 $$ \begin{align*} \phi(x \otimes f)=Df \otimes Cx & =(DJ)(Jf \otimes Jx)(CJ)^* \\ & =(DJ)(J(x \otimes f)J)^*(CJ)^* =(DJ)(J(x \otimes f)^*J)(CJ)^* \end{align*} $$
$$ \begin{align*} \phi(x \otimes f)=Df \otimes Cx & =(DJ)(Jf \otimes Jx)(CJ)^* \\ & =(DJ)(J(x \otimes f)J)^*(CJ)^* =(DJ)(J(x \otimes f)^*J)(CJ)^* \end{align*} $$
for any
![]() $x \otimes f \in \operatorname {Alg}\mathcal {N}$
. By the linearity of
$x \otimes f \in \operatorname {Alg}\mathcal {N}$
. By the linearity of
![]() $\phi |_{F(\mathcal {N})}$
and the continuity of
$\phi |_{F(\mathcal {N})}$
and the continuity of
![]() $\phi $
, we have
$\phi $
, we have
![]() $\phi (A)=(DJ)(JA^*J)(CJ)^*$
for any
$\phi (A)=(DJ)(JA^*J)(CJ)^*$
for any
![]() $A \in K(\mathcal {N})$
.
$A \in K(\mathcal {N})$
.
Lemma 2.7.
![]() $\phi (P)\phi (T)^*\phi (P)=\phi (PT^*P)$
for any
$\phi (P)\phi (T)^*\phi (P)=\phi (PT^*P)$
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
and any
$T \in \operatorname {Alg}\mathcal {N}$
and any
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
Proof. By Lemma 2.2,
![]() $\phi _{P, T}(X)=U_{P, T}V_{P, T}^*XV_{P, T}$
or
$\phi _{P, T}(X)=U_{P, T}V_{P, T}^*XV_{P, T}$
or
![]() $\phi _{P, T}(X)=U_{P, T}V_{P, T}^*JX^*JV_{P, T}$
. To simplify the notation, denote
$\phi _{P, T}(X)=U_{P, T}V_{P, T}^*JX^*JV_{P, T}$
. To simplify the notation, denote
![]() $U_{P, T}, V_{P, T}$
by
$U_{P, T}, V_{P, T}$
by
![]() $U, V$
, respectively. For
$U, V$
, respectively. For
![]() $\phi _{P, T}(X)=UV^*XV$
,
$\phi _{P, T}(X)=UV^*XV$
,
 $$ \begin{align*} \begin{aligned} \phi(P)\phi(T)^*\phi(P)&=UV^*PV (UV^*TV)^* UV^*PV =UV^*PT^*PV =UV^*\langle T^*x, f \rangle PV\\ &=\langle T^*x, f \rangle UV^*PV =\langle T^*x, f \rangle \phi(P) =\phi(\langle T^*x, f \rangle P) =\phi(PT^*P). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi(P)\phi(T)^*\phi(P)&=UV^*PV (UV^*TV)^* UV^*PV =UV^*PT^*PV =UV^*\langle T^*x, f \rangle PV\\ &=\langle T^*x, f \rangle UV^*PV =\langle T^*x, f \rangle \phi(P) =\phi(\langle T^*x, f \rangle P) =\phi(PT^*P). \end{aligned} \end{align*} $$
For
![]() $\phi _{P, T}(X)=UV^*JX^*JV$
, using Remark 2.3,
$\phi _{P, T}(X)=UV^*JX^*JV$
, using Remark 2.3,
 $$ \begin{align*} \begin{aligned} \phi(P)\phi(T)^*\phi(P) &=UV^*JP^*JV (UV^*JT^*JV)^* UV^*JP^*JV =UV^*JP^*TP^*JV\\ &=UV^*J(PT^*P)^*JV =UV^*J(\langle T^*x, f \rangle x \otimes f)^*JV\\ &=\langle T^*x, f \rangle UV^*J(x \otimes f)^*JV\\ &=\langle T^*x, f \rangle\phi(P) =\phi(\langle T^*x, f \rangle P) =\phi(PT^*P). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi(P)\phi(T)^*\phi(P) &=UV^*JP^*JV (UV^*JT^*JV)^* UV^*JP^*JV =UV^*JP^*TP^*JV\\ &=UV^*J(PT^*P)^*JV =UV^*J(\langle T^*x, f \rangle x \otimes f)^*JV\\ &=\langle T^*x, f \rangle UV^*J(x \otimes f)^*JV\\ &=\langle T^*x, f \rangle\phi(P) =\phi(\langle T^*x, f \rangle P) =\phi(PT^*P). \end{aligned} \end{align*} $$
Furthermore, if
![]() $\phi $
is the form in Lemma 2.6(1), then
$\phi $
is the form in Lemma 2.6(1), then
![]() $DPC^* \phi (T)^* DPC^*=DPT^*PC^*$
, which implies that
$DPC^* \phi (T)^* DPC^*=DPT^*PC^*$
, which implies that
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
and
$T \in \operatorname {Alg}\mathcal {N}$
and
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
If
![]() $\phi $
is the form in Lemma 2.6(2), then it follows that
$\phi $
is the form in Lemma 2.6(2), then it follows that
 $$ \begin{align*} \begin{aligned} (DJ)JP^*J(CJ)^* \phi(T)^* (DJ)JP^*J(CJ)^*&=(DJ)J(PT^*P)^*J(CJ)^*\\ &=(DJ)(JP^*J)(JTJ)(JP^*J)(CJ)^*, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (DJ)JP^*J(CJ)^* \phi(T)^* (DJ)JP^*J(CJ)^*&=(DJ)J(PT^*P)^*J(CJ)^*\\ &=(DJ)(JP^*J)(JTJ)(JP^*J)(CJ)^*, \end{aligned} \end{align*} $$
which implies that
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
and any
$T \in \operatorname {Alg}\mathcal {N}$
and any
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
.
Under the assumption on
![]() $\mathcal {N}$
, Lemmas 2.8 and 2.9 follow from Proposition 2.2.
$\mathcal {N}$
, Lemmas 2.8 and 2.9 follow from Proposition 2.2.
Lemma 2.8. Let
![]() $\rho : \operatorname {Alg}\mathcal {N} \rightarrow \operatorname {Alg}\mathcal {N}$
be a surjective linear isometry. If Case (1) in Proposition 2.2 holds for
$\rho : \operatorname {Alg}\mathcal {N} \rightarrow \operatorname {Alg}\mathcal {N}$
be a surjective linear isometry. If Case (1) in Proposition 2.2 holds for
![]() $\rho $
, then
$\rho $
, then
![]() $V, V^*$
are in
$V, V^*$
are in
![]() $\operatorname {Alg}\mathcal {N}$
.
$\operatorname {Alg}\mathcal {N}$
.
Proof. It is sufficient to show that
![]() $V^* E V=E$
for all
$V^* E V=E$
for all
![]() $E \in \mathcal {N}$
. We prove it by the principle of transfinite induction.
$E \in \mathcal {N}$
. We prove it by the principle of transfinite induction.
It is evident that
![]() $V^*(0)V=(0)$
. Moreover, for any given
$V^*(0)V=(0)$
. Moreover, for any given
![]() $F \in \mathcal {N}$
, if the equation
$F \in \mathcal {N}$
, if the equation
![]() $V^* G V=G$
holds for all
$V^* G V=G$
holds for all
![]() $G \in \mathcal {N}$
such that
$G \in \mathcal {N}$
such that
![]() $G < F$
, then because
$G < F$
, then because
![]() $E \mapsto V^* E V$
is an order isomorphism from
$E \mapsto V^* E V$
is an order isomorphism from
![]() $\mathcal {N}$
onto
$\mathcal {N}$
onto
![]() $\mathcal {N}$
, it follows that
$\mathcal {N}$
, it follows that
![]() $V^* F V = F$
.
$V^* F V = F$
.
Lemma 2.9. Let
![]() $\rho : \operatorname {Alg}\mathcal {N} \rightarrow \operatorname {Alg}\mathcal {N}$
be a surjective linear isometry. If Case (2) in Proposition 2.2 holds for
$\rho : \operatorname {Alg}\mathcal {N} \rightarrow \operatorname {Alg}\mathcal {N}$
be a surjective linear isometry. If Case (2) in Proposition 2.2 holds for
![]() $\rho $
, then the following statements hold.
$\rho $
, then the following statements hold.
-
(1)
 $E_- \neq E$
for any
$E_- \neq E$
for any
 $E \neq (0), E \in \mathcal {N}$
.
$E \neq (0), E \in \mathcal {N}$
. -
(2)
 $\mathcal {N}$
is finite.
$\mathcal {N}$
is finite. -
(3) We denote
 $\mathcal {N}=\{E_0, E_1, \ldots , E_n\}$
where
$\mathcal {N}=\{E_0, E_1, \ldots , E_n\}$
where
 $(0)=E_0 < E_1 < \cdots <E_n = H$
. Then
$(0)=E_0 < E_1 < \cdots <E_n = H$
. Then
 $V^*$
and V both map
$V^*$
and V both map
 $E_i$
onto
$E_i$
onto
 $I-E_{n-i}$
for
$I-E_{n-i}$
for
 $0 \leq i \leq n$
.
$0 \leq i \leq n$
.
Proof. (1) In the nest
![]() $\mathcal {N^\perp }$
, we denote
$\mathcal {N^\perp }$
, we denote
![]() $E_+^{\mathcal {N^\perp }}=\bigwedge \{F \in \mathcal {N^\perp }: F \nsubseteq E\}$
for any
$E_+^{\mathcal {N^\perp }}=\bigwedge \{F \in \mathcal {N^\perp }: F \nsubseteq E\}$
for any
![]() $E \neq H, E \in \mathcal {N^\perp }$
, and
$E \neq H, E \in \mathcal {N^\perp }$
, and
![]() $E_-^{\mathcal {N^\perp }}=\bigvee \{F \in \mathcal {N^\perp }: F \nsupseteq E\}$
for any
$E_-^{\mathcal {N^\perp }}=\bigvee \{F \in \mathcal {N^\perp }: F \nsupseteq E\}$
for any
![]() $E \neq (0), E \in \mathcal {N^\perp }$
.
$E \neq (0), E \in \mathcal {N^\perp }$
.
Since the map
![]() $\pi : E \mapsto V^* E V$
is an order isomorphism from
$\pi : E \mapsto V^* E V$
is an order isomorphism from
![]() $\mathcal {N}$
onto
$\mathcal {N}$
onto
![]() $\mathcal {N}^{\perp }$
, we have
$\mathcal {N}^{\perp }$
, we have
![]() $(I-E)_+^{\mathcal {N^\perp }}\neq (I-E)$
for any
$(I-E)_+^{\mathcal {N^\perp }}\neq (I-E)$
for any
![]() $I-E \neq H, I-E \in \mathcal {N^\perp }$
. So
$I-E \neq H, I-E \in \mathcal {N^\perp }$
. So
for any
![]() $I-E \neq H, I-E \in \mathcal {N^\perp }$
. It follows that
$I-E \neq H, I-E \in \mathcal {N^\perp }$
. It follows that
![]() $E_- \neq E$
for any
$E_- \neq E$
for any
![]() $E \neq (0) \in \mathcal {N}$
.
$E \neq (0) \in \mathcal {N}$
.
(2) Suppose that
![]() $\mathcal {N}$
is infinite, then there is a sequence
$\mathcal {N}$
is infinite, then there is a sequence
![]() $\{E_i: i \in \mathbb {N}\} \subseteq \mathcal {N}$
such that
$\{E_i: i \in \mathbb {N}\} \subseteq \mathcal {N}$
such that
![]() $E_i \neq (0)$
or H for any
$E_i \neq (0)$
or H for any
![]() $i \in \mathbb {N}$
and
$i \in \mathbb {N}$
and
![]() $E_i < E_j$
when
$E_i < E_j$
when
![]() $i < j$
. Let
$i < j$
. Let
![]() $G=\bigvee \{E_i: i \in \mathbb {N}\}$
. Then
$G=\bigvee \{E_i: i \in \mathbb {N}\}$
. Then
![]() $G_-=\bigvee \{F \in \mathcal {N}: F < G\}\supseteq \bigvee \{E_i: i \in \mathbb {N}\}=G$
which contradicts
$G_-=\bigvee \{F \in \mathcal {N}: F < G\}\supseteq \bigvee \{E_i: i \in \mathbb {N}\}=G$
which contradicts
![]() $G_- \neq G$
. This implies that
$G_- \neq G$
. This implies that
![]() $\mathcal {N}$
is finite.
$\mathcal {N}$
is finite.
(3) Since
![]() $E \mapsto V^* J E J V$
is an order isomorphism from
$E \mapsto V^* J E J V$
is an order isomorphism from
![]() $\mathcal {N}$
onto
$\mathcal {N}$
onto
![]() $\mathcal {N}^{\perp }$
and
$\mathcal {N}^{\perp }$
and
![]() $EJ=JE$
for any
$EJ=JE$
for any
![]() $E \in \mathcal {N}$
, we obtain
$E \in \mathcal {N}$
, we obtain
![]() $E_i \mapsto V^*E_iV=I-E_{n-i}$
for
$E_i \mapsto V^*E_iV=I-E_{n-i}$
for
![]() $0 \leq i \leq n$
. Since V is a unitary operator, it follows that
$0 \leq i \leq n$
. Since V is a unitary operator, it follows that
![]() $V^*$
and V both map
$V^*$
and V both map
![]() $E_i$
onto
$E_i$
onto
![]() $I-E_{n-i}$
for
$I-E_{n-i}$
for
![]() $0 \leq i \leq n$
.
$0 \leq i \leq n$
.
Using the characterisation of the
![]() $\phi _{A, B}$
provided by Proposition 2.2, we divide the proof of Theorem 2.1 into two lemmas based on whether
$\phi _{A, B}$
provided by Proposition 2.2, we divide the proof of Theorem 2.1 into two lemmas based on whether
![]() $\mathcal {N}$
is isomorphic to
$\mathcal {N}$
is isomorphic to
![]() $\mathcal {N}^\perp $
.
$\mathcal {N}^\perp $
.
Lemma 2.10. If
![]() $\mathcal {N}$
is not order isomorphic to
$\mathcal {N}$
is not order isomorphic to
![]() $\mathcal {N}^\perp $
, then
$\mathcal {N}^\perp $
, then
![]() $\phi $
is a surjective linear isometry.
$\phi $
is a surjective linear isometry.
Proof. Since
![]() $\mathcal {N}$
is not order isomorphic to
$\mathcal {N}$
is not order isomorphic to
![]() $\mathcal {N}^\perp $
, every surjective linear isometry of
$\mathcal {N}^\perp $
, every surjective linear isometry of
![]() $\operatorname {Alg}\mathcal {N}$
is of the form in Proposition 2.2(1). We distinguish two cases according to Lemma 2.6.
$\operatorname {Alg}\mathcal {N}$
is of the form in Proposition 2.2(1). We distinguish two cases according to Lemma 2.6.
Case 1. Suppose that Lemma 2.6(1) holds, that is,
![]() $\phi (A)=DAC^*$
for every
$\phi (A)=DAC^*$
for every
![]() $A \in K(\mathcal {N})$
where
$A \in K(\mathcal {N})$
where
![]() $C, D$
are unitary operators. We claim that C and D are both in
$C, D$
are unitary operators. We claim that C and D are both in
![]() $\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
$\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
For any fixed
![]() $E \in \mathcal {N}$
, if
$E \in \mathcal {N}$
, if
![]() $x \neq 0, x \in E$
and
$x \neq 0, x \in E$
and
![]() $f \neq 0, f \in E_-^\perp $
, then it follows from
$f \neq 0, f \in E_-^\perp $
, then it follows from
![]() $\phi (x \otimes f)=Dx \otimes Cf=U_{T, x \otimes f}V^*_{T, x \otimes f}(x \otimes f)V_{T, x \otimes f}$
that
$\phi (x \otimes f)=Dx \otimes Cf=U_{T, x \otimes f}V^*_{T, x \otimes f}(x \otimes f)V_{T, x \otimes f}$
that
 $$ \begin{align*}Dx=\lambda_{T, x \otimes f} U_{T, x \otimes f}V_{T, x \otimes f}^*x \quad\text{and}\quad Cf=\frac{1}{{\overline{\lambda}_{T, x \otimes f}}}V_{T, x \otimes f}^*f,\end{align*} $$
$$ \begin{align*}Dx=\lambda_{T, x \otimes f} U_{T, x \otimes f}V_{T, x \otimes f}^*x \quad\text{and}\quad Cf=\frac{1}{{\overline{\lambda}_{T, x \otimes f}}}V_{T, x \otimes f}^*f,\end{align*} $$
where
![]() $\lambda _{T, x \otimes f} \in \mathbb {C}$
is on the unit circle.
$\lambda _{T, x \otimes f} \in \mathbb {C}$
is on the unit circle.
By Proposition 2.2 and Lemma 2.8,
![]() $U_{T, x \otimes f}, V_{T, x \otimes f}$
are both in
$U_{T, x \otimes f}, V_{T, x \otimes f}$
are both in
![]() $\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
. Fix
$\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
. Fix
![]() $x_0 \neq 0, x_0 \in (0)_+$
. Then
$x_0 \neq 0, x_0 \in (0)_+$
. Then
![]() $x_0 \otimes f$
is in
$x_0 \otimes f$
is in
![]() $\operatorname {Alg}\mathcal {N}$
for any
$\operatorname {Alg}\mathcal {N}$
for any
![]() $f \neq 0, f \in H$
. Thus, for any
$f \neq 0, f \in H$
. Thus, for any
![]() $E \neq (0), E \in \mathcal {N}$
, we have
$E \neq (0), E \in \mathcal {N}$
, we have
![]() $Cf=V_{T, x_0 \otimes f}^*f/{\overline {\lambda }_{T, x_0 \otimes f}} \in E$
for any
$Cf=V_{T, x_0 \otimes f}^*f/{\overline {\lambda }_{T, x_0 \otimes f}} \in E$
for any
![]() $f \neq 0, f \in E$
. Also, for any
$f \neq 0, f \in E$
. Also, for any
![]() $E \neq H, E \in \mathcal {N}$
, we have
$E \neq H, E \in \mathcal {N}$
, we have
![]() $Cf=V_{T, x_0 \otimes f}^*f/{\overline {\lambda }_{T, x_0 \otimes f}} \in E^\perp $
for any
$Cf=V_{T, x_0 \otimes f}^*f/{\overline {\lambda }_{T, x_0 \otimes f}} \in E^\perp $
for any
![]() $f \neq 0, f \in E^\perp $
. This shows that C is in
$f \neq 0, f \in E^\perp $
. This shows that C is in
![]() $\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
$\operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
For any fixed
![]() $E \in \mathcal {J}(\mathcal {N})$
, there exists an
$E \in \mathcal {J}(\mathcal {N})$
, there exists an
![]() $f_0 \neq 0, f_0 \in E_-^\perp $
. It follows that
$f_0 \neq 0, f_0 \in E_-^\perp $
. It follows that
![]() $Dx=\lambda _{T, x \otimes f_0} U_{T, x \otimes f_0}V_{T, x \otimes f_0}^*x \in E$
for any
$Dx=\lambda _{T, x \otimes f_0} U_{T, x \otimes f_0}V_{T, x \otimes f_0}^*x \in E$
for any
![]() $x \neq 0, x \in E$
, which means that
$x \neq 0, x \in E$
, which means that
![]() $D \in \operatorname {Alg}\mathcal {N}$
.
$D \in \operatorname {Alg}\mathcal {N}$
.
Fix
![]() $E \in \mathcal {J}(\mathcal {N})$
. Then, for any
$E \in \mathcal {J}(\mathcal {N})$
. Then, for any
![]() $y \in E$
and any
$y \in E$
and any
![]() $x \in E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\})$
,
$x \in E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\})$
,
 $$ \begin{align*} \begin{aligned} \langle x, D^*y \rangle&=\langle Dx, y \rangle=\langle \lambda_{T, x \otimes f} U_{T, x \otimes f}V_{T, x \otimes f}^*x, y \rangle\\ &=\langle x, \lambda_{T, x \otimes f}^*V_{T, x \otimes f}U_{T, x \otimes f}^* y \rangle \in \langle x, E \rangle = \{0\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \langle x, D^*y \rangle&=\langle Dx, y \rangle=\langle \lambda_{T, x \otimes f} U_{T, x \otimes f}V_{T, x \otimes f}^*x, y \rangle\\ &=\langle x, \lambda_{T, x \otimes f}^*V_{T, x \otimes f}U_{T, x \otimes f}^* y \rangle \in \langle x, E \rangle = \{0\}. \end{aligned} \end{align*} $$
So
![]() $D^*E \perp (E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\}))$
. Since
$D^*E \perp (E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\}))$
. Since
![]() $E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\})$
is dense in
$E^\perp \cap (\bigcup \{F: F \in \mathcal {J}(\mathcal {N})\})$
is dense in
![]() $E^\perp $
, it follows that
$E^\perp $
, it follows that
![]() $D^* \in \operatorname {Alg}\mathcal {N}$
. This completes the claim.
$D^* \in \operatorname {Alg}\mathcal {N}$
. This completes the claim.
For any
![]() $T \in \operatorname {Alg}\mathcal {N}$
, denote
$T \in \operatorname {Alg}\mathcal {N}$
, denote
![]() $G:=C^* \phi (T)^* D-T^*$
. By (2.1),
$G:=C^* \phi (T)^* D-T^*$
. By (2.1),
![]() $f(Gx)x \otimes f=0$
for any
$f(Gx)x \otimes f=0$
for any
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
. Thus, G maps
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
. Thus, G maps
![]() $E_+$
into E for any
$E_+$
into E for any
![]() $E \neq H, E \in \mathcal {N}$
. It is clear that G is in
$E \neq H, E \in \mathcal {N}$
. It is clear that G is in
![]() $\operatorname {Alg}\mathcal {N}^\perp $
, and hence G maps every
$\operatorname {Alg}\mathcal {N}^\perp $
, and hence G maps every
![]() $E^\perp \in \mathcal {N}^\perp $
into
$E^\perp \in \mathcal {N}^\perp $
into
![]() $E^\perp $
. It follows that G maps
$E^\perp $
. It follows that G maps
![]() $E_+ \ominus E=E_+ \cap E^\perp $
into
$E_+ \ominus E=E_+ \cap E^\perp $
into
![]() $E \cap E^\perp $
for any
$E \cap E^\perp $
for any
![]() $E \neq H, E \in \mathcal {N}$
which yields
$E \neq H, E \in \mathcal {N}$
which yields
![]() $G=0$
and
$G=0$
and
![]() $\phi (T)=DTC^*$
.
$\phi (T)=DTC^*$
.
Case 2. Suppose that Lemma 2.6(2) holds, that is,
![]() $\phi (x \otimes f)=D f \otimes C x$
for every
$\phi (x \otimes f)=D f \otimes C x$
for every
![]() $x \otimes f \in \operatorname {Alg}\mathcal {N}$
where
$x \otimes f \in \operatorname {Alg}\mathcal {N}$
where
![]() $C, D$
are conjugate linear operators such that
$C, D$
are conjugate linear operators such that
![]() $CJ, DJ \in B(H)$
are unitary operators.
$CJ, DJ \in B(H)$
are unitary operators.
Then for
![]() $x_0 \neq 0, x_0 \in (0)_+$
and linear independent
$x_0 \neq 0, x_0 \in (0)_+$
and linear independent
![]() $f_1, f_2 \in H$
,
$f_1, f_2 \in H$
,
and
It follows that
![]() $Df_1$
and
$Df_1$
and
![]() $Df_2$
are linearly dependent which leads to a contradiction.
$Df_2$
are linearly dependent which leads to a contradiction.
In conclusion,
![]() $\phi (T)=DTC^*$
for any
$\phi (T)=DTC^*$
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
and it is clear that
$T \in \operatorname {Alg}\mathcal {N}$
and it is clear that
![]() $\phi $
is a surjective linear isometry of
$\phi $
is a surjective linear isometry of
![]() $\operatorname {Alg}\mathcal {N}$
.
$\operatorname {Alg}\mathcal {N}$
.
Lemma 2.11. If
![]() $\mathcal {N}$
is order isomorphic to
$\mathcal {N}$
is order isomorphic to
![]() $\mathcal {N}^\perp $
, then
$\mathcal {N}^\perp $
, then
![]() $\phi $
is a surjective linear isometry.
$\phi $
is a surjective linear isometry.
Proof. According to Lemma 2.9,
![]() $\mathcal {N}$
is finite; denote
$\mathcal {N}$
is finite; denote
![]() $\mathcal {N}=\{E_0, E_1, \ldots , E_n\}$
where
$\mathcal {N}=\{E_0, E_1, \ldots , E_n\}$
where
![]() $(0)=E_0 < E_1 < \cdots <E_n = H$
. We distinguish two cases according to Lemma 2.6.
$(0)=E_0 < E_1 < \cdots <E_n = H$
. We distinguish two cases according to Lemma 2.6.
Case 1. Suppose that Lemma 2.6(1) holds, that is,
![]() $\phi (A)=DAC^*$
for every
$\phi (A)=DAC^*$
for every
![]() $A \in K(\mathcal {N})$
where
$A \in K(\mathcal {N})$
where
![]() $C, D$
are unitary operators. In this case, for any
$C, D$
are unitary operators. In this case, for any
![]() $E \in \mathcal {J}(\mathcal {N})$
satisfying
$E \in \mathcal {J}(\mathcal {N})$
satisfying
![]() $\dim E_-^\perp> 1$
, fix
$\dim E_-^\perp> 1$
, fix
![]() $x_0 \neq 0, x_0 \in E$
. For any linearly independent
$x_0 \neq 0, x_0 \in E$
. For any linearly independent
![]() $f_1, f_2 \in E_-^\perp $
, we have
$f_1, f_2 \in E_-^\perp $
, we have
![]() $x_0 \otimes f_1, x_0 \otimes f_2 \in \operatorname {Alg}\mathcal {N}$
.
$x_0 \otimes f_1, x_0 \otimes f_2 \in \operatorname {Alg}\mathcal {N}$
.
We claim that
![]() $\phi _{x_0 \otimes f_1, x_0 \otimes f_2}$
is not of the form in Proposition 2.2(2). Otherwise,
$\phi _{x_0 \otimes f_1, x_0 \otimes f_2}$
is not of the form in Proposition 2.2(2). Otherwise,
and
It follows that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are linear dependent, leading to a contradiction.
$f_2$
are linear dependent, leading to a contradiction.
Thus, for any
![]() $f_1 \neq 0, f_1 \in H$
, there exist
$f_1 \neq 0, f_1 \in H$
, there exist
![]() $x_0 \neq 0, x_0 \in (0)_+$
and
$x_0 \neq 0, x_0 \in (0)_+$
and
![]() $f_2 \neq 0, f_2 \in H$
such that
$f_2 \neq 0, f_2 \in H$
such that
Hence,
![]() $Dx_0=\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} U_{x_0 \otimes f_1, x_0 \otimes f_2}V_{x_0 \otimes f_1, x_0 \otimes f_2}^*x_0$
and
$Dx_0=\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} U_{x_0 \otimes f_1, x_0 \otimes f_2}V_{x_0 \otimes f_1, x_0 \otimes f_2}^*x_0$
and
![]() $Cf_1=V_{x_0 \otimes f_1, x_0 \otimes f_2}^*f_1/{\overline {\lambda }_{x_0 \otimes f_1, x_0 \otimes f_2}}$
for some
$Cf_1=V_{x_0 \otimes f_1, x_0 \otimes f_2}^*f_1/{\overline {\lambda }_{x_0 \otimes f_1, x_0 \otimes f_2}}$
for some
![]() $\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} \in \mathbb {C}$
on the unit circle. By the arbitrariness of
$\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} \in \mathbb {C}$
on the unit circle. By the arbitrariness of
![]() $f_1$
and
$f_1$
and
![]() $V_{x_0 \otimes f_1, x_0 \otimes f_2}^* \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
, we obtain
$V_{x_0 \otimes f_1, x_0 \otimes f_2}^* \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
, we obtain
![]() $C \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
$C \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
Similarly, for any
![]() $E \in \mathcal {N}$
with
$E \in \mathcal {N}$
with
![]() $\dim E> 1$
, fix
$\dim E> 1$
, fix
![]() $f_0 \in E_-^\perp $
. Let
$f_0 \in E_-^\perp $
. Let
![]() $x_1, x_2 \in E$
be any linearly independent elements. It is impossible for
$x_1, x_2 \in E$
be any linearly independent elements. It is impossible for
![]() $\phi _{x_1 \otimes f_0, x_2 \otimes f_0}$
to be in the form of Lemma 2.2(2). Thus, for any
$\phi _{x_1 \otimes f_0, x_2 \otimes f_0}$
to be in the form of Lemma 2.2(2). Thus, for any
![]() $x_1 \neq 0, x_1 \in H$
, there exist
$x_1 \neq 0, x_1 \in H$
, there exist
![]() $f_0 \neq 0, f_0 \in H_-^\perp $
and
$f_0 \neq 0, f_0 \in H_-^\perp $
and
![]() $x_2 \neq 0, x_2 \in H$
such that
$x_2 \neq 0, x_2 \in H$
such that
It follows that
![]() $D \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
$D \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
.
For any
![]() $T \in \operatorname {Alg}\mathcal {N}$
, denote
$T \in \operatorname {Alg}\mathcal {N}$
, denote
![]() $G:=C^* \phi (T)^* D-T^*$
. Using a similar method to that in Lemma 2.10, we see that G maps
$G:=C^* \phi (T)^* D-T^*$
. Using a similar method to that in Lemma 2.10, we see that G maps
![]() $E_+ \ominus E=E_+ \cap E^\perp $
into
$E_+ \ominus E=E_+ \cap E^\perp $
into
![]() $E \cap E^\perp $
for any
$E \cap E^\perp $
for any
![]() $E \neq H, E \in \mathcal {N}$
, which yields
$E \neq H, E \in \mathcal {N}$
, which yields
![]() $G=0$
and
$G=0$
and
![]() $\phi (T)=DTC^*$
.
$\phi (T)=DTC^*$
.
Case 2. Suppose that Lemma 2.6(2) holds, that is,
![]() $\phi (x \otimes f)=D f \otimes C x$
for every
$\phi (x \otimes f)=D f \otimes C x$
for every
![]() $x \otimes f \in \operatorname {Alg}\mathcal {N}$
where
$x \otimes f \in \operatorname {Alg}\mathcal {N}$
where
![]() $C, D$
are conjugate linear operators such that
$C, D$
are conjugate linear operators such that
![]() $CJ, DJ \in B(H)$
are unitary operators.
$CJ, DJ \in B(H)$
are unitary operators.
In this case, for any
![]() $E \in \mathcal {J}(\mathcal {N})$
with
$E \in \mathcal {J}(\mathcal {N})$
with
![]() $\dim E_-^\perp> 1$
, fix
$\dim E_-^\perp> 1$
, fix
![]() $x_0 \in E$
. For any linearly independent
$x_0 \in E$
. For any linearly independent
![]() $f_1, f_2 \in E_-^\perp $
,
$f_1, f_2 \in E_-^\perp $
,
![]() $x_0 \otimes f_1, x_0 \otimes f_2$
are in
$x_0 \otimes f_1, x_0 \otimes f_2$
are in
![]() $\operatorname {Alg}\mathcal {N}$
. It is impossible for
$\operatorname {Alg}\mathcal {N}$
. It is impossible for
![]() $\phi _{x_0 \otimes f_1, x_0 \otimes f_2}$
to be in the form of Proposition 2.2(1). Otherwise,
$\phi _{x_0 \otimes f_1, x_0 \otimes f_2}$
to be in the form of Proposition 2.2(1). Otherwise,
and
implying that
![]() $f_1, f_2$
are linear dependent, which leads to a contradiction.
$f_1, f_2$
are linear dependent, which leads to a contradiction.
Thus, for any
![]() $f_1 \neq 0, f_1 \in H$
, there exist
$f_1 \neq 0, f_1 \in H$
, there exist
![]() $x_0 \neq 0, x_0 \in (0)_+$
and
$x_0 \neq 0, x_0 \in (0)_+$
and
![]() $f_2 \neq 0, f_2 \in H$
such that
$f_2 \neq 0, f_2 \in H$
such that
So
![]() $Df_1=\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} U_{x_0 \otimes f_1, x_0 \otimes f_2}V_{x_0 \otimes f_1, x_0 \otimes f_2}^*Jf_1$
and
$Df_1=\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} U_{x_0 \otimes f_1, x_0 \otimes f_2}V_{x_0 \otimes f_1, x_0 \otimes f_2}^*Jf_1$
and
![]() $Cx_0=V_{x_0 \otimes f_1, x_0 \otimes f_2}^*Jx_0/{\overline {\lambda }_{x_0 \otimes f_1, x_0 \otimes f_2}}$
for some
$Cx_0=V_{x_0 \otimes f_1, x_0 \otimes f_2}^*Jx_0/{\overline {\lambda }_{x_0 \otimes f_1, x_0 \otimes f_2}}$
for some
![]() $\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} \in \mathbb {C}$
on the unit circle. According to Lemma 2.9,
$\lambda _{x_0 \otimes f_1, x_0 \otimes f_2} \in \mathbb {C}$
on the unit circle. According to Lemma 2.9,
![]() $V_{x_0 \otimes f_1, x_0 \otimes f_2}^*$
and
$V_{x_0 \otimes f_1, x_0 \otimes f_2}^*$
and
![]() $V_{x_0 \otimes f_1, x_0 \otimes f_2}$
both map
$V_{x_0 \otimes f_1, x_0 \otimes f_2}$
both map
![]() $E_i$
onto
$E_i$
onto
![]() $I-E_{n-i}$
for
$I-E_{n-i}$
for
![]() $0 \leq i \leq n$
. Since
$0 \leq i \leq n$
. Since
![]() $EJ=JE$
for any
$EJ=JE$
for any
![]() $E \in \mathcal {N}$
, by the arbitrariness of
$E \in \mathcal {N}$
, by the arbitrariness of
![]() $f_1$
and
$f_1$
and
![]() $U_{x_0 \otimes f_1, x_0 \otimes f_2} \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
, we see that D maps
$U_{x_0 \otimes f_1, x_0 \otimes f_2} \in \operatorname {Alg}\mathcal {N} \cap \operatorname {Alg}\mathcal {N}^\perp $
, we see that D maps
![]() $E_i$
into
$E_i$
into
![]() $I-E_{n-i}$
and
$I-E_{n-i}$
and
![]() $I-E_i$
into
$I-E_i$
into
![]() $E_{n-i}$
for
$E_{n-i}$
for
![]() $0\leq i\leq n$
, respectively.
$0\leq i\leq n$
, respectively.
Similarly, for any
![]() $E \in \mathcal {N}$
with
$E \in \mathcal {N}$
with
![]() $\dim E> 1$
, fix
$\dim E> 1$
, fix
![]() $f_0 \in E_-^\perp $
. For any linearly independent
$f_0 \in E_-^\perp $
. For any linearly independent
![]() $x_1, x_2 \in E$
,
$x_1, x_2 \in E$
,
![]() $x_1 \otimes f_0, x_2 \otimes f_0$
are in
$x_1 \otimes f_0, x_2 \otimes f_0$
are in
![]() $\operatorname {Alg}\mathcal {N}$
. It is impossible for
$\operatorname {Alg}\mathcal {N}$
. It is impossible for
![]() $\phi _{x_1 \otimes f_0, x_2 \otimes f_0}$
to be in the form of Proposition 2.2(1). Thus, for any
$\phi _{x_1 \otimes f_0, x_2 \otimes f_0}$
to be in the form of Proposition 2.2(1). Thus, for any
![]() $x_1 \neq 0, x_1 \in H$
, there exist
$x_1 \neq 0, x_1 \in H$
, there exist
![]() $f_0 \neq 0, f_0 \in H_-^\perp $
and
$f_0 \neq 0, f_0 \in H_-^\perp $
and
![]() $x_2 \neq 0, x_2 \in H$
such that
$x_2 \neq 0, x_2 \in H$
such that
So
![]() $Df_0=\lambda _{x_1 \otimes f_0, x_2 \otimes f_0} U_{x_1 \otimes f_0, x_2 \otimes f_0}V_{x_1 \otimes f_0, x_2 \otimes f_0}^*Jf_0$
and
$Df_0=\lambda _{x_1 \otimes f_0, x_2 \otimes f_0} U_{x_1 \otimes f_0, x_2 \otimes f_0}V_{x_1 \otimes f_0, x_2 \otimes f_0}^*Jf_0$
and
![]() $Cx_1=V_{x_1 \otimes f_0, x_2 \otimes f_0}^*Jx_1/{\overline {\lambda }_{x_1 \otimes f_0, x_2 \otimes f_0}}$
for some
$Cx_1=V_{x_1 \otimes f_0, x_2 \otimes f_0}^*Jx_1/{\overline {\lambda }_{x_1 \otimes f_0, x_2 \otimes f_0}}$
for some
![]() $\lambda _{x_1 \otimes f_0, x_2 \otimes f_0} \in \mathbb {C}$
on the unit circle. Since
$\lambda _{x_1 \otimes f_0, x_2 \otimes f_0} \in \mathbb {C}$
on the unit circle. Since
![]() $V_{x_1 \otimes f_0, x_2 \otimes f_0}^*, V_{x_1 \otimes f_0, x_2 \otimes f_0}$
both map
$V_{x_1 \otimes f_0, x_2 \otimes f_0}^*, V_{x_1 \otimes f_0, x_2 \otimes f_0}$
both map
![]() $E_i$
onto
$E_i$
onto
![]() $I-E_{n-i}$
for any
$I-E_{n-i}$
for any
![]() $0 \leq i \leq n$
and
$0 \leq i \leq n$
and
![]() $EJ=JE$
for any
$EJ=JE$
for any
![]() $E \in \mathcal {N}$
, by the arbitrariness of
$E \in \mathcal {N}$
, by the arbitrariness of
![]() $x_1$
, we see that C maps
$x_1$
, we see that C maps
![]() $E_i$
into
$E_i$
into
![]() $I-E_{n-i}$
and
$I-E_{n-i}$
and
![]() $I-E_i$
into
$I-E_i$
into
![]() $E_{n-i}$
for all
$E_{n-i}$
for all
![]() $0\leq i\leq n$
, respectively.
$0\leq i\leq n$
, respectively.
By (2.2),
![]() $ (JP^*J)((CJ)^* \phi (T)^* (DJ)-(JTJ))(JP^*J)=0 $
for any
$ (JP^*J)((CJ)^* \phi (T)^* (DJ)-(JTJ))(JP^*J)=0 $
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
and any
$T \in \operatorname {Alg}\mathcal {N}$
and any
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
. So
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
. So
![]() $\langle ((CJ)^* \phi (T)^* (DJ)-JTJ)Jf , Jx \rangle =0$
for all
$\langle ((CJ)^* \phi (T)^* (DJ)-JTJ)Jf , Jx \rangle =0$
for all
![]() $P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
which means that
$P=x \otimes f \in \operatorname {Alg}\mathcal {N}$
which means that
![]() $((CJ)^* \phi (T)^* (DJ)-JTJ)$
maps
$((CJ)^* \phi (T)^* (DJ)-JTJ)$
maps
![]() $(E_i)_-^\perp $
into
$(E_i)_-^\perp $
into
![]() $(E_i)^\perp $
.
$(E_i)^\perp $
.
Moreover, for any
![]() $E_i \in \mathcal {N}$
,
$E_i \in \mathcal {N}$
,
and
![]() $JTJ$
maps
$JTJ$
maps
![]() $E_i$
into
$E_i$
into
![]() $E_i$
. It follows that
$E_i$
. It follows that
![]() $((CJ)^* \phi (T)^* (DJ)-JTJ)$
maps
$((CJ)^* \phi (T)^* (DJ)-JTJ)$
maps
![]() $E_i \cap (E_i)_-^\perp $
into
$E_i \cap (E_i)_-^\perp $
into
![]() $E_i \cap E_i^\perp = \{0\}$
. So
$E_i \cap E_i^\perp = \{0\}$
. So
![]() $((CJ)^* \phi (T)^* (DJ)-JTJ)=0$
, which implies that
$((CJ)^* \phi (T)^* (DJ)-JTJ)=0$
, which implies that
![]() $\phi (T)=(DJ) J T^* J (CJ)^*$
for any
$\phi (T)=(DJ) J T^* J (CJ)^*$
for any
![]() $T \in \operatorname {Alg}\mathcal {N}$
. It is easy to check that
$T \in \operatorname {Alg}\mathcal {N}$
. It is easy to check that
![]() $\phi (T)$
is a surjective linear isometry.
$\phi (T)$
is a surjective linear isometry.
Combining Lemmas 2.10 and 2.11 completes the proof of Theorem 2.1.