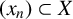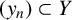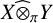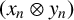1 Weak convergence in projective tensor product
Let X, Y and Z be real Banach spaces. We denote by
![]() $\mathcal {B}(X \times Y , Z)$
the space of continuous bilinear operators from
$\mathcal {B}(X \times Y , Z)$
the space of continuous bilinear operators from
![]() $X \times Y$
into Z. If
$X \times Y$
into Z. If
![]() $Z = \mathbb {R}$
, we simply write
$Z = \mathbb {R}$
, we simply write
![]() $\mathcal {B}(X \times Y)$
. For
$\mathcal {B}(X \times Y)$
. For
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
, define the elementary tensor
$y \in Y$
, define the elementary tensor
![]() $x\otimes y \in \mathcal {B}(X \times Y )^*$
by
$x\otimes y \in \mathcal {B}(X \times Y )^*$
by
We then introduce
![]() $X \otimes Y := \mathrm {span} \{ x\otimes y : x \in X, \, y \in Y\}$
. Recall that the norm on
$X \otimes Y := \mathrm {span} \{ x\otimes y : x \in X, \, y \in Y\}$
. Recall that the norm on
![]() $\mathcal {B}(X~\times ~Y)$
is defined by
$\mathcal {B}(X~\times ~Y)$
is defined by
![]() $\| B \|_{\mathcal {B}(X \times Y)} = \sup _{x \in B_X, y \in B_Y} |B(x,y)|$
. Let
$\| B \|_{\mathcal {B}(X \times Y)} = \sup _{x \in B_X, y \in B_Y} |B(x,y)|$
. Let
![]() $\|\cdot \|_{\pi }$
be the dual norm of
$\|\cdot \|_{\pi }$
be the dual norm of
![]() $\| \cdot \|_{\mathcal {B}(X \times Y)}$
. It is well known (see, for example, [Reference Diestel and Uhl1, Proposition VIII.9.a]) that if
$\| \cdot \|_{\mathcal {B}(X \times Y)}$
. It is well known (see, for example, [Reference Diestel and Uhl1, Proposition VIII.9.a]) that if
![]() $u \in X \otimes Y$
, then
$u \in X \otimes Y$
, then
 $$ \begin{align*} \| u \|_{\pi} = \inf \bigg \{ \sum_{i=1}^n \|x_i\| \|y_i \| : u = \sum_{i=1}^n x_i \otimes y_i \bigg \}.\end{align*} $$
$$ \begin{align*} \| u \|_{\pi} = \inf \bigg \{ \sum_{i=1}^n \|x_i\| \|y_i \| : u = \sum_{i=1}^n x_i \otimes y_i \bigg \}.\end{align*} $$
The projective tensor product of X and Y is defined by
As a consequence of the fundamental linearisation property of tensor products, one can easily deduce the isometric identification
![]() $(X \widehat {\otimes }_\pi Y)^* \equiv \mathcal {B}(X \times Y)$
. Since
$(X \widehat {\otimes }_\pi Y)^* \equiv \mathcal {B}(X \times Y)$
. Since
![]() $\mathcal {B}(X \times Y) \equiv \mathcal {L}(X, Y^*)$
, where
$\mathcal {B}(X \times Y) \equiv \mathcal {L}(X, Y^*)$
, where
![]() $\mathcal {L}(X, Y^*)$
stands for the space of bounded linear operators from X to
$\mathcal {L}(X, Y^*)$
stands for the space of bounded linear operators from X to
![]() $Y^*$
, one also has
$Y^*$
, one also has
![]() $\mathcal {L}(X, Y^*) \equiv (X \widehat {\otimes }_\pi Y)^*$
.
$\mathcal {L}(X, Y^*) \equiv (X \widehat {\otimes }_\pi Y)^*$
.
The aim of this short note is to answer a question of Rodríguez and Rueda Zoca.
Question 1.1 [Reference Rodríguez and Rueda Zoca5, Question 3.9].
Let X and Y be Banach spaces. Let
![]() $(x_n)_{n\in \mathbb {N}}$
and
$(x_n)_{n\in \mathbb {N}}$
and
![]() $(y_n)_{n\in \mathbb {N}}$
be weakly null sequences in X and Y, respectively, such that
$(y_n)_{n\in \mathbb {N}}$
be weakly null sequences in X and Y, respectively, such that
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
![]() $X \widehat {\otimes }_\pi Y$
. Is
$X \widehat {\otimes }_\pi Y$
. Is
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
weakly null in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
weakly null in
![]() $X\widehat {\otimes }_\pi Y$
?
$X\widehat {\otimes }_\pi Y$
?
Let
be the set of elementary tensors in
![]() $X \widehat {\otimes }_\pi Y$
. We shall start with a simple but key observation. Recall that a Banach space X has the approximation property (AP in short) if for every
$X \widehat {\otimes }_\pi Y$
. We shall start with a simple but key observation. Recall that a Banach space X has the approximation property (AP in short) if for every
![]() $\varepsilon>0$
, for every compact subset
$\varepsilon>0$
, for every compact subset
![]() $K \subset X$
, there exists a finite rank operator
$K \subset X$
, there exists a finite rank operator
![]() $T\in \mathcal L(X,X)$
such that
$T\in \mathcal L(X,X)$
such that
![]() $\|Tx -x\| \leq \varepsilon $
for every
$\|Tx -x\| \leq \varepsilon $
for every
![]() $x \in K$
.
$x \in K$
.
Lemma 1.2. Let
![]() $X,Y$
be Banach spaces such that X or Y has the AP. Let
$X,Y$
be Banach spaces such that X or Y has the AP. Let
![]() $T \in X \widehat {\otimes }_\pi Y$
. Then
$T \in X \widehat {\otimes }_\pi Y$
. Then
![]() $T \in \mathcal T$
if and only if every pair of linearly independent families
$T \in \mathcal T$
if and only if every pair of linearly independent families
![]() $\{x_1^*,x_2^* \} \subset X^*$
and
$\{x_1^*,x_2^* \} \subset X^*$
and
![]() $\{y_1^{*},y_2^{*} \} \subset Y^{*}$
satisfies
$\{y_1^{*},y_2^{*} \} \subset Y^{*}$
satisfies
 $$ \begin{align} \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix} = 0. \end{align} $$
$$ \begin{align} \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix} = 0. \end{align} $$
Proof. Thanks to [Reference Ryan6, Proposition 2.8], every
![]() $T\in X \widehat {\otimes }_\pi Y$
can be written as
$T\in X \widehat {\otimes }_\pi Y$
can be written as
 $$ \begin{align*}T = \sum_{n=1}^{\infty} x_n \otimes y_n\end{align*} $$
$$ \begin{align*}T = \sum_{n=1}^{\infty} x_n \otimes y_n\end{align*} $$
with
![]() $\sum _{n=1}^{\infty } \| x_n \| \| y_n \| \leq 2 \|T\|$
. Moreover, the linear map
$\sum _{n=1}^{\infty } \| x_n \| \| y_n \| \leq 2 \|T\|$
. Moreover, the linear map
![]() $\Phi : X \widehat {\otimes }_\pi Y \to \mathcal L(X^*,Y)$
obtained by
$\Phi : X \widehat {\otimes }_\pi Y \to \mathcal L(X^*,Y)$
obtained by
 $$ \begin{align*}\forall x^* \in X^*, \quad \Phi\bigg( \sum_{n=1}^{\infty} x_n \otimes y_n\bigg)(x^*) = \sum_{n=1}^{\infty} x^*(x_n) y_n\end{align*} $$
$$ \begin{align*}\forall x^* \in X^*, \quad \Phi\bigg( \sum_{n=1}^{\infty} x_n \otimes y_n\bigg)(x^*) = \sum_{n=1}^{\infty} x^*(x_n) y_n\end{align*} $$
defines a bounded operator. Since X or Y has the AP,
![]() $\Phi $
is injective (see [Reference Ryan6, Proposition 4.6]).
$\Phi $
is injective (see [Reference Ryan6, Proposition 4.6]).
If
![]() $T = x \otimes y \in \mathcal T$
, then it is straightforward to check that condition
$T = x \otimes y \in \mathcal T$
, then it is straightforward to check that condition
![]() $(\star )$
is verified:
$(\star )$
is verified:
 $$ \begin{align*} \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix} = \begin{vmatrix} x_1^*(x) y_1^{*}(y) & x_1^*(x) y_2^{*}(y) \\ x_2^*(x) y_1^{*}(y) & x_2^*(x) y_2^{*}(y) \end{vmatrix} = 0.\end{align*} $$
$$ \begin{align*} \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix} = \begin{vmatrix} x_1^*(x) y_1^{*}(y) & x_1^*(x) y_2^{*}(y) \\ x_2^*(x) y_1^{*}(y) & x_2^*(x) y_2^{*}(y) \end{vmatrix} = 0.\end{align*} $$
Assume now that
![]() $T \not \in \mathcal T$
. Then
$T \not \in \mathcal T$
. Then
![]() $\Phi (T)$
is an operator of rank greater than 2 in
$\Phi (T)$
is an operator of rank greater than 2 in
![]() $\mathcal L(X^*,Y)$
. Thus, there exists a linearly independent family
$\mathcal L(X^*,Y)$
. Thus, there exists a linearly independent family
![]() $\{x_1^*,x_2^* \} \subset X^*$
such that
$\{x_1^*,x_2^* \} \subset X^*$
such that
![]() $\Phi (T)(x_1^*) \ne 0$
,
$\Phi (T)(x_1^*) \ne 0$
,
![]() $\Phi (T)(x_2^*) \ne 0$
and
$\Phi (T)(x_2^*) \ne 0$
and
![]() $\{\Phi (T)(x_1^*),\Phi (T)(x_2^*) \} \subset Y$
is a linearly independent family. To finish the proof, simply pick a linearly independent family
$\{\Phi (T)(x_1^*),\Phi (T)(x_2^*) \} \subset Y$
is a linearly independent family. To finish the proof, simply pick a linearly independent family
![]() $\{y_1^{*},y_2^{*} \} \subset Y^{*}$
satisfying
$\{y_1^{*},y_2^{*} \} \subset Y^{*}$
satisfying
 $$ \begin{align*} \langle \Phi(T)(x_1^*) , y_1^* \rangle \ne 0 & \quad \langle \Phi(T)(x_1^*) , y_2^* \rangle = 0 \\ \langle \Phi(T)(x_2^*) , y_1^* \rangle = 0 & \quad \langle \Phi(T)(x_2^*) , y_2^* \rangle \ne 0.\\[-2.8pc] \end{align*} $$
$$ \begin{align*} \langle \Phi(T)(x_1^*) , y_1^* \rangle \ne 0 & \quad \langle \Phi(T)(x_1^*) , y_2^* \rangle = 0 \\ \langle \Phi(T)(x_2^*) , y_1^* \rangle = 0 & \quad \langle \Phi(T)(x_2^*) , y_2^* \rangle \ne 0.\\[-2.8pc] \end{align*} $$
Proposition 1.3. Let
![]() $X,Y$
be two Banach spaces such that X or Y has the AP. Then the set of elementary tensors
$X,Y$
be two Banach spaces such that X or Y has the AP. Then the set of elementary tensors
![]() $\mathcal T$
is weakly closed in
$\mathcal T$
is weakly closed in
![]() $X \widehat {\otimes }_\pi Y$
.
$X \widehat {\otimes }_\pi Y$
.
Proof. We let I be the set of all vectors
![]() $(x_1^*,x_2^* ,y_1^{*},y_2^{*})$
such that
$(x_1^*,x_2^* ,y_1^{*},y_2^{*})$
such that
![]() $\{x_1^*,x_2^* \} \subset X^*$
and
$\{x_1^*,x_2^* \} \subset X^*$
and
![]() $\{y_1^{*},y_2^{*} \} \subset Y^{*}$
are both linearly independent families. Next, for every
$\{y_1^{*},y_2^{*} \} \subset Y^{*}$
are both linearly independent families. Next, for every
![]() $T \in X \widehat {\otimes }_\pi Y$
and
$T \in X \widehat {\otimes }_\pi Y$
and
![]() $S=(x_1^*,x_2^* ,y_1^{*},y_2^{*}) \in I$
, we define
$S=(x_1^*,x_2^* ,y_1^{*},y_2^{*}) \in I$
, we define
 $$ \begin{align*}D_S(T) = \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix}.\end{align*} $$
$$ \begin{align*}D_S(T) = \begin{vmatrix} \langle T , x_1^* \otimes y_1^{*} \rangle & \langle T , x_1^* \otimes y_2^{*} \rangle \\ \langle T , x_2^* \otimes y_1^{*} \rangle & \langle T , x_2^* \otimes y_2^{*} \rangle \end{vmatrix}.\end{align*} $$
The result now directly follows from Lemma 1.2 together with the fact that
![]() $D_S$
is continuous with respect to the weak topology. Indeed, one can write
$D_S$
is continuous with respect to the weak topology. Indeed, one can write
![]() $\mathcal T$
as an intersection of weakly closed sets:
$\mathcal T$
as an intersection of weakly closed sets:
The next corollary answers Question 1.1 positively under rather general assumptions.
Corollary 1.4. Let X and Y be Banach spaces such that X or Y has the AP. If
![]() $(x_n)_{n\in \mathbb {N}} \subset X$
converges weakly to x,
$(x_n)_{n\in \mathbb {N}} \subset X$
converges weakly to x,
![]() $(y_n)_{n\in \mathbb {N}} \subset Y$
converges weakly to y and
$(y_n)_{n\in \mathbb {N}} \subset Y$
converges weakly to y and
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
![]() $X \widehat {\otimes }_\pi Y$
, then
$X \widehat {\otimes }_\pi Y$
, then
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
converges weakly to
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
converges weakly to
![]() $x \otimes y$
.
$x \otimes y$
.
Before proving this corollary, let us point out that the canonical basis
![]() $(e_n)_{n \in \mathbb {N}}$
of
$(e_n)_{n \in \mathbb {N}}$
of
![]() $\ell _2$
shows that if
$\ell _2$
shows that if
![]() $(x_n)_{n\in \mathbb {N}}\subset X$
and
$(x_n)_{n\in \mathbb {N}}\subset X$
and
![]() $(y_n)_{n \in \mathbb {N}} \subset Y$
are weakly null sequences, the sequence
$(y_n)_{n \in \mathbb {N}} \subset Y$
are weakly null sequences, the sequence
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
may fail to be weakly null in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
may fail to be weakly null in
![]() $X \widehat {\otimes }_\pi Y$
. Indeed,
$X \widehat {\otimes }_\pi Y$
. Indeed,
![]() $(e_n \otimes e_n)_{n \in \mathbb {N}}$
is isometric to the
$(e_n \otimes e_n)_{n \in \mathbb {N}}$
is isometric to the
![]() $\ell _1$
-canonical basis (see [Reference Ryan6, Example 2.10]).
$\ell _1$
-canonical basis (see [Reference Ryan6, Example 2.10]).
Proof. Assume first that
![]() $(x_n)_{n\in \mathbb {N}} \subset X$
and
$(x_n)_{n\in \mathbb {N}} \subset X$
and
![]() $(y_n)_{n\in \mathbb {N}} \subset Y$
are weakly null sequences such that
$(y_n)_{n\in \mathbb {N}} \subset Y$
are weakly null sequences such that
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
![]() $X \widehat {\otimes }_\pi Y$
. Since
$X \widehat {\otimes }_\pi Y$
. Since
![]() $\mathcal T$
is weakly closed, there exists
$\mathcal T$
is weakly closed, there exists
![]() $x \in X$
and
$x \in X$
and
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $x_n \otimes y_n \to x \otimes y$
in the weak topology. Arguing by contradiction, suppose that
$x_n \otimes y_n \to x \otimes y$
in the weak topology. Arguing by contradiction, suppose that
![]() $x \otimes y \neq 0$
. Pick
$x \otimes y \neq 0$
. Pick
![]() $x^* \in X^*$
and
$x^* \in X^*$
and
![]() $y^* \in Y^*$
such that
$y^* \in Y^*$
such that
![]() $x^*(x) = \|x\| \neq ~0$
and
$x^*(x) = \|x\| \neq ~0$
and
![]() $y^*(y) = \|y\| \neq ~0$
. On the one hand,
$y^*(y) = \|y\| \neq ~0$
. On the one hand,
![]() $x_n \otimes y_n \to x \otimes y$
weakly, so that
$x_n \otimes y_n \to x \otimes y$
weakly, so that
On the other hand, since
![]() $(x_n)_{n\in \mathbb {N}}$
and
$(x_n)_{n\in \mathbb {N}}$
and
![]() $(y_n)_{n\in \mathbb {N}} $
are weakly null, one readily obtains a contradiction:
$(y_n)_{n\in \mathbb {N}} $
are weakly null, one readily obtains a contradiction:
Similarly, if
![]() $(x_n)_{n\in \mathbb {N}} \subset X$
converges weakly to x,
$(x_n)_{n\in \mathbb {N}} \subset X$
converges weakly to x,
![]() $(y_n)_{n\in \mathbb {N}} \subset Y$
converges weakly to y and
$(y_n)_{n\in \mathbb {N}} \subset Y$
converges weakly to y and
![]() $(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
$(x_n \otimes y_n)_{n \in \mathbb {N}}$
is weakly convergent in
![]() $X \widehat {\otimes }_\pi Y$
, then
$X \widehat {\otimes }_\pi Y$
, then
However,
![]() $x \otimes y_n \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
and
$x \otimes y_n \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
and
![]() $x_n \otimes y \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
. Therefore,
$x_n \otimes y \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
. Therefore,
![]() $\big ((x-x_n)\otimes (y-y_n)\big )_{n \in \mathbb {N}}$
converges weakly and, moreover, the weak limit must be 0 thanks to the first part of the proof. This implies that
$\big ((x-x_n)\otimes (y-y_n)\big )_{n \in \mathbb {N}}$
converges weakly and, moreover, the weak limit must be 0 thanks to the first part of the proof. This implies that
![]() $x_n \otimes y_n \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
.
$x_n \otimes y_n \overset {w}{\underset {n\to +\infty }{\longrightarrow }} x\otimes y$
.
In connection with Proposition 1.3, we also wish to mention [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3] which we describe now. If C and D are subsets of X and Y, respectively, then let
As stated in [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3], if C and D are bounded, then
![]() $\overline {C}^w \otimes \overline {D}^w = \overline {C \otimes D}^w$
in
$\overline {C}^w \otimes \overline {D}^w = \overline {C \otimes D}^w$
in
![]() $X \widehat {\otimes }_\pi Y$
. The technique which we introduced in the present note permits us to remove the boundedness assumption in the particular case when C and D are subspaces. It also allows us to slightly simplify the original proof of [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3]. The next lemma is the main ingredient.
$X \widehat {\otimes }_\pi Y$
. The technique which we introduced in the present note permits us to remove the boundedness assumption in the particular case when C and D are subspaces. It also allows us to slightly simplify the original proof of [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3]. The next lemma is the main ingredient.
Lemma 1.5. Let X and Y be Banach spaces such that X or Y has the AP. Let
![]() $(x_s)_s \subset X$
and
$(x_s)_s \subset X$
and
![]() $(y_s)_s \subset Y$
be two nets such that
$(y_s)_s \subset Y$
be two nets such that
![]() $x_s \to x^{**}$
in the weak
$x_s \to x^{**}$
in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $X^{**}$
,
$X^{**}$
,
![]() $y_s \to y^{**}$
in the weak
$y_s \to y^{**}$
in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $Y^{**}$
and
$Y^{**}$
and
![]() $(x_s\otimes y_s)_s$
converges in the weak
$(x_s\otimes y_s)_s$
converges in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $(X \widehat {\otimes }_\pi Y)^{**}$
. Then
$(X \widehat {\otimes }_\pi Y)^{**}$
. Then
![]() $(x_s\otimes y_s)_s$
converges weakly
$(x_s\otimes y_s)_s$
converges weakly
![]() $^*$
to
$^*$
to
![]() $x^{**} \otimes y^{**}$
.
$x^{**} \otimes y^{**}$
.
The proof is essentially the same as that of Corollary 1.4, so we leave the details to the reader.
Corollary 1.6. Let X and Y be Banach spaces such that X or Y has the AP. If C and D are subsets of X and Y, respectively, then
![]() $\overline {C}^w \otimes \overline {D}^w = \overline {C \otimes D}^w$
if one of the following additional assumptions are satisfied:
$\overline {C}^w \otimes \overline {D}^w = \overline {C \otimes D}^w$
if one of the following additional assumptions are satisfied:
-
(i) C and D are subspaces;
-
(ii) C and D are bounded.
Proof. First of all, it is readily seen that
![]() $\overline {C}^w \otimes \overline {D}^w \subset \overline {C \otimes D}^w$
without any additional assumption on C and D (see the first part of the proof of [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3]). Therefore, we only have to prove the reverse inclusion in both cases.
$\overline {C}^w \otimes \overline {D}^w \subset \overline {C \otimes D}^w$
without any additional assumption on C and D (see the first part of the proof of [Reference García-Lirola, Grelier, Martínez-Cervantes and Rueda Zoca2, Theorem 2.3]). Therefore, we only have to prove the reverse inclusion in both cases.
To prove the result under assumption (i), it suffices to apply Proposition 1.3:
To prove the result under assumption (ii), let
![]() $z \in \overline {C \otimes D}^w$
. We fix a net
$z \in \overline {C \otimes D}^w$
. We fix a net
![]() $(x_s \otimes y_s)_s\subset C \otimes D$
which converges weakly to z. Thanks to Proposition 1.3, there exist
$(x_s \otimes y_s)_s\subset C \otimes D$
which converges weakly to z. Thanks to Proposition 1.3, there exist
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $z = x \otimes y$
. Since C and D are bounded, up to taking a suitable subnet, we may assume that both
$z = x \otimes y$
. Since C and D are bounded, up to taking a suitable subnet, we may assume that both
![]() $x_s \to x^{**}$
in the weak
$x_s \to x^{**}$
in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $X^{**}$
and
$X^{**}$
and
![]() ${y_s \to y^{**}}$
in the weak
${y_s \to y^{**}}$
in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $Y^{**}$
. Thanks to Lemma 1.5,
$Y^{**}$
. Thanks to Lemma 1.5,
![]() $x_s \otimes y_s \to x^{**} \otimes y^{**}$
in the weak
$x_s \otimes y_s \to x^{**} \otimes y^{**}$
in the weak
![]() $^*$
-topology of
$^*$
-topology of
![]() $(X \widehat {\otimes }_\pi Y)^{**}$
. By uniqueness of the limit,
$(X \widehat {\otimes }_\pi Y)^{**}$
. By uniqueness of the limit,
![]() $x^{**} \otimes y^{**} = z = x \otimes y$
. We distinguish two cases.
$x^{**} \otimes y^{**} = z = x \otimes y$
. We distinguish two cases.
If
![]() $z = 0$
, then
$z = 0$
, then
![]() $x^{**} = 0$
or
$x^{**} = 0$
or
![]() $y^{**} = 0$
. Say
$y^{**} = 0$
. Say
![]() $x^{**} = 0$
for instance. This means that
$x^{**} = 0$
for instance. This means that
![]() $0 \in \overline {C}^w$
. Now pick any
$0 \in \overline {C}^w$
. Now pick any
![]() $y \in C$
and observe that
$y \in C$
and observe that
![]() $z = 0 \otimes y$
, which was to be shown.
$z = 0 \otimes y$
, which was to be shown.
If
![]() $z \neq 0$
, then it is readily seen that
$z \neq 0$
, then it is readily seen that
![]() $x^{**} \in \mathrm {span}\{x\}$
and
$x^{**} \in \mathrm {span}\{x\}$
and
![]() $y^{**} \in \mathrm {span}\{y\}$
. Therefore,
$y^{**} \in \mathrm {span}\{y\}$
. Therefore,
![]() $x^{**} \in \overline {C}^{w^*} \cap X = \overline {C}^w$
and
$x^{**} \in \overline {C}^{w^*} \cap X = \overline {C}^w$
and
![]() $y^{**} \in \overline {D}^{w^*} \cap Y = \overline {D}^w$
, which concludes the proof.
$y^{**} \in \overline {D}^{w^*} \cap Y = \overline {D}^w$
, which concludes the proof.
2 Applications to vector-valued Lipschitz free spaces
If M is a pointed metric space, with base point
![]() $0 \in M$
, and if X is a real Banach space, then
$0 \in M$
, and if X is a real Banach space, then
![]() $\operatorname {\mathrm {Lip}}_0(M,X)$
stands for the vector space of all Lipschitz maps from M to X which satisfy
$\operatorname {\mathrm {Lip}}_0(M,X)$
stands for the vector space of all Lipschitz maps from M to X which satisfy
![]() $f(0)=0$
. Equipped with the Lipschitz norm,
$f(0)=0$
. Equipped with the Lipschitz norm,
 $$ \begin{align*} \forall f \in \operatorname{\mathrm{Lip}}_0(M,X), \quad \|f\|_L = \sup_{x \neq y \in M} \frac{\|f(x)-f(y)\|_X}{d(x,y)},\end{align*} $$
$$ \begin{align*} \forall f \in \operatorname{\mathrm{Lip}}_0(M,X), \quad \|f\|_L = \sup_{x \neq y \in M} \frac{\|f(x)-f(y)\|_X}{d(x,y)},\end{align*} $$
![]() $\operatorname {\mathrm {Lip}}_0(M,X)$
naturally becomes a Banach space. When
$\operatorname {\mathrm {Lip}}_0(M,X)$
naturally becomes a Banach space. When
![]() $X = \mathbb {R}$
, it is customary to omit the reference to X, that is,
$X = \mathbb {R}$
, it is customary to omit the reference to X, that is,
![]() $\operatorname {\mathrm {Lip}}_0(M):=\operatorname {\mathrm {Lip}}_0(M,\mathbb {R})$
. Next, for
$\operatorname {\mathrm {Lip}}_0(M):=\operatorname {\mathrm {Lip}}_0(M,\mathbb {R})$
. Next, for
![]() $x\in M$
, we let
$x\in M$
, we let
![]() $\delta (x) \in \operatorname {\mathrm {Lip}}_0(M)^*$
be the evaluation functional defined by
$\delta (x) \in \operatorname {\mathrm {Lip}}_0(M)^*$
be the evaluation functional defined by
![]() $\langle \delta (x) , f \rangle = f(x)$
for all
$\langle \delta (x) , f \rangle = f(x)$
for all
![]() $f\in \operatorname {\mathrm {Lip}}_0(M).$
The Lipschitz free space over M is the Banach space
$f\in \operatorname {\mathrm {Lip}}_0(M).$
The Lipschitz free space over M is the Banach space
The universal extension property of Lipschitz free spaces states that for every
![]() $f \in \operatorname {\mathrm {Lip}}_{0}(M,X)$
, there exists a unique continuous linear operator
$f \in \operatorname {\mathrm {Lip}}_{0}(M,X)$
, there exists a unique continuous linear operator
![]() $\overline {f} \in \mathcal {L}(\mathcal {F}(M),X)$
such that:
$\overline {f} \in \mathcal {L}(\mathcal {F}(M),X)$
such that:
-
(i)
 $f=\overline {f} \circ \delta $
; and
$f=\overline {f} \circ \delta $
; and -
(ii)
 $\| \overline {f} \|_{\mathcal {L}(\mathcal {F}(M),X)} = \| f \|_L$
.
$\| \overline {f} \|_{\mathcal {L}(\mathcal {F}(M),X)} = \| f \|_L$
.
In particular, we have the isometric identification
A direct application (in the case
![]() $X = \mathbb {R}$
) provides another basic yet important identification, namely
$X = \mathbb {R}$
) provides another basic yet important identification, namely
It also follows from basic tensor product theory that
![]() $\operatorname {\mathrm {Lip}}_0(M,X^*) \equiv (\mathcal {F}(M) \widehat {\otimes }_\pi X)^*$
, which leads to the next definition (see [Reference García-Lirola, Petitjean and Rueda Zoca4] for more details).
$\operatorname {\mathrm {Lip}}_0(M,X^*) \equiv (\mathcal {F}(M) \widehat {\otimes }_\pi X)^*$
, which leads to the next definition (see [Reference García-Lirola, Petitjean and Rueda Zoca4] for more details).
Definition 2.1 (Vector-valued Lispschitz free spaces).
Let M be a pointed metric space and let X be a Banach space. We define the X-valued Lipschitz free space over M to be
![]() $\mathcal {F}(M,X) := \mathcal {F}(M) \widehat {\otimes }_\pi X$
.
$\mathcal {F}(M,X) := \mathcal {F}(M) \widehat {\otimes }_\pi X$
.
2.1 Weak closure of
 $\delta (M,X)$
$\delta (M,X)$
From [Reference García-Lirola, Petitjean, Procházka and Rueda Zoca3, Proposition 2.9],
![]() $\delta (M) = \{\delta (x) : x \in M \}$
is weakly closed in
$\delta (M) = \{\delta (x) : x \in M \}$
is weakly closed in
![]() $\mathcal {F}(M)$
provided that M is complete. Our first aim is to prove the vector-valued counterpart. For this purpose, we need to identify a set that corresponds to
$\mathcal {F}(M)$
provided that M is complete. Our first aim is to prove the vector-valued counterpart. For this purpose, we need to identify a set that corresponds to
![]() $\delta (M)$
in the vector-valued case. A legitimate set to look at is
$\delta (M)$
in the vector-valued case. A legitimate set to look at is
Notice that this does not exactly correspond to
![]() $\delta (M)$
in the case
$\delta (M)$
in the case
![]() $X = \mathbb {R}$
since we have
$X = \mathbb {R}$
since we have
![]() $\delta (M,\mathbb {R}) = \mathbb {R} \cdot \delta (M)$
. This discrepancy is not a major issue since
$\delta (M,\mathbb {R}) = \mathbb {R} \cdot \delta (M)$
. This discrepancy is not a major issue since
![]() $\mathbb {R} \cdot \delta (M)$
is also a weakly closed set when M is complete. The next result is thus a natural extension to the vector valued setting of [Reference García-Lirola, Petitjean, Procházka and Rueda Zoca3, Proposition 2.9].
$\mathbb {R} \cdot \delta (M)$
is also a weakly closed set when M is complete. The next result is thus a natural extension to the vector valued setting of [Reference García-Lirola, Petitjean, Procházka and Rueda Zoca3, Proposition 2.9].
Proposition 2.2. Let M be a complete pointed metric space and X be a Banach space such that
![]() $\mathcal {F}(M)$
or X have the approximation property. Then
$\mathcal {F}(M)$
or X have the approximation property. Then
![]() $\delta (M,X)$
is weakly closed in
$\delta (M,X)$
is weakly closed in
![]() $\mathcal {F}(M,X)$
.
$\mathcal {F}(M,X)$
.
Proof. In what follows,
![]() $\mathcal T$
denotes the elementary tensors in
$\mathcal T$
denotes the elementary tensors in
![]() $\mathcal {F}(M) \widehat {\otimes }_\pi X$
. Consider a net
$\mathcal {F}(M) \widehat {\otimes }_\pi X$
. Consider a net
![]() $(\delta (m_{\alpha })\otimes x_\alpha )_\alpha \subset \delta (M,X)$
which is weakly convergent. Since
$(\delta (m_{\alpha })\otimes x_\alpha )_\alpha \subset \delta (M,X)$
which is weakly convergent. Since
![]() $\delta (M,X) \subset \mathcal T$
and
$\delta (M,X) \subset \mathcal T$
and
![]() $\mathcal T$
is weakly closed (Proposition 1.3), there exist
$\mathcal T$
is weakly closed (Proposition 1.3), there exist
![]() $\gamma \in \mathcal {F}(M)$
and
$\gamma \in \mathcal {F}(M)$
and
![]() $x\in X$
such that the net goes to
$x\in X$
such that the net goes to
![]() $\gamma \otimes x$
in the weak topology. We may assume that
$\gamma \otimes x$
in the weak topology. We may assume that
![]() $x \neq 0$
, otherwise there is nothing to do. Pick
$x \neq 0$
, otherwise there is nothing to do. Pick
![]() $x^* \in X^*$
such that
$x^* \in X^*$
such that
![]() $x^*(x)\neq 0$
. Then, for every
$x^*(x)\neq 0$
. Then, for every
![]() $f \in \operatorname {\mathrm {Lip}}_0(M)$
, we have
$f \in \operatorname {\mathrm {Lip}}_0(M)$
, we have
![]() $f(m_\alpha )x^*(x_\alpha ) \to f(\gamma ) x^*(x)$
. So the net
$f(m_\alpha )x^*(x_\alpha ) \to f(\gamma ) x^*(x)$
. So the net
![]() $\big (({x^*(x_\alpha )}/{x^*(x)}) \delta (m_\alpha )\big )_\alpha \subset \mathbb {R} \cdot \delta (M)$
weakly converges to
$\big (({x^*(x_\alpha )}/{x^*(x)}) \delta (m_\alpha )\big )_\alpha \subset \mathbb {R} \cdot \delta (M)$
weakly converges to
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\mathbb {R} \cdot \delta (M)$
is weakly closed, there are
$\mathbb {R} \cdot \delta (M)$
is weakly closed, there are
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $m \in M$
such that
$m \in M$
such that
![]() $\gamma = \lambda \delta (m)$
. Consequently,
$\gamma = \lambda \delta (m)$
. Consequently,
![]() $\gamma \otimes x = \delta (m) \otimes \lambda x \in \delta (M,X)$
.
$\gamma \otimes x = \delta (m) \otimes \lambda x \in \delta (M,X)$
.
2.2 Natural preduals
Next, following [Reference García-Lirola, Petitjean, Procházka and Rueda Zoca3, Section 3],
![]() $S \subset \operatorname {\mathrm {Lip}}_0(M)$
is a natural predual of
$S \subset \operatorname {\mathrm {Lip}}_0(M)$
is a natural predual of
![]() $\mathcal {F}(M)$
if
$\mathcal {F}(M)$
if
![]() $S^* \equiv \mathcal {F}(M)$
and
$S^* \equiv \mathcal {F}(M)$
and
![]() $\delta (B(0,r))$
is
$\delta (B(0,r))$
is
![]() $\sigma (\mathcal {F}(M), S)$
-closed for every
$\sigma (\mathcal {F}(M), S)$
-closed for every
![]() $r\geq 0$
. A reasonable extension of this notion in the vector-valued setting is as follows.
$r\geq 0$
. A reasonable extension of this notion in the vector-valued setting is as follows.
Definition 2.3. Let M be a pointed metric space and X be a Banach space with
![]() $\dim (X)\geq 2$
. We say that a Banach space S is a natural predual of
$\dim (X)\geq 2$
. We say that a Banach space S is a natural predual of
![]() $\mathcal {F}(M,X^*)$
if
$\mathcal {F}(M,X^*)$
if
![]() $Y^*\equiv \mathcal {F}(M,X^*)$
and
$Y^*\equiv \mathcal {F}(M,X^*)$
and
is
![]() $\sigma (\mathcal {F}(M,X^*),S)$
-closed for every
$\sigma (\mathcal {F}(M,X^*),S)$
-closed for every
![]() $r \geq 0$
.
$r \geq 0$
.
Notice again that
![]() $\delta (B(0,r),\mathbb {R}) = \mathbb {R} \cdot \delta (B(0,r))$
. In the next statement,
$\delta (B(0,r),\mathbb {R}) = \mathbb {R} \cdot \delta (B(0,r))$
. In the next statement,
![]() $\operatorname {\mathrm {lip}}_0(M)$
denotes the subspace of
$\operatorname {\mathrm {lip}}_0(M)$
denotes the subspace of
![]() $\operatorname {\mathrm {Lip}}_0(M)$
of all uniformly locally flat functions. Recall that
$\operatorname {\mathrm {Lip}}_0(M)$
of all uniformly locally flat functions. Recall that
![]() $f \in \operatorname {\mathrm {Lip}}_0(M)$
is uniformly locally flat if
$f \in \operatorname {\mathrm {Lip}}_0(M)$
is uniformly locally flat if
 $$ \begin{align*} \lim\limits_{d(x,y) \to 0} \frac{|f(x) - f(y)|}{d(x,y)} = 0.\end{align*} $$
$$ \begin{align*} \lim\limits_{d(x,y) \to 0} \frac{|f(x) - f(y)|}{d(x,y)} = 0.\end{align*} $$
Lemma 2.4. Let M be a separable pointed metric space. Suppose that
![]() $S\subset \operatorname {\mathrm {lip}}_0(M)$
is a natural predual of
$S\subset \operatorname {\mathrm {lip}}_0(M)$
is a natural predual of
![]() $\mathcal {F}(M)$
. Then, for every
$\mathcal {F}(M)$
. Then, for every
![]() $r \geq 0$
,
$r \geq 0$
,
![]() $\mathbb {R} \cdot \delta (B(0,r))$
is weak
$\mathbb {R} \cdot \delta (B(0,r))$
is weak
![]() $^*$
closed in
$^*$
closed in
![]() $\mathcal {F}(M)$
.
$\mathcal {F}(M)$
.
Proof. Let us fix
![]() $r \geq 0$
. Let
$r \geq 0$
. Let
![]() $(\lambda _n \delta (x_n))_{n} \subset \mathbb {R} \cdot \delta (B(0,r))$
be a sequence converging to some
$(\lambda _n \delta (x_n))_{n} \subset \mathbb {R} \cdot \delta (B(0,r))$
be a sequence converging to some
![]() $\gamma \in \mathcal {F}(M)$
in the weak
$\gamma \in \mathcal {F}(M)$
in the weak
![]() $^*$
topology. We assume that
$^*$
topology. We assume that
![]() $\gamma \neq 0$
, otherwise there is nothing to do. Since a weak
$\gamma \neq 0$
, otherwise there is nothing to do. Since a weak
![]() $^*$
convergent sequence is bounded, and by weak
$^*$
convergent sequence is bounded, and by weak
![]() $^*$
lower semi-continuity of the norm, we may assume that there exists
$^*$
lower semi-continuity of the norm, we may assume that there exists
![]() $C>0$
such that for every n:
$C>0$
such that for every n:
Thus,
![]() $d(x_n,0) \neq 0$
and
$d(x_n,0) \neq 0$
and
![]() $\lambda _n \neq 0$
for every n. Up to extracting a further subsequence, we may assume that the sequence
$\lambda _n \neq 0$
for every n. Up to extracting a further subsequence, we may assume that the sequence
![]() $(\lambda _n d(x_n,0))_{n}$
converges to some
$(\lambda _n d(x_n,0))_{n}$
converges to some
![]() $\ell \neq 0$
. Since
$\ell \neq 0$
. Since
![]() $(x_n)_{n} \subset B(0,r)$
, we also assume that
$(x_n)_{n} \subset B(0,r)$
, we also assume that
![]() $(d(x_n,0))_{n}$
converges to some d. We will distinguish two cases.
$(d(x_n,0))_{n}$
converges to some d. We will distinguish two cases.
If
![]() $d \neq 0$
, then
$d \neq 0$
, then
![]() $(\lambda _n)_{n}$
converges to
$(\lambda _n)_{n}$
converges to
![]() $\lambda :={\ell }/{d}$
and so
$\lambda :={\ell }/{d}$
and so
![]() $(\delta (x_n))_{n}$
weak
$(\delta (x_n))_{n}$
weak
![]() $^*$
converges to
$^*$
converges to
![]() ${\gamma }/{\lambda }$
. Since S is a natural predual of
${\gamma }/{\lambda }$
. Since S is a natural predual of
![]() $\mathcal {F}(M)$
,
$\mathcal {F}(M)$
,
![]() $\delta (B(0,r))$
is weak
$\delta (B(0,r))$
is weak
![]() $^*$
closed in
$^*$
closed in
![]() $\mathcal {F}(M)$
. So there exists
$\mathcal {F}(M)$
. So there exists
![]() $x \in M$
such that
$x \in M$
such that
![]() $\gamma = \lambda \delta (x)$
.
$\gamma = \lambda \delta (x)$
.
If
![]() $d = 0$
, then
$d = 0$
, then
![]() $(\delta (x_n))_{n}$
converges to
$(\delta (x_n))_{n}$
converges to
![]() $0$
in the norm topology (and
$0$
in the norm topology (and
![]() $(\lambda _n)_{n}$
tends to infinity). Note that we may write
$(\lambda _n)_{n}$
tends to infinity). Note that we may write
Since
![]() $S\subset \operatorname {\mathrm {lip}}_0(M)$
, the sequence
$S\subset \operatorname {\mathrm {lip}}_0(M)$
, the sequence
![]() $({(\delta (x_n) - \delta (0))}/{d(x_n,0)})_{n}$
weak
$({(\delta (x_n) - \delta (0))}/{d(x_n,0)})_{n}$
weak
![]() $^*$
converges to 0. Moreover, the sequence
$^*$
converges to 0. Moreover, the sequence
![]() $(\lambda _n d(x_n,0))_{n}$
converges to
$(\lambda _n d(x_n,0))_{n}$
converges to
![]() $\ell \neq 0$
. Consequently,
$\ell \neq 0$
. Consequently,
![]() $(\lambda _n \delta (x_n))_{n}$
weak
$(\lambda _n \delta (x_n))_{n}$
weak
![]() $^*$
converges to 0 and so
$^*$
converges to 0 and so
![]() $\gamma = 0$
, which is a contradiction.
$\gamma = 0$
, which is a contradiction.
Before going further, we need to introduce the injective tensor product of two Banach spaces. Recall that to define the projective tensor product, we introduced
![]() $x\otimes y$
as an element of
$x\otimes y$
as an element of
![]() $\mathcal {B}(X \times Y)^{*}$
. For the injective tensor product, we change the point of view since we now consider
$\mathcal {B}(X \times Y)^{*}$
. For the injective tensor product, we change the point of view since we now consider
![]() $x\otimes y$
as an element of
$x\otimes y$
as an element of
![]() $\mathcal {B}(X^* \times Y^*)$
defined as follows:
$\mathcal {B}(X^* \times Y^*)$
defined as follows:
In this case, we denote by
![]() $\| \cdot \|_{\varepsilon }$
the canonical norm on
$\| \cdot \|_{\varepsilon }$
the canonical norm on
![]() $\mathcal {B}(X^* \times Y^*)$
. Thus, if
$\mathcal {B}(X^* \times Y^*)$
. Thus, if
![]() $u = \sum _{i=1}^n x_i \otimes y_i \in X \otimes Y$
, then
$u = \sum _{i=1}^n x_i \otimes y_i \in X \otimes Y$
, then
 $$ \begin{align*}\| u \|_{\varepsilon} = \sup \bigg \{ \bigg| \sum_{i=1}^n x^*(x_i) y^*(y_i) \bigg| : x^* \in B_{X^*}, y^* \in B_{Y^*} \bigg \}.\end{align*} $$
$$ \begin{align*}\| u \|_{\varepsilon} = \sup \bigg \{ \bigg| \sum_{i=1}^n x^*(x_i) y^*(y_i) \bigg| : x^* \in B_{X^*}, y^* \in B_{Y^*} \bigg \}.\end{align*} $$
The injective tensor product of X and Y is defined by
In what follows, we will use a classical result from tensor product theory (see, for example, [Reference Ryan6, Theorem 5.33]): if
![]() $X^*$
or
$X^*$
or
![]() $Y^*$
has the Radon–Nikodým property (RNP in short) and
$Y^*$
has the Radon–Nikodým property (RNP in short) and
![]() $X^*$
or
$X^*$
or
![]() $Y^*$
has the AP, then
$Y^*$
has the AP, then
![]() $(X \widehat {\otimes }_\varepsilon Y)^* \equiv X^* \widehat {\otimes }_\pi Y^*$
. The RNP has many characterisations (see [Reference Diestel and Uhl1, Section VII.6] for a nice overview).
$(X \widehat {\otimes }_\varepsilon Y)^* \equiv X^* \widehat {\otimes }_\pi Y^*$
. The RNP has many characterisations (see [Reference Diestel and Uhl1, Section VII.6] for a nice overview).
Assume now that there exists a subspace S of
![]() $\operatorname {\mathrm {Lip}}_0(M)$
such that
$\operatorname {\mathrm {Lip}}_0(M)$
such that
![]() $S^* \equiv \mathcal {F}(M)$
. Then
$S^* \equiv \mathcal {F}(M)$
. Then
whenever either
![]() $\mathcal F(M)$
or
$\mathcal F(M)$
or
![]() $X^*$
has the AP and either
$X^*$
has the AP and either
![]() $\mathcal F(M)$
or
$\mathcal F(M)$
or
![]() $X^*$
has the RNP. It is quite natural to wonder whether there are conditions which ensure that
$X^*$
has the RNP. It is quite natural to wonder whether there are conditions which ensure that
![]() $S \widehat {\otimes }_\varepsilon X$
is a natural predual of
$S \widehat {\otimes }_\varepsilon X$
is a natural predual of
![]() $\mathcal {F}(M,X^*)$
. The next result asserts that this sometimes relies on the scalar case.
$\mathcal {F}(M,X^*)$
. The next result asserts that this sometimes relies on the scalar case.
Proposition 2.5. Let M be a separable pointed metric space,
![]() $S\subset \operatorname {\mathrm {lip}}_0(M)$
be a natural predual of
$S\subset \operatorname {\mathrm {lip}}_0(M)$
be a natural predual of
![]() $\mathcal {F}(M)$
and X be a Banach space (with
$\mathcal {F}(M)$
and X be a Banach space (with
![]() $\dim (X) \geq 2$
). Assume moreover that either
$\dim (X) \geq 2$
). Assume moreover that either
![]() $\mathcal F(M)$
or
$\mathcal F(M)$
or
![]() $X^*$
has the AP and either
$X^*$
has the AP and either
![]() $\mathcal F(M)$
or
$\mathcal F(M)$
or
![]() $X^*$
has the RNP. Then
$X^*$
has the RNP. Then
![]() $S \widehat {\otimes }_\varepsilon X$
is a natural predual of
$S \widehat {\otimes }_\varepsilon X$
is a natural predual of
![]() $\mathcal {F}(M,X^*)$
.
$\mathcal {F}(M,X^*)$
.
Proof. To show that
![]() $S \widehat {\otimes }_\varepsilon X$
is a natural predual, we essentially follow the proof of Proposition 2.2. First of all, we show that
$S \widehat {\otimes }_\varepsilon X$
is a natural predual, we essentially follow the proof of Proposition 2.2. First of all, we show that
![]() $\mathcal T:= \{ \gamma \otimes x^* : \gamma \in \mathcal {F}(M), \, x \in X^* \}$
is weak
$\mathcal T:= \{ \gamma \otimes x^* : \gamma \in \mathcal {F}(M), \, x \in X^* \}$
is weak
![]() $^*$
closed in
$^*$
closed in
![]() $\mathcal {F}(M,X^*)$
. Indeed, it is not hard to show that if
$\mathcal {F}(M,X^*)$
. Indeed, it is not hard to show that if
![]() $T \in \mathcal {F}(M,X^*)$
, then
$T \in \mathcal {F}(M,X^*)$
, then
![]() $T \in \mathcal T$
if and only if for every pair of linearly independent families
$T \in \mathcal T$
if and only if for every pair of linearly independent families
![]() $\{f_1,f_2 \} \subset S$
and
$\{f_1,f_2 \} \subset S$
and
![]() $\{x_1,x_2\} \subset X$
,
$\{x_1,x_2\} \subset X$
,
 $$ \begin{align*}\begin{vmatrix} \langle T , f_1 \otimes x_1 \rangle & \langle T , f_1 \otimes x_2 \rangle \\ \langle T , f_2 \otimes x_1 \rangle & \langle T , f_2 \otimes x_2 \rangle \end{vmatrix} = 0 .\end{align*} $$
$$ \begin{align*}\begin{vmatrix} \langle T , f_1 \otimes x_1 \rangle & \langle T , f_1 \otimes x_2 \rangle \\ \langle T , f_2 \otimes x_1 \rangle & \langle T , f_2 \otimes x_2 \rangle \end{vmatrix} = 0 .\end{align*} $$
Accordingly,
![]() $\mathcal T$
is weak
$\mathcal T$
is weak
![]() $^*$
closed. Fix
$^*$
closed. Fix
![]() $r{\kern-1pt}>{\kern-1pt}0$
and consider a net
$r{\kern-1pt}>{\kern-1pt}0$
and consider a net
![]() $(\delta (m_{\alpha })\otimes x_\alpha ^*)_\alpha {\kern-1pt}\subset{\kern-1pt} \delta (B(0,r),X^*)$
which weak
$(\delta (m_{\alpha })\otimes x_\alpha ^*)_\alpha {\kern-1pt}\subset{\kern-1pt} \delta (B(0,r),X^*)$
which weak
![]() $^*$
converges to some
$^*$
converges to some
![]() $\gamma \otimes x^* \in \mathcal T$
. We may assume that
$\gamma \otimes x^* \in \mathcal T$
. We may assume that
![]() $x^* \neq 0$
otherwise there is nothing to do. Consider
$x^* \neq 0$
otherwise there is nothing to do. Consider
![]() $x \in X$
such that
$x \in X$
such that
![]() $x^*(x)\neq 0$
. Then, for every
$x^*(x)\neq 0$
. Then, for every
![]() $f \in S$
, we have
$f \in S$
, we have
![]() $f(m_\alpha )x^*(x_\alpha ) \to f(\gamma ) x^*(x)$
. So the net
$f(m_\alpha )x^*(x_\alpha ) \to f(\gamma ) x^*(x)$
. So the net
![]() $\big (({x^*(x_\alpha )}/{x^*(x)}) \delta (m_\alpha )\big )_\alpha \subset \mathbb {R} \cdot \delta (M)$
weak
$\big (({x^*(x_\alpha )}/{x^*(x)}) \delta (m_\alpha )\big )_\alpha \subset \mathbb {R} \cdot \delta (M)$
weak
![]() $^*$
converges to
$^*$
converges to
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\mathbb {R} \cdot \delta (M)$
is weak
$\mathbb {R} \cdot \delta (M)$
is weak
![]() $^*$
closed (Lemma 2.4), there are
$^*$
closed (Lemma 2.4), there are
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $m \in M$
such that
$m \in M$
such that
![]() $\gamma = \lambda \delta (m)$
.
$\gamma = \lambda \delta (m)$
.
Acknowledgements
The author thanks Christian Le Merdy and Abraham Rueda Zoca for useful discussions.