Some Trinitarianisms

For the Western Church at least, the definitive statement of the doctrine of the Trinity can be found in the Athanasian Creed. The Athanasian Creed involves forty-four theological theses concerning the doctrines of the Trinity and the Incarnation. Amongst these theses are the following three:

1. (1) ‘We worship one God in Trinity and Trinity in Unity. Neither confounding the Persons nor dividing the Substance.’

2. (2) ‘So the Father is God, the Son is God, and the Holy Spirit is God.’

3. (3) ‘And yet they are not three Gods, but one God.’ (Sullivan (Reference Sullivan1907))

The interpretation of (1)–(3), however, is a matter of some debate. A broad division has arisen over the centuries between two families that disagree about the interpretation of these sentences: Social Trinitarianism and Latin Trinitarianism. Before I say more about these families, I will make one terminological note. The term ‘God’ is often ambiguous between its various possible uses as a proper name and a count noun. So, for the rest of this article, in place of a proper name I shall use the term ‘the Godhead’ and when I intend to use a count noun I will use ‘divinity’.

For both of these families of Trinitarian accounts, (1)–(3) are understood as ruling out both modalism, the heresy that the three persons are different aspects or modes of the same being, and tritheism, the heresy that there are three divinities.

The Social Trinitarian view is best summed up by McCall and Rea:

All versions of Social Trinitarianism are structurally alike in the following respect. The Godhead is something over and above any one of the persons which partly constitute it, and the truth of statements of the form ‘x is divine’ is grounded in x’s possession of certain divine properties rather than any identification of x with the Godhead.

Social Trinitarianism is in contrast to Latin Trinitarianism. Latin Trinitarianism is often characterized as placing greater emphasis on the oneness of the Godhead than on the threeness of the persons. It is amongst Latin accounts of the Trinity that we find the further claim that each of the persons of the Trinity is wholly God. As the Catholic catechism puts it:

Latin accounts of the Trinity rarely express the relation of the persons to the Godhead as one of composition. Rather, it is common for Latin Trinitarians to assert that some relation of numerical sameness holds between each of the persons and the Godhead. However, I believe that it is a mistake to think that Latin Trinitarianism is incompatible with taking the relation between the persons and the Godhead to be one of parthood. For one thing, according to classical mereology, numerical sameness relations are themselves (or at least entail) relations of parthood.Footnote ¹ What I suspect motivates the absence of Latin mereological Trinitarian accounts is the assumption that if each of the persons is part of the Godhead, then none of them can be wholly the Godhead. I wish to explore non-classical mereologies which will avoid this consequence.

For the rest of this article, then, I will be interested in the metaphysical picture that is suggested by this stronger version of the doctrine of the Trinity. I will therefore largely ignore Social Trinitarian accounts,Footnote ² and instead turn to a consideration of the problems that Latin Trinitarianism faces, and an elucidation of the theological desiderata that an orthodox Latin account must satisfy.

Latin Trinitarianism and the logical problem of the Trinity

The central objection to all versions of Latin Trinitarianism is that the proposed interpretations of the sentences (1)–(3) lead to what has become known as ‘the logical problem of the Trinity’. The problem can be stated in many different ways. But I will set it up as follows:

Translate (1) as:

1. (1.1) The Father is not identical with the Son, and the Father is not identical with the Holy Spirit, and the Son is not identical with the Holy Spirit, and there is only one divinity.

Translate (2) as:

1. (1.2) There Father is identical with some divinity, and the Son is identical with some divinity, and the Holy Spirit is identical with some divinity.

Translate (3) as:

1. (1.3) There is some divinity, x, and for any divinity y, x is identical with y.

For the argument that follows we will take (1.1), (1.2), and (1.3) to be theological axioms. From this, however, contradiction follows.

• Proof: There is exactly one divinity (by (1.3)), the Father is identical with this divinity (by (1.2) and (1.3)), the Son is identical with this divinity (by (1.2) and (1.3)), so the Father is identical with the Son (by the Transitivity of Identity). But the Father is not identical with the Son (by 1.1). So we have reached a contradiction.

Thus, assuming classical logic with identity, the theological axioms we began with are inconsistent, therefore false. It seems that the claim that each of the three persons of the Trinity is identical with some divinity leads, via the classical logic of identity, to contradiction. It seems our options are either to abandon the Athanasian Creed, to interpret the theological statements differently from (1.1)–(1.3), or to replace classical logic with some other logic, given which, Argument 1 is invalid. I am interested in the prospects for an orthodox doctrine of the Latin Trinity, so I will assume the truth of the Athanasian Creed. The choice, then, is between a reinterpretation of (1)–(3) or a change in logic. Ceteris paribus, a change in logic will involve a greater mutilation of philosophical orthodoxy than a reinterpretation, which gives us at least some reason to prefer the latter strategy. I will try to do this by suggesting that ‘the Father is God’ does not involve an ‘is’ of identity, but rather an ‘is of constitution’.Footnote ³ To see how this strategy might work, we must first look at some of the basics of orthodox mereology, the study of parts and wholes. The aim will be to establish where the conflict lies between Latin Trinitarianism and classical mereology. This will set up the next section's discussion of possible non-classical mereological models for the Trinity.

Mereology: The Basics

In his classic introduction to the topic, Parts, Peter Simons provides the following gloss on the notions of proper and improper parthood.

Simons (ibid., 26–28) gives the following axioms and definitions (where ‘<<’ stands for ‘. . . is a proper part of . . .’, ‘<’ stands for ‘. . . is a part of . . .’, ‘o’ stands for ‘. . . overlaps. . .’, and ‘I’ stands for ‘. . . is disjoint with . . .’):

• SA0: Any axiom set sufficient for first-order predicate calculus with identity

• SA1 (Anti-Symmetry of Proper Parthood): x ≪ y → ~y ≪ x

• SA2 (Transitivity of Proper Parthood): x ≪ y & y ≪ z → x ≪ z

• SD1 (Definition of Parthood): x < y ↔ x ≪ y V x = y

• SD2 (Definition of Overlap): x o y ↔ (∃z) (z < x & z < y)

• SD3 (Definition of Disjoint): x|y ↔ ~x o y

He adds,

To eliminate this, as Simons sees it, problematic model (as well as others) Simons proposes a set of additional axioms:

• SA3 (Weak Supplementation Principle): x ≪ y → (∃z) (z ≪ y & z|x)

• SA4 (Proper Parts Principle): (∃z) (z ≪ x) & (z) (z ≪ x → z ≪ y) → x < y

• SA5 (Strong Supplementation Principle): ~x < y → (∃z) (z < x & z|y) SA6: x o y → (∃z) (w) (w < z ↔ w < x & w < y)

These axioms (and definitions) characterize Simons's Minimal Extensional Mereology. From these, many theorems can be derived, of which the following will be significant for this article:

• SCT1 (Anti-Reflexivity of Proper Parthood): ~x ≪ x

• SCT2 (Reflexivity of Parthood): x < x

• SCT3 (Asymmetry of Parthood): x = y ↔ x < y & y < x

• SCT7Footnote ⁵ (Extensionality of Parthood): x = y ↔ (z) (z < x ↔ z < y)Footnote ⁶

• SCT71: (Extensionality of Proper Parthood) (∃z) (z ≪ x) V (∃z) (z ≪ y) → ( (z) (z ≪ x ↔ z ≪ y) → x = y)

It is worth noting the difference between SCT7 and SCT71. The former says that any x and y are identical if and only if they share all their parts. The second says more or less the same about proper parts, though it involves a restriction which leaves open the possibility of two atoms (objects with no proper parts) being non-identical although they (trivially) have all their proper parts in common. The latter, Extensionality of Proper Parts, is controversial and most of the models I will be presenting involve its rejection. The former, Extensionality of Parts, is generally thought to be uncontroversial. However, the model that I think best captures the theological doctrine is one that would reject SCT7, as we shall see in due course.

The two formal systems which provide the inspiration for Simons's work, those of Lésniewski (Reference Lésniewski and Surma1992a, Reference Lésniewski and Surma1992b) and Leonard and Goodman (Reference Leonard and Goodman1940), both have definitions, axioms, or theorems which correspond to SA0–SA6 and SD1–SD3. Any system which involves these, regardless of whether they appear as definitions, axioms, or theorems, I shall count as a version of classical mereology. I will not concern myself with the additional axioms that might be added to classical mereology to generate stronger systems than Minimal Extensional Mereology, for SA0–SA6 and SD1–SD3 present the doctrine of the Trinity with troubles enough as it is. In the next section, I will consider which of these must be rejected in order to find a model consistent with a Latin account of the Trinity.

Mereological models

The models that I present in this section are to be judged on the basis of their independent plausibility, their relative degree of divergence from classical mereology, and their success in accommodating the central theological desiderata, which can be enumerated as follows:

1. (2.1) There is only one divinity.

2. (2.2) On the model it is false that ‘the Father is identical with the Son’, ‘the Son is identical with the Holy Spirit’ and ‘the Holy Spirit is identical with the Father’.

3. (2.3) For some sense of the word ‘. . . is wholly. . .’, it is true on the model that ‘the Father is wholly the Godhead’, ‘the Son is wholly the Godhead’, and ‘the Holy Spirit is wholly the Godhead’.

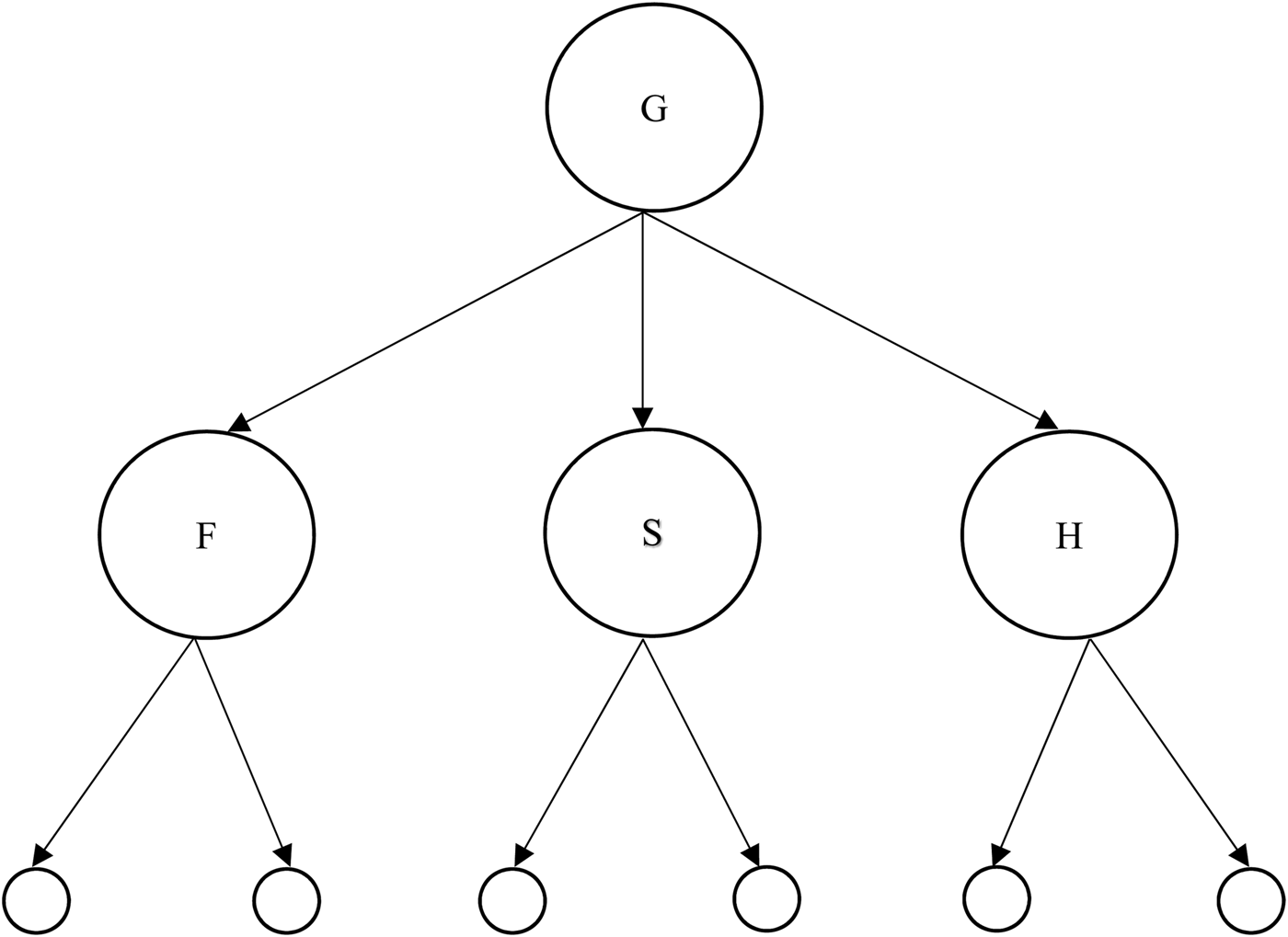
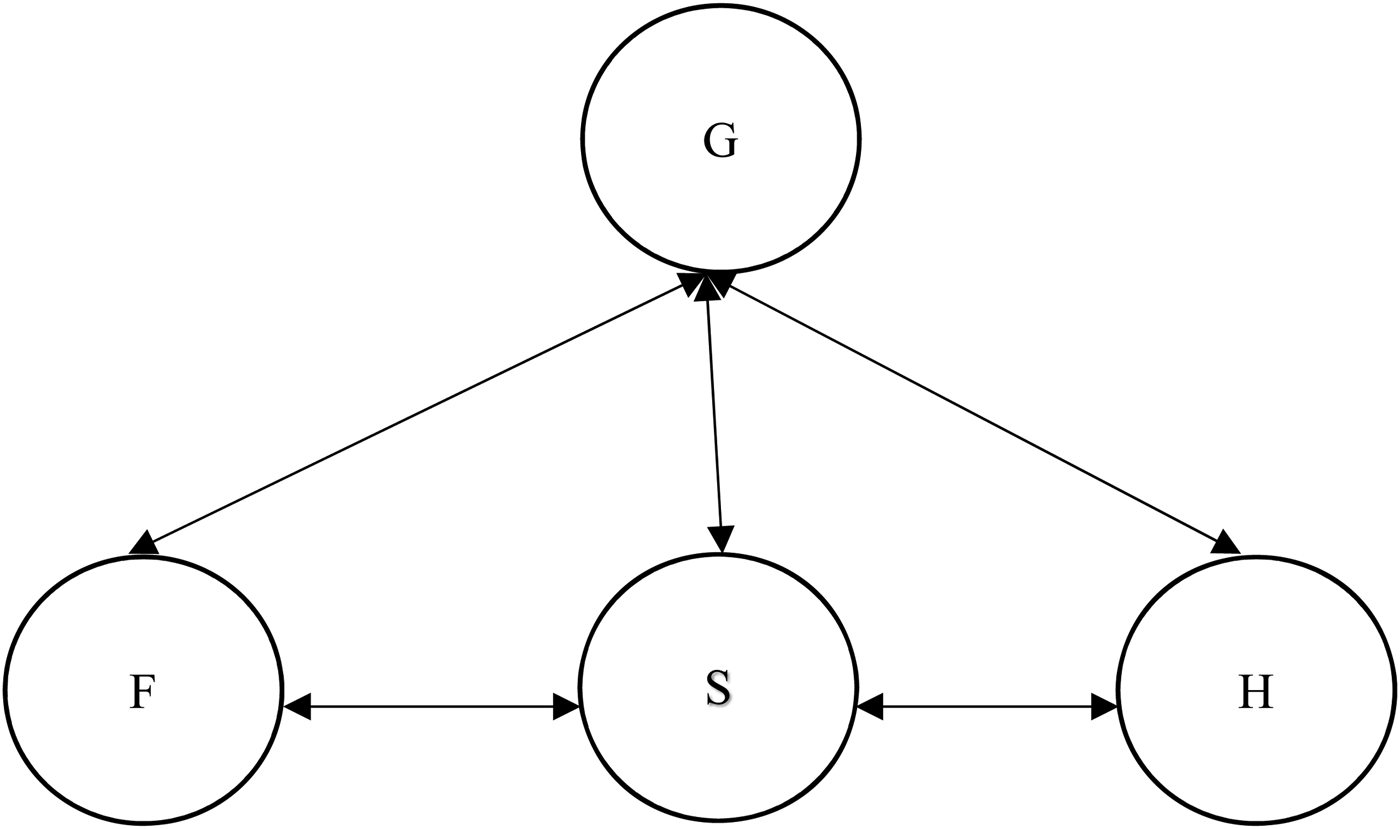
As a starting point, let use consider the mereological model of the Trinity suggested by Social Trinitarianism.Footnote ⁷ On this view, the Godhead is something like a society or family with three members. This suggests that each of the persons is a proper part of the Godhead, each is disjoint from one another (though some versions might involve some common parts between the persons, and verions committed to some kind of divine simplicity might reject the existence of proper parts of the persons entirely). The corresponding model may be pictured as follows, where the straight lines represent the proper parthood relation, ‘G’ stands for the Godhead, ‘F’ for the Father, ‘H’ for the Holy Spirit, ‘S’ for the Son, and unnamed circles show the proper parts of the persons. (Social Trinitarianism does not involve any particular commitment to what or how many these might be.)

There is no incompatibility between this picture and any of the traditional axioms of mereology. Moreover, according to this picture, each of the persons of the Trinity is (a proper part of) the Godhead (the arrows representing the proper parthood relation, with the arrow head pointed at the proper part), but they are distinct from one another, so this picture avoids modalism. As parts of the Godhead, they do not represent separate divinities according to defenders of this view, so tritheism is avoided, or so a hypothetical defender of MODEL A (fig 1) might claim. We can see at a glance, though, that the mereological picture implied by Social Trinitarianism rules out any of the persons being wholly the Godhead. On this model, for each of the persons, there is some other non-identical entity which is not a part of it, but is a proper part of the Godhead. The Godhead, then, on the Social Trinitarian mereology is something over-and-above each of the persons. This model, therefore, does not satisfy all the theological desiderata, as it fails (2.3).

Fig. 1 Model A.

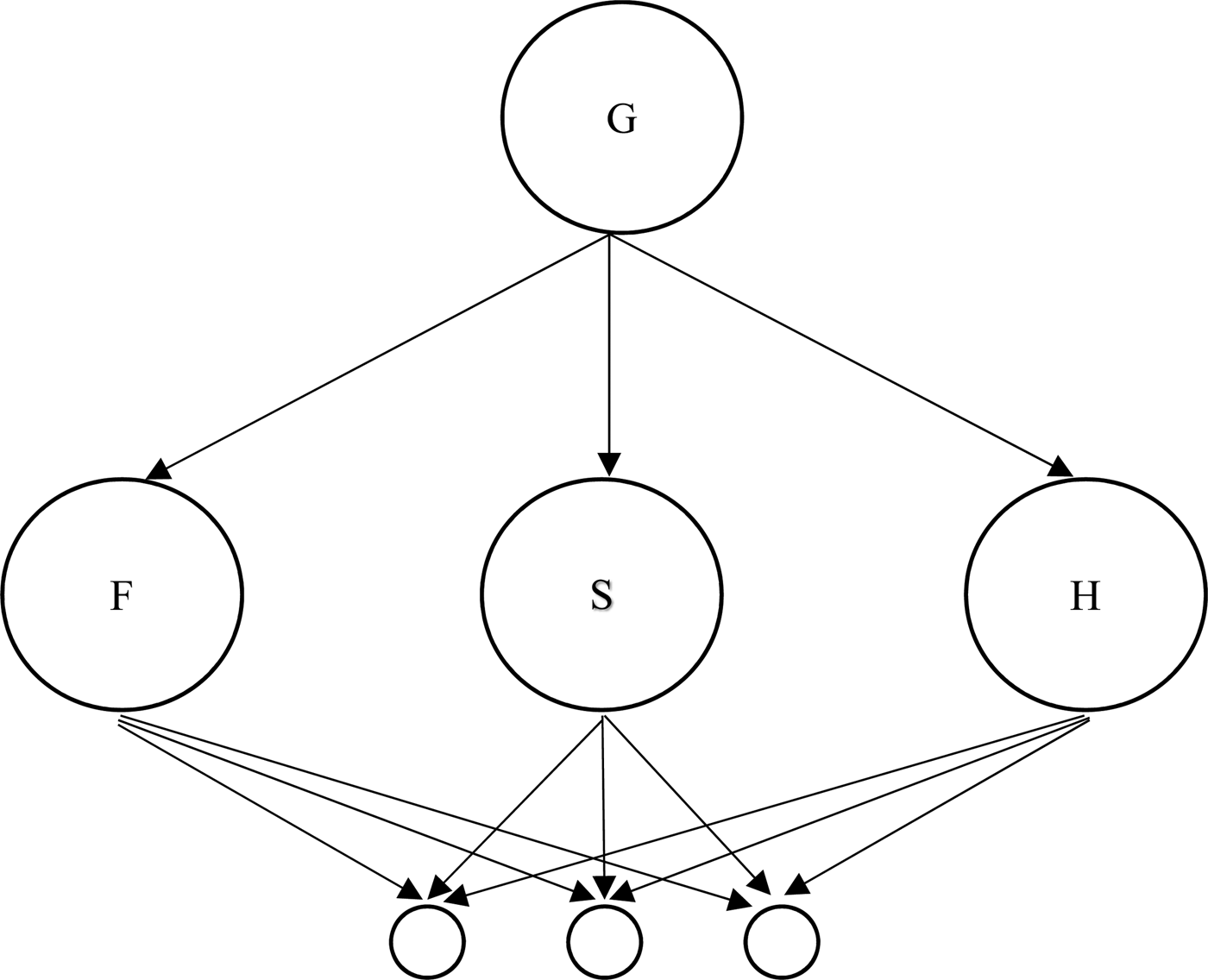
So the Social Trinitarian mereology cannot capture the claim that each of the persons of the Trinity is wholly the Godhead. What alterations to this model might be required? One simple alternative would be as follows:

In this model, the proper parts of the divine persons are all shared in common. The major theological worry here, however, is modalism, the idea being that, if each of the persons is composed of just the same proper parts as each of the other persons, then they must be different guises for one and the same person. In order to respond to the modalist worry, this model cannot allow for the inference from sameness of proper parts to identity. This is to reject the Extensionality of Proper Parts Principle, which says that if x and y have proper parts and have all their proper parts in common, they are identical, and therefore indiscernible.

• Proof: Assume SCT71. By MODEL B (fig 2), (∃x) x ≪ F, moreover, on the model, (x) x ≪ F ↔ x ≪ S, so by conjunction introduction, (∃x) x ≪ F & (y) y ≪ F ↔ y ≪ S. From this, by SCT71, infer F = S. But this is modalism.

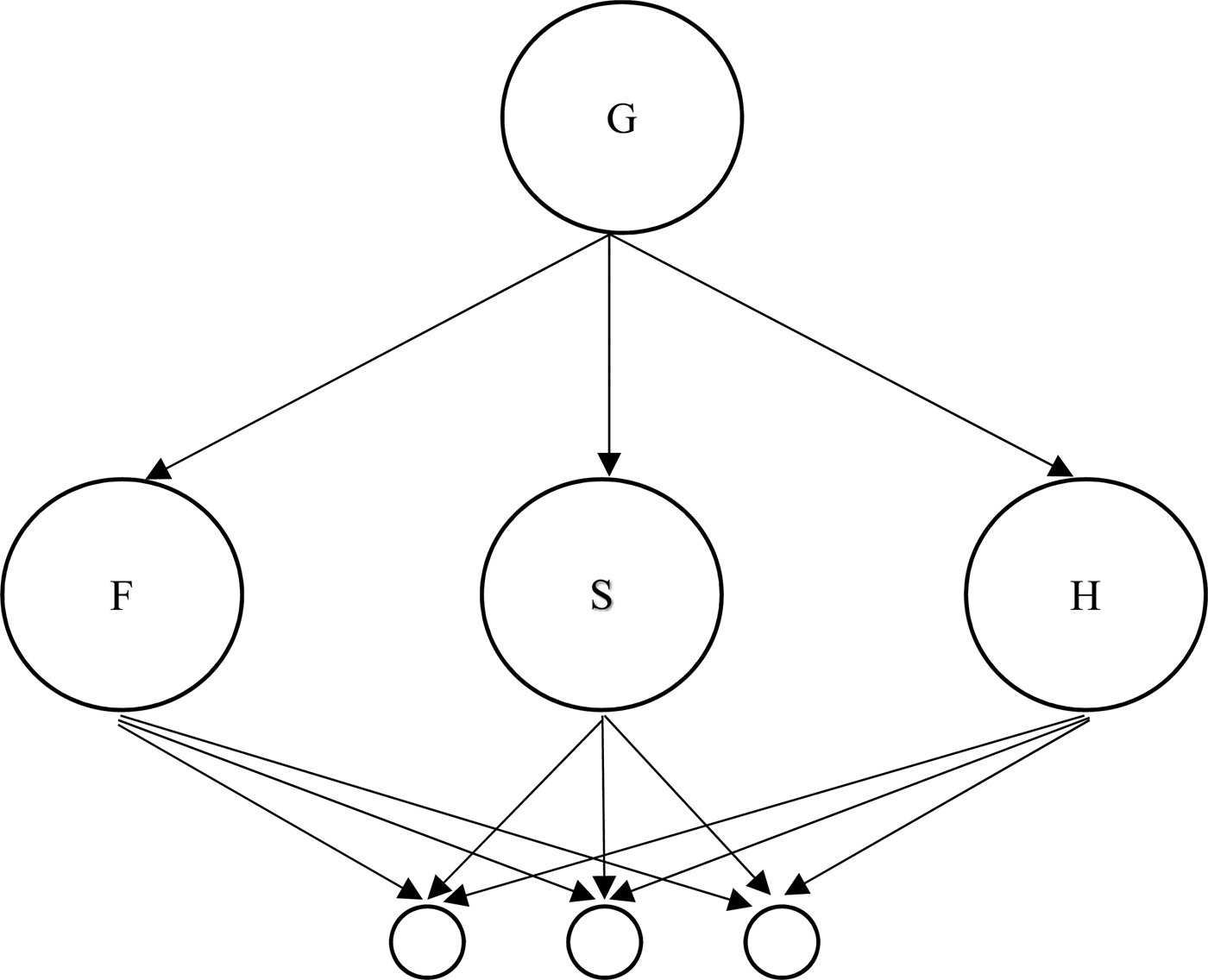
Fig. 2 Model B.

If the Extensionality of Proper Parts is rejected, then it is possible that the persons of the Trinity have exactly the same proper parts and have distinguishing properties (properties that are not grounding in particular parts), and therefore might not turn out to be identical.

However, Extensionality of Proper Parts, in Simons's system, is a theorem (SCT71). This means that this model also involves the rejection of Weak Supplementation (and therefore both the Strong Supplementation Principle and the Proper Parts Principle), because as Varzi (Reference Varzi2008) has shown, Weak Supplementation entails the Extensionality of Proper Parts and Simons has shown the same for Strong Supplementation (Simons (Reference Simons2000), 28–29).Footnote ⁸ The philosophical cost then, is that MODEL B dispenses with (perhaps) independently plausible Extensionality and Supplementation principles, and is committed to the existence of properties of objects that are not grounded in the existence of parts of those objects (a view implicit, under plausible assumptions, in the rejection of Extensionality of Proper Parts).

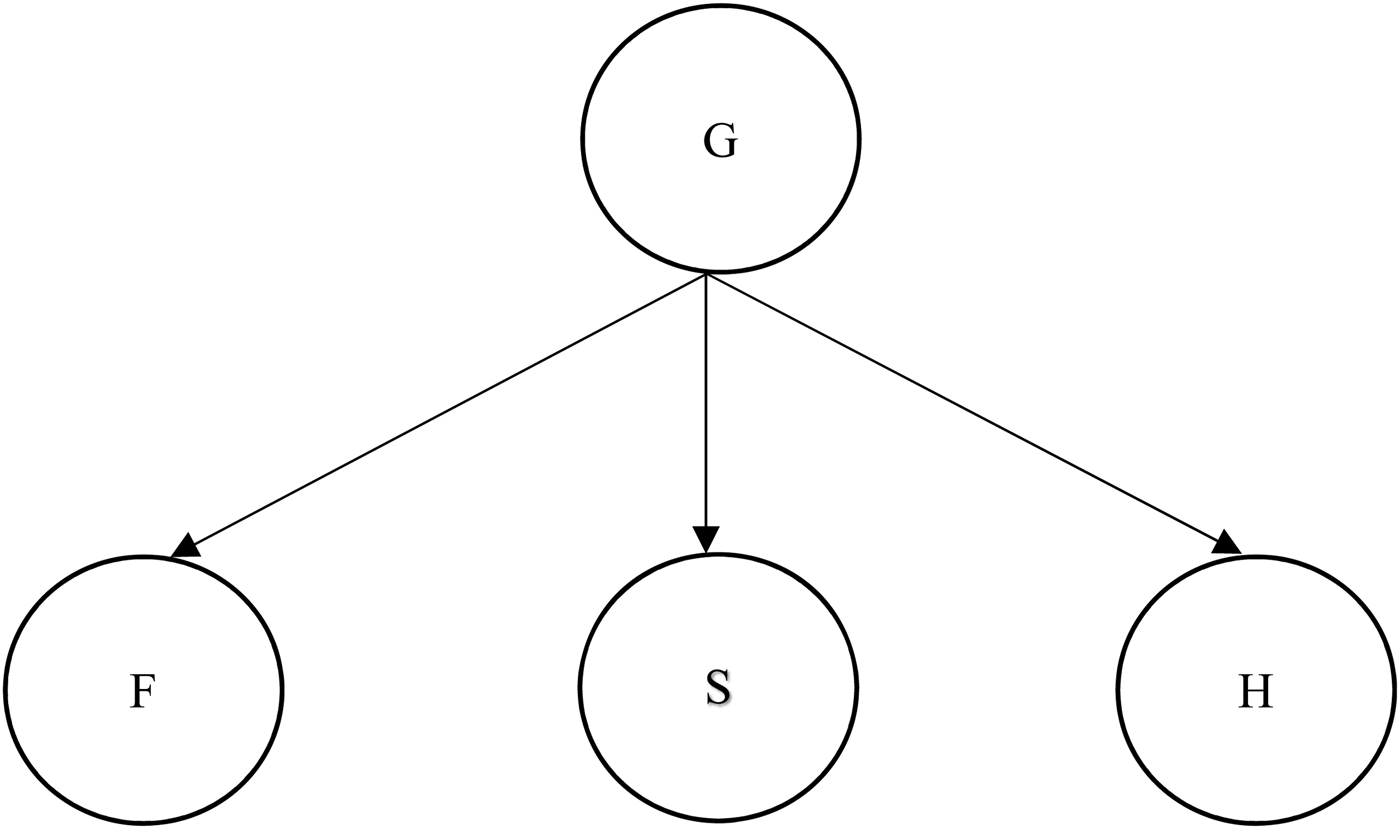
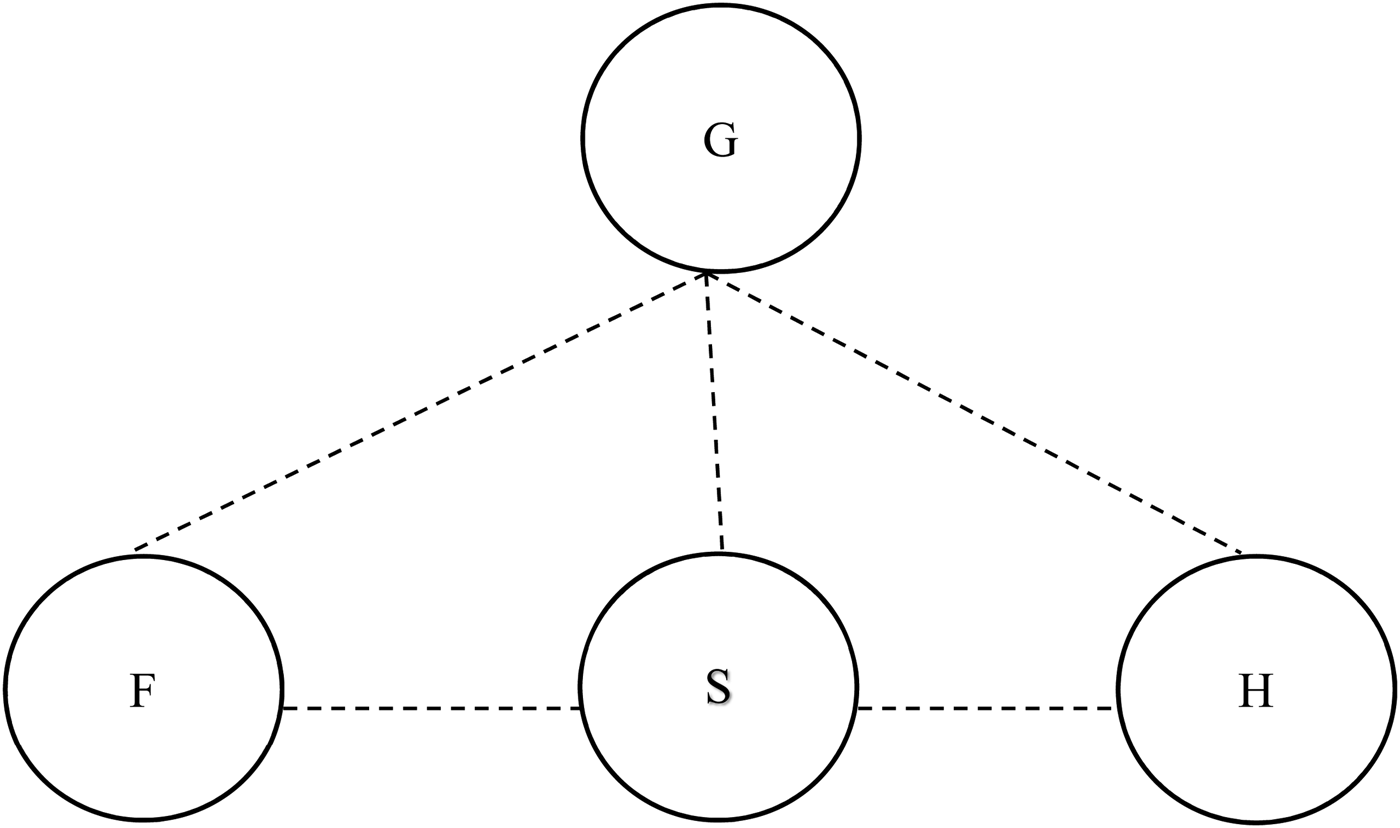
An alternative and closely related model would involve stipulating that the individual persons of the Trinity do not themselves have proper parts. This would go some way to accommodating the views of philosophers like Abelard and Aquinas who believed that the Godhead was simple:

This model is almost simple; the Godhead is not proper partless, but the only proper parts that the Godhead has are the persons themselves. This may be seen as a cost or a benefit depending on one's views of divine simplicity. Unlike MODEL B, this model is compatible with the Extensionality of Proper Parts,Footnote ⁹ and so comes without the philosophical costs of the previous model.

With respect to the theological desiderata, however, MODEL C (fig 3) comes out less well than MODEL B. MODEL B and MODEL C both satisfy (2.1), the denial of tritheism, if MODEL A does, and possibly even if it does not. MODEL B in particular might be in a better position with respect to avoiding tritheism than MODEL A, in virtue of the closer connection between the persons at the level of their proper parts. On both models, so long as Extensionality of Proper Parts is rejected in the case of MODEL B, desideratum (2.2), the denial of modalism, is met. Turning, then, to the final desideratum, we note that according to both these models, the only proper parts that the Godhead has that the Father lacks are the Son and the Holy Spirit. In virtue of this, I think that both of these models come somewhat closer to satisfying desideratum (2.3), that each of the persons be wholly the Godhead, than does MODEL A. For every compositional level below that of the persons themselves, everything that is a proper part of the Godhead is a proper part of the Father, of the Son, and of the Holy Spirit. However, MODEL C can hardly be said to truly be capturing the natural interpretation of (2.3). If there is no compositional level below that of the persons, that is to say, if the divine persons are each simple, then the fact that the Godhead has the persons as proper parts is sufficient for it being false on the model that any of the persons is wholly the Godhead. So MODEL C does not satisfy (2.3). MODEL B comes closer. Once again, on this model, no person of the Trinity has all the same parts as the Godhead (that Father is a part of the Godhead, but not a part of the Son), but in this case, this might more plausibly be taken as a reasonable exception given that the persons have their proper parts in common non-trivially. Whether MODEL B does, in fact, satisfy (2.3) will depend ultimately on the interpretation of that thesis. If one interprets (2.3) as rejecting any ‘sharing out’ of the Godhead between the three persons, as per the passage from the Catholic Catechism quoted earlier, then, as sharing out still seems to be happening on MODEL B, orthodoxy requires yet a further model. I will assume this stronger reading of (2.3) and will therefore continue to look for an alternative that would eliminate this worry.

Fig. 3 MODEL C.

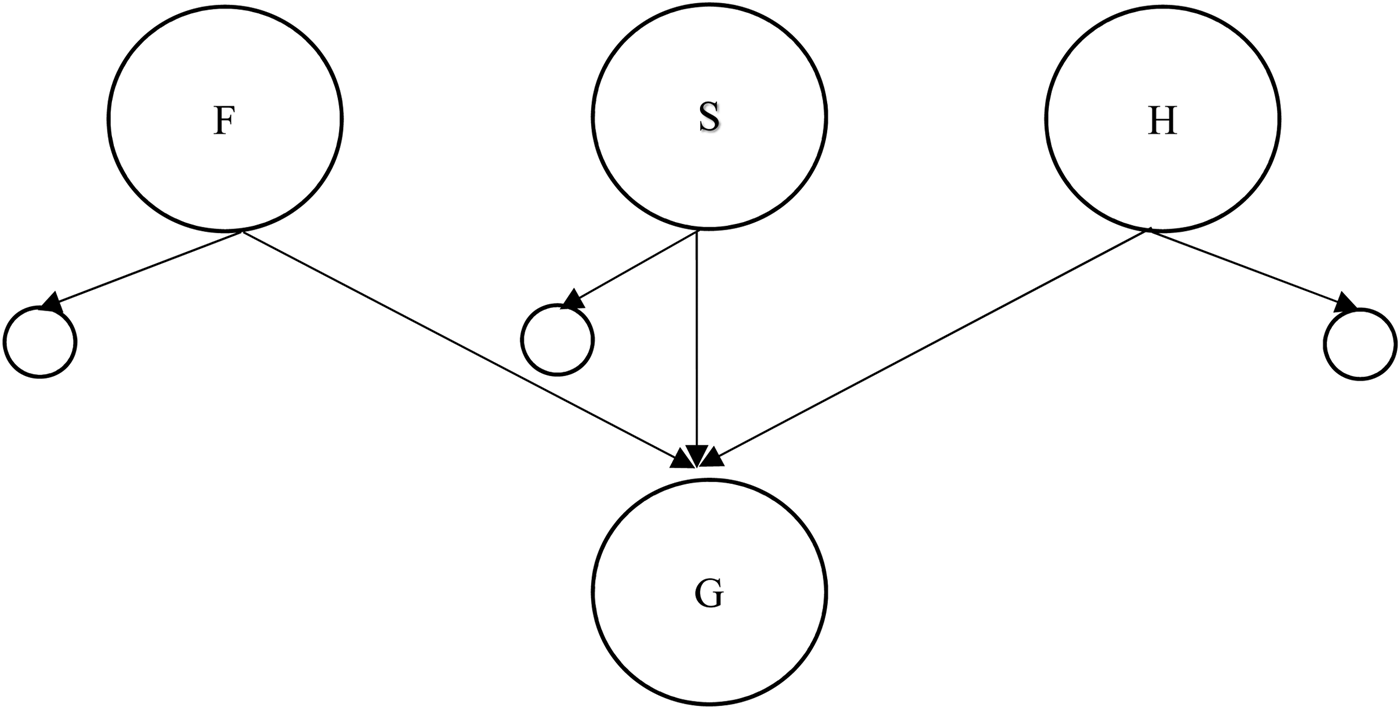
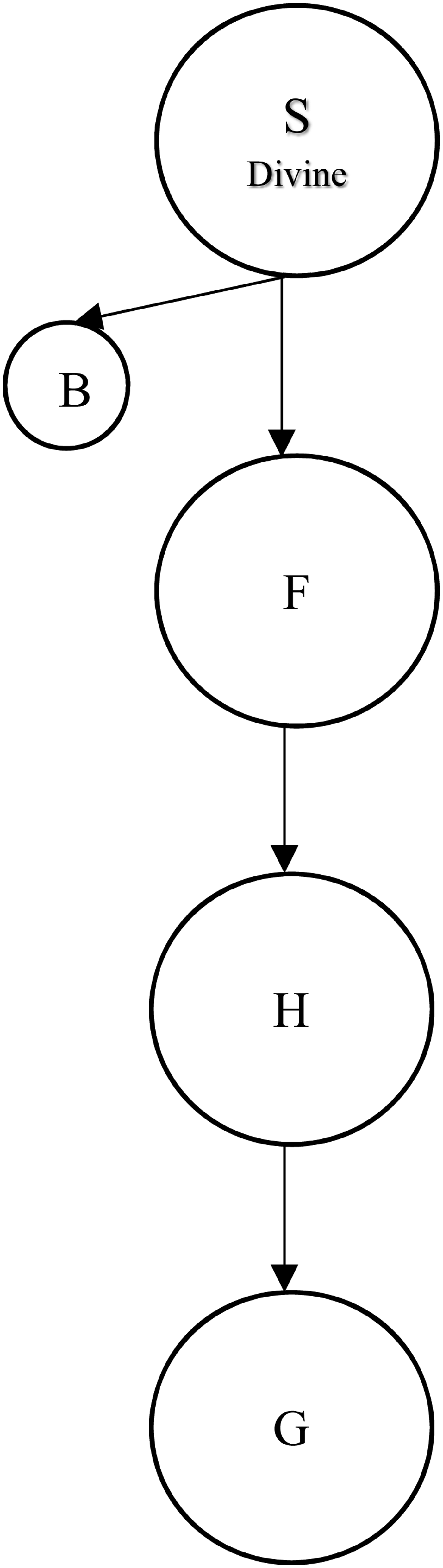
One way that this can be achieved is by turning the diagram on its head, so that the Godhead is a proper part of each of the three persons of the Trinity, but none of the persons are proper parts of the Godhead, as in MODEL D (fig 4) and its closely related variant, MODEL Da (fig 5):

Fig. 4 MODEL D.

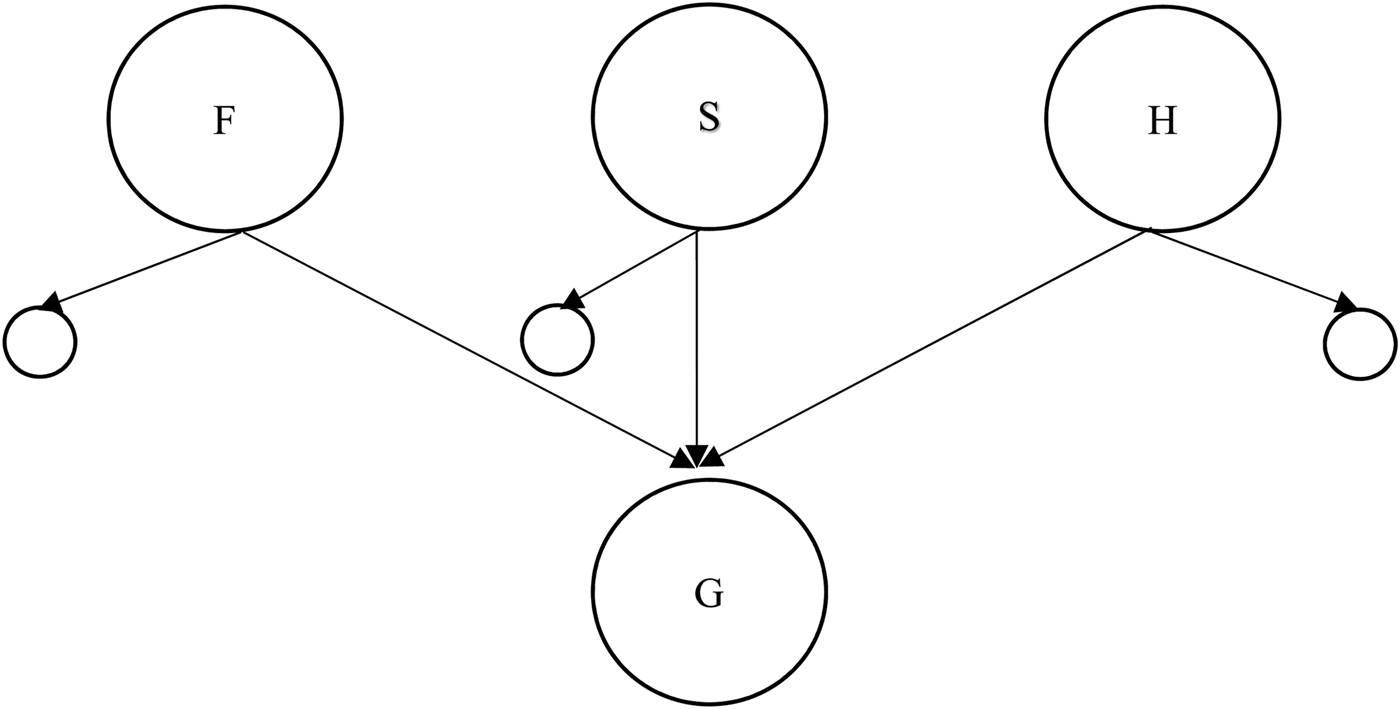
Fig. 5 MODEL Da.

These models more clearly satisfy desiderata (2.3), because, according to this model, there are no parts of the Godhead that are not parts of each of the persons. As with MODEL B, in order to escape modalism, MODEL D must involve the rejection of the Extensionality of Proper Parts principle (and the supplementation principles) for the same reasons as above. However, MODEL Da is compatible with the Extensionality of Proper Parts principle without risking modalism because each of the persons is differentiated in virtue of some proper part which is not a proper part of the Godhead. On the model, they have all the proper parts of the Godhead, but not all the proper parts of one another.Footnote ¹⁰ However, this philosophical benefit comes at a theological cost, because MODEL Da involves non-divine proper parts of the divine persons, or at least parts that are not divine in the same way as the person itself is. Other theological worries face both models. These include the worries concerning simplicity (note that these models are actually, not just almost, simple), though this can be easily remedied by adding proper parts to the Godhead. But there is a more serious worry, namely the oddity of holding that the Godhead is a part of the persons of the Trinity and not the other way around. This seems to turn models D and Da into forms of panentheism (I think this looks particularly true in the case of MODEL Da), where the divinity of the persons of the Trinity is grounded in their partial composition by a particular divine part. Moreover, I think these models look suspiciously tritheistic as well, and therefore fail to satisfy desideratum (2.1). Whereas the Social Trinitarian mereological account claims to be monotheist because the persons derive their divinity by common inclusion in the same Godhead, models D and Da can only claim that the persons are divine in virtue of overlapping with respect to a common divine part. This seems to me to provide even less justification than MODEL A has in claiming that, on the model, there is exactly one God. The search then, continues for a model which satisfies all three desiderata.

So far, we have considered models (excepting MODEL A and MODEL Da) in which each of the persons has just the same proper parts as the Godhead and yet, by stipulation, is not identical with the Godhead. I have suggested that this makes some headway towards accommodating desiderata (2.3), the claim that each of the persons is wholly the Godhead, but might not go far enough. If we take (2.3) to rule out any sharing out of the Godhead among the three persons, I think further alterations to classical mereology would be required. In particular, I think we would need to say that the Godhead and each of the persons have all their parts (proper and improper) in common. There are, I think, two ways in which this idea might be modelled.

In the first model, we reject SA1, the principle of the Anti-Symmetry of Proper Parthood, and allow non-identical entities to be proper parts of one another. Such a model would look like this:

As we will shortly see, Aaron Cotnoir and Andrew Bacon (Reference French and Krause2012) have, in passing, suggested using a non-classical mereology to explain the doctrine of the Trinity, and it is something like this model which I imagine they have in mind. According to this model, each of the persons is a proper part of the Godhead and the Godhead is a proper part of each of the persons.Footnote ¹¹ We can see immediately the theological benefits of this model. It satisfies (2.1), the rejection of tritheism, at least as well as anything we have considered so far. There is exactly one God, namely the Godhead, yet each of the three persons is divine by virtue of being, in Hilary of Poitiers's words, ‘permanently enveloped’ and ‘reciprocally contained’ within the Godhead. This model escapes modalism, and therefore satisfies (2.2) simply by virtue of the model involving a stipulation that each of the persons is non-identical with each of the others. Finally, on this picture it is easy to verify that there is quite a strong interpretation of (2.3) that is satisfied. Namely, it is true on this model that every part of each of the persons is a part of the Godhead and vice versa. That is the sense in which each of the persons is wholly God.

The trouble is that SA1 seems very much like a conceptual truth about proper parts (it seems more intuitive to me, at any rate, than anything we have considered rejecting with earlier models). I will not argue here that the rejection of SA1 is incoherent. Indeed, in the next section we will note a number of philosophers who have taken this possibility very seriously. However, I think that the worries are substantial enough that it is worthwhile to note an alternative that promises the same benefits at, I suggest, a small conceptual cost.

Specifically, I think we can achieve, in effect, the same results while doing less conceptual damage to our system if we expand our notion of an improper part by providing an alternative definition of ‘part’ (SD1 in Simons's system), rather than our tampering with our formalization of the notion of a proper part. By doing this, I think we can arrive at a model, which offers the clearest satisfaction of (2.1)–(2.3). The model that I have in mind is this (the broken lines stand for improper part relations):

According to the traditional definition implicit in Simons's system, x is an improper part of y if and only if x is identical with y. SD1 in Simons's system tells us the x is a part of y if and only if x is a proper part of y or x is identical with y. In this system, then, improper parthood is equivalent to identity. However, if MODEL F (fig 7) is modelling orthodoxy, in particular if it is to escape modalism, it must certainly reject that improper parthood implies identity. MODEL F depends, then, on there being a notion of improper parthood which is such that each of the persons and the Godhead may hold this relation to one another, while not being identical. There is no question that such a relation can be stipulatively defined, but would it be any more plausible as a formalization of a pre-theoretic parthood relation than one which rejects the Anti-Symmetry of Proper Parthood (i.e. that employed in MODEL E (fig 6))? In fact, I think it is considerably more plausible.

Fig. 6 MODEL E.

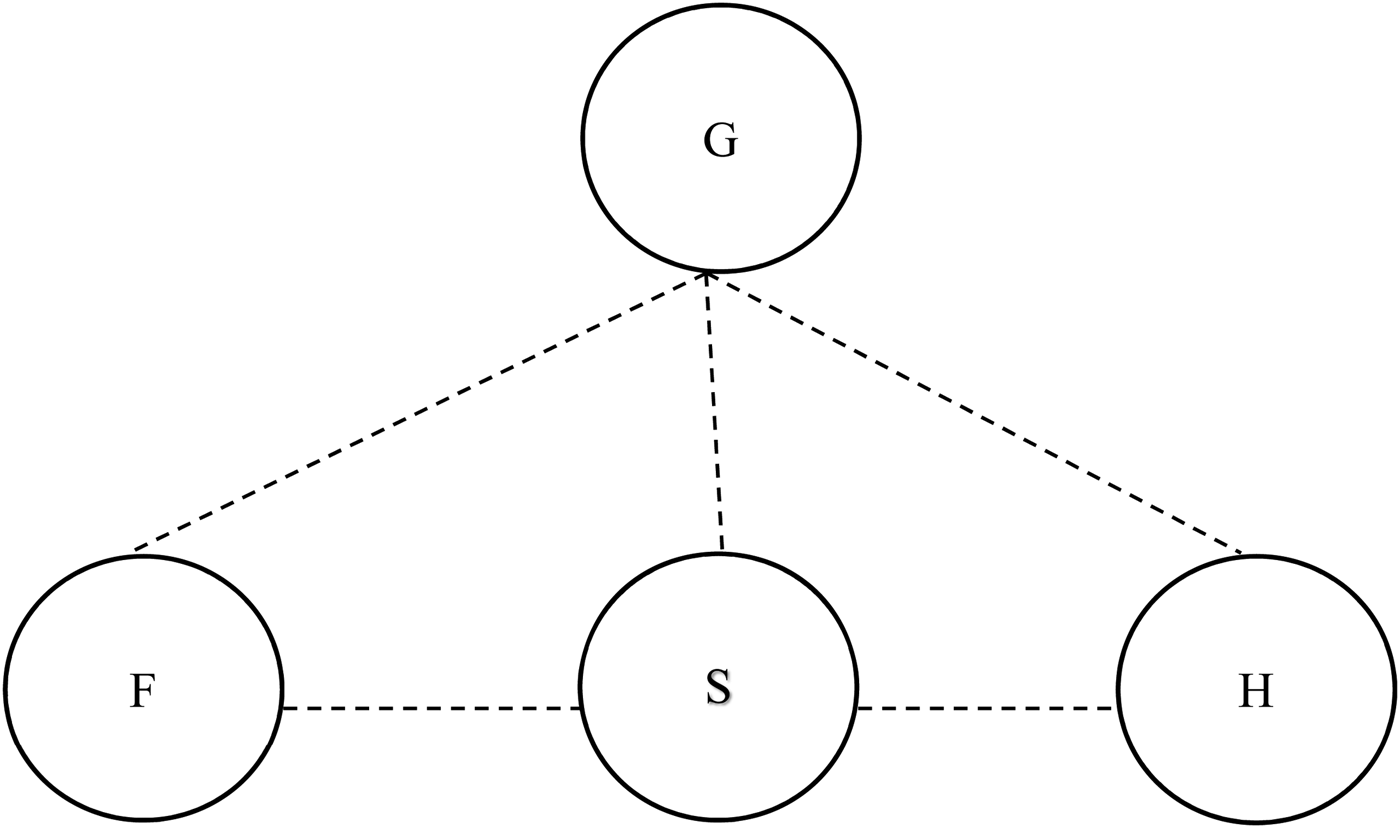
Fig. 7 MODEL F.

In my view, if SA1 is rejected, it is unclear how the term ‘proper part’ is being used. But, I think that we have a quite reasonable grasp of the notion of an improper part, quite separate from our grasp of the identity relation. Consider that it is normal to take the proper part relation as basic and give a definition of part which involves proper parthood in the definiens. After all the latter relation is what the average person probably has in mind when they use the word ‘part’.Footnote ¹² The need for introducing the defined term ‘part’ at all, if we recall, was that it was algebraically more convenient for the same reason as the mathematical relation ‘less-than-or-equal-to’ is more convenient than ‘less-than’ (Simons (1987), 11).

The value of using ‘less-than-or-equal-to’ in place of ‘less-than’, however, is simply that the latter excludes the limit case of the relation, while the former does not. Although Simons goes on to claim that it is essential to his system that identity is recognized as a parthood relation, it is not clear that the reasons he has given justify that claim. If the notion of an improper part is introduced as the limit case of the notion of a proper part, we may well ask why the limit case of the proper part relation should be the relation of identity? It is not at all obvious at first glance that there is some close connection between the two notions. The answer, I think, is this. In Classical Extensional Mereology, and many other classical mereological systems, it is assumed that every property of an object is grounded in the existence of some part of that object. If this is so, then, on the assumption that some suitable second-order version of the Identity of Indiscernibles Principle can be formulated, any x and y that share all their proper parts in common must have all their properties in common, and so are identical. In turn, if this is so (that is to say, if the Extensionality of Proper Parts holds), then it is quite appropriate to take the limit case of the proper part relation to be the identity relation. However, most of the models we have been considering reject the Extensionality of Proper Parts. Without this principle, there is no reason for identity to be the limit case of the proper part relation, and the notions of improper part and identity come apart. That is to say, reject the Extensionality of Proper Parts and SD1 needs replacing.

An alternative definition to Simons's SD1 immediately presents itself:

• SD1′: x < y ↔ x ≪ y ∨ (∃z) (z ≪ x) & (x’) (x’ ≪ x ↔ x’ ≪ y)

In other words, x is a part of y if and only if x is a proper part of y or x and y have all their proper parts in common non-trivially. This is the notion of parthood that MODEL F employs. With this definition in hand, we are free to stipulate that, on MODEL F, objects F, S, H, and the Godhead are all non-identical. We can verify, though, that they have all their proper parts in common. The relation that holds, then, between each of the persons of the Trinity and the Godhead, and between each of the persons and each of the other persons, on this model, is the relation of improper parthood.

Note that, on MODELS E and F, the persons are going to be parts of all the other persons and of the Godhead (proper parts in the case of MODEL E). Similarly, the Godhead is a part of each of the persons. This does not, of course, rule out adding further parts (including proper parts) to the persons or to the Godhead, but if a part is added to any of the four objects in the model, it is added to all of them in virtue of the Transitivity of Parthood.

Once again, on these models, the Extensionality of Proper Parts must be rejected. If the principle is rejected, modalism is avoided, at least arguably so, in which case the model satisfies desiderata (2.2).This model satisfies (2.3) since no person of the Trinity lacks any part of the Godhead. Finally, this model is compatible with monotheism, (2.1), in that there is only one Godhead, and it might plausibly be maintained that each of the persons is divine in virtue of being improper parts of the Godhead. The theological desiderata, therefore, appear to be met. In my next section, I will consider whether the deviation from classical mereology can be justified by independent support.

Some non-theological reasons for non-asymmetrical, non-identity parthood relations

What models E and F have in common, which is key to their capacity to model the three theological desiderata, is that they are incompatible with SCT3 of Simons's system, namely the misnamed Asymmetry of Parthood, which states that x and y are identical if and only if they are parts of one another. The Asymmetry of Parthood is derivable in the system using SD1, Simons's Definition of Parthood and SA1, the axiom of the Anti-Symmetry of Proper Parthood. One of these, SD1 and SA1, then, must be rejected by any system relative to which MODELS E and F are consistent. We have seen that MODEL E corresponds to the rejection of SA1 and MODEL F corresponds to the rejection of SD1. I have suggested that SA1 is a conceptual truth, and suggested that SD1 is not a conceptual truth and not the natural definition of parthood (at least not unless one is committed to the Extensionality of Proper Parts). I think, therefore, that a system without the Asymmetry of Parthood should involve a rejection of SD1, rather than SA1, and that consequently, MODEL F is the most promising model for desiderata (2.1)–(2.3).

What I have not done, so far, is to argue that the Asymmetry of Parthood should be rejected. The only reasons I have so far presented for its rejection are theological in nature. In this section, I will propose some further philosophical benefits to rejecting SCT3. I will not try to argue conclusively for the falsity of SCT3, my aim is merely to support a theological model by noting some secular philosophical benefits that result from its deviance from classical mereology.

Simons himself countenances the failure of Asymmetry of Parthood. While discussing the arguments of Nicholas Rescher against Extensionality,Footnote ¹³ Simons considers whether apparent counter-examples to Extensionality are better captured by a different notion of parthood, rather than that implicit in SD1. He proposes the following alternative:

• SD15: x ⩽ y ↔ ((∃z) (z ≪ x) → (z) (z ≪ x → z ≪ y)) & (~∃z (z ≪ x) → x ≪ y V x = y)

The notion of parthood that ‘⩽’ is supposed to stand for here, which is connected to the one I proposed in the last section, is intended by Simons to stand beside extensional parthood, as defined by SD1, rather than to replace it. Among plausible candidates answering to this alternative notion of parthood, Simons lists ‘the buildings Committee may have the same members as the Personnel Committee’ and ‘the Family Robinson may at the same time be the Basketball Team Robinson’, but the example he considers most plausible is the time-honoured case of a person and their body.

Ultimately, Simons argues that persons and bodies do jointly hold a kind of parthood relation to one another according to which they are neither proper parts of one another nor identical to one another. However, the relation that Simons thinks holds between so-called temporal coincidents is a temporally restricted parthood relation (Simons (Reference Simons2000), 180). The case instance of this alternative notion of parthood that I am interested does not involve temporal coincidents, not if God is outside time, anyway, and the relevant parthood relations in the case must hold eternally. Nevertheless, Simons's support for an alternative notion that of parthood which is not captured by SD1 and allows for joint satisfaction by entities that are not mereologically equivalent, not proper parts of one another, and not identical provides, I think, some support for the coherence of the picture I sketched in the previous section.

Further support comes from the work of Aaron Cotnoir, particularly his 2012 article with Andrew Bacon, ‘Non-Wellfounded Mereologies’,Footnote ¹⁴ in which they argue for the failure of the Asymmetry of Parthood. As mentioned earlier, Bacon and Cotnoir list the doctrine of the Trinity as a possible motivation for their view (Cotnoir & Bacon (Reference Cotnoir and Bacon2012), 187). However, the cases Cotnoir and Bacon think most plausibly motivate the rejection of Asymmetry are similar to those considered by Simons. Cotnoir and Bacon note as an example,

Bacon and Cotnoir's suggestion, in effect, is to reject SA1, so that we may take the statue and clay to be non-identical proper parts of one another at t. We may note in passing, though, that we can escape the problem equally by adopting a definition of parthood different from SD1 such that the statue and clay may be different parts of one another, but not different proper parts.

Statue and clay type cases, then, provide apparent support for rejecting the Asymmetry of Parthood (that is, ST3). But there are other examples. Another case which might lend support to the idea that there is a genuine parthood relation that two non-identical objects may hold to one another, when they share all of their proper parts in common, is the case of vague objects.

Imagine a case where two objects determinately have just the same parts, but both have fuzzy boundaries with respect to some other non-mereological properties. Let us assume that we are discussing de re vagueness, if such a notion makes sense. In this case, given that there is no part that one of the objects has that the other lacks (nor is there any indeterminacy in the relation of the objects to their parts), it follows that they are extensionally equivalent. And yet, given that they are indeterminate with respect to the same set of non-mereological properties, there is a strong temptation, I think, to say that the objects are, at most, indeterminately identical (again, if such a notion makes sense). If this case is possible, then it would represent a case of objects having all their proper parts in common and yet not being identical. This would be a counter-example to the Asymmetry of Parthood.

I will close this section with one final case. Cotnoir (Reference Cotnoir2013, 838–839) suggests that the compositional status of quantum particles might cause some trouble for classical mereology. I agree. I think that, at least on one view of quantum physics, Anti-Symmetry does fail. Specifically, if we take seriously Schrödinger's view that quantum particles are not self-identical, then Anti-Symmetry will not hold of them. To see why this is, we can briefly turn to one recent philosophical exposition of this view of quantum physics.

Quasi-set theory is an alternative to Z-F set theory originally developed in Decio Krause's article ‘On a Quasi-Set Theory’ (Krause (Reference Krause1992)) and subsequently, in more detail by Krause together with Steven French (Reference French and Krause2006, Reference French and Krause2010). The theory of quasi-sets involves sets with elements of two different kinds: one labelled ‘M-atoms’; objects for which all the traditional laws of logic (including identity) apply. These are no different from the Ur-elements of Z-F set theory. The other entities are called ‘m-atoms’. As Krause explains:

Krause and French, therefore, accept two kinds of entities into their domain of discourse: M-atoms, to which the notion of absolute identity does apply, and m-atoms, to which the notion of absolute identity does not apply. Or, more specifically, for any m-atom, x, it is not the case that x is absolutely identical with x.

Krause goes on,

This entails, of course, that we cannot individuate single m-atoms. We cannot, for example, name individual m-atoms, though we can quantify over them.

The significance of all this is that, if Krause and French are right that quasi-set theory can be used to model the world of quantum particles, then there is good reason to think that Asymmetry of Parthood fails for this class of objects.

Assuming that quantum particles can enter into compositional relationships, there is some m-atom, x and there is some m-atom y, such that y is a proper part of x. From this fact a number of interesting results follow.

If we assume the Reflexivity of Parthood, and SA1, then there are improper parts that are not identical (and so Asymmetry of Parthood fails). To see this, assume (∃_mx) x < x (by the Reflexivity of Parthood), but note that ~x ≪ x (by the Anti-Reflexivity of Proper Parthood), however x ≠ x (by definition of m-atoms in quasi-set theory as being non-self-identical), so (∃_mx) x < x & x < x x ≠ x (by &-introduction). This is a counter-example to SD1.

On the other hand, if we assume the Reflexivity of Parthood and the definition of improper parts then we can show that there is something that is a proper part of itself (and so Asymmetry again fails). To see this, assume (∃_mx), x < x (by the Reflexivity of Parthood), x ≠ x (by the definition of m-atoms in quasi-set theory) so x ≪ x (by SD1).Footnote ¹⁶

Krause and French's formal work has not yet encompassed a formal theory of mereology to complement their set-theoretic apparatus; indeed they list this as a future project. However, we can see, at least in some respects, what such a theory might be like. Under a few very plausible assumptions, it must either be possible for some m-atoms x and y to be proper parts of one another, or to be improper parts of one another, but in either case they cannot be identical to each other. This means that Anti-Symmetry must fail for m-atoms in one of two ways. This provides at least some independent motivation for rejecting Anti-Symmetry. These last two cases, the Schrödinger notion of quantum particles and a certain view of de re vagueness show that the Asymmetry of Parthood will be undermined if there are any objects that lack identity conditions but are capable of entering into parthood relations. This, combined with the statue and clay cases, provides at least some independent support for the rejection of the Asymmetry of Parthood. This is all I will say in defence against possible philosophical objections to the models I have sketched. In the next section, however, I will raise a final, theological worry.

The Body of Christ Problem

The objection goes like this: the interest of models B–F partly depends on the persons of the Trinity and the Godhead having all their proper parts in common and yet being non-identical. This, it was suggested is how a mereological model might exemplify the claim that each of the persons is wholly God. However, there is quite plausibly at least one proper part of one of the persons that cannot be a proper part of the Godhead because, at least on the models considered above, that would entail that the proper part is a proper part of each of the other persons as well, and that is heretical. The proper part I have in mind is, one might have guessed, the body of Christ. I have suggested above that mereological equivalence may not be the same thing as identity, because there may be non-mereologically grounded properties that distinguish two extensionally equivalent objects. However, this is a moot point if it turns out that, on the model, the Father has the body of Christ as a proper part, for it is overwhelmingly plausible to suppose that any model in which the body of Christ is a proper part of the Father is one on which the Father died on the Cross and this is the heresy of Patripassianism, a form of modalism rejected by all orthodox Christian denominations.

What responses are available to salvage the project of modelling the Latin Trinity mereologically? It seems to me that there are at least three: one could deny the Transitivity of Proper Parthood, or once could deny that the body of Christ can be analysed mereologically, or once could develop a new model on which the body of Christ bears some other mereological relation to the Son than proper parthood.

I wish to avoid the first option if possible, as I find the Transitivity of Proper Parthood to be highly plausible. The second option also offends against intuition. Bodies, being material objects, have parts and it seems intuitive to think of them as parts of corresponding persons. I wish to consider, instead, the third option.

One possible model which escapes the problem (proposed to me by Martin Pickup at the Metaphysics of the Trinity: New Directions conference at Oxford) is as follows, where ‘B’ stands for the body of Christ:

According to this model, the body of Christ is a proper part of the Son but not of any of the other persons of the Trinity, or of the Godhead. Given that the relation posited by this model is proper parthood, the proper parts transfer over up the line, but not down it. So the Godhead is a proper part of the Son, by Transitivity, but the body of Christ is not a proper part of the Godhead. The problem with this model, however, is obvious: it exacerbates the worry from MODEL D. In this model not only is the Godhead a proper part of the persons, but the Father is proper part of the Son. The ordering between the Father and the Holy Spirit is up for grabs in this model, but to ensure that the body of Christ is a proper part of only the Son, the Son must not be a proper part of any of the other persons. This makes the required ordering of this model particularly awkward theologically, because the obvious sources that one might turn to in order to justify an ordering amongst the persons of the Trinity will give an ordering different from the one in MODEL G (fig 8). For example, if the Trinity were ordered by the relation ‘. . . precedes from . . .’ as it is found in the Western Nicene creed, the Son would fall in the middle, not at the top. The notion of ordering the persons by the proper parthood relation seems suspect at best, and without some better theological justification for this, it would be well to consider alternatives.

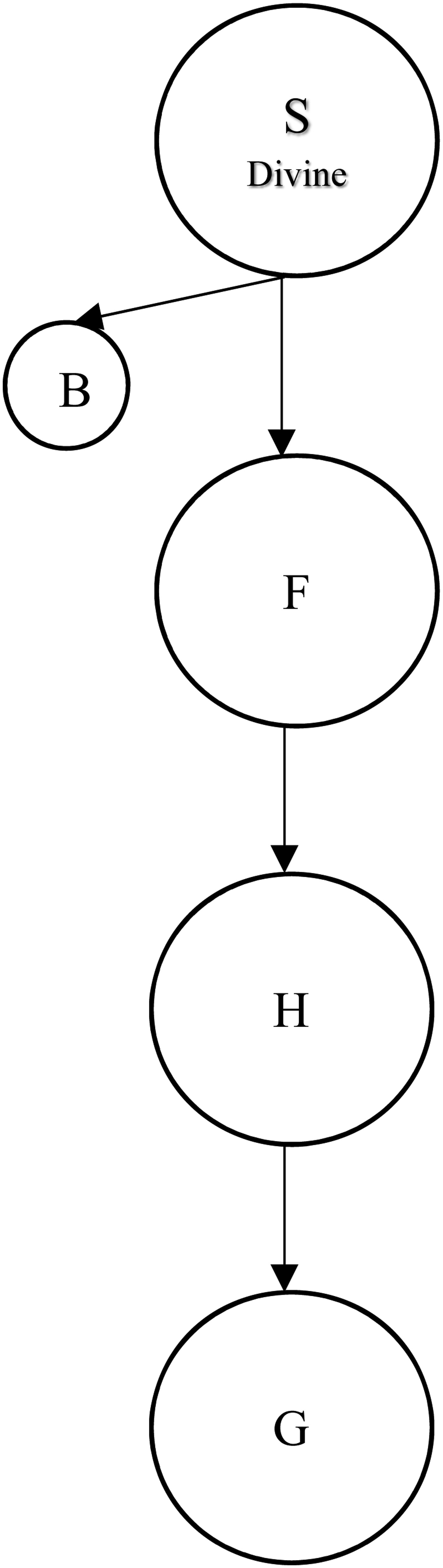
Fig. 8 MODEL G.

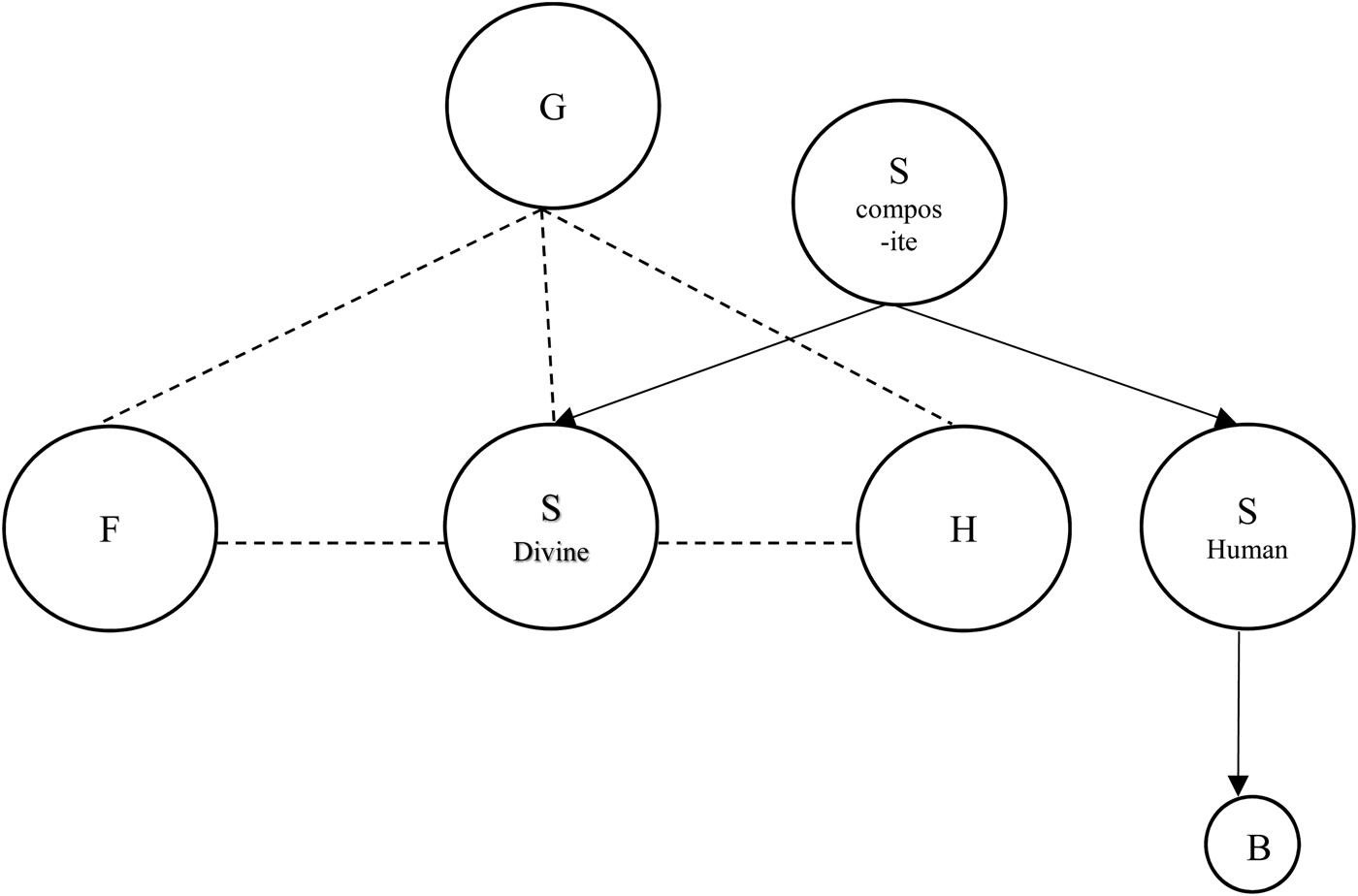
An alternative to this would be to extend MODEL F by involving a more detailed Christological picture, in the following way,

This model has the same philosophical costs as MODEL F, and can claim the same theological benefits, with the additional benefit that the model escapes the body of Christ problem. In this model, the body of Christ is a proper part of the human nature of the Son, but not a proper part of the divine nature. Given this, and the fact that only the latter is in a relation of parthood with the Godhead and the other persons of the Trinity, the threat of Patripassianism disappears, so the body of Christ does not turn out to be a proper part of the Father on this model. MODEL H (fig 9) seems to me to provide the only obvious way of developing MODEL F to tackle the body of Christ problem. It nevertheless faces several possible objections.

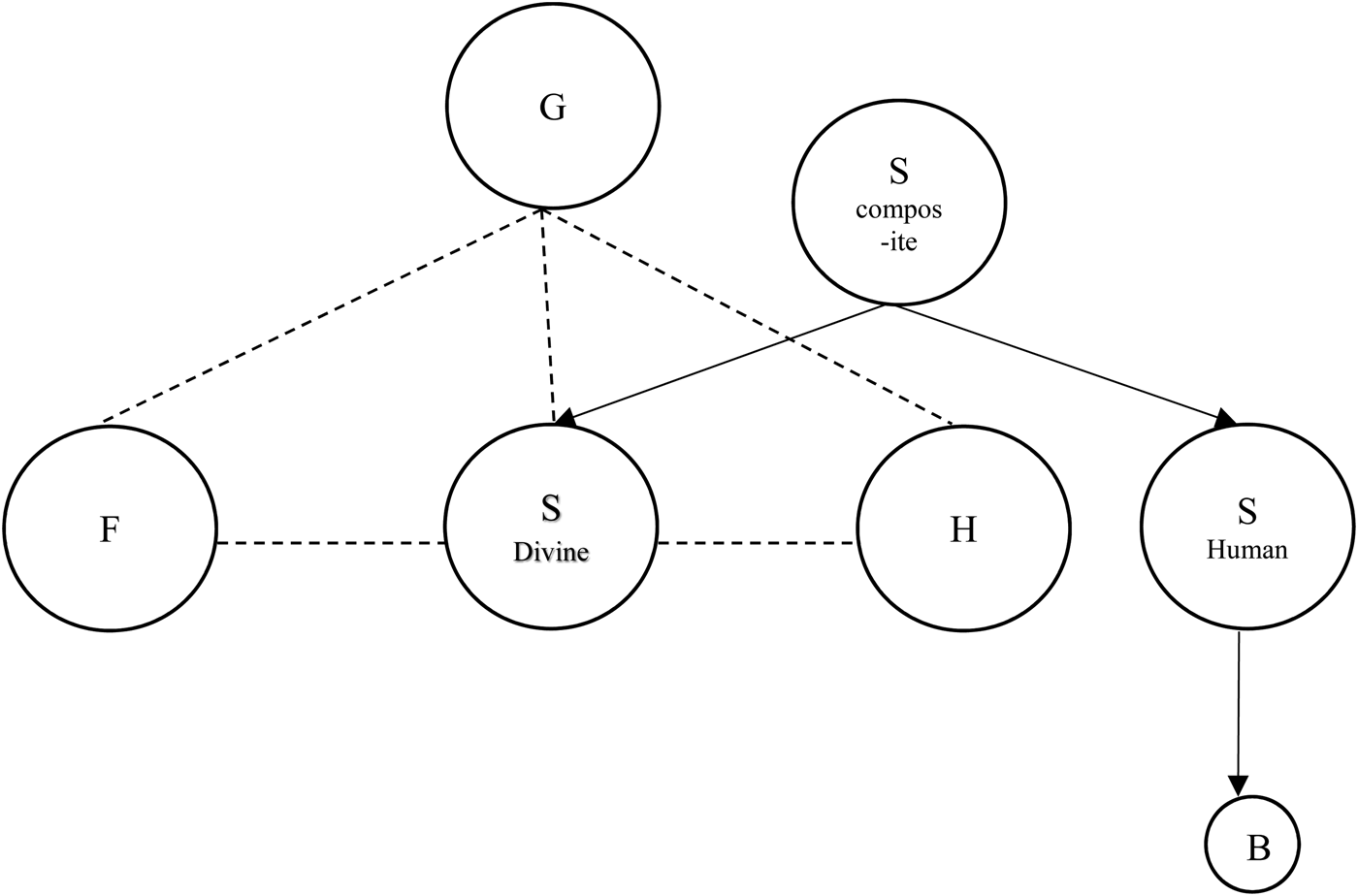
Fig. 9 MODEL H.

The major source of worry about this model might concern the fact that the composite Son (human and divine nature taken together) does not have the same relation to the Godhead that the Father and the Holy Spirit have. This may once again raise the spectre of Arianism. On the other hand, perhaps this model is simply expressing the fact that the composite Son is divine in virtue of holding a particular relation to the divine nature of the Son. It might further be objected, though, that MODEL H involves driving a wedge between the two natures of the Son. In other words, this model might be thought to be a form of Nestorianism.Footnote ¹⁷ However, the controversy that Nestorius caused was in rejecting the doctrine of Hypostatic Union, that is, that Christ's two natures are part of one and the same substance. I do not think that MODEL H is committed to this consequence, and therefore it is not obvious that the model is committed to Nestorianism.

Ultimately, whether MODEL H is compatible with the other theological commitments of Latin Trinitarians is a matter that would need to be decided by theologians. I will rest content by repeating that, if it is rejected, no other obvious mereological model presents itself. In that case, the options are to abandon the project of modelling the Latin Trinity mereologically, or at the very least abandon the attempt to find a place for the body of Christ in such a model, or, alternatively, to make more dramatic alterations to classical mereology in order to find an orthodox model. The former course would seem to me to be unfortunate, for a mereological account of the Trinity seems to me to offer a possible solution to the logical problem which is much simpler and perhaps less controversial than some of the radical proposals that have been made, such as the relative identity solutions associated with Peter Geach (Reference Geach1962) and Peter van Inwagen (Reference van Inwagen and Morris1988). The latter course seems to me to run into serious conceptual trouble and I am doubtful of the prospects, though perhaps an appeal to the recent work of Karen Bennett (Reference Bennett2013), who argues that objects may have the same part several times over, might offer one possibility.Footnote ¹⁸