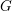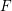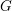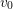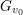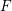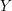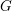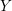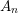1 Introduction
Let  $Y$ be a closed Riemannian manifold of dimension
$Y$ be a closed Riemannian manifold of dimension  $n$ and with Laplace operator
$n$ and with Laplace operator  $\unicode[STIX]{x1D6E5}$. Let
$\unicode[STIX]{x1D6E5}$. Let  $\{\unicode[STIX]{x1D713}_{i}\}$ be an orthonormal basis of Laplace eigenfunctions for
$\{\unicode[STIX]{x1D713}_{i}\}$ be an orthonormal basis of Laplace eigenfunctions for  $L^{2}(Y)$, which satisfy
$L^{2}(Y)$, which satisfy  $\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}=1$ and
$\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}=1$ and  $(\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}_{i}^{2})\unicode[STIX]{x1D713}_{i}=0$. We assume that
$(\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}_{i}^{2})\unicode[STIX]{x1D713}_{i}=0$. We assume that  $\{\unicode[STIX]{x1D713}_{i}\}$ are ordered by eigenvalue, so that
$\{\unicode[STIX]{x1D713}_{i}\}$ are ordered by eigenvalue, so that  $0=\unicode[STIX]{x1D706}_{1}\leqslant \unicode[STIX]{x1D706}_{2}\leqslant \cdots \,$. It is an important question in harmonic analysis to determine the asymptotic size of
$0=\unicode[STIX]{x1D706}_{1}\leqslant \unicode[STIX]{x1D706}_{2}\leqslant \cdots \,$. It is an important question in harmonic analysis to determine the asymptotic size of  $\unicode[STIX]{x1D713}_{i}$, that is, the growth rate of
$\unicode[STIX]{x1D713}_{i}$, that is, the growth rate of  $\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$ in terms of
$\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$ in terms of  $\unicode[STIX]{x1D706}_{i}$. The basic upper bound for
$\unicode[STIX]{x1D706}_{i}$. The basic upper bound for  $\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$, proved by Avacumović [Reference AvacumovićAva56] and Levitan [Reference LevitanLev52], is given by
$\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$, proved by Avacumović [Reference AvacumovićAva56] and Levitan [Reference LevitanLev52], is given by
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\ll \unicode[STIX]{x1D706}_{i}^{(n-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\ll \unicode[STIX]{x1D706}_{i}^{(n-1)/2}.\end{eqnarray}$$ This bound is sharp on the round  $n$-sphere. Indeed, the zonal spherical harmonics have peaks of maximal size at the poles of the axis of rotation. More generally, Sogge and Zelditch [Reference Sogge and ZelditchSZ02] have shown that the compact Riemannian manifolds saturating (1) necessarily have points which are fixed by an appropriately large number of geodesic returns, in the sense that a positive measure subset of geodesics passing through such a point are loops.
$n$-sphere. Indeed, the zonal spherical harmonics have peaks of maximal size at the poles of the axis of rotation. More generally, Sogge and Zelditch [Reference Sogge and ZelditchSZ02] have shown that the compact Riemannian manifolds saturating (1) necessarily have points which are fixed by an appropriately large number of geodesic returns, in the sense that a positive measure subset of geodesics passing through such a point are loops.
On the other hand, if  $Y$ is negatively curved then its geodesic flow is highly chaotic, and one expects this to be reflected in the asymptotics of the eigenfunctions. For example, the quantum ergodicity theorem of Schnirelman [Reference SchnirelmanSch74], Colin de Verdière [Reference Colin de VerdièreCol85] and Zelditch [Reference ZelditchZel87] states that the
$Y$ is negatively curved then its geodesic flow is highly chaotic, and one expects this to be reflected in the asymptotics of the eigenfunctions. For example, the quantum ergodicity theorem of Schnirelman [Reference SchnirelmanSch74], Colin de Verdière [Reference Colin de VerdièreCol85] and Zelditch [Reference ZelditchZel87] states that the  $L^{2}$-mass of a density-one sequence of Laplacian eigenfunctions on a negatively curved manifold equidistributes to the uniform measure. It is likewise reasonable to expect that if
$L^{2}$-mass of a density-one sequence of Laplacian eigenfunctions on a negatively curved manifold equidistributes to the uniform measure. It is likewise reasonable to expect that if  $Y$ has negative curvature then the strong pointwise delocalization bound
$Y$ has negative curvature then the strong pointwise delocalization bound
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\,\ll _{\unicode[STIX]{x1D716}}\,\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D716}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\,\ll _{\unicode[STIX]{x1D716}}\,\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D716}}\end{eqnarray}$$holds with density one. This is akin to the Ramanujan conjecture in the theory of automorphic forms [Reference SarnakSar95]: a generic sequence of eigenfunctions is tempered. Any sequence violating (2) will be called exceptional.
Unlike the weak-* setting of the quantum unique ergodicity conjecture [Reference Rudnick and SarnakRS94], which posits that in negative curvature the  $L^{2}$-mass of any sequence of eigenfunctions equidistributes to the uniform measure, there do in fact exist compact manifolds
$L^{2}$-mass of any sequence of eigenfunctions equidistributes to the uniform measure, there do in fact exist compact manifolds  $Y$ of negative curvature violating (2). The first examples were given in [Reference Rudnick and SarnakRS94], with
$Y$ of negative curvature violating (2). The first examples were given in [Reference Rudnick and SarnakRS94], with  $Y$ being an arithmetic hyperbolic
$Y$ being an arithmetic hyperbolic  $3$-manifold and the exceptional sequences, of density zero, lying in the image of the theta correspondence from
$3$-manifold and the exceptional sequences, of density zero, lying in the image of the theta correspondence from  $\text{Sp}_{2}$.
$\text{Sp}_{2}$.
For surfaces the situation is quite different: Iwaniec and Sarnak [Reference Iwaniec and SarnakIS95] conjecture that hyperbolic surfaces do not support exceptional sequences. This is a very difficult problem which would imply the classical Lindelöf conjecture on the Riemann zeta function in the case of the modular surface.
This leads to the question of when exactly one should expect to find (zero-density) violations of (2). In this paper we give sufficient conditions for a certain class of negatively curved manifolds to support exceptional sequences. Although the question is of interest in this general setting, our techniques are limited to arithmetic locally symmetric spaces. Put succinctly, we show that an arithmetic manifold supports exceptional sequences whenever it has a point with strong Hecke return properties.
1.1 Statement of results
Our main theorem is modelled on a result of Milićević [Reference MilicevicMil11], which, building on [Reference Rudnick and SarnakRS94], provides a structural framework for the class of arithmetic hyperbolic  $3$-manifolds supporting exceptional sequences.
$3$-manifolds supporting exceptional sequences.
First recall that an arithmetic hyperbolic  $3$-manifold arises from the following general construction. Let
$3$-manifold arises from the following general construction. Let  $E$ be a number field having exactly one complex embedding, up to equivalence, and let
$E$ be a number field having exactly one complex embedding, up to equivalence, and let  $F$ be its maximal totally real subfield. For a division quaternion algebra
$F$ be its maximal totally real subfield. For a division quaternion algebra  $B$ over
$B$ over  $E$, ramified at all real places of
$E$, ramified at all real places of  $E$, denote by
$E$, denote by  $G$ the restriction of scalars of
$G$ the restriction of scalars of  $B^{1}$ from
$B^{1}$ from  $E$ to
$E$ to  $F$. Then any arithmetic hyperbolic
$F$. Then any arithmetic hyperbolic  $3$-manifold is commensurable with a congruence manifold associated with
$3$-manifold is commensurable with a congruence manifold associated with  $G$.
$G$.
Following [Reference MilicevicMil11], an arithmetic hyperbolic  $3$-manifold as above is said to be of Maclachlan–Reid type if
$3$-manifold as above is said to be of Maclachlan–Reid type if  $E$ is quadratic over
$E$ is quadratic over  $F$ and there exists a quaternion division algebra
$F$ and there exists a quaternion division algebra  $A$ over
$A$ over  $F$ satisfying
$F$ satisfying  $B=A\,\otimes _{F}\,E$. The main result of [Reference MilicevicMil11] is that Maclachlan–Reid type manifolds support exceptional sequences (in fact, satisfying the same lower bounds as the examples of Rudnick and Sarnak).
$B=A\,\otimes _{F}\,E$. The main result of [Reference MilicevicMil11] is that Maclachlan–Reid type manifolds support exceptional sequences (in fact, satisfying the same lower bounds as the examples of Rudnick and Sarnak).
Notice that when  $B=A\,\otimes _{F}\,E$, the following properties hold. Let
$B=A\,\otimes _{F}\,E$, the following properties hold. Let  $v_{0}$ be the unique archimedean place of
$v_{0}$ be the unique archimedean place of  $F$ which ramifies in
$F$ which ramifies in  $E$. By [Reference Maclachlan and ReidMR03, Theorem 9.5.5] we may assume that
$E$. By [Reference Maclachlan and ReidMR03, Theorem 9.5.5] we may assume that  $A$ is ramified at
$A$ is ramified at  $v_{0}$. Then:
$v_{0}$. Then:
(i)
 $G_{v_{0}}=\text{SL}_{2}(\mathbb{C})$ is non-compact and non-split (as an
$G_{v_{0}}=\text{SL}_{2}(\mathbb{C})$ is non-compact and non-split (as an  $\mathbb{R}$-group);
$\mathbb{R}$-group);(ii)
 $G_{v}=\mathbf{H}^{1}$ (the norm-one Hamiltonian quaternions) is compact for all real
$G_{v}=\mathbf{H}^{1}$ (the norm-one Hamiltonian quaternions) is compact for all real  $v\neq v_{0}$;
$v\neq v_{0}$;(iii) the global involution
 $\unicode[STIX]{x1D703}:g\mapsto \unicode[STIX]{x1D70E}(g)$ of
$\unicode[STIX]{x1D703}:g\mapsto \unicode[STIX]{x1D70E}(g)$ of  $G$, where
$G$, where  $\unicode[STIX]{x1D70E}$ is the unique non-trivial element in the Galois group of
$\unicode[STIX]{x1D70E}$ is the unique non-trivial element in the Galois group of  $E$ over
$E$ over  $F$, induces a Cartan involution on
$F$, induces a Cartan involution on  $G_{v_{0}}$. Indeed,
$G_{v_{0}}$. Indeed,  $G^{\unicode[STIX]{x1D703}}=A^{1}$, so that
$G^{\unicode[STIX]{x1D703}}=A^{1}$, so that  $G^{\unicode[STIX]{x1D703}}(F_{v_{0}})=\mathbf{H}^{1}$ is the maximal compact
$G^{\unicode[STIX]{x1D703}}(F_{v_{0}})=\mathbf{H}^{1}$ is the maximal compact  $\text{SU}(2)$ inside
$\text{SU}(2)$ inside  $G_{v_{0}}=\text{SL}_{2}(\mathbb{C})$.
$G_{v_{0}}=\text{SL}_{2}(\mathbb{C})$.
Our main result is an extension of this to a wide range of compact congruence manifolds.
Theorem 1.1. Let  $F$ be a totally real number field, and let
$F$ be a totally real number field, and let  $v_{0}$ be a real place of
$v_{0}$ be a real place of  $F$. Let
$F$. Let  $G/F$ be a connected anisotropic semisimple
$G/F$ be a connected anisotropic semisimple  $F$-group. We make the following additional assumptions on
$F$-group. We make the following additional assumptions on  $G$:
$G$:
(i)
 $G_{v_{0}}$ is non-compact, non-split and
$G_{v_{0}}$ is non-compact, non-split and  $\mathbb{R}$-almost simple;
$\mathbb{R}$-almost simple;(ii)
 $G_{v}$ is compact for all real
$G_{v}$ is compact for all real  $v\neq v_{0}$;
$v\neq v_{0}$;(iii) there is an involution
 $\unicode[STIX]{x1D703}$ of
$\unicode[STIX]{x1D703}$ of  $G$ defined over
$G$ defined over  $F$ that induces a Cartan involution of
$F$ that induces a Cartan involution of  $G_{v_{0}}$.
$G_{v_{0}}$.
Let  $Y$ be a congruence manifold associated with
$Y$ be a congruence manifold associated with  $G$ as in § 2.10. Then there exist
$G$ as in § 2.10. Then there exist  $\unicode[STIX]{x1D6FF}>0$, depending only on
$\unicode[STIX]{x1D6FF}>0$, depending only on  $G$, and a sequence of linearly independent Laplacian eigenfunctions
$G$, and a sequence of linearly independent Laplacian eigenfunctions  $\unicode[STIX]{x1D713}_{i}$ on
$\unicode[STIX]{x1D713}_{i}$ on  $Y$ that satisfy
$Y$ that satisfy
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}=1,\quad (\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}_{i}^{2})\unicode[STIX]{x1D713}_{i}=0,\quad \text{and}\quad \Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\gg \unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}=1,\quad (\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}_{i}^{2})\unicode[STIX]{x1D713}_{i}=0,\quad \text{and}\quad \Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\gg \unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$ We note that the exponent  $\unicode[STIX]{x1D6FF}$ in Theorem 1.1, and Theorem 1.2 below, is currently logically ineffective. This comes from using a result of Cluckers, Gordon and Halupczok [Reference Shin and TemplierST16, Theorem 14.1] to bound orbital integrals. (Note that Shin and Templier present an alternative, effective proof of [Reference Shin and TemplierST16, Theorem 14.1] in Theorem 7.3 of the same paper, but this has an error as described on S.-W. Shin’s webpage.) The bound of Cluckers, Gordon and Halupczok is ineffective due to their use of model theory. Julia Gordon informs us that, if the residue characteristic is larger than a logically ineffective bound, it may be possible to transfer the constants in their result from the case of positive characteristic and explicate them in that case. However, this is presently unknown. Moreover, even if this were possible, the implied constant in Theorems 1.1 and 1.2 would still be logically ineffective because of the condition that the residue characteristic be sufficiently large.
$\unicode[STIX]{x1D6FF}$ in Theorem 1.1, and Theorem 1.2 below, is currently logically ineffective. This comes from using a result of Cluckers, Gordon and Halupczok [Reference Shin and TemplierST16, Theorem 14.1] to bound orbital integrals. (Note that Shin and Templier present an alternative, effective proof of [Reference Shin and TemplierST16, Theorem 14.1] in Theorem 7.3 of the same paper, but this has an error as described on S.-W. Shin’s webpage.) The bound of Cluckers, Gordon and Halupczok is ineffective due to their use of model theory. Julia Gordon informs us that, if the residue characteristic is larger than a logically ineffective bound, it may be possible to transfer the constants in their result from the case of positive characteristic and explicate them in that case. However, this is presently unknown. Moreover, even if this were possible, the implied constant in Theorems 1.1 and 1.2 would still be logically ineffective because of the condition that the residue characteristic be sufficiently large.
An additional source of ineffectiveness of  $\unicode[STIX]{x1D6FF}$ comes from using theorems of Finis and Lapid [Reference Finis and LapidFL18] when the congruence manifold varies as in Theorem 1.2, although this ineffectiveness is in the weaker sense that the constants are not numerically explicit. Finis and Lapid inform us that their results could probably be made effective with extra work; in fact, as the referee has pointed out, the particular shape of the congruence subgroups, which depend on
$\unicode[STIX]{x1D6FF}$ comes from using theorems of Finis and Lapid [Reference Finis and LapidFL18] when the congruence manifold varies as in Theorem 1.2, although this ineffectiveness is in the weaker sense that the constants are not numerically explicit. Finis and Lapid inform us that their results could probably be made effective with extra work; in fact, as the referee has pointed out, the particular shape of the congruence subgroups, which depend on  $\unicode[STIX]{x1D703}$, in Theorem 1.2 should allow for the exponents arising from their work to be more readily explicated.
$\unicode[STIX]{x1D703}$, in Theorem 1.2 should allow for the exponents arising from their work to be more readily explicated.
1.2 Remarks on the main theorem
A well-known theorem of Borel [Reference BorelBor63] addresses the question of whether one can find many groups satisfying the rationality hypothesis (iii). One consequence of his theorem is that for any connected, simply connected, semisimple algebraic  $\mathbb{R}$-group
$\mathbb{R}$-group  $G$ satisfying condition (i), Theorem 1.1 produces a manifold
$G$ satisfying condition (i), Theorem 1.1 produces a manifold  $Y$ of the form
$Y$ of the form  $\unicode[STIX]{x1D6E4}\backslash G/K$ with an exceptional sequence of eigenfunctions. See § 1.4 for more details and a concrete example.
$\unicode[STIX]{x1D6E4}\backslash G/K$ with an exceptional sequence of eigenfunctions. See § 1.4 for more details and a concrete example.
Theorem 1.1 goes some distance towards answering the basic question of determining the precise conditions under which one should expect a Lindelöf type bound on a compact congruence negatively curved manifold. The three numbered conditions on the group  $G$ are a particularly convenient way of asking that a large enough compact subgroup of
$G$ are a particularly convenient way of asking that a large enough compact subgroup of  $G_{\infty }$ admits a rational structure, which is a key ingredient in our proof. Although the condition that
$G_{\infty }$ admits a rational structure, which is a key ingredient in our proof. Although the condition that  $G_{v_{0}}$ is not split should be necessary, we expect that the other conditions can be relaxed somewhat. For example, throughout most of the paper, the condition that
$G_{v_{0}}$ is not split should be necessary, we expect that the other conditions can be relaxed somewhat. For example, throughout most of the paper, the condition that  $G_{v_{0}}$ is
$G_{v_{0}}$ is  $\mathbb{R}$-almost simple could be weakened to
$\mathbb{R}$-almost simple could be weakened to  $G$ being
$G$ being  $F$-almost simple. The stronger form of this condition is only used in Lemma 4.2, to simplify the application of a theorem of Blomer and Pohl [Reference Blomer and PohlBP16, Theorem 2] and Matz and Templier [Reference Matz and TemplierMT15, Proposition 7.2].
$F$-almost simple. The stronger form of this condition is only used in Lemma 4.2, to simplify the application of a theorem of Blomer and Pohl [Reference Blomer and PohlBP16, Theorem 2] and Matz and Templier [Reference Matz and TemplierMT15, Proposition 7.2].
Besides the results of Rudnick and Sarnak and of Milićević that we have already mentioned, both in the context of arithmetic hyperbolic  $3$-manifolds, there are other results in the literature which provide examples of arithmetic manifolds supporting exceptional sequences. For instance, the techniques of Rudnick and Sarnak were generalized to
$3$-manifolds, there are other results in the literature which provide examples of arithmetic manifolds supporting exceptional sequences. For instance, the techniques of Rudnick and Sarnak were generalized to  $n$-dimensional hyperbolic manifolds for
$n$-dimensional hyperbolic manifolds for  $n\geqslant 5$ by Donnelly [Reference DonnellyDon07]. Later, Lapid and Offen in [Reference Lapid and OffenLO07] discovered a series of arithmetic quotients of
$n\geqslant 5$ by Donnelly [Reference DonnellyDon07]. Later, Lapid and Offen in [Reference Lapid and OffenLO07] discovered a series of arithmetic quotients of  $\text{SL}(n,\mathbb{C})/\text{SU}(n)$ admitting large eigenforms through the link with automorphic
$\text{SL}(n,\mathbb{C})/\text{SU}(n)$ admitting large eigenforms through the link with automorphic  $L$-functions (conditionally on standard conjectures on the size of automorphic
$L$-functions (conditionally on standard conjectures on the size of automorphic  $L$-functions at the edge of the critical strip). To our knowledge [Reference Lapid and OffenLO07] is the only example of power growth lower bounds for sup norms on non-compact quotients, at least if one restricts to a compact set so that the large peaks of eigenfunctions in the cusp do not play a role. Note that Theorem 1.1 includes the examples of Rudnick and Sarnak, of Donnelly, and of Milićević, although without explicit exponents. It is unable to reproduce the examples of Lapid and Offen due to the compactness requirement, but (as was indicated above) it can produce compact quotients of
$L$-functions at the edge of the critical strip). To our knowledge [Reference Lapid and OffenLO07] is the only example of power growth lower bounds for sup norms on non-compact quotients, at least if one restricts to a compact set so that the large peaks of eigenfunctions in the cusp do not play a role. Note that Theorem 1.1 includes the examples of Rudnick and Sarnak, of Donnelly, and of Milićević, although without explicit exponents. It is unable to reproduce the examples of Lapid and Offen due to the compactness requirement, but (as was indicated above) it can produce compact quotients of  $\text{SL}(n,\mathbb{C})/\text{SU}(n)$ with an exceptional sequence of eigenfunctions. In fact, non-compact quotients (of suitable level structure) should also be amenable to our techniques, via an application of simple trace formulae, but we have not pursued this here.
$\text{SL}(n,\mathbb{C})/\text{SU}(n)$ with an exceptional sequence of eigenfunctions. In fact, non-compact quotients (of suitable level structure) should also be amenable to our techniques, via an application of simple trace formulae, but we have not pursued this here.
Finally, while our approach was largely inspired by that of Milićević, we have made an effort to emphasize (in Appendix A) the common features it shares with the techniques of Rudnick and Sarnak and of Lapid and Offen. A synthesis of the subject, as well as a general conjecture restricting the possible limiting exponents for exceptional sequences, can be found in Sarnak’s influential letter [Reference SarnakSar04].
1.3 A hybrid result in the level and eigenvalue aspects
We in fact prove a stronger result than that described in Theorem 1.1, establishing a lower bound in the level and eigenvalue aspects simultaneously. We present this separately, as it requires more care to state; indeed, any notion of non-trivial lower bound must overcome the lower bound one may prove when the eigenspaces have large dimension. More precisely, if  $M$ is a compact Riemannian manifold and
$M$ is a compact Riemannian manifold and  $V$ is the space of
$V$ is the space of  $\unicode[STIX]{x1D713}\in L^{2}(M)$ with a given Laplace eigenvalue, one may show that there is
$\unicode[STIX]{x1D713}\in L^{2}(M)$ with a given Laplace eigenvalue, one may show that there is  $\unicode[STIX]{x1D713}\in V$ satisfying
$\unicode[STIX]{x1D713}\in V$ satisfying  $\Vert \unicode[STIX]{x1D713}\Vert _{\infty }\geqslant \sqrt{\dim V}\Vert \unicode[STIX]{x1D713}\Vert _{2}$.
$\Vert \unicode[STIX]{x1D713}\Vert _{\infty }\geqslant \sqrt{\dim V}\Vert \unicode[STIX]{x1D713}\Vert _{2}$.
If we consider a tower of congruence covers  $Y_{N}$ of
$Y_{N}$ of  $Y$, then the Laplace eigenspaces will have growing dimension because of multiplicities in the corresponding representations at places dividing
$Y$, then the Laplace eigenspaces will have growing dimension because of multiplicities in the corresponding representations at places dividing  $N$. Computationally, one observes that this (and its stronger form involving Arthur packets) is the only source of dimension growth. Although we believe that the dimensions of the joint eigenspaces we consider should be small (partly as a result of our choice of ‘large’ congruence subgroup), we do not know how to prove this in general. As a result, we shall be satisfied if we can beat the bound
$N$. Computationally, one observes that this (and its stronger form involving Arthur packets) is the only source of dimension growth. Although we believe that the dimensions of the joint eigenspaces we consider should be small (partly as a result of our choice of ‘large’ congruence subgroup), we do not know how to prove this in general. As a result, we shall be satisfied if we can beat the bound  $\sqrt{\dim V}$, where
$\sqrt{\dim V}$, where  $V$ is now a space of Hecke–Maass forms with the same Laplace and Hecke eigenvalues. This motivates the following definitions.
$V$ is now a space of Hecke–Maass forms with the same Laplace and Hecke eigenvalues. This motivates the following definitions.
Let  $G$ be as in Theorem 1.1. Let
$G$ be as in Theorem 1.1. Let  $H$ be the identity component of the group of fixed points of
$H$ be the identity component of the group of fixed points of  $\unicode[STIX]{x1D703}$. We let
$\unicode[STIX]{x1D703}$. We let  $D$ be a positive integer such that
$D$ be a positive integer such that  $G$ and
$G$ and  $H$ are unramified at places away from
$H$ are unramified at places away from  $D$ and
$D$ and  $\infty$; see § 2.1 for a precise definition. Let
$\infty$; see § 2.1 for a precise definition. Let  $K$ and
$K$ and  $K_{H}$ be compact open subgroups of
$K_{H}$ be compact open subgroups of  $G(\mathbb{A}_{f})$ and
$G(\mathbb{A}_{f})$ and  $H(\mathbb{A}_{f})$ that are hyperspecial away from
$H(\mathbb{A}_{f})$ that are hyperspecial away from  $D$, as in §§2.4 and 2.10. If
$D$, as in §§2.4 and 2.10. If  $N$ is a positive integer prime to
$N$ is a positive integer prime to  $D$, we let
$D$, we let  $K(N)$ be the corresponding principal congruence subgroup of
$K(N)$ be the corresponding principal congruence subgroup of  $K$, and define
$K$, and define  $Y_{N}=G(F)\backslash G(\mathbb{A})/K(N)K_{H}K_{\infty }$. We give each
$Y_{N}=G(F)\backslash G(\mathbb{A})/K(N)K_{H}K_{\infty }$. We give each  $Y_{N}$ the probability volume measure.
$Y_{N}$ the probability volume measure.
Let  $A\subset G_{\infty }$ be a maximal
$A\subset G_{\infty }$ be a maximal  $\mathbb{R}$-split torus with real Lie algebra
$\mathbb{R}$-split torus with real Lie algebra  $\mathfrak{a}$ and Weyl group
$\mathfrak{a}$ and Weyl group  $W$. We let
$W$. We let  $\mathfrak{a}_{\mathbb{C}}=\mathfrak{a}\otimes \mathbb{C}$. Let
$\mathfrak{a}_{\mathbb{C}}=\mathfrak{a}\otimes \mathbb{C}$. Let  $G_{\infty }^{0}$ be the connected component of
$G_{\infty }^{0}$ be the connected component of  $G_{\infty }$ in the real topology. Any unramified irreducible unitary representation of
$G_{\infty }$ in the real topology. Any unramified irreducible unitary representation of  $G_{\infty }^{0}$ gives rise to an element
$G_{\infty }^{0}$ gives rise to an element  $\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ via the Harish-Chandra isomorphism, which we have normalized so that the tempered spectrum corresponds to
$\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ via the Harish-Chandra isomorphism, which we have normalized so that the tempered spectrum corresponds to  $\mathfrak{a}^{\ast }/W$. We let
$\mathfrak{a}^{\ast }/W$. We let  $\Vert \cdot \Vert$ be the norm on
$\Vert \cdot \Vert$ be the norm on  $\mathfrak{a}$ and
$\mathfrak{a}$ and  $\mathfrak{a}^{\ast }$ coming from the Killing form and extend it naturally to their complexifications. If
$\mathfrak{a}^{\ast }$ coming from the Killing form and extend it naturally to their complexifications. If  $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ we will sometimes abuse notation and write
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ we will sometimes abuse notation and write  $\Vert \unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}\Vert$ to mean the minimum of this norm over representatives for the
$\Vert \unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}\Vert$ to mean the minimum of this norm over representatives for the  $W$-orbits.
$W$-orbits.
By a Hecke–Maass form we mean a joint eigenfunction  $\unicode[STIX]{x1D713}\in L^{2}(Y_{N})$ for the Hecke algebra (away from
$\unicode[STIX]{x1D713}\in L^{2}(Y_{N})$ for the Hecke algebra (away from  $N$ and
$N$ and  $D$) and the ring of invariant differential operators
$D$) and the ring of invariant differential operators  ${\mathcal{D}}$ on
${\mathcal{D}}$ on  $Y_{N}$. We may view the associated eigenvalues as elements in the unramified unitary dual of
$Y_{N}$. We may view the associated eigenvalues as elements in the unramified unitary dual of  $G_{v}$ at finite places
$G_{v}$ at finite places  $v$ (via the Satake isomorphism), while at infinity they determine an element
$v$ (via the Satake isomorphism), while at infinity they determine an element  $\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$. We define a spectral datum
$\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$. We define a spectral datum  $c$ for
$c$ for  $(G,N)$ to be a choice of element
$(G,N)$ to be a choice of element  $\unicode[STIX]{x1D709}(c)\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ and an element
$\unicode[STIX]{x1D709}(c)\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W$ and an element  $\unicode[STIX]{x1D70B}_{v}(c)$ in the unramified unitary dual of
$\unicode[STIX]{x1D70B}_{v}(c)$ in the unramified unitary dual of  $G_{v}$ for all
$G_{v}$ for all  $v\nmid ND\infty$. Given a spectral datum
$v\nmid ND\infty$. Given a spectral datum  $c$ for
$c$ for  $(G,N)$, we define
$(G,N)$, we define  $V(N,c)$ to be the space of Hecke–Maass forms on
$V(N,c)$ to be the space of Hecke–Maass forms on  $Y_{N}$ whose
$Y_{N}$ whose  ${\mathcal{D}}$-eigenvalues are given by
${\mathcal{D}}$-eigenvalues are given by  $\unicode[STIX]{x1D709}(c)$ (the spectral parameter) and whose Hecke eigenvalues at
$\unicode[STIX]{x1D709}(c)$ (the spectral parameter) and whose Hecke eigenvalues at  $v\nmid ND\infty$ are given by
$v\nmid ND\infty$ are given by  $\unicode[STIX]{x1D70B}_{v}(c)$.
$\unicode[STIX]{x1D70B}_{v}(c)$.
Theorem 1.2. With the notation and hypotheses of Theorem 1.1, there exist  $\unicode[STIX]{x1D6FF}>0$, depending only on
$\unicode[STIX]{x1D6FF}>0$, depending only on  $G$ and
$G$ and  $\unicode[STIX]{x1D703}$, and
$\unicode[STIX]{x1D703}$, and  $Q>1$ with the following property. For any positive integer
$Q>1$ with the following property. For any positive integer  $N$ with
$N$ with  $(N,D)=1$ and spectral parameter
$(N,D)=1$ and spectral parameter  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ such that
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ such that  $N(1+\Vert \unicode[STIX]{x1D709}\Vert )$ is sufficiently large, there exist a spectral datum
$N(1+\Vert \unicode[STIX]{x1D709}\Vert )$ is sufficiently large, there exist a spectral datum  $c$ for
$c$ for  $(G,N)$ with
$(G,N)$ with  $\Vert \unicode[STIX]{x1D709}(c)-\unicode[STIX]{x1D709}\Vert \leqslant Q$ and a Hecke–Maass form
$\Vert \unicode[STIX]{x1D709}(c)-\unicode[STIX]{x1D709}\Vert \leqslant Q$ and a Hecke–Maass form  $\unicode[STIX]{x1D713}\in V(N,c)$ such that
$\unicode[STIX]{x1D713}\in V(N,c)$ such that
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\infty }\gg N^{\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{\unicode[STIX]{x1D6FF}}\sqrt{\dim V(N,c)}\Vert \unicode[STIX]{x1D713}\Vert _{2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\infty }\gg N^{\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{\unicode[STIX]{x1D6FF}}\sqrt{\dim V(N,c)}\Vert \unicode[STIX]{x1D713}\Vert _{2}.\end{eqnarray}$$ Note that a Hecke–Maass form as in Theorem 1.1 has Laplacian eigenvalue of size roughly  $(1+\Vert \unicode[STIX]{x1D709}\Vert )^{2}$. Theorem 1.2 therefore implies Theorem 1.1. Moreover, taking
$(1+\Vert \unicode[STIX]{x1D709}\Vert )^{2}$. Theorem 1.2 therefore implies Theorem 1.1. Moreover, taking  $\unicode[STIX]{x1D709}$ at distance at least
$\unicode[STIX]{x1D709}$ at distance at least  $Q$ from the root hyperplanes ensures that the eigenfunction
$Q$ from the root hyperplanes ensures that the eigenfunction  $\unicode[STIX]{x1D713}$ produced by the theorem is tempered at infinity. As in Theorem 1.1, the exponent
$\unicode[STIX]{x1D713}$ produced by the theorem is tempered at infinity. As in Theorem 1.1, the exponent  $\unicode[STIX]{x1D6FF}$ is ineffective.
$\unicode[STIX]{x1D6FF}$ is ineffective.
The only previous results giving lower bounds in the level aspect are for  $\text{GL}_{2}$ over a number field, due to Saha [Reference SahaSah15] and Templier [Reference TemplierTem14]. They use the fact that local Whittaker functions of highly ramified
$\text{GL}_{2}$ over a number field, due to Saha [Reference SahaSah15] and Templier [Reference TemplierTem14]. They use the fact that local Whittaker functions of highly ramified  $p$-adic representations are large high in the cusp, and in particular rely on the non-compactness of the manifold.
$p$-adic representations are large high in the cusp, and in particular rely on the non-compactness of the manifold.
1.4 Borel’s theorem and a concrete example
A classical theorem of Borel on the existence of rationally defined Cartan involutions on real semisimple Lie algebras can be used to provide examples of groups satisfying the hypotheses of Theorem 1.1.Footnote 1 We state this as the following result and provide details for how to extract this statement from the work of Borel in § 2.9.
Proposition 1.3. Let  $G^{\prime }/\mathbb{R}$ be connected, simply connected and
$G^{\prime }/\mathbb{R}$ be connected, simply connected and  $\mathbb{R}$-almost simple. Let
$\mathbb{R}$-almost simple. Let  $F$ be a totally real number field, and let
$F$ be a totally real number field, and let  $v_{0}$ be a real place of
$v_{0}$ be a real place of  $F$. There is a connected semisimple group
$F$. There is a connected semisimple group  $G/F$ with
$G/F$ with  $G_{v_{0}}\simeq G^{\prime }$ that satisfies conditions (ii) and (iii) of Theorem 1.1.
$G_{v_{0}}\simeq G^{\prime }$ that satisfies conditions (ii) and (iii) of Theorem 1.1.
We now give a concrete example of a family of manifolds to which our theorem can be applied, and which to our knowledge does not already appear in the literature.
Let  $F$ be a totally real number field, and let
$F$ be a totally real number field, and let  $E$ be a CM extension of
$E$ be a CM extension of  $F$. Let the rings of integers of these fields be
$F$. Let the rings of integers of these fields be  ${\mathcal{O}}_{F}$ and
${\mathcal{O}}_{F}$ and  ${\mathcal{O}}_{E}$, respectively. Let
${\mathcal{O}}_{E}$, respectively. Let  $v_{0}$ be a distinguished real place of
$v_{0}$ be a distinguished real place of  $F$, and let
$F$, and let  $w_{0}$ be the place of
$w_{0}$ be the place of  $E$ over
$E$ over  $v_{0}$. Let
$v_{0}$. Let  $V$ be a vector space of dimension
$V$ be a vector space of dimension  $n+1$ over
$n+1$ over  $E$ with a Hermitian form
$E$ with a Hermitian form  $\langle \cdot ,\cdot \rangle$ with respect to
$\langle \cdot ,\cdot \rangle$ with respect to  $E/F$. Assume that
$E/F$. Assume that  $\langle \cdot ,\cdot \rangle$ has signature
$\langle \cdot ,\cdot \rangle$ has signature  $(n,1)$ at
$(n,1)$ at  $w_{0}$ and is definite at all other infinite places of
$w_{0}$ and is definite at all other infinite places of  $E$. Let
$E$. Let  $G$ be the
$G$ be the  $F$-algebraic group
$F$-algebraic group  $\text{SU}(V,\langle \cdot ,\cdot \rangle )$, so that
$\text{SU}(V,\langle \cdot ,\cdot \rangle )$, so that  $G_{v_{0}}\simeq \text{SU}(n,1)$.
$G_{v_{0}}\simeq \text{SU}(n,1)$.
Let  $L\subset V$ be an
$L\subset V$ be an  ${\mathcal{O}}_{E}$ lattice on which the form
${\mathcal{O}}_{E}$ lattice on which the form  $\langle \cdot ,\cdot \rangle$ is integral. Let
$\langle \cdot ,\cdot \rangle$ is integral. Let  $L^{\ast }$ be the dual lattice
$L^{\ast }$ be the dual lattice  $L^{\ast }=\{x\in V:\langle x,y\rangle \in {\mathcal{O}}_{E}\text{ for all }y\in L\}$. Let
$L^{\ast }=\{x\in V:\langle x,y\rangle \in {\mathcal{O}}_{E}\text{ for all }y\in L\}$. Let  $\unicode[STIX]{x1D6E4}$ be the group of isometries of
$\unicode[STIX]{x1D6E4}$ be the group of isometries of  $V$ that have determinant 1, preserve
$V$ that have determinant 1, preserve  $L$, and act trivially on
$L$, and act trivially on  $L^{\ast }/L$. If
$L^{\ast }/L$. If  $F\neq \mathbb{Q}$, completion at
$F\neq \mathbb{Q}$, completion at  $w_{0}$ allows us to consider
$w_{0}$ allows us to consider  $\unicode[STIX]{x1D6E4}$ as a discrete, cocompact subgroup of
$\unicode[STIX]{x1D6E4}$ as a discrete, cocompact subgroup of  $\text{SU}(n,1)$, which will be torsion-free if
$\text{SU}(n,1)$, which will be torsion-free if  $L$ is chosen sufficiently small.
$L$ is chosen sufficiently small.
One may associate a complex hyperbolic manifold with  $\unicode[STIX]{x1D6E4}$ in the following way. Let
$\unicode[STIX]{x1D6E4}$ in the following way. Let  $D$ denote the space of lines in
$D$ denote the space of lines in  $V_{w_{0}}$ on which the Hermitian form is negative definite.
$V_{w_{0}}$ on which the Hermitian form is negative definite.  $\text{SU}(n,1)$ acts on
$\text{SU}(n,1)$ acts on  $D$, and
$D$, and  $D$ carries a natural
$D$ carries a natural  $\text{SU}(n,1)$-invariant metric under which it becomes a model for complex hyperbolic
$\text{SU}(n,1)$-invariant metric under which it becomes a model for complex hyperbolic  $n$-space. The quotient
$n$-space. The quotient  $Y=\unicode[STIX]{x1D6E4}\backslash D$ is then a compact complex hyperbolic
$Y=\unicode[STIX]{x1D6E4}\backslash D$ is then a compact complex hyperbolic  $n$-manifold, and is an example of a congruence manifold associated with
$n$-manifold, and is an example of a congruence manifold associated with  $G$ as in Theorem 1.1.
$G$ as in Theorem 1.1.
If  $n\geqslant 2$,
$n\geqslant 2$,  $G$ satisfies conditions (i) and (ii) of Theorem 1.1. We now show that (iii) is satisfied. Let
$G$ satisfies conditions (i) and (ii) of Theorem 1.1. We now show that (iii) is satisfied. Let  $W\subset V$ be a codimension-1 subspace defined over
$W\subset V$ be a codimension-1 subspace defined over  $E$ such that the Hermitian form is positive definite on
$E$ such that the Hermitian form is positive definite on  $W_{w_{0}}$. Let
$W_{w_{0}}$. Let  $\unicode[STIX]{x1D703}$ be the isometry of reflection in
$\unicode[STIX]{x1D703}$ be the isometry of reflection in  $W$. Then
$W$. Then  $g\mapsto \unicode[STIX]{x1D703}g\unicode[STIX]{x1D703}^{-1}$ gives an
$g\mapsto \unicode[STIX]{x1D703}g\unicode[STIX]{x1D703}^{-1}$ gives an  $F$-involution of
$F$-involution of  $G$ that is a Cartan involution on
$G$ that is a Cartan involution on  $G_{v_{0}}$, as required. Theorem 1.1 then implies that there is a sequence of Laplace eigenfunctions
$G_{v_{0}}$, as required. Theorem 1.1 then implies that there is a sequence of Laplace eigenfunctions  $\{\unicode[STIX]{x1D713}_{i}\}$ on
$\{\unicode[STIX]{x1D713}_{i}\}$ on  $Y$ satisfying
$Y$ satisfying  $\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\gg \unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D6FF}}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}$.
$\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }\gg \unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D6FF}}\Vert \unicode[STIX]{x1D713}_{i}\Vert _{2}$.
1.5 The method of proof
The proof of power growth for arithmetic hyperbolic  $3$-manifolds of Maclachlan–Reid type by Milićević [Reference MilicevicMil11] compares an amplified trace and pre-trace formula. Our proof works by extending this method to general groups. The bulk of the work lies in proving asymptotics for the trace formula.
$3$-manifolds of Maclachlan–Reid type by Milićević [Reference MilicevicMil11] compares an amplified trace and pre-trace formula. Our proof works by extending this method to general groups. The bulk of the work lies in proving asymptotics for the trace formula.
More precisely, our proof of Theorem 1.2 proceeds by comparing a trace formula on  $G$ with a relative trace formula for
$G$ with a relative trace formula for  $G$ with respect to
$G$ with respect to  $H$. If we choose a test function
$H$. If we choose a test function  $k\in C_{c}^{\infty }(G(\mathbb{A}))$, the main geometric terms of these trace formulae are
$k\in C_{c}^{\infty }(G(\mathbb{A}))$, the main geometric terms of these trace formulae are  $k(1)$ and
$k(1)$ and  $\unicode[STIX]{x1D6F1}_{H}k(1)$ respectively, where
$\unicode[STIX]{x1D6F1}_{H}k(1)$ respectively, where  $\unicode[STIX]{x1D6F1}_{H}:L^{1}(G(\mathbb{A}))\rightarrow L^{1}(X(\mathbb{A}))$ is given by integration over
$\unicode[STIX]{x1D6F1}_{H}:L^{1}(G(\mathbb{A}))\rightarrow L^{1}(X(\mathbb{A}))$ is given by integration over  $H$. In fact, we need to choose test functions of the form
$H$. In fact, we need to choose test functions of the form  $k=\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast }$ so that their action on
$k=\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast }$ so that their action on  $L^{2}(G(F)\backslash G(\mathbb{A}))$ is positive semidefinite. After controlling the other geometric terms, we wish to find
$L^{2}(G(F)\backslash G(\mathbb{A}))$ is positive semidefinite. After controlling the other geometric terms, we wish to find  $\unicode[STIX]{x1D714}$ that makes
$\unicode[STIX]{x1D714}$ that makes  $\unicode[STIX]{x1D6F1}_{H}k(1)$ large relative to
$\unicode[STIX]{x1D6F1}_{H}k(1)$ large relative to  $k(1)$. At finite places, we shall take for
$k(1)$. At finite places, we shall take for  $\unicode[STIX]{x1D714}_{f}$ an appropriately large sum of
$\unicode[STIX]{x1D714}_{f}$ an appropriately large sum of  $L^{2}$-normalized basic Hecke operators
$L^{2}$-normalized basic Hecke operators  $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v)$, supported on
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v)$, supported on  $K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v}$, where
$K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v}$, where  $\unicode[STIX]{x1D708}$ is a cocharacter of
$\unicode[STIX]{x1D708}$ is a cocharacter of  $G$. The condition that
$G$. The condition that  $\unicode[STIX]{x1D6F1}_{H}k(1)$ be large then boils down to
$\unicode[STIX]{x1D6F1}_{H}k(1)$ be large then boils down to
 $$\begin{eqnarray}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v))(1)=\frac{\text{vol}(H_{v}\cap K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})}{\text{vol}(K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})^{1/2}}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v))(1)=\frac{\text{vol}(H_{v}\cap K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})}{\text{vol}(K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})^{1/2}}\end{eqnarray}$$ being large, for enough places  $v$. Note that this corresponds to our informal description in terms of Hecke returns at the beginning of the introduction: if the projection of the
$v$. Note that this corresponds to our informal description in terms of Hecke returns at the beginning of the introduction: if the projection of the  $H$-period onto the given locally symmetric
$H$-period onto the given locally symmetric  $Y$ is simply a point
$Y$ is simply a point  $p$ (rather than a finite collection of such), the right-hand side above is roughly the multiplicity with which
$p$ (rather than a finite collection of such), the right-hand side above is roughly the multiplicity with which  $p$ appears in its image by the Hecke correspondence
$p$ appears in its image by the Hecke correspondence  $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v)$. In any case, we bound this quantity from below in Lemma 4.6, in terms of the
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D708},v)$. In any case, we bound this quantity from below in Lemma 4.6, in terms of the  $H$-relative size of
$H$-relative size of  $\unicode[STIX]{x1D708}$. The latter is a certain cocharacter inequality, which we show in Lemma 2.2 is verified under the conditions of our main theorem.
$\unicode[STIX]{x1D708}$. The latter is a certain cocharacter inequality, which we show in Lemma 2.2 is verified under the conditions of our main theorem.
While we were writing this paper, Erez Lapid pointed out to us that there was another approach to proving Theorems 1.1 and 1.2 based on a theorem of Sakellaridis on the unramified  $C^{\infty }$ spectrum of symmetric varieties. We have included a discussion of this in Appendix A. We have also included an explanation of why the condition of
$C^{\infty }$ spectrum of symmetric varieties. We have included a discussion of this in Appendix A. We have also included an explanation of why the condition of  $G$ being non-split at
$G$ being non-split at  $v_{0}$ is natural, and motivated our choice of test functions in the trace formula, based on a related conjecture of Sakellaridis and Venkatesh on the
$v_{0}$ is natural, and motivated our choice of test functions in the trace formula, based on a related conjecture of Sakellaridis and Venkatesh on the  $L^{2}$ spectrum.
$L^{2}$ spectrum.
2 Notation and proof of Proposition 1.3
2.1 Algebraic groups
Let  ${\mathcal{O}}$ denote the ring of integers of
${\mathcal{O}}$ denote the ring of integers of  $F$. Let
$F$. Let  $\mathbb{A}$ and
$\mathbb{A}$ and  $\mathbb{A}_{f}$ be the adeles and finite adeles of
$\mathbb{A}_{f}$ be the adeles and finite adeles of  $F$.
$F$.
Let  $G$ and
$G$ and  $\unicode[STIX]{x1D703}$ be as in Theorems 1.1 and 1.2. Let
$\unicode[STIX]{x1D703}$ be as in Theorems 1.1 and 1.2. Let  $H$ again denote the identity component of the group of fixed points of
$H$ again denote the identity component of the group of fixed points of  $\unicode[STIX]{x1D703}$. We let
$\unicode[STIX]{x1D703}$. We let  $T\subset G$ and
$T\subset G$ and  $T_{H}\subset H$ be maximal tori defined over
$T_{H}\subset H$ be maximal tori defined over  $F$ with
$F$ with  $T_{H}\subset T$. We fix an
$T_{H}\subset T$. We fix an  $F$-embedding
$F$-embedding  $\unicode[STIX]{x1D70C}:G\rightarrow \text{SL}_{d}$. Let
$\unicode[STIX]{x1D70C}:G\rightarrow \text{SL}_{d}$. Let  $Z$ be the centre of
$Z$ be the centre of  $G$.
$G$.
Consider  $\text{SL}_{d}$ as a group scheme over
$\text{SL}_{d}$ as a group scheme over  ${\mathcal{O}}$ in the standard way, and take the schematic closures of
${\mathcal{O}}$ in the standard way, and take the schematic closures of  $T_{H}$,
$T_{H}$,  $T$,
$T$,  $H$, and
$H$, and  $G$ in
$G$ in  $\text{SL}_{d}/{\mathcal{O}}$. These closures are group schemes over
$\text{SL}_{d}/{\mathcal{O}}$. These closures are group schemes over  ${\mathcal{O}}$, and all the inclusions between them over
${\mathcal{O}}$, and all the inclusions between them over  $F$ extend to closed embeddings over
$F$ extend to closed embeddings over  ${\mathcal{O}}$. By [Reference TitsTit79, 3.9], we may choose
${\mathcal{O}}$. By [Reference TitsTit79, 3.9], we may choose  $D\in \mathbb{N}$ such that, over
$D\in \mathbb{N}$ such that, over  ${\mathcal{O}}[1/D]$, all fibers of these group schemes are smooth, connected and reductive.
${\mathcal{O}}[1/D]$, all fibers of these group schemes are smooth, connected and reductive.
Let  $X^{\ast }(T)$ and
$X^{\ast }(T)$ and  $X_{\ast }(T)$ denote the group of characters and cocharacters of
$X_{\ast }(T)$ denote the group of characters and cocharacters of  $T\times _{F}\overline{F}$. Let
$T\times _{F}\overline{F}$. Let  $\unicode[STIX]{x1D6E5}$ be the set of roots of
$\unicode[STIX]{x1D6E5}$ be the set of roots of  $T$ in
$T$ in  $G$, and let
$G$, and let  $\unicode[STIX]{x1D6E5}^{+}$ be a choice of positive roots. Let
$\unicode[STIX]{x1D6E5}^{+}$ be a choice of positive roots. Let  $W$ be the Weyl group of
$W$ be the Weyl group of  $(G,T)$ over
$(G,T)$ over  $\overline{F}$. We define
$\overline{F}$. We define
 $$\begin{eqnarray}X_{\ast }^{+}(T)=\{\unicode[STIX]{x1D707}\in X_{\ast }(T):\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle \geqslant 0,\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}\}.\end{eqnarray}$$
$$\begin{eqnarray}X_{\ast }^{+}(T)=\{\unicode[STIX]{x1D707}\in X_{\ast }(T):\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle \geqslant 0,\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}\}.\end{eqnarray}$$ Similarly, we may define  $\unicode[STIX]{x1D6E5}_{H},\unicode[STIX]{x1D6E5}_{H}^{+}$,
$\unicode[STIX]{x1D6E5}_{H},\unicode[STIX]{x1D6E5}_{H}^{+}$,  $W_{H}$ and
$W_{H}$ and  $X_{\ast }^{+}(T_{H})$. Letting
$X_{\ast }^{+}(T_{H})$. Letting  $\unicode[STIX]{x1D70C}$ and
$\unicode[STIX]{x1D70C}$ and  $\unicode[STIX]{x1D70C}_{H}$ denote, as usual, the half-sum of positive roots for
$\unicode[STIX]{x1D70C}_{H}$ denote, as usual, the half-sum of positive roots for  $G$ and
$G$ and  $H$, we introduce the functions
$H$, we introduce the functions
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D707}\Vert ^{\ast } & = & \displaystyle \underset{w\in W}{\max }\langle w\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}\rangle ,\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast } & = & \displaystyle \underset{w\in W_{H}}{\max }\langle w\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}_{H}\rangle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D707}\Vert ^{\ast } & = & \displaystyle \underset{w\in W}{\max }\langle w\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}\rangle ,\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast } & = & \displaystyle \underset{w\in W_{H}}{\max }\langle w\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}_{H}\rangle \nonumber\end{eqnarray}$$ on  $X_{\ast }(T)$ and
$X_{\ast }(T)$ and  $X_{\ast }(T_{H})$, respectively. Our assumption that
$X_{\ast }(T_{H})$, respectively. Our assumption that  $G$ is semisimple implies that
$G$ is semisimple implies that  $\Vert \!\unicode[STIX]{x1D707}\!\Vert ^{\ast }$ is a norm; the condition that
$\Vert \!\unicode[STIX]{x1D707}\!\Vert ^{\ast }$ is a norm; the condition that  $\Vert \unicode[STIX]{x1D707}\Vert ^{\ast }=\Vert -\unicode[STIX]{x1D707}\Vert ^{\ast }$ follows from the fact that
$\Vert \unicode[STIX]{x1D707}\Vert ^{\ast }=\Vert -\unicode[STIX]{x1D707}\Vert ^{\ast }$ follows from the fact that  $\unicode[STIX]{x1D70C}$ and
$\unicode[STIX]{x1D70C}$ and  $-\unicode[STIX]{x1D70C}$ lie in the same Weyl orbit. While
$-\unicode[STIX]{x1D70C}$ lie in the same Weyl orbit. While  $\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }$ also has the property that
$\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }$ also has the property that  $\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }=\Vert -\unicode[STIX]{x1D707}\Vert _{H}^{\ast }$, it is trivial on cocharacters arising from the centre of
$\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }=\Vert -\unicode[STIX]{x1D707}\Vert _{H}^{\ast }$, it is trivial on cocharacters arising from the centre of  $H$.
$H$.
Definition 2.1. We say that  $G$ is
$G$ is  $H$-large if there exists a non-zero
$H$-large if there exists a non-zero  $\unicode[STIX]{x1D707}\in X_{\ast }(T_{H})$ such that
$\unicode[STIX]{x1D707}\in X_{\ast }(T_{H})$ such that
 $$\begin{eqnarray}2\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }\geqslant \Vert \unicode[STIX]{x1D707}\Vert ^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}2\Vert \unicode[STIX]{x1D707}\Vert _{H}^{\ast }\geqslant \Vert \unicode[STIX]{x1D707}\Vert ^{\ast }.\end{eqnarray}$$ Note that this definition is exactly the opposite of the definition of  $H$ being small in
$H$ being small in  $G$ given in [Reference MarshallMar14, Definition 8.1]. By [Reference MarshallMar14, Lemma 8.2], the definition of
$G$ given in [Reference MarshallMar14, Definition 8.1]. By [Reference MarshallMar14, Lemma 8.2], the definition of  $H$-large is independent of the choice of tori
$H$-large is independent of the choice of tori  $T_{H}\subset T$.
$T_{H}\subset T$.
Lemma 2.2. A group  $G$ satisfying the hypotheses of Theorem 1.1 is
$G$ satisfying the hypotheses of Theorem 1.1 is  $H$-large.
$H$-large.
Proof. This follows from [Reference MarshallMar14, Theorem 8.3]. Indeed, [Reference BorelBor91, p. 277] implies that the compact subgroup  $H_{v_{0}}$ is connected in the real topology; by passing to the Lie algebra, this implies that
$H_{v_{0}}$ is connected in the real topology; by passing to the Lie algebra, this implies that  $H_{v_{0}}$ is a maximal compact connected subgroup of
$H_{v_{0}}$ is a maximal compact connected subgroup of  $G_{v_{0}}$. We then deduce from [Reference MarshallMar14, Theorem 8.3] that
$G_{v_{0}}$. We then deduce from [Reference MarshallMar14, Theorem 8.3] that  $H_{v_{0}}$ is not small in
$H_{v_{0}}$ is not small in  $G_{v_{0}}$, and invariance of smallness under field extension then implies that
$G_{v_{0}}$, and invariance of smallness under field extension then implies that  $G$ is
$G$ is  $H$-large.◻
$H$-large.◻
2.2 Local fields
If  $v$ is a place of
$v$ is a place of  $F$, we denote the completion by
$F$, we denote the completion by  $F_{v}$. If
$F_{v}$. If  $v$ is finite, we denote the ring of integers, uniformizer and cardinality of the residue field by
$v$ is finite, we denote the ring of integers, uniformizer and cardinality of the residue field by  ${\mathcal{O}}_{v}$,
${\mathcal{O}}_{v}$,  $\unicode[STIX]{x1D71B}_{v}$ and
$\unicode[STIX]{x1D71B}_{v}$ and  $q_{v}$, respectively. If
$q_{v}$, respectively. If  $v\nmid D\infty$, we have the following consequences of our assumptions on
$v\nmid D\infty$, we have the following consequences of our assumptions on  $D$ and
$D$ and  $\unicode[STIX]{x1D70C}$ above.
$\unicode[STIX]{x1D70C}$ above.
(i) We have
 $G({\mathcal{O}}_{v})=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v}))$ and
$G({\mathcal{O}}_{v})=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v}))$ and  $H({\mathcal{O}}_{v})=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(H_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v}))$, so that
$H({\mathcal{O}}_{v})=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(H_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v}))$, so that  $G({\mathcal{O}}_{v})\cap H_{v}=H({\mathcal{O}}_{v})$.
$G({\mathcal{O}}_{v})\cap H_{v}=H({\mathcal{O}}_{v})$.(ii)
 $G({\mathcal{O}}_{v})$ and
$G({\mathcal{O}}_{v})$ and  $H({\mathcal{O}}_{v})$ are hyperspecial maximal compact subgroups of
$H({\mathcal{O}}_{v})$ are hyperspecial maximal compact subgroups of  $G_{v}$ and
$G_{v}$ and  $H_{v}$, respectively.
$H_{v}$, respectively.(iii) If
 $T$ (and hence
$T$ (and hence  $T_{H}$) split at
$T_{H}$) split at  $v$, the subgroups
$v$, the subgroups  $G({\mathcal{O}}_{v})$ and
$G({\mathcal{O}}_{v})$ and  $H({\mathcal{O}}_{v})$ correspond to points in the Bruhat–Tits buildings of
$H({\mathcal{O}}_{v})$ correspond to points in the Bruhat–Tits buildings of  $G_{v}$ and
$G_{v}$ and  $H_{v}$ that lie in the apartments of
$H_{v}$ that lie in the apartments of  $T$ and
$T$ and  $T_{H}$, respectively.
$T_{H}$, respectively.
Property (i) is a consequence of the inclusions  $H\subset G\subset \text{SL}_{d}$ extending to closed embeddings over
$H\subset G\subset \text{SL}_{d}$ extending to closed embeddings over  ${\mathcal{O}}_{v}$. Property (ii) is [Reference TitsTit79, 3.8] or [Reference Bruhat and TitsBT84, 5.1.40]. Property (iii) is [Reference Bruhat and TitsBT84, 5.1.33], once we use [Reference Bruhat and TitsBT84, 5.1.40] to show that the
${\mathcal{O}}_{v}$. Property (ii) is [Reference TitsTit79, 3.8] or [Reference Bruhat and TitsBT84, 5.1.40]. Property (iii) is [Reference Bruhat and TitsBT84, 5.1.33], once we use [Reference Bruhat and TitsBT84, 5.1.40] to show that the  ${\mathcal{O}}_{v}$ group scheme
${\mathcal{O}}_{v}$ group scheme  $T/{\mathcal{O}}_{v}$ is the standard one associated with
$T/{\mathcal{O}}_{v}$ is the standard one associated with  $T_{v}$. We let
$T_{v}$. We let  ${\mathcal{P}}$ be the set of finite places of
${\mathcal{P}}$ be the set of finite places of  $F$ that do not divide
$F$ that do not divide  $D$ and at which
$D$ and at which  $T$ splits. If
$T$ splits. If  $v\in {\mathcal{P}}$, our assumptions imply that
$v\in {\mathcal{P}}$, our assumptions imply that  $G_{v}$ has a Cartan decomposition
$G_{v}$ has a Cartan decomposition
 $$\begin{eqnarray}G_{v}=\coprod _{\unicode[STIX]{x1D707}\in X_{\ast }^{+}(T)}G({\mathcal{O}}_{v})\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})G({\mathcal{O}}_{v})\end{eqnarray}$$
$$\begin{eqnarray}G_{v}=\coprod _{\unicode[STIX]{x1D707}\in X_{\ast }^{+}(T)}G({\mathcal{O}}_{v})\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})G({\mathcal{O}}_{v})\end{eqnarray}$$ with respect to  $G({\mathcal{O}}_{v})$ and
$G({\mathcal{O}}_{v})$ and  $T$.
$T$.
2.3 Metrics
For any place  $v$ of
$v$ of  $F$ and
$F$ and  $g\in G(F_{v})$ let
$g\in G(F_{v})$ let  $\Vert g\Vert _{v}$ denote the maximum of the
$\Vert g\Vert _{v}$ denote the maximum of the  $v$-adic norms of the matrix entries of
$v$-adic norms of the matrix entries of  $\unicode[STIX]{x1D70C}(g)$. For
$\unicode[STIX]{x1D70C}(g)$. For  $g\in G(\mathbb{A}_{f})$, let
$g\in G(\mathbb{A}_{f})$, let  $\Vert g\Vert _{f}=\prod _{v\nmid \infty }\Vert g_{v}\Vert _{v}$. Fix a left-invariant Riemannian metric on
$\Vert g\Vert _{f}=\prod _{v\nmid \infty }\Vert g_{v}\Vert _{v}$. Fix a left-invariant Riemannian metric on  $G(F_{v_{0}})$. Let
$G(F_{v_{0}})$. Let  $d(\cdot ,\cdot )$ be the associated distance function. We define
$d(\cdot ,\cdot )$ be the associated distance function. We define  $d(x,y)=\infty$ when
$d(x,y)=\infty$ when  $x$ and
$x$ and  $y$ are in different connected components of
$y$ are in different connected components of  $G(F_{v_{0}})$ with the topology of a real manifold.
$G(F_{v_{0}})$ with the topology of a real manifold.
2.4 Compact subgroups
We choose compact subgroups  $K_{v}$ of
$K_{v}$ of  $G_{v}$ for all
$G_{v}$ for all  $v$ such that:
$v$ such that:
∙
 $K_{v_{0}}=H_{v_{0}}$;
$K_{v_{0}}=H_{v_{0}}$;∙
 $K_{v}=G_{v}$ for all other real places;
$K_{v}=G_{v}$ for all other real places;∙
 $\unicode[STIX]{x1D70C}(K_{v})\subset \text{SL}_{d}({\mathcal{O}}_{v})$ for all finite
$\unicode[STIX]{x1D70C}(K_{v})\subset \text{SL}_{d}({\mathcal{O}}_{v})$ for all finite  $v$;
$v$;∙
 $K_{v}=G({\mathcal{O}}_{v})$ for finite places
$K_{v}=G({\mathcal{O}}_{v})$ for finite places  $v\nmid D$; and
$v\nmid D$; and∙
 $K=\prod _{v\nmid \infty }K_{v}$ is open in
$K=\prod _{v\nmid \infty }K_{v}$ is open in  $G(\mathbb{A}_{f})$.
$G(\mathbb{A}_{f})$.
By the remarks in the proof of Lemma 2.2,  $K_{v_{0}}$ is a maximal compact connected subgroup of
$K_{v_{0}}$ is a maximal compact connected subgroup of  $G_{v_{0}}$. We shall suppose that
$G_{v_{0}}$. We shall suppose that  $K_{v}$ for
$K_{v}$ for  $v|D$ is sufficiently small to ensure that the finite group
$v|D$ is sufficiently small to ensure that the finite group  $Z(F)\cap K$ is reduced to
$Z(F)\cap K$ is reduced to  $\{e\}$.
$\{e\}$.
2.5 Measure normalizations
For any place  $v$ of
$v$ of  $F$, let
$F$, let  $\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ be the canonical measure on
$\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ be the canonical measure on  $G(F_{v})$ as defined by Gross in [Reference GrossGro97, § 11]; we recall this construction in § 6.1. Then for all finite places
$G(F_{v})$ as defined by Gross in [Reference GrossGro97, § 11]; we recall this construction in § 6.1. Then for all finite places  $v\nmid D$ we have
$v\nmid D$ we have  $\unicode[STIX]{x1D707}_{G,v}^{\text{can}}(K_{v})=1$. We may then form the product measure
$\unicode[STIX]{x1D707}_{G,v}^{\text{can}}(K_{v})=1$. We may then form the product measure  $\unicode[STIX]{x1D707}_{G}^{\text{can}}=\prod _{v}\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ on
$\unicode[STIX]{x1D707}_{G}^{\text{can}}=\prod _{v}\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ on  $G(\mathbb{A})$. All convolutions (local and global) on
$G(\mathbb{A})$. All convolutions (local and global) on  $G$ will be defined with respect to these measures. If
$G$ will be defined with respect to these measures. If  $f\in C_{c}^{\infty }(G(\mathbb{A}))$, we define the operator
$f\in C_{c}^{\infty }(G(\mathbb{A}))$, we define the operator  $\unicode[STIX]{x1D70B}(f)$ on
$\unicode[STIX]{x1D70B}(f)$ on  $L^{2}(G(F)\backslash G(\mathbb{A}))$ by
$L^{2}(G(F)\backslash G(\mathbb{A}))$ by
 $$\begin{eqnarray}[\unicode[STIX]{x1D70B}(f)\unicode[STIX]{x1D719}](x)=\int _{G(\mathbb{A})}\unicode[STIX]{x1D719}(xg)f(g)\,d\unicode[STIX]{x1D707}_{G}^{\text{can}}(g).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D70B}(f)\unicode[STIX]{x1D719}](x)=\int _{G(\mathbb{A})}\unicode[STIX]{x1D719}(xg)f(g)\,d\unicode[STIX]{x1D707}_{G}^{\text{can}}(g).\end{eqnarray}$$ If  $f\in C_{c}^{\infty }(G(\mathbb{A}))$, we define
$f\in C_{c}^{\infty }(G(\mathbb{A}))$, we define  $f^{\ast }$ by
$f^{\ast }$ by  $f^{\ast }(g)=\overline{f}(g^{-1})$, so that
$f^{\ast }(g)=\overline{f}(g^{-1})$, so that  $\unicode[STIX]{x1D70B}(f)$ and
$\unicode[STIX]{x1D70B}(f)$ and  $\unicode[STIX]{x1D70B}(f^{\ast })$ are adjoints.
$\unicode[STIX]{x1D70B}(f^{\ast })$ are adjoints.
The choice of canonical measure for  $G$ is imposed by the use of the Arthur–Selberg trace formula in § 6; indeed, we want a uniform way of normalizing measures on the collection of connected reductive groups appearing as centralizers. We can afford to be more casual with measure normalizations for
$G$ is imposed by the use of the Arthur–Selberg trace formula in § 6; indeed, we want a uniform way of normalizing measures on the collection of connected reductive groups appearing as centralizers. We can afford to be more casual with measure normalizations for  $H$, in light of our treatment of the geometric side of the relative trace formula in § 5. For finite places
$H$, in light of our treatment of the geometric side of the relative trace formula in § 5. For finite places  $v$ we choose Haar measures
$v$ we choose Haar measures  $dh_{v}$ on
$dh_{v}$ on  $H(F_{v})$ so that
$H(F_{v})$ so that  $H(F_{v})\cap K_{v}$ is assigned measure 1. Because
$H(F_{v})\cap K_{v}$ is assigned measure 1. Because  $H_{v}$ is compact for archimedean
$H_{v}$ is compact for archimedean  $v$, at these places we choose Haar measures
$v$, at these places we choose Haar measures  $dh_{v}$ so that
$dh_{v}$ so that  $H_{v}$ has volume 1. We set
$H_{v}$ has volume 1. We set  $dh=\prod _{v}dh_{v}$.
$dh=\prod _{v}dh_{v}$.
2.6 Hecke algebras
If  $S$ is any finite set of finite places prime to
$S$ is any finite set of finite places prime to  $D$, let
$D$, let  ${\mathcal{H}}_{S}$ be the convolution algebra of functions on
${\mathcal{H}}_{S}$ be the convolution algebra of functions on  $G(F_{S})$ that are compactly supported and bi-invariant under
$G(F_{S})$ that are compactly supported and bi-invariant under  $K_{S}$. Similarly,
$K_{S}$. Similarly,  ${\mathcal{H}}_{f}$ is the convolution algebra of functions on
${\mathcal{H}}_{f}$ is the convolution algebra of functions on  $G(\mathbb{A}_{f}^{D})$ that are compactly supported and bi-invariant under
$G(\mathbb{A}_{f}^{D})$ that are compactly supported and bi-invariant under  $K^{D}$. We identify
$K^{D}$. We identify  ${\mathcal{H}}_{S}$ and
${\mathcal{H}}_{S}$ and  ${\mathcal{H}}_{f}$ with subalgebras of
${\mathcal{H}}_{f}$ with subalgebras of  $C_{c}^{\infty }(G(\mathbb{A}_{f}))$ in the natural way. If
$C_{c}^{\infty }(G(\mathbb{A}_{f}))$ in the natural way. If  $G_{\infty }^{0}$ denotes the connected component of the identity in
$G_{\infty }^{0}$ denotes the connected component of the identity in  $G_{\infty }$ in the real topology, we define
$G_{\infty }$ in the real topology, we define  ${\mathcal{H}}_{\infty }$ to be the subspace of
${\mathcal{H}}_{\infty }$ to be the subspace of  $C_{c}^{\infty }(G_{\infty }^{0})$ consisting of functions that are bi-invariant under
$C_{c}^{\infty }(G_{\infty }^{0})$ consisting of functions that are bi-invariant under  $K_{\infty }$, and define
$K_{\infty }$, and define  ${\mathcal{H}}={\mathcal{H}}_{\infty }\otimes {\mathcal{H}}_{f}$.
${\mathcal{H}}={\mathcal{H}}_{\infty }\otimes {\mathcal{H}}_{f}$.
To control for the degree of Hecke operators in our later estimates, it will be convenient to work with the truncated Hecke algebras defined in [Reference Shin and TemplierST16]. Recall from § 2.1 the Weyl-invariant norm  $\Vert \cdot \Vert ^{\ast }$ on
$\Vert \cdot \Vert ^{\ast }$ on  $X_{\ast }(T)$. Let
$X_{\ast }(T)$. Let  $v$ be a finite place not dividing
$v$ be a finite place not dividing  $D$. Because
$D$. Because  $G_{v}$ is unramified, there is a maximal
$G_{v}$ is unramified, there is a maximal  $F_{v}$-split torus
$F_{v}$-split torus  $A_{v}$ in
$A_{v}$ in  $G_{v}$ such that
$G_{v}$ such that  $K_{v}$ corresponds to a point in the apartment of
$K_{v}$ corresponds to a point in the apartment of  $A_{v}$. We may conjugate
$A_{v}$. We may conjugate  $A_{v}$ inside
$A_{v}$ inside  $T$ over
$T$ over  $\overline{F}_{v}$, and obtain a norm
$\overline{F}_{v}$, and obtain a norm  $\Vert \cdot \Vert _{v}$ on
$\Vert \cdot \Vert _{v}$ on  $X_{\ast }(A_{v})$. We then define
$X_{\ast }(A_{v})$. We then define
 $$\begin{eqnarray}{\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}=\text{span}_{\mathbb{ C}}\,\{\mathbf{1}_{K_{v}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})K_{v}}:\unicode[STIX]{x1D707}\in X_{\ast }(A_{v}),\,\Vert \unicode[STIX]{x1D707}\Vert _{v}\leqslant \unicode[STIX]{x1D705}\};\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}=\text{span}_{\mathbb{ C}}\,\{\mathbf{1}_{K_{v}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})K_{v}}:\unicode[STIX]{x1D707}\in X_{\ast }(A_{v}),\,\Vert \unicode[STIX]{x1D707}\Vert _{v}\leqslant \unicode[STIX]{x1D705}\};\end{eqnarray}$$ note that here and elsewhere,  $\mathbf{1}_{A}$ denotes the characteristic function of the set
$\mathbf{1}_{A}$ denotes the characteristic function of the set  $A$. If
$A$. If  $S$ is any finite set of finite places not dividing
$S$ is any finite set of finite places not dividing  $D$, we set
$D$, we set 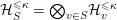 ${\mathcal{H}}_{S}^{{\leqslant}\unicode[STIX]{x1D705}}=\bigotimes _{v\in S}{\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$.
${\mathcal{H}}_{S}^{{\leqslant}\unicode[STIX]{x1D705}}=\bigotimes _{v\in S}{\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$.
We note that  ${\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$ is independent of the choices made in its definition. First, the norm
${\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$ is independent of the choices made in its definition. First, the norm  $\Vert \cdot \Vert _{v}$ is independent of the conjugation of
$\Vert \cdot \Vert _{v}$ is independent of the conjugation of  $A_{v}$ inside
$A_{v}$ inside  $T$. To see this, we note that
$T$. To see this, we note that  $\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }$ can also be defined by taking
$\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }$ can also be defined by taking  $\mathbb{G}_{m}\overset{\unicode[STIX]{x1D706}}{\longrightarrow }T\overset{\text{Ad}}{\longrightarrow }\text{GL}(\mathfrak{g})$, decomposing the representation of
$\mathbb{G}_{m}\overset{\unicode[STIX]{x1D706}}{\longrightarrow }T\overset{\text{Ad}}{\longrightarrow }\text{GL}(\mathfrak{g})$, decomposing the representation of  $\mathbb{G}_{m}$ on
$\mathbb{G}_{m}$ on  $\mathfrak{g}$ into characters in
$\mathfrak{g}$ into characters in  $X^{\ast }(\mathbb{G}_{m})\simeq \mathbb{Z}$, and taking half the sum of the positive terms. This lets us extend
$X^{\ast }(\mathbb{G}_{m})\simeq \mathbb{Z}$, and taking half the sum of the positive terms. This lets us extend  $\Vert \cdot \Vert ^{\ast }$ to all of
$\Vert \cdot \Vert ^{\ast }$ to all of  $X_{\ast }(G)$ in a conjugation-invariant way, and
$X_{\ast }(G)$ in a conjugation-invariant way, and  $\Vert \cdot \Vert _{v}$ is the restriction of this to
$\Vert \cdot \Vert _{v}$ is the restriction of this to  $X_{\ast }(A_{v})$. Secondly, if
$X_{\ast }(A_{v})$. Secondly, if  $A_{v}$ and
$A_{v}$ and  $A_{v}^{\prime }$ are two tori whose apartments contain the point corresponding to
$A_{v}^{\prime }$ are two tori whose apartments contain the point corresponding to  $K_{v}$, then by [Reference TitsTit79, § 2.2.1] they are conjugate by an element of
$K_{v}$, then by [Reference TitsTit79, § 2.2.1] they are conjugate by an element of  $K_{v}$, and this conjugation respects the norms on
$K_{v}$, and this conjugation respects the norms on  $X_{\ast }(A_{v})$ and
$X_{\ast }(A_{v})$ and  $X_{\ast }(A_{v}^{\prime })$. This implies that
$X_{\ast }(A_{v}^{\prime })$. This implies that  ${\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$ is independent of
${\mathcal{H}}_{v}^{{\leqslant}\unicode[STIX]{x1D705}}$ is independent of  $A_{v}$.
$A_{v}$.
2.7 A lemma on double cosets
We shall need bounds on the volume of the support of Hecke operators on  $G_{v}$ and
$G_{v}$ and  $H_{v}$ at places where these groups are split. Such bounds are proved by Macdonald [Reference MacdonaldMac71] for split simply connected semisimple groups, but we shall need them in the general split reductive case, and derive them now from a result of Gross [Reference GrossGro96].
$H_{v}$ at places where these groups are split. Such bounds are proved by Macdonald [Reference MacdonaldMac71] for split simply connected semisimple groups, but we shall need them in the general split reductive case, and derive them now from a result of Gross [Reference GrossGro96].
In this subsection we let  $F$ be a
$F$ be a  $p$-adic field with integer ring
$p$-adic field with integer ring  ${\mathcal{O}}$, uniformizer
${\mathcal{O}}$, uniformizer  $\unicode[STIX]{x1D71B}$, and residue field
$\unicode[STIX]{x1D71B}$, and residue field  $k$, and let
$k$, and let  $q=\#k$. We let
$q=\#k$. We let  $G$ be a split connected reductive group over
$G$ be a split connected reductive group over  $F$. Let
$F$. Let  $T\subset G$ be a maximal split torus, and
$T\subset G$ be a maximal split torus, and  $K\subset G$ a hyperspecial maximal compact subgroup corresponding to a point in the apartment of
$K\subset G$ a hyperspecial maximal compact subgroup corresponding to a point in the apartment of  $T$. Let
$T$. Let  $\Vert \cdot \Vert ^{\ast }$ be the function on
$\Vert \cdot \Vert ^{\ast }$ be the function on  $X_{\ast }(T)$ as in § 2.1.
$X_{\ast }(T)$ as in § 2.1.
Lemma 2.3. We have  $\#K\unicode[STIX]{x1D706}(\unicode[STIX]{x1D71B})K/K\sim q^{2\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }}$ for all
$\#K\unicode[STIX]{x1D706}(\unicode[STIX]{x1D71B})K/K\sim q^{2\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }}$ for all  $\unicode[STIX]{x1D706}\in X_{\ast }(T)$, where the implied constants depend only on
$\unicode[STIX]{x1D706}\in X_{\ast }(T)$, where the implied constants depend only on  $\dim G$.
$\dim G$.
Proof. Let  $P_{\unicode[STIX]{x1D706}}$ be the parabolic subgroup associated with
$P_{\unicode[STIX]{x1D706}}$ be the parabolic subgroup associated with  $\unicode[STIX]{x1D706}$, so that
$\unicode[STIX]{x1D706}$, so that
 $$\begin{eqnarray}\text{Lie}(P_{\unicode[STIX]{x1D706}})=\text{Lie}(T)+\bigoplus _{\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706}\rangle \geqslant 0}\text{Lie}(G)_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Lie}(P_{\unicode[STIX]{x1D706}})=\text{Lie}(T)+\bigoplus _{\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706}\rangle \geqslant 0}\text{Lie}(G)_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$ By Proposition 7.4 of [Reference GrossGro96], we have  $\#K\unicode[STIX]{x1D706}(\unicode[STIX]{x1D71B})K/K=q^{2\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }-\dim (G/P_{\unicode[STIX]{x1D706}})}\#(G/P_{\unicode[STIX]{x1D706}})(k)$. Now
$\#K\unicode[STIX]{x1D706}(\unicode[STIX]{x1D71B})K/K=q^{2\Vert \unicode[STIX]{x1D706}\Vert ^{\ast }-\dim (G/P_{\unicode[STIX]{x1D706}})}\#(G/P_{\unicode[STIX]{x1D706}})(k)$. Now
 $$\begin{eqnarray}\#(G/P_{\unicode[STIX]{x1D706}})(k)=\#G(k)/\#P_{\unicode[STIX]{x1D706}}(k)\quad \text{and}\quad \#P_{\unicode[STIX]{x1D706}}(k)=\#M_{\unicode[STIX]{x1D706}}(k)q^{\dim U_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$
$$\begin{eqnarray}\#(G/P_{\unicode[STIX]{x1D706}})(k)=\#G(k)/\#P_{\unicode[STIX]{x1D706}}(k)\quad \text{and}\quad \#P_{\unicode[STIX]{x1D706}}(k)=\#M_{\unicode[STIX]{x1D706}}(k)q^{\dim U_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$ where  $P_{\unicode[STIX]{x1D706}}=M_{\unicode[STIX]{x1D706}}U_{\unicode[STIX]{x1D706}}$ is the standard Levi decomposition, and the first equality follows from [Reference BorelBor91, Corollary 16.5]. It follows that
$P_{\unicode[STIX]{x1D706}}=M_{\unicode[STIX]{x1D706}}U_{\unicode[STIX]{x1D706}}$ is the standard Levi decomposition, and the first equality follows from [Reference BorelBor91, Corollary 16.5]. It follows that
 $$\begin{eqnarray}q^{-\text{dim}(G/P_{\unicode[STIX]{x1D706}})}\#(G/P_{\unicode[STIX]{x1D706}})(k)=q^{\dim M_{\unicode[STIX]{x1D706}}-\dim G}\#G(k)/\#M_{\unicode[STIX]{x1D706}}(k).\end{eqnarray}$$
$$\begin{eqnarray}q^{-\text{dim}(G/P_{\unicode[STIX]{x1D706}})}\#(G/P_{\unicode[STIX]{x1D706}})(k)=q^{\dim M_{\unicode[STIX]{x1D706}}-\dim G}\#G(k)/\#M_{\unicode[STIX]{x1D706}}(k).\end{eqnarray}$$ The formula of Steinberg [Reference SteinbergSte68] for the number of points of a reductive group over a finite field implies that  $\#G(k)/q^{\dim G}=f(q^{-1})$ and
$\#G(k)/q^{\dim G}=f(q^{-1})$ and  $\#M_{\unicode[STIX]{x1D706}}(k)/q^{\dim M_{\unicode[STIX]{x1D706}}}=f_{\unicode[STIX]{x1D706}}(q^{-1})$, where
$\#M_{\unicode[STIX]{x1D706}}(k)/q^{\dim M_{\unicode[STIX]{x1D706}}}=f_{\unicode[STIX]{x1D706}}(q^{-1})$, where  $f$ and
$f$ and  $f_{\unicode[STIX]{x1D706}}$ are polynomials with constant term 1 that depend only on the root data of
$f_{\unicode[STIX]{x1D706}}$ are polynomials with constant term 1 that depend only on the root data of  $G$ and
$G$ and  $M_{\unicode[STIX]{x1D706}}$, respectively. This completes the proof.◻
$M_{\unicode[STIX]{x1D706}}$, respectively. This completes the proof.◻
2.8 Lie algebras
Let  $\mathfrak{g}$ be the real Lie algebra of
$\mathfrak{g}$ be the real Lie algebra of  $G(F_{\infty })$, and let
$G(F_{\infty })$, and let  $\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$ be the Cartan decomposition associated with
$\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$ be the Cartan decomposition associated with  $K_{\infty }$. Let
$K_{\infty }$. Let  $\mathfrak{a}\subset \mathfrak{p}$ be a maximal abelian subalgebra. We let
$\mathfrak{a}\subset \mathfrak{p}$ be a maximal abelian subalgebra. We let  $\unicode[STIX]{x1D6E5}_{\mathbb{R}}$ be the roots of
$\unicode[STIX]{x1D6E5}_{\mathbb{R}}$ be the roots of  $\mathfrak{a}$ in
$\mathfrak{a}$ in  $\mathfrak{g}$, and let
$\mathfrak{g}$, and let  $\unicode[STIX]{x1D6E5}_{\mathbb{R}}^{+}$ be a choice of positive roots. We let
$\unicode[STIX]{x1D6E5}_{\mathbb{R}}^{+}$ be a choice of positive roots. We let  $W_{\mathbb{R}}$ be the Weyl group of
$W_{\mathbb{R}}$ be the Weyl group of  $\unicode[STIX]{x1D6E5}_{\mathbb{R}}$. For
$\unicode[STIX]{x1D6E5}_{\mathbb{R}}$. For  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\mathbb{R}}$, we let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\mathbb{R}}$, we let  $m(\unicode[STIX]{x1D6FC})$ denote the dimension of the corresponding root space. We denote the Killing form on
$m(\unicode[STIX]{x1D6FC})$ denote the dimension of the corresponding root space. We denote the Killing form on  $\mathfrak{g}$ and
$\mathfrak{g}$ and  $\mathfrak{g}^{\ast }$ by
$\mathfrak{g}^{\ast }$ by  $\langle \cdot ,\cdot \rangle$, and let
$\langle \cdot ,\cdot \rangle$, and let  $\Vert \cdot \Vert$ be the associated norm on
$\Vert \cdot \Vert$ be the associated norm on  $\mathfrak{a}$ and
$\mathfrak{a}$ and  $\mathfrak{a}^{\ast }$.
$\mathfrak{a}^{\ast }$.
Let  $c(\unicode[STIX]{x1D709})$ be Harish-Chandra’s
$c(\unicode[STIX]{x1D709})$ be Harish-Chandra’s  $c$-function; see [Reference HelgasonHel08, ch. II, § 3.3]. Then it is known [Reference Duistermaat, Kolk and VaradarajanDKV79, (3.44)] that the upper bound
$c$-function; see [Reference HelgasonHel08, ch. II, § 3.3]. Then it is known [Reference Duistermaat, Kolk and VaradarajanDKV79, (3.44)] that the upper bound
 $$\begin{eqnarray}|c(\unicode[STIX]{x1D709})|^{-2}\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})\end{eqnarray}$$
$$\begin{eqnarray}|c(\unicode[STIX]{x1D709})|^{-2}\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})\end{eqnarray}$$ holds for all  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$, where we have put
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$, where we have put
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\mathbb{R}}^{+}}(1+|\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle |)^{m(\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\mathbb{R}}^{+}}(1+|\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle |)^{m(\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$2.9 Proof of Proposition 1.3
We now recall Borel’s theorem on the existence of rationally defined Cartan involutions on real semisimple Lie algebras. This is the central ingredient in the proof of Proposition 1.3.
Proposition 2.4 (Borel).
Let  $F$ be a totally real number field, and let
$F$ be a totally real number field, and let  $v_{0}$ be a real place of
$v_{0}$ be a real place of  $F$. Let
$F$. Let  $\mathfrak{g}^{\prime }$ be a real semisimple Lie algebra. There exists
$\mathfrak{g}^{\prime }$ be a real semisimple Lie algebra. There exists  $\mathfrak{g}/F$ with an involution
$\mathfrak{g}/F$ with an involution  $\unicode[STIX]{x1D703}$ defined over
$\unicode[STIX]{x1D703}$ defined over  $F$ such that
$F$ such that  $\mathfrak{g}_{v_{0}}\simeq \mathfrak{g}^{\prime }$,
$\mathfrak{g}_{v_{0}}\simeq \mathfrak{g}^{\prime }$,  $\mathfrak{g}_{v}$ is of compact type for all real
$\mathfrak{g}_{v}$ is of compact type for all real  $v\neq v_{0}$, and
$v\neq v_{0}$, and  $\unicode[STIX]{x1D703}$ induces a Cartan involution of
$\unicode[STIX]{x1D703}$ induces a Cartan involution of  $\mathfrak{g}_{v_{0}}$.
$\mathfrak{g}_{v_{0}}$.
Proof. The statement can be extracted from the proof of [Reference BorelBor63, Proposition 3.8]. For completeness we provide details.
By [Reference BorelBor63, Proposition 3.7], there exist  $\mathfrak{g}_{0}/\mathbb{Q}$ and a
$\mathfrak{g}_{0}/\mathbb{Q}$ and a  $\mathbb{Q}$-involution
$\mathbb{Q}$-involution  $\unicode[STIX]{x1D703}$ of
$\unicode[STIX]{x1D703}$ of  $\mathfrak{g}_{0}$ such that
$\mathfrak{g}_{0}$ such that  $\mathfrak{g}_{0}\,\otimes \,\mathbb{R}\simeq \mathfrak{g}^{\prime }$, and
$\mathfrak{g}_{0}\,\otimes \,\mathbb{R}\simeq \mathfrak{g}^{\prime }$, and  $\unicode[STIX]{x1D703}$ induces a Cartan involution of
$\unicode[STIX]{x1D703}$ induces a Cartan involution of  $\mathfrak{g}_{0}\,\otimes \,\mathbb{R}$. Let
$\mathfrak{g}_{0}\,\otimes \,\mathbb{R}$. Let  $\mathfrak{g}_{0}=\mathfrak{k}_{0}+\mathfrak{p}_{0}$ be the rational Cartan decomposition associated with
$\mathfrak{g}_{0}=\mathfrak{k}_{0}+\mathfrak{p}_{0}$ be the rational Cartan decomposition associated with  $\unicode[STIX]{x1D703}$. Choose
$\unicode[STIX]{x1D703}$. Choose  $\unicode[STIX]{x1D6FC}\in F$ such that
$\unicode[STIX]{x1D6FC}\in F$ such that  $F=\mathbb{Q}(\unicode[STIX]{x1D6FC})$ and
$F=\mathbb{Q}(\unicode[STIX]{x1D6FC})$ and  $\unicode[STIX]{x1D6FC}_{v_{0}}>0$, and
$\unicode[STIX]{x1D6FC}_{v_{0}}>0$, and  $\unicode[STIX]{x1D6FC}_{v}<0$ for all other real
$\unicode[STIX]{x1D6FC}_{v}<0$ for all other real  $v$. Define
$v$. Define  $\mathfrak{g}=\mathfrak{k}_{0}\otimes F+\sqrt{\unicode[STIX]{x1D6FC}}\,\mathfrak{p}_{0}\otimes F\subset \mathfrak{g}_{0}\otimes \overline{\mathbb{Q}}$. We extend
$\mathfrak{g}=\mathfrak{k}_{0}\otimes F+\sqrt{\unicode[STIX]{x1D6FC}}\,\mathfrak{p}_{0}\otimes F\subset \mathfrak{g}_{0}\otimes \overline{\mathbb{Q}}$. We extend  $\unicode[STIX]{x1D703}$ to an involution of
$\unicode[STIX]{x1D703}$ to an involution of  $\mathfrak{g}$ defined over
$\mathfrak{g}$ defined over  $F$.
$F$.
We have  $\mathfrak{g}_{v_{0}}\simeq \mathfrak{g}_{0}\otimes \mathbb{R}\simeq \mathfrak{g}^{\prime }$, and it is clear that
$\mathfrak{g}_{v_{0}}\simeq \mathfrak{g}_{0}\otimes \mathbb{R}\simeq \mathfrak{g}^{\prime }$, and it is clear that  $\unicode[STIX]{x1D703}$ induces a Cartan involution of
$\unicode[STIX]{x1D703}$ induces a Cartan involution of  $\mathfrak{g}_{v_{0}}$. If
$\mathfrak{g}_{v_{0}}$. If  $v\neq v_{0}$ is real, we have
$v\neq v_{0}$ is real, we have  $\mathfrak{g}_{v}=\mathfrak{k}_{0}\otimes \mathbb{R}+i\mathfrak{p}_{0}\otimes \mathbb{R}\subset \mathfrak{g}_{0}\otimes \mathbb{C}$ so that
$\mathfrak{g}_{v}=\mathfrak{k}_{0}\otimes \mathbb{R}+i\mathfrak{p}_{0}\otimes \mathbb{R}\subset \mathfrak{g}_{0}\otimes \mathbb{C}$ so that  $\mathfrak{g}_{v}$ is of compact type.◻
$\mathfrak{g}_{v}$ is of compact type.◻
The corresponding statement for simply connected semisimple groups, Proposition 1.3, can be deduced from the Lie algebra version, as follows.
Let  $G^{\prime }$ be as in Proposition 1.3 and let
$G^{\prime }$ be as in Proposition 1.3 and let  $\mathfrak{g}^{\prime }/\mathbb{R}$ be its Lie algebra. Let
$\mathfrak{g}^{\prime }/\mathbb{R}$ be its Lie algebra. Let  $F$ be a totally real number field and
$F$ be a totally real number field and  $v_{0}$ a real place of
$v_{0}$ a real place of  $F$. Applying Proposition 2.4 to
$F$. Applying Proposition 2.4 to  $\mathfrak{g}^{\prime }$ with this choice of
$\mathfrak{g}^{\prime }$ with this choice of  $F$ and
$F$ and  $v_{0}$, we obtain a corresponding
$v_{0}$, we obtain a corresponding  $\mathfrak{g}/F$ and involution
$\mathfrak{g}/F$ and involution  $\unicode[STIX]{x1D703}$. Let
$\unicode[STIX]{x1D703}$. Let  $\text{Int}(\mathfrak{g})$ be the identity component of
$\text{Int}(\mathfrak{g})$ be the identity component of  $\text{Aut}(\mathfrak{g})$, and let
$\text{Aut}(\mathfrak{g})$, and let  $G$ be the simply connected cover of
$G$ be the simply connected cover of  $\text{Int}(\mathfrak{g})$. Then
$\text{Int}(\mathfrak{g})$. Then  $G$ has Lie algebra
$G$ has Lie algebra  $\mathfrak{g}$, and
$\mathfrak{g}$, and  $\unicode[STIX]{x1D703}$ induces an involution of
$\unicode[STIX]{x1D703}$ induces an involution of  $G$ which we also denote by
$G$ which we also denote by  $\unicode[STIX]{x1D703}$ (as the derivative at the identity of the former is equal to the latter). Because
$\unicode[STIX]{x1D703}$ (as the derivative at the identity of the former is equal to the latter). Because  $G^{\prime }$ and
$G^{\prime }$ and  $G_{v_{0}}$ are connected, simply connected semisimple groups with isomorphic Lie algebras, they are isomorphic. If
$G_{v_{0}}$ are connected, simply connected semisimple groups with isomorphic Lie algebras, they are isomorphic. If  $v\neq v_{0}$ is real, then
$v\neq v_{0}$ is real, then  $\mathfrak{g}_{v}$ is of compact type and
$\mathfrak{g}_{v}$ is of compact type and  $G(F_{v})$ is compact.
$G(F_{v})$ is compact.
By Proposition 2.4,  $\unicode[STIX]{x1D703}$ induces a Cartan involution of
$\unicode[STIX]{x1D703}$ induces a Cartan involution of  $\mathfrak{g}_{v_{0}}$. Because
$\mathfrak{g}_{v_{0}}$. Because  $G$ is simply connected,
$G$ is simply connected,  $G_{v_{0}}$ is connected in the real topology by the Cartan connectedness theorem [Reference Onishchik and VinbergOV94, ch. 4, §2.2, Theorem 2.2], and it follows that
$G_{v_{0}}$ is connected in the real topology by the Cartan connectedness theorem [Reference Onishchik and VinbergOV94, ch. 4, §2.2, Theorem 2.2], and it follows that  $\unicode[STIX]{x1D703}$ also induces a Cartan involution of
$\unicode[STIX]{x1D703}$ also induces a Cartan involution of  $G_{v_{0}}$ (in the sense that the fixed point set
$G_{v_{0}}$ (in the sense that the fixed point set  $G_{v_{0}}^{\unicode[STIX]{x1D703}}$ is a maximal compact subgroup of
$G_{v_{0}}^{\unicode[STIX]{x1D703}}$ is a maximal compact subgroup of  $G_{v_{0}}$). This completes the proof of Proposition 1.3.
$G_{v_{0}}$). This completes the proof of Proposition 1.3.
2.10 Congruence subgroups and adelic quotients
Recall from § 2.1 the integer  $D$, and from § 2.4 the compact open subgroups
$D$, and from § 2.4 the compact open subgroups  $K_{v}$ for finite places
$K_{v}$ for finite places  $v$ and their product
$v$ and their product  $K=\prod _{v\nmid \infty }K_{v}$ inside
$K=\prod _{v\nmid \infty }K_{v}$ inside  $G(\mathbb{A}_{f})$. We now define congruence subgroups of
$G(\mathbb{A}_{f})$. We now define congruence subgroups of  $K_{v}$ and
$K_{v}$ and  $K$ to be used throughout the paper.
$K$ to be used throughout the paper.
Fix an integer  $N\geqslant 1$ prime to
$N\geqslant 1$ prime to  $D$. For
$D$. For  $v\nmid D\infty$ we write
$v\nmid D\infty$ we write  $K_{v}(N)$ for the level
$K_{v}(N)$ for the level  $N$ principal congruence subgroup, given by
$N$ principal congruence subgroup, given by  $K_{v}(N)=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v})(N))$. Here
$K_{v}(N)=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G_{v})\cap \text{SL}_{d}({\mathcal{O}}_{v})(N))$. Here  $\text{SL}_{d}({\mathcal{O}}_{v})(N)$ denotes the principal congruence subgroup of
$\text{SL}_{d}({\mathcal{O}}_{v})(N)$ denotes the principal congruence subgroup of  $\text{SL}_{d}({\mathcal{O}}_{v})$. Let
$\text{SL}_{d}({\mathcal{O}}_{v})$. Let  $S$ be a finite set of finite places prime to
$S$ be a finite set of finite places prime to  $D$. Then we put
$D$. Then we put
 $$\begin{eqnarray}K(N)=\mathop{\prod }_{v\nmid D\infty }K_{v}(N)\mathop{\prod }_{v\mid D}K_{v}\quad \text{and}\quad K^{S}(N)=\mathop{\prod }_{\substack{ v\nmid D\infty \\ v\notin S}}K_{v}(N)\mathop{\prod }_{v\mid D}K_{v}.\end{eqnarray}$$
$$\begin{eqnarray}K(N)=\mathop{\prod }_{v\nmid D\infty }K_{v}(N)\mathop{\prod }_{v\mid D}K_{v}\quad \text{and}\quad K^{S}(N)=\mathop{\prod }_{\substack{ v\nmid D\infty \\ v\notin S}}K_{v}(N)\mathop{\prod }_{v\mid D}K_{v}.\end{eqnarray}$$ For every finite  $v$ we define
$v$ we define  $K_{H,v}=H_{v}\cap K_{v}$. Letting
$K_{H,v}=H_{v}\cap K_{v}$. Letting
 $$\begin{eqnarray}K_{H}=\mathop{\prod }_{v\nmid \infty }K_{H,v}\quad \text{and}\quad K_{H}^{S}=\mathop{\prod }_{v\notin S\cup \infty }K_{H,v},\end{eqnarray}$$
$$\begin{eqnarray}K_{H}=\mathop{\prod }_{v\nmid \infty }K_{H,v}\quad \text{and}\quad K_{H}^{S}=\mathop{\prod }_{v\notin S\cup \infty }K_{H,v},\end{eqnarray}$$then the congruence manifold of interest to us is
 $$\begin{eqnarray}Y_{N}=G(F)\backslash G(\mathbb{A})/K(N)K_{H}K_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}Y_{N}=G(F)\backslash G(\mathbb{A})/K(N)K_{H}K_{\infty }.\end{eqnarray}$$ Let  $\text{Vol}_{N}$ be the volume assigned by
$\text{Vol}_{N}$ be the volume assigned by  $\prod _{v\nmid \infty }\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ to the compact open subgroup
$\prod _{v\nmid \infty }\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ to the compact open subgroup  $K(N)K_{H}$.
$K(N)K_{H}$.
Finally, we write
 $$\begin{eqnarray}[G]=G(F)\backslash G(\mathbb{A})\quad \text{and}\quad [H]=H(F)\backslash H(\mathbb{A})\end{eqnarray}$$
$$\begin{eqnarray}[G]=G(F)\backslash G(\mathbb{A})\quad \text{and}\quad [H]=H(F)\backslash H(\mathbb{A})\end{eqnarray}$$ for the automorphic spaces associated with  $G$ and
$G$ and  $H$. We shall identify
$H$. We shall identify  $L^{2}(Y_{N})$ with the functions in
$L^{2}(Y_{N})$ with the functions in  $L^{2}([G])$ fixed under
$L^{2}([G])$ fixed under  $K(N)K_{H}K_{\infty }$.
$K(N)K_{H}K_{\infty }$.
2.11 Hecke–Maass forms
Let  ${\mathcal{D}}$ be the algebra of differential operators on
${\mathcal{D}}$ be the algebra of differential operators on  $G_{\infty }^{0}/K_{\infty }$ that are invariant under the left action of
$G_{\infty }^{0}/K_{\infty }$ that are invariant under the left action of  $G_{\infty }^{0}$. Note that if we define
$G_{\infty }^{0}$. Note that if we define  $K_{v_{0}}^{+}$ to be the group of fixed points of
$K_{v_{0}}^{+}$ to be the group of fixed points of  $\unicode[STIX]{x1D703}$ on
$\unicode[STIX]{x1D703}$ on  $G_{v_{0}}$, and let
$G_{v_{0}}$, and let  $K_{\infty }^{+}$ be the group obtained by replacing
$K_{\infty }^{+}$ be the group obtained by replacing  $K_{v_{0}}$ with
$K_{v_{0}}$ with  $K_{v_{0}}^{+}$ in the definition of
$K_{v_{0}}^{+}$ in the definition of  $K_{\infty }$, then
$K_{\infty }$, then  $K_{\infty }^{+}$ is a maximal compact subgroup of
$K_{\infty }^{+}$ is a maximal compact subgroup of  $G_{\infty }$, we have
$G_{\infty }$, we have  $G_{\infty }/K_{\infty }^{+}\simeq G_{\infty }^{0}/K_{\infty }$, and the elements of
$G_{\infty }/K_{\infty }^{+}\simeq G_{\infty }^{0}/K_{\infty }$, and the elements of  ${\mathcal{D}}$ are also invariant under the larger group
${\mathcal{D}}$ are also invariant under the larger group  $G_{\infty }$. It follows that
$G_{\infty }$. It follows that  ${\mathcal{D}}$ descends to an algebra of operators on
${\mathcal{D}}$ descends to an algebra of operators on  $Y_{N}$ in a natural way.
$Y_{N}$ in a natural way.
We define a Hecke–Maass form to be a function on  $Y_{N}$ that is an eigenfunction of the ring
$Y_{N}$ that is an eigenfunction of the ring  ${\mathcal{D}}$ on
${\mathcal{D}}$ on  $Y_{N}$ and the Hecke algebra
$Y_{N}$ and the Hecke algebra  ${\mathcal{H}}_{f}$ (and hence of
${\mathcal{H}}_{f}$ (and hence of  ${\mathcal{H}}$). If
${\mathcal{H}}$). If  $\unicode[STIX]{x1D713}$ is a Hecke–Maass form and
$\unicode[STIX]{x1D713}$ is a Hecke–Maass form and  $\unicode[STIX]{x1D714}\in {\mathcal{H}}$, then, using the notation in § 2.5, we define
$\unicode[STIX]{x1D714}\in {\mathcal{H}}$, then, using the notation in § 2.5, we define  $\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D713})$ by the equation
$\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D713})$ by the equation  $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D714})\unicode[STIX]{x1D713}=\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D713})\unicode[STIX]{x1D713}$. We define the spectral parameter of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D714})\unicode[STIX]{x1D713}=\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D713})\unicode[STIX]{x1D713}$. We define the spectral parameter of  $\unicode[STIX]{x1D713}$ to be the unique
$\unicode[STIX]{x1D713}$ to be the unique  $\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W_{\mathbb{R}}$ such that
$\unicode[STIX]{x1D709}\in \mathfrak{a}_{\mathbb{C}}^{\ast }/W_{\mathbb{R}}$ such that  $\unicode[STIX]{x1D713}$ has the same eigenvalues under the action of
$\unicode[STIX]{x1D713}$ has the same eigenvalues under the action of  ${\mathcal{D}}$ as the associated spherical function
${\mathcal{D}}$ as the associated spherical function  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}}$. The Laplace eigenvalue of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}}$. The Laplace eigenvalue of  $\unicode[STIX]{x1D713}$ is given by
$\unicode[STIX]{x1D713}$ is given by  $(\unicode[STIX]{x1D6E5}+C_{1}(G)+\langle \unicode[STIX]{x1D709},\unicode[STIX]{x1D709}\rangle )\unicode[STIX]{x1D713}=0$ for some
$(\unicode[STIX]{x1D6E5}+C_{1}(G)+\langle \unicode[STIX]{x1D709},\unicode[STIX]{x1D709}\rangle )\unicode[STIX]{x1D713}=0$ for some  $C_{1}(G)\in \mathbb{R}$.
$C_{1}(G)\in \mathbb{R}$.
3 A comparison of trace formulae
In the next two sections, we state without proof a trace formula and relative trace formula, and deduce Theorems 1.1 and 1.2 from them. The trace formulae will be proved in §§5 and 6.
3.1 The trace formula
Let  $N$ be a positive integer prime to
$N$ be a positive integer prime to  $D$. Let
$D$. Let  $D^{\prime }$ be a sufficiently large multiple of
$D^{\prime }$ be a sufficiently large multiple of  $D$, depending only on
$D$, depending only on  $G$, to be chosen in § 6.4. Let
$G$, to be chosen in § 6.4. Let  $T$ be a finite set of finite places prime to
$T$ be a finite set of finite places prime to  $D^{\prime }$ and
$D^{\prime }$ and  $N$. Let
$N$. Let  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. We will use the trace formula to count Hecke–Maass forms on
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. We will use the trace formula to count Hecke–Maass forms on  $Y_{N}$ with spectral parameter near
$Y_{N}$ with spectral parameter near  $\unicode[STIX]{x1D709}$, weighted by a Hecke operator at
$\unicode[STIX]{x1D709}$, weighted by a Hecke operator at  $T$. To do this, we shall consider test functions of the form
$T$. To do this, we shall consider test functions of the form  $\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{T}\otimes k_{T}\otimes k_{\unicode[STIX]{x1D709}}$, for
$\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{T}\otimes k_{T}\otimes k_{\unicode[STIX]{x1D709}}$, for  $k_{T}\in {\mathcal{H}}_{T}$ and
$k_{T}\in {\mathcal{H}}_{T}$ and  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$, where we have put
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$, where we have put
 $$\begin{eqnarray}\mathbf{1}_{N}^{T}=\mathbf{1}_{K^{T}(N)K_{H}^{T}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}_{N}^{T}=\mathbf{1}_{K^{T}(N)K_{H}^{T}}.\end{eqnarray}$$ We introduce the following condition on  $k_{\unicode[STIX]{x1D709}}$.
$k_{\unicode[STIX]{x1D709}}$.
 $(\mathsf{P}_{\!\!\infty })$:
$(\mathsf{P}_{\!\!\infty })$: $k_{\unicode[STIX]{x1D709}}$ is supported in
$k_{\unicode[STIX]{x1D709}}$ is supported in  $\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$ and satisfies
$\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$ and satisfies  $$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(g)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(g)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-1/2}.\end{eqnarray}$$
If  $U$ is any finite set of finite places, we define
$U$ is any finite set of finite places, we define  $q_{U}=\prod _{v\in U}q_{v}$. Our asymptotic trace formula is given in the following theorem.
$q_{U}=\prod _{v\in U}q_{v}$. Our asymptotic trace formula is given in the following theorem.
Theorem 3.1. There are constants  $A,B,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}>0$ such that the following statement holds. Let
$A,B,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}>0$ such that the following statement holds. Let  $N$,
$N$,  $T$ and
$T$ and  $\unicode[STIX]{x1D709}$ be as above, and let
$\unicode[STIX]{x1D709}$ be as above, and let  $\unicode[STIX]{x1D705}\geqslant 0$. For any
$\unicode[STIX]{x1D705}\geqslant 0$. For any  $k_{T}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ and any
$k_{T}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ and any  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfying
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfying  $(\mathsf{P}_{\infty })$ we have
$(\mathsf{P}_{\infty })$ we have
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{T}\otimes k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+O(N^{-\unicode[STIX]{x1D6FF}}q_{T}^{A\unicode[STIX]{x1D705}+B}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\Vert k_{T}\Vert _{\infty }),\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{T}\otimes k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+O(N^{-\unicode[STIX]{x1D6FF}}q_{T}^{A\unicode[STIX]{x1D705}+B}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\Vert k_{T}\Vert _{\infty }),\end{eqnarray}$$ where  $\{\unicode[STIX]{x1D713}_{i}\}$ runs over an orthonormal basis of Hecke–Maass forms for
$\{\unicode[STIX]{x1D713}_{i}\}$ runs over an orthonormal basis of Hecke–Maass forms for  $L^{2}(Y_{N})$. The implied constant depends only on
$L^{2}(Y_{N})$. The implied constant depends only on  $G$,
$G$,  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $K$.
$K$.
We note that the exponents  $A$,
$A$,  $B$ and
$B$ and  $\unicode[STIX]{x1D6FF}$ are ineffective, and this is the only source of ineffectiveness of the exponent in Theorems 1.1 and 1.2. As discussed in § 1.1, this comes from using theorems of Finis and Lapid and of Cluckers, Gordon and Halupczok to bound orbital integrals.
$\unicode[STIX]{x1D6FF}$ are ineffective, and this is the only source of ineffectiveness of the exponent in Theorems 1.1 and 1.2. As discussed in § 1.1, this comes from using theorems of Finis and Lapid and of Cluckers, Gordon and Halupczok to bound orbital integrals.
3.2 The relative trace formula
For  $\unicode[STIX]{x1D713}\in C^{\infty }(G(F)\backslash G(\mathbb{A}))$ we consider the
$\unicode[STIX]{x1D713}\in C^{\infty }(G(F)\backslash G(\mathbb{A}))$ we consider the  $H$-automorphic period
$H$-automorphic period
 $$\begin{eqnarray}{\mathcal{P}}_{H}(\unicode[STIX]{x1D713})=\int _{H(F)\backslash H(\mathbb{A})}\unicode[STIX]{x1D713}(h)\,dh.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{H}(\unicode[STIX]{x1D713})=\int _{H(F)\backslash H(\mathbb{A})}\unicode[STIX]{x1D713}(h)\,dh.\end{eqnarray}$$ Our relative trace formula will give the average size of these periods over an orthonormal basis  $\{\unicode[STIX]{x1D713}_{i}\}$ of Hecke–Maass forms for
$\{\unicode[STIX]{x1D713}_{i}\}$ of Hecke–Maass forms for  $L^{2}(Y_{N})$.
$L^{2}(Y_{N})$.
Let  $N$ be a positive integer prime to
$N$ be a positive integer prime to  $D$,
$D$,  $S$ a finite set of finite places prime to
$S$ a finite set of finite places prime to  $D$ and
$D$ and  $N$, and
$N$, and  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. We now consider test functions of the form
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. We now consider test functions of the form  $\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$, for
$\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$, for  $k_{S}\in {\mathcal{H}}_{S}$ and
$k_{S}\in {\mathcal{H}}_{S}$ and  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$. As well as condition
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$. As well as condition  $(\mathsf{P}_{\infty })$, we shall use the following condition on
$(\mathsf{P}_{\infty })$, we shall use the following condition on  $k_{S}$.
$k_{S}$.
 $(\mathsf{P}_{S})$:
$(\mathsf{P}_{S})$:There is
 $R>1$ such that
$R>1$ such that  $\Vert g\Vert _{S}\leqslant R$ for all
$\Vert g\Vert _{S}\leqslant R$ for all  $g\in \text{supp}(k_{S})$.
$g\in \text{supp}(k_{S})$.
The main term of our formula is expressed in terms of the averaging map
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}:L^{1}(G(F_{S}))\longrightarrow L^{1}(G(F_{S})/H(F_{S}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}:L^{1}(G(F_{S}))\longrightarrow L^{1}(G(F_{S})/H(F_{S}))\end{eqnarray}$$given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}k_{S}(g)=\int _{H(F_{S})}k_{S}(gh)\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}k_{S}(g)=\int _{H(F_{S})}k_{S}(gh)\,dh.\end{eqnarray}$$With this notation in hand, we may state our asymptotic relative trace formula.
Proposition 3.2. There is  $A>0$ such that the following statement holds. Let
$A>0$ such that the following statement holds. Let  $N$,
$N$,  $S$ and
$S$ and  $\unicode[STIX]{x1D709}$ be as above. Let
$\unicode[STIX]{x1D709}$ be as above. Let  $k_{S}\in {\mathcal{H}}_{S}$ satisfy
$k_{S}\in {\mathcal{H}}_{S}$ satisfy  $(\mathsf{P}_{S})$ and
$(\mathsf{P}_{S})$ and  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy  $(\mathsf{P}_{\!\!\infty })$. Then
$(\mathsf{P}_{\!\!\infty })$. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\text{vol}([H])\unicode[STIX]{x1D6F1}_{H}k_{S}(1)k_{\unicode[STIX]{x1D709}}(1)+O\big(\#(\text{supp}\,k_{S}/K_{S})\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A}\Vert k_{S}\Vert _{\infty }\big),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\text{vol}([H])\unicode[STIX]{x1D6F1}_{H}k_{S}(1)k_{\unicode[STIX]{x1D709}}(1)+O\big(\#(\text{supp}\,k_{S}/K_{S})\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A}\Vert k_{S}\Vert _{\infty }\big),\nonumber\end{eqnarray}$$ where  $\{\unicode[STIX]{x1D713}_{i}\}$ runs over an orthonormal basis of Hecke–Maass forms for
$\{\unicode[STIX]{x1D713}_{i}\}$ runs over an orthonormal basis of Hecke–Maass forms for  $L^{2}(Y_{N})$.
$L^{2}(Y_{N})$.
3.3 Proof of Theorems 1.1 and 1.2
Recall from § 2.2 that  ${\mathcal{P}}$ denotes the set of finite places of
${\mathcal{P}}$ denotes the set of finite places of  $F$ that do not divide
$F$ that do not divide  $D$ and at which
$D$ and at which  $T$ splits. For
$T$ splits. For  $v\in {\mathcal{P}}$ and
$v\in {\mathcal{P}}$ and  $\unicode[STIX]{x1D707}\in X_{\ast }(T)$, we define
$\unicode[STIX]{x1D707}\in X_{\ast }(T)$, we define  $\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D707})\in {\mathcal{H}}_{v}$ to be the function supported on
$\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D707})\in {\mathcal{H}}_{v}$ to be the function supported on  $K_{v}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})K_{v}$ and taking the value
$K_{v}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})K_{v}$ and taking the value  $q_{v}^{-\Vert \unicode[STIX]{x1D707}\Vert ^{\ast }}$ there. Let
$q_{v}^{-\Vert \unicode[STIX]{x1D707}\Vert ^{\ast }}$ there. Let  $P$ be a positive integer and put
$P$ be a positive integer and put
 $$\begin{eqnarray}S=\{v\in {\mathcal{P}}:P/2\leqslant q_{v}<P,\;v\nmid N,\;v\nmid D^{\prime }\}.\end{eqnarray}$$
$$\begin{eqnarray}S=\{v\in {\mathcal{P}}:P/2\leqslant q_{v}<P,\;v\nmid N,\;v\nmid D^{\prime }\}.\end{eqnarray}$$ Choose any non-zero  $\unicode[STIX]{x1D708}\in X_{\ast }(T)$, and let
$\unicode[STIX]{x1D708}\in X_{\ast }(T)$, and let
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{S}=\mathop{\sum }_{v\in S}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{S}=\mathop{\sum }_{v\in S}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}),\end{eqnarray}$$ where, as in § 2.6, we are identifying  ${\mathcal{H}}_{v}$ with a subalgebra of
${\mathcal{H}}_{v}$ with a subalgebra of  ${\mathcal{H}}_{S}$ in the natural way.
${\mathcal{H}}_{S}$ in the natural way.
In § 4 we will deduce the following weighted bounds from our two trace formulae.
Proposition 3.3. For any  $\unicode[STIX]{x1D708}$ and
$\unicode[STIX]{x1D708}$ and  $P$, we have
$P$, we have
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}\ll P\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}\ll P\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$ In addition, if 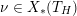 $\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies the
$\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies the  $H$-large inequality (3), then there is
$H$-large inequality (3), then there is  $Q>0$ depending on
$Q>0$ depending on  $\unicode[STIX]{x1D708}$ such that
$\unicode[STIX]{x1D708}$ such that
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})).\end{eqnarray}$$ The exponent  $A$ and the implied constants depend on the choice of
$A$ and the implied constants depend on the choice of  $\unicode[STIX]{x1D708}$.
$\unicode[STIX]{x1D708}$.
Theorems 1.1 and 1.2 follow easily from Proposition 3.3, as we now explain. Choose  $0\neq \unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfying (3), and choose
$0\neq \unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfying (3), and choose  $P$ to be a small power of
$P$ to be a small power of  $(1+\Vert \unicode[STIX]{x1D709}\Vert )N$. We then find
$(1+\Vert \unicode[STIX]{x1D709}\Vert )N$. We then find  $\unicode[STIX]{x1D6FF}>0$ such that for
$\unicode[STIX]{x1D6FF}>0$ such that for  $(1+\Vert \unicode[STIX]{x1D709}\Vert )N$ sufficiently large,
$(1+\Vert \unicode[STIX]{x1D709}\Vert )N$ sufficiently large,
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{\unicode[STIX]{x1D6FF}}N^{\unicode[STIX]{x1D6FF}}\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{\unicode[STIX]{x1D6FF}}N^{\unicode[STIX]{x1D6FF}}\end{eqnarray}$$and
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\gg _{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{2\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}}N^{2\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\gg _{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{2\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}}N^{2\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}}.\end{eqnarray}$$ Comparing (9) and (10) we find that there exist  $\unicode[STIX]{x1D6FF}>0$ and
$\unicode[STIX]{x1D6FF}>0$ and  $Q>1$ such that, for every
$Q>1$ such that, for every  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ and every
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ and every  $N$ with
$N$ with  $(1+\Vert \unicode[STIX]{x1D709}\Vert )N$ large, there is a Hecke–Maass form
$(1+\Vert \unicode[STIX]{x1D709}\Vert )N$ large, there is a Hecke–Maass form  $\unicode[STIX]{x1D713}_{i}$ on
$\unicode[STIX]{x1D713}_{i}$ on  $Y_{N}$ with spectral parameter
$Y_{N}$ with spectral parameter  $\Vert \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q$ and satisfying
$\Vert \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q$ and satisfying  $|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|\gg (1+\Vert \unicode[STIX]{x1D709}_{i}\Vert )^{\unicode[STIX]{x1D6FF}}N^{\unicode[STIX]{x1D6FF}}$. This implies the same lower bound on
$|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|\gg (1+\Vert \unicode[STIX]{x1D709}_{i}\Vert )^{\unicode[STIX]{x1D6FF}}N^{\unicode[STIX]{x1D6FF}}$. This implies the same lower bound on  $\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$, and in particular proves Theorem 1.1.
$\Vert \unicode[STIX]{x1D713}_{i}\Vert _{\infty }$, and in particular proves Theorem 1.1.
It remains to refine this power growth to obtain the stated lower bounds of Theorem 1.2. For this, we will make a special choice of orthonormal basis of Hecke–Maass forms for  $L^{2}(Y_{N})$. First recall that we have a Hilbert direct sum decomposition
$L^{2}(Y_{N})$. First recall that we have a Hilbert direct sum decomposition
 $$\begin{eqnarray}L^{2}(Y_{N})=\bigoplus _{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }},\end{eqnarray}$$
$$\begin{eqnarray}L^{2}(Y_{N})=\bigoplus _{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }},\end{eqnarray}$$ the sum ranging over irreducible representations of  $G_{\infty }^{0}\times G(\mathbb{A}_{f})$ in
$G_{\infty }^{0}\times G(\mathbb{A}_{f})$ in  $L^{2}(G(F)\backslash G(\mathbb{A}))$ satisfying
$L^{2}(G(F)\backslash G(\mathbb{A}))$ satisfying  $\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }}\neq 0$, each occurring with multiplicity
$\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }}\neq 0$, each occurring with multiplicity  $m(\unicode[STIX]{x1D70B})$. Each
$m(\unicode[STIX]{x1D70B})$. Each  $\unicode[STIX]{x1D70B}$ gives rise to a spectral datum
$\unicode[STIX]{x1D70B}$ gives rise to a spectral datum  $c_{\unicode[STIX]{x1D70B}}$ (as defined in the paragraph preceding Theorem 1.2), and this assignment
$c_{\unicode[STIX]{x1D70B}}$ (as defined in the paragraph preceding Theorem 1.2), and this assignment  $\unicode[STIX]{x1D70B}\mapsto c_{\unicode[STIX]{x1D70B}}$ is finite-to-one. Given a spectral datum
$\unicode[STIX]{x1D70B}\mapsto c_{\unicode[STIX]{x1D70B}}$ is finite-to-one. Given a spectral datum  $c$ for
$c$ for  $(G,N)$, the space
$(G,N)$, the space  $V(N,c)$ is the direct sum of
$V(N,c)$ is the direct sum of  $m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }}$ over all
$m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}^{K(N)K_{H}K_{\infty }}$ over all  $\unicode[STIX]{x1D70B}$ in the fiber over
$\unicode[STIX]{x1D70B}$ in the fiber over  $c$.
$c$.
Let  $\{c_{i}\}$ be an enumeration of the spectral data, and for each
$\{c_{i}\}$ be an enumeration of the spectral data, and for each  $c_{i}$ write
$c_{i}$ write  $V_{i}=V(N,c_{i})$ and
$V_{i}=V(N,c_{i})$ and  $\unicode[STIX]{x1D709}_{i}=\unicode[STIX]{x1D709}(c_{i})$. The automorphic period
$\unicode[STIX]{x1D709}_{i}=\unicode[STIX]{x1D709}(c_{i})$. The automorphic period  ${\mathcal{P}}_{H}$ defines a linear functional on each finite-dimensional vector space
${\mathcal{P}}_{H}$ defines a linear functional on each finite-dimensional vector space  $V_{i}$, and its kernel is of codimension at most 1. If the kernel is of codimension 1 we let
$V_{i}$, and its kernel is of codimension at most 1. If the kernel is of codimension 1 we let  $\unicode[STIX]{x1D719}_{i}\in V_{i}$ be a unit normal to it, and otherwise choose
$\unicode[STIX]{x1D719}_{i}\in V_{i}$ be a unit normal to it, and otherwise choose  $\unicode[STIX]{x1D719}_{i}\in V_{i}$ to be an arbitrary unit vector. We may complete this set of vectors to an orthonormal basis of Hecke–Maass forms for
$\unicode[STIX]{x1D719}_{i}\in V_{i}$ to be an arbitrary unit vector. We may complete this set of vectors to an orthonormal basis of Hecke–Maass forms for  $L^{2}(Y_{N})$, to which we apply (9) and (10). Since
$L^{2}(Y_{N})$, to which we apply (9) and (10). Since  ${\mathcal{H}}$ acts as a scalar on
${\mathcal{H}}$ acts as a scalar on  $V_{i}$ we may write the left-hand side of (9) as
$V_{i}$ we may write the left-hand side of (9) as
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\substack{ c_{i} \\ \Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D719}_{i})|^{2}\dim V_{i},\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\substack{ c_{i} \\ \Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D719}_{i})|^{2}\dim V_{i},\end{eqnarray}$$and the left-hand side of (10) as
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\substack{ c_{i} \\ \Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D719}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D719}_{i})|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\substack{ c_{i} \\ \Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D719}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D719}_{i})|^{2}.\end{eqnarray}$$We obtain Theorem 1.2 by comparing the right-hand sides of (9) and (10) as before. ◻
4 Bounds for average periods
We now deduce the average period bounds of Proposition 3.3 from Theorem 3.1 and Proposition 3.2. For this, we must choose test functions  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ and
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ and  $k_{S}\in {\mathcal{H}}_{S}$ to insert into Theorem 3.1 and Proposition 3.2 and explicate the error terms in those results.
$k_{S}\in {\mathcal{H}}_{S}$ to insert into Theorem 3.1 and Proposition 3.2 and explicate the error terms in those results.
4.1 The archimedean test function
Let  $G_{\infty }^{0}$ denote the connected component of the identity in
$G_{\infty }^{0}$ denote the connected component of the identity in  $G_{\infty }$ in the real topology. If
$G_{\infty }$ in the real topology. If  $\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$, we define
$\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$, we define  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ to be the corresponding spherical function on
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ to be the corresponding spherical function on  $G_{\infty }^{0}$. If
$G_{\infty }^{0}$. If  $k_{\infty }\in C_{c}^{\infty }(G_{\infty }^{0})$, we define its Harish-Chandra transform by
$k_{\infty }\in C_{c}^{\infty }(G_{\infty }^{0})$, we define its Harish-Chandra transform by
 $$\begin{eqnarray}\widehat{k}_{\infty }(\unicode[STIX]{x1D707})=\int _{G_{\infty }^{0}}k_{\infty }(g)\unicode[STIX]{x1D711}_{-\unicode[STIX]{x1D707}}(g)\,d\unicode[STIX]{x1D707}_{G,\infty }^{\text{can}}(g).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{k}_{\infty }(\unicode[STIX]{x1D707})=\int _{G_{\infty }^{0}}k_{\infty }(g)\unicode[STIX]{x1D711}_{-\unicode[STIX]{x1D707}}(g)\,d\unicode[STIX]{x1D707}_{G,\infty }^{\text{can}}(g).\end{eqnarray}$$ Note that this is related to our earlier notation as follows: if  $\unicode[STIX]{x1D713}$ is a Maass form with spectral parameter
$\unicode[STIX]{x1D713}$ is a Maass form with spectral parameter  $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $k_{\infty }$ is bi-
$k_{\infty }$ is bi- $K_{\infty }$-invariant, then
$K_{\infty }$-invariant, then  $\widehat{k}_{\infty }(\unicode[STIX]{x1D713})=\widehat{k}_{\infty }(-\unicode[STIX]{x1D707})$.
$\widehat{k}_{\infty }(\unicode[STIX]{x1D713})=\widehat{k}_{\infty }(-\unicode[STIX]{x1D707})$.
We shall choose  $k_{\unicode[STIX]{x1D709}}$ so that its Harish-Chandra transform concentrates around
$k_{\unicode[STIX]{x1D709}}$ so that its Harish-Chandra transform concentrates around  $-\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. For this we first take a function
$-\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$. For this we first take a function  $h_{0}\in C^{\infty }(\mathfrak{a}^{\ast })$ of Paley–Wiener type that is real, non-negative and satisfies
$h_{0}\in C^{\infty }(\mathfrak{a}^{\ast })$ of Paley–Wiener type that is real, non-negative and satisfies  $h_{0}(0)=1$. We implicitly extend
$h_{0}(0)=1$. We implicitly extend  $h_{0}$ to a function on
$h_{0}$ to a function on  $\mathfrak{a}_{\mathbb{C}}^{\ast }$. Let
$\mathfrak{a}_{\mathbb{C}}^{\ast }$. Let
 $$\begin{eqnarray}h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D708})=\mathop{\sum }_{w\in W_{\mathbb{R}}}h_{0}(w\unicode[STIX]{x1D708}-\unicode[STIX]{x1D709}),\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D708})=\mathop{\sum }_{w\in W_{\mathbb{R}}}h_{0}(w\unicode[STIX]{x1D708}-\unicode[STIX]{x1D709}),\end{eqnarray}$$ and let  $k_{\unicode[STIX]{x1D709}}^{0}$ be the bi-
$k_{\unicode[STIX]{x1D709}}^{0}$ be the bi- $K_{\infty }$-invariant function on
$K_{\infty }$-invariant function on  $G_{\infty }^{0}$ satisfying
$G_{\infty }^{0}$ satisfying  $\widehat{k}_{\unicode[STIX]{x1D709}}^{0}(-\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})$. We define
$\widehat{k}_{\unicode[STIX]{x1D709}}^{0}(-\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})$. We define  $k_{\unicode[STIX]{x1D709}}=k_{\unicode[STIX]{x1D709}}^{0}\ast k_{\unicode[STIX]{x1D709}}^{0}$ and
$k_{\unicode[STIX]{x1D709}}=k_{\unicode[STIX]{x1D709}}^{0}\ast k_{\unicode[STIX]{x1D709}}^{0}$ and  $h_{\unicode[STIX]{x1D709}}=(h_{\unicode[STIX]{x1D709}}^{0})^{2}$. We have
$h_{\unicode[STIX]{x1D709}}=(h_{\unicode[STIX]{x1D709}}^{0})^{2}$. We have  $\widehat{k}_{\unicode[STIX]{x1D709}}(-\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})$, so that if
$\widehat{k}_{\unicode[STIX]{x1D709}}(-\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})$, so that if  $\unicode[STIX]{x1D713}$ has spectral parameter
$\unicode[STIX]{x1D713}$ has spectral parameter  $\unicode[STIX]{x1D707}$ as before then
$\unicode[STIX]{x1D707}$ as before then  $\widehat{k}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D713})=h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})$. We define a unitary spectral parameter to be a spectral parameter of a spherical unitary representation of
$\widehat{k}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D713})=h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})$. We define a unitary spectral parameter to be a spectral parameter of a spherical unitary representation of  $G_{\infty }^{0}$. We have
$G_{\infty }^{0}$. We have  $\Vert \Im \unicode[STIX]{x1D707}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$ for any unitary spectral parameter
$\Vert \Im \unicode[STIX]{x1D707}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$ for any unitary spectral parameter  $\unicode[STIX]{x1D707}$ [Reference HelgasonHel00, ch. IV, Theorem 8.1]. If
$\unicode[STIX]{x1D707}$ [Reference HelgasonHel00, ch. IV, Theorem 8.1]. If  $\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is unitary, Lemma 4.1 implies that
$\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is unitary, Lemma 4.1 implies that  $h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})h_{\unicode[STIX]{x1D709}}^{0}(\overline{\unicode[STIX]{x1D707}})=|h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})|^{2}\geqslant 0$.
$h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})=h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})h_{\unicode[STIX]{x1D709}}^{0}(\overline{\unicode[STIX]{x1D707}})=|h_{\unicode[STIX]{x1D709}}^{0}(\unicode[STIX]{x1D707})|^{2}\geqslant 0$.
Lemma 4.1. If  $\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is a unitary spectral parameter, then
$\unicode[STIX]{x1D707}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is a unitary spectral parameter, then  $W_{\mathbb{R}}\unicode[STIX]{x1D707}=W_{\mathbb{R}}\overline{\unicode[STIX]{x1D707}}$.
$W_{\mathbb{R}}\unicode[STIX]{x1D707}=W_{\mathbb{R}}\overline{\unicode[STIX]{x1D707}}$.
Proof. It suffices to show that  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D711}_{\overline{\unicode[STIX]{x1D707}}}$. Realizing
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D711}_{\overline{\unicode[STIX]{x1D707}}}$. Realizing  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ as a matrix coefficient of a unitary representation gives
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ as a matrix coefficient of a unitary representation gives  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(g)=\overline{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D707}}(g^{-1})$ for all
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(g)=\overline{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D707}}(g^{-1})$ for all  $g$. The usual formula for
$g$. The usual formula for  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ as a
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$ as a  $K_{\infty }$-integral gives
$K_{\infty }$-integral gives  $\overline{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D707}}(g^{-1})=\unicode[STIX]{x1D711}_{-\overline{\unicode[STIX]{x1D707}}}(g^{-1})$. The identity
$\overline{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D707}}(g^{-1})=\unicode[STIX]{x1D711}_{-\overline{\unicode[STIX]{x1D707}}}(g^{-1})$. The identity  $\unicode[STIX]{x1D711}_{-\overline{\unicode[STIX]{x1D707}}}(g^{-1})=\unicode[STIX]{x1D711}_{\overline{\unicode[STIX]{x1D707}}}(g)$, obtained for example by setting
$\unicode[STIX]{x1D711}_{-\overline{\unicode[STIX]{x1D707}}}(g^{-1})=\unicode[STIX]{x1D711}_{\overline{\unicode[STIX]{x1D707}}}(g)$, obtained for example by setting  $h=1$ in [Reference HelgasonHel00, ch. IV, Lemma 4.4] and comparing with Theorem 4.3 there, completes the proof.◻
$h=1$ in [Reference HelgasonHel00, ch. IV, Lemma 4.4] and comparing with Theorem 4.3 there, completes the proof.◻
Lemma 4.2. The function  $k_{\unicode[STIX]{x1D709}}$ satisfies property
$k_{\unicode[STIX]{x1D709}}$ satisfies property  $(\mathsf{P}_{\!\!\infty })$.
$(\mathsf{P}_{\!\!\infty })$.
Proof. Note that  $k_{\unicode[STIX]{x1D709}}$ is of compact support independent of
$k_{\unicode[STIX]{x1D709}}$ is of compact support independent of  $\unicode[STIX]{x1D709}$ from the Paley–Wiener theorem of [Reference GangolliGan71]; we may thus take
$\unicode[STIX]{x1D709}$ from the Paley–Wiener theorem of [Reference GangolliGan71]; we may thus take  $h_{0}$ so that the support of
$h_{0}$ so that the support of  $k_{\unicode[STIX]{x1D709}}$ lies in
$k_{\unicode[STIX]{x1D709}}$ lies in  $\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$ for all
$\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$ for all  $\unicode[STIX]{x1D709}$.
$\unicode[STIX]{x1D709}$.
We have the inversion formula
 $$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(g)=\frac{1}{|W_{\mathbb{R}}|}\int _{\mathfrak{a}^{\ast }}\widehat{k}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(g)|c(\unicode[STIX]{x1D707})|^{-2}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(g)=\frac{1}{|W_{\mathbb{R}}|}\int _{\mathfrak{a}^{\ast }}\widehat{k}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(g)|c(\unicode[STIX]{x1D707})|^{-2}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$ We can now quote either [Reference Blomer and PohlBP16, Theorem 2] or [Reference Matz and TemplierMT15, Proposition 7.2] and apply our conditions on  $G_{\infty }$, to find
$G_{\infty }$, to find
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(x)\,\ll _{C}\,(1+\Vert \unicode[STIX]{x1D707}\Vert d(x,K_{\infty }))^{-1/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}(x)\,\ll _{C}\,(1+\Vert \unicode[STIX]{x1D707}\Vert d(x,K_{\infty }))^{-1/2},\end{eqnarray}$$ for  $\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$ and
$\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$ and  $x$ in a compact set
$x$ in a compact set  $C\subset G_{\infty }$. In the inversion formula (11), we apply (4) to bound the Plancherel density function, (12) to bound the spherical function, and recall the concentration of
$C\subset G_{\infty }$. In the inversion formula (11), we apply (4) to bound the Plancherel density function, (12) to bound the spherical function, and recall the concentration of  $\widehat{k}_{\unicode[STIX]{x1D709}}$ around
$\widehat{k}_{\unicode[STIX]{x1D709}}$ around  $-\unicode[STIX]{x1D709}$, to obtain
$-\unicode[STIX]{x1D709}$, to obtain
 $$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(x)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(x,K_{\infty }))^{-1/2},\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D709}}(x)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(x,K_{\infty }))^{-1/2},\end{eqnarray}$$whence the claim. ◻
The following lemma will be helpful when truncating spectral sums. We let  $B(\unicode[STIX]{x1D707})\subset \mathfrak{a}^{\ast }$ denote the unit ball around
$B(\unicode[STIX]{x1D707})\subset \mathfrak{a}^{\ast }$ denote the unit ball around  $\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$.
$\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$.
Lemma 4.3. We may choose the function  $h_{0}$ so that the functions
$h_{0}$ so that the functions  $h_{\unicode[STIX]{x1D707}}$,
$h_{\unicode[STIX]{x1D707}}$,  $\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$, have the following property: if
$\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$, have the following property: if  $\unicode[STIX]{x1D706}$ is a unitary spectral parameter with
$\unicode[STIX]{x1D706}$ is a unitary spectral parameter with  $\Re \unicode[STIX]{x1D706}\in B(\unicode[STIX]{x1D707})$, then
$\Re \unicode[STIX]{x1D706}\in B(\unicode[STIX]{x1D707})$, then  $h_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D706})\geqslant c>0$ for some
$h_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D706})\geqslant c>0$ for some  $c$ depending only on
$c$ depending only on  $G$.
$G$.
Proof. Let  $0<\unicode[STIX]{x1D6FF}<1$. Let
$0<\unicode[STIX]{x1D6FF}<1$. Let  $b\in C_{0}^{\infty }(\mathfrak{a})$ be non-negative, supported in the
$b\in C_{0}^{\infty }(\mathfrak{a})$ be non-negative, supported in the  $\unicode[STIX]{x1D6FF}$-ball around
$\unicode[STIX]{x1D6FF}$-ball around  $0$, and satisfy
$0$, and satisfy  $\int b=1$. We further assume that
$\int b=1$. We further assume that  $b=b_{0}\ast b_{0}$ for some even real-valued
$b=b_{0}\ast b_{0}$ for some even real-valued  $b_{0}$, which ensures that
$b_{0}$, which ensures that  $\widehat{b}(\unicode[STIX]{x1D708})$ is non-negative for
$\widehat{b}(\unicode[STIX]{x1D708})$ is non-negative for  $\unicode[STIX]{x1D708}\in \mathfrak{a}^{\ast }$. We will show that
$\unicode[STIX]{x1D708}\in \mathfrak{a}^{\ast }$. We will show that  $h_{0}=\widehat{b}$ suffices in our construction of
$h_{0}=\widehat{b}$ suffices in our construction of  $h_{\unicode[STIX]{x1D707}}$.
$h_{\unicode[STIX]{x1D707}}$.
We let  $C>0$ be a constant depending only on
$C>0$ be a constant depending only on  $G$ that may vary from line to line. We start by showing that
$G$ that may vary from line to line. We start by showing that  $\Re \widehat{b}(\unicode[STIX]{x1D708})\geqslant -C\unicode[STIX]{x1D6FF}$ for all
$\Re \widehat{b}(\unicode[STIX]{x1D708})\geqslant -C\unicode[STIX]{x1D6FF}$ for all  $\unicode[STIX]{x1D708}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ with
$\unicode[STIX]{x1D708}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ with  $\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$. We have
$\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$. We have
 $$\begin{eqnarray}\displaystyle \widehat{b}(\unicode[STIX]{x1D708}) & = & \displaystyle \int _{\mathfrak{a}}b(H)e^{-i\unicode[STIX]{x1D708}(H)}\,dH\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathfrak{a}}b(H)[e^{-i\Re \unicode[STIX]{x1D708}(H)}+(e^{-i\unicode[STIX]{x1D708}(H)}-e^{-i\Re \unicode[STIX]{x1D708}(H)})]\,dH\nonumber\\ \displaystyle & = & \displaystyle \widehat{b}(\Re \unicode[STIX]{x1D708})+\int _{\mathfrak{a}}b(H)e^{-i\Re \unicode[STIX]{x1D708}(H)}(e^{\Im \unicode[STIX]{x1D708}(H)}-1)\,dH.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{b}(\unicode[STIX]{x1D708}) & = & \displaystyle \int _{\mathfrak{a}}b(H)e^{-i\unicode[STIX]{x1D708}(H)}\,dH\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathfrak{a}}b(H)[e^{-i\Re \unicode[STIX]{x1D708}(H)}+(e^{-i\unicode[STIX]{x1D708}(H)}-e^{-i\Re \unicode[STIX]{x1D708}(H)})]\,dH\nonumber\\ \displaystyle & = & \displaystyle \widehat{b}(\Re \unicode[STIX]{x1D708})+\int _{\mathfrak{a}}b(H)e^{-i\Re \unicode[STIX]{x1D708}(H)}(e^{\Im \unicode[STIX]{x1D708}(H)}-1)\,dH.\nonumber\end{eqnarray}$$ As  $\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$, we have
$\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$, we have  $|e^{\Im \unicode[STIX]{x1D708}(H)}-1|\leqslant C\unicode[STIX]{x1D6FF}$ for all
$|e^{\Im \unicode[STIX]{x1D708}(H)}-1|\leqslant C\unicode[STIX]{x1D6FF}$ for all  $H\in \text{supp}(b)$, so that
$H\in \text{supp}(b)$, so that
 $$\begin{eqnarray}\Re \widehat{b}(\unicode[STIX]{x1D708})\geqslant \widehat{b}(\Re \unicode[STIX]{x1D708})-C\unicode[STIX]{x1D6FF}\geqslant -C\unicode[STIX]{x1D6FF}\end{eqnarray}$$
$$\begin{eqnarray}\Re \widehat{b}(\unicode[STIX]{x1D708})\geqslant \widehat{b}(\Re \unicode[STIX]{x1D708})-C\unicode[STIX]{x1D6FF}\geqslant -C\unicode[STIX]{x1D6FF}\end{eqnarray}$$as required.
We now take  $h_{0}=\widehat{b}$, and construct
$h_{0}=\widehat{b}$, and construct  $h_{\unicode[STIX]{x1D707}}^{0}$ and
$h_{\unicode[STIX]{x1D707}}^{0}$ and  $h_{\unicode[STIX]{x1D707}}$ as before. If we choose
$h_{\unicode[STIX]{x1D707}}$ as before. If we choose  $\unicode[STIX]{x1D6FF}$ small, we will have
$\unicode[STIX]{x1D6FF}$ small, we will have  $\Re h_{0}(\unicode[STIX]{x1D708})\geqslant 1/2$ for all
$\Re h_{0}(\unicode[STIX]{x1D708})\geqslant 1/2$ for all  $\unicode[STIX]{x1D708}$ with
$\unicode[STIX]{x1D708}$ with  $\Vert \Re \unicode[STIX]{x1D708}\Vert \leqslant 1$,
$\Vert \Re \unicode[STIX]{x1D708}\Vert \leqslant 1$,  $\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$. Therefore if
$\Vert \Im \unicode[STIX]{x1D708}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$. Therefore if  $\unicode[STIX]{x1D706}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is unitary with
$\unicode[STIX]{x1D706}\in \mathfrak{a}_{\mathbb{C}}^{\ast }$ is unitary with  $\Re \unicode[STIX]{x1D706}\in B(\unicode[STIX]{x1D707})$, the bound
$\Re \unicode[STIX]{x1D706}\in B(\unicode[STIX]{x1D707})$, the bound  $\Vert \Im \unicode[STIX]{x1D706}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$ implies that
$\Vert \Im \unicode[STIX]{x1D706}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$ implies that
 $$\begin{eqnarray}\displaystyle \Re h_{\unicode[STIX]{x1D707}}^{0}(\unicode[STIX]{x1D706}) & = & \displaystyle \mathop{\sum }_{w\in W_{\mathbb{R}}}\Re h_{0}(w\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \Re h_{0}(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707})-C\unicode[STIX]{x1D6FF}\geqslant 1/4.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Re h_{\unicode[STIX]{x1D707}}^{0}(\unicode[STIX]{x1D706}) & = & \displaystyle \mathop{\sum }_{w\in W_{\mathbb{R}}}\Re h_{0}(w\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \Re h_{0}(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707})-C\unicode[STIX]{x1D6FF}\geqslant 1/4.\nonumber\end{eqnarray}$$ This gives  $h_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D706})=|h_{\unicode[STIX]{x1D707}}^{0}(\unicode[STIX]{x1D706})|^{2}\geqslant 1/16$ as required.◻
$h_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D706})=|h_{\unicode[STIX]{x1D707}}^{0}(\unicode[STIX]{x1D706})|^{2}\geqslant 1/16$ as required.◻
4.2 The  $S$-adic test function
$S$-adic test function
We choose the test function at places in  $S$ to be
$S$ to be  $k_{S}=\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }\in {\mathcal{H}}_{S}$, where
$k_{S}=\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }\in {\mathcal{H}}_{S}$, where  $\unicode[STIX]{x1D714}_{S}$ is as in § 3.3.
$\unicode[STIX]{x1D714}_{S}$ is as in § 3.3.
Lemma 4.4. The function  $k_{S}$ satisfies the following properties.
$k_{S}$ satisfies the following properties.
(a) There is
 $B>0$ such that
$B>0$ such that  $\Vert g\Vert _{S}\ll P^{B}$ for all
$\Vert g\Vert _{S}\ll P^{B}$ for all  $g\in \text{supp}(k_{S})$.
$g\in \text{supp}(k_{S})$.(b) We have
 $\Vert k_{S}\Vert _{\infty }\ll P$.
$\Vert k_{S}\Vert _{\infty }\ll P$.(c) There is
 $C>0$ such that
$C>0$ such that  $\#(\text{supp}\,k_{S}/K_{S})\ll P^{C}$.
$\#(\text{supp}\,k_{S}/K_{S})\ll P^{C}$.
The exponents  $B$ and
$B$ and  $C$ depend on the underlying choice of
$C$ depend on the underlying choice of  $\unicode[STIX]{x1D708}$ in the definition of
$\unicode[STIX]{x1D708}$ in the definition of  $k_{S}$. All implied constants depend on
$k_{S}$. All implied constants depend on  $G$ and
$G$ and  $\unicode[STIX]{x1D708}$.
$\unicode[STIX]{x1D708}$.
Proof. (a) Because supports add under convolution, it suffices to show this for  $g\in \text{supp}(\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}))$ (or
$g\in \text{supp}(\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}))$ (or  $\text{supp}(\unicode[STIX]{x1D70F}(v,-\unicode[STIX]{x1D708}))$, which is similar and we omit) for some
$\text{supp}(\unicode[STIX]{x1D70F}(v,-\unicode[STIX]{x1D708}))$, which is similar and we omit) for some  $v\in S$. Our assumption that
$v\in S$. Our assumption that  $\unicode[STIX]{x1D70C}(K_{w})\subset \text{SL}_{d}({\mathcal{O}}_{w})$ for all finite
$\unicode[STIX]{x1D70C}(K_{w})\subset \text{SL}_{d}({\mathcal{O}}_{w})$ for all finite  $w$ means that we only need to estimate
$w$ means that we only need to estimate  $\Vert \unicode[STIX]{x1D70C}(g)\Vert _{v}$. Consider
$\Vert \unicode[STIX]{x1D70C}(g)\Vert _{v}$. Consider  $\unicode[STIX]{x1D70C}$ as a representation of
$\unicode[STIX]{x1D70C}$ as a representation of  $G$, and let
$G$, and let  $\unicode[STIX]{x1D6FA}\subset X^{\ast }(T)$ be the multiset of weights of this representation. It follows that
$\unicode[STIX]{x1D6FA}\subset X^{\ast }(T)$ be the multiset of weights of this representation. It follows that  $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))$ is semisimple with eigenvalues
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))$ is semisimple with eigenvalues  $\{\unicode[STIX]{x1D71B}_{v}^{\langle \unicode[STIX]{x1D714},\unicode[STIX]{x1D708}\rangle }:\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}\}$. By [Reference Shin and TemplierST16, Lemma 2.17], there is
$\{\unicode[STIX]{x1D71B}_{v}^{\langle \unicode[STIX]{x1D714},\unicode[STIX]{x1D708}\rangle }:\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}\}$. By [Reference Shin and TemplierST16, Lemma 2.17], there is  $x\in \text{GL}_{d}({\mathcal{O}}_{v})$ such that
$x\in \text{GL}_{d}({\mathcal{O}}_{v})$ such that  $x\unicode[STIX]{x1D70C}(T_{v})x^{-1}$ is diagonal, and so if we define
$x\unicode[STIX]{x1D70C}(T_{v})x^{-1}$ is diagonal, and so if we define  $A=\max \{-\langle \unicode[STIX]{x1D714},\unicode[STIX]{x1D708}\rangle :\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}\}$ then we have
$A=\max \{-\langle \unicode[STIX]{x1D714},\unicode[STIX]{x1D708}\rangle :\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}\}$ then we have  $\Vert \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))\Vert _{v}=\Vert x\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))x^{-1}\Vert _{v}=q_{v}^{A}<P^{A}$. Because
$\Vert \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))\Vert _{v}=\Vert x\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v}))x^{-1}\Vert _{v}=q_{v}^{A}<P^{A}$. Because  $\unicode[STIX]{x1D70C}(G({\mathcal{O}}_{v}))\subset \text{SL}_{d}({\mathcal{O}}_{v})$, the same holds for
$\unicode[STIX]{x1D70C}(G({\mathcal{O}}_{v}))\subset \text{SL}_{d}({\mathcal{O}}_{v})$, the same holds for  $g\in \text{supp}(\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}))$.
$g\in \text{supp}(\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708}))$.
(b) We note that
 $$\begin{eqnarray}k_{S}=\mathop{\sum }_{v\in S}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})^{\ast }+\mathop{\sum }_{\substack{ v,w\in S \\ v\neq w}}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}k_{S}=\mathop{\sum }_{v\in S}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})^{\ast }+\mathop{\sum }_{\substack{ v,w\in S \\ v\neq w}}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }.\end{eqnarray}$$ The bound is clear for the second sum, because the terms satisfy  $\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\Vert _{\infty }\leqslant 1$ and the supports of the terms are disjoint. For the first sum, we have
$\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\Vert _{\infty }\leqslant 1$ and the supports of the terms are disjoint. For the first sum, we have
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})^{\ast }\Vert _{\infty }\leqslant \Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\Vert _{2}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})^{\ast }\Vert _{\infty }\leqslant \Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\Vert _{2}^{2},\end{eqnarray}$$ and  $\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\Vert _{2}\ll 1$ follows from Lemma 2.3.
$\Vert \unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\Vert _{2}\ll 1$ follows from Lemma 2.3.
(c) We may write the first sum in (13) as a linear combination of  $\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D707})$ with
$\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D707})$ with  $\unicode[STIX]{x1D707}$ lying in a finite set depending on
$\unicode[STIX]{x1D707}$ lying in a finite set depending on  $\unicode[STIX]{x1D708}$. The bound now follows from Lemma 2.3. The second sum may be treated similarly.◻
$\unicode[STIX]{x1D708}$. The bound now follows from Lemma 2.3. The second sum may be treated similarly.◻
4.3 Proof of Proposition 3.3
We are now in a position to prove Proposition 3.3. We first note that  $k_{\unicode[STIX]{x1D709}}(1)\asymp \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$, where the upper and lower bounds follow from property (
$k_{\unicode[STIX]{x1D709}}(1)\asymp \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$, where the upper and lower bounds follow from property ( $\mathsf{P}_{\infty }$) and [Reference Duistermaat, Kolk and VaradarajanDKV79, (3.44a)], respectively. Moreover,
$\mathsf{P}_{\infty }$) and [Reference Duistermaat, Kolk and VaradarajanDKV79, (3.44a)], respectively. Moreover,  $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$ is bounded above (and below) by a power of
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$ is bounded above (and below) by a power of  $(1+\Vert \unicode[STIX]{x1D709}\Vert )$.
$(1+\Vert \unicode[STIX]{x1D709}\Vert )$.
We now apply Proposition 3.2 with test functions  $k_{S}k_{\unicode[STIX]{x1D709}}$. Moreover, for every pair
$k_{S}k_{\unicode[STIX]{x1D709}}$. Moreover, for every pair  $v,w\in S$ we put
$v,w\in S$ we put  $T=\{v,w\}$ and apply Theorem 3.1 with test function
$T=\{v,w\}$ and apply Theorem 3.1 with test function  $k_{T}k_{\unicode[STIX]{x1D709}}$ where
$k_{T}k_{\unicode[STIX]{x1D709}}$ where  $k_{T}=\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }$; we then sum over such pairs
$k_{T}=\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }$; we then sum over such pairs  $v,w$. As a result, we deduce the existence of constants
$v,w$. As a result, we deduce the existence of constants  $A>2$ (depending on
$A>2$ (depending on  $\unicode[STIX]{x1D708}$) and
$\unicode[STIX]{x1D708}$) and  $\unicode[STIX]{x1D6FF}>0$ such that
$\unicode[STIX]{x1D6FF}>0$ such that
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})\end{eqnarray}$$and
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$ The error term in (14) was obtained by observing that  $\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, for some
$\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, for some  $\unicode[STIX]{x1D705}$ depending only on
$\unicode[STIX]{x1D705}$ depending only on  $\unicode[STIX]{x1D708}$, and
$\unicode[STIX]{x1D708}$, and  $q_{T}=q_{v}q_{w}<P^{2}$, so that
$q_{T}=q_{v}q_{w}<P^{2}$, so that  $q_{T}^{A\unicode[STIX]{x1D705}+B}$ is bounded by a power of
$q_{T}^{A\unicode[STIX]{x1D705}+B}$ is bounded by a power of  $P$; we must also insert the
$P$; we must also insert the  $L^{\infty }$ norm estimate for
$L^{\infty }$ norm estimate for  $k_{T}$ coming from the proof of Lemma 4.4. The error term in (15) was obtained by taking
$k_{T}$ coming from the proof of Lemma 4.4. The error term in (15) was obtained by taking  $B$ as in Lemma 4.4 and setting
$B$ as in Lemma 4.4 and setting  $R=P^{B}$ in condition
$R=P^{B}$ in condition  $(\mathsf{P}_{S})$, and inserting the
$(\mathsf{P}_{S})$, and inserting the  $L^{\infty }$ norm estimate of Lemma 4.4. It remains then to explicate the size of
$L^{\infty }$ norm estimate of Lemma 4.4. It remains then to explicate the size of  $\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)$ and
$\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)$ and  $\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)$ (the latter under our extra condition on
$\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)$ (the latter under our extra condition on  $\unicode[STIX]{x1D708}$), and truncate the spectral sums. We continue to use the convention that the values of the exponents
$\unicode[STIX]{x1D708}$), and truncate the spectral sums. We continue to use the convention that the values of the exponents  $A,\unicode[STIX]{x1D6FF}>0$ can vary from line to line.
$A,\unicode[STIX]{x1D6FF}>0$ can vary from line to line.
We begin with (14). Lemma 4.4 (b) gives  $\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\ll P$. By positivity we may truncate the spectral sum to obtain the upper bound
$\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\ll P$. By positivity we may truncate the spectral sum to obtain the upper bound
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\ll P\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\ll P\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$Combined with Lemma 4.3, this implies (7).
We next examine (15). We begin by observing that if  $\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$, then we may again truncate the spectral sum and apply Lemma 4.3 to obtain
$\unicode[STIX]{x1D707}\in \mathfrak{a}^{\ast }$, then we may again truncate the spectral sum and apply Lemma 4.3 to obtain
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D707}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\ll \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707})+P^{A}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707})(1+\Vert \unicode[STIX]{x1D707}\Vert )^{-\unicode[STIX]{x1D6FF}}N^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D707}\Vert \leqslant 1}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}\ll \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707})+P^{A}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707})(1+\Vert \unicode[STIX]{x1D707}\Vert )^{-\unicode[STIX]{x1D6FF}}N^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$ We next use this to truncate the spectral sum about  $\unicode[STIX]{x1D709}$.
$\unicode[STIX]{x1D709}$.
Lemma 4.5. For any 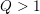 $Q>1$ the left-hand side of (15) can be written as
$Q>1$ the left-hand side of (15) can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\nonumber\\ \displaystyle & & \displaystyle \quad +\,O_{M}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\nonumber\\ \displaystyle & & \displaystyle \quad +\,O_{M}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\nonumber\end{eqnarray}$$Proof. We must show that the sum
 $$\begin{eqnarray}\mathfrak{S}=\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert >Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}=\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert >Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\end{eqnarray}$$satisfies
 $$\begin{eqnarray}\mathfrak{S}=O_{M}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}=O_{M}(\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$ Break the region in the positive chamber  $\mathfrak{a}_{+}^{\ast }$ defined by
$\mathfrak{a}_{+}^{\ast }$ defined by  $\Vert \unicode[STIX]{x1D707}-\unicode[STIX]{x1D709}\Vert >Q$ into an overlapping union of unit balls
$\Vert \unicode[STIX]{x1D707}-\unicode[STIX]{x1D709}\Vert >Q$ into an overlapping union of unit balls  $B(\unicode[STIX]{x1D707}_{n})$ centred at points
$B(\unicode[STIX]{x1D707}_{n})$ centred at points  $\unicode[STIX]{x1D707}_{n}\in \mathfrak{a}^{\ast }$. Because unitary spectral parameters
$\unicode[STIX]{x1D707}_{n}\in \mathfrak{a}^{\ast }$. Because unitary spectral parameters  $\unicode[STIX]{x1D707}$ satisfy
$\unicode[STIX]{x1D707}$ satisfy  $\Vert \Im \unicode[STIX]{x1D707}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$, they also satisfy the rapid decay estimate
$\Vert \Im \unicode[STIX]{x1D707}\Vert \leqslant \Vert \unicode[STIX]{x1D70C}\Vert$, they also satisfy the rapid decay estimate  $h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})\,\ll _{M}\,\Vert \Re \unicode[STIX]{x1D707}-\unicode[STIX]{x1D709}\Vert ^{-M}$. Applying this on each ball gives
$h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D707})\,\ll _{M}\,\Vert \Re \unicode[STIX]{x1D707}-\unicode[STIX]{x1D709}\Vert ^{-M}$. Applying this on each ball gives
 $$\begin{eqnarray}\mathop{\sum }_{\Re \unicode[STIX]{x1D709}_{i}\in B(\unicode[STIX]{x1D707}_{n})}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\,\ll _{M}\,\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}\mathop{\sum }_{\Re \unicode[STIX]{x1D709}_{i}\in B(\unicode[STIX]{x1D707}_{n})}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\Re \unicode[STIX]{x1D709}_{i}\in B(\unicode[STIX]{x1D707}_{n})}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\,\ll _{M}\,\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}\mathop{\sum }_{\Re \unicode[STIX]{x1D709}_{i}\in B(\unicode[STIX]{x1D707}_{n})}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}.\end{eqnarray}$$ Applying (16) and summing over  $n$, we obtain
$n$, we obtain
 $$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n})+P^{A}N^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}(1+\Vert \unicode[STIX]{x1D707}_{n}\Vert )^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n})+P^{A}N^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}(1+\Vert \unicode[STIX]{x1D707}_{n}\Vert )^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n}).\end{eqnarray}$$ From  $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n})\ll \Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{k}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$, where
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D707}_{n})\ll \Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{k}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})$, where  $k$ is the number of roots of
$k$ is the number of roots of  $G$ counted with multiplicity, we may simplify this to
$G$ counted with multiplicity, we may simplify this to
 $$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})P^{A}N^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}(1+\Vert \unicode[STIX]{x1D707}_{n}\Vert )^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})P^{A}N^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{n}\Vert \unicode[STIX]{x1D707}_{n}-\unicode[STIX]{x1D709}\Vert ^{-M}(1+\Vert \unicode[STIX]{x1D707}_{n}\Vert )^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$ The first sum is  $\ll _{M}\,Q^{-M}$. We bound the second sum by breaking it into
$\ll _{M}\,Q^{-M}$. We bound the second sum by breaking it into  $\Vert \unicode[STIX]{x1D707}_{n}\Vert \leqslant \Vert \unicode[STIX]{x1D709}\Vert /2$ and the complement. The first sum is
$\Vert \unicode[STIX]{x1D707}_{n}\Vert \leqslant \Vert \unicode[STIX]{x1D709}\Vert /2$ and the complement. The first sum is  $\ll (1+\Vert \unicode[STIX]{x1D709}\Vert )^{-M}$, and the second is
$\ll (1+\Vert \unicode[STIX]{x1D709}\Vert )^{-M}$, and the second is  $\ll Q^{-M}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}$. Both of these are dominated by
$\ll Q^{-M}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}$. Both of these are dominated by  $(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}$, which finally shows that
$(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}$, which finally shows that
 $$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M}+P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}\,\ll _{M}\,\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})Q^{-M}+P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}},\end{eqnarray}$$as desired. ◻
We combine Lemma 4.5 (taking any  $M>0$ and large enough
$M>0$ and large enough  $Q$) and (15) to obtain
$Q$) and (15) to obtain
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\asymp \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$ We now make use of the critical assumptions that  $G$ is
$G$ is  $H$-large, and
$H$-large, and  $\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3), to bound the right-hand side from below.
$\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3), to bound the right-hand side from below.
Lemma 4.6. If  $\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3) then
$\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3) then  $\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}$.
$\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}_{S}\unicode[STIX]{x1D714}_{S}^{\ast }(1)\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}$.
Proof. Note that for any  $v\in {\mathcal{P}}$ and
$v\in {\mathcal{P}}$ and  $\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ we have
$\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ we have
 $$\begin{eqnarray}q_{v}^{\Vert \unicode[STIX]{x1D708}\Vert ^{\ast }}\int _{H_{v}}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})(x)\,dx=\text{vol}(H_{v}\cap K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})\geqslant \text{vol}(K_{H,v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{H,v})\gg q_{v}^{2\Vert \unicode[STIX]{x1D708}\Vert _{H}^{\ast }},\end{eqnarray}$$
$$\begin{eqnarray}q_{v}^{\Vert \unicode[STIX]{x1D708}\Vert ^{\ast }}\int _{H_{v}}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})(x)\,dx=\text{vol}(H_{v}\cap K_{v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{v})\geqslant \text{vol}(K_{H,v}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{v})K_{H,v})\gg q_{v}^{2\Vert \unicode[STIX]{x1D708}\Vert _{H}^{\ast }},\end{eqnarray}$$ where we have used our assumption that  $T$, and hence
$T$, and hence  $T_{H}$, is split at
$T_{H}$, is split at  $v$, and applied the lower bound from Lemma 2.3. If
$v$, and applied the lower bound from Lemma 2.3. If  $\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3), then so does
$\unicode[STIX]{x1D708}\in X_{\ast }(T_{H})$ satisfies (3), then so does  $-\unicode[STIX]{x1D708}$, and applying the above bound with
$-\unicode[STIX]{x1D708}$, and applying the above bound with  $\pm \unicode[STIX]{x1D708}$, we get
$\pm \unicode[STIX]{x1D708}$, we get  $\int _{H(F_{S})}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\gg 1$ if
$\int _{H(F_{S})}\unicode[STIX]{x1D70F}(v,\unicode[STIX]{x1D708})\unicode[STIX]{x1D70F}(w,\unicode[STIX]{x1D708})^{\ast }\gg 1$ if  $v\neq w$. Summing over
$v\neq w$. Summing over  $v,w\in S$ yields the claim.◻
$v,w\in S$ yields the claim.◻
We deduce from the above lemma that
 $$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}_{N}\mathop{\sum }_{\Vert \Re \unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D709}\Vert \leqslant Q}|\widehat{\unicode[STIX]{x1D714}_{S}}(\unicode[STIX]{x1D713}_{i})|^{2}|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\gg _{\unicode[STIX]{x1D716}}P^{2-\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+O(P^{A}N^{-\unicode[STIX]{x1D6FF}}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D6FF}})).\end{eqnarray}$$ The bound  $h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\ll 1$ completes the proof of (8).
$h_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i})\ll 1$ completes the proof of (8).
5 The amplified relative trace formula
We now prove Proposition 3.2. Recall the notation introduced in § 3.2. For  $\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$ we let
$\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$ we let
 $$\begin{eqnarray}K(x,y)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in G(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\quad \text{and}\quad K_{H}(x,y)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y).\end{eqnarray}$$
$$\begin{eqnarray}K(x,y)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in G(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\quad \text{and}\quad K_{H}(x,y)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y).\end{eqnarray}$$Integrating the spectral expansion
 $$\begin{eqnarray}K(x,y)=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})\unicode[STIX]{x1D713}_{i}(x)\overline{\unicode[STIX]{x1D713}_{i}(y)}\end{eqnarray}$$
$$\begin{eqnarray}K(x,y)=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})\unicode[STIX]{x1D713}_{i}(x)\overline{\unicode[STIX]{x1D713}_{i}(y)}\end{eqnarray}$$ over  $[H]\times [H]$, we obtain
$[H]\times [H]$, we obtain
 $$\begin{eqnarray}\int _{[H]\times [H]}K(x,y)\,dx\,dy=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{[H]\times [H]}K(x,y)\,dx\,dy=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i})|{\mathcal{P}}_{H}(\unicode[STIX]{x1D713}_{i})|^{2}.\end{eqnarray}$$On the other hand, by unfolding we have
 $$\begin{eqnarray}\int _{[H]\times [H]}K_{H}(x,y)\,dx\,dy=\text{vol}([H])\int _{H(\mathbb{A})}\unicode[STIX]{x1D719}(x)\,dx=\text{vol}([H])\unicode[STIX]{x1D6F1}_{H}k_{S}(1)k_{\unicode[STIX]{x1D709}}(1).\end{eqnarray}$$
$$\begin{eqnarray}\int _{[H]\times [H]}K_{H}(x,y)\,dx\,dy=\text{vol}([H])\int _{H(\mathbb{A})}\unicode[STIX]{x1D719}(x)\,dx=\text{vol}([H])\unicode[STIX]{x1D6F1}_{H}k_{S}(1)k_{\unicode[STIX]{x1D709}}(1).\end{eqnarray}$$ We have used the fact that  $K^{S}(N)K_{H}^{S}\cap H(\mathbb{A}_{f}^{S})=K_{H}^{S}$ and the volume of this is
$K^{S}(N)K_{H}^{S}\cap H(\mathbb{A}_{f}^{S})=K_{H}^{S}$ and the volume of this is  $\text{vol}\,K_{H}^{S}=1$.
$\text{vol}\,K_{H}^{S}=1$.
For the remaining terms, first observe that if  $x,y\in H(\mathbb{A})$ we have
$x,y\in H(\mathbb{A})$ we have
 $$\begin{eqnarray}\#\{G(F)\cap \text{supp}(\unicode[STIX]{x1D719}(x^{-1}\cdot y))\}=\#\{x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})\}\ll \#(\text{supp}\,k_{S}/K_{S}),\end{eqnarray}$$
$$\begin{eqnarray}\#\{G(F)\cap \text{supp}(\unicode[STIX]{x1D719}(x^{-1}\cdot y))\}=\#\{x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})\}\ll \#(\text{supp}\,k_{S}/K_{S}),\end{eqnarray}$$ uniformly in  $x$,
$x$,  $y$ and
$y$ and  $N$. Note that the left-hand side of this bound only depends on the image of
$N$. Note that the left-hand side of this bound only depends on the image of  $x$ and
$x$ and  $y$ in
$y$ in  $[H]$, so we may assume that they lie in a fixed compact set. To prove (17), let
$[H]$, so we may assume that they lie in a fixed compact set. To prove (17), let  $g,g^{\prime }\in x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})$ with
$g,g^{\prime }\in x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})$ with  $g=x^{-1}\unicode[STIX]{x1D6FE}y$,
$g=x^{-1}\unicode[STIX]{x1D6FE}y$,  $g^{\prime }=x^{-1}\unicode[STIX]{x1D6FE}^{\prime }y$, and suppose that
$g^{\prime }=x^{-1}\unicode[STIX]{x1D6FE}^{\prime }y$, and suppose that  $g,g^{\prime }$ lie in the same coset in
$g,g^{\prime }$ lie in the same coset in  $\text{supp}\,k_{S}/K_{S}$. Then
$\text{supp}\,k_{S}/K_{S}$. Then  $g_{\infty }^{-1}g_{\infty }^{\prime }$ lies in a fixed compact set and
$g_{\infty }^{-1}g_{\infty }^{\prime }$ lies in a fixed compact set and  $g_{f}^{-1}g_{f}^{\prime }\in K$, so that
$g_{f}^{-1}g_{f}^{\prime }\in K$, so that  $g^{-1}g^{\prime }$ also lies in a fixed compact set. We have
$g^{-1}g^{\prime }$ also lies in a fixed compact set. We have  $g^{-1}g^{\prime }=y^{-1}\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }y$, so that
$g^{-1}g^{\prime }=y^{-1}\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }y$, so that  $\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }$ lies in a fixed compact set, and so if
$\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }$ lies in a fixed compact set, and so if  $g$ is fixed there are only finitely many possibilities for
$g$ is fixed there are only finitely many possibilities for  $g^{\prime }$. Therefore the map
$g^{\prime }$. Therefore the map  $x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})\rightarrow \text{supp}\,k_{S}/K_{S}$ has
$x^{-1}G(F)y\cap \text{supp}(\unicode[STIX]{x1D719})\rightarrow \text{supp}\,k_{S}/K_{S}$ has  $O(1)$ fibres, which proves (17). Using this, we simply estimate
$O(1)$ fibres, which proves (17). Using this, we simply estimate
 $$\begin{eqnarray}\int _{[H]\times [H]}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in G(F)-H(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\,dx\,dy\end{eqnarray}$$
$$\begin{eqnarray}\int _{[H]\times [H]}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in G(F)-H(F)}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\,dx\,dy\end{eqnarray}$$with the pointwise bounds of Corollary 5.2.
5.1 Bounding the off-diagonal contributions
In this section we establish Corollary 5.2, which was used in the proof of Proposition 3.2 above. It is based on the following Diophantine lemma which shows, roughly speaking, that any  $\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ cannot be too close to
$\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ cannot be too close to  $H_{v}$ for various
$H_{v}$ for various  $v$. We shall use the notation introduced in § 2.3.
$v$. We shall use the notation introduced in § 2.3.
Lemma 5.1. If  $C>0$ is given, there are
$C>0$ is given, there are  $A,C_{1},C_{2}>0$ such that the following properties hold for any
$A,C_{1},C_{2}>0$ such that the following properties hold for any  $\unicode[STIX]{x1D6FE}\in G(F)-H(F)$:
$\unicode[STIX]{x1D6FE}\in G(F)-H(F)$:
(i)
 $d(\unicode[STIX]{x1D6FE},H_{v_{0}})\geqslant C_{1}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}$;
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})\geqslant C_{1}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}$;(ii) if
 $(N,D)=1$ is such that
$(N,D)=1$ is such that  $N>C_{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$, and
$N>C_{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$, and  $d(\unicode[STIX]{x1D6FE},H_{v_{0}})<C$, then there is a place
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})<C$, then there is a place  $v|N$ such that
$v|N$ such that  $\unicode[STIX]{x1D6FE}_{v}\notin K(N)_{v}K_{H,v}$.
$\unicode[STIX]{x1D6FE}_{v}\notin K(N)_{v}K_{H,v}$.
Proof. We consider  $H$ and
$H$ and  $G$ as subvarieties of
$G$ as subvarieties of  $F^{d^{2}}$ via the embedding
$F^{d^{2}}$ via the embedding  $\unicode[STIX]{x1D70C}$. Let
$\unicode[STIX]{x1D70C}$. Let  $p_{1},\ldots ,p_{k}\in {\mathcal{O}}[1/D,x_{1},\ldots ,x_{d^{2}}]$ be a set of defining polynomials for
$p_{1},\ldots ,p_{k}\in {\mathcal{O}}[1/D,x_{1},\ldots ,x_{d^{2}}]$ be a set of defining polynomials for  $H$ that are integral over
$H$ that are integral over  ${\mathcal{O}}[1/D]$. Now if
${\mathcal{O}}[1/D]$. Now if  $\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ then
$\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ then  $p_{i}(\unicode[STIX]{x1D6FE})\neq 0$ for some
$p_{i}(\unicode[STIX]{x1D6FE})\neq 0$ for some  $i$.
$i$.
There are  $A,C_{3}>0$ such that for all
$A,C_{3}>0$ such that for all  $\unicode[STIX]{x1D6FE}\in G(F)$ we have
$\unicode[STIX]{x1D6FE}\in G(F)$ we have  $\prod _{v\nmid \infty }|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant C_{3}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$. For
$\prod _{v\nmid \infty }|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant C_{3}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$. For  $\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ the product formula applied to
$\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ the product formula applied to  $p_{i}(\unicode[STIX]{x1D6FE})\in F^{\times }$ implies that the archimedean norms satisfy
$p_{i}(\unicode[STIX]{x1D6FE})\in F^{\times }$ implies that the archimedean norms satisfy  $\prod _{v\mid \infty }|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\geqslant \Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}/C_{3}$. Because
$\prod _{v\mid \infty }|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\geqslant \Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}/C_{3}$. Because  $G_{v}$ is compact for all
$G_{v}$ is compact for all  $v\mid \infty$ other than
$v\mid \infty$ other than  $v_{0}$,
$v_{0}$,  $|p_{i}(\unicode[STIX]{x1D6FE})|_{v}$ is bounded for all such
$|p_{i}(\unicode[STIX]{x1D6FE})|_{v}$ is bounded for all such  $v$. But then we have
$v$. But then we have  $|p_{i}(\unicode[STIX]{x1D6FE})|_{v_{0}}\geqslant C_{1}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}$ for some
$|p_{i}(\unicode[STIX]{x1D6FE})|_{v_{0}}\geqslant C_{1}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{-A}$ for some  $C_{1}>0$, and so
$C_{1}>0$, and so  $d(\unicode[STIX]{x1D6FE},H_{v_{0}})$ satisfies the same bound. This establishes (i).
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})$ satisfies the same bound. This establishes (i).
As above, there are  $A_{1},C_{3}>0$ such that
$A_{1},C_{3}>0$ such that  $\prod _{v\nmid \infty N}|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant C_{3}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A_{1}}$ for all
$\prod _{v\nmid \infty N}|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant C_{3}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A_{1}}$ for all  $\unicode[STIX]{x1D6FE}\in G(F)$. Moreover, we have
$\unicode[STIX]{x1D6FE}\in G(F)$. Moreover, we have  $|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\ll 1$ for
$|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\ll 1$ for  $v|\infty$ by our assumption
$v|\infty$ by our assumption  $d(\unicode[STIX]{x1D6FE},H_{v_{0}})<C$. Now
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})<C$. Now  $p_{i}$ descends to a map
$p_{i}$ descends to a map  $K_{v}/K(N)_{v}\rightarrow {\mathcal{O}}_{v}/N{\mathcal{O}}_{v}$ which is trivial on
$K_{v}/K(N)_{v}\rightarrow {\mathcal{O}}_{v}/N{\mathcal{O}}_{v}$ which is trivial on  $K_{H,v}$. Thus if
$K_{H,v}$. Thus if  $\unicode[STIX]{x1D6FE}_{v}\in K(N)_{v}K_{H,v}$ then
$\unicode[STIX]{x1D6FE}_{v}\in K(N)_{v}K_{H,v}$ then  $|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant |N|_{v}$. If we then suppose that
$|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant |N|_{v}$. If we then suppose that  $\unicode[STIX]{x1D6FE}_{v}\in K(N)_{v}K_{H,v}$ for all
$\unicode[STIX]{x1D6FE}_{v}\in K(N)_{v}K_{H,v}$ for all  $v|N$ it would follow that
$v|N$ it would follow that  $\prod _{v|N}|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant N^{-|F:\mathbb{Q}|}$. But if
$\prod _{v|N}|p_{i}(\unicode[STIX]{x1D6FE})|_{v}\leqslant N^{-|F:\mathbb{Q}|}$. But if  $N>C_{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$ for suitable
$N>C_{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{f}^{A}$ for suitable  $A,C_{2}>0$, we obtain a contradiction by again applying the product formula to
$A,C_{2}>0$, we obtain a contradiction by again applying the product formula to  $p_{i}(\unicode[STIX]{x1D6FE})\in F^{\times }$. This establishes (ii).◻
$p_{i}(\unicode[STIX]{x1D6FE})\in F^{\times }$. This establishes (ii).◻
Corollary 5.2. There is  $A>0$ such that the following statement holds. Let
$A>0$ such that the following statement holds. Let  $N$,
$N$,  $S$ and
$S$ and  $\unicode[STIX]{x1D709}$ be as in § 3.2. Let
$\unicode[STIX]{x1D709}$ be as in § 3.2. Let  $k_{S}\in {\mathcal{H}}_{S}$ satisfy
$k_{S}\in {\mathcal{H}}_{S}$ satisfy  $(\mathsf{P}_{S})$ and
$(\mathsf{P}_{S})$ and  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy  $(\mathsf{P}_{\!\!\infty })$. Put
$(\mathsf{P}_{\!\!\infty })$. Put  $\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$. Then, for all
$\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{S}\,\otimes \,k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}}$. Then, for all  $\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ and all
$\unicode[STIX]{x1D6FE}\in G(F)-H(F)$ and all  $x,y\in H(\mathbb{A})$, we have
$x,y\in H(\mathbb{A})$, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A}\Vert k_{S}\Vert _{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A}\Vert k_{S}\Vert _{\infty }.\end{eqnarray}$$Proof. Let  $\unicode[STIX]{x1D6FA}_{H}\subset H(\mathbb{A})$ be a compact set containing a fundamental domain for
$\unicode[STIX]{x1D6FA}_{H}\subset H(\mathbb{A})$ be a compact set containing a fundamental domain for  $[H]$. We assume that
$[H]$. We assume that  $\unicode[STIX]{x1D6FA}_{H}=\unicode[STIX]{x1D6FA}_{H,D\infty }\times \prod _{v\nmid D\infty }K_{H,v}$ after possibly enlarging
$\unicode[STIX]{x1D6FA}_{H}=\unicode[STIX]{x1D6FA}_{H,D\infty }\times \prod _{v\nmid D\infty }K_{H,v}$ after possibly enlarging  $D$. Because
$D$. Because  $G(F)-H(F)$ is bi-invariant under
$G(F)-H(F)$ is bi-invariant under  $H(F)$, we may assume that
$H(F)$, we may assume that  $x,y\in \unicode[STIX]{x1D6FA}_{H}$.
$x,y\in \unicode[STIX]{x1D6FA}_{H}$.
We may also clearly assume that  $\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\neq 0$. It then follows from Property
$\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\neq 0$. It then follows from Property  $(\mathsf{P}_{S})$ that
$(\mathsf{P}_{S})$ that  $\Vert x^{-1}\unicode[STIX]{x1D6FE}y\Vert _{S}\leqslant R$; in fact we have
$\Vert x^{-1}\unicode[STIX]{x1D6FE}y\Vert _{S}\leqslant R$; in fact we have  $\Vert x^{-1}\unicode[STIX]{x1D6FE}y\Vert _{f}\leqslant R$, using the condition
$\Vert x^{-1}\unicode[STIX]{x1D6FE}y\Vert _{f}\leqslant R$, using the condition  $x^{-1}\unicode[STIX]{x1D6FE}y\in K^{S}(N)K_{H}^{S}\subset K^{S}$. When combined with
$x^{-1}\unicode[STIX]{x1D6FE}y\in K^{S}(N)K_{H}^{S}\subset K^{S}$. When combined with  $x,y\in \unicode[STIX]{x1D6FA}_{H}$, this gives
$x,y\in \unicode[STIX]{x1D6FA}_{H}$, this gives  $\Vert \unicode[STIX]{x1D6FE}\Vert _{f}\ll R$. We may now apply part (i) of Lemma 5.1, to find that
$\Vert \unicode[STIX]{x1D6FE}\Vert _{f}\ll R$. We may now apply part (i) of Lemma 5.1, to find that  $d(\unicode[STIX]{x1D6FE},H_{v_{0}})\gg R^{-A}$. All together, since
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})\gg R^{-A}$. All together, since  $x,y\in H_{v_{0}}$, we deduce that
$x,y\in H_{v_{0}}$, we deduce that  $d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})\gg R^{-A}$. Similarly, from
$d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})\gg R^{-A}$. Similarly, from  $k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y)\neq 0$ and Property
$k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y)\neq 0$ and Property  $(\mathsf{P}_{\!\!\infty })$ it follows that
$(\mathsf{P}_{\!\!\infty })$ it follows that  $d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})<1$, and hence
$d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})<1$, and hence  $d(\unicode[STIX]{x1D6FE},H_{v_{0}})\ll 1$.
$d(\unicode[STIX]{x1D6FE},H_{v_{0}})\ll 1$.
Suppose that  $1+\Vert \unicode[STIX]{x1D709}\Vert \geqslant N$. We have
$1+\Vert \unicode[STIX]{x1D709}\Vert \geqslant N$. We have  $(k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}})(x^{-1}\unicode[STIX]{x1D6FE}y)\leqslant \Vert k_{S}\Vert _{\infty }k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y)$. We then combine
$(k_{S}\,\otimes \,k_{\unicode[STIX]{x1D709}})(x^{-1}\unicode[STIX]{x1D6FE}y)\leqslant \Vert k_{S}\Vert _{\infty }k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y)$. We then combine  $(\mathsf{P}_{\!\!\infty })$ with
$(\mathsf{P}_{\!\!\infty })$ with  $d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})\gg R^{-A}$ to get
$d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}})\gg R^{-A}$ to get
 $$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y) & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}}))^{-1/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert R^{-A})^{-1/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/2}R^{A/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A/2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D709}}(x^{-1}\unicode[STIX]{x1D6FE}y) & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(x^{-1}\unicode[STIX]{x1D6FE}y,H_{v_{0}}))^{-1/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert R^{-A})^{-1/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/2}R^{A/2}\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/4}N^{-1/4}R^{A/2},\nonumber\end{eqnarray}$$which completes the proof in this case.
Now suppose that  $1+\Vert \unicode[STIX]{x1D709}\Vert <N$. Because
$1+\Vert \unicode[STIX]{x1D709}\Vert <N$. Because  $\Vert \unicode[STIX]{x1D6FE}\Vert _{f}\ll R$, part (ii) of Lemma 5.1 implies that there are
$\Vert \unicode[STIX]{x1D6FE}\Vert _{f}\ll R$, part (ii) of Lemma 5.1 implies that there are  $A,C>0$ such that if
$A,C>0$ such that if  $N>CR^{A}$, then there is a place
$N>CR^{A}$, then there is a place  $v|N$ for which
$v|N$ for which  $\unicode[STIX]{x1D6FE}_{v}\notin K(N)_{v}K_{H,v}$. Because
$\unicode[STIX]{x1D6FE}_{v}\notin K(N)_{v}K_{H,v}$. Because  $x,y\in \unicode[STIX]{x1D6FA}_{H}$, we have
$x,y\in \unicode[STIX]{x1D6FA}_{H}$, we have  $x,y\in K_{H,v}$, and so
$x,y\in K_{H,v}$, and so  $x^{-1}\unicode[STIX]{x1D6FE}y\notin K(N)_{v}K_{H,v}$. It follows that if
$x^{-1}\unicode[STIX]{x1D6FE}y\notin K(N)_{v}K_{H,v}$. It follows that if  $N>CR^{A}$, then
$N>CR^{A}$, then  $\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)=0$. We may rephrase this as saying that
$\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)=0$. We may rephrase this as saying that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\leqslant \Vert k_{S}k_{\unicode[STIX]{x1D709}}\Vert _{\infty }N^{-1}CR^{A}\ll \Vert k_{S}\Vert _{\infty }\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})N^{-1}R^{A},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}y)\leqslant \Vert k_{S}k_{\unicode[STIX]{x1D709}}\Vert _{\infty }N^{-1}CR^{A}\ll \Vert k_{S}\Vert _{\infty }\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})N^{-1}R^{A},\end{eqnarray}$$ and the bound  $N^{-1}\leqslant N^{-1/2}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/2}$ completes the proof.◻
$N^{-1}\leqslant N^{-1/2}(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-1/2}$ completes the proof.◻
6 The amplified trace formula
We now prove Theorem 3.1, our trace formula asymptotic with uniform error term. Throughout this section, we can and will relax our condition that  $G_{v_{0}}$ is
$G_{v_{0}}$ is  $\mathbb{R}$-almost simple to the condition that
$\mathbb{R}$-almost simple to the condition that  $G$ is
$G$ is  $F$-almost simple.
$F$-almost simple.
Our proof relies crucially on recent work of Shin and Templier and of Cluckers, Gordon and Halupczok [Reference Shin and TemplierST16] on bounding centralizer volumes and  $p$-adic orbital integrals, as well as work of Finis and Lapid [Reference Finis and LapidFL18] bounding intersection volumes of conjugacy classes with congruence subgroups. We must supply our own bounds on archimedean orbital integrals; these are proven in § 7.
$p$-adic orbital integrals, as well as work of Finis and Lapid [Reference Finis and LapidFL18] bounding intersection volumes of conjugacy classes with congruence subgroups. We must supply our own bounds on archimedean orbital integrals; these are proven in § 7.
6.1 Canonical and Tamagawa measures
If  $G$ is a general connected reductive group over
$G$ is a general connected reductive group over  $F$, Gross [Reference GrossGro97, (1.5)] attaches to
$F$, Gross [Reference GrossGro97, (1.5)] attaches to  $G$ an Artin–Tate motive
$G$ an Artin–Tate motive
 $$\begin{eqnarray}M_{G}=\bigoplus _{d\geqslant 1}M_{G,d}(1-d)\end{eqnarray}$$
$$\begin{eqnarray}M_{G}=\bigoplus _{d\geqslant 1}M_{G,d}(1-d)\end{eqnarray}$$ with coefficients in  $\mathbb{Q}$. Here
$\mathbb{Q}$. Here  $M_{G,d}$ is an Artin motive and
$M_{G,d}$ is an Artin motive and  $(1-d)$ denotes the Tate twist. We let
$(1-d)$ denotes the Tate twist. We let  $\unicode[STIX]{x1D716}(M_{G})$ be the
$\unicode[STIX]{x1D716}(M_{G})$ be the  $\unicode[STIX]{x1D716}$-factor of this motive, which is given by
$\unicode[STIX]{x1D716}$-factor of this motive, which is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D716}(M_{G})=|d_{F}|^{\dim G/2}\mathop{\prod }_{d\geqslant 1}{\mathcal{N}}_{F/\mathbb{Q}}(\mathfrak{f}(M_{G,d}))^{d-1/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}(M_{G})=|d_{F}|^{\dim G/2}\mathop{\prod }_{d\geqslant 1}{\mathcal{N}}_{F/\mathbb{Q}}(\mathfrak{f}(M_{G,d}))^{d-1/2},\end{eqnarray}$$ where  $\mathfrak{f}(M_{G,d})$ denotes the conductor of the Artin motive
$\mathfrak{f}(M_{G,d})$ denotes the conductor of the Artin motive  $M_{G,d}$ (see [Reference GrossGro97, (9.8)]). We let
$M_{G,d}$ (see [Reference GrossGro97, (9.8)]). We let  $L(M_{G_{v}}^{\vee }(1))$ denote the
$L(M_{G_{v}}^{\vee }(1))$ denote the  $L$-function of the local motive
$L$-function of the local motive  $M_{G_{v}}^{\vee }(1)$, and
$M_{G_{v}}^{\vee }(1)$, and  $L(M_{G}^{\vee }(1))$ and
$L(M_{G}^{\vee }(1))$ and  $\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))$ denote the finite and completed
$\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))$ denote the finite and completed  $L$-functions of
$L$-functions of  $M_{G}^{\vee }(1)$. Then
$M_{G}^{\vee }(1)$. Then  $L(M_{G_{v}}^{\vee }(1))$ is a positive real number, and
$L(M_{G_{v}}^{\vee }(1))$ is a positive real number, and  $L(M_{G}^{\vee }(1))$ and
$L(M_{G}^{\vee }(1))$ and  $\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))$ are finite if
$\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))$ are finite if  $Z(G)$ does not contain an
$Z(G)$ does not contain an  $F$-split torus (see [Reference GrossGro97, Proposition 9.4]). From now on we shall assume that
$F$-split torus (see [Reference GrossGro97, Proposition 9.4]). From now on we shall assume that  $G$ satisfies this condition.
$G$ satisfies this condition.
In [Reference GrossGro97, § 11] Gross defines a canonical measure 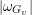 $|\unicode[STIX]{x1D714}_{G_{v}}|$ on
$|\unicode[STIX]{x1D714}_{G_{v}}|$ on  $G_{v}$ at any place of
$G_{v}$ at any place of  $F$. We define
$F$. We define  $\unicode[STIX]{x1D707}_{G,v}^{\text{can}}=L(M_{G_{v}}^{\vee }(1))\cdot |\unicode[STIX]{x1D714}_{G_{v}}|$ as in [Reference GrossGro97]. When
$\unicode[STIX]{x1D707}_{G,v}^{\text{can}}=L(M_{G_{v}}^{\vee }(1))\cdot |\unicode[STIX]{x1D714}_{G_{v}}|$ as in [Reference GrossGro97]. When  $v$ is finite and
$v$ is finite and  $G$ is unramified at
$G$ is unramified at  $v$,
$v$,  $\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ assigns volume 1 to a hyperspecial subgroup of
$\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ assigns volume 1 to a hyperspecial subgroup of  $G(F_{v})$, and so we can define the measure
$G(F_{v})$, and so we can define the measure  $\unicode[STIX]{x1D707}_{G}^{\text{can}}=\prod _{v}\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ on
$\unicode[STIX]{x1D707}_{G}^{\text{can}}=\prod _{v}\unicode[STIX]{x1D707}_{G,v}^{\text{can}}$ on  $G(\mathbb{A})$.
$G(\mathbb{A})$.
Now let  $\unicode[STIX]{x1D714}$ be a non-zero differential form of top degree on
$\unicode[STIX]{x1D714}$ be a non-zero differential form of top degree on  $G$ defined over
$G$ defined over  $F$. For each
$F$. For each  $v$, one may associate with
$v$, one may associate with  $\unicode[STIX]{x1D714}$ a Haar measure
$\unicode[STIX]{x1D714}$ a Haar measure  $|\unicode[STIX]{x1D714}|_{v}$ on
$|\unicode[STIX]{x1D714}|_{v}$ on  $G(F_{v})$. For almost all
$G(F_{v})$. For almost all  $v$,
$v$,  $L(M_{G_{v}}^{\vee }(1))\cdot |\unicode[STIX]{x1D714}|_{v}$ assigns volume 1 to a hyperspecial subgroup of
$L(M_{G_{v}}^{\vee }(1))\cdot |\unicode[STIX]{x1D714}|_{v}$ assigns volume 1 to a hyperspecial subgroup of  $G(F_{v})$. Let
$G(F_{v})$. Let  $\unicode[STIX]{x1D707}_{G}^{\text{Tam}}$ be the Tamagawa measure on
$\unicode[STIX]{x1D707}_{G}^{\text{Tam}}$ be the Tamagawa measure on  $G(\mathbb{A})$, which is defined by
$G(\mathbb{A})$, which is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G}^{\text{Tam}}=\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))^{-1}|d_{F}|^{-\text{dim}\,G/2}\bigotimes _{v}L(M_{G_{v}}^{\vee }(1))|\unicode[STIX]{x1D714}|_{v}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G}^{\text{Tam}}=\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1))^{-1}|d_{F}|^{-\text{dim}\,G/2}\bigotimes _{v}L(M_{G_{v}}^{\vee }(1))|\unicode[STIX]{x1D714}|_{v}\end{eqnarray}$$(see [Reference GrossGro97, (10.2)]) and satisfies [Reference KottwitzKot88, p. 629]
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G}^{\text{Tam}}(G(F)\backslash G(\mathbb{A}))=|\unicode[STIX]{x1D70B}_{0}(Z(\widehat{G})^{\text{Gal}(\overline{F}/F)})||\text{ker}^{1}(F,Z(\widehat{G}))|^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G}^{\text{Tam}}(G(F)\backslash G(\mathbb{A}))=|\unicode[STIX]{x1D70B}_{0}(Z(\widehat{G})^{\text{Gal}(\overline{F}/F)})||\text{ker}^{1}(F,Z(\widehat{G}))|^{-1}.\end{eqnarray}$$ The comparison between  $\unicode[STIX]{x1D707}_{G}^{\text{can}}$ and
$\unicode[STIX]{x1D707}_{G}^{\text{can}}$ and  $\unicode[STIX]{x1D707}_{G}^{\text{Tam}}$ is given by [Reference GrossGro97, Theorem 11.5]
$\unicode[STIX]{x1D707}_{G}^{\text{Tam}}$ is given by [Reference GrossGro97, Theorem 11.5]
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{G}^{\text{can}}}{\unicode[STIX]{x1D707}_{G}^{\text{Tam}}}=\unicode[STIX]{x1D716}(M_{G})\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1)).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{G}^{\text{can}}}{\unicode[STIX]{x1D707}_{G}^{\text{Tam}}}=\unicode[STIX]{x1D716}(M_{G})\unicode[STIX]{x1D6EC}(M_{G}^{\vee }(1)).\end{eqnarray}$$6.2 The trace formula
We now assume that  $G$ is anisotropic. The trace formula is a distributional identity
$G$ is anisotropic. The trace formula is a distributional identity
 $$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}}),\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}}),\end{eqnarray}$$ for  $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(G(\mathbb{A}))$. More precisely,
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(G(\mathbb{A}))$. More precisely,
 $$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\mathop{\sum }_{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\text{tr}(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D719})),\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\mathop{\sum }_{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\text{tr}(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D719})),\end{eqnarray}$$ where  $\unicode[STIX]{x1D70B}$ runs over all irreducible subrepresentations of
$\unicode[STIX]{x1D70B}$ runs over all irreducible subrepresentations of  $L^{2}(G(F)\backslash G(\mathbb{A}))$ occurring with multiplicity
$L^{2}(G(F)\backslash G(\mathbb{A}))$ occurring with multiplicity  $m(\unicode[STIX]{x1D70B})$, and
$m(\unicode[STIX]{x1D70B})$, and
 $$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\mathop{\sum }_{\{\unicode[STIX]{x1D6FE}\}}\frac{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))}{|G_{\unicode[STIX]{x1D6FE}}(F):I_{\unicode[STIX]{x1D6FE}}(F)|}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}),\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\mathop{\sum }_{\{\unicode[STIX]{x1D6FE}\}}\frac{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))}{|G_{\unicode[STIX]{x1D6FE}}(F):I_{\unicode[STIX]{x1D6FE}}(F)|}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}),\end{eqnarray}$$ where  $\{\unicode[STIX]{x1D6FE}\}$ runs over all
$\{\unicode[STIX]{x1D6FE}\}$ runs over all  $G(F)$-conjugacy classes,
$G(F)$-conjugacy classes,  $G_{\unicode[STIX]{x1D6FE}}$ is the centralizer of
$G_{\unicode[STIX]{x1D6FE}}$ is the centralizer of  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in  $G$,
$G$,  $I_{\unicode[STIX]{x1D6FE}}$ is the connected component of
$I_{\unicode[STIX]{x1D6FE}}$ is the connected component of  $G_{\unicode[STIX]{x1D6FE}}$, and
$G_{\unicode[STIX]{x1D6FE}}$, and
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719})=\int _{I_{\unicode[STIX]{x1D6FE}}(\mathbb{A})\backslash G(\mathbb{A})}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}x)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(x).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719})=\int _{I_{\unicode[STIX]{x1D6FE}}(\mathbb{A})\backslash G(\mathbb{A})}\unicode[STIX]{x1D719}(x^{-1}\unicode[STIX]{x1D6FE}x)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(x).\end{eqnarray}$$ (See, for example, [Reference KottwitzKot86, § 9.1] for this formulation of the geometric side.) The measure  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}$ above denotes the quotient measure
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}$ above denotes the quotient measure  $d\unicode[STIX]{x1D707}_{G}^{\text{can}}/d\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$.
$d\unicode[STIX]{x1D707}_{G}^{\text{can}}/d\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$.
We shall bound the terms in  $I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})$ using the Weyl discriminant. For any
$I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})$ using the Weyl discriminant. For any  $v$ and
$v$ and  $\unicode[STIX]{x1D6FE}\in G_{v}$, this is defined by
$\unicode[STIX]{x1D6FE}\in G_{v}$, this is defined by
 $$\begin{eqnarray}D_{v}(\unicode[STIX]{x1D6FE})=|\!\det (1-\text{Ad}(\unicode[STIX]{x1D6FE})_{|\mathfrak{g}_{v}/\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}})|_{v},\end{eqnarray}$$
$$\begin{eqnarray}D_{v}(\unicode[STIX]{x1D6FE})=|\!\det (1-\text{Ad}(\unicode[STIX]{x1D6FE})_{|\mathfrak{g}_{v}/\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}})|_{v},\end{eqnarray}$$ where  $\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}$ denotes the centralizer of
$\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}$ denotes the centralizer of  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in  $\mathfrak{g}_{v}$. If
$\mathfrak{g}_{v}$. If  $S$ is any set of places and
$S$ is any set of places and  $\unicode[STIX]{x1D6FE}\in G(F)$, we define
$\unicode[STIX]{x1D6FE}\in G(F)$, we define  $D_{S}(\unicode[STIX]{x1D6FE})=\prod _{v\in S}D_{v}(\unicode[STIX]{x1D6FE})$ and
$D_{S}(\unicode[STIX]{x1D6FE})=\prod _{v\in S}D_{v}(\unicode[STIX]{x1D6FE})$ and  $D^{S}(\unicode[STIX]{x1D6FE})=\prod _{v\notin S}D_{v}(\unicode[STIX]{x1D6FE})$.
$D^{S}(\unicode[STIX]{x1D6FE})=\prod _{v\notin S}D_{v}(\unicode[STIX]{x1D6FE})$.
6.3 Bounding volumes
We again let  $G$ denote a group satisfying the conditions of Theorem 1.1. Throughout the rest of this section,
$G$ denote a group satisfying the conditions of Theorem 1.1. Throughout the rest of this section,  $A,B$ and
$A,B$ and  $C$ will denote sufficiently large positive constants that may vary from line to line, and will never depend on a choice of place of
$C$ will denote sufficiently large positive constants that may vary from line to line, and will never depend on a choice of place of  $F$.
$F$.
In preparation for the following result, we introduce some additional notation. Given  $\unicode[STIX]{x1D705}\geqslant 0$ and a finite set of finite places
$\unicode[STIX]{x1D705}\geqslant 0$ and a finite set of finite places  $T$ away from
$T$ away from  $D$, we write
$D$, we write  $U_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ for the open compact subset
$U_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ for the open compact subset  $\text{supp}\,{\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$. Furthermore, we denote by
$\text{supp}\,{\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$. Furthermore, we denote by  ${\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ the set of
${\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ the set of  $G(F)$-conjugacy classes of elements in
$G(F)$-conjugacy classes of elements in  $G(F)-Z(F)$ whose
$G(F)-Z(F)$ whose  $G(\mathbb{A})$-conjugacy classes have non-empty intersection with
$G(\mathbb{A})$-conjugacy classes have non-empty intersection with  $K^{T}\cdot U_{T}^{{\leqslant}\unicode[STIX]{x1D705}}\cdot U_{\infty }$, where
$K^{T}\cdot U_{T}^{{\leqslant}\unicode[STIX]{x1D705}}\cdot U_{\infty }$, where  $U_{\infty }=\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$.
$U_{\infty }=\{g\in G(F_{\infty }):d(g,H_{v_{0}})<1\}$.
Proposition 6.1. There exist  $A,B>0$ such that for any
$A,B>0$ such that for any  $\unicode[STIX]{x1D705}\geqslant 0$, any finite set of finite places
$\unicode[STIX]{x1D705}\geqslant 0$, any finite set of finite places  $T$ away from
$T$ away from  $D$, and any
$D$, and any  $\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, we have
$\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll q_{T}^{A\unicode[STIX]{x1D705}+B}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll q_{T}^{A\unicode[STIX]{x1D705}+B}.\end{eqnarray}$$ The implied constant depends only on  $G$.
$G$.
Proof. Let  $S_{D}$ denote the set of places dividing
$S_{D}$ denote the set of places dividing  $D$. Put
$D$. Put  $S_{\unicode[STIX]{x1D6FE}}=\{v\notin S_{D}\cup \infty \cup T:D_{v}(\unicode[STIX]{x1D6FE})\neq 1\}$. We begin by noting that for any
$S_{\unicode[STIX]{x1D6FE}}=\{v\notin S_{D}\cup \infty \cup T:D_{v}(\unicode[STIX]{x1D6FE})\neq 1\}$. We begin by noting that for any  $\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
$\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll q_{S_{\unicode[STIX]{x1D6FE}}}^{B}q_{T}^{B},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll q_{S_{\unicode[STIX]{x1D6FE}}}^{B}q_{T}^{B},\end{eqnarray}$$ where the implied constant depends only on  $G$. Indeed, from the proof of [Reference Shin and TemplierST16, Corollary 6.16] we have
$G$. Indeed, from the proof of [Reference Shin and TemplierST16, Corollary 6.16] we have
 $$\begin{eqnarray}\unicode[STIX]{x1D716}(M_{I_{\unicode[STIX]{x1D6FE}}})L(M_{I_{\unicode[STIX]{x1D6FE}}}^{\vee }(1))\ll \mathop{\prod }_{v\in \text{Ram}(I_{\unicode[STIX]{x1D6FE}})}q_{v}^{B}\ll q_{S_{\unicode[STIX]{x1D6FE}}}^{B}q_{T}^{B},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}(M_{I_{\unicode[STIX]{x1D6FE}}})L(M_{I_{\unicode[STIX]{x1D6FE}}}^{\vee }(1))\ll \mathop{\prod }_{v\in \text{Ram}(I_{\unicode[STIX]{x1D6FE}})}q_{v}^{B}\ll q_{S_{\unicode[STIX]{x1D6FE}}}^{B}q_{T}^{B},\end{eqnarray}$$ where  $\text{Ram}(I_{\unicode[STIX]{x1D6FE}})$ is the set of finite places where
$\text{Ram}(I_{\unicode[STIX]{x1D6FE}})$ is the set of finite places where  $I_{\unicode[STIX]{x1D6FE}}$ is ramified. Note that the last bound follows from the inclusion
$I_{\unicode[STIX]{x1D6FE}}$ is ramified. Note that the last bound follows from the inclusion  $\text{Ram}(I_{\unicode[STIX]{x1D6FE}})\subset S_{D}\cup S_{\unicode[STIX]{x1D6FE}}\cup T$, which follows from [Reference KottwitzKot86, Proposition 7.1]. Moreover, from the definition of the local archimedean factors in [Reference GrossGro97, (7.1) and (7.2)], combined with [Reference Shin and TemplierST16, Proposition 6.3], we find that
$\text{Ram}(I_{\unicode[STIX]{x1D6FE}})\subset S_{D}\cup S_{\unicode[STIX]{x1D6FE}}\cup T$, which follows from [Reference KottwitzKot86, Proposition 7.1]. Moreover, from the definition of the local archimedean factors in [Reference GrossGro97, (7.1) and (7.2)], combined with [Reference Shin and TemplierST16, Proposition 6.3], we find that  $L_{\infty }(M_{I_{\unicode[STIX]{x1D6FE}}}^{\vee }(1))\ll 1$, the implied constant depending only on
$L_{\infty }(M_{I_{\unicode[STIX]{x1D6FE}}}^{\vee }(1))\ll 1$, the implied constant depending only on  $G$. Finally, Corollary 8.12 and Lemma 8.13 of [Reference Shin and TemplierST16] imply
$G$. Finally, Corollary 8.12 and Lemma 8.13 of [Reference Shin and TemplierST16] imply  $\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{Tam}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll 1$. By combining these estimates with (18) we obtain (19).
$\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{Tam}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))\ll 1$. By combining these estimates with (18) we obtain (19).
Now for  $\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
$\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
 $$\begin{eqnarray}D_{v}(\unicode[STIX]{x1D6FE})\leqslant \left\{\begin{array}{@{}ll@{}}q_{v}^{A\unicode[STIX]{x1D705}+B}\quad & \text{ for }v\in T,\\ C\quad & \text{ for }v\mid \infty ,\\ 1\quad & \text{ for }v\notin T\cup \infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}D_{v}(\unicode[STIX]{x1D6FE})\leqslant \left\{\begin{array}{@{}ll@{}}q_{v}^{A\unicode[STIX]{x1D705}+B}\quad & \text{ for }v\in T,\\ C\quad & \text{ for }v\mid \infty ,\\ 1\quad & \text{ for }v\notin T\cup \infty .\end{array}\right.\end{eqnarray}$$From this and the product formula we deduce that
 $$\begin{eqnarray}1=\mathop{\prod }_{v\in T}D_{v}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{v\in S_{D}\cup \infty }D_{v}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}D_{v}(\unicode[STIX]{x1D6FE})\ll q_{T}^{A\unicode[STIX]{x1D705}+B}q_{S_{\unicode[STIX]{x1D6FE}}}^{-1},\end{eqnarray}$$
$$\begin{eqnarray}1=\mathop{\prod }_{v\in T}D_{v}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{v\in S_{D}\cup \infty }D_{v}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}D_{v}(\unicode[STIX]{x1D6FE})\ll q_{T}^{A\unicode[STIX]{x1D705}+B}q_{S_{\unicode[STIX]{x1D6FE}}}^{-1},\end{eqnarray}$$ since  $D_{v}(\unicode[STIX]{x1D6FE})\leqslant q_{v}^{-1}$ for every
$D_{v}(\unicode[STIX]{x1D6FE})\leqslant q_{v}^{-1}$ for every  $v\in S_{\unicode[STIX]{x1D6FE}}$. Inserting this into (19) gives the proposition.◻
$v\in S_{\unicode[STIX]{x1D6FE}}$. Inserting this into (19) gives the proposition.◻
6.4 Bounding adelic orbital integrals
We shall prove Theorem 3.1 by inserting test functions of the form  $\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{T}\,\otimes \,k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}}$ into the trace formula, where
$\unicode[STIX]{x1D719}=\mathbf{1}_{N}^{T}\,\otimes \,k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}}$ into the trace formula, where  $k_{T}\in {\mathcal{H}}_{T}$,
$k_{T}\in {\mathcal{H}}_{T}$,  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$, and
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$, and  $\mathbf{1}_{N}^{T}$ was defined in (5). We now estimate the orbital integrals of these functions.
$\mathbf{1}_{N}^{T}$ was defined in (5). We now estimate the orbital integrals of these functions.
Proposition 6.2. There are constants  $A,B,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}>0$ such that the following statement holds. Let
$A,B,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}>0$ such that the following statement holds. Let  $T$ be a finite set of finite places away from
$T$ be a finite set of finite places away from  $N$ and
$N$ and  $D^{\prime }$. Let
$D^{\prime }$. Let  $\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ and
$\unicode[STIX]{x1D709}\in \mathfrak{a}^{\ast }$ and  $\unicode[STIX]{x1D705}\geqslant 0$. Then, for
$\unicode[STIX]{x1D705}\geqslant 0$. Then, for  $k_{T}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, any
$k_{T}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, any  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfying
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfying  $(\mathsf{P}_{\infty })$, and any
$(\mathsf{P}_{\infty })$, and any  $\unicode[STIX]{x1D6FE}\in G(F)-Z(F)$, we have
$\unicode[STIX]{x1D6FE}\in G(F)-Z(F)$, we have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{N}^{T}\,\otimes \,k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}})\ll N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}q_{T}^{A\unicode[STIX]{x1D705}+B}\Vert k_{T}\Vert _{\infty },\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{N}^{T}\,\otimes \,k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}})\ll N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}q_{T}^{A\unicode[STIX]{x1D705}+B}\Vert k_{T}\Vert _{\infty },\end{eqnarray}$$ where the implied constant depends only on  $G$,
$G$,  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $K$.
$K$.
Proof. We may write  $k_{T}$ as a linear combination of at most
$k_{T}$ as a linear combination of at most  $q_{T}^{A\unicode[STIX]{x1D705}+B}$ terms of the form
$q_{T}^{A\unicode[STIX]{x1D705}+B}$ terms of the form  $\bigotimes _{v\in T}\,1_{K_{v}\unicode[STIX]{x1D707}_{v}(\unicode[STIX]{x1D71B}_{v})K_{v}}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, whose sup norms are all bounded by
$\bigotimes _{v\in T}\,1_{K_{v}\unicode[STIX]{x1D707}_{v}(\unicode[STIX]{x1D71B}_{v})K_{v}}\in {\mathcal{H}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$, whose sup norms are all bounded by  $\Vert k_{T}\Vert _{\infty }$. We may therefore assume that
$\Vert k_{T}\Vert _{\infty }$. We may therefore assume that  $k_{T}$ is a multiple of
$k_{T}$ is a multiple of  $\bigotimes _{v\in T}\,1_{K_{v}\unicode[STIX]{x1D707}_{v}(\unicode[STIX]{x1D71B}_{v})K_{v}}$. This assumption implies that the orbital integral factorizes as
$\bigotimes _{v\in T}\,1_{K_{v}\unicode[STIX]{x1D707}_{v}(\unicode[STIX]{x1D71B}_{v})K_{v}}$. This assumption implies that the orbital integral factorizes as  $\prod _{v}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}_{v})$, where for any
$\prod _{v}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}_{v})$, where for any  $\unicode[STIX]{x1D6FE}_{v}\in G(F_{v})$ we have
$\unicode[STIX]{x1D6FE}_{v}\in G(F_{v})$ we have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}_{v}}(\unicode[STIX]{x1D719}_{v})=\int _{I_{\unicode[STIX]{x1D6FE}_{v}}(F_{v})\backslash G(F_{v})}\unicode[STIX]{x1D719}_{v}(x_{v}^{-1}\unicode[STIX]{x1D6FE}_{v}x_{v})\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},v}(x_{v})\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}_{v}}(\unicode[STIX]{x1D719}_{v})=\int _{I_{\unicode[STIX]{x1D6FE}_{v}}(F_{v})\backslash G(F_{v})}\unicode[STIX]{x1D719}_{v}(x_{v}^{-1}\unicode[STIX]{x1D6FE}_{v}x_{v})\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},v}(x_{v})\end{eqnarray}$$ and  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},v}=\unicode[STIX]{x1D707}_{G,v}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}_{v}},v}^{\text{can}}$. It therefore suffices to work place by place.
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},v}=\unicode[STIX]{x1D707}_{G,v}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}_{v}},v}^{\text{can}}$. It therefore suffices to work place by place.
In [Reference Shin and TemplierST16, Theorem 14.1] it is shown that, if we choose  $D^{\prime }$ to be a sufficiently large (ineffective) multiple of
$D^{\prime }$ to be a sufficiently large (ineffective) multiple of  $D$ depending only on
$D$ depending only on  $G$, then
$G$, then
 $$\begin{eqnarray}|O_{\unicode[STIX]{x1D6FE}}(k_{T})|\leqslant q_{T}^{A\unicode[STIX]{x1D705}+B}D_{T}(\unicode[STIX]{x1D6FE})^{-1/2}\Vert k_{T}\Vert _{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}|O_{\unicode[STIX]{x1D6FE}}(k_{T})|\leqslant q_{T}^{A\unicode[STIX]{x1D705}+B}D_{T}(\unicode[STIX]{x1D6FE})^{-1/2}\Vert k_{T}\Vert _{\infty }.\end{eqnarray}$$We may prove the following bound for the integral at infinity using the results of § 7.
Lemma 6.3. For any  $0<\unicode[STIX]{x1D702}<1/2$, we have the bound
$0<\unicode[STIX]{x1D702}<1/2$, we have the bound
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}D_{\infty }(\unicode[STIX]{x1D6FE})^{-3/4}.\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}D_{\infty }(\unicode[STIX]{x1D6FE})^{-3/4}.\end{eqnarray}$$Proof. Let  $G_{\text{cpt}}$ and
$G_{\text{cpt}}$ and  $G_{\text{cpt},v_{0}}$ be the groups associated with
$G_{\text{cpt},v_{0}}$ be the groups associated with  $G_{\infty }$ and
$G_{\infty }$ and  $G_{v_{0}}$ by Definition 7.2. We begin by showing that, as a consequence of Proposition 7.3, the following statement holds. Let
$G_{v_{0}}$ by Definition 7.2. We begin by showing that, as a consequence of Proposition 7.3, the following statement holds. Let  $0<\unicode[STIX]{x1D702}<1/2$, and let
$0<\unicode[STIX]{x1D702}<1/2$, and let  $k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy property
$k_{\unicode[STIX]{x1D709}}\in {\mathcal{H}}_{\infty }$ satisfy property  $(\mathsf{P}_{\infty })$. Then
$(\mathsf{P}_{\infty })$. Then
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}D_{\infty }(\unicode[STIX]{x1D6FE})^{-3/4}\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}D_{\infty }(\unicode[STIX]{x1D6FE})^{-3/4}\end{eqnarray}$$ for every semisimple  $\unicode[STIX]{x1D6FE}\in G_{\infty }-G_{\text{cpt}}$.
$\unicode[STIX]{x1D6FE}\in G_{\infty }-G_{\text{cpt}}$.
To see how (22) follows from Proposition 7.3, first note that for any non-negative  $f\in C_{c}^{\infty }(G_{\infty }^{0})$ such that
$f\in C_{c}^{\infty }(G_{\infty }^{0})$ such that  $f=1$ on the support of
$f=1$ on the support of  $k_{\unicode[STIX]{x1D709}}$, we have, using property
$k_{\unicode[STIX]{x1D709}}$, we have, using property  $(\mathsf{P}_{\infty })$,
$(\mathsf{P}_{\infty })$,
 $$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D709}}(g) & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-1/2}f(g)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-\unicode[STIX]{x1D702}}f(g)\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\,d(g,H_{v_{0}})^{-\unicode[STIX]{x1D702}}f(g).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D709}}(g) & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-1/2}f(g)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert d(g,H_{v_{0}}))^{-\unicode[STIX]{x1D702}}f(g)\nonumber\\ \displaystyle & \ll & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\,d(g,H_{v_{0}})^{-\unicode[STIX]{x1D702}}f(g).\nonumber\end{eqnarray}$$Thus
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}O_{\unicode[STIX]{x1D6FE}}(fd(\cdot ,H_{v_{0}})^{-\unicode[STIX]{x1D702}}),\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(k_{\unicode[STIX]{x1D709}})\ll \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}O_{\unicode[STIX]{x1D6FE}}(fd(\cdot ,H_{v_{0}})^{-\unicode[STIX]{x1D702}}),\end{eqnarray}$$ to which we may apply (27). Indeed, since  $Z(G)$ is finite, the function
$Z(G)$ is finite, the function  $\Vert X(g)\Vert _{0}$ used there satisfies
$\Vert X(g)\Vert _{0}$ used there satisfies  $\Vert X(g)\Vert _{0}\ll d(g,H_{v_{0}})$.
$\Vert X(g)\Vert _{0}\ll d(g,H_{v_{0}})$.
The proof of Lemma 6.3 then follows from (22) once we have verified that a non-central element  $\unicode[STIX]{x1D6FE}\in G(F)$ cannot lie in
$\unicode[STIX]{x1D6FE}\in G(F)$ cannot lie in  $G_{\text{cpt}}$. Because
$G_{\text{cpt}}$. Because  $G_{\infty }=\prod _{v|\infty }G_{v}$, we have
$G_{\infty }=\prod _{v|\infty }G_{v}$, we have  $G_{\text{cpt}}=G_{\text{cpt},v_{0}}\times \prod _{v\neq v_{0}}G_{v}$, and so it suffices to verify that
$G_{\text{cpt}}=G_{\text{cpt},v_{0}}\times \prod _{v\neq v_{0}}G_{v}$, and so it suffices to verify that  $\unicode[STIX]{x1D6FE}_{v_{0}}\notin G_{\text{cpt},v_{0}}$.
$\unicode[STIX]{x1D6FE}_{v_{0}}\notin G_{\text{cpt},v_{0}}$.
In the case at hand,  $G_{\text{cpt},v_{0}}$ is a normal subgroup of
$G_{\text{cpt},v_{0}}$ is a normal subgroup of  $G_{v_{0}}$ which, as
$G_{v_{0}}$ which, as  $G$ is semisimple, is compact. If we let
$G$ is semisimple, is compact. If we let  $H^{+}$ be the fixed point set of
$H^{+}$ be the fixed point set of  $\unicode[STIX]{x1D703}$ in
$\unicode[STIX]{x1D703}$ in  $G$ (we write
$G$ (we write  $H^{+}$ to distinguish it from its identity component
$H^{+}$ to distinguish it from its identity component  $H$), then
$H$), then  $H_{v_{0}}^{+}$ is a maximal compact subgroup of
$H_{v_{0}}^{+}$ is a maximal compact subgroup of  $G_{v_{0}}$, and so we have
$G_{v_{0}}$, and so we have  $G_{\text{cpt},v_{0}}\subset gH_{v_{0}}^{+}g^{-1}$ for all
$G_{\text{cpt},v_{0}}\subset gH_{v_{0}}^{+}g^{-1}$ for all  $g\in G_{v_{0}}$. Thus, if
$g\in G_{v_{0}}$. Thus, if  $\unicode[STIX]{x1D6FE}_{v_{0}}\in G_{\text{cpt},v_{0}}$, we have
$\unicode[STIX]{x1D6FE}_{v_{0}}\in G_{\text{cpt},v_{0}}$, we have  $\unicode[STIX]{x1D6FE}\in gH^{+}(F)g^{-1}$ for all
$\unicode[STIX]{x1D6FE}\in gH^{+}(F)g^{-1}$ for all  $g\in G(F)$. The group
$g\in G(F)$. The group
 $$\begin{eqnarray}\mathop{\bigcap }_{g\in G(F)}gH^{+}g^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcap }_{g\in G(F)}gH^{+}g^{-1}\end{eqnarray}$$ is a proper  $F$-subgroup of
$F$-subgroup of  $G$; it is normal, since its normalizer contains the Zariski-dense set
$G$; it is normal, since its normalizer contains the Zariski-dense set  $G(F)$. Our assumption that
$G(F)$. Our assumption that  $G$ is
$G$ is  $F$-almost simple implies that it must be contained in
$F$-almost simple implies that it must be contained in  $Z(G)$. We therefore have
$Z(G)$. We therefore have  $\unicode[STIX]{x1D6FE}\in Z(F)$, a contradiction.◻
$\unicode[STIX]{x1D6FE}\in Z(F)$, a contradiction.◻
It remains then to address the size of the orbital integral at finite places away from  $T$. This is provided by the following result. We retain the set-up from the statement of Proposition 6.2; in particular, we recall the notation
$T$. This is provided by the following result. We retain the set-up from the statement of Proposition 6.2; in particular, we recall the notation  $\mathbf{1}_{N}^{T}$ from (5).
$\mathbf{1}_{N}^{T}$ from (5).
Lemma 6.4. There are constants  $\unicode[STIX]{x1D6FF},A,B,C>0$ such that for
$\unicode[STIX]{x1D6FF},A,B,C>0$ such that for  $\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
$\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{N}^{T})\ll N^{-\unicode[STIX]{x1D6FF}}q_{T}^{A\unicode[STIX]{x1D705}+B}D^{T\infty }(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{N}^{T})\ll N^{-\unicode[STIX]{x1D6FF}}q_{T}^{A\unicode[STIX]{x1D705}+B}D^{T\infty }(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$Proof. Recall the sets  $S_{D}$ and
$S_{D}$ and  $S_{\unicode[STIX]{x1D6FE}}$ from the proof of Proposition 6.1. Let
$S_{\unicode[STIX]{x1D6FE}}$ from the proof of Proposition 6.1. Let  $S_{N}$ denote the set of places dividing
$S_{N}$ denote the set of places dividing  $N$.
$N$.
∙ If
 $v\notin S_{D}\cup S_{N}\cup S_{\unicode[STIX]{x1D6FE}}\cup T\cup \infty$, then
$v\notin S_{D}\cup S_{N}\cup S_{\unicode[STIX]{x1D6FE}}\cup T\cup \infty$, then  $K_{v}(N)K_{H_{v}}=K_{v}$ and we have
$K_{v}(N)K_{H_{v}}=K_{v}$ and we have  $O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})=1$; see, for example, [Reference KottwitzKot86, Corollary 7.3].
$O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})=1$; see, for example, [Reference KottwitzKot86, Corollary 7.3].∙ If
 $v\in S_{D}$, then
$v\in S_{D}$, then  $K_{v}(N)K_{H_{v}}=K_{v}K_{H_{v}}$ and a general bound of Kottwitz [Reference Shin and TemplierST16, Theorem 13.1] establishes that
$K_{v}(N)K_{H_{v}}=K_{v}K_{H_{v}}$ and a general bound of Kottwitz [Reference Shin and TemplierST16, Theorem 13.1] establishes that  $O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}K_{H_{v}}})\,\ll _{v}\,D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$.
$O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}K_{H_{v}}})\,\ll _{v}\,D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$.∙ If
 $v\in S_{N}\cup S_{\unicode[STIX]{x1D6FE}}$ we argue as follows.
$v\in S_{N}\cup S_{\unicode[STIX]{x1D6FE}}$ we argue as follows.
We begin by estimating the orbital integrals at places  $v\in S_{N}$, for which we will use as a critical input the work of Finis and Lapid [Reference Finis and LapidFL18]. As the setting of [Reference Finis and LapidFL18] is that of
$v\in S_{N}$, for which we will use as a critical input the work of Finis and Lapid [Reference Finis and LapidFL18]. As the setting of [Reference Finis and LapidFL18] is that of  $\mathbb{Q}$-groups, we shall need to restrict scalars from
$\mathbb{Q}$-groups, we shall need to restrict scalars from  $F$ to
$F$ to  $\mathbb{Q}$ to properly invoke their results. We thus let
$\mathbb{Q}$ to properly invoke their results. We thus let  $p$ denote the rational prime over which
$p$ denote the rational prime over which  $v$ lies, and we note that all places lying over
$v$ lies, and we note that all places lying over  $p$ belong to
$p$ belong to  $S_{N}$. We set
$S_{N}$. We set  $K_{p}=\prod _{v\mid p}K_{v}$, and
$K_{p}=\prod _{v\mid p}K_{v}$, and  $K_{p}(N)K_{H,p}=\prod _{v\mid p}K_{v}(N)K_{H,v}$. Factorize
$K_{p}(N)K_{H,p}=\prod _{v\mid p}K_{v}(N)K_{H,v}$. Factorize  $N=\prod _{p|N}p^{n_{p}}$ and put
$N=\prod _{p|N}p^{n_{p}}$ and put  $N_{p}=p^{n_{p}}$.
$N_{p}=p^{n_{p}}$.
Let  $\unicode[STIX]{x1D707}_{G,p}^{\text{can}}$ (respectively,
$\unicode[STIX]{x1D707}_{G,p}^{\text{can}}$ (respectively,  $\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}$) be the product measure on
$\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}$) be the product measure on  $G_{p}=\prod _{v\mid p}G_{v}$ (respectively,
$G_{p}=\prod _{v\mid p}G_{v}$ (respectively,  $I_{\unicode[STIX]{x1D6FE},p}=\prod _{v\mid p}I_{\unicode[STIX]{x1D6FE},v}$), and let
$I_{\unicode[STIX]{x1D6FE},p}=\prod _{v\mid p}I_{\unicode[STIX]{x1D6FE},v}$), and let  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}$ be the quotient measure. Let
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}$ be the quotient measure. Let  $\text{Ad}:I_{\unicode[STIX]{x1D6FE},p}\backslash G_{p}\rightarrow G_{p}$ be the map
$\text{Ad}:I_{\unicode[STIX]{x1D6FE},p}\backslash G_{p}\rightarrow G_{p}$ be the map  $g\mapsto g^{-1}\unicode[STIX]{x1D6FE}g$, which is a proper map as
$g\mapsto g^{-1}\unicode[STIX]{x1D6FE}g$, which is a proper map as  $\unicode[STIX]{x1D6FE}$ is semisimple. By definition,
$\unicode[STIX]{x1D6FE}$ is semisimple. By definition,
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\text{Ad}^{-1}(K_{p}(N)K_{H_{p}})).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\text{Ad}^{-1}(K_{p}(N)K_{H_{p}})).\end{eqnarray}$$ As  $\text{Ad}^{-1}(K_{p})$ is compact and right-invariant under
$\text{Ad}^{-1}(K_{p})$ is compact and right-invariant under  $K_{p}$, we may break it up into a finite number of orbits
$K_{p}$, we may break it up into a finite number of orbits  $\coprod \overline{g}_{i}K_{p}$, where
$\coprod \overline{g}_{i}K_{p}$, where  $g_{i}\in G_{p}$ and
$g_{i}\in G_{p}$ and  $\overline{g}_{i}$ denotes its image in
$\overline{g}_{i}$ denotes its image in  $I_{\unicode[STIX]{x1D6FE},p}\backslash G_{p}$. This gives
$I_{\unicode[STIX]{x1D6FE},p}\backslash G_{p}$. This gives
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})=\mathop{\sum }_{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p}\cap \text{Ad}^{-1}(K_{p}(N)K_{H_{p}})).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})=\mathop{\sum }_{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p}\cap \text{Ad}^{-1}(K_{p}(N)K_{H_{p}})).\end{eqnarray}$$ Let  $g\in G_{p}$ be such that
$g\in G_{p}$ be such that  $x:=g^{-1}\unicode[STIX]{x1D6FE}g\in K_{p}$. The fibers of the reduction map
$x:=g^{-1}\unicode[STIX]{x1D6FE}g\in K_{p}$. The fibers of the reduction map  $gK_{p}\rightarrow \overline{g}K_{p}$ are the left orbits of
$gK_{p}\rightarrow \overline{g}K_{p}$ are the left orbits of  $I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1}$, so for any
$I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1}$, so for any  $K_{p}^{\prime }\subset K_{p}$ we have
$K_{p}^{\prime }\subset K_{p}$ we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p}\cap \text{Ad}^{-1}(K_{p}^{\prime })) & = & \displaystyle \frac{\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(h\in gK_{p}:h^{-1}\unicode[STIX]{x1D6FE}h\in K_{p}^{\prime })}{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}(I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1})}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}^{\prime })}{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}(I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p}\cap \text{Ad}^{-1}(K_{p}^{\prime })) & = & \displaystyle \frac{\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(h\in gK_{p}:h^{-1}\unicode[STIX]{x1D6FE}h\in K_{p}^{\prime })}{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}(I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1})}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}^{\prime })}{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}},p}^{\text{can}}(I_{\unicode[STIX]{x1D6FE},p}\cap gK_{p}g^{-1})}.\nonumber\end{eqnarray}$$ Taking the quotient of these with  $K_{p}^{\prime }$ equal to
$K_{p}^{\prime }$ equal to  $K_{p}$ and
$K_{p}$ and  $K_{p}(N)K_{H_{p}}$, and using the fact that
$K_{p}(N)K_{H_{p}}$, and using the fact that  $\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(K_{p})=1$ for all
$\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(K_{p})=1$ for all  $v\notin S_{D}\cup \infty$, gives
$v\notin S_{D}\cup \infty$, gives
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p}\cap \text{Ad}^{-1}(K_{p}(N)K_{H_{p}}))}{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p})}=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}(N)K_{H_{p}}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p}\cap \text{Ad}^{-1}(K_{p}(N)K_{H_{p}}))}{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}K_{p})}=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}(N)K_{H_{p}}).\end{eqnarray}$$ One can deduce from [Reference Finis and LapidFL18, Propositions 5.10 and 5.11] (see § 6.5 below) that there are constants  $\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}>0$ (independent of
$\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}>0$ (independent of  $p$) such that if
$p$) such that if  $x\in K_{p}$ is conjugate to an element of
$x\in K_{p}$ is conjugate to an element of  $G(F)-Z(F)$ and satisfies
$G(F)-Z(F)$ and satisfies  $D_{p}(x)>N_{p}^{-\unicode[STIX]{x1D716}}$ then
$D_{p}(x)>N_{p}^{-\unicode[STIX]{x1D716}}$ then
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}(N)K_{H,p})\ll N_{p}^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}(N)K_{H,p})\ll N_{p}^{-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$ (In particular, the implied constant is independent of  $p$.) On the other hand,
$p$.) On the other hand,  $\sum _{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\text{Ad}^{-1}(K_{p}))=O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}})$. Noting that
$\sum _{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\text{Ad}^{-1}(K_{p}))=O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}})$. Noting that  $D_{p}(\unicode[STIX]{x1D6FE})=D_{p}(g_{i}^{-1}\unicode[STIX]{x1D6FE}g_{i})$ for all
$D_{p}(\unicode[STIX]{x1D6FE})=D_{p}(g_{i}^{-1}\unicode[STIX]{x1D6FE}g_{i})$ for all  $i$, we deduce that for
$i$, we deduce that for  $D_{p}(\unicode[STIX]{x1D6FE})>N_{p}^{-\unicode[STIX]{x1D716}}$ we have
$D_{p}(\unicode[STIX]{x1D6FE})>N_{p}^{-\unicode[STIX]{x1D716}}$ we have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})\ll N_{p}^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p})=N_{p}^{-\unicode[STIX]{x1D6FF}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})\ll N_{p}^{-\unicode[STIX]{x1D6FF}}\mathop{\sum }_{i}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE},p}(\overline{g}_{i}K_{p})=N_{p}^{-\unicode[STIX]{x1D6FF}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}}).\end{eqnarray}$$ In the remaining range  $D_{p}(\unicode[STIX]{x1D6FE})\leqslant N_{p}^{-\unicode[STIX]{x1D716}}$, we have
$D_{p}(\unicode[STIX]{x1D6FE})\leqslant N_{p}^{-\unicode[STIX]{x1D716}}$, we have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})\leqslant O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}})\leqslant N_{p}^{-\unicode[STIX]{x1D6FF}}D_{p}(\unicode[STIX]{x1D6FE})^{-\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D716}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}(N)K_{H_{p}}})\leqslant O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}})\leqslant N_{p}^{-\unicode[STIX]{x1D6FF}}D_{p}(\unicode[STIX]{x1D6FE})^{-\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D716}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{p}}).\end{eqnarray}$$ Since  $D_{v}(\unicode[STIX]{x1D6FE})\leqslant 1$ for all
$D_{v}(\unicode[STIX]{x1D6FE})\leqslant 1$ for all  $v\notin T\cup \infty$, we may combine these as
$v\notin T\cup \infty$, we may combine these as
 $$\begin{eqnarray}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}(N)K_{H_{v}}})\ll N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}(N)K_{H_{v}}})\ll N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}).\end{eqnarray}$$ Note that we may shrink  $\unicode[STIX]{x1D6FF}$ to absorb the implied constant in (25) for
$\unicode[STIX]{x1D6FF}$ to absorb the implied constant in (25) for  $p$ sufficiently large, so that the implied constant above only depends on
$p$ sufficiently large, so that the implied constant above only depends on  $G$ and not the number of factors of
$G$ and not the number of factors of  $N$.
$N$.
We now return to the product of orbital integrals over all  $v\in S_{N}\cup S_{\unicode[STIX]{x1D6FE}}$. Recalling that
$v\in S_{N}\cup S_{\unicode[STIX]{x1D6FE}}$. Recalling that  $O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})=1$ for
$O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})=1$ for  $v\notin S_{\unicode[STIX]{x1D6FE}}$, we have just shown that
$v\notin S_{\unicode[STIX]{x1D6FE}}$, we have just shown that
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}(N)K_{H_{v}}})\mathop{\prod }_{\substack{ v\in S_{\unicode[STIX]{x1D6FE}} \\ v\notin S_{N}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}) & \ll & \displaystyle N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\mathop{\prod }_{\substack{ v\in S_{\unicode[STIX]{x1D6FE}} \\ v\notin S_{N}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\nonumber\\ \displaystyle & = & \displaystyle N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}(N)K_{H_{v}}})\mathop{\prod }_{\substack{ v\in S_{\unicode[STIX]{x1D6FE}} \\ v\notin S_{N}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}) & \ll & \displaystyle N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{N}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\mathop{\prod }_{\substack{ v\in S_{\unicode[STIX]{x1D6FE}} \\ v\notin S_{N}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\nonumber\\ \displaystyle & = & \displaystyle N^{-\unicode[STIX]{x1D6FF}}D_{S_{N}}(\unicode[STIX]{x1D6FE})^{-C}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}}).\nonumber\end{eqnarray}$$ For  $v\in S_{\unicode[STIX]{x1D6FE}}$, we proceed as follows. If
$v\in S_{\unicode[STIX]{x1D6FE}}$, we proceed as follows. If  $v\nmid D^{\prime }$ we again apply [Reference Shin and TemplierST16, Theorem 14.1] to get
$v\nmid D^{\prime }$ we again apply [Reference Shin and TemplierST16, Theorem 14.1] to get  $O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{v}^{B}D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$, and if
$O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{v}^{B}D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$, and if  $v\mid D^{\prime }$ we apply [Reference Shin and TemplierST16, Theorem 13.1] to get
$v\mid D^{\prime }$ we apply [Reference Shin and TemplierST16, Theorem 13.1] to get  $O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\,\ll _{v}\,D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$. Combining these gives
$O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\,\ll _{v}\,D_{v}(\unicode[STIX]{x1D6FE})^{-1/2}$. Combining these gives
 $$\begin{eqnarray}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{S_{\unicode[STIX]{x1D6FE}}}^{B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{S_{\unicode[STIX]{x1D6FE}}}^{B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$ Since  $\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we may invoke (20) to obtain
$\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ we may invoke (20) to obtain
 $$\begin{eqnarray}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{S_{\unicode[STIX]{x1D6FE}}}^{B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}\ll q_{T}^{A\unicode[STIX]{x1D705}+B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S_{\unicode[STIX]{x1D6FE}}}O_{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{K_{v}})\leqslant q_{S_{\unicode[STIX]{x1D6FE}}}^{B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}\ll q_{T}^{A\unicode[STIX]{x1D705}+B}D_{S_{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D6FE})^{-C}.\end{eqnarray}$$Putting these estimates together completes the proof of Lemma 6.4. ◻
Remark 6.5. As the authors point out in [Reference Shin and TemplierST16, Remark 7.4], the bound [Reference Shin and TemplierST16, Theorem 14.1] is uniform in the place  $v\nmid D^{\prime }$ whereas the bound [Reference Shin and TemplierST16, Theorem 13.1] of Kottwitz applies to
$v\nmid D^{\prime }$ whereas the bound [Reference Shin and TemplierST16, Theorem 13.1] of Kottwitz applies to  $v\mid D^{\prime }$ but is not uniform in
$v\mid D^{\prime }$ but is not uniform in  $v$. As we allow the implied constant in Proposition 6.2 to depend on the group, this non-uniformity is not an issue.
$v$. As we allow the implied constant in Proposition 6.2 to depend on the group, this non-uniformity is not an issue.
Taken together (and using the product rule for the product of Weyl discriminants), the estimates in (21), Lemma 6.3 and Lemma 6.4 imply Proposition 6.2.◻
6.5 The work of Finis and Lapid
We now explain how to extract from [Reference Finis and LapidFL18, Propositions 5.10 and 5.11] the bound we stated in (24). Recall the notation  $G_{p}=\prod _{v\mid p}G_{v}$,
$G_{p}=\prod _{v\mid p}G_{v}$,  $K_{p}=\prod _{v\mid p}K_{v}$, and so on, from the proof of Lemma 6.4. In what follows, we simplify notation by writing
$K_{p}=\prod _{v\mid p}K_{v}$, and so on, from the proof of Lemma 6.4. In what follows, we simplify notation by writing  $K_{p}^{\prime }$ for
$K_{p}^{\prime }$ for  $K_{p}(N)K_{H,p}$. We recall that
$K_{p}(N)K_{H,p}$. We recall that  $N=\prod _{p\mid N}p^{n_{p}}$ and that
$N=\prod _{p\mid N}p^{n_{p}}$ and that  $x$ is taken to lie in
$x$ is taken to lie in  $K_{p}$.
$K_{p}$.
We first remark that we may assume that  $x$ lies in
$x$ lies in  $K_{p}^{\prime }$, for if there is no such representative then the left-hand side of (24) is zero. We then have
$K_{p}^{\prime }$, for if there is no such representative then the left-hand side of (24) is zero. We then have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}^{\prime })=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:[k,x]\in K_{p}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:k^{-1}xk\in K_{p}^{\prime })=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:[k,x]\in K_{p}^{\prime }),\end{eqnarray}$$ where  $[k,x]:=kxk^{-1}x^{-1}$ is the commutator. Finis and Lapid’s bounds are stated in terms of the adjoint group
$[k,x]:=kxk^{-1}x^{-1}$ is the commutator. Finis and Lapid’s bounds are stated in terms of the adjoint group  $G^{\text{ad}}$. They choose an embedding
$G^{\text{ad}}$. They choose an embedding  $\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}}:\text{Res}_{F/\mathbb{Q}}G^{\text{ad}}\rightarrow \text{GL}(N^{\text{ad}})$, and for every
$\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}}:\text{Res}_{F/\mathbb{Q}}G^{\text{ad}}\rightarrow \text{GL}(N^{\text{ad}})$, and for every  $p$ define
$p$ define  $K_{p}^{\text{ad}}=(\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}})^{-1}(\text{GL}(N^{\text{ad}},\mathbb{Z}_{p}))$. In [Reference Finis and LapidFL18, Definition 5.1], they define the function
$K_{p}^{\text{ad}}=(\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}})^{-1}(\text{GL}(N^{\text{ad}},\mathbb{Z}_{p}))$. In [Reference Finis and LapidFL18, Definition 5.1], they define the function
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(x)=\text{vol}(k\in K_{p}^{\text{ad}}:[k,x]\in K_{p}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(x)=\text{vol}(k\in K_{p}^{\text{ad}}:[k,x]\in K_{p}^{\prime })\end{eqnarray}$$ for  $x\in K_{p}^{\text{ad}}$, where
$x\in K_{p}^{\text{ad}}$, where  $\text{vol}$ is the probability Haar measure on
$\text{vol}$ is the probability Haar measure on  $K_{p}^{\text{ad}}$.Footnote 2 We first relate the two quantities.
$K_{p}^{\text{ad}}$.Footnote 2 We first relate the two quantities.
Lemma 6.6. Let  $\unicode[STIX]{x1D70B}:G\rightarrow G^{\text{ad}}$ be the natural projection map. Then for any
$\unicode[STIX]{x1D70B}:G\rightarrow G^{\text{ad}}$ be the natural projection map. Then for any  $x\in K_{p}$,
$x\in K_{p}$,
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:[k,x]\in K_{p}^{\prime })\ll \unicode[STIX]{x1D719}_{K_{p}^{\prime }}(\unicode[STIX]{x1D70B}(x)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(k\in K_{p}:[k,x]\in K_{p}^{\prime })\ll \unicode[STIX]{x1D719}_{K_{p}^{\prime }}(\unicode[STIX]{x1D70B}(x)),\end{eqnarray}$$ the implied constant depending only on  $G$.
$G$.
Proof. We first claim that  $\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ for almost all
$\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ for almost all  $p$. To see this, we choose a
$p$. To see this, we choose a  $\mathbb{Q}$-embedding
$\mathbb{Q}$-embedding  $\unicode[STIX]{x1D70C}_{\mathbb{Q}}:\text{Res}_{F/\mathbb{Q}}G\rightarrow \text{GL}(N^{\prime })$ with
$\unicode[STIX]{x1D70C}_{\mathbb{Q}}:\text{Res}_{F/\mathbb{Q}}G\rightarrow \text{GL}(N^{\prime })$ with  $K_{p}=\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{-1}(\text{GL}(N^{\prime },\mathbb{Z}_{p}))$ for almost all
$K_{p}=\unicode[STIX]{x1D70C}_{\mathbb{Q}}^{-1}(\text{GL}(N^{\prime },\mathbb{Z}_{p}))$ for almost all  $p$. The embedding
$p$. The embedding
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}:\text{Res}_{F/\mathbb{Q}}G\xrightarrow[{}]{\text{id}\times \unicode[STIX]{x1D70B}}\text{Res}_{F/\mathbb{Q}}G\times \text{Res}_{F/\mathbb{Q}}G^{\text{ad}}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{\mathbb{Q}}\times \unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}}}\text{GL}(N^{\prime }+N^{\text{ad}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}:\text{Res}_{F/\mathbb{Q}}G\xrightarrow[{}]{\text{id}\times \unicode[STIX]{x1D70B}}\text{Res}_{F/\mathbb{Q}}G\times \text{Res}_{F/\mathbb{Q}}G^{\text{ad}}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{\mathbb{Q}}\times \unicode[STIX]{x1D70C}_{\mathbb{Q}}^{\text{ad}}}\text{GL}(N^{\prime }+N^{\text{ad}})\end{eqnarray}$$ is such that  $\unicode[STIX]{x1D6E5}^{-1}(\text{GL}(N^{\prime }+N^{\text{ad}},\mathbb{Z}_{p}))\subset K_{p}$ is hyperspecial for almost all
$\unicode[STIX]{x1D6E5}^{-1}(\text{GL}(N^{\prime }+N^{\text{ad}},\mathbb{Z}_{p}))\subset K_{p}$ is hyperspecial for almost all  $p$, whence the claim. Increasing
$p$, whence the claim. Increasing  $D$ if necessary, we may then assume that
$D$ if necessary, we may then assume that  $\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ for all
$\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ for all  $p\nmid D$.
$p\nmid D$.
For convenience, let us write
 $$\begin{eqnarray}U=\{k\in K_{p}:[k,x]\in K_{p}^{\prime }\}\quad \text{and}\quad V=\{k\in K_{p}^{\text{ad}}:[k,\unicode[STIX]{x1D70B}(x)]\in K_{p}^{\prime }\}.\end{eqnarray}$$
$$\begin{eqnarray}U=\{k\in K_{p}:[k,x]\in K_{p}^{\prime }\}\quad \text{and}\quad V=\{k\in K_{p}^{\text{ad}}:[k,\unicode[STIX]{x1D70B}(x)]\in K_{p}^{\prime }\}.\end{eqnarray}$$ We want to show that  $\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(U)\ll \text{vol}(V)$. From the inclusion
$\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(U)\ll \text{vol}(V)$. From the inclusion  $\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ it follows that
$\unicode[STIX]{x1D70B}(K_{p})\subset K_{p}^{\text{ad}}$ it follows that  $\unicode[STIX]{x1D70B}(U)$ is contained in both
$\unicode[STIX]{x1D70B}(U)$ is contained in both  $\unicode[STIX]{x1D70B}(K_{p})$ and
$\unicode[STIX]{x1D70B}(K_{p})$ and  $V$, yielding
$V$, yielding
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(U)\leqslant \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(\unicode[STIX]{x1D70B}(U))\leqslant \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(V\cap \unicode[STIX]{x1D70B}(K_{p})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(U)\leqslant \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(\unicode[STIX]{x1D70B}(U))\leqslant \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(V\cap \unicode[STIX]{x1D70B}(K_{p})).\end{eqnarray}$$ Now, on  $\unicode[STIX]{x1D70B}(K_{p})$ the push-forward measure
$\unicode[STIX]{x1D70B}(K_{p})$ the push-forward measure  $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}$ is just
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}$ is just  $[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}$. Indeed, since
$[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}$. Indeed, since  $K_{p}$ is maximal compact we have
$K_{p}$ is maximal compact we have  $\unicode[STIX]{x1D70B}^{-1}(K_{p}^{\text{ad}})=K_{p}$ so that
$\unicode[STIX]{x1D70B}^{-1}(K_{p}^{\text{ad}})=K_{p}$ so that  $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(\unicode[STIX]{x1D70B}(K_{p}))=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(K_{p})=1$, while
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(\unicode[STIX]{x1D70B}(K_{p}))=\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(K_{p})=1$, while  $\text{vol}(\unicode[STIX]{x1D70B}(K_{p}))=[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]^{-1}$. We deduce that
$\text{vol}(\unicode[STIX]{x1D70B}(K_{p}))=[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]^{-1}$. We deduce that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(V\cap \unicode[STIX]{x1D70B}(K_{p}))=[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}(V\cap \unicode[STIX]{x1D70B}(K_{p}))\leqslant [K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}(V).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{G,p}^{\text{can}}(V\cap \unicode[STIX]{x1D70B}(K_{p}))=[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}(V\cap \unicode[STIX]{x1D70B}(K_{p}))\leqslant [K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\text{vol}(V).\end{eqnarray}$$ Finally,  $\unicode[STIX]{x1D70B}(K_{p})=K_{p}^{\text{ad}}\cap \unicode[STIX]{x1D70B}(G_{p})$ so that
$\unicode[STIX]{x1D70B}(K_{p})=K_{p}^{\text{ad}}\cap \unicode[STIX]{x1D70B}(G_{p})$ so that  $[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\leqslant [G_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(G_{p})]$, which is bounded in terms of
$[K_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(K_{p})]\leqslant [G_{p}^{\text{ad}}:\unicode[STIX]{x1D70B}(G_{p})]$, which is bounded in terms of  $G$.◻
$G$.◻
We now fix a  $\mathbb{Z}$-lattice
$\mathbb{Z}$-lattice  $\unicode[STIX]{x1D6EC}$ in
$\unicode[STIX]{x1D6EC}$ in  $\text{Res}_{F/\mathbb{Q}}(\mathfrak{g})$ such that
$\text{Res}_{F/\mathbb{Q}}(\mathfrak{g})$ such that  $\unicode[STIX]{x1D6EC}\,\otimes \,\widehat{\mathbb{Z}}$ is
$\unicode[STIX]{x1D6EC}\,\otimes \,\widehat{\mathbb{Z}}$ is  $K^{\text{ad}}$-stable. For
$K^{\text{ad}}$-stable. For  $y\in G_{p}^{\text{ad}}$ define
$y\in G_{p}^{\text{ad}}$ define  $\unicode[STIX]{x1D706}_{p}(y)$ as in [Reference Finis and LapidFL18, Definition 5.2], namely,
$\unicode[STIX]{x1D706}_{p}(y)$ as in [Reference Finis and LapidFL18, Definition 5.2], namely,
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{p}(y)=\max \{n\in \mathbb{Z}\cup \{\infty \}:(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{n}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\text{ for some }\mathfrak{h}\neq 0\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{p}(y)=\max \{n\in \mathbb{Z}\cup \{\infty \}:(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{n}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\text{ for some }\mathfrak{h}\neq 0\},\end{eqnarray}$$ where  $\mathfrak{h}$ ranges over the non-trivial
$\mathfrak{h}$ ranges over the non-trivial  $\mathbb{Q}_{p}$-ideals of
$\mathbb{Q}_{p}$-ideals of  $\mathfrak{g}_{p}=\prod _{v\mid p}\mathfrak{g}_{v}$ and
$\mathfrak{g}_{p}=\prod _{v\mid p}\mathfrak{g}_{v}$ and  $\text{Pr}_{\mathfrak{h}}$ denotes the corresponding projection
$\text{Pr}_{\mathfrak{h}}$ denotes the corresponding projection  $\mathfrak{g}_{p}\rightarrow \mathfrak{h}\subset \mathfrak{g}_{p}$.
$\mathfrak{g}_{p}\rightarrow \mathfrak{h}\subset \mathfrak{g}_{p}$.
We first show how  $\unicode[STIX]{x1D706}_{p}(y)$ controls the size of
$\unicode[STIX]{x1D706}_{p}(y)$ controls the size of  $\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)$, using a combination of Propositions 5.10 and 5.11Footnote 3 of [Reference Finis and LapidFL18]. The argument is already present in [Reference Finis and LapidFL18, § 5.2] in the deduction of the global result [Reference Finis and LapidFL18, Theorem 5.3] from these two local results.
$\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)$, using a combination of Propositions 5.10 and 5.11Footnote 3 of [Reference Finis and LapidFL18]. The argument is already present in [Reference Finis and LapidFL18, § 5.2] in the deduction of the global result [Reference Finis and LapidFL18, Theorem 5.3] from these two local results.
Lemma 6.7. For every  $\unicode[STIX]{x1D716}>0$ small enough there is
$\unicode[STIX]{x1D716}>0$ small enough there is  $\unicode[STIX]{x1D6FF}>0$ such that whenever
$\unicode[STIX]{x1D6FF}>0$ such that whenever  $y\in K_{p}^{\text{ad}}$ satisfies
$y\in K_{p}^{\text{ad}}$ satisfies  $\unicode[STIX]{x1D706}_{p}(y)<\unicode[STIX]{x1D716}n_{p}$ we have
$\unicode[STIX]{x1D706}_{p}(y)<\unicode[STIX]{x1D716}n_{p}$ we have  $\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\,\ll _{G}\,p^{-\unicode[STIX]{x1D6FF}n_{p}}$.
$\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\,\ll _{G}\,p^{-\unicode[STIX]{x1D6FF}n_{p}}$.
Proof. From [Reference Finis and LapidFL18, Proposition 5.11] it follows that there are positive constants  $a,b>0$ and
$a,b>0$ and  $c\geqslant 0$ (depending only on
$c\geqslant 0$ (depending only on  $G$) such that
$G$) such that  $\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\leqslant p^{a(c+\unicode[STIX]{x1D706}_{p}(x)-bn_{p})}$. The constant
$\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\leqslant p^{a(c+\unicode[STIX]{x1D706}_{p}(x)-bn_{p})}$. The constant  $c$ renders this bound useless for small
$c$ renders this bound useless for small  $n_{p}$. Taking
$n_{p}$. Taking  $\unicode[STIX]{x1D716}$ small enough to satisfy
$\unicode[STIX]{x1D716}$ small enough to satisfy  $0<\unicode[STIX]{x1D716}<(c+1)^{-1}b$, we shall apply this bound only in the range
$0<\unicode[STIX]{x1D716}<(c+1)^{-1}b$, we shall apply this bound only in the range  $n_{p}>\unicode[STIX]{x1D716}^{-1}$; we obtain
$n_{p}>\unicode[STIX]{x1D716}^{-1}$; we obtain  $\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\leqslant p^{-a(b-\unicode[STIX]{x1D716}(c+1))n_{p}}$. In the remaining range
$\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\leqslant p^{-a(b-\unicode[STIX]{x1D716}(c+1))n_{p}}$. In the remaining range  $n_{p}\leqslant \unicode[STIX]{x1D716}^{-1}$ we see that
$n_{p}\leqslant \unicode[STIX]{x1D716}^{-1}$ we see that  $\unicode[STIX]{x1D706}_{p}(y)<1$ so that in fact
$\unicode[STIX]{x1D706}_{p}(y)<1$ so that in fact  $\unicode[STIX]{x1D706}_{p}(y)=0$. In this case [Reference Finis and LapidFL18, Proposition 5.10] ensures that
$\unicode[STIX]{x1D706}_{p}(y)=0$. In this case [Reference Finis and LapidFL18, Proposition 5.10] ensures that  $\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\,\ll _{G}\,p^{-1}\leqslant p^{-\unicode[STIX]{x1D716}n_{p}}$. Taking
$\unicode[STIX]{x1D719}_{K_{p}^{\prime }}(y)\,\ll _{G}\,p^{-1}\leqslant p^{-\unicode[STIX]{x1D716}n_{p}}$. Taking  $\unicode[STIX]{x1D6FF}=\min \{\unicode[STIX]{x1D716},a(b-\unicode[STIX]{x1D716}(c+1))\}$, we establish the claim.◻
$\unicode[STIX]{x1D6FF}=\min \{\unicode[STIX]{x1D716},a(b-\unicode[STIX]{x1D716}(c+1))\}$, we establish the claim.◻
It remains to understand the relation between  $D_{p}(y)$ and
$D_{p}(y)$ and  $\unicode[STIX]{x1D706}_{p}(y)$, for
$\unicode[STIX]{x1D706}_{p}(y)$, for  $y\in K_{p}^{\text{ad}}$. For this, the following lemma will be helpful.
$y\in K_{p}^{\text{ad}}$. For this, the following lemma will be helpful.
Lemma 6.8. If  $\unicode[STIX]{x1D6FE}\in G(F)-Z(F)$,
$\unicode[STIX]{x1D6FE}\in G(F)-Z(F)$,  $\text{Ad}(\unicode[STIX]{x1D6FE})$ acts non-trivially on every non-trivial
$\text{Ad}(\unicode[STIX]{x1D6FE})$ acts non-trivially on every non-trivial  $\mathbb{Q}_{p}$-ideal of
$\mathbb{Q}_{p}$-ideal of  $\mathfrak{g}_{p}$.
$\mathfrak{g}_{p}$.
Proof. Suppose that  $\mathfrak{h}\subset \mathfrak{g}_{p}$ is a non-trivial
$\mathfrak{h}\subset \mathfrak{g}_{p}$ is a non-trivial  $\mathbb{Q}_{p}$-ideal on which
$\mathbb{Q}_{p}$-ideal on which  $\text{Ad}(\unicode[STIX]{x1D6FE})$ acts trivially. Let
$\text{Ad}(\unicode[STIX]{x1D6FE})$ acts trivially. Let  $v|p$ be a place for which
$v|p$ be a place for which  $\text{Pr}_{\mathfrak{g}_{v}}\mathfrak{h}\neq 0$, and let
$\text{Pr}_{\mathfrak{g}_{v}}\mathfrak{h}\neq 0$, and let  $\mathfrak{h}_{v}$ be the
$\mathfrak{h}_{v}$ be the  $F_{v}$-linear span of
$F_{v}$-linear span of  $\text{Pr}_{\mathfrak{g}_{v}}\mathfrak{h}$. Then
$\text{Pr}_{\mathfrak{g}_{v}}\mathfrak{h}$. Then  $\mathfrak{h}_{v}$ is a non-trivial ideal of
$\mathfrak{h}_{v}$ is a non-trivial ideal of  $\mathfrak{g}_{v}$ on which
$\mathfrak{g}_{v}$ on which  $\text{Ad}(\unicode[STIX]{x1D6FE})$ acts trivially, or equivalently such that
$\text{Ad}(\unicode[STIX]{x1D6FE})$ acts trivially, or equivalently such that  $\mathfrak{h}_{v}\subset \mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}$. Since
$\mathfrak{h}_{v}\subset \mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}$. Since  $G$ is
$G$ is  $F$-almost simple we have
$F$-almost simple we have  $\bigcap _{g\in G(F)}gG_{\unicode[STIX]{x1D6FE}}g^{-1}\subset Z(G)$ as in Lemma 6.3. This implies that
$\bigcap _{g\in G(F)}gG_{\unicode[STIX]{x1D6FE}}g^{-1}\subset Z(G)$ as in Lemma 6.3. This implies that  $\bigcap _{g\in G(F)}\text{Ad}(g)\mathfrak{g}_{\unicode[STIX]{x1D6FE}}=0$, and hence
$\bigcap _{g\in G(F)}\text{Ad}(g)\mathfrak{g}_{\unicode[STIX]{x1D6FE}}=0$, and hence  $\bigcap _{g\in G(F)}\text{Ad}(g)\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}=0$. However, this is a contradiction as
$\bigcap _{g\in G(F)}\text{Ad}(g)\mathfrak{g}_{v,\unicode[STIX]{x1D6FE}}=0$. However, this is a contradiction as  $\text{Ad}(g)\mathfrak{h}_{v}=\mathfrak{h}_{v}$ for all
$\text{Ad}(g)\mathfrak{h}_{v}=\mathfrak{h}_{v}$ for all  $g\in G_{v}$.◻
$g\in G_{v}$.◻
Finally, we complete the proof of (24). Note that we have assumed that the  $x\in K_{p}$ to which we apply (24) are
$x\in K_{p}$ to which we apply (24) are  $G_{p}$-conjugate to an element in
$G_{p}$-conjugate to an element in  $G(F)-Z(F)$. We may therefore apply the conclusion of Lemma 6.8 to
$G(F)-Z(F)$. We may therefore apply the conclusion of Lemma 6.8 to  $x$, and thus to
$x$, and thus to  $y=\unicode[STIX]{x1D70B}(x)\in K_{p}^{\text{ad}}$.
$y=\unicode[STIX]{x1D70B}(x)\in K_{p}^{\text{ad}}$.
Lemma 6.9. Let  $y\in K_{p}^{\text{ad}}$ be semisimple. Assume that
$y\in K_{p}^{\text{ad}}$ be semisimple. Assume that  $\text{Ad}(y)$ is non-trivial on every non-trivial
$\text{Ad}(y)$ is non-trivial on every non-trivial  $\mathbb{Q}_{p}$-ideal of
$\mathbb{Q}_{p}$-ideal of  $\mathfrak{g}_{p}$ and
$\mathfrak{g}_{p}$ and  $D_{p}(y)>p^{-\unicode[STIX]{x1D716}n_{p}}$. Then
$D_{p}(y)>p^{-\unicode[STIX]{x1D716}n_{p}}$. Then 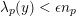 $\unicode[STIX]{x1D706}_{p}(y)<\unicode[STIX]{x1D716}n_{p}$.
$\unicode[STIX]{x1D706}_{p}(y)<\unicode[STIX]{x1D716}n_{p}$.
Proof. Let 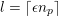 $l=\lceil \unicode[STIX]{x1D716}n_{p}\rceil$. Now if
$l=\lceil \unicode[STIX]{x1D716}n_{p}\rceil$. Now if  $\unicode[STIX]{x1D706}_{p}(y)\geqslant \unicode[STIX]{x1D716}n_{p}$ then, by definition, there is some non-trivial
$\unicode[STIX]{x1D706}_{p}(y)\geqslant \unicode[STIX]{x1D716}n_{p}$ then, by definition, there is some non-trivial  $\mathbb{Q}_{p}$-ideal
$\mathbb{Q}_{p}$-ideal  $\mathfrak{h}$ of
$\mathfrak{h}$ of  $\mathfrak{g}_{p}$ such that
$\mathfrak{g}_{p}$ such that
 $$\begin{eqnarray}(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{l}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{l}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p}).\end{eqnarray}$$ As  $\text{Ad}(y)$ preserves
$\text{Ad}(y)$ preserves  $\mathfrak{h}$, this implies that
$\mathfrak{h}$, this implies that
 $$\begin{eqnarray}(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{l}\text{Pr}_{\mathfrak{ h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}(\text{Ad}(y)-1)\text{Pr}_{\mathfrak{h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p})\subset p^{l}\text{Pr}_{\mathfrak{ h}}(\unicode[STIX]{x1D6EC}\,\otimes \,\mathbb{Z}_{p}).\end{eqnarray}$$ This implies that all eigenvalues of  $\text{Ad}(y)-1$, considered as an endomorphism of the
$\text{Ad}(y)-1$, considered as an endomorphism of the  $\mathbb{Q}_{p}$ vector space
$\mathbb{Q}_{p}$ vector space  $\mathfrak{h}$, must have
$\mathfrak{h}$, must have  $p$-adic valuation at least
$p$-adic valuation at least  $l$. Moreover, as
$l$. Moreover, as  $y$ is semisimple and
$y$ is semisimple and  $\text{Ad}(y)$ is non-trivial on
$\text{Ad}(y)$ is non-trivial on  $\mathfrak{h}$, one of these eigenvalues must be non-zero. As
$\mathfrak{h}$, one of these eigenvalues must be non-zero. As  $D_{p}(y)=|\!\det (1-\text{Ad}(y))_{\mathfrak{g}_{p}/\mathfrak{g}_{p,y}}|_{p}$, we therefore have
$D_{p}(y)=|\!\det (1-\text{Ad}(y))_{\mathfrak{g}_{p}/\mathfrak{g}_{p,y}}|_{p}$, we therefore have  $D_{p}(y)\leqslant p^{-\unicode[STIX]{x1D716}n_{p}}$, a contradiction.◻
$D_{p}(y)\leqslant p^{-\unicode[STIX]{x1D716}n_{p}}$, a contradiction.◻
6.6 Proof of Theorem 3.1
We recall the test function  $\unicode[STIX]{x1D719}$ from the statement of Proposition 6.2, and the set
$\unicode[STIX]{x1D719}$ from the statement of Proposition 6.2, and the set  ${\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ from § 6.3. Then
${\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}$ from § 6.3. Then
 $$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i}),\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{spec}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\text{Vol}_{N}\mathop{\sum }_{i\geqslant 0}\widehat{k_{T}\,\otimes \,k_{\unicode[STIX]{x1D709}}}(\unicode[STIX]{x1D713}_{i}),\end{eqnarray}$$ the sum ranging over an orthonormal basis of Hecke–Maass forms for  $Y_{N}$, and
$Y_{N}$, and
 $$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+\mathop{\sum }_{\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}}\frac{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))}{|G_{\unicode[STIX]{x1D6FE}}(F):I_{\unicode[STIX]{x1D6FE}}(F)|}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}).\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+\mathop{\sum }_{\{\unicode[STIX]{x1D6FE}\}\in {\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}}\frac{\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}(F)\backslash I_{\unicode[STIX]{x1D6FE}}(\mathbb{A}))}{|G_{\unicode[STIX]{x1D6FE}}(F):I_{\unicode[STIX]{x1D6FE}}(F)|}O_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D719}).\end{eqnarray}$$ Here we have used the hypothesis on  $K$ from § 2.4 that
$K$ from § 2.4 that  $Z(F)\cap K=\{e\}$. Now by [Reference Shin and TemplierST16, Corollary 8.10] we have
$Z(F)\cap K=\{e\}$. Now by [Reference Shin and TemplierST16, Corollary 8.10] we have  $|{\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}|\ll q_{T}^{A\unicode[STIX]{x1D705}+B}$. From this and Propositions 6.1 and 6.2 we find
$|{\mathcal{C}}_{T}^{{\leqslant}\unicode[STIX]{x1D705}}|\ll q_{T}^{A\unicode[STIX]{x1D705}+B}$. From this and Propositions 6.1 and 6.2 we find
 $$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+O(q_{T}^{A\unicode[STIX]{x1D705}+B}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\Vert k_{T}\Vert _{\infty }),\end{eqnarray}$$
$$\begin{eqnarray}I_{\text{geom}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D707}_{G}^{\text{can}})=\unicode[STIX]{x1D707}_{G}^{\text{can}}([G])k_{T}(1)k_{\unicode[STIX]{x1D709}}(1)+O(q_{T}^{A\unicode[STIX]{x1D705}+B}N^{-\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})(1+\Vert \unicode[STIX]{x1D709}\Vert )^{-\unicode[STIX]{x1D702}}\Vert k_{T}\Vert _{\infty }),\end{eqnarray}$$as desired. This completes the proof of Theorem 3.1.
7 Bounds for real orbital integrals
The aim of this section is to prove Proposition 7.3, which establishes the uniform bounds on real orbital integrals that were used in the proof of the global bounds of Proposition 6.2.
7.1 Notation
We adopt the following notation in this section.
–
 $G$ is a connected reductive group over
$G$ is a connected reductive group over  $\mathbb{R}$ with real Lie algebra
$\mathbb{R}$ with real Lie algebra  $\mathfrak{g}$.
$\mathfrak{g}$.–
 $\unicode[STIX]{x1D703}$ is a Cartan involution of
$\unicode[STIX]{x1D703}$ is a Cartan involution of  $G$.
$G$.–
 $K$ is the fixed point set of
$K$ is the fixed point set of  $\unicode[STIX]{x1D703}$, so that
$\unicode[STIX]{x1D703}$, so that  $K$ is a maximal compact subgroup of
$K$ is a maximal compact subgroup of  $G$.
$G$.–
 $\mathfrak{g}=\mathfrak{p}+\mathfrak{k}$ is the Cartan decomposition associated with
$\mathfrak{g}=\mathfrak{p}+\mathfrak{k}$ is the Cartan decomposition associated with  $\unicode[STIX]{x1D703}$.
$\unicode[STIX]{x1D703}$.–
 $A$ and
$A$ and  $A_{G}$ are maximal split tori in
$A_{G}$ are maximal split tori in  $G$ and
$G$ and  $Z(G)$, respectively. We assume that
$Z(G)$, respectively. We assume that  $\unicode[STIX]{x1D703}$ acts by
$\unicode[STIX]{x1D703}$ acts by  $-1$ on
$-1$ on  $A$ and
$A$ and  $A_{G}$; see, for example, [Reference BorelBor91, § 24.C].
$A_{G}$; see, for example, [Reference BorelBor91, § 24.C].–
 $A^{0}$ is the connected component of
$A^{0}$ is the connected component of  $A$ in the real topology.
$A$ in the real topology.–
 $\mathfrak{a}$ and
$\mathfrak{a}$ and  $\mathfrak{a}_{G}$ are the Lie algebras of
$\mathfrak{a}_{G}$ are the Lie algebras of  $A$ and
$A$ and  $A_{G}$.
$A_{G}$.–
 $W$ is the Weyl group of
$W$ is the Weyl group of  $\mathfrak{a}$. We recall [Reference BorelBor91, § 24.C] that this is equal to
$\mathfrak{a}$. We recall [Reference BorelBor91, § 24.C] that this is equal to  $N_{G}(A)/Z_{G}(A)$,
$N_{G}(A)/Z_{G}(A)$,  $N_{K}(A)/Z_{K}(A)$, and the group generated by reflections in the roots of
$N_{K}(A)/Z_{K}(A)$, and the group generated by reflections in the roots of  $\mathfrak{a}$ in
$\mathfrak{a}$ in  $\mathfrak{g}$.
$\mathfrak{g}$.–
 $\mathfrak{a}^{+}$ is a choice of open Weyl chamber in
$\mathfrak{a}^{+}$ is a choice of open Weyl chamber in  $\mathfrak{a}$.
$\mathfrak{a}$.–
 $\langle \cdot ,\cdot \rangle$ is an Ad-invariant bilinear form on
$\langle \cdot ,\cdot \rangle$ is an Ad-invariant bilinear form on  $\mathfrak{g}$ that is positive on
$\mathfrak{g}$ that is positive on  $\mathfrak{p}$ and negative on
$\mathfrak{p}$ and negative on  $\mathfrak{k}$.
$\mathfrak{k}$.–
 $\langle \cdot ,\cdot \rangle _{+}$ is the positive definite inner product on
$\langle \cdot ,\cdot \rangle _{+}$ is the positive definite inner product on  $\mathfrak{g}$ given by
$\mathfrak{g}$ given by  $\langle u,v\rangle _{+}=-\langle \unicode[STIX]{x1D703}u,v\rangle$. We let
$\langle u,v\rangle _{+}=-\langle \unicode[STIX]{x1D703}u,v\rangle$. We let  $\Vert \cdot \Vert$ be the associated norm.
$\Vert \cdot \Vert$ be the associated norm.
For a semisimple element  $\unicode[STIX]{x1D6FE}\in G$ let
$\unicode[STIX]{x1D6FE}\in G$ let  $G_{\unicode[STIX]{x1D6FE}}$ be its centralizer, and let
$G_{\unicode[STIX]{x1D6FE}}$ be its centralizer, and let  $I_{\unicode[STIX]{x1D6FE}}$ be the neutral component of
$I_{\unicode[STIX]{x1D6FE}}$ be the neutral component of  $G_{\unicode[STIX]{x1D6FE}}$. The Lie algebra of
$G_{\unicode[STIX]{x1D6FE}}$. The Lie algebra of  $G_{\unicode[STIX]{x1D6FE}}$ is denoted by
$G_{\unicode[STIX]{x1D6FE}}$ is denoted by  $\mathfrak{g}_{\unicode[STIX]{x1D6FE}}$. By [Reference KnappKna02, Theorem 7.39],
$\mathfrak{g}_{\unicode[STIX]{x1D6FE}}$. By [Reference KnappKna02, Theorem 7.39],  $G$ has a Cartan decomposition
$G$ has a Cartan decomposition  $G=KA^{0}K$, and any
$G=KA^{0}K$, and any  $g\in G$ may be written as
$g\in G$ may be written as  $g=k_{1}e^{H}k_{2}$ for a unique
$g=k_{1}e^{H}k_{2}$ for a unique  $H\in \overline{\mathfrak{a}}^{+}$. We use this to define a map
$H\in \overline{\mathfrak{a}}^{+}$. We use this to define a map  $X:G\rightarrow \overline{\mathfrak{a}}^{+}$ by
$X:G\rightarrow \overline{\mathfrak{a}}^{+}$ by  $g\in Ke^{X(g)}K$. We let
$g\in Ke^{X(g)}K$. We let  $D^{G}$ (or
$D^{G}$ (or  $D$ if there is no confusion) denote the Weyl discriminant. A Levi subgroup or parabolic of
$D$ if there is no confusion) denote the Weyl discriminant. A Levi subgroup or parabolic of  $G$ will be called semi-standard if it contains
$G$ will be called semi-standard if it contains  $A$. We will always choose the Levi of a semi-standard parabolic to be semi-standard.
$A$. We will always choose the Levi of a semi-standard parabolic to be semi-standard.
7.2 Orbital integrals of continuous functions
We shall derive Proposition 7.3 from the following result, which bounds  $O_{\unicode[STIX]{x1D6FE}}(f)$ for semisimple
$O_{\unicode[STIX]{x1D6FE}}(f)$ for semisimple  $\unicode[STIX]{x1D6FE}\in G$ and non-singular test functions
$\unicode[STIX]{x1D6FE}\in G$ and non-singular test functions  $f\in C(G)$. It is the archimedean analogue of a result of Kottwitz [Reference Shin and TemplierST16, Theorem 13.1] in the
$f\in C(G)$. It is the archimedean analogue of a result of Kottwitz [Reference Shin and TemplierST16, Theorem 13.1] in the  $p$-adic case.
$p$-adic case.
Proposition 7.1. If  $f\in C^{\infty }(G)$ is bounded and compactly supported modulo centre, then we have
$f\in C^{\infty }(G)$ is bounded and compactly supported modulo centre, then we have  $O_{\unicode[STIX]{x1D6FE}}(f)\,\ll _{f}\,D(\unicode[STIX]{x1D6FE})^{-1/2}$ for every semisimple
$O_{\unicode[STIX]{x1D6FE}}(f)\,\ll _{f}\,D(\unicode[STIX]{x1D6FE})^{-1/2}$ for every semisimple  $\unicode[STIX]{x1D6FE}\in G$.
$\unicode[STIX]{x1D6FE}\in G$.
Proof. The stated inequality is proved in [Har57, Theorem 2] for  $\unicode[STIX]{x1D6FE}$ regular semisimple. The extension of this bound to all semisimple
$\unicode[STIX]{x1D6FE}$ regular semisimple. The extension of this bound to all semisimple  $\unicode[STIX]{x1D6FE}$ follows immediately from Harish-Chandra’s derivative formula [Har66, Lemma 23], which expresses
$\unicode[STIX]{x1D6FE}$ follows immediately from Harish-Chandra’s derivative formula [Har66, Lemma 23], which expresses  $O_{\unicode[STIX]{x1D6FE}}(f)$ as the derivative of (a quantity closely related to)
$O_{\unicode[STIX]{x1D6FE}}(f)$ as the derivative of (a quantity closely related to)  $D(\unicode[STIX]{x1D70E})^{1/2}O_{\unicode[STIX]{x1D70E}}(f)$, for regular semisimple
$D(\unicode[STIX]{x1D70E})^{1/2}O_{\unicode[STIX]{x1D70E}}(f)$, for regular semisimple  $\unicode[STIX]{x1D70E}$ in a neighbourhood of
$\unicode[STIX]{x1D70E}$ in a neighbourhood of  $\unicode[STIX]{x1D6FE}$. The idea is that the latter is bounded independently of
$\unicode[STIX]{x1D6FE}$. The idea is that the latter is bounded independently of  $\unicode[STIX]{x1D6FE}$, and examining the constant that appears there gives the proposition.
$\unicode[STIX]{x1D6FE}$, and examining the constant that appears there gives the proposition.
We now explain this idea in more detail. We recall that a maximal torus  $T$ in a connected reductive group
$T$ in a connected reductive group  $H$ is called fundamental if the compact part of
$H$ is called fundamental if the compact part of  $T$ has maximum possible dimension. For any semisimple
$T$ has maximum possible dimension. For any semisimple  $\unicode[STIX]{x1D6FE}\in G$, we may choose a fundamental maximal torus
$\unicode[STIX]{x1D6FE}\in G$, we may choose a fundamental maximal torus  $T$ in
$T$ in  $I_{\unicode[STIX]{x1D6FE}}$. Note that
$I_{\unicode[STIX]{x1D6FE}}$. Note that  $\unicode[STIX]{x1D6FE}\in I_{\unicode[STIX]{x1D6FE}}$, which implies that
$\unicode[STIX]{x1D6FE}\in I_{\unicode[STIX]{x1D6FE}}$, which implies that  $\unicode[STIX]{x1D6FE}\in T$. As there are only finitely many possibilities for
$\unicode[STIX]{x1D6FE}\in T$. As there are only finitely many possibilities for  $T$ up to conjugacy, we may assume that
$T$ up to conjugacy, we may assume that  $T$ is fixed. Once
$T$ is fixed. Once  $T$ is fixed there are finitely many possibilities for
$T$ is fixed there are finitely many possibilities for  $I_{\unicode[STIX]{x1D6FE}}$, so we also assume
$I_{\unicode[STIX]{x1D6FE}}$, so we also assume  $I_{\unicode[STIX]{x1D6FE}}$ is fixed. Note that we need to choose
$I_{\unicode[STIX]{x1D6FE}}$ is fixed. Note that we need to choose  $T$ fundamental in order for (26) below to hold with a non-zero constant
$T$ fundamental in order for (26) below to hold with a non-zero constant  $c$.
$c$.
We let  $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ be the roots of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ be the roots of  $T$ in
$T$ in  $G$ and
$G$ and  $I_{\unicode[STIX]{x1D6FE}}$. We choose a system of positive roots
$I_{\unicode[STIX]{x1D6FE}}$. We choose a system of positive roots  $\unicode[STIX]{x1D6E5}^{+}$, and let
$\unicode[STIX]{x1D6E5}^{+}$, and let  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}\cap \unicode[STIX]{x1D6E5}^{+}$. We let
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}\cap \unicode[STIX]{x1D6E5}^{+}$. We let  $\unicode[STIX]{x1D70C}$ be a branch of the square root of the modular character, that is, a smooth function on
$\unicode[STIX]{x1D70C}$ be a branch of the square root of the modular character, that is, a smooth function on  $T$ defined near
$T$ defined near  $\unicode[STIX]{x1D6FE}$ so that
$\unicode[STIX]{x1D6FE}$ so that  $\unicode[STIX]{x1D70C}^{2}=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}}\unicode[STIX]{x1D6FC}$. Let
$\unicode[STIX]{x1D70C}^{2}=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}}\unicode[STIX]{x1D6FC}$. Let  $G_{\text{reg}}$ be the set of strongly regular elements in
$G_{\text{reg}}$ be the set of strongly regular elements in  $G$, which we recall is the set of
$G$, which we recall is the set of  $\unicode[STIX]{x1D70E}$ such that
$\unicode[STIX]{x1D70E}$ such that  $G_{\unicode[STIX]{x1D70E}}$ is a torus, and define
$G_{\unicode[STIX]{x1D70E}}$ is a torus, and define  $T_{\text{reg}}=T\cap G_{\text{reg}}$. Let
$T_{\text{reg}}=T\cap G_{\text{reg}}$. Let  $\unicode[STIX]{x1D6FA}$ be a connected component of
$\unicode[STIX]{x1D6FA}$ be a connected component of  $T_{\text{reg}}$ such that
$T_{\text{reg}}$ such that  $\unicode[STIX]{x1D6FE}\in \overline{\unicode[STIX]{x1D6FA}}$, and let
$\unicode[STIX]{x1D6FE}\in \overline{\unicode[STIX]{x1D6FA}}$, and let  $V\subset \unicode[STIX]{x1D6FA}$ be the intersection of
$V\subset \unicode[STIX]{x1D6FA}$ be the intersection of  $\unicode[STIX]{x1D6FA}$ with an open neighbourhood of
$\unicode[STIX]{x1D6FA}$ with an open neighbourhood of  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in  $T$. For
$T$. For  $\unicode[STIX]{x1D70E}\in V$, we define
$\unicode[STIX]{x1D70E}\in V$, we define
 $$\begin{eqnarray}F_{f}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}}(1-\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70E})^{-1})\int _{T\backslash G}f(x^{-1}\unicode[STIX]{x1D70E}x)\,dx.\end{eqnarray}$$
$$\begin{eqnarray}F_{f}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}}(1-\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70E})^{-1})\int _{T\backslash G}f(x^{-1}\unicode[STIX]{x1D70E}x)\,dx.\end{eqnarray}$$ For any  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ let  $H_{\unicode[STIX]{x1D6FC}}\in \text{Lie}(T)$ be as defined in [Har64, § 4]. Define
$H_{\unicode[STIX]{x1D6FC}}\in \text{Lie}(T)$ be as defined in [Har64, § 4]. Define  $D_{I}$ to be the translation-invariant differential operator on
$D_{I}$ to be the translation-invariant differential operator on  $T$ corresponding to
$T$ corresponding to  $\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}}H_{\unicode[STIX]{x1D6FC}}$. By [Har66, Lemma 23] (adapted to the real algebraic case), we may show that
$\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}}H_{\unicode[STIX]{x1D6FC}}$. By [Har66, Lemma 23] (adapted to the real algebraic case), we may show that
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D70E}\rightarrow \unicode[STIX]{x1D6FE}}{\lim }D_{I}F_{f}(\unicode[STIX]{x1D70E})=c\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}-\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}}(1-\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})^{-1})\int _{I_{\unicode[STIX]{x1D6FE}}\backslash G}f(x^{-1}\unicode[STIX]{x1D6FE}x)\,dx,\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D70E}\rightarrow \unicode[STIX]{x1D6FE}}{\lim }D_{I}F_{f}(\unicode[STIX]{x1D70E})=c\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}^{+}-\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{+}}(1-\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})^{-1})\int _{I_{\unicode[STIX]{x1D6FE}}\backslash G}f(x^{-1}\unicode[STIX]{x1D6FE}x)\,dx,\end{eqnarray}$$ where  $c\neq 0$ depends only on the isomorphism class of
$c\neq 0$ depends only on the isomorphism class of  $I_{\unicode[STIX]{x1D6FE}}$.
$I_{\unicode[STIX]{x1D6FE}}$.
On the other hand, it is known [Har57, Theorem 2] that  $F_{f}\in C^{\infty }(V)$, and if
$F_{f}\in C^{\infty }(V)$, and if  $X$ is any translation-invariant differential operator on
$X$ is any translation-invariant differential operator on  $T$, we have
$T$, we have
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D70E}\in V}{\sup }|XF_{f}(\unicode[STIX]{x1D70E})|\,\ll _{X,f}\,1.\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D70E}\in V}{\sup }|XF_{f}(\unicode[STIX]{x1D70E})|\,\ll _{X,f}\,1.\end{eqnarray}$$Combined with (26), this gives the proposition. ◻
7.3 Orbital integrals of singular functions
We now arrive at the main result of this section. We define  $\Vert \cdot \Vert _{0}$ to be the seminorm on
$\Vert \cdot \Vert _{0}$ to be the seminorm on  $\mathfrak{a}$ obtained from the Killing form, which descends to a norm on
$\mathfrak{a}$ obtained from the Killing form, which descends to a norm on  $\mathfrak{a}/\mathfrak{a}_{G}$.
$\mathfrak{a}/\mathfrak{a}_{G}$.
Definition 7.2. We define  $G_{\text{cpt}}$ to be the elements of
$G_{\text{cpt}}$ to be the elements of  $G$ such that
$G$ such that  $\text{Ad}(g)$ is trivial on all the
$\text{Ad}(g)$ is trivial on all the  $\mathbb{R}$-simple factors of
$\mathbb{R}$-simple factors of  $\mathfrak{g}$ of non-compact type.
$\mathfrak{g}$ of non-compact type.
It is clear that  $G_{\text{cpt}}$ is a normal subgroup of
$G_{\text{cpt}}$ is a normal subgroup of  $G$, and because its image under
$G$, and because its image under  $\text{Ad}$ is compact,
$\text{Ad}$ is compact,  $G_{\text{cpt}}$ is compact if and only if
$G_{\text{cpt}}$ is compact if and only if  $A_{G}$ is trivial.
$A_{G}$ is trivial.
Proposition 7.3. Suppose that  $G$ is not a torus. Let
$G$ is not a torus. Let  $0<\unicode[STIX]{x1D702}<1/2$ and let
$0<\unicode[STIX]{x1D702}<1/2$ and let  $f\in C(G)$ be bounded and compactly supported modulo centre. Then
$f\in C(G)$ be bounded and compactly supported modulo centre. Then  $O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})$ converges absolutely, and there is a constant
$O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})$ converges absolutely, and there is a constant  $c(\unicode[STIX]{x1D702},f)>0$ such that
$c(\unicode[STIX]{x1D702},f)>0$ such that
 $$\begin{eqnarray}|O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})|<c(\unicode[STIX]{x1D702},f)D(\unicode[STIX]{x1D6FE})^{-3/4}\end{eqnarray}$$
$$\begin{eqnarray}|O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})|<c(\unicode[STIX]{x1D702},f)D(\unicode[STIX]{x1D6FE})^{-3/4}\end{eqnarray}$$ for every semisimple  $\unicode[STIX]{x1D6FE}\in G-G_{\text{cpt}}$.
$\unicode[STIX]{x1D6FE}\in G-G_{\text{cpt}}$.
Remark 7.4. It may be seen that the bound (27) cannot hold for all semisimple  $\unicode[STIX]{x1D6FE}\in G$. For instance, if
$\unicode[STIX]{x1D6FE}\in G$. For instance, if  $\unicode[STIX]{x1D6FE}$ lies in a compact normal subgroup of
$\unicode[STIX]{x1D6FE}$ lies in a compact normal subgroup of  $G$ (and hence in
$G$ (and hence in  $G_{\text{cpt}}$) then the conjugacy class of
$G_{\text{cpt}}$) then the conjugacy class of  $\unicode[STIX]{x1D6FE}$ will be contained in
$\unicode[STIX]{x1D6FE}$ will be contained in  $K$, and the function
$K$, and the function  $f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}}$ will be singular everywhere on the conjugacy class.
$f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}}$ will be singular everywhere on the conjugacy class.
We sketch the proof of Proposition 7.3, which will occupy the remaining subsections. In § 7.4 we begin by reducing to the case where  $Z(G)$ is anisotropic. This is simple; if
$Z(G)$ is anisotropic. This is simple; if  $A_{G}$ is the maximal split torus in
$A_{G}$ is the maximal split torus in  $Z(G)$, we simply push the orbital integrals forward to
$Z(G)$, we simply push the orbital integrals forward to  $G/A_{G}$. We then divide the proof into two cases, based on the following definition.
$G/A_{G}$. We then divide the proof into two cases, based on the following definition.
Definition 7.5. We say that  $\unicode[STIX]{x1D6FE}\in G$ is elliptic if it is semisimple and
$\unicode[STIX]{x1D6FE}\in G$ is elliptic if it is semisimple and  $Z(G_{\unicode[STIX]{x1D6FE}})$ is anisotropic.
$Z(G_{\unicode[STIX]{x1D6FE}})$ is anisotropic.
If our semisimple  $\unicode[STIX]{x1D6FE}$ is not elliptic, we may choose a non-trivial split torus
$\unicode[STIX]{x1D6FE}$ is not elliptic, we may choose a non-trivial split torus  $S\subset Z(G_{\unicode[STIX]{x1D6FE}})$ and define
$S\subset Z(G_{\unicode[STIX]{x1D6FE}})$ and define  $M$ to be the centralizer of
$M$ to be the centralizer of  $S$ in
$S$ in  $G$. Because we have assumed that
$G$. Because we have assumed that  $Z(G)$ is anisotropic,
$Z(G)$ is anisotropic,  $M$ is a proper Levi subgroup satisfying
$M$ is a proper Levi subgroup satisfying  $G_{\unicode[STIX]{x1D6FE}}\subset M$, and we may apply parabolic descent as well as Proposition 7.1. This is executed in § 7.5.
$G_{\unicode[STIX]{x1D6FE}}\subset M$, and we may apply parabolic descent as well as Proposition 7.1. This is executed in § 7.5.
If  $\unicode[STIX]{x1D6FE}$ is elliptic, we may assume without loss of generality that
$\unicode[STIX]{x1D6FE}$ is elliptic, we may assume without loss of generality that  $\unicode[STIX]{x1D6FE}\in K$. For
$\unicode[STIX]{x1D6FE}\in K$. For  $\unicode[STIX]{x1D716}>0$, define
$\unicode[STIX]{x1D716}>0$, define  $K(\unicode[STIX]{x1D716})=\{g\in G:\Vert X(g)\Vert <\unicode[STIX]{x1D716}\}$. Proving Proposition 7.3 in this case is roughly equivalent to controlling the volume of the conjugacy class of
$K(\unicode[STIX]{x1D716})=\{g\in G:\Vert X(g)\Vert <\unicode[STIX]{x1D716}\}$. Proving Proposition 7.3 in this case is roughly equivalent to controlling the volume of the conjugacy class of  $\unicode[STIX]{x1D6FE}$ that lies inside
$\unicode[STIX]{x1D6FE}$ that lies inside  $K(\unicode[STIX]{x1D716})$, uniformly in
$K(\unicode[STIX]{x1D716})$, uniformly in  $\unicode[STIX]{x1D716}$ and
$\unicode[STIX]{x1D716}$ and  $D(\unicode[STIX]{x1D6FE})$. This turns out to be equivalent to bounding the set of points in
$D(\unicode[STIX]{x1D6FE})$. This turns out to be equivalent to bounding the set of points in  $G/K$ that are moved a distance at most
$G/K$ that are moved a distance at most  $\unicode[STIX]{x1D716}$ by the rotation
$\unicode[STIX]{x1D716}$ by the rotation  $\unicode[STIX]{x1D6FE}$. Note that this set will be non-compact if
$\unicode[STIX]{x1D6FE}$. Note that this set will be non-compact if  $I_{\unicode[STIX]{x1D6FE}}$ is non-compact. We do this in § 7.6 using a geometric argument and Proposition 7.1.
$I_{\unicode[STIX]{x1D6FE}}$ is non-compact. We do this in § 7.6 using a geometric argument and Proposition 7.1.
7.4 Reduction to the case of  $Z(G)$ anisotropic
$Z(G)$ anisotropic
Let  $\overline{G}=G/A_{G}$. We wish to show that if Proposition 7.3 holds for
$\overline{G}=G/A_{G}$. We wish to show that if Proposition 7.3 holds for  $\overline{G}$ then it holds for
$\overline{G}$ then it holds for  $G$. We have an exact sequence
$G$. We have an exact sequence  $1\rightarrow A_{G}\rightarrow G\rightarrow \overline{G}\rightarrow 1$ of algebraic groups over
$1\rightarrow A_{G}\rightarrow G\rightarrow \overline{G}\rightarrow 1$ of algebraic groups over  $\mathbb{R}$, and by Hilbert 90 this gives an exact sequence on points. If
$\mathbb{R}$, and by Hilbert 90 this gives an exact sequence on points. If  $\unicode[STIX]{x1D6FE}\in G$, we denote its image in
$\unicode[STIX]{x1D6FE}\in G$, we denote its image in  $\overline{G}$ by
$\overline{G}$ by  $\overline{\unicode[STIX]{x1D6FE}}$. We denote the connected centralizer of
$\overline{\unicode[STIX]{x1D6FE}}$. We denote the connected centralizer of  $\overline{\unicode[STIX]{x1D6FE}}$ by
$\overline{\unicode[STIX]{x1D6FE}}$ by  $\overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}$. There is an exact sequence
$\overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}$. There is an exact sequence  $1\rightarrow A_{G}\rightarrow I_{\unicode[STIX]{x1D6FE}}\rightarrow \overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}\rightarrow 1$, and so
$1\rightarrow A_{G}\rightarrow I_{\unicode[STIX]{x1D6FE}}\rightarrow \overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}\rightarrow 1$, and so  $G\rightarrow \overline{G}$ induces a bijection
$G\rightarrow \overline{G}$ induces a bijection  $I_{\unicode[STIX]{x1D6FE}}\backslash G\simeq \overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}\backslash \overline{G}$. Moreover, under this bijection we have
$I_{\unicode[STIX]{x1D6FE}}\backslash G\simeq \overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}\backslash \overline{G}$. Moreover, under this bijection we have  $\unicode[STIX]{x1D707}_{G}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}=C\unicode[STIX]{x1D707}_{\overline{G}}^{\text{can}}/\unicode[STIX]{x1D707}_{\overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}}^{\text{can}}$ for some
$\unicode[STIX]{x1D707}_{G}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}=C\unicode[STIX]{x1D707}_{\overline{G}}^{\text{can}}/\unicode[STIX]{x1D707}_{\overline{I}_{\overline{\unicode[STIX]{x1D6FE}}}}^{\text{can}}$ for some  $C>0$, and the function
$C>0$, and the function  $\Vert X(\cdot )\Vert _{0}$ pushes forward to
$\Vert X(\cdot )\Vert _{0}$ pushes forward to  $\Vert X(\cdot )\Vert$. It follows that if
$\Vert X(\cdot )\Vert$. It follows that if  $f\in C(G)$ is invariant under
$f\in C(G)$ is invariant under  $A_{G}$, and its reduction
$A_{G}$, and its reduction  $\overline{f}$ lies in
$\overline{f}$ lies in  $C_{c}(\overline{G})$, we have
$C_{c}(\overline{G})$, we have  $O_{\unicode[STIX]{x1D6FE}}^{G}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})=C\cdot O_{\overline{\unicode[STIX]{x1D6FE}}}^{\overline{G}}(\overline{f}\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})$.
$O_{\unicode[STIX]{x1D6FE}}^{G}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})=C\cdot O_{\overline{\unicode[STIX]{x1D6FE}}}^{\overline{G}}(\overline{f}\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})$.
Let  $f\in C(G)$ be bounded and compactly supported modulo centre. We may assume without loss of generality that
$f\in C(G)$ be bounded and compactly supported modulo centre. We may assume without loss of generality that  $f\geqslant 0$, by replacing
$f\geqslant 0$, by replacing  $f$ by its absolute value. Since
$f$ by its absolute value. Since  $f$ is compactly supported modulo centre, we may choose
$f$ is compactly supported modulo centre, we may choose  $h\in C(G)$ that is invariant under
$h\in C(G)$ that is invariant under  $A_{G}$, satisfies
$A_{G}$, satisfies  $h\geqslant f$, and has reduction
$h\geqslant f$, and has reduction  $\overline{h}$ lying in
$\overline{h}$ lying in  $C_{c}(\overline{G})$. We have
$C_{c}(\overline{G})$. We have
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})\leqslant O_{\unicode[STIX]{x1D6FE}}^{G}(h\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})=C\cdot O_{\overline{\unicode[STIX]{x1D6FE}}}^{\overline{G}}(\overline{h}\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(f\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})\leqslant O_{\unicode[STIX]{x1D6FE}}^{G}(h\Vert X(\cdot )\Vert _{0}^{-\unicode[STIX]{x1D702}})=C\cdot O_{\overline{\unicode[STIX]{x1D6FE}}}^{\overline{G}}(\overline{h}\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}).\end{eqnarray}$$ Because  $D(\unicode[STIX]{x1D6FE})=D(\overline{\unicode[STIX]{x1D6FE}})$, if Proposition 7.3 holds for
$D(\unicode[STIX]{x1D6FE})=D(\overline{\unicode[STIX]{x1D6FE}})$, if Proposition 7.3 holds for  $\overline{G}$ then it holds for
$\overline{G}$ then it holds for  $G$.
$G$.
We may henceforth assume that  $Z(G)$ is anisotropic. We may then take the function
$Z(G)$ is anisotropic. We may then take the function  $f$ of Proposition 7.3 to lie in
$f$ of Proposition 7.3 to lie in  $C_{c}(G)$, and work with
$C_{c}(G)$, and work with  $\Vert X(\cdot )\Vert$ instead of
$\Vert X(\cdot )\Vert$ instead of  $\Vert X(\cdot )\Vert _{0}$. As in § 6, we write
$\Vert X(\cdot )\Vert _{0}$. As in § 6, we write  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D707}_{G}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$.
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D707}_{G}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$.
7.5 The case when  $\unicode[STIX]{x1D6FE}$ is not elliptic
$\unicode[STIX]{x1D6FE}$ is not elliptic
We handle the case when  $\unicode[STIX]{x1D6FE}$ is not elliptic by the process of parabolic descent, which we now recall. Let
$\unicode[STIX]{x1D6FE}$ is not elliptic by the process of parabolic descent, which we now recall. Let  $P=MN$ be a semi-standard parabolic subgroup of
$P=MN$ be a semi-standard parabolic subgroup of  $G$. Choose Haar measures on
$G$. Choose Haar measures on  $N$ and
$N$ and  $K$ so that
$K$ so that  $dk$ gives
$dk$ gives  $K$ measure 1, and for which
$K$ measure 1, and for which  $d\unicode[STIX]{x1D707}_{G}^{\text{can}}=d\unicode[STIX]{x1D707}_{M}^{\text{can}}\,dn\,dk$ in Langlands
$d\unicode[STIX]{x1D707}_{G}^{\text{can}}=d\unicode[STIX]{x1D707}_{M}^{\text{can}}\,dn\,dk$ in Langlands  $MNK$ co-ordinates. For functions in
$MNK$ co-ordinates. For functions in  $C_{c}(G)$, the parabolic descent along
$C_{c}(G)$, the parabolic descent along  $P$ is defined by
$P$ is defined by
 $$\begin{eqnarray}f\in C_{c}(G)\mapsto f^{P}\in C_{c}(M),\end{eqnarray}$$
$$\begin{eqnarray}f\in C_{c}(G)\mapsto f^{P}\in C_{c}(M),\end{eqnarray}$$where
 $$\begin{eqnarray}f^{P}(m)=\unicode[STIX]{x1D6FF}_{P}^{1/2}(m)\int _{N}\int _{K}f(k^{-1}mnk)\,dn\,dk.\end{eqnarray}$$
$$\begin{eqnarray}f^{P}(m)=\unicode[STIX]{x1D6FF}_{P}^{1/2}(m)\int _{N}\int _{K}f(k^{-1}mnk)\,dn\,dk.\end{eqnarray}$$ If  $\unicode[STIX]{x1D6FE}\in M$, we define
$\unicode[STIX]{x1D6FE}\in M$, we define  $D_{M}^{G}(\unicode[STIX]{x1D6FE})$ by choosing a maximal torus
$D_{M}^{G}(\unicode[STIX]{x1D6FE})$ by choosing a maximal torus  $\unicode[STIX]{x1D6FE}\in T\subset M$, letting
$\unicode[STIX]{x1D6FE}\in T\subset M$, letting  $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6E5}_{M}$ be the roots of
$\unicode[STIX]{x1D6E5}_{M}$ be the roots of  $T$ in
$T$ in  $G$ and
$G$ and  $M$, and setting
$M$, and setting  $D_{M}^{G}(\unicode[STIX]{x1D6FE})=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D6E5}_{M}}|\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})-1|$. It may be seen that this is independent of the choice of
$D_{M}^{G}(\unicode[STIX]{x1D6FE})=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D6E5}_{M}}|\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})-1|$. It may be seen that this is independent of the choice of  $T$. We say that
$T$. We say that  $\unicode[STIX]{x1D6FE}\in M$ is
$\unicode[STIX]{x1D6FE}\in M$ is  $(G,M)$-regular if
$(G,M)$-regular if  $D_{M}^{G}(\unicode[STIX]{x1D6FE})\neq 0$. We recall the descent relation between the orbital integrals of
$D_{M}^{G}(\unicode[STIX]{x1D6FE})\neq 0$. We recall the descent relation between the orbital integrals of  $f$ and
$f$ and  $f^{P}$.
$f^{P}$.
Lemma 7.6. If  $\unicode[STIX]{x1D6FE}\in M$ is
$\unicode[STIX]{x1D6FE}\in M$ is  $(G,M)$-regular and
$(G,M)$-regular and  $f\in C_{c}(G)$, we have
$f\in C_{c}(G)$, we have
 $$\begin{eqnarray}D_{M}^{G}(\unicode[STIX]{x1D6FE})^{1/2}O_{\unicode[STIX]{x1D6FE}}(f)=O_{\unicode[STIX]{x1D6FE}}^{M}(f^{P}).\end{eqnarray}$$
$$\begin{eqnarray}D_{M}^{G}(\unicode[STIX]{x1D6FE})^{1/2}O_{\unicode[STIX]{x1D6FE}}(f)=O_{\unicode[STIX]{x1D6FE}}^{M}(f^{P}).\end{eqnarray}$$Proof. Because  $\unicode[STIX]{x1D6FE}$ is
$\unicode[STIX]{x1D6FE}$ is  $(G,M)$-regular, we have
$(G,M)$-regular, we have  $I_{\unicode[STIX]{x1D6FE}}\subset M$. Let
$I_{\unicode[STIX]{x1D6FE}}\subset M$. Let  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}=\unicode[STIX]{x1D707}_{M}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$. We may parametrize
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}=\unicode[STIX]{x1D707}_{M}^{\text{can}}/\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}$. We may parametrize  $I_{\unicode[STIX]{x1D6FE}}\backslash G$ in Langlands coordinates as
$I_{\unicode[STIX]{x1D6FE}}\backslash G$ in Langlands coordinates as  $(I_{\unicode[STIX]{x1D6FE}}\backslash M)NK$, which allows us to write
$(I_{\unicode[STIX]{x1D6FE}}\backslash M)NK$, which allows us to write
 $$\begin{eqnarray}\displaystyle O_{\unicode[STIX]{x1D6FE}}(f) & = & \displaystyle \int _{I_{\unicode[STIX]{x1D6FE}}\backslash G}f(x^{-1}\unicode[STIX]{x1D6FE}x)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(x)\nonumber\\ \displaystyle & = & \displaystyle \int _{I_{\unicode[STIX]{x1D6FE}}\backslash M}\int _{N}\int _{K}f(k^{-1}n^{-1}m^{-1}\unicode[STIX]{x1D6FE}mnk)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}(m)\,dn\,dk\nonumber\\ \displaystyle & = & \displaystyle D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}\unicode[STIX]{x1D6FF}_{P}(\unicode[STIX]{x1D6FE})^{1/2}\int _{I_{\unicode[STIX]{x1D6FE}}\backslash M}\int _{N}\int _{K}f(k^{-1}m^{-1}\unicode[STIX]{x1D6FE}mnk)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}(m)\,dn\,dk\nonumber\\ \displaystyle & = & \displaystyle D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(f^{P}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle O_{\unicode[STIX]{x1D6FE}}(f) & = & \displaystyle \int _{I_{\unicode[STIX]{x1D6FE}}\backslash G}f(x^{-1}\unicode[STIX]{x1D6FE}x)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(x)\nonumber\\ \displaystyle & = & \displaystyle \int _{I_{\unicode[STIX]{x1D6FE}}\backslash M}\int _{N}\int _{K}f(k^{-1}n^{-1}m^{-1}\unicode[STIX]{x1D6FE}mnk)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}(m)\,dn\,dk\nonumber\\ \displaystyle & = & \displaystyle D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}\unicode[STIX]{x1D6FF}_{P}(\unicode[STIX]{x1D6FE})^{1/2}\int _{I_{\unicode[STIX]{x1D6FE}}\backslash M}\int _{N}\int _{K}f(k^{-1}m^{-1}\unicode[STIX]{x1D6FE}mnk)\,d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}^{M}(m)\,dn\,dk\nonumber\\ \displaystyle & = & \displaystyle D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(f^{P}),\nonumber\end{eqnarray}$$as desired. ◻
We shall need a version of Lemma 7.6 that can be applied to the singular functions  $f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. This is Lemma 7.10 below, which we prove by adapting methods from [Reference Matz and TemplierMT15], where similar statements were established for
$f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. This is Lemma 7.10 below, which we prove by adapting methods from [Reference Matz and TemplierMT15], where similar statements were established for  $A_{G}\backslash \text{GL}_{n}(\mathbb{R})$. If
$A_{G}\backslash \text{GL}_{n}(\mathbb{R})$. If  $A\in \text{GL}(\mathfrak{g})$, define
$A\in \text{GL}(\mathfrak{g})$, define  $^{\text{t}}\!A$ to be the transpose with respect to
$^{\text{t}}\!A$ to be the transpose with respect to  $\langle \cdot ,\cdot \rangle _{+}$. As in [Reference Matz and TemplierMT15, §4.2], we define the functions
$\langle \cdot ,\cdot \rangle _{+}$. As in [Reference Matz and TemplierMT15, §4.2], we define the functions  ${\mathcal{L}},{\mathcal{N}}:\text{GL}(\mathfrak{g})\rightarrow \mathbb{R}$ by
${\mathcal{L}},{\mathcal{N}}:\text{GL}(\mathfrak{g})\rightarrow \mathbb{R}$ by  ${\mathcal{L}}(A)=\log (\text{tr}(A\,^{\text{t}}\!A)/\text{dim}\,\mathfrak{g})$ and
${\mathcal{L}}(A)=\log (\text{tr}(A\,^{\text{t}}\!A)/\text{dim}\,\mathfrak{g})$ and  ${\mathcal{N}}(A)=\text{tr}(A\,^{\text{t}}\!A)/\text{dim}\,\mathfrak{g}$.
${\mathcal{N}}(A)=\text{tr}(A\,^{\text{t}}\!A)/\text{dim}\,\mathfrak{g}$.
Lemma 7.7. We have  $0\leqslant {\mathcal{L}}(\text{Ad}(g))\leqslant 2\Vert X(g)\Vert$ for all
$0\leqslant {\mathcal{L}}(\text{Ad}(g))\leqslant 2\Vert X(g)\Vert$ for all  $g\in G$.
$g\in G$.
Proof. We follow [Reference Matz and TemplierMT15, Lemma 4.2]. It may be seen that  $^{\text{t}}\!\text{Ad}(g)=\text{Ad}(\unicode[STIX]{x1D703}(g))^{-1}$ for
$^{\text{t}}\!\text{Ad}(g)=\text{Ad}(\unicode[STIX]{x1D703}(g))^{-1}$ for  $g\in G$. We write
$g\in G$. We write  $g\in G$ as
$g\in G$ as  $k_{1}e^{X(g)}k_{2}$, so that
$k_{1}e^{X(g)}k_{2}$, so that  $\text{Ad}(g)\,^{\text{t}}\!\text{Ad}(g)=\text{Ad}(g\unicode[STIX]{x1D703}(g)^{-1})=\text{Ad}(k_{1}e^{2X(g)}k_{1}^{-1})$. Taking traces gives
$\text{Ad}(g)\,^{\text{t}}\!\text{Ad}(g)=\text{Ad}(g\unicode[STIX]{x1D703}(g)^{-1})=\text{Ad}(k_{1}e^{2X(g)}k_{1}^{-1})$. Taking traces gives
 $$\begin{eqnarray}{\mathcal{N}}(\text{Ad}(g))=\text{tr}(\text{Ad}(e^{2X(g)}))/\text{dim}\,\mathfrak{g}\leqslant e^{2\Vert X(g)\Vert },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}(\text{Ad}(g))=\text{tr}(\text{Ad}(e^{2X(g)}))/\text{dim}\,\mathfrak{g}\leqslant e^{2\Vert X(g)\Vert },\end{eqnarray}$$ and taking logs gives the upper bound. One sees that  $\text{tr}(\text{Ad}(e^{2X(g)}))\geqslant \dim \mathfrak{g}$ by applying the arithmetic mean–geometric mean inequality to opposite pairs of root spaces of
$\text{tr}(\text{Ad}(e^{2X(g)}))\geqslant \dim \mathfrak{g}$ by applying the arithmetic mean–geometric mean inequality to opposite pairs of root spaces of  $\mathfrak{g}$, which gives the lower bound.◻
$\mathfrak{g}$, which gives the lower bound.◻
We let  $P=MN$ be as above, and let
$P=MN$ be as above, and let  $\mathfrak{n}$ be the Lie algebra of
$\mathfrak{n}$ be the Lie algebra of  $N$.
$N$.
Lemma 7.8. Let  $B_{M}\subset M$ and
$B_{M}\subset M$ and  $B_{\mathfrak{n}}\subset \mathfrak{n}$ be compact. There is
$B_{\mathfrak{n}}\subset \mathfrak{n}$ be compact. There is  $C>0$ depending on
$C>0$ depending on  $B_{M}$ and
$B_{M}$ and  $B_{\mathfrak{n}}$ such that for all
$B_{\mathfrak{n}}$ such that for all  $m\in B_{M}$,
$m\in B_{M}$,  $V\in B_{\mathfrak{n}}$, we have
$V\in B_{\mathfrak{n}}$, we have  ${\mathcal{N}}(\text{Ad}(me^{V}))\geqslant 1+C\Vert V\Vert ^{2}$.
${\mathcal{N}}(\text{Ad}(me^{V}))\geqslant 1+C\Vert V\Vert ^{2}$.
Proof. Choose a basis for  $\mathfrak{g}$ subordinate to the root space decomposition
$\mathfrak{g}$ subordinate to the root space decomposition  $\mathfrak{g}=Z_{\mathfrak{g}}(\mathfrak{a})\oplus \bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$ that is orthonormal with respect to
$\mathfrak{g}=Z_{\mathfrak{g}}(\mathfrak{a})\oplus \bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$ that is orthonormal with respect to  $\langle \cdot ,\cdot \rangle _{+}$, where
$\langle \cdot ,\cdot \rangle _{+}$, where  $\unicode[STIX]{x1D6E5}$ are the roots of
$\unicode[STIX]{x1D6E5}$ are the roots of  $\mathfrak{a}$ in
$\mathfrak{a}$ in  $\mathfrak{g}$. It may be seen that the non-zero entries of
$\mathfrak{g}$. It may be seen that the non-zero entries of  $\text{Ad}(m)$ and
$\text{Ad}(m)$ and  $\text{Ad}(m)(\text{Ad}(e^{V})-1)$ with respect to this basis are disjoint, so we have
$\text{Ad}(m)(\text{Ad}(e^{V})-1)$ with respect to this basis are disjoint, so we have
 $$\begin{eqnarray}{\mathcal{N}}(\text{Ad}(me^{V}))={\mathcal{N}}(\text{Ad}(m))+{\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1))\geqslant 1+{\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}(\text{Ad}(me^{V}))={\mathcal{N}}(\text{Ad}(m))+{\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1))\geqslant 1+{\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1)).\end{eqnarray}$$ It follows that if  ${\mathcal{N}}(\text{Ad}(me^{V}))=1$ then
${\mathcal{N}}(\text{Ad}(me^{V}))=1$ then  ${\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1))=0$, so
${\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1))=0$, so  $V=0$. By a compactness argument, we may therefore assume that
$V=0$. By a compactness argument, we may therefore assume that  $\Vert V\Vert$ is less than an arbitrarily small constant. We deal with small
$\Vert V\Vert$ is less than an arbitrarily small constant. We deal with small  $V$ by applying the Taylor expansion of
$V$ by applying the Taylor expansion of  $e^{V}$, which gives
$e^{V}$, which gives
 $$\begin{eqnarray}\displaystyle \text{Ad}(m)(\text{Ad}(e^{V})-1) & = & \displaystyle \text{Ad}(m)\text{ad}(V)+O_{B_{M}}(\Vert V\Vert ^{2}),\nonumber\\ \displaystyle \text{Ad}(m)(\text{Ad}(e^{V})-1)\,^{\text{t}}[\text{Ad}(m)(\text{Ad}(e^{V})-1)] & = & \displaystyle \text{Ad}(m)\text{ad}(V)\,^{\text{t}}[\text{Ad}(m)\text{ad}(V)]+O_{B_{M}}(\Vert V\Vert ^{3}),\nonumber\\ \displaystyle {\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1)) & = & \displaystyle {\mathcal{N}}(\text{Ad}(m)\text{ad}(V))+O_{B_{M}}(\Vert V\Vert ^{3}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Ad}(m)(\text{Ad}(e^{V})-1) & = & \displaystyle \text{Ad}(m)\text{ad}(V)+O_{B_{M}}(\Vert V\Vert ^{2}),\nonumber\\ \displaystyle \text{Ad}(m)(\text{Ad}(e^{V})-1)\,^{\text{t}}[\text{Ad}(m)(\text{Ad}(e^{V})-1)] & = & \displaystyle \text{Ad}(m)\text{ad}(V)\,^{\text{t}}[\text{Ad}(m)\text{ad}(V)]+O_{B_{M}}(\Vert V\Vert ^{3}),\nonumber\\ \displaystyle {\mathcal{N}}(\text{Ad}(m)(\text{Ad}(e^{V})-1)) & = & \displaystyle {\mathcal{N}}(\text{Ad}(m)\text{ad}(V))+O_{B_{M}}(\Vert V\Vert ^{3}).\nonumber\end{eqnarray}$$ By compactness, we have  ${\mathcal{N}}(\text{Ad}(m)\text{ad}(V))\geqslant C>0$ for all
${\mathcal{N}}(\text{Ad}(m)\text{ad}(V))\geqslant C>0$ for all  $\Vert V\Vert =1$ and
$\Vert V\Vert =1$ and  $m\in B_{M}$. As
$m\in B_{M}$. As  ${\mathcal{N}}$ is quadratic, we have
${\mathcal{N}}$ is quadratic, we have  ${\mathcal{N}}(\text{Ad}(m)\text{ad}(V))\geqslant C\Vert V\Vert ^{2}$ for all
${\mathcal{N}}(\text{Ad}(m)\text{ad}(V))\geqslant C\Vert V\Vert ^{2}$ for all  $V$ and
$V$ and  $m\in B_{M}$, which completes the proof.◻
$m\in B_{M}$, which completes the proof.◻
We next show that the parabolic descent integral of  $f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$ along
$f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$ along  $P$ converges and defines a bounded function on
$P$ converges and defines a bounded function on  $M$.
$M$.
Lemma 7.9. Let  $f\in C_{c}(G)$, and for
$f\in C_{c}(G)$, and for  $0<\unicode[STIX]{x1D702}<1/2$ define
$0<\unicode[STIX]{x1D702}<1/2$ define  $F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. Then:
$F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. Then:
(i) the integral defining
 $F_{\unicode[STIX]{x1D702}}^{P}(m)$ converges absolutely for any
$F_{\unicode[STIX]{x1D702}}^{P}(m)$ converges absolutely for any  $m\in M$;
$m\in M$;(ii) there exists
 $f_{1}\in C_{c}(M)$ depending only on
$f_{1}\in C_{c}(M)$ depending only on  $f$ and
$f$ and  $\unicode[STIX]{x1D702}$ such that
$\unicode[STIX]{x1D702}$ such that  $|F_{\unicode[STIX]{x1D702}}^{P}(m)|\leqslant f_{1}(m)$ for all
$|F_{\unicode[STIX]{x1D702}}^{P}(m)|\leqslant f_{1}(m)$ for all  $m\in M$.
$m\in M$.
Proof. We are free to replace  $f$ by its absolute value, so that
$f$ by its absolute value, so that  $f\geqslant 0$. It follows that
$f\geqslant 0$. It follows that  $F_{\unicode[STIX]{x1D702}}^{P}(m)$ is defined everywhere as a value in
$F_{\unicode[STIX]{x1D702}}^{P}(m)$ is defined everywhere as a value in  $[0,\infty ]$. We may also assume that
$[0,\infty ]$. We may also assume that  $f$ is bi-
$f$ is bi- $K$-invariant. Let
$K$-invariant. Let  $B\subset G$ be a compact set containing
$B\subset G$ be a compact set containing  $\text{supp}(f)$. There are compact sets
$\text{supp}(f)$. There are compact sets  $B_{M}\subset M$ and
$B_{M}\subset M$ and  $B_{\mathfrak{n}}\subset \mathfrak{n}$ depending only on
$B_{\mathfrak{n}}\subset \mathfrak{n}$ depending only on  $B$ such that
$B$ such that  $me^{V}\in B$ implies
$me^{V}\in B$ implies  $m\in B_{M}$ and
$m\in B_{M}$ and  $V\in B_{\mathfrak{n}}$. It follows that
$V\in B_{\mathfrak{n}}$. It follows that  $\text{supp}(F_{\unicode[STIX]{x1D702}}^{P})\subset B_{M}$.
$\text{supp}(F_{\unicode[STIX]{x1D702}}^{P})\subset B_{M}$.
Lemma 7.7 implies that
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}}^{P}(m)\unicode[STIX]{x1D6FF}_{P}^{-1/2}(m)=\int _{N}f(mn)\Vert X(mn)\Vert ^{-\unicode[STIX]{x1D702}}\,dn\ll \int _{N}f(mn){\mathcal{L}}(\text{Ad}(mn))^{-\unicode[STIX]{x1D702}}\,dn.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}}^{P}(m)\unicode[STIX]{x1D6FF}_{P}^{-1/2}(m)=\int _{N}f(mn)\Vert X(mn)\Vert ^{-\unicode[STIX]{x1D702}}\,dn\ll \int _{N}f(mn){\mathcal{L}}(\text{Ad}(mn))^{-\unicode[STIX]{x1D702}}\,dn.\end{eqnarray}$$ Writing  $n=e^{V}$ and applying Lemma 7.8 gives
$n=e^{V}$ and applying Lemma 7.8 gives
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}}^{P}(m)\unicode[STIX]{x1D6FF}_{P}^{-1/2}(m)\ll \int _{\mathfrak{ n}}f(me^{V})\Vert V\Vert ^{-2\unicode[STIX]{x1D702}}\,dV.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}}^{P}(m)\unicode[STIX]{x1D6FF}_{P}^{-1/2}(m)\ll \int _{\mathfrak{ n}}f(me^{V})\Vert V\Vert ^{-2\unicode[STIX]{x1D702}}\,dV.\end{eqnarray}$$ In view of our assumption  $0<\unicode[STIX]{x1D702}<1/2$, the right-hand side is bounded by
$0<\unicode[STIX]{x1D702}<1/2$, the right-hand side is bounded by  $C(B,\unicode[STIX]{x1D702})\Vert f\Vert _{\infty }$. This proves (i), and (ii) follows by combining this with
$C(B,\unicode[STIX]{x1D702})\Vert f\Vert _{\infty }$. This proves (i), and (ii) follows by combining this with  $\text{supp}(F_{\unicode[STIX]{x1D702}}^{P})\subset B_{M}$.◻
$\text{supp}(F_{\unicode[STIX]{x1D702}}^{P})\subset B_{M}$.◻
Combining Lemmas 7.6 and 7.9 gives our next result.
Lemma 7.10. Let  $f\in C_{c}(G)$, and for
$f\in C_{c}(G)$, and for  $0<\unicode[STIX]{x1D702}<1/2$ define
$0<\unicode[STIX]{x1D702}<1/2$ define  $F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. If
$F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. If  $\unicode[STIX]{x1D6FE}\in M$ is
$\unicode[STIX]{x1D6FE}\in M$ is  $(G,M)$-regular, then the integral
$(G,M)$-regular, then the integral  $O_{\unicode[STIX]{x1D6FE}}(F_{\unicode[STIX]{x1D702}})$ converges absolutely, and we have
$O_{\unicode[STIX]{x1D6FE}}(F_{\unicode[STIX]{x1D702}})$ converges absolutely, and we have
 $$\begin{eqnarray}D_{M}^{G}(\unicode[STIX]{x1D6FE})^{1/2}O_{\unicode[STIX]{x1D6FE}}(F_{\unicode[STIX]{x1D702}})=O_{\unicode[STIX]{x1D6FE}}^{M}(F_{\unicode[STIX]{x1D702}}^{P}).\end{eqnarray}$$
$$\begin{eqnarray}D_{M}^{G}(\unicode[STIX]{x1D6FE})^{1/2}O_{\unicode[STIX]{x1D6FE}}(F_{\unicode[STIX]{x1D702}})=O_{\unicode[STIX]{x1D6FE}}^{M}(F_{\unicode[STIX]{x1D702}}^{P}).\end{eqnarray}$$ We return now to the proof of Proposition 7.3. Let  $0<\unicode[STIX]{x1D702}<1/2$, and let
$0<\unicode[STIX]{x1D702}<1/2$, and let  $f\in C_{c}(G)$ and
$f\in C_{c}(G)$ and  $F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. We assume that
$F_{\unicode[STIX]{x1D702}}=f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}$. We assume that  $f\geqslant 0$. As
$f\geqslant 0$. As  $\unicode[STIX]{x1D6FE}$ is not elliptic, we may let
$\unicode[STIX]{x1D6FE}$ is not elliptic, we may let  $M$ be a proper Levi subgroup with
$M$ be a proper Levi subgroup with  $G_{\unicode[STIX]{x1D6FE}}\subset M$. Because
$G_{\unicode[STIX]{x1D6FE}}\subset M$. Because  $G_{\unicode[STIX]{x1D6FE}}\subset M$,
$G_{\unicode[STIX]{x1D6FE}}\subset M$,  $\text{Ad}(\unicode[STIX]{x1D6FE})-1$ must be invertible on
$\text{Ad}(\unicode[STIX]{x1D6FE})-1$ must be invertible on  $\mathfrak{g}/\text{Lie}(M)$, so that
$\mathfrak{g}/\text{Lie}(M)$, so that  $\unicode[STIX]{x1D6FE}$ is
$\unicode[STIX]{x1D6FE}$ is  $(G,M)$-regular. Let
$(G,M)$-regular. Let  $P$ be a parabolic with Levi
$P$ be a parabolic with Levi  $M$. By conjugation, we may assume that
$M$. By conjugation, we may assume that  $P$ and
$P$ and  $M$ are semi-standard. We apply Lemma 7.9 to
$M$ are semi-standard. We apply Lemma 7.9 to  $F_{\unicode[STIX]{x1D702}}$ to obtain
$F_{\unicode[STIX]{x1D702}}$ to obtain  $f_{1}\in C_{c}(M)$ such that
$f_{1}\in C_{c}(M)$ such that  $F_{\unicode[STIX]{x1D702}}^{P}(m)\leqslant f_{1}(m)$ for all
$F_{\unicode[STIX]{x1D702}}^{P}(m)\leqslant f_{1}(m)$ for all  $m\in M$. Lemma 7.10 gives
$m\in M$. Lemma 7.10 gives
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(F_{\unicode[STIX]{x1D702}})=D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(F_{\unicode[STIX]{x1D702}}^{P})\leqslant D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(f_{1}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(F_{\unicode[STIX]{x1D702}})=D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(F_{\unicode[STIX]{x1D702}}^{P})\leqslant D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}O_{\unicode[STIX]{x1D6FE}}^{M}(f_{1}).\end{eqnarray}$$ From this and Proposition 7.1, applied on  $M$, we obtain
$M$, we obtain
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(F_{\unicode[STIX]{x1D702}})<c(\unicode[STIX]{x1D702},f)D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}D^{M}(\unicode[STIX]{x1D6FE})^{-1/2}<c^{\prime }(\unicode[STIX]{x1D702},f)D^{G}(\unicode[STIX]{x1D6FE})^{-1/2},\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}^{G}(F_{\unicode[STIX]{x1D702}})<c(\unicode[STIX]{x1D702},f)D_{M}^{G}(\unicode[STIX]{x1D6FE})^{-1/2}D^{M}(\unicode[STIX]{x1D6FE})^{-1/2}<c^{\prime }(\unicode[STIX]{x1D702},f)D^{G}(\unicode[STIX]{x1D6FE})^{-1/2},\end{eqnarray}$$as desired.
7.6 The case of  $\unicode[STIX]{x1D6FE}$ elliptic
$\unicode[STIX]{x1D6FE}$ elliptic
We first observe that, if  $\unicode[STIX]{x1D6FE}\in G$ is elliptic, then it is conjugate to an element of
$\unicode[STIX]{x1D6FE}\in G$ is elliptic, then it is conjugate to an element of  $K$. This is because if
$K$. This is because if  $Z(G_{\unicode[STIX]{x1D6FE}})$ is anisotropic then it is compact and therefore conjugate to a subgroup of
$Z(G_{\unicode[STIX]{x1D6FE}})$ is anisotropic then it is compact and therefore conjugate to a subgroup of  $K$.
$K$.
We shall assume  $\unicode[STIX]{x1D6FE}\in K-G_{\text{cpt}}$, and note that for such
$\unicode[STIX]{x1D6FE}\in K-G_{\text{cpt}}$, and note that for such  $\unicode[STIX]{x1D6FE}$ we have
$\unicode[STIX]{x1D6FE}$ we have  $D(\unicode[STIX]{x1D6FE})\ll 1$, where the implied constant depends only on
$D(\unicode[STIX]{x1D6FE})\ll 1$, where the implied constant depends only on  $G$. For
$G$. For  $\unicode[STIX]{x1D716}>0$ we put
$\unicode[STIX]{x1D716}>0$ we put  $K(\unicode[STIX]{x1D716})=\{g\in G:\Vert X(g)\Vert <\unicode[STIX]{x1D716}\}$ and write
$K(\unicode[STIX]{x1D716})=\{g\in G:\Vert X(g)\Vert <\unicode[STIX]{x1D716}\}$ and write  $1_{K(\unicode[STIX]{x1D716})}$ for the characteristic function of
$1_{K(\unicode[STIX]{x1D716})}$ for the characteristic function of  $K(\unicode[STIX]{x1D716})$. Proposition 7.3 will follow from a bound for
$K(\unicode[STIX]{x1D716})$. Proposition 7.3 will follow from a bound for  $O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})$ that is uniform in
$O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})$ that is uniform in  $\unicode[STIX]{x1D716}$ and
$\unicode[STIX]{x1D716}$ and  $D(\unicode[STIX]{x1D6FE})$, as provided by the following lemma.
$D(\unicode[STIX]{x1D6FE})$, as provided by the following lemma.
Lemma 7.11. For all  $\unicode[STIX]{x1D6FE}\in K-G_{\text{cpt}}$ and
$\unicode[STIX]{x1D6FE}\in K-G_{\text{cpt}}$ and  $0<\unicode[STIX]{x1D716}\leqslant 2D(\unicode[STIX]{x1D6FE})^{1/2}$, we have
$0<\unicode[STIX]{x1D716}\leqslant 2D(\unicode[STIX]{x1D6FE})^{1/2}$, we have  $O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})\ll \unicode[STIX]{x1D716}^{d_{\unicode[STIX]{x1D6FE}}}D(\unicode[STIX]{x1D6FE})^{-d_{\unicode[STIX]{x1D6FE}}/2}$, where
$O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})\ll \unicode[STIX]{x1D716}^{d_{\unicode[STIX]{x1D6FE}}}D(\unicode[STIX]{x1D6FE})^{-d_{\unicode[STIX]{x1D6FE}}/2}$, where  $d_{\unicode[STIX]{x1D6FE}}\geqslant 1$ is the codimension of
$d_{\unicode[STIX]{x1D6FE}}\geqslant 1$ is the codimension of  $I_{\unicode[STIX]{x1D6FE}}K$ in
$I_{\unicode[STIX]{x1D6FE}}K$ in  $G$.
$G$.
Proof. We first convert the problem to one on the symmetric space  $S=G/K$. Let
$S=G/K$. Let  $ds$ be the metric tensor on
$ds$ be the metric tensor on  $S$ associated with the norm
$S$ associated with the norm  $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on  $\mathfrak{p}$. We note that the distance function
$\mathfrak{p}$. We note that the distance function  $d_{S}$ attached to
$d_{S}$ attached to  $ds$ is given by
$ds$ is given by  $d_{S}(g_{1},g_{2})=\Vert X(g_{1}^{-1}g_{2})\Vert$.
$d_{S}(g_{1},g_{2})=\Vert X(g_{1}^{-1}g_{2})\Vert$.
We observe that  $O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716}))$, where
$O_{\unicode[STIX]{x1D6FE}}(1_{K(\unicode[STIX]{x1D716})})=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716}))$, where  $G(\unicode[STIX]{x1D716})=\{x\in G:x^{-1}\unicode[STIX]{x1D6FE}x\in K(\unicode[STIX]{x1D716})\}$. The set
$G(\unicode[STIX]{x1D716})=\{x\in G:x^{-1}\unicode[STIX]{x1D6FE}x\in K(\unicode[STIX]{x1D716})\}$. The set  $G(\unicode[STIX]{x1D716})$ is right
$G(\unicode[STIX]{x1D716})$ is right  $K$-invariant, and
$K$-invariant, and  $G(\unicode[STIX]{x1D716})/K$ is the set of points
$G(\unicode[STIX]{x1D716})/K$ is the set of points  $x\in S$ such that
$x\in S$ such that  $d_{S}(x,\unicode[STIX]{x1D6FE}x)<\unicode[STIX]{x1D716}$. Moreover,
$d_{S}(x,\unicode[STIX]{x1D6FE}x)<\unicode[STIX]{x1D716}$. Moreover,  $G(\unicode[STIX]{x1D716})$ is left
$G(\unicode[STIX]{x1D716})$ is left  $I_{\unicode[STIX]{x1D6FE}}$-invariant, and we will see it is roughly a tube around
$I_{\unicode[STIX]{x1D6FE}}$-invariant, and we will see it is roughly a tube around  $I_{\unicode[STIX]{x1D6FE}}$. Bounding the volume of
$I_{\unicode[STIX]{x1D6FE}}$. Bounding the volume of  $I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716})$ is therefore roughly equivalent to finding the radius of this tube, in a way which we now make precise.
$I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716})$ is therefore roughly equivalent to finding the radius of this tube, in a way which we now make precise.
Because  $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$,
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$,  $\mathfrak{g}_{\unicode[STIX]{x1D6FE}}$ is
$\mathfrak{g}_{\unicode[STIX]{x1D6FE}}$ is  $\unicode[STIX]{x1D703}$-stable. We may then write
$\unicode[STIX]{x1D703}$-stable. We may then write  $\mathfrak{g}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}_{\unicode[STIX]{x1D6FE}}+\mathfrak{k}_{\unicode[STIX]{x1D6FE}}$ where
$\mathfrak{g}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}_{\unicode[STIX]{x1D6FE}}+\mathfrak{k}_{\unicode[STIX]{x1D6FE}}$ where  $\mathfrak{k}_{\unicode[STIX]{x1D6FE}}=\mathfrak{k}\cap \mathfrak{g}_{\unicode[STIX]{x1D6FE}}$ and
$\mathfrak{k}_{\unicode[STIX]{x1D6FE}}=\mathfrak{k}\cap \mathfrak{g}_{\unicode[STIX]{x1D6FE}}$ and  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}\cap \mathfrak{g}_{\unicode[STIX]{x1D6FE}}$. Let
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}\cap \mathfrak{g}_{\unicode[STIX]{x1D6FE}}$. Let  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ be the orthocomplement of
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ be the orthocomplement of  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}$ in
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}$ in  $\mathfrak{p}$. We note that
$\mathfrak{p}$. We note that  $\unicode[STIX]{x1D6FE}\notin G_{\text{cpt}}$ implies that
$\unicode[STIX]{x1D6FE}\notin G_{\text{cpt}}$ implies that  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}\neq \mathfrak{p}$. Indeed, if
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}\neq \mathfrak{p}$. Indeed, if  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}$ then
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}=\mathfrak{p}$ then  $\text{Ad}(\unicode[STIX]{x1D6FE})$ fixes
$\text{Ad}(\unicode[STIX]{x1D6FE})$ fixes  $\mathfrak{p}$, and hence
$\mathfrak{p}$, and hence  $[\mathfrak{p},\mathfrak{p}]$. However,
$[\mathfrak{p},\mathfrak{p}]$. However,  $\mathfrak{p}+[\mathfrak{p},\mathfrak{p}]$ is the product of the
$\mathfrak{p}+[\mathfrak{p},\mathfrak{p}]$ is the product of the  $\mathbb{R}$-simple factors of
$\mathbb{R}$-simple factors of  $\mathfrak{g}$ of non-compact type (see [Reference HelgasonHel01, ch. V, Theorem 1.1] and the subsequent proof). In particular, the codimension
$\mathfrak{g}$ of non-compact type (see [Reference HelgasonHel01, ch. V, Theorem 1.1] and the subsequent proof). In particular, the codimension  $d_{\unicode[STIX]{x1D6FE}}$ of
$d_{\unicode[STIX]{x1D6FE}}$ of  $I_{\unicode[STIX]{x1D6FE}}K$ in
$I_{\unicode[STIX]{x1D6FE}}K$ in  $G$ is at least 1.
$G$ is at least 1.
Let  $x\in G(\unicode[STIX]{x1D716})$. By [Reference HelgasonHel01, ch. VI, Theorem 1.4], we may write
$x\in G(\unicode[STIX]{x1D716})$. By [Reference HelgasonHel01, ch. VI, Theorem 1.4], we may write  $x=e^{X_{\unicode[STIX]{x1D6FE}}}e^{X^{\unicode[STIX]{x1D6FE}}}k$ with
$x=e^{X_{\unicode[STIX]{x1D6FE}}}e^{X^{\unicode[STIX]{x1D6FE}}}k$ with  $X_{\unicode[STIX]{x1D6FE}}\in \mathfrak{p}_{\unicode[STIX]{x1D6FE}}$,
$X_{\unicode[STIX]{x1D6FE}}\in \mathfrak{p}_{\unicode[STIX]{x1D6FE}}$,  $X^{\unicode[STIX]{x1D6FE}}\in \mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ and
$X^{\unicode[STIX]{x1D6FE}}\in \mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ and  $k\in K$. The condition
$k\in K$. The condition  $x^{-1}\unicode[STIX]{x1D6FE}x\in K(\unicode[STIX]{x1D716})$ simplifies to
$x^{-1}\unicode[STIX]{x1D6FE}x\in K(\unicode[STIX]{x1D716})$ simplifies to  $e^{-X^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FE}e^{X^{\unicode[STIX]{x1D6FE}}}\in K(\unicode[STIX]{x1D716})$, which (since
$e^{-X^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FE}e^{X^{\unicode[STIX]{x1D6FE}}}\in K(\unicode[STIX]{x1D716})$, which (since  $\unicode[STIX]{x1D6FE}\in K$) is equivalent to
$\unicode[STIX]{x1D6FE}\in K$) is equivalent to  $e^{-X^{\unicode[STIX]{x1D6FE}}}e^{\text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}}\in K(\unicode[STIX]{x1D716})$. This implies that
$e^{-X^{\unicode[STIX]{x1D6FE}}}e^{\text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}}\in K(\unicode[STIX]{x1D716})$. This implies that  $d_{S}(e^{X^{\unicode[STIX]{x1D6FE}}},e^{\text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}})<\unicode[STIX]{x1D716}$: the element
$d_{S}(e^{X^{\unicode[STIX]{x1D6FE}}},e^{\text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}})<\unicode[STIX]{x1D716}$: the element  $e^{X^{\unicode[STIX]{x1D6FE}}}$ is rotated by
$e^{X^{\unicode[STIX]{x1D6FE}}}$ is rotated by  $\unicode[STIX]{x1D6FE}$ by a distance at most
$\unicode[STIX]{x1D6FE}$ by a distance at most  $\unicode[STIX]{x1D716}$. The Cartan–Hadamard theorem [Reference HelgasonHel01, ch. I, Theorem 13.1] then implies that
$\unicode[STIX]{x1D716}$. The Cartan–Hadamard theorem [Reference HelgasonHel01, ch. I, Theorem 13.1] then implies that  $\Vert \text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}-X^{\unicode[STIX]{x1D6FE}}\Vert <\unicode[STIX]{x1D716}$. Because all eigenvalues of
$\Vert \text{Ad}(\unicode[STIX]{x1D6FE})X^{\unicode[STIX]{x1D6FE}}-X^{\unicode[STIX]{x1D6FE}}\Vert <\unicode[STIX]{x1D716}$. Because all eigenvalues of  $\text{Ad}(\unicode[STIX]{x1D6FE})-1$ on
$\text{Ad}(\unicode[STIX]{x1D6FE})-1$ on  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ have absolute value at most 2, and they occur in complex conjugate pairs, their absolute value is at least
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ have absolute value at most 2, and they occur in complex conjugate pairs, their absolute value is at least  $CD(\unicode[STIX]{x1D6FE})^{1/2}$ for
$CD(\unicode[STIX]{x1D6FE})^{1/2}$ for  $C>0$ depending only on
$C>0$ depending only on  $G$. It follows that
$G$. It follows that  $\Vert X^{\unicode[STIX]{x1D6FE}}\Vert \leqslant C\unicode[STIX]{x1D716}D(\unicode[STIX]{x1D6FE})^{-1/2}$. If we let
$\Vert X^{\unicode[STIX]{x1D6FE}}\Vert \leqslant C\unicode[STIX]{x1D716}D(\unicode[STIX]{x1D6FE})^{-1/2}$. If we let  $B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r)$ be the ball of radius
$B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r)$ be the ball of radius  $r$ around 0 in
$r$ around 0 in  $\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ with respect to
$\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }$ with respect to  $\Vert \cdot \Vert$, it follows that
$\Vert \cdot \Vert$, it follows that  $G(\unicode[STIX]{x1D716})\subset I_{\unicode[STIX]{x1D6FE}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K$ with
$G(\unicode[STIX]{x1D716})\subset I_{\unicode[STIX]{x1D6FE}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K$ with  $r_{0}=C\unicode[STIX]{x1D716}D(\unicode[STIX]{x1D6FE})^{-1/2}\leqslant 2C$.
$r_{0}=C\unicode[STIX]{x1D716}D(\unicode[STIX]{x1D6FE})^{-1/2}\leqslant 2C$.
Let  $I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\subset I_{\unicode[STIX]{x1D6FE}}$ be a compact set such that
$I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\subset I_{\unicode[STIX]{x1D6FE}}$ be a compact set such that  $\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}^{\text{c}})=1$. Then from the preceding paragraph we deduce that
$\unicode[STIX]{x1D707}_{I_{\unicode[STIX]{x1D6FE}}}^{\text{can}}(I_{\unicode[STIX]{x1D6FE}}^{\text{c}})=1$. Then from the preceding paragraph we deduce that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716}))\leqslant \unicode[STIX]{x1D707}_{G}(I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}(I_{\unicode[STIX]{x1D6FE}}\backslash G(\unicode[STIX]{x1D716}))\leqslant \unicode[STIX]{x1D707}_{G}(I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K).\end{eqnarray}$$ Let  $B_{\mathfrak{p}}(r)$ denote the ball of radius
$B_{\mathfrak{p}}(r)$ denote the ball of radius  $r$ around 0 in
$r$ around 0 in  $\mathfrak{p}$ with respect to
$\mathfrak{p}$ with respect to  $\Vert \cdot \Vert$. We have
$\Vert \cdot \Vert$. We have
 $$\begin{eqnarray}I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K\subset I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}}(r_{0}))K=I_{\unicode[STIX]{x1D6FE}}^{\text{c}}K\exp (B_{\mathfrak{p}}(r_{0})).\end{eqnarray}$$
$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}_{\unicode[STIX]{x1D6FE}}^{\bot }}(r_{0}))K\subset I_{\unicode[STIX]{x1D6FE}}^{\text{c}}\exp (B_{\mathfrak{p}}(r_{0}))K=I_{\unicode[STIX]{x1D6FE}}^{\text{c}}K\exp (B_{\mathfrak{p}}(r_{0})).\end{eqnarray}$$ Because  $I_{\unicode[STIX]{x1D6FE}}^{\text{c}}K$ is compact and contained in
$I_{\unicode[STIX]{x1D6FE}}^{\text{c}}K$ is compact and contained in  $I_{\unicode[STIX]{x1D6FE}}K$, the result follows from the expression for
$I_{\unicode[STIX]{x1D6FE}}K$, the result follows from the expression for  $r_{0}$, provided we show that our bounds do not depend on the choice of
$r_{0}$, provided we show that our bounds do not depend on the choice of  $I_{\unicode[STIX]{x1D6FE}}^{\text{c}}$.
$I_{\unicode[STIX]{x1D6FE}}^{\text{c}}$.
We show that, after conjugating  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in  $G$ to another element of
$G$ to another element of  $K$, there are only finitely many possibilities for
$K$, there are only finitely many possibilities for  $I_{\unicode[STIX]{x1D6FE}}$.Footnote 4 Let
$I_{\unicode[STIX]{x1D6FE}}$.Footnote 4 Let  $T_{1},\ldots ,T_{n}$ be representatives for the conjugacy classes of maximal
$T_{1},\ldots ,T_{n}$ be representatives for the conjugacy classes of maximal  $\mathbb{R}$-tori in
$\mathbb{R}$-tori in  $G$. If
$G$. If  $T_{i}^{\text{c}}$ denotes the maximal compact subgroup of
$T_{i}^{\text{c}}$ denotes the maximal compact subgroup of  $T_{i}(\mathbb{R})$, we may assume that
$T_{i}(\mathbb{R})$, we may assume that  $T_{i}^{\text{c}}\subset K$ for all
$T_{i}^{\text{c}}\subset K$ for all  $i$. As we are free to replace
$i$. As we are free to replace  $\unicode[STIX]{x1D6FE}$ by any conjugate, we may assume that
$\unicode[STIX]{x1D6FE}$ by any conjugate, we may assume that  $\unicode[STIX]{x1D6FE}\in T_{i}$ for some
$\unicode[STIX]{x1D6FE}\in T_{i}$ for some  $i$, which implies that
$i$, which implies that  $\unicode[STIX]{x1D6FE}\in T_{i}^{\text{c}}\subset K$. There are now finitely many possibilities for
$\unicode[STIX]{x1D6FE}\in T_{i}^{\text{c}}\subset K$. There are now finitely many possibilities for  $I_{\unicode[STIX]{x1D6FE}}$.◻
$I_{\unicode[STIX]{x1D6FE}}$.◻
We now return to the proof of Proposition 7.3. Choose a compact set  $B$ containing
$B$ containing  $\text{supp}(f)$, so that
$\text{supp}(f)$, so that
 $$\begin{eqnarray}f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}\,\ll _{f}\,1_{B}+\mathop{\sum }_{k=1}^{\infty }2^{\unicode[STIX]{x1D702}k}1_{K(2^{-k})}.\end{eqnarray}$$
$$\begin{eqnarray}f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}}\,\ll _{f}\,1_{B}+\mathop{\sum }_{k=1}^{\infty }2^{\unicode[STIX]{x1D702}k}1_{K(2^{-k})}.\end{eqnarray}$$We deduce that
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})\,\ll _{f}\,O_{\unicode[STIX]{x1D6FE}}(1_{B})+\mathop{\sum }_{k=1}^{\infty }2^{\unicode[STIX]{x1D702}k}O_{\unicode[STIX]{x1D6FE}}(1_{K(2^{-k})}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})\,\ll _{f}\,O_{\unicode[STIX]{x1D6FE}}(1_{B})+\mathop{\sum }_{k=1}^{\infty }2^{\unicode[STIX]{x1D702}k}O_{\unicode[STIX]{x1D6FE}}(1_{K(2^{-k})}).\end{eqnarray}$$An application of Proposition 7.1 and Lemma 7.11 yields
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})\,\ll _{f}\,D(\unicode[STIX]{x1D6FE})^{-1/2}+\mathop{\sum }_{2^{k+1}\geqslant D(\unicode[STIX]{x1D6FE})^{-1/2}}2^{\unicode[STIX]{x1D702}k-k}D(\unicode[STIX]{x1D6FE})^{-1/2}+\mathop{\sum }_{2^{k+1}<D(\unicode[STIX]{x1D6FE})^{-1/2}}2^{\unicode[STIX]{x1D702}k}D(\unicode[STIX]{x1D6FE})^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D6FE}}(f\Vert X(\cdot )\Vert ^{-\unicode[STIX]{x1D702}})\,\ll _{f}\,D(\unicode[STIX]{x1D6FE})^{-1/2}+\mathop{\sum }_{2^{k+1}\geqslant D(\unicode[STIX]{x1D6FE})^{-1/2}}2^{\unicode[STIX]{x1D702}k-k}D(\unicode[STIX]{x1D6FE})^{-1/2}+\mathop{\sum }_{2^{k+1}<D(\unicode[STIX]{x1D6FE})^{-1/2}}2^{\unicode[STIX]{x1D702}k}D(\unicode[STIX]{x1D6FE})^{-1/2}.\end{eqnarray}$$ Our assumption that  $0<\unicode[STIX]{x1D702}<1/2$ implies that both geometric series are bounded by
$0<\unicode[STIX]{x1D702}<1/2$ implies that both geometric series are bounded by  $D(\unicode[STIX]{x1D6FE})^{-3/4}$, completing the proof of Proposition 7.3.
$D(\unicode[STIX]{x1D6FE})^{-3/4}$, completing the proof of Proposition 7.3.
Acknowledgements
We would like to thank Tobias Finis, Erez Lapid, Zeev Rudnick, Yiannis Sakellaridis, Sug Woo Shin, Nicolas Templier, and Akshay Venkatesh for helpful conversations during the elaboration of this paper. The first author benefited from many enlightening discussions with Nicolas Bergeron and Djordje Milićević. We would also like to thank the referees for suggestions that greatly improved the paper.
Appendix A Distinction principles and the  $C^{\infty }$ spectrum of symmetric varieties
$C^{\infty }$ spectrum of symmetric varieties
There are several methods that may be used to prove power growth of eigenfunctions on arithmetic manifolds. The original proof of Rudnick and Sarnak uses a distinction principle. This means that, for certain period integrals, if an automorphic form  $\unicode[STIX]{x1D719}$ has a non-zero period then
$\unicode[STIX]{x1D719}$ has a non-zero period then  $\unicode[STIX]{x1D719}$ is exceptional in some sense, which can mean being a transfer from a smaller group, or being non-tempered.
$\unicode[STIX]{x1D719}$ is exceptional in some sense, which can mean being a transfer from a smaller group, or being non-tempered.
In this appendix we review the method of Rudnick and Sarnak and describe an alternative approach to proving Theorems 1.1 and 1.2 which retains much of the spirit of their approach. It is based on a theorem of Sakellaridis on the unramified  $C^{\infty }$ spectrum of spherical varieties, which we apply in the case of symmetric varieties. In short, we replace the global distinction principle of Rudnick and Sarnak which implies being in the image of a functorial lift by a local distinction principle which implies having non-tempered Satake parameters. What both of these implied properties have in common is that they are rare. Counting arguments can then be used to produce power growth.
$C^{\infty }$ spectrum of spherical varieties, which we apply in the case of symmetric varieties. In short, we replace the global distinction principle of Rudnick and Sarnak which implies being in the image of a functorial lift by a local distinction principle which implies having non-tempered Satake parameters. What both of these implied properties have in common is that they are rare. Counting arguments can then be used to produce power growth.
A.1 The global distinction argument
We illustrate the distinction argument in a special case, taken from Rudnick and Sarnak’s proof [Reference Rudnick and SarnakRS94].
Let  $Q$ be the quadratic form
$Q$ be the quadratic form  $Q(x)=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-7x_{4}^{2}$. If we let
$Q(x)=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-7x_{4}^{2}$. If we let  $V=\{x\in \mathbb{R}^{4}:Q(x)=-1\}$, then
$V=\{x\in \mathbb{R}^{4}:Q(x)=-1\}$, then  $V$ is a two-sheeted hyperboloid and the upper sheet is a model for
$V$ is a two-sheeted hyperboloid and the upper sheet is a model for  $\mathbb{H}^{3}$. If we let
$\mathbb{H}^{3}$. If we let  $\unicode[STIX]{x1D6E4}$ be the intersection of
$\unicode[STIX]{x1D6E4}$ be the intersection of  $\text{O}(Q,\mathbb{Z})$ with the identity component of
$\text{O}(Q,\mathbb{Z})$ with the identity component of  $\text{O}(Q,\mathbb{R})$, then
$\text{O}(Q,\mathbb{R})$, then  $Y=\unicode[STIX]{x1D6E4}\backslash \mathbb{H}^{3}$ is a compact hyperbolic 3-manifold. The distinction result that Rudnick and Sarnak prove is that if
$Y=\unicode[STIX]{x1D6E4}\backslash \mathbb{H}^{3}$ is a compact hyperbolic 3-manifold. The distinction result that Rudnick and Sarnak prove is that if  $\unicode[STIX]{x1D713}\in L^{2}(Y)$ is orthogonal to all theta lifts of cusp forms of weight 1 on
$\unicode[STIX]{x1D713}\in L^{2}(Y)$ is orthogonal to all theta lifts of cusp forms of weight 1 on  $\unicode[STIX]{x1D6E4}_{1}(28)$, then
$\unicode[STIX]{x1D6E4}_{1}(28)$, then  $\unicode[STIX]{x1D713}((2,1,1,1))=0$. The result then follows from the local Weyl law and a counting argument. Indeed, the local Weyl law says that the average size of
$\unicode[STIX]{x1D713}((2,1,1,1))=0$. The result then follows from the local Weyl law and a counting argument. Indeed, the local Weyl law says that the average size of  $|\unicode[STIX]{x1D713}((2,1,1,1))|^{2}$ must be 1. However, the number of eigenfunctions on
$|\unicode[STIX]{x1D713}((2,1,1,1))|^{2}$ must be 1. However, the number of eigenfunctions on  $X$ with eigenvalue
$X$ with eigenvalue  $\unicode[STIX]{x1D706}\leqslant R$ is roughly
$\unicode[STIX]{x1D706}\leqslant R$ is roughly  $R^{3}$, while the number of theta lifts in this range is roughly
$R^{3}$, while the number of theta lifts in this range is roughly  $R^{2}$. Because the number of non-vanishing eigenfunctions is small, their values must be large to make up the right average.
$R^{2}$. Because the number of non-vanishing eigenfunctions is small, their values must be large to make up the right average.
The generalization of this principle, namely that an automorphic form on  $\text{SO}(n,1)$ that is orthogonal to theta lifts from
$\text{SO}(n,1)$ that is orthogonal to theta lifts from  $\text{SL}_{2}$ must have vanishing
$\text{SL}_{2}$ must have vanishing  $\text{SO}(n)$ periods, was used by Donnelly [Reference DonnellyDon07]. It is likely that this could be used to prove Theorem 1.1 on other groups of the form
$\text{SO}(n)$ periods, was used by Donnelly [Reference DonnellyDon07]. It is likely that this could be used to prove Theorem 1.1 on other groups of the form  $\text{SO}(m,n)$,
$\text{SO}(m,n)$,  $\text{U}(m,n)$, or
$\text{U}(m,n)$, or  $\text{Sp}(m,n)$. Another distinction principle that one could apply is due to Jacquet [Reference JacquetJac05] (and later refined by Feigon, Lapid and Offen in [Reference Feigon, Lapid and OffenFLO12, Reference Lapid and OffenLO07]), which states that a form on
$\text{Sp}(m,n)$. Another distinction principle that one could apply is due to Jacquet [Reference JacquetJac05] (and later refined by Feigon, Lapid and Offen in [Reference Feigon, Lapid and OffenFLO12, Reference Lapid and OffenLO07]), which states that a form on  $\text{GL}(n,\mathbb{C})$ with a non-vanishing
$\text{GL}(n,\mathbb{C})$ with a non-vanishing  $\text{U}(n)$ period must come from quadratic base change. See [Reference Jacquet, Lai and RallisJLR93] for a general discussion of these ideas.
$\text{U}(n)$ period must come from quadratic base change. See [Reference Jacquet, Lai and RallisJLR93] for a general discussion of these ideas.
A.2 Symmetric varieties
Let  $F$ be a field of characteristic 0. A symmetric variety over
$F$ be a field of characteristic 0. A symmetric variety over  $F$ is a variety
$F$ is a variety  $X=G/H$ where
$X=G/H$ where  $G$ is a reductive
$G$ is a reductive  $F$-group,
$F$-group,  $\unicode[STIX]{x1D703}$ is an involution of
$\unicode[STIX]{x1D703}$ is an involution of  $G$ over
$G$ over  $F$, and
$F$, and  $H$ is an open
$H$ is an open  $F$-subgroup of the fixed point group
$F$-subgroup of the fixed point group  $G^{\unicode[STIX]{x1D703}}$. We refer the reader to [Reference Helminck and WangHW93, Reference VustVus74] for background on these varieties.
$G^{\unicode[STIX]{x1D703}}$. We refer the reader to [Reference Helminck and WangHW93, Reference VustVus74] for background on these varieties.
If  $S\subset G$ is a
$S\subset G$ is a  $\unicode[STIX]{x1D703}$-stable torus, let
$\unicode[STIX]{x1D703}$-stable torus, let  $S^{+}$ and
$S^{+}$ and  $S^{-}$ be the neutral component of
$S^{-}$ be the neutral component of  $S^{\unicode[STIX]{x1D703}}$ and
$S^{\unicode[STIX]{x1D703}}$ and  $\{x\in S:\unicode[STIX]{x1D703}(x)=x^{-1}\}$ respectively, so that
$\{x\in S:\unicode[STIX]{x1D703}(x)=x^{-1}\}$ respectively, so that  $S^{+}\times S^{-}\rightarrow S$ is an isogeny. A
$S^{+}\times S^{-}\rightarrow S$ is an isogeny. A  $\unicode[STIX]{x1D703}$-stable torus
$\unicode[STIX]{x1D703}$-stable torus  $S$ is said to be
$S$ is said to be  $(F,\unicode[STIX]{x1D703})$-split if it is
$(F,\unicode[STIX]{x1D703})$-split if it is  $F$-split and
$F$-split and  $\unicode[STIX]{x1D703}$ acts on it by inversion. A parabolic subgroup
$\unicode[STIX]{x1D703}$ acts on it by inversion. A parabolic subgroup  $P$ of
$P$ of  $G$ is said to be
$G$ is said to be  $\unicode[STIX]{x1D703}$-split if
$\unicode[STIX]{x1D703}$-split if  $P$ and
$P$ and  $\unicode[STIX]{x1D703}P$ are opposed. In this case,
$\unicode[STIX]{x1D703}P$ are opposed. In this case,  $P\cap \unicode[STIX]{x1D703}(P)$ is the unique
$P\cap \unicode[STIX]{x1D703}(P)$ is the unique  $\unicode[STIX]{x1D703}$-stable Levi of both
$\unicode[STIX]{x1D703}$-stable Levi of both  $P$ and
$P$ and  $\unicode[STIX]{x1D703}P$. All maximal
$\unicode[STIX]{x1D703}P$. All maximal  $(F,\unicode[STIX]{x1D703})$-split tori and all minimal
$(F,\unicode[STIX]{x1D703})$-split tori and all minimal  $\unicode[STIX]{x1D703}$-split parabolic
$\unicode[STIX]{x1D703}$-split parabolic  $F$-subgroups are conjugate under
$F$-subgroups are conjugate under  $G(\overline{F})$. We define the
$G(\overline{F})$. We define the  $\unicode[STIX]{x1D703}$-split rank of
$\unicode[STIX]{x1D703}$-split rank of  $G$ to be the common dimension of such tori. We say that
$G$ to be the common dimension of such tori. We say that  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-split if its
$\unicode[STIX]{x1D703}$-split if its  $\unicode[STIX]{x1D703}$-split rank is equal to its absolute rank, that is, if
$\unicode[STIX]{x1D703}$-split rank is equal to its absolute rank, that is, if  $G$ contains an
$G$ contains an  $(F,\unicode[STIX]{x1D703})$-split maximal torus. We say that
$(F,\unicode[STIX]{x1D703})$-split maximal torus. We say that  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-quasi-split if
$\unicode[STIX]{x1D703}$-quasi-split if  $G$ contains a
$G$ contains a  $\unicode[STIX]{x1D703}$-split Borel defined over
$\unicode[STIX]{x1D703}$-split Borel defined over  $F$. In this case,
$F$. In this case,  $B\cap \unicode[STIX]{x1D703}(B)$ is a
$B\cap \unicode[STIX]{x1D703}(B)$ is a  $\unicode[STIX]{x1D703}$-stable torus, which may or may not be
$\unicode[STIX]{x1D703}$-stable torus, which may or may not be  $\unicode[STIX]{x1D703}$-split.
$\unicode[STIX]{x1D703}$-split.
From now on we shall assume  $G$split over
$G$split over  $F$. The following lemma then implies that
$F$. The following lemma then implies that  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-(quasi-)split if and only if
$\unicode[STIX]{x1D703}$-(quasi-)split if and only if  $G\times \overline{F}$ is.
$G\times \overline{F}$ is.
Lemma A.1. A maximal  $(F,\unicode[STIX]{x1D703})$-split torus in
$(F,\unicode[STIX]{x1D703})$-split torus in  $G$ is also a maximal
$G$ is also a maximal  $\unicode[STIX]{x1D703}$-split torus in
$\unicode[STIX]{x1D703}$-split torus in  $G\times \overline{F}$, and a minimal
$G\times \overline{F}$, and a minimal  $\unicode[STIX]{x1D703}$-split
$\unicode[STIX]{x1D703}$-split  $F$-parabolic in
$F$-parabolic in  $G$ is also a minimal
$G$ is also a minimal  $\unicode[STIX]{x1D703}$-split parabolic in
$\unicode[STIX]{x1D703}$-split parabolic in  $G\times \overline{F}$.
$G\times \overline{F}$.
Proof. Let  $S$ be such a torus, and let
$S$ be such a torus, and let  $A$ be a maximal
$A$ be a maximal  $F$-split torus containing
$F$-split torus containing  $S$. As in [Reference Helminck and WangHW93, Lemma 4.5], let
$S$. As in [Reference Helminck and WangHW93, Lemma 4.5], let  $C$,
$C$,  $M_{1}$ and
$M_{1}$ and  $M_{2}$ be the central, anisotropic and isotropic factors of
$M_{2}$ be the central, anisotropic and isotropic factors of  $Z_{G}(S)$ over
$Z_{G}(S)$ over  $F$. Because
$F$. Because  $Z_{G}(A)=A$, [Reference Helminck and WangHW93] gives
$Z_{G}(A)=A$, [Reference Helminck and WangHW93] gives  $CM_{1}\subset A$ so that
$CM_{1}\subset A$ so that  $M_{1}$ is trivial and
$M_{1}$ is trivial and  $C$ is split. We have
$C$ is split. We have  $S\subset C$, and
$S\subset C$, and  $C$ is
$C$ is  $\unicode[STIX]{x1D703}$-stable, so by the maximality of
$\unicode[STIX]{x1D703}$-stable, so by the maximality of  $S$ we must have
$S$ we must have  $S=C^{-}$. As
$S=C^{-}$. As  $M_{2}\subset G^{\unicode[STIX]{x1D703}}$ by [Reference Helminck and WangHW93],
$M_{2}\subset G^{\unicode[STIX]{x1D703}}$ by [Reference Helminck and WangHW93],  $\unicode[STIX]{x1D703}$ acts trivially on
$\unicode[STIX]{x1D703}$ acts trivially on  $Z_{G}(S)/C^{-}$ so there is no strictly larger
$Z_{G}(S)/C^{-}$ so there is no strictly larger  $\unicode[STIX]{x1D703}$-split torus containing
$\unicode[STIX]{x1D703}$-split torus containing  $S$ over
$S$ over  $\overline{F}$.
$\overline{F}$.
Let  $P$ be such a parabolic. By [Reference Helminck and WangHW93, Lemma 2.4] we may let
$P$ be such a parabolic. By [Reference Helminck and WangHW93, Lemma 2.4] we may let  $A\subset P$ be a
$A\subset P$ be a  $\unicode[STIX]{x1D703}$-stable maximal
$\unicode[STIX]{x1D703}$-stable maximal  $F$-split torus of
$F$-split torus of  $G$. Then [Reference Helminck and WangHW93, Proposition 4.7] implies that
$G$. Then [Reference Helminck and WangHW93, Proposition 4.7] implies that  $A^{-}$ is a maximal
$A^{-}$ is a maximal  $(F,\unicode[STIX]{x1D703})$-split torus of
$(F,\unicode[STIX]{x1D703})$-split torus of  $G$, and
$G$, and  $Z_{G}(A^{-})=P\cap \unicode[STIX]{x1D703}(P)$. We have shown that
$Z_{G}(A^{-})=P\cap \unicode[STIX]{x1D703}(P)$. We have shown that  $A^{-}$ is a maximal
$A^{-}$ is a maximal  $\unicode[STIX]{x1D703}$-split torus in
$\unicode[STIX]{x1D703}$-split torus in  $G\times \overline{F}$, and applying [Reference Helminck and WangHW93] again gives that
$G\times \overline{F}$, and applying [Reference Helminck and WangHW93] again gives that  $P$ is minimal
$P$ is minimal  $\unicode[STIX]{x1D703}$-split in
$\unicode[STIX]{x1D703}$-split in  $G\times \overline{F}$.◻
$G\times \overline{F}$.◻
A.3 A result of Sakellaridis on the unramified  $C^{\infty }$ spectrum
$C^{\infty }$ spectrum
In [Reference SakellaridisSak08, Reference SakellaridisSak13], Sakellaridis describes the unramified  $C^{\infty }$ spectrum of a spherical variety. We reprise his results below in the symmetric case, and use them to describe an alternative approach to Theorems 1.1 and 1.2 in the case when
$C^{\infty }$ spectrum of a spherical variety. We reprise his results below in the symmetric case, and use them to describe an alternative approach to Theorems 1.1 and 1.2 in the case when  $G_{v_{0}}$ is not quasi-split. Throughout,
$G_{v_{0}}$ is not quasi-split. Throughout,  $F$ will be a
$F$ will be a  $p$-adic field and, as in § A.2, the group
$p$-adic field and, as in § A.2, the group  $G$ will be split over
$G$ will be split over  $F$.
$F$.
Let  $A$ and
$A$ and  $B$ be the
$B$ be the  $\unicode[STIX]{x1D703}$-stable maximal split torus and Borel of
$\unicode[STIX]{x1D703}$-stable maximal split torus and Borel of  $G$ chosen in Lemma A.4. Let
$G$ chosen in Lemma A.4. Let  $\unicode[STIX]{x1D6FF}$ denote the modular character of
$\unicode[STIX]{x1D6FF}$ denote the modular character of  $A$ with respect to
$A$ with respect to  $B$. Let
$B$. Let  ${\check{A}}$ be the complex dual torus of
${\check{A}}$ be the complex dual torus of  $A$, so that unramified characters of
$A$, so that unramified characters of  $A$ correspond to elements of
$A$ correspond to elements of  ${\check{A}}$. Let
${\check{A}}$. Let  $W$ be the Weyl group of
$W$ be the Weyl group of  $A$ and
$A$ and  ${\check{A}}$. Recall that the irreducible unramified representations of
${\check{A}}$. Recall that the irreducible unramified representations of  $G$ are in bijection with
$G$ are in bijection with  ${\check{A}}/W$, via the map taking
${\check{A}}/W$, via the map taking  $\unicode[STIX]{x1D70B}$ to its Satake parameter. We introduce the torus
$\unicode[STIX]{x1D70B}$ to its Satake parameter. We introduce the torus  $A_{X}=A/A\cap H$ and write
$A_{X}=A/A\cap H$ and write  ${\check{A}}_{X}$ for its dual torus. We then have a map
${\check{A}}_{X}$ for its dual torus. We then have a map  $\unicode[STIX]{x1D704}:{\check{A}}_{X}\rightarrow {\check{A}}$ with finite kernel. If
$\unicode[STIX]{x1D704}:{\check{A}}_{X}\rightarrow {\check{A}}$ with finite kernel. If  $\unicode[STIX]{x1D712}$ is an unramified character of
$\unicode[STIX]{x1D712}$ is an unramified character of  $A$, let
$A$, let  $I(\unicode[STIX]{x1D712})$ be the corresponding unitarily normalized induced representation of
$I(\unicode[STIX]{x1D712})$ be the corresponding unitarily normalized induced representation of  $G$.
$G$.
The following result of Sakellaridis [Reference SakellaridisSak08, Theorem 1.2.1] describes the unramified  $H$-distinguished
$H$-distinguished  $C^{\infty }$ spectrum in terms of the image
$C^{\infty }$ spectrum in terms of the image  $\unicode[STIX]{x1D704}({\check{A}}_{X})$ in
$\unicode[STIX]{x1D704}({\check{A}}_{X})$ in  ${\check{A}}$, denoted by
${\check{A}}$, denoted by  $A_{X}^{\ast }$.
$A_{X}^{\ast }$.
Theorem A.2 (Sakellaridis).
There exists a non-zero morphism  $C_{c}^{\infty }(X)\rightarrow I(\unicode[STIX]{x1D712})$ only if
$C_{c}^{\infty }(X)\rightarrow I(\unicode[STIX]{x1D712})$ only if  $\unicode[STIX]{x1D712}$ lies in a
$\unicode[STIX]{x1D712}$ lies in a  $W$-translate of
$W$-translate of  $\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$.
$\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$.
From this we may deduce the following consequence.
Corollary A.3. If  $G$ is not
$G$ is not  $\unicode[STIX]{x1D703}$-quasi-split, any irreducible unramified representation
$\unicode[STIX]{x1D703}$-quasi-split, any irreducible unramified representation  $\unicode[STIX]{x1D70B}$ of
$\unicode[STIX]{x1D70B}$ of  $G$ that occurs as a subrepresentation of
$G$ that occurs as a subrepresentation of  $C^{\infty }(X)$ must be non-tempered.
$C^{\infty }(X)$ must be non-tempered.
To see how Corollary A.3 follows from Theorem A.2, we must convert from Sakellaridis’ notation to ours. Sakellaridis defines the tori  $A$ and
$A$ and  $A_{X}$ using an open Borel orbit
$A_{X}$ using an open Borel orbit  $\mathring{X}\subset X$ and its stabilizer, a parabolic subgroup called the associated parabolic. The following lemma translates his definitions to the symmetric case.
$\mathring{X}\subset X$ and its stabilizer, a parabolic subgroup called the associated parabolic. The following lemma translates his definitions to the symmetric case.
Lemma A.4. Let notation be as in § A.2. In particular,  $G$ is assumed split. Let
$G$ is assumed split. Let  $x_{0}=H$ denote the identity coset in
$x_{0}=H$ denote the identity coset in  $X=G/H$. We may choose
$X=G/H$. We may choose
– a
 $\unicode[STIX]{x1D703}$-stable maximal
$\unicode[STIX]{x1D703}$-stable maximal  $F$-split torus
$F$-split torus  $A$,
$A$,– a Borel subgroup
 $B$ defined over
$B$ defined over  $F$, and
$F$, and– a minimal
 $\unicode[STIX]{x1D703}$-split parabolic
$\unicode[STIX]{x1D703}$-split parabolic  $F$-subgroup
$F$-subgroup  $P$
$P$
such that  $A\subset B\subset P$ and
$A\subset B\subset P$ and
– the orbit
 $Bx_{0}$ is open,
$Bx_{0}$ is open,–
 $P=\text{stab}_{G}(Bx_{0})$ is the parabolic associated with the open orbit, and
$P=\text{stab}_{G}(Bx_{0})$ is the parabolic associated with the open orbit, and– the tori
 $A$ and
$A$ and  $A_{X}=A/A\cap H$ are the same as those associated with
$A_{X}=A/A\cap H$ are the same as those associated with  $B$ and
$B$ and  $P$ in [Reference SakellaridisSak13, p. 8].
$P$ in [Reference SakellaridisSak13, p. 8].
Proof. Let  $P$ be a minimal
$P$ be a minimal  $\unicode[STIX]{x1D703}$-split parabolic
$\unicode[STIX]{x1D703}$-split parabolic  $F$-subgroup, and let
$F$-subgroup, and let  $A\subset P$ be a
$A\subset P$ be a  $\unicode[STIX]{x1D703}$-stable maximal
$\unicode[STIX]{x1D703}$-stable maximal  $F$-split torus of
$F$-split torus of  $G$. We may choose a Borel subgroup
$G$. We may choose a Borel subgroup  $A\subset B\subset P$. By [Reference Helminck and WangHW93, Lemma 4.8],
$A\subset B\subset P$. By [Reference Helminck and WangHW93, Lemma 4.8],  $Bx_{0}$ is open in
$Bx_{0}$ is open in  $X$, and
$X$, and  $P$ stabilizes this open orbit. It is also known that
$P$ stabilizes this open orbit. It is also known that  $P=\text{stab}_{G}(Bx_{0})$; see, for example, [Reference SakellaridisSak13, p. 8]. Let
$P=\text{stab}_{G}(Bx_{0})$; see, for example, [Reference SakellaridisSak13, p. 8]. Let  $L=Z_{G}(A^{-})$ be the
$L=Z_{G}(A^{-})$ be the  $\unicode[STIX]{x1D703}$-stable Levi of
$\unicode[STIX]{x1D703}$-stable Levi of  $P$, so that
$P$, so that  $A\subset B\cap L$. It follows that our choices of
$A\subset B\cap L$. It follows that our choices of  $A$,
$A$,  $B$,
$B$,  $P$ and
$P$ and  $L$ are compatible with those in [Reference SakellaridisSak13, p. 8] in the special case of a symmetric variety. Sakellaridis defines
$L$ are compatible with those in [Reference SakellaridisSak13, p. 8] in the special case of a symmetric variety. Sakellaridis defines  $A_{X}=L/L\cap H$ in [Reference SakellaridisSak13, p. 8]. As
$A_{X}=L/L\cap H$ in [Reference SakellaridisSak13, p. 8]. As  $A$ is a maximal torus in
$A$ is a maximal torus in  $L$ and
$L$ and  $[L,L]\subset H$ [Reference VustVus74, Proposition 2(ii)], we have an exact sequence
$[L,L]\subset H$ [Reference VustVus74, Proposition 2(ii)], we have an exact sequence  $1\rightarrow A\,\cap \,H\rightarrow A\rightarrow L/L\,\cap \,H\rightarrow 1$ so
$1\rightarrow A\,\cap \,H\rightarrow A\rightarrow L/L\,\cap \,H\rightarrow 1$ so  $A_{X}\simeq A/A\cap H$, which completes the proof.◻
$A_{X}\simeq A/A\cap H$, which completes the proof.◻
We next show that if  $G$ is not
$G$ is not  $\unicode[STIX]{x1D703}$-quasi-split, then
$\unicode[STIX]{x1D703}$-quasi-split, then  $\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$ does not intersect the maximal bounded subgroup of
$\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$ does not intersect the maximal bounded subgroup of  ${\check{A}}$. If there is some unitary
${\check{A}}$. If there is some unitary  $\unicode[STIX]{x1D712}\in {\check{A}}$ that lies in
$\unicode[STIX]{x1D712}\in {\check{A}}$ that lies in  $\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$, then we have
$\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$, then we have  $\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{1/2}\in A_{X}^{\ast }$. As
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{1/2}\in A_{X}^{\ast }$. As  $A_{X}^{\ast }$ is the set of characters of
$A_{X}^{\ast }$ is the set of characters of  $A$ that arise by pullback from
$A$ that arise by pullback from  $A_{X}$, this implies that
$A_{X}$, this implies that  $\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{1/2}$ is trivial on
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{1/2}$ is trivial on  $A\cap H$, and that
$A\cap H$, and that  $\unicode[STIX]{x1D6FF}$ is unitary on
$\unicode[STIX]{x1D6FF}$ is unitary on  $A\cap H$. However, this contradicts the following lemma.
$A\cap H$. However, this contradicts the following lemma.
Lemma A.5.  $\unicode[STIX]{x1D6FF}$ is unitary on
$\unicode[STIX]{x1D6FF}$ is unitary on  $A^{+}$ if and only if
$A^{+}$ if and only if  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-quasi-split.
$\unicode[STIX]{x1D703}$-quasi-split.
Proof. Let  $P=LU$. We have
$P=LU$. We have  $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{L}\unicode[STIX]{x1D6FF}_{U}$, where
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{L}\unicode[STIX]{x1D6FF}_{U}$, where  $\unicode[STIX]{x1D6FF}_{L}$ and
$\unicode[STIX]{x1D6FF}_{L}$ and  $\unicode[STIX]{x1D6FF}_{U}$ are the modular characters of
$\unicode[STIX]{x1D6FF}_{U}$ are the modular characters of  $B\,\cap \,L$ and
$B\,\cap \,L$ and  $U$, respectively. Because
$U$, respectively. Because  $P$ and
$P$ and  $\unicode[STIX]{x1D703}(P)$ are opposed, we have
$\unicode[STIX]{x1D703}(P)$ are opposed, we have  $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FF}_{U})=\unicode[STIX]{x1D6FF}_{U}^{-1}$, so that
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FF}_{U})=\unicode[STIX]{x1D6FF}_{U}^{-1}$, so that  $\unicode[STIX]{x1D6FF}_{U}^{2}=1$ on
$\unicode[STIX]{x1D6FF}_{U}^{2}=1$ on  $A^{+}$; by positivity,
$A^{+}$; by positivity,  $\unicode[STIX]{x1D6FF}_{U}=1$ on
$\unicode[STIX]{x1D6FF}_{U}=1$ on  $A^{+}$. Therefore
$A^{+}$. Therefore  $\unicode[STIX]{x1D6FF}|_{A^{+}}$ is unitary if and only if
$\unicode[STIX]{x1D6FF}|_{A^{+}}$ is unitary if and only if  $\unicode[STIX]{x1D6FF}_{L}|_{A^{+}}$ is. As
$\unicode[STIX]{x1D6FF}_{L}|_{A^{+}}$ is. As  $\unicode[STIX]{x1D6FF}_{L}$ is trivial on
$\unicode[STIX]{x1D6FF}_{L}$ is trivial on  $A^{-}$, this is equivalent to
$A^{-}$, this is equivalent to  $\unicode[STIX]{x1D6FF}_{L}$ being unitary, or to
$\unicode[STIX]{x1D6FF}_{L}$ being unitary, or to  $L$ being a torus. This completes the proof.◻
$L$ being a torus. This completes the proof.◻
We now turn to the proof of Corollary A.3. Assume that  $G$ is not
$G$ is not  $\unicode[STIX]{x1D703}$-quasi-split, and let
$\unicode[STIX]{x1D703}$-quasi-split, and let  $\unicode[STIX]{x1D70B}\subset C^{\infty }(X)$ be irreducible, unramified and tempered. Let
$\unicode[STIX]{x1D70B}\subset C^{\infty }(X)$ be irreducible, unramified and tempered. Let  $\unicode[STIX]{x1D712}\in {\check{A}}/W$ be the Satake parameter of
$\unicode[STIX]{x1D712}\in {\check{A}}/W$ be the Satake parameter of  $\unicode[STIX]{x1D70B}$. The contragredient
$\unicode[STIX]{x1D70B}$. The contragredient  $\unicode[STIX]{x1D70B}^{\vee }$ has Satake parameter
$\unicode[STIX]{x1D70B}^{\vee }$ has Satake parameter  $\unicode[STIX]{x1D712}^{-1}$, and we have a non-zero map
$\unicode[STIX]{x1D712}^{-1}$, and we have a non-zero map  $C_{c}^{\infty }(X)\rightarrow \unicode[STIX]{x1D70B}^{\vee }$. By [Reference CasselmanCas80, Proposition 2.6] we may choose a representative for
$C_{c}^{\infty }(X)\rightarrow \unicode[STIX]{x1D70B}^{\vee }$. By [Reference CasselmanCas80, Proposition 2.6] we may choose a representative for  $\unicode[STIX]{x1D712}^{-1}$ in
$\unicode[STIX]{x1D712}^{-1}$ in  ${\check{A}}$ such that
${\check{A}}$ such that  $\unicode[STIX]{x1D70B}^{\vee }\subset I(\unicode[STIX]{x1D712}^{-1})$. We now have a non-zero map
$\unicode[STIX]{x1D70B}^{\vee }\subset I(\unicode[STIX]{x1D712}^{-1})$. We now have a non-zero map  $C_{c}^{\infty }(X)\rightarrow I(\unicode[STIX]{x1D712}^{-1})$, so that by Theorem A.2,
$C_{c}^{\infty }(X)\rightarrow I(\unicode[STIX]{x1D712}^{-1})$, so that by Theorem A.2,  $W\unicode[STIX]{x1D712}^{-1}$ must intersect
$W\unicode[STIX]{x1D712}^{-1}$ must intersect  $\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$, but this contradicts our assertion above as
$\unicode[STIX]{x1D6FF}^{-1/2}A_{X}^{\ast }$, but this contradicts our assertion above as  $\unicode[STIX]{x1D712}$ is unitary.
$\unicode[STIX]{x1D712}$ is unitary.
A.4 An alternative approach to Theorems 1.1 and 1.2
We now describe how one might use Corollary A.3 to prove asymptotic lower bounds for periods. The argument is in the same style as that of Rudnick and Sarnak described in § A.1.
We return to the global situation of Theorems 1.1 and 1.2, and freely use the notation of those statements. We note that the compact subgroup  $K_{\infty }$ is given by
$K_{\infty }$ is given by  $K_{v_{0}}=H_{v_{0}}$ and
$K_{v_{0}}=H_{v_{0}}$ and  $K_{v}=G_{v}$ at all other infinite places. We shall let
$K_{v}=G_{v}$ at all other infinite places. We shall let  $N=1$ for simplicity, and write
$N=1$ for simplicity, and write  $Y=G(F)\backslash G(\mathbb{A})/K_{\infty }K$. The image of
$Y=G(F)\backslash G(\mathbb{A})/K_{\infty }K$. The image of  $H(\mathbb{A})$ in
$H(\mathbb{A})$ in  $Y$ is a finite number of points, and we shall assume for simplicity that it is a single point
$Y$ is a finite number of points, and we shall assume for simplicity that it is a single point  $p$. Let
$p$. Let  ${\mathcal{P}}_{H}:C^{\infty }(G(F)\backslash G(\mathbb{A}))\rightarrow \mathbb{C}$ be the period map
${\mathcal{P}}_{H}:C^{\infty }(G(F)\backslash G(\mathbb{A}))\rightarrow \mathbb{C}$ be the period map  $f\mapsto \int _{H(F)\backslash H(\mathbb{A})}f\,dh$. When restricted to
$f\mapsto \int _{H(F)\backslash H(\mathbb{A})}f\,dh$. When restricted to  $C^{\infty }(Y)$,
$C^{\infty }(Y)$,  ${\mathcal{P}}_{H}$ is just evaluation at
${\mathcal{P}}_{H}$ is just evaluation at  $p$.
$p$.
Note that a general connected real reductive group  $G^{\prime }$ with Cartan involution
$G^{\prime }$ with Cartan involution  $\unicode[STIX]{x1D703}$ is (quasi-)split over
$\unicode[STIX]{x1D703}$ is (quasi-)split over  $\mathbb{R}$ if and only if
$\mathbb{R}$ if and only if  $G^{\prime }\times \mathbb{C}$ is
$G^{\prime }\times \mathbb{C}$ is  $\unicode[STIX]{x1D703}$-(quasi-)split. If we assume that
$\unicode[STIX]{x1D703}$-(quasi-)split. If we assume that  $G_{v_{0}}$ is not quasi-split over
$G_{v_{0}}$ is not quasi-split over  $\mathbb{R}$ then this, together with the invariance of
$\mathbb{R}$ then this, together with the invariance of  $\unicode[STIX]{x1D703}$-(quasi-)splitness under extension of algebraically closed fields, and Lemma A.1, implies that
$\unicode[STIX]{x1D703}$-(quasi-)splitness under extension of algebraically closed fields, and Lemma A.1, implies that  $G_{v}$ is not
$G_{v}$ is not  $\unicode[STIX]{x1D703}$-quasi-split at any finite
$\unicode[STIX]{x1D703}$-quasi-split at any finite  $v$ at which
$v$ at which  $G$ splits. Corollary A.3 then gives that any unramified representation
$G$ splits. Corollary A.3 then gives that any unramified representation  $\unicode[STIX]{x1D70B}_{v}$ occurring in
$\unicode[STIX]{x1D70B}_{v}$ occurring in  $C^{\infty }(G_{v}/H_{v})$ must be non-tempered.
$C^{\infty }(G_{v}/H_{v})$ must be non-tempered.
Let  $\unicode[STIX]{x1D70B}$ be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$ be a cuspidal automorphic representation of  $G$, and let
$G$, and let  $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D70B}$ be invariant under
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D70B}$ be invariant under  $K_{\infty }K$. If
$K_{\infty }K$. If  ${\mathcal{P}}_{H}(\unicode[STIX]{x1D713})\neq 0$, this implies that each factor
${\mathcal{P}}_{H}(\unicode[STIX]{x1D713})\neq 0$, this implies that each factor  $\unicode[STIX]{x1D70B}_{v}$ admits a non-zero smooth linear functional invariant under
$\unicode[STIX]{x1D70B}_{v}$ admits a non-zero smooth linear functional invariant under  $H_{v}$. This is equivalent to the existence of an embedding
$H_{v}$. This is equivalent to the existence of an embedding  $\unicode[STIX]{x1D70B}_{v}\rightarrow C^{\infty }(G_{v}/H_{v})$, so that if
$\unicode[STIX]{x1D70B}_{v}\rightarrow C^{\infty }(G_{v}/H_{v})$, so that if  $v$ is finite,
$v$ is finite,  $G$ splits at
$G$ splits at  $v$, and all data are unramified, then
$v$, and all data are unramified, then  $\unicode[STIX]{x1D70B}_{v}$ is non-tempered. The strategy would then be to use the trace formula to show that the number of such
$\unicode[STIX]{x1D70B}_{v}$ is non-tempered. The strategy would then be to use the trace formula to show that the number of such  $\unicode[STIX]{x1D713}$ is a power smaller than the total number of
$\unicode[STIX]{x1D713}$ is a power smaller than the total number of  $\unicode[STIX]{x1D713}$. Combining this with the local Weyl law would then produce asymptotic growth.
$\unicode[STIX]{x1D713}$. Combining this with the local Weyl law would then produce asymptotic growth.
Note that in the case when  $G_{v_{0}}$ is quasi-split but not split over
$G_{v_{0}}$ is quasi-split but not split over  $\mathbb{R}$, Theorem A.2 only implies that the Satake parameters of the distinguished
$\mathbb{R}$, Theorem A.2 only implies that the Satake parameters of the distinguished  $\unicode[STIX]{x1D70B}$ lie in a fixed lower-dimensional subset of
$\unicode[STIX]{x1D70B}$ lie in a fixed lower-dimensional subset of  ${\check{A}}$. It may also be possible to use this to prove a power saving for the number of such
${\check{A}}$. It may also be possible to use this to prove a power saving for the number of such  $\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70B}$.
A.5 Higher-dimensional periods
One advantage of the method described in § A.4 is that it applies equally well to periods along positive-dimensional submanifolds of  $Y$ arising from rational symmetric subgroups. Note that this would produce a result of the form ‘there are certain eigenfunctions whose periods are larger than the average by a power of the eigenvalue’, while determining the size of the average period is a separate problem. It should be pointed out that the average size of a positive-dimensional period should be a negative power of the eigenvalue, so even if one could improve over this one would not necessarily obtain power growth of sup norms as a result.
$Y$ arising from rational symmetric subgroups. Note that this would produce a result of the form ‘there are certain eigenfunctions whose periods are larger than the average by a power of the eigenvalue’, while determining the size of the average period is a separate problem. It should be pointed out that the average size of a positive-dimensional period should be a negative power of the eigenvalue, so even if one could improve over this one would not necessarily obtain power growth of sup norms as a result.
In comparison, the relative trace formula approach we use is more difficult in the positive-dimensional case, because the analysis of the error terms becomes much more complicated. In the case of a point, one needs to bound the value of a spherical function  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D706}}$ away from its centre of symmetry. In the positive-dimensional case, one needs to bound the value of an oscillatory integral whose kernel is constructed from
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D706}}$ away from its centre of symmetry. In the positive-dimensional case, one needs to bound the value of an oscillatory integral whose kernel is constructed from  $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D706}}$, and which is taken over two copies of the submanifold in question. Moreover, the bound obtained must be uniform as the submanifolds move.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D706}}$, and which is taken over two copies of the submanifold in question. Moreover, the bound obtained must be uniform as the submanifolds move.
Appendix B Hecke operators and the  $L^{2}$ spectrum of symmetric varieties
$L^{2}$ spectrum of symmetric varieties
We have sketched two proofs of Theorems 1.1 and 1.2, the one described in § 1.5, which we carry out to completion in this paper, and the one outlined in § A.4. In the latter, no Hecke operators appear; in the former, no distinction principle is used. What is their connection, if any?
In this section we describe how a conjecture of Sakellaridis and Venkatesh on the  $L^{2}$ spectrum of symmetric varieties relates to the method we have used in this paper, in particular to our choices of test functions in the trace formula. As their conjecture is expressed in terms of
$L^{2}$ spectrum of symmetric varieties relates to the method we have used in this paper, in particular to our choices of test functions in the trace formula. As their conjecture is expressed in terms of  $X$-distinguished Arthur parameters, it acts in a sense as a bridge between the two methods.
$X$-distinguished Arthur parameters, it acts in a sense as a bridge between the two methods.
B.1 Plancherel measures
Recall from § 1.5 that a comparison of trace formulae reduces the problem of finding exceptional sequences of Maass forms to that of finding  $\unicode[STIX]{x1D714}$ in the global Hecke algebra with the property that
$\unicode[STIX]{x1D714}$ in the global Hecke algebra with the property that  $\unicode[STIX]{x1D6F1}_{H}(\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast })(1)$ is large relative to
$\unicode[STIX]{x1D6F1}_{H}(\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast })(1)$ is large relative to  $(\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast })(1)$. Indeed, these are just the identity distributions on the geometric side of the
$(\unicode[STIX]{x1D714}\ast \unicode[STIX]{x1D714}^{\ast })(1)$. Indeed, these are just the identity distributions on the geometric side of the  $H$-relative trace formula and the Arthur–Selberg trace formula. The latter question may in turn be reduced to a local problem, namely that of finding an
$H$-relative trace formula and the Arthur–Selberg trace formula. The latter question may in turn be reduced to a local problem, namely that of finding an  $L^{2}$ normalized
$L^{2}$ normalized  $\unicode[STIX]{x1D70F}\in {\mathcal{H}}_{v}$ satisfying
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}_{v}$ satisfying
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(1)=0\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(1)\gg 1,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(1)=0\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(1)\gg 1,\end{eqnarray}$$ for  $v$ in a set of places having positive density. In § 1.5 we explained how these two conditions can be interpreted geometrically, in terms of Hecke returns to a fixed point. We would now like to interpret these same conditions spectrally.
$v$ in a set of places having positive density. In § 1.5 we explained how these two conditions can be interpreted geometrically, in terms of Hecke returns to a fixed point. We would now like to interpret these same conditions spectrally.
Until § B.3 we let  $F$ be a
$F$ be a  $p$-adic field. We let
$p$-adic field. We let  $G$ be a split reductive group over
$G$ be a split reductive group over  $F$, and let
$F$, and let  $K$ be a hyperspecial maximal compact subgroup. We assume that the Haar measure on
$K$ be a hyperspecial maximal compact subgroup. We assume that the Haar measure on  $G$ gives
$G$ gives  $K$ measure 1. We let
$K$ measure 1. We let  ${\mathcal{H}}$ be the spherical Hecke algebra with respect to
${\mathcal{H}}$ be the spherical Hecke algebra with respect to  $K$. We let
$K$. We let  $\widehat{G}$ be the unitary dual of
$\widehat{G}$ be the unitary dual of  $G$, and let
$G$, and let  $\widehat{G}^{\text{sph}}$ be the spherical unitary dual with respect to
$\widehat{G}^{\text{sph}}$ be the spherical unitary dual with respect to  $K$.
$K$.
Then the first condition in (B.1) can be expressed, via the Plancherel inversion formula, as
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{G}^{\text{sph}}(\unicode[STIX]{x1D708})=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{G}^{\text{sph}}(\unicode[STIX]{x1D708})=0.\end{eqnarray}$$ In other words,  $\unicode[STIX]{x1D70F}$ must be such that its Satake transform
$\unicode[STIX]{x1D70F}$ must be such that its Satake transform  $\widehat{\unicode[STIX]{x1D70F}}$ is oscillatory along the support of
$\widehat{\unicode[STIX]{x1D70F}}$ is oscillatory along the support of  $\unicode[STIX]{x1D707}_{G}^{\text{sph}}$, the tempered spectrum
$\unicode[STIX]{x1D707}_{G}^{\text{sph}}$, the tempered spectrum  $\widehat{G}^{\text{sph,temp}}$.
$\widehat{G}^{\text{sph,temp}}$.
A similar Plancherel inversion formula can be used to express the second condition in (B.1). Let  $X=G/H$ be a symmetric variety. We recall the existence of a Plancherel measure
$X=G/H$ be a symmetric variety. We recall the existence of a Plancherel measure  $\unicode[STIX]{x1D707}_{X}$ associated with the separable Hilbert space
$\unicode[STIX]{x1D707}_{X}$ associated with the separable Hilbert space  $L^{2}(X)$, viewed as a
$L^{2}(X)$, viewed as a  $G$-representation; roughly speaking, this is a measure on
$G$-representation; roughly speaking, this is a measure on  $\widehat{G}$ satisfying
$\widehat{G}$ satisfying
 $$\begin{eqnarray}L^{2}(X)=\int _{\widehat{G}}M(\unicode[STIX]{x1D70B})\,\otimes \,\unicode[STIX]{x1D70B}\;d\unicode[STIX]{x1D707}_{X}(\unicode[STIX]{x1D70B}),\end{eqnarray}$$
$$\begin{eqnarray}L^{2}(X)=\int _{\widehat{G}}M(\unicode[STIX]{x1D70B})\,\otimes \,\unicode[STIX]{x1D70B}\;d\unicode[STIX]{x1D707}_{X}(\unicode[STIX]{x1D70B}),\end{eqnarray}$$ where  $M(\unicode[STIX]{x1D70B})$ is some multiplicity space. Notice that
$M(\unicode[STIX]{x1D70B})$ is some multiplicity space. Notice that  $\unicode[STIX]{x1D707}_{X}$ is only defined up to absolutely continuous equivalence (we shall only be concerned with its support).
$\unicode[STIX]{x1D707}_{X}$ is only defined up to absolutely continuous equivalence (we shall only be concerned with its support).
We let  $\unicode[STIX]{x1D6F1}_{H}:L^{1}(G)\rightarrow L^{1}(X)$ be given by integration over
$\unicode[STIX]{x1D6F1}_{H}:L^{1}(G)\rightarrow L^{1}(X)$ be given by integration over  $H$. If we let
$H$. If we let  $v^{0}=\unicode[STIX]{x1D6F1}_{H}(\mathbf{1}_{K})$, there is a second measure, the spherical Plancherel measure
$v^{0}=\unicode[STIX]{x1D6F1}_{H}(\mathbf{1}_{K})$, there is a second measure, the spherical Plancherel measure  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$, which satisfies
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$, which satisfies
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D714}\cdot v^{0},v^{0}\rangle _{L^{2}(X)}=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708})\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D714}\cdot v^{0},v^{0}\rangle _{L^{2}(X)}=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708})\end{eqnarray}$$ for all  $\unicode[STIX]{x1D714}\in {\mathcal{H}}$. In particular, the support of
$\unicode[STIX]{x1D714}\in {\mathcal{H}}$. In particular, the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in the support of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in the support of  $\unicode[STIX]{x1D707}_{X}$. Note that
$\unicode[STIX]{x1D707}_{X}$. Note that  $\unicode[STIX]{x1D714}\cdot v^{0}$ denotes the action of
$\unicode[STIX]{x1D714}\cdot v^{0}$ denotes the action of  $\unicode[STIX]{x1D714}$ on
$\unicode[STIX]{x1D714}$ on  $v^{0}$, given by
$v^{0}$, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D714}\cdot v^{0}=\int _{G}\unicode[STIX]{x1D714}(g)(g\cdot v^{0})\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}\cdot v^{0}=\int _{G}\unicode[STIX]{x1D714}(g)(g\cdot v^{0})\,dg.\end{eqnarray}$$ By a simple unfolding argument, one may show that for any  $\unicode[STIX]{x1D714}\in {\mathcal{H}}$ we have
$\unicode[STIX]{x1D714}\in {\mathcal{H}}$ we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D714}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708}),\end{eqnarray}$$ so that  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ determines the period of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ determines the period of  $\unicode[STIX]{x1D714}$ along
$\unicode[STIX]{x1D714}$ along  $H$. Using this, we may now rephrase the second condition in (B.1) as
$H$. Using this, we may now rephrase the second condition in (B.1) as
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708})\gg 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{H}\unicode[STIX]{x1D70F}(1)=\int _{\widehat{G}^{\text{sph}}}\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})\,d\unicode[STIX]{x1D707}_{X}^{\text{sph}}(\unicode[STIX]{x1D708})\gg 1.\end{eqnarray}$$ In other words,  $\unicode[STIX]{x1D70F}$ must be such that its Satake transform
$\unicode[STIX]{x1D70F}$ must be such that its Satake transform  $\widehat{\unicode[STIX]{x1D70F}}$ does not oscillate too much on the support of
$\widehat{\unicode[STIX]{x1D70F}}$ does not oscillate too much on the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$.
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$.
Having expressed the two conditions in (B.1) spectrally, we see that the existence of appropriate test functions  $\unicode[STIX]{x1D70F}$ can be read off from the support of
$\unicode[STIX]{x1D70F}$ can be read off from the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$, in particular relative to the tempered spectrum. We say that
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$, in particular relative to the tempered spectrum. We say that  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is tempered if the support of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is tempered if the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in  $\widehat{G}^{\text{sph,temp}}$ and strongly tempered if
$\widehat{G}^{\text{sph,temp}}$ and strongly tempered if  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}\leqslant C\unicode[STIX]{x1D707}_{G}^{\text{sph}}$ for some
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}\leqslant C\unicode[STIX]{x1D707}_{G}^{\text{sph}}$ for some  $C>0$, where
$C>0$, where  $\unicode[STIX]{x1D707}_{G}^{\text{sph}}$ is the spherical Plancherel measure on
$\unicode[STIX]{x1D707}_{G}^{\text{sph}}$ is the spherical Plancherel measure on  $G$. With this terminology, we summarize our discussion as follows:
$G$. With this terminology, we summarize our discussion as follows:
- (ST):
if
 $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is strongly tempered the oscillation of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is strongly tempered the oscillation of  $\widehat{\unicode[STIX]{x1D70F}}$ should prevent one from simultaneously achieving both (B.2) and (B.3);
$\widehat{\unicode[STIX]{x1D70F}}$ should prevent one from simultaneously achieving both (B.2) and (B.3);- (T):
if
 $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is tempered but not strongly tempered, the existence of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is tempered but not strongly tempered, the existence of  $\unicode[STIX]{x1D70F}$ satisfying both (B.2) and (B.3) depends on how singular
$\unicode[STIX]{x1D70F}$ satisfying both (B.2) and (B.3) depends on how singular  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is relative to
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is relative to  $\unicode[STIX]{x1D707}_{G}^{\text{sph}}$;
$\unicode[STIX]{x1D707}_{G}^{\text{sph}}$;- (NT):
if
 $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is non-tempered, the exponential growth of
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is non-tempered, the exponential growth of  $\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})$ away from
$\widehat{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D708})$ away from  $\widehat{G}^{\text{sph,temp}}$ should allow one (barring unforseen cancellation) to ensure both conditions (B.2) and (B.3).
$\widehat{G}^{\text{sph,temp}}$ should allow one (barring unforseen cancellation) to ensure both conditions (B.2) and (B.3).
In the next subsection we shall see how recent conjectures of Sakelleridis and Venkatesh relate the tempered properties of  $\unicode[STIX]{x1D707}_{X}$ to the weak containment properties of
$\unicode[STIX]{x1D707}_{X}$ to the weak containment properties of  $H$-distinguished representations.
$H$-distinguished representations.
B.2 The conjecture of Sakellaridis and Venkatesh
Recall the dual torus  ${\check{A}}_{X}$ and the map
${\check{A}}_{X}$ and the map  ${\check{A}}_{X}\rightarrow {\check{A}}$, which were of critical use in describing the local distinction argument of Appendix A. Let
${\check{A}}_{X}\rightarrow {\check{A}}$, which were of critical use in describing the local distinction argument of Appendix A. Let  ${\check{G}}$ denote the Langlands dual group of
${\check{G}}$ denote the Langlands dual group of  $G$, containing
$G$, containing  ${\check{A}}$ as a maximal torus. In [Reference Sakellaridis and VenkateshSV17, §2.2], Sakellaridis and Venkatesh define a dual group
${\check{A}}$ as a maximal torus. In [Reference Sakellaridis and VenkateshSV17, §2.2], Sakellaridis and Venkatesh define a dual group  ${\check{G}}_{X}$ associated with
${\check{G}}_{X}$ associated with  $X$ and a homomorphism
$X$ and a homomorphism  $\unicode[STIX]{x1D704}:{\check{G}}_{X}\times \text{SL}(2,\mathbb{C})\rightarrow {\check{G}}$ whose restriction to
$\unicode[STIX]{x1D704}:{\check{G}}_{X}\times \text{SL}(2,\mathbb{C})\rightarrow {\check{G}}$ whose restriction to  ${\check{G}}_{X}$ has finite kernel. (Note that this requires imposing certain conditions on
${\check{G}}_{X}$ has finite kernel. (Note that this requires imposing certain conditions on  $X$, which we shall ignore as this section is purely expository.) The torus
$X$, which we shall ignore as this section is purely expository.) The torus  ${\check{A}}_{X}$ sits in the complex reductive algebraic group
${\check{A}}_{X}$ sits in the complex reductive algebraic group  ${\check{G}}_{X}$ as a maximal torus, and the map
${\check{G}}_{X}$ as a maximal torus, and the map  $\unicode[STIX]{x1D704}:{\check{G}}_{X}\rightarrow {\check{G}}$ restricts to the natural map
$\unicode[STIX]{x1D704}:{\check{G}}_{X}\rightarrow {\check{G}}$ restricts to the natural map  ${\check{A}}_{X}\rightarrow {\check{A}}$ above.
${\check{A}}_{X}\rightarrow {\check{A}}$ above.
Again under technical assumptions that we shall ignore,  $\unicode[STIX]{x1D704}({\check{G}}_{X})$ is equal to a group constructed by Gaitsgory and Nadler; see [Reference Sakellaridis and VenkateshSV17, §3], in particular §3.2. Moreover, in the case of symmetric varieties, the group of Gaitsgory and Nadler is equal to the group
$\unicode[STIX]{x1D704}({\check{G}}_{X})$ is equal to a group constructed by Gaitsgory and Nadler; see [Reference Sakellaridis and VenkateshSV17, §3], in particular §3.2. Moreover, in the case of symmetric varieties, the group of Gaitsgory and Nadler is equal to the group  $\check{H}$ constructed by Nadler in [Reference NadlerNad05].Footnote 5 We continue to assume that
$\check{H}$ constructed by Nadler in [Reference NadlerNad05].Footnote 5 We continue to assume that  $X$ is symmetric and now recall the following facts about
$X$ is symmetric and now recall the following facts about  ${\check{G}}_{X}$ and
${\check{G}}_{X}$ and  $\unicode[STIX]{x1D704}$.
$\unicode[STIX]{x1D704}$.
– The rank of
 ${\check{G}}_{X}$ is equal to the
${\check{G}}_{X}$ is equal to the  $\unicode[STIX]{x1D703}$-split rank of
$\unicode[STIX]{x1D703}$-split rank of  $G$.
$G$.–
 $\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ if and only if
$\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ if and only if  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-split.
$\unicode[STIX]{x1D703}$-split.–
 $\unicode[STIX]{x1D704}$ is trivial on the
$\unicode[STIX]{x1D704}$ is trivial on the  $\text{SL}(2,\mathbb{C})$ factor if and only if
$\text{SL}(2,\mathbb{C})$ factor if and only if  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-quasi-split.
$\unicode[STIX]{x1D703}$-quasi-split.
The first claim is stated in [Reference NadlerNad05, §1.1 and Proposition 10.6.1]. The fact that  $\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ when
$\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ when  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-split is also stated in §1.1 there, and the reverse implication follows by considering ranks. The third claim follows from the condition that
$\unicode[STIX]{x1D703}$-split is also stated in §1.1 there, and the reverse implication follows by considering ranks. The third claim follows from the condition that  $\unicode[STIX]{x1D704}$ be a distinguished morphism, as defined in the comment before [Reference Sakellaridis and VenkateshSV17, §2.2, Theorem 2.2.3]. Indeed, the group
$\unicode[STIX]{x1D704}$ be a distinguished morphism, as defined in the comment before [Reference Sakellaridis and VenkateshSV17, §2.2, Theorem 2.2.3]. Indeed, the group  $L$ in that comment is the Levi of a minimal
$L$ in that comment is the Levi of a minimal  $\unicode[STIX]{x1D703}$-split parabolic, and
$\unicode[STIX]{x1D703}$-split parabolic, and  $\unicode[STIX]{x1D70C}_{L}$ is the half sum of its positive roots, so that
$\unicode[STIX]{x1D70C}_{L}$ is the half sum of its positive roots, so that  $\unicode[STIX]{x1D704}$ is trivial on
$\unicode[STIX]{x1D704}$ is trivial on  $\text{SL}(2,\mathbb{C})$ if and only if
$\text{SL}(2,\mathbb{C})$ if and only if  $\unicode[STIX]{x1D70C}_{L}$ is trivial, that is,
$\unicode[STIX]{x1D70C}_{L}$ is trivial, that is,  $L$ is a torus. Sakellaridis and Venkatesh conjecture [Reference Sakellaridis and VenkateshSV17, Conjecture 16.2.2] that the support of
$L$ is a torus. Sakellaridis and Venkatesh conjecture [Reference Sakellaridis and VenkateshSV17, Conjecture 16.2.2] that the support of  $\unicode[STIX]{x1D707}_{X}$ may be described in terms of the tempered dual of
$\unicode[STIX]{x1D707}_{X}$ may be described in terms of the tempered dual of  ${\check{G}}_{X}$ and the map
${\check{G}}_{X}$ and the map  $\unicode[STIX]{x1D704}$. They define an
$\unicode[STIX]{x1D704}$. They define an  $X$-distinguished Arthur parameter to be a commutative diagram
$X$-distinguished Arthur parameter to be a commutative diagram

where  ${\mathcal{L}}_{F}$ is the local Langlands group of
${\mathcal{L}}_{F}$ is the local Langlands group of  $F$, and
$F$, and  $\unicode[STIX]{x1D719}$ is a tempered Langlands parameter for
$\unicode[STIX]{x1D719}$ is a tempered Langlands parameter for  ${\check{G}}_{X}$. This naturally gives rise to an Arthur parameter for
${\check{G}}_{X}$. This naturally gives rise to an Arthur parameter for  ${\check{G}}$. We shall say that an Arthur parameter for
${\check{G}}$. We shall say that an Arthur parameter for  ${\check{G}}$ is
${\check{G}}$ is  $X$-distinguished if it arises from such a diagram, and likewise for an
$X$-distinguished if it arises from such a diagram, and likewise for an  $X$-distinguished Arthur packet.
$X$-distinguished Arthur packet.
Conjecture 1 (Sakellaridis and Venkatesh).
The support of  $\unicode[STIX]{x1D707}_{X}$ is contained in the Fell closure of the union of the
$\unicode[STIX]{x1D707}_{X}$ is contained in the Fell closure of the union of the  $X$-distinguished Arthur packets for
$X$-distinguished Arthur packets for  ${\check{G}}$.
${\check{G}}$.
Note that the unramified members of a given Arthur packet should be contained in the associated  $L$-packet, and we assume this from now on without further comment. Thus the above conjecture implies, in particular, that the support of the spherical measure
$L$-packet, and we assume this from now on without further comment. Thus the above conjecture implies, in particular, that the support of the spherical measure  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in the Fell closure of the union of the
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is contained in the Fell closure of the union of the  $L$-packets associated with
$L$-packets associated with  $X$-distinguished Arthur parameters. The latter statement has in fact been proved in [Reference SakellaridisSak13] under certain combinatorial assumptions. Let us now discuss what Conjecture 1 implies for
$X$-distinguished Arthur parameters. The latter statement has in fact been proved in [Reference SakellaridisSak13] under certain combinatorial assumptions. Let us now discuss what Conjecture 1 implies for  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ under the assumptions that
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ under the assumptions that  $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-split,
$\unicode[STIX]{x1D703}$-split,  $\unicode[STIX]{x1D703}$-quasi-split, or neither.
$\unicode[STIX]{x1D703}$-quasi-split, or neither.
- (ST):
If
 $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-split, then
$\unicode[STIX]{x1D703}$-split, then  $\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ and
$\unicode[STIX]{x1D704}({\check{G}}_{X})={\check{G}}$ and  $\unicode[STIX]{x1D704}$ is trivial on
$\unicode[STIX]{x1D704}$ is trivial on  $\text{SL}(2,\mathbb{C})$. Conjecture 1 then implies that
$\text{SL}(2,\mathbb{C})$. Conjecture 1 then implies that  $\unicode[STIX]{x1D707}_{X}$ is supported on the tempered dual of
$\unicode[STIX]{x1D707}_{X}$ is supported on the tempered dual of  $G$. In fact, it may be shown in this case that
$G$. In fact, it may be shown in this case that  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is strongly tempered.
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ is strongly tempered.- (T):
If
 $G$ is
$G$ is  $\unicode[STIX]{x1D703}$-quasi-split but not
$\unicode[STIX]{x1D703}$-quasi-split but not  $\unicode[STIX]{x1D703}$-split,
$\unicode[STIX]{x1D703}$-split,  $\unicode[STIX]{x1D704}$ is still trivial on the
$\unicode[STIX]{x1D704}$ is still trivial on the  $\text{SL}(2,\mathbb{C})$ factor. This implies that
$\text{SL}(2,\mathbb{C})$ factor. This implies that  $\unicode[STIX]{x1D707}_{X}$ is still tempered. However, because
$\unicode[STIX]{x1D707}_{X}$ is still tempered. However, because  $\text{rank}({\check{G}}_{X})<\text{rank}({\check{G}})$, if we identify the tempered spherical dual of
$\text{rank}({\check{G}}_{X})<\text{rank}({\check{G}})$, if we identify the tempered spherical dual of  $G$ with a quotient of a compact torus by the Weyl group, the support of
$G$ with a quotient of a compact torus by the Weyl group, the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ will be contained in a union of lower-dimensional tori. In particular,
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ will be contained in a union of lower-dimensional tori. In particular,  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ will not be strongly tempered.
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$ will not be strongly tempered.- (NT):
If
 $G$ is not
$G$ is not  $\unicode[STIX]{x1D703}$-quasi-split, then an
$\unicode[STIX]{x1D703}$-quasi-split, then an  $X$-distinguished Arthur parameter has non-trivial
$X$-distinguished Arthur parameter has non-trivial  $\text{SL}(2,\mathbb{C})$ factor. Its underlying Langlands parameter is therefore non-tempered, and so then are all members of the associated
$\text{SL}(2,\mathbb{C})$ factor. Its underlying Langlands parameter is therefore non-tempered, and so then are all members of the associated  $L$-packet. It follows that if
$L$-packet. It follows that if  $\unicode[STIX]{x1D713}$ is
$\unicode[STIX]{x1D713}$ is  $X$-distinguished with packet
$X$-distinguished with packet  $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D713}}$, and
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D713}}$, and  $\unicode[STIX]{x1D70B}\in \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D713}}$ is spherical, then
$\unicode[STIX]{x1D70B}\in \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D713}}$ is spherical, then  $\unicode[STIX]{x1D70B}$ must be non-tempered. From Conjecture 1 we deduce that the same is true for any
$\unicode[STIX]{x1D70B}$ must be non-tempered. From Conjecture 1 we deduce that the same is true for any  $\unicode[STIX]{x1D70B}$ in the support of
$\unicode[STIX]{x1D70B}$ in the support of  $\unicode[STIX]{x1D707}_{X}^{\text{sph}}$.
$\unicode[STIX]{x1D707}_{X}^{\text{sph}}$.
B.3 Existence of test functions
Finally, we return to the global situation of Theorems 1.1 and 1.2. We freely use the notation of those statements, with the exception that we drop the assumption that  $G_{v_{0}}$ is not split. Let
$G_{v_{0}}$ is not split. Let  $v$ be a finite place at which
$v$ be a finite place at which  $G$ is split and all data are unramified. We let
$G$ is split and all data are unramified. We let  $\unicode[STIX]{x1D707}_{G,v}^{\text{sph}}$ and
$\unicode[STIX]{x1D707}_{G,v}^{\text{sph}}$ and  $\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ denote the spherical Plancherel measures of
$\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ denote the spherical Plancherel measures of  $G_{v}$ and
$G_{v}$ and  $X_{v}=G_{v}/H_{v}$. As before,
$X_{v}=G_{v}/H_{v}$. As before,  $G_{v_{0}}$ is (quasi-)split over
$G_{v_{0}}$ is (quasi-)split over  $\mathbb{R}$ if and only if
$\mathbb{R}$ if and only if  $G_{v}$ is
$G_{v}$ is  $\unicode[STIX]{x1D703}$-(quasi-)split.
$\unicode[STIX]{x1D703}$-(quasi-)split.
Comparing the conditions from §§B.1 and B.2, we obtain the following consequences of Conjecture 1 for the existence of  $\unicode[STIX]{x1D70F}$ satisfying both conditions in (B.1).
$\unicode[STIX]{x1D70F}$ satisfying both conditions in (B.1).
- (ST):
If
 $G_{v_{0}}$ is split, then
$G_{v_{0}}$ is split, then  $\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is strongly tempered, and such
$\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is strongly tempered, and such  $\unicode[STIX]{x1D70F}$ should not exist.
$\unicode[STIX]{x1D70F}$ should not exist.- (T):
If
 $G_{v_{0}}$ is quasi-split but not split, the existence of such
$G_{v_{0}}$ is quasi-split but not split, the existence of such  $\unicode[STIX]{x1D70F}$ depends on how singular
$\unicode[STIX]{x1D70F}$ depends on how singular  $\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is.
$\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is.- (NT):
If
 $G_{v_{0}}$ is not quasi-split,
$G_{v_{0}}$ is not quasi-split,  $\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ has non-tempered support, and such
$\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ has non-tempered support, and such  $\unicode[STIX]{x1D70F}$ should exist.
$\unicode[STIX]{x1D70F}$ should exist.
Recalling our remarks at the end of § A.4, it seems that in the case (T) above the measure  $\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is still singular enough to allow (B.1) to be satisfied. This of course aligns with the conditions of our theorems, which only require
$\unicode[STIX]{x1D707}_{X,v}^{\text{sph}}$ is still singular enough to allow (B.1) to be satisfied. This of course aligns with the conditions of our theorems, which only require  $G_{v_{0}}$ to be non-split.
$G_{v_{0}}$ to be non-split.