We prove two results about the width of words in $\operatorname{SL}_{n}(\mathbb{Z})$. The first is that, for every $n\geqslant 3$, there is a constant $C(n)$ such that the width of any word in $\operatorname{SL}_{n}(\mathbb{Z})$ is less than $C(n)$. The second result is that, for any word $w$, if $n$ is big enough, the width of $w$ in $\operatorname{SL}_{n}(\mathbb{Z})$ is at most 87.

We study the problem of how the dual complex of the special fiber of a strict normal crossings degeneration 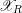$\mathscr{X}_{R}$ changes under products. We view the dual complex as a skeleton inside the Berkovich space associated to 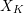$X_{K}$. Using the Kato fan, we define a skeleton 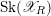$\text{Sk}(\mathscr{X}_{R})$ when the model 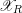$\mathscr{X}_{R}$ is log-regular. We show that if 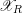$\mathscr{X}_{R}$ and 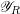$\mathscr{Y}_{R}$ are log-smooth, and at least one is semistable, then 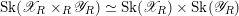$\text{Sk}(\mathscr{X}_{R}\times _{R}\mathscr{Y}_{R})\simeq \text{Sk}(\mathscr{X}_{R})\times \text{Sk}(\mathscr{Y}_{R})$. The essential skeleton 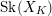$\text{Sk}(X_{K})$, defined by Mustaţă and Nicaise, is a birational invariant of 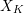$X_{K}$ and is independent of the choice of $R$-model. We extend their definition to pairs, and show that if both $X_{K}$ and $Y_{K}$ admit semistable models, 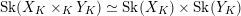$\text{Sk}(X_{K}\times _{K}Y_{K})\simeq \text{Sk}(X_{K})\times \text{Sk}(Y_{K})$. As an application, we compute the homeomorphism type of the dual complex of some degenerations of hyper-Kähler varieties. We consider both the case of the Hilbert scheme of a semistable degeneration of K3 surfaces, and the generalized Kummer construction applied to a semistable degeneration of abelian surfaces. In both cases we find that the dual complex of the 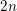$2n$-dimensional degeneration is homeomorphic to a point, $n$-simplex, or $\mathbb{C}\mathbb{P}^{n}$, depending on the type of the degeneration.

We study the realization of acyclic cluster algebras as coordinate rings of Coxeter double Bruhat cells in Kac–Moody groups. We prove that all cluster monomials with $\mathbf{g}$-vector lying in the doubled Cambrian fan are restrictions of principal generalized minors. As a corollary, cluster algebras of finite and affine type admit a complete and non-recursive description via (ind-)algebraic group representations, in a way similar in spirit to the Caldero–Chapoton description via quiver representations. In type $A_{1}^{(1)}$, we further show that elements of several canonical bases (generic, triangular, and theta) which complete the partial basis of cluster monomials are composed entirely of restrictions of minors. The discrepancy among these bases is accounted for by continuous parameters appearing in the classification of irreducible level-zero representations of affine Lie groups. We discuss how our results illuminate certain parallels between the classification of representations of finite-dimensional algebras and of integrable weight representations of Kac–Moody algebras.

In this article we construct a p-adic three-dimensional eigenvariety for the group $U$(2,1)($E$), where $E$ is a quadratic imaginary field and $p$ is inert in $E$. The eigenvariety parametrizes Hecke eigensystems on the space of overconvergent, locally analytic, cuspidal Picard modular forms of finite slope. The method generalized the one developed in Andreatta, Iovita and Stevens [$p$-adic families of Siegel modular cuspforms Ann. of Math. (2) 181, (2015), 623–697] by interpolating the coherent automorphic sheaves when the ordinary locus is empty. As an application of this construction, we reprove a particular case of the Bloch–Kato conjecture for some Galois characters of $E$, extending the results of Bellaiche and Chenevier to the case of a positive sign.

We give an integrability criterion on a real-valued non-increasing function $\unicode[STIX]{x1D713}$ guaranteeing that for almost all (or almost no) pairs $(A,\mathbf{b})$, where $A$ is a real $m\times n$ matrix and $\mathbf{b}\in \mathbb{R}^{m}$, the system

$$\begin{eqnarray}\Vert A\mathbf{q}+\mathbf{b}-\mathbf{p}\Vert ^{m}<\unicode[STIX]{x1D713}(T),\quad \Vert \mathbf{q}\Vert ^{n}<T,\end{eqnarray}$$

$\mathbf{p}\in \mathbb{Z}^{m}$

$\mathbf{q}\in \mathbb{Z}^{n}$

$T$

$\mathbb{R}^{m+n}$

$m=n=1$

Using a recent computation of the rational minus part of $SH(k)$ by Ananyevskiy, Levine and Panin, a theorem of Cisinski and Déglise and a version of the Röndigs and Østvær theorem, rational stable motivic homotopy theory over an infinite perfect field of characteristic different from 2 is recovered in this paper from finite Milnor–Witt correspondences in the sense of Calmès and Fasel.

We study the Iitaka–Kodaira dimension of nef relative anti-canonical divisors. As a consequence, we prove that given a complex projective variety with klt singularities, if the anti-canonical divisor is nef, then the dimension of a general fibre of the maximal rationally connected fibration is at least the Iitaka–Kodaira dimension of the anti-canonical divisor.