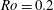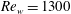1 Introduction
Turbulence is a ubiquitous state for many flows in nature and engineering applications. In stationary turbulence, the flow is assumed to be ergodic. Even though instantaneous properties are sensitive to initial conditions, statistical averages of the instantaneous properties, such as mean velocity profile in wall-bounded turbulence, are unique at any fixed set of parameters. The unique state in turbulence makes it possible to extrapolate data from lower Reynolds number to higher ones. In fact, Kolmogorov (Reference Kolmogorov1941a ,Reference Kolmogorov b ) had proposed a theory and suggested that there would be only one state for turbulent flows with large Reynolds numbers.
Figure 1. Sketch of plane Couette flow with spanwise rotation (RPCF).
Nevertheless, several flow problems, transitional as well as fully turbulent, with multiple states have been reported in wall-bounded flows. In transitional flows, experiments on boundary layer flow, Taylor–Couette flow (TCF), pipe flow as well as plane Couette and plane Poiseuille flows, showed that triggering turbulence depends sensitively on initial conditions (Andereck, Liu & Swinney Reference Andereck, Liu and Swinney1986; Kachanov Reference Kachanov1994; Eckhardt, Schneider & Hof Reference Eckhardt, Schneider, Hof and Westerweel2007; Lee & Wu Reference Lee and Wu2008; Martínez-Arias, Peixinho & Crumeyrolle Reference Martínez-Arias, Peixinho, Crumeyrolle and Mutabazi2014). At a certain fixed parameter (such as Reynolds number), the flow might be laminar with some initial conditions, while it could also be turbulent if some proper initial disturbances were introduced. In turbulent flows, multiple states were also reported for von Kármán flow (Ravelet, Marié & Chiffaudel Reference Ravelet, Marié, Chiffaudel and Daviaud2004; Ravelet, Chiffaudel & Daviaud Reference Ravelet, Chiffaudel and Daviaud2008; Cortet, Chiffaudel & Daviaud Reference Cortet, Chiffaudel, Daviaud and Dubrulle2010), Rayleigh–Bénard convection (Xi & Xia Reference Xi and Xia2008; Ahlers, Funfschilling & Bodenschatz Reference Ahlers, Funfschilling and Bodenschatz2011; Grossmann & Lohse Reference Grossmann and Lohse2011; van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2011; Weiss & Ahlers Reference Weiss and Ahlers2013), spherical–Couette flow (Zimmerman, Triana & Lathrop Reference Zimmerman, Triana and Lathrop2011), random Kolmogorov flow (Iyer, Bonaccorso & Biferale Reference Iyer, Bonaccorso, Biferale and Toschi2017) as well as TCF at the ultimate turbulence regime (Huisman, van der Veen & Sun Reference Huisman, van der Veen, Sun and Lohse2014; Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016; Van der Veen, Huisman & Dung Reference Van der Veen, Huisman, Dung, Tang, Sun and Lohse2016). In the work by Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014), they found that multiple stable turbulent states can occur for the same driving parameters in TCF with
$0.17<a<0.51$
(
$a$
is the rotation ratio of the outer to the inner cylinder) and
$Re=O(10^{6})$
, and different turbulent states correspond to different flow structures (three or four roll cells in top half of the system). They concluded that the coherent structures and their selectability are very important in highly turbulent flows and suggested that the related topics demand continued effort and investigations. Recently, this work was followed by Van der Veen et al. (Reference Van der Veen, Huisman, Dung, Tang, Sun and Lohse2016), who investigated the problems in the range of Taylor number
$Ta=10^{11}$
to
$9\times 10^{12}$
. The multiple states were found to be very robust and were expected to persist beyond
$Ta=10^{13}$
. Furthermore, they investigated the multiple states in a second system with a larger aspect ratio, and found that even richer roll structure phenomena, including an antisymmetric roll state, could exist for this larger aspect ratio system.
It is well accepted that TCF becomes plane Couette flow (PCF) (Faisst & Eckhardt Reference Faisst and Eckhardt2000; Brauckmann, Salewski & Eckhardt Reference Brauckmann, Salewski and Eckhardt2016) if the ratio between the radii of the inner and outer cylinder approaches one. The connections between TCF and PCF (with or without system rotation) inspires us to explore the possibility of multiple states in turbulent PCF. Due to its simple geometry, PCF with spanwise rotation (RPCF) (see sketch in figure 1) has served as one of the benchmark problems in rotating wall-bounded turbulence (Jakirlić, Hanjalić & Tropea Reference Jakirlić, Hanjalić and Tropea2002). In the past, great effort, through both experiments and numerical simulations, has been devoted to investigating RPCF (Bech & Andersson Reference Bech and Andersson1996, Reference Bech and Andersson1997; Tillmark & Alfredsson Reference Tillmark, Alfredsson, Gavrilakis, Machiels and Monkewitz1996; Nagata Reference Nagata1998; Alfredsson & Tillmark Reference Alfredsson, Tillmark, Mullin and Kerswell2005; Barri & Andersson Reference Barri, Andersson, Palma and Silva Lopes2007, Reference Barri and Andersson2010; Hiwatashi, Alfredsson & Tillmark Reference Hiwatashi, Alfredsson, Tillmark and Nagata2007; Tsukahara, Tillmark & Alfredsson Reference Tsukahara, Tillmark and Alfredsson2010; Tsukahara Reference Tsukahara2011; Suryadi, Segalini & Alfredsson Reference Suryadi, Segalini and Alfredsson2014; Salewski & Eckhardt Reference Salewski and Eckhardt2015; Gai, Xia & Cai Reference Gai, Xia, Cai and Chen2016; Kawata & Alfredsson Reference Kawata and Alfredsson2016a ,Reference Kawata and Alfredsson b ). Although comprehensive experimental and numerical results have been published in the past twenty years, no multiple turbulent states have been reported yet. In this paper, we present the first numerical evidence that multiple turbulent states could exist in RPCF at certain Reynolds and rotation numbers.
2 Numerical set-up
In a previous work (Gai et al.
Reference Gai, Xia, Cai and Chen2016), a series of direct numerical simulations (DNSs) were carried out on RPCF at a Reynolds number of
$Re_{w}=U_{w}h/\unicode[STIX]{x1D708}=1300$
, with rotation number
$Ro=2\unicode[STIX]{x1D6FA}_{z}h/U_{w}$
covering 0–0.9, where
$U_{w}$
is half of the wall velocity difference,
$h$
is the half-channel height,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D6FA}_{z}$
is the constant angular velocity in the spanwise direction. The flow field was simulated on a computational box
$10\unicode[STIX]{x03C0}h\times 2h\times 4\unicode[STIX]{x03C0}h$
with
$256\times 71\times 256$
grid points by using an accurate Fourier–Chebyshev pseudospectral method. Periodic boundary conditions are applied in the wall-parallel directions, while the no-slip boundary condition is adopted at the two walls, which are moving with velocity difference
$2U_{w}$
. The related turbulent statistics and flow structures were analysed. They reported that system rotation will enhance the secondary flows at lower rotation rates, but it would suppress the secondary flows if the rotation is too strong due to the Taylor–Proudman effect (Kundu, Cohen & Dowling Reference Kundu, Cohen, Dowling and Tryggvason2015), as those reported in rotating Rayleigh–Bénard flow (Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2012) and TCF (Huisman Reference Huisman2010; Grossmann et al.
Reference Grossmann, Lohse and Sun2016). One remarkable result is that a negative mean velocity gradient was found in the central plane of the channel at
$Ro=0.02$
. In fact, the negative mean velocity gradient in the centre of the channel was also reported in the DNS at
$Re_{w}=5200$
with box size
$4\unicode[STIX]{x03C0}h\times 2h\times 2\unicode[STIX]{x03C0}h$
by Salewski & Eckhardt (Reference Salewski and Eckhardt2015) and the experimental measurements at
$Re_{w}\geqslant 1000$
by Kawata & Alfredsson (Reference Kawata and Alfredsson2016b
) at a similar rotation number. As shown in Gai et al. (Reference Gai, Xia, Cai and Chen2016), there are three pairs of roll cells when the flow are averaged for
$200h/U_{w}\approx 6.37L_{x}/U_{w}$
. However, long-time simulations will give different results. When the flow starts with a laminar flow and some perturbations, the flow in a box of width
$4\unicode[STIX]{x03C0}h$
first evolves at a state with three pairs of roll cells and a negative mean velocity gradient in the centre. But when the simulation continues, the flow will finally evolves to a state with two pairs of roll cells and a positive mean velocity gradient in the centre.
In this paper, two DNSs with grid resolution
$256\times 97\times 256$
at
$Re_{w}=1300$
and
$Ro=0.2$
, which are anti-cyclonic, were carried out, using the same code as Gai et al. (Reference Gai, Xia, Cai and Chen2016). These two DNSs were initialized with flow fields at two different stages at
$Ro=0.02$
, that is, one at an earlier stage with three pairs of roll cells and the other at a later stage with two pairs of roll cells. After the simulations reached their stationary states, another time duration of
$750h/U_{w}\approx 23.85L_{x}/U_{w}$
, which is much longer than the time duration used in Gai et al. (Reference Gai, Xia, Cai and Chen2016), was continued to perform the statistics. In this time duration, 1501 flow fields with sampling time interval
$\unicode[STIX]{x0394}T=0.5h/U_{w}$
were stored and used for the statistics. The results showed that RPCF at
$Re_{w}=1300$
and
$Ro=0.2$
did have multiple states. In order to show that the multiple states are not illusory results of the computation, two more simulations with grid resolution
$512\times 97\times 512$
were run for
$1000h/U_{w}$
with initial fields interpolated from the coarser ones. The samples from the last
$750h/U_{w}$
were used to perform the flow statistics. The results, as shown below and listed in table 1, are consistent with the ones at coarser grid, which again confirmed the existence of these two turbulent states. In the following discussions, the cases will be denoted as ‘Rm_N’ with ‘
$m$
’ being the pair number of roll cells and ‘
$N$
’ being the grid points in the streamwise and spanwise directions.
Figure 2. Temporally and spatially averaged profiles of the streamwise velocity: (a) in the whole channel; (b) zoomed-in view for
$-0.9\leqslant y/h\leqslant 0.9$
.
Table 1. Averaged quantities at two different states. The number of collocation points in the wall-normal direction is
$N_{y}=97$
.
3 Results
Following Reynolds’ strategy (Reynolds Reference Reynolds1894), the instantaneous flow field
$u_{i}(x,y,z,t)$
(
$i=1,2$
or
$3$
refers to the
$x$
,
$y$
and
$z$
directions, respectively;
$u$
,
$v$
,
$w$
are used interchangeably with
$u_{1}$
,
$u_{2}$
,
$u_{3}$
) is decomposed into a mean part and a fluctuating part. In the present study,
$$\begin{eqnarray}\displaystyle & \displaystyle u_{i}(x,y,z,t)=\langle u_{i}\rangle (y)+u_{i}^{\prime }(x,y,z,t). & \displaystyle\end{eqnarray}$$
Here,
$\langle u_{i}\rangle (y)$
is the temporally and spatially averaged velocity (TS mean velocity), while
$u_{i}^{\prime }(x,y,z,t)$
are the corresponding fluctuations. In RPCF,
$\langle u_{2}\rangle =\langle u_{3}\rangle =0$
, and
$\langle u_{1}\rangle (y)=\langle u\rangle (y)$
is the only non-zero TS mean velocity component. Figure 2(a) shows the profiles of
$\langle u\rangle (y)$
from all four simulations. It is seen that the lines of
$\langle u\rangle$
can be divided into two groups (see the zoomed-in view shown in figure 2(b)). One is the from simulations R2_512 and R2_256, and the other is from R3_512 and R3_256, which illustrate the existence of two states. The lines from simulations with three pairs of roll cells have larger slopes in the region
$-0.7h\lesssim y\lesssim 0.7h$
and larger wall friction Reynolds numbers
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}$
. Here
$u_{\unicode[STIX]{x1D70F}}=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
is the friction velocity with
$\unicode[STIX]{x1D70F}_{w}$
and
$\unicode[STIX]{x1D70C}$
being the wall shear stress and the fluid density, respectively. The detailed values of
$Re_{\unicode[STIX]{x1D70F}}$
and mean shear rate at the centreline (
$\unicode[STIX]{x1D6F9}$
) from all simulations are listed in table 1. It is evident that the deviations are negligible for
$Re_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D6F9}$
within each group, while apparent discrepancies can be detected between groups, around
$5.5\,\%$
for
$Re_{\unicode[STIX]{x1D70F}}$
and
$28.3\,\%$
for
$\unicode[STIX]{x1D6F9}$
at 256 resolutions. These non-negligible discrepancies between two groups suggest the existence of the two states.
Figure 3. Time series of
$\unicode[STIX]{x1D713}$
.
In order to explore mean shear rate at the centreline more clearly, the time series of the spatially averaged mean shear rate at the centreline
$\unicode[STIX]{x1D713}(t)=\text{d}[u(x,0,z,t)]_{x,z}/\,\text{d}y$
is shown in figure 3. Here,
$[\cdot ]_{x,z}$
denotes quantities that are averaged in
$x$
and
$z$
directions. From the definition,
$\unicode[STIX]{x1D6F9}$
can be estimated by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F9}=\frac{1}{N_{t}}\mathop{\sum }_{i=1}^{N_{t}}\unicode[STIX]{x1D713}(t_{i}). & \displaystyle\end{eqnarray}$$
Here,
$N_{t}=1501$
is the number of the sampling field. It is evident from figure 3 that
$\unicode[STIX]{x1D713}$
from four simulations oscillates around two different mean values.
$\unicode[STIX]{x1D713}$
from R3_512 and R3_256 oscillates around 0.2 while those from R2_512 and R2_256 oscillate around 0.14. This means that the vorticity ratios
$S=-2\unicode[STIX]{x1D6FA}/(\text{d}\langle u\rangle /\text{d}y)$
in the centre part of the channel from the three-pair state and the two-pair state are approximately
$-1$
and
$-1.43$
respectively. The absolute vorticity at the former state is close to zero and the flow is neutrally stable in the centre core region (Gai et al.
Reference Gai, Xia, Cai and Chen2016), whereas at the latter state, the system rotation will stabilize the flow in the core region (Kristoffersen & Andersson Reference Kristoffersen and Andersson1993). These might explain the lower turbulent kinetic level (
$\langle u^{\prime }u^{\prime }+v^{\prime }v^{\prime }+w^{\prime }w^{\prime }\rangle /2$
) in the centre part of the channel. The standard deviation
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D713}}$
of
$\unicode[STIX]{x1D713}$
from both states are computed by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D713}}=\sqrt{\frac{1}{N_{t}}\mathop{\sum }_{i=1}^{N_{t}}(\unicode[STIX]{x1D713}(t_{i})-\unicode[STIX]{x1D6F9})^{2}}, & \displaystyle\end{eqnarray}$$
and are listed in table 1 too. The variances are much smaller (around
$1/3$
) than the differences between two states, which is approximately
$5.8\times 10^{-2}$
.
Figure 4. Reynolds stresses from all four simulations: (a)
$\langle u^{\prime }u^{\prime }\rangle$
, (b)
$\langle v^{\prime }v^{\prime }\rangle$
, (c)
$\langle w^{\prime }w^{\prime }\rangle$
and (d)
$-\langle u^{\prime }v^{\prime }\rangle$
. All quantities are normalized by
$4U_{w}^{2}$
.
In fact, the deviations are more obvious in higher-order statistics. Figure 4 shows the normalized diagonal components of Reynolds stresses
$\langle u^{\prime }u^{\prime }\rangle$
,
$\langle v^{\prime }v^{\prime }\rangle$
and
$\langle w^{\prime }w^{\prime }\rangle$
and the normalized Reynolds shear stress
$-\langle u^{\prime }v^{\prime }\rangle$
(by
$4U_{w}^{2}$
) from different simulations. Again, apparent deviations can be observed for the Reynolds stresses from the flow states with different pairs of roll cells, which again confirms that these two states are turbulent and statistically different. It should be emphasized here that the lines from the same state but with different grid resolutions match well with each other. This verifies that the present simulation results are valid.
Figure 5. (a) Instantaneous three-dimensional flow structures shown by iso-surfaces of
$Qh^{2}/U_{w}^{2}\geqslant 1.5$
and (b) the instantaneous velocity vectors and contours of
$Qh^{2}/U_{w}^{2}$
at the streamwise section
$x=0$
from simulation R2_512.
Figure 6. (a) Instantaneous three-dimensional flow structures shown by iso-surfaces of
$Qh^{2}/U_{w}^{2}\geqslant 1.5$
and (b) the instantaneous velocity vectors and contours of
$Qh^{2}/U_{w}^{2}$
at the streamwise section
$x=0$
from simulation R3_512.
In order to further characterize the flow differences, the flow structures are analysed. Figures 5 and 6 display the instantaneous three-dimensional flow structures represented by iso-surfaces of
$Qh^{2}/U_{w}^{2}\geqslant 1.5$
(here
$Q=-(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j})(\unicode[STIX]{x2202}u_{j}^{\prime }/\unicode[STIX]{x2202}x_{i})$
), and the instantaneous velocity vectors
$(v,w)$
and the contours of
$Qh^{2}/U_{w}^{2}$
at the streamwise section
$x=0$
from R2_512 and R3_512, respectively. The iso-surfaces of
$Q$
were used to identify the vortex structures by Kasagi, Sumitani & Suzuki (Reference Kasagi, Sumitani, Suzuki and Iida1995), Tsukahara (Reference Tsukahara2011) and Gai et al. (Reference Gai, Xia, Cai and Chen2016). It is seen from figures 5 and 6 that the vortex structures are gathered together into clusters, and most of them are located between two counter-rotating roll cells. Furthermore, two pairs of roll cells (or four roll cells) can be identified from figure 5 while three pairs of roll cells (or six roll cells) can be recognized from figure 6, and these roll cells are straight in the streamwise direction. These flow structures are rather stable and will not disappear during the simulations. This scenario is quite similar to that reported by Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014). In their work, they reported different turbulent states in TCF with different number of turbulent Taylor vortices (rolls).
Figure 7. Contours of
$v(0,0,z,t)$
from (a) R2_512 and (b) R3_512.
It is interesting to notice that these large-scale roll cells structures are not fixed in space, but they are moving in the spanwise directions (since the periodic boundary condition is used in the spanwise directions). In the present study, the instantaneous wall-normal velocity at the centre plane is used to indicate the location of the roll cells, since a local peak value, either maximum or minimum, will appear around the boundaries of each roll cell. This is different from those used by Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014), where they used the peak locations of azimuthal velocity at the centre between two cylinders as the boundaries of rolls. We must emphasize that the present method can only show the approximate locations of roll cells at different time steps. Figure 7(a,b) shows the contours of
$v(0,0,z,t)$
from R2_512 and R3_512 at
$(z,t)$
spaces, respectively. Similar results can be obtained for streamwise averaged wall-normal velocity
$v^{x}(z,t)=1/L_{x}\int _{0}^{L_{x}}v(x,0,z,t)\,\text{d}x$
(not shown here). It is apparent from figure 7 that four roll cells can be recognized at R2_512 while six roll cells can be identified at R3_512. It can also be observed from figure 7 that the travelling velocities of roll cells during
$0<tU_{w}/h\lesssim 300$
are not constant for both cases, but for
$300<tU_{w}/h\lesssim 750$
, they vary very slowly and asymptotically go to an almost constant drift velocity. The speed from R2_512 is much larger than that from R3_512; see supplementary movies 1 and 2 (available at https://doi.org/10.1017/jfm.2017.869) of velocity vectors at the slice
$x=0$
. We have computed the statistics by using the flow fields at
$300<tU_{w}/h\lesssim 750$
, and no clear deviations can be observed between this shorter averaging period and the original
$750h/U_{w}$
(not shown here). Nevertheless, the present time averaging period might not be long enough to show the effect of this locomotion, since the travelling speeds in the spanwise direction of the roll cells at both states are of order
$0.01U_{w}$
, which are much slower than the speed of the wall. Another important point, which deserves further discussion, noted from figure 7 is that the unidirectional spanwise translation of roll cells breaks the spanwise reflection symmetry. At the present simulation with
$tU_{w}/h\lesssim 750$
(1750 for R2_256 cases), the roll cells travel in the same direction. If this unidirectional translation of roll cells was a stable feature of the flow solution, there should be another one that translates in the opposite direction. Alternatively, there could be the third possibility that the spanwise translation oscillates from one direction to the other with an extremely long time scale. In the future, simulations with much longer durations should be performed to investigate the detailed feature of the roll cells’ translation and their influences on the mean statistics. Furthermore, more simulations with different initial flow fields need to be carried out to study the influence of initial conditions on the spanwise motion of the roll cells.
In RPCF, a triple decomposition approach (Moser & Moin Reference Moser and Moin1987; Lee & Kim Reference Lee, Kim and Durst1991; Bech & Andersson Reference Bech and Andersson1996; Gai et al. Reference Gai, Xia, Cai and Chen2016) is usually used to decompose the instantaneous velocity field into three parts in order to see the large-scale structures more clearly. That is,
$$\begin{eqnarray}\displaystyle u_{i}(x,y,z,t) & = & \displaystyle \langle u_{i}\rangle (y)+u_{i}^{\prime }(x,y,z,t)\nonumber\\ \displaystyle & = & \displaystyle \bar{u}_{i}(y,z)+u_{i}^{\prime \prime }(x,y,z,t)\nonumber\\ \displaystyle & = & \displaystyle \langle u_{i}\rangle (y)+u_{i}^{s}(y,z)+u_{i}^{\prime \prime }(x,y,z,t).\end{eqnarray}$$
Here,
$\bar{u}_{i}(y,z)$
is the averaged velocity with respect to
$t$
and
$x$
,
$u_{i}^{s}(y,z)=\bar{u}_{i}(y,z)-\langle u_{i}\rangle (y)$
corresponds to the secondary flow, usually occurring as roll cells. However, if the traditional triple decomposition is adopted to extract the secondary roll cells, the secondary flows will be weakened apparently due to the locomotion of roll cells in the spanwise direction. In order to correctly extract the secondary flows, the following roll-cell-fixed averaging procedure is adopted. First, the instantaneous flow field
$u_{i}(x,y,z,t)$
from each sample is averaged in the
$x$
direction to get
$u_{i}^{x}(y,z,t)$
. Then, the cross-section field
$u_{i}^{x}$
is translated along the
$z$
direction with the implementation of the periodic boundary condition to shift the maximum of
$v^{x}(0,z,t)$
to
$z=0$
. Finally, all the shifted samples are averaged in time to get the mean field
$\tilde{u} _{i}(y,z)$
. The secondary flows are then defined as
$u_{i}^{s}(y,z)=\tilde{u} _{i}(y,z)-\langle u_{i}\rangle (y)$
. It should be noted that the roll-cell-fixed averaging procedure is the same as the traditional triple decomposition if the roll cells are fixed in the spanwise direction.
Figure 8. Velocity vectors
$(v^{s},w^{s})$
from cases (a) R2_512 and (b) R3_512. The vector lengths are proportional to their magnitudes. The contours show the values of
$u^{s}$
.
Figure 8 shows the velocity vectors
$(v^{s},w^{s})$
obtained from the roll-cell-fixed averaging process at the
$y{-}z$
plane with their corresponding streamwise component
$u^{s}$
at R2_512 and R3_512. Consistent with the instantaneous contours shown in figure 5 and figure 6, two and three pairs of roll cells can be identified at these two simulations, respectively. The rolls are more oblate in the state with two pairs of roll cells with width around
$\unicode[STIX]{x03C0}h$
, while they are nearly circular with width around
$2.09h$
in the state with three pairs of roll cells. Furthermore, the regions with larger values of
$u^{s}$
are located between the roll cells. Since the top wall moves with velocity
$2U_{w}$
in our studies, the counter-rotating roll cells bring down fluid with higher speed from the top but bring up fluid with lower speed from the bottom, as shown by the sign of
$u^{s}$
.
4 Influence of the computational domain size
In the previous section, we have shown that two different flow states can exist in one computational domain size which can contain only two or three pairs of roll cells. Whether multiple states can still exist in a larger computational box is an open question. In this section, the influence of the computational domain size is investigated by carrying out two more DNSs at a computational box
$20\unicode[STIX]{x03C0}h\times 2h\times 8\unicode[STIX]{x03C0}h$
, which is twice as large as the one used above in the
$x$
and
$z$
directions, with
$512\times 97\times 512$
grid points. The initial flow fields were generated by periodic extensions, in both streamwise and spanwise directions, of the flow fields at R2_256 and R3_256. The simulations were run for
$1200h/U_{w}$
, and the flow fields from the last
$750h/U_{w}$
were used to get the statistics. Figure 9 shows the mean velocity profiles and Reynolds stress components from the two new simulations, which are denoted as R4_512 and R6_512 respectively since there are 4 pairs and 6 pairs of roll cells in the
$8\unicode[STIX]{x03C0}h$
spanwise domain as depicted in figure 10. In order to be compared with the original simulations with
$L_{z}=4\unicode[STIX]{x03C0}h$
, the results from R2_256 and R3_256 are also shown in figure 9. It is apparent that two different flow statistics can still be observed at the same domain size, which further confirms the existence of two states in this flow problems. Furthermore, the deviations between R2_256 and R4_512 are negligible, and so are the differences between R3_256 and R6_512. These may suggest that the original computational domain size
$10\unicode[STIX]{x03C0}h\times 2h\times 4\unicode[STIX]{x03C0}h$
is long enough in the streamwise direction for the investigation of RPCF at the present parameters.
Figure 9. (a) Mean velocity profiles normalized by
$U_{w}$
, and Reynolds stresses (b)
$\langle u^{\prime }u^{\prime }\rangle$
and
$\langle v^{\prime }v^{\prime }\rangle$
; (c)
$\langle w^{\prime }w^{\prime }\rangle$
and (d)
$-\langle u^{\prime }v^{\prime }\rangle$
from R2_256, R3_256, R4_512 and R6_512. Reynolds stresses are normalized by
$4U_{w}^{2}$
.
Figure 10. Velocity vectors
$(v^{s},w^{s})$
from cases (a) R4_512 and (b) R6_512. The vector lengths are proportional to their magnitudes. The contours show the values of
$u^{s}$
.
We admit that the present investigation on the domain size effect is quite elementary. We suspect that differences in box size, especially the spanwise size, might lead to different results. This would also be true for experiments, since the number of pairs of large-scale roll cells will be different if the experimental systems are different in size. Van der Veen et al. (Reference Van der Veen, Huisman, Dung, Tang, Sun and Lohse2016) found richer roll structure phenomena in TCF with a larger aspect ratio system. More work needs to be done, such as the minimal flow unit (Jiménez & Moin Reference Jiménez and Moin1991; Hsieh & Biringen Reference Hsieh and Biringen2016), to investigate the effects of computational box size in the future.
5 Conclusions and remarks
In this paper, we have shown through direct numerical simulation that multiple turbulent states can occur in RPCF at
$Re_{w}=1300$
and
$Ro=0.2$
. With the same computational domain size, two different flow states, which have different number of streamwise large-scale roll cells, were obtained by using different initial flow fields. At these two different states, the turbulent statistics, including temporally and spatially mean streamwise velocity and Reynolds stresses, show different profiles. Although this is only a numerical result, experimental measurements and theoretical understanding on this point are still lacking; the present highly accurate DNS result documents that multiple states could exist in RPCF with spanwise rotation. Given the similarity of the present results and the results reported by Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014), we infer that the streamwise large-scale vortices (roll cells) play a key role in the multiple states of turbulent flows and their selectability. Therefore, special attention should be paid when flow problems with roll cells are encountered.
Finally, we would like to make several comments. First, the present work is only numerical evidence for a certain computational box, and differences in box size might lead to different results. This would also be true for experiments, since the number of pairs of large-scale roll cells will be different if the experimental systems are different in size. Van der Veen et al. (Reference Van der Veen, Huisman, Dung, Tang, Sun and Lohse2016) found richer roll structure phenomena in TCF with a larger aspect ratio system. More work needs to be done to investigate the effects of computational box size. A companion work by Huang, Xia & Wan (Reference Huang, Xia, Wan and Chen2017) has been carried out to systematically investigate the domain size effect on the flow structures at
$Ro=0.02$
. Similar states transitions were found at the different domain sizes investigated during the flow evolves. Second, the multiple states are not constrained on the rotation number
$Ro=0.2$
at this Reynolds number. It is possible that multiple states can also exist at a wider rotation range, which deserves a comprehensive investigation, and this is currently being investigated. Third, the present results are not in conflict with the Kolmogorov’s theory, since Kolmogorov’s theory assumed that the flow is ergodic with very high Reynolds number. However, the Reynolds number in the present study is quite low. Furthermore, the present two states are stable for time duration
$T\leqslant 1000h/U_{w}$
, but we cannot rule out the possibility of states exchange at longer time duration. Whether the multiple turbulent states could still exist at much higher Reynolds number, or whether the states will exchange at longer time duration are still open questions and demand further investigations.
Acknowledgements
The authors thank the referees for their constructive comments, which clearly improved the quality of the manuscript. We appreciate J. Wang and C. Sun for many useful discussions. This work was supported by the National Science Foundation of China (NSFC grant nos. 11772297, 11521091 and 11672123). M.W. acknowledges support from the Science and Technology Research Fund of Shenzhen under grant no. JCYJ20170412151759222. The simulations were partially run on the TH-1A super computer in Tianjin and TH-2A super computer in Guangzhou.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.869.
