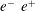1 Introduction
The fireball is a promising model for the generation of
![]() $\unicode[STIX]{x1D6FE}$
-ray bursts (GRBs) (Cavallo & Rees Reference Cavallo and Rees1978; Goodman Reference Goodman1986; Paczynski Reference Paczynski1986; Rees & Meszaros Reference Rees and Meszaros1992; Piran Reference Piran1996, Reference Piran2002). The model relies on the dissipation of kinetic energy of an ultra-relativistic flow, which emits
$\unicode[STIX]{x1D6FE}$
-ray bursts (GRBs) (Cavallo & Rees Reference Cavallo and Rees1978; Goodman Reference Goodman1986; Paczynski Reference Paczynski1986; Rees & Meszaros Reference Rees and Meszaros1992; Piran Reference Piran1996, Reference Piran2002). The model relies on the dissipation of kinetic energy of an ultra-relativistic flow, which emits
![]() $\unicode[STIX]{x1D6FE}$
-rays via synchrotron or synchrotron self-Compton emission. As a result, dense radiation and
$\unicode[STIX]{x1D6FE}$
-rays via synchrotron or synchrotron self-Compton emission. As a result, dense radiation and
![]() $e^{-}~e^{+}$
pair fluids are produced, known as a fireball (Bahcall & Ostriker Reference Bahcall and Ostriker1997). The interaction of the fireball beam, characterized by relativistic factors ranging from
$e^{-}~e^{+}$
pair fluids are produced, known as a fireball (Bahcall & Ostriker Reference Bahcall and Ostriker1997). The interaction of the fireball beam, characterized by relativistic factors ranging from
![]() $10^{2}{-}10^{6}$
, with the external medium can drive field structures that accelerate particles to high energies. As particles accelerate, they will also emit strong radiation bursts, with wavelengths ranging from
$10^{2}{-}10^{6}$
, with the external medium can drive field structures that accelerate particles to high energies. As particles accelerate, they will also emit strong radiation bursts, with wavelengths ranging from
![]() $\unicode[STIX]{x1D6FE}$
-rays to radio waves. Astrophysical observations indicate that the main process leading to radiation emission is synchrotron radiation, which requires large amplitude magnetic fields of the order of Gauss to operate (Piran Reference Piran2005; Uzdensky & Rightley Reference Uzdensky and Rightley2014). The origin of magnetic fields and their amplification to these extreme values are pressing challenges in astrophysics (Kronberg Reference Kronberg2002; Widrow Reference Widrow2002).
$\unicode[STIX]{x1D6FE}$
-rays to radio waves. Astrophysical observations indicate that the main process leading to radiation emission is synchrotron radiation, which requires large amplitude magnetic fields of the order of Gauss to operate (Piran Reference Piran2005; Uzdensky & Rightley Reference Uzdensky and Rightley2014). The origin of magnetic fields and their amplification to these extreme values are pressing challenges in astrophysics (Kronberg Reference Kronberg2002; Widrow Reference Widrow2002).
There has been an extensive effort, based on theoretical and numerical advances, with the objective of understanding the mechanisms by which strong magnetic fields are formed in astrophysical scenarios (Weibel Reference Weibel1959; Tzoufras et al.
Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva2006; Hantao & Zweibel Reference Hantao and Zweibel2015). Medvedev, Waxman and Loeb (Medvedev & Leob Reference Medvedev and Leob1999; Waxman & Loeb Reference Waxman and Loeb2009) proposed that the current filamentation/Weibel instability (CFI/WI) is a leading mechanism allowing for the growth of magnetic fields in the astrophysical context. The corresponding growth rates range from a few microseconds to a few tenths of a second, consistent with the time scales of GRBs (Schlickeiser Reference Schlickeiser2005). These instabilities arise due to an anisotropic velocity distribution in the plasma (WI) or due to a counter-streaming flow of plasma slabs (CFI). Numerical calculations have shown that these instabilities are capable of generating strong magnetic fields with
![]() $10^{-5}$
–
$10^{-5}$
–
![]() $10^{-1}$
of the energy density equipartition (Medvedev et al.
Reference Medvedev, Massimiliano, Fonseca, Silva and Mori2005; Dieckmann, Shukla & Stenflo Reference Dieckmann, Shukla and Stenflo2009; Shukla & Shukla Reference Shukla and Shukla2010; Chakraborti et al.
Reference Chakraborti, Ray, Soderberg, Loeb and Chandra2011; Fiuza et al.
Reference Fiuza, Fonseca, Tonge, Mori and Silva2012; Stockem & et al.
Reference Stockem, Bret, Fonseca and Silva2015).
$10^{-1}$
of the energy density equipartition (Medvedev et al.
Reference Medvedev, Massimiliano, Fonseca, Silva and Mori2005; Dieckmann, Shukla & Stenflo Reference Dieckmann, Shukla and Stenflo2009; Shukla & Shukla Reference Shukla and Shukla2010; Chakraborti et al.
Reference Chakraborti, Ray, Soderberg, Loeb and Chandra2011; Fiuza et al.
Reference Fiuza, Fonseca, Tonge, Mori and Silva2012; Stockem & et al.
Reference Stockem, Bret, Fonseca and Silva2015).
Similar observational evidence of electron–positron (
![]() $e^{-}~e^{+}$
) pair production has been found in TeV blazers (Gould & Schréder Reference Gould and Schréder1967; Salamon & Stecker Reference Salamon and Stecker1998; Neronov & Semikoz Reference Neronov and Semikoz2009; Chang, Broderick & Pfrommer Reference Chang, Broderick and Pfrommer2012; Schlickeiser et al.
Reference Schlickeiser, Elyiv, Ibscher and Miniati2012), where the interaction of TeV photons with the extragalactic background light produces ultra-relativistic
$e^{-}~e^{+}$
) pair production has been found in TeV blazers (Gould & Schréder Reference Gould and Schréder1967; Salamon & Stecker Reference Salamon and Stecker1998; Neronov & Semikoz Reference Neronov and Semikoz2009; Chang, Broderick & Pfrommer Reference Chang, Broderick and Pfrommer2012; Schlickeiser et al.
Reference Schlickeiser, Elyiv, Ibscher and Miniati2012), where the interaction of TeV photons with the extragalactic background light produces ultra-relativistic
![]() $e^{-}~e^{+}$
beams. As these
$e^{-}~e^{+}$
beams. As these
![]() $e^{-}~e^{+}$
beams stream through the intergalactic medium (IGM), the collective beam–plasma instabilities can be relevant. The impact of beam–plasma instabilities upon the
$e^{-}~e^{+}$
beams stream through the intergalactic medium (IGM), the collective beam–plasma instabilities can be relevant. The impact of beam–plasma instabilities upon the
![]() $\unicode[STIX]{x1D6FE}$
-ray emission of bright TeV sources and their subsequent cosmological consequences have been previously investigated theoretically and numerically using realistic parameters (Schlickeiser, Krakau & Supsar Reference Schlickeiser, Krakau and Supsar2013; Broderick et al.
Reference Broderick, Pfrommer, Puchwein and Chang2014; Chang et al.
Reference Chang, Broderick, Pfrommer, Puchwein, Lamberts and Shalaby2014; Sironi & Giannios Reference Sironi and Giannios2014; Chang et al.
Reference Chang, Broderick, Pfrommer, Puchwein, Lamberts, Shalaby and Vasil2016; Shalaby et al.
Reference Shalaby, Broderick, Chang, Pfrommer, Lamberts and Puchwein2017). The goal of this work is to identify conditions to explore such instabilities in laboratory conditions by using realistic finite size fireball beams. Leveraging on fully kinetic one-to-one particle-in-cell (PIC) simulations, we define the criteria for probing the oblique instability (OBI) and the CFI experimentally.
$\unicode[STIX]{x1D6FE}$
-ray emission of bright TeV sources and their subsequent cosmological consequences have been previously investigated theoretically and numerically using realistic parameters (Schlickeiser, Krakau & Supsar Reference Schlickeiser, Krakau and Supsar2013; Broderick et al.
Reference Broderick, Pfrommer, Puchwein and Chang2014; Chang et al.
Reference Chang, Broderick, Pfrommer, Puchwein, Lamberts and Shalaby2014; Sironi & Giannios Reference Sironi and Giannios2014; Chang et al.
Reference Chang, Broderick, Pfrommer, Puchwein, Lamberts, Shalaby and Vasil2016; Shalaby et al.
Reference Shalaby, Broderick, Chang, Pfrommer, Lamberts and Puchwein2017). The goal of this work is to identify conditions to explore such instabilities in laboratory conditions by using realistic finite size fireball beams. Leveraging on fully kinetic one-to-one particle-in-cell (PIC) simulations, we define the criteria for probing the oblique instability (OBI) and the CFI experimentally.
Exploring laboratory surrogates capable of reproducing these mechanisms under controlled conditions is a promising path to gain physical insights that would be otherwise inaccessible. One of the configurations that have been identified towards this goal is the study of the propagation of quasi-neutral relativistic fireball beams in the plasma (Muggli et al.
Reference Muggli, Martins, Vieira and Silva2013). A globally neutral fireball beam is composed of equal amounts of electrons and positrons with identical density and spectral distributions. Recent experimental developments (Sarri et al.
Reference Sarri, Poder, Cole and Schumaker2015) promise to make this exploration possible. The generation of quasi-neutral electron–positron fireball beams, with maximum energy
![]() $\simeq 400~\text{MeV}$
(average
$\simeq 400~\text{MeV}$
(average
![]() $\unicode[STIX]{x1D6FE}\sim 15$
), has been achieved in a laser–plasma accelerator. These beams have large energy spreads, they have a finite length and transverse size and have limited charge.
$\unicode[STIX]{x1D6FE}\sim 15$
), has been achieved in a laser–plasma accelerator. These beams have large energy spreads, they have a finite length and transverse size and have limited charge.
Another method for generating a fireball beam is to superimpose electron
![]() $e^{-}$
and positron
$e^{-}$
and positron
![]() $e^{+}$
bunches as could be done for example at SLAC (Hogan et al.
Reference Hogan, Raubenheimer, Seryi, Muggli, Katsouleas, Huang, Lu, An, Marsh and Mori2010). Numerical simulations show that this extremely relativistic fireball beam
$e^{+}$
bunches as could be done for example at SLAC (Hogan et al.
Reference Hogan, Raubenheimer, Seryi, Muggli, Katsouleas, Huang, Lu, An, Marsh and Mori2010). Numerical simulations show that this extremely relativistic fireball beam
![]() $\unicode[STIX]{x1D6FE}=40\,000$
is also subject to CFI (Muggli et al.
Reference Muggli, Martins, Vieira and Silva2013). Note that CFI of a mildly relativistic
$\unicode[STIX]{x1D6FE}=40\,000$
is also subject to CFI (Muggli et al.
Reference Muggli, Martins, Vieira and Silva2013). Note that CFI of a mildly relativistic
![]() $e^{-}$
bunch
$e^{-}$
bunch
![]() $\unicode[STIX]{x1D6FE}=112$
was observed showing filamentation and its coalescence (Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012). Thus, although there have been efforts to understand the generation of magnetic fields through the Weibel/CFI under ideal conditions (i.e. infinitely wide planar plasma slabs) (Frederiksen et al.
Reference Frederiksen, Hededal, Haugblle and Nordlund1999; Fonseca et al.
Reference Fonseca, Silva, Tonge, Hemker, Dawson and Mori2002a
; Nishikawa et al.
Reference Nishikawa, Niemiec, Hardee, Medvedev, Sol, Mizuno, Zhang, Pohl, Oka and Hartmann2009; Shukla et al.
Reference Shukla, Stockem, Fiuza and Silva2012), the role of realistic beam parameters in the growth of these instabilities remains to be understood in detail.
$\unicode[STIX]{x1D6FE}=112$
was observed showing filamentation and its coalescence (Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012). Thus, although there have been efforts to understand the generation of magnetic fields through the Weibel/CFI under ideal conditions (i.e. infinitely wide planar plasma slabs) (Frederiksen et al.
Reference Frederiksen, Hededal, Haugblle and Nordlund1999; Fonseca et al.
Reference Fonseca, Silva, Tonge, Hemker, Dawson and Mori2002a
; Nishikawa et al.
Reference Nishikawa, Niemiec, Hardee, Medvedev, Sol, Mizuno, Zhang, Pohl, Oka and Hartmann2009; Shukla et al.
Reference Shukla, Stockem, Fiuza and Silva2012), the role of realistic beam parameters in the growth of these instabilities remains to be understood in detail.
In this work, we perform a detailed numerical and theoretical study of the interaction of a realistic fireball beam (with a length comparable to or shorter than the plasma wavelength) in a uniform plasma using ab initio two-dimensional PIC simulations with the PIC code OSIRIS (Fonseca et al.
Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee and Katsouleas2002b
, Reference Fonseca, Martins, Silva, Tonge, Tsung and Mori2008, Reference Fonseca, Vieira, Fiuza, Davidson, Tsung, Mori and Silva2013). We examine in detail the temporal growth of the magnetic field that arises during the interaction between the fireball beam with the plasma. We then find that the growth of electrostatic modes, associated with competing instabilities, can be suppressed as long as the ratio between the beam density and the plasma density is sufficiently high. To make a connection with recent experiments (Sarri et al.
Reference Sarri, Poder, Cole and Schumaker2015), we also investigate the role of the finite beam emittance in the beam dynamics and find a threshold beam emittance for the occurrence of CFI. In addition, we found that the beam energy spread will not affect the growth of the CFI significantly. We consider ultra-relativistic fireball beams, with Lorentz factor
![]() $\unicode[STIX]{x1D6FE}$
ranging from
$\unicode[STIX]{x1D6FE}$
ranging from
![]() ${\sim}10^{3}{-}10^{4}$
, propagating in the plasma with densities ranging from
${\sim}10^{3}{-}10^{4}$
, propagating in the plasma with densities ranging from
![]() $10^{15}{-}10^{17}~\text{cm}^{-3}$
. These are parameters that can be explored in the laboratory. Our results show that the physics of OBI or CFI could be tested in the laboratory using presently or soon to be available electron–positron fireball beams.
$10^{15}{-}10^{17}~\text{cm}^{-3}$
. These are parameters that can be explored in the laboratory. Our results show that the physics of OBI or CFI could be tested in the laboratory using presently or soon to be available electron–positron fireball beams.
2 Simulations of the current filamentation instability
The onset of CFI occurs when the ratio between the transverse beam size (
![]() $\unicode[STIX]{x1D70E}_{y}$
) and the plasma skin depth (
$\unicode[STIX]{x1D70E}_{y}$
) and the plasma skin depth (
![]() $k_{p}^{-1}=c/\unicode[STIX]{x1D714}_{p}$
), is
$k_{p}^{-1}=c/\unicode[STIX]{x1D714}_{p}$
), is
![]() $k_{p}\unicode[STIX]{x1D70E}_{y}\geqslant 1$
(Roswell & Martin Reference Roswell and Martin1973; Chen et al.
Reference Chen, Su, Katsouleas, Wilks and Dawson1987; Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987; Sentoku et al.
Reference Sentoku, Mima, Kaw and Nishikawa2003; Blumenfeld et al.
Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012), where
$k_{p}\unicode[STIX]{x1D70E}_{y}\geqslant 1$
(Roswell & Martin Reference Roswell and Martin1973; Chen et al.
Reference Chen, Su, Katsouleas, Wilks and Dawson1987; Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987; Sentoku et al.
Reference Sentoku, Mima, Kaw and Nishikawa2003; Blumenfeld et al.
Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012), where
![]() $\unicode[STIX]{x1D714}_{p}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$
is the plasma frequency,
$\unicode[STIX]{x1D714}_{p}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$
is the plasma frequency,
![]() $n_{e}$
the background plasma density,
$n_{e}$
the background plasma density,
![]() $m_{e}$
the mass of the electron,
$m_{e}$
the mass of the electron,
![]() $e$
the charge of the electron and
$e$
the charge of the electron and
![]() $c$
the speed of light. When the transverse beam size is larger than the plasma skin depth the plasmas return currents can flow through the beam leading to the growth of CFI. If this condition does not hold, i.e. when
$c$
the speed of light. When the transverse beam size is larger than the plasma skin depth the plasmas return currents can flow through the beam leading to the growth of CFI. If this condition does not hold, i.e. when
![]() $\unicode[STIX]{x1D70E}_{y}\leqslant c/\unicode[STIX]{x1D714}_{p}$
, the CFI does not grow (Roswell & Martin Reference Roswell and Martin1973; Chen et al.
Reference Chen, Su, Katsouleas, Wilks and Dawson1987; Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987; Sentoku et al.
Reference Sentoku, Mima, Kaw and Nishikawa2003; Blumenfeld et al.
Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012).
$\unicode[STIX]{x1D70E}_{y}\leqslant c/\unicode[STIX]{x1D714}_{p}$
, the CFI does not grow (Roswell & Martin Reference Roswell and Martin1973; Chen et al.
Reference Chen, Su, Katsouleas, Wilks and Dawson1987; Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987; Sentoku et al.
Reference Sentoku, Mima, Kaw and Nishikawa2003; Blumenfeld et al.
Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Allen et al.
Reference Allen, Yakimenko, Babzien, Fedurin, Kusche and Muggli2012).
In order to illustrate the generation of magnetic fields through the CFI, we start by describing the results from two-dimensional (2-D) OSIRIS PIC simulations (Fonseca et al.
Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee and Katsouleas2002b
, Reference Fonseca, Martins, Silva, Tonge, Tsung and Mori2008, Reference Fonseca, Vieira, Fiuza, Davidson, Tsung, Mori and Silva2013). The simulations use a moving window travelling at
![]() $c$
. The simulation box has absorbing boundary conditions for the fields and for the particles in the transverse direction. The globally neutral fireball beam is initialized at the entrance of a stationary plasma with
$c$
. The simulation box has absorbing boundary conditions for the fields and for the particles in the transverse direction. The globally neutral fireball beam is initialized at the entrance of a stationary plasma with
![]() $n_{e}=10^{17}~\text{cm}^{-3}$
. The plasma is composed of electrons and stationary ions forming an immobile neutralizing fluid background. The initial density profile for the electron and positron fireball beam is given by
$n_{e}=10^{17}~\text{cm}^{-3}$
. The plasma is composed of electrons and stationary ions forming an immobile neutralizing fluid background. The initial density profile for the electron and positron fireball beam is given by
![]() $n_{b}=n_{b0}\exp (-x^{2}/\unicode[STIX]{x1D70E}_{x}^{2}-y^{2}/\unicode[STIX]{x1D70E}_{y}^{2})$
where
$n_{b}=n_{b0}\exp (-x^{2}/\unicode[STIX]{x1D70E}_{x}^{2}-y^{2}/\unicode[STIX]{x1D70E}_{y}^{2})$
where
![]() $n_{b0}=n_{e}=10^{17}~\text{cm}^{-3}$
,
$n_{b0}=n_{e}=10^{17}~\text{cm}^{-3}$
,
![]() $\unicode[STIX]{x1D70E}_{x}=0.99~c/\unicode[STIX]{x1D714}_{p}=10.2~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D70E}_{x}=0.99~c/\unicode[STIX]{x1D714}_{p}=10.2~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D70E}_{y}=2~c/\unicode[STIX]{x1D714}_{p}=20.4~\unicode[STIX]{x03BC}\text{m}$
are the bunch peak density, length and transverse waist, respectively. The beam propagates along the
$\unicode[STIX]{x1D70E}_{y}=2~c/\unicode[STIX]{x1D714}_{p}=20.4~\unicode[STIX]{x03BC}\text{m}$
are the bunch peak density, length and transverse waist, respectively. The beam propagates along the
![]() $x$
-axis with Lorentz factor
$x$
-axis with Lorentz factor
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}=5.6\times 10^{4}$
, with transverse velocity spread
$\unicode[STIX]{x1D6FE}_{\text{b}}=5.6\times 10^{4}$
, with transverse velocity spread
![]() $v_{th}/c=1.7\times 10^{-5}$
and with no momentum spread in the longitudinal direction. The simulation box dimensions are
$v_{th}/c=1.7\times 10^{-5}$
and with no momentum spread in the longitudinal direction. The simulation box dimensions are
![]() $L_{x}=8.02~c/\unicode[STIX]{x1D714}_{p}$
and
$L_{x}=8.02~c/\unicode[STIX]{x1D714}_{p}$
and
![]() $L_{y}=20.0~c/\unicode[STIX]{x1D714}_{p}$
with a moving window travelling at
$L_{y}=20.0~c/\unicode[STIX]{x1D714}_{p}$
with a moving window travelling at
![]() $c$
along
$c$
along
![]() $x$
. The box is divided into
$x$
. The box is divided into
![]() $128\times 512$
cells with
$128\times 512$
cells with
![]() $2\times 2$
particles per cell.
$2\times 2$
particles per cell.

Figure 1. The interaction of a neutral
![]() $e^{-}$
,
$e^{-}$
,
![]() $e^{+}$
fireball beam having a Gaussian profile with
$e^{+}$
fireball beam having a Gaussian profile with
![]() $\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D70E}_{y}=20.4~\unicode[STIX]{x03BC}\text{m}$
, peak density
$\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D70E}_{y}=20.4~\unicode[STIX]{x03BC}\text{m}$
, peak density
![]() $n_{b}=2.7\times 10^{15}~\text{m}^{-3}$
,
$n_{b}=2.7\times 10^{15}~\text{m}^{-3}$
,
![]() $\unicode[STIX]{x1D6FE}_{b}=5.6\times 10^{4}$
with a static plasma with
$\unicode[STIX]{x1D6FE}_{b}=5.6\times 10^{4}$
with a static plasma with
![]() $n_{e}=n_{b}$
. (a) Evolution of Transverse magnetic
$n_{e}=n_{b}$
. (a) Evolution of Transverse magnetic
![]() $\unicode[STIX]{x1D716}_{bz}$
(red), Longitudinal
$\unicode[STIX]{x1D716}_{bz}$
(red), Longitudinal
![]() $\unicode[STIX]{x1D716}_{ex}$
(green) and transverse electric
$\unicode[STIX]{x1D716}_{ex}$
(green) and transverse electric
![]() $\unicode[STIX]{x1D716}_{ey}$
(blue) field energies as function of distance normalized to the initial kinetic energy of the beam
$\unicode[STIX]{x1D716}_{ey}$
(blue) field energies as function of distance normalized to the initial kinetic energy of the beam
![]() $\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V$
, where
$\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V$
, where
![]() $V_{b}=\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y}$
is the volume of the beam. The dotted line represents the simulation growth rate of the CFI. At time
$V_{b}=\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y}$
is the volume of the beam. The dotted line represents the simulation growth rate of the CFI. At time
![]() $t=1900.09~[1/\unicode[STIX]{x1D714}_{p}]$
, we show (b) the density filaments corresponds to the electron
$t=1900.09~[1/\unicode[STIX]{x1D714}_{p}]$
, we show (b) the density filaments corresponds to the electron
![]() $e^{-}$
(blue) and positron
$e^{-}$
(blue) and positron
![]() $e^{+}$
(red) spatially separated from each other (c) the associated transverse magnetic (
$e^{+}$
(red) spatially separated from each other (c) the associated transverse magnetic (
![]() $B_{z}$
) filaments at linear regime after 0.02 m (d) due to space charge radial electric field (
$B_{z}$
) filaments at linear regime after 0.02 m (d) due to space charge radial electric field (
![]() $E_{x}$
) created.
$E_{x}$
) created.
Figure 1 depicts the growth of the transverse magnetic field energy (a), the beam filaments due to the CFI (b), and the typical electromagnetic field structure (c) and (d). Figure 1(a) shows that the growth of the magnetic field energy as a function of the propagation distance is exponential as expected from the CFI. In figure 1(a), the electromagnetic field is normalized with respect to the initial kinetic energy of the particles
![]() $\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V_{b}$
, where
$\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V_{b}$
, where
![]() $V_{b}=(\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y})$
is the volume of the beam. Simulations reveal that the field energy grows at the expense of the total kinetic energy of the fireball beam. The measured simulation linear growth rate (
$V_{b}=(\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y})$
is the volume of the beam. Simulations reveal that the field energy grows at the expense of the total kinetic energy of the fireball beam. The measured simulation linear growth rate (
![]() $\unicode[STIX]{x1D6E4}_{\text{CFI}}/\unicode[STIX]{x1D714}_{p}\simeq 6.0\times 10^{-3}$
) is within the range predicted by the dispersion relation for the purely transverse CFI (Silva et al.
Reference Silva, Fonseca, Tonge, Mori and Dawson2002). As a consequence of the instability, the beam breaks up into narrow (with a width of the order of
$\unicode[STIX]{x1D6E4}_{\text{CFI}}/\unicode[STIX]{x1D714}_{p}\simeq 6.0\times 10^{-3}$
) is within the range predicted by the dispersion relation for the purely transverse CFI (Silva et al.
Reference Silva, Fonseca, Tonge, Mori and Dawson2002). As a consequence of the instability, the beam breaks up into narrow (with a width of the order of
![]() $0.5\,c/\unicode[STIX]{x1D714}_{p}$
, which correspond to
$0.5\,c/\unicode[STIX]{x1D714}_{p}$
, which correspond to
![]() $5~\unicode[STIX]{x03BC}\text{m}$
for our baseline parameters) and high current density filaments. Figure 1(b) shows that these electron–positron filaments are spatially separated from each other. Each filament carries strong currents, which lead to the generation of strong out-of-the-plane (i.e. azimuthal) magnetic fields with amplitudes beyond 20 T. The azimuthal magnetic fields are also filamented, as shown in figure 1(c). Because of their finite transverse momentum, simulations show that current filaments can merge.
$5~\unicode[STIX]{x03BC}\text{m}$
for our baseline parameters) and high current density filaments. Figure 1(b) shows that these electron–positron filaments are spatially separated from each other. Each filament carries strong currents, which lead to the generation of strong out-of-the-plane (i.e. azimuthal) magnetic fields with amplitudes beyond 20 T. The azimuthal magnetic fields are also filamented, as shown in figure 1(c). Because of their finite transverse momentum, simulations show that current filaments can merge.
As merging occurs, the width of the filaments increases, until the beam filaments width becomes comparable to the initial bunch transverse size. At this point, the CFI stops growing, and no more beam energy flows into the generation of azimuthal magnetic fields. Simultaneously, radial electric fields above
![]() $10~\text{GV}~\text{m}^{-1}$
are also generated (figure 1
d) which can be attributed to space charge effects and due to inductive effects. The beam transverse size is larger than the plasma skin depth, which corresponds to the spatial scales where the instability growth rate is maximum (Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987). Our simulations show a clear transition from the linear to nonlinear stage of CFI due to the merging of fireball bunch filaments and we expect that the mechanisms leading to the saturation of the magnetic fields in our simulations will not differ from well-known saturation mechanisms, described in Yang, Arons & Langdo (Reference Yang, Arons and Langdo1994), Silva et al. (Reference Silva, Fonseca, Tonge, Dawson, Mori and Medvedev2003), Medvedev et al. (Reference Medvedev, Massimiliano, Fonseca, Silva and Mori2005), Achterberg, Wiersma & Norman (Reference Achterberg, Wiersma and Norman2007).
$10~\text{GV}~\text{m}^{-1}$
are also generated (figure 1
d) which can be attributed to space charge effects and due to inductive effects. The beam transverse size is larger than the plasma skin depth, which corresponds to the spatial scales where the instability growth rate is maximum (Su et al.
Reference Su, Katsouleas, Dawson, Chen, Jones and Keinigs1987). Our simulations show a clear transition from the linear to nonlinear stage of CFI due to the merging of fireball bunch filaments and we expect that the mechanisms leading to the saturation of the magnetic fields in our simulations will not differ from well-known saturation mechanisms, described in Yang, Arons & Langdo (Reference Yang, Arons and Langdo1994), Silva et al. (Reference Silva, Fonseca, Tonge, Dawson, Mori and Medvedev2003), Medvedev et al. (Reference Medvedev, Massimiliano, Fonseca, Silva and Mori2005), Achterberg, Wiersma & Norman (Reference Achterberg, Wiersma and Norman2007).
3 Role of the peak beam density and beam duration in the growth of current filamentation instability
In the previous section, and for illustration purposes only, we have considered that the total beam density was twice the background plasma density. In this section, we will investigate the propagation of beams with lower peak densities. In order to keep the number of particles constant, we then increase the beam length, such that
![]() $\unicode[STIX]{x1D70E}_{x}\geqslant \unicode[STIX]{x1D706}_{p}$
. In these conditions, the OBI competes with the CFI (Bret Reference Bret2009). The OBI can grow when the wave vector is at an angle with respect to the flow velocity direction, and it leads to the generation of both electric and magnetic field components. The maximum growth rate for the CFI and the OBI, assuming the beams are infinitely long, are given by
$\unicode[STIX]{x1D70E}_{x}\geqslant \unicode[STIX]{x1D706}_{p}$
. In these conditions, the OBI competes with the CFI (Bret Reference Bret2009). The OBI can grow when the wave vector is at an angle with respect to the flow velocity direction, and it leads to the generation of both electric and magnetic field components. The maximum growth rate for the CFI and the OBI, assuming the beams are infinitely long, are given by
![]() $\unicode[STIX]{x1D6E4}_{\text{CFI}}\sim \sqrt{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FE}_{\text{b}}}\,\unicode[STIX]{x1D6FD}_{b0}$
and
$\unicode[STIX]{x1D6E4}_{\text{CFI}}\sim \sqrt{\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FE}_{\text{b}}}\,\unicode[STIX]{x1D6FD}_{b0}$
and
![]() $\unicode[STIX]{x1D6E4}_{\text{OBI}}\sim \sqrt{3}/2^{4/3}(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FE}_{\text{b}})^{1/3}$
respectively (Bret & Gremillet Reference Bret and Gremillet2006), where
$\unicode[STIX]{x1D6E4}_{\text{OBI}}\sim \sqrt{3}/2^{4/3}(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FE}_{\text{b}})^{1/3}$
respectively (Bret & Gremillet Reference Bret and Gremillet2006), where
![]() $\unicode[STIX]{x1D6FC}$
is the beam (
$\unicode[STIX]{x1D6FC}$
is the beam (
![]() $n_{b}$
) to plasma density (
$n_{b}$
) to plasma density (
![]() $n_{e}$
) ratio and
$n_{e}$
) ratio and
![]() $\unicode[STIX]{x1D6FD}_{b0}=v_{b}/c$
is the normalized velocity of the beam. Thus, the ratio between the CFI growth rate and the OBI growth rate is given by:
$\unicode[STIX]{x1D6FD}_{b0}=v_{b}/c$
is the normalized velocity of the beam. Thus, the ratio between the CFI growth rate and the OBI growth rate is given by:
Equation (3.1) provides criteria for determining which of the two instabilities will dominate. The OBI is almost universally faster than the CFI. However, due to the weak dependence on
![]() $\unicode[STIX]{x1D6FE}_{b}/\unicode[STIX]{x1D6FC}$
, given
$\unicode[STIX]{x1D6FE}_{b}/\unicode[STIX]{x1D6FC}$
, given
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}\sim 10^{4}$
the OBI will begin to dominate when
$\unicode[STIX]{x1D6FE}_{\text{b}}\sim 10^{4}$
the OBI will begin to dominate when
![]() $\unicode[STIX]{x1D6FC}$
is much smaller 1.
$\unicode[STIX]{x1D6FC}$
is much smaller 1.
In order to verify this hypothesis, we have carried out additional two-dimensional OSIRIS PIC simulations using the initial set-up described in § 2, varying
![]() $\unicode[STIX]{x1D70E}_{x}$
between
$\unicode[STIX]{x1D70E}_{x}$
between
![]() $2\unicode[STIX]{x1D706}_{p}$
and
$2\unicode[STIX]{x1D706}_{p}$
and
![]() $10\unicode[STIX]{x1D706}_{p}$
, for which
$10\unicode[STIX]{x1D706}_{p}$
, for which
![]() $\unicode[STIX]{x1D6FC}$
varies between
$\unicode[STIX]{x1D6FC}$
varies between
![]() $0.0026$
and
$0.0026$
and
![]() $1.0$
. In all these cases, our results have consistently shown evidence of the OBI growth.
$1.0$
. In all these cases, our results have consistently shown evidence of the OBI growth.

Figure 2. Interaction of a neutral
![]() $e^{-}$
,
$e^{-}$
,
![]() $e^{+}$
fireball beam with longitudinal size
$e^{+}$
fireball beam with longitudinal size
![]() $\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D706}_{p}$
and a static plasma by keeping constant beam particle number. (a) Evolution of transverse magnetic
$\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D706}_{p}$
and a static plasma by keeping constant beam particle number. (a) Evolution of transverse magnetic
![]() $\unicode[STIX]{x1D716}_{bz}$
(red), longitudinal
$\unicode[STIX]{x1D716}_{bz}$
(red), longitudinal
![]() $\unicode[STIX]{x1D716}_{ex}$
(green) and transverse electric
$\unicode[STIX]{x1D716}_{ex}$
(green) and transverse electric
![]() $\unicode[STIX]{x1D716}_{ey}$
(blue) field energy as function of distance normalized to the initial kinetic energy of the beam
$\unicode[STIX]{x1D716}_{ey}$
(blue) field energy as function of distance normalized to the initial kinetic energy of the beam
![]() $\unicode[STIX]{x1D716}_{p}$
. The dotted line represents the growth rate of OBI. Dashed red line is the evolution of the out of the plane magnetic field for the condition of the simulation shown in figure 1(a). At time
$\unicode[STIX]{x1D716}_{p}$
. The dotted line represents the growth rate of OBI. Dashed red line is the evolution of the out of the plane magnetic field for the condition of the simulation shown in figure 1(a). At time
![]() $t=8880.07~[1/\unicode[STIX]{x1D714}_{p}]$
, we show (b) the density filaments corresponding to the electron
$t=8880.07~[1/\unicode[STIX]{x1D714}_{p}]$
, we show (b) the density filaments corresponding to the electron
![]() $e^{-}$
(blue) and positron
$e^{-}$
(blue) and positron
![]() $e^{+}$
(red) spatially separated from each other (c) the associated transverse magnetic (
$e^{+}$
(red) spatially separated from each other (c) the associated transverse magnetic (
![]() $B_{z}$
) filaments in the linear regime between
$B_{z}$
) filaments in the linear regime between
![]() $x_{1}=0.0551-0.0556~\text{m}$
(d) the space charge separation leads to longitudinal electric field (
$x_{1}=0.0551-0.0556~\text{m}$
(d) the space charge separation leads to longitudinal electric field (
![]() $E_{x}$
).
$E_{x}$
).
In figure 2, we show an illustrative simulation result considering
![]() $\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D706}_{p}$
, with
$\unicode[STIX]{x1D70E}_{x}=2\unicode[STIX]{x1D706}_{p}$
, with
![]() $n_{b}=1.274\times 10^{15}~\text{cm}^{-3}$
, for which
$n_{b}=1.274\times 10^{15}~\text{cm}^{-3}$
, for which
![]() $\unicode[STIX]{x1D6FC}=0.01274$
. In order to describe the propagation of a longer beam, we have increased the simulation box length. We then increased the longitudinal simulation box length to
$\unicode[STIX]{x1D6FC}=0.01274$
. In order to describe the propagation of a longer beam, we have increased the simulation box length. We then increased the longitudinal simulation box length to
![]() $L_{x}=63\,c/\unicode[STIX]{x1D714}_{p}$
(
$L_{x}=63\,c/\unicode[STIX]{x1D714}_{p}$
(
![]() $L_{y}=20\,c/\unicode[STIX]{x1D714}_{p}$
remains identical to that of § 2). The simulation box is now divided into
$L_{y}=20\,c/\unicode[STIX]{x1D714}_{p}$
remains identical to that of § 2). The simulation box is now divided into
![]() $1024\times 512$
cells with
$1024\times 512$
cells with
![]() $2\times 2$
particles per cell for each species.
$2\times 2$
particles per cell for each species.
Figure 2(a) illustrates the evolution of the longitudinal and transverse electric and transverse magnetic energy (normalized to
![]() $\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V_{b}$
, where
$\unicode[STIX]{x1D716}_{p}=(\unicode[STIX]{x1D6FE}_{\text{b}}-1)V_{b}$
, where
![]() $V_{b}=(\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y})$
is the volume of the beam). The emergence of oblique modes can be seen in figure 2(b), which shows tilted beam filaments. In a multi-dimensional configuration, the oblique wave vector couples the transverse (filamentation) and longitudinal (two-stream) instabilities resulting in the electromagnetic beam–plasma instability. Unlike figure 1, the simulation results in figure 2 show that the transverse electric field (
$V_{b}=(\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}_{x}\unicode[STIX]{x1D70E}_{y})$
is the volume of the beam). The emergence of oblique modes can be seen in figure 2(b), which shows tilted beam filaments. In a multi-dimensional configuration, the oblique wave vector couples the transverse (filamentation) and longitudinal (two-stream) instabilities resulting in the electromagnetic beam–plasma instability. Unlike figure 1, the simulation results in figure 2 show that the transverse electric field (
![]() $E_{y}$
) component provides the dominant contribution to the total field energy. The plasma is only weakly magnetized
$E_{y}$
) component provides the dominant contribution to the total field energy. The plasma is only weakly magnetized
![]() $\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D714}_{p}=0.01$
, much lower than in figure 1(c), where
$\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D714}_{p}=0.01$
, much lower than in figure 1(c), where
![]() $\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D714}_{p}\simeq 0.6$
, and the CFI does not play a critical role in the beam propagation. The longitudinal and transverse electric fields grow exponentially, as predicted by the linear analysis of the OBI, matching well the simulation results. The growth rate measured in the simulations is
$\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D714}_{p}\simeq 0.6$
, and the CFI does not play a critical role in the beam propagation. The longitudinal and transverse electric fields grow exponentially, as predicted by the linear analysis of the OBI, matching well the simulation results. The growth rate measured in the simulations is
![]() $\unicode[STIX]{x1D6E4}_{\text{max}}/\unicode[STIX]{x1D714}_{p}\simeq \unicode[STIX]{x1D6E4}_{\text{OBI}}\simeq 2.1\times 10^{-3}$
, in good agreement with Fainberg, Shapiro & Shevchenko (Reference Fainberg, Shapiro and Shevchenko1970). The OBI generates plasma waves with strong radial electric fields in excess of
$\unicode[STIX]{x1D6E4}_{\text{max}}/\unicode[STIX]{x1D714}_{p}\simeq \unicode[STIX]{x1D6E4}_{\text{OBI}}\simeq 2.1\times 10^{-3}$
, in good agreement with Fainberg, Shapiro & Shevchenko (Reference Fainberg, Shapiro and Shevchenko1970). The OBI generates plasma waves with strong radial electric fields in excess of
![]() $1~\text{GV}~\text{m}^{-1}$
(figure 2
d). After 20 cm, the OBI saturates. Despite being limits of the same instability, the electromagnetic beam plasma instability, we will refer to the CFI and the OBI as the manifestation of qualitatively different behaviour of the same instability.
$1~\text{GV}~\text{m}^{-1}$
(figure 2
d). After 20 cm, the OBI saturates. Despite being limits of the same instability, the electromagnetic beam plasma instability, we will refer to the CFI and the OBI as the manifestation of qualitatively different behaviour of the same instability.
4 Effects of finite beam waist and emittance
Theoretical and numerical studies performed to identify the effect of beam emittance on the growth of plasma instabilities and their saturation (Fonseca et al.
Reference Fonseca, Silva, Tonge, Hemker, Dawson and Mori2002a
; Silva et al.
Reference Silva, Fonseca, Tonge, Mori and Dawson2002; Shukla et al.
Reference Shukla, Stockem, Fiuza and Silva2012) typically assume that the beam is infinitely wide. In this section, we will investigate the role of the beam emittance considering finite beam size effects, in order to make closer contact with laboratory conditions. To study the influence of the beam emittance on the propagation, we first consider the equation for the evolution of the beam waist
![]() $\unicode[STIX]{x1D70E}_{y}$
in vacuum (Schroeder & Benedetti Reference Schroeder and Benedetti2011)
$\unicode[STIX]{x1D70E}_{y}$
in vacuum (Schroeder & Benedetti Reference Schroeder and Benedetti2011)
where
![]() $\unicode[STIX]{x1D70E}_{y}$
is the beam radius,
$\unicode[STIX]{x1D70E}_{y}$
is the beam radius,
![]() $\unicode[STIX]{x1D716}_{N}\simeq \unicode[STIX]{x0394}p_{\text{y}}\unicode[STIX]{x1D70E}_{y}$
is a figure for the beam emittance (corresponding to the area of the beam transverse phase space) and
$\unicode[STIX]{x1D716}_{N}\simeq \unicode[STIX]{x0394}p_{\text{y}}\unicode[STIX]{x1D70E}_{y}$
is a figure for the beam emittance (corresponding to the area of the beam transverse phase space) and
![]() $\unicode[STIX]{x0394}p_{\text{y}}$
is the transverse momentum spread. According to (4.1), the evolution for
$\unicode[STIX]{x0394}p_{\text{y}}$
is the transverse momentum spread. According to (4.1), the evolution for
![]() $\unicode[STIX]{x1D70E}_{y}$
and for sufficiently early times is given by:
$\unicode[STIX]{x1D70E}_{y}$
and for sufficiently early times is given by:
where
![]() $\unicode[STIX]{x1D70E}_{y0}$
is the initial beam radius. Hence, according to (4.1), the rate at which
$\unicode[STIX]{x1D70E}_{y0}$
is the initial beam radius. Hence, according to (4.1), the rate at which
![]() $\unicode[STIX]{x1D70E}_{y}$
increases is:
$\unicode[STIX]{x1D70E}_{y}$
increases is:
Equation (4.3) indicates that the beam expands in vacuum due to its transverse momentum spread. As the beam expands,
![]() $n_{b}$
decreases as
$n_{b}$
decreases as
![]() $n_{b}/n_{e}\sim (\unicode[STIX]{x1D70E}_{y0}/\unicode[STIX]{x1D70E}_{y})^{2}$
, in three dimensions, and as
$n_{b}/n_{e}\sim (\unicode[STIX]{x1D70E}_{y0}/\unicode[STIX]{x1D70E}_{y})^{2}$
, in three dimensions, and as
![]() $(\unicode[STIX]{x1D70E}_{y0}/\unicode[STIX]{x1D70E}_{y})$
, in two dimensions. Because of the reduction of
$(\unicode[STIX]{x1D70E}_{y0}/\unicode[STIX]{x1D70E}_{y})$
, in two dimensions. Because of the reduction of
![]() $n_{b}/n_{e}$
, the growth rates for the CFI and for the OBI will also decrease. We then estimate that these instabilities (i.e. CFI and OBI) are suppressed when the rate at which
$n_{b}/n_{e}$
, the growth rates for the CFI and for the OBI will also decrease. We then estimate that these instabilities (i.e. CFI and OBI) are suppressed when the rate at which
![]() $n_{b}/n_{e}$
decreases is much higher than the instability growth rate. Matching the rate at which the beam density drops, which in two dimensions is given by
$n_{b}/n_{e}$
decreases is much higher than the instability growth rate. Matching the rate at which the beam density drops, which in two dimensions is given by
![]() $(1/\unicode[STIX]{x1D70E}_{y})~(\text{d}\unicode[STIX]{x1D70E}_{y}/\text{d}t)$
, to the growth rate of the instability (
$(1/\unicode[STIX]{x1D70E}_{y})~(\text{d}\unicode[STIX]{x1D70E}_{y}/\text{d}t)$
, to the growth rate of the instability (
![]() $\unicode[STIX]{x1D6E4}$
) gives an upper limit for the maximum beam divergence
$\unicode[STIX]{x1D6E4}$
) gives an upper limit for the maximum beam divergence
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x0394}p_{\text{y}}/\unicode[STIX]{x1D6FE}_{\text{b}}$
(and emittance
$\unicode[STIX]{x1D703}=\unicode[STIX]{x0394}p_{\text{y}}/\unicode[STIX]{x1D6FE}_{\text{b}}$
(and emittance
![]() $\unicode[STIX]{x1D716}_{N}\approx \unicode[STIX]{x1D70E}_{y}(\langle p_{y}^{2}\rangle )^{1/2}$
) allowed for the growth of the CFI/OBI:
$\unicode[STIX]{x1D716}_{N}\approx \unicode[STIX]{x1D70E}_{y}(\langle p_{y}^{2}\rangle )^{1/2}$
) allowed for the growth of the CFI/OBI:
where we have considered that
![]() $t\sim L_{\text{growth}}/c$
in (4.4), with
$t\sim L_{\text{growth}}/c$
in (4.4), with
![]() $L_{\text{growth}}$
the growth length of the CFI/OBI instability. Equation (4.4) then gives the threshold beam divergence, beyond which the CFI/OBI will be suppressed. It indicates that beams with higher energy can support higher thermal spreads and still be subject to the growth of the CFI because the beam expands slowly in comparison to lower energy beams. Similarly, beams with higher
$L_{\text{growth}}$
the growth length of the CFI/OBI instability. Equation (4.4) then gives the threshold beam divergence, beyond which the CFI/OBI will be suppressed. It indicates that beams with higher energy can support higher thermal spreads and still be subject to the growth of the CFI because the beam expands slowly in comparison to lower energy beams. Similarly, beams with higher
![]() $\unicode[STIX]{x1D70E}_{y0}$
also support higher emittance than narrower beams because of the slower expansion rate.
$\unicode[STIX]{x1D70E}_{y0}$
also support higher emittance than narrower beams because of the slower expansion rate.
To confirm our theoretical findings, we performed additional two-dimensional simulations using fireball beams with relativistic factors
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}=700,1050,1400$
(the lower
$\unicode[STIX]{x1D6FE}_{\text{b}}=700,1050,1400$
(the lower
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}$
factors used now, in comparison to § 2, to minimize the computational requirements). We use
$\unicode[STIX]{x1D6FE}_{\text{b}}$
factors used now, in comparison to § 2, to minimize the computational requirements). We use
![]() $\unicode[STIX]{x1D70E}_{x}=0.22~c/\unicode[STIX]{x1D714}_{p}=11.7~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D70E}_{x}=0.22~c/\unicode[STIX]{x1D714}_{p}=11.7~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D70E}_{y}=10~c/\unicode[STIX]{x1D714}_{p}=530~\unicode[STIX]{x03BC}\text{m}$
with peak density
$\unicode[STIX]{x1D70E}_{y}=10~c/\unicode[STIX]{x1D714}_{p}=530~\unicode[STIX]{x03BC}\text{m}$
with peak density
![]() $n_{b0}=10~n_{e}=10^{15}~\text{cm}^{-3}$
. For each case, we varied the transverse temperature
$n_{b0}=10~n_{e}=10^{15}~\text{cm}^{-3}$
. For each case, we varied the transverse temperature
![]() $\unicode[STIX]{x0394}p_{\text{y}}=\unicode[STIX]{x1D6FE}_{\text{b}}\unicode[STIX]{x1D703}=1,3,5,7,10$
and
$\unicode[STIX]{x0394}p_{\text{y}}=\unicode[STIX]{x1D6FE}_{\text{b}}\unicode[STIX]{x1D703}=1,3,5,7,10$
and
![]() $20$
in order to determine the threshold beam spread for the occurrence of instability. We note that we have used the classical addition of velocities in the beam thermal spread initialization in order to more clearly identify the dependence of evolution of the instabilities with emittance.
$20$
in order to determine the threshold beam spread for the occurrence of instability. We note that we have used the classical addition of velocities in the beam thermal spread initialization in order to more clearly identify the dependence of evolution of the instabilities with emittance.

Figure 3. (a) Temporal evolution of the transverse magnetic field energy for different beam emittance (b) Thermal velocities as function of Lorentz factor
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}$
, filamentation suppressed for higher thermal velocities. The red line represents a linear fit of the simulation data. At time
$\unicode[STIX]{x1D6FE}_{\text{b}}$
, filamentation suppressed for higher thermal velocities. The red line represents a linear fit of the simulation data. At time
![]() $t=705.60~[1/\unicode[STIX]{x1D714}_{p}]$
, panels (c,d) show beam filaments for thermal velocities
$t=705.60~[1/\unicode[STIX]{x1D714}_{p}]$
, panels (c,d) show beam filaments for thermal velocities
![]() $\unicode[STIX]{x0394}p_{\text{y}}=1,10$
from 2-D PIC simulations.
$\unicode[STIX]{x0394}p_{\text{y}}=1,10$
from 2-D PIC simulations.
Figure 3(a) shows that the magnetic field energy decreases with increasing transverse momentum spread. Figure 3(a) also shows a transition in the evolution of the magnetic energy between
![]() $\unicode[STIX]{x0394}p_{\text{y}}=10$
, where the magnetic field (B-field) still grows at the end of the simulation, and
$\unicode[STIX]{x0394}p_{\text{y}}=10$
, where the magnetic field (B-field) still grows at the end of the simulation, and
![]() $\unicode[STIX]{x0394}p_{\text{y}}=20$
, where the B-field decreases with propagation distance. According to (4.4), using
$\unicode[STIX]{x0394}p_{\text{y}}=20$
, where the B-field decreases with propagation distance. According to (4.4), using
![]() $L_{\text{growth}}\sim 0.037~\text{m}$
and
$L_{\text{growth}}\sim 0.037~\text{m}$
and
![]() $\unicode[STIX]{x1D6E4}_{\text{CFI}}\sim 1.657\times 10^{11}\text{s}^{-1}$
, we obtain the threshold
$\unicode[STIX]{x1D6E4}_{\text{CFI}}\sim 1.657\times 10^{11}\text{s}^{-1}$
, we obtain the threshold
![]() $\unicode[STIX]{x1D703}\sim 0.12$
for the shutdown of the instability. This is in good agreement with figure 3(a). The instability is suppressed for higher beam emittance because the beam to plasma density ratio drops faster than the growth rate of the instability, hence the beam expands in the transverse direction and does not have enough time for the CFI to grow. The threshold for emittance should be taken as only a guide to design experiments, and provides an upper limit required to observe the instabilities. The emittance should thus be much smaller than the values predicted in the model.
$\unicode[STIX]{x1D703}\sim 0.12$
for the shutdown of the instability. This is in good agreement with figure 3(a). The instability is suppressed for higher beam emittance because the beam to plasma density ratio drops faster than the growth rate of the instability, hence the beam expands in the transverse direction and does not have enough time for the CFI to grow. The threshold for emittance should be taken as only a guide to design experiments, and provides an upper limit required to observe the instabilities. The emittance should thus be much smaller than the values predicted in the model.
Figure 3(b) depicts the dependence of the threshold beam emittance on the fireball beam energy. Figure 3(c,d) shows the positron density for two simulations, where all the parameters are kept constant, except for the beam emittance. In particular, in figure 3(c) a beam emittance of
![]() $\unicode[STIX]{x0394}p_{\text{y}}=1$
, much smaller than the threshold value given by (4.4), has been considered. In this case, the CFI develops, leading to the filamentation of the beam (see figure 3
c) and to the exponential growth of the magnetic field energy (see figure 3
a, red curve). However, in the second case (figure 3
d) a higher beam emittance
$\unicode[STIX]{x0394}p_{\text{y}}=1$
, much smaller than the threshold value given by (4.4), has been considered. In this case, the CFI develops, leading to the filamentation of the beam (see figure 3
c) and to the exponential growth of the magnetic field energy (see figure 3
a, red curve). However, in the second case (figure 3
d) a higher beam emittance
![]() $\unicode[STIX]{x0394}p_{\text{y}}=10$
is considered. This suppresses the growth of the magnetic field energy (see figure 3
a, orange curve). As a result, the beam expands before the development of the CFI. These results show that the growth of CFI can only be achieved if the beam emittance is sufficiently small.
$\unicode[STIX]{x0394}p_{\text{y}}=10$
is considered. This suppresses the growth of the magnetic field energy (see figure 3
a, orange curve). As a result, the beam expands before the development of the CFI. These results show that the growth of CFI can only be achieved if the beam emittance is sufficiently small.
5 Effect of beam energy spread
In typical laboratory settings (Sarri et al.
Reference Sarri, Poder, Cole and Schumaker2015), electron–positron fireball beams can contain finite energy spreads. It is, therefore, important to evaluate the potentially deleterious role of the energy spread in the growth of CFI. In this section, we then present simulation results with finite longitudinal momentum spreads. We consider that the central beam relativistic factor is
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}=700$
, and compare two simulations with
$\unicode[STIX]{x1D6FE}_{\text{b}}=700$
, and compare two simulations with
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
and
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
and
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
(
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
(
![]() $\unicode[STIX]{x0394}p_{\text{x}}$
is the longitudinal momentum spread). All other simulation parameters are similar to those described in § 4.
$\unicode[STIX]{x0394}p_{\text{x}}$
is the longitudinal momentum spread). All other simulation parameters are similar to those described in § 4.

Figure 4. (a,b) Temporal evolution
![]() $(t=705.60~[1/\unicode[STIX]{x1D714}_{p}])$
of positron density exhibits the filaments for energy spread
$(t=705.60~[1/\unicode[STIX]{x1D714}_{p}])$
of positron density exhibits the filaments for energy spread
![]() $\unicode[STIX]{x0394}p_{\text{x}}=90,200$
; (c) (colour) the spectrum of two different energy spreads; (d) the solid line represents the simulation growth rate of the CFI for different beam energies.
$\unicode[STIX]{x0394}p_{\text{x}}=90,200$
; (c) (colour) the spectrum of two different energy spreads; (d) the solid line represents the simulation growth rate of the CFI for different beam energies.
Figure 4(a,b) shows the temporal evolution of the beam electron density for
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
(figure 4
a) and for
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
(figure 4
a) and for
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
(figure 4
b). The initial energy spectra of these two beams are shown in figure 4(c). Figure 4(d) shows the comparison of the magnetic field energy evolution. The blue curve shows the growth of magnetic field energy generated by the fireball beam with energy spread
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
(figure 4
b). The initial energy spectra of these two beams are shown in figure 4(c). Figure 4(d) shows the comparison of the magnetic field energy evolution. The blue curve shows the growth of magnetic field energy generated by the fireball beam with energy spread
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
, while the red curve is associated with the lower energy spread
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.29$
, while the red curve is associated with the lower energy spread
![]() $\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
.
$\unicode[STIX]{x0394}p_{\text{x}}/\unicode[STIX]{x1D6FE}_{\text{b}}=0.13$
.
The simulation growth rate (
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D714}_{p}\simeq 2.8\times 10^{-2}$
; shown by the dotted black line in figure 4
d) is consistent with the theoretical growth rate predicted for the purely transverse CFI (Pegoraro et al.
Reference Pegoraro, Bulanov, Califano and Lontano1996; Inglebert et al.
Reference Inglebert, Ghizzo, Reveille, Sarto, Bertrand and Califano2012). We notice that one to one comparisons with the simulation growth rate are non-trivial. We speculate that the differences are probably due to the finite beam size and non-uniform density profile in the transverse directions. We have performed additional simulations, which confirmed that numerical results converge to theoretical predictions as simulations considered progressively wider beams. In fact, to the best our knowledge, the excitation of these modes for finite length finite width modes has not been investigated. Thus, this work also motivates further theoretical developments that could predict the exact growth rate for non-uniform density profiles. However, this discussion does not prevent the main purpose of this section, namely, the energy spread naturally present in laser-produced fireball beams will not prevent the CFI occurring.
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D714}_{p}\simeq 2.8\times 10^{-2}$
; shown by the dotted black line in figure 4
d) is consistent with the theoretical growth rate predicted for the purely transverse CFI (Pegoraro et al.
Reference Pegoraro, Bulanov, Califano and Lontano1996; Inglebert et al.
Reference Inglebert, Ghizzo, Reveille, Sarto, Bertrand and Califano2012). We notice that one to one comparisons with the simulation growth rate are non-trivial. We speculate that the differences are probably due to the finite beam size and non-uniform density profile in the transverse directions. We have performed additional simulations, which confirmed that numerical results converge to theoretical predictions as simulations considered progressively wider beams. In fact, to the best our knowledge, the excitation of these modes for finite length finite width modes has not been investigated. Thus, this work also motivates further theoretical developments that could predict the exact growth rate for non-uniform density profiles. However, this discussion does not prevent the main purpose of this section, namely, the energy spread naturally present in laser-produced fireball beams will not prevent the CFI occurring.
6 Summary and conclusions
In summary, the growth and saturation of an ultra-relativistic beam propagating through plasma have been investigated using particle-in-cell (PIC) simulations. We have shown that short fireball beams, i.e. beams shorter than the plasma wavelength, interacting with uniform plasmas lead to the growth of the CFI. For typical parameters available for experiments, the instability can generate strong transverse magnetic field of the order of MGauss. We found that in typical laboratory settings, the incoming fireball beam filamentation saturates after 10 cm of propagation for the SLAC parameters (Muggli et al. Reference Muggli, Martins, Vieira and Silva2013), while for the laser–plasma generated fireball beam produced recently (Sarri et al. Reference Sarri, Poder, Cole and Schumaker2015) it saturates after 4.4 cm.
We have demonstrated that the beam density needs to be higher than the background plasma density to suppress the growth of the competing OBI instability, which leads to the growth of electrostatic modes (instead of electromagnetic). Beams with lower peak densities will then drive the OBI, which results in tilted filaments and the generation of mostly electrostatic plasma waves. We have also shown that the beam emittance needs to be minimized, reducing transverse beam defocusing effects, which can shut down the CFI or the OBI if the beam defocuses before these instabilities grow. We have also extended our numerical studies to investigate the effect of finite fireball energy spreads on the growth of CFI, and showed that the energy spreads of currently available fireball beams allow for the growth of CFI in the laboratory.
In conclusion, we have identified the factors for the generation of strong magnetic fields via CFI. We expect that the results will influence our understanding of astrophysical scenarios, by revealing the laboratory conditions where these effects can be studied.
Acknowledgements
This work was partially supported by the European Research Council (ERC-2016-InPairs 695088). Simulations were performed at the IST cluster (Lisbon, Portugal). N.S. would like to thank Dr K. M. Schoeffler and Dr E. Boella for helpful discussions. J.V. acknowledges the support for FCT (Portugal).