1. INTRODUCTION
In contradistinction to the main-stream fast ignition scenario (FIS), based on collisional stopping in the compressed deuterium tritium (DT)-fuel of relativistic electron beams (REB), in the 1–2 MeV energy range (ER) (Deutsch et al., Reference Deutsch, Furukawa, Mima, Murakami and Nishihara1996, Reference Deutsch, Furukawa, Mima, Murakami and Nishihara1997), we consider an ultra relativistic extension of a previous attempt (Malkin & Fisch, Reference Malkin and Fisch2002) by using REB in the several tenths of MeV ER, and stopping them in target through turbulence. Motivations for such an endeavor are obviously two-fold. First, conditions involving less initial intensity and easier “piercing” of the DT-precompressed core are electromagnetic instabilities. Moreover, the consideration of fast ignition guided with gold (Au) cone (Fig. 1) (Kodama et al., Reference Kodama, Shiraga, Shigemori, Toyama, Fujioka, Azechi, Fujiita, Habara, Hall, Izawa, Jitsuno, Kitagawa, Krushelnick, Lancaster, Mima, Nagai, Nakai, Nishimura, Norimatsu, Norreys, Sakabe, Tanaka, Youssef and Zepf2002) opens an opportunity of producing hard X- and γ-rays in the cone, which altogether with REB can pave the way to producing many high energy nuclear reactions based on the exchange of virtual photons, i.e., nonhadronic.

Fig. 1. (Color online) Cone-guided fast ignition with γ-production, through REB-Au interaction (after Kodama et al., 2002).
We therefore stress the additional and substantial contribution to REB stopping of strongly inelastic reactions, such as the Trident production of electron-positron pairs. In the 100 MeV and higher ER bremsstrahlung turns significant and hard Gamma come also into play to enhance these processes. We thus specifically emphasize electro-disintegrating deuterons and tritons, first in nucleons and eventually at higher energy with negative pion production included. In the latter case, it seems attractive to considerer pion-catalyzed DT fusion in very dense and hot plasma with no sticking. This claim is supported by preliminary estimates based on Debye like diatomic plasma orbitals. More interplay between resulting positrons and pions of either sign are also seen to contribute to in situ stopping of ultra-relativistic REB. The latter would then drive efficiently a fast ignition target with significantly reduced beam intensity and no further hole boring issues.
2. REB INTERACTION WITH INSTABILITIES
2.1. Electromagnetic Instabilities (EMI)
At moderate relativistic energy, i.e., for a Lorentz factor

v b denoting a monochromatic REB velocity, one is mostly concerned with beam propagation (Fig. 1) through electromagnetic instabilities (EMI) arising in the combined beam (density n b)-target plasma (electron density n p, plasma frequency ωp). EMI are unfortunately able to spoil easily and degrade REB initial qualities through increased emittance, energy spread, beam break-up… Such a possibility is already quantified in the initial linear regime. Most significant EMI growth rates feature two-stream (TS), filamentation (F), and a TSF combination of both (Bret & Deutsch, Reference Bret and Deutsch2005), for the dimensionless Zz = kzV p/ωp~1 with a maximum growth rate in ωp units
In the direction normal to the beam, the filamentation δ behaves for small
Z x = k xV p/ωp as
and then saturates for Z x ≫ V b/c at
Absolute maximum growth rate for oblique wave vector is obtained with Z z ~ 1 and Z x ≫ 1. We shall denote this maximum two-stream/filamentation growth rate as δTSF with
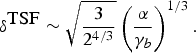
As far as the hierarchy of these unstable modes is concerned, it is obvious that δTSF > δTS for any sets of parameters, except in the non-relativistic regime γb = 1 where both growth rates are equal
2.2. Strong Langmuir Turbulence
On the other hand, at very high γb ≫ 1 values, the nonlinear evolution of the EMI toward an electrostatic regime could induce an appropriate REB collective stopping in precompressed target (Malkin & Fisch, Reference Malkin and Fisch2002). The latter is then monitored by ![]() between initial REB direction and Langmuir (L) wave's number direction, while contrasting W r, energy density in L waves resonating with REB to thermal energy density W th ~ n pT p2 /m ec 2 in target.
between initial REB direction and Langmuir (L) wave's number direction, while contrasting W r, energy density in L waves resonating with REB to thermal energy density W th ~ n pT p2 /m ec 2 in target.
Local REB relaxation length in turbulence thus features
For ωp ~ 6 × 1017 s−1 and T e ~ 5 keV, this simplifies to
If W r > W th, this length would not exceed 50 µm for γbΔθ ≤ 5
2.3. EMHD
It has also been recently documented (Yabuuchi et al., Reference Yabuuchi, Das, Kumar, Habaara, Kam, Kodama, Mima, Norreys, Sengupta and Tanaka2009) that electron magneto-hydrodynamic shock formation, i.e., with immobile ions, could stop high γb REB in the inhomogeneous density region (see Fig. 1). Such a mechanism seems to interpret the stopping of 15 MeV REB, in appropriate target with density ρ ~ 50–100 g/cm3 recently observed experimentally at ILE (Osaka).
3. REB STOPPING ON TARGET ELECTRONS (γB ≫ 1)
The stopping of uncorrelated and ultrarelativistic electron projectiles on target electrons taken as mostly classical (T p ≥ 1 keV) is accurately accounted for by a complete relativistic expression (Deutsch et al., Reference Deutsch, Furukawa, Mima, Murakami and Nishihara1996, Reference Deutsch, Furukawa, Mima, Murakami and Nishihara2000) well approximated by a simple Bethelike one (Starikov & Deutsch, Reference Starikov and Deutsch2005) given as

and also expressed in terms of an equivalent stopping cross-sections σ. For instance, at REB energy E = 200 MeV, one thus witnesses for n e ~ 1026 e-cm−3 (FIS conditions), σ ~ 10−25 cm2, a hundred times the Trident process for electro-production of electron-position pairs on target ions. It is also of quantitative interest to notice that Eqs. (5) displays a slight logarithmic increase, V b being fixed at c, above E > 200 MeV.
4. REB STOPPING ON TARGET IONS (γb ≫ 1)
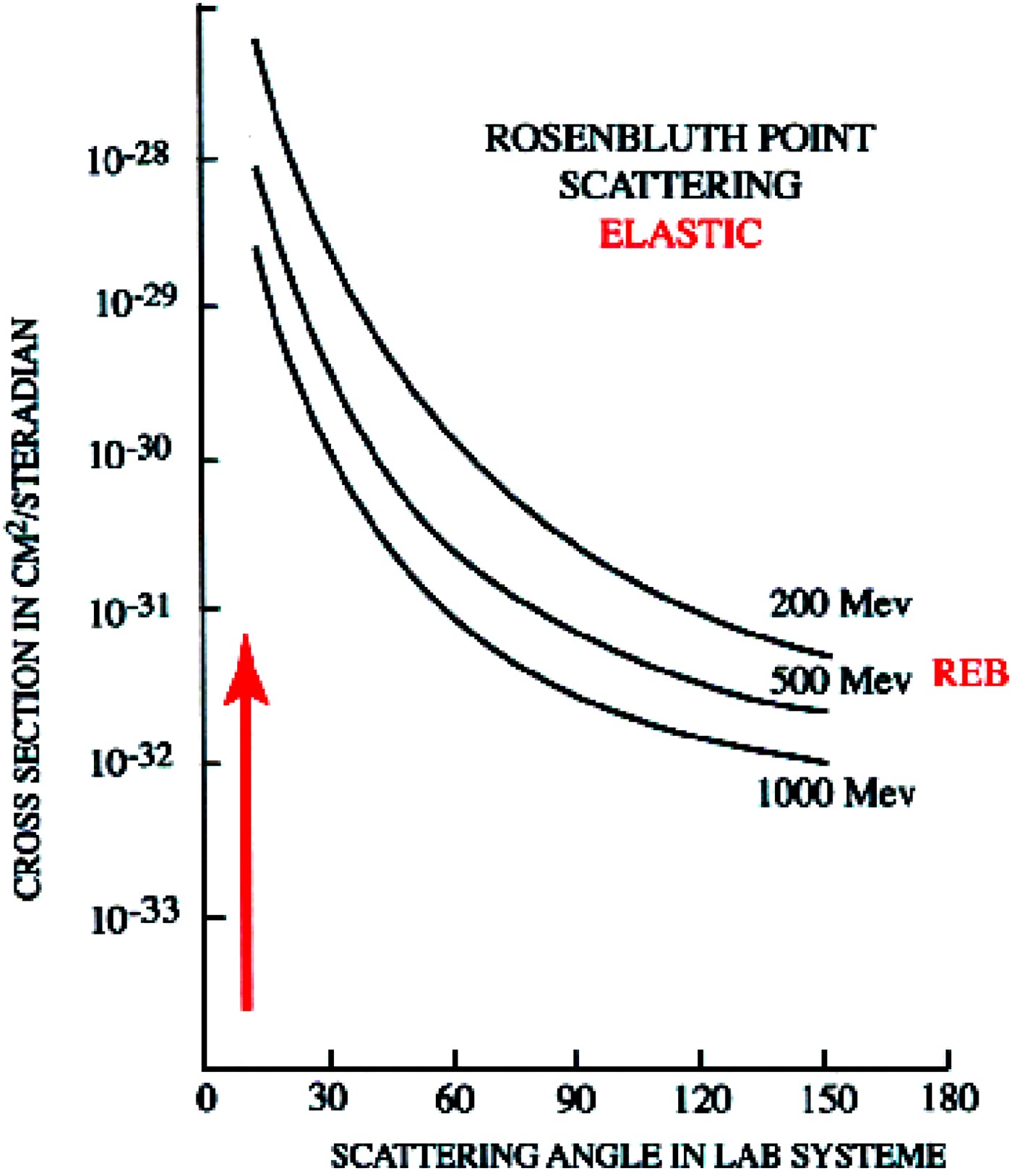
At ultra relativistic energy, the above elastic interaction with target electrons has to be supplemented by elastic interaction on target ions, which then exhibit their extended charge structure through electric and magnetic form factors (Hofstadter, Reference Hofstadter1963).
Elastic scattering of high-energy electrons by the magnetic moment of the proton had actually been predicted by Rosenbluth (Reference Rosenbluth1950), who showed that there is a contribution to the elastic scattering from both the Dirac and the Pauli components of the proton's magnetic moment. The Pauli moment is usually referred to as the “anomalous” part of the proton's magnetic moment. These arguments may be rationalized as follows. For a protonic point charge with masse M and point magnetic moment (in nuclear magnetic n.m.), the differential cross section reads as
![\eqalign {&\left({\displaystyle{{{\rm d}\sigma } \over {{\rm d}{\rm \Omega} }}} \right)_{\rm R}=\left({\displaystyle{{{e}^2 } \over {2{E}_{b} }}} \right)^2 \displaystyle{{\cos ^2 {\rm \theta} /2} \over {\sin ^4{\rm \theta} /2}}\displaystyle{1 \over {1+\displaystyle{{2{E}_{b} } \over {{Mc}^2 }}}}\sin ^2{\rm \theta} /2 \cr & \left\{{1+\displaystyle{{\hbar ^2 {q}^2 } \over {4{M}^2 {c}^2 }}\left[{2\lpar 1+{\rm K}\rpar ^2 \tan ^2{\rm \theta} /2+{\rm K}^2 } \right]} \right\}\cr & \lpar {\rm \mu} _{p}=1+{\rm K}=2.79 {\rm n.m}.\rpar .} \eqno\lpar 6\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021092105787-0842:S026303461000073X_eqn6.gif?pub-status=live)
in terms of momentum
![q = {2 \over {\rm \lambda} } - \left[{1 + \lpar 2{E}_{b} /{\rm M}\rpar \sin ^2 \displaystyle{1 \over 2}{\rm \theta} } \right]^{1/2}\comma \; \eqno\lpar 7\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021092105787-0842:S026303461000073X_eqn7.gif?pub-status=live)
and reduced De Broglie wavelength
of the electron projectile. θ denote the departure with respect to initial REB initial/direction. Eq. (6) is pictured in Figure 2 for several E b values.
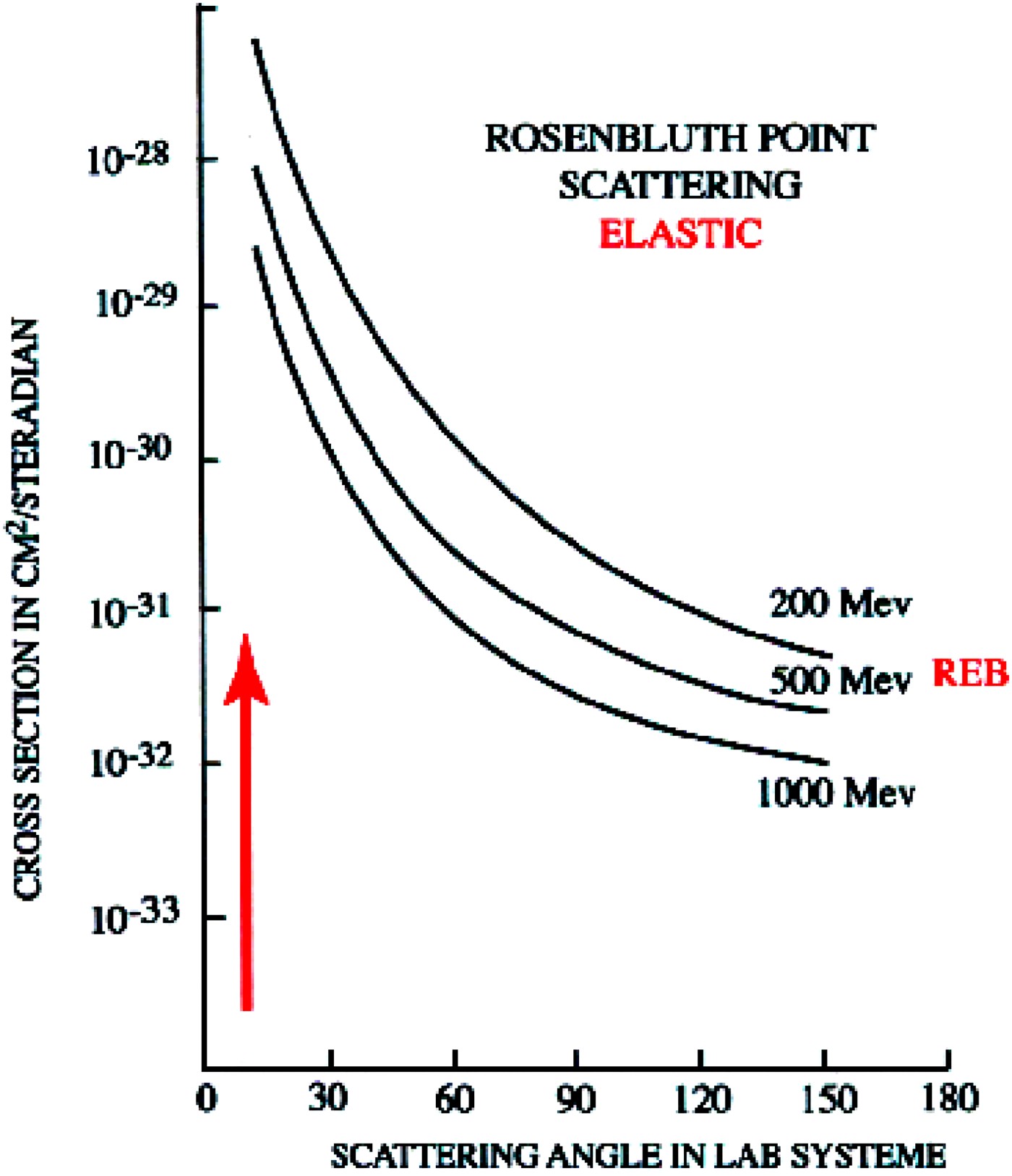
Fig. 2. (Color online) Rosenbluth-point scattering for point-protons with real values of nuclear spin and magnetic moment. The appropriate cross section is given with K = 1.79 nuclear magnetons, μ = 2.79 n.m. (after Hofstadter, Reference Hofstadter1963)
Switching to deuterium, Eq. (6) gets extended to
![\left({{{{\rm d}\sigma } \over {{\rm d}{\rm \Omega} }}} \right)_{\rm R}=\sigma _{\rm NS} \left\{{1+{2 \over 3}{{{q}^2 } \over {4{M}_{D}^2 }}\left[{2{\rm \mu} _{\rm D}^2 \tan ^2 \displaystyle{1 \over 2}{\rm \theta}+{\rm \mu} _{\rm D}^2 } \right]} \right\}{F}_{D}^2\comma \; \eqno\lpar 8\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021092105787-0842:S026303461000073X_eqn8.gif?pub-status=live)
in terms of
M D = deuteron mass
µD is the static deuteron magnetic moment, and F D is the form factor obtainable from the deuteron's charge density, as determined from the wave function of the deuteron in its ground state. The second term in the bracket is the magnetic term. The spin of the deuteron is 1 and this accounts for the difference in the coefficient of the q 2 term between Eqs. (6) and (8).
In the case of breakup of the deuteron, involving inelastic scattering, for large moment transfers one gets (Hofstadter, Reference Hofstadter1963) the inelastic cross-section
![\eqalign{\sigma_{\rm D}^{\rm in} \lpar {\rm \theta}\rpar &= \sigma_{\rm NS} \left\{1 - {F}_{D}^2 + {{q}^2 \over 4{M}2} \left[2\lpar {\rm \mu}_{ p}^2 + {\rm \mu}_{n}^2 - {F}_{D}^2\rpar \tan^2 {1 / 2}{\rm \theta} \right. \right. \cr &\quad \left. \left. + {\rm \mu}_{ p}^2 + {\rm \mu}_{ n}^2 - 3 {F}_{D}^2 \right]\right\}.} \eqno\lpar 9\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021092105787-0842:S026303461000073X_eqn9.gif?pub-status=live)
µp and µn are the proton and neutron magnetic moments, respectively, and F D is the deuteron elastic form factor. When the momentum transfer is large, F D ≅ 0. Similar extensions may also be worked out for tritium. The above elastic expressions (Fig. 2) display a strong maximum in the forward (θ = 0) direction. Corresponding integrated cross-sections then peak in the mbarn (10−27 cm2) range.
5. ELECTRO- AND PHOTO-PRODUCTION OF ELECTRON-POSITRON PAIRS
At the equivalent mb level for the total cross-section, one also encounters the well-known Trident process (Figs. 3 and 4) (Shearer et al., Reference Shearer, Garrison, Wong and Swain1972) for the inelastic production of electron-position pairs on target ions with charge Z. This process gets even significantly enhanced when triggered out by γ rays produced in the cone area of the FIS target (Fig. 1). The given photons are then copiously produced in Au (Z = 79) through the ratio

reaching unity for E = 10.35 MeV in Au and E = 817.16 in DT that leads to the ratio (Myatt et al., Reference Myatt, Delettrez, Maximov, Meyerhofer, Shory, Stoeckl and Storm2009)
![\eqalign{{\sigma_{\rm T} \over \sigma_{{\rm \gamma} \rightarrow {\rm e}^ + {\rm e}^ - }} &= {{\rm \alpha} \over {\rm \pi} }\left[\ln \left({{E} \over {m}_{e} {c}^2 } \right)\ln \left({{E} \over 2.137{m}_{e} {c}^2 Z^{ - 1/3}} \right)\right. \cr & \quad \left. + {1 \over 3}\ln^2 \lpar 2.137 {\rm Z}^{ - 1/3} \rpar \right]\cr &= \hbox{0.017 at 5 MeV in Au}\comma} \eqno\lpar 10\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021092105787-0842:S026303461000073X_eqn10.gif?pub-status=live)
where α = 1/137.036 is the quantum electrodynamics fine structure constant.

Fig. 3. (a) Trident process for pair production. (b) Trident Feynman graph for e++D+T+ → e++ e−+T+D+.
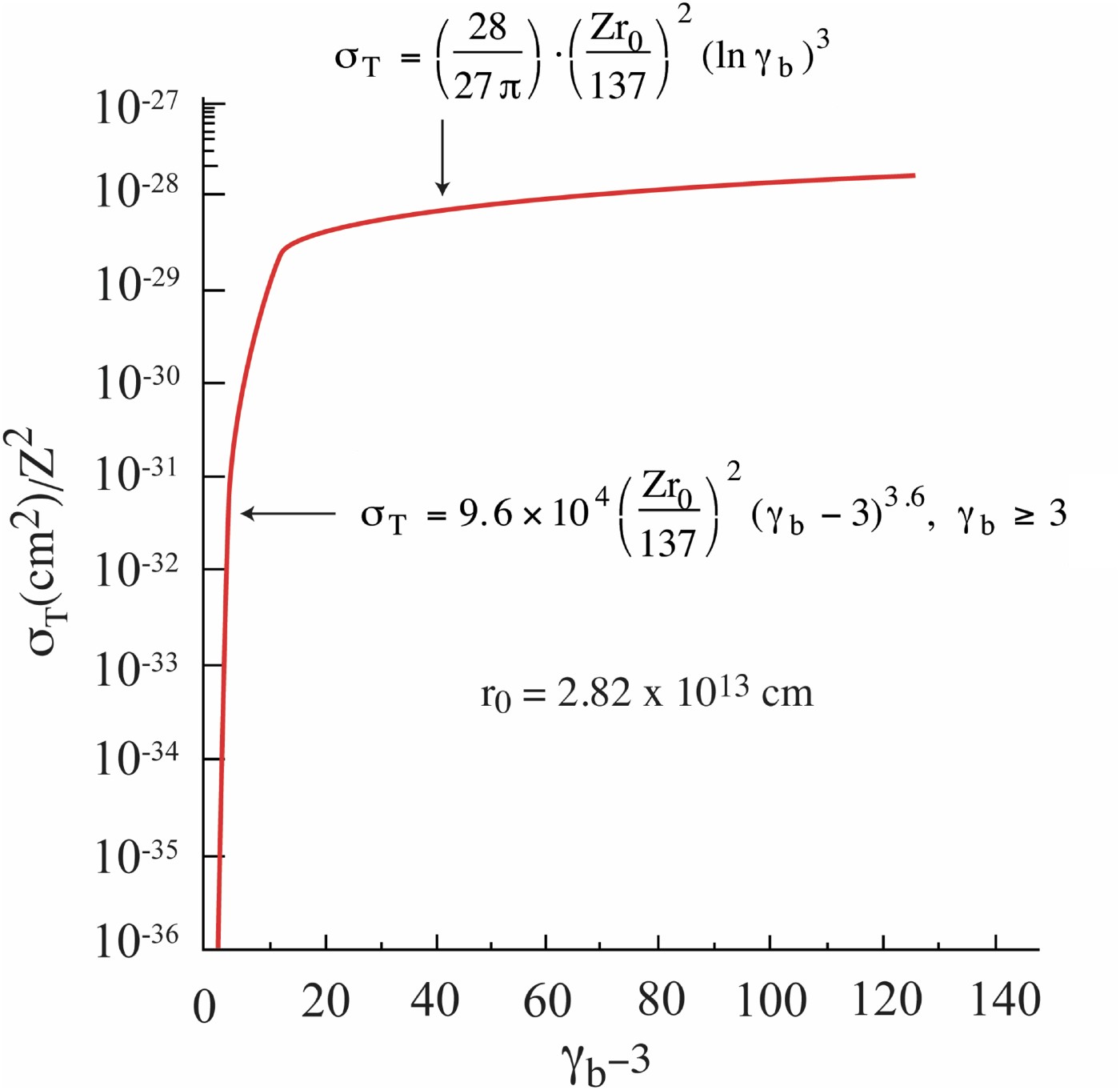
Fig. 4. (Color online) Total cross section σT of the Trident process plotted versus the dimensionless electron-energy excess above the threshold. Here γb = E b/m ec 2. Z denotes target ion nuclear charge.
6. NEGATIVE PION ELECTRO-PRODUCTION
Turning attention to the many channels available to nuclei electro-disintegration, we first focus on the basic Möller diagram (Fig. 5a) pictured à la Feynman with the exchange of one single virtual photon. Its robustness up to E b = 1 GeV is highlighted by the very low level of requested radiative corrections, and the negligibility of multiple and virtual proton exchange. A preliminary disintegration stage involves proton out of deuterium, and deuterium out of tritium. However, as soon as E b ≥ 145 MeV, the channels of negative pion production open up (Figs. 5b, 5c). Pertaining totally differential cross sections then range at a rather low n b (10−33cm2) level.

Fig. 5. (Color online) (a) Electron-electron covariant Möller diagram. (b) D-Electro-disintegration and (c) T- Electrodisintegration. In (b) and (c) π− appears when E b ≥ 150 MeV. Robin Hood pictures a PW-laser (after N. Deutsch)
However, when suitably averaged over the many angular degrees of freedom and at higher energy, the total cross-section may well be lifted up at mb level. Nuclei disintegration offer a first opportunity to correlated proton stopping (Figs. 5b, 5c), which can be pictured as a charge Z = 2, yielding a factor of 4 increase over single proton stopping (Deutsch & Tahir, Reference Deutsch and Tahir1992). Moreover, the π behavior in the given hot and ultradense target may prove highly productive to the hot spot ignition. First, it releases energy through its stopping mechanism. However the most intriguing contribution seems to arise from the various π-catalytic cycles available to DD, TT, and DT nuclear reactions. Its 28 ns lifetime is likely to secure its integrity during the whole compression time available to target.
7. PION CATALYSIS
A typical catalytic cycle is pictured in Figure 6; it straight-forwardly highlights the three main advantages of π-catalyzed thermonuclear fusion in a FIS target: (1) The negative pion is already available at E b ≥ 150 MeV, while it requires 5–8 GeV in conventional and cold μCF operating in liquid hydrogen at room temperature and n LHD = 4.25 × 1022/cm3 (Nagamine, Reference Nagamine2001). (2) The catalytic cycle is trailed a thousand time faster because of the vastly enhanced FIS target density n p = 1026cm−3 (Breunlich et al., Reference Breunlich, Kammel, Cohen and Leon1989; Jandel et al., Reference Jandel, Froelich, Larson and Stodden1989; Harley, Reference Harley1992; Pahlavani & Motevalli, Reference Pahlavani and Motevalli2009). (3) The density and temperature in highly collisional plasma (T p ≥ 1 keV) also secure a catalytic cycle free of the final sticking process of the pion on the resulting alpha particle or other light ions.

Fig. 6. Pion catalyzed D-T fusion cycle with indications of mains processes (after K. Nagamine, Hyp. Int. 138, 5–13 (2001)).
Moreover, the given super compressed DT-target offers many opportunities of stable 3-4- or 5-body molecular arrangements able to contribute to the catalytic cycle (Rebane, Reference Rebane2009). 4-body systems such as the m 1+m 2+m 3−m 4− neutral ones formed by four particles of unit charge, q 1 = q 2 = 1, and q 3 = q 4 = −1 with masses m 1, m 2, m 3, and m 4 and m 1+m 2+m 3− three-particle ions.
Assuming the mass ordering m 1 ≥ m 2, m 3 ≥ m 4, m 2 ≥ m 4, the lowest dissociation threshold for the four-particle system, E th, in the system of Hartree a.u.(![]() ) is
) is
while the lowest dissociation (ionization) threshold for the three-particle system is
It then follows (Rebane, Reference Rebane2009) that combinations m 1+m 2+m 3−m 4−, fulfilling
are obviously stable. This criterion makes it possible to establish stability against dissociation of tens of 4 particles meso molecules, combinations of electrons (e), protons (p), pions (π) deuterons (d), tritons (t), muons (µ) … If the mass of the lightest particle in the system is much smaller than the masses of the other particles, s is outside the interval in Eq. (13). So, the criterion turns inapplicable. See for example, the t +d +p −e − system (s = 0.0007). More generally, from the stability of the m 1+m 2+m 3− three-particle system, it follows that the m 1+m 2+m 3−m 4− four-particle system containing an additional particle of mass satisfying the condition m 4− ≤ m 3− is stable.
In this regard, it is also rather encouraging that the given transitory molecular arrangements can be treated within a Debye approximation. For instance, in an igniting plasma (n p ~ 1026/cc, T p ~ 3-5 keV) one can witness a persistence of (MuDT)+ molecular ions (Kar & Ho, Reference Kar and Ho2008) with a binding energy ~ 400 eV in a state (γ = 0, J = 0) relative to dπ and tπ atomic structures. Such bound states are equivalent to excited hydrogenic atoms with n = 12, and exhibiting anisotropy due to a nearly D+ or T+ ion. So, the probability of hadronic π-capture remains very small, in accordance with the strong inequality (a, scattering length)
thus securing an essentially electromagnetic cycling rate (Fig. 6).
Another intriguing effect able to lower by orders of magnitude the tunneling barrier between fusioning nuclei may arise from the frustration experienced by the pion when simultaneously attracted by so density packed D+ and T+ nuclei (Kimura & Bonasera, Reference Kimura and Bonasera2004).
8. PROVISIONAL CONCLUSIONS
Potential benefits of ICF fast ignition with ultra relativistic electron beams (γb ≫ 1), obviously include: (1) Less initial intensity requested. (2) Easier “piercing” through electromagnetic instabilities. (3) Novel stopping mechanism available. (4) Strong Langmuir and EMHD stopping efficient at γb ≫ 1. (5) Huge number of possible collisional stopping channels available. Final state interactions seem to offer new prospects to pion-catalyzed fusion with very low production cost, negligible sticking in the very dense and hot FIS plasma, and much faster cycling rate, when contrasted to the usual LHD cold approach. It remains to evaluate potentialities of laser produced proton beams in the 20–40 MeV energy range. Pertaining inelastic hadronic reactions feature differential cross-sections in the mb range. So, their investigation in a FIS framework looks highly promising, too.