1. INTRODUCTION
Ship surveillance is an important area of maritime management, especially for illegal activity detection in the Exclusive Economic Zone (EEZ), such as illegal fishing and smuggling. Many countries have established maritime surveillance systems using various marine sensors (Zhao et al., Reference Zhao, Ji, Xing, Zou and Zhou2014a).
Synthetic Aperture Radar (SAR), High Frequency Surface Wave Radar (HFSWR) and the Automatic Identification System (AIS) are three main sensors for surveillance of large maritime areas. Both space-borne and air-borne SAR detect ships by comparing the return signal from the ship and the ocean (Pichel et al., Reference Pichel, Clemente-Colon, Wackerman and Friedman2004). Space-borne SAR has wide coverage and high resolution, and does not have weather restrictions. However, it can only detect ships during satellite transit periods (Ji et al., Reference Ji, Zhang, Meng and Wang2014). Air-borne SAR is usually applied for ship identification or verification during a low-attitude pass (Fingas and Brown, Reference Fingas and Brown2001). Due to different Doppler shifts, HFSWR can detect and track ships by discriminating the echoes from ships and the ocean (Ponsford and Wang, Reference Ponsford and Wang2010). HFSWR has the advantages of continuous surveillance, long range and direct velocity estimation (Grosdidier et al., Reference Grosdidier, Baussard and Khenchaf2010; Maresca et al., Reference Maresca, Braca, Horstmann and Grasso2014). However, it has a low space resolution (Gurgel et al., Reference Gurgel, Schlick, Horstmann and Maresca2010). AIS transmits ship information, i.e., position, ship length, ship width, velocity and heading, for ship collision avoidance, but not all ships carry AIS equipment. The ships with installed AIS equipment are usually defined as cooperative ships, while the others are non-cooperative ships (Ji et al., Reference Ji, Zhang, Meng and Wang2014). To sum up, these sensors have their merits and shortcomings in ship surveillance. We cannot obtain an accurate ship traffic image via one sensor alone. Multi-sensor fusion can combine data from different sensors and gain more accurate and specific information than one single sensor (Hall and Llinas, Reference Hall and Llinas1997).
Many methods have been exploited in the fusion of space-borne SAR, HFSWR and AIS. The main research is concentrated on the fusion of space-borne SAR and AIS and the fusion of HFSWR and AIS. Within the framework of space-borne SAR and AIS fusion, AIS is usually applied to verify the SAR measurement. Brusch et al. (Reference Brusch, Lehner, Fritz, Soccorsi, Soloviev and Van Schie2011) introduced a ship surveillance algorithm using the TerraSAR-X SAR image, and compared their results with satellite AIS for validation. Zhao et al. (Reference Zhao, Ji, Xing, Zou and Zhou2014a; Reference Zhao, Ji, Xing, Zou and Zhou2014b) pointed out the lack of systematic theories in SAR and AIS fusion and further proposed an improved association method based on multiple features. This method can be used to identify and track ships. A ship recognition system, including four steps: time matching, position matching, size matching and speed matching, is established using the SAR and AIS data, and this system can identify the ship in nearly real time (Chaturvedi et al., Reference Chaturvedi, Yang, Ouchi and Shanmugam2012). As for HFSWR and AIS fusion, Dzvonkovskaya et al. (Reference Dzvonkovskaya, Gurgel, Rohling and Schlick2008) and Dzvonkovskaya and Rohling (Reference Dzvonkovskaya and Rohling2010) adopted a statistical method to analyse the HFSWR detection capacity for various ship types. In their work, the data from HFSWR and AIS was correlated. Recently, we (Zhang et al., Reference Zhang, Liu, Zhang, Ji and Zheng2015) presented a Point Tracks Optimal Algorithm to correlate the data of HFSWR and AIS. The state-of-the-art algorithms for the fusion of radar and AIS data are the measurement-level fusion (Habtemariam et al., Reference Habtemariam, Tharmarasa, Mcdonald and Kirubarajan2015) and knowledge-based track fusion (Vivone et al., Reference Vivone, Braca and Horstmann2015). On the aspect of the fusion of three sensors, Gurgel et al. (Reference Gurgel, Schlick, Horstmann and Maresca2010) first used AIS and SAR data to verify HF-radar data. Ji et al. (Reference Ji, Zhang, Meng and Wang2014) proposed a point association analysis of SAR, HFSWR and AIS to recognise non-cooperative ships under different conditions.
Data association is fundamental to data fusion. The aim of this work is to associate ship measurements from space-borne SAR, HFSWR and AIS, and identify the cooperative ships and suspect non-cooperative ships. Furthermore, the start point of non-cooperative ship tracking can be found from the associated results.
It is known that the simultaneous measurements of space-borne SAR, HFSWR and AIS can only be obtained during the satellite transit period. Space-borne SAR measurements are extracted from SAR images. The measurements mainly contain the position, length, width and heading of ships. HFSWR provides measurements about the ship position (range, and azimuth) and radial velocity. AIS provides the ship position, ship features (including the length, width and ship type), velocity (Speed Over Ground – SOG, Course Over Ground - COG) and heading. It is noted that ship position is the common measurement of three sensors, while ship length, width and heading are the common measurements between space-borne SAR and AIS. Moreover, ship velocity is the common measurement between the HFSWR and AIS.
According to the features of the three sensors, we constructed ship measurement models, and formulated the association of space-borne SAR, HFSWR and AIS as a multi-dimensional assignment problem. In this association problem, the Maximum Likelihood (ML) of the measurements were defined as an association cost. The traditional position-only ML was extended to multi-feature ML, which could improve association accuracy rate.
Based on the models, pair gating technology and an iterative search algorithm were applied to partition the measurements into three types. Different association strategies have been used for different types. The Jonker-Volgenant-Castanon (JVC) algorithm was employed to solve the two-dimensional (2-D) assignment problem (Malkoff, Reference Malkoff1997; Jonker and Volgenant, Reference Jonker and Volgenant1987), and Lagrangian relaxation algorithm was used to work out the 3-D association problem. The three-dimensional (3-D) assignment problem belongs to the Non-deterministic Polynomial-time hard (NP hard) problem generally solved by heuristic and relaxation algorithms. The Lagrangian relaxation approach was proved suitable in solving the NP hard problem in performance and real-time application (Deb et al., Reference Deb, Yeddanapudi, Pattipati and Bar-Shalom1997).
The organisation of this paper is as follows. Section 2 introduces the ship measurement models. The association problem is formulated as an assignment problem in Section 3. The data association procedure is presented in Section 4. Section 5 gives both the experiment results of the simulation data and the real detected data. Conclusions are given in Section 6.
2. SHIP MEASUREMENT MODEL
SAR position and AIS position are measured in the World Geodetic System 84 (WGS84), while HFSWR position is measured in the radar polar coordinates system. For convenience, the measurement model is constructed in Cartesian coordinates.
2.1. Ship Measurement Model
The ship state vector at time k is defined as
where
![]() $x(k)$
,
$x(k)$
,
![]() $y(k)$
and
$y(k)$
and
![]() $\dot x(k)$
,
$\dot x(k)$
,
![]() $\dot y(k)$
are the position and velocity components in x, y directions.
$\dot y(k)$
are the position and velocity components in x, y directions.
![]() $\left( \cdot \right)^{T} $
is the transpose function (Maresca et al., Reference Maresca, Braca, Horstmann and Grasso2014). The ship measurement model is defined as
$\left( \cdot \right)^{T} $
is the transpose function (Maresca et al., Reference Maresca, Braca, Horstmann and Grasso2014). The ship measurement model is defined as
where
![]() ${\bi z}\left( k \right)$
is the measurement vector,
${\bi z}\left( k \right)$
is the measurement vector,
![]() $h\left( {{\bi X}\left( k \right)} \right)$
is the measurement function and w(k) is the measurement noise (Habtemariam et al., Reference Habtemariam, Tharmarasa, Mcdonald and Kirubarajan2015; Li and Jilkov, Reference Li and Jilkov2003).
$h\left( {{\bi X}\left( k \right)} \right)$
is the measurement function and w(k) is the measurement noise (Habtemariam et al., Reference Habtemariam, Tharmarasa, Mcdonald and Kirubarajan2015; Li and Jilkov, Reference Li and Jilkov2003).
2.2. SAR Measurement Model
Space-borne SAR only provides measurements at the satellite transit time T tran . Therefore, the measurement model of SAR is defined as
where
![]() $h_s \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {x\left( k \right)} & {y\left( k \right)} & {l\left( k \right)} & {w\left( k \right)} & {h\left( k \right)} \cr}} \right]^T $
is the measurement function of SAR.
$h_s \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {x\left( k \right)} & {y\left( k \right)} & {l\left( k \right)} & {w\left( k \right)} & {h\left( k \right)} \cr}} \right]^T $
is the measurement function of SAR.
![]() $l\left( k \right)$
is ship length,
$l\left( k \right)$
is ship length,
![]() $w\left( k \right)$
is ship width, and
$w\left( k \right)$
is ship width, and
![]() $h\left( k \right)$
is ship heading. w
s
(k) is the SAR measurement noise. The measurement noise is assumed to be zero-mean white Gaussian, and the covariance
R
s
is defined as
$h\left( k \right)$
is ship heading. w
s
(k) is the SAR measurement noise. The measurement noise is assumed to be zero-mean white Gaussian, and the covariance
R
s
is defined as
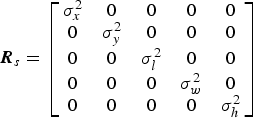 $${\bi R}_s = \left[ {\matrix{ {\sigma _x^2} & 0 & 0 & 0 & 0 \cr 0 & {\sigma _y^2} & 0 & 0 & 0 \cr 0 & 0 & {\sigma _l^2} & 0 & 0 \cr 0 & 0 & 0 & {\sigma _w^2} & 0 \cr 0 & 0 & 0 & 0 & {\sigma _h^2} \cr}} \right]$$
$${\bi R}_s = \left[ {\matrix{ {\sigma _x^2} & 0 & 0 & 0 & 0 \cr 0 & {\sigma _y^2} & 0 & 0 & 0 \cr 0 & 0 & {\sigma _l^2} & 0 & 0 \cr 0 & 0 & 0 & {\sigma _w^2} & 0 \cr 0 & 0 & 0 & 0 & {\sigma _h^2} \cr}} \right]$$
where σ is the standard deviation.
2.3. HFSWR Measurement Model
HFSWR detects the ship target in continuous-time and the HFSWR measurement model is given by
where
![]() $h_h \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {r\left( k \right)} & {\theta \left( k \right)} & {v_r \left( k \right)} \cr}} \right]^T $
is the measurement function of HFSWR. r(k) is the range,
$h_h \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {r\left( k \right)} & {\theta \left( k \right)} & {v_r \left( k \right)} \cr}} \right]^T $
is the measurement function of HFSWR. r(k) is the range,
![]() $\theta (k)$
is the azimuth, and
$\theta (k)$
is the azimuth, and
![]() ${\rm v}_r \left( k \right)$
is the radial velocity. The measurement equations are listed as follows.
${\rm v}_r \left( k \right)$
is the radial velocity. The measurement equations are listed as follows.
 $$v_r\left( k \right) = \displaystyle{{\left( {x\left( k \right) - x_s} \right)\dot x\left( k \right) + \left( {y\left( k \right) - y_s} \right)\dot y\left( k \right)} \over {\sqrt {{\left( {x\left( k \right) - x_s} \right)}^2 + {\left( {y\left( k \right) - y_s} \right)}^2} }}$$
$$v_r\left( k \right) = \displaystyle{{\left( {x\left( k \right) - x_s} \right)\dot x\left( k \right) + \left( {y\left( k \right) - y_s} \right)\dot y\left( k \right)} \over {\sqrt {{\left( {x\left( k \right) - x_s} \right)}^2 + {\left( {y\left( k \right) - y_s} \right)}^2} }}$$
where x s and y s describe the position of the radar stations. w h (k) is the HFSWR measurement noise, which is assumed to be zero-mean white Gaussian. The covariance R h is defined as
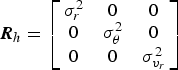 $${\bi R}_h = \left[ {\matrix{ {\sigma _r^2} & 0 & 0 \cr 0 & {\sigma _\theta ^2} & 0 \cr 0 & 0 & {\sigma _{{v}_r} ^2} \cr}} \right]$$
$${\bi R}_h = \left[ {\matrix{ {\sigma _r^2} & 0 & 0 \cr 0 & {\sigma _\theta ^2} & 0 \cr 0 & 0 & {\sigma _{{v}_r} ^2} \cr}} \right]$$
2.4. AIS Measurement Model
The time interval for AIS measurements reporting depends on the types of AIS equipment and ship's dynamic state (Xiao et al., Reference Xiao, Ligteringen, Van Gulijk and Ale2015; Habtemariam et al., Reference Habtemariam, Tharmarasa, Mcdonald and Kirubarajan2015). So the AIS measurement model is defined as
where
![]() $h_a \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {x\left( k \right)} & {y\left( k \right)} & {v_{sog} \left( k \right)} & {\theta _{cog} \left( k \right)} \cr}} \right]^T $
is the measurement function of AIS and
$h_a \left( {{\bi X}\left( k \right)} \right) = \left[ {\matrix{ {x\left( k \right)} & {y\left( k \right)} & {v_{sog} \left( k \right)} & {\theta _{cog} \left( k \right)} \cr}} \right]^T $
is the measurement function of AIS and
![]() $DR\left( {{\bi X}\left( k \right)} \right)$
is a Dead Reckoning (DR) function.
$DR\left( {{\bi X}\left( k \right)} \right)$
is a Dead Reckoning (DR) function.
![]() $v_{sog} \left( k \right)$
is the speed over ground, and
$v_{sog} \left( k \right)$
is the speed over ground, and
![]() $\theta _{cog} \left( k \right)$
is course over ground. If the sampling time k equals the mth AIS report time
$\theta _{cog} \left( k \right)$
is course over ground. If the sampling time k equals the mth AIS report time
![]() $t_{report}^{m} $
, the AIS measurements are directly provided by the AIS reports. If not, the DR method is employed to predict the AIS position and velocity by the AIS reports (Chaturvedi et al., Reference Chaturvedi, Yang, Ouchi and Shanmugam2012). Herein, it is assumed that there are no false alarms and missed detections of the AIS measurements and the measurement noise w
a
(k) is zero.
$t_{report}^{m} $
, the AIS measurements are directly provided by the AIS reports. If not, the DR method is employed to predict the AIS position and velocity by the AIS reports (Chaturvedi et al., Reference Chaturvedi, Yang, Ouchi and Shanmugam2012). Herein, it is assumed that there are no false alarms and missed detections of the AIS measurements and the measurement noise w
a
(k) is zero.
3. PROBLEM FORMULATION
Based on the measurement models established in Section 2, we formulated the association problem as an N-Dimensional (N-D) assignment problem. We extended the previous work of Pattipati et al. (Reference Pattipati, Deb, Bar-Shalom and Washburn1992) and Deb et al. (Reference Deb, Yeddanapudi, Pattipati and Bar-Shalom1997) to the maritime surveillance scenario.
The association is under the assumptions:
-
• The SAR and HFSWR measurements may contain missed detections and false alarms, while the AIS measurements have no missed detections and false alarms.
-
• The cooperative ships should provide ship information to AIS.
-
• The non-cooperative ships should be detected by both SAR and HFSWR, but do not provide information to AIS.
-
• Ships which did not provide the information to AIS and are detected by only one of either SAR and HFSWR sensors, cannot be recognised as non-cooperative ships.
Considering the missed detections in association, we define a dummy measurement in each sensor.
![]() ${\bi z}_{s0} \left( {\rm k} \right)$
and
${\bi z}_{s0} \left( {\rm k} \right)$
and
![]() ${\bi z}_{h0} \left( {\rm k} \right)$
represents the missed detection caused by SAR and HFSWR, while
${\bi z}_{h0} \left( {\rm k} \right)$
represents the missed detection caused by SAR and HFSWR, while
![]() ${\bi z}_{a0} \left( {\rm k} \right)$
represents the missed detection caused by non-cooperative ships in AIS.
${\bi z}_{a0} \left( {\rm k} \right)$
represents the missed detection caused by non-cooperative ships in AIS.
A complete set
![]() ${\bi Z}\left( {\rm k} \right)$
, i.e., the union of all three measurements at time k, is defined as
${\bi Z}\left( {\rm k} \right)$
, i.e., the union of all three measurements at time k, is defined as
n s , nh , and n a are the numbers of SAR, HFSWR and AIS measurements, respectively. i s , ih and i a are the detection indices of each measurement. Since time k is a constant value in the association of space-borne SAR, HFSWR and AIS, k is omitted below.
The union set of all feasible partitions is defined as ζ = {γ
0, γ
1, γ
2, · · · , γ
α
}.
![]() $\gamma _{\rm i} \left( {i \ne 0} \right)$
is one of the feasible partitions and
$\gamma _{\rm i} \left( {i \ne 0} \right)$
is one of the feasible partitions and
![]() $\gamma _0 = \left\{ {{\bi Z} = \phi} \right\}$
represents where the measurements of SAR and HFSWR are all false alarms.
$\gamma _0 = \left\{ {{\bi Z} = \phi} \right\}$
represents where the measurements of SAR and HFSWR are all false alarms.
Based on the definitions above, the association problem can be described as a problem of solving the maximum probability defined as
where
![]() ${p}\left( \cdot \right)$
is the probability of partitions γ and
${p}\left( \cdot \right)$
is the probability of partitions γ and
![]() $ \Gamma $
is the event. Our goal is to choose the partition γ to find the most probable event. Here, the ML ratio
$ \Gamma $
is the event. Our goal is to choose the partition γ to find the most probable event. Here, the ML ratio
![]() $\mathop {\max} \limits_{\gamma \in \zeta} \displaystyle{{L(\gamma )} \over {L(\gamma _0 )}}$
is used to replace p in Equation (10).
$\mathop {\max} \limits_{\gamma \in \zeta} \displaystyle{{L(\gamma )} \over {L(\gamma _0 )}}$
is used to replace p in Equation (10).
![]() $L(\gamma )$
is the ML of partition γ. The traditional ML only about the target position is defined as
$L(\gamma )$
is the ML of partition γ. The traditional ML only about the target position is defined as
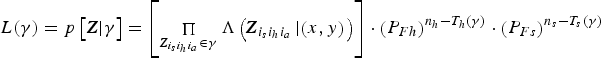 $$L(\gamma ) = p\left[ {{\bi Z} \vert \gamma} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {\left( {x,y} \right)} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
$$L(\gamma ) = p\left[ {{\bi Z} \vert \gamma} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {\left( {x,y} \right)} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
where
![]() $\Lambda \left( {{\bi Z}_{i_s i_h i_a} \left\vert {\left( {x,y} \right)} \right.} \right)$
is the likelihood that the measurements
$\Lambda \left( {{\bi Z}_{i_s i_h i_a} \left\vert {\left( {x,y} \right)} \right.} \right)$
is the likelihood that the measurements
![]() ${\bi Z}_{i_s i_h i_a} $
originate from the target in (x, y) position. P
Fs
and P
Fh
are the false alarm probabilities of SAR and HFSWR, respectively.
${\bi Z}_{i_s i_h i_a} $
originate from the target in (x, y) position. P
Fs
and P
Fh
are the false alarm probabilities of SAR and HFSWR, respectively.
![]() $T_{\rm s} (\gamma )$
and
$T_{\rm s} (\gamma )$
and
![]() $T_{h} (\gamma )$
are the numbers of targets in SAR and HFSWR measurements, respectively. Because of the poor position resolution of HFSWR measurements, the association based only on the position may lead to the wrong association. Alternatively, multi-feature ML is used to improve the association accuracy rate. This is defined as
$T_{h} (\gamma )$
are the numbers of targets in SAR and HFSWR measurements, respectively. Because of the poor position resolution of HFSWR measurements, the association based only on the position may lead to the wrong association. Alternatively, multi-feature ML is used to improve the association accuracy rate. This is defined as
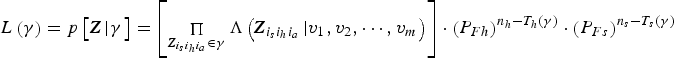 $$L\left( \gamma \right) = p\left[ {{\bi Z}\left \vert \gamma \right.} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {v_1, v_2, \cdots, v_m} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
$$L\left( \gamma \right) = p\left[ {{\bi Z}\left \vert \gamma \right.} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {v_1, v_2, \cdots, v_m} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
where v
1, v
2, · · · v
m
are the different features of target.
![]() $\Lambda \left( {{\bi Z}_{i_s i_h i_a} \left\vert {v_1, v_2, \cdots, v_m} \right.} \right)$
represents the probability of measurement
$\Lambda \left( {{\bi Z}_{i_s i_h i_a} \left\vert {v_1, v_2, \cdots, v_m} \right.} \right)$
represents the probability of measurement
![]() ${\bi Z}_{i_s i_h i_a} $
which originates from the target with the feature vector v
1, v
2, · · · v
m
.
${\bi Z}_{i_s i_h i_a} $
which originates from the target with the feature vector v
1, v
2, · · · v
m
.
Since the features vector of a target is unknown in the association, the v 1, v 2, · · · v m is replaced by the estimate value given by
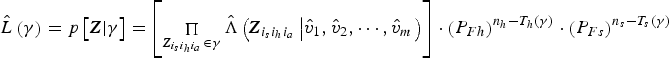 $$\hat L\left( \gamma \right) = {p}\left[ {{\bi Z} \vert \gamma} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \hat \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {\hat v_1, \hat v_2, \cdots, \hat v_m} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
$$\hat L\left( \gamma \right) = {p}\left[ {{\bi Z} \vert \gamma} \right] = \left[ {\mathop \Pi \limits_{{\bi Z}_{i_s i_h i_a} \in \gamma} \hat \Lambda \left( {{\bi Z}_{i_s i_h i_a} \left \vert {\hat v_1, \hat v_2, \cdots, \hat v_m} \right.} \right)} \right] \cdot \left( {P_{Fh}} \right)^{n_h - T_h \left( \gamma \right)} \cdot \left( {P_{Fs}} \right)^{n_s - T_s \left( \gamma \right)} $$
where
![]() $\hat L\left( \gamma \right)$
is the estimated value of
$\hat L\left( \gamma \right)$
is the estimated value of
![]() $L\left( \gamma \right)$
. For cooperative ships, AIS information is treated as the estimated value. For non-cooperative ships, SAR position information is treated as the estimated value. The range and azimuth of AIS measurements are converted from the position (x, y) by Equation (6). The radial velocity is converted from course over ground θ
cog
and speed over ground v
sog
by
$L\left( \gamma \right)$
. For cooperative ships, AIS information is treated as the estimated value. For non-cooperative ships, SAR position information is treated as the estimated value. The range and azimuth of AIS measurements are converted from the position (x, y) by Equation (6). The radial velocity is converted from course over ground θ
cog
and speed over ground v
sog
by
v r is a positive number when the ship sails towards the radar station, and v r is a negative number when the ship sails away from the station.
According to the features of the three sensors, different features are used in the association of different sensor pairs. The ship position, length, width and heading can be selected as the feature vector for SAR and AIS ML. The ship position and radial velocity can be selected as the feature vector for HFSWR and AIS. Only the position feature can be selected for SAR and HFSWR. Table 1 shows the details. For the association with HFSWR, position of (range, azimuth) is more suitable than position of (x, y) because the HFSWR measurement error of position (x, y) increases with an increase in range.
Table 1. The features used in the association of different sensor pair.

Here, we assumed that all the feature measurements are normally distributed with the standard deviation σ, and are independent. Therefore,
![]() $\hat L(\gamma )$
is given by
$\hat L(\gamma )$
is given by
 $$\eqalign{& \hat L\left( \gamma \right) = \left[ {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2} \right) \cdot N\left( {\hat y,\sigma _y^2} \right) \cdot N\left( {\hat l,\sigma _l^2} \right) \cdot N\left( {\hat w,\sigma _w^2} \right) \cdot N\left( {\hat h,\sigma _h^2} \right)} \right]^{1 - \delta _{0i_s}} \cdot \left[ {1 - P_{Ds}} \right]^{\delta _{0i_s}} \cr & \cdot \left( {P_{Fs}} \right)^{n_s - T_s (\gamma )} \cdot \left[ {P_{Dh} \cdot N\left( {{\hat r},\sigma _r^2} \right) \cdot N\left( {\hat \theta, \sigma _\theta ^2} \right) \cdot N\left( {\hat v_r, \sigma _{v_{r}} ^2} \right)} \right]^{1 - \delta _{0i_h}} \cdot \left[ {1 - P_{Dh}} \right]^{\delta _{0i_h}} \cdot \left( {P_{Fh}} \right)^{n_h - T_h (\gamma )}} $$
$$\eqalign{& \hat L\left( \gamma \right) = \left[ {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2} \right) \cdot N\left( {\hat y,\sigma _y^2} \right) \cdot N\left( {\hat l,\sigma _l^2} \right) \cdot N\left( {\hat w,\sigma _w^2} \right) \cdot N\left( {\hat h,\sigma _h^2} \right)} \right]^{1 - \delta _{0i_s}} \cdot \left[ {1 - P_{Ds}} \right]^{\delta _{0i_s}} \cr & \cdot \left( {P_{Fs}} \right)^{n_s - T_s (\gamma )} \cdot \left[ {P_{Dh} \cdot N\left( {{\hat r},\sigma _r^2} \right) \cdot N\left( {\hat \theta, \sigma _\theta ^2} \right) \cdot N\left( {\hat v_r, \sigma _{v_{r}} ^2} \right)} \right]^{1 - \delta _{0i_h}} \cdot \left[ {1 - P_{Dh}} \right]^{\delta _{0i_h}} \cdot \left( {P_{Fh}} \right)^{n_h - T_h (\gamma )}} $$
where P
Ds
and P
Dh
are the detection probabilities of SAR and HFSWR, respectively.
![]() $N\left( {\mu, \sigma _{}^2} \right)$
is given by
$N\left( {\mu, \sigma _{}^2} \right)$
is given by
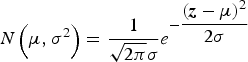 $$N\left( {\mu, \sigma _{}^2} \right) = \displaystyle{1 \over {\sqrt {2\pi} \sigma _{}}} e^{ - \displaystyle{{({\bi z} - \mu )^2} \over {2\sigma}}} $$
$$N\left( {\mu, \sigma _{}^2} \right) = \displaystyle{1 \over {\sqrt {2\pi} \sigma _{}}} e^{ - \displaystyle{{({\bi z} - \mu )^2} \over {2\sigma}}} $$
if taking into account the missed detections in the association, the indicator δ 0i is given as
![]() $L\left( {\gamma _0} \right)$
is given by
$L\left( {\gamma _0} \right)$
is given by
let
![]() $\mathop {\min} \limits_{\gamma \in \zeta} \displaystyle{{L\left( {\gamma _0} \right)} \over {\hat L\left( \gamma \right)}}$
replace
$\mathop {\min} \limits_{\gamma \in \zeta} \displaystyle{{L\left( {\gamma _0} \right)} \over {\hat L\left( \gamma \right)}}$
replace
![]() $\mathop {\max} \limits_{\gamma \in \zeta} \displaystyle{{\hat L\left( \gamma \right)} \over {L\left( {\gamma _0} \right)}}$
, the maximum problem becomes a minimum one
$\mathop {\max} \limits_{\gamma \in \zeta} \displaystyle{{\hat L\left( \gamma \right)} \over {L\left( {\gamma _0} \right)}}$
, the maximum problem becomes a minimum one
then, the association problem can be formulated as a multi-assignment one
 $$J(\rho ) = \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_h = 0}^{n_h} {\sum\limits_{i_a = 0}^{n_a} {c_{i_s i_h i_a} \rho _{i_s i_h i_a}}}} $$
$$J(\rho ) = \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_h = 0}^{n_h} {\sum\limits_{i_a = 0}^{n_a} {c_{i_s i_h i_a} \rho _{i_s i_h i_a}}}} $$
subject to
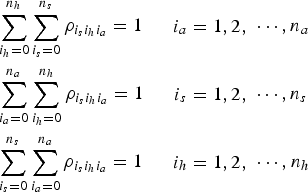 $$\eqalign{& \sum\limits_{i_h = 0}^{n_h} {\sum\limits_{i_s = 0}^{n_s} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_a = 1,2,} \cr}} \cr} \cdots, n_a \cr & \sum\limits_{i_a = 0}^{n_a} {\sum\limits_{i_h = 0}^{n_h} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_s = 1,2,} \cr}} \cr} \cdots, n_s \cr & \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_a = 0}^{n_a} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_h = 1,2,} \cr}} \cr} \cdots, n_h} $$
$$\eqalign{& \sum\limits_{i_h = 0}^{n_h} {\sum\limits_{i_s = 0}^{n_s} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_a = 1,2,} \cr}} \cr} \cdots, n_a \cr & \sum\limits_{i_a = 0}^{n_a} {\sum\limits_{i_h = 0}^{n_h} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_s = 1,2,} \cr}} \cr} \cdots, n_s \cr & \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_a = 0}^{n_a} {\rho _{i_s i_h i_a}}} = 1\matrix{ {} & {\matrix{ {} \cr} \matrix{ {i_h = 1,2,} \cr}} \cr} \cdots, n_h} $$
in which the defined two-valued variables
![]() $\rho _{{i_s} {i_h} {i_a}} $
are given by
$\rho _{{i_s} {i_h} {i_a}} $
are given by
and the association cost
![]() $c_{{i_s} {i_h} {i_a}} $
is defined by
$c_{{i_s} {i_h} {i_a}} $
is defined by
 $$\eqalign{c_{{i_s} {i_h} {i_a}} & = \ln L\left( {\gamma {}_0} \right) - \ln \hat L\left( \gamma \right) \cr & = \left( {1 - \delta _{0i_s}} \right)\left( {\ln \left( {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2 } \right) \cdot N\left( {\hat y,\sigma _y^2 } \right) \cdot N\left( {\hat l,\sigma _l^2 } \right) \cdot N\left( {\hat w,\sigma _w^2 } \right) \cdot N\left( {\hat h,\sigma _h^2 } \right)} \right)} \right) \cr & \quad- \delta _{0i_s}\ln \left( {1 - P_{Ds}} \right) \cr & \quad+ \left( {1 - \delta _{0i_h}} \right)\left( {\ln \left( {P_{Dh} \cdot N\left( {\hat r,\sigma _r^2 } \right) \cdot N\left( {\hat \theta ,\sigma _\theta ^2 } \right) \cdot N\left( {\hat v,\sigma _v^2 } \right)} \right)} \right) - \delta _{0i_h}\ln \left( {1 - P_{Dh}} \right) \cr & \quad+ T_h\left( \gamma \right)\left( {\ln P_{Fh}} \right) + T_s(\gamma )\left( {\ln P_{Fs}} \right)} $$
$$\eqalign{c_{{i_s} {i_h} {i_a}} & = \ln L\left( {\gamma {}_0} \right) - \ln \hat L\left( \gamma \right) \cr & = \left( {1 - \delta _{0i_s}} \right)\left( {\ln \left( {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2 } \right) \cdot N\left( {\hat y,\sigma _y^2 } \right) \cdot N\left( {\hat l,\sigma _l^2 } \right) \cdot N\left( {\hat w,\sigma _w^2 } \right) \cdot N\left( {\hat h,\sigma _h^2 } \right)} \right)} \right) \cr & \quad- \delta _{0i_s}\ln \left( {1 - P_{Ds}} \right) \cr & \quad+ \left( {1 - \delta _{0i_h}} \right)\left( {\ln \left( {P_{Dh} \cdot N\left( {\hat r,\sigma _r^2 } \right) \cdot N\left( {\hat \theta ,\sigma _\theta ^2 } \right) \cdot N\left( {\hat v,\sigma _v^2 } \right)} \right)} \right) - \delta _{0i_h}\ln \left( {1 - P_{Dh}} \right) \cr & \quad+ T_h\left( \gamma \right)\left( {\ln P_{Fh}} \right) + T_s(\gamma )\left( {\ln P_{Fs}} \right)} $$
since the number and probability of false alarms are constant,
![]() $c_{{i_s} {i_h} {i_a}} $
is not affected by the two latter terms. It can be simplified as
$c_{{i_s} {i_h} {i_a}} $
is not affected by the two latter terms. It can be simplified as
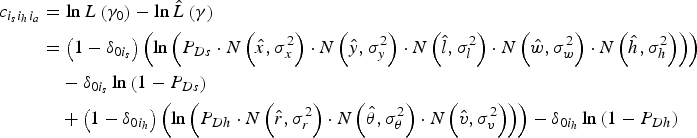 $$\eqalign{c_{{i_s} {i_h} {i_a}} & = \ln L\left( {\gamma _0} \right) - \ln \hat L\left( \gamma \right) \cr & = \left( {1 - \delta _{0i_s}} \right)\left( {\ln \left( {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2 } \right) \cdot N\left( {\hat y,\sigma _y^2 } \right) \cdot N\left( {\hat l,\sigma _l^2 } \right) \cdot N\left( {\hat w,\sigma _w^2 } \right) \cdot N\left( {\hat h,\sigma _h^2 } \right)} \right)} \right) \cr & \quad - \delta _{0i_s}\ln \left( {1 - P_{Ds}} \right) \cr & \quad+ \left( {1 - \delta _{0i_h}} \right)\left( {\ln \left( {P_{Dh} \cdot N\left( {\hat r,\sigma _r^2 } \right) \cdot N\left( {\hat \theta ,\sigma _\theta ^2 } \right) \cdot N\left( {\hat v,\sigma _v^2 } \right)} \right)} \right) - \delta _{0i_h}\ln \left( {1 - P_{Dh}} \right)} $$
$$\eqalign{c_{{i_s} {i_h} {i_a}} & = \ln L\left( {\gamma _0} \right) - \ln \hat L\left( \gamma \right) \cr & = \left( {1 - \delta _{0i_s}} \right)\left( {\ln \left( {P_{Ds} \cdot N\left( {\hat x,\sigma _x^2 } \right) \cdot N\left( {\hat y,\sigma _y^2 } \right) \cdot N\left( {\hat l,\sigma _l^2 } \right) \cdot N\left( {\hat w,\sigma _w^2 } \right) \cdot N\left( {\hat h,\sigma _h^2 } \right)} \right)} \right) \cr & \quad - \delta _{0i_s}\ln \left( {1 - P_{Ds}} \right) \cr & \quad+ \left( {1 - \delta _{0i_h}} \right)\left( {\ln \left( {P_{Dh} \cdot N\left( {\hat r,\sigma _r^2 } \right) \cdot N\left( {\hat \theta ,\sigma _\theta ^2 } \right) \cdot N\left( {\hat v,\sigma _v^2 } \right)} \right)} \right) - \delta _{0i_h}\ln \left( {1 - P_{Dh}} \right)} $$
4. DATA ASSOCIATION FOR SAR, HFSWR AND AIS
The data association procedure contains two phases: measurement partition and data association.
4.1. Measurement Partition
In order to apply the multi-assignment algorithm, the complete set
![]() ${\bi Z}$
is firstly divided into many different combinations. These combinations contain all the possible associated measurements. The pair gating method is used to find the feasible associated target measurements between each pair of sensors. Furthermore, an iterative search method is employed to ensure that the divided combination covers all the possible associated target measurements.
${\bi Z}$
is firstly divided into many different combinations. These combinations contain all the possible associated measurements. The pair gating method is used to find the feasible associated target measurements between each pair of sensors. Furthermore, an iterative search method is employed to ensure that the divided combination covers all the possible associated target measurements.
4.1.1. Pair Gating
Different sensor pairs have different gating thresholds. The three gating thresholds are defined as follows.
-
• The gating threshold between AIS and SAR measurements is given by
(25)where $${\rm D}\left( {i_a, i_s} \right) = \sqrt {\left \vert {{\bi z}_{ai_{a}} \left( x \right) - {\bi z}_{si_s} \left( x \right)} \right \vert ^2 + \left \vert {{\bi z}_{ai_{a}} \left( y \right) - {\bi z}_{si_s} \left( y \right)} \right \vert ^2} \le D_{\max} $$
$${\rm D}\left( {i_a, i_s} \right) = \sqrt {\left \vert {{\bi z}_{ai_{a}} \left( x \right) - {\bi z}_{si_s} \left( x \right)} \right \vert ^2 + \left \vert {{\bi z}_{ai_{a}} \left( y \right) - {\bi z}_{si_s} \left( y \right)} \right \vert ^2} \le D_{\max} $$
 ${\rm D}\left( {i_a, i_s} \right)$
denotes the Euclidean distance between the i
a
th AIS and i
s
th SAR measurement. D
max is the Euclidean distance threshold between the SAR and AIS measurement. It is related to the target space positioning accuracy of SAR. The space positioning accuracy is affected mainly by geometric positioning accuracy and resolution of SAR. D
max is also influenced by the azimuth displacement, which is caused by the Doppler shift of a fast moving target (Tunaley, Reference Tunaley2003). Here, based on SAR resolution and the experiment's statistical data, D
max selected here is 2 km.
${\rm D}\left( {i_a, i_s} \right)$
denotes the Euclidean distance between the i
a
th AIS and i
s
th SAR measurement. D
max is the Euclidean distance threshold between the SAR and AIS measurement. It is related to the target space positioning accuracy of SAR. The space positioning accuracy is affected mainly by geometric positioning accuracy and resolution of SAR. D
max is also influenced by the azimuth displacement, which is caused by the Doppler shift of a fast moving target (Tunaley, Reference Tunaley2003). Here, based on SAR resolution and the experiment's statistical data, D
max selected here is 2 km.
-
• The gating threshold between AIS and HFSWR measurements is given by
(26)The range, azimuth and radial velocity of AIS measurement can be computed by Equations (6) and (14). r max, θ max and V max are the range, azimuth and radial velocity gating threshold of the HFSWR and AIS. These three gating thresholds can refer to the accuracy of the HFSWR detection, and the accuracy is related to the HFSWR resolution. HFSWR range resolution is determined by the signal bandwidth, azimuth resolution is related to the antenna aperture and radial velocity resolution is related to the radar coherent integration time. The value of r max selected here is 2 km, θ max selected here is 5°, and V max selected here is 2 km/h. $$\matrix{ {\left \vert {{\bi z}_{hi_h} \left( r \right) - {\bi z}_{ai_a} \left( r \right)} \right \vert \le r_{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( \theta \right) - {\bi z}_{ai_a} \left( \theta \right)} \right \vert \le \theta _{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( {v_r} \right) - {\bi z}_{ai_a} \left( {v_r} \right)} \right \vert \le V_{\max}} \cr} $$
$$\matrix{ {\left \vert {{\bi z}_{hi_h} \left( r \right) - {\bi z}_{ai_a} \left( r \right)} \right \vert \le r_{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( \theta \right) - {\bi z}_{ai_a} \left( \theta \right)} \right \vert \le \theta _{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( {v_r} \right) - {\bi z}_{ai_a} \left( {v_r} \right)} \right \vert \le V_{\max}} \cr} $$
-
• The gating threshold between SAR and HFSWR measurements is given by
(27) $$\matrix{ {\left \vert {{\bi z}_{hi_h} \left( r \right) - {\bi z}_{si_s} \left( r \right)} \right \vert \le r_{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( \theta \right) - {\bi z}_{si_s} \left( \theta \right)} \right \vert \le \theta _{\max}} \cr} $$
$$\matrix{ {\left \vert {{\bi z}_{hi_h} \left( r \right) - {\bi z}_{si_s} \left( r \right)} \right \vert \le r_{\max}} \cr {\left \vert {{\bi z}_{hi_h} \left( \theta \right) - {\bi z}_{si_s} \left( \theta \right)} \right \vert \le \theta _{\max}} \cr} $$
since the measurement error of HFSWR is greater than the error of SAR, r max and θ max are also selected as the gating threshold between the SAR and HFSWR. The range and azimuth value of SAR are converted by Equation (6).
4.1.2 Iterative Search
The iterative search method can select all the possible associated target measurements and put them into one combination. Thus, all data can be divided into several combinations. The method can begin with any measurement of any sensor. Here, we use the i a th AIS measurement as the start point to demonstrate the iterative search method. The main steps are as follows:
-
• Step 1: AIS set, only one measurement
 ${\bi z}_{ai_{a}} $
, is defined. Furthermore, two empty sets, SAR and HFSWR set, are defined.
${\bi z}_{ai_{a}} $
, is defined. Furthermore, two empty sets, SAR and HFSWR set, are defined. -
• Step 2: Record the elements number of AIS, SAR and HFSWR set.
-
• Step 3: Use every measurement in AIS set, traverse all the SAR measurements, find all the SAR measurements that meet the gating threshold in Equation (25) with AIS measurements, and add them into SAR set; Also, HFSWR set is added with the same step.
-
• Step 4: Use every measurement in SAR set, traverse all the HFSWR measurements, find all the HFSWR measurements meeting the gating threshold in Equation (27) with SAR measurements, and add them into HFSWR set; Also, AIS set is added with the same step.
-
• Step 5: Use every measurement in HFSWR set, traverse all the AIS measurements, find all the AIS measurements that meet the gating threshold in Equation (26) with HFSWR measurements, and add them into HFSWR set; Also, SAR set is added with the same step.
-
• Step 6: if the present elements number of AIS, SAR and HFSWR set are all equal to the elements number in Step 2, go to Step 7; else, go to Step 2 for iteration.
-
• Step 7: The union of AIS, SAR and HFSWR set are the iterative search results.
After the iterative search, we can divide all the measurements into different combinations. These combinations have three types:
-
• Type 1: The union of AIS, SAR and HFSWR set has measurements of one sensor.
-
• Type 2: The union of AIS, SAR and HFSWR set has measurements of two sensors. These measurements may originate from the non-cooperative ships or the cooperative ships with missed detections.
-
• Type 3: The union of AIS, SAR and HFSWR set has measurements of three sensors. These measurements may originate from the cooperative ships.
4.2. Data Association
As for the divided combinations, different association algorithms are applied. For the combinations of Type 1, the SAR and HFSWR measurements are generally regarded as false alarms and the AIS measurements are regarded as the cooperative ships. For the combinations of Type 2, the association problem is a 2-D assignment problem and can be solved by the JVC algorithm. For the combinations of Type 3, the association problem is a 3-D assignment problem and can be solved by a Lagrangian relaxation algorithm.
4.2.1. JVC Algorithms
For the traditional 2-D assignment problem, JVC algorithms can provide an optimal solution in polynomial time (Kadar et al., Reference Kadar, Eadan and Gassner1997). When the combinations have measurements of two sensors, the 2-D assignment algorithm is formulated as follows.
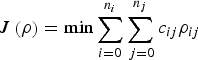 $$J\left( \rho \right) = \min \sum\limits_{i = 0}^{n_i} {\sum\limits_{\,j = 0}^{n_j} {c_{ij} \rho _{ij}}} $$
$$J\left( \rho \right) = \min \sum\limits_{i = 0}^{n_i} {\sum\limits_{\,j = 0}^{n_j} {c_{ij} \rho _{ij}}} $$
subject to
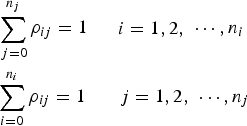 $$\eqalign{& \sum\limits_{\,j = 0}^{n_j} {\rho _{ij}} = 1\matrix{ & {\matrix{ \cr} \matrix{ {i = 1,2,} \cr}} \cr} \cdots, n_i \cr & \sum\limits_{i = 0}^{n_i} {\rho _{ij}} = 1\matrix{ & {\matrix{ \cr} \matrix{ {\,j = 1,2,} \cr}} \cr} \cdots, n_j} $$
$$\eqalign{& \sum\limits_{\,j = 0}^{n_j} {\rho _{ij}} = 1\matrix{ & {\matrix{ \cr} \matrix{ {i = 1,2,} \cr}} \cr} \cdots, n_i \cr & \sum\limits_{i = 0}^{n_i} {\rho _{ij}} = 1\matrix{ & {\matrix{ \cr} \matrix{ {\,j = 1,2,} \cr}} \cr} \cdots, n_j} $$
The value of c ij can be obtained from Equation (24). The optimal solution is to find the point to point assignment so that the sum of c ij is the minimum value. We applied the JVC algorithm to solve the HFSWR and AIS association problem in our previous work (Zhang et al., Reference Zhang, Liu, Zhang, Ji and Zheng2015). Its results showed that the JVC algorithm is feasible for the 2-D assignment problem in both performance and real time.
4.2.2. Lagrangian Relaxation Algorithm
A Lagrangian relaxation algorithm is a suboptimal solution of the 3-D assignment, which can provide the upper and lower bounds of the assignment problem (Poore and Robertson III, Reference Poore and Robertson1997). The lower bound can be usually obtained by the relaxed 2-D assignment solutions. The upper bound can be obtained by the feasible solutions of 3-D assignment (Deb et al., Reference Deb, Yeddanapudi, Pattipati and Bar-Shalom1997).
The main steps of the Lagrangian relaxation algorithm are as follows:
-
• Initial Step: Initialise the value of variables.
-
• Lagrangian multiplier
 $u_{ai_a} = 0$
, iterate time iter = 0, maximum iterate times maxiter = 200, upper bound f
upper
= ∞, and lower bound f
lower = −∞. The gap is defined as Equation (30), and minimum gap threshold mingap = 0.
(30)
$u_{ai_a} = 0$
, iterate time iter = 0, maximum iterate times maxiter = 200, upper bound f
upper
= ∞, and lower bound f
lower = −∞. The gap is defined as Equation (30), and minimum gap threshold mingap = 0.
(30) $$gap = {{\left( {\,f_{upper} - f_{lower}} \right)} / {\left \vert {\,f_{lower}} \right \vert}} $$
$$gap = {{\left( {\,f_{upper} - f_{lower}} \right)} / {\left \vert {\,f_{lower}} \right \vert}} $$
-
• Iteration Step: firstly, the reduced costs are computed as
(31) $$d_{{i_s} {i_h}} ^2 = \mathop {\min} \limits_{i_a} \left( {c_{{i_s} {i_h} {i_a}} - u_{ai_a}} \right)$$
$$d_{{i_s} {i_h}} ^2 = \mathop {\min} \limits_{i_a} \left( {c_{{i_s} {i_h} {i_a}} - u_{ai_a}} \right)$$
Secondly, the 3-D assignment is relaxed as a 2-D assignment problem with
![]() $d_{{i_s} {i_h}} ^2 $
and a new two-valued variable
$d_{{i_s} {i_h}} ^2 $
and a new two-valued variable
![]() ${w_{{i_s} {i_h}}}$
is given by
${w_{{i_s} {i_h}}}$
is given by
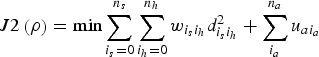 $$J2\left( \rho \right) = \min \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_h = 0}^{n_h} {w_{{i_s}{i_h}} d_{{i_s}{i_h}}^2 } } + \sum\limits_{i_a}^{n_a} {u_{ai_a}}$$
$$J2\left( \rho \right) = \min \sum\limits_{i_s = 0}^{n_s} {\sum\limits_{i_h = 0}^{n_h} {w_{{i_s}{i_h}} d_{{i_s}{i_h}}^2 } } + \sum\limits_{i_a}^{n_a} {u_{ai_a}}$$
subject to
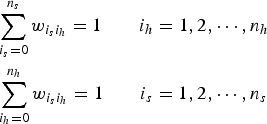 $$\eqalign{& \sum\limits_{i_s = 0}^{n_s} {w_{{i_s} {i_h}}} = 1 \quad \quad {i_h = 1,2,} \cdots ,n_h \cr & \sum\limits_{i_h = 0}^{n_h} {w_{{i_s} {i_h}}} = 1 \quad \quad {i_s = 1,2,} \cdots ,n_s} $$
$$\eqalign{& \sum\limits_{i_s = 0}^{n_s} {w_{{i_s} {i_h}}} = 1 \quad \quad {i_h = 1,2,} \cdots ,n_h \cr & \sum\limits_{i_h = 0}^{n_h} {w_{{i_s} {i_h}}} = 1 \quad \quad {i_s = 1,2,} \cdots ,n_s} $$
This 2-D problem is solved by a JVC algorithm. Then, based on the results of the 2-D problem, the 3-D problem is solved as another 2-D problem as
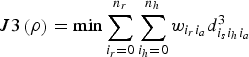 $$J3\left( \rho \right) = \min \sum\limits_{i_r = 0}^{n_r} {\sum\limits_{{i_h} = 0}^{n_h} {w_{{i_r} {i_a}} d_{{i_s} {i_h} {i_a}} ^3}} $$
$$J3\left( \rho \right) = \min \sum\limits_{i_r = 0}^{n_r} {\sum\limits_{{i_h} = 0}^{n_h} {w_{{i_r} {i_a}} d_{{i_s} {i_h} {i_a}} ^3}} $$
Subject to
 $$\eqalign{& \sum\limits_{i_r = 0}^{n_r} {w_{{i_r} {i_a}}} = 1 \quad \quad {i_a = 1,2,} \cdots ,n_a \cr & \sum\limits_{i_a = 0}^{n_a} {w_{{i_r} {i_a}}} = 1 \quad \quad {i_r = 1,2,} \cdots ,n_r} $$
$$\eqalign{& \sum\limits_{i_r = 0}^{n_r} {w_{{i_r} {i_a}}} = 1 \quad \quad {i_a = 1,2,} \cdots ,n_a \cr & \sum\limits_{i_a = 0}^{n_a} {w_{{i_r} {i_a}}} = 1 \quad \quad {i_r = 1,2,} \cdots ,n_r} $$
where i
r
are the 2-D assignment results of Equation (32), which are the index of assignment results for SAR and HFSWR. n
r
is the number of 2-D assignment results. The value of
![]() $d_{{i_s} {i_h} {i_a}} ^3 $
equals
$d_{{i_s} {i_h} {i_a}} ^3 $
equals
![]() $c_{{i_s} {i_h} {i_a}} $
. Finally, Lagrangian Multiplier
$c_{{i_s} {i_h} {i_a}} $
. Finally, Lagrangian Multiplier
![]() $u_{ai_a} $
is updated with the new price update algorithm (Pattipati et al., Reference Pattipati, Deb, Bar-Shalom and Washburn1992).
$u_{ai_a} $
is updated with the new price update algorithm (Pattipati et al., Reference Pattipati, Deb, Bar-Shalom and Washburn1992).
-
• Results output Step: Update the value of gap as Equation (30), and update the value of f upper , f lower and iter by
(36) $$\eqalign{& f_{{\rm lower}} = \max \left( {\,f_{lower}, J2} \right) \cr & f_{upper} = \min \left( {\,f_{upper}, J3} \right) \cr & {iter} = {iter} + {\it 1}} $$
$$\eqalign{& f_{{\rm lower}} = \max \left( {\,f_{lower}, J2} \right) \cr & f_{upper} = \min \left( {\,f_{upper}, J3} \right) \cr & {iter} = {iter} + {\it 1}} $$
If the iteration meets the terminate condition (gap < mingap) or (iter > maxiter), association results are output. Otherwise, the iteration step is continued.
5. EXPERIMENT RESULTS
In this section, the evaluation metric is first presented for association of SAR, HFSWR, and AIS. Then, the proposed method is verified by simulated and real data.
5.1. Evaluation Metric
Since the errors of SAR and HFSWR are different orders of magnitude, different metrics are used to evaluate the association performance. The evaluation metrics are defined as follows:
-
• Mean position error: mean position error between SAR and AIS is defined as
(37) $$\bar \varepsilon _{{\rm pos}} = \displaystyle{1 \over {num\_s}}\sum\limits_{num = 1}^{num\_s} {\sqrt {\left( {\hat x - {\bi z}_{si_s} \left( x \right)} \right)^2 + \left( {\hat y - {\bi z}_{si_s} \left( y \right)} \right)^2}} $$
$$\bar \varepsilon _{{\rm pos}} = \displaystyle{1 \over {num\_s}}\sum\limits_{num = 1}^{num\_s} {\sqrt {\left( {\hat x - {\bi z}_{si_s} \left( x \right)} \right)^2 + \left( {\hat y - {\bi z}_{si_s} \left( y \right)} \right)^2}} $$
-
• where num_s is the number of SAR and AIS association results.
 $\hat x$
,
$\hat x$
,
 ${\hat y}$
are the estimated value.
${\hat y}$
are the estimated value. -
• Mean range error, mean azimuth error, mean radial Velocity error: the mean error between HFSWR and AIS or SAR is defined as
(38) $$\bar \varepsilon = \displaystyle{1 \over {num\_h}}\sum\limits_{num = 1}^{num\_h} {\left \vert {{\hat {\bi z}} - {\bi z}_{hi_h}} \right \vert} $$
$$\bar \varepsilon = \displaystyle{1 \over {num\_h}}\sum\limits_{num = 1}^{num\_h} {\left \vert {{\hat {\bi z}} - {\bi z}_{hi_h}} \right \vert} $$
-
• where the num_h is the number of HFSWR and AIS or SAR association results.
 ${\hat {\bi z}}$
is the estimated value.
${\hat {\bi z}}$
is the estimated value. -
• Accuracy rate. The association accuracy rate is defined for the evaluation of the simulated data, which is given by
(39) $${acc}\_{rate} = \displaystyle{{num\_right} \over {num\_associate}}$$
$${acc}\_{rate} = \displaystyle{{num\_right} \over {num\_associate}}$$
where num_right is the number of correctly associated measurements, and num_associate is the number of associated results.
5.2. Simulated Data Association
The simulated data contains cooperative ships, non-cooperative ships and false alarms.
5.2.1. Simulated Data Parameters
The cooperative ships data is simulated based on AIS measurements in a real ship detection scenario. These measurements are extracted from a Terrestrial AIS report from 06:47 to 06:57 on November 13, 2013. The Dead Reckoning (DR) method is employed to predict the AIS position and velocity at 06:52. The SAR and HFSWR measurements of cooperative ships are simulated with the AIS data plus the measurement noise w s (k) and w h (k), with the detect probability P Ds and P Dh . For non-cooperative ships, the simulated data are uniformly distributed in the measurement area. These measurements are detected by SAR and HFSWR with the detection probability P Ds and P Dh , and not detected by AIS. False alarms are simulated with only SAR or HFSWR measurements, and the false alarm probability is P Fs and P Fh , respectively.
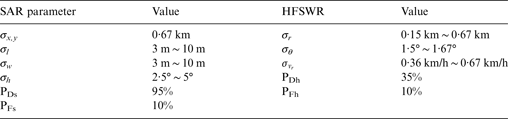
Different resolutions SAR and HFSWR measurements are simulated in this section. Three resolution SAR images are usually used in ship detection: high resolution (pixel resolution less than 3 m), medium resolution (pixel resolution about 8 to 10 m) and low resolution SAR images (pixel resolution about 25 m). Due to the limitations of the resolution, it is hard to identify the exact ship length and width from the low resolution SAR images. Thus, only high and medium resolution SAR scenarios are simulated. The maximum errors of ship length and width extracted from the SAR images are about three pixels of image compared with the real ship. In medium resolution SAR images, the ship heading is estimated through the Radon transform (Margarit and Tabasco, Reference Margarit and Tabasco2011), the maximum heading error is about 15°. In high resolution SAR images, the maximum heading error is about 7·5°. For the HFSWR simulation, the Wellen Radar (WERA) has high resolution on ship detection. Referring to Maresca et al. (Reference Maresca, Braca, Horstmann and Grasso2014), the simulation data on WERA is selected as the parameters set for high resolution HFSWR, and our HFSWR parameters are selected as the parameters set for low resolution.
Table 2 highlights the main parameters of our simulated scenarios, in which the value of standard deviations σ are one-third of the maximum errors, and detection and false alarm probabilities are derived from the experimental statistics.
Table 2. Main parameters of the simulated scenarios.
5.2.2. Monte Carlo simulations
The influence of different features and parameters is evaluated by 102 Monte Carlo (MC) simulations. From the simulation results, we draw conclusions as follows:
-
• Association with ship length and radial velocity features can improve the association accuracy rate. Its association accuracy rate is always higher than the ML association without those features.
-
• Association with ship heading and azimuth features cannot improve the association rate. Association accuracy rate is always lower than the ML association without those features.
-
• Association with ship width feature can improve the association accuracy rate when σ w ≥ 6 m. This means that association with the ship width feature can improve the association accuracy rate only in high resolution SAR.
Real data association, considered in this paper, is the association of medium resolution SAR and low resolution HFSWR. The simulated results of this scenario are analysed as follows. The maximum standard deviations of Table 2 are selected as the simulated parameters. Table 3 shows the results of the different features combination with the multi-feature ML association algorithm. The accuracy rate of multi-feature with position, ship length, range and radial velocity is the highest. Table 4 compares three association algorithms. Multi-feature ML association brings the 12·4% percentage points improvement of the association accuracy rate, compared with the traditional position-only ML association. Figure 1 shows the association accuracy rate of three association algorithms in 102 MC simulations.

Figure 1. Association results of NN, position ML and Multi-feature ML association.
Table 3. The association results of different features in the Multi-feature association algorithm.
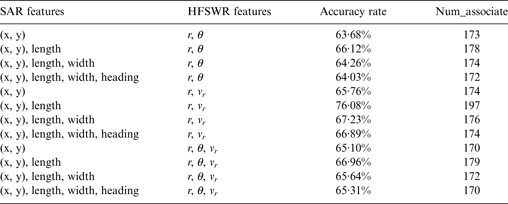
Table 4. The comparison of three association algorithms.

5.3. Real Data Association
Experiments are conducted on a real ship detection scenario on 13 November 2013. The association experiments are based on data from space-borne SAR, coastal HFSWR and Terrestrial AIS.
5.3.1. Real Data information
The SAR image is acquired from RADARSAT2 on 06:52, 13 November 2013, which is wide mode, Vertical Transmit and Vertical Receive (VV) polarisation, with 25*25 m spatial resolution and 10 m pixel spacing. Figure 2(a) shows the SAR image. The SAR measurements are detected by the sliding window Constant False Alarm Rate (CFAR) algorithm (Ji et al., Reference Ji, Zhang, Meng and Zhang2010). The ship length is extracted by the rotation and pixel counting method (Margarit and Tabasco, Reference Margarit and Tabasco2011).

Figure 2. The SAR image and SAR, HFSWR, AIS measurements on 13 November 2013.
The HFSWR data is collected from coastal HFSWR, whose working frequency is 4·70 MHz. The number of antenna array elements is eight, and the distance of antenna elements is 14·5 m. The time span of data collected is 1 min. The HFSWR measurements are detected with the CFAR method of Adaptive Power Regression Thresholding (APRT) (Dzvonkovskaya and Hermann, Reference Dzvonkovskaya and Hermann2007).
The AIS data are collected from Terrestrial AIS. Since the AIS report time relies on the type of AIS equipment and ship dynamic state, the time span of AIS report is from 06:47 to 06:57 on 13 November 2013. The DR method is used to deduce the ship dynamic state at the satellite transit time using the AIS report.
Figure 2(b) presents the distribution of three sensors measurements, which covers the range of Northern latitude 37·5° ~ 39° and East longitude 120·2° ~122°. The square points represent the AIS measurements; the triangular points represent the HFSWR measurements; the circular points represent the SAR measurements. The number of AIS, HFSWR and SAR measurements is 672, 212, and 478, respectively.
5.3.2. Real Data association result
Table 5 shows the association results. The number of cooperative ships detected by at least two sensors is 299. This is because the AIS coverage area is wider than the SAR and HFSWR, and the rest of the 373 cooperative ships are only detected by AIS. The number of non-cooperative ships is 58.
Table 5. The association results of the real ship detection scenario.

The association error is also analysed. Figure 3 illustrates the distribution of the different errors. The position errors are in the range 0 ~ 2 km, and mean position error is about 0·53 km. The signed range errors are in the range of −2 ~ 2 km, and the mean range error is about 0·93 km. The signed azimuth errors are distributed between −5 and 5°, and mean azimuth error is 2·13°. The signed Radial Velocity Errors lie between −2 ~ 2 km/h, and mean radial velocity error is about 1·08 km/h.

Figure 3. The distribution of Mean position, range azimuth and radial velocity error.
A local area data is also employed to demonstrate the effect of different association algorithms. Figure 4 shows the local area, the range of Northern latitude 37·91° ~ 37·97° and East longitude 121·09° ~121·15°. There are five AIS measurements, four HFSWR measurements and six SAR measurements, which are labelled by the symbols and number. Figure 5(a) is the corresponding SAR image of the local area, in which only five ships are clearly identified. The SAR measurement 3 in Figure 4 possibly originates from a false alarm, and the other five ship images are all labelled in Figure 4. Figure 5 (b) highlights the radial velocity direction of the AIS and HFSWR measurements. The arrow of the solid line represents the course over ground of AIS measurements, and the arrow of the dotted line represents the direction of radial velocity. Table 6 shows the speed of the AIS and HFSWR measurements.

Figure 4. The local area of Figure 2.

Figure 5. Ships in the SAR image and the radial velocity diagram.
Table 6. The speed of AIS and HFSWR measurements.
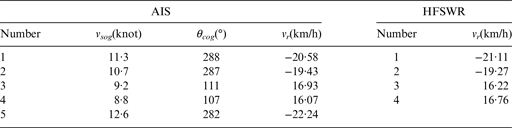
Table 7 shows the association results of three algorithms. The results set {i a , ih, is } means that the i a th AIS measurement, the i h th HFSWR measurement and the i s th SAR measurement all originate from the same target. i = 0 means that the target is missed by this sensor. The NN and position ML algorithms made a mistake in the association because of the presence of the SAR measurement 3. Multi-feature ML association results are more reasonable.
Table 7. The association results of three algorithms.

Details of multi-feature ML association results are analysed as follows. The results {1, 1, 1} and {2, 2, 2} originate from two cooperative ships, which are detected by all three sensors. From the fusion information, it is derived that the ship of {1, 1, 1} is an oil tanker, whose length is 93 m, the other ship of {2, 2, 2} is a cargo vessel, whose length is 98 m. The result {5, 0, 6} is a cooperative ship detected by the SAR and AIS, which is mis-detected by the HFSWR. The direction of HFSWR measurement 4 radial velocity is inconsistent with direction of the AIS measurement 5 radial velocity. Therefore, The HFSWR point 4 does not originate from the target {5, 0, 6}. The merit of multi-feature ML association is demonstrated in the association of the measurements {3, 3, 4} and {4, 4, 5}. When we considered the multi-feature (ship length and radial velocity) in the association, the wrong association, caused by the SAR measurement 3, can be avoided. We deduced that the target {3, 3, 4} is a cooperative cargo and the target {4, 4, 5} is a cooperative oil tanker.
6. CONCLUSIONS
Data fusion of Space-borne SAR, HFSWR and AIS for ship detection can improve the detection accuracy and reduce false alarms. Data association is the key step in data fusion. In order to make full use of the measurements, a multi-feature ML association algorithm is proposed in this paper. Besides the traditional position information, we employed the ship length, width, heading and radial velocity data in the data association. Results from simulated data demonstrated that ship width and heading for SAR, and azimuth for the HFSW did not improve the results of the association of medium resolution SAR and low resolution HFSWR. Real data results showed that the multi-feature ML association algorithm can improve the association accuracy under the condition of measurements with some false alarms. From the association results, we can further identify the information of cooperative ships and suspected non-cooperative ships. The non-cooperative ships are regarded as the track start point for the non-cooperative ship tracking. Since the medium resolution Space-borne SAR measurements cannot provide accurate target velocity, the association of SAR and HFSWR measurements can only depend on the position data, which reduced the association accuracy. Future work will be concentrated on obtaining more high resolution information from SAR and HFSWR.
FINANCIAL SUPPORT
This work was supported by the National Natural Science Foundation of China (Grant number 61362002), Marine scientific research special funds for public welfare (Grant No. 201505002), and the Postgraduate Scientific Research Innovation Key Foundation of Inner Mongolia (Grant number 1402020201).


















