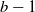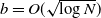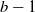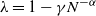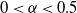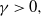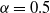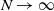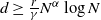1. Introduction
This paper studies the steady-state performance of load-balancing algorithms in many-server systems. We consider a system with N identical servers with buffer size ![]() $b-1$ such that
$b-1$ such that ![]() $b=O\left(\sqrt{\log N}\right)$; in other words, each server can hold at most b jobs, one job in service and
$b=O\left(\sqrt{\log N}\right)$; in other words, each server can hold at most b jobs, one job in service and ![]() $b-1$ jobs in a buffer. We assume jobs arrive according to a Poisson process with rate
$b-1$ jobs in a buffer. We assume jobs arrive according to a Poisson process with rate ![]() $\lambda N$, where
$\lambda N$, where ![]() $\lambda = 1 - \gamma N^{-\alpha}$ for
$\lambda = 1 - \gamma N^{-\alpha}$ for ![]() $0<\alpha<0.5$ and
$0<\alpha<0.5$ and ![]() $\gamma >0$, and have independent and identically distributed (i.i.d.) exponential service times with mean 1. When a job arrives, the load balancer immediately routes the job to one of the servers. If the server’s buffer is full, the job is discarded. We study a class of load-balancing algorithms, which includes join-the-shortest-queue (JSQ), idle-one-first (I1F) [Reference Gupta and Walton9], join-the-idle-queue (JIQ) [Reference Lu, Xie, Kliot, Geller, Larus and Greenberg11, Reference Stolyar14], and power-of-d-choices (Pod) with
$\gamma >0$, and have independent and identically distributed (i.i.d.) exponential service times with mean 1. When a job arrives, the load balancer immediately routes the job to one of the servers. If the server’s buffer is full, the job is discarded. We study a class of load-balancing algorithms, which includes join-the-shortest-queue (JSQ), idle-one-first (I1F) [Reference Gupta and Walton9], join-the-idle-queue (JIQ) [Reference Lu, Xie, Kliot, Geller, Larus and Greenberg11, Reference Stolyar14], and power-of-d-choices (Pod) with ![]() $d\geq \frac{r}{\gamma}N^\alpha\log N$ [Reference Mitzenmacher12, Reference Vvedenskaya, Dobrushin and Karpelevich17], and establish moment bounds on some function of the queue lengths. From the moment bounds, we show that under JSQ, I1F, JIQ, and Pod with
$d\geq \frac{r}{\gamma}N^\alpha\log N$ [Reference Mitzenmacher12, Reference Vvedenskaya, Dobrushin and Karpelevich17], and establish moment bounds on some function of the queue lengths. From the moment bounds, we show that under JSQ, I1F, JIQ, and Pod with ![]() $d\geq \frac{r}{\gamma}N^\alpha\log N$, both the probability that a job is routed to a non-idle server and the expected waiting time per job are
$d\geq \frac{r}{\gamma}N^\alpha\log N$, both the probability that a job is routed to a non-idle server and the expected waiting time per job are ![]() $\smash{O\big(\frac{b}{N^{r(0.5-\alpha)}}\big)}$, where r is any positive integer such that
$\smash{O\big(\frac{b}{N^{r(0.5-\alpha)}}\big)}$, where r is any positive integer such that ![]() $\smash{r \leq \frac{\log N}{72(b-1)^2}}$.
$\smash{r \leq \frac{\log N}{72(b-1)^2}}$.
1.1. Related work and our contributions
Performance analysis of many-server systems is one of the most fundamental and widely studied problems in queueing theory. The stationary distribution of the classic M/M/N system (called the Erlang C model) was one of the earliest subjects studied. For systems with distributed queues where each server maintains a separate queue, it is well known that the JSQ algorithm is delay optimal [Reference Weber19, Reference Winston20] under fairly general conditions. However, the exact stationary distribution of many-server systems under JSQ remains an open problem. A recent breakthrough in this area is [Reference Eschenfeldt and Gamarnik6], which shows that in the Halfin–Whitt regime (![]() $\alpha=0.5$) the diffusion-scaled process converges to a two-dimensional diffusion limit, from which it can be shown that most servers have one job in service and
$\alpha=0.5$) the diffusion-scaled process converges to a two-dimensional diffusion limit, from which it can be shown that most servers have one job in service and ![]() $\Theta\big(\sqrt{N}\big)$ servers have two jobs (one in service and one in a buffer). This seminal work has led to several significant developments: (i) [Reference Braverman3] proved that the stationary distribution indeed converges to the stationary distribution of the two-dimensional diffusion limit based on Stein’s method; (ii) via stochastic coupling, [Reference Mukherjee, Borst, van Leeuwaarden and Whiting13] showed that the diffusion limit of Pod converges to that of JSQ in the Halfin–Whitt regime at the process level (over finite time) when
$\Theta\big(\sqrt{N}\big)$ servers have two jobs (one in service and one in a buffer). This seminal work has led to several significant developments: (i) [Reference Braverman3] proved that the stationary distribution indeed converges to the stationary distribution of the two-dimensional diffusion limit based on Stein’s method; (ii) via stochastic coupling, [Reference Mukherjee, Borst, van Leeuwaarden and Whiting13] showed that the diffusion limit of Pod converges to that of JSQ in the Halfin–Whitt regime at the process level (over finite time) when ![]() $d=\Theta\big(\sqrt{N}\log N\big)$; and (iii) when
$d=\Theta\big(\sqrt{N}\log N\big)$; and (iii) when ![]() $\alpha<1/6$, [Reference Liu and Ying10] proved that the waiting probability of a job is asymptotically zero with
$\alpha<1/6$, [Reference Liu and Ying10] proved that the waiting probability of a job is asymptotically zero with ![]() $\smash{d=\Omega\left(\frac{\log N}{1-\lambda}\right)}$ at the steady state, based on Stein’s method. Interested readers can find a comprehensive survey of recent results in [Reference van der Boor, Borst, van Leeuwaarden and Mukherjee16].
$\smash{d=\Omega\left(\frac{\log N}{1-\lambda}\right)}$ at the steady state, based on Stein’s method. Interested readers can find a comprehensive survey of recent results in [Reference van der Boor, Borst, van Leeuwaarden and Mukherjee16].
Let ![]() $S_i$ denote the fraction of servers with at least i jobs, including the one in service, at steady state. In this paper we prove that if a load-balancing algorithm routes an incoming job to an idle server with probability at least
$S_i$ denote the fraction of servers with at least i jobs, including the one in service, at steady state. In this paper we prove that if a load-balancing algorithm routes an incoming job to an idle server with probability at least ![]() $1-\frac{1}{\sqrt{N}\,}$ when the fraction of busy servers is no more than
$1-\frac{1}{\sqrt{N}\,}$ when the fraction of busy servers is no more than ![]() $\smash{\lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$, then the following bound holds for any positive integer
$\smash{\lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$, then the following bound holds for any positive integer ![]() $\smash{r \leq \frac{\log N}{72(b-1)^2}}$:
$\smash{r \leq \frac{\log N}{72(b-1)^2}}$:
 \begin{align*}\mathbb{E}\Bigg[\Bigg(\max\Bigg\{\sum_{i=1}^b S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\Bigg\}\Bigg)^r\Bigg]\leq 10\left(\frac{5r(b-1)}{\sqrt{N}\log N}\right)^r, \qquad {\bar k}=1+\frac{1}{2(b-1)}.\end{align*}
\begin{align*}\mathbb{E}\Bigg[\Bigg(\max\Bigg\{\sum_{i=1}^b S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\Bigg\}\Bigg)^r\Bigg]\leq 10\left(\frac{5r(b-1)}{\sqrt{N}\log N}\right)^r, \qquad {\bar k}=1+\frac{1}{2(b-1)}.\end{align*}This result implies that
 \begin{align*}\mathbb{E}\Bigg[\sum_{i=1}^b {S}_i\Bigg]\leq \lambda +\frac{{11\lambda b+11}}{N^{r(0.5-\alpha)}}, \end{align*}
\begin{align*}\mathbb{E}\Bigg[\sum_{i=1}^b {S}_i\Bigg]\leq \lambda +\frac{{11\lambda b+11}}{N^{r(0.5-\alpha)}}, \end{align*}
i.e. the expected queue length per server exceeds ![]() $\lambda$ by at most
$\lambda$ by at most ![]() $\frac{{11\lambda b+11}}{N^{r(0.5-\alpha)}}$, and that under JSQ, I1F, JIQ, and Pod (
$\frac{{11\lambda b+11}}{N^{r(0.5-\alpha)}}$, and that under JSQ, I1F, JIQ, and Pod (![]() $d\geq \frac{r}{\gamma}N^{\alpha}\log N$), the stationary probability that an incoming job is routed to a non-idle server is asymptotically zero (as
$d\geq \frac{r}{\gamma}N^{\alpha}\log N$), the stationary probability that an incoming job is routed to a non-idle server is asymptotically zero (as ![]() $N \to \infty$), which will be proved in Corollary 2.1.
$N \to \infty$), which will be proved in Corollary 2.1.
To the best of our knowledge, there are only a few papers that deal with the steady-state analysis of many-server systems with distributed queues [Reference Banerjee and Mukherjee1, Reference Braverman3, Reference Liu and Ying10]. [Reference Banerjee and Mukherjee1] and [Reference Braverman3] analyze the steady-state distribution of JSQ in the Halfin–Whitt regime, and [Reference Liu and Ying10] studies Pod with ![]() $\alpha<1/6$. This paper complements all three, as it applies to a class of load-balancing algorithms and to any sub-Halfin–Whitt regime. Table 1 summarizes the comparison between our results and existing ones in the literature. Since the existing works focused on steady-state queue length, we also present our results in terms of
$\alpha<1/6$. This paper complements all three, as it applies to a class of load-balancing algorithms and to any sub-Halfin–Whitt regime. Table 1 summarizes the comparison between our results and existing ones in the literature. Since the existing works focused on steady-state queue length, we also present our results in terms of ![]() ${\textrm E}[S_i]$ for comparison purposes.
${\textrm E}[S_i]$ for comparison purposes.
Table 1: Our contributions and related work.

Similar to [Reference Braverman3] and [Reference Liu and Ying10], the result of this paper is proved using the mean-field approximation (fluid-limit approximation) based on Stein’s method. The execution of Stein’s method here, however, is quite different from [Reference Braverman3, Reference Liu and Ying10].
In our proof we consider a simple fluid system with arrival rate ![]() $\lambda$ and departure rate
$\lambda$ and departure rate ![]() $\lambda+\frac{\log N}{\sqrt{N}}$, so
$\lambda+\frac{\log N}{\sqrt{N}}$, so
x can be viewed as a fluid approximation of the normalized total queue length ![]() $\sum_{i=1}^b S_i$, and
$\sum_{i=1}^b S_i$, and ![]() $\dot x$ is the derivative of x with respect to time t. The dynamic of this fluid system (1) is a good approximation of the generator of the stochastic system only when the normalized service rate of the stochastic system is close to
$\dot x$ is the derivative of x with respect to time t. The dynamic of this fluid system (1) is a good approximation of the generator of the stochastic system only when the normalized service rate of the stochastic system is close to ![]() $\lambda+\frac{\log N}{\sqrt{N}}$, i.e. when
$\lambda+\frac{\log N}{\sqrt{N}}$, i.e. when ![]() $S_1\approx \lambda+\frac{\log N}{\sqrt{N}}$. Our analysis consider three regimes of the state space:
$S_1\approx \lambda+\frac{\log N}{\sqrt{N}}$. Our analysis consider three regimes of the state space:
• Regime 1:
 $S_1$ is close to
$S_1$ is close to  $\lambda+\frac{\log N}{\sqrt{N}}$. In this regime, the simple fluid system can approximate the generator of the stochastic system. Via Stein’s method, we can quantify the approximation error.
$\lambda+\frac{\log N}{\sqrt{N}}$. In this regime, the simple fluid system can approximate the generator of the stochastic system. Via Stein’s method, we can quantify the approximation error.• Regime 2:
 $\sum_{i=2}^b S_i \leq \frac{c\log N}{\sqrt{N}}$ for some
$\sum_{i=2}^b S_i \leq \frac{c\log N}{\sqrt{N}}$ for some  $c>0$. Since
$c>0$. Since  $S_1\leq 1$, in this regime the normalized total queue length is close to one.
$S_1\leq 1$, in this regime the normalized total queue length is close to one.• Regime 3: The state is in neither regime 1 nor regime 2. In this case we apply the tail bound in [Reference Bertsimas, Gamarnik and Tsitsiklis2] to prove that the probability it occurs is small, and negligible as N increases. This is equivalent to the state-space-collapse argument, which shows that at steady state, the system ‘lives’ in a lower-dimensional space instead of in the full state space.
Pioneered in [Reference Stolyar15] (and called the drift-based fluid limits method) for fluid-limit analysis and in [Reference Braverman and Dai4, Reference Braverman, Dai and Feng5] for steady-state diffusion approximation, the power of Stein’s method for steady-state approximations has been recognized in a number of recent papers [Reference Braverman3, Reference Braverman and Dai4, Reference Braverman, Dai and Feng5, Reference Gast7, Reference Gast and Van Houdt8, Reference Stolyar15, Reference Ying21, Reference Ying22].
The surprising part of our analysis is that the simple fluid system, which only ‘partially’ approximates the generator of the stochastic system, is sufficient for executing Stein’s method when combining with the state-space-collapse approach. The advantage of using such a simple fluid system is that Stein’s equation can be solved easily, which is often the key difficulty of applying Stein’s method for queueing systems.
Finally, we would like to note that all the proofs in this paper are elementary. Therefore, this paper is another example that demonstrates the power of Stein’s method for analyzing complex queueing systems with elementary probability methods.
2. Model and main results
Consider a many-server system with N homogeneous servers, where job arrival follows a Poisson process with rate ![]() $\lambda N$ and service times are i.i.d. exponential random variables with rate 1. We consider the sub-Halfin–Whitt regime such that
$\lambda N$ and service times are i.i.d. exponential random variables with rate 1. We consider the sub-Halfin–Whitt regime such that ![]() $\lambda=1-\gamma N^{-\alpha}$ for some
$\lambda=1-\gamma N^{-\alpha}$ for some ![]() $0<\alpha<0.5$ and
$0<\alpha<0.5$ and ![]() $\gamma >0$. As shown in Figure 1, each server maintains a separate queue and we assume a buffer size of
$\gamma >0$. As shown in Figure 1, each server maintains a separate queue and we assume a buffer size of ![]() $b-1$ (i.e. each server can have one job in service and
$b-1$ (i.e. each server can have one job in service and ![]() $b-1$ jobs in the queue).
$b-1$ jobs in the queue).

Figure 1. Load balancing in many-server systems.
Let ![]() $S_i(t)$ denote the fraction of servers with at least i jobs at time
$S_i(t)$ denote the fraction of servers with at least i jobs at time ![]() $t \geq 0$. Under the finite buffer assumption with buffer size
$t \geq 0$. Under the finite buffer assumption with buffer size ![]() $b-1$, we define
$b-1$, we define ![]() $S_i(t) = 0$ for all
$S_i(t) = 0$ for all ![]() $i \geq b+1$ and all
$i \geq b+1$ and all ![]() $t\geq 0$ for notational convenience. Furthermore, define the set
$t\geq 0$ for notational convenience. Furthermore, define the set ![]() ${\mathbb S}\subseteq {\mathbb R}^b$ such that
${\mathbb S}\subseteq {\mathbb R}^b$ such that
We then have ![]() $S(t) = [S_1(t), S_2(t), \ldots ,S_b(t)]^\top \in \mathbb S$ for any
$S(t) = [S_1(t), S_2(t), \ldots ,S_b(t)]^\top \in \mathbb S$ for any ![]() $t\geq 0$. We consider a class of load-balancing algorithms which route each incoming job to a server upon its arrival based on S(t) so that (
$t\geq 0$. We consider a class of load-balancing algorithms which route each incoming job to a server upon its arrival based on S(t) so that (![]() $S(t)\,{:}\,t\geq 0$) is a finite-state and irreducible continuous-time Markov chain (CTMC), which implies that (
$S(t)\,{:}\,t\geq 0$) is a finite-state and irreducible continuous-time Markov chain (CTMC), which implies that (![]() $S(t)\,{:}\,t\geq 0$) has a unique stationary distribution. Let
$S(t)\,{:}\,t\geq 0$) has a unique stationary distribution. Let ![]() $S \in \mathbb S$ be the random variables having the stationary distribution of (
$S \in \mathbb S$ be the random variables having the stationary distribution of (![]() $S(t)\,{:}\,t\geq 0$). Note that
$S(t)\,{:}\,t\geq 0$). Note that ![]() $\lambda$, (
$\lambda$, (![]() $S(t)\,{:}\,t\geq 0$), and S all depend on N, the number of servers in the system. Let
$S(t)\,{:}\,t\geq 0$), and S all depend on N, the number of servers in the system. Let ![]() $A_1(s)$ denote the probability that an incoming job is routed to a busy server when the system is in state
$A_1(s)$ denote the probability that an incoming job is routed to a busy server when the system is in state ![]() $s \in \mathbb S$, i.e.
$s \in \mathbb S$, i.e.
The main result of this paper is the following theorem.
Theorem 2.1. Assume ![]() $\lambda=1-\gamma N^{-\alpha}$ for
$\lambda=1-\gamma N^{-\alpha}$ for ![]() $0<\alpha<0.5$ and
$0<\alpha<0.5$ and ![]() $\gamma >0$, and
$\gamma >0$, and ![]() $b \leq 1+\frac{\sqrt{\log N}}{{9}}$. If a load-balancing algorithm guarantees
$b \leq 1+\frac{\sqrt{\log N}}{{9}}$. If a load-balancing algorithm guarantees ![]() $A_1(s)\leq \frac{1}{\sqrt{N}\,}$ for any
$A_1(s)\leq \frac{1}{\sqrt{N}\,}$ for any ![]() $s \in \mathbb S$ such that
$s \in \mathbb S$ such that ![]() $s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, then for any integers N and r such that
$s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, then for any integers N and r such that ![]() $\smash{N\geq \big(\frac{{4}{\bar k}\log N}{\gamma}\big)^{\frac{1}{^{0.5-\alpha} }}}$ and
$\smash{N\geq \big(\frac{{4}{\bar k}\log N}{\gamma}\big)^{\frac{1}{^{0.5-\alpha} }}}$ and ![]() $1\leq r\leq {\frac{\log N}{72 (b-1)^2}}$, the following bound holds at steady state:
$1\leq r\leq {\frac{\log N}{72 (b-1)^2}}$, the following bound holds at steady state:
 \begin{align*}\mathbb{E}\Bigg[\Bigg(\max\Bigg\{\sum_{i=1}^{b} S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\Bigg\}\Bigg)^r\Bigg]\leq 10\Bigg(\frac{5r(b-1)}{\sqrt{N}\log N}\Bigg)^r,\end{align*}
\begin{align*}\mathbb{E}\Bigg[\Bigg(\max\Bigg\{\sum_{i=1}^{b} S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\Bigg\}\Bigg)^r\Bigg]\leq 10\Bigg(\frac{5r(b-1)}{\sqrt{N}\log N}\Bigg)^r,\end{align*}
where ![]() ${\bar k = 1+\frac{1}{2(b-1)}}$.
${\bar k = 1+\frac{1}{2(b-1)}}$.
Note that the expectation in Theorem 2.1 is with respect to the stationary distribution of the CTMC (![]() $S(t)\,{:}\,t\geq 0$) according to the definition of S. The condition
$S(t)\,{:}\,t\geq 0$) according to the definition of S. The condition ![]() $A_1(s)\leq \frac{1}{\sqrt{N}\,}$ when
$A_1(s)\leq \frac{1}{\sqrt{N}\,}$ when ![]() $\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$ requires the following: for any given state s in which at least the fraction
$\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$ requires the following: for any given state s in which at least the fraction ![]() $\frac{\gamma}{N^{\alpha}}-\frac{{\bar k}\log N}{\sqrt{N}}$ of servers are idle, an incoming job should be routed to an idle server with probability at least
$\frac{\gamma}{N^{\alpha}}-\frac{{\bar k}\log N}{\sqrt{N}}$ of servers are idle, an incoming job should be routed to an idle server with probability at least ![]() $\smash{1-\frac{1}{\sqrt{N}\,}}$. Note that
$\smash{1-\frac{1}{\sqrt{N}\,}}$. Note that ![]() $\smash{N\geq \left(\frac{{4}{\bar k}\log N}{\gamma}\right)^{\frac{1}{^{0.5-\alpha} }}}$ implies
$\smash{N\geq \left(\frac{{4}{\bar k}\log N}{\gamma}\right)^{\frac{1}{^{0.5-\alpha} }}}$ implies ![]() $\smash{\frac{\gamma}{N^\alpha} \geq \frac{4{\bar k}\log N}{\sqrt{N}}}$, which guarantee that
$\smash{\frac{\gamma}{N^\alpha} \geq \frac{4{\bar k}\log N}{\sqrt{N}}}$, which guarantee that ![]() $\lambda+\frac{{\bar k}\log N}{\sqrt{N}} < 1$ and
$\lambda+\frac{{\bar k}\log N}{\sqrt{N}} < 1$ and ![]() $\frac{\gamma}{N^{\alpha}} > \frac{{\bar k}\log N}{\sqrt{N}}$. There are several well-known policies that satisfy this condition:
$\frac{\gamma}{N^{\alpha}} > \frac{{\bar k}\log N}{\sqrt{N}}$. There are several well-known policies that satisfy this condition:
• JSQ routes an incoming job to the least-loaded server in the system, so
 $A_1(s)=0$ when
$A_1(s)=0$ when  $\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.
$\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.• I1F routes an incoming job to an idle server, if available, or to a server with one job, if available. Otherwise, the job is routed to a randomly selected server. Therefore,
 $A_1(s)=0$ when
$A_1(s)=0$ when  $s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$.
$s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$.• JIQ routes an incoming job to an idle server if possible; otherwise, it routes the job to a server chosen uniformly at random. Therefore,
 $A_1(s)=0$ when
$A_1(s)=0$ when  $\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.
$\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.• Pod samples d servers uniformly at random and dispatches the job to the least-loaded server among the d servers. Ties are broken uniformly at random. Given
 $d \geq \frac{{r}}{\gamma}N^\alpha\log N,$
$d \geq \frac{{r}}{\gamma}N^\alpha\log N,$ $\smash{A_1(s)\leq \frac{1}{\sqrt{N}\,}}$ when
$\smash{A_1(s)\leq \frac{1}{\sqrt{N}\,}}$ when  $\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.
$\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$.
A direct consequence of Theorem 2.1 is asymptotic zero waiting (![]() $N \to \infty$) at steady state. Let
$N \to \infty$) at steady state. Let ![]() $\mathcal W$ denote the event that an incoming job is routed to a busy server, and
$\mathcal W$ denote the event that an incoming job is routed to a busy server, and ![]() $p_{\mathcal W}$ denote the probability of this event at steady state. Let
$p_{\mathcal W}$ denote the probability of this event at steady state. Let ![]() $\mathcal B$ denote the event that an incoming job is blocked (discarded) and
$\mathcal B$ denote the event that an incoming job is blocked (discarded) and ![]() $p_{\mathcal B}$ denote the probability of this event at steady state. Note that
$p_{\mathcal B}$ denote the probability of this event at steady state. Note that ![]() ${\mathcal B}\subseteq {\mathcal W}$, because an incoming job is blocked when being routed to a busy server with b jobs. Furthermore, let W denote the waiting time of jobs that are not blocked at steady state. We have the following results based on the main theorem.
${\mathcal B}\subseteq {\mathcal W}$, because an incoming job is blocked when being routed to a busy server with b jobs. Furthermore, let W denote the waiting time of jobs that are not blocked at steady state. We have the following results based on the main theorem.
Corollary 2.1. Assume ![]() $\lambda=1-\gamma N^{-\alpha}$ for
$\lambda=1-\gamma N^{-\alpha}$ for ![]() $0<\alpha<0.5$ and
$0<\alpha<0.5$ and ![]() $\gamma >0,$ and
$\gamma >0,$ and ![]() $b \leq 1+ \frac{\sqrt{\log N}}{{9}}$. If a load-balancing algorithm guarantees
$b \leq 1+ \frac{\sqrt{\log N}}{{9}}$. If a load-balancing algorithm guarantees ![]() $A_1(s)\leq \frac{1}{N^{0.5r}}$ for any
$A_1(s)\leq \frac{1}{N^{0.5r}}$ for any ![]() $s \in \mathbb S$ such that
$s \in \mathbb S$ such that ![]() $\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$, then the following results hold for any integers N and r such that
$\smash{s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}}$, then the following results hold for any integers N and r such that ![]() $\smash{N \geq \big(\frac{{4}{\bar k}\log N}{\gamma}\big)^{\frac{1}{0.5-\alpha}}}$ and
$\smash{N \geq \big(\frac{{4}{\bar k}\log N}{\gamma}\big)^{\frac{1}{0.5-\alpha}}}$ and ![]() $1\leq r\leq \frac{\log N}{72(b-1)^2}$ at steady state:
$1\leq r\leq \frac{\log N}{72(b-1)^2}$ at steady state:
 \begin{equation}{Number\ of\ buffered\ jobs\ per\ server:}\quad \mathbb{E}\left[\sum_{i=2}^b S_i\right]\leq \frac{11\lambda b + 11}{{\gamma^r}N^{r(0.5-\alpha)}}. \end{equation}
\begin{equation}{Number\ of\ buffered\ jobs\ per\ server:}\quad \mathbb{E}\left[\sum_{i=2}^b S_i\right]\leq \frac{11\lambda b + 11}{{\gamma^r}N^{r(0.5-\alpha)}}. \end{equation} The proof of this corollary is an application of the Markov inequality and Little’s law, and can be found in Section 4. We note that the corollary above requires ![]() $A_1(s)\leq \frac{1}{N^{0.5 r}}$ for any
$A_1(s)\leq \frac{1}{N^{0.5 r}}$ for any ![]() $s \in \mathbb S$ such that
$s \in \mathbb S$ such that ![]() $s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, which is more restrictive than the assumption in the theorem that only requires
$s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, which is more restrictive than the assumption in the theorem that only requires ![]() $A_1(s)\leq \frac{1}{\sqrt{N}\,}$ for the same s. However, it is easy to verify that JSQ, I1F, JIQ, and Pod with
$A_1(s)\leq \frac{1}{\sqrt{N}\,}$ for the same s. However, it is easy to verify that JSQ, I1F, JIQ, and Pod with ![]() $d\geq \frac{r}{\gamma}N^\alpha \log N$ also satisfy this condition. We further remark that the probability of waiting and the expected waiting time are both
$d\geq \frac{r}{\gamma}N^\alpha \log N$ also satisfy this condition. We further remark that the probability of waiting and the expected waiting time are both ![]() $O\big(\frac{{b}}{N^{r(0.5-\alpha)}}\big)$. Under the assumption that
$O\big(\frac{{b}}{N^{r(0.5-\alpha)}}\big)$. Under the assumption that ![]() $b=O\big(\sqrt{\log N}\big)$ for any positive integer r, we can find a sufficiently large N such that r satisfies the condition in the corollary. The significance of this is that it implies that the waiting probability and the mean waiting time decay faster than any polynomial function of
$b=O\big(\sqrt{\log N}\big)$ for any positive integer r, we can find a sufficiently large N such that r satisfies the condition in the corollary. The significance of this is that it implies that the waiting probability and the mean waiting time decay faster than any polynomial function of ![]() $1/N$ in the sub-Halfin–Whitt regime. Furthermore, from (2), we have
$1/N$ in the sub-Halfin–Whitt regime. Furthermore, from (2), we have
 \begin{equation*}\mathbb{E}\Bigg[\sum_{i=2}^b NS_i\Bigg]\leq \frac{11\lambda b + 11}{{\gamma^r}N^{r(0.5-\alpha)-1}}.\end{equation*}
\begin{equation*}\mathbb{E}\Bigg[\sum_{i=2}^b NS_i\Bigg]\leq \frac{11\lambda b + 11}{{\gamma^r}N^{r(0.5-\alpha)-1}}.\end{equation*}
Note that ![]() $\sum_{i=2}^b NS_i$ is the total number of jobs in the buffers at steady state, so our result shows that, for sufficiently large N, not only is the expected number of buffered jobs per server almost zero, but so also is the total number of buffered jobs in all N servers.
$\sum_{i=2}^b NS_i$ is the total number of jobs in the buffers at steady state, so our result shows that, for sufficiently large N, not only is the expected number of buffered jobs per server almost zero, but so also is the total number of buffered jobs in all N servers.
3. Proof of Theorem 2.1
In this section, we present the proof, based on Stein’s method, of our main theorem. As modularized in [Reference Braverman and Dai4], this approach includes three key ingredients: generator approximation, gradient bounds, and state space collapse (SSC).
3.1. Generator approximation
Define ![]() $e_i \in \mathbb R^b$ to be a b-dimensional vector such that the ith entry is
$e_i \in \mathbb R^b$ to be a b-dimensional vector such that the ith entry is ![]() $1/N$ and all other
$1/N$ and all other ![]() $b-1$ entries are zero. Furthermore, define
$b-1$ entries are zero. Furthermore, define ![]() $A_i(s)$ to be the probability that an incoming job is routed to a server with at least i jobs when the system is in state s, i.e.
$A_i(s)$ to be the probability that an incoming job is routed to a server with at least i jobs when the system is in state s, i.e.
From this definition, we have ![]() $A_0(s)=1$. Given the definition above, the CTMC transits from state s to
$A_0(s)=1$. Given the definition above, the CTMC transits from state s to ![]() $s+e_i$ with rate
$s+e_i$ with rate ![]() $\lambda N\left(A_{i-1}(s)-A_i(s)\right)$, which occurs when an arrival comes and is routed to a server with
$\lambda N\left(A_{i-1}(s)-A_i(s)\right)$, which occurs when an arrival comes and is routed to a server with ![]() $i-1$ jobs, and transits from state s to
$i-1$ jobs, and transits from state s to ![]() $s-e_i$ with rate
$s-e_i$ with rate ![]() $N(s_i-s_{i+1})$, which occurs when a job leaves a server with i jobs.
$N(s_i-s_{i+1})$, which occurs when a job leaves a server with i jobs.
Let G be the generator of the CTMC (![]() $S(t)\,{:}\,t\geq 0$). Given a function
$S(t)\,{:}\,t\geq 0$). Given a function ![]() $f\,{:}\, \mathbb S \to \mathbb R$, we have
$f\,{:}\, \mathbb S \to \mathbb R$, we have
 \begin{align*}G f(s) = & \sum_{i=1}^{b} \left(\lambda N (A_{i-1}(s)-A_i(s)) (\,f(s + e_i) - f(s)) \right.\nonumber\\[5pt]
& + N (s_i - s_{i+1}) (\,f(s - e_i)-f(s))). \end{align*}
\begin{align*}G f(s) = & \sum_{i=1}^{b} \left(\lambda N (A_{i-1}(s)-A_i(s)) (\,f(s + e_i) - f(s)) \right.\nonumber\\[5pt]
& + N (s_i - s_{i+1}) (\,f(s - e_i)-f(s))). \end{align*}
For any bounded function ![]() $f\,{:}\, \mathbb S \to \mathbb R$ we have
$f\,{:}\, \mathbb S \to \mathbb R$ we have ![]() $\mathbb{E}[ G f(S) ] = 0$, which can be easily verified by using the global balance equations and the fact that S represents the steady state of the CTMC.
$\mathbb{E}[ G f(S) ] = 0$, which can be easily verified by using the global balance equations and the fact that S represents the steady state of the CTMC.
To understand the steady-state performance of a load-balancing algorithm, we will establish moment bounds on the following function:
 \begin{equation*}\max\left\{\sum_{i=1}^b S_i-\lambda-\frac{k \log N}{\sqrt{N}},0\right\},\end{equation*}
\begin{equation*}\max\left\{\sum_{i=1}^b S_i-\lambda-\frac{k \log N}{\sqrt{N}},0\right\},\end{equation*}
where ![]() $\smash{\bar k-\frac{r}{\sqrt{N}\log N}\leq k \leq \bar k.}$ The moment bounds are used to bound the probability that the total number of jobs in the system
$\smash{\bar k-\frac{r}{\sqrt{N}\log N}\leq k \leq \bar k.}$ The moment bounds are used to bound the probability that the total number of jobs in the system ![]() $\big(N\sum_{i=1}^b S_i\big)$ exceeds
$\big(N\sum_{i=1}^b S_i\big)$ exceeds ![]() $N\lambda+k\sqrt{N}\log N$ at steady state, and can also be used to bound the probability that an incoming job is routed to an idle server in Corollary 2.1.
$N\lambda+k\sqrt{N}\log N$ at steady state, and can also be used to bound the probability that an incoming job is routed to an idle server in Corollary 2.1.
We consider a simple fluid system with arrival rate ![]() $\lambda$ and departure rate
$\lambda$ and departure rate ![]() $\lambda+\frac{\log N}{\sqrt{N}}$, i.e.
$\lambda+\frac{\log N}{\sqrt{N}}$, i.e.
and a function g(x) which is the solution of the following Stein’s equation [Reference Ying21]:
 \begin{align}g'(x) \Bigg(-\frac{\log N}{\sqrt{N}}\Bigg) = \Bigg(\max\Bigg\{x-\lambda-\frac{k \log N}{\sqrt{N}},0\Bigg\}\Bigg)^r \quad \text{for all } x, \end{align}
\begin{align}g'(x) \Bigg(-\frac{\log N}{\sqrt{N}}\Bigg) = \Bigg(\max\Bigg\{x-\lambda-\frac{k \log N}{\sqrt{N}},0\Bigg\}\Bigg)^r \quad \text{for all } x, \end{align}
where ![]() $g'(x) = \frac{{\textrm d} g(x)}{{\textrm d} x}$ and r is a positive integer. The left-hand side of (3) is applying the generator of the simple fluid system to the function g(x), i.e.
$g'(x) = \frac{{\textrm d} g(x)}{{\textrm d} x}$ and r is a positive integer. The left-hand side of (3) is applying the generator of the simple fluid system to the function g(x), i.e.
It is easy to verify that the solution to (3) is
and
We note that the simple fluid system is a one-dimensional system and the stochastic system is b dimensional. In order to couple these two systems, we define
 \begin{equation}f(s)=g\left(\sum_{i=1}^b s_i\right),\end{equation}
\begin{equation}f(s)=g\left(\sum_{i=1}^b s_i\right),\end{equation}and use this f(s) in Stein’s method.
Since ![]() $\sum_{i=1}^b s_i\leq b$ for
$\sum_{i=1}^b s_i\leq b$ for ![]() $s\in \mathbb{S},$f(s) is bounded for
$s\in \mathbb{S},$f(s) is bounded for ![]() $s\in\mathbb{S}.$ So,
$s\in\mathbb{S}.$ So,
 \begin{equation}\mathbb{E}[Gf(S)]=E\left[Gg\left(\sum_{i=1}^b S_i\right)\right]=0.\end{equation}
\begin{equation}\mathbb{E}[Gf(S)]=E\left[Gg\left(\sum_{i=1}^b S_i\right)\right]=0.\end{equation}Now define
Based on (3) and (7), we obtain
 \begin{align}\mathbb{E}\Bigg[{h^r_k}\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg] &= \mathbb{E}\Bigg[ g'\Bigg(\sum_{i=1}^b S_i\Bigg) \Bigg(-\frac{\log N}{\sqrt{N}}\Bigg) - Gg\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg].\end{align}
\begin{align}\mathbb{E}\Bigg[{h^r_k}\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg] &= \mathbb{E}\Bigg[ g'\Bigg(\sum_{i=1}^b S_i\Bigg) \Bigg(-\frac{\log N}{\sqrt{N}}\Bigg) - Gg\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg].\end{align} Note that, according to the definitions of f(s) in (6) and ![]() $e_j$, we have
$e_j$, we have
 \begin{equation*}f(s+e_j)=g\Bigg(\sum_{i=1}^b s_i+\frac{1}{N}\Bigg)\end{equation*}
\begin{equation*}f(s+e_j)=g\Bigg(\sum_{i=1}^b s_i+\frac{1}{N}\Bigg)\end{equation*}and
 \begin{equation*}f(s-e_j)=g\Bigg(\sum_{i=1}^b s_i-\frac{1}{N}\Bigg)\end{equation*}
\begin{equation*}f(s-e_j)=g\Bigg(\sum_{i=1}^b s_i-\frac{1}{N}\Bigg)\end{equation*}
for any ![]() $1\leq j \leq b.$ Therefore,
$1\leq j \leq b.$ Therefore,
 \begin{align*}Gg\Bigg(\sum_{i=1}^b s_i\Bigg)&=N\lambda(1-A_b(s))\Bigg(g\Bigg(\sum_{i=1}^b s_i+\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b s_i\Bigg)\Bigg)\\& \quad + Ns_1\Bigg(g\Bigg(\sum_{i=1}^b s_i-\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b s_i\Bigg)\Bigg).\end{align*}
\begin{align*}Gg\Bigg(\sum_{i=1}^b s_i\Bigg)&=N\lambda(1-A_b(s))\Bigg(g\Bigg(\sum_{i=1}^b s_i+\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b s_i\Bigg)\Bigg)\\& \quad + Ns_1\Bigg(g\Bigg(\sum_{i=1}^b s_i-\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b s_i\Bigg)\Bigg).\end{align*}Substituting the equation above into (8), we have
 \begin{align}& \mathbb{E}\Bigg[h^r_k\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg]\nonumber\\
& \quad= \mathbb{E}\Bigg[g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(-\frac{\log N}{\sqrt{N}}\Bigg)-N\lambda(1-A_b(S))\Bigg(g\Bigg(\sum_{i=1}^b S_i+\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg) \nonumber\\
& \qquad\qquad\qquad\qquad\qquad\qquad\quad -NS_1\Bigg(g\Bigg(\sum_{i=1}^b S_i-\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg)\Bigg]. \end{align}
\begin{align}& \mathbb{E}\Bigg[h^r_k\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg]\nonumber\\
& \quad= \mathbb{E}\Bigg[g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(-\frac{\log N}{\sqrt{N}}\Bigg)-N\lambda(1-A_b(S))\Bigg(g\Bigg(\sum_{i=1}^b S_i+\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg) \nonumber\\
& \qquad\qquad\qquad\qquad\qquad\qquad\quad -NS_1\Bigg(g\Bigg(\sum_{i=1}^b S_i-\frac{1}{N}\Bigg)-g\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg)\Bigg]. \end{align} Let ![]() $\eta = \lambda +\frac{k\log N}{\sqrt{N}}$ to simplify the notation. From the closed forms of g and g' in (4) and (5), note that, for any
$\eta = \lambda +\frac{k\log N}{\sqrt{N}}$ to simplify the notation. From the closed forms of g and g' in (4) and (5), note that, for any ![]() $x < \eta$,
$x < \eta$, ![]() $g(x) = g'\left(x\right)=0$. Also note that when
$g(x) = g'\left(x\right)=0$. Also note that when ![]() $x>\eta+\frac{1}{N}$,
$x>\eta+\frac{1}{N}$,
so for ![]() $x>\eta+\frac{1}{N},$
$x>\eta+\frac{1}{N},$
By using the mean-value theorem in the region ![]() $\big[\eta-\frac{1}{N}, \eta+\frac{1}{N}\big]$ and Taylor’s theorem in the region
$\big[\eta-\frac{1}{N}, \eta+\frac{1}{N}\big]$ and Taylor’s theorem in the region ![]() $\big(\eta+\frac{1}{N}, \infty\big)$, we have
$\big(\eta+\frac{1}{N}, \infty\big)$, we have
 \begin{align}g\Big(x+\frac{1}{N}\Big)-g(x) & = \Big(g\Big(x+\frac{1}{N}\Big)-g(x)\Big) \Big(\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \textbf{1}_{ x > \eta+\frac{1}{N}} \Big) \nonumber\\[5pt]
& = \frac{g'(\xi)}{N}\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \left(\frac{g'(x)}{N} + \frac{g''(\zeta)}{2N^2}\right) \textbf{1}_{ x > \eta+\frac{1}{N}} , \end{align}
\begin{align}g\Big(x+\frac{1}{N}\Big)-g(x) & = \Big(g\Big(x+\frac{1}{N}\Big)-g(x)\Big) \Big(\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \textbf{1}_{ x > \eta+\frac{1}{N}} \Big) \nonumber\\[5pt]
& = \frac{g'(\xi)}{N}\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \left(\frac{g'(x)}{N} + \frac{g''(\zeta)}{2N^2}\right) \textbf{1}_{ x > \eta+\frac{1}{N}} , \end{align} \begin{align}g\Big(x-\frac{1}{N}\Big)-g(x) & = \Big(g\Big(x-\frac{1}{N}\Big)-g(x)\Big) \Big(\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \textbf{1}_{ x > \eta+\frac{1}{N}} \Big) \nonumber\\[5pt]
& = -\frac{g'(\tilde{\xi})}{N}\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \Big(-\frac{g'(x)}{N} + \frac{g''(\tilde{\zeta})}{2N^2}\Big) \textbf{1}_{ x > \eta+\frac{1}{N}} , \end{align}
\begin{align}g\Big(x-\frac{1}{N}\Big)-g(x) & = \Big(g\Big(x-\frac{1}{N}\Big)-g(x)\Big) \Big(\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \textbf{1}_{ x > \eta+\frac{1}{N}} \Big) \nonumber\\[5pt]
& = -\frac{g'(\tilde{\xi})}{N}\textbf{1}_{\eta-\frac{1}{N} \leq x \leq \eta+\frac{1}{N}} + \Big(-\frac{g'(x)}{N} + \frac{g''(\tilde{\zeta})}{2N^2}\Big) \textbf{1}_{ x > \eta+\frac{1}{N}} , \end{align}
where ![]() $\xi, \zeta \in \big(x,x+\frac{1}{N}\big)$ and
$\xi, \zeta \in \big(x,x+\frac{1}{N}\big)$ and ![]() $\tilde{\xi}, \tilde{\zeta} \in \big(x-\frac{1}{N},x\big)$. Substituting (10) and (11) into the generator difference in (9), we have
$\tilde{\xi}, \tilde{\zeta} \in \big(x-\frac{1}{N},x\big)$. Substituting (10) and (11) into the generator difference in (9), we have
 \begin{align}\hspace*{-90pt}\mathbb{E}&\Bigg[h^r_k\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg]\nonumber\\[5pt]
& = \mathbb{E}\Bigg[g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(\lambda A_b(S)- \lambda-\frac{\log N}{\sqrt{N}}+S_1\Bigg)\textbf{1}_{\sum_{i=1}^b S_i> \eta +\frac{1}{N}}\Bigg] \hspace*{90pt}\end{align}
\begin{align}\hspace*{-90pt}\mathbb{E}&\Bigg[h^r_k\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg]\nonumber\\[5pt]
& = \mathbb{E}\Bigg[g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(\lambda A_b(S)- \lambda-\frac{\log N}{\sqrt{N}}+S_1\Bigg)\textbf{1}_{\sum_{i=1}^b S_i> \eta +\frac{1}{N}}\Bigg] \hspace*{90pt}\end{align} \begin{align}&\quad + \mathbb{E}\Bigg[\Bigg(g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(-\frac{\log N}{\sqrt{N}}\Bigg)-\lambda(1-A_b(S))g'(\xi) + S_1g'(\tilde{\xi})\Bigg)\textbf{1}_{\eta-\frac{1}{N} \leq \sum_{i=1}^b S_i \leq \eta+\frac{1}{N}}\Bigg] \end{align}
\begin{align}&\quad + \mathbb{E}\Bigg[\Bigg(g'\Bigg(\sum_{i=1}^b S_i\Bigg)\Bigg(-\frac{\log N}{\sqrt{N}}\Bigg)-\lambda(1-A_b(S))g'(\xi) + S_1g'(\tilde{\xi})\Bigg)\textbf{1}_{\eta-\frac{1}{N} \leq \sum_{i=1}^b S_i \leq \eta+\frac{1}{N}}\Bigg] \end{align}
Note that in (12) and (14), ![]() $\xi,\zeta \in \Big(\sum_{i=1}^b S_i,\sum_{i=1}^b S_i+\frac{1}{N}\Big)$ and
$\xi,\zeta \in \Big(\sum_{i=1}^b S_i,\sum_{i=1}^b S_i+\frac{1}{N}\Big)$ and ![]() $\tilde{\xi},\tilde{\zeta}\in \Big(\sum_{i=1}^b S_i-\frac{1}{N},\break \sum_{i=1}^b S_i\Big)$ are random variables whose values depend on
$\tilde{\xi},\tilde{\zeta}\in \Big(\sum_{i=1}^b S_i-\frac{1}{N},\break \sum_{i=1}^b S_i\Big)$ are random variables whose values depend on ![]() $\sum_{i=1}^b S_i.$ We do not include
$\sum_{i=1}^b S_i.$ We do not include ![]() $\sum_{i=1}^b S_i$ in the notation for simplicity.
$\sum_{i=1}^b S_i$ in the notation for simplicity.
Next, we study g' and g'' to bound the terms in (13) and (14), and SSC to bound the term in (12).
3.2. Gradient bounds
We summarize the bounds on g' and g'' in the following two lemmas.
Lemma 3.1. For any ![]() $x\in\left[ \lambda +\frac{k\log N}{\sqrt{N}} -\frac{2}{N}, \lambda +\frac{k\log N}{\sqrt{N}} +\frac{2}{N}\right]$, we have
$x\in\left[ \lambda +\frac{k\log N}{\sqrt{N}} -\frac{2}{N}, \lambda +\frac{k\log N}{\sqrt{N}} +\frac{2}{N}\right]$, we have
Proof. For any ![]() $x\in\left[ \lambda +\frac{k\log N}{\sqrt{N}} -\frac{2}{N}, \lambda +\frac{k\log N}{\sqrt{N}} +\frac{2}{N}\right]$, from the closed-form expression of g' in (5) we have
$x\in\left[ \lambda +\frac{k\log N}{\sqrt{N}} -\frac{2}{N}, \lambda +\frac{k\log N}{\sqrt{N}} +\frac{2}{N}\right]$, from the closed-form expression of g' in (5) we have
Lemma 3.2. For ![]() $x>\lambda +\frac{k\log N}{\sqrt{N}}$, we have
$x>\lambda +\frac{k\log N}{\sqrt{N}}$, we have
Proof. For ![]() $x> \lambda +\frac{k\log N}{\sqrt{N}},$ we have
$x> \lambda +\frac{k\log N}{\sqrt{N}},$ we have
 \begin{equation*}g'(x)=\frac{\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r}{-\frac{\log N}{\sqrt{N}}},\end{equation*}
\begin{equation*}g'(x)=\frac{\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r}{-\frac{\log N}{\sqrt{N}}},\end{equation*}which implies
 \begin{eqnarray*}g''(x)= \frac{r\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^{r-1}}{-\frac{\log N}{\sqrt{N}}} \end{eqnarray*}
\begin{eqnarray*}g''(x)= \frac{r\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^{r-1}}{-\frac{\log N}{\sqrt{N}}} \end{eqnarray*}and
 \begin{equation*}\hspace*{27pt}|g''(x)|=\left|\frac{r\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^{r-1}}{-\frac{\log N}{\sqrt{N}}}\right|\leq\frac{r\sqrt{N}}{\log{N}}\left(\max\left\{x-\lambda -\frac{k\log N}{\sqrt{N}}, 0\right\}\right)^{r-1}. \hspace*{27pt}{\square}\end{equation*}
\begin{equation*}\hspace*{27pt}|g''(x)|=\left|\frac{r\left(x-\lambda -\frac{k\log N}{\sqrt{N}}\right)^{r-1}}{-\frac{\log N}{\sqrt{N}}}\right|\leq\frac{r\sqrt{N}}{\log{N}}\left(\max\left\{x-\lambda -\frac{k\log N}{\sqrt{N}}, 0\right\}\right)^{r-1}. \hspace*{27pt}{\square}\end{equation*}Based on Lemma 3.1, we bound the term (13):
 \begin{align} & \mathbb{E}\Bigg[\Bigg(g'\left(\sum_{i=1}^b S_i\right)\left(-\frac{\log N}{\sqrt{N}}\right)-\lambda(1-A_b(S))g'(\xi) + S_1g'(\tilde{\xi})\Bigg)\textbf{1}_{\eta-\frac{1}{N} \leq \sum_{i=1}^b S_i \leq \eta+\frac{1}{N}}\Bigg]\nonumber\\[5pt]
& \qquad\qquad\qquad\leq \left(\lambda+\frac{\log N}{\sqrt{N}}+1\right)\frac{2^r}{N^{r-0.5}\log N} \leq \frac{2^{r+1}}{N^{r-0.5}\log N}, \end{align}
\begin{align} & \mathbb{E}\Bigg[\Bigg(g'\left(\sum_{i=1}^b S_i\right)\left(-\frac{\log N}{\sqrt{N}}\right)-\lambda(1-A_b(S))g'(\xi) + S_1g'(\tilde{\xi})\Bigg)\textbf{1}_{\eta-\frac{1}{N} \leq \sum_{i=1}^b S_i \leq \eta+\frac{1}{N}}\Bigg]\nonumber\\[5pt]
& \qquad\qquad\qquad\leq \left(\lambda+\frac{\log N}{\sqrt{N}}+1\right)\frac{2^r}{N^{r-0.5}\log N} \leq \frac{2^{r+1}}{N^{r-0.5}\log N}, \end{align}
where ![]() $\lambda+\frac{\log N}{\sqrt{N}} \leq 1$ in the first inequality according to the assumption
$\lambda+\frac{\log N}{\sqrt{N}} \leq 1$ in the first inequality according to the assumption ![]() $N \geq \left(\frac{4{\bar k}\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ in Theorem 2.1.
$N \geq \left(\frac{4{\bar k}\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ in Theorem 2.1.
Based on Lemma 3.2, we bound the term (14):
 \begin{align}& -\mathbb{E}\left[\frac{1}{2N}(\lambda(1-A_b(S))g''(\zeta) + S_1g''(\tilde{\zeta}))\textbf{1}_{ \sum_{i=1}^b S_i > \eta+\frac{1}{N}}\right]\nonumber\\[5pt]
& \qquad\qquad\qquad \leq \mathbb{E}\left[\frac{1}{2N}(\lambda|g''(\zeta)| + S_1|g''(\tilde{\zeta})|)\textbf{1}_{ \sum_{i=1}^b S_i > \eta+\frac{1}{N}}\right] \leq \frac{r \mathbb{E}\left[{h^{r-1}_k}\left(\sum_{i=1}^b S_i +{\frac{1}{N}}\right)\right]}{\sqrt{N}\log N}. \end{align}
\begin{align}& -\mathbb{E}\left[\frac{1}{2N}(\lambda(1-A_b(S))g''(\zeta) + S_1g''(\tilde{\zeta}))\textbf{1}_{ \sum_{i=1}^b S_i > \eta+\frac{1}{N}}\right]\nonumber\\[5pt]
& \qquad\qquad\qquad \leq \mathbb{E}\left[\frac{1}{2N}(\lambda|g''(\zeta)| + S_1|g''(\tilde{\zeta})|)\textbf{1}_{ \sum_{i=1}^b S_i > \eta+\frac{1}{N}}\right] \leq \frac{r \mathbb{E}\left[{h^{r-1}_k}\left(\sum_{i=1}^b S_i +{\frac{1}{N}}\right)\right]}{\sqrt{N}\log N}. \end{align}3.3. State space collapse
In this section we consider the term in (12):
 \begin{align}\mathbb{E}&\left[g'\left(\sum_{i=1}^{b} S_i\right)\left(\lambda A_b(S)-\lambda-\frac{\log N}{\sqrt{N}} +S_1\right) \textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta + \frac{1}{N}}\right]\nonumber\\[8pt]
& = \mathbb{E}\Bigg[-\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda A_b(S)-\lambda- \frac{\log N}{\sqrt{N}} + S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta+ \frac{1}{N}}\Bigg] \nonumber\displaybreak\\
& = \mathbb{E}\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda+ \frac{\log N}{\sqrt{N}} - S_1-\lambda A_b(S)\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta + \frac{1}{N}}\right] \nonumber\\[5pt]
& \leq \mathbb{E}\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda+ \frac{\log N}{\sqrt{N}} - S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta+\frac{1}{N}}\right] , \end{align}
\begin{align}\mathbb{E}&\left[g'\left(\sum_{i=1}^{b} S_i\right)\left(\lambda A_b(S)-\lambda-\frac{\log N}{\sqrt{N}} +S_1\right) \textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta + \frac{1}{N}}\right]\nonumber\\[8pt]
& = \mathbb{E}\Bigg[-\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda A_b(S)-\lambda- \frac{\log N}{\sqrt{N}} + S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta+ \frac{1}{N}}\Bigg] \nonumber\displaybreak\\
& = \mathbb{E}\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda+ \frac{\log N}{\sqrt{N}} - S_1-\lambda A_b(S)\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta + \frac{1}{N}}\right] \nonumber\\[5pt]
& \leq \mathbb{E}\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda-\frac{k\log N}{\sqrt{N}} \right)^r\left(\lambda+ \frac{\log N}{\sqrt{N}} - S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta+\frac{1}{N}}\right] , \end{align}where the last inequality holds because
 \begin{equation*}\left(\sum_{i=1}^{b} s_i-\lambda-\frac{k\log N}{\sqrt{N}}\right)^r\textbf{1}_{\sum_{i=1}^{b} s_i \gt \eta + \frac{1}{N}}\geq 0\end{equation*}
\begin{equation*}\left(\sum_{i=1}^{b} s_i-\lambda-\frac{k\log N}{\sqrt{N}}\right)^r\textbf{1}_{\sum_{i=1}^{b} s_i \gt \eta + \frac{1}{N}}\geq 0\end{equation*}
for any ![]() $s \in \mathbb S$.
$s \in \mathbb S$.
We define a Lyapunov function ![]() $V\,{:}\,\mathbb S \to \mathbb R$ to be
$V\,{:}\,\mathbb S \to \mathbb R$ to be
 \begin{align}V(s)=\min\left\{\sum_{i=2}^{b} s_i, \lambda+\frac{k\log N}{\sqrt{N}} -s_1 \right\}. \end{align}
\begin{align}V(s)=\min\left\{\sum_{i=2}^{b} s_i, \lambda+\frac{k\log N}{\sqrt{N}} -s_1 \right\}. \end{align}Lemma 3.3. Under any load-balancing algorithm such that ![]() $A_1(s)\leq \frac{1}{\sqrt{N}\,}$ when
$A_1(s)\leq \frac{1}{\sqrt{N}\,}$ when ![]() $s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, we have, for
$s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, we have, for ![]() $N \geq \left(\frac{{4}{\bar k}\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$, that
$N \geq \left(\frac{{4}{\bar k}\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$, that
for any state ![]() $s \in \mathbb S$ such that
$s \in \mathbb S$ such that ![]() $V(s)\geq \frac{\log N}{\sqrt{N}}$.
$V(s)\geq \frac{\log N}{\sqrt{N}}$.
Proof. For the Lyapunov function defined in (18), the Lyapunov drift is
 \begin{align*}\triangledown V(s)&=\mathbb{E}\left[GV(S) \mid S=s\right]\\& = \sum_{i=1}^{b}\left(\lambda N (A_{i-1}(s)-A_i(s)) (V(s + e_i) - V(s)) + N (s_i - s_{i+1}) (V(s - e_i)-V(s))\right). \end{align*}
\begin{align*}\triangledown V(s)&=\mathbb{E}\left[GV(S) \mid S=s\right]\\& = \sum_{i=1}^{b}\left(\lambda N (A_{i-1}(s)-A_i(s)) (V(s + e_i) - V(s)) + N (s_i - s_{i+1}) (V(s - e_i)-V(s))\right). \end{align*}
Given ![]() $V(s)\geq \frac{\log N}{\sqrt{N}}$, we consider the following two cases.
$V(s)\geq \frac{\log N}{\sqrt{N}}$, we consider the following two cases.
Case 1: Assume ![]() $\sum_{i=2}^{b} s_i\leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1$. Note that
$\sum_{i=2}^{b} s_i\leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1$. Note that
 \begin{alignat*}{2}V(s+e_1) & \leq \sum_{i=2}^{b} s_i, & V(s-e_1) & = \sum_{i=2}^{b} s_i,\\V(s+e_j) & \leq \sum_{i=2}^{b} s_i+\frac{1}{N}, \qquad & V(s-e_j) & = \sum_{i=2}^{b} s_i - \frac{1}{N}, \quad \text{for all } 2 \leq j \leq b.\end{alignat*}
\begin{alignat*}{2}V(s+e_1) & \leq \sum_{i=2}^{b} s_i, & V(s-e_1) & = \sum_{i=2}^{b} s_i,\\V(s+e_j) & \leq \sum_{i=2}^{b} s_i+\frac{1}{N}, \qquad & V(s-e_j) & = \sum_{i=2}^{b} s_i - \frac{1}{N}, \quad \text{for all } 2 \leq j \leq b.\end{alignat*}
Furthermore, ![]() $V(s)=\sum_{i=2}^{b} s_i\geq \frac{\log N}{\sqrt{N}}$, which implies
$V(s)=\sum_{i=2}^{b} s_i\geq \frac{\log N}{\sqrt{N}}$, which implies ![]() $s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$ because
$s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$ because ![]() $s_2\geq s_3\geq \cdots \geq s_b.$ Therefore, we have
$s_2\geq s_3\geq \cdots \geq s_b.$ Therefore, we have
where the last inequality holds because ![]() $\sum_{i=1}^{b} s_i\leq \lambda+\frac{k\log N}{\sqrt{N}}$ implies that
$\sum_{i=1}^{b} s_i\leq \lambda+\frac{k\log N}{\sqrt{N}}$ implies that ![]() $s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, which further implies that
$s_1\leq \lambda+\frac{{\bar k}\log N}{\sqrt{N}}$, which further implies that ![]() $A_1(s)\leq \frac{1}{\sqrt{N}\,}$.
$A_1(s)\leq \frac{1}{\sqrt{N}\,}$.
Case 2: Assume ![]() $\sum_{i=2}^{b} s_i>\lambda+\frac{k\log N}{\sqrt{N}}-s_1$. Note that
$\sum_{i=2}^{b} s_i>\lambda+\frac{k\log N}{\sqrt{N}}-s_1$. Note that
 \begin{alignat*}{2}V(s + e_1) & = \lambda+\frac{k\log N}{\sqrt{N}}-s_1- \frac{1}{N}, &\,\, V(s - e_1) & \leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1+\frac{1}{N}, \\[8pt]
V(s + e_j) & = \lambda+\frac{k\log N}{\sqrt{N}}-s_1, & V(s- e_j) & \leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1, \text{ for all } 2 \leq j \leq b.\end{alignat*}
\begin{alignat*}{2}V(s + e_1) & = \lambda+\frac{k\log N}{\sqrt{N}}-s_1- \frac{1}{N}, &\,\, V(s - e_1) & \leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1+\frac{1}{N}, \\[8pt]
V(s + e_j) & = \lambda+\frac{k\log N}{\sqrt{N}}-s_1, & V(s- e_j) & \leq \lambda+\frac{k\log N}{\sqrt{N}}-s_1, \text{ for all } 2 \leq j \leq b.\end{alignat*}
In this case ![]() $\sum_{i=2}^b s_i\geq V(s)=\lambda+\frac{k\log N}{\sqrt{N}}-s_1\geq \frac{\log N}{\sqrt{N}}$, which also implies
$\sum_{i=2}^b s_i\geq V(s)=\lambda+\frac{k\log N}{\sqrt{N}}-s_1\geq \frac{\log N}{\sqrt{N}}$, which also implies ![]() $s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$. Therefore, we have
$s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$. Therefore, we have
 \begin{align*}\triangledown V(s) & \leq -\lambda(1-A_1(s))+(s_1-s_2)\\[4pt]
& = s_1-s_2-\lambda+\lambda A_1(s)\\[4pt]
& \leq (k-1)\frac{\log N}{\sqrt{N}}-s_2+\lambda A_1(s)\\[4pt]
& \leq \left(k-1-\frac{1}{b-1}\right)\frac{\log N}{\sqrt{N}}+ \frac{1}{\sqrt{N}\,} \\[4pt]
& {\leq} -\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}+ \frac{1}{\sqrt{N}\,} ,\end{align*}
\begin{align*}\triangledown V(s) & \leq -\lambda(1-A_1(s))+(s_1-s_2)\\[4pt]
& = s_1-s_2-\lambda+\lambda A_1(s)\\[4pt]
& \leq (k-1)\frac{\log N}{\sqrt{N}}-s_2+\lambda A_1(s)\\[4pt]
& \leq \left(k-1-\frac{1}{b-1}\right)\frac{\log N}{\sqrt{N}}+ \frac{1}{\sqrt{N}\,} \\[4pt]
& {\leq} -\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}+ \frac{1}{\sqrt{N}\,} ,\end{align*}
where the second inequality holds because ![]() $s_1\leq \lambda+(k-1)\frac{\log N}{\sqrt{N}}$ and it implies
$s_1\leq \lambda+(k-1)\frac{\log N}{\sqrt{N}}$ and it implies ![]() $A_1(s) \leq \frac{1}{\sqrt{N}\,}$, the last inequality holds because
$A_1(s) \leq \frac{1}{\sqrt{N}\,}$, the last inequality holds because ![]() $s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$, and the last equality holds because
$s_2\geq \frac{1}{b-1}\frac{\log N}{\sqrt{N}}$, and the last equality holds because ![]() $1+\frac{1}{2(b-1)}-\frac{r}{\sqrt{N}\log N} \leq k \leq 1+\frac{1}{2(b-1)}$.
$1+\frac{1}{2(b-1)}-\frac{r}{\sqrt{N}\log N} \leq k \leq 1+\frac{1}{2(b-1)}$.
Before moving forward, we present the following result from [Reference Bertsimas, Gamarnik and Tsitsiklis2]. The following version of the lemma is from [Reference Wang, Maguluri, Srikant and Ying18], but the result was proved in [Reference Bertsimas, Gamarnik and Tsitsiklis2].
Lemma 3.4. Let ![]() $(X (t)\,{:}\, t \geq 0)$ be a continuous-time Markov chain over a countable state space
$(X (t)\,{:}\, t \geq 0)$ be a continuous-time Markov chain over a countable state space ![]() $\mathbb X$. Suppose that it is irreducible, nonexplosive, and positive recurrent, and X denotes the steady state of
$\mathbb X$. Suppose that it is irreducible, nonexplosive, and positive recurrent, and X denotes the steady state of ![]() $(X (t)\,{:}\, t \geq 0)$. Consider a Lyapunov function
$(X (t)\,{:}\, t \geq 0)$. Consider a Lyapunov function ![]() $V\,{:}\, \mathbb X \to \mathbb{R}^{+}$ and define the drift of V at a state
$V\,{:}\, \mathbb X \to \mathbb{R}^{+}$ and define the drift of V at a state ![]() $i \in \mathbb X$ as
$i \in \mathbb X$ as
where ![]() $q_{ii'}$ is the transition rate from i to i'. Suppose that the drift satisfies the following conditions:
$q_{ii'}$ is the transition rate from i to i'. Suppose that the drift satisfies the following conditions:
(i) There exist constants
 $\gamma > 0$ and
$\gamma > 0$ and  $B > 0$ such that
$B > 0$ such that  $\Delta V (i) \leq -\gamma$ for any
$\Delta V (i) \leq -\gamma$ for any  $i \in \mathbb X$ with
$i \in \mathbb X$ with  $V(i) > B$.
$V(i) > B$.(ii)
 $\nu_{\max} := \sup\limits_{i,i'\in \mathbb X: q_{i i'} >0} |V(i') - V(i)|< \infty$.
$\nu_{\max} := \sup\limits_{i,i'\in \mathbb X: q_{i i'} >0} |V(i') - V(i)|< \infty$.(iii)
 $\bar q := \sup\limits_{i \in \mathbb X} (-q_{ii}) < \infty$.
$\bar q := \sup\limits_{i \in \mathbb X} (-q_{ii}) < \infty$.
Then, for any non-negative integer j, we have
where
Based on the drift analysis in Lemmas 3.3 and 3.4 (Lemma B.1 in [Reference Wang, Maguluri, Srikant and Ying18]), we have the following tail bound on V(S).
Lemma 3.5. Given the Lyapunov function defined in (18) and denoting ![]() $\tilde{k} = 1+\frac{1}{4(b-1)}$, we have
$\tilde{k} = 1+\frac{1}{4(b-1)}$, we have
 \begin{equation*}\mathbb{P}\left(V(S)\geq \frac{\tilde{k}\log N}{\sqrt{N}}\right)\leq \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{{8}(b-1)}\Bigg\}.\end{equation*}
\begin{equation*}\mathbb{P}\left(V(S)\geq \frac{\tilde{k}\log N}{\sqrt{N}}\right)\leq \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{{8}(b-1)}\Bigg\}.\end{equation*}Proof. From Lemma 3.3, we have
and it is easy to verify that ![]() $q_{\max}\leq N$ and
$q_{\max}\leq N$ and ![]() $v_{\max}\leq \frac{1}{N}$.
$v_{\max}\leq \frac{1}{N}$.
Based on Lemma 3.4 with ![]() $j=\frac{\sqrt{N}\log N}{8(b-1)}$, we have
$j=\frac{\sqrt{N}\log N}{8(b-1)}$, we have
 \begin{align*}\mathbb{P}\left(V(S)\geq \frac{\tilde{k}\log N}{\sqrt{N}}\right) & \leq \left(\frac{1}{1+\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}-\frac{1}{\sqrt{N}\,}}\right)^{\frac{\sqrt{N}\log N}{8(b-1)}+1}\\& \leq \left(1 - \frac{1}{4(b-1)}\frac{\log N}{\sqrt{N}}+\frac{1}{2\sqrt{N}\,}\right)^{\frac{\sqrt{N}\log N}{8(b-1)}}\\ & \leq \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\} , \end{align*}
\begin{align*}\mathbb{P}\left(V(S)\geq \frac{\tilde{k}\log N}{\sqrt{N}}\right) & \leq \left(\frac{1}{1+\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}-\frac{1}{\sqrt{N}\,}}\right)^{\frac{\sqrt{N}\log N}{8(b-1)}+1}\\& \leq \left(1 - \frac{1}{4(b-1)}\frac{\log N}{\sqrt{N}}+\frac{1}{2\sqrt{N}\,}\right)^{\frac{\sqrt{N}\log N}{8(b-1)}}\\ & \leq \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\} , \end{align*}
where the second inequality holds because ![]() $\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}\leq1 + \frac{1}{\sqrt{N}\,}$ for large N.
$\frac{1}{2(b-1)}\frac{\log N}{\sqrt{N}}\leq1 + \frac{1}{\sqrt{N}\,}$ for large N.
Given the SSC result in Lemma 3.5, we now bound (12) (continuing from (17)) by considering two regimes, ![]() $V(s)\leq \frac{\tilde{k}\log N}{\sqrt{N}}$ and
$V(s)\leq \frac{\tilde{k}\log N}{\sqrt{N}}$ and ![]() $V(s) > \frac{\tilde{k}\log N}{\sqrt{N}}$, as follows:
$V(s) > \frac{\tilde{k}\log N}{\sqrt{N}}$, as follows:
 \begin{align}\mathbb{E}&\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\right]\nonumber\\& = \mathbb{E}\Bigg[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{V(S)\leq \frac{\tilde{k}\log N}{\sqrt{N}}}\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\Bigg]\end{align}
\begin{align}\mathbb{E}&\left[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\right]\nonumber\\& = \mathbb{E}\Bigg[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{V(S)\leq \frac{\tilde{k}\log N}{\sqrt{N}}}\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\Bigg]\end{align} \begin{align}&\,\,\,\quad + \mathbb{E}\Bigg[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{V(S)>\frac{\tilde{k}\log N}{\sqrt{N}}}\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\Bigg].\quad\end{align}
\begin{align}&\,\,\,\quad + \mathbb{E}\Bigg[\frac{\sqrt{N}}{\log N}\left(\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}}\right)^r\left(\lambda+\frac{\log N}{\sqrt{N}}-S_1\right)\textbf{1}_{V(S)>\frac{\tilde{k}\log N}{\sqrt{N}}}\textbf{1}_{\sum_{i=1}^{b} S_i> \eta+\frac{1}{N}}\Bigg].\quad\end{align} To bound (19), we consider state s such that ![]() $\textbf{1}_{V(s)\leq \frac{\tilde{k}\log N}{\sqrt{N}}}=1$ and
$\textbf{1}_{V(s)\leq \frac{\tilde{k}\log N}{\sqrt{N}}}=1$ and ![]() $\textbf{1}_{\sum_{i=1}^{b} s_i> \eta+\frac{1}{N}} = 1$, because otherwise (19)
$\textbf{1}_{\sum_{i=1}^{b} s_i> \eta+\frac{1}{N}} = 1$, because otherwise (19)![]() $\,=0$. For any state s such that
$\,=0$. For any state s such that ![]() $\smash{\sum_{i=1}^{b} s_i> \eta +\frac{1}{N}= \lambda +\frac{k\log N}{\sqrt{N}}+\frac{1}{N}}$, we have
$\smash{\sum_{i=1}^{b} s_i> \eta +\frac{1}{N}= \lambda +\frac{k\log N}{\sqrt{N}}+\frac{1}{N}}$, we have
Given (21), ![]() $V(s) \leq \frac{\tilde{k} \log N}{\sqrt{N}}$ means
$V(s) \leq \frac{\tilde{k} \log N}{\sqrt{N}}$ means
Therefore, we have
 \begin{align}(\linkref{disp19}{19}) \leq \left(1 - \frac{1}{5(b-1)} \right)\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}},0\right\}\right)^r\right]. \end{align}
\begin{align}(\linkref{disp19}{19}) \leq \left(1 - \frac{1}{5(b-1)} \right)\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}},0\right\}\right)^r\right]. \end{align}To bound (20), we have
 \begin{align}(\linkref{disp20}{20}) & \leq \frac{{b^r}\sqrt{N}}{\log N} \mathbb{E}\left[\textbf{1}_{V(S)>\frac{\tilde{k}\log N}{\sqrt{N}}}\right] \nonumber\\[8pt]
& \leq \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\} , \end{align}
\begin{align}(\linkref{disp20}{20}) & \leq \frac{{b^r}\sqrt{N}}{\log N} \mathbb{E}\left[\textbf{1}_{V(S)>\frac{\tilde{k}\log N}{\sqrt{N}}}\right] \nonumber\\[8pt]
& \leq \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\} , \end{align}
where the first inequality holds because ![]() $\sum_{i=1}^{b} s_i-\lambda -\frac{k\log N}{\sqrt{N}} \leq \sum_{i=1}^{b} s_i \leq b$ and
$\sum_{i=1}^{b} s_i-\lambda -\frac{k\log N}{\sqrt{N}} \leq \sum_{i=1}^{b} s_i \leq b$ and ![]() $\lambda+\frac{\log N}{\sqrt{N}}-s_1 \leq 1$ for large N, and the second inequality holds due to Lemma 3.5.
$\lambda+\frac{\log N}{\sqrt{N}}-s_1 \leq 1$ for large N, and the second inequality holds due to Lemma 3.5.
Based on (22) and (23), we obtain the following upper bound on (12):
 \begin{align}& \mathbb{E}\left[g^{\prime}\left(\sum_{i=1}^{b} S_i\right)\left(\lambda B(S)-\lambda-\frac{\log N}{\sqrt{N}}+S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta}\right]\nonumber\\[2pt]
& \qquad\qquad\leq \left(1 - \frac{1}{5(b-1)} \right)\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}},0\right\}\right)^r\right]\nonumber\\[5pt]
& \qquad\qquad\qquad+ \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}.\end{align}
\begin{align}& \mathbb{E}\left[g^{\prime}\left(\sum_{i=1}^{b} S_i\right)\left(\lambda B(S)-\lambda-\frac{\log N}{\sqrt{N}}+S_1\right)\textbf{1}_{\sum_{i=1}^{b} S_i \gt \eta}\right]\nonumber\\[2pt]
& \qquad\qquad\leq \left(1 - \frac{1}{5(b-1)} \right)\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{k\log N}{\sqrt{N}},0\right\}\right)^r\right]\nonumber\\[5pt]
& \qquad\qquad\qquad+ \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}.\end{align}3.4. Higher moment bounds
Given the results (24), (15), and (16), which bound (12), (13), and (14), respectively, we have
 \begin{align}\mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right]& \leq \left(1 - \frac{1}{5(b-1)}\right) \mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right] \nonumber \\[5pt]
& \quad + \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}\nonumber\displaybreak\\
& \quad + \frac{2^{r+1}}{N^{r-0.5}\log N} + \frac{r}{\sqrt{N}\log N}\mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i\right)\right] \nonumber\\[5pt]
& \leq \left(1 - \frac{1}{5(b-1)}\right) \mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right] + \frac{1+2^{r+1}}{N^{r-0.5}\log N} \end{align}
\begin{align}\mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right]& \leq \left(1 - \frac{1}{5(b-1)}\right) \mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right] \nonumber \\[5pt]
& \quad + \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}\nonumber\displaybreak\\
& \quad + \frac{2^{r+1}}{N^{r-0.5}\log N} + \frac{r}{\sqrt{N}\log N}\mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i\right)\right] \nonumber\\[5pt]
& \leq \left(1 - \frac{1}{5(b-1)}\right) \mathbb{E}\left[h^r_k\left(\sum_{i=1}^{b} S_i\right)\right] + \frac{1+2^{r+1}}{N^{r-0.5}\log N} \end{align} \begin{align}& \qquad\quad\,\, + \frac{r}{\sqrt{N}\log N}\mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i+{\frac{1}{N}}\right)\right] ,\end{align}
\begin{align}& \qquad\quad\,\, + \frac{r}{\sqrt{N}\log N}\mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i+{\frac{1}{N}}\right)\right] ,\end{align}
where the second inequality holds because, given ![]() $0\leq b \leq 1 + \frac{\sqrt{\log N}}{9}$ and
$0\leq b \leq 1 + \frac{\sqrt{\log N}}{9}$ and ![]() $1\leq r\leq \frac{\log N}{72(b-1)^2}$, we have
$1\leq r\leq \frac{\log N}{72(b-1)^2}$, we have
 \begin{align*}\frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}& \leq \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{36(b-1)^2}\Bigg\} \\[8pt]
\leq \frac{{b^r}\sqrt{N}}{\log N} {\textrm e}^{-2r\log N}& = \frac{{b^r}}{N^{2r-0.5} \log N} \leq \frac{1}{N^{r-0.5}\log N}.\end{align*}
\begin{align*}\frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{32(b-1)^2}+\frac{\log N}{16(b-1)}\Bigg\}& \leq \frac{{b^r}\sqrt{N}}{\log N} \exp\Bigg\{-\frac{\log^2 N}{36(b-1)^2}\Bigg\} \\[8pt]
\leq \frac{{b^r}\sqrt{N}}{\log N} {\textrm e}^{-2r\log N}& = \frac{{b^r}}{N^{2r-0.5} \log N} \leq \frac{1}{N^{r-0.5}\log N}.\end{align*}
Finally, by moving the first term in (25) to the left-hand side of the inequality and then multiplying by ![]() $4(b-1)$ on both sides of the inequality, we obtain
$4(b-1)$ on both sides of the inequality, we obtain
 \begin{align*}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^b S_i\right)\right]\leq \frac{4(1+2^{r+1})(b-1)}{N^{r-0.5}\log N}+\frac{4r(b-1)}{\sqrt{N}\log N} \mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i + {\frac{1}{N}}\right)\right],\end{align*}
\begin{align*}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^b S_i\right)\right]\leq \frac{4(1+2^{r+1})(b-1)}{N^{r-0.5}\log N}+\frac{4r(b-1)}{\sqrt{N}\log N} \mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i + {\frac{1}{N}}\right)\right],\end{align*}
where ![]() $\bar k - \frac{r}{\sqrt{N}\log N} \leq k \leq \bar k$.
$\bar k - \frac{r}{\sqrt{N}\log N} \leq k \leq \bar k$.
Define ![]() $w_r = \frac{5r(b-1)}{\sqrt{N}\log N}$ and
$w_r = \frac{5r(b-1)}{\sqrt{N}\log N}$ and ![]() $z_r = \frac{5(1+2^{r+1})(b-1)}{N^{r-0.5}\log N}$. The inequality above can be written as
$z_r = \frac{5(1+2^{r+1})(b-1)}{N^{r-0.5}\log N}$. The inequality above can be written as
 \begin{align*}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^b S_i\right)\right]\leq w_r \mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i+ {\frac{1}{N}}\right)\right] + z_r.\end{align*}
\begin{align*}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^b S_i\right)\right]\leq w_r \mathbb{E}\left[h^{r-1}_k\left(\sum_{i=1}^b S_i+ {\frac{1}{N}}\right)\right] + z_r.\end{align*}By recursively applying this inequality, we obtain
 \begin{align*}\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\right\}\right)^r\right] &\leq \prod_{j=1}^r w_j + \sum_{i=1}^{r} z_i \left(\prod_{j=i+1}^r w_j\right),\end{align*}
\begin{align*}\mathbb{E}\left[\left(\max\left\{\sum_{i=1}^{b} S_i-\lambda -\frac{{\bar k}\log N}{\sqrt{N}},0\right\}\right)^r\right] &\leq \prod_{j=1}^r w_j + \sum_{i=1}^{r} z_i \left(\prod_{j=i+1}^r w_j\right),\end{align*}
where we define ![]() $\prod_{j=r+1}^r w_j=1$ for notational convenience. We note that
$\prod_{j=r+1}^r w_j=1$ for notational convenience. We note that ![]() $z_i \prod_{j=i+1}^r w_j$ is a decreasing sequence in i for
$z_i \prod_{j=i+1}^r w_j$ is a decreasing sequence in i for ![]() $2 \leq i \leq r$, because
$2 \leq i \leq r$, because
and
 \begin{equation*}\prod_{j=1}^r w_j \leq z_1 \prod_{j=2}^r w_j\end{equation*}
\begin{equation*}\prod_{j=1}^r w_j \leq z_1 \prod_{j=2}^r w_j\end{equation*}
because ![]() $w_1=\frac{5(b-1)}{\sqrt{N}\log N} \leq z_1=\frac{25(b-1)}{\sqrt{N}\log N}$. Therefore,
$w_1=\frac{5(b-1)}{\sqrt{N}\log N} \leq z_1=\frac{25(b-1)}{\sqrt{N}\log N}$. Therefore,
 \begin{align}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^{b} S_i\right)\right]& \leq (r+1) z_1 \prod_{j=2}^r w_j \nonumber\\[5pt]
& \leq (r+1) z_1(w_r)^{r-1} \end{align}
\begin{align}\mathbb{E}\left[h^{r}_k\left(\sum_{i=1}^{b} S_i\right)\right]& \leq (r+1) z_1 \prod_{j=2}^r w_j \nonumber\\[5pt]
& \leq (r+1) z_1(w_r)^{r-1} \end{align}
where the inequality (27) holds because ![]() $w_i$ is increasing in i, and (28) holds by substituting
$w_i$ is increasing in i, and (28) holds by substituting ![]() $z_1$ and
$z_1$ and ![]() $w_r$. This concludes the proof.
$w_r$. This concludes the proof.
4. Proof of Corollary 2.1
Based on the moment bound in Theorem 2.1, we study the waiting probability ![]() $p_{\mathcal W}$ and the waiting time
$p_{\mathcal W}$ and the waiting time ![]() $\mathbb{E}[W]$,
$\mathbb{E}[W]$, ![]() $\mathbb{E}[S_1]$, and
$\mathbb{E}[S_1]$, and ![]() $\mathbb{E}[\sum_{i=2}^b S_i]$ for JSQ, I1F, and JIQ. The analysis for Pod is similar and will be provided later. We begin with the waiting probability
$\mathbb{E}[\sum_{i=2}^b S_i]$ for JSQ, I1F, and JIQ. The analysis for Pod is similar and will be provided later. We begin with the waiting probability ![]() $p_{\mathcal W}$:
$p_{\mathcal W}$:
 \begin{align}p_{\mathcal W}& = \mathbb{P}\left(S_1=1\right)\leq \mathbb{P}\left(\sum_{i=1}^bS_i\geq 1\right) \nonumber\\[5pt]
& \leq \mathbb{P}\left(h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\geq \left(\frac{\gamma}{N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r\right)\nonumber\\[5pt]
& \leq \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r} \end{align}
\begin{align}p_{\mathcal W}& = \mathbb{P}\left(S_1=1\right)\leq \mathbb{P}\left(\sum_{i=1}^bS_i\geq 1\right) \nonumber\\[5pt]
& \leq \mathbb{P}\left(h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\geq \left(\frac{\gamma}{N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r\right)\nonumber\\[5pt]
& \leq \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r} \end{align} \begin{align}\hspace*{-32pt} \leq \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{2N^{\alpha}}\right)^r} \hspace*{32pt}\end{align}
\begin{align}\hspace*{-32pt} \leq \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{2N^{\alpha}}\right)^r} \hspace*{32pt}\end{align}
where (29) is a result of Markov’s inequality, (30) holds because ![]() $N \geq \left(\frac{{4}\bar k\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ implies
$N \geq \left(\frac{{4}\bar k\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ implies ![]() $\frac{\bar k\log N}{\sqrt{N}} \leq \frac{\gamma}{2N^{\alpha}}$, (31) holds by substituting (28), and (32) holds because
$\frac{\bar k\log N}{\sqrt{N}} \leq \frac{\gamma}{2N^{\alpha}}$, (31) holds by substituting (28), and (32) holds because ![]() $r\leq \frac{\log N}{72(b-1)^2}$ implies
$r\leq \frac{\log N}{72(b-1)^2}$ implies ![]() $\log N \geq 10r(b-1).$
$\log N \geq 10r(b-1).$
From ![]() $p_{\mathcal W}$, we can obtain an upper bound on
$p_{\mathcal W}$, we can obtain an upper bound on ![]() $\mathbb{E}[W]$:
$\mathbb{E}[W]$:
where the last inequality holds because the expected waiting time for a job routed to a busy server is at most ![]() $b-1$.
$b-1$.
Moreover, for jobs that are not discarded, the average queueing delay according to Little’s law is
 \begin{equation*}\mathbb{E}[W]=\frac{\mathbb{E}\left[\sum_{i=1}^bS_i\right]}{\lambda(1-p_{\mathcal B})}-1.\end{equation*}
\begin{equation*}\mathbb{E}[W]=\frac{\mathbb{E}\left[\sum_{i=1}^bS_i\right]}{\lambda(1-p_{\mathcal B})}-1.\end{equation*}Therefore, we have
 \begin{align*}\mathbb{E}\left[\sum_{i=1}^b S_i\right] & = \lambda\left(1-p_{\mathcal B}\right)\left( \mathbb{E}[W]+1\right) \\[5pt]
& \leq \lambda \mathbb{E}[W]+\lambda \\[5pt]
& \leq \lambda b \cdot p_{\mathcal W} + \lambda \\[5pt]
& \leq \frac{10\lambda b}{{\gamma^r} N^{r(0.5-\alpha)}} + \lambda.\end{align*}
\begin{align*}\mathbb{E}\left[\sum_{i=1}^b S_i\right] & = \lambda\left(1-p_{\mathcal B}\right)\left( \mathbb{E}[W]+1\right) \\[5pt]
& \leq \lambda \mathbb{E}[W]+\lambda \\[5pt]
& \leq \lambda b \cdot p_{\mathcal W} + \lambda \\[5pt]
& \leq \frac{10\lambda b}{{\gamma^r} N^{r(0.5-\alpha)}} + \lambda.\end{align*}
Further, according to the work conservation law, we have the following lower bound on ![]() $\mathbb{E}[S_1]$:
$\mathbb{E}[S_1]$:
which yields an upper bound on ![]() $\mathbb{E}\left[\sum_{i=2}^b {S}_i\right]$:
$\mathbb{E}\left[\sum_{i=2}^b {S}_i\right]$:
 \begin{equation*}\mathbb{E}\left[\sum_{i=2}^b {S}_i\right]\leq \frac{10\lambda b + 10}{{\gamma^r} N^{r(0.5-\alpha)}}.\end{equation*}
\begin{equation*}\mathbb{E}\left[\sum_{i=2}^b {S}_i\right]\leq \frac{10\lambda b + 10}{{\gamma^r} N^{r(0.5-\alpha)}}.\end{equation*} The analysis for Pod with ![]() ${d\geq \frac{r}{\gamma}N^\alpha \log N}$ is similar, except the waiting probability
${d\geq \frac{r}{\gamma}N^\alpha \log N}$ is similar, except the waiting probability ![]() $p_{\mathcal W}$ in the first step becomes
$p_{\mathcal W}$ in the first step becomes
 \begin{align}p_{\mathcal W} & = \mathbb{P}\left(\mathcal W \, \left| \, S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right.\right)\mathbb{P}\left(S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \quad + \mathbb{P}\left(\mathcal W \, \left| \, S_1> 1-\frac{\gamma}{2N^{\alpha}}\right.\right)\mathbb{P}\left(S_1> 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq \mathbb{P}\left(\mathcal W \, \left| \, S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right.\right)+\mathbb{P}\left(S_1> 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq {\left(1-\frac{\gamma}{2N^{\alpha}}\right)^{\frac{r}{\gamma}N^\alpha \log N}}+\mathbb{P}\left(\sum_{i=1}^b S_i>1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq {N^{-\frac{r}{2}}} + \mathbb{P}\left(h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\geq \left(\frac{\gamma}{2N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r\right)\end{align}
\begin{align}p_{\mathcal W} & = \mathbb{P}\left(\mathcal W \, \left| \, S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right.\right)\mathbb{P}\left(S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \quad + \mathbb{P}\left(\mathcal W \, \left| \, S_1> 1-\frac{\gamma}{2N^{\alpha}}\right.\right)\mathbb{P}\left(S_1> 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq \mathbb{P}\left(\mathcal W \, \left| \, S_1\leq 1-\frac{\gamma}{2N^{\alpha}}\right.\right)+\mathbb{P}\left(S_1> 1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq {\left(1-\frac{\gamma}{2N^{\alpha}}\right)^{\frac{r}{\gamma}N^\alpha \log N}}+\mathbb{P}\left(\sum_{i=1}^b S_i>1-\frac{\gamma}{2N^{\alpha}}\right)\nonumber\\[5pt]
& \leq {N^{-\frac{r}{2}}} + \mathbb{P}\left(h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\geq \left(\frac{\gamma}{2N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r\right)\end{align} \begin{align}\hspace*{-34pt} \leq \frac{1}{N^{0.5r}} + \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{2N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r} \hspace*{34pt}\end{align}
\begin{align}\hspace*{-34pt} \leq \frac{1}{N^{0.5r}} + \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{2N^{\alpha}}-\frac{\bar k\log N}{\sqrt{N}}\right)^r} \hspace*{34pt}\end{align} \begin{align}\hspace*{-30pt}\leq \frac{1}{N^{0.5r}} + \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{4N^{\alpha}}\right)^r}\hspace*{30pt}\end{align}
\begin{align}\hspace*{-30pt}\leq \frac{1}{N^{0.5r}} + \frac{\mathbb{E}\left [h^r_{\bar k}\left(\sum_{i=1}^bS_i\right)\right]}{\left(\frac{\gamma}{4N^{\alpha}}\right)^r}\hspace*{30pt}\end{align} \begin{align}\hspace*{-120pt}& \leq \frac{1}{N^{0.5r}} + \frac{10}{\gamma^r N^{r(0.5-\alpha)}} \nonumber \\[4pt] & \leq \frac{11}{\gamma^r N^{r(0.5-\alpha)}} ,\hspace*{120pt}\end{align}
\begin{align}\hspace*{-120pt}& \leq \frac{1}{N^{0.5r}} + \frac{10}{\gamma^r N^{r(0.5-\alpha)}} \nonumber \\[4pt] & \leq \frac{11}{\gamma^r N^{r(0.5-\alpha)}} ,\hspace*{120pt}\end{align}
where (33) holds because ![]() $\big(1-\frac{1}{x}\big)^x\leq \frac{1}{{\textrm e}}$ for
$\big(1-\frac{1}{x}\big)^x\leq \frac{1}{{\textrm e}}$ for ![]() $x\geq 1$, (34) is a result of the Markov inequality, (35) holds because
$x\geq 1$, (34) is a result of the Markov inequality, (35) holds because ![]() $N \geq \left(\frac{{4}\bar k\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ implies
$N \geq \left(\frac{{4}\bar k\log N}{\gamma}\right)^{\frac{1}{0.5-\alpha}}$ implies ![]() $\frac{\gamma}{4N^{\alpha}}\geq \frac{\bar k\log N}{\sqrt{N}}$, (36) holds by substituting (28), and (37) holds because
$\frac{\gamma}{4N^{\alpha}}\geq \frac{\bar k\log N}{\sqrt{N}}$, (36) holds by substituting (28), and (37) holds because ![]() $r\leq \frac{\log N}{72 (b-1)^2}$ implies
$r\leq \frac{\log N}{72 (b-1)^2}$ implies ![]() $\log N \geq 20r(b-1).$ The remaining analysis to obtain
$\log N \geq 20r(b-1).$ The remaining analysis to obtain ![]() $\mathbb{E}[W]$,
$\mathbb{E}[W]$, ![]() $\mathbb{E}[S_1]$, and
$\mathbb{E}[S_1]$, and ![]() $\mathbb{E}[\sum_{i=1}^b S_i]$ is the same as the analysis for JSQ.
$\mathbb{E}[\sum_{i=1}^b S_i]$ is the same as the analysis for JSQ.
5. Conclusion and discussion
In this paper we have studied the steady-state performance of a class of load-balancing algorithms for many-server (N servers) systems in the sub-Halfin–Whitt regime (![]() $\alpha < 0.5$). We established an upper bound on the higher moment on a distance function of the queue length with Stein’s method, and studied the probability that an incoming job is routed to a busy server under JSQ, I1F, JIQ, and Pod.
$\alpha < 0.5$). We established an upper bound on the higher moment on a distance function of the queue length with Stein’s method, and studied the probability that an incoming job is routed to a busy server under JSQ, I1F, JIQ, and Pod.
We studied the sub-Halfin–Whitt regime (![]() $\alpha < 0.5$); one interesting extension is to consider a ‘heavier’ traffic regimes where
$\alpha < 0.5$); one interesting extension is to consider a ‘heavier’ traffic regimes where ![]() $0.5 \leq \alpha < 1$. In such a regime, the above state space collapse result does not hold. It would require a different fluid model and a different state space collapse analysis, which is an interesting problem to be studied in the future.
$0.5 \leq \alpha < 1$. In such a regime, the above state space collapse result does not hold. It would require a different fluid model and a different state space collapse analysis, which is an interesting problem to be studied in the future.
Acknowledgements
The authors would like to thank Anton Braverman and Weina Wang for stimulating discussions that led to this result. This work was supported in part by NSF CNS-1824393, ECCS-1547294, ECCS-1609202, ECCS-1739344, and the U.S. Office of Naval Research (ONR Grant No. N00014-15-1-2169).