Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T15:06:16.575Z Has data issue: false hasContentIssue false
  • English
  • Français

RFNC–VNIITF multifunctional shock tube for investigating the evolution of instabilities in nonstationary gas dynamic flows

Published online by Cambridge University Press:  03 March 2004

Yu.A. KUCHERENKO ,
O.E. SHESTACHENKO ,
S.I. BALABIN  and
A.P. PYLAEV
Yu.A. KUCHERENKO
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics (RFNC–VNIITF), Chelyabinsk, Russia
O.E. SHESTACHENKO
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics (RFNC–VNIITF), Chelyabinsk, Russia
S.I. BALABIN
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics (RFNC–VNIITF), Chelyabinsk, Russia
A.P. PYLAEV
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics (RFNC–VNIITF), Chelyabinsk, Russia
Rights & Permissions [Opens in a new window]

Abstract

The design, operation, and functionality of the multifunctional shock tube (MST) facility at the Russian Federal Nuclear Center–VNIITF are described. When complete, the versatile MST consists of three different driver sections that permit the execution of three different classes of experiments on the compressible turbulent mixing of gases induced by the (1) Richtmyer–Meshkov instability (generated by a stationary shock wave with shock Mach numbers <5), (2) Rayleigh–Taylor instability (generated by compression wave such that acceleration of the interface is <105g0, where g0 = 9.8 m/s2), and (3) combined Richtmyer–Meshkov and Rayleigh–Taylor instability (generated by a nonstationary shock wave with initial pressure at the front 5 × 106 Pa and acceleration of ≤106g0 of the interface). For each of these types of experiments, the density ratio of the gases is ρ2 /ρ1 ≤ 34. Perturbations are imposed on a thin membrane, embedded in a thin wire array of microconductors that is destroyed by an electric current. In addition, various limitations of experimental techniques used in the study of interfacial instability generated turbulent mixing are also briefly discussed.

Keywords

Compression waveNonstationary shockStationary shockTurbulent mixing
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 381 - 384
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

In spite of a great number of investigations performed with an objective to study the evolution of hydrodynamic instabilities and turbulent mixing associated with them in gases, there are many questions that have not been studied as a result of the experimental technique limitations. When studying the turbulence induced by the action of the Richtmyer–Meshkov instability, a great uncertainty takes place that is associated with the parameters of diaphragms separating the different density gases at the initial instant of time. At the same time, the influence of a diaphragm is such that the obtained turbulent flow “does not forget” the initial conditions. This leads to the turbulent flow structure distortion and, as a consequence, to great errors when measuring the turbulence parameters.

When studying the turbulence induced by the action of the Rayleigh–Taylor instability, the role of the separating diaphragm is also rather important. This problem is especially significant when studying the self-similar mode of mixing at which it is important to have the self-similar spectrum of perturbations at the contact boundary of different density gases. A great uncertainty is, possibly, associated with this circumstance in the determination of the nondimensional rate of different density gases in the self-similar mode. This mode is characterized by the constant rate of the mixing zone width growth. At the same time, the mixing zone width L depends only on the density ratio of miscible media n or Atwood number A = (n − 1)/(n + 1), the contact boundary acceleration g1 and time t:

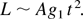
The self-similar mode of the gravitational turbulent mixing is everywhere used both for the calibration of the semiempirical models of mixing and for the mathematical modeling of mixing processes due to the minimum number of parameters determining this mode. The proportionality coefficient in the relation (1), which represents the nondimensional rate of mixing, is determined in experiments and is estimated at the numerical modeling.

It is known (Kucherenko et al., 1991) that the gravitational turbulent mixing process of different density media is asymmetric in the sense that the fronts of the penetration of the light medium into the heavy one and the heavy medium into the light one are spreading with different velocity. Historically the nondimensional rate αb of spreading of the light medium front into the heavy one is assumed to be the characteristic of the gravitational turbulent mixing (Read, 1984). Denoting the distance of the light medium penetration front coordinate subtracted from the contact boundary as L12, it is possible to write down

where S = gt2/2.

Results obtained in experiments with different density liquids (Read, 1984; Kucherenko et al., 1988, 1991; Youngs, 1991) give the value of α being found in the range of α = 0.06–0.07

At the same time, the results obtained in the work of Vasilenko et al. (1991) with different density gases give the magnitude of this value, which exceeds the one shown above by more than a factor of two. The reasons for such a difference have not been elucidated up to now. It may be proposed that in the work of Vasilenko et al. (1991) either the conditions of self-similarity were not satisfied in the setup of the experiments or the measurements were made in the linear stage of the Rayleigh–Taylor instability evolution, when the initial experimental conditions “were not yet forgotten.” The last argument is supported by the absence of the direct control of the initial conditions when performing experiments in this work. Moreover, the factor of compressibility can exert an influence on the result in the work of Vasilenko et al. (1991). However, the investigations performed in the work of Zaitsev et al. (2000) with compressible media have shown that the values of αb for different combinations of gases are found in the range of α = 0.052–0.098.

In the works of Youngs (1991) and Anuchina et al. (1997), the numerical three-dimensional modeling of the gravitational turbulent mixing evolution was carried out by means of different mathematical codes. In the work of Anuchina et al. (1997) the value of α ≈ 0.052 was obtained, but in the work of Youngs (1991), this value is in the range of α = 0.04–0.06.

Thus, it is seen that the results obtained in the work of Vasilenko et al. (1991) for gases are contradictory. This contradiction is, most likely, associated with imperfections in the experimental technique. The study of the turbulence induced by the successive action of the Richtmyer–Meshkov and Rayleigh–Taylor instabilities has not yet been performed. However, this situation is often realized when studying the operation of laser targets in the problem of inertial thermonuclear fusion. The absence of such work being set up under laboratory conditions is, apparently, associated with the absence of the appropriate experimental technique.

The multifunctional shock tube (MST) being developed at present at the RFNC–VNIITF will make it possible to solve a number of fundamental problems of nonstationary turbulence that were described above. In the present work, three modes of the MST operation associated with the shown problems are described. This development was the result of the RFNC–VNIITF and Lawrence Livermore National Laboratory (LLNL) collaboration and initially it was known as Project “BIZON.”

2. MULTIFUNCTIONAL SHOCK TUBE WITH DRIVER I

The physical scheme of the MST with driver I is presented in Figure 1. This driver is intended for studying the Richtmyer–Meshkov instability and the turbulent mixing induced by it. One of the investigated gases with density ρ1 is located in measuring section I (4) and the second gas with density ρ2 in measuring section II (6). At the initial instant of time a separating membrane (5) is found between gases. The composition of driver I includes a high pressure chamber (1), a high pressure membrane (2), a transitional section (3), and a part of the measuring section I. Driver I operates as follows. Gas is forced into the high-pressure chamber up to such pressure P0, at which the high-pressure membrane is opened. The gas flow rushes into the transitional section and then into measuring section I creating a shock wave (SW). The function of the transitional section consists of coordinating the round cross section A–A of the high-pressure chamber with the square cross section C–C of measuring section I. The cross section A–A of the high-pressure chamber is chosen to be round proceeding from the considerations of its strength and technology to mount the high-pressure membrane on it. C–C and D–D cross sections of the measuring sections were chosen to be right-angled (square), proceeding from the convenience to register the turbulent mixing parameters by the light techniques. The cross section of the other form would induce difficulties associated either with taking into account the additional refraction of light beams or with mounting the plane transparent windows on the nonplanar walls of the measuring sections. The transitional section along the axis x is of a variable cross-section F(x) which changes from the round cross section to the square one. At the same time, the gas flow form is smoothly changed. The intensity of the SW being created is determined by the value of pressure P0. A part of measuring section I is used to generate a stationary SW propagating through a low-pressure gas. The required length of the stationary SW determines the length of this part of the measuring section. As a result of the SW passage through the contact boundary of gases, the contact boundary undergoes the impulsive acceleration whose character is shown in the right part of Figure 1. Mach number of the stationary SW generated by the driver I amounts to M ≤ 5.

Physical scheme of MST with driver I.

The separating membrane (5) performs two functions. First, it stabilizes the contact boundary (CB) of different density gases while preventing the mixing of gases prior to the SW arrival at CB. Second, by means of this membrane, at the initial instant of time, the zone of initial perturbations with specified parameters is created at the contact boundary. Such a membrane has, actually, been developed and has been named the “specter-diaphragm.” Its distinctive features are its initiation from the external force and its disappearance just after the creation of the initial perturbations zone.

The length of measuring section II is chosen depending on the problem being solved. If a single passage of SW through the zone of mixture is required, then the outlet section (7) is used for this purpose, which prevents from the creation of the reflected shock waves.

3. MULTIFUNCTIONAL SHOCK TUBE WITH DRIVER II

The physical scheme of MST with driver II is presented in Figure 2. This driver is intended for investigating the successive action of the Richtmyer–Meshkov and Rayleigh–Taylor instabilities and the turbulent mixing induced by them. One of the gases (the heavier one) being investigated and having density ρ2 is placed into measuring section I (5), but the lighter gas of density ρ1 is placed into measuring section II (7). At the initial instant of time, the separating membrane (5) separates gases. This membrane performs the same function as in the case with driver I. Driver II includes a vacuum section (1), a restraining membrane (2), a section of the electrically exploded foil (EEF; 3) and the electrically exploded metal foil (4). The metal foil separates measuring section I from the section of EEF. The restraining membrane separates the section of EEF from the vacuum section. At the moment of the metal foil blasting a SW is formed that propagates into both sides. When SW reaches the restraining membrane (2), it ruptures it, and gas moving behind SW begins to flow into vacuum. As a result, a rarefaction wave is formed that propagates toward the side of measuring section I. This rarefaction wave overtakes SW, which propagates along measuring section I. As a result, a nonstationary SW with pressure sharply dropping at the back front falls on the contact boundary. Pressure at the leading front of SW can reach 5 * 105 Pa at a distance of 500 mm from the point of the electrically exploded foil location. Thus, the leading front of the shock wave creates the Richtmyer–Meshkov instability after passing through the contact boundary of gases, and then the different density gases undergo the action of the Rayleigh–Taylor instability in the region of the contact boundary, because the gradients of pressure and density are directed to the opposite sides. For the MST with driver II, the contact boundary acceleration dependence on time is shown in the right part of Figure 2. At first, the contact boundary is accelerated in the pulsed mode, then it moves with almost constant acceleration. In case of the MST with driver II, all the sections have the same square cross section.

Physical scheme of MST with driver II.

4. MULTIFUNCTIONAL SHOCK TUBE WITH DRIVER III

The physical scheme of the MST with driver III is presented in Figure 3. This driver is intended for studying the Rayleigh–Taylor instability and the turbulent mixing induced by this instability. The lighter gas of density ρ1 is placed into measuring section I (5); the other heavier gas of density ρ2 is located in measuring section II (7). The separating membrane (6) separates gases. This membrane performs the same functions as in two preceding cases with drivers II and I. Driver III includes a high-pressure chamber (1), a high-pressure membrane (2), a transitional section (3), and a piston (4). The high-pressure chamber, the high-pressure membrane (2), and the transitional section of driver III perform the same functions as in the driver I. However, here the gas flow does not form the stationary shock wave after passing through the transitional section, but accelerates the light piston. The piston accelerating creates a compression wave before itself, which is transformed into a shock wave in time. In the case of driver III, the separating membrane and, consequently, the contact boundary of gases should be arranged at some distance from the initial position of the piston so that, by the moment of the arrival at the contact boundary, the compression wave cannot be transformed into SW. The pressure profile in the compression wave is such that pressure drops in the positive direction of the axis x. Therefore, the gradients of pressure and density in the region of the contact boundary of different density gases will be directed to the opposite sides, and therefore, the contact boundary of the gases will be Rayleigh–Taylor unstable. This boundary will move along the axis x with almost constant acceleration whose dependence on time is shown in the right part of Figure 3. The maximum value of the contact boundary acceleration may reach the value of g1 = 105 g, where g is the acceleration of the Earth's gravitational field. The measurement of the evolution process of the instability and the turbulent mixing of gases in the region of the contact boundary during its motion with acceleration is completed in measuring section II before the piston reaches this region. Subsequently, the piston will get into the outlet section (8) where its deceleration takes place. For the same reasons given when we described MST with driver I, the high-pressure chamber cross section is chosen to be round, but the cross section of the measuring sections is square. The transitional section is of the variable cross section F(x) that ensures the smooth change of the form of the gas flow at its transition from the high-pressure chamber to the measuring section I.

Physical scheme of MST with driver III.

5. CONCLUSION

The multifunctional shock tube, which has been developed in RFNC–VNIITF in collaboration with colleagues from LLNL and which has made it possible to realize three different modes of nonstationary gas dynamic flows, will provide the possibility to accomplish applied tasks in the interests of solving the inertial thermonuclear fusion problems and for the development of different cumulative devices.

The multifunctional shock tube provides the following parameters of gas dynamic flows:

  • in the mode with driver I, a stationary shock wave with Mach number M ≤ 5 is generated;
  • in the mode with driver II, a nonstationary shock wave is generated whose initial pressure at the front is 5 * 106 Pa with the acceleration of the contact boundary of different density gases behind the wave front g1 ≤ 106 g, where g is the acceleration of the Earth's gravitational field;
  • in the mode with driver III, a compression wave is generated that ensures the acceleration of the contact boundaries of different density gases g1 ≤ 105 g.

In all three modes the gases with density ration p2/p1 ≤ 34 may be used.

References

REFERENCES

Anuchina, N.N. et al. (1997). Three-dimensional numerical simulation of Rayleigh–Taylor instability by MAH-3 code. Proc. 6th Int. Workshop on Physics of Compressible Turbulent Mixing.
Kucherenko, Yu.A. et al. (1988). Experimental investigation of the gravitational turbulent mixing in self-similar mode. Rus. J. VANT, Series Theoretical and Applied Physics 1.
Kucherenko, Yu.A. et al. (1991). Experimental study of the gravitational turbulent mixing in self-similar mode. Proc. 3rd Int. Workshop on Physics of Compressible Turbulent Mixing.
Read, K. (1984). Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12.Google Scholar
Vasilenko, A.M. et al. (1991). Experimental investigations for turbulent mixing of gases at the interface under the influence of the decelerating shock wave. Proc. 3rd Int. Workshop on Physics of Compressible Turbulent Mixing.
Youngs, D.L. (1991). Three-dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids A 3.Google Scholar
Zaitsev, S.G. et al. (2000). Evolution of the Rayleigh–Taylor instability in compressible media. Report under ISTC Project No. 96-029.
Figure 0

Physical scheme of MST with driver I.

Figure 1

Physical scheme of MST with driver II.

Figure 2

Physical scheme of MST with driver III.