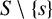1 Introduction
The minimal number of generators of a finite group G is denoted by
![]() $d(G).$
A generating set S for a group G is independent (sometimes called irredundant) if
$d(G).$
A generating set S for a group G is independent (sometimes called irredundant) if
Let
![]() $m(G)$
denote the maximal size of an independent generating set for
$m(G)$
denote the maximal size of an independent generating set for
![]() $G.$
$G.$
The finite groups with
![]() $m(G)=d(G)$
are classified by Apisa and Klopsch.
$m(G)=d(G)$
are classified by Apisa and Klopsch.
Theorem 1.1 (Apisa–Klopsch, [Reference Apisa and Klopsch1, Theorem 1.6]).
If
![]() $d(G)=m(G)$
, then G is soluble. Moreover, either
$d(G)=m(G)$
, then G is soluble. Moreover, either
-
•
 $G/\operatorname {\mathrm {Frat}}(G)$
is an elementary abelian p-group for some prime p; or
$G/\operatorname {\mathrm {Frat}}(G)$
is an elementary abelian p-group for some prime p; or -
•
 $G/\operatorname {\mathrm {Frat}}(G)=PQ,$
where P is an elementary abelian p-group and Q is a nontrivial cyclic q-group for distinct primes p and
$G/\operatorname {\mathrm {Frat}}(G)=PQ,$
where P is an elementary abelian p-group and Q is a nontrivial cyclic q-group for distinct primes p and
 $q,$
such that Q acts by conjugation faithfully on P and P (viewed as a module for Q) is a direct sum of
$q,$
such that Q acts by conjugation faithfully on P and P (viewed as a module for Q) is a direct sum of
 $m(G)-1$
isomorphic copies of one simple Q-module.
$m(G)-1$
isomorphic copies of one simple Q-module.
In view of this result, Apisa and Klopsch suggest a natural ‘classification problem’: given a nonnegative integer c, characterise all finite groups G which satisfy
![]() $m(G) - d(G) \leq c$
. The particular case
$m(G) - d(G) \leq c$
. The particular case
![]() $c=1$
has been recently highlighted by Glasby (see [Reference Glasby7, Problem 2.3]).
$c=1$
has been recently highlighted by Glasby (see [Reference Glasby7, Problem 2.3]).
A nice result in universal algebra, due to Tarski and known as the Tarski irredundant basis theorem (see for example [Reference Burris and Sankappanavar3, Theorem 4.4]), implies that, for every positive integer k with
![]() $d(G)\leq k\leq m(G), G$
contains an independent generating set of cardinality
$d(G)\leq k\leq m(G), G$
contains an independent generating set of cardinality
![]() $k.$
So the condition
$k.$
So the condition
![]() $m(G) - d(G)= 1$
is equivalent to the fact that there are only two possible cardinalities for an independent generating set of
$m(G) - d(G)= 1$
is equivalent to the fact that there are only two possible cardinalities for an independent generating set of
![]() $G.$
$G.$
Let G be a finite group. We recall that the socle of G, denoted
![]() $\operatorname {\mathrm {soc}}(G)$
, is the subgroup generated by the minimal normal subgroups of G; moreover, G is said to be monolithic primitive if G has a unique minimal normal subgroup and the Frattini subgroup
$\operatorname {\mathrm {soc}}(G)$
, is the subgroup generated by the minimal normal subgroups of G; moreover, G is said to be monolithic primitive if G has a unique minimal normal subgroup and the Frattini subgroup
![]() $\operatorname {\mathrm {Frat}}(G)$
of G is the identity.
$\operatorname {\mathrm {Frat}}(G)$
of G is the identity.
In this paper, we prove the following two main results.
Theorem 1.2. Let G be a finite group with
![]() $\operatorname {\mathrm {Frat}}(G)=1$
and
$\operatorname {\mathrm {Frat}}(G)=1$
and
![]() $m(G)=d(G)+1.$
If G is not soluble, then
$m(G)=d(G)+1.$
If G is not soluble, then
![]() $d(G)=2$
, G is a monolithic primitive group and
$d(G)=2$
, G is a monolithic primitive group and
![]() $G/\operatorname {\mathrm {soc}}(G)$
is cyclic of prime power order.
$G/\operatorname {\mathrm {soc}}(G)$
is cyclic of prime power order.
It was proved by Whiston and Saxl [Reference Whiston and Saxl15] that
![]() $m(\operatorname {\mathrm {PSL}}(2,p))=3$
for any prime p with p not congruent to
$m(\operatorname {\mathrm {PSL}}(2,p))=3$
for any prime p with p not congruent to
![]() $\pm 1$
modulo 8 or 10. In particular, as
$\pm 1$
modulo 8 or 10. In particular, as
![]() $d(S)=2$
for every nonabelian simple group, we deduce that there are infinitely many nonabelian simple groups G with
$d(S)=2$
for every nonabelian simple group, we deduce that there are infinitely many nonabelian simple groups G with
![]() $m(G)=d(G)+1$
. We also give examples of nonsimple groups G having
$m(G)=d(G)+1$
. We also give examples of nonsimple groups G having
![]() ${m(G)=d(G)+1}$
in Section 4.
${m(G)=d(G)+1}$
in Section 4.
Theorem 1.3. Let G be a finite group with
![]() $\operatorname {\mathrm {Frat}}(G)=1$
and
$\operatorname {\mathrm {Frat}}(G)=1$
and
![]() $m(G)=d(G)+1.$
If G is soluble, then one of the following occurs:
$m(G)=d(G)+1.$
If G is soluble, then one of the following occurs:
-
(1)
 $G\cong V\rtimes P$
, where P is a finite noncyclic p-group and V is an irreducible P-module, which is not a p-group; in this case,
$G\cong V\rtimes P$
, where P is a finite noncyclic p-group and V is an irreducible P-module, which is not a p-group; in this case,
 $d(G)=d(P)$
;
$d(G)=d(P)$
; -
(2)
 $G\cong V^t \rtimes H,$
where V is a faithful irreducible H-module,
$G\cong V^t \rtimes H,$
where V is a faithful irreducible H-module,
 $m(H)=2$
and either
$m(H)=2$
and either
 $t=1$
or H is abelian; in this case,
$t=1$
or H is abelian; in this case,
 $d(G)=t+1$
;
$d(G)=t+1$
; -
(3) there exist two normal subgroups
 $N_1$
,
$N_1$
,
 $N_2$
such that
$N_2$
such that
 $1 \lneq N_1 \leq N_2, N_1$
is an abelian minimal normal subgroup of
$1 \lneq N_1 \leq N_2, N_1$
is an abelian minimal normal subgroup of
 $G, N_2/N_1\leq \operatorname {\mathrm {Frat}}(G/N_1)$
and
$G, N_2/N_1\leq \operatorname {\mathrm {Frat}}(G/N_1)$
and
 $G/N_2\cong V^t\rtimes H$
, where V is an irreducible H-module and H is a nontrivial cyclic group of prime power order; in this case,
$G/N_2\cong V^t\rtimes H$
, where V is an irreducible H-module and H is a nontrivial cyclic group of prime power order; in this case,
 $d(G)=t+1.$
$d(G)=t+1.$
In Section 4, we give examples of finite soluble groups G with
![]() $m(G)=d(G)+1$
for each of the three possibilities arising in Theorem 1.3.
$m(G)=d(G)+1$
for each of the three possibilities arising in Theorem 1.3.
2 Preliminary results
Let L be a monolithic primitive group and let A be its unique minimal normal subgroup. For each positive integer k, let
![]() $L^k$
be the k-fold direct product of L. The crown-based power of L of size k is the subgroup
$L^k$
be the k-fold direct product of L. The crown-based power of L of size k is the subgroup
![]() $L_k$
of
$L_k$
of
![]() $L^k$
defined by
$L^k$
defined by
In [Reference Dalla Volta and Lucchini4], it is proved that for every finite group G, there exists a monolithic group L and a homomorphic image
![]() $L_k$
of G such that
$L_k$
of G such that
-
(1)
 $ d(L/\operatorname {\mathrm {soc}} L) < d(G) $
; and
$ d(L/\operatorname {\mathrm {soc}} L) < d(G) $
; and -
(2)
 $d(L_k) =d(G).$
$d(L_k) =d(G).$
A group
![]() $L_{k}$
with this property is called a generating crown-based power for G.
$L_{k}$
with this property is called a generating crown-based power for G.
In [Reference Dalla Volta and Lucchini4], it is explained how
![]() $d(L_{k})$
can be explicitly computed in terms of k and the structure of L. A key ingredient (when one wants to determine
$d(L_{k})$
can be explicitly computed in terms of k and the structure of L. A key ingredient (when one wants to determine
![]() $d(G)$
from the behaviour of the crown-based power homomorphic images of G) is to evaluate, for each monolithic group L, the maximal k such that
$d(G)$
from the behaviour of the crown-based power homomorphic images of G) is to evaluate, for each monolithic group L, the maximal k such that
![]() $L_{k}$
is a homomorphic image of G. This integer k arises from an equivalence relation among the chief factors of G. In what follows, we give some details.
$L_{k}$
is a homomorphic image of G. This integer k arises from an equivalence relation among the chief factors of G. In what follows, we give some details.
Given groups G and A, we say that A is a G-group if G acts on A via automorphisms. In addition, A is irreducible if G does not stabilise any nontrivial proper subgroups of A. Two G-groups A and B are G-isomorphic if there exists a group isomorphism
![]() $\phi : A\to B$
such that
$\phi : A\to B$
such that
![]() $\phi (g(a))=g(\phi (a))$
for all
$\phi (g(a))=g(\phi (a))$
for all
![]() $a\in A$
and
$a\in A$
and
![]() $g\in G.$
Following [Reference Jiménez-Seral and Lafuente8], we say that two irreducible G-groups A and B are G-equivalent, denoted
$g\in G.$
Following [Reference Jiménez-Seral and Lafuente8], we say that two irreducible G-groups A and B are G-equivalent, denoted
![]() $A \sim _G B$
, if there is an isomorphism
$A \sim _G B$
, if there is an isomorphism
![]() $\Phi : A\rtimes G \rightarrow B\rtimes G$
which restricts to a G-isomorphism
$\Phi : A\rtimes G \rightarrow B\rtimes G$
which restricts to a G-isomorphism
![]() $\phi \colon A \to B$
and induces the identity
$\phi \colon A \to B$
and induces the identity
![]() $G \cong AG/A \to BG/B \cong G$
, in other words, such that the following diagram commutes:
$G \cong AG/A \to BG/B \cong G$
, in other words, such that the following diagram commutes:

Observe that two G-isomorphic G-groups are G-equivalent, and the converse holds if A and B are abelian.
Let
![]() $A=X/Y$
be a chief factor of G. A complement U of A in G is a subgroup of G such that
$A=X/Y$
be a chief factor of G. A complement U of A in G is a subgroup of G such that
We say that
![]() $A=X/Y$
is a Frattini chief factor if
$A=X/Y$
is a Frattini chief factor if
![]() $X/Y$
is contained in the Frattini subgroup of
$X/Y$
is contained in the Frattini subgroup of
![]() $G/Y$
; this is equivalent to saying that A is abelian and there is no complement to A in G. The number
$G/Y$
; this is equivalent to saying that A is abelian and there is no complement to A in G. The number
![]() $\delta _G(A)$
of non-Frattini chief factors that are G-equivalent to A, in any chief series of G, does not depend on the particular choice of such a series.
$\delta _G(A)$
of non-Frattini chief factors that are G-equivalent to A, in any chief series of G, does not depend on the particular choice of such a series.
Now, we denote by
![]() $L_G(A)$
the
monolithic primitive group associated to A, that is,
$L_G(A)$
the
monolithic primitive group associated to A, that is,
 $$ \begin{align*}L_G(A):= \begin{cases} A\rtimes (G/\mathbf{C}_G(A)) & \text{ if }A\text{ is abelian}, \\ G/\mathbf{C}_G(A)& \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}L_G(A):= \begin{cases} A\rtimes (G/\mathbf{C}_G(A)) & \text{ if }A\text{ is abelian}, \\ G/\mathbf{C}_G(A)& \text{ otherwise}. \end{cases} \end{align*} $$
If A is a non-Frattini chief factor of G, then
![]() $L_G(A)$
is a homomorphic image of G. More precisely, there exists a normal subgroup N such that
$L_G(A)$
is a homomorphic image of G. More precisely, there exists a normal subgroup N such that
![]() $G/N \cong L_G(A)$
and
$G/N \cong L_G(A)$
and
![]() $\operatorname {\mathrm {soc}} (G/N) \sim _G~A$
. We identify
$\operatorname {\mathrm {soc}} (G/N) \sim _G~A$
. We identify
![]() $\operatorname {\mathrm {soc}}( L_G(A))$
with A, as G-groups.
$\operatorname {\mathrm {soc}}( L_G(A))$
with A, as G-groups.
Consider now all the normal subgroups N of G with the property that
![]() ${G/N \cong L_G(A)}$
and
${G/N \cong L_G(A)}$
and
![]() $\operatorname {\mathrm {soc}} (G/N) \sim _G A$
. The intersection
$\operatorname {\mathrm {soc}} (G/N) \sim _G A$
. The intersection
![]() $R_G(A)$
of all these subgroups has the property that
$R_G(A)$
of all these subgroups has the property that
![]() $G/R_G(A)$
is isomorphic to the crown-based power
$G/R_G(A)$
is isomorphic to the crown-based power
![]() $(L_G(A))_{\delta _G(A)}$
. The socle
$(L_G(A))_{\delta _G(A)}$
. The socle
![]() $I_G(A)/R_G(A)$
of
$I_G(A)/R_G(A)$
of
![]() $G/R_G(A)$
is called the A-crown of G and it is a direct product of
$G/R_G(A)$
is called the A-crown of G and it is a direct product of
![]() $\delta _G(A)$
minimal normal subgroups G-equivalent to A.
$\delta _G(A)$
minimal normal subgroups G-equivalent to A.
Note that if L is monolithic primitive and
![]() $L_k$
is a homomorphic image of G for some
$L_k$
is a homomorphic image of G for some
![]() $k\geq 1$
, then
$k\geq 1$
, then
![]() $L \cong L_G(A)$
for some non-Frattini chief factor A of G and
$L \cong L_G(A)$
for some non-Frattini chief factor A of G and
![]() $k \leq \delta _G(A)$
. Furthermore, if
$k \leq \delta _G(A)$
. Furthermore, if
![]() $(L_G(A))_k$
is a generating crown-based power, then so is
$(L_G(A))_k$
is a generating crown-based power, then so is
![]() $(L_G(A))_{\delta _G(A)}$
; in this case, we say that A is a generating chief factor for G.
$(L_G(A))_{\delta _G(A)}$
; in this case, we say that A is a generating chief factor for G.
For an irreducible G-module M, set
 $$ \begin{align*} r_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)}M,\\ s_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)} H^1(G,M), \\ t_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)} H^1(G/\mathbf{C}_G(M),M). \end{align*} $$
$$ \begin{align*} r_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)}M,\\ s_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)} H^1(G,M), \\ t_G(M)&:=\dim_{\operatorname{\mathrm{End}}_G(M)} H^1(G/\mathbf{C}_G(M),M). \end{align*} $$
It can be seen that
(see for example [Reference Lucchini10, 1.2]). Now, define
 $$ \begin{align*}h_{G}(M):= \begin{cases} \delta_G(M)&\text{if }M\text{ is a trivial } G\textrm{-module}, \\ \displaystyle \bigg\lfloor\frac{s_G(M)-1}{r_G(M)}\bigg\rfloor+2=\bigg\lfloor\frac{\delta_G(M)+t_G(M)-1}{r_G(M)}\bigg\rfloor+2& \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}h_{G}(M):= \begin{cases} \delta_G(M)&\text{if }M\text{ is a trivial } G\textrm{-module}, \\ \displaystyle \bigg\lfloor\frac{s_G(M)-1}{r_G(M)}\bigg\rfloor+2=\bigg\lfloor\frac{\delta_G(M)+t_G(M)-1}{r_G(M)}\bigg\rfloor+2& \text{otherwise}. \end{cases} \end{align*} $$
By [Reference Aschbacher and Guralnick2, Theorem A],
![]() $t_G(M)<r_G(M)$
for any irreducible G-module M, and therefore
$t_G(M)<r_G(M)$
for any irreducible G-module M, and therefore
The importance of
![]() $h_G(M)$
is clarified by the following proposition.
$h_G(M)$
is clarified by the following proposition.
Proposition 2.1 [Reference Detomi and Lucchini6, Proposition 2.1].
If there exists an abelian generating chief factor A of G, then
![]() $ d(G)=h_G(A)$
.
$ d(G)=h_G(A)$
.
When G admits a nonabelian generating chief factor A, a relation between
![]() $\delta _G(A)$
and
$\delta _G(A)$
and
![]() $d(G)$
is provided by the following result.
$d(G)$
is provided by the following result.
Proposition 2.2. If
![]() $d(G)\geq 3$
and there exists a nonabelian generating chief factor A of G, then
$d(G)\geq 3$
and there exists a nonabelian generating chief factor A of G, then
 $$ \begin{align*}\delta_G(A)>\frac{|A|^{d(G)-1}}{2|\mathbf{C}_{\operatorname{\mathrm{Aut}} A}(L_G(A)/A)|}\geq \frac{|A|^{d(G)-2}}{2\log_2|A|}. \end{align*} $$
$$ \begin{align*}\delta_G(A)>\frac{|A|^{d(G)-1}}{2|\mathbf{C}_{\operatorname{\mathrm{Aut}} A}(L_G(A)/A)|}\geq \frac{|A|^{d(G)-2}}{2\log_2|A|}. \end{align*} $$
Proof. Suppose that
![]() $d(G)\ge 3$
and let A be a nonabelian generating chief factor of G.
$d(G)\ge 3$
and let A be a nonabelian generating chief factor of G.
For a finite group X, let
![]() $\phi _X(m)$
denote the number of ordered m-tuples
$\phi _X(m)$
denote the number of ordered m-tuples
![]() $(x_1,\ldots ,x_m)$
of elements of X generating X. Define
$(x_1,\ldots ,x_m)$
of elements of X generating X. Define
 $$ \begin{align*} L&:=L_G(A),\\ \gamma&:=|\mathbf{C}_{\operatorname{\mathrm{Aut}} A}(L/A)|,\\ \delta&:=\delta_G(A),\\ d&:=d(G). \end{align*} $$
$$ \begin{align*} L&:=L_G(A),\\ \gamma&:=|\mathbf{C}_{\operatorname{\mathrm{Aut}} A}(L/A)|,\\ \delta&:=\delta_G(A),\\ d&:=d(G). \end{align*} $$
In [Reference Dalla Volta and Lucchini4], it is proved that if
![]() $m\geq d(L),$
then
$m\geq d(L),$
then
 $$ \begin{align}d(L_k)\leq m \quad {\text {if and only if}} \quad k\leq \frac{\phi_{L/A}(m)}{\phi_L(m)\gamma}. \end{align} $$
$$ \begin{align}d(L_k)\leq m \quad {\text {if and only if}} \quad k\leq \frac{\phi_{L/A}(m)}{\phi_L(m)\gamma}. \end{align} $$
By the main result in [Reference Lucchini and Menegazzo13],
![]() $d(L)=\max (2,d(L/A))$
. Since A is a generating chief factor, from the definition, we have
$d(L)=\max (2,d(L/A))$
. Since A is a generating chief factor, from the definition, we have
![]() $d(L/A) < d(L_{\delta _G(A)})=d(G)$
. As
$d(L/A) < d(L_{\delta _G(A)})=d(G)$
. As
![]() $2 < d(G),$
it follows
$2 < d(G),$
it follows
![]() ${d(L)<d(G).}$
Now, by applying (2.2) with
${d(L)<d(G).}$
Now, by applying (2.2) with
![]() $k=\delta _G(A)$
and
$k=\delta _G(A)$
and
![]() $m=d(G)-1,$
we deduce that
$m=d(G)-1,$
we deduce that
 $$ \begin{align}\delta_G(A)>\frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)\gamma}.\end{align} $$
$$ \begin{align}\delta_G(A)>\frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)\gamma}.\end{align} $$
By [Reference Detomi and Lucchini6, Corollary 1.2],
 $$ \begin{align}\frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)}\geq \frac{|A|^{d(G)-1}}{2}.\end{align} $$
$$ \begin{align}\frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)}\geq \frac{|A|^{d(G)-1}}{2}.\end{align} $$
Moreover,
![]() $A\cong S^n$
, where n is a positive integer and S is a nonabelian simple group. In the proof of Lemma 1 in [Reference Dalla Volta and Lucchini5], it is shown that
$A\cong S^n$
, where n is a positive integer and S is a nonabelian simple group. In the proof of Lemma 1 in [Reference Dalla Volta and Lucchini5], it is shown that
Now, [Reference Kohl9] shows that
![]() $|{\operatorname {\mathrm {Out}}}(S)| \leq \log _2(|S|)$
and hence
$|{\operatorname {\mathrm {Out}}}(S)| \leq \log _2(|S|)$
and hence
From (2.3), (2.4) and (2.5), we obtain
 $$ \begin{align*} \delta_G(A)> \frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)\gamma}\geq \frac{|A|^{d(G)-1}}{2|A|\log_2|A|}=\frac{|A|^{d(G)-2}}{2\log_2|A|}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \delta_G(A)> \frac{\phi_{L/A}(d(G)-1)}{\phi_L(d(G)-1)\gamma}\geq \frac{|A|^{d(G)-1}}{2|A|\log_2|A|}=\frac{|A|^{d(G)-2}}{2\log_2|A|}.\\[-42pt] \end{align*} $$
Recall that
![]() $m(G)$
is the largest cardinality of an independent generating set of G.
$m(G)$
is the largest cardinality of an independent generating set of G.
Theorem 2.3 [Reference Lucchini and Spiga14, Theorem 1.3].
Let G be a finite group. Then
![]() $m(G)\geq a+b,$
where a and b are, respectively, the number of non-Frattini and nonabelian factors in a chief series of G. Moreover, if G is soluble, then
$m(G)\geq a+b,$
where a and b are, respectively, the number of non-Frattini and nonabelian factors in a chief series of G. Moreover, if G is soluble, then
![]() $m(G)=a.$
$m(G)=a.$
Corollary 2.4. Assume that G is a finite group with a unique minimal normal subgroup A. If A is nonabelian, then
![]() $m(G)\geq 3.$
$m(G)\geq 3.$
Proof. Suppose first that G is simple. Let l be an element of G of order 2. Since
![]() $G=\langle l^x\mid x\in G\rangle $
, the set
$G=\langle l^x\mid x\in G\rangle $
, the set
![]() $\{l ^x\mid x \in G\}$
contains a minimal generating set of
$\{l ^x\mid x \in G\}$
contains a minimal generating set of
![]() $G.$
Since G cannot be generated by two involutions, this minimal generating set has cardinality at least three. Thus,
$G.$
Since G cannot be generated by two involutions, this minimal generating set has cardinality at least three. Thus,
![]() $m(G)\ge 3$
.
$m(G)\ge 3$
.
Suppose next that G is not simple. Let a and b be the number of non-Frattini and nonabelian factors in a chief series of G. As G is not simple, there exists a maximal normal subgroup N of G containing A and we have a chief series
![]() $1\unlhd N_1\unlhd \cdots \unlhd N_{t-1}\unlhd N_t=G$
with
$1\unlhd N_1\unlhd \cdots \unlhd N_{t-1}\unlhd N_t=G$
with
![]() $N_1=A$
and
$N_1=A$
and
![]() $N_{t-1}=N.$
Then,
$N_{t-1}=N.$
Then,
![]() $a\geq 2$
,
$a\geq 2$
,
![]() $b\geq 1$
and
$b\geq 1$
and
![]() $m(G)\geq a+b\geq 3$
by Theorem 2.3.
$m(G)\geq a+b\geq 3$
by Theorem 2.3.
3 Proof of the main results
Let G be a finite group, let
![]() $d:=d(G)$
and let
$d:=d(G)$
and let
![]() $m:=m(G)$
. Suppose that
$m:=m(G)$
. Suppose that
![]() $m=d+1.$
Let A be a generating chief factor of G and let
$m=d+1.$
Let A be a generating chief factor of G and let
![]() $\delta :=\delta _G(A)$
,
$\delta :=\delta _G(A)$
,
![]() $L:=L_G(A).$
$L:=L_G(A).$
3.1 A is nonabelian
First, suppose that
![]() $\delta \geq 2.$
By Theorem 2.3,
$\delta \geq 2.$
By Theorem 2.3,
![]() $m\geq 2\delta $
and therefore
$m\geq 2\delta $
and therefore
![]() $d\geq 2\delta -1\geq 3.$
By Proposition 2.2,
$d\geq 2\delta -1\geq 3.$
By Proposition 2.2,
 $$ \begin{align*}\delta> \frac{|A|^{d-2}}{2\log_2|A|}\geq \frac{ |A|^{2\delta-3}}{2\log_2|A|}\geq \frac{60^{2\delta-3}}{2\log_260},\end{align*} $$
$$ \begin{align*}\delta> \frac{|A|^{d-2}}{2\log_2|A|}\geq \frac{ |A|^{2\delta-3}}{2\log_2|A|}\geq \frac{60^{2\delta-3}}{2\log_260},\end{align*} $$
but this is never true.
Suppose now that
![]() $\delta =1$
. In this case, by the main theorem in [Reference Lucchini and Menegazzo13],
$\delta =1$
. In this case, by the main theorem in [Reference Lucchini and Menegazzo13],
![]() $d=d(L)=\max (2,d(L/A))=2$
and therefore
$d=d(L)=\max (2,d(L/A))=2$
and therefore
![]() $m=3.$
Since L is an epimorphic image of G, we must have
$m=3.$
Since L is an epimorphic image of G, we must have
![]() $m(L)\leq 3$
. However,
$m(L)\leq 3$
. However,
![]() $m(L)\geq 3$
by Corollary 2.4. Hence,
$m(L)\geq 3$
by Corollary 2.4. Hence,
![]() $m(L)=m=3$
and therefore it follows from [Reference Lucchini11, Lemma 11] that
$m(L)=m=3$
and therefore it follows from [Reference Lucchini11, Lemma 11] that
![]() $G/\operatorname {\mathrm {Frat}}(G)\cong L.$
Finally, by Theorem 2.3,
$G/\operatorname {\mathrm {Frat}}(G)\cong L.$
Finally, by Theorem 2.3,
![]() $m(L)=3$
implies
$m(L)=3$
implies
![]() $m(L/A)\leq 1,$
and this is possible only if
$m(L/A)\leq 1,$
and this is possible only if
![]() $L/A$
is a cyclic p-group. This concludes the proof of Theorem 1.2.
$L/A$
is a cyclic p-group. This concludes the proof of Theorem 1.2.
3.2 A is abelian
It follows from Proposition 2.1 and (2.1) that
If
![]() $d=\delta -1,$
then
$d=\delta -1,$
then
![]() $m=\delta $
and this is possible if
$m=\delta $
and this is possible if
![]() $G/\operatorname {\mathrm {Frat}}(G)\cong A^\delta .$
However, in this case, A would be a trivial G-module and therefore
$G/\operatorname {\mathrm {Frat}}(G)\cong A^\delta .$
However, in this case, A would be a trivial G-module and therefore
![]() $d=h_G(A)=\delta =m,$
which is a contradiction.
$d=h_G(A)=\delta =m,$
which is a contradiction.
Now suppose that
![]() $d=\delta .$
By Theorem 2.3, G is soluble and contains only one non-Frattini chief factor which is not G-isomorphic to
$d=\delta .$
By Theorem 2.3, G is soluble and contains only one non-Frattini chief factor which is not G-isomorphic to
![]() $A.$
If A is noncentral in G, then
$A.$
If A is noncentral in G, then
![]() $G/\operatorname {\mathrm {Frat}}(G)\cong L_\delta $
and
$G/\operatorname {\mathrm {Frat}}(G)\cong L_\delta $
and
![]() $L/A$
is a cyclic p-group. However, this implies
$L/A$
is a cyclic p-group. However, this implies
![]() $r_G(A)\,{=}\,1,\ t_G(A)\,{=}\,0$
and
$r_G(A)\,{=}\,1,\ t_G(A)\,{=}\,0$
and
![]() $d=h_G(A)=\delta +1,$
which is a contradiction. If A is central, then
$d=h_G(A)=\delta +1,$
which is a contradiction. If A is central, then
![]() $G/\operatorname {\mathrm {Frat}}(G)\cong V\rtimes P$
, where P is a finite p-group, V is an irreducible P-module and
$G/\operatorname {\mathrm {Frat}}(G)\cong V\rtimes P$
, where P is a finite p-group, V is an irreducible P-module and
![]() $d(P)=d.$
In particular, we obtain item (1) in Theorem 1.3.
$d(P)=d.$
In particular, we obtain item (1) in Theorem 1.3.
Finally assume
![]() $d=\delta +1.$
Notice that in this case,
$d=\delta +1.$
Notice that in this case,
![]() $L=A\rtimes H,$
where A is a faithful, nontrivial, irreducible H-module, and
$L=A\rtimes H,$
where A is a faithful, nontrivial, irreducible H-module, and
In particular, by Corollary 2.4, H is soluble.
If
![]() $m(H)=2,$
then
$m(H)=2,$
then
![]() $G/\operatorname {\mathrm {Frat}}(G)\cong L_\delta .$
In particular, we obtain item (2) in Theorem 1.3.
$G/\operatorname {\mathrm {Frat}}(G)\cong L_\delta .$
In particular, we obtain item (2) in Theorem 1.3.
If
![]() $m(H)=1,$
then there exist two normal subgroups
$m(H)=1,$
then there exist two normal subgroups
![]() $N_1$
and
$N_1$
and
![]() $N_2$
of G such that
$N_2$
of G such that
![]() $1 \lneq N_1 \leq N_2, G/N_2\cong L_\delta , N_2/N_1\leq \operatorname {\mathrm {Frat}}(G/N_1)$
and
$1 \lneq N_1 \leq N_2, G/N_2\cong L_\delta , N_2/N_1\leq \operatorname {\mathrm {Frat}}(G/N_1)$
and
![]() $N_1/\operatorname {\mathrm {Frat}}(G)$
is an abelian minimal normal subgroup of
$N_1/\operatorname {\mathrm {Frat}}(G)$
is an abelian minimal normal subgroup of
![]() $G/\operatorname {\mathrm {Frat}}(G).$
As
$G/\operatorname {\mathrm {Frat}}(G).$
As
![]() $m(H)=1$
, H is cyclic of prime power order. In particular, we obtain item (3) in Theorem 1.3.
$m(H)=1$
, H is cyclic of prime power order. In particular, we obtain item (3) in Theorem 1.3.
4 Examples for Theorems 1.2 and 1.3
4.1 Monolithic groups: examples for Theorem 1.2
Let G be monolithic primitive with nonabelian socle
![]() $N= S_1\times \cdots \times S_n$
, with
$N= S_1\times \cdots \times S_n$
, with
![]() $S\cong S_i$
for each
$S\cong S_i$
for each
![]() $1\leq i \leq n.$
The number
$1\leq i \leq n.$
The number
![]() $\mu (G)=m(G)-m(G/N)$
has been investigated in [Reference Lucchini12]. The group G acts by conjugation on the set
$\mu (G)=m(G)-m(G/N)$
has been investigated in [Reference Lucchini12]. The group G acts by conjugation on the set
![]() $\{S_1,\ldots ,S_n\}$
of the simple components of
$\{S_1,\ldots ,S_n\}$
of the simple components of
![]() $N.$
This produces a group homomorphism
$N.$
This produces a group homomorphism
![]() $G\to \operatorname {\mathrm {Sym}}(n)$
and the image K of G under this homomorphism is a transitive subgroup of
$G\to \operatorname {\mathrm {Sym}}(n)$
and the image K of G under this homomorphism is a transitive subgroup of
![]() $\operatorname {\mathrm {Sym}}(n).$
Moreover, the subgroup X of
$\operatorname {\mathrm {Sym}}(n).$
Moreover, the subgroup X of
![]() $\operatorname {\mathrm {Aut}} S$
induced by the conjugation action of
$\operatorname {\mathrm {Aut}} S$
induced by the conjugation action of
![]() $\textbf {N}_G(S_1)$
on the first factor
$\textbf {N}_G(S_1)$
on the first factor
![]() $S_1$
is an almost simple group with socle
$S_1$
is an almost simple group with socle
![]() $S.$
$S.$
By [Reference Lucchini12, Proposition 4],
![]() $\mu (G)\geq \mu (X)=m(X)-m(X/S).$
Assume
$\mu (G)\geq \mu (X)=m(X)-m(X/S).$
Assume
![]() $m(G)=3.$
Observe that by Theorems 1.1 and 1.2,
$m(G)=3.$
Observe that by Theorems 1.1 and 1.2,
![]() $G/N$
is cyclic of prime power order. If
$G/N$
is cyclic of prime power order. If
![]() $X=S$
, then
$X=S$
, then
 $$ \begin{align*} 3=m(G)=m(G/N)+\mu(G)& \geq m(G/N)+\mu(X)= m(G/N)+m(S)\\ &\geq m(G/N)+3. \end{align*} $$
$$ \begin{align*} 3=m(G)=m(G/N)+\mu(G)& \geq m(G/N)+\mu(X)= m(G/N)+m(S)\\ &\geq m(G/N)+3. \end{align*} $$
This implies that
![]() $G/N=1$
and
$G/N=1$
and
![]() $G=S$
is a simple group. If
$G=S$
is a simple group. If
![]() $X\neq S$
, then
$X\neq S$
, then
![]() $G\neq N$
and
$G\neq N$
and
Moreover,
![]() $X/S$
is a nontrivial cyclic group of prime power order, so
$X/S$
is a nontrivial cyclic group of prime power order, so
By Corollary 2.4,
![]() $m(X)=3.$
$m(X)=3.$
The groups
are currently the only known examples (to the best knowledge of the authors) of almost simple groups X with
![]() $X\neq \operatorname {\mathrm {soc}}(X)$
and
$X\neq \operatorname {\mathrm {soc}}(X)$
and
![]() $m(X)=3.$
We believe that there are other such examples, but our current computer codes are not efficient enough to carry out a thorough investigation.
$m(X)=3.$
We believe that there are other such examples, but our current computer codes are not efficient enough to carry out a thorough investigation.
Let
![]() $S:=\mathrm {PSL}_2(7)$
and
$S:=\mathrm {PSL}_2(7)$
and
![]() $H:=\mathrm {Aut}(\mathrm {PSL}_2(7)),$
or let
$H:=\mathrm {Aut}(\mathrm {PSL}_2(7)),$
or let
![]() $S:=\mathrm {PSL}_2(9)$
and
$S:=\mathrm {PSL}_2(9)$
and
![]() $H\in \{\mathrm {P}\Sigma \mathrm {L}_2(9), M_{10}\}$
. Consider the wreath product
$H\in \{\mathrm {P}\Sigma \mathrm {L}_2(9), M_{10}\}$
. Consider the wreath product
![]() $W:=H \wr \operatorname {\mathrm {Sym}}(n)$
. Any element
$W:=H \wr \operatorname {\mathrm {Sym}}(n)$
. Any element
![]() $w\in W$
can be written as
$w\in W$
can be written as
![]() $w=\pi (a_1,\ldots ,a_n),$
with
$w=\pi (a_1,\ldots ,a_n),$
with
![]() $\pi \in \operatorname {\mathrm {Sym}}(n)$
and
$\pi \in \operatorname {\mathrm {Sym}}(n)$
and
![]() $a_i\in H$
for
$a_i\in H$
for
![]() $1\leq i\leq n$
. In particular,
$1\leq i\leq n$
. In particular,
![]() $N=\operatorname {\mathrm {soc}}(W) =S_1\times \cdots \times S_n=\{(s_1,\ldots ,s_n)\mid s_i \in S\}$
.
$N=\operatorname {\mathrm {soc}}(W) =S_1\times \cdots \times S_n=\{(s_1,\ldots ,s_n)\mid s_i \in S\}$
.
Proposition 4.1. Let G be the subgroup of W generated by
![]() $N=\operatorname {\mathrm {soc}}(W)$
and
$N=\operatorname {\mathrm {soc}}(W)$
and
![]() $\gamma =\sigma (a,1,\ldots ,1),$
where
$\gamma =\sigma (a,1,\ldots ,1),$
where
![]() $\sigma =(1\,2\cdots n)\in \operatorname {\mathrm {Sym}}(n)$
and
$\sigma =(1\,2\cdots n)\in \operatorname {\mathrm {Sym}}(n)$
and
![]() $a\in H\setminus S.$
If
$a\in H\setminus S.$
If
![]() $n=2^t$
for some positive integer
$n=2^t$
for some positive integer
![]() $t,$
then
$t,$
then
![]() $m(G)=3.$
$m(G)=3.$
In particular, this gives infinitely many examples of nonsimple, nonsoluble groups G with
![]() $m(G)=d(G)+1$
in Theorem 1.2.
$m(G)=d(G)+1$
in Theorem 1.2.
Proof. Suppose that
![]() $n=2^t$
for some positive integer t. Let
$n=2^t$
for some positive integer t. Let
![]() $r:=m(G)$
; we aim to prove that
$r:=m(G)$
; we aim to prove that
![]() $r=3$
.
$r=3$
.
Let
![]() $\{g_1,\ldots ,g_r\}$
be an independent generating set of
$\{g_1,\ldots ,g_r\}$
be an independent generating set of
![]() $G.$
Observe that
$G.$
Observe that
and hence
![]() $G/N$
is cyclic of order
$G/N$
is cyclic of order
![]() $2^{t+1}.$
Therefore, relabelling the elements of the independent generating set if necessary, we may assume
$2^{t+1}.$
Therefore, relabelling the elements of the independent generating set if necessary, we may assume
![]() $G=\langle g_1, N\rangle $
. Hence,
$G=\langle g_1, N\rangle $
. Hence,
![]() ${g_1=\sigma (as_1,s_2,\ldots ,s_n)}$
with
${g_1=\sigma (as_1,s_2,\ldots ,s_n)}$
with
![]() $s_1,\ldots ,s_n\in S.$
Moreover, for
$s_1,\ldots ,s_n\in S.$
Moreover, for
![]() $2\leq i\leq r,$
there exists
$2\leq i\leq r,$
there exists
![]() $u_i\in \mathbb Z$
such that
$u_i\in \mathbb Z$
such that
![]() $g_ig_1^{u_i}\in N$
. Observe that
$g_ig_1^{u_i}\in N$
. Observe that
![]() $\{g_1,g_2g_1^{u_2},\ldots ,g_rg_1^{u_r}\}$
is still an independent generating set having cardinality r.
$\{g_1,g_2g_1^{u_2},\ldots ,g_rg_1^{u_r}\}$
is still an independent generating set having cardinality r.
Let
Then,
![]() $Y=\{g_1^m,(g_2g_1^{u_2})^m,\ldots ,(g_rg_1^{u_r})^m\}$
is another independent generating set for G having cardinality r. We have
$Y=\{g_1^m,(g_2g_1^{u_2})^m,\ldots ,(g_rg_1^{u_r})^m\}$
is another independent generating set for G having cardinality r. We have
with
![]() $b=as_1\cdots s_n \in \operatorname {\mathrm {Aut}} S\setminus S,$
and for
$b=as_1\cdots s_n \in \operatorname {\mathrm {Aut}} S\setminus S,$
and for
![]() $2\leq i\leq r,$
there exist
$2\leq i\leq r,$
there exist
![]() $s_{i1},\ldots s_{in}\in S$
such that
$s_{i1},\ldots s_{in}\in S$
such that
Let
![]() $Z:=\{b, s_{ij} \mid 2\leq i\leq r, 1\leq j\leq n\}$
and
$Z:=\{b, s_{ij} \mid 2\leq i\leq r, 1\leq j\leq n\}$
and
![]() $T=\langle Z\rangle .$
Since
$T=\langle Z\rangle .$
Since
![]() $G=\langle y_1,\ldots ,y_t\rangle \leq T \wr \langle \sigma \rangle ,$
we must have
$G=\langle y_1,\ldots ,y_t\rangle \leq T \wr \langle \sigma \rangle ,$
we must have
![]() $\operatorname {\mathrm {Aut}}(S)=T.$
However,
$\operatorname {\mathrm {Aut}}(S)=T.$
However,
![]() $m(\operatorname {\mathrm {Aut}}(S))=3,$
so
$m(\operatorname {\mathrm {Aut}}(S))=3,$
so
![]() $\operatorname {\mathrm {Aut}}(S)=\langle b, s_{iu}, s_{jv}\rangle $
for suitable
$\operatorname {\mathrm {Aut}}(S)=\langle b, s_{iu}, s_{jv}\rangle $
for suitable
![]() $2\leq i,j\leq r$
and
$2\leq i,j\leq r$
and
![]() $2\leq u, v\leq n.$
$2\leq u, v\leq n.$
Let
![]() $H:=\langle y_1, y_i, y_j\rangle $
and, for
$H:=\langle y_1, y_i, y_j\rangle $
and, for
![]() $1\leq k\leq n,$
consider the projection
$1\leq k\leq n,$
consider the projection
![]() $\pi _k: N\to S$
sending
$\pi _k: N\to S$
sending
![]() $(s_1,\ldots ,s_n)$
to
$(s_1,\ldots ,s_n)$
to
![]() $s_k.$
Notice that
$s_k.$
Notice that
![]() $\pi _1(y_1^n)=b, \pi _1((y_i)^{y_1^{1-u}})=s_{iu}, \pi _1((y_j)^{y_1^{1-v}})=s_{jv}.$
In particular,
$\pi _1(y_1^n)=b, \pi _1((y_i)^{y_1^{1-u}})=s_{iu}, \pi _1((y_j)^{y_1^{1-v}})=s_{jv}.$
In particular,
![]() $\pi _1(H\cap N)=S$
and
$\pi _1(H\cap N)=S$
and
![]() $H\cap N$
is a subdirect product of
$H\cap N$
is a subdirect product of
![]() $N= S_1\times \cdots \times S_n$
.
$N= S_1\times \cdots \times S_n$
.
Recall that a subgroup D of
![]() $N=S_1\times \cdots \times S_n$
is said to lie fully diagonally in N if each projection
$N=S_1\times \cdots \times S_n$
is said to lie fully diagonally in N if each projection
![]() $\pi _i: D\to S_i$
is an isomorphism. To each pair
$\pi _i: D\to S_i$
is an isomorphism. To each pair
![]() $(\Phi ,\alpha )$
, where
$(\Phi ,\alpha )$
, where
![]() ${\Phi =\{B_1,\ldots ,B_c\}}$
is a partition of the set
${\Phi =\{B_1,\ldots ,B_c\}}$
is a partition of the set
![]() $\{1,\ldots ,n\}$
and
$\{1,\ldots ,n\}$
and
![]() $\alpha =(\alpha _1,\ldots ,\alpha _n)\in (\operatorname {\mathrm {Aut}} S)^n$
, we associate a direct product
$\alpha =(\alpha _1,\ldots ,\alpha _n)\in (\operatorname {\mathrm {Aut}} S)^n$
, we associate a direct product
![]() $\Delta (\Phi ,\alpha )=D_1\times \cdots \times D_c$
, where each factor
$\Delta (\Phi ,\alpha )=D_1\times \cdots \times D_c$
, where each factor
![]() $D_j=\{(x^{\alpha _{i_1}},\ldots , x^{\alpha _{i_d}})\mid x\in S\}$
is a full diagonal subgroup of the direct product
$D_j=\{(x^{\alpha _{i_1}},\ldots , x^{\alpha _{i_d}})\mid x\in S\}$
is a full diagonal subgroup of the direct product
![]() $S_{i_1} \times \cdots \times S_{i_d}$
corresponding to the block
$S_{i_1} \times \cdots \times S_{i_d}$
corresponding to the block
![]() $B_j=\{i_1,\ldots ,i_d\}$
in
$B_j=\{i_1,\ldots ,i_d\}$
in
![]() $\Phi .$
$\Phi .$
Since
![]() $H\cap N$
is a subdirect product of
$H\cap N$
is a subdirect product of
![]() $N,$
we must have
$N,$
we must have
![]() $H\cap N=\Delta (\Phi ,\alpha )$
for a suitable choice of the pair
$H\cap N=\Delta (\Phi ,\alpha )$
for a suitable choice of the pair
![]() $(\Phi ,\alpha ).$
As
$(\Phi ,\alpha ).$
As
![]() $G=\langle H,N\rangle $
, the action by conjugation of H on
$G=\langle H,N\rangle $
, the action by conjugation of H on
![]() $\{S_1,\ldots ,S_n\}$
is transitive and hence the partition
$\{S_1,\ldots ,S_n\}$
is transitive and hence the partition
![]() $\{B_1,\ldots ,B_c\}$
corresponds to an imprimitive system for the permutation action of
$\{B_1,\ldots ,B_c\}$
corresponds to an imprimitive system for the permutation action of
![]() $\langle \sigma \rangle $
on
$\langle \sigma \rangle $
on
![]() $\{1,\ldots ,n\}.$
So there exist
$\{1,\ldots ,n\}.$
So there exist
![]() $c=2^\gamma $
and
$c=2^\gamma $
and
![]() $d=2^\delta $
with
$d=2^\delta $
with
![]() $c\cdot d=n$
such that
$c\cdot d=n$
such that
Notice that
![]() $y_1\in H$
normalises
$y_1\in H$
normalises
![]() $\Delta (\Phi ,\alpha )$
. In particular,
$\Delta (\Phi ,\alpha )$
. In particular,
![]() $y_1^c$
normalises
$y_1^c$
normalises
![]() $\Delta (\Phi ,\alpha ).$
However,
$\Delta (\Phi ,\alpha ).$
However,
![]() $y_1^c$
normalises
$y_1^c$
normalises
![]() $L=S_1\times S_{1+c}\times \cdots \times S_{1+(d-1)c}$
and acts on L as
$L=S_1\times S_{1+c}\times \cdots \times S_{1+(d-1)c}$
and acts on L as
![]() $\pi \cdot l,$
where
$\pi \cdot l,$
where
![]() $\pi $
is the d-cycle
$\pi $
is the d-cycle
![]() $(1,1+c,\ldots ,1+(d-1)c)$
and
$(1,1+c,\ldots ,1+(d-1)c)$
and
![]() $l=(b,1,\ldots ,1)\in L.$
In particular,
$l=(b,1,\ldots ,1)\in L.$
In particular,
![]() $\pi \cdot l$
normalises the full diagonal subgroup
$\pi \cdot l$
normalises the full diagonal subgroup
![]() $D_1$
of L. Therefore, setting
$D_1$
of L. Therefore, setting
![]() $\phi _i=\alpha _{1+(i-1)c}$
, for every
$\phi _i=\alpha _{1+(i-1)c}$
, for every
![]() $s\in S$
, there exists
$s\in S$
, there exists
![]() $t\in T$
such that
$t\in T$
such that
It follows that
 $$ \begin{align*}\begin{aligned} \phi_{d}b\phi_1^{-1}\phi_2&=\phi_1,\\ \phi_{d}b\phi_1^{-1}\phi_3&=\phi_{2},\\ \cdots\\ \phi_{d}b\phi_1^{-1}\phi_d&=\phi_{d-1}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \phi_{d}b\phi_1^{-1}\phi_2&=\phi_1,\\ \phi_{d}b\phi_1^{-1}\phi_3&=\phi_{2},\\ \cdots\\ \phi_{d}b\phi_1^{-1}\phi_d&=\phi_{d-1}. \end{aligned}\end{align*} $$
In particular,
![]() $(\phi _1\phi _d^{-1})^d\equiv b^{d-1}$
modulo
$(\phi _1\phi _d^{-1})^d\equiv b^{d-1}$
modulo
![]() $S.$
If d is even, then
$S.$
If d is even, then
![]() $b\in \langle x^2\mid x\in \operatorname {\mathrm {Aut}}(S)\rangle =S,$
against our assumption. Thus,
$b\in \langle x^2\mid x\in \operatorname {\mathrm {Aut}}(S)\rangle =S,$
against our assumption. Thus,
![]() $d=1$
and hence
$d=1$
and hence
![]() $c=n$
. However, this implies that
$c=n$
. However, this implies that
![]() ${H\cap N=N}$
and consequently
${H\cap N=N}$
and consequently
![]() $H=G.$
Thus,
$H=G.$
Thus,
![]() $m(G)=r\leq 3$
. However,
$m(G)=r\leq 3$
. However,
![]() $m(G)\geq 3$
by Theorem 2.3. So we conclude that
$m(G)\geq 3$
by Theorem 2.3. So we conclude that
![]() $m(G)=3.$
$m(G)=3.$
4.2 Soluble groups: examples for Theorem 1.3
We give three elementary examples, but with the same ideas, one can construct more complicated examples. Let
![]() $S_n$
be the symmetric group of degree n and let
$S_n$
be the symmetric group of degree n and let
![]() $C_n$
be the cyclic group of order n.
$C_n$
be the cyclic group of order n.
The group
![]() $G:=S_3 \times C_2^t = C_3 : C_2^{t+1}$
with
$G:=S_3 \times C_2^t = C_3 : C_2^{t+1}$
with
![]() $t\ge 1$
satisfies
$t\ge 1$
satisfies
![]() $d(G)=t+1$
and
$d(G)=t+1$
and
![]() ${m(G)=t+2}$
. This gives examples of groups satisfying item (1) in Theorem 1.3.
${m(G)=t+2}$
. This gives examples of groups satisfying item (1) in Theorem 1.3.
The group
![]() $G:=S_4=K:S_3$
with K the Klein subgroup of
$G:=S_4=K:S_3$
with K the Klein subgroup of
![]() $S_4$
and the group
$S_4$
and the group
![]() ${G:=(C_3^t : C_2) \times C_2}$
with
${G:=(C_3^t : C_2) \times C_2}$
with
![]() $C_2$
acting on
$C_2$
acting on
![]() $C_3^t$
by inversion also satisfy
$C_3^t$
by inversion also satisfy
![]() $m(G)=d(G)+1$
. These two examples yield groups satisfying item (2) in Theorem 1.3 with
$m(G)=d(G)+1$
. These two examples yield groups satisfying item (2) in Theorem 1.3 with
![]() $m(H)=2$
in the first case and with H abelian in the second case.
$m(H)=2$
in the first case and with H abelian in the second case.
As above, let K be the Klein subgroup of
![]() $S_4$
and let
$S_4$
and let
![]() $G:=K:(S_3\times C_2^{t-1})$
. This gives examples of groups satisfying item (3) in Theorem 1.3.
$G:=K:(S_3\times C_2^{t-1})$
. This gives examples of groups satisfying item (3) in Theorem 1.3.