DISPOSITION: ANOMALY OF PLASMA BLOCK GENERATION

It was necessary for the new developments on laser fusion with ps laser pulses that powers above TW had to be generated. This was achieved by discovering the chirped pulse amplification (CPA) (Mourou & Tajima, Reference Mourou, Tajima, Tanaka, Meyerhofer and Meyer-Ter-Vehn2002) or the amplification of sub-ps dye laser pulses, e.g., in inverted excimer laser media (Schäfer, Reference Schäfer1986; Szatmari et al., Reference Szatmari and Schäfer1988). The second new aspect is to depart from the usual scheme of laser fusion with spherical compression of fuel pellets in favor of a side-on ignition of modestly compressed or uncompressed solid density fuel of large volume, which is still purely within the conditions solely for power generation—otherwise the scheme of Nuckolls and Wood (Reference Nuckolls and Wood2002, Reference Nuckolls and Wood2005) could never have been disclosed—and the similar scheme (Hora, Reference Hora2002) could not have been declassified.

Irradiating (TW to PW)-ps laser pulses (Cowan et al., Reference Cowan, Parry, Key, Dittmire, Hatchett, Henry, Mody, Moran, Pennington, Phillips, Sangster, Sefcik, Singh, Snavely, Stoyer, Wilks, Young, Takahashi, Dong, Fountain, Parnell, Johnson, Hunt and Kuhl1999; Ledingham et al., Reference Ledingham, Spencer, Mccanny, Singhal, Santala, Clark, Watts, Beg, Zepf, Krushelnik, Tatarakis, Dangor, Norreys, Allott, Neely, Clark, Machacek, Wark, Cresswell, Sanderson and Magill2002; Leemans et al., Reference Leemans, Rodgers, Castravas, Geddes, Fubiani, Esarey, Shadwick, Donahue and Smith2001; Magill et al., Reference Magill, Schwoerer, Ewald, Galy, Schenkel and Sauerbrey2003) usually results in extreme relativistic effects as the generation of highly directed electron beams with more than MeV energy, in highly charged GeV ions, in gamma bursts with subsequent photonuclear reactions, and nuclear transmutations, in positron pair production, and high intensity very hard X-ray emission. In contrast to these usual observations, few very different anomalous measurements were reported. What was most important in these few cases is that the laser pulses with TW and higher power could be prepared in a most exceptional way to have a suppression of prepulses by a factor 10⁸ (contrast ratio), or higher for times a few dozens of ps before the main pulse is hitting the target. These very clean laser pulses were most exceptional only and especially possible by using the Schäfer-Szatmari method with excimer lasers (Sauerbrey, Reference Sauerbrey1996) or with CPA using titanium-sapphire lasers by Zhang et al. (Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998) and by Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999) using neodymium glass lasers. These exceptional conditions could be understood from the results of very detailed one-dimensional computations of laser-plasma interaction with dominating nonlinear (ponderomotive) forces (Hora, Reference Hora2003, Reference Hora2004). It was shown (Hora, Reference Hora2004, Fig. 3) that irradiation of a deuterium plasma block of specially selected initial density (bi-Rayleigh profile), with a neodymium glass laser intensity of 10¹⁸ W/cm², resulted within 1.5 ps in a thick plasma block moving against the laser light, with velocities above 10⁹ cm/s and another similar block moving with the laser direction into the plasma interior. However, such a generation of plasma blocks was never observed because in all experiments, a minor prepulse produced plasma in front of the target, where the laser beam was shrinking to about one wavelength diameter with extremely high intensities due to relativistic or ponderomotive self-focusing (Hora, Reference Hora1975).

The acceleration was then dominated by the nonlinear force f _NL given by the time averaged values of the amplitudes of the electric field E and the magnetic field H of the laser in this simplified geometry at perpendicular incidences in the x-direction as (Hora, Reference Hora2000)

(1)

where n is the complex index of refraction in the plasma. The first expression is the reminds of the ponderomotive forces derived by Kelvin for electrostatics before the Maxwellian theory while the second expression represents the force density as gradient of the energy density given in general by the Maxwellian stress tensor. Thanks to the clean laser pulses of the Schäfer-Szatmari method, it was for the first time ever that Sauerbrey (Reference Sauerbrey1996) could avoid the self-focusing and measure the generated plasma block moving against the laser light with an acceleration derived from Doppler shift. This was very accurately reproduced by the nonlinear force theory (Hora et al., 2007b).

The second crucial experiments with the anomaly were performed with clean laser pulses of about 30 wavelength diameters by Zhang et al. (Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998) and irradiating the target with 300 fs laser pulses. There was only a modest X-ray emission, not the usually very intense hard X-rays. When taking out a weak pulse and pre-irradiating this at times t* few ps before the main pulse, the X-rays were unchanged. But as soon as t* was increased to 70 ps, the usual hard X-rays were observed. It was estimated (Hora & Wang, Reference Hora and Wang2001) that 70 ps were needed to build-up the plasma plume before the target, which are necessary for providing relativistic self-focusing with the subsequent usual relativistic effects.

A third crucial observation was made by Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999) when irradiation of copper targets with half TW very clean laser pulses of a few ps duration were studied. Instead of the expected and usually measured 22 MeV fast copper ions, the fast ions had only 0.5 MeV energy. Furthermore, it was observed that the number of the fast ions (in difference to the slow thermal ions) was constant when varying the laser power by a factor of 30. From this it could be concluded that the acceleration was from the unchanged volume of the skin layer at the target surface where the nonlinear force produced the generation of a highly directed plane plasma block moving against the laser (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002; Hora, Reference Hora2003). This skin layer acceleration by the nonlinear force (SLANF) with avoiding self-focusing was then confirmed experimentally in all details, especially from high directivity of the fast ions and the generation of a plasma block toward the plasma interior, as measured at irradiation of thin foils (Badziak et al., Reference Badziak, Glowacz, Jablonski, Pahys, Wolowski and Hora2004, Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005).

Most significant was the result (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002; Hora, Reference Hora2003) that the SLANF-generated directed quasi-neutral plasma blocks should have an ion current density of 10¹¹ As/cm² as confirmed experimentally later (Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005). This was 1000 times higher (Badziak et al., Reference Badziak, Glowacz, Hora, Jablonski and Wolowski2006) than concluded from other mechanisms considered for a proton beam FI scheme of laser fusion (Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Geissel, Habs, Hegelich, Karsch, Ledingham, Neely, Ruhl, Schlegel and Schreiber2005). The measured ion beam current densities with block ignition are more than a million times higher than any accelerator could provide for beam fusion.

This also led to a reconsideration of the scheme of direct ignition of solid state or modestly compressed DT by the plasma blocks (Hora, Reference Hora2000, Reference Hora2003) for fusion energy production similar to the scheme of Nuckolls and Wood (Reference Nuckolls and Wood2002, Reference Nuckolls and Wood2005) using very intense 5 MeV electron beams generated by 10 PW-ps laser pulses. The only difficulty for igniting solid-state density DT is that there is the need of an exorbitantly high energy flux density

(2)

derived by Chu (Reference Chu1972) and confirmed by Bobin (Reference Bobin, Schwarz and Hora1974). The measurements by Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999, Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) were well reaching near 10⁶ J/cm², but the higher threshold (2) seemed to be prohibitive. One way out may be by using a conical reduction of the cross section of the plasma block with highly directed ions and a modest temperature (Fig. 1) (Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007).

Fig. 1. Schematic description of a spherical laser irradiation on a DT layer (area A ₁) producing a block layer accelerated against the laser and another one of thickness d ₁ moving as quasineutral plasma into the cone. The radially directed ions have energies of about 80 keV. The modestly heated block expands to a higher thickness d ₂ but smaller area A ₂ to hit solid DT at a radius R for igniting fusion (Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007).

In the following section, mechanisms are studied, which explain how the thickness d of the plasma block in the direct laser-plasma interaction area A can be enlarged. In the following section, mechanisms of the ignition in the area A ₁ are studied showing to what extend the initial results of Chu (Reference Chu1972) may lead to a lower threshold, and in the following section, parameters are considered, which describe the possibility to ignite an exothermic reaction for gaining fusion energy from solid DT using the laser driven block ignition based on SLANF.

PLASMA BLOCKS WITH DIELECTRIC INCREASED THICKNESS

For aiming block ignition for laser fusion following Figure 1, it is important that the initially laser accelerated block in the area A should receive the highest possible thickness by the nonlinear force acceleration. It is well known from one-dimensional hydrodynamic computations before 1980 (Lawrence, Reference Lawrence1978; Hora, Reference Hora1981) and selected for laser irradiation with 10¹⁸ W/cm² laser intensities (Hora, Reference Hora2004, see Fig. 3), that a deuterium plasma which received 15 vacuum wavelength thick blocks accelerated to velocities of about 10⁹ cm/s within 1.5 ps irradiation. Another example of these results is shown in Figure 2, where a compressing plasma block with a thickness of nearly 60 vacuum wave lengths was generated after 450 fs irradiation by a 10¹⁶ W/cm² laser intensity on a deuterium plasma with very specifically prepared initial density (Lawrence, Reference Lawrence1978, p 104). The following new computations are using the genuine two-fluid hydrodynamic codes (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984; Cang et al., Reference Cang, Osman, Hora, Zhang, Badziak, Wolowski, Jungwirth, Rohlena and Ullschmied2005) resulting in many details of this thick block generation (Sadighi et al., 2009; Yazdani et al., Reference Yazdani, Cang, Sadaghi-Bonaz and Hora2009).

Fig. 2. (Color online) Genuine two-fluid computation for laser interaction with deuterium plasma. Velocity at irradiation for a 10¹⁶ W/cm² neodymium glass laser irradiation between 500 and 650 fs with an initially 100 µm Rayleigh density profile of 100 eV temperatures resulting in a 10 µm thick compressing plasma block.

Fig. 3. (Color online) Same as Figure 3 with other view of diagram.

The problem is related to the propagation of electromagnetic waves in media with varying refractive index n = 1 – (n _e/n _ec)/(1 + iν/ω), where n _e is the electron density, n _ec is the critical electron density where the plasma frequency is equal to the laser frequency ω, ν is the electron collision frequency depending on the locally varying electron density, the temperature of the plasma including nonlinear generalizations by the electron quiver motion in the laser field, and on relativistic effects (Hora, Reference Hora1981, Section 6). The plasma frequency satisfies ω_p = (4πe ²n _e/m)^1/2. Due to the local (x-dependent) variation of n, the wave equation cannot be solved by elementary functions (as sine or cosine) but by higher (Bessel-, Legendre-, etc.) functions covering most of the mathematics of the 19th-century about differential equations. Approximate solutions were necessary within quantum mechanics, so using the Wentzel-Krames-Brillouin-Jordan (WKBJ) method.

One exception of a solution by elementary functions was possible for the very special case where the spatial variation along the x-coordinate for collisionless plasma was given by Rayleigh (Reference Rayleigh1880)

(3)

where the solutions for the wave equation of the electric field E of the laser were exactly expressed by elementary functions with an amplitude E ₀

(4)

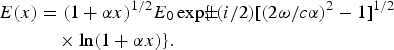
These exact solutions shows only two kinds of waves in the inhomogeneous medium, one moving to the positive, the other to the negative x-direction (Schlick, Reference Schlick1904) without any internal reflections. At the interface between a homogeneous medium and the Rayleigh medium with a continuous connection and a jump in the refractive index, the phase shift causes a reflection only at the point of connection, which usually can be very small as expected for the inhomogeneous medium from works performed in optics to suppress reflection. However, there is a range of α-values where total reflection can occur, even for perpendicular incidence, what is never possible, e.g., at the boundary between two homogenous media. It was clarified by Hora (Reference Hora1957) that the result is very significant following Eq. (4) that there are only two exact solutions in the inhomogeneous optical medium for a wave-moving to +x and one moving to −x, and no internal reflection is present. There were no internal reflections as it was wrongly suggested from the many-layer approximation (Hora, Reference Hora1981, Chapter 7). This result of no internal reflection was then shown generally for any medium (not only for the Rayleigh case) as a rather surprise by Osterberg (Reference Osterberg1958).

The Rayleigh medium has another special importance when studying the nonlinear (ponderomotive) forces generated by a laser field in plasmas. It was known from electrostatics that electrons can be moved by a ponderomotive force if there are gradients in the electric field E given by −∇E ². It was the merit of Weibel (Reference Weibel1958) to demonstrate that the same forces on electrons in vacuum appear also considering the time average in the high frequency fields of microwaves. The evaluation of these forces for laser propagation in plasmas including the inhomogeneous dielectric properties (Hora, Reference Hora1969) resulted in the nonlinear force density (Hora, Reference Hora2000)

(5)

after subtracting the gas dynamic, thermo-kinetic forces, where H is the laser field vector, 1 is the unity tensor, ω is the laser radian frequency, c is the vacuum speed of light, and n is the (complex) refractive index. To prove that these and only these terms of the force are correct, derived from momentum conservation for the non-transient case (Hora, Reference Hora1969), and by symmetry reasons for the transient case (Hora, Reference Hora1985). For simplified geometry (Hora, Reference Hora2000, see Eqs. (4)–(10), the force (5) can be reduced to the time averaged value of Eq. (1)

(6)

where E _v is the amplitude of the electric field of the laser. Within the plasma, the square of the electric field is increased by a swelling factor

(7)

With respect to the result of the Rayleigh profiles (Eq. (4)), the main limitation is that propagating waves are to be considered requiring an oscillating exponential function. This is fulfilled as long as

(8)

where the limit for α is given for the neodymium glass lasers.

The very unique property of the Rayleigh profile consists in the fact that the interaction of the laser field in such a medium causes a (nearly) constant force producing a uniform acceleration and a motion of the whole block to a (nearly) undistorted DT plasma block, corresponding to monochromatic ions. Considering mostly cases where (n² –1) = −n _e/n _ec is close to unity, where n _ec is the critical density with ω = ω_p, the Rayleigh profile (3) results in a constant force because of

(9)

confirming that the whole plasma is then accelerated as an undistorted block. This property of the Rayleigh profile with respect to the nonlinear (ponderomotive) force is very significant and important to generate uniformly fast moving plasma blocks for the applications.

Vacuum wave length by laser irradiation of Rayleigh density profiles was seen in the numerical hydrodynamic one-fluid studies (Hora, Reference Hora2004, Fig. 3; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007, Fig. 1) concerning nonlinear force acceleration in plane geometry. This was many years preceding the confirmation by the first exact measurement by Sauerbrey (Reference Sauerbrey1996; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) thanks to his first use of TW-ps laser pulses with a contrast ratio above 10⁸. The appearance of undistorted plasma blocks of a thickness of up to 20 times the thickness of the skin layer in the Rayleigh profile with the appropriately selected α-value was increased by the swelling factor S = 1/n, the value of which could well be higher than 20 µm. This was possible even with inclusion of the collision frequency (Hora, Reference Hora1983, see Eq. (6.48)). The example of a block of even 60 vacuum wave lengths thickness, described by these computations, is shown in Figure 2.

This all was essential in the clarification of the anomaly of TW-ps laser pulse interaction with targets for driving the plasma in area A of Figure 1 as a SLANF process by avoiding relativistic self-focusing. The reasonable result of the one-fluid computation (Hora, Reference Hora2004, Fig. 3; Hora et al. (Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007), Fig. 1) can be understood from the following estimations. A neodymium glass laser pulse of 10¹⁸ W/cm² irradiated a deuterium plasma of initially 100 eV temperature with a Rayleigh profile with α = 2 × 10⁴ cm⁻¹. At the interaction time of 1.5 ps, the electric field E of the laser was so strongly swelled that the laser field energy density was more than 15 times higher than in vacuum. In the same way, the thickness of the skin layer was increased by a similar factor and a plasma block of more than 15 vacuum wavelengths depth was moving against the laser light nearly undistorted with a velocity of up to a few 10⁹ cm/s. A similar block was moving into the plasma below the critical density.

It was evident that the conditions had to be selected in some very specific way. On the one hand, the laser intensity had to be of such a value that heating was not much influencing the profiles in the plasma to avoid optical reflection, partially standing waves, and subsequent density rippling as seen before (Hora, Reference Hora1981, Figs 10.20a and 10.20b) at times after 2.5 ps while the block conditions were well preserved at the time 1.5 ps. On the other hand, the laser intensity had to be rather high, close to 10¹⁸ W/cm², to adjust to the DT fusion conditions.

Figure 3 shows an example of the generation of a compressing plasma block of nearly 20 wavelength depth appearing at early times of 0.40 ps after the irradiation of a laser pulse of 10¹⁶ W/cm² using the genuine two-fluid code (Cang et al., Reference Cang, Osman, Hora, Zhang, Badziak, Wolowski, Jungwirth, Rohlena and Ullschmied2005) for comparison with Figure 2. The compressing block has indeed a lower depth than that shown in Figure 2. For the acceleration of the plasma against the laser light, one finds a value of 2 × 10¹⁹ cm/s² in some analogy to the results of Sauerbrey (Reference Sauerbrey1996). Based on the vacuum electric field of the laser for the intensity of 10¹⁶ W/cm², a swelling factor (Eq. (7)) of S = 3.75 could be derived. This is similar to the evaluation (Hora, Reference Hora2003) of the swelling factor at the initial SLANF experiments (Badziak et al., Reference Badziak, Glowacz, Jablonski, Pahys, Wolowski and Hora2004). In these estimations, the plasma density was approximated by the value of the critical density of 3.3 × 10⁻³ g/cm³ of deuterium plasma.

For cases closer to the conditions of the geometry in area A of Figure 1, calculations were performed with bi-Rayleigh deuterium plasma targets of initial thickness of 20 µm. Figure 4 shows the result for a laser intensity of 10¹⁵ W/cm² of a 300 fs pulse on a plasma with an initial temperature of 10 eV, where the compressing block has a depth of 8 vacuum wave lengths. Figure 5 represents the result for 10¹⁵ W/cm² where the compressing block of 10 µm is not with a fully homogenous velocity (monochromatic ions) to show an example how the initial conditions for the computations have to be fit for the aim of achieving thick blocks for the laser fusion scheme according to Figure 1. Details of the computations are reported in related papers (Yazdani et al., Reference Yazdani, Cang, Sadaghi-Bonaz and Hora2009).

Fig. 4. Genuine two fluid calculation of ion velocity for an initially bi-Rayleigh density profile of 20 µm depth with α = 1.02 ×10⁴ cm⁻¹ and 10 eV temperature by neodymium glass laser irradiation of intensity 10¹⁵ W/cm² of 300 fs duration.

Fig. 5. Results for the same conditions as in Figure 4 at irradiation with 10¹⁶ W/cm² neodymium glass laser intensity. The compressing plasma block between –4 and +4 µm depth has the highest velocities at the end time of irradiation.

REDUCTION OF THE IGNTION THRESHOLD

Studies about the mechanism on how the directed plasma blocks interact at area A ₁ of Figure 1 with a DT target were based on the work of Chu (Reference Chu1972). This regards a hydrodynamic model and one has to be aware that the mechanisms of the interpenetration of the hot plasma hitting the cold DT fuel may need another more detailed model. An earlier attempt (Hora, Reference Hora1983) leads to a reduction of the hydrodynamic ignition threshold by a factor of 20. A more detailed study could be based on a treatment with PIC techniques (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004), which fact has to be taken into account when this chapter is treating only the hydrodynamic side of the process.

The question is about the exorbitantly high energy flux density E* (Eq. (2)) needed for ignition of uncompressed DT. When Chu (Reference Chu1972) derived this value, several later discovered processes in plasmas were not known. This refers manly to two phenomena: (1) the reduction of the thermal conductivity between hot and cold plasma given by the inhibition factor F* and (2) the reduction of the stopping length of the generated alpha particles from the fusion reaction in the plasma due to collective effects.

Inhibition factor

The reduction of the thermal conductivity of the electrons by the inhibition factor F* was discovered in an empirical way from the evaluation of experiments for laser fusion. Experiments were performed with targets of different layers, and the diagnostics by X-rays etc. resulted in a reduction of the thermal conduction by a factor F* = 33 (Young et al., Reference Young, Whitlock, Decoste, Ripin, Hagel, Stamper, Mcmahon and Bodner1977). Other experiments resulted in a reduction by a factor 100 (Deng et al., Reference Deng, Tao and Wang1982). Several theories tried to explain these results assuming magnetic fields, ion-acoustic turbulence, or Weibel instabilities. The theory which described the facts best was that of Tan and Min (Reference Tan and Min1985) based on the Krook equation (Lifshitz & Pitaevski, Reference Lifshitz and Pitaevski1961, p. 177) leading to pressure effects since these are causing ambipolar fields and therefore internal electric fields.

The final solution was the theory of electric double layers with their strong internal electric fields within the plasma (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984; Hora, Reference Hora1991). To illustrate this, the problems with these internal electric fields in inhomogeneous plasmas have to be explained. How difficult it was to understand the physics of these fields follows from the fact that these fields were fully known to the Stockholm school working on the ionospheric plasmas, see the review by Fälthammar (Reference Fälthammar1988), but in contrast, nearly all physicists believed that there are no electric fields inside the plasmas. Kulsrud (Reference Kulsrud1983) reviewed Alfven's (Reference Alfven1981) book just after Alfven had received the Nobel Prize with the statement “Alfven's electric fields which are intuitively not clear.” Indeed there is some relation between the Alfven magneto-hydrodynamic waves and the electric fields as these appeared in the laser interaction with plasmas as the nonlinear ponderomotive forces (Hora, Reference Hora1991, Section 12.4), based on the same mathematical formulation. The knowledge of these fields was fully familiar from the studies of plasmas above the atmosphere for nearly 100 years, e.g., from the studies of the polar light of the Stockholm pioneering plasma school beginning with Birkeland (see Fälthammar, Reference Fälthammar1988) who qualitatively suggested some particle emission from the sun. This phenomenon was then discovered as a phenomenon of the solar wind whose velocity and ion current density of the involved protons was calculated quantitatively first by Biermann (Reference Biermann1951) from evaluating the photographs of a comet motion in agreement with later measurements with space crafts.

The mentioning of Kulsrud's (Reference Kulsrud1983) book review should not be understood as a criticism. This remark was most helpful to overcome an insufficiency within the then existing usual knowledge of the plasma state. It had been tacitly assumed, that all plasmas cannot have internal electric fields due to the fact that the electric conductivity of plasmas is of similar orders of magnitudes as in metals. Undergraduate students learn how in a homogeneous metal, any generated electric field is decaying on timescales of atto- or fs. If a piece of metal is located within an external electric field, this decay of any internal field leads to the generation of electric double layers at the surface of the metal, and then the discussion of electrostatics without any time dependence is beginning. The fact that there is a most complicated time dependent mechanism involved for this generation of the electron layers at the metal surface could always be neglected because of the short times. However, since the recently discovered mechanisms due to atto- or fs laser pulses are known, these dynamics of the electric fields in plasmas, as in metals, cannot be ignored. It should be underlined that the situation in a metal at times longer than fs is correct only within a uniform (homogeneous) metal. What is significant is that under inhomogeneous spatially and/or temporally conditions as in plasmas, the mentioned conclusions, even for much longer timescales, are highly complicated.

The merit of Kulsrud is the shake up against the usually assumed prejudice in plasma theory. He formulated it while most of all other authorities tacitly and without any doubt went ahead “intuitively” with the wrong assumption. The very detailed knowledge of the Stockholm school about the internal electric fields in plasmas was ignored or marginalized as a kind of heresy, though most of the plasma experiments for magnetic confinement fusion or at laser-plasma interaction are always inhomogeneous plasmas, even with inclusion to complicated temporal dependences which otherwise even lead to further complications. The excuse for the situation in extraterrestrial plasmas is just in the fact that there is a long time dependence at these very low density plasmas, and there is the very large spatial geometry, so that the internal electric fields in the plasma could not be ignored. It also should respectfully be admitted that the action of electric fields in the equation of motion of a plasma, in the generalized Ohm's law as an expression of diffusion (Hora, Reference Hora2000, see Eq. (4.62)), and in the ambipolar term were related to pressure gradients.

The elimination of any electric field was the principle of Schlüter's (Reference Schlüter1950) plasma hydrodynamic equations, which was valid for spatial dimensions larger than the Debye length

(10)

describing the plasma temperature by T, the Boltzmann constant by k, the electron density by n _e and, the charge of the electrons by e. For spatial scales larger than the Debye length, one may use the approximation of space charge neutrality. Then, from the Euler equations of motion for the electrons and ions follows for the force density in the plasma

(11)

where the thermokinetic force

(12)

is given by the gas-dynamic pressure p, and the general nonlinear force is described by Eq. (5). This equation is algebraically identical (Hora, Reference Hora1969, Reference Hora2000) with

(13)

It was shown that these identical Eqs. (5) and (13) are the final and general expressions of the time dependent (transient) equation of motion derived by solving a long controversial discussion (Hora, Reference Hora1985) containing all and only all terms of Eqs. (5) or (13).

The Eq. (13) is that of the Maxwellian stress tensor including the dielectric response and the transient (time dependent) behavior of the fields. Eq. (13) explains the parts acting in the nonlinear force. Here, one recognizes on the right-hand side first the Lorentz term f_Lorentz = j × H/c with the plasma current density j and the vacuum velocity of light c, then the Coulomb term Eρ with the electric charge density ρ and as the third term the Kelvin ponderomotive term (see Hora, Reference Hora2000, Eq. (1.1))

(14)

The remaining terms in Eq. (13) are new nonlinear terms which were derived for the general equation of motion in plasmas from the studies of laser interaction. The proof for the final generality of Eq. (13) was given by momentum conservation for the non-transient case (∂/∂t = 0) and for the transient case by symmetry (Hora, Reference Hora1985). The inclusion of the term Eρ in Eq. (13) was enforced by momentum conservation (Hora, Reference Hora1969) for electric charges ρ due to oscillations with the laser radiation frequency ω.

For the correct interpretation, it is necessary to mention that Kelvin's ponderomotive force is identical with the nonlinear Schlüter term

(15)

remembering the definition of the electric polarization P and the refractive index without collisions

(16)

This term in Eq. (15) was the only nonlinear term in Eq. (13), which was derived in a very sophisticated way by Schlüter (Reference Schlüter1950), which did not appear in the derivation from the kinetic Boltzmann equations (Spitzer, Reference Spitzer1956). All other, also the transient terms, were the result of studies on laser-plasma interaction (Hora, Reference Hora1969, Reference Hora1985).

From Kelvin's ponderomotive force in Eq. (14) follows formally an expression of the “field gradient force” (as a more general expression than Eq. (6)), or the “electrostriction” for collisionless plasma (n without imaginary part).

(17)

This can be used for the case of perpendicular incidence of plane laser waves on an inhomogeneous plasma of one-dimensional geometry e.g., along the coordinate x. For the same conditions, the stress tensor description produces a force density into the x-direction as it was used in Eq. (6).

Eq. (17) led to the common expression “ponderomotive force.” As is known for (plane wave) perpendicular incidence of laser radiation on plasma, the Schlüter term is then zero. Nevertheless there is a force in the form of Eq. (17). In this case, however, the nonlinear force f_NL is the result of the Lorentz term in Eq. (13). This confusion of the definitions is avoided if one uses the general expression of the nonlinear force (13) for the electrodynamic part of the force density in plasma. This is valid for any incidence, for plasmas with collisions and including a time dependence of the fields.

These results for the nonlinear force, with clear proofs by experiments (Hora, Reference Hora1991, Section 10.4), were derived for the quasi-neutral plasma. Nevertheless, this was the access to see the internal electric fields within high density plasmas similar to “Alfven electric fields” (Kulsrud, Reference Kulsrud1983) leading to a direct understanding of the inhibition factor.

The derivation of Eqs. (5) and (13) for the single particle motion (Hora, Reference Hora1991, see Sections 8.7 to 8.9, and 10.7) demonstrated that the forces are mostly acting on the electron cloud within the (space charge neutrally assumed) plasma and push or pull the electron clouds generating electric double layers such that the ion cloud is following the electrostatic attraction. These are exactly the electric fields of the space plasma following Alfven (Reference Alfven1981) as seen also in experiments (Hora, Reference Hora2000) between two homogeneous plasmas, each having different density or temperature to produce the ambipolar field as a double layer in a transition region. The whole dynamic mechanisms of these electric fields including plasma collisions could be studied by the genuine two fluid hydrodynamics (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984; Hora, Reference Hora1991) leading to an established and detailed knowledge about the double layers with Alfven's (Reference Alfven1981) electric fields.

As an example of how the electric field in plasmas was marginalized, it should be mentioned (Eliezer & Hora, Reference Eliezer and Hora1989) how the radial electric field in magnetically confined discharge plasma causes a high speed rotation by the E ×B forces. This happens also in mirror machines and in tokomaks and can be used for isotope separation (Hora et al., Reference Hora and Karger1977). This rotation was measured from side on observed Doppler shifts of H _α-lines exactly arriving at the calculated velocities from the E ×B forces, while the explanation (Sigmar et al., Reference Sigmar, Clarke, Neidigh and Vandersluis1974) ignored this and related it to a banana-plateau regime consistent with neoclassical theory. The clear rotation in tokomaks was then measured by Bell (Reference Bell1979) and Razumova (Reference Razumova1984). The realization of electric fields in plasmas and double layers led to the surface tension in plasmas (Hora et al., Reference Hora, Min, Eleizer, Lalousis, Pease and Szichman1989) and to the first quantum theory of surface tension in metals. A further generalization of this Debye layer model led to nuclear forces with consequences for quark-gluon plasmas (Hora, Reference Hora2006a; Ghahramani et al., Reference Ghahramani, Hora, Miley, Ghanaatian, Hooshmand, Philberth and Osman2008).

Based on this knowledge, it was then straightforward to understand the inhibition factor F* as a double layer effect (Cicchitelli et al., Reference Cicchitelli, Elijah, Eliezer, Ghatak, Goldsworthy, Hora and Lalousis1984; Hora & Ghatak, Reference Hora and Ghatak1985). For simplified conditions of a plasma surface expanding into vacuum (Hora, Reference Hora1991, see Fig. 2.2), or at the interface between hot and cold plasma as in the following conditions of the hydrodynamic computations of Chu (Reference Chu1972), or at a wall confining plasma, the Debye layer is generated showing a depletion of electrons. The electrons from the plasma interior are electrically reflected at the ions which remain in the double layer whose positive charge results in an electron return current of the electrons back into the plasma (Fig. 6). The potential step given by kT/2 (one dimension!) corresponds to the work function of the plasma similar to that of a metal surface following the generalization of the Richardson equation for the transmission of exceptionally energetic electrons to produce the thermionic emission. The thermal conduction is performed by the ions only, and in the equation of energy conservation for the electrons one has to take the ionic thermal conductivity

(18)

instead of the electron conductivity K _e, determined by the mass m _e of the electrons and that m _i of the ions. Using the average ion mass of a 50:50 DT plasma, the square root in Eq. (18) defines the inhibition factor of F* = 67.5 in agreement with the semi-empirical evaluation with values between 33 (Young et al., Reference Young, Whitlock, Decoste, Ripin, Hagel, Stamper, Mcmahon and Bodner1977) and 100 (Deng et al., Reference Deng, Tao and Wang1982). For a wide-spread double layer of inhomogeneous plasma the hydrodynamic evaluation results in summary into the same potential step (Alfven, Reference Alfven1981; Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984) to justify the same inhibition in general, see also Chu (Reference Chu1972), Niu et al. (Reference Niu, He, Qiao and Zhou2008).

Fig. 6. Double layer between hot and cold plasma (Cicchitelli et al., Reference Cicchitelli, Elijah, Eliezer, Ghatak, Goldsworthy, Hora and Lalousis1984) with depletion of the high velocity electrons until the ions produce such a potential that the electrons in the hot part are reflected. Thermal transport is determined by the ion thermal conductivity.

COLLECTIVE EFFECT FOR THE STOPPING OF ALPHA PARTICLES

After the just discussed problem of thermal transport, the question of the transport properties for the stopping of the DT fusion produced alpha particles in plasma are important for the ignition. Chu (Reference Chu1972, see Eq. (7)) used the Winterberg approximation for the binary collisions combining roughly all the numerical models mostly following the Bethe-Bloch theory. A comprehensive summary of these models was given by Stepanek, especially for the alpha particles of the DT reaction (Stepanek, Reference Stepanek, Schwarz, Hora, Lubin and Yaakobi1981, see Fig. 6) where the Bethe-Bloch stopping length R increases as

(19)

with the plasma temperature T.

A visible discrepancy appeared with the measurements by Kerns et al. (Reference Kerns, Rogers and Clark1972) at the Air Force Weapons Laboratory of the Kirtland Air Force Base where an electron beam with 2 MeV energy and 0.5 MA current of 2 mm diameter was hitting deuterated polyethylene CD₂. The penetration depth of the electrons was measured by changing the thickness d of the CD₂ and the saturation of the emission of fusion neutrons at d = 3 mm was a proof of the much stronger stopping than in the Bethe-Bloch theory predicted. An explanation of the value d was immediately possible when Bagge and Hora (Reference Bagge and Hora1974) theory of the stopping of cosmic rays was applied, where the interaction of the charged energetic particles was to be taken considering the whole electron cloud in a Debye sphere with the Debye potential for the electrons, and not by binary electron collisions. The discovery of this collective interaction was by Gabor (Reference Gabor1952) following the work of S. R. Milner who derived the Debye screening before Debye. Detailed results were reported (Ray et al., Reference Ray, Hora, Schwarz and Hora1977a, Reference Ray and Hora1977b) based on an analysis using the Fokker-Planck equation and quantum electrodynamics. Another drastic difference of the stopping length of the Bethe-Bloch theory was measured in a direct way (Hoffmann et al., Reference Hoffmann, Weyrich, Wahl, Gardes, Bimbot and Fleurier1990).

In strong contrast to the T ^3/2 dependence (Eq. (19)), the stopping length was nearly temperature independent. The results for the 2.89 MeV alpha particles in a hydrogen-boron (11) plasma in Figure 7 are nearly identical with those from the DT reaction (Stepanek, Reference Stepanek, Schwarz, Hora, Lubin and Yaakobi1981, see Fig. 6). It can immediately be expected that such a discrepancy will change the fusion ignition significantly. This was the reason that a strong reheat occurred in an inertially confined DT fusion pellet leading to the discovery of the volume ignition for inertial fusion energy (IFE) (Hora & Ray, Reference Hora and Ray1978) later confirmed by Kirkpartick and Wheeler (Reference Kirkpatrick and Wheeler1981), where John Wheeler's close knowledge of the related physics was helpful. This was further confirmed by numerous other authors (Basko, Reference Basko1990; He & Li, Reference He and Li1994; Martinez-Val et al., Reference Martinez-Val, Eliezer and Piera1994; Atzeni, Reference Atzeni1995), where the robustness of volume ignition against spark ignition (Lindl, Reference Lindl, Hora and Miley2005) with nearly the same fusion gains was underlined by Lackner et al. (Reference Lackner, Colgate, Johnson, Kirkpatrick, Menikoff, Petschek and Miley1994). The ideal and natural adiabatic hydrodynamics of the reacting DT plasma has shown, that only the reheat guaranteed the highest measured fusion gains (Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998) on the way to ignition (Miley et al., Reference Miley, Hora, Osman, Evans and Toups2005).

Fig. 7. Temperature dependence of the stopping length R (range) for alpha particles of 2.89 MeV in a hydrogen-boron(11) plasma with binary electron collisions [Fokker-Planck F.P. collisions and quantum electrodynamic (Pauli) cut-off] and collisions with the electron collective in a Debye sphere (Ray et al., 1977) corresponding to the summary by Stepanek (Reference Stepanek, Schwarz, Hora, Lubin and Yaakobi1981, Fig. 6; Malekynia et al., Reference Malekynia, Hora, Ghoranneviss and Miley2009, Fig. 1) where corrections to the binary collision theory with screened Debye potential and the Balescu (Reference Balescu1997) model decreases the result of binary collisions, but not as far as the Gabor (Reference Gabor1952) collective effect.

The more precise expression describing a very slight decrease of the stopping length R with the temperature T for DT, as shown by Stepanek (1991, Fig. 6), can be approximated by

(20)

where the temperature T is in keV.

HYDRODYNAMIC CALCULATIONS

For studying the interaction with solid DT of the nonlinear force driven plasma blocks from area A in Figure 1 after conical guiding to area A ₁, the ignition is following the scheme of Chu (Reference Chu1972) modified by the later discovered inhibition factor and of the collective effect for the stopping power. To be as close as possible to the treatment of Chu (Reference Chu1972), the same hydrodynamic Eqs. (2) to (6) were used and are not repeated here. The first modification is to use the thermal condition of the electrons with the inhibition factor F*. The energy transfer terms W ₁ and W ₂ in the equations of energy conservation (Chu, Reference Chu1972, Eqs. (5) and (6)) were based on computations of the bremsstrahlung using the electron temperature T _e working with Eq. (15) of Chu (Reference Chu1972) with the maximum at x = 0, thus,

(21)

where Eqs. (17) and (20) of Chu (Reference Chu1972) differ a little-bit as there T _i = T _eI was assumed, while the following computations with the collective stopping have to be valid for any temperature relation.

The α particles are assumed to deposit their energy in the plasma. They have a mean free path in the case of a plasma of solid state density DT in the approximation of Chu (Reference Chu1972, Eq. (7)), which is given by the Winterberg approximation for binary collisions within the Bethe-Bloch theory, and in the following computation according to the stopping length at collective effect it is given by Eq. (20). The action of the stopping with the collective effect is expressed by the temperature T from Eq. (20). For the calculation of the collective effect we added the term P on the right hand of Eq. (21). Thus,

(22)

P is the thermonuclear heating rate per unit time obtained from the burn rate and the fractional alpha particle deposition

(23)

(24)

E_α = 3.5 Mev and f is the fraction of alpha particle energy absorbed by electrons or ions, which is given by

(25)

In the equations after (21), the temperatures of the electrons and the ions were used to be equal to T, as used in Eq. (20), for the following numerical evaluations.

Figure 8 reproduced the results of Chu (Reference Chu1972) for the temperature T on an irradiated solid state DT target depending on time, where the most characteristic case is that for the ignition energy flux density E* = 4.3 × 10¹⁵ erg/cm² = 4.3 × 10⁸ J/cm² where the temperature approaches with the time a constant value. This E* is the ignition threshold E _t* as explained in more detail by Chu (Reference Chu1972) in full agreement with Bobin (1984).

Fig. 8. Characteristics of the dependence of the temperature T on time t for parameters E* of energy flux density in ergs/cm² for ignition of fusion at solid state DT reproduced from Figure 2 of Chu (Reference Chu1972).

Results and comparison of the thresholds of chu

The following numerical evaluations are based on the characteristic plots for comparison with the results of Chu (Reference Chu1972) where first the results without inhibition factor F*, but with and without collective effect, were performed as reported by Malekynia et al. (Reference Malekynia, Hora, Ghoranneviss and Miley2009). Figure 3 in this paper reproduces the temperatures reported by Chu (Reference Chu1972) very well at times above about 1 ns, when collective effects are not taken into account. The discrepancies at lower time's t are not essential and may be due to some differences in the computation codes. Some details about these discrepancies were discussed before for cases without collective effect, but only with the inhibition factor, where specific numerical evaluations were shown and an effect of a slightly retrograde dependence was elaborated (Ghoranneviss, Reference Ghoranneviss, Malekynia, Hora, Miley and He2008). As expected, the results with the collective effects arrive at higher temperatures T. In order to find the threshold temperature at these conditions, results at lower parameter E* were shown by Malekynia et al. (Reference Malekynia, Hora, Ghoranneviss and Miley2009, Fig. 4), where the characteristics show ignition at E* at about 10⁸ J/cm².

After these first corrections to the Chu (Reference Chu1972) results, it was most interesting to achieve the computation for both corrections including the inhibition factor F* = 67.5 and the collective effect. Results for the characteristics are presented in Figure 9. The ignition threshold is then

(26)

Fig. 9. Results for recalculation of the characteristics as in Figure 8, with incident energy flux density as parameter. Upper curves with inhibition factor and with collective effect for alpha particle stopping, lower curves as in the case of Chu (Reference Chu1972) Figure 8. The ignition threshold with collective effect and with inhibition of E*_ot = 2 × 10⁷ J/cm² I reduced from E* = 4.3 × 10⁸ J/cm² as achieved by Chu (Reference Chu1972).

This result shows a decrease of the ignition threshold due to the inhibition mechanism and due to the collective effect for the stopping of the alpha particles of the DT reaction by a factor of 21.5 (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008).

This again—as mentioned before—appears to be a high value which may not simplify the conditions for block ignition (Hora, Reference Hora2002, Reference Hora2003; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007), though this hydrodynamic analysis is only part of the problem. The interpenetration problem cannot be covered by hydrodynamics, and there are good arguments that Wilk's et al. (Reference Wilks, Kruer, Tabak and Landgon1992) code techniques (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Chen & Wilks, Reference Chen and Wilks2005; Klimo & Limpouch et al., Reference Limpouch, Psikal, Andreev, Platinov and Kawata2008) may lead to further clarification of the ignition problem, though recently the transport problems with respect to heat conduction and stopping power may be on a stronger basis using hydrodynamics. An encouraging preliminary result about the interpenetration was achieved before (Hora, Reference Hora1983) with another eventually possible reduction by a factor 20. Adding up the estimated reduction of the threshold may then arrive at

(27)

as the most optimistic limit.

It should be mentioned that the ignition of hydrogen-boron-11 (p-¹¹B) fusion fuel, following the hydrodynamic analysis with inclusion of inhibition and collective effects similar to the here presented treatment for DT, arrives at the surprising result (Azizi et al., Reference Azizi, Hora, Miley, Malekynia, Ghoranneviss and He2009) that the plane geometry ignition threshold without compression is only within one order of magnitude higher than that for DT, while the spherical compression and volume ignition is extremely more difficult.

SUMMARY OF RESULTS: IGNITION OF DT AT LOW COMPRESSION

Limitations for the block ignition are given by the just reported minimum thresholds of the energy flux density E* of the energy irradiated on the DT fuel how this is compatible with the need of not too high laser intensities I. These have to be, e.g., for neodymium glass lasers between 10¹⁷ and (closer to) 10¹⁸ W/cm². The limit for I is given by the condition that the energy of the accelerated ion has to be close to 80 keV, corresponding to the resonance maximum of the DT reaction cross section. This intensity has to be modified by the swelling factor, Eq. (7), which depends on the chosen parameters of the nonlinear (ponderomotive) force interaction of the laser beam with the plasma layer in the area A of Figure 1, for which some examples were given above.

From a very preliminary estimation for a special case, one may conclude that the irradiation of a laser pulse of 10 kJ energy during 1 ps on a cross-section of 10⁻² cm² corresponds to an intensity of 10¹⁸ W/cm⁻². Up to 0.5 times of the irradiated laser energy can be converted into the kinetic energy of the DT ion block, which is equivalent to an energy flux density of 5 × 10⁵ J/cm². The thickness of the compressing block moving parallel to the direction of the laser beam is assumed to be 10 µm by choosing the conditions as explained above. If a conical motion of this block as shown in Figure 1 is performed up to a cross section of 10⁻⁴ cm^2, a block of plasma with the directed energy of the DT ions of 80 keV will be achieved at about 0.1 mm cylindrical diameter and about 1 mm length. The energy flux density of 5 × 10⁷ J/cm² should just meet the requirements for ignition of solid DT as elaborated above.

This is an example only for demonstration that the there discussed conditions for ignition may be fulfilled. A number of questions for this ignition by the laser driven ion beam are still open, similar to the consideration about driving with the 5 MeV electron beam (Nuckolls & Wood, Reference Nuckolls and Wood2002). The following points play an important role considering the interpenetration of the energetic plasma block within the DT fuel: (1) whether the 1 mm length of the block is optimized, (2) what the details will be for preparing the DT layer in the area A of Figure 1 (Yazdani et al., Reference Yazdani, Cang, Sadaghi-Bonaz and Hora2009) for generating the block as considered with respect to a block with a minimum of distortion and optimized swelling, (3) whether the optimized temperature in the range around 100 eV of the generated block due to thermalizing mechanisms during the interaction at A, or (4) how to fit with the lengthening of the block before reaching the area A ₁, and others. In any case, the results gained at present based on the new anomalies of nonlinear force driven block acceleration and the new steps to improve the Chu (Reference Chu1972) ignition—also in view of the electron beam ignition (Nuckolls & Wood, Reference Nuckolls and Wood2002)—may open aspects for a very low cost fusion energy generation or space propulsion if generalized to proton-boron11 fuel (Hora, Reference Hora2002; Miley et al., Reference Miley, Hora, Cang, Osman, Badziak, Wolowski, Sheng, Zhang, Zhang and He2008; Azizi et al., Reference Azizi, Hora, Miley, Malekynia, Ghoranneviss and He2009).