Introduction
The early detection and treatment of psychoses already in their prodromal stage have become widely accepted goals in psychiatry during the last two decades (Fusar-Poli et al. Reference Fusar-Poli, Borgwardt, Bechdolf, Addington, Riecher-Rössler, Schultze-Lutter, Keshavan, Wood, Ruhrmann, Seidman, Valmaggia, Cannon, Velthorst, De Haan, Cornblatt, Bonoldi, Birchwood, McGlashan, Carpenter, McGorry, Klosterkötter, McGuire and Yung2013 b). Consequently, a number of operational criteria aiming at identifying patients with a clinical high risk (CHR) for psychosis have been established internationally. However, meta-analyses suggest that – among help-seeking individuals – about one-third of those meeting internationally established CHR criteria will develop psychosis within 5 years (Fusar-Poli et al. Reference Fusar-Poli, Bonoldi, Yung, Borgwardt, Kempton, Valmaggia, Barale, Caverzasi and McGuire2012; Schultze-Lutter et al. Reference Schultze-Lutter, Michel, Schmidt, Schimmelmann, Maric, Salokangas, Riecher-Rössler, van der Gaag, Nordentoft, Raballo, Meneghelli, Marshall, Morrison, Ruhrmann and Klosterkötter2015), with about 73% of these developing schizophrenic psychoses (Fusar-Poli et al. Reference Fusar-Poli, Bechdolf, Taylor, Bonoldi, Carpenter, Yung and McGuire2013 a) and about one-third is having a clinical remission within 2 years (Simon et al. Reference Simon, Borgwardt, Riecher-Rössler, Velthorst, de Haan and Fusar-Poli2013). Hence, risk stratification of CHR patients offers great potential for enhancing clinical decision making and improving the cost–benefit ratio of preventive interventions (Ruhrmann et al. Reference Ruhrmann, Klosterkötter, Bodatsch, Nikolaides, Julkowski, Hilboll and Schultz-Lutter2012). Accordingly, recent research efforts have been increasingly directed toward estimating the risk of developing psychosis on an individual level. The trend towards indicated prevention and personalized medicine in early stages of psychosis is exemplified by the fact that several large multicenter studies [i.e. Personalised Prognostic Tools for Early Psychosis Management (PRONIA), PSYSCAN and North American Prodrome Longitudinal Study (NAPLS) III] are currently underway aiming at developing prognostic tools in CHR patients. Furthermore, an ever-increasing number of studies are seeking to improve the prediction of psychosis in CHR patients by incorporating single risk factors and indicators into multivariable prediction models (e.g. Cannon et al. Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008; Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009; Ruhrmann et al. Reference Ruhrmann, Schultze-Lutter, Salokangas, Heinimaa, Linszen, Dingemans, Birchwood, Patterson, Juckel, Heinz, Morrison, Lewis, von Reventlow and Klosterkötter2010). By using the term ‘multivariable models’, we refer to models with multiple predictor variables (i.e. independent variables) and one outcome variable (i.e. dependent variable) as opposed to multivariate models, which have multiple outcome variables (Hidalgo & Goodman, Reference Hidalgo and Goodman2013).
However, despite considerable research efforts, no psychosis risk prediction model has yet been adopted in clinical practice. The most likely explanation for this is that none of the published models has yet been convincingly demonstrated to have sufficient validity and clinical utility. While a lack of progress in this area could be partly attributed to the fact that psychoses are complex disorders with large phenomenological, pathophysiological and etiological heterogeneity (Keshavan et al. Reference Keshavan, Nasrallah and Tandon2011) and that there are heterogeneous subgroups within CHR samples (Fusar-Poli et al. Reference Fusar-Poli, Cappucciati, Borgwardt, Woods, Addington, Nelson, Nieman, Stahl, Rutigliano, Riecher-Rössler, Simon, Mizuno, Lee, Kwon, Lam, Perez, Keri, Amminger, Metzler, Kawohl, Rössler, Lee, Labad, Ziermans, An, Liu, Woodberry, Braham, Corcoran, McGorry, Yung and McGuire2016), another important obstacle to consider is the widespread use of poor (i.e. biased and inefficient) modeling strategies, which can severely compromise the reliability and validity of the developed models. Examples of poor modeling strategies are relying on small event per variable (EPV) ratios (i.e. small number of patients with transition to psychosis relative to the number of considered predictor variables), using biased methods to select predictor variables for inclusion into the multivariable prediction model among a set of candidate predictor variables, not properly assessing the predictive accuracy of the model, using inappropriate model types, and not efficiently dealing with missing data (D'Amico et al. Reference D'Amico, Malizia and D'Amico2016; Wynants et al. Reference Wynants, Collins and Van Calster2016). Systematic reviews on the methodology of studies developing clinical prediction models for type 2 diabetes (Collins et al. Reference Collins, Mallett, Omar and Yu2011), cancer (Mallett et al. Reference Mallett, Royston, Dutton, Waters and Altman2010), traumatic brain injury outcome (Mushkudiani et al. Reference Mushkudiani, Hukkelhoven, Hernandez, Murray, Choi, Maas and Steyerberg2008), kidney disease (Collins et al. Reference Collins, Omar, Shanyinde and Yu2013) or medicine in general (Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012) all found that the use of such methods is widespread. Hence, it is reasonable to assume that poor methods are also a widespread problem in prediction of psychosis research.
Unfortunately, a systematic review on the methodology and reporting of studies developing or validating models predicting psychosis in CHR patients using rigorous quality criteria has not yet been conducted. Although one systematic review (Strobl et al. Reference Strobl, Eack, Swaminathan and Visweswaran2012) has focused on methods and performance of models predicting the onset of psychosis, several critical aspects, such as EPV ratios, selection of predictor variables, assessment of predictive performance and dealing with missing data, were not addressed. This might be because up until recently, no guidance existed to help form a well-defined review question and determine which details to extract and critically appraise from prediction modeling studies (Moons et al. Reference Moons, de Groot, Bouwmeester, Vergouwe, Mallett, Altman, Reitsma and Collins2014). Fortunately, such guidance has now become available with the publication of the Checklist for critical Appraisal and data extraction for systematic Reviews of Prediction Modeling Studies (CHARMS; Moons et al. Reference Moons, de Groot, Bouwmeester, Vergouwe, Mallett, Altman, Reitsma and Collins2014) which was developed by a panel of experts of the Cochrane Prognosis Methods Group.
The present systematic review therefore aims to critically appraise the methodology and reporting of studies developing or validating models predicting psychosis in CHR patients. We reviewed prediction modeling studies regardless of the domains that predictor variables were selected from. In accordance with the recently published CHARMS and other guidelines on clinical prediction modeling (e.g. Altman et al. Reference Altman, McShane, Sauerbrei and Taube2012; Collins et al. Reference Collins, Reitsma, Altman and Moons2015), all important methodological issues are addressed, including effective sample size, type of model used, selection and transformation of variables, assessment of predictive performance, internal and external validation, and treatment of missing data. The ultimate goal of this paper is to enhance the methodology and reporting of future studies not only by identifying frequent sources of bias but also by giving recommendations for improvement. To facilitate understanding, brief explanations of key statistical concepts in prognostic modeling are provided in Table 1 (see also Fusar-Poli & Schultze-Lutter, Reference Fusar-Poli and Schultze-Lutter2016).
Table 1. Definitions of key terms used in developing and validating prognostic models a

a Descriptions are adapted from Steyerberg (Reference Steyerberg2009).
Method
Search strategy
A literature search was carried out (up to 14 March 2016) in the databases of Medline, Embase, PsycINFO and Web of Science using the following search terms: (predict* OR ‘vulnerability marker’ OR ‘risk factors for transition’) AND psychosis AND (‘clinically at high risk’ OR ‘clinically at risk’ OR ‘clinical high risk’ OR ‘ultra high risk’ OR prodrom* OR ‘at risk mental state’ OR ‘risk of psychosis’). The search was restricted to English-language papers published from 1998 onwards because this marks the time when the first prospective studies with patients meeting validated CHR criteria were published (Yung et al. Reference Yung, Phillips, McGorry, McFarlane, Francey, Harrigan, Patton and Jackson1998). The publication type was restricted to articles only, thus excluding meeting abstracts, editorials, letters, reviews and comments. In addition, the reference lists of the included studies were screened to identify further potentially relevant studies.
Study selection
Studies were included if they met the following criteria: (1) involved subjects with a CHR for psychosis that were prospectively followed up; (2) developed or validated a prognostic model that predicted later transition to psychosis from variables obtained at baseline; (3) included at least two predictor variables in the prognostic model.
CHR for psychosis was required to be diagnosed by internationally established criteria. That is, subjects had to fulfill either ultra-high-risk, basic symptom or unspecific prodromal symptom criteria (for a review, see Fusar-Poli et al. Reference Fusar-Poli, Borgwardt, Bechdolf, Addington, Riecher-Rössler, Schultze-Lutter, Keshavan, Wood, Ruhrmann, Seidman, Valmaggia, Cannon, Velthorst, De Haan, Cornblatt, Bonoldi, Birchwood, McGlashan, Carpenter, McGorry, Klosterkötter, McGuire and Yung2013 b). Studies with overlapping samples were not excluded since the focus of our review was on methodology and reporting and not on the predictive performance of different models or the predictive potential of different predictor variables.
Studies were selected in a two-step procedure: First, all references retrieved from the databases were screened based on their titles and abstracts. Next, articles that were found to be potentially eligible were further evaluated based on their full texts. The study selection was performed by the first author (E.S.) and randomly checked by the second author (A.R.). Discrepancies in the final classification were discussed until consensus was reached.
Data extraction
We developed a comprehensive item list based on current methodological recommendations for developing and reporting clinical prediction models. To this end, we studied the item lists of previous systematic reviews evaluating prediction research in other medical fields (Mushkudiani et al. Reference Mushkudiani, Hukkelhoven, Hernandez, Murray, Choi, Maas and Steyerberg2008; Mallett et al. Reference Mallett, Royston, Dutton, Waters and Altman2010; Collins et al. Reference Collins, Mallett, Omar and Yu2011, Reference Collins, Omar, Shanyinde and Yu2013; Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012; van Oort et al. Reference van Oort, van den Berg, Koes, de Vet, Anema, Heymans and Verhagen2012), existing reporting statements and checklists [i.e. the CHARMS, Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD; Collins et al. Reference Collins, Reitsma, Altman and Moons2015) and Reporting Recommendations for Tumor Marker Prognostic Studies (REMARK; Altman et al. Reference Altman, McShane, Sauerbrei and Taube2012)], as well as current text books (Harrell, Reference Harrell2001; Steyerberg, Reference Steyerberg2009) and articles (Altman et al. Reference Altman, Vergouwe, Royston and Moons2009; Moons et al. Reference Moons, Altman, Vergouwe and Royston2009 a, b; Royston et al. Reference Royston, Moons, Altman and Vergouwe2009; Steyerberg et al. Reference Steyerberg, Vickers, Cook, Gerds, Gonen, Obuchowski, Pencina and Kattan2010) on clinical prediction modeling. The first author (E.S.) extracted all data, which were randomly checked by the second author (A.R.). Discrepancies were resolved by mutual discussions.
Data analysis
In line with a recent systematic review on clinical prediction research (Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012), we distinguished between predictor finding studies, prediction model development studies and external validation studies. Predictor finding studies primarily aim to explore which predictors independently contribute to the prediction of the outcome, i.e. are associated with the outcome (Moons et al. Reference Moons, Royston, Vergouwe, Grobbee and Altman2009 b; Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012). By contrast, model development studies aim to develop multivariable prediction models for clinical practice (i.e. for informed decision making) that predict the outcome as accurately as possible. While both types of studies make use of multivariable prediction models, the focus of the first is more on causal explanation and hypothesis testing whereas the latter is more concerned with accurate prediction. Although there are clear similarities in the design and analysis of etiological and prognostic studies, there are several aspects in which they differ. For example, calibration and discrimination are highly relevant to prognostic research but meaningless in etiological research (Moons et al. Reference Moons, Royston, Vergouwe, Grobbee and Altman2009 b). Furthermore, establishing unbiased estimates of each individual predictor with the outcome is important in etiological research but not in prognostic research (for more details on the difference between prognostic and etiological research, see Moons et al. Reference Moons, Royston, Vergouwe, Grobbee and Altman2009 b; Seel et al. Reference Seel, Steyerberg, Malec, Sherer and Macciocchi2012).
Studies were categorized as predictor model development studies if it was clearly stated in the paper that the aim was developing a model for clinical practice and not merely testing the predictive potential of certain predictor variables or domains. Studies were categorized as external validation studies if their aim was to assess the performance of a previously reported prediction model using new participant data that were not used in the development process. All other studies fulfilling inclusion criteria were termed predictor finding studies.
Since it would have been unfair to evaluate the different study types by exactly the same criteria, we grouped results by study type whenever necessary. Each extracted item was summarized in terms of absolute and relative frequencies and the results are reported according to the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (Moher et al. Reference Moher, Liberati, Tetzlaff, Altman and Group2009).
Results
Literature search results
The literature search identified 91 articles eligible for full review (see Fig. 1). The included studies were published between November 2002 and February 2016. The number of studies published per year was increasing, with only a single study published in 2002 and 14 studies published in 2015. Three journals accounted for almost half of the publications: 28 articles (31%) appeared in Schizophrenia Research, nine (10%) in Schizophrenia Bulletin and eight (9%) in Biological Psychiatry. The full list of included studies is presented in online Supplementary Table S1.

Fig. 1. Flowchart of the literature search.
Study aims
Only seven studies (Cannon et al. Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008; Ruhrmann et al. Reference Ruhrmann, Schultze-Lutter, Salokangas, Heinimaa, Linszen, Dingemans, Birchwood, Patterson, Juckel, Heinz, Morrison, Lewis, von Reventlow and Klosterkötter2010; Michel et al. Reference Michel, Ruhrmann, Schimmelmann, Klosterkötter and Schultze-Lutter2014; Nieman et al. Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Chan et al. Reference Chan, Krebs, Cox, Guest, Yolken, Rahmoune, Rothermundt, Steiner, Leweke, van Beveren, Niebuhr, Weber, Cowan, Suarez-Pinilla, Crespo-Facorro, Mam-Lam-Fook, Bourgin, Wenstrup, Kaldate, Cooper and Bahn2015; Perkins et al. Reference Perkins, Jeffries, Addington, Bearden, Cadenhead, Cannon, Cornblatt, Mathalon, McGlashan, Seidman, Tsuang, Walker, Woods and Heinssen2015 a, b) (8%) aimed at developing a clinical prediction model for application in clinical practice and thus were categorized as model development studies. All other studies (92%) were considered predictor finding studies.
We did not identify any true external validation studies. Although Mason et al. (Reference Mason, Startup, Halpin, Schall, Conrad and Carr2004) aimed at replicating the results of Yung et al. (Reference Yung, Phillips, Yuen and McGorry2004) and Thompson et al. (Reference Thompson, Nelson and Yung2011) aimed at replicating the results of Cannon et al. (Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008), both studies did not evaluate an exact published model (i.e. applied a regression formula to new data) but re-estimated regression coefficients of previously identified predictors. As frequently pointed out in the literature (e.g. Royston & Altman, Reference Royston and Altman2013; Moons et al. Reference Moons, de Groot, Bouwmeester, Vergouwe, Mallett, Altman, Reitsma and Collins2014), such studies are not model validation studies, but should be considered model re-development studies.
Study designs
All studies were cohort studies, except one (Thompson et al. Reference Thompson, Nelson and Yung2011), which used a nested cohort design. Of the studies, 66 (73%) were single-center and 25 (27%) were multicenter studies. Data were collected at 27 different centers. Many studies had overlapping samples. For instance, more than one-quarter (25.3%) of the published studies were based on data collected at the Personal Assessment and Crisis Evaluation (PACE) clinic in Melbourne, although not always from the same time periods. The criteria used for identifying CHR patients and assessing transition to psychosis are displayed in online Supplementary Table S2. The length and frequency of follow-up differed markedly between studies. Whereas some studies assessed transition to psychosis on a monthly basis in the first year (e.g. Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009), others conducted follow-up assessments only on a yearly or less frequent basis, which poses the risk of missing at least some transitions and might lead to a less accurate estimation of the time to transition. The average follow-up duration (from the 84 studies it could be determined) was 33.1 months (median 27.9 months, range 12–90 months). Of these studies, 17% had a follow-up duration of only 1 year, 33% of less than 2 years, and 60% of less than 3 years.
Number of patients and transitions
The average number of included CHR patients per study was 128 (s.d. 134) and the average number of transitions was 29.8 (s.d. 25.2). Although model development studies tended to have a higher number of included patients and transitions than predictor finding studies (252 v. 118 and 56.1 v. 27.6, respectively), these differences did not reach statistical significance. The average proportion of patients with later transition to psychosis was 27% (median 26%, range 5–53%). Since for a binary or a time-to-event outcome the effective sample size is the smaller of the two outcome frequencies (Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015), the effective sample size in the included studies almost always corresponded to the number of cases with later transition to psychosis and thus on average was only about one-quarter of the number of included CHR patients.
Number and type of considered predictor variables
The number of considered predictor variables could be determined in 85 studies (93%) and was 23.7 on average (median 12, s.d. 36.9, range 2–225). Model development studies considered significantly more predictor variables than predictor finding studies (97 v. 17.1 predictors, p = 0.040). The most frequently covered domains were positive symptoms, followed by negative symptoms, sociodemographic characteristics, and general, social and occupational functioning (see Fig. 2).

Fig. 2. Frequency of domains covered by candidate predictors. EEG, Electroencephalogram; MRI, magnetic resonance imaging.
EPV ratio
The average number of events per considered predictor variable (EPV) was 3 (median 1.8, s.d. 3, range 0.1–14.3). Although model development studies tended to have smaller average EPV than predictor finding studies (1.8 v. 3.1), this difference did not reach statistical significance. Only three studies (Velthorst et al. Reference Velthorst, Derks, Schothorst, Becker, Durston, Ziermans, Nieman and de Haan2013 a; Walder et al. Reference Walder, Holtzman, Addington, Cadenhead, Tsuang, Cornblatt, Cannon, McGlashan, Woods, Perkins, Seidman, Heinssen and Walker2013; Stowkowy et al. Reference Stowkowy, Liu, Cadenhead, Cannon, Cornblatt, McGlashan, Perkins, Seidman, Tsuang, Walker, Woods, Bearden, Mathalon and Addington2016) (3.5%), all of which were predictor finding studies, had an EPV of at least 10.
Missing data
Missing data at baseline were only explicitly mentioned in 28 studies (31%). The number of subjects with missing data was reported in 24 studies (26%), the number of missing values for each predictor in 11 studies (12%), and the number of subjects lost to follow-up in 35 studies (38%). Of the studies, nine (10%) reported to have omitted at least one predictor with missing values. The vast majority of studies handled missing data by performing complete case analyses, although this was only made explicit in 26 studies (29%) and must be assumed for those studies that did not mention missing data (Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Multiple imputation was only used in four studies (4%) (Seidman et al. Reference Seidman, Giuliano, Meyer, Addington, Cadenhead, Cannon, McGlashan, Perkins, Tsuang, Walker, Woods, Bearden, Christensen, Hawkins, Heaton, Keefe, Heinssen and Cornblatt2010; Nieman et al. Reference Nieman, Velthorst, Becker, de Haan, Dingemans, Linszen, Birchwood, Patterson, Salokangas, Heinimaa, Heinz, Juckel, von Reventlow, Morrison, Schultze-Lutter, Klosterkotter and Ruhrmann2013, Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Rüsch et al. Reference Rüsch, Heekeren, Theodoridou, Muller, Corrigan, Mayer, Metzler, Dvorsky, Walitza and Rossler2015) while single imputation was applied in two studies (2%) (Demjaha et al. Reference Demjaha, Valmaggia, Stahl, Byrne and McGuire2012; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015).
Model types
The most frequently used model types were Cox proportional hazard and logistic regression models, which were used in 51 (56%) and 23 (25%) studies, respectively. Of the studies, five (5.5%) had fitted both of these models. A small number of studies applied more modern statistical learning methods, such as support vector machines (Koutsouleris et al. Reference Koutsouleris, Meisenzahl, Davatzikos, Bottlender, Frodl, Scheuerecker, Schmitt, Zetzsche, Decker, Reiser, Moller and Gaser2009, Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, b, Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015) (4%), least absolute shrinkage and selection operator (LASSO) (Chan et al. Reference Chan, Krebs, Cox, Guest, Yolken, Rahmoune, Rothermundt, Steiner, Leweke, van Beveren, Niebuhr, Weber, Cowan, Suarez-Pinilla, Crespo-Facorro, Mam-Lam-Fook, Bourgin, Wenstrup, Kaldate, Cooper and Bahn2015; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016) (2%), greedy algorithm (Perkins et al. Reference Perkins, Jeffries, Addington, Bearden, Cadenhead, Cannon, Cornblatt, Mathalon, McGlashan, Seidman, Tsuang, Walker, Woods and Heinssen2015 a, b) (2%), partial least squares discriminant analysis (Huang et al. Reference Huang, Leweke, Tsang, Koethe, Kranaster, Gerth, Gross, Schreiber, Ruhrmann, Schultze-Lutter, Klosterkötter, Holmes and Bahn2007) (1%) and convex hull classification (Bedi et al. Reference Bedi, Carrillo, Cecchi, Slezak, Sigman, Mota, Ribeiro, Javitt, Copelli and Corcoran2015) (1%). Linear discriminant analysis was used in one study (Mittal et al. Reference Mittal, Walker, Bearden, Walder, Trottman, Daley, Simone and Cannon2010) (1%). One study (Healey et al. Reference Healey, Penn, Perkins, Woods and Addington2013) (1%) appeared to have used an ordinary least square regression model with a binary outcome, which clearly violates modeling assumptions.
Selection of predictor variables and dimensionality reduction
Pre-selection of candidate predictors for inclusion in the multivariable analyses based on univariable predictor–outcome associations was performed in 32 studies (35%). Of the studies, six reduced the number of predictors before inclusion to the final models by applying dimensionality reduction methods, such as principal component analysis (Huang et al. Reference Huang, Leweke, Tsang, Koethe, Kranaster, Gerth, Gross, Schreiber, Ruhrmann, Schultze-Lutter, Klosterkötter, Holmes and Bahn2007; Koutsouleris et al. Reference Koutsouleris, Meisenzahl, Davatzikos, Bottlender, Frodl, Scheuerecker, Schmitt, Zetzsche, Decker, Reiser, Moller and Gaser2009, Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015; Raballo et al. Reference Raballo, Nelson, Thompson and Yung2011), exploratory factor analysis (Demjaha et al. Reference Demjaha, Valmaggia, Stahl, Byrne and McGuire2012) and latent class factor analysis (Velthorst et al. Reference Velthorst, Derks, Schothorst, Becker, Durston, Ziermans, Nieman and de Haan2013 a).
For selecting predictors within multivariable models, 34 studies (37%) used stepwise methods. Most of these used backward elimination methods, but six studies also used forward and backward stepwise, five used forward stepwise and two did not describe the specific stepwise method. Of the studies, nine (10%) applied stepwise variable selections in multiple steps, that is, first to each of several domains, and then to the variables retained in each domain. The most frequently used significance threshold for stepwise variable selection was p = 0.05. Automated variable selection within multivariable models using non-stepwise-methods was conducted in only four studies. Two of these (Chan et al. Reference Chan, Krebs, Cox, Guest, Yolken, Rahmoune, Rothermundt, Steiner, Leweke, van Beveren, Niebuhr, Weber, Cowan, Suarez-Pinilla, Crespo-Facorro, Mam-Lam-Fook, Bourgin, Wenstrup, Kaldate, Cooper and Bahn2015; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016) used the LASSO and two (Perkins et al. Reference Perkins, Jeffries, Addington, Bearden, Cadenhead, Cannon, Cornblatt, Mathalon, McGlashan, Seidman, Tsuang, Walker, Woods and Heinssen2015 a, b) a greedy algorithm.
Transformation of predictor variables
Three of the model development studies (Cannon et al. Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008; Ruhrmann et al. Reference Ruhrmann, Schultze-Lutter, Salokangas, Heinimaa, Linszen, Dingemans, Birchwood, Patterson, Juckel, Heinz, Morrison, Lewis, von Reventlow and Klosterkötter2010; Perkins et al. Reference Perkins, Jeffries, Cornblatt, Woods, Addington, Bearden, Cadenhead, Cannon, Heinssen, Mathalon, Seidman, Tsuang, Walker and McGlashan2015 b) (43%) and 10 of the predictor finding studies (Yung et al. Reference Yung, Phillips, Yuen, Francey, McFarlane, Hallgren and McGorry2003, Reference Yung, Phillips, Yuen and McGorry2004; Mason et al. Reference Mason, Startup, Halpin, Schall, Conrad and Carr2004; Amminger et al. Reference Amminger, Leicester, Yung, Phillips, Berger, Francey, Yuen and McGorry2006; Thompson et al. Reference Thompson, Nelson and Yung2011; Nelson et al. Reference Nelson, Yuen, Wood, Lin, Spiliotacopoulos, Bruxner, Broussard, Simmons, Foley, Brewer, Francey, Amminger, Thompson, McGorry and Yung2013; Velthorst et al. Reference Velthorst, Nelson, Wiltink, de Haan, Wood, Lin and Yung2013 b; DeVylder et al. Reference DeVylder, Muchomba, Gill, Ben-David, Walder, Malaspina and Corcoran2014; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015; O'Donoghue et al. Reference O'Donoghue, Nelson, Yuen, Lane, Wood, Thompson, Lin, McGorry and Yung2015) (12%) fitted prediction models based on categorized or dichotomized continuous variables. Of these, six (Yung et al. Reference Yung, Phillips, Yuen, Francey, McFarlane, Hallgren and McGorry2003, Reference Yung, Phillips, Yuen and McGorry2004; Mason et al. Reference Mason, Startup, Halpin, Schall, Conrad and Carr2004; Cannon et al. Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008; Thompson et al. Reference Thompson, Nelson and Yung2011; Nelson et al. Reference Nelson, Yuen, Wood, Lin, Spiliotacopoulos, Bruxner, Broussard, Simmons, Foley, Brewer, Francey, Amminger, Thompson, McGorry and Yung2013) chose categorization cut-points based on the lowest p value, one (DeVylder et al. Reference DeVylder, Muchomba, Gill, Ben-David, Walder, Malaspina and Corcoran2014) based on the maximal area under the receiver operating characteristic curve (AUC), one (O'Donoghue et al. Reference O'Donoghue, Nelson, Yuen, Lane, Wood, Thompson, Lin, McGorry and Yung2015) based on quartiles, and five studies (Amminger et al. Reference Amminger, Leicester, Yung, Phillips, Berger, Francey, Yuen and McGorry2006; Cannon et al. Reference Cannon, Cadenhead, Cornblatt, Woods, Addington, Walker, Seidman, Perkins, Tsuang, McGlashan and Heinssen2008; Ruhrmann et al. Reference Ruhrmann, Schultze-Lutter, Salokangas, Heinimaa, Linszen, Dingemans, Birchwood, Patterson, Juckel, Heinz, Morrison, Lewis, von Reventlow and Klosterkötter2010; Velthorst et al. Reference Velthorst, Nelson, Wiltink, de Haan, Wood, Lin and Yung2013 b; Perkins et al. Reference Perkins, Jeffries, Cornblatt, Woods, Addington, Bearden, Cadenhead, Cannon, Heinssen, Mathalon, Seidman, Tsuang, Walker and McGlashan2015 b) did not provide explanations for the chosen cut-points. In at least four studies (Yung et al. Reference Yung, Phillips, Yuen, Francey, McFarlane, Hallgren and McGorry2003, Reference Yung, Phillips, Yuen and McGorry2004; Mason et al. Reference Mason, Startup, Halpin, Schall, Conrad and Carr2004; Nelson et al. Reference Nelson, Yuen, Wood, Lin, Spiliotacopoulos, Bruxner, Broussard, Simmons, Foley, Brewer, Francey, Amminger, Thompson, McGorry and Yung2013) the reason of dichotomizing continuous predictor variables was to provide a simple scoring rule.
Model performance
Table 2 displays the frequency of reporting different performance measures stratified by study aim. Whereas all model development studies reported at least one model performance measure, this was only the case in 28 (33%) of the predictor finding studies. If model performance was assessed, this was mainly done using classification measures, such as sensitivity and specificity, and less frequently using overall performance and discrimination measures. Calibration was not assessed in any of the model development studies and only in five (5%) of the predictor finding studies. Four of these (Piskulic et al. Reference Piskulic, Addington, Cadenhead, Cannon, Cornblatt, Heinssen, Perkins, Seidman, Tsuang, Walker, Woods and McGlashan2012; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015; Rüsch et al. Reference Rüsch, Heekeren, Theodoridou, Muller, Corrigan, Mayer, Metzler, Dvorsky, Walitza and Rossler2015; Xu et al. Reference Xu, Zhang, Zheng, Li, Tang, Luo, Sheng and Wang2016) used the Hosmer–Lemeshow statistic and one (Perkins et al. Reference Perkins, Jeffries, Cornblatt, Woods, Addington, Bearden, Cadenhead, Cannon, Heinssen, Mathalon, Seidman, Tsuang, Walker and McGlashan2015 b) a calibration plot. From the 31 studies reporting at least one classification measure, 19 did not report the probability threshold for classification and whether it was chosen from the data or set a priori, three used model types that did not predict a probability, and eight chose the probability threshold from the data. From the 35 studies (38%) reporting at least one performance measure, 21 (60%) only reported the so-called apparent performance.
Table 2. Model performance measures, stratified by type of prediction study

Data are given as number of studies (percentage).
AUC, Area under the receiver operator characteristic curve; BAC, balanced accuracy; DOR, diagnostic odds ratio; FPR, false positive rate; LR, likelihood ratio; NPV, negative predictive value; PPV, positive predictive value; TNR, true negative rate; TPR, true positive rate.
Model evaluation
Internal cross-validation was carried out in only four of the model development studies (57%) (Michel et al. Reference Michel, Ruhrmann, Schimmelmann, Klosterkötter and Schultze-Lutter2014; Nieman et al. Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Perkins et al. Reference Perkins, Jeffries, Addington, Bearden, Cadenhead, Cannon, Cornblatt, Mathalon, McGlashan, Seidman, Tsuang, Walker, Woods and Heinssen2015 a, b) and 10 of the predictor finding studies (12%) (Schultze-Lutter et al. Reference Schultze-Lutter, Klosterkötter, Picker, Steinmeyer and Ruhrmann2007; Koutsouleris et al. Reference Koutsouleris, Meisenzahl, Davatzikos, Bottlender, Frodl, Scheuerecker, Schmitt, Zetzsche, Decker, Reiser, Moller and Gaser2009, Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, b, Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015; Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009; Mittal et al. Reference Mittal, Walker, Bearden, Walder, Trottman, Daley, Simone and Cannon2010; Bedi et al. Reference Bedi, Carrillo, Cecchi, Slezak, Sigman, Mota, Ribeiro, Javitt, Copelli and Corcoran2015; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016). Of these, six (Koutsouleris et al. Reference Koutsouleris, Meisenzahl, Davatzikos, Bottlender, Frodl, Scheuerecker, Schmitt, Zetzsche, Decker, Reiser, Moller and Gaser2009, Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, b; Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015; Perkins et al. Reference Perkins, Jeffries, Addington, Bearden, Cadenhead, Cannon, Cornblatt, Mathalon, McGlashan, Seidman, Tsuang, Walker, Woods and Heinssen2015 a; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016) used k-fold cross-validation, three (Michel et al. Reference Michel, Ruhrmann, Schimmelmann, Klosterkötter and Schultze-Lutter2014; Nieman et al. Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015) used bootstrapping, three (Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009; Mittal et al. Reference Mittal, Walker, Bearden, Walder, Trottman, Daley, Simone and Cannon2010; Bedi et al. Reference Bedi, Carrillo, Cecchi, Slezak, Sigman, Mota, Ribeiro, Javitt, Copelli and Corcoran2015) used leave-one-out cross-validation and two (Schultze-Lutter et al. Reference Schultze-Lutter, Klosterkötter, Picker, Steinmeyer and Ruhrmann2007; Perkins et al. Reference Perkins, Jeffries, Cornblatt, Woods, Addington, Bearden, Cadenhead, Cannon, Heinssen, Mathalon, Seidman, Tsuang, Walker and McGlashan2015 b) used a split-sampling approach. However, five of these studies (Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009; Mittal et al. Reference Mittal, Walker, Bearden, Walder, Trottman, Daley, Simone and Cannon2010; Michel et al. Reference Michel, Ruhrmann, Schimmelmann, Klosterkötter and Schultze-Lutter2014; Nieman et al. Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Cornblatt et al. Reference Cornblatt, Carrion, Auther, McLaughlin, Olsen, John and Correll2015) only cross-validated the final model and therefore did not take into account the uncertainty introduced by the variable selection and transformation. Only four studies (Koutsouleris et al. Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, b, Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016) used nested repeated cross-validation, which is considered the best approach for training and testing a prediction model in one sample (Krstajic et al. Reference Krstajic, Buturovic, Leahy and Thomas2014).
Model presentation
Only four studies (Schultze-Lutter et al. Reference Schultze-Lutter, Klosterkötter, Picker, Steinmeyer and Ruhrmann2007, Reference Schultze-Lutter, Klosterkötter, Michel, Winkler and Ruhrmann2012; Ziermans et al. Reference Ziermans, de Wit, Schothorst, Sprong, van Engeland, Kahn and Durston2014; Xu et al. Reference Xu, Zhang, Zheng, Li, Tang, Luo, Sheng and Wang2016) (4%) provided the full model formula, seven (8%) used model types that cannot be easily described with a model formula (e.g. support vector machine), 20 (22%) only provided p values but not regression coefficients of predictors, and 60 studies (66%) only provided regression coefficients of the predictor variables but not the intercept or baseline survival function, which are required in logistic and Cox regression, respectively, to properly assess calibration (Royston & Altman, Reference Royston and Altman2013; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Three studies (Lencz et al. Reference Lencz, Smith, McLaughlin, Auther, Nakayama, Hovey and Cornblatt2006; Riecher-Rössler et al. Reference Riecher-Rössler, Pflueger, Aston, Borgwardt, Brewer, Gschwandtner and Stieglitz2009; Bang et al. Reference Bang, Kim, Song, Baek, Lee and An2015) also only provided regression coefficients for standardized or otherwise transformed variables without giving enough details to exactly replicate the variable transformation in a new dataset.
Discussion
Our systematic review identified 91 studies using a multivariable clinical prediction model for predicting the transition to psychosis in CHR patients. The vast majority of these studies (n = 84) were classified as predictor finding studies because they primarily aimed at hypothesis testing or evaluating the predictive potential of certain predictors or assessment domains. Only seven studies stated explicitly that they aimed at developing a prediction model for clinical practice and therefore were classified as model development studies. Thus, in prediction of psychosis research, studies seem to focus much more often on etiology/explanation than maximizing prognostic accuracy (for a more detailed explanation of the difference between prognostic and etiological research, see Moons et al. Reference Moons, Royston, Vergouwe, Grobbee and Altman2009 b; Seel et al. Reference Seel, Steyerberg, Malec, Sherer and Macciocchi2012). However, it should be noted that this distinction was not always clear-cut as many authors did not clearly describe the aim of the study or possibly tried to achieve both accurate prognosis and a better understanding of causal relationships.
We found that poor conduct and reporting were widespread in both predictor finding and model developed studies and that almost all aspects of the modeling process were affected. The results of this review are therefore consistent with reviews of prediction modeling studies in other medical fields (Mushkudiani et al. Reference Mushkudiani, Hukkelhoven, Hernandez, Murray, Choi, Maas and Steyerberg2008; Mallett et al. Reference Mallett, Royston, Dutton, Waters and Altman2010; Collins et al. Reference Collins, Mallett, Omar and Yu2011; Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012; Collins et al. Reference Collins, Omar, Shanyinde and Yu2013).
One of the biggest concerns is that most studies relied on small effective sample sizes and number of events (i.e. patients with later transitions to psychosis) relative to the number of considered predictor variables (EPV). Small EPV ratios increase the risk of overfitting and overestimating the performance of the model, if it is developed and assessed in the same sample (Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Furthermore, it can lead to biased regression coefficients and unstable variable selection (Mushkudiani et al. Reference Mushkudiani, Hukkelhoven, Hernandez, Murray, Choi, Maas and Steyerberg2008). Current guidelines and textbooks therefore recommend EPV ratios of at least 10 (Steyerberg, Reference Steyerberg2009; Moons et al. Reference Moons, de Groot, Bouwmeester, Vergouwe, Mallett, Altman, Reitsma and Collins2014; Collins et al. Reference Collins, Reitsma, Altman and Moons2015). Unfortunately, in this review, an EPV of at least 10 was only achieved in three studies (Velthorst et al. Reference Velthorst, Derks, Schothorst, Becker, Durston, Ziermans, Nieman and de Haan2013 a; Walder et al. Reference Walder, Holtzman, Addington, Cadenhead, Tsuang, Cornblatt, Cannon, McGlashan, Woods, Perkins, Seidman, Heinssen and Walker2013; Stowkowy et al. Reference Stowkowy, Liu, Cadenhead, Cannon, Cornblatt, McGlashan, Perkins, Seidman, Tsuang, Walker, Woods, Bearden, Mathalon and Addington2016) and the median EPV was only 1.8. While low EPV ratios have also frequently been criticized in other fields of clinical prediction research (Collins et al. Reference Collins, Mallett, Omar and Yu2011; Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012), the problem seems to be particularly severe in prediction of psychosis as reviews on studies developing models predicting cancer (Mallett et al. Reference Mallett, Royston, Dutton, Waters and Altman2010), kidney disease (Collins et al. Reference Collins, Omar, Shanyinde and Yu2013), type 2 diabetes (Collins et al. Reference Collins, Mallett, Omar and Yu2011) and cardiovascular disease (Wessler et al. Reference Wessler, Lai Yh, Kramer, Cangelosi, Raman, Lutz and Kent2015) have reported median EPV ratios of 10, 29, 19 and 11–34, respectively. The much lower sample sizes in prediction of psychosis research can be at least partially explained by the fact that CHR patients are difficult to recruit and follow-up durations of at least 2 years are needed to detect most later transitions to psychosis (Kempton et al. Reference Kempton, Bonoldi, Valmaggia, McGuire and Fusar-Poli2015).
However, although missing data are expected to be frequent in medical research in general (Sterne et al. Reference Sterne, White, Carlin, Spratt, Royston, Kenward, Wood and Carpenter2009) and in early psychosis research in particular, only about one-third of the included studies mentioned any missing data. Furthermore, reporting on the type and frequency of missing data was often poor. Moreover, only four studies (Seidman et al. Reference Seidman, Giuliano, Meyer, Addington, Cadenhead, Cannon, McGlashan, Perkins, Tsuang, Walker, Woods, Bearden, Christensen, Hawkins, Heaton, Keefe, Heinssen and Cornblatt2010; Nieman et al. Reference Nieman, Velthorst, Becker, de Haan, Dingemans, Linszen, Birchwood, Patterson, Salokangas, Heinimaa, Heinz, Juckel, von Reventlow, Morrison, Schultze-Lutter, Klosterkotter and Ruhrmann2013, Reference Nieman, Ruhrmann, Dragt, Soen, van Tricht, Koelman, Bour, Velthorst, Becker, Weiser, Linszen and de Haan2014; Rüsch et al. Reference Rüsch, Heekeren, Theodoridou, Muller, Corrigan, Mayer, Metzler, Dvorsky, Walitza and Rossler2015) (4%) performed multiple imputation, which is generally acknowledged as the preferred method for handling incomplete data (Sterne et al. Reference Sterne, White, Carlin, Spratt, Royston, Kenward, Wood and Carpenter2009; Moons et al. Reference Moons, de Groot, Bouwmeester, Vergouwe, Mallett, Altman, Reitsma and Collins2014). Hence, it is likely that most studies had excluded subjects or variables with incomplete data, which not only leads to a waste of data and reduced power, but can also negatively affect the representativeness of the sample and consequently the generalizability of the resulting prediction model (Gorelick, Reference Gorelick2006; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Unfortunately, poor handling and reporting of missing data are widespread in any medical field (Bouwmeester et al. Reference Bouwmeester, Zuithoff, Mallett, Geerlings, Vergouwe, Steyerberg, Altman and Moons2012). However, in prediction of psychosis the consequences might be particularly severe as samples are already quite small and a further loss of data can be less afforded.
Approximately 60% of both predictor finding and model development studies used Cox regression and thus treated the outcome as a time-to-event variable, whereas the remaining studies used models with a binary outcome (i.e. transition v. non-transition). For prospective studies with longer-term diagnostic outcomes and regular follow-up assessments, as is the case in prediction of psychosis studies, time-to-event outcome models are more appropriate because they use more information, have more statistical power, and can deal with censoring (i.e. cases with incomplete follow-up) (van der Net et al. Reference van der Net, Janssens, Eijkemans, Kastelein, Sijbrands and Steyerberg2008; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Since loss to follow-up is frequent in prediction of psychosis research and follow-up durations often too short to capture all transitions (Schultze-Lutter et al. Reference Schultze-Lutter, Michel, Schmidt, Schimmelmann, Maric, Salokangas, Riecher-Rössler, van der Gaag, Nordentoft, Raballo, Meneghelli, Marshall, Morrison, Ruhrmann and Klosterkötter2015), the 40% of studies that have applied a binary outcome model are mainly faced with two shortcomings. First, they had to exclude non-transitioned cases with short follow-up durations, which again further aggravated the problem of already existing small sample sizes and might have hampered the representativeness of the sample. Second, patients with late transition to psychosis might have been misclassified as non-transitioned cases.
Several studies (Koutsouleris et al. Reference Koutsouleris, Meisenzahl, Davatzikos, Bottlender, Frodl, Scheuerecker, Schmitt, Zetzsche, Decker, Reiser, Moller and Gaser2009, Reference Koutsouleris, Borgwardt, Meisenzahl, Bottlender, Moller and Riecher-Rössler2012 a, b, Reference Koutsouleris, Riecher-Rössler, Meisenzahl, Smieskova, Studerus, Kambeitz-Ilankovic, von Saldern, Cabral, Reiser, Falkai and Borgwardt2015) used so-called machine learning or pattern recognition methods, such as support vector machines. In line with Steyerberg et al. (Reference Steyerberg, van der Ploeg and Van Calster2014), we herein use the term ‘machine learning method’ to refer to the more modern and flexible statistical learning methods originally developed in the field of computer science, such as random forest or neural networks, which can automatically capture highly complex non-linear relationships between predictor and response variables, and separate them from regression-based methods traditionally used in clinical prediction modeling, such as logistic and Cox regression or penalized versions thereof (i.e. models in which regression coefficients are shrunken towards zero, such as LASSO). Since the first results with machine learning methods have been encouraging, a more widespread use of these methods in the field of early detection of psychosis is now considered by many authors a promising strategy to improve the prediction of psychosis (Pettersson-Yeo et al. Reference Pettersson-Yeo, Benetti, Marquand, Dell'acqua, Williams, Allen, Prata, McGuire and Mechelli2013; Koutsouleris & Kambeitz, Reference Koutsouleris, Kambeitz, Riecher-Rössler and McGorry2016). However, many methodologists in the field of clinical prediction modeling (Steyerberg et al. Reference Steyerberg, van der Ploeg and Van Calster2014; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015) do not share this enthusiasm for the following reasons: First, due to their higher flexibility, machine learning methods are more prone to overfitting than regression-based approaches, particularly in small datasets (van der Ploeg et al. Reference van der Ploeg, Austin and Steyerberg2014). Hence, when sample sizes are small, as is frequently the case in prediction of psychosis research, their performance advantage resulting from the increased ability to capture the true underlying relationship between predictors and response might not be high enough to compensate for the increased tendency to overfit (Steyerberg et al. Reference Steyerberg, van der Ploeg and Van Calster2014). Accordingly, van der Ploeg et al. (Reference van der Ploeg, Nieboer and Steyerberg2016) have shown that logistic regression outperformed support vector machines, random forests and neural networks in external validation, when predicting 6-month mortality in traumatic brain injury patients from sociodemographic, computed tomography, and laboratory data. Similarly, logistic regression outperformed random forest and support vector machines, when predicting treatment resistance in major depressive disorder (Perlis, Reference Perlis2013). Of course, this does not mean that machine learning methods would also perform worse in every prediction of psychosis scenario (for example, they might still be superior when predicting psychosis from neuroimaging data). However, based on the above findings, it seems rather unlikely that they would be vastly superior in most scenarios. Second, machine learning methods are less interpretable and more difficult to communicate to clinicians (Steyerberg et al. Reference Steyerberg, van der Ploeg and Van Calster2014). For example, regression models can transparently be presented, with insight in relative effects of predictors by odds or hazard ratios, while many machine learning models are essentially black boxes with highly complex prediction equations. Third, while traditional methods can be easily adjusted to local settings (e.g. by changing the model intercept), this is more difficult for machine learning methods (Steyerberg et al. Reference Steyerberg, van der Ploeg and Van Calster2014). However, the ability to adjust the model, also called re-calibration (Steyerberg, Reference Steyerberg2009), is important in prediction of psychosis, as rates of transition to psychosis have been shown to vary considerably across time and location (Fusar-Poli et al. Reference Fusar-Poli, Bonoldi, Yung, Borgwardt, Kempton, Valmaggia, Barale, Caverzasi and McGuire2012).
With regard to variable selection strategies, we found that univariable screening of candidate predictors and/or stepwise variable selection were frequently conducted in both predictor finding and model development studies. However, these methods have long been criticized on multiple grounds (Harrell, Reference Harrell2001; Steyerberg, Reference Steyerberg2009; Núñez et al. Reference Núñez, Steyerberg and Núñez2011). Specifically, when the EPV ratio is low, the variable selection is unstable, the size and significance of the estimated regression coefficients are systematically overestimated, and the performance of the selected model is overoptimistic (Derksen & Keselman, Reference Derksen and Keselman1992; Sun et al. Reference Sun, Shook and Kay1996; Steyerberg et al. Reference Steyerberg, Eijkemans and Habbema1999; Steyerberg & Vergouwe, Reference Steyerberg and Vergouwe2014). Since the bias introduced by these methods is more severe when EPV ratios are low, their use in prediction of psychosis research is particularly problematic. Unfortunately, we also found that most studies relied on high significance thresholds, such as p < 0.05, for variable selection, which leads to more bias and worse cross-validated predictive performance than higher thresholds, particularly in small datasets (Steyerberg et al. Reference Steyerberg, Eijkemans and Habbema1999, Reference Steyerberg, Eijkemans, Harrell and Habbema2001). Furthermore, we found that several studies performed forward stepwise instead of the more recommended backward stepwise selection (Steyerberg, Reference Steyerberg2009; Núñez et al. Reference Núñez, Steyerberg and Núñez2011). Given that sample sizes in the field of early psychosis research are small, a more sensible approach for variable selection would be to rely more on external knowledge. For example, candidate predictors could be pre-selected by performing meta-analyses or based on theory. If external knowledge is not available, a more stable set of predictor variables and reduced overfitting can be achieved by applying shrinkage methods (Steyerberg et al. Reference Steyerberg, Eijkemans, Harrell and Habbema2001; Núñez et al. Reference Núñez, Steyerberg and Núñez2011), such as the LASSO (Tibshirani, Reference Tibshirani1997), which have only been used in two (Chan et al. Reference Chan, Krebs, Cox, Guest, Yolken, Rahmoune, Rothermundt, Steiner, Leweke, van Beveren, Niebuhr, Weber, Cowan, Suarez-Pinilla, Crespo-Facorro, Mam-Lam-Fook, Bourgin, Wenstrup, Kaldate, Cooper and Bahn2015; Ramyead et al. Reference Ramyead, Studerus, Kometer, Uttinger, Gschwandtner, Fuhr and Riecher-Rössler2016) of the included studies.
We also found several studies that categorized or even dichotomized continuous predictor variables, which has been strongly discouraged by methodologists because it leads to a considerable loss of information, reduced statistical power, residual confounding, and decreased predictive accuracy (Royston et al. Reference Royston, Altman and Sauerbrei2006; Altman et al. Reference Altman, McShane, Sauerbrei and Taube2012; Collins et al. Reference Collins, Ogundimu, Cook, Manach and Altman2016). Furthermore, many of these studies chose cut-points by taking the value that produced the lowest p or highest AUC value, which can lead to a serious inflation of the type I error and to an overestimation of the prognostic effect (Hollander et al. Reference Hollander, Sauerbrei and Schumacher2004; Altman et al. Reference Altman, McShane, Sauerbrei and Taube2012).
Another area that needs considerable improvement concerns model performance assessment and evaluation, although this is clearly more important for model development and less so for predictor finding studies. We found that none of the proposed models has been externally validated and internal cross-validation was carried out in only 57% of model development studies and 12% of predictor finding studies. Furthermore, half of these used poor internal cross-validation strategies, such as split-sampling, which wastes half of the data and leads to highly uncertain estimates of model performance (Austin & Steyerberg, Reference Austin and Steyerberg2014; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015), or cross-validating only the final model after having conducted data-driven variable selection in the whole sample, which leads to highly overoptimistic performance estimates (Krstajic et al. Reference Krstajic, Buturovic, Leahy and Thomas2014).
Since internal cross-validation was conducted infrequently, most studies only reported the so called ‘apparent’ performance, which tends to be strongly overoptimistic because it is calculated in the same data as used for model building (Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Furthermore, most studies did not report the whole spectrum of recommended performance measures. For example, calibration, which is a key aspect of the model performance (Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015), was rarely assessed and mostly using the Hosmer–Lemeshow statistic instead of the more recommended calibration-in-the-large and calibration slope (Steyerberg et al. Reference Steyerberg, Vickers, Cook, Gerds, Gonen, Obuchowski, Pencina and Kattan2010; Collins et al. Reference Collins, Reitsma, Altman and Moons2015). Moreover, many studies reporting classification measures (i.e. sensitivity and specificity) had searched for optimal probability thresholds for classification in the same sample as they used for testing, which again probably contributed to overoptimism (Leeflang et al. Reference Leeflang, Moons, Reitsma and Zwinderman2008).
We also found major deficiencies in the way that models were presented. Most importantly, most studies did not provide enough details to exactly apply the model in a new dataset, which might at least partially explain why none of these models has yet been externally validated. Furthermore, several studies only provided enough details to apply a simplified scoring rule but not the original model. However, as explained above, the perceived advantage of simplification/categorization comes at high costs. A much better way of facilitating the clinical application would be the creation of an online risk calculator (Steyerberg & Vergouwe, Reference Steyerberg and Vergouwe2014). This would also allow the clinical use and external validation of more complex models (e.g. machine learning algorithms) that cannot be described with a simple model formula (Steyerberg et al. Reference Steyerberg, van der Ploeg and Van Calster2014).
Limitations
Our literature search was restricted to English-language journal articles only. Thus, it is possible that some relevant literature has been missed. A further limitation is that choosing an appropriate modeling strategy is complex and depends on many different factors, including research question, study design, sample size and number of variables. Although we grouped studies by their aim and relied on guidelines (i.e. the CHARMS) for critically appraising the methodology and reporting of the included studies as much as possible, some studies might have been treated unfairly due to not taking all specific factors into account.
Conclusion
Taken together, we found that most studies developing a model for predicting the transition to psychosis in CHR patients were poorly conducted and reported. Biased and inefficient methods, such as complete case analysis, modeling a time-to-event outcome as a binary outcome, data-driven univariable and stepwise selection of candidate variables, categorization of continuous predictors, and assessing only the apparent predictive performance, were widespread and often applied together and in datasets with small EPV ratios, which probably potentiated their harmful consequences. Consequently, most published predictive performance estimates in this field are likely to be considerably overoptimistic. Unfortunately, this was rarely acknowledged, since proper internal validation was infrequent and external validation not attempted. An essential requirement for future studies is therefore to improve model validation. While we acknowledge that – due to differences in measurement methods across centers – external validation is often difficult, internal validation can and should always be performed (Moons et al. Reference Moons, Kengne, Woodward, Royston, Vergouwe, Altman and Grobbee2012). To further enhance progress, future studies should more strictly adhere to current checklists and guidelines on clinical prediction models, such as the recently published TRIPOD statement (Collins et al. Reference Collins, Reitsma, Altman and Moons2015; Moons et al. Reference Moons, Altman, Reitsma, Ioannidis, Macaskill, Steyerberg, Vickers, Ransohoff and Collins2015). Since EPV ratios in prediction of psychosis research are small compared with other fields of prediction research, researchers in this field should take extra care to not waste valuable information and to avoid overfitting, for example, by more strongly relying on external information and applying models that are not too adaptive. In Table 3, we have summarized our recommendations for improved methodology and reporting in prediction of psychosis studies.
Table 3. Recommendations for improved methodology and reporting
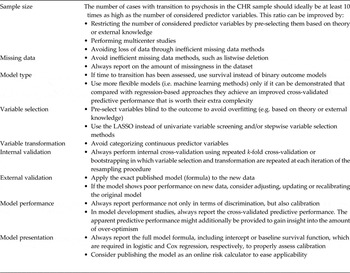
CHR, Clinical high risk; LASSO, least absolute shrinkage and selection operator.
Supplementary material
The supplementary material for this article can be found at http://doi.org/10.1017/S0033291716003494
Acknowledgements
This work was supported by the Swiss National Science Foundation (P2BSP3-165392).
Declaration of Interest
None.







