Published online by Cambridge University Press: 31 August 2005
To compare two multivariate random vectors of the same dimension, we define a new stochastic order called upper orthant dispersive ordering and study its properties. We study its relationship with positive dependence and multivariate hazard rate ordering as defined by Hu, Khaledi, and Shaked (Journal of Multivariate Analysis, 2002). It is shown that if two random vectors have a common copula and if their marginal distributions are ordered according to dispersive ordering in the same direction, then the two random vectors are ordered according to this new upper orthant dispersive ordering. Also, it is shown that the marginal distributions of two upper orthant dispersive ordered random vectors are also dispersive ordered. Examples and applications are given.
It is of interest to compare two random variables in terms of their variability. Although this topic has been studied extensively in the univariate case, several attempts have been made to extend it to the multivariate case. Important contributions in this case have been made by Giovagnoli and Wynn [8], Shaked and Shanthikumar [21], and Fernandez-Ponce and Suarez-Llorens [7], among others.
Let X and Y be two univariate random variables with distribution functions F and G and with survival functions F and G, respectively. A basic concept for comparing variability in distributions is that of dispersive ordering. X is said to be less dispersed than Y (denoted by X ≤disp Y) if
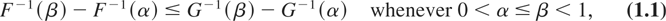
where F−1 and G−1 are the right continuous inverses of the distribution functions F and G, respectively. This means that the difference between any two quantiles of X is smaller than the difference between the corresponding quantiles of Y. In case the random variables X and Y are of continuous type with hazard rates rF and rG, respectively, then X ≤disp Y if and only if
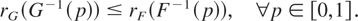
For more details on dispersive ordering, see Shaked and Shanthikumar [20, Sec.2B].
In analogy with the characterization (1.2) of the univariate dispersive ordering, we introduce a new order in the multivariate case, which we call upper orthant dispersive ordering and study its properties. According to (1.2), X ≤disp Y if and only if the hazard rates of X and Y at the quantiles of the same order p are ordered for all values of p ∈ [0,1]. To this end, we first recall the definition of hazard rate (or hazard gradient) in the multivariate case. Consider a random vector X = (X1,…,Xn) with a partially differentiable survival function F(x) = P{X > x}. The function R = −logF is called the hazard function of X, and the vector rX of partial derivatives, defined by

for all x ∈ {x : F(x) > 0}, is called the hazard gradient of X (see Johnson and Kotz [11] and Marshall [15]). Note that rX(i)(x) can be interpreted as the conditional hazard rate of Xi evaluated at xi, given that Xj > xj for all j ≠ i; that is,
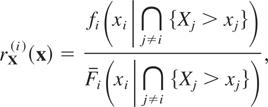
where fi(·|∩j≠i{Xj > xj}) and Fi(·|∩j≠i{Xj > xj}) are respectively the conditional density and the conditional survival functions of Xi, given that Xj > xj for all j ≠ i. For convenience, here and below we set rX(i)(x) = ∞ for all x ∈ {x : F(x) = 0}. Now, we define upper orthant dispersive ordering.
Definition 1.1: Let X = (X1,…,Xn) and Y = (Y1,…,Yn) be two random vectors with respective survival functions F and G. We say that X is smaller than Y according to upper orthant dispersive ordering (denoted by

) if for all uj ∈ [0,1], j = 1,…,n, j ≠ i,
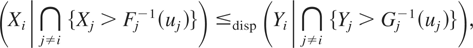
for i = 1,…,n.
In case the distributions under consideration are absolutely continuous, the upper orthant dispersive ordering can be equivalently expressed in terms of the hazard gradients at the quantiles of the same orders of the conditional distributions. If we denote by xi(β;u) and yi(β;u), the βth quantiles of the conditional distributions (Xi|∩j≠i{Xj > Fj−1(uj)}) and (Yi|∩j≠i{Yj > Gj−1(uj)}), respectively, then
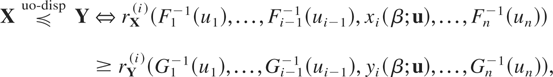
for every β ∈ [0,1], u ∈ [0,1]n−1, and i = 1,…,n, where rX(i) and rY(i) stand for the ith components of the hazard gradients of X and Y, respectively.
The following slightly modified version of a theorem of Saunders and Moran [19] provides a useful tool for establishing dispersive ordering among members of a parametric family of distributions.
Theorem 1.1: Let Xa be a random variable with distribution function Fa for each a ∈ R such that the following hold:
(i) Fa is supported on some interval (x−(a),x+(a)) ⊆ (−∞,∞) and has density fa that does not vanish on any subinterval of (x−(a),x+(a)).
(ii) The derivative of Fa with respect to a exists and is denoted by Fa′.
Then
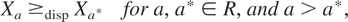
if and only if,
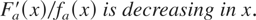
In the next example we identify conditions under which two bivariate normal random vectors are ordered according to upper orthant dispersive ordering. More examples are discussed in Section 4.
Example 1.1 (Bivariate Normal Distribution): Let X and Y follow bivariate Normal distributions, each with mean vector (0,0) and with dispersion matrices

respectively, with σi > 0 for i = 1,2. For the time being, we are assuming that the marginal distributions of X and Y are identical. The general case is considered later. We use Theorem 1.1 to prove that in case ρ and ρ′ are of the same sign, then

Let us denote by Gρ, the distribution function of {X1|X2 > y} (we are suppressing its dependence on y for the clarity of notation). Then

and the corresponding conditional density function is
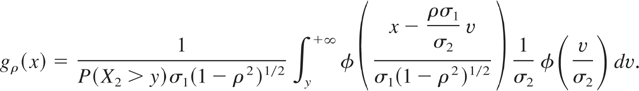
Now we compute

which simplifies to

Similarly, the conditional density function gρ(x) can be written as

This gives
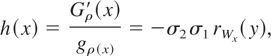
where rWx(.) denotes the hazard rate of Wx, a normal random variable with mean ρxσ2 /σ1 and variance σ22(1 − ρ2). It is known that the family of normal random variables with a fixed variance but with different means is ordered according to hazard rate order and the one with the smaller mean has the greater hazard rate. Using this fact, it follows that if ρ > 0, then h(x) is increasing in x. Hence, by Theorem 1.1,

. If ρ < 0, then h(x) is decreasing in x; hence, (X1,X2) is increasing in ρ in the sense of upper orthant dispersive ordering. This proves the required result. █
The organization of the article is as follows. In Section 2 we study some properties of the upper orthant dispersive ordering as defined earlier. It is proved that if two random vectors have the same dependence structure (copula), then they are ordered according to upper orthant dispersive ordering if and only if their corresponding marginals are ordered according to univariate dispersive ordering. In Section 3 we consider the special case of nonnegative random variables (more generally, if the conditional distributions have common left end points of their supports). It is shown that if two random vectors have the same marginal distributions and they are ordered according to upper orthant dispersive ordering, then their bivariate copulas are ordered, implying that one random vector is more dependent in the sense of positive quadrant dependence than the other. We also study the connection between upper orthant dispersive ordering and multivariate hazard rate ordering as introduced by Hu, Khaledi, and Shaked [9]. The last section is devoted to some examples and applications. It is shown that if two univariate distributions are ordered according to dispersive ordering, then the corresponding vectors of order statistics from them are ordered according to upper orthant dispersive ordering.
In this section we establish an interesting property of the upper orthant dispersive ordering that if two n-dimensional random vectors X and Y have the same dependence structure in the sense that they have the same copula, then dispersive ordering among the marginal distributions implies upper orthant dispersive ordering and vice versa. The notion of copula has been introduced by Sklar [23], and studied by, among others, Kimeldrof and Sampson [13] under the name of uniform representation and by Deheuvels [5] under the name of dependence function. A copula C is a cumulative distribution function with uniform margins on [0,1]. Given a copula C, if one defines
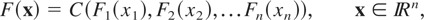
then F is a multivariate distribution function with margins as F1,F2,…,Fn. For any multivariate distribution function F with margins as F1,F2,…,Fn, there exists a copula C such that (2.1) holds. If F is continuous, then C is unique and can be constructed as follows:
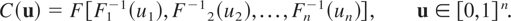
It follows that if X and Y are two n-dimensional random vectors with margins as (F1,F2,…,Fn) and (G1,G2,…,Gn), respectively, and if they have the same copula, then
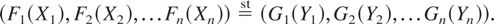
For i = 1,…,n, let us denote by Hi,uX the cumulative distribution function (cdf) of the conditional distribution (Xi|∩j≠i{Xj > Fj−1(uj)}) and by Hi,uY that of (Yi|∩j≠i{Yj > Gj−1(uj)}). To prove the next theorem, we first prove the following lemma, which may be of independent interest.
Lemma 2.1: If two n-dimensional random vectors X and Y have the same copula, then, for i = 1,…n,
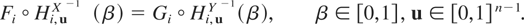
Proof: Proving (2.4) is equivalent to proving that for i = 1,…n and u ∈ [0,1]n−1,

which is true because of (2.3), since X and Y have the same copula. █
Theorem 2.1: Let X and Y be two n-dimensional random vectors with the same copula. Then

if and only if Xi ≤disp Yi, i = 1,…,n.
Proof: By definition,

It follows from (2.4) that if X and Y have the same copula, then for i = 1,…n and u ∈ [0,1]n−1,
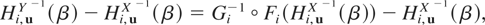
for i = 1,…n and for every β ∈ [0,1].
It is easy to see that the right-hand side of (2.6) is increasing in β if and only if Gi−1 Fi(x) − x is increasing in x (i.e., if and only if Xi ≤disp Yi, i = 1,…,n). This proves the desired result. █
Recently, Müller and Scarsini [16] have investigated some other multivariate stochastic orders for which results parallel to Theorem 2.1 hold for those orders. The following interesting property of the upper orthant dispersive ordering immediately follows from Theorem 2.1.
Corollary 2.1: Let Y = (a1 X1 + b1,a2 X2 + b2,…,an Xn + bn). Then for

.
Proof: Since X and Y have the same copula, the required result follows immediately from Theorem 2.1. █
Example 2.1 (Multivariate Normal Distributions): Let X follow the p-variate multivariate Normal distribution with mean vector μ and dispersion matrix Σ = ((σij)), with σij = ρijσiσj, ρii = 1, σi > 0, and i,j = 1,…,p. Let Y follow the p-variate multivariate Normal distribution with mean vector μ′ and dispersion matrix Σ′ = ((σij′)), with σij′ = ρijσi′σj′, σi′ > 0, and i,j = 1,…,p. It is known that X and Y have the same copula. It follows from Theorem 2.1 that

if and only if σi ≤ σi′ for i = 1,…,p. This result in conjunction with Example 1.1 leads us to the following result for comparing two bivariate Normal distributions.
Let X and Y follow bivariate Normal distributions with dispersion matrices
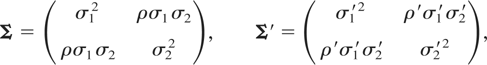
respectively. If 0 < σi ≤ σi′ for i = 1,2 and |ρ′| ≤ |ρ| < 1, then
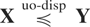
.
It will be interesting to find necessary and sufficient conditions under which two multivariate normal random vectors will be ordered according to upper orthant dispersive ordering in the general case.
It follows immediately that if two random vectors are ordered according to upper orthant dispersive ordering, then so are their corresponding subsets. In particular, their marginal distributions will be then ordered according to univariate dispersive ordering.
Theorem 2.2: Let X and Y be two n-dimensional random vectors such that

. Then

where I = {i1,i2,…,ik} ⊂ {1,2,…,n}, XI = (Xi1,…,Xik), YI = (Yi1,…,Yik), and k = 1,…,n.
The proof of the next result is also immediate.
Theorem 2.3: Let X1,…,Xm be a set of independent random vectors for which the dimension of Xi is ki, i = 1,…,m. Let Y1,…,Ym be another set of independent random variables for which the dimension of Yi is ki, i = 1,…,m. Then
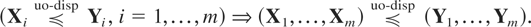
Remark 2.1: A consequence of (2.7) is that if X1,…,Xn is a collection of independent univariate random variables and Y1,…,Yn is another set of independent random variables, then Xi ≤disp Yi, i = 1,…,n implies
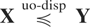
.
In general, there does not seem to be any direct connection between upper orthant dispersive ordering and the multivariate dispersive ordering as introduced by Fernandez-Ponce and Suarez-Llorens [7]. According to their definition, X ≤disp Y may not imply that Xi ≤disp Yi for i = 1,…,n. Also, the multivariate dispersive ordering as defined by them may not be preserved under permutations of the variables. On the other hand, the upper orthant dispersive ordering is invariant under the same permutation of the two vectors and their marginals are also ordered according to univariate dispersive ordering. Obviously, if

, then tr ΣX ≤ tr ΣY, where ΣX and ΣY denote the dispersion matrices of X and Y, respectively.
In this section, we will restrict our attention to the case in which the random vectors under consideration are nonnegative or, more generally, they have a finite common left end point of their supports. We will see that certain results hold in this case that may not hold in the general case. The following assumption will be made at some places in this article.
Assumption A: The random variables {Xi|∩j≠i{Xj > Fj−1(uj)}} and {Yi|∩j≠i{Yj > Gj−1(uj)}} have a finite common left endpoint of their supports for all u and for i = 1,…,n.
In the univariate case, for nonnegative random variables, there is an intimate connection between hazard rate ordering and dispersive ordering and which is made more explicit in the following result of Bagai and Kochar [1]. We use this theorem to prove some of the results of this section.
Theorem 3.1: Let X and Y be two univariate random variables with distribution functions F and G, respectively, such that F(0) = G(0) = 0. Then the following hold:
(a) If Y ≤hr X and either F or G is DFR (decreasing failure rate), then Y ≤disp X.
(b) If Y ≤disp X and either F or G is IFR (increasing failure rate), then Y ≤hr X.
For a bivariate random vector (S,T), we say that T is right tail increasing in S if P[T > t|S > s] is increasing in s for all t, and we denote this relationship by RTI(T |S). If S and T are continuous lifetimes, then T is right tail increasing in S if and only if r(s|T > t) ≤ r(s|T > 0) = rS(s) for all s > 0 and for each fixed t. The RTI property is weaker than the RCSI (right corner set increasing) property, but stronger than PQD (positive quadrant dependence). In the next theorem, we study the effect of positive dependence on upper orthant dispersive ordering for nonnegative random vectors.
Theorem 3.2: Let X = (X1,X2) be a bivariate random vector such that the left end point of the support of {Xi|Xj > Fj−1(u)} is finite and independent of u ∈ [0,1] for i,j = 1,2. Let XI = (X1I,X2I) be a random vector of independent random variables such that
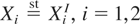
.
(a) If Xi is RTI in Xj, i ≠ j, and Xi is DFR for i,j = 1,2, then
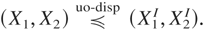
(b) If
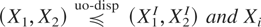
is IFR for i = 1,2, then Xi is RTI in Xj, i ≠ j, i,j = 1,2.
Proof:
(a) Note that RTI(Xi|Xj) if and only if, for all u ≥ 0,
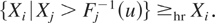
It follows from Theorem 3.1(a) that if, in addition, Xi is DFR, then
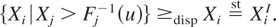
Since this holds for i,j = 1,2, the required result follows.
(b)

implies for all u ≥ 0,
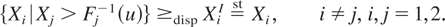
This together with the assumption that X1 and X2 are IFR implies (3.2) by Theorem 3.1(b). This proves that RTI(Xi|Xj), i ≠ j, i,j = 1,2. █
Theorem 3.3: Let X and Y be two n-dimensional random vectors satisfying Assumption A and such that

. Then

implies that
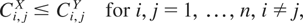
where Ci,jX (Ci,jY) denotes the copula of (Xi,Xj) ((Yi,Yj)).
Proof:
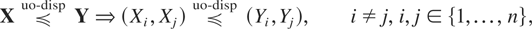
from which it follows that

and which, in turn, implies

under Assumption A since dispersive ordering implies stochastic ordering when the random variables have a finite common left end point of their supports. If we denote by Fi,j (Gi,j) the joint survival function of (Xi,Xj) ((Yi,Yj)), then (3.6) can be written as

where C(u,v) = 1 − u − v + C(u.v). █
If (3.4) holds and the margins of (Xi,Xj) and (Yi,Yj) are equal, then we say that (Yi,Yj) is more PQD than (Xi,Xj) (cf. [10, p.36]). Note that Ci,jX(ui,uj) ≡ uiuj in the case Xi and Xj are independent and Ci,jX(ui,uj) ≥ uiuj for all ui,uj ∈ [0,1] in the case Xi and Xj are PQD. Thus, according to Theorem 3.3, if Assumption A holds and if X and Y have the same margins and

, then the Yi's are more dependent than the Xi's according to PQD ordering. We obtain the following result as a special case.
Corollary 3.1: Let X = (X1,X2) be a bivariate random vector such that the left end point of the support of {Xi|Xj > Fj−1(u)} is finite and independent of u ∈ [0,1], for i ≠ j and i,j = 1,2. Let XI = (X1I,X2I) be a random vector of independent random variables such that

. Then
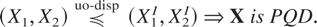
Contrast this result with Theorem 3.2(b), which is a stronger one since RTI implies PQD. However, here no assumption on the monotonicity of the hazard rates is made in the second case.
Remark 3.1: Assumption A is very crucial for Theorem 3.3 and Corollary 3.1 to hold. As a counterexample, let Y1 and Y2 be two independent U(0,1) random variables. Let X1 = X2 be uniformly distributed over (0,1) also. Note that X1 and X2 are strongly positively dependent, as they satisfy the Frechet upper bound. Let us compare (X1,X2) with (Y1,Y2) according to upper orthant dispersive ordering. The relevant conditional distributions to compare are

The left-hand conditional distribution is U(u,1) and the right-hand conditional distribution is U(0,1). Hence,
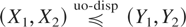
, but C1,2X ≥ C1,2Y, contradictory to (3.4). The reason for this contradiction is that unless Assumption A is satisfied, dispersive ordering may not imply stochastic ordering.
Theorem 3.4: Let X and Y be two n-dimensional random vectors satisfying Assumption A and such that

. Then

implies
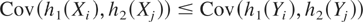
for all increasing convex functions h1 and h2 for which the above covariances exist.
Proof: Without loss of generality, let i = 1 and j = 2. The survival functions of (h1(X1),h2(X2)), h1(X1), and h2(X2) are, respectively, H(x1,x2) = F(h1−1(x1), h2−1(x2)), H1(x1) = F1(h1−1(x1)), and H2(x2) = F2(h2−1(x2)). Similarly, the survival functions of (h1(Y1),h2(Y2)), h1(Y1), and h2(Y2) are, respectively, K(x1,x2) = G(h1−1(x1),h2−1(x2)), K1(x1) = G1(h1−1(x1)), and K2(x2) = G2(h2−1(x2)). Covariance between h1(X1) and h2(X2), if it exists, can be expressed as

where h1−1(x1) = F1−1(u) and h2−1(x2) = F2−1(v). The assumption

implies that Xi ≤disp Yi, from which it follows that fi(Fi−1(u)) ≥ gi(Gi−1(u)) and Fi−1(u) ≤ Gi−1(u), i = 1,2, under Assumption A. Now hi′(x) is increasing in x since h(x) is convex. Combining these facts, the required result follows from (3.8). █
Theorem 3.5: Let X and Y be two n-dimensional random vectors satisfying the Assumption A and let φ1,…,φn be increasing convex functions on

. Then
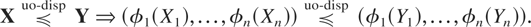
Proof: Note that the cdf of φj(Xj) is Fφj(x) = Fj(φj−1(x)), with its inverse as Fφj−1(u) = φj(Fj−1(u)). We have to prove that for i = 1,…,n, uj ∈ (0,1), j = 1,…,n, j ≠ i,
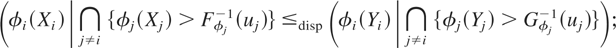
that is,

which is equivalent to
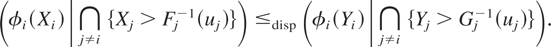
Using Assumption A, for i = 1,…,n, uj ∈ (0,1), j = 1,…,n, j ≠ i,

implies
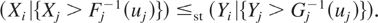
Now the required result follows from Theorem 2.2 of Rojo and He [18] since φi's are increasing convex functions. █
Hu et al. [9] gave the following definition of multivariate (weak) hazard rate ordering.
Definition 3.1: Let X and Y be n-dimensional random vectors with hazard gradients rX and rY, respectively. We say that X is smaller than Y according to weak hazard rate ordering (written as X ≤whr Y) if

for

; that is, if
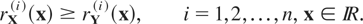
In the next theorem we establish results analogous to Theorem 3.1 between upper orthant dispersive ordering and multivariate weak hazard rate ordering under Assumption A.
Theorem 3.6: Let X and Y be two n-dimensional random vectors satisfying Assumption A.

Proof:
(a) Under Assumption A, Y ≤whr X implies that Yi ≤st Xi, i = 1,…,n, which is equivalent to Gi−1(u) ≤ Fi−1(u), for u ∈ [0,1], i = 1,…,n. Again, Y ≤whr X implies that for i = 1,…,n, (Yi|∩j≠i{Yj > xj}) ≤st (Xi|∩j≠i{Xj > xj}). Taking xj = Fj−1(uj), j = 1,…,n,j ≠ i, we find that this implies yi′(β;u) ≤ xi(β;u), where yi′(β;u) is the βth quantiles of the conditional distribution (Yi|∩j≠i{Yj > Fj−1(uj)}) and xi(β;u) is as defined earlier. On the other hand, rY(i)(x) decreasing in x implies that

for xj ≤ xj′, j = 1…,n, j ≠ i. This, along with Gi−1(ui) ≤ Fi−1(ui), implies that
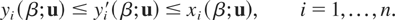
Using these observations, we obtain
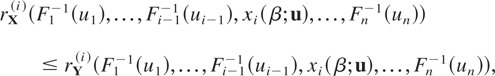
since Y ≤whr X. The right-hand side of this inequality is less than or equal to
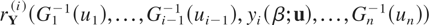
since rY(i)(x) is decreasing in x. This completes the proof of (a).
(b) From the assumption

, it follows that
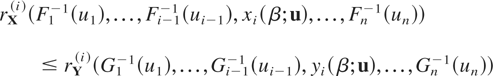
and

which implies that xi(β;u) ≥ yi(β;u) and Fj−1(uj) ≥ Gj−1(uj), j = 1,…,n, j ≠ i. Using these facts and the assumption that rY(i)(x) is increasing in x, it follows that, for i = 1,…,n, the right-hand side of (3.11) is less than or equal to
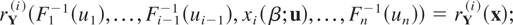
that is, we have shown that for i = 1,…,n,

and hence the required result. █
Remark 3.2: If rX(i)(x1,…,xi,…,xn) increases in xi for i = 1,…,n, then we say that the random vector X has a multivariate increasing hazard rate distribution (cf. Johnson and Kotz [11]). The condition rX(i)(x1,…,xi,…,xn) increasing in xj, j = 1,…,n, j ≠ i, i = 1,…,n describes a condition of positive dependence that is equivalent to saying that the random vector X has RCSI; that is,

increases in xi′, i = 1,…,n.
We will now study some preservation properties of the upper orthant dispersive order under random compositions. Such results are often referred to as preservations under “random mapping” (see Shaked and Wong [22]), or preservations of “stochastic convexity” (see Shaked and Shanthikumar [20, Chap.6] and Denuit, Lefèvre, and Utev [6], and references therein).
Let

be a family of n-dimensional survival functions, where

is a subset of the real line. Let X(θ) denote a random vector with survival function Fθ. For any random variable Θ with support in

and with distribution function H, let us denote by X(Θ) a random vector with survival function G given by

Theorem 3.7: Consider a family of n-dimensional survival functions
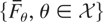
as above. Let Θ1 and Θ2 be two random variables with supports in

and distribution functions H1 and H2, respectively. Let Y1 and Y2 be two random vectors such that Yi =st X(Θi), i = 1,2; that is, suppose that the survival function of Yi is given by
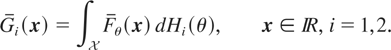
If
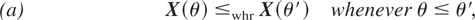
(b) Θ1 and Θ2 are ordered in the univariate hazard rate order; that is,
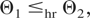
(c) rX(θ)(i)(x1,…,xn) is decreasing in xj, j = 1,…,n, i = 1,…,n,
then
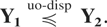
Proof: Hu et al. [9] proved that assumptions (a) and (b) imply that Y1 ≤whr Y2. Now, we show that for i = 1,…,n, rY1(i)(x1,…,xn) is decreasing in xj, j = 1,…,n, then the required result will follow from Theorem 3.6(a). Assumption (a) is equivalent to Fθ(x) being TP2 (recall from Karlin [12] that a function
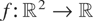
is said to be totally positive of order 2 (TP2) if f (x1,y1) f (x2,y2) ≥ f (x1,y2) f (x2,y1), for x2 ≥ x1 and y2 ≥ y1) in (θ,xj), j = 1,…,n. rX(θ)(i)(x1,…,xn) decreasing in xj, j = 1,…,n, j ≠ i is equivalent to Fθ(x1,…,xn) being TP2 in (xi,xj), i,j = 1,…,n, j ≠ i. Using these observations, it follows that G1(x) is TP2 in (xi,xj), i,j = 1,…,n (cf. Karlin [12]), which is equivalent to rY1(i)(x1,…,xn) decreasing in xj, j = 1,…,n, j ≠ i. It is worth noting that rX(θ)(i)(x1,…,xn) decreasing in xi is equivalent to the fact that {Xi|∩j≠i{Xj > xj}} is a DFR random variable, i = 1,…,n. Now, G1(x) can be written as

that is, (Y1,…,Yn) is a sort of mixture of DFR random variables; therefore, −∂ log Gj(x)/∂xi is decreasing in xi, which is equivalent to rY1(i)(x1,…,xn) decreasing in xi. This completes the proof. █
Example 4.1 (Multivariate Pareto Distributions): For a > 0, let Xa = (Xa,1,…,Xa,n) have the survival function Fa given by

see, for example, Kotz, Balakrishnan, and Johnson [14, p.600]. The corresponding density function is given by
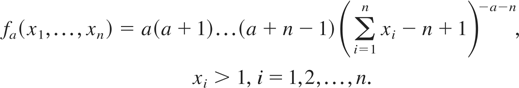
Hu et al. [9] showed that Xa1 ≤whr Xa2 whenever a1 ≥ a2. On the other hand,
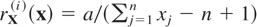
, is decreasing in xj, j = 1,…,n. Then from Theorem 3.6(a) it follows that
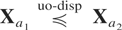
whenever a1 ≥ a2.
Example 4.2 (Bivariate Farlie–Gumbel–Morgenstern Distributions): For α ∈ (−1, 1), let Xα = (Xα,1,Xα,2) have the survival function Fα given by
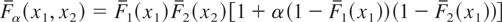
and Yα = (Yα,1,Yα,2) have the survival function Gα given by

where F1, F2, G1, and G2 are arbitrary univariate survival functions (which happen to be the marginal survival functions of Xα,1, Xα,2, Yα,1, and Yα,2, respectively, independently of α). Assume that Xα,i ≤disp Yα,i, i = 1,2. It is easy to see that CXα(u,v) = CYα(u,v). Then, from Theorem 2.1, it follows that
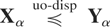
.
Example 4.3 (Multivariate Gumbel Exponential Distributions): For positive parameters λ = {λI : I ⊆ {1,2,…,n},I ≠ [empty ]}, let Xλ = (X1,X2,…,Xn) have the survival function Fλ given by

see Kotz et al. [14, p.406]. For another set of positive parameters λ* = {λI* : I ⊆ {1,2,…,n},I ≠ [empty ]}, let Yλ* = (Y1,Y2,…,Yn) have the survival function Gλ*. Let Xi =st Yi, i = 1,…,n; that is, λi = λi*. We show that if λ ≥ λ*, then for i = 1,…,n,
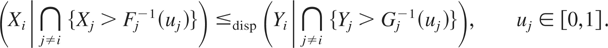
Since Xi =st Yi, i = 1,…,n, (4.1) is equivalent to
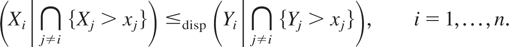
Let xi = (x1,…,xi−1,xi+1,…,n) . The survival function of (Xi|∩j≠i{Xj > xj}), denoted by Fi(xi;xi), is
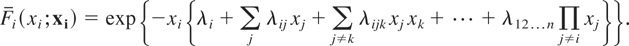
Similarly, the survival function of {Yi|Yj > xj, j ≠ i}, denoted by Gi(xi;xi), is

Now, the ratio
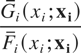
is increasing in xi; that is,
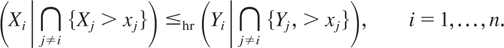
On the other hand, the random variable {Xi|Xj > xj, j ≠ i} has an exponential distribution that is DFR. Combining this observation with (4.6), it follows from Theorem 3.1(a) that (4.2) holds. Now, applying Theorem 3.3 to this example, we get that Ci,jλ is decreasing in λ, where Ci,jλ denotes the copula of (Xi,Xj)
Application 4.1 (Order Statistics): Let X1,…,Xn (Y1,…,Yn) be a random sample from a univariate distribution with strictly increasing distribution function F (G). Bartoszewicz [3] has shown that F ≤disp G implies Xi:n ≤disp Yi:n, i = 1,…,n, where Xi:n (Yi:n) is the ith-order statistic of the X sample (Y sample). We will strengthen this result to prove that F ≤disp G implies
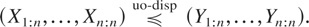
We first show that in the case of random samples from continuous distributions, the copulas of order statistics are independent of the parent distributions. Note that

. Since the function G−1F is strictly increasing, it follows from Theorem 2.4.3 of Nelsen [17] that C(Xi:n,Xj:n) = C(Yi:n,Yj:n), for i,j = 1,…,n. It now immediately follows from Theorem 2.1 that F ≤disp G implies (4.7).
Since the order statistics from a random sample are positively associated (cf. Boland, Hollander, Joag-Dev, and Kochar [4]) and since (X1:n,…,Xn:n) and (Y1:n,…,Yn:n) have the same copula, the conditions of Theorem 3.4 are satisfied. Hence, for i,j ∈ {1,…,n},

for all increasing convex functions h1 and h2 for which the above covariances exist. This result was originally proved by Bartoszewicz [2] using a different method. A similar result can be established for record values.
Application 4.2 (Record Values): Let X1,…,Xn,… (Y1,…,Yn,…) be a sequence of random variables from a univariate distribution F (G). It is known that F ≤disp G implies RmX ≤disp RmY, where RmX (RmY) is the mth record value of the X sequence (Y sequence). We first show that in the case of random sequences from continuous distributions, the copulas of record values are independent of the parent distributions. Then it will immediately follow from Theorem 2.1 that F ≤disp G implies
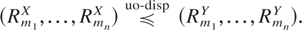
Let M(x) = −log F(x); then the distribution function of RmX can be expressed as FRmX(x) = Gm(M(x)), where Gm(x) is the distribution function of a Gamma random variable with scale parameter one and shape parameter m. Similarly, let N(x) = −log G(x); then the distribution function of RmY is FRmY(x) = Gm(N(x)). Now, both M(X1),…,M(Xn),… and N(Y1),…,N(Yn),… are sequences of independent and identically distributed (i.i.d.) exponential random variables with mean one. Using this observation, it follows that

where Rm* is the mth record value of a sequence of i.i.d. exponential random variables with mean one.

This proves the desired result.
Research by the first author was partially supported by the Statistical Research Center, Tehran, Iran. The authors are grateful to the referees for their helpful comments and suggestions, which have greatly improved the presentation of the article.