Introduction
The human cochlea is a small, spiral shaped structure with approximately two and a half turns.Reference Skinner, Ketten, Holden, Harding, Smith and Gates1 Typically, artificial cochlear implant insertion involves electrode placement in the inner ear, which exerts force upon the inner wall of the scala tympani, in both the basal turn and apex turn regions. The insertion force during an electrode placement is composed of forward pressure from the insertion, accompanying frictional forces, electrode recoil forces, and adhesion forces between the electrode and the inner cochlea.Reference Todd, Naghdy and Svehla2 The main factors influencing force during electrode implantation are surgical technique and electrode design.Reference Todd, Naghdy and Svehla2 Variations in these factors, in addition to natural variations in cochlear spiral length in the patient population, result in a range of possible electrode insertion forces. In practice, however, the applied force during electrode insertion is most heavily dependent on surgical technique and expertise, with a high risk of damage to the cochlea.Reference Zrunek and Burian3 In recent years, numerous protocols have been developed regarding electrode insertion force and contour path, in order to optimise electrode insertion and minimise damage to the cochlea.Reference Rebscher, Heilmann, Bruszewski, Talbot, Snyder and Merzenich4–Reference Xu, Briggs, Tykocinski, Newbold, Risi and Cowan8
Prior research has applied three-dimensional (3D) helicon-spiral modelling,Reference Yoo, Wang, Rubinstein and Vannier9 geometry modellingReference Vogel10 and finite element micromechanical modellingReference Kolston and Ashmore11 to approach and simulate human cochlear geometry, using the said mathematical models to describe the various parts of the cochlea in detail. Histological sectioning has been used to measure cochlear curvature, while liquid volume measurements have been used to assess cochlear volume.Reference Saito, Igarashi, Alford and Guilford12, Reference Xiang, Zhao, Xiao, Luo, Wei and Zhao13 The cochlear spiral has also been measured using orthogonal projection with computed tomography (CT) to reconstruct images of histological sections.Reference Manoussaki, Chadwick, Ketten, Arruda, Dimitriadis and O'Malley14 However, all the above experimental methods have been used on in vitro samples alone; none have included in vivo data.
The advancement of medical imaging techniques has led to the use of non-invasive modalities, CT and magnetic resonance imaging (MRI), for characterising anatomical geometry.Reference Purcell, Fischbein, Patel, Johnson and Lalwani15–Reference Chen, Chen, Chang, Huang, Su and Hsieh21 The development of 3D reconstruction technology has allowed two-dimensional images to be rendered into 3D volume images.Reference Morita, Kariya, Farajzadeh Deroee, Cureoglu, Nomiya and Nomiya22–Reference Migueis, Melo Freitas and Cordeiro24 These techniques have resulted in significant advances in inner-ear imaging.
The inherent nature of CT provides good in vivo delineation of bony anatomy in general, and the bony labyrinth in particular.Reference Tomandl, Hastreiter, Eberhardt, Rezk-Salama, Naraghi and Greess25 However, during cochlear implantation procedures, the electrode must pass the basal membrane of the membranous labyrinth, a soft tissue structure.Reference Kha, Chen and Clark26, Reference Hanekom27 Therefore, MRI is arguably the optimum imaging modality with which to visualise and measure inner-ear anatomy, including any deformities. Thus, some researchers have opted to use MRI for inner-ear imaging. The modality has been used to aid surgeons in their clinical evaluation of the inner ear.Reference Lane, Ward, Witte, Bernstein and Driscoll28 Another study used CT imaging to identify inner-ear deformities in patients with sensorineural hearing loss and investigate the deformities' role in hearing loss.Reference Chen, Gittleman, Barnes and Chang29 However, radiation is a concern when using CT imaging. Therefore, MRI could be an appropriate technology that enables reproducible findings in the measurement of the inner ear.
This study utilised MRI to non-invasively image the human bilateral cochlea in vivo. Image processing was used to obtain 3D volume images of right and left inner ears, and the bilateral cochlear spiral in particular. This was used to measure the length and curvature of each of the basal turn, middle turn and apex turn segments. These measurements provide an individual's geometry for pre-artificial cochlear implant assessment. The measurements can be used to plan the electrode insertion method and route, thus minimising potential damage by reducing the frictional, electrode recoil and adhesion forces during implantation.
Materials and methods
Cochlear imaging
A 3 T Magnetom Trio MRI scanner (Siemens, Erlangen, Germany) was used to acquire imaging data. The scanner produced images using a constructive interference in steady state (‘CISS’) gradient echo sequence, with a scanning repetition time and echo time of 5.65 ms and 2.6 ms respectively. Image data sets were comprised of 48 slices, with a pixel dimension of 0.5 mm × 0.5 mm × 0.5 mm.
Subjects
Eight human subjects (six male and two female) with no known inner-ear pathology were recruited. Four left inner ears and eight right inner ears were imaged.
The study was approved by the Institutional Review Board of Chang Gung Memorial Hospital (permit number: 99-1700B) and was conducted in accordance with the Declaration of Helsinki. Written informed consent was obtained from all subjects enrolled in the study.
Cochlear image processing
The length and curvature measurements will vary depending on the measurement location in the cochlear spiral. Thus, in order to standardise measurement, and obtain accurate and reproducible readings, the cochlear spiral volume image was manipulated and a fixed methodology was used to quantify the cochlear spiral length. The steps involved are described below.
The images of the inner ear were threshold-adjusted to segment the image data corresponding to the inner ear. The data were subsequently reconstructed and rendered to generate a 3D image representing the inner ear, as demonstrated in Figure 1.
Fig. 1 A reconstructed, rendered three-dimensional image of the inner ear demonstrating: the semicircular canal (‘a’), the ampullae (‘b’) and the cochlea (‘c’).
As electrode implantation requires insertion into the scala tympani, adjacent to the basal membrane of the membranous labyrinth, further image manipulation was required for this region.Reference Kha, Chen and Clark26, Reference Hanekom27 The basal membrane was delineated from the scala tympani on the MRI image slices by eye, generating a further 3D volume representing the scala tympani.
In order to show the cochlear spiral path, the cochlea was displayed as a semi-transparent volume, represented by the outlined scala tympani, as shown in Figure 2.
Fig. 2 A rendered three-dimensional, semi-transparent image of the cochlear spiral line (arrow).
The resulting spiral was then divided into three segments: the basal segment, the middle turn segment and the apex turn segment. Two of the segments were subdivided as follows: those in the basal turn segment were numbered sections 1–3 and those in the middle turn segment were numbered sections 4–6. The apex turn segment was left undivided and numbered section 7, as shown in Figure 3.
Fig. 3 Division of the cochlear spiral into base, middle and apex turn segments. The base and middle turn segments are subdivided into smaller segments. The segments are numbered thus: base turn segments (1–3), middle turn segment (4–6) and apex turn segment (7).
Cochlear curvature measurements
Following division of the spiral into segments, the 3D co-ordinates of the mid and end points in each spiral segment (Xw, Yw, Zw) were identified, as shown in Figure 4, where the index ‘w’ denotes the point under consideration. The set of points are non-coplanar. A series of transformations were performed to place all points in a target plane.
Fig. 4 Identification of the co-ordinates of the mid-point (‘a’) and end points (‘b’ and ‘c’) of each segment.
Firstly, using equation (1), (Xw, Yw, Zw) was transformed by (tx, ty, tz), to the new co-ordinates (X, Y, Z), holding the vector direction consistent. Note that ‘T’ is the transform function.
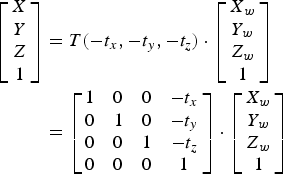$$\eqalign{\left[ {\matrix{ X \cr Y \cr Z \cr 1 \cr}} \right] & = T( - {t_x}, - {t_y}, - {t_z}) \cdot \left[ {\matrix{ {{X_w}} \cr {{Y_w}} \cr {{Z_w}} \cr 1 \cr}} \right] \cr & = \left[ {\matrix{ 1 & 0 & 0 & { - {t_x}} \cr 0 & 1 & 0 & { - {t_y}} \cr 0 & 0 & 1 & { - {t_z}} \cr 0 & 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ {{X_w}} \cr {{Y_w}} \cr {{Z_w}} \cr 1 \cr}} \right]} $$Secondly, the points were rotationally transformed θ degrees about the X, Y, and Z axes using equations (2), (3) and (4) respectively.
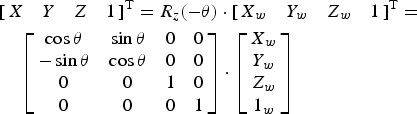$$\eqalign{& {\left[ {\matrix{ X & Y & Z & 1 \cr}} \right]^{\rm T}} = {R_z}( - \theta ) \cdot {\left[ {\matrix{ {{X_w}} & {{Y_w}} & {{Z_w}} & 1 \cr}} \right]^{\rm T}} = \cr & \quad \left[ {\matrix{ {\cos \theta} & {\sin \theta} & 0 & 0 \cr { - \sin \theta} & {\cos \theta} & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ {{X_w}} \cr {{Y_w}} \cr {{Z_w}} \cr {{1_w}} \cr}} \right]} $$
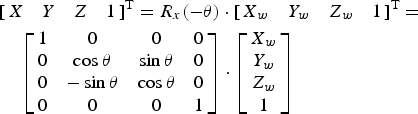$$\eqalign{& {\left[ {\matrix{ X & Y & Z & 1 \cr}} \right]^{\rm T}} = {R_x}( - \theta ) \cdot {\left[ {\matrix{ {{X_w}} & {{Y_w}} & {{Z_w}} & 1 \cr}} \right]^{\rm T}} = \cr & \quad \left[ {\matrix{ 1 & 0 & 0 & 0 \cr 0 & {\cos \theta} & {\sin \theta} & 0 \cr 0 & { - \sin \theta} & {\cos \theta} & 0 \cr 0 & 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ {{X_w}} \cr {{Y_w}} \cr {{Z_w}} \cr 1 \cr}} \right]} $$
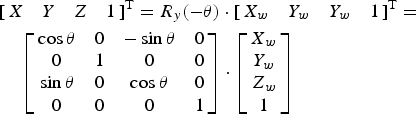$$\eqalign{& {\left[ {\matrix{ X & Y & Z & 1 \cr}} \right]^{\rm T}} = {R_y}( - \theta ) \cdot {\left[ {\matrix{ {{X_w}} & {{Y_w}} & {{Y_w}} & 1 \cr}} \right]^{\rm T}} = \cr & \quad \left[ {\matrix{ {\cos \theta} & 0 & { - \sin \theta} & 0 \cr 0 & 1 & 0 & 0 \cr {\sin \theta} & 0 & {\cos \theta} & 0 \cr 0 & 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ {{X_w}} \cr {{Y_w}} \cr {{Z_w}} \cr 1 \cr}} \right]} $$The resulting target plane is shown in Figure 5.
Fig. 5 Transformation of the non-coplanar mid-point (‘a’) and end point (‘b’ and ‘c’) co-ordinates into a target plane.
AutoCAD computer-aided design and drafting software (Autodesk, San Rafael, California, USA) was used to fit a curve between the three points in the target plane, the curvature of which was assumed to be the curvature of a given segment of the cochlea. AutoCAD was then used to measure the length and curvature radius, R, as shown in Figure 6. Curvature, ρ, is the inverse of curvature radius and was calculated using the formula ρ = 1 / R.
Fig. 6 The transformed target plane demonstrates mid-point (‘a’) and end points (‘b’ and ‘c’), using AutoCAD software to calculate the curvature radius ‘R’.
Results
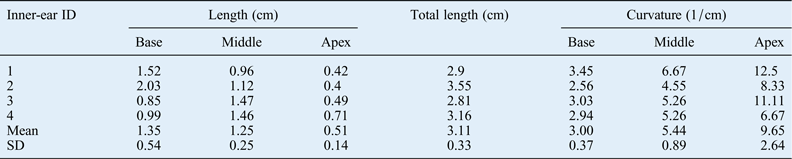
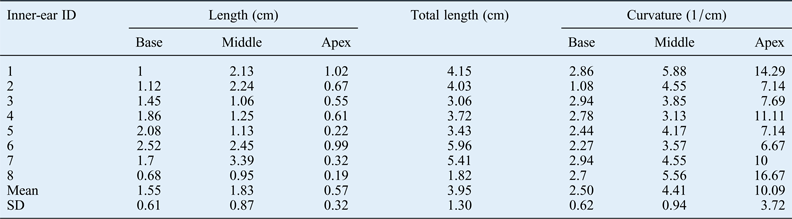
Measurements of segment length and total cochlear length are demonstrated in Table I for the left cochlea and Table II for the right cochlea. The mean total left ear cochlear length was 3.11 cm (range, 2.81–3.55 cm). The mean total right ear cochlear length was 3.95 cm (range, 1.82–5.96 cm). This is in line with data in the literature.Reference Yost30 For the left cochlea, the mean basal turn segment length was 1.35 cm (range, 0.85–2.03 cm), the mean middle turn segment length was 1.25 cm (range, 0.96–1.47 cm) and the mean apex turn segment length was 0.51 cm (range, 0.4–0.71 cm). For the right cochlea, the mean basal turn segment length was 1.55 cm (range, 0.68–2.52 cm), the mean middle turn segment was 1.83 cm (range, 0.95–3.39 cm), and the mean apex turn segment length was 0.57 cm (range, 0.19–1.02 cm).
Table I Length and curvature values for left base, middle and apex cochleae
ID = identification; SD = standard deviation
Table II Length and curvature values for right base, middle and apex cochleae
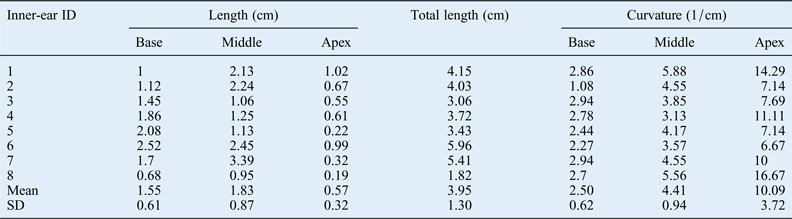
ID = identification; SD = standard deviation
In the left ear, the mean basal turn segment curvature was 3 cm−1 (range, 2.56–3.45 cm−1), the mean middle turn segment curvature was 5.44 cm−1 (range, 4.55– 6.67 cm−1) and the mean apex turn segment curvature was 9.65 cm−1 (range, 6.67–12.5 cm−1). In the right ear, the mean basal turn segment curvature was 2.5 cm−1 (range, 1.08–2.94 cm−1), the mean middle turn segment curvature range was 4.41 cm−1 (range, 3.13–5.88 cm−1) and the mean apex turn segment curvature was 10.09 cm−1 (range, 6.67–16.67 cm−1).
Discussion
During an artificial cochlear implant procedure, the surgeons often have no prior knowledge of a patient's cochlear spiral anatomy. Thus, the force applied during insertion is largely a function of the surgeon's clinical acumen and experience, resulting in a potentially high risk of damage to the patient's scala tympani, with an associated risk of implant failure.Reference Todd, Naghdy and Svehla2 If a patient's cochlear spiral curvature measurements are obtained prior to the implantation procedure using medical imaging, surgeons may plan the optimum insertion track prior to the procedure, minimising excess force during insertion and reducing the risk of injury.
Measurements of right and left ears are compared in Figure 7. The mean total cochlear length is longer in the right ears examined, as are each of the individual cochlear segments. However, this difference does not reach statistical significance. Overall, the apex turn segment of the cochlea had the greatest degree of curvature for bilateral cochleae, as seen in Figure 8 (p < 0.05). The cochlear curvature was found to be greater in the basal and middle turn segments in the left ear compared to the right, while the apex turn segment's curvature was greater in the right ear compared to the left (Figure 8). These data highlight the differences that can exist in cochlear length and curvature between left and right cochleae.
• This study quantified the geometric shape of the human inner-ear cochlea in vivo
• Specifically, raw magnetic resonance imaging data were reconstructed to generate a three-dimensional image of the cochlea
• A detailed description of the cochlear spiral is provided, using curvature and length measurements
• Right cochleae mean total length was greater than left cochleae mean total length
• The data provide a valuable reference for cochlear implantation procedure development, to minimise potential implantation damage
Fig. 7 Mean segment lengths and mean total lengths (with error bars) for the left and right cochleae.
Fig. 8 Mean segment curvature measurements (with error bars) for the left and right cochleae.
The data presented emphasise the need to describe each cochlea individually. It is hoped that the methodology described here will enable the provision of important anatomical information. Note that the head movement of subjects during the MRI scan will affect the imaging quality of the cochleae, which is a limitation of the present study. Furthermore, this methodology will allow pre-operative evaluation, and assessment of the electrode insertion technique and route, thus reducing the risk of damage to the cochlea. For bilateral cochleae, curvature changes can lead to excessive friction, pressure and adhesion forces in the apex turn segment during a cochlear implant procedure. The gradual increase in curvature, moving towards the apex turn segment, makes control of the electrode insertion position more difficult, highlighting the importance of an appreciation of cochlear length and curvature.
Conclusion
This study quantified the geometric shape of the human inner-ear cochlea in vivo, by reconstructing raw MRI data to generate a 3D image of the cochlea and its spirals. The spiral was separated into basal, middle and apex turn segments, and the lengths and curvatures of each section were measured. A comparison of left and right ears demonstrated that the right cochleae mean total length was greater than the left cochleae mean total length. Measurements showed greater curvature in the basal and middle turn segments of the left ear compared to the right ear, while the converse was true for the apex turn segment. On the basis of these results, in clinical terms, if bilateral artificial cochlear implants are required, each cochlea should be measured and assessed prior to surgery.
Pre-operative cochlear length and curvature measurements provide valuable information for surgeons, enabling them to evaluate the optimal electrode insertion method and route. This information increases insertion accuracy and reduces the risk of damage to the cochlea that may arise from excessive force. The data may also be used to improve and customise artificial cochlear design, such that the electrode adheres more closely to the basal membrane of the membranous labyrinth.
Acknowledgements
Support for this project was provided by Chang Gung Memorial Hospital (CMRPD190463). Facilities were provided by the Biomedical Engineering Center in Chang Gung University, Taiwan.
