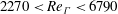1 Introduction
Studies of the vortex ring has been of great interest to researchers as it has a simple torus shape, propagates with a self-induced velocity for long distances retaining its shape and shows some spectacular instability patterns after which it breaks down into smaller vortical structures. Also, vortex rings can be generated easily by impulsively pushing a slug of fluid through a sharp edged orifice or a nozzle. These properties allow researchers to study the interaction of a free vortex structure with flow, with similar or different vortical structures and with objects of different shapes.
Historically, evidence of scientific studies on vortex rings exists since the early nineteenth century, although tobacco rings were well known before in artistic work. An interesting review on the early observations and studies of vortex rings can be obtained from the article of Velasco Fuentes (Reference Velasco Fuentes2014). Probably the first important early mathematical study on vorticity dynamics and the vortex ring was by the German physicist Helmholtz (Reference Helmholtz1858). In the same year Rogers (Reference Rogers1858) observed vortex rings experimentally and determined their motion to be similar to that obtained by Capocci (Reference Capocci1846). Dyson (Reference Dyson1893) first calculated the velocity potential of the vortex ring. Later, many theoretical formulations for the velocity potential of the induced flow field of the vortex ring were proposed. Most of the present knowledge and understanding of the generation, formation and evolution characteristics of vortex rings are well depicted in the reviews of Shariff & Leonard (Reference Shariff and Leonard1992), Lim & Nickels (Reference Lim, Nickels and Green1995) and Sullivan et al. (Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008). The understanding of the propagation mechanism of vortex rings revived with the introduction of the localised induction effect of a curved vortex filament on itself by Arms & Hama (Reference Arms and Hama1965). However, when the method is used for a circular line vortex, the propagation velocity is predicted to be infinite. This singularity was removed by Tung & Ting (Reference Tung and Ting1967) by asymptotic matching of the inner viscous core to the outer potential flow. Later, Saffman (Reference Saffman1970) and Pullin (Reference Pullin1979) derived expressions for the vortex ring trajectory, circulation and its diameter using similarity theory. An important study in this period is by Fraenkel (Reference Fraenkel1972) who used Hamilton’s equation to find the translational velocity of the vortex rings as the derivative of the energy with respect to impulse. Das et al. (Reference Das, Bansal and Manghnani2016) has shown that this model is best for predicting translational velocity when the experimental values of the core diameter and circulation are used and the data of Tung & Ting (Reference Tung and Ting1967) are close to these values only when the vortex ring is pinched off from the trailing jet. Fukumoto (Reference Fukumoto2010) gives a detailed overview of the growing knowledge of translational speed of an axisymmetric vortex ring, with focus on the influence of viscosity. Recently, Sullivan et al. (Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008) performed experiments on thin core vortex rings generated using a piston gun in water. They also gave empirical equations for the calculation of radius, core size, circulation and bubble dimension of the vortex ring. Based on the ratio of core radius (
$a$
) to vortex ring radius (
$R$
), (
$\unicode[STIX]{x1D6FD}=a/R$
) a vortex ring is termed as thin core (
$\unicode[STIX]{x1D6FD}<0.1$
) or thick core (
$\unicode[STIX]{x1D6FD}>0.1$
) (Fraenkel Reference Fraenkel1972).
The important parameters that characterize the free vortex ring are its diameter (
$D$
), circulation (
$\unicode[STIX]{x1D6E4}$
) and core radius (
$a$
). The dynamic behaviour is often understood from the self-induced translational velocity (
$U$
) which is a function of these parameters or alternatively can be written as function of its impulse (
$P$
) and energy (
$E$
). The basic characteristics are largely available as models and discussed in detail in earlier studies (Tung & Ting Reference Tung and Ting1967, Saffman Reference Saffman1970, Fraenkel Reference Fraenkel1972). The translational velocity observed in the experiments in earlier studies are always influenced by either the piston vortex, stopping vortex or orifice lip generated tiny vortices. This is because the most commonly used method of producing vortex rings in experiments is to eject a slug of fluid out of an orifice or nozzle by impulsively moving a piston (Maxworthy Reference Maxworthy1977, Didden Reference Didden1979, Blondeaux & De Bernardinis Reference Blondeaux and De Bernardinis1983, Auerbach Reference Auerbach1987, Irdmusa & Garris Reference Irdmusa and Garris1987, Glezer Reference Glezer1988, Glezer & Coles Reference Glezer and Coles1990, Auerbach Reference Auerbach1991, Lim & Nickels Reference Lim, Nickels and Green1995, Weigand & Gharib Reference Weigand and Gharib1997, Shusser & Gharib Reference Shusser and Gharib2000, Allen & Auvity Reference Allen and Auvity2002, Cater et al.
Reference Cater, Soria and Lim2004, Sullivan et al.
Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008). The properties of such experimentally produced vortex rings often depend on the generating apparatus. The differences found in the numerous experimental investigations and also between the experiments and theoretical predictions have been the subject of much research due to the presence of a stopping vortex and piston vortex. The effects of a stopping vortex and piston vortex are predominantly visible in the variation of the diameter of a vortex ring with time, which shows a dip after reaching its maximum value. This is an effect of the stopping vortex and piston vortex as explained by Maxworthy (Reference Maxworthy1977), Didden (Reference Didden1979), Pullin (Reference Pullin1979), Blondeaux & De Bernardinis (Reference Blondeaux and De Bernardinis1983), Auerbach (Reference Auerbach1987), Irdmusa & Garris (Reference Irdmusa and Garris1987), Glezer (Reference Glezer1988), Auerbach (Reference Auerbach1991), Weigand & Gharib (Reference Weigand and Gharib1997), Allen & Auvity (Reference Allen and Auvity2002) and Cater et al. (Reference Cater, Soria and Lim2004). Das et al. (Reference Das, Bansal and Manghnani2016) have developed a novel vortex ring generating apparatus that eliminates the effect of the piston vortex and stopping vortex. The same generating apparatus has been used in the present study.
Besides the study of a free vortex ring in an unbounded fluid, the research into vortex rings also encompasses the investigation of the interaction of this fundamental fluid dynamical structure with generic-shaped bodies. The apparent simple flow structure while propagating and interacting with different objects produces spectacular flow features. In interaction studies of incompressible vortex rings with objects or a wall, mostly the axis of the vortex ring intersects the wall surface and the interaction is either normal (Magarvey & MacLatchy Reference Magarvey and MacLatchy1964, Boldes & Ferreri Reference Boldes and Ferreri1973, Walker et al. Reference Walker, Smith, Cerra and Doligalski1987, Orlandi & Verzicco Reference Orlandi and Verzicco1993, Allen et al. Reference Allen, Jouanne and Shashikanth2007) or oblique (Lim Reference Lim1989, Kachman et al. Reference Kachman, Kshimoto, Bernal, Sahin, Tlyggvason and Schreyer1991, Scherer & Bernal Reference Scherer and Bernal1993) to the surface. The present study is different in this respect as the axis of the vortex ring is neither normal nor oblique to the surface with which it is interacting. Here, the vortex ring is coaxial with the cylinder while translating over it.
Amongst the normal interaction studies, the experiments of Magarvey & MacLatchy (Reference Magarvey and MacLatchy1964) and Boldes & Ferreri (Reference Boldes and Ferreri1973) are some of the earlier works where effects of interaction on the trajectory of the vortex ring are studied. The stretching and rebounding of the vortex ring were observed. Walker et al. (Reference Walker, Smith, Cerra and Doligalski1987) observed the separation of the induced boundary layer and formation of secondary and tertiary vortices similar to the observations of Peace & Riley (Reference Peace and Riley1983) who studied numerically the interaction of a two-dimensional vortex pair approaching a wall. Flow visualization experiments of Lim et al. (Reference Lim, Nickels and Chong1991) for normal interaction of a vortex ring with a wall and head-on collision of two identical vortex rings confirmed that the rebounding of the primary vortex ring from the wall is due to formation of the secondary vortex ring and not due to the distortion of the core, as conjectured earlier by Barker & Crow (Reference Barker and Crow1977). This phenomenon was also explained by Harvey & Perry (Reference Harvey and Perry1971) and Cerra & Smith (Reference Cerra and Smith1983). The stretching, rebounding and instability of the interacting vortex ring are also studied by Orlandi & Verzicco (Reference Orlandi and Verzicco1993), Riley & Stevens (Reference Riley and Stevens1993) and Chu et al. (Reference Chu, Wang and Chang1995).
Brasseur (Reference Brasseur1986) studied the propagation of a vortex ring in a tube due to its application in arterial stenoses. The inviscid analysis revealed that the outer streamlines of the vortex ring turn parallel to the wall, resulting in an increase in the amount of axial flow near the tube walls. The closed form integral solution for the velocity potential of such a flow configuration was also developed. Experiments were conducted over a wide range of Reynolds numbers to characterise the flow when vortex ring is placed axisymmetrically inside the tube. This is the only study that addresses the axial interaction of a vortex ring with a body where the axis of the vortex ring coincides with the axis of the interacting body. In all other interaction studies of incompressible vortex rings, the axis of vortex ring intersects the surface and the interaction is either normal or oblique to the surface.
Recently Lucey et al. (Reference Lucey, Gher, Cooper and Richter2003) devised methods for various applications of vortex rings such as, pumping fluid through a flexible tube and removal of surface deposits from a tube. They also used a vortex ring as a heat exchanger where heat is transferred from a heated tubular plate to the vortex ring that carries it to a heat sink. In their work, a vortex ring moves over a concentric rod which may be a flexible tube, rod with erodible surface or a heated rigid rod. In such situations, the impulsive vortical flow field is one of the major factors that determines the efficiency of these devices.
In this work an attempt is made to address the related problem of Brasseur (Reference Brasseur1986) where the vortex ring is passed over a cylinder axisymmetrically, as in the case of the above study of Lucey et al. (Reference Lucey, Gher, Cooper and Richter2003). In order to study the effect of such axial interaction, flow visualization and particle image velocimetry (PIV) experiments are carried out to evaluate the change in velocity of the interacting vortex ring in comparison with the free travelling vortex ring and then an analytical expression is derived which would predict the above observation theoretically.
Figure 1. Schematic of experimental set-up.
2 Experiments
Experiments are carried out to observe the motion of a vortex ring as it propagates over a cylinder. Flow visualization based measurements have been used to study the evolution of vortex ring diameter and translational velocity with time. These measurements are combined with PIV measurements to obtain the detailed flow field, circulation and core diameter. Circulation and core diameter obtained from PIV measurements are used as input in the theoretical analysis which is carried out later.
2.1 Experimental set-up
A schematic of the experimental set-up used for vortex ring generation is shown in figure 1. The experimental set-up consists of a large glass tank which is divided into two compartments: a driving section with a piston attached to one of its end and a test section. The piston is driven by a loudspeaker (100 W) and is used to push a slug of air volume through a circular nozzle, which is used to generate the vortex ring. The details of the nozzle and the set-up can be obtained from Das et al. (Reference Das, Bansal and Manghnani2016). The exit of the nozzle is chamfered while the other end is attached to a bell-mouth-shaped entrance for smooth entry of the flow. An opening at the top of the driving section is used before the experiments to introduce seeding particles into the compartment from a seed generator for the purpose of visualization and PIV measurements and closed during experiments.
For study of an interacting vortex ring, a cylindrical glass rod of diameter 6 mm is placed inside the test section as shown in figure 1. The cylinder is placed at a distance of approximately
$2D_{o}$
(
$D_{o}$
is the nozzle diameter) from the nozzle exit so that the vortex ring can be considered to be fully formed (Maxworthy Reference Maxworthy1977) before it starts interacting with the rod. The leading edge of the rod is conical shaped to minimize disturbance to the vortex ring streamlines as it approaches the rod. This arrangement allows smooth movement of the vortex ring over the rod.
An important feature of this set-up is the elimination of the stopping vortex and the piston vortex. The influence of the piston vortex, previously studied by Allen & Auvity (Reference Allen and Auvity2002) is avoided in this set-up by separating the piston from the nozzle, as shown in figure 1. As the piston is large, its required displacement is small to create a nearly impulsive momentum at nozzle exit that forms the vortex ring. The piston is also connected by a semi-flexible polythene sheet with the wall (to avoid leakage) which further avoids scrapping of the boundary layer from the wall and the formation of even a tiny piston vortex. The stopping vortex is avoided with a controlled motion of the piston. It is observed that if the piston is decelerated slowly, rather than impulsively or very rapidly, the stopping vortex is either not formed or very weak. It is noticed that if the impulse (defined as the integral of the square of piston velocity over time) associated with the deceleration time of the piston velocity is more than 15 % of the total impulse delivered by the piston, stopping vortex effects are avoided. Also, the length of the long nozzle is chosen such that the effect of the image vortex from the wall that separates the driver and driven compartments is negligible. Additionally, the long nozzle ensures that the slug of fluid that comes out and forms the vortex ring is from the front portion of it and does not have the disturbed fluid from the corner. The bell-mouth entry at the nozzle reduces other disturbances that may affect the vortex ring. More details can be obtained from Das et al. (Reference Das, Bansal and Manghnani2016). This ensured that the diameter and the corresponding velocity evolution of the vortex ring did not show a dip after reaching its maximum value, an effect of the stopping vortex as explained by Didden (Reference Didden1979), Maxworthy (Reference Maxworthy1977) and Weigand & Gharib (Reference Weigand and Gharib1997). Elimination of piston vortex and stopping vortex effects are essential to show the effect of the cylinder on the vortex ring motion in this study, as small changes in the vortex ring characteristics become important, as will be shown later.
For flow visualization, the vortex ring generated from the nozzle in the test section compartment is visualized using a continuous laser (1.2 W, 532 nm) and a high-speed camera of resolution
$1028\times 1296$
pixels with capacity to capture at 2000 frames per second (f.p.s.) at full resolution. The laser sheet is passed through a cylindrical lens to obtain the light sheet lying in the vertical plane passing through the cylinder’s axis. Due to refraction from the glass cylinder, only one half of the vertical plane is illuminated properly. Hence, images of only one half of the vortex ring are taken for the interacting cases.
The PIV technique has been used for measuring the velocity field of the vortex ring. For this, a double-pulsed Nd-YAG laser (
$300~\text{mJ}~\text{pulse}^{-1}$
, 10 Hz) is used for illuminating the flow field. The beam is delivered from laser head to the experimental zone by an articulated arm with a sheet forming optics at the end. The sheet forming optics consists of two spherical lenses and one cylindrical lens. The thickness of the sheet is approximately 1 mm. The light sheet lies in the vertical plane and passes through the cylinder’s axis. A 12-bit CCD camera of 4 MP resolution is used for capturing the images. The frame rate of the camera is 4 Hz in double-frame mode. The PIV acquisition system comprises of a synchronizer (NI PCI-6602 timer box), which synchronizes the laser and camera with reference to the wave front signal that is used to drive the piston.
Fog is used for seeding in all the experiments. The driving section is filled with fog prior to the start of the experiment. The diameter of the seeding particles is approximately
$1~\unicode[STIX]{x03BC}\text{m}$
. Density of the fluid used is
$1.353~\text{kg}~\text{m}^{-3}$
. In order to estimate how strictly the seed particles follow the flow and their response to high velocity gradients, particle Stokes number has been calculated. Stokes number (
$St_{k}$
), is defined as the ratio of the particle relaxation time (
$\unicode[STIX]{x1D70F}_{pr}$
) to the characteristic time scale of the flow (
$\unicode[STIX]{x1D70F}_{fs}$
). The particle relaxation time was given by Melling, Durst & Whitalaw (Reference Melling, Durst and Whitalaw1976) as:
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{pr}=\frac{\unicode[STIX]{x1D70C}_{pr}D_{pr}^{2}}{18\unicode[STIX]{x1D707}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}_{pr}$
is the particle density,
$D_{pr}$
is the diameter of the particle and
$\unicode[STIX]{x1D707}$
is the fluid viscosity. The flow time scale is given as:
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{fs}=\frac{L_{fs}}{U_{fs}},\end{eqnarray}$$
where
$L_{fs}$
is the characteristic length and
$U_{fs}$
is the characteristic velocity for the flow. The inner diameter of the nozzle is taken as
$L_{fs}$
and the slug flow velocity (average velocity at which flow comes out of the nozzle) is taken as
$U_{fs}$
.
Using this information, it is found that Stokes number is much smaller than unity (i.e.
$St_{k}\ll 1$
). For this condition, the tracing accuracy error of the particles is below 1 % (Tropea, Yarin & Foss Reference Tropea, Yarin and Foss2007).
Cylindrical coordinate system (
$\unicode[STIX]{x1D70C},z$
) has been used throughout as shown in figure 1. For piston motion, the origin is placed at the centre of the piston at its starting position. For vortex ring motion, the origin is at the centre of the nozzle exit.
2.2 Piston motion analysis
The piston is the driving unit for vortex ring generation. Some of the terminologies associated with its motion are as follows:
-
(i) stroke length (
$L_{p}$
): the distance moved by the piston after providing the signal; -
(ii) stroke time (
$T_{p}$
): the time taken by the piston to push the fluid out of the nozzle.
A trapezoidal signal with smooth corners is fed to the speaker from a signal generator. The signal’s peak-to-peak voltage range determines the stroke length (
$L_{p}$
), while the rise time of the signal is the stroke time (
$T_{p}$
). A typical trajectory of the piston and its corresponding velocity (
$V$
) versus time (
$t$
) graph is shown in figure 2. The displacement of the piston is tracked using a high-speed camera. A considerable amount of stopping time is ensured, so that the vortex ring formed will not be disturbed by the suction of air caused by the receding of the piston.
Figure 2. (a) Displacement–time graph and (b) velocity–time graph for piston motion.
Using the slug flow model given by Maxworthy (Reference Maxworthy1977), the slug length (
$L_{m}$
) (length of fluid pushed out of the nozzle to form the vortex ring) and slug velocity
$U_{m}$
(velocity at which fluid ejects out of the nozzle) are defined as:
$$\begin{eqnarray}\displaystyle & \displaystyle L_{m}=L_{p}\times \frac{A_{p}}{A_{o}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{m}=U_{p}\times \frac{A_{p}}{A_{o}}, & \displaystyle\end{eqnarray}$$
$A_{p}$
is the area of the piston which is taken to be same as cross-sectional area of the chamber and
$A_{o}$
is the cross-sectional area of the nozzle.
$U_{p}$
is the maximum velocity achieved by piston during its motion as is shown in figure 2. Using this, the jet Reynolds number based on the diameter of the nozzle (
$D_{o}$
) is defined as
$Re_{jet}=(U_{m}D_{o})/\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of air. The value of
$\unicode[STIX]{x1D708}$
is taken as
$1.511\times 10^{-5}$
for case 1 and case 4, while
$1.568\times 10^{-5}$
for case 2, case 3 and case 5.
In the present study, to determine the characteristics of free and interacting vortex rings for different jet Reynolds numbers,
$U_{m}$
is varied, whereas the exit diameter of the nozzle is kept constant. Table 1 shows the combinations of stroke length and stroke time that have been used in this study and their corresponding jet Reynolds numbers.
Table 1. List of all the cases for which experimental study was performed.
3 Experimental results
3.1 Flow visualization results
Flow visualization experiments are performed in two sets, first for a free vortex ring (without the interacting cylinder) and second for an interacting vortex ring (with a cylinder of diameter 6 mm). Flow visualization images are taken at 200 f.p.s. For each of the cases the following data are obtained for the vortex ring:
-
(i)
$x(t)$
, the distance travelled from the nozzle exit with time, i.e. the trajectory; -
(ii)
$D(t)$
, the diameter of the vortex ring obtained by noting the radial position of the core centre in a diametrical plane with time.
3.1.1 Evolution of free vortex ring
Dynamic evolution of the free vortex rings are discussed first, as the changes in the characteristics of these vortex rings are noted, while they are interacting axially with the cylinder in later sections. The evolution process from the detachment of the vortex ring from the nozzle exit to its propagation along the axial direction as observed during flow visualization have been shown for two representative cases, case 1 and case 5 in figures 3 and 4 respectively. The effect of stroke time and slug velocity or
$Re_{jet}$
is clearly visible between these two figures.
$T_{p}$
and
$Re_{jet}$
being small for case 1 (figure 3), the trailing jet is weak and no shear layer vortex is observed. While for case 5, both
$T_{p}$
and
$U_{m}$
are large resulting a stronger trailing jet with shear layer vortices. In the present experiments, in interacting cases the cylindrical rod is placed at a distance
$2D_{o}$
and hence, interact only when the vortex ring is fully formed (Maxworthy Reference Maxworthy1977) but not pinched off from the jet and no shear layer vortex ring is present in close proximity of the primary vortex ring.
Figure 3. Evolution of free vortex ring for case 1.
Figure 4. Evolution of free vortex ring for case 5.
The translational velocity of the free vortex ring,
$U_{f}$
is calculated from the axial position by using a 5 point central differencing scheme. Figure 5 shows the variation of diameter (
$D_{f}$
) and translational velocity (
$U_{f}$
) of the free vortex ring with time for all the cases. Note that the diameter variation does not show the dip in its value after reaching its maximum value, which is the effect of elimination of piston vortex and stopping vortex. For non-dimensional values, nozzle diameter (
$D_{o}$
) is used as length scale and slug flow velocity (
$U_{m}$
) is used for velocity scale. Therefore, non-dimensional time is defined as
$t^{\ast }=t(D_{o}/U_{m})$
.
Figure 5. Variations of (a) diameter and (b) translational velocity with time for free vortex ring (all quantities are non-dimensional).
Figure 6. Evolution of interacting vortex ring for case 1.
For all the cases, it can be seen that the vortex ring diameter and velocity increase gradually with time before reaching nearly constant values. It is at this state the vortex ring interacts with the cylindrical rod. It is also observed that at this state
$D_{f}$
and
$U_{f}$
increase with
$Re_{jet}$
. However, the initial state of development depends on the time history of the piston motion. With respect to the diameters of cases 2, 3 and 5, although their magnitudes are very close to each other, they also follow this trend.
Figure 7. Evolution of interacting vortex ring for case 5.
Figure 8. Variations of (a) diameter and (b) translational velocity with time for interacting vortex ring (all quantities are non-dimensional).
3.1.2 Evolution of interacting vortex ring
Flow visualization for the interacting vortex ring is carried out to observe the effect of the cylindrical rod as well as the induced axisymmetric boundary layer formed over the surface of the cylinder on the vortex ring diameter (
$D_{int}$
) and translational velocity (
$U_{int}$
). The motion of the vortex ring over the cylinder as obtained from flow visualization experiments is shown in figures 6 and 7 for cases 1 and 5 respectively. It can be observed from figure 6 at
$t^{\ast }=9.8$
that the vortex ring smoothly passes over the cylinder and induces a boundary layer. The boundary layer is subjected to favourable pressure gradient upstream of the vortex plane (plane passing through vortex core centre and perpendicular to the axial direction) and adverse pressure gradient downstream of it. As the vortex ring moves over the cylinder, the boundary layer separates from the surface in the adverse pressure gradient zone (see figure 6 at
$t^{\ast }=15.63$
). The separated boundary layer forms a secondary vortex ring which gets convected into the wake after encircling the primary vortex ring. This convection occurs due to the induced velocity field of the primary–secondary vortex ring interaction. Depending on the strength (Reynolds number) of the vortex ring, the secondary ring can merge with the primary ring, convect in the wake region or form a mushroom-like structure in cross-sectional view and lift off (as shown in figure 6 at
$t^{\ast }=18.14$
). However, the focus of the present study is on the motion of the vortex ring prior to the separation of the induced boundary layer. The evolution history of the vortex ring diameters and translational velocities with time for interaction cases are shown in figure 8.
The evolution of the interacting vortex ring diameter is seen to be similar to that for the free vortex ring up to a certain distance. After that a gradual increase in the diameter of the interacting vortex ring is observed as the boundary layer starts to separate from the surface of the cylinder. The effect of boundary layer separation can also be seen in the form of a decrease in the velocity of propagation of the vortex ring. The diameter and velocity of the vortex ring increase with an increase in Reynolds number for the interacting vortex ring as well.
It can be seen in the visualization images that the trailing jet is connected with the vortex ring for a long distance/time. However, it is appropriate to have the vortex ring free from the trailing jet while interacting. In reality, the visualization images do not portray the proper picture as smoke traces do not indicate the actual velocity and vorticity fields. Actual velocity and vorticity fields (obtained from PIV) presented in § 3.2 rather show that the vortex ring is detached at a much earlier time than what is observed in flow visualization. Thus, one has to be careful while using flow visualization alone to determine the detachment time.
3.2 PIV results
To find the details of the flow field and the properties of the core of the vortex ring, PIV measurements are carried out. PIV images show the velocity vectors (
$v_{z}$
and
$v_{\unicode[STIX]{x1D70C}}$
) in the laboratory frame of reference. Figures 9 and 10 depict the vorticity contours for the free vortex rings for cases 1 and 5 respectively, whereas figures 11 and 12 show the vorticity contours for the same cases respectively, when the vortex ring is interacting with the cylinder.
$Z\text{-Vorticity}$
is the azimuthal component of vorticity calculated from the measured velocity field and non-dimensional vorticity is defined as
$Z\text{-Vorticity}\_\text{nd}=Z\text{-Vorticity}(D_{o}/U_{m})$
. Data for interacting cases are taken from a distance such that the fluid velocities in the induced boundary layer are measured with sufficient spatial accuracy. In theoretical estimation of translational velocity, the value of circulation within the boundary layer, obtained from velocity data, is used. It is important to note that the exact time of detachment of the vortex ring from the trailing jet can be obtained from PIV data and is different from that observed in flow visualization.
Figure 9. Vorticity field of free vortex ring for case 1.
Figure 10. Vorticity field of free vortex ring for case 5.
Figure 11. Vorticity field of interacting vortex ring for case 1.
Figure 12. Vorticity field of interacting vortex ring for case 5.
In figure 11, because of the lower
$Re$
, the separation of the boundary layer is observed within the visualized area whereas in figure 12, due to higher
$Re$
, the boundary layer remains attached for a longer distance. An important phenomenon that can be observed, particularly for high
$Re$
cases, is that the fluid layer containing trailing jet shear layer vorticity gets entrained into the primary vortex ring as the vortex ring approaches the cylinder and moves axisymmetrically over it (see figure 12 at
$t^{\ast }=15.71$
and
$t^{\ast }=17.46$
).
3.2.1 Flow field – circulation
The experimental value for core circulation of the vortex ring is obtained from the PIV data. To calculate the circulation values, the velocity vector is line integrated along the unit tangent of a polygonal path as shown in figure 13(a). The circulation value initially increases with time until the vortex ring gets fully formed and then it stabilizes at a certain value. In this study, the time variation of the circulation is not important as the vortex ring interacts in a fully formed state. Details of the variations of
$\unicode[STIX]{x1D6E4}$
with time can be obtained from Das et al. (Reference Das, Bansal and Manghnani2016) for different Reynolds numbers for a free travelling vortex ring. Table 2 shows the steady state circulation values obtained for both free and interacting vortex rings and also
$Re_{\unicode[STIX]{x1D6E4}}$
(
$Re_{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708}$
) of the free vortex ring for all 5 cases. Non-dimensional circulation (
$\unicode[STIX]{x1D6E4}_{n}$
) is obtained by dividing
$\unicode[STIX]{x1D6E4}$
by
$U_{m}\,D_{o}$
. It is observed in table 2 that there is an increase in circulation for all the interacting cases in comparison to the fully formed free vortex ring circulation. The reason for this is discussed in § 3.3. The maximum error in the measurement of circulation is 2.3 % (see table 2 for individual standard deviations in non-dimensional circulation values).
Figure 13. Contour for calculation of (a) core circulation and (b) core diameter.
Table 2. Core circulation for free and interacting vortex rings for all cases.
3.2.2 Core structure – core diameter
For a vortex ring, vorticity is mostly concentrated inside the core region and defining the core appropriately is crucial for using the existing formulas of translational velocities. The core is usually defined as the distance between the peaks in the velocity profile (in the laboratory frame of reference) across the core centreline which contains nearly 90 % of the vorticity containing fluid (Maxworthy Reference Maxworthy1977, Weigand & Gharib Reference Weigand and Gharib1997, Arakeri et al.
Reference Arakeri, Das, Krothapalli and Lourenco2004 and Das et al.
Reference Das, Bansal and Manghnani2016). The velocity profile passing through the core centre along two axes, one perpendicular to the axis (vertical) and the other parallel to the axis (horizontal) (see figure 13
b) is used to determine the core diameter. The corresponding velocity profiles for free and interacting vortex rings for case 1 are shown in figures 14 and 15 respectively. For other cases, the nature of the velocity profiles remain the same, only the values are different. To calculate the core diameter from the velocity profile plots, distance between the peak values of velocities (Maxworthy Reference Maxworthy1977) is considered. Other definitions of core diameter are discussed in detail in Das et al. (Reference Das, Bansal and Manghnani2016) and it is shown that the above mentioned definition includes nearly 90 % of maximum vorticity (note the vorticity distribution is nearly Gaussian) in the core. Accordingly, the core diameters are specified in table 3. Non-dimensional core diameter (
$2a_{n}$
) is obtained by dividing the dimensional value with the length scale
$D_{o}$
. Comparing the corresponding estimates of the core diameter along the two profiles for all the cases suggests that the core is not exactly circular, as has been observed in many of the previous investigations. It has more of an elliptical shape with the horizontal diameter (profile 1) slightly larger than the vertical diameter (profile 2). However, for simplification, the core is assumed to be circular and hence the average of the two values along both the profiles is taken. Also, it is observed that the core diameter in the interacting cases is larger in comparison to that of a free vortex ring. The maximum error in the measurement of core diameter is 6.5 % (see table 3 for individual standard deviations in non-dimensional core diameter values).
Figure 14. Plots for (a)
$v_{\unicode[STIX]{x1D70C}}/U_{m}$
versus
$z/D_{o}$
(profile 1) and (b)
$v_{z}/U_{m}$
versus
$\unicode[STIX]{x1D70C}/D_{o}$
(profile 2) for free vortex ring case 1.
Figure 15. Plots for (a)
$v_{\unicode[STIX]{x1D70C}}/U_{m}$
versus
$z/D_{o}$
(profile 1) and (b)
$v_{z}/U_{m}$
versus
$\unicode[STIX]{x1D70C}/D_{o}$
(profile 2) for interacting vortex ring case 1.
Table 3. Core diameter of free and interacting vortex rings for all cases.
3.3 Comparison between free and interacting vortex ring
In this section, a comparison of velocity (
$U$
) and ring diameters (
$D$
) of free and interacting vortex rings have been shown for the same cases. As discussed before, after a certain time the values of
$D$
and
$U$
reach a steady state condition. It is observed that, both
$D$
and
$U$
(see figures 16 and 17) change due to the presence of the cylinder. From figure 16, it is observed that for cases 1 and 2,
$D_{int}<D_{f}$
, for cases 3 and 4,
$D_{int}\approx D_{f}$
and for case 5,
$D_{int}>D_{f}$
. However, the presence of the cylinder increases the velocity for all the cases (see figure 17). The change in velocity is small for cases 1 and 3 compared to the other three cases. These observations are explained by consideration of the displacement effect and the acceleration effect, discussed next.
Figure 16. Comparisons between diameters of free and interacting vortex ring for (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
Figure 17. Comparisons between translational velocity of free and interacting vortex ring for (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
3.3.1 Displacement effect
In an interacting case, the presence of the cylinder and viscous boundary layer over it displace the streamlines by a certain amount in radial direction compared to the streamline of the free travelling vortex ring. Thereby, it is expected that the diameter of the vortex ring will increase due to interaction. The displacement thickness (
$\unicode[STIX]{x1D6FF}^{\ast }$
) is expected to be a direct function of stroke time. This argument has been verified from the detailed experimental study of the development of the boundary layer due to the axial interaction of a vortex ring with a cylinder carried out by Sohoni (Reference Sohoni2013). Figure 18 shows a comparison between
$\unicode[STIX]{x1D6FF}^{\ast }$
for the two cases with different stroke times and hence
$Re_{\unicode[STIX]{x1D6E4}}$
(
$T_{p}=410~\text{ms}$
,
$Re_{\unicode[STIX]{x1D6E4}}=5903$
and
$T_{p}=430~\text{ms}$
,
$Re_{\unicode[STIX]{x1D6E4}}=8114$
respectively). This has been shown for
$t=90~\text{ms}$
(figure 18
a) and
$t=130~\text{ms}$
(figure 18
b), where
$t=0$
is the time at which the vortex ring reaches the cylinder and
$z=0$
is the tip of the cylinder. It can be observed that the displacement of the streamlines is larger for the case with a larger stroke time.
Figure 18. Comparison of displacement thickness over the cylinder (
$z=0$
is tip of the cylinder) for different stroke times (
$T_{p}=410~\text{ms}$
,
$Re_{\unicode[STIX]{x1D6E4}}=5903$
and
$T_{p}=430~\text{ms}$
,
$Re_{\unicode[STIX]{x1D6E4}}=8114$
) (a)
$t=90~\text{ms}$
and (b)
$t=130~\text{ms}$
.
3.3.2 Acceleration effect
Along with the displacement effect there is an opposite effect that decreases the vortex ring diameter. This effect is due to the fluid acceleration between the vortex core and the cylinder which reduces the pressure in this region. The fluid acceleration should occur to maintain the same mass flow rate of the induced velocity field between the cylinder and vortex core. This can be considered as the effect of the blockage due to the cylinder also. To show this effect, a comparison of flow velocity between a free and interacting vortex ring for the same case when the vortex ring is at the same location (see figure 19) is performed. A comparison between velocity profiles taken at
$z/D_{o}=2.03$
(figure 19) for case 4 is shown in figure 20. It can be observed that the velocity in the interacting case is more than the velocity in the free case due to the acceleration of flow in this region.
Figure 19. Contour along which velocity profile is compared between the free and interacting case for case 4.
Figure 20. Comparison of velocity profile between free and interacting vortex ring for case 4 (
$Re_{\unicode[STIX]{x1D6E4}}=6790,T_{P}=240~\text{ms}$
).
The net result is a combination of the displacement and acceleration effects and depending upon which effect dominates, the diameter may increase or decrease. The boundary layer thickness is expected to be proportional to the square root of the stroke time which implies that the displacement effect is highest for case 5 and is more dominant, thereby leading to an increase in the ring diameter. Cases 1 and 2 have smaller stroke times and smaller translational velocities, hence the acceleration effect plays a more defining role causing a decrease in ring diameter, as can be seen in figure 16. For cases 3 and 4, the acceleration effect is equally strong as the displacement effect and hence not much change in vortex ring diameter is observed. Note, if
$\unicode[STIX]{x1D6E4}$
remains same, the translational velocity should be increasing as the diameter decreases and vice versa. However, the translational velocity is increasing for all the cases.
Also, from the PIV results in § 3.2, it has been noticed that the circulation and core diameter values of the interacting vortex ring are slightly more than those of the free vortex ring. This is explained by the acceleration effect, as a result of which a part of the shear layer gets entrained within the primary vortex ring (see figure 19) which in turn leads to an increase in the core diameter. This entrained shear layer fluid adds some circulation to the primary ring circulation and hence the net value of
$\unicode[STIX]{x1D6E4}$
for the interacting vortex ring is larger. This phenomenon is very clearly seen in figure 12 at
$t^{\ast }=12.22$
. However for a non-interacting vortex ring under the same case, (see figure 10) the particles in the shear layer are separated from the primary ring (pinching off) in the same location where the cylinder (
$z/D_{o}=2.03$
) is placed.
The change in the translational velocity of the primary vortex ring may be occurring either due to the inviscid interactions or due to the viscous boundary layer formed over the cylinder. To find out which factor plays a more substantial role, a theoretical analysis has been performed in § 4.
3.3.3 Uncertainty check
The increase in the values of the velocity for the interacting vortex ring that has been observed are small and could also be attributed to chance or uncertainty. To eliminate this possibility, a test of hypothesis was performed using two sample unpaired
$t$
tests (Rice Reference Rice2006) for all 5 cases. The samples of velocity comprised of points only from the steady state condition. The null hypothesis (
$H_{o}$
) was that there is no significant change in the velocity of the vortex ring due to the presence of the cylinder and the variation is due to chance. The alternate hypothesis (
$H_{1}$
) being that the velocity of the interacting vortex ring is more than that of the free vortex ring in a steady state condition. The test was performed for a 95 % confidence level, which is standard practice. The results obtained are shown in table 4.
Table 4. Test of hypothesis using two sample
$t$
tests (all values are non-dimensional).
Since the
$p$
values (probability of observing a sample statistic as extreme as the test statistic) for all the cases is less than 5 %, the the null hypothesis (
$H_{o}$
) is rejected and it can be confidently said that the increase in velocity is due to an assignable cause and not a chance variation.
4 Inviscid analysis
In this section, an analytical solution for the flow of a vortex ring of strength
$\unicode[STIX]{x1D6E4}$
and radius
$R$
over an infinite, stationary, rigid, circular cylinder of radius
$R_{c}$
is obtained. The flow is considered to be inviscid and incompressible. The self-induced velocity of the vortex ring is affected due to the presence of the cylinder. To study the effect of axial interactions, the classical model of a vortex ring is used. Due to axisymmetry, a cylindrical polar coordinate system (
$\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703},z$
) with origin located at the centre of the circular filament is used. The choice of origin has been taken to be such that at any instant of time
$t$
, the vortex filament is located in the
$z=0$
plane (refer figure 21). The vortex ring and the frame of reference are moving in
$+z$
direction with a speed
$U$
.
In classical theory, the vortex ring is assumed to be a circular line vortex of zero cross-section. The analytical formulation of streamfunction
$\unicode[STIX]{x1D6F9}$
of a circular vortex filament given by Lamb (Reference Lamb1945) and Maxworthy (Reference Maxworthy1977) is as follows:
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}=-\frac{\unicode[STIX]{x1D6E4}}{2\unicode[STIX]{x03C0}}(r_{1}+r_{2})[K(\unicode[STIX]{x1D706})-E(\unicode[STIX]{x1D706})],\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}=(r_{2}-r_{1})/(r_{2}+r_{1})$
;
$r_{1}$
,
$r_{2}$
are the shortest and the longest distance from a point to the vortex ring, as shown in figure 22, and
$K(\unicode[STIX]{x1D706})$
and
$E(\unicode[STIX]{x1D706})$
are complete elliptic integrals of the first and second kind respectively.
In the vicinity of the core of the vortex (
$s/R\ll 1$
), the modulus of the elliptic integrals tends to 1 (i.e.
$\unicode[STIX]{x1D706}\rightarrow 1$
). Hence the elliptic integrals can be replaced with the asymptotic forms given in Dwight (Reference Dwight1961) and Gradshteyn & Ryzhik (Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger1965), which leads to the following equation for the streamfunction:
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}=-\frac{\unicode[STIX]{x1D6E4}R}{2\unicode[STIX]{x03C0}}\left[\ln \left(\frac{8R}{s}\right)+\left(\frac{s\cos (\unicode[STIX]{x1D6FC})}{2R}\right)\left(\ln \left(\frac{8R}{s}\right)-1\right)\right].\end{eqnarray}$$
The streamfunction is expressed in terms of polar coordinates (
$s,\unicode[STIX]{x1D6FC}$
) with the origin at centre of vortex core. However, far away from the core, the modulus of the elliptic integrals tends to 0 (i.e.
$\unicode[STIX]{x1D706}\rightarrow 0$
) and the following polynomial series expansions for the elliptic integrals can be used:
$$\begin{eqnarray}\displaystyle & \displaystyle K(\unicode[STIX]{x1D706})=\frac{\unicode[STIX]{x03C0}}{2}\left[1+\frac{\unicode[STIX]{x1D706}^{2}}{4}+\frac{9\unicode[STIX]{x1D706}^{4}}{64}+\frac{25\unicode[STIX]{x1D706}^{6}}{256}+\cdots \!\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E(\unicode[STIX]{x1D706})=\frac{\unicode[STIX]{x03C0}}{2}\left[1-\frac{\unicode[STIX]{x1D706}^{2}}{4}\left(1+\frac{3\unicode[STIX]{x1D706}^{2}}{16}+\frac{5\unicode[STIX]{x1D706}^{4}}{64}\right)+\cdots \!\right]. & \displaystyle\end{eqnarray}$$
Therefore, using (4.3) and (4.4), the expression for
$\unicode[STIX]{x1D6F9}$
outside the core region can be written as:
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}=\frac{\unicode[STIX]{x1D6E4}}{4}(r_{1}+r_{2})\left[\frac{\unicode[STIX]{x1D706}^{2}}{2}+\frac{3\unicode[STIX]{x1D706}^{4}}{16}+\frac{15\unicode[STIX]{x1D706}^{6}}{128}+\cdots \!\right].\end{eqnarray}$$
The inviscid interaction between the vortex ring and cylinder is modelled using the method of images. The flow field caused by the vortex ring moving over a cylinder (referred to as the combined flow field) in an inviscid medium can be thought of as the combination of the flow field produced by a lone vortex ring (referred to as the primary vortex ring) and that of a complementing flow structure (referred to as the image vortex ring) simulating the effect of the cylinder. A perturbation parameter,
$\unicode[STIX]{x1D716}$
(the ratio of two length scales) is defined as follows:
$$\begin{eqnarray}\unicode[STIX]{x1D716}=\frac{R_{c}}{R}.\end{eqnarray}$$
Figure 21. Schematic of vortex ring over a cylinder in cylindrical coordinates.
Figure 22. A circular vortex ring with zero cross-section.
An image vortex ring of strength
$-\unicode[STIX]{x1D6E4}^{\ast }$
is considered with its core centre located at the inverse point (Saffman Reference Saffman1992). The inverse point for a cylinder of radius
$R_{c}$
and a vortex ring having radius
$R$
is given by:
$$\begin{eqnarray}R_{inv}=\frac{R_{c}^{2}}{R}=\unicode[STIX]{x1D716}R_{c}.\end{eqnarray}$$
Therefore, the radius of the image vortex ring is
$R_{i}=R_{inv}$
.
The radius of the cylinder is 3 mm and the radius of the primary vortex ring as obtained experimentally from flow visualization is in the range of 35 to 45 mm. The core radius of the vortex ring as obtained from the PIV experiments is in the range of 10 to 15 mm. Therefore, the surface of the cylinder is located significantly far away from the core of the vortex ring. Hence, the formulation of the streamfunction given in (4.5) is valid near to the cylinder’s surface. Similarly, for the image vortex ring, the core is located at a distance of the order of 0.1 mm (using
$R\sim 40~\text{mm}$
) from centreline, while the cylinder surface is at a distance 3 mm from the centreline. Hence the flow field due to image vortex ring on cylinder surface will also be governed by (4.5).
The circulation
$\unicode[STIX]{x1D6E4}^{\ast }$
of the image vortex ring is taken with a negative sign because it is opposite to that of the primary ring. The induced effect of the image ring will lead to an increase in velocity of the primary ring. The value of
$\unicode[STIX]{x1D6E4}^{\ast }$
is calculated using the zero normal velocity boundary condition at the surface of the cylinder. The normal velocity (
$U_{n}$
) of the flow at any point is:
$$\begin{eqnarray}U_{n}(\unicode[STIX]{x1D70C},z)=-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}z}.\end{eqnarray}$$
Using
$r_{1}\,=\,\sqrt{\!(\unicode[STIX]{x1D70C}-R)^{2}+z^{2}}$
and
$r_{2}\,=\,\sqrt{\!(\unicode[STIX]{x1D70C}+R)^{2}+z^{2}}$
and differentiating equation (4.5) gives:
$$\begin{eqnarray}U_{n}(\unicode[STIX]{x1D70C},z)=\frac{\unicode[STIX]{x1D6E4}}{4}\left(\frac{z}{r_{1}}+\frac{z}{r_{2}}\right)\left(\frac{1}{2}\unicode[STIX]{x1D706}^{2}+\frac{3}{16}\unicode[STIX]{x1D706}^{4}+\frac{15}{128}\unicode[STIX]{x1D706}^{6}+\cdots \!\right).\end{eqnarray}$$
The normal velocity at the surface of the cylinder must be zero. Hence:
$$\begin{eqnarray}U_{n}(\unicode[STIX]{x1D70C},z)_{primary}+U_{n}(\unicode[STIX]{x1D70C},z)_{image}=0.\end{eqnarray}$$
Figure 23. Comparison of induced normal velocity at the cylinder surface between primary and image vortex rings for (a) old boundary condition and (b) modified boundary condition.
The plots of normal velocity due to the primary and image vortex rings at the surface of the cylinder (
$\unicode[STIX]{x1D70C}=R_{c}$
) with respect to
$z$
(assuming
$\unicode[STIX]{x1D6E4}=-\unicode[STIX]{x1D6E4}^{\ast }=1$
), is as shown in figure 23(a). The plot suggests that the velocity profile due to the image vortex has shrunk in comparison to that of the primary vortex ring. Therefore, the velocity profile of image ring has to be stretched with a suitable factor in order to match with the primary rings velocity profile. This factor is found to be
$\unicode[STIX]{x1D716}=R_{c}/R$
. The normal velocity of the image structure is modified as follows:
$$\begin{eqnarray}U_{n}(\unicode[STIX]{x1D70C},z)_{image,stretched}=U_{n}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}z)_{image}.\end{eqnarray}$$
Thus the modified boundary condition equation is:
$$\begin{eqnarray}U_{n}(\unicode[STIX]{x1D70C},z)_{primary}+U_{n}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}z)_{image}=0.\end{eqnarray}$$
The modified plot of radial velocity at the surface of the cylinder is shown in figure 23(b). The two profiles exactly match each other, which implies that
$\unicode[STIX]{x1D6E4}^{\ast }=-\unicode[STIX]{x1D6E4}$
as these plots were obtained for same magnitudes of
$\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}^{\ast }$
.
Here, it is important to understand that the image vortex structure is not just a vortex ring of radius
$R_{inv}$
, but a stretched version of it, or it would not satisfy the boundary condition.
In the experiments, it is observed that the presence of the cylinder increases the propagation velocity of the vortex ring. In order to quantitatively estimate the change in velocity due to inviscid axial interactions, the induced axial velocity by the image vortex ring on the primary vortex ring has to be evaluated. The axial velocity induced by a vortex ring at any point is given by:
$$\begin{eqnarray}U(\unicode[STIX]{x1D70C},z)=-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F9}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
On solving this for the image vortex ring (
$R=R_{i}$
) and substituting
$\unicode[STIX]{x1D70C}=R$
and
$z=0$
for the core centre of the primary vortex ring, the induced velocity due to the image vortex ring only is obtained as:
$$\begin{eqnarray}\unicode[STIX]{x0394}U=\frac{\unicode[STIX]{x1D6E4}}{2R}\left(\frac{3}{2}\unicode[STIX]{x1D716}^{4}+\frac{15}{16}\unicode[STIX]{x1D716}^{8}+\frac{105}{128}\unicode[STIX]{x1D716}^{12}+\cdots \!\right).\end{eqnarray}$$
An alternate and a much more useful form of this equation is:
$$\begin{eqnarray}\unicode[STIX]{x0394}U=\frac{\unicode[STIX]{x1D6E4}}{2R}\left(\frac{3}{2}\unicode[STIX]{x1D6FE}^{2}+\frac{15}{16}\unicode[STIX]{x1D6FE}^{4}+\frac{105}{128}\unicode[STIX]{x1D6FE}^{6}+\cdots \!\right),\end{eqnarray}$$
where,
$\unicode[STIX]{x1D6FE}=R^{\prime }/R=\unicode[STIX]{x1D716}^{2}$
,
$R^{\prime }$
is the radius of the vortex ring whose effect is being taken into account (in this case it is the image vortex ring) and
$R$
is the radius of the vortex ring on which the effect is being calculated.
$$\begin{eqnarray}\therefore \quad U_{int}=U_{f}+\unicode[STIX]{x0394}U.\end{eqnarray}$$
Here,
$U_{int}$
and
$U_{f}$
are the velocities of the interacting and free vortex rings respectively. It can be noted that the increase in velocity of the vortex ring due to the image structure depends on
$\unicode[STIX]{x1D716}$
. Also, the radius and circulation of the primary vortex ring play an important role in the determination of the induced velocity. The theoretical values of velocity for the free vortex ring are obtained using three different models: Saffman’s thin core model (Saffman Reference Saffman1992), Tung and Ting’s finite core model (Tung & Ting Reference Tung and Ting1967) and Fraenkel’s energy-impulse model (Fraenkel Reference Fraenkel1972). The corresponding equations for these models are:
$$\begin{eqnarray}\displaystyle & \displaystyle U=\frac{\unicode[STIX]{x1D6E4}}{4\unicode[STIX]{x03C0}R}\left(\ln \left(\frac{8R}{a}\right)-0.558\right)\quad \text{(Saffman's model)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U=\frac{\unicode[STIX]{x1D6E4}}{4\unicode[STIX]{x03C0}R}\left(\ln \left(\frac{8R}{\sqrt{4\unicode[STIX]{x1D708}t}}\right)-0.688\right)\quad \text{(Tung and Ting's model)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E=\frac{1}{2}\unicode[STIX]{x1D70C}R\unicode[STIX]{x1D6E4}^{2}\left(\ln \left(\frac{8R}{a}\right)-\frac{7}{4}+\frac{3}{16}\left(\frac{R}{a}\right)^{2}\ln \left(\frac{8R}{a}\right)\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6E4}\unicode[STIX]{x03C0}R^{2}\left(1+\frac{3}{4}\left(\frac{R}{a}\right)^{2}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U=\frac{\unicode[STIX]{x2202}E}{\unicode[STIX]{x2202}P}\quad \text{(Fraenkel's model)}. & \displaystyle\end{eqnarray}$$
Table 5 shows the comparison of the theoretical free vortex ring translational velocities (
$U_{f}$
) with the experimental values (
$U_{fe}$
). Then, a comparison of the ratio of increase in velocity obtained for all the cases using (4.15) with respect to
$U_{fe}$
is done with the corresponding ratio of increase in the experimental velocity. All the velocity values are non-dimensionalized with respect to
$U_{m}$
.
Table 5. Comparison between experimental and theoretical
$\unicode[STIX]{x0394}U$
from inviscid and viscous analysis. (All velocities are non-dimensionalized with respect to
$U_{m}$
and velocity differences are non-dimensionalized with respect to
$U_{fe}$
).).
The finite core model given by Tung & Ting (Reference Tung and Ting1967) and the energy-impulse base model of Fraenkel (Reference Fraenkel1972) give velocities much closer to the experimental values for a free vortex ring compared to Saffman’s thin core model (see table 5). Also, there is an order of magnitude difference between the experimentally determined
$\unicode[STIX]{x0394}U_{e}$
and
$\unicode[STIX]{x0394}U_{inv}$
, obtained from the inviscid analysis. This leads to the conclusion that the pure inviscid interaction of the vortex ring with the cylinder is not significant in the parameter range in which the present experiments are performed and probably it is the viscous effects which dominate. However, if a vortex ring is generated with appropriate
$\unicode[STIX]{x1D6E4}$
,
$D$
and
$\unicode[STIX]{x1D716}$
such that the inviscid effects are larger compared to viscous boundary layer effects, the inviscid theory can be verified. Equation (4.15) suggests that such an experiment would require large
$\unicode[STIX]{x1D6E4}$
, small
$R$
and large
$\unicode[STIX]{x1D716}$
(large
$R^{\prime }$
). Experiments with these parameters would actually lead to the creation of a stronger induced boundary layer and viscous effects. Arresting the growth of the induced boundary layer through some flow control technique is probably the only way the inviscid theory can be verified with experiments. However, an indirect proof of the inviscid theory is established when the effect of the induced boundary layer vorticity is taken into consideration in the next section.
5 Effects of induced axisymmetric boundary layer
When the vortex ring starts to interact with the cylinder, a boundary layer is formed around its surface due to viscous interactions. This can be seen in the PIV images shown in figures 11 and 12. In the absence of availability of any theory for an axisymmetric boundary layer, a simplistic analysis is carried out where the boundary layer is assumed to be an annulus sheet of vorticity with varying strength along the axial direction. The detailed analysis is given below.
The boundary layer has its own vorticity and hence a vorticity flux i.e. circulation per unit area. A contour integral of velocity along a rectangular box, as depicted in figure 24(a), surrounding the boundary layer completely will give an estimation of this circulation. This circulation has the opposite sense compared to the primary vortex ring, and hence would contribute to an increase in velocity of the vortex ring. As can be seen in figure 24(a), the boundary layer thickness varies along the length of the cylinder. Therefore, to incorporate the effect of the boundary layer accurately, the entire region is divided into small rectangular zones, as shown in figure 24(b). Each small section is considered as an independent vortex ring with some circulation which is calculated by performing a line integral of the velocity vector along its perimeter.
Figure 24. (a) Contour for calculation of boundary layer circulation and (b) boundary layer divided into small rectangular zones for case 1 (
$Re_{\unicode[STIX]{x1D6E4}}=2270$
,
$T_{p}=210~\text{ms}$
).
To calculate the radius of the series of annuli considered as strips of vortex rings, a vertical line is drawn through the middle of each rectangular section and the variation of vorticity is plotted along the line (see figure 25). The point of maximum vorticity is taken as the centre of the vortex ring strip and its distance from the cylinder axis is taken to be the radius of the vortex ring (
$R_{B.L}$
). The effect of each and every vortex ring strip is evaluated on the primary vortex ring and added together to obtain their total effect. Equation (4.15) is used to obtain the induced velocity due to one section in the direction perpendicular to the line joining the centre of the primary vortex ring core and the centre of the boundary layer section. The axial component of this induced velocity is obtained to find the change in the axial velocity of the primary vortex ring.
Figure 25. Vorticity distribution along a boundary layer section for case 1 (
$Re_{\unicode[STIX]{x1D6E4}}=2270,T_{p}=210~\text{ms}$
).
The boundary layer formed over the cylinder is also going to have an image structure at its own inverse point. This image will have a circulation in the same sense as the primary vortex ring and hence would contribute toward a decrease in translational velocity. Thus, the overall change in the velocity of the primary vortex ring is going to be the net summation of changes due to (i) the image vortex ring, (ii) the boundary layer vortex and (iii) the boundary layer image vortex. Table 5 shows the comparison of the net theoretical change in velocity (
$\unicode[STIX]{x0394}U_{vis}$
) due to all of the factors with the experimental values (
$\unicode[STIX]{x0394}U_{e}$
) obtained from flow visualization. After incorporating the effects of boundary layer vorticity, the comparison of the theoretical changes in the velocities with the experimental values shows a close match. Therefore, it can be said that the boundary layer vorticity is responsible for the increase in translational velocity for the cases considered here.
6 Conclusion
A detailed study of axial interaction of a vortex ring with a circular cylinder is carried out with flow visualization, particle image velocity measurements and analytical investigation. High-speed flow visualization experiments reveal the development of flow structure and trajectory. Translational velocity and diameter of the free and interacting vortex ring are also obtained quantitatively from it. Additional information required to understand the dynamics of the interaction process are the core diameter and core circulation, obtained from the detailed velocity field measurement using PIV. It is observed that, due to presence of the cylinder, there is an increase in the translational velocity of the vortex ring. Changes in the characteristic properties of the vortex ring such as core circulation (
$\unicode[STIX]{x1D6E4}$
), core radius (
$a$
) and ring diameter (
$D$
) are also measured due to the interaction. It is observed that for all cases, the translational velocity (
$U$
) of the interacting vortex ring is higher (figure 17) when compared with that of a free travelling vortex ring. However, the change in diameter,
$D$
, can be an increase or decrease or it can remain almost the same (figure 16). This is due to some interesting dynamics of the interacting flow field revealed by the PIV measurements. The presence of the cylinder displaces the streamlines near the cylinder as it acts as blockage to the freely translating flow. The induced boundary layer aids the displacement. However, displacements of the streamlines do not always enlarge or stretch the vortex ring diameter. To pass the same induced mass flow through the region between the vortex ring and the cylinder, the fluid accelerates more when compared to the freely translating ring. The acceleration of the irrotational central region flow reduces the local pressure, which tries to decrease
$D$
. Thus, these two opposite competing effects determine the nature of the diameter of the interacting vortex ring when compared to that of the freely translating ring. Further, the accelerated flow entrains some of the shear layer fluid into the core of the vortex ring and increases both
$a$
and
$\unicode[STIX]{x1D6E4}$
.
To explain the observed increase in translational velocity, an analytical study under an inviscid assumption is performed. In this analysis, the method of images is used to determine the effect of the image flow structure on the vortex ring using Lamb’s formulation of the streamfunction. The strength of the image vortex ring is determined from the zero normal velocity boundary condition. It is found that the image vortex structure is not just a vortex ring of radius
$R_{inv}$
, but a stretched version of it, satisfying the wall boundary condition. The inviscid theory does predict an increase in velocity of the interacting vortex ring. However, it fails to predict the values of the increased velocity obtained from the present experiments. This is due to the fact that the values of
$\unicode[STIX]{x1D6E4}$
,
$R$
,
$R^{\prime }$
and
$\unicode[STIX]{x1D716}$
used in the present experiments lead to the formation of an axisymmetric boundary layer, the effects of which dominate the results. To determine its effects, the boundary layer region over the cylinder, which is an annular vortex sheet of variable strength along the axis, is modelled as a series of vortex rings. Inviscid induction of these vortex rings and their images in the velocity of the primary vortex ring are obtained from the developed theory. The change in translational velocity obtained from this model matches closely with the experimental observations.
