2. ELLIPSOID BUBBLE FORMATION

In this section, bubble formation next to the intense laser pulse is analyzed by a simple analytical description. In the bubble regime, a cavity free from electrons is formed behind the laser pulse instead of the plasma wave. In this regime, the electron dynamics are defined by the pondermotive force of the laser pulse and electromagnetic fields of the bubble. Correctly, the bubble includes the cavity with the large ion charge, the electrons sheath around the cavity forming the bubble boundaries, and the bunch of accelerated electrons at the base of the cavity. At the beginning of the interaction, there is no bunch yet, and the cavity shape is determined only by the pondermotive potential of the laser pulse. The transverse size of the cavity reaches a maximum near the middle plane which passes through the cavity center. The bubble moves through the plasma background with the group velocity of the laser pulse. In the excess of the laser pulse and bubble fields, the plasma background's ions are stationary due to its large mass approximately. But the plasma electrons are expelled by the pondermotive force. On the bubble boundary, the pondermotive force on the electrons in the definite distance from the laser axis is nearly balanced by the attracting force of the bubble. These electrons remain on the sheath around the bubble and make the bubble boundaries. In continue, we will focus on these electrons and write an expression for balancing the forces on them.

Electric and magnetic fields of the ellipsoid bubble which move with group velocity of the laser pulse are (Zobdeh et al., Reference Zobdeh, Bonabi and Afarideh2009; Bonabi et al., Reference Bonabi, Navid and Zobdeh2009),

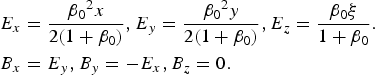(1)$$\eqalign{{E_x} & = \displaystyle{{{{\rm \beta} _0}^2 x} \over {2(1 + {{\rm \beta} _0})}},{E_y} = \displaystyle{{{{\rm \beta} _0}^2 y} \over {2(1 + {{\rm \beta} _0})}},{E_z} = \displaystyle{{{{\rm \beta} _0}{\rm \xi}} \over {1 + {{\rm \beta} _0}}}. \cr {B_x} & = {E_y},{B_y} = - {E_x},{B_z} = 0.} $$

In which variables are normalized as follows:

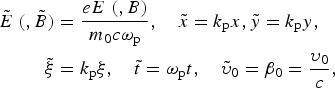(2)$$\eqalign{\tilde E\;(,\tilde B) & = \displaystyle{{eE\;(,B)} \over {{m_0}c{{\rm \omega} _{\rm p}}}},\quad \tilde x = {k_{\rm p}}x,\tilde y = {k_{\rm p}}y, \cr \tilde {\rm \xi} & = {k_{\rm p}}{\rm \xi}, \quad \tilde t = {{\rm \omega} _{\rm p}}t,\quad {{\tilde {\rm \upsilon}} _0} = {{\rm \beta} _0} = \displaystyle{{{{\rm \upsilon} _0}} \over c},} $$

and ξ = z − ν₀t, is the bubble-moving coordinate and v ₀ = c(1–ω_p²/ω²)^1/2 is the group velocity of the laser pulse. We assume that the bubble center is located at origin in t = 0 (its center remains at ξ = 0 for all time). For this situation, the normalized longitudinal and transverse electromagnetic force components of the bubble on the test electron are,

(3)$${F_{{\rm bub}}}^r = - \displaystyle{{{{\rm \beta} _0}^2 r} \over {2(1 + {{\rm \beta} _0})}},{F_{{\rm bub}}}^z = - \displaystyle{{{{\rm \beta} _0}{\rm \xi}} \over {1 + {{\rm \beta} _0}}}.$$

Furthermore, we assume the normalized vector potential of the laser pulse with longitudinal and transverse Gaussian profiles as,

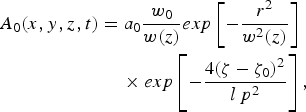(4)$$\eqalign{{A_0}(x,y,z,t) & = {a_0}\displaystyle{{{w_0}} \over {w(z)}}exp\left[ { - \displaystyle{{{r^2}} \over {{w^2}{{(z)}^{}}}}} \right] \cr &\quad\, \times exp\left[ { - \displaystyle{{4{{({\rm \zeta} - {{\rm \zeta} _0})}^2}} \over {l{\,p^2}}}} \right],} $$

where

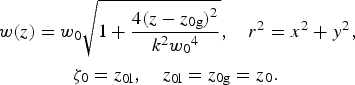(5)$$\eqalign{w(z) & = {w_0}\sqrt {1 + \displaystyle{{4{{(z - {z_{{\rm 0g}}})}^2}} \over {{k^2}{w_0}^4}}}, \quad {r^2} = {x^2} + {y^2}, \cr & \quad \quad {{\rm \zeta} _0} = {z_{{\rm 0l}}},\quad {z_{{\rm 0l}}} = {z_{{\rm 0g}}} = {z_0}.}$$

We assume, for simplicity, that the center of the laser pulse z _0l is located at the Gaussian beam waist z _0g, at t = 0. The pondermotive force can be expressed by ${\overrightarrow F _{{\rm pond}}} = - \nabla {V_{{\rm pond}}}$$(x,y,z,t),$ in which the normalized pondermotive potential is defined as,

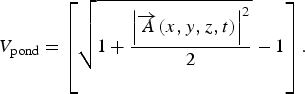(6)$${V_{{\rm pond}}} = \left[ {\sqrt {1 + \displaystyle{{{{\left \vert {\overrightarrow A (x,y,z,t)} \right \vert} ^2}} \over 2}} - 1} \right].$$

In this manner, the normalized longitudinal and transverse components of the scattering pondermotive force are obtained as follows:

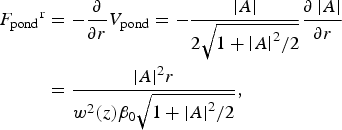$$\eqalign{{F_{{\rm pond}}}^{\rm r} & = - \displaystyle{\partial \over {\partial r}}{V_{{\rm pond}}} = - \displaystyle{{\left \vert A \right \vert} \over {2\sqrt {1 + {{\left \vert A \right \vert} ^2}/2}}} \displaystyle{{\partial \left \vert A \right \vert} \over {\partial r}} \cr &= \displaystyle{{{{\left \vert A \right \vert} ^2}r} \over {{w^2}(z){{\rm \beta} _0}\sqrt {1 + {{\left \vert A \right \vert} ^2}/2}}},} $$

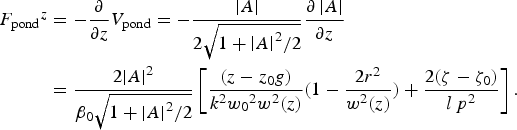(7)$$\eqalign{{F_{{\rm pond}}}^z & = - \displaystyle{\partial \over {\partial z}}{V_{{\rm pond}}} = - \displaystyle{{\left \vert A \right \vert} \over {2\sqrt {1 + {{\left \vert A \right \vert} ^2}/2}}} \displaystyle{{\partial \left \vert A \right \vert} \over {\partial z}} \cr & = \displaystyle{{2{{\left \vert A \right \vert} ^2}} \over {{{\rm \beta} _0}\sqrt {1 + {{\left \vert A \right \vert} ^2}/2}}} \left[ {\displaystyle{{(z - {z_0}g)} \over {{k^2}{w_0}^2 {w^2}(z)}}(1 - \displaystyle{{2{r^2}} \over {{w^2}(z)}}) + \displaystyle{{2({\rm \zeta} - {{\rm \zeta} _0})} \over {l{\,p^2}}}} \right].} $$

Moreover, in the bubble regime of the LWFA, the bubble structure passing through the background plasma with the group velocity of the laser pulse. In the equilibrium (quasi-static) state, some background electrons lay in the electron sheath layer around the bubble boundaries. These electrons introduce an electron sheath around the bubble which shield electrostatic field of the bubble out of the bubble boundaries. Of course, some of these electrons trap and accelerate toward the longitudinal axis in the rear part of the first bubble. In the laboratory reference frame, the electrons in the inner boundary of this sheath are in quasi-equilibrium in the longitudinal direction when they go along the sheath layer of the bubble. Now parameter α defines as follows to indicate longitudinal force balance condition for the electrons on the bubble boundaries,

(8)$${\rm \alpha} = {F_{{\rm bub}}}^z + {F_{{\rm pond}}}^z. $$

Adiabatic variation of the bubble shape through the interaction of intense laser pulse is neglected in our equilibrium condition, and the bubble is assumed in a steady-state situation.

In the next section, we will follow numerical results for the derivation of spatial points around the driver laser pulse which have minimum values of parameter α. In this new formalism, the ellipsoid boundary in the front side of the bubble (interaction zone with laser pulse) is recognized. The rear side of the bubble has an ellipsoid structure with an approximately identical transverse radius but with different (stretched) longitudinal radius, R’_z. Figure 1 shows this structure by a cylindrical 2D simulation (Fig. 1 from Benedetti et al., Reference Benedetti, Schroeder, Esarey, Rossi and Leemans2013). We obtain longitudinal and transverse radiuses of the bubble front side (R _z, R_r), and compare them with simulation results of this recent work. This twofold ellipsoid structure was observed in other multidimensional simulation results (see, for example, Pukhov & Meyer-Ter-vehn, Reference Pukhov and Meyer-Ter-vehn2002; Kostyukova et al., Reference Kostyukova, Pukhov and Kiselev2004; Kalmykov et al., Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter2011; Cowan et al., Reference Cowan, Kalmykov, Beck, Davoine, Bunkers, Lifshitz, Lefebvre, Bruhwiler, Shadwick and Umstadter2012; Benedetti et al., Reference Benedetti, Schroeder, Esarey, Rossi and Leemans2013). Asymmetric behavior of the ellipsoid in the front and rear sides is a consequence of the misallocation of the laser center with the ellipsoid's center. Discontinuity and scattering of the electrons in this point was shown in previous multidimensional simulations (Wu et al., Reference Wu, Xie, Liu, Hong, Zhang and Yu2009; Cowan et al., Reference Cowan, Kalmykov, Beck, Davoine, Bunkers, Lifshitz, Lefebvre, Bruhwiler, Shadwick and Umstadter2012; Kalmykov et al., Reference Kalmykov, Beck, Davoine, Lefebvre and Shadwick2012).

Fig. 1. The twofold (egg shape) ellipsoid structure of the bubble in highly nonlinear regime of LWFA by 2D simulation from Benedetti et al., Reference Benedetti, Schroeder, Esarey, Rossi and Leemans2013. R _r is the transverse radius and R _z (R’_z) is the longitudinal radius of the front (rear) side of the bubble. Allocation of laser pulse and its orientation approximately are illustrated by the red curve and two ellipsoids are drawn with white curves.

In the next section, we obtain the analytical form of the R _z and R _r, as a function of the normalized laser pulse amplitude a ₀, pulse length l _p, laser beam waist w ₀, and its normalized frequency ω/ω_p (plasma density scale).

3. NUMERICAL RESULTS

In this section, ellipsoid dimensions are obtained as a function of laser amplitude a ₀, waist w ₀, pulse length l _p, and normalized frequency ω/ω_p (which defines plasma density). For each value of these parameters, the location of points in the front side of the bubble boundaries is obtained by numerical minimization of α Eq. (8). After each minimization procedure, ellipsoid equation ${y^2}/R_r^2 + {z^2}/R_z^2 = 1$ is fitted on these points. In this equation, R _r and R _z are transverse (radial) and longitudinal radiuses of the ellipsoid bubble, respectively. For simplicity, in numerical results we assume that t = 0, center of the laser pulse and its beam waist are located at, z _0l = z _0g = z ₀.

In the first step, we assume that ellipsoid cavity has enough large dimensions which spread all considered space, but in continue ellipsoid dimensions are obtained. Longitudinal force α is plotted in Figure 2 for some values of z ₀, distance between laser pulse and bubble centers.

Fig. 2. Total longitudinal force α, for different z ₀. Maximum slope occurred for z ₀ = 0.678 at equilibrium condition, α = 0.

In this figure, center of ellipsoid cavity is located at the origin and laser pulse is located at the front (rear) of bubble, z ₀ > 0 (z ₀ < 0). For each value of z ₀, the longitudinal force has maximal three roots. First root (z ₁ at the front of the cavity) shows the stable equilibrium point for allocation of electron sheath in front boundary of the ellipsoid cavity. Background plasma electrons in this point experience restoring force which returns any longitudinal displacement from equilibrium.

In continue, we obtain feasible value for z ₀, in which maximum restoring force or maximum stability is occurred. Figure 3 shows the slope of the longitudinal forcedα/dz|z ₁, at the first root, as a function of z ₀. Equilibrium with the maximum stability occurred for $z_0^{{\rm max}} $, in which |dα/dz| is maximized. In this formalism, distance between the ellipsoid and laser pulse centers z ₀, and longitudinal radius of the ellipsoid R _z = z ₁ are obtained simultaneously. Transverse radius of the ellipsoid is obtained by a fitting procedure of the spatial points in the r–z plane for which α is minimized. In the fitting procedure, R _z (and z ₀) is known by the above-mentioned method and suitable value of R _r is obtained by fitting ellipsoid equation. With this formalism, ellipsoid dimensions and its location are obtained in the wide range of the interaction parameters.

Fig. 3. Slope of the restoring force at the equilibrium for different z ₀ values.

Figure 4a shows spatial points in the r–z plane for which α is minimized for normalized laser parameters l _p = 2.0, w ₀ = 3.6, ω/ω_p = 10, and for different values of the normalized laser amplitude between 2 and 20. For small values of laser amplitude (a ₀ <2), there is no suitable numerical solution. This result is in good agreement with nonlinear the relativistic nature of the wake-field acceleration in the bubble regime (a ₀ > 1).

Fig. 4. (a) Bubble boundary in the r–z plane for different values of the normalized laser pulse amplitude. (b) Bubble dimensions as a function of the laser amplitude (l _p = 2.0, w ₀ = 3.6, ω/ω_p = 10).

In figure 4b, ellipsoid parameters are shown as a function of normalized laser amplitude a ₀. Bubble dimensions interpolates by the following polynomials:

$${R_z}\left( {{a_0}} \right) = \left\{ {\matrix{ {0.6508\; {a_0} - 0.1536, \quad \quad 2 \lt {a_0} \le 10,\;} \cr {0.033\; {a_0} + 5.896, \quad \quad {a_0} \gt 10\;.} \cr}} \right.$$

$${R_r}\left( {{a_0}} \right) = - 0.021\; a_0^2 + 0.8622\; {a_0} + 1.942.$$

(9)$${{z_0}\left( {{a_0}} \right) = \left\{ {\matrix{{0.6183\;{a_0} - 1.099,} \hfill & {2{\rm \lt }{a_0} \le 10,} \cr 5 \hfill & {{a_0}{\rm \gt }10} \cr}}\right.}. $$

It is clear that the bubble has minimum dimensions in the moderate relativistic case, R _r = 3.58 and R _z = 0.977 (at a ₀ ≳ 2), and then it grows asymptotically, with increasing laser amplitude throughout the highly relativistic regime, R _r = 10.8 and R _z = 6.5 (a ≈ 20). For all laser amplitudes, the radial diameter is greater than the longitudinal diameter (oblate bubble), and the laser pulse locates in the front of the bubble center, Z ₀(a ₀) > 0.

In this step, we compare variation of the ellipsoid radius in terms of the laser pulse amplitude with the 2D PIC simulation results in Benedetti et al., Reference Benedetti, Schroeder, Esarey, Rossi and Leemans2013. Linear fitting of our results in the defined range of the laser amplitude (2 < a ₀ < 7) in this reference are presented in Figure 5. Linear fitting of the transverse radius is in agreement with the linear fitting of the PIC simulation in the prescribed range (Fig. 5a), but a big difference exists for the longitudinal radius (Fig. 5b). This difference between the rear and front ellipsoid longitudinal radiuses distinguished in the cavity structure obtained in 2D results of the PIC simulation in Figure 1. Comparison between these results (fig. 5b) shows that the rear side radius is approximately, few times greater than the front side of the bubble.

Fig. 5. Transverse (a) and longitudinal (b) radiuses of the bubble in terms of the normalized laser pulse amplitude from our formalism (blue line) and 2D PIC results (red dashed line) from Benedetti et al. (Reference Benedetti, Schroeder, Esarey, Rossi and Leemans2013).

Figure 6a shows the bubble parameters (vs.) the different normalized laser pulse length (1 < k _pl _p < 6) for a ₀ = 10, w ₀ = 3.6, and ω/ω_p = 10. It is known that the resonance condition in the bubble regime is occurred for l _p ≈ λ_p/2. Our numerical minimization procedure has failed for the laser pulses shorter than ${{\rm \lambda} _{\rm p}}/6\;({k_{\rm p}}{l_{\rm p}} {\mathop {\lt} \limits_{\sim}} 1) ({k_{\rm p}}{l_{\rm p}}{\mathop {\lt} \limits_{\sim}} 1$.

Fig. 6. (a) Bubble boundary in the r–z  plane for different values of laser pulse duration. (b) Bubble dimensions as a function of pulse duration (a ₀ = 10, w ₀ = 3.6, ω/ω_p = 10).

Multiple definition functions are fitted for the bubble dimensions. Breaking at k _pl _p ≈ 2 (l _p ≈ λ_p/3), indicates the resonance condition for the pulse length, where bubble reaches to its maximum dimensions.

$${R_z}\left( {{l_{\rm p}}} \right) = \left\{ {\matrix{ {0.465\;{l_{\rm p}} + 5.273,} \hfill & {{l_{\rm p}} \le 2,} \cr \quad {12.28\;{l_{\rm p}}^{ - 0.8523} - 0.5665,} \hfill & {{l_{\rm p}} \gt 2,} \cr } } \right.$$

(10)$${{R_r}\left( {{l_{\rm p}}} \right) = \left\{ {\matrix{{12,} \hfill & {{l_{\rm p}} \le 1.5,} \cr \quad {21.85\;{l_{\rm p}}^{ - 1.743} + 1.419,} \hfill & {{l_{\rm p}}{\rm \gt }1.5.} \cr } } \right.} $$

Figure 7 shows the bubble parameters (vs.) the different laser spot size (w ₀) for l _p = 2.0, a ₀ = 10, and ω/ω_p = 10. It must be mentioned that the numerical procedure does not have a suitable solution beyond the prescribed range (3.0 < w ₀ < 4.2) which is in agreement with optimum condition on the laser beam waist, ${k_{\rm p}}{w_0} = \sqrt {{a_0}} = 3.16$, for bubble excitation. Noticably, bubble structure exchanges from oblate to prolate for w ₀ ≤ 3.

subsequently, linear functions are fitted on the bubble dimensions in figure 5,

$${R_z}\left( {{w_0}} \right) = 6.2,$$

(11)$${R_r}\left( {{w_0}} \right) = - 0.9041\; {w_0}^2 + 10.08\; {w_0} - 16.$$

Fig. 7. (a) Bubble boundary in  the r–z plane. Numerical allowed spot size range (3.0–4.2) is in good agreement with optimum bubble creation condition, ${k_{\rm p}}{w_0} = \sqrt {{a_0}} = 3.16$. (b) Bubble dimensions as a function of beam waist (l _p = 2.0, a ₀ = 10, ω/ω_p = 10).

Finally, Figure 8 shows the bubble dimensions (vs.) the different normalized laser frequency (ω/ω_p) for l _p = 5.1, a ₀ = 10, and  w ₀ = 3.6. Normalized laser frequency identifies plasma density scale (relative to the critical density). Subsequently, power dependencies are fitted suitably on the points,

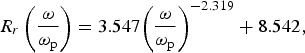$${R_r}\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = 3.547{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 2.319}} + 8.542,$$

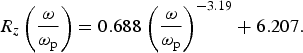(12)$${R_z}\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = 0.688\; {\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 3.19}} + 6.207.$$

Fig. 8. (a) Bubble boundary in the r–z plan. (b) Bubble dimensions as a function of normalized laser frequency (l _p = 2, a ₀ = 10, w ₀ = 3.6). Bubble dimensions are minimized (R _r ≃ 8.5 and R _z ≃ 6.2) for the dilute plasma (ω/ω_p > 10).

Ellipsoid bubble dimensions reach the values R _r ≃ 8.5 and R _z ≃ 6.2, asymptotically for dilute plasma (ω/ω_p ≫ 1). However, its dimensions increase with decreasing laser frequency (or increasing plasma density) up to a near-critical condition $({\rm \omega} / {\rm \omega}_{\rm p} {\mathop {\gt} \limits_{\sim}} 1)$, to R _r ≃ 12.1 and R _z ≃ 6.9. Furthermore, the front side of the bubble remains oblate for all selected parameters.

By combining Eqs. (9)–(12), the bubble parameters have the following dependency to the laser characteristics, for two cases: 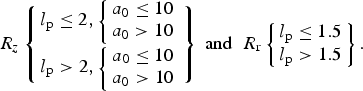${R_z}\left\{ {\matrix{ {{l_{\rm p}} \le 2,\left\{ {\matrix{ {{a_0} \le 10} \cr {{a_0} \gt 10} \cr}} \right.} \cr {{l_{\rm p}} \gt 2,\left\{ {\matrix{ {{a_0} \le 10} \cr {{a_0} \gt 10} \cr}} \right.} \cr}} \right\}\;{\rm and}\;\; {R_{\rm r}}\left\{ {\matrix{ {{l_{\rm p}} \le 1.5} \cr {{l_{\rm p}} \gt 1.5} \cr}} \right\}.$

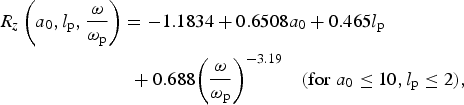$$\eqalign{& {R_z}\left( {{a_0},{l_{\rm p}},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = - 1.1834 + 0.6508{a_0} + 0.465{l_{\rm p}} \cr &\qquad{\hskip50pt} + 0.688{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 3.19}}\quad ({\rm for}\; {a_0} \le 10,{l_{\rm p}} \le 2),}$$

$$\eqalign{& {R_z}\left( {{a_0},{l_{\rm p}},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = 4.9516 + 0.033{a_0} + 0.465{l_{\rm p}} \cr & \qquad{\hskip50pt} + 0.688{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 3.19}}\quad ({\rm for\;} \; {a_0} \gt 10,{l_{\rm p}} \le 2),} $$

$$\eqalign{& {R_z}\left( {{a_0},{l_{\rm p}},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = - 7.0445 + 0.6508{a_0} + 0.688{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 3.19}} \cr & \qquad{\hskip50pt} + 12.28l_{\rm p}^{ - 0.8523} \quad ({\rm for}\; \; {a_0} \le 10,\; {l_{\rm p}} \gt 2),} $$

$$\eqalign{& {R_z}\left( {{a_0},{l_{\rm p}},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = - 0.9093 + 0.033{a_0} + 0.688{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 3.19}} \cr & \qquad{\hskip50pt} + 12.28l_{\rm p}^{ - 0.8523} \quad ({\rm for\;} {a_0} \gt 10,\;\; {l_{\rm p}} \gt 2),} $$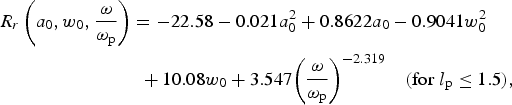

$$\eqalign{& {R_r}\left( {{a_0},{w_0},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = - 22.58 - 0.021a_0^2 + 0.8622{a_0} - 0.9041w_0^2 \cr & \qquad{\hskip55pt} + 10.08{w_0} + 3.547{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 2.319}}\quad ({\rm for}\; {l_{\rm p}} \le 1.5),} $$

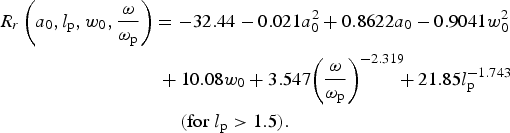(13)$$\eqalign{& {R_r}\left( {{a_0},{l_{\rm p}},{w_0},\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right) = - 32.44 - 0.021a_0^2 + 0.8622{a_0} - 0.9041w_0^2 \cr & \qquad{\hskip65pt} + 10.08{w_0} + 3.547{\left( {\displaystyle{{\rm \omega} \over {{{\rm \omega} _{\rm p}}}}} \right)^{ - 2.319}} \!\!\!+ 21.85l_{\rm p}^{ - 1.743} \; \cr & \qquad{\hskip77pt} ({\rm for}\; {l_{\rm p}} \gt 1.5).} $$

Figure 9a shows the variation of transverse radius of the bubble in terms of normalized laser pulse amplitude and beam waist. In figure (9b), the schematic deformation of the bubble is shown through the propagation of a Gaussian laser pulse in many Rayleigh lengths around the focus point. The ellipsoid bubble remains oblate in this path, but its compression is minimized in focus.

Fig. 9. (a) Transverse radius of the bubble in terms of normalized laser pulse amplitude and beam waist. (b) The schematic deformation of the bubble trough the propagation of a Gaussian laser pulse.

Figure 10 shows ellipsoid bubble radiuses as a function of normalized laser pulse amplitude and frequency. A great variation of the bubble dimensions in the moderate relativistic amplitude and near-critical plasmas $({\rm \omega} /{\rm \omega} _{\rm p} {\mathop {\gt} \limits_{\sim}} 1)$ reaches to the stable dimensions in the highly relativistic amplitude and dilute plasmas asymptotically (ω/ω_p ≫ 1).

Fig. 10. Transverse (a) and longitudinal (b) radiuses of the bubble in terms of normalized laser pulse amplitude and frequency.

Figure 11 shows bubble dimensions as a function of the normalized laser pulse amplitude and pulse length. Disconnection in the curves is occurred around the resonance condition, k _pl _p ≈ 2 (l _p ≈ λ_p/3).

Fig. 11. Transverse (a) and longitudinal (b) radiuses of the bubble in terms of the normalized laser pulse amplitude and the laser pulse duration.