In Theory of International Politics, Kenneth Waltz famously analogized states in international relations to firms in an oligopolistic industry.Footnote 1 Firms choose prices (or quantities) in an effort to maximize profits, but in the limiting case of perfect competition they earn no profit because of a strategic incentive to undercut each other. Given their preferences, anti-trust law, and “the structure of the situation,” the firms face what amounts to a Prisoners' Dilemma. Waltz saw this model as exactly parallel to the idea that international anarchy leads states to choose policies—arming, allying, and attacking, in particular—that can make them worse off than if they could instead commit themselves to cooperate. For Waltz, the microeconomic analogy was a way of developing and putting on solid ground the traditional realist intuition that there is something fundamentally different about interstate relations, something that makes them inevitably tragic in a way that domestic politics need not be.
Theory of International Politics was written before developments in game theory reworked the field of industrial organization, and in particular before elaboration of the idea that repeated interactions could allow firms to construct self-enforcing agreements that would sustain higher prices and profits.Footnote 2 Robert Axelrod and Robert Keohane applied this idea to international relations, suggesting that it undermined the claim that they must necessarily be conflictual and tragic.Footnote 3 Joseph Grieco argued in response that if states have an intrinsic preference for “relative gains,” it could be impossible to sustain a cooperative interstate agreement by implicit threats of ceasing cooperation if the other cheats.Footnote 4 Robert Powell argued that the right realist counter should not be to make a different assumption about state preferences, but to understand that in anarchy force can enable states to convert relative advantage into absolute gain.Footnote 5 Depending on military technology and costs for fighting, this possibility might prevent states from cooperating despite a “shadow of the future” (i.e., repeated interactions). Tragedy restored, but with qualifications.
Parallel to this neoliberal-neorealist exchange, an ongoing debate among realists centers on a different objection to the idea that anarchy implies a great deal of tragedy. Robert Jervis argued that tragic outcomes resulted from a “security dilemma” whose severity depends on the degree to which military technology and geography favor offense or defense. Jervis's core arguments, developed further by a number of scholars taking a similar approach, picture state leaders as uncertain about whether other states are satisfied with the territorial status quo or have expansionist preferences. When defense is favored in the “offense-defense balance,” arms levels can safely be lower and cooperation is less risky if another state is in fact expansionist. Using this theoretical basis, “defensive realists” maintain that because offense is disadvantaged by balancing behavior and because nuclear weapons effectively favor defenders, international anarchy needn't or shouldn't be the source of large costs.Footnote 6 “Offensive realists” disagree because of reservations about the offense-defense balance concept and because they think that even a small probability of facing an expansionist type is enough to make major powers expansionist or defensively aggressive in turn.Footnote 7
Routinely taught in graduate international relations (IR) seminars, these various arguments are interesting and important. They conflict in some places but overlap in others.Footnote 8 It is not clear whether or exactly how they might emerge and survive as implications of a common set of premises.Footnote 9
In this article I develop a two-state model built on realist premises. States in the model (1) interact in the absence of a third party that can reliably guarantee agreements between them (anarchy); (2) can gain from coordinating their interactions but have some degree of conflicting preferences over issues of mutual concern, which may include territory; (3) have the ability to generate and use armed force against each other; and (4) find both the provision and use of arms costly, at least to some extent. The goal is a baseline model that succinctly characterizes central strategic problems faced by states interacting in international anarchy, and that yields clear implications on what determines variation in the costs of anarchy over time and across states.
In the model, two states choose arms levels and whether to attack in successive periods. If there is no war, relative military strength determines the resolution of a set of issues through an unspecified bargaining process. If there is a war, territory is put into play so that the winner gets not only control of the issues but also the loser's territory. I show that repeated interactions can be used to enable mutually beneficial cooperation between the states on the issues, but subject to a war constraint: arms levels cannot be so low that a state would prefer to “break out” by rapidly mobilizing and going to war. Thus, as “neoliberal institutionalists” like Keohane and Axelrod argued, there can be considerable scope for cooperation despite anarchy because of the possibility of self-enforcing agreements that rely on repeated interactions. However, in line with the traditional realist intuition, this mechanism cannot in general support the first-best outcome of no war and no costly armament (or other competitive effort). Some costs of anarchy are avoidable without supranational government, some are not. At least for the two-state case, the model shows just what follows from a set of standard premises—states that have the capacity to use force, some conflict of interest, but also a common interest in avoiding wasteful and dangerous competition.
The baseline model yields propositions on the size of the unavoidable costs of anarchy. In line with Jervis although by a different logic, the war constraint is less severe, and thus the potential depth of interstate cooperation is greater, the more geography and military technology favor defense relative to offense. The war constraint is also less tight the less intrinsic value the states put on controlling the other's territory, which can be an effect of industrialization, democracy, or nationalism when agreement on homelands and borders exists. Greater interdependence or “gains from trade”—meaning more potential value to be divided up that is separate from homeland territory—may either increase or decrease the war constraint, as a result of offsetting effects. Protectionism, or any factor that lowers the efficiency of exploiting gains from trade between independent states, tightens the war constraint, raising the arms level necessary for a stable peace. In dyads where one state has greater military potential than the other, the smaller state is predicted to have a higher arms burden, but the model reveals offsetting forces that push in the direction of military burdens being only weakly related to state size.
Although not normally stated in terms of arms as a measure of international cooperation, some of these implications will seem familiar to IR theory adepts. In particular, some results from the baseline model look like a synthesis of positions argued by “defensive realism,” “neoclassical realism,” and “neoliberal institutionalism,” with additional implications on conflict and trade reminiscent of ideas from, for example, Cordell Hull and Richard Rosecrance.Footnote 10 Other positions, such as several associated with offensive realism, are not supported.
What is new then? First, theoretical synthesis. These and other implications emerge in a connected and transparent way from a single strategic model. This is in contrast to the standard presentation of arguments as competing schools of thought that are based on or stress different assumptions or issue domains.
Second, the model provides an alternative theoretical foundation, since the logic that generates the implications differs markedly from standard arguments. The closest thing to a clear baseline model in the existing literature—and also the theory undergirding defensive realism—is Jervis's treatment of the security dilemma and its subsequent development.Footnote 11 There, great-power politics are driven primarily by states' uncertainty about other states' preferences for territorial expansion. By contrast, while it could be added in principle, this model has no uncertainty about types at all. We still get, however, standard security-dilemma-like results concerning the offense-defense balance. Indeed, the model suggests a novel way of formalizing the somewhat mysterious idea of the security dilemma. Even without any uncertainty about states' preferences, in the model greater offensive advantage leads to greater equilibrium arms levels, which lower states' values for living with the status quo and so make the gamble of war more attractive. More broadly, an important feature of the baseline model is that it puts the guns-butter tradeoff at the heart of the theory, a political economy dimension entirely missing from the “anarchy arguments” glossed earlier.Footnote 12
Third, some implications of the model are new—such as the results on state size and arms burdens—or revise existing theories. For example, existing conceptualizations of the offense-defense balance define it in terms of the prospects or costs of successful attack versus defense, taking force levels as exogenously given. But as becomes clear in the model, states choose force levels endogenously in light of military technology and geography to affect prospects for successful offense or defense. This point undermines or even inverts standard offense-defense hypotheses about how these factors matter. For instance, relative offensive advantage in technology or geography causes states to arm to higher levels, and at these levels the odds of successful attack can actually be lower than if defensive advantages in technology were greater. Thus, railroads increased rapid mobilization capacity in late nineteenth-century Europe, which drove increases in equilibrium armament levels, which in turn made the status quo less desirable but conquest less easy than it would have been at lower arms levels.
Fourth, compared to existing theory, the baseline model yields more determinate and testable implications for a measurable proxy for the costs of anarchy—military burdens and force sizes. For lack of space I briefly consider only broad patterns in military spending and force size among the major powers over the last 150 years in light of the model's implications, leaving an assessment based on panel data to other work.Footnote 13
Regarding the model, the closest papers in the literature are by Powell and Matthew Jackson and Massimo Morelli.Footnote 14 Powell's underappreciated article was the first to explicitly model state choices about how much to arm and whether to attack in a fully dynamic setting. He identified the tradeoff that lies behind the war constraint in the model here: higher peacetime arms levels reduce an adversary's ability to “break out” and attack, but they also reduce the state's values for living with a peaceful status quo by reducing consumption. The costs of deterrence can make war to eliminate or lessen the need for deterrence a more attractive, if tragically inefficient, option.Footnote 15
Whereas in Powell's model the only issue at stake is control of one's own or the other state's territory, the model here adds an international issue over which the states have conflicting preferences. This could be anything, for example, the terms of a trade deal, the division of Poland or spheres of influence, support for rebels in a third country, or the value of getting one's way on all disputed issues apart from control of homeland territory. This addition allows the model to speak to the IR debate on cooperation and conflict as it developed after Waltz. Arming in the model is not just about attack or deterrence, but also about gaining bargaining leverage on contested issues. The states have an incentive to arm for bargaining leverage but wish to avoid wasted effort. In effect they face a classic “repeated Prisoners' Dilemma” problem with respect to the contested issues, but this problem is embedded in a larger context where the use of force puts sovereignty at risk.
Jackson and Morelli examine models similar to Powell's but their states choose arms levels simultaneously rather than sequentially. The minor timing difference proves to have oddly large consequences. With simultaneous arming there is no pure strategy equilibrium because at levels high enough that neither wants to break out and attack, a state could do better by temporarily lowering arms spending before the other has a chance to react. This may seem like a technical artifact, but it raises a substantive question. If arms levels are just about deterrence, why aren't states constantly trying to save on spending by short-run cuts not large enough to draw an attack? The model here suggests one possible resolution. Arms are valuable not only for deterrence but also for bargaining leverage. Cuts that would not lead to an all-out attack by a rival would nonetheless disadvantage the state in issue bargaining. The model has simultaneous arming decisions, but stable arms levels when peace is supportable.Footnote 16
The literature on “the bargaining model of war” focuses on frictions that might explain costly armed conflict, such as private information and incentives to misrepresent, and commitment problems occasioned by power shifts.Footnote 17 While war can be an equilibrium outcome in the model I present in the next section (arising from “costly deterrence,” a commitment problem) its focus is not on explaining specific wars but instead is about the quality of interstate relations more generally. The main choice of interest is arms levels (or military effort), which emerge as a theoretically defensible measure of the degree of inefficiency in an interstate system that might be attributed to, or blamed on, the condition of anarchy. The model highlights how arms levels feed back on states' values for living with a peaceful status quo and thus affect their willingness to run war risk. But specific paths to war are not the focus (as indicated, for example, by the assumption of efficient issue bargaining).
Model
Two states, 1 and 2, interact in successive periods t = 0, 1, 2, …. They each get resources normalized to size 1 each period. Resources can be consumed or converted, one-for-one, into arms. For simplicity and clarity, in this section the two states are identical in terms of resources and other parameters, such as value for taking territory.
In each period, the states simultaneously choose arms levels ![]() $a_i^t \in [0,1]$, next observe
$a_i^t \in [0,1]$, next observe ![]() $a^t = (a_1^t, a_2^t )$, and then simultaneously choose whether to attack. (When there is no need to be explicit about the period, I use (a 1, a 2) for arms levels.) If either attacks, war occurs, one side wins, taking all the resources or territory, and the strategic interaction ends. If neither attacks they move to the next period. Payoffs are discounted by the common factor δ ∈ [0, 1) each period.
$a^t = (a_1^t, a_2^t )$, and then simultaneously choose whether to attack. (When there is no need to be explicit about the period, I use (a 1, a 2) for arms levels.) If either attacks, war occurs, one side wins, taking all the resources or territory, and the strategic interaction ends. If neither attacks they move to the next period. Payoffs are discounted by the common factor δ ∈ [0, 1) each period.
In every period t, there is an international issue worth γ > 0 that can be divided up between them. This could stand for a different issue in every period, or it could be the same issue, always subject to renegotiation. The most natural interpretation is that γ stands for many issues, summarizing their total value to the two states. In the discussion of empirical implications, I will refer to γ as the degree of interdependence or the gains from trade. Conceptually, the distinction between γ and the resources that each state controls is that the states are “sovereign” over those resources, but cannot unilaterally decide the allocation of γ.
Since the focus here is not on inefficiencies in bargaining over γ, I assume that if war does not occur, the states divide up γ in each period as a function of relative military strength. Suppose that if force levels are (a 1, a 2) and there is no war, then state 1's payoff is 1 − a 1 + γq(a 1, a 2) while state 2 gets 1 − a 2 + γ(1 − q(a 1, a 2)). This says that a state's payoff if war does not occur is what it doesn't spend on arms plus its value for the issue resolution. A number between 0 and 1, q(a 1, a 2) is state 1's share of the division on the issues γ.
The function q(a 1, a 2) has the usual properties of a “contest success function.”Footnote 18 It is symmetric, which implies an equal split when a 1 = a 2, and it is increasing in a 1 and decreasing in a 2. Thus a state can gain a larger share on the issues by increasing its arms. The value taken by q(a 1, a 2) can be interpreted as the probability that state 1 wins a limited military conflict over γ that would occur if bargaining failed, and thus a component of the “disagreement point” that determines the bargaining outcome.
If state i ∈ {1, 2} chooses to attack j in a period (and j stays on defense), then we will assume that i wins the all-out war that occurs with probability p i(a i, a j; m), where m ≥ 0 is an exogenous parameter that indexes offensive advantage. A factor will be said to increase offensive advantage if for any given positive force levels at the time of attack, its presence improves an attacker's odds.Footnote 19
To give a specific example, consider
Thus for values of m less than 1, the defending state j gets an advantage against the attacking state i, for (say) equal force sizes. In the specific case of (1), m can also be interpreted as a measure of “the offense-defense balance” in that 1/m is the ratio of attacker to defender forces that gives an attacker a 50–50 chance of victory.
Finally, state i’s expected payoff from period t forward if it attacks defender j in period t is
For simplicity war is treated as a costly lottery. The loser is eliminated, getting a payoff of 0 henceforth. The winner gets full control of the issues in the present and all future periods, as well as the loser's territory and resources starting in the next period.Footnote 20 We assume that each state values the other side's territory at μ ∈ [0, 1], which allows us to vary how “greedy” they are.Footnote 21 Small μ means that they don't get as much value out of ruling the other state's territory as they do their own (which is worth 1). This could be for several reasons, including costs of ruling hostile foreigners, lack of interest in territory not considered to be historic homeland, or democratic values that support self-determination or political equality. The parameter c ≥ 0 is broken out to represent additional costs of fighting, such as destructive impact.Footnote 22
I focus on conditions for an undominated pure-strategy subgame perfect equilibria with no war, and conditions in which war is the only equilibrium outcome.Footnote 23
By assuming that the most a state can arm in a period is 1, we have also assumed that whatever value the states derive from the issue dimension, it cannot be converted into military capability. This is not necessary. We could have ![]() $a_i^t \in [0,1 + \gamma q(a_i^{t - 1}, a_j^{t - 1} )]$, so that last period's total resources can be used for this period's arms. Allowing γ to be usable for military capability may or may not tighten the war constraint in the analysis that follows, but does not change qualitative results.
$a_i^t \in [0,1 + \gamma q(a_i^{t - 1}, a_j^{t - 1} )]$, so that last period's total resources can be used for this period's arms. Allowing γ to be usable for military capability may or may not tighten the war constraint in the analysis that follows, but does not change qualitative results.
For simplicity and generality the bargaining over the issues represented by γ is treated in a reduced-form way. As discussed in the online appendix, several common bargaining protocols can give rise to a function q(a 1, a 2) as described. These include a stage game in which each state has an equal chance of finding itself in a position to change the status quo on the issue and the other can then choose whether to use force to try to reverse a fait accompli; and a game where we simply select the Nash bargaining solution over division of γ, with disagreement being a costly conflict lottery over γ. The key assumption, which is entirely consistent with the realist tradition, is that relative military power translates into more favorable issue outcomes on average. This is not true for all issues all the time; for instance, if both sides must agree to change the status quo, then a challenger's threats to use force may be hard to make credible. The assumption here is that it is true often enough that states expect that reducing military strength could disadvantage them in issue bargaining in the future.
Results
How much “cooperation under anarchy” is possible in this two-state model? If peace can be sustained (no attacks in equilibrium), then cooperation in the model is measured by the equilibrium level of arms. More arms, less cooperation. This is because arms spending is just wasteful. If the states spend positive amounts (a 1, a 2) and divide γ in shares q(a 1, a 2) and 1 − q(a 1, a 2), they could be better off spending at lower levels that yield the same division. The most efficient outcome, or maximum cooperation, would be a peaceful equilibrium in which neither spends anything on arms and the issue is divided equally in every period, yielding per-period payoffs of 1 + γ/2.
Two temptations work against the feasibility of the first best. The first is the war constraint: if one state has no arms then the other may prefer to build and attack to gain control of the issues and more territory (if it values more territory). The second temptation is that independent of the incentive to arm and attack, arming would confer bargaining leverage and yield more favorable issue resolutions.
Cooperating on International Issues
It is useful to begin by forgetting the war constraint and considering the problem of cooperation over the issues. A state can get more favorable issue resolutions by increasing military strength, but if the other replies in kind both are worse off than if they had not armed up. If they fail to construct what would amount to an arms-control agreement, a spheres-of-influence agreement, an agreement to demarcate or demilitarize a border, or the like, then the noncooperative outcome is the pair of arms levels such that neither wants to spend more given what the other is spending. This is the level a NE (“NE” for Nash equilibrium in the stage game) such that the marginal issue benefit of spending more equals the marginal arms cost of 1 when both choose it (assuming an interior solution):
If, as is natural, we assume that the bargaining returns to a given increment of arms are lower at higher levels, then it is easy to show that the more the states care about the issue conflict (larger γ), the more effort they waste on the competition (larger a NE).Footnote 24
However, as Axelrod, Keohane, and others argued, the states can use “the shadow of the future” to construct deals to support more cooperative outcomes. They agree to spend or compete less and to compromise on the issues, with the understanding that if either reneges they will return to costly competition. Consider an arms level ![]() $\hat a \lt a^{NE}$. Using a trigger strategy as the implicit punishment threat, the states prefer to stick with cooperating at â provided that
$\hat a \lt a^{NE}$. Using a trigger strategy as the implicit punishment threat, the states prefer to stick with cooperating at â provided that
The left-hand side is the payoff for sticking with the deal. The right-hand side is the best a state can do by arming up in a period, which will then be followed by a return to costly competition. Multiplying through by 1 − δ and considering what happens as δ approaches 1—that is, as states put more weight on their welfare in future periods, or as the time it takes to perceive and respond to arms changes by the other side lessens—we get the following result.
Proposition 1
If military power can be used to influence issue resolutions beyond state borders but not for conquest of the other state's territory, then for large enough δ the states in the model can support cooperation on any ![]() $\hat a \lt a^{NE}$, including maximum cooperation at
$\hat a \lt a^{NE}$, including maximum cooperation at ![]() $\hat a = 0$ in all periods, as an equilibrium outcome.
$\hat a = 0$ in all periods, as an equilibrium outcome.
So far, so neoliberal. If the “if” condition in the proposition held universally, the fact of anarchy would in principle pose little or no problem for states in international politics, and there would be no grounds for viewing international relations as a necessarily tragic realm.
But that condition need not hold. If state j has no military, state i might prefer to arm and attack to take territory. To keep things simple, suppose that p i(a i, a j) is such that when a j = 0 state i can win for sure at minimal cost in arms.Footnote 25 Then i prefers to arm a little and take over j if
which is the case if
This condition means that if the costs of fighting do not outweigh the value the states put on acquiring new territory and full determination of the issues, the first-best outcome of maximal cooperation (no arms spending) and no war is not possible because each would be tempted to arm up and invade.
The War Constraint
Given (2), then, stable peace requires that both states arm enough that neither would want to “break out,” arming rapidly and attacking, as Hitler did in the 1930s. Putting the incentive to compete on the issues to the side for the moment, suppose both states are choosing arms level ![]() $\hat a \gt 0$. For this to be an equilibrium each must prefer peace at â to mobilizing and attacking:
$\hat a \gt 0$. For this to be an equilibrium each must prefer peace at â to mobilizing and attacking:
This is the war constraint, the condition on arms that must be satisfied for states not to want to mobilize and attack. Multiplying through by 1 − δ, we have
Although not necessary for the results that follow, we can simplify and get a clearer understanding of the strategic dilemma by considering the problem for discount factors close to 1. If the “shadow of the future” is long enough, a state maximizes the value of the breakout option by spending all available resources on arms in a period (i.e., a = 1) to maximize the chance of victory in war.Footnote 26 So the war constraint simplifies to
Figure 1 graphically depicts the war constraint in two possible cases. In the first, there are values of â that satisfy the constraint and there is a minimum value a* that satisfies it with equality. In the second, there is no arms level high enough that neither prefers to mobilize and attack but low enough that a peaceful status quo is preferable to trying war in hopes of getting rid of the need for costly deterrence.Footnote 27 In this second case, war is inevitable and in fact must occur in the first period in equilibrium. The cause can be attributed to anarchy (and condition 2) in that the states would prefer it if they could commit to zero arms and no attacks. Note as well that inefficient conflict arises in this case despite the “shadow of the future” being as long as it can be. For preferences and a military technology such that the war constraint cannot be met, the states' capacity to attack and possibly eliminate the other undermines cooperation based on repeated interactions.Footnote 28
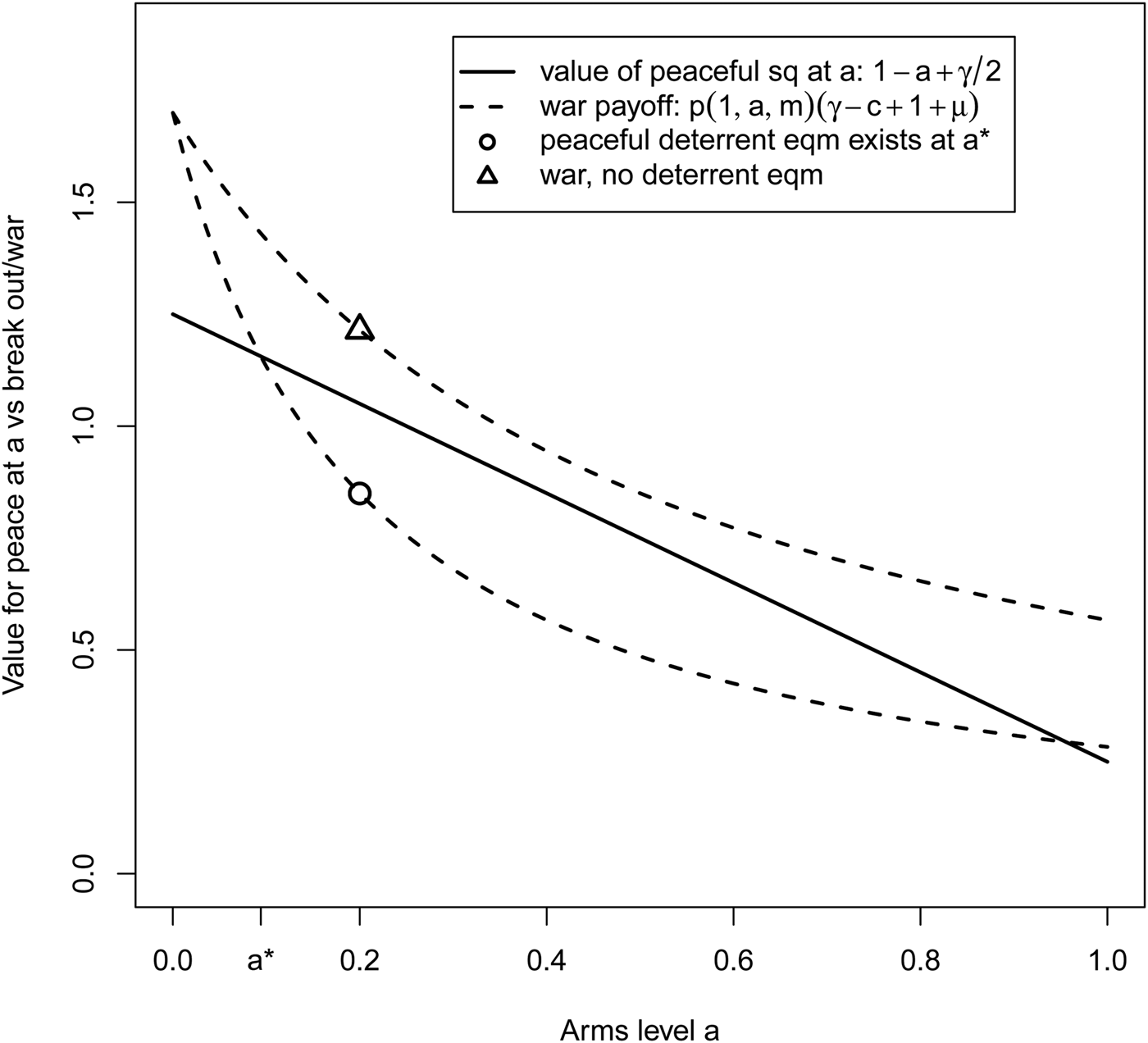
Figure 1. Equilibria with and without stable deterrence
Suppose parameters are such that the war constraint can be satisfied. This is necessary for a peaceful equilibrium to exist, but not quite sufficient. It must also be that neither state would want to decrease its arms level enough in one period to save on costs but not so much as to draw an attack. As the following main result details, neither wants to do this if reducing arms spending would hurt the state enough in bargaining over disputed issues.
Proposition 2
If there is a smallest a* that solves the war constraint (4) with equality, and a* ≤ a NE, then for large enough δ the game has peaceful equilibria in which, on the path of play, the states choose ![]() $\hat a \in [a^{\ast},\bar a]$ in every period, where
$\hat a \in [a^{\ast},\bar a]$ in every period, where ![]() $\bar a \le a^{NE}$ is determined by specific parameters. Thus in the most cooperative equilibrium the states choose a* in all periods on the path. Further, if defensive advantage is sufficiently large ( m is small enough), such an a* definitely exists and a* < a NE.
$\bar a \le a^{NE}$ is determined by specific parameters. Thus in the most cooperative equilibrium the states choose a* in all periods on the path. Further, if defensive advantage is sufficiently large ( m is small enough), such an a* definitely exists and a* < a NE.
Using standard assumptions about states' preferences and capabilities, Proposition 2 provides an answer to the question of how much cooperation under anarchy is possible. As neoliberal institutionalists argued, states can use repeated interactions and the shadow of the future to construct regimes or tacit deals that make them better off than they would be without such formal or informal institutions. (By “institutions” I mean simply coordination on more efficient outcomes that requires acting against short-run interests; in practice this is often facilitated by international organizations whose roles are not modeled here.) Without institutions, states in the model engage in costly competition at the myopic Nash outcome of a NE.
However even with institutions—coordination on an a* < a NE—there are still unavoidable costs of anarchy. The depth of cooperation is constrained by the inability to commit not to go to war if the other state's military effort is low enough.
Issue competition plays a subtle strategic role. If there are no disagreements over international issues (γ = 0), then the cooperative equilibria just described do not exist. With γ = 0 the states have no reason to arm for bargaining leverage (a NE = 0), so there is no immediate penalty for short-run cuts not large enough to undermine deterrence of invasion. For small enough γ but enough “greed” about territory that condition (2) still holds, the model becomes close to that of Jackson and Morelli.Footnote 29 Mixed-strategy equilibria with random arms levels and positive odds of attack result. Empirically, however, we do not see states constantly and arbitrarily varying their military spending.Footnote 30
Introducing issue competition provides one empirically plausible way to resolve the puzzle. When a* < a NE, undercutting on military strength leads to less favorable outcomes on international issues the state cares about. In other words, arming or other costly competitive effort is valuable not only for deterrence of invasion but also for helping to get one's way in the random and diverse disputes that make up international affairs. “Diplomacy without arms is like music without instruments,” as Frederick the Great put it.Footnote 31
In this deliberately spare, “pure IR” model, a state's only reasons to want arms and a military have to do with foreign policy. Their sole functions are to deter or attack another state and to gain leverage in international bargaining. But of course rulers want armies for domestic political reasons as well. They need guns and soldiers to deter or put down organized rebellions. For many countries, domestic demand for arms could be the explanation for why they don't have an incentive to undercut to save money, getting into the unstable dynamic that Jackson and Morelli discuss. Let a D be the spending level a state's leadership would choose if there were no international threats or bargaining considerations whatsoever. If a* < a D, then peaceful pure-strategy equilibria may be feasible, although international cooperation would not be able to reduce arms levels to the minimum that satisfies the war constraint. Indeed, such a domestically insecure state's demand for a larger-than-necessary military could aggravate international conflict by increasing neighbors' military burdens.
At least since the end of the Cold War many small states' borders are de facto protected by the expectation that the US, the European Union, and perhaps the UN would impose sanctions or worse if they were openly invaded by a neighbor. (In the two-state model, this amounts to aggressors having higher costs to attack because of expected reactions by more powerful states.) These states' arms levels may be entirely determined by domestic political considerations and not at all by considerations of deterrence or competition on interstate issues.
How Deep Can Interstate Cooperation Be?
Focused on the claim that anarchy makes international politics inevitably conflictual, Waltz had little to say about what explains variation in international cooperation. His main variable was the number of major powers. In arguments that greatly influenced realists, he suggested that “unit level” factors—state characteristics other than relative power, like regime type or territorial preferences—should not be part of a “systemic” IR theory and also are not likely to have large and consistent effects on levels of conflict and cooperation.
Writing at about the same time, Jervis argued that variation in the extent of international conflict and cooperation depends on factors influencing states' ability to arm up and invade, and also to distinguish offensive from defensive forces. For example, states separated by distance and water should find it easier to cooperate, as should nuclear weapons states with secure second-strike forces, because these make invasion and conquest nearly impossible. Jervis's logic relied on the idea that states are always uncertain about whether their counterparts might be aggressive types. When offense is advantaged, it is more dangerous to cooperate (e.g., to lower your arms levels) because you are in deeper trouble if the other side turns out to be aggressive.Footnote 32
For neoliberal institutionalists the main variables determining international cooperation's feasibility were the “shadow of the future” (leaders' discount rates) and a somewhat generic notion of degree of conflict of interest.Footnote 33 Whether because the shadow of the future is difficult to measure or because leader discount rates don't explain much variation in international cooperation, the cooperation-under-anarchy program has been more successful at explaining the basis for much international cooperation and many international institutions than at explaining variation over time or across states.
What determines maximum feasible cooperation in the model presented here?
Proposition 3
Maximum feasible international cooperation (smaller a*) is (1) decreasing in the value the states derive from controlling the other's territory ( μ ); (2) increasing in defensive advantage (smaller m ) and war costs (larger c ); and (3) may increase or decrease with the extent of interdependence ( γ).
Value for Territory
The less “greedy” the states are about additional territory, the less they need to arm for deterrence (or otherwise compete) and thus the greater the scope for cooperation on other issues. This is an intuitive implication of this fundamentally realist model, consistent with the claims of neoclassical realists who argue that most international conflict stems from states with revisionist preferences rather than “tragic” conflict between fearful, uncertain security seekers.Footnote 34 In the model, however, it is precisely revisionist preferences that make for tragedy, in the sense of inefficient arming that makes war more attractive and that could be avoided but for interstate anarchy. Here, more “greed” makes for more inefficiency, not less. (Note that standard security-dilemma arguments conceptualize inefficient outcomes only in terms of conflict between security seekers.)
The mechanism is not simply that more value for additional territory makes conquest more valuable, but instead involves a feedback loop. Suppose a new leadership comes to power in state A that puts greater intrinsic value on controlling territory beyond its current borders (an increase in μ A in an asymmetric version of the model). At prior arms levels, state A would want to arm up and attack. Understanding this, state B arms to a higher level to deter A. But this makes a peaceful status quo less attractive for state B since it now has to spend on an ongoing policy of “containment.” So in turn A needs to arm more to deter attack by state B, even if state B is a pure status quo type that has zero intrinsic value for controlling more territory (μ B = 0). In turn, A’s need to deter B from attacking to get rid of the threat arising from A’s revisionist preference lowers A’s value for a peaceful status quo relative to war, feeding back again on B’s need for arms (and so on up to equilibrium levels, if a peaceful equilibrium exists).Footnote 35
Two points follow on this example. First, it shows how the model captures the Waltzian insight that “systemic forces” can override the influence of particular “unit level” state desires or characteristics. A state with no intrinsic value for acquiring more territory or deposing another regime might be driven to do so by a neighbor's greed along with system effects of its own response. The idea of “liberal imperialism” or “making the world safe for democracy” is based on this logic.Footnote 36 Second, it nonetheless does not follow that states' intrinsic value for territory is irrelevant for the level of international cooperation, or that all states are driven by anarchy to be expansionist, as “offensive realists” like Mearsheimer maintain.Footnote 37 Rather, this state-level characteristic is a natural component of a realist, structural model, and its variation has an important influence on outcomes.
There has been little analysis in IR of the determinants of states' intrinsic value for controlling additional territory, whether by critics of realism or realist critics of Waltz's and offensive realists' skepticism. And perhaps because of a lack of theory linking revisionist territorial preferences to the costs of anarchy, we have not seen extensive efforts to measure variation in territorial preferences to check whether this might explain significant variation in the costs of anarchy.Footnote 38 The baseline model suggests how the international effects of plausibly important state-level factors—such as democracy, nationalism, and industrialization—can be incorporated in a structural model and analyzed for their impact on the costs of anarchy, via their effect on states' values for territorial conquest. A very partial sketch follows.
What determines a state's value for ruling new territory? In ancien regime days it might have been the productivity of the peasants and towns that a ruling noble could tax. Nowadays it can still have to do with the material value of land. For instance, high arms levels around the Persian Gulf are plausibly related to the presence of valuable oil reserves. But probably more often it has to do with nationalist ideologies and attachments. Where there is agreement that borders correctly divide national territories, values for adding more are lower than where there is disagreement, other things equal. Empirically, arms levels tend to be much higher while cooperation and international institutions are less evident where there are dissatified nationalisms. Consider Israel and its neighbors, North and South Korea, Eritrea and Ethiopia, Armenia and Azerbaijan, or India and Pakistan (who disagree about Kashmir).
Table 1 lists the top and bottom fifteen states on two measures of military effort—military spending as a share of gross domestic product (GDP) and armed forces per 1,000 population—for both the Cold War years and the period 1991–2010.Footnote 39 The first superscript on the country name indicates the number of territorial rivalries the state was involved in according to codings by William Thompson and David Dreyer. These are cases where Thompson and Dreyer judge that two states view each other as “threatening competitors” that “contest the exclusive control of territory.”Footnote 40 Most often these territorial rivalries are linked to competing nationalist ideologies concerning what land properly belongs to the nation, or in the case of the two Koreas (which Thompson and Dreyer do not code as a territorial rivalry) which regime should rule the territory that belongs to the Korean nation. Territorial rivalries are clearly much more common among the high-military-effort states, which are often the smaller state in a dyad with an intense nationalist conflict—for instance, Eritrea, Armenia, Israel (versus its several larger neighbors), Kuwait, Greece, Taiwan, and North Korea.Footnote 41
Table 1. Top and bottom 15 states on two measures of arms levels

Notes: First superscript is number of territorial rivalries in period; second is number of states with a “positional,” “ideological,” or “interventional” rivalry (Thompson and Dreyer Reference Thompson and Dreyer2012). Some high-spending states like North Korea are missing data on military burden and so do not appear in the military burden lists. Post-Cold War is after 1990.
Regarding variation over time, there are good reasons to think that industrialization, the spread of democracy, and the sorting of people and boundaries according to nationalist ideologies have—on average and over the last 200 years—reduced states' intrinsic value for acquiring new territory. Concerning industrialization, when income comes mainly from human capital and manufactured tradables rather than land, it is arguably harder to profit from military conquest, and less necessary since trade can provide a cheaper alternative.Footnote 42 Next, democracies have less economic rationale for military conquest than do narrowly held autocracies if the rents must be shared more broadly, or if a strong norm of political equality (which might have an instrumental basis) implies that people in conquered territory would have to be treated as citizens on equal terms.Footnote 43 Concerning nationalism, the aftermath of two world wars, decolonization, and the break-up of the Soviet Union all contributed to greater congruence between interstate borders and conceptions of common nationality, albeit with a number of important exceptions that continue to stimulate conflict and arming.
Figure 2 shows striking declines over the last 190 years in the number of territorial rivalries per independent state, again using Thompson and Dreyer's codings. The change is particularly large for the militarily strongest states in the international system, which saw a steep and persistent drop in territorial rivalries in the years around World War II. To be sure, this is not a perfect measure of average values for μ, for reasons I will discuss. But since territorial rivalries involve public claims on a neighbor's territory sufficient to cause perception of serious threat, their decline is at least consistent with the proposition that on average states' value for acquiring new territory has declined. Further, the cases behind the large drop for major powers from 1939 to 1945 are consistent with the idea that democratization and more nationalism-congruent borders have contributed to the long-run reduction. These include the end of three disputes associated with Italy's switch from fascism to democracy; four territorial rivalries associated with the end of imperial Japan; and two rivalries associated with the end of Nazi Germany and the redrawing of borders (and possibly the ethnic cleansing of German speakers) in Eastern Europe.

Figure 2. Territorial rivalry over time
The Offense-Defense Balance
In the model, deeper cooperation is possible when the odds of successful attack are lower for any given force levels, which is how greater defensive advantage is defined here. Since Jervis the canonical justification for this claim has been that states are uncertain about others' preferences over territory or issues (μ and γ in the model), and guessing wrong is more dangerous when offense is relatively advantaged. Extensions of the core idea hold that offensive advantage makes “spirals of hostility” and preemptive war more likely between what are in fact security-seeking states.Footnote 44
A weakness in these arguments is that it is not clear why genuinely security-seeking states that have no territorial or issue conflicts would be unable to credibly signal this to each other over time.Footnote 45 Another issue is that it is not empirically plausible that any state has ever been a pure security seeker. Surely all states have things about the political world they would like to change if they faced no external constraints. Perhaps this is just a matter of degree, so that the Jervis-Glaser-Kydd “two type” model is still a good approximation for some cases, such as US policymakers' thinking about the Soviet Union during the Cold War. But there are many other cases where one or both states correctly understand that the other has significant revisionist preferences and these are at the root of the conflict. Standard security-dilemma arguments either rule out or have no way of conceptualizing tragic outcomes (inefficient arming, conflict) in these settings.Footnote 46
In the baseline model the states have no uncertainty at all about each other's preferences and neither is a pure security seeker (if μ > 0 or γ > 0). Thus the standard security-dilemma arguments do not apply. Instead, relative advantage for offense increases arming and lowers cooperation because more arms are needed to deter break out, and deterrence is needed because the states have some revisionist preferences. Worse, offensive advantage has a perverse multiplier effect: The more arms a state needs to deter attack by a potential adversary, the less desirable living with the status quo becomes for that state. This makes war relatively more attractive, which means that the other state has to spend more, which makes the status quo less good for it, and so on. As Powell showed and as Figure 1 represents, the net result can be that there is no arms level high enough to deter break out but low enough to make peace preferable to fighting.
Literally interpreted, the “no peaceful equilibrium” case in Figure 1 may be quite rare. But it is plausible that a state's value for living with the territorial status quo—and thus its willingness to risk war—depends in part on how much it has to spend to maintain it. The model clarifies how states' value for (living with) the status quo is endogenous to the strategic dilemma posed by anarchy, with the political economy tradeoff between guns and butter playing a central role.Footnote 47
What determines variation in the offense-defense balance and are these things related to observed patterns of international cooperation and conflict? Answering this question requires, first, additional interpretation of “offensive/defensive advantage,” a difficult concept that is the source of much debate. In almost all cases, scholars define offense-defense advantage or “balance” in terms of the ease or cost of offensive operations, either given a defender's forces or without specifying the force levels at which cost is to be evaluated. In the most detailed analysis, Glaser and Kaufmann define the balance as “the ratio of the cost of the forces the attacker requires to take territory to the cost of the forces the defender has deployed.”Footnote 48
But defenders choose forces in light of what they think is needed to deter, and defender force size strongly affects an adversary's costs or ability to arm up to a force ratio favorable for attack. So if a technological change renders existing force sizes too small for comfortable deterrence—say, railroads make the movement and supply of mass armies more feasible—then states may arm to higher peacetime levels to offset what would have been good odds for an attacker “breaking out” from the old force levels. The cost or ease of offense from the new equilibrium force levels thus need not be any different from what it was before the technological change that favored offense. Put differently, the underlying technological influences on offensive prospects (summarized by the exogenous parameter m in the model) have a direct, positive effect on the odds of successful attack for any given force levels. But this direct effect can be undone by the indirect effect a larger m has via increased equilibrium arms levels.
Indeed, the baseline model yields the following general implication, which is surprising and interesting in light of the existing literature.
Proposition 4
Consider the model with any contest success function p i(a i, a j; m), where m indexes offensive advantage in the sense that p i is increasing in m for positive arms levels. In a peaceful equilibrium with arms levels a*, the probability that a break-out attack would succeed is decreasing in offensive advantage.
So greater offensive advantage implies higher equilibrium force levels (from Proposition 3), but a smaller chance that an offensive would succeed at those force levels! The intuition is straightforward: higher arms levels make the status quo less appealing. Thus for peace to continue to be feasible at these levels, mobilizing and going to war must become less attractive, which means that its odds of success must decline. The effect of the endogenous increase in arms levels must more than offset the direct impact of an offense-favoring technological change.Footnote 49
To illustrate, consider two examples, the first hypothetical. Two kingdoms are separated by a broad river. Given the river, each requires a standing army of only, say, 1,000 soldiers to deter the other from “arming up” and invading with the maximum capacity of (say) 5,000 soldiers. A massive earthquake upstream causes the river to run dry. Now 1,000 is not enough to deter breakout because a defender no longer has the advantage provided by the river. So both sides arm to a new equilibrium level at, say, 3,000 soldiers, which is much costlier to maintain. Because war is now more attractive than before in terms of the long-run cost savings from defeating the other kingdom, arms levels have to be high enough that breakout and attack are even less likely to succeed than before to maintain deterrence. This is so despite the fact that for any fixed force levels, the elimination of the river unambiguously favors offense.
Second, consider that many have argued that Europe on the eve of World War I was characterized by a high level of defense dominance, in fact if not in leaders' perceptions. The evidence comes from the war itself, which showed that greatly improved firepower (better rifles and machines guns) had rendered taking defended terrain extremely difficult. At the same time, however, railroads and better roads had made it possible for the continental powers to mobilize vastly larger numbers of soldiers and deliver them to a front much more quickly than before the 1860s. This meant that at low initial force levels, a breakout—mobilization and rapid delivery of a mass army to the front—could give a state a good chance of victory by a crushing blow, even despite some machine guns on the other side. To deter, states thus needed to arm up to peace-time levels high enough that such a course would not be sufficiently promising.
Thus the conventional IR wisdom about this famous case may have it backwards. A situation of increased offensive advantage may have caused states to try to arm to levels high enough that breakout would not be so promising as to make attack appealing. There could have been increased offensive advantage even though at equilibrium force levels driven by this technological condition, offense was not highly likely to succeed.Footnote 50 Arms levels determine the likelihood that an attack will succeed, but at the same time the likelihood that attack will succeed determines arms levels. In equilibrium, it may appear that “defense dominance” prevails because many machine guns and sophisticated use of railroads by a defender could probably stop an attack. But the need for many machine guns and many quickly mobilizable troops in peacetime is driven by an offensive advantage (the ability to generate a massive, mobile army quickly). Further, high levels of costly arms and military preparedness, or the anticipation of ruinous arms racing, makes a peaceful status quo less appealing.Footnote 51
To summarize, offense is more advantaged the greater the odds that an attacker wins for any given force levels, and the more forces mobilization can add before an adversary can effectively counter. Greater offensive advantage in these two senses implies higher equilibrium arms levels and other forms of costly competition (less international cooperation); probably greater odds of large-scale war; but not greater odds that attackers will actually win their wars.Footnote 52
With the offense-defense balance so understood, in a conventional world any technological or doctrinal innovations that enable states to mobilize and deploy troops more quickly favor offense and so should make for higher arms levels and less international cooperation. By contrast, because the threat to use nuclear weapons becomes increasingly credible as a nuclear-armed state loses homeland territory in conventional war, nuclear weapons make old-style territorial conquest difficult to imagine. As Jervis and others argued, this technological development implies a major shift in the direction of defense dominance among nuclear states, and probably even among states that could acquire nuclear weapons on short notice. With secure second-strike forces, a break-out attack to overwhelm an adversary becomes suicidal for any disparity in conventional arms.
The empirical expectation, then, is that prior to the nuclear era the major powers should have seen increasing arms levels and decreasing international cooperation after Prussia's demonstration of how railroads, good roads, and organization could be used to rapidly deploy mass armies in the Austro-Prussian and Franco-Prussian wars of 1866 and 1870. Onorato, Scheve, and Stasavage document how the share of major power populations mobilized during interstate wars increased enormously in the period from 1859 to 1970 (or 1954), compared to wars in previous and subsequent years.Footnote 53 They argue that this was largely a result of the railroad. This is direct evidence for a large increase in offensive advantage in a sense specified here—railroads and other technological and organizational innovations caused a substantial increase in capacity to mobilize and deploy large numbers of troops rapidly. Thus the results from the baseline model imply that we should see, for the major powers, a general tendency for peacetime force levels to be increasing, until the impact of nuclear weapons begins to be felt, after which there should be declines.Footnote 54
The solid black lines in Figure 3 display armed forces per 1,000 population for nine major powers for 1816 to 2007, during years when the state was not engaged in an interstate war. The lines have wide dashes for years of interstate war. The small-dashed line is a smooth of the solid black line, thus showing the trend for peacetime armed forces in the state (wartime force levels are not included in the smooth).Footnote 55
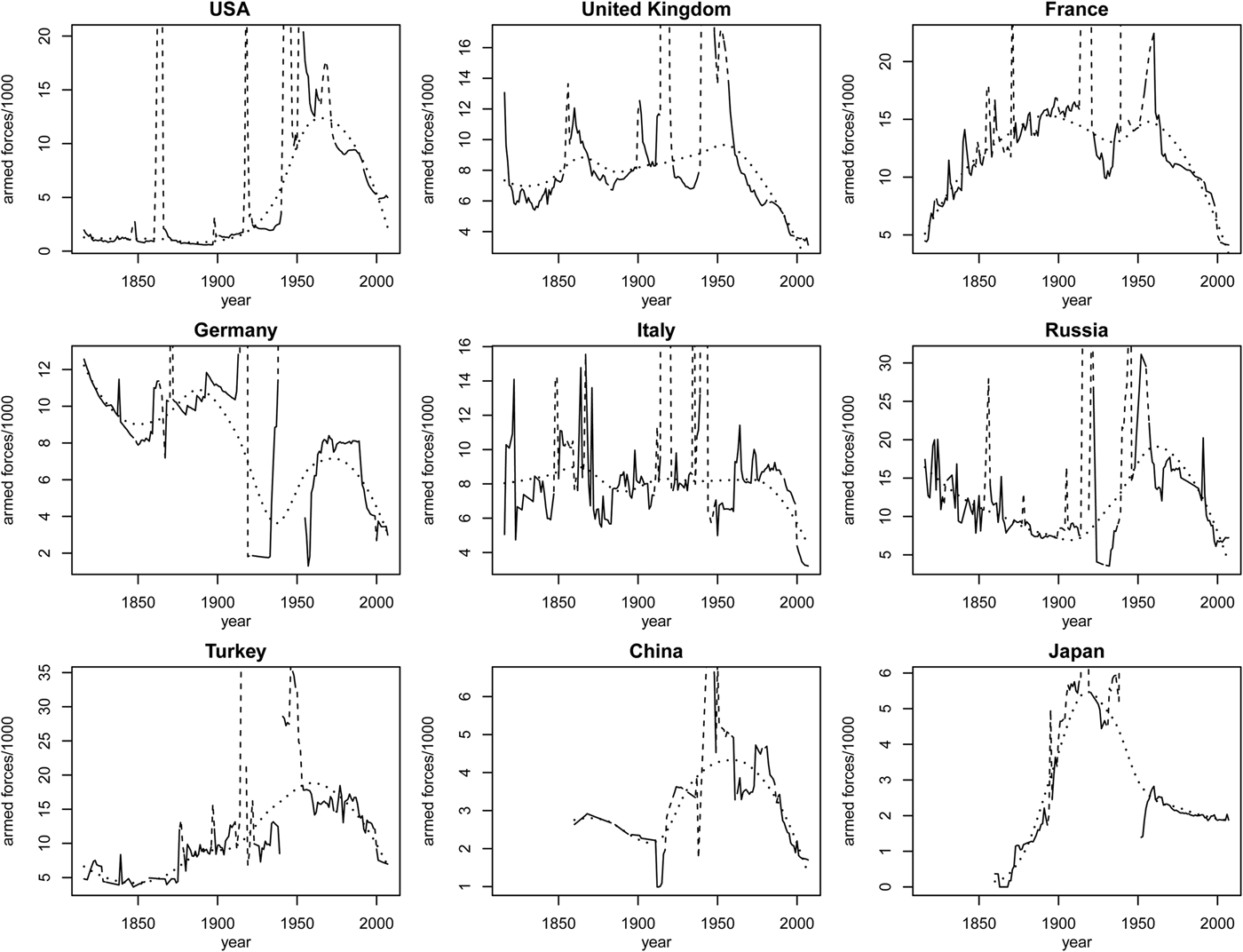
Figure 3. Peacetime armed forces per 1,000 population
The patterns—mainly “inverse-U” shaped—are largely though not entirely consistent with the expectations based on the broad system-level variations in the offense-defense balance I described. First, all of these states see declines (and mainly large declines) in armed forces from the mid-1950s to the present. Although in a few cases the decline occurs mostly after the end of the Cold War, for most it takes place throughout. This is consistent with the major powers adjusting gradually to a new world in which, in contrast to the period from (at least) 1900 to 1950, they do not need to worry about being able to quickly raise a mass army to defeat a possible attack by another major power in a total war. Of course, other factors may contribute to more cooperation and less competition among the major powers since World War II. More are democracies and there are fewer nationalist disagreements about which nations should own what land in Europe or Northeast Asia since the postwar settlements. Both factors may lower values for annexing territory, which in the baseline model implies lower arms levels. But the pattern is nonetheless also consistent with the large increase in defensive advantage arising from the advent of nuclear weapons.Footnote 56
On the other side of 1945, in various degrees France, Britain, Germany, the US, Japan, and Turkey (Ottoman Empire) all see increasing force levels in the years leading up to World War I, consistent with the implications of increased offensive advantage in the second part of the nineteenth century. Russia, Italy, and China do not, however, with these data. Russia may be explained by the fact that its absolute army sizes were growing rapidly as a result of its large population and moderate population growth.Footnote 57 Note also that after 1860 almost all European powers moved to conscription and shorter periods of service to increase reserve forces and the number of young men trained to fight. By contrast, in the nuclear era the major powers have moved back to smaller professional armies with long service periods, and smaller reserve forces.Footnote 58 Historians have often stressed increasing military competition and arms racing in the decades leading up to World War I.Footnote 59
For the interwar period, the German army abided by the force size limitations of the Versailles Treaty until 1933 when Hitler began his rearmament drive. Faced with a major power regime that appeared to have greater value for territorial expansion than before, the other European powers and the US followed quickly, though not quickly enough. Joseph Maiolo details the politics of the European and Asian arms races of the 1930s. Military and civilian leaders in all the major powers had concluded from the Great War that “a modern war is a war of nations rather than armies,” so that peacetime forces and military industry had to be capable of rapid expansion.Footnote 60 He argues that the strain of mobilizing to get to higher peacetime arms levels in the midst of the Depression was an important factor driving Europe to war. The much larger mobilization capacity of a hostile Soviet Union meant that deterrence would require high and possibly unsustainable levels of peacetime armament in Germany. Similarly, Dale Copeland shows how concern about the inability to match Soviet military capacity in the long run motivated both Hitler and his generals to plan for preventive war from 1933 on.Footnote 61
Value for Issues Other Than Territory
The term γ represents the states' value for issues other than homeland territory, and which cannot be determined unilaterally by either state. The larger γ, the more each state's welfare depends on the other's actions, and the greater the potential for cooperation in the neoliberal institutionalist sense of agreements to share gains from mutual restraint on competitive policies.Footnote 62 The empirical example of greatest interest, given an extensive literature and debate, concerns gains from international trade. Clearly, greater potential gains from trade imply greater potential for international cooperation, as might occur if trade costs decline (because of, for instance, steam power or containerized shipping, or with geographic proximity). But how do greater gains from trade affect the costs of anarchy, here measured by a*, the smallest arms level consistent with a stable peace?
In contrast to value for territory or war costs, increasing the gains from trade has competing effects. On the one hand, greater gains from trade increase the value of a peaceful status quo in which these are shared, but on the other hand, there is more value to be captured from a successful all-out war. The first effect favors lower arms levels, the second higher.
Virtually the entire literature on interdependence and war neglects the second effect. The standard argument is that more trade between two states increases the opportunity cost of war, a claim that does not consider what happens to trade after one side wins a war. If the winner takes over or sets the policies of the loser, it can capture all gains from trade for itself.Footnote 63
The competing effects of greater gains from trade tip in the direction of relaxing the war constraint the more the states have decreasing value for additional gains (the baseline assumes risk neutrality for simplicity). This is because an international agreement that divides the gains gives a state a “bird in the hand,” whereas trying to grab all via war is a gamble on “two in the bush.”
The results on γ also depend on how we envision domestic politics affecting the distribution of gains from successful war. For an autocrat or a democracy willing to economically oppress the people in a defeated country, successful war might double the “gains from trade” via the increased tax base that results from conquest. But to the extent that the winning state would not disproportionately tax people in the defeated territory, then increased gains from trade simply increase the value of a neoliberal deal between independent states, so reducing international competition (a*).Footnote 64
Finally, note that increasing the gains from trade in the model is not the same thing as reducing protectionism. The analysis assumed that gains from trade are fully exploited in a neoliberal deal between states—γ is divided equally and fully. To model protectionism or other barriers to full efficiency when the states are sovereign, let the gains available in peace be γ p < γ, p for “protectionism.” Now it is immediate that greater protectionism implies a tighter war constraint and greater a*, since there is now a greater economic efficiency motivation for war.Footnote 65
Protectionist and colonial trade blocs in the 1930s were thought to have favored war by increasing the returns to acquiring territory where a major power could guarantee a flow of resources and benefit from trade based on comparative advantage. Rosecrance and others have argued that free trade favors peace because it provides states with a cheaper means of obtaining benefits that, in a world with less free trade, might require conquest to obtain.Footnote 66 The model formalizes and extends this argument. Free trade favors lower costs of anarchy not because it is a benefit foregone while fighting, but because it reduces the relative economic appeal of successful conquest. Thus freer trade should allow states to maintain lower equilibrium arms levels. Lower costs of anarchy in turn make a peaceful status quo more beneficial and so more robust against temptations for war.Footnote 67
Differences in Relative Power and Greed, and Multipolarity
For clarity the baseline model assumed two states with equal resources, the same preferences over territory, and the same war costs. I next consider a variant that allows for asymmetries, and briefly discuss the restriction to two states.
Relative Power and Arms Levels
Existing IR theory makes no predictions about how the military burdens of two adversaries should be expected to vary with relative resources.Footnote 68 If state A grows larger than state B, how will force sizes or military spending change? Empirically, examples from Table 1 suggest a tendency for the smaller state in a rivalrous dyad to make a larger military effort, relative to resource base. Perhaps this makes intuitive sense—the smaller state needs to spend a larger fraction of income to match the arms levels produced by an even smaller fraction spent by the larger state.
Analysis of an asymmetric version of the baseline model largely supports this intuition, but with qualifications. In the online appendix I consider an extension in which the states have resources r 1 and r 2 that they can spend on arms, where R = r 1/r 2 indexes state 1's “relative power.” The analysis identifies offsetting strategic dynamics. First, greater resources for state 1 means that it can get a bigger advantage from mobilizing and attacking, which implies that a smaller state 2 needs a larger peacetime military burden to maintain deterrence. However, greater resources for state 1 also means that state 2 has more to gain from successful conquest, a motivation that presses the larger state to spend more to deter. The second strategic logic is referenced by President Theodore Roosevelt's remark that “undefended wealth invites aggression,” suggesting that rich countries need to spend more to deter invasion.Footnote 69
Nonetheless, further analysis shows that under a plausible assumption about how war costs vary with relative size—namely, that the smaller state faces higher costs—the smaller state in a rivalry will tend to have the larger military burden. Let i’s costs for war with j be c ir j. In the case of the ratio-form military technology, a closed-form solution for the lowest feasible equilibrium military burdens, ![]() $b_i^{\ast} = a_i^{\ast} /r_i$, can be derived. Figure 4 shows how state 1's military burden varies as we vary the ratio of its total resources to state 2's (that is, R = r 1/r 2), for two levels of offensive advantage and two levels of “greed.”Footnote 70
$b_i^{\ast} = a_i^{\ast} /r_i$, can be derived. Figure 4 shows how state 1's military burden varies as we vary the ratio of its total resources to state 2's (that is, R = r 1/r 2), for two levels of offensive advantage and two levels of “greed.”Footnote 70
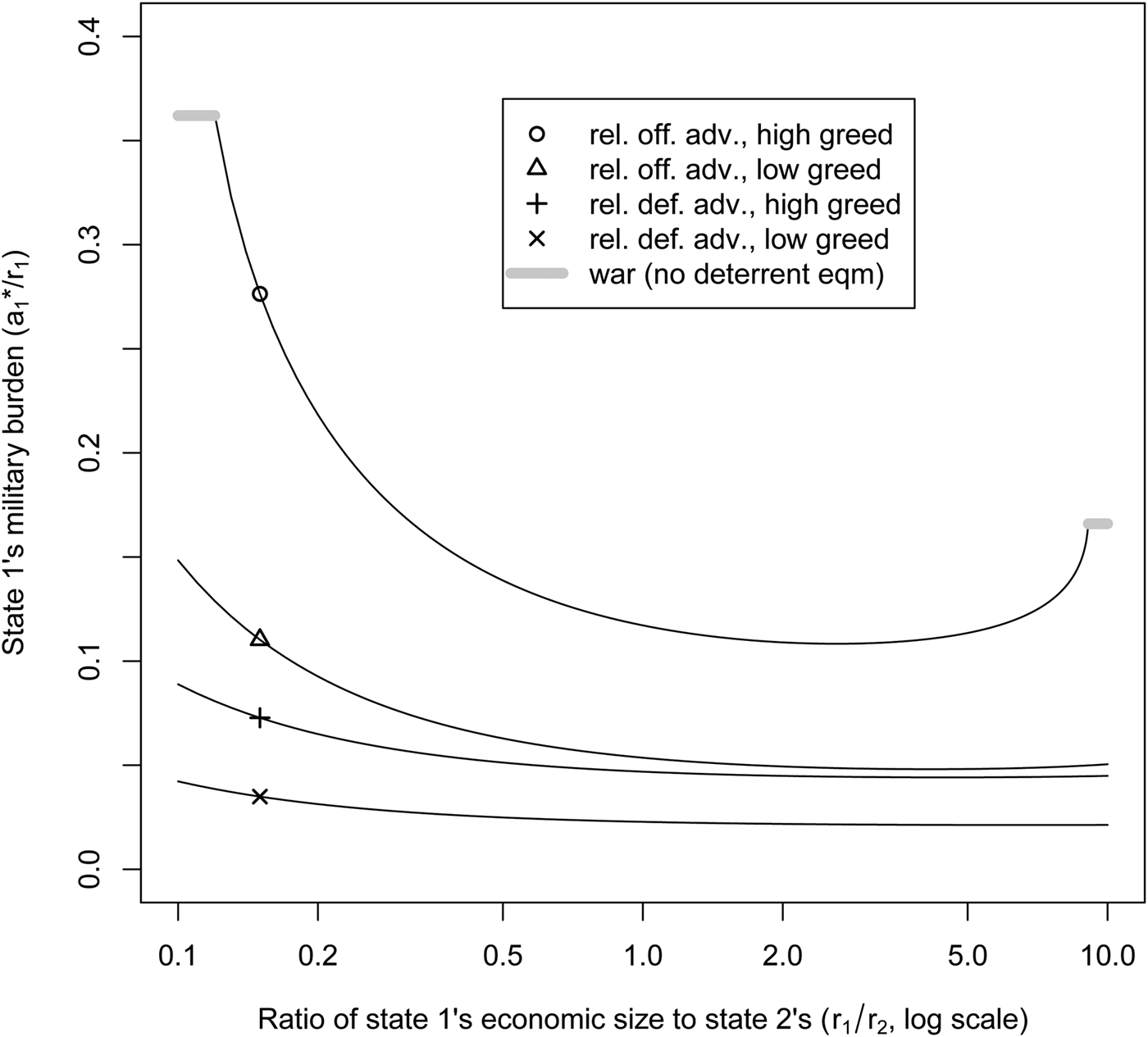
Figure 4. Relative power and military burdens
The smaller state has the larger equilibrium military burden, and its burden increases as the power disparity grows. The size of these effects increases with greed and offensive advantage, and decreases with greater war costs. Except in the case of high greed and high offensive advantage, military burdens are quite insensitive to relative power ratios. This is a result of the offsetting strategic forces just described.Footnote 71
Asymmetric Greed or War Costs
States can differ not only in relative size but also in the value they put on acquiring new territory or costs of fighting relative to value for new territory. To extend possible asymmetries to these factors, let μ i ∈ [0, 1] be the weight state i puts on control of j’s territory, and c i be i’s costs for war. Consider a version of the model in which there is no issue competition and states arm sequentially, as in Powell's formulation. We then have
Proposition 5
Let w i(r i, r j, μ i, c i) be state i ’s value for winning a war, and suppose that w i is increasing in μ i and decreasing in c i. Then for any military technology, increasing the value i puts on control of j ’s territory, or reducing i ’s costs for fighting j, implies greater equilibrium military burdens for both states.
The key point here is feedback effects—security externalities that work through increased costs of deterrence. In an extreme case, a sufficiently greedy state could lead a status quo state—one with zero intrinsic value for additional territory—to prefer war to eliminate the greedy regime and so reduce the need for costly deterrence and competition. US entry into World War II, and arguably the Iraq War of 2003, were partly motivated by this logic, which accords more generally with the idea behind Wilson's notion of war to make the world “safe for democracy.”Footnote 72
With issue competition (γ > 0) and simultaneous arms decisions, if state i's value for territory increases then j's equilibrium arms level must increase. However, state i's arms level can stay approximately the same or even decline slightly. The reason is that while more arms increase j's costs of deterrence, they also improve its outcomes in issue disputes, so weakening its motivation for all-out war against i. In arming up to deter an expansionist adversary, a state with little or no intrinsic value for acquiring more territory gets the side benefit of greater power in international disputes. These make living with the expansionist state marginally more palatable, so weakening the threat to the expansionist. By a different mechanism, there is a parallel here to David Lake’s argument for why democracies may be “powerful pacifists,” in the sense of having little interest in territorial acquisition but strong military capability.Footnote 73
More Than Two States
Waltz proposed to explain variation in major power war risk by the number of major powers. He argued that more than two (“multipolarity”) implied higher risk from greater odds of miscalculation about who would fight with whom, because of complexity and incentives for “buck passing.” But he also argued that states balance, allying with the weaker side against a stronger aggressor. This tendency should create expectations of coalitions forming against aggressors under multipolarity, thus some effect in the opposite direction.Footnote 74
Multipolar balance-of-power models in which coalitions can form are complex, sensitive to what seem like fairly arbitrary assumptions, and appear to support few general results.Footnote 75 In addition, to date they abstract from features such as geography that have been critical influences on what coalitions are likely to form in, say, European great-power politics.Footnote 76 These are reasons that it makes sense for a baseline model to begin with relations between just two states. But it also means that some important strategic dynamics cannot be addressed by the model, such as the US or Britain entering continental wars out of fear that victory by France or Germany would harm them in the future.
Nonetheless, for an empirically common case of multipolar politics we can get a useful implication from the baseline model. If there is a “balancer” state that would intervene on behalf of state j when state i attacks j, this amounts to defense dominance in the model: either the war costs of the attacker are increased, or the odds of victory are decreased (smaller m). By results summarized in Propositions 3 and 5, in both instances the war constraint is relaxed and greater cooperation becomes feasible between i and j.
The UN order and decolonization after World War II created a system with many small, poor, formally independent countries, mainly in Africa and Asia. Invasions in the developing world with the goal of conquest or annexation of territory have been extremely rare, in some part because of developing states' “recognition that they will probably meet strong Western opposition if they embark on territorial aggression.”Footnote 77 The implication from the model is that these states can afford to have smaller militaries than they otherwise might. Indeed, for many countries that do not have a significant nationalist land dispute with any neighbors, the size of their military may not reflect interstate deterrence at all, but instead is a matter of domestic demand (a D as discussed earlier). In other words, for large parts of the world, there is no binding war constraint on arms levels and international cooperation. The costs of interstate anarchy are low for these states as a result of major power policies.
Conclusion
States can use military effort to change the world beyond their borders in directions they like and also to invade other states or defend against invasion. But because military effort is costly (there is a guns-butter tradeoff), they face a strategic problem akin to repeated Prisoners' Dilemma (PD). Threats or use of force can gain short-run advantage on various issues, but if other states do the same they end up spending more for no long-run benefit. Thus agreements to limit costly competition by strategies of conditional cooperation (e.g., tit for tat), often facilitated by international institutions, make sense, even for highly “greedy” states.
However, because the strategic problem states face in anarchy is not a standard repeated PD, this “neoliberal institutionalist” mechanism cannot in general be used to reduce the costs of anarchy to zero. Unlike in repeated PD, a cooperating state can be eliminated or permanently disadvantaged (made unable to retaliate effectively) if the other state “defects.” As seen in the baseline model, the extent of international cooperation is limited by states' need to maintain enough arms to deter mobilization and attack by potential adversaries. This “war constraint” sets a lower bound on the costs of anarchy. In the model, the lower bound is determined by the offense-defense balance, the intrinsic value both states put on controlling additional territory, and the extent of gains from cooperation on issues beyond homeland territory.
The model shows how diverse and apparently conflicting theoretical arguments can be synthesized in the sense of being derived in a clear, connected fashion from a small set of realist premises. Some of its main implications are similar to those of the closest thing to a baseline model in the literature, the two-type security-dilemma theory posed by Jervis and developed by Glaser, Kydd, and others.Footnote 78 However, its core strategic logic is different. In this way it suggests an alternative theoretical foundation.
In the model, the costs due ultimately to anarchy arise not from states' uncertainty about others' territorial aims, but instead from a strategic dynamic rooted in political economy. For instance, state A’s revisionism forces B to spend more to deter, which lowers B’s value for the status quo, forcing A to spend more to deter B, which lowers A’s value for the status quo further, and so on. Greater equilibrium military competition makes states more willing to risk war in crises or try preventive war to avoid oppressive defense burdens in the future.Footnote 79 Greater offensive advantage in geography or military technology means that states have to arm more to get the same degree of deterrence, thus endogenously lowering states' values for living with the status quo and exacerbating a “security dilemma” as this theory would understand it.
The standard two-type model has no way to understand tragic inefficiency between states with some revisionist preferences. Here, by contrast, anarchy can cause tragedy for any set of states not all known to be pure security seekers, as a result of security externalities of costly competition in arms or other military effort.Footnote 80
Extensions to the complete-information model might introduce incomplete information about preferences for territory (μ). Its absence is not intended to suggest that uncertainty about motivations is unimportant for interstate interactions. Jervis, and much work following him, demonstrates otherwise.Footnote 81 Starting with a complete-information baseline is useful for multiple reasons, including clarifying the sources of the costs of anarchy and allowing us to understand just what incomplete information about motivation would add.
Moreover, not all interstate competition is driven by uncertainty about the other side's intrinsic preference for territorial expansion. For instance, it seems plausible that Chinese and US leaders understand perfectly well that China would like to revise the “territorial” status quo in the East and South China seas, and that the US would prefer that they did not. Likewise, the leaders of North Korea and Iran correctly view US administrations as having revisionist preferences concerning their regime type, so that the US can't easily commit not to support avowedly democratic challengers in these states in the event of domestic uprisings (as in Libya). This known US revisionism can then add to the incentive to develop nuclear arms.Footnote 82 Such interactions may not be best analyzed in terms of status quo types' uncertainty about whether the other is revisionist, and yet—by the strategic logic developed here—they can still be very costly and inefficient as a result of anarchy.
Even though the costs of anarchy have been at the center of arguments in IR for years, there have been almost no efforts to measure them empirically, beyond studies of patterns of interstate war. The analysis here suggests that arms levels provide a theoretically defensible measure because failures of cooperation in areas where repeated interactions could in principle support deals should not be blamed on anarchy. Moreover, arms levels are a convenient measure both for gauging welfare consequences of anarchy across time and space and for assessing how much a “third-image” logic influences these costs. Regarding welfare consequences, arguably a couple percent of GDP for most countries these days—the median was about 1.5 percent in 2012—is not that much tragedy, especially if one considers that for many countries, some large fraction of this is wholly about domestic stability or military politics rather than interstate competition. An important point, consistent with “defensive realism” and critics who stress domestic determinants of territorial preferences, is that low costs of anarchy in a nuclear world with many industrialized, free-trading, nationalism-satisfied major-power democracies is implied by a realist baseline model.Footnote 83
If antitrust law permitted it, profit-seeking firms would merge to form a monopoly. Likewise, the two states in the model could in principle completely eliminate the costs of anarchy by merging or federating, after which they could end military efforts directed at external defense. The condition of anarchy among states is not a natural given but instead an endogenous choice made by state leaders. States do not merge for the same two main reasons that combatants in civil wars find it so difficult to agree on power-sharing arrangements. First, it is risky to trust that a new government's paper constitution will protect one from attack and expropriation after one has disarmed or ceded control to a powerful higher-level military force. Second, in the modern period when nationalist sentiment can be very strong, a leader and his or her constituents may simply have a large “consumption value” for formal independence, so that the costs of anarchy are a price of nationalist satisfaction. The higher the price, the stronger the incentive for small states to merge or accept protectorate status, and for major powers to seek stronger institutions at international or regional levels. But strong international institutions will be harder to build because of the underlying conditions that create the need for costly deterrence. When the costs of anarchy are low (for example, at present, for the reasons suggested), genuine pooling of sovereignty might be more feasible but there is also less call for it, and more scope for international institutions and conditional cooperation between independent states.Footnote 84
Supplementary Material
Supplementary material for this article is available at <https://doi.org/10.1017/S0020818318000115>.







