2. PIC SIMULATIONS

We apply a PIC method to simulate the interaction of a plasma layer with an intense ultrashort laser pulse. The method is based on the electromagnetic PIC and is appropriate for analysis of the dynamics of overdense plasmas created by arbitrarily polarized, obliquely incident laser pulses. The 2D (using a Cartesian coordinate system) relativistic, electromagnetic code (Satou et al., 2001) is used to calculate the interaction of an intense laser pulse with an overdense plasma. Calculations with ion mobility allowed were carried out for a plasma with the initial density profile shown in Figure 1. Simulations were performed for laser wavelengths of λ = 1 μm and laser intensities I_L ≥ 10¹⁹ W/cm². The laser pulse was linearly polarized, normally incident, and the intensity distribution was Gaussian in shape and time with the duration of t_L = 40 fs. The time step is chosen to be 0.03/ω_L, where ω_L is the laser frequency, and the mesh size is chosen to be 0.03 c/ω_L. The number of x-axis grid points is 10⁴ and the maximum electron density is n_emax = 4n_c, where n_c is the critical density. The size of the simulation region is 50 μm × 70 μm and the number of electrons ∼10⁷ (the same for ions). Initial electron temperature is 1 keV and ion temperature is 800 eV. Thickness of the plasma layer l_p (foil thickness) varied from 1 μm to several microns. Plasma density gradient L varied from 0.1 μm to several microns. The plasma layer was initially localized in some runs at 220 ≤ ω_L x/c ≤ 238 (see Fig. 1). For simplicity, uniformity in the z-direction is assumed. The relativistic equations of motion and Maxwell's equations are solved for the components x, y, p_x, p_y, p_z, and E_x, E_y, and B_z:

Here q_j, m_j, and γ_j indicate the charge and the mass of a particle and the Lorentz factor, respectively, and j_j is the current density. PIC simulation results are shown in Figures 2, 3, 4, 5, 6, and 7 and will be discussed below together with the analytical model.

Target density profile and target position in the simulation area. The plasma layer is initially localized at 220 < ωL x/c < 238 inside the simulation box of size 0 < ωL x/c ≤ 450; 0 ≤ ωL y/c ≤ 315.

Electron and ion energies and the absorption coefficient dependence on the normalized plasma density gradient ωL L/c at ωL t = 133. Maximum electron density ne = 4nc, the plasma slab length is 2 μm, Z = 1. The laser beam radius R = 2μm, tL = 40 fs is the pulse duration, the intensity IL = 1020 W/cm2 for electron and ion energies, and IL = 1019 W/cm2 for the absorption coefficient.

Electron distribution function at ωL t = 500. The laser beam and plasma parameters are the same as in Figure 2.

Spatial distribution of the ion density at both sides of the foil target at time ωL /t = 333. The laser and plasma parameters are the same as in Figure 2. The plasma density gradient length L = 1 μm.

a: Ion distribution in the velocity phase space at ωL t = 166. The laser beam parameters and target parameters are the same as in Figure 2. b: The same as in a, but at ωL t = 333.

Dependence of the fast ion velocity rate (vy /vx) on the laser intensity at ωL t = 333. The upper curve is the PIC simulation result, whereas the lower one is the result from Eq. (13). Target parameters are the same as in Figure 2.

Positions of 10 fast ions at time ωL t = 0 (+), ωL t = 300 (x), ωL t = 400 (*), ωL t = 600 (□), ejected from the foil rear with different y-coordinates. Solid curves are the ion energy spatial distributions at the same moments. The laser beam and plasma parameters are the same as in Figure 2.

3. FAST ELECTRON GENERATION

Ion acceleration depends critically on the efficiency of the transfer of laser energy into high-energy electrons, because these electrons are the source of the requisite strong electrostatic fields. Numerical simulations show that for the intensity I_L ∼ 10¹⁹ W/cm² and for a short (40 fs) laser pulse, the absorption coefficient is independent of the angle of incidence, with the absorption of about 14% when no prepulse is used (see Fig. 2). Close absolute values of the absorption coefficient (10%) and a dependence of the absorption coefficient on the plasma gradient L similar to Figure 2 were obtained by Lefebvre and Bonnaud (1997) for a 130-fs pulse duration and 4·10¹⁹ W/cm² intensity. An immobile ion approximation was assumed in this paper in contrast to our model. A small difference in results means that the ion movement for such a laser pulse and intensity is insignificant and has no influence on the absorption. For a bigger laser intensity of 10²⁰ W/cm² the absorption coefficient, according to our simulations (Andreev et al., 2003), increases up to 30%, which means a significant influence of ion movement on absorption at higher intensity even for a very short pulse duration.

We estimate the number of fast electrons accelerated by the laser pulse to be N_eh = K_e(I_L)ε_L /ε_eh, where ε_L is the laser pulse energy, K_e(I_L) is the transformation coefficient of laser energy into fast electron energy, and ε_eh is the average energy of the fast electrons. It has been shown (Key et al., 1998) that in the range 10¹⁸–10²⁰ W/cm², K_e(I_L) increases linearly from 0.03 up to the plasma absorption coefficient η for subpicosecond laser pulses. For laser intensities of more than 10¹⁹ W/cm², K_e(I_L) ≈ η. This means that initially all of the laser energy absorbed by the plasma is assumed to be transferred to high-energy electrons and then fast electrons transfer energy to fast ions and other loss channels. The analytical scaling from Andreev et al. (2003) of average η(L,I_L) is close to the PIC simulation data:

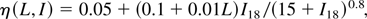
where I₁₈ is the laser intensity in units 10¹⁸ W/cm² and L = Lω/c. Formula (1) is correct at a laser intensity interval 10¹⁸–10²⁰ W/cm². Let us mark that the PIC simulation gives a local maximum of η(L) dependence, shown in Figure 2, but analytical scaling (1) gives only the average value of the absorption coefficient and therefore shows a smooth increase with L. This maximum is connected with the resonance ponderomotive absorption (Andreev et al., 2003).

The average energy of the fast electrons is then calculated from the ponderomotive potential (Wilks et al., 2001):

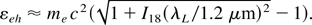
As an example, for the laser intensity I_L = 10²⁰ W/cm², the average fast electron energy (2) is ε_eh ∼ 4.3 MeV, and it is close to the electron energy from Figure 2. The number of fast electrons is N_eh ∼ 2.2 × 10¹¹K_e(I_L) ≈ η ≈ 0.3 and the laser beam radius R = 2μm.

In underdense plasmas with a large scale of plasma inhomogeneity L, an additional electron acceleration occurs, giving electron energies approximately proportional to I₁₈^3/2 (Maksimchuk et al., 2002) and therefore a dependence of electron energy on the laser intensity, ε_ch(I₁₈), sharper than I₁₈^1/2. For example, an experimentally observed relationship of ε_eh(I₁₈) ∼ I₁₈^α, α = 0.8 has been reported (Nemoto et al., 2002). In our case, the scale of plasma inhomogeneity L is less than or of the order of the laser wavelength, and Eq. (2) is valid as an estimate of the electron energy over the range of laser intensities of 10¹⁸–10²⁰ W/cm².

We consider the propagation of laser-generated fast electrons through the foil target in order to find its distribution and the number that propagate from inside the target to the vacuum at the target rear. The effects of surface curvature and the modulation change the angular distribution of fast electrons propagating inside the target. The effect of surface curvature is important here because we consider a laser beam of small radius, ∼2 μm. At the equilibrium where the ponderomotive pressure and the ambipolar field balance each other, the electron density is

where n_i(x) is ion density, Δ = ∂²/∂x² + ∂²/∂y², and a_L = eA_I /mc² is the normalized vector potential of the laser wave. A Gaussian (as in the 2D PIC simulation) dependence of the laser beam intensity on the transverse coordinate y is assumed, as is an exponential drop in the skin layer l_s inside the plasma:

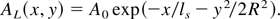
From (3) and (4) and by equating n_e = n_c, the critical density surface x = x(y) can be found. The derivative of this, dx/dy, is then used to calculate the average angle between the normal to this surface and the axis x:

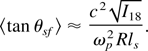
This angle increases with the increasing laser intensity and the gradient and with the decreasing spot size R. For the laser parameters used in the simulations, (5) gives θ_sf ∼ 6° (at ω_L l_s /2c ∼ 0.3), which agrees well with the simulation results. We should note that Eq. (5) gives only an averaged estimate of the angle. The detail dependence of θ_sf on the transverse coordinate is given in our paper (Andreev et al., 2003). Near the laser beam center, where the intensity has a maximum and the electrons of a maximal energy are generated, the angle is less than 2° and only at a half beam radius does this angle reach the estimate (5). Let us mark that an increase of the critical surface curvature stops at larger laser intensities (or pulse durations) because of the instability development, which perturbs the critical surface. The growth rate estimate for this instability approximately corresponds to 1/(40 fs) at 10²⁰ W/cm².

An initial curvature of the target surface ∝ θ_sf can then compensate such a critical density surface curvature and therefore the electron beam divergence. An additional divergence of the fast electron bunch θ₀ is produced by the direct interaction with the laser field. Electrons receive a pulse of transverse momentum from the laser electric field E₀ over a time t_a = l_s /v_x. Because the longitudinal electron velocity v_x ∼ c, t_a << 1/ω_L and the accelerating force eE₀(1 − υ_x /c) ≈ eE₀ /2γ_e², the angle θ₀ can be estimated as

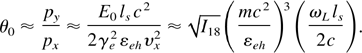
PIC simulation results of the electron distribution function are shown in Figure 3 for the plasma density gradient L of 1 μm and the slab length of 2 μm. For very fast electrons, γ_e ∼ 5, ω_L l_s /2c ∼ 0.3 and therefore from Eq. (6), θ₀ ∼ 5° as in the simulations. The electrons of a smaller energy, γ_e ∼ 1, have a wider angle distribution (see Fig. 3). The simulation also agrees with the analytic result of Eq. (6) that the fast electron divergence decreases with the increasing laser intensity, despite the fact that the angle (5) increases with the intensity. This effect is described by our selection of a maximal energy of electrons from the distribution function in Figure 3. As we already mentioned above, such electrons are generated near the beam center where the intensity has a maximum. The critical surface has a minimal curvature at this area (this surface approximately reproduces the transverse profile of the laser beam). Therefore the angles of propagation of such fast electrons fall down with the laser intensity. The total electron divergence θ_e = θ_sf + θ₀ does not significantly increase with the propagation of the electron jet through the foil, because the Coulomb binary scattering angle θ_sc is very small for the parameters used in the simulations: n_c = 4n_c, ε_ch ∼ 1 MeV, L_foil ∼ 2 μm give θ_sc ≤ 1°, which is not significant. The self-generated magnetic field has more influence on the electron beam propagation. The beam current J_eh = eN_eh /t_L is much bigger than the Alfven current J_A = m_e c³/e. Therefore, the direct current produces a return current to compensate its magnetic field. In a real plasma with a finite conductivity, the magnetic field can be as large as a few MG and the gyro-radius of a fast electron can reach the foil thickness. The electron spatial distribution in such a magnetic field looks like a ring. PIC simulations (Pukhov, 2001; Cowan et al., 2002) reproduced such a ring for a thick foil (near 100 μm), but for our case of 2 μm it is a small effect. The plasma density filaments initially produced by the plasma surface modulation could be merged by the self-generated magnetic field (Pukhov & Meyer-ter-Vehn, 1997) and do not increase the electron bunch divergence. In our simulations we did not get a large development of such an instability.

The angular distribution of fast electrons ejected from the skin layer has been simulated by Ruhl and Mulser (1995) and is reproduced well by θ_e(I₁₈) calculated from Eqs. (5) and (6). For example, the angle of ejection of electron jets from Ruhl and Mulser (1995) is 20° and from Eqs. (5) and (6), for the same parameters, is near 15°.

The radius of the electron jet is approximately R + 1(θ₀ + θ_sf ) ∼ 2.5 μm and length is approximately l ∼ ct_L ∼ 12 μm for a 40-fs laser pulse. As the foil thickness is only 2 μm, the electrons are leaving the foil. The ejected electrons induce an attracting, opposite charge at the surface of the foil and partially come back to the foil.

The maximum distance h from the foil that the electrons can travel can be easily estimated by equating the electrostatic energy of the rear surface electrons e²N_eh⁽¹⁾²/2R (here N_eh⁽¹⁾ = πR²hn_eh) to the total energy of the same electrons N_eh⁽¹⁾ε_eh giving

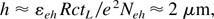
where n_eh ≈ N_ehπR²ct_L. The ejected electrons induce an attracting, opposite charge at the surface of the foil. The time for the electrons to fall back to the surface is t = mcγ_e R²/eQ, where Q ∼ Rε_eh /e, so that the length of the propagation path of the electrons along the surface is ct_b ∼ 2R. This “fountain” effect produces a volume ring of noncompensated electric charge at the foil surface with the internal radius R, the external radius R_ext ∼ 2R, and the height h. The target surface inside the ring of radius R has a positive charge of approximately Q = N_eh⁽¹⁾e (there are N_ch⁽¹⁾ electrons in a circle of radius ∼ R, and another N_eh⁽²⁾ in the outside ring; see Fig. 8). This nonequilibrium condition continues for some period of time after the laser pulse has terminated, allowing outside thermal electrons to balance the electric charge. The electron ring and its movement can be seen in our simulations. The transverse velocities of electrons near the target surfaces are estimated from the simulations to be much less than the speed of light, indicating that electrons are bound by fields near the surfaces. Only approximately 10% of fast electrons contribute to the acceleration of ions via the ambipolar field; therefore the electron losses from the front side of the target can be neglected. These processes continue for 10s of femtoseconds after charges have equilibrated. The ion pulse starts at the beginning of the laser pulse and continues during this time. Because of its low velocity (∼8 × 10⁸ cm/s) compared to that of the electrons, it only moves a small distance of ∼1 μm during the acceleration stage.

A general scheme of laser plasma foil interaction and the ion bunch generation.

Let us mark that a small number N_ef of ultrafast electrons with the energy ε_ef = (γ_ef − 1)mc² overcome the electrostatic barrier when γ_ef > N_eh e²/mc²R and propagate into the vacuum with a small angular divergence θ_ef . Estimating the electron bunch radial electrostatic field from the Poisson's equation as E_r ≅ 2πen_ef R, and the acceleration time as the time to double the bunch size, one arrives at the following estimate of the ultrafast electron beam divergence (Tikhonchuk, 2002):

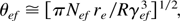
where r_e is the classical electron radius. These ultrafast electrons are shown in PIC simulations in Figure 3 and the scheme in Figure 8.

4. FAST ION PRODUCTION FROM THE REAR SIDE OF THE FOIL

In the previous section we concluded that during the laser pulse, fast electrons at a density of n_eh = eN_eh⁽¹⁾/πR²h move at a distance r_d = v_eh /ω_ph ∼ h in front of the ions, where ω_ph = (4πe²n_eh c²/ε_eh)^1/2. This generates the electric field

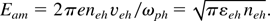
We assume that the foil plasma has a sharp rear boundary, because the laser pulse is too short to allow time for the shock wave to reach the rear surface. The velocity of ions accelerated by the ambipolar force is then v_i = (Z/m_i)E_am t_a, and their energy

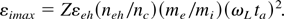
The total time during which ions are accelerated, t_a, is the sum of the duration of the laser pulse, t_L, and relaxation time of the ambipolar field, ω_ph⁻¹. Equation (10) is thus obviously valid over acceleration times that are short enough that ions travelling at a reference velocity v_i do not completely traverse the accelerating field of width cω_ph⁻¹, that is, for t_a < ω_ph⁻¹ c/v_i. For longer pulses, the approximation of fixed ions is no longer valid, and the ion energy in this case is given by Gurevich and Meshcherkin (1981):

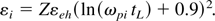
In our case t_L ∼ t_a ≤ ω_ph⁻¹ c/v_i and Eqs. (10) and (11) give approximately the same energy. To verify Eq. (10), the velocity of the ion front was estimated from the position of ions at ω_L t = 500 as shown in Figure 4, giving a velocity of v_i ∼ 3 × 10⁸ cm/s, that is, two thirds of the value given by Eq. (10). The scaling ε_i ∼ I₁₈^0.5 that follows from Eq. (10) has been confirmed by numerical calculations for a plasma with a sharp rear surface and it agrees with the experimental data from Wilks et al. (2001).

5. ION BEAM TRANSPORT FROM THE FOIL REAR TO VACUUM

In the initial stage of the acceleration process (t < ω_ph⁻¹ c/v_i), the electrons move away from the ions. The electron ring discussed in the previous section is only one of the factors influencing the ion motion. The equation for the ion acceleration along the foil surface is

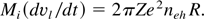
From this equation, the angle of ion divergence can be estimated as

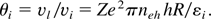
This indicates that ions propagate from the target at relatively wide angles in the initial stage, as confirmed by the simulation results (see Fig. 5a). After this, the separated charges recombine, with the electrons from the ring having returned to charged plasma surface. As a result, at ω_L t = 333, the ion divergence has decreased, as can be seen in Figure 5b. The PIC simulation results of the dependence of fast ion direction (v_y /v_x) on the laser intensity are shown in Figure 6 for a plasma density gradient L of 1 μm and the slab length of 2 μm (upper curve). Simulations thus agree well with the analytic result of Eq. (13) (lower curve).

At time t >> R/v_i, the ion jet has a stretched shape and we can approximate the electric and magnetic fields as cylindrical:

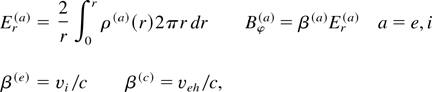
where ρ^(a) is the charge density of particles of type a. The radial ion motion equation is then

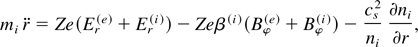
where c_s is the speed of ion sound. We make a simple approximation of axial particle motion, x = v_i t at a stationary beam current n_i R² ∼ const. Then for r = R, the particle trajectory (β⁽ⁱ⁾ << 1) is given by

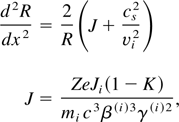
where J_i is the total electric current of the ion beam, K = n_eh /Zn_i < 1 is the degree of compensating of ion beam charge by electrons, and γ⁽ⁱ⁾ is the Lorentz factor of the ions. The initial conditions of the ion jets are:

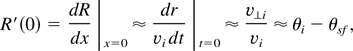
where θ_sr is the angle of surface curvature (angle between surface normal and x-axis). Then from Eq. (16), we find an approximate dependence of the rate of divergence on the laser intensity. Following from Eq. (16), emittance ε_μ = RdR/dx is given by

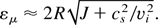
This gives ε_μ ∼ 10⁻¹ mm·rad for the parameters used in the simulations. From Eq. (16) we conclude that the particle beam emittance depends on the parameter K, and for K ∼ 1, emittance is very low (J < c_s²/v_i²). It is generated only by the thermal pressure. The ion jet shown in Figure 4 propagates with little divergence or convergence. It is confirmed also by the shape of separate ion trajectories at various target points, as is shown in Figure 7. The numerical calculation of the magnitude K for a bunch of ejected ions reveals an almost complete charge compensation by electrons: K ≈ 0.98.

Thus, convergence of the ion beam can be achieved by rearranging the foil target into a curve. The distance from the foil at which the beam is focused depends on the foil profile and the laser beam parameters. We consider the focusing effect in more detail. From Eq. (16), the equation of the trajectory of boundary particles of the beam is

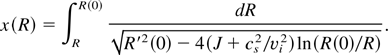
The minimum radius of the focused beam is achieved when the expression under the square root in Eq. (19) is zero:

The minimum radius of a bunch is reached where the transverse component of the kinetic energy of a bunch is transformed completely into the potential energy of the pressure and Coulomb forces. Equation (20) also gives the basics for the formulation of requirements for focusing a bunch of ions. As R′(0) ∼ 1, the charge compensation needs to be such that J << 1. The ion distribution function needs to be arranged such that the fluctuation of velocity is much less than average velocity c_s << v_i. The focal length is then given by

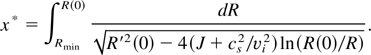
These formulae are convenient for determining the order of magnitude of focusing for a given set of parameters, as all essential effects are taken into account: the Coulomb repulsion, thermal expansion, magnetic field of a bunch, surface curvature, and angular scatter of ejected ions. At relativistic ion velocities, the ion bunches are squeezed by their own magnetic field (factor 1 − β⁽ⁱ⁾² reducing the value of J). From Eq. (16), for the ions ejected from a flat surface (R′(0) = 0) and under only the thermal pressure, the ion bunch radius will increase according to the following formula: R − R(0) ≈ 2c_s x/v_i = 2c_s t. A similar result follows from Gurevich and Meshcherkin (1981) and Kovalev et al. (2001).

The produced ion bunch can be unstable during propagation in vacuum. The main type of ion instability for our condition is electrostatic Budker instability (Meshkov, 1991). We calculated the development of transverse filamentation for a general case; then the threshold value of the instability scale is given by

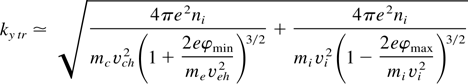
and the growth rate of this instability is

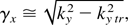
where φ_max > φ_min,(eφ_max ≤ m_i v_i² ∼ m_e v_e²) limit values of the electrostatic potential inside the bunch (φ corresponds to the electric field from (14)). As we see from these formulae, the threshold value of the transverse scale of instability is close to the longitudinal Debye radius of the bunch and the growth rate increases with k_y. Such a rise is limited by the condition on

, where ε_i⊥ is the transversal component of the ion kinetic energy. Therefore

For example, at v_i = 8 × 10⁸ cm/c, ω_pi = 10¹³ c⁻¹, θ_i ≈ 5°, the threshold and the minimal scale of instabilities are λ_tr = 2π/k_{y tr} ≈ 2μm, λ_min ≈ 200 nm. Note that such an instability develops faster if the foil rear density is modulated with the scale ∼c/ω_ph. At the nonlinear stage, the ion bunch is divided in separated filaments of a diameter λ_min and the bunch divergence is decreased. This physical picture is represented in Figure 8, where also the basic parameters entered in the article are shown.