1 Introduction
The motion of suspended particles in viscous fluids is a much studied research topic and finds a wide range of applications in industrial and natural settings, as well as in the study of fluid flows. A number of industrial processes involve the transport of particles over long distances over which segregation of particles (and therefore possible destabilization of a suspension) can be a practical concern. By contrast, it may be desirable to engineer devices that induce controlled particle segregation based on a physical property of the particle such as its size or shape, e.g. field flow fractionation (Giddings, Yang & Myers Reference Giddings, Yang and Myers1976). In situations where particles faithfully follow fluid trajectories, i.e. when they behave as passive tracers, their motion is commonly used to characterize and visualize the flow itself.
An accurate quantification of the hydrodynamic resistance to the motion of a suspended particle is key to describing its motion. The classical Stokes law for the drag on a particle was modified by Faxén to include the effect of an externally imposed pressure gradient and by Oseen to account for finite fluid inertia (Happel & Brenner Reference Happel and Brenner1965; Leal Reference Leal1980). Saffman (Reference Saffman1965) showed that a particle experiences a lift force in a shear flow at small but finite Reynolds numbers due to Oseen corrections, and various generalizations have been obtained subsequently (McLaughlin Reference McLaughlin1991; Asmolov Reference Asmolov1995). The effect of an unsteady background flow on the motion of a sphere in an unbounded fluid has also been studied (Lovalenti & Brady Reference Lovalenti and Brady1993, Reference Lovalenti and Brady1995; Asmolov & McLaughlin Reference Asmolov and McLaughlin1999).
Many flows with particles, such as the flow of a suspension through a pipe or a microfluidic channel, or the flow of particles around an obstacle, involve motion near a solid boundary. The presence of the boundary modifies the hydrodynamics of particles suspended in the flow, in particular at low Reynolds numbers where hydrodynamic interactions are long range. A number of studies have quantified the dynamics of a single sphere near a wall in the Stokes flow limit (Brenner Reference Brenner1961; Goldman, Cox & Brenner Reference Goldman, Cox and Brenner1967a ,Reference Goldman, Cox and Brenner b ), and several others have quantified the effect of inertia in such configurations (Segré & Silberberg Reference Segré and Silberberg1962; Ho & Leal Reference Ho and Leal1974; Vasseur & Cox Reference Vasseur and Cox1977; McLaughlin Reference McLaughlin1993; Hogg Reference Hogg1994; Hood, Lee & Roper Reference Hood, Lee and Roper2015). Much research has focused on the hydrodynamics of dilute suspensions in which boundary effects are weak (Batchelor & Green Reference Batchelor and Green1972a ; Hinch Reference Hinch1977; Haber & Brenner Reference Haber and Brenner1999; Bhattacharya, Bławzdziewicz & Wajnryb Reference Bhattacharya, Bławzdziewicz and Wajnryb2006; Zurita-Gotor, Bławzdziewicz & Wajnryb Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007; Feuillebois et al. Reference Feuillebois, Ekiel-Jeżewska, Wajnryb, Sellier and Bławzdziewicz2015) and on the dynamics of pairs of spheres in linear flows (Goldman, Cox & Brenner Reference Goldman, Cox and Brenner1966; Batchelor & Green Reference Batchelor and Green1972b ; Nir & Acrivos Reference Nir and Acrivos1973; Jeffrey & Onishi Reference Jeffrey and Onishi1984; Swan & Brady Reference Swan and Brady2007). Other studies have considered close-range particle–particle and particle–wall interactions (Goren & O’Neill Reference Goren and O’Neill1971; Sangani, Acrivos & Peyla Reference Sangani, Acrivos and Peyla2011; Cardinaels & Stone Reference Cardinaels and Stone2015).
Several researchers have, to good effect, combined far-field descriptions of particle hydrodynamics with near-field corrections for lubrication when particles are close to each other or to other boundaries in the flow (Durlofsky, Brady & Bossis Reference Durlofsky, Brady and Bossis1987; Brady & Bossis Reference Brady and Bossis1988; Bossis, Meunier & Sherwood Reference Bossis, Meunier and Sherwood1991; Swan & Brady Reference Swan and Brady2011; Aponte-Rivera & Zia Reference Aponte-Rivera and Zia2016; Gallier et al. Reference Gallier, Lemaire, Lobry and Peters2016). Another approach is to simulate the flow numerically accounting for the presence of suspended particles, thereby computing both the flow and the particle trajectory simultaneously (Dance & Maxey Reference Dance and Maxey2003; Kempe & Fröhlich Reference Kempe and Fröhlich2012b ; Haddadi & Morris Reference Haddadi and Morris2015). Such methods, however, also typically require additional corrections for lubrication when separation distances between solid surfaces are small (Ladd & Verberg Reference Ladd and Verberg2001; Nguyen & Ladd Reference Nguyen and Ladd2002; Kempe & Fröhlich Reference Kempe and Fröhlich2012a ; Izard, Bonometti & Lacaze Reference Izard, Bonometti and Lacaze2014).
In this paper, we develop a general theory of the force on a rigid spherical particle suspended in a general quadratic background flow in the vicinity of a large obstacle; we determine the force on the particle in a direction normal to the surface of the obstacle. Working within the Stokes flow limit, we use the Lorentz reciprocal theorem along with a local expansion of the background flow about the particle centre to obtain explicit expressions for the normal force as a function of the particle motion and the local properties of the background flow. The theory provides exact results for arbitrary distances between the surface of the particle and the obstacle, whose boundary is allowed to be either rigid or a free surface. To aid the analysis, we focus on situations where the obstacle’s surface is itself spherical, although some general conclusions can be drawn for non-spherical obstacle boundaries, as discussed in subsequent sections.
Employing a quadratic expansion of the background flow about the spherical particle’s centre (see figure 1), we obtain a general expression for the normal component of the force of the form
 $$\begin{eqnarray}\displaystyle F_{\bot }=\boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{\bot } & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a\bigg[\bigg\{-{\mathcal{A}}\,(\boldsymbol{v}_{p}-\boldsymbol{u})-a\,{\mathcal{B}}\,(\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{a^{2}}{2}{\mathcal{C}}\,(\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})+\frac{a^{2}}{2}{\mathcal{D}}\,\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\bigg\}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }\bigg]_{\boldsymbol{x}_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\bot }=\boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{\bot } & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a\bigg[\bigg\{-{\mathcal{A}}\,(\boldsymbol{v}_{p}-\boldsymbol{u})-a\,{\mathcal{B}}\,(\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{a^{2}}{2}{\mathcal{C}}\,(\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})+\frac{a^{2}}{2}{\mathcal{D}}\,\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\bigg\}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }\bigg]_{\boldsymbol{x}_{p}},\end{eqnarray}$$
where
![]() $\boldsymbol{e}_{\bot }$
is the unit normal to the obstacle pointing towards the particle centre,
$\boldsymbol{e}_{\bot }$
is the unit normal to the obstacle pointing towards the particle centre,
![]() $a$
is the particle’s radius and
$a$
is the particle’s radius and
![]() $\unicode[STIX]{x1D707}$
is the viscosity of the fluid. Also,
$\unicode[STIX]{x1D707}$
is the viscosity of the fluid. Also,
![]() $\boldsymbol{v}_{p}$
and
$\boldsymbol{v}_{p}$
and
![]() $\boldsymbol{u}$
are, respectively, the particle and ambient flow velocity and
$\boldsymbol{u}$
are, respectively, the particle and ambient flow velocity and
![]() $\boldsymbol{x}_{p}$
represents the position of the particle’s centre; cf. figure 1. The scalar quantities
$\boldsymbol{x}_{p}$
represents the position of the particle’s centre; cf. figure 1. The scalar quantities
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
are dimensionless hydrodynamic resistances that depend on (i) the separation distance between the particle and the obstacle and (ii) the size of the particle relative to that of the obstacle; these resistances are calculated explicitly in this paper. We recover Faxén’s law and the results of lubrication theory, respectively, for large and small separations between the sphere and the boundary. The results of the theory can be used to compute approximate trajectories of particles near boundaries consistently without the need to include additional lubrication terms to prevent surface-to-surface contact.
${\mathcal{D}}$
are dimensionless hydrodynamic resistances that depend on (i) the separation distance between the particle and the obstacle and (ii) the size of the particle relative to that of the obstacle; these resistances are calculated explicitly in this paper. We recover Faxén’s law and the results of lubrication theory, respectively, for large and small separations between the sphere and the boundary. The results of the theory can be used to compute approximate trajectories of particles near boundaries consistently without the need to include additional lubrication terms to prevent surface-to-surface contact.

Figure 1. (a) General set-up of the problem of a small spherical particle of radius
![]() $a$
immersed in a background flow field
$a$
immersed in a background flow field
![]() $\boldsymbol{u}(\boldsymbol{x})$
at a distance
$\boldsymbol{u}(\boldsymbol{x})$
at a distance
![]() $h$
from a large obstacle of radius of curvature
$h$
from a large obstacle of radius of curvature
![]() $R$
. The characteristic scale of the flow is
$R$
. The characteristic scale of the flow is
![]() $\ell \gg a$
;
$\ell \gg a$
;
![]() $\ell =O(R)$
in many situations. (b) A sketch of the geometry relevant to the disturbance flow problem in the vicinity of the particle. The obstacle surface is assumed to be locally spherical with a radius
$\ell =O(R)$
in many situations. (b) A sketch of the geometry relevant to the disturbance flow problem in the vicinity of the particle. The obstacle surface is assumed to be locally spherical with a radius
![]() $R\gtrsim \ell \gg a$
. (c) An example with
$R\gtrsim \ell \gg a$
. (c) An example with
![]() $\ell \ll R$
is the pressure-driven flow of particle-laden fluids through channels of non-uniform shape; as sketched, the walls are locally planar.
$\ell \ll R$
is the pressure-driven flow of particle-laden fluids through channels of non-uniform shape; as sketched, the walls are locally planar.
The paper is organized as follows. Section 2 introduces the mathematical problem and briefly presents the scaling of the hydrodynamic force with particle size and the flow properties. In § 3, we obtain a general expression for the normal force on the particle by using the Lorentz reciprocal theorem for Stokes flow. We show that the normal force, up to cubic order in particle size, contains four different contributions involving moments of the background flow in the vicinity of the particle. In § 4, we obtain analytic expressions for these force contributions as functions of the distance of the particle from the boundary. In § 5, we discuss the asymptotic behaviour of the forces for large and small separations between the sphere and the boundary, showing that extensional contributions to the normal force are important even for modestly large separations between the particle and the obstacle. We also discuss the implications of the theory for the trapping of particles near surfaces and the motion of a force-free particle.
2 Problem set-up and general theory
We consider the flow of a viscous fluid (density
![]() $\unicode[STIX]{x1D70C}$
and viscosity
$\unicode[STIX]{x1D70C}$
and viscosity
![]() $\unicode[STIX]{x1D707}$
) in the vicinity of a large obstacle of characteristic radius of curvature
$\unicode[STIX]{x1D707}$
) in the vicinity of a large obstacle of characteristic radius of curvature
![]() $R$
, which is described by a velocity field
$R$
, which is described by a velocity field
![]() $\boldsymbol{u}(\boldsymbol{x})$
that is assumed to be fully known. The flow has a characteristic velocity scale
$\boldsymbol{u}(\boldsymbol{x})$
that is assumed to be fully known. The flow has a characteristic velocity scale
![]() $u_{0}$
and a characteristic length scale
$u_{0}$
and a characteristic length scale
![]() $\ell$
that, in general, may or may not be related to
$\ell$
that, in general, may or may not be related to
![]() $R$
, cf. figure 1. As an example, gradients of flow past a large curved obstacle depend on the size of the obstacle (i.e.
$R$
, cf. figure 1. As an example, gradients of flow past a large curved obstacle depend on the size of the obstacle (i.e.
![]() $\ell \sim R$
). By contrast, in pressure-driven flow through a channel with plane walls (
$\ell \sim R$
). By contrast, in pressure-driven flow through a channel with plane walls (
![]() $R\rightarrow \infty$
), flow gradients are determined by the width of the channel
$R\rightarrow \infty$
), flow gradients are determined by the width of the channel
![]() $(\ell \ll R)$
. Similarly, hydrodynamic interactions in dilute suspensions are associated with flow gradients on the scale of the interparticle separation
$(\ell \ll R)$
. Similarly, hydrodynamic interactions in dilute suspensions are associated with flow gradients on the scale of the interparticle separation
![]() $\ell$
and are generally unrelated to the curvature of nearby walls (Swan & Brady Reference Swan and Brady2007).
$\ell$
and are generally unrelated to the curvature of nearby walls (Swan & Brady Reference Swan and Brady2007).
At small Reynolds numbers (
![]() $Re_{u}\equiv \unicode[STIX]{x1D70C}u_{0}\ell /\unicode[STIX]{x1D707}\ll 1$
), the flow is described by the Stokes equations
$Re_{u}\equiv \unicode[STIX]{x1D70C}u_{0}\ell /\unicode[STIX]{x1D707}\ll 1$
), the flow is described by the Stokes equations
where
![]() $\unicode[STIX]{x1D748}_{u}=-p_{u}\unicode[STIX]{x1D644}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the stress tensor and
$\unicode[STIX]{x1D748}_{u}=-p_{u}\unicode[STIX]{x1D644}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the stress tensor and
![]() $p_{u}$
is the pressure. Although the precise shape of the obstacle is not ultimately important for the formalism developed here, we consider two classes of obstacles widely encountered in physical systems. The first corresponds to solid obstacles on whose surface the flow must satisfy the no-slip boundary condition (denoted BC I), and the second corresponds to obstacles with free surfaces, e.g. a clean gas bubble, on which tangential components of stress vanish (denoted BC II). The boundary conditions satisfied by the flow (
$p_{u}$
is the pressure. Although the precise shape of the obstacle is not ultimately important for the formalism developed here, we consider two classes of obstacles widely encountered in physical systems. The first corresponds to solid obstacles on whose surface the flow must satisfy the no-slip boundary condition (denoted BC I), and the second corresponds to obstacles with free surfaces, e.g. a clean gas bubble, on which tangential components of stress vanish (denoted BC II). The boundary conditions satisfied by the flow (
![]() $\boldsymbol{u},\unicode[STIX]{x1D748}_{u}$
) on the surface
$\boldsymbol{u},\unicode[STIX]{x1D748}_{u}$
) on the surface
![]() $S_{w}$
of the obstacle are accordingly either
$S_{w}$
of the obstacle are accordingly either
where
![]() $\boldsymbol{m}$
denotes the unit normal to the surface of the obstacle, directed into the fluid (figure 1). The flow (
$\boldsymbol{m}$
denotes the unit normal to the surface of the obstacle, directed into the fluid (figure 1). The flow (
![]() $\boldsymbol{u},\,\unicode[STIX]{x1D748}_{u}$
), which we refer to as the ‘background flow’, may satisfy some generally inhomogeneous boundary conditions at infinity.
$\boldsymbol{u},\,\unicode[STIX]{x1D748}_{u}$
), which we refer to as the ‘background flow’, may satisfy some generally inhomogeneous boundary conditions at infinity.
We now introduce to the flow a rigid spherical particle of radius
![]() $a$
with a centre at a distance
$a$
with a centre at a distance
![]() $h$
from the surface of the obstacle. The particle, whose centre is at a position
$h$
from the surface of the obstacle. The particle, whose centre is at a position
![]() $\boldsymbol{x}_{p}(t)$
translates with velocity
$\boldsymbol{x}_{p}(t)$
translates with velocity
![]() $\boldsymbol{v}_{p}$
and rotates with angular velocity
$\boldsymbol{v}_{p}$
and rotates with angular velocity
![]() $\unicode[STIX]{x1D734}_{p}$
, as indicated in figure 1. Due to the motion of the particle, the velocity field is no longer
$\unicode[STIX]{x1D734}_{p}$
, as indicated in figure 1. Due to the motion of the particle, the velocity field is no longer
![]() $\boldsymbol{u}(\boldsymbol{x})$
, but rather
$\boldsymbol{u}(\boldsymbol{x})$
, but rather
where
![]() $\boldsymbol{v}(\boldsymbol{x})$
is the disturbance flow due to the moving particle. Assuming that the disturbance velocity scale
$\boldsymbol{v}(\boldsymbol{x})$
is the disturbance flow due to the moving particle. Assuming that the disturbance velocity scale
![]() $v_{0}$
is at most of the order of
$v_{0}$
is at most of the order of
![]() $u_{0}$
, the net flow
$u_{0}$
, the net flow
![]() $\boldsymbol{U}$
also satisfies the Stokes equations, the boundary conditions at the wall (either BC I or BC II as appropriate) and the conditions at infinity satisfied by
$\boldsymbol{U}$
also satisfies the Stokes equations, the boundary conditions at the wall (either BC I or BC II as appropriate) and the conditions at infinity satisfied by
![]() $\boldsymbol{u}$
. In addition, to observe the no-slip condition on the surface
$\boldsymbol{u}$
. In addition, to observe the no-slip condition on the surface
![]() $S_{p}$
of the rigid particle,
$S_{p}$
of the rigid particle,
![]() $\boldsymbol{U}$
must satisfy
$\boldsymbol{U}$
must satisfy
where
![]() $\boldsymbol{r}\equiv \boldsymbol{x}-\boldsymbol{x}_{p}$
is the position of a point in space relative to the particle centre.
$\boldsymbol{r}\equiv \boldsymbol{x}-\boldsymbol{x}_{p}$
is the position of a point in space relative to the particle centre.
The disturbance flow
![]() $\boldsymbol{v}$
is therefore governed by
$\boldsymbol{v}$
is therefore governed by
Here,
![]() $\unicode[STIX]{x1D748}_{v}=-p_{v}\unicode[STIX]{x1D644}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D735}\boldsymbol{v}+\unicode[STIX]{x1D735}\boldsymbol{v}^{\text{T}})$
is the stress tensor associated with the disturbance flow
$\unicode[STIX]{x1D748}_{v}=-p_{v}\unicode[STIX]{x1D644}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D735}\boldsymbol{v}+\unicode[STIX]{x1D735}\boldsymbol{v}^{\text{T}})$
is the stress tensor associated with the disturbance flow
![]() $\boldsymbol{v}$
(with
$\boldsymbol{v}$
(with
![]() $p_{v}$
being the pressure). Also,
$p_{v}$
being the pressure). Also,
![]() $\boldsymbol{w}(\boldsymbol{x})$
is the disturbance flow surface velocity distribution on the sphere required for the net flow
$\boldsymbol{w}(\boldsymbol{x})$
is the disturbance flow surface velocity distribution on the sphere required for the net flow
![]() $\boldsymbol{U}$
to satisfy the no-slip condition on the particle.
$\boldsymbol{U}$
to satisfy the no-slip condition on the particle.
Since disturbance flow quantities depend on the local background flow properties through (2.5c
),
![]() $\boldsymbol{v}(\boldsymbol{x})$
is generally also time dependent along the trajectory of the particle. Inertial effects associated with this time dependence are small for
$\boldsymbol{v}(\boldsymbol{x})$
is generally also time dependent along the trajectory of the particle. Inertial effects associated with this time dependence are small for
![]() $\mathit{Re}_{u}\ll 1$
and are neglected here, making the disturbance flow
$\mathit{Re}_{u}\ll 1$
and are neglected here, making the disturbance flow
![]() $\boldsymbol{v}(\boldsymbol{x})$
quasi-steady and the time dependence of the flow implicit; see Lovalenti & Brady (Reference Lovalenti and Brady1993, Reference Lovalenti and Brady1995) for a detailed discussion. We also note that the boundary conditions (2.5e
) assume that the introduction of the particle does not produce stresses that deform the surface of the obstacle. For a free surface in particular, this assumption only holds if the disturbance pressure is small relative to the Laplace–Young pressure jump across the interface. The deformation of the interface is much smaller than the particle size if the capillary number
$\boldsymbol{v}(\boldsymbol{x})$
quasi-steady and the time dependence of the flow implicit; see Lovalenti & Brady (Reference Lovalenti and Brady1993, Reference Lovalenti and Brady1995) for a detailed discussion. We also note that the boundary conditions (2.5e
) assume that the introduction of the particle does not produce stresses that deform the surface of the obstacle. For a free surface in particular, this assumption only holds if the disturbance pressure is small relative to the Laplace–Young pressure jump across the interface. The deformation of the interface is much smaller than the particle size if the capillary number
![]() $\mathit{Ca}\equiv (\ell /a)^{2}\unicode[STIX]{x1D707}u_{0}/\unicode[STIX]{x1D6FE}\ll 1$
,
$\mathit{Ca}\equiv (\ell /a)^{2}\unicode[STIX]{x1D707}u_{0}/\unicode[STIX]{x1D6FE}\ll 1$
,
![]() $\unicode[STIX]{x1D6FE}$
being the surface tension of the interface
$\unicode[STIX]{x1D6FE}$
being the surface tension of the interface
![]() $S_{w}$
. This condition is satisfied in typical micron-scale applications.
$S_{w}$
. This condition is satisfied in typical micron-scale applications.
The flow
![]() $\boldsymbol{u}(\boldsymbol{x})$
and the geometry of the obstacle’s surface
$\boldsymbol{u}(\boldsymbol{x})$
and the geometry of the obstacle’s surface
![]() $S_{w}$
have so far not been specified. To make analytical progress, we restrict our attention to particles that are small relative to the ambient flow scale, i.e.
$S_{w}$
have so far not been specified. To make analytical progress, we restrict our attention to particles that are small relative to the ambient flow scale, i.e.
![]() $a/\ell \ll 1$
. In addition, we only consider obstacles
$a/\ell \ll 1$
. In addition, we only consider obstacles
![]() $S_{w}$
with spherical boundaries (this includes planar surfaces), and thereby draw upon the well-developed literature for two-sphere hydrodynamic interactions (Stimson & Jeffery Reference Stimson and Jeffery1926; Brenner Reference Brenner1961; Maude Reference Maude1961). Henceforth, ‘sphere’ and ‘particle’ will both refer to the spherical particle
$S_{w}$
with spherical boundaries (this includes planar surfaces), and thereby draw upon the well-developed literature for two-sphere hydrodynamic interactions (Stimson & Jeffery Reference Stimson and Jeffery1926; Brenner Reference Brenner1961; Maude Reference Maude1961). Henceforth, ‘sphere’ and ‘particle’ will both refer to the spherical particle
![]() $S_{p}$
.
$S_{p}$
.
With no loss of generality, we take
![]() $\boldsymbol{x}=\mathbf{0}$
to represent the point on
$\boldsymbol{x}=\mathbf{0}$
to represent the point on
![]() $S_{w}$
closest to the surface of the particle
$S_{w}$
closest to the surface of the particle
![]() $S_{p}$
and
$S_{p}$
and
![]() $\boldsymbol{e}_{\bot }$
to represent the unit normal to
$\boldsymbol{e}_{\bot }$
to represent the unit normal to
![]() $S_{w}$
at this point, cf. figure 1. By construction,
$S_{w}$
at this point, cf. figure 1. By construction,
![]() $\boldsymbol{e}_{\bot }$
points toward the centre of the particle, so that
$\boldsymbol{e}_{\bot }$
points toward the centre of the particle, so that
![]() $\boldsymbol{x}_{p}=h\boldsymbol{e}_{\bot }$
. It is also convenient to introduce cylindrical coordinates
$\boldsymbol{x}_{p}=h\boldsymbol{e}_{\bot }$
. It is also convenient to introduce cylindrical coordinates
![]() $(r,\unicode[STIX]{x1D703},z)$
with origin at the centre of the particle as indicated in figure 1. The position of a point relative to the particle centre is then
$(r,\unicode[STIX]{x1D703},z)$
with origin at the centre of the particle as indicated in figure 1. The position of a point relative to the particle centre is then
![]() $\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{x}_{p}=r\boldsymbol{e}_{r}+z\boldsymbol{e}_{z}$
; note that
$\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{x}_{p}=r\boldsymbol{e}_{r}+z\boldsymbol{e}_{z}$
; note that
![]() $\boldsymbol{e}_{z}=\boldsymbol{e}_{\bot }$
. Although our primary focus in on the case where the particle is small relative to the obstacle (
$\boldsymbol{e}_{z}=\boldsymbol{e}_{\bot }$
. Although our primary focus in on the case where the particle is small relative to the obstacle (
![]() $a/R\ll 1$
), the formalism that we develop here is valid for arbitrary
$a/R\ll 1$
), the formalism that we develop here is valid for arbitrary
![]() $a/R$
and can therefore be applied more generally to sphere–sphere interactions.
$a/R$
and can therefore be applied more generally to sphere–sphere interactions.
Gradients of
![]() $\boldsymbol{u}(\boldsymbol{x})$
are set by
$\boldsymbol{u}(\boldsymbol{x})$
are set by
![]() $\ell$
, while those of
$\ell$
, while those of
![]() $\boldsymbol{v}(\boldsymbol{x})$
are determined by the radius of the particle
$\boldsymbol{v}(\boldsymbol{x})$
are determined by the radius of the particle
![]() $a$
, owing to the no-slip condition (2.5c
) on its surface. The background velocity field
$a$
, owing to the no-slip condition (2.5c
) on its surface. The background velocity field
![]() $\boldsymbol{u}(\boldsymbol{x})$
in the vicinity of a small particle (
$\boldsymbol{u}(\boldsymbol{x})$
in the vicinity of a small particle (
![]() $a/\ell \ll 1$
) can be approximated by a Taylor expansion about its centre. To quadratic order in distance from the particle centre, we can write
$a/\ell \ll 1$
) can be approximated by a Taylor expansion about its centre. To quadratic order in distance from the particle centre, we can write
Then, the surface velocity distribution
![]() $\boldsymbol{w}(\boldsymbol{x})$
in (2.5c
) is
$\boldsymbol{w}(\boldsymbol{x})$
in (2.5c
) is
with
Here,
![]() $\unicode[STIX]{x1D640}$
,
$\unicode[STIX]{x1D640}$
,
![]() $\unicode[STIX]{x1D74E}$
and
$\unicode[STIX]{x1D74E}$
and
![]() $\unicode[STIX]{x1D642}$
are background flow properties evaluated at the particle centre
$\unicode[STIX]{x1D642}$
are background flow properties evaluated at the particle centre
![]() $\boldsymbol{x}_{p}$
, viz. the rate-of-strain tensor
$\boldsymbol{x}_{p}$
, viz. the rate-of-strain tensor
![]() $(\unicode[STIX]{x1D640})$
, the vorticity (
$(\unicode[STIX]{x1D640})$
, the vorticity (
![]() $\unicode[STIX]{x1D74E}$
) and a rank-3 tensor (
$\unicode[STIX]{x1D74E}$
) and a rank-3 tensor (
![]() $\unicode[STIX]{x1D642}$
) that quantifies the curvature of the background flow (Nadim & Stone Reference Nadim and Stone1991).
$\unicode[STIX]{x1D642}$
) that quantifies the curvature of the background flow (Nadim & Stone Reference Nadim and Stone1991).
The hydrodynamic force on the particle under the net flow
![]() $\boldsymbol{U}=\boldsymbol{u}+\boldsymbol{v}$
is given by
$\boldsymbol{U}=\boldsymbol{u}+\boldsymbol{v}$
is given by
![]() $\boldsymbol{F}=\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{v}\,\text{d}S,$
where
$\boldsymbol{F}=\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{v}\,\text{d}S,$
where
![]() $\boldsymbol{n}$
is the unit normal on the particle surface directed into the fluid. Due to linearity, each
$\boldsymbol{n}$
is the unit normal on the particle surface directed into the fluid. Due to linearity, each
![]() $\boldsymbol{w}^{(i)}$
in (2.8) can be associated with a flow (
$\boldsymbol{w}^{(i)}$
in (2.8) can be associated with a flow (
![]() $\boldsymbol{v}^{(i)},\unicode[STIX]{x1D748}_{v}^{(i)}$
). The force on the particle is then expressible as
$\boldsymbol{v}^{(i)},\unicode[STIX]{x1D748}_{v}^{(i)}$
). The force on the particle is then expressible as
where
![]() $\boldsymbol{F}^{(i)}=\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{v}^{(i)}\,\text{d}S$
is the force associated with the surface velocity distribution
$\boldsymbol{F}^{(i)}=\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{v}^{(i)}\,\text{d}S$
is the force associated with the surface velocity distribution
![]() $\boldsymbol{w}^{(i)}$
in (2.8). Thus,
$\boldsymbol{w}^{(i)}$
in (2.8). Thus,
![]() $\boldsymbol{F}^{(0)}$
is the hydrodynamic force due to the translation of the sphere relative to the mean local background velocity,
$\boldsymbol{F}^{(0)}$
is the hydrodynamic force due to the translation of the sphere relative to the mean local background velocity,
![]() $\boldsymbol{F}^{(1)}$
is due to the background velocity gradient and the rotation of the sphere and
$\boldsymbol{F}^{(1)}$
is due to the background velocity gradient and the rotation of the sphere and
![]() $\boldsymbol{F}^{(2)}$
is the contribution of the curvature of the background velocity field in the vicinity of the particle. In the absence of the boundary
$\boldsymbol{F}^{(2)}$
is the contribution of the curvature of the background velocity field in the vicinity of the particle. In the absence of the boundary
![]() $S_{w}$
(i.e. in an infinite medium)
$S_{w}$
(i.e. in an infinite medium)
![]() $\boldsymbol{F}^{(0)}$
reduces to the Stokes drag, while
$\boldsymbol{F}^{(0)}$
reduces to the Stokes drag, while
![]() $\boldsymbol{F}^{(2)}$
becomes the Faxén contribution to the force, proportional to
$\boldsymbol{F}^{(2)}$
becomes the Faxén contribution to the force, proportional to
![]() $\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
. By contrast, the
$\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
. By contrast, the
![]() $\boldsymbol{F}^{(1)}$
contribution, which depends on gradient of the background velocity, is identically zero for a sphere in an unbounded fluid (Happel & Brenner Reference Happel and Brenner1965; Batchelor Reference Batchelor1970). However, the introduction of the boundary
$\boldsymbol{F}^{(1)}$
contribution, which depends on gradient of the background velocity, is identically zero for a sphere in an unbounded fluid (Happel & Brenner Reference Happel and Brenner1965; Batchelor Reference Batchelor1970). However, the introduction of the boundary
![]() $S_{w}$
breaks the symmetry of the disturbance flow
$S_{w}$
breaks the symmetry of the disturbance flow
![]() $\boldsymbol{v}$
around the sphere, making
$\boldsymbol{v}$
around the sphere, making
![]() $\boldsymbol{F}^{(1)}$
generally non-zero, as we show in subsequent sections.
$\boldsymbol{F}^{(1)}$
generally non-zero, as we show in subsequent sections.
If we use the representative scale
![]() $v_{p}$
for the translational speed of the particle and take length scales
$v_{p}$
for the translational speed of the particle and take length scales
![]() $\ell$
and
$\ell$
and
![]() $a$
, respectively, to measure gradients of
$a$
, respectively, to measure gradients of
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\boldsymbol{v}$
, we obtain from (2.8) and (2.10) that the different force contributions scale as
$\boldsymbol{v}$
, we obtain from (2.8) and (2.10) that the different force contributions scale as
The force on a sphere moving in free space in the Stokes flow limit is described exactly by a combination of the Stokes drag
![]() $\boldsymbol{F}^{(0)}$
and the Faxén contribution
$\boldsymbol{F}^{(0)}$
and the Faxén contribution
![]() $\boldsymbol{F}^{(2)}$
, i.e. Faxén’s law. In the presence of a nearby boundary, however,
$\boldsymbol{F}^{(2)}$
, i.e. Faxén’s law. In the presence of a nearby boundary, however,
![]() $\boldsymbol{F}^{(1)}$
is non-zero and can, in particular, exceed
$\boldsymbol{F}^{(1)}$
is non-zero and can, in particular, exceed
![]() $\boldsymbol{F}^{(2)}$
since it is nominally
$\boldsymbol{F}^{(2)}$
since it is nominally
![]() $O(\ell /a)$
greater than the Faxén force contribution.
$O(\ell /a)$
greater than the Faxén force contribution.
Here, we seek to develop analytical expressions for the force on the particle for arbitrary separations
![]() $h$
(relative to
$h$
(relative to
![]() $a$
) between the particle and the obstacle. We further focus our attention on the force normal to the obstacle, which, as we will show, can be obtained by exploiting the geometric symmetry. The computations for the force parallel to the wall are beyond the focus of this paper, but can be obtained using the techniques presented in the following sections.
$a$
) between the particle and the obstacle. We further focus our attention on the force normal to the obstacle, which, as we will show, can be obtained by exploiting the geometric symmetry. The computations for the force parallel to the wall are beyond the focus of this paper, but can be obtained using the techniques presented in the following sections.
3 A reciprocal relation for the force normal to the obstacle
In this paper, we focus on the hydrodynamic force normal to the surface
![]() $S_{w}$
of the obstacle,
$S_{w}$
of the obstacle,
![]() $F_{z}=\boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{z}$
, for which we use the reciprocal theorem for Stokes flows. To this effect, we introduce as a model problem the Stokes flow due to a spherical particle translating normal to the surface of a stationary spherical obstacle (either no slip or no stress) at a velocity
$F_{z}=\boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{z}$
, for which we use the reciprocal theorem for Stokes flows. To this effect, we introduce as a model problem the Stokes flow due to a spherical particle translating normal to the surface of a stationary spherical obstacle (either no slip or no stress) at a velocity
![]() $V^{\prime }$
in a quiescent background fluid of viscosity
$V^{\prime }$
in a quiescent background fluid of viscosity
![]() $\unicode[STIX]{x1D707}$
. As in the main problem introduced in § 2, we take the radius of the spherical particle to be
$\unicode[STIX]{x1D707}$
. As in the main problem introduced in § 2, we take the radius of the spherical particle to be
![]() $a$
, the radius of the obstacle as
$a$
, the radius of the obstacle as
![]() $R$
and the perpendicular distance of the particle’s centre to the surface of the obstacle as
$R$
and the perpendicular distance of the particle’s centre to the surface of the obstacle as
![]() $h$
.
$h$
.
It is convenient to describe the model problem in dimensionless form using the characteristic scales
![]() $a$
,
$a$
,
![]() $V^{\prime }$
and
$V^{\prime }$
and
![]() $\unicode[STIX]{x1D707}V^{\prime }/a$
, respectively, to scale distances, velocities and stresses. Defining
$\unicode[STIX]{x1D707}V^{\prime }/a$
, respectively, to scale distances, velocities and stresses. Defining
![]() $\tilde{\boldsymbol{r}}=\boldsymbol{r}/a$
, and dimensionless model velocity and stress fields by
$\tilde{\boldsymbol{r}}=\boldsymbol{r}/a$
, and dimensionless model velocity and stress fields by
![]() $\boldsymbol{v}^{\prime }$
and
$\boldsymbol{v}^{\prime }$
and
![]() $\unicode[STIX]{x1D748}^{\prime }$
, respectively, the model problem satisfies
$\unicode[STIX]{x1D748}^{\prime }$
, respectively, the model problem satisfies
Solutions to the model problem (both for the no-slip and stress-free cases) depend on the dimensionless geometric ratios (i)
![]() $h/a$
, which quantifies the separation distance of the particle from the surface
$h/a$
, which quantifies the separation distance of the particle from the surface
![]() $S_{w}$
of obstacle and (ii) the curvature ratio
$S_{w}$
of obstacle and (ii) the curvature ratio
![]() $a/R$
. Exact solutions to the model problem can be constructed for arbitrary
$a/R$
. Exact solutions to the model problem can be constructed for arbitrary
![]() $h/a$
and
$h/a$
and
![]() $a/R$
using known results (Brenner Reference Brenner1961; Maude Reference Maude1961; Adamczyk, Adamczyk & Van de Ven Reference Adamczyk, Adamczyk and Van de Ven1983) and are summarized in appendix A. An approach similar to the one used in this paper was adopted to evaluate wall effects on the motion of a sphere in a viscoelastic fluid (Becker, McKinley & Stone Reference Becker, McKinley and Stone1996).
$a/R$
using known results (Brenner Reference Brenner1961; Maude Reference Maude1961; Adamczyk, Adamczyk & Van de Ven Reference Adamczyk, Adamczyk and Van de Ven1983) and are summarized in appendix A. An approach similar to the one used in this paper was adopted to evaluate wall effects on the motion of a sphere in a viscoelastic fluid (Becker, McKinley & Stone Reference Becker, McKinley and Stone1996).
Note that while the model flow (
![]() $\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime }$
) is expressed in dimensionless form, we continue to express the main disturbance flow (
$\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime }$
) is expressed in dimensionless form, we continue to express the main disturbance flow (
![]() $\boldsymbol{v},\unicode[STIX]{x1D748}_{v}$
) in dimensional terms due to its dependence on the arbitrary background flow
$\boldsymbol{v},\unicode[STIX]{x1D748}_{v}$
) in dimensional terms due to its dependence on the arbitrary background flow
![]() $\boldsymbol{u}(\boldsymbol{x})$
. For the two Stokes flows
$\boldsymbol{u}(\boldsymbol{x})$
. For the two Stokes flows
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{v}^{\prime }$
the reciprocal theorem has the form
$\boldsymbol{v}^{\prime }$
the reciprocal theorem has the form
where
![]() $S_{\infty }$
refers to a bounding surface at infinity and
$S_{\infty }$
refers to a bounding surface at infinity and
![]() $\boldsymbol{n}$
is the unit normal directed into the fluid. The factor
$\boldsymbol{n}$
is the unit normal directed into the fluid. The factor
![]() $\unicode[STIX]{x1D707}/a$
in (3.2) is due to the definition of the dimensionless stress tensor
$\unicode[STIX]{x1D707}/a$
in (3.2) is due to the definition of the dimensionless stress tensor
![]() $\unicode[STIX]{x1D748}^{\prime }$
in the model problem. The integral over
$\unicode[STIX]{x1D748}^{\prime }$
in the model problem. The integral over
![]() $S_{\infty }$
vanishes since
$S_{\infty }$
vanishes since
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{v}^{\prime }$
decay to zero as
$\boldsymbol{v}^{\prime }$
decay to zero as
![]() $|\boldsymbol{r}|\rightarrow \infty$
. Additionally, both
$|\boldsymbol{r}|\rightarrow \infty$
. Additionally, both
![]() $(\boldsymbol{v},\unicode[STIX]{x1D748}_{v})$
and
$(\boldsymbol{v},\unicode[STIX]{x1D748}_{v})$
and
![]() $(\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime })$
either have zero velocities on a rigid wall, or vanishing tangential stress and normal velocity components at a plane interface, due to which the surface integrals on
$(\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime })$
either have zero velocities on a rigid wall, or vanishing tangential stress and normal velocity components at a plane interface, due to which the surface integrals on
![]() $S_{w}$
in (3.2) are identically zero. On applying the boundary conditions for
$S_{w}$
in (3.2) are identically zero. On applying the boundary conditions for
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{v}^{\prime }$
on
$\boldsymbol{v}^{\prime }$
on
![]() $S_{p}$
, the reciprocal relationship gives the normal component of the hydrodynamic force on the sphere as
$S_{p}$
, the reciprocal relationship gives the normal component of the hydrodynamic force on the sphere as
where
![]() $\text{d}\tilde{S}\equiv a^{-2}\,\text{d}S$
is a dimensionless differential area element and we recall that
$\text{d}\tilde{S}\equiv a^{-2}\,\text{d}S$
is a dimensionless differential area element and we recall that
![]() $\boldsymbol{e}_{z}=\boldsymbol{e}_{\bot }$
.
$\boldsymbol{e}_{z}=\boldsymbol{e}_{\bot }$
.
Using the decomposition of
![]() $\boldsymbol{w}(\boldsymbol{x})$
in (2.7) we can write
$\boldsymbol{w}(\boldsymbol{x})$
in (2.7) we can write
 $$\begin{eqnarray}\displaystyle F_{z}^{(1)} & = & \displaystyle \unicode[STIX]{x1D707}a\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\boldsymbol{w}^{(1)}\,\text{d}\tilde{S}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D707}a^{2}\!\left\{-\unicode[STIX]{x1D640}\boldsymbol{ : }\!\int _{S_{p}}\tilde{\boldsymbol{r}}(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime })\,\text{d}\tilde{S}+\left(\unicode[STIX]{x1D734}_{p}-\frac{1}{2}\unicode[STIX]{x1D74E}\right)\!\boldsymbol{\cdot }\!\int _{S_{p}}\tilde{\boldsymbol{r}}\times (\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime })\,\text{d}\tilde{S}\right\}\quad \text{and}\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{z}^{(1)} & = & \displaystyle \unicode[STIX]{x1D707}a\int _{S_{p}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\boldsymbol{w}^{(1)}\,\text{d}\tilde{S}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D707}a^{2}\!\left\{-\unicode[STIX]{x1D640}\boldsymbol{ : }\!\int _{S_{p}}\tilde{\boldsymbol{r}}(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime })\,\text{d}\tilde{S}+\left(\unicode[STIX]{x1D734}_{p}-\frac{1}{2}\unicode[STIX]{x1D74E}\right)\!\boldsymbol{\cdot }\!\int _{S_{p}}\tilde{\boldsymbol{r}}\times (\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime })\,\text{d}\tilde{S}\right\}\quad \text{and}\quad\end{eqnarray}$$
The above expressions involve only integrals on the particle surface
![]() $S_{p}$
. Thus, they are generally valid for an arbitrary particle suspended in a quadratic flow as long as the model flow
$S_{p}$
. Thus, they are generally valid for an arbitrary particle suspended in a quadratic flow as long as the model flow
![]() $(\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime })$
satisfies (3.1), although we note that the solution to the corresponding model problem may not be known for arbitrary geometries. We also remark that a more general application of the reciprocal theorem, with the appropriate choice of model problem, can be used to compute the full mobility matrix for a sphere near a boundary; see e.g. Becker et al. (Reference Becker, McKinley and Stone1996), Haber & Brenner (Reference Haber and Brenner1999). While solutions to the relevant model problems (wall-parallel translation and rotation of a sphere) are known (Dean & O’Neill Reference Dean and O’Neill1963; O’Neill Reference O’Neill1964), we do not attempt these more involved calculations here. Rather, we focus on the normal force component, which can be computed explicitly by utilizing the symmetry in the model problem (3.1).
$(\boldsymbol{v}^{\prime },\unicode[STIX]{x1D748}^{\prime })$
satisfies (3.1), although we note that the solution to the corresponding model problem may not be known for arbitrary geometries. We also remark that a more general application of the reciprocal theorem, with the appropriate choice of model problem, can be used to compute the full mobility matrix for a sphere near a boundary; see e.g. Becker et al. (Reference Becker, McKinley and Stone1996), Haber & Brenner (Reference Haber and Brenner1999). While solutions to the relevant model problems (wall-parallel translation and rotation of a sphere) are known (Dean & O’Neill Reference Dean and O’Neill1963; O’Neill Reference O’Neill1964), we do not attempt these more involved calculations here. Rather, we focus on the normal force component, which can be computed explicitly by utilizing the symmetry in the model problem (3.1).
3.1 Axisymmetry of the model problem
To exploit the spherical symmetry, we parametrize the surface of the particle in the
![]() $rz$
section through using intrinsic coordinates, see e.g. Stimson & Jeffery (Reference Stimson and Jeffery1926), Happel & Brenner (Reference Happel and Brenner1965). As shown in figure 2, we define
$rz$
section through using intrinsic coordinates, see e.g. Stimson & Jeffery (Reference Stimson and Jeffery1926), Happel & Brenner (Reference Happel and Brenner1965). As shown in figure 2, we define
![]() $s$
as the dimensionless arc length in the
$s$
as the dimensionless arc length in the
![]() $rz$
plane (non-dimensionalized using the particle radius
$rz$
plane (non-dimensionalized using the particle radius
![]() $a$
), such that
$a$
), such that
![]() $s=0$
and
$s=0$
and
![]() $s=\unicode[STIX]{x03C0}$
correspond, respectively, to the points on the sphere farthest and closest to
$s=\unicode[STIX]{x03C0}$
correspond, respectively, to the points on the sphere farthest and closest to
![]() $S_{w}$
, i.e.
$S_{w}$
, i.e.
for an arbitrary scalar field
![]() $f$
defined on the spherical particle surface
$f$
defined on the spherical particle surface
![]() $S_{p}$
.
$S_{p}$
.

Figure 2. Parametrization of the particle surface in polar coordinates (
![]() $\tilde{r},\tilde{z}$
), showing intrinsic coordinates (
$\tilde{r},\tilde{z}$
), showing intrinsic coordinates (
![]() $s$
,
$s$
,
![]() $n$
). The evaluation of the force ultimately involves bipolar coordinates (
$n$
). The evaluation of the force ultimately involves bipolar coordinates (
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
), which are introduced in § 4. Here,
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
), which are introduced in § 4. Here,
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are dimensionless quantities relevant to the bipolar coordinate system that are related to
$\unicode[STIX]{x1D6FD}$
are dimensionless quantities relevant to the bipolar coordinate system that are related to
![]() $h/a$
and
$h/a$
and
![]() $R/a$
and are defined in § 4.
$R/a$
and are defined in § 4.
Due to the boundary conditions and the geometry (spherical particle and obstacle surfaces), the model problem is axisymmetric about the
![]() $z$
-axis. The
$z$
-axis. The
![]() $\unicode[STIX]{x1D703}$
integration in the surface integrals of (3.4), when written using (3.6), can then be immediately evaluated without explicit knowledge of
$\unicode[STIX]{x1D703}$
integration in the surface integrals of (3.4), when written using (3.6), can then be immediately evaluated without explicit knowledge of
![]() $\unicode[STIX]{x1D748}^{\prime }$
. Defining
$\unicode[STIX]{x1D748}^{\prime }$
. Defining
one can write
Substituting (2.8) into (3.7) and using the symmetries of the tensors
![]() $\unicode[STIX]{x1D640}$
and
$\unicode[STIX]{x1D640}$
and
![]() $\unicode[STIX]{x1D642}$
, we obtain
$\unicode[STIX]{x1D642}$
, we obtain
The unit tangent and outward normal vectors
![]() $\boldsymbol{s}$
and
$\boldsymbol{s}$
and
![]() $\boldsymbol{n}$
, respectively, to the surface of the sphere are by definition
$\boldsymbol{n}$
, respectively, to the surface of the sphere are by definition
Under the axisymmetry of the model flow, we can then write
where
![]() $p^{\prime }$
is the dimensionless pressure (in units of
$p^{\prime }$
is the dimensionless pressure (in units of
![]() $\unicode[STIX]{x1D707}V^{\prime }/a$
) and
$\unicode[STIX]{x1D707}V^{\prime }/a$
) and
![]() $\unicode[STIX]{x1D714}^{\prime }=\boldsymbol{e}_{\unicode[STIX]{x1D703}}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{v}^{\prime })$
is the dimensionless vorticity field (in units of
$\unicode[STIX]{x1D714}^{\prime }=\boldsymbol{e}_{\unicode[STIX]{x1D703}}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{v}^{\prime })$
is the dimensionless vorticity field (in units of
![]() $V^{\prime }/a$
) of the model problem (Happel & Brenner Reference Happel and Brenner1965). The no-slip condition on the sphere in the model problem (
$V^{\prime }/a$
) of the model problem (Happel & Brenner Reference Happel and Brenner1965). The no-slip condition on the sphere in the model problem (
![]() $\boldsymbol{v}^{\prime }=\boldsymbol{e}_{z}$
on
$\boldsymbol{v}^{\prime }=\boldsymbol{e}_{z}$
on
![]() $S_{p}$
, cf. equation 3.1c
), ensures that the term in parentheses in (3.11) is identically zero. Substituting (3.10) and (3.11) into (3.8) then results in
$S_{p}$
, cf. equation 3.1c
), ensures that the term in parentheses in (3.11) is identically zero. Substituting (3.10) and (3.11) into (3.8) then results in
 $$\begin{eqnarray}\displaystyle F_{z}^{(2)} & = & \displaystyle -2\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D60E}_{zzz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{-p^{\prime }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{\tilde{r}^{2}\tilde{z}^{2}}{2}-\frac{\tilde{r}^{4}}{8}\right)+\unicode[STIX]{x1D714}^{\prime }\left(\frac{\tilde{r}\tilde{z}}{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{\tilde{z}^{2}-\tilde{r}^{2}}{2}\right)-\frac{\tilde{r}^{3}}{2}\frac{\unicode[STIX]{x2202}\tilde{z}}{\unicode[STIX]{x2202}s}\right)\right\}\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D60E}_{jjz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{-p^{\prime }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\!\!\left(\frac{\tilde{r}^{4}}{8}\right)+\unicode[STIX]{x1D714}^{\prime }\frac{\tilde{r}^{3}}{2}\frac{\unicode[STIX]{x2202}\tilde{z}}{\unicode[STIX]{x2202}s}\right\}\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{z}^{(2)} & = & \displaystyle -2\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D60E}_{zzz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{-p^{\prime }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{\tilde{r}^{2}\tilde{z}^{2}}{2}-\frac{\tilde{r}^{4}}{8}\right)+\unicode[STIX]{x1D714}^{\prime }\left(\frac{\tilde{r}\tilde{z}}{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{\tilde{z}^{2}-\tilde{r}^{2}}{2}\right)-\frac{\tilde{r}^{3}}{2}\frac{\unicode[STIX]{x2202}\tilde{z}}{\unicode[STIX]{x2202}s}\right)\right\}\text{d}s\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D60E}_{jjz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{-p^{\prime }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\!\!\left(\frac{\tilde{r}^{4}}{8}\right)+\unicode[STIX]{x1D714}^{\prime }\frac{\tilde{r}^{3}}{2}\frac{\unicode[STIX]{x2202}\tilde{z}}{\unicode[STIX]{x2202}s}\right\}\text{d}s,\end{eqnarray}$$
Through an integration by parts, integrals involving
![]() $p^{\prime }$
can be recast in terms of integrals involving
$p^{\prime }$
can be recast in terms of integrals involving
![]() $\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}s$
; boundary terms are identically zero since
$\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}s$
; boundary terms are identically zero since
![]() $\tilde{r}=0$
for both
$\tilde{r}=0$
for both
![]() $s=0$
and
$s=0$
and
![]() $s=\unicode[STIX]{x03C0}$
. Writing
$s=\unicode[STIX]{x03C0}$
. Writing
![]() $\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}s=\boldsymbol{s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p^{\prime }$
and noting that the momentum equation for the axisymmetric dimensionless model problem can be expressed as
$\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}s=\boldsymbol{s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p^{\prime }$
and noting that the momentum equation for the axisymmetric dimensionless model problem can be expressed as
![]() $\unicode[STIX]{x1D735}p^{\prime }=-\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D714}^{\prime }\boldsymbol{e}_{\unicode[STIX]{x1D703}})$
, we write
$\unicode[STIX]{x1D735}p^{\prime }=-\unicode[STIX]{x1D735}\times (\unicode[STIX]{x1D714}^{\prime }\boldsymbol{e}_{\unicode[STIX]{x1D703}})$
, we write
where
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}n=\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the derivative normal to the surface of the sphere. Thus, on eliminating the pressure
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}n=\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the derivative normal to the surface of the sphere. Thus, on eliminating the pressure
![]() $p^{\prime }$
from (3.12) in favour of the vorticity
$p^{\prime }$
from (3.12) in favour of the vorticity
![]() $\unicode[STIX]{x1D714}^{\prime }$
using (3.13), the expressions for
$\unicode[STIX]{x1D714}^{\prime }$
using (3.13), the expressions for
![]() $F_{z}^{(0)}$
,
$F_{z}^{(0)}$
,
![]() $F_{z}^{(1)}$
and
$F_{z}^{(1)}$
and
![]() $F_{z}^{(2)}$
become
$F_{z}^{(2)}$
become
 $$\begin{eqnarray}\displaystyle F_{z}^{(2)} & = & \displaystyle -\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a^{3}\left[\unicode[STIX]{x1D60E}_{zzz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{\tilde{r}^{3}\tilde{z}^{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{1}{\tilde{z}^{2}}\frac{\unicode[STIX]{x1D714}^{\prime }}{r}\right)-\frac{r^{7}}{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{\unicode[STIX]{x1D714}^{\prime }}{\tilde{r}^{3}}\right)\right\}\text{d}s\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\unicode[STIX]{x1D60E}_{jjz}\int _{0}^{\unicode[STIX]{x03C0}}\frac{\tilde{r}^{7}}{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{\unicode[STIX]{x1D714}^{\prime }}{\tilde{r}^{3}}\right)\text{d}s\,\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{z}^{(2)} & = & \displaystyle -\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a^{3}\left[\unicode[STIX]{x1D60E}_{zzz}\int _{0}^{\unicode[STIX]{x03C0}}\left\{\tilde{r}^{3}\tilde{z}^{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{1}{\tilde{z}^{2}}\frac{\unicode[STIX]{x1D714}^{\prime }}{r}\right)-\frac{r^{7}}{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{\unicode[STIX]{x1D714}^{\prime }}{\tilde{r}^{3}}\right)\right\}\text{d}s\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\unicode[STIX]{x1D60E}_{jjz}\int _{0}^{\unicode[STIX]{x03C0}}\frac{\tilde{r}^{7}}{4}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{\unicode[STIX]{x1D714}^{\prime }}{\tilde{r}^{3}}\right)\text{d}s\,\right].\end{eqnarray}$$
Note that since
![]() $F_{z}^{(0)}$
depends on the translational velocity of the sphere relative to the fluid, it is related to the force on the particle in the model problem
$F_{z}^{(0)}$
depends on the translational velocity of the sphere relative to the fluid, it is related to the force on the particle in the model problem
![]() $F_{z}^{\prime }$
as
$F_{z}^{\prime }$
as
![]() $F_{z}^{(0)}=F_{z}^{\prime }(w_{z}^{(0)}/V^{\prime })$
. This contribution to the force is already well known (Brenner Reference Brenner1961; Cox & Brenner Reference Cox and Brenner1967) for a translating sphere in a quiescent fluid, but is obtained here as the leading term of a more general expansion of the background flow. The expressions for
$F_{z}^{(0)}=F_{z}^{\prime }(w_{z}^{(0)}/V^{\prime })$
. This contribution to the force is already well known (Brenner Reference Brenner1961; Cox & Brenner Reference Cox and Brenner1967) for a translating sphere in a quiescent fluid, but is obtained here as the leading term of a more general expansion of the background flow. The expressions for
![]() $F_{z}^{(1)}$
and
$F_{z}^{(1)}$
and
![]() $F_{z}^{(2)}$
have a similar structure to
$F_{z}^{(2)}$
have a similar structure to
![]() $F_{z}^{(0)}$
and are calculated in the next section.
$F_{z}^{(0)}$
and are calculated in the next section.
4 Evaluation of the normal force on the sphere
4.1 Vorticity field in the model problem
The normal force on the sphere, equation (3.14), can be computed given the vorticity field in the model problem, which corresponds to the translation of a spherical particle normal to a stationary spherical obstacle (on which the flow satisfies either no-slip or stress-free conditions) in a quiescent fluid. For arbitrary
![]() $a/h$
and
$a/h$
and
![]() $a/R$
, the solution to the model problem can be expressed using bipolar coordinates
$a/R$
, the solution to the model problem can be expressed using bipolar coordinates
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, in which the particle surface
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, in which the particle surface
![]() $S_{p}$
and the obstacle surface
$S_{p}$
and the obstacle surface
![]() $S_{w}$
are delineated by the coordinate lines
$S_{w}$
are delineated by the coordinate lines
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}$
, respectively (see figure 2), where (Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983)
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}$
, respectively (see figure 2), where (Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983)
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}\equiv \cosh ^{-1}\left({\displaystyle \frac{\left({\displaystyle \frac{h}{a}}+{\displaystyle \frac{R}{a}}\right)^{2}-\left({\displaystyle \frac{R}{a}}\right)^{2}+1}{2\left({\displaystyle \frac{h}{a}}+{\displaystyle \frac{R}{a}}\right)}}\right)\quad \text{and}\quad {\displaystyle \frac{\sinh \unicode[STIX]{x1D6FD}}{\sinh \unicode[STIX]{x1D6FC}}}\equiv -\frac{a}{R}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\equiv \cosh ^{-1}\left({\displaystyle \frac{\left({\displaystyle \frac{h}{a}}+{\displaystyle \frac{R}{a}}\right)^{2}-\left({\displaystyle \frac{R}{a}}\right)^{2}+1}{2\left({\displaystyle \frac{h}{a}}+{\displaystyle \frac{R}{a}}\right)}}\right)\quad \text{and}\quad {\displaystyle \frac{\sinh \unicode[STIX]{x1D6FD}}{\sinh \unicode[STIX]{x1D6FC}}}\equiv -\frac{a}{R}.\end{eqnarray}$$
Taken together, the values of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
specify both
$\unicode[STIX]{x1D6FD}$
specify both
![]() $a/h$
and
$a/h$
and
![]() $a/R$
and therefore uniquely determine the geometry of the problem. The coordinates
$a/R$
and therefore uniquely determine the geometry of the problem. The coordinates
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
are related to the cylindrical coordinates
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
are related to the cylindrical coordinates
![]() $(r,z)$
as (Stimson & Jeffery Reference Stimson and Jeffery1926)
$(r,z)$
as (Stimson & Jeffery Reference Stimson and Jeffery1926)
Thus,
![]() $\unicode[STIX]{x1D709}$
takes values in the range
$\unicode[STIX]{x1D709}$
takes values in the range
![]() $[\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}]$
, where we take
$[\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}]$
, where we take
![]() $\unicode[STIX]{x1D6FD}<0$
and
$\unicode[STIX]{x1D6FD}<0$
and
![]() $\unicode[STIX]{x1D6FC}>0$
without loss of generality, cf. (4.1). The coordinate
$\unicode[STIX]{x1D6FC}>0$
without loss of generality, cf. (4.1). The coordinate
![]() $\unicode[STIX]{x1D702}$
lies in
$\unicode[STIX]{x1D702}$
lies in
![]() $[0,\unicode[STIX]{x03C0}]$
; on the particle
$[0,\unicode[STIX]{x03C0}]$
; on the particle
![]() $S_{p}$
,
$S_{p}$
,
![]() $\unicode[STIX]{x1D702}=0\;\Longleftrightarrow \;s=0$
and
$\unicode[STIX]{x1D702}=0\;\Longleftrightarrow \;s=0$
and
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x03C0}\;\Longleftrightarrow \;s=\unicode[STIX]{x03C0}$
, cf. figure 2. We note that for a fixed curvature ratio
$\unicode[STIX]{x1D702}=\unicode[STIX]{x03C0}\;\Longleftrightarrow \;s=\unicode[STIX]{x03C0}$
, cf. figure 2. We note that for a fixed curvature ratio
![]() $a/R$
, the limit
$a/R$
, the limit
![]() $\unicode[STIX]{x1D6FC}\rightarrow 0$
corresponds to the case where the surfaces are touching
$\unicode[STIX]{x1D6FC}\rightarrow 0$
corresponds to the case where the surfaces are touching
![]() $(h\rightarrow a)$
and
$(h\rightarrow a)$
and
![]() $\unicode[STIX]{x1D6FC}\rightarrow \infty$
to large separations (
$\unicode[STIX]{x1D6FC}\rightarrow \infty$
to large separations (
![]() $h/a\rightarrow \infty$
).
$h/a\rightarrow \infty$
).
The model vorticity field
![]() $\unicode[STIX]{x1D714}^{\prime }$
can be described in these coordinates, for arbitrary
$\unicode[STIX]{x1D714}^{\prime }$
can be described in these coordinates, for arbitrary
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
, by first defining the functions
$\unicode[STIX]{x1D6FD}$
, by first defining the functions
where
 $$\begin{eqnarray}\displaystyle g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}) & = & \displaystyle (\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{5/2}\mathop{\sum }_{n=0}^{\infty }\bigg[V_{n}(\unicode[STIX]{x1D70F})\bigg\{\frac{\text{d}^{2}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}^{2}}-\frac{2\sinh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{4}\frac{\cosh \unicode[STIX]{x1D709}+3\unicode[STIX]{x1D70F}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}U_{n}(\unicode[STIX]{x1D709})\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D70F}^{2})\,U_{n}(\unicode[STIX]{x1D709})\left\{\frac{\text{d}^{2}V_{n}(\unicode[STIX]{x1D70F})}{\text{d}\unicode[STIX]{x1D70F}^{2}}+\frac{2}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}V_{n}(\unicode[STIX]{x1D70F})}{\text{d}\unicode[STIX]{x1D70F}}\right\}\bigg].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}) & = & \displaystyle (\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{5/2}\mathop{\sum }_{n=0}^{\infty }\bigg[V_{n}(\unicode[STIX]{x1D70F})\bigg\{\frac{\text{d}^{2}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}^{2}}-\frac{2\sinh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{4}\frac{\cosh \unicode[STIX]{x1D709}+3\unicode[STIX]{x1D70F}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}U_{n}(\unicode[STIX]{x1D709})\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D70F}^{2})\,U_{n}(\unicode[STIX]{x1D709})\left\{\frac{\text{d}^{2}V_{n}(\unicode[STIX]{x1D70F})}{\text{d}\unicode[STIX]{x1D70F}^{2}}+\frac{2}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}V_{n}(\unicode[STIX]{x1D70F})}{\text{d}\unicode[STIX]{x1D70F}}\right\}\bigg].\end{eqnarray}$$
This completes the description of the model vorticity field
![]() $\unicode[STIX]{x1D714}^{\prime }$
required to calculate the normal force on the particle using (3.14). We remark that the curvature ratio
$\unicode[STIX]{x1D714}^{\prime }$
required to calculate the normal force on the particle using (3.14). We remark that the curvature ratio
![]() $a/R$
and boundary conditions on both surfaces enter the problem through the coefficients
$a/R$
and boundary conditions on both surfaces enter the problem through the coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
, which depend on both
$d_{n}$
, which depend on both
![]() $a/h$
and
$a/h$
and
![]() $a/R$
(via
$a/R$
(via
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
). In the limit
$\unicode[STIX]{x1D6FD}$
). In the limit
![]() $a/R\rightarrow 0$
(planar
$a/R\rightarrow 0$
(planar
![]() $S_{w}$
), we find from (4.1) that
$S_{w}$
), we find from (4.1) that
![]() $\unicode[STIX]{x1D6FC}\rightarrow \cosh ^{-1}(h/a)$
and
$\unicode[STIX]{x1D6FC}\rightarrow \cosh ^{-1}(h/a)$
and
![]() $\unicode[STIX]{x1D6FD}\rightarrow 0$
. The solutions to the model problems (both no-slip and stress-free cases) in this limit are given by Brenner (Reference Brenner1961) for arbitrary
$\unicode[STIX]{x1D6FD}\rightarrow 0$
. The solutions to the model problems (both no-slip and stress-free cases) in this limit are given by Brenner (Reference Brenner1961) for arbitrary
![]() $h/a$
(i.e. arbitrary
$h/a$
(i.e. arbitrary
![]() $\unicode[STIX]{x1D6FC}$
). For the general case of a curved obstacle (
$\unicode[STIX]{x1D6FC}$
). For the general case of a curved obstacle (
![]() $\unicode[STIX]{x1D6FD}\neq 0$
) and no-slip surfaces (BC I), the appropriate expressions for the coefficients
$\unicode[STIX]{x1D6FD}\neq 0$
) and no-slip surfaces (BC I), the appropriate expressions for the coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
can be constructed using two-sphere solutions (Maude Reference Maude1961; Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983) and depend on both
$d_{n}$
can be constructed using two-sphere solutions (Maude Reference Maude1961; Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983) and depend on both
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
(see appendix A). The coefficients corresponding to a stress-free curved obstacle
$\unicode[STIX]{x1D6FD}$
(see appendix A). The coefficients corresponding to a stress-free curved obstacle
![]() $S_{w}$
(
$S_{w}$
(
![]() $\unicode[STIX]{x1D6FD}\neq 0$
; BC II) have been computed in appendix A.
$\unicode[STIX]{x1D6FD}\neq 0$
; BC II) have been computed in appendix A.
4.2 Expressions for the force
To utilize the expression (4.4) for
![]() $\unicode[STIX]{x1D714}^{\prime }$
in the integrals of (3.14), it is necessary to transform
$\unicode[STIX]{x1D714}^{\prime }$
in the integrals of (3.14), it is necessary to transform
![]() $\text{d}s$
and
$\text{d}s$
and
![]() $\text{d}n$
to bipolar coordinates. Writing
$\text{d}n$
to bipolar coordinates. Writing
![]() $\text{d}n=\boldsymbol{n}\boldsymbol{\cdot }\text{d}\boldsymbol{r}$
and
$\text{d}n=\boldsymbol{n}\boldsymbol{\cdot }\text{d}\boldsymbol{r}$
and
![]() $\text{d}s=\boldsymbol{s}\boldsymbol{\cdot }\text{d}\boldsymbol{r}$
in (3.10) and using the transformation (4.2), we obtain
$\text{d}s=\boldsymbol{s}\boldsymbol{\cdot }\text{d}\boldsymbol{r}$
in (3.10) and using the transformation (4.2), we obtain
so that
for any function
![]() $f$
. Substituting the expressions (4.2)–(4.7) for the coordinate transformation
$f$
. Substituting the expressions (4.2)–(4.7) for the coordinate transformation
![]() $(r,z)\mapsto (\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
and the model vorticity field
$(r,z)\mapsto (\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
and the model vorticity field
![]() $\unicode[STIX]{x1D714}^{\prime }$
into (3.14), we obtain
$\unicode[STIX]{x1D714}^{\prime }$
into (3.14), we obtain
The explicit evaluation of
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
utilizes some properties of the Legendre polynomials that appear in
${\mathcal{J}}$
utilizes some properties of the Legendre polynomials that appear in
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
; the details are given in appendix B. The integration ultimately results in expressions for the force in terms of the coefficients
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
; the details are given in appendix B. The integration ultimately results in expressions for the force in terms of the coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
of the model flow, which we express as
$d_{n}$
of the model flow, which we express as
 $$\begin{eqnarray}\displaystyle {\mathcal{C}} & = & \displaystyle 2{\mathcal{B}}\cosh \unicode[STIX]{x1D6FC}-{\mathcal{A}}\cosh ^{2}\unicode[STIX]{x1D6FC}-\frac{\sqrt{2}\sinh \unicode[STIX]{x1D6FC}}{9}\mathop{\sum }_{n=0}^{\infty }\big[n(n+1)(a_{n}+b_{n}+c_{n}+d_{n})\nonumber\\ \displaystyle & & \displaystyle +\,\{(2n-1)^{2}(a_{n}+b_{n})+(2n+3)^{2}(c_{n}+d_{n})\}\big],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{C}} & = & \displaystyle 2{\mathcal{B}}\cosh \unicode[STIX]{x1D6FC}-{\mathcal{A}}\cosh ^{2}\unicode[STIX]{x1D6FC}-\frac{\sqrt{2}\sinh \unicode[STIX]{x1D6FC}}{9}\mathop{\sum }_{n=0}^{\infty }\big[n(n+1)(a_{n}+b_{n}+c_{n}+d_{n})\nonumber\\ \displaystyle & & \displaystyle +\,\{(2n-1)^{2}(a_{n}+b_{n})+(2n+3)^{2}(c_{n}+d_{n})\}\big],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\mathcal{D}} & = & \displaystyle \frac{{\mathcal{A}}}{3}-\frac{{\mathcal{C}}}{5}+\frac{2\sqrt{2}}{45}\mathop{\sum }_{n=0}^{\infty }\big[(2(2n+1)-\coth \unicode[STIX]{x1D6FC})\{(a_{n}-b_{n})\text{e}^{\unicode[STIX]{x1D6FC}}+(c_{n}-d_{n})\text{e}^{-\unicode[STIX]{x1D6FC}}\}\nonumber\\ \displaystyle & & \displaystyle -\,5\{(a_{n}-b_{n})\text{e}^{\unicode[STIX]{x1D6FC}}-(c_{n}-d_{n})\text{e}^{-\unicode[STIX]{x1D6FC}}\}\big]\text{e}^{-(2n+1)\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}} & = & \displaystyle \frac{{\mathcal{A}}}{3}-\frac{{\mathcal{C}}}{5}+\frac{2\sqrt{2}}{45}\mathop{\sum }_{n=0}^{\infty }\big[(2(2n+1)-\coth \unicode[STIX]{x1D6FC})\{(a_{n}-b_{n})\text{e}^{\unicode[STIX]{x1D6FC}}+(c_{n}-d_{n})\text{e}^{-\unicode[STIX]{x1D6FC}}\}\nonumber\\ \displaystyle & & \displaystyle -\,5\{(a_{n}-b_{n})\text{e}^{\unicode[STIX]{x1D6FC}}-(c_{n}-d_{n})\text{e}^{-\unicode[STIX]{x1D6FC}}\}\big]\text{e}^{-(2n+1)\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
Thus, we have obtained general expressions for the hydrodynamic resistances of a spherical particle near a stationary spherical obstacle suspended in a locally quadratic background flow. The component of the hydrodynamic force on the sphere normal to the obstacle, accurate up to the quadratic moment of the flow, is therefore
 $$\begin{eqnarray}\displaystyle F_{\bot }\equiv \boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{\bot } & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a\bigg[\bigg\{-{\mathcal{A}}\,(\boldsymbol{v}_{p}-\boldsymbol{u})-a\,{\mathcal{B}}\,(\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u})\nonumber\\ \displaystyle & & \displaystyle +\frac{a^{2}}{2}{\mathcal{C}}\,(\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})+\frac{a^{2}}{2}{\mathcal{D}}\,\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\bigg\}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }\bigg]_{\boldsymbol{x}_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\bot }\equiv \boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{e}_{\bot } & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a\bigg[\bigg\{-{\mathcal{A}}\,(\boldsymbol{v}_{p}-\boldsymbol{u})-a\,{\mathcal{B}}\,(\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u})\nonumber\\ \displaystyle & & \displaystyle +\frac{a^{2}}{2}{\mathcal{C}}\,(\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})+\frac{a^{2}}{2}{\mathcal{D}}\,\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\bigg\}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }\bigg]_{\boldsymbol{x}_{p}}.\end{eqnarray}$$
5 Discussion
The general expression for the normal force (4.12) shows that there are four distinct contributions up to the second moment of the background flow. The first of these, proportional to
![]() ${\mathcal{A}}$
, is due to the translation of the particle relative to the mean background flow in its vicinity, and is identical to the general expression obtained by Brenner (Reference Brenner1961). The term proportional to
${\mathcal{A}}$
, is due to the translation of the particle relative to the mean background flow in its vicinity, and is identical to the general expression obtained by Brenner (Reference Brenner1961). The term proportional to
![]() ${\mathcal{B}}$
arises due to extensional gradients of the background flow. This contribution is identically zero for a sphere in an infinite medium (Happel & Brenner Reference Happel and Brenner1965; Batchelor Reference Batchelor1970), but as we will show shortly, is generally non-zero for finite
${\mathcal{B}}$
arises due to extensional gradients of the background flow. This contribution is identically zero for a sphere in an infinite medium (Happel & Brenner Reference Happel and Brenner1965; Batchelor Reference Batchelor1970), but as we will show shortly, is generally non-zero for finite
![]() $h/a$
and is ultimately important in determining the motion of the particle close to the obstacle. Second moments of the background flow result in two separate contributions to the force: one that is proportional to
$h/a$
and is ultimately important in determining the motion of the particle close to the obstacle. Second moments of the background flow result in two separate contributions to the force: one that is proportional to
![]() ${\mathcal{C}}$
and depends on the curvature of the background velocity normal to the plane (
${\mathcal{C}}$
and depends on the curvature of the background velocity normal to the plane (
![]() $\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u}$
) and another that is proportional to
$\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u}$
) and another that is proportional to
![]() ${\mathcal{D}}$
and depends on
${\mathcal{D}}$
and depends on
![]() $\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
. In the discussion that follows, the subscripts
$\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
. In the discussion that follows, the subscripts
![]() $\text{I}$
or
$\text{I}$
or
![]() $\text{II}$
will be used, when necessary, to distinguish between the cases in which the surface of the obstacle is a no-slip boundary or a no-stress interface, respectively.
$\text{II}$
will be used, when necessary, to distinguish between the cases in which the surface of the obstacle is a no-slip boundary or a no-stress interface, respectively.
We now discuss the asymptotic behaviour of the hydrodynamic resistance coefficients in the limits of large and small separations of the sphere from the obstacle. It is convenient to describe the limiting behaviour in terms of a dimensionless parameter
which is the minimum surface-to-surface distance relative to the radius of the particle. The hydrodynamic resistances depend on the two dimensionless parameters
![]() $h/a$
and
$h/a$
and
![]() $R/a$
.
$R/a$
.

Figure 3. Resistance coefficients for the cases of an obstacle with (a) a solid surface and (b) a stress-free interface in the limit of a weakly curved obstacle (
![]() $a/R\rightarrow 0\;\Longleftrightarrow \;\unicode[STIX]{x1D6FD}\rightarrow 0$
). Dashed lines indicate the leading asymptotic behaviour for large and small
$a/R\rightarrow 0\;\Longleftrightarrow \;\unicode[STIX]{x1D6FD}\rightarrow 0$
). Dashed lines indicate the leading asymptotic behaviour for large and small
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Although the formalism is general for arbitrary
![]() $a/R$
, we restrict our attention to situations with small particles (
$a/R$
, we restrict our attention to situations with small particles (
![]() $a/R\ll 1$
). Hydrodynamic interactions are weak for very large separations with
$a/R\ll 1$
). Hydrodynamic interactions are weak for very large separations with
![]() $h\gg R\gg a$
and are well described by interactions between point objects using the method of reflections (Haber & Brenner Reference Haber and Brenner1999). We focus here on the stronger interactions associated with separation distances satisfying
$h\gg R\gg a$
and are well described by interactions between point objects using the method of reflections (Haber & Brenner Reference Haber and Brenner1999). We focus here on the stronger interactions associated with separation distances satisfying
![]() $R\gg h\gtrsim a$
(including
$R\gg h\gtrsim a$
(including
![]() $R\gg h\gg a$
), which corresponds to
$R\gg h\gg a$
), which corresponds to
![]() $|\unicode[STIX]{x1D6FD}|\ll \unicode[STIX]{x1D6FC}$
, cf. (4.1). Thus, a Taylor expansion of (4.11) about
$|\unicode[STIX]{x1D6FD}|\ll \unicode[STIX]{x1D6FC}$
, cf. (4.1). Thus, a Taylor expansion of (4.11) about
![]() $\unicode[STIX]{x1D6FD}=0$
(i.e. the limit of a planar obstacle,
$\unicode[STIX]{x1D6FD}=0$
(i.e. the limit of a planar obstacle,
![]() $a/R\rightarrow 0$
) using the results of appendix A is appropriate. The leading-order forms of the resistances
$a/R\rightarrow 0$
) using the results of appendix A is appropriate. The leading-order forms of the resistances
![]() ${\mathcal{A}}_{\text{I}}$
,
${\mathcal{A}}_{\text{I}}$
,
![]() ${\mathcal{B}}_{\text{I}}$
,
${\mathcal{B}}_{\text{I}}$
,
![]() ${\mathcal{C}}_{\text{I}}$
and
${\mathcal{C}}_{\text{I}}$
and
![]() ${\mathcal{D}}_{\text{I}}$
(no-slip wall) and
${\mathcal{D}}_{\text{I}}$
(no-slip wall) and
![]() ${\mathcal{A}}_{\text{II}}$
,
${\mathcal{A}}_{\text{II}}$
,
![]() ${\mathcal{B}}_{\text{II}}$
,
${\mathcal{B}}_{\text{II}}$
,
![]() ${\mathcal{C}}_{\text{II}}$
and
${\mathcal{C}}_{\text{II}}$
and
![]() ${\mathcal{D}}_{\text{II}}$
(no-stress interface) for
${\mathcal{D}}_{\text{II}}$
(no-stress interface) for
![]() $|\unicode[STIX]{x1D6FD}|\ll 1$
are plotted in figure 3(a,b), respectively, as functions of
$|\unicode[STIX]{x1D6FD}|\ll 1$
are plotted in figure 3(a,b), respectively, as functions of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
5.1 Asymptotic behaviour for small and large separations
The asymptotic behaviour of
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
for large separations
${\mathcal{D}}$
for large separations
![]() $\unicode[STIX]{x1D6E5}\gg 1$
(in the limit
$\unicode[STIX]{x1D6E5}\gg 1$
(in the limit
![]() $a/R\rightarrow 0$
) is obtained by a term-by-term Taylor series expansion of the expressions in (C 3) for large
$a/R\rightarrow 0$
) is obtained by a term-by-term Taylor series expansion of the expressions in (C 3) for large
![]() $\unicode[STIX]{x1D6FC}$
(note that
$\unicode[STIX]{x1D6FC}$
(note that
![]() $\unicode[STIX]{x1D6E5}\gg 1\;\Longrightarrow \;\unicode[STIX]{x1D6FC}\gg 1$
), and then evaluating the sum. Only the first few terms of the series are required to obtain asymptotically accurate results.
$\unicode[STIX]{x1D6E5}\gg 1\;\Longrightarrow \;\unicode[STIX]{x1D6FC}\gg 1$
), and then evaluating the sum. Only the first few terms of the series are required to obtain asymptotically accurate results.
For arbitrarily large separations
![]() $\unicode[STIX]{x1D6E5}\rightarrow \infty$
, only
$\unicode[STIX]{x1D6E5}\rightarrow \infty$
, only
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{D}}$
are non-zero, with
${\mathcal{D}}$
are non-zero, with
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() ${\mathcal{C}}$
decaying algebraically to zero. Independent of the boundary condition at the wall
${\mathcal{C}}$
decaying algebraically to zero. Independent of the boundary condition at the wall
![]() $S_{w}$
, we obtain
$S_{w}$
, we obtain
In this limit, from (4.12) we recover Faxén’s law for the force on a sphere in an unbounded fluid:
We find additionally that
![]() ${\mathcal{B}}\propto \unicode[STIX]{x1D6E5}^{-2}$
and
${\mathcal{B}}\propto \unicode[STIX]{x1D6E5}^{-2}$
and
![]() ${\mathcal{C}}\propto \unicode[STIX]{x1D6E5}^{-3}$
for large
${\mathcal{C}}\propto \unicode[STIX]{x1D6E5}^{-3}$
for large
![]() $\unicode[STIX]{x1D6E5}\gg 1$
, with
$\unicode[STIX]{x1D6E5}\gg 1$
, with
![]() $O(1)$
prefactors that depend on the boundary conditions at
$O(1)$
prefactors that depend on the boundary conditions at
![]() $S_{w}$
; specifically, we obtain
$S_{w}$
; specifically, we obtain
The above far-field expressions are in agreement with the resistances calculated using the method of reflections (Haber & Brenner Reference Haber and Brenner1999; Swan & Brady Reference Swan and Brady2007).
Table 1. Asymptotic behaviour of the resistance coefficients for small and large separations for small particles
![]() $(a\lesssim h\ll R\;\Longleftrightarrow \;|\unicode[STIX]{x1D6FD}|\ll 1)$
, with subscripts
$(a\lesssim h\ll R\;\Longleftrightarrow \;|\unicode[STIX]{x1D6FD}|\ll 1)$
, with subscripts
![]() $\text{I}$
and
$\text{I}$
and
![]() $\text{II}$
indicating, respectively, no-slip and stress-free obstacle boundaries, e.g. equation (2.2). The
$\text{II}$
indicating, respectively, no-slip and stress-free obstacle boundaries, e.g. equation (2.2). The
![]() $\unicode[STIX]{x1D6E5}\ll 1$
asymptotes are obtained applying the method of Cox & Brenner (Reference Cox and Brenner1967) to the expressions (C 3). The
$\unicode[STIX]{x1D6E5}\ll 1$
asymptotes are obtained applying the method of Cox & Brenner (Reference Cox and Brenner1967) to the expressions (C 3). The
![]() $O(\unicode[STIX]{x1D6E5}^{0})$
constants in the
$O(\unicode[STIX]{x1D6E5}^{0})$
constants in the
![]() $\unicode[STIX]{x1D6E5}\ll 1$
expressions are computed by a numerical integration of known analytic functions involving polynomials and hyperbolic functions. The asymptotes for
$\unicode[STIX]{x1D6E5}\ll 1$
expressions are computed by a numerical integration of known analytic functions involving polynomials and hyperbolic functions. The asymptotes for
![]() $R/a\gg \unicode[STIX]{x1D6E5}\gg 1$
are calculated by a regular perturbation expansion of (C 3) for large
$R/a\gg \unicode[STIX]{x1D6E5}\gg 1$
are calculated by a regular perturbation expansion of (C 3) for large
![]() $\unicode[STIX]{x1D6FC}$
; curvature corrections of relative order
$\unicode[STIX]{x1D6FC}$
; curvature corrections of relative order
![]() $h/R\ll 1$
have been retained in this limit.
$h/R\ll 1$
have been retained in this limit.

For small separations
![]() $(\unicode[STIX]{x1D6E5}\ll 1)$
, the asymptotic forms of
$(\unicode[STIX]{x1D6E5}\ll 1)$
, the asymptotic forms of
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
cannot in general be evaluated to arbitrary order in
${\mathcal{D}}$
cannot in general be evaluated to arbitrary order in
![]() $\unicode[STIX]{x1D6E5}$
(in particular beyond
$\unicode[STIX]{x1D6E5}$
(in particular beyond
![]() $O(\unicode[STIX]{x1D6E5}^{-1})$
terms) using a term-by-term expansion of (C 3). Instead, a more sophisticated approach involving matched asymptotic expansions of the infinite series in (C 3) is required (Cox & Brenner Reference Cox and Brenner1967), using which we obtain at leading order:
$O(\unicode[STIX]{x1D6E5}^{-1})$
terms) using a term-by-term expansion of (C 3). Instead, a more sophisticated approach involving matched asymptotic expansions of the infinite series in (C 3) is required (Cox & Brenner Reference Cox and Brenner1967), using which we obtain at leading order:
Here
![]() $K=K_{\text{I}}=1$
for a no-slip wall, and
$K=K_{\text{I}}=1$
for a no-slip wall, and
![]() $K=K_{\text{II}}=1/4$
for a stress-free surface. These leading-order asymptotes in the small
$K=K_{\text{II}}=1/4$
for a stress-free surface. These leading-order asymptotes in the small
![]() $\unicode[STIX]{x1D6E5}$
limit can also be obtained by using the well-known description of the model flow from lubrication theory, rather than the exact solution in terms of bipolar coordinates. We verify that using the lubrication theory prediction for the model vorticity
$\unicode[STIX]{x1D6E5}$
limit can also be obtained by using the well-known description of the model flow from lubrication theory, rather than the exact solution in terms of bipolar coordinates. We verify that using the lubrication theory prediction for the model vorticity
![]() $\unicode[STIX]{x1D714}^{\prime }$
(O’Neill & Stewartson Reference O’Neill and Stewartson1967; Jeffrey & Onishi Reference Jeffrey and Onishi1981) in the general formulas (3.14) recovers the leading-order asymptotes (5.5) obtained from analysing the full expressions in (C 3). The asymptotic forms of the resistance coefficients for large and small
$\unicode[STIX]{x1D714}^{\prime }$
(O’Neill & Stewartson Reference O’Neill and Stewartson1967; Jeffrey & Onishi Reference Jeffrey and Onishi1981) in the general formulas (3.14) recovers the leading-order asymptotes (5.5) obtained from analysing the full expressions in (C 3). The asymptotic forms of the resistance coefficients for large and small
![]() $\unicode[STIX]{x1D6E5}$
in the limit
$\unicode[STIX]{x1D6E5}$
in the limit
![]() $a/R\rightarrow 0$
are indicated in figure 3 as dashed lines. These asymptotes, along with leading-order corrections in
$a/R\rightarrow 0$
are indicated in figure 3 as dashed lines. These asymptotes, along with leading-order corrections in
![]() $a/R$
, are tabulated in table 1. The logarithmic and
$a/R$
, are tabulated in table 1. The logarithmic and
![]() $O(\unicode[STIX]{x1D6E5}^{0})$
terms in the
$O(\unicode[STIX]{x1D6E5}^{0})$
terms in the
![]() $\unicode[STIX]{x1D6E5}\ll 1$
limit (table 1) are found using the method detailed in Cox & Brenner (Reference Cox and Brenner1967), with the
$\unicode[STIX]{x1D6E5}\ll 1$
limit (table 1) are found using the method detailed in Cox & Brenner (Reference Cox and Brenner1967), with the
![]() $O(\unicode[STIX]{x1D6E5}^{0})$
terms obtained from a numerical integration of known analytic functions.
$O(\unicode[STIX]{x1D6E5}^{0})$
terms obtained from a numerical integration of known analytic functions.
While the analysis formally applies to spherical particles near spherical obstacles, some general quantitative conclusions can be drawn for non-spherical obstacles. Consider obstacles that are only locally spherical, i.e. the principle radii of curvature are both locally equal to
![]() $R$
(cf. figure 1). If (i) the particle radius and its distance from the obstacle are small (
$R$
(cf. figure 1). If (i) the particle radius and its distance from the obstacle are small (
![]() $a\lesssim h\ll R$
) and (ii) gradients in the curvature of the obstacle’s surface occur over length scales of
$a\lesssim h\ll R$
) and (ii) gradients in the curvature of the obstacle’s surface occur over length scales of
![]() $O(R)$
, these curvature gradients have a small effect on the normal force since the disturbance flow due to the particle decays at most over a characteristic length scale of
$O(R)$
, these curvature gradients have a small effect on the normal force since the disturbance flow due to the particle decays at most over a characteristic length scale of
![]() $h\ll R$
. In this case, the results in table 1 remain applicable to first approximation. For
$h\ll R$
. In this case, the results in table 1 remain applicable to first approximation. For
![]() $h\gtrsim O(R)$
, the disturbance flow caused by the particle must conform to the detailed shape of the obstacle boundary and a local description does not suffice. Similar arguments apply if the principle radii of curvature of the obstacle, say
$h\gtrsim O(R)$
, the disturbance flow caused by the particle must conform to the detailed shape of the obstacle boundary and a local description does not suffice. Similar arguments apply if the principle radii of curvature of the obstacle, say
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
, are distinct, although it is noted that for a small particle that is close to the obstacle surface (
$R_{2}$
, are distinct, although it is noted that for a small particle that is close to the obstacle surface (
![]() $a\lesssim h\ll R_{1}$
,
$a\lesssim h\ll R_{1}$
,
![]() $a\lesssim h\ll R_{2}$
,
$a\lesssim h\ll R_{2}$
,
![]() $R_{1}\neq R_{2}$
), only the terms independent of
$R_{1}\neq R_{2}$
), only the terms independent of
![]() $a/R$
in table 1 are meaningful.
$a/R$
in table 1 are meaningful.
5.2 Force on a stationary particle near an obstacle
We now compute the external force that must be applied in order to hold a particle stationary on the symmetry axis of a normally incident stagnation flow near an obstacle (figure 4). By symmetry, the only component of the external force required to keep the particle stationary is in the direction normal to the surface. In the near-field limit
![]() $(\unicode[STIX]{x1D6E5}\ll 1)$
the background flow may be alternately expressed using a Taylor expansion about the point on the obstacle closest to the particle surface,
$(\unicode[STIX]{x1D6E5}\ll 1)$
the background flow may be alternately expressed using a Taylor expansion about the point on the obstacle closest to the particle surface,
![]() $\boldsymbol{x}=\mathbf{0}$
, as
$\boldsymbol{x}=\mathbf{0}$
, as
![]() $\boldsymbol{u}(\boldsymbol{x})\sim \boldsymbol{u}|_{\boldsymbol{x}=\mathbf{0}}+\boldsymbol{x}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{u})_{\boldsymbol{x}=\mathbf{0}}+(1/2)\boldsymbol{x}\boldsymbol{x}\boldsymbol{ : }(\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})_{\boldsymbol{x}=\mathbf{0}}+\cdots \,$
, cf. figure 4. To compute the normal component of the force, one need consider only the normal velocity
$\boldsymbol{u}(\boldsymbol{x})\sim \boldsymbol{u}|_{\boldsymbol{x}=\mathbf{0}}+\boldsymbol{x}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{u})_{\boldsymbol{x}=\mathbf{0}}+(1/2)\boldsymbol{x}\boldsymbol{x}\boldsymbol{ : }(\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{u})_{\boldsymbol{x}=\mathbf{0}}+\cdots \,$
, cf. figure 4. To compute the normal component of the force, one need consider only the normal velocity
![]() $\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }$
due to the form of (4.12). Evaluating moments of this velocity field at the particle centre
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{\bot }$
due to the form of (4.12). Evaluating moments of this velocity field at the particle centre
![]() $\boldsymbol{x}_{p}=h\boldsymbol{e}_{\bot }$
and applying (4.12) results in an expression for the normal force
$\boldsymbol{x}_{p}=h\boldsymbol{e}_{\bot }$
and applying (4.12) results in an expression for the normal force
![]() $F_{\bot }$
.
$F_{\bot }$
.

Figure 4. A particle held stationary in a normally incident stagnation flow
![]() $\boldsymbol{u}(\boldsymbol{x})$
near an obstacle. In the limit of small separations
$\boldsymbol{u}(\boldsymbol{x})$
near an obstacle. In the limit of small separations
![]() $\unicode[STIX]{x1D6E5}\equiv (h/a)-1\ll 1$
,
$\unicode[STIX]{x1D6E5}\equiv (h/a)-1\ll 1$
,
![]() $\boldsymbol{u}(\boldsymbol{x})$
can be approximated using a Taylor expansion about the point
$\boldsymbol{u}(\boldsymbol{x})$
can be approximated using a Taylor expansion about the point
![]() $\boldsymbol{x}=\mathbf{0}$
and has a generic structure that depends critically on the boundary conditions at
$\boldsymbol{x}=\mathbf{0}$
and has a generic structure that depends critically on the boundary conditions at
![]() $S_{w}$
. As a result, the external force required to keep the particle stationary close to the obstacle surface is much greater for a stress-free
$S_{w}$
. As a result, the external force required to keep the particle stationary close to the obstacle surface is much greater for a stress-free
![]() $S_{w}$
in comparison with that for a no-slip
$S_{w}$
in comparison with that for a no-slip
![]() $S_{w}$
due to the generally larger surface velocities in the former, see (5.6), (5.7). In both cases, the force on the stationary particle becomes independent of
$S_{w}$
due to the generally larger surface velocities in the former, see (5.6), (5.7). In both cases, the force on the stationary particle becomes independent of
![]() $\unicode[STIX]{x1D6E5}$
for
$\unicode[STIX]{x1D6E5}$
for
![]() $\unicode[STIX]{x1D6E5}\ll 1$
.
$\unicode[STIX]{x1D6E5}\ll 1$
.
For a no-slip surface
![]() $S_{w}$
, both the normal velocity and the extension rate at the surface of the obstacle are zero. In this case, we find that force contributions proportional to
$S_{w}$
, both the normal velocity and the extension rate at the surface of the obstacle are zero. In this case, we find that force contributions proportional to
![]() $\unicode[STIX]{x1D6E5}^{-1}$
and
$\unicode[STIX]{x1D6E5}^{-1}$
and
![]() $\log \unicode[STIX]{x1D6E5}^{-1}$
both vanish, so that to leading order in
$\log \unicode[STIX]{x1D6E5}^{-1}$
both vanish, so that to leading order in
![]() $a/R$
, we are left with
$a/R$
, we are left with
in agreement with the results of Goren & O’Neill (Reference Goren and O’Neill1971) for a planar no-slip surface. If the obstacle has a stress-free surface (e.g. a gas bubble), the above result changes qualitatively due to the generally non-zero extension rates at its surface. Using the resistances in table 1, we now find (to leading order in
![]() $a/R$
)
$a/R$
)
Thus, for a stress-free
![]() $S_{w}$
, the normal force scales with
$S_{w}$
, the normal force scales with
![]() $a^{2}$
at leading order and depends on the extension rate of the flow. We note that for both no-slip and stress-free surfaces, the normal force is independent of
$a^{2}$
at leading order and depends on the extension rate of the flow. We note that for both no-slip and stress-free surfaces, the normal force is independent of
![]() $\unicode[STIX]{x1D6E5}$
for
$\unicode[STIX]{x1D6E5}$
for
![]() $\unicode[STIX]{x1D6E5}\ll 1$
. We remark that explicit dependence of the force on the curvature of the obstacle appears only as
$\unicode[STIX]{x1D6E5}\ll 1$
. We remark that explicit dependence of the force on the curvature of the obstacle appears only as
![]() $O(a/R)$
corrections to the numerical factors in (5.6) and (5.7), although we recognize that the background flow
$O(a/R)$
corrections to the numerical factors in (5.6) and (5.7), although we recognize that the background flow
![]() $\boldsymbol{u}(\boldsymbol{x})$
carries an implicit dependence on the curvature of the boundary
$\boldsymbol{u}(\boldsymbol{x})$
carries an implicit dependence on the curvature of the boundary
![]() $S_{w}$
.
$S_{w}$
.
Since objects in Stokes flows are free of net force, the external force required to hold the particle in place has a normal component
![]() $F_{\bot }^{ext}=-F_{\bot }$
. From (5.6) and (5.7), it is evident that the normal component of the force required to keep a small particle (
$F_{\bot }^{ext}=-F_{\bot }$
. From (5.6) and (5.7), it is evident that the normal component of the force required to keep a small particle (
![]() $a/\ell \ll 1$
,
$a/\ell \ll 1$
,
![]() $a/R\ll 1$
) stationary near a stress-free surface is an
$a/R\ll 1$
) stationary near a stress-free surface is an
![]() $O(\ell /a)$
greater than the corresponding force for a particle near a no-slip boundary. While the origin of this feature is evident from the vanishing value of the extension rate
$O(\ell /a)$
greater than the corresponding force for a particle near a no-slip boundary. While the origin of this feature is evident from the vanishing value of the extension rate
![]() $\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\!\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{u}$
near a no-slip surface, it is a somewhat counterintuitive result given that the hydrodynamic force experienced by a particle translating normal to a surface at a given velocity and separation distance is smaller for a stress-free surface than for a no-slip surface (by a factor of
$\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\!\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{u}$
near a no-slip surface, it is a somewhat counterintuitive result given that the hydrodynamic force experienced by a particle translating normal to a surface at a given velocity and separation distance is smaller for a stress-free surface than for a no-slip surface (by a factor of
![]() $1/4$
for
$1/4$
for
![]() $\unicode[STIX]{x1D6E5}\ll 1$
, cf. table 1). The qualitative difference between forces on stationary particles near no-slip and stress-free surfaces has implications for the flow-driven trapping of particles at interfaces.
$\unicode[STIX]{x1D6E5}\ll 1$
, cf. table 1). The qualitative difference between forces on stationary particles near no-slip and stress-free surfaces has implications for the flow-driven trapping of particles at interfaces.
5.3 Motion of a force-free particle
To analyse the motion of a particle moving under zero external force, it is convenient to scale the background velocity by
![]() $u_{0}$
and lengths by
$u_{0}$
and lengths by
![]() $\ell$
and introduce
$\ell$
and introduce
![]() $\boldsymbol{U}=\boldsymbol{u}/u_{0}$
and
$\boldsymbol{U}=\boldsymbol{u}/u_{0}$
and
![]() $\boldsymbol{X}=\boldsymbol{x}/\ell$
. Denoting the dimensionless position of a particle by
$\boldsymbol{X}=\boldsymbol{x}/\ell$
. Denoting the dimensionless position of a particle by
![]() $\boldsymbol{X}_{p}\equiv \boldsymbol{x}_{p}/\ell$
and neglecting both particle and fluid inertia, the trajectory of a particle with no external force is given as
$\boldsymbol{X}_{p}\equiv \boldsymbol{x}_{p}/\ell$
and neglecting both particle and fluid inertia, the trajectory of a particle with no external force is given as
where
![]() $t$
is a dimensionless time (in units of
$t$
is a dimensionless time (in units of
![]() $\ell /u_{0}$
). Here,
$\ell /u_{0}$
). Here,
![]() $\boldsymbol{W}$
is the velocity of the sphere relative to the mean fluid velocity in its vicinity, which becomes zero when
$\boldsymbol{W}$
is the velocity of the sphere relative to the mean fluid velocity in its vicinity, which becomes zero when
![]() $a/\ell =0$
. From the expression (4.12), the normal component of the relative velocity
$a/\ell =0$
. From the expression (4.12), the normal component of the relative velocity
![]() $\boldsymbol{W}$
of a force-free particle can be written as
$\boldsymbol{W}$
of a force-free particle can be written as
 $$\begin{eqnarray}\displaystyle W_{\bot }\equiv \boldsymbol{e}_{\bot }\boldsymbol{\cdot }\boldsymbol{W} & = & \displaystyle \boldsymbol{e}_{\bot }\boldsymbol{\cdot }\left\{-\frac{a}{\ell }\frac{{\mathcal{B}}}{{\mathcal{A}}}\,\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}+\frac{1}{2}\left(\frac{a}{\ell }\right)^{2}\frac{{\mathcal{C}}}{{\mathcal{A}}}\,\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}+\frac{1}{2}\left(\frac{a}{\ell }\right)^{2}\frac{{\mathcal{D}}}{{\mathcal{A}}}\,\tilde{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{U}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\left|\frac{a^{3}}{\ell ^{3}}\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}\right|\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{\bot }\equiv \boldsymbol{e}_{\bot }\boldsymbol{\cdot }\boldsymbol{W} & = & \displaystyle \boldsymbol{e}_{\bot }\boldsymbol{\cdot }\left\{-\frac{a}{\ell }\frac{{\mathcal{B}}}{{\mathcal{A}}}\,\boldsymbol{e}_{\bot }\boldsymbol{\cdot }\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}+\frac{1}{2}\left(\frac{a}{\ell }\right)^{2}\frac{{\mathcal{C}}}{{\mathcal{A}}}\,\boldsymbol{e}_{\bot }\boldsymbol{e}_{\bot }\boldsymbol{ : }\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}+\frac{1}{2}\left(\frac{a}{\ell }\right)^{2}\frac{{\mathcal{D}}}{{\mathcal{A}}}\,\tilde{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{U}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\left|\frac{a^{3}}{\ell ^{3}}\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\tilde{\unicode[STIX]{x1D735}}\boldsymbol{U}\right|\right),\end{eqnarray}$$
where
![]() $\tilde{\unicode[STIX]{x1D735}}=\ell \unicode[STIX]{x1D735}$
is a dimensionless gradient operator.
$\tilde{\unicode[STIX]{x1D735}}=\ell \unicode[STIX]{x1D735}$
is a dimensionless gradient operator.

Figure 5. Ratios
![]() ${\mathcal{B}}/{\mathcal{A}}$
,
${\mathcal{B}}/{\mathcal{A}}$
,
![]() ${\mathcal{C}}/2{\mathcal{A}}$
and
${\mathcal{C}}/2{\mathcal{A}}$
and
![]() ${\mathcal{D}}/2{\mathcal{A}}$
that govern the motion of a force-free particle relative to the fluid for (a) no-slip and (b) stress-free conditions on the obstacle in the limit
${\mathcal{D}}/2{\mathcal{A}}$
that govern the motion of a force-free particle relative to the fluid for (a) no-slip and (b) stress-free conditions on the obstacle in the limit
![]() $a/R\rightarrow 0$
. Note that the velocity of the particle relative to the fluid due to flow curvature (coefficients
$a/R\rightarrow 0$
. Note that the velocity of the particle relative to the fluid due to flow curvature (coefficients
![]() ${\mathcal{C}}/2{\mathcal{A}}$
and
${\mathcal{C}}/2{\mathcal{A}}$
and
![]() ${\mathcal{D}}/2{\mathcal{A}}$
) is multiplied by an
${\mathcal{D}}/2{\mathcal{A}}$
) is multiplied by an
![]() $O(a^{2}/\ell ^{2})$
factor, while the contribution of extensional flow gradients (quantified by
$O(a^{2}/\ell ^{2})$
factor, while the contribution of extensional flow gradients (quantified by
![]() ${\mathcal{B}}/2{\mathcal{A}}$
) is multiplied by a much larger
${\mathcal{B}}/2{\mathcal{A}}$
) is multiplied by a much larger
![]() $O(a/\ell )$
factor. The relative importance of the terms therefore depends both on
$O(a/\ell )$
factor. The relative importance of the terms therefore depends both on
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $a/\ell$
in addition to the flow properties. Dashed lines are leading-order asymptotes for large and small
$a/\ell$
in addition to the flow properties. Dashed lines are leading-order asymptotes for large and small
![]() $\unicode[STIX]{x1D6E5}$
and follow from the results in table 1.
$\unicode[STIX]{x1D6E5}$
and follow from the results in table 1.
The ratios of the resistance coefficients in (5.9) for particles near rigid and stress-free boundaries are reported in figure 5. As
![]() $\unicode[STIX]{x1D6E5}\rightarrow \infty$
, both
$\unicode[STIX]{x1D6E5}\rightarrow \infty$
, both
![]() ${\mathcal{B}}/{\mathcal{A}}$
and
${\mathcal{B}}/{\mathcal{A}}$
and
![]() ${\mathcal{C}}/{\mathcal{A}}$
decay to zero, while
${\mathcal{C}}/{\mathcal{A}}$
decay to zero, while
![]() ${\mathcal{D}}/{\mathcal{A}}\rightarrow 1/3$
, resulting in
${\mathcal{D}}/{\mathcal{A}}\rightarrow 1/3$
, resulting in
![]() $\boldsymbol{W}\sim (1/6)(a/\ell )^{2}\tilde{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{U}$
as per Faxén’s law (quadratic in
$\boldsymbol{W}\sim (1/6)(a/\ell )^{2}\tilde{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{U}$
as per Faxén’s law (quadratic in
![]() $a/\ell$
). However, the effect of the extensional gradient term, although decaying with
$a/\ell$
). However, the effect of the extensional gradient term, although decaying with
![]() $\unicode[STIX]{x1D6E5}$
, can be significant due to its linear dependence on
$\unicode[STIX]{x1D6E5}$
, can be significant due to its linear dependence on
![]() $a/\ell$
. The contribution of background flow gradients to the relative velocity is important as long as
$a/\ell$
. The contribution of background flow gradients to the relative velocity is important as long as
For small separations (
![]() $\unicode[STIX]{x1D6E5}\ll 1$
), it follows from the asymptotic forms of
$\unicode[STIX]{x1D6E5}\ll 1$
), it follows from the asymptotic forms of
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
that
${\mathcal{D}}$
that
Thus, from (5.9), the extensional gradient contribution to the relative velocity is dominant over the curvature contributions at small separations. Also, we note that the contribution from curvature terms proportional to
![]() ${\mathcal{C}}$
are much greater than those proportional to
${\mathcal{C}}$
are much greater than those proportional to
![]() ${\mathcal{D}}$
for
${\mathcal{D}}$
for
![]() $\unicode[STIX]{x1D6E5}\lesssim 1$
.
$\unicode[STIX]{x1D6E5}\lesssim 1$
.
In the limit
![]() $\unicode[STIX]{x1D6E5}\gg 1$
, we find
$\unicode[STIX]{x1D6E5}\gg 1$
, we find
![]() ${\mathcal{B}}\propto \unicode[STIX]{x1D6E5}^{-2}$
,
${\mathcal{B}}\propto \unicode[STIX]{x1D6E5}^{-2}$
,
![]() ${\mathcal{C}}\propto \unicode[STIX]{x1D6E5}^{-3}$
and
${\mathcal{C}}\propto \unicode[STIX]{x1D6E5}^{-3}$
and
![]() ${\mathcal{D}}\sim 1/3$
with
${\mathcal{D}}\sim 1/3$
with
![]() $O(1)$
prefactors for
$O(1)$
prefactors for
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() ${\mathcal{C}}$
, both for the no-slip and no-stress cases (cf. table 1). For large separations, the effect of the extensional gradient term is therefore important for distances of the particle to the boundary up to
${\mathcal{C}}$
, both for the no-slip and no-stress cases (cf. table 1). For large separations, the effect of the extensional gradient term is therefore important for distances of the particle to the boundary up to
Thus, the classical Faxén’s law for spheres only applies when
![]() $h\gg \sqrt{a\ell }\gg a$
, and boundary effects become important even for modest distances from no-slip or stress-free boundaries. The contribution of extensional flow gradients to the relative velocity of the particle to the fluid becomes increasingly important with decreasing
$h\gg \sqrt{a\ell }\gg a$
, and boundary effects become important even for modest distances from no-slip or stress-free boundaries. The contribution of extensional flow gradients to the relative velocity of the particle to the fluid becomes increasingly important with decreasing
![]() $h$
and is ultimately dominant when the separation between the two surfaces is comparable to the particle size, i.e. when
$h$
and is ultimately dominant when the separation between the two surfaces is comparable to the particle size, i.e. when
![]() $\unicode[STIX]{x1D6E5}=O(1)$
.
$\unicode[STIX]{x1D6E5}=O(1)$
.
The above conclusions remain valid when corrections for the finite curvature of the boundary are taken into account, provided that
![]() $a\lesssim h\ll R$
. In particular, since the motion of the particle relative to the fluid depends on ratios of the dimensionless hydrodynamic resistances, the resulting relative velocity
$a\lesssim h\ll R$
. In particular, since the motion of the particle relative to the fluid depends on ratios of the dimensionless hydrodynamic resistances, the resulting relative velocity
![]() $W_{\bot }$
in (5.9) is given to leading order by its
$W_{\bot }$
in (5.9) is given to leading order by its
![]() $a/R\rightarrow 0$
limit (planar surface
$a/R\rightarrow 0$
limit (planar surface
![]() $S_{w}$
) and has corrections of
$S_{w}$
) and has corrections of
![]() $O(a/R)$
, cf. table 1.
$O(a/R)$
, cf. table 1.
By calculating tangential components of the force in terms of moments of the background flow, expressions similar to (5.9) can be developed for the tangential components of the relative velocity of a force-free particle. It is noted that the presence of boundaries in general couples rotation with wall-parallel translation, so that an additional condition on the external torque acting on the particle must be specified to uniquely determine its motion (e.g. zero external torque acts on particles in several common applications). These mobility relations are known to varying degree of accuracy in linear flows (Goldman et al.
Reference Goldman, Cox and Brenner1967b
; Jeffrey Reference Jeffrey1992; Swan & Brady Reference Swan and Brady2007; Aponte-Rivera & Zia Reference Aponte-Rivera and Zia2016) and in the far field
![]() $(h\gg a)$
for quadratic flows (Haber & Brenner Reference Haber and Brenner1999). The present results can be integrated with well-developed numerical techniques for particle dynamics (Brady & Bossis Reference Brady and Bossis1988; Sierou & Brady Reference Sierou and Brady2001; Swan & Brady Reference Swan and Brady2011) to accurately compute the trajectories of particles in many-body systems.
$(h\gg a)$
for quadratic flows (Haber & Brenner Reference Haber and Brenner1999). The present results can be integrated with well-developed numerical techniques for particle dynamics (Brady & Bossis Reference Brady and Bossis1988; Sierou & Brady Reference Sierou and Brady2001; Swan & Brady Reference Swan and Brady2011) to accurately compute the trajectories of particles in many-body systems.
6 Conclusions
We have determined the hydrodynamic force, normal to a large obstacle, on a nearby spherical particle immersed in a background flow. By a local expansion of the background flow up to quadratic order, we obtained analytical expressions for the normal force in terms of moments of the background flow in the vicinity of the particle. Our results, which hold for spheres both near rigid walls as well as near free surfaces in the small capillary number limit, provide a first step towards a systematic generalization of Faxén’s law in confined systems.
We identify two important modifications that relate to Faxén-like contributions when a spherical particle is near a boundary. First, there is a contribution to the force proportional to extensional flow gradients, which forms the dominant contribution to the relative velocity between the particle and the fluid when the separation between the particle and the obstacle is comparable to the particle size. Second, we show that in addition to the Faxén force term, an extra force contribution proportional to curvature of the flow normal to the obstacle becomes important when the distance to the wall is comparable to the particle size. The near-field force contributions automatically recover the results of lubrication theory and can be integrated into dynamical simulations of particle trajectories near obstacles. We apply our theory to show that the force required to hold a particle stationary in the vicinity of an obstacle is generally much greater if the obstacle surface is stress free than if the obstacle has a no-slip surface.
Analytical expressions for the normal force have been obtained for arbitrary distances of the particle to the obstacle and the asymptotic behaviour of the force for large and small separations between the particle and the obstacle have been calculated. Both the exact and asymptotic results are useful in describing the transport of particles at low Reynolds numbers in confined geometries, such as in microfluidic devices or in biological systems. The generality of the results obtained here allow them to be used in simulations of particles near physical boundaries without the need to resolve the flow on the scale of individual particles and the thin lubrication layers between surfaces in near contact.
Acknowledgements
We thank the Carbon Mitigation Initiative of Princeton University for partial support of this research. We also thank the referees for pointing out the influence of boundary curvature.
Appendix A. Coefficients
 $a_{n}$
,
$a_{n}$
,
 $b_{n}$
,
$b_{n}$
,
 $c_{n}$
and
$c_{n}$
and
 $d_{n}$
in the model flow problem
$d_{n}$
in the model flow problem
The model problem consists of the viscous flow driven by the translation of a sphere of radius
![]() $a$
normal to a fixed spherical obstacle of radius
$a$
normal to a fixed spherical obstacle of radius
![]() $R$
in an otherwise unbounded fluid that is quiescent at infinity. The flow is axisymmetric and can thus be expressed in terms of a dimensionless streamfunction
$R$
in an otherwise unbounded fluid that is quiescent at infinity. The flow is axisymmetric and can thus be expressed in terms of a dimensionless streamfunction
![]() $\unicode[STIX]{x1D713}^{\prime }(\tilde{r},\tilde{z})$
(in units of
$\unicode[STIX]{x1D713}^{\prime }(\tilde{r},\tilde{z})$
(in units of
![]() $V^{\prime }a^{2}$
) that is related to dimensionless velocity components (in units of
$V^{\prime }a^{2}$
) that is related to dimensionless velocity components (in units of
![]() $V^{\prime }$
) by
$V^{\prime }$
) by
![]() $v_{r}^{\prime }=\tilde{r}^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}^{\prime }/\unicode[STIX]{x2202}\tilde{z}$
and
$v_{r}^{\prime }=\tilde{r}^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}^{\prime }/\unicode[STIX]{x2202}\tilde{z}$
and
![]() $v_{z}^{\prime }=-\tilde{r}^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}^{\prime }/\unicode[STIX]{x2202}\tilde{r}$
. In bipolar coordinates
$v_{z}^{\prime }=-\tilde{r}^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}^{\prime }/\unicode[STIX]{x2202}\tilde{r}$
. In bipolar coordinates
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, the streamfunction
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, the streamfunction
![]() $\unicode[STIX]{x1D713}^{\prime }$
in the model problem can be generally expressed as
$\unicode[STIX]{x1D713}^{\prime }$
in the model problem can be generally expressed as
![]() $\unicode[STIX]{x1D713}^{\prime }=\sum _{n=1}^{\infty }U_{n}(\unicode[STIX]{x1D709})V_{n}(\unicode[STIX]{x1D70F}),$
with
$\unicode[STIX]{x1D713}^{\prime }=\sum _{n=1}^{\infty }U_{n}(\unicode[STIX]{x1D709})V_{n}(\unicode[STIX]{x1D70F}),$
with
![]() $U_{n}$
and
$U_{n}$
and
![]() $V_{n}(\unicode[STIX]{x1D70F})$
are defined in (4.3). The coefficients
$V_{n}(\unicode[STIX]{x1D70F})$
are defined in (4.3). The coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
in
$d_{n}$
in
![]() $U_{n}$
are determined by the boundary conditions at the two spherical surfaces of the particle
$U_{n}$
are determined by the boundary conditions at the two spherical surfaces of the particle
![]() $S_{p}$
and the obstacle
$S_{p}$
and the obstacle
![]() $S_{w}$
and depend on
$S_{w}$
and depend on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
, which are related to the dimensionless separation distance
$\unicode[STIX]{x1D6FD}$
, which are related to the dimensionless separation distance
![]() $h/a$
and the curvature ratio
$h/a$
and the curvature ratio
![]() $a/R$
, cf. (4.1).
$a/R$
, cf. (4.1).
For the case where
![]() $S_{w}$
is a no-slip surface, the coefficients
$S_{w}$
is a no-slip surface, the coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
can be reconstructed as a superposition of the results of Maude (Reference Maude1961) (summarized in Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983) for co-moving and counter-moving solid spheres normal to their line of centres. Defining
$d_{n}$
can be reconstructed as a superposition of the results of Maude (Reference Maude1961) (summarized in Adamczyk et al.
Reference Adamczyk, Adamczyk and Van de Ven1983) for co-moving and counter-moving solid spheres normal to their line of centres. Defining
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{X}}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD},\quad {\mathcal{Y}}=\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}\quad \text{and}\\ \displaystyle \unicode[STIX]{x1D705}_{\text{I}}=\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)(2n+3)\left\{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}-(2n+1)^{2}\sinh ^{2}{\mathcal{Y}}\right\}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{X}}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD},\quad {\mathcal{Y}}=\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}\quad \text{and}\\ \displaystyle \unicode[STIX]{x1D705}_{\text{I}}=\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)(2n+3)\left\{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}-(2n+1)^{2}\sinh ^{2}{\mathcal{Y}}\right\}},\end{array}\right\}\end{eqnarray}$$
the coefficients are
 $$\begin{eqnarray}\displaystyle a_{n,\text{I}} & = & \displaystyle \frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n+3)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n-1)\text{e}^{-{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,2(2n+1)\text{e}^{-(n-1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{3}{2}}\right){\mathcal{Y}}+2(2n-1)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle +\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{n,\text{I}} & = & \displaystyle \frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n+3)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n-1)\text{e}^{-{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,2(2n+1)\text{e}^{-(n-1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{3}{2}}\right){\mathcal{Y}}+2(2n-1)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle +\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle b_{n,\text{I}} & = & \displaystyle -\frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n+3)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n-1)\text{e}^{-{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,2(2n+1)\text{e}^{-(n-1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{3}{2}}\right){\mathcal{Y}}-2(2n-1)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle +\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{n,\text{I}} & = & \displaystyle -\frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n+3)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n-1)\text{e}^{-{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,2(2n+1)\text{e}^{-(n-1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{3}{2}}\right){\mathcal{Y}}-2(2n-1)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle +\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle c_{n,\text{I}} & = & \displaystyle \frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n-1)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{-{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n+3)\text{e}^{{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,2(2n+1)\text{e}^{-(n+3/2){\mathcal{X}}}\sinh \left(n-{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}+2(2n+3)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle -\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\}\quad \text{and}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{n,\text{I}} & = & \displaystyle \frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n-1)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{-{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n+3)\text{e}^{{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,2(2n+1)\text{e}^{-(n+3/2){\mathcal{X}}}\sinh \left(n-{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}+2(2n+3)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle -\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\}\quad \text{and}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle d_{n,\text{I}} & = & \displaystyle -\frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n-1)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{-{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n+3)\text{e}^{{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,2(2n+1)\text{e}^{-(n+3/2){\mathcal{X}}}\sinh \left(n-{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}-2(2n+3)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle -\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{n,\text{I}} & = & \displaystyle -\frac{\unicode[STIX]{x1D705}_{\text{I}}}{2}(2n-1)\left\{\vphantom{\left(n+{\displaystyle \frac{1}{2}}\right)}(2n+1)^{2}\text{e}^{-{\mathcal{Y}}}\sinh {\mathcal{Y}}-(2n+1)(2n+3)\text{e}^{{\mathcal{X}}}\sinh {\mathcal{Y}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,2(2n+1)\text{e}^{-(n+3/2){\mathcal{X}}}\sinh \left(n-{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}-2(2n+3)\text{e}^{-(n+1/2){\mathcal{X}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\nonumber\\ \displaystyle & & \displaystyle -\left.4\text{e}^{-(n+1/2){\mathcal{Y}}}\sinh \left(n+{\displaystyle \frac{1}{2}}\right){\mathcal{Y}}\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle a_{n,\text{I}} & = & \displaystyle -c_{n,\text{I}}=\frac{n(n+1)(2n+1)\sinh ^{4}\unicode[STIX]{x1D6FC}}{\sqrt{2}\left[4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}\right]},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{n,\text{I}} & = & \displaystyle -c_{n,\text{I}}=\frac{n(n+1)(2n+1)\sinh ^{4}\unicode[STIX]{x1D6FC}}{\sqrt{2}\left[4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}\right]},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle b_{n,\text{I}} & = & \displaystyle -\frac{2n+3}{2n-1}d_{n,\text{I}}\nonumber\\ \displaystyle & = & \displaystyle \frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)}\left[1-\frac{2\sinh (2n+1)\unicode[STIX]{x1D6FC}+(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{n,\text{I}} & = & \displaystyle -\frac{2n+3}{2n-1}d_{n,\text{I}}\nonumber\\ \displaystyle & = & \displaystyle \frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)}\left[1-\frac{2\sinh (2n+1)\unicode[STIX]{x1D6FC}+(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}\right].\end{eqnarray}$$
Two-sphere relations similar to (A 2) can also be obtained for the hydrodynamic interaction of a no-slip spherical particle
![]() $S_{p}$
at
$S_{p}$
at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
with a stationary stress-free spherical surface
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
with a stationary stress-free spherical surface
![]() $S_{w}$
at
$S_{w}$
at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}$
by the appropriate choice of the coefficients
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}$
by the appropriate choice of the coefficients
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
. These coefficients are calculated here using an approach similar to that of Brenner (Reference Brenner1961); defining
$d_{n}$
. These coefficients are calculated here using an approach similar to that of Brenner (Reference Brenner1961); defining
we find
where the subscript
![]() $\text{II}$
denotes an association with BC II (stress-free obstacle). The results of Brenner (Reference Brenner1961) for a sphere translating normal to a planar stress-free surface can be recovered by setting
$\text{II}$
denotes an association with BC II (stress-free obstacle). The results of Brenner (Reference Brenner1961) for a sphere translating normal to a planar stress-free surface can be recovered by setting
![]() $\unicode[STIX]{x1D6FD}=0$
in the above expressions; in this case the coefficients reduce to
$\unicode[STIX]{x1D6FD}=0$
in the above expressions; in this case the coefficients reduce to
 $$\begin{eqnarray}\displaystyle & \displaystyle b_{n,\text{II}}=\displaystyle -\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)}\left[\frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}+2(2n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{2n\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}-1\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{n,\text{II}}=\displaystyle -\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n-1)}\left[\frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}+2(2n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{2n\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}-1\right], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle d_{n,\text{II}}=\displaystyle -\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n+3)}\left[1-\frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-2(2n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{2n\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}\right]. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{n,\text{II}}=\displaystyle -\frac{n(n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{\sqrt{2}(2n+3)}\left[1-\frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-2(2n+1)\sinh ^{2}\unicode[STIX]{x1D6FC}}{2n\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}\right]. & \displaystyle\end{eqnarray}$$
Appendix B. Evaluating the integrals for the force
The expression for the force in (4.8) relies on computing the integrals
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
defined in (4.9), which we give here again:
${\mathcal{J}}$
defined in (4.9), which we give here again:
Both
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
involve integration with respect to
${\mathcal{J}}$
involve integration with respect to
![]() $\unicode[STIX]{x1D70F}$
(which parametrizes the surface of the sphere), and have kernels containing
$\unicode[STIX]{x1D70F}$
(which parametrizes the surface of the sphere), and have kernels containing
![]() $V_{n}(\unicode[STIX]{x1D70F})$
, which enter through
$V_{n}(\unicode[STIX]{x1D70F})$
, which enter through
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
. We recall the definition of
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
. We recall the definition of
![]() $V_{n}(\unicode[STIX]{x1D70F})$
in terms of Legendre polynomials
$V_{n}(\unicode[STIX]{x1D70F})$
in terms of Legendre polynomials
![]() $P_{n}(\unicode[STIX]{x1D70F})$
and give some properties (Stimson & Jeffery Reference Stimson and Jeffery1926) that are useful in the evaluation of the integrals:
$P_{n}(\unicode[STIX]{x1D70F})$
and give some properties (Stimson & Jeffery Reference Stimson and Jeffery1926) that are useful in the evaluation of the integrals:
 $$\begin{eqnarray}\displaystyle g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}) & = & \displaystyle (\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{5/2}\mathop{\sum }_{n=0}^{\infty }\Bigg[V_{n}(\unicode[STIX]{x1D70F})\left\{\frac{\text{d}^{2}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}^{2}}-\frac{2\sinh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(\frac{3\cosh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}-\frac{9}{4}-n(n+1)\right)U_{n}(\unicode[STIX]{x1D709})\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\,U_{n}(\unicode[STIX]{x1D709})}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\left\{\frac{n(n-1)}{2n+1}V_{n-1}(\unicode[STIX]{x1D70F})-\frac{(n+1)(n+2)}{2n+1}V_{n+1}(\unicode[STIX]{x1D70F})\right\}\Bigg],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}) & = & \displaystyle (\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{5/2}\mathop{\sum }_{n=0}^{\infty }\Bigg[V_{n}(\unicode[STIX]{x1D70F})\left\{\frac{\text{d}^{2}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}^{2}}-\frac{2\sinh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\frac{\text{d}U_{n}(\unicode[STIX]{x1D709})}{\text{d}\unicode[STIX]{x1D709}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left(\frac{3\cosh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}-\frac{9}{4}-n(n+1)\right)U_{n}(\unicode[STIX]{x1D709})\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2\,U_{n}(\unicode[STIX]{x1D709})}{\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F}}\left\{\frac{n(n-1)}{2n+1}V_{n-1}(\unicode[STIX]{x1D70F})-\frac{(n+1)(n+2)}{2n+1}V_{n+1}(\unicode[STIX]{x1D70F})\right\}\Bigg],\end{eqnarray}$$
where
![]() $U_{n}(\unicode[STIX]{x1D709})$
is defined in (4.3a
). We observe that
$U_{n}(\unicode[STIX]{x1D709})$
is defined in (4.3a
). We observe that
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
is a linear combination of
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
is a linear combination of
![]() $V_{n}(\unicode[STIX]{x1D70F})$
for different
$V_{n}(\unicode[STIX]{x1D70F})$
for different
![]() $n$
with coefficients that depend only on
$n$
with coefficients that depend only on
![]() $\unicode[STIX]{x1D709}$
. Note also that
$\unicode[STIX]{x1D709}$
. Note also that
![]() $(1-\unicode[STIX]{x1D70F}^{2})V_{n}$
, which appears in the kernel of
$(1-\unicode[STIX]{x1D70F}^{2})V_{n}$
, which appears in the kernel of
![]() ${\mathcal{J}}$
, can be written in terms of
${\mathcal{J}}$
, can be written in terms of
![]() $V_{n-2}$
,
$V_{n-2}$
,
![]() $V_{n}$
and
$V_{n}$
and
![]() $V_{n+1}$
using (B 2).
$V_{n+1}$
using (B 2).
Any additional
![]() $\unicode[STIX]{x1D70F}$
dependence (i.e. outside of
$\unicode[STIX]{x1D70F}$
dependence (i.e. outside of
![]() $V_{n}(\unicode[STIX]{x1D70F})$
) in
$V_{n}(\unicode[STIX]{x1D70F})$
) in
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
, and therefore in the kernels of
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$
, and therefore in the kernels of
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
, is entirely due to factors of
${\mathcal{J}}$
, is entirely due to factors of
![]() $(\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{m/2}$
, where
$(\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{m/2}$
, where
![]() $m$
is an odd integer. Both
$m$
is an odd integer. Both
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
can therefore be written as superposition of integrals
${\mathcal{J}}$
can therefore be written as superposition of integrals
![]() ${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
defined by
${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
defined by
The coefficients of the superposition, which are obtained by substituting (B 3) into (B 1) and rearranging, are functions of
![]() $\unicode[STIX]{x1D709}$
only, and remain constant throughout the integration. Taking a
$\unicode[STIX]{x1D709}$
only, and remain constant throughout the integration. Taking a
![]() $\unicode[STIX]{x1D709}$
derivative of (B 4) immediately results in an expression for
$\unicode[STIX]{x1D709}$
derivative of (B 4) immediately results in an expression for
![]() ${\mathcal{K}}_{m+2,n}(\unicode[STIX]{x1D709})$
in terms of
${\mathcal{K}}_{m+2,n}(\unicode[STIX]{x1D709})$
in terms of
![]() ${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
, thus providing a recursion relation. Applying the formula for
${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
, thus providing a recursion relation. Applying the formula for
![]() ${\mathcal{K}}_{1,n}(\unicode[STIX]{x1D709})$
given by Stimson & Jeffery (Reference Stimson and Jeffery1926), we obtain
${\mathcal{K}}_{1,n}(\unicode[STIX]{x1D709})$
given by Stimson & Jeffery (Reference Stimson and Jeffery1926), we obtain
with
which can be used to compute
![]() ${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
for any odd
${\mathcal{K}}_{m,n}(\unicode[STIX]{x1D709})$
for any odd
![]() $m$
. Substituting these expressions into
$m$
. Substituting these expressions into
![]() ${\mathcal{I}}_{k}$
and
${\mathcal{I}}_{k}$
and
![]() ${\mathcal{J}}$
results, after evaluation at
${\mathcal{J}}$
results, after evaluation at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
, in formulas only involving
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}$
, in formulas only involving
![]() $\unicode[STIX]{x1D6FC}$
and the coefficients
$\unicode[STIX]{x1D6FC}$
and the coefficients
![]() $a_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
,
$a_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
,
![]() $b_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
,
$b_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
,
![]() $c_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
and
$c_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
and
![]() $d_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, which enter through
$d_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, which enter through
![]() $U_{n}(\unicode[STIX]{x1D709})$
. The expressions for the force (4.10) and resistance coefficients (4.11) in terms of
$U_{n}(\unicode[STIX]{x1D709})$
. The expressions for the force (4.10) and resistance coefficients (4.11) in terms of
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
then follow directly.
$d_{n}$
then follow directly.
Appendix C. Expressions for the hydrodynamic resistances for a spherical particle near a planar obstacle (
 $\unicode[STIX]{x1D6FD}=0$
)
$\unicode[STIX]{x1D6FD}=0$
)
Analytical expressions for the dimensionless hydrodynamic resistances
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
can be obtained by substituting the expressions for
${\mathcal{D}}$
can be obtained by substituting the expressions for
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
and
$c_{n}$
and
![]() $d_{n}$
from either (A 3) or (A 9) as appropriate, into (4.11). This yields infinite series representations for
$d_{n}$
from either (A 3) or (A 9) as appropriate, into (4.11). This yields infinite series representations for
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
in terms of
${\mathcal{D}}$
in terms of
![]() $\unicode[STIX]{x1D6FC}=\cosh ^{-1}(h/a)$
only, for both no-slip and no-stress cases, which we provide here. We first define
$\unicode[STIX]{x1D6FC}=\cosh ^{-1}(h/a)$
only, for both no-slip and no-stress cases, which we provide here. We first define
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{L}}_{n}(\unicode[STIX]{x1D6FC})\equiv -{\displaystyle \frac{\sqrt{2}}{3\sinh \unicode[STIX]{x1D6FC}}}\{a_{n}+b_{n}+c_{n}+d_{n}\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}l@{}}{\displaystyle \frac{4\sinh \unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)}{(2n-1)(2n+3)}}\left[{\displaystyle \frac{2\sinh (2n+1)\unicode[STIX]{x1D6FC}+(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}}-1\right],\quad \\ \quad \text{for BC I}\quad \\ {\displaystyle \frac{4\sinh \unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)}{(2n-1)(2n+3)}}\left[{\displaystyle \frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}+(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}{2\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}}-1\right],\quad \\ \quad \text{for BC II},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{L}}_{n}(\unicode[STIX]{x1D6FC})\equiv -{\displaystyle \frac{\sqrt{2}}{3\sinh \unicode[STIX]{x1D6FC}}}\{a_{n}+b_{n}+c_{n}+d_{n}\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}l@{}}{\displaystyle \frac{4\sinh \unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)}{(2n-1)(2n+3)}}\left[{\displaystyle \frac{2\sinh (2n+1)\unicode[STIX]{x1D6FC}+(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}}-1\right],\quad \\ \quad \text{for BC I}\quad \\ {\displaystyle \frac{4\sinh \unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)}{(2n-1)(2n+3)}}\left[{\displaystyle \frac{4\cosh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}+(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}{2\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}}-1\right],\quad \\ \quad \text{for BC II},\quad \end{array}\right.\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{n}(\unicode[STIX]{x1D6FC})\equiv {\displaystyle \frac{\sqrt{2}}{3}}\Big\{(2n-1)(a_{n}+b_{n})+(2n+3)(c_{n}+d_{n})\Big\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}l@{}}-{\displaystyle \frac{4\sinh ^{4}\unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)(2n+1)}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}},\quad \text{for BC I}\quad \\ -{\displaystyle \frac{4\sinh ^{4}\unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)(2n+1)}{2\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}},\quad \text{for BC II},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{n}(\unicode[STIX]{x1D6FC})\equiv {\displaystyle \frac{\sqrt{2}}{3}}\Big\{(2n-1)(a_{n}+b_{n})+(2n+3)(c_{n}+d_{n})\Big\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}l@{}}-{\displaystyle \frac{4\sinh ^{4}\unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)(2n+1)}{4\sinh ^{2}\left(n+{\displaystyle \frac{1}{2}}\right)\unicode[STIX]{x1D6FC}-(2n+1)^{2}\sinh ^{2}\unicode[STIX]{x1D6FC}}},\quad \text{for BC I}\quad \\ -{\displaystyle \frac{4\sinh ^{4}\unicode[STIX]{x1D6FC}}{3}}{\displaystyle \frac{n(n+1)(2n+1)}{2\sinh (2n+1)\unicode[STIX]{x1D6FC}-(2n+1)\sinh 2\unicode[STIX]{x1D6FC}}},\quad \text{for BC II},\quad \end{array}\right.\end{eqnarray}$$
where BC I and BC II represent, respectively, no-slip or stress-free conditions on the surface
![]() $S_{w}$
of the obstacle.
$S_{w}$
of the obstacle.
The dimensionless hydrodynamic resistances
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{D}}$
are then
${\mathcal{D}}$
are then
 $$\begin{eqnarray}\displaystyle {\mathcal{C}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle 2{\mathcal{B}}\cosh \unicode[STIX]{x1D6FC}-{\mathcal{A}}\cosh ^{2}\unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & & \displaystyle -\mathop{\sum }_{n=0}^{\infty }\left\{(n^{2}+n-1){\mathcal{L}}_{n}\,\sinh ^{2}\unicode[STIX]{x1D6FC}+{\displaystyle \frac{2}{3}}(2n+1){\mathcal{M}}_{n}\sinh \unicode[STIX]{x1D6FC}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{C}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle 2{\mathcal{B}}\cosh \unicode[STIX]{x1D6FC}-{\mathcal{A}}\cosh ^{2}\unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & & \displaystyle -\mathop{\sum }_{n=0}^{\infty }\left\{(n^{2}+n-1){\mathcal{L}}_{n}\,\sinh ^{2}\unicode[STIX]{x1D6FC}+{\displaystyle \frac{2}{3}}(2n+1){\mathcal{M}}_{n}\sinh \unicode[STIX]{x1D6FC}\right\},\end{eqnarray}$$
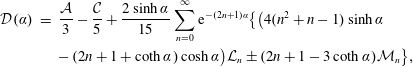 $$\begin{eqnarray}\displaystyle {\mathcal{D}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle {\displaystyle \frac{{\mathcal{A}}}{3}}-{\displaystyle \frac{{\mathcal{C}}}{5}}+{\displaystyle \frac{2\sinh \unicode[STIX]{x1D6FC}}{15}}\mathop{\sum }_{n=0}^{\infty }\text{e}^{-(2n+1)\unicode[STIX]{x1D6FC}}\big\{\big(4(n^{2}+n-1)\sinh \unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & & \displaystyle -\,(2n+1+\coth \unicode[STIX]{x1D6FC})\cosh \unicode[STIX]{x1D6FC}\big){\mathcal{L}}_{n}\pm (2n+1-3\coth \unicode[STIX]{x1D6FC}){\mathcal{M}}_{n}\big\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle {\displaystyle \frac{{\mathcal{A}}}{3}}-{\displaystyle \frac{{\mathcal{C}}}{5}}+{\displaystyle \frac{2\sinh \unicode[STIX]{x1D6FC}}{15}}\mathop{\sum }_{n=0}^{\infty }\text{e}^{-(2n+1)\unicode[STIX]{x1D6FC}}\big\{\big(4(n^{2}+n-1)\sinh \unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & & \displaystyle -\,(2n+1+\coth \unicode[STIX]{x1D6FC})\cosh \unicode[STIX]{x1D6FC}\big){\mathcal{L}}_{n}\pm (2n+1-3\coth \unicode[STIX]{x1D6FC}){\mathcal{M}}_{n}\big\},\end{eqnarray}$$









