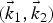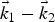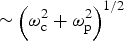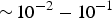1. INTRODUCTION
The scientific community has wide ranging usages for the whole electromagnetic (EM) spectrum. However, the complexity of production of usable intensity differs for different parts of spectrum. The terahertz (THz) radiation is located in the spectral region 0.1–10 THz between the microwave and the infrared portion of the EM spectrum (Sizov, Reference Sizov2010). THz radiation has wide range of applications due to its attractive features as (Leemans et al., Reference Leemans, Tilborg, Faure, Geddes, Toth, Schroeder, Esarey, Fubioni and Dugan2004): (i) it can transmit through cloths and most packaging materials such as paper or plastics, (ii) many substances have “fingerprint” spectra in the THz range, (iii) its low photon energy (about one million times less than X rays) makes THz radiation is non-ionizing and therefore not dangerous for human beings. These properties make THz systems a promising tool for different types of applications such as medical diagnostic, quality control, biological imaging, remote sensing, material characterization, chemical & security identification, outer space communication & submillimeter radars, spectroscopic identifications of complex molecules, explosive detection (Yoshii et al., Reference Yoshii, Lai, Katsouleas, Joshi and Mori1997; Carr et al., Reference Carr, Martin, McKinney, Jordan, Neil and Williams2002; Abo-Bakr et al., Reference Abo-Bakr, Feikes, Holldack, Kuske, Peatman, Schade, Wustefeld and Hübers2003; Dragoman & Dragoman, Reference Dragoman and Dragoman2004; Leemans et al., Reference Leemans, Tilborg, Faure, Geddes, Toth, Schroeder, Esarey, Fubioni and Dugan2004; Schroeder et al., Reference Schroeder, Esarey, Tilborg and Leemans2004; Siegel, Reference Siegel2004), etc.
A variety of schemes have been proposed for developing THz sources, for example, interaction of short laser pulses with large band gap semiconductors (Sprangle et al., Reference Sprangle, Penano, Hafizi and Kapetanakos2004), metallic surfaces (Antonsen et al., Reference Antonsen, Palastra and Milchberg2007), electro-optical crystals (Schillinger & Sauerbrey, Reference Schillinger and Sauerbrey1999), such as ZnSe, GaP, ZnTe LiNbO3. But due to lower damage threshold and low conversion efficiencies in these materials, it is not possible to generate efficient and strong THz pulses. In last few years, various plasma-based schemes have emerged as potential candidate for THz radiation generation. The plasma, being a broken medium, can handle very high fields, and can provide strong THz pulses in comparison with other mediums. Hamster et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993) proposed a scheme of high-power THz generation from short pulse laser-produced plasma, employing 1 TW, 100 fs laser beam focused on gas and solid targets. They also observed THz radiation in a laser-induced plasma channel where ponderomotive force drives radiation (Hamster et al., Reference Hamster, Sullivan, Gordon and Falcone1994). Penano et al. (Reference Penano, Sprangle, Hafizi, Gordon and Serafim2010) have examined a model for THz generation by the beating of the two laser beams, which generates a finite nonlinear current density due to large electron collisions driving the THz wave.
THz radiation generation by mixing of two laser beams with different intensities in different media (collisional and non-collisional plasma) has shown tremendous potential in terms of amplitude, tunability, efficiency, and directionality (Bhasin & Tripathi, Reference Bhasin and Tripathi2009; Liu & Tripathi, Reference Liu and Tripathi2009; Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010; Malik et al., Reference Malik, Malik and Nishida2011, Reference Malik, Malik and Stroth2012b ; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013; Singh & Malik, Reference Singh and Malik2014; Reference Singh and Malik2015, Reference Singh and Malik2016; Varshney et al., Reference Varshney, Sajal, Chauhan, Kumar and Sharma2014; Malik, Reference Malik2015). Malik et al. (Reference Malik, Malik and Nishida2011) proposed a model for tunable THz radiation generation by beating of two femtosecond laser pulses. They utilized tunnel ionization mechanism for THz radiation generation with some phase difference of two laser pulses and external magnetic field. They observed significant enhancement in the frequency and power of the emitted THz radiation. Singh & Malik (Reference Singh and Malik2015, Reference Singh and Malik2016) and Malik (Reference Malik2015) studied THz radiation generation by mixing of two laser beams in realistic plasma, where electron–neutral and electron–positron collisions persist. They observe lower THz field and efficiency in the collisional plasma. Few studies have also been made on tunable and efficient THz generation by using various laser profiles such as cosh-Gaussian (Singh et al., Reference Singh, Singh and Sharma2013), Gaussian beams (Malik et al., Reference Malik, Malik and Nishida2011, Reference Malik, Malik and Stroth2012b ), super Gaussian beams (Varshney et al., Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015), rounded triangular (Malik & Malik, Reference Malik and Malik2013), and triangular beams (Varshney et al., Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015), but most of these schemes lack on parametric studies of focusing, directionality, and collimation on generated THz wave. In particular, the cosh-Gaussian intensity profile of a laser beam that can be considered as an optical beam with null intensity at the center, has been a subject of considerable interest due to its high utility in the field of plasma, atomic, and modern optics because it can be used as an effective tool to guide, focus, and trap neutral atoms (Singh et al., Reference Singh, Singh and Sharma2013). In the present paper, we propose a scheme of THz generation by beating of two cosh-Gaussian lasers. The cosh-Gaussian beams (decentered Gaussian beams) also have raised considerable interest in recent times on account of their wide and attractive applications. The issue of high amplitude and power of THz radiation is addressed by employing cosh-Gaussian profiles and issues of directionality and tunability are addressed by applying dc static magnetic field in the transverse direction. Both the beating lasers and generated THz radiation have the same state of polarization because the THz emission is maximum when the polarization of laser beams and the THz are aligned. The propagation properties of cosh-Gaussian laser beams are important technological issue, since these beams control higher efficient power with flat-top beam shape and hollow-Gaussian lasers beam in comparison with that of a Gaussian beam. Contrary to the case of two spatial profiles of Gaussian lasers, THz radiation can be focused at a desired position by choosing a suitable decentered parameter of cosh-Gaussian lasers. Two cosh-Gaussian laser beams exert a nonlinear ponderomotive force, which is acting on the plasma electrons. Due to velocity perturbation this ponderomotive force couples with density ripples of appropriate periodicity and excites a nonlinear current. The density ripple provides the phase-matching condition and resonant excitation of emitted radiation with an enhancement in the efficiency. In Section II, we calculate the expressions for ponderomotive force, density perturbation, and nonlinear current density. The amplitude and efficiency of THz wave are derived in Section III. Conclusion is given in Section IV.
2. BASIC EQUATIONS FOR EVALUATION OF NONLINEAR CURRENT DENSITY
We consider two cosh-Gaussian lasers with different frequencies (ω1 and ω2) and wave numbers (
![]() $\vec k_1 $
and
$\vec k_1 $
and
![]() $\vec k_2 $
) co-propagating in a magnetized plasma
$\vec k_2 $
) co-propagating in a magnetized plasma
![]() $(B_0 \,\hat z)$
having corrugated plasma density given by n = n
0 + n′, n′ = n
α0
e
iαx
, where n
α0 is the amplitude of ripple and α is the repetition factor for corrugation ripples. These density ripples may be produced using various techniques involving transmissive ring grating and a patterned mask (Hazra et al.,
Reference Hazra, Chini, Sanyal, Grenzer and Pietsch2004; Malik et al., Reference Malik, Singh and Sajal2014; Malik & Malik, Reference Malik and Malik2011, Reference Malik and Malik2012; Kuo et al., Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007). Here we can control ripple parameter by changing the groove period, groove structure, and duty cycle in such a grating and by adjusting the period and size of the masks. The profile of laser electric fields is given as
$(B_0 \,\hat z)$
having corrugated plasma density given by n = n
0 + n′, n′ = n
α0
e
iαx
, where n
α0 is the amplitude of ripple and α is the repetition factor for corrugation ripples. These density ripples may be produced using various techniques involving transmissive ring grating and a patterned mask (Hazra et al.,
Reference Hazra, Chini, Sanyal, Grenzer and Pietsch2004; Malik et al., Reference Malik, Singh and Sajal2014; Malik & Malik, Reference Malik and Malik2011, Reference Malik and Malik2012; Kuo et al., Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007). Here we can control ripple parameter by changing the groove period, groove structure, and duty cycle in such a grating and by adjusting the period and size of the masks. The profile of laser electric fields is given as
where j = 1,2 for two lasers, a 0 is the initial beam width, and b is the decentered parameter. The electric field profile given by Eq. (1) is plotted in Figure 1. One can notice that as a decentered parameter of the cosh-Gaussian laser beam changes from b = 0 to 5, the profile changes its shape in the following sequences: (1) Gaussian (b = 0), (ii) cosh-Gaussian (b = 1), (iii) flat-top (b = 1.45), (iv) ring shape (b = 2), and (v) hollow-Gaussian (b = 5).

Fig. 1. Normalized cosh-Gaussian laser field amplitude as a function of transverse distance y for de-centered parameters 0 < b ≤ 5. Other laser parameters are a 0 = 0.05 mm, ω1 = 2.4 × 1014 rad/s.
Beating lasers exert a nonlinear ponderomotive force
![]() $\vec F_{\rm p} ( = F_{\,px} \hat x + F_{\,py} \hat y)$
on plasma electron having oscillatory velocity (due to the electric field of beating lasers)
$\vec F_{\rm p} ( = F_{\,px} \hat x + F_{\,py} \hat y)$
on plasma electron having oscillatory velocity (due to the electric field of beating lasers)
![]() $\vec v_j = e[ - {\rm \omega} _{\rm c} \hat x + {\rm \omega} _j \hat y]/ m({\rm \omega} _j^2 - {\rm \omega} _{\rm c}^2 )\,E_{\,jy} $
at frequency ω = ω1 − ω2 and wave vector
$\vec v_j = e[ - {\rm \omega} _{\rm c} \hat x + {\rm \omega} _j \hat y]/ m({\rm \omega} _j^2 - {\rm \omega} _{\rm c}^2 )\,E_{\,jy} $
at frequency ω = ω1 − ω2 and wave vector
![]() $\vec k'' = \vec k_1 - \vec k_2 $
. The components of the ponderomotive force F
px
and F
py
are as follows:
$\vec k'' = \vec k_1 - \vec k_2 $
. The components of the ponderomotive force F
px
and F
py
are as follows:
 $$F_{{\rm p}x} = \displaystyle{{e^2 E_0^2} \over {2m}}\,\left[ {{\rm \delta} _{11} - {\rm \delta} _{12} {\rm \Delta}} \right]\cosh ^2 \left( {\displaystyle{{yb} \over {a_0}}} \right)e^{ - 2{{y^2} / {a_0^2}}},$$
$$F_{{\rm p}x} = \displaystyle{{e^2 E_0^2} \over {2m}}\,\left[ {{\rm \delta} _{11} - {\rm \delta} _{12} {\rm \Delta}} \right]\cosh ^2 \left( {\displaystyle{{yb} \over {a_0}}} \right)e^{ - 2{{y^2} / {a_0^2}}},$$
 $$F_{{\rm p}y} = \displaystyle{{e^2 E_0^2} \over {2m}}\,\left[ {{\rm \delta} _{21} - {\rm \delta} _{22} {\rm \Delta}} \right]\cosh ^2 \left( {\displaystyle{{yb} \over {a_0}}} \right)e^{ - 2{{y^2} / {a_0^2}}},$$
$$F_{{\rm p}y} = \displaystyle{{e^2 E_0^2} \over {2m}}\,\left[ {{\rm \delta} _{21} - {\rm \delta} _{22} {\rm \Delta}} \right]\cosh ^2 \left( {\displaystyle{{yb} \over {a_0}}} \right)e^{ - 2{{y^2} / {a_0^2}}},$$
where
![]() ${\rm \delta} _{12} = [i{\rm \omega} _{\rm c} {\rm \omega} /({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )]$
,
${\rm \delta} _{12} = [i{\rm \omega} _{\rm c} {\rm \omega} /({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )]$
,
 $$\eqalign{{\rm \delta} _{11} = \left[ {\displaystyle{{i{\rm \omega} _1 k_2} \over {{\rm \omega} _2 ({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{i{\rm \omega} _2 k_1} \over {{\rm \omega} _1 ({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right. \left. { - \displaystyle{{i{\rm \omega} _{\rm c}^2 k^{\prime \prime}} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right],} $$
$$\eqalign{{\rm \delta} _{11} = \left[ {\displaystyle{{i{\rm \omega} _1 k_2} \over {{\rm \omega} _2 ({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{i{\rm \omega} _2 k_1} \over {{\rm \omega} _1 ({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right. \left. { - \displaystyle{{i{\rm \omega} _{\rm c}^2 k^{\prime \prime}} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right],} $$
 $$\eqalign{{\rm \delta} _{21} &= \left[ {\displaystyle{{ - {\rm \omega} _{\rm c} k_1} \over {{\rm \omega} _1 ({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{{\rm \omega} _{\rm c} k_2} \over {{\rm \omega} _2 ({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}} \right. \cr & \left. {\quad - \displaystyle{{{\rm \omega} _{\rm c} {\rm \omega} _2 k_2} \over {({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{{\rm \omega} _{\rm c} {\rm \omega} _1 k_1} \over {({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}} \right],} $$
$$\eqalign{{\rm \delta} _{21} &= \left[ {\displaystyle{{ - {\rm \omega} _{\rm c} k_1} \over {{\rm \omega} _1 ({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{{\rm \omega} _{\rm c} k_2} \over {{\rm \omega} _2 ({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}} \right. \cr & \left. {\quad - \displaystyle{{{\rm \omega} _{\rm c} {\rm \omega} _2 k_2} \over {({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{{\rm \omega} _{\rm c} {\rm \omega} _1 k_1} \over {({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}} \right],} $$
 $${\rm \delta} _{22} = \left[ {\displaystyle{{2i{\rm \omega} _1 {\rm \omega} _2} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )\,({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right],$$
$${\rm \delta} _{22} = \left[ {\displaystyle{{2i{\rm \omega} _1 {\rm \omega} _2} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )\,({\rm \omega} _2^2 - {\rm \omega} _{\rm c}^2 )}}} \right],$$
where ωc = eB 0/m
Figure 2 shows the variation of ponderomotive force as a function of decentered parameter b. The ponderomotive force couples with pre-existing space-charge mode (of negligible amplitude) having potential φ at frequency ω = ω1 − ω2 and wave number
![]() $\vec k'' = \vec k_1 - \vec k_2 $
, to provide oscillatory velocity to plasma electrons in the presence of transverse magnetic field, given by
$\vec k'' = \vec k_1 - \vec k_2 $
, to provide oscillatory velocity to plasma electrons in the presence of transverse magnetic field, given by
The oscillations of plasma electron perturb the equilibrium of plasma and, density perturbation due to this can be calculated by substituting Eq. (3) into continuity equation. The density perturbation n = n
NL + n
L consists of both linear part (due to space-charge mode) and nonlinear part (due to the ponderomotive force). Here, density perturbation is assumed to be small as compared with the density ripple. Substituting n = n
L + n
NL in the Poisson's equation
![]() $\nabla ^2 {\rm \varphi} = 4{\rm \pi} ne$
, we obtain
$\nabla ^2 {\rm \varphi} = 4{\rm \pi} ne$
, we obtain
where ε = 1 + χ and
![]() ${\rm \chi} = - {\rm \omega} _{\rm p}^2 /({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )$
. On rearranging Eqs. (3) and (4), we obtain the oscillatory velocity components of plasma electrons:
${\rm \chi} = - {\rm \omega} _{\rm p}^2 /({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )$
. On rearranging Eqs. (3) and (4), we obtain the oscillatory velocity components of plasma electrons:
 $$v_z = \displaystyle{{ - {\rm \omega} _{\rm c}} \over {m({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 )}}F_{px} + i\displaystyle{{({\rm \omega} ^2 - {\rm \omega} _{\rm p}^2 )} \over {m({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 ){\rm \omega}}} F_{{\rm p}y},$$
$$v_z = \displaystyle{{ - {\rm \omega} _{\rm c}} \over {m({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 )}}F_{px} + i\displaystyle{{({\rm \omega} ^2 - {\rm \omega} _{\rm p}^2 )} \over {m({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 ){\rm \omega}}} F_{{\rm p}y},$$
where
![]() ${\rm \omega} _{\rm h} = \sqrt {{\rm \omega} _{\rm c}^2 + {\rm \omega} _{\rm p}^2} $
. In the presence of density ripple n
α0
e
iαx
, the oscillatory velocity excites a nonlinear current density at
${\rm \omega} _{\rm h} = \sqrt {{\rm \omega} _{\rm c}^2 + {\rm \omega} _{\rm p}^2} $
. In the presence of density ripple n
α0
e
iαx
, the oscillatory velocity excites a nonlinear current density at
![]() $({\rm \omega}, \,\vec k_1 - \vec k_2 + \vec {\rm \alpha} ),$
which can be written as
$({\rm \omega}, \,\vec k_1 - \vec k_2 + \vec {\rm \alpha} ),$
which can be written as
It can be seen that the nonlinear current oscillates at frequency difference ω = ω1 − ω2 similar to the ponderomotive force, but its wave number
![]() $\vec k( = \vec k_1 - \vec k_2 + \vec {\rm \alpha} )$
is different from the ponderomotive force.
$\vec k( = \vec k_1 - \vec k_2 + \vec {\rm \alpha} )$
is different from the ponderomotive force.

Fig. 2. Plot of normalized ponderomotive force F p/eE 1 as a function of decentered parameter b.
3. THz AMPLITUDE
Now, we solve the wave equation to find the amplitude of the THz wave
where
![]() $\overline{\overline \varepsilon } $
is the plasma permittivity tensor at ω. We can separate out the coupled
$\overline{\overline \varepsilon } $
is the plasma permittivity tensor at ω. We can separate out the coupled
![]() $\hat x$
and
$\hat x$
and
![]() $\hat y$
components of
$\hat y$
components of
![]() $\vec E$
. On neglecting second-order term
$\vec E$
. On neglecting second-order term
![]() $\hat y$
component of THz radiation is given by
$\hat y$
component of THz radiation is given by
 $$\eqalign{& - \displaystyle{{2ikc^2} \over {{\rm \omega} ^2}} \displaystyle{{\partial E_y} \over {\partial z}} + \left( {\displaystyle{{k^2 c^2} \over {{\rm \omega} ^2}} - {\rm \varepsilon} _{yy} + \displaystyle{{{\rm \varepsilon} _{yx} {\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right) \cr & \quad E_y = \displaystyle{{4{\rm \pi} i} \over {\rm \omega}} J_y^{{\rm NL}} - \displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}} \displaystyle{{4{\rm \pi} i} \over {\rm \omega}} J_x^{{\rm NL}},} $$
$$\eqalign{& - \displaystyle{{2ikc^2} \over {{\rm \omega} ^2}} \displaystyle{{\partial E_y} \over {\partial z}} + \left( {\displaystyle{{k^2 c^2} \over {{\rm \omega} ^2}} - {\rm \varepsilon} _{yy} + \displaystyle{{{\rm \varepsilon} _{yx} {\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right) \cr & \quad E_y = \displaystyle{{4{\rm \pi} i} \over {\rm \omega}} J_y^{{\rm NL}} - \displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}} \displaystyle{{4{\rm \pi} i} \over {\rm \omega}} J_x^{{\rm NL}},} $$
where
![]() ${\rm \varepsilon} _{yy} \!=\! [1 \!\!-\! ({\rm \omega} _{\rm p}^2 /{\rm \omega} _{}^2 \!\!-\! {\rm \omega} _{\rm c}^2 )]$
and
${\rm \varepsilon} _{yy} \!=\! [1 \!\!-\! ({\rm \omega} _{\rm p}^2 /{\rm \omega} _{}^2 \!\!-\! {\rm \omega} _{\rm c}^2 )]$
and
![]() ${\rm \varepsilon} _{xy} \!=\! - i[{\rm \omega} _{\rm c} {\rm \omega} _{\rm p}^2 /({\rm \omega} /{\rm \omega} _{}^2 \!-\! {\rm \omega} _{\rm c}^2 )]$
are components of the dielectric tensor. One can conclude from Eq. (8) that THz radiation generation has to satisfy the following dispersion relation for exact phase-matching condition in the corrugated magnetized plasma, which includes the corrugation factor and suggests that the maximum energy transfer from beating lasers to oscillating electrons will take place at resonance condition leading to the maximum THz radiation
${\rm \varepsilon} _{xy} \!=\! - i[{\rm \omega} _{\rm c} {\rm \omega} _{\rm p}^2 /({\rm \omega} /{\rm \omega} _{}^2 \!-\! {\rm \omega} _{\rm c}^2 )]$
are components of the dielectric tensor. One can conclude from Eq. (8) that THz radiation generation has to satisfy the following dispersion relation for exact phase-matching condition in the corrugated magnetized plasma, which includes the corrugation factor and suggests that the maximum energy transfer from beating lasers to oscillating electrons will take place at resonance condition leading to the maximum THz radiation
The corrugation factor (periodicity of density ripples) required for the fine tuning of maximum energy transfer is calculated utilizing Eq. (9a) along with resonance conditions
![]() $\vec k = \vec k_1 - \vec k_2 + {\rm \alpha} $
and ω = ω1 − ω2 ≈ ωh. The corrugation factor comes out as follows:
$\vec k = \vec k_1 - \vec k_2 + {\rm \alpha} $
and ω = ω1 − ω2 ≈ ωh. The corrugation factor comes out as follows:
Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013, Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015) have shown that the wave number of density ripples (α) increases with THz frequency (ω), attains maximum value at
![]() ${\rm \omega} \sim {\rm \omega} _{\rm h} $
(resonance), and then starts decreasing. On combining Eqs. (8) and (9), we obtain the phase-matched normalized amplitude of THz radiation as follows:
${\rm \omega} \sim {\rm \omega} _{\rm h} $
(resonance), and then starts decreasing. On combining Eqs. (8) and (9), we obtain the phase-matched normalized amplitude of THz radiation as follows:
 $$\eqalign{& \left \vert {\displaystyle{{E_y} \over {E_0}}} \right \vert = \displaystyle{1 \over {4k^{\prime}}}\displaystyle{{n_{q0}} \over {n_0}} \displaystyle{1 \over {{\rm \omega} ^{\prime}({\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2} )}} \cr & \quad x^{\prime}\left[ {\left \vert {\left( {\displaystyle{{{\rm \omega} ^{\prime 2} - 1} \over {{\rm \omega} ^{\prime}}} - \left \vert {\displaystyle{{{\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right \vert {\rm \omega} ^{\prime}_{\rm c}} \right)F_{{\rm p}y} + \left( {{\rm \omega} ^{\prime}_{\rm c} - {\rm \omega} ^{\prime}\left \vert {\displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right)F_{{\rm p}x}} \right \vert} \right],} $$
$$\eqalign{& \left \vert {\displaystyle{{E_y} \over {E_0}}} \right \vert = \displaystyle{1 \over {4k^{\prime}}}\displaystyle{{n_{q0}} \over {n_0}} \displaystyle{1 \over {{\rm \omega} ^{\prime}({\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2} )}} \cr & \quad x^{\prime}\left[ {\left \vert {\left( {\displaystyle{{{\rm \omega} ^{\prime 2} - 1} \over {{\rm \omega} ^{\prime}}} - \left \vert {\displaystyle{{{\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right \vert {\rm \omega} ^{\prime}_{\rm c}} \right)F_{{\rm p}y} + \left( {{\rm \omega} ^{\prime}_{\rm c} - {\rm \omega} ^{\prime}\left \vert {\displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right)F_{{\rm p}x}} \right \vert} \right],} $$
where k′ = kc/ωp, ω′ = ω/ωp, ω′c = ωc/ωp, and x′ = xω p/c. Substituting the ponderomotive force into Eq. (10), we obtain normalized amplitude of THz wave as follows:
 $$\eqalign{\left \vert {\displaystyle{{E_y} \over {E_0}}} \right \vert &=\! \left[ \matrix{{\rm \xi}_1^{\prime} {\rm \delta}_{11}^{\prime} +\! \displaystyle{{2y^{\prime}{\rm \xi}_1^{\prime} {\rm \delta}_{12}^{\prime}} \over {a_0^{\prime 2}}} - \displaystyle{{b{\rm \xi}_1^{\prime} {\rm \delta}_{12}^{\prime}} \over {a_0^{\prime}}} \tanh \left( {\displaystyle{{y^{\prime}b} \over {a_0^{\prime}}}} \right) \hfill +\! {\rm \xi}_2^{\prime} {\rm \delta}_{21}^{\prime} \!+ \displaystyle{{4y^{\prime}{\rm \xi}_2^{\prime} {\rm \delta}_{22}^{\prime}} \over {a_0^{\prime 2}}} \hfill \cr - \displaystyle{{b{\rm \xi}_2^{\prime} {\rm \delta}_{22}^{\prime}} \over {a_0^{\prime}}} \tanh \left( {\displaystyle{{yb} \over {a_0^{\prime}}}} \right) \hfill} \right] \cr & \quad \cosh ^2 \left( {\displaystyle{{y^{\prime}b} \over {a_0^{\prime}}}} \right)e^{ - 2\left( {{{y^{\prime 2}} / {a_0^{\prime 2}}}} \right)},} $$
$$\eqalign{\left \vert {\displaystyle{{E_y} \over {E_0}}} \right \vert &=\! \left[ \matrix{{\rm \xi}_1^{\prime} {\rm \delta}_{11}^{\prime} +\! \displaystyle{{2y^{\prime}{\rm \xi}_1^{\prime} {\rm \delta}_{12}^{\prime}} \over {a_0^{\prime 2}}} - \displaystyle{{b{\rm \xi}_1^{\prime} {\rm \delta}_{12}^{\prime}} \over {a_0^{\prime}}} \tanh \left( {\displaystyle{{y^{\prime}b} \over {a_0^{\prime}}}} \right) \hfill +\! {\rm \xi}_2^{\prime} {\rm \delta}_{21}^{\prime} \!+ \displaystyle{{4y^{\prime}{\rm \xi}_2^{\prime} {\rm \delta}_{22}^{\prime}} \over {a_0^{\prime 2}}} \hfill \cr - \displaystyle{{b{\rm \xi}_2^{\prime} {\rm \delta}_{22}^{\prime}} \over {a_0^{\prime}}} \tanh \left( {\displaystyle{{yb} \over {a_0^{\prime}}}} \right) \hfill} \right] \cr & \quad \cosh ^2 \left( {\displaystyle{{y^{\prime}b} \over {a_0^{\prime}}}} \right)e^{ - 2\left( {{{y^{\prime 2}} / {a_0^{\prime 2}}}} \right)},} $$
where y′ = yω
p/c, a′0 = a
0ωp/c,
![]() ${\rm \delta} '_{12} = {\rm \delta} _{12} /{\rm \omega} _{\rm p}^{\rm 2} $
, δ′11 = δ11/cω
p, δ′21 = δ21/cω
p,
${\rm \delta} '_{12} = {\rm \delta} _{12} /{\rm \omega} _{\rm p}^{\rm 2} $
, δ′11 = δ11/cω
p, δ′21 = δ21/cω
p,
![]() ${\rm \delta} '_{22} = {\rm \delta} _{22} /{\rm \omega} _{\rm p}^2 $
,
${\rm \delta} '_{22} = {\rm \delta} _{22} /{\rm \omega} _{\rm p}^2 $
,
 $${\rm \xi}_1^{\prime} = c{\rm \omega} _{\rm p} \left[ {\displaystyle{1 \over {8k^{\prime}}}\displaystyle{{n_{{\rm \alpha} 0}} \over {n_0}} \left( {\displaystyle{{{\rm \omega} ^{\prime}{\rm \omega}_2^{\prime}} \over {{\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2}}} x^{\prime}v_2^{\prime} \left\{ {{\rm \omega} ^{\prime} + {\rm \omega}_{\rm c}^{\prime} \left \vert {\displaystyle{{{\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right\}} \right)} \right],$$
$${\rm \xi}_1^{\prime} = c{\rm \omega} _{\rm p} \left[ {\displaystyle{1 \over {8k^{\prime}}}\displaystyle{{n_{{\rm \alpha} 0}} \over {n_0}} \left( {\displaystyle{{{\rm \omega} ^{\prime}{\rm \omega}_2^{\prime}} \over {{\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2}}} x^{\prime}v_2^{\prime} \left\{ {{\rm \omega} ^{\prime} + {\rm \omega}_{\rm c}^{\prime} \left \vert {\displaystyle{{{\rm \varepsilon} _{xy}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right\}} \right)} \right],$$
 $${\rm \xi}_2^{\prime} = c{\rm \omega} _{\rm p} \left[ {\displaystyle{1 \over {8k^{\prime}}}\displaystyle{{n_{{\rm \alpha} 0}} \over {n_0}} \left( {\displaystyle{{{\rm \omega} ^{\prime}{\rm \omega}_2^{\prime}} \over {{\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2}}} x^{\prime}v_2^{\prime} \left\{ {{\rm \omega}_{\rm c}^{\prime} + \displaystyle{{{\rm \omega} ^{\prime 2} - 1} \over {{\rm \omega} ^{\prime}}}\left \vert {\displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right\}} \right)} \right].$$
$${\rm \xi}_2^{\prime} = c{\rm \omega} _{\rm p} \left[ {\displaystyle{1 \over {8k^{\prime}}}\displaystyle{{n_{{\rm \alpha} 0}} \over {n_0}} \left( {\displaystyle{{{\rm \omega} ^{\prime}{\rm \omega}_2^{\prime}} \over {{\rm \omega} ^{\prime 2} - {\rm \omega}_{\rm h}^{\prime 2}}} x^{\prime}v_2^{\prime} \left\{ {{\rm \omega}_{\rm c}^{\prime} + \displaystyle{{{\rm \omega} ^{\prime 2} - 1} \over {{\rm \omega} ^{\prime}}}\left \vert {\displaystyle{{{\rm \varepsilon} _{yx}} \over {{\rm \varepsilon} _{xx}}}} \right \vert} \right\}} \right)} \right].$$
Equation (10) exhibits that greater the value of corrugation amplitude (n
α0/n
0), greater will be the amplitude of excited THz radiation due to larger number of oscillating electrons involved in the process of nonlinear current generation at
![]() $({\rm \omega}, \,\vec k)$
. In Figure 3a and 3b, the normalized THz amplitude is plotted as a function of normalized THz frequency (ω/ωp) for different laser profiles (corresponding to decentralized parameter b = 0, 0.5, 1.0, 1.4, 3, 4, 5) respectively at ωc/ωp = 0.2 (B
0 = 71 kG) and ωc/ωp = 0.3 (B
0 = 107 kG). The maximum THz amplitude is obtained at resonance condition ω ≈ ωh irrespective of laser profiles. It can be attributed to the factor
$({\rm \omega}, \,\vec k)$
. In Figure 3a and 3b, the normalized THz amplitude is plotted as a function of normalized THz frequency (ω/ωp) for different laser profiles (corresponding to decentralized parameter b = 0, 0.5, 1.0, 1.4, 3, 4, 5) respectively at ωc/ωp = 0.2 (B
0 = 71 kG) and ωc/ωp = 0.3 (B
0 = 107 kG). The maximum THz amplitude is obtained at resonance condition ω ≈ ωh irrespective of laser profiles. It can be attributed to the factor
![]() $({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 )$
present in the expression of nonlinear current
$({\rm \omega} ^2 - {\rm \omega} _{\rm h}^2 )$
present in the expression of nonlinear current
![]() $\vec J_{{\rm NL}} $
given by Eq. (6) (in
$\vec J_{{\rm NL}} $
given by Eq. (6) (in
![]() ${\vec v}\,_{\rm \omega}^{{\rm NL}} $
). This factor is introduced in Eq. (4) (potential φ of space charge mode of plasma) due to the presence of perpendicular magnetic field. In the presence of magnetic field, the potential of space-charge mode will achieve its peak value at ω ≅ ωh and energy transfer in beat wave process will be maximal. This maximally developed space-charge mode along with density ripple gives rise to strong nonlinear current responsible for the maximum THz amplitude. The amplitude of THz wave decreases as one moves away from the resonance position. At the same time α has maximum value (or λc is small) at resonance
${\vec v}\,_{\rm \omega}^{{\rm NL}} $
). This factor is introduced in Eq. (4) (potential φ of space charge mode of plasma) due to the presence of perpendicular magnetic field. In the presence of magnetic field, the potential of space-charge mode will achieve its peak value at ω ≅ ωh and energy transfer in beat wave process will be maximal. This maximally developed space-charge mode along with density ripple gives rise to strong nonlinear current responsible for the maximum THz amplitude. The amplitude of THz wave decreases as one moves away from the resonance position. At the same time α has maximum value (or λc is small) at resonance
![]() ${\rm \omega} \sim {\rm \omega} _{\rm h} ;$
thus, density ripples with small corrugation factor (λc) are best suited for efficient THz excitation. This result matches with the observation of Antonsen et al. (Reference Antonsen, Palastra and Milchberg2007), who proposed that the phase-matching requirements for efficient energy transfer from laser pulse to THz can be matched in a parabolic plasma channel (in radius) by z sequence of δ-function peaks with period d and strength triangle Δ, in axial distance, that is,
${\rm \omega} \sim {\rm \omega} _{\rm h} ;$
thus, density ripples with small corrugation factor (λc) are best suited for efficient THz excitation. This result matches with the observation of Antonsen et al. (Reference Antonsen, Palastra and Milchberg2007), who proposed that the phase-matching requirements for efficient energy transfer from laser pulse to THz can be matched in a parabolic plasma channel (in radius) by z sequence of δ-function peaks with period d and strength triangle Δ, in axial distance, that is,
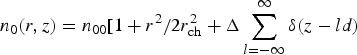 $n_0 (r,z) = n_{00} [1 + {{r^2} / {2r_{{\rm ch}}^2}} + {\rm \Delta} \sum\limits_{l = - \infty} ^\infty {{\rm \delta} (z - ld)} $
.
$n_0 (r,z) = n_{00} [1 + {{r^2} / {2r_{{\rm ch}}^2}} + {\rm \Delta} \sum\limits_{l = - \infty} ^\infty {{\rm \delta} (z - ld)} $
.

Fig. 3. (a) Plot of normalized THz amplitude (E y /E 1) as a function of normalized THz frequency (ω/ωp) for different values of decentered parameter 0 < b ≤ 1.4. All other parameters are same as Figure 1. (b) Plot of normalized THz amplitude (E y /E 1) as a function of normalized THz frequency (ω/ωp) for different values of decentered parameter 1.5 < b ≤ 5. All plasma parameters are same as Figure 1.
Here, δ function-type axial coagulated plasma density acts as ripples. This inhomogeneity couples with the density perturbation provided by ponderomotive force and gives rise to a nonlinear current responsible for THz generation. Figure 3a shows that the THz amplitude increases with b for b < 1.5. The maximum amplitude (E
y
) is obtained for Gaussian laser profile (b = 0) at resonance condition ω ≈ ωh. For higher value of decenterd parameter (1.5 ≤ b ≤ 5), the normalized THz amplitude increases with b and the maximum amplitude is again achieved at THz frequency
![]() ${\rm \omega} \sim {\rm \omega} _{\rm h} $
as shown in Figure 3b. THz amplitude (E
y
) achieves maximum value for hollow-Gaussian beating lasers (with b = 5). The variation of THz amplitude with b can be attributed to the variation of nonlinear ponderomotive force, which depends upon the shape of beating lasers beams as shown in Figure 2. Figure 3 also exhibits that the normalized THz field amplitude decreases and peak shifts toward higher value of THz due to new resonance frequency
${\rm \omega} \sim {\rm \omega} _{\rm h} $
as shown in Figure 3b. THz amplitude (E
y
) achieves maximum value for hollow-Gaussian beating lasers (with b = 5). The variation of THz amplitude with b can be attributed to the variation of nonlinear ponderomotive force, which depends upon the shape of beating lasers beams as shown in Figure 2. Figure 3 also exhibits that the normalized THz field amplitude decreases and peak shifts toward higher value of THz due to new resonance frequency
![]() $\sqrt {{\rm \omega} _{\rm p}^2 + {\rm \omega} _{\rm c}^2} $
by varying applied magnetic field from B
0 = 71 kG (ωc/ωp = 0.2) to B
0 = 107 kG (ωc/ωp = 0.3). Thus, THz amplitude (at a particular THz frequency) can be tuned by changing dc magnetic field.
$\sqrt {{\rm \omega} _{\rm p}^2 + {\rm \omega} _{\rm c}^2} $
by varying applied magnetic field from B
0 = 71 kG (ωc/ωp = 0.2) to B
0 = 107 kG (ωc/ωp = 0.3). Thus, THz amplitude (at a particular THz frequency) can be tuned by changing dc magnetic field.
Finally, we calculate the efficiency (η) of the present scheme. Average EM energy stored per unit volume in electric and magnetic fields are given by the relations (Malik et al., Reference Malik, Malik and Nishida2011, Reference Malik, Malik and Stroth2012b
; Singh et al., Reference Singh, Singh and Sharma2013; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013, Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015)
![]() $\left\langle {W_{E{\rm i}}} \right\rangle = \displaystyle{1 \over {8{\rm \pi}}} {\rm \varepsilon} _0 \displaystyle{\partial \over {\partial {\rm \omega} _{\rm i}}} \left[ {{\rm \omega} _{\rm i} \left( {1 - {{{\rm \omega} _{\rm p}^2} / {{\rm \omega} _{\rm i}^2}}} \right)} \right]\left\langle {\left\vert {E_{\rm i}} \right\vert^2} \right\rangle $
and
$\left\langle {W_{E{\rm i}}} \right\rangle = \displaystyle{1 \over {8{\rm \pi}}} {\rm \varepsilon} _0 \displaystyle{\partial \over {\partial {\rm \omega} _{\rm i}}} \left[ {{\rm \omega} _{\rm i} \left( {1 - {{{\rm \omega} _{\rm p}^2} / {{\rm \omega} _{\rm i}^2}}} \right)} \right]\left\langle {\left\vert {E_{\rm i}} \right\vert^2} \right\rangle $
and
![]() ${\rm } \,\left\langle {W_{B{\rm i}}} \right\rangle = {{\left\langle {\left\vert {B_{\rm i} ^2} \right\vert} \right\rangle} / {8{\rm \pi} {\rm \mu} _0}}, $
respectively; where 〈B
i〉 = k〈E
i〉/ωi. The energy densities of the incident lasers (W
pump) and emitted radiation (W
THz) are as follows:
${\rm } \,\left\langle {W_{B{\rm i}}} \right\rangle = {{\left\langle {\left\vert {B_{\rm i} ^2} \right\vert} \right\rangle} / {8{\rm \pi} {\rm \mu} _0}}, $
respectively; where 〈B
i〉 = k〈E
i〉/ωi. The energy densities of the incident lasers (W
pump) and emitted radiation (W
THz) are as follows:
and
 $$W_{{\rm THz}} = {\rm \varepsilon} _0 \left \vert {E_0} \right \vert ^2 \left[ \matrix{\displaystyle{1 \over 2}\sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{11}^2 + {\rm \xi} _2^2 {\rm \delta} _{21}^2} \right)a_0 \{ 1 + e^{b^2 /2} \} \hfill \cr + \displaystyle{1 \over 2}\sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{12}^2 + 4{\rm \xi} _2^2 {\rm \delta} _{22}^2} \right)a_0 \{ 1 + (1 + b^2 )e^{b^2 /2} \} \hfill \cr - \displaystyle{{b^2} \over {a_0^{}}} \sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{12}^2 + {\rm \xi} _2^2 {\rm \delta} _{22}^2} \right)\{ - 1 + e^{b^2 /2} \} \hfill} \right].$$
$$W_{{\rm THz}} = {\rm \varepsilon} _0 \left \vert {E_0} \right \vert ^2 \left[ \matrix{\displaystyle{1 \over 2}\sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{11}^2 + {\rm \xi} _2^2 {\rm \delta} _{21}^2} \right)a_0 \{ 1 + e^{b^2 /2} \} \hfill \cr + \displaystyle{1 \over 2}\sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{12}^2 + 4{\rm \xi} _2^2 {\rm \delta} _{22}^2} \right)a_0 \{ 1 + (1 + b^2 )e^{b^2 /2} \} \hfill \cr - \displaystyle{{b^2} \over {a_0^{}}} \sqrt {\displaystyle{{\rm \pi} \over 2}} \left( {{\rm \xi} _1^2 {\rm \delta} _{12}^2 + {\rm \xi} _2^2 {\rm \delta} _{22}^2} \right)\{ - 1 + e^{b^2 /2} \} \hfill} \right].$$
The normalized efficiency of THz radiation generation is evaluated
 $$\eqalign{& {\rm \eta} = \displaystyle{{W_{{\rm THz}}} \over {W_{{\rm pump}}}} = \left[ {\left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{11}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{21}^{\prime 2}} \right) + \displaystyle{1 \over {a_0^{\prime 2}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + 4{\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)} \vphantom{\quad \displaystyle{{\{ 1 + (1 + b^2 )e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}} + \displaystyle{{b^2} \over {a_0^{\prime}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)\displaystyle{{\{ 1 - e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}}} \right.. \cr & \left. {\quad \displaystyle{{\{ 1 + (1 + b^2 )e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}} + \displaystyle{{b^2} \over {a_0^{\prime}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)\displaystyle{{\{ 1 - e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}}} \right].} $$
$$\eqalign{& {\rm \eta} = \displaystyle{{W_{{\rm THz}}} \over {W_{{\rm pump}}}} = \left[ {\left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{11}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{21}^{\prime 2}} \right) + \displaystyle{1 \over {a_0^{\prime 2}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + 4{\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)} \vphantom{\quad \displaystyle{{\{ 1 + (1 + b^2 )e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}} + \displaystyle{{b^2} \over {a_0^{\prime}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)\displaystyle{{\{ 1 - e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}}} \right.. \cr & \left. {\quad \displaystyle{{\{ 1 + (1 + b^2 )e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}} + \displaystyle{{b^2} \over {a_0^{\prime}}} \left( {{\rm \xi}_1^{\prime 2} {\rm \delta}_{12}^{\prime 2} + {\rm \xi}_2^{\prime 2} {\rm \delta}_{22}^{\prime 2}} \right)\displaystyle{{\{ 1 - e^{b^2 /2} \}} \over {\{ 1 + e^{b^2 /2} \}}}} \right].} $$
Figure 4 shows that the efficiency η of the present scheme increases with decentered parameter (b) and decrease with laser beam width (a
0). The efficiency can be optimized with an applied static magnetic field corresponding to THz frequency. An efficiency ~20% is achieved by frequency mixing of two hollow-Gaussian laser beams at beam width
![]() $a_0 \sim 3c/5{\rm \omega} _{\rm p} $
and dc magnetic field
$a_0 \sim 3c/5{\rm \omega} _{\rm p} $
and dc magnetic field
![]() $B_0 \sim 107\,{\rm kG}$
. Wu et al. (Reference Wu, Sheng and Zhang2008) achieved energy conversion efficiency ~0.005 in inhomogeneous plasma at peak laser intensity 5.48 × 1012 W/cm2, which is much lower than the present model. Malik et al. (Reference Malik, Malik and Nishida2011, Reference Malik, Malik and Stroth2012b
) have reported the conversion efficiency ~0.002 and ~0.006 by beating of two spatial-Gaussian lasers and two super Gaussian lasers, respectively. Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have reported the conversion efficiency
$B_0 \sim 107\,{\rm kG}$
. Wu et al. (Reference Wu, Sheng and Zhang2008) achieved energy conversion efficiency ~0.005 in inhomogeneous plasma at peak laser intensity 5.48 × 1012 W/cm2, which is much lower than the present model. Malik et al. (Reference Malik, Malik and Nishida2011, Reference Malik, Malik and Stroth2012b
) have reported the conversion efficiency ~0.002 and ~0.006 by beating of two spatial-Gaussian lasers and two super Gaussian lasers, respectively. Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have reported the conversion efficiency
![]() $\sim\!10^{ - 3} $
by beating of two planer x-mode lasers in a magnetized plasma. Further Varshney et al. (Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015) improved one order of conversion efficiency and achieved ~10−2 by photomixing of two super-Gaussian laser. Malik et al. (Reference Malik, Singh and Sajal2014) obtain efficiency about 15% by frequency mixing of two top-hat lasers in the magnetized plasma.
$\sim\!10^{ - 3} $
by beating of two planer x-mode lasers in a magnetized plasma. Further Varshney et al. (Reference Varshney, Sajal, Sharma, Chauhan and Kumar2015) improved one order of conversion efficiency and achieved ~10−2 by photomixing of two super-Gaussian laser. Malik et al. (Reference Malik, Singh and Sajal2014) obtain efficiency about 15% by frequency mixing of two top-hat lasers in the magnetized plasma.

Fig. 4. Plot of THz efficiency (η) as a function of normalized laser beam width a oωp/c for different values of b and ωc/ωp. Other normalized parameters are same as in Figure 1.
4. CONCLUSIONS
The resonant excitation of THz radiation by beating of two cosh-Gaussian laser beams in preformed corrugated plasma in the presence of magnetic field is found to be quite efficient technique for obtaining intense, focused, and tunable THz beam. Nonlinear photomixing of laser beams result into a strong nonlinear ponderomotive force on plasma electrons, which in turn resonantly excites a nonlinear current responsible for THz radiation generation. The ponderomotive force depends upon the laser profile (which depends upon the decentralized parameter of cosh-Gaussian laser beams). Ponderomotive force decreases from b = 0 (Gaussian) to b = 1.4 (flat-top), and then starts increasing and maximizes for b = 5 (hollow-Gaussian). As a result, nonlinear current generated by using hollow-Gaussian laser beams exhibit the maximum THz field amplitude. THz field amplitude is optimized utilizing externally applied dc magnetic field. Here magnetic field plays two roles. It controls the phase velocity and group velocity of beating lasers on one side and the polarization of generated THz wave on the other. THz field amplitude acquires large values as ω approaches toward resonance frequency (~ωh). Stronger magnetic field leads to THz amplitude with the enhanced efficiency of the process, and intense radiation have been achieved when the lasers of lower beam width are used under the effect of stronger magnetic field and larger amplitude of the density ripples. In the presence of a stronger magnetic field, the ripples in the density are required to be created at comparatively smaller distances. Thus, the presence of transverse magnetic field makes the present scheme more tunable in terms of THz frequency. The efficiency can be further enhanced by using large amplitude density ripples.
ACKNOWLEDGEMENTS
One of the authors, P. V. acknowledges SERB-DST, Government of India for providing financial support.