2. Governing equations and numerical technique

Consider the flow in a circular cylinder of radius $R$ and length $L$ , with no-slip boundary conditions, and with an imposed temperature profile at the cylinder wall. The bottom endwall has a fixed temperature $T_{0}^{\ast }$ except for a disk of diameter $D$ at the bottom centre with a hotter temperature $T_{h}^{\ast }$ . The top endwall is kept at a temperature $T_{t}^{\ast }$ , and the temperature varies linearly along the sidewall between $T_{0}^{\ast }$ at the bottom and $T_{t}^{\ast }$ at the top, resulting in a stable stratification, but for the hot spot at the bottom. There are horizontal and vertical temperature gradients, driven by the differences $T_{h}^{\ast }-T_{0}^{\ast }$ and $T_{t}^{\ast }-T_{0}^{\ast }$ respectively. Figure 1(a) shows a schematic of the cylinder. The boundary conditions for the temperature (not considering the hot disk) result in a stable stratification ${\it\rho}(z^{\ast })={\it\rho}_{0}(1-{\it\alpha}(T^{\ast }(z^{\ast })-T_{0}^{\ast }))={\it\rho}_{0}(1-{\it\alpha}(T_{t}^{\ast }-T_{0}^{\ast })z^{\ast }/L)$ , and the corresponding Brunt–Väisälä frequency $N_{BV}$ is

where ${\it\alpha}$ is the coefficient of thermal expansion and ${\it\rho}_{0}$ is the density at temperature  $T_{0}^{\ast }$ .

Figure 1. (a) Schematic of the apparatus with contours of non-dimensional temperature $T$ showing a laminar thermal plume emerging from the localized heating at the base centre for $Gr=10^{5}$ , ${\it\sigma}=7$ , $A_{r}=A_{z}=2$ and $A_{T}=1$ . (b) Radial temperature profile at the bottom wall (2.7) along a diameter, for the same geometry as (a), $C=7.4$ and ${\it\epsilon}=1/3$ .

The Boussinesq approximation is implemented, treating all fluid properties as constant except for a linear variation of density with temperature in the gravitational buoyancy term. The system is non-dimensionalized using $L$ as the length scale, $L^{2}/{\it\kappa}$ as the time scale ( ${\it\kappa}$ is the thermal diffusivity), $T_{h}^{\ast }-T_{0}^{\ast }$ as the temperature scale, and ${\it\kappa}^{2}{\it\rho}_{0}/L^{2}$ as the pressure scale. The non-dimensional governing equations are

where $\boldsymbol{u}=(u,v,w)$ is the velocity in cylindrical coordinates $(r,{\it\theta},z)\in [0,A_{r}/A_{z}]\times [0,2{\rm\pi}]\times [0,1]=\mathscr{D}$ , the corresponding vorticity is ${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}=({\it\xi},{\it\eta},{\it\zeta})$ , $p$ is the dynamic pressure, $\boldsymbol{e}_{z}=(0,0,1)$ is the vertical unit vector in the $z$ -direction and $T=(T^{\ast }-T_{0}^{\ast })/(T_{h}^{\ast }-T_{0}^{\ast })$ is the non-dimensional temperature, while $T^{\ast }$ is the dimensional temperature. $N$ is the non-dimensional Brunt–Väisälä frequency $N=N_{BV}L^{2}/{\it\kappa}$ . The non-dimensional parameters are

where ${\it\nu}$ is the kinematic viscosity and $g$ is the acceleration due to gravity. We have introduced a Grashof number based on the hot-spot diameter $D$ , as is typically done in natural convection problems due to localized heating (Torrance Reference Torrance1979), rather than a dimension of the container. The relationship between the Grashof number and the non-dimensional Brunt–Väisälä frequency is

The boundary conditions are:

The temperature profile at the bottom wall has been regularized so that instead of a step function, it is of the form

where $1/(2A_{z})=D/(2L)$ is the non-dimensional radius of the hot disk, and ${\it\epsilon}$ is the non-dimensional length where most of the temperature variation takes place. We have taken $C=7.4$ so that 95 % of the temperature variation takes place in an interval of length ${\it\epsilon}$ centred at the hot-disk radius, $r\in [(1-{\it\epsilon})/(2A_{z}),(1+{\it\epsilon})/(2A_{z})]$ . Figure 1(b) shows the radial temperature profile imposed at the bottom wall, for ${\it\epsilon}=1/3$ , which is the value used for the simulations. In practice it is impossible to maintain a sharp temperature jump, so the regularization (2.7) mimics the real physical situation, and also helps to improve the convergence of the spectral method used in the numerical simulations.

The main parameter that controls the validity of the Boussinesq approximation is ${\it\alpha}(T_{t}^{\ast }-T_{0}^{\ast })$ , which is independent of the other governing parameters; validity requires ${\it\alpha}(T_{t}^{\ast }-T_{0}^{\ast })\ll 1$ (Busse Reference Busse1967; Gray & Giorgini Reference Gray and Giorgini1976). For the Grashof numbers considered in this study, $\mathit{Gr}\leqslant 3.5\times 10^{5}$ , this requirement is easily satisfied with typical laboratory-scale experiments. For example, using water and $D=3\ \text{cm}$ (corresponding to a cylinder of radius and height of $6\ \text{cm}$ ), and $T_{t}^{\ast }-T_{0}^{\ast }<8\,^{\circ }\text{C}$ , $\mathit{Gr}\sim 4.5\times 10^{5}$ can be achieved while ${\it\alpha}(T_{t}^{\ast }-T_{0}^{\ast })<2\times 10^{-3}\ll 1$ . For air, using $D=12\ \text{cm}$ (corresponding to a cylinder of radius and height of $24\ \text{cm}$ ), and $T_{t}^{\ast }-T_{0}^{\ast }<2\,^{\circ }\text{C}$ , $\mathit{Gr}\sim 5\times 10^{5}$ can be achieved while ${\it\alpha}(T_{t}^{\ast }-T_{0}^{\ast })<7\times 10^{-3}\ll 1$ . Of course, using a larger apparatus and/or different fluids, there is ample room for reaching even larger Grashof numbers while maintaining the validity of the Boussinesq approximation.

The governing equations have been solved using a second-order time-splitting method, with space discretized via a Galerkin–Fourier expansion in ${\it\theta}$ and Chebyshev collocation in $r$ and $z$ . The spectral solver is based on that described by Mercader, Batiste & Alonso (Reference Mercader, Batiste and Alonso2010) and it has recently been used in our previous study of plumes in an isothermal (non-stratified) ambient (Lopez & Marques Reference Lopez and Marques2013). For the solutions presented here, with $A_{r}=A_{z}=2$ and $A_{T}=1$ , we have used up to $n_{r}=256$ and $n_{z}=128$ Chebyshev modes in the radial and axial directions and $n_{{\it\theta}}=36$ azimuthal Fourier modes. The number of Chebyshev spectral modes is high in order to well-resolve the plume structure and the rapid variation of the temperature and the boundary layer forming at the bottom wall. The solution is well-resolved with at least four orders of magnitude of decay in the modal energies.

The $L_{2}$ -norms of the azimuthal Fourier modes of a given solution,

where $\boldsymbol{u}_{m}$ is the $m$ th Fourier mode of the velocity field and $\boldsymbol{u}_{m}^{\ast }$ is its complex conjugate, provide a convenient way to characterize the non-axisymmetric states. For axisymmetric states, $E_{0}$ is the non-dimensional kinetic energy of the flow.

The governing equations and boundary conditions are invariant under arbitrary rotations around the cylinder axis and reflections about meridional planes. These symmetries (orthogonal transformations) act simultaneously on the points in the fluid domain and also on vector fields. If $\unicode[STIX]{x1D64E}$ is the matrix of one of these symmetry transformations, its action ${\it\tau}(\unicode[STIX]{x1D64E})$ on the velocity field $\boldsymbol{u}(\boldsymbol{r})$ is given by ${\it\tau}(\unicode[STIX]{x1D64E})\boldsymbol{u}(\boldsymbol{r})=\unicode[STIX]{x1D64E}\boldsymbol{u}(\unicode[STIX]{x1D64E}^{-1}\boldsymbol{r})$ (see Chossat & Lauterbach Reference Chossat and Lauterbach2000, § 1.2.4), or equivalently ${\it\tau}(\unicode[STIX]{x1D64E})\boldsymbol{u}(\unicode[STIX]{x1D64E}\boldsymbol{r})=\unicode[STIX]{x1D64E}\boldsymbol{u}(\boldsymbol{r})$ . These equations say that in order to obtain the symmetrically related velocity field, ${\it\tau}(\unicode[STIX]{x1D64E})\boldsymbol{u}$ , of a given field $\boldsymbol{u}$ , one takes the velocity vector at a point $\boldsymbol{r}$ , transforms it according to $\unicode[STIX]{x1D64E}$ , and translates the result to the transformed point $\unicode[STIX]{x1D64E}\boldsymbol{r}$ . Using cylindrical coordinates and the cylindrical components of the velocity field, the action of the two symmetries in our problem is given by

where ${\it\alpha}$ and ${\it\beta}$ are arbitrary angles, $R_{{\it\alpha}}$ is the rotation of angle ${\it\alpha}$ about the cylinder axis, and $K_{{\it\beta}}$ is the reflection about the meridional plane ${\it\theta}={\it\beta}$ . $R_{{\it\alpha}}$ and $K_{{\it\beta}}$ do not commute ( $K_{{\it\beta}}R_{{\it\alpha}}=R_{-{\it\alpha}}K_{{\it\beta}}$ ), and generate the group $O(2)$ (orthogonal matrices in two dimensions) acting on the periodic azimuthal ${\it\theta}$ -direction. The action of these symmetries on the vorticity is given by A vector field is $\unicode[STIX]{x1D64E}$ -symmetric, or equivariant under $\unicode[STIX]{x1D64E}$ , if ${\it\tau}(\unicode[STIX]{x1D64E})\boldsymbol{u}(\boldsymbol{r})=\boldsymbol{u}(\boldsymbol{r})$ , i.e. it coincides with the $\unicode[STIX]{x1D64E}$ -transformed field; an equivalent expression is $\unicode[STIX]{x1D64E}\boldsymbol{u}(\boldsymbol{r})=\boldsymbol{u}(\unicode[STIX]{x1D64E}\boldsymbol{r})$ . As a consequence, the basic steady flow, which possesses all the symmetries of the problem, is axisymmetric (independent of ${\it\theta}$ ), and also equivariant under meridional reflections $K_{{\it\beta}}$ . A field that is equivariant under $K_{{\it\beta}}$ is said to be parity symmetric.

Another useful quantity is the helicity $\mathit{He}$ of a given solution, defined as the integral over the fluid domain $\mathscr{D}$ of the scalar product of the velocity and vorticity fields:

The local helicity $\boldsymbol{u}\boldsymbol{\cdot }{\bf\omega}$ is invariant under rotations $R_{{\it\alpha}}$ , but is not invariant under parity (the action of $K_{{\it\beta}}$ ):

An important consequence is that parity-symmetric solutions (invariant under $K_{{\it\beta}}$ ) have zero helicity, and therefore $\mathit{He}$ is a good measure of the parity breaking processes that are related to the spontaneous generation of swirl.

3. Basic state

For moderate values of the Grashof number, $\mathit{Gr}$ , the solution of the governing equations is a steady and axisymmetric basic state, BS. For the results presented here, we have fixed all the other parameters at $A_{r}=2,A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ , and have varied $\mathit{Gr}$ over several decades. The choice of $A_{T}=1$ means that the centre of the hot spot on the bottom is at the same temperature as the top endwall, and so the neutral buoyancy level of a well-developed plume will be roughly halfway between the top and bottom. Keeping $A_{T}$ fixed means that the strength of the stratification is then proportional to $\mathit{Gr}$ , and this is reflected in the buoyancy frequency squared being proportional to $\mathit{Gr}$ . The Prandtl number ${\it\sigma}=7$ nominally corresponds to water as the working fluid. The solutions are quantitatively dependent on the geometric parameters $A_{r}$ and $A_{z}$ but, for reasonable variations, the results are qualitatively independent of these.

The localized heating in the centre of the bottom endwall means that there is a non-zero radial temperature gradient for any non-zero $\mathit{Gr}$ . This radial temperature gradient locally produces azimuthal vorticity resulting in a meridional circulation drawing fluid radially inward above the heated portion of the lower endwall and upward along the axis, eventually forming a thermal plume for larger $\mathit{Gr}$ . The vertical extent of this axial plume is limited by the vertical stratification, and the diffusion of both temperature and vorticity.

Figure 2 shows the structure of the base state in terms of isotherms and streamlines at $\mathit{Gr}=10,10^{3}$ and $10^{5}$ . In this range of $\mathit{Gr}$ , the base state is stable and there are substantial changes in the flow structure. The streamlines are isolevels of the streamfunction ${\it\psi}$ , where the meridional velocity components are $(u,w)=(-\partial {\it\psi}/\partial z,\partial {\it\psi}/\partial r)/r$ . For $\mathit{Gr}=10^{2}$ and smaller, the flow is conduction dominated; the velocity is very small, as can be observed from the values of the streamfunction and the spacing between the streamlines, and the hot-spot temperature diffuses throughout the whole domain. For larger Grashof numbers ( $\mathit{Gr}\sim 10^{3}$ ) the velocity intensifies above the hot spot and a thermal plume begins to form. As the plume fluid rises, its temperature dissipates, and when the temperature of the rising fluid matches the ambient temperature, it stops rising and spreads out radially, creating a large-scale circulation in the bottom half of the container (up to the neutral buoyancy level), while in the upper part of the container the fluid is essentially stagnant and linearly stratified.

Figure 2. Isotherms (a,c,e) and streamlines (b,d,f) of the steady axisymmetric basic state BS at $A_{r}=2,A_{z}=2,A_{T}=1,{\it\sigma}=7$ and $\mathit{Gr}$ as indicated. There are 10 contour levels with $T\in [-0.5,0.5]$ , and ${\it\psi}\in [-0.042,0.042]$ for $\mathit{Gr}=10,{\it\psi}\in [-0.92,0.92]$ for $\mathit{Gr}=10^{3}$ , and ${\it\psi}\in [-3.5,3.5]$ for $\mathit{Gr}=10^{5}$ ; solid lines (red) are positive and dashed lines (yellow) are negative.

By $\mathit{Gr}=10^{5}$ , a well-developed plume has formed (see figure 2 e,f). The temperature in the plume still drops as the fluid rises, as in the lower- $\mathit{Gr}$ cases, but now as the plume fluid reaches the neutral buoyancy level it retains upward momentum resulting in an overshoot beyond the neutral buoyancy level before it stagnates vertically, falls back to the neutral level and continues to flow out radially. In the upper part, the flow is essentially stagnant and linearly stratified, matching the imposed linear temperature profile imposed on the sidewall. In the lower part, the return flow of the plume generates a meridional circulation. The meridional circulation generates a thermal boundary layer at the sidewall, and between this boundary layer and the plume, the temperature is essentially linearly stratified, but with a slightly different stratification from the imposed linear profile at the sidewall.

Figure 3. Profiles of temperature $T(z)$ and vertical velocity $w(z)$ of the steady axisymmetric basic state BS at $A_{r}=2$ , $A_{z}=2$ , $A_{T}=1$ and ${\it\sigma}=7$ , for $\mathit{Gr}$ as indicted. The solid black lines are the profiles at the plume centre, $r=0$ . The dashed grey (red online ) lines are the profiles at mid-radius $r=0.5\,A_{r}$ . The grey line in (c) is the imposed temperature profile at the sidewall, $r=A_{r}$ , and the vertical short-dashed line at $w=0$ in (d–f) is the vertical axis to help assess the rising or descending flow in the ambient.

Figure 4. Variation of the plume height, $z_{PH}$ , and neutral buoyancy level, $z_{NB}$ , with $\mathit{Gr}$ for $A_{r}=2$ , $A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ .

Figure 3 shows vertical profiles at the axis of the temperature $T(r=0,z)$ and the vertical velocity $w(r=0,z)$ . We have used these profiles for a quantitative measurement of the plume height, $z_{PH}$ , defined as the stagnation point of the plume where $w(r=0,z_{PH})=0$ , and the neutral buoyancy level $z_{NB}$ , defined as the height at which the plume temperature (and density) equals the ambient temperature. The long-dashed lines in figure 3 are the $T$ - and $w$ -profiles at mid-radius ( $r=0.5A_{r}$ ). Figure 4 shows the variations in $z_{PH}$ and $z_{NB}$ over a range of $\mathit{Gr}$ for which the base state is stable. For small $\mathit{Gr}\lesssim 10^{3}$ , the plume is not well-developed and so the plume height is ill-defined (see figure 3 a,d where there is a global meridional circulation driven by the hot spot, but the flow does not stagnate on the axis except at the top and bottom endwalls). The neutral buoyancy level is lower than the top endwall for $\mathit{Gr}>10$ and decreases with increasing $\mathit{Gr}$ for small $\mathit{Gr}$ until the flow begins to undergo the transition from being conduction dominated to convection dominated and the plume begins to be well-established, at approximately $\mathit{Gr}=300$ . With further increases in $\mathit{Gr}$ , the neutral buoyancy level grows monotonically with $\mathit{Gr}$ . The plume height is always larger than the neutral buoyancy level; it decreases with increasing $\mathit{Gr}$ until $\mathit{Gr}\approx 2\times 10^{4}$ , suggesting that the transition regime from conduction- to convection-dominated flow is broadly between $\mathit{Gr}=300$ and $\mathit{Gr}=2\times 10^{4}$ . The weaker stratification below the neutral buoyancy height, mentioned earlier, is clearly seen in figure 3(c) by comparing the vertical temperature profile in the ambient (at mid-radius, drawn as a dashed grey curve, red online) to the imposed linear temperature profile at the sidewall (drawn as a solid grey line).

Figure 5. Isotherms (a) and azimuthal vorticity contours (b) of the axisymmetric periodic puffing plume state at $\mathit{Gr}=3.5\times 10^{5},A_{r}=2,A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ at four equispaced phases over one puffing period $2{\rm\pi}/{\it\omega}_{0}\approx 3.9\times 10^{4}$ ; there are 20 contour levels with $T\in [-0.5,0.5]$ and ${\it\eta}\in [-10^{5},10^{5}]$ ; solid lines (red) are positive and dashed lines (yellow) are negative. See associated online movies 1 and 2.

4. Axisymmetric puffing plume

By increasing the Grashof number above $10^{5}$ and keeping the simulations axisymmetric, the basic state ceases to be stable, and a periodic solution appears. In terms of dynamical systems theory, we say that the basic state undergoes a Hopf bifurcation. The instability is due to the development of a buoyancy anomaly near the hot spot; this develops into a localized blob of fluid which rises faster than the fluid in the plume in the underlying unstable steady solution. This limit-cycle mode from an axisymmetric instability is very much the same as in the non-stratified ambient localized heating problem (Lopez & Marques Reference Lopez and Marques2013), the so-called puffing plume. The onset of the puffing plume, for the parameters considered here, is at $\mathit{Gr}\approx 2.84\times 10^{5}$ . Figure 5 shows four snapshots over one puffing period at $\mathit{Gr}=3.5\times 10^{5}$ ; the supplementary movies 1 and 2 available online at http://dx.doi.org/10.1017/jfm.2014.628 clearly shows the development of the puffs. For a range of $\mathit{Gr}$ following the Hopf bifurcation, the puffing frequency, ${\it\omega}_{0}$ , grows monotonically with $\mathit{Gr}$ , as does the buoyancy frequency $N$ ( $N\sim \sqrt{\mathit{Gr}}$ ); ${\it\omega}_{0}$ is larger than $N$ ( ${\it\omega}_{0}\sim 1.4N$ ), and so the puffing plume does not drive internal waves. From both the online movies 1 and 2 and figure 5, it is clear that the azimuthal vorticity is localized on the hot spot and in the plume up to about the neutral buoyancy height, as are the radial temperature gradients.

Figure 6. Isotherms (a) and azimuthal vorticity contours (b) of the axisymmetric periodic puffing plume state at $\mathit{Gr}=1\times 10^{6}$ , $A_{r}=2,A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ at four phases over one period $2{\rm\pi}/{\it\omega}\approx 4{\rm\pi}/{\it\omega}_{0}\approx 4.1\times 10^{4}$ ; there are 20 contour levels with $T\in [-0.5,0.5]$ and ${\it\eta}\in [-2\times 10^{5},2\times 10^{5}]$ ; solid lines (red) are positive and dashed lines are negative. See associated online movies 3 and 4.

At $\mathit{Gr}\approx 4.7\times 10^{5}$ , the puffing plume undergoes a period-doubling bifurcation: the blob in the plume develops into a vortex ring whose radius expands while the central plume column remains intact. At the next cycle the remains of the ring are still there, impeding the subsequent blob developing into a ring, and the blob instead travels up the central column which overshoots the neutral buoyancy level higher than in the previous cycle. The next cycle coincides with the previous one, resulting in a period-doubling bifurcation. Figure 6 shows four equispaced snapshots of the period-doubled puffing plume, over one period at $\mathit{Gr}=1\times 10^{6}$ ; the first two snapshots clearly show the formation of the vortex ring, which rises to about half the neutral buoyancy height. The last two snapshots, corresponding to the next puffing cycle, do not have an outer ring, and the central plume rises higher. The movies 3 and 4 available online shows further details of the period-doubled state.

Figure 7. Times series of $E_{0}$ over a time interval of 0.01, taken some time after transients had died down, for various values of $\mathit{Gr}$ as indicated.

Figure 7 shows time series of the global kinetic energy $E_{0}$ after transients had died down, for various values of $\mathit{Gr}$ . Figure 7(a) is for a periodic puffing state at $\mathit{Gr}=3.5\times 10^{5}$ with (primary) frequency ${\it\omega}_{0}$ , where each peak corresponds to a puffing event. Figure 7(b) shows the period-doubled state at $\mathit{Gr}=6\times 10^{5}$ . Each peak corresponds to a puffing event, but the energy of consecutive puffs is different due to the detachment between the outer ring and the central hot column, and so the state shown is periodic, with a (primary) frequency of half the puffing frequency. In figure 7(c) at $\mathit{Gr}=8\times 10^{5}$ the frequencies associated with the central column and outer ring are not in a rational ratio, so the resultant regime is quasi-periodic. These states have a primary frequency close to ${\it\omega}_{0}/2$ and an additional low beating frequency. In figure 7(d) at $\mathit{Gr}=1\times 10^{6}$ they have synchronized again, and the primary frequency is ${\it\omega}_{0}/2$ .

Figure 8. (a) Variation of the primary frequency of the axisymmetric puffing plumes ${\it\omega}$ versus $\mathit{Gr}$ ; the curve is the non-dimensional buoyancy frequency $N$ , the open symbols correspond to limit cycle puffing states and the filled symbols are various puffing states that are generally quasi-periodic, but some have frequency locked to being periodic. The puffing frequency is ${\it\omega}_{0}$ . (b) The same results scaled by $N$ ; the three horizontal lines are at ${\it\omega}_{0}/N=2/\sqrt{2}$ , 1, and $1/\sqrt{2}$ .

The period doubling results in the time-dependent flow having a frequency peak at half the puffing frequency. This new frequency peak is lower than $N$ and internal waves result. Figure 8 shows how the frequency varies with $\mathit{Gr}$ , and compares it to $N$ . For $\mathit{Gr}>4.8\times 10^{5}$ , the flow is quite complicated temporally, becoming quasi-periodic and then synchronizing, then quasi-periodic again, with some very long-period modulations over short intervals in $\mathit{Gr}$ , suggesting that there are resonant dynamics at play. Nevertheless, there is a strong temporal signal such that the associated frequency, ${\it\omega}_{0}/2$ , results in internal waves at approximately $40^{\circ }$ to the vertical. This angle comes from the dispersion relation for internal waves, and is given by $\arccos ({\it\omega}_{0}/2N)$ , although in actuality it is the local buoyancy frequency rather than that corresponding to the imposed sidewall boundary temperature profile that is relevant. From figure 3 we see that these two buoyancy frequencies are quite similar in the region above the neutral buoyancy height. This is consistent with many experimental observations of internal waves emerging from regions with localized instabilities and turbulence into a stratified region having frequencies in a narrow band about the local buoyancy frequency divided by $\sqrt{2}$ (Munroe & Sutherland Reference Munroe and Sutherland2014), and Sutherland & Linden (Reference Sutherland and Linden1998) have shown using a linear theory that internal waves within this band of frequencies are the most efficient in extracting energy from the turbulent region and transporting it through the stratified region. They also suggest that these waves feed back upon the turbulent region and modify its mean properties to the extent that waves in this preferred frequency band are further enhanced. Similar mechanisms seem to be in play in the puffing plume regime.

5. Spontaneous generation of swirl

The puffing plume dynamics described in the previous section were from simulations restricted to the axisymmetric subspace. When the dynamics is not restricted and general three-dimensional perturbations are allowed, the base state BS loses stability at $\mathit{Gr}$ lower than that for the onset of the axisymmetric puffing mode. For the parameter values studied here, instability to three-dimensional flow occurs at $\mathit{Gr}\approx 1.18\times 10^{5}$ .

It is well-known (Crawford & Knobloch Reference Crawford and Knobloch1991; Knobloch Reference Knobloch1996) that breaking $O(2)$ symmetry can result in either standing or rotating waves if the bifurcating eigenvalue is complex (symmetry-breaking Hopf bifurcation), and which one occurs is very much problem dependent. Moreover, due to the reflection symmetry, the rotating wave’s sense of rotation can be positive or negative; both solutions bifurcate simultaneously, and which one is observed depends on the initial conditions. In our problem, the base state becomes unstable and a periodic solution in the form of a rotating wave with azimuthal wavenumber $m=1$ appears. Figure 9 shows the modal energies $E_{0}$ and $E_{1}$ of the solutions obtained up to $\mathit{Gr}=4\times 10^{5}$ . The rotating wave solution branch RW undergoes a number of subsequent bifurcations as $\mathit{Gr}$ is increased, which are described below. We begin by describing the characteristics of the rotating wave state.

Figure 9. Variation of the modal energies (see (2.8)),  $E_{0}$ and $E_{1}$ , with $\mathit{Gr}$ of the various states as indicated.

Figure 10. Variations of (a) precession frequency scaled by $N$ and (b) helicity with $\mathit{Gr}$ of the rotating wave state RW, showing the supercritical character of the Hopf bifurcation (absolute values are shown as RW come as conjugate pairs with opposite senses of rotation).

Figure 10(a) shows the variation of the absolute value of the precession frequency ${\it\omega}_{pr}$ , scaled by $N$ , with $\mathit{Gr}$ . It shows that $|{\it\omega}_{pr}|/N\sim 1/\sqrt{2}$ , and so internal waves are excited by the rotating wave state, RW, and are emitted at approximately $45^{\circ }$ , much like the internal waves in the period-doubled axisymmetric puffing plume. The RW state has non-trivial swirl, as measured by the helicity. Figure 10(b) shows how $\mathit{He}$ grows from zero at the Hopf bifurcation at which RW emerges. Near onset, $|\mathit{He}|\sim \mathit{Gr}\sim N^{2}$ , and since $\mathit{He}$ is a quadratic quantity, the bifurcating velocity perturbation magnitude scales with $\sqrt{\mathit{Gr}}\sim N$ , in agreement with the theory of a supercritical Hopf bifurcation (Kuznetsov Reference Kuznetsov2004).

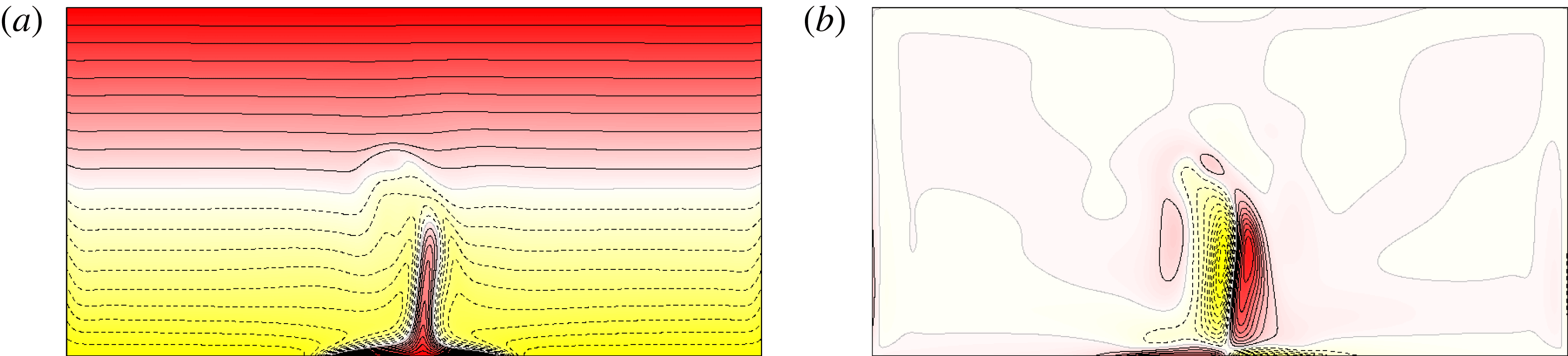
Figure 11. Snapshots of (a) isotherms and (b) azimuthal vorticity contours in a meridional plane, at an instant in time of the rotating wave state RW at $\mathit{Gr}=2\times 10^{5},A_{r}=2,A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ . There are 10 contour levels with $T\in [-0.5,0.5]$ and ${\it\eta}\in [-5\times 10^{4},5\times 10^{4}]$ ; solid lines (red) are positive and dashed lines (yellow) are negative.

Figure 12. (a) Three-dimensional isosurfaces of azimuthal vorticity ${\it\eta}$ , at an instant in time of the rotating wave state RW at $\mathit{Gr}=2\times 10^{5},A_{r}=2,A_{z}=2,A_{T}=1$ and ${\it\sigma}=7$ , and the isosurface levels are at ${\it\eta}=\pm 10^{3}$ . The online movie 5 show the isosurfaces over one precession period $2{\rm\pi}/{\it\omega}_{pr}\approx 5\times 10^{-4}$ . Three-dimensional isosurfaces of vertical vorticity ${\it\xi}$ of the same state, at levels (b) ${\it\xi}=\pm 2000$ and (c) ${\it\xi}=\pm 4000$ .

Figure 11 shows isotherms and contours of azimuthal vorticity in a meridional plane for the RW state at $\mathit{Gr}=2\times 10^{5}$ . It clearly shows that the plume is tilted, and therefore the reflection symmetry is broken. As is well-known from bifurcation theory (Knobloch Reference Knobloch1996), a Hopf bifurcation breaking axisymmetry from an $O(2)$ -symmetric state may result in rotating waves when the reflection symmetry is broken, or standing waves when it is preserved. Figure 12(a) show isosurfaces of azimuthal vorticity ${\it\eta}$ of this solution, indicating that it has azimuthal wavenumber $m=1$ , and the online movie 5 shows that it is a rotating wave: the plume does not change shape, but precesses about the vertical axis at a constant rate ${\it\omega}_{pr}$ , given in figure 10(a). The RW solutions come in pairs, one rotating clockwise and the other rotating counter-clockwise. This symmetry-breaking process is responsible for the spontaneous generation of swirl. Figure 12(b) shows the structure of the plume: the isosurfaces of axial vorticity at ${\it\xi}=\pm 2000$ show that the plume consists of two intertwined vortices with opposite sense of rotation. Both vortices have positive vertical velocity, but opposite ${\it\xi}$ , therefore their local helicities are of opposite sign. Figure 12(c) shows isosurfaces of axial vorticity at higher ${\it\xi}=\pm 4000$ , illustrating that the two vortices are of different strengths. The strongest vortex is the light grey (yellow online) isosurface, corresponding to negative ${\it\xi}$ , and therefore the total helicity of this solution is negative, corresponding to a clockwise precession of the thermal plume, as can be seen in the online movie 5.

Figure 13. Isotherms of MRW at $\mathit{Gr}=2.5\times 10^{5}$ in the inertial (stationary) frame (a) and a precessing frame (b) with frequency ${\it\omega}_{pr}=7435.0$ . There are 10 contour levels with $T\in [-0.5,0.5]$ ; solid lines (red) are positive and dashed lines (yellow) are negative.

6. Discussion and conclusions

This study was motivated by the long-standing puzzle that for many plumes, including some geophysical plumes, swirl is sometimes observed, and yet there is not a generally accepted explanation of where it comes from, particularly for plumes whose scales are such that the Coriolis force is not expected to be a primary factor. For the most part, explanations rely on the focusing and amplification of background rotation or shear near the ground by the updraft from the plume. The important issue is to determine if the swirl arises due to extraneous effects (ambient rotation or ambient shear) or due to intrinsic effects. The only way to determine this is to eliminate external disturbances, and this is done by employing an enclosed geometry. The laboratory experiments of Torrance (Reference Torrance1979) considered a plume in a completely enclosed cylinder driven by a localized hot spot on the bottom boundary. In a parameter regime where the ambient stratification is not too weak or too strong, the onset of swirl in a plume was observed, but no details of the flow nor any explanation of what the swirl was due to were offered. Nevertheless, the completely enclosed experiments suggest that the onset of swirl could be intrinsic to the plume dynamics.

In order to investigate this idea, we have simulated the flow in a stationary fully enclosed cylinder driven by a localized hot spot at the bottom, in a stratified ambient that is maintained by a linearly decreasing fixed temperature up the sidewall. We fix the ratio of the temperature difference between the top and bottom of the sidewall to the temperature difference between the centre of the hot spot and the bottom of the side to be $A_{T}=1$ (this results in the plume’s neutral buoyancy level being at about the cylinder half-height), as well as fixing the geometry and fluid (water), and we explore the dynamics of the plume as the Grashof number $\mathit{Gr}$ is increased. Increasing the Grashof number corresponds to increasing the temperature of the centre of the hot spot relative to the temperature of the bottom of the sidewall, and since $A_{T}=1$ this also means that the buoyancy frequency of the ambient stratification is increased proportionally with $\sqrt{\mathit{Gr}}$ .

When the simulations are restricted to being axisymmetric, the steady plume flow loses stability to a puffing mode via a Hopf bifurcation at $\mathit{Gr}\approx 2.84\times 10^{5}$ . The features of the puffing mode are very similar to those of the puffing mode in an isothermal ambient (Lopez & Marques Reference Lopez and Marques2013), with the one notable difference being that the plume in the stratified ambient does not penetrate all the way to the ceiling. In both the isothermal ambient and the present stratified ambient cases, the steady axisymmetric plume state loses stability to three-dimensional disturbances at $\mathit{Gr}$ significantly lower than the critical $\mathit{Gr}$ for the axisymmetric puffing mode instability. However, the manner in which axisymmetry is broken in the two cases is very different. They both break the invariance to rotations, $R_{{\it\alpha}}$ , but while the plume in an isothermal ambient preserves parity, $K_{{\it\beta}}$ , parity is broken in the stratified ambient case. It is this parity-breaking Hopf bifurcation which results in the swirling plume. Near onset ( $\mathit{Gr}\gtrsim 1.18\times 10^{5}$ ), the swirling plume is a rotating wave possessing non-zero mean helicity, and its precession frequency is approximately $1/\sqrt{2}$ times the buoyancy frequency, and so internal waves are emitted at approximately $45^{\circ }$ . On further increasing $\mathit{Gr}>2.4\times 10^{5}$ , the swirling plume is modulated. The modulation is due to a puff of hot fluid propagating upwards along the tilted swirling plume. We find that the precession frequency is exciting the puffing mode subharmonically at $\mathit{Gr}$ values a little below where the puffing mode sets in in the absence of the swirl; the precession frequency is about half the puffing frequency. As $\mathit{Gr}$ is increased beyond approximately $2.8\times 10^{5}$ , the plume is further modulated by a very low frequency. We show that this results from a global bifurcation and this very low-frequency modulated plume is close to a heteroclinic cycle where the flow slowly drifts from a state resembling the axisymmetric puffing mode to a state resembling the rotating wave swirling plume. In summary, swirl results spontaneously from an intrinsic instability breaking parity symmetry. Subsequent instabilities lead to quite complicated spatio-temporal behaviour. These results provides a new perspective with which to re-visit the question of how do naturally occurring plumes, such as dust devils, acquire their swirl.