INTRODUCTION
The question whether majority rule leads to predictable and stable decisions is of central importance for democratic theory (e.g. Dahl, Reference Dahl1989; Riker, Reference Riker1982). The so-called chaos theorems imply that in case of an empty core outcomes of majority decisions are unrestricted as any alternative might be selected, given the appropriate agenda (McKelvey Reference McKelvey1976; Schofield Reference Schofield1978). Committee experiments are a perfect setting for empirically testing these theoretical implications, and existing studies provide evidence for the attractiveness of the core and the absence of chaos if the core is empty.Footnote 1 These experiments usually employ a static one-shot setting where committees make single binding decisions. However, as I argue below, a dynamic setting might be a more appropriate design for testing the properties of majority rule. Therefore, I present experiments where committees make multiple decisions over time in this study. Compared to previous research, I find a substantially lower attractiveness of the core. In fact, results diverge from the core in the course of the experiment. However, in line with previous research I find no evidence that decisions in a setting with an empty core are characterized by higher majority rule instability.
The design of Fiorina's and Plott's (Reference Fiorina and Plott1978) (in the following FP) committee experiments has become the standard setting for analyzing majority decision making in small groups. In the experiment, five-person committees have to select points from a two-dimensional policy space. Every subject is represented by its ideal point, and payoffs decrease the greater the distance between a subject's ideal point and the outcome chosen by the committee. While the locations of all ideal points are common knowledge, subjects only know their own payoff functions.
FP's experiment is designed as a one-shot game. Hence, committees have to make a single binding decision. Decision making starts from a point at the margin of the policy space. Upon recognition by the experimenter, any committee member can propose an amendment to the current motion, and the committee may discuss and vote on the proposal. If the proposal receives a majority of at least three votes, it becomes the new motion. The amendment process continues until one committee member makes a proposal to conclude the debate. If a majority of the committee members accepts this proposal, the current motion becomes the final binding result of the committee decision. Otherwise, the floor is open to new amendments. Decision making ends with a successful proposal to conclude the debate.
Series 1 of FP's experiment fulfills Plott's (Reference Plott1967) symmetry condition. Hence, assuming rationally acting and egoistically motivated individuals, social choice theory makes an exact point prediction (Player A's ideal-point) for the outcome of the group decisions. Experimental results show that the core is the best prediction among all competing approaches tested by FP. Although committees only rarely choose the predicted point exactly, results cluster closely around the core. Several other studies confirm the predictive power of the core (e.g. Berl et al., Reference Berl, McKelvey, Ordeshook and Winer1976; Isaac and Plott, Reference Isaac, Plott and Ordeshook1978; McKelvey and Ordeshook, Reference McKelvey and Ordeshook1984). Moreover, Wilson (Reference Wilson, Plott and Smith2008) finds convergence towards the core in the course of decision making. Contrary to all earlier studies on committee decision making in two-dimensional policy spaces, committees in Wilson's experiment do not communicate directly face-to-face. Instead, subjects interact via a computer network. This allows Wilson to analyze the complete decision-making process in detail. His results show that every successful amendment moves the current motion on the floor closer to the core in the course of a group decision.
In Series 3 of the experiment, the configuration of ideal points induces an empty core. FP finds hardly any differences comparing behavior in Series 1 and Series 3. Although the variance of chosen points is slightly higher in Series 3 than in Series 1, an empty core is not associated with chaos. Moreover, subjects in Series 3 have no greater difficulties selecting a point than subjects in Series 1.
Although FP's two central findings—the attractiveness of the core and the absence of chaos if the core is empty—seem to be pretty robust (McKelvey and Ordeshook, Reference McKelvey, Ordeshook, Enelow and Hinich1990; Miller, Reference Miller, Druckman, Green, Kuklinski and Lupia2011), some open questions remain. For instance, Wilson's (Reference Wilson, Plott and Smith2008) discovery that the decision-making process converges on the core, yet seldom ends up exactly in the core raises the question whether the convergence process had been concluded by the end of the experiment or whether committees would have reached the core if they had made multiple decisions. This cannot be answered in a one-shot setting. Moreover, the implication of the theorems by McKelvey (Reference McKelvey1976) and Schofield (Reference Schofield1978) that there is no stable committee decision if the core is empty should also be tested in a dynamic setting. If majority rule actually exhibits the theoretically predicted instability, results should cycle through the policy space over time. In the following, I present an experimental design examining these open questions in a setting where committees make multiple decisions over time on the basis of the same configurations of ideal points as in FP's Series 1 and Series 3.
EXPERIMENTAL DESIGN AND PROCEDURES
Committees in my experiment consist of five members and have to choose points in a two-dimensional policy space consisting of 200 by 150 units. I study two treatments. Treatment 1 uses the configuration of ideal points from FP's Series 1 with a core (Player A's ideal point) and Treatment 2 employs the locations of ideal points in FP's Series 3 with an empty core.Footnote 2 Subjects earn tokens during the experiment.Footnote 3 At the end of the experiment, all tokens earned are converted into money. 1,000 tokens yield €1.00.
The experiment is programmed in z-Tree (Fischbacher Reference Fischbacher2007), and subjects interact via a computer network. Hence, there is no communication between subjects besides voting. The game is played over 20 periods. In the first period, a point at the right top margin of the policy space (190|140) serves as the status quo. At the beginning of every period, the computer randomly picks one committee member as the agenda setter of the current period. Before making her decision, the agenda setter can examine all options of the decision space by clicking on the alternatives.Footnote 4 In order to control for the level of information of subjects, the experimental design employs complete information. When the agenda setter clicks on a point in the policy space, she gets to know her own potential payoff for the respective point and the payoffs of all other committee members. She also knows the complete distribution of payoffs for the current status quo point.
The agenda setter has two options. She can either propose a new point which is then put to a vote to the whole committee, or the agenda setter can maintain the current status quo. If the agenda setter maintains the status quo, the status quo point is the result of the current period. However, if the agenda setter makes a proposal, the other committee members decide by majority voting between the proposed point and the status quo.Footnote 5 Committee members also possess complete information. They get to know their own potential payoffs for the proposed point and the status quo as well as the potential payoffs of all other committee members resulting from the proposal and the status quo. Committee members vote simultaneously. Hence, they do not get to know the other members’ voting decisions while still deciding between the proposal and the status quo. The alternative supported by a majority of the committee members is the result of the current period. At the end of a period, subjects receive information about the distribution of votes in the current period (if a vote was necessary), the distribution of payouts in the current period and the cumulative distribution of payouts from all previous periods. Afterwards a new period starts, and the computer again assigns the role of the agenda setter randomly to a committee member. The chosen point from the previous period serves as the status quo of the new period.
Committees make 20 consecutive decisions under the same rules. The experimental design uses partner matching. Hence, the composition of committees remains constant throughout the whole experiment. Moreover, locations of ideal points and payout functions do not change during the course of play.
Procedures
The experiments took place in December 2012 in the Cologne Laboratory for Economic Research at the University of Cologne. Participants were recruited using ORSEE (Greiner Reference Greiner, Kremer and Macho2004) from a subject pool comprising about 3,000 subjects. Overall, 120 subjects participated in the experiment. In both treatments, 60 subjects formed 12 committees.Footnote 6 At the beginning of the experiment, subjects were individually assigned to cubicles in order to preclude uncontrolled interactions among participants. Then, subjects received written instructions explaining the task in context-free language.Footnote 7 Each session took about 90 minutes. Subjects were paid privately in cash directly after the experiment. On average, they earned €15.44.
EXPERIMENTAL RESULTS
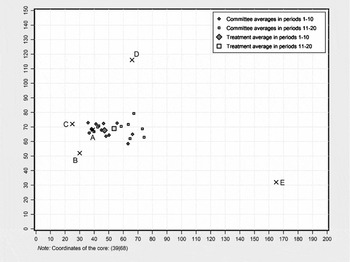
The experimental results from Treatment 1 confirm the finding from prior experiments that committees rarely choose the core alternative exactly. 21.25% (51 out of 240) of the decisions resulted in the selection of the core. Only four of the twelve committees chose the core in at least one period of the experiment. While three committees stuck to the core after its first selection until the end of the experiment, one committee left it again after having selected it for six periods. The low selection rate of the core is due to the fact that it was rarely proposed. Only six agenda setters proposed the core during the experiment, and two times the committee voted against the proposal.Footnote 8 Deviations from the core are not randomly distributed around the core. The average outcome over all twenty periods is (50.3|68.3) and differs significantly from the core (39|68) along the x-axis.Footnote 9 Thus, committees chose points systematically to the right of the predicted equilibrium.
When the core is not empty, all feasible winning alternatives lie closer to the core than the current status quo. Thus theoretically, outcomes should converge to the core in the course of the experiment. However, in 27 decisions committees chose points located further from the core than the status quo. Figure 1 shows the development of chosen points over time. In the first ten periods of the experiment the average outcome in Treatment 1 is (47.1|67.7). The average outcome in the second half is (53.6|68.9). Hence, there is no evidence of results converging on the core when committees make multiple decisions over time. In fact, contrary to the theoretical expectation, results significantly diverged from the predicted equilibrium along the x-axis in the course of the experiment.Footnote 10
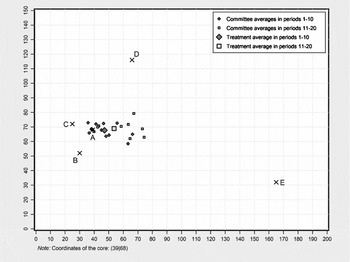
Figure 1 10-period Average Committee Decisions in Treatment 1.
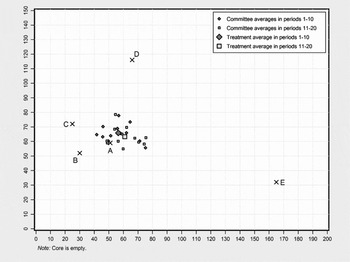
In Treatment 2, the mean outcome over all 20 periods is (58.7|64.5). Figure 2 shows that there is also a slight movement of results to the right during the experiment. In the first half, the average outcome is (56.5|65.8). In the second half it is (61.0|63.2). The difference is significant on the x-axis.Footnote 11
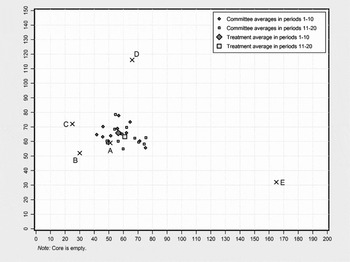
Figure 2 10-period Average Committee Decisions in Treatment 2.
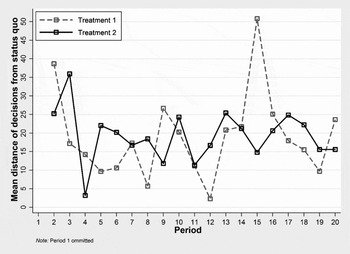
In order to compare the stability of committee decisions over time in the two treatments, I compute the difference between the chosen point and the status quo for each committee in a period. Figure 3 shows the treatment averages per period. As the two curves intersect repeatedly, it is obvious that there is no significant difference between the two treatments.Footnote 12 Hence, there is no evidence that an empty core reduces the stability of decision making. Moreover, committees in Treatment 2 did not have greater difficulties reaching a decision than committees in Treatment 1. On average, decision making per period in Treatment 1 took 87 seconds while an average decision in Treatment 2 took 83 seconds.
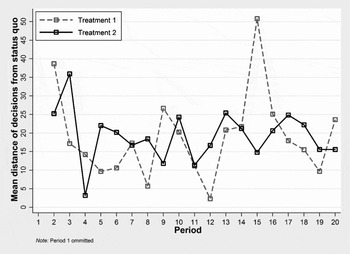
Figure 3 Variation of Outcomes Over Time.
Results from Treatment 2 corroborate prior findings that an empty core does not cause unstable majority decisions. For instance, Bianco et al. (Reference Bianco, Lynch, Miller and Sened2006) reexamine the existing experimental evidence on committee decision making with an empty core and find that 94% of the outcomes lie in the uncovered set. In Treatment 2, 113 out of all 240 committee decisions (47.1%) lie inside the uncovered set, and 127 decisions (52.9%) result in points outside the uncovered set.Footnote 13 As the uncovered set comprises only 13.8% of the Pareto set, it performs significantly better than expected if committees chose points randomly from the Pareto set.Footnote 14
DISCUSSION AND CONCLUSION
Studying committee decision making in a dynamic setting over time provides new insights into the workings of majority rule. Especially the finding that results diverge from the core during the experiment in Treatment 1 deserves further attention. A possible explanation for this pattern is the influence of social preferences. Committee experiments with a discrete set of alternatives have produced ample evidence that subjects take distributional consequences of their decisions into account (e.g. Eavey and Miller, Reference Eavey and Miller1984; Miller and Oppenheimer, Reference Miller and Oppenheimer1982; Sauermann and Kaiser, Reference Sauermann and Kaiser2010). Possibly, spatial committee decisions follow similar patterns.
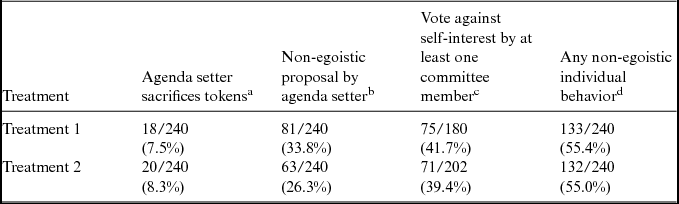
Individual decisions of agenda setters provide first evidence for the influence of distributional concerns of committee members. The possible effect of social preferences is most obvious when an agenda setter makes a proposal offering her less tokens than the status quo. As column 2 of Table 1 shows, this happened 18 times in Treatment 1 and 20 times in Treatment 2. Agenda setters sacrificed on average 312 points in Treatment 1 and 352 points in Treatment 2 by making proposals leaving them worse-off than the status quo. However, there might be more instances in which agenda setters relinquished own material payoffs. Before submitting a decision, agenda setters can examine the payoff consequences of points in the policy space by clicking on them. Conducting the experiment via a computer network allows me to track these examined points for all agenda setter decisions. Column 3 of Table 1 lists the number of agenda setter decisions where the agenda setter analyzed points in the policy space offering her more tokens than the finally submitted proposal and offering more tokens than the current status quo to at least two additional committee members. In both treatments, agenda setters frequently proposed points despite being aware of points preferred by the majority offering higher individual payouts to themselves.
Table 1 Non-egoistic Behavior of Agenda Setters and Voters
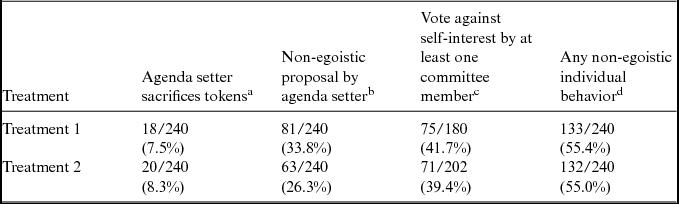
aAgenda setter makes a proposal offering her less tokens than the current status quo.
bBefore submitting her decision in a period, the agenda setter has clicked on points in the policy space which offer her more tokens than the later submitted proposal and which offer more tokens than the current status quo to at least two additional committee members.
cAt least one committee member votes for an alternative offering her less tokens than the other alternative.
dAgenda setter sacrifices tokens OR Non-egoisitic proposal OR Non-egoistic vote.
In the voting stage committee members have to choose between the proposal and the current status quo. As payoff consequences for both options are common knowledge, a vote in favor of the alternative offering less tokens is most likely driven by social preferences. Column 4 of Table 1 shows that in about 40% of all decisions where committees had to vote, at least one committee member voted against her self-interest. Finally, the last column of Table 1 displays the number of committee decisions per treatment in which at least one committee member—i.e. the agenda setter or at least one voter—displayed behavior against her immediate self-interest. In both treatments, non-egoistic individual behavior occurs in about 55% of all decisions.
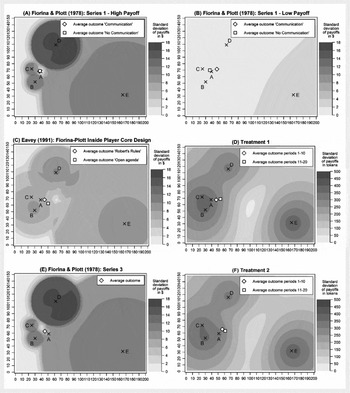
A comparison of the fairness properties of the policy space and selected outcomes of the current experiment to previous experimental studies on majority rule in Figure 4 offers further indications for the influence of social preferences.Footnote 15 The region closely around the core in FP's high payout condition (cf. Panel A) is the only region in the Pareto set providing a relatively equal distribution of payouts. In accordance with the idea that subjects value distributional fairness, average committee decisions are very close to the core. In the low payoff condition of FP's experiment (Panel B), almost all alternatives of the policy space offer a relatively equal distribution of payouts. The lack of strong incentives in that experimental condition is a likely explanation for the higher variance of final outcomes compared to the high payouts condition. Eavey (Reference Eavey1991) uses the same ideal-point configuration as FP's Series 1, yet employs different payoff functions (cf. Panel C). Just like the core in Treatment 1 (Panel D), the core in Eavey's experiment is characterized by high inequality, whereas the area to the right of the core provides a more equal distribution of payouts. In both experiments, results differ from the core and committees choose more equally distributed alternatives.
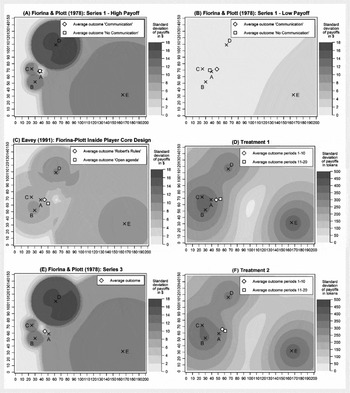
Figure 4 Variation of Outcomes Over Time.
Panels E and F of Figure 4 show that experiments with an empty core seem to be influenced by distributional concerns as well. In FP's Series 3, the area to the top left of Player A offers the most equally distributed payoffs, and average outcomes are located exactly there. In Treatment 2, the region to the right of Player A offers the most equally distributed alternatives, and average outcomes track the shift of the fair alternatives.
Overall, the findings presented in this study suggest that social preferences, i.e. preferences for a fair distribution of payouts, deserve more attention as a possible motivational factor in committee decisions. However, there are also plausible alternative explanations. For example, the agenda process employed in this study is very different from previous committee experiments and might be responsible for the behavioral differences compared to previous studies.
The experimental literature on multilateral bargaining suggests that the lack of communication might explain the other-regarding behavior observed in this study. Experiments frequently find systematic deviations from the predictions of the Baron and Ferejohn (Reference Baron and Ferejohn1989) legislative bargaining model (e.g. Diermeier and Morton, Reference Diermeier, Morton, Austen-Smith and Duggan2005; Fréchette et al., Reference Fréchette, Kagel and Lehrer2003). In particular, proposers usually gain substantially lower amounts than theoretically predicted. Preferences for a fair distribution could explain this pattern. In a recent experiment, however, Agranov and Tergiman (Reference Agranov and Tergiman2014) show that proposers gain significantly more when communication within the group is allowed. This finding suggests that proposers do not offer more than theoretically predicted because they want to be fair. Rather, proposers make equal proposals because other group members cannot communicate their willingness to accept lower proposals. Communication greatly reduces proposers’ uncertainty and allows them to make proposals that are more selfish. Hence, voters’ inability to communicate their willingness to accept certain distributions could provide an alternative explanation for the experimental findings presented above. Differentiating between the possible causal mechanisms calls for further experiments on committee decision making in the future.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/XPS.2015.16.