Peace is not made with friends, peace is made with
enemies.
Making peace is risky business. At the international level, ending
or reducing conflict often requires governments to take risky actions
that leave them vulnerable to exploitation, such as making territorial
concessions, cutting armaments, or opening commercial and financial
relations. These risks are compounded by uncertainty and distrust over
the other side's intentions: Are they committed to peaceful relations
or do they seek a unilateral advantage? At the domestic level, there can
be serious disagreements over the desirability of risking peace,
disagreements that manifest themselves in political conflict between
“hawkish” and “dovish” factions. As a result,
what happens between states can affect the personal and political
fortunes of actors within them. Particularly in democratic political
systems, efforts at cooperation take place under the gaze of voters who
must decide which leaders they want to guide their country's
foreign policy. Governments that attempt to make peace risk being
undermined by political opponents seeking to capitalize on voters'
fear and distrust.1
Given these risks, under what conditions will a government attempt
peace with a distrusted rival? Under what conditions will those
attempts be successful in bringing about robust cooperation? What are
the domestic political costs and benefits of trying to initiate
cooperation? Such questions are vitally important to our understanding
of international conflict and its resolution. As the research into
“enduring rivalries” notes, the vast majority of
militarized conflicts take place in the context of long-running
adversarial relationships: for example, France and Germany, India and
Pakistan, Greece and Turkey, Britain and Russia, Israel and its Arab
neighbors, the United States and any number of rivals such as the
Soviet Union, China, Cuba, North Korea, and Iran.2
Interest in this problem has given rise in recent years to studies,
mostly empirical, that explore the timing of rivalry termination,
3 when adversaries make concessions in
long-running territorial disputes,
4 See
Huth and Allee 2002; and Chiozza and Choi
2003.
and whether repeated conflicts
can be tamed by bilateral norms.
5 Nevertheless, this area of inquiry remains undertheorized,
particularly in connecting the international and domestic sides of the
problem.6
As one study notes,
“Rapprochement … has attracted much less attention than war
and peace.”
7 Many international conflict
models assume a peaceful status quo and then examine governments'
incentives to threaten or use military force to change that status
quo.
8 See, for example, Bueno de Mesquita
and Lalman 1992; and Powell 1999.
Less systematic attention has been
paid to the opposite process: starting from a status quo of conflict
and distrust and considering the incentives to initiate peaceful, or at
least more cooperative, relations.
9 Exceptions include Ward 1989 and
Kydd 2000. I note that there is a growing
literature on bargaining to end wars; see, for example, Wagner 2000; Smith and Stam 2003; and Slantchev 2003.
The model developed here focuses on the problems of cooperation under
distrust, rather than the problem of bargaining during costly
conflict.
Likewise, the vast literature on cooperation that
grew out of the analysis of repeated games focuses on whether or not
cooperative equilibria exist, but it does not explicitly model the
transition from conflict to cooperation.
10 See, for example, Axelrod 1984.
This article develops a two-level game that examines a
government's decision to risk cooperation, taking into account the
strategic interdependence of the international and domestic levels. At
the international level, states must decide whether or not to agree to
some mutually accommodating deal. In each of two periods, one state
decides either to cooperate or defect, and then the other chooses to
cooperate or defect in response.11
The
international component of the game is similar to that in Kydd 2000.
Each state leader is uncertain about
the preferences of the other. Possible types include hard-liners, who
have strong incentives to exploit cooperation by the other side;
moderates, who will reciprocate both cooperation and defection; and
soft-liners, who would rather cooperate on exploitative terms than risk
mutual defection. The interaction at this level highlights a number of
problems previously identified in the literature on cooperation under
uncertainty.
12 A confrontational policy
can signal toughness and may deter the adversary from thinking the state
can be exploited; on the other hand, such a policy may also lead to an
unwanted conflict spiral. A cooperative strategy can open the door to
peaceful relations, but it also leaves the state vulnerable to
exploitation by the other side and may tempt the adversary to defect in
the future as well.
The domestic component of the game captures electoral competition
between two parties within one of the states. The international
interaction takes place in the view of an electorate that must try to
decide which of two parties it wants to run the state's foreign
policy. One party is known to have more hawkish preferences, on
average, than the other, although the exact preferences of any
particular government are uncertain and depend on whether the party is
controlled by moderate or extremist factions. The strategy of the
incumbent and the foreign state's response give voters a chance to
learn about the preferences of both the current government and the
adversary. I assume that the median voter is moderate, meaning that the
voter is dogmatically neither soft- nor hard-line. Rather, the voter
would be willing to cooperate with the rival state if the voter trusted
it to respond in kind—a trust that is initially lacking but may
be acquired over the course of the game. Given this assumption, the
electorate wants a government that is neither so dovish that it will
not defend the national interest if challenged nor so hawkish that it
will create unnecessary conflict.13
Thus in deciding whether or not to attempt
cooperation, governments must worry not only about how the foreign
adversary will respond, but also on how voters will react to their
decisions.
The model generates a number of predictions about the conditions that
lead to cooperation and conflict at the international level and the
domestic political repercussions of the possible international
outcomes. For the purposes of this article, I focus on the different
incentives that leaders of hawkish and dovish parties have to initiate
cooperation under conditions of high distrust. Are hawks or doves more
likely to initiate cooperation with a distrusted adversary? How does
the foreign state's response vary depending on which party is in
power? Are hawks or doves better at eliciting long-term cooperation? In
other words: do doves deliver the olive branch, or does it take a
“Nixon to go to China”?
I derive two main results. First, when trust is low but the costs
from continued conflict are high, the type of government most likely to
initiate cooperation is one with a hawkish reputation but moderate
preferences. Second, while leaders from dovish parties can be better at
promoting mutual cooperation in the short term, cooperation initiated
by a hawkish leader is more robust to future shocks in the relationship
and thus is more likely to be longer lasting. Hence, the model suggests
that hawks enjoy a number of political and strategic advantages in
trying to make peace. While it may not require a Nixon to go to China,
it certainty helps to have one. That said, the model also shows that
hawks may not always want to take advantage of their superior ability
to make peace. If the hawkish party is dominated by hard-liners or if
the costs of continued conflict are low, then hawks may choose to
perpetuate an international rivalry rather than risk peacemaking. The
model specifies conditions under which hawks' incentives to risk
peace align with their political and strategic advantages in doing
so.
In developing these results, I depart from and extend the
conventional argument for why hawks can be better peacemakers than
doves. This story, formalized most prominently by Cukierman and
Tommasi, hinges on the leader's credibility with his domestic
electorate.14
Cukierman and Tommasi 1998; see also Cowen and Sutter 1998.
If voters are unsure whether peace
is in the nation's interests, they are more likely to approve of a
deal endorsed by a hawk than one endorsed by a dove. After all, when
President Richard Nixon said that peace with China was in U.S.
interests, this was more credible than if the message had come from a
leader with less obvious anticommunist credentials.
15 This logic is a natural extension of Calvert's
argument about the value of biased information sources; see Calvert
1985.
While probably correct in some measure, this conventional wisdom is
incomplete in at least two respects. First, this argument says little
about the incentives of the government to take the risky action of
initiating cooperation. Even if hawks are better at selling cooperation
to their electorates, when do they have the incentive to even try?16
Cukierman and Tommasi generate an electoral
incentive for hawks to promote cooperation by assuming that candidates
are committed to carrying out their proposals. Hence, a hawk that
proposes peace becomes desirable to voters by convincing them that a
more accommodative policy is in their interests and, at the same time,
committing to pursue such a policy after the election. Without this
exogenous commitment mechanism, voters might be inclined to elect a
dove after learning from the hawk that peace is a good idea, weakening
the latter's incentive ever to make such a proposal; see Cukierman
and Tommasi 1998. The model in this article
assumes that politicians cannot precommit to future actions.
Are hawks or doves more likely to try to initiate cooperation? Second,
by focusing solely on the leader's credibility with the domestic
electorate, this story ignores a very important actor in this
interaction: the foreign state. As the literature on two-level games
suggests, choices at the international and domestic levels are
strategically interdependent.
17 See,
especially, Putnam 1988.
Hence, it
makes little sense to think of the interaction between leaders and
voters in isolation from the interaction between states. How does the
hawkishness or dovishness of the leader affect the way a foreign state
responds to a cooperative gesture?
The model developed in this article fills these gaps by considering
not only the electorate's response, but also the leader's
incentives to initiate cooperation and the foreign state's
incentives in responding. Which kind of government is most likely to
initiate cooperation depends in part on the cost of continued conflict.
When the payoff from mutual defection is relatively tolerable, only a
soft-line dove will initiate cooperation. When the costs of mutual
defection become large, however, cooperation is most likely to be
initiated by a moderate hawk. Moderate hawks are likely to test the
waters of cooperation in large part because it is electorally safer for
them to do so. The model shows that the costs and benefits of risking
peace fall asymmetrically on hawkish and dovish governments. When
parties have different reputations, the same policy—for example,
cooperation—leads voters to make different inferences about the
preferences that prevail in that party. A dovish government that
cooperates is considered to be extreme, while a hawkish government that
cooperates is believed to be moderate. As a result, initiating
cooperation can be an electoral boon for a hawk but electoral suicide
for a dove. This difference derives from the fact that moderates in
each party have to pursue different strategies to signal their type.
Doves have to guard against being seen as soft-liners, while hawks have
to guard against being seen as hard-liners. Moderates of each party
consequently reveal themselves in different ways: doves by defecting,
hawks by cooperating.18
In a related
context, Nincic refers to this phenomenon as the “politics of
opposites”; see Nincic 1988.
Hence, a moderate hawk is the most likely type to initiate
cooperation.
I then show that cooperation initiated by hawks is more likely to
endure than is cooperation initiated by doves. This result stems from
the foreign state's incentives in responding to cooperative
gestures from the two kinds of parties. In brief, cooperation is
tempting when coming from a dove but reassuring when coming from a
hawk. Since a dove that cooperates reveals itself to be exploitable,
hard-liners in the foreign state have some incentive to keep such
leaders in power. Consequently, they may reciprocate cooperation by a
dove in the short term, with the hope of exploiting the dove down the
line. As a result, a cooperative gesture by a dove can elicit
cooperation in the short run, but such cooperation need not endure into
the future—as hard-liners who initially cooperated only for
tactical reasons later reveal their true type. The same incentive does
not exist when a hawk initiates cooperation. A hawk who cooperates
reveals itself to be moderate, which means that it can be trusted to
reciprocate cooperation but it cannot be exploited. The result, I show,
is that a cooperative gesture by a hawk more faithfully reveals whether
or not the foreign state has moderate preferences, thereby laying the
groundwork for a stable cooperative relationship, if indeed such a
relationship is possible.
This article proceeds as follows. The first section lays out the main
assumptions of the model. The second and third sections sketch the main
features of the equilibria that exist when trust between the states is
low. While formal details of the solution are in the Appendix, these
sections highlight the incentives actors have in this strategic
setting, and particularly the choices that they face in initiating or
responding to a cooperative gesture. The fourth section then directly
compares the equilibrium strategies and outcomes for hawkish and dovish
governments, focusing particularly on which government is most likely
to initiate cooperation and on the prospects that cooperation will
endure. The final section offers concluding remarks and discusses the
model's empirical implications.
The Model
Actors and Sequence of Moves
The model captures interactions on both the international and
domestic levels. At the international level, the game is similar to
that developed by Kydd.19
There are two states, A and B, which
interact over two periods. In each period, one state decides whether to
cooperate (
c) or defect (
d); and then the other
state, after observing the first one's choice, decides whether to
cooperate or defect in return. In period 1, state A moves first, and in
period 2, state B moves first. Because the risk of exploitation falls
mainly on the state that moves first, this alternating structure means
that both states get a turn being exposed to that risk. The uncertainty
is greater for state A, because it does not have the benefit of
observing one round of play before its move.
To capture the domestic component of the game, I assume that state A
is composed of three actors: an electorate and two political parties,
the Hawks and the Doves. At the start of the game, one of these parties
is in government and the other is in opposition. In the first period,
the governing party determines whether A cooperates or defects. After
observing B's response, but before the second period begins, the
electorate decides either to retain the incumbent or to replace it with
a leader from the opposition party. The party that wins the election
controls the state's foreign policy in period 2. State B observes
the outcome of the election before making its decision in that
period.
Outcomes and Payoffs
In each period, there are four possible outcomes at the international
level: mutual cooperation (cc), mutual defection
(dd), unilateral defection by A (dc), and unilateral
defection by B (cd). The international payoffs associated with
each outcome are as shown in Figure 1. I
assume that r > t > w > 0. Hence,
if α and β were zero, the actors would have the payoff
orderings of the familiar Stag Hunt game—that is, each would
prefer to cooperate if the other cooperates and to defect if the other
defects. In addition, I assume here that cooperation is relatively
risky, in the sense that the spread between the payoffs that can be
obtained from cooperating (r or 0) is large relative to the
spread between the payoffs that can be obtained from defecting
(t or w).20
In
particular, I assume that r > 2*(t −
w). This assumption is not particularly strong and is made
largely for convenience. The preference ordering alone ensures that
r > t − w. As t −
w approaches r, the difference between cooperation
and defection vanishes, as both strategies yield the same payoff
regardless of the other side's response. Hence, assuming that
r > 2*(t − w) ensures that the
difference between cooperation and defection is sufficiently
meaningful.
International outcomes and their payoffs
The parameters α and β index how hawkish the actors are, with
higher values indicating a greater willingness to engage in
noncooperative or conflictual policies. The values of these parameters
determine the actors' preference orderings over the possible
outcomes. Different values of α, for example, induce five different
preference orderings for actor A:
- Pacifist. When α < −t, then A's
ordering is cc > cd > dc >
dd, and A prefers any outcome in which it cooperates to an
outcome in which it defects.
- Soft-liner. When −t ≤ α <
−w, then A's ordering is cc >
dc > cd > dd. A soft-liner would
rather cooperate under unfavorable terms (cd) than to
experience mutual conflict (dd).
- Moderate. When −w ≤ α <
r − t, then A's ordering is cc
> dc > dd > cd, which are the Stag
Hunt preferences just described.
- Hard-liner. When r − t ≤ α
< r − w , then A's ordering is
dc > cc > dd > cd. In this
case, A prefers unilateral defection to mutual cooperation, but still
prefers mutual cooperation to mutual defection. This ordering of
outcomes is the same as in the prisoner's dilemma.
- Warmonger. When α ≥ r − w,
then A's ordering is dc > dd > cc
> cd. A prefers any outcome in which it defects over any
outcome in which it cooperates.
One can similarly identify five kinds of state B depending on the
value of β.
As with any game-theoretic model, this one is silent about why actors
have different preferences over international outcomes; rather, it
takes preferences as given and explores the strategic implications.
Nevertheless, it is easy to see how such heterogeneity can arise.
Actors can have different assessments of the state's national
interests or identity, different views about the utility and
desirability of using force, different costs and benefits from
conflict, or different attitudes toward risk. In some cases, hard-line
and warmonger preferences arise from an ideological antipathy toward
the adversary: for example, anticommunism in the United States, Hindu
nationalism in India, and militant Islam in Pakistan and some Arab
states. In other cases, hard-line preferences can be rooted in the
material interests of those who might stand to lose from a peace deal,
such as Cuban exiles in the United States or Israeli settlers in the
West Bank. Soft-line or pacifist types might arise from an ideological
aversion to confrontation and militarism or in constituencies that bear
the costs of continued conflict. For example, groups that benefit from
trade with an adversary might be willing to cooperate on exploitative
terms if continued conflict would jeopardize that trade.21
See, for example, Papayoanou 1997.
It is also quite likely that the
influence of third countries can induce softer preferences in the
bilateral relationship being modeled. In the 1970s, for example, the
New Democracy party in Greece was open to the charge of being overly
accommodating to Turkey because of its pro-Western orientation at a
time when the Western allies were pushing for Greek concessions to end
the rivalry.
22 And if Nixon had moderate preferences
with respect to China in the early 1970s, this was in large part
because of his recognition that rapprochement with China could help the
United States in its conflict with the Soviet Union.
Whatever their type, all actors value the international outcome in
each period.23
I assume that there is no
discounting of future payoffs. This assumption simplifies the solution
of the model and focuses attention on how current decisions are shaped
by their future consequences.
Hence, the leader, the
opposition, and the voters in state A all get a payoff from the
international interaction that is determined by their specific values
of α. Let α
H, α
D,
and α
V denote the hawkishness of the Hawk party
leader, the Dove party leader, and the pivotal voter, respectively. In
addition, politicians value holding office. In particular, assume that
the leader who holds office in each period receives an additional
benefit,
V > 0.
Because members of different parties tend to have different policy
preferences, the party labels inform voters and foreign decision makers
about the likely preferences of the incumbent and opposition
leader.24
See, for example, Kiewiet and
McCubbins 1991; Cox and McCubbins 1993; and Aldrich 1995.
I assume that the Hawk party is
identifiably more hawkish than the Dove party, in the sense that a
leader affiliated with the Hawks is likely to have higher payoffs from
confrontational outcomes than does a leader affiliated with the Doves.
Because party cleavages rarely form solely or even primarily over
foreign policy issues, however, the party labels do not perfectly
predict preferences on this dimension; rather, they suggest tendencies.
Thus while Hawks tend to be more hawkish than Doves, the distributions
of foreign policy preferences within the two parties overlap: there can
be relatively dovish Hawks and relatively hawkish Doves.
In particular, I assume that each party has moderate and extremist
factions. The Hawk party is composed of moderates, for whom
αH = 0, and extremists, for whom
αH = αH* >
r − t. Notice that the extremist Hawks can be
either hard-liners or warmongers, or some mix of the two; none of the
results depend on how extreme this faction is. As a short-hand,
however, I will generally refer to the extremist Hawks as hard-liners.
Similarly, the Dove party is composed of moderates, for whom,
αD = 0, and extremists, for whom
αD = αD* <
−w. Again, one needs not specify whether the extremist
Doves are soft-liners or pacifists or both, though I will generally use
the term soft-liner as a short-hand to refer to this faction.25
These assumptions do not rule out the
existence of other preference types within each party, for example,
hard-liners or warmongers in the Dove party. I simply assume that these
preferences cannot be dominant in that party.
The actual
preferences of a Hawk or Dove government depend on which faction in the
party calls the shots, which I take to be a key source of uncertainty
in the model, as specified below.
The electorate in state A consists of numerous individuals with
potentially heterogeneous preferences covering the entire spectrum. I
show below that standard median voter results will hold in this
context, which means that one needs only concentrate on the preferences
of the median or pivotal voter. Here, I assume that the pivotal voter
is a moderate, with αV = 0.26
There is no loss in generality in fixing this parameter to
zero.
While this assumption need not always be true, this is
the most interesting assumption from a strategic perspective, because
it means that the median voter does not have a natural affinity for one
party or the other. As a result, the electoral outcome is maximally
dependent on the actors' choices. Assuming that the median voter
is moderate is not the same as asserting that the median voter always
prefers to cooperate. A moderate prefers to cooperate only if it
expects the other side will as well. Hence, whether a moderate prefers
cooperation or defection depends strongly on its beliefs about the
rival. More extreme types, by contrast, tend to prefer one strategy or
the other regardless of the other state's expected response. The
best indicator of moderation, then, is a willingness to revise policy
preferences—in either a cooperative or conflictual
direction—in response to changing beliefs about the adversary.
Studies of public opinion in a variety of conflicts—involving the
United States,
27 See Page and Shapiro
1992; Peffley and Hurwitz 1992; and Nincic 1988.
Israel,
28 and India
29—show that aggregate opinion, at least,
tends to move in this way. That said, most of the core results
developed here would continue to hold if the median voter were assumed
to be hard-line rather than moderate.
30 Proofs are available from the author.
Information and Beliefs
All actors are incompletely informed about the preferences of other
actors in the game, with the exception of the pivotal voter, who is
known to be moderate. Let pH and
pD denote the prior probability that the
Hawk and Dove governments, respectively, are controlled by their
moderate factions. With the complementary probabilities, the parties
are controlled by their extremist factions. These assumptions imply
that there is some chance the party leaders have the same preferences
as the pivotal voter, but there is also some chance that they are more
extreme, in either the hawkish or dovish direction.31
Though the two-type model is simple, it can capture a
variety of party systems, including highly polarized systems in which
both parties are likely to be extremist
(pD, pH both
low), moderate systems (pD,
pH both high), “militant”
systems in which the parties tend in the hawkish direction
(pH low, pD
high), and “pacifist” systems in which the parties tend in
the dovish direction (pH high,
pD low). While equilibrium behavior varies
in its particulars depending on the actual values of these parameters,
the general results discussed here hold for all combinations
(pD, pH) such
that 0 < pD < 1 and 0 <
pH < 1.
The uncertainty
surrounds not only the specific party leader's personal views, but
also the relative strength of the factions within the party, the
leader's need to cater to those factions, and so on. This
interpretation takes the focus away from just the preferences of
individual leaders, and puts it as well on the dynamics of intraparty
politics. For example, even if one believes that the Hawk leader is
personally a moderate, there may be uncertainty as to whether he can
act on those preferences if the hard-line faction in the party is too
strong.
32 By fixing the probabilities
with which different factions control the parties, I have made
intraparty politics exogenous to the game. This is an assumption that I
hope to relax in future versions of the model.
In the case of state B, I assume that the government is either
moderate, in which case β = 0, or hard-line, in which case β =
β* with r − w > β* > r
− t. This assumption captures the distrust that actors
in A have about B's intentions. There is some possibility that B
is moderate, in which case mutually beneficial cooperation is possible,
but there is also some chance that B is hard-line and will exploit
cooperation when given the chance. As before, it is useful to interpret
this assumption as deriving from factional politics within B—that
is, B contains both moderates and hard-liners, and that A's
uncertainty is over which faction actually calls the shots. Let
q denote the prior probability that state B is moderate.33
This prior probability is shared by all
actors in state A. It would be interesting to extend the model to
permit heterogeneous prior beliefs about B's type.
This
probability roughly corresponds to how much A initially trusts B.
34 Equating trust with a prior belief about
preferences is consistent with the usage in Kydd
forthcoming, who has a nice justification for this treatment of
the term.
When
q is low, actors in A think it quite
likely that B is controlled by hard-liners and hence is not trustworthy.
Because I am interested in situations involving high distrust, the
discussion in this article focuses on the equilibria that exist when
q is low.
The Incentive to Appear Moderate:
Equilibrium Behavior the Second Period
The main intuition that emerges from equilibrium play in the second
period is that governments in state A, whether Hawk or Dove, have
strong incentives to convince both voters and the foreign state that
they have moderate preferences. At the international level, generating
a posterior belief that one is moderate is helpful for eliciting
cooperation from state B. After all, a moderate will not exploit
cooperation, nor can it be exploited. Hence, if state B is convinced
that it is facing a moderate government, it will cooperate regardless
of whether it has moderate or hard-line preferences. At the domestic
level, convincing voters that one is moderate is also useful for
getting reelected. The median voter prefers moderate leaders, not
simply because the voter is moderate, but also because governments that
are known to be moderate elicit cooperation from the adversary, and
they reciprocate in kind, hence giving voters their best possible
outcome.35
The fact that the second
period generates this simple intuition may help counter skepticism that
the results in this article are driven by a rather restrictive game
structure—particularly, the assumptions that there are only two
periods and the states alternate moving first. While this structure is
not necessarily realistic, it does induce realistic incentives on the
actors' first-period choices.
At the very last node of the game, the government in A must decide
how to respond to B's second-period strategy. This decision is
quite straightforward and depends only on the current government's
type. If A is a soft-liner, then it will cooperate regardless of what B
did. If A is a hard-liner or warmonger, then it will defect regardless
of what B did. If A is moderate, then it will reciprocate whatever B
did: cooperating in response to cooperation, and defecting in response
to defection. Notice that this means that a Dove will always
reciprocate cooperation in the second period and may or may not defect
in response to defection; a Hawk will always reciprocate defection and
may or may not reciprocate cooperation.
Now consider B's strategy. Informally, both types of B want to
cooperate if they are sufficiently convinced that the government in A
is moderate. This is because even a hard-liner prefers mutual
cooperation to mutual defection, and a moderate will respond to either
strategy in kind. If B is sufficiently convinced that A is hard-line,
then both types of B will defect. If B thinks that the government in A
is soft-line, then a moderate B will want to cooperate, while a
hard-line B will be tempted to defect.
Formally, consider first the case in which the Dove is in power in
the second period. Let
pDh denote the
probability that the Dove is a moderate given the history of the game
to this point. If the Dove was in office in the first period, then
pDh is a posterior
belief, updated based on what the Dove did in the earlier period; if
the Hawk was in office in the first period, then
pDh =
pD, because there is no history on which
to update the prior belief about the Dove. Because B knows that a Dove
is certain to reciprocate cooperation,
If B defects, then with probability
pDh, the Dove is a
moderate and will defect, and with the complementary probability the
Dove is an extremist and will cooperate, allowing itself to be
exploited. Thus,
Comparing these equations, one finds that B will cooperate if
Because
,
a moderate B, for whom β = 0, will always cooperate when a Dove is
in power. A hard-line B will cooperate with a Dove if and only if
.
Notice that
is increasing in the posterior belief that the Dove is a moderate,
pDh. This means that
an increase in the probability that the Dove is moderate increases the
range of conditions under which a hard-line B will cooperate.
Similar calculations show that, if a Hawk is in power in the second
period, then B will cooperate if
where pHh is defined
analogously to pDh.
This means that a moderate B will cooperate with a Hawk if
,
and a hard-line B will cooperate with a Hawk if
.
Once again, because
is increasing in pHh, a
higher posterior probability that the Hawk is moderate makes these
conditions easier to meet and hence increases the chances that B will
cooperate.
Continuing up the tree, one next considers the voters' decision
to keep or replace the first-period incumbent. The election hinges on
which party is expected to deliver a better outcome in the second
period, where the expectations depend in large part on the first-round
history. Hence, voting is prospective in the sense that the electorate
wants to maximize future payoffs, and retrospective in the sense that
the outcome in the previous period shapes the voters' beliefs
about the type of the incumbent and foreign state.
Formally, let σDh and
σHh denote the expected
probabilities that B will cooperate in the second period with a Dove
and Hawk, respectively, given the history of the game. For any given
voter i, with hawkishness αi, the
expected utility of electing a Dove and a Hawk, respectively, are:
Because these equations are all linear in αi,
it is easy to show that there will exist some cutpoint
α such that all voters with αi
< α will prefer one party (generally the Doves), and
all voters with αi < α will
prefer the other (generally the Hawks). This result justifies the focus
on a single, pivotal voter, which in the case of majority rule voting
would correspond to the median voter. Whichever party the pivotal voter
prefers will win the election.
Given the assumption that the median voter is moderate, with
αV = 0, one can readily show that the
voter's expected utility from electing a given party is weakly
increasing in the posterior probability that its leader is moderate.
This result stems from two sources, one direct and the other indirect.
The direct effect derives from the fact that a moderate voter always
does better with a moderate leader, regardless of what the foreign
state does. Holding constant the strategy of state B, the expected
utility from each party is increasing in the probability that it is
moderate, pDh or
pHh. The indirect
effect derives from the fact that a moderate voter is always better off
if state B cooperates, and, as shown above, the probability that B will
cooperate with a given leader is weakly increasing in the probability
that the leader is moderate. Hence, government's help their
reelection changes by encouraging the belief that they are moderate.
Of course, it is not always possible for voters to pick a candidate
who is certain to be a moderate. In this case, voters have to decide
which kind of extremist they are more willing to risk having in office,
a choice that depends on their beliefs about B. The more the voters
have reason to trust B after the first period, the more willing they
will be to risk putting an extremist Dove in power. The less they trust
B after the first period, the more willing they will be to risk
electing an extremist Hawk. This observation suggests that hawkish
parties often enjoy an advantage when trust is low. Under such
conditions, even a known hard-liner can get reelected if the
alternative is putting in place a government that might be too soft.
This result recalls Iklé's observation that, during times
of war, doves are generally more vulnerable to the charge of treason
than hawks are to the charge of “adventurism.”36
Initiating Cooperation: Equilibrium
Behavior in the First Period
I now turn to the first-period strategies. The full derivation of
these can be found in the Appendix. Here, my main goal is to discuss
the basic form the equilibria take when q is low and to focus
particularly on the conditions under which the government initiates
cooperation and how B reacts in that event. Because the game can start
with either the Dove or the Hawk in power, one needs to consider each
scenario in turn.
Dove in Power
For low values of q, the equilibrium strategies in the first
period are as follows:
- A moderate Dove defects. A soft-line Dove cooperates with
probability sD and defects with
probability 1 − sD, where
sD can be zero, one, or some number in
between.
- In response to cooperation, a moderate B always cooperates, while a
hard-line B plays a mixed strategy, cooperating with probability
σDc and defecting with
probability 1 −
σDc.
- In response to defection, a moderate B may cooperate or defect,
while a hard-line B always defects.
Several observations flow from these equilibrium strategies.
The main result is that Doves are hesitant to initiate cooperation. A
moderate Dove always defects, and even a soft-line Dove generally
defects some or all of the time. (There does exist an equilibrium in
which the soft-line Dove always cooperates, or
sD = 1, but as I note below, the
conditions under which it holds seem implausible.) The reason for this
hesitance is that cooperation is risky for a Dove, both because of what
it reveals about the government and because of how the rival state
responds. When trust is low, the only type of Dove that cooperates is
an extremist.37
When the soft-line Dove
is the only type to cooperate with nonzero probability, this is
trivially true. In the pooling equilibrium in which the soft-line Dove
always defects, it is assumed that, off the equilibrium path, a Dove
that cooperates must be soft-line.
The political danger of
this revelation is most clearly evident in the event that B does not
reciprocate. Following a
cd outcome, the Dove is known to be
soft-line, and B is known to be hard-line. Under these conditions, the
voters know that keeping the Dove will encourage B to defect, the
soft-line government will cooperate in response, and voters will get
the “sucker's payoff” of zero. Alternatively, they can
put the Hawk in power, and the worst result will be mutual defection,
for a payoff of
w. Because
w > 0, the pivotal
voter always prefers to remove the Dove following a
cd
outcome. Thus the international cost to being unilaterally exploited is
compounded by a domestic political cost, creating a disincentive for
Doves to cooperate. This result captures the standard story for the
electoral defeat of Israeli Prime Minister Ehud Barak after the
breakdown of talks with the Palestinians in September 2000 and the
onset of the second Intifada. To many in Israel, Palestinian rejection
of the terms offered by the Labor leader at Camp David represented
unilateral defection in the face of a cooperative gesture. This act
convinced much of the Israeli electorate that Palestinian leader Yasir
Arafat was a hard-liner (or worse) and had the effect, domestically, of
shifting the Israeli public to the right.
38 See, for example, Arian 2002.
The landslide election of the more
hawkish Likud leader, Ariel Sharon, and the diminished political
standing of the Labor party, which had been closely associated with the
Oslo peace process, were natural outgrowths of this development.
Even if cooperation is reciprocated by state B, this outcome is not
without political risks for a Dove government. The reason has to do
with B's equilibrium response to cooperation.39
In the event that the soft-line Dove defects in
equilibrium, the responses to cooperation by state B and the electorate
are off the path of play and are based on the off-the-path belief
described in fn. 37.
While a moderate B will always
reciprocate cooperation, a hard-line B does so as well with some
nonzero probability. This is because a hard-line B knows that, if it
defects in response to cooperation, it will surely face the Hawk in the
next period. On the other hand, if there is a good chance that the Dove
will be kept after a
cc outcome, then there is some incentive
to cooperate in order to keep the Dove in power. In doing so, it
foregoes the temptation payoff in the first period to enhance the
electoral prospects of the soft-line Dove, whose reelection allows the
hard-liner to get the temptation payoff in the second period. Thus the
hard-line B may resist the temptation to defect unilaterally in period
1 because it would rather have the Dove than the Hawk as its opponent
in period 2.
As a result of this logic, the electorate does not necessarily keep a
Dove that cooperates even if B reciprocates. Though the Dove has
delivered the best possible outcome in the first period, it has
revealed itself to be soft-line, and B's cooperative response is
only partly reassuring. After a cc outcome, there remains some
lingering doubt that B is a wolf in sheep's clothing: a hard-liner
who has cooperated purely for tactical reasons, to prevent the election
of a Hawk. I show in the Appendix that the electorate must play a mixed
strategy in this event, reelecting the Dove with probability
kDcc ∈ (0,1) and
removing the Dove with the complementary probability.
This result recalls the fate of French Prime Minister Joseph
Caillaux, who attempted to resolve the Franco-German colonial rivalry
in Africa in the wake of the 1911 Agadir incident. Caillaux struck an
advantageous deal: Germany renounced all political rights in Morocco in
exchange for some territorial concessions in the Congo. In the process,
he was aided not only by British support, but also by the threat that,
if Germany's intransigence undermined Caillaux's center-left
government, the Germans would end up having to deal with the much more
hawkish Georges Clemenceau.40
Hence,
German decision makers were aware of the hawk waiting in the wings.
Even so, the German concessions did not save Caillaux. As details of
the deal emerged, he fell victim to strident attacks from the right,
alleging that he would seek deeper reconciliation with Germany at the
expense of French colonial interests.
41 His government collapsed in the face of this
criticism. Thus Caillaux lost power despite the advantageous deal
because the outcome raised doubts about his firmness in dealing with
Germany while doing nothing to dispel distrust of that adversary.
The political risks of cooperation for a Dove are underscored by the
conditions that are required to support the separating equilibrium in
which the soft-line Dove always cooperates. This equilibrium exists
only when the value of office is low, the soft-line type is extremely
averse to conflict, and the Hawk party is very likely to be run by
moderates. When these conditions hold, an extremist Dove strictly
prefers to cooperate largely because it is content to commit electoral
suicide. Since office is not all that valuable and a new Hawk
government is likely to elicit and reciprocate cooperation, a soft-line
Dove would rather cooperate and see the Hawk elected than engage in the
noncooperative action that would help its political fortunes. While the
model shows that this behavior is logically possible, the conditions
under which it makes sense are unlikely to be observed empirically.
Under more plausible conditions, then, even soft-line Doves defect at
least some of the time.
Hawk in Power
When the Hawk is in power to start that game, the equilibrium can
take two different forms, reflecting the mixed incentives that Hawks
have. On the one hand, moderate Hawks have strong electoral incentives
to attempt peace in order to reveal their moderation; in doing so, they
benefit from the fact that, as Hawks, they are less vulnerable than
Doves to the charge of being soft. On the other hand, as I noted
earlier, Hawks enjoy a natural electoral advantage over Doves when
trust is low because, under these conditions, voters fear hard-liners
less than they fear soft-liners. Hence, Hawks sometimes have an
incentive to perpetuate the rivalry to maintain this advantage. Which
incentive is stronger turns out to depend on how bad the mutual
defection outcome, w, is and, in particular, whether it is
above or below some threshold,
,
which I derive in the Appendix. When
,
then mutual defection is a relatively tolerable outcome, and the incentive
to try to initiate peaceful relations is low. When
,
then mutual defection is relatively unattractive, increasing the incentive
to attempt peace.
Not surprisingly, then, if
and q is sufficiently low, a Hawkish government will always defect
in the first period, regardless of whether it is moderate or hard-line.
Likewise, both kinds of state B will defect in response, and all actors
will enter the second period with their beliefs unchanged. Because
voters do not have an opportunity to revise their initial distrust of
the foreign adversary, they will generally retain the Hawk given this
outcome. Thus when trust is low and mutual defection is relatively
tolerable, a Hawkish government in A will not initiate cooperation,
thereby perpetuating the rivalry and their party's natural
electoral advantage.
When
,
the prospects for cooperation are more promising. When q is
between zero and a threshold derived in the Appendix, the equilibrium
strategies take the following form:
- A moderate Hawk cooperates, and a hard-line Hawks defects.
- In response to cooperation, a moderate B cooperates, and a
hard-line B defects.
- In response to defection, a moderate B cooperates, and a hard-line
B defects.
Notice that these strategies are all separating, in the sense that
different types always take different actions, thereby revealing their
preferences unambiguously. Several implications follow from this.
Because a Hawk that cooperates reveals itself to be a moderate, the
electorate will almost always reelect such a government, regardless of
how B responds.42
The
“almost” caveat is needed because there exists a set of
conditions under which the electorate removes the Hawk with nonzero
probability after the cd outcome. Nevertheless, the
probability that a Hawk will be reelected after a cd outcome
is always greater than zero and hence always greater than the
corresponding probability for a Dove.
As discussed above, a
known moderate is the best possible leader for the pivotal voter,
because such a leader elicits and reciprocates cooperation in the
second period. Hence, whether B's response to the cooperative
gesture reveals it to be moderate or hard-line, the electorate is happy
to retain the Hawk.
Unlike when a Dove cooperates, then, the hard-line B has no incentive
in this case to disguise itself in the first period to influence the
electoral outcome. It simply cannot change the fact that the moderate
Hawk will be reelected. While the hard-line B will cooperate with the
moderate Hawk in the second period—when it must go first—it
will exploit the Hawk's cooperation in the first period. The
moderate B, on the other hand, is happy to know that it is dealing with
a moderate, and so it reciprocates cooperation in the first period and
offers cooperation again in the second. Because the hard-line and
moderate types of B respond differently to cooperation by a Hawk,
B's choice in this event perfectly reveals its type. As I will
note below, the superior information elicited by a Hawk's
cooperative gesture can promote the stability of cooperation in the
long run.
Given the political and diplomatic benefits that accrue to a Hawk
that cooperates, it might seem puzzling that a hard-line Hawk does not
also cooperate, at least some of the time. Indeed, there is an
interesting asymmetry in the equilibria between Hawks and Doves: while
an extremist Dove might sometimes mimic its moderate counterpart by
defecting, the extremist Hawk does not mimic its moderate counterpart
by cooperating. This asymmetry arises from the assumption of low trust.
Under this condition, the danger of revealing oneself to be a
hard-liner is much lower than the danger of revealing oneself to be a
soft-liner. When q is low, the most likely response to a
Hawk's defection is defection by a hard-line B. Once B has
revealed itself to be hard-line, the electorate has no reason to dump a
hard-line Hawk, since the Dove can do no better and may do much worse.
Thus the initial condition of low trust means that the hard-line Hawk
has little to fear by revealing itself.
Comparing Hawks and Doves
One can now answer the questions set out at the beginning of this
article. Under conditions of high mistrust, are hawks or doves more
likely to initiate cooperation? Are hawks or doves better at eliciting
cooperation from the foreign state and at promoting mutual cooperation
over the long run?
Who Initiates Cooperation?
As I have shown, the Hawk and Dove governments have different first
period strategies. In the case of the Dove, there is a semi-separating
equilibrium in which the moderate Dove always defects and the soft-line
Dove plays a mixed strategy, cooperating with some probability
sD ∈ [0,1] . In the case of
the Hawk, there is either a pooling equilibrium in which both types defect
or a separating equilibrium in which the moderate Hawk cooperates and the
hard-line Hawk defects
.
Table 1 summarizes the probability that cooperation
will be initiated by different types of government.
The probability of initiating cooperation by party and type
There are several results here. When payoff from mutual conflict is
relatively high, only a soft-line Dove will initiate cooperation. This
makes intuitive sense: when the prospects for cooperation are at their
worst—that is, when trust is lacking and the continued conflict
is tolerable—only the most conciliatory will try to make peace.
When the payoff from mutual defection is low, however, the type that is
most likely to initiate cooperation is a moderate Hawk. This is
especially so given the implausibility, noted above, of the
sD = 1 equilibrium. Partisan politics
aside, these results collectively mean the probability that any
government will initiate cooperation is highest when continued conflict
is particularly costly, or
.
This observation recalls Zartman's finding that a “mutually
hurting stalemate” helps to make a rivalry “ripe for
resolution.”
43 Notice that these results do not imply that any Hawk
government is necessarily more likely to cooperate than is any Dove
government. The ex ante probability of cooperation by a Hawk
is the probability that moderates control that party,
pH, while the ex ante probability
of cooperation by a Dove is (1 −
pD)sD.
Depending on the actual distribution of types within each party, either
of these probabilities could be the larger. In particular, if the Hawk
party contains no moderates (pH ≈ 0),
then cooperation by a Hawk is unlikely. Only if extremists are
relatively rare is a Hawkish leader more likely to initiate cooperation
than a Dovish leader (and then only when
).
This result arises from the signaling aspects of the decision to
cooperate. As noted earlier, leaders are trying to achieve the same
goal: convincing foreign and domestic audiences that they have moderate
preferences. Though this incentive is common to both parties, the
strategies that they must use to generate these beliefs are different.
A moderate Hawk must convince everyone that it is not hard-line. To do
this, it must choose a strategy that a hard-line type is reluctant to
mimic: cooperation. A moderate Dove, by contrast, must convince
everyone that it is not too soft. It does so by selecting a strategy
that a soft-line Dove finds costly to mimic: defection. Interestingly,
this means that two moderates with identical preferences but from
different parties will behave differently in otherwise exactly similar
situations. Put another way, the same policy—cooperation—is
a moderate policy coming from a Hawk, but an extremist policy coming
from a Dove.
Because of this asymmetry, cooperation is politically much riskier
for the Dove than for the Hawk. This is easiest to see when the
government cooperates and the adversary defects, thereby revealing that
it is hard-line. After this result, the voters prefer to have a Hawk in
power. Thus when a Hawk extends a gesture of cooperation, it knows that
a defection by the adversary, while bad from a foreign policy
perspective, will not destroy its reelection prospects. By contrast,
when a Dove cooperates, defection by the adversary leads both to a
foreign policy and an electoral defeat. Moreover, even when the foreign
state reciprocates cooperation in the first round, the Hawk is
electorally more secure than the Dove. Under conditions of low trust, a
Dove that cooperates reveals itself to be an extremist. Because voters
cannot rule out the possibility that B is hard-line, they may remove
the Dove in spite of the optimistic first-round outcome. In sum, the
parties' domestic political incentives make cooperation relatively
safer for the Hawk.
Will Cooperation Be Reciprocated, and Will It Last?
The second set of results deals with the probability that the states
will achieve mutual cooperation in the short and long term. There are
two subtly different findings here. First, consider the probability
that an initial gesture of cooperation will be reciprocated. When a
Hawk attempts cooperation, only a moderate B will reciprocate
cooperation. When a Dove initiates cooperation, a moderate B will
always reciprocate, and a hard-line B does likewise with positive
probability. Hence, the probability that a cooperative gesture will be
reciprocated in the first period is higher under the Dove.
Mutual cooperation in the first period, however, does not guarantee
future cooperation. The problem stems from the fact that a hard-line B
might reciprocate cooperation from a Dove, hoping to appear moderate to
take advantage of the Dove after it is reelected. Knowing this, voters
may reject a Dove government even after a cc outcome. As a
result, mutual cooperation initiated by a Dove in the first period can
break down in the second period in two different ways. First, there is
a lingering danger that B is a hard-liner who is waiting until the
second period to reveal itself. Second, a skeptical electorate may
replace the Dove with a Hawk, in which case there is some chance that
the new government will be hard-line, making continued cooperation
impossible. Either way, the high hopes for peace coming out of the
first period can be dashed in the second.
The fragility of cooperation initiated by the dovish party is evident
in the efforts of Democratic President Bill Clinton to rein in North
Korea's nuclear program in the mid-1990s. The 1994 Framework
Agreement—in which North Korea agreed to halt its program and
readmit inspectors in exchange for energy assistance and other
guarantees—eventually unraveled because of one or both of the
shocks identified here. Republicans immediately questioned the wisdom
of the deal, arguing that Clinton had given into blackmail and that
North Korea could not be trusted to carry out its end of the
bargain.44
This criticism took
greater force when Republicans took over control of the Congress a
month after the deal was struck. Without walking away from the
agreement altogether, Congress dragged its feet on funding the U.S.
commitments, citing the concern that North Korea was not living up to
its side of the bargain. With the election of Republican George W. Bush
as president, confrontational rhetoric and charges of cheating
intensified. The distrust was not unwarranted. In October 2002, the
North Koreans admitted that they had been secretly reprocessing uranium
in violation of the deal, and shortly thereafter they restarted the
reactor that had been closed by the Framework Agreement, expelled
inspectors, and withdrew from the Nonproliferation Treaty.
45 See, for example, Alvarez 2003.
These actions are consistent with
the view that North Korea's cooperation in 1994 was a temporary,
tactical shift to defuse the current crisis, not a signal of the
regime's moderation. While each side claims that it was merely
responding to the provocations of the other, it is evident that
hard-liners reasserted themselves in at least one of the states,
leading cooperation to collapse.
By contrast, mutual cooperation initiated by a Hawk is more robust.
Cooperation by a Hawk not only reveals its moderate preferences, but
also induces the two types of B to separate, with the moderate type
reciprocating cooperation and the hard-line type defecting. Hence,
after an initial round of mutual cooperation, it is common knowledge
that both the Hawk party and state B are run by moderates. Under these
conditions, cooperation in the second round is assured.
Furthermore, if the game were to go on for additional periods, the
superior information generated by the Hawk's initial gesture of
cooperation would have a lasting and beneficial effect. After the Hawk
and state B both cooperate in the first round, it is common knowledge
that none of the actors in the game are hard-line. Given this, future
cooperation is robust to an alternation in power within A. The only
shock that could upset this cooperative equilibrium would be a takeover
of the Hawk party or state B by hard-liners (a possibility that is
outside the scope of the current model). By contrast, even if the Doves
manage to achieve mutual cooperation over two periods, this cooperation
might not survive a future change in power within A. The lingering
possibility that the Hawk is hard-line could cause trust to break down.
Hence, mutual cooperation initiated by a Dove is vulnerable to a wider
range of shocks than is cooperation initiated by a Hawk. In
expectation, then, the latter should be longer-lasting. In sum, while
Doves may be more successful in promoting cooperation in the short run,
lasting cooperation is more likely if the first step is initiated by a
Hawk.
Conclusion: Implications and Illustrations
The model in this article is obviously quite stylized. The order of
moves is fixed somewhat arbitrarily, and the interaction ends after
only two periods. An election is assumed to follow predictably between
the periods, and its outcome hinges entirely on the international
outcome. None of these assumptions is realistic. As with any model, the
one developed here exists to highlight some key strategic dilemmas and
trade-offs that governments encounter when they consider risking peace.
It captures an interaction in which there are potential gains from
cooperation coupled with a danger of exploitation, a lack of trust that
arises from uncertainty about the adversary's preferences, and
domestic political competition among factions that have different
preferences about the desirability of risking cooperation. To do so, it
marries a canonical model of trust with a simple game of two-party
electoral choice. Although assuming that the election swings entirely
on the international outcome is unrealistic, doing so brings out in
starkest detail the influence of domestic political incentives on
foreign policy choice.
The model yields several key results regarding the initiation and
robustness of mutual cooperation. When trust is lacking and the costs
of continued conflict are relatively tolerable, then it takes a
pacifist to attempt peace. Under these conditions, a soft-line Dove is
the only type willing to take the risky steps that are needed to learn
whether mutual cooperation is possible. On the other hand, when trust
is low but costs of mutual defection are high, efforts to initiate
cooperation are most likely to come from moderate Hawks. Moreover,
mutual cooperation initiated by such a government has a better chance
of enduring over the long run than does cooperation initiated by a
Dovish government. Moderate Hawks enjoy greater electoral security when
risking cooperation, and foreign states respond to their cooperative
gestures in a way that promotes robust cooperation over the long
term.
These results suggest a number of potentially testable empirical
implications, though there are nontrivial challenges in measurement and
operationalization. The hypotheses cover three areas: the probability
of initiating cooperation, the political effects of attempting peace,
and the likelihood that cooperation, once started, will endure.
The Probability of Initiating Cooperation
The first hypothesis from the model is that, as the costs of conflict
increase, a moderate from the hawkish party becomes the most likely
type to initiate cooperation. Considerable care must be taken in
testing this hypothesis because the prediction is conditional on two
things that may, in practice, be hard to measure. First, whether a
moderate Hawk or soft-line Dove is the most likely type to initiate
cooperation depends on the magnitude of w relative to other
parameters. This suggests that this effect is most likely to be evident
in the context of particularly dangerous and costly rivalries.
Second, this hypothesis does not say that any Hawk government is more
likely to initiate peace than any Dove government. As noted above, the
ex ante probability of initiating cooperation depends on the
probabilities that each party is controlled by moderates. Hence, it is
useful to have ex ante indicators of the Hawk party's
moderation. Several factors might help free the Hawk party from the
influence of its hard-line faction. First, majoritarian, rather than
proportional representation, electoral rules tend to empower moderates
over extremists. Second, if there are other issues that bind the
hard-liners to the Hawkish party, then they may not have a credible
exit threat, again diminishing their influence over the party's
policies. Third, if a hawkish government enjoys a sizable majority
among voters or in the legislature, then it may be less vulnerable to
pressure from its extremist wing. This last point is consistent with
Huth and Allee's finding that governments with large legislative
majorities are more likely to offer concessions in territorial
disputes.46
All three of these factors are evident in the rapprochement between
Greece and Turkey in the 1930s. In that conflict, the most potent
hard-line faction in Greece consisted of Greek refugees who had been
forced to flee Turkey after their war in 1921–22 and who demanded
compensation for property left behind. The refugees were a hard bloc to
ignore not only because of their passion for the issue, but also
because of sheer numbers: they accounted for roughly 20 percent of the
Greek population at the time. Ultimately, though, refugee interests
would be sacrificed on the altar of Greco-Turkish rapprochement, as the
agreements signed in 1930 absolved Turkey of all claims by the
refugees. Interestingly, the man who delivered this deal was
Eleutherios Venizelos, who had not only been a long-time champion of
Greek irredentism, but who also counted the refugees as key supporters
of his Liberal party.47
For this reason,
contemporary reports of Venizelos' visit to Turkey in 1930 express
the same surprise that accompanied Nixon's visit to China in
1972.
48 See, for example, New York
Times, 27 October 1930, 9.
Several factors freed Venizelos from the hard-line interests within
his party. First, an electoral reform enacted before the 1928 election
changed the voting rules from proportional representation to plurality.
This change, combined with Venizelos's high personal popularity,
led to a thoroughly lopsided electoral result. While Venizelos's
Liberal party received 46.9 percent of the vote, it won 71.2 percent of
the seats in the Chamber of Deputies; adding several smaller
pro-Venizelos parties, the Greek prime minister could count on the
support of more than 90 percent of the legislature.49
This dominance meant that Venizelos had unprecedented autonomy to
ignore the refugee bloc, which made up only 13.6 percent of the
chamber.
50 Moreover, the refugees were
ideologically tied to the Liberal party, meaning that they could not
credibly threaten to defect to the opposition. The main cleavage in the
Greek political system at the time was between those who supported
Venizelos and the republic, and those who supported the old monarchy.
For a variety of reasons, the refugees were adamantly prorepublic and
personally loyal to Venizelos.
51 These
tight bonds diluted the power that this large voting bloc might
otherwise have exercised. Hence, once Venizelos had come to the
realization that continued conflict with Turkey was no longer in Greek
interests, he was politically free to act on those moderate
preferences.
52 For a discussion of why
Venizelos had become a moderate by 1930, see Psomiades
1962, chap. 14.
The Political Effects of Risking Peace
The next set of predictions deals with the electoral implications of
international outcomes. The model predicts a fundamental asymmetry
between hawkish and dovish parties in the political costs and benefits
of risking peace. Testing the waters of cooperation is politically
risky for doves, especially, but not exclusively, when the other side
responds aggressively. For a hawkish government, on the other hand,
initiating a cooperative gesture can be a political boon, by reassuring
voters that its preferences are moderate. Colaresi finds evidence that
a record of unreciprocated cooperation toward a rival can shorten a
leader's tenure in office, but his tests do not differentiate
between leaders based on reputation or party affiliation.53
Elsewhere, I use counterfactual
simulations on survey data from the 1968 National Election Study to
show such an effect in the canonical case of “Nixon going to
China”: U.S. rapprochement with China in the late 1960s and early
1970s.
54 The evidence presented in that
article shows that a hypothetical proposal to open ties with that
communist nation would have been electorally rewarding in the 1968
presidential race for the Republican candidate, Nixon, but politically
costly for the Democratic candidate, Hubert Humphrey.
A corollary hypothesis that would provide indirect evidence of this
asymmetry deals with the timing of peace initiatives. The logic here
suggests that Doves might prefer to make their initiatives early in the
electoral cycle, when they are relatively secure, while Hawks might be
tempted to attempt peace as an election approaches to boost their
standing.55
Huth and Allee 2002 and Chiozza and Choi 2003 present evidence that democratic leaders are
more likely to make concessions in territorial disputes early in the
term rather than later, but neither test for a conditional relationship
of the type hypothesized here.
Nixon, again, provides the
classic example, delivering not only his China trip, but also the
Strategic Arms Limitations Treaty and the Anti-Ballistic Missile treaty
with the Soviet Union within months of the 1972 election—all rare
instances of bold peacemaking in an election year.
56 Other peace initiatives by hawks share this
timing. In 1988, just a year before a general election, Greek Prime
Minister Andreas Papandreou abandoned his Socialist party's
long-standing position against talks with Turkey and helped to initiate
one of the most significant efforts at rapprochement between those
countries. The so-called “Davos process” failed to resolve
the ongoing conflicts over Cyprus and the Aegean, and Papandreou
eventually lost power because of ill health and scandals. Nevertheless,
his conversion from hard-liner to peacemaker a year before an election
has been interpreted as political opportunism.
57
Moreover, Papandreou's choice of timing stands in marked contrast
with that of the previous New Democracy government, which was known to
have a much more flexible position on Turkey.
58
The most prominent initiative of then Prime Minister Constantine
Caramanlis—a summit meeting with his Turkish counterpart in March
1978—took place only four months after a general election.
Indeed, Caramanlis had called early elections in order to have them
behind him when he entered the negotiations.
59 Washington Post, 20 September 1977,
A14.
While I have mostly emphasized the implications of a decision to
cooperate, the model also suggests that Doves might enjoy political
benefits from a tough strategy. Just as cooperation is an electoral
boon for a Hawk, defecting can boost the political fortunes of a Dove.
Borker, Kriesberg, and Abdul-Quader present evidence consistent with
this hypothesis. Updating and refining Mueller's model of rally
events and presidential popularity, they distinguish between
conciliatory and confrontational events and show that public reactions
to each depended on the president at the time. In particular,
conciliatory events tended to boost the popularity of Presidents Dwight
D. Eisenhower, Lyndon B. Johnson, and Nixon—arguably the three
presidents with the most hawkish reputations during the period covered
(1945–80)—while confrontational events increased the
popularity of Presidents John F. Kennedy and Jimmy Carter—the
most dovish of the lot.60
See Borker,
Kriesberg, and Abdul-Quader 1985; and Mueller
1973.
The Probability That Cooperation Will Endure
The final prediction is that cooperative arrangements delivered by
hawks are more likely to endure than are deals delivered by doves. With
an appropriate data set on such agreements, this hypothesis could be
tested using duration analysis, much as Werner and Fortna test the
duration of settlements that emerge from interstate wars.61
To date, however, a
comprehensive data set on agreements—especially one that includes
peace plans that do not directly emerge from wars—is lacking.
In the absence of systematic proof at this stage, there is suggestive
evidence for this third hypothesis in a number cases in which enduring
rivals were able to achieve long-lasting settlements of core disputes.
In many prominent rivalries that were successfully terminated, the
governments that brought about rapprochement counted hard-line elements
in society among their core supporters.62
See Bennett 1998 for a coding of
rivalry termination.
Nixon bucked the anticommunists in the
Republican party to bring about the opening with China.
63 As already noted,
Venizelos and the Greek Liberal party sacrificed the interests of the
refugees to make peace with Turkey. In early twentieth-century Britain,
those most opposed to rapprochement with Russia were Radicals who
loathed the tsarist political system and adamantly opposed any dealings
with it.
64 Nevertheless, it was the Liberal
party that silenced its Radical wing to settle those countries'
rivalry in Central Asia in 1907.
65
In Israel, the hard-line opposition to peace with the Arab states and
Palestinians comes from a mixture of ideological considerations and the
material interests of those who have settled on lands taken by Israel
in the 1967 war. In delivering peace with Egypt in 1979, Israeli Prime
Minister Menachim Begin overrode these constituencies in spite of the
fact that they were central in his Likud coalition.
66 Such
cases suggest a pattern in which successful conflict resolution was
achieved by a government that counted among its core supporters those
most opposed to peace.
Of course, hawkish governments do not always deliver peace. In the
ongoing conflict between Israel and the Palestinian Authority,
hard-liners who support continued settlement of the West Bank and the
Gaza Strip form a strong voting bloc for the Likud party. While the
results of this article suggest that a Likud-led government is in a
better position to deliver a lasting peace than is a Labor government,
it is not at all clear that moderate voices in that party have
sufficient clout. For example, in a May 2004 referendum, 60 percent of
Likud members voted against a plan put forward by their own prime
minister, Ariel Sharon, to withdraw Israeli soldiers and settlers from
the Gaza Strip.67
New York
Times, 3 May 2004, 1.
The weight of this faction,
combined with Likud's dependence on several far-right parties to
maintain its governing majority, suggests a case in which
pH is very low.
Together with the theoretical results, this last observation suggests
an unfortunate dilemma arising from the potential mismatch between a
government's preferences and its political incentives. Doves want
peace, but they may not have the electoral security or credibility to
deliver it. Hawks enjoy both electoral security and credibility in
attempting cooperation, but they may not want to try.
Appendix
This Appendix presents formal derivations of the equilibria to this
game. The full proofs are quite long, so I focus only on the equilibria
that hold under certain initial conditions. A complete treatment is
available from the author. Proposition 1 considers the case in which a
Dove is in power at the start of the game. Proposition 2 deals with the
case in which a Hawk is initially in power and the payoff from mutual
defection, w, is relatively low. As noted in the text, this
condition is associated with the separating equilibrium that is at the
heart of the claim that Hawks make good peacemakers.
In the event that the opposition is elected at the start of the
second period, conditions (3) and (4) determine how different types of
B will respond to the new government. A moderate B will always
cooperate with a Dove, while a hard-line B will cooperate with a new
Dove only if pD > (β* −
r + t)/(t − w).
Similarly, a moderate B will cooperate with a new Hawk if
pH > w/r, and a
hard-line B will cooperate with a new Hawk if
pH > (β* +
w)/r. Collectively, these conditions create six
possible configurations of the prior probabilities
pH and pD.
Here, I present the proofs of the equilibria that hold when
pD < (β* − r +
t)/(t − w) and (β* +
w)/r > pH >
w/r. Under these conditions, a moderate B will
cooperate with, and a hard-line B will defect against, either kind of
new government.
In all equilibria, state A's behavior at the last node of the
game follows trivially from the payoffs. In response to cooperation,
the government in A cooperates if α < r −
t defects otherwise. In response to defection, the government
in A defects if α > −w, and cooperates otherwise.
To save space, these strategies will not be repeated in the statements
of the equilibria that follow.
Proposition 1. The following strategies and the beliefs they
generate through Bayes's rule describe a perfect Bayesian
equilibrium to this game when a Dove is in power to start the game and
q <
min[q1,q2] , with
q1 and q2 to be defined
below.
Proof. The moderate B's strategy in (1.4a) follows from
the fact that a Dove will always reciprocate cooperation. The
strategies in (1.4b) follow from the conditions on
pH described at the introduction to this
appendix.
Consider first the subgame that follows first-round cooperation by
the Dove. From (1.1), a Dove that cooperated in period 1 must be
soft-line. If a moderate B cooperates, it gets a first-period payoff of
r, and, if it defects, it gets a first-period payoff of
t. In addition, B knows that its strategy will influence which
party wins the election. It is conjectured in (1.3b) that, if B
defects, the Dove will be replaced by a Hawk. It follows from (1.4b)
that the expected value to a moderate B of playing the second round
against a new Hawk is pH r.
Putting this all together,
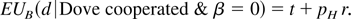
If B cooperates, let
kDcc be the
probability that the Dove is retained after a cc outcome.
Then,
It is trivial to see that equation (A2) is greater than (A1) for any
value of kDcc. This
confirms (1.2a). Because a moderate B will reciprocate cooperation, a B
that fails to do so must be a hard-liner, and the electorate will
certainly replace the soft-line Dove with the Hawk at the election,
confirming (1.3b).
Now consider the hard-line B's response to cooperation by a
Dove. Based solely on first-period payoffs, a hard-line B prefers
defection, for a payoff of t + β*, over cooperation, for a
payoff of r. It knows, however, that defection will lead to
the election of a Hawk, while cooperation will lead to the Dove's
being reelected with probability
kDcc. In the second
period, a hard-line B defects against a Dove that is known to be
soft-line as well as a new Hawk. Thus,
Thus, a hard-line B prefers to cooperate if
Now consider the electorate's response to a cc outcome.
Let qDcc denote the
posterior probability that B is a moderate in this event. If the
electorate keeps the Dove, then it will enjoy mutual cooperation in the
second period if B is a moderate and the sucker's payoff if B is
hard-line. Thus,
If the voters elect the Hawk, then B will cooperate if it is moderate
and defect if it is hard-line, and the Hawk government's response
will depend on its type:
Hence, the median voter prefers the Dove if
The following lemma now establishes that, when q is
sufficiently low, the hard-line B's response to cooperation and
the electorate's response to the cc outcome are given by
the mixed strategies proposed in (1.2a) and (1.3b).
Lemma. If q meets the conditions set out in the
statement of the proposition, then a hard-line B will reciprocate
cooperation with some probability
σDc ∈ (0,1), and the
electorate will keep the Dove after a cc outcome with some
probability kDcc
∈ (0,1).
Proof. Assume instead that the electorate always retains the
Dove after cc, or
kDcc = 1. By (A5), the
hard-line B would always want to reciprocate cooperation in period 1.
Because both types of B respond the same way,
qDcc = q. It
can be shown that q < q1 (the
expression for which is in [A24] below) implies that
q < w/[w + (1
−pH)(r −
t)]. By equation (A8), the electorate will remove the
Dove after cc. This contradicts the initial assumption that
kDcc = 1.
Now assume that the voters always remove the Dove after cc,
or kDcc = 0. By
equation (A5), a hard-line B would always defect in the first period.
In that case, only a moderate B would reciprocate cooperation, so
qDcc = 1. By equation
(A8), the electorate would want to keep the Dove after cc,
which contradicts the assumption that
kDcc = 0.
Hence, under these conditions, there is no equilibrium in which the
hard-line B plays a pure strategy in response to cooperation and the
electorate plays pure strategy in response to cc.
To sustain this mixed strategy equilibrium in the subgame following
cooperation by a Dove, it must be the case that a hard-line B is
indifferent between cooperating and defecting. This is achieved by
making equation (A5) an equality, providing an exact expression for
kDcc. To encourage the
electorate to play a mixed strategy after cc, it must be the
case that the pivotal voter is indifferent between the soft-line Dove
and a new Hawk given beliefs
qDcc. Applying
Bayes's rule and substituting into equation (A8), the electorate
is indifferent when
I have now characterized the subgame that follows cooperation by a
Dove. Putting it all together, the expected value of cooperating for a
moderate and soft-line Dove, respectively, are:
Now consider the subgame that follows a first-round defection by the
Dove. For a hard-line B to play a mixed strategy against the Dove in
the second period, as proposed in (1.4a), it must be indifferent
between cooperating and defecting, which happens (from equation
[3]) when
Applying Bayes's rule and substituting into (A13) yields
Assume, as conjectured in (1.2b), that only a moderate B would
cooperate in response to defection. This means that, following a
dc outcome, the electorate knows that B is a moderate. Because
a moderate B will always cooperate with a Dove in the second period,
the electorate wants to keep the Dove in this event, as proposed in
(1.3a). A moderate B's expected utility of cooperating and
defecting, respectively, are:
Comparing these, one finds that a moderate B will cooperate in
response to defection if
as proposed in (1.2b). If the electorate retains the Dove that
defected, the hard-line B is indifferent between cooperating and
defecting in the second period; this means that its expected value of
play with a Dove in the second period must be r. Hence,
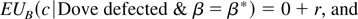
Comparing these, one finds that a hard-line B will cooperate in
response to defection if
It can be shown that β* > r − t and
r > 2(t − w) ensure that the
right-hand side of this expression is negative. This confirms that a
hard-line B always defects in response to defection, as proposed in
(1.2b).
This proof has already established that the electorate retains the
Dove after a history of dc. Now consider the electorate's
response to dd. Define
qDdd to be the
electorate's posterior belief that B is moderate given this
history. There are two cases to consider. If equation (A16) holds, then
the moderate B always cooperates in response to defection and
qDdd = 0. The
electorate's choice under these conditions is between
Setting these two equations equal, one finds that the electorate is
indifferent between the Dove and the Hawk when
If equation (A16) does not hold, then the moderate B always defects
in response to defection and
qDdd = q.
From the equilibrium strategies,
Setting these two equal and rearranging them yields the expression
for σDdd that holds in this
case. This expression is not particularly interesting except to note
that, for σDdd to be a true
probability, it must be the case that
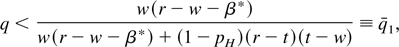
which is assumed in the statement of the proposition. It can also be
shown that the mix probability
σDdd that creates
indifference between equations (A22) and (A23) is lower than the
corresponding value given in (A21).
I have now characterized the subgame that follows defection by a
Dove. As shown above, there are two possible strategies for the
moderate B in response to defection. For ease of notation, define
σDd as the probability that
a moderate B will cooperate in this event; or
Putting all of it together, the expected values of defecting for a
moderate and soft-line Dove, respectively, are
For the soft-line Dove to play a mixed strategy at its first node, it
must be indifferent between cooperating and defecting. This
indifference is created by finding the value of
kDdd that makes
expected value of defection in equation (A27) equal to the expected
value of cooperation in (A11). Let
denote this critical value when
σDd = 0, and let
denote the critical value when
σDd = 1. It is
straightforward to show that
:
as the moderate B's response to defection becomes less rewarding,
the Dove must be compensated by a higher probability of reelection.
This result ensures that at least one of the strategy pairs shown in
equation (A25) holds in equilibrium.
68 Note that, if
,
there exist two equilibria: one in which the moderate B always defects
in response to defection and one in which the moderate B always
cooperates in response to defection. This possibility has no impact on
the results discussed in the text.
In either event, the indifference condition can only be met if
q is not too high. The key here is that, as q rises,
cooperation becomes more attractive relative to defection. To maintain
indifference between the two,
kDdd must rise with
q. The upper bound on q can be derived by finding the
value of q at which
kDdd must equal one in
order to make the soft-line Dove indifferent. Let
q2 denote this upper bound. To prove that there
exists a q2 > 0, it can be shown that, for
q arbitrarily close to zero, there exists a
kDdd < 1 that
creates the necessary indifference. Then, because
kDdd increases with
q, it must be the case that q2 is
greater than zero.
As q → 0, we know from equation (A11) that
and from equation (A27) that
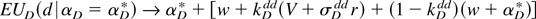
Indifference between equations (A28) and (A29) is achieved when
which must be in (0,1), recalling that w +
αD* < 0.
The final element of the proof is to note that, if the soft-line Dove
is indifferent between cooperating and defecting, then the moderate
Dove strictly prefers to defect, as proposed in (1.1).
Proposition 2. The following strategies and the beliefs they
generate through Bayes's rule describe a perfect Bayesian
equilibrium to this game when a Hawk is in power to start the game,
2w < r , and q <
(αH* − t +
2w)/(αH* − t +
2w + V).
Proof. As before, B's strategy in (2.4b)—that is,
moderates cooperate with a new Dove, while hard-liners defect—is
ensured by the conditions on pD assumed at
the outset. B's proposed strategy in (2.4a) follows from the
beliefs generated by the Hawk's first-period strategy. A Hawk that
cooperated is certainly a moderate, so both types of B want to
cooperate. A Hawk that defected is certainly a hard-liner, so both
types of B want to defect.
Now consider the electorate's strategy in (2.3). A Hawk that
cooperated is certainly a moderate, and because both kinds of B will
cooperate with a known moderate, the electorate keeps the Hawk, thereby
ensuring its best possible payoff, r. A Hawk that defected is
certainly hard-line. If B cooperated in response the Hawk's
defection, then it is certainly a moderate, and the electorate would
rather have the Dove in office, again ensuring a cooperative outcome.
If B defected, then it is certainly a hard-liner, and the best the
electorate can do is to keep the hard-line Hawk in power, because a
hard-line B will defect on either a new Dove or a hard-line Hawk, but
the former might cave in response.
Now consider B's response to cooperation by a Hawk. Because B
knows that the Hawk will be retained regardless of what it does in the
first period, there is no reason for either type of B to act
deceptively. Hence, each type acts to maximize its first-period
payoff—that is, the moderate reciprocates cooperation while the
hard-liner defects. If the Hawk defected, then B can either
cooperate—getting the sucker's payoff but also ensuring the
election of the Dove in the next period—or it can defect and
ensure the reelection of the extremist Hawk. For a moderate B, the
expected utility from cooperating and defecting are:
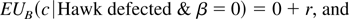
Thus the moderate type cooperates if r > 2w,
which is stipulated to be true in the statement of the proposition. For
a hard-line B,
Comparing these, one finds that a hard-line B defects if
This condition is ensured by the assumptions that β* >
r − t and r > 2(t −
w). This confirms B's strategies as proposed in (2.2).
Finally, I turn to the Hawk's first-period strategy, starting
first with the moderate type. If it plays its equilibrium strategy and
cooperates, the moderate Hawk expects
The expected value of deviating to defection is
Comparing these, one finds that a moderate B prefers cooperation if
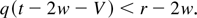
Because r > t, r − 2w
> t − 2w − V, so this
condition must be true for all q ∈ [0,1] . Thus
the moderate Hawk strictly prefers to cooperate. For the hard-line
Hawk, the expected value of defecting is
The expected value of deviating to cooperation is
because the extremist, by acting like a moderate, can take advantage
of B in the second period. Comparing these, one finds that the
hard-line Hawk prefers to defect if
which is the condition given in the statement of the proposition.
