Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-14T09:52:13.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisors computing minimal log discrepancies on lc surfaces

Part of: Birational geometry Local theory

Published online by Cambridge University Press:  14 February 2023

JIHAO LIU  and
LINGYAO XIE
JIHAO LIU
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Rd, Evanston, IL 60208, U.S.A. e-mail: jliu@northwestern.edu
LINGYAO XIE
Affiliation:
Department of Mathematics, The University of Utah, Salt Lake City, UT 84112, U.S.A. e-mail: lingyao@math.utah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

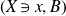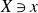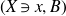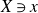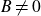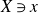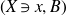Let $(X\ni x,B)$ be an lc surface germ. If $X\ni x$ is klt, we show that there exists a divisor computing the minimal log discrepancy of $(X\ni x,B)$ that is a Kollár component of $X\ni x$ . If $B\not=0$ or $X\ni x$ is not Du Val, we show that any divisor computing the minimal log discrepancy of $(X\ni x,B)$ is a potential lc place of 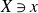$X\ni x$ . This extends a result of Blum and Kawakita who independently showed that any divisor computing the minimal log discrepancy on a smooth surface is a potential lc place.

MSC classification

Primary: 14E30: Minimal model program (Mori theory, extremal rays)
Secondary: 14B05: Singularities
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 1 , July 2023 , pp. 107 - 128
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexeev, V.. Two two–dimensional terminations. Duke Math. J. 69 (1993), no. 3, 527–545.Google Scholar
Ambro, F.. On minimal log discrepancies. Math. Res. Lett. 6 (1999), no. 5–6, 573–580.Google Scholar
Ambro, F.. The set of toric minimal log discrepancies. Cent. Eur. J. Math. 4 (2006), no. 3, 358–370.Google Scholar
Birkar, C., Cascini, P., C. D. Hacon J. McKernan. Existence of minimal models for varieties of log general type. J. Amer. Math. Soc. 23 (2010), no. 2, 405–468.Google Scholar
Blum, H.. On divisors computing MLD’s and LCT’s. Bull. Korean Math. Soc. 58 (2021), no. 1, 113–132.Google Scholar
Borisov, A. A.. Minimal discrepancies of toric singularities. Manuscripta Math. 92 (1997), no. 1, 33–45.Google Scholar
Chen, B.. Upper bound of discrepancies of divisors computing minimal log discrepancies on surfaces. arXiv:2009.03613v1.Google Scholar
G. Chen J. Han. Boundedness of inline923-complements for surfaces. Adv. Math. 383 (2021), 107703, 40pp.CrossRefGoogle Scholar
Chen, W., Di Cerbo, G., Han, J., Jiang, C., Svaldi, R.. Birational boundedness of rationally connected Calabi–Yau 3-folds. Adv. Math. 378 (2021), 107541, 32pp.CrossRefGoogle Scholar
Nolla de Celis, A.. Dihedral groups and G-Hilbert schemes. Ph.D. thesis. University of Warwick (2008).Google Scholar
Ein, L. Mustaţă, M.. Inversion of adjunction for local complete intersection varieties. Amer. J. Math. 126 (2004), no. 6, 1355–1365.Google Scholar
Ein, L., Mustaţă, M., Yasuda, T.. Jet schemes, log discrepancies and inversion of adjunction. Invent. Math. 153 (2003), no. 3, 519–535.Google Scholar
Han, J., Liu, J., Shokurov, V. V.. ACC for minimal log discrepancies for exceptional singularities. arXiv:1903.04338v2.Google Scholar
Han, J., Liu, Y., Qi, L.. ACC for local volumes and boundedness of singularities. arXiv:2011.06509v2.Google Scholar
J. Han Y. Luo. On boundedness of divisors computing minimal log discrepancies for surfaces. arXiv:2005.09626v2.Google Scholar
Hartshorne, R.. Algebraic Geometry. Graduate Texts in Math. no. 52 (Springer-Verlag, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Ishii, S.. The minimal log discrepancies on a smooth surface in positive characteristic. Math. Z. 297 (2021) 389–397 (2021).CrossRefGoogle Scholar
Jiang, C.. A gap theorem for minimal log discrepancies of non-canonical singularities in dimension three. J. Algebraic Geom. 30 (2021), 759–800.CrossRefGoogle Scholar
Kawakita, M.. Towards boundedness of minimal log discrepancies by the Riemann–Roch theorem. Amer. J. Math. 133 (2011), no. 5, 1299–1311.Google Scholar
Kawakita, M.. Discreteness of log discrepancies over log canonical triples on a fixed pair. J. Algebraic Geom. 23 (2014), no. 4, 765–774.CrossRefGoogle Scholar
Kawakita, M.. A connectedness theorem over the spectrum of a formal power series ring. Internat. J. Math. 26 (2015), no. 11, 1550088, 27pp.CrossRefGoogle Scholar
Kawakita, M.. Divisors computing the minimal log discrepancy on a smooth surface. Math. Proc. Camb. Phil. Soc. 163 (2017), no. 1, 187–192.Google Scholar
Kawakita, M.. On equivalent conjectures for minimal log discrepancies on smooth threefolds. J. Algebraic Geom. 30 (2021), 97–149.CrossRefGoogle Scholar
Kollár, J.. Exercises in the birational geometry of algebraic varieties. arXiv:0809.02579v2.Google Scholar
J. Kollár S. Mori. Birational Geometry of Algebraic Varieties. Cambridge Tracts in Math. no. 134 (Cambridge University Press, 1998).CrossRefGoogle Scholar
Kudryavtsev, S. A.. Pure log terminal blow-ups. Math. Notes 69 (2001), no. 5, 814–819.Google Scholar
Li, C.. Minimizing normalized volumes of valuations. Math. Z. 289 (2018), no. 1–2, 491–513.Google Scholar
C. Li C. Xu. Stability of valuations and Kollár components. J. Eur. Math. Soc. 22 (2020), no. 8, 2573–2627.Google Scholar
Liu, J.. Toward the equivalence of the ACC for a-log canonical thresholds and the ACC for minimal log discrepancies. arXiv:1809.04839v3.Google Scholar
Liu, J. and Xiao, L.. An optimal gap of minimal log discrepancies of threefold non-canonical singularities. J. Pure Appl. Algebra 225 (2021), no. 9, 106674, 23 pp.CrossRefGoogle Scholar
Mustaţă, M. Nakamura, Y.. A boundedness conjecture for minimal log discrepancies on a fixed germ. Local and global methods in algebraic geometry. Contemp. Math. no. 712 (2018), 287–306.CrossRefGoogle Scholar
Nakamura, Y.. On semi-continuity problems for minimal log discrepancies. J. Reine Angew. Math. 711 (2016), 167–187.CrossRefGoogle Scholar
Nakamura, Y.. On minimal log discrepancies on varieties with fixed Gorenstein index. Michigan Math. J. 65 (2016), no. 1, 165–187.Google Scholar
Y. Nakamura K. Shibata. Inversion of adjunction for quotient singularities. arXiv:2011.07300v2.Google Scholar
Prokhorov, Y. G.. Blow-ups of canonical singularities. Algebra (Moscow, 1998) (2000), 301–318.Google Scholar
Shibata, K.. Minimal log discrepancies in positive characteristic. Comm. Algebra 50 (2022), no. 2, 571–582.Google Scholar
V. V. Shokurov. A.c.c. in codimension 2. (1994), preprint.Google Scholar
Shokurov, V. V.. 3–fold log models. J. Math. Sciences 81 (1996), 2677–2699.Google Scholar
Shokurov, V. V.. Complements on surfaces. J. Math. Sci. (New York) 102 (2000), no. 2, 3876–3932.Google Scholar
Shokurov, V. V.. Letters of a bi-rationalist, V. Minimal log discrepancies and termination of log flips (Russian). Tr. Mat. Inst. Steklova 246 (2004), Algebr. Geom. Metody, Svyazi i Prilozh., 328–351; translation in Proc. Steklov Inst. Math. 246 (2004), no. 3, 315–336.Google Scholar
Xu, C.. Finiteness of algebraic fundamental groups. Compositio Math. 150 (2014), no. 3, 409–414.Google Scholar