Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T15:40:29.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of the influence of the stabilizing properties of transitional layers on the turbulent mixing evolution

Published online by Cambridge University Press:  03 March 2004

Yu.A. KUCHERENKO ,
S.I. BALABIN ,
R.I. ARDASHOVA ,
O.E. KOZELKOV ,
A.V. DULOV  and
I.A. ROMANOV
Yu.A. KUCHERENKO
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
S.I. BALABIN
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
R.I. ARDASHOVA
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
O.E. KOZELKOV
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
A.V. DULOV
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
I.A. ROMANOV
Affiliation:
Russian Federal Nuclear Center, Academician E.I. Zababakhin, All-Russian Research Institute of Technical Physics, Chelyabinsk, Russia
Rights & Permissions [Opens in a new window]

Abstract

Experiments conducted on the EKAP facility at the Russian Federal Nuclear Center–VNIITF concerning the stabilization of Rayleigh–Taylor instability-induced mixing in miscible liquids by the formation of a molecular diffusion (or transitional) layer between the liquids initially were described. The experiments had an Atwood number of 1/3. The acceleration was 3500 times that of Earth's gravity, and several values of diffusion layer thickness were considered. The experiments showed that the growth of the turbulent mixing zone could be delayed by adjusting the amplitude of the initial perturbations and the characteristic thickness of the diffusion layer. This has been observed in experiments conducted with water and mercury. The mixing layer evolution was imaged using X-ray radiography.

Keywords

Mixing delayMixing stabilizationTransitional layerTurbulent mixing
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 369 - 373
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

A nonstationary one-dimensional (1D) gas dynamic flow in layered systems is unstable in a number of gases. When the lighter fluid accelerates the heavy one, or vice versa, the heavy fluid is decelerated, and the turbulent mixing arises almost immediately between them on the contact boundary. Such situations take place, for example, in highly intensive shock and explosive processes, such as in laser thermonuclear fusion when compressing the targets. Taking into account these processes is especially important when compressing the special target in the problem of the inertial thermonuclear fusion (ITF). These processes exert an immediate influence on the dynamics of targets compression. Therefore, the investigation of methods for stabilizing or suppressing the mixing at the contact boundary is of great importance.

When studying the turbulent mixing evolution in the gravitationally unstable system, at the modeling installation EKAP, two possibilities were observed for the delay of the mixing evolution at the unstable contact boundaries. The first possibility is associated with decreasing the initial perturbations on the contact boundary or eliminating them. Thus, in the experiments with mercury–water, where no special measures were applied to generate small-scale perturbations, the delay in the mixing evolution was observed. The second possibility is associated with the location of the transitional layer with the continuous distribution of density on the contact boundary. In the experiments performed with some gravitationally unstable systems, a period of time was observed during which mutual penetration of the liquids was not observed. In the evolution of perturbations some latent period occurred. E. I. Zababakhin (1988) proposed that smearing the sharp boundary due to molecular diffusion when using mutually soluble liquids in experiments might induce the latent period. The works, in particular the work of Zababakhin (1988), in which in the linear approximation it is shown that in the systems with the continuous distribution of density the increment of the growth of the perturbation amplitude is less than in the case of the density jump at the same values of acceleration, g, and the drop of densities, n, can be the basis for this. Nevertheless, this did not make it possible to determine the time of the latent period in the evolution of initial perturbations. In such systems, the definite delay in the mixing evolution is observed depending on the relation of the characteristic size of the perturbation region L0 to the characteristic thickness of the transitional layer h (Anuchina et al., 1978; Neuvazhayev, 1983). In a system with a transitional layer it is possible to attain any desired delay in the turbulent mixing evolution, and if necessary to create systems with L0 /h = 0.

In the present work the delay was determined experimentally in the gravitational turbulent mixing in systems with a transitional layer, density ratio 2, and density perturbations in the transitional layer center.

2. SETUP OF EXPERIMENTS AND TECHNIQUES OF MEASUREMENTS

The study of the influence of the stabilizing properties of the transitional layer on the turbulent mixing evolution has been performed in the following setup given in Figures 1 and 2.

Physical scheme of the system being investigated.

Scheme of the experiments setup.

The system being investigated and consisting of two mutually soluble liquids having densities ρ1 and ρ2 was located in the ampoule 1 (Fig. 1). A transitional layer 2 with continuous distribution of density, whose density is changed according to the law placed ρ(y), ρ1 < ρ(y) < ρ2, was formed as a result of the mutual diffusion of these liquids. The transitional diffusion layer width was determined as the distance h* between the points with densities 1.1ρ1 and 0.9ρ2. The transitional layer contains the initial perturbation zone whose size is equal to L0. The initial perturbation zone size L0 can be equal to the transitional layer width or smaller, or it can be larger. The investigations were carried out with artificially created initial perturbations having their size ZB and a complex form. As a result, the perturbations were three-dimensional and their spectrum had a wide set of wavelengths. The maximum of the spectrum was usually at the wavelength λ ≈ 1 mm. For the spectrum maximum, the relation of the perturbation amplitude to the wavelength of the perturbation amounted to α/λ ≈ 0.4. In addition to perturbations specified by particles, in the experiments there were background perturbations induced by the irregular vibrations of the ampoule and the whole installation in the process of acceleration. Figure 3 shows X-ray photographs of the systems with the continuous distribution of density for different h*. It is possible to see the structural elements of the ampoule 1, heavy (a dark field) and light (a light field) liquids, reference benchmarks P on the ampoule, and the region of initial perturbation in the form of a light band that was formed by particle 2.

X-ray photographs of the systems with the continuous distribution of density for different h*(t).

The experiments were performed as follows (Fig. 2). Ampoule 1 was secured on piston 2, which was sealed in the channel of gas accelerator 4 by membrane 3. By means of a high pressure system, gas was forced into the gas accelerator (GA), and when pressure in the gas accelerator channel reached the pressure equal to that of breakdown, the destruction of membrane 3 took place, and ampoule 1 began to be accelerated in measuring section 5 in the direction of the Earth's gravitational field g. When the ampoule moved the distance S, electromechanical contact 6 was closed, which led to the action of two pulsed X-ray tubes. The X radiation of these tubes made it possible to obtain the shadow image of the turbulent mixing evolution on stationary X-ray film 7. Reference benchmarks 8 on the measuring section and the benchmarks on the ampoule made it possible to determine the distance S which was passed by the ampoule at the moment of its imaging. Then the ampoule got into damping device 10, where its deceleration to rest took place.

3. EXPERIMENTAL RESULTS

Experiments to determine the delay in the evolution of the gravitational turbulent mixing (GTM) in the system with the transitional layer were performed on a single pair of liquids with n = 2. Two groups of experiments were carried out. The first group of experiments had a density jump at the contact boundary (h* = 0), the second one was performed on the systems with the continuous density distribution (h* > 0). Water with ρ1 = 1 g/cm3 was used as a light liquid, Klerichi liquid (formic-malonic acid talium) with ρ2 = 2 g/cm3 was used as a heavy one. When performing the experiments, an ampoule with a square section of working volume S = 50 × 50 mm2 and 110 mm in length was used. The experiments were carried out at an initial acceleration of 3500 g in the range of 0 < S < 1100 mm with the transitional layer of different width h* and with the relation L0 /h*.

Figure 4 shows the characteristic X-ray photographs obtained in the experiments of the second group. It is seen that at the displacement at a distance S = 370 mm, the position of initial perturbations has not changed. They occupy the same position as at the instant of time t = 0.

Stages in the turbulent mixing evolution in the systems with the transitional layer (h* = 10.6 mm, L0 = 0.8 mm).

On the following photos, it is seen that the evolving perturbations go beyond the diffusion layer, and the size L of the mixing region of the two liquids is growing. Hence, it follows that in the experiments the delay in the turbulent mixing is observed. We shall call the duration of this delay as time T and the displacement

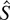
at which the failure of the transitional layer region being visible on X-ray photographs takes place. The size L21 depending of S is given in Figure 5 for different values of h* (and L0 /h*). In the same figure the dotted line shows the dependence of the mixing front in the light liquid L21 (S) at h* = 0.

Dependence of the mixing front coordinate on the contact boundary displacement S.

It is seen that the larger h (the less L0), the larger

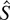
and the greater the delay T. The same conclusion is supported by the results of other series of experiments in which the relation L0 /h* was changed within wide limits due to a change in h* as well as due to a change in L0. The results of these experiments in the dimensionless form

are given in Figure 6.

Dependence of the delay in the mixing evolution.

From this figure it follows that the dependence

in the investigated range is L0 /h* > 0.2. However, with a decreasing initial perturbation region and with an increasing transitional layer width, the delay in the mixing evolution increases sharply. In this regard, the results of experiments without particle perturbations, that is, with L0 /h* = 0, are of interest. The perturbations in these experiments were only the background ones and, as was previously noted, they occur as a result of vibrations of the structural elements of the installation and the ampoule after applying the acceleration.

In these experiments, the instability evolution begins somewhat later. At the same time, the instability along the ampoule walls evolves earlier. From X-ray photographs, shown in Figure 7, it is seen that the transitional layer is not involved in the turbulent motion, but along the walls the instability evolves in the form of tongues elongated along the wall. This does not make it possible to determine the exact value of

.

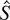
Stages in the turbulent mixing development in the system with the transitional layer at L0 /h* = 0.

4. CONCLUSION

1. At the installation EKAP, the experimental determination of the delay in the gravitational turbulent mixing evolution has been carried out in two-layered systems with n = 2, with the available transitional layer having a continuous distribution of density. The transitional layer with the characteristic size h* was formed as a result of mutual diffusion of mutually soluble liquids.

2. Investigations were performed using such liquids as water (ρ1 = 1 g/cm3) and “Klerichi” liquid (ρ2 = 2 g/cm3). The zone of initial perturbations with the characteristic size L0 was formed by solid particles with their average size Z.

Nine series of experiments differing in the relation L0 /h*(0.01 < L0 /h* < 0.6) have been carried out at an initial acceleration of 3500 g. In each series of experiments, the average value of the coordinate L2.1 of the mixing front was determined in the light liquid depending on the contact boundary displacement S. The value of the delay in the evolution of gravitational turbulent mixing was determined as the distance that was traversed by the ampoule at the moment when the mixing front in the light liquid went out beyond the transitional layer size h.

3. For all the values of L0 /h*, the value of the delay

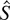
in the gravitational turbulent mixing evolution has been determined. It has been shown that the less L0 /h*, the greater the value of the delay. The dependence

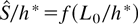
is of nonlinear character. In experiments with L0 /h* = 0, the long-wavelength perturbations (in the first place near the ampoule walls) develop. At the same time, the turbulent mixing in the center of the ampoule is not observed during a long interval of time.

References

REFERENCES

Anuchina, N.N. et al. (1978). Turbulent mixing at the accelerating boundary of different density liquids. Mech. Fluid 6.
Neuvazhayev, V.E. (1983). Properties of the model of the turbulent mixing of the interface between different density liquids being accelerated. Rus. J. PMTF 5.
Zababakhin, E.I. et al. (1988). Convective instability limitations. Rus. J.VANT 1, 4.Google Scholar
Figure 0

Physical scheme of the system being investigated.

Figure 1

Scheme of the experiments setup.

Figure 2

X-ray photographs of the systems with the continuous distribution of density for different h*(t).

Figure 3

Stages in the turbulent mixing evolution in the systems with the transitional layer (h* = 10.6 mm, L0 = 0.8 mm).

Figure 4

Dependence of the mixing front coordinate on the contact boundary displacement S.

Figure 5

Dependence of the delay in the mixing evolution.

Figure 6

Stages in the turbulent mixing development in the system with the transitional layer at L0 /h* = 0.