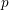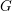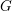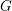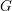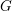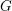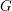1 Introduction
A major motivation for the study of the representation theory of  $p$-adic groups is, via the local Langlands correspondence, to understand Galois representations. The arithmetic core of these representations, which is rather mysterious on the Galois side, is encoded in restriction to wild inertia. On the automorphic side, this restriction corresponds to looking at certain representations of pro-
$p$-adic groups is, via the local Langlands correspondence, to understand Galois representations. The arithmetic core of these representations, which is rather mysterious on the Galois side, is encoded in restriction to wild inertia. On the automorphic side, this restriction corresponds to looking at certain representations of pro- $p$-subgroups.
$p$-subgroups.
For  $p$-adic general linear groups, Bushnell and Kutzko [Reference Bushnell and KutzkoBK93] constructed, and classified, all cuspidal irreducible representations. At the heart of this classification sit the so-called “simple characters”; these are very particular arithmetically defined characters of pro-
$p$-adic general linear groups, Bushnell and Kutzko [Reference Bushnell and KutzkoBK93] constructed, and classified, all cuspidal irreducible representations. At the heart of this classification sit the so-called “simple characters”; these are very particular arithmetically defined characters of pro- $p$-subgroups, which exhibit remarkable rigidity properties (see below for details). These properties were exploited, and extended, by Bushnell and Henniart [Reference Bushnell and HenniartBH96], who defined the notion of an “endo-class” and hence proved a ramification theorem [Reference Bushnell and HenniartBH03] for the local Langlands correspondence for general linear groups: there is a bijection between the set of endo-classes and the set of orbits (under the Weil group) of irreducible representations of the wild inertia group. More recently, they have extended this, using the fundamental structural properties of simple characters to prove a higher ramification theorem [Reference Bushnell and HenniartBH17].
$p$-subgroups, which exhibit remarkable rigidity properties (see below for details). These properties were exploited, and extended, by Bushnell and Henniart [Reference Bushnell and HenniartBH96], who defined the notion of an “endo-class” and hence proved a ramification theorem [Reference Bushnell and HenniartBH03] for the local Langlands correspondence for general linear groups: there is a bijection between the set of endo-classes and the set of orbits (under the Weil group) of irreducible representations of the wild inertia group. More recently, they have extended this, using the fundamental structural properties of simple characters to prove a higher ramification theorem [Reference Bushnell and HenniartBH17].
For  $p$-adic classical groups—that is, symplectic, special orthogonal and unitary groups—in odd residual characteristic, analogous characters were constructed by the second author [Reference StevensSte05] as a fundamental step in the construction of all cuspidal irreducible representations [Reference StevensSte08]. This required first extending the theory of simple characters to the case of “semisimple characters” (see also the work of Dat [Reference DatDat09]). However, the rigidity results which allowed Bushnell and Kutzko to obtain a classification were missing—partly because some of them are false.
$p$-adic classical groups—that is, symplectic, special orthogonal and unitary groups—in odd residual characteristic, analogous characters were constructed by the second author [Reference StevensSte05] as a fundamental step in the construction of all cuspidal irreducible representations [Reference StevensSte08]. This required first extending the theory of simple characters to the case of “semisimple characters” (see also the work of Dat [Reference DatDat09]). However, the rigidity results which allowed Bushnell and Kutzko to obtain a classification were missing—partly because some of them are false.
In this paper, we prove many of these rigidity results for semisimple characters, which are new even in the case of general linear groups—in particular, we prove “intertwining implies conjugacy” and Skolem–Noether results (see below for details). In a sequel [Reference Kurinczuk, Skodlerack and StevensKSS16], jointly with Kurinczuk, we are then able to put this together with other work of Kurinczuk and the second author [Reference Kurinczuk and StevensKS15], to turn the construction of cuspidal representations into a classification, for both complex and  $\ell$-modular representations, with
$\ell$-modular representations, with  $\ell \neq p$ prime. More precisely, we establish the following conjugacy result for cuspidal types in
$\ell \neq p$ prime. More precisely, we establish the following conjugacy result for cuspidal types in  $p$-adic classical groups: if
$p$-adic classical groups: if  $(J,\unicode[STIX]{x1D706})$ and
$(J,\unicode[STIX]{x1D706})$ and  $(J^{\prime },\unicode[STIX]{x1D706}^{\prime })$ are two types from the construction in [Reference StevensSte08] which induce to give equivalent irreducible cuspidal representations, then they are conjugate.
$(J^{\prime },\unicode[STIX]{x1D706}^{\prime })$ are two types from the construction in [Reference StevensSte08] which induce to give equivalent irreducible cuspidal representations, then they are conjugate.
We anticipate further work to come from these rigidity results. Semisimple characters (or, more precisely, their endo-classes) will give a decomposition of the category of smooth  $\ell$-modular representations of classical groups, and each subcategory should be equivalent to the subcategory of depth zero representations of some other (endoscopic) group, for which other techniques are available. Current work of the first author (see [Reference SkodlerackSko17] for the start of this) aims at generalizing the results proved here to proper inner forms of classical groups, where additional problems arise, analogous to those in the case of inner forms of general linear groups [Reference Broussous, Sécherre and StevensBSS12]. One would then expect that a Jacquet–Langlands correspondence between inner forms would respect the decompositions of the categories by endo-class, as for general linear groups [Reference Sécherre and StevensSS16], and that this would be a major step in making such a correspondence explicit. Finally, it would be interesting to explore whether our results on semisimple characters for general linear groups can be extended to semisimple types: suppose
$\ell$-modular representations of classical groups, and each subcategory should be equivalent to the subcategory of depth zero representations of some other (endoscopic) group, for which other techniques are available. Current work of the first author (see [Reference SkodlerackSko17] for the start of this) aims at generalizing the results proved here to proper inner forms of classical groups, where additional problems arise, analogous to those in the case of inner forms of general linear groups [Reference Broussous, Sécherre and StevensBSS12]. One would then expect that a Jacquet–Langlands correspondence between inner forms would respect the decompositions of the categories by endo-class, as for general linear groups [Reference Sécherre and StevensSS16], and that this would be a major step in making such a correspondence explicit. Finally, it would be interesting to explore whether our results on semisimple characters for general linear groups can be extended to semisimple types: suppose  $(J,\unicode[STIX]{x1D706})$ and
$(J,\unicode[STIX]{x1D706})$ and  $(J^{\prime },\unicode[STIX]{x1D706}^{\prime })$ are Bushnell–Kutzko semisimple types for the same Bernstein component of a
$(J^{\prime },\unicode[STIX]{x1D706}^{\prime })$ are Bushnell–Kutzko semisimple types for the same Bernstein component of a  $p$-adic general linear group, so that they intertwine; what extra condition on the associated lattice sequences is required to be able to conclude that the types are conjugate? The same question can also be asked in classical groups.
$p$-adic general linear group, so that they intertwine; what extra condition on the associated lattice sequences is required to be able to conclude that the types are conjugate? The same question can also be asked in classical groups.
Now we state our results more precisely. Let  $F$ be a non-archimedean local field of odd residual characteristic. Let
$F$ be a non-archimedean local field of odd residual characteristic. Let  $G$ be the isometry group of an
$G$ be the isometry group of an  $\unicode[STIX]{x1D716}$-hermitian space with respect to some automorphism of
$\unicode[STIX]{x1D716}$-hermitian space with respect to some automorphism of  $F$ of order at most two, so that
$F$ of order at most two, so that  $G$ is the group of fixed points under an involution on the full automorphism group
$G$ is the group of fixed points under an involution on the full automorphism group  $\tilde{G}$ of the underlying
$\tilde{G}$ of the underlying  $F$-vector space
$F$-vector space  $V$. We similarly regard the Lie algebra of
$V$. We similarly regard the Lie algebra of  $G$ as the fixed points of an involution on
$G$ as the fixed points of an involution on  $A=\operatorname{End}_{F}(V)$. Note that, when
$A=\operatorname{End}_{F}(V)$. Note that, when  $\unicode[STIX]{x1D716}=1$ and the involution on
$\unicode[STIX]{x1D716}=1$ and the involution on  $F$ is trivial, we are working with the full orthogonal group; however, the set of semisimple characters for the full orthogonal group and for the special orthogonal group coincide.
$F$ is trivial, we are working with the full orthogonal group; however, the set of semisimple characters for the full orthogonal group and for the special orthogonal group coincide.
The starting point in the construction of semisimple characters is an algebraic combinatorial object, a so-called semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$. The principal data here are: an element
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$. The principal data here are: an element  $\unicode[STIX]{x1D6FD}\in A$ which generates a sum of field extensions
$\unicode[STIX]{x1D6FD}\in A$ which generates a sum of field extensions  $E=F[\unicode[STIX]{x1D6FD}]=\bigoplus _{i\in I}E_{i}$; and a rational point
$E=F[\unicode[STIX]{x1D6FD}]=\bigoplus _{i\in I}E_{i}$; and a rational point  $\unicode[STIX]{x1D6EC}$ in the (enlarged) Bruhat–Tits building of the centralizer of
$\unicode[STIX]{x1D6EC}$ in the (enlarged) Bruhat–Tits building of the centralizer of  $\unicode[STIX]{x1D6FD}$ in
$\unicode[STIX]{x1D6FD}$ in  $G$, which we think of as a lattice sequence in
$G$, which we think of as a lattice sequence in  $V$ (see [Reference Broussous and LemaireBL02]). Associated to
$V$ (see [Reference Broussous and LemaireBL02]). Associated to  $\unicode[STIX]{x1D6EC}$, we have a filtration
$\unicode[STIX]{x1D6EC}$, we have a filtration  $(\mathfrak{a}_{n})_{n\in \mathbb{Z}}$ of
$(\mathfrak{a}_{n})_{n\in \mathbb{Z}}$ of  $A$ (which is the Moy–Prasad filtration) and the integer
$A$ (which is the Moy–Prasad filtration) and the integer  $q$ is defined by
$q$ is defined by  $\unicode[STIX]{x1D6FD}\in \mathfrak{a}_{-q}\setminus \mathfrak{a}_{1-q}$; this is required to be positive. Finally,
$\unicode[STIX]{x1D6FD}\in \mathfrak{a}_{-q}\setminus \mathfrak{a}_{1-q}$; this is required to be positive. Finally,  $r$ is an integer between 0 and
$r$ is an integer between 0 and  $q$ which is small enough in the following approximate sense: the stratum
$q$ which is small enough in the following approximate sense: the stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ corresponds to the coset
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ corresponds to the coset  $\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r}$ and
$\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r}$ and  $r$ must be small enough so that the formal intertwining of the coset has a nice formula involving the centralizer of
$r$ must be small enough so that the formal intertwining of the coset has a nice formula involving the centralizer of  $\unicode[STIX]{x1D6FD}$. (See Section 6 for more details, and a precise definition.) A semisimple stratum
$\unicode[STIX]{x1D6FD}$. (See Section 6 for more details, and a precise definition.) A semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ as above splits according to the primitive idempotents
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ as above splits according to the primitive idempotents  $1^{i}$ of
$1^{i}$ of  $E$, giving simple strata
$E$, giving simple strata  $[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ in
$[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ in  $V^{i}=1^{i}V$, which are studied in [Reference Bushnell and KutzkoBK93]. In particular, a semisimple stratum is simple if and only if its indexing set
$V^{i}=1^{i}V$, which are studied in [Reference Bushnell and KutzkoBK93]. In particular, a semisimple stratum is simple if and only if its indexing set  $I$ has cardinality one.
$I$ has cardinality one.
Associated to any semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, and for any integer
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, and for any integer  $m\geqslant 0$, we have a family
$m\geqslant 0$, we have a family  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ of semisimple characters. We do not recall the definition here (see Section 9) but note only that, by applying the idempotents, we obtain from a semisimple character
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ of semisimple characters. We do not recall the definition here (see Section 9) but note only that, by applying the idempotents, we obtain from a semisimple character  $\unicode[STIX]{x1D703}$ a collection of simple characters
$\unicode[STIX]{x1D703}$ a collection of simple characters  $\unicode[STIX]{x1D703}_{i}$, for
$\unicode[STIX]{x1D703}_{i}$, for  $i\in I$. For simple characters, the fundamental rigidity property proved in [Reference Bushnell and KutzkoBK93] for lattice chains (that is, sequences without repetition), is the following:
$i\in I$. For simple characters, the fundamental rigidity property proved in [Reference Bushnell and KutzkoBK93] for lattice chains (that is, sequences without repetition), is the following:
Suppose  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ are simple characters which intertwine in
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ are simple characters which intertwine in  $\tilde{G}$. Then they are conjugate in the parahoric subgroup
$\tilde{G}$. Then they are conjugate in the parahoric subgroup  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
In the case of semisimple characters, this result is false as soon as  $\#I>1$: the essential reason is that one can have two lattice sequences (or even chains)
$\#I>1$: the essential reason is that one can have two lattice sequences (or even chains)  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ which are conjugate in
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ which are conjugate in  $\tilde{G}$ but such that the separate pieces
$\tilde{G}$ but such that the separate pieces  $\unicode[STIX]{x1D6EC}^{i},\unicode[STIX]{x1D6EC}^{\prime i}$ are not (all) conjugate in
$\unicode[STIX]{x1D6EC}^{i},\unicode[STIX]{x1D6EC}^{\prime i}$ are not (all) conjugate in  $\operatorname{Aut}_{F}(V^{i})$. Equivalently, there are points in the building of a proper Levi subgroup of
$\operatorname{Aut}_{F}(V^{i})$. Equivalently, there are points in the building of a proper Levi subgroup of  $\tilde{G}$ which are not conjugate under the Levi but are conjugate under
$\tilde{G}$ which are not conjugate under the Levi but are conjugate under  $\tilde{G}$. For similar reasons, the result would remain false if one weakened the conclusion to only conjugacy under
$\tilde{G}$. For similar reasons, the result would remain false if one weakened the conclusion to only conjugacy under  $\tilde{G}$. Thus one needs an extra condition to ensure that intertwining implies conjugacy. In order to describe this condition, we need a “matching theorem” for semisimple characters which intertwine:
$\tilde{G}$. Thus one needs an extra condition to ensure that intertwining implies conjugacy. In order to describe this condition, we need a “matching theorem” for semisimple characters which intertwine:
Theorem. (See Theorem 10.1) Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine in
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine in  $\tilde{G}$ and suppose that
$\tilde{G}$ and suppose that  $\unicode[STIX]{x1D6EC}$ and
$\unicode[STIX]{x1D6EC}$ and  $\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then there is a unique bijection
$\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then there is a unique bijection  $\unicode[STIX]{x1D701}$ between the index sets
$\unicode[STIX]{x1D701}$ between the index sets  $I$ and
$I$ and  $I^{\prime }$ such that the simple characters
$I^{\prime }$ such that the simple characters  $\unicode[STIX]{x1D703}_{i}$ and
$\unicode[STIX]{x1D703}_{i}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ are intertwined by an isomorphism in
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ are intertwined by an isomorphism in  $\operatorname{Hom}_{F}(V^{i},V^{\prime \unicode[STIX]{x1D701}(i)})$.
$\operatorname{Hom}_{F}(V^{i},V^{\prime \unicode[STIX]{x1D701}(i)})$.
This matching theorem allows us to describe a condition which is certainly necessary for conjugacy: if  $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$ as in the theorem are conjugate by an element of the parahoric subgroup
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$ as in the theorem are conjugate by an element of the parahoric subgroup  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ then, with
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ then, with  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ the matching given by the previous theorem, we have
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ the matching given by the previous theorem, we have
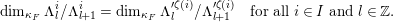 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}=\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{l}^{\prime \unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{l+1}^{\prime \unicode[STIX]{x1D701}(i)}\quad \text{for all}~i\in I~\text{and}~l\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}=\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{l}^{\prime \unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{l+1}^{\prime \unicode[STIX]{x1D701}(i)}\quad \text{for all}~i\in I~\text{and}~l\in \mathbb{Z}.\end{eqnarray}$$ Equivalently, the isomorphism in the theorem which intertwines the characters maps the point in the building corresponding to  $\unicode[STIX]{x1D6EC}^{i}$ to a point conjugate to the point corresponding to
$\unicode[STIX]{x1D6EC}^{i}$ to a point conjugate to the point corresponding to  $\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)}$. It turns out that this condition is also sufficient to obtain an “intertwining implies conjugacy” result:
$\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)}$. It turns out that this condition is also sufficient to obtain an “intertwining implies conjugacy” result:
Theorem. (See Theorem 10.2) Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine in
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine in  $\tilde{G}$, let
$\tilde{G}$, let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Theorem 10.1, and suppose that the condition (1.1) holds. Then
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Theorem 10.1, and suppose that the condition (1.1) holds. Then  $\unicode[STIX]{x1D703}$ is conjugate to
$\unicode[STIX]{x1D703}$ is conjugate to  $\unicode[STIX]{x1D703}^{\prime }$ by an element of
$\unicode[STIX]{x1D703}^{\prime }$ by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
Now we turn to our results for classical groups. Suppose that our underlying strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ are skew—that is,
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ are skew—that is,  $\unicode[STIX]{x1D6FD}$ is in the Lie algebra of
$\unicode[STIX]{x1D6FD}$ is in the Lie algebra of  $G$, the associated decomposition of
$G$, the associated decomposition of  $V$ is orthogonal with respect to the hermitian form, and
$V$ is orthogonal with respect to the hermitian form, and  $\unicode[STIX]{x1D6EC}$ is in the building of the centralizer in
$\unicode[STIX]{x1D6EC}$ is in the building of the centralizer in  $G$ of
$G$ of  $\unicode[STIX]{x1D6FD}$ (see [Reference Broussous and StevensBS09]). Our first main result here is a Skolem–Noether theorem for semisimple strata, which is crucial in the sequel [Reference Kurinczuk, Skodlerack and StevensKSS16].
$\unicode[STIX]{x1D6FD}$ (see [Reference Broussous and StevensBS09]). Our first main result here is a Skolem–Noether theorem for semisimple strata, which is crucial in the sequel [Reference Kurinczuk, Skodlerack and StevensKSS16].
Theorem. (See Theorem 7.12) Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata which intertwine in
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata which intertwine in  $G$, and suppose that
$G$, and suppose that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. Then, there is an element
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. Then, there is an element  $g\in G$ such that
$g\in G$ such that  $g\unicode[STIX]{x1D6FD}g^{-1}=\unicode[STIX]{x1D6FD}^{\prime }$.
$g\unicode[STIX]{x1D6FD}g^{-1}=\unicode[STIX]{x1D6FD}^{\prime }$.
Note that, for  $\unicode[STIX]{x1D6FD}$ as in the theorem, the number of
$\unicode[STIX]{x1D6FD}$ as in the theorem, the number of  $G$-orbits in the Lie algebra of
$G$-orbits in the Lie algebra of  $G$ with the same characteristic polynomial as
$G$ with the same characteristic polynomial as  $\unicode[STIX]{x1D6FD}$ is
$\unicode[STIX]{x1D6FD}$ is  $2^{\#I}$,
$2^{\#I}$,  $2^{\#I-1}$ or
$2^{\#I-1}$ or  $2^{\#I-2}$, depending on
$2^{\#I-2}$, depending on  $G$ and
$G$ and  $\unicode[STIX]{x1D6FD}$; thus some additional condition is certainly necessary to conclude that
$\unicode[STIX]{x1D6FD}$; thus some additional condition is certainly necessary to conclude that  $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }$ are conjugate.
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }$ are conjugate.
Given a skew-semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, the set
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, the set  ${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ of semisimple characters for
${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ of semisimple characters for  $G$ is obtained by restricting the semisimple characters in
$G$ is obtained by restricting the semisimple characters in  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Equivalently, one may just restrict those semisimple characters which are invariant under the involution defining
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Equivalently, one may just restrict those semisimple characters which are invariant under the involution defining  $G$. Our final result is an “intertwining implies conjugacy” theorem for semisimple characters for
$G$. Our final result is an “intertwining implies conjugacy” theorem for semisimple characters for  $G$.
$G$.
Theorem. (See Theorem 10.3) Let  $\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two semisimple characters of
$\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two semisimple characters of  $G$, which intertwine over
$G$, which intertwine over  $G$, and assume that their matching satisfies (1.1). Then,
$G$, and assume that their matching satisfies (1.1). Then,  $\unicode[STIX]{x1D703}_{-}$ and
$\unicode[STIX]{x1D703}_{-}$ and  $\unicode[STIX]{x1D703}_{-}^{\prime }$ are conjugate under
$\unicode[STIX]{x1D703}_{-}^{\prime }$ are conjugate under  $\operatorname{U}(\unicode[STIX]{x1D6EC})=\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap G$.
$\operatorname{U}(\unicode[STIX]{x1D6EC})=\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap G$.
This is the first step in an “intertwining implies conjugacy” result for cuspidal types proved in the sequel [Reference Kurinczuk, Skodlerack and StevensKSS16], which then completes the classification of cuspidal representations of  $G$.
$G$.
Let us say a few words about the proofs of these results, beginning with those for general linear groups. Since a semisimple character is defined in terms of a semisimple stratum underlying it, we must first prove similar results for strata. One major complication here is that, although a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ determines the associated splitting
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ determines the associated splitting  $V=\bigoplus _{i\in I}V^{i}$, since it comes from the idempotents of
$V=\bigoplus _{i\in I}V^{i}$, since it comes from the idempotents of  $E=F[\unicode[STIX]{x1D6FD}]$, one may have equivalent strata with different splittings.
$E=F[\unicode[STIX]{x1D6FD}]$, one may have equivalent strata with different splittings.
Thus we prove that, given two semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ which intertwine and such that
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ which intertwine and such that  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, there is a canonical matching between the index sets
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, there is a canonical matching between the index sets  $I,I^{\prime }$ of their splittings (see Proposition 7.1). The proof of this is by induction: when the strata are minimal (that is,
$I,I^{\prime }$ of their splittings (see Proposition 7.1). The proof of this is by induction: when the strata are minimal (that is,  $r=q-1$), we match the primary factors of the characteristic polynomials of the strata (see Definition 6.6), which are equal by intertwining. The inductive step requires a careful analysis of the derived strata of a semisimple stratum. As a consequence of this, one sees that if the initial strata are in fact equivalent, then there is an element of
$r=q-1$), we match the primary factors of the characteristic polynomials of the strata (see Definition 6.6), which are equal by intertwining. The inductive step requires a careful analysis of the derived strata of a semisimple stratum. As a consequence of this, one sees that if the initial strata are in fact equivalent, then there is an element of  $\tilde{G}$ which normalizes the (equivalence class of the) strata and conjugates the two splittings (see Lemma 7.18).
$\tilde{G}$ which normalizes the (equivalence class of the) strata and conjugates the two splittings (see Lemma 7.18).
As is the case for simple characters, the fact that a semisimple character does not determine the underlying stratum (even up to equivalence) presents additional difficulties. First, when we have a semisimple character  $\unicode[STIX]{x1D703}$ which can be defined relative to two different strata, we need a matching between their associated splittings, which is given by conjugation by an element of the normalizer of
$\unicode[STIX]{x1D703}$ which can be defined relative to two different strata, we need a matching between their associated splittings, which is given by conjugation by an element of the normalizer of  $\unicode[STIX]{x1D703}$ (see Proposition 9.9). The key result, which allows one to perform induction along defining sequences for semisimple characters, is an analogue of Bushnell–Kutzko’s “Translation Principle” for simple characters (see Theorem 9.16). A crucial step in this is to characterize when a stratum of the form
$\unicode[STIX]{x1D703}$ (see Proposition 9.9). The key result, which allows one to perform induction along defining sequences for semisimple characters, is an analogue of Bushnell–Kutzko’s “Translation Principle” for simple characters (see Theorem 9.16). A crucial step in this is to characterize when a stratum of the form  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple one (see Proposition 6.11). With these tools all to hand, we are able to prove the main matching and “intertwining implies conjugacy” theorems for semisimple characters.
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple one (see Proposition 6.11). With these tools all to hand, we are able to prove the main matching and “intertwining implies conjugacy” theorems for semisimple characters.
Now we pass our attention to the skew-semisimple case. We begin with an analysis of the Witt groups  $W_{\ast }(E)$ of finite field extensions
$W_{\ast }(E)$ of finite field extensions  $E$ of
$E$ of  $F$. Given a non-zero equivariant form
$F$. Given a non-zero equivariant form  $\unicode[STIX]{x1D706}:E\rightarrow F$, we get a trace map from
$\unicode[STIX]{x1D706}:E\rightarrow F$, we get a trace map from  $W_{\ast }(E)$ and
$W_{\ast }(E)$ and  $W_{\ast }(F)$ and it is the understanding of this map that allows us to make progress. In particular, the map takes hermitian
$W_{\ast }(F)$ and it is the understanding of this map that allows us to make progress. In particular, the map takes hermitian  $E$-spaces of maximal anisotropic dimension to hermitian
$E$-spaces of maximal anisotropic dimension to hermitian  $F$-spaces of maximal anisotropic dimension (see Theorem 4.4); moreover, outside the symplectic case the map is injective on spaces of a given dimension. One deduces from this that, again outside the symplectic case, when there is a self-dual embedding of a field extension
$F$-spaces of maximal anisotropic dimension (see Theorem 4.4); moreover, outside the symplectic case the map is injective on spaces of a given dimension. One deduces from this that, again outside the symplectic case, when there is a self-dual embedding of a field extension  $E$ into a hermitian
$E$ into a hermitian  $F$-space, it is unique up to conjugation. In the symplectic case, this is not true but we prove a Skolem–Noether for simple strata which intertwine (see Theorem 5.2); this is proved by using the strata to twist the symplectic form into orthogonal forms and then using a result on lifting approximate isometries.
$F$-space, it is unique up to conjugation. In the symplectic case, this is not true but we prove a Skolem–Noether for simple strata which intertwine (see Theorem 5.2); this is proved by using the strata to twist the symplectic form into orthogonal forms and then using a result on lifting approximate isometries.
With this to hand, the scheme of proof of “intertwining implies conjugacy” for skew-semisimple characters is formally very similar to the case of  $\tilde{G}$ described above, beginning with the strata and then proceeding to characters, but we must prove that the matchings obtained along the way give isometries between the spaces
$\tilde{G}$ described above, beginning with the strata and then proceeding to characters, but we must prove that the matchings obtained along the way give isometries between the spaces  $V^{i}$ (which are all hermitian spaces). In general the major difficulty occurs at the base step of an induction; for example, the base case of Proposition 7.10—that the matching for skew-semisimple strata which intertwine gives isometries—is proved using an idempotent lifting result.
$V^{i}$ (which are all hermitian spaces). In general the major difficulty occurs at the base step of an induction; for example, the base case of Proposition 7.10—that the matching for skew-semisimple strata which intertwine gives isometries—is proved using an idempotent lifting result.
We finish with a brief description of the organization of the paper. After setting up notation, we begin with some basic results on classical groups: in Section 3 we prove results on the lifting of approximate isometries in a hermitian space; in Section 4 we analyze the Witt groups  $W_{\ast }(E)$ of finite field extensions
$W_{\ast }(E)$ of finite field extensions  $E$ of
$E$ of  $F$ and trace-like maps from
$F$ and trace-like maps from  $W_{\ast }(E)$ to
$W_{\ast }(E)$ to  $W_{\ast }(F)$; and in Section 5 we prove the first Skolem–Noether result, for embeddings of a field (the simple case). Next we look at semisimple strata: in Section 6 we recall the definitions and some fundamental results; in Section 7 we prove that intertwining semisimple strata have a matching, and prove the Skolem–Noether theorem above; and in Section 8 we prove an intertwining implies conjugacy result for semisimple strata. Finally, we turn to semisimple characters: in Section 9 we recall the definitions and recall or prove many basic results, in particular the translation principles; and in Section 10 we prove the remaining main results.
$W_{\ast }(F)$; and in Section 5 we prove the first Skolem–Noether result, for embeddings of a field (the simple case). Next we look at semisimple strata: in Section 6 we recall the definitions and some fundamental results; in Section 7 we prove that intertwining semisimple strata have a matching, and prove the Skolem–Noether theorem above; and in Section 8 we prove an intertwining implies conjugacy result for semisimple strata. Finally, we turn to semisimple characters: in Section 9 we recall the definitions and recall or prove many basic results, in particular the translation principles; and in Section 10 we prove the remaining main results.
2 Notation
Let  $F$ be a non-archimedean local field of odd residual characteristic with valuation
$F$ be a non-archimedean local field of odd residual characteristic with valuation  $\unicode[STIX]{x1D708}_{F}$ and equipped with an involution
$\unicode[STIX]{x1D708}_{F}$ and equipped with an involution  $\unicode[STIX]{x1D70C}$ (which may be trivial) with fixed field
$\unicode[STIX]{x1D70C}$ (which may be trivial) with fixed field  $F_{0}$. We write
$F_{0}$. We write  $o_{F},\mathfrak{p}_{F}$ and
$o_{F},\mathfrak{p}_{F}$ and  $\unicode[STIX]{x1D705}_{F}$ for the valuation ring, its maximal ideal and the residue field of
$\unicode[STIX]{x1D705}_{F}$ for the valuation ring, its maximal ideal and the residue field of  $F$, respectively, and we assume that the image of the additive valuation
$F$, respectively, and we assume that the image of the additive valuation  $\unicode[STIX]{x1D708}:=\unicode[STIX]{x1D708}_{F}$ is
$\unicode[STIX]{x1D708}:=\unicode[STIX]{x1D708}_{F}$ is  $\mathbb{Z}\cup \{\infty \}$. We also denote by
$\mathbb{Z}\cup \{\infty \}$. We also denote by  $x\mapsto \bar{x}$ the reduction map
$x\mapsto \bar{x}$ the reduction map  $o_{F}{\twoheadrightarrow}\unicode[STIX]{x1D705}_{F}=o_{F}/\mathfrak{p}_{F}$. We fix a symmetric or skew-symmetric uniformizer
$o_{F}{\twoheadrightarrow}\unicode[STIX]{x1D705}_{F}=o_{F}/\mathfrak{p}_{F}$. We fix a symmetric or skew-symmetric uniformizer  $\unicode[STIX]{x1D71B}\in \mathfrak{p}_{F}\setminus \mathfrak{p}_{F}^{2}$: symmetric in the case
$\unicode[STIX]{x1D71B}\in \mathfrak{p}_{F}\setminus \mathfrak{p}_{F}^{2}$: symmetric in the case  $F/F_{0}$ is unramified and skew-symmetric otherwise. We use similar notation for other non-archimedean local fields. If
$F/F_{0}$ is unramified and skew-symmetric otherwise. We use similar notation for other non-archimedean local fields. If  $E|F$ is an algebraic field extension then we write
$E|F$ is an algebraic field extension then we write  $E^{ur}$ for the maximal unramified subextension of
$E^{ur}$ for the maximal unramified subextension of  $E|F$.
$E|F$.
Let  $h$ be an
$h$ be an  $\unicode[STIX]{x1D716}$-hermitian form (with
$\unicode[STIX]{x1D716}$-hermitian form (with  $\unicode[STIX]{x1D716}=\pm 1$) on an
$\unicode[STIX]{x1D716}=\pm 1$) on an  $F$-vector space
$F$-vector space  $V$ of finite dimension, that is, for all
$V$ of finite dimension, that is, for all  $v_{1},v_{2}\in V$ and
$v_{1},v_{2}\in V$ and  $x,y\in F$ the biadditive form
$x,y\in F$ the biadditive form  $h$ is non-degenerate and satisfies
$h$ is non-degenerate and satisfies
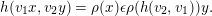 $$\begin{eqnarray}h(v_{1}x,v_{2}y)=\unicode[STIX]{x1D70C}(x)\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(h(v_{2},v_{1}))y.\end{eqnarray}$$
$$\begin{eqnarray}h(v_{1}x,v_{2}y)=\unicode[STIX]{x1D70C}(x)\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(h(v_{2},v_{1}))y.\end{eqnarray}$$ We denote the ring of  $F$-endomorphisms of
$F$-endomorphisms of  $V$ by
$V$ by  $A$ and its group of units
$A$ and its group of units  $A^{\times }$ by
$A^{\times }$ by  $\tilde{G}$. Let
$\tilde{G}$. Let  $G$ be the group of all elements
$G$ be the group of all elements  $g$ of
$g$ of  $\tilde{G}$ such that
$\tilde{G}$ such that  $h(gv_{1},gv_{2})$ is equal to
$h(gv_{1},gv_{2})$ is equal to  $h(v_{1},v_{2})$, for all vectors
$h(v_{1},v_{2})$, for all vectors  $v_{1},v_{2}$; this is the group of points of a reductive group over
$v_{1},v_{2}$; this is the group of points of a reductive group over  $F_{0}$, which is connected unless
$F_{0}$, which is connected unless  $F=F_{0}$ and
$F=F_{0}$ and  $\unicode[STIX]{x1D716}=+1$, in which case it is the full orthogonal group. Let
$\unicode[STIX]{x1D716}=+1$, in which case it is the full orthogonal group. Let  $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{h}$ be the adjoint anti-involution of
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{h}$ be the adjoint anti-involution of  $h$ on
$h$ on  $A$. For a
$A$. For a  $\unicode[STIX]{x1D70E}$-stable subset
$\unicode[STIX]{x1D70E}$-stable subset  $M$ of
$M$ of  $A$, we write
$A$, we write  $M_{+}$ for the set of symmetric elements and
$M_{+}$ for the set of symmetric elements and  $M_{-}$ for the set of skew-symmetric elements.
$M_{-}$ for the set of skew-symmetric elements.
An  $o_{F}$-lattice in
$o_{F}$-lattice in  $V$ is a free
$V$ is a free  $o_{F}$-module
$o_{F}$-module  $M$ of dimension
$M$ of dimension  $m$. The dual
$m$. The dual  $M^{\#}$ of
$M^{\#}$ of  $M$ with respect to
$M$ with respect to  $h$ is the set of all vectors
$h$ is the set of all vectors  $v$ of
$v$ of  $V$ such that
$V$ such that  $h(v,M)$ is a subset of
$h(v,M)$ is a subset of  $\mathfrak{p}_{F}$. A lattice sequence in
$\mathfrak{p}_{F}$. A lattice sequence in  $V$ is a map
$V$ is a map  $\unicode[STIX]{x1D6EC}$ from
$\unicode[STIX]{x1D6EC}$ from  $\mathbb{Z}$ to the set of
$\mathbb{Z}$ to the set of  $o_{F}$-lattices of
$o_{F}$-lattices of  $V$ satisfying:
$V$ satisfying:
(i)
 $\unicode[STIX]{x1D6EC}_{s}\subseteq \unicode[STIX]{x1D6EC}_{t}$, for all integers
$\unicode[STIX]{x1D6EC}_{s}\subseteq \unicode[STIX]{x1D6EC}_{t}$, for all integers  $s>t$; and
$s>t$; and(ii)
 $\unicode[STIX]{x1D6EC}_{s}\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D6EC}_{s+e}$ for some (unique) integer
$\unicode[STIX]{x1D6EC}_{s}\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D6EC}_{s+e}$ for some (unique) integer  $e$ and all integers
$e$ and all integers  $s$.
$s$.
We call  $e=:e(\unicode[STIX]{x1D6EC}|o_{F})$ the
$e=:e(\unicode[STIX]{x1D6EC}|o_{F})$ the  $o_{F}$-period of
$o_{F}$-period of  $\unicode[STIX]{x1D6EC}$. An injective lattice sequence is called a lattice chain. For each integer
$\unicode[STIX]{x1D6EC}$. An injective lattice sequence is called a lattice chain. For each integer  $s$, we denote by
$s$, we denote by  $x\mapsto \bar{x}$ the reduction map
$x\mapsto \bar{x}$ the reduction map  $\unicode[STIX]{x1D6EC}_{s}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{s}/\unicode[STIX]{x1D6EC}_{s+1}$. A lattice sequence
$\unicode[STIX]{x1D6EC}_{s}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{s}/\unicode[STIX]{x1D6EC}_{s+1}$. A lattice sequence  $\unicode[STIX]{x1D6EC}$ is called self-dual if there is an integer
$\unicode[STIX]{x1D6EC}$ is called self-dual if there is an integer  $u$ such that
$u$ such that  $(\unicode[STIX]{x1D6EC}_{s})^{\#}=\unicode[STIX]{x1D6EC}_{u-s}$.
$(\unicode[STIX]{x1D6EC}_{s})^{\#}=\unicode[STIX]{x1D6EC}_{u-s}$.
As usual, a lattice sequence  $\unicode[STIX]{x1D6EC}$ determines the following filtrations of
$\unicode[STIX]{x1D6EC}$ determines the following filtrations of  $A$ and
$A$ and  $A_{-}$ (if
$A_{-}$ (if  $\unicode[STIX]{x1D6EC}$ is self-dual):
$\unicode[STIX]{x1D6EC}$ is self-dual):  $\mathfrak{a}_{i}(\unicode[STIX]{x1D6EC})$ is the set of all elements of
$\mathfrak{a}_{i}(\unicode[STIX]{x1D6EC})$ is the set of all elements of  $A$ which map
$A$ which map  $\unicode[STIX]{x1D6EC}_{s}$ into
$\unicode[STIX]{x1D6EC}_{s}$ into  $\unicode[STIX]{x1D6EC}_{s+i}$ for all integers
$\unicode[STIX]{x1D6EC}_{s+i}$ for all integers  $s$ and
$s$ and  $\mathfrak{a}_{i,-}(\unicode[STIX]{x1D6EC})$ is the intersection of
$\mathfrak{a}_{i,-}(\unicode[STIX]{x1D6EC})$ is the intersection of  $\mathfrak{a}_{i}(\unicode[STIX]{x1D6EC})$ with
$\mathfrak{a}_{i}(\unicode[STIX]{x1D6EC})$ with  $A_{-}$. We skip the argument
$A_{-}$. We skip the argument  $\unicode[STIX]{x1D6EC}$ if there is no cause of confusion and we write
$\unicode[STIX]{x1D6EC}$ if there is no cause of confusion and we write  $\mathfrak{a}_{i}^{\prime }$ if there is a second lattice sequence
$\mathfrak{a}_{i}^{\prime }$ if there is a second lattice sequence  $\unicode[STIX]{x1D6EC}^{\prime }$ given.
$\unicode[STIX]{x1D6EC}^{\prime }$ given.
The sequence  $\unicode[STIX]{x1D6EC}$ also induces filtrations on
$\unicode[STIX]{x1D6EC}$ also induces filtrations on  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}):=\mathfrak{a}_{0}^{\times }$ by
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}):=\mathfrak{a}_{0}^{\times }$ by  $\tilde{\operatorname{U}}^{i}(\unicode[STIX]{x1D6EC})=1+\mathfrak{a}_{i}$ and, when
$\tilde{\operatorname{U}}^{i}(\unicode[STIX]{x1D6EC})=1+\mathfrak{a}_{i}$ and, when  $\unicode[STIX]{x1D6EC}$ is self-dual, on
$\unicode[STIX]{x1D6EC}$ is self-dual, on  $\operatorname{U}(\unicode[STIX]{x1D6EC}):=\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap G$ by
$\operatorname{U}(\unicode[STIX]{x1D6EC}):=\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap G$ by  $\operatorname{U}^{i}(\unicode[STIX]{x1D6EC})=\tilde{\operatorname{U}}^{i}(\unicode[STIX]{x1D6EC})\cap G$ for
$\operatorname{U}^{i}(\unicode[STIX]{x1D6EC})=\tilde{\operatorname{U}}^{i}(\unicode[STIX]{x1D6EC})\cap G$ for  $i\in \mathbb{N}$. The filtration on
$i\in \mathbb{N}$. The filtration on  $A$ defines a “valuation map”
$A$ defines a “valuation map”  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}$ as follows: for
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}$ as follows: for  $\unicode[STIX]{x1D6FD}\in A$, we put
$\unicode[STIX]{x1D6FD}\in A$, we put  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=\sup \{i\mid \unicode[STIX]{x1D6FD}\in \mathfrak{a}_{i}\}$, an integer or
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=\sup \{i\mid \unicode[STIX]{x1D6FD}\in \mathfrak{a}_{i}\}$, an integer or  $\infty$. The normalizer
$\infty$. The normalizer  $\mathfrak{n}(\unicode[STIX]{x1D6EC})$ of
$\mathfrak{n}(\unicode[STIX]{x1D6EC})$ of  $\unicode[STIX]{x1D6EC}$ is the set of elements
$\unicode[STIX]{x1D6EC}$ is the set of elements  $g\in A^{\times }$ such that
$g\in A^{\times }$ such that  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(g^{-1})=-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(g)$.
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(g^{-1})=-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(g)$.
The translation of  $\unicode[STIX]{x1D6EC}$ by
$\unicode[STIX]{x1D6EC}$ by  $s\in \mathbb{Z}$ is the lattice sequence
$s\in \mathbb{Z}$ is the lattice sequence  $(\unicode[STIX]{x1D6EC}+s)_{i}:=\unicode[STIX]{x1D6EC}_{i-s}$, and we define the direct sum
$(\unicode[STIX]{x1D6EC}+s)_{i}:=\unicode[STIX]{x1D6EC}_{i-s}$, and we define the direct sum  $\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\prime }$ of two lattice sequences
$\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\prime }$ of two lattice sequences  $\unicode[STIX]{x1D6EC}$ and
$\unicode[STIX]{x1D6EC}$ and  $\unicode[STIX]{x1D6EC}^{\prime }$ of the same period as
$\unicode[STIX]{x1D6EC}^{\prime }$ of the same period as  $(\unicode[STIX]{x1D6EC}_{j}\oplus \unicode[STIX]{x1D6EC}_{j}^{\prime })_{j\in \operatorname{Z}}$. The lattice sequence
$(\unicode[STIX]{x1D6EC}_{j}\oplus \unicode[STIX]{x1D6EC}_{j}^{\prime })_{j\in \operatorname{Z}}$. The lattice sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\oplus (\unicode[STIX]{x1D6EC}+1)\oplus \cdots \oplus (\unicode[STIX]{x1D6EC}+e(\unicode[STIX]{x1D6EC}|o_{F})-1)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\oplus (\unicode[STIX]{x1D6EC}+1)\oplus \cdots \oplus (\unicode[STIX]{x1D6EC}+e(\unicode[STIX]{x1D6EC}|o_{F})-1)\end{eqnarray}$$ is always a lattice chain. By this construction, many theorems in [Reference Bushnell and KutzkoBK93] proven for lattice chains are valid for lattice sequences (cf. [Reference StevensSte05], and also [Reference Kurinczuk and StevensKS15], where this is called a  $\dagger$-construction). If this is the case, or the proof of a result for lattice chains is valid for lattice sequences without change, then, in the following, we just refer to the statement for lattice chains.
$\dagger$-construction). If this is the case, or the proof of a result for lattice chains is valid for lattice sequences without change, then, in the following, we just refer to the statement for lattice chains.
Finally, for  $x$ a real number, we denote by
$x$ a real number, we denote by  $\lfloor x\rfloor$ the greatest integer not greater than
$\lfloor x\rfloor$ the greatest integer not greater than  $x$.
$x$.
3 Lifting isometries
The isomorphism type of the hermitian space  $(V,h)$ is encoded in any self-dual lattice sequence of
$(V,h)$ is encoded in any self-dual lattice sequence of  $V$, as explained in this section. The main results are Proposition 3.1 and Corollary 3.2, which explain how an approximate isometry (for example, one which induces an isometry at the level of residue fields) can be lifted to a genuine isometry. Let us state the main proposition:
$V$, as explained in this section. The main results are Proposition 3.1 and Corollary 3.2, which explain how an approximate isometry (for example, one which induces an isometry at the level of residue fields) can be lifted to a genuine isometry. Let us state the main proposition:
Proposition 3.1. Let  $F|F^{\prime }$ be a finite field extension. Suppose we are given two finite-dimensional
$F|F^{\prime }$ be a finite field extension. Suppose we are given two finite-dimensional  $\unicode[STIX]{x1D716}$-hermitian spaces
$\unicode[STIX]{x1D716}$-hermitian spaces  $(V,h)$ and
$(V,h)$ and  $(V^{\prime },h^{\prime })$ with respect to
$(V^{\prime },h^{\prime })$ with respect to  $(F,\unicode[STIX]{x1D70C})$, an
$(F,\unicode[STIX]{x1D70C})$, an  $F^{\prime }$-linear isomorphism
$F^{\prime }$-linear isomorphism  $f:V\rightarrow V^{\prime }$ and two self-dual
$f:V\rightarrow V^{\prime }$ and two self-dual  $o_{F}$-lattice sequences
$o_{F}$-lattice sequences  $\unicode[STIX]{x1D6EC}$ and
$\unicode[STIX]{x1D6EC}$ and  $\unicode[STIX]{x1D6EC}^{\prime }$ of
$\unicode[STIX]{x1D6EC}^{\prime }$ of  $(V,h)$ and
$(V,h)$ and  $(V^{\prime },h^{\prime })$, respectively, such that, for all
$(V^{\prime },h^{\prime })$, respectively, such that, for all  $i\in \mathbb{Z}$,
$i\in \mathbb{Z}$,
∙
 $f(\unicode[STIX]{x1D6EC}_{i})=\unicode[STIX]{x1D6EC}_{i}^{\prime }$,
$f(\unicode[STIX]{x1D6EC}_{i})=\unicode[STIX]{x1D6EC}_{i}^{\prime }$,∙
 $f((\unicode[STIX]{x1D6EC}_{i})^{\#})=f(\unicode[STIX]{x1D6EC}_{i})^{\#}$,
$f((\unicode[STIX]{x1D6EC}_{i})^{\#})=f(\unicode[STIX]{x1D6EC}_{i})^{\#}$,∙
 $\overline{h^{\prime }(f(v),f(w))}=\overline{h(v,w)}\in \unicode[STIX]{x1D705}_{F}$, for all
$\overline{h^{\prime }(f(v),f(w))}=\overline{h(v,w)}\in \unicode[STIX]{x1D705}_{F}$, for all  $v\in \unicode[STIX]{x1D6EC}_{i}$,
$v\in \unicode[STIX]{x1D6EC}_{i}$,  $w\in (\unicode[STIX]{x1D6EC}_{i+1})^{\#}$ and
$w\in (\unicode[STIX]{x1D6EC}_{i+1})^{\#}$ and∙
 $\overline{f(vx)}=\overline{f(v)x}\in \unicode[STIX]{x1D6EC}_{i+e(\unicode[STIX]{x1D6EC}^{\prime }|o_{F})\unicode[STIX]{x1D708}_{F}(x)}^{\prime }/\unicode[STIX]{x1D6EC}_{1+i+e(\unicode[STIX]{x1D6EC}^{\prime }|o_{F})\unicode[STIX]{x1D708}_{F}(x)}^{\prime }$, for all
$\overline{f(vx)}=\overline{f(v)x}\in \unicode[STIX]{x1D6EC}_{i+e(\unicode[STIX]{x1D6EC}^{\prime }|o_{F})\unicode[STIX]{x1D708}_{F}(x)}^{\prime }/\unicode[STIX]{x1D6EC}_{1+i+e(\unicode[STIX]{x1D6EC}^{\prime }|o_{F})\unicode[STIX]{x1D708}_{F}(x)}^{\prime }$, for all  $v\in \unicode[STIX]{x1D6EC}_{i}$,
$v\in \unicode[STIX]{x1D6EC}_{i}$,  $x\in F^{\times }$.
$x\in F^{\times }$.
Then there is an  $F$-linear isometry
$F$-linear isometry  $g$ from
$g$ from  $(V,h)$ to
$(V,h)$ to  $(V^{\prime },h^{\prime })$ mapping
$(V^{\prime },h^{\prime })$ mapping  $\unicode[STIX]{x1D6EC}$ to
$\unicode[STIX]{x1D6EC}$ to  $\unicode[STIX]{x1D6EC}^{\prime }$ such that
$\unicode[STIX]{x1D6EC}^{\prime }$ such that  $(f-g)(\unicode[STIX]{x1D6EC}_{i})\subseteq \unicode[STIX]{x1D6EC}_{i+1}^{\prime }$ for all integers
$(f-g)(\unicode[STIX]{x1D6EC}_{i})\subseteq \unicode[STIX]{x1D6EC}_{i+1}^{\prime }$ for all integers  $i$.
$i$.
Later it will be useful to have a stronger approximation statement. For that we introduce a generalization of the adjoint anti-involution. For two finite-dimensional  $\unicode[STIX]{x1D716}$-hermitian spaces
$\unicode[STIX]{x1D716}$-hermitian spaces  $(V,h)$ and
$(V,h)$ and  $(V^{\prime },h^{\prime })$ with respect to
$(V^{\prime },h^{\prime })$ with respect to  $(F,\unicode[STIX]{x1D70C})$ there is a map
$(F,\unicode[STIX]{x1D70C})$ there is a map  $\unicode[STIX]{x1D70E}_{h,h^{\prime }}$ from
$\unicode[STIX]{x1D70E}_{h,h^{\prime }}$ from  $\operatorname{Hom}_{F}(V,V^{\prime })$ to
$\operatorname{Hom}_{F}(V,V^{\prime })$ to  $\operatorname{Hom}_{F}(V^{\prime },V)$ defined, for
$\operatorname{Hom}_{F}(V^{\prime },V)$ defined, for  $f\in \operatorname{Hom}_{F}(V,V^{\prime })$, by the equation
$f\in \operatorname{Hom}_{F}(V,V^{\prime })$, by the equation
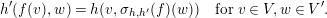 $$\begin{eqnarray}h^{\prime }(f(v),w)=h(v,\unicode[STIX]{x1D70E}_{h,h^{\prime }}(f)(w))\quad \text{for}~v\in V,w\in V^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}h^{\prime }(f(v),w)=h(v,\unicode[STIX]{x1D70E}_{h,h^{\prime }}(f)(w))\quad \text{for}~v\in V,w\in V^{\prime }.\end{eqnarray}$$Corollary 3.2. Let  $(V^{1},h_{1})$ and
$(V^{1},h_{1})$ and  $(V^{2},h_{2})$ be two
$(V^{2},h_{2})$ be two  $\unicode[STIX]{x1D716}$-hermitian spaces over
$\unicode[STIX]{x1D716}$-hermitian spaces over  $F$ (for the same
$F$ (for the same  $\unicode[STIX]{x1D716}$), let
$\unicode[STIX]{x1D716}$), let  $\unicode[STIX]{x1D6EC}^{1}$ be a self-dual lattice sequence and let
$\unicode[STIX]{x1D6EC}^{1}$ be a self-dual lattice sequence and let  $f:V^{1}\rightarrow V^{2}$ be an
$f:V^{1}\rightarrow V^{2}$ be an  $F$-linear isomorphism such that
$F$-linear isomorphism such that  $\unicode[STIX]{x1D6EC}^{2}:=f(\unicode[STIX]{x1D6EC}^{1})$ is self-dual. Suppose
$\unicode[STIX]{x1D6EC}^{2}:=f(\unicode[STIX]{x1D6EC}^{1})$ is self-dual. Suppose  $U_{i}$ is a closed subgroup of
$U_{i}$ is a closed subgroup of  $\tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}^{i})$ which is invariant under
$\tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}^{i})$ which is invariant under  $\unicode[STIX]{x1D70E}_{h_{i}}$ for
$\unicode[STIX]{x1D70E}_{h_{i}}$ for  $i=1,2$, such that
$i=1,2$, such that  $\unicode[STIX]{x1D70E}_{h_{1},h_{2}}(f)\in U_{1}f^{-1}U_{2}$. Then there is an isometry from
$\unicode[STIX]{x1D70E}_{h_{1},h_{2}}(f)\in U_{1}f^{-1}U_{2}$. Then there is an isometry from  $(V^{1},h_{1})$ to
$(V^{1},h_{1})$ to  $(V^{2},h_{2})$ contained in
$(V^{2},h_{2})$ contained in  $U_{2}fU_{1}$.
$U_{2}fU_{1}$.
Proof. The  $\unicode[STIX]{x1D716}$-hermitian spaces
$\unicode[STIX]{x1D716}$-hermitian spaces  $(V_{1},h_{1})$ and
$(V_{1},h_{1})$ and  $(V_{2},h_{2})$ are isometric by a map which sends
$(V_{2},h_{2})$ are isometric by a map which sends  $\unicode[STIX]{x1D6EC}^{1}$ to
$\unicode[STIX]{x1D6EC}^{1}$ to  $\unicode[STIX]{x1D6EC}^{2}$, by Proposition 3.1. Thus we can restrict to the case where
$\unicode[STIX]{x1D6EC}^{2}$, by Proposition 3.1. Thus we can restrict to the case where  $(V_{1},h_{1})=(V_{2},h_{2})=:(V,h)$ and
$(V_{1},h_{1})=(V_{2},h_{2})=:(V,h)$ and  $\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6EC}_{2}=\unicode[STIX]{x1D6EC}$. By assumption, the double coset
$\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6EC}_{2}=\unicode[STIX]{x1D6EC}$. By assumption, the double coset  $U_{2}fU_{1}$ is invariant under the automorphism
$U_{2}fU_{1}$ is invariant under the automorphism  $g\mapsto \unicode[STIX]{x1D70E}_{h}(g^{-1})$, and this double coset thus has a fixed point, by [Reference Kurinczuk and StevensKS15, 2.7(ii)(a)] and [Reference StevensSte01a, 2.2].◻
$g\mapsto \unicode[STIX]{x1D70E}_{h}(g^{-1})$, and this double coset thus has a fixed point, by [Reference Kurinczuk and StevensKS15, 2.7(ii)(a)] and [Reference StevensSte01a, 2.2].◻
We need a sequence of lemmas to prove Proposition 3.1.
Lemma 3.3. Suppose that  $\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period
$\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period  $1$ such that
$1$ such that  $\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{1}$. Consider the form
$\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{1}$. Consider the form
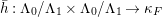 $$\begin{eqnarray}\bar{h}:\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}_{F}\end{eqnarray}$$
$$\begin{eqnarray}\bar{h}:\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}_{F}\end{eqnarray}$$ defined by  $\bar{h}(\bar{v},\bar{w})=\overline{h(v,w)}$. Then every Witt basis of
$\bar{h}(\bar{v},\bar{w})=\overline{h(v,w)}$. Then every Witt basis of  $(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$ lifts to a Witt basis of
$(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$ lifts to a Witt basis of  $(V,h)$ contained in
$(V,h)$ contained in  $\unicode[STIX]{x1D6EC}_{0}$, under the projection
$\unicode[STIX]{x1D6EC}_{0}$, under the projection  $\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$.
$\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$.
Proof. Let  ${\mathcal{B}}$ be a Witt basis of
${\mathcal{B}}$ be a Witt basis of  $\bar{h}$. We have
$\bar{h}$. We have
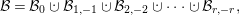
where  ${\mathcal{B}}_{i,-i}$ spans a hyperbolic plane,
${\mathcal{B}}_{i,-i}$ spans a hyperbolic plane,  ${\mathcal{B}}_{0}$ spans an anisotropic space, and all these spaces are pairwise orthogonal to each other in
${\mathcal{B}}_{0}$ spans an anisotropic space, and all these spaces are pairwise orthogonal to each other in  $\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$. Further we have a decomposition
$\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$. Further we have a decomposition
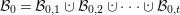
into pairwise orthogonal sets of cardinality one. Take an arbitrary lift  ${\mathcal{B}}^{\prime (0)}$ of
${\mathcal{B}}^{\prime (0)}$ of  ${\mathcal{B}}$ to
${\mathcal{B}}$ to  $\unicode[STIX]{x1D6EC}_{0}$; for an element
$\unicode[STIX]{x1D6EC}_{0}$; for an element  $\bar{v}\in {\mathcal{B}}$, we write
$\bar{v}\in {\mathcal{B}}$, we write  $v\in {\mathcal{B}}^{\prime (0)}$ for its lift.
$v\in {\mathcal{B}}^{\prime (0)}$ for its lift.
Step 1. Consider  ${\mathcal{B}}_{0,1}=\{\bar{v}_{0}\}$; put
${\mathcal{B}}_{0,1}=\{\bar{v}_{0}\}$; put  $W:=v_{0}^{\bot }$ and define
$W:=v_{0}^{\bot }$ and define
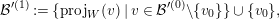 $$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\{\operatorname{proj}_{W}(v)\mid v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{0}\}\}\cup \{v_{0}\},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\{\operatorname{proj}_{W}(v)\mid v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{0}\}\}\cup \{v_{0}\},\end{eqnarray}$$ where  $\operatorname{proj}_{W}$ denotes the orthogonal projection onto
$\operatorname{proj}_{W}$ denotes the orthogonal projection onto  $W$. We recall the formula
$W$. We recall the formula
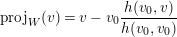 $$\begin{eqnarray}\operatorname{proj}_{W}(v)=v-v_{0}\frac{h(v_{0},v)}{h(v_{0},v_{0})}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{proj}_{W}(v)=v-v_{0}\frac{h(v_{0},v)}{h(v_{0},v_{0})}\end{eqnarray}$$ and conclude that  $\overline{h(\operatorname{proj}_{W}(v),\operatorname{proj}_{W}(v^{\prime }))}$ is equal to
$\overline{h(\operatorname{proj}_{W}(v),\operatorname{proj}_{W}(v^{\prime }))}$ is equal to
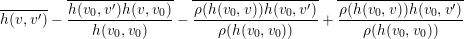 $$\begin{eqnarray}\overline{h(v,v^{\prime })}-\overline{\frac{h(v_{0},v^{\prime })h(v,v_{0})}{h(v_{0},v_{0})}}-\overline{\frac{\unicode[STIX]{x1D70C}(h(v_{0},v))h(v_{0},v^{\prime })}{\unicode[STIX]{x1D70C}(h(v_{0},v_{0}))}}+\overline{\frac{\unicode[STIX]{x1D70C}(h(v_{0},v))h(v_{0},v^{\prime })}{\unicode[STIX]{x1D70C}(h(v_{0},v_{0}))}}\end{eqnarray}$$
$$\begin{eqnarray}\overline{h(v,v^{\prime })}-\overline{\frac{h(v_{0},v^{\prime })h(v,v_{0})}{h(v_{0},v_{0})}}-\overline{\frac{\unicode[STIX]{x1D70C}(h(v_{0},v))h(v_{0},v^{\prime })}{\unicode[STIX]{x1D70C}(h(v_{0},v_{0}))}}+\overline{\frac{\unicode[STIX]{x1D70C}(h(v_{0},v))h(v_{0},v^{\prime })}{\unicode[STIX]{x1D70C}(h(v_{0},v_{0}))}}\end{eqnarray}$$ and therefore equal to  $\overline{h(v,v^{\prime })}$ for all
$\overline{h(v,v^{\prime })}$ for all  $v,v^{\prime }\in B^{\prime (0)}\setminus \{v_{0}\}$. Thus, replacing
$v,v^{\prime }\in B^{\prime (0)}\setminus \{v_{0}\}$. Thus, replacing  $(V,h)$ by
$(V,h)$ by  $(W,h_{|W})$ and
$(W,h_{|W})$ and  $\unicode[STIX]{x1D6EC}$ by its intersection with
$\unicode[STIX]{x1D6EC}$ by its intersection with  $W$ and then repeating, we can assume that
$W$ and then repeating, we can assume that  ${\mathcal{B}}_{0}$ is empty.
${\mathcal{B}}_{0}$ is empty.
Step 2. Consider  ${\mathcal{B}}_{1,-1}=\{\bar{v}_{1},\bar{v}_{-1}\}$ and define now
${\mathcal{B}}_{1,-1}=\{\bar{v}_{1},\bar{v}_{-1}\}$ and define now  $W:=\{v_{1},v_{-1}\}\text{}^{\bot }$. Then, as in Step 1, elements
$W:=\{v_{1},v_{-1}\}\text{}^{\bot }$. Then, as in Step 1, elements  $v$ and
$v$ and  $v^{\prime }$ of
$v^{\prime }$ of
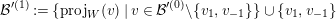 $$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\{\operatorname{proj}_{W}(v)\mid v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{1},v_{-1}\}\}\cup \{v_{1},v_{-1}\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\{\operatorname{proj}_{W}(v)\mid v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{1},v_{-1}\}\}\cup \{v_{1},v_{-1}\}\end{eqnarray}$$ satisfy  $\overline{h(\operatorname{proj}_{w}(v),\operatorname{proj}_{W}(v^{\prime }))}=\overline{h(v,v^{\prime })}$, because if
$\overline{h(\operatorname{proj}_{w}(v),\operatorname{proj}_{W}(v^{\prime }))}=\overline{h(v,v^{\prime })}$, because if  $v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{1},v_{-1}\}$ then
$v\in {\mathcal{B}}^{\prime (0)}\setminus \{v_{1},v_{-1}\}$ then
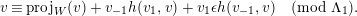 $$\begin{eqnarray}v\equiv \operatorname{proj}_{W}(v)+v_{-1}h(v_{1},v)+v_{1}\unicode[STIX]{x1D716}h(v_{-1},v)\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6EC}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}v\equiv \operatorname{proj}_{W}(v)+v_{-1}h(v_{1},v)+v_{1}\unicode[STIX]{x1D716}h(v_{-1},v)\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6EC}_{1}).\end{eqnarray}$$ Thus we have reduced to the hyperbolic case that  ${\mathcal{B}}$ is equal to
${\mathcal{B}}$ is equal to  ${\mathcal{B}}_{1,-1}$.
${\mathcal{B}}_{1,-1}$.
Step 3. We have  ${\mathcal{B}}={\mathcal{B}}_{1,-1}=\{\bar{v}_{1},\bar{v}_{-1}\}$. The sequence
${\mathcal{B}}={\mathcal{B}}_{1,-1}=\{\bar{v}_{1},\bar{v}_{-1}\}$. The sequence  $(w_{i})_{i\geqslant 1}$, defined by
$(w_{i})_{i\geqslant 1}$, defined by  $w_{1}:=v_{1}$ and
$w_{1}:=v_{1}$ and
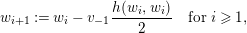 $$\begin{eqnarray}w_{i+1}:=w_{i}-v_{-1}\frac{h(w_{i},w_{i})}{2}\quad \text{for}~i\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}w_{i+1}:=w_{i}-v_{-1}\frac{h(w_{i},w_{i})}{2}\quad \text{for}~i\geqslant 1,\end{eqnarray}$$ has a limit  $v_{1}^{\prime }$ which satisfies
$v_{1}^{\prime }$ which satisfies  $h(v_{1}^{\prime },v_{1}^{\prime })=0$ and
$h(v_{1}^{\prime },v_{1}^{\prime })=0$ and  $\bar{v}_{1}^{\prime }=\bar{v}_{1}$, and analogously we find
$\bar{v}_{1}^{\prime }=\bar{v}_{1}$, and analogously we find  $v_{-1}^{\prime }$ with similar properties. Then
$v_{-1}^{\prime }$ with similar properties. Then
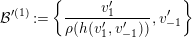 $$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\left\{\frac{v_{1}^{\prime }}{\unicode[STIX]{x1D70C}(h(v_{1}^{\prime },v_{-1}^{\prime }))},v_{-1}^{\prime }\right\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}^{\prime (1)}:=\left\{\frac{v_{1}^{\prime }}{\unicode[STIX]{x1D70C}(h(v_{1}^{\prime },v_{-1}^{\prime }))},v_{-1}^{\prime }\right\}\end{eqnarray}$$ is a Witt basis of  $V$ which lifts
$V$ which lifts  ${\mathcal{B}}$.◻
${\mathcal{B}}$.◻
Lemma 3.4. Suppose that  $\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period
$\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period  $1$ such that
$1$ such that  $\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$. Consider the form
$\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$. Consider the form
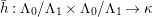 $$\begin{eqnarray}\bar{h}:\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}\end{eqnarray}$$
$$\begin{eqnarray}\bar{h}:\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}\end{eqnarray}$$ defined by  $\bar{h}(\bar{v},\bar{w})=\overline{h(v,w)\unicode[STIX]{x1D71B}^{-1}}$. For every Witt basis
$\bar{h}(\bar{v},\bar{w})=\overline{h(v,w)\unicode[STIX]{x1D71B}^{-1}}$. For every Witt basis  of
of  $(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$, with isotropic parts
$(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$, with isotropic parts  ${\mathcal{B}}^{-}$ and
${\mathcal{B}}^{-}$ and  ${\mathcal{B}}^{+}$ and anisotropic part
${\mathcal{B}}^{+}$ and anisotropic part  ${\mathcal{B}}_{0}$, there is a Witt basis
${\mathcal{B}}_{0}$, there is a Witt basis  contained in
contained in  $\unicode[STIX]{x1D6EC}_{-1}$ of
$\unicode[STIX]{x1D6EC}_{-1}$ of  $(V,h)$ such that
$(V,h)$ such that  ${\mathcal{B}}_{0}^{\prime },{\mathcal{B}}^{\prime +}$ and
${\mathcal{B}}_{0}^{\prime },{\mathcal{B}}^{\prime +}$ and  ${\mathcal{B}}^{\prime -}\unicode[STIX]{x1D71B}$ are lifts of
${\mathcal{B}}^{\prime -}\unicode[STIX]{x1D71B}$ are lifts of  ${\mathcal{B}}_{0}$,
${\mathcal{B}}_{0}$,  ${\mathcal{B}}^{+}$ and
${\mathcal{B}}^{+}$ and  ${\mathcal{B}}^{-}$ under the projection
${\mathcal{B}}^{-}$ under the projection  $\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$, respectively.
$\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$, respectively.
Here we explicitly make use of the fact that  $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D71B})\in \{\unicode[STIX]{x1D71B},-\unicode[STIX]{x1D71B}\}$.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D71B})\in \{\unicode[STIX]{x1D71B},-\unicode[STIX]{x1D71B}\}$.
Proof. This follows directly from Lemma 3.3 if we substitute  $h$ by
$h$ by  $h\unicode[STIX]{x1D71B}^{-1}$. ◻
$h\unicode[STIX]{x1D71B}^{-1}$. ◻
We need a third base case for period 2.
Lemma 3.5. Suppose that  $\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period
$\unicode[STIX]{x1D6EC}$ is a self-dual lattice chain of period  $2$ such that
$2$ such that  $\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$. Then
$\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$. Then  $h$ has anisotropic dimension zero and for any basis
$h$ has anisotropic dimension zero and for any basis  ${\mathcal{B}}_{0}$ of
${\mathcal{B}}_{0}$ of  $\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$ there is a Witt basis for
$\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$ there is a Witt basis for  $h$,
$h$,
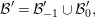 $$\begin{eqnarray}{\mathcal{B}}^{\prime }={\mathcal{B}}_{-1}^{\prime }\cup {\mathcal{B}}_{0}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}^{\prime }={\mathcal{B}}_{-1}^{\prime }\cup {\mathcal{B}}_{0}^{\prime },\end{eqnarray}$$ such that  ${\mathcal{B}}_{i}^{\prime }$ is a subset of
${\mathcal{B}}_{i}^{\prime }$ is a subset of  $\unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1}$ for all
$\unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1}$ for all  $i$ and such that
$i$ and such that  ${\mathcal{B}}_{0}^{\prime }$ is a lift of
${\mathcal{B}}_{0}^{\prime }$ is a lift of  ${\mathcal{B}}_{0}$ under the projection
${\mathcal{B}}_{0}$ under the projection  $\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$. Further,
$\unicode[STIX]{x1D6EC}_{0}{\twoheadrightarrow}\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$. Further,  $h$ vanishes on
$h$ vanishes on  ${\mathcal{B}}_{0}^{\prime }\times {\mathcal{B}}_{0}^{\prime }$.
${\mathcal{B}}_{0}^{\prime }\times {\mathcal{B}}_{0}^{\prime }$.
Proof. First we prove that  $h$ is hyperbolic. Suppose for contradiction that it has positive anisotropic dimension, that is, let
$h$ is hyperbolic. Suppose for contradiction that it has positive anisotropic dimension, that is, let  $v$ be an anisotropic vector and part of a Witt basis for
$v$ be an anisotropic vector and part of a Witt basis for  $h$ which splits
$h$ which splits  $\unicode[STIX]{x1D6EC}$. We can multiply
$\unicode[STIX]{x1D6EC}$. We can multiply  $v$ by a scalar such that
$v$ by a scalar such that  $h(v,v)$ is a unit or a uniformizer of
$h(v,v)$ is a unit or a uniformizer of  $F$. We treat only the second case, because the first one is similar. There is an index
$F$. We treat only the second case, because the first one is similar. There is an index  $i$ such that
$i$ such that  $\unicode[STIX]{x1D6EC}_{i}\cap vF$ is equal to
$\unicode[STIX]{x1D6EC}_{i}\cap vF$ is equal to  $vo_{F}$, and then this is equal to
$vo_{F}$, and then this is equal to  $\unicode[STIX]{x1D6EC}_{i}^{\#}\cap vF$ because
$\unicode[STIX]{x1D6EC}_{i}^{\#}\cap vF$ because  $h(v,v)$ is uniformizer. Since, for all lattices in the image of
$h(v,v)$ is uniformizer. Since, for all lattices in the image of  $\unicode[STIX]{x1D6EC}$ the homothety class is invariant under dualization, we obtain that the index has to be zero. Thus,
$\unicode[STIX]{x1D6EC}$ the homothety class is invariant under dualization, we obtain that the index has to be zero. Thus,  $\unicode[STIX]{x1D6EC}_{-1}\cap vF=v\mathfrak{p}_{F}^{-1}$ is equal to
$\unicode[STIX]{x1D6EC}_{-1}\cap vF=v\mathfrak{p}_{F}^{-1}$ is equal to  $\unicode[STIX]{x1D71B}^{-2}(\unicode[STIX]{x1D6EC}_{1}\cap vF)$, which is a contradiction.
$\unicode[STIX]{x1D71B}^{-2}(\unicode[STIX]{x1D6EC}_{1}\cap vF)$, which is a contradiction.
Now let us construct the lift. We start with a Witt basis  ${\mathcal{B}}^{\prime \prime }$ for
${\mathcal{B}}^{\prime \prime }$ for  $h$ which splits
$h$ which splits  $\unicode[STIX]{x1D6EC}$. Let
$\unicode[STIX]{x1D6EC}$. Let  ${\mathcal{B}}_{0}^{\prime \prime }$ be the set of elements
${\mathcal{B}}_{0}^{\prime \prime }$ be the set of elements  $v$ of
$v$ of  ${\mathcal{B}}^{\prime \prime }$ such that
${\mathcal{B}}^{\prime \prime }$ such that
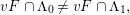 $$\begin{eqnarray}vF\cap \unicode[STIX]{x1D6EC}_{0}\neq vF\cap \unicode[STIX]{x1D6EC}_{1},\end{eqnarray}$$
$$\begin{eqnarray}vF\cap \unicode[STIX]{x1D6EC}_{0}\neq vF\cap \unicode[STIX]{x1D6EC}_{1},\end{eqnarray}$$ and let  $W_{0}$ be the span of
$W_{0}$ be the span of  ${\mathcal{B}}_{0}^{\prime \prime }$. We prove that the restriction of
${\mathcal{B}}_{0}^{\prime \prime }$. We prove that the restriction of  $h$ to
$h$ to  $W_{0}$ is zero. We define, for
$W_{0}$ is zero. We define, for  $v\in {\mathcal{B}}^{\prime \prime }$, the element
$v\in {\mathcal{B}}^{\prime \prime }$, the element  $v^{\ast }$ to be the element of
$v^{\ast }$ to be the element of  ${\mathcal{B}}^{\prime \prime }$ such that
${\mathcal{B}}^{\prime \prime }$ such that  $h(v,v^{\ast })$ is non-zero, that is equal to
$h(v,v^{\ast })$ is non-zero, that is equal to  $1$ or
$1$ or  $-1$. If there is an element
$-1$. If there is an element  $v\in {\mathcal{B}}_{0}^{\prime \prime }$ such that
$v\in {\mathcal{B}}_{0}^{\prime \prime }$ such that  $v^{\ast }\in W_{0}$ then
$v^{\ast }\in W_{0}$ then  $\unicode[STIX]{x1D6EC}_{-1}\cap (vF+v^{\ast }F)=\unicode[STIX]{x1D6EC}_{0}\cap (vF+v^{\ast }F)$ and thus this coincides with
$\unicode[STIX]{x1D6EC}_{-1}\cap (vF+v^{\ast }F)=\unicode[STIX]{x1D6EC}_{0}\cap (vF+v^{\ast }F)$ and thus this coincides with  $(\unicode[STIX]{x1D6EC}_{-1})^{\#}\cap (vF+v^{\ast }F)$. This is a contradiction because
$(\unicode[STIX]{x1D6EC}_{-1})^{\#}\cap (vF+v^{\ast }F)$. This is a contradiction because  $(\unicode[STIX]{x1D6EC}_{-1})^{\#}$ is equal to
$(\unicode[STIX]{x1D6EC}_{-1})^{\#}$ is equal to  $\unicode[STIX]{x1D6EC}_{1}$. This shows that
$\unicode[STIX]{x1D6EC}_{1}$. This shows that  $h$ is zero on
$h$ is zero on  $W_{0}$. Thus, multiplying elements of
$W_{0}$. Thus, multiplying elements of  ${\mathcal{B}}_{0}^{\prime \prime }$ by scalars if necessary, we can assume that
${\mathcal{B}}_{0}^{\prime \prime }$ by scalars if necessary, we can assume that  ${\mathcal{B}}_{0}^{\prime \prime }$ is a subset of
${\mathcal{B}}_{0}^{\prime \prime }$ is a subset of  $\unicode[STIX]{x1D6EC}_{0}\setminus \unicode[STIX]{x1D6EC}_{1}$. By the definition of
$\unicode[STIX]{x1D6EC}_{0}\setminus \unicode[STIX]{x1D6EC}_{1}$. By the definition of  ${\mathcal{B}}_{0}^{\prime \prime }$ we have that, for all
${\mathcal{B}}_{0}^{\prime \prime }$ we have that, for all  $v\in {\mathcal{B}}_{0}^{\prime \prime }$, the intersection of
$v\in {\mathcal{B}}_{0}^{\prime \prime }$, the intersection of  $vF$ with
$vF$ with  $\unicode[STIX]{x1D6EC}_{-1}$ is
$\unicode[STIX]{x1D6EC}_{-1}$ is  $vo_{F}$ for all
$vo_{F}$ for all  $v\in {\mathcal{B}}_{0}^{\prime \prime }$ and thus taking duals we get that the intersection of
$v\in {\mathcal{B}}_{0}^{\prime \prime }$ and thus taking duals we get that the intersection of  $v^{\ast }F$ with
$v^{\ast }F$ with  $\unicode[STIX]{x1D6EC}_{1}$ is
$\unicode[STIX]{x1D6EC}_{1}$ is  $v^{\ast }\mathfrak{p}_{F}$, and thus
$v^{\ast }\mathfrak{p}_{F}$, and thus  ${\mathcal{B}}^{\prime \prime }\setminus {\mathcal{B}}_{0}^{\prime \prime }$ is a subset of
${\mathcal{B}}^{\prime \prime }\setminus {\mathcal{B}}_{0}^{\prime \prime }$ is a subset of  $\unicode[STIX]{x1D6EC}_{-1}\setminus \unicode[STIX]{x1D6EC}_{0}$. Thus, we have now found a basis
$\unicode[STIX]{x1D6EC}_{-1}\setminus \unicode[STIX]{x1D6EC}_{0}$. Thus, we have now found a basis  ${\mathcal{B}}^{\prime \prime }$ satisfying all the conditions except that
${\mathcal{B}}^{\prime \prime }$ satisfying all the conditions except that  ${\mathcal{B}}_{0}^{\prime \prime }$ need not be a lift of
${\mathcal{B}}_{0}^{\prime \prime }$ need not be a lift of  ${\mathcal{B}}_{0}$. Now a base change from
${\mathcal{B}}_{0}$. Now a base change from  ${\mathcal{B}}_{0}^{\prime \prime }$ to a lift of
${\mathcal{B}}_{0}^{\prime \prime }$ to a lift of  ${\mathcal{B}}_{0}$ in
${\mathcal{B}}_{0}$ in  $W_{0}$, together with the adjoint base change on the span of
$W_{0}$, together with the adjoint base change on the span of  ${\mathcal{B}}^{\prime \prime }\setminus {\mathcal{B}}_{0}^{\prime \prime }$, finishes the proof.◻
${\mathcal{B}}^{\prime \prime }\setminus {\mathcal{B}}_{0}^{\prime \prime }$, finishes the proof.◻
Corollary 3.6. Under the assumptions of Lemma 3.5 there is a unique  $\unicode[STIX]{x1D705}$-basis
$\unicode[STIX]{x1D705}$-basis  ${\mathcal{B}}_{-1}$ of
${\mathcal{B}}_{-1}$ of  $\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}$ such that, for all elements
$\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}$ such that, for all elements  $x$ of
$x$ of  ${\mathcal{B}}_{0}$, there is exactly one element
${\mathcal{B}}_{0}$, there is exactly one element  $y$ of
$y$ of  ${\mathcal{B}}_{-1}$ such that
${\mathcal{B}}_{-1}$ such that
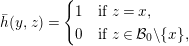 $$\begin{eqnarray}\bar{h}(y,z)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~z=x,\\ 0\quad & \text{if}~z\in {\mathcal{B}}_{0}\setminus \{x\},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\bar{h}(y,z)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~z=x,\\ 0\quad & \text{if}~z\in {\mathcal{B}}_{0}\setminus \{x\},\end{array}\right.\end{eqnarray}$$ where  $\bar{h}:\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}$ is the form induced from
$\bar{h}:\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}\times \unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D705}$ is the form induced from  $h$. Further, there is a Witt basis for
$h$. Further, there is a Witt basis for  $h$ which lifts
$h$ which lifts  ${\mathcal{B}}_{0}\cup {\mathcal{B}}_{-1}$.
${\mathcal{B}}_{0}\cup {\mathcal{B}}_{-1}$.
Proof. By Lemma 3.5 the form  $\bar{h}$ is non-degenerate and thus identifies the dual of
$\bar{h}$ is non-degenerate and thus identifies the dual of  $\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$ with
$\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1}$ with  $\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}$ with
$\unicode[STIX]{x1D6EC}_{-1}/\unicode[STIX]{x1D6EC}_{0}$ with  $\unicode[STIX]{x1D70E}$-twisted
$\unicode[STIX]{x1D70E}$-twisted  $\unicode[STIX]{x1D705}$-action. We take for
$\unicode[STIX]{x1D705}$-action. We take for  ${\mathcal{B}}_{-1}$ the basis dual to
${\mathcal{B}}_{-1}$ the basis dual to  ${\mathcal{B}}_{0}$. The remaining part follows from Lemma 3.5.◻
${\mathcal{B}}_{0}$. The remaining part follows from Lemma 3.5.◻
We put together the two previous results to treat the general case.
Lemma 3.7. Let  $\unicode[STIX]{x1D6EC}$ be a self-dual lattice chain of period
$\unicode[STIX]{x1D6EC}$ be a self-dual lattice chain of period  $e$ and set
$e$ and set  $N=\lfloor (e-1)/2\rfloor$ if
$N=\lfloor (e-1)/2\rfloor$ if  $\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$, and
$\unicode[STIX]{x1D6EC}_{0}^{\#}=\unicode[STIX]{x1D6EC}_{0}$, and  $N=\lfloor e/2\rfloor$ otherwise. Let
$N=\lfloor e/2\rfloor$ otherwise. Let  ${\mathcal{B}}$ be a subset of
${\mathcal{B}}$ be a subset of  $V$ satisfying the following conditions:
$V$ satisfying the following conditions:
(i)
 $(\unicode[STIX]{x1D6EC}_{0})^{\#}\in \{\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1}\}$;
$(\unicode[STIX]{x1D6EC}_{0})^{\#}\in \{\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1}\}$;(ii)
 ${\mathcal{B}}=\bigcup _{i=N+1-e}^{N}{\mathcal{B}}_{i}$, with
${\mathcal{B}}=\bigcup _{i=N+1-e}^{N}{\mathcal{B}}_{i}$, with  ${\mathcal{B}}_{i}\subseteq \unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1}$;
${\mathcal{B}}_{i}\subseteq \unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1}$;(iii)
 $\bar{{\mathcal{B}}}_{i}$, the image of
$\bar{{\mathcal{B}}}_{i}$, the image of  ${\mathcal{B}}_{i}$ in
${\mathcal{B}}_{i}$ in  $\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$, is a basis of
$\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$, is a basis of  $\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$;
$\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$;(iv) for all
 $i\in \{0,1,\ldots ,N\}$ with
$i\in \{0,1,\ldots ,N\}$ with  $(\unicode[STIX]{x1D6EC}_{i})^{\#}\not \in \{\unicode[STIX]{x1D6EC}_{i+1},\unicode[STIX]{x1D6EC}_{i+1-e}\}$ and all
$(\unicode[STIX]{x1D6EC}_{i})^{\#}\not \in \{\unicode[STIX]{x1D6EC}_{i+1},\unicode[STIX]{x1D6EC}_{i+1-e}\}$ and all  $v\in {\mathcal{B}}_{i}$ there exists a unique
$v\in {\mathcal{B}}_{i}$ there exists a unique  $v^{\prime }\in {\mathcal{B}}\cap (\unicode[STIX]{x1D6EC}_{i+1})^{\#}\setminus (\unicode[STIX]{x1D6EC}_{i})^{\#}$ such that
$v^{\prime }\in {\mathcal{B}}\cap (\unicode[STIX]{x1D6EC}_{i+1})^{\#}\setminus (\unicode[STIX]{x1D6EC}_{i})^{\#}$ such that  $\overline{h(v,v^{\prime })}=\bar{1}$;
$\overline{h(v,v^{\prime })}=\bar{1}$;(v) if
 $(\unicode[STIX]{x1D6EC}_{0})^{\#}=\unicode[STIX]{x1D6EC}_{1}$ then
$(\unicode[STIX]{x1D6EC}_{0})^{\#}=\unicode[STIX]{x1D6EC}_{1}$ then  $\bar{{\mathcal{B}}}_{0}$ is a Witt basis for
$\bar{{\mathcal{B}}}_{0}$ is a Witt basis for  $(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$;
$(\unicode[STIX]{x1D6EC}_{0}/\unicode[STIX]{x1D6EC}_{1},\bar{h})$;(vi) if
 $(\unicode[STIX]{x1D6EC}_{N})^{\#}=\unicode[STIX]{x1D6EC}_{N+1-e}$ then
$(\unicode[STIX]{x1D6EC}_{N})^{\#}=\unicode[STIX]{x1D6EC}_{N+1-e}$ then  $\bar{{\mathcal{B}}}_{N}$ is a Witt basis of
$\bar{{\mathcal{B}}}_{N}$ is a Witt basis of  $(\unicode[STIX]{x1D6EC}_{N}/\unicode[STIX]{x1D6EC}_{N+1},\overline{h\unicode[STIX]{x1D71B}^{-1}})$.
$(\unicode[STIX]{x1D6EC}_{N}/\unicode[STIX]{x1D6EC}_{N+1},\overline{h\unicode[STIX]{x1D71B}^{-1}})$.
Then there is a basis  ${\mathcal{B}}^{\prime }$ of
${\mathcal{B}}^{\prime }$ of  $(V,h)$ such that:
$(V,h)$ such that:
(a)
 ${\mathcal{B}}^{\prime }=\bigcup _{i=N+1-e}^{N}{\mathcal{B}}_{i}^{\prime }$, where
${\mathcal{B}}^{\prime }=\bigcup _{i=N+1-e}^{N}{\mathcal{B}}_{i}^{\prime }$, where  ${\mathcal{B}}_{i}^{\prime }:={\mathcal{B}}^{\prime }\cap (\unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1})$, for all
${\mathcal{B}}_{i}^{\prime }:={\mathcal{B}}^{\prime }\cap (\unicode[STIX]{x1D6EC}_{i}\setminus \unicode[STIX]{x1D6EC}_{i+1})$, for all  $i$;
$i$;(b)
 $\bar{{\mathcal{B}}^{\prime }}_{i}=\bar{{\mathcal{B}}}_{i}$, for all
$\bar{{\mathcal{B}}^{\prime }}_{i}=\bar{{\mathcal{B}}}_{i}$, for all  $i$; and
$i$; and(c)
 ${\mathcal{B}}^{\prime }$ is a Witt basis of
${\mathcal{B}}^{\prime }$ is a Witt basis of  $(V,h)$ up to multiplication of some isotropic elements of
$(V,h)$ up to multiplication of some isotropic elements of  ${\mathcal{B}}_{N}^{\prime }$ by
${\mathcal{B}}_{N}^{\prime }$ by  $\unicode[STIX]{x1D71B}^{-1}$.
$\unicode[STIX]{x1D71B}^{-1}$.
Proof. The lattice chain  $\unicode[STIX]{x1D6EC}$ is split by a Witt decomposition; that is, there are pairwise orthogonal
$\unicode[STIX]{x1D6EC}$ is split by a Witt decomposition; that is, there are pairwise orthogonal  $\unicode[STIX]{x1D716}$-hermitian spaces
$\unicode[STIX]{x1D716}$-hermitian spaces  $V^{i},i\in \{0,\ldots ,N\}$ whose sum is
$V^{i},i\in \{0,\ldots ,N\}$ whose sum is  $V$ such that
$V$ such that
 $$\begin{eqnarray}(V^{i}\cap \unicode[STIX]{x1D6EC}_{i})+\unicode[STIX]{x1D6EC}_{i+1}=\unicode[STIX]{x1D6EC}_{i}~\text{and}~V^{i}\cap (\unicode[STIX]{x1D6EC}_{i+1})^{\#}+(\unicode[STIX]{x1D6EC}_{i})^{\#}=(\unicode[STIX]{x1D6EC}_{i+1})^{\#}.\end{eqnarray}$$
$$\begin{eqnarray}(V^{i}\cap \unicode[STIX]{x1D6EC}_{i})+\unicode[STIX]{x1D6EC}_{i+1}=\unicode[STIX]{x1D6EC}_{i}~\text{and}~V^{i}\cap (\unicode[STIX]{x1D6EC}_{i+1})^{\#}+(\unicode[STIX]{x1D6EC}_{i})^{\#}=(\unicode[STIX]{x1D6EC}_{i+1})^{\#}.\end{eqnarray}$$ Counting dimensions we deduce that  $V^{i}\cap \unicode[STIX]{x1D6EC}_{j}$ is a subset of
$V^{i}\cap \unicode[STIX]{x1D6EC}_{j}$ is a subset of  $\unicode[STIX]{x1D6EC}_{j+1}$ for all
$\unicode[STIX]{x1D6EC}_{j+1}$ for all  $j$ with
$j$ with  $\unicode[STIX]{x1D6EC}_{j}\not \in \{\unicode[STIX]{x1D6EC}_{i}a,(\unicode[STIX]{x1D6EC}_{i+1})^{\#}a\mid a\in F^{\times }\}$. Now consider, for
$\unicode[STIX]{x1D6EC}_{j}\not \in \{\unicode[STIX]{x1D6EC}_{i}a,(\unicode[STIX]{x1D6EC}_{i+1})^{\#}a\mid a\in F^{\times }\}$. Now consider, for  $0\leqslant i\leqslant N$,
$0\leqslant i\leqslant N$,
 $$\begin{eqnarray}\tilde{{\mathcal{B}}_{i}}:=\{\operatorname{proj}_{V^{i}}(v)\mid v\in {\mathcal{B}}_{j}~\text{and}~\unicode[STIX]{x1D6EC}_{j}\in \{\unicode[STIX]{x1D6EC}_{i},(\unicode[STIX]{x1D6EC}_{i+1})^{\#}\}\}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{B}}_{i}}:=\{\operatorname{proj}_{V^{i}}(v)\mid v\in {\mathcal{B}}_{j}~\text{and}~\unicode[STIX]{x1D6EC}_{j}\in \{\unicode[STIX]{x1D6EC}_{i},(\unicode[STIX]{x1D6EC}_{i+1})^{\#}\}\}.\end{eqnarray}$$ For each  $i$, by removing repetitions we obtain from the lattice sequence
$i$, by removing repetitions we obtain from the lattice sequence  $\unicode[STIX]{x1D6EC}\cap V^{i}$ in
$\unicode[STIX]{x1D6EC}\cap V^{i}$ in  $V^{i}$ a lattice chain of period 1 or 2 with a self-dual lattice if
$V^{i}$ a lattice chain of period 1 or 2 with a self-dual lattice if  $i$ is positive. Thus, after scaling, we can apply Lemma 3.3 or 3.4 or Corollary 3.6 to
$i$ is positive. Thus, after scaling, we can apply Lemma 3.3 or 3.4 or Corollary 3.6 to  $(V^{i},\unicode[STIX]{x1D6EC}\cap V^{i},\bar{\tilde{{\mathcal{B}}_{i}}})$ to obtain
$(V^{i},\unicode[STIX]{x1D6EC}\cap V^{i},\bar{\tilde{{\mathcal{B}}_{i}}})$ to obtain  ${\mathcal{B}}_{i}^{\prime }$.◻
${\mathcal{B}}_{i}^{\prime }$.◻
Proof of Proposition 3.1.
We only have to prove that we can replace  $f$ by an
$f$ by an  $F$-linear isomorphism, that is that we can reduce the argument to
$F$-linear isomorphism, that is that we can reduce the argument to  $F=F^{\prime }$. The rest follows directly from Lemma 3.7.
$F=F^{\prime }$. The rest follows directly from Lemma 3.7.
Since the statement depends only on  $\operatorname{im}(\unicode[STIX]{x1D6EC})$, without loss of generality assume that
$\operatorname{im}(\unicode[STIX]{x1D6EC})$, without loss of generality assume that  $\unicode[STIX]{x1D6EC}$, and therefore
$\unicode[STIX]{x1D6EC}$, and therefore  $\unicode[STIX]{x1D6EC}^{\prime }$ also, is a chain. Take a
$\unicode[STIX]{x1D6EC}^{\prime }$ also, is a chain. Take a  $\unicode[STIX]{x1D705}_{F}$-basis
$\unicode[STIX]{x1D705}_{F}$-basis  $(\bar{v}_{ij})_{j}$ of
$(\bar{v}_{ij})_{j}$ of  $\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$ and lift it to
$\unicode[STIX]{x1D6EC}_{i}/\unicode[STIX]{x1D6EC}_{i+1}$ and lift it to  $(v_{ij})_{j}$, for
$(v_{ij})_{j}$, for  $i=1,\ldots ,e(\unicode[STIX]{x1D6EC}|o_{F})$. Then
$i=1,\ldots ,e(\unicode[STIX]{x1D6EC}|o_{F})$. Then  $(v_{ij})_{ij}$ is an
$(v_{ij})_{ij}$ is an  $F$-splitting basis of
$F$-splitting basis of  $\unicode[STIX]{x1D6EC}$. Similarly we choose a lift
$\unicode[STIX]{x1D6EC}$. Similarly we choose a lift  $(w_{ij})_{ij}$ for
$(w_{ij})_{ij}$ for  $(\overline{f(v_{ij})})_{ij}$. The
$(\overline{f(v_{ij})})_{ij}$. The  $F$-linear map
$F$-linear map  $\tilde{f}$ which maps
$\tilde{f}$ which maps  $v_{ij}$ to
$v_{ij}$ to  $w_{ij}$ satisfies the assumptions of the Proposition and
$w_{ij}$ satisfies the assumptions of the Proposition and  $(f-\tilde{f})(\unicode[STIX]{x1D6EC}_{i})\subseteq \unicode[STIX]{x1D6EC}_{i+1}$, for all
$(f-\tilde{f})(\unicode[STIX]{x1D6EC}_{i})\subseteq \unicode[STIX]{x1D6EC}_{i+1}$, for all  $i\in \mathbb{Z}$. Thus we can replace
$i\in \mathbb{Z}$. Thus we can replace  $f$ by
$f$ by  $\tilde{f}$.◻
$\tilde{f}$.◻
4 Witt groups
In this section we fix a finite field extension  $E|F$ and an involution
$E|F$ and an involution  $\unicode[STIX]{x1D70C}^{\prime }$ extending
$\unicode[STIX]{x1D70C}^{\prime }$ extending  $\unicode[STIX]{x1D70C}$ and we denote by
$\unicode[STIX]{x1D70C}$ and we denote by  $E_{0}$ the set of
$E_{0}$ the set of  $\unicode[STIX]{x1D70C}^{\prime }$-fixed points in
$\unicode[STIX]{x1D70C}^{\prime }$-fixed points in  $E$. We fix a non-zero
$E$. We fix a non-zero  $\unicode[STIX]{x1D70C}^{\prime }$–
$\unicode[STIX]{x1D70C}^{\prime }$– $\unicode[STIX]{x1D70C}$-equivariant
$\unicode[STIX]{x1D70C}$-equivariant  $F$-linear map
$F$-linear map
 $$\begin{eqnarray}\unicode[STIX]{x1D706}:E\rightarrow F.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}:E\rightarrow F.\end{eqnarray}$$ We heavily use in this section that the residue characteristic of  $F$ is odd. We will see that the map
$F$ is odd. We will see that the map  $\unicode[STIX]{x1D706}$ induces in a natural way a map from the Witt group
$\unicode[STIX]{x1D706}$ induces in a natural way a map from the Witt group  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ of
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ of  $(\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716})$-hermitian forms over
$(\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716})$-hermitian forms over  $E$ to the Witt group
$E$ to the Witt group  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$.
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$.
We recall that the Witt group  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is the set of equivalence classes of
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is the set of equivalence classes of  $(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716})$-hermitian forms over
$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716})$-hermitian forms over  $F$, where we say two such forms are equivalent if their maximal anisotropic direct summands are isometric. We write
$F$, where we say two such forms are equivalent if their maximal anisotropic direct summands are isometric. We write  $\langle h\rangle$ for the class in
$\langle h\rangle$ for the class in  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ of signed forms equivalent to
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ of signed forms equivalent to  $h$; similarly, for a (skew-) symmetric matrix
$h$; similarly, for a (skew-) symmetric matrix  $M$, we write
$M$, we write  $\langle M\rangle$ for the class of signed hermitian forms equivalent to the form with Gram matrix
$\langle M\rangle$ for the class of signed hermitian forms equivalent to the form with Gram matrix  $M$ under the standard basis.
$M$ under the standard basis.
The group structure on  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is induced by the orthogonal sum. Let us recall its structure:
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is induced by the orthogonal sum. Let us recall its structure:
Theorem 4.1. The Witt group  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is isomorphic to:
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is isomorphic to:
(i) the trivial group if
 $\unicode[STIX]{x1D70C}$ is trivial and
$\unicode[STIX]{x1D70C}$ is trivial and  $\unicode[STIX]{x1D716}=-1$;
$\unicode[STIX]{x1D716}=-1$;(ii)
 $C_{2}\times C_{2}$ if
$C_{2}\times C_{2}$ if  $-1\in (F^{\times })^{2}$ and
$-1\in (F^{\times })^{2}$ and  $\unicode[STIX]{x1D70C}$ is non-trivial;
$\unicode[STIX]{x1D70C}$ is non-trivial;(iii)
 $C_{4}$ if
$C_{4}$ if  $\unicode[STIX]{x1D70C}$ is non-trivial and
$\unicode[STIX]{x1D70C}$ is non-trivial and  $-1\not \in (F^{\times })^{2}$;
$-1\not \in (F^{\times })^{2}$;(iv)
 $C_{2}\times C_{2}\times C_{2}\times C_{2}$ if
$C_{2}\times C_{2}\times C_{2}\times C_{2}$ if  $-1\in (F^{\times })^{2}$,
$-1\in (F^{\times })^{2}$,  $\unicode[STIX]{x1D716}=1$ and
$\unicode[STIX]{x1D716}=1$ and  $\unicode[STIX]{x1D70C}$ is trivial;
$\unicode[STIX]{x1D70C}$ is trivial;(v)
 $C_{4}\times C_{4}$ if
$C_{4}\times C_{4}$ if  $-1\not \in (F^{\times })^{2}$,
$-1\not \in (F^{\times })^{2}$,  $\unicode[STIX]{x1D716}=1$ and
$\unicode[STIX]{x1D716}=1$ and  $\unicode[STIX]{x1D70C}$ is trivial.
$\unicode[STIX]{x1D70C}$ is trivial.
Proof. The proof is an easy conclusion of the classification of the hermitian forms using Witt bases, given for example in [Reference Bruhat and TitsBT87, 1.14], and is left to the reader. ◻
When it is non-trivial, the group  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is generated by the classes of one-dimensional anisotropic spaces. For example, if
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ is generated by the classes of one-dimensional anisotropic spaces. For example, if  $\unicode[STIX]{x1D716}=1$ then: in the case
$\unicode[STIX]{x1D716}=1$ then: in the case  $F\neq F_{0}$, the one-dimensional anisotropic spaces are
$F\neq F_{0}$, the one-dimensional anisotropic spaces are  $\langle (1)\rangle$ and
$\langle (1)\rangle$ and  $\langle (\unicode[STIX]{x1D6FF})\rangle$, with
$\langle (\unicode[STIX]{x1D6FF})\rangle$, with  $\unicode[STIX]{x1D6FF}\in F_{0}^{\times }\setminus N_{F/F_{0}}(F^{\times })$; in the case
$\unicode[STIX]{x1D6FF}\in F_{0}^{\times }\setminus N_{F/F_{0}}(F^{\times })$; in the case  $F=F_{0}$, the one-dimensional anisotropic spaces are
$F=F_{0}$, the one-dimensional anisotropic spaces are  $\langle (1)\rangle$,
$\langle (1)\rangle$,  $\langle (\unicode[STIX]{x1D71B})\rangle$,
$\langle (\unicode[STIX]{x1D71B})\rangle$,  $\langle (\unicode[STIX]{x1D6FF})\rangle$ and
$\langle (\unicode[STIX]{x1D6FF})\rangle$ and  $\langle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D71B})\rangle$, with
$\langle (\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D71B})\rangle$, with  $\unicode[STIX]{x1D6FF}$ a non-square unit in
$\unicode[STIX]{x1D6FF}$ a non-square unit in  $o_{F}$.
$o_{F}$.
Definition 4.2. We define  $\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}$ from
$\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}$ from  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ to
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ to  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ by
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ by
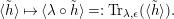 $$\begin{eqnarray}\langle \tilde{h}\rangle \mapsto \langle \unicode[STIX]{x1D706}\circ \tilde{h}\rangle =:\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}(\langle \tilde{h}\rangle ).\end{eqnarray}$$
$$\begin{eqnarray}\langle \tilde{h}\rangle \mapsto \langle \unicode[STIX]{x1D706}\circ \tilde{h}\rangle =:\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}(\langle \tilde{h}\rangle ).\end{eqnarray}$$ If  $E|F$ is tamely ramified and
$E|F$ is tamely ramified and  $\unicode[STIX]{x1D706}=\operatorname{tr}_{E|F}$ then we write
$\unicode[STIX]{x1D706}=\operatorname{tr}_{E|F}$ then we write  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ for
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ for  $\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}$.
$\operatorname{Tr}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D716}}$.
For the remainder of the section we often skip the subscripts in  $\operatorname{Tr}$.
$\operatorname{Tr}$.
Example 4.3. In general, the map  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ is not injective, even if
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ is not injective, even if  $\unicode[STIX]{x1D716}\,=\,1$. For example consider
$\unicode[STIX]{x1D716}\,=\,1$. For example consider  $E\,=\,\mathbb{Q}_{3}(\sqrt{3},\sqrt{5})$,
$E\,=\,\mathbb{Q}_{3}(\sqrt{3},\sqrt{5})$,  $F\,=\,\mathbb{Q}_{3}(\sqrt{5})$ and
$F\,=\,\mathbb{Q}_{3}(\sqrt{5})$ and  $\unicode[STIX]{x1D70C}^{\prime }(\sqrt{5})\,=\,-\sqrt{5}$. Then
$\unicode[STIX]{x1D70C}^{\prime }(\sqrt{5})\,=\,-\sqrt{5}$. Then
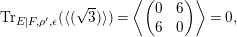 $$\begin{eqnarray}\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(\langle (\sqrt{3})\rangle )=\left\langle \left(\begin{array}{@{}cc@{}}0 & 6\\ 6 & 0\end{array}\right)\right\rangle =0,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(\langle (\sqrt{3})\rangle )=\left\langle \left(\begin{array}{@{}cc@{}}0 & 6\\ 6 & 0\end{array}\right)\right\rangle =0,\end{eqnarray}$$ so that  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ is not injective. On the other hand, we have that
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ is not injective. On the other hand, we have that
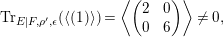 $$\begin{eqnarray}\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(\langle (1)\rangle )=\left\langle \left(\begin{array}{@{}cc@{}}2 & 0\\ 0 & 6\end{array}\right)\right\rangle \neq 0,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(\langle (1)\rangle )=\left\langle \left(\begin{array}{@{}cc@{}}2 & 0\\ 0 & 6\end{array}\right)\right\rangle \neq 0,\end{eqnarray}$$ In particular,  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ maps the class
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}$ maps the class  $\langle (\sqrt{3})\oplus (1)\rangle$ of maximal anisotropic dimension to the class in
$\langle (\sqrt{3})\oplus (1)\rangle$ of maximal anisotropic dimension to the class in  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ of maximal anisotropic dimension. We will see that this is always the case.
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ of maximal anisotropic dimension. We will see that this is always the case.
There is a unique element  $X$ in
$X$ in  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ with maximal anisotropic dimension, which we denote by
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ with maximal anisotropic dimension, which we denote by  $X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$. The main result of this section is the following theorem:
$X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$. The main result of this section is the following theorem:
Theorem 4.4.  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}(X_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716},E})=X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$.
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}(X_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716},E})=X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$.
The following definition will be useful both in the proof of Theorem 4.4 and in several other proofs later.
Definition 4.5. Let  $\unicode[STIX]{x1D6FE}$ be a non-singular (skew-)symmetric element of
$\unicode[STIX]{x1D6FE}$ be a non-singular (skew-)symmetric element of  $\operatorname{Aut}_{F}(V)$. We define the signed hermitian form
$\operatorname{Aut}_{F}(V)$. We define the signed hermitian form
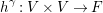 $$\begin{eqnarray}h^{\unicode[STIX]{x1D6FE}}:V\times V\rightarrow F\end{eqnarray}$$
$$\begin{eqnarray}h^{\unicode[STIX]{x1D6FE}}:V\times V\rightarrow F\end{eqnarray}$$via
 $$\begin{eqnarray}h^{\unicode[STIX]{x1D6FE}}(v,w):=h(v,\unicode[STIX]{x1D6FE}w),\quad v,w\in V.\end{eqnarray}$$
$$\begin{eqnarray}h^{\unicode[STIX]{x1D6FE}}(v,w):=h(v,\unicode[STIX]{x1D6FE}w),\quad v,w\in V.\end{eqnarray}$$ We call  $h^{\unicode[STIX]{x1D6FE}}$ the (skew-)symmetric twist of
$h^{\unicode[STIX]{x1D6FE}}$ the (skew-)symmetric twist of  $h$by
$h$by  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
Note that, if  $h$ is an
$h$ is an  $\unicode[STIX]{x1D716}$-hermitian form, then
$\unicode[STIX]{x1D716}$-hermitian form, then  $h^{\unicode[STIX]{x1D6FE}}$ is
$h^{\unicode[STIX]{x1D6FE}}$ is  $\unicode[STIX]{x1D716}$-hermitian when
$\unicode[STIX]{x1D716}$-hermitian when  $\unicode[STIX]{x1D6FE}$ is symmetric, and
$\unicode[STIX]{x1D6FE}$ is symmetric, and  $(-\unicode[STIX]{x1D716})$-hermitian when
$(-\unicode[STIX]{x1D716})$-hermitian when  $\unicode[STIX]{x1D6FE}$ is skew-symmetric. Twisting by a non-singular symmetric element
$\unicode[STIX]{x1D6FE}$ is skew-symmetric. Twisting by a non-singular symmetric element  $\unicode[STIX]{x1D6FE}$ induces a permutation of
$\unicode[STIX]{x1D6FE}$ induces a permutation of  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ and we observe that, by an easy check, the only classes in
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ and we observe that, by an easy check, the only classes in  $W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ which are preserved by every symmetric twist are the trivial class and the class
$W_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716}}(F)$ which are preserved by every symmetric twist are the trivial class and the class  $X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$ of maximal anisotropic dimension. Indeed, twisting by all symmetric elements gives a transitive action on the classes of spaces of fixed odd (anisotropic) dimension.
$X_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D716},F}$ of maximal anisotropic dimension. Indeed, twisting by all symmetric elements gives a transitive action on the classes of spaces of fixed odd (anisotropic) dimension.
Proposition 4.6. If  $E|F$ has odd degree, then,
$E|F$ has odd degree, then,  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is injective.
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is injective.
Proof. There is nothing to say in the symplectic case, so we assume  $\unicode[STIX]{x1D716}=1$ or
$\unicode[STIX]{x1D716}=1$ or  $F\neq F_{0}$. Moreover, we can assume that
$F\neq F_{0}$. Moreover, we can assume that  $\unicode[STIX]{x1D716}=1$ because, if
$\unicode[STIX]{x1D716}=1$ because, if  $F\neq F_{0}$ then a twist by a skew-symmetric element of
$F\neq F_{0}$ then a twist by a skew-symmetric element of  $F^{\times }$ induces bijections
$F^{\times }$ induces bijections  $W_{\unicode[STIX]{x1D70C}^{\prime },1}(E)\rightarrow W_{\unicode[STIX]{x1D70C}^{\prime },-1}(E)$ and
$W_{\unicode[STIX]{x1D70C}^{\prime },1}(E)\rightarrow W_{\unicode[STIX]{x1D70C}^{\prime },-1}(E)$ and  $W_{\unicode[STIX]{x1D70C},1}(F)\rightarrow W_{\unicode[STIX]{x1D70C},-1}(F)$, commuting with
$W_{\unicode[STIX]{x1D70C},1}(F)\rightarrow W_{\unicode[STIX]{x1D70C},-1}(F)$, commuting with  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}$. Now
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}$. Now  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle (1)\rangle )$ is a class of odd anisotropic dimension, all classes of this anisotropic dimension are symmetric twists of
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle (1)\rangle )$ is a class of odd anisotropic dimension, all classes of this anisotropic dimension are symmetric twists of  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle (1)\rangle )$ and they generate
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle (1)\rangle )$ and they generate  $W_{\unicode[STIX]{x1D70C},1}(F)$. Thus
$W_{\unicode[STIX]{x1D70C},1}(F)$. Thus  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is surjective and, moreover, bijective, since
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is surjective and, moreover, bijective, since  $W_{\unicode[STIX]{x1D70C},1}(F)$ is isomorphic to
$W_{\unicode[STIX]{x1D70C},1}(F)$ is isomorphic to  $W_{\unicode[STIX]{x1D70C}^{\prime },1}(E)$ as groups.◻
$W_{\unicode[STIX]{x1D70C}^{\prime },1}(E)$ as groups.◻
Lemma 4.7. Suppose  $E|F$ is of degree
$E|F$ is of degree  $2$ and
$2$ and  $F=F_{0}$. Then
$F=F_{0}$. Then  $\operatorname{im}(\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1})$ has at least four elements. Further:
$\operatorname{im}(\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1})$ has at least four elements. Further:
(i) If
 $E\neq E_{0}$ then
$E\neq E_{0}$ then  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ is injective.
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ is injective.(ii) If
 $E=E_{0}$ then the kernel of
$E=E_{0}$ then the kernel of  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ has exactly four elements and they have anisotropic dimension at most
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ has exactly four elements and they have anisotropic dimension at most  $2$.
$2$.
Proof. Take an element  $\unicode[STIX]{x1D6FF}\in E_{0}^{\times }$ and a uniformizer
$\unicode[STIX]{x1D6FF}\in E_{0}^{\times }$ and a uniformizer  $\unicode[STIX]{x1D6FC}$ of
$\unicode[STIX]{x1D6FC}$ of  $E$ which is skew-symmetric with respect to the generator
$E$ which is skew-symmetric with respect to the generator  $\unicode[STIX]{x1D70F}$ of
$\unicode[STIX]{x1D70F}$ of  $\operatorname{Gal}(E|F)$. Then
$\operatorname{Gal}(E|F)$. Then  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle \unicode[STIX]{x1D6FF}\rangle )$ has Gram matrix
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle \unicode[STIX]{x1D6FF}\rangle )$ has Gram matrix
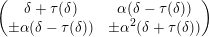 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}) & \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))\\ \pm \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF})) & \pm \unicode[STIX]{x1D6FC}^{2}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}) & \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))\\ \pm \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF})) & \pm \unicode[STIX]{x1D6FC}^{2}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))\end{array}\right)\end{eqnarray}$$ with respect to the  $F$-basis
$F$-basis  $\{1,\unicode[STIX]{x1D6FC}\}$, where we have
$\{1,\unicode[STIX]{x1D6FC}\}$, where we have  $+$ if
$+$ if  $\unicode[STIX]{x1D70C}^{\prime }$ is trivial and
$\unicode[STIX]{x1D70C}^{\prime }$ is trivial and  $-$ if not. Its determinant is
$-$ if not. Its determinant is  $d:=\pm 4\unicode[STIX]{x1D6FC}^{2}N_{E|F}(\unicode[STIX]{x1D6FF})$ and we only have to choose
$d:=\pm 4\unicode[STIX]{x1D6FC}^{2}N_{E|F}(\unicode[STIX]{x1D6FF})$ and we only have to choose  $\unicode[STIX]{x1D6FF}$ such that
$\unicode[STIX]{x1D6FF}$ such that  $-d$ is not a square in
$-d$ is not a square in  $F$ to get that
$F$ to get that  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ is non-zero.
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ is non-zero.
If  $-1\in (E^{\times })^{2}$ then, since
$-1\in (E^{\times })^{2}$ then, since  $p$ is odd, also
$p$ is odd, also  $-1\in N_{E|F}(E^{\times })$ and thus we can find
$-1\in N_{E|F}(E^{\times })$ and thus we can find  $\unicode[STIX]{x1D6FF}\in E_{0}^{\times }$ such that
$\unicode[STIX]{x1D6FF}\in E_{0}^{\times }$ such that  $-d=4\unicode[STIX]{x1D6FC}^{2}$; this is not a square in
$-d=4\unicode[STIX]{x1D6FC}^{2}$; this is not a square in  $F^{\times }$ because
$F^{\times }$ because  $\unicode[STIX]{x1D6FC}\not \in F$. If
$\unicode[STIX]{x1D6FC}\not \in F$. If  $-1\not \in (E^{\times })^{2}$ then
$-1\not \in (E^{\times })^{2}$ then  $E|F$ is ramified and
$E|F$ is ramified and  $\unicode[STIX]{x1D708}_{F}(\unicode[STIX]{x1D6FC}^{2})=1$ so we can take
$\unicode[STIX]{x1D708}_{F}(\unicode[STIX]{x1D6FC}^{2})=1$ so we can take  $\unicode[STIX]{x1D6FF}=1$ to get
$\unicode[STIX]{x1D6FF}=1$ to get  $-d\not \in (F^{\times })^{2}$.
$-d\not \in (F^{\times })^{2}$.
In either case, we have that  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ is non-zero for a suitable
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ is non-zero for a suitable  $\unicode[STIX]{x1D6FF}$, and thus of anisotropic dimension 2. Taking symmetric twists of
$\unicode[STIX]{x1D6FF}$, and thus of anisotropic dimension 2. Taking symmetric twists of  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ by elements of
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(\langle (\unicode[STIX]{x1D6FF})\rangle )$ by elements of  $F$ (which commute with
$F$ (which commute with  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$), we see that the image of
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$), we see that the image of  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ has at least two non-trivial elements and thus, as a subgroup of a 2-group, at least four elements in total. This also shows (i).
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$ has at least two non-trivial elements and thus, as a subgroup of a 2-group, at least four elements in total. This also shows (i).
We consider now the case  $E=E_{0}$. Take
$E=E_{0}$. Take  $y\in o_{F}$ to be a non-square unit if
$y\in o_{F}$ to be a non-square unit if  $E|F$ is ramified and a uniformizer of
$E|F$ is ramified and a uniformizer of  $F$ if
$F$ if  $E|F$ is unramified. Then
$E|F$ is unramified. Then  $(\unicode[STIX]{x1D6FC})$ and
$(\unicode[STIX]{x1D6FC})$ and  $(y\unicode[STIX]{x1D6FC})$ are not isomorphic and both are in the kernel of
$(y\unicode[STIX]{x1D6FC})$ are not isomorphic and both are in the kernel of  $\operatorname{Tr}_{E|F,\operatorname{id},1}$. Since the kernel consists of at most four elements, it is the subgroup generated by
$\operatorname{Tr}_{E|F,\operatorname{id},1}$. Since the kernel consists of at most four elements, it is the subgroup generated by  $\langle (\unicode[STIX]{x1D6FC})\rangle$ and
$\langle (\unicode[STIX]{x1D6FC})\rangle$ and  $\langle (y\unicode[STIX]{x1D6FC})\rangle$, which is of order four and consists of classes of spaces of anisotropic dimensions
$\langle (y\unicode[STIX]{x1D6FC})\rangle$, which is of order four and consists of classes of spaces of anisotropic dimensions  $0,1,1,2$.◻
$0,1,1,2$.◻
Proof of Theorem 4.4.
As in the proof of Proposition 4.6, we may assume that  $\unicode[STIX]{x1D716}=1$. We only need to prove the statement for one
$\unicode[STIX]{x1D716}=1$. We only need to prove the statement for one  $\unicode[STIX]{x1D706}$, because given two such maps
$\unicode[STIX]{x1D706}$, because given two such maps  $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$ there is a symmetric element
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$ there is a symmetric element  $z$ of
$z$ of  $E$ such that
$E$ such that  $\unicode[STIX]{x1D706}_{1}(zx)=\unicode[STIX]{x1D706}_{2}(x)$ for all
$\unicode[STIX]{x1D706}_{1}(zx)=\unicode[STIX]{x1D706}_{2}(x)$ for all  $x\in E$. (We thank R. Kurinczuk for pointing this out.) Moreover, we only have to prove that
$x\in E$. (We thank R. Kurinczuk for pointing this out.) Moreover, we only have to prove that  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero for a suitable
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero for a suitable  $\unicode[STIX]{x1D706}$, since its image is invariant under any symmetric twist with an element of
$\unicode[STIX]{x1D706}$, since its image is invariant under any symmetric twist with an element of  $F_{0}^{\times }$, so must be trivial or
$F_{0}^{\times }$, so must be trivial or  $X_{\unicode[STIX]{x1D70C},1,F}$.
$X_{\unicode[STIX]{x1D70C},1,F}$.
If  $E/F$ is of odd degree then the result follows immediately from Proposition 4.6. Since the result is transitive in towers of extensions, this means we can reduce to the case that
$E/F$ is of odd degree then the result follows immediately from Proposition 4.6. Since the result is transitive in towers of extensions, this means we can reduce to the case that  $E/F$ is quadratic; in particular,
$E/F$ is quadratic; in particular,  $E|F$ is at worst tamely ramified and we can take
$E|F$ is at worst tamely ramified and we can take  $\unicode[STIX]{x1D706}=\operatorname{tr}_{E|F}$. Moreover, we may replace
$\unicode[STIX]{x1D706}=\operatorname{tr}_{E|F}$. Moreover, we may replace  $E|F$ by
$E|F$ by  $E|F_{0}$ since, if
$E|F_{0}$ since, if  $\operatorname{Tr}_{E|F_{0},\unicode[STIX]{x1D70C}^{\prime },1}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero then
$\operatorname{Tr}_{E|F_{0},\unicode[STIX]{x1D70C}^{\prime },1}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero then  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero also. But then, by transitivity again and considering the extensions
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}(X_{\unicode[STIX]{x1D70C}^{\prime },1,E})$ is non-zero also. But then, by transitivity again and considering the extensions  $E|E_{0}$ and
$E|E_{0}$ and  $E_{0}|F_{0}$, we reduce to the case
$E_{0}|F_{0}$, we reduce to the case  $E|F$ quadratic with
$E|F$ quadratic with  $F=F_{0}$. Now Lemma 4.7 implies that
$F=F_{0}$. Now Lemma 4.7 implies that  $X_{\unicode[STIX]{x1D70C}^{\prime },1,E}$ is not in the kernel of
$X_{\unicode[STIX]{x1D70C}^{\prime },1,E}$ is not in the kernel of  $\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$, as required.◻
$\operatorname{Tr}_{E|F,\unicode[STIX]{x1D70C}^{\prime },1}$, as required.◻
5 Skolem–Noether
In this section we consider Skolem–Noether-like theorems for classical groups. We take the notation  $E,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D706}$ from Section 4. We fix two
$E,\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D706}$ from Section 4. We fix two  $\unicode[STIX]{x1D70C}^{\prime }$–
$\unicode[STIX]{x1D70C}^{\prime }$– $\unicode[STIX]{x1D70E}$-equivariant
$\unicode[STIX]{x1D70E}$-equivariant  $F$-algebra embeddings
$F$-algebra embeddings
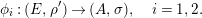 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}:(E,\unicode[STIX]{x1D70C}^{\prime })\rightarrow (A,\unicode[STIX]{x1D70E}),\quad i=1,2.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}:(E,\unicode[STIX]{x1D70C}^{\prime })\rightarrow (A,\unicode[STIX]{x1D70E}),\quad i=1,2.\end{eqnarray}$$ We attach to each  $\unicode[STIX]{x1D719}_{i}$ an
$\unicode[STIX]{x1D719}_{i}$ an  $\unicode[STIX]{x1D716}$-hermitian form
$\unicode[STIX]{x1D716}$-hermitian form
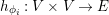 $$\begin{eqnarray}h_{\unicode[STIX]{x1D719}_{i}}:V\times V\rightarrow E\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D719}_{i}}:V\times V\rightarrow E\end{eqnarray}$$ with respect to  $\unicode[STIX]{x1D70C}^{\prime }$ such that
$\unicode[STIX]{x1D70C}^{\prime }$ such that
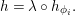 $$\begin{eqnarray}h=\unicode[STIX]{x1D706}\circ h_{\unicode[STIX]{x1D719}_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}h=\unicode[STIX]{x1D706}\circ h_{\unicode[STIX]{x1D719}_{i}}.\end{eqnarray}$$ For the proof that such a form exists and is unique, see [Reference Broussous and StevensBS09]. Note that the  $\unicode[STIX]{x1D716}$-hermitian forms
$\unicode[STIX]{x1D716}$-hermitian forms  $h_{\unicode[STIX]{x1D719}_{i}}$ may differ because the maps
$h_{\unicode[STIX]{x1D719}_{i}}$ may differ because the maps  $\unicode[STIX]{x1D719}_{i}$ may induce different
$\unicode[STIX]{x1D719}_{i}$ may induce different  $E$-actions on
$E$-actions on  $V$. In particular, two such embeddings
$V$. In particular, two such embeddings  $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of  $G$ if and only if
$G$ if and only if  $(V,h_{\unicode[STIX]{x1D719}_{1}})$ is isomorphic to
$(V,h_{\unicode[STIX]{x1D719}_{1}})$ is isomorphic to  $(V,h_{\unicode[STIX]{x1D719}_{2}})$ as a hermitian
$(V,h_{\unicode[STIX]{x1D719}_{2}})$ as a hermitian  $E$-space.
$E$-space.
We then get the following corollary of Theorem 4.4.
Corollary 5.1. Suppose that  $\unicode[STIX]{x1D70C}^{\prime }$ is non-trivial and that
$\unicode[STIX]{x1D70C}^{\prime }$ is non-trivial and that  $\unicode[STIX]{x1D716}=1$ or
$\unicode[STIX]{x1D716}=1$ or  $F\neq F_{0}$. Then
$F\neq F_{0}$. Then  $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of  $g\in G$, that is
$g\in G$, that is
 $$\begin{eqnarray}g\unicode[STIX]{x1D719}_{1}(x)g^{-1}=\unicode[STIX]{x1D719}_{2}(x)\quad \text{for all}~x\in E.\end{eqnarray}$$
$$\begin{eqnarray}g\unicode[STIX]{x1D719}_{1}(x)g^{-1}=\unicode[STIX]{x1D719}_{2}(x)\quad \text{for all}~x\in E.\end{eqnarray}$$Proof. We write  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$ for the set of classes of
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$ for the set of classes of  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ with even-dimensional anisotropic part. Then
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)$ with even-dimensional anisotropic part. Then  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$ only consists of the trivial element and
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$ only consists of the trivial element and  $X_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716},E}$ so, by Theorem 4.4, there is a map
$X_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716},E}$ so, by Theorem 4.4, there is a map  $\unicode[STIX]{x1D706}$ such that
$\unicode[STIX]{x1D706}$ such that  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is injective on
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}$ is injective on  $W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$. Since
$W_{\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D716}}(E)^{0}$. Since  $\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle h_{\unicode[STIX]{x1D719}_{i}}\rangle )=\langle h\rangle$, we deduce that
$\operatorname{Tr}_{\unicode[STIX]{x1D706}}(\langle h_{\unicode[STIX]{x1D719}_{i}}\rangle )=\langle h\rangle$, we deduce that  $(V,h_{\unicode[STIX]{x1D719}_{1}})$ and
$(V,h_{\unicode[STIX]{x1D719}_{1}})$ and  $(V,h_{\unicode[STIX]{x1D719}_{2}})$ are isomorphic as hermitian
$(V,h_{\unicode[STIX]{x1D719}_{2}})$ are isomorphic as hermitian  $E$-spaces and the result follows.◻
$E$-spaces and the result follows.◻
In the symplectic case, the analogous result is false without further hypotheses. The following theorem gives a sufficient additional condition which will be useful.
Theorem 5.2. For  $i=1,2$, let
$i=1,2$, let  $\unicode[STIX]{x1D6EC}^{i}$ be a self-dual lattice sequence in
$\unicode[STIX]{x1D6EC}^{i}$ be a self-dual lattice sequence in  $V$ normalized by
$V$ normalized by  $\unicode[STIX]{x1D719}_{i}(E)^{\times }$. Let
$\unicode[STIX]{x1D719}_{i}(E)^{\times }$. Let  $\unicode[STIX]{x1D6FD}$ be a non-zero skew-symmetric element generating
$\unicode[STIX]{x1D6FD}$ be a non-zero skew-symmetric element generating  $E$ over
$E$ over  $F$ and write
$F$ and write  $r_{i}:=1+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}^{i}}(\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD}))$. Suppose that there is an element
$r_{i}:=1+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}^{i}}(\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD}))$. Suppose that there is an element  $g$ of
$g$ of  $G$ such that
$G$ such that
 $$\begin{eqnarray}g^{-1}(\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{1},-}(\unicode[STIX]{x1D6EC}^{1}))g\cap (\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{2},-}(\unicode[STIX]{x1D6EC}^{2}))\neq \varnothing .\end{eqnarray}$$
$$\begin{eqnarray}g^{-1}(\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{1},-}(\unicode[STIX]{x1D6EC}^{1}))g\cap (\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{2},-}(\unicode[STIX]{x1D6EC}^{2}))\neq \varnothing .\end{eqnarray}$$ Then  $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of  $G$.
$G$.
In the language of strata below (see Section 6), the hypotheses here say that the pure skew strata  $[\unicode[STIX]{x1D6EC}^{i},-r_{i}+1,-r_{i},\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})]$ intertwine. We will need the following lemma, where we recall that
$[\unicode[STIX]{x1D6EC}^{i},-r_{i}+1,-r_{i},\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})]$ intertwine. We will need the following lemma, where we recall that  $h^{\unicode[STIX]{x1D6FE}}$ denotes the twist of
$h^{\unicode[STIX]{x1D6FE}}$ denotes the twist of  $h$ by a (skew-)symmetric element
$h$ by a (skew-)symmetric element  $\unicode[STIX]{x1D6FE}$ (see Definition 4.5).
$\unicode[STIX]{x1D6FE}$ (see Definition 4.5).
Lemma 5.3. Let  $\unicode[STIX]{x1D6EC}$ be a self-dual lattice sequence and let
$\unicode[STIX]{x1D6EC}$ be a self-dual lattice sequence and let  $a_{1},a_{2}$ be two non-zero symmetric or skew-symmetric elements of the normalizer of
$a_{1},a_{2}$ be two non-zero symmetric or skew-symmetric elements of the normalizer of  $\unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6EC}$ such that  $a_{1}a_{2}^{-1}\in \tilde{\operatorname{U}}^{s}(\unicode[STIX]{x1D6EC})$, for some
$a_{1}a_{2}^{-1}\in \tilde{\operatorname{U}}^{s}(\unicode[STIX]{x1D6EC})$, for some  $s>0$. Then there is an
$s>0$. Then there is an  $F$-linear isometry from
$F$-linear isometry from  $(V,h^{a_{1}})$ to
$(V,h^{a_{1}})$ to  $(V,h^{a_{2}})$ in
$(V,h^{a_{2}})$ in  $\tilde{\operatorname{U}}^{s}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}^{s}(\unicode[STIX]{x1D6EC})$.
Proof. We apply Proposition 3.1 for  $f=\operatorname{id}_{V}$ to see that the spaces
$f=\operatorname{id}_{V}$ to see that the spaces  $(V,h^{a_{1}})$ and
$(V,h^{a_{1}})$ and  $(V,h^{a_{2}})$ are isometric. Now we apply Corollary 3.2, with
$(V,h^{a_{2}})$ are isometric. Now we apply Corollary 3.2, with  $f=\operatorname{id}_{V}$ again, to finish the proof.◻
$f=\operatorname{id}_{V}$ again, to finish the proof.◻
Proof of Theorem 5.2.
By Corollary 5.1 we only need to treat the case that  $F=F_{0}$ and
$F=F_{0}$ and  $\unicode[STIX]{x1D716}=-1$. By hypothesis, there are elements
$\unicode[STIX]{x1D716}=-1$. By hypothesis, there are elements  $g\in G$ and
$g\in G$ and  $c_{i}\in \unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{i},-}(\unicode[STIX]{x1D6EC}^{i})$ such that
$c_{i}\in \unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})+\mathfrak{a}_{r_{i},-}(\unicode[STIX]{x1D6EC}^{i})$ such that  $gc_{1}g^{-1}=c_{2}$. Thus, by Lemma 5.3, we have isometries
$gc_{1}g^{-1}=c_{2}$. Thus, by Lemma 5.3, we have isometries
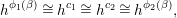 $$\begin{eqnarray}h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}\cong h^{c_{1}}\cong h^{c_{2}}\cong h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})},\end{eqnarray}$$
$$\begin{eqnarray}h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}\cong h^{c_{1}}\cong h^{c_{2}}\cong h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})},\end{eqnarray}$$ where the middle isomorphism is given by  $g$. Let
$g$. Let  $f$ be an isomorphism from
$f$ be an isomorphism from  $h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}$ to
$h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}$ to  $h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})}$. Since
$h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})}$. Since  $h^{\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})}$ are orthogonal forms, Corollary 5.1 applied to the embeddings
$h^{\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D6FD})}$ are orthogonal forms, Corollary 5.1 applied to the embeddings  $x\mapsto f\unicode[STIX]{x1D719}_{1}(x)f^{-1}$ and
$x\mapsto f\unicode[STIX]{x1D719}_{1}(x)f^{-1}$ and  $\unicode[STIX]{x1D719}_{2}$ implies that there is an isomorphism from
$\unicode[STIX]{x1D719}_{2}$ implies that there is an isomorphism from  $h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}$ to
$h^{\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D6FD})}$ to  $h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})}$ which conjugates
$h^{\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D6FD})}$ which conjugates  $\unicode[STIX]{x1D719}_{1}$ to
$\unicode[STIX]{x1D719}_{1}$ to  $\unicode[STIX]{x1D719}_{2}$. But any such isomorphism is an isometry of
$\unicode[STIX]{x1D719}_{2}$. But any such isomorphism is an isometry of  $(V,h)$, as required.◻
$(V,h)$, as required.◻
We will also need the following integral version of the Skolem–Noether theorem:
Proposition 5.4. [Reference SkodlerackSko14, Theorem 1.2]
Let  $\unicode[STIX]{x1D719}_{i}:(E,\unicode[STIX]{x1D70C}^{\prime })\rightarrow (A,\unicode[STIX]{x1D70E})$ be a
$\unicode[STIX]{x1D719}_{i}:(E,\unicode[STIX]{x1D70C}^{\prime })\rightarrow (A,\unicode[STIX]{x1D70E})$ be a  $\unicode[STIX]{x1D70C}^{\prime }$–
$\unicode[STIX]{x1D70C}^{\prime }$– $\unicode[STIX]{x1D70E}$-equivariant
$\unicode[STIX]{x1D70E}$-equivariant  $F$-algebra embedding, for
$F$-algebra embedding, for  $i=1,2$. Suppose further that
$i=1,2$. Suppose further that  $(V,h_{\unicode[STIX]{x1D719}_{1}})$ is isomorphic to
$(V,h_{\unicode[STIX]{x1D719}_{1}})$ is isomorphic to  $(V,h_{\unicode[STIX]{x1D719}_{2}})$ as hermitian
$(V,h_{\unicode[STIX]{x1D719}_{2}})$ as hermitian  $E$-spaces and that there is a self-dual lattice chain
$E$-spaces and that there is a self-dual lattice chain  $\unicode[STIX]{x1D6EC}$ normalized by
$\unicode[STIX]{x1D6EC}$ normalized by  $\unicode[STIX]{x1D719}_{i}(E)^{\times }$,
$\unicode[STIX]{x1D719}_{i}(E)^{\times }$,  $i=1,2$. Then
$i=1,2$. Then  $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$ are conjugate by an element of  $\operatorname{U}(\unicode[STIX]{x1D6EC})$.
$\operatorname{U}(\unicode[STIX]{x1D6EC})$.
6 Semisimple strata
We now turn to the notion of semisimple stratum for  $G$. The background can be found in [Reference Bushnell and KutzkoBK93, Reference StevensSte02, Reference StevensSte05], whose notation we adopt. However, many of the results in the literature are only available for lattice chains, while other results on semisimple strata were omitted in [Reference StevensSte05] (jumping directly to semisimple characters). Thus we gather together here various results which we will need in our work.
$G$. The background can be found in [Reference Bushnell and KutzkoBK93, Reference StevensSte02, Reference StevensSte05], whose notation we adopt. However, many of the results in the literature are only available for lattice chains, while other results on semisimple strata were omitted in [Reference StevensSte05] (jumping directly to semisimple characters). Thus we gather together here various results which we will need in our work.
A stratum is a quadruple  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ consisting of an
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ consisting of an  $o_{F}$-lattice sequence
$o_{F}$-lattice sequence  $\unicode[STIX]{x1D6EC}$, non-negative integers
$\unicode[STIX]{x1D6EC}$, non-negative integers  $q\geqslant r$ and an element
$q\geqslant r$ and an element  $b\in \mathfrak{a}_{-q}(\unicode[STIX]{x1D6EC})$. This stratum is called strict if
$b\in \mathfrak{a}_{-q}(\unicode[STIX]{x1D6EC})$. This stratum is called strict if  $\unicode[STIX]{x1D6EC}$ is a lattice chain. The stratum is skew if
$\unicode[STIX]{x1D6EC}$ is a lattice chain. The stratum is skew if  $\unicode[STIX]{x1D6FD}\in A_{-}$ and
$\unicode[STIX]{x1D6FD}\in A_{-}$ and  $\unicode[STIX]{x1D6EC}$ is self-dual, and it is called null if
$\unicode[STIX]{x1D6EC}$ is self-dual, and it is called null if  $\unicode[STIX]{x1D6FD}=0$ and
$\unicode[STIX]{x1D6FD}=0$ and  $q=r$.
$q=r$.
Two strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent if
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent if  $\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r-j}=\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }-j}^{\prime }$, for all non-negative integers
$\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r-j}=\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }-j}^{\prime }$, for all non-negative integers  $j$. This is equivalent to saying that
$j$. This is equivalent to saying that  $\unicode[STIX]{x1D6EC}$ is a translate of
$\unicode[STIX]{x1D6EC}$ is a translate of  $\unicode[STIX]{x1D6EC}^{\prime }$,
$\unicode[STIX]{x1D6EC}^{\prime }$,  $r=r^{\prime }$ and the cosets
$r=r^{\prime }$ and the cosets  $\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r}=\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime }$ coincide. They intertwine under a subgroup
$\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r}=\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime }$ coincide. They intertwine under a subgroup  $H$ of
$H$ of  $\tilde{G}$ if there is an element
$\tilde{G}$ if there is an element  $g$ of
$g$ of  $H$ such that
$H$ such that  $g(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r})g^{-1}$ intersects
$g(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r})g^{-1}$ intersects  $\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime }$. We denote the set of such elements by
$\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime }$. We denote the set of such elements by  $I_{H}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }])$. If both strata are equal we skip the second argument and if
$I_{H}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }])$. If both strata are equal we skip the second argument and if  $H$ is
$H$ is  $\tilde{G}$ we skip
$\tilde{G}$ we skip  $H$ in the notation. The two strata are conjugate under
$H$ in the notation. The two strata are conjugate under  $H$ if there is a
$H$ if there is a  $g\in H$ such that
$g\in H$ such that  $[g\unicode[STIX]{x1D6EC},q,r,g\unicode[STIX]{x1D6FD}g^{-1}]$ is equal to
$[g\unicode[STIX]{x1D6EC},q,r,g\unicode[STIX]{x1D6FD}g^{-1}]$ is equal to  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$. Two equivalence classes of strata are called conjugate under
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$. Two equivalence classes of strata are called conjugate under  $H$ if there are representatives of either classes which are conjugate under
$H$ if there are representatives of either classes which are conjugate under  $H$.
$H$.
Definition 6.1. (Simple stratum)
A stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is called:
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is called:
(i) pure if
 $F[\unicode[STIX]{x1D6FD}]$ is a field such that
$F[\unicode[STIX]{x1D6FD}]$ is a field such that  $F[\unicode[STIX]{x1D6FD}]^{\times }\subseteq \mathfrak{n}(\unicode[STIX]{x1D6EC})$ and
$F[\unicode[STIX]{x1D6FD}]^{\times }\subseteq \mathfrak{n}(\unicode[STIX]{x1D6EC})$ and  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q<-r$;
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q<-r$;(ii) simple if either it is null, or it is pure and the degree
 $[F[\unicode[STIX]{x1D6FD}]:F]$ is minimal among all equivalent pure strata.
$[F[\unicode[STIX]{x1D6FD}]:F]$ is minimal among all equivalent pure strata.
This is equivalent to [Reference StevensSte05, Definition 1.5], or [Reference Bushnell and KutzkoBK93] in the case of lattice chains (see Proposition 6.4 below).
We now want to consider strata where  $F[\unicode[STIX]{x1D6FD}]$ is a direct sum of (not necessarily separable) field extensions. Given a decomposition
$F[\unicode[STIX]{x1D6FD}]$ is a direct sum of (not necessarily separable) field extensions. Given a decomposition  $V=\bigoplus _{i}V^{i}$ we write
$V=\bigoplus _{i}V^{i}$ we write  $A^{i,j}$ for
$A^{i,j}$ for  $\operatorname{Hom}_{F}(V^{j},V^{i})$ and
$\operatorname{Hom}_{F}(V^{j},V^{i})$ and  $1^{i}$ for the projection onto
$1^{i}$ for the projection onto  $V^{i}$ with kernel
$V^{i}$ with kernel  $\bigoplus _{j\neq i}V^{j}$. A stratum
$\bigoplus _{j\neq i}V^{j}$. A stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is split by the decomposition if
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is split by the decomposition if  $1^{i}\unicode[STIX]{x1D6FD}1^{j}=0$ for
$1^{i}\unicode[STIX]{x1D6FD}1^{j}=0$ for  $i\neq j$ and if the decomposition splits
$i\neq j$ and if the decomposition splits  $\unicode[STIX]{x1D6EC}$, that is,
$\unicode[STIX]{x1D6EC}$, that is,  $\unicode[STIX]{x1D6EC}$ is the direct sum of the lattice sequences
$\unicode[STIX]{x1D6EC}$ is the direct sum of the lattice sequences  $\unicode[STIX]{x1D6EC}^{i}:=\unicode[STIX]{x1D6EC}\cap V^{i}$. We write
$\unicode[STIX]{x1D6EC}^{i}:=\unicode[STIX]{x1D6EC}\cap V^{i}$. We write  $\unicode[STIX]{x1D6FD}_{i}:=1^{i}\unicode[STIX]{x1D6FD}1^{i}$ and
$\unicode[STIX]{x1D6FD}_{i}:=1^{i}\unicode[STIX]{x1D6FD}1^{i}$ and  $q_{i}:=-\text{min}\{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}_{i}),-r\}$. We are now in a position to define a semisimple stratum.
$q_{i}:=-\text{min}\{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}_{i}),-r\}$. We are now in a position to define a semisimple stratum.
Definition 6.2. [Reference StevensSte05, Definition 3.2]
A stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is called semisimple if either it is null or
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is called semisimple if either it is null or  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q<-r$ and there is a splitting
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q<-r$ and there is a splitting  $V=\bigoplus _{i}V^{i}$ such that:
$V=\bigoplus _{i}V^{i}$ such that:
(i) for every
 $i$ the stratum
$i$ the stratum  $[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ in
$[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ in  $A^{i,i}$ is simple;
$A^{i,i}$ is simple;(ii) for all
 $i\neq j$ the stratum
$i\neq j$ the stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ is not equivalent to a simple stratum.
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ is not equivalent to a simple stratum.
A semisimple stratum is called skew-semisimple if the decomposition of  $V$ is orthogonal and all strata occurring in (i) are skew.
$V$ is orthogonal and all strata occurring in (i) are skew.
For later, to describe the intertwining of  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, we need an integer
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, we need an integer  $k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ which characterizes the semisimplicity of a stratum. Denote by
$k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ which characterizes the semisimplicity of a stratum. Denote by  $a_{\unicode[STIX]{x1D6FD}}:A\rightarrow A$ the map
$a_{\unicode[STIX]{x1D6FD}}:A\rightarrow A$ the map  $a_{\unicode[STIX]{x1D6FD}}(x)=\unicode[STIX]{x1D6FD}x-x\unicode[STIX]{x1D6FD}$ and put
$a_{\unicode[STIX]{x1D6FD}}(x)=\unicode[STIX]{x1D6FD}x-x\unicode[STIX]{x1D6FD}$ and put  $\mathfrak{n}_{l}=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{l})\cap \mathfrak{a}_{0}$.
$\mathfrak{n}_{l}=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{l})\cap \mathfrak{a}_{0}$.
If  $F[\unicode[STIX]{x1D6FD}]$ is a field we define, as in [Reference StevensSte05, Definition 1.4]:
$F[\unicode[STIX]{x1D6FD}]$ is a field we define, as in [Reference StevensSte05, Definition 1.4]:
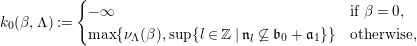 $$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\left\{\begin{array}{@{}ll@{}}-\infty \quad & \text{if}~\unicode[STIX]{x1D6FD}=0,\\ \max \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}),\sup \{l\in \mathbb{ Z}\mid \mathfrak{ n}_{l}\not \subseteq \mathfrak{b}_{0}+\mathfrak{a}_{1}\}\}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\left\{\begin{array}{@{}ll@{}}-\infty \quad & \text{if}~\unicode[STIX]{x1D6FD}=0,\\ \max \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}),\sup \{l\in \mathbb{ Z}\mid \mathfrak{ n}_{l}\not \subseteq \mathfrak{b}_{0}+\mathfrak{a}_{1}\}\}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$ and one writes  $k_{F}(\unicode[STIX]{x1D6FD})$ for
$k_{F}(\unicode[STIX]{x1D6FD})$ for  $k_{0}(\unicode[STIX]{x1D6FD},\mathfrak{p}_{E}^{\mathbb{Z}})$, where
$k_{0}(\unicode[STIX]{x1D6FD},\mathfrak{p}_{E}^{\mathbb{Z}})$, where  $\mathfrak{p}_{E}^{\mathbb{Z}}$ denotes the lattice sequence
$\mathfrak{p}_{E}^{\mathbb{Z}}$ denotes the lattice sequence  $i\mapsto \mathfrak{p}_{E}^{i}$, the unique
$i\mapsto \mathfrak{p}_{E}^{i}$, the unique  $o_{F}$-lattice chain in the
$o_{F}$-lattice chain in the  $F$-vector space
$F$-vector space  $E$ whose normalizer contains
$E$ whose normalizer contains  $E^{\times }$. We have that
$E^{\times }$. We have that
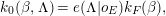 $$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=e(\unicode[STIX]{x1D6EC}|o_{E})k_{F}(\unicode[STIX]{x1D6FD}),\end{eqnarray}$$
$$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=e(\unicode[STIX]{x1D6EC}|o_{E})k_{F}(\unicode[STIX]{x1D6FD}),\end{eqnarray}$$by the remark after [Reference StevensSte01a, Lemma 5.6]. We now prove that Definition 6.1 is equivalent to that in [Reference StevensSte05, 1.5]
Proposition 6.4. Given a non-negative integer  $s$, a pure stratum
$s$, a pure stratum  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is simple if and only if
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is simple if and only if  $-s>k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Further, writing
$-s>k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Further, writing  $\tilde{\unicode[STIX]{x1D6EC}}=\bigoplus _{l=0}^{e-1}(\unicode[STIX]{x1D6EC}-l)$, with
$\tilde{\unicode[STIX]{x1D6EC}}=\bigoplus _{l=0}^{e-1}(\unicode[STIX]{x1D6EC}-l)$, with  $e=e(\unicode[STIX]{x1D6EC}|o_{F})$, we have
$e=e(\unicode[STIX]{x1D6EC}|o_{F})$, we have  $k_{0}(\unicode[STIX]{x1D6FD}^{\oplus e},\tilde{\unicode[STIX]{x1D6EC}})=k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
$k_{0}(\unicode[STIX]{x1D6FD}^{\oplus e},\tilde{\unicode[STIX]{x1D6EC}})=k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
Note that the lattice sequence  $\tilde{\unicode[STIX]{x1D6EC}}$ in the statement is in fact a lattice chain, with the same period as
$\tilde{\unicode[STIX]{x1D6EC}}$ in the statement is in fact a lattice chain, with the same period as  $\unicode[STIX]{x1D6EC}$.
$\unicode[STIX]{x1D6EC}$.
Proof. The second assertion follows directly from (6.3), and we thus only concentrate on the first, which is true if  $\unicode[STIX]{x1D6EC}$ is a lattice chain by [Reference Bushnell and KutzkoBK93, Theorem 2.4.1]. We compare the two notions of simple: a stratum which is simple in the sense of Definition 6.1 is called degree-simple, and a stratum which is either null or pure satisfying
$\unicode[STIX]{x1D6EC}$ is a lattice chain by [Reference Bushnell and KutzkoBK93, Theorem 2.4.1]. We compare the two notions of simple: a stratum which is simple in the sense of Definition 6.1 is called degree-simple, and a stratum which is either null or pure satisfying  $-s>k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is called
$-s>k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is called  $k_{0}$-simple.
$k_{0}$-simple.
If  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is  $k_{0}$-simple then so is
$k_{0}$-simple then so is  $[\tilde{\unicode[STIX]{x1D6EC}},q,s,\unicode[STIX]{x1D6FD}^{\oplus e}]$, by the second assertion, and thus it is degree-simple, because
$[\tilde{\unicode[STIX]{x1D6EC}},q,s,\unicode[STIX]{x1D6FD}^{\oplus e}]$, by the second assertion, and thus it is degree-simple, because  $\tilde{\unicode[STIX]{x1D6EC}}$ is a lattice chain. Thus
$\tilde{\unicode[STIX]{x1D6EC}}$ is a lattice chain. Thus  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is degree-simple.
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is degree-simple.
If  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is degree-simple but not
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is degree-simple but not  $k_{0}$-simple, then the stratum [
$k_{0}$-simple, then the stratum [ $\mathfrak{p}_{E}^{\mathbb{Z}}$,
$\mathfrak{p}_{E}^{\mathbb{Z}}$,  $-\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD})$,
$-\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD})$,  $\lfloor s/(e(\unicode[STIX]{x1D6EC}|o_{E}))\rfloor ,\unicode[STIX]{x1D6FD}$] is not
$\lfloor s/(e(\unicode[STIX]{x1D6EC}|o_{E}))\rfloor ,\unicode[STIX]{x1D6FD}$] is not  $k_{0}$-simple. But then, the latter is not degree-simple, because
$k_{0}$-simple. But then, the latter is not degree-simple, because  $\mathfrak{p}_{E}^{\mathbb{Z}}$ is a lattice chain, and thus
$\mathfrak{p}_{E}^{\mathbb{Z}}$ is a lattice chain, and thus  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is not degree-simple, using a
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is not degree-simple, using a  $(W,E)$-decomposition as in [Reference Bushnell and KutzkoBK99, 5.3].◻
$(W,E)$-decomposition as in [Reference Bushnell and KutzkoBK99, 5.3].◻
Corollary 6.5.  $[\bigoplus _{l=0}^{e-1}(\unicode[STIX]{x1D6EC}-l),q,s,\unicode[STIX]{x1D6FD}^{\oplus e}]$ is simple if and only if
$[\bigoplus _{l=0}^{e-1}(\unicode[STIX]{x1D6EC}-l),q,s,\unicode[STIX]{x1D6FD}^{\oplus e}]$ is simple if and only if  $[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is simple.
$[\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]$ is simple.
If  $F[\unicode[STIX]{x1D6FD}]$ is not a field we define for a semisimple stratum
$F[\unicode[STIX]{x1D6FD}]$ is not a field we define for a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, as in [Reference StevensSte05, (3.6)],
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, as in [Reference StevensSte05, (3.6)],
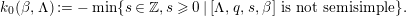 $$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=-\min \{s\in \mathbb{Z},s\geqslant 0\mid [\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]~\text{is not semisimple}\}.\end{eqnarray}$$
$$\begin{eqnarray}k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=-\min \{s\in \mathbb{Z},s\geqslant 0\mid [\unicode[STIX]{x1D6EC},q,s,\unicode[STIX]{x1D6FD}]~\text{is not semisimple}\}.\end{eqnarray}$$Minimal strata
We begin now with an analysis of semisimple strata of the form  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$. For the simple case, we recall that an element
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$. For the simple case, we recall that an element  $\unicode[STIX]{x1D6FD}$ of an extension
$\unicode[STIX]{x1D6FD}$ of an extension  $E|F$ is called minimal if it satisfies the following two conditions:
$E|F$ is called minimal if it satisfies the following two conditions:
(i)
 $\text{gcd}(\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD}),e(E|F))=1$;
$\text{gcd}(\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD}),e(E|F))=1$;(ii)
 $\unicode[STIX]{x1D6FD}^{e(E|F)}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD})}+\mathfrak{p}_{E}$ generates the extension
$\unicode[STIX]{x1D6FD}^{e(E|F)}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D708}_{E}(\unicode[STIX]{x1D6FD})}+\mathfrak{p}_{E}$ generates the extension  $\unicode[STIX]{x1D705}_{E}|\unicode[STIX]{x1D705}_{F}$.
$\unicode[STIX]{x1D705}_{E}|\unicode[STIX]{x1D705}_{F}$.
Then, by [Reference Bushnell and KutzkoBK93, 1.4.13(ii), 1.4.15], a pure stratum  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is simple if and only if
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is simple if and only if  $\unicode[STIX]{x1D6FD}$ is minimal. By a slight abuse, we call a semisimple stratum of the form
$\unicode[STIX]{x1D6FD}$ is minimal. By a slight abuse, we call a semisimple stratum of the form  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ a minimal semisimple stratum.
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ a minimal semisimple stratum.
For minimal semisimple strata, the characteristic polynomial is very important for distinguishing the summands. For  $b$ an element of a finite-dimensional semisimple algebra
$b$ an element of a finite-dimensional semisimple algebra  $B$ over some field
$B$ over some field  $K$, we denote the reduced characteristic polynomial of
$K$, we denote the reduced characteristic polynomial of  $b$ in
$b$ in  $B|K$, defined in [Reference ReinerRei03, (9.20)], by
$B|K$, defined in [Reference ReinerRei03, (9.20)], by  $\unicode[STIX]{x1D712}_{b,B|K}$, and the minimal polynomial by
$\unicode[STIX]{x1D712}_{b,B|K}$, and the minimal polynomial by  $\unicode[STIX]{x1D707}_{b,B|K}$.
$\unicode[STIX]{x1D707}_{b,B|K}$.
Definition 6.6. Let  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ be a stratum with
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ be a stratum with  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q$ and set
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD})=-q$ and set  $y_{\unicode[STIX]{x1D6FD}}:=\unicode[STIX]{x1D6FD}^{e/g}\unicode[STIX]{x1D71B}^{q/g}$, where
$y_{\unicode[STIX]{x1D6FD}}:=\unicode[STIX]{x1D6FD}^{e/g}\unicode[STIX]{x1D71B}^{q/g}$, where  $g=\text{gcd}(e,q)$, with characteristic polynomial
$g=\text{gcd}(e,q)$, with characteristic polynomial  $\unicode[STIX]{x1D6F7}(X)=\unicode[STIX]{x1D712}_{y_{\unicode[STIX]{x1D6FD}},A|F}\in o_{F}[X]$. We define the characteristic polynomial of the stratum
$\unicode[STIX]{x1D6F7}(X)=\unicode[STIX]{x1D712}_{y_{\unicode[STIX]{x1D6FD}},A|F}\in o_{F}[X]$. We define the characteristic polynomial of the stratum  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ to be the reduction
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ to be the reduction  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}:=\bar{\unicode[STIX]{x1D6F7}}\in \unicode[STIX]{x1D705}_{F}[X]$. It depends only on the equivalence class of the stratum.
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}:=\bar{\unicode[STIX]{x1D6F7}}\in \unicode[STIX]{x1D705}_{F}[X]$. It depends only on the equivalence class of the stratum.
For a null stratum we define  $y_{0}:=0$ and
$y_{0}:=0$ and  $\unicode[STIX]{x1D719}_{0}(X):=X^{N}$, where
$\unicode[STIX]{x1D719}_{0}(X):=X^{N}$, where  $N=\dim _{F}(V)$.
$N=\dim _{F}(V)$.
Remark 6.7. If  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FE}]$ intertwine then
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FE}]$ intertwine then  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}}$.
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}}$.
Proposition 6.8. If  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is semisimple with associated splitting
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is semisimple with associated splitting  $V=\bigoplus _{i\in I}V^{i}$, then we have the following:
$V=\bigoplus _{i\in I}V^{i}$, then we have the following:
(i)
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$ is the product of the polynomials
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$ is the product of the polynomials  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$, which are pairwise coprime polynomials;
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$, which are pairwise coprime polynomials;(ii) each polynomial
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$ is a power of an irreducible polynomial;
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$ is a power of an irreducible polynomial;(iii) the
 $F$-algebra homomorphism induced by
$F$-algebra homomorphism induced by  $\unicode[STIX]{x1D6FD}\mapsto \sum _{i\in I}\unicode[STIX]{x1D6FD}_{i}$ is a bijection from
$\unicode[STIX]{x1D6FD}\mapsto \sum _{i\in I}\unicode[STIX]{x1D6FD}_{i}$ is a bijection from  $F[\unicode[STIX]{x1D6FD}]$ to the product of the
$F[\unicode[STIX]{x1D6FD}]$ to the product of the  $E_{i}:=F[\unicode[STIX]{x1D6FD}_{i}]$;
$E_{i}:=F[\unicode[STIX]{x1D6FD}_{i}]$;(iv)
 $\unicode[STIX]{x1D705}_{F}[\bar{y}_{\unicode[STIX]{x1D6FD}}]$ is canonically isomorphic to
$\unicode[STIX]{x1D705}_{F}[\bar{y}_{\unicode[STIX]{x1D6FD}}]$ is canonically isomorphic to  $\prod _{i\in I}\unicode[STIX]{x1D705}_{F}[\bar{y}_{\unicode[STIX]{x1D6FD}_{i}}]$.
$\prod _{i\in I}\unicode[STIX]{x1D705}_{F}[\bar{y}_{\unicode[STIX]{x1D6FD}_{i}}]$.
Proof. For all indices  $i$, we have
$i$, we have  $e=e(\unicode[STIX]{x1D6EC}|o_{F})=e(\unicode[STIX]{x1D6EC}^{i}|o_{F})$ and
$e=e(\unicode[STIX]{x1D6EC}|o_{F})=e(\unicode[STIX]{x1D6EC}^{i}|o_{F})$ and  $q=q_{i}$ for all indices
$q=q_{i}$ for all indices  $i$ with
$i$ with  $\unicode[STIX]{x1D6FD}_{i}\neq 0$. Since also
$\unicode[STIX]{x1D6FD}_{i}\neq 0$. Since also  $\unicode[STIX]{x1D6FD}=\sum _{i}\unicode[STIX]{x1D6FD}_{i}$ with
$\unicode[STIX]{x1D6FD}=\sum _{i}\unicode[STIX]{x1D6FD}_{i}$ with  $\unicode[STIX]{x1D6FD}_{i}\in A^{i,i}$, we get
$\unicode[STIX]{x1D6FD}_{i}\in A^{i,i}$, we get
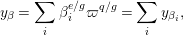 $$\begin{eqnarray}y_{\unicode[STIX]{x1D6FD}}=\mathop{\sum }_{i}\unicode[STIX]{x1D6FD}_{i}^{e/g}\unicode[STIX]{x1D71B}^{q/g}=\mathop{\sum }_{i}y_{\unicode[STIX]{x1D6FD}_{i}},\end{eqnarray}$$
$$\begin{eqnarray}y_{\unicode[STIX]{x1D6FD}}=\mathop{\sum }_{i}\unicode[STIX]{x1D6FD}_{i}^{e/g}\unicode[STIX]{x1D71B}^{q/g}=\mathop{\sum }_{i}y_{\unicode[STIX]{x1D6FD}_{i}},\end{eqnarray}$$ and  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$ is equal to the product of the
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$ is equal to the product of the  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$. That
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$. That  $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$ is primary now follows from the fact that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}_{i}}$ is primary now follows from the fact that  $[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ is a simple stratum and the remaining assertions are a consequence of [Reference StevensSte05, Remark 3.3].◻
$[\unicode[STIX]{x1D6EC}^{i},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ is a simple stratum and the remaining assertions are a consequence of [Reference StevensSte05, Remark 3.3].◻
It will also be useful to have another criterion by which to recognize a minimal semisimple stratum. Recall that a stratum  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is called fundamental if the coset
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is called fundamental if the coset  $\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q}$ contains no nilpotent elements; in this case, the rational number
$\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q}$ contains no nilpotent elements; in this case, the rational number  $q/e$ is called the level of the stratum, where
$q/e$ is called the level of the stratum, where  $e=e(\unicode[STIX]{x1D6EC}|o_{F})$. We also define the level of the null stratum
$e=e(\unicode[STIX]{x1D6EC}|o_{F})$. We also define the level of the null stratum  $[\unicode[STIX]{x1D6EC},q,q,0]$ to be
$[\unicode[STIX]{x1D6EC},q,q,0]$ to be  $q/e$.
$q/e$.
Proposition 6.9. A stratum  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is fundamental if and only if its characteristic polynomial is not a power of
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is fundamental if and only if its characteristic polynomial is not a power of  $X$. Two fundamental strata which intertwine have the same level. A fundamental stratum cannot intertwine a null stratum of strictly smaller level.
$X$. Two fundamental strata which intertwine have the same level. A fundamental stratum cannot intertwine a null stratum of strictly smaller level.
Proof. Suppose  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ has characteristic polynomial
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ has characteristic polynomial  $X^{m}$ and put
$X^{m}$ and put  $e=e(\unicode[STIX]{x1D6EC}|o_{F})$; then the element
$e=e(\unicode[STIX]{x1D6EC}|o_{F})$; then the element  $\unicode[STIX]{x1D6FD}$ satisfies
$\unicode[STIX]{x1D6FD}$ satisfies
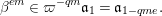 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}^{em}\in \unicode[STIX]{x1D71B}^{-qm}\mathfrak{a}_{1}=\mathfrak{a}_{1-qme}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}^{em}\in \unicode[STIX]{x1D71B}^{-qm}\mathfrak{a}_{1}=\mathfrak{a}_{1-qme}.\end{eqnarray}$$ Then, by [Reference BushnellBus87, Lemma 2.1], there is a nilpotent element in  $\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q}$, so the stratum is not fundamental. (The proof of that Lemma is valid for lattice sequences if one allows block matrices with block sizes
$\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q}$, so the stratum is not fundamental. (The proof of that Lemma is valid for lattice sequences if one allows block matrices with block sizes  $0\times l$ or
$0\times l$ or  $l\times 0$.) Conversely, if
$l\times 0$.) Conversely, if  $[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is not fundamental, then
$[\unicode[STIX]{x1D6EC},q,q-1,\unicode[STIX]{x1D6FD}]$ is not fundamental, then  $y_{\unicode[STIX]{x1D6FD}}$ is congruent to a nilpotent element modulo
$y_{\unicode[STIX]{x1D6FD}}$ is congruent to a nilpotent element modulo  $\mathfrak{a}_{1}$, and thus the characteristic polynomial of the stratum is a power of
$\mathfrak{a}_{1}$, and thus the characteristic polynomial of the stratum is a power of  $X$. The remaining assertions now follow easily, because if one of them were false, then there would be a fundamental stratum whose characteristic polynomial is a power of
$X$. The remaining assertions now follow easily, because if one of them were false, then there would be a fundamental stratum whose characteristic polynomial is a power of  $X$.◻
$X$.◻
We now give criteria for a fundamental stratum to be simple or semisimple. We recall that a fundamental stratum is called non-split if the characteristic polynomial of the stratum is a power of an irreducible polynomial. Given a fundamental stratum  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ we define the following
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ we define the following  $\unicode[STIX]{x1D705}_{F}$-algebra
$\unicode[STIX]{x1D705}_{F}$-algebra
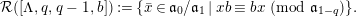 $$\begin{eqnarray}{\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b]):=\{\bar{x}\in \mathfrak{a}_{0}/\mathfrak{a}_{1}\mid xb\equiv bx~(\text{mod}~\mathfrak{a}_{1-q})\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b]):=\{\bar{x}\in \mathfrak{a}_{0}/\mathfrak{a}_{1}\mid xb\equiv bx~(\text{mod}~\mathfrak{a}_{1-q})\}.\end{eqnarray}$$ The following result is stated in [Reference Bushnell and KutzkoBK93, 2.4.13] for strict strata but, because the quotient  $\mathfrak{a}_{0}/\mathfrak{a}_{1}$ depends only on the image of
$\mathfrak{a}_{0}/\mathfrak{a}_{1}$ depends only on the image of  $\unicode[STIX]{x1D6EC}$ and the element
$\unicode[STIX]{x1D6EC}$ and the element  $b$ of a non-split fundamental stratum normalizes
$b$ of a non-split fundamental stratum normalizes  $\unicode[STIX]{x1D6EC}$, is also valid for arbitrary lattice sequences.
$\unicode[STIX]{x1D6EC}$, is also valid for arbitrary lattice sequences.
Proposition 6.10. [Reference Bushnell and KutzkoBK93, 2.4.13]
A non-split fundamental stratum  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a simple stratum if and only if
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a simple stratum if and only if  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple.
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple.
To get a similar result for semisimple strata we need, for an element  $b\in \mathfrak{a}_{-q}(\unicode[STIX]{x1D6EC})$ and an integer
$b\in \mathfrak{a}_{-q}(\unicode[STIX]{x1D6EC})$ and an integer  $n$, the map
$n$, the map
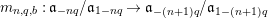 $$\begin{eqnarray}m_{n,q,b}:\mathfrak{a}_{-nq}/\mathfrak{a}_{1-nq}\rightarrow \mathfrak{a}_{-(n+1)q}/\mathfrak{a}_{1-(n+1)q}\end{eqnarray}$$
$$\begin{eqnarray}m_{n,q,b}:\mathfrak{a}_{-nq}/\mathfrak{a}_{1-nq}\rightarrow \mathfrak{a}_{-(n+1)q}/\mathfrak{a}_{1-(n+1)q}\end{eqnarray}$$ induced by multiplication by  $b$.
$b$.
Proposition 6.11. A fundamental stratum  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a semisimple stratum if and only if
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a semisimple stratum if and only if  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple and, for all non-negative integers
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple and, for all non-negative integers  $n$, the kernel of
$n$, the kernel of  $m_{n+1,q,b}$ and the image of
$m_{n+1,q,b}$ and the image of  $m_{n,q,b}$ intersect trivially.
$m_{n,q,b}$ intersect trivially.
Proof. Since the algebra  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ and the maps
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ and the maps  $m_{n,q,b}$ depend only on the equivalence class of the stratum, we are free to move to an equivalent stratum at any point.
$m_{n,q,b}$ depend only on the equivalence class of the stratum, we are free to move to an equivalent stratum at any point.
Suppose first that  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple and, for all non-negative integers
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])$ is semisimple and, for all non-negative integers  $n$, the kernel of
$n$, the kernel of  $m_{n+1,q,b}$ and the image of
$m_{n+1,q,b}$ and the image of  $m_{n,q,b}$ intersect trivially. We inductively find a splitting. For this, assume that
$m_{n,q,b}$ intersect trivially. We inductively find a splitting. For this, assume that  $\unicode[STIX]{x1D719}_{b}$ is a product of two coprime monic factors
$\unicode[STIX]{x1D719}_{b}$ is a product of two coprime monic factors  $\bar{f_{0}}$ and
$\bar{f_{0}}$ and  $\bar{f_{1}}$. Let
$\bar{f_{1}}$. Let  $\unicode[STIX]{x1D6F7}$ be the characteristic polynomial of
$\unicode[STIX]{x1D6F7}$ be the characteristic polynomial of  $y_{b}=\unicode[STIX]{x1D71B}^{q/g}b^{e/g}$, where
$y_{b}=\unicode[STIX]{x1D71B}^{q/g}b^{e/g}$, where  $g$ is the greatest common divisor of
$g$ is the greatest common divisor of  $e=e(\unicode[STIX]{x1D6EC}|o_{F})$ and
$e=e(\unicode[STIX]{x1D6EC}|o_{F})$ and  $q$. Hensel’s Lemma implies that we can factorize
$q$. Hensel’s Lemma implies that we can factorize  $\unicode[STIX]{x1D6F7}$ as
$\unicode[STIX]{x1D6F7}$ as  $f_{0}f_{1}$ where
$f_{0}f_{1}$ where  $f_{i}$ is a monic lift of
$f_{i}$ is a monic lift of  $\bar{f_{i}}$. By Bézout’s Lemma, there are polynomials
$\bar{f_{i}}$. By Bézout’s Lemma, there are polynomials  $a_{0},a_{1}\in o_{F}[X]$ such that
$a_{0},a_{1}\in o_{F}[X]$ such that  $a_{0}f_{0}+a_{1}f_{1}=1$. The map
$a_{0}f_{0}+a_{1}f_{1}=1$. The map  $1_{i}=a_{i}(y_{b})f_{i}(y_{b})$ is the projection onto the kernel of
$1_{i}=a_{i}(y_{b})f_{i}(y_{b})$ is the projection onto the kernel of  $f_{1-i}$, and the sum
$f_{1-i}$, and the sum  $\ker (f_{0})\oplus \ker (f_{1})=V$ splits the stratum
$\ker (f_{0})\oplus \ker (f_{1})=V$ splits the stratum  $[\unicode[STIX]{x1D6EC},q,q-1,b]$. Moreover, we have
$[\unicode[STIX]{x1D6EC},q,q-1,b]$. Moreover, we have  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])\simeq {\mathcal{R}}([\unicode[STIX]{x1D6EC}^{0},q_{0},q-1,b_{0}])\oplus {\mathcal{R}}([\unicode[STIX]{x1D6EC}^{1},q_{1},q-1,b_{1}])$, by the coprimality of
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])\simeq {\mathcal{R}}([\unicode[STIX]{x1D6EC}^{0},q_{0},q-1,b_{0}])\oplus {\mathcal{R}}([\unicode[STIX]{x1D6EC}^{1},q_{1},q-1,b_{1}])$, by the coprimality of  $f_{0},f_{1}$, so that both
$f_{0},f_{1}$, so that both  ${\mathcal{R}}([\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}])$ are semisimple.
${\mathcal{R}}([\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}])$ are semisimple.
Thus, by Propositions 6.10 and 6.8, we only have to show that strata equivalent to null strata are the only non-fundamental strata for which the kernel of  $m_{n+1,q,b}$ and the image of
$m_{n+1,q,b}$ and the image of  $m_{n,q,b}$ intersect trivially. Now let us assume that
$m_{n,q,b}$ intersect trivially. Now let us assume that  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ is non-fundamental. Then without loss of generality we can assume that
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ is non-fundamental. Then without loss of generality we can assume that  $b$ is nilpotent. The conditions on the maps imply that
$b$ is nilpotent. The conditions on the maps imply that  $m_{n,q,b}\circ m_{(n-1),q,b}\circ \cdots \circ m_{1,q,b}$ is injective on the image of
$m_{n,q,b}\circ m_{(n-1),q,b}\circ \cdots \circ m_{1,q,b}$ is injective on the image of  $m_{0,q,b}$. If
$m_{0,q,b}$. If  $n$ is big enough, the first product is the zero map, so the image of
$n$ is big enough, the first product is the zero map, so the image of  $m_{0,q,b}$ is zero, that is,
$m_{0,q,b}$ is zero, that is,  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a null stratum.
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ is equivalent to a null stratum.
For the converse, suppose that  $[\unicode[STIX]{x1D6EC},q,q-1,b]$ is a semisimple stratum with associated splitting
$[\unicode[STIX]{x1D6EC},q,q-1,b]$ is a semisimple stratum with associated splitting  $V=\bigoplus _{i\in I}V^{i}$. Since the characteristic polynomials
$V=\bigoplus _{i\in I}V^{i}$. Since the characteristic polynomials  $\unicode[STIX]{x1D719}_{b_{i}}$ are pairwise coprime, we have
$\unicode[STIX]{x1D719}_{b_{i}}$ are pairwise coprime, we have  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])\simeq \bigoplus _{i\in I}{\mathcal{R}}([\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}])$ and, since each stratum
${\mathcal{R}}([\unicode[STIX]{x1D6EC},q,q-1,b])\simeq \bigoplus _{i\in I}{\mathcal{R}}([\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}])$ and, since each stratum  $[\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}]$ is simple, this algebra is semisimple by Proposition 6.10. (Note that the algebra is clearly semisimple for the null stratum.)
$[\unicode[STIX]{x1D6EC}^{i},q_{i},q-1,b_{i}]$ is simple, this algebra is semisimple by Proposition 6.10. (Note that the algebra is clearly semisimple for the null stratum.)
The maps  $m_{n,q,b}$ preserve the decomposition
$m_{n,q,b}$ preserve the decomposition  $A=\bigoplus _{i,j}A^{i,j}$ so we may work blockwise. On the diagonal blocks
$A=\bigoplus _{i,j}A^{i,j}$ so we may work blockwise. On the diagonal blocks  $A^{i,i}$, the map
$A^{i,i}$, the map  $m_{n,q,b}$ is either zero (in the case
$m_{n,q,b}$ is either zero (in the case  $b_{i}=0$) or bijective. On the non-diagonal blocks
$b_{i}=0$) or bijective. On the non-diagonal blocks  $A^{i,j}$, with
$A^{i,j}$, with  $i\neq j$, the map is bijective or zero by [Reference Bushnell and KutzkoBK99, 3.7 Lemma 4].◻
$i\neq j$, the map is bijective or zero by [Reference Bushnell and KutzkoBK99, 3.7 Lemma 4].◻
Semisimple strata
Now we turn to the case of general semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$. A very important tool to prove properties of semisimple strata by an inductive procedure is the tame corestriction map, which was introduced in [Reference Bushnell and KutzkoBK93, 1.3.3] in the simple case.
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$. A very important tool to prove properties of semisimple strata by an inductive procedure is the tame corestriction map, which was introduced in [Reference Bushnell and KutzkoBK93, 1.3.3] in the simple case.
Definition 6.12. Let  $E|F$ be a field extension and
$E|F$ be a field extension and  $B$ be the centralizer of
$B$ be the centralizer of  $E$ in
$E$ in  $A$. A non-zero
$A$. A non-zero  $B$–
$B$– $B$-bimodule map
$B$-bimodule map  $s:A\rightarrow B$ is called a tame corestriction (relative to
$s:A\rightarrow B$ is called a tame corestriction (relative to  $E|F$) if, for all
$E|F$) if, for all  $\mathfrak{o}_{F}$-lattice sequences
$\mathfrak{o}_{F}$-lattice sequences  $\unicode[STIX]{x1D6EC}$ normalized by
$\unicode[STIX]{x1D6EC}$ normalized by  $E^{\times }$, we have
$E^{\times }$, we have
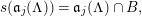 $$\begin{eqnarray}s(\mathfrak{a}_{j}(\unicode[STIX]{x1D6EC}))=\mathfrak{a}_{j}(\unicode[STIX]{x1D6EC})\cap B,\end{eqnarray}$$
$$\begin{eqnarray}s(\mathfrak{a}_{j}(\unicode[STIX]{x1D6EC}))=\mathfrak{a}_{j}(\unicode[STIX]{x1D6EC})\cap B,\end{eqnarray}$$ for all integers  $j$.
$j$.
If  $E=F[\unicode[STIX]{x1D6FE}]$ we often write
$E=F[\unicode[STIX]{x1D6FE}]$ we often write  $s_{\unicode[STIX]{x1D6FE}}$ for a (choice of) tame corestriction relative to
$s_{\unicode[STIX]{x1D6FE}}$ for a (choice of) tame corestriction relative to  $E|F$.
$E|F$.
(i) By [Reference Bushnell and KutzkoBK93, 1.3.4], tame corestrictions exist: if
 $\unicode[STIX]{x1D713}_{F}$ and
$\unicode[STIX]{x1D713}_{F}$ and  $\unicode[STIX]{x1D713}_{E}$ are additive characters of
$\unicode[STIX]{x1D713}_{E}$ are additive characters of  $F$ and
$F$ and  $E$, with conductors
$E$, with conductors  $\mathfrak{p}_{F}$ and
$\mathfrak{p}_{F}$ and  $\mathfrak{p}_{E}$, respectively, then there is a unique map
$\mathfrak{p}_{E}$, respectively, then there is a unique map  $s:A\rightarrow B$ such that This map is a tame corestriction and every tame corestriction arises in this way. Moreover, tame corestrictions are unique up to multiplication by an element of
$s:A\rightarrow B$ such that This map is a tame corestriction and every tame corestriction arises in this way. Moreover, tame corestrictions are unique up to multiplication by an element of $$\begin{eqnarray}\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}(ab)=\unicode[STIX]{x1D713}_{E}\circ \operatorname{tr}_{B|E}(s(a)b),\quad a\in A,b\in B.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}(ab)=\unicode[STIX]{x1D713}_{E}\circ \operatorname{tr}_{B|E}(s(a)b),\quad a\in A,b\in B.\end{eqnarray}$$ $o_{E}^{\times }$.
$o_{E}^{\times }$.(ii) If
 $\unicode[STIX]{x1D6FE}$ generates the extension
$\unicode[STIX]{x1D6FE}$ generates the extension  $E|F$ then, by [Reference Bushnell and KutzkoBK93, 1.3.2 (i)], the kernel of
$E|F$ then, by [Reference Bushnell and KutzkoBK93, 1.3.2 (i)], the kernel of  $s_{\unicode[STIX]{x1D6FE}}$ is equal to the image of the adjoint map
$s_{\unicode[STIX]{x1D6FE}}$ is equal to the image of the adjoint map  $a_{\unicode[STIX]{x1D6FE}}:A\rightarrow A$.
$a_{\unicode[STIX]{x1D6FE}}:A\rightarrow A$.(iii) If
 $E$ is
$E$ is  $\unicode[STIX]{x1D70E}$-invariant, we can arrange the additive characters
$\unicode[STIX]{x1D70E}$-invariant, we can arrange the additive characters  $\unicode[STIX]{x1D713}_{F}$ and
$\unicode[STIX]{x1D713}_{F}$ and  $\unicode[STIX]{x1D713}_{E}$ in (i) to be
$\unicode[STIX]{x1D713}_{E}$ in (i) to be  $\unicode[STIX]{x1D70E}$-invariant also, and then the tame corestriction
$\unicode[STIX]{x1D70E}$-invariant also, and then the tame corestriction  $s$ is
$s$ is  $\unicode[STIX]{x1D70E}$-equivariant.
$\unicode[STIX]{x1D70E}$-equivariant.
Given a simple stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ in
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ in  $A$ and an element
$A$ and an element  $c\in \mathfrak{a}_{-r}$, the tame corestriction map allows us to define a derived stratum
$c\in \mathfrak{a}_{-r}$, the tame corestriction map allows us to define a derived stratum  $[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(c)]$ in
$[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(c)]$ in  $B_{\unicode[STIX]{x1D6FE}}$, the centralizer in
$B_{\unicode[STIX]{x1D6FE}}$, the centralizer in  $A$ of
$A$ of  $\unicode[STIX]{x1D6FE}$, and we can ask whether this derived stratum is (equivalent to) a fundamental or simple stratum. The following theorem is particularly useful.
$\unicode[STIX]{x1D6FE}$, and we can ask whether this derived stratum is (equivalent to) a fundamental or simple stratum. The following theorem is particularly useful.
Theorem 6.14. [Reference Bushnell and KutzkoBK93, Theorems 2.2.8, 2.4.1]
Let  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ be a stratum equivalent to a simple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ be a stratum equivalent to a simple stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Then
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Then  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum if and only if the derived stratum
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum if and only if the derived stratum  $[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a simple stratum.
$[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a simple stratum.
As an immediate corollary, we get the following result on semisimple strata.
Corollary 6.15. Let  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ be a stratum equivalent to a simple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ be a stratum equivalent to a simple stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Assume that we have a decomposition
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Assume that we have a decomposition  $V=\bigoplus _{i}V^{i}$ into
$V=\bigoplus _{i}V^{i}$ into  $\unicode[STIX]{x1D6FD}$- and
$\unicode[STIX]{x1D6FD}$- and  $\unicode[STIX]{x1D6FE}$-invariant
$\unicode[STIX]{x1D6FE}$-invariant  $F$-subspaces. Then
$F$-subspaces. Then  $[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a semisimple stratum with associated splitting
$[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a semisimple stratum with associated splitting  $V=\bigoplus _{i}V^{i}$ if and only if
$V=\bigoplus _{i}V^{i}$ if and only if  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum with associated splitting
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum with associated splitting  $V=\bigoplus _{i}V^{i}$.
$V=\bigoplus _{i}V^{i}$.
Suppose now that  $[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$ is semisimple so that, for any
$[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$ is semisimple so that, for any  $0\leqslant r<q$, the stratum
$0\leqslant r<q$, the stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Then we can realize the assumption on
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$. Then we can realize the assumption on  $\unicode[STIX]{x1D6FE}$ in the previous corollary (that is, we can find
$\unicode[STIX]{x1D6FE}$ in the previous corollary (that is, we can find  $\unicode[STIX]{x1D6FE}$ such that the splitting associated to
$\unicode[STIX]{x1D6FE}$ such that the splitting associated to  $[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$ is preserved by
$[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$ is preserved by  $\unicode[STIX]{x1D6FE}$) by the following theorem.
$\unicode[STIX]{x1D6FE}$) by the following theorem.
Theorem 6.16. ([Reference StevensSte05, 3.4], [Reference StevensSte01b, 1.10])
Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a (skew)-stratum split by
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a (skew)-stratum split by  such that every stratum
such that every stratum  $[\unicode[STIX]{x1D6EC},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ is equivalent to a simple stratum, and such that
$[\unicode[STIX]{x1D6EC},q_{i},r,\unicode[STIX]{x1D6FD}_{i}]$ is equivalent to a simple stratum, and such that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum. Then
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum. Then  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a (skew)-simple stratum
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to a (skew)-simple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ split by the same direct sum.
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ split by the same direct sum.
Proof. We observe only that, although this is not quite the statement in [Reference StevensSte05, 3.4], this is what the proof there actually demonstrates. The skew case then follows immediately by applying [Reference StevensSte01b, 1.10]. ◻
In particular, if  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum with splitting
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum with splitting  $V=\bigoplus _{i}V^{i}$ and
$V=\bigoplus _{i}V^{i}$ and  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a simple stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ such that
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ such that  $\unicode[STIX]{x1D6FE}V^{i}\subseteq V^{i}$ for each
$\unicode[STIX]{x1D6FE}V^{i}\subseteq V^{i}$ for each  $i$, then Corollary 6.15 implies that the derived stratum
$i$, then Corollary 6.15 implies that the derived stratum  $[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a semisimple stratum with the same splitting
$[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})]$ is equivalent to a semisimple stratum with the same splitting  $V=\bigoplus _{i}V^{i}$.
$V=\bigoplus _{i}V^{i}$.
Notation 6.17. For the rest of the article we use the following notation:  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ always denotes a stratum, and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ always denotes a stratum, and  $B$ the centralizer of
$B$ the centralizer of  $\unicode[STIX]{x1D6FD}$ in
$\unicode[STIX]{x1D6FD}$ in  $A$. If
$A$. If  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is semisimple then
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is semisimple then  $V=\bigoplus _{i\in I}V^{i}$ is the associated splitting and we have
$V=\bigoplus _{i\in I}V^{i}$ is the associated splitting and we have  $A=\bigoplus _{i,j}A^{i,j}$ and
$A=\bigoplus _{i,j}A^{i,j}$ and  $B=\bigoplus _{i\in I}B^{i,i}$, where
$B=\bigoplus _{i\in I}B^{i,i}$, where  $B^{i,i}$ is the centralizer of
$B^{i,i}$ is the centralizer of  $E_{i}=F[\unicode[STIX]{x1D6FD}_{i}]$ in
$E_{i}=F[\unicode[STIX]{x1D6FD}_{i}]$ in  $A^{i,i}$. Further, we write
$A^{i,i}$. Further, we write  $\mathfrak{b}_{l}$ for the intersection of
$\mathfrak{b}_{l}$ for the intersection of  $\mathfrak{a}_{l}$ with
$\mathfrak{a}_{l}$ with  $B$. We use analogous notations for a second stratum
$B$. We use analogous notations for a second stratum  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ but all with
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ but all with  $(\,)^{\prime }$. If we want to specify the centralizer of
$(\,)^{\prime }$. If we want to specify the centralizer of  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in  $A$, for an arbitrary element
$A$, for an arbitrary element  $\unicode[STIX]{x1D6FE}$, we write
$\unicode[STIX]{x1D6FE}$, we write  $B_{\unicode[STIX]{x1D6FE}}$.
$B_{\unicode[STIX]{x1D6FE}}$.
Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum. We define a tame corestriction
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum. We define a tame corestriction  $s_{\unicode[STIX]{x1D6FD}}:A\rightarrow B$ for
$s_{\unicode[STIX]{x1D6FD}}:A\rightarrow B$ for  $\unicode[STIX]{x1D6FD}$ by
$\unicode[STIX]{x1D6FD}$ by  $s_{\unicode[STIX]{x1D6FD}}(a):=\sum _{i}s_{i}(a_{ii})$, where
$s_{\unicode[STIX]{x1D6FD}}(a):=\sum _{i}s_{i}(a_{ii})$, where  $s_{i}$ is a tame corestriction for
$s_{i}$ is a tame corestriction for  $\unicode[STIX]{x1D6FD}_{i}$ as in Definition 6.12. If
$\unicode[STIX]{x1D6FD}_{i}$ as in Definition 6.12. If  $s_{i}$ is defined relative to additive characters
$s_{i}$ is defined relative to additive characters  $\unicode[STIX]{x1D713}_{F},\unicode[STIX]{x1D713}_{E^{i}}$ as in Remark 6.13(i), then we put
$\unicode[STIX]{x1D713}_{F},\unicode[STIX]{x1D713}_{E^{i}}$ as in Remark 6.13(i), then we put  $\unicode[STIX]{x1D713}_{B^{i,i}}=\unicode[STIX]{x1D713}_{E^{i}}\circ \operatorname{tr}_{B^{i,i}|E^{i}}$ and define an additive character of
$\unicode[STIX]{x1D713}_{B^{i,i}}=\unicode[STIX]{x1D713}_{E^{i}}\circ \operatorname{tr}_{B^{i,i}|E^{i}}$ and define an additive character of  $B$ by
$B$ by
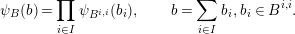 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{B}(b)=\mathop{\prod }_{i\in I}\unicode[STIX]{x1D713}_{B^{i,i}}(b_{i}),\qquad b=\mathop{\sum }_{i\in I}b_{i},b_{i}\in B^{i,i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{B}(b)=\mathop{\prod }_{i\in I}\unicode[STIX]{x1D713}_{B^{i,i}}(b_{i}),\qquad b=\mathop{\sum }_{i\in I}b_{i},b_{i}\in B^{i,i}.\end{eqnarray}$$ Writing  $\unicode[STIX]{x1D713}_{A}=\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}$, the map
$\unicode[STIX]{x1D713}_{A}=\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}$, the map  $s_{\unicode[STIX]{x1D6FD}}$ is then a non-zero
$s_{\unicode[STIX]{x1D6FD}}$ is then a non-zero  $(B,B)$-bimodule homomorphism satisfying
$(B,B)$-bimodule homomorphism satisfying
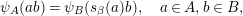 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{A}(ab)=\unicode[STIX]{x1D713}_{B}(s_{\unicode[STIX]{x1D6FD}}(a)b),\quad a\in A,b\in B,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{A}(ab)=\unicode[STIX]{x1D713}_{B}(s_{\unicode[STIX]{x1D6FD}}(a)b),\quad a\in A,b\in B,\end{eqnarray}$$and
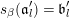 $$\begin{eqnarray}s_{\unicode[STIX]{x1D6FD}}(\mathfrak{a}_{l}^{\prime })=\mathfrak{b}_{l}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}s_{\unicode[STIX]{x1D6FD}}(\mathfrak{a}_{l}^{\prime })=\mathfrak{b}_{l}^{\prime }\end{eqnarray}$$ for all lattice sequences  $\unicode[STIX]{x1D6EC}^{\prime }$ which are split by
$\unicode[STIX]{x1D6EC}^{\prime }$ which are split by  $V=\bigoplus _{i}V^{i}$ into a direct sum of
$V=\bigoplus _{i}V^{i}$ into a direct sum of  $o_{E^{i}}$-lattice sequences.
$o_{E^{i}}$-lattice sequences.
Lemma 6.18. The sequence  $A\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }A\stackrel{s_{\unicode[STIX]{x1D6FD}}}{\rightarrow }B$ is exact and the kernel of
$A\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }A\stackrel{s_{\unicode[STIX]{x1D6FD}}}{\rightarrow }B$ is exact and the kernel of  $s_{\unicode[STIX]{x1D6FD}}$ is split by the decomposition
$s_{\unicode[STIX]{x1D6FD}}$ is split by the decomposition  $A=\bigoplus A^{i,j}$.
$A=\bigoplus A^{i,j}$.
Proof. By definition, the kernel of  $s_{\unicode[STIX]{x1D6FD}}$ is the direct sum of the
$s_{\unicode[STIX]{x1D6FD}}$ is the direct sum of the  $A^{i,j}$, for
$A^{i,j}$, for  $i\neq j$, and of the kernels of
$i\neq j$, and of the kernels of  $s_{i}$, for
$s_{i}$, for  $i\in I$. The sequence is exact on the
$i\in I$. The sequence is exact on the  $(i,i)$ components, by [Reference Bushnell and KutzkoBK93, 1.3.2], and it is therefore enough to prove that for
$(i,i)$ components, by [Reference Bushnell and KutzkoBK93, 1.3.2], and it is therefore enough to prove that for  $j\neq i$ the restriction of
$j\neq i$ the restriction of  $a_{\unicode[STIX]{x1D6FD}}$ on
$a_{\unicode[STIX]{x1D6FD}}$ on  $A^{i,j}$ is bijective onto
$A^{i,j}$ is bijective onto  $A^{i,j}$. It has the form
$A^{i,j}$. It has the form  $a_{\unicode[STIX]{x1D6FD}}(a_{ij})=\unicode[STIX]{x1D6FD}_{i}a_{ij}-a_{ij}\unicode[STIX]{x1D6FD}_{j}$, which is injective because
$a_{\unicode[STIX]{x1D6FD}}(a_{ij})=\unicode[STIX]{x1D6FD}_{i}a_{ij}-a_{ij}\unicode[STIX]{x1D6FD}_{j}$, which is injective because  $\unicode[STIX]{x1D6FD}_{i}$ and
$\unicode[STIX]{x1D6FD}_{i}$ and  $\unicode[STIX]{x1D6FD}_{j}$ have no common eigenvalue, because their minimal polynomials are coprime since
$\unicode[STIX]{x1D6FD}_{j}$ have no common eigenvalue, because their minimal polynomials are coprime since  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ is not equivalent to a simple stratum.◻
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ is not equivalent to a simple stratum.◻
To describe the intertwining of a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, recall that we have defined the integer
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$, recall that we have defined the integer  $k_{0}=k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and the lattices
$k_{0}=k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and the lattices  $\mathfrak{n}_{l}=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{l})\cap \mathfrak{a}_{0}$, for
$\mathfrak{n}_{l}=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{l})\cap \mathfrak{a}_{0}$, for  $l$ an integer. We will also need the unit subgroups
$l$ an integer. We will also need the unit subgroups  $1+\mathfrak{m}_{l}$, where
$1+\mathfrak{m}_{l}$, where  $\mathfrak{m}_{l}=\mathfrak{n}_{l+k_{0}}\cap \mathfrak{a}_{l}$, for integers
$\mathfrak{m}_{l}=\mathfrak{n}_{l+k_{0}}\cap \mathfrak{a}_{l}$, for integers  $l\geqslant 1$. As the first of several intertwining results we have:
$l\geqslant 1$. As the first of several intertwining results we have:
Theorem 6.19. (See [Reference StevensSte01a, 4.6], [Reference Bushnell and KutzkoBK93, 1.5.8] for simple strata)
Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum.
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum.
(i)
 $I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}])=(1+\mathfrak{m}_{-(k_{0}+r)})B^{\times }(1+\mathfrak{m}_{-(k_{0}+r)})$.
$I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}])=(1+\mathfrak{m}_{-(k_{0}+r)})B^{\times }(1+\mathfrak{m}_{-(k_{0}+r)})$.(ii) If the stratum is skew then
 $$\begin{eqnarray}I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}])=((1+\mathfrak{m}_{-(k_{0}+r)})\cap G)(B^{\times }\cap G)((1+\mathfrak{m}_{-(k_{0}+r)})\cap G).\end{eqnarray}$$
$$\begin{eqnarray}I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}])=((1+\mathfrak{m}_{-(k_{0}+r)})\cap G)(B^{\times }\cap G)((1+\mathfrak{m}_{-(k_{0}+r)})\cap G).\end{eqnarray}$$
The crucial ingredient for the proof is:
Lemma 6.20. [Reference StevensSte05, 3.7]
For all integers  $s$ we have:
$s$ we have:
(i)
 $\mathfrak{n}_{-s}^{i,j}\subseteq \mathfrak{a}_{-(k_{0}+s)}$ for
$\mathfrak{n}_{-s}^{i,j}\subseteq \mathfrak{a}_{-(k_{0}+s)}$ for  $i\neq j$;
$i\neq j$;(ii)
 $\mathfrak{n}_{-s}=\mathfrak{b}_{0}+\mathfrak{n}_{-s}\cap \mathfrak{a}_{-(k_{0}+s)}$.
$\mathfrak{n}_{-s}=\mathfrak{b}_{0}+\mathfrak{n}_{-s}\cap \mathfrak{a}_{-(k_{0}+s)}$.
In [Reference StevensSte05], this lemma was formulated for  $s\leqslant -k_{0}$, but the case
$s\leqslant -k_{0}$, but the case  $s\geqslant -k_{0}$ is trivial. From this we deduce
$s\geqslant -k_{0}$ is trivial. From this we deduce
Lemma 6.21. Take  $i\neq j$. The restriction of
$i\neq j$. The restriction of  $a_{\unicode[STIX]{x1D6FD}}$ to
$a_{\unicode[STIX]{x1D6FD}}$ to  $A^{i,j}$ is an
$A^{i,j}$ is an  $F$-linear homeomorphism and
$F$-linear homeomorphism and  $a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ is equal to
$a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ is equal to  $\mathfrak{n}_{s}^{i,j}$ for all integers
$\mathfrak{n}_{s}^{i,j}$ for all integers  $s\geqslant k_{0}$.
$s\geqslant k_{0}$.
Proof. The map  $a_{\unicode[STIX]{x1D6FD}}$ is a linear automorphism on
$a_{\unicode[STIX]{x1D6FD}}$ is a linear automorphism on  $A^{i,j}$ by Lemma 6.18; thus the image of an
$A^{i,j}$ by Lemma 6.18; thus the image of an  $o_{F}$-lattice contains an
$o_{F}$-lattice contains an  $o_{F}$-lattice and the restriction of
$o_{F}$-lattice and the restriction of  $a_{\unicode[STIX]{x1D6FD}}$ to
$a_{\unicode[STIX]{x1D6FD}}$ to  $A^{i,j}$ is a homeomorphism. It follows that, for
$A^{i,j}$ is a homeomorphism. It follows that, for  $s$ big enough, we have that
$s$ big enough, we have that  $a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}:=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})\cap A^{i,j}$ is contained in
$a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}:=a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})\cap A^{i,j}$ is contained in  $\mathfrak{a}_{0}^{i,j}$ and is therefore equal to
$\mathfrak{a}_{0}^{i,j}$ and is therefore equal to  $\mathfrak{n}_{s}^{i,j}$; in particular, it is contained in
$\mathfrak{n}_{s}^{i,j}$; in particular, it is contained in  $\mathfrak{a}_{-k_{0}+s}^{i,j}$ by Lemma 6.20(i). By periodicity we have that
$\mathfrak{a}_{-k_{0}+s}^{i,j}$ by Lemma 6.20(i). By periodicity we have that  $a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ is contained in
$a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ is contained in  $\mathfrak{a}_{-k_{0}+s}^{i,j}$ for all integers
$\mathfrak{a}_{-k_{0}+s}^{i,j}$ for all integers  $s$ and thus
$s$ and thus  $\mathfrak{n}_{s}^{i,j}$ is equal to
$\mathfrak{n}_{s}^{i,j}$ is equal to  $a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ for all integers
$a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{s})^{i,j}$ for all integers  $s$ with
$s$ with  $s\geqslant k_{0}$.◻
$s\geqslant k_{0}$.◻
Proof of Theorem 6.19.
We follow the proof of [Reference Bushnell and KutzkoBK93, 1.5.8]. For a null stratum there is nothing to prove, so we assume the stratum is non-null. The main ingredients which have to be verified are the exact sequences of [Reference Bushnell and KutzkoBK93, 1.4.10], which hold by Lemma 6.20, and the analogue of [Reference Bushnell and KutzkoBK93, 1.4.16], which we prove now. We write  $d$ for
$d$ for  $-(r+k_{0})$ and put:
$-(r+k_{0})$ and put:
∙
 $M=\mathfrak{n}_{t+jd+k_{0}}\cap \mathfrak{a}_{t+jd}\cap (\unicode[STIX]{x1D6FE}_{1}(\mathfrak{n}_{-r}\cap \mathfrak{a}_{d})+(\mathfrak{n}_{-r}\cap \mathfrak{a}_{d})\unicode[STIX]{x1D6FE}_{2}+(\mathfrak{n}_{t+jd-r}\cap \mathfrak{a}_{t+(j+1)d}))$;
$M=\mathfrak{n}_{t+jd+k_{0}}\cap \mathfrak{a}_{t+jd}\cap (\unicode[STIX]{x1D6FE}_{1}(\mathfrak{n}_{-r}\cap \mathfrak{a}_{d})+(\mathfrak{n}_{-r}\cap \mathfrak{a}_{d})\unicode[STIX]{x1D6FE}_{2}+(\mathfrak{n}_{t+jd-r}\cap \mathfrak{a}_{t+(j+1)d}))$;∙
 $L=\mathfrak{a}_{t+jd+k_{0}}\cap (\unicode[STIX]{x1D6FE}_{1}\mathfrak{a}_{-r}+\mathfrak{a}_{-r}\unicode[STIX]{x1D6FE}_{2}+\mathfrak{a}_{t+jd-r})$;
$L=\mathfrak{a}_{t+jd+k_{0}}\cap (\unicode[STIX]{x1D6FE}_{1}\mathfrak{a}_{-r}+\mathfrak{a}_{-r}\unicode[STIX]{x1D6FE}_{2}+\mathfrak{a}_{t+jd-r})$;
for integers  $t\geqslant 0,j\geqslant 1$ and elements
$t\geqslant 0,j\geqslant 1$ and elements  $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$ of
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$ of  $B^{\times }$. The sequence
$B^{\times }$. The sequence  $M\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }L\stackrel{s_{\unicode[STIX]{x1D6FD}}}{\rightarrow }B$ is exact if all its restrictions on the
$M\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }L\stackrel{s_{\unicode[STIX]{x1D6FD}}}{\rightarrow }B$ is exact if all its restrictions on the  $A^{i,j}$ are exact. For
$A^{i,j}$ are exact. For  $i=j$ the proof is done in [Reference StevensSte01a, (5.2)] and for
$i=j$ the proof is done in [Reference StevensSte01a, (5.2)] and for  $i\neq j$ it follows from Lemmas 6.20(i), 6.21 and 6.18. The same cohomology argument as in [Reference StevensSte01a, Corollary 4.14] followed by the simple case in [Reference StevensSte01a, Theorem 4.6] proves (ii).◻
$i\neq j$ it follows from Lemmas 6.20(i), 6.21 and 6.18. The same cohomology argument as in [Reference StevensSte01a, Corollary 4.14] followed by the simple case in [Reference StevensSte01a, Theorem 4.6] proves (ii).◻
A completely analogous proof using the exercise [Reference Bushnell and KutzkoBK93, 1.5.12] (or, alternatively, using the  $\dagger$-construction as in [Reference Kurinczuk and StevensKS15, Theorem 3.9]) provides:
$\dagger$-construction as in [Reference Kurinczuk and StevensKS15, Theorem 3.9]) provides:
Theorem 6.22. Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}]$ be semisimple strata in
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}]$ be semisimple strata in  $A$. Then:
$A$. Then:
(i)
 $I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}])=(1+\mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime })B^{\times }(1+\mathfrak{m}_{-(k_{0}+r)})$;
$I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}])=(1+\mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime })B^{\times }(1+\mathfrak{m}_{-(k_{0}+r)})$;(ii) if both strata are skew then
 $$\begin{eqnarray}\displaystyle & & \displaystyle I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}])\nonumber\\ \displaystyle & & \displaystyle \quad =((1+\mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime })\cap G)(B^{\times }\cap G)((1+\mathfrak{m}_{-(k_{0}+r)})\cap G).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}])\nonumber\\ \displaystyle & & \displaystyle \quad =((1+\mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime })\cap G)(B^{\times }\cap G)((1+\mathfrak{m}_{-(k_{0}+r)})\cap G).\nonumber\end{eqnarray}$$
7 Matching for intertwining strata
In this chapter we show that, if we have semisimple strata which intertwine, then there is a canonical bijection between their associated splittings. This will then allow us to deduce a Skolem–Noether theorem for skew-semisimple strata which intertwine.
7.1 For general linear groups
We fix a pair of semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$,
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$,  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$, with associated splittings
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$, with associated splittings  $\bigoplus _{i\in I}V^{i}$ and
$\bigoplus _{i\in I}V^{i}$ and  $\bigoplus _{j\in I^{\prime }}V^{\prime j}$, respectively. The main result of this subsection is:
$\bigoplus _{j\in I^{\prime }}V^{\prime j}$, respectively. The main result of this subsection is:
Proposition 7.1. Suppose that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ intertwines
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ intertwines  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$, that
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$, that  $r=r^{\prime }$ and that
$r=r^{\prime }$ and that  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then:
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then:
(i) if one stratum is null, then
 $q=q^{\prime }$ and the other stratum is null;
$q=q^{\prime }$ and the other stratum is null;(ii) if both strata are non-null then
 $q=q^{\prime }$ and there is a unique bijection
$q=q^{\prime }$ and there is a unique bijection  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, for all indices
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, for all indices  $i\in I$. Moreover,
$i\in I$. Moreover,  $V^{i}$ and
$V^{i}$ and  $V^{\prime \unicode[STIX]{x1D701}(i)}$ have the same
$V^{\prime \unicode[STIX]{x1D701}(i)}$ have the same  $F$-dimension.
$F$-dimension.
Note that, in case (i), both splittings are trivial so we trivially have a (unique) bijection  $\unicode[STIX]{x1D701}$ as in (ii). We call the bijection
$\unicode[STIX]{x1D701}$ as in (ii). We call the bijection  $\unicode[STIX]{x1D701}$ a matching of
$\unicode[STIX]{x1D701}$ a matching of  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r,\unicode[STIX]{x1D6FD}^{\prime }]$ and
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r,\unicode[STIX]{x1D6FD}^{\prime }]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$.
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$.
Remark 7.2. If  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ do not have the same period then we can scale them so that they do. In particular, the requirement in Proposition 7.1 that they have the same period is not a genuine constraint.
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ do not have the same period then we can scale them so that they do. In particular, the requirement in Proposition 7.1 that they have the same period is not a genuine constraint.
To prove Proposition 7.1 (and, later, other results on semisimple strata), we introduce the notion of a defining sequence for a semisimple stratum, which allows us to prove properties of semisimple strata by an inductive process (cf. [Reference Bushnell and KutzkoBK93] for the simple case). Let  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a (skew)-semisimple stratum with associated splitting
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ be a (skew)-semisimple stratum with associated splitting  $V=\bigoplus _{i\in I}V^{i}$. A defining sequence for
$V=\bigoplus _{i\in I}V^{i}$. A defining sequence for  $\unicode[STIX]{x1D6E5}$ is a finite sequence of (skew)-semisimple strata
$\unicode[STIX]{x1D6E5}$ is a finite sequence of (skew)-semisimple strata  $(\unicode[STIX]{x1D6E5}^{k})_{k=0,\ldots ,q-r}$ defined as follows:
$(\unicode[STIX]{x1D6E5}^{k})_{k=0,\ldots ,q-r}$ defined as follows:
∙
 $\unicode[STIX]{x1D6E5}^{0}=\unicode[STIX]{x1D6E5}$;
$\unicode[STIX]{x1D6E5}^{0}=\unicode[STIX]{x1D6E5}$;∙ for
 $0<k\leqslant q-r$, we have
$0<k\leqslant q-r$, we have  $\unicode[STIX]{x1D6E5}^{k}=[\unicode[STIX]{x1D6EC},q,r+k,\unicode[STIX]{x1D6FE}_{k}]$ a (skew)-semisimple stratum equivalent to
$\unicode[STIX]{x1D6E5}^{k}=[\unicode[STIX]{x1D6EC},q,r+k,\unicode[STIX]{x1D6FE}_{k}]$ a (skew)-semisimple stratum equivalent to  $[\unicode[STIX]{x1D6EC},q,r+k,\unicode[STIX]{x1D6FD}]$ with
$[\unicode[STIX]{x1D6EC},q,r+k,\unicode[STIX]{x1D6FD}]$ with  $\unicode[STIX]{x1D6FE}_{k}\in \prod _{i}A^{i,i}$ (see Theorem 6.16).
$\unicode[STIX]{x1D6FE}_{k}\in \prod _{i}A^{i,i}$ (see Theorem 6.16).
Note that there is a significant degree of choice in producing a defining sequence for a (skew)-semisimple stratum.
Suppose now we want to prove a statement  $P(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$ for all pairs of semisimple strata
$P(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$ for all pairs of semisimple strata  $\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$. The inductive procedure, which we call strata induction, to prove
$\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$. The inductive procedure, which we call strata induction, to prove  $P$ is given by the following steps.
$P$ is given by the following steps.
∙ The base case: Here one proves
 $P$ for all minimal semisimple strata and null strata.
$P$ for all minimal semisimple strata and null strata.∙ The induction step:
(i) The step
 $r+1$ to
$r+1$ to  $r$: from the induction hypothesis and possibly an auxiliary statement (S1) we restrict to the case where the first elements
$r$: from the induction hypothesis and possibly an auxiliary statement (S1) we restrict to the case where the first elements  $\unicode[STIX]{x1D6E5}^{(1)}$ and
$\unicode[STIX]{x1D6E5}^{(1)}$ and  $\unicode[STIX]{x1D6E5}^{\prime (1)}$ of defining sequences of
$\unicode[STIX]{x1D6E5}^{\prime (1)}$ of defining sequences of  $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6E5}^{\prime }$ have the same element
$\unicode[STIX]{x1D6E5}^{\prime }$ have the same element  $\unicode[STIX]{x1D6FE}$, and hence the same associated splitting.
$\unicode[STIX]{x1D6FE}$, and hence the same associated splitting.(ii) Taking a second auxiliary statement (S2), we show that the derived strata
 $s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5})$ and
$s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5})$ and  $s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}^{\prime })$ satisfy the assumptions of
$s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}^{\prime })$ satisfy the assumptions of  $P$. In this article, (S2) will always be the description of the intertwining of
$P$. In this article, (S2) will always be the description of the intertwining of  $\unicode[STIX]{x1D6E5}^{(1)}$ with
$\unicode[STIX]{x1D6E5}^{(1)}$ with  $\unicode[STIX]{x1D6E5}^{\prime (1)}$ (see Proposition 7.3 below).
$\unicode[STIX]{x1D6E5}^{\prime (1)}$ (see Proposition 7.3 below).(iii) The base case shows
 $P(s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}),s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}^{\prime }))$ and, together with a third auxiliary statement (S3), provides
$P(s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}),s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6E5}^{\prime }))$ and, together with a third auxiliary statement (S3), provides  $P(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$. For (S3) we will use Theorem 6.14.
$P(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$. For (S3) we will use Theorem 6.14.
Strata induction can be restricted to simple strata by substituting the word semisimple by simple.
In the following, we use the notation for tame corestrictions as in the previous section.
Proposition 7.3. Suppose  $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }$ and we are given elements
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }$ and we are given elements  $a\in \mathfrak{a}_{-r}$ and
$a\in \mathfrak{a}_{-r}$ and  $a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$ such that there is an element
$a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$ such that there is an element  $g$ of
$g$ of  $\tilde{G}$ which intertwines
$\tilde{G}$ which intertwines  $[\unicode[STIX]{x1D6EC},q,r-1,\unicode[STIX]{x1D6FD}+a]$ with
$[\unicode[STIX]{x1D6EC},q,r-1,\unicode[STIX]{x1D6FD}+a]$ with  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime }-1,\unicode[STIX]{x1D6FD}+a^{\prime }]$. Using Theorem 6.22, write
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime }-1,\unicode[STIX]{x1D6FD}+a^{\prime }]$. Using Theorem 6.22, write  $g=(1+u^{\prime })b(1+v)$, with
$g=(1+u^{\prime })b(1+v)$, with  $b\in B^{\times }$,
$b\in B^{\times }$,  $u^{\prime }\in \mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime }$ and
$u^{\prime }\in \mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime }$ and  $v\in \mathfrak{m}_{-(k_{0}+r)}$. Then the component
$v\in \mathfrak{m}_{-(k_{0}+r)}$. Then the component  $b^{i,i}$ intertwines
$b^{i,i}$ intertwines  $[\unicode[STIX]{x1D6EC},r,r-1,s_{i}(a^{i,i})]$ with
$[\unicode[STIX]{x1D6EC},r,r-1,s_{i}(a^{i,i})]$ with  $[\unicode[STIX]{x1D6EC}^{\prime },r^{\prime },r^{\prime }-1,s_{i}(a^{\prime i,i})]$, for all
$[\unicode[STIX]{x1D6EC}^{\prime },r^{\prime },r^{\prime }-1,s_{i}(a^{\prime i,i})]$, for all  $i\in I$.
$i\in I$.
Proof. Again we only have to consider a non-zero element  $\unicode[STIX]{x1D6FD}$. This is essentially the calculation in [Reference Bushnell and KutzkoBK93, 2.6.1] which we want to recall, to show its validity for different semisimple strata.
$\unicode[STIX]{x1D6FD}$. This is essentially the calculation in [Reference Bushnell and KutzkoBK93, 2.6.1] which we want to recall, to show its validity for different semisimple strata.
Let  $(1+w^{\prime })$ be the inverse of
$(1+w^{\prime })$ be the inverse of  $(1+u^{\prime })$. By the intertwining property of
$(1+u^{\prime })$. By the intertwining property of  $g$, we have
$g$, we have
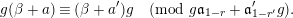 $$\begin{eqnarray}g(\unicode[STIX]{x1D6FD}+a)\equiv (\unicode[STIX]{x1D6FD}+a^{\prime })g\hspace{0.6em}({\rm mod}\hspace{0.2em}g\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }g).\end{eqnarray}$$
$$\begin{eqnarray}g(\unicode[STIX]{x1D6FD}+a)\equiv (\unicode[STIX]{x1D6FD}+a^{\prime })g\hspace{0.6em}({\rm mod}\hspace{0.2em}g\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }g).\end{eqnarray}$$ Multiplying by  $(1+w^{\prime })$ on the left and
$(1+w^{\prime })$ on the left and  $(1+v)^{-1}$ on the right we obtain
$(1+v)^{-1}$ on the right we obtain
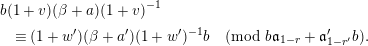 $$\begin{eqnarray}\displaystyle & & \displaystyle b(1+v)(\unicode[STIX]{x1D6FD}+a)(1+v)^{-1}\nonumber\\ \displaystyle & & \displaystyle \quad \equiv (1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime })(1+w^{\prime })^{-1}b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }b).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle b(1+v)(\unicode[STIX]{x1D6FD}+a)(1+v)^{-1}\nonumber\\ \displaystyle & & \displaystyle \quad \equiv (1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime })(1+w^{\prime })^{-1}b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }b).\end{eqnarray}$$We first consider the right hand side.
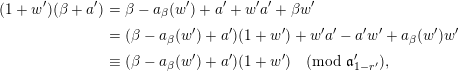 $$\begin{eqnarray}\displaystyle (1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime }) & = & \displaystyle \unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime }+w^{\prime }a^{\prime }+\unicode[STIX]{x1D6FD}w^{\prime }\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })(1+w^{\prime })+w^{\prime }a^{\prime }-a^{\prime }w^{\prime }+a_{\unicode[STIX]{x1D6FD}}(w^{\prime })w^{\prime }\nonumber\\ \displaystyle & \equiv & \displaystyle (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })(1+w^{\prime })\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-r^{\prime }}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime }) & = & \displaystyle \unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime }+w^{\prime }a^{\prime }+\unicode[STIX]{x1D6FD}w^{\prime }\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })(1+w^{\prime })+w^{\prime }a^{\prime }-a^{\prime }w^{\prime }+a_{\unicode[STIX]{x1D6FD}}(w^{\prime })w^{\prime }\nonumber\\ \displaystyle & \equiv & \displaystyle (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })(1+w^{\prime })\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-r^{\prime }}^{\prime }),\nonumber\end{eqnarray}$$ because  $a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$,
$a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$,  $w^{\prime }\in \mathfrak{a}_{1}^{\prime }$ and
$w^{\prime }\in \mathfrak{a}_{1}^{\prime }$ and  $a_{\unicode[STIX]{x1D6FD}}(w^{\prime })\in \mathfrak{a}_{-r^{\prime }}^{\prime }$. A similar calculation for the left hand side and equation (7.4) leads to
$a_{\unicode[STIX]{x1D6FD}}(w^{\prime })\in \mathfrak{a}_{-r^{\prime }}^{\prime }$. A similar calculation for the left hand side and equation (7.4) leads to
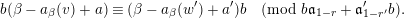 $$\begin{eqnarray}b(\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(v)+a)\equiv (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }b).\end{eqnarray}$$
$$\begin{eqnarray}b(\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(v)+a)\equiv (\unicode[STIX]{x1D6FD}-a_{\unicode[STIX]{x1D6FD}}(w^{\prime })+a^{\prime })b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }b).\end{eqnarray}$$ We apply  $s_{\unicode[STIX]{x1D6FD}}$ to get
$s_{\unicode[STIX]{x1D6FD}}$ to get
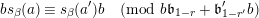 $$\begin{eqnarray}bs_{\unicode[STIX]{x1D6FD}}(a)\equiv s_{\unicode[STIX]{x1D6FD}}(a^{\prime })b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{b}_{1-r}+\mathfrak{b}_{1-r^{\prime }}^{\prime }b)\end{eqnarray}$$
$$\begin{eqnarray}bs_{\unicode[STIX]{x1D6FD}}(a)\equiv s_{\unicode[STIX]{x1D6FD}}(a^{\prime })b\hspace{0.6em}({\rm mod}\hspace{0.2em}b\mathfrak{b}_{1-r}+\mathfrak{b}_{1-r^{\prime }}^{\prime }b)\end{eqnarray}$$ and thus  $b^{i,i}$ intertwines the derived strata
$b^{i,i}$ intertwines the derived strata  $[\unicode[STIX]{x1D6EC},r,r-1,s_{i}(a^{i,i})]$ and
$[\unicode[STIX]{x1D6EC},r,r-1,s_{i}(a^{i,i})]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },r^{\prime },r^{\prime }-1,s_{i}(a^{\prime i,i})]$, for all
$[\unicode[STIX]{x1D6EC}^{\prime },r^{\prime },r^{\prime }-1,s_{i}(a^{\prime i,i})]$, for all  $i\in I$.◻
$i\in I$.◻
Proposition 7.6. (Cf. [Reference Bushnell and KutzkoBK93, 2.2.1])
Suppose that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}]$ are simple and that there are
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}]$ are simple and that there are  $a\in \mathfrak{a}_{-r}$ and
$a\in \mathfrak{a}_{-r}$ and  $a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$ such that
$a^{\prime }\in \mathfrak{a}_{-r^{\prime }}^{\prime }$ such that  $s_{\unicode[STIX]{x1D6FD}}(a)\equiv s_{\unicode[STIX]{x1D6FD}}(a^{\prime })\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{b}_{1-r}+\mathfrak{b}_{1-r^{\prime }}^{\prime })$. Then, there are elements
$s_{\unicode[STIX]{x1D6FD}}(a)\equiv s_{\unicode[STIX]{x1D6FD}}(a^{\prime })\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{b}_{1-r}+\mathfrak{b}_{1-r^{\prime }}^{\prime })$. Then, there are elements  $w^{\prime }\in \mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime }$ and
$w^{\prime }\in \mathfrak{m}_{-(k_{0}^{\prime }+r^{\prime })}^{\prime }$ and  $v\in \mathfrak{m}_{-(k_{0}+r)}$ such that
$v\in \mathfrak{m}_{-(k_{0}+r)}$ such that
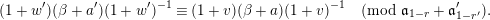 $$\begin{eqnarray}(1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime })(1+w^{\prime })^{-1}\equiv (1+v)(\unicode[STIX]{x1D6FD}+a)(1+v)^{-1}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(1+w^{\prime })(\unicode[STIX]{x1D6FD}+a^{\prime })(1+w^{\prime })^{-1}\equiv (1+v)(\unicode[STIX]{x1D6FD}+a)(1+v)^{-1}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-r}+\mathfrak{a}_{1-r^{\prime }}^{\prime }).\end{eqnarray}$$ Moreover, if the strata and the elements  $a$ and
$a$ and  $a^{\prime }$ are skew and the strata intertwine in
$a^{\prime }$ are skew and the strata intertwine in  $G$, then we can choose
$G$, then we can choose  $1+v$ and
$1+v$ and  $1+w^{\prime }$ in
$1+w^{\prime }$ in  $G$.
$G$.
Before the proof let us recall that the Cayley transform of an element  $v$ of
$v$ of  $(\mathfrak{a}_{1})_{-}$ is the element
$(\mathfrak{a}_{1})_{-}$ is the element  $(1+v/2)(1-v/2)^{-1}$. It is an element of
$(1+v/2)(1-v/2)^{-1}$. It is an element of  $\operatorname{U}^{1}(\unicode[STIX]{x1D6EC})\subset G$.
$\operatorname{U}^{1}(\unicode[STIX]{x1D6EC})\subset G$.
Proof. Let  $\unicode[STIX]{x1D6FD}$ be non-zero and write
$\unicode[STIX]{x1D6FD}$ be non-zero and write  $C$ for the kernel of
$C$ for the kernel of  $s_{\unicode[STIX]{x1D6FD}}$. Without loss of generality, we can assume that
$s_{\unicode[STIX]{x1D6FD}}$. Without loss of generality, we can assume that  $s_{\unicode[STIX]{x1D6FD}}(a)$ and
$s_{\unicode[STIX]{x1D6FD}}(a)$ and  $s_{\unicode[STIX]{x1D6FD}}(a^{\prime })$ are equal, since the map
$s_{\unicode[STIX]{x1D6FD}}(a^{\prime })$ are equal, since the map  $s_{\unicode[STIX]{x1D6FD}}:\mathfrak{a}_{1-r}\rightarrow \mathfrak{b}_{1-r}$ is surjective. The map
$s_{\unicode[STIX]{x1D6FD}}:\mathfrak{a}_{1-r}\rightarrow \mathfrak{b}_{1-r}$ is surjective. The map
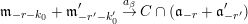 $$\begin{eqnarray}\mathfrak{m}_{-r-k_{0}}+\mathfrak{m}_{-r^{\prime }-k_{0}^{\prime }}^{\prime }\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }C\cap (\mathfrak{a}_{-r}+\mathfrak{a}_{-r^{\prime }}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}_{-r-k_{0}}+\mathfrak{m}_{-r^{\prime }-k_{0}^{\prime }}^{\prime }\stackrel{a_{\unicode[STIX]{x1D6FD}}}{\rightarrow }C\cap (\mathfrak{a}_{-r}+\mathfrak{a}_{-r^{\prime }}^{\prime })\end{eqnarray}$$ is surjective because  $C\cap (\mathfrak{a}_{-r}+\mathfrak{a}_{-r^{\prime }}^{\prime })$ is equal to
$C\cap (\mathfrak{a}_{-r}+\mathfrak{a}_{-r^{\prime }}^{\prime })$ is equal to  $(C\cap \mathfrak{a}_{-r})+(C\cap \mathfrak{a}_{-r^{\prime }}^{\prime })$ by [Reference Bushnell and KutzkoBK93, 1.3.17] and
$(C\cap \mathfrak{a}_{-r})+(C\cap \mathfrak{a}_{-r^{\prime }}^{\prime })$ by [Reference Bushnell and KutzkoBK93, 1.3.17] and  $a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{-r})$ is a subset of
$a_{\unicode[STIX]{x1D6FD}}^{-1}(\mathfrak{a}_{-r})$ is a subset of  $B+\mathfrak{m}_{-r-k_{0}}$ by Lemma 6.20(ii). Thus, we can find
$B+\mathfrak{m}_{-r-k_{0}}$ by Lemma 6.20(ii). Thus, we can find  $w^{\prime }\in \mathfrak{m}_{-r^{\prime }-k_{0}^{\prime }}$ and
$w^{\prime }\in \mathfrak{m}_{-r^{\prime }-k_{0}^{\prime }}$ and  $v\in \mathfrak{m}_{-r-k_{0}}$ to satisfy (7.5) for
$v\in \mathfrak{m}_{-r-k_{0}}$ to satisfy (7.5) for  $b=1$. We now follow the calculation in the proof of Proposition 7.3 backwards to show the desired congruence. In the skew situation we can find skew-symmetric elements, say
$b=1$. We now follow the calculation in the proof of Proposition 7.3 backwards to show the desired congruence. In the skew situation we can find skew-symmetric elements, say  $\tilde{v}$ and
$\tilde{v}$ and  $\tilde{w^{\prime }}$, which satisfy (7.5) and we define
$\tilde{w^{\prime }}$, which satisfy (7.5) and we define  $1+v$ and
$1+v$ and  $1+w^{\prime }$ to be the Cayley transforms of
$1+w^{\prime }$ to be the Cayley transforms of  $\tilde{v}$ and
$\tilde{v}$ and  $\tilde{w^{\prime }}$, respectively.◻
$\tilde{w^{\prime }}$, respectively.◻
We need one final lemma before we can prove Proposition 7.1, which will play the role of (S1).
Lemma 7.7. Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata, with lattice sequences of the same period, for which there is a (unique) bijection
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata, with lattice sequences of the same period, for which there is a (unique) bijection  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, for all indices
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, for all indices  $i\in I$, and
$i\in I$, and  $\dim _{F}V^{i}=\dim _{F}V^{\prime \unicode[STIX]{x1D701}(i)}$. Then there are an element
$\dim _{F}V^{i}=\dim _{F}V^{\prime \unicode[STIX]{x1D701}(i)}$. Then there are an element  $g$ of
$g$ of  $\tilde{G}$ and an element
$\tilde{G}$ and an element  $\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$ such that
$\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$ such that  $V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, for all indices
$V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, for all indices  $i\in I$, and:
$i\in I$, and:
∙
 $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ is equivalent to
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ is equivalent to  $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$;
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$;∙
 $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$; and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$; and∙
 $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$ and
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ are semisimple strata with the same associated splitting
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ are semisimple strata with the same associated splitting  $V=\bigoplus _{i\in I}V^{i}$.
$V=\bigoplus _{i\in I}V^{i}$.
Proof. Applying Theorem 6.16 to the strata  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$, for each
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$, for each  $i$, we find an equivalent simple stratum
$i$, we find an equivalent simple stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$; in particular,
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$; in particular,  $\unicode[STIX]{x1D6FE}_{i}$ and
$\unicode[STIX]{x1D6FE}_{i}$ and  $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ have the same irreducible minimal polynomial, and the same characteristic polynomial since
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ have the same irreducible minimal polynomial, and the same characteristic polynomial since  $\dim _{F}V^{i}=\dim _{F}V^{\prime \unicode[STIX]{x1D701}(i)}$.
$\dim _{F}V^{i}=\dim _{F}V^{\prime \unicode[STIX]{x1D701}(i)}$.
Further, for  $i\neq j$ in
$i\neq j$ in  $I$, the stratum
$I$, the stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D6FE}_{j}]$ is equivalent to
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D6FE}_{j}]$ is equivalent to  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$, which is not equivalent to a simple stratum, so that the stratum
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},\max \{q_{i},q_{j}\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$, which is not equivalent to a simple stratum, so that the stratum  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ is semisimple, where
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ is semisimple, where  $\unicode[STIX]{x1D6FE}=\sum _{i\in I}\unicode[STIX]{x1D6FE}_{i}$. The same applies to
$\unicode[STIX]{x1D6FE}=\sum _{i\in I}\unicode[STIX]{x1D6FE}_{i}$. The same applies to  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}^{\prime }]$, where
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}^{\prime }]$, where  $\unicode[STIX]{x1D6FE}^{\prime }=\sum _{i\in I}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$. Finally, since
$\unicode[STIX]{x1D6FE}^{\prime }=\sum _{i\in I}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$. Finally, since  $\unicode[STIX]{x1D6FE}_{i}$ and
$\unicode[STIX]{x1D6FE}_{i}$ and  $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ have the same characteristic polynomial, we can find
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ have the same characteristic polynomial, we can find  $g\in \tilde{G}$ such that
$g\in \tilde{G}$ such that  $V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$ and
$V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$ and  $g\unicode[STIX]{x1D6FE}^{\prime }g^{-1}=\unicode[STIX]{x1D6FE}$, and the result follows.◻
$g\unicode[STIX]{x1D6FE}^{\prime }g^{-1}=\unicode[STIX]{x1D6FE}$, and the result follows.◻
Proof of Proposition 7.1.
The equality  $q=q^{\prime }$ in (i) follows from the results on level in Proposition 6.9. The existence of
$q=q^{\prime }$ in (i) follows from the results on level in Proposition 6.9. The existence of  $\unicode[STIX]{x1D701}$ in (ii) is proved by strata induction, where we take Lemma 7.7 for (S1), Proposition 7.3 for (S2), and Theorem 6.14 for (S3). The base case follows because the characteristic polynomials are equal, so we match the primary factors using [Reference StevensSte05, 3.3(ii)]. The equality of dimensions follows from the fact that the degree of the
$\unicode[STIX]{x1D701}$ in (ii) is proved by strata induction, where we take Lemma 7.7 for (S1), Proposition 7.3 for (S2), and Theorem 6.14 for (S3). The base case follows because the characteristic polynomials are equal, so we match the primary factors using [Reference StevensSte05, 3.3(ii)]. The equality of dimensions follows from the fact that the degree of the  $i$th primary factor is the dimension of
$i$th primary factor is the dimension of  $V^{i}$.
$V^{i}$.
For the inductive step, suppose that  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are semisimple strata as in the proposition which intertwine. Then the stratum
$\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are semisimple strata as in the proposition which intertwine. Then the stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a semisimple stratum  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}=[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ whose splitting is a coarsening of that of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}=[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ whose splitting is a coarsening of that of  $\unicode[STIX]{x1D6E5}$, by Theorem 6.16; similarly we have a semisimple stratum
$\unicode[STIX]{x1D6E5}$, by Theorem 6.16; similarly we have a semisimple stratum  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r+1,\unicode[STIX]{x1D6FE}^{\prime }]$. Since the strata
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r+1,\unicode[STIX]{x1D6FE}^{\prime }]$. Since the strata  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$,  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ intertwine, we may apply the inductive hypothesis to them. In particular, they satisfy the hypotheses of Lemma 7.7 and, replacing
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ intertwine, we may apply the inductive hypothesis to them. In particular, they satisfy the hypotheses of Lemma 7.7 and, replacing  $\unicode[STIX]{x1D6E5}^{\prime }$ by its conjugate
$\unicode[STIX]{x1D6E5}^{\prime }$ by its conjugate  $g\unicode[STIX]{x1D6E5}^{\prime }$, we may assume
$g\unicode[STIX]{x1D6E5}^{\prime }$, we may assume  $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
Now we apply (S2)—Proposition 7.3—to the strata  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ and  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$, with
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$, with  $a=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$ and
$a=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$ and  $a^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}$. The conclusion is that the derived strata intertwine so that the base case gives us a bijection between the index sets
$a^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}$. The conclusion is that the derived strata intertwine so that the base case gives us a bijection between the index sets  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that, for each
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that, for each  $i\in I$, the stratum
$i\in I$, the stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},r+1,r,s_{\unicode[STIX]{x1D6FE}_{i}}(\unicode[STIX]{x1D6FD}_{i}-\unicode[STIX]{x1D6FE}_{i})+s_{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}}(\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }-\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)})]$ is equivalent to a simple stratum. (Here
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},r+1,r,s_{\unicode[STIX]{x1D6FE}_{i}}(\unicode[STIX]{x1D6FD}_{i}-\unicode[STIX]{x1D6FE}_{i})+s_{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}}(\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }-\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)})]$ is equivalent to a simple stratum. (Here  $\unicode[STIX]{x1D6FE}_{i}=1^{i}\unicode[STIX]{x1D6FE}1^{i}$, where
$\unicode[STIX]{x1D6FE}_{i}=1^{i}\unicode[STIX]{x1D6FE}1^{i}$, where  $1^{i}$ is the idempotent corresponding to
$1^{i}$ is the idempotent corresponding to  $V^{i}$, and similarly
$V^{i}$, and similarly  $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}=1^{\prime \unicode[STIX]{x1D701}(i)}\unicode[STIX]{x1D6FE}1^{\prime \unicode[STIX]{x1D701}(i)}$, corresponding to
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}=1^{\prime \unicode[STIX]{x1D701}(i)}\unicode[STIX]{x1D6FE}1^{\prime \unicode[STIX]{x1D701}(i)}$, corresponding to  $V^{\prime \unicode[STIX]{x1D701}(i)}$; note also that
$V^{\prime \unicode[STIX]{x1D701}(i)}$; note also that  $\unicode[STIX]{x1D6FE}_{i}$ and
$\unicode[STIX]{x1D6FE}_{i}$ and  $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}$ have the same characteristic polynomial so that we can view both
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}$ have the same characteristic polynomial so that we can view both  $V^{i}$ and
$V^{i}$ and  $V^{\prime \unicode[STIX]{x1D701}(i)}$ as
$V^{\prime \unicode[STIX]{x1D701}(i)}$ as  $F[\unicode[STIX]{x1D6FE}_{i}]$-vector spaces.) But then
$F[\unicode[STIX]{x1D6FE}_{i}]$-vector spaces.) But then  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, by (S3)—Theorem 6.14.
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},\max \{q_{i},q_{\unicode[STIX]{x1D701}(i)}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }]$ is equivalent to a simple stratum, by (S3)—Theorem 6.14.
The existence of  $\unicode[STIX]{x1D701}$ implies, in particular, that both strata have the same number of blocks, that is, the sets
$\unicode[STIX]{x1D701}$ implies, in particular, that both strata have the same number of blocks, that is, the sets  $I$ and
$I$ and  $I^{\prime }$ have the same cardinality. Finally, we prove the uniqueness of
$I^{\prime }$ have the same cardinality. Finally, we prove the uniqueness of  $\unicode[STIX]{x1D701}$. Assume, for contradiction, that there are two distinct indices
$\unicode[STIX]{x1D701}$. Assume, for contradiction, that there are two distinct indices  $i,j\in I$ and an index
$i,j\in I$ and an index  $i^{\prime }\in I^{\prime }$ such that
$i^{\prime }\in I^{\prime }$ such that  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime i^{\prime }},\max \{q_{i},q_{i^{\prime }}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{i^{\prime }}^{\prime }]$ and
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{\prime i^{\prime }},\max \{q_{i},q_{i^{\prime }}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{i^{\prime }}^{\prime }]$ and  $[\unicode[STIX]{x1D6EC}^{j}\oplus \unicode[STIX]{x1D6EC}^{\prime i^{\prime }},\max \{q_{j},q_{i^{\prime }}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{j}+\unicode[STIX]{x1D6FD}_{i^{\prime }}^{\prime }]$ are both equivalent to simple strata. From this (and the equality of periods) it follows that the integers
$[\unicode[STIX]{x1D6EC}^{j}\oplus \unicode[STIX]{x1D6EC}^{\prime i^{\prime }},\max \{q_{j},q_{i^{\prime }}^{\prime }\},r,\unicode[STIX]{x1D6FD}_{j}+\unicode[STIX]{x1D6FD}_{i^{\prime }}^{\prime }]$ are both equivalent to simple strata. From this (and the equality of periods) it follows that the integers  $q_{i}$,
$q_{i}$,  $q_{j}$ and
$q_{j}$ and  $q_{i^{\prime }}^{\prime }$ are all equal; we denote this integer by
$q_{i^{\prime }}^{\prime }$ are all equal; we denote this integer by  $q$.
$q$.
By the proof of the existence, the spaces  $V^{i}$ and
$V^{i}$ and  $V^{i^{\prime }}$ have the same dimension, and thus, by conjugating, we can assume that they are equal. By Theorem 6.16, the strata
$V^{i^{\prime }}$ have the same dimension, and thus, by conjugating, we can assume that they are equal. By Theorem 6.16, the strata  $[\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}]$ and
$[\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime i^{\prime }},q,r,\unicode[STIX]{x1D6FD}_{i^{\prime }}]$ intertwine. Then the stratum
$[\unicode[STIX]{x1D6EC}^{\prime i^{\prime }},q,r,\unicode[STIX]{x1D6FD}_{i^{\prime }}]$ intertwine. Then the stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ intertwines with
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$ intertwines with  $[\unicode[STIX]{x1D6EC}^{\prime i^{\prime }}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i^{\prime }}+\unicode[STIX]{x1D6FD}_{j}]$ and the latter is equivalent to a simple stratum. Thus the semisimple stratum
$[\unicode[STIX]{x1D6EC}^{\prime i^{\prime }}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i^{\prime }}+\unicode[STIX]{x1D6FD}_{j}]$ and the latter is equivalent to a simple stratum. Thus the semisimple stratum  $[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$, which has two blocks, is intertwined with a simple stratum, which has only one block. This is a contradiction since the existence shows that semisimple strata which intertwine have the same number of blocks.◻
$[\unicode[STIX]{x1D6EC}^{i}\oplus \unicode[STIX]{x1D6EC}^{j},q,r,\unicode[STIX]{x1D6FD}_{i}+\unicode[STIX]{x1D6FD}_{j}]$, which has two blocks, is intertwined with a simple stratum, which has only one block. This is a contradiction since the existence shows that semisimple strata which intertwine have the same number of blocks.◻
As a useful consequence, we see that, given two semisimple strata which intertwine, we can find equivalent semisimple strata with elements which are conjugate.
Corollary 7.8. Suppose that the semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ intertwine and that
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ intertwine and that  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, and let
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, and let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching between their index sets. Then there are semisimple strata
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching between their index sets. Then there are semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\tilde{\unicode[STIX]{x1D6FD}}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\tilde{\unicode[STIX]{x1D6FD}}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\tilde{\unicode[STIX]{x1D6FD}}^{\prime }]$, equivalent to, and with the same associated splitting as,
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\tilde{\unicode[STIX]{x1D6FD}}^{\prime }]$, equivalent to, and with the same associated splitting as,  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$, respectively, such that
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$, respectively, such that  $\tilde{\unicode[STIX]{x1D6FD}}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ has the same characteristic polynomial as
$\tilde{\unicode[STIX]{x1D6FD}}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ has the same characteristic polynomial as  $\tilde{\unicode[STIX]{x1D6FD}}_{i}$, for all indices
$\tilde{\unicode[STIX]{x1D6FD}}_{i}$, for all indices  $i\in I$.
$i\in I$.
Proof. This follows immediately from Lemma 7.7 (whose hypotheses are satisfied, thanks to Proposition 7.1) by putting, in the notation of the Lemma,  $\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FE}$ and
$\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FE}$ and  $\tilde{\unicode[STIX]{x1D6FD}}^{\prime }=g^{-1}\unicode[STIX]{x1D6FE}g$.◻
$\tilde{\unicode[STIX]{x1D6FD}}^{\prime }=g^{-1}\unicode[STIX]{x1D6FE}g$.◻
If  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ are strata in spaces
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$ are strata in spaces  $V$ and
$V$ and  $V^{\prime }$, respectively, then we put
$V^{\prime }$, respectively, then we put
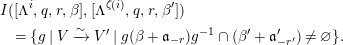 $$\begin{eqnarray}\displaystyle & & \displaystyle I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime }])\nonumber\\ \displaystyle & & \displaystyle \quad =\{g\mid V\xrightarrow[{}]{{\sim}}V^{\prime }\mid g(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r})g^{-1}\cap (\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime })\neq \varnothing \}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime }])\nonumber\\ \displaystyle & & \displaystyle \quad =\{g\mid V\xrightarrow[{}]{{\sim}}V^{\prime }\mid g(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{-r})g^{-1}\cap (\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{-r^{\prime }}^{\prime })\neq \varnothing \}.\nonumber\end{eqnarray}$$ This generalizes the notion of intertwining and we say that any element of this set intertwines  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ with
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ with  $[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$.
$[\unicode[STIX]{x1D6EC}^{\prime },q^{\prime },r^{\prime },\unicode[STIX]{x1D6FD}^{\prime }]$.
Corollary 7.9. Suppose that the semisimple strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ intertwine and that
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ intertwine and that  $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, and let
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }$ have the same period, and let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching between their index sets. Then the intertwining set
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching between their index sets. Then the intertwining set  $I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }])$ is equal to
$I([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }])$ is equal to
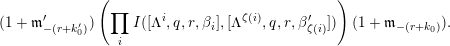 $$\begin{eqnarray}(1+\mathfrak{m}_{-(r+k_{0}^{\prime })}^{\prime })\left(\mathop{\prod }_{i}I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}],[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }])\right)(1+\mathfrak{m}_{-(r+k_{0})}).\end{eqnarray}$$
$$\begin{eqnarray}(1+\mathfrak{m}_{-(r+k_{0}^{\prime })}^{\prime })\left(\mathop{\prod }_{i}I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}],[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }])\right)(1+\mathfrak{m}_{-(r+k_{0})}).\end{eqnarray}$$Proof. By Corollary 7.8 we may replace the strata with equivalent strata such that there is  $g\in \tilde{G}$ such that
$g\in \tilde{G}$ such that  $\unicode[STIX]{x1D6FD}^{\prime }=g^{-1}\unicode[STIX]{x1D6FD}g$. The result now follows by applying Theorem 6.22 to the strata
$\unicode[STIX]{x1D6FD}^{\prime }=g^{-1}\unicode[STIX]{x1D6FD}g$. The result now follows by applying Theorem 6.22 to the strata  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}]$.◻
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}]$.◻
7.2 For classical groups
We continue with the notation from the previous section but assume now that all our strata are skew. We will prove the following strengthening of Proposition 7.1 in this case.
Proposition 7.10. Suppose that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two skew-semisimple strata which intertwine in
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two skew-semisimple strata which intertwine in  $G$ and let
$G$ and let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Proposition 7.1. Then:
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Proposition 7.1. Then:
(i)
 $(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, for all
$(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, for all  $i\in I$;
$i\in I$;(ii) the intertwining set
 $I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }])$ is equal to where
$I_{G}([\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}],[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }])$ is equal to where $$\begin{eqnarray}((1+\mathfrak{m}_{-(r+k_{0}^{\prime })}^{\prime })\cap G)\left(\left(\mathop{\prod }_{i}I_{i}\right)\cap G\right)((1+\mathfrak{m}_{-(r+k_{0})})\cap G),\end{eqnarray}$$
$$\begin{eqnarray}((1+\mathfrak{m}_{-(r+k_{0}^{\prime })}^{\prime })\cap G)\left(\left(\mathop{\prod }_{i}I_{i}\right)\cap G\right)((1+\mathfrak{m}_{-(r+k_{0})})\cap G),\end{eqnarray}$$ $I_{i}=I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}],[\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }])$.
$I_{i}=I([\unicode[STIX]{x1D6EC}^{i},q,r,\unicode[STIX]{x1D6FD}_{i}],[\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }])$.
Remark 7.11. Part (ii) of Proposition 7.10 is a consequence of (i): indeed, if (i) is true then, by conjugating, we can assume that  $V^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all
$V^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all  $i\in I$, and (ii) follows from Corollary 7.9 and a simple cohomology argument as in [Reference StevensSte01a, Corollary 4.14].
$i\in I$, and (ii) follows from Corollary 7.9 and a simple cohomology argument as in [Reference StevensSte01a, Corollary 4.14].
As an immediate consequence of Proposition 7.10 and the simple Skolem–Noether theorem 5.2, we get a Skolem–Noether theorem for semisimple strata.
Theorem 7.12. Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata which intertwine in
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata which intertwine in  $G$, and suppose that
$G$, and suppose that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. Then there is an element
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. Then there is an element  $g\in G$ such that
$g\in G$ such that  $g\unicode[STIX]{x1D6FD}g^{-1}$ is equal to
$g\unicode[STIX]{x1D6FD}g^{-1}$ is equal to  $\unicode[STIX]{x1D6FD}^{\prime }$.
$\unicode[STIX]{x1D6FD}^{\prime }$.
For the proof of Proposition 7.10 we need the following idempotent lifting lemma.
Lemma 7.13. Let  $(\mathfrak{k}_{r})_{r\geqslant 0}$ be a decreasing sequence of
$(\mathfrak{k}_{r})_{r\geqslant 0}$ be a decreasing sequence of  $o_{F}$-lattices in
$o_{F}$-lattices in  $A$ such that
$A$ such that  $\mathfrak{k}_{r}\mathfrak{k}_{s}\subseteq \mathfrak{k}_{r+s}$, for all
$\mathfrak{k}_{r}\mathfrak{k}_{s}\subseteq \mathfrak{k}_{r+s}$, for all  $r,s\geqslant 0$, and
$r,s\geqslant 0$, and  $\bigcap _{r\geqslant 1}\mathfrak{k}_{r}=\{0\}$. Suppose there is an element
$\bigcap _{r\geqslant 1}\mathfrak{k}_{r}=\{0\}$. Suppose there is an element  $\unicode[STIX]{x1D6FC}$ of
$\unicode[STIX]{x1D6FC}$ of  $\mathfrak{k}_{0}$ which satisfies
$\mathfrak{k}_{0}$ which satisfies  $\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FC}\in \mathfrak{k}_{1}$. Then there is an idempotent
$\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FC}\in \mathfrak{k}_{1}$. Then there is an idempotent  $\tilde{\unicode[STIX]{x1D6FC}}\in \mathfrak{k}_{0}$ such that
$\tilde{\unicode[STIX]{x1D6FC}}\in \mathfrak{k}_{0}$ such that  $\tilde{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D6FC}\in \mathfrak{k}_{1}$. Moreover, if
$\tilde{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D6FC}\in \mathfrak{k}_{1}$. Moreover, if  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FC}$ then we can choose
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FC}$ then we can choose  $\tilde{\unicode[STIX]{x1D6FC}}$ such that
$\tilde{\unicode[STIX]{x1D6FC}}$ such that  $\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}})=\tilde{\unicode[STIX]{x1D6FC}}$.
$\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}})=\tilde{\unicode[STIX]{x1D6FC}}$.
Proof. We define  $e_{0}:=\unicode[STIX]{x1D6FC}$, and put
$e_{0}:=\unicode[STIX]{x1D6FC}$, and put  $e_{1}:=3e_{0}^{2}-2e_{0}^{3}\in \mathfrak{k}_{0}$. A straightforward calculation shows that
$e_{1}:=3e_{0}^{2}-2e_{0}^{3}\in \mathfrak{k}_{0}$. A straightforward calculation shows that
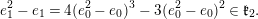 $$\begin{eqnarray}e_{1}^{2}-e_{1}=4(e_{0}^{2}-e_{0})^{3}-3(e_{0}^{2}-e_{0})^{2}\in \mathfrak{k}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}e_{1}^{2}-e_{1}=4(e_{0}^{2}-e_{0})^{3}-3(e_{0}^{2}-e_{0})^{2}\in \mathfrak{k}_{2}.\end{eqnarray}$$ Continuing this process, we construct a sequence  $(e_{n})_{n\geqslant 0}$ in
$(e_{n})_{n\geqslant 0}$ in  $\mathfrak{k}_{0}$ which satisfies:
$\mathfrak{k}_{0}$ which satisfies:
(i)
 $e_{n}\equiv e_{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{2^{i}})$; and
$e_{n}\equiv e_{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{2^{i}})$; and(ii)
 $e_{n}\equiv e_{n}^{2}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{2^{n}})$,
$e_{n}\equiv e_{n}^{2}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{2^{n}})$,
for all non-negative integers  $i<n$. This sequence has a limit
$i<n$. This sequence has a limit  $\tilde{\unicode[STIX]{x1D6FC}}$ in
$\tilde{\unicode[STIX]{x1D6FC}}$ in  $\mathfrak{k}_{0}$ which is, by construction, an idempotent congruent to
$\mathfrak{k}_{0}$ which is, by construction, an idempotent congruent to  $\unicode[STIX]{x1D6FC}$ modulo
$\unicode[STIX]{x1D6FC}$ modulo  $\mathfrak{k}_{1}$. Moreover, by construction the sequence
$\mathfrak{k}_{1}$. Moreover, by construction the sequence  $(e_{n})$ is symmetric if
$(e_{n})$ is symmetric if  $\unicode[STIX]{x1D6FC}$ is, in which case the limit
$\unicode[STIX]{x1D6FC}$ is, in which case the limit  $\tilde{\unicode[STIX]{x1D6FC}}$ is also symmetric.◻
$\tilde{\unicode[STIX]{x1D6FC}}$ is also symmetric.◻
Corollary 7.14. Let  $(\mathfrak{k}_{r})_{r\geqslant 0}$ be as in Lemma 7.13. Suppose that
$(\mathfrak{k}_{r})_{r\geqslant 0}$ be as in Lemma 7.13. Suppose that  $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}$ are elements of
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}$ are elements of  $\mathfrak{k}_{0}$ such that
$\mathfrak{k}_{0}$ such that  $\unicode[STIX]{x1D6FC}_{i}^{2}-\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{k}_{1}$ and
$\unicode[STIX]{x1D6FC}_{i}^{2}-\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{k}_{1}$ and  $\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FC}_{j}\in \mathfrak{k}_{1}$, for all
$\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FC}_{j}\in \mathfrak{k}_{1}$, for all  $i\neq j$. Suppose further that
$i\neq j$. Suppose further that  $\sum _{i}\unicode[STIX]{x1D6FC}_{i}\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{1})$. Then there are idempotents
$\sum _{i}\unicode[STIX]{x1D6FC}_{i}\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{k}_{1})$. Then there are idempotents  $\tilde{\unicode[STIX]{x1D6FC}}_{i}$ such that
$\tilde{\unicode[STIX]{x1D6FC}}_{i}$ such that  $\tilde{\unicode[STIX]{x1D6FC}}_{i}-\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{k}_{1}$, with
$\tilde{\unicode[STIX]{x1D6FC}}_{i}-\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{k}_{1}$, with  $\tilde{\unicode[STIX]{x1D6FC}}_{i}\tilde{\unicode[STIX]{x1D6FC}}_{j}=0$, for
$\tilde{\unicode[STIX]{x1D6FC}}_{i}\tilde{\unicode[STIX]{x1D6FC}}_{j}=0$, for  $i\neq j$, and
$i\neq j$, and  $\sum _{i}\tilde{\unicode[STIX]{x1D6FC}}_{i}=1$. If further
$\sum _{i}\tilde{\unicode[STIX]{x1D6FC}}_{i}=1$. If further  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{i})=\unicode[STIX]{x1D6FC}_{i}$, for all
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{i})=\unicode[STIX]{x1D6FC}_{i}$, for all  $i$, then we can choose the
$i$, then we can choose the  $\tilde{\unicode[STIX]{x1D6FC}}_{i}$ such that
$\tilde{\unicode[STIX]{x1D6FC}}_{i}$ such that  $\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}}_{i})=\tilde{\unicode[STIX]{x1D6FC}}_{i}$, for all
$\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}}_{i})=\tilde{\unicode[STIX]{x1D6FC}}_{i}$, for all  $i$.
$i$.
Proof. We find  $\tilde{\unicode[STIX]{x1D6FC}}_{1}$ by Lemma 7.13 and set
$\tilde{\unicode[STIX]{x1D6FC}}_{1}$ by Lemma 7.13 and set  $\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }=1-\tilde{\unicode[STIX]{x1D6FC}}_{1}$. Consider the space
$\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }=1-\tilde{\unicode[STIX]{x1D6FC}}_{1}$. Consider the space  $V^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }V$, the lattices
$V^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }V$, the lattices  $\mathfrak{k}_{r}^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }\mathfrak{k}_{r}\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }$ and the elements
$\mathfrak{k}_{r}^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }\mathfrak{k}_{r}\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }$ and the elements  $\unicode[STIX]{x1D6FC}_{i}^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }\unicode[STIX]{x1D6FC}_{i}\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }$ for
$\unicode[STIX]{x1D6FC}_{i}^{(1)}:=\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }\unicode[STIX]{x1D6FC}_{i}\tilde{\unicode[STIX]{x1D6FC}}_{1}^{\bot }$ for  $i\geqslant 2$. These satisfy the hypotheses of the corollary, which now follows by induction. If
$i\geqslant 2$. These satisfy the hypotheses of the corollary, which now follows by induction. If  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{1})=\unicode[STIX]{x1D6FC}_{1}$ then we choose
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{1})=\unicode[STIX]{x1D6FC}_{1}$ then we choose  $\tilde{\unicode[STIX]{x1D6FC}}_{1}$ such that
$\tilde{\unicode[STIX]{x1D6FC}}_{1}$ such that  $\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}}_{1})=\tilde{\unicode[STIX]{x1D6FC}}_{1}$, and
$\unicode[STIX]{x1D70E}(\tilde{\unicode[STIX]{x1D6FC}}_{1})=\tilde{\unicode[STIX]{x1D6FC}}_{1}$, and  $V^{(1)}$ is then the orthogonal complement of
$V^{(1)}$ is then the orthogonal complement of  $\tilde{\unicode[STIX]{x1D6FC}}_{1}V$ so that the result again follows by induction.◻
$\tilde{\unicode[STIX]{x1D6FC}}_{1}V$ so that the result again follows by induction.◻
We also need the classical group analogue of Lemma 7.7.
Lemma 7.15. Let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata which intertwine in
$[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata which intertwine in  $G$ and let
$G$ and let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Proposition 7.1. Suppose moreover that
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Proposition 7.1. Suppose moreover that  $(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, for all
$(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, for all  $i\in I$. Then there are an element
$i\in I$. Then there are an element  $g\in G$ and a skew element
$g\in G$ and a skew element  $\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$ such that
$\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$ such that  $V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, for all indices
$V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, for all indices  $i\in I$, and:
$i\in I$, and:
∙
 $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ is equivalent to
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ is equivalent to  $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$;
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$;∙
 $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ is equivalent to  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$; and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$; and∙
 $[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$ and
$[g\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ are skew-semisimple strata with the same associated splitting
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$ are skew-semisimple strata with the same associated splitting  $V=\bigoplus _{i\in I}V^{i}$.
$V=\bigoplus _{i\in I}V^{i}$.
Proof. The proof is the same as that of Lemma 7.7. We only need to note that, once we have found  $\unicode[STIX]{x1D6FE}_{i}$ and
$\unicode[STIX]{x1D6FE}_{i}$ and  $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ with the same irreducible minimal polynomial then there is an element
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ with the same irreducible minimal polynomial then there is an element  $g\in G$ such that
$g\in G$ such that  $V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, since
$V^{i}=gV^{\prime \unicode[STIX]{x1D701}(i)}$, since  $(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, and then the elements
$(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, and then the elements  $g\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }g^{-1}$ and
$g\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D701}(i)}^{\prime }g^{-1}$ and  $\unicode[STIX]{x1D6FE}_{i}$ are conjugate in
$\unicode[STIX]{x1D6FE}_{i}$ are conjugate in  $G_{i}=A^{i,i}\cap G$ by Remark 7.11 and Theorem 5.2.◻
$G_{i}=A^{i,i}\cap G$ by Remark 7.11 and Theorem 5.2.◻
Proof of Proposition 7.10.
The case  $q=r$ is trivial (since both strata are then null) so we assume
$q=r$ is trivial (since both strata are then null) so we assume  $q>r$. It is sufficient to prove (i) by Remark 7.11. We prove (i) by strata induction, giving first the inductive step. Suppose that
$q>r$. It is sufficient to prove (i) by Remark 7.11. We prove (i) by strata induction, giving first the inductive step. Suppose that  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are skew-semisimple strata as in the proposition which intertwine in
$\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are skew-semisimple strata as in the proposition which intertwine in  $G$. Then the stratum
$G$. Then the stratum  $[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a skew-semisimple stratum
$[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FD}]$ is equivalent to a skew-semisimple stratum  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}=[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ whose splitting is a coarsening of that of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}=[\unicode[STIX]{x1D6EC},q,r+1,\unicode[STIX]{x1D6FE}]$ whose splitting is a coarsening of that of  $\unicode[STIX]{x1D6E5}$, by Theorem 6.16; similarly we have a skew-semisimple stratum
$\unicode[STIX]{x1D6E5}$, by Theorem 6.16; similarly we have a skew-semisimple stratum  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r+1,\unicode[STIX]{x1D6FE}^{\prime }]$. Since the strata
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }=[\unicode[STIX]{x1D6EC}^{\prime },q,r+1,\unicode[STIX]{x1D6FE}^{\prime }]$. Since the strata  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$,  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ intertwine, we may apply Lemma 7.15 and, replacing
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ intertwine, we may apply Lemma 7.15 and, replacing  $\unicode[STIX]{x1D6E5}^{\prime }$ by its conjugate
$\unicode[STIX]{x1D6E5}^{\prime }$ by its conjugate  $g\unicode[STIX]{x1D6E5}^{\prime }$, we may assume
$g\unicode[STIX]{x1D6E5}^{\prime }$, we may assume  $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
Now, if  $h\in G$ intertwines the strata
$h\in G$ intertwines the strata  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$ and  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ then Theorem 6.22 allows us to write
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{\prime }$ then Theorem 6.22 allows us to write  $h=xby$, with
$h=xby$, with  $b\in B_{\unicode[STIX]{x1D6FE}}\cap G$ (and
$b\in B_{\unicode[STIX]{x1D6FE}}\cap G$ (and  $x,y$ in certain compact subgroups). Then Proposition 7.3, applied as in the proof of Proposition 7.1, implies that the derived strata
$x,y$ in certain compact subgroups). Then Proposition 7.3, applied as in the proof of Proposition 7.1, implies that the derived strata  $[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE})]$ and
$[\unicode[STIX]{x1D6EC},r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE})]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ intertwine (blockwise). Then we may assume that
$[\unicode[STIX]{x1D6EC}^{\prime },r+1,r,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ intertwine (blockwise). Then we may assume that  $\unicode[STIX]{x1D6FE}$ is simple. On the other hand, these derived strata are equivalent to skew-semisimple strata; moreover, either both are equivalent to a null stratum or neither is, by Proposition 6.9. Take a
$\unicode[STIX]{x1D6FE}$ is simple. On the other hand, these derived strata are equivalent to skew-semisimple strata; moreover, either both are equivalent to a null stratum or neither is, by Proposition 6.9. Take a  $\unicode[STIX]{x1D70E}$-equivariant non-zero form
$\unicode[STIX]{x1D70E}$-equivariant non-zero form  $\unicode[STIX]{x1D706}$ from
$\unicode[STIX]{x1D706}$ from  $F[\unicode[STIX]{x1D6FE}]$ to
$F[\unicode[STIX]{x1D6FE}]$ to  $F$. The base step (below) now implies that the bijection
$F$. The base step (below) now implies that the bijection  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ has the property that
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ has the property that  $(V^{i},h_{\unicode[STIX]{x1D6FE}}|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h_{\unicode[STIX]{x1D6FE}}|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, with
$(V^{i},h_{\unicode[STIX]{x1D6FE}}|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h_{\unicode[STIX]{x1D6FE}}|_{V^{\prime \unicode[STIX]{x1D701}(i)}})$, with  $h=\unicode[STIX]{x1D706}\circ h_{\unicode[STIX]{x1D6FE}}$. But then we also have
$h=\unicode[STIX]{x1D706}\circ h_{\unicode[STIX]{x1D6FE}}$. But then we also have  $(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime }\unicode[STIX]{x1D701}(i)})$, as required.
$(V^{i},h|_{V^{i}})\cong (V^{\prime \unicode[STIX]{x1D701}(i)},h|_{V^{\prime }\unicode[STIX]{x1D701}(i)})$, as required.
It remains to show the base case  $r=q-1$. Replacing
$r=q-1$. Replacing  $[\unicode[STIX]{x1D6EC}^{\prime },q,q-1,\unicode[STIX]{x1D6FD}^{\prime }]$ by a conjugate if necessary, we may assume that the strata are intertwined by 1 so that
$[\unicode[STIX]{x1D6EC}^{\prime },q,q-1,\unicode[STIX]{x1D6FD}^{\prime }]$ by a conjugate if necessary, we may assume that the strata are intertwined by 1 so that
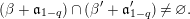 $$\begin{eqnarray}(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q})\cap (\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{1-q}^{\prime })\neq \varnothing .\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FD}+\mathfrak{a}_{1-q})\cap (\unicode[STIX]{x1D6FD}^{\prime }+\mathfrak{a}_{1-q}^{\prime })\neq \varnothing .\end{eqnarray}$$ Thus there are elements  $a\in \mathfrak{a}_{1}$ and
$a\in \mathfrak{a}_{1}$ and  $a^{\prime }\in \mathfrak{a}_{1}^{\prime }$ such that
$a^{\prime }\in \mathfrak{a}_{1}^{\prime }$ such that
 $$\begin{eqnarray}z:=y_{\unicode[STIX]{x1D6FD}}+a=y_{\unicode[STIX]{x1D6FD}^{\prime }}+a^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}z:=y_{\unicode[STIX]{x1D6FD}}+a=y_{\unicode[STIX]{x1D6FD}^{\prime }}+a^{\prime }.\end{eqnarray}$$ By the bijectivity of  $\unicode[STIX]{x1D701}$ we can assume that
$\unicode[STIX]{x1D701}$ we can assume that  $I=I^{\prime }$ and
$I=I^{\prime }$ and  $\unicode[STIX]{x1D701}$ is the identity. Let
$\unicode[STIX]{x1D701}$ is the identity. Let  $i\in I$.
$i\in I$.
We show that there is an idempotent  $e$ such that
$e$ such that  $e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$ and
$e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$ and  $e\equiv 1^{\prime i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}^{\prime })$: there is a polynomial
$e\equiv 1^{\prime i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}^{\prime })$: there is a polynomial  $Q\in o_{F}[X]$ such that
$Q\in o_{F}[X]$ such that  $Q(y_{\unicode[STIX]{x1D6FD}})\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$. Moreover, by replacing
$Q(y_{\unicode[STIX]{x1D6FD}})\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$. Moreover, by replacing  $Q(X)$ by
$Q(X)$ by  $(1/2)(Q(X)+\unicode[STIX]{x1D70E}(Q)(\pm X))$, we can choose
$(1/2)(Q(X)+\unicode[STIX]{x1D70E}(Q)(\pm X))$, we can choose  $Q$ such that, for all
$Q$ such that, for all  $j$, the coefficient of
$j$, the coefficient of  $X^{j}$ is symmetric (resp. skew-symmetric) if and only if
$X^{j}$ is symmetric (resp. skew-symmetric) if and only if  $y_{\unicode[STIX]{x1D6FD}}^{j}$ is symmetric (resp. skew-symmetric). We have a canonical isomorphism from
$y_{\unicode[STIX]{x1D6FD}}^{j}$ is symmetric (resp. skew-symmetric). We have a canonical isomorphism from  $\unicode[STIX]{x1D705}[\bar{y}_{\unicode[STIX]{x1D6FD}}]$ to
$\unicode[STIX]{x1D705}[\bar{y}_{\unicode[STIX]{x1D6FD}}]$ to  $\unicode[STIX]{x1D705}[\bar{y}_{\unicode[STIX]{x1D6FD}^{\prime }}]$ (mapping
$\unicode[STIX]{x1D705}[\bar{y}_{\unicode[STIX]{x1D6FD}^{\prime }}]$ (mapping  $\bar{y}_{\unicode[STIX]{x1D6FD}}$ to
$\bar{y}_{\unicode[STIX]{x1D6FD}}$ to  $\bar{y}_{\unicode[STIX]{x1D6FD}^{\prime }}$) so
$\bar{y}_{\unicode[STIX]{x1D6FD}^{\prime }}$) so  $Q(y_{\unicode[STIX]{x1D6FD}^{\prime }})$ is congruent to some idempotent modulo
$Q(y_{\unicode[STIX]{x1D6FD}^{\prime }})$ is congruent to some idempotent modulo  $\mathfrak{a}_{1}^{\prime }$, and indeed
$\mathfrak{a}_{1}^{\prime }$, and indeed  $Q(y_{\unicode[STIX]{x1D6FD}^{\prime }})\equiv 1^{\prime i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}^{\prime })$ since the matching
$Q(y_{\unicode[STIX]{x1D6FD}^{\prime }})\equiv 1^{\prime i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}^{\prime })$ since the matching  $\unicode[STIX]{x1D701}$ is given by matching minimal polynomials. By Proposition 7.13 applied with
$\unicode[STIX]{x1D701}$ is given by matching minimal polynomials. By Proposition 7.13 applied with  $\mathfrak{k}_{r}=\mathfrak{a}_{r}\cap \mathfrak{a}_{r}^{\prime }$, there is a symmetric idempotent
$\mathfrak{k}_{r}=\mathfrak{a}_{r}\cap \mathfrak{a}_{r}^{\prime }$, there is a symmetric idempotent  $e\in \mathfrak{a}_{0}\cap \mathfrak{a}_{0}^{\prime }$ congruent to
$e\in \mathfrak{a}_{0}\cap \mathfrak{a}_{0}^{\prime }$ congruent to  $Q(z)$ modulo both radicals.
$Q(z)$ modulo both radicals.
The idempotent  $e$ gives a new splitting
$e$ gives a new splitting  $V=\tilde{V}^{i}\oplus (\tilde{V}^{i})^{\bot }$ for both lattice sequences.
$V=\tilde{V}^{i}\oplus (\tilde{V}^{i})^{\bot }$ for both lattice sequences.
Finally, we show that  $V^{i}$ and
$V^{i}$ and  $\tilde{V}^{i}$ are isomorphic signed hermitian spaces. We define the map
$\tilde{V}^{i}$ are isomorphic signed hermitian spaces. We define the map  $\unicode[STIX]{x1D713}:V^{i}\rightarrow \tilde{V}^{i}$ to be the restriction of
$\unicode[STIX]{x1D713}:V^{i}\rightarrow \tilde{V}^{i}$ to be the restriction of  $e$ to
$e$ to  $V^{i}$. We first show that the map is injective. If
$V^{i}$. We first show that the map is injective. If  $v$ is a non-zero element of its kernel, then there is an integer
$v$ is a non-zero element of its kernel, then there is an integer  $l$ such that
$l$ such that  $v\in \unicode[STIX]{x1D6EC}_{l}^{i}\setminus \unicode[STIX]{x1D6EC}_{l+1}^{i}$. But then
$v\in \unicode[STIX]{x1D6EC}_{l}^{i}\setminus \unicode[STIX]{x1D6EC}_{l+1}^{i}$. But then
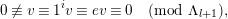 $$\begin{eqnarray}0\not \equiv v\equiv 1^{i}v\equiv ev\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6EC}_{l+1}),\end{eqnarray}$$
$$\begin{eqnarray}0\not \equiv v\equiv 1^{i}v\equiv ev\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6EC}_{l+1}),\end{eqnarray}$$ where the third congruence uses that  $e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$. Similarly, the restriction of
$e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$. Similarly, the restriction of  $1^{i}$ to
$1^{i}$ to  $\tilde{V}^{i}$ is injective and these maps induce pairwise inverse
$\tilde{V}^{i}$ is injective and these maps induce pairwise inverse  $\unicode[STIX]{x1D705}_{F}$-isomorphisms between
$\unicode[STIX]{x1D705}_{F}$-isomorphisms between  $\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}$ and
$\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}$ and  $\tilde{\unicode[STIX]{x1D6EC}}_{l}^{i}/\tilde{\unicode[STIX]{x1D6EC}}_{l+1}^{i}$ where
$\tilde{\unicode[STIX]{x1D6EC}}_{l}^{i}/\tilde{\unicode[STIX]{x1D6EC}}_{l+1}^{i}$ where  $\tilde{\unicode[STIX]{x1D6EC}}_{l}^{i}$ is the intersection of
$\tilde{\unicode[STIX]{x1D6EC}}_{l}^{i}$ is the intersection of  $\unicode[STIX]{x1D6EC}_{l}$ with
$\unicode[STIX]{x1D6EC}_{l}$ with  $\tilde{V}^{i}$. Thus
$\tilde{V}^{i}$. Thus  $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6EC}^{i})$ is equal to
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6EC}^{i})$ is equal to  $\tilde{\unicode[STIX]{x1D6EC}}^{i}$.
$\tilde{\unicode[STIX]{x1D6EC}}^{i}$.
We now compare the hermitian structures. For  $v\in \unicode[STIX]{x1D6EC}_{l}^{i}$ and
$v\in \unicode[STIX]{x1D6EC}_{l}^{i}$ and  $w\in (\unicode[STIX]{x1D6EC}_{l+1}^{i})^{\#}$ we have
$w\in (\unicode[STIX]{x1D6EC}_{l+1}^{i})^{\#}$ we have
 $$\begin{eqnarray}\overline{h(v,w)}=\overline{h(v,1^{i}w)}=\overline{h(v,ew)}=\overline{h(v,e^{2}w)}=\overline{h(ev,ew)}=\overline{h(\unicode[STIX]{x1D713}(v),\unicode[STIX]{x1D713}(w))}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{h(v,w)}=\overline{h(v,1^{i}w)}=\overline{h(v,ew)}=\overline{h(v,e^{2}w)}=\overline{h(ev,ew)}=\overline{h(\unicode[STIX]{x1D713}(v),\unicode[STIX]{x1D713}(w))}.\end{eqnarray}$$ By Proposition 3.1 there is an  $F$-linear isometry
$F$-linear isometry
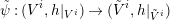 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D713}}:(V^{i},h|_{V^{i}})\rightarrow (\tilde{V}^{i},h|_{\tilde{V}^{i}})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D713}}:(V^{i},h|_{V^{i}})\rightarrow (\tilde{V}^{i},h|_{\tilde{V}^{i}})\end{eqnarray}$$such that
∙
 $\tilde{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D6EC}^{i})=\tilde{\unicode[STIX]{x1D6EC}}^{i}$ and
$\tilde{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D6EC}^{i})=\tilde{\unicode[STIX]{x1D6EC}}^{i}$ and∙
 $\tilde{\unicode[STIX]{x1D713}}$ and
$\tilde{\unicode[STIX]{x1D713}}$ and  $\unicode[STIX]{x1D713}$ induce the same isomorphism on
$\unicode[STIX]{x1D713}$ induce the same isomorphism on  $\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}$, for all integers
$\unicode[STIX]{x1D6EC}_{l}^{i}/\unicode[STIX]{x1D6EC}_{l+1}^{i}$, for all integers  $l$.
$l$.
Thus,  $V^{i}$,
$V^{i}$,  $\tilde{V}^{i}$, and similarly
$\tilde{V}^{i}$, and similarly  $V^{\prime i}$, are isomorphic signed hermitian spaces.◻
$V^{\prime i}$, are isomorphic signed hermitian spaces.◻
7.3 Matching for equivalent strata
We need to understand the matching between two equivalent strata, and for that reason we have the following three results.
Lemma 7.16. Suppose that  $e$ is an idempotent in
$e$ is an idempotent in  $\prod _{i}A^{i,i}$ such that every non-zero element
$\prod _{i}A^{i,i}$ such that every non-zero element  $x$ of
$x$ of  $\prod _{i}A^{i,i}$ satisfies
$\prod _{i}A^{i,i}$ satisfies  $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(ex-xe)>\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(x)$. Then
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(ex-xe)>\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(x)$. Then  $e$ is a central idempotent of
$e$ is a central idempotent of  $\prod _{i}A^{i,i}$, that is, commutes with all elements of
$\prod _{i}A^{i,i}$, that is, commutes with all elements of  $\prod _{i}A^{i,i}$.
$\prod _{i}A^{i,i}$.
Proof. Let  $x$ be an element of
$x$ be an element of  $\prod _{i}A^{i,i}$ and put
$\prod _{i}A^{i,i}$ and put  $x^{\prime }=a_{e}(x)=ex-xe$. Then
$x^{\prime }=a_{e}(x)=ex-xe$. Then  $ex^{\prime }e$ is zero and one checks
$ex^{\prime }e$ is zero and one checks  $a_{e}(a_{e}(x^{\prime }))=x^{\prime }$. The condition on
$a_{e}(a_{e}(x^{\prime }))=x^{\prime }$. The condition on  $e$ now implies
$e$ now implies  $x^{\prime }=0$ and thus
$x^{\prime }=0$ and thus  $e$ is central.◻
$e$ is central.◻
Lemma 7.17. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be two semisimple strata, such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be two semisimple strata, such that
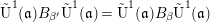 $$\begin{eqnarray}\tilde{\operatorname{U}}^{1}(\mathfrak{a})B_{\unicode[STIX]{x1D6FD}^{\prime }}\tilde{\operatorname{U}}^{1}(\mathfrak{a})=\tilde{\operatorname{U}}^{1}(\mathfrak{a})B_{\unicode[STIX]{x1D6FD}}\tilde{\operatorname{U}}^{1}(\mathfrak{a})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\operatorname{U}}^{1}(\mathfrak{a})B_{\unicode[STIX]{x1D6FD}^{\prime }}\tilde{\operatorname{U}}^{1}(\mathfrak{a})=\tilde{\operatorname{U}}^{1}(\mathfrak{a})B_{\unicode[STIX]{x1D6FD}}\tilde{\operatorname{U}}^{1}(\mathfrak{a})\end{eqnarray}$$ then there are a bijection  $\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ and an element
$\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ and an element  $g$ of
$g$ of  $\tilde{\operatorname{U}}^{1}(\mathfrak{a})$ such that:
$\tilde{\operatorname{U}}^{1}(\mathfrak{a})$ such that:
(i)
 $1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$; and
$1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$; and(ii)
 $g1^{i}g^{-1}=1^{\unicode[STIX]{x1D70F}(i)}$;
$g1^{i}g^{-1}=1^{\unicode[STIX]{x1D70F}(i)}$;
for all indices  $i\in I$. Moreover, the bijection
$i\in I$. Moreover, the bijection  $\unicode[STIX]{x1D70F}$ satisfies
$\unicode[STIX]{x1D70F}$ satisfies
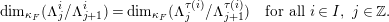 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D70F}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D70F}(i)})\quad \text{for all}~i\in I,~j\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D70F}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D70F}(i)})\quad \text{for all}~i\in I,~j\in \mathbb{Z}.\end{eqnarray}$$Proof. By the equality of the two sets and Lemmas 7.13 and 7.16, every primitive central idempotent of  $B_{\unicode[STIX]{x1D6FD}}$ has to be congruent modulo
$B_{\unicode[STIX]{x1D6FD}}$ has to be congruent modulo  $\mathfrak{a}_{1}(\unicode[STIX]{x1D6EC})$ to a sum of primitive central idempotents of
$\mathfrak{a}_{1}(\unicode[STIX]{x1D6EC})$ to a sum of primitive central idempotents of  $B_{\unicode[STIX]{x1D6FD}^{\prime }}$, and vice versa. The first part follows from this. For the second part, take the map
$B_{\unicode[STIX]{x1D6FD}^{\prime }}$, and vice versa. The first part follows from this. For the second part, take the map  $g$ which sends
$g$ which sends  $v\in V$ to
$v\in V$ to  $\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}v$. Finally, the map
$\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}v$. Finally, the map  $v\mapsto 1^{i}v$ induces, for each
$v\mapsto 1^{i}v$ induces, for each  $j\in \mathbb{Z}$, a linear map
$j\in \mathbb{Z}$, a linear map  $\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D70F}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D70F}(i)}\rightarrow \unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i}$ whose inverse is induced by
$\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D70F}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D70F}(i)}\rightarrow \unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i}$ whose inverse is induced by  $v\mapsto 1^{\unicode[STIX]{x1D70F}(i)}v$.◻
$v\mapsto 1^{\unicode[STIX]{x1D70F}(i)}v$.◻
Lemma 7.18. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be equivalent semisimple strata. Then there is an element
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be equivalent semisimple strata. Then there is an element  $g$ of
$g$ of  $1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ such that
$1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ such that  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ have the same associated splitting.
$[\unicode[STIX]{x1D6EC},q,m,g\unicode[STIX]{x1D6FD}^{\prime }g^{-1}]$ have the same associated splitting.
Proof. Note that we may replace  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ by an equivalent stratum with the same splitting (and likewise for
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ by an equivalent stratum with the same splitting (and likewise for  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$). Thus, by applying Corollary 7.8, we may assume that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$). Thus, by applying Corollary 7.8, we may assume that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial and thus there is an element
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial and thus there is an element  $x$ of
$x$ of  $\tilde{G}$ such that
$\tilde{G}$ such that  $x\unicode[STIX]{x1D6FD}x^{-1}=\unicode[STIX]{x1D6FD}^{\prime }$.
$x\unicode[STIX]{x1D6FD}x^{-1}=\unicode[STIX]{x1D6FD}^{\prime }$.
Since the strata intertwine, Proposition 7.1 gives us a matching  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that the minimal polynomials satisfy
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that the minimal polynomials satisfy  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}_{i}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }}$ and
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}_{i}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}(i)}^{\prime }}$ and  $\dim _{F}V^{i}=\dim _{F}V^{\unicode[STIX]{x1D701}(i)}$, for each
$\dim _{F}V^{i}=\dim _{F}V^{\unicode[STIX]{x1D701}(i)}$, for each  $i\in I$. Note that this implies that
$i\in I$. Note that this implies that  $xV^{i}=V^{\unicode[STIX]{x1D701}(i)}$. We can also compare the intertwining sets of the strata (which are equal) and then Lemma 7.17 gives us a map
$xV^{i}=V^{\unicode[STIX]{x1D701}(i)}$. We can also compare the intertwining sets of the strata (which are equal) and then Lemma 7.17 gives us a map  $\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ such that
$\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ such that  $1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, for all
$1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, for all  $i\in I$. Since the identity intertwines the two strata, Corollary 7.9 implies that we can write the identity as
$i\in I$. Since the identity intertwines the two strata, Corollary 7.9 implies that we can write the identity as  $uyv$, with
$uyv$, with  $u,v\in \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ and
$u,v\in \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ and  $y=\prod _{i\in I}y_{i}$ such that
$y=\prod _{i\in I}y_{i}$ such that  $y_{i}V^{i}=V^{\unicode[STIX]{x1D701}(i)}$. Moreover, we have
$y_{i}V^{i}=V^{\unicode[STIX]{x1D701}(i)}$. Moreover, we have  $y=u^{-1}v^{-1}\in \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ so that
$y=u^{-1}v^{-1}\in \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ so that  $y_{i}\unicode[STIX]{x1D6EC}^{i}=\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$. Thus
$y_{i}\unicode[STIX]{x1D6EC}^{i}=\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$. Thus
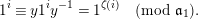 $$\begin{eqnarray}1^{i}\equiv y1^{i}y^{-1}=1^{\unicode[STIX]{x1D701}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}1^{i}\equiv y1^{i}y^{-1}=1^{\unicode[STIX]{x1D701}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1}).\end{eqnarray}$$ In particular, we get  $1^{\unicode[STIX]{x1D70F}(i)}\equiv 1^{\unicode[STIX]{x1D701}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$ so that
$1^{\unicode[STIX]{x1D70F}(i)}\equiv 1^{\unicode[STIX]{x1D701}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$ so that  $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70F}$, and then Lemma 7.17 also implies that
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70F}$, and then Lemma 7.17 also implies that  $\unicode[STIX]{x1D701}$ satisfies the extra condition
$\unicode[STIX]{x1D701}$ satisfies the extra condition
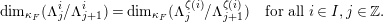 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D701}(i)})\quad \text{for all}~i\in I,j\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D701}(i)})\quad \text{for all}~i\in I,j\in \mathbb{Z}.\end{eqnarray}$$ Now  $\unicode[STIX]{x1D6EC}^{i}$ and
$\unicode[STIX]{x1D6EC}^{i}$ and  $x^{-1}\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$ are
$x^{-1}\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$ are  $o_{F[\unicode[STIX]{x1D6FD}_{i}]}$-lattice sequences in
$o_{F[\unicode[STIX]{x1D6FD}_{i}]}$-lattice sequences in  $V^{i}$ with successive quotients of the same dimensions so there is an element
$V^{i}$ with successive quotients of the same dimensions so there is an element  $z_{i}$ of
$z_{i}$ of  $B_{\unicode[STIX]{x1D6FD}_{i}}^{\times }$ such that
$B_{\unicode[STIX]{x1D6FD}_{i}}^{\times }$ such that  $z_{i}\unicode[STIX]{x1D6EC}^{i}=x^{-1}\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$. In particular, writing
$z_{i}\unicode[STIX]{x1D6EC}^{i}=x^{-1}\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$. In particular, writing  $z=\prod _{i\in I}z_{i}$, the element
$z=\prod _{i\in I}z_{i}$, the element  $xz$ conjugates
$xz$ conjugates  $\unicode[STIX]{x1D6FD}$ to
$\unicode[STIX]{x1D6FD}$ to  $\unicode[STIX]{x1D6FD}^{\prime }$ and lies in
$\unicode[STIX]{x1D6FD}^{\prime }$ and lies in  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
Finally, since the strata  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent, the element
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent, the element  $xz$ also lies in
$xz$ also lies in  $\mathfrak{n}_{-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which, by Lemma 6.20, is
$\mathfrak{n}_{-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which, by Lemma 6.20, is  $(1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}))\mathfrak{b}_{0}^{\times }$. Hence we can write
$(1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}))\mathfrak{b}_{0}^{\times }$. Hence we can write  $xz=gb$, with
$xz=gb$, with  $b\in \mathfrak{b}_{0}^{\times }$ and
$b\in \mathfrak{b}_{0}^{\times }$ and  $g\in 1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.◻
$g\in 1+\mathfrak{m}_{-(k_{0}+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.◻
We end this section with a criterion for a minimal semisimple stratum to be equivalent to a skew-semisimple stratum, in terms of its characteristic polynomial.
Lemma 7.19. Suppose  $[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum such that
$[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum such that  $\unicode[STIX]{x1D6EC}$ is self-dual and
$\unicode[STIX]{x1D6EC}$ is self-dual and  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})\equiv -\unicode[STIX]{x1D6FD}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-m})$. Put
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})\equiv -\unicode[STIX]{x1D6FD}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1-m})$. Put  $e_{0}=e(F|F_{0})$,
$e_{0}=e(F|F_{0})$,  $e=e(\unicode[STIX]{x1D6EC}|\mathfrak{o}_{F})$ and
$e=e(\unicode[STIX]{x1D6EC}|\mathfrak{o}_{F})$ and  $g=\gcd (m,e)$, and set
$g=\gcd (m,e)$, and set  $\unicode[STIX]{x1D702}=(-1)^{(2m+ee_{0})/ge_{0}}$. Let
$\unicode[STIX]{x1D702}=(-1)^{(2m+ee_{0})/ge_{0}}$. Let  $\unicode[STIX]{x1D719}$ be the characteristic polynomial of
$\unicode[STIX]{x1D719}$ be the characteristic polynomial of  $[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ and suppose that its primary factors
$[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ and suppose that its primary factors  $\unicode[STIX]{x1D719}_{i}$ satisfy
$\unicode[STIX]{x1D719}_{i}$ satisfy
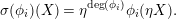 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)=\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{i})}\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D702}X).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)=\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{i})}\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D702}X).\end{eqnarray}$$Then the stratum is equivalent to a skew-semisimple stratum.
Proof. Let  $(1^{i})$ be the idempotents of the associated splitting of
$(1^{i})$ be the idempotents of the associated splitting of  $\unicode[STIX]{x1D6FD}$. By hypothesis, the stratum
$\unicode[STIX]{x1D6FD}$. By hypothesis, the stratum  $[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ is equivalent to
$[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ is equivalent to  $[\unicode[STIX]{x1D6EC},m,m-1,-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})]$, which is also semisimple, with associated idempotents
$[\unicode[STIX]{x1D6EC},m,m-1,-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})]$, which is also semisimple, with associated idempotents  $(\unicode[STIX]{x1D70E}(1^{i}))$. Then Lemma 7.17 implies that there is a bijection
$(\unicode[STIX]{x1D70E}(1^{i}))$. Then Lemma 7.17 implies that there is a bijection  $\unicode[STIX]{x1D70F}$ of
$\unicode[STIX]{x1D70F}$ of  $I$ such that
$I$ such that  $\unicode[STIX]{x1D70E}(1^{i})$ is congruent to
$\unicode[STIX]{x1D70E}(1^{i})$ is congruent to  $1^{\unicode[STIX]{x1D70F}(i)}$ modulo
$1^{\unicode[STIX]{x1D70F}(i)}$ modulo  $\mathfrak{a}_{1}$, for all indices
$\mathfrak{a}_{1}$, for all indices  $i$. Recalling that
$i$. Recalling that  $\unicode[STIX]{x1D719}$ is the characteristic polynomial of (the reduction of)
$\unicode[STIX]{x1D719}$ is the characteristic polynomial of (the reduction of)  $y_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}^{e/g}\unicode[STIX]{x1D71B}^{m/g}$ and noting that
$y_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}^{e/g}\unicode[STIX]{x1D71B}^{m/g}$ and noting that  $\unicode[STIX]{x1D70E}(y_{\unicode[STIX]{x1D6FD}})$ is congruent to
$\unicode[STIX]{x1D70E}(y_{\unicode[STIX]{x1D6FD}})$ is congruent to  $\unicode[STIX]{x1D702}y_{\unicode[STIX]{x1D6FD}}$ modulo
$\unicode[STIX]{x1D702}y_{\unicode[STIX]{x1D6FD}}$ modulo  $\mathfrak{a}_{1}$, it follows that
$\mathfrak{a}_{1}$, it follows that  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)$ is equal to
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)$ is equal to  $\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)}(\unicode[STIX]{x1D702}X)$, whence
$\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)}(\unicode[STIX]{x1D702}X)$, whence  $\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)}$, by the hypotheses of the lemma. However, the characteristic polynomials for different simple blocks (that is, for different
$\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}(i)}$, by the hypotheses of the lemma. However, the characteristic polynomials for different simple blocks (that is, for different  $i$) are coprime and thus
$i$) are coprime and thus  $\unicode[STIX]{x1D70F}(i)=i$ for all
$\unicode[STIX]{x1D70F}(i)=i$ for all  $i$.
$i$.
Now we apply Corollary 7.14 to the elements  $(1^{i}+\unicode[STIX]{x1D70E}(1^{i}))/2$ (and
$(1^{i}+\unicode[STIX]{x1D70E}(1^{i}))/2$ (and  $\mathfrak{k}_{r}=\mathfrak{a}_{r}$) to obtain pairwise orthogonal symmetric idempotents
$\mathfrak{k}_{r}=\mathfrak{a}_{r}$) to obtain pairwise orthogonal symmetric idempotents  $e_{i}$ with
$e_{i}$ with  $\sum _{i}e_{i}=1$. Then we conjugate the stratum by
$\sum _{i}e_{i}=1$. Then we conjugate the stratum by  $\sum _{i}e_{i}1^{i}$ to obtain a stratum equivalent to
$\sum _{i}e_{i}1^{i}$ to obtain a stratum equivalent to  $[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ whose simple blocks are equivalent to skew-simple strata by [Reference StevensSte01b, 1.10]. This finishes the proof.◻
$[\unicode[STIX]{x1D6EC},m,m-1,\unicode[STIX]{x1D6FD}]$ whose simple blocks are equivalent to skew-simple strata by [Reference StevensSte01b, 1.10]. This finishes the proof.◻
8 Intertwining and conjugacy for semisimple strata
In the case of simple strata on a fixed lattice chain, intertwining implies conjugacy up to equivalence (see [Reference Bushnell and KutzkoBK93, 2.6.1]). The same result is true for arbitrary lattice sequences and, as we prove here, for simple skew strata (that is,  $G$-intertwining implies
$G$-intertwining implies  $G$-conjugacy). However, the analogous result is no longer true for semisimple strata. As well as giving some examples to illustrate this, we give a useful sufficient additional condition to guarantee that the strata are indeed conjugate.
$G$-conjugacy). However, the analogous result is no longer true for semisimple strata. As well as giving some examples to illustrate this, we give a useful sufficient additional condition to guarantee that the strata are indeed conjugate.
8.1 For general linear groups
Theorem 8.1. (Cf. [Reference Bushnell and KutzkoBK93, 2.6.1])
Suppose  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are simple strata which intertwine. Then, up to equivalence they are conjugate by an element of
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are simple strata which intertwine. Then, up to equivalence they are conjugate by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
Proof. By Corollary 7.8, we can assume that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. By [Reference Bushnell and HenniartBH96, Lemma 1.6], there is an element of
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same characteristic polynomial. By [Reference Bushnell and HenniartBH96, Lemma 1.6], there is an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which conjugates
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which conjugates  $\unicode[STIX]{x1D6FD}$ to
$\unicode[STIX]{x1D6FD}$ to  $\unicode[STIX]{x1D6FD}^{\prime }$.◻
$\unicode[STIX]{x1D6FD}^{\prime }$.◻
In contrast to simple strata we cannot achieve intertwining implies conjugacy for semisimple strata.
Example 8.2. Let  $V$ be a 4-dimensional vector space over
$V$ be a 4-dimensional vector space over  $F$ with basis
$F$ with basis  $v_{1},\ldots ,v_{4}$ and let
$v_{1},\ldots ,v_{4}$ and let  $\unicode[STIX]{x1D6EC}$ be the lattice chain of period 2 such that
$\unicode[STIX]{x1D6EC}$ be the lattice chain of period 2 such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{0}=v_{1}o_{F}+v_{2}o_{F}+v_{3}o_{F}+v_{4}o_{F},\qquad \unicode[STIX]{x1D6EC}_{1}=v_{1}o_{F}+v_{2}o_{F}+v_{3}o_{F}+v_{4}\mathfrak{p}_{F}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{0}=v_{1}o_{F}+v_{2}o_{F}+v_{3}o_{F}+v_{4}o_{F},\qquad \unicode[STIX]{x1D6EC}_{1}=v_{1}o_{F}+v_{2}o_{F}+v_{3}o_{F}+v_{4}\mathfrak{p}_{F}.\end{eqnarray}$$ Then, with respect to the basis,  $\mathfrak{a}_{0}(\unicode[STIX]{x1D6EC})$ is
$\mathfrak{a}_{0}(\unicode[STIX]{x1D6EC})$ is
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}o_{F} & o_{F} & o_{F} & o_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ \mathfrak{ p}_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F} & o_{F}\\ \end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}o_{F} & o_{F} & o_{F} & o_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ \mathfrak{ p}_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F} & o_{F}\\ \end{array}\right)\end{eqnarray}$$The two elements:
 $$\begin{eqnarray}\displaystyle & b:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1}), & \displaystyle \nonumber\\ \displaystyle & b^{\prime }:=\operatorname{diag}(-\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & b:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1}), & \displaystyle \nonumber\\ \displaystyle & b^{\prime }:=\operatorname{diag}(-\unicode[STIX]{x1D71B}^{-1},-\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1}) & \displaystyle \nonumber\end{eqnarray}$$ give two semisimple strata  $[\unicode[STIX]{x1D6EC},2,1,b]$ and
$[\unicode[STIX]{x1D6EC},2,1,b]$ and  $[\unicode[STIX]{x1D6EC},2,1,b^{\prime }]$ which intertwine but whose equivalence classes are not conjugate over
$[\unicode[STIX]{x1D6EC},2,1,b^{\prime }]$ which intertwine but whose equivalence classes are not conjugate over  $\operatorname{Aut}_{F}(V)$. Indeed, suppose for contradiction that the strata are conjugate under an element of
$\operatorname{Aut}_{F}(V)$. Indeed, suppose for contradiction that the strata are conjugate under an element of  $\tilde{G}$; then this element has to be an element of the normalizer of
$\tilde{G}$; then this element has to be an element of the normalizer of  $\unicode[STIX]{x1D6EC}$ and thus by Lemma 7.18 we can assume after conjugation that the associated splittings, which are the same for both strata, are conjugated to each other. Note that this splitting is given by
$\unicode[STIX]{x1D6EC}$ and thus by Lemma 7.18 we can assume after conjugation that the associated splittings, which are the same for both strata, are conjugated to each other. Note that this splitting is given by  $V^{1}=v_{1}F+v_{2}F$ and
$V^{1}=v_{1}F+v_{2}F$ and  $V^{2}=v_{3}F+v_{4}F$. The minimal polynomials of the strata force that the matching has to be given by exchanging the two blocks
$V^{2}=v_{3}F+v_{4}F$. The minimal polynomials of the strata force that the matching has to be given by exchanging the two blocks  $V^{1}$ and
$V^{1}$ and  $V^{2}$. But this is not possible, because the image of
$V^{2}$. But this is not possible, because the image of  $\unicode[STIX]{x1D6EC}^{1}=\unicode[STIX]{x1D6EC}\cap V^{1}$ contains only one homothety class of lattices, while the image of
$\unicode[STIX]{x1D6EC}^{1}=\unicode[STIX]{x1D6EC}\cap V^{1}$ contains only one homothety class of lattices, while the image of  $\unicode[STIX]{x1D6EC}^{2}=\unicode[STIX]{x1D6EC}\cap V^{2}$ contains two.
$\unicode[STIX]{x1D6EC}^{2}=\unicode[STIX]{x1D6EC}\cap V^{2}$ contains two.
Thus we impose an extra condition in the following theorem.
Theorem 8.3. Suppose that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two non-null semisimple strata which intertwine and let
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two non-null semisimple strata which intertwine and let  $\unicode[STIX]{x1D701}$ be the matching between their index sets. Suppose moreover that
$\unicode[STIX]{x1D701}$ be the matching between their index sets. Suppose moreover that
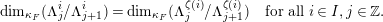 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D701}(i)})\quad \text{for all}~i\in I,j\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{i}/\unicode[STIX]{x1D6EC}_{j+1}^{i})=\dim _{\unicode[STIX]{x1D705}_{F}}(\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}/\unicode[STIX]{x1D6EC}_{j+1}^{\unicode[STIX]{x1D701}(i)})\quad \text{for all}~i\in I,j\in \mathbb{Z}.\end{eqnarray}$$ Then the strata are conjugate by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$.
Proof. Fix an index  $i$ of
$i$ of  $I$. By Corollary 7.9 there is an
$I$. By Corollary 7.9 there is an  $F$-linear isomorphism
$F$-linear isomorphism  $g_{i}:V^{i}\rightarrow V^{\unicode[STIX]{x1D701}(i)}$ such that
$g_{i}:V^{i}\rightarrow V^{\unicode[STIX]{x1D701}(i)}$ such that  $[g_{i}\unicode[STIX]{x1D6EC}^{i},q,r,g_{i}\unicode[STIX]{x1D6FD}^{i}g_{i}^{-1}]$ intertwines
$[g_{i}\unicode[STIX]{x1D6EC}^{i},q,r,g_{i}\unicode[STIX]{x1D6FD}^{i}g_{i}^{-1}]$ intertwines  $[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime \unicode[STIX]{x1D701}(i)}]$. Now condition (8.4) implies that the lattice sequences
$[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime \unicode[STIX]{x1D701}(i)}]$. Now condition (8.4) implies that the lattice sequences  $g_{i}\unicode[STIX]{x1D6EC}^{i}$ and
$g_{i}\unicode[STIX]{x1D6EC}^{i}$ and  $\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$ are conjugate so, modifying
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)}$ are conjugate so, modifying  $g_{i}$ if necessary, we may assume
$g_{i}$ if necessary, we may assume  $g_{i}\unicode[STIX]{x1D6EC}_{j}^{i}=\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}$, for each
$g_{i}\unicode[STIX]{x1D6EC}_{j}^{i}=\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}$, for each  $j\in \mathbb{Z}$. Now we can apply Theorem 8.1 so that, replacing
$j\in \mathbb{Z}$. Now we can apply Theorem 8.1 so that, replacing  $g_{i}$ by a translate by an element of
$g_{i}$ by a translate by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)})$, we can assume that
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)})$, we can assume that  $[g_{i}\unicode[STIX]{x1D6EC}^{i},q,r,g_{i}\unicode[STIX]{x1D6FD}^{i}g_{i}^{-1}]$ is equivalent to
$[g_{i}\unicode[STIX]{x1D6EC}^{i},q,r,g_{i}\unicode[STIX]{x1D6FD}^{i}g_{i}^{-1}]$ is equivalent to  $[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime \unicode[STIX]{x1D701}(i)}]$. Then
$[\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D701}(i)},q,r,\unicode[STIX]{x1D6FD}^{\prime \unicode[STIX]{x1D701}(i)}]$. Then
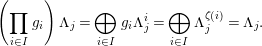 $$\begin{eqnarray}\left(\mathop{\prod }_{i\in I}g_{i}\right)\unicode[STIX]{x1D6EC}_{j}=\bigoplus _{i\in I}g_{i}\unicode[STIX]{x1D6EC}_{j}^{i}=\bigoplus _{i\in I}\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}=\unicode[STIX]{x1D6EC}_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\mathop{\prod }_{i\in I}g_{i}\right)\unicode[STIX]{x1D6EC}_{j}=\bigoplus _{i\in I}g_{i}\unicode[STIX]{x1D6EC}_{j}^{i}=\bigoplus _{i\in I}\unicode[STIX]{x1D6EC}_{j}^{\unicode[STIX]{x1D701}(i)}=\unicode[STIX]{x1D6EC}_{j}.\end{eqnarray}$$ so that  $\prod _{i\in I}g_{i}\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ conjugates the first to the second stratum.◻
$\prod _{i\in I}g_{i}\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ conjugates the first to the second stratum.◻
8.2 For classical groups
We give here the similar “intertwining implies conjugacy” statements for skew-semisimple strata, beginning with the simple case.
Theorem 8.5. Suppose  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two skew-simple strata which intertwine in
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two skew-simple strata which intertwine in  $G$. Then they are conjugate over
$G$. Then they are conjugate over  $\operatorname{U}(\unicode[STIX]{x1D6EC})$.
$\operatorname{U}(\unicode[STIX]{x1D6EC})$.
Proof. The proof is mutatis mutandis that of Theorem 8.1: we apply Lemma 7.15, then Theorem 5.2, and then Proposition 5.4. ◻
As in the non-skew case, this is no longer true if one replaces simple by semisimple.
Example 8.6. Consider a ramified quadratic field extension  $F|F_{0}$ and a skew-hermitian form on
$F|F_{0}$ and a skew-hermitian form on  $V=F^{4}$ whose Gram matrix
$V=F^{4}$ whose Gram matrix  $(h_{ij})$ with respect to the standard basis is the antidiagonal matrix with entries
$(h_{ij})$ with respect to the standard basis is the antidiagonal matrix with entries
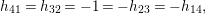 $$\begin{eqnarray}h_{41}=h_{32}=-1=-h_{23}=-h_{14},\end{eqnarray}$$
$$\begin{eqnarray}h_{41}=h_{32}=-1=-h_{23}=-h_{14},\end{eqnarray}$$ and write  $G$ for the isometry group of this form. Let
$G$ for the isometry group of this form. Let  $\unicode[STIX]{x1D71B}$ be a skew-symmetric uniformizer of
$\unicode[STIX]{x1D71B}$ be a skew-symmetric uniformizer of  $F$ and let
$F$ and let  $z$ be a non-square unit in
$z$ be a non-square unit in  $F_{0}$. Let
$F_{0}$. Let  $\unicode[STIX]{x1D6EC}$ be a self-dual lattice chain corresponding to the hereditary order
$\unicode[STIX]{x1D6EC}$ be a self-dual lattice chain corresponding to the hereditary order
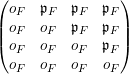 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}o_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & o_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ \end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}o_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & \mathfrak{p}_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & o_{F} & \mathfrak{p}_{F}\\ o_{F} & o_{F} & o_{F} & o_{F}\\ \end{array}\right)\end{eqnarray}$$We define the skew-symmetric elements:
 $$\begin{eqnarray}b:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},z\unicode[STIX]{x1D71B}^{-1}),\qquad b^{\prime }:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}b:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1},z\unicode[STIX]{x1D71B}^{-1}),\qquad b^{\prime }:=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-1},\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1}z,\unicode[STIX]{x1D71B}^{-1}).\end{eqnarray}$$ The minimal skew-semisimple strata  $[\unicode[STIX]{x1D6EC},4,3,b]$ and
$[\unicode[STIX]{x1D6EC},4,3,b]$ and  $[\unicode[STIX]{x1D6EC},4,3,b^{\prime }]$ intertwine over
$[\unicode[STIX]{x1D6EC},4,3,b^{\prime }]$ intertwine over  $G$ because
$G$ because  $b$ is conjugate to
$b$ is conjugate to  $b^{\prime }$ under
$b^{\prime }$ under  $G$, but the strata are not conjugate under
$G$, but the strata are not conjugate under  $G$ because they are not conjugate under
$G$ because they are not conjugate under  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
As an immediate consequence of Proposition 7.10, [Reference SkodlerackSko14, Proposition 5.2] and Theorem 8.5 (as in the non-skew case above) we have:
Theorem 8.7. Suppose that  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two non-null skew-semisimple strata which intertwine in
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}^{\prime }]$ are two non-null skew-semisimple strata which intertwine in  $G$, with matching
$G$, with matching  $\unicode[STIX]{x1D701}$, such that (8.4) holds. Then the strata are conjugate by an element of
$\unicode[STIX]{x1D701}$, such that (8.4) holds. Then the strata are conjugate by an element of  $\operatorname{U}(\unicode[STIX]{x1D6EC})$.
$\operatorname{U}(\unicode[STIX]{x1D6EC})$.
9 Semisimple characters
Associated to the semisimple strata studied in the previous sections, we have sets of characters of certain compact open subgroups, which are called semisimple characters. The purpose of this section is both briefly to recall their definitions and properties (from [Reference Bushnell and KutzkoBK93] and [Reference StevensSte05]) and to ensure that all the results we need are available for arbitrary lattice sequences.
9.1 Semisimple characters for  $\tilde{G}$
$\tilde{G}$
Fix a non-null semisimple stratum  $[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$. Define
$[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$. Define  $r:=-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$and let
$r:=-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$and let  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$be a semisimple stratum equivalent to
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FE}]$be a semisimple stratum equivalent to  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$such that
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$such that  $\unicode[STIX]{x1D6FE}$commutes with the projections
$\unicode[STIX]{x1D6FE}$commutes with the projections  $1^{i}$of the associated splitting of
$1^{i}$of the associated splitting of  $\unicode[STIX]{x1D6FD}$. If
$\unicode[STIX]{x1D6FD}$. If  $[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$is minimal then we take
$[\unicode[STIX]{x1D6EC},q,r,\unicode[STIX]{x1D6FD}]$is minimal then we take  $\unicode[STIX]{x1D6FE}$to be zero.
$\unicode[STIX]{x1D6FE}$to be zero.
The rings of a semisimple stratum (cf. [Reference Bushnell and KutzkoBK93, 3.1])
We start with the orders  $\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and
$\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and  $\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, defined inductively by
$\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, defined inductively by
∙
 $\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{h}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{\lfloor r/2\rfloor +1}$,
$\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{h}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{\lfloor r/2\rfloor +1}$,∙
 $\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{j}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{\lfloor r+1/2\rfloor }$,
$\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{j}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{\lfloor r+1/2\rfloor }$,
with  $\mathfrak{h}(0,\unicode[STIX]{x1D6EC})=\mathfrak{j}(0,\unicode[STIX]{x1D6EC})=\mathfrak{a}_{0}$. We define now the groups
$\mathfrak{h}(0,\unicode[STIX]{x1D6EC})=\mathfrak{j}(0,\unicode[STIX]{x1D6EC})=\mathfrak{a}_{0}$. We define now the groups
 $$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}),\qquad J^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}),\end{eqnarray}$$
$$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}),\qquad J^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}):=\mathfrak{j}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}),\end{eqnarray}$$ for  $m\geqslant -1$, and write
$m\geqslant -1$, and write  $H$ and
$H$ and  $J$ instead of
$J$ instead of  $H^{0}$ and
$H^{0}$ and  $J^{0}$.
$J^{0}$.
We now begin the proofs of the statements in [Reference Bushnell and KutzkoBK93, Section 3.1] for semisimple strata. (Note that some of these are already in [Reference StevensSte05].)
Proposition 9.1. (Cf. [Reference Bushnell and KutzkoBK93, (3.1.9)])
(i) For all
 $-1\leqslant t\leqslant r$, the lattice
$-1\leqslant t\leqslant r$, the lattice  $\mathfrak{h}^{\lfloor \frac{t}{2}\rfloor +1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a bimodule over the ring
$\mathfrak{h}^{\lfloor \frac{t}{2}\rfloor +1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a bimodule over the ring  $\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
$\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.(ii) If
 $r<q$,
$r<q$,  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ for
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ for  $k\geqslant \lfloor r/2\rfloor +1$.
$k\geqslant \lfloor r/2\rfloor +1$.(iii) For
 $k\geqslant 0$,
$k\geqslant 0$,  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a  $\mathfrak{b}_{\unicode[STIX]{x1D6FD}}$-bimodule.
$\mathfrak{b}_{\unicode[STIX]{x1D6FD}}$-bimodule.(iv)
 $\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a ring and in particular an
$\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a ring and in particular an  $o_{F}$-order in
$o_{F}$-order in  $A$ and
$A$ and  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a two-sided ideal of
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a two-sided ideal of  $\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, for all non-negative integers
$\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, for all non-negative integers  $k$.
$k$.(v) Let
 $t\leqslant r-1$ and let
$t\leqslant r-1$ and let  $[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}^{\prime }]$ be a semisimple stratum equivalent to
$[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}^{\prime }]$ be a semisimple stratum equivalent to  $[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}]$. Then
$[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}]$. Then  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$, for all non-negative integers
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$, for all non-negative integers  $k>t-\lfloor (r+1)/2\rfloor$.
$k>t-\lfloor (r+1)/2\rfloor$.(vi) The definition of
 $\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ does not depend on the choice of
$\mathfrak{h}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ does not depend on the choice of  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
Proof. In [Reference Bushnell and KutzkoBK93, (3.1.9)] the statement is proven for strict simple strata. In the case of a non-strict simple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, the stratum
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, the stratum
 $$\begin{eqnarray}\left[\bigoplus _{l=0}^{e(\unicode[STIX]{x1D6EC})-1}(\unicode[STIX]{x1D6EC}-l),q,m,\unicode[STIX]{x1D6FD}^{\oplus e}\right]\end{eqnarray}$$
$$\begin{eqnarray}\left[\bigoplus _{l=0}^{e(\unicode[STIX]{x1D6EC})-1}(\unicode[STIX]{x1D6EC}-l),q,m,\unicode[STIX]{x1D6FD}^{\oplus e}\right]\end{eqnarray}$$is a strict simple stratum and, using the identity
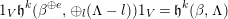 $$\begin{eqnarray}1_{V}\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\oplus e},\oplus _{l}(\unicode[STIX]{x1D6EC}-l))1_{V}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}1_{V}\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\oplus e},\oplus _{l}(\unicode[STIX]{x1D6EC}-l))1_{V}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\end{eqnarray}$$ (where  $1_{V}$ denotes projection onto the first copy of
$1_{V}$ denotes projection onto the first copy of  $V$ in
$V$ in  $\bigoplus _{l=0}^{e(\unicode[STIX]{x1D6EC})-1}V$) we get the result for all simple strata. Thus we continue with the case of semisimple strata.
$\bigoplus _{l=0}^{e(\unicode[STIX]{x1D6EC})-1}V$) we get the result for all simple strata. Thus we continue with the case of semisimple strata.
We are going to prove the semisimple case via induction along  $\unicode[STIX]{x1D6FD}$, but (v) only for the case where the strata in (v) have the same associated splitting; we prove the general case after the next four lemmas. We start with the inductive step and begin with (v). We use the idea of [Reference StevensSte05, Lemma 3.9]. Assume that
$\unicode[STIX]{x1D6FD}$, but (v) only for the case where the strata in (v) have the same associated splitting; we prove the general case after the next four lemmas. We start with the inductive step and begin with (v). We use the idea of [Reference StevensSte05, Lemma 3.9]. Assume that  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ and  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ are defined using the same
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ are defined using the same  $\unicode[STIX]{x1D6FE}$ and that
$\unicode[STIX]{x1D6FE}$ and that  $[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}^{\prime }]$ has the same associated splitting as
$[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}^{\prime }]$ has the same associated splitting as  $[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}]$. In particular, we immediately get that
$[\unicode[STIX]{x1D6EC},q,t,\unicode[STIX]{x1D6FD}]$. In particular, we immediately get that  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,j}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap A^{i,j}$, for
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,j}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap A^{i,j}$, for  $i\neq j$, because
$i\neq j$, because  $\mathfrak{h}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ is a bi-
$\mathfrak{h}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ is a bi- $\mathfrak{b}_{\unicode[STIX]{x1D6FE}}$-module, while
$\mathfrak{b}_{\unicode[STIX]{x1D6FE}}$-module, while  $\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,i}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap A^{i,i}$ follows from the simple case. The proof of (ii) is similar, and (v) for
$\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,i}=\mathfrak{h}^{k}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap A^{i,i}$ follows from the simple case. The proof of (ii) is similar, and (v) for  $\unicode[STIX]{x1D6FE}$ implies (vi). Now (i) follows from [Reference StevensSte05, 3.10(ii)], (iii) follows from (i) for
$\unicode[STIX]{x1D6FE}$ implies (vi). Now (i) follows from [Reference StevensSte05, 3.10(ii)], (iii) follows from (i) for  $t=-1$, and finally (iv) follows from (iii), (ii), and (iv) for
$t=-1$, and finally (iv) follows from (iii), (ii), and (iv) for  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
For the base case (when  $\unicode[STIX]{x1D6FE}=0$) (i) and (v) are shown as in the induction step and the remaining assertions are obvious.
$\unicode[STIX]{x1D6FE}=0$) (i) and (v) are shown as in the induction step and the remaining assertions are obvious.
To prove Proposition 9.1(v) in general we need the following sequence of lemmas.
Lemma 9.2.  $\mathfrak{h}^{\max \{0,1+t-\lfloor (r+1)/2\rfloor \}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is an
$\mathfrak{h}^{\max \{0,1+t-\lfloor (r+1)/2\rfloor \}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is an  $\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$-bimodule for all
$\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$-bimodule for all  $r\geqslant t\geqslant 0$.
$r\geqslant t\geqslant 0$.
For this we need the analogue of [Reference StevensSte05, Lemma 3.10] for  $\mathfrak{h}$ instead of
$\mathfrak{h}$ instead of  $\mathfrak{j}$ (see the sentence following loc. cit.).
$\mathfrak{j}$ (see the sentence following loc. cit.).
Lemma 9.3. (Cf. [Reference StevensSte05, Lemma 3.10(i)])
(i) For all integers
 $k\geqslant \lfloor r/2\rfloor +1$, we have
$k\geqslant \lfloor r/2\rfloor +1$, we have  $\mathfrak{n}_{k-r}\cap \mathfrak{a}_{k}\subseteq \mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
$\mathfrak{n}_{k-r}\cap \mathfrak{a}_{k}\subseteq \mathfrak{h}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.(ii) For all integers
 $k\geqslant \lfloor (r+1)/2\rfloor$, we have
$k\geqslant \lfloor (r+1)/2\rfloor$, we have  $\mathfrak{n}_{k-r}\cap \mathfrak{a}_{k}\subseteq \mathfrak{j}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
$\mathfrak{n}_{k-r}\cap \mathfrak{a}_{k}\subseteq \mathfrak{j}^{k}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$.
Proof of Lemma 9.2.
The proof is by induction on  $r=-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. We have the two important identities:
$r=-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. We have the two important identities:
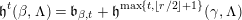 $$\begin{eqnarray}\mathfrak{h}^{t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}+\mathfrak{h}^{\max \{t,\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{h}^{t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}+\mathfrak{h}^{\max \{t,\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\end{eqnarray}$$and
 $$\begin{eqnarray}\mathfrak{n}_{-t}=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{n}_{-t}=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}+\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}\end{eqnarray}$$ We write  $t_{0}$ for
$t_{0}$ for  $\max \{0,1+t-\lfloor (r+1)/2\rfloor \}$ so that
$\max \{0,1+t-\lfloor (r+1)/2\rfloor \}$ so that
 $$\begin{eqnarray}t_{0}+r-t\geqslant 1+\left\lfloor \frac{r}{2}\right\rfloor \qquad \text{and}\qquad 2(r-t+t_{0})>r.\end{eqnarray}$$
$$\begin{eqnarray}t_{0}+r-t\geqslant 1+\left\lfloor \frac{r}{2}\right\rfloor \qquad \text{and}\qquad 2(r-t+t_{0})>r.\end{eqnarray}$$ We have to show that  $\mathfrak{n}_{-t}\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a subset of
$\mathfrak{n}_{-t}\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a subset of  $\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. We have
$\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. We have
∙
 $\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a
$\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a  $\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}$-module.
$\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}$-module.∙
 $(\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t})\mathfrak{b}_{\unicode[STIX]{x1D6FD},t_{0}}$ is contained in
$(\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t})\mathfrak{b}_{\unicode[STIX]{x1D6FD},t_{0}}$ is contained in  $\mathfrak{n}_{t_{0}-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{t_{0}+r-t}$, which is a subset of
$\mathfrak{n}_{t_{0}-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{t_{0}+r-t}$, which is a subset of  $\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ by (9.4) and Lemma 9.3.
$\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ by (9.4) and Lemma 9.3.
The last containment we need, that  $(\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t})\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ is a subset of
$(\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t})\mathfrak{h}^{\max \{t_{0},\lfloor r/2\rfloor +1\}}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ is a subset of  $\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, is proved by induction. The case of
$\mathfrak{h}^{t_{0}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$, is proved by induction. The case of  $\unicode[STIX]{x1D6FE}=0$ is trivial, while the induction step is a result of the equality
$\unicode[STIX]{x1D6FE}=0$ is trivial, while the induction step is a result of the equality  $\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}=\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}$ and the induction hypothesis.◻
$\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}=\mathfrak{n}_{-t}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})\cap \mathfrak{a}_{r-t}$ and the induction hypothesis.◻
Finally, we see that the proof of the general case of Proposition 9.1(v) follows from Lemmas 9.2 and 7.18. ◻
Given now the preliminary results on semisimple strata that we have obtained in previous sections and Proposition 9.1, we can follow the definitions and proofs of [Reference Bushnell and KutzkoBK93, Section 3.1], from (3.1.3) to (3.1.21), to see that if one makes the obvious substitution
∙ “replace
 $\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}\mathfrak{n}_{l}$ by
$\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}\mathfrak{n}_{l}$ by  $\mathfrak{a}_{t}\cap \mathfrak{n}_{t+l}$”, for
$\mathfrak{a}_{t}\cap \mathfrak{n}_{t+l}$”, for  $t\geqslant 0$,
$t\geqslant 0$,
then everything is true except possibly for the equalities in (3.1.9)(iii), in (3.1.10)(iii) and in (3.1.11). (Some of these are already described in [Reference StevensSte05].) Thus, from now on, we will use these statements from [Reference Bushnell and KutzkoBK93] for semisimple strata by referring to [Reference Bushnell and KutzkoBK93] (and giving the reference to [Reference StevensSte05] if there is one).
Characters (Cf. [Reference Bushnell and KutzkoBK93, 3.2])
Here we introduce the semisimple characters and their groups exactly the same way as it was done in [Reference Bushnell and KutzkoBK93, Section 3.2] for simple characters. This definition is equivalent to the definition given in [Reference StevensSte05, Section 3]. We fix an additive character  $\unicode[STIX]{x1D713}_{F}$ of
$\unicode[STIX]{x1D713}_{F}$ of  $F$ of level one (that is, trivial on
$F$ of level one (that is, trivial on  $\mathfrak{p}_{F}$ but not on
$\mathfrak{p}_{F}$ but not on  $o_{F}$). We define
$o_{F}$). We define  $\unicode[STIX]{x1D713}_{A}:=\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}$ and a character
$\unicode[STIX]{x1D713}_{A}:=\unicode[STIX]{x1D713}_{F}\circ \operatorname{tr}_{A|F}$ and a character
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}:\tilde{\operatorname{U}}^{\lfloor q/2\rfloor +1}(\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times },\qquad \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}(1+x):=\unicode[STIX]{x1D713}_{A}(\unicode[STIX]{x1D6FD}x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}:\tilde{\operatorname{U}}^{\lfloor q/2\rfloor +1}(\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times },\qquad \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}(1+x):=\unicode[STIX]{x1D713}_{A}(\unicode[STIX]{x1D6FD}x).\end{eqnarray}$$ The kernel of  $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}$ contains
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}$ contains  $\tilde{\operatorname{U}}^{q+1}(\unicode[STIX]{x1D6EC})$ because
$\tilde{\operatorname{U}}^{q+1}(\unicode[STIX]{x1D6EC})$ because  $\unicode[STIX]{x1D713}_{F}$ has level one.
$\unicode[STIX]{x1D713}_{F}$ has level one.
Definition 9.5. Suppose  $0\leqslant m<r$. If
$0\leqslant m<r$. If  $q=r$ then we define the set
$q=r$ then we define the set  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to be the set of all characters
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to be the set of all characters  $\unicode[STIX]{x1D703}:H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times }$ such that:
$\unicode[STIX]{x1D703}:H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times }$ such that:
(i) the restriction of
 $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{\lfloor q/2\rfloor +1}(\unicode[STIX]{x1D6EC})$ is equal to
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap \tilde{\operatorname{U}}^{\lfloor q/2\rfloor +1}(\unicode[STIX]{x1D6EC})$ is equal to  $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}$;
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}$;(ii) the restriction of
 $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$ factors through the determinant map
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$ factors through the determinant map  $\det _{B_{\unicode[STIX]{x1D6FD}}}:B_{\unicode[STIX]{x1D6FD}}^{\times }\rightarrow F[\unicode[STIX]{x1D6FD}]^{\times }$.
$\det _{B_{\unicode[STIX]{x1D6FD}}}:B_{\unicode[STIX]{x1D6FD}}^{\times }\rightarrow F[\unicode[STIX]{x1D6FD}]^{\times }$.
If  $q>r$ then we define
$q>r$ then we define  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ inductively to be the set of all characters
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ inductively to be the set of all characters  $\unicode[STIX]{x1D703}:H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times }$ such that:
$\unicode[STIX]{x1D703}:H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\rightarrow \mathbb{C}^{\times }$ such that:
(i)
 $\unicode[STIX]{x1D703}$ is normalized by
$\unicode[STIX]{x1D703}$ is normalized by  $\mathfrak{n}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$;
$\mathfrak{n}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$;(ii) the restriction of
 $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$ factors through the determinant map
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FD}}^{\times }$ factors through the determinant map  $\det _{B_{\unicode[STIX]{x1D6FD}}}:B_{\unicode[STIX]{x1D6FD}}^{\times }\rightarrow F[\unicode[STIX]{x1D6FD}]^{\times }$;
$\det _{B_{\unicode[STIX]{x1D6FD}}}:B_{\unicode[STIX]{x1D6FD}}^{\times }\rightarrow F[\unicode[STIX]{x1D6FD}]^{\times }$;(iii) if
 $m^{\prime }=\max (m,\lfloor r/2\rfloor )$, then
$m^{\prime }=\max (m,\lfloor r/2\rfloor )$, then  $\unicode[STIX]{x1D703}|_{H^{m^{\prime }+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})}$ is of the form
$\unicode[STIX]{x1D703}|_{H^{m^{\prime }+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})}$ is of the form  $\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{c}$, for some
$\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{c}$, for some  $\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m^{\prime },\unicode[STIX]{x1D6FE})$ and
$\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m^{\prime },\unicode[STIX]{x1D6FE})$ and  $c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$.
$c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$.
We also define  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,0)$ to be the set consisting of the trivial character on
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,0)$ to be the set consisting of the trivial character on  $\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.
(i) For
 $m\geqslant \lfloor q/2\rfloor$ we have
$m\geqslant \lfloor q/2\rfloor$ we have  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=\{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}\}$.
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=\{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}\}$.(ii) This definition of the set of semisimple characters is a priori different from the one introduced in [Reference StevensSte05, 3.13], which we temporarily call
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$:
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$:(a) If
 $\unicode[STIX]{x1D6EC}$ is strict and the stratum is simple then
$\unicode[STIX]{x1D6EC}$ is strict and the stratum is simple then  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined as in Definition 9.5, see [Reference Bushnell and KutzkoBK93, (3.2.1)(3.2.3)]. In [Reference StevensSte05], the set
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined as in Definition 9.5, see [Reference Bushnell and KutzkoBK93, (3.2.1)(3.2.3)]. In [Reference StevensSte05], the set  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,0)_{BKS}$ is defined to be the set consisting of the trivial character on
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,0)_{BKS}$ is defined to be the set consisting of the trivial character on  $\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.(b) If
 $\unicode[STIX]{x1D6EC}$ is a lattice sequence and the stratum is simple then
$\unicode[STIX]{x1D6EC}$ is a lattice sequence and the stratum is simple then  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined in [Reference Bushnell and KutzkoBK94, Section 5] in the following way. We take an
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined in [Reference Bushnell and KutzkoBK94, Section 5] in the following way. We take an  $o_{E}$-lattice chain
$o_{E}$-lattice chain  $\unicode[STIX]{x1D6EC}^{0}$ of the same period as
$\unicode[STIX]{x1D6EC}^{0}$ of the same period as  $\unicode[STIX]{x1D6EC}$, in some space
$\unicode[STIX]{x1D6EC}$, in some space  $V^{0}$, and restrict all elements of
$V^{0}$, and restrict all elements of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{0}\oplus \unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD})_{BKS}$ to
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{0}\oplus \unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD})_{BKS}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. The obtained restrictions form the set
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. The obtained restrictions form the set  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$.
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$.(c) If
 $\unicode[STIX]{x1D6EC}$ is a lattice sequence and the stratum is semisimple and non-null with associated splitting
$\unicode[STIX]{x1D6EC}$ is a lattice sequence and the stratum is semisimple and non-null with associated splitting  $V=\bigoplus _{i}V^{i}$ then
$V=\bigoplus _{i}V^{i}$ then  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined to be the set of characters
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is defined to be the set of characters  $\unicode[STIX]{x1D703}$ such that
$\unicode[STIX]{x1D703}$ such that  $\unicode[STIX]{x1D703}_{i}:=\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of
$\unicode[STIX]{x1D703}_{i}:=\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ and, for
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ and, for  $m^{\prime }=\max (m,\lfloor (-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}))/2\rfloor )$, the restriction of
$m^{\prime }=\max (m,\lfloor (-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}))/2\rfloor )$, the restriction of  $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m^{\prime }+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to
$H^{m^{\prime }+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to  $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D703}_{0}$ for some element
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D703}_{0}$ for some element  $\unicode[STIX]{x1D703}_{0}$ of
$\unicode[STIX]{x1D703}_{0}$ of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m^{\prime },\unicode[STIX]{x1D6FE})_{BKS}$ where
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m^{\prime },\unicode[STIX]{x1D6FE})_{BKS}$ where  $[\unicode[STIX]{x1D6EC},q,-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}),\unicode[STIX]{x1D6FE}]$ is an element of a defining sequence of the stratum with
$[\unicode[STIX]{x1D6EC},q,-k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}),\unicode[STIX]{x1D6FE}]$ is an element of a defining sequence of the stratum with  $\unicode[STIX]{x1D6FD}$ (see [Reference StevensSte05, 3.13]).
$\unicode[STIX]{x1D6FD}$ (see [Reference StevensSte05, 3.13]).
We write  $I_{H}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ for the intertwining of two characters in a group
$I_{H}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ for the intertwining of two characters in a group  $H$, that is,
$H$, that is,  $g\in H$ is an element of
$g\in H$ is an element of  $I_{H}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ if and only if
$I_{H}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ if and only if  $\unicode[STIX]{x1D703}^{g}:x\mapsto \unicode[STIX]{x1D703}(gxg^{-1})$ and
$\unicode[STIX]{x1D703}^{g}:x\mapsto \unicode[STIX]{x1D703}(gxg^{-1})$ and  $\unicode[STIX]{x1D703}^{\prime }$ agree on the intersection of their domains. In the case
$\unicode[STIX]{x1D703}^{\prime }$ agree on the intersection of their domains. In the case  $H=\tilde{G}$ we omit the subscript.
$H=\tilde{G}$ we omit the subscript.
Proposition 9.7. The sets  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ coincide. In particular the definition is independent of the choice of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ coincide. In particular the definition is independent of the choice of  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
Proof. Let us first remark that the definition of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is independent of the choice of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is independent of the choice of  $\unicode[STIX]{x1D6FE}$ once we have established the equality for all possible strata which can occur as a first member with respect to a jump sequence of
$\unicode[STIX]{x1D6FE}$ once we have established the equality for all possible strata which can occur as a first member with respect to a jump sequence of  $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FD})$, by [Reference StevensSte05, 3.14(ii)]. We prove the equality at first for simple strata. Note that we fix here
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FD})$, by [Reference StevensSte05, 3.14(ii)]. We prove the equality at first for simple strata. Note that we fix here  $q$ and that we do an induction on the critical exponent
$q$ and that we do an induction on the critical exponent  $k_{0}$. If the stratum is null, then both sets only consist of the trivial character on
$k_{0}$. If the stratum is null, then both sets only consist of the trivial character on  $\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.
$\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})$.
Suppose now that  $k_{0}\geqslant -q$: the set
$k_{0}\geqslant -q$: the set  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is a subset of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is a subset of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ because of [Reference Bushnell and KutzkoBK93, (3.2.1)(3.2.3)]. (The normalizing property is also satisfied in the case of lattice sequences because the lattice chain
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ because of [Reference Bushnell and KutzkoBK93, (3.2.1)(3.2.3)]. (The normalizing property is also satisfied in the case of lattice sequences because the lattice chain  $\unicode[STIX]{x1D6EC}^{0}$ in Remark 9.6(ii)(b) can be chosen to be principal.)
$\unicode[STIX]{x1D6EC}^{0}$ in Remark 9.6(ii)(b) can be chosen to be principal.)
For the other containment in the case of  $m\geqslant \lfloor -k_{0}/2\rfloor$ we have that
$m\geqslant \lfloor -k_{0}/2\rfloor$ we have that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is contained in
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is contained in  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}$ which is equal to
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}$ which is equal to
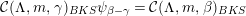 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})_{BKS}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})_{BKS}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}}={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}\end{eqnarray}$$ by induction hypothesis. In the case  $m<\lfloor -k_{0}/2\rfloor$ we follow an induction on
$m<\lfloor -k_{0}/2\rfloor$ we follow an induction on  $m$, where we use
$m$, where we use  $\lfloor -k_{0}/2\rfloor$ as the start for the induction, which is known by the first case.
$\lfloor -k_{0}/2\rfloor$ as the start for the induction, which is known by the first case.
Take an element  $\unicode[STIX]{x1D703}$ of
$\unicode[STIX]{x1D703}$ of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Consider Case (ii)(b) in Remark 9.6. Writing
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Consider Case (ii)(b) in Remark 9.6. Writing  $\bar{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}^{0}\oplus \unicode[STIX]{x1D6EC}$, we have to show that there is an element of
$\bar{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}^{0}\oplus \unicode[STIX]{x1D6EC}$, we have to show that there is an element of  ${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m,\unicode[STIX]{x1D6FD}\,\oplus \,\unicode[STIX]{x1D6FD})_{BKS}$ which restricts to
${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m,\unicode[STIX]{x1D6FD}\,\oplus \,\unicode[STIX]{x1D6FD})_{BKS}$ which restricts to  $\unicode[STIX]{x1D703}$. By the induction hypothesis on
$\unicode[STIX]{x1D703}$. By the induction hypothesis on  $m$ there is a character
$m$ there is a character  $\tilde{\unicode[STIX]{x1D703}}$ in
$\tilde{\unicode[STIX]{x1D703}}$ in  ${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m+1,\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD})_{BKS}$ which restricts to
${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m+1,\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD})_{BKS}$ which restricts to  $\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})}$. On the other hand, by definition
$\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})}$. On the other hand, by definition  $\unicode[STIX]{x1D703}|_{\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}_{E})}$ factorizes through the determinant, that is, has the form
$\unicode[STIX]{x1D703}|_{\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}_{E})}$ factorizes through the determinant, that is, has the form  $\unicode[STIX]{x1D712}\circ \det _{B}$, with
$\unicode[STIX]{x1D712}\circ \det _{B}$, with  $\unicode[STIX]{x1D712}$ a smooth character of
$\unicode[STIX]{x1D712}$ a smooth character of  $E^{\times }$. We define
$E^{\times }$. We define  $\bar{\unicode[STIX]{x1D703}}$ a character on
$\bar{\unicode[STIX]{x1D703}}$ a character on
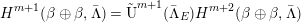 $$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6EC}})=\tilde{\operatorname{U}}^{m+1}(\bar{\unicode[STIX]{x1D6EC}}_{E})H^{m+2}(\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
$$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6EC}})=\tilde{\operatorname{U}}^{m+1}(\bar{\unicode[STIX]{x1D6EC}}_{E})H^{m+2}(\unicode[STIX]{x1D6FD}\oplus \unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$ via  $\bar{\unicode[STIX]{x1D703}}(bx)=\unicode[STIX]{x1D712}(\det _{\bar{B}}(b))\tilde{\unicode[STIX]{x1D703}}(x)$. If this is well defined then it lies in
$\bar{\unicode[STIX]{x1D703}}(bx)=\unicode[STIX]{x1D712}(\det _{\bar{B}}(b))\tilde{\unicode[STIX]{x1D703}}(x)$. If this is well defined then it lies in  ${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m,\unicode[STIX]{x1D6FD}\,\oplus \,\unicode[STIX]{x1D6FD})_{BKS}$ and its restriction to
${\mathcal{C}}(\bar{\unicode[STIX]{x1D6EC}},m,\unicode[STIX]{x1D6FD}\,\oplus \,\unicode[STIX]{x1D6FD})_{BKS}$ and its restriction to  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is  $\unicode[STIX]{x1D703}$.
$\unicode[STIX]{x1D703}$.
For  $\bar{\unicode[STIX]{x1D703}}$ to be well defined we only need that
$\bar{\unicode[STIX]{x1D703}}$ to be well defined we only need that  $\unicode[STIX]{x1D712}\circ \det _{\bar{B}}|_{\tilde{\operatorname{U}}^{m+1}(\bar{\unicode[STIX]{x1D6EC}}_{E})}$ and
$\unicode[STIX]{x1D712}\circ \det _{\bar{B}}|_{\tilde{\operatorname{U}}^{m+1}(\bar{\unicode[STIX]{x1D6EC}}_{E})}$ and  $\tilde{\unicode[STIX]{x1D703}}$ coincide on the intersection of their domains, which is
$\tilde{\unicode[STIX]{x1D703}}$ coincide on the intersection of their domains, which is  $\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$. The image of
$\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$. The image of  $\det _{\bar{B}}$ on
$\det _{\bar{B}}$ on  $\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$ coincides with the image of
$\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$ coincides with the image of  $\det _{B}$ on
$\det _{B}$ on  $\tilde{\operatorname{U}}^{m+2}(\unicode[STIX]{x1D6EC}_{E})$ (it is equal to
$\tilde{\operatorname{U}}^{m+2}(\unicode[STIX]{x1D6EC}_{E})$ (it is equal to  $\tilde{\operatorname{U}}^{\lfloor (m+1)/e(\unicode[STIX]{x1D6EC}_{E})\rfloor +1}(o_{E})$) and the restriction of
$\tilde{\operatorname{U}}^{\lfloor (m+1)/e(\unicode[STIX]{x1D6EC}_{E})\rfloor +1}(o_{E})$) and the restriction of  $\tilde{\unicode[STIX]{x1D703}}$ to
$\tilde{\unicode[STIX]{x1D703}}$ to  $\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$ factorizes through
$\tilde{\operatorname{U}}^{m+2}(\bar{\unicode[STIX]{x1D6EC}}_{E})$ factorizes through  $\det _{\bar{B}}$. Thus this restriction has to be equal to the corresponding restriction of
$\det _{\bar{B}}$. Thus this restriction has to be equal to the corresponding restriction of  $\unicode[STIX]{x1D712}\circ \det _{\bar{B}}$ because
$\unicode[STIX]{x1D712}\circ \det _{\bar{B}}$ because  $\tilde{\unicode[STIX]{x1D703}}$ and
$\tilde{\unicode[STIX]{x1D703}}$ and  $\unicode[STIX]{x1D703}$ coincide on
$\unicode[STIX]{x1D703}$ coincide on  $\tilde{\operatorname{U}}^{m+2}(\unicode[STIX]{x1D6EC}_{E})$. This finishes the proof in the simple case.
$\tilde{\operatorname{U}}^{m+2}(\unicode[STIX]{x1D6EC}_{E})$. This finishes the proof in the simple case.
We consider now the semisimple case for  $k_{0}\geqslant -q$. We have that
$k_{0}\geqslant -q$. We have that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is a subset of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})_{BKS}$ is a subset of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ because the simple restrictions of an element
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ because the simple restrictions of an element  $\unicode[STIX]{x1D703}$ of the first set satisfy the normalizing and the factorizing condition and
$\unicode[STIX]{x1D703}$ of the first set satisfy the normalizing and the factorizing condition and  $\unicode[STIX]{x1D703}$ is trivial on the unipotent parts of the Iwahori decomposition of
$\unicode[STIX]{x1D703}$ is trivial on the unipotent parts of the Iwahori decomposition of  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ with respect to
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ with respect to  $\unicode[STIX]{x1D6FD}$ by [Reference StevensSte05, 3.15]. For the other containment the case
$\unicode[STIX]{x1D6FD}$ by [Reference StevensSte05, 3.15]. For the other containment the case  $m\geqslant \lfloor -k_{0}/2\rfloor$ follows as in the simple case. If
$m\geqslant \lfloor -k_{0}/2\rfloor$ follows as in the simple case. If  $m<\lfloor -k_{0}/2\rfloor$ then we show by induction on
$m<\lfloor -k_{0}/2\rfloor$ then we show by induction on  $m$ that the restriction
$m$ that the restriction  $\unicode[STIX]{x1D703}_{i}$ of an element
$\unicode[STIX]{x1D703}_{i}$ of an element  $\unicode[STIX]{x1D703}$ of
$\unicode[STIX]{x1D703}$ of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is an element of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$. By induction hypothesis
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$. By induction hypothesis  $\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of
$\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m+1,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ and the axioms for
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m+1,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ and the axioms for  $\unicode[STIX]{x1D703}$ imply the factorization condition for
$\unicode[STIX]{x1D703}$ imply the factorization condition for  $\unicode[STIX]{x1D703}_{i}$. Thus
$\unicode[STIX]{x1D703}_{i}$. Thus  $\unicode[STIX]{x1D703}_{i}$ is an element of
$\unicode[STIX]{x1D703}_{i}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})$ because it is normalized by
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})$ because it is normalized by  $\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E_{i}}^{i})$ (because
$\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E_{i}}^{i})$ (because  $\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ and
$\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ and  $\unicode[STIX]{x1D703}_{i}|_{\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}_{E_{i}}^{i})}$ are) and because
$\unicode[STIX]{x1D703}_{i}|_{\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC}_{E_{i}}^{i})}$ are) and because  $\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of
$\unicode[STIX]{x1D703}_{i}|_{H^{m+2}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m+1,\unicode[STIX]{x1D6FD}_{i})$ by the simple case. Thus
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m+1,\unicode[STIX]{x1D6FD}_{i})$ by the simple case. Thus  $\unicode[STIX]{x1D703}_{i}$ is an element of
$\unicode[STIX]{x1D703}_{i}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ again by the simple case. This finishes the proof.◻
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i})_{BKS}$ again by the simple case. This finishes the proof.◻
Let us recall the intertwining formula for a semisimple character:
Proposition 9.8. ([Reference StevensSte05, 3.16, 3.22], [Reference Bushnell and KutzkoBK93, (3.3.2)])
The intertwining of a semisimple character  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is given by
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is given by  $S_{m}(\unicode[STIX]{x1D6FD})B_{\unicode[STIX]{x1D6FD}}^{\times }S_{m}(\unicode[STIX]{x1D6FD})$ where
$S_{m}(\unicode[STIX]{x1D6FD})B_{\unicode[STIX]{x1D6FD}}^{\times }S_{m}(\unicode[STIX]{x1D6FD})$ where
 $$\begin{eqnarray}S_{m}(\unicode[STIX]{x1D6FD})=S(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=1+\mathfrak{m}_{-k_{0}-m}+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}S_{m}(\unicode[STIX]{x1D6FD})=S(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=1+\mathfrak{m}_{-k_{0}-m}+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}).\end{eqnarray}$$ Moreover, the normalizer  $\mathfrak{n}(\unicode[STIX]{x1D703})$ of
$\mathfrak{n}(\unicode[STIX]{x1D703})$ of  $\unicode[STIX]{x1D703}$ contains
$\unicode[STIX]{x1D703}$ contains  $S_{m}(\unicode[STIX]{x1D6FD})$.
$S_{m}(\unicode[STIX]{x1D6FD})$.
Reading the proofs of [Reference Bushnell and KutzkoBK93] from (3.2.1) to (3.5.9) we see that all statements except the statements (3.3.17) and (3.5.1) are true for semisimple characters (replacing  $\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}\mathfrak{n}_{l}$ by
$\mathfrak{b}_{\unicode[STIX]{x1D6FD},t}\mathfrak{n}_{l}$ by  $\mathfrak{a}_{t}\cap \mathfrak{n}_{t+l}$ throughout), after making the following assumptions:
$\mathfrak{a}_{t}\cap \mathfrak{n}_{t+l}$ throughout), after making the following assumptions:
∙ For the statements (3.3.20) and (3.5.2) until (3.5.9) the elements
 $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}$ and
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}$ and  $\unicode[STIX]{x1D6FD}_{1}^{\prime }$ need to be assumed to have the same associated splitting;
$\unicode[STIX]{x1D6FD}_{1}^{\prime }$ need to be assumed to have the same associated splitting;∙ The element
 $b$ in (3.5.2) and (3.5.6) is assumed to be split by the splitting of
$b$ in (3.5.2) and (3.5.6) is assumed to be split by the splitting of  $\unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FD}$.
However (3.3.20) is also true without the additional assumption, by Lemma 7.18, and we will see that there are obvious modifications of (3.3.17) and (3.5.1) which are still true.
Proposition 9.9. (See [Reference Bushnell and KutzkoBK93, (3.5.1)])
Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata such that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ is non-empty. Then there is a bijection
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ is non-empty. Then there is a bijection  $\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ such that
$\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ such that  $1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, and:
$1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, and:
(i)
 $k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=k_{0}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$;
$k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=k_{0}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$;(ii) the field extensions
 $E_{i}|F$ and
$E_{i}|F$ and  $E_{\unicode[STIX]{x1D70F}(i)}^{\prime }|F$ have the same inertia degree and the same ramification index;
$E_{\unicode[STIX]{x1D70F}(i)}^{\prime }|F$ have the same inertia degree and the same ramification index;(iii) the dimensions of
 $V^{i}$ and
$V^{i}$ and  $V^{\unicode[STIX]{x1D70F}(i)}$ as
$V^{\unicode[STIX]{x1D70F}(i)}$ as  $F$-vector spaces coincide;
$F$-vector spaces coincide;(iv) there is an element
 $g$ of
$g$ of  $S_{m}(\unicode[STIX]{x1D6FD})$ such that
$S_{m}(\unicode[STIX]{x1D6FD})$ such that  $gV^{i}$ is equal to
$gV^{i}$ is equal to  $V^{\unicode[STIX]{x1D70F}(i)}$. In fact, the element
$V^{\unicode[STIX]{x1D70F}(i)}$. In fact, the element  $g=\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ is an example.
$g=\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ is an example.
Proof. The existence of  $\unicode[STIX]{x1D70F}$ follows from taking the topological closure of the two descriptions of the intertwining of an element
$\unicode[STIX]{x1D70F}$ follows from taking the topological closure of the two descriptions of the intertwining of an element  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$,
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$,
 $$\begin{eqnarray}I(\unicode[STIX]{x1D703})=S_{m}(\unicode[STIX]{x1D6FD})B_{\unicode[STIX]{x1D6FD}}^{\times }S_{m}(\unicode[STIX]{x1D6FD})=S_{m}(\unicode[STIX]{x1D6FD}^{\prime })B_{\unicode[STIX]{x1D6FD}^{\prime }}^{\times }S_{m}(\unicode[STIX]{x1D6FD}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}I(\unicode[STIX]{x1D703})=S_{m}(\unicode[STIX]{x1D6FD})B_{\unicode[STIX]{x1D6FD}}^{\times }S_{m}(\unicode[STIX]{x1D6FD})=S_{m}(\unicode[STIX]{x1D6FD}^{\prime })B_{\unicode[STIX]{x1D6FD}^{\prime }}^{\times }S_{m}(\unicode[STIX]{x1D6FD}^{\prime }),\end{eqnarray}$$ together with Lemma 7.17. We now follow the proof of [Reference Bushnell and KutzkoBK93, (3.5.1)] to get that  $\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}/\mathfrak{b}_{\unicode[STIX]{x1D6FD},1}$ is isomorphic to
$\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}/\mathfrak{b}_{\unicode[STIX]{x1D6FD},1}$ is isomorphic to  $\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime },0}/\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime },1}$, by an isomorphism of
$\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime },0}/\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime },1}$, by an isomorphism of  $\unicode[STIX]{x1D705}_{F}$-algebras which maps
$\unicode[STIX]{x1D705}_{F}$-algebras which maps  $1^{i}$ to
$1^{i}$ to  $1^{\unicode[STIX]{x1D70F}(i)}$. We also have that
$1^{\unicode[STIX]{x1D70F}(i)}$. We also have that  $(1^{i}\mathfrak{a}_{0}1^{i})/\mathfrak{a}_{1}=(1^{\unicode[STIX]{x1D70F}(i)}\mathfrak{a}_{0}1^{\unicode[STIX]{x1D70F}(i)})/\mathfrak{a}_{1}$ and thus, as in the proof of [Reference Bushnell and KutzkoBK93, (2.1.4)], we get the desired equalities in (ii) and (iii).
$(1^{i}\mathfrak{a}_{0}1^{i})/\mathfrak{a}_{1}=(1^{\unicode[STIX]{x1D70F}(i)}\mathfrak{a}_{0}1^{\unicode[STIX]{x1D70F}(i)})/\mathfrak{a}_{1}$ and thus, as in the proof of [Reference Bushnell and KutzkoBK93, (2.1.4)], we get the desired equalities in (ii) and (iii).
The equality of the additive closures of the intertwining set  $I(\unicode[STIX]{x1D703})\cap \mathfrak{a}_{0}$ in terms of
$I(\unicode[STIX]{x1D703})\cap \mathfrak{a}_{0}$ in terms of  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ implies that, for each
$\unicode[STIX]{x1D6FD}^{\prime }$ implies that, for each  $i\in I$, we can write
$i\in I$, we can write  $1^{\unicode[STIX]{x1D70F}(i)}=b+u$ with
$1^{\unicode[STIX]{x1D70F}(i)}=b+u$ with  $1+u\in S_{m}(\unicode[STIX]{x1D6FD})$ and
$1+u\in S_{m}(\unicode[STIX]{x1D6FD})$ and  $b\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}}$. By Lemma 7.13 applied with
$b\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}}$. By Lemma 7.13 applied with  $\mathfrak{k}_{0}=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}$ and
$\mathfrak{k}_{0}=\mathfrak{b}_{\unicode[STIX]{x1D6FD},0}$ and  $\mathfrak{k}_{l}=(S_{m}(\unicode[STIX]{x1D6FD})-1)\cap \mathfrak{b}_{\unicode[STIX]{x1D6FD},l}$, there is an idempotent
$\mathfrak{k}_{l}=(S_{m}(\unicode[STIX]{x1D6FD})-1)\cap \mathfrak{b}_{\unicode[STIX]{x1D6FD},l}$, there is an idempotent  $e$ in
$e$ in  $B_{\unicode[STIX]{x1D6FD}}$ which is congruent to
$B_{\unicode[STIX]{x1D6FD}}$ which is congruent to  $b\hspace{0.6em}({\rm mod}\hspace{0.2em}S_{m}(\unicode[STIX]{x1D6FD})-1)$. Since, in particular,
$b\hspace{0.6em}({\rm mod}\hspace{0.2em}S_{m}(\unicode[STIX]{x1D6FD})-1)$. Since, in particular,  $e\equiv b\equiv 1^{\unicode[STIX]{x1D70F}(i)}\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, Lemma 7.16 implies that
$e\equiv b\equiv 1^{\unicode[STIX]{x1D70F}(i)}\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, Lemma 7.16 implies that  $e$ is a central idempotent in
$e$ is a central idempotent in  $B_{\unicode[STIX]{x1D6FD}}$, in particular a sum of primitive central idempotents of
$B_{\unicode[STIX]{x1D6FD}}$, in particular a sum of primitive central idempotents of  $B_{\unicode[STIX]{x1D6FD}}$. Since
$B_{\unicode[STIX]{x1D6FD}}$. Since  $e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, we see that in fact
$e\equiv 1^{i}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$, we see that in fact  $e=1^{i}$. Thus in fact
$e=1^{i}$. Thus in fact  $1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}S_{m}(\unicode[STIX]{x1D6FD})-1)$ and we deduce that
$1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}S_{m}(\unicode[STIX]{x1D6FD})-1)$ and we deduce that  $g=\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ is an element of
$g=\sum _{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ is an element of  $S_{m}(\unicode[STIX]{x1D6FD})$ with the required property (iv).
$S_{m}(\unicode[STIX]{x1D6FD})$ with the required property (iv).
We write  $k_{0}$ and
$k_{0}$ and  $k_{0}^{\prime }$ for the corresponding critical exponents. By (iv) and Proposition 9.8 we can suppose that
$k_{0}^{\prime }$ for the corresponding critical exponents. By (iv) and Proposition 9.8 we can suppose that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same associated splitting. Assume
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same associated splitting. Assume  $k_{0}>k_{0}^{\prime }$ and take a semisimple stratum
$k_{0}>k_{0}^{\prime }$ and take a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,-k_{0},\unicode[STIX]{x1D6FE}]$ equivalent to
$[\unicode[STIX]{x1D6EC},q,-k_{0},\unicode[STIX]{x1D6FE}]$ equivalent to  $[\unicode[STIX]{x1D6EC},q,-k_{0},\unicode[STIX]{x1D6FD}]$ such that
$[\unicode[STIX]{x1D6EC},q,-k_{0},\unicode[STIX]{x1D6FD}]$ such that  $\unicode[STIX]{x1D6FE}\in \prod _{i}A^{ii}$. We have
$\unicode[STIX]{x1D6FE}\in \prod _{i}A^{ii}$. We have  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},-k_{0},\unicode[STIX]{x1D6FD}^{\prime })\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},-k_{0},\unicode[STIX]{x1D6FE})\neq \varnothing$ and thus
${\mathcal{C}}(\unicode[STIX]{x1D6EC},-k_{0},\unicode[STIX]{x1D6FD}^{\prime })\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},-k_{0},\unicode[STIX]{x1D6FE})\neq \varnothing$ and thus  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FD}$ have the same associated splitting by the existence of the map
$\unicode[STIX]{x1D6FD}$ have the same associated splitting by the existence of the map  $\unicode[STIX]{x1D70F}$ for
$\unicode[STIX]{x1D70F}$ for  $\unicode[STIX]{x1D6FD}^{\prime }$ and
$\unicode[STIX]{x1D6FD}^{\prime }$ and  $\unicode[STIX]{x1D6FE}$. Then the fact that
$\unicode[STIX]{x1D6FE}$. Then the fact that  $k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})<k_{0}$ implies that there is an index
$k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})<k_{0}$ implies that there is an index  $i_{0}$ such that
$i_{0}$ such that  $[\unicode[STIX]{x1D6EC}^{i_{0}},-,-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}]$ is not simple. It is still either pure or equivalent to a null stratum. Since (ii) implies that
$[\unicode[STIX]{x1D6EC}^{i_{0}},-,-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}]$ is not simple. It is still either pure or equivalent to a null stratum. Since (ii) implies that
 $$\begin{eqnarray}\dim _{F}F[\unicode[STIX]{x1D6FE}_{i_{0}}]=\dim _{F}F[\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }]=\dim _{F}F[\unicode[STIX]{x1D6FD}_{i_{0}}],\end{eqnarray}$$
$$\begin{eqnarray}\dim _{F}F[\unicode[STIX]{x1D6FE}_{i_{0}}]=\dim _{F}F[\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }]=\dim _{F}F[\unicode[STIX]{x1D6FD}_{i_{0}}],\end{eqnarray}$$ it follows from simplicity that  $\unicode[STIX]{x1D6FE}_{i_{0}}=0$ (see Definition 6.1). This forces the restriction of an element
$\unicode[STIX]{x1D6FE}_{i_{0}}=0$ (see Definition 6.1). This forces the restriction of an element  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to  $H^{-k_{0}+1}(\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime },\unicode[STIX]{x1D6EC}^{i_{0}})$ to be trivial and therefore
$H^{-k_{0}+1}(\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime },\unicode[STIX]{x1D6EC}^{i_{0}})$ to be trivial and therefore  $\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }=0$. (Otherwise
$\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }=0$. (Otherwise  $q_{i_{0}}^{\prime }:=-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime })>-k_{0}$, by simplicity of
$q_{i_{0}}^{\prime }:=-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime })>-k_{0}$, by simplicity of  $[\unicode[STIX]{x1D6EC}^{i_{0}},q_{i_{0}}^{\prime },-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }]$, and
$[\unicode[STIX]{x1D6EC}^{i_{0}},q_{i_{0}}^{\prime },-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }]$, and  $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }}$ is not trivial on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}_{i_{0}}^{\prime }}$ is not trivial on  $\tilde{U} ^{q_{i_{0}}^{\prime }}(\unicode[STIX]{x1D6EC}^{i_{0}})$ by Proposition 6.9.)
$\tilde{U} ^{q_{i_{0}}^{\prime }}(\unicode[STIX]{x1D6EC}^{i_{0}})$ by Proposition 6.9.)
Thus  $\unicode[STIX]{x1D703}_{i_{0}}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i_{0}},m,0)\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i_{0}},m,\unicode[STIX]{x1D6FD}_{i_{0}})$ is trivial and by the same argument we obtain
$\unicode[STIX]{x1D703}_{i_{0}}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i_{0}},m,0)\cap {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{i_{0}},m,\unicode[STIX]{x1D6FD}_{i_{0}})$ is trivial and by the same argument we obtain  $\unicode[STIX]{x1D6FD}_{i_{0}}=0$. But this is a contradiction to the non-simplicity of
$\unicode[STIX]{x1D6FD}_{i_{0}}=0$. But this is a contradiction to the non-simplicity of  $[\unicode[STIX]{x1D6EC}^{i_{0}},-,-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}]$.◻
$[\unicode[STIX]{x1D6EC}^{i_{0}},-,-k_{0},\unicode[STIX]{x1D6FD}_{i_{0}}]$.◻
Remark 9.10. Recall that a semisimple character  $\unicode[STIX]{x1D703}$ is called simple if there is a simple stratum
$\unicode[STIX]{x1D703}$ is called simple if there is a simple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ such that  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$; then, by Proposition 9.9, every semisimple stratum
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$; then, by Proposition 9.9, every semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ such that  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ has to be simple.
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ has to be simple.
Proposition 9.11. (See [Reference Bushnell and KutzkoBK93, (3.3.17)])
For every element of  $\unicode[STIX]{x1D703}$ of
$\unicode[STIX]{x1D703}$ of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ the intersection of the normalizer
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ the intersection of the normalizer  $\mathfrak{n}(\unicode[STIX]{x1D703})$ with
$\mathfrak{n}(\unicode[STIX]{x1D703})$ with  $\mathfrak{n}(\unicode[STIX]{x1D6EC})$ is the set
$\mathfrak{n}(\unicode[STIX]{x1D6EC})$ is the set  $S_{m}(\unicode[STIX]{x1D6FD})\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$. In particular, the intersection of
$S_{m}(\unicode[STIX]{x1D6FD})\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$. In particular, the intersection of  $\mathfrak{n}(\unicode[STIX]{x1D703})$ with
$\mathfrak{n}(\unicode[STIX]{x1D703})$ with  $\tilde{\operatorname{U}}_{1}(\unicode[STIX]{x1D6EC})$ is equal to
$\tilde{\operatorname{U}}_{1}(\unicode[STIX]{x1D6EC})$ is equal to
 $$\begin{eqnarray}1+\mathfrak{b}_{1}+\mathfrak{m}_{-k_{0}-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}1+\mathfrak{b}_{1}+\mathfrak{m}_{-k_{0}-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\end{eqnarray}$$ and  $(\tilde{\operatorname{U}}_{1}(\unicode[STIX]{x1D6EC})\cap \mathfrak{n}(\unicode[STIX]{x1D703}))-1$ is a
$(\tilde{\operatorname{U}}_{1}(\unicode[STIX]{x1D6EC})\cap \mathfrak{n}(\unicode[STIX]{x1D703}))-1$ is a  $\mathfrak{b}_{0}$-bimodule and is closed under multiplication.
$\mathfrak{b}_{0}$-bimodule and is closed under multiplication.
Proof. The set  $\mathfrak{c}:=\mathfrak{m}_{-k_{0}-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a
$\mathfrak{c}:=\mathfrak{m}_{-k_{0}-m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+\mathfrak{j}^{\lfloor (-k_{0}+1)/2\rfloor }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is a  $\mathfrak{b}_{0}$-bimodule and closed under multiplication by [Reference Bushnell and KutzkoBK93, (3.1.10)]. Thus (9.12) is equal to
$\mathfrak{b}_{0}$-bimodule and closed under multiplication by [Reference Bushnell and KutzkoBK93, (3.1.10)]. Thus (9.12) is equal to  $(1+\mathfrak{b}_{1})(1+\mathfrak{c})$.
$(1+\mathfrak{b}_{1})(1+\mathfrak{c})$.
An element of  $\mathfrak{n}(\unicode[STIX]{x1D703})\cap \mathfrak{n}(\unicode[STIX]{x1D6EC})$ intertwines
$\mathfrak{n}(\unicode[STIX]{x1D703})\cap \mathfrak{n}(\unicode[STIX]{x1D6EC})$ intertwines  $\unicode[STIX]{x1D703}$ and normalizes
$\unicode[STIX]{x1D703}$ and normalizes  $\unicode[STIX]{x1D6EC}$ thus it is contained in
$\unicode[STIX]{x1D6EC}$ thus it is contained in  $S_{m}(\unicode[STIX]{x1D6FD})\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$ by the intertwining formula. The latter set is contained in the normalizer of
$S_{m}(\unicode[STIX]{x1D6FD})\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$ by the intertwining formula. The latter set is contained in the normalizer of  $\unicode[STIX]{x1D703}$ because
$\unicode[STIX]{x1D703}$ because  $S_{m}(\unicode[STIX]{x1D6FD})$ and
$S_{m}(\unicode[STIX]{x1D6FD})$ and  $\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$ are. This finishes the proof of the first statement. If we intersect the set
$\mathfrak{n}(\unicode[STIX]{x1D6EC}_{E})$ are. This finishes the proof of the first statement. If we intersect the set  $\mathfrak{n}(\unicode[STIX]{x1D703})\cap \mathfrak{n}(\unicode[STIX]{x1D6EC})$ further with
$\mathfrak{n}(\unicode[STIX]{x1D703})\cap \mathfrak{n}(\unicode[STIX]{x1D6EC})$ further with  $\tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ then we obtain the formula (9.12).◻
$\tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ then we obtain the formula (9.12).◻
By [Reference Bushnell and KutzkoBK93, Theorem 3.5.8], a non-trivial intersection of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ with
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ with  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ implies equality of the sets. We will generalize this theorem to a blockwise version. If
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ implies equality of the sets. We will generalize this theorem to a blockwise version. If  $V=\bigoplus _{k}V^{k}$ is a splitting for
$V=\bigoplus _{k}V^{k}$ is a splitting for  $V$ which splits a semisimple stratum
$V$ which splits a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, we write
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, we write  $\unicode[STIX]{x1D703}_{k}$ for the restriction of
$\unicode[STIX]{x1D703}_{k}$ for the restriction of  $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6EC}^{k})$.
$H^{m+1}(\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6EC}^{k})$.
Lemma 9.13. Suppose that  $V=\bigoplus _{k}V^{k}$ is a splitting which refines the associated splittings of two semisimple strata
$V=\bigoplus _{k}V^{k}$ is a splitting which refines the associated splittings of two semisimple strata  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$. Suppose further that the sets
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$. Suppose further that the sets  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD})$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD}^{\prime })$ coincide and that
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD}^{\prime })$ coincide and that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k})$ is equal to
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k})$ is equal to  ${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k}^{\prime })$, for all
${\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k}^{\prime })$, for all  $k$. Let
$k$. Let  $a\in \mathfrak{a}_{-m-1}\cap \prod _{k}A^{k,k}$,
$a\in \mathfrak{a}_{-m-1}\cap \prod _{k}A^{k,k}$,  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be given such that
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be given such that  $\unicode[STIX]{x1D703}_{k}$ coincides with
$\unicode[STIX]{x1D703}_{k}$ coincides with  $\unicode[STIX]{x1D703}_{k}^{\prime }\unicode[STIX]{x1D713}_{a_{k}}$ for all indices
$\unicode[STIX]{x1D703}_{k}^{\prime }\unicode[STIX]{x1D713}_{a_{k}}$ for all indices  $k$. Then
$k$. Then  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum with the same associated splitting as
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum with the same associated splitting as  $\unicode[STIX]{x1D6FD}$, and the sets
$\unicode[STIX]{x1D6FD}$, and the sets  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D713}_{a}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ coincide and both contain
$\unicode[STIX]{x1D713}_{a}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ coincide and both contain  $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D713}_{a}$.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D713}_{a}$.
Note the abuse of notation here: If  $r=m+1$ we mean by
$r=m+1$ we mean by  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD})$ the set
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FD})$ the set  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$.
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$.
Proof. The group  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is the same as
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is the same as  $H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ by Proposition 9.1(ii) and [Reference Bushnell and KutzkoBK93, (3.5.9)]. More precisely, it is a combination of both statements, where we apply (3.5.9) in the case that
$H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ by Proposition 9.1(ii) and [Reference Bushnell and KutzkoBK93, (3.5.9)]. More precisely, it is a combination of both statements, where we apply (3.5.9) in the case that  $k_{0}$ is equal to
$k_{0}$ is equal to  $k_{0}^{\prime }$ and smaller than
$k_{0}^{\prime }$ and smaller than  $-(m+1)$. To do this, we must first show that, in this case,
$-(m+1)$. To do this, we must first show that, in this case,  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime }$ have the same associated splitting.
$\unicode[STIX]{x1D6FD}^{\prime }$ have the same associated splitting.
The corresponding idempotents  $(1^{i})_{i}$ and
$(1^{i})_{i}$ and  $(1^{i^{\prime }})_{i^{\prime }}$ of the associated splittings commute because the idempotents
$(1^{i^{\prime }})_{i^{\prime }}$ of the associated splittings commute because the idempotents  $(1^{k})_{k}$ commute with all of them and are a refinement of both. By Proposition 9.9 there is a bijection
$(1^{k})_{k}$ commute with all of them and are a refinement of both. By Proposition 9.9 there is a bijection  $\unicode[STIX]{x1D70F}$ from
$\unicode[STIX]{x1D70F}$ from  $I$ to
$I$ to  $I^{\prime }$ such that
$I^{\prime }$ such that  $1^{\unicode[STIX]{x1D70F}(i)}$ is congruent to
$1^{\unicode[STIX]{x1D70F}(i)}$ is congruent to  $1^{i}$ modulo
$1^{i}$ modulo  $\mathfrak{a}_{1}$. The product
$\mathfrak{a}_{1}$. The product  $1^{i}1^{i^{\prime }}$ is congruent to zero for
$1^{i}1^{i^{\prime }}$ is congruent to zero for  $i^{\prime }\neq \unicode[STIX]{x1D70F}(i)$ and thus it is zero, because they commute (take powers). Thus
$i^{\prime }\neq \unicode[STIX]{x1D70F}(i)$ and thus it is zero, because they commute (take powers). Thus  $1^{i}$ and
$1^{i}$ and  $1^{\unicode[STIX]{x1D70F}(i)}$ coincide, that is, the splittings coincide.
$1^{\unicode[STIX]{x1D70F}(i)}$ coincide, that is, the splittings coincide.
We now go back to the general case and show that  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ which is split by
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ which is split by  $V=\bigoplus _{k}V^{k}$. Let
$V=\bigoplus _{k}V^{k}$. Let  $s^{\prime }$ be a tame corestriction with respect to
$s^{\prime }$ be a tame corestriction with respect to  $\unicode[STIX]{x1D6FE}^{\prime }$, a parameter for a first member of a defining sequence for
$\unicode[STIX]{x1D6FE}^{\prime }$, a parameter for a first member of a defining sequence for  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$. Since
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$. Since  $\unicode[STIX]{x1D703}_{k}^{\prime }\unicode[STIX]{x1D713}_{-a_{k}}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k}^{\prime })$, we have that the coset
$\unicode[STIX]{x1D703}_{k}^{\prime }\unicode[STIX]{x1D713}_{-a_{k}}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{k},m,\unicode[STIX]{x1D6FD}_{k}^{\prime })$, we have that the coset  $s^{\prime }(a_{k})+\mathfrak{b}_{\unicode[STIX]{x1D6FE}_{k}^{\prime },-m}^{\prime }$ is intertwined by the centralizer of
$s^{\prime }(a_{k})+\mathfrak{b}_{\unicode[STIX]{x1D6FE}_{k}^{\prime },-m}^{\prime }$ is intertwined by the centralizer of  $\unicode[STIX]{x1D6FE}_{k}^{\prime }$ and thus
$\unicode[STIX]{x1D6FE}_{k}^{\prime }$ and thus  $s^{\prime }(a_{k})$ is congruent to an element of
$s^{\prime }(a_{k})$ is congruent to an element of  $F[\unicode[STIX]{x1D6FE}_{k}^{\prime }]$ modulo
$F[\unicode[STIX]{x1D6FE}_{k}^{\prime }]$ modulo  $\mathfrak{a}_{-m}$. Further, the stratum
$\mathfrak{a}_{-m}$. Further, the stratum  $[\unicode[STIX]{x1D6EC}^{k},m+1,m,s^{\prime }(\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FE}_{k}^{\prime })]$ is equivalent to a simple stratum because
$[\unicode[STIX]{x1D6EC}^{k},m+1,m,s^{\prime }(\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FE}_{k}^{\prime })]$ is equivalent to a simple stratum because  $[\unicode[STIX]{x1D6EC}^{k},q,m,\unicode[STIX]{x1D6FD}_{k}^{\prime }]$ is simple. Thus the stratum
$[\unicode[STIX]{x1D6EC}^{k},q,m,\unicode[STIX]{x1D6FD}_{k}^{\prime }]$ is simple. Thus the stratum  $[\unicode[STIX]{x1D6EC}^{k},m+1,m,s^{\prime }(\unicode[STIX]{x1D6FD}_{k}^{\prime }+a_{k}-\unicode[STIX]{x1D6FE}_{k}^{\prime })]$ is equivalent to a simple stratum and it follows that
$[\unicode[STIX]{x1D6EC}^{k},m+1,m,s^{\prime }(\unicode[STIX]{x1D6FD}_{k}^{\prime }+a_{k}-\unicode[STIX]{x1D6FE}_{k}^{\prime })]$ is equivalent to a simple stratum and it follows that  $[\unicode[STIX]{x1D6EC}^{k},q,m,\unicode[STIX]{x1D6FD}_{k}^{\prime }+a_{k}]$ is equivalent to a simple stratum by Corollary 6.15. By coarsening the splitting
$[\unicode[STIX]{x1D6EC}^{k},q,m,\unicode[STIX]{x1D6FD}_{k}^{\prime }+a_{k}]$ is equivalent to a simple stratum by Corollary 6.15. By coarsening the splitting  $\bigoplus _{k}V^{k}$ we find a semisimple stratum
$\bigoplus _{k}V^{k}$ we find a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ and by Theorem 6.16 we can choose the desired stratum to be split by
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ and by Theorem 6.16 we can choose the desired stratum to be split by  $\bigoplus _{k}V^{k}$.
$\bigoplus _{k}V^{k}$.
Since  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to the semisimple stratum
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to the semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$, it follows that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$, it follows that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })$ is equal to
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })$ is equal to  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })\unicode[STIX]{x1D713}_{a}$ (see for example [Reference StevensSte05, Remark 3.14(ii)]) and intersects
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })\unicode[STIX]{x1D713}_{a}$ (see for example [Reference StevensSte05, Remark 3.14(ii)]) and intersects  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ non-trivially. Following the same argument as earlier, we see that
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ non-trivially. Following the same argument as earlier, we see that  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FD}^{\prime \prime }$ have the same associated splitting, and it now follows from [Reference Bushnell and KutzkoBK93, Theorem 3.5.8] that the sets
$\unicode[STIX]{x1D6FD}^{\prime \prime }$ have the same associated splitting, and it now follows from [Reference Bushnell and KutzkoBK93, Theorem 3.5.8] that the sets  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ coincide.◻
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ coincide.◻
Corollary 9.14. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata.
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata.
(i) Suppose that
 $V=\bigoplus _{k}V^{k}$ is a splitting which refines the two splittings associated to
$V=\bigoplus _{k}V^{k}$ is a splitting which refines the two splittings associated to  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, and suppose that there are semisimple characters
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, and suppose that there are semisimple characters  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ such that for every index
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ such that for every index  $k$ the characters
$k$ the characters  $\unicode[STIX]{x1D703}_{k}$ and
$\unicode[STIX]{x1D703}_{k}$ and  $\unicode[STIX]{x1D703}_{k}^{\prime }$ coincide. Then
$\unicode[STIX]{x1D703}_{k}^{\prime }$ coincide. Then  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and both contain
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and both contain  $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}^{\prime }$.(ii) Suppose that the sets
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ intersect non-trivially. Then they coincide.
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ intersect non-trivially. Then they coincide.(iii) Suppose
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and  $m>0$. Then
$m>0$. Then  $H^{m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ and
$H^{m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ and  $S_{m}(\unicode[STIX]{x1D6FD})$ normalizes them.
$S_{m}(\unicode[STIX]{x1D6FD})$ normalizes them.
Proof. The first assertion follows inductively from Lemma 9.13 with  $a=0$ and the second follows from the first one by using Proposition 9.9(iv) and Proposition 9.8. The group
$a=0$ and the second follows from the first one by using Proposition 9.9(iv) and Proposition 9.8. The group  $S_{m}(\unicode[STIX]{x1D6FD})$ normalizes
$S_{m}(\unicode[STIX]{x1D6FD})$ normalizes  $H^{m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ by Proposition 9.1(i) and [Reference Bushnell and KutzkoBK93, (3.1.15)(iii)]. Then (iii) follows in a similar way to (ii) by applying [Reference Bushnell and KutzkoBK93, (3.5.9)] to the case where the associated splittings coincide.◻
$H^{m}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ by Proposition 9.1(i) and [Reference Bushnell and KutzkoBK93, (3.1.15)(iii)]. Then (iii) follows in a similar way to (ii) by applying [Reference Bushnell and KutzkoBK93, (3.5.9)] to the case where the associated splittings coincide.◻
9.2 The transfer principle for  $\tilde{G}$
$\tilde{G}$
We would like to be able to get an analogue of strata induction for semisimple characters, for which we need:
∙ the “translation principle” initially introduced for simple characters in [Reference Bushnell and KutzkoBK94, 2.11], and
∙ a result on “derived characters” (see Proposition 9.17 below).
From now on the element  $\unicode[STIX]{x1D6FE}$can be arbitrary, that is, we free
$\unicode[STIX]{x1D6FE}$can be arbitrary, that is, we free  $\unicode[STIX]{x1D6FE}$from the requirements of the beginning of the previous section.
$\unicode[STIX]{x1D6FE}$from the requirements of the beginning of the previous section.
In the following we use the notation  $\mathfrak{m}(\unicode[STIX]{x1D6E5})$ for the set
$\mathfrak{m}(\unicode[STIX]{x1D6E5})$ for the set  $\mathfrak{m}_{-(k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ for a stratum
$\mathfrak{m}_{-(k_{0}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})+m)}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ for a stratum  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$. Equivalent strata
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$. Equivalent strata  $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6E5}^{\prime }$ give coinciding sets
$\unicode[STIX]{x1D6E5}^{\prime }$ give coinciding sets  $\mathfrak{m}(\unicode[STIX]{x1D6E5})=\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime })$.
$\mathfrak{m}(\unicode[STIX]{x1D6E5})=\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime })$.
Lemma 9.15. Suppose  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum split by
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ is a semisimple stratum split by  $V=\bigoplus _{i}V^{i}$ and
$V=\bigoplus _{i}V^{i}$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ is a semisimple stratum equivalent to
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ is a semisimple stratum equivalent to  $\unicode[STIX]{x1D6E5}$. Then there is an element
$\unicode[STIX]{x1D6E5}$. Then there is an element  $u$ of
$u$ of  $1+\mathfrak{m}(\unicode[STIX]{x1D6E5})$ such that
$1+\mathfrak{m}(\unicode[STIX]{x1D6E5})$ such that  $u\unicode[STIX]{x1D6FD}^{\prime }u^{-1}$ is split by
$u\unicode[STIX]{x1D6FD}^{\prime }u^{-1}$ is split by  $V=\bigoplus _{i}V^{i}$.
$V=\bigoplus _{i}V^{i}$.
Proof. By the intertwining formula, taking the intersection with  $\mathfrak{a}$ and then the additive closure, we get
$\mathfrak{a}$ and then the additive closure, we get
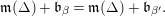 $$\begin{eqnarray}\mathfrak{m}(\unicode[STIX]{x1D6E5})+\mathfrak{b}_{\unicode[STIX]{x1D6FD}}=\mathfrak{m}(\unicode[STIX]{x1D6E5})+\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}(\unicode[STIX]{x1D6E5})+\mathfrak{b}_{\unicode[STIX]{x1D6FD}}=\mathfrak{m}(\unicode[STIX]{x1D6E5})+\mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}.\end{eqnarray}$$ Thus for every index  $i$ there is an element
$i$ there is an element  $\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to the idempotent
$\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to the idempotent  $1^{i}$ modulo
$1^{i}$ modulo  $\mathfrak{m}(\unicode[STIX]{x1D6E5})$. Corollary 7.14 provides idempotents
$\mathfrak{m}(\unicode[STIX]{x1D6E5})$. Corollary 7.14 provides idempotents  $1^{\prime i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to
$1^{\prime i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to  $1^{i}$ which sum to 1. The element
$1^{i}$ which sum to 1. The element  $u=\sum _{i}1^{i}1^{\prime i}$ has the desired property.◻
$u=\sum _{i}1^{i}1^{\prime i}$ has the desired property.◻
Theorem 9.16. Let  $\unicode[STIX]{x1D6E5}:=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$\unicode[STIX]{x1D6E5}:=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $\unicode[STIX]{x1D6E5}^{\prime }:=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ be semisimple strata with the same associated splitting
$\unicode[STIX]{x1D6E5}^{\prime }:=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ be semisimple strata with the same associated splitting  $V=\bigoplus _{j}V^{j}$ such that
$V=\bigoplus _{j}V^{j}$ such that
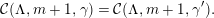 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime }).\end{eqnarray}$$ Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum with associated splitting
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ be a semisimple stratum with associated splitting  $V=\bigoplus _{i\in I}V^{i}$ such that
$V=\bigoplus _{i\in I}V^{i}$ such that  $\unicode[STIX]{x1D6E5}$ is equivalent to
$\unicode[STIX]{x1D6E5}$ is equivalent to  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ and  $\unicode[STIX]{x1D6FE}$ is an element of
$\unicode[STIX]{x1D6FE}$ is an element of  $\prod _{i\in I}A^{i,i}$. Then there exist a semisimple stratum
$\prod _{i\in I}A^{i,i}$. Then there exist a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ with associated splitting
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ with associated splitting  $V=\bigoplus _{i^{\prime }\in I^{\prime }}V^{\prime i^{\prime }}$ and an element
$V=\bigoplus _{i^{\prime }\in I^{\prime }}V^{\prime i^{\prime }}$ and an element  $u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}$ such that
$u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}$ such that  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime }]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime }]$ is equivalent to  $\unicode[STIX]{x1D6E5}^{\prime }$, with
$\unicode[STIX]{x1D6E5}^{\prime }$, with  $u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime }\in I^{\prime }}A^{i^{\prime },i^{\prime }}$ and
$u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime }\in I^{\prime }}A^{i^{\prime },i^{\prime }}$ and
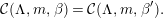 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$(i) Let us first remark that, given a semisimple stratum
 $\unicode[STIX]{x1D6E5}^{\prime \prime }=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime \prime }]$ with the same associated splitting as
$\unicode[STIX]{x1D6E5}^{\prime \prime }=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime \prime }]$ with the same associated splitting as  $\unicode[STIX]{x1D6FE}$, once we know the assertion for
$\unicode[STIX]{x1D6FE}$, once we know the assertion for  $(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$ and for
$(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime })$ and for  $(u.\unicode[STIX]{x1D6E5}^{\prime },\unicode[STIX]{x1D6E5}^{\prime \prime })$, for every
$(u.\unicode[STIX]{x1D6E5}^{\prime },\unicode[STIX]{x1D6E5}^{\prime \prime })$, for every  $u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}$, then we know it also for
$u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}$, then we know it also for  $(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime \prime })$.
$(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime \prime })$.(ii) The case where
 $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6E5}^{\prime }$ are equivalent follows directly from Lemma 9.15 applied (blockwise) to
$\unicode[STIX]{x1D6E5}^{\prime }$ are equivalent follows directly from Lemma 9.15 applied (blockwise) to  $\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$, taking
$\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$, taking  $u$ to be as there and
$u$ to be as there and  $\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}$.(iii) We now reduce to the case that
 $\unicode[STIX]{x1D6E5}$ is simple so assume that the result has already been proven in this case. Then, applying this to the strata
$\unicode[STIX]{x1D6E5}$ is simple so assume that the result has already been proven in this case. Then, applying this to the strata  $[\unicode[STIX]{x1D6EC}^{j},q,m,\unicode[STIX]{x1D6FD}_{j}]$, for each
$[\unicode[STIX]{x1D6EC}^{j},q,m,\unicode[STIX]{x1D6FD}_{j}]$, for each  $j$, we can find
$j$, we can find  $[\unicode[STIX]{x1D6EC}^{j},q,m,\unicode[STIX]{x1D6FD}_{j}^{\prime }]$ and elements
$[\unicode[STIX]{x1D6EC}^{j},q,m,\unicode[STIX]{x1D6FD}_{j}^{\prime }]$ and elements  $u_{j}\in 1+\mathfrak{m}(\unicode[STIX]{x1D6E5}_{j}^{\prime })$ such that
$u_{j}\in 1+\mathfrak{m}(\unicode[STIX]{x1D6E5}_{j}^{\prime })$ such that  $C(\unicode[STIX]{x1D6EC}^{j},m,\unicode[STIX]{x1D6FD}_{j})$ is equal to
$C(\unicode[STIX]{x1D6EC}^{j},m,\unicode[STIX]{x1D6FD}_{j})$ is equal to  $C(\unicode[STIX]{x1D6EC}^{j},m,\unicode[STIX]{x1D6FD}_{j}^{\prime })$ and
$C(\unicode[STIX]{x1D6EC}^{j},m,\unicode[STIX]{x1D6FD}_{j}^{\prime })$ and  $u_{j}\unicode[STIX]{x1D6FE}_{j}^{\prime }u_{j}^{-1}$ is split by the associated splitting of
$u_{j}\unicode[STIX]{x1D6FE}_{j}^{\prime }u_{j}^{-1}$ is split by the associated splitting of  $\unicode[STIX]{x1D6FD}_{j}^{\prime }$. Moreover, by conjugating
$\unicode[STIX]{x1D6FD}_{j}^{\prime }$. Moreover, by conjugating  $\unicode[STIX]{x1D6FD}_{j}$ with an element of
$\unicode[STIX]{x1D6FD}_{j}$ with an element of  $S_{m}(\unicode[STIX]{x1D6FD}_{j})$ we can assume that
$S_{m}(\unicode[STIX]{x1D6FD}_{j})$ we can assume that  $\unicode[STIX]{x1D6FD}_{j}$ and
$\unicode[STIX]{x1D6FD}_{j}$ and  $\unicode[STIX]{x1D6FD}_{j}^{\prime }$ have the same associated splitting, see Proposition 9.9(iv). The stratum
$\unicode[STIX]{x1D6FD}_{j}^{\prime }$ have the same associated splitting, see Proposition 9.9(iv). The stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ is semisimple, where
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ is semisimple, where  $\unicode[STIX]{x1D6FD}^{\prime }=\sum _{j}\unicode[STIX]{x1D6FD}_{j}^{\prime }$, using Theorem 6.16, and
$\unicode[STIX]{x1D6FD}^{\prime }=\sum _{j}\unicode[STIX]{x1D6FD}_{j}^{\prime }$, using Theorem 6.16, and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ have the same associated splitting.
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ have the same associated splitting.Take
 $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Although we know that, for each
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$. Although we know that, for each  $i$, the restriction of
$i$, the restriction of  $\unicode[STIX]{x1D703}$ to block
$\unicode[STIX]{x1D703}$ to block  $i$ lies in
$i$ lies in  $C(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i}^{\prime })$, it does not follow that
$C(\unicode[STIX]{x1D6EC}^{i},m,\unicode[STIX]{x1D6FD}_{i}^{\prime })$, it does not follow that  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$, since the definition of semisimple character entails a certain compatibility between the blocks. However, there is an element
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$, since the definition of semisimple character entails a certain compatibility between the blocks. However, there is an element  $a\in \prod _{i}A^{i,i}\cap \mathfrak{a}_{-m-1}$ such that
$a\in \prod _{i}A^{i,i}\cap \mathfrak{a}_{-m-1}$ such that  $\unicode[STIX]{x1D703}\unicode[STIX]{x1D713}_{-a}$ is an element of
$\unicode[STIX]{x1D703}\unicode[STIX]{x1D713}_{-a}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$. Then, by Lemma 9.13, the stratum
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$. Then, by Lemma 9.13, the stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum with the same associated splitting as
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a semisimple stratum with the same associated splitting as  $\unicode[STIX]{x1D6FD}$, and thus as
$\unicode[STIX]{x1D6FD}$, and thus as  $\unicode[STIX]{x1D6FD}^{\prime }$, with the same set of semisimple characters as the stratum with entry
$\unicode[STIX]{x1D6FD}^{\prime }$, with the same set of semisimple characters as the stratum with entry  $\unicode[STIX]{x1D6FD}$. This finishes the proof of this case.
$\unicode[STIX]{x1D6FD}$. This finishes the proof of this case.(iv) Finally, we assume that
 $\unicode[STIX]{x1D6E5}$ is simple, so that
$\unicode[STIX]{x1D6E5}$ is simple, so that  $\unicode[STIX]{x1D6E5}^{\prime }$ is simple too, by Proposition 9.9. By [Reference Bushnell and KutzkoBK93, (3.5.9)] there is a simple stratum
$\unicode[STIX]{x1D6E5}^{\prime }$ is simple too, by Proposition 9.9. By [Reference Bushnell and KutzkoBK93, (3.5.9)] there is a simple stratum  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime \prime }]$, equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime \prime }]$, equivalent to  $\unicode[STIX]{x1D6E5}^{\prime }$, such that
$\unicode[STIX]{x1D6E5}^{\prime }$, such that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ is equal to
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ is equal to  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime \prime })$. Thus by (i) and (ii) we can assume
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime \prime })$. Thus by (i) and (ii) we can assume  $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}^{\prime \prime }$. As in [Reference Bushnell and KutzkoBK94, 5.2(iii)], we take two tame corestrictions
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}^{\prime \prime }$. As in [Reference Bushnell and KutzkoBK94, 5.2(iii)], we take two tame corestrictions  $s$ and
$s$ and  $s^{\prime }$ for
$s^{\prime }$ for  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$ such that
$\unicode[STIX]{x1D6FE}^{\prime }$ such that  $s(x)\equiv s^{\prime }(x)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{t+1})$, for all elements
$s(x)\equiv s^{\prime }(x)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{t+1})$, for all elements  $x$ of
$x$ of  $\mathfrak{a}_{t}$ and all integers
$\mathfrak{a}_{t}$ and all integers  $t$.
$t$.We put
 $c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$. Then
$c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$. Then  $[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is equivalent to a semisimple stratum by Corollary 6.15. As in [Reference Bushnell and KutzkoBK94, 5.3], the fact that
$[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is equivalent to a semisimple stratum by Corollary 6.15. As in [Reference Bushnell and KutzkoBK94, 5.3], the fact that  $[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is fundamental implies that
$[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is fundamental implies that  $[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ is fundamental too; however, we need that the latter stratum also satisfies the criterion on the maps
$[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ is fundamental too; however, we need that the latter stratum also satisfies the criterion on the maps  $m_{n,m+1,s^{\prime }(c)}$ of Proposition 6.11. Note that the same proposition implies that the maps
$m_{n,m+1,s^{\prime }(c)}$ of Proposition 6.11. Note that the same proposition implies that the maps  $m_{n,m+1,s(c)}$ do satisfy this criterion.
$m_{n,m+1,s(c)}$ do satisfy this criterion.The tame corestrictions
 $s$ and
$s$ and  $s^{\prime }$ are surjective as maps from
$s^{\prime }$ are surjective as maps from  $\mathfrak{a}_{t}$ to
$\mathfrak{a}_{t}$ to  $\mathfrak{b}_{\unicode[STIX]{x1D6FE},t}$ and to
$\mathfrak{b}_{\unicode[STIX]{x1D6FE},t}$ and to  $\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t}$, respectively, and thus we obtain an isomorphism of
$\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t}$, respectively, and thus we obtain an isomorphism of  $\unicode[STIX]{x1D705}_{F}$-vector spaces
$\unicode[STIX]{x1D705}_{F}$-vector spaces  $\unicode[STIX]{x1D719}_{t}$ from
$\unicode[STIX]{x1D719}_{t}$ from  $\mathfrak{b}_{\unicode[STIX]{x1D6FE},t}/\mathfrak{b}_{\unicode[STIX]{x1D6FE},t+1}$ to
$\mathfrak{b}_{\unicode[STIX]{x1D6FE},t}/\mathfrak{b}_{\unicode[STIX]{x1D6FE},t+1}$ to  $\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t}/\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t+1}$, for all integers
$\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t}/\mathfrak{b}_{\unicode[STIX]{x1D6FE}^{\prime },t+1}$, for all integers  $t$, by sending the class of
$t$, by sending the class of  $s(x)$ to that of
$s(x)$ to that of  $s^{\prime }(x)$; note that this is well defined by the choice of
$s^{\prime }(x)$; note that this is well defined by the choice of  $s$ and
$s$ and  $s^{\prime }$. Then
$s^{\prime }$. Then  $m_{n,m+1,s^{\prime }(c)}$ is equal to
$m_{n,m+1,s^{\prime }(c)}$ is equal to  $\unicode[STIX]{x1D719}_{n-m-1}\circ m_{n,m+1,s(c)}\circ \unicode[STIX]{x1D719}_{n}^{-1}$ and thus, varying
$\unicode[STIX]{x1D719}_{n-m-1}\circ m_{n,m+1,s(c)}\circ \unicode[STIX]{x1D719}_{n}^{-1}$ and thus, varying  $n$, the maps
$n$, the maps  $m_{n,m+1,s^{\prime }(c)}$ satisfy the additional criterion of Proposition 6.11.
$m_{n,m+1,s^{\prime }(c)}$ satisfy the additional criterion of Proposition 6.11.The arguments after [Reference Bushnell and KutzkoBK94, (5.4)] show that the algebras
 ${\mathcal{R}}([\unicode[STIX]{x1D6EC},m+1,m,s(c)])$ and
${\mathcal{R}}([\unicode[STIX]{x1D6EC},m+1,m,s(c)])$ and  ${\mathcal{R}}([\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)])$ are isomorphic, which implies, by Proposition 6.11, that
${\mathcal{R}}([\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)])$ are isomorphic, which implies, by Proposition 6.11, that  $[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ is equivalent to a semisimple stratum, say with associated splitting
$[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ is equivalent to a semisimple stratum, say with associated splitting  $(1^{i^{\prime }})$. By Corollary 6.15 the stratum
$(1^{i^{\prime }})$. By Corollary 6.15 the stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FE}^{\prime }+\sum _{i^{\prime }}1^{i^{\prime }}c1^{i^{\prime }}]$ is equivalent to a semisimple stratum
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FE}^{\prime }+\sum _{i^{\prime }}1^{i^{\prime }}c1^{i^{\prime }}]$ is equivalent to a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ with the same splitting and by Proposition 7.6 there is an element
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ with the same splitting and by Proposition 7.6 there is an element  $u$ of
$u$ of  $1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime })$ such that
$1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime })$ such that  $u\unicode[STIX]{x1D6FD}^{\prime \prime }u^{-1}$ is equivalent to
$u\unicode[STIX]{x1D6FD}^{\prime \prime }u^{-1}$ is equivalent to  $\unicode[STIX]{x1D6FE}^{\prime }+c$ modulo
$\unicode[STIX]{x1D6FE}^{\prime }+c$ modulo  $\mathfrak{a}_{-m}$. Thus, setting
$\mathfrak{a}_{-m}$. Thus, setting  $\unicode[STIX]{x1D6FD}^{\prime }=u\unicode[STIX]{x1D6FD}^{\prime \prime }u^{-1}$, the stratum
$\unicode[STIX]{x1D6FD}^{\prime }=u\unicode[STIX]{x1D6FD}^{\prime \prime }u^{-1}$, the stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ satisfies the desired properties, as where the last equality follows from [Reference Bushnell and KutzkoBK93, (3.3.20)]—see the remark after Proposition 9.8. ◻
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ satisfies the desired properties, as where the last equality follows from [Reference Bushnell and KutzkoBK93, (3.3.20)]—see the remark after Proposition 9.8. ◻ $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D713}_{c}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D713}_{c}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D713}_{c}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D713}_{c}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }),\end{eqnarray}$$
Proposition 9.17. Suppose  $m<q-1$ and let
$m<q-1$ and let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata which have defining sequences with a common first element
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata which have defining sequences with a common first element  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$. Suppose
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$. Suppose  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ are semisimple characters which agree on restriction to
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ are semisimple characters which agree on restriction to  $H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$, so that we can write
$H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$, so that we can write  $\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and
$\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and  $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}$, for some
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}$, for some  $\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ and
$\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ and  $c\in \mathfrak{a}_{-(m+1)}$. Let
$c\in \mathfrak{a}_{-(m+1)}$. Let  $s_{\unicode[STIX]{x1D6FE}}$ be a tame corestriction with respect to
$s_{\unicode[STIX]{x1D6FE}}$ be a tame corestriction with respect to  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
(i) For any
 $g\in I(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ there are elements
$g\in I(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ there are elements  $x,y\in S_{m+1}(\unicode[STIX]{x1D6FE})$ and
$x,y\in S_{m+1}(\unicode[STIX]{x1D6FE})$ and  $g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}$ such that
$g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}$ such that  $g=xg^{\prime }y$; moreover,
$g=xg^{\prime }y$; moreover,  $g^{\prime }$ intertwines
$g^{\prime }$ intertwines  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.(ii) For any
 $g^{\prime }\in I_{B_{\unicode[STIX]{x1D6FE}}^{\times }}(\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})})$, there are elements
$g^{\prime }\in I_{B_{\unicode[STIX]{x1D6FE}}^{\times }}(\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})})$, there are elements  $x,y$ of
$x,y$ of  $1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that
$1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that  $xg^{\prime }y$ intertwines
$xg^{\prime }y$ intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{\prime }$.(iii) If the characters
 $\unicode[STIX]{x1D713}_{s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ and
$\unicode[STIX]{x1D713}_{s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ and  $\unicode[STIX]{x1D713}_{s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ are equal, then there is
$\unicode[STIX]{x1D713}_{s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ are equal, then there is  $z\in 1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that
$z\in 1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that  $\unicode[STIX]{x1D703}^{z}=\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{z}=\unicode[STIX]{x1D703}^{\prime }$.
Remark 9.18. The strategy of the proof of Proposition 9.17(ii) is as follows: we take  $x$ and
$x$ and  $y$ such that
$y$ such that  $xg^{\prime }y$ intertwines the stratum
$xg^{\prime }y$ intertwines the stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ with
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ with  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}+c]$ (see also Proposition 7.6) and prove that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}+c]$ (see also Proposition 7.6) and prove that  $xg^{\prime }y$ intertwines
$xg^{\prime }y$ intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$. Thus, if
$\unicode[STIX]{x1D703}^{\prime }$. Thus, if  $c$ is an element of
$c$ is an element of  $\prod _{i}A^{i,i}$ and
$\prod _{i}A^{i,i}$ and  $g^{\prime }$ maps the splitting associated to
$g^{\prime }$ maps the splitting associated to  $\unicode[STIX]{x1D6FD}^{\prime }$ to that of
$\unicode[STIX]{x1D6FD}^{\prime }$ to that of  $\unicode[STIX]{x1D6FD}$, then we can choose
$\unicode[STIX]{x1D6FD}$, then we can choose  $x\in \prod _{i}A^{i,i}$ and
$x\in \prod _{i}A^{i,i}$ and  $y\in \prod _{i^{\prime }}A^{i^{\prime }i^{\prime }}$ which satisfy the assertions of Proposition 9.17(ii).
$y\in \prod _{i^{\prime }}A^{i^{\prime }i^{\prime }}$ which satisfy the assertions of Proposition 9.17(ii).
Proof. We have  $H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ by [Reference Bushnell and KutzkoBK93, (3.1.9),(3.5.9)], so we just write
$H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})$ by [Reference Bushnell and KutzkoBK93, (3.1.9),(3.5.9)], so we just write  $H^{m+1}$.
$H^{m+1}$.
(i) The decomposition
 $g=xg^{\prime }y$ follows directly from Proposition 9.8. The elements
$g=xg^{\prime }y$ follows directly from Proposition 9.8. The elements  $x$ and
$x$ and  $y$ normalize
$y$ normalize  $H^{m+1}$ by Corollary 9.14(iii). Thus
$H^{m+1}$ by Corollary 9.14(iii). Thus  $g^{\prime }\in I(\unicode[STIX]{x1D703}^{x},\unicode[STIX]{x1D703}^{\prime y^{-1}})$. By [Reference Bushnell and KutzkoBK93, (3.3.9)] we have We have
$g^{\prime }\in I(\unicode[STIX]{x1D703}^{x},\unicode[STIX]{x1D703}^{\prime y^{-1}})$. By [Reference Bushnell and KutzkoBK93, (3.3.9)] we have We have $$\begin{eqnarray}\unicode[STIX]{x1D703}^{x}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c},\qquad \text{and}\qquad \unicode[STIX]{x1D703}^{\prime y^{-1}}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FE}y^{-1}-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{x}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c},\qquad \text{and}\qquad \unicode[STIX]{x1D703}^{\prime y^{-1}}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FE}y^{-1}-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$ $\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D713}_{a_{\unicode[STIX]{x1D6FE}}(x)}$ and
$\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D713}_{a_{\unicode[STIX]{x1D6FE}}(x)}$ and  $\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FE}y^{-1}-\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D713}_{-a_{\unicode[STIX]{x1D6FE}}(y)}$ (as characters of
$\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FE}y^{-1}-\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D713}_{-a_{\unicode[STIX]{x1D6FE}}(y)}$ (as characters of  $H^{m+1}$) and thus their restrictions to
$H^{m+1}$) and thus their restrictions to  $\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}^{\times }$ are trivial. Thus, on
$\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}^{\times }$ are trivial. Thus, on  $\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}^{\times }$, we have and analogously for
$\tilde{\operatorname{U}}^{m+1}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}^{\times }$, we have and analogously for $$\begin{eqnarray}\unicode[STIX]{x1D703}^{x}=\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{x}=\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\end{eqnarray}$$ $\unicode[STIX]{x1D703}^{y^{-1}}$. Since
$\unicode[STIX]{x1D703}^{y^{-1}}$. Since  $g^{\prime }$ intertwines
$g^{\prime }$ intertwines  $\unicode[STIX]{x1D703}^{x}$ with
$\unicode[STIX]{x1D703}^{x}$ with  $\unicode[STIX]{x1D703}^{y^{-1}}$ and
$\unicode[STIX]{x1D703}^{y^{-1}}$ and  $\unicode[STIX]{x1D703}_{0}$ with itself, it also intertwines
$\unicode[STIX]{x1D703}_{0}$ with itself, it also intertwines  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.(ii) If some element
 $g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}^{\times }$ intertwines
$g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}^{\times }$ intertwines  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ then it intertwines the stratum
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ then it intertwines the stratum  $[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with
$[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with  $[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$ and thus, by Proposition 7.6, there are elements
$[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$ and thus, by Proposition 7.6, there are elements  $x,y$ of
$x,y$ of  $1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that
$1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1}$ such that  $g^{\prime }$ intertwines
$g^{\prime }$ intertwines  $[\unicode[STIX]{x1D6EC},q,m,y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}]$ with
$[\unicode[STIX]{x1D6EC},q,m,y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}]$ with  $[\unicode[STIX]{x1D6EC},q,m,x^{-1}(\unicode[STIX]{x1D6FD}+c)x]$; that is,
$[\unicode[STIX]{x1D6EC},q,m,x^{-1}(\unicode[STIX]{x1D6FD}+c)x]$; that is,  $g^{\prime }$ is an element of
$g^{\prime }$ is an element of  $I(\unicode[STIX]{x1D713}_{x^{-1}(\unicode[STIX]{x1D6FD}+c)x},\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}})$. Now we have and an analogous equation for
$I(\unicode[STIX]{x1D713}_{x^{-1}(\unicode[STIX]{x1D6FD}+c)x},\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}})$. Now we have and an analogous equation for $$\begin{eqnarray}\unicode[STIX]{x1D713}_{x^{-1}(\unicode[STIX]{x1D6FD}+c)x}=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}+c-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{x^{-1}(\unicode[STIX]{x1D6FD}+c)x}=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}+c-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{x^{-1}\unicode[STIX]{x1D6FE}x-\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}},\end{eqnarray}$$ $\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}}$. Since
$\unicode[STIX]{x1D713}_{y\unicode[STIX]{x1D6FD}^{\prime }y^{-1}}$. Since  $g^{\prime }$ intertwines each of
$g^{\prime }$ intertwines each of  $\unicode[STIX]{x1D703}_{0}$ and
$\unicode[STIX]{x1D703}_{0}$ and  $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}}|_{H^{m+1}}$ with themselves, we deduce that
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}}|_{H^{m+1}}$ with themselves, we deduce that  $g^{\prime }$ intertwines
$g^{\prime }$ intertwines  $\unicode[STIX]{x1D703}^{x}$ with
$\unicode[STIX]{x1D703}^{x}$ with  $\unicode[STIX]{x1D703}^{\prime y^{-1}}$.
$\unicode[STIX]{x1D703}^{\prime y^{-1}}$.(iii) This follows immediately from (ii) applied to the identity element by putting
 $z=xy$, which normalizes
$z=xy$, which normalizes  $H^{m+1}$. ◻
$H^{m+1}$. ◻
Corollary 9.19. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata which have semisimple approximations
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be semisimple strata which have semisimple approximations  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ from defining sequences respectively with a common associated splitting
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ from defining sequences respectively with a common associated splitting  $V=\bigoplus _{j}V^{j}$. Suppose that
$V=\bigoplus _{j}V^{j}$. Suppose that  $H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to
$H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to  $H^{m+2}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ and let
$H^{m+2}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$ and let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two intertwining semisimple characters which coincide on
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two intertwining semisimple characters which coincide on  $H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Then there is an element in
$H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Then there is an element in  $\prod _{j}(A^{j,j})^{\times }$ which intertwines
$\prod _{j}(A^{j,j})^{\times }$ which intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{\prime }$.
Proof. By the translation principle, Theorem 9.16, there are  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$, a semisimple stratum which has
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$, a semisimple stratum which has  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ as an approximation, and an element
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ as an approximation, and an element  $u\in (1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}})\cap \prod A^{j,j}$ such that
$u\in (1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}})\cap \prod A^{j,j}$ such that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ and  $u\unicode[STIX]{x1D6FE}u^{-1}$ is split by the associated splitting of
$u\unicode[STIX]{x1D6FE}u^{-1}$ is split by the associated splitting of  $\unicode[STIX]{x1D6FD}^{\prime \prime }$. Replacing
$\unicode[STIX]{x1D6FD}^{\prime \prime }$. Replacing  $\unicode[STIX]{x1D6FD}^{\prime }$ by
$\unicode[STIX]{x1D6FD}^{\prime }$ by  $u^{-1}\unicode[STIX]{x1D6FD}^{\prime \prime }u$, we reduce to the case where
$u^{-1}\unicode[STIX]{x1D6FD}^{\prime \prime }u$, we reduce to the case where  $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$.
Now set  $\unicode[STIX]{x1D703}_{0}=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$. Then there is an element
$\unicode[STIX]{x1D703}_{0}=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$. Then there is an element  $c\in \bigoplus _{j}A^{j,j}$ such that
$c\in \bigoplus _{j}A^{j,j}$ such that  $\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}+c}$, because
$\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}+c}$, because  $\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and
$\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and  $\unicode[STIX]{x1D703}^{\prime }$ are trivial on the lower and upper unipotent parts of the Iwahori decomposition with respect to
$\unicode[STIX]{x1D703}^{\prime }$ are trivial on the lower and upper unipotent parts of the Iwahori decomposition with respect to  $V=\bigoplus _{j}V^{j}$. As we know that
$V=\bigoplus _{j}V^{j}$. As we know that  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D703}^{\prime }$ intertwine, Proposition 9.17(i) provides an element of
$\unicode[STIX]{x1D703}^{\prime }$ intertwine, Proposition 9.17(i) provides an element of  $\prod _{j}(B_{\unicode[STIX]{x1D6FE}}^{j,j})^{\times }$ which intertwines the corresponding derived characters. Now fix a block
$\prod _{j}(B_{\unicode[STIX]{x1D6FE}}^{j,j})^{\times }$ which intertwines the corresponding derived characters. Now fix a block  $j$, then Proposition 9.17(ii) provides an element
$j$, then Proposition 9.17(ii) provides an element  $g_{j}$ of
$g_{j}$ of  $(A^{j,j})^{\times }$ which intertwines
$(A^{j,j})^{\times }$ which intertwines  $\unicode[STIX]{x1D703}_{j}$ with
$\unicode[STIX]{x1D703}_{j}$ with  $\unicode[STIX]{x1D703}_{j}^{\prime }$. Thus
$\unicode[STIX]{x1D703}_{j}^{\prime }$. Thus  $g=(g_{j})$ intertwines
$g=(g_{j})$ intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$ because both characters are trivial on the unipotent parts of the Iwahori decomposition with respect to
$\unicode[STIX]{x1D703}^{\prime }$ because both characters are trivial on the unipotent parts of the Iwahori decomposition with respect to  $V=\bigoplus _{j}V^{j}$.◻
$V=\bigoplus _{j}V^{j}$.◻
9.3 Semisimple characters for  $G$
$G$
Suppose now that  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ is a skew-semisimple stratum and continue with the notation of the previous subsection. The adjoint anti-involution
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ is a skew-semisimple stratum and continue with the notation of the previous subsection. The adjoint anti-involution  $\unicode[STIX]{x1D70E}$ of the signed hermitian form
$\unicode[STIX]{x1D70E}$ of the signed hermitian form  $h$ acts on
$h$ acts on  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ via
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ via
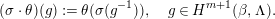 $$\begin{eqnarray}(\unicode[STIX]{x1D70E}\cdot \unicode[STIX]{x1D703})(g):=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70E}(g^{-1})),\quad g\in H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E}\cdot \unicode[STIX]{x1D703})(g):=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70E}(g^{-1})),\quad g\in H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC}).\end{eqnarray}$$Definition 9.20. We define the set of semisimple characters  ${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to be the set of all restrictions
${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ to be the set of all restrictions  $\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FD})\cap G}$ where
$\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FD})\cap G}$ where  $\unicode[STIX]{x1D703}$ run through all elements of
$\unicode[STIX]{x1D703}$ run through all elements of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$, the set of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$, the set of  $\unicode[STIX]{x1D70E}$-fixed points.
$\unicode[STIX]{x1D70E}$-fixed points.
We call an element of  ${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ a semisimple character for
${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ a semisimple character for  $G$.
$G$.
Remark 9.21. ([Reference StevensSte05, 3.6], [Reference StevensSte01b, 2.5])
(i) The restriction map from
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ to
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ to  ${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is bijective, in particular injective.
${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ is bijective, in particular injective.(ii) For two skew-semisimple strata
 $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$,
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$,  $g\in G$, and characters
$g\in G$, and characters  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ the following conditions are equivalent:
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ the following conditions are equivalent:∙
 $g\in I_{G}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$;
$g\in I_{G}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$;∙
 $g\in I_{G}(\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap G},\unicode[STIX]{x1D703}^{\prime }|_{H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap G})$.
$g\in I_{G}(\unicode[STIX]{x1D703}|_{H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap G},\unicode[STIX]{x1D703}^{\prime }|_{H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})\cap G})$.
We have an analogous description to that of Proposition 9.8 of the intertwining of a semisimple character for  $G$.
$G$.
Proposition 9.22. [Reference StevensSte05, 3.27]
For  $\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ a semisimple character of
$\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ a semisimple character of  $G$, we have
$G$, we have
 $$\begin{eqnarray}I_{G}(\unicode[STIX]{x1D703}_{-})=(S_{m}(\unicode[STIX]{x1D6FD})\cap G)(B_{\unicode[STIX]{x1D6FD}}\cap G)(S_{m}(\unicode[STIX]{x1D6FD})\cap G).\end{eqnarray}$$
$$\begin{eqnarray}I_{G}(\unicode[STIX]{x1D703}_{-})=(S_{m}(\unicode[STIX]{x1D6FD})\cap G)(B_{\unicode[STIX]{x1D6FD}}\cap G)(S_{m}(\unicode[STIX]{x1D6FD})\cap G).\end{eqnarray}$$For two skew-semisimple strata giving the same set of semisimple characters we have a stronger version of Proposition 9.9.
Proposition 9.23. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata such that the intersection
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata such that the intersection  ${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ is non-empty.
${\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ is non-empty.
(i) The sets
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ coincide.
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ coincide.
Let  $\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ be the bijection given by Proposition 9.9, such that
$\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime }$ be the bijection given by Proposition 9.9, such that  $1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$.
$1^{i}\equiv 1^{\unicode[STIX]{x1D70F}(i)}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{1})$.
(ii) The spaces
 $V^{i}$ and
$V^{i}$ and  $V^{\unicode[STIX]{x1D70F}(i)}$ are isomorphic as hermitian spaces, for all indices
$V^{\unicode[STIX]{x1D70F}(i)}$ are isomorphic as hermitian spaces, for all indices  $i\in I$
$i\in I$(iii) There is an element of
 $\operatorname{U}^{1}(\unicode[STIX]{x1D6EC})$ which normalizes every element of
$\operatorname{U}^{1}(\unicode[STIX]{x1D6EC})$ which normalizes every element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and sends
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and sends  $V^{i}$ onto
$V^{i}$ onto  $V^{\unicode[STIX]{x1D70F}(i)}$.
$V^{\unicode[STIX]{x1D70F}(i)}$.
Proof. We prove the first statement by induction on  $m$. If
$m$. If  $m=q$ then
$m=q$ then  $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }=0$ and both sets only contain the trivial character on
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{\prime }=0$ and both sets only contain the trivial character on  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$, that is, they coincide, so we suppose
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$, that is, they coincide, so we suppose  $m<q$. Let
$m<q$. Let  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$ be entries of a first member of defining sequences of the skew-semisimple strata
$\unicode[STIX]{x1D6FE}^{\prime }$ be entries of a first member of defining sequences of the skew-semisimple strata  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, respectively. Then by the induction hypothesis we can assume that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, respectively. Then by the induction hypothesis we can assume that  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime })$ coincide so, by Proposition 9.1(ii) and Corollary 9.14(iii), we have
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime })$ coincide so, by Proposition 9.1(ii) and Corollary 9.14(iii), we have
 $$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC}),\end{eqnarray}$$
$$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC}),\end{eqnarray}$$ a group which we denote by  $H^{m+1}$. There is, by Glauberman’s correspondence, then a unique
$H^{m+1}$. There is, by Glauberman’s correspondence, then a unique  $\unicode[STIX]{x1D70E}$-invariant lift of an element
$\unicode[STIX]{x1D70E}$-invariant lift of an element  $\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ to
$\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})\cap {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ to  $H^{m+1}$, and this lies in both
$H^{m+1}$, and this lies in both  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$. The result now follows by Corollary 9.14(ii).
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$. The result now follows by Corollary 9.14(ii).
The second statement follows directly from Proposition 3.1 applied to the map  $f:v\mapsto \sum _{i\in I}1^{\unicode[STIX]{x1D70F}(i)}1^{i}v$, which lies in
$f:v\mapsto \sum _{i\in I}1^{\unicode[STIX]{x1D70F}(i)}1^{i}v$, which lies in  $\tilde{U} ^{1}(\unicode[STIX]{x1D6EC})$. We are left to prove the third statement. We write the map
$\tilde{U} ^{1}(\unicode[STIX]{x1D6EC})$. We are left to prove the third statement. We write the map  $f$ as a tuple
$f$ as a tuple  $f=(f_{i})$ where
$f=(f_{i})$ where  $f_{i}=1^{\unicode[STIX]{x1D70F}(i)}1^{i}$. We write
$f_{i}=1^{\unicode[STIX]{x1D70F}(i)}1^{i}$. We write  $S_{m}(\unicode[STIX]{x1D6FD})_{i}$ for
$S_{m}(\unicode[STIX]{x1D6FD})_{i}$ for  $1^{i}S_{m}(\unicode[STIX]{x1D6FD})1^{i}$. Then
$1^{i}S_{m}(\unicode[STIX]{x1D6FD})1^{i}$. Then  $\unicode[STIX]{x1D70E}(f_{i})f_{i}=1^{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}\in S_{m}(\unicode[STIX]{x1D6FD})_{i}$ so the double coset
$\unicode[STIX]{x1D70E}(f_{i})f_{i}=1^{i}1^{\unicode[STIX]{x1D70F}(i)}1^{i}\in S_{m}(\unicode[STIX]{x1D6FD})_{i}$ so the double coset  $S_{m}(\unicode[STIX]{x1D6FD}^{\prime })_{\unicode[STIX]{x1D70F}(i)}f_{i}S_{m}(\unicode[STIX]{x1D6FD})_{i}$ contains an isometry, by Corollary 3.2. We can write this isometry as
$S_{m}(\unicode[STIX]{x1D6FD}^{\prime })_{\unicode[STIX]{x1D70F}(i)}f_{i}S_{m}(\unicode[STIX]{x1D6FD})_{i}$ contains an isometry, by Corollary 3.2. We can write this isometry as  $(1^{\unicode[STIX]{x1D70F}(i)}+u_{\unicode[STIX]{x1D70F}(i)})(1^{i}+v_{i})$, since
$(1^{\unicode[STIX]{x1D70F}(i)}+u_{\unicode[STIX]{x1D70F}(i)})(1^{i}+v_{i})$, since  $f_{i}=1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ can be absorbed into the other terms. We define
$f_{i}=1^{\unicode[STIX]{x1D70F}(i)}1^{i}$ can be absorbed into the other terms. We define  $g=\sum _{i}(1^{\unicode[STIX]{x1D70F}(i)}+u_{\unicode[STIX]{x1D70F}(i)})(1^{i}+v_{i})\in G$ so we have to show that
$g=\sum _{i}(1^{\unicode[STIX]{x1D70F}(i)}+u_{\unicode[STIX]{x1D70F}(i)})(1^{i}+v_{i})\in G$ so we have to show that  $g$ is an element of
$g$ is an element of  $\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$.
$\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$.
By Proposition 9.11 the set  $(\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}))-1$ is a
$(\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}))-1$ is a  $\mathfrak{b}_{0}$- and a
$\mathfrak{b}_{0}$- and a  $\mathfrak{b}_{0}^{\prime }$-bimodule, and is closed under multiplication. Thus the products
$\mathfrak{b}_{0}^{\prime }$-bimodule, and is closed under multiplication. Thus the products  $u_{\unicode[STIX]{x1D70F}(i)}v_{i}$,
$u_{\unicode[STIX]{x1D70F}(i)}v_{i}$,  $u_{\unicode[STIX]{x1D70F}(i)}1^{i}$,
$u_{\unicode[STIX]{x1D70F}(i)}1^{i}$,  $1^{\unicode[STIX]{x1D70F}(i)}v_{i}$ and
$1^{\unicode[STIX]{x1D70F}(i)}v_{i}$ and  $(1^{\unicode[STIX]{x1D70F}(i)}-1^{i})1^{i}$ are all elements of
$(1^{\unicode[STIX]{x1D70F}(i)}-1^{i})1^{i}$ are all elements of  $(\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}))-1$, and
$(\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC}))-1$, and  $g$ is an element of
$g$ is an element of  $\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ as required.◻
$\mathfrak{n}(\unicode[STIX]{x1D703})\cap \tilde{\operatorname{U}}^{1}(\unicode[STIX]{x1D6EC})$ as required.◻
We also get an analogue to [Reference Bushnell and KutzkoBK93, 3.5.9] for semisimple characters for  $G$.
$G$.
Proposition 9.24. Suppose  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ are skew-semisimple strata with the same associated splitting, such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ are skew-semisimple strata with the same associated splitting, such that  $m>0$ and
$m>0$ and
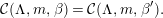 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$ Then  $H^{m}(\unicode[STIX]{x1D6FD})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime })$ and there is a skew-semisimple stratum
$H^{m}(\unicode[STIX]{x1D6FD})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime })$ and there is a skew-semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, with the same associated splitting, such that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$, with the same associated splitting, such that
 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$Proof. Corollary 9.14(iii) gives  $H^{m}(\unicode[STIX]{x1D6FD})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime })$. Now we take a character
$H^{m}(\unicode[STIX]{x1D6FD})=H^{m}(\unicode[STIX]{x1D6FD}^{\prime })$. Now we take a character  $\unicode[STIX]{x1D703}$ in
$\unicode[STIX]{x1D703}$ in  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and a skew-symmetric element
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and a skew-symmetric element  $b$ of
$b$ of  $\mathfrak{a}_{-m}(\unicode[STIX]{x1D6EC})$ in
$\mathfrak{a}_{-m}(\unicode[STIX]{x1D6EC})$ in  $\prod _{i}A^{i,i}$ such that
$\prod _{i}A^{i,i}$ such that  $\unicode[STIX]{x1D703}\unicode[STIX]{x1D713}_{b}$ is an element of
$\unicode[STIX]{x1D703}\unicode[STIX]{x1D713}_{b}$ is an element of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime })$. The same proof as in the second part of [Reference Bushnell and KutzkoBK93, 3.5.9] shows that there is a semisimple stratum
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime })$. The same proof as in the second part of [Reference Bushnell and KutzkoBK93, 3.5.9] shows that there is a semisimple stratum  $[\unicode[STIX]{x1D6EC},n,m-1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to
$[\unicode[STIX]{x1D6EC},n,m-1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ equivalent to  $[\unicode[STIX]{x1D6EC},n,m-1,\unicode[STIX]{x1D6FD}+b]$ such that
$[\unicode[STIX]{x1D6EC},n,m-1,\unicode[STIX]{x1D6FD}+b]$ such that  $\unicode[STIX]{x1D6FD}^{\prime \prime }\in \prod _{i}A^{i,i}$. Since
$\unicode[STIX]{x1D6FD}^{\prime \prime }\in \prod _{i}A^{i,i}$. Since  $\unicode[STIX]{x1D6FD}+b$ is skew-symmetric,
$\unicode[STIX]{x1D6FD}+b$ is skew-symmetric,  $\unicode[STIX]{x1D6FD}^{\prime \prime }$ can be chosen skew-symmetric, by [Reference StevensSte01b, 1.10]. Then
$\unicode[STIX]{x1D6FD}^{\prime \prime }$ can be chosen skew-symmetric, by [Reference StevensSte01b, 1.10]. Then
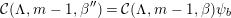 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D713}_{b}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D713}_{b}\end{eqnarray}$$ has a non-trivial intersection with  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime })$, and thus they are equal by Corollary 9.14(ii).◻
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m-1,\unicode[STIX]{x1D6FD}^{\prime })$, and thus they are equal by Corollary 9.14(ii).◻
Next we obtain an analogue of the translation principle, Theorem 9.16, for which we need the following lemma.
Lemma 9.25. Suppose  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent skew-simple strata and suppose that
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ are equivalent skew-simple strata and suppose that  $\unicode[STIX]{x1D6E5}$ is split by the orthogonal sum
$\unicode[STIX]{x1D6E5}$ is split by the orthogonal sum  $\bigoplus _{i}V^{i}$. Then there is an element
$\bigoplus _{i}V^{i}$. Then there is an element  $u$ of
$u$ of  $(1+\mathfrak{m}(\unicode[STIX]{x1D6E5}))\cap G$ such that
$(1+\mathfrak{m}(\unicode[STIX]{x1D6E5}))\cap G$ such that  $u\unicode[STIX]{x1D6FD}^{\prime }u^{-1}$ is an element of
$u\unicode[STIX]{x1D6FD}^{\prime }u^{-1}$ is an element of  $\prod _{i}A^{i,i}$.
$\prod _{i}A^{i,i}$.
Proof. As in the proof of Lemma 9.15 we find elements  $\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to
$\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{b}_{\unicode[STIX]{x1D6FD}^{\prime }}$ congruent to  $1^{i}$ modulo
$1^{i}$ modulo  $\mathfrak{m}(\unicode[STIX]{x1D6E5})$. We can replace
$\mathfrak{m}(\unicode[STIX]{x1D6E5})$. We can replace  $\unicode[STIX]{x1D6FC}_{i}$ by
$\unicode[STIX]{x1D6FC}_{i}$ by  $(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{i}))/2$ to ensure that the elements
$(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}_{i}))/2$ to ensure that the elements  $\unicode[STIX]{x1D6FC}_{i}$ are symmetric. By Corollary 7.14 we obtain pairwise orthogonal symmetric idempotents
$\unicode[STIX]{x1D6FC}_{i}$ are symmetric. By Corollary 7.14 we obtain pairwise orthogonal symmetric idempotents  $1^{\prime i}$ congruent to
$1^{\prime i}$ congruent to  $\unicode[STIX]{x1D6FC}_{i}$ who sum up to 1. As in the proof of Proposition 9.23(iii) we see that
$\unicode[STIX]{x1D6FC}_{i}$ who sum up to 1. As in the proof of Proposition 9.23(iii) we see that  $(1^{\prime i}+1^{\prime i}\mathfrak{m}(\unicode[STIX]{x1D6E5})1^{\prime i})(1^{i}+1^{i}\mathfrak{m}(\unicode[STIX]{x1D6E5})1^{i})$ contains an isometry, say
$(1^{\prime i}+1^{\prime i}\mathfrak{m}(\unicode[STIX]{x1D6E5})1^{\prime i})(1^{i}+1^{i}\mathfrak{m}(\unicode[STIX]{x1D6E5})1^{i})$ contains an isometry, say  $u_{i}^{\prime }u_{i}$. Then
$u_{i}^{\prime }u_{i}$. Then  $g:=\sum _{i}u_{i}^{\prime }u_{i}$ has the desired property.◻
$g:=\sum _{i}u_{i}^{\prime }u_{i}$ has the desired property.◻
Theorem 9.26. Let  $\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$\unicode[STIX]{x1D6E5}=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ be skew-semisimple strata with the same associated splitting
$\unicode[STIX]{x1D6E5}^{\prime }=[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ be skew-semisimple strata with the same associated splitting  $V=\bigoplus _{j}V^{j}$ such that
$V=\bigoplus _{j}V^{j}$ such that
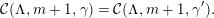 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE}^{\prime }).\end{eqnarray}$$ Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ be a skew-semisimple stratum, with associated splitting
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ be a skew-semisimple stratum, with associated splitting  $V=\bigoplus _{i\in I}V^{i}$, such that
$V=\bigoplus _{i\in I}V^{i}$, such that  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ is equivalent to  $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and  $\unicode[STIX]{x1D6FE}$ is an element of
$\unicode[STIX]{x1D6FE}$ is an element of  $\prod _{i\in I}A^{i,i}$. Then, there exists a skew-semisimple stratum
$\prod _{i\in I}A^{i,i}$. Then, there exists a skew-semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, with splitting
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$, with splitting  $V=\bigoplus _{i^{\prime }\in I^{\prime }}V^{\prime i^{\prime }}$ and an element
$V=\bigoplus _{i^{\prime }\in I^{\prime }}V^{\prime i^{\prime }}$ and an element  $u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}\cap G$, such that
$u\in (1+\mathfrak{m}(\unicode[STIX]{x1D6E5}^{\prime }))\cap \prod _{j}A^{j,j}\cap G$, such that  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime }]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime }]$ is equivalent to  $\unicode[STIX]{x1D6E5}^{\prime }$, with
$\unicode[STIX]{x1D6E5}^{\prime }$, with  $u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime }\in I^{\prime }}A^{i^{\prime }i^{\prime }}$ and
$u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime }\in I^{\prime }}A^{i^{\prime }i^{\prime }}$ and
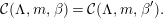 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime }).\end{eqnarray}$$Proof. The proof is analogous to the proof of Theorem 9.16, following the same four steps. Step (i) is the same (with the added requirement that  $u\in G$), while step (ii), the case where
$u\in G$), while step (ii), the case where  $\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$ are equivalent, follows from Lemma 9.25. Step (iii), the reduction from the semisimple to the simple case, is line by line the same because we can take the element
$\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E5}^{\prime }$ are equivalent, follows from Lemma 9.25. Step (iii), the reduction from the semisimple to the simple case, is line by line the same because we can take the element  $a$ blockwise skew and Theorem 6.16 ensures that the stratum
$a$ blockwise skew and Theorem 6.16 ensures that the stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a skew-semisimple stratum with the same associated splitting as
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }+a]$ is equivalent to a skew-semisimple stratum with the same associated splitting as  $\unicode[STIX]{x1D6FD}^{\prime }$; the splitting of
$\unicode[STIX]{x1D6FD}^{\prime }$; the splitting of  $\unicode[STIX]{x1D6FD}_{j}$ is conjugate in
$\unicode[STIX]{x1D6FD}_{j}$ is conjugate in  $G$ to that of
$G$ to that of  $\unicode[STIX]{x1D6FD}_{j}^{\prime }$ by Proposition 9.23(iii).
$\unicode[STIX]{x1D6FD}_{j}^{\prime }$ by Proposition 9.23(iii).
There is more to say in step (iv), the case where  $\unicode[STIX]{x1D6E5}$ is simple. We can modify
$\unicode[STIX]{x1D6E5}$ is simple. We can modify  $\unicode[STIX]{x1D6FE}^{\prime }$ by Proposition 9.24 to assume
$\unicode[STIX]{x1D6FE}^{\prime }$ by Proposition 9.24 to assume  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime })$. We choose
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE}^{\prime })$. We choose  $s$ a
$s$ a  $\unicode[STIX]{x1D70E}$-equivariant tame corestriction relative to
$\unicode[STIX]{x1D70E}$-equivariant tame corestriction relative to  $\unicode[STIX]{x1D6FE}$, and likewise
$\unicode[STIX]{x1D6FE}$, and likewise  $s^{\prime }$ relative to
$s^{\prime }$ relative to  $\unicode[STIX]{x1D6FE}^{\prime }$. The proof of [Reference Bushnell and KutzkoBK94, 5.2(iii)] shows that there is
$\unicode[STIX]{x1D6FE}^{\prime }$. The proof of [Reference Bushnell and KutzkoBK94, 5.2(iii)] shows that there is  $\unicode[STIX]{x1D706}\in k_{F[\unicode[STIX]{x1D6FE}]}^{\times }$ such that
$\unicode[STIX]{x1D706}\in k_{F[\unicode[STIX]{x1D6FE}]}^{\times }$ such that  $s(x)+\mathfrak{a}_{t+1}=\unicode[STIX]{x1D706}(s^{\prime }(x)+\mathfrak{a}_{t+1})$, for all
$s(x)+\mathfrak{a}_{t+1}=\unicode[STIX]{x1D706}(s^{\prime }(x)+\mathfrak{a}_{t+1})$, for all  $x\in \mathfrak{a}_{t}$ and all integers
$x\in \mathfrak{a}_{t}$ and all integers  $t$. Since
$t$. Since  $s,s^{\prime }$ are
$s,s^{\prime }$ are  $\unicode[STIX]{x1D70E}$-equivariant, we deduce that
$\unicode[STIX]{x1D70E}$-equivariant, we deduce that  $\unicode[STIX]{x1D706}$ is symmetric, that is,
$\unicode[STIX]{x1D706}$ is symmetric, that is,  $\bar{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}$. Then, choosing a symmetric lift
$\bar{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}$. Then, choosing a symmetric lift  $\hat{\unicode[STIX]{x1D706}}$ of
$\hat{\unicode[STIX]{x1D706}}$ of  $\unicode[STIX]{x1D706}$ to
$\unicode[STIX]{x1D706}$ to  $o_{F[\unicode[STIX]{x1D6FE}]}^{\times }$ and replacing
$o_{F[\unicode[STIX]{x1D6FE}]}^{\times }$ and replacing  $s^{\prime }$ by
$s^{\prime }$ by  $\hat{\unicode[STIX]{x1D706}}s^{\prime }$, we see that we may assume that
$\hat{\unicode[STIX]{x1D706}}s^{\prime }$, we see that we may assume that  $s(x)\equiv s^{\prime }(x)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{t+1})$, for all
$s(x)\equiv s^{\prime }(x)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{a}_{t+1})$, for all  $x\in \mathfrak{a}_{t}$ and all integers
$x\in \mathfrak{a}_{t}$ and all integers  $t$.
$t$.
We put  $c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$, so that the derived stratum
$c=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}$, so that the derived stratum  $[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is equivalent to a skew-semisimple stratum by Corollary 6.15 and [Reference StevensSte01b, 1.10]. In particular, denoting by
$[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ is equivalent to a skew-semisimple stratum by Corollary 6.15 and [Reference StevensSte01b, 1.10]. In particular, denoting by  $\unicode[STIX]{x1D719}_{i}\in k_{F[\unicode[STIX]{x1D6FE}]}(X)$ the primary factors of its characteristic polynomial, we have
$\unicode[STIX]{x1D719}_{i}\in k_{F[\unicode[STIX]{x1D6FE}]}(X)$ the primary factors of its characteristic polynomial, we have  $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)=\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{i})}\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D702}X)$, where
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{i})(X)=\unicode[STIX]{x1D702}^{\deg (\unicode[STIX]{x1D719}_{i})}\unicode[STIX]{x1D719}_{i}(\unicode[STIX]{x1D702}X)$, where  $\unicode[STIX]{x1D702}=(-1)^{(2(m+1)+ee_{0})/ge_{0}}$ for
$\unicode[STIX]{x1D702}=(-1)^{(2(m+1)+ee_{0})/ge_{0}}$ for  $e=e(\unicode[STIX]{x1D6EC}|\mathfrak{o}_{F[\unicode[STIX]{x1D6FE}]})$,
$e=e(\unicode[STIX]{x1D6EC}|\mathfrak{o}_{F[\unicode[STIX]{x1D6FE}]})$,  $e_{0}=e(F[\unicode[STIX]{x1D6FE}]|F[\unicode[STIX]{x1D6FE}]_{0})$ and
$e_{0}=e(F[\unicode[STIX]{x1D6FE}]|F[\unicode[STIX]{x1D6FE}]_{0})$ and  $g=\gcd (m+1,e)$.
$g=\gcd (m+1,e)$.
Now the strata  $[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ and
$[\unicode[STIX]{x1D6EC},m+1,m,s(c)]$ and  $[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ have the same characteristic polynomial, by the choice of
$[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ have the same characteristic polynomial, by the choice of  $s,s^{\prime }$, and the duality
$s,s^{\prime }$, and the duality  $\unicode[STIX]{x1D70E}$ acts in the same way on the residue fields
$\unicode[STIX]{x1D70E}$ acts in the same way on the residue fields  $k_{F[\unicode[STIX]{x1D6FE}]},k_{F[\unicode[STIX]{x1D6FE}^{\prime }]}$, since they have the same image in
$k_{F[\unicode[STIX]{x1D6FE}]},k_{F[\unicode[STIX]{x1D6FE}^{\prime }]}$, since they have the same image in  $\mathfrak{a}_{0}/\mathfrak{a}_{1}$ by [Reference Bushnell and KutzkoBK94, 5.2]. Hence
$\mathfrak{a}_{0}/\mathfrak{a}_{1}$ by [Reference Bushnell and KutzkoBK94, 5.2]. Hence  $[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ satisfies the hypotheses of Lemma 7.19 and is equivalent to a skew-semisimple stratum. The argument now finishes as in step (iv) of Theorem 9.16.◻
$[\unicode[STIX]{x1D6EC},m+1,m,s^{\prime }(c)]$ satisfies the hypotheses of Lemma 7.19 and is equivalent to a skew-semisimple stratum. The argument now finishes as in step (iv) of Theorem 9.16.◻
Finally, we get an analogue of Proposition 9.17, with the same proof (replacing the reference to Proposition 9.8 by Proposition 9.22).
Proposition 9.27. Suppose  $m<q-1$ and let
$m<q-1$ and let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$,
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$,  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata which have defining sequences with a common first element
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata which have defining sequences with a common first element  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$. Let
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$. Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ be semisimple characters which agree on
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ be semisimple characters which agree on  $H^{m+2}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FE})$, so that we can write
$H^{m+2}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6FE})$, so that we can write  $\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and
$\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}}$ and  $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}$, for some
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c}$, for some  $\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})^{\unicode[STIX]{x1D70E}}$ and  $c\in \mathfrak{a}_{-(m+1),-}$. Let
$c\in \mathfrak{a}_{-(m+1),-}$. Let  $s_{\unicode[STIX]{x1D6FE}}$ be a
$s_{\unicode[STIX]{x1D6FE}}$ be a  $\unicode[STIX]{x1D70E}$-equivariant tame corestriction with respect to
$\unicode[STIX]{x1D70E}$-equivariant tame corestriction with respect to  $\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FE}$.
(i) For any
 $g\in I_{G}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ there are elements
$g\in I_{G}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ there are elements  $x,y\in S_{m+1}(\unicode[STIX]{x1D6FE})\cap G$ and
$x,y\in S_{m+1}(\unicode[STIX]{x1D6FE})\cap G$ and  $g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}\cap G$ such that
$g^{\prime }\in B_{\unicode[STIX]{x1D6FE}}\cap G$ such that  $g=xg^{\prime }y$; moreover,
$g=xg^{\prime }y$; moreover,  $g^{\prime }$ intertwines
$g^{\prime }$ intertwines  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}$ with  $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$.(ii) For any
 $g^{\prime }\in I_{B_{\unicode[STIX]{x1D6FE}}\cap G}(\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})})$, there are elements
$g^{\prime }\in I_{B_{\unicode[STIX]{x1D6FE}}\cap G}(\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)},\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})})$, there are elements  $x,y\in (1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1})\cap G$ such that
$x,y\in (1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1})\cap G$ such that  $xg^{\prime }y$ intertwines
$xg^{\prime }y$ intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{\prime }$.(iii) If
 $\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}=\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ then there is
$\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)}=\unicode[STIX]{x1D713}_{s_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})}$ then there is  $z\in (1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1})\cap G$ such that
$z\in (1+\mathfrak{m}_{-k_{0}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})-m-1})\cap G$ such that  $\unicode[STIX]{x1D703}^{z}=\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{z}=\unicode[STIX]{x1D703}^{\prime }$.
Corollary 9.28. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata such that we can chose elements
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be two skew-semisimple strata such that we can chose elements  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ in defining sequences (with skew strata) such that
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ in defining sequences (with skew strata) such that  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$ have a common associated splitting, say
$\unicode[STIX]{x1D6FE}^{\prime }$ have a common associated splitting, say  $(V^{j})$, and such that
$(V^{j})$, and such that  $H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to
$H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$ is equal to  $H^{m+2}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$. Let
$H^{m+2}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC})$. Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ be two semisimple characters which are intertwined by an element of
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ be two semisimple characters which are intertwined by an element of  $G$ and which coincide on
$G$ and which coincide on  $H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Then there is an element in
$H^{m+2}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})$. Then there is an element in  $\prod _{j}(A^{j,j})^{\times }\cap G$ which intertwines
$\prod _{j}(A^{j,j})^{\times }\cap G$ which intertwines  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$.
$\unicode[STIX]{x1D703}^{\prime }$.
10 Matching and conjugacy for semisimple characters
In this final section we prove that there is an analogue of the matching Proposition 7.1 for semisimple characters which intertwine. One might think that this matching could just come from that for the underlying semisimple strata, but these do not necessarily intertwine so this is not possible. Then the sufficient condition (8.4) for an “intertwining implies conjugacy” result for semisimple strata is also sufficient for semisimple characters, also in the case of semisimple characters for  $G$.
$G$.
10.1 For general linear groups
For a semisimple character  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$, with decomposition
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$, with decomposition  $V=\bigoplus _{i\in I}V^{i}$ associated to
$V=\bigoplus _{i\in I}V^{i}$ associated to  $[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$, we write
$[\unicode[STIX]{x1D6EC},q,0,\unicode[STIX]{x1D6FD}]$, we write  $\unicode[STIX]{x1D703}_{i}$ for the restriction of
$\unicode[STIX]{x1D703}_{i}$ for the restriction of  $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $H^{m+1}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})=H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,i}$, for each index
$H^{m+1}(\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6EC}^{i})=H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})\cap A^{i,i}$, for each index  $i\in I$.
$i\in I$.
Theorem 10.1. Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine and suppose that
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine and suppose that  $\unicode[STIX]{x1D6EC}$ and
$\unicode[STIX]{x1D6EC}$ and  $\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then there is a unique bijection
$\unicode[STIX]{x1D6EC}^{\prime }$ have the same period. Then there is a unique bijection  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that there is an element
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ such that there is an element  $g\in \tilde{G}$ with
$g\in \tilde{G}$ with
(i)
 $gV^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all
$gV^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all  $i\in I$;
$i\in I$;(ii)
 $\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and
$\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, for all
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, for all  $i\in I$.
$i\in I$.
Moreover, all elements of  $\tilde{G}$ which satisfy (i) also satisfy (ii).
$\tilde{G}$ which satisfy (i) also satisfy (ii).
Proof. First we prove the uniqueness of  $\unicode[STIX]{x1D701}$ under the assumption that the existence statement is proven. If there are two bijections from
$\unicode[STIX]{x1D701}$ under the assumption that the existence statement is proven. If there are two bijections from  $I$ to
$I$ to  $I^{\prime }$ satisfying the assertions of the theorem then there are indices
$I^{\prime }$ satisfying the assertions of the theorem then there are indices  $i_{1},i_{2}\in I$ and
$i_{1},i_{2}\in I$ and  $i^{\prime }\in I^{\prime }$ such that
$i^{\prime }\in I^{\prime }$ such that  $\unicode[STIX]{x1D703}_{i_{1}}$ and
$\unicode[STIX]{x1D703}_{i_{1}}$ and  $\unicode[STIX]{x1D703}_{i_{2}}$ intertwine with
$\unicode[STIX]{x1D703}_{i_{2}}$ intertwine with  $\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$. By (i), we can conjugate
$\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$. By (i), we can conjugate  $\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$ to
$\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$ to  $V^{i_{1}}$ and to
$V^{i_{1}}$ and to  $V^{i_{2}}$, and afterward
$V^{i_{2}}$, and afterward  $\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }\otimes \unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$ is the Levi-part (under an Iwahori decomposition) of a simple character, which intertwines with
$\unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }\otimes \unicode[STIX]{x1D703}_{i^{\prime }}^{\prime }$ is the Levi-part (under an Iwahori decomposition) of a simple character, which intertwines with  $\unicode[STIX]{x1D703}_{i_{1}}\otimes \unicode[STIX]{x1D703}_{i_{2}}$. The index set of the latter two semisimple characters has different cardinalities and we obtain a contradiction.
$\unicode[STIX]{x1D703}_{i_{1}}\otimes \unicode[STIX]{x1D703}_{i_{2}}$. The index set of the latter two semisimple characters has different cardinalities and we obtain a contradiction.
To prove the final assertion of the statement let us assume that  $g^{\prime }$ is another element of
$g^{\prime }$ is another element of  $\tilde{G}$ which satisfies (i). Then the characters
$\tilde{G}$ which satisfies (i). Then the characters  $\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and
$\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and  $\unicode[STIX]{x1D703}_{i}^{g^{\prime -1}}$ are conjugate by the restriction of
$\unicode[STIX]{x1D703}_{i}^{g^{\prime -1}}$ are conjugate by the restriction of  $g^{\prime }g^{-1}$ to
$g^{\prime }g^{-1}$ to  $V^{\prime \unicode[STIX]{x1D701}(i)}$. Thus
$V^{\prime \unicode[STIX]{x1D701}(i)}$. Thus  $\unicode[STIX]{x1D703}_{i}^{g^{\prime -1}}$ and
$\unicode[STIX]{x1D703}_{i}^{g^{\prime -1}}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, because
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, because  $\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and
$\unicode[STIX]{x1D703}_{i}^{g^{-1}}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ do.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ do.
We now turn to the existence proof. First we reduce to the case of lattice chains, in fact to the case where both lattice chains are blockwise principal lattice chains—that is, for each index  $i$ the dimension
$i$ the dimension  $\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{k}^{i}/\unicode[STIX]{x1D6EC}_{k+1}^{i}$ is independent of
$\dim _{\unicode[STIX]{x1D705}_{F}}\unicode[STIX]{x1D6EC}_{k}^{i}/\unicode[STIX]{x1D6EC}_{k+1}^{i}$ is independent of  $k$. For that we repeat the
$k$. For that we repeat the  $\dagger$-construction
$\dagger$-construction  $\unicode[STIX]{x1D6EC}^{\dagger }:=\bigoplus _{j=0}^{e-1}(\unicode[STIX]{x1D6EC}-j)$, where
$\unicode[STIX]{x1D6EC}^{\dagger }:=\bigoplus _{j=0}^{e-1}(\unicode[STIX]{x1D6EC}-j)$, where  $e$ is the period of
$e$ is the period of  $\unicode[STIX]{x1D6EC}$ (which we assume coincides with that of
$\unicode[STIX]{x1D6EC}$ (which we assume coincides with that of  $\unicode[STIX]{x1D6EC}^{\prime }$), and
$\unicode[STIX]{x1D6EC}^{\prime }$), and  $\unicode[STIX]{x1D6EC}^{\prime \dagger }$ similarly. Let us remark that
$\unicode[STIX]{x1D6EC}^{\prime \dagger }$ similarly. Let us remark that  $\unicode[STIX]{x1D6EC}^{\dagger }$ is the direct sum of the
$\unicode[STIX]{x1D6EC}^{\dagger }$ is the direct sum of the  $(\unicode[STIX]{x1D6EC}^{i})^{\dagger }$. We will also need to use the notion of endo-equivalence of simple characters, for which we refer the reader to [Reference Bushnell and HenniartBH96] and [Reference Broussous, Sécherre and StevensBSS12].
$(\unicode[STIX]{x1D6EC}^{i})^{\dagger }$. We will also need to use the notion of endo-equivalence of simple characters, for which we refer the reader to [Reference Bushnell and HenniartBH96] and [Reference Broussous, Sécherre and StevensBSS12].
By assumption,  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D703}^{\prime }$ intertwine and thus
$\unicode[STIX]{x1D703}^{\prime }$ intertwine and thus  $\unicode[STIX]{x1D703}^{\dagger }$ and
$\unicode[STIX]{x1D703}^{\dagger }$ and  $\unicode[STIX]{x1D703}^{\prime \dagger }$ intertwine. Assume that we have proven the existence of
$\unicode[STIX]{x1D703}^{\prime \dagger }$ intertwine. Assume that we have proven the existence of  $\unicode[STIX]{x1D701}$ for the case of blockwise principal lattice chains. In particular we find an element
$\unicode[STIX]{x1D701}$ for the case of blockwise principal lattice chains. In particular we find an element  $g$ which maps, for each index
$g$ which maps, for each index  $i$, the vector space
$i$, the vector space  $(V^{i})^{\dagger }$ to
$(V^{i})^{\dagger }$ to  $(V^{\prime \unicode[STIX]{x1D701}(i)})^{\dagger }$, and then
$(V^{\prime \unicode[STIX]{x1D701}(i)})^{\dagger }$, and then  $(\unicode[STIX]{x1D703}_{i}^{\dagger })^{g^{-1}}$ and
$(\unicode[STIX]{x1D703}_{i}^{\dagger })^{g^{-1}}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime \dagger }$ intertwine. In particular, this implies that
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime \dagger }$ intertwine. In particular, this implies that  $V^{\unicode[STIX]{x1D701}(i)}$ and
$V^{\unicode[STIX]{x1D701}(i)}$ and  $V^{i}$ have the same dimension and that
$V^{i}$ have the same dimension and that  $\unicode[STIX]{x1D703}_{i}^{\dagger }$ and
$\unicode[STIX]{x1D703}_{i}^{\dagger }$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime \dagger }$ are endo-equivalent. (More precisely, they are realizations of endo-equivalent ps-characters.) Thus there is an isomorphism
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime \dagger }$ are endo-equivalent. (More precisely, they are realizations of endo-equivalent ps-characters.) Thus there is an isomorphism  $g_{i}:V^{i}\rightarrow V^{\prime \unicode[STIX]{x1D701}(i)}$ and, for any such, the simple characters
$g_{i}:V^{i}\rightarrow V^{\prime \unicode[STIX]{x1D701}(i)}$ and, for any such, the simple characters  $\unicode[STIX]{x1D703}_{i}^{g_{i}^{-1}}$ and
$\unicode[STIX]{x1D703}_{i}^{g_{i}^{-1}}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, since they are realizations of endo-equivalent ps-characters on the same space. Thus the element
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}(i)}^{\prime }$ intertwine, since they are realizations of endo-equivalent ps-characters on the same space. Thus the element  $\sum _{i\in I}g_{i}$ has all the required properties. This finishes the proof of the reduction to the blockwise principal case.
$\sum _{i\in I}g_{i}$ has all the required properties. This finishes the proof of the reduction to the blockwise principal case.
Now we assume we are in the blockwise principal case and prove the existence of  $\unicode[STIX]{x1D701}$. We proceed via induction on
$\unicode[STIX]{x1D701}$. We proceed via induction on  $m$, with the case
$m$, with the case  $m\geqslant \lfloor q/2\rfloor$ following directly from Proposition 7.1. For
$m\geqslant \lfloor q/2\rfloor$ following directly from Proposition 7.1. For  $m<\lfloor q/2\rfloor$, let
$m<\lfloor q/2\rfloor$, let  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ be a semisimple stratum equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ be a semisimple stratum equivalent to  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ with
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}]$ with  $\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$, and similarly for
$\unicode[STIX]{x1D6FE}\in \prod _{i}A^{i,i}$, and similarly for  $[\unicode[STIX]{x1D6EC}^{\prime },q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$. We write
$[\unicode[STIX]{x1D6EC}^{\prime },q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$. We write  $J$ for the index set of the splitting of
$J$ for the index set of the splitting of  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$, and similarly
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$, and similarly  $J^{\prime }$. We have the character
$J^{\prime }$. We have the character  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$, and similarly
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m+1,\unicode[STIX]{x1D6FE})$, and similarly  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}^{\prime }$, and these characters intertwine. In particular, by induction, there are a bijection
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}^{\prime }$, and these characters intertwine. In particular, by induction, there are a bijection  $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}:J\rightarrow J^{\prime }$ and
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}:J\rightarrow J^{\prime }$ and  $g\in \tilde{G}$ such that
$g\in \tilde{G}$ such that  $gV^{j}=V^{\prime \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}$ and
$gV^{j}=V^{\prime \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}^{g^{-1}}$ intertwines
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}^{g^{-1}}$ intertwines  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}^{\prime }$ for all
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}^{\prime }$ for all  $j\in J$, where
$j\in J$, where  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}|_{H^{m+2}(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6EC}^{j})}$. Since
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}|_{H^{m+2}(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6EC}^{j})}$. Since  $g\unicode[STIX]{x1D6EC}^{j}$ and
$g\unicode[STIX]{x1D6EC}^{j}$ and  $\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}$ are then principal lattice chains of the same period in the same space, they are conjugate so, changing
$\unicode[STIX]{x1D6EC}^{\prime \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}(j)}$ are then principal lattice chains of the same period in the same space, they are conjugate so, changing  $g$, we may assume they are equal; that is,
$g$, we may assume they are equal; that is,  $g\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
$g\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$.
In particular, conjugating everything by  $g$, we may assume that the strata
$g$, we may assume that the strata  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ have the same associated splitting,
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ have the same associated splitting,  $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}$ is the identity and
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FE}}$ is the identity and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}$ intertwines
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}$ intertwines  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },j}^{\prime }$. Since then
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },j}^{\prime }$. Since then  $\unicode[STIX]{x1D6EC}^{j}=\unicode[STIX]{x1D6EC}^{\prime j}$, for all indices
$\unicode[STIX]{x1D6EC}^{j}=\unicode[STIX]{x1D6EC}^{\prime j}$, for all indices  $j$, [Reference Bushnell and KutzkoBK93, Theorem 3.5.11] implies that
$j$, [Reference Bushnell and KutzkoBK93, Theorem 3.5.11] implies that  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}$ and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE},j}$ and  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },j}^{\prime }$ are conjugate by an element of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime },j}^{\prime }$ are conjugate by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}^{j})$ so, by conjugating, we can assume they are equal. By Corollary 9.14(i) this implies that
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC}^{j})$ so, by conjugating, we can assume they are equal. By Corollary 9.14(i) this implies that  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}$ is equal to
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}$ is equal to  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}$. Corollary 9.19 provides an intertwiner for
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}$. Corollary 9.19 provides an intertwiner for  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D703}^{\prime }$ which preserves every
$\unicode[STIX]{x1D703}^{\prime }$ which preserves every  $V^{j}$. Now, since we can then prove the existence of
$V^{j}$. Now, since we can then prove the existence of  $\unicode[STIX]{x1D701}$ separately for each block
$\unicode[STIX]{x1D701}$ separately for each block  $V^{j}$, we may assume that
$V^{j}$, we may assume that  $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}$ is simple. By Corollary 9.14(iii) we then have that
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}^{\prime }}$ is simple. By Corollary 9.14(iii) we then have that
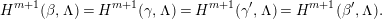 $$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}H^{m+1}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})=H^{m+1}(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6EC}).\end{eqnarray}$$ Thus we abbreviate  $H^{m+1}$, and similarly
$H^{m+1}$, and similarly  $H^{m+2}$. By the translation principle Theorem 9.16, we can find a semisimple stratum
$H^{m+2}$. By the translation principle Theorem 9.16, we can find a semisimple stratum  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ with splitting
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ with splitting  $V=\bigoplus _{i\in I^{\prime \prime }}V^{\prime \prime i^{\prime \prime }}$ and an element
$V=\bigoplus _{i\in I^{\prime \prime }}V^{\prime \prime i^{\prime \prime }}$ and an element  $u\in (1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}^{\prime }})\cap \prod _{j}A^{j,j}$ such that
$u\in (1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}^{\prime }})\cap \prod _{j}A^{j,j}$ such that
∙
 $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ is equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ is equivalent to  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$;
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$;∙
 ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$; and
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$; and∙
 $u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime \prime }}A^{i^{\prime \prime }i^{\prime \prime }}$.
$u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}\in \prod _{i^{\prime \prime }}A^{i^{\prime \prime }i^{\prime \prime }}$.
Note that  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ is then also equivalent to
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FD}^{\prime \prime }]$ is then also equivalent to  $[\unicode[STIX]{x1D6EC},q,m+1,u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}]$. Since
$[\unicode[STIX]{x1D6EC},q,m+1,u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}]$. Since  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$, Proposition 9.9 implies that we have a bijection
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$, Proposition 9.9 implies that we have a bijection  $\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime \prime }$ and
$\unicode[STIX]{x1D70F}:I\rightarrow I^{\prime \prime }$ and  $y\in S_{m}(\unicode[STIX]{x1D6FD})$ such that
$y\in S_{m}(\unicode[STIX]{x1D6FD})$ such that  $yV^{i}={V^{\prime }}^{\prime \unicode[STIX]{x1D70F}(i)}$. Moreover, the element
$yV^{i}={V^{\prime }}^{\prime \unicode[STIX]{x1D70F}(i)}$. Moreover, the element  $y$ normalizes
$y$ normalizes  $\unicode[STIX]{x1D703}$, thus
$\unicode[STIX]{x1D703}$, thus  $\unicode[STIX]{x1D703}_{i}^{y^{-1}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70F}(i)}$. In particular, we may replace the pair
$\unicode[STIX]{x1D703}_{i}^{y^{-1}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70F}(i)}$. In particular, we may replace the pair  $(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$ by
$(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$ by  $(\unicode[STIX]{x1D6FD}^{\prime \prime },u\unicode[STIX]{x1D6FE}^{\prime }u^{-1})$, since we can then compose the bijection
$(\unicode[STIX]{x1D6FD}^{\prime \prime },u\unicode[STIX]{x1D6FE}^{\prime }u^{-1})$, since we can then compose the bijection  $\unicode[STIX]{x1D701}:I^{\prime \prime }\rightarrow I^{\prime }$ that we obtain with
$\unicode[STIX]{x1D701}:I^{\prime \prime }\rightarrow I^{\prime }$ that we obtain with  $\unicode[STIX]{x1D70F}$ (and right multiply the element
$\unicode[STIX]{x1D70F}$ (and right multiply the element  $g$ we obtain by
$g$ we obtain by  $y$). Thus we may assume that
$y$). Thus we may assume that  $\unicode[STIX]{x1D6FE}=u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}$. Now conjugating back with
$\unicode[STIX]{x1D6FE}=u\unicode[STIX]{x1D6FE}^{\prime }u^{-1}$. Now conjugating back with  $u$ (that is, replacing
$u$ (that is, replacing  $(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D703})$ by
$(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D703})$ by  $(u^{-1}\unicode[STIX]{x1D6FD}u,u^{-1}\unicode[STIX]{x1D6FE}u,\unicode[STIX]{x1D703}^{u})$), we may assume that
$(u^{-1}\unicode[STIX]{x1D6FD}u,u^{-1}\unicode[STIX]{x1D6FE}u,\unicode[STIX]{x1D703}^{u})$), we may assume that  $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }$.
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }$.
Now let  $s_{\unicode[STIX]{x1D6FE}}$ be a tame corestriction with respect to
$s_{\unicode[STIX]{x1D6FE}}$ be a tame corestriction with respect to  $\unicode[STIX]{x1D6FE}$. We write
$\unicode[STIX]{x1D6FE}$. We write  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D703}^{\prime }$ as in Proposition 9.17,
$\unicode[STIX]{x1D703}^{\prime }$ as in Proposition 9.17,
 $$\begin{eqnarray}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c},\qquad \text{and}\qquad \unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c},\qquad \text{and}\qquad \unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE}},\end{eqnarray}$$ with  $\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ and
$\unicode[STIX]{x1D703}_{0}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$ and  $c\in \mathfrak{a}_{-(m+1)}$. Moreover, by Remark 9.18, we can assume that
$c\in \mathfrak{a}_{-(m+1)}$. Moreover, by Remark 9.18, we can assume that  $c$ is decomposed by the splitting
$c$ is decomposed by the splitting  $V=\bigoplus _{i\in I}V^{i}$. Since
$V=\bigoplus _{i\in I}V^{i}$. Since  $\unicode[STIX]{x1D703}_{0}$ and
$\unicode[STIX]{x1D703}_{0}$ and  $\unicode[STIX]{x1D713}_{c}\unicode[STIX]{x1D703}_{0}$ are both elements of
$\unicode[STIX]{x1D713}_{c}\unicode[STIX]{x1D703}_{0}$ are both elements of  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$, both are intertwined by every element of
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FE})$, both are intertwined by every element of  $B_{\unicode[STIX]{x1D6FE}}^{\times }$; in particular, we deduce that the derived stratum
$B_{\unicode[STIX]{x1D6FE}}^{\times }$; in particular, we deduce that the derived stratum  $[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(c)]$ is intertwined by every element of
$[\unicode[STIX]{x1D6EC},m+1,m,s_{\unicode[STIX]{x1D6FE}}(c)]$ is intertwined by every element of  $B_{\unicode[STIX]{x1D6FE}}^{\times }$ and thus
$B_{\unicode[STIX]{x1D6FE}}^{\times }$ and thus  $s_{\unicode[STIX]{x1D6FE}}(c)$ is an element of
$s_{\unicode[STIX]{x1D6FE}}(c)$ is an element of  $F[\unicode[STIX]{x1D6FE}]+\mathfrak{b}_{\unicode[STIX]{x1D6FE},-m}$, by [Reference Bushnell and KutzkoBK93, Lemma 2.4.11]. Then, since
$F[\unicode[STIX]{x1D6FE}]+\mathfrak{b}_{\unicode[STIX]{x1D6FE},-m}$, by [Reference Bushnell and KutzkoBK93, Lemma 2.4.11]. Then, since  $c,\unicode[STIX]{x1D6FD}$ are both decomposed by the splitting
$c,\unicode[STIX]{x1D6FD}$ are both decomposed by the splitting  $V=\bigoplus _{i\in I}V^{i}$, there is a semisimple stratum
$V=\bigoplus _{i\in I}V^{i}$, there is a semisimple stratum  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ equivalent to
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ equivalent to  $[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$ with splitting
$[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$ with splitting  $V=\bigoplus _{i\in I}V^{i}$. Similarly, there is a semisimple stratum
$V=\bigoplus _{i\in I}V^{i}$. Similarly, there is a semisimple stratum  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$ equivalent to
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$ equivalent to  $[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with splitting
$[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with splitting  $V=\bigoplus _{i\in I^{\prime }}V^{i^{\prime }}$.
$V=\bigoplus _{i\in I^{\prime }}V^{i^{\prime }}$.
By Proposition 9.17 there is an element of  $B_{\unicode[STIX]{x1D6FE}}^{\times }$ which intertwines
$B_{\unicode[STIX]{x1D6FE}}^{\times }$ which intertwines  $[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with
$[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FE})]$ with  $[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$, so intertwines the semisimple strata
$[\unicode[STIX]{x1D6EC},m+1,m,s(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}+c)]$, so intertwines the semisimple strata  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ and
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ and  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$. Then the matching for semisimple strata, Proposition 7.1, implies that there is
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$. Then the matching for semisimple strata, Proposition 7.1, implies that there is  $g\in B_{\unicode[STIX]{x1D6FE}}^{\times }$ which matches their splittings; indeed, since we are in the blockwise principal case, we may choose such
$g\in B_{\unicode[STIX]{x1D6FE}}^{\times }$ which matches their splittings; indeed, since we are in the blockwise principal case, we may choose such  $g\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}$. In particular, conjugating by this element (which centralizes
$g\in \tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}$. In particular, conjugating by this element (which centralizes  $\unicode[STIX]{x1D6FE}$), we may assume that
$\unicode[STIX]{x1D6FE}$), we may assume that  $I=I^{\prime }$ and the strata
$I=I^{\prime }$ and the strata  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ and
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}]$ and  $[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$ are intertwined by an element of
$[\unicode[STIX]{x1D6EC},m+1,m,\unicode[STIX]{x1D6FF}^{\prime }]$ are intertwined by an element of  $B_{\unicode[STIX]{x1D6FE}}\cap \prod _{i}A^{i,i}$. But then, by Proposition 9.17 again,
$B_{\unicode[STIX]{x1D6FE}}\cap \prod _{i}A^{i,i}$. But then, by Proposition 9.17 again,  $\unicode[STIX]{x1D703}_{i}$ intertwines with
$\unicode[STIX]{x1D703}_{i}$ intertwines with  $\unicode[STIX]{x1D703}_{i}^{\prime }$ for all
$\unicode[STIX]{x1D703}_{i}^{\prime }$ for all  $i\in I$, which finishes the proof.◻
$i\in I$, which finishes the proof.◻
Theorem 10.2. Let  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine, let
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be semisimple characters which intertwine, let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Theorem 10.1, and suppose that condition (8.4) holds. Then
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching given by Theorem 10.1, and suppose that condition (8.4) holds. Then  $\unicode[STIX]{x1D703}$ is conjugate to
$\unicode[STIX]{x1D703}$ is conjugate to  $\unicode[STIX]{x1D703}^{\prime }$ by an element of
$\unicode[STIX]{x1D703}^{\prime }$ by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$.
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$.
Proof. We first remark that the result is transitive: that is, if the hypotheses are also satisfied for a pair  $(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D703}^{\prime \prime })$ of semisimple characters then the conclusion for the pairs
$(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D703}^{\prime \prime })$ of semisimple characters then the conclusion for the pairs  $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ and
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ and  $(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D703}^{\prime \prime })$ implies that for
$(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D703}^{\prime \prime })$ implies that for  $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime \prime })$. Similarly, if
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime \prime })$. Similarly, if  $(\unicode[STIX]{x1D703}^{\prime \prime },\unicode[STIX]{x1D6FD}^{\prime \prime })$ is conjugate to
$(\unicode[STIX]{x1D703}^{\prime \prime },\unicode[STIX]{x1D6FD}^{\prime \prime })$ is conjugate to  $(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$ by an element of
$(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$ by an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$, then the result for
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$, then the result for  $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ is equivalent to that for
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })$ is equivalent to that for  $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime \prime })$.
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime \prime })$.
We need to consider three steps.
(i) Suppose first that
 $\unicode[STIX]{x1D703}$ is equal to
$\unicode[STIX]{x1D703}$ is equal to  $\unicode[STIX]{x1D703}^{\prime }$. Then, by Proposition 9.9(iv) we can find an element of
$\unicode[STIX]{x1D703}^{\prime }$. Then, by Proposition 9.9(iv) we can find an element of  $S_{m}(\unicode[STIX]{x1D6FD})$ which maps
$S_{m}(\unicode[STIX]{x1D6FD})$ which maps  $V^{i}$ onto
$V^{i}$ onto  $V^{\unicode[STIX]{x1D701}(i)}$. This element normalizes
$V^{\unicode[STIX]{x1D701}(i)}$. This element normalizes  $\unicode[STIX]{x1D703}$.
$\unicode[STIX]{x1D703}$.(ii) Suppose
 $q>m$ and that
$q>m$ and that  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ have simple strata
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ have simple strata  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}]$ and  $[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ in their defining sequences, respectively, and suppose that
$[\unicode[STIX]{x1D6EC},q,m+1,\unicode[STIX]{x1D6FE}^{\prime }]$ in their defining sequences, respectively, and suppose that  $\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}$ and
$\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}$ and  $\unicode[STIX]{x1D703}^{\prime }|_{H^{m+2}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})}$ coincide; in particular the sets of simple characters for the strata for
$\unicode[STIX]{x1D703}^{\prime }|_{H^{m+2}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})}$ coincide; in particular the sets of simple characters for the strata for  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$ coincide. Then the translation principle Proposition 9.16 provides a semisimple stratum with element
$\unicode[STIX]{x1D6FE}^{\prime }$ coincide. Then the translation principle Proposition 9.16 provides a semisimple stratum with element  $\unicode[STIX]{x1D6FD}^{\prime \prime }$, such that
$\unicode[STIX]{x1D6FD}^{\prime \prime }$, such that  $\unicode[STIX]{x1D6FD}^{\prime \prime }-\unicode[STIX]{x1D6FE}$ is an element of
$\unicode[STIX]{x1D6FD}^{\prime \prime }-\unicode[STIX]{x1D6FE}$ is an element of  $\mathfrak{a}_{-m-1}$ and
$\mathfrak{a}_{-m-1}$ and  ${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$, and an element
${\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime \prime })={\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$, and an element  $u$ of
$u$ of  $1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$ such that
$1+\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$ such that  $u\unicode[STIX]{x1D6FE}u^{-1}$ is split by the associated splitting of
$u\unicode[STIX]{x1D6FE}u^{-1}$ is split by the associated splitting of  $\unicode[STIX]{x1D6FD}^{\prime \prime }$.
$\unicode[STIX]{x1D6FD}^{\prime \prime }$.Now we can apply part (i) to
 $(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$ and
$(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$ and  $(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime \prime })$ so, by transitivity, we reduce to the case where
$(\unicode[STIX]{x1D703}^{\prime },\unicode[STIX]{x1D6FD}^{\prime \prime })$ so, by transitivity, we reduce to the case where  $\unicode[STIX]{x1D6FE}^{\prime }=u\unicode[STIX]{x1D6FE}u^{-1}$. Then, by conjugating by
$\unicode[STIX]{x1D6FE}^{\prime }=u\unicode[STIX]{x1D6FE}u^{-1}$. Then, by conjugating by  $u$, we reduce to the case where
$u$, we reduce to the case where  $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }$. Now writing
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }$. Now writing  $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$ as in Proposition 9.17, we get that the derived strata intertwine so, by Theorem 8.3, are conjugate by elements of
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$ as in Proposition 9.17, we get that the derived strata intertwine so, by Theorem 8.3, are conjugate by elements of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}$. But then Proposition 9.17(iii) gives us an element of
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap B_{\unicode[STIX]{x1D6FE}}$. But then Proposition 9.17(iii) gives us an element of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which conjugates
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})$ which conjugates  $\unicode[STIX]{x1D703}$ to
$\unicode[STIX]{x1D703}$ to  $\unicode[STIX]{x1D703}^{\prime }$. Part (i) enables us to modify the conjugating element such that
$\unicode[STIX]{x1D703}^{\prime }$. Part (i) enables us to modify the conjugating element such that  $V^{i}$ is mapped to
$V^{i}$ is mapped to  $V^{\unicode[STIX]{x1D701}(i)}$ for all indices
$V^{\unicode[STIX]{x1D701}(i)}$ for all indices  $i$.
$i$.(iii) We now prove the general case by induction on
 $m$. If the strata are null strata (
$m$. If the strata are null strata ( $m=q$), then we can take the identity as the conjugating element. Suppose now
$m=q$), then we can take the identity as the conjugating element. Suppose now  $m<q$. Take for the strata first members of the defining sequences with entries
$m<q$. Take for the strata first members of the defining sequences with entries  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$, respectively. By the induction hypothesis
$\unicode[STIX]{x1D6FE}^{\prime }$, respectively. By the induction hypothesis  $\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}$ is conjugate to
$\unicode[STIX]{x1D703}|_{H^{m+2}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6EC})}$ is conjugate to  $\unicode[STIX]{x1D703}^{\prime }|_{H^{m+2}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})}$ by an element which conjugates the splittings; thus, by conjugating, we may assume that these restrictions are equal, and further that
$\unicode[STIX]{x1D703}^{\prime }|_{H^{m+2}(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D6EC})}$ by an element which conjugates the splittings; thus, by conjugating, we may assume that these restrictions are equal, and further that  $\unicode[STIX]{x1D6FE}$ and
$\unicode[STIX]{x1D6FE}$ and  $\unicode[STIX]{x1D6FE}^{\prime }$ have the same associated splitting, say
$\unicode[STIX]{x1D6FE}^{\prime }$ have the same associated splitting, say  $V=\bigoplus _{j}V^{j}$. Now Corollary 9.19 provides an intertwiner of
$V=\bigoplus _{j}V^{j}$. Now Corollary 9.19 provides an intertwiner of  $\unicode[STIX]{x1D703}$ with
$\unicode[STIX]{x1D703}$ with  $\unicode[STIX]{x1D703}^{\prime }$ which preserves
$\unicode[STIX]{x1D703}^{\prime }$ which preserves  $V^{j}$, for all indices
$V^{j}$, for all indices  $j$. We apply Part (ii) for each
$j$. We apply Part (ii) for each  $j$ to obtain an element
$j$ to obtain an element  $g=(g_{j})$ of
$g=(g_{j})$ of  $\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$ which conjugates
$\tilde{\operatorname{U}}(\unicode[STIX]{x1D6EC})\cap \prod _{i}A^{i,\unicode[STIX]{x1D701}(i)}$ which conjugates  $\unicode[STIX]{x1D703}_{j}$ to
$\unicode[STIX]{x1D703}_{j}$ to  $\unicode[STIX]{x1D703}_{j}^{\prime }$ for all indices
$\unicode[STIX]{x1D703}_{j}^{\prime }$ for all indices  $j$. Finally, Corollary 9.14(i) applied to
$j$. Finally, Corollary 9.14(i) applied to  $\unicode[STIX]{x1D703}^{g^{-1}}$ and
$\unicode[STIX]{x1D703}^{g^{-1}}$ and  $\unicode[STIX]{x1D703}^{\prime }$ and the splitting
$\unicode[STIX]{x1D703}^{\prime }$ and the splitting  $\bigoplus _{i}V^{\unicode[STIX]{x1D701}(i)}$ gives that
$\bigoplus _{i}V^{\unicode[STIX]{x1D701}(i)}$ gives that  $\unicode[STIX]{x1D703}^{g^{-1}}$ and
$\unicode[STIX]{x1D703}^{g^{-1}}$ and  $\unicode[STIX]{x1D703}^{\prime }$ coincide, and the element
$\unicode[STIX]{x1D703}^{\prime }$ coincide, and the element  $g$ is as required. ◻
$g$ is as required. ◻
10.2 For classical groups
If two characters  $\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ intertwine then their lifts
$\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ intertwine then their lifts  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ intertwine and we get a matching
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ intertwine and we get a matching  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ from Theorem 10.1. Let us state the main theorem:
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ from Theorem 10.1. Let us state the main theorem:
Theorem 10.3. Let  $\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and
$\unicode[STIX]{x1D703}_{-}\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two semisimple characters of
$\unicode[STIX]{x1D703}_{-}^{\prime }\in {\mathcal{C}}_{-}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD}^{\prime })$ be two semisimple characters of  $G$, which intertwine in
$G$, which intertwine in  $G$, and assume that their matching satisfies (8.4). Then,
$G$, and assume that their matching satisfies (8.4). Then,  $\unicode[STIX]{x1D703}_{-}$ and
$\unicode[STIX]{x1D703}_{-}$ and  $\unicode[STIX]{x1D703}_{-}^{\prime }$ are
$\unicode[STIX]{x1D703}_{-}^{\prime }$ are  $\operatorname{U}(\unicode[STIX]{x1D6EC})\cap (\prod _{i}A^{i,i})$-conjugate.
$\operatorname{U}(\unicode[STIX]{x1D6EC})\cap (\prod _{i}A^{i,i})$-conjugate.
Proof. The proof is completely the same as for Theorem 10.2 by using  $\unicode[STIX]{x1D70E}$-fixed lifts of the characters and the relevant results for
$\unicode[STIX]{x1D70E}$-fixed lifts of the characters and the relevant results for  $G$ in place of those for
$G$ in place of those for  $\tilde{G}$. Specifically: in step (i), we use Proposition 9.23(iii). In step (ii), we use the translation principle for
$\tilde{G}$. Specifically: in step (i), we use Proposition 9.23(iii). In step (ii), we use the translation principle for  $G$, Theorem 9.26, to reduce to the case of a common
$G$, Theorem 9.26, to reduce to the case of a common  $\unicode[STIX]{x1D6FE}$ and we use Proposition 9.27(i) to reduce to the derived strata; the case of minimal strata is done in Theorem 8.7. In step (iii), we use Corollary 9.28 to reduce to the case where the stratum with
$\unicode[STIX]{x1D6FE}$ and we use Proposition 9.27(i) to reduce to the derived strata; the case of minimal strata is done in Theorem 8.7. In step (iii), we use Corollary 9.28 to reduce to the case where the stratum with  $\unicode[STIX]{x1D6FE}$ is simple.◻
$\unicode[STIX]{x1D6FE}$ is simple.◻
We also conjecture a more natural version of the matching Theorem 10.1 for  $G$.
$G$.
Conjecture 10.4. Let  $[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and
$[\unicode[STIX]{x1D6EC},q,m,\unicode[STIX]{x1D6FD}]$ and  $[\unicode[STIX]{x1D6EC}^{\prime },q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata and
$[\unicode[STIX]{x1D6EC}^{\prime },q,m,\unicode[STIX]{x1D6FD}^{\prime }]$ be skew-semisimple strata and  $\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and
$\unicode[STIX]{x1D703}\in {\mathcal{C}}(\unicode[STIX]{x1D6EC},m,\unicode[STIX]{x1D6FD})^{\unicode[STIX]{x1D70E}}$ and  $\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ two semisimple characters which are intertwined by an element of
$\unicode[STIX]{x1D703}^{\prime }\in {\mathcal{C}}(\unicode[STIX]{x1D6EC}^{\prime },m,\unicode[STIX]{x1D6FD}^{\prime })^{\unicode[STIX]{x1D70E}}$ two semisimple characters which are intertwined by an element of  $G$. Let
$G$. Let  $\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching from Theorem 10.1. Then, there is an element
$\unicode[STIX]{x1D701}:I\rightarrow I^{\prime }$ be the matching from Theorem 10.1. Then, there is an element  $g\in G$ such that
$g\in G$ such that  $gV^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all
$gV^{i}=V^{\prime \unicode[STIX]{x1D701}(i)}$, for all  $i\in I$.
$i\in I$.