1. INTRODUCTION
The development of laser-plasma interaction during the last few years using the terawatt to petawatt laser pulses of about picosecond duration developed into a number of new relativistic effects and nonlinearities (Osman et al., 2004; Beech & Osman, 2005; Bret et al., 2006; Deutsch et al., 2005; Jablonski et al., 2005; Glowacz et al., 2006). This was subsequently reported in the broad stream of experimental research (Zhang et al., 1998; Cowan et al., 1999; Roth et al., 2005; Badziak et al., 2005; Hora et al., 2005; Hora, 2005; Schaumann et al., 2005; Hoffmann et al., 2005; Glinec et al., 2005; Chen & Wilks, 2005) where phenomena as 100 MeV electron bursts (Nakamura et al., 2006), GeV ions and electron beams (Lifschitz et al., 2006), pair production, gamma bursts with subsequent nuclear transmutations etc. were observed. Application to fast ignition for laser fusion (Tabak et al., 1994; Kodama and Fast Ignitor Consortium, 2002; Key, 2001; Gus'kov, 2005; Sakagami et al., 2006) emerged for different schemes mostly involving relativistic effects. In view of this, the theory of the forces involved was essential (Hora, 2000), especially the final general expression of the nonlinear ponderomotive force (Hora, 1985). The relativistic foundation as a four-force was elaborated (Rowlands, 1990, 1997).
This paper reports on a relativistic investigation of the laser interaction with plasma. This will involve converting the best nonlinear ponderomotive force expression to its relativistic counterpart. Having achieved this, it will be established that the resultant four-force obeys the fundamental conservation laws including both Lorentz and gauge invariance. The stress-energy tensor of this force will be investigated.
It is apparent that a way to treat macroscopic plasma is to employ a fluid mechanical approach. This approach was taken by Alfvén in 1942 (Shercliff, 1965; Davies, 2006) and it was him who coined the term “Magneto-hydrodynamics.” Magneto-hydrodynamics consists of combining the momentum and conservation equations for the charges in plasma. These are then constrained by the Maxwell equations for the interactions of the charge fluids with the electromagnetic fields.
Alfvén treated plasma as a fluid consisting of a single charge species. He linearized the fluid equations and derived substantial results from these linearized equations. Schlüter (1950) later derived a nonlinear treatment of the two fluid approaches. The total force of the laser-plasma system at an arbitrary temperature is composed of both the ponderomotive force (linear or nonlinear) and the thermo-kinetic force. Thus, it should be noted that the ponderomotive force is in fact the total force acting on the system minus the thermo-kinetic force. It is convenient to talk about the ponderomotive force instead of the total force as this provides a more illuminating picture. Here we will consider all terms of the nonlinear ponderomotive force including those terms that are not classically ponderomotive.
2. THE TIME-INDEPENDENT PONDEROMOTIVE FORCE
Following the manner of Kentwell and Jones (1987), we will consider the basic time-independent treatment of laser light upon plasma. The assumptions are that there is a single species plasma, overall charge neutrality, an internally field free plasma, and that the only fields considered are high frequency impinging electromagnetic fields. The electromagnetic force on the charges causes the charges to react hydrodynamically and this leads to ponderomotive force being given by

This simple result has also been derived via the oscillation center theory and the stress tensor approaches.
The acceptance of this expression is almost universal since the force is the same as that derived by Helmholtz and Kelvin for electrostatics (Kentwell & Jones, 1987). It has been called the electrostriction force or field gradient force. It was hoped that this force would lead to fusion since it has the effect of pushing the plasma into the nodes of the laser beam. In three dimensions, this will force the plasma into a much localized region. The problem with this scheme is that absorption processes overcome the confining forces before fusion can occur.
Schlüter (1950) derived a time-independent nonlinear ponderomotive force from the two fluid Euler equations, one for each charge species. Neutral charge species were considered to have negligible affect upon the plasma motions. Schlüter's force expression is given by
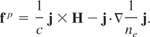
This force can be recast in a more enlightening form (Hora, 1969) as

The last term, the “Schlüter Term,” is in fact, nonlinear. This is due to it being quadratic in the electric field. These force equations stimulated considerable interest in this area of study.
The ponderomotive force equation allows an expression for the current to be deduced. The current is important because it is an observable system. Hora (1969) suggested that a current J will be induced according to

where J is the current induced, ν is the collision frequency, and ω is the frequency of the incident electromagnetic radiation. It should be noted that this is a form of Ohm's law and in the absence of collisions, ν = 0.
The problem with Schlüter's ponderomotive force was that it predicted shear forces at the surface of the collisionless plasma. A “net force appeared along the plasma surface [that] could not be possible because of momentum transfer” (Hora et al., 1990).
By considering momentum transfer, additional terms were added (Hora, 1969) to the nonlinear ponderomotive force. This force is given by

It should be noted that the refractive index is the complex refractive index; a function of the plasma frequency, collision frequency, and the incident radiation frequency. It is given by
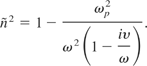
The nonlinear ponderomotive force can be recast by considering its components which is equivalent to (Hora, 1969)
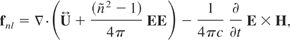
where U is the Maxwellian stress tensor. It should be noted that U is the three-space stress tensor and not the four-space stress-energy tensor.
3. THE TIME-INDEPENDENT PONDEROMOTIVE FORCE
An exact expression was derived for the nonlinear time-dependent ponderomotive force (Hora, 1985). He obtained this by following on from the work of Zeidler et al. (1985) who compared the different expressions for the transient ponderomotive force. They state that the force can be broken into a gradient and a time-dependent term. They derive their own time-dependent term as well as giving a summary of time-dependent terms derived by other authors. Hora (1985) had noticed that the addition of a logarithmic term would result in an equation which encompassed the nonlinear terms derived previously. This formally completed the time-dependent nonlinear ponderomotive force. The new time-dependent nonlinear ponderomotive force is

This can be expressed (by utilizing to the Maxwell stress tensor) as

It is noteworthy that the last term in the equation (which is the time variation of the Poynting vector) and the divergence of the Maxwellian three-space tensor would combine to form the divergence of the Maxwellian four-space tensor. This fact was recognized and used in investigating the time-dependent ponderomotive nonlinear four-force (Rowlands, 1990).
4. DERIVATION OF THE PONDEROMOTIVE FOUR-FORCE AND ITS STRESS-ENERGY TENSOR
The investigation starts with Hora's (1985) nonlinear time-dependent ponderomotive three-force (which does not include the thermo-kinetic term for simplicity):
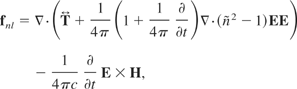
where

is the complex refractive index and ∂ is the frequency of the incident laser light, which has electric and magnetic fields denoted by E and H, respectively. The symbol
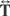
represents the Maxwell stress tensor (a three-dimensional object that depends upon electric and magnetic fields).
By making the following identifications:
refractive term:
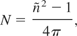
Poynting term:
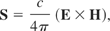
Maxwellian term:
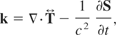
conductivity term:
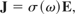
thus we obtain the following equation:
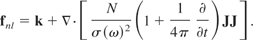
It should be noted that k is comprised of the pure Maxwellian three-force components. As in Rowlands (1990) the above nonlinear three-force can be converted to a four-force by the following procedure: convert all derivatives to their three-dimensional tensorial expressions (Latin indices), and then adjust the index range to cover four dimensions (Greek indices) if it is suitable to do so.
The force derived from the electromagnetic stress-energy tensor portion (i.e., k) is defined for a general reference frame to make it easy to convert it into four dimensions. The remainder of the ponderomotive force expression is defined in a special reference frame (i.e., the rest frame) since there are no magnetic fields, and relative motion generates magnetic fields. To obtain the general reference frame expression, it is necessary to replace J(E) by J(E,H) which is given by
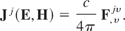
Where
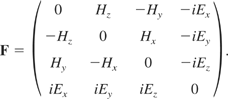
The ponderomotive four-force must then take the same form as the three-force expression, but with the indices ranging over time, so that m → ν and j → μ. Thus, the final four-force becomes

The fourth component of the ponderomotive four-force describes the rate of change of relative energy, due to the rate that energy is being supplied to the plasma by the laser beam. The relative energy is the sum of the relative kinetic energy and the rest energy. Since the rest energy is constant, the rate of change of relative energy can also be interpreted as the rate of change of kinetic energy. Thus, the first three components of the ponderomotive four-force describe the motion and the fourth component describes the change in kinetic energy. The Maxwell stress-energy tensor can be defined (Marion & Heald, 1980) as follows:
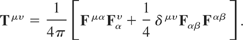
This definition allows the ponderomotive four-force to be described totally in terms of the electromagnetic field tensor:
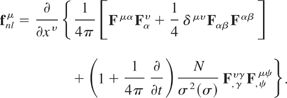
The four-force is related to its stress-energy tensor by the following relation:
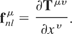
Thus the ponderomotive stress-energy tensor is
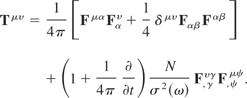
4.1. Lorentz invariance of the ponderomotive four-force
If the total stress-energy tensor can be shown to be Lorentz invariant, then the force derived from this tensor must also be Lorentz invariant. It is well known that the electromagnetic field tensor obeys Lorentz invariance (Aitchison, 1984). Partial differentials with respect to space-time indices (Greek indices) are Lorentz invariant. Thus, the electromagnetic field tensor derivatives are Lorentz invariant. Since
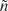
squared is a scalar, N is also a scalar. The frequency ω is also a scalar. A scalar transforms according to the Lorentz transformations. Since all parts of the total stress-energy tensor are Lorentz invariant, the four-force derived from it is also Lorentz invariant. Therefore, the nonlinear force is Lorentz invariant.
4.2. Gauge invariance of the ponderomotive four-force
The gauge invariance of these terms can be informally ascertained by investigated the expression for the ponderomotive four-force. The electromagnetic field tensor is the only tensor involved. This tensor is gauge invariant and its divergence is gauge invariance. Thus the ponderomotive four-force must be gauge invariant also.
4.2.1. Gauge invariance of the electromagnetic (faraday) tensor
The electromagnetic field tensor can be defined in terms of the four-potentials. The four-potential A is defined as follows
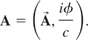
The electromagnetic field tensor is defined as
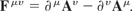
The gauge transformations can be defined as

where x is a scalar differentiable function of position. The primes denote the object that has been transformed by a gauge transformation. It is well known (Aitchison, 1984) that the form of the electromagnetic field tensor is unchanged after application of the gauge transformations. That is, the electromagnetic field tensor is invariant under gauge transformations.
4.2.2. The nonlinear ponderomotive four-force
The nonlinear time-dependent ponderomotive four-force can be shown to be comprised of two portions. One is a Maxwellian portion and the other is a dielectric response portion.
Maxwellian:
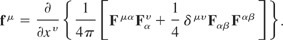
Dielectric:

In order to discover the gauge invariance of the above expression it is necessary to treat each portion separately. It is reasonable to assert that the Maxwellian portion will be gauge invariant, but it needs to be proved.
4.2.2.1. The gauge invariance of the Maxwellian portion Let the Maxwellian portion be denoted by Mμ. It is convenient to take Mμ and break it up into two smaller parts. The gauge invariance of each of these parts will then be tested.Let the portions of Mμ be denoted by part one and part two:
Part one:

Part two:
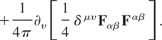
4.2.2.1.1. The gauge invariance of part one Lets expand part one into its four potential terms. This involves substituting for the electromagnetic field terms
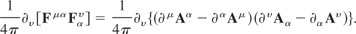
Define the appropriate gauge transformations as
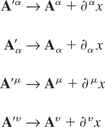
Thus part one primed becomes, after substituting in the above gauge transformations

Factor and collect terms to obtain

i.e.,
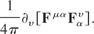
This is exactly the form of part one before the gauge transformations were applied. Thus, part one is gauge invariant.
4.2.2.1.2. The gauge invariance of part two Let's expand part two into its 4-potential terms. This involves substituting for the electromagnetic field terms to obtain
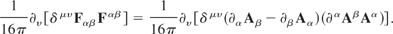
Define the following gauge transformations
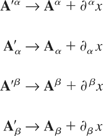
and apply them to part two. Part two primed is thus

i.e.,
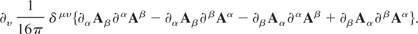
Collecting terms results in
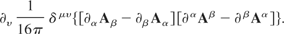
Using the definitions of the electromagnetic field tensors leads to
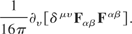
This is of the same form as the expression before the gauge transformations were applied. We have
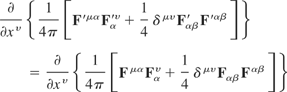
i.e.,

Thus, part two is gauge invariant.
It has been shown that both parts one and two of the Maxwellian portion are gauge invariant. Thus, as expected, the entire Maxwellian portion is invariant under gauge transformations. For the total nonlinear four-force to be gauge invariant, it remains to be shown that the dielectric response portion is gauge invariant.
4.2.2.2. The gauge invariance of the dielectric response portion For simplicity, as in the preceding section, the dielectric response portion can be expressed in terms of two parts. To obtain these two parts, we will need to recast the dielectric response portion in a more suitable form. Start with the dielectric response portion defined as
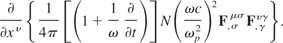
This can be redefined as
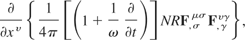
where R is a scalar function given by

Note that N is complex due to the complex refractive index. Thus, the product of R and N can be considered to be a simple complex function. That is, RN can be replaced by (a + ib) and still retain validity. Hence,
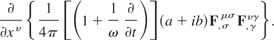
This can be broken into two parts, by expansion giving
Part three:
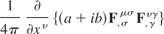
Part four:
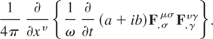
There are some common elements between parts three and four. First of all, there is the factor of 1/4π in each part. This is a scaling factor only and plays no part in determining the invariance under gauge transformations. Second, there is the (a + ib)F,σμσF,γυγ term.
Now,
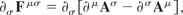
i.e.,
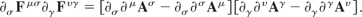
This leads to

This must be multiplied by (a + ib) to obtain

In order to show the gauge invariance of the above expanded expression, it will be necessary to substitute in the gauge potentials.
4.2.2.2.1. The gauge invariance of part three Note that we will be dropping the 1/4π factor from this proof as it is only a scaling factor and will not affect the gauge invariance. Part three is
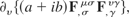
and by using the earlier result, this can be expanded to get

We must now apply the gauge transformations to the above expression giving

The specific gauge transformations are defined as follows:
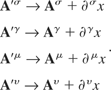
Substituting these into the right-hand side gives the following expression

Expand the above to give an expression for part three under gauge transformations as follows:

By collecting terms, this simplifies to
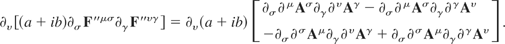
We can rearrange this to give
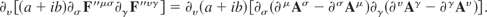
Thus, after substituting in for the terms in parenthesis, we now have
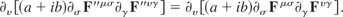
This is exactly the form of part three before the gauge transformations were applied. Therefore, part three is gauge invariant.
4.2.2.2.2. The gauge invariance of part four Part four can be restated as
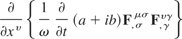
remembering that there is a scaling factor of 1/4π that has no effect on the gauge invariance. Now, this is the same as part three except that a and ib are prefixed by (1/ω)(∂/∂t). The gauge transformed form of part four is

Substituting in the expressions for the gauge transformations which are given by
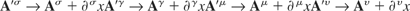
and then multiplying out yields the following expression for the right-hand side

Collection of terms results in
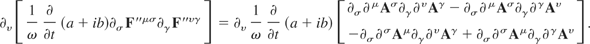
Rearrange to give
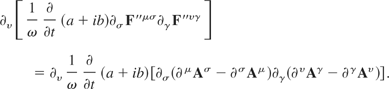
Thus, after substituting in for the terms in parenthesis we have
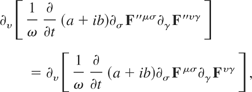
this is of the same form as the expression before the gauge transformations were applied. Therefore part four is gauge invariant.
Since both part three and part four are gauge invariant, the dielectric response portion is gauge invariant. Both the Maxwellian and dielectric response portions of the nonlinear four-force have been shown to be gauge invariant. Thus, the total nonlinear four-force is gauge invariant.
This was to be expected since there are no free potential terms. All the potentials were differentiated and subtracted. Thus, the effect of the gauge scalar was cancelled. The inclusion of the electromagnetic field tensor and its derivatives ensured gauge invariance.
5. RELATIVISTIC PLASMA THEORY AND THE PLASMA MAGNETIC RESPONSE
These methods do not provide an exact derivation of the magnetic permeability. The relativistic approaches do not explicitly derive the magnetic permeability. The non-relativistic approaches are either not rigorous or not considered in general plasma.
In order to fill this apparent gap in current knowledge, I developed a relativistic model of the interaction of electromagnetic waves with general plasma, which includes the magnetic response explicitly. This gauge and Lorentz invariant model of the propagation of electromagnetic waves naturally includes plasma variables such as the plasma frequency without explicitly adding them. Further analysis of this elegant model allows a value for the magnetic permeability to be easily generated.
5.1. Relativistic plasmas and electromagnetic waves
There have been a number of non-relativistic treatments of the interaction of electromagnetic radiation with plasma (Kentwell & Jones, 1987; Hora, 1985). Some of these have been modified to partially include relativistic effects. There have also been some fully relativistic theories of electromagnetic interaction with plasma. The way in which they incorporated the magnetic permeability and the electric susceptibility will also be investigated.
The work of Anile (1990) demonstrates how the perturbation theory can be used to examine electromagnetic waves in cold relativistic plasma. Initially, the problem is the set-up with nonlinear equations which are then linearized.
The nonlinear sets of equations are:
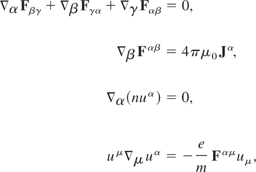
where F is the free space electromagnetic tensor, J is the current, u is the electrons velocity, e and m are the electron charge and mass, respectively, and n is the number density of the charges.
Let the system undergo locally plane wave perturbations to each of the main variables, and linearize these equations, this will lead via much algebra to the following

Ωp is to be identified as the plasma frequency and hence the above equation is the dispersion relation. This model carries the permeability and the permittivity, but does not explicitly derive or use them.
The seminal work of Friedrichs (1974) treated the relativistic plasma by mathematically studying the set of hyperbolic equations that constitute the conservation equations of the system. Although he treats the cases of polarized electric and magnetic fields, he does not derive any expression for the magnetic permeability.
Buneman (1968) used relativistic Boltzmann or “Vlasov” equations to describe a covariant dispersion theory with constant magnetic fields. The Boltzmann function is constant along particle orbits in phase (position, momentum) space. He looked at the change from steady state distribution functions under a perturbing electromagnetic field.
The perturbed function F is
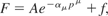
where A is a scaling factor, p is the momenta of the electrons, f is the perturbed distribution function, and α is a time-like vector that describes a drift velocity, and whose length is the inverse of the temperature of the system.
By looking at the conservation law which expresses the Boltzmann equation, a Fresnel type integral is obtained

where fμν are the perturbing field's tensor and the Δx are used to correct the phase. This theory then leads to an admittance tensor given by

where N is the number density, k is the wave-vector of the perturbing electromagnetic field, ταβ is the Lorentz rotator, K2 and K3 are the Bessel functions of the second and third order, and τ is the proper time. The magnetic permeability cannot be accessed directly and thus its value can't be calculated.
Pfirsch and Morrison (1991) used a relativistic linearized Maxwell-Vlasov technique in their derivation of an energy-momentum tensor. This was facilitated by the use of variational techniques.
A Hamiltonian is developed in a phase space based on the variables p and q, where the first three members of the set of p are the momenta, and the first three members of the set of q are identified as the position variables. This gauge invariant Hamiltonian is of the form

where A and φ are the magnetic and electric potentials of the magnetic and electric fields B and E.
The Vlasov equations can be defined in the following way:
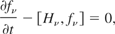
where the functions f are derived from the density functions. These functions f are a general solutions to the Van Vleck determinant as well as the Vlasov equations.
The system is described by a Lagrangian L which is dependent upon the gauge invariant Hamiltonian. Now, the second order Lagrangian describes the linearized system. Thus, the four-derivation of the linearized energy-momentum tensor is
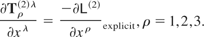
This is also an expression for the force. In this whole description, there has been no mention of the optical variables. They are carried in a hidden way in this theory.
Bauer et al. (1995) took a relativistic oscillation center approach to deriving an expression for the ponderomotive force. They started with a relativistic Lagrangian of a charge q and mass m in an arbitrary electromagnetic field defined by the magnetic and electric potentials A and φ. This Lagrangian is

where the Lorentz factor is
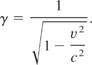
This is then transformed to the oscillation center via the action and angle variables S(x,t) and η = η(x,t). Varying the action S over the angle η and assuming that η is normalized to 2π gives a cycle-averaged Lagrangian
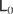
. This Lagrangian system is given by
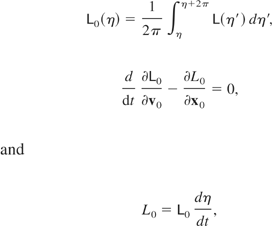
where the subscript zero denoted the oscillation center variables.
Consider a test particle injected into a non-relativistic Langmuir wave of the form

with the potential being
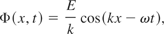
where the hat denotes slowly varying quantities.
For the case of no explicit time dependence, we have the ponderomotive force as

where V0 is the oscillation center velocity normalized to the phase velocity (i.e., the ratio of the oscillation center velocity to the phase velocity). The phase velocity is defined as vφ = ω/k. In this case, the permittivity and the permeability are not defined, but their information is carried implicitly within the ponderomotive force.
Hartemann and Toffano (1990) looked at a linear isotropic medium. They applied relativistic transformations to Maxwell's sourced equations in a vacuum. These transformed equations then undergo a four-dimensional Fourier analysis, using the assumption that the medium is non-magnetic (i.e., μ = 1). They arrive at the following dispersion relation (in Standard International units)
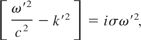
where the primed quantities are those defined in the rest frame of the medium. In the above equation, the frequency and wave-vector are given by ω and k, respectively, and the conductivity are given by σ. The magnetic permeability and the electric permittivity are bound in the conductivity. They are not derived explicitly.
Novak (1981) in his Ph.D. thesis and various papers (Novak, 1980, 1989) studied this sort of interaction using quantum mechanical methods. His conclusion was that this interaction is governed by the Proca Lagrangian (which is the Lagrangian for a massive spin one vector field). This has the form

where F is the Faraday field tensor, A is the electromagnetic potential four-vector, and μ is the mass term. It is well known that this Lagrangian is a Lorentz invariant, but is not gauge invariant due to its description in terms of four-potentials.
Novak derives Maxwell's equations in a curved space-time
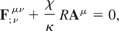
where χ is a coupling constant, κ is the gravitational coupling constant, and R is the scalar of curvature. He compares these with the Proca equations in a flat space-time
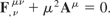
He then concludes that a photon traveling through a medium (equivalent to a curved empty space) can act like it had a mass of
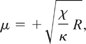
in an empty flat space-time.
The magnetic permeability and the electric permittivity are bound in this description within the mass term for the photon. The difficulty in obtaining the value of the optical constants from this approach is the same as that of deriving the metric.
This method used the curved medium approach to derive the dynamics of the photon in space-time, which has taken on mass by having “clothed” itself in the medium. In this case, it is not gauge invariant, and the permittivity and permeability are bound in the metric.
Under the general relativistic formalism, electromagnetism in a moving medium can be described by replacing the medium with an optical metric. This metric is given by
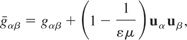
where the four-velocity is given by u.
Thus, the electromagnetic wave must obey the relations
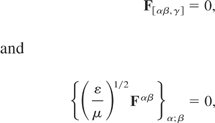
where ε and μ are the permittivity and permeability, respectively, of the medium.
Zhu and Shen (1987) showed that for a medium with a constant less than light-speed velocity in the x direction, a non-unity refractive index as well as circularly polarized light, the ponderomotive force is

with
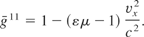
This expression does carry the permittivity and permeability as the square of the refractive index. Again, a ponderomotive force is defined in terms of these variables, but no attempt is made to derive a value for these variables.
All these methods relativistically describe the interaction of electromagnetic radiation with a plasma (or in some cases a more general medium), but do not elucidate a method of easily calculating the magnetic permeability of a general plasma. The authors have concentrated on developing the dynamics of their models and have not investigated further the optical constants.
5.2. The magnetic response of non-relativistic plasmas
In this section, non-relativistic investigations into a relation or value for the magnetic permeability of plasma are investigated. The initial approaches were just plausibility arguments. Schlüter (1960) gave a case for the magnetic permeability of plasma having a value of unity. He noted that the response of the electrons to a magnetic field is gyration. Thus the magnetic field due to the motion in one direction by an electron is cancelled by the countermotion of the neighboring electron. Such that, in the worst case, a net surface current around the plasma remains, this is sufficiently small if the plasma volume is sufficiently large.
Kadomtsev (1996) gave a good review of tokomak plasmas, and Grad (1967) done extensive work on the question of magnetic permeability of plasma in a tokomak. In a study of “some new stable toroidal plasma configurations,” he discussed multiple fields based on the condition that the guiding center distribution is the same on all flux surfaces. After finding multiple allowable configurations, he then tested the stability of the system, if it is assumed to display paramagnetic or diamagnetic behavior. He found that this system doesn't preclude the plasma being diamagnetic or paramagnetic and is stable under both conditions.
Grad (1968) then considered a non-parallel current with a guiding center distribution of f (ε,μ). He then asked whether a diamagnetic or paramagnetic signal is induced in a conducting loop surrounding the plasma. Using plasma confined within a tokomak, and with the plasma parameters at their equilibrium values and a zero plasma pressure, he was able to show that the plasma cannot be diamagnetic. It should be emphasized that a tokomak is plasma confined to a specific geometry and hence one cannot imply that this result is true for the general case.
Grad (1971) reviewed all of his work up until 1970. In this paper, he examines the hypothesis that plasma is diamagnetic. He finds that “a scalar pressure plasma is … globally diamagnetic; even with inverted pressure profiles. A force-free field [with parallel currents only] is “normally” paramagnetic … [but] it can give a diamagnetic signal.”
Grad concluded that “Diamagnetism is not a basic plasma property; it is not a thermal requisite or a consequence of Lenz's law; nor is it a correlative of stability—it is only somewhat more common than paramagnetism.”
The tokomak being a confined plasma system does not necessarily illuminate the case of the general unconfined plasma. Ginzburg (1970) takes an inherently non-relativistic approach by treating plasma as a non-degenerate electron gas and arrives at the conclusion that the magnetic permeability is approximately unity as long as the plasma is non-degenerate. So, it is important to ask at what temperature below which this plasma becomes degenerate and does not obey the above formulae. This temperature is given approximately by
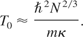
For laser induced plasma, it must be kept above 10000° K for a density of 3.8 × 1022 per cm3 in order for the plasma to stay non-degenerate.
5.3. Relativistic derivation of a value for the magnetic permeability
I will develop a totally relativistic, coordinate system independent and general theory of the plasma response. This will lead to a correct and general derivation of an expression for the magnetic permeability. The very important result that the value of the magnetic permeability is unity will be obtained.
The plasma model used is a one fluid plasma model. It could be electron plasma or ion plasma. Overall, charge density consistency is assumed, but local variation of charge density could occur. The collisions between any particles are assumed to be negligible.
The effect of radiation on the plasma is given by the following prescription. The plasma is described by fluid mechanics and the electromagnetic force is described via the Lorentz force. It is reasonable to assert that the Lorentz force generates a force in the fluid (plasma) which is labeled the magneto-hydrodynamical approach (Hora, 1981).
The Lorentz invariance will be assured by utilizing covariant expressions for both the electromagnetic force and the fluid force. The gauge invariance will be assured by being manifestly gauge invariant from the outset. This relies upon using gauge invariant expressions for the field descriptions. The fluid force contains no four-potentials and hence is gauge invariant. The Lorentz force contains the electromagnetic field tensor (which is the only four-potential dependent object). Now, the electromagnetic field tensor Fαβ is manifestly gauging invariant. Thus, the Lorentz force is gauge invariant. Since the entire system is described by gauge invariant forces, the system will be manifestly gauging invariant. It should be noted that the system of units employed are the Gaussian system of units.
All equations are defined relative to a general reference frame and all quantities in the rest frame are denoted by the adjective “proper.” The following definitions will be referred to by a single symbol:
Lorentz factor:
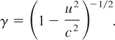
Four-Velocity:

Proper Mass Density:
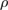
Proper Charge Density:
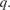
5.3.1. The Lorentz force density
First we will investigate the Lorentz force in order to set-up the model into an appropriate form. Let fα be the Lorentz force density of the incident electromagnetic radiation which is defined, thus
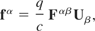
where q is the proper charge density of the fluid, U is the fluid element's four-velocity, and Fαβ is the electromagnetic field tensor. The electromagnetic field tensor is a six-form and is given by the following:
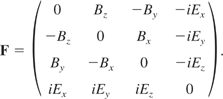
It is convenient to describe the Lorentz force totally in terms of the field tensor. In order to do this, both the inhomogeneous Maxwell's equations are utilized. They are both given by
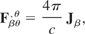
which implies the equation of continuity (Marion & Heald, 1980), therefore the equation of continuity does not have to be explicitly included. Identify that the four-current J can be written as
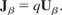
Thus by inserting Eq. (5) into Eq. (4) we obtain
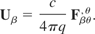
Now, Eq. (6) can be placed in Eq. (3) giving
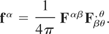
The above equation is the Lorentz force cast solely in terms of the electromagnetic field tensor.
5.3.2. The charged fluid force density
The second part of this model describes the fluid response to a force. The fluid force density Γ is equal to the mass density ρ by the fluid four-acceleration. This acceleration is nonlinear in terms of four-velocity. Thus,
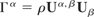
where U is the fluid element's four-velocity.
Eqs. (4) and (5) can be written as the following by using the metric tensor:
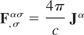
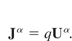
Insert Eq. (10) into Eq. (9) and rearranged to give
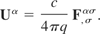
Differentiate this with respect to dxβ and along with Eq. (6), insert into Eq. (8) to obtain
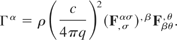
We now have the fluid force density expressed in terms of the electromagnetic field tensor only.
There is an interesting point of interpretation. The motion of the charge can be implied from the incident fields or the incident fields can be implied from studying the motion of the charges. Both methods are equivalent to each other.
5.3.3. Equating the forces
Set the Lorentz force density (Eq. 7) equal to the fluid force density (Eq. 12) and rearranged to obtain the following

where
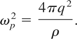
It is interesting to note that the plasma frequency has appeared in this model as a constant without explicitly introducing it. Without loss of generality we can write
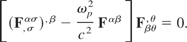
Eq. (15) allows three cases. The first case is nonlinear and won't be considered here, although nonlinear treatments have previously been examined (Kentwell & Jones, 1987; Rowlands, 1990, 1997; Hora, 1981, 1985). The second case is trivial Fβθ,θ = 0, that is, there are no four-currents in the fluid, which is not physically possible for a charged fluid. The third case,
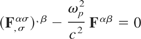
is a wave equation in terms of the electromagnetic field tensor.
5.3.4. The four-current wave equation
It can be seen that Eq. (16) is dependent on the electromagnetic field tensor. This is an object that has six independent components. The four-current, which can be derived from it, contains only four independent components and thus reduces the complexity of the calculations.
The four-current wave equation can be derived from the field tensor wave equation by inserting Eq. (9) into Eq. (16) to obtain
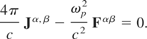
Differentiate this with respect to dxβ and then insert Eq. (9) (after changing the dummy index from σ → β) giving
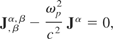
which can be written as
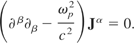
5.3.5. A solution to the wave equation
Try a solution of
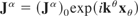
where
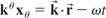
with
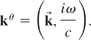
The d'Alembertian can be written as

So, the d'Alembertian operating on the four-current gives
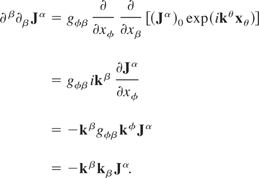
Eq. (19) reduces to
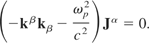
So, either there are no four-currents or
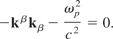
This equation gives the dispersion relation of the wave equation (19) using the solution (20).
5.3.6. The dispersion relation for the four-current wave equation
Now, an invariant of Eq. (22) is
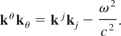
An invariant of Eq. (23) is also obtained after a little algebra
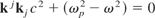
where kjkj is the length of the vector
.
Eq. (24) is the dispersion relation of the ordinary wave through the plasma. It must be noted that this derivation includes the effect of magnetic fields as nothing was assumed about the form of the electromagnetic field tensor. This dispersion relation is also a relativistic invariant (due to the squares) and has zero length in all reference frames. That is, it is a null vector.
Also from Eq. (24), it can be seen that when
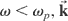
is imaginary and the wave will reflect. This has ascribed a physical meaning to the plasma frequency and it is no longer just a numerical constant.
5.3.7. The electric and magnetic response of the charged fluid
An alternate and simpler derivation of the preceding section is the following:
Set Eq. (8) equal to Eq. (3):
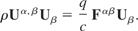
After some rearrangement, we have
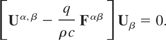
So, for the linear cases, either Uβ = 0 (No velocity caused by the incident electromagnetic radiation which is not physically possible) or
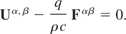
Differentiate with respect to dxβ and insert Eq. (9) and Eq. (10) to obtain
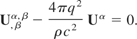
Now, use Eq. (14) to obtain
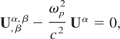
i.e.,

where the d'Alembertian is defined by
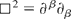
.
Thus, Uα obeys the same wave equation as the four-current. This is to be expected since the four-current can be defined as a linear function of the velocity. The solution to the wave Eq. (27) is
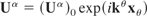
with the dispersion relation given by Eq. (24). It should be noted that the above is valid for all magnetic fields as it makes no assumption as to the form of the electromagnetic field tensor.
5.3.8. The derivation of the Magnetic permeability of plasma
Utilizing the above model, further physical insights can be gained about the interaction of electromagnetic radiation with plasma. Specifically we will investigate the magnetic response of the plasma.
Now, rearrange Eq. (25) to give
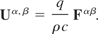
It is a collection of equations and individual sets of equations that can be selected by a suitable choice of index. To select the time derivatives of the spatial components of the four-velocity, let α → j and β → 4, so we obtain
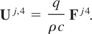
By utilizing the definition of the electromagnetic field tensor, Eq. (29) becomes
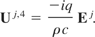
This equation can be recasted utilizing the fact that dx4 = icdt as follows:
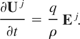
Eq. (31) now describes Eq. (29) in space + time terminology. It is to be noted that this expression is for the general reference frame such that all the Lorentz factors are implicit.
Using the fact that the velocities Uj are the time derivative of the displacements rj and then rearranging, an expression for the displacements becomes
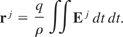
Apply an oscillating electric field to the charged fluid. The form of the oscillating field is:
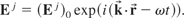
Inserting Eq. (33) into Eq. (32) and doing the dual integrals with respect to time leads to the following:
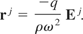
The polarization three-vector

is defined in component form as
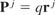
which when Eq. (34) is introduced becomes
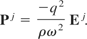
There is an alternative expression for the polarization 3-vector using the permeability χe
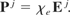
Thus, χe can be identified as
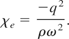
From Eq. (14), Eq. (37) can be recasted as follows
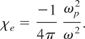
It must be noted that ω is the frequency of the incident radiation and that ωρ is the plasma frequency.
The dielectric constant can be determined from the relation
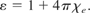
Insert Eq. (38) into the dielectric expression to obtain
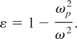
The above equation shows that the plasma is dispersive since ε depends on frequency. That is, different frequencies propagate at different rates. From the dispersion relation (24), it can be seen that there are some frequencies at which the electromagnetic wave will not propagate.
The dispersion relation (24) can be used to identify the refractive index η for the plasma. Using
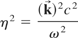
Eq. (24) can be rearranged to get
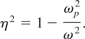
The expression for the dielectric of the plasma is derived from the electric field component of the incident radiation. The permeability can be derived from using both the refractive index and the dielectric constant. The expression required is
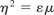
where μ is the magnetic permeability of this plasma.
Insert Eqs. (39) and (40) into Eq. (41). Then rearrange to get μ being of unit value. Since
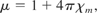
it is clear that χm = 0. This means that the magnetic susceptibility χm is zero in the plasma.
The collisionless plasma under the influence of a magnetic field is neither para, ferro, or diamagnetic. There is no response of the plasma to an applied electromagnetic field other than the Lorentz motion of the macroscopic particle (fluid element). This is a result of fundamental importance to all plasma researches who have assumed this result for many decades without rigorous proof or knowledge of the generality of its application.
5.3.9. A pressure based modification to the model
Here we will investigate a fluid that has a pressure profile. In this model, Eq. (3) is unmodified, so
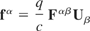
but Eq. (8) is modified to give (Synge, 1965; Schutz, 1985)

where p is the pressure and is a scalar.
As done previously, equate Eqs. (3) and (42) and define the following
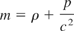
to give
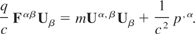
Rearranging and collecting like terms gives

Now if the pressure is constant or is slowly varying in space and time, then the derivative of the pressure is approximately zero. Hence Eq. (44) becomes

The nonlinear case will not be treated here. The linear cases allow only the bracketed section as the non trivial solution. Thus,
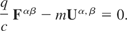
To investigate the wave properties implied by Eq. (45), the equation must be differentiated with respect to dxβ giving

Eq. (43) differentiates to
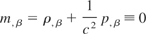
and so gives

This is similar to Eq. (26) before Eq. (9) is inserted. It will then lead directly to a wave equation of the form (27), but noting that the mass density term in the plasma frequency (14) is replaced by the modified mass density term (43).
Mathematically speaking, Eq. (46) implies that modified mass density term (43) can directly substitute the mass density term, and any derivative can be treated as if the modified mass density term is constant. This is borne out by the fact that the wave equation is the same as Eq. (27) except the modified mass density term substitutes for the mass density term.
Thus, the conclusion that the magnetic permeability is unity still holds under the pressure conditions pursuant to the above analysis.
6. CONCLUSIONS AND FURTHER WORK
This paper has been a relativistic investigation of electromagnetic radiation and it's interaction with matter in which I have investigated the form of the response of the medium to incident electromagnetic waves.
By investigating in detail the existing status of plasma theory, a common weakness was identified. Most authors assumed the magnetic response of the medium to be negligible and did not consider all relativistic effects. By extending and modifying such theories, a more complete description can be obtained. I have rendered the nonlinear time-dependent ponderomotive force of Hora in its most complete form by casting it as a four-force. The resulting four-force obeys gauge and Lorentz invariance principles and has a symmetric stress-energy tensor. This ponderomotive four-force now contains the magnetic response terms which renders it more complete. This force has the added strength of obeying the appropriate relativistic conservation laws. This reformulation will be of great importance to those who are attempting to attain inertial confinement fusion by clarifying and extending the existing theory.
Many authors have assumed that the magnetic permeability is unity in plasma. A number of plausibility arguments have been given to justify this assumption, but no rigorous proof has been offered. By creating a formulation which from the outset contains the magnetic response factors, I have proven from first principles the fundamental result that the value of the magnetic permeability is indeed unity. I have further shown that this result is valid in the general reference frame. This theory also contained variables like the plasma frequency in a way that was not contrived. This theory has the added strength of obeying Lorentz and gauge invariance principles. Being Lorentz invariant, this four-force has the added advantage of containing the magnetic and electric fields in a single “Faraday” tensor and hence involves magnetic response terms. This allows plasma physicists to continue secure in the knowledge that their base assumption is correct over a general range of velocities.
Throughout this paper, the Gaussian set of units was used. The reason for these units still being utilized in the plasma physics field is historic. In Appendix B of the PhD Thesis of Rowlands (1997), an argument is made for the use of Natural Gaussian units (c = 1 etc.). “Standard International units are not as symmetric in the expressions relating electric and magnetic phenomena. This adds weight to the fact that the symmetries implied in a space-time formulation should be carried through to the constituent equations in order to have the simplest defined system. That is to say, that the best system of units defined in 3-space may not necessarily translate to being the best system of units in a space-time manifold.” Thus, when natural units are used, the Gaussian system of units has inherent symmetries that are not readily apparent in the standard international system of units.
Further work could be done by codifying the dynamics of the nonlinear ponderomotive four-force into a computer simulation. This would be advantageous to understanding any relativistic consequences of this force e.g., how the extra magnetic field terms would affect the dynamics of the plasma. An investigation as to the effect of intense magnetic fields on the plasma should provide some interesting physics.


