INTRODUCTION
Interaction of intense laser pulses with matter and the effect of lasers on molecular processes such as dissociation, ionization, and conversion of fragments into the desired products are subjects of considerable interest (Tzallas et al., Reference Tzallas and Langeley2000; Hora, Reference Hora2004; Reference Hora2007; Malka & Fritzler, Reference Malka and Fritzler2004; Maslova et al., Reference Maslova, Shvedunov, Tunkin and Vinogradov2008; Brumer & Sharipo, Reference Brumer and Shapiro2009; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Navid and Zobdeh2009; Reference Sadighi-Bonabi, Yazdani, Cang and Hora2010a; Reference Sadighi-Bonabi, Hora, Riazi, Yazdani and Sadighi2010b; Sadighi-Bonabi & Rahimatollahpur, Reference Sadighi-Bonabi and Rahmatollahpur2010). The old dream of understanding the dynamics of photo-chemistry and achieving valuable products became transparent by real time observations of the transition-state region between reagents and products in 1994 (Zewail, Reference Zewail1994). Methane as an abundant natural gas is the most stable hydrocarbon at room temperature and is one of the major greenhouse gases with very high global warming potential.
Although, methane is a clean fuel among other conventional fuels and it is a primary fossil fuel however, the conversion of methane into higher hydrocarbons and hydrogen has many advantages (Lunsford, Reference Lunsford2000; Yamani, Reference Yamani2005). These products may provide new feed stocks for chemical processes. In addition, the transportation of methane across remote and inaccessible geographic locations is a big challenge, which can be resolved by conversion techniques (Gondal et al., Reference Gondal, Yamani, Dastageer, Ali and Arfaj2003; Heng & Suhaili Idrus, Reference Heng and Suhaili Idrus2004). Moreover, on site liquefaction of methane can prevent contributing to the build-up of greenhouse gases. Because of the stability of methane the required energy is very high in the present large scale technologies such as indirect method of Fischer-Tropsch process or partial oxidation. These processes can be performed at very high temperatures and high pressures with expensive catalysts (Zepeda et al., Reference Zepeda, Villagómez and Joseph-Nathan1998; Dry, Reference Dry2002). Recently, researchers tried to unlock the secret of direct method of conversion of methane by studying the photo-catalytic conversion of methane, which have some advantages including partially selecting and low temperature processing of some desired chemical products (Gondal et al., Reference Gondal, Hameed, Yamani and Arfaj2004; Yuliati et al., Reference Yuliati, Itoh and Yoshida2008). However, this is an expensive method and wasting of valuable catalyst during this process. As a consequence, some other techniques should be sought.
One of the attractive alternative methods in resolving this problem is using intense pulse lasers without any catalysts (Gondal et al., Reference Gondal, Yamani, Dastageer, Ali and Arfaj2003). The control of organic chemistry with intense laser fields capable of controlling a system toward prescribed desired valuable products has been a main goal. However, the conversion amounts were not considerable.
Rapid advances in the development of intense short pulse lasers and the appearance of femtosecond laser pulses in the 1980s and an experienced pulse shaping technology the objective of controlling chemical reactions with coherent light was accomplished (Assion et al., Reference Assion, Baumert, Bergt, Brixner, Kiefer, Seyfried, Strehle and Gerber1998, Lezius et al., Reference Lezius, Blanchet, Rayner, Villeneave, Stolow and Yu2000). The production of ultra-short laser pulses allowed for the probe of reaction dynamics and molecular dynamic simulations at a time scale of nuclear motion and direct observation of molecular alignment (He et al., Reference He and Becker2008; Baker, Reference Baker, Robinson, Lein, Chirilă, Torres, Bandulet, Comtois, Kieffer, Villeneuve, Tisch and Marangos2008). Modern chemistry and optimal control theory is dedicated to the study of chemical reactions and ways to control the outcome of the reactions to maximize the yield of a desired product among other competing products. Nowadays femtosecond lasers are widely used in controlling chemical reactions and choosing the desired dissociation channels (Graham et al., Reference Graham, Fang, Ledingham, Sinohal, Mccanny, Smith, Kosmidis and Harrevelt2000; Bauer & Ceccherini, Reference Bauer and Ceccherini2001; Picon et al., Reference Picon, Bahabad, Kapteyn, Murnane and Becker2011; Irani et al., Reference Irani, Zare, Navid, Dehghani and Sadighi-Bonabi2012). There have been a number of reports focused on the interaction of intense laser field with methane, most abundant organic trace gas in the atmosphere (Chen et al., Reference Chen, Wang, Wei, Lin, Hutton and Zou2011). Hering and Cornaggia (Reference Hering and Cornaggia1998) have studied the dissociation of methane and their results are based on the multi-electron ionization in the high intensity regime with quasi-classical trajectory calculation (Hering & Cornaggia, Reference Hering and Cornaggia1998).
During the dissociation of methane the produced methyl and methylene radicals constitute the building blocks of higher hydrocarbons (Sagan et al., Reference Sagan and Chyba1997; Harrevelt, 2006). Some other studies on the methane photo-chemistry also have appeared in atmospheric chemistry of planets and nanotechnology (Swain et al., Reference Swain, Vasisht and Tinetti2008; Bartus & Bródka, Reference Bartus and Bródka2011).
The photo dissociation of methane has been studied extensively based on the theoretical approaches (Wang et al., Reference Wang, Tang, Gao, Elshakre and Kong2003; Reference Wang, Song, Liu and Kong2006; Zare et al., Reference Zare, Irani, Navid, Dehghani, Anvari and Sadighi-Bonabi2013), however the important role of nine internal degrees of methane, does not allow explaining the process explicitly (Abu-samha & Madsen, Reference Abu-Samha and Madsen2009; Son & Chu, Reference Son and Chu2009). The experimental results can help to have better insight into the theoretical studies. To the best of our knowledge a comprehensive experimental conversion of methane by intense ultraviolet laser without any catalyst at atmospheric pressures was not reported.
In this paper, following our recent study on dissociation of methane (Zare et al., Reference Zare, Irani, Navid, Dehghani, Anvari and Sadighi-Bonabi2013), we investigated the dissociation of CH4 molecule and conversion into higher hydrocarbons using two wavelengths of 248 nm KrF laser and 355 nm of third harmonic of Nd:YAG laser both experimentally and theoretically. In the experimental part of this paper, the conversion of methane into other hydrocarbons and main yields are measured and analyzed in detail. In the theoretical part, the conversion efficiency of methane is calculated and compared with the experimental results.
EXPERIMENTAL SETUP
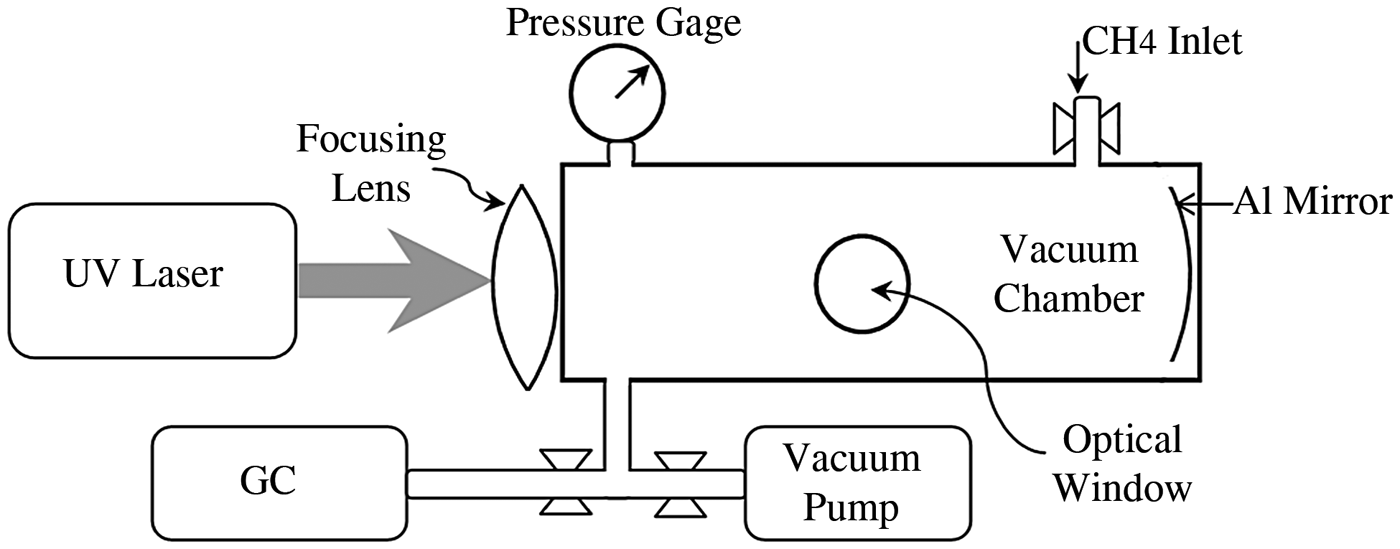
A schematic experimental setup is shown in Figure 1. Methane is exposed to ultraviolet laser sources in a cylindrical aluminum chamber with internal diameter and length of 3 cm and 10 cm, respectively, which is about 71 cm3 of chamber volume. The laser beam is focused by fused silica lens longitudinally through quartz window at the center of the cell. A pressure gauge is used to determine the gas pressure of the reaction chamber. Optical window is used to analyze the fluorescence light of unstable products such as CH, CH2, and CH3. A concave shaped aluminum plate at the end of the chamber reflects back the beam into the chamber for further absorption. Two mass flow controllers are used to evacuate the reaction chamber by a vacuum pump in order to fill it with proper methane gas. A gas chromatograph (GC) series B 5890 equipped with packed column and a flame ionization detector (FID) is used to analyze the reaction products. Helium was used as a carrier gas and acetylene, ethylene, and ethane were used as references. The reactor was evacuated to below 0.001 Pa and then pressurized with research-grade (99.999%) methane gas. Following the ultraviolet laser exposure, the reactor content was injected into the packed column of GC and the concentrations of final stable products were measured.
Fig. 1. Schematic view of the experimental setup.
EXPERIMENTAL RESULTS
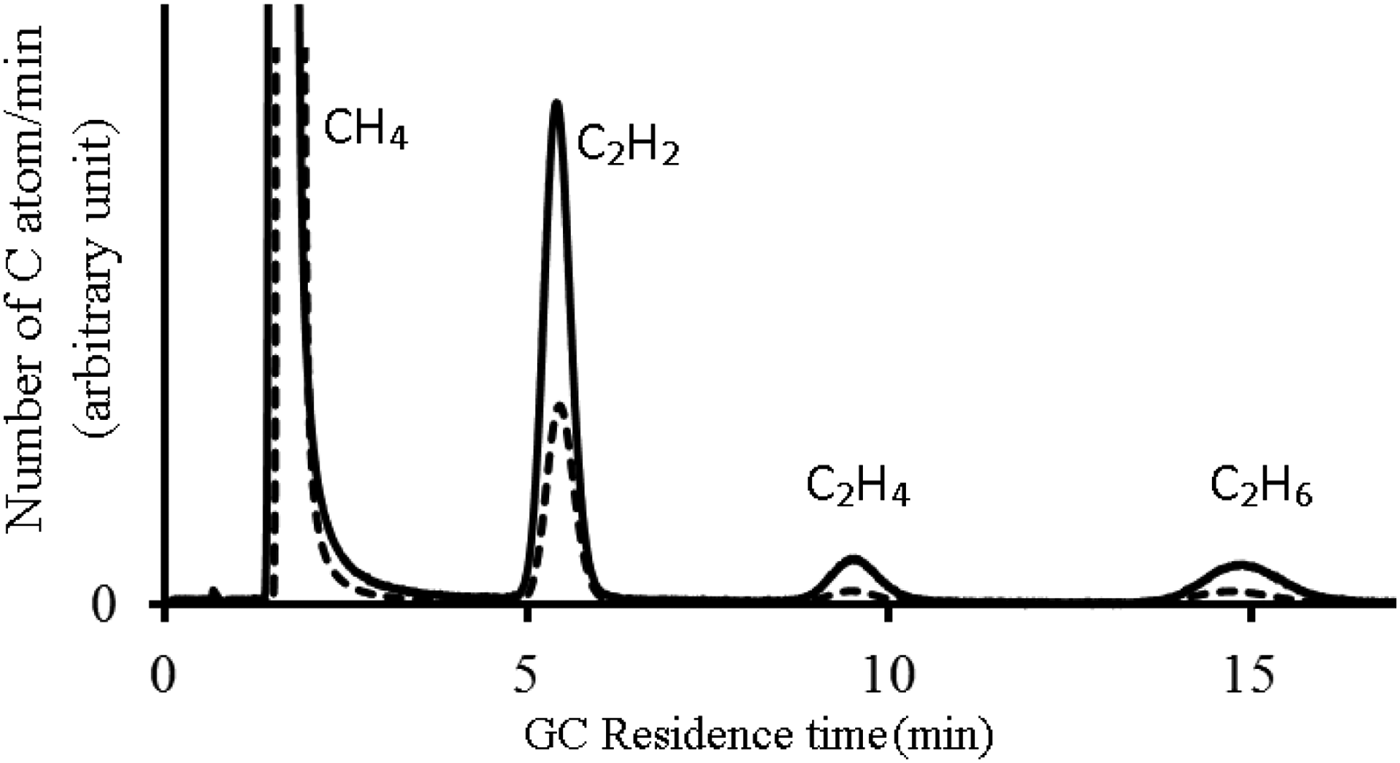
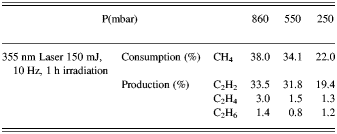
CH4 gas is irradiated with 355 nm (third harmonic of Nd:YAG) laser, for irradiation time of 1 h, repetition rate of 10 Hz, energy of 150 mJ per pulse and pulse duration of 10 ns for pressures of 250 mbar, 550 mbar, and 860 mbar. The chromatogram of conversion of methane into higher hydrocarbons of C2H2, C2H4, and C2H6 are indicated in Figure 2. It should be mentioned that in this GC system the FID response increases linearly with carbon number. Therefore, in chromatography graphs the area under each graph of every component is proportional to its carbon number. For 250 mbar pressure, the amount of this area for methane, acetylene, ethylene, and ethane are equal to 64.0, 31.9, 2.17, and 1.99, respectively (dashed line in Fig. 2). According to the number of carbon atoms for each component the amounts of 78%, 19.4%, 1.32%, and 1.2% are achieved for methane, acetylene, ethylene, and ethane, respectively. For 560 mbar pressure, the conversion efficiency of 65.9%, 31.76%, 1.5%, and 0.8% for methane, acetylene, ethylene and ethane are obtained, respectively (dotted line in Fig. 2). For 860 mbar pressure, the amounts of 62.0%, 33.5%, 3.0%, and 1.4% are achieved for the above mentioned order of components (solid line in Fig. 2).
Fig. 2. Chromatogram of conversion of methane into higher hydrocarbons using 355 nm Nd: YAG laser, for irradiation time of 1 h, repetition rate of 10 Hz, energy of 150 mJ per pulse and pulse duration of 10 ns for pressure of 250 mbar (dashed line), 550 mbar (dotted line) and 860 mbar (solid line). The peaks of the graph correspond to methane, acetylene, ethylene and ethane. The horizontal and vertical axes represent the GC residence time in minutes and the number of carbon atoms/min of produced components in arbitrary unit, respectively.
Considering the results of 355 nm laser the conversion efficiency of methane is improved by increasing the pressure. If this result is true for higher pressure it will be a promising result for higher conversion efficiency considerations which can be investigated in other works.
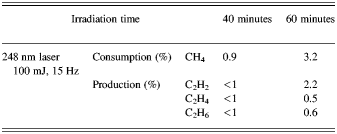
The results of conversion process using KrF laser at 248 nm is shown in Figure 3 for two different irradiation times. The chromatograms are for repetition rate 15 Hz, energy of 100 mJ per pulse, duration of 20 ns, pressure of 860 mbar for irradiation time of 40 min (dashed line) and 60 min. (solid line). The amounts of 99.1% for methane and less than 1% for three other components are obtained for 40 min irradiation time. In the case of 60 min irradiation time, the amount of methane is 96.7%, and the amount of produced components of acetylene, ethylene, and ethane are 2.2%, 0.5%, 0.6%, respectively. These results are much higher than the previous obtained values, which were obtained in some different experimental conditions (Romanzin et al., Reference Romanzin, Arzoumanian, Es-Sebbar, Jolly, Perrier, Gazeau and Bénilan2010).
Fig. 3. Chromatogram of conversion of methane into higher hydrocarbons using 248 nm KrF laser, for repetition rate 15 Hz, energy of 100 mJ per pulse, duration of 20 ns for pressure of 860 mbar for irradiation times of 40 min (dashed line) and 60 min (solid line). The peak values correspond to methane, acetylene, ethylene and ethane respectively. The horizontal and vertical axes represent the GC residence time in minutes and the number of carbon atoms/min of produced components in arbitrary unit, respectively.
In all experiments, temperature and pressure changes were not considerable. The total average power of irradiation of methane was 1.5 W by both laser systems. From the results presented for Nd:YAG laser, it is concluded that the conversion efficiency of methane increases with pressure and the maximum amount of methane consumption was 38.0% at 860 mbar. The experimental results are listed in Tables 1 and 2.
Table 1. The results of photo-conversion of methane by 355 nm Nd: YAG laser
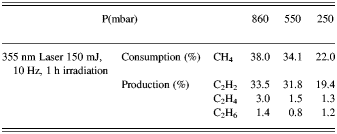
Table 2. The results of photo-conversion of methane by 248 nm KrF laser
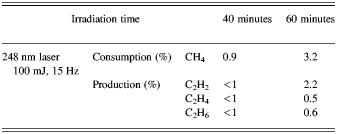
Based on the obtained data, despite of our first intuition, the conversion efficiency of 355 nm is much higher than the amounts measured for 248 nm. Laser beam characteristics are listed in Table 3.
Table 3. Characteristics of lasers used in experiments
NUMERICAL MODEL AND THEORETICAL CALCULATIONS
The dissociation of methane has been studied extensively using conventional ultraviolet sources (Mebel et al., Reference Mebel, Lin and Chang1997), ultraviolet or visible nanosecond lasers (Gondal et al., Reference Gondal, Yamani, Dastageer, Ali and Arfaj2003), and high power femtosecond lasers (Wang et al., Reference Wang, Tang, Gao, Elshakre and Kong2003; Kong et al., Reference Kong, Luo, Xu, Sharifi, Song and Leang2006). According to the dissociation energy of methane the multi-photon absorption is assumed to be the dominant process. Considering the calculated energy for excited states of methane, it is supposed that the methane goes to disintegration following the absorption of two and three photons from wavelengths of 248 nm and 355 nm, respectively from the first singlet electronic excited state. Theoretical study of multi-photon absorption of molecules is studied before (Bauer, Reference Bauer2002; Sugimori et al., Reference Sugimori, Ito, Takta, Ichitani, Nagao and Nishikawa2007).
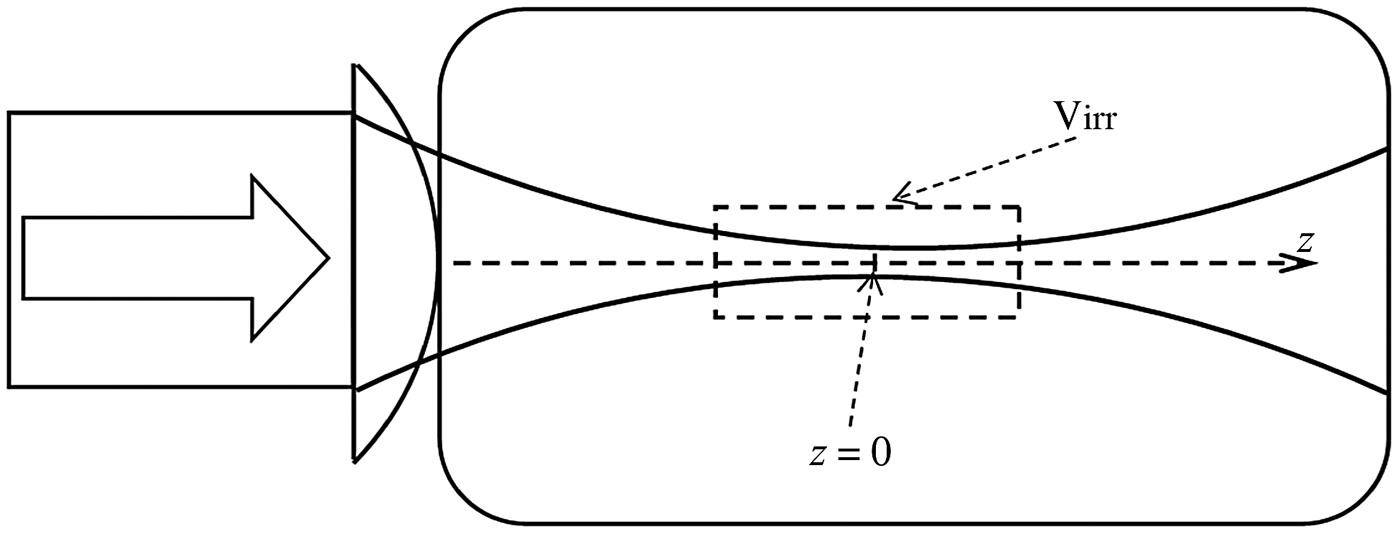
To clarify the conversion process and compare the theoretical values with the experimental results, the conversion efficiency of methane is also calculated theoretically. In order to simplify the calculations and assuming a model similar to the experimental condition of the interaction of laser pulses with methane, a spatial Gaussian beam is considered. Figure 4 indicates the focused laser beam by convex spherical lens and its propagation inside the reaction cell. The interaction of laser beam with methane gas occurs in a small region around the center of the cell. For a Gaussian laser beam, it is assumed that the reactions occur in a volume determined by Rayleigh length of the beam. The border of irradiation volume, V irr, around the focal length z = 0, is shown (dashed line) in Figure 4.
Fig. 4. Propagation of Gaussian laser beam through the reaction chamber. The border of the irradiation volume Virr is shown (dashed line) around focal point of the beam z = 0.
Considering the corrections due to the small irradiated volume in the cell (Romanzin et al., Reference Romanzin, Arzoumanian, Es-Sebbar, Jolly, Perrier, Gazeau and Bénilan2010) and applying the correction factor of V irr /V cell, the rate of n photon absorption of methane, γ, ( in photon·s−1·cm−2) can be written as
$${\rm \gamma}=\displaystyle{{V_{irr} } \over {V_{cell} }}{\rm \sigma} _n F_0 \lpar t\rpar ^n [ CH_4 ] \comma \;$$σn (photon−(n-1)·sn-1·cm2n·moleule−1) is the absorption cross section of n photons for methane, F 0 (t) is the photon flux (photon·s−1·cm−2) at z = 0 and at time t, and [CH 4 ] is the density of methane gas (molecule·cm−3). The value of σn for methane is used according to reference (Galasso, Reference Galasso1992).
By considering the z = 0 as focal point of a Gaussian beam, the cross-section S(z) at distance z from the focal point is given by
$$S\lpar z\rpar =S_0 [ 1+\lpar z/z_0 \rpar ^2 ] .$$Here, z 0 is the Rayleigh length of the Gaussian beam. The cross-section of the beam, S 0 , is estimated to be 0.63 mm2 and 1.4 × 10−3 mm2 for KrF and Nd: YAG lasers using ZEMAX optical software, respectively. The irradiated volume is taken as
$$V_{irr}=6z_0 A_0 .$$In order to computational simplicity the pulsed laser sources are approximated with an equivalent continuous photon source. For this purpose the quantity of F 0(t)n Eq. (1) is substituted by its average during one second:
$$\overline {F^n }=f \times \int\nolimits_{ - \infty }^{+\infty } {dt} F_0 \lpar t\rpar ^n .$$f is the repetition rate of the pulsed laser.
Previous studies indicate that the dissociation of methane is followed by different channels (Wang et al., Reference Wang, Liu, Min, Su, Bersohn, Preses and Larese2000):
$$CH_4 \buildrel {hv} \over \rightarrow \left\{\matrix{CH_3+H \hfill& & \lpar a\rpar \hfill \cr CH_2+H_2 \hfill & & \lpar b\rpar \hfill \cr ^1 CH_2+H+H & & \lpar c\rpar \hfill \cr ^3 \, CH_2+H+H & &\lpar d\rpar \hfill \cr CH+H_2+H & & \, \lpar e\rpar \hfill} \right.$$In this study, the dissociation probabilities of different channels for one photon of 121.6 nm wavelength absorption are also taken as an approximate value for n photon absorption process. Following the dissociation of methane, unstable components of CH x (x = 1,2,3) are produced at the reaction cell, which react with other fragments to form stable products. It is indicated that higher hydrocarbons formed by insertion of CH x radicals into C-C bonds. Immediately after the production of CH, CH2, CH3, H2, and H components, chemical reactions form new components. For the calculation of reaction products, we consider only components containing hydrogen and carbon atoms. Components with one to three carbon atoms are considered in chemical reactions for simplicity. The final components are the results of many complicated reactions. One of the reactions that contribute to the formation of C2H6 is:
$$\eqalign{& CH_4 \buildrel {hv} \over \rightarrow CH_3+H \cr & CH_4+CH_3 \leftrightarrow H+C_2 H_6 \cr & H+H\lpar +M\rpar \leftrightarrow H_2 \lpar +M\rpar }$$M is a particle that removes the kinetic energy of H atom and takes no part in the reaction. As a result, the final reaction can be summarized as
$$2CH_4 \to C_2 H_6+H_2 .$$According to the ionization energy (12.61 eV) of methane, the ionized components are neglected in this model and in the numerical calculations the 46 reactions containing 16 components of C, CH, 1CH2, 3CH2, CH3, CH4, C2H, C2H2, C2H3,C2H4, C2H5,C2H6, C3H7, C3H8, H, H2 are considered. The differential equation governing the rate of change of density of component α, Aα, is determined by
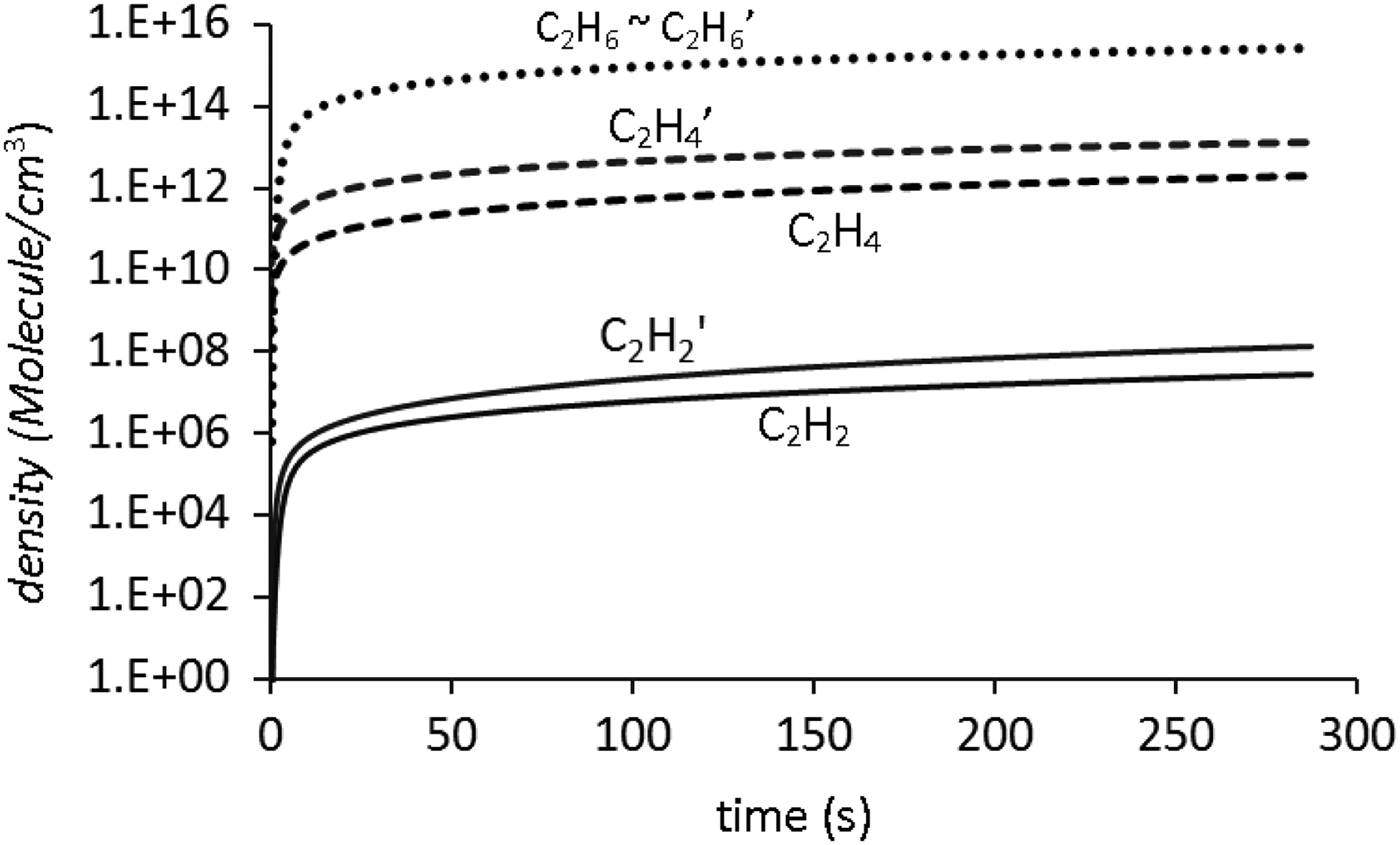
$$\displaystyle{d \over {dt}}A_{\rm \alpha}=R_{\rm \alpha}+R^{\prime}_{\rm \alpha}\comma \; \, {\rm \alpha}=1\comma \; ...\comma \; 16.$$where R α and R′a are the rate of change of the component α due to laser radiation and chemical reactions, respectively. Reaction rate constants are given in the literature (Tsang et al., Reference Tsang and Hampson1986). The number of 16 differential equations are solved numerically by the fourth order Runge-Kutta method. Figure 5 shows the calculated density of stable hydrocarbons as a function of time at atmospheric pressure from t = 0 to t = 300 second in the cell for KrF and Nd:YAG lasers, respectively.
Fig. 5. Numerical results of densities of C2H2, C2H4 and C2H6 as a function of time for about 5 minutes, in the cell. Primed and unprimed notations are used for Nd: YAG and KrF laser irradiation results, respectively. The calculated results are obtained for data of Table 3 at atmospheric pressure.
It is shown in Figure 5 that C2H6 has approximately the same value for two lasers, however, for C2H2 and C2H4 it is different. According to these results the most of the methane molecules are converted to C2H6. This result emerges from the above assumptions that have been supposed for different channels. Simply for two and three photon absorption of methane the probability of different dissociation channels may be different from those of 121.6 nm wavelength. Moreover, methane may absorb more than two and three photons, from 355 nm and 248 nm laser sources, respectively. According to the ionization energy of methane this assumption leads to ionization followed by dissociation mechanism of methane. The theoretical results may lead to good agreement with experimental results by considering the mentioned factors and introducing the complete ion molecular reactions as
$$\eqalign {& \rm CH_{4}^{+}+ CH_{4}^{+}\rightarrow CH_{5}^{+}+CH_{3}\comma \; CH_{5}^{+}+ CH_{4}\rightarrow C_{2} H_{5}^{+}\cr & \rm\quad + 2H_{2}\comma \; CH^{+}+ CH_{4}\rightarrow C_{2}H_{5}^{+}\comma \; CH^{+}+ C_{2}H_{2} \rightarrow C_{2} H_{3}^{+}\cr & \rm \quad + C\comma \; CH_{2}^{+}+ CH_{4}\rightarrow C_{2}H_{6}^{+}\comma \; CH_{3}^{+}+ CH_{4} \rightarrow C_{2} H_{5}^{+}\cr & \rm \quad + H_{2}\comma \; CH_{4}^{+}+ C_{2}H_{4}\rightarrow C_{2} H_{5}^{+}+ CH_{3}\comma \; \cr & \quad \rm CH_{4}^{+} + H_{2} \rightarrow CH_{5}^{+}+ H\comma \; C_{2} H^{+}+ C_{2}H_{2}\rightarrow C_{2}H_{3}^{+}+ \cr & \quad \rm C_{2}\comma \; C_{2}H^{+}+ H_{2} \rightarrow C_{2}H_{3}^{+}\comma \; C_{2}H_{2} ^{+}+ CH_{4}\rightarrow C_{2} H_{3}^{+}\cr & \quad + \rm CH_{3}\comma \; C_{2}H_{2}^{+}+ C_{2}H_{2}\rightarrow C_{2}H_{3}^{+}+ C_{2}H\comma \; C_{2}H_{2}^{+}+ \cr & \quad \rm C_{2}H_{4}\rightarrow C_{2}H_{4}^{+}+ C_{2}H_{2\comma } C_{2}H_{2}^{+}+ H_{2}\rightarrow \cr & \quad \rm C_{2}H_{3}^{+}+ H\comma \; C_{2}H_{3}^{+}+ H_{2}\rightarrow C_{2}H_{4}^{+}+ H\comma \; }$$where components containing one and two carbon numbers are considered (Sieck & Lias, Reference Sieck and Lias1976). Comparing the numerical results of two lasers show that the conversion efficiency with 355 nm laser is remarkable in comparison to 248 nm laser for C2H2 and C2H4 products, which is the result of intensity considerations. In this study Nd: YAG laser is focused to smaller volumes than KrF laser with little spherical aberrations and produces higher intensities than 248 nm KrF laser. Therefore the numerical results depend strongly on focused intensity that is a logical result for multi-photon process.
CONCLUSIONS
In this paper, the experimental and theoretical conversion of methane into higher hydrocarbons is investigated in order to estimate the products. According to the experimental results the final products of C2H2, C2H4, and C2H6 are the same kind for both lasers. However, their amounts are very different. As a remarkable feature of experimental results, for one hour irradiation of methane by 1.5 watts average power at the pressure of 860 mbar, C2H2 has the highest conversion yield with the amounts of 33.5% and 2.2% for Nd:YAG and KrF lasers, respectively. On the theoretical study the conversion efficiency of methane is implemented using fourth order Runge-Kutta method. In the numerical model, C2H6 has the highest density which is the result of current assumptions. It is concluded that other theoretical approach of ionized components in reaction cell should be considered to explain these measurements, properly.
As satisfying result, the wavelength dependence conversion of methane shows the selective capability in this process. If there is possible to change the laser parameters, the output products will be controllable. In this regard genetic algorithms can be the best choice to maximize the desired products.
ACKNOWLEDGMENTS
The authors want to thank Pars oil and gas company of ministry of oil for their support of this project through contract number PT131. We also acknowledge the research deputy of Sharif University of Technology.
