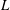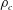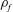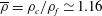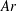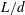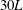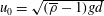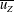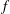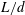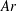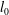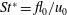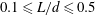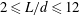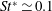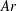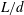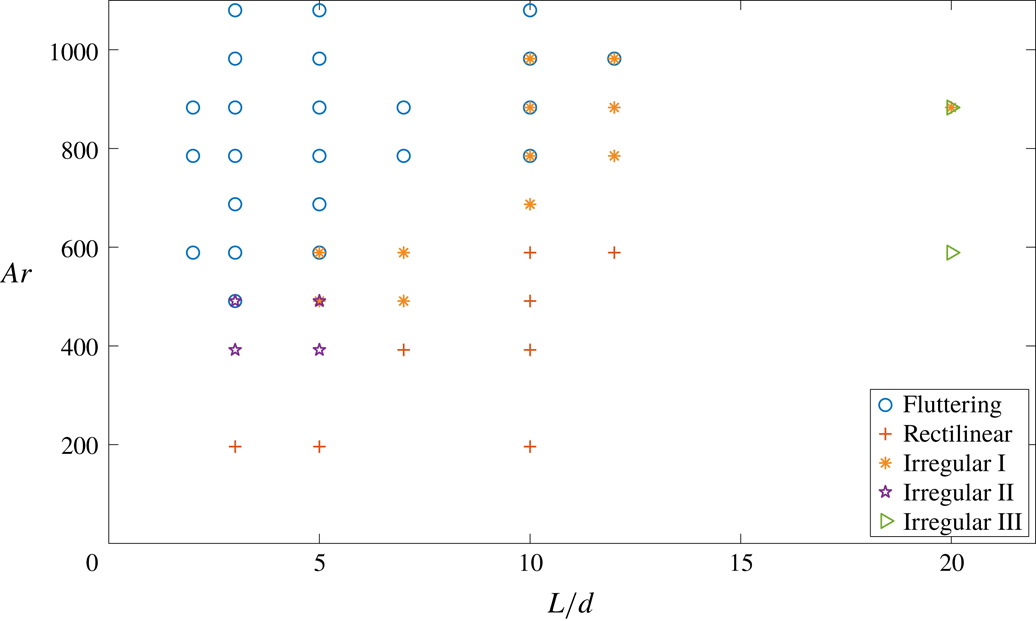1 Introduction
Three-dimensional bodies falling or rising under the effect of buoyancy in a fluid at rest have been a subject of continuous interest for the variety and attractiveness of the types of path that they display. Non-vertical (e.g. oblique) or non-rectilinear (e.g. periodic, chaotic,
![]() $\ldots$
) paths are known to be the result of the complex coupling between the flow generated by the body motion (in particular, the wake structure) and the degrees of freedom in translation and rotation of the body. The case of the freely moving sphere illustrates the strong influence of the control parameters on the coupling between the fluid and the moving body, providing a remarkable diversity in the styles of path and associated wakes (see Auguste & Magnaudet Reference Auguste and Magnaudet2018, and references therein). For this singular geometry, the control parameters are the body to fluid relative density
$\ldots$
) paths are known to be the result of the complex coupling between the flow generated by the body motion (in particular, the wake structure) and the degrees of freedom in translation and rotation of the body. The case of the freely moving sphere illustrates the strong influence of the control parameters on the coupling between the fluid and the moving body, providing a remarkable diversity in the styles of path and associated wakes (see Auguste & Magnaudet Reference Auguste and Magnaudet2018, and references therein). For this singular geometry, the control parameters are the body to fluid relative density
![]() $\overline{\unicode[STIX]{x1D70C}}$
, and the Archimedes number
$\overline{\unicode[STIX]{x1D70C}}$
, and the Archimedes number
![]() $Ar$
comparing buoyancy and viscosity effects, defined as
$Ar$
comparing buoyancy and viscosity effects, defined as
where
![]() $\unicode[STIX]{x1D70C}_{c}$
is the density of the solid body,
$\unicode[STIX]{x1D70C}_{c}$
is the density of the solid body,
![]() $\unicode[STIX]{x1D70C}_{f}$
is the fluid density,
$\unicode[STIX]{x1D70C}_{f}$
is the fluid density,
![]() $\unicode[STIX]{x1D708}$
is the fluid kinematic viscosity,
$\unicode[STIX]{x1D708}$
is the fluid kinematic viscosity,
![]() $g=9.81~\text{m}~\text{s}^{-2}$
is the magnitude of the gravitational acceleration and
$g=9.81~\text{m}~\text{s}^{-2}$
is the magnitude of the gravitational acceleration and
![]() $D$
is a characteristic dimension of the body, the diameter in the case of a sphere. Once the mean rise/fall velocity of the body is known, a Reynolds number
$D$
is a characteristic dimension of the body, the diameter in the case of a sphere. Once the mean rise/fall velocity of the body is known, a Reynolds number
![]() $Re$
can be defined, enabling the comparison with the case of a fixed body, the corresponding velocity being then the upcoming mean flow velocity. In the case of non-spherical bodies, the anisotropy of the body has also an influence on the fluid–body coupling, by impacting the flow structure as well as the response of the body to the hydrodynamic loads. Wake instability depends on the body geometry and vortex formation is modified as soon as the symmetry axis of the body changes its orientation with respect to the body velocity. As well, non-sphericity makes anisotropic the generalized inertia tensors, involving proper and added-mass contributions, so that the ability of the body to react to hydrodynamic efforts is anisotropic. The influence of a control parameter characterizing the body non-sphericity on the properties and characteristics of the different paths, as well as on the transitions between them, is emphasized in the investigations on freely moving disks of various thickness-to-diameter ratios or two-dimensional plates of various thickness-to-width ratios (see Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). At variance with the latter geometries, the free motion of elongated finite-length circular cylinders received until now little attention. It is however one of the simplest three-dimensional geometries, characterized by the elongation ratio,
$Re$
can be defined, enabling the comparison with the case of a fixed body, the corresponding velocity being then the upcoming mean flow velocity. In the case of non-spherical bodies, the anisotropy of the body has also an influence on the fluid–body coupling, by impacting the flow structure as well as the response of the body to the hydrodynamic loads. Wake instability depends on the body geometry and vortex formation is modified as soon as the symmetry axis of the body changes its orientation with respect to the body velocity. As well, non-sphericity makes anisotropic the generalized inertia tensors, involving proper and added-mass contributions, so that the ability of the body to react to hydrodynamic efforts is anisotropic. The influence of a control parameter characterizing the body non-sphericity on the properties and characteristics of the different paths, as well as on the transitions between them, is emphasized in the investigations on freely moving disks of various thickness-to-diameter ratios or two-dimensional plates of various thickness-to-width ratios (see Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). At variance with the latter geometries, the free motion of elongated finite-length circular cylinders received until now little attention. It is however one of the simplest three-dimensional geometries, characterized by the elongation ratio,
![]() $L/d$
, where
$L/d$
, where
![]() $d$
is the diameter and
$d$
is the diameter and
![]() $L$
the length of the cylinder. Moreover, this geometry aroused the surge of developments concerning wake instability and three-dimensional aspects of nominally two-dimensional wake flows about fixed cylinders (see Williamson Reference Williamson1996; Inoue & Sakuragi Reference Inoue and Sakuragi2008) and elastically mounted cylinders undergoing vortex-induced vibrations (see Williamson & Govardhan Reference Williamson and Govardhan2004). It is therefore the focus of the present investigation.
$L$
the length of the cylinder. Moreover, this geometry aroused the surge of developments concerning wake instability and three-dimensional aspects of nominally two-dimensional wake flows about fixed cylinders (see Williamson Reference Williamson1996; Inoue & Sakuragi Reference Inoue and Sakuragi2008) and elastically mounted cylinders undergoing vortex-induced vibrations (see Williamson & Govardhan Reference Williamson and Govardhan2004). It is therefore the focus of the present investigation.
The problem of an infinitely long circular cylinder free to move in any direction perpendicular to its axis is a two-dimensional counterpart to the case of the sphere, and its characteristic dimension
![]() $D$
is the cylinder diameter. To investigate the coupling between the wake instability and path oscillations, Namkoong, Yoo & Choi (Reference Namkoong, Yoo and Choi2008) performed numerical simulations of the two-dimensional motion of a freely falling/rising infinitely long circular cylinder in an infinite fluid, but considered also situations of partially restrained motion in translation and rotation of the body. They focused on density ratios
$D$
is the cylinder diameter. To investigate the coupling between the wake instability and path oscillations, Namkoong, Yoo & Choi (Reference Namkoong, Yoo and Choi2008) performed numerical simulations of the two-dimensional motion of a freely falling/rising infinitely long circular cylinder in an infinite fluid, but considered also situations of partially restrained motion in translation and rotation of the body. They focused on density ratios
![]() $0.5<\overline{\unicode[STIX]{x1D70C}}<4$
and Reynolds numbers between
$0.5<\overline{\unicode[STIX]{x1D70C}}<4$
and Reynolds numbers between
![]() $65$
and
$65$
and
![]() $185$
, corresponding to an unsteady wake exhibiting periodic vortex shedding in the case of a fixed cylinder. They observed that vortex shedding induces a low-amplitude periodic motion of the cylinder, both in translation and rotation, with transverse displacements typically lower than
$185$
, corresponding to an unsteady wake exhibiting periodic vortex shedding in the case of a fixed cylinder. They observed that vortex shedding induces a low-amplitude periodic motion of the cylinder, both in translation and rotation, with transverse displacements typically lower than
![]() $0.1D$
(for instance
$0.1D$
(for instance
![]() $0.08D$
for
$0.08D$
for
![]() $Re\simeq 160$
and
$Re\simeq 160$
and
![]() $\overline{\unicode[STIX]{x1D70C}}=1.01$
). By partially restraining the cylinder translation or rotation, they further showed that the transverse motion of the cylinder delays the onset of vortex shedding, thus reducing the Strouhal number (of less than
$\overline{\unicode[STIX]{x1D70C}}=1.01$
). By partially restraining the cylinder translation or rotation, they further showed that the transverse motion of the cylinder delays the onset of vortex shedding, thus reducing the Strouhal number (of less than
![]() $15\,\%$
), whereas rotation has a negligible effect. A similar behaviour is found experimentally by Horowitz & Williamson (Reference Horowitz and Williamson2006, Reference Horowitz and Williamson2010) for cylinders with also two degrees of freedom in translation and one in rotation, although at much higher Reynolds numbers (
$15\,\%$
), whereas rotation has a negligible effect. A similar behaviour is found experimentally by Horowitz & Williamson (Reference Horowitz and Williamson2006, Reference Horowitz and Williamson2010) for cylinders with also two degrees of freedom in translation and one in rotation, although at much higher Reynolds numbers (
![]() $3500<Re<7000$
). For density ratios
$3500<Re<7000$
). For density ratios
![]() $\overline{\unicode[STIX]{x1D70C}}>0.54$
, they observed small-amplitude oscillations (about
$\overline{\unicode[STIX]{x1D70C}}>0.54$
, they observed small-amplitude oscillations (about
![]() $0.05D$
for
$0.05D$
for
![]() $Re\simeq 3800$
and
$Re\simeq 3800$
and
![]() $\overline{\unicode[STIX]{x1D70C}}=2.0$
), occurring at a frequency equal to the vortex shedding frequency for a stationary cylinder, and consistent with the Bénard–von Kármán vortex street observed in the wake of the body. This path was considered rectilinear by the authors owing to the negligible amplitudes involved, but also in contrast to the large-amplitude oscillatory motion observed for light cylinders (
$\overline{\unicode[STIX]{x1D70C}}=2.0$
), occurring at a frequency equal to the vortex shedding frequency for a stationary cylinder, and consistent with the Bénard–von Kármán vortex street observed in the wake of the body. This path was considered rectilinear by the authors owing to the negligible amplitudes involved, but also in contrast to the large-amplitude oscillatory motion observed for light cylinders (
![]() $\overline{\unicode[STIX]{x1D70C}}<0.54$
). In the latter case, they recorded displacement oscillations of amplitude of the order of
$\overline{\unicode[STIX]{x1D70C}}<0.54$
). In the latter case, they recorded displacement oscillations of amplitude of the order of
![]() $D$
in the transverse direction at a frequency approximately
$D$
in the transverse direction at a frequency approximately
![]() $1.3$
times smaller (and
$1.3$
times smaller (and
![]() $0.3D$
in the vertical direction at twice this frequency), in association with a wake structure comprising two vortex pairs generated per cycle. In the same configuration, Mathai et al. (Reference Mathai, Zhu, Sun and Lohse2017) investigated numerically the effect of both
$0.3D$
in the vertical direction at twice this frequency), in association with a wake structure comprising two vortex pairs generated per cycle. In the same configuration, Mathai et al. (Reference Mathai, Zhu, Sun and Lohse2017) investigated numerically the effect of both
![]() $\overline{\unicode[STIX]{x1D70C}}$
and
$\overline{\unicode[STIX]{x1D70C}}$
and
![]() $I^{\ast }=I_{p}/I_{f}$
, the particle moment of inertia
$I^{\ast }=I_{p}/I_{f}$
, the particle moment of inertia
![]() $I_{p}$
relative to that of the fluid
$I_{p}$
relative to that of the fluid
![]() $I_{f}$
, by varying them separately in the range
$I_{f}$
, by varying them separately in the range
![]() $[0.1,10]$
, thus covering heavy (
$[0.1,10]$
, thus covering heavy (
![]() $\overline{\unicode[STIX]{x1D70C}}\simeq 10$
) to light (
$\overline{\unicode[STIX]{x1D70C}}\simeq 10$
) to light (
![]() $\overline{\unicode[STIX]{x1D70C}}\simeq 0.1$
) cylinders. They separate for
$\overline{\unicode[STIX]{x1D70C}}\simeq 0.1$
) cylinders. They separate for
![]() $Ar\simeq 220$
(the corresponding
$Ar\simeq 220$
(the corresponding
![]() $Re$
is not specified) a regime of cylinder oscillation with weak to intermediate displacement amplitudes,
$Re$
is not specified) a regime of cylinder oscillation with weak to intermediate displacement amplitudes,
![]() $0<A<0.3D$
, dominated by the effect of the parameter
$0<A<0.3D$
, dominated by the effect of the parameter
![]() $\overline{\unicode[STIX]{x1D70C}}$
, from a regime dominated by the effect of the moment of inertia and the rotational degree of freedom, corresponding to higher amplitudes,
$\overline{\unicode[STIX]{x1D70C}}$
, from a regime dominated by the effect of the moment of inertia and the rotational degree of freedom, corresponding to higher amplitudes,
![]() $0.4D<A<0.75D$
. For
$0.4D<A<0.75D$
. For
![]() $Ar\simeq 500$
, the mass dominated regime extends until
$Ar\simeq 500$
, the mass dominated regime extends until
![]() $A\simeq 0.5D$
, and in the moment of inertia dominated regime, amplitudes almost double (ranging from
$A\simeq 0.5D$
, and in the moment of inertia dominated regime, amplitudes almost double (ranging from
![]() $0.6D$
to
$0.6D$
to
![]() $1.2D$
) when
$1.2D$
) when
![]() $I^{\ast }$
is varied. They also noted that the gradual transition from one regime to the other is accompanied by a change in the wake pattern, from the two single vortex shedding mode to the two vortex pair shedding mode identified by Horowitz & Williamson (Reference Horowitz and Williamson2010). They concluded that the rotational degree of freedom can have a significant influence on the trajectories, in particular on the frequency and amplitude of the body displacement, and on the wakes of freely rising isotropic bodies.
$I^{\ast }$
is varied. They also noted that the gradual transition from one regime to the other is accompanied by a change in the wake pattern, from the two single vortex shedding mode to the two vortex pair shedding mode identified by Horowitz & Williamson (Reference Horowitz and Williamson2010). They concluded that the rotational degree of freedom can have a significant influence on the trajectories, in particular on the frequency and amplitude of the body displacement, and on the wakes of freely rising isotropic bodies.
A question that can now be asked is whether the additional degrees of freedom associated with the free ends of a finite-length cylinder would result in different paths. In other words, what would be the effect of leaving free the cylinder ends; and of allowing the six degrees of freedom of the body to be excited by the surrounding flow structure, and to be coupled with it? Two lengths now characterize the body geometry, the diameter
![]() $d$
and the length
$d$
and the length
![]() $L$
. The behaviour of circular cylinders of finite span-length moving through still water by buoyancy was studied by Marchildon, Clamen & Gauvin (Reference Marchildon, Clamen and Gauvin1964) for
$L$
. The behaviour of circular cylinders of finite span-length moving through still water by buoyancy was studied by Marchildon, Clamen & Gauvin (Reference Marchildon, Clamen and Gauvin1964) for
![]() $70<Re<2400$
(
$70<Re<2400$
(
![]() $Re$
is based on
$Re$
is based on
![]() $d$
) and
$d$
) and
![]() $1.46<L/d<35$
, and by Chow & Adams (Reference Chow and Adams2011) for
$1.46<L/d<35$
, and by Chow & Adams (Reference Chow and Adams2011) for
![]() $200<Re<6000$
and
$200<Re<6000$
and
![]() $1\leqslant L/d\leqslant 90$
, in both cases for a wide range of cylinder materials and therefore densities, ranging from wood (
$1\leqslant L/d\leqslant 90$
, in both cases for a wide range of cylinder materials and therefore densities, ranging from wood (
![]() $\unicode[STIX]{x1D70C}_{c}=0.74~\text{g}~\text{cm}^{-3}$
) to gold alloy (
$\unicode[STIX]{x1D70C}_{c}=0.74~\text{g}~\text{cm}^{-3}$
) to gold alloy (
![]() $\unicode[STIX]{x1D70C}_{c}=11.7~\text{g}~\text{cm}^{-3}$
). For these extensive ranges of parameters, both studies record a periodic motion of the cylinder consisting of an angular oscillation of the symmetry axis (of amplitude larger than
$\unicode[STIX]{x1D70C}_{c}=11.7~\text{g}~\text{cm}^{-3}$
). For these extensive ranges of parameters, both studies record a periodic motion of the cylinder consisting of an angular oscillation of the symmetry axis (of amplitude larger than
![]() $20^{\circ }$
in Chow & Adams (Reference Chow and Adams2011)) associated with a periodic lateral deviation of the centre of gravity, about the cylinder configuration corresponding to the rectilinear path with the symmetry axis perpendicular to the mean fall velocity. Numerical simulations by Romero-Gomez & Richmond (Reference Romero-Gomez and Richmond2016) reproduced the results of Chow & Adams (Reference Chow and Adams2011). Jayaweera & Mason (Reference Jayaweera and Mason1965) investigated small cylinders made either of Perspex, steel or aluminium falling in liquid paraffin, sugar solutions of different concentrations or water, for Reynolds numbers ranging from less than 0.01 to approximately 1000. They observed that when eddies break away from the edges as well as the sides, the cylinder flutters with an amplitude of oscillation comparatively larger for shorter cylinders, but decreasing as the length increases, so that longer cylinders fall stably. They further mentioned that the transition from steady fall to fluttering is not abrupt. They however observed that it depends on
$20^{\circ }$
in Chow & Adams (Reference Chow and Adams2011)) associated with a periodic lateral deviation of the centre of gravity, about the cylinder configuration corresponding to the rectilinear path with the symmetry axis perpendicular to the mean fall velocity. Numerical simulations by Romero-Gomez & Richmond (Reference Romero-Gomez and Richmond2016) reproduced the results of Chow & Adams (Reference Chow and Adams2011). Jayaweera & Mason (Reference Jayaweera and Mason1965) investigated small cylinders made either of Perspex, steel or aluminium falling in liquid paraffin, sugar solutions of different concentrations or water, for Reynolds numbers ranging from less than 0.01 to approximately 1000. They observed that when eddies break away from the edges as well as the sides, the cylinder flutters with an amplitude of oscillation comparatively larger for shorter cylinders, but decreasing as the length increases, so that longer cylinders fall stably. They further mentioned that the transition from steady fall to fluttering is not abrupt. They however observed that it depends on
![]() $\overline{\unicode[STIX]{x1D70C}}$
, and that the critical value of
$\overline{\unicode[STIX]{x1D70C}}$
, and that the critical value of
![]() $Re$
above which fluttering occurs increases with increasing
$Re$
above which fluttering occurs increases with increasing
![]() $L/d$
; for steel cylinders with
$L/d$
; for steel cylinders with
![]() $L/d$
about
$L/d$
about
![]() $10$
, their critical value of
$10$
, their critical value of
![]() $Re$
is approximately
$Re$
is approximately
![]() $50$
. Marchildon et al. (Reference Marchildon, Clamen and Gauvin1964) observed the secondary motion for
$50$
. Marchildon et al. (Reference Marchildon, Clamen and Gauvin1964) observed the secondary motion for
![]() $Re$
greater than
$Re$
greater than
![]() $300$
, and in some cases as low as
$300$
, and in some cases as low as
![]() $80$
. It is worth pointing out that the latter value is higher than the critical Reynolds number corresponding to the onset of unsteadiness in the wake behind a fixed two-dimensional cylinder of infinite span,
$80$
. It is worth pointing out that the latter value is higher than the critical Reynolds number corresponding to the onset of unsteadiness in the wake behind a fixed two-dimensional cylinder of infinite span,
![]() $Re_{c}\simeq 47$
. However, for a cylinder held in an upcoming flow, the transition of its wake from a stationary to a periodic state is strongly dependent on the elongation ratio
$Re_{c}\simeq 47$
. However, for a cylinder held in an upcoming flow, the transition of its wake from a stationary to a periodic state is strongly dependent on the elongation ratio
![]() $L/d$
of the cylinder. The experiments by Schouveiler & Provansal (Reference Schouveiler and Provansal2001) and Provansal, Schouveiler & Leweke (Reference Provansal, Schouveiler and Leweke2004) for cylinders with free hemispherical ends and the numerical simulations by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with free flat faces indicate that this transition occurs at increasing critical Reynolds numbers
$L/d$
of the cylinder. The experiments by Schouveiler & Provansal (Reference Schouveiler and Provansal2001) and Provansal, Schouveiler & Leweke (Reference Provansal, Schouveiler and Leweke2004) for cylinders with free hemispherical ends and the numerical simulations by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with free flat faces indicate that this transition occurs at increasing critical Reynolds numbers
![]() $Re_{c}$
when the elongation ratio decreases, typically
$Re_{c}$
when the elongation ratio decreases, typically
![]() $Re_{c}\simeq 100$
for
$Re_{c}\simeq 100$
for
![]() $L/d=5$
and
$L/d=5$
and
![]() $Re_{c}\simeq 200$
for
$Re_{c}\simeq 200$
for
![]() $L/d=1$
. Furthermore, the numerical investigation by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) disclose the existence of a variety of wake structures for
$L/d=1$
. Furthermore, the numerical investigation by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) disclose the existence of a variety of wake structures for
![]() $40\leqslant Re\leqslant 300$
and
$40\leqslant Re\leqslant 300$
and
![]() $1<L/d<100$
. Depending on the governing parameters, they identify five different vortex shedding patterns, corresponding to different equilibria reached from the vortical contributions generated from the flat bases or from the circular side of the cylinder. A question thus arises regarding what would be the paths associated with these different wake structures, or how would these be modified by the degrees of freedom of the cylinder.
$1<L/d<100$
. Depending on the governing parameters, they identify five different vortex shedding patterns, corresponding to different equilibria reached from the vortical contributions generated from the flat bases or from the circular side of the cylinder. A question thus arises regarding what would be the paths associated with these different wake structures, or how would these be modified by the degrees of freedom of the cylinder.
Besides the diversity of paths that could be observed, we have seen that the question of the existence of contrasted periodic motions of either low or large amplitude associated with different types of wake structure, permeates the literature on freely moving two-dimensional cylinders. As this feature is shared with disks, or spheres, conviction has grown steadily stronger that it constitutes a central question concerning the behaviour of freely moving bodies (Ern et al. Reference Ern, Risso, Fabre and Magnaudet2012). A decisive step forward to clarifying this question was achieved recently for short-length cylinders (‘disks’ of variable thickness), by a joint effort in both direct numerical simulations (Auguste, Magnaudet & Fabre Reference Auguste, Magnaudet and Fabre2013; Chrust, Bouchet & Dušek Reference Chrust, Bouchet and Dušek2013) and stability analysis of the fluid–body system (Tchoufag, Fabre & Magnaudet Reference Tchoufag, Fabre and Magnaudet2014). Tchoufag et al. (Reference Tchoufag, Fabre and Magnaudet2014) showed that instability of the fluid–body system leads to contrasted instability modes corresponding to different strengths of coupling between the body and the fluid depending on the time scales involved, resulting in different types of paths, in particular periodic motions of contrasted amplitude, but also involving different symmetry properties, embodied in planar or spiralling paths, or intermediate paths. The existence of modes corresponding to different strengths of coupling between the fluid and the body may also be expected to occur for finite-length elongated cylinders. Furthermore, these complex regimes are more likely to happen close to the onset of path instability where the rectilinear path gives way to periodic paths.
With the aim of shedding some light on the questions raised in this introduction, the present paper addresses experimentally the problem of freely falling finite-length cylinders for a large range of elongation ratios and Archimedes numbers corresponding to paths transitioning from rectilinear to periodic. The general guideline of this work is the following. We first present the experimental approach, in particular the experimental set-up allowing us to track the motion of the cylinders, and the image processing procedure implemented to have a non-biased and accurate description of it. A technical appendix complements the latter. We then present an overview of the different paths observed. The following sections are devoted to the quantitative characterization of the rectilinear and fluttering paths, presenting the measurement results and the corresponding scaling laws for the mean vertical motion as well as for the oscillatory translational and rotational motion of the body. A qualitative description is further provided, when possible, of the wake structure associated with the different paths. The paper ends with a discussion and concluding remarks.
2 Experimental tools
The bodies used in the experiments are ‘3D printed’ elongated circular cylinders of length
![]() $L$
and diameter
$L$
and diameter
![]() $d$
. The 3D printer was a ProJet®3510HD, and the material, VisiJet®M3-X, an ABS-like plastic. The choice of 3D printing allowed us for a very good control of the dimensions of the cylinders, with a resolution of
$d$
. The 3D printer was a ProJet®3510HD, and the material, VisiJet®M3-X, an ABS-like plastic. The choice of 3D printing allowed us for a very good control of the dimensions of the cylinders, with a resolution of
![]() $32~\unicode[STIX]{x03BC}\text{m}$
and an accuracy of
$32~\unicode[STIX]{x03BC}\text{m}$
and an accuracy of
![]() $\pm 2\unicode[STIX]{x2030}$
. When possible, cylinders were printed with their axis pointing upwards, so that the layers of material were deposited along the length of the cylinder, which allowed for a better accuracy when printing the rounded sides of the cylinder. However, this could not be done for very long cylinders (
$\pm 2\unicode[STIX]{x2030}$
. When possible, cylinders were printed with their axis pointing upwards, so that the layers of material were deposited along the length of the cylinder, which allowed for a better accuracy when printing the rounded sides of the cylinder. However, this could not be done for very long cylinders (
![]() $L/d=20$
), for they would bend during the printing process. Consequently, the latter were printed with their axis horizontal. The diameter of the cylinders ranged from 1.17 to 5.47 mm, and their lengths from 5.26 to 50.86 mm. The elongation ratio of the cylinders
$L/d=20$
), for they would bend during the printing process. Consequently, the latter were printed with their axis horizontal. The diameter of the cylinders ranged from 1.17 to 5.47 mm, and their lengths from 5.26 to 50.86 mm. The elongation ratio of the cylinders
![]() $L/d$
ranged from 2 to 20 and was known to within
$L/d$
ranged from 2 to 20 and was known to within
![]() $\pm 4.3\times 10^{-2}$
. The mass of all cylinders was measured using a scale accurate up to
$\pm 4.3\times 10^{-2}$
. The mass of all cylinders was measured using a scale accurate up to
![]() $10^{-4}$
g, which allowed us to know the density
$10^{-4}$
g, which allowed us to know the density
![]() $\unicode[STIX]{x1D70C}_{c}$
of the cylinders with an accuracy of
$\unicode[STIX]{x1D70C}_{c}$
of the cylinders with an accuracy of
![]() $\pm 0.2~\text{kg}~\text{m}^{-3}$
. The measured densities ranged from
$\pm 0.2~\text{kg}~\text{m}^{-3}$
. The measured densities ranged from
![]() $1140.0$
to
$1140.0$
to
![]() $1190.0~\text{kg}~\text{m}^{-3}$
, with two cylinders out of 163 having a measured density of
$1190.0~\text{kg}~\text{m}^{-3}$
, with two cylinders out of 163 having a measured density of
![]() $1111.0~\text{kg}~\text{m}^{-3}$
. The cylinders were kept submerged in water at all times to ensure that the porosity of the 3D printing material was constantly saturated with water, so that the body density would not change during the course of the experiments. At the minimum three different cylinders were printed for each couple of parameters
$1111.0~\text{kg}~\text{m}^{-3}$
. The cylinders were kept submerged in water at all times to ensure that the porosity of the 3D printing material was constantly saturated with water, so that the body density would not change during the course of the experiments. At the minimum three different cylinders were printed for each couple of parameters
![]() $(L,d)$
. No significant difference in behaviour was observed across all bodies having same dimensions
$(L,d)$
. No significant difference in behaviour was observed across all bodies having same dimensions
![]() $(L,d)$
, which ensures that the 3D printing was consistent both with dimensions and density of the bodies.
$(L,d)$
, which ensures that the 3D printing was consistent both with dimensions and density of the bodies.
The experiments were performed in a 1.70 m high glass tank with a square cross-section of 0.4 m (eight to eighty times larger than the particle length), filled with filtered tap water. The tank was located in an air-conditioned laboratory at
![]() $19\pm 1\,^{\circ }\text{C}$
. Water temperature was measured everyday using two thermocouples located at the top of the tank below the free surface, and at the bottom of the tank. Temperature differences between the top and the bottom of the tank were always smaller than
$19\pm 1\,^{\circ }\text{C}$
. Water temperature was measured everyday using two thermocouples located at the top of the tank below the free surface, and at the bottom of the tank. Temperature differences between the top and the bottom of the tank were always smaller than
![]() $1.1\,^{\circ }\text{C}$
. The water density was assumed to be
$1.1\,^{\circ }\text{C}$
. The water density was assumed to be
![]() $\unicode[STIX]{x1D70C}_{f}=1000~\text{kg}~\text{m}^{-3}$
, giving a density ratio of
$\unicode[STIX]{x1D70C}_{f}=1000~\text{kg}~\text{m}^{-3}$
, giving a density ratio of
![]() $\overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}=1.16\pm 1\,\%$
for all experiments.
$\overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}=1.16\pm 1\,\%$
for all experiments.
In addition to the density ratio
![]() $\overline{\unicode[STIX]{x1D70C}}$
and the elongation ratio
$\overline{\unicode[STIX]{x1D70C}}$
and the elongation ratio
![]() $L/d$
, the problem also depends on the Archimedes number, introduced previously and defined as,
$L/d$
, the problem also depends on the Archimedes number, introduced previously and defined as,
where the diameter of the sphere having a volume equal to that of the cylinder is taken here as the characteristic dimension of the body
![]() $D$
. With this definition of
$D$
. With this definition of
![]() $Ar$
based on
$Ar$
based on
![]() $D$
, experiments performed for various
$D$
, experiments performed for various
![]() $L/d$
at given
$L/d$
at given
![]() $Ar$
and
$Ar$
and
![]() $\overline{\unicode[STIX]{x1D70C}}$
allow us to investigate for given volume, and thus given buoyancy force, the influence of the cylinder elongation ratio on its behaviour.
$\overline{\unicode[STIX]{x1D70C}}$
allow us to investigate for given volume, and thus given buoyancy force, the influence of the cylinder elongation ratio on its behaviour.
The cylinders were released at the top of the tank, below the free surface, using tweezers. The release conditions were found to have no effect on the final behaviour of the cylinder. Even when released with their axis vertical, the cylinders rotated so that their axis was horizontal after a transient distance of fall less than
![]() $10d$
. The time between two releases was kept above
$10d$
. The time between two releases was kept above
![]() $5$
min, so that fluid perturbations in the tank caused by the fall of the previous cylinder could dissipate.
$5$
min, so that fluid perturbations in the tank caused by the fall of the previous cylinder could dissipate.
The cylinders were tracked along their fall with a travelling cart embarking two orthogonal cameras and the corresponding backlights allowing the observation of the bodies by shadowgraphy (figure 1
a,b). Travelling followed the cylinders over a distance of at least
![]() $200d$
. The elevation of the cart was recorded using a magnetic encoder with an accuracy of
$200d$
. The elevation of the cart was recorded using a magnetic encoder with an accuracy of
![]() $\pm 5~\unicode[STIX]{x03BC}\text{m}$
and an acquisition frequency of 1000 Hz. Since the shadowgraphy technique could not provide any information on the cylinder rotation about its axis, a pattern of random dots was drawn on a single cylinder out of the three available for each set of parameters
$\pm 5~\unicode[STIX]{x03BC}\text{m}$
and an acquisition frequency of 1000 Hz. Since the shadowgraphy technique could not provide any information on the cylinder rotation about its axis, a pattern of random dots was drawn on a single cylinder out of the three available for each set of parameters
![]() $(Ar,L/d,\overline{\unicode[STIX]{x1D70C}})$
. Use of front lightning allowed visualization of these patterns. No significant rotation of the cylinders about their axes was observed across all experiments, except in some cases during the short transient period following the release of the body from rest.
$(Ar,L/d,\overline{\unicode[STIX]{x1D70C}})$
. Use of front lightning allowed visualization of these patterns. No significant rotation of the cylinders about their axes was observed across all experiments, except in some cases during the short transient period following the release of the body from rest.

Figure 1. (a–b) Lateral and top view of the experimental set-up; (c) schematic view of the cylinder; (b–c) definition of the coordinate systems.
![]() $Z$
labels the vertical coordinate,
$Z$
labels the vertical coordinate,
![]() $(X,Y)$
the horizontal plane defined by the positions of the cameras. Origin O is fixed; axis
$(X,Y)$
the horizontal plane defined by the positions of the cameras. Origin O is fixed; axis
![]() $(\text{O}x)$
is parallel to the cylinder axis;
$(\text{O}x)$
is parallel to the cylinder axis;
![]() $(\text{O}z)$
is parallel to the horizontal plane
$(\text{O}z)$
is parallel to the horizontal plane
![]() $(X,Y)$
; plane
$(X,Y)$
; plane
![]() $(x,y)$
is vertical.
$(x,y)$
is vertical.
In addition, specific experiments were carried out to uncover the wake associated with the different types of path. The wake of the falling cylinders was visualized by coating the bodies with ink before releasing them in the tank. The ink chosen was highly concentrated and miscible in water. The cylinders were left submerged in pure ink during
![]() $15$
to 30 min before being released in the tank, to ensure that the amount of ink on the cylinder surface was sufficiently high so that it would be released during a satisfactory amount of time. The ink trail left by the cylinders during their fall was recorded with the same cameras and backlights used for shadowgraphy.
$15$
to 30 min before being released in the tank, to ensure that the amount of ink on the cylinder surface was sufficiently high so that it would be released during a satisfactory amount of time. The ink trail left by the cylinders during their fall was recorded with the same cameras and backlights used for shadowgraphy.
3 Image and signal processing
The images were acquired by two orthogonal cameras using shadowgraphy, i.e. by shedding light from behind the cylinder, which projects its shadow on the camera (figure 1
b). The output of the cameras is two grey scale image sequences in the planes
![]() $(X,Z)$
and
$(X,Z)$
and
![]() $(Y,Z)$
, where
$(Y,Z)$
, where
![]() $Z$
is the vertical coordinate and
$Z$
is the vertical coordinate and
![]() $(X,Y)$
map the horizontal plane. Two different sets of cameras were used. PCO2000® acquired
$(X,Y)$
map the horizontal plane. Two different sets of cameras were used. PCO2000® acquired
![]() $2048\times 2048$
pixels images at 14 Hz for recording slow periodic motions, and LaVision® sCMOS acquired
$2048\times 2048$
pixels images at 14 Hz for recording slow periodic motions, and LaVision® sCMOS acquired
![]() $2560\times 2160$
pixels images at 50 Hz for faster oscillations. The grey scale images were converted to black and white images using a thresholding operation. After binarization, the cylinder shadows on both cameras appear as a black area on a white background. The list of pixels belonging to the borders between black and white regions was then retrieved and labelled as the projection contours of the cylinder. Following the routine described in Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007), camera calibration was performed using a metallic cylinder of known diameter, which was placed at different known positions
$2560\times 2160$
pixels images at 50 Hz for faster oscillations. The grey scale images were converted to black and white images using a thresholding operation. After binarization, the cylinder shadows on both cameras appear as a black area on a white background. The list of pixels belonging to the borders between black and white regions was then retrieved and labelled as the projection contours of the cylinder. Following the routine described in Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007), camera calibration was performed using a metallic cylinder of known diameter, which was placed at different known positions
![]() $(X_{cal},Y_{cal})$
in the cameras field of view. The optical scale factor obtained with the camera calibration was used to convert the pixel data of the images in metres. Then, an iterative procedure crossing the information provided by the two cameras allowed the estimation of the three-dimensional (3-D) coordinates of the cylinder centre of gravity as those of the isobarycentres of the contour points of the cylinder projections. This method is however not sufficient to determine accurately the centre of gravity and orientation of the body, as it does not account for the deformations of the cylinder contour induced by the perspective projections onto the image plane of the cameras. It provides however a first estimation of the distance of the body centre to the camera which is used as an initialization of the refined following step implemented to correct perspective effects. This advanced technique, described in more details in the Appendix, is based on a geometric reprojection of the cylinder contour (Huang, Chen & Chia Reference Huang, Chen and Chia1996). It outputs the centre of the two flat faces of the cylinder, denoted
$(X_{cal},Y_{cal})$
in the cameras field of view. The optical scale factor obtained with the camera calibration was used to convert the pixel data of the images in metres. Then, an iterative procedure crossing the information provided by the two cameras allowed the estimation of the three-dimensional (3-D) coordinates of the cylinder centre of gravity as those of the isobarycentres of the contour points of the cylinder projections. This method is however not sufficient to determine accurately the centre of gravity and orientation of the body, as it does not account for the deformations of the cylinder contour induced by the perspective projections onto the image plane of the cameras. It provides however a first estimation of the distance of the body centre to the camera which is used as an initialization of the refined following step implemented to correct perspective effects. This advanced technique, described in more details in the Appendix, is based on a geometric reprojection of the cylinder contour (Huang, Chen & Chia Reference Huang, Chen and Chia1996). It outputs the centre of the two flat faces of the cylinder, denoted
![]() $S$
and
$S$
and
![]() $T$
, in a frame tied to the camera position. Using the vertical position of the travelling cart embarking the cameras, given by the magnetic encoder, the positions of
$T$
, in a frame tied to the camera position. Using the vertical position of the travelling cart embarking the cameras, given by the magnetic encoder, the positions of
![]() $S$
and
$S$
and
![]() $T$
can then be expressed in a frame tied to the tank (thereafter termed the laboratory frame), which is independent of the position of the travelling cart, and corresponding to the coordinate system
$T$
can then be expressed in a frame tied to the tank (thereafter termed the laboratory frame), which is independent of the position of the travelling cart, and corresponding to the coordinate system
![]() $(X,Y,Z)$
.
$(X,Y,Z)$
.
From the 3-D coordinates of
![]() $S$
and
$S$
and
![]() $T$
, the position of the cylinder centre of gravity can easily be deduced, as well as the angle
$T$
, the position of the cylinder centre of gravity can easily be deduced, as well as the angle
![]() $\unicode[STIX]{x1D703}$
between the cylinder axis and the horizontal, and the azimuthal angle
$\unicode[STIX]{x1D703}$
between the cylinder axis and the horizontal, and the azimuthal angle
![]() $\unicode[STIX]{x1D713}$
(see figure 1
c). Note that, as mentioned in § 2, experiments showed that no rotation of the cylinder about its symmetry axis could be observed, apart from the initial transient in some cases. However, transients, mainly related to the release of the body from rest, are discarded in the analysis and results that follow. The 3-D coordinates of the cylinder centre of gravity in the laboratory frame are hereafter denoted
$\unicode[STIX]{x1D713}$
(see figure 1
c). Note that, as mentioned in § 2, experiments showed that no rotation of the cylinder about its symmetry axis could be observed, apart from the initial transient in some cases. However, transients, mainly related to the release of the body from rest, are discarded in the analysis and results that follow. The 3-D coordinates of the cylinder centre of gravity in the laboratory frame are hereafter denoted
![]() $(X,Y,Z)$
, and the corresponding velocities
$(X,Y,Z)$
, and the corresponding velocities
![]() $(u_{X},u_{Y},u_{Z})$
. An example of the time evolution of the quantities characterizing the cylinder position and orientation can be seen in figure 2(a–d). In addition to the oscillatory behaviour, a slight drift is observed for the spatial coordinates
$(u_{X},u_{Y},u_{Z})$
. An example of the time evolution of the quantities characterizing the cylinder position and orientation can be seen in figure 2(a–d). In addition to the oscillatory behaviour, a slight drift is observed for the spatial coordinates
![]() $X$
and
$X$
and
![]() $Y$
, as well as for the azimuthal angle
$Y$
, as well as for the azimuthal angle
![]() $\unicode[STIX]{x1D713}$
. This drift was measured to be always less than
$\unicode[STIX]{x1D713}$
. This drift was measured to be always less than
![]() $6\,\%$
of the total falling height, to be not reproducible and could not be linked to any of the governing parameters. Its existence is attributed to large-scale low-velocity fluid motions in the tank, as they are difficult to avoid in a large tank. Similar irregular weak motions were observed in other experiments, and are mentioned in particular by Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007) for the study of rising disks. Following their approach that considers this drift as uncoupled with the main oscillatory motion of the body, a low-frequency filtering is applied to the time evolutions of the quantities characterizing the oscillatory behaviour of the body. The amplitude and phases of the periodic signals are then obtained using the Hilbert transform.
$6\,\%$
of the total falling height, to be not reproducible and could not be linked to any of the governing parameters. Its existence is attributed to large-scale low-velocity fluid motions in the tank, as they are difficult to avoid in a large tank. Similar irregular weak motions were observed in other experiments, and are mentioned in particular by Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007) for the study of rising disks. Following their approach that considers this drift as uncoupled with the main oscillatory motion of the body, a low-frequency filtering is applied to the time evolutions of the quantities characterizing the oscillatory behaviour of the body. The amplitude and phases of the periodic signals are then obtained using the Hilbert transform.

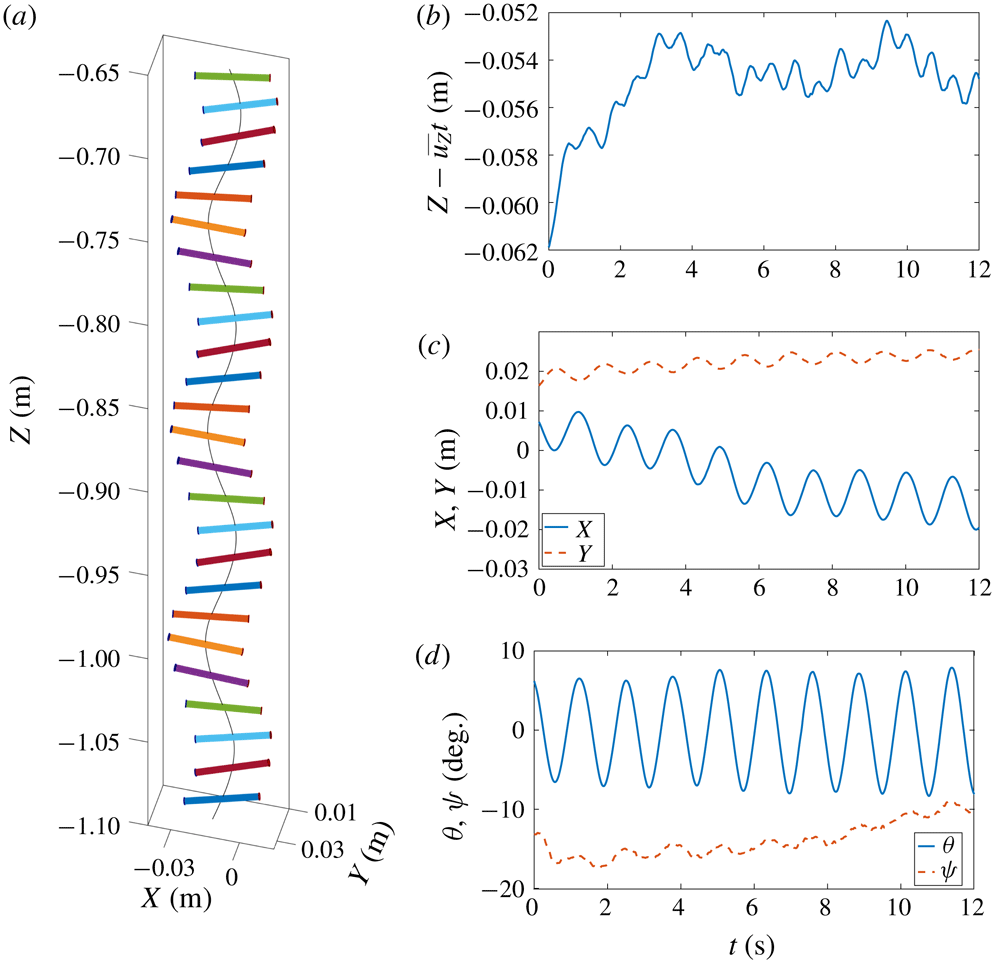
Figure 2. Illustration of the cylinder motion in the fluttering regime: (a) three-dimensional plot, with an angle of view chosen close to perpendicular to the azimuthal plane to avoid perspective effects; corresponding time period 5.5 s to 10.5 s; the cylinder is plotted every 0.18 s. (b–d) Typical evolutions in time of the: (b) vertical displacement, (c) horizontal coordinates, (d) angles
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D713}$
;
$\unicode[STIX]{x1D713}$
;
![]() $Ar=800$
,
$Ar=800$
,
![]() $L/d=10$
,
$L/d=10$
,
![]() $d=3~\text{mm}$
,
$d=3~\text{mm}$
,
![]() $\overline{u_{Z}}=10~\text{cm}~\text{s}^{-1}$
.
$\overline{u_{Z}}=10~\text{cm}~\text{s}^{-1}$
.
The coordinate system provided by the cameras being arbitrary, it is not the best suited to describe the body motion. Several coordinates systems can be introduced to get a better characterization of the body motion. For planar trajectories of the cylinders, a simpler and good description of their path is in fact manifest in the azimuthal plane defined by the cylinder axis and the vertical direction, and obtained by rotating the laboratory frame coordinates
![]() $(X,Y,Z)$
by the angle
$(X,Y,Z)$
by the angle
![]() $\unicode[STIX]{x1D713}$
, as
$\unicode[STIX]{x1D713}$
, as
 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}c@{}}X_{azi}\\ Y_{azi}\\ Z_{azi}\end{array}\right]=R_{\unicode[STIX]{x1D713}}\left[\begin{array}{@{}c@{}}X\\ Y\\ Z\end{array}\right]\quad \text{with }R_{\unicode[STIX]{x1D713}}=\left(\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D713} & \sin \unicode[STIX]{x1D713} & 0\\ -\sin \unicode[STIX]{x1D713} & \cos \unicode[STIX]{x1D713} & 0\\ 0 & 0 & 1\end{array}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}c@{}}X_{azi}\\ Y_{azi}\\ Z_{azi}\end{array}\right]=R_{\unicode[STIX]{x1D713}}\left[\begin{array}{@{}c@{}}X\\ Y\\ Z\end{array}\right]\quad \text{with }R_{\unicode[STIX]{x1D713}}=\left(\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D713} & \sin \unicode[STIX]{x1D713} & 0\\ -\sin \unicode[STIX]{x1D713} & \cos \unicode[STIX]{x1D713} & 0\\ 0 & 0 & 1\end{array}\right). & & \displaystyle\end{eqnarray}$$
However, while it is often the case, we will see later that not all trajectories lie in this plane. We therefore opt to work within the frame, hereafter termed the body frame, having its origin O fixed and axes
![]() $(x,y,z)$
rotating with the body (Lamb Reference Lamb1993). Axis
$(x,y,z)$
rotating with the body (Lamb Reference Lamb1993). Axis
![]() $(\text{O}x)$
is chosen parallel to the cylinder axis and the plane
$(\text{O}x)$
is chosen parallel to the cylinder axis and the plane
![]() $(x,y)$
vertical (see figure 1
c). In this frame, the cylinder velocity components are denoted
$(x,y)$
vertical (see figure 1
c). In this frame, the cylinder velocity components are denoted
![]() $(u,v,w)$
and are deduced from the velocity components in the laboratory frame
$(u,v,w)$
and are deduced from the velocity components in the laboratory frame
![]() $(u_{X},u_{Y},u_{Z})$
by two rotations of angle
$(u_{X},u_{Y},u_{Z})$
by two rotations of angle
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D713}$
respectively,
$\unicode[STIX]{x1D713}$
respectively,
 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}c@{}}u\\ v\\ w\end{array}\right]=R_{\unicode[STIX]{x1D703}}R_{\unicode[STIX]{x1D713}}\left[\begin{array}{@{}c@{}}u_{X}\\ u_{Y}\\ u_{Z}\end{array}\right]\quad \text{with }R_{\unicode[STIX]{x1D703}}=\left(\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D703} & 0 & \sin \unicode[STIX]{x1D703}\\ 0 & 1 & 0\\ -\sin \unicode[STIX]{x1D703} & 0 & \cos \unicode[STIX]{x1D703}\end{array}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}c@{}}u\\ v\\ w\end{array}\right]=R_{\unicode[STIX]{x1D703}}R_{\unicode[STIX]{x1D713}}\left[\begin{array}{@{}c@{}}u_{X}\\ u_{Y}\\ u_{Z}\end{array}\right]\quad \text{with }R_{\unicode[STIX]{x1D703}}=\left(\begin{array}{@{}ccc@{}}\cos \unicode[STIX]{x1D703} & 0 & \sin \unicode[STIX]{x1D703}\\ 0 & 1 & 0\\ -\sin \unicode[STIX]{x1D703} & 0 & \cos \unicode[STIX]{x1D703}\end{array}\right). & & \displaystyle\end{eqnarray}$$
Note that the axis
![]() $z$
, corresponding to the velocity component
$z$
, corresponding to the velocity component
![]() $w$
, has been chosen perpendicular to the vertical plane
$w$
, has been chosen perpendicular to the vertical plane
![]() $(x,y)$
, and is therefore horizontal. As can be seen in the example in figure 3, the body frame provides a simpler and more relevant description of the body motion than the laboratory frame, figure 3(b) indicating that in this case, the trajectory is nearly planar and contained in the azimuthal plane.
$(x,y)$
, and is therefore horizontal. As can be seen in the example in figure 3, the body frame provides a simpler and more relevant description of the body motion than the laboratory frame, figure 3(b) indicating that in this case, the trajectory is nearly planar and contained in the azimuthal plane.
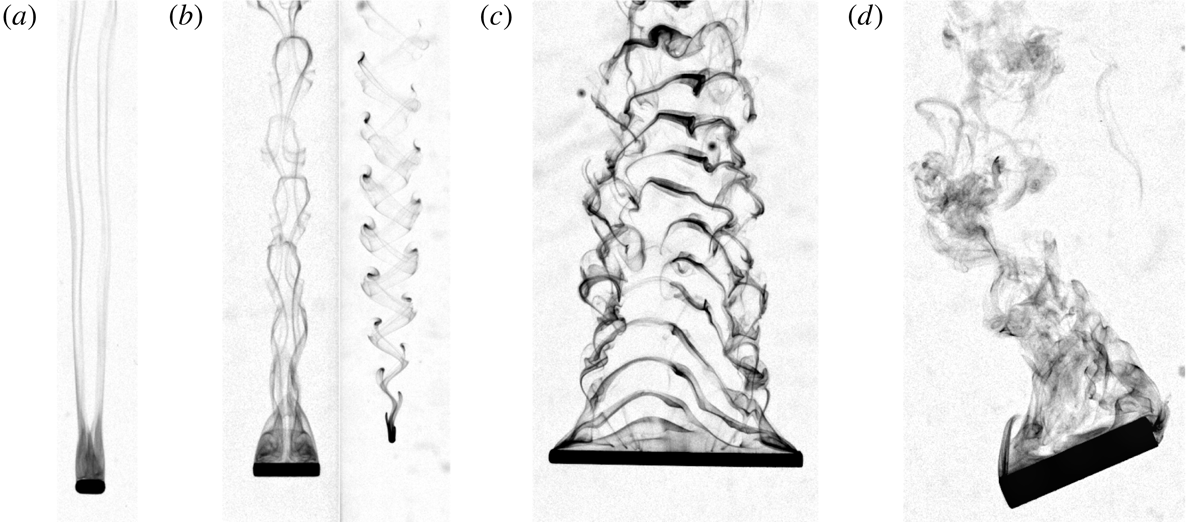
4 Overview of the different paths observed
In this section we provide an overview of the different types of path observed within the space of parameters
![]() $(Ar,L/d)$
investigated for 195 cylinders. As can be seen in figure 4, three main types of motion are observed in the range
$(Ar,L/d)$
investigated for 195 cylinders. As can be seen in figure 4, three main types of motion are observed in the range
![]() $Ar\in [200,1100]$
,
$Ar\in [200,1100]$
,
![]() $L/d\in [2,20]$
. The first two correspond to stationary regimes: the rectilinear fall and the regular oscillatory motion called fluttering. In addition, in the transitional region of parameters separating the domains of occurrence of these regimes, oscillatory motions of weak and irregular amplitude are detected. Based on their distinctive features, we separate them in three types (termed Irregular I to III).
$L/d\in [2,20]$
. The first two correspond to stationary regimes: the rectilinear fall and the regular oscillatory motion called fluttering. In addition, in the transitional region of parameters separating the domains of occurrence of these regimes, oscillatory motions of weak and irregular amplitude are detected. Based on their distinctive features, we separate them in three types (termed Irregular I to III).

Figure 3. Comparison of the velocity components (a) in the laboratory frame, and (b) in the system of axes rotating with the body defined in figure 1(c);
![]() $Ar=800,L/d=10$
.
$Ar=800,L/d=10$
.

Figure 4. Map of the different paths observed in the plane
![]() $(Ar,L/d)$
for
$(Ar,L/d)$
for
![]() $\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}\simeq 1.16$
. For all
$\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}\simeq 1.16$
. For all
![]() $(Ar,L/d)$
, each type of path is observed using different cylinders. For some
$(Ar,L/d)$
, each type of path is observed using different cylinders. For some
![]() $(Ar,L/d)$
, different types of path can be observed with the same cylinder in different runs.
$(Ar,L/d)$
, different types of path can be observed with the same cylinder in different runs.

Figure 5. Examples of the time evolution of
![]() $\unicode[STIX]{x1D703}$
for the fluttering motion
$\unicode[STIX]{x1D703}$
for the fluttering motion
![]() $(Ar=785,L/d=10)$
, for the rectilinear motion
$(Ar=785,L/d=10)$
, for the rectilinear motion
![]() $(Ar=200,L/d=3)$
, for the Irregular I motion
$(Ar=200,L/d=3)$
, for the Irregular I motion
![]() $(Ar=500,L/d=5)$
and for the Irregular II motion
$(Ar=500,L/d=5)$
and for the Irregular II motion
![]() $(Ar=400,L/d=3)$
.
$(Ar=400,L/d=3)$
.
The fluttering motion is a periodic oscillatory motion of regular amplitude, observed here for Archimedes numbers ranging from 490 to 1080, and
![]() $L/d$
from 2 to 12 (figure 4). An illustration of this path is shown in figure 2(b–d), where the evolution in time of the five measured degrees of freedom are plotted. The evolution of the body along its path is also displayed in the three-dimensional plot of figure 2(a). Fluttering typically occurs for heavier and shorter cylinders, at a frequency of approximately
$L/d$
from 2 to 12 (figure 4). An illustration of this path is shown in figure 2(b–d), where the evolution in time of the five measured degrees of freedom are plotted. The evolution of the body along its path is also displayed in the three-dimensional plot of figure 2(a). Fluttering typically occurs for heavier and shorter cylinders, at a frequency of approximately
![]() $1$
Hz. It is characterized by oscillations of the cylinder centre of gravity (horizontal displacement in the azimuthal direction ranging approximately from
$1$
Hz. It is characterized by oscillations of the cylinder centre of gravity (horizontal displacement in the azimuthal direction ranging approximately from
![]() $0.1L$
to
$0.1L$
to
![]() $0.3L$
, or
$0.3L$
, or
![]() $0.35d$
to
$0.35d$
to
![]() $2.8d$
) coupled with oscillations of the inclination angle
$2.8d$
) coupled with oscillations of the inclination angle
![]() $\unicode[STIX]{x1D703}$
(ranging from
$\unicode[STIX]{x1D703}$
(ranging from
![]() $7^{\circ }$
to
$7^{\circ }$
to
![]() $20^{\circ }$
). Oscillations of horizontal velocity components (
$20^{\circ }$
). Oscillations of horizontal velocity components (
![]() $u_{X}$
,
$u_{X}$
,
![]() $u_{Y}$
) and of
$u_{Y}$
) and of
![]() $\unicode[STIX]{x1D703}$
occur at the same frequency
$\unicode[STIX]{x1D703}$
occur at the same frequency
![]() $f$
and their amplitudes remain constant during the fall. Owing to symmetry properties, oscillations of the vertical velocity component
$f$
and their amplitudes remain constant during the fall. Owing to symmetry properties, oscillations of the vertical velocity component
![]() $u_{Z}$
occur at twice the fluttering frequency,
$u_{Z}$
occur at twice the fluttering frequency,
![]() $2f$
. Weak oscillations of
$2f$
. Weak oscillations of
![]() $\unicode[STIX]{x1D713}$
(typically lower than
$\unicode[STIX]{x1D713}$
(typically lower than
![]() $6^{\circ }$
) can also be observed at the fluttering frequency, and are stronger for cylinders with smaller elongation ratios (
$6^{\circ }$
) can also be observed at the fluttering frequency, and are stronger for cylinders with smaller elongation ratios (
![]() $L/d<5$
). The kinematics of the fluttering regime will be described in detail in § 6. Similar zigzag periodic motions were observed for finite-length cylinders covering a large range of density ratios (see for instance Marchildon et al.
Reference Marchildon, Clamen and Gauvin1964; Chow & Adams Reference Chow and Adams2011), and are also known to exist for plates (see for instance Belmonte, Eisenberg & Moses Reference Belmonte, Eisenberg and Moses1998; Andersen, Pesavento & Wang Reference Andersen, Pesavento and Wang2005b
) and disks (see for instance Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007; Auguste et al.
Reference Auguste, Magnaudet and Fabre2013).
$L/d<5$
). The kinematics of the fluttering regime will be described in detail in § 6. Similar zigzag periodic motions were observed for finite-length cylinders covering a large range of density ratios (see for instance Marchildon et al.
Reference Marchildon, Clamen and Gauvin1964; Chow & Adams Reference Chow and Adams2011), and are also known to exist for plates (see for instance Belmonte, Eisenberg & Moses Reference Belmonte, Eisenberg and Moses1998; Andersen, Pesavento & Wang Reference Andersen, Pesavento and Wang2005b
) and disks (see for instance Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007; Auguste et al.
Reference Auguste, Magnaudet and Fabre2013).
During the rectilinear vertical fall, the cylinder axis remains horizontal. This kind of motion is observed in a subspace of
![]() $Ar\in [200,1000]$
and
$Ar\in [200,1000]$
and
![]() $L/d\in [3,12]$
(figure 4). For this type of path, a slight horizontal drift might be observed on the motion of the centre of gravity, but it is weak (for all cases it is lower than
$L/d\in [3,12]$
(figure 4). For this type of path, a slight horizontal drift might be observed on the motion of the centre of gravity, but it is weak (for all cases it is lower than
![]() $3\,\%$
of the total falling height), non-reproducible and does not present a preferential direction related to the body geometry. No significant and regular horizontal motion could be observed for these cylinders so that their path is termed rectilinear. However, low-amplitude high-frequency oscillations (approximately six times larger than typical fluttering frequencies
$3\,\%$
of the total falling height), non-reproducible and does not present a preferential direction related to the body geometry. No significant and regular horizontal motion could be observed for these cylinders so that their path is termed rectilinear. However, low-amplitude high-frequency oscillations (approximately six times larger than typical fluttering frequencies
![]() $f$
) were detected on the vertical velocity
$f$
) were detected on the vertical velocity
![]() $u_{Z}$
(or on
$u_{Z}$
(or on
![]() $v$
) in the range
$v$
) in the range
![]() $L/d\in [2,12]$
and
$L/d\in [2,12]$
and
![]() $Ar\in [390,1080]$
investigated with a 50 Hz acquisition frequency of the camera, and covering both some rectilinear and fluttering paths. These oscillations will be discussed in more detail in § 7.
$Ar\in [390,1080]$
investigated with a 50 Hz acquisition frequency of the camera, and covering both some rectilinear and fluttering paths. These oscillations will be discussed in more detail in § 7.
In the transitional region separating the rectilinear fall and the fluttering regime, different types of weak irregular oscillations can be observed, markedly in contrast with the rectilinear and fluttering regime. Though they are hard to disentangle from noise, some distinctive features can be pointed out to suggest a classification. The regime Irregular I is attributed to cylinder oscillations of weak and irregular amplitude in both displacement and inclination angle
![]() $\unicode[STIX]{x1D703}$
. These occur at frequencies close to those of the fluttering motion but with amplitudes significantly smaller (typically
$\unicode[STIX]{x1D703}$
. These occur at frequencies close to those of the fluttering motion but with amplitudes significantly smaller (typically
![]() $\unicode[STIX]{x1D703}<3^{\circ }$
) and less regular than the ones observed for fluttering cylinders. An illustration is provided in figure 5. In the regime Irregular II observed here for
$\unicode[STIX]{x1D703}<3^{\circ }$
) and less regular than the ones observed for fluttering cylinders. An illustration is provided in figure 5. In the regime Irregular II observed here for
![]() $Ar\in [400,500]$
and
$Ar\in [400,500]$
and
![]() $L/d\in [3,5]$
, the oscillations of the cylinder axis (close to the fluttering frequency
$L/d\in [3,5]$
, the oscillations of the cylinder axis (close to the fluttering frequency
![]() $f$
) are modulated by a low-frequency oscillation (for instance, six times slower), as shown in figure 5. The amplitude reached in the bursts is higher than that observed in the regime Irregular I (for instance, an amplitude of
$f$
) are modulated by a low-frequency oscillation (for instance, six times slower), as shown in figure 5. The amplitude reached in the bursts is higher than that observed in the regime Irregular I (for instance, an amplitude of
![]() $10^{\circ }$
can be reached). As for now, the origin of this mode is unclear, but it might be related to a complex wake structure occurring for this range of parameters. In fact, it is worth pointing out that low-frequency modulations of wake oscillations have been observed in several studies for fixed finite-length cylinders with free ends in comparable ranges of
$10^{\circ }$
can be reached). As for now, the origin of this mode is unclear, but it might be related to a complex wake structure occurring for this range of parameters. In fact, it is worth pointing out that low-frequency modulations of wake oscillations have been observed in several studies for fixed finite-length cylinders with free ends in comparable ranges of
![]() $L/d$
and
$L/d$
and
![]() $Re$
. Dauchy, Dušek & Fraunié (Reference Dauchy, Dušek and Fraunié1997) observed a slow modulation of the oscillations in the wake of cylinders with
$Re$
. Dauchy, Dušek & Fraunié (Reference Dauchy, Dušek and Fraunié1997) observed a slow modulation of the oscillations in the wake of cylinders with
![]() $L/d$
about
$L/d$
about
![]() $10$
and
$10$
and
![]() $20$
for
$20$
for
![]() $52\leqslant Re\leqslant 100$
, as the result of a secondary instability setting in at approximately
$52\leqslant Re\leqslant 100$
, as the result of a secondary instability setting in at approximately
![]() $20\,\%$
above the primary instability threshold. Numerical simulations by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with
$20\,\%$
above the primary instability threshold. Numerical simulations by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with
![]() $20\leqslant L/d\leqslant 50$
and
$20\leqslant L/d\leqslant 50$
and
![]() $Re=60$
also revealed the existence of a low-frequency modulation in the wake signal, but the beat in this case was attributed to bistability of the flow and the alternate appearance of two different modes of instability (namely Type II and III described here in § 7). Note that the frequency of the wake primary instability is different in both studies, both values being approximately seven times larger than the frequency
$Re=60$
also revealed the existence of a low-frequency modulation in the wake signal, but the beat in this case was attributed to bistability of the flow and the alternate appearance of two different modes of instability (namely Type II and III described here in § 7). Note that the frequency of the wake primary instability is different in both studies, both values being approximately seven times larger than the frequency
![]() $f$
of the modulated oscillation observed here. Regimes Irregular I and II are difficult to distinguish from what would be the fluttering regime when it sets in. And in fact, figure 4 shows that for different cylinders having same
$f$
of the modulated oscillation observed here. Regimes Irregular I and II are difficult to distinguish from what would be the fluttering regime when it sets in. And in fact, figure 4 shows that for different cylinders having same
![]() $(Ar,L/d)$
, different types of path (fluttering, Irregular I or II) can be observed. This underlines the difficulty of experimentation for these parameters. However, as will be seen later in figure 12, there is a significant jump in the oscillation amplitude of
$(Ar,L/d)$
, different types of path (fluttering, Irregular I or II) can be observed. This underlines the difficulty of experimentation for these parameters. However, as will be seen later in figure 12, there is a significant jump in the oscillation amplitude of
![]() $\unicode[STIX]{x1D703}$
between the regime Irregular I and the fluttering one. Finally, in the case of long cylinders (
$\unicode[STIX]{x1D703}$
between the regime Irregular I and the fluttering one. Finally, in the case of long cylinders (
![]() $L/d=20$
,
$L/d=20$
,
![]() $Ar=590$
and
$Ar=590$
and
![]() $Ar=890$
), a different rotational low-amplitude oscillatory mode is observed, called Irregular III. At variance with the fluttering mode that affects the inclination angle
$Ar=890$
), a different rotational low-amplitude oscillatory mode is observed, called Irregular III. At variance with the fluttering mode that affects the inclination angle
![]() $\unicode[STIX]{x1D703}$
, regime Irregular III is characterized by oscillations in the azimuthal angle of the cylinder,
$\unicode[STIX]{x1D703}$
, regime Irregular III is characterized by oscillations in the azimuthal angle of the cylinder,
![]() $\unicode[STIX]{x1D713}$
, occurring at a higher frequency than the fluttering one, approximately 4 Hz. The amplitude of this motion is of extremely low amplitude, approximately
$\unicode[STIX]{x1D713}$
, occurring at a higher frequency than the fluttering one, approximately 4 Hz. The amplitude of this motion is of extremely low amplitude, approximately
![]() $0.2^{\circ }$
.
$0.2^{\circ }$
.
We have seen that a wide variety of paths occurs for cylinders in the range of parameters investigated here. The existence of low-amplitude oscillatory motions and the subsequent transition to stronger oscillations, when control parameters are changed (in this case for given
![]() $L/d$
when increasing the volume of the body, i.e. when increasing
$L/d$
when increasing the volume of the body, i.e. when increasing
![]() $Ar$
) has been observed in previous works for bodies with contrasted geometries (disks, short-length cylinders, two-dimensional cylinders, spheres, etc
$Ar$
) has been observed in previous works for bodies with contrasted geometries (disks, short-length cylinders, two-dimensional cylinders, spheres, etc
![]() $\ldots$
) as reviewed by Ern et al. (Reference Ern, Risso, Fabre and Magnaudet2012). As the experimental determination of these motions, termed A-regimes or quasi-vertical regimes in the literature, may be hindered or modified by noise or residual disturbances in the fluid, numerical simulations appear today as the most suitable tool for their investigation (Auguste et al.
Reference Auguste, Magnaudet and Fabre2013; Chrust et al.
Reference Chrust, Bouchet and Dušek2013). We therefore turn now our attention to the quantitative analysis of mean fall velocity and mean drag (§ 5), before focusing on the properties of the large-amplitude oscillatory motion corresponding to the fluttering regime (§ 6).
$\ldots$
) as reviewed by Ern et al. (Reference Ern, Risso, Fabre and Magnaudet2012). As the experimental determination of these motions, termed A-regimes or quasi-vertical regimes in the literature, may be hindered or modified by noise or residual disturbances in the fluid, numerical simulations appear today as the most suitable tool for their investigation (Auguste et al.
Reference Auguste, Magnaudet and Fabre2013; Chrust et al.
Reference Chrust, Bouchet and Dušek2013). We therefore turn now our attention to the quantitative analysis of mean fall velocity and mean drag (§ 5), before focusing on the properties of the large-amplitude oscillatory motion corresponding to the fluttering regime (§ 6).

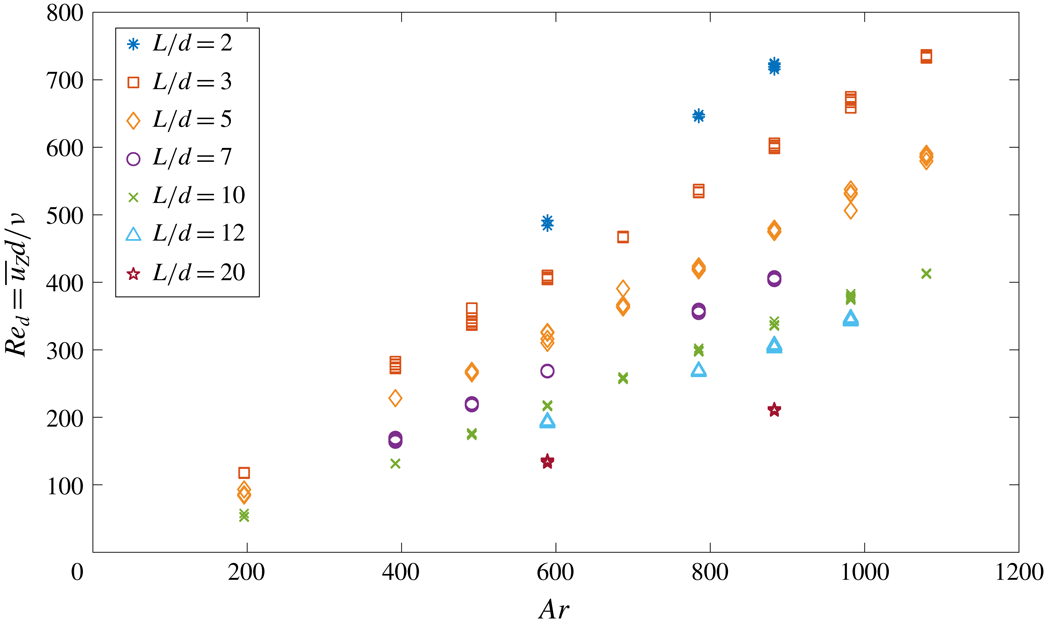
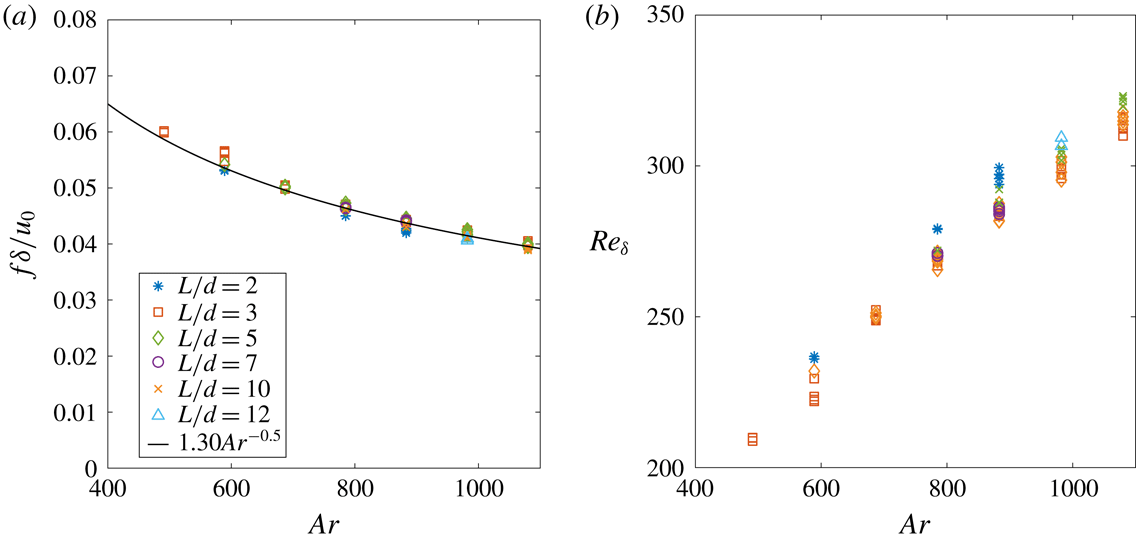
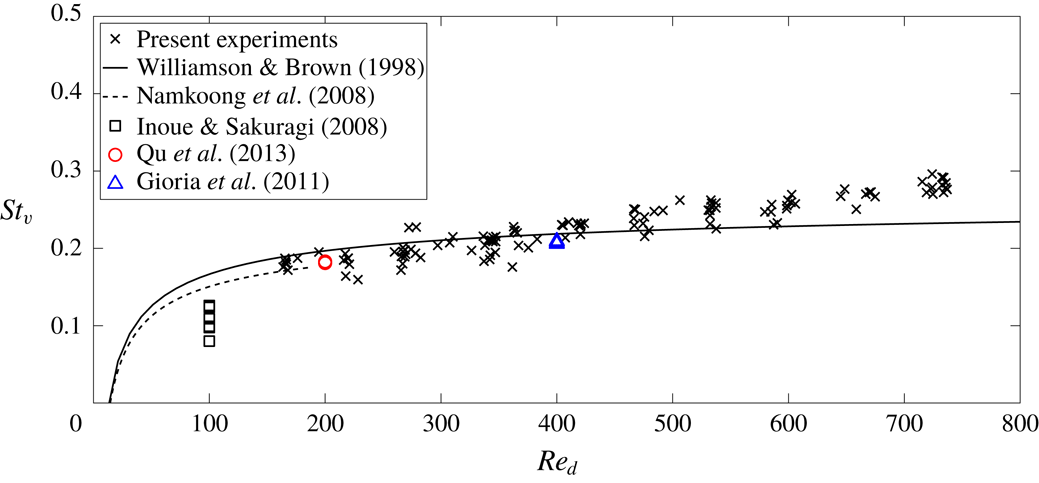
Figure 6. Reynolds number versus Archimedes number for various elongation ratios.
5 Mean fall velocity of the cylinder
After the initial transient following the release of the body from rest, a mean vertical velocity of the body can be determined. Its absolute value, denoted
![]() $\overline{u_{Z}}$
, typically ranges from
$\overline{u_{Z}}$
, typically ranges from
![]() $4$
to
$4$
to
![]() $13.5~\text{cm}~\text{s}^{-1}$
. For a given couple
$13.5~\text{cm}~\text{s}^{-1}$
. For a given couple
![]() $(Ar,L/d)$
, data scattering between different runs indicates on average a relative error for
$(Ar,L/d)$
, data scattering between different runs indicates on average a relative error for
![]() $\overline{u_{Z}}$
less than
$\overline{u_{Z}}$
less than
![]() $1\,\%$
for the whole data, with a maximum of dispersion of
$1\,\%$
for the whole data, with a maximum of dispersion of
![]() $4.5\,\%$
. The velocity
$4.5\,\%$
. The velocity
![]() $\overline{u_{Z}}$
can be used to create the Reynolds number
$\overline{u_{Z}}$
can be used to create the Reynolds number
![]() $Re_{d}=\overline{u_{Z}}d/\unicode[STIX]{x1D708}$
based on the cylinder diameter, which is particularly useful for the comparison with fixed or with two-dimensional cylinders, as will be done in § 7. Figure 6 shows
$Re_{d}=\overline{u_{Z}}d/\unicode[STIX]{x1D708}$
based on the cylinder diameter, which is particularly useful for the comparison with fixed or with two-dimensional cylinders, as will be done in § 7. Figure 6 shows
![]() $Re_{d}$
plotted versus the Archimedes number for various
$Re_{d}$
plotted versus the Archimedes number for various
![]() $L/d$
. For a given volume of the body, corresponding to a given Archimedes number, a strong effect of the elongation ratio is visible, lower
$L/d$
. For a given volume of the body, corresponding to a given Archimedes number, a strong effect of the elongation ratio is visible, lower
![]() $L/d$
corresponding to higher
$L/d$
corresponding to higher
![]() $Re_{d}$
. For all elongation ratios and all types of motion, the evolution of
$Re_{d}$
. For all elongation ratios and all types of motion, the evolution of
![]() $Re_{d}$
versus
$Re_{d}$
versus
![]() $Ar$
is very close to linear, though for
$Ar$
is very close to linear, though for
![]() $L/d\leqslant 5$
and
$L/d\leqslant 5$
and
![]() $Ar\leqslant 500$
, data more notably separate from the global trend.
$Ar\leqslant 500$
, data more notably separate from the global trend.
A drag coefficient can also be deduced from
![]() $\overline{u_{Z}}$
, via a force balance between the drag force and the buoyancy force, as
$\overline{u_{Z}}$
, via a force balance between the drag force and the buoyancy force, as
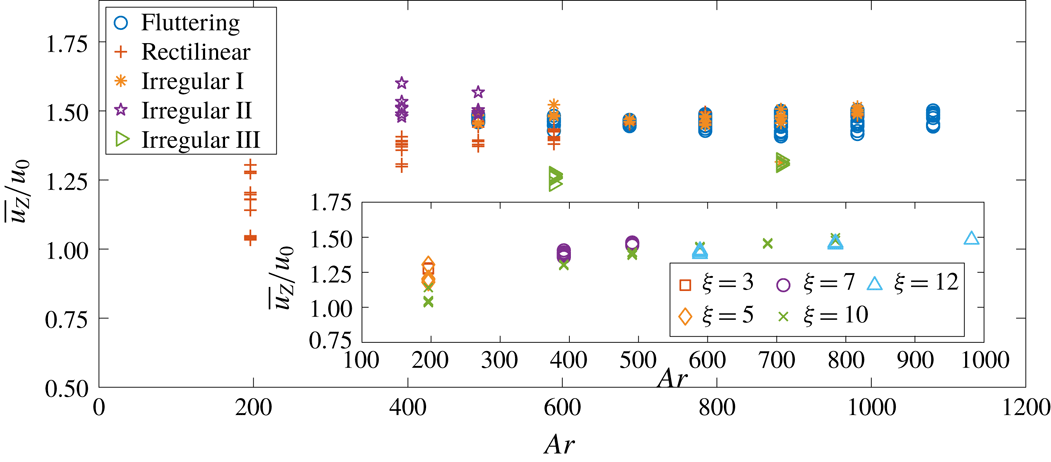
Figure 7 shows the evolution of
![]() $C_{d}$
with the Reynolds number for the different types of motion. The drag coefficients are nearly constant at 0.70 for the fluttering and Irregular I regime, for the Reynolds numbers and elongation ratios considered here, and for rectilinear paths with
$C_{d}$
with the Reynolds number for the different types of motion. The drag coefficients are nearly constant at 0.70 for the fluttering and Irregular I regime, for the Reynolds numbers and elongation ratios considered here, and for rectilinear paths with
![]() $Re_{d}>250$
. Irregular II paths also correspond to comparable values of
$Re_{d}>250$
. Irregular II paths also correspond to comparable values of
![]() $C_{d}$
. For rectilinear paths with
$C_{d}$
. For rectilinear paths with
![]() $Re$
increasing from 50 to 250, the drag coefficient decreases from about
$Re$
increasing from 50 to 250, the drag coefficient decreases from about
![]() $1.45$
to
$1.45$
to
![]() $0.70$
. Cylinders undergoing Irregular III oscillations have a higher
$0.70$
. Cylinders undergoing Irregular III oscillations have a higher
![]() $C_{d}$
than those falling rectilinearly at the same
$C_{d}$
than those falling rectilinearly at the same
![]() $Re_{d}$
, an increase of approximately 0.1 being observed for
$Re_{d}$
, an increase of approximately 0.1 being observed for
![]() $Re_{d}\simeq 100$
and of 0.15 for
$Re_{d}\simeq 100$
and of 0.15 for
![]() $Re_{d}\simeq 200$
. For comparison, we also plot the drag coefficients obtained experimentally by Jayaweera & Mason (Reference Jayaweera and Mason1965) for metal cylinders with
$Re_{d}\simeq 200$
. For comparison, we also plot the drag coefficients obtained experimentally by Jayaweera & Mason (Reference Jayaweera and Mason1965) for metal cylinders with
![]() $L/d>100$
falling through liquid paraffin, sugar solutions or water. The trend is similar, but the two sets of measurements separate on parallel curves for
$L/d>100$
falling through liquid paraffin, sugar solutions or water. The trend is similar, but the two sets of measurements separate on parallel curves for
![]() $Re_{d}>50$
, a difference that may come from the differences in
$Re_{d}>50$
, a difference that may come from the differences in
![]() $\overline{\unicode[STIX]{x1D70C}}$
and
$\overline{\unicode[STIX]{x1D70C}}$
and
![]() $L/d$
. For
$L/d$
. For
![]() $10<Re_{d}<50$
, we also compare with the coefficients provided by the numerical simulations of Vakil & Green (Reference Vakil and Green2009) for fixed finite-length cylinders. Their results are consistent with those of Jayaweera & Mason (Reference Jayaweera and Mason1965) and with the trend of our data. In this range of
$10<Re_{d}<50$
, we also compare with the coefficients provided by the numerical simulations of Vakil & Green (Reference Vakil and Green2009) for fixed finite-length cylinders. Their results are consistent with those of Jayaweera & Mason (Reference Jayaweera and Mason1965) and with the trend of our data. In this range of
![]() $Re$
, no significant effect of
$Re$
, no significant effect of
![]() $L/d$
is observed by Vakil & Green (Reference Vakil and Green2009). In their experimental study on the drag coefficient of freely falling cylinders for
$L/d$
is observed by Vakil & Green (Reference Vakil and Green2009). In their experimental study on the drag coefficient of freely falling cylinders for
![]() $200<Re_{d}<6000$
, Chow & Adams (Reference Chow and Adams2011) review the different correlations of the literature based on
$200<Re_{d}<6000$
, Chow & Adams (Reference Chow and Adams2011) review the different correlations of the literature based on
![]() $\overline{\unicode[STIX]{x1D70C}}$
and
$\overline{\unicode[STIX]{x1D70C}}$
and
![]() $L/d$
, and propose an expression depending on
$L/d$
, and propose an expression depending on
![]() $I^{\ast }=\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
. In the present study, the drag coefficient depends on the Reynolds number for
$I^{\ast }=\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
. In the present study, the drag coefficient depends on the Reynolds number for
![]() $Re_{d}<200$
, which lies outside the range of
$Re_{d}<200$
, which lies outside the range of
![]() $Re_{d}$
studied by Chow & Adams (Reference Chow and Adams2011). However, significant differences in
$Re_{d}$
studied by Chow & Adams (Reference Chow and Adams2011). However, significant differences in
![]() $C_{d}$
are also observed with this work for
$C_{d}$
are also observed with this work for
![]() $Re_{d}>200$
for the same values of
$Re_{d}>200$
for the same values of
![]() $\overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}$
and
$\overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}$
and
![]() $L/d$
. Chow & Adams (Reference Chow and Adams2011) measured
$L/d$
. Chow & Adams (Reference Chow and Adams2011) measured
![]() $C_{d}$
ranging from approximately 0.8 to 1 for
$C_{d}$
ranging from approximately 0.8 to 1 for
![]() $I^{\ast }$
ranging from 0.25 to 1, whereas the present
$I^{\ast }$
ranging from 0.25 to 1, whereas the present
![]() $C_{d}$
is nearly constant at 0.7 over the same range of
$C_{d}$
is nearly constant at 0.7 over the same range of
![]() $I^{\ast }$
. This difference might be linked with the fact that the fluttering motion observed by Chow & Adams (Reference Chow and Adams2011) is of a much greater amplitude (
$I^{\ast }$
. This difference might be linked with the fact that the fluttering motion observed by Chow & Adams (Reference Chow and Adams2011) is of a much greater amplitude (
![]() $20^{\circ }<\tilde{\unicode[STIX]{x1D703}}<50^{\circ }$
) than the one observed in the present study, where
$20^{\circ }<\tilde{\unicode[STIX]{x1D703}}<50^{\circ }$
) than the one observed in the present study, where
![]() $\tilde{\unicode[STIX]{x1D703}}<25^{\circ }$
.
$\tilde{\unicode[STIX]{x1D703}}<25^{\circ }$
.

Figure 7. Drag coefficient of the freely falling cylinders versus Reynolds number
![]() $Re_{d}=\overline{u_{Z}}d/\unicode[STIX]{x1D708}$
for the different types of motion, and comparison with some previous works.
$Re_{d}=\overline{u_{Z}}d/\unicode[STIX]{x1D708}$
for the different types of motion, and comparison with some previous works.

Figure 8. Average vertical velocity scaled by the gravitational velocity versus the Archimedes number for the different types of motion. The inset shows the effect of the elongation ratio on the velocities of cylinders displaying a rectilinear motion.
The remarkable trend displayed by the evolution of
![]() $C_{d}$
with
$C_{d}$
with
![]() $Re_{d}$
in figure 7 allows us to infer from equation (5.2) that the characteristic velocity scale for the mean fall is given by the gravitational velocity
$Re_{d}$
in figure 7 allows us to infer from equation (5.2) that the characteristic velocity scale for the mean fall is given by the gravitational velocity
![]() $u_{0}=((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gd)^{1/2}$
. The dimensionless mean fall velocity
$u_{0}=((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gd)^{1/2}$
. The dimensionless mean fall velocity
![]() $\overline{u_{Z}}/u_{0}$
is shown in figure 8 for all the Archimedes numbers and elongation ratios investigated. For fluttering and Irregular I regimes, as well as rectilinear paths with
$\overline{u_{Z}}/u_{0}$
is shown in figure 8 for all the Archimedes numbers and elongation ratios investigated. For fluttering and Irregular I regimes, as well as rectilinear paths with
![]() $Ar>600$
, the dimensionless velocity is remarkably independent of the Archimedes number;
$Ar>600$
, the dimensionless velocity is remarkably independent of the Archimedes number;
![]() $\overline{u_{Z}}/u_{0}$
is almost constant at approximately
$\overline{u_{Z}}/u_{0}$
is almost constant at approximately
![]() $1.46$
for all the
$1.46$
for all the
![]() $Ar$
and
$Ar$
and
![]() $L/d$
considered here. In the case of cylinders falling rectilinearly with Archimedes numbers rising from approximately
$L/d$
considered here. In the case of cylinders falling rectilinearly with Archimedes numbers rising from approximately
![]() $200$
to
$200$
to
![]() $600$
, the fall velocity increases from approximately
$600$
, the fall velocity increases from approximately
![]() $1$
to
$1$
to
![]() $1.5$
and depends on the elongation ratio, as can be seen in the inset of figure 8. The effect is stronger at lower
$1.5$
and depends on the elongation ratio, as can be seen in the inset of figure 8. The effect is stronger at lower
![]() $Ar$
. For
$Ar$
. For
![]() $Ar=200$
, a difference of about 0.2 is observed between
$Ar=200$
, a difference of about 0.2 is observed between
![]() $L/d=10$
and
$L/d=10$
and
![]() $L/d=3$
, longer cylinders being the slower ones. A slight effect of the type of motion is also visible. Cylinders undergoing modulated oscillations (regime Irregular II) have a slightly higher dimensionless fall velocity than those displaying fluttering and rectilinear paths (difference of approximately
$L/d=3$
, longer cylinders being the slower ones. A slight effect of the type of motion is also visible. Cylinders undergoing modulated oscillations (regime Irregular II) have a slightly higher dimensionless fall velocity than those displaying fluttering and rectilinear paths (difference of approximately
![]() $10\,\%$
for
$10\,\%$
for
![]() $Ar=400$
and
$Ar=400$
and
![]() $5\,\%$
for
$5\,\%$
for
![]() $Ar=500$
), while cylinders undergoing weak azimuthal oscillations (regime Irregular III) have a lower (approximately
$Ar=500$
), while cylinders undergoing weak azimuthal oscillations (regime Irregular III) have a lower (approximately
![]() $20\,\%$
) dimensionless fall velocity than the other ones. Interestingly, for bodies undergoing a fluttering motion, the mean fall velocity of the elongated finite-length cylinders considered here scales with the gravitational velocity
$20\,\%$
) dimensionless fall velocity than the other ones. Interestingly, for bodies undergoing a fluttering motion, the mean fall velocity of the elongated finite-length cylinders considered here scales with the gravitational velocity
![]() $u_{0}$
based on their diameter
$u_{0}$
based on their diameter
![]() $d$
independently of their length
$d$
independently of their length
![]() $L$
, in the same way the mean fall/rise velocity of short-length cylinders (disks of finite thickness) scales with the gravitational velocity based on their length or thickness
$L$
, in the same way the mean fall/rise velocity of short-length cylinders (disks of finite thickness) scales with the gravitational velocity based on their length or thickness
![]() $L$
, independently of the body diameter (Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007).
$L$
, independently of the body diameter (Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007).
6 Fluttering regime of the cylinders
This section focuses on the study of the body kinematics in the oscillatory regime, called fluttering in § 4, and characterized by oscillations of the body centre of gravity and of the body inclination,
![]() $\unicode[STIX]{x1D703}$
. These oscillations occur at the frequency
$\unicode[STIX]{x1D703}$
. These oscillations occur at the frequency
![]() $f$
with
$f$
with
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
, while oscillations at
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
, while oscillations at
![]() $2\unicode[STIX]{x1D714}$
are observed on the vertical velocity of the body. The fluttering frequency
$2\unicode[STIX]{x1D714}$
are observed on the vertical velocity of the body. The fluttering frequency
![]() $f$
was measured via a spectral analysis of the oscillations of
$f$
was measured via a spectral analysis of the oscillations of
![]() $\unicode[STIX]{x1D703}$
over the time span corresponding to a constant amplitude. The frequency ranges from 0.65 to 1.5 Hz and decreases as
$\unicode[STIX]{x1D703}$
over the time span corresponding to a constant amplitude. The frequency ranges from 0.65 to 1.5 Hz and decreases as
![]() $Ar$
increases, whatever the elongation ratio. For
$Ar$
increases, whatever the elongation ratio. For
![]() $L/d=2$
, a frequency decrease from approximately 1.5 to 1.2 Hz is observed for
$L/d=2$
, a frequency decrease from approximately 1.5 to 1.2 Hz is observed for
![]() $Ar$
going from approximately 590 to 880. For
$Ar$
going from approximately 590 to 880. For
![]() $L/d=10$
,
$L/d=10$
,
![]() $f$
goes from 0.80 to 0.75 Hz for
$f$
goes from 0.80 to 0.75 Hz for
![]() $Ar$
increasing from 785 to 1090. To build a Strouhal number, a characteristic length scale has to be chosen as a complement to the gravitational velocity determined in the previous section,
$Ar$
increasing from 785 to 1090. To build a Strouhal number, a characteristic length scale has to be chosen as a complement to the gravitational velocity determined in the previous section,
![]() $u_{0}$
. Considering the classical interpretation of the Archimedes number as a Reynolds number, we note that
$u_{0}$
. Considering the classical interpretation of the Archimedes number as a Reynolds number, we note that
![]() $Ar=\sqrt{3/2}u_{0}l_{0}/\unicode[STIX]{x1D708}$
, with
$Ar=\sqrt{3/2}u_{0}l_{0}/\unicode[STIX]{x1D708}$
, with
![]() $l_{0}=\sqrt{dL}$
. The characteristic length and velocity scales,
$l_{0}=\sqrt{dL}$
. The characteristic length and velocity scales,
![]() $l_{0}$
and
$l_{0}$
and
![]() $u_{0}$
, can then be used to form the Strouhal number,
$u_{0}$
, can then be used to form the Strouhal number,
Figure 9 shows that
![]() $St^{\ast }$
is nearly independent of
$St^{\ast }$
is nearly independent of
![]() $Ar$
and
$Ar$
and
![]() $L/d$
in the range considered, with
$L/d$
in the range considered, with
![]() $St^{\ast }\simeq 0.11$
. Furthermore, this result turns out to be general for short and elongated finite-length cylinders. For short-length cylinders with
$St^{\ast }\simeq 0.11$
. Furthermore, this result turns out to be general for short and elongated finite-length cylinders. For short-length cylinders with
![]() $L/d$
ranging from 0.1 to 0.5 and a density contrast close to 1, Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007) obtained the relation
$L/d$
ranging from 0.1 to 0.5 and a density contrast close to 1, Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007) obtained the relation
![]() $St^{\ast }=fd/((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gd)^{1/2}\simeq 0.1$
which is retrieved from the expression (6.1) proposed here, considering that the gravitational velocity scale
$St^{\ast }=fd/((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gd)^{1/2}\simeq 0.1$
which is retrieved from the expression (6.1) proposed here, considering that the gravitational velocity scale
![]() $u_{0}$
for these bodies is
$u_{0}$
for these bodies is
![]() $((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gL)^{1/2}$
,
$((\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}-1)gL)^{1/2}$
,
![]() $L$
being the cylinder length or disk thickness. It is worth pointing out that the Strouhal number
$L$
being the cylinder length or disk thickness. It is worth pointing out that the Strouhal number
![]() $St_{L}$
based on the inertial time scale
$St_{L}$
based on the inertial time scale
![]() $L/u_{0}$
is also nearly independent of
$L/u_{0}$
is also nearly independent of
![]() $Ar$
for all
$Ar$
for all
![]() $L/d$
but contrastingly shows a strong dependence in
$L/d$
but contrastingly shows a strong dependence in
![]() $L/d$
, increasing from approximately
$L/d$
, increasing from approximately
![]() $0.15$
for
$0.15$
for
![]() $L/d=2$
to approximately
$L/d=2$
to approximately
![]() $0.4$
for
$0.4$
for
![]() $L/d=12$
. In fact,
$L/d=12$
. In fact,
![]() $St_{L}$
scales with
$St_{L}$
scales with
![]() $(L/d)^{1/2}$
, so that
$(L/d)^{1/2}$
, so that
![]() $St_{L}/(L/d)^{1/2}\simeq 0.11$
for all elongation ratios and
$St_{L}/(L/d)^{1/2}\simeq 0.11$
for all elongation ratios and
![]() $Ar$
considered here. A similar expression can be straightforwardly obtained for the Strouhal number based on the diameter
$Ar$
considered here. A similar expression can be straightforwardly obtained for the Strouhal number based on the diameter
![]() $d$
.
$d$
.

Figure 9. Strouhal number
![]() $St^{\ast }=f\sqrt{Ld}/u_{0}$
of the fluttering motion versus the Archimedes number
$St^{\ast }=f\sqrt{Ld}/u_{0}$
of the fluttering motion versus the Archimedes number
![]() $Ar$
for various elongation ratios.
$Ar$
for various elongation ratios.
This result can be compared with the expression
![]() $f_{lit}\simeq 0.126\sqrt{(\overline{\unicode[STIX]{x1D70C}}-1)g/\overline{\unicode[STIX]{x1D70C}}L}$
proposed by Marchildon et al. (Reference Marchildon, Clamen and Gauvin1964) to represent the oscillation frequencies they measured experimentally for cylinders with
$f_{lit}\simeq 0.126\sqrt{(\overline{\unicode[STIX]{x1D70C}}-1)g/\overline{\unicode[STIX]{x1D70C}}L}$
proposed by Marchildon et al. (Reference Marchildon, Clamen and Gauvin1964) to represent the oscillation frequencies they measured experimentally for cylinders with
![]() $\overline{\unicode[STIX]{x1D70C}}\in [1.14,11.7]$
and by Chow & Adams (Reference Chow and Adams2011) for cylinders with
$\overline{\unicode[STIX]{x1D70C}}\in [1.14,11.7]$
and by Chow & Adams (Reference Chow and Adams2011) for cylinders with
![]() $\overline{\unicode[STIX]{x1D70C}}\in [1.13,8.51]$
. This expression fits, with only a very slight overestimation, the measured oscillation frequencies
$\overline{\unicode[STIX]{x1D70C}}\in [1.13,8.51]$
. This expression fits, with only a very slight overestimation, the measured oscillation frequencies
![]() $f$
of the present paper, since
$f$
of the present paper, since
![]() $f_{lit}\simeq 1.14f/\sqrt{\overline{\unicode[STIX]{x1D70C}}}\simeq 1.06f$
for
$f_{lit}\simeq 1.14f/\sqrt{\overline{\unicode[STIX]{x1D70C}}}\simeq 1.06f$
for
![]() $\overline{\unicode[STIX]{x1D70C}}=1.16$
. However, the two predictions significantly depart from each other for stronger density contrast
$\overline{\unicode[STIX]{x1D70C}}=1.16$
. However, the two predictions significantly depart from each other for stronger density contrast
![]() $\overline{\unicode[STIX]{x1D70C}}$
. A factor
$\overline{\unicode[STIX]{x1D70C}}$
. A factor
![]() $2$
between the two expressions would typically be found for metal cylinders falling in water. It is therefore worth pointing out that both expressions have to be considered with caution. The expression proposed here, which also applies to short-length cylinders, was only determined for bodies with a density close to that of the surrounding liquid. As in the case of short-length cylinders (or disks), at different
$2$
between the two expressions would typically be found for metal cylinders falling in water. It is therefore worth pointing out that both expressions have to be considered with caution. The expression proposed here, which also applies to short-length cylinders, was only determined for bodies with a density close to that of the surrounding liquid. As in the case of short-length cylinders (or disks), at different
![]() $\overline{\unicode[STIX]{x1D70C}}$
, different modes of oscillatory motion may be expected to occur (Tchoufag et al.
Reference Tchoufag, Fabre and Magnaudet2014). As regards the expression for
$\overline{\unicode[STIX]{x1D70C}}$
, different modes of oscillatory motion may be expected to occur (Tchoufag et al.
Reference Tchoufag, Fabre and Magnaudet2014). As regards the expression for
![]() $f_{lit}$
, it is based on a torque balance on the body, assuming that the moment of momentum of the cylinder compensates for a pressure torque due to the asymmetry of the flow surrounding the cylinder, as soon as its axis is no longer perpendicular to its velocity. However, this balance omits the added-mass torque related to the existence of both axial and transversal velocity components, and which has been lately shown to provide a crucial contribution for anisotropic bodies, for instance for plates (Andersen, Pesavento & Wang Reference Andersen, Pesavento and Wang2005a
) and short-length cylinders (Fernandes et al.
Reference Fernandes, Ern, Risso and Magnaudet2008). Like for these bodies, the selection of the fluttering frequency is therefore concealed in the intricate equilibrium between the proper and added inertia terms and the vortical contributions accounting for viscous and wake effects.
$f_{lit}$
, it is based on a torque balance on the body, assuming that the moment of momentum of the cylinder compensates for a pressure torque due to the asymmetry of the flow surrounding the cylinder, as soon as its axis is no longer perpendicular to its velocity. However, this balance omits the added-mass torque related to the existence of both axial and transversal velocity components, and which has been lately shown to provide a crucial contribution for anisotropic bodies, for instance for plates (Andersen, Pesavento & Wang Reference Andersen, Pesavento and Wang2005a
) and short-length cylinders (Fernandes et al.
Reference Fernandes, Ern, Risso and Magnaudet2008). Like for these bodies, the selection of the fluttering frequency is therefore concealed in the intricate equilibrium between the proper and added inertia terms and the vortical contributions accounting for viscous and wake effects.

Figure 10. Oscillatory viscous wavelength
![]() $\unicode[STIX]{x1D6FF}$
versus
$\unicode[STIX]{x1D6FF}$
versus
![]() $Ar$
for various elongation ratios, normalized with (a) the cylinder diameter
$Ar$
for various elongation ratios, normalized with (a) the cylinder diameter
![]() $d$
; (b)
$d$
; (b)
![]() $l_{0}=\sqrt{dL}$
. Same legend for both panels.
$l_{0}=\sqrt{dL}$
. Same legend for both panels.
Following this line, the analysis can be pushed ahead by investigating the characteristics of the unsteady boundary layer existing at the surface of a body oscillating in a fluid otherwise at rest at the fluttering frequency
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
. This frequency is much larger than the viscous diffusion frequency
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
. This frequency is much larger than the viscous diffusion frequency
![]() $\unicode[STIX]{x1D708}/d^{2}$
(typically
$\unicode[STIX]{x1D708}/d^{2}$
(typically
![]() $50$
times for
$50$
times for
![]() $L/d=2$
and
$L/d=2$
and
![]() $200$
times for
$200$
times for
![]() $L/d=10$
), so that viscous diffusion of vorticity away from the body surface is strongly limited, the velocity changing sharply to adapt to the no-slip condition. The associated characteristic length scale can be introduced in the form of the oscillatory viscous wavelength,
$L/d=10$
), so that viscous diffusion of vorticity away from the body surface is strongly limited, the velocity changing sharply to adapt to the no-slip condition. The associated characteristic length scale can be introduced in the form of the oscillatory viscous wavelength,
![]() $\unicode[STIX]{x1D6FF}=2\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$
. Figure 10(a) shows that
$\unicode[STIX]{x1D6FF}=2\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$
. Figure 10(a) shows that
![]() $\unicode[STIX]{x1D6FF}$
is here of the order of the diameter
$\unicode[STIX]{x1D6FF}$
is here of the order of the diameter
![]() $d$
of the cylinder and depends both on
$d$
of the cylinder and depends both on
![]() $Ar$
and
$Ar$
and
![]() $L/d$
. Furthermore, figure 10(b) shows that it scales with
$L/d$
. Furthermore, figure 10(b) shows that it scales with
![]() $l_{0}=\sqrt{dL}$
, since
$l_{0}=\sqrt{dL}$
, since
![]() $\unicode[STIX]{x1D6FF}/l_{0}$
is independent of the elongation ratio, within experimental accuracy. This provides a possible physical interpretation for the length scale
$\unicode[STIX]{x1D6FF}/l_{0}$
is independent of the elongation ratio, within experimental accuracy. This provides a possible physical interpretation for the length scale
![]() $l_{0}$
. Since the effect of the elongation ratio is well captured by the length scale
$l_{0}$
. Since the effect of the elongation ratio is well captured by the length scale
![]() $l_{0}$
as well as by the length scale
$l_{0}$
as well as by the length scale
![]() $\unicode[STIX]{x1D6FF}$
, the results presented in figures 9 and 10 can then be expressed in two other forms. The first, illustrated in figure 11(a), is that the Strouhal number based on the thickness
$\unicode[STIX]{x1D6FF}$
, the results presented in figures 9 and 10 can then be expressed in two other forms. The first, illustrated in figure 11(a), is that the Strouhal number based on the thickness
![]() $\unicode[STIX]{x1D6FF}$
is independent of the elongation ratio. It displays an evolution with
$\unicode[STIX]{x1D6FF}$
is independent of the elongation ratio. It displays an evolution with
![]() $Ar$
that can be modelled by
$Ar$
that can be modelled by
![]() $1.3Ar^{-0.5}$
, leading to the scaling
$1.3Ar^{-0.5}$
, leading to the scaling
![]() $St^{\ast }\simeq 0.11$
. The second is that the Reynolds number based on the thickness of the unsteady boundary layer
$St^{\ast }\simeq 0.11$
. The second is that the Reynolds number based on the thickness of the unsteady boundary layer
![]() $Re_{\unicode[STIX]{x1D6FF}}=u_{0}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
is also independent of
$Re_{\unicode[STIX]{x1D6FF}}=u_{0}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
is also independent of
![]() $L/d$
, as shown in figure 11(b). The result is highlighted by contrasting this figure with figure 6. The dependence on
$L/d$
, as shown in figure 11(b). The result is highlighted by contrasting this figure with figure 6. The dependence on
![]() $Ar$
and independence of
$Ar$
and independence of
![]() $L/d$
observed in figure 11(a,b) indicate that, for these quantities, the volume of the body is important as expected (buoyancy being the driving force), yet no longer the exact shape of the body (i.e. its elongation ratio), suggesting a crucial role of the sharp edges of the cylinder (formed where its flat bases join its circular side) in the control of the extension of the unsteady boundary layers created by viscosity in the vicinity of the moving body.
$L/d$
observed in figure 11(a,b) indicate that, for these quantities, the volume of the body is important as expected (buoyancy being the driving force), yet no longer the exact shape of the body (i.e. its elongation ratio), suggesting a crucial role of the sharp edges of the cylinder (formed where its flat bases join its circular side) in the control of the extension of the unsteady boundary layers created by viscosity in the vicinity of the moving body.
Figure 11. (a) Strouhal number,
![]() $f\unicode[STIX]{x1D6FF}/u_{0}$
, versus
$f\unicode[STIX]{x1D6FF}/u_{0}$
, versus
![]() $Ar$
for various elongation ratios, indicating an evolution close to
$Ar$
for various elongation ratios, indicating an evolution close to
![]() $Ar^{-0.5}$
; (b) Reynolds number
$Ar^{-0.5}$
; (b) Reynolds number
![]() $Re_{\unicode[STIX]{x1D6FF}}=u_{0}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
based on the Stokes oscillatory wavelength for various elongation ratios as a function of the Archimedes number
$Re_{\unicode[STIX]{x1D6FF}}=u_{0}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
based on the Stokes oscillatory wavelength for various elongation ratios as a function of the Archimedes number
![]() $Ar$
.
$Ar$
.
We now turn our attention to the amplitudes of the translational and rotational oscillatory motions of the cylinder. During the fluttering regime, the inclination of the cylinder axis relative to the horizontal,
![]() $\unicode[STIX]{x1D703}$
, oscillates periodically and regularly, so that it can be modelled by an harmonic function,
$\unicode[STIX]{x1D703}$
, oscillates periodically and regularly, so that it can be modelled by an harmonic function,
![]() $\unicode[STIX]{x1D703}=\tilde{\unicode[STIX]{x1D703}}\sin (\unicode[STIX]{x1D714}t-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}})$
. Figure 12 shows that the amplitude
$\unicode[STIX]{x1D703}=\tilde{\unicode[STIX]{x1D703}}\sin (\unicode[STIX]{x1D714}t-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}})$
. Figure 12 shows that the amplitude
![]() $\tilde{\unicode[STIX]{x1D703}}$
depends both on
$\tilde{\unicode[STIX]{x1D703}}$
depends both on
![]() $Ar$
and
$Ar$
and
![]() $L/d$
, ranging from approximately
$L/d$
, ranging from approximately
![]() $20^{\circ }$
for
$20^{\circ }$
for
![]() $L/d=2$
to approximately
$L/d=2$
to approximately
![]() $7^{\circ }$
for
$7^{\circ }$
for
![]() $L/d=12$
, shorter cylinders displaying a greater oscillation amplitude of their axis. For a given elongation ratio,
$L/d=12$
, shorter cylinders displaying a greater oscillation amplitude of their axis. For a given elongation ratio,
![]() $\tilde{\unicode[STIX]{x1D703}}$
increases slightly with
$\tilde{\unicode[STIX]{x1D703}}$
increases slightly with
![]() $Ar$
. A larger increase, of approximately
$Ar$
. A larger increase, of approximately
![]() $2.5^{\circ }$
, is observed for
$2.5^{\circ }$
, is observed for
![]() $L/d=3$
and
$L/d=3$
and
![]() $Ar$
going from
$Ar$
going from
![]() $490$
to
$490$
to
![]() $590$
, which is not observed for higher elongation ratios for the values of
$590$
, which is not observed for higher elongation ratios for the values of
![]() $Ar$
that could be explored. For
$Ar$
that could be explored. For
![]() $L/d\geqslant 5$
, a jump is in fact observed in a short interval of
$L/d\geqslant 5$
, a jump is in fact observed in a short interval of
![]() $Ar$
from the values corresponding to the regime Irregular I,
$Ar$
from the values corresponding to the regime Irregular I,
![]() $\tilde{\unicode[STIX]{x1D703}}<3^{\circ }$
, to those of the fluttering regime,
$\tilde{\unicode[STIX]{x1D703}}<3^{\circ }$
, to those of the fluttering regime,
![]() $\tilde{\unicode[STIX]{x1D703}}$
growing further slowly and nearly linearly with
$\tilde{\unicode[STIX]{x1D703}}$
growing further slowly and nearly linearly with
![]() $Ar$
.
$Ar$
.

Figure 12. Amplitude
![]() $\tilde{\unicode[STIX]{x1D703}}$
of the oscillations of
$\tilde{\unicode[STIX]{x1D703}}$
of the oscillations of
![]() $\unicode[STIX]{x1D703}$
versus
$\unicode[STIX]{x1D703}$
versus
![]() $Ar$
for various elongation ratios for the fluttering and Irregular I regimes. Amplitudes corresponding to the latter regime are plotted using filled markers, except those for
$Ar$
for various elongation ratios for the fluttering and Irregular I regimes. Amplitudes corresponding to the latter regime are plotted using filled markers, except those for
![]() $L/d=10$
which are plotted using ticked boxes. The difference in amplitude between the two regimes is conspicuous.
$L/d=10$
which are plotted using ticked boxes. The difference in amplitude between the two regimes is conspicuous.
Chow & Adams (Reference Chow and Adams2011) measured
![]() $\tilde{\unicode[STIX]{x1D703}}$
in their experiments for freely falling cylinders with
$\tilde{\unicode[STIX]{x1D703}}$
in their experiments for freely falling cylinders with
![]() $\overline{\unicode[STIX]{x1D70C}}\in [1.13,8.5]$
,
$\overline{\unicode[STIX]{x1D70C}}\in [1.13,8.5]$
,
![]() $L/d\in [1,90]$
and
$L/d\in [1,90]$
and
![]() $Ar\in [200,6000]$
. By considering that the oscillation velocity of the ends of the cylinders is of the same order of magnitude as the mean fall velocity, and that it scales as its excursion over its period,
$Ar\in [200,6000]$
. By considering that the oscillation velocity of the ends of the cylinders is of the same order of magnitude as the mean fall velocity, and that it scales as its excursion over its period,
![]() $f_{lit}L\tilde{\unicode[STIX]{x1D703}}$
, they propose that
$f_{lit}L\tilde{\unicode[STIX]{x1D703}}$
, they propose that
![]() $\tilde{\unicode[STIX]{x1D703}}$
is only dependent on the density and elongation ratio,
$\tilde{\unicode[STIX]{x1D703}}$
is only dependent on the density and elongation ratio,
![]() $\tilde{\unicode[STIX]{x1D703}}\sim \sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
. They measured
$\tilde{\unicode[STIX]{x1D703}}\sim \sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
. They measured
![]() $20^{\circ }<\tilde{\unicode[STIX]{x1D703}}<40^{\circ }$
for
$20^{\circ }<\tilde{\unicode[STIX]{x1D703}}<40^{\circ }$
for
![]() $0.3<\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}<0.9$
. In the present study,
$0.3<\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}<0.9$
. In the present study,
![]() $\tilde{\unicode[STIX]{x1D703}}$
cannot be determined using only
$\tilde{\unicode[STIX]{x1D703}}$
cannot be determined using only
![]() $\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
, as it is also dependent on the Archimedes number. Moreover, the amplitude of the oscillations are here significantly smaller than those obtained by Chow & Adams (Reference Chow and Adams2011) for similar
$\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
, as it is also dependent on the Archimedes number. Moreover, the amplitude of the oscillations are here significantly smaller than those obtained by Chow & Adams (Reference Chow and Adams2011) for similar
![]() $\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
(ranging here from 0.30 to 0.75).
$\sqrt{\overline{\unicode[STIX]{x1D70C}}/(L/d)}$
(ranging here from 0.30 to 0.75).

Figure 13. Angular velocity of the cylinder
![]() $\unicode[STIX]{x1D714}\tilde{\unicode[STIX]{x1D703}}L$
normalized with the gravitational velocity
$\unicode[STIX]{x1D714}\tilde{\unicode[STIX]{x1D703}}L$
normalized with the gravitational velocity
![]() $u_{0}$
as a function of the Archimedes number
$u_{0}$
as a function of the Archimedes number
![]() $Ar$
for various
$Ar$
for various
![]() $L/d$
.
$L/d$
.
From the inclination angle of the body, we can determine the rotation rate of the body and its amplitude
![]() $\unicode[STIX]{x1D714}\tilde{\unicode[STIX]{x1D703}}$
, which is expected to scale with the inertial frequency associated with the mean fall,
$\unicode[STIX]{x1D714}\tilde{\unicode[STIX]{x1D703}}$
, which is expected to scale with the inertial frequency associated with the mean fall,
![]() $u_{0}/L$
. This scaling is displayed in figure 13, versus the Archimedes number, showing a remarkable gathering of the data points independently of the elongation ratio
$u_{0}/L$
. This scaling is displayed in figure 13, versus the Archimedes number, showing a remarkable gathering of the data points independently of the elongation ratio
![]() $L/d$
. Furthermore, the evolution with the Archimedes number is close to a constant, except for
$L/d$
. Furthermore, the evolution with the Archimedes number is close to a constant, except for
![]() $Ar\simeq 500$
at
$Ar\simeq 500$
at
![]() $L/d=3$
, for which the rotation rate is in fact slightly lower, as seen previously for the inclination angle
$L/d=3$
, for which the rotation rate is in fact slightly lower, as seen previously for the inclination angle
![]() $\tilde{\unicode[STIX]{x1D703}}$
.
$\tilde{\unicode[STIX]{x1D703}}$
.

Figure 14. Amplitude of oscillation of the velocity component along the cylinder axis,
![]() $\tilde{u}$
, normalized with
$\tilde{u}$
, normalized with
![]() $u_{0}$
versus
$u_{0}$
versus
![]() $Ar$
for various elongation ratios.
$Ar$
for various elongation ratios.
During the periodic motion, the oscillations of
![]() $\unicode[STIX]{x1D703}$
are coupled with oscillations of the cylinder centre of gravity. These can be characterized by the component of the body velocity along the cylinder axis,
$\unicode[STIX]{x1D703}$
are coupled with oscillations of the cylinder centre of gravity. These can be characterized by the component of the body velocity along the cylinder axis,
![]() $u$
, which oscillates at the fluttering frequency
$u$
, which oscillates at the fluttering frequency
![]() $f$
, and similarly to
$f$
, and similarly to
![]() $\unicode[STIX]{x1D703}$
, can be accurately represented by an harmonic function,
$\unicode[STIX]{x1D703}$
, can be accurately represented by an harmonic function,
![]() $u=\tilde{u} \sin (\unicode[STIX]{x1D714}t-\unicode[STIX]{x1D719}_{u})$
,
$u=\tilde{u} \sin (\unicode[STIX]{x1D714}t-\unicode[STIX]{x1D719}_{u})$
,
![]() $\tilde{u}$
being the oscillation amplitude and
$\tilde{u}$
being the oscillation amplitude and
![]() $\unicode[STIX]{x1D719}_{u}$
the phase. Figure 14 shows that the amplitude
$\unicode[STIX]{x1D719}_{u}$
the phase. Figure 14 shows that the amplitude
![]() $\tilde{u}$
normalized with
$\tilde{u}$
normalized with
![]() $u_{0}$
ranges between 0.2 and 0.7 for all the cases investigated. For a given elongation ratio,
$u_{0}$
ranges between 0.2 and 0.7 for all the cases investigated. For a given elongation ratio,
![]() $\tilde{u} /u_{0}$
increases with
$\tilde{u} /u_{0}$
increases with
![]() $Ar$
. At variance with the amplitude
$Ar$
. At variance with the amplitude
![]() $\tilde{\unicode[STIX]{x1D703}}$
, it also increases with
$\tilde{\unicode[STIX]{x1D703}}$
, it also increases with
![]() $L/d$
. The periodic motion of cylinders with increasing elongation ratios is therefore characterized by stronger axial velocity components and lower inclination angles. The phase difference,
$L/d$
. The periodic motion of cylinders with increasing elongation ratios is therefore characterized by stronger axial velocity components and lower inclination angles. The phase difference,
![]() $\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}}$
, between the oscillations of
$\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}}$
, between the oscillations of
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D703}$
is plotted as a function of
$\unicode[STIX]{x1D703}$
is plotted as a function of
![]() $Ar$
for various
$Ar$
for various
![]() $L/d$
in figure 15. Values remarkably gather along a master curve increasing slightly from approximately
$L/d$
in figure 15. Values remarkably gather along a master curve increasing slightly from approximately
![]() $9\unicode[STIX]{x03C0}/8$
to a constant value of approximately
$9\unicode[STIX]{x03C0}/8$
to a constant value of approximately
![]() $5\unicode[STIX]{x03C0}/4$
for
$5\unicode[STIX]{x03C0}/4$
for
![]() $Ar\geqslant 690$
. In the range of parameters considered here, no significant effect of
$Ar\geqslant 690$
. In the range of parameters considered here, no significant effect of
![]() $Ar$
nor of the elongation ratio
$Ar$
nor of the elongation ratio
![]() $L/d$
is observed on the phase difference between the oscillations of body inclination and axial velocity, at variance with the results for short-length cylinders (Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007).
$L/d$
is observed on the phase difference between the oscillations of body inclination and axial velocity, at variance with the results for short-length cylinders (Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007).

Figure 15. Phase difference between the oscillations of
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D703}$
versus
$\unicode[STIX]{x1D703}$
versus
![]() $Ar$
for various elongation ratios.
$Ar$
for various elongation ratios.
As mentioned in § 2, not all trajectories in the fluttering regime are planar zigzag paths contained in the azimuthal frame. The ellipticity of the path can be characterized by the ratio of
![]() $\tilde{w}/\tilde{u}$
,
$\tilde{w}/\tilde{u}$
,
![]() $\tilde{w}$
being the amplitude of the oscillations of the velocity component
$\tilde{w}$
being the amplitude of the oscillations of the velocity component
![]() $w$
in the direction perpendicular to the azimuthal plane (see figure 1
c). This quantity is displayed in figure 16. Mean values of
$w$
in the direction perpendicular to the azimuthal plane (see figure 1
c). This quantity is displayed in figure 16. Mean values of
![]() $\tilde{w}/\tilde{u}$
are plotted in the inset of figure 16 versus
$\tilde{w}/\tilde{u}$
are plotted in the inset of figure 16 versus
![]() $L/d$
. The figures indicate that the elongation ratio has a decisive impact on the type of trajectory observed. For long cylinders (
$L/d$
. The figures indicate that the elongation ratio has a decisive impact on the type of trajectory observed. For long cylinders (
![]() $L/d=7$
,
$L/d=7$
,
![]() $10$
and
$10$
and
![]() $12$
), the trajectory is very close to a planar zigzag, with
$12$
), the trajectory is very close to a planar zigzag, with
![]() $\tilde{w}/\tilde{u} <7\,\%$
for all cases. This behaviour changes with decreasing
$\tilde{w}/\tilde{u} <7\,\%$
for all cases. This behaviour changes with decreasing
![]() $L/d$
, with
$L/d$
, with
![]() $\tilde{w}/\tilde{u} \sim 0.1$
for all cylinders at
$\tilde{w}/\tilde{u} \sim 0.1$
for all cylinders at
![]() $L/d=5$
. For
$L/d=5$
. For
![]() $L/d=3$
, we find
$L/d=3$
, we find
![]() $\tilde{w}/\tilde{u} \sim 0.2$
, and for
$\tilde{w}/\tilde{u} \sim 0.2$
, and for
![]() $L/d=2$
,
$L/d=2$
,
![]() $\tilde{w}/\tilde{u} \sim 0.3$
. A slight increase of
$\tilde{w}/\tilde{u} \sim 0.3$
. A slight increase of
![]() $\tilde{w}/\tilde{u}$
with
$\tilde{w}/\tilde{u}$
with
![]() $Ar$
can be seen for
$Ar$
can be seen for
![]() $L/d=3$
, even though the data are dispersed due to difficulties in measuring
$L/d=3$
, even though the data are dispersed due to difficulties in measuring
![]() $w$
, which remains small (typically, lower than
$w$
, which remains small (typically, lower than
![]() $1.5~\text{cm}~\text{s}^{-1}$
). The body motion gets more complex and three-dimensional as the elongation ratio decreases. The existence of the
$1.5~\text{cm}~\text{s}^{-1}$
). The body motion gets more complex and three-dimensional as the elongation ratio decreases. The existence of the
![]() $w$
component in the fluttering regime is probably related to the existence of oscillations in the azimuthal angle
$w$
component in the fluttering regime is probably related to the existence of oscillations in the azimuthal angle
![]() $\unicode[STIX]{x1D713}$
. We were able to detect weak oscillations of
$\unicode[STIX]{x1D713}$
. We were able to detect weak oscillations of
![]() $\unicode[STIX]{x1D713}$
of amplitude slightly increasing with
$\unicode[STIX]{x1D713}$
of amplitude slightly increasing with
![]() $Ar$
, approximately
$Ar$
, approximately
![]() $6^{\circ }$
for
$6^{\circ }$
for
![]() $L/d=2$
, dispersed between
$L/d=2$
, dispersed between
![]() $3^{\circ }$
and
$3^{\circ }$
and
![]() $7^{\circ }$
for
$7^{\circ }$
for
![]() $L/d=3$
, lower than
$L/d=3$
, lower than
![]() $4^{\circ }$
for
$4^{\circ }$
for
![]() $L/d=5$
and than
$L/d=5$
and than
![]() $2^{\circ }$
for
$2^{\circ }$
for
![]() $L/d=10$
. However, the path of shorter cylinders (
$L/d=10$
. However, the path of shorter cylinders (
![]() $L/d=2$
and
$L/d=2$
and
![]() $3$
) could not be fully described, owing to the difficulty in determining properly the phases of
$3$
) could not be fully described, owing to the difficulty in determining properly the phases of
![]() $w$
and
$w$
and
![]() $\unicode[STIX]{x1D713}$
relative to those of
$\unicode[STIX]{x1D713}$
relative to those of
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.

Figure 16. Ratio between the amplitude of the oscillations of
![]() $u$
and
$u$
and
![]() $w$
, versus
$w$
, versus
![]() $Ar$
for various elongation ratios. The inset shows the mean values of
$Ar$
for various elongation ratios. The inset shows the mean values of
![]() $\tilde{w}/\tilde{u}$
for each
$\tilde{w}/\tilde{u}$
for each
![]() $L/d$
as a function of
$L/d$
as a function of
![]() $L/d$
.
$L/d$
.
7 Wake visualization and analysis
We now turn our attention to the structure and nature of the wake associated with the various paths observed here for freely falling cylinders. Wake visualization was performed by coating the cylinders in ink before releasing them into the tank. This provides a good qualitative visualization of the wake of the cylinders, as can be seen in figure 17. Several different types of wake are observed in the space of parameters
![]() $(Ar,L/d)$
covered here, for cylinders undergoing a rectilinear fall (figure 17
a,b), Irregular III oscillations (figure 17
c) or strong fluttering (figure 17
d). In the case of cylinders presenting a rectilinear motion, a comparison can directly be made with the numerical study by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for fixed cylinders with finite lengths and free ends.
$(Ar,L/d)$
covered here, for cylinders undergoing a rectilinear fall (figure 17
a,b), Irregular III oscillations (figure 17
c) or strong fluttering (figure 17
d). In the case of cylinders presenting a rectilinear motion, a comparison can directly be made with the numerical study by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for fixed cylinders with finite lengths and free ends.

Figure 17. Different types of wake observed. (a) Steady wake with two pairs of longitudinal vortices observed for a cylinder in rectilinear motion with
![]() $(Ar=200,L/d=3)$
. (b) Periodic release of hairpin vortices observed for cylinders following rectilinear paths with
$(Ar=200,L/d=3)$
. (b) Periodic release of hairpin vortices observed for cylinders following rectilinear paths with
![]() $(Ar=200,L/d=5)$
on the left and
$(Ar=200,L/d=5)$
on the left and
![]() $(Ar=200,L/d=10)$
on the right. (c) Wake for long cylinders
$(Ar=200,L/d=10)$
on the right. (c) Wake for long cylinders
![]() $(Ar=600,L/d=20)$
displaying weak azimuthal oscillations. (d) Fluttering regime
$(Ar=600,L/d=20)$
displaying weak azimuthal oscillations. (d) Fluttering regime
![]() $(Ar=1100,L/d=5)$
.
$(Ar=1100,L/d=5)$
.
We observe a single case of steady wake for
![]() $Ar=200$
and
$Ar=200$
and
![]() $L/d=3$
, corresponding to
$L/d=3$
, corresponding to
![]() $Re_{d}=120$
and to the lightest cylinder tested in our experiment which displays a rectilinear fall (see figure 17
a). This wake is characterized by the formation of four longitudinal dye streaks, alike the steady wake observed numerically by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for
$Re_{d}=120$
and to the lightest cylinder tested in our experiment which displays a rectilinear fall (see figure 17
a). This wake is characterized by the formation of four longitudinal dye streaks, alike the steady wake observed numerically by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for
![]() $Re_{d}=150$
and
$Re_{d}=150$
and
![]() $L/d=1$
(denoted Type IV in their work) and composed of two pairs of counter-rotating longitudinal vortices (see their figures 5b and 6). To our knowledge, this is the first experimental evidence of the existence of the wake structure uncovered numerically by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with slightly different parameters, and corresponding to the shedding of two steady counter-rotating vortex pairs behind the cylinder.
$L/d=1$
(denoted Type IV in their work) and composed of two pairs of counter-rotating longitudinal vortices (see their figures 5b and 6). To our knowledge, this is the first experimental evidence of the existence of the wake structure uncovered numerically by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for cylinders with slightly different parameters, and corresponding to the shedding of two steady counter-rotating vortex pairs behind the cylinder.
For
![]() $Ar=200$
,
$Ar=200$
,
![]() $L/d=5$
and
$L/d=5$
and
![]() $10$
(corresponding to
$10$
(corresponding to
![]() $Re_{d}=80$
and
$Re_{d}=80$
and
![]() $50$
respectively), we observe a periodic double-sided shedding of hairpin vortices (figure 17
b). It should be noted that in both cases, no significant horizontal displacement of the body was detected. The vortex shedding frequency was estimated to be approximately 7 Hz. Inoue & Sakuragi (Reference Inoue and Sakuragi2008) observed similar shedding of vortices for
$50$
respectively), we observe a periodic double-sided shedding of hairpin vortices (figure 17
b). It should be noted that in both cases, no significant horizontal displacement of the body was detected. The vortex shedding frequency was estimated to be approximately 7 Hz. Inoue & Sakuragi (Reference Inoue and Sakuragi2008) observed similar shedding of vortices for
![]() $Re_{d}=150$
and
$Re_{d}=150$
and
![]() $L/d=5$
, for
$L/d=5$
, for
![]() $Re_{d}=100$
and
$Re_{d}=100$
and
![]() $L/d=10$
, and for
$L/d=10$
, and for
![]() $Re_{d}=60$
and
$Re_{d}=60$
and
![]() $L/d=13$
, referenced as Type III (see their figure 5a). This type of wake is, according to Inoue & Sakuragi (Reference Inoue and Sakuragi2008), characterized by disconnected hairpin-shaped vortices shed alternatively from opposite sides of the curved surface of the cylinder, in contrast to vortices shed in Types I and II, to be discussed hereafter. An experimental illustration of a similar wake is also provided by Jayaweera & Mason (Reference Jayaweera and Mason1965) for
$L/d=13$
, referenced as Type III (see their figure 5a). This type of wake is, according to Inoue & Sakuragi (Reference Inoue and Sakuragi2008), characterized by disconnected hairpin-shaped vortices shed alternatively from opposite sides of the curved surface of the cylinder, in contrast to vortices shed in Types I and II, to be discussed hereafter. An experimental illustration of a similar wake is also provided by Jayaweera & Mason (Reference Jayaweera and Mason1965) for
![]() $Re_{d}=70$
and
$Re_{d}=70$
and
![]() $L/d=10$
.
$L/d=10$
.
Figure 17(c) shows the wake of a cylinder with
![]() $Ar\simeq 600$
and
$Ar\simeq 600$
and
![]() $L/d=20$
(
$L/d=20$
(
![]() $Re_{d}\simeq 130$
) corresponding to regime Irregular III. The wake for this freely moving long cylinder can be compared to the observations for fixed long cylinders with free ends from the numerical study by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) and without free ends from the experimental results by Williamson (Reference Williamson1989). The instantaneous structure of the wake observed in this case is similar to that referred to as Type II by Inoue & Sakuragi (Reference Inoue and Sakuragi2008), and as oblique vortex shedding by Williamson (Reference Williamson1989). However, the cylinder shown in figure 17(c) presents weak regular azimuthal oscillations, which are coupled to the wake. A periodic beating of the wake is in fact observed here near the ends of the cylinder, at the oscillation frequency of the azimuthal angle
$Re_{d}\simeq 130$
) corresponding to regime Irregular III. The wake for this freely moving long cylinder can be compared to the observations for fixed long cylinders with free ends from the numerical study by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) and without free ends from the experimental results by Williamson (Reference Williamson1989). The instantaneous structure of the wake observed in this case is similar to that referred to as Type II by Inoue & Sakuragi (Reference Inoue and Sakuragi2008), and as oblique vortex shedding by Williamson (Reference Williamson1989). However, the cylinder shown in figure 17(c) presents weak regular azimuthal oscillations, which are coupled to the wake. A periodic beating of the wake is in fact observed here near the ends of the cylinder, at the oscillation frequency of the azimuthal angle
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
In the case of fluttering cylinders, the coupling between the wake and the motion of the body leads to a significantly different wake structure, strongly influenced by the orientation of the body and of its flat faces relative to its velocity. An example is shown on figure 17(d) for
![]() $Ar\simeq 1100$
and
$Ar\simeq 1100$
and
![]() $L/d=5$
(
$L/d=5$
(
![]() $Re_{d}\simeq 585$
) for a body displaying a fluttering motion of amplitude
$Re_{d}\simeq 585$
) for a body displaying a fluttering motion of amplitude
![]() $\unicode[STIX]{x1D703}\simeq 12^{\circ }$
.
$\unicode[STIX]{x1D703}\simeq 12^{\circ }$
.

Figure 18. Strouhal number based on the high-frequency vertical oscillation of
![]() $v$
,
$v$
,
![]() $St_{v}=f_{v}d/\overline{u_{Z}}$
, versus the Reynolds number.
$St_{v}=f_{v}d/\overline{u_{Z}}$
, versus the Reynolds number.
Flow visualization thus revealed that an unsteady wake is observed even for bodies maintaining a rectilinear motion. A deeper analysis of the cylinder kinematics was therefore carried out in order to uncover possible effects of the wake unsteadiness in their path. This revealed that high-frequency oscillations of the vertical velocity of the cylinder (which can be seen on
![]() $v$
, as
$v$
, as
![]() $v\simeq u_{Z}$
for all cases) are observed on most cylinders recorded with an acquisition frequency of 50 Hz. These oscillations occur at a frequency
$v\simeq u_{Z}$
for all cases) are observed on most cylinders recorded with an acquisition frequency of 50 Hz. These oscillations occur at a frequency
![]() $f_{v}\sim 7$
Hz measured by the spectral analysis of
$f_{v}\sim 7$
Hz measured by the spectral analysis of
![]() $v$
(figure 18), and are observed for cylinders presenting rectilinear as well as fluttering paths. The amplitude of this vertical oscillation is very low, less than
$v$
(figure 18), and are observed for cylinders presenting rectilinear as well as fluttering paths. The amplitude of this vertical oscillation is very low, less than
![]() $4\,\%$
of
$4\,\%$
of
![]() $\overline{u_{Z}}$
for all cases, and was difficult to measure accurately.
$\overline{u_{Z}}$
for all cases, and was difficult to measure accurately.
![]() $f_{v}$
is remarkably constant with
$f_{v}$
is remarkably constant with
![]() $Re_{d}$
, with 6 Hz
$Re_{d}$
, with 6 Hz
![]() ${<}f_{v}<7.2~\text{Hz}$
for all cases but 2, being at approximately 8 Hz. No effect of
${<}f_{v}<7.2~\text{Hz}$
for all cases but 2, being at approximately 8 Hz. No effect of
![]() $L/d$
was detected on
$L/d$
was detected on
![]() $f_{v}$
. Vortex shedding from the curved side of the cylinder is a plausible cause for these oscillations, as they occur for all cylinders independently of their path,
$f_{v}$
. Vortex shedding from the curved side of the cylinder is a plausible cause for these oscillations, as they occur for all cylinders independently of their path,
![]() $L/d$
and
$L/d$
and
![]() $Re_{d}$
. Furthermore, this frequency is close to the estimated vortex shedding frequency from wake visualization videos for instance for
$Re_{d}$
. Furthermore, this frequency is close to the estimated vortex shedding frequency from wake visualization videos for instance for
![]() $Re_{d}=50$
and
$Re_{d}=50$
and
![]() $L/d=10$
(figure 17
b).
$L/d=10$
(figure 17
b).
A corresponding Strouhal number can be built as
![]() $St_{v}=f_{v}d/\overline{u_{Z}}$
.
$St_{v}=f_{v}d/\overline{u_{Z}}$
.
![]() $St_{v}$
increases with
$St_{v}$
increases with
![]() $Re_{d}$
and ranges from approximately 0.16 to 0.30 (figure 18). The elongation ratio has seemingly no impact on
$Re_{d}$
and ranges from approximately 0.16 to 0.30 (figure 18). The elongation ratio has seemingly no impact on
![]() $St_{v}$
in the range explored. Comparison of
$St_{v}$
in the range explored. Comparison of
![]() $St_{v}$
with previous results of the literature can be seen in figure 19. Williamson & Brown (Reference Williamson and Brown1998) proposed a fit in series of
$St_{v}$
with previous results of the literature can be seen in figure 19. Williamson & Brown (Reference Williamson and Brown1998) proposed a fit in series of
![]() $Re_{d}^{-1/2}$
for the Strouhal number corresponding to the Bénard–von Kármán instability about a fixed cylinder,
$Re_{d}^{-1/2}$
for the Strouhal number corresponding to the Bénard–von Kármán instability about a fixed cylinder,
![]() $St_{BvK}=0.2731-1.1129Re_{d}^{-1/2}+0.4821Re_{d}^{-1}$
for
$St_{BvK}=0.2731-1.1129Re_{d}^{-1/2}+0.4821Re_{d}^{-1}$
for
![]() $Re_{d}\leqslant 1000$
. For approximately
$Re_{d}\leqslant 1000$
. For approximately
![]() $160<Re_{d}<400$
corresponding to rectilinear and Irregular I paths (figure 7), the present results for
$160<Re_{d}<400$
corresponding to rectilinear and Irregular I paths (figure 7), the present results for
![]() $St_{v}$
are in good agreement with this expression. The Strouhal number values, computed by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for fixed cylinders with free ends at
$St_{v}$
are in good agreement with this expression. The Strouhal number values, computed by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) for fixed cylinders with free ends at
![]() $Re_{d}=100$
, are also plotted in figure 19. They are significantly smaller than the results for infinite cylinders, ranging from approximately 0.08 for
$Re_{d}=100$
, are also plotted in figure 19. They are significantly smaller than the results for infinite cylinders, ranging from approximately 0.08 for
![]() $L/d\simeq 3$
to 0.13 for
$L/d\simeq 3$
to 0.13 for
![]() $L/d\simeq 20$
. Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) and Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011) performed numerical studies of the flow past a cylinder using domains of varying spanwise length. Although measuring
$L/d\simeq 20$
. Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) and Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011) performed numerical studies of the flow past a cylinder using domains of varying spanwise length. Although measuring
![]() $St_{BvK}$
was not the primary aim of their work, they provided values of
$St_{BvK}$
was not the primary aim of their work, they provided values of
![]() $St_{BvK}$
for some Reynolds numbers. Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) studied cylinders of spanwise length
$St_{BvK}$
for some Reynolds numbers. Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) studied cylinders of spanwise length
![]() $L=10d$
and
$L=10d$
and
![]() $12d$
at
$12d$
at
![]() $Re_{d}=200$
providing
$Re_{d}=200$
providing
![]() $St_{BvK}\simeq 0.18$
, and Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011) cylinders of spanwise length
$St_{BvK}\simeq 0.18$
, and Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011) cylinders of spanwise length
![]() $L=6d$
and
$L=6d$
and
![]() $12d$
at
$12d$
at
![]() $Re_{d}=400$
yielding
$Re_{d}=400$
yielding
![]() $St_{BvK}\simeq 0.21$
. Both
$St_{BvK}\simeq 0.21$
. Both
![]() $St_{BvK}$
values are in good agreement with the present experimental results. It should be noted that Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) also performed numerical simulations for infinite cylinders, and that the values of
$St_{BvK}$
values are in good agreement with the present experimental results. It should be noted that Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013) also performed numerical simulations for infinite cylinders, and that the values of
![]() $St_{BvK}$
they found were in remarkable agreement with the model of Williamson & Brown (Reference Williamson and Brown1998). For the same
$St_{BvK}$
they found were in remarkable agreement with the model of Williamson & Brown (Reference Williamson and Brown1998). For the same
![]() $Re_{d}$
, the Strouhal number values they computed were thus lower for cylinders of fixed spanwise length. Finally, it can be pointed out that Namkoong et al. (Reference Namkoong, Yoo and Choi2008) observed numerically that for
$Re_{d}$
, the Strouhal number values they computed were thus lower for cylinders of fixed spanwise length. Finally, it can be pointed out that Namkoong et al. (Reference Namkoong, Yoo and Choi2008) observed numerically that for
![]() $66<Re_{d}<185$
the degrees of freedom in rotation and translation of an infinitely long (i.e. two-dimensional) cylinder lead to a slight decrease in the frequency of vortex shedding and of the associated oscillatory motion of the cylinder, with typically
$66<Re_{d}<185$
the degrees of freedom in rotation and translation of an infinitely long (i.e. two-dimensional) cylinder lead to a slight decrease in the frequency of vortex shedding and of the associated oscillatory motion of the cylinder, with typically
![]() $St_{BvK}\simeq 0.17$
for
$St_{BvK}\simeq 0.17$
for
![]() $\overline{\unicode[STIX]{x1D70C}}=1.01$
and
$\overline{\unicode[STIX]{x1D70C}}=1.01$
and
![]() $Re_{d}=156$
, corresponding to the trend observed here for lower
$Re_{d}=156$
, corresponding to the trend observed here for lower
![]() $Re_{d}$
(figure 19). For
$Re_{d}$
(figure 19). For
![]() $Re_{d}$
larger than approximately
$Re_{d}$
larger than approximately
![]() $400$
, corresponding to cylinders displaying in our configuration a fluttering motion (figure 7), we find values for the Strouhal number
$400$
, corresponding to cylinders displaying in our configuration a fluttering motion (figure 7), we find values for the Strouhal number
![]() $St_{v}$
higher than those of
$St_{v}$
higher than those of
![]() $St_{BvK}$
. The high-frequency mode is therefore observed to coexist, and most possibly is coupled, with the fluttering mode, as oscillations of
$St_{BvK}$
. The high-frequency mode is therefore observed to coexist, and most possibly is coupled, with the fluttering mode, as oscillations of
![]() $v$
at
$v$
at
![]() $f_{v}$
are detected to be superimposed to those at twice the fluttering frequency.
$f_{v}$
are detected to be superimposed to those at twice the fluttering frequency.

Figure 19. Strouhal number based on the high-frequency vertical oscillation of
![]() $v$
,
$v$
,
![]() $St_{v}=f_{v}d/\overline{u_{Z}}$
, versus
$St_{v}=f_{v}d/\overline{u_{Z}}$
, versus
![]() $Re_{d}$
, comparison with results from Williamson & Brown (Reference Williamson and Brown1998), Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013), Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011). The dashed line corresponds to the expression
$Re_{d}$
, comparison with results from Williamson & Brown (Reference Williamson and Brown1998), Qu et al. (Reference Qu, Norberg, Davidson, Peng and Wang2013), Gioria et al. (Reference Gioria, Meneghini, Aranha, Barbeiro and Carmo2011). The dashed line corresponds to the expression
![]() $St_{v}=0.2429-0.9238Re_{d}^{-1/2}$
from Namkoong et al. (Reference Namkoong, Yoo and Choi2008).
$St_{v}=0.2429-0.9238Re_{d}^{-1/2}$
from Namkoong et al. (Reference Namkoong, Yoo and Choi2008).
The correspondence between the Strouhal numbers provided by the oscillations of
![]() $v$
measured in our experiments, by the wake visualizations and by various numerical and experimental data on vortex shedding in the wake of fixed cylinders suggests that vortex shedding from the curved side of the cylinder may be responsible for the weak oscillations of the vertical velocity observed here for freely falling cylinders. An associated rotation of the cylinder about its axis could possibly exist along with the high-frequency vertical oscillation of the body, as observed by Namkoong et al. (Reference Namkoong, Yoo and Choi2008). In our experiments, no such motion could be detected across all experiments outside the transient period following the release of the body from rest. However, the measurement method for the rotation is not accurate enough to determine such low-amplitude motions (rotational and translational oscillations with amplitudes, respectively, of approximately
$v$
measured in our experiments, by the wake visualizations and by various numerical and experimental data on vortex shedding in the wake of fixed cylinders suggests that vortex shedding from the curved side of the cylinder may be responsible for the weak oscillations of the vertical velocity observed here for freely falling cylinders. An associated rotation of the cylinder about its axis could possibly exist along with the high-frequency vertical oscillation of the body, as observed by Namkoong et al. (Reference Namkoong, Yoo and Choi2008). In our experiments, no such motion could be detected across all experiments outside the transient period following the release of the body from rest. However, the measurement method for the rotation is not accurate enough to determine such low-amplitude motions (rotational and translational oscillations with amplitudes, respectively, of approximately
![]() $0.7^{\circ }$
and
$0.7^{\circ }$
and
![]() $0.1d$
for
$0.1d$
for
![]() $\overline{\unicode[STIX]{x1D70C}}=1.01$
and
$\overline{\unicode[STIX]{x1D70C}}=1.01$
and
![]() $Re_{d}=156$
in the simulations by Namkoong et al. (Reference Namkoong, Yoo and Choi2008) for freely falling two-dimensional cylinders). Numerical simulation may be a more adapted and accurate tool to carry further the investigation of the different regimes of low-amplitude oscillations of the cylinders.
$Re_{d}=156$
in the simulations by Namkoong et al. (Reference Namkoong, Yoo and Choi2008) for freely falling two-dimensional cylinders). Numerical simulation may be a more adapted and accurate tool to carry further the investigation of the different regimes of low-amplitude oscillations of the cylinders.
8 Conclusion
We investigated the motion of freely falling elongated cylinders (length-to-diameter ratio ranging from 2 to 20) in a liquid otherwise at rest, for the density ratio
![]() $\overline{\unicode[STIX]{x1D70C}}\simeq 1.16$
and for Archimedes numbers ranging from
$\overline{\unicode[STIX]{x1D70C}}\simeq 1.16$
and for Archimedes numbers ranging from
![]() $200$
to
$200$
to
![]() $1100$
. The Archimedes numbers are based on the body equivalent diameter, enabling us to investigate, at given
$1100$
. The Archimedes numbers are based on the body equivalent diameter, enabling us to investigate, at given
![]() $Ar$
, and therefore at given volume of the body and given buoyancy force (
$Ar$
, and therefore at given volume of the body and given buoyancy force (
![]() $\overline{\unicode[STIX]{x1D70C}}$
being fixed), the effect of the elongation ratios of the cylinders on their behaviour. A shadowgraphy technique involving two cameras and two backlights mounted on a travelling cart was used to track the cylinders along their fall. A dedicated image processing algorithm was further implemented to properly reconstruct the position and orientation of the cylinder in the 3-D space. In the range of parameters explored, we identified three main types of path, matching regimes known to exist for three-dimensional bodies (disks and spheres). Two of these are stationary, the rectilinear motion and the large-amplitude oscillatory motion (also referred to as fluttering or zigzag motion). The third one comprises irregular oscillatory motions of low amplitude (denoted here Irregular I to III) that may be assimilated to A-regimes or quasi-vertical regimes of the literature (see for instance Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). The rectilinear motion observed here is twofold. On the one hand, a steady vertical fall associated with a steady wake composed by two pairs of longitudinal vortices generated behind the cylinder is observed (here, only for
$\overline{\unicode[STIX]{x1D70C}}$
being fixed), the effect of the elongation ratios of the cylinders on their behaviour. A shadowgraphy technique involving two cameras and two backlights mounted on a travelling cart was used to track the cylinders along their fall. A dedicated image processing algorithm was further implemented to properly reconstruct the position and orientation of the cylinder in the 3-D space. In the range of parameters explored, we identified three main types of path, matching regimes known to exist for three-dimensional bodies (disks and spheres). Two of these are stationary, the rectilinear motion and the large-amplitude oscillatory motion (also referred to as fluttering or zigzag motion). The third one comprises irregular oscillatory motions of low amplitude (denoted here Irregular I to III) that may be assimilated to A-regimes or quasi-vertical regimes of the literature (see for instance Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). The rectilinear motion observed here is twofold. On the one hand, a steady vertical fall associated with a steady wake composed by two pairs of longitudinal vortices generated behind the cylinder is observed (here, only for
![]() $Ar=200$
and
$Ar=200$
and
![]() $L/d=3$
). On the other hand, a vertical rectilinear motion with very light vertical oscillations at a Strouhal number
$L/d=3$
). On the other hand, a vertical rectilinear motion with very light vertical oscillations at a Strouhal number
![]() $St_{v}$
(frequency
$St_{v}$
(frequency
![]() $f_{v}$
) close to that of the Bénard–von Kármán instability is observed in association with an unsteady wake, displaying in some range of parameters a periodic shedding of hairpin vortices. No additional motion of the body could be detected here experimentally, but horizontal or rotational motions of the body could possibly occur for these bodies. Their path would then belong to the second class of paths identified here, the low-amplitude rotational oscillatory regimes. The low-amplitude rotational regimes observed here present oscillations of irregular amplitude, that are difficult to disentangle from noise. Nevertheless, we tried to grasp some distinctive features and classified them in three groups. Irregular III corresponds to oscillations essentially of the azimuthal angle
$f_{v}$
) close to that of the Bénard–von Kármán instability is observed in association with an unsteady wake, displaying in some range of parameters a periodic shedding of hairpin vortices. No additional motion of the body could be detected here experimentally, but horizontal or rotational motions of the body could possibly occur for these bodies. Their path would then belong to the second class of paths identified here, the low-amplitude rotational oscillatory regimes. The low-amplitude rotational regimes observed here present oscillations of irregular amplitude, that are difficult to disentangle from noise. Nevertheless, we tried to grasp some distinctive features and classified them in three groups. Irregular III corresponds to oscillations essentially of the azimuthal angle
![]() $\unicode[STIX]{x1D713}$
of the cylinder at Strouhal numbers about
$\unicode[STIX]{x1D713}$
of the cylinder at Strouhal numbers about
![]() $St_{v}$
for long cylinders (
$St_{v}$
for long cylinders (
![]() $L/d=20$
). Irregular I and Irregular II present irregular oscillations of the inclination angle
$L/d=20$
). Irregular I and Irregular II present irregular oscillations of the inclination angle
![]() $\unicode[STIX]{x1D703}$
and of the body centre of gravity position at a frequency close to the fluttering frequency
$\unicode[STIX]{x1D703}$
and of the body centre of gravity position at a frequency close to the fluttering frequency
![]() $f$
, that stay weak (lower than
$f$
, that stay weak (lower than
![]() $3^{\circ }$
) over the whole time sequence (Irregular I) or are low-frequency modulated (Irregular II), amplitudes varying in this case from less than
$3^{\circ }$
) over the whole time sequence (Irregular I) or are low-frequency modulated (Irregular II), amplitudes varying in this case from less than
![]() $3^{\circ }$
to sometimes approximately
$3^{\circ }$
to sometimes approximately
![]() $10^{\circ }$
. These salient features are proposed here as a basis for future developments and improved analysis of these paths, as it must be stressed that experimentation, at least the one carried out here, is not accurate enough to elaborate a full characterization of these complex paths. Interestingly, though no significant oscillatory motion of the cylinder is clearly visible in these regimes, a significant agitation due to wake unsteadiness is present in the liquid, featuring in particular three-dimensional vortex shedding. A sharp distinction between these regimes and the fluttering regime is conspicuous, for large-amplitude oscillations in both orientation and translation of the body are manifest in the latter. In the fluttering regime, the rotation of the body as well as its tendency to slide along its symmetry axis are strongly coupled with an unsteady wake that has a distinct outline, and whose characteristic features are related to the fact that the flat sides of the cylinder contoured by sharp edges tend now to face the direction of motion. Still, closer examination of the temporal signals of the body vertical motion revealed coexistence in the fluttering regime of oscillations at frequencies
$10^{\circ }$
. These salient features are proposed here as a basis for future developments and improved analysis of these paths, as it must be stressed that experimentation, at least the one carried out here, is not accurate enough to elaborate a full characterization of these complex paths. Interestingly, though no significant oscillatory motion of the cylinder is clearly visible in these regimes, a significant agitation due to wake unsteadiness is present in the liquid, featuring in particular three-dimensional vortex shedding. A sharp distinction between these regimes and the fluttering regime is conspicuous, for large-amplitude oscillations in both orientation and translation of the body are manifest in the latter. In the fluttering regime, the rotation of the body as well as its tendency to slide along its symmetry axis are strongly coupled with an unsteady wake that has a distinct outline, and whose characteristic features are related to the fact that the flat sides of the cylinder contoured by sharp edges tend now to face the direction of motion. Still, closer examination of the temporal signals of the body vertical motion revealed coexistence in the fluttering regime of oscillations at frequencies
![]() $2f$
(fluttering behaviour) and
$2f$
(fluttering behaviour) and
![]() $f_{v}$
, suggesting a complex shedding of vortices originating both from the curved side of the cylinder and from the flat faces.
$f_{v}$
, suggesting a complex shedding of vortices originating both from the curved side of the cylinder and from the flat faces.
The detailed analysis of the body kinematics in the fluttering regime brought to light a series of remarkable properties of this motion. In the range of parameters
![]() $Ar$
and
$Ar$
and
![]() $L/d$
investigated here for
$L/d$
investigated here for
![]() $\overline{\unicode[STIX]{x1D70C}}\simeq 1.16$
, the values of the mean vertical velocity of the body gather together into the relation
$\overline{\unicode[STIX]{x1D70C}}\simeq 1.16$
, the values of the mean vertical velocity of the body gather together into the relation
![]() $\overline{u_{Z}}\simeq 1.46u_{0}$
, where
$\overline{u_{Z}}\simeq 1.46u_{0}$
, where
![]() $u_{0}=((\overline{\unicode[STIX]{x1D70C}}-1)gd)^{1/2}$
is the gravitational velocity based on the cylinder diameter
$u_{0}=((\overline{\unicode[STIX]{x1D70C}}-1)gd)^{1/2}$
is the gravitational velocity based on the cylinder diameter
![]() $d$
. The mean fall velocity of the cylinder appears therefore independent of its length, depending solely on its diameter, in the same way the mean velocity of the finite-length disk is independent of its diameter, depending solely on its length or thickness (see for instance Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007, where
$d$
. The mean fall velocity of the cylinder appears therefore independent of its length, depending solely on its diameter, in the same way the mean velocity of the finite-length disk is independent of its diameter, depending solely on its length or thickness (see for instance Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007, where
![]() $u_{0}=(|\overline{\unicode[STIX]{x1D70C}}-1|gL)^{1/2}$
,
$u_{0}=(|\overline{\unicode[STIX]{x1D70C}}-1|gL)^{1/2}$
,
![]() $\overline{\unicode[STIX]{x1D70C}}\simeq 0.99$
and
$\overline{\unicode[STIX]{x1D70C}}\simeq 0.99$
and
![]() $0.1\leqslant L/d\leqslant 0.5$
). Proceeding along with this parallel, a unified view of the fluttering frequency
$0.1\leqslant L/d\leqslant 0.5$
). Proceeding along with this parallel, a unified view of the fluttering frequency
![]() $f$
of finite-length cylinders (either short or elongated) with density ratios close to unity is provided by the Strouhal number,
$f$
of finite-length cylinders (either short or elongated) with density ratios close to unity is provided by the Strouhal number,
featuring the length scale
![]() $l_{0}$
and the gravitational velocity scale based on the dimension of the cylinder corresponding to the direction of its mean vertical motion (the length for a short-length cylinder and the diameter for an elongated cylinder), yielding
$l_{0}$
and the gravitational velocity scale based on the dimension of the cylinder corresponding to the direction of its mean vertical motion (the length for a short-length cylinder and the diameter for an elongated cylinder), yielding
![]() $St^{\ast }\simeq 0.11$
for elongated cylinders, and
$St^{\ast }\simeq 0.11$
for elongated cylinders, and
![]() $St^{\ast }\simeq 0.1$
for disks in Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007). These results bring to the fore that the characteristic length and velocity scales of the body motion are respectively
$St^{\ast }\simeq 0.1$
for disks in Fernandes et al. (Reference Fernandes, Risso, Ern and Magnaudet2007). These results bring to the fore that the characteristic length and velocity scales of the body motion are respectively
![]() $l_{0}$
and
$l_{0}$
and
![]() $u_{0}$
. When made dimensionless using these scales, the mean vertical velocity and the frequency of the oscillations are almost independent of
$u_{0}$
. When made dimensionless using these scales, the mean vertical velocity and the frequency of the oscillations are almost independent of
![]() $L/d$
and
$L/d$
and
![]() $Ar$
. Their relevance is further intensified by considering that the Archimedes number defined using the equivalent diameter of the cylinder
$Ar$
. Their relevance is further intensified by considering that the Archimedes number defined using the equivalent diameter of the cylinder
![]() $D$
as mentioned previously, can be expressed as the Reynolds number built with
$D$
as mentioned previously, can be expressed as the Reynolds number built with
![]() $u_{0}$
and
$u_{0}$
and
![]() $l_{0}$
,
$l_{0}$
,
![]() $Ar=\sqrt{3/2}u_{0}l_{0}/\unicode[STIX]{x1D708}$
.
$Ar=\sqrt{3/2}u_{0}l_{0}/\unicode[STIX]{x1D708}$
.
Moving beyond this point to improve our understanding is not an easy task with the results at hand. The scaling proposed for the fluttering frequency appears as purely inertial, based on the inertial time scale
![]() $l_{0}/u_{0}$
. However, primary causes of frequency selection could lie deeper in the flow organization in the vicinity of the body due to the effect of viscosity. The fluttering period is an order of magnitude shorter than the viscous diffusion time scale
$l_{0}/u_{0}$
. However, primary causes of frequency selection could lie deeper in the flow organization in the vicinity of the body due to the effect of viscosity. The fluttering period is an order of magnitude shorter than the viscous diffusion time scale
![]() $d^{2}/\unicode[STIX]{x1D708}$
, so that the liquid velocity changes sharply to satisfy the no-slip condition on the cylinder surface and viscous effects are responsible for flow reversal in the vicinity of the cylinder. The extension of the recirculation region can be estimated with the oscillatory viscous wavelength,
$d^{2}/\unicode[STIX]{x1D708}$
, so that the liquid velocity changes sharply to satisfy the no-slip condition on the cylinder surface and viscous effects are responsible for flow reversal in the vicinity of the cylinder. The extension of the recirculation region can be estimated with the oscillatory viscous wavelength,
![]() $\unicode[STIX]{x1D6FF}=2\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$
, which scales with
$\unicode[STIX]{x1D6FF}=2\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$
, which scales with
![]() $l_{0}=\sqrt{dL}$
, since
$l_{0}=\sqrt{dL}$
, since
![]() $\unicode[STIX]{x1D6FF}/l_{0}$
is found to be, within experimental accuracy, independent of the elongation ratio for given
$\unicode[STIX]{x1D6FF}/l_{0}$
is found to be, within experimental accuracy, independent of the elongation ratio for given
![]() $Ar$
. We therefore suggest that the origin of the length scale
$Ar$
. We therefore suggest that the origin of the length scale
![]() $l_{0}$
is related to viscosity, as a characteristic recirculation length scale. For the unsteady boundary layers at rather high frequencies involved here, flow reversal might be expected to occur simultaneously both on the face and side of the cylinder surface, coupling therefore the two characteristic dimensions of the body,
$l_{0}$
is related to viscosity, as a characteristic recirculation length scale. For the unsteady boundary layers at rather high frequencies involved here, flow reversal might be expected to occur simultaneously both on the face and side of the cylinder surface, coupling therefore the two characteristic dimensions of the body,
![]() $d$
and
$d$
and
![]() $L$
.
$L$
.
We further explored the characteristics of the amplitudes of oscillation in translation and rotation of the body and showed that cylinders with higher elongation ratios display a higher axial velocity component
![]() $u$
and lower inclination angle
$u$
and lower inclination angle
![]() $\unicode[STIX]{x1D703}$
. The rotation rate of the cylinders scales with the inertial frequency scale,
$\unicode[STIX]{x1D703}$
. The rotation rate of the cylinders scales with the inertial frequency scale,
![]() $u_{0}/L$
, depending only slightly on
$u_{0}/L$
, depending only slightly on
![]() $Ar$
and
$Ar$
and
![]() $L/d$
. One of the most remarkable results is however provided by the phase difference
$L/d$
. One of the most remarkable results is however provided by the phase difference
![]() $(\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}})$
between the oscillations of
$(\unicode[STIX]{x1D719}_{u}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D703}})$
between the oscillations of
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D703}$
, which increases slightly from approximately
$\unicode[STIX]{x1D703}$
, which increases slightly from approximately
![]() $9\unicode[STIX]{x03C0}/8$
to a constant value of
$9\unicode[STIX]{x03C0}/8$
to a constant value of
![]() $5\unicode[STIX]{x03C0}/4$
for larger
$5\unicode[STIX]{x03C0}/4$
for larger
![]() $Ar$
, whatever the elongation ratio
$Ar$
, whatever the elongation ratio
![]() $L/d$
. This result is markedly at variance with the behaviour of disks, where a strong influence of the disk aspect ratio on the phase difference is observed, changing by approximately
$L/d$
. This result is markedly at variance with the behaviour of disks, where a strong influence of the disk aspect ratio on the phase difference is observed, changing by approximately
![]() $\unicode[STIX]{x03C0}/2$
when
$\unicode[STIX]{x03C0}/2$
when
![]() $L/d$
varies between
$L/d$
varies between
![]() $0.1$
and
$0.1$
and
![]() $0.5$
(Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007). In spite of these properties, it is worth pointing out that the path of the cylinders remains complex. The fluttering motion is moderately three-dimensional (ellipticity lower than
$0.5$
(Fernandes et al.
Reference Fernandes, Risso, Ern and Magnaudet2007). In spite of these properties, it is worth pointing out that the path of the cylinders remains complex. The fluttering motion is moderately three-dimensional (ellipticity lower than
![]() $0.3$
), becoming more planar as the elongation ratio of the body increases, tending towards a path contained in the plane formed by the body symmetry axis and the vertical. Since the motion in the perpendicular direction to this plane is weak, its characterization requires a specific investigation, which is beyond the scope of the present paper.
$0.3$
), becoming more planar as the elongation ratio of the body increases, tending towards a path contained in the plane formed by the body symmetry axis and the vertical. Since the motion in the perpendicular direction to this plane is weak, its characterization requires a specific investigation, which is beyond the scope of the present paper.
Acknowledgements
The authors are grateful to S. Cazin, G. Ehses and R. Soeparno for the technical support provided for the experiments. They also gratefully acknowledge financial support by IFP Energies Nouvelles, Solaize, France and warmly thank D. Ferré and R. Brahem (from department R1240S), C. P. da Fonte and L. Gamet (R1510S), as well as J. L. Pierson (R04) for their interest in the problem.
Appendix. Three-dimensional reconstruction of a cylinder using its projected contour
When observing a 3-D object through a camera using shadowgraphy, only the 2-D projection of its contour is seen. This projected contour loses some properties of the 3-D object, such as symmetries. In our study, we need to determine accurately the pose, i.e. the accurate position in a 3-D space, of the cylinders. In the case of a cylinder, the projected contour on the camera plane loses the planar symmetry property of the cylinder. Moreover, the distortion is not even for all contour points, and the ones further from the camera axis are more distorted. As a result, the shape and orientation of the projected cylinder contour are vastly different from its physical ones. Furthermore, no contour point is easily matchable to a physical point of the cylinder. In consequence, determining the exact features of the 3-D object using solely its projection is not a trivial matter. The 3-D reconstruction (also called pose estimation) of a cylinder using its projected contour is a problem investigated by several computer vision studies due to its difficulty and numerous applications (Huang et al. Reference Huang, Chen and Chia1996; Doignon & de Mathelin Reference Doignon and de Mathelin2007; Shiu & Huang Reference Shiu and Huang1993; Navab & Appel Reference Navab and Appel2006). Huang et al. (Reference Huang, Chen and Chia1996) presented a pose determination method using only the straight line projection of the sides of the cylinder, based on the image from a single camera. Being based on a geometric transformation, it can be implemented directly on the cylinder contour (versus on the images, which is computationally heavier) and runs fast. Consequently, the method of Huang et al. (Reference Huang, Chen and Chia1996) was chosen in the present work to solve the problem of the 3-D reconstruction of the cylinder.
As mentioned before, the perspective distortion of a cylinder depends on its position in the camera field of view. Features of the cylinder can only be accurately extracted when its axis is perfectly orthogonal to the camera optical axis. In our experiments, the rotation and fall velocity of the cylinder made it impossible to keep it in that configuration at all times. Additionally, the projected contour of the cylinder only has smooth surfaces, and no angular point can be identified and matched to a physical point of the cylinder. Therefore, other geometric properties of the cylinder contour that can be easily identified have to be found. Huang et al. (Reference Huang, Chen and Chia1996) chose to use the projection of the straight sides of the cylinder as such features. Once the contour points belonging to the cylinder straight sides have been properly identified, it is possible to determine the equation of the two planes containing each the centre of projection of the camera and one of these lines. Then, a new image plane, called the canonical image plane, is created. The cylinder contour points in this new plane correspond to what would have appeared on the original image plane if the cylinder axis had been orthogonal to the camera optical axis. Specific features of cylinder contour in the canonical image plane can be used to determine the position and orientation of the cylinder in the laboratory frame. Once these points have been identified, they are located in the original image plane using the inverse projection transformation to the one used to go from the original image plane to the canonical one. Then, their positions in the laboratory frame are deduced from the camera calibration. The output from this method is the centre of the two flat faces of the cylinder.
The method described in Huang et al. (Reference Huang, Chen and Chia1996) was developed to be used with a single camera. In our experimental set-up, we have two orthogonal cameras. Given the nature of a camera, the method of Huang et al. (Reference Huang, Chen and Chia1996) is very accurate to determine the two coordinates corresponding to its image plane, but less so for the third one, corresponding to its depth of field. In the present work, the method of Huang et al. (Reference Huang, Chen and Chia1996) was adapted so that for each frame, a camera was used to give the two coordinates corresponding to its image plane, and the remaining coordinate was given by the other camera. The camera outputting two coordinates was chosen to be the one having the best view angle of the cylinder. This adaptation proved to increase significantly the accuracy of the reconstruction method.
Given the vast number of operations involved in the method of Huang et al. (Reference Huang, Chen and Chia1996), it is difficult to estimate quantitatively its accuracy. Huang et al. (Reference Huang, Chen and Chia1996) suggest to use the computed cylinder length, deduced from the coordinates of the two flat faces of the cylinder, and to compare it to the actual cylinder length to have an estimation of the accuracy. All the data we provide in this work have an associated mean relative error of
![]() $4.5\,\%$
for the length, with a maximum error of
$4.5\,\%$
for the length, with a maximum error of
![]() $10\,\%$
and a root-mean-square value of
$10\,\%$
and a root-mean-square value of
![]() $4\,\%$
. When the error was greater than
$4\,\%$
. When the error was greater than
![]() $10\,\%$
, the data were discarded. This occurred in 22 out of 248 runs.
$10\,\%$
, the data were discarded. This occurred in 22 out of 248 runs.