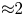1. Introduction
Investigations of magnetic reconnection are paramount for understanding particle acceleration in astrophysical plasma environments (Biskamp Reference Biskamp1986; Büchner Reference Büchner1999; Ji & Daughton Reference Ji and Daughton2011; Gonzalez & Parker Reference Gonzalez and Parker2016; Nalewajko Reference Nalewajko2016; Howes Reference Howes2018; Ji et al. Reference Ji2019). The two-dimensional (2-D) Sweet–Parker model of reconnection has been studied and verified by numerous state-of-the-art spheromak and tokamak apparatuses (e.g. Ji et al. Reference Ji, Yamada, Hsu and Kulsrud1998; Brown, Cothran & Fung Reference Brown, Cothran and Fung2006; Egedal et al. Reference Egedal, Fox, Katz, Porkolab, Reim and Zhang2007; Ji et al. Reference Ji2014; Yamada et al. Reference Yamada, Yoo, Jara-Almonte, Ji, Kulsrud and Myers2014). However, to the authors’ knowledge, there is no operational experiment dedicated to studying driven reconnection about a three-dimensional (3-D) magnetic null point (figure 1) featuring the fan-spine topology (Parnell et al. Reference Parnell, Smith, Neukirch and Priest1996, Reference Parnell, Neukirch, Smith and Priest1997). To date, only the 3-D electron magnetohydrodynamic (MHD) experiment at UCLA was designed to study whistler wave propagation and magnetic reconnection in the fan-spine topology due to relaxation dynamics (Stenzel et al. Reference Stenzel, Urrutia, Griskey and Strohmaier2001, Reference Stenzel, Urrutia, Griskey and Strohmaier2002). A complete understanding of reconnection in astrophysical environments, such as in the solar corona (Longcope & Parnell Reference Longcope and Parnell2009; Pontin, Priest & Galsgaard Reference Pontin, Priest and Galsgaard2013; Edwards & Parnell Reference Edwards and Parnell2015) and dynamic particle acceleration in collimated plasma jets (Liu et al. Reference Liu, Berger, Title, Tarbell and Low2011; Nishizuka et al. Reference Nishizuka, Hayashi, Tanabe, Kuwahata, Kaminou, Ono, Inomoto and Shimizu2012; Thurgood, Pontin & McLaughlin Reference Thurgood, Pontin and McLaughlin2017), requires an experimental application that investigates driven modes of torsional magnetic reconnection (Priest & Pontin Reference Priest and Pontin2009; Pontin Reference Pontin2011, Reference Pontin2012) that lie beyond the capabilities of the classical quasi-stationary X-line geometry (Zweibel & Yamada Reference Zweibel and Yamada2016).

Figure 1. Geometry of a 3-D null point.
Torsional modes of magnetic reconnection are driven by rotational magnetic field dynamics embedded within the plasma (Pontin & Galsgaard Reference Pontin and Galsgaard2007; Pontin, Al-Hachami & Galsgaard Reference Pontin, Al-Hachami and Galsgaard2011; Thurgood et al. Reference Thurgood, Pontin and McLaughlin2017). Any experiment for investigating the plasma and magnetic field dynamics leading to and resulting from torsional reconnection must also be able to resolve such driving mechanisms. Since magnetic reconnection in the kinetic regime involves a kinetic physics on the scale of the electron inertial length $d_{e}$![]() (Stenzel & Urrutia Reference Stenzel and Urrutia1998; Stenzel Reference Stenzel1999; Stenzel, Urrutia & Griskey Reference Stenzel, Urrutia and Griskey1999; Stenzel et al. Reference Stenzel, Urrutia, Griskey and Strohmaier2001, Reference Stenzel, Urrutia, Griskey and Strohmaier2002; Chesny, Orange & Dempsey Reference Chesny, Orange and Dempsey2021), a first laboratory torsional reconnection experiment must feature a plasma with a sufficiently large $d_{e}$
(Stenzel & Urrutia Reference Stenzel and Urrutia1998; Stenzel Reference Stenzel1999; Stenzel, Urrutia & Griskey Reference Stenzel, Urrutia and Griskey1999; Stenzel et al. Reference Stenzel, Urrutia, Griskey and Strohmaier2001, Reference Stenzel, Urrutia, Griskey and Strohmaier2002; Chesny, Orange & Dempsey Reference Chesny, Orange and Dempsey2021), a first laboratory torsional reconnection experiment must feature a plasma with a sufficiently large $d_{e}$![]() for resolvable diagnostics, while also providing the MHD plasma conditions required for reconnection (i.e. Lundquist number $S > 1$
for resolvable diagnostics, while also providing the MHD plasma conditions required for reconnection (i.e. Lundquist number $S > 1$![]() , see § 3.2). Here, we investigate a well-studied plasma condition that is applied to satisfy such conditions in a unique configuration (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017), including the feasibility for enabling reconnection, as shown by the computed plasma parameters and their resulting particle acceleration profiles. Of particular interest to the plasma physics community would be the exploration of plasma drifting into a 3-D null point region waiting for the plasma to envelope it and feasibly resulting in a moving reconnection site (Lukin & Linton Reference Lukin and Linton2011; Chesny et al. Reference Chesny, Orange and Dempsey2021).
, see § 3.2). Here, we investigate a well-studied plasma condition that is applied to satisfy such conditions in a unique configuration (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017), including the feasibility for enabling reconnection, as shown by the computed plasma parameters and their resulting particle acceleration profiles. Of particular interest to the plasma physics community would be the exploration of plasma drifting into a 3-D null point region waiting for the plasma to envelope it and feasibly resulting in a moving reconnection site (Lukin & Linton Reference Lukin and Linton2011; Chesny et al. Reference Chesny, Orange and Dempsey2021).
Preliminary predictions of torsional reconnection at laboratory scales require demonstrating the two main aspects mentioned above. First, that certain laboratory- generated plasmas satisfy MHD conditions for reconnection and, second, that existing experimental hardware components that form these MHD plasmas can mimic the magnetic field dynamics of torsional reconnection (Pontin & Galsgaard Reference Pontin and Galsgaard2007; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011). The initial study of Chesny et al. (Reference Chesny, Orange, Oluseyi and Valletta2017) described a feasible apparatus that achieved both of the previous conditions, but stopped short of demonstrating particle response to reconnection. Numerous authors (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Stanier, Browning & Dalla Reference Stanier, Browning and Dalla2012; Hosseinpour, Mehdizade & Mohammadi Reference Hosseinpour, Mehdizade and Mohammadi2014; Gascoyne Reference Gascoyne2015; Threlfall et al. Reference Threlfall, Neukirch, Parnell and Eradat Oskoui2015; Pallister, Pontin & Wyper Reference Pallister, Pontin and Wyper2019) have employed a test particle approach to demonstrate relativistic particle acceleration in torsional reconnection under collisionless solar plasma conditions. These studies were able to broadly confirm satellite observations of the acceleration of protons to $\sim 10$![]() MeV levels and the formation of collimated, bidirectional jets.
MeV levels and the formation of collimated, bidirectional jets.
To begin to close the knowledge gap between the predictions of particle acceleration in torsional modes of reconnection and the design of a next-generation experiment, we combine an MHD test particle algorithm featuring a localized resistivity profile with plasma parameters that are achievable with a well known experimental device. The effect of this enforced resistivity is to approximate the input plasma geometry of the device which localizes the non-ideal region required for reconnection (Pontin, Hornig & Priest Reference Pontin, Hornig and Priest2004, Reference Pontin, Hornig and Priest2005; Wyper & Jain Reference Wyper and Jain2011). Our approach assumes a simple configuration of circular coils to produce a background, 3-D null point magnetic field (Chesny & Orange Reference Chesny and Orange2020; Chesny et al. Reference Chesny, Orange and Dempsey2021) along with an established plasma sheath generation model (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017; Chesny & Orange Reference Chesny and Orange2018). A generalized configuration of these hardware components is shown to approximate theoretical electrodynamics of torsional fan reconnection. Any realistic prediction of particle acceleration resulting from this configuration must employ magnetic and electric field solutions to the steady-state, kinematic, resistive MHD equations at energy and length scales achievable with these devices. We combine the resistive MHD solutions of Wyper & Jain (Reference Wyper and Jain2010) and Wyper & Jain (Reference Wyper and Jain2011) with a full-orbit test particle algorithm (e.g. Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Gascoyne Reference Gascoyne2015) to investigate particle acceleration at these achievable plasma scales. An important distinction between previous studies and the one presented here is the manner in which charged particles are introduced into the system. Whereas a broad collection of particles with randomized momenta is sufficient for mimicking an astrophysical plasma environment (Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008; Hosseinpour Reference Hosseinpour2015), a geometrically controlled injection of particles with localized resistivity and uniform momenta will more closely approximate the investigated hardware infrastructure (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017; Chesny & Orange Reference Chesny and Orange2018).
Of the three modes of torsional reconnection (torsional fan, torsional spine and spine-fan; e.g. Priest & Pontin (Reference Priest and Pontin2009)), we limit this study to focused jet formation resulting from the torsional fan case due to the dynamics of plasma formation and propagation within the hardware system (see § 3). A thin, axially propagating plasma sheath with an azimuthal magnetic field profile will be shown to mimic the application of a rotational perturbation to the spine axis (torsional fan case; Pontin & Galsgaard (Reference Pontin and Galsgaard2007) and Pontin et al. (Reference Pontin, Al-Hachami and Galsgaard2011)) and to provide the conditions for magnetic reconnection – resulting in a focused jet of accelerated ions. While an alternative investigation of torsional spine reconnection in this architecture is certainly an open question, this work is focused on particle response in the torsional fan mode alone.
In addition to advancements in basic plasma science, laboratory investigations of torsional reconnection resulting in plasma jets may have significant implications for technology fields such as spacecraft propulsion (Chesny Reference Chesny2013; Cazzola et al. Reference Cazzola, Curreli, Markidis and Lapenta2016; Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017; Bathgate et al. Reference Bathgate, Bilek, Cairns and McKenzie2018; Cazzola, Curreli & Lapenta Reference Cazzola, Curreli and Lapenta2018; Ebrahimi Reference Ebrahimi2020). This novel concept of exploiting magnetic reconnection for in-space propulsion faces competing architectures. Inducing the 2-D model of Sweet–Parker reconnection (Cazzola et al. Reference Cazzola, Curreli and Lapenta2018), although demonstrably more mature in terms of experimentation (e.g. Yamada et al. Reference Yamada, Yoo, Jara-Almonte, Ji, Kulsrud and Myers2014), faces the prospect of suppressing one side of a bidirectional outflow to produce thrust. The suppression would require an asymmetric density profile for the input plasma, but there is seemingly not yet a technological solution to imposing this asymmetry. The 2-D concept has recently been tested using a scaled-down, operational prototype (Bathgate et al. Reference Bathgate, Bilek, Cairns and McKenzie2018) which marks the first test of a reconnection-based thruster. However, its efficiency was low (${<}1\,\%$![]() ) and would require the addition of a magnetic mirror at one end to reflect the bidirectional flow and produce a net thrust. The recent application of the 2-D model via azimuthally symmetric plasmoid reconnection was simulated by Ebrahimi (Reference Ebrahimi2020). Further steps toward this operational thruster will require considerations of the pulsed nature of the reconnection process and how the plasmoid instability can operate at high frequencies. As simulated in this paper, the 3-D torsional fan mode may suggest a way to inject plasma and induce a perturbation resulting in a single, unidirectional jet of directed energy, where a majority of the plasma within the azimuthal perturbation region may be accelerated along one side of the spine axis which is the only outlet (§ 4).
) and would require the addition of a magnetic mirror at one end to reflect the bidirectional flow and produce a net thrust. The recent application of the 2-D model via azimuthally symmetric plasmoid reconnection was simulated by Ebrahimi (Reference Ebrahimi2020). Further steps toward this operational thruster will require considerations of the pulsed nature of the reconnection process and how the plasmoid instability can operate at high frequencies. As simulated in this paper, the 3-D torsional fan mode may suggest a way to inject plasma and induce a perturbation resulting in a single, unidirectional jet of directed energy, where a majority of the plasma within the azimuthal perturbation region may be accelerated along one side of the spine axis which is the only outlet (§ 4).
This paper uses a full-orbit test particle approach to investigate the kinetic response of helium ions in a resistive, collisional plasma to solutions of the steady-state, kinematic, resistive MHD equations with a localized resistivity profile. Building predictive models that are able to constrain the performance characteristics of future experiments of torsional reconnection at 3-D nulls will become important for an intimate understanding of the physics of astrophysical and laboratory observations. We first outline our governing equations and computational infrastructure in § 2, then introduce our choice of laboratory scaling and hardware in § 3. Results of the response of the constrained injection of helium ions to torsional fan reconnection are presented in § 4 with a discussion of dynamics and potential applications in §§ 5 and 6.
2. Computational routine
All routines were written in Python and used standard NumPy and SciPy packages. Three-dimensional visualizations are created using the Mayavi package (Ramachandran & Varoquaux Reference Ramachandran and Varoquaux2011) and FreeCAD.
2.1. Field structure
We use the 3-D magnetic field and electric potential solutions to the steady-state, kinematic, resistive MHD equations given by Wyper & Jain (Reference Wyper and Jain2010) and Wyper & Jain (Reference Wyper and Jain2011). For the torsional fan case, the twist in the magnetic field is localized to two flat, disk-like regions above and below the fan plane and is given in cylindrical coordinates ($r$![]() , $\theta$
, $\theta$![]() , $z$
, $z$![]() ). This magnetic field is of the form,
). This magnetic field is of the form,
where distances are scaled to a characteristic length described in §§ 2.2 and 3.2, $j$![]() , $l$
, $l$![]() and $c$
and $c$![]() govern the degree and spatial extent of the twist, and $\beta$
govern the degree and spatial extent of the twist, and $\beta$![]() and $\gamma$
and $\gamma$![]() are positive integers. Throughout this paper, we set $j = 5$
are positive integers. Throughout this paper, we set $j = 5$![]() , $\gamma = 3$
, $\gamma = 3$![]() , $l = 1$
, $l = 1$![]() and $\beta = c = 0$
and $\beta = c = 0$![]() , corresponding to a generic radially linear perturbation, and consistent with the torsional fan reconnection simulations of Hosseinpour (Reference Hosseinpour2015), Hosseinpour (Reference Hosseinpour2014a) and Hosseinpour et al. (Reference Hosseinpour, Mehdizade and Mohammadi2014). Using these values, (2.1) reduces to
, corresponding to a generic radially linear perturbation, and consistent with the torsional fan reconnection simulations of Hosseinpour (Reference Hosseinpour2015), Hosseinpour (Reference Hosseinpour2014a) and Hosseinpour et al. (Reference Hosseinpour, Mehdizade and Mohammadi2014). Using these values, (2.1) reduces to
Figure 2 displays $XZ$![]() and $XY$
and $XY$![]() streamlines of (2.2), with the distance scaled to a characteristic length (see below). The location of greatest twist is in the $XY$
streamlines of (2.2), with the distance scaled to a characteristic length (see below). The location of greatest twist is in the $XY$![]() plane at height $Z = \sqrt {1.5}$
plane at height $Z = \sqrt {1.5}$![]() defined by the $\theta$
defined by the $\theta$![]() term in (2.2). To approximate a controlled injection of plasma, we apply a resistivity profile $\eta$
term in (2.2). To approximate a controlled injection of plasma, we apply a resistivity profile $\eta$![]() depending only on height $z$
depending only on height $z$![]() as
as
where $\eta _{0} = m_{e} \nu _{e,i} / n_{e} \, \textrm {e}^{2}$![]() is the plasma resistivity calculated from the characteristic parameters of electron mass $m_{e}$
is the plasma resistivity calculated from the characteristic parameters of electron mass $m_{e}$![]() , electron–ion collision frequency $\nu _{e,i}$
, electron–ion collision frequency $\nu _{e,i}$![]() , electron number density $n_{e}$
, electron number density $n_{e}$![]() and the elementary charge $e$
and the elementary charge $e$![]() (see § 3.2). We set $\delta = 2$
(see § 3.2). We set $\delta = 2$![]() to localize the resistivity profile to the height $Z = \sqrt {1.5}$
to localize the resistivity profile to the height $Z = \sqrt {1.5}$![]() of maximum magnetic field twist predicted by (2.2). This choice, as will be shown in § 3.3, inherently confines and localizes the injected plasma sheath to the region of stressed, non-potential magnetic field. This choice also satisfies the constraints for realistic solutions when the sum of parameters $\gamma + \delta \ge 3$
of maximum magnetic field twist predicted by (2.2). This choice, as will be shown in § 3.3, inherently confines and localizes the injected plasma sheath to the region of stressed, non-potential magnetic field. This choice also satisfies the constraints for realistic solutions when the sum of parameters $\gamma + \delta \ge 3$![]() and is odd (Wyper & Jain Reference Wyper and Jain2011). The electric potential in torsional fan reconnection with the above resistivity profile is of the form
and is odd (Wyper & Jain Reference Wyper and Jain2011). The electric potential in torsional fan reconnection with the above resistivity profile is of the form
with the recurrence relation for $G(z, \lambda )$![]() being
being
and solutions for all values of $\lambda$![]() found using
found using
and
As in Wyper & Jain (Reference Wyper and Jain2011), the initial electric potential $\varPhi _{0}$![]() is in units of volts and depends on the current density $j_{0}$
is in units of volts and depends on the current density $j_{0}$![]() and normalized distances as $\varPhi _{0} = j_{0} \eta _{0} L_{0}$
and normalized distances as $\varPhi _{0} = j_{0} \eta _{0} L_{0}$![]() . The electric field can then be derived using $\boldsymbol {E} = - \boldsymbol {\nabla } \varPhi$
. The electric field can then be derived using $\boldsymbol {E} = - \boldsymbol {\nabla } \varPhi$![]() . Using our numerical parameters, these equations reduce to
. Using our numerical parameters, these equations reduce to
and

Figure 2. Magnetic field streamlines of torsional fan reconnection. (a) In the $XZ$![]() plane, the greatest azimuthal twist is localized to $Z = \sqrt {1.5}$
plane, the greatest azimuthal twist is localized to $Z = \sqrt {1.5}$![]() . (b) Spine field lines can be seen to twist in the $XY$
. (b) Spine field lines can be seen to twist in the $XY$![]() plane.
plane.
Figure 3 displays cross-sections of the vector and scalar fields of the torsional fan magnetic field (figure 3a,b, (2.2)), electric potential (figure 3c,d, (2.8)) and the electric field (figure 3e,f, (2.9)). Blue contours denote the extents of the plasma sheath injected into these fields, and will be described in more detail in § 3.3. Figure 4 shows the vector drift velocity (top row) calculated from
with the bottom row displaying the scalar resistivity profile of (2.3) localized to the region of maximum magnetic twist at $Z = \sqrt {1.5}$![]() .
.

Figure 3. Vector and scalar fields of torsional fan reconnection using $B_{0}=1$![]() T, $L_{0}=10$
T, $L_{0}=10$![]() cm, $\varPhi _{0}=6$
cm, $\varPhi _{0}=6$![]() kV and $E_{0}=60$
kV and $E_{0}=60$![]() kV m$^{-1}$
kV m$^{-1}$![]() . Vertical extents of panels’ (a,c,e) images are expanded to [$-2 \sqrt {1.5}$
. Vertical extents of panels’ (a,c,e) images are expanded to [$-2 \sqrt {1.5}$![]() , $2 \sqrt {1.5}$
, $2 \sqrt {1.5}$![]() ]. In all images, blue lines show extent of particle input sheath (see § 3.3). Here (a) $XZ$
]. In all images, blue lines show extent of particle input sheath (see § 3.3). Here (a) $XZ$![]() magnetic field at $Y = 0$
magnetic field at $Y = 0$![]() with units of Tesla; (b) $XY$
with units of Tesla; (b) $XY$![]() magnetic field twist at $Z = \sqrt {1.5}$
magnetic field twist at $Z = \sqrt {1.5}$![]() ; (c) $XZ$
; (c) $XZ$![]() electric potential at $Y = 0$
electric potential at $Y = 0$![]() ; (d) $XY$
; (d) $XY$![]() electric potential at $Z = \sqrt {1.5}$
electric potential at $Z = \sqrt {1.5}$![]() ; (e) $XZ$
; (e) $XZ$![]() electric field at $Y = 0$
electric field at $Y = 0$![]() ; (f) $XY$
; (f) $XY$![]() electric field at $Z = \sqrt {1.5}$
electric field at $Z = \sqrt {1.5}$![]() .
.

Figure 4. Vector and scalar quantities of torsional fan reconnection fields in figure 3 using $B_{0}=1$![]() T, $L_{0}=10$
T, $L_{0}=10$![]() cm, $\varPhi _{0}=6$
cm, $\varPhi _{0}=6$![]() kV and $E_{0}=60$
kV and $E_{0}=60$![]() kV m$^{-1}$
kV m$^{-1}$![]() . The plasma resistivity $\eta _{0}$
. The plasma resistivity $\eta _{0}$![]() is calculated from parameters in § 3.2. Vertical extents of panels’ (a,c) images are expanded to [$-2 \sqrt {1.5}$
is calculated from parameters in § 3.2. Vertical extents of panels’ (a,c) images are expanded to [$-2 \sqrt {1.5}$![]() , $2 \sqrt {1.5}$
, $2 \sqrt {1.5}$![]() ]. In all images, blue lines show extent of particle input sheath (see § 3.3). Here (a) $XZ$
]. In all images, blue lines show extent of particle input sheath (see § 3.3). Here (a) $XZ$![]() drift velocity at $Y = 0$
drift velocity at $Y = 0$![]() ; (b) $XY$
; (b) $XY$![]() drift velocity at $Z = \sqrt {1.5}$
drift velocity at $Z = \sqrt {1.5}$![]() ; (c) $XZ$
; (c) $XZ$![]() resistivity profile at $Y = 0$
resistivity profile at $Y = 0$![]() ; (d) uniform $XY$
; (d) uniform $XY$![]() resistivity profile at $Z = \sqrt {1.5}$
resistivity profile at $Z = \sqrt {1.5}$![]() .
.
2.2. Particle trajectories
Particle trajectories are computed using the relativistic equations of motion for momentum $\boldsymbol {p}$![]() , namely
, namely
and the Lorentz force in a collisional plasma
where $\boldsymbol {r}$![]() is the 3-D Cartesian position, $e$
is the 3-D Cartesian position, $e$![]() is the charge of a singly ionized particle, $A$
is the charge of a singly ionized particle, $A$![]() is the atomic mass, $m_{p}$
is the atomic mass, $m_{p}$![]() is the proton rest mass in MeV c$^{-2}$
is the proton rest mass in MeV c$^{-2}$![]() and $\nu _{in}$
and $\nu _{in}$![]() is the ion–neutral collision frequency (see below). Within the code, (2.11) and (2.12) are solved in dimensionless form, with distance scaled to a characteristic length $\boldsymbol {r} = L_{0} \boldsymbol {x}$
is the ion–neutral collision frequency (see below). Within the code, (2.11) and (2.12) are solved in dimensionless form, with distance scaled to a characteristic length $\boldsymbol {r} = L_{0} \boldsymbol {x}$![]() , momentum scaled to the initial momentum $\boldsymbol {p} = p_{0} \boldsymbol {n}$
, momentum scaled to the initial momentum $\boldsymbol {p} = p_{0} \boldsymbol {n}$![]() , magnetic field to a characteristic strength $\boldsymbol {B} = B_{0} \boldsymbol {b}$
, magnetic field to a characteristic strength $\boldsymbol {B} = B_{0} \boldsymbol {b}$![]() , time to the characteristic non-relativistic gyroperiod $t = \tau _{0} t^{\prime }$
, time to the characteristic non-relativistic gyroperiod $t = \tau _{0} t^{\prime }$![]() , with $\tau _{0} = 2 {\rm \pi}m_{0} / e B_{0}$
, with $\tau _{0} = 2 {\rm \pi}m_{0} / e B_{0}$![]() (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008). The initial momentum in MeV c$^{-1}$
(Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008). The initial momentum in MeV c$^{-1}$![]() is calculated from the initial particle kinetic energy $K_{0}$
is calculated from the initial particle kinetic energy $K_{0}$![]() in eV as $p_{0} = (K_{0}^{2} + 2 A m_{p} K_{0} )^{1/2}$
in eV as $p_{0} = (K_{0}^{2} + 2 A m_{p} K_{0} )^{1/2}$![]() . Our choices of $L_{0}$
. Our choices of $L_{0}$![]() and $B_{0}$
and $B_{0}$![]() will be described in § 3.2.
will be described in § 3.2.
Since full orbit particle tracing in plasmas is not limited by inelastic collisions (e.g. Marchand Reference Marchand2010; Homma et al. Reference Homma, Hoshino, Tokunaga, Yamoto, Hatayama, Asakura, Sakamoto and Tobita2018), the effects of collisions are accounted for in the final term on the right-hand side of (2.12). The addition of this collisional term has been shown to be effective in particle tracking studies of magnetic reconnection in high density laser plasmas up to $\sim 10^{25}$![]() m$^{-3}$
m$^{-3}$![]() (Zhong et al. Reference Zhong2016). The collision frequency is determined by our choice of plasma parameters in § 3.2. Most laboratory plasmas are weakly ionized, where the degree of ionization is dependent on the ion ($n_{i}$
(Zhong et al. Reference Zhong2016). The collision frequency is determined by our choice of plasma parameters in § 3.2. Most laboratory plasmas are weakly ionized, where the degree of ionization is dependent on the ion ($n_{i}$![]() ) and neutral gas ($n_{g}$
) and neutral gas ($n_{g}$![]() ) number densities $\chi = n_{i} / ( n_{g} + n_{i} )$
) number densities $\chi = n_{i} / ( n_{g} + n_{i} )$![]() and $\chi \ll 1$
and $\chi \ll 1$![]() . Weakly ionized plasmas are further defined by the electron–ion collision frequency $\nu _{ei}$
. Weakly ionized plasmas are further defined by the electron–ion collision frequency $\nu _{ei}$![]() being less than the electron–neutral collision frequency $\nu _{en}$
being less than the electron–neutral collision frequency $\nu _{en}$![]() ($\nu _{ei} < \nu _{en}$
($\nu _{ei} < \nu _{en}$![]() ; Park et al. Reference Park, Choe, Moon and Yoo2019). In the case of low-energy electrons (a few eV), the main collisional process in a weakly ionized plasma is dominated by polarization scattering of ions against neutral particles $\nu _{in}$
; Park et al. Reference Park, Choe, Moon and Yoo2019). In the case of low-energy electrons (a few eV), the main collisional process in a weakly ionized plasma is dominated by polarization scattering of ions against neutral particles $\nu _{in}$![]() (Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005). Electron and ion polarization scattering rate constants in units of cm$^{3}$
(Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005). Electron and ion polarization scattering rate constants in units of cm$^{3}$![]() s$^{-1}$
s$^{-1}$![]() are calculated from
are calculated from
and
respectively, where $\alpha _{R}$![]() is the species-dependent relative polarizability ($\alpha _{R, He} = 1.384$
is the species-dependent relative polarizability ($\alpha _{R, He} = 1.384$![]() for helium;
for helium;
Schwerdtfeger & Nagle (Reference Schwerdtfeger and Nagle2019)). The charged particle collision frequencies against neutrals are then calculated using
Parameters using typical laboratory values given in table 1 demonstrate numerically that the chosen helium plasma is weakly ionized ($\chi = 1\,\%$![]() and $\nu _{ei} < \nu _{en}$
and $\nu _{ei} < \nu _{en}$![]() ) and polarization scattering is the dominant collisional process.
) and polarization scattering is the dominant collisional process.
Table 1. Helium plasma parameters used for the CPG plasma regime. Assumes a capacitor bank discharge of 6 kV over 10 cm ($E=60$![]() kV m$^{-1}$
kV m$^{-1}$![]() ).
).

The dimensionless forms of (2.11) and (2.12) are solved numerically using the scipy.integrate.odeint package which uses LSODA from the FORTRAN library to dynamically monitor data and reduce errors by automatically switching between stiff and non-stiff methods. Numerical validation of this routine first verified the relativistic ion gyroradius $r_{g,i} = \gamma A m_{p} v_{\bot } / e B$![]() within uniform magnetic fields ($\boldsymbol {E} = 0$
within uniform magnetic fields ($\boldsymbol {E} = 0$![]() V m$^{-1}$
V m$^{-1}$![]() ). Then, summing the kinetic and electric potential energies throughout test runs with collisionless single particle trajectories when $\boldsymbol {E} \neq 0$
). Then, summing the kinetic and electric potential energies throughout test runs with collisionless single particle trajectories when $\boldsymbol {E} \neq 0$![]() V m$^{-1}$
V m$^{-1}$![]() demonstrated total energy conservation to five significant figures, of the order of $0.1$
demonstrated total energy conservation to five significant figures, of the order of $0.1$![]() eV, using (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Gascoyne Reference Gascoyne2015)
eV, using (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Gascoyne Reference Gascoyne2015)
Monitoring the total energy in the collisional plasma regime will elucidate the energy loss and energy loss rate due to collisions and scattering.
3. Plasma scaling parameters
3.1. Electrodynamic simulation of hardware
Here, we motivate our choice of particle injection geometry by simulating the electrodynamics of a hardware infrastructure that mimics the analytical requirements for torsional fan reconnection. In torsional fan reconnection, it is an azimuthal perturbation to the spine axis of a 3-D null point topology that provides the driver. In previous investigations of the torsional fan mode, the $r$![]() and $z$
and $z$![]() components of the fan-spine topology are subjected to a non-zero $\theta$
components of the fan-spine topology are subjected to a non-zero $\theta$![]() component (Galsgaard, Priest & Titov Reference Galsgaard, Priest and Titov2003; Pontin & Galsgaard Reference Pontin and Galsgaard2007; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011; Wyper & Jain Reference Wyper and Jain2011, Reference Wyper and Jain2010) as in (2.2). Consider a region of a spine axis consisting of vertical, potential magnetic field lines where the perturbation is to be imposed (such as in figure 1). A localized plasma injection imposing this azimuthal perturbation upon these spine axis field lines has the effect of pushing the vertical spine axis field lines toward their nearest neighbour (such as in figure 2), thus becoming a localized non-potential field with current density $\boldsymbol {J} \neq 0$
component (Galsgaard, Priest & Titov Reference Galsgaard, Priest and Titov2003; Pontin & Galsgaard Reference Pontin and Galsgaard2007; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011; Wyper & Jain Reference Wyper and Jain2011, Reference Wyper and Jain2010) as in (2.2). Consider a region of a spine axis consisting of vertical, potential magnetic field lines where the perturbation is to be imposed (such as in figure 1). A localized plasma injection imposing this azimuthal perturbation upon these spine axis field lines has the effect of pushing the vertical spine axis field lines toward their nearest neighbour (such as in figure 2), thus becoming a localized non-potential field with current density $\boldsymbol {J} \neq 0$![]() . The stronger the azimuthal component, the more horizontal these spine axis field lines become in the localized region, and are thus in very close proximity to one another. If the magnetic field is initially frozen into the plasma, as characterized by a Lundquist number $S > 1$
. The stronger the azimuthal component, the more horizontal these spine axis field lines become in the localized region, and are thus in very close proximity to one another. If the magnetic field is initially frozen into the plasma, as characterized by a Lundquist number $S > 1$![]() (§ 3.2), then a sufficiently narrow spatial extent exists within which current sheets can form (as defined by solving for the transition length from frozen-in condition effects while $S > 1$
(§ 3.2), then a sufficiently narrow spatial extent exists within which current sheets can form (as defined by solving for the transition length from frozen-in condition effects while $S > 1$![]() to resistive diffusion effects when $S < 1$
to resistive diffusion effects when $S < 1$![]() ; $L_{cs} = m_{e} \nu _{ei} / \mu _{0} v_{A} n_{e,i} \, \textrm {e}^{2}$
; $L_{cs} = m_{e} \nu _{ei} / \mu _{0} v_{A} n_{e,i} \, \textrm {e}^{2}$![]() when $S = 1$
when $S = 1$![]() ). It is within these narrow current sheets that $S \lesssim 1$
). It is within these narrow current sheets that $S \lesssim 1$![]() and where diffusion of magnetic field lines through the plasma and non-ideal effects take over. In these current sheet regions, the magnetic field lines can diffuse through the plasma and re-form the initial potential spine axis configuration. This reconnection to the original potential configuration has the effect of directly converting the stored magnetic field energy into kinetic energy of the surrounding plasma due to the strong electric fields that are generated by the current sheet in the twisted region.
and where diffusion of magnetic field lines through the plasma and non-ideal effects take over. In these current sheet regions, the magnetic field lines can diffuse through the plasma and re-form the initial potential spine axis configuration. This reconnection to the original potential configuration has the effect of directly converting the stored magnetic field energy into kinetic energy of the surrounding plasma due to the strong electric fields that are generated by the current sheet in the twisted region.
Expanding on the general design of Chesny et al. (Reference Chesny, Orange, Oluseyi and Valletta2017), a first-order, 3-D fan-spine magnetic null point topology is created by a four-coil solenoid as shown in figure 5(a,b). The coils are distributed axially every 10 cm, each with radius 15 cm and carrying constant current $I = 200$![]() kA. The current is reversed for each symmetric half to create a central, positive magnetic null ( Parnell et al. (Reference Parnell, Smith, Neukirch and Priest1996); field vectors point in along the spine, out along the fan) with magnitude chosen to generate a field approaching 1 T at 10 cm from the null point. This will correspond directly to our choice of characteristic length in the system of MHD equations discussed below. We stress that the considered solenoid is only one of many possible coil configurations for producing a qualitative fan-spine topology (Chesny & Orange Reference Chesny and Orange2020). As such, the authors leave quantitative analyses of more complex coil configurations and modulated currents as a topic for a future study. The fan-spine topology of the magnetic field of this considered configuration is solved via the analytical expressions for circular, current carrying coils given by Simpson et al. (Reference Simpson, Lane, Immer and Youngquist2001).
kA. The current is reversed for each symmetric half to create a central, positive magnetic null ( Parnell et al. (Reference Parnell, Smith, Neukirch and Priest1996); field vectors point in along the spine, out along the fan) with magnitude chosen to generate a field approaching 1 T at 10 cm from the null point. This will correspond directly to our choice of characteristic length in the system of MHD equations discussed below. We stress that the considered solenoid is only one of many possible coil configurations for producing a qualitative fan-spine topology (Chesny & Orange Reference Chesny and Orange2020). As such, the authors leave quantitative analyses of more complex coil configurations and modulated currents as a topic for a future study. The fan-spine topology of the magnetic field of this considered configuration is solved via the analytical expressions for circular, current carrying coils given by Simpson et al. (Reference Simpson, Lane, Immer and Youngquist2001).

Figure 5. (a) Radial view of streamlines for an arbitrary, solenoidal fan-spine topology, spaced over 40 cm, each with radius 15 cm and $I=100$![]() kA. (b) Axial view of fan plane. (c) Computer-aided design of axially aligned CPG at an arbitrary spine axis location with plasma sheath illustrated in green. The CPG discharge produces an azimuthal magnetic field. (d) Axial view of azimuthal CPG magnetic field. (e) Simulated coil fan-spine topology with localized CPG field superimposed. (f) Simulated superposition of localized CPG magnetic field upon coil fan plane magnetic field at $Z=12.25$
kA. (b) Axial view of fan plane. (c) Computer-aided design of axially aligned CPG at an arbitrary spine axis location with plasma sheath illustrated in green. The CPG discharge produces an azimuthal magnetic field. (d) Axial view of azimuthal CPG magnetic field. (e) Simulated coil fan-spine topology with localized CPG field superimposed. (f) Simulated superposition of localized CPG magnetic field upon coil fan plane magnetic field at $Z=12.25$![]() cm with units of Tesla.
cm with units of Tesla.
To provide an azimuthal perturbation to one side of this coil-generated spine axis, we consider the magnetic field of a generalized coaxial plasma gun (CPG) (e.g. Larson, Liebing & Dethlefsen Reference Larson, Liebing and Dethlefsen1966; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002) with plasma sheath parameters and run-down phase dynamics identical to a dense plasma focus apparatus (DPF) (see below). A CPG is constructed from a thin, cylindrical anode a few centimetres in length insulated from an outer, concentric cathode. The cathode is often a solid cylindrical shell surrounding the anode, but for visual purposes we illustrate the outer electrodes as long, thin rods, as common in DPF geometries (Krishnan Reference Krishnan2012). The CPG is aligned axially with one side of the spine axis within the coils as shown in the computer-aided design in figure 5(c,d). Here, we describe the general process of CPG plasma sheath generation for argument purposes only, as it is well documented in literature. A high voltage capacitor bank discharge ionizes the gas in-between the CPG electrodes, thus forming a plasma sheath at the insulating base (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003). This plasma current density and the azimuthal magnetic field of the CPG generate a $\boldsymbol {J} \times \boldsymbol {B}$![]() force so the plasma sheath lifts off of the insulator and propagates down the electrode axis (e.g. Krishnan & Thompson Reference Krishnan and Thompson2010). This propagating plasma sheath sustains and amplifies an azimuthal magnetic field internal to the plasma (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961), which is centred around the spine axis of the conducting coil field. We consider this description to be the source of both the plasma and in situ azimuthal perturbation magnetic field (figure 2) required for the breakdown of ideal MHD in torsional fan reconnection as described earlier. In the hardware configuration of figure 5(c,d), the thin plasma sheath (green) is injected axially along the spine, subjecting it to a magnetic twist.
force so the plasma sheath lifts off of the insulator and propagates down the electrode axis (e.g. Krishnan & Thompson Reference Krishnan and Thompson2010). This propagating plasma sheath sustains and amplifies an azimuthal magnetic field internal to the plasma (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961), which is centred around the spine axis of the conducting coil field. We consider this description to be the source of both the plasma and in situ azimuthal perturbation magnetic field (figure 2) required for the breakdown of ideal MHD in torsional fan reconnection as described earlier. In the hardware configuration of figure 5(c,d), the thin plasma sheath (green) is injected axially along the spine, subjecting it to a magnetic twist.
Chesny et al. (Reference Chesny, Orange, Oluseyi and Valletta2017) modelled the dynamic magnetic field of a capacitor bank discharge across CPG electrodes as
where $R$![]() is the resistance, $C$
is the resistance, $C$![]() is the capacitance, $r$
is the capacitance, $r$![]() is the radial distance and $t$
is the radial distance and $t$![]() is the time elapsed since the discharge. Typical values of CPG discharges, $V_{0} = 6$
is the time elapsed since the discharge. Typical values of CPG discharges, $V_{0} = 6$![]() kV, $R = 1$
kV, $R = 1$![]() m$\varOmega$
m$\varOmega$![]() and $C = 330 \mathrm {\mu }$
and $C = 330 \mathrm {\mu }$![]() F, were adopted to approximate this magnetic field (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961; Larson et al. Reference Larson, Liebing and Dethlefsen1966; Schaer Reference Schaer1994; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Heo & Park Reference Heo and Park2002; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002; Witherspoon et al. Reference Witherspoon, Case, Messer, Bomgardner, Phillips, Brockington and Elton2009). Figures 5(e) and 5(f) show the simulated electrodynamics of the hardware architecture and demonstrate the feasibility of this configuration to provide the required driving of torsional fan reconnection under proper MHD plasma conditions. Time $t \approx 8.2 \times 10^{-7}$
F, were adopted to approximate this magnetic field (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961; Larson et al. Reference Larson, Liebing and Dethlefsen1966; Schaer Reference Schaer1994; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Heo & Park Reference Heo and Park2002; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002; Witherspoon et al. Reference Witherspoon, Case, Messer, Bomgardner, Phillips, Brockington and Elton2009). Figures 5(e) and 5(f) show the simulated electrodynamics of the hardware architecture and demonstrate the feasibility of this configuration to provide the required driving of torsional fan reconnection under proper MHD plasma conditions. Time $t \approx 8.2 \times 10^{-7}$![]() s was solved from (3.1) under the constraints of a magnetic field of $B_{\theta }=1$
s was solved from (3.1) under the constraints of a magnetic field of $B_{\theta }=1$![]() T located $r=10$
T located $r=10$![]() cm from the null. This magnetic field is solved in a plane at $Z=10$
cm from the null. This magnetic field is solved in a plane at $Z=10$![]() cm and superimposed upon the initial potential spine axis of the coil-generated fan-spine topology (figure 5a). Figure 5(e) shows streamlines of this localized magnetic twist upon the spine axis of the coil field in figure 5(a) and mimics the azimuthal twist of figure 2, i.e. the analytical perturbation imposed in (2.2). Vector field superposition in this $Z=10$
cm and superimposed upon the initial potential spine axis of the coil-generated fan-spine topology (figure 5a). Figure 5(e) shows streamlines of this localized magnetic twist upon the spine axis of the coil field in figure 5(a) and mimics the azimuthal twist of figure 2, i.e. the analytical perturbation imposed in (2.2). Vector field superposition in this $Z=10$![]() cm plane is plotted in figure 5(f), showing the magnitude of the twist applied to the fan-spine topology from an approximated CPG discharge, which is consistent with ${\approx }1$
cm plane is plotted in figure 5(f), showing the magnitude of the twist applied to the fan-spine topology from an approximated CPG discharge, which is consistent with ${\approx }1$![]() T magnetic fields internal to the plasma sheath in robust MHD models (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004). A full description of the superposition of these fields would require a full 2-D or 3-D MHD or kinetic simulation where the background fan-spine topology is threaded within the initial plasma formation and evolution. The following section will present the quantitative plasma parameters that satisfy the kinetic and MHD requirements for reconnection to predict particle response to the torsional fan mode.
T magnetic fields internal to the plasma sheath in robust MHD models (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004). A full description of the superposition of these fields would require a full 2-D or 3-D MHD or kinetic simulation where the background fan-spine topology is threaded within the initial plasma formation and evolution. The following section will present the quantitative plasma parameters that satisfy the kinetic and MHD requirements for reconnection to predict particle response to the torsional fan mode.
3.2. Plasma parameters
Kinetic and MHD plasma parameters are calculated in table 1. The parameters listed in the top portion of the table give the characteristic values used to numerically solve (2.1) to (2.16). Coaxial plasma gun specifications from previous experiments (Larson et al. Reference Larson, Liebing and Dethlefsen1966; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002) are used to show in table 1 that such a configuration can satisfy the requirements for reconnection to occur from an induced breakdown of ideal MHD plasma conditions (Büchner Reference Büchner1999; Ryutov, Drake & Remington Reference Ryutov, Drake and Remington2000; Kallenrode Reference Kallenrode2004). Helium CPG plasma sheaths ($A=4$![]() ) are formed at discharge voltages of $\lesssim 10$
) are formed at discharge voltages of $\lesssim 10$![]() kV and densities of $\sim 10^{20}$
kV and densities of $\sim 10^{20}$![]() m$^{-3}$
m$^{-3}$![]() (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961; Larson et al. Reference Larson, Liebing and Dethlefsen1966; Schaer Reference Schaer1994; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Heo & Park Reference Heo and Park2002; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002). The electric potential value $\varPhi _{0}$
(Lindberg & Jacobsen Reference Lindberg and Jacobsen1961; Larson et al. Reference Larson, Liebing and Dethlefsen1966; Schaer Reference Schaer1994; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Heo & Park Reference Heo and Park2002; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002). The electric potential value $\varPhi _{0}$![]() is derived from a capacitor bank discharge voltage $V_{0} = 6$
is derived from a capacitor bank discharge voltage $V_{0} = 6$![]() kV typical of CPG helium gas breakdown across ${\approx }10$
kV typical of CPG helium gas breakdown across ${\approx }10$![]() cm (Larson et al. Reference Larson, Liebing and Dethlefsen1966; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002), corresponding to electric fields of ${\approx }60$
cm (Larson et al. Reference Larson, Liebing and Dethlefsen1966; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002), corresponding to electric fields of ${\approx }60$![]() kV m$^{-1}$
kV m$^{-1}$![]() . A characteristic magnetic field $B_{0} = 1$
. A characteristic magnetic field $B_{0} = 1$![]() T, as the one simulated in § 3.1, is achievable with high-temperature superconductors (Goodzeit, Meinke & Ball Reference Goodzeit, Meinke and Ball2005; Levin et al. Reference Levin, Barnes, Murphy, Brunke, Long, Horwath and Turgut2008; Squire et al. Reference Squire, Carter, Chang Diaz, Giambusso, Ilin, Ogilve-Araya, Olsen, Bering and Longmier2013). In figure 3, the simulated particle sheath is immersed at the location of maximum twist $Z=\sqrt {1.5}$
T, as the one simulated in § 3.1, is achievable with high-temperature superconductors (Goodzeit, Meinke & Ball Reference Goodzeit, Meinke and Ball2005; Levin et al. Reference Levin, Barnes, Murphy, Brunke, Long, Horwath and Turgut2008; Squire et al. Reference Squire, Carter, Chang Diaz, Giambusso, Ilin, Ogilve-Araya, Olsen, Bering and Longmier2013). In figure 3, the simulated particle sheath is immersed at the location of maximum twist $Z=\sqrt {1.5}$![]() (§ 3.3). The initial MHD condition of this helium plasma is demonstrated by a Lundquist number $S \approx 3000$
(§ 3.3). The initial MHD condition of this helium plasma is demonstrated by a Lundquist number $S \approx 3000$![]() with motions dominated by the magnetic field pressure (plasma $\beta < 1$
with motions dominated by the magnetic field pressure (plasma $\beta < 1$![]() ). The plasma resistivity $\eta _{0} = 4.5 \times 10^{-5} \varOmega$
). The plasma resistivity $\eta _{0} = 4.5 \times 10^{-5} \varOmega$![]() -m is used to solve for the localized resistivity profile and the solutions of Wyper & Jain (Reference Wyper and Jain2011) and Wyper & Jain (Reference Wyper and Jain2010), within which ideal MHD can break down and reconnection can be initiated. The calculation of each relevant collision frequency demonstrates that the condition for a weakly ionized laboratory plasma is satisfied ($\nu _{ei} < \nu _{en}$
-m is used to solve for the localized resistivity profile and the solutions of Wyper & Jain (Reference Wyper and Jain2011) and Wyper & Jain (Reference Wyper and Jain2010), within which ideal MHD can break down and reconnection can be initiated. The calculation of each relevant collision frequency demonstrates that the condition for a weakly ionized laboratory plasma is satisfied ($\nu _{ei} < \nu _{en}$![]() ) and that the ion–neutral scattering frequency becomes the dominant term in (2.12). The collision time scale compared with the gyroperiod is $1/\nu _{in} \tau _{0} \approx 0.7$
) and that the ion–neutral scattering frequency becomes the dominant term in (2.12). The collision time scale compared with the gyroperiod is $1/\nu _{in} \tau _{0} \approx 0.7$![]() , demonstrating the need for the collisional term in (2.12), which is further highlighted by the ion mean free path of 0.2 mm being significantly less than the chosen length scale. External fields can penetrate the plasma, as the electron skin depth $d_{e} = 0.5$
, demonstrating the need for the collisional term in (2.12), which is further highlighted by the ion mean free path of 0.2 mm being significantly less than the chosen length scale. External fields can penetrate the plasma, as the electron skin depth $d_{e} = 0.5$![]() mm is of the same order of the ion gyroradius $r_{g,i} = 1$
mm is of the same order of the ion gyroradius $r_{g,i} = 1$![]() mm (Fridman & Kennedy Reference Fridman and Kennedy2004). These are typical order-of-magnitude values and by no means limit the possible ranges of CPG/DPF parameters.
mm (Fridman & Kennedy Reference Fridman and Kennedy2004). These are typical order-of-magnitude values and by no means limit the possible ranges of CPG/DPF parameters.
3.3. Particle injection
While previous authors considered the response of a randomized injection of a collection of particles to torsional fan reconnection (e.g. within the boundaries of a sphere and centred around the null;
Dalla & Browning (Reference Dalla and Browning2006), Dalla & Browning (Reference Dalla and Browning2008) and Hosseinpour (Reference Hosseinpour2015)), we consider the geometrically controlled injection of particles typical of a CPG device. The initial kinetic energy and momentum ($K_{0} \approx 10$![]() eV; Larson et al. (Reference Larson, Liebing and Dethlefsen1966), Schaer (Reference Schaer1994), Scheuer et al. (Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994) ,Thio et al. (Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002) and Witherspoon et al. (Reference Witherspoon, Case, Messer, Bomgardner, Phillips, Brockington and Elton2009)) of each helium ion in the sheath will follow the generalized snowplough model of a CPG plasma sheath rundown phase (Lee Reference Lee1983; Lee & Serban Reference Lee and Serban1996; Ziemer & Choueiri Reference Ziemer and Choueiri2001; Tang, Adams & Rusnak Reference Tang, Adams and Rusnak2010), and be taken to be in the $+Z$
eV; Larson et al. (Reference Larson, Liebing and Dethlefsen1966), Schaer (Reference Schaer1994), Scheuer et al. (Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994) ,Thio et al. (Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002) and Witherspoon et al. (Reference Witherspoon, Case, Messer, Bomgardner, Phillips, Brockington and Elton2009)) of each helium ion in the sheath will follow the generalized snowplough model of a CPG plasma sheath rundown phase (Lee Reference Lee1983; Lee & Serban Reference Lee and Serban1996; Ziemer & Choueiri Reference Ziemer and Choueiri2001; Tang, Adams & Rusnak Reference Tang, Adams and Rusnak2010), and be taken to be in the $+Z$![]() direction. The sheath injection height is set to $Z = \sqrt {1.5}$
direction. The sheath injection height is set to $Z = \sqrt {1.5}$![]() , corresponding to the $+Z$
, corresponding to the $+Z$![]() location of greatest magnetic field twist (see § 5 for a discussion of the exclusion of the $-Z$
location of greatest magnetic field twist (see § 5 for a discussion of the exclusion of the $-Z$![]() location twist). It will be confined in the radial $XY$
location twist). It will be confined in the radial $XY$![]() plane to an inner ($r_{in} = 0.1$
plane to an inner ($r_{in} = 0.1$![]() ) and outer ($r_{out} = 1.0$
) and outer ($r_{out} = 1.0$![]() ) radius, corresponding to the inner (1 cm) and outer electrode (10 cm) radii, respectively, of an approximated CPG device. Since the initial plasma temperature $T$
) radius, corresponding to the inner (1 cm) and outer electrode (10 cm) radii, respectively, of an approximated CPG device. Since the initial plasma temperature $T$![]() will be much smaller than the discharge electric potential $\varPhi _{0}$
will be much smaller than the discharge electric potential $\varPhi _{0}$![]() , the finite thickness of the sheath $s$
, the finite thickness of the sheath $s$![]() can be modelled to follow the Child sheath law (Fridman & Kennedy Reference Fridman and Kennedy2004; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005)
can be modelled to follow the Child sheath law (Fridman & Kennedy Reference Fridman and Kennedy2004; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005)

where $\lambda _{D}=(\epsilon _{0} T_{eV} / e n_{e,i})^{1/2}$![]() is the Debye length. In table 1, the sheath thickness $s \sim 10^{2} \lambda _{D}$
is the Debye length. In table 1, the sheath thickness $s \sim 10^{2} \lambda _{D}$![]() , is consistent with expectations for high voltage discharges (Fridman & Kennedy Reference Fridman and Kennedy2004; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005). The positions and momenta of $10\,000$
, is consistent with expectations for high voltage discharges (Fridman & Kennedy Reference Fridman and Kennedy2004; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005). The positions and momenta of $10\,000$![]() input particles are shown in figure 6 with streamlines of the magnetic field present for comparison.
input particles are shown in figure 6 with streamlines of the magnetic field present for comparison.

Figure 6. Particle injection geometry. (a) The $10\,000$![]() particle sheath disk is confined to a radius of $0.1 \leq r \leq 1.0$
particle sheath disk is confined to a radius of $0.1 \leq r \leq 1.0$![]() in the $XY$
in the $XY$![]() plane at $Z = \sqrt {1.5}$
plane at $Z = \sqrt {1.5}$![]() , with Child sheath thickness $s$
, with Child sheath thickness $s$![]() . (b) Each helium ion has initial kinetic energy of 10 eV with its momentum in the $+Z$
. (b) Each helium ion has initial kinetic energy of 10 eV with its momentum in the $+Z$![]() direction.
direction.
An important note on the injection position of this sheath refers back to the localized resistivity profile shown in figure 4(c,d) calculated from (2.3). The vertical position ($Z = \sqrt {1.5}$![]() ) of the input sheath is centred within the peak resistivity, i.e. the diffusion region, where the non-ideal effects of magnetic field connectivity changes must occur in our investigated geometry.
) of the input sheath is centred within the peak resistivity, i.e. the diffusion region, where the non-ideal effects of magnetic field connectivity changes must occur in our investigated geometry.
4. Results
4.1. Single particle behaviour
Per particle, trajectories were computed for four characteristic times ($4 \tau _{0}$![]() ; 4000 time steps at a resolution of $dt = 0.001$
; 4000 time steps at a resolution of $dt = 0.001$![]() ), through which the final particle kinetic energies are shown to reach their maxima, and then subsequently lose most of their energy through collisions. Here, we present the results of two individual particle trajectories from the inner and outer extents of the sheath at initial positions of $\boldsymbol {r}_{in} = [0.1, 0.0, \sqrt {1.5}]$
), through which the final particle kinetic energies are shown to reach their maxima, and then subsequently lose most of their energy through collisions. Here, we present the results of two individual particle trajectories from the inner and outer extents of the sheath at initial positions of $\boldsymbol {r}_{in} = [0.1, 0.0, \sqrt {1.5}]$![]() and $\boldsymbol {r}_{out} = [1.0, 0.0, \sqrt {1.5}]$
and $\boldsymbol {r}_{out} = [1.0, 0.0, \sqrt {1.5}]$![]() . In this sense, these two simulated particle trajectories can be taken as representative samples of the whole sheath. While the details of their orbital motions, including bounce motions and drifts, are of interest, their details are out of the scope of this study and are left to future analyses. Figure 7(a) shows a visualization of these particle trajectories (blue to red) as they are accelerated toward the spine axis and in the $+Z$
. In this sense, these two simulated particle trajectories can be taken as representative samples of the whole sheath. While the details of their orbital motions, including bounce motions and drifts, are of interest, their details are out of the scope of this study and are left to future analyses. Figure 7(a) shows a visualization of these particle trajectories (blue to red) as they are accelerated toward the spine axis and in the $+Z$![]() direction (red). The geometry of the end of their trajectories will be addressed along with the results of a bulk particle injection in § 4.2.
direction (red). The geometry of the end of their trajectories will be addressed along with the results of a bulk particle injection in § 4.2.

Figure 7. Single particle trajectories and total energy evolution. (a) Side view of simulation particles at $\boldsymbol {r}_{in}$![]() and $\boldsymbol {r}_{out}$
and $\boldsymbol {r}_{out}$![]() and acceleration momenta directions along the spine axis. (b) Inner particle total energy evolution as a function of time. Inner particle kinetic energy as functions of (c) time and (d) $Z$
and acceleration momenta directions along the spine axis. (b) Inner particle total energy evolution as a function of time. Inner particle kinetic energy as functions of (c) time and (d) $Z$![]() position. The inner particle gains a maximum kinetic energy of ${\approx }2.4$
position. The inner particle gains a maximum kinetic energy of ${\approx }2.4$![]() keV of kinetic energy. (e) Outer particle total energy evolution as a function of time. Outer particle kinetic energy as functions of (f) time and (g) $Z$
keV of kinetic energy. (e) Outer particle total energy evolution as a function of time. Outer particle kinetic energy as functions of (f) time and (g) $Z$![]() -position. The outer particle gains a maximum kinetic energy of ${\approx }1.7$
-position. The outer particle gains a maximum kinetic energy of ${\approx }1.7$![]() keV of kinetic energy.
keV of kinetic energy.
Figure 7(b–g) shows the energy evolution of these two inner and outer sheath particles. Figure 7(b–d) shows the energy evolution of the inner particle as a function of time (figure 7b,c) and $Z$![]() -position along the spine axis direction (figure 7d), while figure 7(e–g) shows the respective energy evolutions for the outer particle. Both particles begin in a region of positive electric potential (green lines) and gain ${\approx }2$
-position along the spine axis direction (figure 7d), while figure 7(e–g) shows the respective energy evolutions for the outer particle. Both particles begin in a region of positive electric potential (green lines) and gain ${\approx }2$![]() keV of kinetic energy (red lines) during propagation over ${\approx }16$
keV of kinetic energy (red lines) during propagation over ${\approx }16$![]() cm along the spine direction. It is seen by the initial energy state at $t = 0$
cm along the spine direction. It is seen by the initial energy state at $t = 0$![]() that in the absence of collisions the peak possible kinetic energy gain of the ions is $\approx$
that in the absence of collisions the peak possible kinetic energy gain of the ions is $\approx$![]() 8–10 keV, as given by (2.4) and (2.8). However, the specific effect of collisions on the kinetic energy gains can be seen by calculating the total number of collisions during the simulation time as $4 \tau _{0} \nu _{in} \approx 5.5$
8–10 keV, as given by (2.4) and (2.8). However, the specific effect of collisions on the kinetic energy gains can be seen by calculating the total number of collisions during the simulation time as $4 \tau _{0} \nu _{in} \approx 5.5$![]() corresponding to a loss of nearly all of the initial potential energy over the full simulation time. These resultant effects on individual particle trajectories can only be determined numerically as in this paper ((2.11) and (2.12)), or by detailed investigation of individual particle trajectories, which is outside the scope of this study. After this peak kinetic energy gain, the total energy of each particle is rapidly lost due to collisional effects ((2.16), black dotted lines) as the particles propagate away from the regions of strong electric potential. The shape of the initially rapid kinetic energy gains of the acceleration phases (red lines, figure 7c,f and figure 7d,g; $\approx$
corresponding to a loss of nearly all of the initial potential energy over the full simulation time. These resultant effects on individual particle trajectories can only be determined numerically as in this paper ((2.11) and (2.12)), or by detailed investigation of individual particle trajectories, which is outside the scope of this study. After this peak kinetic energy gain, the total energy of each particle is rapidly lost due to collisional effects ((2.16), black dotted lines) as the particles propagate away from the regions of strong electric potential. The shape of the initially rapid kinetic energy gains of the acceleration phases (red lines, figure 7c,f and figure 7d,g; $\approx$![]() 1300–1600 time steps) follow the behaviour found in similar particle energization simulations of both torsional fan and torsional spine reconnection (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Stanier et al. Reference Stanier, Browning and Dalla2012; Hosseinpour Reference Hosseinpour2014a,Reference Hosseinpourb, Reference Hosseinpour2015; Hosseinpour et al. Reference Hosseinpour, Mehdizade and Mohammadi2014; Gascoyne Reference Gascoyne2015). However, those simulations were rooted in the collisionless nature of solar coronal conditions, whereas here a more resistive plasma nature contributes strongly to total energy loss. In fact, we have run identical simulations suppressing the collisional term in (2.12) as a numerical check, which demonstrated total energy conservation to order $10^{-1}$
1300–1600 time steps) follow the behaviour found in similar particle energization simulations of both torsional fan and torsional spine reconnection (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Stanier et al. Reference Stanier, Browning and Dalla2012; Hosseinpour Reference Hosseinpour2014a,Reference Hosseinpourb, Reference Hosseinpour2015; Hosseinpour et al. Reference Hosseinpour, Mehdizade and Mohammadi2014; Gascoyne Reference Gascoyne2015). However, those simulations were rooted in the collisionless nature of solar coronal conditions, whereas here a more resistive plasma nature contributes strongly to total energy loss. In fact, we have run identical simulations suppressing the collisional term in (2.12) as a numerical check, which demonstrated total energy conservation to order $10^{-1}$![]() eV.
eV.
The dash–dotted lines in figure 8 show the magnetic moment of the inner and outer particles as a function of time, each plotted as a ratio to each particle's initial quantity $\mu / \mu _{0}$![]() , respectively ($\mu = m_{i} v_{\bot }^{2} / 2 B$
, respectively ($\mu = m_{i} v_{\bot }^{2} / 2 B$![]() ). For comparison, during plasma confinement in a general magnetic mirror configuration, a particle's magnetic moment is a conserved quantity along its trajectory. These results clearly show that the magnetic moment in torsional fan reconnection is not a conserved quantity even at smaller spatial scales than the solar corona (Hosseinpour Reference Hosseinpour2014a,Reference Hosseinpourb). The solid lines in figure 8(a,b) show the calculation of the ratio of parallel to perpendicular momenta $p_{\parallel } / p_{\bot }$
). For comparison, during plasma confinement in a general magnetic mirror configuration, a particle's magnetic moment is a conserved quantity along its trajectory. These results clearly show that the magnetic moment in torsional fan reconnection is not a conserved quantity even at smaller spatial scales than the solar corona (Hosseinpour Reference Hosseinpour2014a,Reference Hosseinpourb). The solid lines in figure 8(a,b) show the calculation of the ratio of parallel to perpendicular momenta $p_{\parallel } / p_{\bot }$![]() , per particle, along the local vector magnetic field lines as a function of time. In both cases, the parallel component dominates during the particle acceleration ($p_{\parallel } / p_{\bot } \gg 1$
, per particle, along the local vector magnetic field lines as a function of time. In both cases, the parallel component dominates during the particle acceleration ($p_{\parallel } / p_{\bot } \gg 1$![]() ; note the log$_{10}$
; note the log$_{10}$![]() scale) up to the time of peak kinetic energy gain (vertical dotted lines). During the rapid acceleration phase of each particle, both the momentum ratio and the magnetic moment oscillate at the particle gyrofrequency, and are precisely out of phase with one another. This inverse behaviour is expected since each of these quantities are separately dominated by parallel and perpendicular quantities, respectively. As the particles traverse up the spine axis, their dominant parallel momenta correspondingly reduce the numerator in the magnetic moment equation. Overall, the momentum ratio is always greater than unity during its trajectory far from the reconnection region, and the magnetic moment is not conserved. Thus, particle acceleration in torsional fan reconnection occurs along open magnetic field lines where the ions are never trapped and can escape along the spine axis. This hints to important aspects of technology development applications that will be discussed in § 5.
scale) up to the time of peak kinetic energy gain (vertical dotted lines). During the rapid acceleration phase of each particle, both the momentum ratio and the magnetic moment oscillate at the particle gyrofrequency, and are precisely out of phase with one another. This inverse behaviour is expected since each of these quantities are separately dominated by parallel and perpendicular quantities, respectively. As the particles traverse up the spine axis, their dominant parallel momenta correspondingly reduce the numerator in the magnetic moment equation. Overall, the momentum ratio is always greater than unity during its trajectory far from the reconnection region, and the magnetic moment is not conserved. Thus, particle acceleration in torsional fan reconnection occurs along open magnetic field lines where the ions are never trapped and can escape along the spine axis. This hints to important aspects of technology development applications that will be discussed in § 5.

Figure 8. Per particle, ratios of scaled magnetic moment $\mu / \mu _{0}$![]() (dot–dashed lines) and parallel to perpendicular momenta $p_{\parallel } / p_{\bot }$
(dot–dashed lines) and parallel to perpendicular momenta $p_{\parallel } / p_{\bot }$![]() (solid lines, log$_{10}$
(solid lines, log$_{10}$![]() scale) as functions of time. (a) Inner particle ratios. (b) Outer particle ratios. For each particle, the $p_{\parallel } / p_{\bot }$
scale) as functions of time. (a) Inner particle ratios. (b) Outer particle ratios. For each particle, the $p_{\parallel } / p_{\bot }$![]() ratios are above unity, demonstrating that accelerated particles are never trapped about the null and will inherently escape along the spine axis.
ratios are above unity, demonstrating that accelerated particles are never trapped about the null and will inherently escape along the spine axis.
4.2. Bulk injection
Figure 9 displays limited visual results of 500 of the full $10\,000$![]() particles simulated in the input sheath. Figure 9(a–c) shows the bulk trajectories through the first 1633 time steps, corresponding to the time of peak kinetic energy of the outer particle $\vec {r} = [1.0, 0.0, \sqrt {1.5}]$
particles simulated in the input sheath. Figure 9(a–c) shows the bulk trajectories through the first 1633 time steps, corresponding to the time of peak kinetic energy of the outer particle $\vec {r} = [1.0, 0.0, \sqrt {1.5}]$![]() in figure 7. The sheath is seen to accelerate from $Z = \sqrt {1.5}$
in figure 7. The sheath is seen to accelerate from $Z = \sqrt {1.5}$![]() to $Z \lesssim 2$
to $Z \lesssim 2$![]() at this time of peak kinetic energy, mimicking a small-scale jet formation after propagating $\lesssim 10$
at this time of peak kinetic energy, mimicking a small-scale jet formation after propagating $\lesssim 10$![]() cm along the spine axis direction. Figure 9(d–f) shows each particle running through the full simulation time (4000 time steps, $dt = 0.001$
cm along the spine axis direction. Figure 9(d–f) shows each particle running through the full simulation time (4000 time steps, $dt = 0.001$![]() ) and travelling far from the reconnection region (blue-to-red). All particle trajectories move along the spine axis in the $+Z$
) and travelling far from the reconnection region (blue-to-red). All particle trajectories move along the spine axis in the $+Z$![]() direction in figure 9 and qualitatively become focused toward the $Z$
direction in figure 9 and qualitatively become focused toward the $Z$![]() axis. Despite the parallax of this 3-D image, the inner particles reach a maximum height of $Z \gtrsim 3$
axis. Despite the parallax of this 3-D image, the inner particles reach a maximum height of $Z \gtrsim 3$![]() , corresponding to the spine axis extent shown in figure 7(d). A histogram of the particle maximum kinetic energies (figure 10a) follows a relatively narrow energy distribution, from $1.67 \lesssim KE \lesssim 2.38$
, corresponding to the spine axis extent shown in figure 7(d). A histogram of the particle maximum kinetic energies (figure 10a) follows a relatively narrow energy distribution, from $1.67 \lesssim KE \lesssim 2.38$![]() keV, corresponding to particle speeds of $283 \lesssim v \lesssim 338$
keV, corresponding to particle speeds of $283 \lesssim v \lesssim 338$![]() km s$^{-1}$
km s$^{-1}$![]() . The root mean squared (r.m.s.) maximum kinetic energy of the particle distribution is 2.03 keV (312 km s$^{-1}$
. The root mean squared (r.m.s.) maximum kinetic energy of the particle distribution is 2.03 keV (312 km s$^{-1}$![]() ). In figure 10(b), both the maximum kinetic energy and injection potential are plotted as a function of sheath $XY$
). In figure 10(b), both the maximum kinetic energy and injection potential are plotted as a function of sheath $XY$![]() injection radius (at height $Z = \sqrt {1.5}$
injection radius (at height $Z = \sqrt {1.5}$![]() ). This behaviour shows that particles injected at smaller radii reach higher kinetic energy maxima, and that the final bulk particle energy profile can be predicted from (2.8) and figure 3(c,d) where the inner particles begin in a region of higher electric potential with $-r^{2}$
). This behaviour shows that particles injected at smaller radii reach higher kinetic energy maxima, and that the final bulk particle energy profile can be predicted from (2.8) and figure 3(c,d) where the inner particles begin in a region of higher electric potential with $-r^{2}$![]() dependence at $Z = \sqrt {1.5}$
dependence at $Z = \sqrt {1.5}$![]() . The collisional nature of the investigated plasma (${\approx }5.5$
. The collisional nature of the investigated plasma (${\approx }5.5$![]() collisions per trajectory) shows a similar total energy loss per particle, independent of the injection radius. The kinetic energy gains and losses are uniquely dependent on the dominant collisional process as determined by the plasma parameters and require computational algorithms, such as particle tracking, to quantify. A consequence of the rotational drift velocity in figure 4(b) is that the bulk motion of particles should mimic helical motions, such as those observed in solar jets (Pariat et al. Reference Pariat, Dalmasse, DeVore, Antiochos and Karpen2016) that are evident in 2-D reconnection experiments (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990). This effect is qualitatively seen at the base of the jet-like structure in figure 9(a,b) and explicitly in the end-on view of figure 9(c).
collisions per trajectory) shows a similar total energy loss per particle, independent of the injection radius. The kinetic energy gains and losses are uniquely dependent on the dominant collisional process as determined by the plasma parameters and require computational algorithms, such as particle tracking, to quantify. A consequence of the rotational drift velocity in figure 4(b) is that the bulk motion of particles should mimic helical motions, such as those observed in solar jets (Pariat et al. Reference Pariat, Dalmasse, DeVore, Antiochos and Karpen2016) that are evident in 2-D reconnection experiments (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990). This effect is qualitatively seen at the base of the jet-like structure in figure 9(a,b) and explicitly in the end-on view of figure 9(c).

Figure 9. Limited results of 500 out of $10\,000$![]() particle tracks through [top row] 1633 time steps, and (d–f) all 4000 simulation time steps (blue-to-red; $4 \tau _{0}$
particle tracks through [top row] 1633 time steps, and (d–f) all 4000 simulation time steps (blue-to-red; $4 \tau _{0}$![]() at $dt=0.001$
at $dt=0.001$![]() ). The $XYZ$
). The $XYZ$![]() magnetic field streamlines are visible for scale (black). Note that while the vertical axes of the magnetic streamlines and particle tracks may look offset in relative size due to parallax in the 3-D plotting, they are identical. (a,d) All particles are accelerated along the $+Z$
magnetic field streamlines are visible for scale (black). Note that while the vertical axes of the magnetic streamlines and particle tracks may look offset in relative size due to parallax in the 3-D plotting, they are identical. (a,d) All particles are accelerated along the $+Z$![]() spine axis in a jet-like formation. (b,e) Side $XZ$
spine axis in a jet-like formation. (b,e) Side $XZ$![]() view of jet-like formation and propagation. (c,f) End-on $XY$
view of jet-like formation and propagation. (c,f) End-on $XY$![]() view of helical particle motions about the $Z$
view of helical particle motions about the $Z$![]() spine axis.
spine axis.

Figure 10. (a) Histogram of maximum jet kinetic energies for the 4000 simulation particles with r.m.s. energy of 2.03 keV (speed 312 km s$^{-1})$![]() . (b) Maximum kinetic energy distribution of $10\,000$
. (b) Maximum kinetic energy distribution of $10\,000$![]() test particles as a function of input sheath $XY$
test particles as a function of input sheath $XY$![]() radius, compared with their injection potential values.
radius, compared with their injection potential values.
5. Discussion
The modelling results in this paper predict particle acceleration dynamics resulting from resistive torsional fan magnetic reconnection using numerical input parameters typical of laboratory plasma generation devices. By using resistive MHD models (Wyper & Jain Reference Wyper and Jain2010, Reference Wyper and Jain2011), the quantitative evidence of torsional reconnection-based particle acceleration provided here suggests that a new generation of laboratory experiments may be feasible. A confined injection of helium ions, derived from the snowplough model of CPGs (Lindberg & Jacobsen Reference Lindberg and Jacobsen1961; Larson et al. Reference Larson, Liebing and Dethlefsen1966; Heo & Park Reference Heo and Park2002; Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004; Bures, Krishnan & James Reference Bures, Krishnan and James2012; Mitrofanov et al. Reference Mitrofanov, Krauz, Kubes, Scholz, Paduch and Zielinska2014; Caballero Bendixsen et al. Reference Caballero Bendixsen, Bott-Suzuki, Cordaro, Krishnan, Chapman, Coleman and Chittenden2016), results in impulsive particle acceleration from 10 eV to ${\approx }2$![]() keV kinetic energy profiles into a focused and accelerated plasma structure ${\approx }16$
keV kinetic energy profiles into a focused and accelerated plasma structure ${\approx }16$![]() cm in length (figures 9 and 10), indicating the formation of a jet. These results are significant because if such particle acceleration and dynamics could be replicated in a laboratory setting, a much more intimate understanding of the physics of 3-D modes of magnetic reconnection would emerge.
cm in length (figures 9 and 10), indicating the formation of a jet. These results are significant because if such particle acceleration and dynamics could be replicated in a laboratory setting, a much more intimate understanding of the physics of 3-D modes of magnetic reconnection would emerge.
It is important to put our results in context with the previously cited literature. Our considered 10 cm scale plasma put tight spatial and momentum constraints on the injected population of particles (figure 6), whereas solar conditions were more generally treated with a randomized population of isotropic particle injection momenta within a finite spherical volume centred about the null point (e.g. Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008). These constraints are justified for two reasons. First, laboratory-generated MHD plasmas that feature the azimuthal magnetic field profile required for torsional reconnection (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017) are highly constrained in energy–momentum space (e.g. Larson et al. Reference Larson, Liebing and Dethlefsen1966; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002; Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004; Gonzalez et al. Reference Gonzalez, Clausse, Bruzzone and Florido2004; Krishnan Reference Krishnan2012; Caballero Bendixsen et al. Reference Caballero Bendixsen, Bott-Suzuki, Cordaro, Krishnan, Chapman, Coleman and Chittenden2016). Second, in this design of experimentally induced reconnection, the perturbation to the potential 3-D null point field is inherently confined within the localized, in situ plasma volume. This placed the fundamental requirement on imposing a localized resistivity profile within our system of equations so that these first approximations of non-ideal effects on the resulting plasma flow can be made (Wyper & Jain Reference Wyper and Jain2011). The localized resistivity profile simulates the plasma sheath considered to be the reconnection diffusion region. For this reason, the particle sheath in figure 6 is constrained to the location of maximum twist in the torsional fan regime. Although the localized twist in (2.1) is mathematically symmetric about the fan plane ($Z$![]() -axis), physically there is no link between the two planar twists. Specifically, in 3-D resistive MHD simulations of torsional fan reconnection (Pontin & Galsgaard Reference Pontin and Galsgaard2007), the disturbances to the surrounding plasma from the localized twist travel along the local magnetic field lines and there is neither a flow, nor a magnetic connection between the two sides of the fan plane. Thus, it is feasible that a single perturbation on one side of the fan plane would be sufficient to provide the twist to induce torsional fan reconnection and a singular, unidirectional plasma jet. This is in contrast to the bidirectional jets resulting from a wider, randomized particle injection within the analytically symmetric fields (Dalla & Browning Reference Dalla and Browning2006; Hosseinpour Reference Hosseinpour2015).
-axis), physically there is no link between the two planar twists. Specifically, in 3-D resistive MHD simulations of torsional fan reconnection (Pontin & Galsgaard Reference Pontin and Galsgaard2007), the disturbances to the surrounding plasma from the localized twist travel along the local magnetic field lines and there is neither a flow, nor a magnetic connection between the two sides of the fan plane. Thus, it is feasible that a single perturbation on one side of the fan plane would be sufficient to provide the twist to induce torsional fan reconnection and a singular, unidirectional plasma jet. This is in contrast to the bidirectional jets resulting from a wider, randomized particle injection within the analytically symmetric fields (Dalla & Browning Reference Dalla and Browning2006; Hosseinpour Reference Hosseinpour2015).
In developing these algorithms and testing specific cases of field strengths, we have also found results consistent with Dalla & Browning (Reference Dalla and Browning2006) under changes to the scaling of the magnetic and electric fields. While not shown in this paper explicitly, when $B_{0}$![]() is increased, the stronger fields act to confine (i.e. mirror) the particles around the null and suppress acceleration. Conversely, increasing $E_{0}$
is increased, the stronger fields act to confine (i.e. mirror) the particles around the null and suppress acceleration. Conversely, increasing $E_{0}$![]() provides more rapid acceleration to higher energies, but the particles are not focused along the spine and more closely follow the electric field lines in figure 3(c). This aspect points to the effectiveness of computational modelling to predict and inform future experimental designs, and the scalability of jet formation across spatial and energy scales is worthy of future study.
provides more rapid acceleration to higher energies, but the particles are not focused along the spine and more closely follow the electric field lines in figure 3(c). This aspect points to the effectiveness of computational modelling to predict and inform future experimental designs, and the scalability of jet formation across spatial and energy scales is worthy of future study.
These results point to a possible consistency between astrophysical and feasible laboratory plasma dynamics, where high-energy jet formation observed in environments such as the solar atmosphere (Pontin et al. Reference Pontin, Priest and Galsgaard2013) and active galactic nuclei (Petropoulou et al. Reference Petropoulou, Sironi, Spitkovsky and Giannios2019) have been associated with magnetic reconnection. Controlling scaled-down manifestations of these dynamics could lead to a more complete understanding of their initiation and evolution. This includes possible high temporal resolution observations of current sheet formation and radial magnetic field line slippages within the plasma sheath. Such time scale resolution will need to be very fast ($\lesssim 1 \ \mathrm {\mu }$![]() s) and will likely require advanced diagnostics to decipher fine scale dynamics (see below). Recent observations from the Parker Solar Probe have shown that impulsive particle acceleration occurs very near the Sun (McComas et al. Reference McComas2019), and solar wind formation via reconnection originates near 3-D null point configurations seen by the Solar Dynamics Observatory (Mason, Antiochos & Viall Reference Mason, Antiochos and Viall2019). More specific origins of these impulsive accelerations along open magnetic field lines will be determined by further observations of forced reconnection (Srivastava et al. Reference Srivastava, Mishra, Jelınek, Samanta, Tian, Pant, Kayshap, Banerjee, Doyle and Dwivedi2019), and may end up being associated with torsional modes (Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008; Hosseinpour et al. Reference Hosseinpour, Mehdizade and Mohammadi2014; Hosseinpour Reference Hosseinpour2015). An experimental infrastructure that can reproduce torsional reconnection and form plasma jets along open magnetic field lines will be able to probe laboratory manifestations of these dynamics seen across astrophysical plasma scales (Ji et al. Reference Ji2019). Further efforts to establish this infrastructure may be able to use this model and these results to inform design constraints (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017).
s) and will likely require advanced diagnostics to decipher fine scale dynamics (see below). Recent observations from the Parker Solar Probe have shown that impulsive particle acceleration occurs very near the Sun (McComas et al. Reference McComas2019), and solar wind formation via reconnection originates near 3-D null point configurations seen by the Solar Dynamics Observatory (Mason, Antiochos & Viall Reference Mason, Antiochos and Viall2019). More specific origins of these impulsive accelerations along open magnetic field lines will be determined by further observations of forced reconnection (Srivastava et al. Reference Srivastava, Mishra, Jelınek, Samanta, Tian, Pant, Kayshap, Banerjee, Doyle and Dwivedi2019), and may end up being associated with torsional modes (Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008; Hosseinpour et al. Reference Hosseinpour, Mehdizade and Mohammadi2014; Hosseinpour Reference Hosseinpour2015). An experimental infrastructure that can reproduce torsional reconnection and form plasma jets along open magnetic field lines will be able to probe laboratory manifestations of these dynamics seen across astrophysical plasma scales (Ji et al. Reference Ji2019). Further efforts to establish this infrastructure may be able to use this model and these results to inform design constraints (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017).
In terms of laboratory infrastructure, the injection and acceleration of the plasma sheath will likely strongly depend on the geometric radial-to-axial aspect ratio of CPG devices (e.g. Larson et al. Reference Larson, Liebing and Dethlefsen1966; Schaer Reference Schaer1994; Scheuer et al. Reference Scheuer, Schoenberg, Henins, Gerwin, Moses, Garcia, Gribble, Hoyt, Black and Mayo1994; Thio et al. Reference Thio, Eskridge, Lee, Smith, Martin, Markusic and Cassibry2002; Witherspoon et al. Reference Witherspoon, Case, Messer, Bomgardner, Phillips, Brockington and Elton2009), including the form of the plasma formation surface (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004). The plasma sheath following the general snowplough model of particle injection (Lee Reference Lee1983; Lee & Serban Reference Lee and Serban1996; Gonzalez et al. Reference Gonzalez, Clausse, Bruzzone and Florido2004; Tang et al. Reference Tang, Adams and Rusnak2010) is a first approximation, and more accurate representations of the sheath geometry will further inform experimental design using simulations such as the ones presented here. Additionally, the analytic solutions of (2.1) and (2.4) denote a rotational perturbation increasing in strength radially outward from the spine axis (figure 3). However, the observed magnetic field profile of both CPG and DPF sheaths demonstrate that the strongest field strengths occur closest to the inner electrode ($\sim 1/r$![]() dependence; Willenborg & Hendricks (Reference Willenborg and Hendricks1976) and Esaulov et al. (Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003)), and this was confirmed analytically by (3.1) in figure 5(e,f). Not only does this result in the perturbation occurring closer to the spine, but it contributes to an enhanced axial velocity from the $\boldsymbol {J} \times \boldsymbol {B}$
dependence; Willenborg & Hendricks (Reference Willenborg and Hendricks1976) and Esaulov et al. (Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003)), and this was confirmed analytically by (3.1) in figure 5(e,f). Not only does this result in the perturbation occurring closer to the spine, but it contributes to an enhanced axial velocity from the $\boldsymbol {J} \times \boldsymbol {B}$![]() force driving the sheath propagation (Kwek, Tou & Lee Reference Kwek, Tou and Lee1990; Krishnan & Thompson Reference Krishnan and Thompson2010; Krishnan Reference Krishnan2012). Such alterations to the sheath (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004) and perturbation profiles should be the subject of more in depth studies of plasma response. Additionally, diagnosing the plasma response to fast torsional modes on submicrosecond scales and magnetic field line slippages (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017) may require advanced diagnostics such as laser-induced fluorescence or two-photon laser-induced fluorescence (e.g. Thakur et al. Reference Thakur, Adriany, Gosselin, McKee, Scime, Sears and Tynan2016; Schmidt et al. Reference Schmidt, Sands, Scofield, Gord and Roy2017). However, experiments utilizing the plasma conditions considered in this paper with sufficiently large electron inertial length $d_{e} = 0.5$
force driving the sheath propagation (Kwek, Tou & Lee Reference Kwek, Tou and Lee1990; Krishnan & Thompson Reference Krishnan and Thompson2010; Krishnan Reference Krishnan2012). Such alterations to the sheath (Esaulov et al. Reference Esaulov, Makhin, Bauer, Siemon, Sotnikov, Paraschiv, Presura, Freeman, Hagen, Ziegler, Lindemuth and Sheehey2003, Reference Esaulov, Bauer, Lindemuth, Makhin, Presura, Ryutov, Sheehey, Siemon and Sotnikov2004) and perturbation profiles should be the subject of more in depth studies of plasma response. Additionally, diagnosing the plasma response to fast torsional modes on submicrosecond scales and magnetic field line slippages (Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017) may require advanced diagnostics such as laser-induced fluorescence or two-photon laser-induced fluorescence (e.g. Thakur et al. Reference Thakur, Adriany, Gosselin, McKee, Scime, Sears and Tynan2016; Schmidt et al. Reference Schmidt, Sands, Scofield, Gord and Roy2017). However, experiments utilizing the plasma conditions considered in this paper with sufficiently large electron inertial length $d_{e} = 0.5$![]() mmmay only require diagnostics achievable using 3-D magnetic B-dot probes and Langmuir probes (e.g. Stenzel et al. Reference Stenzel, Urrutia and Griskey1999; Urrutia et al. Reference Urrutia, Stenzel, Griskey and Strohmaier2003).
mmmay only require diagnostics achievable using 3-D magnetic B-dot probes and Langmuir probes (e.g. Stenzel et al. Reference Stenzel, Urrutia and Griskey1999; Urrutia et al. Reference Urrutia, Stenzel, Griskey and Strohmaier2003).
Referring to the application of magnetic reconnection to space propulsion, the hardware configuration simulated in figure 5 is similar to that of a magnetoplasmadynamic thruster (MPD) (Sovey et al. Reference Sovey, Mantenieks, Haag, Raitano and Parkes1989; Myers, Mantenieks & Sovey Reference Myers, Mantenieks and Sovey1990; Mantenieks & Myers Reference Mantenieks and Myers1993; Mikellides, Turchi & Roderick Reference Mikellides, Turchi and Roderick2000; Tang et al. Reference Tang, Cheng, Liu and York2012a,Reference Tang, Cheng, Liu and Yorkb), where a CPG is axially aligned with an external solenoid magnetic field. However, there are two major differences between external field MPDs and the configuration investigated here. First, the external magnetic field in MPDs is solenoidal, with all coils carrying current in the same direction forming a uniform axial vector magnetic field in the plasma region. Although the axial field lines in a solenoidal magnetic field mimic the localized topology of a spine axis, any current sheet accumulation and amplification achieved would likely not be constructed similar to those achieved in the fan-spine topology (Pontin & Galsgaard Reference Pontin and Galsgaard2007; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011). Second, and most importantly, the resistive plasma state considered in this paper is crucial to the onset of the reconnection process. Referring to the fundamental plasma parameters in table 1, the collisional nature of the CPG plasma state ($n_{i} \sim 10^{20}$![]() m$^{-3}$
m$^{-3}$![]() , $\nu _{in} \sim 10^{6}$
, $\nu _{in} \sim 10^{6}$![]() s$^{-1}$
s$^{-1}$![]() ) is such that the diffusion of stressed magnetic field lines through the plasma is possible ($S \approx 3000$
) is such that the diffusion of stressed magnetic field lines through the plasma is possible ($S \approx 3000$![]() ) within thin, resistive current sheets as simulated here. Magnetoplasmadynamic thrusters have produced plasmas with electron temperatures of the order of $T_{e} = 0.15\text {--}20$
) within thin, resistive current sheets as simulated here. Magnetoplasmadynamic thrusters have produced plasmas with electron temperatures of the order of $T_{e} = 0.15\text {--}20$![]() eV; however, the plasma densities seemed to be too low ($10^{15}$
eV; however, the plasma densities seemed to be too low ($10^{15}$![]() m$^{-3}$
m$^{-3}$![]() , Tang et al. (Reference Tang, Cheng, Liu and York2012b); $10^{16}$
, Tang et al. (Reference Tang, Cheng, Liu and York2012b); $10^{16}$![]() –$10^{18}$
–$10^{18}$![]() m$^{-3}$
m$^{-3}$![]() ,
,
Myers et al. (Reference Myers, Mantenieks and Sovey1990)) with insufficient electron ion collision frequencies ($\nu _{ei} \approx 2 \times 10^{7}$![]() s$^{-1}$
s$^{-1}$![]() , Myers et al. (Reference Myers, Mantenieks and Sovey1990)) to induce the resistive effects of reconnection. This effect has been quantified by showing that the primary plasma acceleration process in MPDs is thermal energy conversion (Mikellides et al. Reference Mikellides, Turchi and Roderick2000) where the rotation of the plasma is limited by viscous drag (Mikellides & Turchi Reference Mikellides and Turchi2000).
, Myers et al. (Reference Myers, Mantenieks and Sovey1990)) to induce the resistive effects of reconnection. This effect has been quantified by showing that the primary plasma acceleration process in MPDs is thermal energy conversion (Mikellides et al. Reference Mikellides, Turchi and Roderick2000) where the rotation of the plasma is limited by viscous drag (Mikellides & Turchi Reference Mikellides and Turchi2000).
When considering the competing architectures of magnetic reconnection propulsion (Cazzola et al. Reference Cazzola, Curreli, Markidis and Lapenta2016; Chesny et al. Reference Chesny, Orange, Oluseyi and Valletta2017; Bathgate et al. Reference Bathgate, Bilek, Cairns and McKenzie2018; Ebrahimi Reference Ebrahimi2020), it is anticipated that 3-D torsional reconnection may provide a pathway to more efficient plasma propulsion in comparison with the 2-D model, along with offering high specific impulse capabilities (2.03 keV $\approx$![]() 312 km s$^{-1}$
312 km s$^{-1}$![]() ). Additionally, since acceleration and peak kinetic energies in torsional fan reconnection occur while particles are travelling along open magnetic field lines (figures 7 and 9) with dominant parallel momenta (figure 8), reconnection may significantly reduce or even eliminate the requirements of a magnetic nozzle to transfer particle momentum and produce thrust (Arefiev & Breizman Reference Arefiev and Breizman2004; Olsen et al. Reference Olsen, Ballenger, Carter, Díaz, Giambusso, Glover, Ilin, Squire, Longmier, Bering and Cloutier2015). The response of heavier ions more suitable for propulsion applications (i.e. Ar, Xe) will be a useful future investigation. As a final note on efficiency, external field MPDs have been shown to be ${\approx }20\,\%$
). Additionally, since acceleration and peak kinetic energies in torsional fan reconnection occur while particles are travelling along open magnetic field lines (figures 7 and 9) with dominant parallel momenta (figure 8), reconnection may significantly reduce or even eliminate the requirements of a magnetic nozzle to transfer particle momentum and produce thrust (Arefiev & Breizman Reference Arefiev and Breizman2004; Olsen et al. Reference Olsen, Ballenger, Carter, Díaz, Giambusso, Glover, Ilin, Squire, Longmier, Bering and Cloutier2015). The response of heavier ions more suitable for propulsion applications (i.e. Ar, Xe) will be a useful future investigation. As a final note on efficiency, external field MPDs have been shown to be ${\approx }20\,\%$![]() –$60\,\%$
–$60\,\%$![]() efficient (Sovey et al. Reference Sovey, Mantenieks, Haag, Raitano and Parkes1989; Myers et al. Reference Myers, Mantenieks and Sovey1990). Since MPDs are thermal plasma accelerators, much of the magnetic energy from both the rotational plasma sheath and the external solenoid field is stored, but unused. If magnetic reconnection can be induced to release this stored energy in a similar configuration, the system electric-to-particle efficiency can be significantly improved, thus resulting in a strong coupling between the fields and the plasma.
efficient (Sovey et al. Reference Sovey, Mantenieks, Haag, Raitano and Parkes1989; Myers et al. Reference Myers, Mantenieks and Sovey1990). Since MPDs are thermal plasma accelerators, much of the magnetic energy from both the rotational plasma sheath and the external solenoid field is stored, but unused. If magnetic reconnection can be induced to release this stored energy in a similar configuration, the system electric-to-particle efficiency can be significantly improved, thus resulting in a strong coupling between the fields and the plasma.
Finally, moving beyond collisional particle tracking methods to further verify the efficacy of this investigated architecture will necessitate the use of more complex numerical techniques such as particle-in-cell. Modelling plasma formation and propagation into a fan-spine topology, along with subsequent magnetic field line twisting and non-ideal effects of field line diffusion through the plasma require comprehensive plasma simulation techniques. While the relative low density of the plasma scales investigated here suggest the formation of jet-like features while accounting for collisions, the particle tracking technique does not consider either the feedback of particle-generated fields or more complex interactions between particles. These effects are non-negligible at higher plasma densities when the plasma $\beta$![]() approaches or exceeds unity (table 1). These more robust numerical techniques can examine a wider range of plasma parameters at various degrees of collisionality and determine whether these dynamics enhance or degrade the formation of jet-like phenomena.
approaches or exceeds unity (table 1). These more robust numerical techniques can examine a wider range of plasma parameters at various degrees of collisionality and determine whether these dynamics enhance or degrade the formation of jet-like phenomena.
6. Conclusion
Here, particle acceleration resulting from the 3-D torsional fan magnetic reconnection mode has been investigated in a resistive plasma at scales achievable with laboratory equipment. Previously, such studies have been limited to solar coronal conditions (Dalla & Browning Reference Dalla and Browning2005, Reference Dalla and Browning2006, Reference Dalla and Browning2008; Stanier et al. Reference Stanier, Browning and Dalla2012; Hosseinpour Reference Hosseinpour2014a,Reference Hosseinpourb, Reference Hosseinpour2015; Hosseinpour et al. Reference Hosseinpour, Mehdizade and Mohammadi2014; Gascoyne Reference Gascoyne2015; Threlfall et al. Reference Threlfall, Neukirch, Parnell and Eradat Oskoui2015; Pallister et al. Reference Pallister, Pontin and Wyper2019) as this is the most easily studied astrophysical plasma environment where 3-D null points reside (Longcope & Parnell Reference Longcope and Parnell2009; Edwards & Parnell Reference Edwards and Parnell2015). The initial attempt to establish a link between torsional reconnection modes in observable 3-D null point topologies with existing technologies in the laboratory constrained a range of length and energy scales on which kinetic and MHD conditions were satisfied (Chesny et al. (Reference Chesny, Orange, Oluseyi and Valletta2017), $B_{0} = 1$![]() T and $L_{0} = 1$
T and $L_{0} = 1$![]() cm, therein). The results in this paper build upon those initial assumptions and take similar scales further down the path toward next-generation magnetic reconnection experiments to move beyond the 2-D model (e.g. Egedal et al. Reference Egedal, Fox, Katz, Porkolab, Reim and Zhang2007; Yamada et al. Reference Yamada, Yoo, Jara-Almonte, Ji, Kulsrud and Myers2014) and focus on torsional modes (Pontin Reference Pontin2011). We have used experimental scaling parameters ($L_{0}$
cm, therein). The results in this paper build upon those initial assumptions and take similar scales further down the path toward next-generation magnetic reconnection experiments to move beyond the 2-D model (e.g. Egedal et al. Reference Egedal, Fox, Katz, Porkolab, Reim and Zhang2007; Yamada et al. Reference Yamada, Yoo, Jara-Almonte, Ji, Kulsrud and Myers2014) and focus on torsional modes (Pontin Reference Pontin2011). We have used experimental scaling parameters ($L_{0}$![]() , $B_{0}$
, $B_{0}$![]() , $\varPhi _{0}$
, $\varPhi _{0}$![]() , $E_{0}$
, $E_{0}$![]() ) to study the response of a controlled injection of 10 eV helium ions to the solutions of the steady-state, kinematic, resistive MHD equations in torsional fan reconnection (Wyper & Jain Reference Wyper and Jain2010, Reference Wyper and Jain2011). Imposing a localized resistivity profile mimicked the injection of a resistive dense plasma sheath confined to the location of maximum magnetic field twist where torsional fan reconnection occurs. Our relativistic, collisional particle tracking routine demonstrated the rapid acceleration and focusing of a plasma jet to ${\approx }2$
) to study the response of a controlled injection of 10 eV helium ions to the solutions of the steady-state, kinematic, resistive MHD equations in torsional fan reconnection (Wyper & Jain Reference Wyper and Jain2010, Reference Wyper and Jain2011). Imposing a localized resistivity profile mimicked the injection of a resistive dense plasma sheath confined to the location of maximum magnetic field twist where torsional fan reconnection occurs. Our relativistic, collisional particle tracking routine demonstrated the rapid acceleration and focusing of a plasma jet to ${\approx }2$![]() keV energies along open magnetic field lines and propagating away from the reconnection region, consistent with dynamics found in solar plasma jets (Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008; Hosseinpour Reference Hosseinpour2015).
keV energies along open magnetic field lines and propagating away from the reconnection region, consistent with dynamics found in solar plasma jets (Dalla & Browning Reference Dalla and Browning2006, Reference Dalla and Browning2008; Hosseinpour Reference Hosseinpour2015).
Collisional plasma simulations combined with experimental infrastructures for discovery science designed to induce and study 3-D reconnection modes (torsional fan, torsional spine and spine-fan) will provide both plasma physicists and heliophysicists the important ability to intimately study the details of astrophysical particle acceleration first-hand, particularly in terms of injecting a plasma into a vacuum 3-D null point region (Lukin & Linton Reference Lukin and Linton2011; Chesny et al. Reference Chesny, Orange and Dempsey2021). If eventually demonstrated to induce driven torsional reconnection modes, the simulated experimental infrastructure may help address open questions in fundamental reconnection science, including the multiscaled nature of the reconnection process, reconnection rates and the dispersion between thermal and kinetic energies. This instrument can also decipher unique reconnection dynamics in the fan-spine topology, such as the build-up of magnetic twist, current sheet formation and the diffusion of radial magnetic field lines through plasma by using sufficiently advanced plasma diagnostics. This infrastructure may also be used to directly verify analytical models of 3-D reconnection modes (Pontin & Galsgaard Reference Pontin and Galsgaard2007; Priest & Pontin Reference Priest and Pontin2009; Pontin Reference Pontin2011; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011). Demonstrating a reconnection-induced plasma jet in the laboratory will help to confirm and refine both theoretical and computational models of the complex reconnection process (Parnell et al. Reference Parnell, Neukirch, Smith and Priest1997; Pontin & Galsgaard Reference Pontin and Galsgaard2007; Wyper & Jain Reference Wyper and Jain2010; Pontin et al. Reference Pontin, Al-Hachami and Galsgaard2011, Reference Pontin, Priest and Galsgaard2013; Thurgood et al. Reference Thurgood, Pontin and McLaughlin2017), particularly with respect to particle velocity distributions (Howes Reference Howes2018) and helical jets (Pariat et al. Reference Pariat, Dalmasse, DeVore, Antiochos and Karpen2016).
Acknowledgements
The authors greatly appreciate the anonymous reviewers whose comments and suggestions significantly improved the quality of this manuscript.
Editor T. Carter thanks the referees for their advice in evaluating this article.
Funding
D.L. Chesny would like to thank S. Dalla for helpful discussions on particle tracking. N.B. Orange acknowledges financial support from NASA MUREP MIRO (grant number NNX15AP95A), NASA MUREP MIRO (grant number 80NSSC21M0001) and the South Carolina Space Grant (grant number NNX15AL49H), a NASA-sponsored program administered by the College of Charleston. D.L. Chesny received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interest
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.